张量分析第一章

合集下载

第一章张量分析初步

eijk eijk 6
证明见例题
eijk与ij间的关系
由排列符号的性质 : ei e j eijk ek
ei e j • ek eijk
由于ei e j • ek表示的是混合积,其物理意义是单位立方体的体积.
另外,由矢量分析知, 平行六面体的体积可以表示成其三个棱的行

i e1, j e2, k e3
X1
X3 P(x1, x2, x3)
O
X2
➢ 再对上述代换结果进行简写P点改写为： P(x1,x2,x3)P(xi, i=1,2,3)P(xi)
➢ 基向量：ei, i=1,2,3 ei ➢ 则称上述字母i为指标，i的取值i=1,2,3为指标i的取值
列式形式.
eeij
(i1, ( j1
i2,i3 , j2,
)
j3
)
ek (k1,k 2 ,k3)
ei,ej,ek为3个单位基向量， i,j,k互不相等。
i1 i2 i3 ei e j • ek j1 j2 j3 eijk
k1 k2 k3

a13 x3 a23 x3

b1 b2

a31x1 a32 x2 a33 x3 b3
如何用一个最简单的式子来表示？
用矩阵？还有更简单的表示方法吗? 可总结为：aij x j bi
aij, xj, bi是些什么量？
§1.1 指标记号及两个特殊符号
两种方式:
将左式展开，再给定每一个i值，求左右是否相等；
只有当i=j时ij才不等于“0”，
∴
a j ij ai ii ( ii不求和) ai

黄克智版张量分析第一章习题解析

k az bz
a y bz a z by i a z bx a xbz j a xby a y bx k 0
即
a y bz a z b y 0 a z bx a x bz 0 a x b y a y bx 0
或故
ax a y az c bx by bz
C i C j C k A B C B C A B C B C A B C D i D j D k C A B D B D B A D A D D A B C B C B A C A C i C A B D B D B A D A D D A B C B C B A C A C j C A B D B D B A D A D D A B C B C B A C A C k
a c mb i 2 j 3k m2i j 2k 1 2m i 2 m j 3 2m k
b a 2i j 2k 1 2m i 2 m j 3 2m k 21 2m 2 m 23 2m 2 9m 0
x y z x y z z y y z x x z z x x y z x y z x x z z x y y x x y z x x z z x y y x y x y z z y z x y y x y x y z z y z x y y x z x y z z y y z x x z z x y z z y y z x x z
证明：参见：1.2.2.4 由协变基矢量求逆变基矢量式（1.2.17）及式（1.2.25 ）。
1.10 已知：以i，j，k 表示三维空间中笛卡坐标基矢量，

张量分析书籍附详尽易懂

n个
称为n维仿射空间。E n 中旳每一种元素称为点。
记：
o (0, ,0),
x (x1,, xn ) ,
(x1, , xn )
且分别称为放射空间旳原点、位置矢量和负矢量。
对于n维仿射空间，全部旳位置矢量构成一种集合：
V0 x (x1,, xn ) xi , xi F,1 i n
(1 t)(1,1) t(1,1) a t b
(1 2t,1 2t) a t b
当 t b 时：
(2t 1,2t 1) (1,1)
当 t a 时：
(2t 1,2t 1) (1,1)
由此可得 a 0 ，b 1 。显然 r1 等 r2 价。
r1 与 r5 ： (取 s b5 b1 )
域上旳矢量空间。且仍记为V0 。
数域上旳矢量空间V0 具有如下性质：x, y, z V0 ,、 F
（1）
x yyx
（2）
(x y) z x ( y z)
（3）V0中存在称为有关加法旳单位元素o，使得：
xo x
x V0
（4）V0中每一种元素x都存在唯一旳(-x )，使得：
x (x) o
当t=b时：位置矢量标
定b点。即：
S
(4b 2,3 2b) (2,1)
由此拟定b=1 。
x2
当t=a时：位置矢量标
3
2
定a点。即：
1
(4a 2,3 2a) (1,1.5 )
由此拟定a=0.75 。
图中画出了计算成果。
x2 3
2 u ab
1
2 (a)
u xy
x1
4
6
u xy u ab
1
2
。 Vx空间中旳矢量称为约束矢量。

张量分析提纲及部分习题答案

y
对静止的连续介质，有
ζ n fd 0 ， ζd fd 0 ，
A
ζ f 0。
（21）证明应力是一个张量；记 ij ：表示在给定基 g i 下，在面 g j 上，单位面积受力 F j 在 g i 方向上的分量为
对斜圆锥面上任一点（图中黑点处），不难由相似三角形得到，
z z R cos C i R sin j zk ，进而可得， H H r Rz sin zR cos r R cos C R g i j， gz i sin j k ， H H z H H r
dx g dx I g dx II 1 4 x I 2 dx I 6 x I x II 2 dx II Pdx I Q dx II 11 12 1 1 I 。 2 4 dxII g 21dx I g 22 dx II 6 x I x II dx I 9 x II dx II P2 dx I Q2 dx II
Pi Qi 时，坐标 xI , xII 才可能存在。即向量场 P, Q 无旋时，其在两点间 x II x I Pi Qi 的路径积分与路径无关，积出的值就是坐标。本例中， II I ，故相应的“协 x x
当变坐标”不存在。（正因为如此，坐标也没有逆变、协变之说。）（9）有点类似曲面第一基本型（1.3.12）。（10） Lame 常数定义（1.3.13）在非正交系中也成立，但此时（1.3.12a）不成立。
1.9-1.13：略； 1.14：注意，所谓斜圆锥是指， O 点沿 z 方向在大圆平面上的投影 M 在大圆的直径上。

第一章张量分析基础知识

第⼀章张量分析基础知识晶体物理性能南京⼤学物理系由于近代科学技术的发展，单晶体⼈⼯培养技术的成熟，单晶体的各⽅⾯物理性能（如⼒、声、热、电、磁、光）以及它们之间相互作⽤的物理效应，在各尖端科学技术领域⾥，都得到了某些应⽤．特别是⽯英⼀类压电晶体作为换能器、稳定频率的晶体谐振器、晶体滤波器等在电⼦技术中，⽐较早地在⼯业规模上进⾏⼤批⽣产和⼴泛应⽤．激光问世的四⼗多年来，单晶体在激光的调制、调Q、锁模、倍频、参量转换等光电技术应⽤中，已成单晶体应⽤中极为活跃的领域．《晶体物理性能》是我系晶体物理专业的专业课程之⼀，⽬的就是希望对晶体特别是光电技术中使⽤的晶体（包括基质晶体与⾮线性光学晶体）的有关物理性能及其应⽤⽅⾯的基本知识，有⼀个了解．对今后从事光电晶体的⽣长、检测和应⽤的⼯作，在分析问题、解决问题⽅⾯有所帮助，同时要在今后⼯作中不断从实践和理论两个⽅⾯扩⼤知识领域，有⼀个基础．考虑到本专业属于晶体材料性质的专业特点，本课程不仅对晶体物理性能的各个⽅⾯作深⼊全⾯的介绍，也将侧重于激光晶体有关的⼀些性能及其应⽤．鉴于以上考虑，《晶体物理性能》讲义将以离⼦晶体为主要对象，以光电技术上应⽤为线索组织内容，共分为⼋章．着重于从宏观⾓度结合微观机制介绍晶体基本物理性能以及各种交互作⽤过程的物理效应和它们在光电技术中的某些应⽤，包括弹性与弹性波（第⼆章），晶体光学中的各向异性（第五章），压电与铁电现象（第四章），电光效应（第七章），光学参量过程（第六章），声光效应（第⼋章）．由于晶体物理性能的各向异性的特点和晶体对称性有密切关系，通常正确、⽅便地描述这些物理性能必须使⽤张量来表⽰．因此，在第⼀章，我们介绍了关于张量分析基础知识⽅⾯的内容．由于⽔平有限，实践经验缺乏，时间仓促，因⽽内容安排不妥、取舍不当、错误之处⼀定很多，希望同学们提出宝贵意见，批评指正．第⼀章张量的基础知识§１．１标量、⽮量和⼆阶张量…………………………………………………………………２§１．２坐标变换和变换矩阵……………………………………………………………………§１．３正交变换矩阵的性质……………………………………………………………………§１．４晶体对称操作的变换矩阵……………………………………………………………§１．５⼆阶张量的变换与张量的定义………………………………………………………§１．６张量的⾜符互换对称…………………………………………………………………§１．７张量的矩阵表⽰和矩阵的代数运算…………………………………………………§１．８⼆阶对称张量的⼏何表⽰和⼆阶张量的主轴………………………………………§１．９⼆阶对称张量主轴的确定……………………………………………………………§１．10晶体张量与晶体对称性的关系………………………………………………………第⼆章晶体的弹性与弹性波§２．１弹性性质与原⼦间⼒…………………………………………………………………§２．２应变……………………………………………………………………………………§２．３应⼒……………………………………………………………………………………§２．４推⼴的虎克定律、弹性系数…………………………………………………………§２．５⽴⽅晶体的弹性系数…………………………………………………………………§２．６各向同性材料的弹性系数……………………………………………………………§２．７弹性扰动的传播――弹性波…………………………………………………………§２．８简谐振动和驻波……………………………………………………………………§２．９弹性常数及振动衰减因⼦的测量⽅法……………………………………………第三章晶体的介电性质§３．１介质中的宏观电场强度与极化强度………………………………………………§３．２晶体中的有效场……………………………………………………………………§３．３⾼频电场的介电极化（光的⾊散与吸收）………………………………………§３．４介电常数的测量……………………………………………………………………§３．５离⼦晶体的静电击穿………………………………………………………………§３．６激光的电击穿（激光的电击穿损伤）……………………………………………第四章铁电与压电物理§４．１铁电体的⼀般性质…………………………………………………………………§４．２常⽤铁电体的实验规律……………………………………………………………§４．３铁电体的相变热⼒学………………………………………………………………§４．４铁电体相变的微观机制……………………………………………………………§４．５晶体的压电效应……………………………………………………………………§４．６压电⽅程和机电耦合系数…………………………………………………………§４．７压电晶体的应⽤实例――⽯英……………………………………………………第五章晶体光学§５．１光学各向异性晶体…………………………………………………………………§５．２各向异性介质中光的传播…………………………………………………………§５．３折射椭球与折射率曲⾯……………………………………………………………§５．４晶体表⾯上的折射…………………………………………………………………§５．５晶体偏光⼲涉及其应⽤……………………………………………………………第六章倍频与参量频率转换§６．１⾮线性极化…………………………………………………………………………§６．２⾮线性极化系数……………………………………………………………………§６．３⾮线性介质中电磁场耦合⽅程……………………………………………………§６．４光倍频………………………………………………………………………………§６．５光倍频的相匹配……………………………………………………………………§６．６第II类相匹配………………………………………………………………………§６．７⾓度匹配和温度匹配扫描实验曲线………………………………………………§６．８内腔倍频……………………………………………………………………………§６．９光参量放⼤…………………………………………………………………………§６．10参量振荡器…………………………………………………………………………§６．11参量振荡器的调谐⽅法……………………………………………………………§６．12参量频率上转换……………………………………………………………………§６．13⾮线性材料的性能要求……………………………………………………………第七章电光效应及其应⽤§７．１线性电光效应………………………………………………………………………§７．２两种典型材料的电光效应…………………………………………………………§７．３电光滞后……………………………………………………………………………§７．４电光调制原理………………………………………………………………………§７．５实际调制器的⼏个问题……………………………………………………………§７．６晶体电光开关………………………………………………………………………§７．７电光Q开关…………………………………………………………………………§７．８电光偏转……………………………………………………………………………§７．９电光材料……………………………………………………………………………§７．10晶体均匀性的实验检测……………………………………………………………§７．11晶体的激光损伤……………………………………………………………………§７．12晶体均匀性实验检测………………………………………………………………第⼋章声光效应及其应⽤§８．１弹光效应……………………………………………………………………………§８．２声光交互作⽤产⽣的衍射现象……………………………………………………§８．３声光交互作⽤的理论………………………………………………………………§８．４声光效应在⼀些物理常数测量中的应⽤…………………………………………§８．５声光调制器…………………………………………………………………………§８．６声光偏转器…………………………………………………………………………§８．７声光调Q……………………………………………………………………………§８．８声光材料……………………………………………………………………………附录A．３２点群投影图…………………………………………………………………………B．各阶张量在不同点群中的矩阵形式……………………………………………………C．主要常数表………………………………………………………………………………D．单轴晶体中光线离散⾓α的推导………………………………………………………E．双轴晶体中双折射⾯相差Γ的推导……………………………………………………F．贝塞尔函数的基本性质…………………………………………………………………第⼀章张量分析基础知识以前学的课程中，有关⼒学、热学、电学、光学等的性质都是以各向同性介质来表述的或以⼀维问题来说明问题，这对于突出某些物理现象的微观的物理原因⽅⾯是必要的，但晶体物理性能是讲晶体中的⼒学、电学、光学、声学、磁学、热学等物理性能，⽽晶体的各向异性却是⼀种很普遍的特性，特别是很多现象如热电、压电、电光、声光、⾮线性光学效应……等等物理现象则完全因为晶体具有各向异性性质才能表现出来．因此，晶体结构对称性和这些性质之间的关系成为问题的主要⽅⾯。

张量分析第一章习题答案

j
一阶张量一阶张量根据张量识别定理: δ ij 是1+1阶即二阶张量. (2) 对于任意二阶张量 b jk 缩并:
∑ε
j ,k
ijk
b jk
一阶张量
∑ε
j ,k
1 jk b jk = b23 − b32
∑ε
j ,k
2 jk
b jk = b31 − b13
∑ε
j ,k
3 jk
b jk = b12 − b21
∑
i1i2 ⋅⋅⋅iµ j1 j2 ⋅⋅⋅ jµ
得 Ai1′i 1 Ai2′i2 ⋅⋅⋅ Aiµ′iµ Aj1′ j1 Aj2′ j2 ⋅⋅⋅ Ajν ′ jν ai1i2 ⋅⋅⋅iµ j1 j2 ⋅⋅⋅ jν 命题得证！命题得证！
ci1′i2′ ⋅⋅⋅iµ′ =
∑ ∑
i1i2 ⋅⋅⋅iν j1 j2 ⋅⋅⋅ jν
得
i1i2 ⋅⋅⋅iµ j1′ j2′ ⋅⋅⋅ jν ′ j1 j2 ⋅⋅⋅ jν
在新坐标系中: ci1′i2′ ⋅⋅⋅iµ′ = ∑ ai1′i2′ ⋅⋅⋅iµ′ j1′ j2′ ⋅⋅⋅ jν ′ b j1′ j2′ ⋅⋅⋅ jν ′
j1′ j2′ ⋅⋅⋅ jν ′
比较
ai1′i2′ ⋅⋅⋅iµ′ j1′ j2′ ⋅⋅⋅ jν ′ =
ai1′i2′ ⋅⋅⋅iµ′ =
∑
i1i2 ⋅⋅⋅iµ
得 Ai1′i 1 Ai2′i2 ⋅⋅⋅ Aiµ′iµ ai1i2 ⋅⋅⋅iµ
命题得证！命题得证！
6. 根据张量识别定理证明:δ ij是二阶张量, ε ijk 为三阶张量. 证: (1) 对于任意一阶张量对于任意阶张量 a j ∑ δij a j = ai

张量分析-第1讲LJ

a2 F3 a3 F2 a c b1 a b c1 a3 F1 a1 F3 a c b2 a b c2 a1 F2 a2 F1 a c b3 a b c3
所以有： a b c a c b a b c
g1和g 2
g1和g 2 不是单位矢量，即它们有量纲的，一般地说，
其长度也不为单位长度。此外它们也并不正交。矢量F可以在 g1和g 2 上分解:
F F g1 F g 2
1 2
(平行四边形法则)
则有: F g 1 F 1g 1 g 1 F 2 g 2 g 1
F g 1 F 1g 1 g 1 F 2 g 2 g 1
e2 b2 c2
e3
e3 b3 b2 c3 b3 c2 e 1 b3 c1 b1c3 e 2 b1c2 b2 c1 e 3 c3
b3 a 2 F3 a3 F2 e 1 a3 F1 a1 F3 e 2 a1 F2 a 2 F1 e 3 F3
j 1
F2 ' e 2 ' e1 F1 e 2 ' e 2 F2 e 2 ' e 3 F3 2 ' j F j
j 1 3
3
F3' e 3' e1 F1 e 3' e 2 F2 e 3' e 3 F3 3' j F j
j 1
矢量场函数的散度: 矢量场函数的旋度:
i F x Fx j y Fy
Fx Fy Fz F z y x
k Fz Fy Fx Fz Fy Fx i k j y z y z z x x Fz

教材张量分析及场论

张量分析与场论第一章张量代数任何物理现象的发展都是按照自身的规律进行的，这是客观的存在，而不以人们的意志为转移。

但是，在研究、分析这些物理现象时，采用什么样的方法则是由人们的意志决定的。

无数事实证明，研究方法的选取与当时人们对客观事物的认识水平有关，而研究方法的好坏则直接关系到求解问题的繁简程度。

由于物理量的分量与坐标的选择有关，所以由物理量的分量表示的方程，其形式就必然与坐标系的选取有关。

在建立基本方程时，每选用一种坐标系都要作一些繁琐的推导。

张量分析能以简洁的表达式，清晰的推导过程，有效地描述复杂问题的本质，并突出现象的几何和物理特点。

张量分析成功应用的根本在于由它表示的方程具有坐标变换下不变的性质，即由张量表示的方程，其形式不随坐标的选择而变化。

第一章中将着重介绍直角坐标系中的张量代数，第二章介绍正交曲线坐标系的张量分析及场论，作为进一步的学习的基础，在第三章还对一般曲线坐标系中的张量做了简单的介绍。

1.1点积、矢量分量及记号ij δ我们在以前的学习中已熟悉了用箭头表示的矢量，如位移u ρ，力F ρ等。

这些量满足平行四边形运算的矢量加法法则，即设u ρ，v ρ为矢量，则v u w ρρρ+=的运算如右图所示。

在理论力学中我们还知道，如u ρ表示某一点的位移，F ρ表示作用在该点上的力，则该力对物体质点所做的功为其中F ρ、|u ρ|分别表示矢量F ρ、u ρ的大小，θ表示矢量F ρ与矢量u ρ之间的夹角，这就定义了一种称为点积的运算。

点积的定义：设u ρ，v ρ为两个任意矢量，设|u ρ|，|v ρ|分别为其大小（也称为模）。

θ为这两个矢量之间的夹角，则u ρ与v ρ的点积为由点积定义可知，点积具有交换律，即u ρ•v ρ=v ρ•u ρ。

可以用几何的方法证明点积也具有分配率，即如w ρ=u ρ+v ρ，则或可写为如果0v u =⋅ρρ则称u ρ垂直于v ρ，记为u ρ⊥v ρ。

由点积的定义可知，2u u u ρρρ=⋅。

张量第一章

系中也必为零。
2、设，为r阶张量，方程
为张量方程。在张量方程中的每一项都有相同的张量特性。因此在
所有能够容许变换到的坐标系普遍有效。
若将张量方程两边同乘以变换系数，则
所以方程具有张量性质。
张量分析的重要性在于，由物理关系得到的方程如果是张量方程，
那它就在所有容许变换的坐标系成立了，避免了它在各种不同坐标系中
张量相乘提高了阶数，又称为张量外积。
3、张量的缩并对r阶张量进行缩并，就是对张量的某两个指标求和（如使j=k），
所得到的仍是张量，阶数比缩并前的原张量少2，即变为r-2阶张量。缩并使张量降阶，又称为张量内积。例如：对三阶张量，使j=k，缩并为缩并也可由乘法定义。
例：对的j、k进行缩并，则二阶张量缩并后得到标量，是它的不变量。
变换，则这九个量的集合称二阶张量，每个元素称张量分量。为单位二阶张量
二阶张量分量可组成一个二阶张量矩阵。二阶张量的另一个定义：设,为任意矢量的分量，若九个分量能与它们构成标量
则这九个分量定义一个二阶张量。高阶张量定义：在三维空间中，当直角坐标系旋转变换到时，基矢量和坐标按前述
规律变化。如果中确定的个分量与在中确定的之间服从相同的变换规律，即按式
个张量中的每一个分量，它们所组成的集合仍然是一个张量，称为第一个张量乘以第二个张量的乘积。积张量的阶数等于因子张量阶数之和。
例如：一矢量乘以一个二阶张量，乘积为 = 为一个三阶张量。
张量乘法服从分配律和结合律，但不服从交换律。高阶张量的乘积也可表示为不变式。张量与的乘积表示为（，可以是任意阶张量）
五：求导的简化法
数量场Φ的梯度
向量场散度：
向量场的旋度：
§1.2 坐标变换

张量分析1

第一章张量的概念§ 1.1 引言什么是张量？这是读者在开始学习本课程时会提出的问题，现从读者已有的力学知识出发，举例对这个问题作一些初步的阐述，使读者对张量这个新的概念，有个初步的理解。

有三维空间，一个矢量（例如力矢量、速度矢量等）在某些参考坐标系中，有三个分量，这三个分量的集合，规定了这个矢量。

当坐标变化换时，这些分量按一定的变换法则变换。

在力学中还有一些更复杂的量。

例如受力物体内一点的应力状态，有9个应力分量，如以直角坐标表示，用矩阵形式列出，则有()⎪⎪⎪⎭⎫⎝⎛σσσσσσσσσ=σzz zyzxyz yy yxxz xy xx ij 这9个分量的集合，规定了一点的应力状态，称为应力张量。

当坐标变换时，应力张量的分量按一定的变换法则变换，再如，一点的应力状态，具有和应力张量相似的性质，称为应变张量。

把上述的力矢量、速度矢量、应力张量、应变张量等量的性质抽象化，撇开它们所表示的量的物理性质，抽出其数学上的共性，便得出抽象的张量概念。

所谓张量是一个物理量或几何量，它由在某参考坐标系中一定数目的分量的集合所规定，当坐标变换时，这些分量按一定的变换法则变换。

张量有不同的“阶”和“结构”，这由它们所遵循的不同的变换法则来区分。

矢量是一阶张量；应力张量、应变张量是二阶张量；还有三阶、四阶、......等高阶张量。

可以看出，张量是矢量概念的推广。

关于张量的严密的解析定义，将在 § 1.8中讨论。

由张量的特性可以看出，它是一种不依赖于特定坐标系的表达物理定律的方式。

采用张量记法表示的方程，在某一坐标系中成立，则在容许变换的其它坐标系中也成立，即张量方程具有不变性。

这使它特别适合于表达物理定律，因为物理定律与人们为了描述它所采用的坐标系无关。

因此，张量分析为人们提供了推导基本方程的有力工具。

此外，张量记法简洁，是一种非常精炼的数学语言。

张量这个名词是沃伊特（V oigt ）首先提出的，用来表示晶体的应力（张力）状态，可见张量分析与弹性力学关系的密切。

张量第一章

第一章笛卡儿张量§1.1 指标表示法一：指标标号，自由指标x x =1 y x =2 z x =3 i x 1=i ，2，3基矢量i e =1 j e =2 k e =3i e 1=i ，2，3 任意一个矢量 i a 1=i ，2，3 332211e a e a e a a ++=二：求和约定哑标在一个单项式中，同一个指标重复出现两次，则将该指标按顺序1，2，3轮换求和。

该重复出现的指标为哑标。

如：332211b a b a b a b a i i ++=三：Kroneker ij δ⎨⎧≠==ji j i ij1δii δ=3 ， ijj i j ij ij i j ij ijhj ih e e x x x a δλδαλδδδ=-=-=)(四：Levi —Civita 符号 i j k e⎪⎩⎪⎨⎧-=非循环序列逆循环序列（循环序列),,(0),,1),,(1k j i k j i k j i e ijk1、循环序列： 1312231123===e e e2、逆循环序列： 1132213321-===e e e3、非循环序列： i ,j ,k 中有两个以上的指标取相同值4、奇置换和偶置换：在i ,j ,k 的具体序列中将指标顺序进行调换，奇数次为奇置换，偶数次为偶置换，序列偶置换属于原序列，奇置换则循环↔逆循环，非循环序列任何置换均为非循环序列。

kj ijk i kk j j i i k j i ijk b a e c b a e b a c e c c e b b e a a ba c a a a e a a a a a a a a a a ==⨯====⨯===222321333231232221131211五：求导的简化法()()i ix ,=∂∂()i ix ,ϕϕ=∂∂()jk i kj i u x x u ,2=∂∂∂数量场Φ的梯度 i i e e x e x e x g r a d ,332211φφφφφ=∂∂+∂∂+∂∂=向量场v 散度： i i v x v x v x v v d i v ,332211=∂∂+∂∂+∂∂=向量场的旋度：ki j k i j e e v e x v x v e x v x v e x v x v r o t v ,321122133113223)()()(=∂∂-∂∂+∂∂-∂∂+∂∂-∂∂=§1.2 坐标变换旧坐标系 321x x ox ：321,,e e e新坐标系 321x x x o ''' ：321,,e e e ''''11新旧坐标系间方向余弦为：332313333222122231211111332211)()()()()()('''''''''''''''αααααααααe x e x e x e x e x e x则新旧坐标关系为：⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡''''''''''''321332313322212312111321x x x x x x ααααααααα ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡'''⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡'''''''''321333231232221131211321x x x x x x ααααααααα j j i i x x '='α k j k j x x ''=α基矢量关系为j j i i e e ''=α k j k j e e ''=α k i j k j i ''''=δαα jk k i j i δαα='' 即变换系数矩阵为正交矩阵对a ， j j i i e a e a a =='' k j k j i i e a e a ''''=α 两边点乘j e ' ，有： j j j j a a ''=αj j i i a a ''=α k j k j a a ''=α即：矢量分量变换与坐标变换服从相同规律。

张量分析各章要点

各章要点第一章：矢量和张量指标记法：哑指标求和约定：同一项中出现一对相同的协、逆变指标则对该指标求和自由指标规则：同一项中只能出现一次，不同项中保持在同一水平线上协变基底和逆变基底：ki k i i x ∂∂==∂ξ∂ξr g e j j i i ⋅=δg giik k x∂ξ=∂g e123 ===g g g 张量概念i i'i'i =βg g i'i'ii =βg g i k i k j j''''ββ=δ i'i'i i v v =β ii 'i 'iv v =β i 'j'i 'j'k l ij ..k 'l'i j k 'l'..kl T T =ββββ i i i i v v ==v g g ..kl ij ijk l T =⊗⊗⊗T g g g g 度量张量ij i i i j i i g =⊗=⊗=⊗G g g g g g g⋅=⋅=⋅=⋅=v G G v v T G G T T.j kj i ik T T g =张量的商法则lm ijk T(i,j,k,l,m)S U = ijk...lmT(i,j,k,l,m)T = 置换符号312n 1n123n i i i i i 123n 1n i i i ...i A a a a ......a a e -- i j k Lmnijk .L.m .n a a a e e A = i j k .L .m .n ijk Lmn a a a e e A =置换张量i j k ijk ijk i j k =ε⊗⊗=ε⊗⊗εg g g g g gijk i j k ()e ε=⋅⨯=g g gijk ijk i j k ()ε=⋅⨯=g g gi j k ijk ijk i j k a b a b ()::()⨯=ε=ε=⊗=⊗a b g g a b εεa b广义δ符号i ii r s tj j j ijk ijk ijk r s t rst rst rst k k k r s te e δδδδδδ==εε=δδδδijk j k j k jk ist s t t s st δ=δδ-δδδijk k ijt t 2δ=δijk ijk 6δ=性质：是张量重要矢量等式：()()()⨯⨯=⋅-⋅a b c a c b a b c第二章：二阶张量重要性质：T =T.u u.T 主不变量i 1.i Tr()T ζ==T i j l m2l m .i .j 1T T 2ζ=δ 3det()ζ=T1()()(())(())()⋅⋅⨯⋅⋅⨯⋅⨯⋅=ζ⋅⨯T u v w +u T v w +u v T w u v w2)[)][()(]()[()]()⋅⋅⋅⨯⋅⋅⨯⋅⋅⋅⨯⋅=ξ⋅⨯T u (T v w +u T v T w)+T u (v T w u v w （ ()[()()]det()()⋅⋅⋅⨯⋅=⋅⨯T u T v T w T u v w 标准形1. 特征值、特征向量⋅=λT v v ()-λ⋅=T G v 0 321230λ-ζλ+ζλ-ζ= 2. 实对称二阶张量标准形i 123i 112233=⋅⊗=λ⊗+λ⊗+λ⊗N N g g g g g gg g 3. 正交张量（了解方法）12112233(cos()sin())(sin()cos())=ϕ+ϕ⊗+-ϕ+ϕ⊗+⊗R e e e e e e e e4. 反对称二阶张量的标准形21123=μ⊗-μ⊗=μ⨯Ωe e e e e G⋅=⨯Ωu ωu31:2=-=μ⨯ωεΩe u=-⋅Ωεω5. 正则张量极分解=⋅=⋅T R U V R第三章张量函数概念：各项同性张量函数、解析函数计算 e T ， sin()T 重要定理：1. Hamilton-Cayley 定理：32321231230λ-ζλ+ζλ-ζ=⇒-ζ+ζ-ζ=T T T G 0 2.对称各向同性张量函数表示定理：2012f ()k k k ==++H N G N N ；其中T T ;==H H N N ；而系数i k 是N 的主不变量的函数。

【张量分析ppt课件】张量分析课件第一章线性空间-50页精选文档

（2）∵ x y z ( x 1 y 1 ) z 1 , , ( x n y n ) z n
( x 1 y 1 z 1 , ,x n y n z n )
x ( y z ) ( x 1 ( y 1 z 1 ) , , ( x n ( y n z n ))
( x 1 y 1 z 1 , ,x n y n z n )
∴ x + (y + z )= ( x + y )+ z = x + y + z （4）∵ o(0, ,0)V0 x o (x 1 0 , x n 0 )(x1, ,xn)
∴ xox
（5）∵ ()x ()(x 1 , ,xn) (()x 1 , ,()xn)
∴
(x 1 , ,xn) (x 1 ), ,)xn)
第一章线性空间
若记实数集合为F，F中的元素记为a、b、c、…。
则加法法则将F中的任意两个元素 a, bF ; c F
+ (a, b)c
abc
乘法法则将F中的任意两个元素 a, bF ; c F
× (a, b)c
abc
显然具有加法法则和乘法则所确定的实数集中元
素间确定关系使得实数集构成一个空间。并记为：
所有以x点为起点的矢量按：
u x yu x z(y 1 x 1 , ,y n x n ) (z 1 x 1 , ,z n x n )
(y 1 ( x 1 ) (z 1 x 1 ) ,,(y n x n ) (z n x n ))
u xy (y1x1, ,ynxn) ((y1x1) ,,(ynxn)) F
a, b,xF
（6） (a b ) x a x b x
a, b,xF

第1章张量分析基础剖析

张量分析与连续介质力学教材：《The Mechanics and Thermodynamics of Continua》M.E. Gurtin, E. Fried, L. Anand. Cambridge University Press, 2010教学参考书：1、《An Introduction to Continuum Mechanics》, M.E. Gurtin, AcademicPress, 1981. （中译本：郭仲衡等译，连续介质力学引论，高等教育出版社，1992）2、《连续介质力学基础》，熊祝华等，湖南大学出版社，19973、《连续介质力学基础》，黄筑平，高等教育出版社，20034、《非线性连续介质力学》，匡正邦，上海交大出版社，2002x vy第一章张量分析基础第一节矢量和张量代数一、矢量代数本课程只在三维欧氏空间内讨论连续介质力学的基础原理。

1、点——反应一定的空间位置，由x表示2、矢量——具有大小和方向且满足一定规则的空间实体，用v来表示。

（两点间的距离可由一矢量表示）（点x和矢量v之和是另一个点y）3、矢量的点积和叉积1）点积（θ为两个矢量间的夹角）u 表示矢量的大小，为一标量，有u u u ⋅=。

2）叉积w v u =⨯ （为一新的矢量）v u ⨯表示由u 和v 构成的平行四边形的面积。

θsin v u v u =⨯且u w ⊥，v w ⊥3）混合积()w v u ⨯⋅()w⋅表示由u，v和w三个矢量围成的体的体积。

vu⨯●如果该体的体积不为零，则称u，v和w线性无关。

●如果对于不为零的常数a，b，c，有：u cabv+w=+则称u，v和w线性相关。

不满足线性相关的矢量则是线性无关的。

4、矢量空间及其性质由欧氏空间ε中对应的点构成的矢量形成的空间称为矢量空间ν。

如果u，v和w是线性无关的，则{}wu,构成矢量空间ν的基，即ν中任一矢量v,都可以表示为：w v u γβα++=a1）如果()0>⨯⋅w v u ，则基{}w v ,u,是正向的（右手法则）。

第1章张量分析(清华大学张量分析,你值得拥有)

jigggg一般来说张量的对称化与反对称化若四阶张量满足ijgggg则称张量t对其12指标是对称张量用来表示其转置张量ijjiklkl若四阶张量满足ijgggg则称张量t对其12指标是反对称张量用ijjiklkl张量的对称化与反对称化可立即得出反对称张量的对角分量均为零同为对称结构加任意载荷均可分为对称和反对称
g1 1
gi xi g2 ix1 sin x2 jx1 cos x2
g2 r
曲线坐标系：斜角直线坐标系的延伸
※三维球坐标系
(x, y, z) (x1, x2, x3)
(r, , ) (x1, x2 , x3 )
x3
r
gr g
g
x2
r x1i x2 j x3k xigi x1
新、老坐标之间的变换和逆变换： xi = xi xi'
gidxi gi' dx i'
dxi
=
xi xi'
dx i '
dx i
i'
i'
→
gi
i i'
dx
i'
g i
'
dx
i'
再由：
gidxi
g i
'
dx
i
'
→
gi'
i i'
gi
dxi'
=
xi' xi
dxi
i i
'
dx
i
→
gidxi
gi'
i i
'
dx
定义式（实体形式，几何表达）：
u v u v cos
v cos

张量分析答案完整版

证明： ∂ν m ∂ν n − ∂x n ∂x m ∂x m 则由 vm ' = β m = ' ' v m vm ∂x m m ∂v ' ∂x m ∂v m ∂x n ∂x m 可知: m ' = + ' ' ' ' vm n ∂x m ∂x ∂x n ∂x m ∂x n ∂x n ∂v ' ∂x n ∂v n ∂x m ∂x n 同理可得： n ' = + ' ' ' ' vn m ∂x m ∂x n ∂x ∂x m ∂x m ∂x n ∂v ' ∂v ' ∂x m ∂v m ∂x n ∂x m 则 T( m ' . n ' ) = m ' − n ' = + ' ' ' ' n ∂x n ∂x m ∂x m ∂x ∂x n ∂x m ∂x n 令 T ( m .n ) = 由于： ∂x m
T i j k = βri βs j βt k T rst T
' ' i 'j k ' ' '
' ' '
'
'
'
= β ir β js β kt Trst
' ' ' ' ' ' '
T..ik j = βri βs j β kt T..trs T. ij k = βri β s βt T r j k .st
∴T 与S具有相同的主不变量。
2.4 求证：（1） [T ⋅ u v w ] + [u v T ⋅ w ] + [u v T ⋅ w ] = φ1T [u v w ]

张量分析

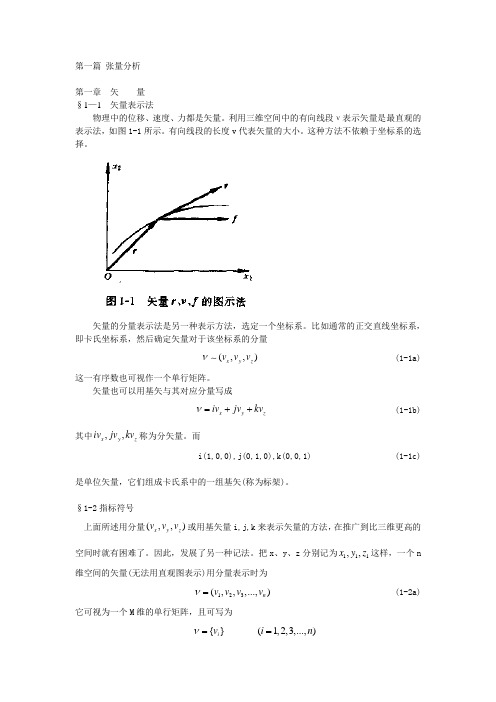
第一篇张量分析第一章矢量 §1—1 矢量表示法物理中的位移、速度、力都是矢量。

利用三维空间中的有向线段ν表示矢量是最直观的表示法，如图1-1所示。

有向线段的长度v 代表矢量的大小。

这种方法不依赖于坐标系的选择。

矢量的分量表示法是另一种表示方法，选定一个坐标系。

比如通常的正交直线坐标系，即卡氏坐标系，然后确定矢量对于该坐标系的分量(,,)x y z v v v ν(1-1a)这一有序数也可视作一个单行矩阵。

矢量也可以用基矢与其对应分量写成x y z iv jv kv ν=++ (1-1b)其中,,x y z iv jv kv 称为分矢量。

而i(1,0,0),j(0,1,0),k(0,0,1) (1-1c)是单位矢量，它们组成卡氏系中的一组基矢(称为标架)。

§1-2指标符号上面所述用分量(,,)x y z v v v 或用基矢量i,j,k 来表示矢量的方法，在推广到比三维更高的空间时就有困难了。

因此，发展了另一种记法。

把x 、y 、z 分别记为111,,x y z 这样，一个n 维空间的矢量(无法用直观图表示)用分量表示时为123(,,,...,)n v v v v ν= (1-2a)它可视为一个M 维的单行矩阵，且可写为{}i v ν= (1,2,3,...,)i n =同理，基矢i,j,k 可分别写为123,,e e e ，n 维空间的基矢i e (1,2,3,...,)i n =。

而与式(1-1b)对应的写法为112233n n e v e v e v e v ν=++++ (1-2b)相应的分矢量为11,,,i i e v e v ，其中1e =(0,…,0,1,0,…,0) (1-2c)↑ 顺序第i 个这里i 叫做v 的下标，也有记作jv (如本书第三章以后章节所出现)的，这时j 称为上标。

有些量比矢量更复杂，只用一个下(或上)指标还不够，还要采用更多的指标，比如,,,ij ij ijk A B C ，等等。

张量分析第一章

第一章 张量分析初步

黄克智版张量分析第一章习题解析

张量分析书籍附详尽易懂

最新张量分析第一章ppt课件

张量分析提纲及部分习题答案

第一章张量分析基础知识

张量分析第一章 习题答案

张量分析-第1讲LJ

教材张量分析及场论

张量第一章

张量分析1

张量第一章

张量分析各章要点

【张量分析ppt课件】张量分析课件第一章 线性空间-50页精选文档

第1章 张量分析基础剖析

第1章 张量分析(清华大学张量分析,你值得拥有)

张量分析答案完整版

张量分析

第一章张量分析初步

张量分析第一章习题答案

【张量分析ppt课件】张量分析课件第一章线性空间-50页精选文档

第1章张量分析基础剖析

第1章张量分析(清华大学张量分析,你值得拥有)