张量分析简答题
张量分析(Tensor Analysis)

ds 2 (dx1 ) 2 (dx 2 ) 2 (dx3 ) 2
利用克罗内克符号,上式可写成:
ds ij dx dx
2 i
j
克罗内克符号的一些常用性质:
i j xi x j
x j ij x i
i
j i k
j k
D) 置换符号
置换符号eijk=eijk定义为:
r i dr i dx x
空间一点P的位置矢量可用直角坐标表示为:
r z ji j
式中 ij 为沿坐标轴 zj 方向的单位矢量。
r r z j z j j i i ij i x z x x
r 上式表明, i 是单位矢量 ij 的线性组合,因此也是矢量。 x
基矢量(续)
r r i 变化时位置矢量r的变化,因此 i i 表征当 x i 的方向是沿坐标曲线 x x x r 的切线方向。矢量 i 可以取作曲线坐标系的基矢量(协变基矢量): x
r z j gi i i i j x x
注意:对于在曲线坐标系中的每一点,都有三个基 矢量。 基矢量一般不是单位矢量,彼此也不正交; 基矢量可以有量纲,但一点的三个基矢量的量纲可以不同;
1 张量的概念
在三维空间,一个矢量(例如力矢量、速度矢量等)在某参考坐标系中, 有三个分量;这三个分量的集合,规定了这个矢量;当坐标变换时,这些 分量按一定的变换法则变换。
在力学中还有一些更复杂的量。例如受力 物体内一点的应力状态,有9个应力分量, 如以直角坐标表示,用矩阵形式列出,则 有:
xx xy xz ij yx yy yz zx zy zz
克罗内克符号 i j 的定义是:
张量考试试卷

张量考试试卷一、选择题(每题2分,共20分)1. 张量是多维数组的推广,它在数学中通常用来描述什么?A. 向量场B. 线性变换C. 标量场D. 矩阵2. 以下哪个不是张量的属性?A. 阶数B. 维度C. 线性D. 可微性3. 在张量代数中,两个张量的乘积被称为什么?A. 张量积B. 外积C. 内积D. 张量和4. 张量场在物理学中通常用来描述什么?A. 力B. 温度C. 位移D. 速度5. 张量的阶数是指什么?A. 张量中元素的数量B. 张量可以展开的维度数C. 张量在空间中的自由度D. 张量中非零元素的个数6. 张量分析中,哪种操作可以改变张量的阶数?A. 张量积B. 张量和C. 张量外积D. 张量内积7. 在连续介质力学中,应力张量是如何描述的?A. 描述物体内部的力B. 描述物体的位移C. 描述物体的变形D. 描述物体的体积变化8. 张量运算中的“缩并”操作是指什么?A. 将张量简化为更低阶的张量B. 将两个张量合并为一个C. 将张量中的某些维度进行求和D. 将张量中的元素进行排序9. 在张量代数中,张量的转置操作会改变张量的什么?A. 阶数B. 维度C. 元素的值D. 元素的排列顺序10. 张量场在广义相对论中扮演什么角色?A. 描述时空的曲率B. 描述物体的质量分布C. 描述物体的动量D. 描述物体的角动量二、简答题(每题10分,共30分)1. 简述张量与矩阵的区别,并给出一个张量的例子。
2. 解释什么是协变导数,并说明它在张量场中的应用。
3. 描述张量积与外积的区别,并给出一个具体的例子。
三、计算题(每题25分,共50分)1. 给定一个二阶张量 \( A \),其元素为 \( A_{ij} \),计算 \( A \) 的迹(trace)。
2. 考虑一个四维空间中的张量场 \( T^{ab}_{cd} \),其中 \( a, b, c, d \) 都是从0到3的整数。
如果 \( T^{ab}_{cd} \) 在某一点\( P \) 处满足 \( T^{ab}_{cd} = T^{ba}_{dc} \),计算在该点\( T \) 的对称化(symmetrized)形式。
张量分析——精选推荐

《连续介质力学》例题和习题第一张、矢量和张量分析第一节 矢量与张量代数一、 矢量代数令 11223A A A =++A e e e 112233B B B =++B e e e 则有 11223A A A αααα=++A e e e 11122233()()()A B A B A B +=+++++A B e ee 1122331122331122()()A A A B B B A B A B A B ∙=++∙++=++A B e e e e e e112233112233111112121313212122222323313132323333()() A A A B B B A B A B A B A B A B A B A B A B A B ⨯=++⨯++=⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯A B e e e e e e e e e e e e e e e e e e e e e e e e 又因为 11⨯=e e 0 123⨯=e e e 132⨯=-e e e 213⨯=-e e e 22⨯=e e 0 231⨯=e e e 312⨯=e e e 321⨯=-e e e 33⨯=e e 0则 2332131132122(_)()()A B A B A B A B A B A B⨯=+-+-A B e e e习题1、证明下列恒等式:1)[]2()()()()⨯∙⨯⨯⨯=∙⨯A B B C C A A B C2) [][]()()()()⨯∙⨯=∙⨯-∙⨯A B C D A C D B B C D A2、请判断下列矢量是否线性无关?1232=-+A e e e 23=--B e e 12=-+C e e .其中i e 单位为正交的基矢量。
*补充知识:矩阵及矩阵运算1、定义:[]()111213212223313233,1,2,3ij A A A A A A A i j A AA ⎡⎤⎢⎥⎡⎤===⎣⎦⎢⎥⎢⎥⎣⎦A i 表示行,j 表示列;m 和n 相等表示为方阵,称为m (或n )阶矩阵。
张量分析试卷

班 级: 姓 名: 学 号: 考试日期:密 封 线拟题人: 2011-2012 学 年 1 学 期 张量分析(A ) 试卷 校对人:一. 简答题(每题2分,共10分)1. ij j a b 与k ikb a 是否相等? 2. *ij δ是如何定义的?3. 张力张量的阶数与对称性如何? 4. 对偶基的定义。
5. 阶数大于等于2的张量的分量有几种类型?二. 给出坐标变换*i ij j x x α=,其中 0()1000ij α⎛= ⎪ ⎪ ⎪ ⎪⎝⎭(a) 若在i x -坐标系中12322,A i i i =-+ 求它在*i x -坐标系中的分量。
(5分)(b) 若**132,B i i =+ 求它在i x -坐标系中的分量。
(5分) (c) 计算在i x -坐标系中的A B ⨯。
(5分)三. 平面应力12()21i j s -⎛⎫= ⎪-⎝⎭,求:(1)与单位向量n =+垂直的面上的应力。
(5分) (2)这个面上的法应力与切应力。
(5分)四. 一个二阶张量的分量如下给出:()400021012ij I ⎛⎫⎪= ⎪ ⎪⎝⎭(a) 求此张量的特征值及主轴。
(8分)(b) 写出在以主轴为坐标轴的坐标系中此惯性矩张量的分量。
(2分)五. 写出下列张量的散度223121222233112222312()ij x x x x x x s x x x x x x x x x x ⎛⎫-⎪=+ ⎪ ⎪-⎝⎭ (10分)六. 写出由给定基决定的ix -坐标系与*ix -坐标系间的转换:1212122,e i i e i i =+=-+;*1*212122,2.e i i e i i =+=-+(10分)七. 令()ix φ为直角笛卡尔坐标系i x 中的数量场,且令**i i jj x x α=为由这个直角笛卡尔坐标系到一个斜坐标系*ix 的坐标转换。
证明:(1,2,3)ii xφ∂=∂是φ的梯度的共变分量。
(10分) 八. 已知两个斜笛卡尔坐标系ix -坐标系与*ix -坐标系,分别由下列基确定:1232133132,,;e i i e i i e i i i =+=+=++*1*2*311312,2,2.e i e i i e i i ==+=+在ix -坐标系中,一个二阶笛卡尔张量的共变和反变分量分别为:()()120161825203,182532032253242ij ij a a ---⎛⎫⎛⎫⎪⎪==-- ⎪ ⎪ ⎪ ⎪--⎝⎭⎝⎭写出这个二阶张量在*ix-坐标系中的共变分量及反变分量。
张量分析作业答案

张量分析作业1.2题 证明:()()()()()()()()()()()()()()()()()()()()()()()()()C B AD D B A C D C B A U B A D C B A D C A B U B A U A B B A U A B U BA U AB U B A U B A DC wv u v w u w v u U D C B A D C D C B A ⨯∙-⨯∙=⨯⨯⨯=⨯⨯∙-⨯∙=∙-∙=∙+∙-∙+∙-=⨯⨯-=⨯⨯⨯-∙-∙=⨯⨯=⨯⨯⨯⨯-=⨯⨯⨯令同理可证得:利用点积交换律得:得:,利用公式设1.5 求证:0a b ⨯=⇔,a b 线性相关。
证明: a b ⨯=xy z xy zij ka a ab b b =()()()0y z z y z x x z x y y x a b a b i a b a b j a b a b k -+-+-= ∴i j j i a b a b =即i ji ja a kb b == i i a kb = i j k i j k k k k a i a j a k b i b j b k ∴++=++即k =a b ,a b ∴线性相关 同理可证 当,a b 线性相关时,0a b ⨯= ∴0a b ⨯=⇔,a b 线性相关。
1-7解:c mb a =+ ()1,2,3c =()2,,2mb m m m =- (),,a x y z =22021223x y z m x m y z m +-=+=+=-=解得1320234,,,9999x y z m ====-132023999a i j k =++1.8 试求线元d kx 的长度d k s 。
解:d d d d =d d d k ki k k ki i i x g x x x g r g r r δ=⇒==⇒1.10、解:(1)由公式g 1=g1(g 2×g 3)g 2=g 1(g 3×g 1)g 3=g1(g 1×g 2)又g =[g 1 g 2 g 3]=k ×i ·j ,得g 1=j i k jk i k j i ∙⨯⨯+⨯+⨯g 2=j i k kj k i j i ∙⨯⨯+⨯+⨯g 3=ji k jk k i j i ∙⨯⨯+⨯+⨯(2)g rs =323121g g g g g g g g s r ∙+∙+∙=⨯=()()()()()()j i k i j i k j k i k j +∙+++∙+++∙+ =222j k i ++1-10、解:(1)由公式g 1=g1(g 2×g 3)g 2=g 1(g 3×g 1)g 3=g1(g 1×g 2)又g =[g 1 g 2 g 3]=k ×i ·j ,得g 1=j i k jk i k j i ∙⨯⨯+⨯+⨯g 2=j i k kj k i j i ∙⨯⨯+⨯+⨯g 3=ji k jk k i j i ∙⨯⨯+⨯+⨯(2)g rs =323121g g g g g g g g s r ∙+∙+∙=⨯=()()()()()()j i k i j i k j k i k j +∙+++∙+++∙+ =222j k i ++1.17求:题1.13所示圆柱坐标和球坐标i x ,与笛卡尔坐标j x '的转换系数'i j β与'j i β。
张量分析答案完整版.

1.1 求证: u × (v × w ) = ( u • w) v − ( u • v) w
黄克智版张量分析课后习题答案完整版
并问: u × ( v × w ) 与 (u × v) × w 是否相等? u 、v、w 为矢量 证明:因为 u= (u x , u y , u z ) ; v= ( vx , vy , vz ) ; w= ( wx , wy , wz ) ;
左边= u × (v × w ) = (u x , u y , u z ) × [ ( vx , vy , vz ) × ( wx , wy , wz ) ]
g11g1 + g 12g 2 + g 13g 3 = 2g1 + g 2 + g 3
= j + k = g1
1.11 根据上题结果验算公式: g j = g jig i 1 1 1 由上题结果: g = 2 , g1 = ( −i + j + k ) , g 2 = (i − j + k ) , g3 = ( i + j − k ) 2 2 2
=[
⎧2 g rs = ⎨ ⎩1
及: g1 = g11g1 + g12g 2 + g13g3
所以 u × (v × w) ≠(u × v) ×w
第一章
同理; g 21g1 + g 22g 2 + g 23g3 = g1 + 2g 2 + g 3 当r=s 当r ≠ s
=
=
, u y ( vx wy − wx v y ) − u z ( wxv z − v x wz ) u x ( wx vz − vx wz ) − u y ( v y wz − w yv z ) ] 所以: u × (v × w ) = (u • w)v − ( u • v) w 同理可证: ( u × v ) × w = ( u • w) v − ( v • w) u
张量分析第一章 习题答案

一阶张量 一阶张量 根据张量识别定理: δ ij 是1+1阶即二阶张量. (2) 对于任意二阶张量 b jk 缩并:
∑ε
j ,k
ijk
b jk
一阶张量
∑ε
j ,k
1 jk b jk = b23 − b32
∑ε
j ,k
2 jk
b jk = b31 − b13
∑ε
j ,k
3 jk
b jk = b12 − b21
∑
i1i2 ⋅⋅⋅iµ j1 j2 ⋅⋅⋅ jµ
得 Ai1′i 1 Ai2′i2 ⋅⋅⋅ Aiµ′iµ Aj1′ j1 Aj2′ j2 ⋅⋅⋅ Ajν ′ jν ai1i2 ⋅⋅⋅iµ j1 j2 ⋅⋅⋅ jν 命题得证! 命题得证!
ci1′i2′ ⋅⋅⋅iµ′ =
∑ ∑
i1i2 ⋅⋅⋅iν j1 j2 ⋅⋅⋅ jν
得
i1i2 ⋅⋅⋅iµ j1′ j2′ ⋅⋅⋅ jν ′ j1 j2 ⋅⋅⋅ jν
在新坐标系中: ci1′i2′ ⋅⋅⋅iµ′ = ∑ ai1′i2′ ⋅⋅⋅iµ′ j1′ j2′ ⋅⋅⋅ jν ′ b j1′ j2′ ⋅⋅⋅ jν ′
j1′ j2′ ⋅⋅⋅ jν ′
比较
ai1′i2′ ⋅⋅⋅iµ′ j1′ j2′ ⋅⋅⋅ jν ′ =
ai1′i2′ ⋅⋅⋅iµ′ =
∑
i1i2 ⋅⋅⋅iµ
得 Ai1′i 1 Ai2′i2 ⋅⋅⋅ Aiµ′iµ ai1i2 ⋅⋅⋅iµ
命题得证! 命题得证!
6. 根据张量识别定理证明:δ ij是二阶张量, ε ijk 为三阶张量. 证: (1) 对于任意一阶张量 对于任意 阶张量 a j ∑ δij a j = ai
张量分析与材料应力张量习题解答

练习题Ⅱ(金属所)1. 用下标符号证明:C B A B C A C B A )()()(⋅-⋅=⨯⨯。
2. 证明nknj ni mk mj mi lklj li lmn ijk δδδδδδδδδ=∈∈3. 证明ijk klm =(δil δjm -δim δjl )4. 证明ijk ikj =-6。
5. 证明ijkmik =-2δjm 。
6. 证明具有中心对称的晶体不具有由奇阶张量描述的物理性质,但由偶阶张量描述的物理性质也具有中心对称的特性。
7. B 为矢量,M 为二阶张量,证明:(div M )⋅B =div(M ⋅B )-{ (B ∇)∶M } 8. 设在P 点的应力张量 σ如下:求法线方向为]221[的面上的正应力。
⎪⎪⎪⎭⎫ ⎝⎛----=211121112)(ij σ9. 设在P 点的应力张量 σ如下:求该处的主应力及主方向。
并验证主方向是相互正交的。
⎪⎪⎪⎭⎫ ⎝⎛=740473037)(ij σ10. 位移场u 在给定坐标系下的分量分别是:u 1= ax 2+bx 3,u 2=ax 1cx 3,u 3= bx 2+cx 3;其中a 、b 、c 皆为常数。
求这个位移场的应变张量Γ。
11. 弹性体的的应变张量场如下所示,这个应变张量场合理吗?⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡++--=32222111216112226226)(x x x x x x x ij ε12. 在立方晶体中承受一均匀应力场,以]101[、]211[和[111]为x 1、x 2和x 3坐标轴的应力分量只有σ13和σ23两项,求以三个晶轴作坐标系的各应力分量σ’ij 。
练习题Ⅱ解答(金属所)1. 用下标符号证明: C B A B C A C B A )()()(⋅-⋅=⨯⨯。
解:CB A BC A e e e e e C B C B A )()()(()()()(⋅-⋅=-==∈∈=∈=∈⨯=∈⨯⨯i i j j j i j i jl im jm il m l j i klm ijk m l j ik m l klm j ijk i k j ijk c b a c b a )δ-δδδc b a c b a c b a a 2. 证明nknj ni mk mj mi lklj li lmn ijk δδδδδδδδδ=∈∈解:a ij 的行列式为333231232221131211det a a a a a a a a a A = 当行列式行与行、列与列对换一次行列式的值就变号一次,任意换行后有A a a a a a a a a a lmn n n n m m m l l l det 321321321=∈ 任意换列后有A a a a a a a a a a ijk kjik j i kj i det 333222111=∈ 因此,任意行与行、列与列交换后有A a a a a a a a a a lmn ijk nkmkninj mj mi nimi li det ∈=∈ 令a ij =δij ,det A =1,则有lmn ijk nknj ni mk mj mi lklj li ∈=∈δδδδδδδδδ 3. 证明ijk klm =(δil δjm -δim δjl ) 解:根据上题的结果,有)()3()3()()(im jl mj li li mj mj li mi lj mj li mi lj jl im li kj mk ki mj lk mi lj kk mj li kk mi lk kj mk lj ki mkmj mi lklj li kkkj ki klm ijk δδδδδδδδδδδδδδδδδδδδδδδδδδδδδδδδδδδδδδδδδδδ-=++-++=++-++==∈∈4. 证明ijk ikj =-6解:ijk ikj =-ijk kij =-(δii δjj -δij δji )=-(33-δii )=-(9-3)=-65. 证明ijk mik =-2δjm解:ijk mik =ijk kmi =(δim δji -δii δjm )= (δjm -3δjm )=-2δjm6.证明具有中心对称的晶体不具有由奇阶张量描述的物理性质,但由偶阶张量描述的物理性质也具有中心对称的特性。
张量分析习题答案

张量分析习题答案张量分析习题答案张量分析是数学中的一个重要分支,它在物理学、工程学和计算机科学等领域中有着广泛的应用。
学习张量分析需要掌握一定的数学知识和技巧,通过解答习题可以更好地理解和应用这一理论。
本文将给出一些张量分析习题的详细解答,帮助读者更好地掌握这一领域的知识。
1. 习题一:设有一个二阶张量A,其分量为Aij = 2i + j,求A的迹和对称部分。
解答:首先,迹是指一个方阵的主对角线上元素的和。
对于二阶张量A,其迹为Aii,即A的两个主对角线元素之和。
根据题目给出的分量表达式,可以得到A的迹为A11 + A22 = 2(1) + 1 + 2(2) + 2 = 9。
其次,对称部分是指一个张量的分量满足Aij = Aji的部分。
对于二阶张量A,其对称部分为(A + A^T)/2,其中A^T表示A的转置。
根据题目给出的分量表达式,可以得到A的转置矩阵为:A^T = [A11 A21][A12 A22]= [2(1) + 1 2(2) + 2][1 2]将A和A^T代入对称部分的表达式中,可以得到对称部分为:(A + A^T)/2 = [(2(1) + 1) + (2(1) + 1)]/2 [(2(2) + 2) + 2]/2[(1 + 1) + 1]/2 [(2 + 2) + 2]/2[3 4][1 2]2. 习题二:设有一个三阶张量B,其分量为Bijk = i^2 + j^2 + k^2,求B的迹和对称部分。
解答:对于三阶张量B,其迹为Biii,即B的三个主对角线元素之和。
根据题目给出的分量表达式,可以得到B的迹为B111 + B222 + B333 = (1^2 + 1^2 + 1^2) + (2^2 + 2^2 + 2^2) + (3^2 + 3^2 + 3^2) = 9 + 12 + 27 = 48。
对于三阶张量B,其对称部分为(B + B^T)/2,其中B^T表示B的转置。
根据题目给出的分量表达式,可以得到B的转置张量为:B^T = [B111 B211 B311][B121 B221 B321][B131 B231 B331]= [1^2 + 1^2 + 1^2 2^2 + 1^2 + 1^2 3^2 + 1^2 + 1^2][1^2 + 2^2 + 1^2 2^2 + 2^2 + 1^2 3^2 + 2^2 + 1^2][1^2 + 3^2 + 1^2 2^2 + 3^2 + 1^2 3^2 + 3^2 + 1^2]= [3 6 9][6 9 14][9 14 19]将B和B^T代入对称部分的表达式中,可以得到对称部分为:(B + B^T)/2 = [(1^2 + 1^2 + 1^2) + (3)]/2 [(2^2 + 1^2 + 1^2) + (6)]/2 [(3^2 + 1^2 + 1^2) + (9)]/2[(1^2 + 2^2 + 1^2) + (6)]/2 [(2^2 + 2^2 + 1^2) + (9)]/2 [(3^2 + 2^2 +1^2) + (14)]/2[(1^2 + 3^2 + 1^2) + (9)]/2 [(2^2 + 3^2 + 1^2) + (14)]/2 [(3^2 + 3^2 + 1^2) + (19)]/2[5 8 10][8 11 16][10 16 24]通过以上习题的解答,我们可以更好地理解和应用张量分析的知识。
第二章 张量分析
P P x1' , x 2' , x 3' P x i'
这种坐标系记为 xi。' 这两组变量
x1 , 和x 2 , x 3 表示x同1' 一, x空2' , x 3'
间点的位置。两者由下列坐标变换联系起来:
xi xi xi'
aigi a jg j aia j gi g j
aiaj 0
令
gij gi g j
g ij g i g j
gi j gi g j g j gi
它们分别称为协变度量张量、逆变度量张量和混合度量张量
考虑到矢量a的任意性 g ji gi g j i j
可知:基矢量 g与i 是g i 正交的,它们称为互逆基矢量 互逆基矢量间具有下列关系:
gig j g k gi g j g k gig j g k eijk
这两个量定义为爱丁顿(Eddington)张量并分别记为 和ijk 。ijk
由此定义可知
123 g1g 2g3
123 g1g 2g3
对于矢量 a 0 ,则有
a 2 a a a i g i a j g j a i a j g i g j ai gi a j g j ai a j gi g j
(ii) x 2' (常 数 C)为2 通过z轴的平面; (iii) x3' (常z 数 C)3为垂直于z轴的平面;
和坐标曲线:
(i) x1' 和r C1 x的2' 交线 (zC线2 )是直线; (ii) x 2' 和 C2 的x3'交线z (r线C3)是直线;
张量分析(最后附题目)

x2
5
2 常用总体坐标系(正交系)
z
O
(x0 y0 z0)
·
z (ρ0 ϕ0 z0)
·
θ
O
·(r r
0
θ0 ϕ0 )
y
x
x
ϕ
O
ρ
y
x
ϕ
直角坐标系
柱坐标系
v e v A
v v v e x , e y , ez v v v Ax , Ay , Az
v v v e ρ , eϕ , e z 曲线 v v v 正交 Aρ , Aϕ , Az
●
矢量微分元
Байду номын сангаас
线元,面元,体元v v v v 例: ∫ F ⋅ dl , ∫ B ⋅ dS , ∫ ρ dV
v v 其中:dl , dS dV 称为微分元。
v dl
v dS
A.直角坐标系 在直角坐标系中,坐标变量为(x,y,z),如图,做一微分体元。 v v r r 线元: dlx = dxa x 面元: dS x = dydzax v v r r dS y = dxdza y dl y = dya y v r v r dS z = dxdyaz dlz = dzaz v r r r 体元: dV = dxdydz dl = dxax + dya y + dzaz
(对各向同性、线性电介质) 电极化率,表征了电介质的性质 r r 对各向异性、非线性电介质, 并不和 E 简单成正比, P 其方向也不一定平行,“电极化率”不是一个简单的数。 r r r P 当 E 不太强时, 和 E 的对应关系仍然是线性关系, 可以用分量表示为:
r r ∑ pi 单位体积内所有分子 电极化强度矢量:P = 的电偶极矩矢量和 ΔV r r P = αE
关于张量分析的数学原理和实际应用案例

关于张量分析的数学原理和实际应用案例引言张量分析是一门重要的数学分支,在科学和工程领域有着广泛的应用。
作为一种多维量、多方向、多变量的数据结构,张量在物理、力学、电磁学、地球物理学等领域的描述、建模与计算中起着不可或缺的作用。
本文将介绍张量分析的数学原理以及实际应用案例,旨在帮助读者更好地了解这门学科。
第一部分数学原理1.张量的定义按照一般的定义,张量是一个可用于表示多维量和多向量之间关系的数学对象。
它可以看做是一种多维矩阵,其中每个元素都有多个指标。
与标量和向量不同,张量的指标可以有多个,我们常常用字母来表示。
2.张量的运算在张量分析中,张量的运算包括加、减、乘等。
与标量和向量不同,张量的乘法并不等同于代数乘法,而是采用了一种特殊的“卷积运算”。
例如,两个二阶张量相乘的结果是一个四阶张量。
这种方法既能描述多维多向量之间的关系,又可以实现基本的数学运算。
3.张量的变换由于张量具有多个指标,所以张量的变换涉及到各个指标的变化。
例如,一个二阶张量在坐标系变换后,其各个分量会发生相应的变化。
我们可以通过矩阵变换来描述张量的变换规律。
这一点在物理领域的应用尤其常见。
第二部分实际应用案例1. 电磁场模拟电磁场模拟是利用计算机模拟电磁场分布的方法,是工程和科学研究中的一项重要任务。
在这个过程中,张量分析被广泛应用。
例如,可以用张量表示电场强度、磁场强度等物理量,通过各种运算描述它们之间的关系。
同时,也可以用张量来描述电磁波的传播规律,实现电磁场的精确计算。
这种方法被广泛应用于电子器件设计、通讯技术等领域。
2. 生物医学图像处理生物医学图像处理是生物医学领域研究的一个重要方向,包括了图像采集、处理、分析等各个环节。
其中,张量分析被广泛应用于图像处理中。
例如,可以用张量表示医学图像中的像素强度、颜色等信息,通过各种运算分析其空间分布与统计规律,实现对生物组织的诊断、治疗等应用。
这种方法在医学影像学、神经科学等领域有着广泛的应用。
张量分析部分习题答案

2 6 0 1 3
1 6 1 2 1 3
1 6 1 2 1 3
(d) 略 2. (a) 1
1, 2 2, 3 5
A1 i 2 i3 , A2 i1 , A3 i 2 i3
1 0 0 * ( I ij ) 0 2 0 0 0 5
t jibj
则: (e1
e2 e3 ) (b1 b2 b3 )(tij ) 5 1 0
(c)
b1 tij ai b j ai tij b j (a1 a 2 a3 )(tij ) b2 3 b 3 2 2 1 0 2 3 ( sij ) 2 3 2 , (tij ) 2 0 0 1 2 1 3 0 0
(b) 对 i ,散度分量为
aj
tij xi
,
a1 1, a2 0, a3 x2 ;
7
对
j ,散度分量为 bi x j
tij
,
b1 1, b2 0, b3 1
5.证明:
* aij * aij a pq xr a pq ip jq kr * * xk a pq xr xk xr
* 3 0 反向 4 1 * 1 1 * 2 e i1 , e i 1 i ,2, 2 2
18.
1 * 1
1 2 1 , 2
X * * X 1 2 *1 1 x x x 2 1 x*2 x1 x 2 2
a2 3b 2 3 a 3b 1 3 1a b 3 2
3 2
a b
3 3
3 3
6.(a)
张量分析答案完整版

T i j k = βri βs j βt k T rst T
' ' i 'j k ' ' '
' ' '
'
'
'
= β ir β js β kt Trst
' ' ' ' ' ' '
T..ik j = βri βs j β kt T..trs T. ij k = βri β s βt T r j k .st
∴T 与S具有相同的主不变量。
2.4 求证: (1) [T ⋅ u v w ] + [u v T ⋅ w ] + [u v T ⋅ w ] = φ1T [u v w ]
黄克智版张量分析 习题解析

因为 detU≠0,所以 vx=vy=vz=0 是唯一零解,即:v=0。
1.4 已知:矢量 u,v,求证: u v u v
证明: u v u v sinu,v u v
1.5 求证: a b 0 a,b 线性相关。
证明: 即
i jk a b ax ay az
bx by bz
aybz azby i azbx axbz j axby aybx k 0
wy uyvz uzvy wx uzvx uxvz k
uv w uv w
1.2 求证: (A×B) ×(C×D)=B(A·C×D) -A(B·C×D) =C(A·B×D) -D(A·B×C)
证明:
i jk
A B Ax Ay Az Bx By Bz
Ay Bz Az By i Az Bx AxBz j AxBy Ay Bx k
2
ui u j gij , vi v j gij
uu12 u3
g11 g21 g31
g12 g22 g32
g13 g23 g33
u1 u 2 u 3
ห้องสมุดไป่ตู้
2 1 1
1 2 1
1 2 6
1231
7 3
v1 g11
v2 v3
g21 g31
g12 g22 g32
g13 g23 g33
i jk B D Bx By Bz
Dx Dy Dz
By Dz Bz Dy i Bz Dx BxDz j BxDy By Dx k
i
A B C D Ay Bz Az By
Cy Dz Cz Dy
j Az Bx Ax Bz Cz Dx Cx Dz
k Ax By Ay Bx Cx Dy Cy Dx
张量习题答案

张量习题答案张量习题答案张量是数学中一个重要的概念,广泛应用于物理学、工程学等领域。
它是一个多维数组,可以用来表示向量、矩阵和更高维的数据结构。
张量的运算和性质十分复杂,因此在学习张量的过程中,习题是不可或缺的一部分。
下面我将为大家提供一些张量习题的答案,希望能对大家的学习有所帮助。
1. 习题:给定两个向量a = (1, 2, 3)和b = (4, 5, 6),求a和b的内积。
答案:内积是两个向量对应分量的乘积之和。
所以,a和b的内积可以表示为:a·b = 1×4 + 2×5 + 3×6 = 4 + 10 + 18 = 32。
2. 习题:已知一个3×3的矩阵A = [[1, 2, 3], [4, 5, 6], [7, 8, 9]],求矩阵A的转置。
答案:矩阵的转置是将矩阵的行和列互换得到的新矩阵。
对于矩阵A来说,它的转置可以表示为:A^T = [[1, 4, 7], [2, 5, 8], [3, 6, 9]]。
3. 习题:已知一个2×2的矩阵B = [[2, 3], [4, 5]],求矩阵B的特征值和特征向量。
答案:特征值和特征向量是矩阵在线性代数中的重要概念。
对于矩阵B来说,我们可以通过求解特征方程来求得其特征值和特征向量。
特征方程可以表示为:det(B - λI) = 0,其中I是单位矩阵,det表示行列式。
解特征方程可以得到矩阵B的特征值。
然后,将每个特征值代入(B - λI)x = 0,求解得到特征向量。
具体计算过程略。
4. 习题:已知一个3维张量C,其形状为(2, 3, 4),求张量C的元素个数。
答案:张量的元素个数等于各个维度的乘积。
对于张量C来说,其元素个数可以计算为:2 × 3 × 4 = 24。
5. 习题:已知一个2维张量D,其形状为(3, 3),求张量D的逆矩阵。
答案:逆矩阵是在线性代数中常用的概念,对于方阵来说,如果存在逆矩阵,那么该矩阵是可逆的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
22
张量分析
Tensor Analysis
x2
x1'
x2' x2
x
' 2
e2'
e2 e1'
x1' x1
e1
令:αi' j cos(ei' ,e j )
x1
( i' , j 1,2 )
则:αi' j
ccooss((ee21''
,e1 ) ,e1 )
cos(e1' cos(e2'
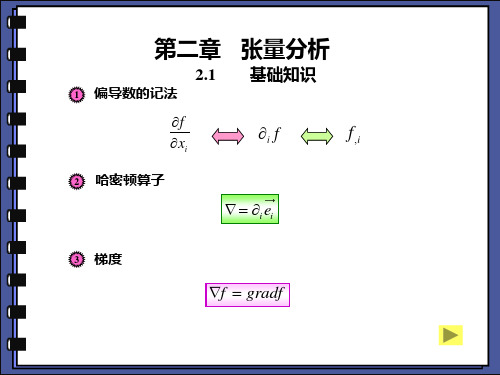
标为哑指标。如:
ai xi (i 1,2, n)
a1x1 a2 x2 an xn
n i 1
ai
xi
又如: ii jj 11 22 33 x y z
11
张量分析
Tensor Analysis
1
求和约定仅对字母指标有效,如 33 z
Aij jk Aik
ij jk ik
ij jk kl il
xi x j
xi, j
ij
aii a jk
jk
18
张量分析
Tensor Analysis
§A-2 张量的定义和代数运算
1. 矢量的基本运算
矢量a 分量ai
a a1e1 a2e2 a3e3 aiei
23
31 32 33
x xy xz
yx
y
yz
zx zy z
10
张量分析
Tensor Analysis
一.若干约定 哑标和自由标 1. Einstein求和约定
凡在某一项内,重复一次且仅重复一次的指标,表 示对该指标在它的取值范围内求和,并称这样的指
(rot vr )z
1 (rv ) 1 vr
r r r
0
所以除原点有旋外,其他点的流体均作无旋运动
O
7
张量分析
Tensor Analysis
三、不参考本课程教案的前提下,请独立完成你认为学的最好或最有用的知 识点做15分钟的PPT。
答:我觉得以下内容学的比较好,因为可以更加深刻的理解高等流体力 中各种物理量的定义以及相关公式的推导。
=
1( w 2 y
v z
)
2
=
1( 2
u z
w x
),3
=
1( v 2 x
u y
),于是 =i
ei
1( w v 2 y z
)i
i jk
1(
u
w
)k
1(
v
u)j ,源自依据场论写成
=
1
u
=
1
2 z x
其中
S =sij
1( ui 2 x j
+
uj xi
)称为应变率张量,是一个对称张量,
描述流体微团的变形运动。A=aij
1( ui 2 x j
u j )称为旋转率张 xi
量,是一个反对称张量。描述流体微团的旋转运动。把aij的三个
独立分量看作矢量的三个分量1,2,3,对应于1
2
度变化,此即速度分解定理。
6
张量分析
Tensor Analysis
利用速度分解定理分析下列两种现象 1.剪切流动速度场
y
ur
u ay
但是,因为:(rot vr )z a 0
vw0
x
o
所以其为有旋场,处处有旋,流体作有旋运动
2.点涡运动速度场
vr 0
v
b r
当 r 时0 ,
同样:xx12
1211''
1
2'
2 2'
x1' x2'
i '
j
T
xx12''
由()式得
x1 x2
i '
j
1
xx12''
基矢量e1 e2 e3 ( 3个坐标方向的单位矢量)
1 任意矢量可以表示为基矢量的线性组合
2
基矢量不是唯一的
19
张量分析
Tensor Analysis
1 基矢量点积 ei e j δij
2 任意两矢量的点积
a b aiei bje j aibjδij aibi a jbj
所以任意一个二阶张量总可以分解为对称张量和反对称张量两部分
1
张量分析
Tensor Analysis
不理解的地方:令Bij
1 2
( Aij
Aji )后,为什么就有Bji
1 2
(
Aji
Aij )
既然这里A为任意二阶张量,那么应该还有
1 2
( Aji
Aij )=
1 2
( Aij
Aji )=Bij为什么就有了Bij
=B
j
,
i
这里i和j位置交换后对二阶张量Bij元素的排列难
道没影响吗?还有一点,令Cij
=
1 2
( Aij
Aji
)后,
为什么有
1 2
( Aij
Aji
)=
1 2
( Aji
Aij
),而不是这样
1 2
( Aij
Aji )=
-
1 2
( Aji
Aij
),还有C ji
=
1 2
( Aji
Aij
)
不太明白。 2
ei e j ij
ei' e j' i' j'
考虑一位置矢量
x x je j x j' e j'
x je j ei' x j' e j' ei'
x j cos(e j ,ei' ) x j' j'i' xi'
(
),ij
2( ) xi x j
uk ,ij
2u xi x j
13
张量分析
Tensor Analysis
3.自由标
定义:凡在同一项内不重复出现的指标。如
a ji xi bj
j为自由标
j=1 a11x1 a12 x2 a13 x3 b1
14
张量分析
Tensor Analysis
A2
A3
Aj
j 1 j2 j3
ds2 dx2 dy2 dz2 dxidxi ij dxidx j
17
张量分析
性质:
Tensor Analysis
ijij ii 11 22 33 3
Aijij Aii Ajj A11 A22 A33
x y z
u
x
v
w
=
v x
v y
v w
=
y z
,式中
ui x j
或
v x
v y
v
w
w w w
w w w
x y z
)
1 2
( Aij
Aji
).
令
Bij
1 2
( Aij
Aji
), Cij
=
1 2
( Aij
Aji
)
则
1
1
Bij = 2 ( Aij Aji )= 2 ( Aji Aij )=Bji
Cij
=
1 2
( Aij
Aji )=
1 2
( Aji
Aij )=-C ji
从而Bij为二阶对称张量,Cij为二阶反对称张量
§A-1 指标符号
§A-2 张量的定义和代数运算
§A-3 张量分析
8
张量分析
Tensor Analysis
§A-1 指标符号
x1,x2 xn 记作 xi (i 1,2, n)
下标符号 i 称为指标;n 为维数 指标 i 可以是下标,如 xi也可以是上标,如 xi
指标的取值范围如不作说明,均表示从1~3
1 同一个方程中各项自由标必须相同
2 不能改变某一项的自由标,但所有项的 自由标可以改变
如: a ji xi bj aki xi bj aki xi bk
15
张量分析
Tensor Analysis
二.克罗内克(Kronecker-δ)符号
定义:
ij 10
当i j 当i j
由定义
1 0 0 11 12 13
I 0
1
0 21
22
23
ij
0 0 1 31 32 33
