张量分析(1)
2019-【张量分析ppt课件】张量分析课件第一章 线性空间-PPT精品文档-文档资料

4
r2 3 a 2 b1 2 1
b2 b3 r3 a3
( 1 t ) ( 3 , 1 ) t ( 4 , 1 ) 0 t 1 , t F : r 1 与 r 2 :(取 sb b ) a b ( 1 t ) ( a s ) t ( b s )a t b 2 2 1 1 ( 1 t ) ( 2 1 . 65 , 2 . 3 0 ) t ( 1 1 . 65 , 2 2 . 3 )a t b ( 0 . 35 t , 2 . 3 2 t )a t b ( 0 . 35 t , 2 . 3 2 t ) ( 0 . 65 , 4 . 3 ) 当 t b 时: ( 0 . 35 t , 2 . 3 2 t ) ( 0 , 3 ) 当 t a 时: .35 b 1 。显然由(1.1-7)式可知 r 1∥r 2 ,但 由此可得 a0 , 0 . 3 5 0 由(1.2-1)式可知 r1 和 r 2 不等价(因为 a )。
确定的矢量 u x x y 所构成的一类矢量,称为矢量 y的等价类。V 0 中所有矢量按(1.2-1)所构成 的等价类的集合称为自由矢量集合。记为 V 0 。 应当注意的是自由矢量的集合中的一个元素是 一类按平行性等价的约束矢量,而不是一个矢 量。
r1 : ( 1 t ) ( 2 , 0 ) t ( 1 , 2 ) 0 t 1 , t F
定义实数域上位置矢量的加法运算和数乘运算:
x ( xxxx ,, ) ( ,, )(,, x x )
1 n 1 n 1 n
x y ( x y ,x y ) ( zz , n ) z 1 1 n n 1
08张量分析1

z = x3
图 1-1
向量的定义
k = i3
a
P
y = x2
i = i1
O
j = i2
x = x1
向量的位置(作用点)效应可用向量函数来反映。如图 1-2,水流各点的流速可用向量函数 v ( x , y , z ) 表示, x , y , z 表示 v 作用点的空间坐标。
图 1-2
流速场
A B C
vA vB vC
a + b = b + a 交换律
(a + b) + c = a + (b + c ) 结合律
( λµ ) a = λ ( µ a )
λ (a + b ) = λ a + λ b
1a = a
结合律 分配律
a+0 = a
a + (−a ) = 0
零向量 负向量
(λ + µ ) a = λ a + µ a 分配律
(
)
ɶ1 , a ɶ2 , a ɶ3 = a ɶj = a ɶ je j a= a
(
)
1.2 点积与欧氏空间
★ 同义词 : 点积、 点积、内积、 内积、数量积、 数量积、标量积 在线性空间里,没有长度和夹角的概念,从而没有几何度量的概念,此外几何上求向量在数轴上的投影, 物理上功与功率的计算等等,都需引入的点积的概念。
式中,小写指标 k , ℓ , m 为整型变量,称自由标,可在默认范围内取任意值。本书仅讨论 3 维线性 空间,自由标默认取值为 1 , 2 , 3 (n 维线性空间中,自由标默认取值为 1 ,… ,n) 。字母带自由标不 仅简化了数 (向量) 组的表示, 而且具有双重意义: 它既可代表数 (向量) 组全体(当视自由标为变量时), 亦可表示数(向量)中某-分量(当视自由标为某-数值时)。
张量分析

张量分析张量分析,又称张量微积分,是一门研究多维空间中的向量和张量的数学工具。
它在物理学、工程学、计算机科学等领域有着广泛的应用。
张量分析的核心思想是通过张量的计算和运算,来描述和解释多维空间中的现象和问题。
在数学中,张量是一种广义的向量概念。
它不仅可以表示标量和向量,还可以表示具有更高维度的物理量。
例如,二阶张量可以表示物体的形变和应力分布,三阶张量可以表示电磁场的分布,四阶张量可以表示弹性材料的性质等。
张量分析的基本概念包括张量的定义和表示、张量的变换规律以及张量的运算。
对于二阶张量,可以用一个矩阵来表示。
张量的变换规律与坐标系的选择有关,不同的坐标系下,同一个张量可以表示为不同的矩阵形式。
张量的运算包括加法、数乘、内积和外积等。
这些运算在物理和工程问题中具有重要的意义,可以帮助研究人员推导和解决实际问题。
在物理学中,张量分析被广泛应用于描述和分析物体的运动、形变、应力等问题。
例如,通过分析物体的应力张量,可以判断物体是否会发生破坏或变形。
在工程学中,张量分析可以用于解决弹性力学、流体力学、电磁学等问题。
在计算机科学中,张量分析可以用于图像处理、模式识别等领域。
张量分析的发展离不开数学家们的努力。
早在19世纪,克里斯托弗·亚当斯(Christopher Adams)就提出了张量的概念。
20世纪初,爱因斯坦在相对论的研究中也广泛应用了张量分析。
随着计算机的发展和计算能力的提高,张量分析在科学研究中的应用也越来越广泛。
虽然张量分析在各个领域中都有广泛的应用,但它的理论和方法并不容易掌握。
要学好张量分析,需要对线性代数、微积分和向量分析等数学知识有扎实的掌握。
此外,也需要具备一定的物理学和工程学的基础知识。
对于初学者来说,可以通过学习相关的教材和参考资料,同时结合实际问题进行练习和应用。
总之,张量分析是一门重要的数学工具,对于描述和解决多维空间中的问题具有重要的意义。
它在物理学、工程学、计算机科学等领域有着广泛的应用。
张量分析提纲及部分习题答案

y
对静止的连续介质,有
ζ n fd 0 , ζd fd 0 ,
A
ζ f 0。
(21) 证明应力是一个张量; 记 ij :表示在给定基 g i 下,在面 g j 上,单位面积受力 F j 在 g i 方向上的分量为
对斜圆锥面上任一点 (图中黑点处) , 不难由相似三角形得到,
z z R cos C i R sin j zk ,进而可得, H H r Rz sin zR cos r R cos C R g i j, gz i sin j k , H H z H H r
dx g dx I g dx II 1 4 x I 2 dx I 6 x I x II 2 dx II Pdx I Q dx II 11 12 1 1 I 。 2 4 dxII g 21dx I g 22 dx II 6 x I x II dx I 9 x II dx II P2 dx I Q2 dx II
Pi Qi 时,坐标 xI , xII 才可能存在。即向量场 P, Q 无旋时,其在两点间 x II x I Pi Qi 的路径积分与路径无关,积出的值就是坐标。本例中, II I ,故相应的“协 x x
当 变坐标”不存在。 (正因为如此,坐标也没有逆变、协变之说。 ) (9) 有点类似曲面第一基本型(1.3.12) 。 (10) Lame 常数定义(1.3.13)在非正交系中也成立,但此时(1.3.12a)不成立。
1.9-1.13:略; 1.14: 注意,所谓斜圆锥是指, O 点沿 z 方向在大圆平面上的投影 M 在大圆的直径上。
第一章张量分析基础知识

第⼀章张量分析基础知识晶体物理性能南京⼤学物理系由于近代科学技术的发展,单晶体⼈⼯培养技术的成熟,单晶体的各⽅⾯物理性能(如⼒、声、热、电、磁、光)以及它们之间相互作⽤的物理效应,在各尖端科学技术领域⾥,都得到了某些应⽤.特别是⽯英⼀类压电晶体作为换能器、稳定频率的晶体谐振器、晶体滤波器等在电⼦技术中,⽐较早地在⼯业规模上进⾏⼤批⽣产和⼴泛应⽤.激光问世的四⼗多年来,单晶体在激光的调制、调Q、锁模、倍频、参量转换等光电技术应⽤中,已成单晶体应⽤中极为活跃的领域.《晶体物理性能》是我系晶体物理专业的专业课程之⼀,⽬的就是希望对晶体特别是光电技术中使⽤的晶体(包括基质晶体与⾮线性光学晶体)的有关物理性能及其应⽤⽅⾯的基本知识,有⼀个了解.对今后从事光电晶体的⽣长、检测和应⽤的⼯作,在分析问题、解决问题⽅⾯有所帮助,同时要在今后⼯作中不断从实践和理论两个⽅⾯扩⼤知识领域,有⼀个基础.考虑到本专业属于晶体材料性质的专业特点,本课程不仅对晶体物理性能的各个⽅⾯作深⼊全⾯的介绍,也将侧重于激光晶体有关的⼀些性能及其应⽤.鉴于以上考虑,《晶体物理性能》讲义将以离⼦晶体为主要对象,以光电技术上应⽤为线索组织内容,共分为⼋章.着重于从宏观⾓度结合微观机制介绍晶体基本物理性能以及各种交互作⽤过程的物理效应和它们在光电技术中的某些应⽤,包括弹性与弹性波(第⼆章),晶体光学中的各向异性(第五章),压电与铁电现象(第四章),电光效应(第七章),光学参量过程(第六章),声光效应(第⼋章).由于晶体物理性能的各向异性的特点和晶体对称性有密切关系,通常正确、⽅便地描述这些物理性能必须使⽤张量来表⽰.因此,在第⼀章,我们介绍了关于张量分析基础知识⽅⾯的内容.由于⽔平有限,实践经验缺乏,时间仓促,因⽽内容安排不妥、取舍不当、错误之处⼀定很多,希望同学们提出宝贵意见,批评指正.第⼀章张量的基础知识§1.1标量、⽮量和⼆阶张量…………………………………………………………………2§1.2坐标变换和变换矩阵……………………………………………………………………§1.3正交变换矩阵的性质……………………………………………………………………§1.4晶体对称操作的变换矩阵……………………………………………………………§1.5⼆阶张量的变换与张量的定义………………………………………………………§1.6张量的⾜符互换对称…………………………………………………………………§1.7张量的矩阵表⽰和矩阵的代数运算…………………………………………………§1.8⼆阶对称张量的⼏何表⽰和⼆阶张量的主轴………………………………………§1.9⼆阶对称张量主轴的确定……………………………………………………………§1.10晶体张量与晶体对称性的关系………………………………………………………第⼆章晶体的弹性与弹性波§2.1弹性性质与原⼦间⼒…………………………………………………………………§2.2应变……………………………………………………………………………………§2.3应⼒……………………………………………………………………………………§2.4推⼴的虎克定律、弹性系数…………………………………………………………§2.5⽴⽅晶体的弹性系数…………………………………………………………………§2.6各向同性材料的弹性系数……………………………………………………………§2.7弹性扰动的传播――弹性波…………………………………………………………§2.8简谐振动和驻波……………………………………………………………………§2.9弹性常数及振动衰减因⼦的测量⽅法……………………………………………第三章晶体的介电性质§3.1介质中的宏观电场强度与极化强度………………………………………………§3.2晶体中的有效场……………………………………………………………………§3.3⾼频电场的介电极化(光的⾊散与吸收)………………………………………§3.4介电常数的测量……………………………………………………………………§3.5离⼦晶体的静电击穿………………………………………………………………§3.6激光的电击穿(激光的电击穿损伤)……………………………………………第四章铁电与压电物理§4.1铁电体的⼀般性质…………………………………………………………………§4.2常⽤铁电体的实验规律……………………………………………………………§4.3铁电体的相变热⼒学………………………………………………………………§4.4铁电体相变的微观机制……………………………………………………………§4.5晶体的压电效应……………………………………………………………………§4.6压电⽅程和机电耦合系数…………………………………………………………§4.7压电晶体的应⽤实例――⽯英……………………………………………………第五章晶体光学§5.1光学各向异性晶体…………………………………………………………………§5.2各向异性介质中光的传播…………………………………………………………§5.3折射椭球与折射率曲⾯……………………………………………………………§5.4晶体表⾯上的折射…………………………………………………………………§5.5晶体偏光⼲涉及其应⽤……………………………………………………………第六章倍频与参量频率转换§6.1⾮线性极化…………………………………………………………………………§6.2⾮线性极化系数……………………………………………………………………§6.3⾮线性介质中电磁场耦合⽅程……………………………………………………§6.4光倍频………………………………………………………………………………§6.5光倍频的相匹配……………………………………………………………………§6.6第II类相匹配………………………………………………………………………§6.7⾓度匹配和温度匹配扫描实验曲线………………………………………………§6.8内腔倍频……………………………………………………………………………§6.9光参量放⼤…………………………………………………………………………§6.10参量振荡器…………………………………………………………………………§6.11参量振荡器的调谐⽅法……………………………………………………………§6.12参量频率上转换……………………………………………………………………§6.13⾮线性材料的性能要求……………………………………………………………第七章电光效应及其应⽤§7.1线性电光效应………………………………………………………………………§7.2两种典型材料的电光效应…………………………………………………………§7.3电光滞后……………………………………………………………………………§7.4电光调制原理………………………………………………………………………§7.5实际调制器的⼏个问题……………………………………………………………§7.6晶体电光开关………………………………………………………………………§7.7电光Q开关…………………………………………………………………………§7.8电光偏转……………………………………………………………………………§7.9电光材料……………………………………………………………………………§7.10晶体均匀性的实验检测……………………………………………………………§7.11晶体的激光损伤……………………………………………………………………§7.12晶体均匀性实验检测………………………………………………………………第⼋章声光效应及其应⽤§8.1弹光效应……………………………………………………………………………§8.2声光交互作⽤产⽣的衍射现象……………………………………………………§8.3声光交互作⽤的理论………………………………………………………………§8.4声光效应在⼀些物理常数测量中的应⽤…………………………………………§8.5声光调制器…………………………………………………………………………§8.6声光偏转器…………………………………………………………………………§8.7声光调Q……………………………………………………………………………§8.8声光材料……………………………………………………………………………附录A.32点群投影图…………………………………………………………………………B.各阶张量在不同点群中的矩阵形式……………………………………………………C.主要常数表………………………………………………………………………………D.单轴晶体中光线离散⾓α的推导………………………………………………………E.双轴晶体中双折射⾯相差Γ的推导……………………………………………………F.贝塞尔函数的基本性质…………………………………………………………………第⼀章张量分析基础知识以前学的课程中,有关⼒学、热学、电学、光学等的性质都是以各向同性介质来表述的或以⼀维问题来说明问题,这对于突出某些物理现象的微观的物理原因⽅⾯是必要的,但晶体物理性能是讲晶体中的⼒学、电学、光学、声学、磁学、热学等物理性能,⽽晶体的各向异性却是⼀种很普遍的特性,特别是很多现象如热电、压电、电光、声光、⾮线性光学效应……等等物理现象则完全因为晶体具有各向异性性质才能表现出来.因此,晶体结构对称性和这些性质之间的关系成为问题的主要⽅⾯。
张量分析第一章 习题答案

一阶张量 一阶张量 根据张量识别定理: δ ij 是1+1阶即二阶张量. (2) 对于任意二阶张量 b jk 缩并:
∑ε
j ,k
ijk
b jk
一阶张量
∑ε
j ,k
1 jk b jk = b23 − b32
∑ε
j ,k
2 jk
b jk = b31 − b13
∑ε
j ,k
3 jk
b jk = b12 − b21
∑
i1i2 ⋅⋅⋅iµ j1 j2 ⋅⋅⋅ jµ
得 Ai1′i 1 Ai2′i2 ⋅⋅⋅ Aiµ′iµ Aj1′ j1 Aj2′ j2 ⋅⋅⋅ Ajν ′ jν ai1i2 ⋅⋅⋅iµ j1 j2 ⋅⋅⋅ jν 命题得证! 命题得证!
ci1′i2′ ⋅⋅⋅iµ′ =
∑ ∑
i1i2 ⋅⋅⋅iν j1 j2 ⋅⋅⋅ jν
得
i1i2 ⋅⋅⋅iµ j1′ j2′ ⋅⋅⋅ jν ′ j1 j2 ⋅⋅⋅ jν
在新坐标系中: ci1′i2′ ⋅⋅⋅iµ′ = ∑ ai1′i2′ ⋅⋅⋅iµ′ j1′ j2′ ⋅⋅⋅ jν ′ b j1′ j2′ ⋅⋅⋅ jν ′
j1′ j2′ ⋅⋅⋅ jν ′
比较
ai1′i2′ ⋅⋅⋅iµ′ j1′ j2′ ⋅⋅⋅ jν ′ =
ai1′i2′ ⋅⋅⋅iµ′ =
∑
i1i2 ⋅⋅⋅iµ
得 Ai1′i 1 Ai2′i2 ⋅⋅⋅ Aiµ′iµ ai1i2 ⋅⋅⋅iµ
命题得证! 命题得证!
6. 根据张量识别定理证明:δ ij是二阶张量, ε ijk 为三阶张量. 证: (1) 对于任意一阶张量 对于任意 阶张量 a j ∑ δij a j = ai
张量分析-第1讲LJ

a2 F3 a3 F2 a c b1 a b c1 a3 F1 a1 F3 a c b2 a b c2 a1 F2 a2 F1 a c b3 a b c3
所以有: a b c a c b a b c
g1和g 2
g1和g 2 不是单位矢量,即它们有量纲的, 一般地说,
其长度也不为单位长度。此外它们也并不正交。 矢量F可以在 g1和g 2 上分解:
F F g1 F g 2
1 2
(平行四边形法则)
则有: F g 1 F 1g 1 g 1 F 2 g 2 g 1
F g 1 F 1g 1 g 1 F 2 g 2 g 1
e2 b2 c2
e3
e3 b3 b2 c3 b3 c2 e 1 b3 c1 b1c3 e 2 b1c2 b2 c1 e 3 c3
b3 a 2 F3 a3 F2 e 1 a3 F1 a1 F3 e 2 a1 F2 a 2 F1 e 3 F3
j 1
F2 ' e 2 ' e1 F1 e 2 ' e 2 F2 e 2 ' e 3 F3 2 ' j F j
j 1 3
3
F3' e 3' e1 F1 e 3' e 2 F2 e 3' e 3 F3 3' j F j
j 1
矢量场函数的散度: 矢量场函数的旋度:
i F x Fx j y Fy
Fx Fy Fz F z y x
k Fz Fy Fx Fz Fy Fx i k j y z y z z x x Fz
张量分析

张量分析研一 熊焕君 2017.9.281.引论:我们对标量和矢量都非常熟悉。
标量是在空间中没有方向的量,其基本特征是只需要一个数就可以表示,且当坐标系发生转动时这个数保持不变,因此也称其为不变量。
而矢量是个有方向的量,三维空间中矢量需要一组三个数(分量)来表示,其基本特征是当坐标系发生转动时,这三个数按一定规律而变化。
然而在数学物理问题中,还常出现一些更为复杂的量,如描述连续体中一点的应力状态或一个微元体的变形特征等,仅用标量和矢量不足以刻画出他们的性质。
要描述这些量则有必要将标量和矢量的概念加以引申和扩充,即引入新的量——张量。
在概念上,张量和矢量有许多类同之处。
一方面张量也表示某一客观存在的几何量或物理量,显然张量作为一个整体是与描述它所选取的坐标系无关,可像矢量代数那样,用抽象法进行描述;另一方面也可像矢量一样采用坐标法进行描述,此时张量包含有若干个分量元素,各个分量的取值与具体的坐标系相关联。
张量的主要特征是,在坐标系发生变化时,其分量取值遵守着一定的转化定律。
张量方法的核心内容是研究一个复杂的量集坐标转换规律。
我们知道,一个物理定律如果是正确的,就必须不依赖于用来描述它的任何坐标系,张量方法就是既采用坐标系,而又摆脱具体坐标系的影响的不变方法。
于是我们可以在简单的直角坐标系中建立描述某一运动法则的支配方程,如果需要可以用张量方法将其转换到任意一个曲线坐标系中去。
例如对于很大一类边值问题,若选用恰当的曲线坐标系,其边界条件可以简化的表达,那么我们就可以将支配方程用张量方法转化到所采用的坐标系中来,从而使问题的求解容易处理。
2.记号与约定张量是包含有大量分量元素的复杂量集,必须使用适当的记号和约定,才能使其表达形式简化紧凑,从而使分析和讨论有序地进行。
从某种意义上讲,可以说张量是对记号的研究。
所以我们必须熟悉各种约定记号,才能对张量这个工具运用自如。
在张量方法中对一个量的标记采用字母标号法。
数学中的张量分析方法

数学中的张量分析方法在数学中,张量分析是一种用于描述多维空间中变量关系的数学工具。
它在许多领域中被广泛应用,包括物理学、工程学、计算机科学和经济学等。
本文将介绍张量的基本概念和常见的应用方法。
一、张量的定义和性质1. 张量的定义张量是一个多维数组,可以表示为多个分量的组合。
在欧几里德空间中,一阶张量是向量,二阶张量是矩阵。
高阶张量可以看做是多个矩阵的组合。
2. 张量的性质张量具有坐标系无关性,即其分量在不同坐标系下具有相同的转换法则。
这使得张量在描述物理量时具有普适性和通用性。
二、张量的运算法则1. 张量的加法和减法张量的加法和减法都是对应分量相加或相减。
要求参与运算的张量具有相同的维度。
2. 张量的数乘张量的数乘是将每个分量都乘以一个标量。
数乘并不改变张量的维度。
3. 张量的张量积张量的张量积是两个张量的分量进行乘积并按照一定规则相加得到的新张量。
它在向量叉乘、矩阵乘法等问题中有广泛应用。
4. 张量的缩并运算张量的缩并是对张量的某些分量进行求和,并将结果保留在一个新的张量中。
它常用于求解线性方程组、协方差矩阵等问题。
三、张量的应用举例1. 物理学中的应用张量在物理学中有广泛的应用,如流体力学中的应力张量、电动力学中的麦克斯韦张量等。
它们描述了物质在空间中的运动和相互作用。
2. 工程学中的应用张量在工程学中用于描述物体的形变、应力分布等。
它在结构力学、弹性力学、热传导等领域中有着重要的作用。
3. 计算机科学中的应用张量在图像处理、模式识别、机器学习等领域中被广泛应用。
例如,卷积神经网络中的卷积操作就可以用张量运算进行描述。
4. 经济学中的应用张量在经济学中用于描述多个经济变量之间的关系。
它可以用来分析供求关系、生产函数等经济现象。
结语:张量分析作为一种重要的数学工具,为我们研究和解决各种问题提供了强有力的帮助。
通过对张量的定义、性质和运算法则的了解,我们可以更好地理解和应用张量,进而推动科学的发展和进步。
张量分析1

第一章 张量的概念§ 1.1 引言什么是张量?这是读者在开始学习本课程时会提出的问题,现从读者已有的力学知识出发,举例对这个问题作一些初步的阐述,使读者对张量这个新的概念,有个初步的理解。
有三维空间,一个矢量(例如力矢量、速度矢量等)在某些参考坐标系中,有三个分量,这三个分量的集合,规定了这个矢量。
当坐标变化换时 ,这些分量按一定的变换法则变换。
在力学中还有一些更复杂的量。
例如受力物体内一点的应力状态,有9个应力分量,如以直角坐标表示,用矩阵形式列出,则有()⎪⎪⎪⎭⎫⎝⎛σσσσσσσσσ=σzz zyzxyz yy yxxz xy xx ij 这9个分量的集合,规定了一点的应力状态,称为应力张量。
当坐标变换时,应力张量的分量按一定的变换法则变换,再如,一点的应力状态,具有和应力张量相似的性质,称为应变张量。
把上述的力矢量、速度矢量、应力张量、应变张量等量的性质抽象化,撇开它们所表示的量的物理性质,抽出其数学上的共性,便得出抽象的张量概念。
所谓张量是一个物理量或几何量,它由在某参考坐标系中一定数目的分量的集合所规定,当坐标变换时,这些分量按一定的变换法则变换。
张量有不同的“阶”和“结构”,这由它们所遵循的不同的变换法则来区分。
矢量是一阶张量;应力张量、应变张量是二阶张量;还有三阶、四阶、......等高阶张量。
可以看出,张量是矢量概念的推广。
关于张量的严密的解析定义,将在 § 1.8中讨论。
由张量的特性可以看出,它是一种不依赖于特定坐标系的表达物理定律的方式。
采用张量记法表示的方程,在某一坐标系中成立,则在容许变换的其它坐标系中也成立,即张量方程具有不变性。
这使它特别适合于表达物理定律,因为物理定律与人们为了描述它所采用的坐标系无关。
因此,张量分析为人们提供了推导基本方程的有力工具。
此外,张量记法简洁,是一种非常精炼的数学语言。
张量这个名词是沃伊特(V oigt )首先提出的,用来表示晶体的应力(张力)状态,可见张量分析与弹性力学关系的密切。
张量分析01

附录I 张量分析近代力学在电子计算机的辅助下冲破了数学求解上的重重困难,取得了突飞猛进的发展,力求对复杂的物理现象和工程问题做出更为系统和真实的描述和研究。
张量分析能以简洁的表达形式和清晰的推导过程来有效地描述复杂问题的本质,已被近代力学文献和教科书普遍采用。
作为入门,此处着重介绍笛卡儿坐标系和正交曲线坐标系中的张量。
I.1 矢量和张量的记法,求和约定力学中常用的量可以分成三类:只有大小没有方向性的物理量称为标量。
例如温度T 、密度ρ、时间t 等。
既有大小又有方向性的物理量称为矢量,常用黑体(或加箭头)表示,为与课堂讲述一致,此处选择用上加箭头表示矢量。
例如矢径r 、位移u 、速度v 、力f 等。
具有多重方向性的更为复杂的物理量称为张量,常用黑体(或加下横)表示,为与课堂讲述一致,此处选择用下加横线表示矢量。
例如一点的应力状态要用应力张量来表示,它是具有二重方向性的二阶张量,记为σ。
矢量可以在参考坐标系中分解。
例如图1 中P 点的位移u 在笛卡儿坐标系()321,,x x x 中分解为∑==++=31332211i i i e u e u e u e u u (I.1)其中1u 、2u 、3u 是位移的三个分量,1e 、2e 、3e是沿坐标轴的三个单位基矢量。
由此引出矢量(可推广至张量)的三种记法: ( l )实体记法:把矢量或张量的整个物理实体用一个黑体字母或上加箭头来表示。
例如把位移记为u 。
( 2 )分解式记法:同时写出矢量或张量的分量和相应分解方向的基矢量。
例如用式(I.1)表示位移u 。
( 3 )分量记法:把矢量或张量用其全部分量的集合来表示,省略相应的基矢量。
例如用三个位移分量()3,2,1=i u i 的集合表示位移u 。
下面详细讨论后两种记法中广泛采用的指标符号。
对于一组性质相关的n 个量可以采用指标符号来表示。
例如,n 维空间中矢量a 的n 个分量1a ,2a ,…,n a 可缩写成()n i a i ,,2,1 =。
(完整版)《张量分析》报告

一 爱因斯坦求和约定1.1指标变量的集合:n n y y y x x x ,...,,,...,,2121表示为:n j y n i x j i ...,3,2,1,,...,3,2,1,==写在字符右下角的 指标,例如xi 中的i 称为下标。
写在字符右上角的指标,例如yj 中的j 称为上标;使用上标或下标的涵义是不同的。
用作下标或上标的拉丁字母或希腊字母,除非作了说明,一般取从1到n 的所有整数,其中n 称为指标的范围。
1.2求和约定若在一项中,同一个指标字母在上标和下标中重复出现,则表示要对这个指标遍历其范围1,2,3,…n 求和。
这是一个约定,称为求和约定。
例如:333323213123232221211313212111bx A x A x A b x A x A x A bx A x A x A =++=++=++筒写为:ijijbx A =j——哑指标i——自由指标,在每一项中只出现一次,一个公式中必须相同遍历指标的范围求和的重复指标称为“哑标”或“伪标”。
不求和的指标称为自由指标。
1.3 Kronecker-δ符号(克罗内克符号)和置换符号Kronecker-δ符号定义j i ji ij ji ≠=⎩⎨⎧==当当01δδ置换符号ijkijk e e =定义为:⎪⎩⎪⎨⎧-==的任意二个指标任意k j,i,当021)(213,132,3的奇置换3,2,1是k j,i,当112)(123,231,3的偶置换3,2,1是k j,i,当1ijk ijke ei,j,k 的这些排列分别叫做循环排列、逆循环排列和非循环排列。
置换符号主要可用来展开三阶行列式:231231331221233211231231133221332211333231232221131211a a a a a a a a a a a a a a a a a a a a a a a a a a a a ---++==因此有:ijmjimii i i jijAA aa a a a ==++=δδδδδ332211kijjkiijkkjiikjjikijkee e e e e e ==-=-=-=同时有:ijjijij iiiijijijkj ikilkljkijjjiiijijijkjikiie e aa aa a a a aa δδδδδδδδδδδδδδδδδδδ=⋅=++=========++=332211332211331001010100131211232221333231321333222111321321321-=====δδδδδδδδδδδδδδδδδδδδδδδδδδδe e k j i k j i k j i k k k j j j i i i ijk333222111321321321r q p r q p r q p k k k j j j i i i pqr ijke e δδδδδδδδδδδδδδδδδδ⋅=ipp i p i p i p i δδδδδδδδδ==++11332211krkqkpjrjqjpiriqippqrijke e δδδδδδδδδ=jqirjriqjrjqiriqkqrijke e kp δδδδδδδδ-===321321322311332112312213322113312312332211333231232221131211k j i ijkkjiijkaa a e a a a e aa a a a a a a a a a a a a a a a a aaaa a aaa a A ==---++==Kronecker-δ和置换符号符号的关系为:itjsjtiskstkije e δδδδ-=二 张量代数2.1张量的加法(减法)两个同阶、同变异(结构) 的张量可以相加(或相减)。
第1章 张量分析(清华大学张量分析,你值得拥有)

g1 1
gi xi g2 ix1 sin x2 jx1 cos x2
g2 r
曲线坐标系:斜角直线坐标系的延伸
※三维球坐标系
(x, y, z) (x1, x2, x3)
(r, , ) (x1, x2 , x3 )
x3
r
gr g
g
x2
r x1i x2 j x3k xigi x1
新、老坐标之间的变换和逆变换: xi = xi xi'
gidxi gi' dx i'
dxi
=
xi xi'
dx i '
dx i
i'
i'
→
gi
i i'
dx
i'
g i
'
dx
i'
再由:
gidxi
g i
'
dx
i
'
→
gi'
i i'
gi
dxi'
=
xi' xi
dxi
i i
'
dx
i
→
gidxi
gi'
i i
'
dx
定义式(实体形式,几何表达):
u v u v cos
v cos
张量分析在机器学习中的应用

张量分析在机器学习中的应用在近年来的机器学习领域中,张量分析作为一种强大的工具,被广泛应用于各种复杂的数据模型和算法中。
本文将探讨张量分析在机器学习中的应用,并分析其在不同领域中的优势和局限。
通过了解张量分析的基本概念和常见应用案例,我们可以更好地理解其在机器学习中的作用和价值。
一、张量分析的基本概念张量是一种多维数组,可以包含标量、向量、矩阵等数据类型。
在张量分析中,我们通常使用高阶张量来表示复杂的数据结构。
张量具有多个属性,如阶数、维度和元素等,这些属性可以为机器学习提供丰富的信息。
张量分析的基本概念包括张量的表示、运算和变换等,这些概念为机器学习提供了一种灵活和高效的数据处理方式。
二、1. 张量分解张量分解是一种重要的张量分析技术,可以将高阶张量分解为较低阶的张量,从而降低数据的复杂度。
在机器学习中,张量分解可以用于特征提取、降维和模型简化等任务。
通过张量分解,我们可以从高维数据中提取出有用的特征,减少冗余信息,提高学习算法的效果和效率。
2. 张量网络张量网络是一种基于张量分析的模型,可以用于处理复杂的数据结构和关系。
通过构建张量网络,我们可以将多个张量连接起来形成一个高效的数据流图,从而实现对复杂数据的处理和学习。
在机器学习中,张量网络可以用于图像识别、自然语言处理和推荐系统等任务,取得了很好的效果。
3. 张量分析算法张量分析算法是一种基于张量分析的算法思想,可以解决一些特定的机器学习问题。
例如,张量奇异值分解可以用于处理异常检测和异常值处理,张量回归可以用于处理多任务学习和关系建模等。
这些算法利用了张量分析的特性,将其应用于实际问题中,取得了一定的研究进展和应用效果。
三、张量分析在机器学习中的优势和局限1. 优势张量分析在机器学习中具有以下优势:(1) 多维数据处理:张量可以表示多维数据,可以更好地处理复杂的数据结构和关系。
(2) 特征提取和降维:张量分解可以从高维数据中提取有用的特征,减少数据的冗余信息。
关于张量分析的数学原理和实际应用案例

关于张量分析的数学原理和实际应用案例引言张量分析是一门重要的数学分支,在科学和工程领域有着广泛的应用。
作为一种多维量、多方向、多变量的数据结构,张量在物理、力学、电磁学、地球物理学等领域的描述、建模与计算中起着不可或缺的作用。
本文将介绍张量分析的数学原理以及实际应用案例,旨在帮助读者更好地了解这门学科。
第一部分数学原理1.张量的定义按照一般的定义,张量是一个可用于表示多维量和多向量之间关系的数学对象。
它可以看做是一种多维矩阵,其中每个元素都有多个指标。
与标量和向量不同,张量的指标可以有多个,我们常常用字母来表示。
2.张量的运算在张量分析中,张量的运算包括加、减、乘等。
与标量和向量不同,张量的乘法并不等同于代数乘法,而是采用了一种特殊的“卷积运算”。
例如,两个二阶张量相乘的结果是一个四阶张量。
这种方法既能描述多维多向量之间的关系,又可以实现基本的数学运算。
3.张量的变换由于张量具有多个指标,所以张量的变换涉及到各个指标的变化。
例如,一个二阶张量在坐标系变换后,其各个分量会发生相应的变化。
我们可以通过矩阵变换来描述张量的变换规律。
这一点在物理领域的应用尤其常见。
第二部分实际应用案例1. 电磁场模拟电磁场模拟是利用计算机模拟电磁场分布的方法,是工程和科学研究中的一项重要任务。
在这个过程中,张量分析被广泛应用。
例如,可以用张量表示电场强度、磁场强度等物理量,通过各种运算描述它们之间的关系。
同时,也可以用张量来描述电磁波的传播规律,实现电磁场的精确计算。
这种方法被广泛应用于电子器件设计、通讯技术等领域。
2. 生物医学图像处理生物医学图像处理是生物医学领域研究的一个重要方向,包括了图像采集、处理、分析等各个环节。
其中,张量分析被广泛应用于图像处理中。
例如,可以用张量表示医学图像中的像素强度、颜色等信息,通过各种运算分析其空间分布与统计规律,实现对生物组织的诊断、治疗等应用。
这种方法在医学影像学、神经科学等领域有着广泛的应用。
张量分析
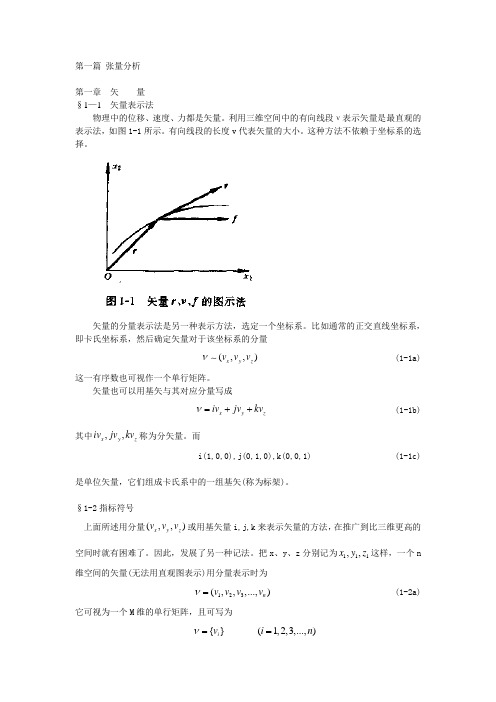
第一篇 张量分析第一章 矢 量 §1—1 矢量表示法物理中的位移、速度、力都是矢量。
利用三维空间中的有向线段ν表示矢量是最直观的表示法,如图1-1所示。
有向线段的长度v 代表矢量的大小。
这种方法不依赖于坐标系的选择。
矢量的分量表示法是另一种表示方法,选定一个坐标系。
比如通常的正交直线坐标系,即卡氏坐标系,然后确定矢量对于该坐标系的分量(,,)x y z v v v ν(1-1a)这一有序数也可视作一个单行矩阵。
矢量也可以用基矢与其对应分量写成x y z iv jv kv ν=++ (1-1b)其中,,x y z iv jv kv 称为分矢量。
而i(1,0,0),j(0,1,0),k(0,0,1) (1-1c)是单位矢量,它们组成卡氏系中的一组基矢(称为标架)。
§1-2指标符号上面所述用分量(,,)x y z v v v 或用基矢量i,j,k 来表示矢量的方法,在推广到比三维更高的空间时就有困难了。
因此,发展了另一种记法。
把x 、y 、z 分别记为111,,x y z 这样,一个n 维空间的矢量(无法用直观图表示)用分量表示时为123(,,,...,)n v v v v ν= (1-2a)它可视为一个M 维的单行矩阵,且可写为{}i v ν= (1,2,3,...,)i n =同理,基矢i,j,k 可分别写为123,,e e e ,n 维空间的基矢i e (1,2,3,...,)i n =。
而与式(1-1b)对应的写法为112233n n e v e v e v e v ν=++++ (1-2b)相应的分矢量为11,,,i i e v e v ,其中1e =(0,…,0,1,0,…,0) (1-2c)↑ 顺序第i 个这里i 叫做v 的下标,也有记作jv (如本书第三章以后章节所出现)的,这时j 称为上标。
有些量比矢量更复杂,只用一个下(或上)指标还不够,还要采用更多的指标,比如,,,ij ij ijk A B C ,等等。
张量分析1

柱坐标系 任意坐标系
uz uz uz uz ur u uz ez r r z t
0.1 张量的特点
du ui j i u u gi j dt t
5
课程特点
研究张量及张量方程的表达、运算、 转换及数学特性 相关的主要先修课为高等数学、线性 代数和大学物理 建议的学习方法——参考文献法
11 12 13 21 22 23 31 32 33
1.1 向量与向量空间 13
由向量代数知,对于给定基向量(右手标准 正交),有如下运算法则成立
相等
a = b 当切仅当 ai = bi
0 ≡ (0 , 0 , 0)
-a ≡(-a1,-a2 ,-a3 )
指标表示法
a ajij ajij
j
j=1,2,3 哑标
爱因斯坦求和约定:若指标中有两个相同, 表示在默认范围内求和。 任意基向量 a ai gi ai a1 , a2 , a3 略去基向量 i=1,2,3 自由标 11 12 13 k,l=1,2,3 kl 21 22 23 ii = (i1, i2 , i3) 32 33 31
由点积可定义 向量的长度和 夹角
a
aa
ab cos ab
17
点积的公理化定义
由几何定义可导出向量点积的四条最基本的运算规律 :
ab ba
la b la b
a b c a c b c
a a 0 当切仅当 a 0 时 a a 0
1.2 点积与欧氏空间
克罗内克符号 ij
ei 标准正交基
黄克智版张量分析第一章习题解析

i B C Bx Cx
j By Cy
k Bz Cz
By C z Bz C y i Bz C x BxC z j BxC y By C x k i B D Bx Dx j By Dy k Bz Dz
By Dz Bz Dy i Bz Dx Bx Dz j Bx Dy By Dx k
1.4
已知:矢量 u,v,求证: u v u v
证明:
u v u v sinu, v u v
1.5 求证: a b 0 a,b 线性相关。 证明:
i a b ax bx
j ay by
k az bz
a y bz a z by i az bx a xbz j a xby a y bx k 0
1 g i j k 2
3
g11 j k j k 2
g12 g 21 j k i k 1 g13 g 31 j k i j 1 g 22 i k i k 2 g 33 i j i j 2 g 23 g 32 i k i j 1
x y z x y z z y y z x x z z x x y z x y z x x z z x y y x x y z x x z z x y y x y x y z z y z x y y x y x y z z y z x y y x z x y z z y y z x x z z x y z z y y z x x z
a bc
或 a,b,c 共面。三维空间中共面的三矢量线性相关。
1.7 已知:矢量 b=2i +j -2k,c=i +2j +3k,i,j,k 为笛卡儿基; 若将 c 分解为与 b 平行的矢量及垂直于 b 的矢量 a 之和,即c=a +mb。 求 a;m(其中 b· =0) a 解:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x2
' x2
e2'
e2 e ' 1
' x1
e1 x1
x1
x2
' x2
' x1
x2
' x2 e2'
e 2 e1'
' x1
e1 x1
x1
令:αi' j cos(ei' ,e j )
( i' , j 1,2 )
则: αi' j
cos(e1' , e1 ) cos(e1' , e2 ) cos sin cos( e , e ) cos( e , e ) ' ' sin cos 1 2 2 2
A B ( Aij Bij )ei e j Tijei e j Τ
符合 φ ijklei e j ek el ,为一新张量
另证:
Ai ' j ' i 'i j ' j Aij Bi ' j ' i 'i j ' j Bij
Ai ' j ' Bi ' j ' i 'i j ' j ( Aij Bij )
xi xi , j ij x j aii jk a jk
三.Ricci 符号
定义:
ei j k
1 1 0
ei j k
即:
e123 e231 e312 1 e213 e132 e321 1 e111 e112 e113 0
故也有定义
( A2 7)
ei j k (ei e j ) ek ei (e j ek )
2
矢量混合积
(a b) c ei j k ai b j ek cr er ei j k ai b j cr δk r ei j k ai b j ck ( A2 6)
x1 x1' 1'1 1' 2 x1 于是: i ' j () x x2 2'2 2' 2 '1 x2
x1 11' 同样: x2 21'
同理
xi ij' x j'
同二维问题,可得
ij j k ik
' '
(正交性)
可试证:
i j jk i k
' '
' '
3. 张量定义
定义:在坐标变换时,满足如下变换关系 的量称为张量
' j ' k ' l ' i 'i j ' j k ' k ijkl i ' jj' kk ' ll ' i ' j ' k ' l ' ijkl ii
自由标数目n--张量的阶数;对于三维空间, 张量分量的个数为3n个,变换式也有3n个。
采用并矢记号(不变性记法或抽象记法)
φ ijklei e j ek el
()
可写成上式的量也称为张量(第二种定义)
讨论
T Tij ei e j Tk 'l' ek' el'
1
上述表达式具有不变性特征;
共27个分量,亦称为排列符号、置换符号
ei j k e j k i ek i j ei k j ek j i e j i k
a11 A a21 a31 a12 a22 a32 a13 a23 a11a22 a33 a12 a23 a31 a13 a21a32 a33
§A-2 矢量的基本运算
矢量a 分量ai
a a1e1 a2e2 a3e3 ai ei
基矢量e1 e2 e 3
( A2 1)
( 3个坐标方向的单位矢量)
说明
1
任意矢量可以表示为基矢量的线性组合 基矢量不是唯一的
2
1.点积
1
基矢量点积
ei e j δij ( A2 2)
如:
a ji xi bj
aki xi b j aki xi bk
wrong right
二.克罗内克(Kronecker-δ)符号 定义:
1 ij 0
由定义
当i j 当i j
1 0 0 11 12 13 I 0 1 0 22 23 ij 21 0 0 1 31 32 33
2. 三维情况
ei e j ij
考虑一位置矢量
ei' e j' i' j'
x x j e j x j' e j' x j e j ei' x j' e j' ei'
x j cos(e j , ei' ) x j' j' i' xi'
xi' i' j x j
2
任意两矢量的点积
a b ai ei b j e j aib j δij aibi a j b j ( A2 3)
2.叉积
1
基矢量的叉积
ei e j ei j k ek
( A2 4 )
由于
ei δi k ek e j δ j k ek
δi1 δi 2 ei e j δ j1 δ j 2 e1 e2
表示的是以 a, b, c 为边长的平行六面体的体积。
4.并矢(并乘)
定义:
ab ai ei b j e j ai b j ei e j
展开共9项,
ei e j
可视为并矢的基
ai bj 为并矢的分解系数或分量
§A-3 坐标变换 与张量的定义
1.平面笛卡儿坐标系旋转变换
x2
' x2 ' x1
A1 ij Ai 1 j A1 2 j A2 3 j A3 A2 A 3 Aj
j 1 j2 j3
ds2 dx2 dy2 dz2 dxi dxi ijdxi dx j
性质:
ij ij ii 11 22 33 3 Aij ij Aii Ajj A11 A22 A33 Aij jk Aik ij jk ik ij jk kl il
δi 3 δ j 3 er s t δi r δ j s et e3
ei j t et ei j k ek
a11 a31 a12 a32 a13 a23 ei j k a1i a2 j a3k ) a33
(比较: A a21 a22
特别地:
e1 e2 e12 k ek e123e3 e3
() ( ),ij xi x j
2
uk ,ij
uk xi x j
2
3.自由标 定义:凡在同一项内不重复出现的指标。如
a ji xi bj
j=1
j 为自由标
a11 x1 a12 x2 a13 x3 b1
1
同一个方程中各项自由标必须相同
2
不能改变某一项的自由标,但所有项的 自由标可以改变
一.若干约定 哑标和自由标
1. Einstein求和约定
凡在某一项内,重复一次且仅重复一次的 指标,表示对该指标在它的取值范围内求和, 并称这样的指标为哑指标。如:
ai xi (i 1,2,n) n a1 x1 a2 x2 an xn i 1 ai xi
又如:
ii jj 11 22 33 x y z
T x ' 12' x1' 1 i ' j 22' x2 ' x2 '
由()式得
1 x ' x1 1 i ' j x x2 2'
第一节 第二节 第三节
问题的提出 矢量的基本运算 坐标变换及张量的定义
自然法则与坐标无关,坐标系的引入方便 分析,但也掩盖了物理本质; 坐标系引入后的相关表达式冗长
引入张量方法
§A-1 指标符号
x1 , x2 xn
记作 xi (i 1,2,n)
下标符号 i 称为指标;n 为维数
指标 i 可以是下标,如 xi
' '
讨论:上式的几何意义
x2
' x2
' x1
x2
' x2 e2'
说明
1
e 2 e1'
' x1
e1 x1
x1
基矢量具有与坐标分量相同的变换规律 e i ' i' j e j
ei ij' e j'
2
矢量的分量也具有与坐标分量相同的变换 规律
vi ' i ' j v j vi ij' v j '
比较 :
' ' i j i j
