数字电路与数字电子技术 课后答案第七章教学提纲
精品课件-数字电子技术-第7章

(D3 23 +D2
22
+D121+D0 20 )
(7.1.2)
第7章 数/模(D/A)与模/数(A/D)转换器
对于n位输入的权电阻网络D/A转换器, 当负反馈电阻取 为R/2时, 输出电压为
vO
=
VREF 2n
(Dn1 2n1 +Dn2 2n2 + …
+D121+D0 20 )
=
VREF 2n
第7章 数/模(D/A)与模/数(A/D)转换器
第7章 数/模(D/A)与模/数(A/D)转换器
7.1 D/A转换器 7.2 A/D转换器 7.3 集成D/A转换器Multisim 10仿真实验 实验与实训 本章小结 习题
第7章 数/模(D/A)与模/数(A/D)转换器
7.1 D/A 7.1.1 权电阻网络D/A
第7章 数/模(D/A)与模/数(A/D)转换器
由图7.1.2所示电路还可以看出, 由于工作在线性反相 输入状态的运算放大电器的反相输入端相当于接地(虚地), 所以无论模拟开关Si合于何种位置, 与Si相连的倒T型2R电阻 支路从效果上看总是接“地”的, 即流经每条倒T型2R电阻 支路的电流与模拟开关Si的状态无关; 从R—2R倒T型电阻网 络的A、 D、 C、 D每个节点向左看, 每个二端网络的等效 电阻均为R, 故从基准电压UREF输出的电流恒为I=UREF/R, 而流经倒T型2R电阻支路的电流从高位到低位按2的负整数幂 递减, 从右到左分别为I3=I/2, I2=I/4, I1=I/8 , I0=I/16。
第7章 数/模(D/A)与模/数(A/D)转换器
由图7.1.2所示电路, 有
iΣ =I3 +I2 +I1+I0
数字电子技术基础习题册答案7-11

第7章 时序逻辑电路【7-1】已知时序逻辑电路如图7.1所示,假设触发器的初始状态均为0。
(1 )写出电路的状态方程和输出方程。
(2) 分别列出X =0和X =1两种情况下的状态转换表,说明其逻辑功能。
(3) 画出X =1时,在CP 脉冲作用下的Q 1、Q 2和输出Z 的波形。
1J 1KC11J 1KC1Q 1Q 2CPXZ1图7.1解:1.电路的状态方程和输出方程n 1n2n 11n 1Q Q Q X Q +=+ n 2n 11n 2Q Q Q ⊕=+ CP Q Q Z 21=2.分别列出X =0和X =1两种情况下的状态转换表,见题表7.1所示。
逻辑功能为 当X =0时,为2位二进制减法计数器;当X =1时,为3进制减法计数器。
3.X =1时,在CP 脉冲作用下的Q 1、Q 2和输出Z 的波形如图7.1(b)所示。
题表7.1Q Q Z图7.1(b)【7-2】电路如图7.2所示,假设初始状态Q a Q b Q c =000。
(1) 写出驱动方程、列出状态转换表、画出完整的状态转换图。
(2) 试分析该电路构成的是几进制的计数器。
Q c图7.2解:1.写出驱动方程1a a ==K J ncn a b b Q Q K J ⋅== n b n a c Q Q J = n a c Q K = 2.写出状态方程n a 1n a Q Q =+ n a n a n a n a n c n a 1n b Q Q Q Q Q Q Q +=+ nc n a n c n b n a 1n b Q Q Q Q Q Q +=+3.列出状态转换表见题表7.2,状态转换图如图7.2(b)所示。
图7.2(b)表7.2状态转换表CP na nbc Q Q Q 0 0 0 0 1 0 0 1 2 0 1 0 3 0 1 1 4 1 0 0 5 1 0 16 0 0 0n4.由FF a 、FF b 和FF c 构成的是六进制的计数器。
精品课件-数字电子技术-第7章

第7章 集成逻辑门电路简介
7.4 已知电路和输入信号的波形如图7.12所示,信号 的重复频率为1 MHz,每个门的平均延迟时间tpd=20 ns,试 画出:(1) 不考虑tpd影响时的波形;(2) 考虑tpd影响
第7章 集成逻辑门电路简介
图7.12 题7.4图
第7章 集成逻辑门电路简介
7.5 电路如图7.13所示。(1) 分别写出Y1、Y2、Y3、 Y4的逻辑函数表达式;(2) 若已知A、B、C的波形,试分别 画出Y1、Y2、Y3、Y4
(4) DE段。当UI≥1.4 V时,V2、V5饱和,V4截止,输 出为低电平, 与非门处于饱和状态, 所以把DE段称为饱和
第7章 集成逻辑门电路简介
4. (1) 输出高电平UOH和输出低电平UOL。电压传输特性 曲线截止区的输出电压为UOH,饱和区的输出电压为UOL。 一般产品规定UOH≥2.4 V,UOL<0.4 V (2) 阈值电压Uth。电压传输特性曲线转折区中点所 对应的输入电压为Uth,也称门槛电压。一般TTL与非门的 Uth≈1.4 V
Y=Y1·Y2
第7章 集成逻辑门电路简介
图7.4 实现“线与”功能的电路
第7章 集成逻辑门电路简介
但是普通TTL逻辑门的输出端是不允许直接相连的,如 图7.5所示电路:设门1的输出为高电平(Y1=1), 门2的输 出为低电平(Y2=0),此时门1的V4管和门2的V5管均饱和导通, 这样在电源UCC的作用下将产生很大的电流流过V4、V5管使V4、 V5
第7章 集成逻辑门电路简介
(3) 关门电平UOFF和开门电平UON。保证输出电平为 额定高电平(2.7 V左右)时,允许输入低电平的最大值, 称为关门电平UOFF。通常UOFF≈1 V , 一般产品要求 UOFF≥0.8 V。 保证输出电平达到额定低电平(0.3 V)时, 允许输入高电平的最小值,称为开门电平UON。通常 UON≈1.4 V,一般产品要求UON≤1.8 V
数字电路第七章答案

第七章可编程逻辑器件PLD第一节基本内容一、基本知识点(一)可编程逻辑器件PLD基本结构可编程逻辑器件PLD是70年代发展起来的新型逻辑器件,相继出现了只读存储器ROM、可编程只读存储器PROM、可编程逻辑阵列PLA、可编程阵列逻辑PAL、通用阵列逻辑GAL 和可擦写编程逻辑器件EPLD等多个品种,它们的组成和工作原理基本相似。
PLD的基本结构由与阵列和或阵列构成。
与阵列用来产生有关与项,或阵列把所有与项构成“与或”形式的逻辑函数。
在数字电路中,任何组合逻辑函数均可表示为与或表达式,因而用“与门-或门”两级电路可实现任何组合电路,又因为任何时序电路是由组合电路加上存储元件(触发器)构成的,因而PLD的“与或”结构对实现数字电路具有普遍意义。
在PLD中,输入电路中为了适应各种输入情况,每一个输入信号都配有一缓冲电路,使其具有足够的驱动能力,同时产生原变量和反变量输出,为与门阵列提供互补信号输入。
输出电路的输出方式有多种,可以由或阵列直接输出,构成组合方式输出,也可以通过寄存器输出,构成时序方式输出。
输出既可以是低电平有效,也可以是高电平有效;既可以直接接外部电路,也可以反馈到输入与阵列,由此可见PLD的输出电路根据不同的可编程逻辑器件有所不同。
(二)可编程逻辑器件分类1.按编程部位分类PLD有着大致相同的基本结构,根据与阵列和或阵列是否可编程,分为三种基本类型:(1)与阵列固定,或阵列可编程(2)与或阵列均可编程(3)与阵列可编程,或阵列固定归纳上述PLD的结构特点,列于表7-1。
表7-1 各种PLD的结构特点2.按编程方式分类(1)掩膜编程(2)熔丝与反熔丝编程(3)紫外线擦除、电可编程(4)电擦除、电可编程(5)在系统编程(Isp)(三)高密度可编程逻辑器件HDPLD243通常衡量可编程逻辑器件芯片的密度是以芯片能容纳等效逻辑门的数量,一般是以2000为界限,即芯片容纳等效逻辑门小于2000门,称它为低密度可编程逻辑器件或简单的可编程逻辑器件(SPLD),若大于2000等效逻辑门,称为高密度可编程逻辑器件(HDPLD)。
数字电子技术第7章习题答案

数字电子技术第7章习题答案
1. 什么是逻辑门?
答:逻辑门是数字电路中的基本组件,用于对输入进行逻辑运算并产生输出。
2. 列举几种常见的逻辑门。
答:与门、或门、非门、异或门、与非门、或非门等。
3. 什么是真值表?
答:真值表是一种用来展示逻辑函数输入与输出关系的表格,其中列出了所有可能的输入和对应的输出。
4. 什么是逻辑电路?
答:逻辑电路是指由逻辑门组成的电路,用于对输入进行逻辑运算并产生输出。
5. 什么是卡诺图?
答:卡诺图是一种用于最小化逻辑函数的图形化工具,通过将函数的真值表转化为图形,可快速找到最小化的逻辑表达式。
6. 什么是多路复用器?
答:多路复用器是一种数字电路,可以选择不同的输入并将其发送到一个输出线上。
7. 什么是解码器?
答:解码器是一种数字电路,用于将二进制数字输入转换为对应的输出,通常用于驱动其他数字电路中的寄存器、计数器等。
8. 什么是编码器?
答:编码器是一种数字电路,用于将多个输入端连接到一个二进制数字输出端,也可以实现将多个开关等输入转换为一个数字信号输出。
9. 什么是计数器?
答:计数器是一种数字电路,可用于记录电路所经过的时间或事件数量,通常用于计时器、频率计等应用。
10. 什么是触发器?
答:触发器是一种数字电路,可用于存储和控制数字信号,通常用于存储器、寄存器等应用。
数字电路与数字电子技术-课后答案第七章

J1= K1= 1,J2= K2= 0,J3= K3= 0,Z = Q1
(3)实现模2计数,只需Q2,Q1翻转其余状态不变。
J1= K1= 1,J2= K2= Q1,Z = Q2Q1
(4)要保持状态不变时则:
J1= K1= 0,J2= K2= 0,J3= K3= 0,Z = 0
DA=QA +QA + QCQD
DB= QD+QB
DC= QC +QB QD
DD=
3检查是否自启动
本计数器具有自启动能力
4画出逻辑电路图
图P7.A12 ( 1 )(c)
(2)画出状态转换卡诺图,从而得到动作卡诺图
图P7.A12 ( 2 )(a)
(3)采用JK触发器在动作卡诺图上求出各触发器激励函数.
解:
(1)写出各触发器的激励函数,列分析表
J1= K1=1 J2= = (Q3+Q4) J3= Q4
K2= K3=
J4= F=
K4=
(2)根据分析表画出状态转换图
图P7.A14 ( a )
(3)写出特征方程画出在CP作用下各触发器和F工作波形
图P7.A14 ( b )
Q1n+1= [ ]↓
Q2n+1= [ (Q3+Q4) +Q1Q2] CP↓
1根据状态转换表,作出状态的响应序列,设y = Q2Q1
X:0 1 1 0 1 1 1 1 1 0
yn:0 0 2 1 0 2 1 3 3 3
yn+1:0 2 1 0 2 1 3 3 3 0
Z:1 1 1 1 1 1 1 0 0 1
2根据状态响应序列画响应的输出波形。
《数字电路-分析与设计》第七章习题及解答(部分1) 北京理工大学出版社
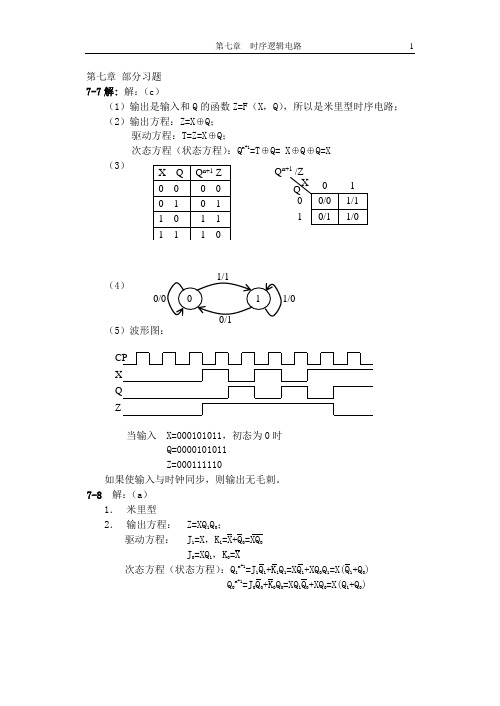
第七章 部分习题 7-7解: 解:(c )(1)输出是输入和Q 的函数Z=F (X ,Q ),所以是米里型时序电路; (2)输出方程:Z=X ⊕Q ;驱动方程:T=Z=X ⊕Q ;次态方程(状态方程):Q n+1=T ⊕Q= X ⊕Q ⊕Q=X(3)(4)(5)波形图:当输入 X=000101011,初态为0时 Q=0000101011 Z=000111110如果使输入与时钟同步,则输出无毛刺。
7-8 解:(a ) 1. 米里型2. 输出方程: Z=XQ 1Q 0;驱动方程: J 1=X ,K 1=X+Q 0=XQ 0J 0=XQ 1,K 0=X次态方程(状态方程):Q 1n+1=J 1Q 1+K 1Q 1=XQ 1+XQ 0Q 1=X(Q 1+Q 0)Q 0n+1=J 0Q 0+K 0Q 0=XQ 1Q 0+XQ 0=X(Q 1+Q 0)Q n+1CP X Q Z3.4.7-12某同步时序电路的逻辑方程如下:驱动方程:nQ X T 01⊕=,n Q X T 10=;输出方程:n Q X Z 1=。
要求: 解:1.同步时序电路的逻辑图示于图,这是米里型的状态机。
2.(a )状态方程: Q 1n+1=T 1⊕Q 1=X ⊕Q 0⊕Q 1Q 0n+1=T 0⊕Q 0=XQ 1⊕Q 0=XQ 1Q 0+XQ 0+Q 1Q 0(b )状态转换表: (c )状态转换图:(Q 1Q 0n+1Q7-15解:(a )“11”检测器,不重叠。
S 0:初始状态,输出0; S 1:输入一个“1”,输出0; S 2:输入两个“1”,输出1;(b ) “101”检测器,可重叠。
S 0:初始状态;S 1:输入序列为“1”;S 2:输入序列为“10”;S 3:输入序列为“101”;(c )(d )略7-34 “011”序列检测器,可重叠。
解:1.采用D(a ) 米里型状态图: S 0:初始状态;S 1:输入序列为“0”; S 2:输入序列为“01”;S 3:输入序列为“011”; (b ) 状态表(两种画法均可):(c ) 状态化简:由观察法知,S 0、S 3等价。
数字电子技术基础--第七章(第五版)课件PPT

相当存1。
A3 A2
A1
A0
该存储器的容量=?
+V D
存储
D
R
R•••
R R 矩阵
Y0
Y1
•
•
位线
•
Y 14
Y 15
•••
S3 I0
I1
I14
I15
S2 S1
16 线 -1 线 数 据 选 择 器
S0
Y
D0
11
二、可编程ROM(PROM)
有一种可编程序的 ROM ,在出厂时全部存 储 “1”,用户可根据需要将某些单元改写为 “0”,但是,只能改写一次,称为 PROM。
地
译
址
码
存储矩阵
输
器
入
控制信号输入
( CS 、R/W)
读/写控制电路
图 8.1.4
数据输入/输出
25
(1)地址译码器
译码 单译码 ---n位地址构成 2n 条地址线。若n=10,则有1024条地址线 方式 双译码 --- 将地址分成两部分,分别由行译码器和列译码器共同译码
其输出为存储矩阵的行列选择线,由它们共同确定欲选择 的地址单元。
0111
1
0101
0110
0
0110
0101
1
0110
0100
0
0111
0100
1
0111
0101
0
1000
1100
1
1000
1111
0
1001
1101
1
1001
1110
0
1010
1111
1
1010
《数字电子技术基础》课后习题及参考答案

第1章习题与参考答案【题1-1】将下列十进制数转换为二进制数、八进制数、十六进制数。
(1)25;(2)43;(3)56;(4)78解:(1)25=(11001)2=(31)8=(19)16(2)43=(101011)2=(53)8=(2B)16(3)56=(111000)2=(70)8=(38)16(4)(1001110)2、(116)8、(4E)16【题1-2】将下列二进制数转换为十进制数。
(1)10110001;(2)10101010;(3)11110001;(4)10001000 解:(1)10110001=177(2)10101010=170(3)11110001=241(4)10001000=136【题1-3】将下列十六进制数转换为十进制数。
(1)FF;(2)3FF;(3)AB;(4)13FF解:(1)(FF)16=255(2)(3FF)16=1023(3)(AB)16=171(4)(13FF)16=5119【题1-4】将下列十六进制数转换为二进制数。
(1)11;(2)9C;(3)B1;(4)AF解:(1)(11)16=(00010001)2(2)(9C)16=(10011100)2(3)(B1)16=(1011 0001)2(4)(AF)16=(10101111)2【题1-5】将下列二进制数转换为十进制数。
(1)1110.01;(2)1010.11;(3)1100.101;(4)1001.0101解:(1)(1110.01)2=14.25(2)(1010.11)2=10.75(3)(1001.0101)2=9.3125【题1-6】将下列十进制数转换为二进制数。
(1)20.7;(2)10.2;(3)5.8;(4)101.71解:(1)20.7=(10100.1011)2(2)10.2=(1010.0011)2(3)5.8=(101.1100)2(4)101.71=(1100101.1011)2【题1-7】写出下列二进制数的反码与补码(最高位为符号位)。
数字电子技术基础数电第六版阎石课后答案第七章

数字电子技术基础数电第六版阎石课后答案第七章第七章:逻辑门和逻辑代数1. 本章节内容概述本章介绍了逻辑门和逻辑代数的基础知识。
首先介绍了逻辑电平和逻辑门的概念,然后详细介绍了与门、或门、非门等基本逻辑门的原理、特性和应用。
接着介绍了与非门、或非门、异或门等组合逻辑门的原理和应用。
最后介绍了逻辑代数的基本概念和运算规则。
2. 逻辑门逻辑门是数字电子电路中使用的基本元件,用于进行逻辑运算。
逻辑门有多种类型,其中最基本的有与门(AND)、或门(OR)和非门(NOT)。
2.1 与门(AND)与门是一种逻辑门,其输出信号仅在所有输入信号都为高电平时才为高电平,否则为低电平。
与门的逻辑符号如下:AND gateAND gate2.2 或门(OR)或门是一种逻辑门,其输出信号在任何输入信号中有一个或多个为高电平时就为高电平,只有所有输入信号都为低电平时才为低电平。
或门的逻辑符号如下:OR gateOR gate2.3 非门(NOT)非门是一种逻辑门,其输出信号和输入信号相反。
当输入信号为低电平时,输出信号为高电平;当输入信号为高电平时,输出信号为低电平。
非门的逻辑符号如下:NOT gateNOT gate3. 组合逻辑门除了基本逻辑门之外,还有一些由基本逻辑门组合而成的组合逻辑门,例如与非门(NAND)、或非门(NOR)和异或门(XOR)等。
3.1 与非门(NAND)与非门是由与门和非门组成的组合逻辑门。
其输出信号在所有输入信号都为高电平时为低电平,否则为高电平。
与非门的逻辑符号如下:NAND gateNAND gate3.2 或非门(NOR)或非门是由或门和非门组成的组合逻辑门。
其输出信号在任何输入信号中有一个或多个为高电平时为低电平,只有所有输入信号都为低电平时才为高电平。
或非门的逻辑符号如下:NOR gateNOR gate3.3 异或门(XOR)异或门是一种比较特殊的组合逻辑门,其输出信号在输入信号中有奇数个高电平时为高电平,否则为低电平。
数字电子技术课后习题答案

ABACBC
BC
A
00 01 11 10
00
1
0
1
11
0
1
0
Y ABC
❖ 3.13某医院有一、二、三、四号病室4间,每室设有 呼叫按钮,同时在护士值班室内对应的装有一号、 二号、三号、四号4个指示灯。
❖ 现要求当一号病室的按钮按下时,无论其它病室的 按钮是否按下,只有一号灯亮。当一号病室的按钮 没有按下而二号病室的按钮按下时,无论三、四号 病室的按钮是否按下,只有二号灯亮。当一、二号 病室的按钮都未按下而三号病室的按钮按下时,无 论四号病室的按钮是否按下,只有三号灯亮。只有 在一、二、三号病室的按钮均未按下四号病室的按 钮时,四号灯才亮。试用优先编码器74148和门电路 设计满足上述控制要求的逻辑电路,给出控制四个 指示灯状态的高、低电平信号。
HP RI/BIN
I0
0/ Z1 0 10 ≥1
I1
1/ Z1 1 11
I2
2/ Z1 2 12 18
YS
I3
3/ Z1 3 13
I4
4/ Z1 4 14
YEX
I5
5/ Z1 5 15
I6
6/ Z1 6 16
I7
7/ Z1 7 17
Y0
V18
Y1
ST
E N
Y2
(b)
74148
(a)引脚图;(b)逻辑符号
A
00 01 11 10
00
0
0
1
11
1
0
1
Y AB BC AC
由于存在AC 项,不存在相切的圈,故无冒险。
❖ 4.1在用或非门组成的基本RS触发器中,已知 输入SD 、RD的波形图如下,试画出输出Q, Q
数字电子技术基础课后习题答案第7章习题答案

题7.1.1 可编程阵列逻辑(PAL)由、和组成。
答:输入缓冲器、与阵列、或阵列输出题7.1.2 通用阵列逻辑(GAL)由、和组成。
答:输入缓冲器、与阵列、或阵列输出逻辑宏单元题7.1.3 可编程阵列逻辑(PAL)可组成种典型的输出组态。
(A)2 (B)3 (C)4 (D)5答:C题7.1.4 通用阵列逻辑(GAL)的输出逻辑宏单元可组成种典型的输出组态。
(A)2 (B)3 (C)4 (D)5答:D题7.1.5 在系统编程器件(isp)和早期的EEPROM在编程方面,前者脱离了束缚。
(A)软件平台(B)编程器(C)电源(D)刷新电路答:B题7.1.6 单片通用阵列逻辑(GAL)的输出逻辑宏单元编程为寄存器组态时,只能应用在场合。
(A)同步时序电路(B)异步时序电路(C)复位电路(D)移位寄存器答:A、D题7.2.1 在系统可编程逻辑器件采用编程单元。
(A)E2CMOS (B)熔丝(C)SRAM (D)隧道型浮栅单元答:A题7.2.2 EPM7000S系列提供的共享乘积项有和。
(A)共享扩展(B)并联扩展(C)串联扩展(D)缓冲扩展答A、B题7.2.3 输入输出单元即可以编程为输入或输出,还可以编程为。
答:双向题7.2.4 编程I/O控制块输出缓冲器的输出电压摆率,可提供较高的。
(A)克服毛刺(B)并联扩展(C)转换速度(D)减低功耗答:C题7.2.5 ispLSI1000系列的ORP可提供GLB到IOC的信号。
(A)输入(B)中间(C)输出(D)时钟答:C题7.2.6 CPLD具有较高的性能,并具有如下特点。
(A)单片多系统(B)异步时序电路(C)动态刷新(D)丰富的查找表8081题7.3.1 现场可编程门阵列(FPGA )静态时无 ,称之为 。
(A) 功耗 (B) 电流(C) 零功耗器件 (D) 有源器件答:A 、C题7.3.2 CPLD 的信号通路固定,系统速度可以 。
FPGA 的内连线是分布在逻辑单元周围,而且编程的种类和编程点很多,使布线相当灵活,但在系统速度方面低于 。
《数字电子技术》教学大纲

《数字电子技术》教学大纲一、课程基本信息课程编码:075112B中文名称:数字电子技术英文名称:Digital Electronic Technology课程类别:专业基础及核心课总学时:64总学分:4适用专业:电子科学与技术专业、电气工程及其自动化专业先修课程:电路分析、模拟电子技术二、课程的性质、目标和任务课程性质:《数字电子技术》是电子科学与技术专业、电气工程及其自动化专业的一门专业基础课程,属于必修课。
课程目标:本课程主要使学生熟悉数字电路的基础知识,理解数字逻辑电路的工作原理,掌握数字逻辑电路的基本分析和设计方法。
培养学生的逻辑思维和分析能力,使学生具有一定的分析、设计数字逻辑电路的能力,为数字系统的硬件设计奠定坚实的基础,并能在控制、信号处理等复杂系统及工程应用中加以利用。
课程任务:本课程要求学生掌握数字电路的基本概念、基本原理和基本方法,掌握常用数制、码制,熟练掌握逻辑运算及逻辑函数的化简,掌握组合逻辑电路的分析和设计方法,熟悉常用中规模组合逻辑器件的功能及应用,掌握同步时序逻辑电路的分析和设计方法,熟悉常用中规模时序逻辑器件的功能及应用,理解脉冲波形产生及整形电路的工作原理,了解存储器在数字电路中的应用,了解常用ADC和DAC芯片的技术指标。
三、课程教学基本要求《数字电子技术》课程的教学环节主要是课堂教学,教师应按照教学大纲精心组织教学内容,每章布置相关习题,并安排适当的习题课。
该课程与《数字电子技术实验》课程结合,帮助学生进一步理解数字电路相关理论知识,提高动手能力,使学生具备一定的数字电路设计能力。
四、课程教学内容及要求第一章数制和码制(4学时)1、教学目标通过本章的学习,使学生掌握常用数制、码制的基本概念、表示方法及运算。
2、教学要求(1)了解二进制、八进制、十六进制等表示。
(2)理解二进制数算术运算的原理和方法。
(3)掌握不同数制之间的转换。
(4)掌握8421BCD码、5421、2421码。
《数字电子技术基础》课后习题答案

《数字电子技术基础》课后习题答案《数字电路与逻辑设计》作业教材:《数字电子技术基础》(高等教育出版社,第2版,2012年第7次印刷)第一章:自测题:一、1、小规模集成电路,中规模集成电路,大规模集成电路,超大规模集成电路5、各位权系数之和,1799、01100101,01100101,01100110;11100101,10011010,10011011二、1、×8、√10、×三、1、A4、B练习题:1.3、解:(1) 十六进制转二进制: 4 5 C0100 0101 1100二进制转八进制:010 001 011 1002 13 4十六进制转十进制:(45C)16=4*162+5*161+12*160=(1116)10所以:(45C)16=(10001011100)2=(2134)8=(1116)10(2) 十六进制转二进制: 6 D E . C 80110 1101 1110 . 1100 1000二进制转八进制:011 011 011 110 . 110 010 0003 3 3 6 . 6 2十六进制转十进制:(6DE.C8)16=6*162+13*161+14*160+13*16-1+8*16-2=(1 758.78125)10所以:(6DE.C8)16=(011011011110. 11001000)2=(3336.62)8=(1758.78125)10(3) 十六进制转二进制:8 F E . F D1000 1111 1110. 1111 1101二进制转八进制:100 011 111 110 . 111111 0104 3 7 6 . 7 7 2十六进制转十进制:(8FE.FD)16=8*162+15*161+14*160+15*16-1+13*1 6-2=(2302.98828125)10所以:(8FE.FD)16=(100011111110.11111101)2=(4376.772)8=(2302.98828125)10(4) 十六进制转二进制:7 9 E . F D0111 1001 1110 . 1111 1101二进制转八进制:011 110 011 110 . 111 111 0103 6 3 6 . 7 7 2十六进制转十进制:(79E.FD)16=7*162+9*161+14*160+15*16-1+13*16 -2=(1950. 98828125)10所以:(8FE.FD)16=(011110011110.11111101)2=(3636.772)8=(1 950.98828125)101.5、解:(74)10 =(0111 0100)8421BCD=(1010 0111)余3BCD (45.36)10=(0100 0101.0011 0110)8421BCD=(0111 1000.0110 1001 )余3BCD(136.45)10=(0001 0011 0110.0100 0101)8421BCD=(0100 0110 1001.0111 1000 )余3BCD (374.51)10=(0011 0111 0100.0101 0001)8421BCD=(0110 1010 0111.1000 0100)余3BCD1.8、解(1)(+35)=(0 100011)原= (0 100011)补(2)(+56 )=(0 111000)原= (0 111000)补(3)(-26)=(1 11010)原= (1 11101)补(4)(-67)=(1 1000011)原= (1 1000110)补第二章:自测题:一、1、与运算、或运算、非运算3、代入规则、反演规则、对偶规则二、2、×4、×三、1、B3、D5、C练习题:2.2:(4)解:Y=AB̅+BD+DCE+A̅D=AB̅+BD+AD+A̅D+DCE=AB̅+BD+D+DCE=AB̅+D (B +1+CE ) =AB̅+D (8)解:Y =(A ̅+B ̅+C ̅)(D ̅+E ̅)̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅(A ̅+B ̅+C ̅+DE ) =[(A ̅+B ̅+C ̅)̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅+(D ̅+E ̅)̅̅̅̅̅̅̅̅̅̅](A ̅+B ̅+C ̅+DE ) =(ABC +DE )(ABC ̅̅̅̅̅̅+DE ) =DE 2.3:(2)证明:左边=A +A ̅(B +C)̅̅̅̅̅̅̅̅̅̅̅̅ =A +A ̅+(B +C)̅̅̅̅̅̅̅̅̅̅=A +B̅C ̅ =右式所以等式成立(4)证明:左边= (A̅B +AB ̅)⨁C = (A̅B +AB ̅)C ̅+ (A ̅B +AB ̅)̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅C = (A ̅BC ̅+AB ̅C ̅)+A ̅B ̅̅̅̅⋅AB̅̅̅̅̅⋅C =A̅BC ̅+AB ̅C ̅+(A +B ̅)(A ̅+B )C =A̅BC ̅+AB ̅C ̅+(AB +A ̅B ̅)C =A̅BC ̅+AB ̅C ̅+ABC +A ̅B ̅C 右边= ABC +(A +B +C )AB ̅̅̅̅⋅BC ̅̅̅̅⋅CA̅̅̅̅ =ABC +(A +B +C )[(A̅+B ̅)(B ̅+C ̅)(C ̅+A ̅)] =ABC +(A +B +C )(A̅B ̅+A ̅C ̅+B ̅+B ̅C ̅)(C ̅+A ̅)=ABC +(A +B +C )(A̅B ̅C ̅+A ̅C ̅+B ̅C ̅+A ̅B ̅) =ABC +AB̅C ̅+A ̅BC ̅+A ̅B ̅C 左边=右边,所以等式成立 2.4(1)Y ′=(A +B ̅C ̅)(A ̅+BC) 2.5(3)Y ̅=A ̅B ̅(C ̅+D ̅)̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅ C ̅D ̅(A ̅+B ̅)̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅ 2.6:(1)Y =AB +AC +BC=AB (C +C̅)+AC (B +B ̅)+BC (A +A ̅) =ABC +ABC ̅+AB ̅C +A ̅BC 2.7:(1)Y =A ̅B ̅+B ̅C ̅+AC +B ̅C 卡诺图如下: B C A 00 0111100 1 1 1111所以,Y=B̅+AC2.8:(2)画卡诺图如下:B C A 0001 11 100 1 1 0 11 1 1 1 1Y(A,B,C)=A+B̅+C̅2.9:(1)画Y(A,B,C,D)=∑m(0,1,2,3,4,6,8)+∑d(10,11,12,13,14)如下:CDAB00 01 11 1000 1 1 1 101 1 111 ×××10 1 ××Y (A,B,C,D )=A̅B ̅+D ̅ 2.10:(3)解:化简最小项式: Y =AB +(A̅B +C ̅)(A ̅B ̅+C ) =AB +(A̅B A ̅B ̅+A ̅BC +A ̅B ̅C ̅+C ̅C ) =AB (C +C̅)+A ̅BC +A ̅B ̅C ̅ =ABC +ABC ̅+A ̅BC +A ̅B ̅C ̅ =∑m (0,3,6,7)最大项式:Y =∏M(1,2,4,5) 2.13:(3)Y =AB̅+BC ̅+AB ̅C ̅+ABC ̅D ̅ =AB̅(1+C ̅)+BC ̅(1+AD ̅) =AB̅+BC ̅ =AB̅+BC ̅̿̿̿̿̿̿̿̿̿̿̿̿ = AB̅̅̅̅̅∙BC ̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅技能题:2.16 解:设三种不同火灾探测器分别为A 、B 、C ,有信号时值为1,无信号时为0,根据题意,画卡诺图如下:B C A 00 01 11 10 0 0 0 1 0 1 0 1 1 1Y =AB +AC +BC=AB +AC +BC ̿̿̿̿̿̿̿̿̿̿̿̿̿̿̿̿̿̿̿=AB ̅̅̅̅⋅AC ̅̅̅̅⋅BC ̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅=(A ̅+B ̅)(A ̅+C ̅)(B ̅+C ̅)̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅=A ̅+B ̅̅̅̅̅̅̅̅̅+A ̅+C ̅̅̅̅̅̅̅̅̅+B ̅+C ̅̅̅̅̅̅̅̅̅第三章:自测题:一、1、饱和,截止7、接高电平,和有用输入端并接,悬空;二、1、√8、√;三、1、A4、D练习题:3.2、解:(a)因为接地电阻4.7k Ω,开门电阻3k Ω,R>R on ,相当于接入高电平1,所以Y =A ̅B ̅1̅̅̅̅̅̅=A +B +0=A +B(e) 因为接地电阻510Ω,关门电0.8k Ω,R<R off ,相当于接入高电平0,所以、Y =A +B +0̅̅̅̅̅̅̅̅̅̅̅̅̅=A̅⋅B ̅∙1̅̅̅̅̅̅̅̅̅̅=A +B +0=A +B3.4、解:(a) Y1=A+B+0̅̅̅̅̅̅̅̅̅̅̅̅̅=A+B̅̅̅̅̅̅̅̅(c) Y3=A+B+1̅̅̅̅̅̅̅̅̅̅̅̅̅=1̅=0(f) Y6=A⋅0+B⋅1̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅=B̅3.7、解:(a) Y1=A⨁B⋅C=(A̅B+AB̅)C=A̅BC+AB̅C3.8、解:输出高电平时,带负载的个数2020400===IHOHOH I I NG 可带20个同类反相器输出低电平时,带负载的个数78.1745.08===ILOLOL I I NG 反相器可带17个同类反相器3.12EN=1时,Y 1=A , Y 2=B ̅EN=0时,Y 1=A ̅, Y 2=B3.17根据题意,设A为具有否决权的股东,其余两位股东为B、C,画卡诺图如下,BCA00 01 11 100 0 0 0 01 0 1 1 1则表达结果Y的表达式为:Y=AB+AC=AB+AC̿̿̿̿̿̿̿̿̿̿̿̿=AB̅̅̅̅⋅AC̅̅̅̅̅̅̅̅̅̅̅̅̅̅逻辑电路如下:技能题:3.20:解:根据题意,A、B、C、D变量的卡诺图如下:CD AB00 01 11 1000 0 0 0 001 0 0 0 011 0 1 1 110 0 0 0 0Y =ABC +ABD =ABC +ABD ̿̿̿̿̿̿̿̿̿̿̿̿̿̿̿̿=ABC ̅̅̅̅̅̅⋅ABD ̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅电路图如下:第四章:自测题:一、2、输入信号,优先级别最高的输入信号7、用以比较两组二进制数的大小或相等的电路,A>B 二、3、√4、√三、5、A7、C练习题:4.1;解:(a) Y =A⨁B +B ̅̅̅̅̅̅̅̅̅̅̅̅̅=A ̅B +AB ̅+B ̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅=A ̅B +B ̅̅̅̅̅̅̅̅̅̅̅=A ̅+B̅̅̅̅̅̅̅̅̅=AB ,所以电路为与门。
数字电路课后题参考答案

习题参考答案注:参考答案,并不是唯一答案或不一定是最好答案。
仅供大家参考。
第一章习题2. C B A D B A C B A F ⋅⋅+⋅⋅+⋅⋅=3. 设:逻辑变量A 、B 、C 、D 分别表示占有40%、30%、20%、10%股份的四个股东,各变量取值为1表示该股东投赞成票;F 表示表决结果,F =1表示表决通过。
F =AB +AC +BCD4. 设:A 、B 开关接至上方为1,接至下方为0;F 灯亮为1,灯灭为0。
F =A ⊙B5. 设:10kW 、15kW 、25kW 三台用电设备分别为A 、B 、C ,设15kW 和25kW 两台发电机组分别为Y 和Z ,且均用“0”表示不工作,用“1”表示工作。
C AB Z BA B A Y ⋅=⋅=6.输入为余3码,用A 、B 、C 、D 表示,输出为8421BCD 码,用Y 0、Y 1、Y 2、Y 3表示。
D C A B A Y CB DC BD B Y DC Y DY ⋅⋅+⋅=⋅+⋅⋅+⋅=⊕==32107. 设:红、绿、黄灯分别用A 、B 、C 表示,灯亮时为1,灯灭时为0;输出用F 表示,灯正常工作时为0,灯出现故障时为1。
C A B A C B A F ⋅+⋅+⋅⋅=8. D C B D A H DC B AD C B A D C B A D C B A G DC B AD C A B A F DC B A E ⋅⋅+⋅=⋅⋅⋅+⋅⋅⋅+⋅⋅⋅+⋅⋅⋅=⋅⋅⋅+⋅⋅+⋅=⋅⋅⋅=第二章习题1. 设:红、绿、黄灯分别用A 、B 、C 表示,灯亮时其值为1,灯灭时其值为0;输出报警信号用Y 表示,灯正常工作时其值为0,灯出现故障时其值为1。
AC AB C B A Y ⋅⋅=2. 设:烟、温度和有害气体三种不同类型的探测器的输出信号用A 、B 、C 表示,作为报警信号电路的输入,有火灾探测信号时用1表示,没有时用0表示。
报警信号电路的书躇用Y 表示,有报警信号时用1表示,没有时用0表示。
数电第七章答案

数电第七章答案7.2解:激励⽅程:211Q Q D ?'=,X Q D +'=22输出⽅程:21'?=Q Q Z 激励/转移表如下:21Q QX0 100 01 10 11 01 10 01 0001 11 01 01)21(21''Q Q D D状态输出表如下:S X Z 0 1A B C DB BCD B B A B0 0 1 0S '⼆者不是对偶关系,因为保存状态的触发器并没有对偶变换,对偶的概念并不适合于状态表。
7.4解:激励⽅程:激励/转移表为:采⽤题中要求的转态命名,状态表为:7.5解:由图形可知1Q =X'3*2*Q Y X Q += '3''*3**Q X Y X Q += 激励/转移表、状态/输出表如下:0 0 0 110 110 011 011 A G G D D 0 0 1 110 110 011 011 B G G D D 0 1 0 110 110 011 011 C G G D D 0 1 1 110 110 011 011 D G G D D 1 0 0 000 100 001 011 E A E B D 1 0 1 000 100 001 011 F A EB D 1 1 0 000 100 001 011 G A E B D 1 1 1 100 100 001 011 H A E B D7.6解:由图⾏可知激励⽅程:1''1*1**Q Y Q Y Q +=2'1''21''2*)**(***Q Q Y X Q Q Y X Q += '2'*Q X Z =激励/转移表、状态/输出表如下:0 0 00,1 01,1 00,0 01,0 A A,1 B,1 A,0 B,0 0 1 01,1 10,1 01,0 00,0 B B,1 C,1 B,0 A,0 1 0 10,0 11,0 10,0 11,0 C C,0 D,0 C,0 D,0 1 1 11,0 00,0 11,0 10,0 D D,0 A,0 D,0 C,07.7 This can be algebraically.If all of the input combinations are covered,the logical sum of the expressions on all the transitions leaving state must be 1.If the sum is not 1,it is 0 for all input combinations that are uncovered.For double-covered input combinations,we look at all possible pairs of transitions leaving a state.The product of a pair of transition equations is 1 for any double-covered input combinations.这部分可以由代数来完成,如果所有的输⼊组合被覆盖,在所有的转换过程中其余的状态的表达式的逻辑和必须为1。
《数字电子技术基础》课后习题答案

《数字电路与逻辑设计》作业教材:《数字电子技术基础》(高等教育出版社,第2版,2012年第7次印刷)第一章:自测题:一、1、小规模集成电路,中规模集成电路,大规模集成电路,超大规模集成电路5、各位权系数之和,1799、01100101,01100101,01100110;11100101,10011010,10011011二、1、×8、√10、×三、1、A4、B练习题:1.3、解:(1)十六进制转二进制:45 C010*********二进制转八进制:010*********2134十六进制转十进制:(45C)16=4*162+5*161+12*160=(1116)10所以:(45C)16=(10001011100)2=(2134)8=(1116)10(2)十六进制转二进制:6D E.C8011011011110.11001000二进制转八进制:011011011110.1100100003336.62十六进制转十进制:(6DE.C8)16=6*162+13*161+14*160+13*16-1+8*16-2=(1758.78125)10所以:(6DE.C8)16=(011011011110. 11001000)2=(3336.62)8=(1758.78125)10(3)十六进制转二进制:8F E.F D100011111110.11111101二进制转八进制:100011111110.1111110104376.772十六进制转十进制:(8FE.FD)16=8*162+15*161+14*160+15*16-1+13*16-2=(2302.98828125)10所以:(8FE.FD)16=(100011111110.11111101)2=(437 6.772)8=(2302.98828125)10 (4)十六进制转二进制:79E.F D011110011110.11111101二进制转八进制:011110011110.1111110103636.772十六进制转十进制:(79E.FD)16=7*162+9*161+14*160+15*16-1+13*16-2=(1950. 98828125)10所以:(8FE.FD)16=(011110011110.11111101)2=(3636.772)8=(1950.98828125)101.5、解:(74)10 =(0111 0100)8421BCD=(1010 0111)余3BCD(45.36)10 =(0100 0101.0011 0110)8421BCD=(0111 1000.0110 1001 )余3BCD(136.45)10 =(0001 0011 0110.0100 0101)8421BCD=(0100 0110 1001.0111 1000 )余3BCD (374.51)10 =(0011 0111 0100.0101 0001)8421BCD=(0110 1010 0111.1000 0100)余3BCD1.8、解(1)(+35)=(0 100011)原= (0 100011)补(2)(+56 )=(0 111000)原= (0 111000)补(3)(-26)=(1 11010)原= (1 11101)补(4)(-67)=(1 1000011)原= (1 1000110)补第二章:自测题:一、1、与运算、或运算、非运算3、代入规则、反演规则、对偶规则 二、 2、×4、× 三、 1、B 3、D5、C练习题:2.2:(4)解:Y =AB̅+BD +DCE +A D =AB̅+BD +AD +A D +DCE =AB̅+BD +D +DCE =AB̅+D (B +1+CE ) =AB̅+D (8)解:Y =(A +B ̅+C )(D ̅+E ̅)̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅(A +B ̅+C +DE ) =[(A +B ̅+C )̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅+(D ̅+E ̅)̅̅̅̅̅̅̅̅̅̅](A +B ̅+C +DE ) =(ABC +DE )(ABC ̅̅̅̅̅̅+DE ) =DE2.3:(2)证明:左边=A +A (B +C)̅̅̅̅̅̅̅̅̅̅̅̅ =A +A +(B +C)̅̅̅̅̅̅̅̅̅̅ =A +B̅C ̅ =右式所以等式成立(4)证明:左边= (A B +AB̅)⨁C = (A B +AB ̅)C + (A B +AB̅)̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅C = (A BC +AB ̅C )+A B ̅̅̅̅⋅AB̅̅̅̅⋅C =A BC +AB̅C +(A +B ̅)(A +B )C =A BC +AB̅C +(AB +A B ̅)C =A BC +AB̅C +ABC +A B ̅C 右边= ABC +(A +B +C )AB̅̅̅̅⋅BC ̅̅̅̅⋅CA ̅̅̅̅ =ABC +(A +B +C )[(A +B̅)(B ̅+C )(C +A )]=ABC +(A +B +C )(A B̅+A C +B ̅+B ̅C )(C +A ) =ABC +(A +B +C )(A B̅C +A C +B ̅C +A B ̅) =ABC +AB̅C +A BC +A B ̅C 左边=右边,所以等式成立 2.4(1)Y ′=(A +B̅C )(A +BC) 2.5(3)Y ̅=A B ̅̅̅̅(C +D ̅)̅̅̅̅̅̅̅̅̅̅̅̅̅̅ C D ̅̅̅̅̅(A +B ̅)̅̅̅̅̅̅̅̅̅̅̅̅̅̅ 2.6:(1)Y =AB +AC +BC=AB (C +C̅)+AC (B +B ̅)+BC (A +A ̅) =ABC +ABC̅+AB ̅C +A ̅BC 2.7:(1)Y =A B̅+B ̅C +AC +B ̅C 卡诺图如下:所以,Y =B2.8:(2)画卡诺图如下:Y(A,B,C)=A +B̅+C2.9:(1)画Y (A,B,C,D )=∑m (0,1,2,3,4,6,8)+∑d(10,11,12,13,14)如下:Y (A,B,C,D )=A B̅+D ̅2.10:(3)解:化简最小项式:Y =AB +(A B +C )(A B̅+C ) =AB +(A B A B̅+A BC +A B ̅C +C C ) =AB (C +C )+A BC +A B̅C =ABC +ABC ̅+A BC +A B ̅C =∑m (0,3,6,7)最大项式:Y =∏M(1,2,4,5)2.13:(3)Y =AB̅+BC +AB ̅C +ABC D ̅ =AB̅(1+C )+BC (1+AD ̅) =AB ̅+BC =AB ̅+BC ̿̿̿̿̿̿̿̿̿̿̿̿ = AB ̅̅̅∙BC ̅̅̅̅̅̅̅̅̅̅̅技能题:2.16 解:设三种不同火灾探测器分别为A 、B 、C ,有信号时值为1,无信号时为0,根据题意,画卡诺图如下:Y =AB +AC +BC =AB +AC +BC ̿̿̿̿̿̿̿̿̿̿̿̿̿̿̿̿̿̿̿ =AB ̅̅̅̅⋅AC̅̅̅̅⋅BC ̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅ =(A +B ̅)(A +C )(B ̅+C )̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅ =A +B ̅̅̅̅̅̅̅̅+A +C ̅̅̅̅̅̅̅̅+B ̅+C̅̅̅̅̅̅̅̅第三章:自测题:一、1、饱和,截止7、接高电平,和有用输入端并接,悬空; 二、 1、√ 8、√; 三、 1、A 4、D练习题:3.2、解:(a)因为接地电阻4.7k Ω,开门电阻3k Ω,R>R on ,相当于接入高电平1,所以Y =A B 1̅̅̅̅̅̅=A +B +0=A +B (e) 因为接地电阻510Ω,关门电0.8k Ω,R<R off ,相当于接入高电平0,所以、 Y =A +B +0̅̅̅̅̅̅̅̅̅̅̅̅̅=A ̅⋅B ̅∙1̅̅̅̅̅̅̅̅̅̅=A +B +0=A +B3.4、解:(a) Y 1=A +B +0̅̅̅̅̅̅̅̅̅̅̅̅̅=A +B ̅̅̅̅̅̅̅(c) Y 3=A +B +1̅̅̅̅̅̅̅̅̅̅̅̅̅=1̅=0(f) Y 6=A ⋅0+B ⋅1̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅=B̅3.7、解:(a) Y 1=A⨁B ⋅C =(A B +AB̅)C =A B C +AB ̅C3.8、解:输出高电平时,带负载的个数2020400===IH OH OH I I N G 可带20个同类反相器输出低电平时,带负载的个数78.1745.08===IL OL OL I I N G 反相器可带17个同类反相器3.12EN=1时,Y 1=A , Y 2=B̅ EN=0时,Y 1=A̅, Y 2=B3.17根据题意,设A 为具有否决权的股东,其余两位股东为B 、C ,画卡诺图如下,则表达结果Y 的表达式为:Y =AB +AC =AB +AC ̿̿̿̿̿̿̿̿̿̿̿=AB ̅̅̅̅⋅AC̅̅̅̅̅̅̅̅̅逻辑电路如下:技能题:3.20:解:根据题意,A 、B 、C 、D 变量的卡诺图如下:Y =ABC +ABD =ABC +ABD ̿̿̿̿̿̿̿̿̿̿̿̿̿̿̿=ABC̅̅̅̅̅̅⋅ABD ̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅电路图如下:第四章:自测题:一、2、输入信号,优先级别最高的输入信号7、用以比较两组二进制数的大小或相等的电路,A>B 二、 3、√ 4、√ 三、 5、A 7、C练习题:4.1;解:(a) Y =A⨁B +B ̅̅̅̅̅̅̅̅̅̅̅̅̅=A B +AB ̅+B ̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅=A B +B ̅̅̅̅̅̅̅̅̅̅̅=A +B ̅̅̅̅̅̅̅̅=AB ,所以电路为与门。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数字电路与数字电子技术课后答案第七章第七章 时序逻辑电路1.电路如图P7.1所示,列出状态转换表,画出状态转换图和波形图,分析电路功能。
图P7.1 解:(1)写出各级的W.Z 。
D 1=21Q Q ,D 2=Q 1,Z=Q 2CP( 2 ) 列分析表( 3 ) 状态转换表(4)状态转换图和波形图。
图7.A1本电路是同步模3计数器。
2. 已知电路状态转换表如表P7.1所示,输入信号波形如图P7.2所示。
若电路的初始状态为Q2Q1 = 00,试画出Q2Q1的波形图(设触发器的下降沿触发)。
Q 2 Q 1 D 2 D 1 Q 2n+1 Q 1n+1 Z0 0 0 1 0 1 00 1 1 0 1 0 01 0 0 0 0 0 11 1 1 0 1 0 1Q 2 Q 1 Q 2n+1 Q 1n+1 Z 0 0 0 1 0 0 1 1 0 0 1 0 0 0 1 1 1 1 0 1 CPCP Q 1 0 Q 1 0 Z ( b ) Q 2 Q 1 /Z( a )01/0 11/1 10/1 00/0解:由状态转换表作出波形图3. 试分析图P7.3所示电路,作出状态转换表及状态转换图,并作出输入信号为0110111110相应的输出波形(设起始状态Q 2Q 1 = 00)。
( a )( b )解:(1)写W.Z 列分析表 J 1 = XQ 2Q Q X K 1 = X表P7.1X Q 2 Q 1 0 1 00 01 10 11 01/1 10/0 10/0 01/1 11/1 10/0 11/0 00/1 Q 2n+1 Q 1n+1/Z CP X Q 1 0 Q 2 0 Z 图P7.2 CP X 图P7.3CPX Q 1 0Q 1 0 Z图P7.A2( 2 ) 作出状态转换表及状态转换图(3)作出输出波形图:1 根据状态转换表,作出状态的响应序列,设y = Q 2Q 1 X : 0 1 1 0 1 1 1 1 1 0 y n : 0 02 1 0 2 13 3 3 y n+1: 0 2 1 0 2 1 3 3 3 0 Z : 1 1 1 1 1 1 1 0 0 12 根据状态响应序列画响应的输出波形。
4.Z 。
X :0 0 1 1 0 0 0 1 1 1 1 1 0 1 … Z :0 0 0 0 0 0 0 0 0 0 1 1 0 0 … 解:(1)建立原始的状态转换图和状态转换表 设:A --- 输入“0”以后的状态。
B --- 输入1个“1”以后的状态。
C --- 输入2个“1”以后的状态。
D --- 输入3个“1”以后的状态。
E ---输入4个“1”以后的状态。
(2(3设:A —00 B —01 C —11 D —10 (4选用JK 触发器,J 是a 必圈0必不圈,其余无关,K 是β必圈1必不圈,其余无关。
J 2 = XQ 1 J 2 =2Q X Z =12Q Q X K 2 =X K1=X +Q 2 =2Q X(5)画出逻辑电路图图P7.A4( e )5. 已知某计数器电路中图P7.4所示,分析它是几进制计数器,并画出工作波形,设电路初始状态Q2Q1 = 00。
图P7.4解:列出分析表:D1=1Q,D2=21Q⊕Q设计数器为4进制计数器,画出工作波形图如下:Q2 Q1 D2 D1 Q2n+1 Q1n+10 0 0 1 0 10 1 1 0 1 01 0 1 1 1 11 1 0 0 0 0图P7.A5( a )00011110CPQ1 0Q1 0图P7.A5 ( b )6. 分析图P7.5所示计数器电路,画出状态转换图,说明是几进制计数器,有无自启功能。
图P7.5解:(1)写出激励函数,列分析表J1=32QQ J2=1Q J3=Q2Q1K1=1 K2= 31QQ =Q1+Q3 K3=1设计数器是具有自启动能力的模4计数器。
( 2 ) 画出状态转换图图P7.A6000 001111110100101010011Q3 Q2 Q1 J3 K3 J2 K2 J1 K1 Q3n+1 Q2n+1 Q1n+10 0 0 0 1 0 0 1 1 0 0 10 0 1 0 1 1 1 0 1 0 1 00 1 0 0 1 0 0 0 1 0 1 10 1 1 1 1 1 1 0 1 1 0 01 0 0 0 1 0 1 1 1 0 0 11 0 1 0 1 1 1 1 1 0 1 01 1 0 0 1 0 1 0 1 0 0 01 1 1 1 1 1 1 1 1 0 0 07.分析图P7.6所示计数器电路,写出各级出发器特征方程,画出状态转换图,说明电路是否具有自启动能力。
图P7.6解:(1)写出激励函数,列分析表J1=1 J2 = Q13Q J3 = Q2Q1K1=1 K2= Q13Q K3 = Q1(2)写出各级触发器特征方程,画出状态转换图。
Q1 n+1 = [1Q]CP↓Q2 n+1 = [Q13Q2Q+231QQQ]CP↓Q3 n+1 = [Q2Q13Q+1Q Q3] CP↓设计数器是具有自启能力的模6计数器。
Q3 Q2 Q1 J3 K3 J2 K2 J1 K1 Q3n+1 Q2n+1 Q1n+10 0 0 0 0 0 0 1 1 0 0 10 0 1 0 1 1 1 1 1 0 1 00 1 0 0 0 0 0 1 1 0 1 10 1 1 1 1 1 1 1 1 1 0 01 0 0 0 0 0 1 1 1 1 0 11 0 1 0 1 1 1 1 1 0 0 01 1 0 0 0 0 1 1 1 1 1 11 1 1 1 1 1 1 1 1 0 1 0图P7.A7000 0011011101001110100118. 用JK 触发器设计同步模9 加法计数器。
解:(1)列出状态转换表,画出动作卡诺图( J 4 = Q 3Q 2Q 1 J 3 = Q 2Q 14 K 4 = 1 K 3 = Q 2Q 1图P7.A8( b )(3)检查是否具有自启能力。
具有自启动能力 (4)画出逻辑电路图图P7.A8( d )9. 用D 触发器设计模7同步加法计数器。
解:(1) 画出状态转换卡诺图,求出激励函数。
由于D 触发器Q n+1 = D ,所以可以Q n+1直接求出D 。
Q 4 Q 3 Q 2 Q 1 J 4 K 4 J 3 K 3 J 2 K 2 J 1 K 1 Q 3n+1 Q 2n+1 Q 1n+1 Z1 0 0 1 0 1 0 0 1 1 0 1 0 0 1 0 1 1 0 1 0 0 1 0 0 0 0 0 1 0 0 1 0 1 1 0 1 1 0 1 1 1 1 1 0 1 0 1 0 0 1 1 1 0 0 0 1 0 0 0 0 0 1 0 1 0 0 1 1 1 0 1 0 1 0 0 1 1 0 1 0 1 1 0 1 1 1 1 0 0 1 0 0 0 0 0 1 0 1 1 0 1 1 1 1 1 1 1 1 1 1 1 0 1 0 0 0 0 111 11 1111 10 10 10 10 10 10 10 10 11 11 11 11 图P7.A8( c )0000 0110 0000 0010 0001 1101 1110 0101 1011 0100 1100 1000 0011 0000 0000 0111图P7.A9( a )D 3 = Q 32Q +Q 2Q 1D 2 = 2Q Q 1+3Q Q 21QD 1 = 3Q 1Q +2Q 1Q Z = Q 3Q 2 (2)检查是否自启动具有自启动能力 (3)画出逻辑电路图Q 3 Q 2 Q 1 D 3 D 2 D 1 Q 3n+1 Q 2n+1 Q 1n+1 Z 1 1 1 1 0 0 1 0 0 1 10 1011 10 10 10 11 图P7.A9( b ) 000 101 111 100 110 001 10 011 010图P7.A9( c )10. 用JK 触发器设计模7同步减法计数器 解:(1((2J 3=2Q J 2=2Q +3Q =31Q Q J 1=1 Z=23Q Q K 3=2Q 1Q K 2= 1Q K 1=Q 2+Q 3=32Q Q(3)检查是否自启动(4图P7.A10( c )11.用JK 触发器设计一个可控计数器,X=0为7进制同步加法计数,X=1为模5同步加法计数。
解:(1)画出状态转换卡诺图,从而画出动作卡诺图图P7.A11( a ) 图P7.A11( a )(2)根据动作卡诺图求出激励函数J 3 = Q 2Q 1 J 2 = Q 1 J 1 =3Q +X 2Q =23Q X •Q K 3 = X K 2 = Q 1+Q 3 =31Q Q K 1=1 (3) 检查是否自启动X Q 3 Q 2 Q 1 00 01 11 10 00 01 11 10 Q 3n+1 Q 2n+1 Q 1n+1001 101 000 001 010 110 xxx 010100 xxx xxx 100 011 000 xxx 011X Q 3 Q 2 Q 1 00 01 11 10 00 01 11 10 W 20 0 0 0 α α X α βX X β 1 β X 1 X Q 3 Q 2 Q 1 0001 11 10 00 01 11 10 W 3 0 0 β 0 0 1 X 0α X X α 0 β X 0X Q 3 Q 2 Q 1 00 01 11 10 00 01 11 10 W 1 αα0α β β X β β X X βα 0 X α有自启动能力(4) 画出逻辑电路图图P7.A11( c )12. 按下列给定状态转换表,设计同步计数器图P7.A12 ( 1 )( a )2 从次态卡诺图求出激励函数D A =Q A C Q +Q A D Q +A Q Q C Q D D B =C Q Q D +Q B D Q D C = Q C D Q +Q B C Q Q D D D =D Q3 检查是否自启动4 画出逻辑电路图图P7.A12 ( 1 )( c )(2) 画出状态转换卡诺图,从而得到动作卡诺图图P7.A12 ( 2 )( a )(3) 采用JK 触发器在动作卡诺图上求出各触发器激励函数. J A = Q B C Q D Q J B = Q C D Q J C =B Q Q D K A =00B Q K B = Q A K C = Q B Q D J D = Q B Q C + A Q B Q C Q = C B A C B Q Q Q •Q QK D = Q B C Q +B Q Q C = C B C B Q Q •Q QQ A Q B Q C Q D00 01 11 10 00 01 11 10 Q 4n+1 Q 3n+1 Q 2n+1 Q 1n+1 0001 0101 1101 1001 0100 0110 1110 1100xxxx 1000 0000 xxxx xxxx 0111 1111 xxxxQ A Q BQ C Q D 00 01 11 100001 11 10 Q A n+1 0 0 1 1 0 0 1 1 X 1 0 XX 0 1 X Q A Q B Q C Q D 00 01 11 10 00 01 11 10 Q C n+1 0 0 0 0 0 1 1 0 X 0 0 X X 1 1 X Q A Q B Q C Q D 00 01 11 10 00 01 11 10 Q D n+1 1 1 1 1 0 0 0 0 X 0 0 X X 1 1 X Q A Q B Q C Q D 00 01 11 10 00 01 11 10 Q B n+10 1 1 0 1 1 1 1 X 1 1 X X 1 1 X(4) 检查是否自启动图P7.A12 ( 2 )( b )电路具有自启动能力 (5)画出逻辑电路图图P7.A12 ( 2 )( c )13.分析图P7.7所示电路逻辑功能,画出状态转换图,说明电路是否具有自启动能力Q A Q B Q C Q D J A K A J B K B J C K C J D K D Q A n+1 Q B n+1 Q C n+1 Q D n+11 0 0 1 0 1 0 1 1 0 0 0 0 0 1 1 1 0 1 0 0 1 1 1 0 0 0 1 0 1 1 0 1 0 1 1 0 1 0 1 1 0 0 1 0 0 1 0 1 1 0 1 0 0 0 1 0 1 0 1 1 0 0 0 1 1 1 0 0 0 1 1 0 0 00 1 0 1 1 1 1 1 1 0 0 0 1 0 1 0 0 1 0 0 1 1101 1000 0000 1001 1100 0100 0101 0001 0111 01101010 0011 00101111 11101011图P7.7解:本电路是异步时序电路,用特征方程法进行分析(1) 写出各触发器的激励函数及特征方程J 1 = K 1 = 1 J 2 = Q 3 J 3 =1 J 4 = K 4 = 1 CP 1= CP ↓ K 2 = 1 K 3 = Q 2 CP 4 = Q 3↓ CP2 = Q 1↓ CP 3 = CP ↓Z =CP Q Q Q Q 4321 Q 1n+1 = [1Q ]CP ↓ Q 2n+1 = [Q 32Q ]Q 1↓Q 3n+1 = [3Q +2Q Q 3] CP ↓= [3Q +2Q ] CP ↓= [23Q Q ] CP ↓ Q 4n+1 = [4Q ] Q 3↓本电路是异步模8计数器,有自启动能力14.分析图P7.8所示电路,写出特征方程,画出状态转换图及在CP 作用下Q 1,Q 2,Q 3,Q 4和F 的工作波形.表P7.A13 Q 4 Q 3 Q 2 Q 1 Q 4n+1 Q 3n+1 Q 2n+1 Q 1n+1 0 0 0 0 0 1 0 1 0 1 0 1 0 1 0 0 0 1 1 0 1 0 1 1 1 0 1 1 1 1 1 0 1 1 0 0 1 1 0 1 1 1 0 1 1 1 0 0 1 1 1 0 0 0 1 1 0 0 1 1 0 1 1 0 0 1 0 0 0 1 0 1 0 1 1 1 1 0 0 0 1 0 0 0 1 1 0 1 1 0 0 1 1 1 0 0 0 0 1 0 0 1 1 1 1 0 1 0 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 1 0 1 0 0图P7.A130001 1010 0010 1000 01110000 1100 0101 0110 1111 1101 0100 0011 1110图P7.8解:(1) 写出各触发器的激励函数,列分析表J 1= K 1=1 J 2 =431Q Q •Q =1Q (Q 3+Q 4) J 3 = Q 41Q K 2 = 1Q K 3 =2Q 1QJ 4 =2Q 3QF=4Q 3Q 2Q 1QK 4 =1Q(2) 根据分析表画出状态转换图 表P7.A14Q A Q B Q C Q D J A K A J B K B J C K C J D K D Q A n+1 Q B n+1 Q C n+1 Q D n+1 F 0 0 0 0 1 1 0 1 0 1 1 1 1 0 0 1 1 0 0 0 1 1 0 0 0 0 0 1 1 1 0 0 0 0 0 0 1 0 0 1 0 0 0 1 1 1 0 0 0 1 0 0 0 1 1 0 0 0 0 0 0 1 1 0 0 1 0 0 0 1 0 0 0 1 0 1 1 1 1 1 0 0 1 1 0 0 1 0 1 0 0 0 0 0 0 1 1 0 1 0 0 0 0 1 1 0 0 1 0 0 1 1 1 1 0 1 0 1 0 0 1 1 1 0 0 0 0 0 0 1 1 0 1 1 0 0 1 0 0 0 1 1 1 1 1 1 1 1 0 1 1 1 0 1 0 0 1 1 0 0 0 0 0 1 1 1 0 1 0 0 1 0 1 0 0 1 1 0 1 1 1 1 0 1 0 1 0 1 0 1 1 0 0 0 0 0 0 1 1 1 0 1 0 0 1 1 0 0 0 1 1 1 1 1 1 1 0 0 1 1 0 1 1 0 1 0 0 0 0 0 0 1 1 1 1 0 0 0 1 1 1 0 0 1 1 0 1 1 1 1 0 1 0 1 0 1 1 1 1 0 0 0 0 0 0 1 1 1 1 1 0 00001 1000 1001 0010 0011 0100 0111 0101 10100110 1011 0000图P7.A14 ( a )(3) 写出特征方程画出在CP作用下各触发器和F工作波形图P7.A14 ( b )Q1n+1 = [1Q]↓Q2n+1 = [1Q(Q3+Q4) 2Q+Q1Q2] CP↓Q3n+1 = [Q41Q3Q+12QQ Q3]↓Q4n+1 = [2Q3Q4Q+Q1Q4] CP↓15. 分析图P7.9所示电路,并画出在CP作用下Q2输出与CP之间的关系图P7.9解:(1) 写出特征方程Q1n+1 = [1Q][ Q2+CP]↑当Q3=1时, CP1 =CP↑,即CP1=CP↓Q2n+1 = [1Q] Q1↑当Q3 = 0时, CP1=CP↑Q3n+1 = [1Q] Q1↑根据特征方程画出工作波形图(1)画波形图Q1 0Q2 0Q2 0Q3 0F 0CPQ1 0Q2 0图P7.A15CP脉冲与Q2之间的关系是Q2的周期为3.5 T CP (T CP为CP的周期)16. 分析图P7.10所示电路,写出特征方程,并画出在CP作用下,输出a、b、c、d、e、f下的各点波形,说明该电路完成什么逻辑功能。
