八年级数学全等三角形“边边边”基础训练含答案
全等三角形边角边判定的练习题.doc

(这个条件可以证得吗?)。
全等三角形边角边判定的基本练习1.如图3,巳知AD〃BC, AD = CB,要用边角边公理证明^ABC竺^CDA,需要三个条件,这三个条件中,已具有两个条件,一是AD = CB(已知),二是;还需要一个条件2.如图4,已知AB = AC, AD=AE, Z1=Z2,要用边角边公理证明△ ABD竺ACE,需要满足的三个条件中,已具有两个条件:一是二是还需要一个条件(这个条件可以证得吗?)o3.已知:AD〃BC, AD= CB(图3)。
求证:AADC^ACBA.4.已知:AB = AC、AD = AE、Z1=Z2(图4)。
求证:Z^ABD 丝Z^ACE。
图45.已知:如图,AB = AC, F、E分别是AB、AC的中点。
求证:△ABE^AACFoC6、己知:点A、F、E、C 在同一条直线上,AF = CE, BE〃DF, BE = DF. 求证:△ABE#ACDF.D C7、已知:如图AB=AC,AD=AE,ZBAC= ZDAE,求证:AABD^AACE8、如图,ZiABC中,AB = AC, AD平分匕BAC,试说明^ABD丝MCD。
B D C9、已矢口:如图,AD〃BC, AD=CB 。
求证:AADC^ACBAo,AD±11、已知:如图,点A、B、C、D在同一条直线上,DB=,垂足分别是A、Do求证:△FDCWA13、如图,在中,D是AB ±一点,DF交AC于点E, FE= , CE= , AB与CF 有什么位置关系?说明你判断的理由。
12、己知:如图,AC= , AE= ,Z1=Z2A14、己知:如图,ZDBA=Z , BD= ° 求证ZC=ZD15、已知:如图,AC和BD相交于点0, 0C= , 0D= 。
求证:DC〃AB。
16、已知:如图,AC和BD相交于点0, DC= , DB= 0求证:ZC=ZB17、已知:如图,D、E分别是^ABC的边AB,AC的中点,点F在DE的延长线上,且EF=DE. 求证:(1)BD=FC (2)AB〃CFB C18、己知:如图,AB=AC, EB=EC, AE的延长线交BC于D.求证:BD=CD19、已知:如图,AB=AC,AD=AE,ZBAC= ZDAE.求证:BD=CE20、已知,AABC和AECD都是等边三角形,且点B, C, D在一条直线上求证:BE=AD21、如图,己知,AB〃DE, AB=DE, AF=DCo请问图中有那儿对全等三角形?请任选一对给予证明。
人教版八年级数学上册第12单元第2节 第1课时 “边边边” 同步练习题(含答案)
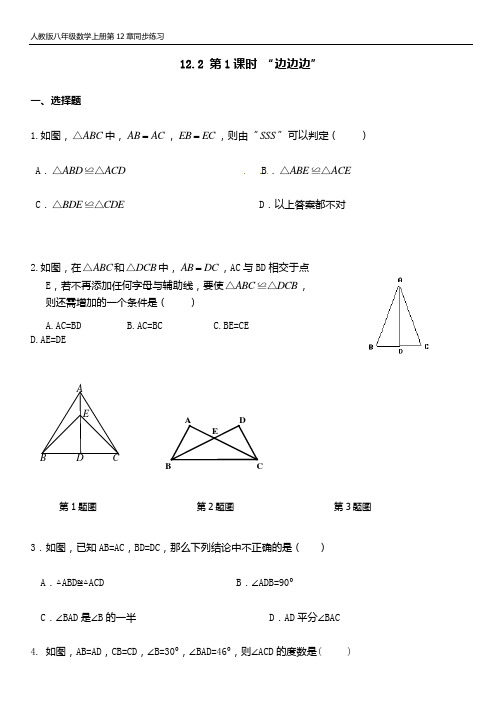
12.2 第1课时 “边边边”一、选择题1.如图,ABC △中,AB AC =,EB EC =,则由“SSS ”可以判定( ) A .ABD ACD △≌△ B .ABE ACE △≌△ C .BDE CDE △≌△D .以上答案都不对2.如图,在ABC △和DCB △中,AB DC =,AC 与BD 相交于点E ,若不再添加任何字母与辅助线,要使ABC DCB △≌△,则还需增加的一个条件是( )A.AC=BDB.AC=BCC.BE=CED.AE=DE3.如图,已知AB=AC ,BD=DC ,那么下列结论中不正确的是( ) A .△ABD ≌△ACD B .∠ADB=90° C .∠BAD 是∠B 的一半D .AD 平分∠BAC4. 如图,AB=AD ,CB=CD ,∠B=30°,∠BAD=46°,则∠ACD 的度数是( )EDCB AA EB D C第1题图第2题图第3题图A.120°B.125°C.127°D.104°第4题图第5题图5. 如图,线段AD与BC交于点O,且AC=BD,AD=BC,则下面的结论中不正确的是( )A.△ABC≌△BADB.∠CAB=∠DBAC.OB=OCD.∠C=∠D6. 如图,AB=CD,BC=DA,E、F是AC上的两点,且AE=CF,DE=BF,,那么图中全等三角形共有()对A.4对 B.3对 C.2对 D.1对7. 如图,AB=CD,BC=AD,则下列结论不一定正确的是().A.AB∥DCB. ∠B=∠DC. ∠A=∠CD. AB=BC第7题图8. 如果△ABC的三边长分别为3,5,7,△DEF的三边长分别为3,3x-2,2x -1,若这两个三角形全等,则x 等于( )A .73B .3C .4D .5二、填空题9.(2011湖北十堰)工人师傅常用角尺平分一个任意角。
做法如下:如图,∠AOB 是一个任意角,在边OA ,OB 上分别取OM=ON ,移动角尺,使角尺 两边相同的刻度分别与M ,N 重合,过角尺顶点C 作射线OC 。
八年级上册《数学》第12章利用“边边边”“边角边”判定三角形全等练习题(含答案)

八年级上册《数学》第12章利用“边边边”“边角边”判定三角形全等练习题第1课时利用“边边边”判定三角形全等一、能力提升1.如图,AC=AD,BC=BD,O是CD的中点,则全等三角形的对数是()A.1B.2C.3D.42.如图,AB=AC,BD=DC,则下列结论不正确的是()A.∠B=∠CB.∠ADB=90°∠BC.∠BAD=12D.AD平分∠BAC3.如图,AB=DE,AC=DF,BC=EF,小新根据这些条件得出了四个结论,你认为结论正确的个数是()①AB∥DE;②AC∥DF;③BF=CE;④∠1=∠2.A.1B.2C.3D.44.如图,在5×5的正方形网格中,以点D,E为两个顶点作位置不同的格点三角形,使所作的格点三角形与△ABC全等,这样的格点三角形最多可以画()A.2个B.4个C.6个D.8个5.如图,以△ABC的顶点A为圆心,以BC长为半径作弧;再以顶点C为圆心,以AB长为半径作弧,两弧交于点D,连接AD,CD.若∠B=65°,则∠ADC的大小为度.6.如图,在△ABC中,AD=DE,AB=BE,∠CED=70°,则∠A=.7.如图,AB=AC,BE与CF交于点O,且BO=CO,求证:∠B=∠C.二、创新应用8.如图,AD=CB,E,F是AC上的两个动点,且有DE=BF.(1)若点E,F运动到图①的位置,且有AF=CE,求证:△ADE≌△CBF;(2)若点E,F运动到图②的位置,仍有AF=CE,则△ADE≌△CBF还成立吗?为什么?答案:一、能力提升1.C△ABC≌△ABD,△AOC≌△AOD,△BOC≌△BOD.2.C3.D在△ABC与△DEF中,{AB=DE, AC=DF, BC=EF,∴△ABC≌△DEF.∴∠B=∠E,∠1=∠2,BC=EF.∵∠B=∠E,∴AB∥DE.∵∠1=∠2,∴∠ACE=∠DFB,∴AC∥DF.∵BC=EF,∴BC+CF=EF+CF,∴BF=CE.即①②③④都正确.4.B这里要考虑满足两个三角形三边相等的所有情况,如图,共有4个.5.656.110°根据“SSS”可得△ABD≌△EBD,则∠A=∠DEB.根据∠CED=70°,可得∠A=∠DEB=110°.7.证明:如图,连接AO ,在△ABO 和△ACO 中.{AB =AC ,AO =AO ,BO =CO ,所以△ABO ≌△ACO. 所以∠B=∠C. 二、创新应用8.分析:在题图①位置时,可以用“SSS ”证明;在题图②位置时,由于AF-EF=CE-EF ,这样有AE=CF ,用“SSS ”也可以证明△ADE ≌△CBF. (1)证明 ∵AF=CE ,∴AF+EF=CE+EF .即AE=CF.在△ADE 与△CBF 中,{AD =CB ,DE =BF ,AE =CF ,∴△ADE ≌△CBF (SSS).(2)解 成立,理由如下:∵AF=CE , ∴AF-EF=CE-EF .即AE=CF.在△ADE 与△CBF 中,{AD =CB ,DE =BF ,AE =CF ,∴△ADE ≌△CBF (SSS).第2课时利用“边角边”判定三角形全等练习题一、能力提升1.如图,在△ABC和△DEF中,已知AB=DE,BC=EF,根据“SAS”判定△ABC≌△DEF,还需的条件是()A.∠A=∠DB.∠B=∠EC.∠C=∠FD.以上三个均可以2.已知A,B,C顺次在一条直线上,分别以AB,BC为边在直线的同侧作正三角形ABE和正三角形BCD,下列结论错误的是()A.△ABD≌△EBCB.∠DAB=∠CEBC.∠ABD=∠EBCD.△ABE≌△BCD3.如图,已知AB=AC,AD=AE,∠BAC=∠DAE.下列结论不正确的是()A.∠BAD=∠CAEB.△ABD≌△ACEC.AB=BCD.BD=CE4.如图,有一面三角形镜子,小明不小心将它打破成1,2两块,现需配成同样大小的一面镜子.为了方便起见,需带上,其理由是.5.如图,已知AC=FE,BC=DE,点A,D,B,F在一条直线上,根据“SAS”判定△ABC≌△FDE,还需添一个条件,这个条件是.6.(2020·江苏无锡中考)如图,已知AB∥CD,AB=CD,BE=CF.求证:(1)△ABF≌△DCE;(2)AF∥DE.7.如图,在△ABC中,BE,CF分别是AC,AB两条边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连接AD,AG.求证:AG⊥AD.8.如图,AD=AE,BD=CE,AF⊥BC于点F,且F是BC的中点,求证:∠D=∠E.二、创新应用9.已知△ABC和△ADE均为等腰三角形,且∠BAC=∠DAE,AB=AC,AD=AE.(1)如图①,点E在BC上,求证:BC=BD+BE;(2)如图②,点E在CB的延长线上,(1)的结论是否成立?若成立,给出证明;若不成立,写出成立的式子并证明.①②答案: 一、能力提升 1.B 2.D3.C 因为∠BAC=∠DAE ,所以∠BAC-∠DAC=∠DAE-∠DAC ,即∠BAD=∠CAE ,选项A 正确. 因为AB=AC ,∠BAD=∠CAE ,AD=AE ,所以根据“SAS ”可知△ABD ≌△ACE ,所以选项B 正确.由全等三角形的对应边相等,得出BD=CE ,所以选项D 正确.只有选项C 没有充分的条件可以证明,故选C .4.1 两边及其夹角分别相等的两个三角形全等5.∠C=∠E6.证明:(1)∵AB ∥CD ,∴∠B=∠C.∵BE=CF ,∴BE-EF=CF-EF ,即BF=CE. 在△ABF 和△DCE 中,{AB =CD ,∠B =∠C ,BF =CE ,∴△ABF ≌△DCE (SAS). (2)由(1)知△ABF ≌△DCE ,∴∠AFB=∠DEC .∴180°-∠AFB=180°-∠DEC .即∠AFC=∠DEB , ∴AF ∥DE.7.证明:∵BE ,CF 分别是AC ,AB 两条边上的高,∴∠ACG+∠CAB=90°.∠DBA+∠CAB=90°. ∴∠ACG=∠DBA.在△AGC 和△DAB 中,{AC =DB ,∠ACG =∠DBA ,CG =AB ,∴△AGC ≌△DAB (SAS). ∴∠G=∠BAD.又∠G+∠GAB=90°,∴∠BAD+∠GAB=90°.即∠GAD=90°.∴AG ⊥AD.8.证明:如图,连接AB ,AC.∵F 是BC 的中点, ∴BF=CF.∵AF ⊥BC ,∴∠AFB=∠AFC=90°.在△ABF 和△ACF 中,{BF =CF ,∠AFB =∠AFC ,AF =AF ,∴△ABF ≌△ACF (SAS). ∴AB=AC.在△ABD 和△ACE 中,{AD =AE ,BD =CE ,AB =AC ,∴△ABD ≌△ACE (SSS). ∴∠D=∠E.二、创新应用9.(1)证明:∵∠BAC=∠DAE ,∴∠BAC-∠BAE=∠DAE-∠BAE .即∠EAC=∠DAB.在△ABD 和△ACE 中,{AB =AC ,∠DAB =∠EAC ,AD =AE ,∴△ABD ≌△ACE (SAS).∴BD=CE.又BC=CE+BE ,∴BC=BD+BE.11 (2)解:(1)的结论不成立,此时BC=BD-BE.证明如下: ∵∠BAC=∠DAE ,∴∠BAC+∠BAE=∠DAE+∠BAE ,即∠EAC=∠DAB.在△ABD 和△ACE 中,{AB =AC ,∠DAB =∠EAC ,AD =AE ,∴△ABD ≌△ACE (SAS).∴BD=CE.又BE+BC=CE ,∴BE+BC=BD .即BC=BD-BE.。
人教版八年级上册数学11.1.1 三角形的边 练习及答案解析

11.1.1三角形的边基础知识一、选择题1.下列图形中三角形的个数是()A.4个B.6个C.9个D.10个答案:D2.下列长度的三条线段,能组成三角形的是( )A.1cm,2 cm,3cm B.2cm,3 cm,6 cmC.4cm,6 cm,8cm D.5cm,6 cm,12cm【答案】C3.已知三条线段的比是:①1:3:4;②1:4:6;③3:3:6;④6:6:10;⑤3:4:5.其中可构成三角形的有( )A.1个B.2个C.3个 C.4个【答案】B4.(2012浙江义乌)如果三角形的两边长分别为3和5,第三边长是偶数,则第三边长可以是【】A.2B.3C.4D.8【答案】C5.(2012广东汕头)已知三角形两边的长分别是4和10,则此三角形第三边的长可能是【】A. 5 B.6 C.11 D.16【答案】C6.(2013•宜昌)下列每组数分别表示三根木棒的长度,将它们首尾连接后,能摆成三角形的一组是()A.1,2,6 B.2,2,4 C.1,2,3 D.2,3,4【答案】D7.已知等腰三角形的周长为24,一边长是4,则另一边长是()A. 16B.10C. 10或16D. 无法确定【答案】B8.有四根长度分别为6cm,5cm,4cm,1cm的木棒,选择其中的三根组成三角形,则可选择的种数有()A. 4B.3C.2D.1【答案】D9.(2013•南通)有3cm,6cm,8cm,9cm的四条线段,任选其中的三条线段组成一个三角形,则最多能组成三角形的个数为()A.1 B.2 C.3 D.4【答案】C10.(2013•海南)一个三角形的三条边长分别为1、2、x,则x的取值范围是()A .1≤x ≤3B .1<x ≤3C .1≤x <3D .1<x <3【答案】D11.如果三角形的两边长分别为3和5,则周长L 的取值范围是( )A. 6<L <15B. 6<L <16C.11<L <13D.10<L <16【答案】D12.在下列长度的四根木棒中,能与4cm 、9cm 两根木棒围成一个三角形是( )A 、4cmB 、5cmC 、13cmD 、9cm【答案】D13.已知等腰三角形的两边长分别为4、9,则它的周长为( )A .22B .17C .17或22D .13【答案】A二、填空题1.如图,图中有 个三角形,它们分别是 .【答案】 6;△AEG, △AEF, △AFG, △ABC, △ABD, △ACD2.若五条线段的长分别是1cm,2cm,3cm,4cm,5cm,则以其中三条线段为边可构成______个三角形.【答案】33.△ABC 的周长是12 cm ,边长分别为a ,b , c , 且 a=b+1 , b=c+1 , 则a= cm , b= cm , c= cm.【答案】5,4,34.在△ABC 中,AB=5,AC=7,那么BC 的长的取值范围是_______.【答案】2<BC <125.若等腰三角形的腰长为6,则它的底边长a 的取值范围是________;若等腰三角形的底边长为4,则它的腰长b 的取值范围是_______.【答案】0<a <12, b >2三、解答题1.已知三角形三边的比是3:4:5,且最大边长与最小边长的差是4,求这个三角形的三边的长.【答案】设每一份长为xcm,根据题意,可列方程5x-3x=4解得 x=2所以三角形的三边分别是6cm,8cm,10cm.2.已知等腰三角形两边长分别为a 和b,且满足︱a-1︱+(2a+3b-11)2=0,求这个等腰三角形的GF E DC B A周长.【答案】因为︱a-1︱≥0,(2a+3b-11)2≥0,又︱a-1︱+(2a+3b-11)2=0,所以a-1=0, 2a+3b-11=0,解得 a=1,b=3,当a=1为腰时,三边为1,1,3,不构成三角形,当b=3为腰时,三边为3,3,1,此时周长为3+3+1=7.3.如图,用火柴棒摆出一系列三角形图案,按这种方式摆下去,当摆到20层(n=20)时,需要多少根火柴?解:3(1+2+3+…+20)=6304.如图,在⊿ABC中,BC边上有n个点(包括B,C两点),则图中共有个三角形.答案:能力提升1.已知三角形的三边长分别为2,x-3,4,求x的取值范围.解:4-2<x-3<4+25<x<92.若a、b、c是△ABC的三边,请化简|a-b-c|+|b-c-a|+|c-a-b|.解:原式=(b+c-a)+(a+c-b)+(a+b-c)=a+b+c3.如图,点P是⊿ABC内一点,试证明:AB+AC>PB+PC.解:延长BP 交AC 于点D.在⊿ABD 中,AB+AD>BP+PD ①在⊿PDC 中,DP+DC>PC ②①+②得AB+AC>PB+PC4.如图,已知点P 是△ABC 内一点,试说明PA+PB+P C >21(AB+BC+AC).【答案】在△ABP 中,PA+P B >AB,同理有 PB+PC >BC,PA+PC >AC,三式相加得 2(PA+PB+PC )>AB+BC+AC,所以有PA+PB+P C >21(AB+BC+AC).5.四边形ABCD 是任意四边形,AC 与BD 交点O .求证:AC+BD >(AB+BC+CD+DA ).证明:在△OAB 中有OA+OB >AB在△OAD 中有 ,在△ODC 中有 ,在△ 中有 , P C B A∴OA+OB+OA+OD+OD+OC+OC+OB>AB+BC+CD+DA即:,即:AC+BD>(AB+BC+CD+DA)答案:OA+OD>AD,OD+OC>CD,OBC,OB+OC>BC,2(AC+BD)>AB+BC+CD+DA.。
17.八年级数学三角形全等的条件(边边边)(练习)(解析版)

第十二章全等三角形12.2.1 三角形全等的条件(边边边)精选练习答案一、单选题(共10小题)1.(2020·呼伦贝尔市期末)如图,小敏做了一个角平分仪ABCD,其中AB=AD,BC=DC,将仪器上的点A与∠PRQ的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE 就是∠PRQ的平分线.此角平分仪的画图原理是:根据仪器结构,可得△ABC≌△ADC,这样就有∠QAE=∠PAE.则说明这两个三角形全等的依据是[来()A.SAS B.ASA C.AAS D.SSS【答案】D【解析】试题解析:在△ADC和△ABC中,AD ABDC BCAC AC⎧⎪⎨⎪⎩===,∴△ADC≌△ABC(SSS),∴∠DAC=∠BAC,即∠QAE=∠PAE.故选D.2.(2020 哈尔滨市期末)如图,AC=BD,AO=BO,CO=DO,∠D=30°,∠A=95°,则∠AOB等于( )A.120°B.125°C.130°D.135°【答案】B基础篇【解析】在△AOC 和△BOD 中AC BD AO BO CO DO =⎧⎪=⎨⎪=⎩,∴△AOC ≌△BOD (SSS ),∴∠C =∠D ,又∵∠D =30°,∴∠C=30°,又∵在△AOC 中,∠A=95°,∴∠AOC=(180-95-30) °=55°,又∵∠AOC+∠AOB=180°(邻补角互补),∴∠AOB=(180-55)°=125 °. 故选B.3.(2018·佛山市期末)如图,用尺规作一个角等于已知角,其作图原理是:由△ODC ≌△O ′D ′C ′得∠AOB =∠A ′O ′B ′,其依据的定理是( )A .SSSB .SASC .ASAD .AAS【答案】A 【解析】详解:在△OCD 与△O′C′D′,∵''''''O C OC O D OD C D CD =⎧⎪=⎨⎪=⎩,∴△OCD ≌△O ′C ′D ′(SSS ),∴∠A ′O ′B ′=∠AOB ,显然运用的判定方法是SSS .故选A.4.(2019·惠州市期中)如图,AB =CD ,AD =CB ,判定△ABD ≌△CDB 的依据是( )A .SSSB .ASAC .SASD .AAS【答案】A 【分析】已知两边对应相等,再加上公共边相等,根据“SSS ”即可得出结论.【详解】在△ABD 和△CDB 中,∵AB =CD ,AD =CB ,BD =DB ,∴△ABD ≌△CDB (SSS ).故选A .5.(2018深圳市期末)如图,在四边形ABCD 中,AB =AD ,BC =DC ,AC 与BD 相交于点O ,则①CA 平分∠BCD ;②AC ⊥BD ;③∠ABC =∠ADC =90°;④四边形ABCD 的面积为AC •BD .上述结论正确的个数是( )A .1个B .2个C .3个D .4个【答案】B【分析】证明△ABC 与△ADC 全等,即可解决问题.【详解】解:在△ABC 与△ADC 中,AB AD BC DC AC AC =⎧⎪=⎨⎪=⎩,∴△ABC ≌△ADC (SSS ),∴∠ACB =∠ACD ,故①正确,∵AB =AD ,BC =DC∴AC 是BD 的垂直平分线,即AC ⊥DB ,故②正确;无法判断∠ABC=∠ADC=90°,故③错误,四边形ABCD的面积=S△ADB+S△BCD=12DB×OA+12DB×OC=12AC•BD,故④错误;故选:B.6.(2019·菏泽市期末)如图,方格纸中△DEF的三个顶点分别在小正方形的顶点上,像这样的三个顶点都在格点上的三角形叫格点三角形,则图中与△DEF全等的格点三角形最多有()A.8个B.7个C.6个D.4个【答案】A【分析】认真观察图形,根据SSS判定两三角形全等即可解答.【详解】如图所示:2×3排列的可找出9个全等的三角形,除去△DEF外有8个与△DEF全等的三角形:△DAF,△BGQ,△CGQ,△NFH,△AFH,△CKR,△KRW,△CGR.故选A.7.(2020·许昌市期中)如图,已知AE=AD,AB=AC,EC=DB,下列结论:①∠C=∠B ;②∠D=∠E ;③∠EAD=∠BAC ;④∠B=∠E ;其中错误的是( )A .①②B .②③C .③④D .只有④ 【答案】D【详解】解:因为AE =AD ,AB =AC ,EC =DB ;所以△ABD ≌△ACE(SSS);所以∠C =∠B ,∠D =∠E ,∠EAC=∠DAB ;所以 ∠EAC-∠DAC=∠DAB-∠DAC ;得∠EAD=∠CAB .所以错误的结论是④,故选D .8.(2019·翁牛特旗期中)如图,在ABC 和BDE 中,点C 在BD 边上,AC 边交BE 边于点F . 若AC BD =, AB ED =,BC BE =,则ACB ∠等于( )A .EDB ∠B .BED ∠C .1AFB 2∠D .2ABF ∠【答案】C 【解析】详解:在△ABC 和△DEB 中,∵AC BD AB ED BC BE =⎧⎪=⎨⎪=⎩,∴△ABC ≌△DEB (SSS ),∴∠ACB=∠DBE ,∵∠AFB 是△BFC 的外角,∴∠ACB+∠DBE=∠AFB ,∴∠ACB=12∠AFB , 故选C .9.(2019·深圳市期中)如图,四边形ABCD 是轴对称图形,且直线AC 是否对称轴,AB ∥CD ,则下列结论:①AC ⊥BD ;②AD ∥BC ;③四边形ABCD 是菱形;④△ABD ≌△CDB .其中结论正确的序号是( )A.①②③B.①②③④C.②③④D.①③④【答案】B【分析】根据轴对称图形的性质,结合菱形的判定方法以及全等三角形的判定方法分析得出答案.【详解】解:如图,因为l是四边形ABCD的对称轴,AB∥CD,则AD=AB,∠1=∠2,∠1=∠4,则∠2=∠4,∴AD=DC,同理可得:AB=AD=BC=DC,所以四边形ABCD是菱形.根据菱形的性质,可以得出以下结论:所以①AC⊥BD,正确;②AD∥BC,正确;③四边形ABCD是菱形,正确;④在△ABD和△CDB中∵AB BC AD DC BD BD=⎧⎪=⎨⎪=⎩,∴△ABD≌△CDB(SSS),正确.故正确的结论是:①②③④.故选B.10.(2017·衡阳市期末)如图所示,已知AB=CD,AD=CB,AC、BD相交于O,则图中全等三角形有()A.2对B.3对C.4对D.5对【答案】C【解析】因为AB=CD,AD=CB,根据SSS可以判定三角形ABD与三角形CDB全等,三角形ABC与三角形CDA,根据平行四边形的性质可得:AO=CO,BO=DO,再利用SSS可以判定三角形AOD和三角形COB全等,三角形AOB和三角形COD全等,共4对,故选C.二、填空题(共5小题)11.(2020·湛江市期末)如图,在ABC中,点A的坐标为()0,1,点B的坐标为()0,4,点C的坐标为()4,3,点D在第二象限,且ABD与ABC全等,点D的坐标是______.【答案】(-4,2)或(-4,3)【详解】把点C向下平移1个单位得到点D(4,2),这时△ABD与△ABC全等,分别作点C,D关于y轴的对称点(-4,3)和(-4,2),所得到的△ABD与△ABC全等.故答案为(-4,2)或(-4,3).12.(2019·重庆市期中)如图,在△ABC中,已知AD=DE,AB=BE,∠A=85°,∠C=45°,则∠CDE=_____度.提升篇【答案】40【分析】先证明△ADB ≌△BDE ,即得∠A=∠DEB ,再利用三角形的外角的性质即可求出.【详解】如图:在△ABC 中,已知AD DE AB BE BD BD ⎧⎪⎨⎪=⎩== ,∴△ADB ≌△BDE ,∴∠A=∠DEB=85°,∵∠CDE=∠DEB -∠C=85°-45°=40°.故答案为4013.(2018·巍山县期中)如图,已知AD=BC ,根据“SSS ”,还需要一个条件_________,可证明△ABC ≌△BAD ;根据“SAS ”,还需要一个条件__________,可证明△ABC ≌△BAD .【答案】DB=CA ∠DAB=∠CBA【分析】图形中隐含条件AB=BA ,找出第三边BD 和AC 即可;找出∠DAB 和∠CBA 即可.【详解】在△ABC 和△BAD 中AD BC CA DB AB BA ⎧⎪⎨⎪⎩=== ,∴△ABC ≌△BAD (SSS );在△ABC 和△BAD 中AD BC DAB CBA AB BA ⎪∠⎪⎩∠⎧⎨=== ,∴△ABC ≌△BAD (SAS ).故答案为: DB=CA ,∠DAB=∠CBA .14.(2018·台东市期中)如图,以△ABC 的顶点A 为圆心,以BC 长为半径作弧;再以顶点C 为圆心,以AB 长为半径作弧,两弧交于点D ;连结AD 、CD .若∠B=65°,则∠ADC 的大小为___度.【答案】65【详解】解:∵以点A为圆心,以BC长为半径作弧;以顶点C为圆心,以AB长为半径作弧,两弧交于点D,∴AB=CD,BC=AD.又∵AC=CA,∴△ABC≌△CDA(SSS).∴∠ADC=∠B=65°.故答案为:65.15.(2018·淮安市期末)如图,在△ABC中,已知AD=DE,AB=BE,∠A=80°,则∠CED=_____度.【答案】100【分析】根据SSS证△ABD≌△EBD,推出∠A=∠DEB,根据∠CED=80°,代入求出∠A=∠DEB=100°即可.【详解】在△ABD和△EBD中∵{AB BE BD BD AD DE===,∴△ABD≌△EBD(SSS),∴∠A=∠DEB,∵∠A=80°,∴∠CED=180°−80°=100°故答案为100°.三、解答题(共2小题)16.(2019·衢州市期中)如图,点A 、D 、C 、F 在同一条直线上,AD=CF ,AB=DE ,BC=EF.(1)求证:ΔABC ≌△DEF ;(2)若∠A=55°,∠B=88°,求∠F 的度数.【答案】(1)证明见解析;(2)37°【解析】(1)∵AC=AD+DC , DF=DC+CF ,且AD=CF∴AC=DF在△ABC 和△DEF 中,AB DE BC EF AC DF =⎧⎪=⎨⎪=⎩∴△ABC ≌△DEF (SSS )(2)由(1)可知,∠F=∠ACB∵∠A=55°,∠B=88°∴∠ACB=180°-(∠A+∠B )=180°-(55°+88°)=37°∴∠F=∠ACB=37°17.(2018·沂水县期中)如图,点B 、E 、C 、F 在一条直线上,AB =DF ,AC =DE ,BE =FC . (1)求证:△ABC ≌△DFE ;(2)连接AF 、BD ,求证:四边形ABDF 是平行四边形.【答案】(1)证明见解析;(2)证明见解析.【分析】(1)由SSS 证明△ABC ≌△DFE 即可;(2)连接AF 、BD ,由全等三角形的性质得出∠ABC=∠DFE ,证出AB ∥DF ,即可得出结论.【详解】详解:证明:,,在和中,,≌;解:如图所示:由知≌,,,,四边形ABDF是平行四边形.。
八年级数学上册第十二章全等三角形必考考点训练(带答案)

八年级数学上册第十二章全等三角形必考考点训练单选题1、如图,锐角△ABC的两条高BD、CE相交于点O,且CE=BD,若∠CBD=20°,则∠A的度数为()A.20°B.40°C.60°D.70°答案:B分析:由BD、CE是高,可得∠BDC=∠CEB=90°,可求∠BCD=70°,可证Rt△BEC≌Rt△CDB(HL),得出∠BCD =∠CBE=70°即可.解:∵BD、CE是高,∠CBD=20°,∴∠BDC=∠CEB=90°,∴∠BCD=180°﹣90°﹣20°=70°,在Rt△BEC和Rt△CDB中,{CE=BD,BC=CB∴Rt△BEC≌Rt△CDB(HL),∴∠BCD=∠CBE=70°,∴∠A=180°﹣70°﹣70°=40°.故选:B.小提示:本题考查三角形高的定义,三角形全等判定与性质,三角形内角和公式,掌握三角形高的定义,三角形全等判定与性质,三角形内角和公式是解题关键.2、如图,已知AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连接BF,CE.下列说法正确的是()①BD=CD;②∠BAD=∠CAD;③△BDF≌△CDE;④BF∥CE;⑤CE=AEA.①②B.③⑤C.①③④D.①④⑤答案:C分析:①根据三角形的中线直接进行判断即可;②一般三角形一条边上的中线不一定是这条边所对的角的平分线;③根据“SAS”直接进行判断即可;④根据三角形全等的性质直接判定∠F=∠DEC,根据平行线的判定方法得出结果;⑤根据全等三角形的性质可以判定CE=BF,不能判定CE=AE.解:①∵AD是△ABC的中线,∴BD=CD,故①正确;②∵AD为△ABC的中线,∴BD=CD,∠BAD和∠CAD不一定相等,故②错误;③在△BDF和△CDE中{BD=CD∠BDF=∠CDEDF=DE,∴△BDF≌△CDE(SAS),故③正确;④∵△BDF≌△CDE,∴∠F=∠DEC,∴BF∥CE,故④正确;⑤∵△BDF≌△CDE,∴CE=BF,故⑤错误;综上分析可知,①③④正确,故C正确.故选:C.小提示:本题考查了全等三角形的判定与性质,三角形中线的定义,熟练掌握三角形全等的判定方法并准确识图,是解题的关键.3、如图,在△ABC中,AB=5,AC=9,AD是BC边上的中线,则AD的取值范围是()A.4<AD<14B.0<AD<14C.2<AD<7D.5<AD<9答案:C分析:延长AD至点E,使得DE=AD,可证△ABD≌△CDE,可得AB=CE,AD=DE,在△ACE中,根据三角形三边关系即可求得AE的取值范围,从而得到AD的取值范围.如图,延长AD至点E,使得DE=AD,∵AD是BC边上的中线,∴BD=CD,在△ABD和△CDE中,{AD=DE∠ADB=∠CDEBD=CD,∴△ABD≌△CDE(SAS),∴AB=CE=5,AD=DE,∵△ACE中,AC-CE<AE<AC+CE,∴4<AE<14,∴2<AD<7.故选:C.小提示:本题主要考查倍长中线法解题,能够做出辅助线证出三角形全等再结合三角形三边关系是解题关键.4、观察下列作图痕迹,所作线段CD为△ABC的角平分线的是()A.B.C.D.答案:C分析:根据角平分线画法逐一进行判断即可.A:所作线段为AB边上的高,选项错误;B:做图痕迹为AB边上的中垂线,CD为AB边上的中线,选项错误;C:CD为∠ACB的角平分线,满足题意。
1.5.1 “边边边” 浙教版八年级数学上册同步练习(含解析)

第1章 三角形的初步知识1.5 三角形全等的判定第1课时 “边边边”基础过关全练知识点1 “边边边”(或“SSS”)1.如图,在△ABC中,AB=AC,BE=EC,AE的延长线交BC于点D,直接使用“SSS”可判定( )A.△ABD≌△ACDB.△ABE≌△EDCC.△ABE≌△ACED.△BED≌△CED2.如图,AB=AD,CB=CD,∠B=30°,∠BAD=46°,则∠ACD的度数是( )A.120°B.125°C.127°D.104°3.如图,在△ABC和△FED中,AC=FD,BC=ED,要利用“SSS”判定△ABC≌△FED,还需添加的条件是 .4.(教材P28变式题)如图,在四边形ABCD中,AB=AD,CB=CD,∠B=105°,则∠D= °.知识点2 三角形的稳定性5.(2022浙江诸暨绍初教育集团期中)如图,人字梯中间一般会设计一“拉杆”,这样做的道理是( )A.两点之间,线段最短B.垂线段最短C.两直线平行,内错角相等D.三角形具有稳定性6.(2022浙江台州和合教育期中)如图,李叔叔家的凳子坏了,于是他给凳子加了两根木条,这样凳子就比较牢固了,他所应用的数学原理是 .知识点3 角平分线的作法7.(2022浙江义乌绣湖中学期中)如图,AB∥CD,以点 B 为圆心,小于 DB 的长为半径作圆EF的长为半径作圆弧,两弧,分别交 BA、BD 于点 E、F,再分别以点 E、F 为圆心,大于12弧交于点 G,作射线 BG 交 CD 于点 H.若∠D=116°,则∠DHB=( )A.8° B.16°C.32° D.64°能力提升全练8.(2022独家原创)如图,点B,D,F,E在同一条直线上,且AB=AC,AD=AE,BD=CE,∠DAF=65°,∠BAE=105°,则∠BEC的度数为( )A.70°B.75°C.80°D.85°9.如图,已知AB=CD,BC=DA,E,F是AC上的两点,且AE=CF,DE=BF,那么图中全等三角形有 对.10.(2022浙江宁波镇海期末)如图,已知△ABC,请按下列要求作出图形.(1)用直角三角尺画BC边上的高线;(2)用直尺和圆规画∠B的平分线.11.(2022浙江杭州三墩中学期中)如图,AB=DC,AC=DB.(1)求证:△ABC≌△DCB;(2)求证:∠ABD=∠DCA.12.(2022浙江宁波春晓中学期中)如图,已知AB=AC,BD=CD.(1)求证:∠B=∠C;(2)若∠B=25°,∠A=2∠C,求∠BDC的度数.素养探究全练13.[数学建模]如图,工人师傅要检查人字梁的∠B和∠C是否相等,但他手边没有量角器,只有一个刻度尺.他是这样操作的:①分别在BA和CA上取BE=CG;②在BC上取BD=CF;③量出DE的长为a米,FG的长为b米.若a=b,则说明∠B和∠C是相等的,他的这种做法合理吗?为什么?答案全解全析基础过关全练1.C 在△ABE与△ACE中,AB=AC,BE=CE,AE=AE,∴△ABE≌△ACE(SSS).故选C.2.C 在△ABC和△ADC中,AB=AD,CB=CD,AC=AC,∴△ABC≌△ADC(SSS),∴∠BAC=∠DAC=12∠BAD=23°,∠ACD=∠ACB,∵∠BAC+∠B+∠ACB=180°,∴∠ACD=∠ACB=180°-30°-23°=127°.故选C.3.AB=FE(答案不唯一)解析 当AB=FE时,在△ABC和△FED中,AC=FD,BC=ED,AB=FE,∴△ABC≌△FED(SSS).答案不唯一.4.105解析 连结AC,在△ABC和△ADC中,AB=AD, CB=CD, AC=AC,∴△ABC≌△ADC(SSS),∴∠D=∠B=105°.5.D 人字梯中间一般设计一“拉杆”,是为了形成三角形,利用三角形具有稳定性来增加其稳定性.故选D.6.三角形的稳定性解析 给凳子加了两根木条之后形成了三角形,而三角形具有稳定性,所以凳子比较牢固的数学原理是三角形的稳定性.7.C ∵AB∥CD,∴∠DHB=∠ABH,∠D+∠ABD=180°,∴∠ABD=180°-116°=64°,根据作图可得∠DBH=∠ABH=12∠ABD=32°,∴∠DHB=∠ABH=32°.故选C.能力提升全练8.D 在△ABD 和△ACE 中,AB =AC ,AD =AE ,BD =CE ,∴△ABD ≌△ACE(SSS),∴∠BAD=∠CAE=12(∠BAE-∠DAF)=20°,∠ADB=∠AEC,∵∠ADB=∠DAE+∠AED,∠AEC=∠AED+∠BEC,∴∠BEC=∠DAE=∠DAF+∠CAE=65°+20°=85°.故选D.9.3解析 在△ADC 和△CBA 中,AD =CB ,AC =CA ,CD =AB ,∴△ADC ≌△CBA(SSS).在△ADE 和△CBF 中,AD =CB ,DE =BF ,AE =CF ,∴△ADE ≌△CBF(SSS).∵AE=CF,∴AE+EF=CF+EF,∴AF=CE.在△DEC 和△BFA 中,DE =BF ,CE =AF ,DC =BA ,∴△DEC ≌△BFA(SSS).综上可知共有3对全等三角形.10.解析 (1)如图,AD 即为BC 边上的高.(2)如图,BE 即为∠ABC 的平分线.11.证明 (1)在△ABC 和△DCB 中,AB =DC ,AC =BD ,BC =CB ,∴△ABC ≌△DCB(SSS).(2)∵△ABC ≌△DCB,∴∠ABC=∠DCB,∠ACB=∠DBC,∴∠ABD=∠DCA.12.解析 (1)证明:如图,连结AD,并延长到E.在△ABD和△ACD中,AB=AC,BD=CD,AD=AD,∴△ABD≌△ACD(SSS),∴∠B=∠C.(2)由(1)得△ABD≌△ACD,∴∠B=∠C,∠BAD=∠CAD,∵∠BAC=2∠C,∴∠BAD=∠CAD=∠C=∠B=25°,∵∠BDE=∠B+∠BAD=50°,∠CDE=∠CAD+∠C=50°,∴∠BDC=∠BDE+∠CDE=100°.素养探究全练13.解析 这种做法合理.理由:若在△BDE和△CFG中,BE=CG,BD=CF,DE=FG,则△BDE≌△CFG(SSS),∴∠B=∠C.。
最新初二上册数学三角形的边练习题及答案

初二上册数学三角形的边练习题及答案一、选择题1.三角形是()2.假设△ABC三条边的长度分别为m,n,p,且,那么这个三角形为()3.试用学过的知识判断,以下说法正确的选项是()角形4.以下长度的三条线段能组成三角形的是()A.1,2,3B.2,2,4C.3,4,5D.3,4,85.一个三角形的两边长分别为3cm和7cm,那么此三角形第三边长可能是()6.一个三角形的两边长分别为3和5,第三边长是偶数,那么第三边长可以是()7.,M是铁丝AD的中点,将该铁丝首尾相接折成△ABC,且∠B=30°,∠C=100°,.那么以下说法正确的选项是()C.点M在BC上,且距点B较近,距点C较远D.点M在BC上,且距点C较近,距点B较远8.为2中三角柱ABCEFG的展开,其中AE、BF、CG、DH是三角柱的边.假设1中,AD=10,CD=2,那么以下何者可为AB长度?()二、填空题9.假设有一条公共边的两个三角形称为一对“共边三角形〞,那么中以BC为公共边的“共边三角形〞有________对10.△AB C的一个外角为50°,那么△ABC一定是________三角形11.假设等腰三角形两边长分别为3和5,那么它的周长是_______________.12.,在三角形中所对的边是________________.13.用7根火柴首尾顺次相接摆成一个三角形,能摆成_______个不同的三角形.14.,在1中互不重叠的三角形共有4个,在2中,互不重叠的三角形共有7个,在3中,互不重叠的三角形共有10个……那么在第n个形中,互不重叠的三角形共有__________个(用含n的代数式表示).15.用12根火柴棒(等长)拼成一个三角形,火柴棒不允许剩余,重叠和折断,那么能摆出不同的三角形的个数有______.16.,1中共有3个三角形,2中共有6个三角形,3中共有10个三角形,…,以此类推,那么6中共有_____个三角形.17.,直角ABC的周长为2022,在其内部有五个小直角三角形,那么这五个小直角三角形的周长为18.平面上有5个点,其中任意三点都不在同一条直线上,那么这些点共可组成__________个不同的三角形.三、解答题19.两条平行直线上各有n个点,用这n对点按如下的规那么连接线段;①平行线之间的点在连线段时,可以有共同的端点,但不能有其它交点;②符合①要求的线段必须全部画出;1展示了当n=1时的情况,此时中三角形的个数为0;2展示了当n=2时的一种情况,此时中三角形的个数为2;(1)当n=3时,请在3中画出使三角形个数最少的形,此时中三角形的个数为__________个;(2)试猜测当n对点时,按上述规那么画出的形中,最少有多少个三角形?(3)当n=2022时,按上述规那么画出的形中,最少有多少个三角形?20.过A、B、C、D、E五个点中任意三点画三角形;(1)其中以AB为一边可以画出__________个三角形;(2)其中以C为顶点可以画出__________个三角形.21.△ABC是某村一遍假设干亩土地的示意,在党的“十六大〞精神的指导下,为进一步加大农村经济结构调整的力度,某村决定把这块土地平均分给四位“花农〞种植,请你帮他们分一分,提供两种分法.要求:画出形,并简要说明分法.22.△ABC中,A1,A2,A3,…,An为AC边上不同的n个点,首先连接BA1,中出现了3个不同的三角形,再连接BA2,中便有6个不同的三角形…(1)完成下表:连接个数出现三角形个数假设出现了45个三角形,那么共连接了多少个点?假设一直连接到An,那么中共有__________个三角形.23.一个三角形三边长之比为2:3:4,周长为36cm,求此三角形的三边长. 练习题答案一、选择题二、填空题三、解答题19.解:(1)4个;(2)当有n对点时,最少可以画2(n-1)个三角形;(3)2×(2022-1)=4010个.答:当n=2022时,最少可以画4010个三角形.20.解:(1),以AB为一边的三角形有△ABC、△ABD、△ABE共3个;(2),以点C为顶点的三角形有△ABC、△BEC、△BCD、△ACE、△ACD、△CDE 共6个.故答案为:(1)3,(2)6.21.解:第一种是取各边的中点,分别取,AB.BC,AC的中点D,E,Y,连接DE,EY和AE,所形成的四个三角形面积相等(如下).第二种,在BC边上取四等分点D,E,F,分别连接AD,AE,AF,所形成的四个三角形面积相等(如下).22.解:(1)连接个数123456出现三角形个数3610152128(2)8个点;(3)1+2+3+…+(n+1)=23.解:设三边长分别为2x,3x,4x,由题意得,2x+3x+4x=36,解得:x=4.故三边长为:8cm,12cm,16cm.。
2022年人教版初中数学8年级上册全等三角形判定二(SSS,AAS)(基础)巩固练习及答案

2022年人教版初中数学8年级上册【巩固练习】一、选择题1.(2020•奉贤区二模)如图,已知AD是△ABC的边BC上的高,下列能使△ABD≌△ACD的条件是()A.∠B=45° B.∠BAC=90° C.BD=AC D.AB=AC2.如图,已知AB=CD,AD=BC,则下列结论中错误的是()A.AB∥DCB.∠B=∠DC.∠A=∠CD.AB=BC3.下列判断正确的是()A.两个等边三角形全等B.三个对应角相等的两个三角形全等C.腰长对应相等的两个等腰三角形全等D.直角三角形与锐角三角形不全等4.如图,AB、CD、EF相交于O,且被O点平分,DF=CE,BF=AE,则图中全等三角形的对数共有()A.1对B.2对C.3对D.4对5.如图,∠1=∠2,∠3=∠4,下面结论中错误的是()A.△ADC≌△BCD B.△ABD≌△BACC.△ABO≌△CDO D.△AOD≌△BOC6.如图,已知AB⊥BD于B,ED⊥BD于D,AB=CD,BC=ED,以下结论不正确的是()A.EC⊥ACB.EC=ACC.ED+AB=DBD.DC=CB二、填空题7.如图,AB=CD,AC=DB,∠ABD=25°,∠AOB=82°,则∠DCB=_________.8.如图,已知:∠1=∠2,∠3=∠4,要证BD=CD,需先证△AEB≌△AEC,根据是,再证△BDE≌△,根据是.9.(2020秋•大同期末)如下图∠1=∠2,由AAS判定△ABD≌△ACD,则需添加的条件是.10.如图,AC=AD,CB=DB,∠2=30°,∠3=26°,则∠CBE=_______.11.如图,点D在AB上,点E在AC上,CD与BE相交于点O,且AD=AE,AB=AC,若∠B=20°,则∠C=_______.12.已知,如图,AB=CD,AC=BD,则△ABC≌,△ADC≌.三、解答题13.(2020•通辽)如图,四边形ABCD中,E点在AD上,其中∠BAE=∠BCE=∠ACD=90°,且BC=CE,求证:△ABC与△DEC全等.14.如图,已知D、E、B三点共线,AE=CE,AE⊥CE,∠D=∠B=90°.求证:CD+AB=DB.15.如图,已知AB=DC,AC=DB,BE=CE求证:AE=DE.【答案与解析】一.选择题1.【答案】D;【解析】解:当AB=AC时,△ABD≌△ACD,∵AD是△ABC的边BC上的高,AB=AC,∴BD=CD,∵在△ABD 和△ADC 中,∴△ABD≌△ACD(SSS).2.【答案】D;【解析】连接AC 或BD 证全等.3.【答案】D;4.【答案】C;【解析】△DOF≌△COE,△BOF≌△AOE,△DOB≌△COA.5.【答案】A;【解析】将两根钢条'AA ,'BB 的中点O 连在一起,说明OA='OA ,OB='OB ,再由对顶角相等可证.6.【答案】D;【解析】△ABC≌△EDC,∠ECD+∠ACB=∠CAB+∠ACB=90°,所以EC⊥AC,ED +AB =BC+CD=DB.二.填空题7.【答案】66°;【解析】可由SSS 证明△ABC≌△DCB,∠OBC=∠OCB=82412︒=︒,所以∠DCB=∠ABC=25°+41°=66°.8.【答案】ASA,CDE,SAS;【解析】△AEB ≌△AEC 后可得BE=CE.9.【答案】∠B=∠C.【解析】解:由图可知,只能是∠B=∠C,才能组成“AAS”.故填∠B=∠C.10.【答案】56°;【解析】∠CBE=26°+30°=56°.11.【答案】20°;【解析】△ABE≌△ACD(SAS).12.【答案】△DCB,△DAB;【解析】注意对应顶点写在相应的位置上.三.解答题13.【解析】解:∵∠BCE=∠ACD=90°,∴∠3+∠4=∠4+∠5,∴∠3=∠5,在△ACD 中,∠ACD=90°,∴∠2+∠D=90°,∵∠BAE=∠1+∠2=90°,∴∠1=∠D,在△ABC 和△DEC 中,,∴△ABC≌△DEC(AAS).14.【解析】证明:∵AE⊥CE,∴∠AEB+∠CED=90°,又∵∠B=90°∴∠A+∠AEB=90°,∴∠A=∠CED,在△AEB 与△ECD 中,A CEDB DAE CE ∠=∠∠=∠=⎧⎪⎨⎪⎩∴△AEB≌△ECD(AAS)∴AB=DE ,BE=CD∵DE+BE=DB∴CD+AB=DB15.【解析】证明:在△ABC 和△DCB 中AB DC AC DB BC =CB ⎧⎪⎨⎪⎩==∴△ABC≌△DCB(SSS)∴∠ABC=∠DCB,在△ABE 和△DCE 中ABC DCB AB DC BE CE =∠=∠=⎧⎪⎨⎪⎩∴△ABE≌△DCE(SAS)∴AE=DE.全等三角形的判定二(SSS,AAS)(基础)【学习目标】1.理解和掌握全等三角形判定方法3——“边边边”,和判定方法4——“角角边”;2.能把证明角相等或线段相等的问题,转化为证明它们所在的两个三角形全等.【要点梳理】要点一、全等三角形判定3——“边边边”全等三角形判定1——“边边边”三边对应相等的两个三角形全等.(可以简写成“边边边”或“SSS”).要点诠释:如图,如果''A B =AB,''A C =AC,''B C =BC,则△ABC≌△'''A B C .要点二、全等三角形判定4——“角角边”1.全等三角形判定4——“角角边”两个角和其中一个角的对边对应相等的两个三角形全等(可以简写成“角角边”或“AAS”)要点诠释:由三角形的内角和等于180°可得两个三角形的第三对角对应相等.这样就可由“角边角”判定两个三角形全等,也就是说,用角边角条件可以证明角角边条件,后者是前者的推论.2.三个角对应相等的两个三角形不一定全等.如图,在△ABC 和△ADE 中,如果DE∥BC,那么∠ADE=∠B,∠AED=∠C,又∠A=∠A,但△ABC 和△ADE 不全等.这说明,三个角对应相等的两个三角形不一定全等.要点三、判定方法的选择1.选择哪种判定方法,要根据具体的已知条件而定,见下表:已知条件可选择的判定方法一边一角对应相等SAS AAS ASA 两角对应相等ASA AAS 两边对应相等SAS SSS2.如何选择三角形证全等(1)可以从求证出发,看求证的线段或角(用等量代换后的线段、角)在哪两个可能全等的三角形中,可以证这两个三角形全等;(2)可以从已知出发,看已知条件确定证哪两个三角形全等;(3)由条件和结论一起出发,看它们一同确定哪两个三角形全等,然后证它们全等;(4)如果以上方法都行不通,就添加辅助线,构造全等三角形.【典型例题】类型一、全等三角形的判定3——“边边边”1、已知:如图,△RPQ 中,RP=RQ,M 为PQ 的中点.求证:RM平分∠PRQ.【思路点拨】由中点的定义得PM=QM,RM 为公共边,则可由SSS 定理证明全等.【答案与解析】证明:∵M 为PQ 的中点(已知),∴PM=QM在△RPM 和△RQM 中,()(),,RP RQ PM QM RM RM ⎧=⎪=⎨⎪=⎩已知公共边∴△RPM≌△RQM(SSS).∴∠PRM=∠QRM(全等三角形对应角相等).即RM 平分∠PRQ.【总结升华】在寻找三角形全等的条件时有的可以从图中直接找到,如:公共边、公共角、对顶角等条件隐含在题目或图形之中.把证明一对角或线段相等的问题,转化为证明它们所在的两个三角形全等,综合应用全等三角形的性质和判定.举一反三:【变式】已知:如图,AD=BC,AC=BD.试证明:∠CAD=∠DBC.【答案】证明:连接DC,在△ACD 与△BDC 中()AD BC AC BD CD DC ⎧=⎪=⎨⎪=⎩公共边∴△ACD≌△BDC(SSS)∴∠CAD=∠DBC(全等三角形对应角相等)类型二、全等三角形的判定4——“角角边”2、已知:如图,AB⊥AE,AD⊥AC,∠E=∠B,DE=CB.求证:AD=AC.【思路点拨】要证AC=AD,就是证含有这两个线段的三角形△BAC≌△EAD.【答案与解析】证明:∵AB⊥AE,AD⊥AC,∴∠CAD=∠BAE=90°∴∠CAD+∠DAB=∠BAE+∠DAB ,即∠BAC=∠EAD在△BAC 和△EAD 中BAC EAD B E CB=DE ∠=∠⎧⎪∠=∠⎨⎪⎩∴△BAC≌△EAD(AAS)∴AC=AD【总结升华】我们要善于把证明一对角或线段相等的问题,转化为证明它们所在的两个三角形全等.举一反三:【变式】如图,AD 是△ABC 的中线,过C、B 分别作AD 及AD 的延长线的垂线CF、BE.求证:BE=CF.【答案】证明:∵AD 为△ABC 的中线∴BD=CD∵BE⊥AD,CF⊥AD,∴∠BED=∠CFD=90°,在△BED 和△CFD 中BED CFD BDE CDF BD CD ∠=∠⎧⎪∠=∠⎨⎪=⎩(对顶角相等)∴△BED≌△CFD(AAS)∴BE=CF3、(2020春•雅安期末)如图:AB=A′B′,∠A=∠A′,若△ABC≌△A′B′C′,则还需添加的一个条件有()种.A.1B.2C.3D.4【思路点拨】本题要证明△ABC≌△A′B′C′,已知了AB=A′B′,∠A=∠A′,可用的判别方法有ASA,AAS,及SAS,所以可添加一对角∠B=∠B′,或∠C=∠C′,或一对边AC=A′C′,分别由已知与所添的条件即可得证.【答案与解析】解:添加的条件可以为:∠B=∠B′;∠C=∠C′;AC=A′C′,共3种.若添加∠B=∠B′,证明:在△ABC 和△A′B′C′中,,∴△ABC≌△A′B′C′(ASA);若添加∠C=∠C′,证明:在△ABC 和△A′B′C′中,,∴△ABC≌△A′B′C′(AAS);若添加AC=A′C′,证明:在△ABC 和△A′B′C′中,,∴△ABC≌△A′B′C′(SAS).故选C.【总结升华】此题考查了全等三角形的判定,是一道条件开放型问题,需要由因索果,逆向推理,逐步探求使结论成立的条件,解决这类问题要注意挖掘隐含的条件,如公共角、公共边、对顶角相等,这类问题的答案往往不唯一,只有合理即可.熟练掌握全等三角形的判定方法是解本题的关键.类型三、全等三角形判定的实际应用4、“三月三,放风筝”.下图是小明制作的风筝,他根据DE=DF,EH=FH,不用度量,就知道∠DEH=∠DFH.请你用所学的知识证明.【答案与解析】证明:在△DEH 和△DFH 中,DE DF EH FH DH DH ⎧⎪⎨⎪=⎩==∴△DEH≌△DFH(SSS)∴∠DEH=∠DFH.【总结升华】证明△DEH≌△DFH,就可以得到∠DEH=∠DFH,我们要善于从实际问题中抽离出来数学模型,这道题用“SSS”定理就能解决问题.举一反三:【变式】(2020秋•紫阳县期末)雨伞的中截面如图所示,伞骨AB=AC,支撑杆OE=OF,AE=AB,AF=AC,当O 沿AD 滑动时,雨伞开闭,问雨伞开闭过程中,∠BAD 与∠CAD 有何关系?说明理由.【答案】解:雨伞开闭过程中二者关系始终是:∠BAD=∠CAD,理由如下:∵AB=AC,AE=AB,AF=AC,∴AE=AF,在△AOE 与△AOF 中,,∴△AOE≌△AOF(SSS),∴∠BAD=∠CAD.【巩固练习】一、选择题1.如图,∠A=∠D,∠B=∠E,BF=CE,下列结论错误的是()A.△ABC≌△DEFB.BF=ECC.AC∥DED.AC=DF2.如图,AB∥EF,DE∥AC,BD=CF,则图中不是全等三角形的是()A.△BAC≌FEDB.△BDA≌FCEC.△DEC≌CADD.△BAC≌FCE3.如图,AB=BD,∠1=∠2,要用AAS判定△ABC≌△DBE,则添加的条件是()A.AE=ECB.∠D=∠AC.BE=BCD.∠DEB=∠C4.下列判断中错误的是()A.有两角和一边对应相等的两个三角形全等B.有两边和一角对应相等的两个三角形全等C.有两边和其中一边上的中线对应相等的两个三角形全等D.有一边对应相等的两个等边三角形全等5.(2020•滕州市校级模拟)如图,在下列条件中,不能证明△ABD≌△ACD的是()A.BD=DC,AB=AC B.∠ADB=∠ADC,BD=DCC.∠B=∠C,∠BAD=∠CAD D.∠B=∠C,BD=DC6.如图,点A在DE上,AC=CE,∠1=∠2=∠3,则DE的长等于()A.DC B.BC C.AB D.AE+AC二、填空题7.(2020春•鹤岗校级期末)如图:在△ABC和△FED中,AD=FC,AB=FE,当添加条件________________时,就可得到△ABC≌△FED.(只需填写一个即可)8.如图,点D在AB上,点E在AC上,且∠B=∠C,在条件①AB=AC,②AD=AE,③BE=CD,④∠AEB=∠ADC中,不能使△ABE≌△ACD的是_______.(填序号)9.已知,如图,AB∥CD,AF∥DE,AF=DE,且BE=2,BC=10,则EF=________.10.如图,AB∥CD,AD∥BC,OE=OF,图中全等三角形共有______对.11.如图,直线l过正方形ABCD的顶点B,点A、C到直线l的距离分别是1和2,则EF的长是___________.12.在△ABC 和△DEF 中(1)AB=DE;(2)BC=EF;(3)AC=DF;(4)∠A=∠D;(5)∠B=∠E;(6)∠C=∠F 从这六个条件中选取三个条件可判定△ABC 与△DEF 全等的方法共有________种.三、解答题13.(2020秋•景洪市校级期中)如图,O 为码头,A,B 两个灯塔与码头的距离相等,OA,OB 为海岸线,一轮船离开码头,计划沿∠AOB 的平分线航行,在航行途中,测得轮船与灯塔A 和灯塔B 的距离相等,试问轮船航行时是否偏离预定航线,请说明理由.14.已知:如图,ABC △中,45ABC ∠=°,CD AB ⊥于D ,BE AC ⊥于E ,BE 与CD 相交于点F .求证:BF AC =.15.如图,DC∥AB,∠BAD 和∠ADC 的角平分线相交于E,过E 的直线分别交DC、AB 于C、B 两点.求证:AD=AB+DC.【答案与解析】一、选择题1.【答案】C;2.【答案】D;3.【答案】D;【解析】满足判定定理AAS的只有D选项.4.【答案】B;【解析】C选项和D选项都可以由SSS定理证全等.5.【答案】D;【解析】解:A、∵在△ABD和△ACD中,∴△ABD≌△ACD(SSS),故本选项错误;B、∵在△ABD和△ACD中,∴△ABD≌△ACD(SAS),故本选项错误;C、∵在△ABD和△ACD中,∴△ABD≌△ACD(AAS),故本选项错误;D、不符合全等三角形的判定定理,不能推出△ABD≌△ACD,故本选项正确;故选D.6.【答案】C;【解析】可证∠BAC=∠E,∠BCA=∠DCE,所以△ABC≌△EDC,DE=AB.二、填空题7.【答案】BC=ED.8.【答案】④【解析】三个角对应相等不能判定三角形全等.9.【答案】6;【解析】△ABF≌△CDE,BE=CF=2,EF=10-2-2=6.10.【答案】6;【解析】△ABO≌△CDO,△AFO≌△CEO,△DFO≌△BEO,△AOD≌△COB,△ABD≌△CDB,△ABC≌△CDA.11.【答案】3;【解析】由AAS证△ABF≌△CBE,EF=FB+BE=CE+AF=2+1=3.12.【答案】13;【解析】ASA类型3种,AAS类型6种,SAS类型3种,SSS类型一种,共13种.三、解答题13.【解析】解:此时轮船没有偏离航线.理由:由题意知:假设轮船在D处,则DA=DB,AO=BO,在△ADC和△BDC中,,∴△ADO≌△BDO(SSS),∴∠AOD=∠BOD,即DO 为∠AOB 的角平分线,∴此时轮船没有偏离航线.14.【解析】证明:∵CD AB⊥∴90BDC CDA ∠=∠=︒∵45ABC ∠=︒∴45DCB ABC ∠=∠=︒∴DB DC=∵BE AC⊥∴90AEB ∠=︒∴90A ABE ∠+∠=︒∵90CDA ∠=︒∴90A ACD ∠+∠=︒∴ABE ACD∠=∠在BDF ∆和CDA ∆中BDC CDADB DC ABE ACD∠=∠⎧⎪=⎨⎪∠=∠⎩∴BDF ∆≌CDA ∆(AAS)∴BF AC =.15.【解析】证明:延长DE 交AB 的延长线于F∴∠CDE=∠F,∠CDA+∠BAD=180º∵DE 平分∠CDA,AE 平分∠DAB ∴∠CDE=∠ADE=21∠CDA,∠DAE=∠EAF=21∠BAD∴∠ADE=∠F,∠EDA+∠DAE=90º∴∠AED=∠AEF=90º在△ADE 与△AFE 中⎪⎩⎪⎨⎧=∠=∠∠=∠AE AE FEA DEA F ADE ∴△ADE≌△AFE (AAS)∴DE=EF,AD=AF在△DCE 与△FBE 中,⎪⎩⎪⎨⎧∠=∠=∠=∠FEB DEC FE DE F CDE ∴△DCE≌△FBE(ASA)∴DC=BF,∴AD=AB+DC.全等三角形的判定二(SSS,AAS)(提高)【学习目标】1.理解和掌握全等三角形判定方法3——“边边边”,和判定方法4——“角角边”;2.能把证明一对角或线段相等的问题,转化为证明它们所在的两个三角形全等.【要点梳理】要点一、全等三角形判定3——“边边边”全等三角形判定1——“边边边”三边对应相等的两个三角形全等.(可以简写成“边边边”或“SSS”).要点诠释:如图,如果''A B =AB,''A C =AC,''B C =BC,则△ABC≌△'''A B C.要点二、全等三角形判定4——“角角边”1.全等三角形判定4——“角角边”两个角和其中一个角的对边对应相等的两个三角形全等(可以简写成“角角边”或“AAS”)要点诠释:由三角形的内角和等于180°可得两个三角形的第三对角对应相等.这样就可由“角边角”判定两个三角形全等,也就是说,用角边角条件可以证明角角边条件,后者是前者的推论.2.三个角对应相等的两个三角形不一定全等.如图,在△ABC 和△ADE 中,如果DE∥BC,那么∠ADE=∠B,∠AED=∠C,又∠A=∠A,但△ABC 和△ADE 不全等.这说明,三个角对应相等的两个三角形不一定全等.要点三、判定方法的选择1.选择哪种判定方法,要根据具体的已知条件而定,见下表:已知条件可选择的判定方法一边一角对应相等SAS AAS ASA 两角对应相等ASA AAS 两边对应相等SASSSS2.如何选择三角形证全等(1)可以从求证出发,看求证的线段或角(用等量代换后的线段、角)在哪两个可能全等的三角形中,可以证这两个三角形全等;(2)可以从已知出发,看已知条件确定证哪两个三角形全等;(3)由条件和结论一起出发,看它们一同确定哪两个三角形全等,然后证它们全等;(4)如果以上方法都行不通,就添加辅助线,构造全等三角形.【典型例题】类型一、全等三角形的判定3——“边边边”1、如图,在△ABC 和△ADE 中,AB=AC,AD=AE,BD=CE,求证:∠BAD=∠CAE.【答案与解析】证明:在△ABD 和△ACE 中,AB AC AD AE BD CE =⎧⎪=⎨⎪=⎩∴△ABD≌△ACE(SSS)∴∠BAD=∠CAE(全等三角形对应角相等).【总结升华】把证明一对角或线段相等的问题,转化为证明它们所在的两个三角形全等,综合应用全等三角形的判定和性质.要证∠BAD=∠CAE,先找出这两个角所在的三角形分别是△BDA 和△CAE,然后证这两个三角形全等.【变式】(2020•静海县模拟)已知点A、D、C、F 在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,还需添加一个条件是.【答案】AC=DF.解:理由是:∵在△ABC 和△DEF中,∴△ABC≌△DEF(SSS),故答案为:AC=DF.类型二、全等三角形的判定4——“角角边”2、已知:如图,∠ACB=90°,AC=BC,CD 是经过点C 的一条直线,过点A、B 分别作AE⊥CD、BF⊥CD,垂足为E、F.求证:CE=BF【答案与解析】证明:∵AE⊥CD、BF⊥CD,∴∠AEC=∠BFC=90°∴∠BCF+∠B=90°∵∠ACB=90°,∴∠BCF+∠ACF=90°∴∠ACF=∠B在△BCF 和△CAE 中⎪⎩⎪⎨⎧=∠=∠∠=∠BC AC B ACE BFC AEC ∴△BCF≌△CAE(AAS)∴CE=BF.【总结升华】要证CE=BF,只需证含有这两个线段的△BCF≌△CAE.同角的余角相等是找角3、平面内有一等腰直角三角板(∠ACB=90°)和一直线MN.过点C 作CE⊥MN 于点E,过点B 作BF⊥MN 于点F.当点E 与点A 重合时(如图1),易证:AF+BF=2CE.当三角板绕点A 顺时针旋转至图2的位置时,上述结论是否仍然成立?若成立,请给予证明;若不成立,线段AF、BF、CE之间又有怎样的数量关系,请直接写出你的猜想,不需证明.【思路点拨】过B 作BH⊥CE 与点H,易证△ACE≌△CBH,根据全等三角形的对应边相等,即可证得AF+BF=2CE.【答案与解析】解:图2,AF+BF=2CE 仍成立,证明:过B 作BH⊥CE 于点H,∵∠CBH+∠BCH=∠ACE+∠BCH=90°∴∠CBH=∠ACE在△ACE 与△CBH 中,90ACH CBH AEC CHB AC BC ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩∴△ACE≌△CBH.(AAS)∴CH=AE,BF=HE,CE=EF,∴AF+BF=AE+EF+BF=CH+EF+HE=CE+EF=2EC.【总结升华】正确作出垂线,构造全等三角形是解决本题的关键.举一反三:【变式】已知Rt△ABC 中,AC=BC,∠C=90°,D 为AB 边的中点,∠EDF=90°,∠EDF 绕D 点旋转,它的两边分别交AC、CB 于E、F.当∠EDF 绕D 点旋转到DE⊥AC 于E 时(如图1),易证12DEF CEF ABC S S S +=△△△;当∠EDF 绕D 点旋转到DE 和AC 不垂直时,在图2情况下,上述结论是否成立?若成立,请给予证明;若不成立,请写出你的猜想,不需证明.图2ADBC E M N F 【答案】解:图2成立;证明图2:过点D 作DM AC DN BC⊥⊥,则90DME DNF MDN ∠=∠=∠=°在△AMD 和△DNB 中,AMD=DNB=90A B AD BD ∠∠︒⎧⎪∠=∠⎨⎪=⎩∴△AMD≌△DNB(AAS)∴DM=DN∵∠MDE+∠EDN=∠NDF+∠EDN=90°,∴∠MDE=∠NDF在△DME 与△DNF 中,90EMD FDN DM DN MDE NDF ∠=∠=︒⎧⎪=⎨⎪∠=∠⎩∴△DME≌△DNF(ASA)∴DME DNFS S =△△∴DEF CEF DMCN DECF S =S =S S .+△△四边形四边形可知ABC DMCN 1S =S 2△四边形,∴12DEF CEF ABC S S S +=△△△.类型三、全等三角形判定的实际应用4、(2020秋•内丘县期中)如图,AD 是一段斜坡,AB 是水平线,现为了测斜坡上一点D 的竖直高度DB 的长度,欢欢在D 处立上一竹竿CD,并保证CD⊥AD,然后在竿顶C 处垂下一根绳CE,与斜坡的交点为点E,他调整好绳子CE 的长度,使得CE=AD,此时他测得DE=2米,求DB 的长度.【思路点拨】延长CE交AB于F,根据等角的余角相等求出∠A=∠C,再利用“角角边”证明△ABD和△CDE全等,根据全等三角形对应边相等可得DB=DE.【答案与解析】解:如图,延长CE交AB于F,则∠A+∠1=90°,∠C+∠2=90°,∵∠1=∠2(对顶角相等),∴∠A=∠C,在△ABD和△CDE中,,∴△ABD≌△CDE(AAS),∴DB=DE,∵DE=2米,∴DB的长度是2米.【总结升华】本题考查了全等三角形的应用,仔细观察图形求出∠A=∠C是解题的关键.。
人教版2022-2023学年数学八年级上学期三角形的三边关系练习题含答案

人教版2022-2023学年数学八年级上学期三角形的三边关系练习题学校:___________姓名:___________班级:___________一、单选题1.如图所示,工人师傅在砌门时,通常用木条BD固定长方形门框ABCD,使其不变形,这样做的数学根据是()A.两点确定一条直线B.两点之间,线段最短C.同角的余角相等D.三角形具有稳定性2.下图所示的五角星是用螺栓将两端打有孔的5根木条连接构成的图形,它的形状不稳定,如果在木条交叉点打孔加装螺栓的办法使其形状稳定,那么至少需要添加()个螺栓A.1B.2C.3D.43.已知三角形的两边长分别为5cm和8cm,则第三边的长可以是()A.2cm B.3cm C.6cm D.13cm4.平行四边形的一边长为10,那么它的两条对角线的长可以是()A.4和6B.6和8C.8和12D.20和30 5.如果三角形的两边长分别为4和7,则周长L的取值范围是()A.3<L<11B.6<L<16C.14<L<22D.10<L<216.一个等腰三角形的底边长是6,腰长是一元二次方程x2−7x+12=0的一根,则此三角形的周长是()A.12B.13C.14D.12或14二、填空题7.若长度分别为3,5,a的三条线段能组成一个三角形,则整数a的最大值为________.8.已知a,b,c是ABC的三边长,则b c a a b c a b c--+-+---=______.9.安排学生住宿,若每间住3人,则还有13人无房可住;若每间住6人,则还有一间不空也不满,则宿舍的房间数量可能为_____.三、解答题10的小数部分为a,8b,求a+b的平方根.11.(1)计算:232cos45°;(2)解不等式组:() 31225233x xx x⎧+>-⎪⎨+≤-⎪⎩.12.请补全证明过程及推理依据.已知:如图,BC//ED,BD平分∠ABC,EF平分∠AED.求证:BD∠EF.证明:∠BD平分∠ABC,EF平分∠AED,∠∠1=12∠AED,∠2=12∠ABC(______________)∠BC∠ED(________)∠∠AED=________(________________)∠12∠AED=12∠ABC∠∠1=________∠BD∠EF(________________).参考答案:1.D【分析】根据三角形具有稳定性解答即可.【详解】解:常用木条固定长方形门框ABCD,使其不变形,这种做法的根据是三角形具有稳定性.故选:D.【点睛】本题考查三角形稳定性的实际应用.三角形的稳定性在实际生活中有着广泛的应用,如钢架桥、房屋架梁等,因此要使一些图形具有稳定的结构,通常会把图形变成分成三角形,熟记三角形具有稳定性是解题的关键.2.A【分析】用木条交叉点打孔加装螺栓的办法去达到使其形状稳定的目的,可用三角形的稳定性解释.【详解】如图,A点加上螺栓后,根据三角形的稳定性,原不稳定的五角星中具有了稳定的各边故答案为:A.【点睛】本题考查了三角形的稳定性的问题,掌握三角形的稳定性是解题的关键.3.C【分析】先确定第三边的取值范围,后根据选项计算选择.【详解】设第三边的长为x,∠ 角形的两边长分别为5cm和8cm,∠3cm<x<13cm,故选C.【点睛】本题考查了三角形三边关系定理,熟练确定第三边的范围是解题的关键.4.D【分析】根据平行四边形对角线互相平分和三角形两边之和大于第三边逐项判断即可.【详解】解:如图,设AB=10,对角线相交于点E,它的两条对角线的长为4和6时,465102AE BE++==<,不符合题意;它的两条对角线的长为6和8时,687102AE BE++==<,不符合题意;它的两条对角线的长为8和12时,812102AE BE++==,不符合题意;它的两条对角线的长为20和30时,设AE=15,BE=10,AB BE AE+>,符合题意;故选:D.【点睛】本题考查了平行四边形的性质和三角形的三边关系,解题关键是明确两条较短边的和大于最长边可构成三角形.5.C【分析】根据三角形的三边关系,可得3<第三边<11,即可求解.【详解】解:∠4+7=11,7﹣4=3,∠3<第三边<11,∠4+7+3<L<11+4+7,即14<L<22.故选:C.【点睛】本题主要考查了三角形的三边关系,熟练掌握三角形的两边之和大于第三边,两边之差小于第三边是解题的关键.6.C【分析】通过解一元二次方程x2-7x+12=0求得等腰三角形的两个腰长,然后求该等腰三角形的周长.【详解】解:由一元二次方程x2-7x+12=0,得(x-3)(x-4)=0,∠x-3=0或x-4=0,解得x=3,或x=4;∠等腰三角形的两腰长是3或4;∠当等腰三角形的腰长是3时,3+3=6,构不成三角形,所以不合题意,舍去;∠当等腰三角形的腰长是4时,0<6<8,所以能构成三角形,所以该等腰三角形的周长=6+4+4=14;故选:C .【点睛】本题综合考查了一元二次方程-因式分解法、三角形的三边关系、等腰三角形的性质.解答该题时,采用了“分类讨论”的数学思想.7.7【分析】根据三角形三边关系定理得出5-3<a <5+3,求出即可.【详解】解:由三角形三边关系定理得:5-3<a <5+3,即2<a <8,即符合的最大整数a 的值是7,故答案为:7.【点睛】本题考查了三角形三边关系定理,能根据定理得出2<a <8是解此题的关键,注意:三角形的两边之和大于第三边,三角形的两边之差小于第三边.8.33a b c -+【分析】根据三角形三边关系定理,确定绝对值中式子的符号后化简即可.【详解】∠a ,b ,c 是ABC 的三边长,∠a +c >b ,b +c >a , ∠b c a a b c a b c --+-+---=a c b a b c a b c +-+-++--=33a b c -+,故答案为:33a b c -+.【点睛】本题考查了三角形三边关系定理,绝对值的化简,熟练掌握三角形三边关系定理是解题的关键.9.5或6【分析】设共有x 间宿舍,则共有(313)x +个学生,然后根据每间住6人,则还有一间不空也不满,列出不等式组进行求解即可.【详解】解:设共有x 间宿舍,则共有(313)x +个学生,依题意得:3136(1)3136x x x x +>-⎧⎨+<⎩,解得:1319 33x<<.又x为正整数,5x∴=或6.故答案为:5或6.【点睛】本题主要考查了一元一次不等式组的应用,解题的关键在于能够准确根据题意列出不等式组进行求解.10.a+b的平方根为±1;34<,43-<-,由不等式的性质求得a、b 的值,再计算求值即可;【详解】解:∠34<,∠526<<,∠43-<-,∠485<<,∠253a=-=,844b==∠a+b=1,∠a+b的平方根为±1;【点睛】本题考查了无理数的估算,不等式的性质,平方根的计算;掌握无理数的估算方法是解题关键.11.(1)82;(2)﹣5<x≤﹣1【分析】(1)根据有理数乘方,最简二次根式,特殊角的三角函数值,二次根式的加减法计算求解;(2)根据一元一次不等式组的解法,先分别求出两个不等式的解集,再确定不等式组的解集.【详解】解:(1)232cos45°=2==82;(2)() 31225233x xx x⎧+>-⎪⎨+≤-⎪⎩①②,不等式∠的解集是:x>﹣5,不等式∠的解集是:x≤﹣1,∠原不等式组的解集是:﹣5<x≤﹣1.【点睛】本主要考查了实数的运算,一元一次不等式组的解法,理解有理数乘方,最简二次根式,特殊角的三角函数值,二次根式的加减法,一元一次不等式组的解法是解答关键.12.角平分线的定义;已知;∠ABC;两直线平行,同位角相等;∠2;同位角相等,两直线平行【分析】根据角平分线的定义得出∠1=12∠AED,∠2=12∠ABC,根据平行线的性质定理得出∠AED=∠ABC,求出∠1=∠2,再根据平行线的判定定理推出即可.【详解】证明:∠BD平分∠ABC,EF平分∠AED,∠∠1=12∠AED,∠2=12∠ABC(角平分线的定义)∠BC∠ED(已知)∠∠AED=∠ABC(两直线平行,同位角相等)∠12∠AED=12∠ABC∠∠1=∠2∠BD∠EF(同位角相等,两直线平行).故答案为:角平分线的定义;已知;∠ABC;两直线平行,同位角相等;∠2;同位角相等,两直线平行.【点睛】本题考查了角平分线的定义,平行线的性质定理和判定定理等知识点,能熟记平行线的性质定理和判定定理是解此题的关键.。
人教版八年级数学上册《三角形全等的判定》课堂同步练习题含答案(6课时)

11 题图
10.如图,已知 AC = FE ,BC = DE ,点 A、D、
B、F 在一条直线上,要使△ ABC ≌△ FDE ,还需添加一.个.条件,这个条件
7
12.2 三角形全等的判定
一、选择题
第 1 课时 边边边(SSS)
1. B 2. A 3.C 4.C 5.C 6.B 7.D 8.B
二、填空题
9. sss
10. AB = FD (答案不惟一,也可以是 AD = FB )
11. 76
12. sss 13 .20 14. AB=AC
16. ②①③ 17. EC, △ABF≌△DCE
[来源:Z+xx+]
21.(2010 浙江金华)如图,在△ABC 中,D 是 BC 边上的点(不与 B,C 重合),
F,E 分别是 AD 及其延长线上的点,CF∥BE. 请你添加一个条件,使△BDE
≌△CDF (不再添 加其它线段,不再标注或使用其他字母),并给出证明.
(1)你添加的条件是: (2)证明:
∴∠A=∠C(全等三角形的对应角相等)
21. 解:(1)
(或点 D 是线段 BC 的中点), FD = ED, CF = BE 中
任选一个即可﹒
(2)以 BD = DC 为例进行证明:
∵CF∥BE,
[来源:]
∴∠FCD﹦∠EBD.
又∵ BD = DC ,∠ FDC﹦∠EDB, ∴△BDE≌△CDF.
A.BC=EC,∠B=∠E
全等三角形判定基础练习(有答案)

全等三角形判定基础练习(有答案)一.选择题(共3小题)1.如图,已知AD=AE,添加下列条件仍无法证明△ABE≌△ACD的是()A.AB=AC B.∠ADC=∠AEB C.∠B=∠C D.BE=CD2.判定两个三角形全等,给出如下四组条件:①两边和一角对应相等;②两角和一边对应相等;③两个直角三角形中斜边和一条直角边对应相等;④三个角对应相等;其中能判定这两个三角形全等的条件是()A.①和②B.①和④C.②和③D.③和④3.如图,下列各组条件中,不能得到△ABC≌△BAD的是()A.BC=AD,∠ABC=∠BAD B.BC=AD,AC=BDC.AC=BD,∠CAB=∠DBA D.BC=AD,∠CAB=∠DBA二.解答题(共6小题)4.如图,AB=CB,BE=BF,∠1=∠2,证明:△ABE≌△CBF.5.如图所示,有两个直角三角形△ABC和△QPA按如图位置摆放C,P,A在同一条直线上,并且BC=PA.当QP与AB垂直时,△ABC能和△QPA全等吗,请说明理由.6.如图,BE⊥AC于E,CF⊥AB于F,CF、BE相交于点D,且BD=CD.求证:AD平分∠BAC.7.如图,在直角三角形ABC中,∠ABC=90°,点D在BC的延长线上,且BD=AB,过B作BE⊥AC,与BD的垂线DE交于点E.求证:△ABC≌△BDE.8.如图,在△ABC中,AB=AC,点D、E在BC上,且BD=CE.求证:△ABE≌△ACD.9.如图,已知点D在AB上,点E在AC上,BE和CD相交于点O,AB=AC,∠B=∠C.求证:△ABE≌△ACD.全等三角形判定(孙雨欣)初中数学组卷参考答案与试题解析一.选择题(共3小题)1.如图,已知AD=AE,添加下列条件仍无法证明△ABE≌△ACD的是()A.AB=AC B.∠ADC=∠AEB C.∠B=∠C D.BE=CD【分析】全等三角形的判定定理有SAS,ASA,AAS,SSS,看看条件是否符合判定定理即可.【解答】解:A、∵在△ABE和△ACD中,,∴△ABE≌△ACD(SAS),正确,故本选项错误;B、∵在△ABE和△ACD中,,∴△ABE≌△ACD(ASA),正确,故本选项错误;C、∵在△ABE和△ACD中,,∴△ABE≌△ACD(AAS),正确,故本选项错误;D、根据AE=AD,BE=CD和∠A=∠A不能推出△ABE和△ACD全等,错误,故本选项正确;故选D.【点评】本题考查了对全等三角形的判定定理的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS.2.判定两个三角形全等,给出如下四组条件:①两边和一角对应相等;②两角和一边对应相等;③两个直角三角形中斜边和一条直角边对应相等;④三个角对应相等;其中能判定这两个三角形全等的条件是()A.①和②B.①和④C.②和③D.③和④【分析】认真分析各选项提供的已知条件,结合全等三角形判定方法对选项提供的已知条件逐一判断.【解答】解:①两边和一角对应相等不正确,应该是两边的夹角,故本选项错误,②两角和一边对应相等,符合AAS,故本选项正确,③两个直角三角形中斜边和一条直角边对应相等,符合SAS,故本选项正确,④三个角对应相等,可以相似不全等,故本选项错误,故选C.【点评】本题主要考查了对全等三角形的判定方法的理解及运用.常用的判定方法有AAS,SSS,SAS 等,难度适中.3.如图,下列各组条件中,不能得到△ABC≌△BAD的是()A.BC=AD,∠ABC=∠BAD B.BC=AD,AC=BDC.AC=BD,∠CAB=∠DBA D.BC=AD,∠CAB=∠DBA【分析】根据图形可得公共边AB=AB,再加上选项所给条件,利用判定定理SSS、SAS、ASA、AAS分别进行分析即可.【解答】解:根据图形可得公共边:AB=AB,A、BC=AD,∠ABC=∠BAD可利用SAS证明△ABC≌△BAD,故此选项不合题意;B、BC=AD,AC=BD可利用SSS证明△ABC≌△BAD,故此选项不合题意;C、AC=BD,∠CAB=∠DBA可利用SAS证明△ABC≌△BAD,故此选项不合题意;D、BC=AD,∠CAB=∠DBA不能证明△ABC≌△BAD,故此选项符合题意;故选:D.【点评】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.二.解答题(共7小题)4.如图,AB=CB,BE=BF,∠1=∠2,证明:△ABE≌△CBF.【分析】利用∠1=∠2,即可得出∠ABE=∠CBF,再利用全等三角形的判定SAS得出即可.【解答】证明:∵∠1=∠2,∴∠1+∠FBE=∠2+∠FBE,即∠ABE=∠CBF,在△ABE与△CBF中,,∴△ABE≌△CBF(SAS).【点评】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.5.如图所示,有两个直角三角形△ABC和△QPA按如图位置摆放C,P,A在同一条直线上,并且BC=PA.当QP与AB垂直时,△ABC能和△QPA全等吗,请说明理由.【分析】首先根据∠QAP=90°,AB⊥PQ可证出∠PQA=∠BAC,在加上条件BC=AP,∠C=∠QAP=90°,可利用AAS定理证明△ABC和△QPA全等.【解答】△ABC能和△QPA全等;证明:∵∠QAP=90°,∴∠PQA+∠QPA=90°,∵QP⊥AB,∴∠BAC+∠APQ=90°,∴∠PQA=∠BAC,在△ABC和△QPA中,,∴△ABC≌△QPA(AAS).【点评】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.6.如图,BE⊥AC于E,CF⊥AB于F,CF、BE相交于点D,且BD=CD.求证:AD平分∠BAC.【分析】要证AD平分∠BAC,只需证DF=DE.可通过证△BDF≌△CDE(AAS)来实现.根据已知条件,利用AAS可直接证明△BDF≌△CDE,从而可得出AD平分∠BAC.【解答】证明:∵BE⊥AC,CF⊥AB,∴∠BFD=∠CED=90°.在△BDF与△CDE中,,∴Rt△BDF≌Rt△CDE(AAS).∴DF=DE,∴AD是∠BAC的平分线.【点评】本题考查了全等三角形的判定和性质,以及到角两边距离相等的点在角平分线上等知识.发现并利用△BDF≌△CDE是正确解答本题的关键.7.如图AB,CD相交于点O,AD=CB,AB⊥DA,CD⊥CB,求证:△ABD≌△CDB.【分析】首先根据AB⊥DA,CD⊥CB,可得∠A=∠C=90°,再利用HL定理证明Rt△ABD≌Rt△CBD即可.【解答】证明:∵AB⊥DA,CD⊥CB,∴∠A=∠C=90°,在Rt△ABD和Rt△CBD中,∴Rt△ABD≌Rt△CBD(HL).【点评】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.8.如图,在△ABC中,AB=AC,点D、E在BC上,且BD=CE.求证:△ABE≌△ACD.【分析】由AB=AC可得∠B=∠C,然后根据BD=CE可证BE=CD,根据SAS即可判定三角形的全等.【解答】证明∵AB=AC,∴∠B=∠C,∵BD=EC,∴BE=CD,在△ABE与△ACD中,,∴△ABE≌△ACD(SAS).【点评】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.9.如图,已知点D在AB上,点E在AC上,BE和CD相交于点O,AB=AC,∠B=∠C.求证:△ABE≌△ACD.【分析】根据全等三角形的判定定理ASA推出即可.【解答】证明:∵在△ABE和△ACD中,∴△ABE≌△ACD(ASA).【点评】本题考查了全等三角形的判定定理的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS.10.如图,在直角三角形ABC中,∠ABC=90°,点D在BC的延长线上,且BD=AB,过B作BE⊥AC,与BD的垂线DE交于点E.求证:△ABC≌△BDE.【分析】利用已知得出∠A=∠DBE,进而利用ASA得出△ABC≌△BDE即可.【解答】证明:在Rt△ABC中,∵∠ABC=90°,∴∠ABE+∠DBE=90°,∵BE⊥AC,∴∠ABE+∠A=90°,∴∠A=∠DBE,∵DE是BD的垂线,∴∠D=90°,在△ABC和△BDE中,∵,∴△ABC≌△BDE(ASA).【点评】此题主要考查了全等三角形的判定,三角形内角和定理的应用,正确发现图形中等量关系∠A=∠DBE是解题关键.。
【最新】人教版八年级数学上册12.2 第1课时 “边边边”精选练习1含答案.doc
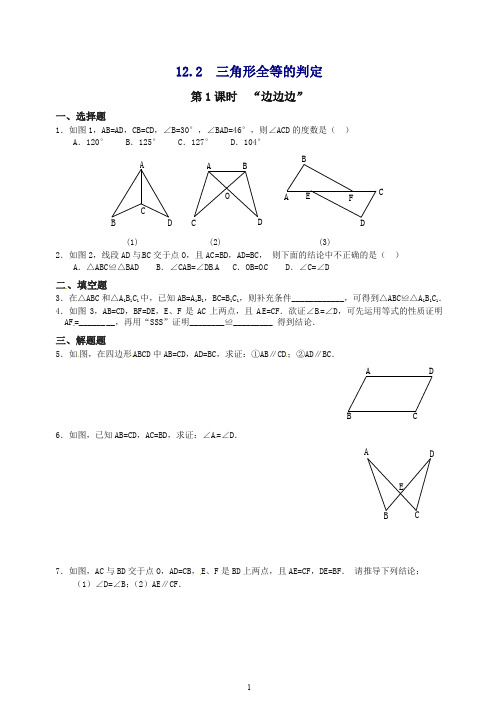
12.2 三角形全等的判定第1课时 “边边边”一、选择题1.如图1,AB=AD ,CB=CD ,∠B=30°,∠BAD=46°,则∠ACD 的度数是( )A .120°B .125°C .127°D .104°DCBAODCBAFEDC BA(1) (2) (3)2.如图2,线段AD 与BC 交于点O ,且AC=BD ,AD=BC ,•则下面的结论中不正确的是( ) A .△ABC ≌△BAD B .∠CAB=∠DB A C .OB=OC D .∠C=∠D二、填空题3.在△ABC 和△A 1B 1C 1中,已知AB=A 1B 1,BC=B 1C 1,则补充条件____________,可得到△ABC ≌△A 1B 1C 1. 4.如图3,AB=CD ,BF=DE ,E 、F 是AC 上两点,且A E=CF .欲证∠B =∠D ,可先运用等式的性质证明AF =________,再用“SSS ”证明________≌_________•得到结论.三、解题题5.如图,在四边形ABCD 中AB=CD ,AD=BC ,求证:①AB ∥CD ;②AD ∥BC .DCBA6.如图,已知AB=CD ,AC=BD ,求证:∠A =∠D .E DCBA7.如图,AC 与BD 交于点O ,AD=CB ,E 、F 是BD 上两点,且AE=CF ,DE=BF .•请推导下列结论:(1)∠D=∠B ;(2)AE ∥CF .O F ED CBA答案:1.C 2.C 3.AC=AC 4.CE;△ABF≌△CDE5.连接AC(或BD) 6.连接BC后证明△ABC≌△DCB7.①证明△ADE≌△CBF;②证明∠AEF=∠CFE。
部编数学八年级上册专题14边边角证全等(解析版)含答案

答卷时应注意事项1、拿到试卷,要认真仔细的先填好自己的考生信息。
2、拿到试卷不要提笔就写,先大致的浏览一遍,有多少大题,每个大题里有几个小题,有什么题型,哪些容易,哪些难,做到心里有底;3、审题,每个题目都要多读几遍,不仅要读大题,还要读小题,不放过每一个字,遇到暂时弄不懂题意的题目,手指点读,多读几遍题目,就能理解题意了;容易混乱的地方也应该多读几遍,比如从小到大,从左到右这样的题;4、每个题目做完了以后,把自己的手从试卷上完全移开,好好的看看有没有被自己的手臂挡住而遗漏的题;试卷第1页和第2页上下衔接的地方一定要注意,仔细看看有没有遗漏的小题;5、中途遇到真的解决不了的难题,注意安排好时间,先把后面会做的做完,再来重新读题,结合平时课堂上所学的知识,解答难题;一定要镇定,不能因此慌了手脚,影响下面的答题;6、卷面要清洁,字迹要清工整,非常重要;7、做完的试卷要检查,这样可以发现刚才可能留下的错误或是可以检查是否有漏题,检查的时候,用手指点读题目,不要管自己的答案,重新分析题意,所有计算题重新计算,判断题重新判断,填空题重新填空,之后把检查的结果与先前做的结果进行对比分析。
亲爱的小朋友,你们好!经过两个月的学习,你们一定有不小的收获吧,用你的自信和智慧,认真答题,相信你一定会闯关成功。
相信你是最棒的!专题14 边边角证全等1.已知如图:∠ABP=∠CBP,P为BN上一点,且PD⊥BC于点D,∠BAP+∠BCP=180°,求证:AB+BC=2BD.【解答】解:过点P作PM⊥AB,垂足为点M,∵PM⊥AB,PD⊥BC,∠ABP=∠CBP,∴PM=PD,BM=BD,∵∠BAP+∠BCP=180°,且∠BAP+∠MAP=180°,∴∠PAM=∠BCP,在△PAM和△PCD中,,∴△PAM≌△PCD,∴AM=CD,∴BM﹣AB=BC﹣BD,∴BD﹣AB=BC﹣BD,∴AB+BC=2BD.2.如图,四边形ABCD中,∠A+∠C=180°,BD平分∠ABC,(1)求证:DC=AD;(2)若BC=21,AB=9,AD=10,求BD的长.【解答】证明:在BC上截取BE=BA,连接DE,∵BD平分∠ABC,∴∠ABD=∠EBD,在△BAD和△BED中,∵,∴△BAD≌△BED(SAS),∴DA=DE,∠A=∠BED,∵∠BED+∠DEC=180°,∠A+∠C=180°,∴∠C=∠DEC,∴DE=DC,∴DC=AD.(2)如图,过点D作DF⊥BC于点F,∵△BAD≌△BED,∴BA=BE=9、AD=DC=10,∵BC=21,∴EC=12,∵DE=DC,∴EF=FC=EC=6,在Rt△DFC中,DF===8,在Rt△BDF中,BD===17.3.如图,在四边形ABCD中,已知BD平分∠ABC,∠A+∠C=180°,试说明AD=CD的理由.【解答】证明:如图,过点D作DE⊥AB交BA的延长线于E,作DF⊥BC于F,所以,∠EDF+∠BAD=180°,∵BD平分∠ABC,∴DE=DF,∵∠BAD与∠BCD互补,∴∠ADE=∠CDF,在△ADE和△CDF中,,∴△ADE≌△CDF(AAS),∴AD=CD.4.如图所示,四边形ABCD中,BC<BA,AD=CD,BD平分∠ABC,求证:∠A+∠C=180°.【解答】证明:如图,过D作出DE⊥BA,DF⊥BC,.∵BD平分∠ABC,DE⊥BA,DF⊥BC,∴DE=DF,∠E=∠DFC=90°,在Rt△DEA和Rt△DFC中,,∴Rt△DEA≌Rt△DFC(HL),∴∠C=∠EAD,∵∠BAD+∠EAD=180°,∴∠BAD+∠C=180°.5.如图,OC平分∠MON,A、B分别为OM、ON上的点,且BO>AO,AC=BC,求证:∠OAC+∠OBC=180°.【解答】解:如图,作CE⊥ON于E,CF⊥OM于F.∵OC平分∠MON,CE⊥ON于E,CF⊥OM于F.∴CE=CF,∵AC=BC,∠CEB=∠CFA=90°,∴Rt△CFA≌Rt△CEB(HL),∴∠ACF=∠ECB,∴∠ACB=∠ECF,∵∠ECF+∠MON=360°﹣90°﹣90°=180°,∴∠ACB+∠AOB=180°,∴∠OAC+∠OBC=180°.6.如图,在四边形ABCD中,∠BAD=∠DCB=90°,AB=AD,延长CD到E,使DE=BC,连接AE ,AC .(1)求证:△ACE 是等腰直角三角形;(2)若AC =6cm ,求四边形ABCD 的面积.【解答】(1)证明:在四边形ABCD 中,∠BAD =∠DCB =90°,∴∠B +∠ADC =360°﹣∠BAD ﹣∠DCB =180°,∵∠ADE +∠ADC =180°,∴∠ADE =∠B ,在△ADE 和△ABC 中,,∴△ADE ≌△ABC (SAS ),∴∠DAE =∠BAC ,AE =AC ,∴∠CAE =∠CAD +∠DAE =∠CAD +∠BAC =∠BAD =90°,∴△ACE 是等腰直角三角形.(2)解:∵△ADE ≌△ABC ,∴S △ADE =S △ABC ,∵△ACE 是等腰直角三角形.AC =6cm ,∴AC =AE =6cm ,∴四边形ABCD 的面积=S △ACD +S △ABC =S △ACD +S △ADE =S △ACE =×6×6=18(cm 2).7.已知:如图,点E 、F 在BC 上,AF 与DE 交于点G ,AB =DC ,GE =GF ,∠B =∠C .求证:AG =DG .【解答】证明:∵GE =GF ,∴△GEF 为等腰三角形,∴∠GEF=∠GFE,∵在△ABF和△DCE中,∠B=∠C,∴∠A=∠D,在△ABF和△DCE中,,∴△ABF≌△DCE(ASA),∴AF=DE,又∵GF=GE,∴AF﹣GF=DE﹣GE,即AG=DG.8.如图,已知AC平分∠BAD,CE⊥AB,CD⊥AD,点E,D分别为垂足,CF=CB.(1)求证:BE=FD.(2)若AF=4,AB=6,求DF.【解答】(1)证明:∵AC平分∠BAD,CE⊥AB,CD⊥AD,∴CD=CE,∠ADC=∠AEC=90°,在Rt△CDF与Rt△CEB中,,∴Rt△CDF≌Rt△CEB(HL),∴BE=FD;(2)解:由(1)知,BE=FD,∠ADC=∠AEC=90°,在Rt△ACD与Rt△ACE中,,∴Rt△ACD≌Rt△ACE(HL),∴AD=AE,∵AB=AE+BE=AD+BE=AF+FD+BE,AF=4,AB=6,∴6=4+FD+BE=4+2•DF,∴DF=1.9.在平面直角坐标系中,点A的坐标为(3,3),AB=BC,AB⊥BC,点B在x轴上.(1)如图1,AC交x轴于点D,若∠DBC=10°,则∠ADB= 55° ;(2)如图1,若点B在x轴正半轴上,点C(1,﹣1),求点B坐标;(3)如图2,若点B在x轴负半轴上,AE⊥x轴于点E,AF⊥y轴于点F,∠BFM=45°,MF 交直线AE于点M,若点B(﹣1,0),BM=5,求EM的长.【解答】解:(1)∠ADB=55°;∵AB=BC,AB⊥BC,∴∠A=∠C=45°,∵∠ADB=∠C+∠DBC,∠DBC=10°,∴∠ADB=45°+10°=55°;(2)解:如图1,过A作AD⊥x轴,CE⊥x轴,垂足分别为D、E,∵AD⊥x轴,CE⊥x轴,∴∠ADB=∠BEC=90°,∴∠DAB+∠ABD=90°,∵AB⊥BC,∴∠EBC+∠ABD=90°,∴∠DAB=∠EBC,在△ADB与△BEC中,,∴△ADB≌△BEC(AAS),∴BD=CE,∵A(3,3),C(1,﹣1),∴OD=3,CE=1,∴OB=OD+BD=OD+CE=3+1=4,∴B(4,0);(3)解:如图2,在AM上截取AN=OB,连接FN,∵A(3,3),∴OF=AF=3,在△BOF与△NAF中,,∴△BOF≌△NAF(SAS),∴∠BFO=∠NFA,BF=NF,∵∠BFM=∠BFO+∠OFM=45°,∴∠NFA+∠OFM=45°,∵∠OFA=90°,∴∠NFM=∠OFA﹣(∠NFA+∠OFM)=90°﹣45°=45°,∴∠BFM=∠NFM,在△BFM与△NFM中,,∴△BFM≌△NFM(SAS),∴BM=NM,∵BM=5,B(﹣1,0),∴MN=5,BO=AN=1,∴EM=MN+AN﹣AE=5+1﹣3=3.10.如图,在四边形ABCD中,BC>BA,AD=CD,BD平分∠ABC,若∠C=50°,求∠BAD的度数.【解答】解:过点D作DE⊥BC于E,过点D作DF⊥AB交BA的延长线于F,∵BD平分∠ABC,∴DE=DF,∠DEC=∠F=90°,在RtCDE和Rt△ADF中,,∴Rt△CDE≌Rt△ADF(HL),∴∠FAD=∠C,∴∠BAD+∠C=∠BAD+∠FAD=180°,∵∠C=50°,∴∠BAD=130°.11.定义:一组邻边相等且对角互补的四边形叫做“等补四边形”.如图1,四边形ABCD中,AD=CD,∠A+∠C=180°,则四边形ABCD叫做“等补四边形”.(1)概念理解①在以下四种图形中,一定是“等补四边形”的是 D .A.平行四边形B.菱形C.矩形D.正方形②等补四边形ABCD中,若∠B:∠C:∠D=2:3:4,则∠A= 90° .(2)知识运用如图1,在四边形ABCD中,BD平分∠ABC,AD=CD,BC>BA.求证:四边形ABCD是等补四边形.(3)探究发现如图2,在等补四边形ABCD中,AB=AD,连接AC,AC是否平分∠BCD?请说明理由.【解答】解:(1)①∵平行四边形的对角相等,不一定互补,对边相等,邻边不一定相等,∴平行四边形不一定是等补四边形,故不选A;∵菱形四边相等,对角相等,但不一定互补,∴菱形不一定是等补四边形,故不选B;∵矩形对角互补,但邻边不一定相等,∴矩形不一定是等补四边形,故不选C;∵正方形四个角是直角,四条边相相等,∴正方形一定是等补四边形,故选D.②∵等补四边形对角互补,∴∠A:∠B:∠C:∠D=3:2:3:4,又∵∠A+∠C=180°,∴∠A=∠C=90°,故填90°.(2)如图1,证明:在BC上截取BE=BA,连接DE,在△BAD和△BED中,,∴△BAD≌△BED(SAS),∴∠A=∠DEB,AD=DE.∵AD=CD,∴DE=DC.∴∠C=∠DEC.∵∠BED+∠DEC=180°,∴∠A+∠C=180°,又∵AD=CD,∴四边形ABCD是等补四边形;(3)如图2,过点A分别作AE⊥BC于E,AF⊥CD于F,则∠AEB=∠AFD=90°,∵四边形ABCD是等补四边形,∴∠B+∠ADC=180°,又∠ADC+∠ADF=180°,∴∠B=∠ADF,∵AB=AD,∴△ABE≌△ADF(AAS),∴AE=AF,∴AC是∠BCF的平分线(在角的内部且到角两边距离相等的点在角平分线上),即AC平分∠BCD.12.已知在∠MON中,A,B分别为ON,OM上一点.(1)如图,若CD⊥OB于D,OC平分∠MON,OA+OB=2OD,求证:∠MON+∠ACB=180°;(2)若CD⊥OB于D,OC平分∠MON,∠MON+∠ACB=180°,求证:OA+OB=2OD.【解答】解:(1)作CH⊥OA垂足为H,∵OC平分∠MON,CD⊥OM,CH⊥OA,∴CD=CH,在RT△OCD和RT△OCH中,,∴△OCD≌△OCH,∴OD=OH,∵OA+OB=2OD,∴OH+AH+OD﹣BD=20D,∴BD=AH,在△CDB和△CHA中,,∴△CDB≌△CHA,∴∠BCD=∠ACH,∴∠DCH=∠BCA,在四边形OHCD中,∵∠MON+∠DCH+∠ODC+∠CHO=360°,∠CDO=∠CHO=90°,∴∠MON+∠DCH=180°,∴∠MON+∠BCA=180°.(2)作CH⊥OA垂足为H,∵OC平分∠MON,CD⊥OM,CH⊥OA,∴CD=CH,在RT△OCD和RT△OCH中,,∴△OCD≌△OCH,∴OD=OH,在四边形OHCD中,∵∠MON+∠DCH+∠ODC+∠CHO=360°,∠CDO=∠CHO=90°,∴∠MON+∠DCH=180°,∵∠MON+∠BCA=180°,∴∠BCA=∠DCH,∴∠BCD=∠ACH,在△CDB和△CHA中,,∴△CDB≌△CHA,∴BD=AH,∴OB+OA=OD﹣BD+OH+AH=2OD.13.(1)问题背景:如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E、F分别是BC,CD上的点,且∠EAF=60°,探究图中线段BE,EF,FD之间的数量关系.小王同学探究此问题的方法是延长FD到点G,使DG=BE,连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是 EF=BE+DF .(2)探索延伸:如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是BC,CD上的点,且∠EAF=∠BAD,上述结论是否仍然成立,并说明理由;(3)结论应用:如图3,等腰直角三角形ABC中,∠BAC=90°,AB=AC,点M,N在边BC上,且∠MAN=45°.若BM=12,CN=16,则MN的长为 20 .【解答】解:(1)EF=BE+DF,证明如下:在△ABE和△ADG中,,∴△ABE≌△ADG(SAS),∴AE=AG,∠BAE=∠DAG,∵∠EAF=∠BAD,∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD﹣∠EAF=∠EAF,∴∠EAF=∠GAF,在△AEF和△AGF中,,∴△AEF≌△AGF(SAS),∴EF=FG,∵FG=DG+DF=BE+DF,∴EF=BE+DF,故答案为:EF=BE+DF;(2)结论EF=BE+DF仍然成立;理由:延长FD到点G,使DG=BE,连接AC,如下图,在△ABE和△ADG中,,∴△ABE≌△ADG(SAS),∴AE=AG,∠BAE=∠DAG,∵∠EAF=∠BAD,∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD﹣∠EAF=∠EAF,∴∠EAF=∠GAF,在△AEF和△AGF中,,∴△AEF≌△AGF(SAS),∴EF=FG,∵FG=DG+DF=BE+DF,∴EF=BE+DF;(3)过点C作CE⊥BC,垂足为点C,截取CE,使CE=BM,连接AE、EN,∵AB=AC,∠BAC=90°,∴∠B=∠ACB=45°,∵CE⊥BC,∴∠ACE=∠B=45°,在△ABM和△ACE中,,∴△ABM≌△ACE(SAS),∴AM=AE,∠BAM=∠CAE,∵∠BAC=90°,∠MAN=45°,∴∠BAM+∠CAN=45°,在△MAN和△EAN中,,∴△MAN≌△EAN(SAS),∴MN=EN,在Rt△ENC中,由勾股定理得EN2=EC2+NC2,∴MN2=BM2+NC2,∵BM=12,CN=16,∴MN==20,故答案为:20.。
人教版八年级数学上册三角形边角边判定三角形全等专项小练习(附答案)

《12.2 三角形全等的判定课时2》基础练易错诊断(打“√”或“×”)1.两边和任一角分别相等的两个三角形全等.()2.有两边及其一边的对角分别相等的两个三角形全等.()3.在△ABC和△DEF中,若AB=DE,∠B=∠E,BC=EF,则△ABC≌△DEF.()对点达标知识点一用“SAS”证明三角形全等1.(2021·昆明质检)如图,AB平分∠DAC,要用SAS条件确定△ABC≌△ABD,还需要有条件()A.DB=CBB.AB=ABC.AD=ACD.∠D=∠C2.根据如图所给信息,可得x的长是()A.16B.18C.20D.16或183.(2021·宿州质检)如图,点E,F在AC上,AD=BC,DF=BE,要使△ADF≌△CBE,还需要添加一个条件是()A.∠A=∠CB.∠D=∠BC.AD∥BCD.DF∥BE4.(2020·柳州中考)如图,已知OC平分∠MON,点A,B分别在射线OM,ON上,且OA=OB.求证:△AOC≌△BOC.5.(2020·兰州中考)如图,在△ABC中,AB=AC,点D,E分别是AC和AB的中点求证:BD=CE.知识点二“SAS”的实际应用6.(2021·武汉期中)如图,将两根钢条AA',BB的中点O连在一起,使AA',BB'可以绕着点O自由旋转,就做成了一个测量工件,则A'B′的长等于内槽宽AB,那么判定△OAB≌△OA'B′的理由是.7.如图,一块三角形玻璃碎成了Ⅰ,Ⅱ两块,现需购买同样大小的一块三角形玻璃,为方便起见,只需带上第块玻璃碎片.8.(2021·济南期中)如图,AD,BC表示两根长度相同的木条,若O是AD,BC的中点,经测量AB=9cm,则容器的内径CD为cm.参考答案易错诊断1.×2.×3.√对点达标1.C2.C3.B4.答案:见解析解析:∵OC平分∠MON,∴∠AOC=∠BOC,在△AOC和△BOC中,OA OBAOC BOC OC OC=⎧⎪∠=∠⎨⎪=⎩,,,∴△AOC≌△BOC(SAS).5. 答案:见解析解析:∵AB=AC,D,E分别为AC,AB的中点,∴AD=AE,在△ABD和△ACE中,AB ACA A AD AE=⎧⎪∠=∠⎨⎪=⎩,,,∴△ABD≌△ACE(SAS),∴BD=CE.6.SAS7.I8.9。
三角形全等的判定“边角边”(7种题型)-2023年新八年级数学常见题型(人教版)(解析版)

三角形全等的判定“边角边”(7种题型)【知识梳理】全等三角形判定——“边角边”1. 全等三角形判定——“边角边”两边和它们的夹角对应相等的两个三角形全等(可以简写成“边角边”或“SAS ”).要点诠释:如图,如果AB = ''A B ,∠A =∠'A ,AC = ''A C ,则△ABC ≌△'''A B C . 注意:这里的角,指的是两组对应边的夹角.2. 有两边和其中一边的对角对应相等,两个三角形不一定全等.如图,△ABC 与△ABD 中,AB =AB ,AC =AD ,∠B =∠B ,但△ABC 与△ABD 不完全重合,故不全等,也就是有两边和其中一边的对角对应相等,两个三角形不一定全等.【考点剖析】题型一:用“边角边”直接证明三角形全等例1.已知:如图,点C 为AB 中点,CD=BE ,CD ∥BE.求证:△ACD ≌△CBE.【解析】证明:∵CD ∥BE ,∴∠ACD=∠B..∵点C 为AB 中点,∴AC=CB.又∵CD=BE ,∴△ACD ≌△CBE (SAS )【变式1】如图,AC DF =,12∠=∠,如果根据“SAS ”判定ABC DEF △≌△,那么需要补充的条件是( )A .A D ∠=∠B .AB DE =C .B E ∠=∠D .BF CE =【答案】D 【详解】解:需要补充的条件是BF=CE ,∴BF+FC=CE+CF ,即BC=EF ,在△ABC 和△DEF 中,12AC DF BC EF =⎧⎪∠=∠⎨⎪=⎩,∴△ABC ≌△DEF (SAS ).故选:D .【变式1】如图,点B ,E ,C ,F 在同一条直线上,AB =DE ,BE =CF ,∠B =∠DEF .求证:△ABC ≌△DEF .【解答】证明:∵BE =CF ,∴BE+CE =CF+EC .∴BC =EF .在△ABC 和△DEF 中,{AB =DE∠B =∠DEF BC =EF,∴△ABC≌△DEF(SAS).【变式3】如图,CA=CD,∠BCE=∠ACD,BC=EC.求证:△ABC≌△DEC.【解答】证明:∵∠BCE=∠ACD,∴∠BCE+∠ACE=∠ACD+∠ACE,∴∠ACB=∠DCE,在△ABC和△DEC中,{AC=DC∠ACB=∠DCE BC=EC,∴△ABC≌△DEC(SAS).【变式4】如图,D、C、F、B四点在一条直线上,AC=EF,AC⊥BD,EF⊥BD,垂足分别为点C、点F,BF=CD.试说明:△ABC≌△EDF.【解答】解:∵AC⊥BD,EF⊥BD,∴∠ACB=∠EFD=90°,∵BF=CD,∴BF+CF=CD+CF,即BC=DF,在△ABC和△EDF中,{BC=DF∠ACB=∠EFD AC=EF,∴△ABC≌△EDF(SAS).【变式5】如图,△ABC 中,AB=AC ,点E ,F 在边BC 上,BE=CF ,点D 在AF 的延长线上,AD=AC ,(1)求证:△ABE ≌△ACF ;(2)若∠BAE=30°,则∠ADC= °.【答案】(1)证明见解析;(2)75.【详解】(1)∵AB=AC ,∴∠B=∠ACF ,在△ABE 和△ACF 中,AB AC B ACFBE CF =⎧⎪∠=∠⎨⎪=⎩,∴△ABE ≌△ACF (SAS );(2)∵△ABE ≌△ACF ,∠BAE=30°,∴∠CAF=∠BAE=30°,∵AD=AC ,∴∠ADC=∠ACD ,∴∠ADC=280013︒−︒=75°,故答案为75. 【变式6】(2023春·江苏·七年级统考期末)如图,在ABC 和ADE V 中,AB AC =,AD AE =,90BAC DAE ∠=∠=︒,连接BD CE 、.(1)求证:ABD ACE ≌△△. (2)图中BD 和CE 有怎样的关系?试证明你的结论.【详解】(1)解:90BAC DAE ∠=∠=︒∴BAC CAD DAE CAD ∠+∠=∠+∠∴BAD EAC ∠=∠AB AC =,AD AE =∴ABD ACE ≌△△. (2)解:如图,设BD 和CE 交点为FABD ACE ≌△△∴ACE ABD ∠=∠90BAC ∠=︒∴90ABD DBC ACB ∠+∠+∠=︒∴90ACE DBC ACB ∠+∠+∠=︒即90ECB DBC ∠+∠=︒∴()18090BFC ECB DBC ∠=︒−∠+∠=︒∴BD CE ⊥.题型二:用“边角边”间接证明三角形全等例2、已知:如图,AB =AD ,AC =AE ,∠1=∠2.求证:BC =DE .【答案与解析】证明: ∵∠1=∠2∴∠1+∠CAD =∠2+∠CAD ,即∠BAC =∠DAE在△ABC 和△ADE 中AB AD BAC DAE AC AE =⎧⎪∠=∠⎨⎪=⎩∴△ABC ≌△ADE (SAS )∴BC =DE (全等三角形对应边相等)【变式1】如图所示,点O 为AC 的中点,也是BD 的中点,那么AB 与CD 的关系是________.【答案】平行且相等【详解】解:∵点O 为AC 的中点,也是BD 的中点,∴AO=OC ,BO=OD ,又∵∠AOB=∠DOC ,∴△AOB ≌△COD (SAS )∴AB=CD ,∠A=∠C ,∴AB//CD,即AB 与CD 的关系是平行且相等,故答案为:平行且相等.【变式2】如图,已知AB ∥CD ,AB =CD ,∠A =∠D .求证:AF =DE .【详解】证明:∵AB//CD ,∴∠B =∠C ,在△ABF 和△DCE 中,A D AB CDB C ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△ABF ≌△DCE (ASA ),∴AF =DE .【变式3】如图,点E 、F 分别是矩形ABCD 的边 AB 、CD 上的一点,且DF =BE .求证:AF=CE .【分析】由SAS 证明△ADF ≌△CBE ,即可得出AF =CE .【详解】证明:∵四边形ABCD 是矩形,∴∠D =∠B =90°,AD =BC ,在△ADF 和△CBE 中,AD BC D B DF BE ⎧⎪∠∠⎨⎪⎩===,∴△ADF ≌△CBE (SAS ),∴AF =CE .【变式4】已知ABN 和ACM △位置如图所示,AB AC =,AD AE =,12∠=∠.(1)试说明:BD CE =;(2)试说明:M N ∠=∠.【详解】解:(1)在△ADB 和△AEC 中,12AB AC AD AE =⎧⎪∠=∠⎨⎪=⎩∴△ADB ≌△AEC (SAS ),∴BD=CE ;(2)∵12∠=∠,∴BAN CAM ∠=∠,∵△ADB ≌△AEC ,∴B C ∠=∠,∴180180B BAN C CAM ︒−∠−∠=︒−∠−∠,即M N ∠=∠.【变式5】如图,将两个一大、一小的等腰直角三角尺拼接 (A 、B 、D 三点共线,AB =CB ,EB =DB ,∠ABC =∠EBD =90°),连接AE 、CD ,试确定AE 与CD 的位置与数量关系,并证明你的结论.【答案】AE =CD ,并且AE ⊥CD证明:延长AE 交CD 于F ,∵△ABC 和△DBE 是等腰直角三角形∴AB =BC ,BD =BE在△ABE 和△CBD 中90AB BC ABE CBD BE BD =⎧⎪∠=∠=︒⎨⎪=⎩∴△ABE ≌△CBD (SAS )∴AE =CD ,∠1=∠2又∵∠1+∠3=90°,∠3=∠4(对顶角相等)∴∠2+∠4=90°,即∠AFC =90°∴AE ⊥CD题型三:边角边与倍长中线例3、如图,AD 是△ABC 的中线,求证:AB +AC >2AD .【答案与解析】 证明:如图,延长AD 到点E ,使AD =DE ,连接CE .在△ABD 和△ECD 中,∴△ABD ≌△ECD (SAS ).∴AB =CE .∵AC +CE >AE ,∴AC +AB >AE =2AD .即AC +AB >2AD .14.如图所示,AD 是△ABC 中BC 边上的中线,若AB =2,AC =6,则AD 的取值范围是__________AD DE ADB EDC BD CD ⎧⎪∠∠⎨⎪⎩===.【答案】2<AD <4【分析】此题要倍长中线,再连接,构造全等三角形.根据三角形的三边关系:任意两边之和大于第三边,任意两边之差小于第三边.即可求解.【详解】解:延长AD 到E ,使AD =DE ,连接BE ,∵AD 是△ABC 的中线,∴BD =CD ,在△ADC 与△EDB 中,BD CD ADC BDE AD DE =⎧⎪∠=∠⎨⎪=⎩∴△ADC ≌△EDB (SAS ),∴EB =AC ,根据三角形的三边关系定理:6-2<6+2,∴2<AD <4,故AD 的取值范围为2<AD <4.【点睛】本题主要考查对全等三角形的性质和判定,三角形的三边关系定理等知识点的理解和掌握,能推出6-2<AE <6+2是解此题的关键.题型四:边角边与截长补短例4、已知,如图:在△ABC 中,∠B =2∠C ,AD ⊥BC ,求证:AB =CD -BD .【答案与解析】 证明:在DC 上取一点E ,使BD =DE∵ AD ⊥BC ,∴∠ADB =∠ADE在△ABD 和△AED 中,∴△ABD ≌△AED (SAS ). ∴AB =AE ,∠B=∠AED .又∵∠B =2∠C =∠AED =∠C +∠EAC .∴∠C =∠EAC .∴AE =EC .∴AB =AE =EC =CD —DE =CD —BD .【变式】已知,如图,在四边形ABCD 中,AC 平分∠BAD ,CE ⊥AB 于E ,并且AE =(AB +AD ), 求证:∠B +∠D =180°.【答案】证明:在线段AE 上,截取EF =EB ,连接FC ,BD DE ADB=ADE AD AD ⎧⎪⎨⎪⎩=∠∠=12A EDC B∵CE ⊥AB ,∴∠CEB =∠CEF =90°在△CBE 和△CFE 中,∴△CBE 和△CFE (SAS )∴∠B =∠CFE∵AE =(AB +AD ),∴2AE = AB +AD∴AD =2AE -AB∵AE =AF +EF ,∴AD =2(AF +EF )-AB =2AF +2EF -AB =AF +AF +EF +EB -AB =AF +AB -AB ,即AD =AF在△AFC 和△ADC 中∴△AFC ≌△ADC (SAS )∴∠AFC =∠D∵∠AFC +∠CFE =180°,∠B =∠CFE.∴∠AFC +∠B =180°,∠B +∠D =180°.题型五:边边角不能判定两个三角形全等例5.如图,已知AC =BD ,添加下列一个条件后,仍无法判定△ABC ≌△BAD 的是()A .∠ABC =∠BADB .∠C =∠D =90° C .∠CAB =∠DBA D .CB =DA【答案】A CEB CEFEC =EC EB EF=⎧⎪∠=∠⎨⎪⎩12(AF ADFAC DAC AC AC =⎧⎪∠=∠⎨⎪=⎩角平分线定义)【分析】根据全等三角形的判定方法即可一一判断;【详解】在△ABC 与△BAD 中,AC =BD ,AB =BA ,A 、SSA 无法判断三角形全等,故本选项符合题意;B 、根据HL 即可判断三角形全等,故本选项不符合题意;C 、根据SAS 即可判断三角形全等,故本选项不符合题意;D 、根据SSS 即可判断三角形全等,故本选项不符合题意;故选:A . 题型六:尺规作图——利用边角边做三角形例6.(2023春·广东揭阳·七年级统考期末)已知:线段a ,c ,α∠.求作:ABC .使BC a =,AB c =,ABC α∠=∠.(要求:尺规作图,不写作法,保留作图痕迹)【详解】解:如图所示:【变式1】(2023春·陕西宝鸡·七年级校考阶段练习)尺规作图:已知:线段m ,n ,∠β.求作:ABC ,使AB m =,BC n =,ABC β∠=∠(保留作图痕迹,不写作法).【详解】解:如图所示:ABC ∴即为所作.题型七:边边边与边角边综合 八年级假期作业)如图,在ABC 中,(1)图中有___________对全等三角形;(2)请选一对加以证明.【详解】(1)图中有3对全等三角形:ABD ACD ≌△△,ABE ACE ≌△△,BDE CDE ≌V V . 故答案为3;(2)∵D 是BC 的中点,∴BD CD =.在ABD △和ACD 中,AB AC BD CDAD AD =⎧⎪=⎨⎪=⎩, ∴()SSS ABD ACD ≌V V ;∴BAE CAE ∠=∠.在ABE 和ACE △中,AB AC BAE CAEAE AE =⎧⎪∠=∠⎨⎪=⎩, ∴()SAS ABE ACE △△≌; ∴BE CE =.在BDE △和CDE 中,BE CE BD CDDE DE =⎧⎪=⎨⎪=⎩, ∴()SSS BDE CDE ≌V V . 【过关检测】一、单选题A .SSSB .SASC .ASAD .AAS【答案】B 【分析】由题意可知根据“边角边”可证OAB OCD VV ≌即可选择.【详解】解:∵在OAB 和OCD 中,OC OA COD AOB OD OB =⎧⎪∠=∠⎨⎪=⎩, ∴()OAB OCD SAS ≌△△.故判定这两个三角形全等的依据是“SAS ”.故选B .【点睛】本题考查三角形全等的判定.熟练掌握判定三角形全等的条件是解题关键. 2.(2023春·江西景德镇·七年级统考期末)如图,AB AC =,点D 、E 分别在AC 和AB 边上,且AD AE =,则可得到ABD ACE △△≌,判定依据是( )A .ASAB .AASC .SASD .SSS【答案】C 【分析】根据SAS 证明ABD ACE △△≌,即可求解. 【详解】解:在ABD △与ACE △中,AB AC BAD CAEAD AE =⎧⎪∠=∠⎨⎪=⎩∴ABD ACE △△≌()SAS ,故选:C . 【点睛】本题考查了全等三角形的判定,熟练掌握全等三角形的判定定理是解题的关键.3.(2023春·四川成都·七年级统考期末)如图,在ABF △和DCE △中,点E 、F 在BC 上,AF DE =,AFB DEC ∠=∠,添加下列一个条件后能用“SAS ”判定ABF DCE ≌△△的是( )A .BE CF =B .BC ∠=∠ C .AD ∠=∠ D .AB DC =【答案】A 【分析】先根据BE CF =得到BF CE =,再根据全等三角形的判定定理进行分析即可.【详解】解:∵BE CF =,∴BE EF CF EF +=+,即BF CE =,A 选项,因为BE CF =,AFB DEC ∠=∠,BF CE =,满足“SAS ”判定ABF DCE ≌△△,符合题意; B 选项,因为B C ∠=∠,AFB DEC ∠=∠,BF CE =,是用“AAS ”判定ABF DCE ≌△△,不符合题意; C 选项,因为A D ∠=∠,AF DE =,AFB DEC ∠=∠,是用“ASA ”判定ABF DCE ≌△△,不符合题意; D 选项,因为AB DC =,AF DE =,AFB DEC ∠=∠,不能判定ABF DCE ≌△△,不符合题意; 故选:A .【点睛】本题考查了全等三角形的判定定理,能熟记全等三角形的判定定理是解此题的关键.4.(2023春·四川达州·七年级统考期末)如图,在2×3的正方形方格中,每个正方形方格的边长都为1,则1∠和2∠的关系是( )A .221∠=∠B .2190∠−∠=︒C .1290∠+∠=︒D .12180∠+∠=︒【答案】C 【分析】先证明ABC CDE △△≌,再利用全等三角形的性质和等量代换求解即可. 【详解】解:如图,在ABC 和CDE 中,2901AC CE ACB CED BC DE ==⎧⎪∠=∠=︒⎨⎪==⎩,∴ABC CDE △△≌()SAS ,∴1DCE ∠=∠, ∵290DCE ∠+∠=︒,∴1290∠+∠=︒,故选:C .【点睛】本题考查了全等三角形的判定与性质,利用网格证明三角形全等是解题的关键.A .20cmB .45cmC .25cmD .65cm【答案】D 【分析】根据题意可得:OF OG =,OC OD =,利用已知条件判断出OFC OGD ≌,得到CF DG =,即可求出答案.【详解】解:如图:∵O 是FG 和CD 的中点,∴OF OG =,OC OD =,在OFC △和OGD 中,OF OG FOC GODOC OD =⎧⎪∠=∠⎨⎪=⎩,∴()SAS OFC OGD ≌,∴CF DG =,又20cm DG =,∴20cm CF DG ==,∴小明离地面的高度=支点到地面的高度452065cm CF +=+=,故D 正确.故选:D .【点睛】本题主要考查了三角形全等知识的应用,用数学方法解决生活中有关的实际问题,把实际问题转换成数学问题,用数学方法加以论证,最后进行求解,是一种十分重要的方法. 七年级统考期末)如图,已知在ABC 和BAD 中,直接判定ABC BAD ≌的依据是( A .SSSB .AASC .ASAD .SAS【答案】D 【分析】找出两个三角形中已知相等的对应边和对应角,然后根据判定方法即可判断.【详解】解:在ABC 和ABD △中,BC AD ABC BAD AB BA =⎧⎪∠=∠⎨⎪=⎩, ∴()ABC BAD SAS ≌.故选:D .【点睛】此题主要考查了三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS 、SAS 、ASA 、AAS 、HL .注意:判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角. 7.(2023春·上海浦东新·七年级校考阶段练习)如图,AD 平分BAC ∠,AB AC =,连接BD 、CD ,并延长交AC 、AB 于F 、E 点,则图中全等的三角形有( )对.A .3对B .4对C .5对D .6对【答案】B 【分析】认真观察图形,确定已知条件在图形上的位置,结合全等三角形的判定方法,仔细寻找.【详解】解:AD 平分BAC ∠,BAD CAD ∴∠=∠,在ABD 与ACD 中,AB AC BAD CADAD AD ⎧⎪∠∠⎨⎪⎩===,()SAS ABD ACD ∴≌,BD CD ∴=,B C ∠=∠,ADB ADC ∠=∠,又EDB FDC ∠=∠,ADE ADF ∴∠=∠,AED AFD ∴≌,BDE CDF ≌,ABF ACE ≌.AED AFD ∴≌,ABD ACD ≌,BDE CDF ≌,ABF ACE ≌,共4对.故选:B .【点睛】本题考查三角形全等的判定方法和全等三角形的性质.注意:AAA 、SSA 不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.8.(2023春·河北保定·七年级校考阶段练习)如图,在AOB 和COD △中,OA OB =,OC OD =,AOB COD ∠=∠,AC ,BD 交于点M ,关于结论Ⅰ,Ⅱ,下列判断正确的是( )结论Ⅰ:AC BD =;结论Ⅱ:CMD COD ∠>∠A .Ⅰ对,Ⅱ错B .Ⅰ错,Ⅱ对C .Ⅰ,Ⅱ都对D .Ⅰ,Ⅱ都错【答案】A 【分析】根据已知条件可知三角形的全等,根据全等三角形的性质可知边相等,再根据三角形的内角和即可求出角的大小.【详解】AOB COD ∠=∠,AOB AOD COD AOD ∴∠+∠=∠+∠,AOC BOD ∴∠=∠,∴在AOC 和BOD 中,∴OA OB AOC BODOC OD =⎧⎪∠=∠⎨⎪=⎩,()AOC BOD SAS ∴≌, AC BD ∴=,故Ⅰ正确;AOC BOD ≌,OCA BDO ∴∠=∠,MDC MDO ODC ∴∠=∠+∠,OCD OCA MCD ∴∠=∠+∠,180()COD OCD ODC ∠=︒−∠+∠,180()CMD MDC MCD ∠=︒−∠+∠,180()CMD MDO ODC MCD ∴∠=︒−∠+∠+∠,180()COD OCA MCD ODC ∠=︒−∠+∠+∠,CMD COD ∴∠=∠,故Ⅱ错误;故选:A .【点睛】本题考查了全等三角形的性质,熟记对应性质和判定定理是解题的关键. 9.(2023春·江苏·七年级统考期末)如图,在四边形ABCD 中,对角线AC 平分BAD ∠,AD AB >,下列结论正确的是( )A .AD AB CD BC −=−B .AD AB CD BC −>− C .AD AB CD BC −<−D .AD AB −与CD BC −的大小关系无法确定【答案】B 【分析】在AD 上截取AE AB =,BAC EAC ≌,由DE CD CE >−即可求解.【详解】解:如图,在AD 上截取AE AB =,AC 平分BAD ∠,BAC EAC ∴∠=∠,在BAC 和EAC 中AB AE BAC EACAC AC =⎧⎪∠=∠⎨⎪=⎩,∴BAC EAC ≌(SAS ),BC EC ∴=,在CDE 中:DE CD CE >−,AD AB AD AE CD BC −=−>−.故选:B .【点睛】本题考查了三角形中三边的关系,三角形全等的判定及性质,掌握性质,并根据题意作出辅助线是解题的关键. 10.(2022秋·云南昭通·八年级统考期末)如图,AD 是ABC 的中线,E ,F 分别是AD 和AD 延长线上的点,且CE BF ,连接BF CE ,,下列说法: ①DE DF =;②ABD 和ACD 面积相等;③CE BF =;④BDF CDE ≌;⑤CEF F ∠∠=. 其中正确的有( )【答案】B 【分析】根据三角形中线的定义可得BD CD =,然后利用“边角边”证明BDF 和CDE 全等,根据全等三角形对应边相等可得CE BF =,全等三角形对应角相等可得F CED ∠∠=,再根据内错角相等,两直线平行可得BF CE ,最后根据等底等高的三角形的面积相等判断出②正确.【详解】解:∵AD 是ABC 的中线,∴BD CD =,在BDF 和CDE 中,BD CD BDF CDEDF DE =⎧⎪∠=∠⎨⎪=⎩,∴()SAS BDF CDE ≌,故④正确∴CE BF F CED ∠∠==,,故①正确,∵CEF CED ∠∠=,∴CEF F ∠∠=,故⑤正确,∴BF CE ,故③正确,∵BD CD =,点A 到BD CD 、的距离相等,∴ABD 和ACD 面积相等,故②正确,综上所述,正确的有5个,故选:B .【点睛】本题考查全等三角形的判定与性质,熟练掌握全等三角形的判定方法并准确识图是解题的关键.二、填空题【答案】120°【分析】先证明,DAG BAC ≌得到GDA CBA ∠=∠,再利用60BAD ∠=︒以及三角形的内角和定理、邻补角的性质可得答案.【详解】解:60,DAE GAC ∠=∠=︒,DAG BAC ∴∠=∠,,AD AB AC AG ==在DAG 与BAC 中,,AD AB DAG BACAG AC =⎧⎪∠=∠⎨⎪=⎩,DAG BAC ∴≌,GDA CBA ∴∠=∠,BEO AED ∠=∠,BOE BAD ∴∠=∠60,BAD ∴∠=︒60,BOE ∴∠=︒120.DOC ∴∠=︒故答案为:120.︒【点睛】本题考查的是三角形全等的判定与性质,等边三角形的判定与性质,邻补角的性质,三角形的内角和定理,掌握以上知识是解题的关键. 七年级统考期末)如图,在锐角ABC 中,24ABC S = 【分析】先根据三角形全等的判定定理与性质可得ME MN =,再根据两点之间线段最短可得BM MN +的最小值为BE ,然后根据垂线段最短可得当BE AC ⊥时,BE 取得最小值,最后利用三角形的面积公式即可得.【详解】如图,在AC 上取一点E ,使AE AN =,连接ME ,AD 是BAC ∠的平分线,EAM NAM ∴∠=∠,在AEM △和ANM 中,AE AN EAM NAMAM AM =⎧⎪∠=∠⎨⎪=⎩,()SAS AEM ANM ∴≌, ME MN ∴=,BM MN BM ME ∴+=+,由两点之间线段最短得:当点,,B M E 共线时,BM ME +取最小值,最小值为BE ,又由垂线段最短得:当BE AC ⊥时,BE 取得最小值,248,ABC S AC ==,1182422AC BE BE ∴⋅=⨯⋅=,解得6BE =,即BM MN +的最小值为6,故答案为:6.【点睛】本题考查了角平分线的定义、三角形全等的判定定理与性质、两点之间线段最短、垂线段最短等知识点,正确找出BM MN +取得最小值时BE 的位置是解题关键. 13.(2023春·广东云浮·八年级校考期中)如图,小明与小红玩跷跷板游戏,已知跷跷板的支点O (即跷跷板的中点)至地面的距离是48cm ,当小红从水平位置CD 下降28cm 时,这时小明离地面的高度是___________cm .【答案】76【分析】根据题意可得:OF OG =,OC OD =,利用已知条件判断出OFC OGD ≌V V ,得到CF DG =,即可【详解】解:如图:∵O 是FG 和CD 的中点,∴OF OG =,OC OD =,在OFC △和OGD 中,OF OG FOC GODOC OD =⎧⎪∠=∠⎨⎪=⎩,∴(SAS)OFC OGD ≌V V ,∴CF DG =,又28cm DG =,∴28cm CF DG ==,∴小明离地面的高度=支点到地面的高度482876cm CF +=+=,故答案为:76.【点睛】本题主要考查了三角形全等知识的应用,用数学方法解决生活中有关的实际问题,把实际问题转换成数学问题,用数学方法加以论证,最后进行求解,是一种十分重要的方法. 14.(2023春·广东佛山·七年级校考期中)在测量一个小口圆形容器的壁厚(厚度均匀)时,小明用“X 型转动钳”按如图方法进行测量,其中OA OD =,OB OC =,测得3cm AB =,5cm EF =,圆形容器的壁厚是______cm .【分析】由题证明AOB DOC ≌,由全等三角形的性质可得,AB CD =,即可解决问题.【详解】在AOB 和DOC △中,OA OD AOB DOCBO OC =⎧⎪∠=∠⎨⎪=⎩,(SAS)AOB DOC ∴≌,3cm AB CD ∴==,cm 5EF =Q ,∴圆柱形容器的壁厚是1(53)1(cm)2⨯−=,故答案为:1.【点睛】本题考查了全等三角形的应用,解题的关键是利用全等三角形的性质解决实际问题.【答案】25米/25m【分析】根据SAS 可证明ACB DCE ≌△△,再根据全等三角形的性质可得AB DE =,进而得到答案. 【详解】解:∵点C 是AD 的中点,也是BE 的中点,∴AC DC =,BC EC =,∵在ACB △和DCE △中,AC DC ACB DCEBC EC =⎧⎪∠=∠⎨⎪=⎩, ∴()SAS ACB DCE ≌,∵25DE =米,∴25AB =米,故答案为:25米.【点睛】此题考查了全等三角形的应用,关键掌握全等三角形的判定定理和性质定理. 16.(2022秋·陕西宝鸡·八年级统考期末)如图,E 是ABC ∆外一点,D 是AE 上一点,AC BC BE ==,DA DB =,EBD CBD ∠=∠,70C ∠=︒,则BED ∠的度数为___________.【答案】35︒/35度【分析】连接DC ,则DC 垂直平分AB ,可得35ADC DCB ∠=∠=︒,再证明BED BCD ∆≅∆,即可得到35BED DCB ∠=∠=︒.【详解】连接DC ,DA DB =,CA CB =,DC ∴是AB 的垂直平分线,1352DCB ACB ∴∠=∠=︒,在BED 和BCD △中BD BD EBD CBDBE BC =⎧⎪∠=∠⎨⎪=⎩(SAS)BED BCD ∴≌,35BED DCB ∴∠=∠=︒,故答案为:35︒.【点睛】本题主要考查等腰三角形的性质,由条件得到DC 是AB 的垂直平分线再想到证明BED BCD △≌△是解题的关键. 17.(2023·全国·八年级假期作业)如图,AB 与CD 相交于点O ,且O 是AB CD ,的中点,则AOC 与BOD 全等的理由是________.【答案】SAS /边角边【分析】根据全等三角形的判定定理求解即可.【详解】解:∵O 是AB CD ,的中点,∴,,OA OB OC OD ==在AOC 和DOB 中,OA OB AOC BOD OC OD =⎧⎪∠=∠⎨⎪=⎩ ∴()SAS AOC DOB ≌, 故答案为:SAS .【点睛】此题考查了全等三角形的判定,熟记全等三角形的判定定理是解题的关键.18.(2022秋·山东聊城·八年级统考期末)如图,在ABC ∆中,已知 AB AC =,BD CF = ,BE CD =.若40A ∠=︒,则EDF ∠的度数为__________.【答案】70°【分析】(1)证△BED ≌△CDF ;(2)利用AB=AC 得到∠B 与∠C(3)利用整体法求得∠EDF【详解】∵AB=AC ,∴∠B=∠C∵BD=CF ,BE=CD∴△BED ≌△CDF ,∴∠FDC=∠BED∵∠A=40°∴∠B=∠C=70°∴在△BED 中,∠BED+∠BDE=110°∴∠EDB+∠FDC=110°∴∠EDF=70°【点睛】求角度,常见的方法有:(1)方程思想;(2)整体思想;(3)转化思想本题就是利用全等,结合整体思想求解的角度三、解答题 19.(2023秋·广东广州·八年级统考期末)已知:如图,12BC DC =∠=∠,,求证:ABC ≌ADC △.【答案】见解析【分析】先证明ACB ACD ∠=∠,再结合AC AC =,BC DC =,即可得到结论.【详解】.证明:12∠=∠,ACB ACD ∴∠=∠,AC AC BC DC ==,,ABC ∴≌ADC △.【点睛】本题考查的是全等三角形的判定,掌握“利用SAS 证明两个三角形全等”是解本题的关键. 20.(2021秋·广东广州·八年级广州市第八十九中学校考期中)如图,点E 、F 在BC 上,BF EC =,AB DC =,B C ∠=∠.求证:A D ∠=∠.【答案】证明见解析【分析】证明()SAS ABF DCE ≌△△,然后根据全等三角形的性质即可得出结论.【详解】证明:在ABF △和DCE △中,AB DC B CBF CE =⎧⎪∠=∠⎨⎪=⎩, ∴()SAS ABF DCE ≌△△, ∵A D ∠=∠.【点睛】本题考查全等三角形的判定和性质.掌握全等三角形的判定是解题的关键.21.(2023春·陕西西安·七年级校考阶段练习)已知:如右图ABCD ,AB CD =.求证:ADC CBA ≌.【答案】见解析【分析】由AB CD ,得ACD CAB ∠=∠,再利用SAS 即可证得结论.【详解】证明:∵ABCD ,∴ACD CAB ∠=∠,在ADC △与CBA △中:AB CD ACD CAB AC CA =⎧⎪∠=∠⎨⎪=⎩, ∴()SAS ADC CBA ≌.【点睛】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS 、SAS 、ASA 、AAS 、HL . 22.(2023春·陕西咸阳·七年级统考期末)如图,点D 在线段BE 上,AB CD ,AB DE =,BD CD =.ABD △和EDC △全等吗?为什么?【答案】ADB ECD △≌△,理由见解析【分析】先根据平行线的性质得到ABD EDC =∠∠,再利用SAS 证明ADB ECD △≌△即可得到结论.【详解】解:ADB ECD △≌△,理由如下:∵AB CD ,∴ABD EDC =∠∠,∵AB ED =,BD DC =,∴()SAS ADB ECD △≌△.【点睛】本题主要考查了全等三角形的判定,平行线的性质,熟知边角边证明三角形全等是解题的关键.(1)求证:AEC DFB △△≌; (2)若6AEC S ∆=,求三角形BEC 的面积.【答案】(1)见解析(2)92BEC S =△【分析】(1)根据AE DF ∥得A D ∠=∠,根据AB CD =得AB BC CD BC +=+,即AC DB =,根据ASA 即可证明AEC DFB △△≌; (2)在AEC △中,以AC 为底作EH 为高,则12AEC S EH AC ∆=⋅,12BCE S EH BC ∆=⋅,根据13AB CD BC ==得43AC BC =,6AEC S ∆=,即可得.【详解】(1)证明:∵AE DF ∥,A D ∴∠=∠, ∵AB CD =,AB BC CD BC ∴+=+AC DB ∴=,在AEC △和DFB △中,AE DF A DAC DB =⎧⎪∠=∠⎨⎪=⎩,SAS AEC DFB ∴≌()△△;(2)解:如图所示,在AEC △中,以AC 为底作EH 为高,12AEC S EH AC ∆∴=⋅,12BCE S EH BC ∆=⋅,∵13AB CD BC ==,43AC BC ∴=,6AEC S ∆=, ΔΔ3 4.54BEC AEC S S ∴==.【点睛】本题考查了三角形的判定与性质,三角形的面积,解题的关键是理解题意,掌握这些知识点. 24.(2023春·福建福州·七年级福州华伦中学校考期末)已知:如图,点,F C 在线段BE 上,AB DE =,B E ∠=∠,BF EC =.求证:A D ∠=∠.【答案】见解析【分析】先根据线段的和差得出BC EF =,进而证明ABC DEF ≌△△,根据全等三角形的性质即可得证. 【详解】证明:∵BF EC =,∴BF FC FC CE +=+,即BC EF =,在,ABC DEF 中,AB DE B EBC EF =⎧⎪∠=∠⎨⎪=⎩,∴ABC DEF ≌△△, ∴A D ∠=∠.【点睛】本题考查了全等三角形的性质与判定,熟练掌握全等三角形的性质与判定是解题的关键.25.(2023·全国·八年级假期作业)如图,在△ABC 中,已知AB AC =,2BAC DAE ∠=∠,且DAE FAE ∆≅∆.求证:ABD ACF ∆≅∆.【答案】见解析【分析】先根据全等三角形的性质以及已知2BAC DAE ∠=∠得出BAD CAF ∠=∠,再利用SAS 即可证出ABD ACF ∆≅∆.【详解】证明:∵DAE FAE ∆≅∆,∴,AD AF DAE FAE =∠=∠.∵2BAC DAE ∠=∠,∴BAD EAC DAE FAE ∠+∠=∠=∠,∵FAC EAC FAE ∠+∠=∠∴BAD CAF ∠=∠.在ABD ∆和ACF ∆中,AB AC BAD CAFAD AF =⎧⎪∠=∠⎨⎪=⎩∴ABD ACF ∆≅∆.【点睛】本题考查了全等三角形的判定和性质,灵活运用这些性质解决问题是本题的关键. 八年级假期作业)如图,在ABC 和V(1)求证:ABD ACE △△≌(2)若35BDA ∠=︒,则【答案】(1)见解析(2)70【分析】(1)根据等式的性质,可得=BAD CAE ∠∠,根据SAS 可得两个三角形全等;(2)根据全等三角形的性质,可得对应角相等,根据等腰三角形的性质,可得ADC AEC ∠∠=,根据等量代换,可得证明结论.【详解】(1)证明:=BAC DAE ∠∠,BAC DAC DAE DAC ∴∠−∠=∠−∠,即=BAD CAE ∠∠.在ABD △和ACE △中,AB AC BAD EACAD AE =⎧⎪∠=∠⎨⎪=⎩,SAS ABD ACE ∴≌();(2)证明:ABD ACE ≌△△, ADB AEC ∴∠=∠,AD AE =ADC AEC ∴∠=∠35BDA ADC ∴∠=∠=︒∴223570BDC BDA ∠∠==⨯︒=︒.故答案为:70.【点睛】本题考查了全等三角形的判定与性质,利用SAS 证明三角形全等,利用全等三角形的性质,证明对应角相等,再利用等量代换得出证明结论. 27.(2023春·全国·七年级专题练习)如图,已知点B ,E ,C ,F 在一条直线上,AB DE =,BF CE =,B E ∠=∠.求证:ABC DEF ≌△△【答案】见解析【分析】用边角边定理进行证明即可.【详解】解:∵BF CE =∴BF FC CE FC +=+即:BC EF =在ABC 和DEF 中AB DE B EBC EF =⎧⎪∠=∠⎨⎪=⎩∴()SAS ABC DEF ≌. 【点睛】本题考查边角边定理证明三角形全等,根据题意找到相应的条件是解题关键. 求证:DE BF =.证明:AD BC (已知)∴∠_______=∠_______(两直线平行,内错角相等)AF CE =∴ADE CBF ∴≌( 【答案】A ;C ;AF EF CE EF −=−;AD BC =;A C ∠=∠;AE CF =;SAS ;全等三角形对应边相等.【分析】根据平行线的性质得到∠A =∠C ,根据等式的性质得到AE CF =,然后证明ADE CBF V V ≌即可得到结论.【详解】证明:AD BC (已知)∴∠A =∠C (两直线平行,内错角相等)AF CE =(已知)∴AF EF CE EF −=−(等式的基本性质)即AE CF =在ADE V 和CBF V 中AD BC A CAE CF =⎧⎪∠=∠⎨⎪=⎩,ADE CBF ∴≌(SAS )DE BF ∴=(全等三角形对应边相等)故答案为:A ;C ;AF EF CE EF −=−;AD BC =;A C ∠=∠;AE CF =;SAS ;全等三角形对应边相等.【点睛】本题考查全等三角形的判定和性质,掌握全等三角形的判定定理是解题的关键.【答案】见解析【分析】根据BE CF =可得BC EF =,根据AC DF ∥可得ACB DFE ∠=∠,即可根据SAS 进行求证.【详解】证明:∵BE CF =,∴BE CE CF CE −=−,即BC EF =,∵AC DF ∥,∴ACB DFE ∠=∠,在ABC 和DEF 中,AC DF ACB DFEBC EF =⎧⎪∠=∠⎨⎪=⎩, ∴()SAS ABC DEF △△≌. 【点睛】本题主要考查了全等三角形的判定,解题的关键是根据题目所给条件,得出相应的边和角度相等,熟练掌握三角形全等的判定定理. 求证:(1)AE CF =;(2)AE CF ∥;(3)∠=∠AFE CEF .【答案】(1)见解析(2)见解析(3)见解析【分析】(1)根据“边角边”证明ABE CDF △≌△,即可证得结论;(2)根据全等三角形的性质可得AEB CFD ∠=∠,进而可得结论;(3)由全等三角形的性质可得AE CF =,根据“边角边”证明AEF CFE △≌△,即可证得结论.【详解】(1)证明:在ABE 和CDF 中,∵AB CD =, B D ∠=∠,BE DF =,∴ABE CDF△≌△()SAS ,∴AE CF =; (2)证明:∵ABE CDF △≌△,∴AEB CFD ∠=∠,∴AE CF ∥;(3)证明:∵ABE CDF △≌△,∴AE CF =,又∵AEB CFD ∠=∠,EF FE =,∴AEF CFE △≌△,∴∠=∠AFE CEF .【点睛】本题考查了全等三角形的判定和性质以及平行线的判定,熟练掌握全等三角形的判定和性质是解题的关键. 求作:ABC ,使 【答案】见解析【分析】先作CAB α∠=∠,再在角的两边上分别截取AC b =,AB c =,从而可得答案.【详解】解:ABC 即为所求.【点睛】本题考查的是作三角形,掌握作一个角等于已知角是解本题的关键. 32.(2023·全国·八年级假期作业)“倍长中线法”是解决几何问题的重要方法.所谓倍长中线法,就是将三角形的中线延长一倍,以便构造出全等三角形,具体做法是:如图,AD 是ABC 的中线,延长AD 到E ,使DE AD =,连接BE ,构造出BED 和CAD .求证:BED CAD △≌△.【答案】见解析【分析】由AD 是ABC 的中线,可得DE AD =,再由EDB ADC ∠=∠,DB DC =,即可证明BED CAD △≌△.【详解】证明:如图所示:,AD 是ABC 的中线,DB DC ∴=,在BED 和CAD 中,ED AD EDB ADCDB DC =⎧⎪∠=∠⎨⎪=⎩,(SAS)BED CAD ∴≌.【点睛】本题主要考查了三角形全等的判定,倍长中线,熟练掌握三角形全等的判定,添加适当的辅助线是解题的关键. 33.(2023春·全国·七年级期末)如图,在ABC 中,D 是BC 延长线上一点,满足CD BA =,过点C 作CE AB ∥,且CE BC =,连接DE 并延长,分别交AC ,AB 于点F ,G .(1)求证:ABC DCE ≅;(2)若12BD =,2AB CE =,求BC 的长度.【答案】(1)见解析(2)4【分析】(1)根据SAS 证明≌ABC DCE 即可;(2)根据全等三角形的性质解答即可.【详解】(1)∵CE AB ∥,∴B ECD ∠=∠,在ABC 与DCE △中,AB CD B ECDBC CE =⎧⎪∠=∠⎨⎪=⎩, ∴()SAS ABC DCE ≌;(2)∵≌ABC DCE ,∴,AB CD BC CE ==,∵2AB CE =,∴2CD BC =,∵12BD =,∴312BD CD BC BC =+==∴4BC =.【点睛】此题考查全等三角形的判定和性质,关键是掌握全等三角形的判定和性质.。
人教版八年级上册数学全等三角形练习题及答案一
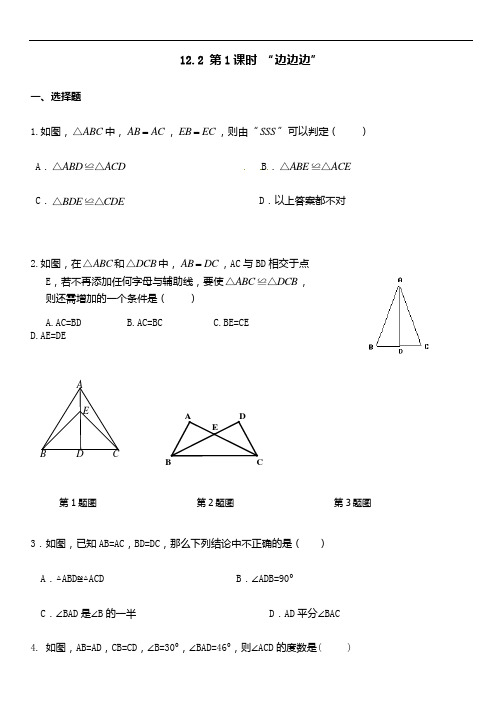
12.2 第1课时 “边边边”一、选择题1.如图,ABC △中,AB AC =,EB EC =,则由“SSS ”可以判定( ) A .ABD ACD △≌△ B .ABE ACE △≌△ C .BDE CDE △≌△D .以上答案都不对2.如图,在ABC △和DCB △中,AB DC =,AC 与BD 相交于点E ,若不再添加任何字母与辅助线,要使ABC DCB △≌△,则还需增加的一个条件是( )A.AC=BDB.AC=BCC.BE=CED.AE=DE3.如图,已知AB=AC ,BD=DC ,那么下列结论中不正确的是( ) A .△ABD ≌△ACD B .∠ADB=90° C .∠BAD 是∠B 的一半D .AD 平分∠BAC4. 如图,AB=AD ,CB=CD ,∠B=30°,∠BAD=46°,则∠ACD 的度数是( )EDCB AA EB D C第1题图第2题图第3题图A.120°B.125°C.127°D.104°第4题图第5题图5. 如图,线段AD与BC交于点O,且AC=BD,AD=BC,则下面的结论中不正确的是( )A.△ABC≌△BADB.∠CAB=∠DBAC.OB=OCD.∠C=∠D6. 如图,AB=CD,BC=DA,E、F是AC上的两点,且AE=CF,DE=BF,,那么图中全等三角形共有()对A.4对 B.3对 C.2对 D.1对7. 如图,AB=CD,BC=AD,则下列结论不一定正确的是().A.AB∥DCB. ∠B=∠DC. ∠A=∠CD. AB=BC第7题图8. 如果△ABC的三边长分别为3,5,7,△DEF的三边长分别为3,3x-2,2x -1,若这两个三角形全等,则x 等于( )A .73B .3C .4D .5二、填空题9.(2011湖北十堰)工人师傅常用角尺平分一个任意角。
做法如下:如图,∠AOB 是一个任意角,在边OA ,OB 上分别取OM=ON ,移动角尺,使角尺 两边相同的刻度分别与M ,N 重合,过角尺顶点C 作射线OC 。
浙教版八年级数学上册__边边边(SSS)__同步练习(解析版)
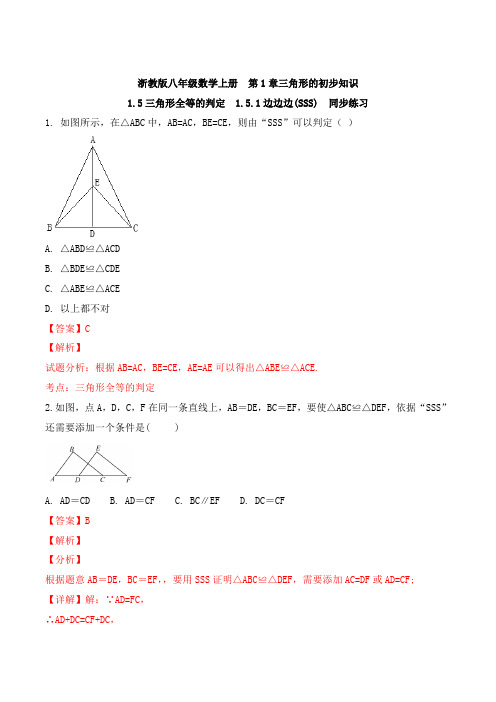
浙教版八年级数学上册第1章三角形的初步知识1.5三角形全等的判定 1.5.1边边边(SSS) 同步练习1. 如图所示,在△ABC中,AB=AC,BE=CE,则由“SSS”可以判定()A. △ABD≌△ACDB. △BDE≌△CDEC. △ABE≌△ACED. 以上都不对【答案】C【解析】试题分析:根据AB=AC,BE=CE,AE=AE可以得出△ABE≌△ACE.考点:三角形全等的判定2.如图,点A,D,C,F在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,依据“SSS”还需要添加一个条件是( )A. AD=CDB. AD=CFC. BC∥EFD. DC=CF【答案】B【解析】【分析】根据题意AB=DE,BC=EF,,要用SSS证明△ABC≌△DEF,需要添加AC=DF或AD=CF;【详解】解:∵AD=FC,∴AD+DC=CF+DC,∴AC=DF,在△ABC和△FED中∴△ABC≌△DEF,故选:B.【点睛】本题考查了全等三角形的判定,证得AC=DF是解题的关键.3.如图,一扇窗户打开后,用窗钩AB可将其固定,这里所运用的几何原理是()A. 垂线段最B. 两点之间线段最短C. 两点确定一条直线D. 三角形的稳定性【答案】D【解析】【分析】根据三角形的稳定性即可解答.【详解】一扇窗户打开后,用窗钩AB可将其固定,这里所运用的几何原理是三角形的稳定性,故选:D.【点睛】本题考查了三角形的稳定性,利用三角形的稳定性是解题的关键.4.如图,在△ABC和△FED中,AC=FD,BC=ED,要利用“SSS”来判定△ABC和△FED全等时,下面的4个条件中:①AE=FB;②AB=FE;③AE=BE;④BF=BE,可利用的是( )A. ①或②B. ②或③C. ①或③D. ①或④【答案】A【解析】由题意可得,要用SSS进行△ABC和△FED全等的判定,需要AB=FE,若添加①AE=FB,则可得AE+BE=FB+BE,即AB=FE,故①可以;若添加AB=FE,则可直接证明两三角形的全等,故②可以。
八年级数学上学期全等三角形判定一(SSS,SAS)(基础)知识讲解——含课后作业与答案

全等三角形判定一(SSS ,SAS )(基础)【学习目标】1.理解和掌握全等三角形判定方法1——“边边边”,和判定方法2——“边角边”;2.能把证明一对角或线段相等的问题,转化为证明它们所在的两个三角形全等.【要点梳理】【高清课堂:379109 全等三角形判定一,基本概念梳理回顾】要点一、全等三角形判定1——“边边边”全等三角形判定1——“边边边”三边对应相等的两个三角形全等.(可以简写成“边边边”或“SSS ”).要点诠释:如图,如果''A B =AB ,''A C =AC ,''B C =BC ,则△ABC ≌△'''A B C .要点二、全等三角形判定2——“边角边”1. 全等三角形判定2——“边角边”两边和它们的夹角对应相等的两个三角形全等(可以简写成“边角边”或“SAS ”).要点诠释:如图,如果AB = ''A B ,∠A =∠'A ,AC = ''A C ,则△ABC ≌△'''A B C . 注意:这里的角,指的是两组对应边的夹角.2. 有两边和其中一边的对角对应相等,两个三角形不一定全等.如图,△ABC 与△ABD 中,AB =AB ,AC =AD ,∠B =∠B ,但△ABC 与△ABD 不完全重合,故不全等,也就是有两边和其中一边的对角对应相等,两个三角形不一定全等.【典型例题】类型一、全等三角形的判定1——“边边边”【高清课堂:379109 全等三角形的判定(一)同步练习4】1、已知:如图,△RPQ 中,RP =RQ ,M 为PQ 的中点.求证:RM 平分∠PRQ .【思路点拨】由中点的定义得PM =QM ,RM 为公共边,则可由SSS 定理证明全等.【答案与解析】证明:∵M 为PQ 的中点(已知),∴PM =QM在△RPM 和△RQM 中,()(),,RP RQ PM QM RM RM ⎧=⎪=⎨⎪=⎩已知公共边 ∴△RPM ≌△RQM (SSS ).∴ ∠PRM =∠QRM (全等三角形对应角相等).即RM 平分∠PRQ.【总结升华】在寻找三角形全等的条件时有的可以从图中直接找到,如:公共边、公共角、对顶角等条件隐含在题目或图形之中. 把证明一对角或线段相等的问题,转化为证明它们所在的两个三角形全等,综合应用全等三角形的性质和判定.类型二、全等三角形的判定2——“边角边”2、(2016•泉州)如图,△ABC 、△CDE 均为等腰直角三角形,∠ACB=∠DCE=90°,点E 在AB 上.求证:△CDA ≌△CEB .【思路点拨】根据等腰直角三角形的性质得出CE=CD ,BC=AC ,再利用全等三角形的判定证明即可.【答案与解析】证明:∵△ABC 、△CDE 均为等腰直角三角形,∠ACB=∠DCE=90°,∴CE=CD ,BC=AC ,∴∠ACB ﹣∠ACE=∠DCE ﹣∠ACE ,∴∠ECB=∠DCA ,在△CDA 与△CEB 中,∴△CDA ≌△CEB .【总结升华】本题考查了全等三角形的判定,熟记等腰直角三角形的性质是解题的关键,同时注意证明角等的方法之一:利用等式的性质,等量加等量,还是等量.举一反三:【变式】(2014•房县三模)如图,C 是线段AB 的中点,CD 平分∠ACE ,CE 平分∠BCD ,CD=CE .求证:△ACD ≌△BCE .【答案】证明:∵C 是线段AB 的中点,∴AC=BC ,∵CD 平分∠ACE ,CE 平分∠BCD ,∴∠ACD=∠ECD ,∠BCE=∠ECD ,∴∠ACD=∠BCE ,在△ACD 和△BCE 中,∴△ACD ≌△BCE (SAS ).3、如图,将两个一大、一小的等腰直角三角尺拼接 (A 、B 、D 三点共线,AB =CB ,EB =DB ,∠ABC =∠EBD =90°),连接AE 、CD ,试确定AE 与CD 的位置与数量关系,并证明你的结论.【答案与解析】AE =CD ,并且AE ⊥CD证明:延长AE 交CD 于F ,∵△ABC 和△DBE 是等腰直角三角形∴AB =BC ,BD =BE在△ABE 和△CBD 中90AB BC ABE CBD BE BD =⎧⎪∠=∠=︒⎨⎪=⎩∴△ABE≌△CBD(SAS)∴AE=CD,∠1=∠2又∵∠1+∠3=90°,∠3=∠4(对顶角相等)∴∠2+∠4=90°,即∠AFC=90°∴AE⊥CD【总结升华】通过观察,我们也可以把△CBD看作是由△ABE绕着B点顺时针旋转90°得到的.尝试着从变换的角度看待全等.举一反三:【变式】已知:如图,AP平分∠BAC,且AB=AC,点Q在PA上,求证:QC=QB【答案】证明:∵ AP平分∠BAC∴∠BAP=∠CAP在△ABQ与△ACQ中∵∴△ABQ≌△ACQ(SAS)∴ QC=QB类型三、全等三角形判定的实际应用4、(2014秋•兰州期末)如图,点D为码头,A,B两个灯塔与码头的距离相等,DA,DB为海岸线.一轮船离开码头,计划沿∠ADB的角平分线航行,在航行途中C点处,测得轮船与灯塔A和灯塔B的距离相等.试问:轮船航行是否偏离指定航线?请说明理由.【思路点拨】只要证明轮船与D点的连线平分∠ADB就说明轮船没有偏离航线,也就是证明∠ADC=∠BDC.要证明角相等,常常通过把角放到两个三角形中,利用题目条件证明这两个三角形全等,从而得出对应角相等.【答案与解析】解:此时轮船没有偏离航线.理由:由题意知:DA=DB,AC=BC,在△ADC和△BDC中,,∴△ADC≌△BDC(SSS),∴∠ADC=∠BDC,即DC为∠ADB的角平分线,∴此时轮船没有偏离航线.【总结升华】本题考查了全等三角形的应用,解答本题的关键是:根据条件设计三角形全等,巧妙地借助两个三角形全等,寻找对应角相等.要学会把实际问题转化为数学问题来解决.举一反三:【变式】工人师傅经常利用角尺平分一个任意角,如图所示,∠AOB是一个任意角,在边OA,边OB上分别取OD=OE,移动角尺,使角尺两边相同的刻度分别与D、E重合,这时过角尺顶点P的射线OP就是∠AOB的平分线,你能先说明△OPE与△OPD全等,再说明OP平分∠AOB吗?【答案】证明:在△OPE与△OPD中∵OE OD OP OP PE PD=⎧⎪=⎨⎪=⎩∴△OPE≌△OPD (SSS)∴∠EOP=∠DOP(全等三角形对应角相等)∴ OP平分∠AOB.【巩固练习】一、选择题1. (2015•莆田)如图,AE∥DF,AE=DF,要使△EAC≌△FDB,需要添加下列选项中的()A.AB=CD B.EC=BF C.∠A=∠D D.AB=BC2. 如图,已知AB =CD ,AD =BC ,则下列结论中错误的是( )A.AB ∥DCB.∠B =∠DC.∠A =∠CD.AB =BC3. (2016春•成安县期末)如图,由∠1=∠2,BC =DC ,AC=EC ,得△ABC ≌△EDC 的根据是( )A.SASB.ASAC.AASD.SSS4. 如图,AB 、CD 、EF 相交于O ,且被O 点平分,DF =CE ,BF =AE ,则图中全等三角形的对数共有( )A. 1对B. 2对C. 3对D. 4对5. 如图,将两根钢条'AA ,'BB 的中点O 连在一起,使'AA ,'BB 可以绕着点O 自由转动,就做成了一个测量工件,则''A B 的长等于内槽宽AB ,那么判定△OAB ≌△''OA B 的理由是( )A.边角边B.角边角C.边边边D.角角边6. 如图,已知AB ⊥BD 于B ,ED ⊥BD 于D ,AB =CD ,BC =ED ,以下结论不正确的是( )A.EC ⊥ACB.EC =ACC.ED +AB =DBD.DC =CB二、填空题7. 如图,AB =CD ,AC =DB ,∠ABD =25°,∠AOB =82°,则∠DCB =_________.8. 如图,在四边形ABCD中,对角线AC、BD互相平分,则图中全等三角形共有_____对.9.(2016•牡丹江)如图,AD和CB相交于点E,BE=DE,请添加一个条件,使△ABE≌△CDE(只添一个即可),你所添加的条件是.10. 如图,AC=AD,CB=DB,∠2=30°,∠3=26°,则∠CBE=_______.11. 如图,点D在AB上,点E在AC上,CD与BE相交于点O,且AD=AE,AB=AC,若∠B =20°,则∠C=_______.12. 已知,如图,AB=CD,AC=BD,则△ABC≌,△ADC≌ .三、解答题13. (2014春•章丘市校级期中)如图A 、B 两点分别位于一座小山脚的两端,小明想要测量A 、B 两点间的距离,请你帮他设计一个测量方案,测出AB 的距离.并说明其中的道理.14. 已知:如图,AB ∥CD ,AB =CD .求证:AD ∥BC .分析:要证AD ∥BC ,只要证∠______=∠______,又需证______≌______.证明:∵ AB ∥CD ( ),∴ ∠______=∠______ ( ),在△______和△______中,⎪⎩⎪⎨⎧===),______(______),______(______),______(______∴ Δ______≌Δ______ ( ).∴ ∠______=∠______ ( ).∴ ______∥______( ).15. 如图,已知AB =DC ,AC =DB ,BE =CE 求证:AE =DE.【答案与解析】一.选择题1. 【答案】A ;【解析】解:∵AE∥FD,∴∠A=∠D,∵AB=CD,∴AC=BD,在△AEC 和△DFB 中,,∴△EAC≌△FDB(SAS ),故选:A .2. 【答案】D ;【解析】连接AC 或BD 证全等.3. 【答案】A ;【解析】通过等量加等量得到∠BCA=∠DCE, 从而由SAS 定理判定全等.4. 【答案】C ;【解析】△DOF ≌△COE ,△BOF ≌△AOE ,△DOB ≌△COA.5. 【答案】A ;【解析】将两根钢条'AA ,'BB 的中点O 连在一起,说明OA ='OA ,OB ='OB ,再由对顶角相等可证.6. 【答案】D ;【解析】△ABC ≌△EDC ,∠ECD +∠ACB =∠CAB +∠ACB =90°,所以EC ⊥AC ,ED +AB =BC +CD =DB.二.填空题7. 【答案】66°;【解析】可由SSS 证明△ABC ≌△DCB ,∠OBC =∠OCB =82412︒=︒, 所以∠DCB = ∠ABC =25°+41°=66°8. 【答案】4;【解析】△AOD ≌△COB ,△AOB ≌△COD ,△ABD ≌△CDB ,△ABC ≌△CDA.9. 【答案】AE=CE ;【解析】由题意得,BE=DE ,∠AEB=∠CED (对顶角),可选择利用SAS 进行全等的判定,答案不唯一.10.【答案】56°;【解析】∠CBE =26°+30°=56°.11.【答案】20°;【解析】△ABE ≌△ACD (SAS )12.【答案】△DCB ,△DAB ;【解析】注意对应顶点写在相应的位置上.三.解答题13.【解析】解:如图所示:在AB 下方找一点O ,连接BO ,并延长使BO=B′O,连接AO ,并延长使AO=A′O,在△AOB 和△A′OB′中:,∴△AOB≌△A′OB′(SAS ),∴AB=A′B′,量出A′B′的长即可.14. 【解析】3,4;ABD ,CDB ;已知;1,2;两直线平行,内错角相等; ABD ,CDB ;AB ,CD ,已知;∠1=∠2,已证;BD =DB ,公共边;ABD ,CDB ,SAS ;3,4,全等三角形对应角相等; AD ,BC ,内错角相等,两直线平行.15.【解析】证明:在△ABC 和△DCB 中AB DC AC DB BC =CB ⎧⎪⎨⎪⎩==∴△ABC ≌△DCB (SSS ) ∴∠ABC =∠DCB , 在△ABE 和△DCE 中ABC DCB AB DC BE CE =⎧⎪∠=∠⎨⎪=⎩∴△ABE ≌△DCE (SAS ) ∴AE =DE.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
用“边边边”判定三角形全等
基础训练
1.如图,下列三角形中,与△ABC 全等的是()
2.如图,已知AC=FE,BC=DE,点A,D,B,F 在一条直线上,要利用“SSS”证明△ABC≌△FDE,还可以添加的一个条件是()
A.AD=FB
B.DE=BD
C.BF=DB
D.以上都不对
3.满足下列条件的两个三角形不一定全等的是(
)A.有一边相等的两个等边三角形
B.有一腰和底边对应相等的两个等腰三角形
C.周长相等的两个三角形
D.斜边和一条直角边对应相等的两个等腰直角三角形
4.如图,在△ABC 和△FED 中,AC=FD,BC=ED,要利用“SSS”来判定△ABC 和△FED 全等时,下面的4个条件中:
①AE=FB;②AB=FE;③AE=BE;④BF=BE,可利用的是(
)
A.①或②
B.②或③
C.①或③
D.①或④5.如图,在方格纸中,以AB 为一边作△ABP,使之与△ABC 全等,从P 1,P 2,P 3,P 4四个点中找出符合条件
的点P,则点P 有()
A.1个
B.2个
C.3个
D.4个
6.如图,AB=DE,AC=DF,BC=EF,则∠D 等于()
A.30°
B.50°
C.60°
D.100°
7.如图,已知AE=AD,AB=AC,EC=DB,下列结论:
①∠C=∠B;②∠D=∠E;③∠EAD=∠BAC;④∠B=∠E.其中错误的是()
A.①②
B.②③
C.③④
D.只有④
8.工人师傅常用角尺平分一个任意角,做法如下:如图,已知∠AOB是任意一个角,在边OA,OB上分别截取OM=ON,移动角尺,使角尺两边相同的刻度分别与M,N重合,过角尺顶点P作射线OP,则OP是∠AOB的平分线,其理由是___________________.
9.王师傅用4根木条钉成一个四边形木架如图所示.
要使这个木架不变形,他至少还要再钉上几根木条?()
A.0根
B.1根
C.2根
D.3根
10.如图,建高楼常需要用塔吊来吊建筑材料,而塔吊的上部是三角形结构,这是应用了三角形的哪个性质?
答:.
10.如图,AB=AC,AD=AE,BE=CD,试说明:△ABD≌△ACE.
参考答案
1.【答案】C
2.【答案】A
解:根据已知条件AC=FE,BC=DE,可知要利用“SSS”证明△ABC≌△FDE,只需要满足AB=FD即可.而当AD=FB时,可得到AB=FD,故选A.
3.【答案】C
4.【答案】A
5.【答案】C
6.【答案】D
7.【答案】D
8.【答案】SSS
解:在△OPM和△OPN中,OM=ON,PM=PN,OP=OP,所以△OPM≌△OPN(SSS),所以∠POM=∠PON,即OP平分∠AOB.
9.【答案】B10.【答案】稳定性。
