第11章+静电场中的导体和电介质1_导体素材
静电场中的导体与电介质

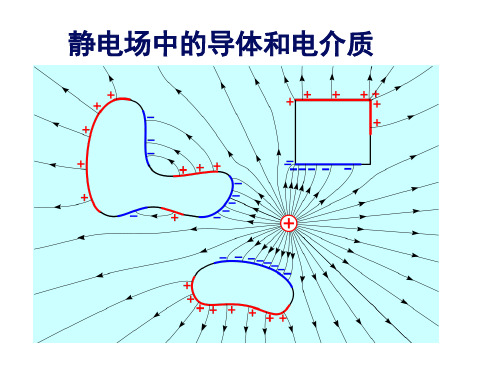
在静电场中平衡时: 1.内部电场强度不为零;2.电介质表面出现极化电荷
真空中的导体和电介质
P
pi
ΔV
P0eE
01
02
实验证
电 考 真空和P 偶 虑 中电c的介o 导质sS 极 一 P,体ln矩 电 pi, 0介 S 极 2质 l, 化 P 斜 0 . 极度定面 化:义V 圆 和 强:p 2i 电 柱 S 0 ,c荷 L So 体 明 各 性 介l0 : 向 质的 s密 在 同 中电co s度
此式对其它情况仍然适 用
D
义:电位移矢量D可, 得:D Dd0ESP S
q0
此既电介质中的高斯定理:通过电场中任意闭合曲面的电位移通量, 等于该闭合曲面所包围的自由电荷的代数和。
仿照电场线,用电位移线来描述电位移在空间的分布。但两者有 区别: 电场线起始于正电荷,终止于负电荷(包括极化电荷) 电位移线只起始于自由正电荷,终止于自由负电荷
在国际单位制中,D 的单位是: 库/米2(C/m2)
对各向同性电介质,因
所以 P0 eE
D 0EP 0 ( 1 ) E
式中 ε = ε0εr 叫电介质的介电常数, εr 称电介质的相对介电常数。
引入D,避免了求极化电荷的复杂问题,可使有电介质存在时解题简化。 只要有电介质,均应先求D 再求E 等。
E E0 E E0 与E 方 向 相 反 :
E
P
E0 // n
E
0 0
0
P cos
P
n
P
e 0E
E
E0
- E
10.4
E0 -
电介
质中0 静电E场0的-基本e
E
静电场中的导体和电解质

Q + + + + ++ + + + + E= 0 S+ + + + + + + + ++
Q q + + + +++ + +-q + + - E= 0 S + 结论: 电荷分布在导体外表面, 导体 + q + + 内部和内表面没净电荷. + - - + + + + ++ 腔内有电荷q: E 0 q 0
i
结论: 电荷分布在导体内外两个表面,内表面感应电荷为-q. 外表面感应电荷为Q+q.
NIZQ
第 5页
大学物理学 静电场中的导体和电介质
结论: 在静电平衡下,导体所带的电荷只能分布在导体的 表面,导体内部没有净电荷. • 静电屏蔽 一个接地的空腔导体可以隔离内 外电场的影响. 1. 空腔导体, 腔内没有电荷 空腔导体起到屏蔽外电场的作用. 2. 空腔导体,腔内存在电荷 接地的空腔导 体可以屏蔽内、 外电场的影响.
NIZQ
第 3页
大学物理学 静电场中的导体和电介质
• 静电平衡时导体中的电场特性
E内 0
场强:
ΔVab
b
a
E dl 0
• 导体内部场强处处为零 E内 0 • 表面场强垂直于导体表面 E表面 // dS
• 导体为一等势体 V 常量 • 导体表面是一个等势面
S
0 E P dS qi
静电场中的导体和电介质

-
目录
静电场中的导体 和电介质
0
静电场中的导体和电介质
静电场中的导体和电介质
静电场是指在没有电流流动的情况下,电荷分布所产生的电场。在静电场中,导体和电介质 是两种不同的物质,它们的特性和作用也不同,本文将探讨导体和电介质在静电场中的性质 和应用 首先,我们需要了解导体和电介质的基本概念。导体是一种具有良好导电性能的物质,常见 的导体包括金属等。导体内的自由电子可以在外加电场的作用下移动,形成电流。而电介质 则是一种不良导电的物质,它的电导率远远低于导体。电介质在外加电场下无法形成连续的 电流,而是通过极化现象来响应电场的作用 在静电场中,导体和电介质的行为有很大的不同。对于导体来说,其特点是在静电平衡状态 下,内部电场为零。这是因为导体内的自由电子能够自由移动,它们会在外加电场的作用下 重新分布,直到达到平衡状态。这种现象被称为电荷运动的屏蔽效应。导体的另一个重要性 质是表面上的电荷分布是均匀的,这也是导体可以用来储存电荷的
与导体不同,电介质在静电场中的响应更加复杂。当外加电场作用于电介质时,电介 质分子会发生极化现象,即分子内部正、负电荷的分离。这种分离会导致电介质内部 产生电位移场,从而相应地改变电场分布。电介质的极化程度可以用极化强度来衡量 ,极化强度与外加电场的强度成正比。除了极化现象,电介质还可能发生击穿现象, 即在电场强度过高时,电介质内部的绝缘失效,导致电流的突然增加
0
静电场中的导体和电介质
导体在静电场中的一个重要应用 是电路中的导线。电路中的导线 由导体制成,它们能够有效地传 导电流。在电力系统中,导体连 接电源和电器设备,将电能传输 到目标地点。此外,在电子设备 制造中,导体用于制作电路板, 连接不同的电子元件,实现电信 号的传输和处理
静电场中的导体与电介质

§2 静电场中的导体和电介质§2-1 静电场中的导体1. 导体的静电平衡条件当电荷静止不动时,电场散布不随转变,该体系就达到了静电平衡。
在导体中存在自由电荷,它们在电场的作用下可以移动,从而改变电荷的散布……导体内自由电荷无宏观运动的状态。
导体的静电平衡的必要条件是其体内图2-1导体的静电平衡场强处处为零。
从静电平衡的条件动身可以取得以下几点推论:推论1)导体是等位体,导体表面是等位面:2)导体表面周围的场强处处与它的表面垂直:因为电力线处处与等位面正交,所以导体外的场强必与它的表面垂直。
(注意:本章所用的方式与第一章不同,而是假定这种平衡以达图2-2导体对等位面的控制作用到,以平衡条件动身结合静电场的普遍规律分析问题。
)2.电荷散布1) 体内无电荷,电荷只散布在导体的表面上:当带电导体处于静电平衡时,导体内部不存在净电荷(即电荷的体密度)电荷仅散布在导体的表面。
可以用高斯定理来证明:设导体内有净电荷,则可在导体内部作一闭合的曲面,将包围起来,依静电条件知S面上处处, 即由高斯定理必有q=02) 面电荷密度与场强的关系:当导体静电平衡时,导体表面周围空间的 与该处导体表面的面电荷密度 有如下关系:论证: 在电荷面密度为 的点取面元设 点为导体表面之外周围空间的点,面元。
充分小,可以为 上的面电荷密度 是均匀的,以为横截面作扁圆柱形高斯面(S ),上底面过P 点,把电荷q= 包围起来. 通太高斯面的电通量是:3) 表面曲率的影响、尖端放电导体电荷如何散布,定量分析研究较复杂,这不仅与这个导体的形状有关,还和它周围有何种带电体有关。
对孤立导体,电荷的散布有以下定性的规律:图2-3导体表面场强与电荷面密度曲率较大的地方(凸出而尖锐处),电荷密度e 较大;曲率较小的地方(较平坦处)电荷密度e 较小;曲率为负的地方(凹进去向)电荷密度e 更小。
1) 端放电的利和弊3 导体壳(腔内无带电体情况)大体性质:当导体壳内无带电体时,在静电平衡当导体壳内无 带电体时,在静电平衡下:导体壳内表面上处处无电荷,电荷仅散布在外 表面;空腔内无带电场,空腔内电位处处相等。
第章静电场中的导体和电介质PPT课件

q2
EA
1 2 o
2 2 o
3 2 o
4 2 o
0
EB
1 2 O
2 2 O
3 2 o
4 2 o
0
1
23
4
由电荷守恒:
1S 2 S q1
A
B
3S 4S q2
1
4
q1 q2 2S
2
3
q1 q2 2S
20
1
4
q1 q2 2S
q1
2
3
q1 q2 2S
1
2
上述结果表明:平板相背的两面带电等
R3 R2
R3
RR11
qq1 1
RR33
问题:电势表
达式能直接写
R2 R1
q1
4 or
2
dr
R3
(q q1 )
4 or 2
dr
出来吗?
q1
4 o
1 R1
1 R2
q q1
4 o R3
V1 V2
同理,球壳的电势为:
V2
E dl
R3
R3
(q
4
q1 ) or 2
dr
q q1
2.内屏蔽
+
+
壳外表面上的电荷分布与腔内带电体的位置无关,只 取于导体外表面的形状。
若将空腔接地,则空腔外表面上的感应电荷被大地电荷 中和,腔外电场消失,腔内电荷不会对空腔外产生影响。即 接地空腔对内部电场起到了屏蔽作用,这是静电屏蔽的另外 一种——内屏蔽。
高压设备用金属导体壳接地做保护。 14
五、利用静电平衡条件和性质作定量计算
例1:半径为R和r的球形导体(R>r),用很长的细导线连 接起来,使两球带电Q、q,求两球表面的电荷面密度。
第十一章静电场中的导体和电介质精品PPT课件

ElQ极化越激烈
E 0 极化现象消失 p 0
21
有极分子
E外 0 每个分子 p 0 l 不变
E
E外 0
F
MpE F
O
H
H
H2O分子
+ -+
2
-
A
C
+
n
-
B
U A BU 1U 2 U n
1 1 1 1 电容减小
A
B
C C1 C2
Cn 电压增加
3.电容器混联 11 1 C C1 C2 C3
q1 q2 q3
UU1U2 U2 U3
C1
C2
C3
U
18
例]
如图所示,三块平行导体板,A、B、C的面积均为S,其中A
板带电量为Q,B板和C板不带电,A和B间相距为d1A和C间 相距为d2,求(1)各导体板上的电荷分布和导体板间的电势 差;(2)将DC导体分别接地再求导体板上的电荷分布和导
平板电容器
球形电容器
柱形电容器
AB
+
d
+
充电
B
R1 A R2
BA
R1
l
R2
电容器的基本作用就是充电与放电
照相闪光: 高能量的瞬间放电 13
一.孤立导体的电容
U 0 若半径R球形导体,带电量Q,则:
Q U
4 0 R
可证:对于任何孤立导体的 Q/U的比值仅与导体的形状大小 有关,而与Q,U无关
定义:电容
接地空腔导体将使外部空间 不受空腔内的电场影响.
接地导体电势为零
+++++++-- - - 仪器 + + + + +11+
静电场中的导体和电介质1课件

➢问:可否在S 内存在两种等量异号的电荷,才使
•
P
S
E内 0
qi 0 (S内) 成立?
➢答:不可能
S是任意取的高斯面,只 要在某点有某种正或者 负电荷存在,我们就可 以取一个小的高斯面将 其包围,这样
qi 0 (S内)
与导体内场强为0矛盾
(2)空腔导体
➢A:空腔内没有带电体时
空腔导体的内表面无电 荷,电荷只能分布在外 表面
应用二:导体空腔与静电屏蔽 Electrostatic Shielding
一、第一类导体空腔 —— [ 腔内无带电体]
腔内无电场 屏蔽(腔内仪器不受外场影响)。
注意:腔外 发电场,腔内
q
E
在腔内也激 0 是因为腔
外表面被 q 感应出异号电荷,
感应场与外场叠加后使腔内: E 0 (合场强为零)。
在一些工厂或实验室里, 存在大量易燃气体, 工作人员要穿 一种特制的鞋, 这种鞋的导电性能很好,能够将电荷导入大地, 避免电荷在人体上的积累, 以免产生火花放电, 引起火灾.
➢4. 闪电
带电云层之间或带电云层和地面之间发生强烈放电时, 产生 耀眼的闪光和巨响, 这就是闪电. 闪电的放电电流可以高达几十万 安培, 会使建筑物遭受严重损坏. 这就是雷击。
二、第二类导体空腔— [腔内有带电体]
(1)腔内电场不受外电场影响。 (可用高斯定理证明)
QQ q
q
q
(2)空腔导体腔外电场不受导体腔内电场影响。
与腔内电荷分布无关,但与腔内 放置的带电体电量有 关。
QQ q
q
q
导体外的电场是Q+q产生的电场的叠加。
由于导体内表面上电量与腔内电荷等量异号,在+q发出 的电场线全部终止在内表面上,则+q及-q在腔外产生 的合场强为0。
静电场中的导体和电介质(大学物理作业,考研真题)

物理(下)作业专业班级:姓名:学号:第十一章静电场中的导体和电介质(1)一、选择题1、两个同心薄金属球壳,半径分别为1R 和2R (1R <2R ),若分别带上电量1q 和2q 的电荷,则两者的电势分别为1U 和2U (选无穷远处为电势零点)。
现用导线将两球壳连接,则它们的电势为(A )、1U ;(B )、2U ;(C )、21U U ;(D )、)(2121U U 。
[]2、两导体板A 和B 相距为d ,并分别带有等量异号电荷。
现将另一不带电的,且厚度为t (t ﹤d )的导体板C 插入A 、B 之间(不与它们接触),则导体板A 和B 之间的电势差U AB 的变化为:(A )、不变;(B )、增大;(C )、减小;(D )、不一定。
[]3、(2018年暨南大学)将一带电量为Q 的金属小球靠近一个不带电的金属导体时,则有:(A )金属导体因静电感应带电,总电量为-Q ;(B )金属导体因感应带电,靠近小球的一端带-Q ,远端带+Q ;(C )金属导体两端带等量异号电荷,且电量q<Q ;(D )当金属小球与金属导体相接触后再分离,金属导体所带电量大于金属小球所带电量。
二、填空题1、导体在达到静电平衡时,其导体内部的场强应为______;整个导体(包括导体表面)的电势应是______;导体表面的场强方向应是______。
2、当空腔导体达到静电平衡时,若腔内无电荷,则给该空腔导体所带的电荷应分布在;若腔内有电荷,则空腔导体上的电荷应分布在。
3、如图所示,两同心导体球壳,内球壳带电量+q ,外球壳带电量-2q 。
静电平衡时,外球壳的内表面带电量为______;外表面带电量为_______。
三、计算题1、同轴传输线是由两个很长且彼此绝缘的同轴金属直圆柱体构成,如图所示。
设内圆柱体的半径为R 1,外圆柱体的内半径为R 2。
并假定内外圆柱导体分别带等量异号电荷,其线电荷密度大小为λ,求内外圆柱导体之间的电场强度分布以及它们之间的电势差。
静电场中的导体和电介质
平行板电容器的电容,与极板的面积成正比,与极板 间的距离成反比。
圆柱形电容器的电容
两柱面间的场强大小 E Q 2 0 Lr 方向沿着径向 两柱面间的电势差
U A U B Edr Q 2 0 L ln R2 R1
R2
Q 2 0 Lr
R1
dr
柱形电容器的电容
dWe we dV
取半径为r,厚为dr的球壳, 电场总能量为: 其体积元为: 2
8r
2
dr
dV 4r dr
2
Q We dWe 8
R2
R1
dr 1 Q2 ( R2 R1 ) 2 r 2 4R2 R1
Q C U
4 0 R
★电量按半径比例进行重新分配
2 1 Q Q 2 Q 3 3 F 2 2 4π 0 R 18π 0 R
二. 电容器及其电容 常见的电容器: 平行板电容器----两块导体薄板; 圆柱形电容器----导体薄柱面; 球形电容器----导体薄球面; 当电容器的两极板分别带有等值异号电荷Q时,电荷Q与 两极板A、B间的电势差 (UA-UB) 的比值定义为电容器的 电容:
外 内
E内 ? S
★电荷只分布在外表面,内表面上处处无电荷
内表=0
E内=0
2、 若导体壳包围的空间(腔)有电荷:
内
q S ★内表面带电总量为-q,内表面上各处 电荷面密度取决于腔内电荷的分布
外
q内表 q
E内 0
3、静电屏蔽
S
A
Q
B
E内 0
在电子仪器中,用金属网罩把电路包起来,使其 不受外界带电体的干扰。 传送微弱电信号的导线,外表用金属丝编成的网 包起来,这种的导线叫屏蔽线。
静电场中的导体和电介质(含答案,大学物理作业,考研真题)

1、一片二氧化钛晶片,其面积为 1.0cm2, 厚度为 0.10mm 。把平行板电容器的两极板紧
贴在晶片两侧。此时电容器的电容为_____________. ;当在电容器的两板上加上 12V 电压时,
极板上的电荷为_____________. ;电容器内的电场强度为_____________ .。(二氧化钛的相
[
]
3、(2018 年暨南大学)将一带电量为 Q 的金属小球靠近一个不带电的金属导体时,则有:
(A)金属导体因静电感应带电,总电量为-Q;
(B)金属导体因感应带电,靠近小球的一端带-Q,远端带+Q;
(C)金属导体两端带等量异号电荷,且电量 q<Q;
(D)当金属小球与金属导体相接触后再分离,金属导体所带电量大于金属小球所带电量。
二、 填空题
1、导体在达到静电平衡时,其导体内部的场强应为______;整个导体(包括导体表面)
的电势应是______;导体表面的场强方向应是______。
2、当空腔导体达到静电平衡时,若腔内无电荷,则给该空腔导体所带的电荷应分布
在
;若腔内有电荷,则空腔导体上的电荷应分布
在
。
3、如图所示,两同心导体球壳,内球壳带电量+q,外球壳带电量-2q。
(C)、使电容增大,但与介质板的位置无关;(D)、使电容增大,但与介质板的位置有关。
[
]
3、(2011 年太原科技大学)两个半径相同的金属球,一为空心,一为实心,把两者各自
孤立时的电容值加以比较,则:
(A)空心球电容值大;
(B)实心球电容值大;
(C)两球电容值相等;
(D)大小关系无法确定
[
]
二、 填空题
(1)若两极上分别带有电荷+Q 和—Q,求各区域的电位移 D,电场强度 E,及电势 U;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
空腔的内表面无电荷,电荷只分布于外表面上; ② 空腔内有电荷+q 时: 空腔的内表面有电荷 –q ,外表面有电荷 Q+q
Q + + + + +
+ + + + + + + +
+q
+ - + Q+q -q + - + + +
+ + +
++
+ + +
+
E
S
E内 dS 0
q 0
3、静电平衡时,导体表面上各处的面电荷密度与其表 面紧邻处的场强大小成正比: E
11.1.4 静电屏蔽
置于静电场中的导体空腔,内部没有电场,所以导 体壳对外界静电场起了隔离作用,导体空腔内的物体不 受腔外电场的影响。 利用这一性质,可将一些精密仪器放置在空腔内, 以避免外界电场的影响。
E=0
被保护仪器
若导体空腔内有带电体,则空腔内存在的电场要影响 到腔外的物体。 为了消除这种影响,可将导体空腔接地,从而隔 绝了腔内带电体(电场)对外界的影响。 结论: 接地的空腔导体可以屏蔽腔内、外电场的相互影响。
因为连接导线很长,利用孤立 导体的电势公式: Q r
q
R
( 1) V
Q 4 0 R
q 4 0 r
Q R 得: q r
可见,大球所带电量Q 比小球所带电量q 多。 (2) 两球的面电荷密度分别为:
Q 1 4R 2
q 2 2 4r
1 Qr2 r 2 2 qR R
两球电荷面密度与半径成反比。
例2:在一个接地的金属球附近有一个电量为q(q > 0) 的点电荷。已知球的半径为R,点电荷与球心距离为 r, 求金属球面上感应电荷的总电量 q’ 。 解: 点电荷q 在球心 o 处的电势:
V1
q
4 0 r
感应电荷 q’ 在球心 o 处的电势:
q
V2
导体的电势:
证: 在导体内部取一很小的封闭面S 为高斯面。 高斯定理: + +++ + E内 0, E + + + S + + q内 0 + + +++ +Q
S
E内 dS 0
所以导体内部无电荷,即电荷只能分布在导体的表面上。
2、空腔导体(设总带电量为 Q)静电平衡时: ① 空腔内无电荷时:
尖端放电: 具有尖端的带电导体,当尖端处的场强超过空气的击 穿场强时,会发生空气被电离的放电现象。 空气的击穿强度为 +
Emax 3 kV / mm
+
+ + ++ + ++ -
P49(绝缘强度)
+
+ +
“电风”
避雷针就是应用尖端放电性质制造的。 另外,高压输电网的导线应采用表面光滑 的粗导线。
0
证:由高斯定理,过P 作很小的圆柱面S,底面为dS
E 侧 内底 外底
EdS
1
0
dS
E en 0
dS
P
E
E 0
E内 0
4、孤立导体处于静电平衡时,其表面各处的面电荷密度 σ与曲率有关。曲率大的地方,面电荷密度σ也大。
1 R
孤立导体表面附近的场强分布也服从同样的规律。 尖端附近的场强最大,平坦的地方次之,凹进去的 地方最弱。
E0
外新分布
静电平衡状态 导体表面出现感应电荷
自由电子宏观 定向运动停止
E内 E E0 0
附加电场 E
静电平衡时导体中的电场特性 (1)静电平衡时,导体内任何一点场强都等于零。 即:导体内不存在电场线。
E内 0
(2)静电平衡时,导体表面上任何一点场强方向都垂 直于导体表面。即:电场线垂直于导体表面。
E 表面
静电平衡时 电势性质:
导体是个等势体, 表面是个等势面 证:在导体内任取两点a、b
E
Vab E内 dl 0
b
E内 0
a b
Va Vb
a
E
也可以从电场强度与电势梯度之间的关系分析。
11.1.3 静电平衡时导体上的电荷分布 (设总带电量为Q)
1、静电平衡时,内部各处无电荷,电荷Q只分布在导 体表面。
电器设备
高压带电作业
屏蔽线
11.1.5 计算示例
导体放入静电场中,电场会影响导体上的电荷分布; 同时导体上的电荷分布也会影响电场的分布。 计算有导体存在时的静电场的基本依据有: (1)电荷守恒定律;
电场高斯定理 (2)静电场基本规律: 静电场环路定理 ( 电势的概念 )
(3)导体的静电平衡条件:
导体内部的场强处处为零;导体表面的场强垂直
于导体的表面:
E内 0, E表 表面
导体内部和导体表面电势处处相等。
例1 : 两个半径分别为 R 和 r 的球形导体(R > r),用 一根很长的细导线连接起来,使这个导体组带电,求两 球表面电荷与半径的关系?
解:两球由导线连接,电势相等。
11.1.2 导体的静电平衡条件
静电感应现象: 在外电场影响下, 导体表面不同部分出现正负(感应) 电荷的现象。 静电平衡状态:导体内部和表面没 有电荷的宏观定向移动的状态。
E - E=0 - F -
+ + + + + + + - + + + +
E0
静电感应现象过程
导体(带电或 不带电)
q
4 0 R
q
r
q
-
-
V
4 0 r
+ + + + +
V V1 V2
q =0
思考2: 两块平行放置的导体大平板带电后,其相对 的两表面上面电荷密度是否一定是大小相等,符号相 反?为什么。
q
q’ =? R r o - -
4 0 R
V V1 V2
R q r
q 4 0r
q 4 0 R
0
q
感应电量 q’ 的值总是小于点电荷电量 q。
思考1:在距一个原来不带电的导体球的中心 r 处放置一 电量为 q 的点电荷。此导体球的电势多大?
o +
q 4 0 r
第11章 静电场中的导体和电介质
11.1 静电场中的金属导体 11.2 静电场中的电介质 11.3 有电介质时的静电场和高斯定理 11.4 电容 电容器
11.5 电场的能量
重点:有导体、电介质存在时的场强和电势计算 电位移D的计算
11.1 静电场中的金属导体
11.1.1 金属导体的电结构
由带正电的晶体点阵(框架)和大量自由电子组成。 任意微小体积元内,自由电子的负 电荷和晶体点阵上的正电荷的数目相 等, 整个导体显现电中性。
