数学：17.1《反比例函数》同步练习(人教新课标八年级下)

合集下载

反比例函数单元测试题新人教版八年级下

第十七章反比例函数单元测试题一、选择题(每小题5分．共25分) 1.下列函数中．y 是x 的反比例函数的是( ) (A)12y x =- (B) 21y x = (C) 11y x =- (D) 11y x =- 2.已知y 与x 成正比例．z 与y 成反比例，那么z 与x 之间的关系是( ) (A)成正比例， (B)成反比例 (c)有可能成正比例，也有可能是反比例 (D)无法确定． 3．如图，函数(1)y k x =+与k y x =在同一坐标系中，图象只能是下图中的( ) 4.三角形的面积为24cm ，底边上的高()y cm 与底边()x cm 之间的函数关系图象大致应为( ) 5.已知反比例函数(0)k y k x =<的图象上有两点1122(,)(,)A x y B x y ,且12x x <则12y y -的值是( ) (A)正数 (B)负数 (C)非正数 (D)不能确定二、填空题(每小题5分,共25分) 6.某奶粉生产厂要制造一种容积为2升(1升＝1立方分米)的圆柱形桶,桶的底面面积S 与桶高h 有怎样的函数关系式 . 7.一水桶的下底面积是盖面积的2倍,如果将其底朝下放在桌子上,它对桌面的压强是600Pa ,翻过来放, 对桌面的压强是 .8.设有反比例函数1k y x +=,1122(,)(,)x y x y 为其图象上两点,若12x x <0<,12y y >则k 的取值范围 .9.直线y kx b =+过一、三、四象限，则函数by kx =的图象在象限，并且在每一个象限内y 随x 的增大而 .10.如图所示是三个反比例函数1k y x =,2k y x =,3ky x =的图象,由此观察1k 、2k 、3k 的大小关系是(用“<”连接).三、解答下列问题.(第11、12两题各10分，13题14分，14题16分，共50分)密封线铜陵第七中学初二（）班姓名：编号：11.已知变量y 与()1x +成反比例,且当2x =时,1y =-,求y 和x 之间的函数关系.12.如图．正比例函数(0)y kx k =>与反比例函数k y x =的图象相交于A 、C 两点，过A 作x 轴的垂线交x 轴于B ，连 BC ，求△ABC 的面积13.某空调厂的装配车间计划组装9000台空调:⑴从组装空调开始,每天组装的台数m (单位:台/天)与生产的时间t (单位:天)之间有怎样的函数关系? ⑵原计划用2个月时间(每月以30天计算)完成,由于气温提前升高,厂家决定这批空调提前十天上市,那么装配车间每天至少要组装多少空调?点B 在函数14.如图,正方形OABC 的面积为9,点O 为坐标原点,(0,0)k y k x x=>>的图象上,点(,)P m n 是函数(0,0)k y k x x =>>的图象上任意一点,边点P 分别作x 轴、y 轴的垂线,垂足分别为E 、F ,并设矩形OEPF 和正方形OABC 不重合部分的面积为S.(提示:考虑点P 在点B 的左侧或右侧两种情况) ⑴求B 点的坐标和k 的值； ⑵当92S =时，求P 点的坐标； ⑶写出S 关于m 的函数关系式.。

数学：第十七章反比例函数单元测试(人教新课标八年级下)

数学：第十七章反比例函数单元测试(人教新课标八年级下)-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN第十七章反比例函数能力检测一、填空（27） 1．已知反比例函数()0≠=k xky 的图象经过点（2，－3），则k 的值是_______,图象在__________象限，当x>0时，y 随x 的减小而__________. 2若反比例函数xk y 3-=的图象位于一、三象限内，正比例函数x k y )92(-=过二、四象限，则k 的整数值是________。

3.在函数xk y 22--=（k 为常数）的图象上有三个点（-2，1y ），(-1，2y )，（21，3y ），函数值1y ，2y ，3y 的大小为； 4．反比例函数22)12(-+=kx k y 在每个象限内y 随x 的增大而增大，则k=5 如果一次函数y=mx+n 与反比例函数xm n y -=3的图象相交于点（21，2），那么这两个函数解析式分别为、6.已知y 1与x 成正比例(比例系数为k 1),y 2与x 成反比例(比例系数为k 2),若函数y=y 1+y 2的图象经过点(1,2),(2, 12),则8k 1+5k 2的值为________. 7 若m ＜－1，则下列函数：①()0 x xmy =;② y =－mx+1; ③ y = mx; ④ y =(m + 1)x 中，y 随x 增大而增大的是___________。

8．老师给出一个函数，甲、乙、丙、丁四人各指出这个函数的一个性质，甲：函数图象不经过第三象限；乙：函数图象经过第一象限；丙：y 随x 的增大而减小；丁：当2<x 时，0>y 。

已知这四人叙述都正确，请构造出满足上述所有性质的一个函数_______________。

9如图2，在x 轴上点P 的右侧有一点D ，过点D 作x 轴的垂线交双曲线xy 1=于点B ，连结BO 交AP 于C ，设△AOP 的面积为S 1，梯O xyABD P C形BCPD 面积为S 2，则S 1与S 2的大小关系是S 1 S 2。

2021年新人教版数学八年级下人教新课标第十七章反比例函数综合检测题

数学:第17章反比例函数综合检测题A(人教新课标八年级下)一、选择题(每小题3分，共30分) 1、反比例函数y ＝xn 5+图象经过点(2，3)，则n 的值是( )． A 、－2 B 、－1 C 、0 D 、12、若反比例函数y ＝x k(k ≠0)的图象经过点(－1，2)，则这个函数的图象一定经过点( )． A 、(2，－1) B 、(－21，2) C 、(－2，－1) D 、(21，2)3、(08双柏县)已知甲、乙两地相距s (km)，汽车从甲地匀速行驶到乙地，则汽车行驶的时间t (h)与行驶速度v (km/h)的函数关系图象大致是( )4、若y 与x 成正比例，x 与z 成反比例，则y 与z 之间的关系是( )．A 、成正比例B 、成反比例C 、不成正比例也不成反比例D 、无法确定 5、一次函数y ＝kx －k ，y 随x 的增大而减小，那么反比例函数y ＝xk满足( )． A 、当x ＞0时，y ＞0 B 、在每个象限内，y 随x 的增大而减小 C 、图象分布在第一、三象限 D 、图象分布在第二、四象限6、如图，点P 是x 轴正半轴上一个动点，过点P 作x 轴的垂线PQ 交双曲线y ＝x1于点Q ，连结OQ ，点P 沿x 轴正方向运动时， Rt △QOP 的面积( )．A 、逐渐增大B 、逐渐减小C 、保持不变D 、无法确定 7、在一个可以改变容积的密闭容器内，装有一定质量m 的某种气体，当改变容积V 时，气体的密度ρ也随之改变．ρ与V 在一定范围内满足ρ＝Vm，它的图象如图所示，则该气体的质量m 为( )．A 、1.4kgB 、5kgC 、6.4kgD 、7kg 8、若A(－3，y 1)，B(－2，y 2)，C(－1，y 3)三点都在函数y ＝－x1的图象上，则y 1，y 2，y 3的大小关系是( )．A 、y 1＞y 2＞y 3B 、y 1＜y 2＜y 3C 、y 1＝y 2＝y 3D 、y 1＜y 3＜y 2 9、已知反比例函数y ＝xm21-的图象上有A(x 1，y 1)、B(x 2，y 2)两点，当x 1＜x 2＜0时，y 1＜y 2，则m 的取值范围是( )．Q pxy ot /h Ot /h O t /hO t /h v /(km/h) O A ． B ． C ．．A 、m ＜0B 、m ＞0C 、m ＜21 D 、m ＞21 10、如图，一次函数与反比例函数的图象相交于A 、B 两点，则图中使反比例函数的值小于一次函数的值的x 的取值范围是( )．A 、x ＜－1B 、x ＞2C 、－1＜x ＜0或x ＞2D 、x ＜－1或0＜x ＜2 二、填空题(每小题3分，共30分)11.某种灯的使用寿命为1000小时，它的可使用天数y 与平均每天使用的小时数x 之间的函数关系式为 . 12、已知反比例函数xky =的图象分布在第二、四象限，则在一次函数b kx y +=中，y 随x 的增大而 (填“增大”或“减小”或“不变”)．13、若反比例函数y ＝xb 3-和一次函数y ＝3x ＋b 的图象有两个交点，且有一个交点的纵坐标为6，则b ＝． 14、反比例函数y ＝(m ＋2)x m2－10的图象分布在第二、四象限内，则m 的值为．15、有一面积为S 的梯形，其上底是下底长的31，若下底长为x ，高为y ，则y 与x 的函数关系是． 16、如图，点M 是反比例函数y ＝xa(a ≠0)的图象上一点，过M 点作x 轴、y 轴的平行线，若S 阴影＝5，则此反比例函数解析式为． 17、使函数y ＝(2m 2－7m －9)x m2－9m ＋19是反比例函数，且图象在每个象限内y 随x 的增大而减小，则可列方程(不等式组)为．18、过双曲线y ＝xk(k ≠0)上任意一点引x 轴和y 轴的垂线，所得长方形的面积为______． 19. 如图，直线y ＝kx(k ＞0)与双曲线xy 4=交于A(x 1，y 1)，B(x 2，y 2)两点，则2x 1y 2－7x 2y 1＝___________．20、如图，长方形AOCB 的两边OC 、OA 分别位于x 轴、 y 轴上，点B 的坐标为B(－320，5)，D 是AB 边上的一点，将△ADO 沿直线OD 翻折，使A 点恰好落在对角线OB 上的点E 处，若点E 在一反比例函数的图象上，那么该函数的解析式是．三、解答题(共60分)21、(8分)如图，P 是反比例函数图象上的一点，且点P 到x轴的距离为3，到y 轴的距离为2，求这个反比例函数的解析式．22、(9分)请你举出一个生活中能用反比例函数关系描述的实例，写出其函数表达式，并画出函数图象．举例:函数表达式:23、(10分)如图，已知A(x 1，y 1)，B(x 2，y 2)是双曲线y ＝xk在第一象限内的分支上的两点，连结OA 、OB ． (1)试说明y 1＜OA ＜y 1＋1y k ； (2)过B 作BC ⊥x 轴于C ，当m ＝4时，求△BOC 的面积．24、(10分)如图，已知反比例函数y ＝－x8与一次函数 y ＝kx ＋b 的图象交于A 、B 两点，且点A 的横坐标和点B 的纵坐标都是－2．求:(1)一次函数的解析式； (2)△AOB 的面积．25、(11分)如图，一次函数y ＝ax ＋b 的图象与反比例函数y ＝xk 的图象交于M 、N 两点．(1)求反比例函数与一次函数的解析式；(2)根据图象写出使反比例函数的值大于一次函数的值的x 的取值范围．26、(12分)如图，已知反比例函数y ＝xk的图象与一次函数y ＝a x ＋b 的图象交于M(2，m)和N(－1，－4)两点． (1)求这两个函数的解析式； (2)求△MON 的面积；(3)请判断点P(4，1)是否在这个反比例函数的图象上，并说明理由．参考答案:一、选择题1、D ；2、A ；3、C ；4、B ；5、D ；6、C7、D ；8、B ；9、D ； 10、D ．二、填空题 11、y ＝x 1000； 12、减小； 13、5 ； 14、－3 ；15、y ＝xs 23 ； 16、y＝－x 5； 17、⎩⎨⎧---=+-0972119922＞m m m m ； 18、|k|； 19、 20； 20、y ＝－x 12．三、解答题 21、y ＝－x6． 22、举例:要编织一块面积为2米2的矩形地毯，地毯的长x(米)与宽y(米)之间的函数关系式为y ＝x2(x ＞0)． x (2)1 1 232 … y…4234 1…(只要是生活中符合反比例函数关系的实例均可) 画函数图象如右图所示．23、(1)过点A 作AD ⊥x 轴于D ，则OD ＝x 1，AD ＝y 1，因为点A(x 1，y 1)在双曲线y ＝xk上，故x 1＝1y k ，又在Rt △OAD 中，AD ＜OA ＜AD ＋OD ，所以y 1＜OA ＜y 1＋1y k ； (2)△BOC 的面积为2．24、(1)由已知易得A(－2，4)，B(4，－2)，代入y ＝kx ＋b 中，求得y ＝－x ＋2；(2)当y ＝0时，x ＝2，则y ＝－x ＋2与x 轴的交点M(2，0)，即|OM|＝2，于是S △AOB ＝S △AOM＋S △BOM ＝21|OM|·|y A |＋21|OM|·|y B |＝21×2×4＋21×2×2＝6．25、(1)将N(－1，－4)代入y ＝xk ，得k ＝4．∴反比例函数的解析式为y ＝x 4．将M(2，m)代入y ＝x 4，得m ＝2．将M(2，2)，N(－1，－4)代入y ＝ax ＋b ，得⎩⎨⎧-=+-=+.b a ,b a 422解得⎩⎨⎧-==.b ,a 22∴一次函数的解析式为y ＝2x －2． (2)由图象可知，当x ＜－1或0＜x ＜2时，反比例函数的值大于一次函数的值．26、解(1)由已知，得－4＝1-k ，k ＝4，∴y ＝x 4．又∵图象过M(2，m)点，∴m ＝24＝2，∵y ＝a x ＋b 图象经过M 、N 两点，∴,422⎩⎨⎧-=+-=+b a b a 解之得,22⎩⎨⎧-==b a ∴y ＝2x －2．(2)如图，对于y ＝2x －2，y ＝0时，x ＝1，∴A(1，0)，OA ＝1，∴S △MON ＝S △MOA ＋S △NOA＝21OA ·MC ＋21OA ·ND ＝21×1×2＋21×1×4＝3． (3)将点P(4，1)的坐标代入y ＝x4，知两边相等，∴P 点在反比例函数图象上．。

初中八下17[1].1.2反比例函数的图像和性质题

人教新课标版初中八下17.1.2反比例函数的图像和性质同步训练题知能点分类训练：知能点1：反比例函数的图像和性质 1. 函数x2y =的自变量x 的取值范围是___________，图像在___________象限。

2. 函数x3y -=的自变量x 的取值范围是___________，图像位于___________象限。

3. 函数x1ky 2+=的自变量x 的取值范围是___________，图像位于___________象限。

4. 设)y ,x (B ),y ,x (A 2211是反比例函数x2y -=图像上的点，若0x x 21<<，则21y y 与之间的关系是（） A 、0y y 12<<B 、0y y 21<<C 、0y y 12>>D 、0y y 21>>5. 在反比例函数x1y -=的图像上，有三点)y ,x (),y ,x (),y ,x (332211，若321x 0x x >>>，则下列各式正确的是（）A 、213y y y >>B 、123y y y >>C 、321y y y >>D 、231y y y >>6. 反比例函数)0k (xk y ≠=的图像经过点（2，5），若点（100，n ）在反比例函数的图像上，则n 等于（）A 、10B 、5C 、2D 、1017. 已知点（2，－6）在函数y=kx 的图像上，则函数xk y =的图像在（）A 、第一、第二象限B 、第二、第三象限C 、第二、第四象限D 、第一、第四象限8. 某函数图像如图17－2－1所示，则该函数关系式可能是（）A 、y=xB 、x1y =C 、2x y =D 、|x |1y =规律方法应用：9. 满足函数)0k (x k y )1x (k y ≠=-=和函数的图像大致是（）10. 当x<0时，函数y=x 与x1y =在同一坐标系中的图像大致是（）11. 如图17－2－4所示，点P 是反比例函数x2y -=上一点，PD ⊥x 轴，垂足为D ，则=∆POD S _____。

17.1反比例函数复习测试题(人教版初中数学八年级下册)

第十七章反比例函数测试题（B ）一、选择题（每小题4分，共40分）1、下列关系式中，哪个等式表示y 是x 的反比例函数（）A ：23y x =B ： 2x y =C ：12y x =+D ：1y x=- 2、反比例函数y=2x的图象位于（）A ：第一、二象限B ：第一、三象限C ：第二、三象限D ：第二、四象限3、函数y=1x与函数y=x 的图象在同一平面直角坐标系内的交点个数是（）． A ：1个 B ：2个 C ：3个 D ：0个4、已知点A （-1，5）在反比例函数(0)ky k x=≠的图象上，则该函数的解析式为（） A ：1y x = B ：25y x = C ：5y x=- D ：5y x =5、若反比例函数(0)ky k x=≠经过（-2，3），则这个反比例函数一定经过（）A ：（-2，-3）B ：（3，2）C ：（3，-2）D ：（-3，-2） 6、某村的粮食总产量为a （a 为常数）吨，设该村的人均粮食产量为y 吨，人口数为x ，则y 与x 之间的函数关系式的大致图像应为（）7、如图，过反比例函数xy 2009=（x ＞0）的图象上任意两点A 、B 分别作x 轴的垂线，垂足分别为C 、D ，连接OA 、OB ，设△AOC 和△BOD 的面积分别是S 1、S 2，比较它们的大小，可得（）A ：S 1＞S 2B ：S 1＝S 2C ：S 1＜S 2D ：大小关系不能确定 8、已知反比例函数(0)ky k x=<的图象上有两点1122(,)(,)A x y B x y ,且12x x <则12y y -的值是( )A ：正数B ：负数C ：非正数D ：不能确定姓名班级A F 1y kx =+ 9、若y 与－3x 成反比例，x 与z4成反比例，则y 是z 的（） A ：正比例函数 B ：反比例函数 C ：一次函数 D ：不能确定10、函数与ky x=在同一坐标系内的大致图象是（）A ：B ：C ：D ：二、填空题（每小题4分，共40分） 11、反比例函数35y x=-中，比例系数k= ； 12、如果函数25(2)ky k x -=-是反比例函数，那么k= ；13、如图：在反比例函数(0)ky k x=≠图象上取一点A 分别作AC ⊥x 轴，AB ⊥y 轴，且S 矩形ABOC = 12，那么这个函数解析式为；14、已知函数(0)k y k x=≠，当12x =-时，6y =，则函数的解析式为； 15、反比例函数k y x =的图象经过3(,5)2-和（a ，－3），则a= ；16、已知正比例函数y kx =和反比例函数3y x=的图象都过A （m ，1），则m= ；正比例函数的解析式为；17、函数2y x=- 的图象，在每一象限内，y 随x 的增大而（填“增大”或“减小”）；18、如果反比例函数ky x=的图象经过点（－3，－4），那么这个函数的图象应分别分布在象限；19、已知y －2与x 成反比例，当x=3时，y=1，则y 与x 的函数关系式为； 20、反比例函数3k y x+=的图象在二、四象限，则k 的取值范围是。

2019年—2020年新人教版八年级数学下册反比例函数同步练习(精品试题)

反比例函数重点：1、概念：一般地，形如xk y =（k 为常数，0≠k ）的函数称为反比例函数，其中x 是自变量，且0≠x ；y 是函数，且0≠y 。

2、反比例函数的三种表示方法：xk y =，k xy =，1-=kx y 。

（0≠k ）3、反比例函数解析式的确定：（待定系数法）已知一个点的坐标),(y x 或一对x 、y 的值或双曲线上的一点即可求出k 的值。

4、反比例函数图像与性质：5、反比例函数)0(≠=k xy 的图像关于原点对称，也会关于直线x y ±=对称。

6、反比例函数)0(≠=k xk y 的图像位置随着k的增大，相对于坐标原点会越来越远。

7、反比例函数的比例系数k 的几何意义：过双曲线上任意一点作坐标轴的垂线所得的矩形面积均为k 。

2k S OPB=∆8、反比例函数与实际问题：运用反比例函数解决实际问题，首先要认真分析题目中所给各量之间的相互关系，然后根据所给的已知条件确定反比例函数关系式，从而进一步解决实际问题。

题型一求反比例函数解析式1. 如右图，某个反比例函数的图象经过点P ，则它的解析式为（） A. )0(1>=x x y B. )0(1>-=x x yC.)0(1<=x x yD.)0(1<-=x xy2. 如图是反比例函数xm y 2-=的图象，那么实数m 的取值范围是。

3. 点（1，2）在反比例函数1k y x-=的图象上，则k 的值是。

题型二反比例函数图像与性质4. 若反比例函数1y x=-的图象上有两点1(1)A y ，，2(2)B y ，，则1y ______2y 。

5. 已知反比例函数xy k =的图象在一、三象限，则直线k k +=x y 的图象经过6. 已知反比例函数y ＝－2x，下列结论不正确．．．的是（） A ．图象经过点（－2，1） B ．图象在第二、四象限C．当x＜0时，y随着x的增大而增大D．当x＞－1时，y＞2 7. 在反比例函数y=xm21-的图象上有两点A（x1,y1）,B (x2,y2),当x1＜0＜x2时，有y1＜y2,则m的取值范围是（）A、m＜0B、m＞0C、m＜21D、m＞218. 已知三点11(,)x y、22(,)x y、33(,)x y均在双曲线4yx=上，且123x x x<<<，则下列各式正确的是（）A、123y y y<<B、213y y y<<C、312y y y<< D、321y y y<<题型三反比例函数图像与几何图形9.如图，点A在双曲线6yx=上，且OA＝4，过A作AC⊥x轴，垂足为C，OA的垂直平分线交OC于B，则△ABC的周长为( )(A) (B)5 (C)10.如图，直线l和双曲线kyx=（0k>）交于A、B两点，P是线段AB上的点（不与A、B重合），过点A、B、P分别向x轴作垂线，垂足分别为C、D、E，连接OA、OB、OP，设△AOC的面积为1S、△BOD的面积为2S、△POE的面积为3S，则( )A．123S S S<<B．123S S S>>C．123S S S=>D．123S S S=<11.如图，平面直角坐标系中，OB在x轴上，∠ABO＝90º，点A的坐标为(1，2)．将△A90º，点O的对应点C恰好落在双曲线y ＝ kx(x ＞0)上，则k ＝（）A ．2B ．3C ．4D ．612．如图，直线ｌ是经过点（1,0）且与y 轴平行的直线．Rt△ABC 中直角边AC=4，BC=3．将BC 边在直线ｌ上滑动，使A ，B 在函数xk y =的图象上．那么k的值是（）A ．3B ．６Ｃ．12 D ．41513. 如图所示，点1A 、2A 、3A 在x 轴上，且32211A A A A OA ==,分别过点1A 、2A 、3A 作y 轴的平行线，与分比例函数)0(8>=x xy 的图像分别交于点1B 、2B 、3B ，分别过点1B 、2B 、3B 作x 轴的平行线，分别与y 轴交于点1C 、2C 、3C ，连接1OB 、2OB 、3OB ,那么图中阴影部分的面积之和为． 14. 如图，矩形ABCD 的对角线BD 经过坐标原点，矩形的边分别平行于坐标轴，点C在反比例函数ky x=的图象上.若点A 的坐标为（－2，－2），则k 的值为（）（）A ．-2B ．2C ．3D ．415.如图，有反比例函数1y x=、1y x=-的图象和一个以原点为圆心，2为半径的圆，则S =阴影．题型四反比例函数与一次函数16.在同一直角坐标系中，函数y=kx+k ，与y=xk -（k 0≠）的图像大致为（）17.如图，一次函数与反比例函数的图像相交于A 、B 两点，则图中使反比例函数的值小于一次函数的值的x 的取值范围是（）A ．x ＜－1B ．－1＜x ＜0，或x＞2C ．x ＞2D ．x ＜－1，或0＜x ＜2 [练习]1、已知反比例函数的图象经过点(21)P -，，则这个函数的图象位于（）A ．第一、三象限B ．第二、三象限C ．第二、四象限D ．第三、四象限2、某反比例函数的图象经过点(23)-，，则此函数图象也经过点（） A ．(23)-，B ．(33)--，C ．(23)，D ．(46)-，3、如图，若点A 在反比例函数(0)k y k x=≠的图象上，AM x ⊥轴于点M ，AMO △的面积为3，则k = ．4、如图是反比例函数xm y 2-=的图象，那么实数m 的取值范围是5、已知直线mx y =与双曲线xk y =的一个交点A 的坐标为（-1，-2）．则m =_____；k =____；它们的另一个交点坐标是______．6、如图,一次函数ｙ1=ｘ－1与反比例函数ｙ2=x2的图像交于点A(2,1),B(－1,－2),则使ｙ1＞ｙ2的ｘ的取值范围是（）A. ｘ＞2B. ｘ＞2 或－1＜ｘ＜0C. －1＜ｘ＜2D. ｘ＞2 或ｘ＜－17、如右图，△OPQ 是边长为2过点P ，则它的解析式是_______。

数学：《反比例函数》同步练习2(人教版八年级下)

数学：《反比例函数》同步练习2（人教版八年级下）一、选择题：1．函数①x y 2=，②x y =，③1-=xy ，④xy 8=中，是反比例函数的个数有（） A ．0个 B ．1个 C ．2个 D ．3个2. 下列函数中y 既不是x 的正比例函数，也不是反比例函数的是（）A. y x=-19B.x y -=10C. 152xy =- D . 214x y =3. 函数y kx b =+与y kxkb =≠()0的图象可能是（）A. B. C. D.4.函数922)2(--+=m mx m y 是反比例函数，则m 的值是（）A. m =4或m =-2B. m =4C. m =-2D. m =-15.在第三象限中，下列函数，y 随x 的增大而减小的有（）①3x y -= ②xy 8= ③52+-=x y ④65--=x y A ．1个 B ．2个 C ．3个 D ．4个6. 函数xy 2=与函数x y =的图象在同一平面直角坐标系内的交点个数是（） A ． 0个 B ．1个 C ．2个 D ．3个7.某气球充满一定质量的气体后，当温度不变时，气球内的气体的气压P （kPa ）是气体体积V （m 3）的反比例函数，其图象如图所示，当气球内的气压大于140kPa 时，•气球将爆炸，为了安全起见，气体体积应（）A ．不大于2435m 3 B ．不小于2435m 3 C ．不大于2437m 3 D ．不小于2437m 3第７题图第８题图8. 如图所示，A 、B 是函数xy 1=的图像上关于原点对称的任意两点，AC ∥y 轴，BC ∥x 轴，△ABC 的面积记为S ，则（）A.1=SB. 21<<SC. 2=SD.2>S9. 函数xy 1-=第四象限的图象上有两点),(11y x A 、),(22y x B 且21x x <，那么下列结论正确的是（） A.21y y < B.21y y > C.21y y = D.1y 与2y 的大小关系不能确定10. 若点（3，4）是反比例函数xm m y 122++=图象上一点，则此函数图象必经过点（）A.（3，－4）B.（2，－6）C.（4，－3）D. （2，6）二、填空题：11. 给出下列x 与y 的函数关系式：①，②，③，④，⑤，⑥13=xy ，其中是反比例函数的有。

第17章反比例函数单元复习测试(含答案)(人教新课标初二下)doc初中数学

337第17章反比例函数单元复习测试（含答案）（人教新课标初二下）doc 初中数学第17章反比例函数（时刻：120分钟分数：120分）得分 _______、选择题〔每题3分，共30分〕11 .以下函数，①y=2x ，②y=x ，③y=x 1，④y= 是反比例函数的个数有〔丨.x 1A . 0个B . 1个C . 2个D . 3个22 .反比例函数y= 的图象位于〔〕xA .第一、二象限B .第一、三象限C .第二、三象限D .第二、四象限3.矩形的面积为10,那么它的长y 与宽x 之间的关系用图象表示大致为〔〕k4.关于x 的函数y=k 〔 x+1丨和y=-〔 k 工0〕它们在同一坐标系中的大致图象是〔？〕.k5 .点〔3, 1〕是双曲线y=-〔 2 0〕上一点，那么以下各点中在该图象上的点是〔丨.x11A .〔 —，-9〕B .〔 3, 1〕C .〔 -1 , 3〕D .〔 6,-—〕326 .某气球充满一定质量的气体后，当温度不变时，气球内的气体的气压P 〔kPa 〕是气体体积 V 〔m 3〕体积应〔丨.24A.不大于一卅B35 不小于24 m33524.不大于一* .不小于2437的反比例函数，其图象如下图，当气球内的气压大于140kPa时，？气球将爆炸，为了安全起见，气体k 11. 一个反比例函数 y=k 〔 k z 0〕的图象通过点 P 〔-2 , -1〕，那么该反比例函数的解析式是 ________________ x12 .关于x 的一次函数y=kx+1和反比例函数 y=—的图象都通过点〔2, m 〕，那么一次函数的解析式是x13 . 一批零件300个，一个工人每小时做 15个，用关系式表示人数 x?与完成任务所需的时刻 y 之间的函数关系式为 _________ .114 .正比例函数y=x 与反比例函数y=—的图象相交于 A C 两点，AB 丄x 轴于B, CD?丄x 轴于D,如下图,x200 150 J (XI50 0.5 t.O L5 2 v (m l )（第6题）（7.某闭合电路中，电源电压为定值，电流中电流I 与电阻R 之间的函数关系的图象，663A . I=B .1=-C . 1=-R RiI 〔 A 〕与电阻那么用电阻2R 〔Q 丨成反比例，如右图所表示的是该电路 R 表示电流I?的函数解析式为〔〕.8 .函数y=—与函数y=x 的图象在同一平面直角坐标系内的交点个数是〔 xB . 2个〕.A . 1个 9 •假设函数 y=〔 m+2C . 3个D . 0个|m|-3是反比例函数，那么 m 的值是〔〕.-2.土 210 .点 A 〔-3 , y i 〕 ,B 〔-2 , y 2〕4,C 〔3, y 3〕都在反比例函数 y=—的图象上，那么〔丨.xA . y i <y 2<y 3B . y 3<y 2<y iC . y 3<y i <y 2D . y 2<y i <y 3二、填空题〔每题分，共27分〕4(0.8,120) It那么四边形ABCD 勺为 ________（第14题）第15题）(第19题）〔用” > 填空〕19 .两个反比例函数 y= — , y=—在第一象限内的图象如下图，点P 1, P 2, P 3 .......... P 2005,在反比例函数y=—X纵坐标分不是1, 3, ?5?……,?共2005年连续奇3y= 的图象交点依次是 Q 1〔X 1, y 1〕，Q 2〔x 2,x\\ . !! \\ . “ \\ !!> 、< 、 — 的图象上, 数，过点 y 2〕，Q 3 x x它们的横坐标分不是 X 1, X 2, X 3,…X 2005, P l , P 2, P 3,…，P 2005分不作y 轴的平行线与〔X 3, y 3〕，…， Q 2005〔 X 2005, y 2005〕，那么 y 2005 = 三、不定项选择题〔每题 4分，共8分，错选一项得 0分，？对而不全酌情给分〕 20 .当>0时，两个函数值1A . y=3x 与 y=x1 C . y=-2x+6 与 y=xy , 一个随x 增大而增大，另一个随x 的增大而减小的是〔？丨.c 匕1 .y=-3x 与 y=x 1 .y=3x-15 ^与 y=-—x1 在y=」的图象中，阴影部分面积为1的有〔〕.x四、运算题.〔8分〕如图，一次函数 y=kx+b y= m 〔 m 甘0〕的图象在第一象限交于x〔1〕求点A 、B 、D 的坐标；22. 〔k z 0〕的图象与x 轴、y 轴分不交于 A 、B?两点，且与反比例函数 C 点，CD 垂直于x 轴，垂足为 D, ?假设OA=OB=OD=1 求一次函数和反比例函数的解析式.15•如图，P 是反比例函数图象在第二象限上的一点，且矩形是 ___________ .3n 916.反比例函数丫=注_9的图象每一象限内，y 随x 的增大而增大，那么n=10 n 2X17. _______________________________________________________________ 一次函数y=3x+m 与反比例函数y= _3的图象有两个交点，当m= ________________________________________ 时有一个交点的纵坐标为 6.x k18. 假设一次函数y=x+b 与反比例函数y= 图象，在第二象限内有两个交点，？那么kxPEOF 勺面积为8，那么反比例函数的表达式x25 .〔 12分〕如图，一次函数 y=kx+b 的图象与反比例函数y=m 的图象交于A B 两点.823.〔 10分〕如图，点 A 〔4, m 〕，B 〔-1 , n 〕在反比例函数 y 的图象上，直线 AB?分不与x 轴，y 轴x相交于C 、D 两点，〔1〕求直线AB 的解析式.〔2〕C D 两点坐标.〔3〕S A AOC : S ^BOD 是多少？24.〔 11分〕y=y i -y 2, y i 与.x 成正比例，y 与x 成反比例，且当 x=1时，y=-14 , x=4时，y=3.求〔1〕y 与x 之间的函数关系式. 〔2〕自变量x 的取值范畴.1〔3〕当x=—时，y 的值.4〔1〕利用图中的条件，求反比例函数和一次函数的解析式. 〔2〕依照图象写出使一次函数的值大于反比例函数的值的x 的取值范畴.526 .〔14分〕如图，双曲线y在第一象限的一支上有一点C〔1, 5〕，?过点C?的直线y=kx+b〔k>0〕x与x轴交于点A〔a, 0〕.〔1〕求点A的横坐标a与k的函数关系式〔不写自变量取值范畴〕.〔2〕当该直线与双曲线在第一象限的另一个交点D的横坐标是9时，求△ COA?勺面积.1答案：1. B 2 . D 3 . A 4 . A 5 . B 6 . B 7 . A 8 . B 9 . A 10 . Dk b 0解得k 1b 1• 一次函数的解析式为 y=x+1 ,••点C 在一次函数y=x+1的图象上，？且CDL x 轴, • C 点的坐标为〔1, 2〕，又••点C 在反比例函数y=m 〔 m^ 0〕的图象上，x〔2〕依照图象可知，一次函数的图象在反比例函数的图象的上方时, 的值，即x>2或-1<x<0 .26.解：〔1 点 C 〔 1, 5〕在直线 y=-kx+b 上，• 5=-k+b ,又•••点 A 〔a , 0〕也在直线 y=-kx+b 上，-ak+b=0，二 b=ak11. y=2 12 . y=x+1 13 x .y=-20 14 . 2x15 . y=--x16. n=-3 17 . m=5 18 .<,> 22.解：〔1〕T OA=OB=OD=1•••点A B 、D 的坐标分不为 19 . 2004. 5 20 . A 、B 21 . A C 、DA 〔-1 , 0〕〔2〕•••点 AB 在一次函数 y=kx+b 〔 k 工 0〕 ,B 〔0, 1〕，的图象上，D 〔 1, 0〕. 23 . 24 . 25 . ••• m=2 ? •••反比例函数的解析式为〔1〕〔1〕 2 y=. x D 〔 0, y=2x-6 ;〔 2〕C 〔3, 0〕， y=2、. x - ^!提示：设 y=k 1 .. x -x自变量x 取值范畴是 -6〕；〔 3〕S A AOC S A BO =1 : k，再代入求k 1, k 2的值.xx>0 . 当 x=-时，y=2 J 1 -16「=255.4 V4解：〔1〕由图中条件可知，双曲线通过点•••仁口，• m=2, •••反比例函数的解析式为2A 〔 2,1〕2 y=_. x又点B 也在双曲线上，• n = — =-2，•点1B 的坐标为〔-1 , -2丨.•••直线y=kx+b 通过点A 、B.1 2k b解得k 12 k b b• 一次函数的解析式为 y=x-1 .?一次函数的值大于反比例函数5 将b=ak 代入5=-k+a 中得5=-k+ak , • a= +1.k 〔2〕由于D点是反比例函数的图象与直线的交点5 y 二9•' ak=5+k，•‘• y=-8k+5③y 9k ak将①代入③得:5 =-8k+5 ,• k=5-,a=1099-X 10X 5=25• A〔10,0〕，又知〔1, 5〕，•'• S^COA =2。

数学：《反比例函数》同步练习1(人教版八年级下)

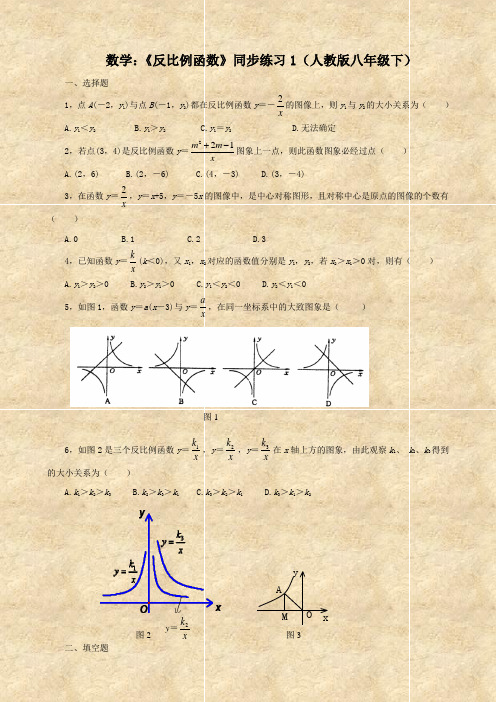
数学：《反比例函数》同步练习1（人教版八年级下）一、选择题1，点A (－2，y 1)与点B (－1，y 2)都在反比例函数y ＝－x 2的图像上，则y 1与y2的大小关系为（） A.y 1＜y 2 B.y 1＞y 2 C.y 1＝y 2 D.无法确定2，若点(3，4)是反比例函数y ＝221m m x+-图象上一点，则此函数图象必经过点（） A.(2，6) B.(2，－6) C.(4，－3) D.(3，－4)3，在函数y ＝x 2，y ＝x +5，y ＝－5x 的图像中，是中心对称图形，且对称中心是原点的图像的个数有（）A.0B.1C.2D.34，已知函数y ＝k x(k ＜0)，又x 1，x 2对应的函数值分别是y 1，y 2，若x 2＞x 1＞0对，则有（） A.y 1＞y 2＞0 B.y 2＞y 1＞0 C.y 1＜y 2＜0 D.y 2＜y 1＜0 5，如图1，函数y ＝a (x －3)与y ＝a x ，在同一坐标系中的大致图象是（）6，如图2是三个反比例函数y ＝1k x ，y ＝2k x ，y ＝3k x 在x 轴上方的图象，由此观察k 1、 k 2、k 3得到的大小关系为（）A.k 1＞k 2＞k 3B.k 2＞k 3＞k 1C.k 3＞k 2＞k 1D.k 3＞k 1＞k 2二、填空题 y ＝2k x 图2 图1图3 O A M xy7，已知反比例函数y ＝k x(k ≠0)与一次函数y ＝x 的图象有交点，则k 的范围是______. 8，已知反比例函数y ＝32m x -，当m ＿＿＿时，其图象的两个分支在第二、四象限内；当m ＿＿＿时，其图象在每个象限内y 随x 的增大而减小.9，若反比例函数y ＝3k x -的图象位于一、三象限内，正比例函数y ＝(2k －9)x 过二、四象限，则k 的整数值是______.10，已知点P (1，a )在反比例函数y ＝k x (k ≠0)的图象上，其中a ＝m 2+2m +3(m 为实数)，则这个函数的图象在第______象限.11，写出一个反比例函数，使它的图象在第二、四象限，这个函数的解析式是_____.12，已知反比例函数y ＝xk (k ≠0)，当x ＞0时，y 随x 的增大而增大，那么一次函数y ＝kx －k 的图像过象限. 三、解答题13，反比例函数的图象过点（2，－2），求函数y 与自变量x 之间的关系式，它的图象在第几象限内？y 随x 的减小如何变化？请画出函数图象，并判断点（－3，0），（－3，－3）是否在图象上？14，若反比例函数y ＝24212-+m x m 的图象经过第二、四象限，求函数的解析式.15，如图3所示，一个反比例函数的图象在第二象限内，点A 是图象上的任意一点，AM ⊥x 轴于M ，O 是原点，若S △AOM ＝3，求该反比例函数的解析式，并写出自变量的取值范围.16，点P ，Q 在y ＝－3x的图象上. （1）若P （1，a ），Q （2，b ），比较a ，b 的大小；（2）若P （－1，a ），Q （－2，b ），比较a ，b 的大小；（3）你能从中发现y 随x 增大时的变化规律吗？（4）若P （x 1，y 1），Q （x 2，y 2），x 1＜x 2，你能比较y 1与y 2的大小吗？17，(08达州市)平行于直线y x =的直线l 不经过第四象限，且与函数3(0)y x x=>和图象交于点A ，过点A 作AB y ⊥轴于点B ，AC x ⊥轴于点C ，四边形ABOC 的周长为8．求直线l 的解析式．18，已知变量y 与x 成反比例，并且当x ＝2时，y ＝－3.（1）求y 与x 的函数关系式；（2）求当y ＝2时x 的值；（3）在直角坐标系内画出（1）小题中函数图象的草图.答案：一、1，A ；2，A ；3，C ；4，C ；5，D ；6，C .二、7，k ＞0；8，＜23、＞23；9，4；0，在一、三象限.提示：因为m 2+2m +3＞0，则a ＞0，点P (1，a )在图象上，则k ＞0；11，答案不唯一，比例系数小于0；12，一、二、四.三、13，y ＝－4x，二、四，在每一象限内y 随x 的减小而减小，略，点（－3，0），（－3，－3）都不在图象上；14，y ＝－9x ；15，y ＝－6x (x ＜0)；16，（1）b ＞a ，（2）a ＞b ，（3）在每个象限内，y 随x 的增大而增大，（4）当位于同一分支上时，y 1＜y 2，当位于不同分支上时，y 1＞y 2；17，【答案】设A 点的坐标为（x,y ）,由题意得2x+2y=8,整理得y= 4-x 即A 的坐标为（x,4-x ）,把A 点代入3(0)y x x=>中，解得x=1或x=3 由此得到A 点的坐标是（1,3）或（3,1）又由题意可设定直线l 的解析式为y=x+b （b ≥0）把（1,3）点代入y=x+b ，解得 b ＝2把（3,1）点代入y=x+b ，解得 b=－2，不合要求，舍去所以直线l 的解析式为y=x+218，y ＝－6x ，（2）x ＝－3，（3）略. A B OCyx 3(0)y x x=> l。

八年级数学下册17.1反比例函数阿基米德杠杆原理素材新人教版

八年级数学下册17.1反比例函数阿基米德杠杆原理素材新人教版阿基米德杠杆原理阿基米德在《论平面图形的平衡》一书中最早提出了杠杆原理.他首先把杠杆实际应用中的一些经验知识当作"不证自明的公理"，然后从这些公理出发，运用几何学通过严密的逻辑论证，得出了杠杆原理.这些公理是：(1)在无重量的杆的两端离支点相等的距离处挂上相等的重量，它们将平衡；(2)在无重量的杆的两端离支点相等的距离处挂上不相等的重量，重的一端将下倾；(3)在无重量的杆的两端离支点不相等距离处挂上相等重量，距离远的一端将下倾；(4)一个重物的作用可以用几个均匀分布的重物的作用来代替，只要重心的位置保持不变.相反，几个均匀分布的重物可以用一个悬挂在它们的重心处的重物来代替；似图形的重心以相似的方式分布……正是从这些公理出发，在"重心"理论的基础上，阿基米德又发现了杠杆原理，即"二重物平衡时，它们离支点的距离与重量成反比."阿基米德对杠杆的研究不仅仅停留在理论方面，而且据此原理还进了一系列的发明创造.据说，他曾经借助杠杆和滑轮组，使停放在沙滩上的桅船顺利下水.在保卫叙拉古免受罗马海军袭击的战斗中，阿基米德利用杠杆原理制造了远、近距离的投石器，利用它射出各种飞弹和巨石攻击敌人，曾把罗马人阻于叙拉古城外达3年之久.这里还要顺便提及的是，在我国历史上也早有关于杠杆的记载.战国时代的墨家曾经总结过这方面的规律，在《墨经》中就有两条专门记载杠杆原理的.这两条对杠杆的平衡说得很全面.里面有等臂的，有不等臂的；有改变两端重量使它偏动的，也有改变两臂长度使它偏动的.这样的记载，在世界物理学史上也是非常有价值的.杠杆平衡条件：要使杠杆平衡，作用在杠杆上的两个力（动力和阻力）的大小跟它们的力臂或反比.动力×动力臂=阻力×阻力臂，用代数式表示为：F· L1=W·L2式中，F表示动力，L1表示动力臂，W表示阻力，L2表示阻力臂.从上式可看出，欲使杠杆达到平衡，动力臂是阻力臂的几倍，动力就是阻力的几分之一.在使用杠杆时，为了省力，就应该用动力臂比阻力臂长的杠杆；如欲省距离，就应该用动力臂比阻力臂短的杠杆.因此使用杠杆可以省力，也可以省距离.但是，要想省力，就必须多移动距离；要想少移动距离，就必须多费些力.要想又省力而又少移动距离，是不可能实现的.杠杆五要素：三点两臂：支点（用O表示），动力（F）作用点，阻力（W）作用点，杠杆的固定转轴就是通常所说的“支点”，从转轴到动力作用线的垂直距离叫“动力臂”，从转轴到阻力作用线的垂直距离叫“阻力臂”.【动力】任何机械，不论是简单的还是复杂的，在工作时，总要受到两种力的作用：一种是推动机械的力叫作“动力”，另一种是阻碍机械运动的力叫作“阻力”.动力可以是人力，也可以是畜力、风力、电力、水力、蒸汽压力等，阻力除了我们要克服的有用阻力之外，还有一些是不可避免的无用阻力.【作用线】通过力的作用点沿力的方向所引的直线，叫作“力的作用线”.【动力臂】从支点到力的作用线的垂直距离叫“力臂”.从支点到动力的作用线的垂直距离L1叫作“动力臂”；从支点到阻力的作用线的垂直距离L2叫作“阻力臂”.如果把从动力点到支点的棒长距离作为动力臂，或把从阻力点到支点的棒长距离作为阻力臂，这种认识是错误的.这是因为对动力臂和阻力臂的概念认识不清所致.【阻力臂】见动力臂条.杠杆的分类及应用：对杠杆的分类一般是两种方法.第一种是以支点、阻力点和动力点所处的位置来分的；另一种是按省力或费力来区分的.无论怎样来划分，总离不开省力、费力、不省力也不费力这几种情况.分别简述如下：第一种分类法第一类杠杆：是动力和有用阻力分别在支点的两边.这类杠杆不省力也不费力.例如，剪金属片用的剪刀，刀口很短，它的机械利益远大于1.这是因为金属板很硬，刀口短，刀把长，即动力臂大于阻力臂，可以少用力.属于这种情况的杠杆还有克丝钳等.家庭裁衣剪布用的剪刀，把与刃基本是等长的，即动力臂等于阻力臂，属于不省力也不费力的类型.因为布的厚度较薄，不需太大的力，剪布要直故刀口要长些，为此用力不大，布剪的也直.属于这种类型的还有物理天平.又如理发用的剪刀，刀口很长，即动力臂小于阻力臂，它的机械利益小于1.这是因为剪发本来不需要多大的力，刀口长一些，能够剪得快一些和齐一些.第二类杠杆：是支点和动力点分别在有用阻力点的两边.这类杠杆的动力臂大于阻力臂，其机械利益总是大于1，所以总是省力的.例如，用铡刀铡草、独轮车等都是这类杠杆.第三类杠杆：是支点和有用阻力点分别在动力点的两边，这类杠杆的动力臂小于阻力臂，其机械利益总是小于1，所以总是费力的.例如，缝纫机的脚踏板、夹食品的竹夹子都属于这类杠杆.第二种分类法第一类杠杆：是省力的杠杆，力点离支点愈远则愈省力，即动力臂大于阻力臂.例如，羊角锤、木工钳、独轮车、汽水板子、铡刀、开瓶器、榨汁器、胡桃钳等等.第二类杠杆：是费力的杠杆，力点离支点愈近就愈费力，即动力臂小于阻力臂.如镊子、钓鱼杆、理发用的剪刀.第三类杠杆：不省力也不费力的杠杆，重点、力点距离支点一样远，就不省力也不费力，即动力臂等于阻力臂，这样的杠杆只是改变了用力的方向.如夭平、定滑轮等.有一些杠杆例如：剪刀、钉锤、拔钉器……可能省力可能费力，也可能既不省力也不费力.这要看力点和支点的距离：1.剪较硬物体：要用较大的力才能剪开硬的物体，这说明阻力较大.用动力臂较长、阻力臂较短的剪刀.2.剪纸或布：用较小的力就能剪开纸或布之类较软的物体，这说明阻力较小，同时为了加快剪切速度，刀口要比较长.用动力臂较短、阻力臂较长的剪刀.3.剪树枝：修剪树枝时，一方面树枝较硬，这就要求剪刀的动力臂要长、阻力臂要短；另一方面，为了加快修剪速度，剪切整齐，要求剪刀刀口要长.用动力臂较长、阻力臂较短，同时刀口较长的剪刀.扳手，门，抽水马桶，秤，天平，自行车脚踏板，剪刀、开罐器、钳子、指甲刀、自动锁、电灯开关，螺丝起子、火车铁轨交换控制杆等等自行车中的杠杆原理前触闸：前触闸是靠杠杆原理制动的.当手握紧闸把时，闸把的另一头将接头、拉杆、拉管向下压，使闸皮向下压至与轮胎接触，产生摩擦制动力.其缺点是刹车效果与轮胎充气程度有关.充气不足时，会使摩擦力减小，影响刹车效果.脚蹬是轮轴，但是轮轴也用了杠杆的原理....自行车是一种机械，它由许多的简单机械构成：执行部分的车把，控制部分中的车闸把，后闸部件中的前曲拐，后曲拐及支架，货架上的弹簧夹，车铃的按钮等部件都属于杠杆. 传动部分中的脚蹬...1：脚踏板是动力，链条是阻力.支点是中间圆盘的轴2：后轮外圈的车胎是阻力，自行车链条是动力.车轮轴是支点控制刹车闸的杠杆：车把上的闸把是省力杠杆，人们用很小的力就能使车闸以比较大的压力上一页下一页。

八年级数学下册 17.1《反比例函数》习题精选新人教版

17.1.1反比例函数的意义姓名【题组练习1】1. 下列函数，①y=2x，②y=x，③y=x -1，④y=11x +是反比例函数的个数有（）． A ．0个 B ．1个 C ．2个 D ．3个 2. 下列函数中，是反比例函数的是（） A. 2x y =-B. 11y x =-C. 12y x=- D. 21y x =3. 若()21a y a x -=-是反比例函数，则a 的值为（）A ． 1B ．-1C ． 0D ．任意实数 4. 函数y=2006x自变量x 的取值范围是（）A ．x ＞0B ．x ＜0C ．x=0D ．x≠0 5.若y 与3x -成反比例，x 与4z成正比例，则y 是z 的（） A 、正比例函数 B 、反比例函数 C 、一次函数 D 、不能确定 6. 若关于x 、y 的函数y=5x 25k -是反比例函数，则k=________．【知识点1小结】把形如ky x=， k 为常数，且0k ≠的函数称为反比例函数。

其中x 是自变量，y 是函数，自变量x 的取值是不等于0的一切实数。

【题组练习2】7. 若函数y=kx中，当x=2时，y=-3，则函数解析式是_______． 8. 已知y -2与x 成反比例，当x =3时，y =1，则y 与x 间的函数关系式为；9. 某厂有煤1500吨，求得这些煤能用的天数y 与平均每天用煤吨数x 之间的函数关系式为。

10. 已知圆柱的侧面积是π102cm ，若圆柱底面半径为r cm ，高为h cm ，则h 与r 的函数关系式是。

【知识点2小结】对于反比例函数解析式k y x=，其中x 、y 都为变量，k 是一个不等于零的常数，只要k 的值确定了，反比例函数的解析式也就确定．也就是说确定一个反比例函数关系的关键是求得非零常数k 的值，可利用待定系数法求k 的值。

12．【易错题】已知y 是x 的反比例函数，且x=0.3时，y=10．（1）写出y 与x 的函数关系式．（2）求当x=2时y 的值．第6题图13．【易错题】已知y=y 1-y 2，y 1与x 成反比例，y 2与x 2成正比例，且当x=-1时y=-5，当x=1时，y=1，求y 与x 之间的函数关系式．17.1.2反比例函数的图像和性质姓名【题组练习1】1. 反比例函数y=kx经过A （-1，3）点，则k 的值为（） A ．2 B ．1.5 C ．-3 D ．-322. 已知点（2，-1）在函数y=kx 的图像上，则函数y=kx图像在第（）象限A ．一、二B ．二、三C ．二、四D ．一、四 3. 反比例函数y=kx（k≠0）的图像经过点（2，5），若点（100，m ）•在反比例函数的图像上，则m 等于（）．A ．10B ．5C ．2D ．1104. 若点(34)，是反比例函数221m m y x+-=图象上一点，则函数图象必经过点（）Ａ．(26)，Ｂ．(26)-，Ｃ．(43)-，Ｄ．(34)-，5. 图象经过点（-2，5）的反比例函数的解析式是 .6. 如图所示，直线y=2x 与双曲线y=kx的图象的一个交点坐标为（2，4），•则它们的另一个交点坐标为 .【知识点1小结】反比例函数ky x=，其中x ，y 都为变量，只有一个待定系数k ，确定了k 的值，也就确定了反比例函数解析式，而由函数图像上的点的坐标，代入y=kx 中即可求出k 的值，从而确定反比例函数的关系式。

新人教版八年级下册第十七章反比例函数学案稿配套练习册(含答案)-1

第十七章反比例函数（答案）一次函数与反比例函数反比例函数反比例函数一次函数一次函数解析式性质图象性质xyox yox yo x yo x yo x yok ＞0k ＜0b ＜0,图象在一三四象限b=0,图象在一三象限b ＞0,图象在一二三象限b ＜0,图象在二三四象限b=0,图象在二四象限b ＞0,图象在一二四象限k ＞k ＜0Y 随x 的增大而增大Y 随x 的增大而减小形如y=kx+b (k.b 为常数，k ≠0)注意：过原点当b=0时，是正比例函数一条直线图象解析式应用应用）为常数，（形如0≠=k k xk y k ＞0k ＜0xyo xyo图象在二四象限图象在一三象限双曲线Y 随x 的增大而减小每一象限内Y 随x 的增大而增大每一象限内k ＞k ＜柱形储藏室轮船卸货力学问题电学问题实际问题，图象在第一象限最优方案17.1.1反比例函数的意义【学习目标】1.能判断一个函数式是否为反比例函数．（重点）2.会利用待定系数法求反比例函数的解析式．（重点、难点）【自主预习】1.在每天从家到学校的过程中，路程S 一定，行走的速度v 越快，到学校所花费的时间t 越少，其中速度v 与时间t 成反比例关系.用一定数额的钱M 购买商品，当单件商品的价格p 越低时，购买的件数n 越多.反之，当单件商品的价格p 越高时，购买的件数n 越少.舞台灯光的亮暗是通过改变电阻R 来控制电流I 的变化实现的。

当电压U=220V 时, 电阻R 越大，电流I 越小，灯光就越暗；电阻R 越小，电流I 越大，灯光就越亮.生活中的反比例关系比比皆是.你能从熟悉的生活环境中举出一些成反比例关系的实例吗？试一试吧！提示：答案不唯一。

例如：人的视觉机能受运动速度的影响很大,行驶中司机在驾驶室内观察前方物体是动态的,车速增加,视野变窄，其车速与视野成反比例关系。

2．用函数解析式表示下列问题中变量之间的对应关系：（1）京沪线铁路全长1463km ，某次列车的平均速度v km/h •随此次列车的全程运行时间t h的变化而变化，其关系可用函数式表示为：t v 1463=．（2）某住宅小区要种植一个面积为1000m 2矩形草坪，草坪的长y m 随宽x m 的变化而变化，可用函数式表示为xy 1000=．（3）已知北京市的总面积为241068.1km ⨯，人均占有的土地面积2km S /人，随全市总人口n 人的变化而变化，其关系可用函数式表示为nS 41068.1⨯=．【自主探究】1.从上面的几个例子中，你有什么发现？发现：①每个例子都涉及两种相关联的量，一种量变化，另一种量也随着变化；②一种量增加了，另一种量就减少，若它减少了，另一种量就增加； ③符合小学所学的反比例关系.v S t =，pM n =，R I 220= 归纳：形如）为常数，（0≠=k k xk y 的函数称为反比例函数. 2.已知y 是x 的反比例函数，当x=2-时，y=6-．（1）写出y 与x 的函数关系式；（2）求当x=4-时y 的值．解：（1）∵y 是x 的反比例函数，∴可设xk y =∵当x=2-时，y=6-，∴62-=-k ，即12=k∴y 与x 的函数关系式为xy 12=（2）当x=4-时，412-=y ，即3-=y【自主检测】1．下列函数中是反比例关系的有 ②③④⑥⑦⑩ （填序号）.①4x y -= ②x y 2-= ③131+=x y ④2=xy ⑤2y x =1 ⑥x y 43-=⑦21xy = ⑧1-=x y ⑨2211x y -= ⑩x ky =k (为常数，)0≠k2．（2008·安徽）函数xky =的图象经过点A （1，—2），则k 的值为（ D ）.A ．21 B. 21- C. 2 D. —23．y=(m-1)2-m x 是反比例函数，则m= -1 ．4.小明家离学校 1.5km ，小明步行上学需x min ，那么小明的步行速度min)/(m y 可以表示为xy 1500=；水平地面上重1500N 的物体，与地面的接触面积为x 2m ，那么该物体对地面的压强)/(2m N y 可以表示为x y 1500=.函数表达式xy 1500=还可以表示许多不同情境中变量之间的函数关系，请你再列举一例.解：某企业要生产1500辆农用车，每天能生产x 辆，那么该企业完成任务的天数y 可以表示为xy 1500=5．已知y 是2x 的反比例函数，当x=12时，y=1．（1）求y 与x 的函数关系式；（2）当x=-14时，求y 的值；（3）当y=-12时，求x 的值．解：（1）∵y 是2x 的反比例函数，∴可设xk y 2=，又∵当x=21时，y=1，∴解得21=k∴y 与x 的函数关系式为x y 21=；（2）当41-=x 时，2-=y ；（3）当y=-12时，1-=x 【自主小结】17.1.2 反比例函数的图像与性质（一）【学习目标】1.会描点画反比例函数的图象. （重点）2.能结合图形分析反比例函数的性质．（重点、难点）【自主预习】我们已经知道一次函数)0(≠+=k b kx y 的函数图像是一条直线，那么反比例函数)0(≠=k k x ky 为常数，的图像是什么样呢？请利用“描点”的方法画出反比例函数xy 4=和x y 4-=的图象．反比例函数概念求函数解析）（0≠=k xky解：（1）列表：x...... -4 -2 -1 1 2 4 (x)y 4=...... -1 -2 -4 4 2 1 (x)y 4-= ……124-4-2-1（2）描点：（图略）（3）连线：【自主探究】1.观察上述图象并与课本上函数xy 6=和x y 6-=的图象进行比较，你有什么发现？归纳：①.反比例函数的图像是双曲线；②.当k >0时，双曲线的两支分别位于第一、第三象限，在每个象限内y 值随x 值的增大而减小；当k <0时，双曲线的两支分别位于第二、第四象限，在每个象限内y 值随x 值的增大而增大；③渐近性：反比例函数的图象无限接近x 轴，y 轴，但永远达不到x 轴，y 轴； ④对称性：反比例函数的图象既是中心对称图形，又是轴对称图形.【自主检测】1．请你写出一个反比例函数的解析式，使它的图象在第一、三象限．解：答案不唯一.例如：xy 1=2．下列图象中，是反比例函数的图象的是（ D ）3．在反比例函数y=kx（k<0）的图象上有两点A （x 1，y 1），B （x 2，y 2），且x 1>x 2>0，则y 1-y 2的值为（ A ）A ．正数 B. 负数 C. 非正数 D. 非负数4．已知反比例函数xm y 1-=，当m < 1 时，在图象的每一支上，y 值随x 的增大而增大．5．已知反比例函数y=2k x-的图象在第一、三象限内，则k >2 ． 6．若一次函数y=kx+b 的图象经过第一、二、四象限，则反比例函数y=kbx的图象一定在第二、四象限．7（拓展）．两个不同的反比例函数的图象是否会相交？为什么？解：两个不同的反比例函数的图象不会相交假设反比例函数x k y 1=与xk y 2=（21k k ≠）的图象相交，则方程组⎪⎩⎪⎨⎧==xk y x k y 21就有解，不妨设解为⎩⎨⎧==ny m x ，则mn k k ==21 矛盾于21k k ≠，所以假设不成立，原命题成立.【自主小结】17.1.2 反比例函数的图像与性质（二）【学习目标】能用反比例函数的定义和性质解决有关的数学问题．（重点、难点）【自主预习】在反比例函数xy 4=的图象上任取一点P ，过这一点分别作x 轴、y 轴的平行线，平行线与坐标轴围成的矩形的面积是多少？矩形的面积会随着点P 的变化而变化吗？请你试一试.解：矩形的面积是4，矩形的面积不会随着点P 的变化而变化设点P 的坐标为()n m ,，∵点P 在函数xy 4=的图象上，∴4=mn 又∵n PA =，m PB =，∴四边形PAOB 的面积为4【自主探究】反比例函数图像：双曲线性质1.已知反比例函数的图象经过点A （2，-6）（1）这个函数的图象分布在哪些象限？y 随x 的增大而如何变化？（2）点B （-3，4）、C （-212，445）和D （2，-5）是否在这个函数的图象上？解：（1）设反比例函数的解析式为xky =，∵反比例函数的图象经过点A （2，-6）∴62-=k，即012<-=k ，∴这个函数的图象分布在第二、四象限，在每个象限内，y 随x 的增大而增大；（2）∵1243-=⨯-，12544212-=⨯-，()121052-≠-=-⨯ ∴点B 、点C 在这个函数的图象上，点D 不在这个函数的图象上. 2.如图，直线y=kx 与反比例函数y=x6-的图象相交于点A 、B ，过点A 作AC 垂直于y 轴于点C ，求ABC S ∆．解：如图，设点A 的坐标为()n m ,-，其中0,0>>n m ，根据函数的对称性，可得()n m B -,，∵过点A 作AC 垂直于y 轴于点C ，∴点C 的坐标为()n ,0 ∴m m AC =-=，AC 边上的高为()n n n 2=-- 又∵直线y=kx 与反比例函数y=x6-的图象相交于点A 、B ， ∴6=mn ，∴6221==⋅=∆mn n AC S ABC【自主检测】1.点（1，3）在反比例函数y=kx的图象上，则k= 3 ，在图象的每一支上，y 随x•的增大而减小．2.已知正比例函数y=k 1x （k 1≠0）与反比例函数y=2k x（k 2≠0）•的图象有一个交点的坐标为（-2，-1），则它的另一个交点的坐标是（2，1）．3.已知函数y=-kx （k ≠0）和y=-4x的图象交于A 、B 两点，过点A 作AC 垂直于y 轴，垂足为C ，则BO C S ∆ =__2___．4．如图，在同一直角坐标系中，函数y=kx-k 与y=kx（k ≠0）的图象大致是（ D ）A B C D5．如图，点A 、B 在反比例函数y=kx的图象上，且点A 、B 的横坐标分别为a ，2a （a>0），AC ⊥x 轴，垂足为点C ，且△AOC 的面积为2．（1）求该反比例函数的解析式；（2）若点（-a ，y 1），（-2a ，y 2）在该反比例函数的图象上，试比较y 1与y 2的大小．解：（1）∵点A 在反比例函数y=kx的图象上，且点A 的横坐标为a ，∴点A 的坐标为⎪⎭⎫⎝⎛a k a ,，∴a k AC =，a OC =∵△AOC 的面积为2，∴ 221=⋅OC AC ，解得4=k∴该反比例函数的解析式为xy 4=（2）∵a>0，∴-a>-2a ，而04>=k∴根据反比例函数的性质，可得y 1<y 2 【自主小结】17.2 实际问题与反比例函数（一）【学习目标】掌握从实际问题中建构反比例函数模型（学科内应用）．（重点、难点）【自主预习】某校科技小组进行野外考察，途中遇到一片十几米宽的烂泥湿地，为了安全，迅速通过这片湿地，他们沿着前进路线铺垫了若干块木板，构筑成一条临时通道，从而顺利完成了任务．（1）请你解释他们这样做的道理.（2）当人和木板对湿地的压力一定时，随着木板面积S （2m ）的变化，人和木板对地面的压强p （Pa ）将如何变化？（3）如果人和木板对湿地的压力合计600N ，那么①用含S 的代数式表示p ，p 是S 的反比例函数吗？为什么？②当木板面积为0.22m 时，压强是多少？③如果要求压强不超过6 000Pa ，木板面积至少要多大？ ④在直角坐标系中，作出相应的函数图象． ⑤请利用图像对（2）和（3）作出直观解释.解：（1）他们这样做主要是为了减少人和木板对地面压强，避免人陷入烂泥湿地；（2）当人和木板对湿地的压力一定时，随着木板面积S （2m ）的增大，人和木板对地面的压强p （Pa ）将减小；当木板面积S （2m ）减小，人和木板对地面的压强p （Pa ）将增大；反比例函数解题技巧数形结合思想待定系数法（3）①SP 600=,P 是S 的反比例函数.因为函数SP 600=符合反比例函数的基本形式，满足反比例函数的概念；②当木板面积为0.22m 时，压强是3000 Pa ；③如果要求压强不超过6 000Pa ，木板面积至少要0.12m ④图略⑤根据图形可知，木板面积越小，人和木板对地面的压强就越大；木板面积越大，人和木板对地面的压强就越小；无论木板面积多大，人和木板对地面的压强始终存在. 【自主探究】如右图，某玻璃器皿制造公司要制造一种容积为1升（1升＝1•立方分米）的圆锥形漏斗．（1）漏斗口的面积S 与漏斗的深d 有怎样的函数关系？（2）如果漏斗口的面积为100厘米2，则漏斗的深为多少？解：（1）根据圆锥的体积公式有：131=Sd ∴漏斗口的面积S 与漏斗的深d 的函数关系为dS 3=（2）如果漏斗口的面积为100厘米2，即1=S 平方分米 ∴漏斗的深3=d 分米30=厘米.【自主检测】1．已知甲、乙两地相距s km ，汽车从甲地匀速行驶到乙地，•如果汽车每小时耗油量为aL ，那么从甲地到乙地汽车的总耗油量y （L ）与汽车的行驶速度v （km/h ）的函数图象大致是（ C ）2．面积为2的△ABC ，一边长为x ，这边上的高为y ，则y 与x•的变化规律用图象表示大致是（ C ）3．（1）已知某矩形的面积为202cm ，写出其长y 与宽x 之间的函数表达式；（2）当矩形的长为12cm 时，求宽为多少？当矩形的宽为4cm ，求其长为多少？（3）如果要求矩形的长不小于8cm ，其宽至多要多少？解：（1）当某矩形的面积为202cm 时，其长y 与宽x 之间的函数表达式为xy 20=；（2）当矩形的长为12cm 时，宽为cm cm 351220= 当矩形的宽为4cm 时，长为cm cm 5420=（3）如果要求矩形的长不小于8cm ，其宽至多cm 5.24．新建成的住宅楼主体工程已经竣工，只剩下楼体外表面需要贴瓷砖，已知楼体外表面的面积为5×103m 2．（1）所需的瓷砖块数n 与每块瓷砖的面积S 有怎样的函数关系？（2）为了使住宅楼的外观更漂亮，开发商决定采用灰、白、蓝三种颜色的瓷砖，每块瓷砖的面积都是80cm 2，灰、白、蓝瓷砖使用比例为2：2：1，•则需要三种瓷砖各多少块？解：（1）所需的瓷砖块数n 与每块瓷砖的面积S 的函数关系为Sn 5000=（2）∵每块瓷砖的面积都是80cm 2=0.008m 2，∴625000008.05000==n （块）∴需要灰瓷砖25000052625000=⨯（块），白瓷砖250000块，蓝瓷砖125000块.【自主小结】17.2 实际问题与反比例函数（二）【学习目标】掌握从实际问题中建构反比例函数模型（生活中应用）．（重点、难点）【自主预习】数学来源于生活又服务于生活.请同学们认真思考以下题目，把你的做法和想法在小组内交流，选取组内最好的意见在全班交流.某商场出售一批进价为2元的贺卡，在市场营销中发现此商品的日销售单价x 元与日销售量y 之间有如下关系：x （元） 3456y （个）20 15 12 10（1）猜测并确定y 与x 之间的函数关系式，并画出图象；（2）设经营此贺卡的销售利润为W 元，试求出W 与x 之间的函数关系式，若物价局规定此贺卡的售价最高不能超过10元／个，请你求出当日销售单价x•定为多少元时，才能获得最大日销售利润？解：（1）y 与x 之间的函数关系式为：xy 60=，图略；（2）∵xx x y x W 1206060)2()2(-=⋅-=⋅-=，而物价局规定此贺卡的售价最高不能超过10元／个∴当10=x 时，才能获得最大日销售利润48=W 元【自主探究】码头工人以每天50吨的速度往一艘轮船上装卸货物，把轮船装载完毕恰好用了8天时间．（1）轮船到达目的地后开始卸货，卸货速度v （单位：吨/天）与卸货时间t （单位：天）之间有怎样的函数关系？（2）由于遇到紧急情况，船上的货物必须在不超过5日内卸反比例函数学科内应用面积问题体积问题图象均在一项限变量取值大于0载完毕，那么平均每天至少要卸多少吨货物？解：（1）轮船到达目的地后开始卸货，卸货速度v （单位：吨/天）与卸货时间t （单位：天）之间的函数关系为tv 400=（2）由于遇到紧急情况，船上的货物必须在不超过5日内卸载完毕，则5400≤=vt ，解得80≥v ，即平均每天至少要卸80吨货物【自主检测】1.一辆汽车往返于甲、乙两地之间，如果汽车以50千米/时的平均速度从甲地出发，则经过6小时可到达乙地．（1）甲、乙两地相距 300 千米；（2）如果汽车把速度提高到v （千米/时），则从甲地到乙地所用时间为t （小时），请写出t 与v 之间的函数关系式vt 300=；（3）因某种原因，这辆汽车需在5小时内从甲地到达乙地，则此时汽车的平均速度至少应是每小时 60 千米；（4）已知汽车的平均速度最大可达80千米/时，那么它从甲地到乙地最快需要 3.75 小时.2.某学校冬季储煤120吨，若每天用煤x 吨，经过y 天可以用完．（1）请写出y 与x 之间的函数关系式；（2）画出函数的图象；（3）当每天的用煤量为1.2～1.5吨时，这些煤可以用的天数在什么范围？解：（1）y 与x 之间的函数关系为xy 120= （2）图象略（3）当2.1=x 时，100=y ；当5.1=x 时，80=y ；∴当每天的用煤量为1.2～1.5吨时，这些煤可以用的天数在80～100天.3.某地上年度电价为0.8元，年用电量为1•亿度，•本年度计划将电价调至0.55～0.75元之间，经测算，若电价调到x 元，则本年度新增用电量y （亿度）与（x-0.4）•元成反比．又当x=0.65元时，y=0.8．（1）求y 与x 之间的函数关系式；（2）若每度电的成本价0.3元，电价调至0.6元，请你预算一下本年度电力部门的纯收入多少？解：（1）∵本年度新增用电量y （亿度）与（x-0.4）•元成反比，∴可设4.0-=x ky又当x=0.65元时，y=0.8，∴4.065.08.0-=k ，解得2.0=k∴y 与x 之间的函数关系式为4.02.0-=x y（2）当电价调至0.6元时，14.06.02.0=-=y ，即本年度新增用电量1亿度∴()()6.0113.06.0=+⨯-（亿元），即本年度电力部门的纯收入为0.6亿元.4.某汽车油箱的容积为70升，小王把油箱注满油后准备驾驶汽车从县城到300千米外的省城接客人，在接到客人后立即原路返回，请回答下列问题：（1）油箱注满油后，汽车能够行驶的总路程a 千米与平均耗油量b 升/千米之间有怎样的函数关系？（2）小王以平均每千米耗油0.1升的速度驾驶汽车到达省城，在返程时由于下雨，小王降低了车速，此时每行驶1千米的耗油量增加了一倍.如果小王一直以此速度行驶，油箱里的油是否能够回到县城？如果不够用，至少还需加多少油？解：（1）油箱注满油后，汽车能够行驶的总路程a 千米与平均耗油量b 升/千米之间的函数关系为ba 70=. （2）由题意得：小王由县城到省城需耗油301.0300=⨯（升），由省城到县城需耗油602.0300=⨯（升），而30+60-70=20，所以油不够用，至少还需加油20升.【自主小结】17.2 实际问题与反比例函数（三）【学习目标】掌握从物理问题中建构反比例函数模型（跨学科应用）．（重点、难点）【自主预习】在现实生活中，人们发现了很多相反的物理现象，并巧妙地运用于生活中.如一般的温度计都是利用热胀冷缩的原理制成的，但在低温物理、航空技术和宇宙航行研究中采用的半导体温度计，是利用半导体的电阻随温度的升高而减小的特性制成的.压力一定时，受力面积越大，压强就越小，为减少压强，越野吉普车的车轮制作得比普通车的宽，等等.所以古希腊哲学家、数学家、物理学家阿基米德曾说过：给我一个支点，我可以移动地球.这句话对吗？它们反映了什么样的函数关系？解：这句话是对的.根据杠杆平衡原理，加在杠杆两端的力与它们的力臂成反比.如图有：G l F l 21=,12l Gl F =如果G 为地球对杠杆的作用力的话，在G ,2l 一定时，若1l 足够大，那么施加很小的力F ，就能移动地球，这在理论上是成立的.反映出当G ,2l 一定时，F 与1l 成反比例关系.【自主探究】1.小伟欲用撬棍橇动一块大石头，已知阻力和阻力臂不变，分别为1500牛顿和0.5米．（1）动力F 与动力臂L 有怎样的函数关系？当动力臂为1.5米时，撬动石头至少需要多大的力？（2）若想使动力F 不超过题（1）中所用力的一半，则动力臂至少要加长多少？解：（1）动力F 与动力臂L 的函数关系为：LF 750=当5.1=L 米时，500=F 牛顿，即撬动石头至少需要500牛顿的力；（2）若想使动力F 不超过题（1）中所用力的一半，则3250750==L （米） ∴动力臂至少要加长1.5米FG2l1l O 反比例函数生活中应用商品销售费用问题 ……图像信息、文字信息表格信息、数形结合 ……2．由物理学知识知道，在力F （N ）的作用下，物体会在力F 的方向上发生位移s （m ），力F 所做的功W （J ）满足：W=Fs ．当W 为定值时，F 与s 之间的函数图象如右上图所示．（1）力F 所做的功的是多少？（2）试确定F 与s 之间的函数表达式；（3）当F=4N 时，s 是多少？解：（1）由图可知，力F 所做的功的是15 J ；（2）F 与s 之间的函数表达式为：sF 15=；（3）当F=4N 时，m s 415=.【自主检测】1.一辆汽车的功率为50马力（1马力=75kg ·m/s ），当汽车的速度达到144km/h 的时候，汽车的牵引力是 93.75 kg ；若汽车在上坡时需要1250kg 的牵引力，则汽车的速度应为 3m/s .2.在某一电路中，保持电压不变，电流I （安培）和电阻R （欧姆）成反比例，当电阻R=5欧姆时，电流I=2安培．（1）求I 与R 之间的函数关系式；（2）当电流I=0.5时，求电阻R 的值．解：（1）∵保持电压不变，电流I （安培）和电阻R （欧姆）成反比例，∴设RU I=∵当电阻R=5欧姆时，电流I=2安培，∴10=U 伏 ∴I 与R 之间的函数关系式为RI 10=；（2）当电流I=0.5时，电阻R 的值为20欧姆.3.一定质量的二氧化碳气体，其体积V （m 3）是密度p （kg/m 3）的反比例函数，•请根据下图中的已知条件求出当密度p=1.1kg/m 3时二氧化碳气体的体积V 的值．解：∵一定质量的二氧化碳气体，其体积V （m 3）是密度p（kg/m 3）的反比例函数，∴设pk V =，由图可知1985k =，解得980=k ，∴p V 980=∴当密度p=1.1kg/m 3时，二氧化碳气体的体积V 的值为3119800m ．4.一个用电器的电阻是可调节的，其范围为110•～220•欧姆，•已知电压为220伏，这个用电器的电路图如图所示:（1）输出功率P 与电阻R 有怎样的函数关系？（2）用电器输出功率的范围多大？解：（1）根据物理学知识，RU P 2=；∴输出功率P 与电阻R 的函数关系为RP 2220=（2）当110=R 欧姆时，440=P 瓦；当220=R 欧姆时，220=P 瓦；∴用电器输出功率的范围为220•～440•瓦. 【自主小结】第17章《反比例函数》回顾与思考【学习目标】1．知道反比例函数概念，能画反比例函数的图象，并掌握其性质．（重点） 2．运用反比例函数的图像和性质解决有关问题．（重点、难点）【自主预习】一、本章知识结构图二、本章主要知识点1.反比例函数的概念：形如）为常数，（0≠=k k x k y 的函数称为反比例函数； 2.反比例函数的图像：双曲线； 3.反比例函数的性质：(1)取值范围：x ≠ 0，y ≠ 0；(2)位置情况：当k > 0时，双曲线的两支分别位于第一、第三象限，当k < 0时，双曲线的两支分别位于第二、第四象限；(3)增减性：当k > 0时，在每个象限内y 值随x 值的增大而减小，当k < 0时，在每个象限内y 值随x 值的增大而增大；(4)渐近性：反比例函数的图象无限接近 x 轴，y 轴，但永远达不到x 轴，y 轴； (5)对称性：反比例函数的图象既是中心对称图形，又是轴对称图形. 【自主探究】一、问题探究探究一：反比例函数的定义如果函数22k y kx -=的图像是双曲线，且在第二、四象限，那么k 的值是 -1 . 探究二：反比例函数的图像及性质函数y x m =+与(0)my m x=≠在同一坐标系内的图象可能是（ B ）y y y y反比例函数跨学科应用物理学公式注意取值范围探究三：反比例函数的综合运用如图，已知一次函数a x y +-=1与x 轴、y 轴分别交于点D 、C 两点和反比例函数xk y =2交于A 、B 两点，且点A 的坐标是（1，3）点B 的坐标是（3，m ） (1)求a ，k ，m 的值；(2)求C 、D 两点的坐标，并求△AOB 的面积；(3)利用图像直接写出，当x 在什么取值范围时，1y ＞2y ？解：(1)∵一次函数与反比例函数交于A 、B 两点，∴31=+-a ，31=k，解得4=a ，3=k ∴41+-=x y ，xy 32=，把点B （3，m ）代入得1=m(2)C 点的坐标为（0，4）、D 点的坐标为（4，0），△AOB 的面积为4142114214421=⨯⨯-⨯⨯-⨯⨯； (3)由图像得，当41<<x 时，21y y >【自主检测】1．当a = 1 时，22)1(-+=a x a y 是反比例函数．2．已知函数y=21k x-在第一象限内，y 随x 增大而减小，则k 的取值范围是（ D ） A ．k<12 B ．k≥12 C ．k=12 D ．k>123．点A （-2，a ），B （-1，b ），C （3，c ）在双曲线y=kx（k<0）上，则a 、b 、c 的大小关系为 b>a>c ．4．已知一次函数y=kx+b 的图象与反比例函数y=6x的图象相交于A 、B 两点，点A 的横坐标是3，点B 的纵坐标是-3，求：(1)一次函数的解析式；(2)当x 为何值时，一次函数的函数值小于0？解：(1)由题意得A(3,2)，B(-2,-3) ∴⎩⎨⎧-=+-=+3223b k b k ，解得⎩⎨⎧-==11b k ，∴一次函数的解析式为1-=x y(2)由0<y 得01<-x ，解得1<x ，∴当x<1时，一次函数的函数值小于0. 5．已知y=y 1+y 2，y 1与x+1成正比例，y 2与x 2成反比例，并且x=1时，y=1；x=3时，y=23+1，•求x=13时y 的值．解：由题意可设22211),1(x k y x k y =+=，∴221)1(xk x k y ++=将数据代入得：()⎪⎩⎪⎨⎧+=++=+132313122121k k k k ，解得⎩⎨⎧-==3221k k ，即23)1(2x x y -+= ∴当x=13时，373-=y .。

17.1.3反比例函数

y=-x
y=x
设 P ( m , n ) 是双曲线 y
k x
( k 0 ) 上任意一点 , 有 :
(1 ) 过 P 作 x 轴的垂线 , 垂足为 A , 则
S OAP 1 2 OA AP 1 2 | m | | n | 1 2 |k |
面积性质（一）
y P(m,n) y P(m,n) o A x
C S 2 , 则___.
y
A.S1>S2 B.S1<S2 C.S1 = S2 D.S1和S2的大小关系不能确定.
由上述性质1可知选C
o
S2
S1
A
B
x
C
D
4 .如图 , 在 y
1 x
( x 0 )的图像上有三点
A, B , C ,
经过三点分别向
x 轴引垂线 , 交 x 轴于 A1 , B 1 , C 1 三点 ,
义务教育课程标准实验教科书人教版《数学》八年级下册
反比例函数的图象和性质： 1.反比例函数的图象是双曲线; 2.图象性质见下表： k y= K>0 K<0
x
图象
当k＞0时，函数图象的两个分支分别在第一、三象限，在每个象限内，y随x的增大而减小. 当k＜0时，函数图象的两个分支分别在第二、四象限，在每个象限内，y随x的增大而增大.
边结 OA , OB , OC , 记 OAA 1 , OBB 1 , OCC 1的面积分别为
A S 1 , S 2 , S 3 , 则有 __ .
y
A S1 B
A.S1 = S2 = S3 B. S1 < S2 < S3 C. S3 < S1 < S2 D. S1 > S2 >S3 解:由性质(1)得

(完整版)人教八年级数学下册同步练习题及答案

1第十六章、分式 16.1.1从分数到分式（第一课时）一、课前小测：1、________________________统称为整式．2、23表示_______÷______的商，那么（2a+b ）÷（m+n ）可以表示为________． 3、甲种水果每千克价格a 元，乙种水果每千克价格b 元，取甲种水果m 千克，乙种水果n 千克，混合后，平均每千克价格是_________．二、基础训练：1、分式24x x -，当x_______时，分式有意义；当x_______时，分式的值为零；当x_______时，分式15x -+的值为正；当x______时，分式241x -+的值为负． 2、有理式①2x ，②5x y +，③12a -，④1x π-中，是分式的有（） A ．①② B ．③④ C ．①③ D ．①②③④23、使分式||1x x -无意义，x 的取值是（） A ．0 B ．1 C ．-1 D ．±1三、综合训练：1、当x______时，分式2134x x +-无意义． 2、当x_______时，分式2212x x x -+-的值为零． 3、当x 取何值时，下列分式有意义？（1）（2）2323x x +-16.1.2分式的基本性质(第二课时)一、课前小测：23+x31.如果分式x211-的值为负数,则的x 取值范围是( ) A.21≤x B.21<x C.21≥x D.21>x 2. 当_____时,分式4312-+x x 无意义.当______时,分式68-x x 有意义二、基础训练：1、分式的基本性质为：_________ ___．用字母表示为：_____________________．2、判断下列约分是否正确：（1）c b c a ++=b a ，（2）22y x y x --=y x +1，（3）nm n m ++=0。

3、根据分式的基本性质，分式a a b --可变形为（） A ．a a b-- B ．a a b + C ．-a a b - D ．a a b + 4、填空：4 (1) x x x 3222+= ()3+x ， (2) 32386b b a =()33a ， 5、约分：（1）c ab b a 2263 （2）532164xyz yz x - 三、综合训练：1、通分：（1）231ab 和b a 272 （2）xx x --21和x x x +-21 2、若a ＝23，则2223712aa a a ---+的值等于______。

人教八年级数学下 17.1反比例函数同步测试A

数学：17.1反比例函数同步测试A （人教新课标八年级下）A 卷（60分）一、选择题1.下列表达式中，表示y 是x 的反比例函数的是（） ①31-=xy ②.x y 63-= ③x y 2-= ④m my (3=是常数，)0≠m A.①②④ B.①③④ C.②③ D.①③2.下列函数关系中是反比例函数的是（）A.等边三角形面积S 与边长a 的关系B.直角三角形两锐角A 与B 的关系C.长方形面积一定时，长y 与宽x 的关系D.等腰三角形顶角A 与底角B 的关系 3. （08甘肃省兰州市）若反比例函数ky x=的图象经过点(3)m m ，，其中0m ≠，则此反比例函数的图象在（） A ．第一、二象限 B ．第一、三象限 C ．第二、四象限D ．第三、四象限4.函数x k y =的图象经过点（-4，6），则下列个点中在xk y =图象上的是（） A.（3，8 ） B.（-3，8） C.（-8，-3） D.（-4，-6）5. 在下图中，反比例函数xk y 12+=的图象大致是（）D6. 已知反比例函数xky =的图象在第二、第四象限内，函数图象上有两点A (72，y 1)、B (5，y 2)，则y 1与y 2的大小关系为（）。

A 、y 1＞y 2B 、y 1＝y 2C 、y 1＜y 2D 、无法确定二、填空题（每小题3分，共18分）7. 写出一个图象在第一、三象限的反比例函数的解析式． 8. 已知反比例函数的图象经过点（3，2）和（m ，－2），则m 的值是＿＿．9. 在ABC △的三个顶点(23)(45)(32)A B C ----，，，，，中，可能在反比例函数(0)ky k x=>的图象上的点是． 10. 某种蓄电池的电压为定值，使用此电源时，电流 I （A ）与可变电阻 R （Ω）之间的函数关系如图所示，当用电器的电流为10A 时，用电器的可变电阻为_______Ω。

11. 反比例函数xky =的图象如图所示，点M 是该函数图象上一点，MN 垂直于x 轴，垂足是点N ，如果S △MON ＝2，则k 的值为 .12. 小明家离学校1.5km ，小明步行上学需min x ，那么小明步行速度(m /min)y 可以表示为1500y x=；水平地面上重1500N 的物体，与地面的接触面积为2m x ，那么该物体对地面压强2(/m )y N可以表示为1500y x=；，函数关系式1500y x=还可以表示许多不同情境中变量之间的关系，请你再列举1．例．：．三、解答题（本大题24分）13.甲、乙两地相距100km ，一辆汽车从甲地开往乙地，把汽车到达乙地所用的时间)(h t 表示为汽车速度)/(h km v 的函数，并画出函数图象.14. 已知一次函数y x 13=-2k 的图象与反比例函数y k x23=-的图象相交，其中一个交点的纵坐标为6。

北京市2020〖人教版〗八年级数学下册期末复习试卷反比例函数同步训练2

北京市2020年〖人教版〗八年级数学下册期末复习试卷反比例函数同步训练一．选择题：1．下列函数中，反比例函数是（）A 1)1(=-y xB 11+=x y C 21xy = D x y 31= 2．已知反比例函数的图像经过点（a ，b ），则它的图像一定也经过（）A (－a ,－b )B (a ,－b )C (－a ，b )D （0，0）3．如果反比例函数xk y =的图像经过点（－3，－4），那么函数的图像应在（） A 第一、三象限 B 第一、二象限 C 第二、四象限 D 第三、四象限 4．若y 与－3x 成反比例，x 与z 4成正比例，则y 是z 的（） A 正比例函数 B 反比例函数 C 一次函数 D 不能确定5．若反比例函数22)12(--=mx m y 的图像在第二、四象限，则m 的值是（） A －1或1 B 小于21 的任意实数 C －1 Ｄ不能确定 6．函数x k y =的图象经过点（－4，6），则下列各点中在x k y =图象上的是（） A （3，8） B （3，－8） C （－8，－3） D （－4，－6）7．正比例函数kx y =和反比例函数k y =在同一坐标系内的图象为（ B CD8．如图，A 为反比例函数xk y =图象上一点，AB 垂直x 轴于B 点，若 S △AOB ＝3，则k 的值为（） A 、 6 B 、 3 C 、 23 D 、不能确定9．如果y 与z 成反比例关系，x 与z 成正比例关系，则y 与x 成（）A ．正比例关系B 反比例关系C ．一次函数关系D ．不同于以上答案10．如图13－8－5，面积为2的ΔABC ，一边长为x ，这边上的高为y ，则y 与x 的变化规律用图象表示大致是（）11．如图13－8－6所示，A （1x ，1y ）、B （2x ，2y ）、C （3x ，3y ）是函数x y 1=的图象在第一象限分支上的三个点，且1x ＜2x ＜3x ，过A 、B 、C 三点分别作坐标轴的垂线，得矩形ADOH 、BEON 、CFOP ，它们的面积分别为S 1、S 2、S 3，则下列结论中正确的是（）A ． S 1<S 2<S 3B ． S 3 <S 2< S 1C ． S 2< S 3<S 1D ． S 1=S 2=S 3二、解答题：已知：反比例函数xk y =和一次函数12-=x y ，其中一次函数的图像经过点（k ，5）. （1）试求反比例函数的解析式；（2）若点A 在第一象限，且同时在上述两函数的图像上，求A 点的坐标；参考答案：一．1．D ；2．A ；3．A ；4．A ；5．C ；6．B ；7．B 、D ；8．A ；9．B ；10．D ；11．D ；二．解：（1）因为一次函数12-=x y 的图像经过点（k ,5）AB O x y所以有 125-=k (3分) 解得 3=k所以反比例函数的解析式为xy 3=（4分）（2）由题意得：⎪⎩⎪⎨⎧-==123x y x y （6分）解这个方程组得：⎪⎩⎪⎨⎧==223y x ⎩⎨⎧-=-=31y x （7分）因为点A 在第一象限，则0>x ，0>y所以点A 的坐标为（23，2）（8分）。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

x y O E F P （第9题）
反比例函数单元测试
一．选择题：（7×4分=28分）
（）1．如果反比例函数k y x
=在每个象限内，y 随x 的增大而减小，那么其图象分布在 A ．第一、二象限 B ．第一、三象限
C ．第二、三象限
D ．第二、四象限
（）2．已知反比例函数y ＝2a x
-的图象在第二、四象限，则a 的取值范围是 A ．a ≤2 B ．a ≥2 C ．a ＜2 D ．a ＞2
（）3．已知反比例函数的图象经过点（a ，b ），则它的图象一定也经过
A ．(－a ，－b)
B ．(a ，－b)
C ．(－a ，b)
D ．（0，0）
（）4．在同一直角坐标平面内，如果直线y=k 1x 与双曲线x
k y 2=没有交点，那么k 1和k 2的关系一定是
A ．k 1 k 2＝0
B ．k 1 k 2＞1
C ．k 1 k 2＞0
D ．k 1 k 2＜0
( )5．在同一直角坐标系中，函数y=k(x －1)与y=
)0(<k x k 的大致图象是
（）6．已知反比例函数k y x
=（k ＜0）的图象上有两点A （x 1，y 1），B （x 2，y 2），且x 1＜x 2＜0，则y 1－y 2的值是
A ．正数
B ．负数
C ．非正数
D ．非负数
（）7.直线l 与双曲线C 在第一象限相交于A 、B 两点，其图象信息如图4
所示，则阴影部分（包括边界）横、纵坐标都是整数的点（俗称格点）有：
A ．4个
B ．5 个
C ．6个
D ．8个
二．填空题：（6×4分=24分）
8． u 与t 成反比，且当u ＝8时，81=t ，这个函数解析式为． 9．写出一个图象位于一、三象限的反比例函数表达式．
10．如图，P 是反比例函数图象在第二象限上一点，且矩形PEOF 的面积是3，则反比例函数的解析式D ． B ． C ． A ．
为．
11．反比例函数x k y =
的图象经过（－23，5）、（a ，－3）及（10，b ）三个点，则k ＝，a ＝，b ＝．
12．已知一次函数23y x =-+的图象与反比例函数()11k y k x
-=≠的图象交于第四象限的一点P （m ，－m ），则这个反比例函数的解析式为_______________．
13.双曲线x
y x y 21==与在第一象限内的图象如图所示，作一条平行于y 轴的直线分别交双曲线于A 、B 两点，连接OA 、OB ，则△AOB 的面积为
三．解答题：
14．反比例函数x
k y =的图象经过点A(2，3)．（1）求这个函数的解析式；（2）请判断点B(1，6)是否在这个反比例函数的图象上，并说明理由．(10分)
15．已知反比例函数3m y x
=-和一次函数1y kx =-的图象都经过点P （m ，－3m ）．（1）求点P 的坐标和一次函数的解析式；（2）若点M （a ，y 1）和点N （a+1，y 2）（a ＞0）都在反比例函数的图象上，试通过计算或利用反比例的性质，说明y 1与y 2的大小．(10分)
16．如图，已知反比例函数y 1=m x
的图像与一次函数y 2=kx+b 的图象交于两点A （-2,1）、B （a ，-2）. （1）求反比例函数和一次函数的解析式；（2）若一次函数y 2=kx+b 的图象交y 轴于点C ，求△AO B 的面积（O 为坐标原点）；（3）求使y 1＞y 2时x 的取值范围.(6+4+4=14分)
17．近年来，我国煤矿安全事故频频发生，其中危害最大的是瓦斯，其主要成分是CO.在一次矿难事件的调查中发现：从零时起，井内空气中CO 的浓度达到4 mg/L ，此后浓度呈直线型增加，在第7小时达到最高值46 mg/L ，发生爆炸；爆炸后，空气中的CO 浓度成反比例下降.如图11，根据题中相关信息回答下列问题：（1）求爆炸前后．．
空气中CO 浓度y 与时间x 的函数关系式，并写出相应的自变量取值范围；（2）当空气中的CO 浓度达到34 mg/L 时，井下3 km 的矿工接到自动报警信号，这时他们至少要以多少km/h 的
速度撤离才能在爆炸前逃生？（3）矿工只有在空气中的CO 浓度降
到4 mg/L 及以下时，才能回到矿井开展生产自救，求矿工至少在
爆炸后多少小时才能下井? (6+4+4=14分)
参考答案：
一．选择题：B ；C ；A ；D ；B ；B ；B
二．填空题：８．t u 1=；９．x y 1=
（答案不唯一）；１０．x y 3-=；１１．43;25;215--；１２．x y 9-=；１３．2
1 三．解答题： 14.(1)x
y 6=,在 15.(1)P(1,-3), y=-2x-1 (2)y 1＜y 2
16..102)3(;2
3)2(;1,2)1(21 x x x y x y 或---=-= 17.（1）因为爆炸前浓度呈直线型增加，
所以可设y 与x 的函数关系式为1y k x b =+
由图象知1y k x b =+过点（0，4）与（7，46）
∴14746b k b =⎧⎨+=⎩. 解得164k b =⎧⎨=⎩
, ∴64y x =+,此时自变量x 的取值范围是0≤x ≤7. (不取x =0不扣分，x =7可放在第二段函数中)
因为爆炸后浓度成反比例下降，
所以可设y 与x 的函数关系式为2k y x =
. 由图象知2k y x =
过点（7,46）， ∴2467
k =. ∴2322k =, ∴322y x
=，此时自变量x 的取值范围是x ＞7. （2）当y =34时，由64y x =+得,6x +4=34，x =5 . ∴撤离的最长时间为7-5=2(小时).
∴撤离的最小速度为3÷2=1.5(km/h).
(3)当y =4时，由322y x
=得, x =80.5，80.5-7=73.5(小时). ∴矿工至少在爆炸后73.5小时能才下井.。