运筹学第十一章 二人有限零和对策
11上管理运筹学复习题

阅读使人充实,会谈使人敏捷,写作使人精确。
——培根11上管理运筹学复习题一、单选题1.能够采用图解法的进行求解的简单线性规划问题的变量个数为 ( )。
A .1个B .2个C .3个D .4个2、在中日篮球比赛(对策论问题)中,称为局中人的是 ( )。
A .双方领导人B .双方的教练C .两个国家的人民D .中日参赛的国家队 3.在决策分析中,以下不属于非确定情况下的决策准则是( )。
A .小中取大准则B .大中取大准则C .大中取小准则D .等可能性准则4.设整数规划为为整数且121212121,0,321..3max x x x x x x x t s x x f ≥≤-≥++= ,则该整数规划属于( )。
A .0—1规划B .混合整数规划C .纯整数规划D .以上答案均不对 5.对某复杂问题进行系统分析,从而得到最满意的行动方案,可能需要做这样一些工作( )(1) 对方案进行分析、比较、评价;(2) 选择满意方案; (3) 阐明问题现状;(4) 提出可行备选方案;(5)明确决策目标。
你认为正确的分析思路与程序应该是( )A. (5)—(3)—(4)—(1)—(2)B. (3)—(4)—(1)—(2)—(5)C. (5)—(4)—(3)—(1)—(2)D. (3)—(5)—(4)—(1)—(2) 6.线性规划一般模型中,自由变量可以用两个非负变量的 ( )代换。
A .和B .差C .积D .商 7.线性规划模型的特点是 ( )。
A .变量个数少 B .约束条件少C .目标函数的表达式短D .约束条件和目标函数都是线性的 8.二人零和对策中“零和”的含义是指 ( )。
A .甲方的赢得值为零B .乙方的赢得值为零C .二人的赢得值都是零D .二人的得失相加为零9.设有参加对抗的局中人A 和B ,A 的赢得矩阵为⎪⎪⎪⎭⎫⎝⎛--205634916321321αααβββ,则最优纯策略的对策值为( )A. 4B. 3C. 9D. 110.对于风险型决策问题,其各自然状态发生的概率是()的。
管理运筹学期末复习资料【韩伯棠】

运筹学(Operational Research)复习资料第一章绪论一、名词解释1.运筹学:运筹学是应用分析、试验、量化的方法,对经济管理系统中的人力、物力、财力等资源进行统筹安排,为决策者提供有依据的最优方案,以实现最有效的管理。
二、选择题1.运筹学的主要分支包括(ABDE )A图论B线性规划C非线性规划D整数规划E目标规划2. 最早运用运筹学理论的是( A )A . 二次世界大战期间,英国军事部门将运筹学运用到军事战略部署B . 美国最早将运筹学运用到农业和人口规划问题上C . 二次世界大战期间,英国政府将运筹学运用到政府制定计划D . 50年代,运筹学运用到研究人口,能源,粮食,第三世界经济发展等问题上第二章线性规划的图解法一、选择题/填空题1.线性规划标准式的特点:(1)目标函数最大化(2)约束条件为等式(3 决策变量为非负(4 ) 右端常数项为非负2. 在一定范围内,约束条件右边常数项增加一个单位:(1)如果对偶价格大于0,则其最优目标函数值得到改进,即求最大值时,最优目标函数值变得更大,求最小值时最优目标函数值变得更小。
(2)如果对偶价格小于0,则其最优目标函数值变坏,即求最大值时,最优目标函数值变小了;求最小值时,最优目标函数值变大了。
(3)如果对偶价格等于0,则其最优目标函数值不变。
3.LP模型(线性规划模型)三要素:(1)决策变量(2)约束条件(3)目标函数4. 数学模型中,“s·t”表示约束条件。
5. 将线性规划模型化成标准形式时,“≤”的约束条件要在不等式左端加上松弛变量。
6. 将线性规划模型化成标准形式时,“≥”的约束条件要在不等式左端减去剩余变量。
7.下列图形中阴影部分构成的集合是凸集的是A【解析】:如何判断是凸集?凸集:两点之间连线在图内凹集:两点之间连线在图外8. 线性规划问题有可行解且凸多边形无界,这时CA没有无界解 B 没有可行解 C 有无界解 D 有有限最优解9. 对于线性规划问题,下列说法正确的是( D )A. 线性规划问题可能没有可行解B. 在图解法上,线性规划问题的可行解区域都是“凸”区域C. 线性规划问题如有最优解,则最优解可在可行解区域顶点上到达D. 上述说法都正确第三章线性规划问题的计算机求解一、名词解释1.相差值:相应的决策变量的目标系数需要改进的数量,使得决策变量为正值。
管理运筹学_北京理工大学中国大学mooc课后章节答案期末考试题库2023年

管理运筹学_北京理工大学中国大学mooc课后章节答案期末考试题库2023年1.需求为随机的单一周期的报童问题是要解决()的问题。
答案:期望损失最小2.在经济订购批量存储模型的灵敏度分析中,当订货费或存储率预测值有误差时,该选择何种存储策略()。
答案:选择原最优存储策略3.下例错误的结论是()答案:检验数就是目标函数的系数4.在报童所订购报纸的模型中,下列哪些不等式不符合最优数量 Q*求解的是()。
答案:__5.【图片】的可行域是():答案:6.根据最大最大原则为以下问题选出最优行动方案?【图片】答案:S27.A工厂生产同一规格的设备,每季度的单位成本依次是1万元、1.2万元、1.3万元、1.5万元。
设备当季度卖出不产生任何存储、维护费用,若积压一季度需存储、维护费用0.05万元,则设备的单位费用(单位:万元)为:答案:8.存储论要解决的问题是:答案:何时补充物资。
_当需要补充物资时,补充的数量是多少。
9.根据动态规划的时间参量是连续的还是离散的、决策过程的演变过程是确定性的还是随机性的,可以将动态规划的决策过程分为哪些决策过程:答案:离散随机性_连续随机性_离散确定性_连续确定性10.下列成本中属于存储成本的是:答案:购买物资所用资金的利息。
_仓库管理人员的劳务费。
_储存仓库的费用。
11.对偶价格小于0时,约束条件的常数项增加一个单位,则对于求min目标函数的线性规划,其最优值的数值会增大。
答案:正确12.关于线性规划的最优解判定,说法不正确的是()答案:求目标函数最大值时,如果所有检验数都小于等于零,则有唯一最优解13.求目标函数值最小的线性规划单纯形表的大M法,在约束条件中加入人工变量是()答案:为了构造约束系数矩阵中的单位矩阵14.求解目标函数值最大的线性规划问题中,在确定出基变量的时,根据minbi/ aij选取入基变量的原因是()答案:确保下一步迭代新得到的bj值都≥015.关于线性规划的原问题和对偶问题的关系,两个问题的最优解的值一致。
两人有限零和博弈例题

两人有限零和博弈例题当谈及“有限零和博弈”,意味着在有限的资源和局势下,两个参与者的利益完全相反,一方的利益增加意味着另一方的利益减少。
以下是一个简单的例题,帮助你理解有限零和博弈的概念:例题:小明和小红的游戏小明和小红正在玩一个有限零和博弈。
他们有一堆糖果,共计10颗。
游戏的规则是,每一轮,小明和小红都可以选择拿走1颗、2颗或3颗糖果,但总共只能拿走5颗。
每轮结束后,剩余的糖果将会由另一方继续选择。
游戏一共进行两轮。
问题:在这个有限零和博弈中,如果小明和小红都追求最大化自己的利益,他们应该如何策略地进行选择,以及最终的结果是什么?解答:在有限零和博弈中,小明和小红的利益完全相反。
一方的利益增加,就意味着另一方的利益减少。
由于这是一个有限博弈,他们只进行两轮,因此可以通过逐轮的分析来找到最佳策略。
第一轮:如果小明拿1颗,小红拿4颗。
小明:1,小红:4。
如果小明拿2颗,小红拿3颗。
小明:2,小红:3。
如果小明拿3颗,小红拿2颗。
小明:3,小红:2。
根据这些选择,小明和小红都应该采取最优策略:在第一轮中,小明拿3颗糖果,小红拿2颗糖果。
第二轮:如果小明拿1颗,小红拿4颗。
小明:1,小红:4。
如果小明拿2颗,小红拿3颗。
小明:2,小红:3。
如果小明拿3颗,小红拿2颗。
小明:3,小红:2。
根据这些选择,同样地,小明和小红都应该采取最优策略:在第二轮中,小明拿1颗糖果,小红拿4颗糖果。
综合两轮结果,最终小明拿3颗糖果,小红拿2颗糖果。
这个例子中,小明和小红通过在每一轮中选择最优策略,最终达到了在有限零和博弈中的最佳结果。
不过需要注意的是,这个结论适用于这个具体的问题,不同的规则和局势可能会导致不同的最优策略。
第十一章二人有限零和对策

二、混合策略对策的解 1、定义:如果混合策略对策
x y
G*={S*,D*;E}满足:
E (x* , y* ) max E (x, y ) min E (x, y ) 则称x , y 分别为局中人甲、乙的最优混合策略.
* *
(x , y )为对策G *的最优解。
6*
易知,G在纯策略意义下无解。
记 xi p( si ) 0 xi 1(i 1, 2) yi p(di ) 0 yi 1(i 1, 2)
d1 s1 7 s2 3 yj y1 d2 4 6 y2 xi x1 x2
x
i 1 2 i 1
2
i
1 1
y
i
E ( X , Y ) aij p( si , d j )
3.对策问题举例 ①下棋、打牌、体育比赛等。
② 齐王赛马:齐王与大将田忌赛马,各自的 马都分为三 等,但齐王的同等马均强于 田忌。孙膑给田忌出主意, 用下----上 ,上----中,中----下, 赢 B 石头 剪子 布 A 结果田忌胜出。 石头 0 1 -1 ③猜手:小孩A与B猜手, 剪子 -1 1 0 若规定赢 得1分, 布 0 1 -1 平得0分,输得 -1分, 则 A的赢得可用右表来 表示。
证明 : 记 min ai* j min max aij max min aij max aij*
j j i i j i
min ai* j ai* j* , max aij* ai* j*
j i
故 aij* ai* j* , ai* j* ai* j aij* ai* j* ai* j 即( si* , d j* )是G的解
运筹学

一、单选题(共40 道试题,共100 分。
)V 1. 对于第二类存储模型——进货能力有限,不允许缺货,下列哪项不属于起假设前提条件()A. 需求是连续,均匀的B. 进货是连续,均匀的C. 当存储降至零时,可以立即得到补充D. 每个周期的定货量需要一次性进入存储,一次性满足标准答案:D2. 在完全不确定下的决策方法不包括下列的哪一项()A. 悲观法B. 乐观法C. 最大收益法D. 等可能性法标准答案:C3. 所谓确定条件下的决策,是指在这种条件下,只存在()A. 一种自然状态B. 两种自然状态C. 三种或三种以上自然状态D. 无穷多种自然状态标准答案:A4. 单纯形法的迭代计算过程是从一个可行解转换到目标函数值更大的另一个可行解。
A. 对B. 错标准答案:B5. 下例错误的说法是A. 标准型的目标函数是求最大值B. 标准型的目标函数是求最小值C. 标准型的常数项非正D. 标准型的变量一定要非负标准答案:C6. 求般获得最好经济效益问题是求如何合理安排决策变量(即如何安排生产)使目标函数最大的问题,求最大的目标函数问题,则记为max Z;若是如何安排生产使成本是最小的问题,则记为min Z .A. 对B. 错标准答案:A7. ()是用来衡量所实现过程优劣的一种数量指标A. 状态B. 决策C. 状态转移D. 指标函数标准答案:D8. 在实际工作中,企业为了保证生产的连续性和均衡性,需要存储一定数量的物资,对于存储方案,下列说法正确的是( )A. 应尽可能多的存储物资,以零风险保证生产的连续性B. 应尽可能少的存储物资,以降低库存造成的浪费C. 应从多方面考虑,制定最优的存储方案D. 以上说法都错误标准答案:C9. 约束条件为AX=b,X≥0 的线性规划问题的可行解集是()A. 补集B. 凸集C. 交集D. 凹集标准答案:B10. 存货台套的运费应列入()A. 订货费用B. 保管费用C. 进厂价D. 其它支出标准答案:C11. 基可行解中的非零变量的个数小于约束条件数时,该LP问题可求得( )。
大工19春《运筹学》在线作业123参考答案

大工19春《运筹学》在线作业123参考答案大工19春《运筹学》在线作业1数学规划的研究对象为()。
A.数值最优化问题B.最短路问题C.整数规划问题D.最大流问题正确答案:A运筹学的基本特点不包括()。
A.考虑系统的整体优化B.多学科交叉与综合C.模型方法的应用D.属于行为科学正确答案:D()是解决多目标决策的定量分析的数学规划方法。
A.线性规划B.非线性规划C.目标规划D.整数规划正确答案:C线性规划问题中决策变量应为()。
A.连续变量B.离散变量C.整数变量D.随机变量正确答案:A数学规划模型的三个要素不包括()。
A.决策变量B.目标函数C.约束条件D.最优解正确答案:D数学规划的应用极为普遍,它的理论和方法已经渗透到自然科学、社会科学和工程技术中。
T.对F.错正确答案:A存储论的对象是一个由补充、存储和需求三个环节构成的现实运行系统,且以存储为中心环节,故称为存储系统。
T.对F.错正确答案:A满足目标要求的可行解称为最优解。
T.对F.错正确答案:A运筹学是运用数学方法,对需要进行管理的问题统筹规划,为决策机构进行决策时提供以数量化为基础的科学方法。
T.对F.错正确谜底:A线性规划的建模是指将用语言文字描述的应用问题转化为用线性规划模型描述的数学问题。
T.对F.错正确答案:A在国际上,通常认为“运筹学”与“管文科学”是具有相同或附近涵义。
T.对F.错正确谜底:A整数规划问题中的整数变量可以分为一般离散型整数变量和连续型整数变量。
T.对F.错正确答案:B线性规划数学模型的三要素包括目标函数、约束条件和解。
T.对F.错正确谜底:B基本解的概念适用于所有的线性规划问题。
T.对F.错正确谜底:B线性规划问题的可行解是满足约束条件的解。
T.对F.错正确谜底:A存储策略是决定多长时间补充一次货物以及每次补充多少数量的策略。
T.对F.错正确谜底:A线性规划的最优解是指使目标函数达到最优的可行解。
T.对F.错正确答案:A线性规划的求解方法包括图解法、纯真形法、椭球法、内点法等。
大连理工20春《运筹学》期末题

大连理工2020年春《运筹学》期末题一、单项选择题1、下列叙述正确的是()。
A.线性规划问题,若有最优解,则必是一个基变量组的可行基解B.线性规划问题一定有可行基解C.线性规划问题的最优解只能在最低点上达到D.单纯形法求解线性规划问题时,每换基迭代一次必使目标函数值下降一次答案:A2、数学规划的研究对象为()。
A.数值最优化问题 B.最短路问题 C.整数规划问题 D.最大流问题答案:A3、下列方法中可以用来求解部分树的方法的为()。
A.闭回路法 B.破圈法 C.踏石法 D.匈牙利算法答案:B4、把各种备选方案、可能出现的状态和概率以及产生的后果绘制在一张图上,称为()。
A.决策树 B.最大流 C.最小支撑树 D.连通图答案:A5、以下说法中,不属于无概率决策问题(不确定型决策问题)的特点的为()。
A.决策人面临多种决策方案B.对每个决策方案对应的几个不同决策状态无法估计其出现概率的大小C.仅凭个人的主观倾向和偏好进行方案选择D.未来情况和条件出现的概率已知答案:D6、线性规划问题中决策变量应为()。
A.连续变量 B.离散变量 C.整数变量 D.随机变量答案:A7、线性规划问题的数学模型由目标函数、约束条件和()三个部分组成。
A.非负条件 B.顶点集合 C.最优解 D.决策变量答案:D8、典型的无概率决策准则,不包括()。
A.乐观准则 B.折中准则 C.等可能准则 D.最大后悔值准则答案:D9、以下说法中不正确的为()。
A.完成各个作业需要的时间最长的路线为关键路线 B.关键路线上的作业称为关键作业C.所有关键作业的总时差为0 D.以上说法均不正确答案:D10、()也称小中取大准则。
这是一种在不确定型决策问题中,充分考虑可能出现的最小收益后,在最小收益中再选取最大者的保守决策方法。
A.悲观准则 B.折中准则 C.等可能准则 D.后悔值准则答案:A11、当某个非基变量检验数为零,则该问题有()。
A.无解B.无穷多最优解C.退化解D.唯一最优解答案:B12、假设对于一个动态规划问题,应用顺推法以及逆推解法得出的最优解分别为P和D,则有()。
天津大学《运筹学》在线作业一-02

《运筹学》在线作业一
对于确定型决策问题,下列说法错误的是()
A:确定型决策就是指在知道某个自然因素必然发生的前提下所作的决策
B:当计算成本或费用时,“选优”原则是取损益值最小的方案
C:当计算利润或收益时,“选优”原则是取损益值最小的方案
D:确定性决策除了满足一般决策问题的四个条件外,还需要加一个条件:只存在一个确定的自然因素
参考选项:C
某咨询公司要解答“筹划一个新超市应设置多少个收银台才合适”的问题,应选择
A:同行类比方法
B:模拟方法
C:数学规划方法
D:马尔柯夫分析方法
参考选项:B
可行流应满足的条件是()
A:容量条件
B:平衡条件
C:容量条件和平衡条件
D:容量条件或平衡条件
参考选项:C
以下叙述不是泊松流具备的条件的是()
A:无后效性
B:无记忆性
C:平稳性
D:普通性
参考选项:B
资源的影子价格是一种()
A:机会成本
B:市场价格
C:均衡价格
D:实际价格
参考选项:A
线性规划可行域的顶点一定是( )
A:基本可行解
B:非基本解
C:非可行解
1。
运筹学教程对策论

Games) §2.矩阵对策(Matrix Games) 2.矩阵对策( 矩阵对策
剪刀、 例2:“石头 、剪刀、布”游戏
局中人2 局中人2 局中人1 局中人1 1(石头) ) 2(剪刀) 剪刀) 3 (布) 0 -1 1 1 0 -1 -1 1 0 1(石头) ) 2(剪刀) 剪刀) 3 (布)
0=0
3.最优纯策略
齐王赛马:
-1<3
3.最优纯策略
定义:一个矩阵对策,如果它的支付矩阵A的元素满足: 定义:一个矩阵对策,如果它的支付矩阵A的元素满足:
则称这个值v为对策的值。如果纯局势(i*,j*)使: 则称这个值v为对策的值。
则称( 为对策G的鞍点( point),也称它是对策G 则称(i*,j*)为对策G的鞍点(Saddle point),也称它是对策G在 纯策略中的解, 分别为局中人1和局中人2的最优解。 纯策略中的解,i*与j*分别为局中人1和局中人2的最优解。
故对策的解为(3,3),即秋季贮煤20吨合理。(决策论中的悲观准则)
3.最优纯策略
例6:甲、乙双方谈判签订一项合同,甲方的“要价”是25万元,而乙方的“ 出价”是20万元,谈判陷于僵局。为打破僵局,双方约定,再各报一个价。以 下述价格成交:谁让步多,取谁出的价;如果双方让步相同,则取双方报价的 中间值。问甲、乙双方应如何报价?最后的成交价是多少? 解 显然,甲、乙双方的报价都在20万元到25万元之间。不妨取整数值,甲 、乙各有6个策略:报价20,21,…,25(单位:万元)。由约定知,甲的支付矩 阵可用表所示。
•局中人: •策略: 自始至终的行动方案; 把局中人的策略全体,称做这个局中人的策略集合; 例如,在齐王与田忌赛马的例子中,如果—开始就要把各人的三匹马排好 次序,然后依次出赛。各局中人都有六个策略:(1)(上、中、下),(2) ( 上、下、中)(3)(中、上、下)(4)(中、下、上),( 5 ) ( 下 、 中 、 上 ) , (6) (下、上、中)。这个策略全体就是局中人的策略集合。 有限,无限
管理运筹学 易错判断题整理

× 5 如果运输问题或者转运问题模型中,Cij 都是产地i到销地j的最小 运输费用,则运输问题同转运问题将得到相同的最优解。
√
第三章:目标规划
主要内容: 1 描述目标规划建模的思路以及他的数学模型同一般线性 数学模型的相同和不同点。 2 解释下列变量:1正负偏差变量 2绝对约束和目标约束 3 优先因子与权系数。 3 目标规划图解法的步骤。 4 目标规划 目标函数特点。 判断题: 1 目标规划模型中,可以不含有绝对约束但是必须含有目 标约束。
第一章:线性规划及单纯形法
2.1单纯形法和两阶段法大M法 主要内容
1 线性规划数学模型的结构及各要素的特征。 2 求解线性规划时可能出现哪几种结果。 3 叙述线性规划问题的可行解、基解、基可行解、最优解 的概念及上述解之间的关系。
4 单纯性法的计算步骤,如何在单纯性表中判别问题是具 有唯一最优解、无穷多最优解、无界解。
√ 4 动态规划的基本方程保证各阶段内决策的独立进行,可以不考虑这之前和之后 决策的如何进行。
√
第六章:网络规划
主要内容:
6.1 1 通常用G=(v,e)表示一个图,试描述符号V,E及表达式的含义。 2 解释下列名词,说明区别。1 端点,相邻,关联边, 2 环,多重边,简单图 3链,初等链 4. 圈,初等圈,简单圈。 5.回路,初等路6.节点的次,悬挂点,悬挂边,孤立点 7. 连通图,连通分图 ,支撑子图8. 有向图,基础图,赋权图 3 描述树,图的支撑树,最小支撑树的概念。 4 描述Dijkstra算法的基本思想和步骤。 5 最大流问题是线性规划问题,说明其线性形式。 6 什么是增光链,为什么不存在关于可行流f的增广链,就是最大流。 7截集,截量以及最大流最小截量定理。 8 最小费用最大流的概念。
矩阵对策的基本理论

A
a21
a22
a2n
am1 am2 amn
(12-3)
为局中人Ⅰ的赢得 矩阵。由于对策为零和的,故局中人 Ⅱ的赢得矩阵为-A。
当局中人Ⅰ、Ⅱ的策略集 S1, S2 及局中人Ⅰ的赢得矩阵 A 确定后,一个矩阵对策就给定
了。因此将矩阵对策表示为 G S1,S2;A.
矩阵对策的最优纯策略
x E m
x
x , x ,, x
12
m
T
,
x i
0, i
1,,
m,
m
x i
i 1
1
S 2
y
E
n
y
y , y ,, y
12
n
T,
y j
0,
j
1,
n,
n
j 1
y j
1
S 和S 1
2
分别称为局中人Ⅰ和Ⅱ的混合策略集;
x
S
1
和y
S
2
分别称为局中人Ⅰ和Ⅱ
的混合策略;当
x
S 1
和y
S
2
其中, T G1
和T G 2
分别为局中人 I 和 II 的策略集。
运筹学
使自己的赢得尽可能的小,理性的选择就应该是从各自可能出现的最不利的情形中争取尽可
能好的结果。
管理运筹学11对策论

2019/10/28
1. 矩阵对策的数学模型
建立二人零和对策的模型就是要根据对实际问 题的叙述,确定甲、乙两个局中人的策略集合以 及相应的赢得矩阵。不难看出在“齐王赛马”的 例子中,齐王的赢得矩阵为:
3 1 1 1 1 -1
义;若抽到黑牌,甲的掷硬币已无意义,只与乙的猜红 或猜黑有关。所以,对于局势“掷硬币,猜红”甲的期 望赢得为:1/2(1/2p-1/2q)+1/2t = 1/4(p-q+2t )
2019/10/28
1. 矩阵对策的示例2
抽到红牌1/2
掷硬币
让乙猜
抽到黑牌1/2 让乙猜
正面 1/2
反面 1/2
猜红
定理1:设矩阵对策G={S1,S2,A}在策略意 义下有解的充分必要条件是存在着局势( i* ,j* ) 使得对于一切i与j都有aij* ai*j* ai*j成立。
定理2:对策矩阵G={S1,S2,A}在混合策略 意义下有解的充分必要条件是存在着
x * S1* , y * S2*使(x *,y *) 为E (x,y) 的 一个鞍点,即对于一切x S1* , y S2* 有
对 策
零和
盟
多人
对
策
无
非零和
限
对 同有限对策
策
第二节:矩阵对策
1.矩阵对策的数学模型 2.矩阵对策解的问题 3.矩阵对策的混合策略 4.矩阵对策的基本定理 5.矩阵对策解的性质
2019/10/28
1.矩阵对策的数学模型
(1)矩阵对策的内涵:二人有限零和对策,即对策双方 的利益是激烈对抗的。
11 对策论

11 对策论1、甲、乙二人零和对策,已知甲的赢得矩阵,求双方的最优策略与对策值。
(1)2124148523A --⎡⎤⎢⎥=⎢⎥⎢⎥-⎣⎦ (2)221344216A ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦(3)963564743A --⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦ (4)176435024A ⎡⎤⎢⎥=--⎢⎥⎢⎥-⎣⎦(5)2314641543322324A --⎡⎤⎢⎥--⎢⎥=⎢⎥⎢⎥--⎣⎦ (6)93180654672433856221A ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦解(1)max[min()]min[max()]ij ij jjiia a ==1甲的最优策略:2α,乙的最有策略:1β;对策值1G V = (2)max[min()]min[max()]ij ij jjiia a ==3甲的最优策略:2α,乙的最有策略:1β;对策值3G V = (3)max[min()]min[max()]ij ij jjiia a ==4甲的最优策略:2α,乙的最有策略:3β;对策值4G V = (4)max[min()]min[max()]ij ij jjiia a ==1甲的最优策略:1α,乙的最有策略:1β;对策值1G V = (5)max[min()]min[max()]ij ij jjiia a ==2甲的最优策略:3α,乙的最有策略:4β;对策值2G V = (6)max[min()]min[max()]ij ij jjiia a ==4甲的最优策略:2α,乙的最有策略:3β;对策值4G V =2、甲、乙二人进行一种游戏,甲先在横轴的[0,1]x ∈区间内任选一个数,不让乙知道;然后乙在纵轴的[0,1]y ∈区间内任选一个数。
双方选定后,乙对甲的支付为22175(,)22224P x y y x xy x y =--++,求甲、乙二人的最优策略和对策值。
7422524px y xp y x y∂⎧=-+⎪∂⎪⎨∂⎪=-+∂⎪⎩因为22222422px py px y ⎧∂=-⎪∂⎪⎪∂⎪=⎨∂⎪⎪∂=-⎪∂∂⎪⎩所以p(x,y)由最小值。
《运筹学》试题及答案(五)

《运筹学》试题及答案(代码:8054)一、填空题(本大题共8小题,每空2分,共20分)1.线性规划闯题中,如果在约束条件中出现等式约束,我们通常用增加_人工变量__的方法来产生初始可行基。
2.线性规划模型有三种参数,其名称分别为价值系数、_技术系数__和_限定系数__。
3.原问题的第1个约束方程是“=”型,则对偶问题相应的变量是_无非负约束(或无约束、或自由__变量。
4.求最小生成树问题,常用的方法有:避圈法和 _破圈法__。
5.排队模型M/M/2中的M,M,2分别表示到达时间为__负指数_分布,服务时间服从负指数分布和服务台数为2。
6.如果有两个以上的决策自然条件,但决策人无法估计各自然状态出现的概率,那么这种决策类型称为__不确定__型决策。
7.在风险型决策问题中,我们一般采用__效用曲线_来反映每个人对待风险的态度。
8.目标规划总是求目标函数的_最小__信,且目标函数中没有线性规划中的价值系数,而是在各偏差变量前加上级别不同的_优先因子(或权重)___。
二、单项选择题(本大题共l0小题,每小题3分,共30分)在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内。
多选无分。
9.使用人工变量法求解极大化线性规划问题时,当所有的检验数在基变量中仍含有非零的人工变量,表明该线性规划问题【 D 】A.有唯一的最优解 B.有无穷多最优解C.为无界解 D.无可行解10.对偶单纯形法解最大化线性规划问题时,每次迭代要求单纯形表中【 D 】A.b列元素不小于零 B.检验数都大于零C.检验数都不小于零 D.检验数都不大于零11.已知某个含10个结点的树图,其中9个结点的次为1,1,3,1,1,1,3,1,3,则另一个结点的次为【 A 】A.3 B.2C.1 D.以上三种情况均有可能12.如果要使目标规划实际实现值不超过目标值。
则相应的偏离变量应满足【 B 】13.在运输方案中出现退化现象,是指数字格的数目【 C 】A.等于 m+n B.等于m+n-1C.小于m+n-1 D.大于m+n-114.关于矩阵对策,下列说法错误的是【 D 】A.矩阵对策的解可以不是唯一的C.矩阵对策中,当局势达到均衡时,任何一方单方面改变自己的策略,都将意味着自己更少的赢得和更大的损失D.矩阵对策的对策值,相当于进行若干次对策后,局中人I的平均赢得或局中人Ⅱ的平均损失值【 A 】A.2 8.—l C.—3 D.116.关于线性规划的原问题和对偶问题,下列说法正确的是【 B 】A.若原问题为元界解,则对偶问题也为无界解B.若原问题无可行解,其对偶问题具有无界解或无可行解c.若原问题存在可行解,其对偶问题必存在可行解D.若原问题存在可行解,其对偶问题无可行解17.下列叙述不属于解决风险决策问题的基本原则的是【 C 】A.最大可能原则 B.渴望水平原则C.最大最小原则 D.期望值最大原则18.下列说法正确的是【 D 】A.线性规划问题的基本解对应可行域的顶点也必是该问题的可行解D.单纯形法解标准的线性规划问题时,按最小比值原则确定换出基变量是为了保证迭代计算后的解仍为基本可行解三、多项选择题(本大题共5小题,每小题2分,共l0分)在每小题列出的四个备选项中至少有两个是符合题目要求的,请将其代码填写在题后的括号内。
运筹学()——精选推荐
4
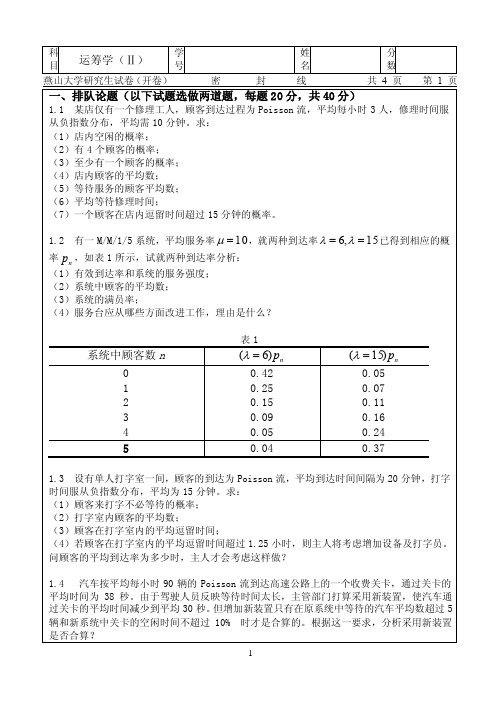
1.3 设有单人打字室一间,顾客的到达为 Poisson 流,平均到达时间间隔为 20 分钟,打字 时间服从负指数分布,平均为 15 分钟。求: (1)顾客来打字不必等待的概率; (2)打字室内顾客的平均数; (3)顾客在打字室内的平均逗留时间; (4)若顾客在打字室内的平均逗留时间超过 1.25 小时,则主人将考虑增加设备及打字员。 问顾客的平均到达率为多少时,主人才会考虑这样做?
(1)根据 / 说明增加工人的原因;
(2)增加工人后店内空闲的概率;店内至少有 2 个或更多的顾客的概率 ;
(3)求 L, Lq ,W ,Wq 。
1.13 某火车站的电话问讯处有 3 部电话,可以视为 M/M/3/3 系统。已知平均每隔 2 分钟 有一次问讯电话(包括接通和未接通的),每次通话平均时间为 3 分钟。试问打来问讯处的 电话能接通的概率为多少?
1.15 顾客以每小时 4 人的平均到达率到一个双人理发店理发,顾客到达过程为 Poisson 流。当顾客到达理发店 时发现理发店已 有顾客在理发, 则该顾客就拒绝 进入此店,并不再 来。若理发店的理发时间服从负指数分布。试问:
(1)若要保证在可能到达的顾客中至多有 40% 的顾客不进入理发店,则每个理发师 必须以怎样的服务率进行服务?
(2)进入理发店的平均顾客数是多少? (3)顾客的平均理发时间是多少?
二、对策论题(以下试题选做一道题,20 分)
2.1 甲、乙两游泳队举行包括两个项目的对抗比赛,两队各有一名健将级运动员(甲队为
李,乙队为王),在 3 个项目上的成绩都很突出。但规则规定他们每人只许参加两项比赛,
每队的其他两名运动员可参加全部 3 项比赛。已知各运动员的平时成绩(秒)见表 2。假定 各运动员在比赛中正常发挥水平,又设比赛的第一名得 5 分,第二名得 3 分,第三名得 1 分。问教练应决定让自己队健将参加那两项比赛,可使本队得分最多?
二人零和有限对策

毕业论文(设计)题目: 二人零和有限对策问题的研究学院: 数理与信息学院学生姓名: 梁世龙学号:060503202专业:数学与应用数学班级:B06数学(2)班指导老师:金丽起止日期:2010.03.01~2010.05.072010 年6 月18 日摘要二人零和有限对策是对策论的分支问题. 而对策论是应用数学的一个分支问题, 目前在生物学, 经济学, 国际关系, 计算机科学, 政治学, 军事战略和其他很多学科都有广泛的应用. 二人零和有限对策是一种最基本的策略, 它的一套比较成熟的理论和算法是研究其他各种对策的基础. 本文主要讨论二人零和有限对策问题的基本理论和算法, 并了解在实际问题中的应用.关键词: 二人零和有限对策; 对策论; 鞍点Finite Two Person Zero-sum GamesAbstractFinite two person zero-sums game is a branch of game theory, and game theory is a branch problem of applied mathematics. It has a wide range of application in biology, economics, international relations, computer science, political science, military strategy and many other disciplines at present. Finite two person zero-sum games is a basic strategy, it has the mature theory and algorithms, it is the basis for study the other game problems. This article focuses on the basic theory and algorithms of Finite two person zero-sums game, and understands the applications of practical problems.Keywords:Finite two person zero-sums game; Game theory; Saddle point目录摘要 (I)Abstract (II)1 前言 (1)2 对策 (2)2.1对策的例子 (2)2.2对策的基本要素 (2)2.3展开型对策 (5)2.4对策的分类 (11)3 二人零和有限对策 (12)3.1矩阵对策的基本概念 (12)3.2混合策略 (17)3.3最大最小定理 (25)3.4矩阵对策的最优策略 (27)3.5矩阵对策与线性规划的关系 (36)3.6矩阵对策的求解 (42)4小结 (54)致谢 (56)1 前言对策论是研究竞争性行为的数学分支. 在日常生活中的下棋、打牌、体育竞赛等, 在社会生活中如战争、企业的竞争等, 都具有竞争或对抗的性质, 我们把这一类行为称为对策行为. 在对策行为里, 参加竞争的个体有不同的目标和利益. 为了实现各自的目标, 每个个体必须考虑对手的各种行动方案, 并尽量选取对自己最有利的策略.二人零和对策是指参与对策的局中人只有两个, 每个人的策略集均是有限集并且两个局中人的赢利之和为零(或某个常数). 在对策论中理论最简单又最完善的部分是二人零和对策, 它是其他各部分理论的基础. 在一个二人对策问题中(例如两人进行对抗性竞赛), 参加者分别为局中人甲和乙, 他们都有自己的策略. 若甲有m 个策略, 乙有n 个策略. 当甲选取第i 个策略时,乙选取第j 个策略, 这便形成一种局势. 此时甲、乙双方会有赢得或损失. 若甲所得为()()(),,1,2,,;1,2,,i j a f x i j i m j n ==== , 乙的所得为(),i ja -, 则(),i ja 为甲取第i 个策略、乙取第j 个策略时甲的支付(或赢得).[1]上述问题可用矩阵方法进行处理. 因此这类对策也称为二人零和矩阵对策. 对策论的中心问题是局中人采取何种策略才能使自己赢得最多(或损失最少).从数学角度看, 二人零和对策问题可以分为二人零和有限对策和二人零和无限对策, 在这里我们只讨论二人零和有限对策.二人零和有限对策是一种最简单、最基本的策略. 说它简单是因为只有两个局中人, 并且每个局中人只有有限个策略; 说他基本是因为它有比较成熟的理论和算法,是研究其他对策的基础. 二人零和有限对策也称为矩阵对策. 在每局中, 两个局中人独立选择一个策略(互相都不知道对方的策略), 而两人的收益总和为零. 在这种对策中, 两个局中人的利益是完全相反的, 因此不可能合作.本文中我们主要介绍二人零和有限对策的理论和矩阵对策问题的求解方法.2 对策2.1 对策的例子[2]例 2.1田忌赛马问题. 战国时期, 齐国的国王与一名叫田忌的大将进行赛马. 双方各出三匹马, 分别为上(等)马、中(等)马、下(等)马各一匹. 比赛时, 每次双方各从自己的三匹马中任选一匹马来比, 输者付给胜者1千两黄金, 共赛三次. 当时, 三种不同等级的马相差非常悬殊, 而同等级的马, 齐王的比田忌的要强. 谋士孙膑给田忌出了个主意: 每次比赛先让齐王牵出他要参赛的马, 然后用下马对齐王的上马, 用中马对齐王的下马, 用上马对齐王的中马. 结果田忌二胜一负, 赢得1千两黄金. 由此看来, 两人采取什么样的策略(出马次序)对胜负是至关重要的.例 2.2 冬季取暖问题. 某单位要在秋季决定冬季取暖所用煤的储量. 在正常的冬季气温下,需要消耗15吨煤, 但在较暖或较冷的时候分别需要10吨和20吨煤. 设煤的价格随着冬季的冷暖程度而有所变动: 在较暖、正常、较冷的气温下分别为每吨100元、120元、150元. 假设在秋季煤价为每吨100元. 问在没有当年冬季准确的气象预报条件下, 秋季储存多少吨煤才合理?例 2.3罪犯两难问题. 甲、乙两人因犯罪而牵涉于某案件中, 但法院只掌握其部分罪证. 如果他们都不承认, 则他们将被作为较小的违法案件的被告而受到惩罚(例如各判刑一年); 如果两人都认罪, 则两人都被判刑, 但考虑其认罪态度, 可以给予减刑(例如各判刑六年); 如果一人认罪, 而另一人拒不承认, 则认罪的可以宽大处理(例如判刑3年), 而拒不认罪者将受到严惩(例如判刑10年), 问甲、乙应该怎样选择才能对自己有利?2.2对策的基本要素对策模型的形式千差万别, 但都必须包括三个基本要素: 局中人, 策略集和支付函数.(1)局中人对策中, 有权决定自己行动方案的参加者称为局中人(player), 一般的用N表示局中人的集合. 在一个对策中至少要有两个局中人. 局中人除了可以是一个自然人外, 还可以是代表着共同利益的一个集团, 例如球队、企业、国家. 在研究人与大自然作斗争时, 人和自然都是局中人.(2) 策略集对策中, 局中人选择的一个实际可行且完整的行动方案称为一个策略(strategy). 参加对策的每个局中人i 都有自己的策略集(strategy set)i S , i N ∈, 它是局中人i 的所有策略的集合.在任何一个对策中, 每个局中人至少要有两个策略, 这是因为, 若某个局中人只有一个策略, 则策略的结果将完全听凭别人摆布, 该局中人就是去了作局中人的资格.例2.1 中, 如果用(上, 中, 下)表示用上马、中马、下马这样一个顺序参加比赛,这 就是一个完整的行动方案, 即一个策略. 则齐王和田忌都有六个策略: (上, 中, 下), (上, 下, 中), (中, 上, 下), (中, 下, 上), (下, 中, 上), (下, 上, 中), 把齐王的策略记为123456,,,,,αααααα, 田忌的策略记为123456,,,,,ββββββ. 例2.2 中, 人有三个策略: 秋季买煤10吨、15吨和20吨, 记为123,,ααα; 大自然也有三个策略: 冬天的气温较暖、正常、较冷, 记为123,,βββ.例2.3中, 罪犯甲有两个策略: 不承认和承认, 记为1α和2α; 罪犯乙同甲一样,也有两个策略: 不承认和承认, 记为1β和2β.要注意的是, 这里的策略强调“完整性”, 并不是指对策中所采取的局部行动方案, 例如, 在下象棋时, 在一局棋中, 某一步走“当头炮”, 只是作为一个策略的组成部分, 而不是一个完整的策略. 又如在田忌赛马问题中, 齐王的三匹马的出场顺序是一个策略, 但每次出哪匹马只是一个策略的一个部分, 并不是一个完整的行动方案.我们从策中每一个局中人的策略集中,各取一个策略组成策略组,则它称之为对策的局势(situation). (3) 支付函数对策的结果是由局势唯一确定的. 对策的结果决定了每个局中人的得失, 这种得与失称之为局中人的支付(payoff). 可见, 局中人的支付都是局势的函数, 因此称支付为支付函数(payoff function). 局中人i 的支付函数可记为,i P i N ∈.通常, 局中人的集合N , 策略集{}i S 和支付函数{}i P , 确定这三个基本要素之后, 一个对策Γ就完全确定了. 记{}{}(),,.i i N S P Γ=这种对策称之为策略型(strategy form)对策或正规型(normal form)对策.在田忌赛马的问题中, 齐王的支付函数可以写成表 2.1 所示的表格:表2. 1 田忌赛马问题中齐王的支付函数1 β2 β3 β4 β5 β6 β1α 3 1 1 1 1 -1 2α1 3 1 1 -1 1 3α 1 -1 3 1 1 1 4α -1 1 1 3 1 5α 1 1 -1 1 3 1 6α1111-13若只考虑数字, 则齐王的支付函数就是一个矩阵:311111131111113111111311111131111113-⎡⎤⎢⎥-⎢⎥⎢⎥-⎢⎥-⎢⎥⎢⎥-⎢⎥-⎣⎦; 相同的, 田忌的支付函数也可写成矩阵:311111131111113111111311111131111113-----⎡⎤⎢⎥-----⎢⎥⎢⎥----⎢⎥-----⎢⎥⎢⎥-----⎢⎥-----⎣⎦. 冬季取暖问题中, 人的支付函数为123123100016002500150015002250200020002000βββααα---⎡⎤⎢⎥---⎢⎥⎢⎥---⎣⎦, 这也是一个矩阵, 大自然的支付函数是100016002500150015002250200020002000⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦.罪犯两难问题, 甲、乙的支付函数分别为12 12120372ββαα--⎡⎤⎢⎥--⎣⎦, 1212 12312072ββαα--⎡⎤⎢⎥--⎣⎦.这也是矩阵的形式.2.3 展开型对策策略型对策中, 局中人的策略集在对策开始之前就已确定了, 但是, 有的对策无法提前确定局中人的一个完整行动方案. 那么, 局中人的每一步需要依据其他局中人的前一步来确定, 我们把这类对策称为展开型(extensive form)对策. (1) 定义定义 2.1[3] 有向图(),D X A =指由一个非空有限集X 和X 中的某些元素的有序对集合A 所构成的二元组(),X A . X 称之为D 的顶点集, 其中的元素称之为顶点; A 称为D 的弧集, 其中的元素称之为弧.若, A 中的元素a 是X 中元素x 与y 的有序对, 即(),a x y =, 那么称x 为a 的尾,y 为a 的头; a 为x 的出弧, 也称为y 的入弧; 还称x 与y 相邻.x X ∀∈, 此时记()(){}()(){},,,,D DN x y Xx y A N x y X y x A +-=∈∈=∈∈分别称为顶点x 在D 中的出邻域(out-neighbour)和入邻域(in-neighbour).若D 中有k 个相异顶点i x X∈()1,2,,i k = , 使()()1,2,3,,i i x x A i k -∈= , 那么称序列12k x x x 为D 的一条从1x 到k x 的路(path).定义2.2 若有向图(),T X A =满足 (1) 存在0x X ∈, 且0x 没有入弧; (2) {}0\,x X x x ∀∈有一条入弧;(3) {}0\,x X x D ∀∈中有唯一的从0x 到x 的路,则称T 为树形图, 并称0x 为T 的根(root), T 中没有出弧的顶点称为T 的梢(tree-top), 记T 中所有树梢的集合为X ∂.定义2.3 假设{}1,2,,N n = 是局中人的集合, 若 (1) 存在树形图(),T X A =, 且X X ≠∂; (2) 存在映射:\X X N ϕ∂→; (3) 存在映射:n p X ∂→ℜ,于是称四元组(),,,N T p ϕ∑=为n 人对策树.下面对对策树中的概念作一些解释.若0x 为树形图T 的根, 并且()0x i N ϕ=∈, 其表示在0x 处行动的局中人为i . 假设局中人i 选取0x 的一条出弧()01,x x , 在1x 处行动的局中人为j , 即()1x j N ϕ=∈, 而且局中人j 又选取弧()12,x x , , 诸如此类.由树形图T 的定义可得, X ω∀∈∂, T 中存在唯一的一条从根0x 到梢ω的路10l i i x x x ω , 我们把这条路称为通往ω的局(play).对于通往ω的局, 对应的有()()()()()12,,,,nn p p p p ωωωω=∈ℜ其中()i p ω表示局中人i 在通往ω的局中所得到的支付, 1,2,,i n = ; 向量()p ω则表示所有局中人通往ω的局中所得到的支付的分布情况.i N ∀∈, 引入集合(){}\,i X x X X x i ϕ=∈∂=它表示局中人i 的行动顶点的集合, 也可以记为()1i ϕ-. 再记()0\\,i i NX X XX ∈⎛⎫=∂ ⎪⎝⎭那么01,,,n X X X 是\X X ∂的一个划分. 若有0x X ∈, 则表示在顶点x 处, 是随机选择行动的. 所以, 我们设: 0x X ∀∈, 在x 的出弧集上给定一个概率分布, 且x 的每条出弧上的概率均为正, 记x p .有了上述概念, 现在可以给出展开型对策的定义. 定义 2.4 展开型n 人对策Γ指定了一下的四个条件: (1) 对策树(),,,N T p ϕ∑=;(2) \X X ∂划分成1n +个子集01,,,n X X X ; (3) 0,x X x ∀∈的出弧集上的概率分布0x p >;(4) i N ∀∈, i X 有一个划分为12,,,ii i it X X X , 则称()1,2,,il i X l t = 为局中人i 的信息集(information set), 其中,il x y X ∀∈, x 与y 不相邻, 并且()()TTN x N y ++=.简单来说, 展开型对策Γ就是一个六元组, 如下所示{}{}()12,,,,,,,,ix i i it i NN T p p X X X ϕ∈Γ= .在展开型对策中, 引进了信息集的概念是为了表达一种情况: 当轮到局中人i 行动时, 他只了解自己处于该信息集内的某个顶点处, 但又不能确定自己到底在哪个顶点上.假设Γ是展开型n 人对策, i N ∈, 如果存在信息集it X 满足2it X ≥, 那么局中人i 只知道自己处于it X 内, 而不能确定具体的位置, 则称局中人i 在it X 中有着不完全信息(imperfect information); 若{}1,2,,i l k ∀∈ , 有1it X =, 那么称Γ有完全信息(perfect information). 如果Γ中的每个局中人都有完全信息, 则Γ有完全信息. 棋类比赛就是具有完全信息的对策, 而桥牌则不是.展开型对策与策略型对策虽然在定义上有所不同, 但它们是可以互相转化的. (2) 策略型对策化为展开型对策假设策略型对策{}{}(),,i i N S P Γ=, 其中{}()()(){}()121,2,,,,,, 1,2,,.i i i i i m N n S s s s i n ===就可以构造一个对策树: 其以0x 为根, 0x 有1m 条出弧()()110,k x x , 111,2,,km = , 分别对应局中人1的1m 个策略; 每个顶点()()11111k x k m ≤≤有2m 条出弧()()()1212,k kx x ,()'22121k k k m =+-, '221,2,,k m = , 它们对应局中人2的2m 个策略; 像这样继续下去,对每个顶点()()1111211n n k n n x k m m m ----≤≤ , 有n m 条出弧()()()11,n nn n k k x x --,()'11n n n n k k k m -=+-, '1,2,,n n k m = , 对应于局中人n 的n m 个策略. 这里{}(){}(){}010112112, ,1, 2,3,,,1;i ni i k ii n k nnX X x X x k m m m i n Xx km m m --=∅==≤≤=∂=≤≤ ()n n k x X ∀∈∂, 在对策树中从根0x 到梢()n n k x 的唯一路对应于Γ的唯一局势s , 则()()()()()()12,,,.nn k np x P s P s P s =说明策略型对策可以转化为展开型对策. 若策略型对策Γ中局中人对自己所采用的策略保密, 则Γ所对应的展开型对策具有不完全信息. (3) 展开型对策化为策略型对策定义 2.5[4]展开型对策Γ中局中人i 的一个策略()i s是定义在局中人i 的信息集{}12,,,i i i it XX X 上的一个映射, 使1i l t ∀≤≤, ()()i il s X 对应于ilX 中, 以顶点为尾的一条弧. 局中人i 的所有策略构成的策略集记为i S , 1,2,,i n = .该定义说明: 策略()i s是局中人i 的一个行动方案, 它指明局中人i 在自己的每一个信息集上该选择哪一条出弧. 每个局中人i 在选定一个策略()()1,2,,i i s S i n ∈= 后, 就组成一个局势()()()()12,,,n s s ss= .x X ∀∈, 对策树中存在从根到x 的唯一的路, 这条路上的弧的集合记为()A x . 特殊的, 局势s 对应对策树只能从根到梢ω的唯一的路, 即s 对应于通往ω的局.在局势()()()()12,,,n s s ss= 下, 在顶点x 处选择出弧(),x y 的概率为()(),,,1, 0, x p x y s x y ⎧⎪=⎨⎪⎩()()()0,,,.i it it x X x X s X x y ∈∈=且其他所以, 在局势s 下, 顶点x 出现的概率为[]()()(),,.y z A x s x s y z ∈=∏则, 在在局势s 下, 到达树梢ω的概率为[]s x , 局中人i 在树梢ω上得到的支付为()i p ω, 所以局中人i 在局势s 下的支付是()()[].i i XP s p s ωωω∈∂=∑则, 当0X =∅时, 假设局势s 对应于通往ω的局, 那么()().i i P s p ω=例 2.4 对于翻摊游戏问题, 在桌上放五根火柴, 甲、乙二人轮流取走一根或两根, 谁取走最后一根或两根则为胜者, 胜者得一分, 输者失1分. 则甲的策略为()()()()()()()()()()11121314152,1,2,2,1,2,1,1,1,1,1,s s s s s ===== 策略中第j 个数为第j 次取的火柴的数量; 乙的策略为()()()()()()()()212223242,1,1,2,1,1,2,s s s s ====相同的, 第j 个数为乙第j 次取的火柴数; 甲的支付函数如表2.2所示.表2.2 翻摊游戏问题中甲的支付函数()21s()22s()23s()24s()11s 1 -1 1 -1 ()12s 1 1 1 1 ()13s 1 -1 1 -1 ()14s -1 1 -1 1 ()15s-11-11而乙的支付函数是上表中数字反号所得的表.下面为0X ≠∅的例子.例 2.5 两张纸牌游戏问题. 设游戏开始时, 甲(局中人1)和乙(局中人2)都压上一元的赌注, 然后甲从两张牌A 和2中抽一张牌给乙, 乙看了后再说话. 如果是A, 乙必须告诉甲是“A”; 如果是2, 乙可以说“A”, 也可以说是“2”. 但若乙说了“2”, 则判定为乙输, 他所压的一元钱就输给甲. 若说“A”, 则乙要再压上一元的赌注, 然后再由甲去判断. 甲如果相信乙, 就等于他输掉了自己所压的一元钱; 甲如果不信, 那么必须同样再压上一元, 然后去翻牌. 如果翻开后是A, 则乙赢甲2元; 如果是2, 则甲赢乙2元.在该对策中, 显然有{}{}{}00134212,,,,.X x X x x X x x ===且这是一个具有不完全信息的对策.可知, 甲有两个策略()11s ={乙说“A ”, 甲相信},(){12s =乙说“A ”, 甲不信};乙也有两个策略(){21s =牌为2, 说2}, (){22s =牌为2, 说A};甲的支付函数如表2.3所示.表2.3 两张纸牌游戏中甲的支付函数()21 s()22 s()11s 0-1()12s1-2因为两张牌中抽一张为A 或2的概率各为12, 则0X 中顶点0x 的两条出弧的概率均为12, 所以()()()()()()()()()()()()()()()()()1211112112121211212211,110,2211,111,22111,21,22211,220.22P s s P s s P s s P s s =⨯-+⨯==⨯-+⨯-=-=⨯-+⨯=-=⨯-+⨯=乙的支付函数是表2.3中数字反号所得的表.由于策略型对策已经有了一套较完善的求局中人“最合理”的行为方案的方法, 而展开型对策不是, 所以任何展开型对策都可转化为策略型对策来求解, 这个转化在展开型对策中有重要的作用. 但是, 展开型对策自身有它的固有特性, 而这些特性在转化为策略型对策之后就失去了, 所以, 就展开型对策本身考虑, 上述转化是否有必要还需研究.2.4 对策的分类对策的种类非常多, 可以根据不同的原则进行分类.(1) 根据每个局中人的策略是否可以在对策开始之前确定, 对策可以分为策略型对策和展开型对策.(2) 根据对策的过程是否和时间有关, 可以把对策分成动态对策和静态对策. 动态对策又称为微分对策(differential game).还有以下分类.只有两个局中人的对策称之为二人对策(two-person game). 有两个以上局中人的对策称之为多人对策(multi-person game). n 个局中人的对策称为n 人对策(n-person game). 如, 例2.1, 例2.2和例2.3都是二人对策.若对策中每个局中人的策略集都是有限的, 则称为有限对策(finite game), 否则称为无限对策(infinite game). 例2.1, 例2.2, 例2.3都为有限对策.在对策中, 若在任一局势中所有局中人的支付之和都为零, 则称为零和对策(zero-sum game); 若在任一局势中的支付之和为一个常数σ, 则称为常和对策(constant-sum game). 显然, 零和对策也为常和对策. 例2.1, 例2.2都为零和对策, 但例2.3不是零和对策, 也不是常和对策.3 二人零和有限对策二人零和有限对策是一种最简单、最基本的策略. 简单是因为只有两个局中人, 而且每个局中人都只有有限个策略; 说它基本是因为它有比较成熟的理论和算法,它是研究其他对策的基础.下文介绍二人零和有限对策的基本概念、解的存在性定理,即最大最小定理、最优策略的性质、与线性规划的关系、求解方法和求最有策略集的方法等内容.3.1 矩阵对策的基本概念假设Γ是二人零和有限对策, 局中人甲和乙的策略集为{}{}112212,,,,,,,.m n S S αααβββ==假设在局势(),i j αβ中, 甲的支付为()1,2,,;1,2,,ij a i m j n == , 那么甲的支付函数可以写成矩阵的形式()ij m nA a ⨯=; 又设在局势(),i j αβ中, 乙的支付为()1,2,,;1,2,,ij b i m j n == , 那么乙的支付函数也可以写成矩阵的形式()ij m nB b ⨯=.由于Γ是零和对策, 那么0ij ij a b +=, 1,2,,;1,2,,,i m j n ==则有B A =-, 所以Γ由甲的支付函数(矩阵)A 唯一确定. 那么二人零和有限对策可以记为()12,;S S A Γ=.因此二人零和有限对策也可称为矩阵对策(matrix game), A 称之为支付矩阵(payoff matrix).矩阵对策中一个局中人的所得就是另一个局中人的损失, 所以矩阵对策是完全对抗的, 则两个局中人绝对不可能合作, 即矩阵对策是非合作二人对策.若甲采用策略i α, 那么他至少可以得到1min i ij j np a ≤≤=.因为甲希望i p 越大越好, 所以它可以选择策略*i α, 使他的所得不少于*111m ax m ax m in i i ij j ni mi n p p a ≤≤≤≤≤≤==.同样的, 若乙采用策略j β, 则他至多损失1max j ij i mq a ≤≤=.因为乙希望j q 越小越少, 所以他可以选择策略*j β, 使他的所失不多于*111m in m in m ax j j ij j nj n i mq q a ≤≤≤≤≤≤==,也就是说, 若乙处理的合适, 甲的所得不会大于*j q .既然甲可以选择策略*i α, 使他至少可以得到*i p , 而乙可以选择策略*j β, 使甲至多得到*j q , 那么这两个值之间的关系是什么样的呢?以田忌赛马问题为例,*1616*1616m ax m in 1,m in m ax 3,i ij j i jij j i p a q a ≤≤≤≤≤≤≤≤==-==即**i j p q <.在冬季取暖问题中,*1313*1313m ax m in 2000,m in m ax 2000,i ij j i j ij j i p a q a ≤≤≤≤≤≤≤≤==-==-即**i j p q =.那么, 我们得到以下的结论.引理 3.1[5] 对于矩阵对策()12,;S S A Γ=, 有1111m ax m in m in m ax ij ij j nj n i m i ma a ≤≤≤≤≤≤≤≤≤ (3.1)证明 因为11m in ,1,2,,;1,2,,,m ax ,1,2,,;1,2,,,ij ij j nij ij i ma a i m j n a a j n i m ≤≤≤≤≤==≤==所以11min max ,1,2,,;1,2,,.ij ij j ni ma a i m j n ≤≤≤≤≤==上式左边与j 无关, 两边对j 取最小值, 得111min min max ,1,2,,,ij ij j nj n i ma a i m ≤≤≤≤≤≤≤=两边再对i 取最大值, 得11max min min max ,ij ij j nj n i mi ma a ≤≤≤≤≤≤≤≤≤这就证明了(3.1)式.定理 3.1[6]矩阵对策()12,;S S A Γ=有等式1111m ax m in m in m ax ij ij j nj n i m i ma a ≤≤≤≤≤≤≤≤= (3.2)成立的充要条件是存在局势()**,i j αβ, 使得****,1,2,,;1,2,,.ij i j i j a a a i m j n ≤≤== (3.3)证明 ()⇐假设Γ存在局势()**,i j αβ使得(3. 3)成立, 从而****1max min ,ij i j i j i j ni ma a a ≤≤≤≤≤≤所以**11min max max min ,ij ij i j i j n i j ni mi m a a a ≤≤≤≤≤≤≤≤≤≤另一方面, 由引理3.1, 有1111m ax m in m in m ax ij ij j nj n i m i ma a ≤≤≤≤≤≤≤≤≤因此**1111max min min max .ij ij i j j nj n i m i ma a a ≤≤≤≤≤≤≤≤==()⇒设(3.2)式成立. 容易知道有**1,1i m j n ≤≤≤≤, 使**111111m in m ax m in ,m ax m in m ax ,ij i j j nj ni m ij ij j n i mi ma a a a ≤≤≤≤≤≤≤≤≤≤≤≤==则由(3.2)式得******1111max min max min ,ij i j i j ij i j j nj ni mi ma a a a a ≤≤≤≤≤≤≤≤=≤≤=于是****,1,2,,;1,2,,.ij i j i j a a a i m j n ≤≤==从(3.3)式可以看出: 当局中人甲采取策略*i α时, 局中人乙为了使自己所失最少, 只有选择策略*j β, 否则就可能失去更多; 同样, 当局中人乙采取策略*j β时, 甲为了得到最多, 也只能选择策略*i α, 否则得到的将更少. 有此可知, 双方的竞争在局势()**,i j αβ下达到一个平衡的状态. 由此给出下面的定义.定义 3.1[6]设矩阵对策()12,;S S A Γ=, 如果存在**12,i j S S αβ∈∈, 使得****,1,2,,;1,2,,,ij i j i j a a a i m j n ≤≤==则称局势()**,i j αβ为Γ的平衡局势(equilibrium situation)或解(solution); *i α与*j β分别称为局中人甲与乙的最优策略(optimal strategy); **i j a 称为Γ的值(value), 记为v Γ.由定理3.1的必要性的证明可得**1111max min min max ij ij i j j nj n i m i mv a a a Γ≤≤≤≤≤≤≤≤===,因此有以下的推论.推论 3.1 如果矩阵对策()12,;S S A Γ=使(3.2)式成立, 那么Γ有解, 而且Γ的值等于(3.2)式的值.在冬季取暖问题中, 由前面的计算可得13131313max min min max 2000,ij ij j j i i a a ≤≤≤≤≤≤≤≤==-所以该对策有解()33,αβ, 即秋季存20吨煤最为合理, 对策的值为-2000.仿照二元函数中鞍点的定义, 又称满足(3.3)式的局势()**,i j αβ是对策Γ的鞍点(saddle point).根据以上讨论, 我们可以给出求矩阵对策()12,;S S A Γ=和鞍点的一个方法[6]: 分别求出支付矩阵A 中第i 行的最小元素()1,2,,i p i m = 和第j 列的最大元素()1,2,,j q j n = , 如果11max min i j j ni mp q ≤≤≤≤=,则Γ有解, 并且满足**11m ax ,m in i i i mjj j np p q q ≤≤≤≤==的局势()**,i j αβ是Γ的鞍点, **i jv p q Γ==.一个矩阵对策的鞍点可能有许多个. 如, 假设矩阵对策的支付矩阵为6595142185750263A ⎡⎤⎢⎥-⎢⎥=⎢⎥⎢⎥⎣⎦, 那么Γ有四个鞍点()()()()12143234,,,,,,,,αβαβαβαβ 且5v Γ=.当对策的鞍点不惟一时, 鞍点之间有如下关系. 定理 3.4[6] 在矩阵对策()12,;S S A Γ=中, 若()11,i jαβ和()22,i j αβ是Γ的两个鞍点,则有 (1) 对策值的无差别性: 1122i j ij a a =;(2)鞍点的可交换性: ()12,i jαβ和()21,i j αβ都是Γ的鞍点.证明 (1) 由鞍点的定义, 有211112122221,,i j i j i j i j i j i j a a a a a a ≤≤≤≤从而2221111222,i j i j i j i j i j a a a a a ≤≤≤≤于是22211112i j i j i j i j v a a a a Γ====.(2) 由鞍点的定义可知, {}1,2,,,i m ∀∈ 有1112122212,,ij i j i j ij i j i j a a a a a a ≤=≤=并且{}1,2,,,j n ∀∈ 有1211121222,,i j i j i j i j i j i j a a a a a a =≤=≤从而21211212,1,2,,;1,2,,,,1,2,,;1,2,,.ij i j i j ij i j i j a a a i m j n a a a i m j n ≤≤==≤≤==这就证明了()12,i jαβ和()21,i j αβ都是Γ的鞍点.3.2 混合策略由3.1节的讨论可知, 在田忌赛马问题中16161616max min 13min max ij ij j j i i a a ≤≤≤≤≤≤≤≤=-<=所以对策无解, 即局中人都找不到各自的最优策略, 也就求不出对策的值.例 3.1 给定矩阵对策()12,;S S A Γ=, 其中3654A ⎡⎤=⎢⎥⎣⎦, 此时12121212m ax m in 4,m in m ax 5.ij j i ij j i a a ≤≤≤≤≤≤≤≤==可知12121212m ax m in m in m ax ij ij j j i i a a ≤≤≤≤≤≤≤≤<.所以Γ无解.这说明按定义3.1中的对策的解的概念会导致许多矩阵对策无解, 因此有必要把对策的解的定义作一些修改.由之前的讨论可以看出, 当两个局中人根据“从最不利情形中选取最有利的结果”的原则选取策略时, 例3.1中的局中人甲应选取2α, 局中人乙应选取1β, 此时甲将会得到5, 比期望得到的4还要多, 所以1β对乙来说并非是最优策略, 所以乙将会考虑采用策略2β. 那么, 甲也会采取相应的办法, 改选1α, 以使他得到6, 而乙又可能仍选1β来对付甲的策略1α. 那么, 甲选1α或2α以及乙选1β或2β的可能性都不能被排除, 对甲、乙双方来说, 不存在一个双方均可接受的平衡局势. 在这样的情形下, 一个相对自然的并且符合实际的想法是: 既然甲、乙双方都没有最优策略可选, 那是不是可以给出一个选取策略的概率分布?若局中人甲选取策略1α的概率是1x , 选取2α的概率是2x ; 乙选取1β的概率是1y ,选取2β的概率是2y , 那么{}{}()1122121212,,,,,,,,,1,1.m m ij m nS S A a x x y y αααβββ⨯===+=+=记()12,x x x =, ()12,y y y =, 则局中人甲的支付的期望值为()()()()111221221111111111(,) 3654 36151411119 4422E x y xAyx y x y x y x y x y x y y x x y x y T==+++=+-+-+--⎛⎫⎛⎫=---+⎪ ⎪⎝⎭⎝⎭ 由上式可知, 当114x =时, (,)E x y =92, 也就是说, 当局中人甲以概率14选取1α时, 他可以得到92, 但这并不能保证他的支付的期望值会超过92. 这是因为, 只要当乙以12的概率选取1β, 就可以控制局中人甲的期望值不会超过92. 所以92是局中人甲的支付的期望值. 同样, 局中人乙以概率12选取1β时, 他的所失的期望值也是92. 于是, 当据局中人甲分别以概率14与34选取1α与2α, 局中人乙以概率12分别选取1β与2β时, 对双方都是最好的选择.若把上述方法推广到一般情况中, 引入如下的概念. 定义 3.2[6] 假设有矩阵对策()12,;S S A Γ=, 其中{}{}()112212,,,,,,,,,m n ij m nS S A a αααβββ⨯=== 记()()*11*2101,2,,, 1,01,2,,, 1,mmi i i n nj j j S x x i m x S y y j n y ==⎧⎫=∈ℜ≥==⎨⎬⎩⎭⎧⎫⎪⎪=∈ℜ≥==⎨⎬⎪⎪⎩⎭∑∑称*1S 和*2S 分别为局中人甲和乙的混合策略集(mixed strategy set); **12,x S y S ∈∈分别为局中人甲和乙的混合策略; **12,x S y S ∀∈∀∈, 称(),x y 为Γ的一个混合局势(mixedsituation), 并称11(,)mniji j i j E x y xAy ax y T====∑∑为局中人甲的期望支付函数(expected payoff function), 或者简称为支付函数. 这样得到的一个新的对策记为()***12,;S SE Γ=,称之为Γ的混合扩充(mixed extension).由定义 3.2, Γ中的策略为*Γ中混合策略的特例, 或称*Γ中的混合策略是Γ中策略的一种扩充. 如, 局中人甲的策略k α等价于局中人甲的混合策略()12,,,m x x x x = , 其中1,0,i x ⎧=⎨⎩,.i k i k =≠为了便于区分, 我们把Γ的策略()1,2,,i i m α= 和()1,2,,j j n β= 统称为纯策略(pure strategy).一个混合策略()*121,,,m x x x x S =∈ 可以假设为两个局中人重复进行对策Γ时, 局中人甲分别采取纯策略12,,,m ααα 的频率. 如果只进行一次对策, 那么混合策略()12,,,m x x x x = 可以假设为局中人甲对各个纯策略的偏爱程度.同3.1节一样, 若两个局中人均按照“从最不利情形中选取最有利的结果”的原则, 那么局中人甲可以保证自己的支付的期望值不少于()**211m ax m in ,;y S x S v E x y ∈∈=。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 -1 2 0
1 d1 d3 -1 d1 d4 2 0
0 4 s3 s1 2 2 s3 s2 0 4
2 d1 d2 4
2 s3 s4 (2) 0
j i i
S={s1,s2,……,sm}—局中人甲的策略集 D={d1,d2,……,dn}—局中人乙的策略集 3.局势:在一局对策中,每个局中人都选定一个策略 后的各策略的组合。表示为(Si,Dj). 4.得失值(赢得函数):局中人选定某策略后相应的 收益值。表示为 R甲(si,dj)—甲的收益 R乙(si,dj)—乙的收益
s1 1 s2 -1 A s3 2 s4 0
d1 d2 d3 d4 s1 s2 s3 s4
1 -1 2 0 0 3 4 4 0 1 d1 d3 2 2 3 d d 4 1 4 1 1
d1 d2 d3 d4
0 3 4 4 0 1 2 2 3 4 1 1
证明 : 记 min ai* j min max aij max min aij max aij*
j j i i j i
min ai* j ai* j* , max aij* ai* j*
j i
故
aij* ai* j* , ai* j* ai* j
i 1, , m
j 1, , n
3.对策问题举例 ①下棋、打牌、体育比赛等。
② 齐王赛马:齐王与大将田忌赛马,各自的 马都分为三 等,但齐王的同等马均强于 田忌。孙膑给田忌出主意, 用下----上 ,上----中,中----下, 赢 B 石头 剪子 布 A 结果田忌胜出。 石头 0 1 -1 ③猜手:小孩A与B猜手, 剪子 -1 1 0 若规定赢 得1分, 布 0 1 -1 平得0分,输得 -1分, 则 A的赢得可用右表来 表示。
-甲的期望收益 -乙的期望损失
二、混合策略对策的解 1、定义:如果混合策略对策
x y
G*={S*,D*;E}满足:
E (x* , y* ) max E (x, y ) min E (x, y) 则称x , y 分别为局中人甲、乙的最优混合策略.
* *
(x* , y* )为对策G *的最优解。 VG * =E(x* ,y* )为对策G *的最优值。
4.对策的分类
动态:是连续时间的动态对策,因此从上一状态到
另一状态的转移用微分描述
对策 零和:得+失=0 二人: 静态: 非零和:得+失≠0 零和
结盟:多人在一起交换策略
多人 不结盟:多人在一起交换策略 和
非零和
零和 非零
二.对策问题的组成(几个基本要素) 1.局中人:一局对策的参加者。
2.策略:局中人在一局对策中对付对手的一个行动方 案。策略全体称为策论集。
d1 d2 s1 s2 s3 s4 d1
1 -1 2 0 0 d1 d2 s s 4 3 1 s3 2 2 d d 1 2 2 s3 s2 0 4 s4 4
'
d1 s3 2 s3 s4
s4 0
s3 2) (
故鞍点为(s3,d1) 对策值为VG*=2
A
练习
先用优超原理简化矩阵,再求解。
A
2 2 5 6
3 4 5 6 1 3 4 0 9 1 0 3 8 3 6 4
11.3二人有限零和对策的混合策略对策模型
一、基本概念 例:已知对策G={S,D;A}
A= 7
3
4
64*Biblioteka A'j对于A' min max aij max min aij 2, 即对策解是(s3 , d1)VG 2。 根据性质3,则X* (0,0,1,0), Y * (1,0,0,0),VG* 2
例7:求解矩阵
S1 A= S2 S3
y(1)= y(2)= y(3)= x(1)= x(2)= x(3)= VG*= 0 0.50000 0.50000 0 0.75000 0.25000 6.50000
aij* ai* j* ai* j 即( si* , d j* )是G的解
aij* ai* j* ai* j i 1, , m max aij* ai* j* min ai* j
i j
j 1, , n
min max aij max aij* ai* j* min ai* j max min aij
7 -2 5 3 -1 -6
VG 3 ( si* , d j* ) ( s2 , d 2 )
8
例3
3
8
7
只有一个鞍点
0 2 2 -3 5 4 3 2 3 4 -4 -2
min max aij 2
j i
max min aij 2
2、定理:设G*=(S*,D*;E)为混合对策,则
E ( x, y ) E ( x , y ) E ( x , y )
* * * *
例6: 求解下列对策
1 -1 A 2 0 0 3 4 4 0 1 2 2 3 4 1 1 0 3 4 4 0 1 2 2 3 4 1 1
对策论:把各式各样的冲突现象抽象成一种 数学模型,然后给出分析这些问题的方法 和解。
对策论-数学角度
博弈论-经济角度
2.对策论的历史
春秋战国时期-孙子兵法
殷代-围棋 19世纪-西方人把对策论应用于经济领 域
40年代中期-对策论作为一种数学理论 1944年,美籍匈牙利数学家-纽曼 (Neuman) 经济学家-曼格斯特 (Morgenstern) 《对策论及其在经济管理中的应用》
j i i j i j
但对于任意A, 有 max min aij min max aij
i j j i
只有ai* j* min max aij max min aij
j i i j
即( si* , d j* )是鞍点 证毕
例2 -2 4 8
2 3 -6
-2 8 2
i j
鞍点不存在, 即在纯策略意义下无解
5
4
2
例4
6 1 8 0
5 5 -1 4 2 -1 5 7 5 5 2 6 2 0 5 6
VG 5 ( si* , d j* ) ( s1 , d 2 ), ( s1 , d 4 ), ( s3 , d 2 ), ( s3 , d 4 ) 鞍点不唯一,但值唯一。
第11章 二人有限零和对策
第11章 二人有限零和对策
11.1基本概念
11.2二人有限零和对策
的纯策略对策模型
11.3二人有限零和对策
的混合策略对策模型
11.1 基本概念
一、对策现象与对策论
1. 对策和对策论
对策:就是竞争或斗争中的决策.
如:政治方面的阶级斗争,经济方面的劳资纠纷, 市场竞争,原料竞争,投标竞争,外贸谈判,军 备竞赛,各种体育比赛等.
d1 d2 10 -1 12 10 6 8
d3 3 -5 5
请你分析,理智情况下,甲、乙两 厂最可能出现什么策略,最大收益 是多少?
分析 :甲 : 当然想出s2
d1 d2 d 3 S1 10 -1 3 -1 乙:当然想出d3 A= S2 12 10 -5 -5 S3 6 8 5* 5* 12 10 5* 对甲而言,先想最坏,再想最好. 则s*=s3,V甲=5=max min aij 对乙而言,先想最坏,再想最好. 则d*=d3,V乙=5=min max aij (s3,d3)即为双方的最优策略,此时甲得5,乙失5。有 唯一最优策略。
甲选 max min aij si* j i 即理智局中人的选择 乙选 min max aij d j* j i
2、纯策略对策的解
(1) 对策G的解和值:使得aij* ai* j* ai* j 的(si* , d j* )称为 G的解,si* 与d j* 分别是 甲,乙的最优纯策略,ai* j* 称为G的值,记为VG 。
3
7
6*
易知,G在纯策略意义下无解。
记 xi p ( si ) 0 xi 1(i 1, 2) yi p (di ) 0 yi 1(i 1, 2)
x
i 1 2 i 1
2
i
1 1
y
i
d1 s1 7 s2 3 yj y1
d2 4 6 y2
xi x1 x2
E ( X , Y ) aij p ( si , d j )
i j
aij p ( si ) p (d j )
i j
aij xi y j
i j
当甲取s1时,最少收益为:min{7x1y1,4x1y2}
当乙取d1时,最大损失为:max{7x1y1,3x2y1}
甲选 max min E ( X , Y ) xi* j i 即理智局中人的选择 乙选 min max E(X,Y) y j* j i
则(x*,y*)-混合策略下的最优解
E(x*,y*)-混合策略下的最优值
二人有限零和对策的混合策略对策模型:
G*={S*,D*;E}
其中:S*={X=(x1,x2,…,xm)T ∑xi=1,xi≥0}
-甲的混合策略集
D*={y=(y1,y2,…,yn)T ∑yj=1,yj≥0}
-乙的混合策略集
E=E(X,Y)= ∑ ∑aijxiyj
M
故称G S ,D,A)为纯策略对策模型(矩阵对策) (
二、纯策略对策的解 1、纯策略分析
例1:今有甲、乙两厂生产同一种产品,它们 都想通过内部改革挖掘,获得更多得市场份额。 已知两厂分别都有三个策略措施。据预测,当 双方采取不同的策略措施后两厂的市场占有份 额变动情况如下所示。
