运筹学教程第五版课后答案
《运筹学教程》胡云权-第五版-运筹学复习

x6
10
[2]
-5
1
0
-1
1
5
3M+2
3-4M
2M-5
0
-M
0
-z
-M
x4
2
0
[7/2 ]
1/2
1
1/2
-1/2
4/7
2
x1
5
1
-5/2
1/2
0
-1/2
1/2
-
0
7M/2+8
M/2-6
0
M/2+1
-3M/2-1
-z
3
x2
4/7
0
1
1/7
2/7
1/7
-1/7
2
x1
45/7
1
0
6/7
5/7
-1/7
1/7
✓ 右端项非负
解的重要概念
可行解(或可行点):满足所有约束条件的向量 x ( x1 , x 2 , x n )
可行域:所有的可行解的全体
D { x Ax b, x 0}
最优解:在可行域中目标函数值最大(或最小)的可行解,最优解的全体
称为最优解集合
O {x D c x c y, y D }
0
x3
0
x4
0
x5
9
4
3
4
5
[ 10 ]
1
0
0
0
1
0
0
0
1
90
40
30
7
12
0
0
0
1
90
bi
360
运筹学5至12章习题参考答案

图6-48
【解】虚拟一个发点和一个收点
v2
8.8
0
8
5
13
4
89.16
v3
8.6
8
0
3
4.8
12
82.16
v4
5.6
5
3
0
7.8
9
71.96
v5
8
13
4.8
7.8
0
9
81.92
v6
6
4
12
9
9
0
82.2
运价
1
1.2
1.6
2.6
3.2
3.4
选第4个工厂最好。
6.10如图6-47,(1)求v1到v10的最大流及最大流量;(2)求最小割集和最小割量。
运筹学5-12章参考答案
习题五
5.2用元素差额法直接给出表5-52及表5-53下列两个运输问题的近似最优解.
表5-52
B1
B2
B3
B4
B5
Ai
A1
19
16
10
21
9
18
A2
14
13
5
24
7
30
A3
25
30
20
11
23
10
A4
7
8
6
10
4
42
运筹学(胡运权)第五版课后答案-运筹作业

运筹学(胡运权)第五版课后答案-运筹作业47页1.1b用图解法找不到满足所有约束条件的公共范围,所以该问题无可行解47页1.1d无界解1 2 3 454321-1-6 -5 -4 -3 -2X2X12x1--2x1+3x1 2 3 44321X12x1+x2=23x1+4x2=X1.2(b)约束方程的系数矩阵A= 1 2 3 42 1 1 2P1 P2 P3 P4基基解是否可行解目标函数值X1 X2 X3 X4P1 P2 -4 11/2 0 0 否P1 P3 2/5 0 11/5 0 是43/5 P1 P4 -1/3 0 0 11/6 否P2 P3 0 1/2 2 0 是 5 P2 P4 0 -1/2 0 2 否P3 P4 0 0 1 1 是 5最优解A=(0 1/2 2 0)T和(0 0 1 1)T49页13题设Xij为第i月租j个月的面积minz=2800x11+2800x21+2800x31+2800x41+4500x12+4500x22+4500x32+6000x1 3 +6000x23+7300x14s.t.x11+x12+x13+x14≥15x12+x13+x14+x21+x22+x23≥10x13+x14+x22+x23+x31+x32≥20x14+x23+x32+x41≥12Xij≥0用excel求解为:( )用LINDO求解:LP OPTIMUM FOUND AT STEP 3 OBJECTIVE FUNCTION V ALUE1) 118400.0V ARIABLE V ALUE REDUCED COSTZ 0.000000 1.000000X11 3.000000 0.000000X21 0.000000 2800.000000X31 8.000000 0.000000X41 0.000000 1100.000000X12 0.000000 1700.000000X22 0.000000 1700.000000X32 0.000000 0.000000X13 0.000000 400.000000X23 0.0000001500.000000X14 12.000000 0.000000ROW SLACK OR SURPLUS DUAL PRICES2) 0.000000 -2800.0000003) 2.000000 0.0000004) 0.000000 -2800.0000005) 0.000000 -1700.000000NO. ITERATIONS= 3答若使所费租借费用最小,需第一个月租一个月租期300平方米,租四个月租期1200平方米,第三个月租一个月租期800平方米,50页14题设a1,a2,a3, a4, a5分别为在A1, A2, B1, B2, B3加工的Ⅰ产品数量,b1,b2,b3分别为在A1, A2, B1加工的Ⅱ产品数量,c1为在A2,B2上加工的Ⅲ产品数量。
胡运权运筹学第五版答案

胡运权运筹学第五版答案【篇一:运筹学基础及应用第四版胡运权主编课后练习答案】xt>习题一 p46 1.1 (a)412该问题有无穷多最优解,即满足4x1z?3。
6x26且0?x2?的所有?x1,x2?,此时目标函数值(b)用图解法找不到满足所有约束条件的公共范围,所以该问题无可行解。
1.2(a) 约束方程组的系数矩阵12a833106?403000200??0?1t最优解x??0,10,0,7,0,0?。
(b) 约束方程组的系数矩阵1a222314??2??最优解1.3(a)(1) 图解法11??2x??,0,,0?5?5?t。
最优解即为?3x14x295x12x28的解x31,2,最大值z352(2)单纯形法首先在各约束条件上添加松弛变量,将问题转化为标准形式 max z?10x1?5x2?0x3?0x4?3x1?4x2?x3?9s.t. ?5x12x2x48则p3,p4组成一个基。
令x1?x2?0得基可行解x??0,0,9,8?,由此列出初始单纯形表12。
??min?898,53?520,??min?2183,??142?2?新的单纯形表为1,20,表明已找到问题最优解x1?1, x2?32,x3?0 , x4?0。
最大值z*352(b) (1) 图解法6x1?2x2x1?x2?最优解即为?6x12x224x1?x2?5的解x73,22?,最大值z172(2) 单纯形法首先在各约束条件上添加松弛变量,将问题转化为标准形式 max z?2x1?x2?0x3?0x4?0x55x2?x3?15??s.t. ?6x1?2x2?x4?24xxx5125则p3,p4,p5组成一个基。
令x1?x2?0得基可行解x??0,0,15,24,5?,由此列出初始单纯形表12。
??min??,245?,??461?155,24,20,??min?3?32?2新的单纯形表为【篇二:运筹学基础及应用第四版胡运权主编课后练习答案】xt>习题一 p46 1.1 (a)41的所有?x1,x2?,此时目标函数值2该问题有无穷多最优解,即满足4x1?6x2?6且0?x2?z?3。
第五版运筹学课后习题答案

第五版运筹学课后习题答案【篇一:运筹学课后习题答案林齐宁版本北邮出版社】>1、某织带厂生产a、b两种纱线和c、d两种纱带,纱带由专门纱线加工而工厂有供纺纱的总工时7200h,织带的总工时1200h。
(1) 列出线性规划模型,以便确定产品的数量使总利润最大;(2) 如果组织这次生产具有一次性的投入20万元,模型有什么变化?对模型的解是否有影响?解:(1)设a的产量为x1,b的产量为x2,c的产量为x3,d的产量为x4,则有线性规划模型如下:max f(x)=(168?42)x1 +(140?28)x2 +(1050?350)x3 +(406?140)x4=126 x1 +112 x2 +700 x3 +266 x4?3x1?2x2?10x3?4x4?7200?s.t. ? 2x3?0.5x4?1200?xi?0, i?1,2,3,4?(2)如果组织这次生产有一次性的投入20万元,由于与产品的生产量无关,故上述模型只需要在目标函数中减去一个常数20万,因此可知对模型的解没有影响。
2、将下列线性规划化为极大化的标准形式minf(x)?2x1?3x2?5x3解:将约束条件中的第一行的右端项变为正值,并添加松弛变量x4,在第二行添加人工变量? x1? x2? x3??5 ???6x1?7x2?9x3?16 x5,将第三行约束的绝对值号打开,变为两s.t. ?|19x1?7x2?5x3|?13个不等式,分别添加松弛变量x6, x7,并令??x,x?0, x?不限3?12x3?x3??x3??,则有max[?f(x)]= {?2 x1 ?3 x2 ?5(x3??x3??)+0 x4 ?m x5+0 x6 +0 x7} ?? x3???x4?5 ?x1 ?x2 ?x3 ???6x?7x?9x??9x?? ?x?1612335????5x3?? ?x6?13 s.t. ? 19x1?7x2?5x3??19x?7x?5x??5x?? ?x7?131233??,x3??,x4,x5,x6,x7?0?x1,x2,x3?3、用单纯形法解下面的线性规划maxf(x)?2x1?5x2?3x3?3x1?2x2?x3?610??x?6x?3x?125 ?123s. t. ???2x1?x2?0.5x3?420?x1,x2,x3?0, ?解:在约束行1,2,3分别添加x4, x5, x6松弛变量,有初始基础可行解和单纯形答:最优解为x1 =244.375, x2 =0, x3 =123.125, 剩余变量x6=847.1875;最优解的目标函数值为858.125。
运筹学课后习题答案

6
5
6
3
σ34=15+50=1;至此;六个闭回路全部计算完 ;σ11=4;σ14=2;σ22=0;σ31=2;σ32=2;σ34=1;即全部检验数σ均 大于或等于0 即用上述三种方法计算中;用沃格尔法计算所
得结果z*=35为最优解
2024/1/10
16
表329
销地 B1
B2
B3
B4
产量
产地
A1
3
7
22
4
A3 销量
4
33
3
3
B3
6 3 28 2
B4 B5 产量
1 4 30
5
⑤
2
0
2②
15 0
6⑧
2
3
③
④
⑦
⑥
①
x11=1;x14=1;x15=3;x21=2;x32=3;x33=2;x34=1;总费用=1×3 +1×4+3×0+2×2+3×3+2×8+1×5=41
2024/1/10
18
②西北角法求解:
3 2 运输问题的基可行解应满足什么条件 试判断形表 326和表327中给出的调运方案是否作为表上作业法迭 代时的基可行解 为什么
2024/1/10
1
表326
销地 B1
B2
B3
B4
产量
产地
A1
0
A2
A3
5
销量
5
15
15
15
10
25
5
15
15
10
解:表326产地个数m=3;销地个数n=4;m+n1=3+41=6个;而 表326中非零个数的分量为5个≠6个;所以表326不可作为表上 作业法时的基可行解
运筹学教程第五版课后答案

运筹学教程第五版课后答案第一章课后答案1.1 选择题答案1.B2.D3.A4.C5.A1.2 填空题答案1.优化2.最优解3.最大化4.变量5.限制条件1.3 解答题答案1.运筹学是指运用数学方法来研究决策问题和优化问题的学科。
它包括数学规划、排队论、图论、线性规划等多个分支领域,并广泛应用于各个领域的管理和决策中。
2.线性规划是数学规划中的一种重要方法,用于解决特定形式的最优化问题。
线性规划的基本模型包括目标函数、决策变量、约束条件等要素。
线性规划的求解过程包括建立数学模型、确定最优解的条件和方法、利用线性规划软件进行求解等步骤。
第二章课后答案2.1 选择题答案1.B2.A3.C4.D5.B2.2 填空题答案1.线性不等式2.解空间3.最优解4.可行解5.凸集2.3 解答题答案1.线性规划模型由目标函数、决策变量和约束条件三部分组成。
其中,目标函数是优化的目标,决策变量是待确定的变量,约束条件是对决策变量的限制。
线性规划模型可以表示为:maximize Z = c1x1 + c2x2 + … + cnxn subject to: a11x1 + a12x2 + … + a1nxn <= b1 a21x1 + a22x2 + … + a2nxn <= b2 … am1x1 + am2x2 + … + amnxn <= bm x1, x2, …, xn >= 0 其中,Z表示要优化的目标函数,ci表示目标函数中的系数,aij表示约束条件中的系数,bi表示约束条件右侧的常数。
2.线性规划应用广泛,包括生产调度、资源分配、运输问题等。
例如,一个工厂生产两种产品,需要确定每种产品的产量使得总利润最大化,可以使用线性规划模型进行建模和求解。
又如,在物流领域中,需要确定货物的最优运输方案,可以使用线性规划模型来解决。
第三章课后答案3.1 选择题答案1.C2.A3.B4.D5.B3.2 填空题答案1.线性规划2.整数规划3.混合整数规划4.松弛问题5.整数线性规划3.3 解答题答案1.整数规划是指在线性规划的基础上,决策变量取整数值的最优化问题。
胡运权运筹学教程答案

胡运权运筹学教程答案胡运权运筹学教程答案【篇一运筹学基础及应用第四版胡运权主编课后练习答案】txt 习题一p461.1a23。
b用亂解法找到满足所打约柬条仲的公it范w,所以该问题无可行解。
1.2a约束方程组的系数矩阵r最优解a.o,iao,7,o,ob约束方程组的系数矩阵fi234、4l22i2,最优解1八,0,11,0八v551.3a1图解法⑵单纯形法首先在各约朿条件上添加松弛变铽,将问题转化为标准形式maxz10a-,5a20x30a4[3a-.4义2a39si.[5a-j2x2a48则a,p4组成个猫令a;c20得-站可行解a_0.0.9,8,山此列出初始单纯形表cr20,0-minj2a新的单纯形农为a,xoxax21414mtq.qco,表明已找到问题垴优解._5__25xi,a-30,a4(b)(1)图解法17最优解即为严aixy52x224的解x卩,2v最大值zii22/单纯形法(2)苘先在外约朿条件.h添加松弛变m,将问题转化为标准形式maxz2.v,x2ox30.v4oa55a2156.y,2x2.v424【篇二运筹学(第五版)习题答案】章(39页)1.1用图解法求解下列线性规划问题,并指出问题是具有唯一最优解、无穷多最优解、无界解还是无可行解。
(1)maxzx1x25x110x250x1x21x24x1,x20x13x23x1x22x1,x20(3)maxz2x12x2x1-x2-1-0.5x1x22x1,x20(4)maxzx1x2x1-x203x1-x2-3x1,x20解(1)(图略)有唯一可行解,maxz14(2)(图略)有唯一可行解,minz9/4(3)(图略)无界解(4)(图略)无可行解1.2将下列线性规划问题变换成标准型,并列出初始单纯形表。
(1)minz-3x14x2-2x35x44x1-x22x3-x4-2x1x23x3-x414-2x13x2-x32x42 x1,x2,x30,x4无约束(2)maxszkpkzkaikxiki1k1xk1mik1i1,...,nxikOi1n;k1,,m1解设z-z,x4x5-x6,x5,x60标准型maxz3x1-4x22x3-5x5-x60x70x8-mx9-mx10s.t.-4x1x2-2x3x5-x6x10 2x1x23x3-x5x6x714-2x13x2-x32x5-2x6-x8x92x1,x2,x3,x5,x6,x7,x8 ,x9,x100⑵解加入人工变量x1,x2,x3,xn,得maxs1/pki1nk1mikxik-mx1-mx2-..-mxns.t.xixik1i1,2,3,nk1mxik0,xi 0,i1,2,3n;k1,2.,m是任意正整数1.3在下面的线性规划问题中找出满足约束条件的所有基解。
(完整word版)运筹学(胡运权)第五版课后答案,运筹作业
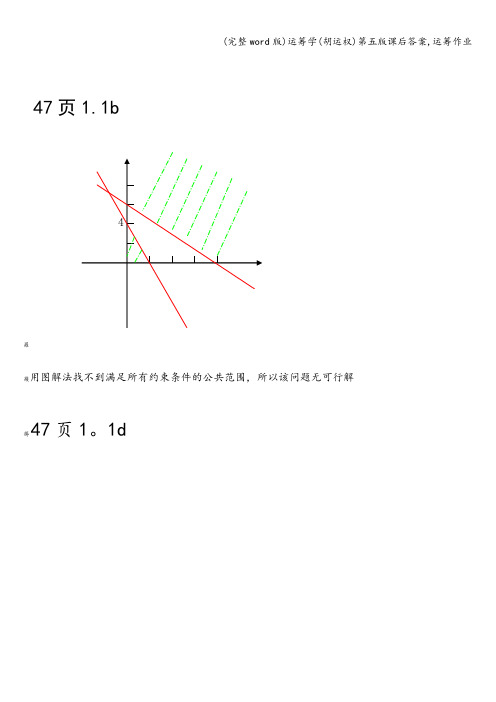
47页1.1b羅蕿用图解法找不到满足所有约束条件的公共范围,所以该问题无可行解薅47页1。
1d蒂无界解(b)衿1.2蕿约束方程的系数矩阵A=1234莇2112蚄P1P2P3P4,运筹作业肀最优解A=(01/220)T和(0011)T页13题肆49膃设Xij为第i月租j个月的面积羄minz=2800x11+2800x21+2800x31+2800x41+4500x12+4500x22+4500x32+6000x13+6000x23+7300x 14螁s.t.聿x11+x12+x13+x14≥15膃x12+x13+x14+x21+x22+x23≥10膀x13+x14+x22+x23+x31+x32≥20艿x14+x23+x32+x41≥12袇Xij≥0芃用excel求解为:薁用LINDO求解:羁LPOPTIMUMFOUNDATSTEP3薆OBJECTIVEFUNCTIONVALUE 蚇1)118400.0羂VARIABLEVALUEREDUCEDCOST 荿Z0.0000001。
000000虿X113.0000000。
000000螇X210。
0000002800。
000000莃X318。
0000000.000000肁X410.0000001100。
000000莈X120.0000001700.000000袆X220.0000001700。
000000螄X320.0000000。
000000蕿X130.000000400.000000膇X230。
0000001500。
000000袆X1412.0000000.000000袁ROWSLACKORSURPLUSDUALPRICES芁2)0。
000000—2800。
000000羆3)2.0000000.000000羆4)0。
000000—2800.000000节5)0。
000000-1700.000000蝿NO。
ITERATIONS=3罿答若使所费租借费用最小,需第一个月租一个月租期300平方米,租四个月租期1200平方米,第三个月租一个月租期800平方米,页14题肆50蚃设a1,a2,a3,a4,a5分别为在A1,A2,B1,B2,B3加工的Ⅰ产品数量,b1,b2,b3分别为在A1,A2,B1加工的Ⅱ产品数量,c1为在A2,B2上加工的Ⅲ产品数量。
《运筹学教程》胡云权 第五版 第四章 动态规划

* u1 ( A) B1
按计算顺序反推得最优决策序列
* u1 ( A) B1
u* (B1 ) C2 2
* u3 (C2 ) D2
u* ( D2 ) E2 4
最优路线: A B1 C2 D2 E2 F
动态规划的基本思想
可见,求解各阶段都利用了以下关系
f k ( sk ) min dk ( sk , uk ) f k 1 ( sk 1 )
• 动态规划应用
多阶段决策过程的最优化
1、最短路线问题
【例1】从A点铺设一条管道到E点,图中两点间连线上数字表示两 点间距离。现需选一条由A到E的铺管线路,使总距离最短。
2 4 B1 4 8 A 5 3 B3 阶段1 9 B2 7 3 阶段2 2 5 C3 阶段3 阶段4 C2 2 4 1 6 D2 C1 6 5 D1 3
B3
3
阶段2
阶段4
• 状态和状态变量 状态:各阶段开始时的客观条件 状态无后效性: 给定了某阶段状态,则在这阶段以后过程的发展 不受这阶段以前各阶段状态的影响。
动态规划的基本概念和原理
4 A 5 3
B1 4
2
C1 6 1
5 D1 3 4 D2 E
8
B2 7
9
2 5
C2 2 C3
6 4
阶段3
基本概念 • 状态和状态变量 sk: 第k个阶段的状态变量 Sk :第k个阶段状态变量的集合,称状态集合
* pk . n P k ,n
当k=1时,f1(s1)就是从初始状态s1到全过程结束的整体最优函数。
动态规划的基本思想
【例】选择一条运输线路,使得A到F的运费最小。
2 4
胡运权运筹学第五版第一章习题讲解

1.3 答案:
●单纯形法:
Cj CB 0 0 基 x3 x4 Cj-Zj 0 x3
10
x1
Cj-Zj
8/5
1
0
2/5
1 1
0
0 5/14
1/5
-2 -3/14
5
x2
3/2
0
10
x1
Cj-Zj
1
1
0
0
0
-1/7
-5/14
2/7
-25/14
Return
课后题答案
z' -3x1 x 2 'x 2 ' '-2x 3 '0x 4 0x 5 - Mx6 - Mx7
台时 限制 6000 1000 0 4000 7000 4000
单位台 时费用 0.05 0.03 0.06 0.11 0.05
6 4 7 0.25 0.36 0.25 0.44 0.25 0.35
6 4 7 0.21 0.36 0.21 0.44 0.21 0.77
8
8 11
0.5 0.48
0.27 0.48
课后题答案
1.1(a)答案: 该问题有无穷多最优解。 取特殊值:(1.5,0) 计算目标函数最优值 得:min z=3。
1.1(a)
1.1(b)答案: 由图可知:该Lp问题没 有可行域,即可得出: 该问题无可行解
1.1(b)
Return
课后题答案
1.2(b)答案:
基解 基
x1 P2 P3 P4 P3 -4 2/5 -113 ) 10 x211 6000 7( x x x ) 9 x 12 x 121 122 123 221 322 10000 6( x111 x121 ) 8( x211 x221 ) 4000 s.t. 4( x112 x122 ) 11x322 7000 7( x113 x123 ) 4000 x111 , x112 , x113 , x121 , x122 , x123 , x211 , x221 , x322 0
管理运筹学(第五版)韩伯棠主编第三章 线性规划问题的计算机求解课后习题参考答案

第三章线性规划问题的计算机求解3-1(1)甲、乙两种柜的日产量是分别是4和8,这时最大利润是2720。
(2)油漆工艺生产增加1小时,可以使总利润提高13.333元。
(3)常数项的上下限是指常数项在指定的范围内变化时,与其对应的约束条件的对偶价格不变。
比如油漆时间变为100,因为100在40和160之间,所以其对偶价格不变仍为13.333。
(4)不变,因为还在120和480之间。
3-2(1)最优决策为截第一种钢板6张,第二种钢板7张。
(2)需要A种规格的小钢板成品个数在12和27范围内时,第一个约束条件的对偶价格不变。
(3)B种规格的小钢板成品的剩余变量值为4,表示此决策下,截得B种规格成品的实际数量比B种规格的成品的需求量多了4个。
3-3(1)农用车有12辆剩余。
(2)300到正无穷范围内。
(3)每增加一辆大卡车,总运费降低192元。
3-4(1)是最优解。
(2)此常数项在-∞到2范围内变化时,约束1的对偶价格不变。
3-5(1)圆桌和衣柜的生产件数分别是350和100件,这时最大利润是3100元。
(2)相差值为0代表,不需要对相应的目标函数系数进行改进就可以生产该产品。
(3)最优解不变,因为C1允许增加量200-6=140;C2允许减少量为100-30=70,所有允许增加百分比和允许减少百分比之和(75-60)/140+(100-90)/70<100%,所以最优解不变。
3-6(1)1150x=,270x=,即产品I的产量为150,产品II的产量为70;目标函数最优值103 000,即最大利润为103 000。
(2)1、3车间的加工工时数已使用完;2、4车间的加工工时数没用完;没用完的加工工时数为2车间330小时,4车间15小时。
(3)50,0,200,0。
含义:1车间每增加1工时,总利润增加50元;3车间每增加1工时,总利润增加200元;2车间与4车间每增加一个工时,总利润不增加。
(4)3车间,因为增加的利润最大。
运筹学(第五版) 习题答案

非基变量 的检验数 =0,所以有无穷多最优解。
(3)解:大M法
加入人工变量,化成标准型:
Max z=10 +15 +12 +0 +0 +0 -M
s.t. 5 +3 + + =9
-5 +6 +15 + =15
2 + + - + =5
, , , , , , 0
当 0,目标函数在原点最大值。
k= 时, , 同号。
当 0时,目标函数在BC线断上任一点有最大值
当 0时,目标函数在原点最大值。
k=0时, =0
当 0时,目标函数在A点有最大值
当 0,目标函数在OC线断上任一点有最大值
(2)当 =0时,max z=
0时,目标函数在C点有最大值
0时,目标函数在OA线断上任一点有最大值
(i=1,2,3…,n)
0, 0, (i=1,2,3…n; k=1,2….,m)
M是任意正整数
初始单纯形表:
-M
-M
…
-M
…
…
…
b
…
…
…
…
-M
1
1
0
…
0
1
1
…
…
0
0
…
0
-M
1
0
1
…
0
0
…
…
0
0
…
0
…
…
…
…
…
…
…
…
…
…
…
…
…
《运筹学(胡运权)》第五版课后习题答案
VARIABLE VALUE REDUCED COST
Z 0.000000 1.000000
X11 3.000000 0.000000
X21 0.000000 2800.000000
X31 8.000000 0.000000
X41 0.000000 1100.000000
X12 0.000000 1700.000000
程序法
6.4a
破圈法
避圈法
最小部分树16
6.4b
最小部分树32
172页6.11
红色曲线为使用一年卖出
蓝色曲线为使用两年卖出
绿色曲线为使用三年卖出
紫色曲线为使用四年卖出
最短路程为3.7万元,路径为v0-v1-v4或v0-v2-v4或v0-v1-v2-v4
三种方案分别为:第一年年初买新车,年末卖掉再买新车,一直用到第四年年末卖掉;
X2 1.000000 2.000000 INFINITY
X3 4.000000 1.000000 1.500000
X1,X2,X3 0.000000 0.000000 INFINITY
RIGHTHAND SIDE RANGES
ROW CURRENT ALLOWABLE ALLOWABLE
RHS INCREASE DECREASE
d)
maxz=3x1+x2+4x3-0.4y
s.t.
6x1+3x2+5x3≤45
3x1+4x2+5x3-y≤30
x1,x2,x3,y≥0
用lomdo求解为
LP OPTIMUM FOUND AT STEP 0
OBJECTIVE FUNCTION VALUE
运筹学第五、六、七、八章答案

运筹学第五、六、七、⼋章答案5.2⽤元素差额法直接给出表5-53及表5-54下列两个运输问题的近似最优解.表5-53表5-54【解】表5-53。
表5-54 Z=4955.3 求表5-55及表5-56所⽰运输问题的最优⽅案.(1)⽤闭回路法求检验数(表5-55)表5-55(2)⽤位势法求检验数(表5-56)表5-56【解】(1)(2)5.4求下列运输问题的最优解(1)C1⽬标函数求最⼩值;(2)C2⽬标函数求最⼤值1359250 648525 111312730C=??903060107856913142015107=C15 45 20 40 60 30 50 40(3)⽬标函数最⼩值,B1的需求为30≤b1≤50, B2的需求为40,B3的需求为20≤b3≤60,A1不可达A4,B4的需求为30.502070109482356794- 【解】(1)(2)5.5(1)建⽴数学模型设x ij (I=1,2,3;j=1,2)为甲、⼄、丙三种型号的客车每天发往B 1,B 2两城市的台班数,则111221223132112131122232111211223132max 40(806560505040)404040400404040600510150(1,2,3;1,2)ij Z x x x x x x x x x x x x x x x x x x x i j =+++++++=??++=??+≤??+≤??+≤?≥==??(2)写平衡运价表(3)最优调度⽅案:即甲第天发5辆车到B 1城市,⼄每天发5辆车到B 1城市,5辆车到B 2城市,丙每天发10辆车到B 2城市,多余5辆,最⼤收⼊为Z=40(5×80+5×60+5×50+10×40)=54000(元)5.6(1)设x ij 为第i ⽉⽣产的产品第j ⽉交货的台数,则此⽣产计划问题的数学模型为1112131421441121314112223242132333431424344411121314212223243132333441424344min 1.15 1.3 1.450.9850406080656565650,(,ij Z x x x x Mx x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x i j =+++++++++=+++=+++=+++=+++≤+++≤+++≤+++≤≥ 1,,4)??=?(2)化为运输问题后运价表(即⽣产费⽤加上存储费⽤)如下,其中第5列是虚设销地费⽤为零,需求量25台,四⽉份交货10台;三⽉份⽣产65台,当⽉交货60台,四⽉份交货5台,4⽉份⽣产65台当⽉交货。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《运筹学》试题(答案)
一、单项选择题。
下列每题给出的四个答案中只有一个是正确的,将表示正确答案的字母填入题后的括号中。
(20分)
1.对一个极大化的线性规划问题用单纯形法求解,若对所有的检验数0
≤j σ,但对某个
非基变量j x ,有0
=j σ,则该线性规划问题( B )
A .有唯一的最优解;
B .有无穷多个最优解;
C .为无界解;
D .无可行解。
2.使用人工变量法求解极大化线性规划问题时,当所有的检验数0
≤j σ,在基变量中仍含有非零的人工变量,表明该线性规划问题( D )
A .有唯一的最优解;
B .有无穷多个最优解;
C .为无界解;
D .无可行解。
3.在对偶问题中,若原问题与对偶问题均具有可行解,则( A ) A .两者均具有最优解,且它们最优解的目标函数值相等;
B .两者均具有最优解,原问题最优解的目标函数值小于对偶问题最优解的目标函数值;
C .若原问题有无界解,则对偶问题无最优解;
D .若原问题有无穷多个最优解,则对偶问题只有唯一最优解;
4.在用对偶单纯形法解最大化线性规划问题时,每次迭代要求单纯形表中( D )
A .b 列元素不小于零;
B .检验数都大于零;
C .检验数都不小于零;
D .检验数都不大于零。
5.在产销平衡运输问题中,设产地为m 个,销地为n 个,那么解中非零变量的个数( A )。
A .不能大于(m +n -1);B .不能小于(m +n -1);C .等于(m +n -1);D .不确定。
6.在运输问题中,每次迭代时,如果有某非基变量的检验数等于零,则该运输问题( B )。
A .无最优解;B .有无穷多个最优解;C .有唯一最优解;D .出现退化解。
7.在目标规划中,求解的基本原则是首先满足高级别的目标,但当高级别目标不能满足时( D )。
A .其后的所有低级别目标一定不能被满足;
B .其后的所有低级别目标一定能被满足;
C .其后的某些低级别目标一定不能被满足;
D .其后的某些低级别目标有可能被满足。
8.若一个指派问题的系数矩阵的某行各元素都加上常数k 得到一个新的矩阵,这一新矩阵对应着一个新的指派问题,则( A )。
A .新问题与原问题有相同的最优解;
B .新问题最优目标值大于原问题最优目标函数值;
C .新问题最优解等于原问题最优解加上k ;
D .新问题最优解小于原问题最优解。
9.如果要使目标规划实际实现值不超过目标值,则相应的偏离变量应满足( B )。
A .0>+d ;
B .0=+d ;
C .0=-d ;
D .
.0,0>>+-d d
10.动态规划问题中最优策略具有性质:( C ) A .每个阶段的决策都是最优的;
B .当前阶段以前的各阶段决策是最优的;
C .无论初始状态与初始决策如何,对于先前决策所形成的状态而言,其以后的所有决策应
构成最优策略;
D .它与初始状态无关。
二、计算题
1.用单纯形法求解以下线性规划问题
⎪⎪⎩⎪⎪⎨
⎧≥≤+≤≤+=0
,18
231224..53max 21212121x x x x x x t s x x z
解:
化为标准型如下
⎪⎪⎩⎪⎪⎨
⎧≥=+
+=+
=+
+=0
,18
231224..53max 215
214
23121x x x x x x x x x t s x x z
所以最优解为x 1=2, x 2=6,最优值为z =36
2.已知线性规划问题:
⎪⎩⎪
⎨⎧≥≤+++≤++++++=0,,,20
23220322..432max 4
3214
3
2143214321x x x x x x x x x x x x t s x x x x z
(1) (1) 写出其对偶问题
(2) (2) 若已知其对偶问题最优解为2.0,2.121==y y ,根据对偶理论求出原问题
的最优解。
解:
(1)其对偶问题为
⎪⎪⎪⎩⎪
⎪⎪⎨⎧≥≥+≥+≥+≥++=0
,4
2333222122020min 212
121212121y y y
y y y y
y y y y y w
(2)将2.0,2.121==y y 代入到对偶问题的四个约束条件可得 1*1.2+2*0.2>1; 2*1.2+0.2>1; 2*1.23*0.2=3; 3*1.2+2*0.2=4
那么由互补松驰性得,x 1=0; x 2=0; x 3>0; x 4>0。
再由y 1, y 2>0得,原问题的两个约束条件均取等号,这样联立方程求解原问题的最优解为,x 1=0; x 2=0; x 3=4; x 4=4,目标函数值z=28.
3.求出下图中从A 到E 的最短路线及其长度。
把整个最短路线问题分为4个阶段,建立模型:A ,B ,C ,D ,E 为5个状态。
当k =4时, f (D 1)=3, f (D 2)=1, f (D 3)=5 当k =3时,
5
455123min 4)(5)(2)(min )(3211=⎪⎭⎪
⎬⎫⎪⎩⎪⎨⎧+++=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧+++=D f D f D f C f ,相应的决策为11*
3)(D C u =
4
254113min 2)(4)(1)(min )(3212=⎪⎭⎪
⎬⎫⎪⎩⎪⎨⎧+++=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧+++=D f D f D f C f ,相应的决策为12*
3)(D C u =
当k =2时,
7
344543min 3)(4)(4)(min )(2111=⎪⎭⎪
⎬⎫⎪⎩⎪⎨⎧+++=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧+++=C f C f D f B f ,相应的决策为
11*
2)(D B u =或21*2)(C B u =
63415min 3)(1)(min )(212=⎭⎬⎫⎩⎨⎧++=⎭⎬⎫⎩⎨⎧++=C f C f B f ,相应的决策为12*
2)(C B u = 8
355435min 3)(5)(3)3(min )(213=⎪
⎭
⎪
⎬⎫
⎪⎩⎪⎨⎧+++=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧+++=C f C f D f B f ,相应的决策为
33*
2)(D B u =或23*
2)(C B u =
当k =1时,
8
182637min 1)(2)(3)(min )(321=⎪
⎭
⎪
⎬⎫
⎪⎩⎪⎨⎧+++=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧+++=B f B f B f A f ,相应的决策为2*
1)(B A u =
所以最短路线为:A->B 2->C 1->D 1->E ,其长度为8。
4.已知A ,B 两人对策时对A 的赢得矩阵如下,求双方各自的最优策略及对策值。
⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--021302412
解:这是一个纯局势下的对策问题,A 取α1,B 取β2为双方的最优纯策略。
A 的蠃得值的1,B 的赢得值为-1。
5.某一决策问题的损益矩阵如下表所示,其中矩阵元素值为年利润。
(1) (1) 若各事件发生的概率j P
是未知的,分别用悲观准则(maxmin 准则)、乐观准则(maxmax 准则)选出决策方案。
(2)
(2) 若1.0,7.0,2.0321===P P P
,则用期望收益值准则会选择哪个方案?
解:参照P378-386。
此处略。
