有理数数轴绝对值知识点习题
有理数练习题:绝对值的几何意义
绝对值的几何意义
【知识点】
一般地,数轴上表示数a的点与原点的距离叫做数a的绝对值,记作a 一个正数的绝对值是它本身;
一个负数的绝对值是它的相反数;
0的绝对值是0
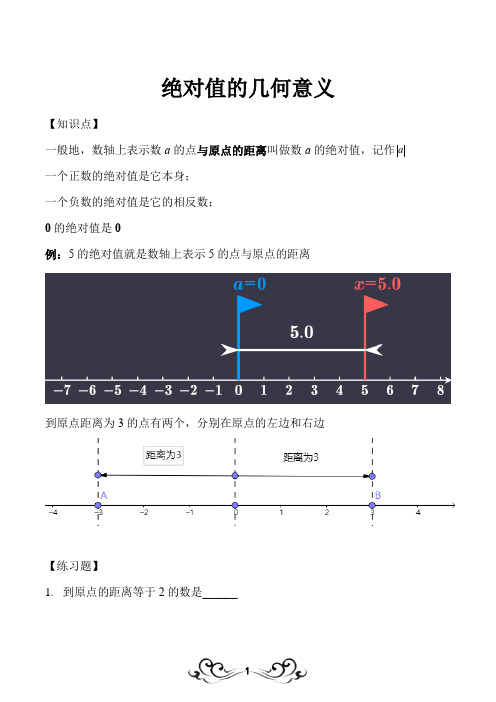
例:5的绝对值就是数轴上表示5的点与原点的距离
到原点距离为3的点有两个,分别在原点的左边和右边
【练习题】
1.到原点的距离等于2的数是______
2.到原点的距离等于1.6的数是______
3.到原点的距离等于2019的数是______
4.到原点的距离等于6的数是______
5.到原点的距离等于1
的数是______
9
的数是______
6.到原点的距离等于7
3
的数是______,在原点左侧的数是______
7.到原点的距离等于2
3
8.到原点的距离等于a(a>0)的数是______
的数是______,其中在原点右侧的数是______ 9.到原点的距离等于7
8
10.到原点的距离等于0.8的数是______,其中在原点右侧的数是______
答案
1. 2或-2
2. 1.6或-1.6
3. 2019或-2019
4. 6或-6
5. 19±
6. 123±
7. 23±,23-
8. a 或-a 9. 78±;78
10. 0.8或-0.8;0.8。
有理数,数轴,绝对值练习

有理数一、填空题1.如果提高10分表示+10分,那么下降8分表示_______,不升不降用_______表示..如果向南走5 km 记为-5 km ,那么向北走10 km 记为____.如果收入2万元用+2万元表示,那么支出3000元,用_______表示..某乒乓球比赛用+1表示赢一局,那么输2局用_______表示,不输不赢用_______表示..某企业以1996年的利润为标准,2000年增加了10%记为+10%,2001年利润为-5%表示的意义是_______..节约用水,如果节约5.6吨水记作+5.6吨,那么浪费3.8吨水,记作_______.2.大于-5.1的所有负整数为_____.3.分数有_____,_____.4.珠穆朗玛峰高出海平面8848米,表示为+8848米.吐鲁番盆地低于海平面155米,表示为____.5.请写出3个大于-1的负分数_____.6.某旅游景点一天门票收入5000元,记作+5000元,则同一天支出水、电、维修等各种费用600元,应记作_____.7.某县外贸局一年出口总额人民币1300万元,表示为+1300万.进口某种原料350万应表示为_____.8.在“学雷锋活动月”活动中,甲乙两组同学上街清扫街道,它们分别在街道的两端同时相向开始打扫,街道总长1200米,两组会合时甲组向南清扫了500米,记作+500米,则乙组向北清扫了_____米,应记作_____.9.某下岗职工购进一批苹果,第一天盈利17元,记作+17元,第二天亏损6元应记作_____. 二、选择题1、下面是关于0的一些说法,其中正确说法的个数是( )①0既不是正数也不是负数;②0是最小的自然数;③0是最小的正数;④0是最小的非负数;⑤0既不是奇数也不是偶数.A.0 B.1 C.2 D.32、在0,21,-51,-8,+10,+19,+3,-3.4中整数的个数是( )A.6B.5C.4D.3 3、下列说法正确的是( )A.零上5℃与零下5℃意思一样,都是5℃.B.正整数集合与负整数集合并在一起是整数集合C.收入-2000元表示支出2000元.D.-a 是负数, a 是正数. 4、下列各数中,大于-21小于21的负数是( ) A.-32B.-31C.31D.05、.负数是指( )A.把某个数的前边加上“-”号B.不大于0的数C.除去正数的其他数D.小于0的数 6、关于零的叙述错误的是( ) A.零大于所有的负数 B.零小于所有的正数 C.零是整数 D.零既是正数,也是负数 7、非负数是( )A.正数 B.零 C.正数和零 D.自然数8、文具店、书店和玩具店依次座落在一条东西走向的大街上,文具店在书店西边20米处,玩具店位于书店东边100米处,小明从书店沿街向东走了40米,接着又向东走了-60米,此时小明的位置在( ) A.文具店 B.玩具 C.文具店西40米处 D.玩具店西60米处三、解答题9、下面是具有相反意义的量,请用箭头标出其对应关系10、某天气预报显示,我国五个地区的最高气温第二天比第一天下降了12℃,这五个地区第一天最高气温如图所示,请填写第二天的最高气温11、某同学语、数、外三科的成绩,高出平均分部分记作正数,低出部分记作负数,如表所示请回答,该生成绩最好和最差的科目分别是什么?12、某公司今年第一季度收入与支出情况如表所示(单位:万元)请问:(1)该公司今年第一季度总收入与总支出各多少万元? (2)如果收入用正数表示,则总收入与总支出应如何表示?(3)该公司第一季度利润为多少万元?13、某地气象站测得某天的四个时刻气温分别为:早晨6点为零下3℃,中午12点为零上1℃,下午4点为0℃,晚上12点为零下9℃.1.用正数或负数表示这四个不同时刻的温度.2.早晨6点比晚上12点高多少度.3.下午4点比中午12点低多少度.?14、找规律(1)1,-2,3,-4,5,-6,7,-8 ,………其中第199个数为 ,第2002个数 ,规律是 ;(2)1,2,-3,4,5,-6,7,8 ,-9 ………其中第345个数为 ,第2002个数 ,规律是 ; (3)-1,2,-3,4,-5,6,-7,8 ,-9…… 其中第279个数为 ,第320个数的符号为 ,规律是 .15、小明的爸爸开的小店昨天获利120元,他在每日收支账本上记下“120元”.今天小店亏了20元,记作__.A :20元B :-20元C :-20D :100元进一步来看,一周来他的账本上的数据为周一 周二 周三 周四 周五 周六 周日 120元 -20元 80元 0元 -10元 150元 100元 如此看来他这一周是赚了还是赔了?有多少?16、某日傍晚,项城的气温由中午的零上2℃下降了7℃,这天傍晚项城的气温是多少?数轴一、选择题1.下列所画的数轴中正确的是( ) A .B .C .D . 2、互为相反数是指( )A 、具有相反意义的两个量B 、一个数的前面添上“–”号所得的数C 、数轴上原点两旁的两个点表示的数D 、只有符号不同的两个数 3、在数轴上距离原点4个单位长度的点所表示的数是( ) A 、4 B 、–4 C 、4或–4 D 、2或–24、大于–2.5而不大于3的整数( )A 、4个B 、5个C 、6个D 、7个5、如图所示,根据有理数a ,–b ,–c ,在数轴上的位置,比较a ,b ,c ,的大小, 则有( ) A 、a<b<c B 、a<c<b C 、b<a<c D 、b<c<a6、下列说法错误的是( )A 、所有的有理数都可以用数轴上的点表示B 、数轴上的原点表示零C 、在数轴上表示–3的点于表示+1的点的距离是2D 、数轴上表示413的点,在原单位左边413个单位 二、填空题7、在数轴上表示+3的点在原点的______侧,距原点的距离是______个单位;表示–5的点原点的_____侧,它离原点的距离是_____个单位;表示+3的点位于表示–5的点的_____侧,根据_____,可得–5<38、若数轴上得点M 和N 点表示的两个数互为相反数,并且这两点间的距离为7.2,则这两个点表示的数分别和______和______. 9、已知A ,B 是数轴上的点.(1)如果点A 表示数–3,将A 向右移动7个单位长度,那么终点表示的数是_______; (2)如果点B 表示数3,将B 向左移动7个单位长度,再向右移动5个单位长度,那么终点表示的数是______.10、正数的相反数是______数,一个数的相反数的相反数是______,0的相反数是______. 11、______的相反数大于它本身,______的相反数小于它本身. 12、在数轴上,点A 对应的数是21,那么在数轴上与点A 相距3个单位长度的点表示的数是______.9.+3的相反数是_____;______的相反数是-1.2;-175与_____互为相反数。
初一数学有理数、数轴、绝对值同步练习(含答案)

2.1有理数测试令狐采学基础检测1、_____、______和______统称为整数;_____和_____统称为分数;______、______、______、______和______统称为有理数; ______和______统称为非负数;______和______统称为非正数;______和______统称为非正整数;______和______统称为非负整数.2、下列不是正有理数的是()A 、-3.14B 、0C 、37 D 、33、既是分数又是正数的是()A 、+2B 、-314 C 、0 D 、2.3拓展提高4、下列说法正确的是()A 、正数、0、负数统称为有理数B 、分数和整数统称为有理数C 、正有理数、负有理数统称为有理数D 、以上都不对5、-a 一定是()A 、正数B 、负数C 、正数或负数D 、正数或零或负数6、下列说法中,错误的有() ①742-是负分数;②1.5不是整数;③非负有理数不包括0;④整数和分数统称为有理数;⑤0是最小的有理数;⑥-1是最小的负整数。
A 、1个B 、2个C 、3个D 、4个7、把下列各数分别填入相应的大括号内:自然数集合{ …};整数集合{ …};正分数集合{ …};非正数集合{ …};8、简答题:(1)-1和0之间还有负数吗?如有,请列举。
(2)-3和-1之间有负整数吗?-2和2之间有哪些整数?(3)有比-1大的负整数吗?有比1小的正整数吗?(4)写出三个大于-105小于-100的有理数。
1.2.2数轴基础检测1、 画出数轴并表示出下列有理数:.0,32,29,5.2,2,2,5.1---2、 在数轴上表示-4的点位于原点的边,与原点的距离是个单位长度。
3、比较大小,在横线上填入“>”、“<”或“=”。
10;0-1;-1-2;-5-3;-2.52.5.拓展提高4.数轴上与原点距离是5的点有个,表示的数是。
5.已知x是整数,并且-3<x<4,那么在数轴上表示x的所有可能的数值有。
(完整版)绝对值有理数比较大小知识点及习题

第三讲:绝对值、有理数比较大小1、 绝对值:一般地,在数轴上表示数a 的点到原点的距离叫做a 的绝对值;(|a|≥0)2、 一个正数的绝对值是其本身;一个负数的绝对值是其相反数;0的绝对值是0;3、 绝对值可表示为:⎪⎩⎪⎨⎧<-=>=)0a (a )0a (0)0a (a a 4、0a 1a a>⇔= ; 0a 1a a <⇔-=;5、 有理数的比较:在数轴上表示有理数,它们从左到右的顺序,就是从小到大的顺序。
即左边的数小于右边的数;(①正数大于0,0大于负数,正数大于负数;②两个负数,其绝对值大的反而小;)一、填空题1、一个正数的绝对值是____,一个负数的绝对值是____,0的绝对值是___2、绝对值小于3的整数有___个,它们是________。
3、用“>”或“<”号填空。
-3__-4, -(-4)__-|-5|, -65__-76 4、若a +|a |=0,则a __0,若a -|a |=0,则a __0。
5、已知|a |=73,|b |=209,且b < a ,则a =___,b =___。
6、若|a -2|+|b +1|=0,则a +b =___。
7、绝对值最小的有理数是___,绝对值等于它本身的数是______,绝对值等于它的相反数的数是______。
8、绝对值小于2的整数有___个,绝对值不大于3的非负整数是_______。
9、一个数的倒数的绝对值是21,则这个数是____。
10、-31的相反数是___,-31的绝对值是___,-31的倒数是___。
11、有理数m ,n 在数轴上的位置如图,二、选择题1、-|-2|的倒数是( )A 、2B 、21C 、-21 D 、-2 2、若|a |=-a ,则a 一定是( )A 、正数B 、负数C 、非正数D 、非负数3、代数式|x -2|+3的最小值是( )A 、0B 、2C 、3D 、54、若|a |=|b |,则a 与b 的关系是( )A 、a =bB 、a =-bC 、a =b 或a =-bD 、不能确定5、下面说法中正确的有( )个①互为相反数的两个数的绝对值相等;②一个数的绝对值是一个正数;③一个数的绝对值的相反数一定是负数;④只有负数的绝对值是它的相反数。
有理数数轴绝对值知识点 习题

⎪⎪⎪⎩⎪⎪⎪⎨⎧有理数⎪⎩⎪⎨⎧)3,2,1:()3,2,1:(ΛΛ如负整数如正整数整数)0(零⎪⎩⎪⎨⎧----)8.4,3.2,31,21:(Λ如负分数分数)8.3,3.5,31,21:(Λ如正分数有理数、数轴、绝对值1、负数的应用,有理数的分类(1)、负数的意义:引入负数是我们实际的需要,我们通常用正、负来表示一对相反意义的量。
Eg1. 上升1m 表示为+1m ,则下降2m 表示为 。
生活中有很多这样的相反的量:前进-后退,向东-向西,等等。
(2)课堂练习:1.将下列各数填到相应的括号内: -,34,-9,,0,,π,1245,-,20% 整数集合: 正分数集合: 非负数集合:分数集合:2. a 一定是正数,-a 一定是负数吗?回答并举例:3. 如果零上5度记作+5度,那么零下3度记作什么?4. 东、西为俩个相反方向,如果—4m 表示一个物体向西运动4m ,那么+2m 表示什么?物体原地不动记作什么?5. 某仓库运进面粉记作+,那么运出面粉应记作什么?2、数轴(1)1、数轴的三要素: 、 、 。
在数轴上,右边的数总比左边的数大。
最小的正整数是 ,最大的负整数是 。
(2)、数轴上的点,右边的数 > 左边的数。
正数 > 0 > 负数(3)、△相反数:两个数只有符号不同,我们称一个是另一个的相反数。
Eg 。
2和-2,a 和-a 。
本质:只有符号不同,其它不变。
特别的:0的相反数是 。
※ x +y 的相反数是 ,a -b 的相反数是牢记:正数的相反数是 ,负数的相反数是 ,相反数等于它本身的数是 。
(4)、相反数的代数意义:a>0时,-a 0; a<0时,-a 0; a =0时,-a 0.(a 可以代表任意有理数)相反数的几何意义: 表示互为相反数的两个点位于原点的 ,且到原点的 相等。
(5)、会进行符号的化简:eg 。
-(-2)= ;+[-(+2)]= ;-(x +y )= ;3、绝对值(1)、概念:在数轴上,一个数所对应的点到原点的 叫做该数的绝对值。
七年级数学有理数混合运算数轴绝对值练习题(附答案)

七年级数学有理数混合运算数轴绝对值练习J2. 泄义[x]为不超过;V 的最大整数,如[3.6] = 3, [0.6] = 0, [-3.6] = -4.对于任意实数X,下列式子 中错误的是()A. [x] = x (x 为整数)B. 0≤x -[x]< 1C. [^+y]≤[-v]+[y]D. [n+x]=n+[x](n 为整数)二. 解答题赢下列各数分别填入相应的集合里・4 22 -23,- 一W ,0,丰,一(一3.14),2006, -什5),+ 1.88(1) 整数集合:{ }:(2) 正数集合:{ };(3) 负分数集合:{ }:(4) 非负有理数集合:{ }•4. 某超市3天内饮料进岀仓库的件数如下(“ + ”表示进库,”表示岀库):+26, -32, ~15, +34, -3&-20。
(1) 经过这3天■库里的饮料是增多还是减少了?(2) 经过这3天,仓库管理员发现库里还存480件饮料,3天前库里有饮料多少件?(3) 如果进出的装卸费都是每件5元,那么这3天共要付多少装卸费?5. 如图,线段AB=24,动点P 从A 出发,以每秒2个单位的速度沿射线AB 运动,运动时间为t 秒 (t>0), M 为AP 的中点•• --- 4 ------ ■ --------- • ---A M P Bb 当点P 在线段AB 上运动时,① 当t 为多少时,PB 二2AM?② 求2BM-BP 的值.2•当P 在AB 延长线上运动时,N 为BP 的中点,说明线段MN 的长度不变,并求出其值・3•在P 点的运动过程中,是否存在这样的t 的值,使M 、N 、B 三点中的一个点是以其余两点为端点 的线段的中点,若有,请求出t 的值;若没有,请说明理由・6. 在数轴上,表示数加与"的点之间的距离可以表示为∖m-n ∖.例如:在数轴上,表示数-3与2的点 之间的距离是5 = ∣-3-2∣表示数r 与—1的点之间的距离是3 = ∣-4-(-l )p.利用上述结论解决如下问题:1. 若|x —5| = 3,求X 的值;2. 点A 、B 为数轴上的两个动点,点A 表示的数是",点B 表示的数是b,且匕―M = 6(">d ),点C 表示的数为-2,若A 、B 、C 三点中的某一个点是另两个点组成的线段的中点,求G 、方的值.D.1122的结果是i ∙i 、2£3‘;P÷2M ,=62; l ,-t ∙2MM j ≡102;根据你观察到的规律求l 3+23÷33+8、阅读第⑴小题的计算方法,再计算第⑵小题。
有理数、数轴、相反数、绝对值练习卷

有理数【2 】.数轴.相反数.绝对值检测卷班级:___________姓名:____________一.填空题1.假如向南走5 km记为-5 km,那么向北走10 km记为____2.大于-5.1的所有负整数为__________________.3.珠穆朗玛峰凌驾海平面8848米,表示为+8848米.吐鲁番盆地低于海平面155米,表示为_________.4.原点表示的数是_______,原点右边的数是________,左边的数是________.5.绝对值是2的数有_____个,它们是_________,绝对值是110的数有_____个,它们是________,0的绝对值记作:_____=_____,-100的绝对值是_____,记作:_____=_____.6.一个数与它的相反数之和等于_____.7._______的倒数是它本身,_______的绝对值是它本身.8.-|-67|=_______,-(-110)=_______,-|+13|=_______,-(+25)=_______,+|-12|=_______,9.若|-x|=|12|,则x=_______.10.一个数的绝对值越小,则该数在数轴上所对应的点,离原点越_____.11.比较大小:(1)-35___|-12| (2)|-15|___0(3)|-65|___|-43| (4)-97___-6512.距原点3个单位长度的数是___________二.断定题1.-13的相反数是3. ()2.划定了正偏向的直线叫数轴. ()3.数轴上表示数0的点叫做原点.()4.假如A.B两点表示两个相邻的整数,那么这两点之间的距离是一个单位长度.()5.若两个数的绝对值相等,则这两个数也相等. ()6.一个有理数的绝对值不小于它自身7.-a的绝对值等于a8.一个数的绝对值是它的相反数,则这个数必定是负数. ( )9.若-a是负数,则a是正数. ()10.正整数聚集与负整数集归并在一路是整数聚集.()三.选择题1.|x|=2,则这个数是()A.2B.2和-2C.-2D.以上都错2.|12a|=-12a,则a必定是()A.负数B.正数C.非正数D.非负数3.假如一个数的绝对值等于这个数的相反数,那么这个数是()A.正数B.负数C.正数.零D.负数.零4.每个有理数都可以用数轴上的以下哪项来表示()A.一个点B.线C.单位D.长度5.下列图形中不是数轴的是()6.下列说法错误的是()A.零是最小的整数B.有最大的负整数,没有最大的正整数C.数轴上两点表示的数分离是-213与-2,那么-2在右边D.所有的有理数都可以用数轴上的点表示出来7.下列各数中,大于-12小于12的负数是()A.-23B.-13 C.13 D.08.负数是指()A.把某个数的前边加上“-”号B.不大于0的数C.除去正数的其他数D.小于0的数9.关于零的论述错误的是()A.零大于所有的负数B.零小于所有的正数C.零是整数D.零既是正数,也是负数10.下面是关于0的一些说法,个中准确说法的个数是()①0既不是正数也不是负数;②0是最小的天然数;③0是最小的正数;④0是最小的非负数;⑤0既不是奇数也不是偶数.A.0B.1C.2D.311.下面准确的是()A.数轴是一条划定了原点,正偏向和长度单位的射线B.离原点近的点所对应的有理数较小C.数轴上的点可以表示随意率性有理数D.原点在数轴的正中央12.关于相反数的论述错误的是()A.两数之和为0,则这两个数为相反数B.假如两数所对应的点到原点的距离相等,这两个数互为相反数C.符号相反的两个数,必定互为相反数D.零的相反数为零13.若数轴上A.B两点所对应的有理数分离为a.b,且b在a的右边,则a-b的成果必定()A.大于零B.小于零C.等于零D.无法肯定14.假如点A .B .C .D 所对应的数为a .b .c .d ,则a .b .c .d 的大小关系为( )A.a <c <d <bB.b <d <a <cC.b <d <c <aD.d <b <c <a15.0,12,-15,-8,+10,+19,+3,-3.4中整数的个数是()A.6B.5C.4D.3四.解答题1.某气象预告显示,我国五个地区的最高气温第二天比第一世界降了12℃,这五个地区第一天最高气温如图所示,请填写第二天的最高气温. 2.在给出的数轴上,标出以下各数及它们的相反数.-1,2,0,52,-43.下图是一个长方体纸盒的睁开图,请把-5,3,5,-1,-3,1分离填入六个长方形,使得按虚线折成长方体后,相对面上的两数互为相反数.4.出租车司机李师傅一世界午的营运满是在器械走向的萧绍路长进行的,假如划定向东行驶为正,他这世界午行车的里程(单位:千米)是: +8, -6, -5, +10, -5, +3, -2, +6, +2, -5(1)若把李师傅下昼动身地记为0,他将最后一名乘客送抵目标地时,李师傅距下昼动身地有多远?(2)假如汽车耗油量为0.41升/千米,那么这世界午汽车共耗油若干升?5.(1)已知ab>0,试求ab ab b b aa ||||||++的值. (2)若|x -2|+|y +3|+|z -5|=0,盘算:①x ,y ,z 的值.②求|x |+|y |+|z |的值.。
专题训练1数轴、相反数、绝对值、有理数的概念及综合应用(24张PPT)数学

解析
3.在数轴上表示-2,0,6.3,15的点中,在原点右边的点有( )A.0个 B.1个 C.2个 D.3个
C
解析 在数轴上表示-2,0,6.3,15的点中,在原点右边的点有6.3,15,共2个,故选C.
答案
解析
例2 数轴上的点A对应的数是-2,与A相距1个单位长度的点B对应的数是__________.
解 由于表示相反数的两个点到原点的距离相等,而点D,B之间的距离为9,可知点D,B表示的数分别为-4.5和4.5,则点D,E,A表示负数,故图中5个点所表示的数中有3个负数;点C表示的数的绝对值最小.
解
类型4
绝对值的应用
例4 某家企业生产瓶装食用调和油,根据质量要求,净含量(不含包装)可以有0.002 1升的误差,现抽查6瓶食用调和油.超过规定净含量的部分记作正数,不足规定净含量的部分记作负数,结果如下(单位:升):+0.001 9,-0.002 2,+0.002 1,-0.001 5,+0.002 4,-0.000 9.请问这6瓶食用调和油中有几瓶符合要求?请用绝对值的知识说明理由.
解 如果|a|>|b|,那么结果为b的质量最符合标准.如果|a|<|b|,那么结果为a的质量最符合标准.如果|a|=|b|,那么两个篮球的质量最符合标准.
解
本课结束
ห้องสมุดไป่ตู้ 同学们再见!
授课老师:
时间:2024年9月1日
2024课件
同学们再见!
授课老师:
时间:2024年9月1日
变式训练10.如图,检测4个足球,其中超过标准质量的克数记为正数,不足标准质量的克数记为负数,从轻重的角度看,最接近标准的是( )
答案
C
11.有一只小昆虫在数轴上爬行,它从原点开始爬,“+”表示此昆虫向右,“-”表示此昆虫向左,总共爬行了10次,其数据统计如下(单位:厘米):+3,-2,-3,+1,+2,-2,-1,+1,-3,+2.如果此昆虫每分钟爬行4厘米,那么在此爬行过程中,它用了几分钟?
人教版七年级数学有理数-绝对值知识总结及练习题(附答案)

1.2.4绝对值定义:一般地,在数轴上表示 数a 的点与原点的距离叫做数a 的绝对值,记作︱a ︱。
1)一个正数的绝对值是它本身;2)零的绝对值是零;3)一个负数的绝对值是它的相反数。
即:4)任何一个有理数的绝对值都是非负数,(即0和正数.) 在数轴上表示的两个数,右边的数总要 大于 左边的数。
也就是:1)、负数 < 0,0 < 正数,正数大于负数.2)、两个负数,绝对值大的 反而小 .练习:1、判断下列说法是否正确:(1)有理数的绝对值一定是正数;(2)如果两个数的绝对值相等,那么这两个数相等;(3)符号相反且绝对值相等的数互为相反数;(4)一个数的绝对值越大,表示它的点在数轴上越靠右;(5)一个数的绝对值越大,表示它的点在数轴上离原点越远。
(7)若a =b ,则|a|=|b|。
(8)若|a|=|b|,则a =b 。
(9)若|a|=-a ,则a 必为负数。
(10)互为相反数的两个数的绝对值相等。
(11)一个数的绝对值是 2 ,则这数是2 。
(12)|5|=|-5|。
(13)|-0.3|=|0.3|。
(14)|3|>0。
(15)|-1.4|<0。
例1、已知052=++-y x ,求x,y 的值。
例2、若3=x ,则x=___。
例3、下列说法中,错误的是( )A 、一个数的绝对值一定是正数B 、互为相反数的两个数的绝对值相等C 、绝对值最小的数是0D 、绝对值等于它本身的数是非负数作业:1化简:=--5___;=--)5(___;=+-)21(_2比较下列各对数的大小:-(-1)___-(+2);)3.0(--___31-; 2--___-(-2)。
4、已知a=-2,b=1,则b a -+得值为___。
5、下列结论中,正确的有( )①符号相反且绝对值相等的数互为相反数;②一个数的绝对值越大,表示它的点在数轴上离原点越远;③两个负数,绝对值大的它本身反而小;④正数大于一切负数;⑤在数轴上,右边的数总大于左边的数。
有理数_数轴-相反数-绝对值练习题

有理数数轴同步练习姓名1.在数轴上表示的两个数中,的数总比的数大。
2.在数轴上,表示-5的数在原点的侧,它到原点的距离是个单位长度。
3.在数轴上,表示+2的点在原点的侧,距原点个单位;表示-7的点在原点的侧,距原点个单位;两点之间的距离为个单位长度。
4.在数轴上,把表示3的点沿着数轴向负方向移动5个单位,则与此位置相对应的数是。
5.与原点距离为2.5个单位长度的点有个,它们表示的有理数是。
6.到原点的距离不大于3的整数有个,它们是:。
7.下列说法正确的是()A.没有最大的正数,却有最大的负数B.数轴上离原点越远,表示数越大C.0大于一切非负数D.在原点左边离原点越远,数就越小8.下列结论正确的有()个:①规定了原点,正方向和单位长度的直线叫数轴②最小的整数是0 ③正数,负数和零统称有理数④数轴上的点都表示有理数A.0B.1C.2D.39.在数轴上,A点和B点所表示的数分别为-2和1,若使A点表示的数是B点表示的数的3倍,应把A点()A.向左移动5个单位B.向右移动5个单位C.向右移动4个单位D.向左移动1个单位或向右移动5个单位10.在数轴上,离原点距离等于3的数是。
11.点A 为数轴上表示-2的动点,当点A 沿数轴移动4个单位长度到B 时,点B所表示的实数是()A.1B.-6C.2或-6D.不同于以上答案12.在数轴上画出下列各点,它们分别表示:+3, 0,-314, 112,-3,-1.25并把它们用“<”连接起来。
相反数与绝对值练习题姓名1、若x=—x,则x一定是()A、正数B、负数C、非正数D、非负数2、下列说法正确的是()A、一个数的绝对值的相反数一定不是负数B、一个数的绝对值的相反数是负数C、一个数的绝对值一定是正数D、一个数的绝对值的一定是非负数3、下列结论正确的是()A、a一定是正数B、—c一定是负数-一定是正数 D、—a一定是非正数C、—a4、如果a+b=0,则a与b的大小关系是()A、a=b=0B、a与b不相等C、a与b互为相反数D、a、b异号5、下列说法不正确的是()A、如果a的绝对值比它本身大,则a一定是负数B、如果两个数不等,则它们的绝对值也必不相等C、两个负有理数,绝对值大的离原点远D、两个负有理数,大的离原点近6、绝对值不大于6的非正整数有。
2023年中考数学《有理数之绝对值》重点知识总及专项练习题(含答案解析)

2023年中考数学《有理数之绝对值》重点知识总及专项练习题(含答案解析)一、重点知识总结1. 绝对值的定义:数轴上表示数a 的点到原点的距离用数a 的绝对值来表示。
即|a |。
离远点越远的数绝对值越大,离原点越近的数绝对值越小。
2. 求绝对值:正数的绝对值等于它本身,负数的绝对值等于它的相反数,0的绝对值是0。
即⎪⎩⎪⎨⎧==−===0000a a a a a a a a a ,则若,则<若,则>若或⎪⎩⎪⎨⎧≤−=≥=00a a a a a a ,则若,则若 3. 绝对值与相反数:互为相反数的两个数绝对值相等。
即a 与b 互为相反数,则b a =。
绝对值相等的两个数要么相等,要么互为相反数。
即b a =,则b a =或b a −=。
绝对值等于一个正数的数有两个,他们互为相反数。
()0>a a x =,则a x ±=。
二、专项练习题1、(2022•黔西南州)﹣3的绝对值是( )A .±3B .3C .﹣3D .﹣31 【分析】根据绝对值的性质:|a |=即可得出答案.【解答】解:﹣3的绝对值:|﹣3|=3,故选:B .2、(2022•黄石)21−的绝对值是( )A .21−B .2﹣1C .1+2D .±(2﹣1) 【分析】直接利用绝对值的定义分别分析得出答案.【解答】解:1﹣的绝对值是﹣1;故选:B .3、(2022•百色)﹣2023的绝对值等于( )A .﹣2023B .2023C .±2023D .2022 【分析】利用绝对值的意义求解.【解答】解:因为负数的绝对值等于它的相反数;所以,﹣2023的绝对值等于2023.故选:B .4、(2022•广东)|﹣2|=( )A .21B .2C .﹣2D .﹣21 【分析】根据绝对值是数轴上的点到原点的距离,可得答案.【解答】解:|﹣2|=2,故选:B .5、(2022•荆门)如果|x |=2,那么x =( )A .2B .﹣2C .2或﹣2D .2或﹣21 【分析】利用绝对值的意义,直接可得结论.【解答】解:∵|±2|=2,∴x =±2.故选:C .6、(2022•聊城)实数a 的绝对值是45,a 的值是( )A .45B .﹣45C .±54D .±45 【分析】根据绝对值的意义直接进行解答【解答】解:∵|a |=,∴a =±.故选:D .。
初一有理数绝对值题50练

初一有理数绝对值题50练一、基础概念理解1、绝对值的定义:数轴上表示一个数的点与原点的距离叫做这个数的绝对值。
正数的绝对值是它本身,负数的绝对值是它的相反数,0 的绝对值是 0。
例如,5 的绝对值是 5,-3 的绝对值是 3,0 的绝对值是 0。
练习 1:求下列各数的绝对值:(1)-7 (2)8 (3)0 (4)-12练习 2:若一个数的绝对值是 4,求这个数。
练习 3:绝对值等于本身的数是()A 正数B 负数C 非负数D 非正数二、简单计算2、计算绝对值的运算。
例如:| 5 + 3 |=| 2 |= 2练习 4:计算:(1)| 7 9 |(2)| 3 + 8 |(3)| 5 12 |练习 5:已知| a |= 3,| b |= 5,且 a < b,求 a + b 的值。
练习 6:若| x 2 |= 5,求 x 的值。
三、比较大小3、利用绝对值比较有理数的大小。
两个负数比较大小,绝对值大的反而小。
例如:比较 3 和 5 的大小。
因为| 3 |= 3,| 5 |= 5,3 <5,所以 3 > 5。
练习 7:比较下列各组数的大小:(1) 1 和 4 (2)0 和 2 (3) 05 和 2练习 8:如果 a < 0,b < 0,且| a |<| b |,那么 a 和 b 的大小关系是()A a > bB a = bC a < bD 无法确定练习 9:有理数 a、b 在数轴上的位置如图所示,比较| a |和| b |的大小。
(数轴略)四、综合应用4、绝对值在实际问题中的应用。
例如:出租车的收费标准是起步价 8 元(3 千米以内),超过 3 千米的部分每千米 15 元。
某人乘坐出租车行驶了 x 千米(x > 3),则应付车费为 8 + 15(| x 3 |)元。
练习 10:某工厂生产一种零件,规定零件的尺寸误差不能超过±05毫米,若生产的零件尺寸为 x 毫米,用绝对值表示零件尺寸的误差范围。
练习 11:一足球队在一场比赛中的胜负情况可以用净胜球数来表示,若净胜球数为正数,则表示赢球;若净胜球数为负数,则表示输球;若净胜球数为 0,则表示平局。
有理数-绝对值的概念知识点以及习题大全

【有理数】➢ 绝对值相反数:只有符号不同的两个数叫做互为相反数。
(1)实数a 的相反数是 -a ; 0的相反数是0(2)a 和b 互为相反数⇔a+b=0像5与-5、-2.5与2.5等等符号不同、绝对值相等的两个数互为相反数,其中一个是另一个的相反数。
(3) 相反数的几何意义:表示互为相反数的两个点(除0外)分别在原点O 的两边,并且到原点的距离相等。
【基础练习】1. ______的相反数是它本身,_____的绝对值是它本身,_______的绝对值是它的相反数.2. 一个数的绝对值是32,那么这个数为______. 3. 已知a=-2,b=1,则b a -+得值为______4. 如果3-=a ,则______=-a ,______=a .5. 若︱m ︱=︱-2︱,则m =__________。
6. ______5=-;______312=-;______31.2=-;______=+π.7. 下列说法中正确的是( )A .a -一定是负数B .只有两个数相等时它们的绝对值才相等C .若a b =则a 与b 互为相反数D .若一个数小于它的绝对值,则这个数是负数8. 若m 是有理数,则|m|-m 一定是( )A.零B.非负数C. 正数 D 负数9. 如果22a a -=-,则a 的取值范围是( )A .a >OB .a ≥OC .a ≤OD .a <O10.给出下列说法:①互为相反数的两个数绝对值相等;②绝对值等于本身的数只有正数;③不相等的两个数绝对值不相等;④绝对值相等的两数一定相等.其中正确的有( )A .0个B .1个C .2个D .3个11. 绝对值等于其相反数的数一定是( )A .负数B .正数C .负数或零D .正数或零12. 在数轴上,若点 A 和 点B 所表示的数互为相反数,点A 在数轴的右边,并且和原点的距离为2,那么点B 表示的数是( )A 、2B 、—2C 、2和—2D 、—3 13. 在数轴上,表示有理数的绝对值的点的位置在( )A 、原点的两旁B 、任何一点C 、原点的右边D 、原点及其右边 14. 绝对值最小的数是 ( )A .1B .-1C .0D .没有15. 求下列各数的绝对值0.5 2 -4 -30 0 -(-3) -∣-2.5∣16. 为体现社会对教师的尊重,教师节这一天上午,出租车司机小王在东西向的公路上免费接送老师。
(完整版)绝对值练习题(经典)100道

绝对值综合练习题1、有理数的绝对值一定是_________。
2、绝对值等于它本身的数有________个。
3、下列说法正确的是( )A、—|a|一定是负数B、只有两个数相等时它们的绝对值才相等C、若|a|=|b|,则a与b互为相反数D、若一个数小于它的绝对值,则这个数为负数4。
若有理数在数轴上的对应点如下图所示,则下列结论中正确的是()A、a>|b|B、a〈bC、|a|>|b|D、|a|〈|b|5、相反数等于—5的数是______,绝对值等于5的数是________.6、—4的倒数的相反数是______.7、绝对值小于2的整数有________。
8、若|-x|=2,则x=____;若|x-3|=0,则x=______;若|x-3|=1,则x=_______。
10、已知|a|+|b|=9,且|a|=2,求b的值.11、已知|a|=3,|b|=2,|c|=1,且a<b<c,求a、b、c的值。
12、如果m〉0, n<0, m〈|n|,那么m,n,-m, -n的大小关系_________________.13、如果,则的取值范围是( )A.>O B.≥O C.≤O D.<O14、绝对值不大于11。
1的整数有()A .11个B .12个C .22个D .23个15、│a │= -a ,a 一定是( )A 、正数B 、负数C 、非正数D 、非负数16、有理数m ,n 在数轴上的位置如图,17、若|x —1| =0, 则x=__________,若|1—x |=1,则x=_______.18、如果,则,.19、已知│x+y+3│=0, 求│x+y │的值。
20、│a -2│+│b -3│+│c -4│=0,则a+2b+3c=21、如果a,b 互为相反数,c 、d 互为倒数,x 的绝对值是1, 求代数式x b a ++x 2+cd 的值。
22、已知│a │=3,│b │=5,a 与b 异号,求│a -b │的值。
有理数、数轴动点、绝对值、求值化简问题(解析版)-初中数学

有理数、数轴动点、绝对值、求值化简问题【题型归纳】题型一:正数与负数1.(2024七年级上·浙江)小戴同学的微信钱包账单如图所示, 5.20+表示收入5.20元,下列说法正确的是( )A . 1.00-表示收入1.00元B . 1.00-表示支出1.00元C . 1.00-表示支出 1.00-元D .收支总和为6.20元【答案】B 【分析】根据 5.20+表示收入5.20元,可以得出“收入”用正数表示,从而“支出”就用负数表示,得出答案.【详解】解:∵ 5.20+表示收入5.20元,“收入”用正数表示,∴“支出”就用负数表示,∴ 1.00-表示支出1.00元,故选:B .2.(2024七年级上·江苏·专题练习)在下列选项中,具有相反意义的量是( )A .上升了6米和后退了7米B .卖出10斤米和盈利10元C .收入20元与支出30元D .向东行30米和向北行30米【答案】C【分析】本题考查了对正负数概念的理解,关键明确正负数是表示一对意义相反的量.根据相反意义的量的概念,逐项判断分析即可解题.【详解】解:A.不是一对具有相反意义的量,不符合题意;B.不是一对具有相反意义的量,不符合题意;C.是一对具有相反意义的量,符合题意;D.不是一对具有相反意义的量,不符合题意.故本题选:C .3.(2024七年级上·江苏·专题练习)机床厂工人加工一种直径为30mm 的机器零件,要求误差不大于0.05mm ,质检员现抽取10个进行检测(超出部分记为正,不足部分记为负,单位:mm )得到数据如下:0.050.040.020.070.030.040.010.010.030.06+--+-+--+-,,,,,,,,,.其中不合格的零件有( )A .1个B .2个C .3个D .4个【答案】B 【分析】本题主要考查了正负数的实际应用,首先审清题意,明确“正”和“负”所表示的意义,找到数值大于0.05的零件数即可得到答案.【详解】解:∵要求误差不大于0.05mm ,∴只有0.07+和0.06-误差大于0.05,∴不合格的零件有2个,故选:B .题型二:有理数的分类4.(2024七年级上·全国·专题练习)下列说法正确的是( )A .正整数、负整数、正分数和负分数统称为有理数B .整数和分数统称有理数C .正数和负数统称有理数D .正整数和负整数统称整数5.(2024七年级上·江苏·专题练习)关于4-,227,0.41,116-,0,3.14这六个数,下列说法错误的是( )A .4-,0是整数B .227,0.41,0,3.14是正数C .4-,227,0.41,116-,0,3.14是有理数D .4-,116-是负数6.(23-24七年级上·贵州黔东南·阶段练习)对于有理数,有下列说法:(1)正整数和负整数的总和就是整数;(2)分数包括了正分数和负分数和0;(3)有理数是整数和分数的统称;(4)0是整数;(5)分数包含有限小数、循环小数,其中说法全正确的有( )A .(1)(2)(3)B .(2)(3)(4)C .(3)(4)(5)D .(1)(4)(5)题型三:利用数轴比较有理数大小7.(23-24七年级上·河南郑州·期末)已知a b ,在数轴上的位置如图所示,则下列结论:①0a b <<,②||||a b <,③0a b->,④b a a b -<+,正确的是( )A .②③B .①②C .①③D .①④【答案】C 【分析】本题考查根据点在数轴上的位置比较代数式大小,熟练掌握利用数轴比较数的大小是解决问题的关键.\故①0a b <<正确;a b >,②错误;由8.(23-24七年级上·四川达州·期末)如图,若A 是有理数a 在数轴上对应的点,则关于a ,a -,1的大小关系表示正确的是( )A .1a a <<-B .1a a <-<C .1a a <-<D .1a a -<<9.(2024·广东广州·二模)有理数a ,b 在数轴上的对应点的位置如图所示,把a ,a -,b 按照从小到大的顺序排列,正确的是( )A .a a b<-<B .a b a -<<C .a a b -<<D .b a a<-<【答案】A 【分析】本题考查了数轴与有理数大小的比较,正确理解数轴与有理数大小的比较的方法是解题的关键.在数轴上标出有理数a 的相反数a -所表示的点,再根据“在数轴上表示的两个数,右边的数总比左边的数大”,即可判断答案.【详解】在数轴上标出有理数a 的相反数a -所表示的点,则a ,a -,b 按照从小到大的顺序排列为a a b <-<.故选:A .题型四:数轴的距离问题10.(2024·福建福州·三模)如图是单位长度为1的数轴,点A,B是数轴上的点,若点A表示的数是3-,则点B 表示的数是()A.1-B.0C.1D.2【答案】C【分析】本题考查了数轴,熟练掌握数轴上两点之间的距离公式是解题的关键.根据数轴上两点之间的距离公式计算即可.【详解】解:Q点A表示的数是3-,点B距离点A有4个单位,\点B表示的数是341-+=,故选:C.11.(2024·北京·二模)在数轴上,点A,B在原点O的两侧,分别表示数a,3,将点A向左平移1个单位长度,=,则a的值为()得到点C.若CO BOA.2-B.1-C.1D.212.(23-24七年级上·河南新乡·期末)如图,在数轴上点A在原点右侧,距离原点5个单位长度,表示的数是5,点B距离点A是6个单位长度,则点B表示的数是()A.6B.6或6-C.11或6-D.11或1-【答案】D【分析】本题考查了数轴上两点之间的距离,根据题意可列的式子,进而求解,求解数轴上两点之间的距离是解题的关键.【详解】解:∵点B 距离点A 是6个单位长度,则5611+=,或561-=-,∴点B 表示的数是11或1-,故选:D .题型五:数轴的动点问题13.(23-24九年级下·河北保定·期中)如图,一个点在数轴上从原点开始先向右移动1个单位长度,再向左移动a 个单位长度后,该点所表示的数为3-,则a 的值是( )A .4-B .4C .3-D .3【答案】B【分析】本题以数轴为背景考查了两点之间距离公式、解一元一次方程等知识,根据题意,数形结合,由数轴上两点之间距离的表示方法列式求解即可得到答案,熟记数轴上两点之间距离的表示方法是解决问题的关键.【详解】解:根据题意可知,13a -=-,∴4a =,故选:B .14.(23-24七年级上·湖南衡阳·期末)一个动点P 从数轴上的原点出发,沿数轴的正方向以前进4个单位,后退2个单位的程序运动,已知点P 每秒前进或后退1个单位.设n x 表示第n 秒点P 在数轴上的位置所对应的数,如22x =,44x =,53x =,则2023x 为( )A .673B .674C .675D .676【答案】C 【分析】本题主要考查了数轴上的动点问题,数字类的规律探索,根据题意可知每6秒点P 完成一次前进和一次后退运动,且每6秒内点P 向数轴正方形运动2个单位,再由202363371¸=K 即可得到答案.【详解】解:∵动点P 从数轴上的原点出发,沿数轴的正方向以前进4个单位,后退2个单位的程序运动,∴每6秒点P 完成一次前进和一次后退运动,且每6秒内点P 向数轴正方形运动2个单位,∵202363371¸=K ,∴2023x 为33721675´+=,故选:C .15.(23-24七年级上·江苏苏州·阶段练习)如图,圆的周长为4个单位长度,在该圆的4等分点处分别标上数字0、1、2、3,先让圆周上表示数字0的点与数轴上表示数1-的点重合,再将数轴按逆时针方向环绕在该圆上,则数轴上表示数2124-的点与圆周上表示数字( )的点重合.A .0B .1C .2D .3【答案】B 【分析】本题主要考查数轴,熟练掌握数轴的特点和围绕圆周对应的数之间的关系的相互关系是解题的关键.根据题意发现规律,即可解得答案.【详解】解:依题意,4次为一个周期,依次为0,3,2,1,21244531¸=,故数轴上表示数2124-的点与圆周上表示数字1的点重合.故选B .题型六:绝对值非负数的应用16.(23-24七年级下·山东潍坊·阶段练习)若5x -与7y +互为相反数,则3x y -的值是( )A .22B .8C .8-D .22-17.(23-24七年级上·河南新乡·阶段练习)若230a b -++=,则a b +的值是( )A .0B .1C .1-D .202118.(23-24七年级上·广东韶关·期末)若320x y -++=,则x y +的值是( ).A .5B .1C .2D .0题型七:化简绝对值问题19.(2024七年级上·全国·专题练习)若0ab ¹,那么a ab b +的取值不可能是( )A .2-B .0C .1D .220.(23-24七年级下·海南省直辖县级单位·期末)实数m 、n 在数轴上的位置如图所示,化简||n m n -+的结果为( )A .mB .m -C .2m n -D .2n m-21.(2024七年级上·江苏·专题练习)若a 、b 、c 均为整数,且||||1a b c a -+-=,则||||||a c c b b a -+-+-的值为( )A .1B .2C .3D .4题型八:有理数的综合问题22.(2024七年级上·浙江·专题练习)把下列各数分别填在表示它所属的横线上:① 3.14-;②(9)++;③425-;④0;⑤(7)+-;⑥13.14;⑦2000;⑧80%-.(填写序号)(1)正数:___________;(2)负数:___________;(3)整数:___________;(4)分数___________.【答案】(1)②⑥⑦(2)①③⑤⑧(3)②④⑤⑦(4)①③⑥⑧【分析】本题考查有理数的分类及定义,掌握有理数的分类及相关定义是解题的关键;(1)根据正数定义进行分类即可;(2)根据负数定义进行分类即可;(3)根据整数定义进行分类即可(4)根据分数定义进行分类即可.【详解】(1)正数:②⑥⑦;故答案为:②⑥⑦;(2)负数:①③⑤⑧;故答案为:①③⑤⑧;(3)整数:②④⑤⑦;故答案为:②④⑤⑦;(4)分数:①③⑥⑧.故答案为:①③⑥⑧.23.(23-24七年级上·广东·单元测试)如图,数轴上的三点A 、B 、C 分别表示有理数a ,b ,c .(1)填空:a b -______0,a c +______0,b c -______0.(用<或>或=号填空)(2)化简:a b a c b c ---+-.24.(23-24七年级下·甘肃陇南·阶段练习)阅读材料:点A ,B 在数轴上分别表示有理数a ,b ,A ,B 两点之间的距离可表示为AB a b =-.例如:7与1-两数在数轴上所对应的两点之间的距离表示为()718--=,6x -的几何意义是数轴上表示有理数x 的点与表示6的点之间的距离.这种数形结合的方法,可以用来解决一些问题.如图,已知数轴上两点A 、B 对应的数分别为1-和2,数轴上另有一个点P 对应的数为有理数x .(1)请根据阅读材料填空:点P 、A 之间的距离PA =________(用含x 的式子表示);若该距离为4,则x =________.(2)根据几何意义,解决下列问题:①若点P 在线段AB 上,则12x x ++-=________.②若125x x ++-=,求点P 表示的有理数x .值等知识.熟练掌握在数轴上表示有理数是,数轴上两点之间的距离,绝对值的几何意义,绝对值方程,化简绝对值是解题的关键.【专题训练】一、单选题25.(23-24七年级上·四川南充)在π223.141500.333 2.010********--¼-¼,,,中,非负数的个数( )A .2个B .3个C .4个D .5个【答案】B【分析】本题考查了非负数的定义,解题的关键是掌握非负数的定义.根据“零和正数统称为非负数”,即可求解.【详解】解:非负数有:3.141502.010010001¼,,,共3个,故选:B .26.(2024七年级上·全国·专题练习)下列各对数中,互为相反数的有( )()1-与1+;()2--与()2+-;12æö--ç÷èø与12æö++ç÷èø;()1-+与()1+-;()2-+与()2--A .1对B .2对C .3对D .4对即互为相反数的有3对.故选:C .27.(2024七年级上·山东青岛·专题练习)下列关于零的说法中,正确的是( )A .零是正数B .零是负数C .零既不是正数,也不是负数D .零仅表示没有【答案】C【分析】本题考查了对数的理解与运用,注意:负数都小于零,正数都大于零,零既不是正数也不是负数,整数包括正整数、零、负整数;零不仅表示没有,还表示一个介于负数与正数之间的一个数.依据题意,零大于负数,小于正数,零既不是正数也不是负数,整数包括正整数、零、负整数,从而即可根据以上内容判断求解.【详解】解:A 、零不是正数,说法错误;B 、零不是负数,说法错误;C 、零既不是正数,也不是负数,说法正确;D 、零不仅仅表示没有,不同情形下,零表示的意义不同,说法错误;故选:C .28.(23-24七年级上·安徽合肥·期末)在()5--,0.8-,0,|6|-四个数中,最小的数是( )A .()5--B .0.8-C .0D .|6|-【答案】B【分析】本题考查了有理数比较大小,正数大于0,0大于负数,两个负数其绝对值大的反而小,负数都小于0是解题关键.根据正数大于0,0大于负数,两个负数其绝对值大的反而小,可得答案.【详解】解:()50.80|6|--<-<<-,故最小的数是5-.故选:B29.(2024七年级上·江苏·专题练习)下列说法正确的是( )A .数轴上的一个点可以表示不同的有理数B .数轴上有两个不同的点可以表示同一个有理数C .任何有理数都可以在数轴上找到与它对应的唯一的点D .有的有理数不能在数轴上表示出来【答案】C【分析】本题考查了数轴的应用,根据数轴上的点与有理数的对应关系进行解答.【详解】解:A .数轴上一个点只能表示一个数,不能表示两个不同的数,故选项错误;B .数轴上两个不同的点表示两个不同的数,故选项错误;C .任何一个有理数都可以在数轴上找到和它对应的唯一的一个点,正确;D .所有的有理数都可以用数轴上的点表示,故选项错误.故本题选:C .30.(23-24七年级上·江苏常州·期末)有理数a ,b 在数轴上的对应点的位置如图所示.把a -,b ,0按照从小到大的顺序排列,正确的是( )A .0a b<-<B .0a b -<<C .0b a <<-D .0b a <-<按照从小到大的顺序排列为0a <-31.(2024七年级上·全国·专题练习)下列有关相反数的说法:①符号相反的数叫相反数;②数轴上原点两旁的数是相反数;③()3--的相反数是3-;④a -一定是负数;⑤若两个数之和为0,则这两个数互为相反数; ⑥若两个数互为相反数,则这两个数一定是一个正数一个负数.其中正确的个数有( )A .2个B .3个C .4个D .5个【答案】A【分析】本题考查相反数的定义,依据相反数的定义进行判断即可.【详解】解:①符号相反的两个数不一定互为相反数,如2-与3,故①错误;②数轴上原点两旁的数不一定互为相反数,如2-和3,故②错误;③()33--=,3的相反数是3-,故③正确;④a -不一定是负数,如0a =时,0a -=,故④错误;⑤若两个数之和为0,则这两个数互为相反数,故⑤正确;⑥0的相反数是0,故⑥错误.故选:A .32.(24-25七年级上·全国·随堂练习)如果0a b c ++=且c b a >>.则下列说法中可能成立的是( )A .a 、b 为正数,c 为负数B .a 、c 为正数,b 为负数C .b 、c 为正数,a 为负数D .a 、b 、c 为正数二、填空题33.(24-25七年级上·河南安阳·开学考试)乒乓球被誉为我国的“国球”,在正规比赛中,乒乓球的标准质量为2.7克.0.15克的乒乓球记作0.15+,那么另一个低于标准质量0.03克的乒乓球记作.【答案】0.03-【分析】本题考查正负数的意义.熟练掌握正负数表示意义相反的量,是解题的关键.【详解】解:把一个超出标准质量0.15克的乒乓球记作0.15+,那么另一个低于标准质量0.03克的乒乓球记作0.03-,故答案为:0.03-.34.(2024七年级上·北京·专题练习)把下列各数填入它所属的集合内3-,30%,215-,0, 5.32-(1)整数集合{____________________……};(2)分数集合{____________________……};(3)非负数集合{____________________……}.【答案】(1)3-,035.(24-25七年级上·河南南阳·开学考试)在56-,2-,0.35,2.4,25%,0,6,1-,97,24,100.2这些数中,( )是自然数,()是整数,( )最大,( )最小.36.(24-25七年级上·全国·随堂练习)已知x 是非负数,且非负数中最小的数是0.(1)已知210a b -+-=,则a b +的值是_________;(2)当a =________时,12a -+有最小值,最小值是______.【答案】(1)337.(2024七年级上·浙江·专题练习)已知m 是有理数,则|2||4||6||8|m m m m -+-+-+-的最小值是.三、解答题38.(2024七年级上·江苏·专题练习)在数轴上表示下列各数的相反数,并比较原数的大小.3, 1.5-,132-,4||5-,0,4-比较原数的大小为:1443 1.50325-<-<-<<-<.39.(2024七年级上·全国·专题练习)化简下列各式的符号,并回答问题:(1)()2--;(2)15æö+-ç÷èø;(3)()4éù---ëû(4)()3.5éù--+ëû;(5)(){}5éù----ëû(6)(){}5éù---+ëû问:①当5+前面有2012个负号,化简后结果是多少?②当5-前面有2013个负号,化简后结果是多少?你能总结出什么规律?(3)()44éù---=-ëû;(4)()3.5 3.5éù--+=ëû;(5)(){}55éù----=ëû;(6)(){}55éù---+=-ëû;①当5+前面有2012个负号,化简后结果是5+;②当5-前面有2013个负号,化简后结果5-,总结规律:一个数的前面有奇数个负号,化简的结果等于它的相反数,有偶数个负号,化简的结果等于它本身.40.(2024七年级上·全国·专题练习)阅读理解:数轴上线段的长度可以用线段端点表示的数进行减法运算得到,例如图,线段()101AB ==--;线段220BC ==-;线段()321AC ==--问题:(1)数轴上点M N 、代表的数分别为9-和1,则线段MN =___________;(2)数轴上点E F 、代表的数分别为6-和3-,则线段EF =___________;(2)解:∵点E F 、代表的数分别为6-和3-,∴线段()363EF =---=;故答案为:3;(3)解:由题可得|2|5m -=,则25m -=或25m -=-,解得7m =或3m =-,∴m 值为7或3-.41.(2024七年级上·江苏·专题练习)同学们都知道,()42--表示4与2-的差的绝对值,实际上也可理解为4与2-两数在数轴上所对应的两点之间的距离;同理3x -也可理解为x 与3两数在数轴上所对应的两点之间的距离.试探索:(1)求()42--= ;(2)若25x -=,则x = ;(3)请你找出所有符合条件的整数x ,使得123x x -++=.。
绝对值练习题(精)100道(DOC)

绝对值综合练习题一1、有理数的绝对值一定是()2、绝对值等于它本身的数有()个3、下列说法正确的是()A、一lai—定是负数B只有两个数相等时它们的绝对值才相等C、若lal=lbl,贝a与b互为相反数D、若一个数小于它的绝对值,则这个数为负数4.若有理数在数轴上的对应点如下图所示,则下列结论中正确的是()A、a>lblB、a<bC、lal>lblD、lal<lbl5、相反数等于-5的数是,绝对值等于5的数是。
6、-4的倒数的相反数是。
7、绝对值小于2的整数有。
8、若l—x|=2,贝x=;若l x-3l=0,贝x=;若lx-3l=1,则x=。
9、实数a、b在数轴上位置如图所示,贝恫、lbl的大小关系是。
丨丨丨丨丨I丨丨.a0b10、已知|a|+|b|=9,且|a|=2,求b的值。
11、已知|a|=3,|b|=2,|c|=1,且a〈b〈c,求a、b、c的值。
12、如果m>0,n〈0,m〈|n|,那么m,n,-m,-n的大小关系()13、如果卜加卜-加,贝仏的取值范围是()A.〉OB.^$OC.^WOD.^VO14、绝对值不大于11.1的整数有A.11个B.12个C.22个D.23个15、|a|二一a,a一定是()A、正数B、负数C、非正数D、非负数16、有理数m,n在数轴上的位置如图,比较大小:-m-n,mn17、若|x—l|=0,贝寸x二,若|]_x|=1,贝寸x二.18、如果八3,贝沖一沪,卩一冬=.19、已知|x+y+3|=0,求|x+y|的值。
20、|a-2|+|b—3|+|c—4|=0,则a+2b+3c=21、如果a,b互为相反数,c,d互为倒数,x的绝对值是1,求代数式ab+x2+cd的值。
x22、已知|a|=3,|b|=5,a与b异号,求|a—b|的值。
23.如果a,b互为相反数,那么a+b=,2a+2b=24.a+5的相反数是3,那么,a=.25.如果a和b表示有理数,在什么条件下,a+b和a—b互为相反数?26、若X的相反数是一5,则X=;若一X的相反数是一3.7,则X=27、若一个数的倒数是1.2,贝这个数的相反数是,绝对值是28、若一a=l,则a二;若一a二一2,则a二;如果一a二a,那么a二29、已知|X—4|+|Y+2|=0,求2X—|Y|的值。
人教版七年级数学上册《有理数的分类、数轴、相反数及绝对值》专题训练-附带答案

人教版七年级数学上册《有理数的分类、数轴、相反数及绝对值》专题训练-附带答案【知识点梳理】考点1 正数和负数1.概念正数:大于0的数叫做正数。
负数:在正数前面加上负号“—”的数叫做负数。
2.意义:在同一个问题上用正数和负数表示具有相反意义的量。
考点2 有理数1.概念整数:正整数、0、负整数统称为整数。
分数:正分数、负分数统称分数。
(有限小数与无限循环小数都是有理数。
)注:正数和零统称为非负数负数和零统称为非正数正整数和零统称为非负整数负整数和零统称为非正整数。
2.分类:两种⑴按正、负性质分类:⑵按整数、分数分类:正有理数正整数正整数有理数正分数整数0零有理数负整数负有理数负整数分数正分数负分数负分数考点3 数轴1.概念:规定了原点、正方向、单位长度的直线叫做数轴。
三要素:原点、正方向、单位长度2.对应关系:数轴上的点和有理数是一一对应的。
比较大小:在数轴上右边的数总比左边的数大。
3.应用求两点之间的距离:两点在原点的同侧作减法在原点的两侧作加法。
(注意不带“+”“—”号)考点4 相反数1.概念代数:只有符号不同的两个数叫做相反数。
(0的相反数是0)几何:在数轴上离原点的距离相等的两个点所表示的数叫做相反数。
2.性质:若a与b互为相反数则a+b=0 即a=-b;反之若a+b=0 则a与b互为相反数。
两个符号:符号相同是正数符号不同是负数。
3.多重符号的化简多个符号:三个或三个以上的符号的化简看负号的个数(:当“—”号的个数是偶数个时结果取正号当“—”号的个数是奇数个时结果取负号)考点5 绝对值1.几何意义:一般地数轴上表示数a的点与原点的距离叫做数a的绝对值。
一个正数的绝对值是它的本身(若|a|=|b| 则a=b或a=﹣b)2.代数意义一个负数的绝对值是它的相反数0的绝对值是03.代数符号意义:a >0 |a|=a 反之|a|=a 则a≥0 |a|=﹣a 则a≦0a = 0 |a|=0a<0 |a|=‐a注:非负数的绝对值是它本身非正数的绝对值是它的相反数。
七上 有理数 数轴 绝对值 课后测试(答案)

七上有理数数轴绝对值课后测试一、选择题:1、下列各数中,比﹣2小的数是()A.﹣3B.﹣1C.0D.12、﹣的相反数是()A.﹣2B.2C.﹣D.3、与﹣3互为倒数的是( )A.﹣B.﹣3C.D.34、|﹣8|的相反数是()A.﹣8B. 8C.D.5、下列说法中正确的是()A.任何有理数的绝对值都是正数B.最大的负有理数是﹣1C.0是最小的数D.如果两个数互为相反数,那么它们的绝对值相等6、实数a在数轴上对应的点如图所示,则a,﹣a,1的大小关系正确的是()A.a<﹣a<1B.﹣a<a<1C.1<﹣a<aD.a<1<﹣a7、下列说法正确的是( )A.没有最小的正数B.﹣a表示负数C.符号相反两个数互为相反数D.一个数的绝对值一定是正数8、若有理数a和b在数轴上所表示的点分别在原点的右边和左边,则︱b︱-︱a-b︱等于()A、aB、-aC、2b+aD、2b-a9、一个数的绝对值小于3,那么这个数不可能是( )A.0B.2C.﹣2D.﹣310、如图,数轴上每相邻两点相距一个单位长度,点A、B、C、D对应的位置如图所示,它们对应的数分别是a、b、c、d,且d﹣b+c=10,那么点A对应的数是( )A.﹣6B.﹣3C.0D.正数二、填空题:11、已知|x|=8,则x= .12、若,则a= .13、﹣a﹣b+c的相反数是 .14、小于﹣3.8的最大整数是.15、把下列各数填在相应的大括号里(将各数用逗号分开):﹣4,0.62,,18,0,﹣8.91,+100 正数:{ …};负数:{ …};整数:{ …};分数:{ …}.16、绝对值不大于5的整数有个.17、数轴上一个点到﹣1所表示的点的距离为4,那么这个点在数轴上所表示的数是_______.18、有理数在数轴上的对应点如图所示,化简: .三、计算题:19、﹣|﹣8| 20、﹣(+7); 21、﹣(﹣5); 22、+︱-10︱四、简答题:23、把下列各数分别填入相应的集合里:+(﹣2),0,﹣0.314,﹣(﹣11),,﹣4,0.,正有理数集合:{ …},负有理数集合:{ …},整数集合:{ …},自然数集合:{ …},分数集合:{ …}.24、已知|a﹣2|与|b﹣3|互为相反数,求3a+2b的值.25、当x为何值时,代数式|3x﹣2|+2取最小值,最小值是多少?26、如图,点P、Q在数轴上表示的数分别是-8、4,点P以每秒2个单位的速度运动,点Q以每秒1个单位的速度运动.设点P、Q同时出发,运动时间为t秒.(1)若点P、Q同时向右运动2秒,则点P表示的数为_______,点P、Q之间的距离是______个单位;(2)经过__________秒后,点P、Q重合;(3)试探究:经过多少秒后,点P、Q两点间的距离为14个单位.参考答案1、A.2、D.3、A.4、A5、D.6、D.7、A.8、B9、D.10、B.11、答案为:±8.12、±2;13、答案为:a+b﹣c.14、答案为:﹣4.15、解:正数:{0.62,,18,+100};负数:{﹣4,﹣8.91};整数:{﹣4,18,0,+100 };分数:{0.62,,﹣8.91};16、1117、答案为:3或﹣5.18、-b+c+a;19、﹣|﹣8|=﹣8;20、﹣(+7)=﹣7;21、﹣(﹣5)=5;22、1023、解:正有理数集合:(﹣(﹣11),,0.,);负有理数集合:(+(﹣2),﹣0.314,﹣4);整数集合:(+(﹣2),0,﹣(﹣11));自然数集合:(0,﹣(﹣11));分数集合:(﹣0.314,,﹣4,0.,). 24、解:∵|a﹣2|与|b﹣3|互为相反数,∴|a﹣2|+|b﹣3|=0,∴a﹣2=0,b﹣3=0,解得a=2,b=3,所以,3a+2b=3×2+2×3=6+6=12.25、解:∵|3x﹣2|≥0,∴当3x﹣2=0,即x=时,|3x﹣2|+2取最小值2.26、解:(1)4,10;(2)4,12(3)①2t+t+12=14,t=.②2t=26+t,t=26;③2t+12=14+t,t=2. 答:经过、26、2秒时,P、Q相距14个单位.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
⎪⎪⎪⎩⎪⎪⎪⎨⎧有理数⎪⎩⎪⎨⎧)3,2,1:()3,2,1:(ΛΛ如负整数如正整数整数)0(零⎪⎩⎪⎨⎧----)8.4,3.2,31,21:(Λ如负分数分数)8.3,3.5,31,21:(Λ如正分数有理数、数轴、绝对值
1、负数的应用,有理数的分类
(1)、负数的意义:引入负数是我们实际的需要,我们通常用正、负来表示一对相反意义的量。
Eg1. 上升1m 表示为+1m ,则下降2m 表示为 。
生活中有很多这样的相反的量:前进-后退,向东-向西,等等。
(2)
课堂练习:
1.将下列各数填到相应的括号内:
-7.2,34,-9,1.4,0,3.14,π,1245
,-2.5,20% 整数集合: 正分数集合: 非负数集合:
分数集合:
2. a 一定是正数,-a 一定是负数吗?回答并举例:
3. 如果零上5度记作+5度,那么零下3度记作什么?
4. 东、西为俩个相反方向,如果—4m 表示一个物体向西运动4m ,那么+2m 表示什么?物体原地不动记作什么?
5. 某仓库运进面粉7.5t 记作+7.5t ,那么运出面粉3.8t 应记作什么?
2、数轴
(1)1、数轴的三要素: 、 、 。
在数轴上,右边的数总比左边的数大。
最小的正整数是 ,最大的负整数是 。
(2)、数轴上的点,右边的数 > 左边的数。
正数 > 0 > 负数
(3)、△相反数:两个数只有符号不同,我们称一个是另一个的相反数。
Eg 。
2和-2,a 和-a 。
本质:只有符号不同,其它不变。
特别的:0的相反数是 。
※ x +y 的相反数是 ,a -b 的相反数是
牢记:正数的相反数是 ,负数的相反数是 ,相反数等于它本身的数是 。
(4)、相反数的代数意义:a>0时,-a 0; a<0时,-a 0; a =0时,-a 0.(a 可以代表任意有理数)
相反数的几何意义: 表示互为相反数的两个点位于原点的 ,且到原点的 相等。
(5)、会进行符号的化简:eg 。
-(-2)= ;+[-(+2)]= ;-(x +y )= ;
3、绝对值
(1)、概念:在数轴上,一个数所对应的点到原点的 叫做该数的绝对值。
记作: △任何数的绝对值一定 0,即:|a| 0.
(2)
、代数意义: ( a>0) 正数的绝对值等于
|a|= (a=0) 0的绝对值是 (a<0) 负数的绝对值等于
绝对值等于本身的数是 ;绝对值等于它的相反数的数是 ;
(3)、几何意义:一个数a 的绝对值就是数轴上表示a 的点到原点的距离。
记作:|a| △绝对值等于正数的数有两个,它们 。
|x|=3,则x =
(4)、利用绝对值比较大小:两个负数,绝对值大的反而小。
-
45 -56, -58 -57
(5)、绝对值化简:即去绝对值号。
把握一个原则:先判断绝对值号内的数的符号,再根据绝对值的代数意义来化简去绝对值号。
已知x<0,y>0,化简|x-y|+|x|+|y|.
课后练习:
1.把下列给数填在相应的大括号里:
-4,0.001,0,-1.7,15,2
3+. 正数集合{ …}, 负数集合{ …},
正整数集合{ …}, 分数集合{ …}
2.0是整数吗?自然数一定是整数吗?0一定是正整数吗?整数一定是自然数吗?
3.在数轴上,表示数-3,2.6,53-,0,314,3
22-,-1的点中,在原点左边的点有 个. 4.在数轴上点A 表示-4,如果把原点O 向负方向移动1.5个单位,那么在新数轴上点A 表示的数是( )
A.215-
B.-4
C.2
12- D.212 5.数轴上与原点的距离是2的点有 个,这些点表示的数是 ;与原点的距离是5的点有 个,这些点表示的数是 。
6.判断:
(1)-2是相反数 (2)-3和+3都是相反数 (3)-3是3的相反数 (4)-3与+3互为相反数
(5)+3是-3的相反数 (6)一个数的相反数不可能是它本身
7.化简下列各数中的符号:
(1))312(--= (2) -(+5)= (3)[])7(--- = (4)[]{})3(+-+-=
8.(1)x 3
2是 的相反数。
(2)如果-a=-9,那么-a 的相反数是 。
9.│-2│等于( )
A .-2
B .2
C .-
12 D .12 10.绝对值为4的数是( )
A .±4
B .4
C .-4
D .2
11.-4的绝对值是________;2的相反数的绝对值是______.
12.若│a │=│-3│,则a=_______.
13.下列计算正确的是( )
A .-|-13|=13
B .|79|=±79
C .-(-3)=3
D .-│-6│=-6 14.如图,在所给数轴上画出表示数-3,-1,│-2│的点.把这组数从小到大用“<”号连接起来. 0
作业:
1.______7.3=-;______0=;______75.0=+-. 2.______31=+;______45=--;______3
2=-+. 3.______510=-+-;______5.55.6=---.
4.______的相反数是它本身,_____的绝对值是它本身,_______的绝对值是它的相反数.
5.一个数的绝对值是3
2,那么这个数为______. 6.绝对值等于4的数是______.
7、比较大小; 0.3 —564;—37 —25 8.绝对值等于其相反数的数一定是…………………………………( )
A .负数
B .正数
C .负数或零
D .正数或零
9.给出下列说法:①互为相反数的两个数绝对值相等;②绝对值等于本身的数只有正数;③不相等的两个数绝对值不相等;④绝对值相等的两数一定相等.其中正确的
有………………………………( )
A .0个
B .1个
C .2个
D .3个
10.7=x ,则______=x ; 7=-x ,则______=x .
11.绝对值不大于11.1的整数有……( )A .11个 B .12个 C .22个 D .23个。
