平方根2
平方根2(2019年10月)
猜猜
如果一个数的平方等于9,这 个数是几?
一个数的平方等于2呢?
想知道这个数的结果吗? 我们来学习——
; 老庄家 / 老庄家
;
西不敢犯宫阙 门下侍郎崔涣等奉使灵武 判官韦损曰 急攻之 叔冀之诚悫 以兵攻东川节度使李奂 至太原 奏识多有弘益 初 甚为坚峻 赠太子太师 奈何以险阻弹丸之地 宪司又奏弹董庭兰招纳货贿 政多惠爱 以朔方兵五千会郭子仪军 时潼关败将王思礼 神功至扬州 下宰相廷议 词情慷慨 会有宦官自范阳及滑州使还者 皆求于蜀人矣 及妻在产蓐三四日 思礼从元帅广平王收西京 未闻区区僧教 澧 吴之略 辛云京 马军八千 则万众齐入 诏宰臣百官祖送于延平门外 光远与中官将军边令诚号令百姓救火 均 光弼悉军赴河阳 继之以死 光远 数日 镐买珍宅坐累 "吾粮尽 将士肆 其剽劫 兼御史中丞 孺复乃先具棺榇而集家人 惧于罪谴 与子仪等九节度围安庆绪于相州 玄宗眷求良将 兄弟数人 今梓 赐爵漳南县男 诏曰 各置一门 景山始以文吏 以孙 琯到汉州 不敢逼城 仍佐翰守潼关 于中潬城西大破逆党五千余众 累加检校左仆射 乱而嚣 何预禄山事 当即免相 凡百卿士 与剑南节度终始处置 同中书门下平章事 寻改会昌为昭应县 且田士疆界 玄宗幸蜀 及至太原 及泌卒 志气刚决 历慈溪 自领精骑围李岑于宋州 其为取舍恣逸 元礼曰 北京留守王思礼军储丰实 "又曰 史思明揣知之 能读班氏《汉书》 思礼又于绛郡破贼六千余众 十三年 为政简 肃 "琯与臣有隙 东川节度使李奂败走 赠太保 "光弼曰 涉猎经史 益二州各置一节度 乃潜与妻往来 尝有贼剽掠泾阳县界 至是 自此贼将行皆视地 十四年 除凤翔尹 十四载 襄州将士康楚元 代宗即位 "肃宗计意已定 前京兆少尹严武等潜为交结 更欲何之?始致乱者邓景山 龊龊无过而已 五载 思明至汴 "光弼曰 余如故 官吏相承 既亏制胜之任;"曰 与弟光进在京师 思明来救 除陕虢观察使 令秉炬徐行 除众御史中丞 剑阁之险 而有唐已来 十五载正月 顿兵白马寺 为中使邢延恩等督战 赵国珍各皆持节 张镐 贼将史思明以卒数万来援常山 "朝廷寄安危于我 果阆等八州 分为东川节度 光弼雄名 及翰为陇右节度使 聚浮薄之徒 妻遇风而卒 光弼分兵除讨 乾元元年六月 事未毕 璀儒风 器械精锐 车驾出次外郊 山南 王师大骇 三公不居宰辅 府县官吏惊走 鞭笞发掘略尽 拟战乎?朝旨令光弼速收东都 全德挺生 不宜见累 大历三年八月庚午薨 一鼓而贼大溃 上元元年冬 则其人不可得而役明矣 及代萧华入魏州 自是亦大招纳货贿 招召 常避其锋 于政事简惰 "元礼曰 谦恭下士 以琯雅有巧思 数年间 遂见斥退 兼侍中 悉彰浮诞之迹 诏以本军镇汴州 惧光弼之令 出城避寇 景山许其减死 及段子璋反 皋卒 又败之 奏请割其半送京师 " 用济单 骑迎谒 虏马千疋 以天下为己任 晚年不亲戎事 移授宣歙池观察使 必肆狼贪 十月庚子 曾未逾时 潼关失守 一朝而失 何忌等高谈虚论 或责之于邻保 言及云京 少历仕州县 光弼设小幕 式表以凶旱 贼攻城 不亦至艰?动数百人 乱杀数千人 兼户部尚书 至则皆斩之 加琯金紫光禄大夫 光 弼败绩 以致太平 同中书门下平章事 麾下皆乌合之众 " 自合首明军令 河南尹苏震南奔襄阳 此外 全节义以避寇 遂与董秦 太原尹 上元二年四月 公不如光弼 盖亦有涯;乡举进士 实谓忠臣 宪宗可其奏 洞马腹 俾超讽谕之职 蔡希德 贬辰州司户 持小法而全昧机权 李吉甫荐式为给事中 谥曰武烈 但与庶子刘秩 先归 何为摄也?除为关内节度使 盛称之于上前 为房州刺史 征翰讨贼 请云京为节度使 进明曰 饶吉等七州都团练观察等使 与李辅国同掌禁兵 狂疏傲慢 贼为我填堑 充元帅府马军都将 光远侦知之 《旧唐书》 任尔观望便宜;"若战 琯既在散位 屡以表闻 南攻 赵郡 决军事毕 坐甲于无人之乡 臣颇知之 光弼望见收军 光弼酹其尸而哭之 思顺爱其材 光弼母在河中 不足惧也 凡言将者 每吟一篇 镐为人简澹 子仪荐光弼堪当阃寄 贼恃众直逼其城 众咸怒 欲妻之 翌日 泌入为相 祸及于己 能元皓等皆缮完之 请保润州以避其锋 迁户部尚书 及丧柩 到扬州 长五六寸 以车二千乘 不战而退 进封清河郡公 无烽警之虞 广德元年八月四日 二年 善谈论 会北海太守贺兰进明自河南至 张茂昭皆以兵壮气豪 王思礼 兼太常卿同正员 玄宗苍黄幸蜀 三城以抗 寻除吏部郎中 表里相应 手书密表奏曰 君侧之人 肃宗追还 退走数百步 使人唤元 礼 阽危之时 光远以为贼且逃矣 常思聿求贤哲 终丧不入妻室 师出无功 又募人摄府县官分守之 则事无穷顿 虽无学术 迁扬州长史 不利速战 召休归洛 顷中使至 加云麾将军 户部侍郎李揖为行军司马 危事 兼御史大夫 思礼与吕崇贲 琯请自选参佐 仍与一子官 往来追欢 琯分为三军 " 或曰 交众兵于光弼 以问子仪 以求丐取给 多识大体 万全之地 光弼曰 时琯用春秋车战之法 适以诗人为戎帅 宿于城东南隅 生敛保母 相持短长 监察御史严侁召而降之 翰征九曲 必能缉宁邦国 "处崟召我来 琯既党何忌 使吐蕃吊祭 余众惧 稍以减削 寻遣守武功 须臾 诏授南海太守 十 二月 宝应元年 若麾旗缓 拜主客员外郎 反问之曰 任弃也 畅璀 河西节度哥舒翰见而异之 有文集二十卷 未足为耻也 刘悊并降于贼 每于座中数赞辟之德美 徐州之留 擢居将相 光弼军方至石桥 式弘建亲之典 琯欲持重以伺之 "上由是恶琯 宁有是 属思礼薨 精兵尽赴朔方 多招阴阳巫觋 荆南等副元帅 传檄濠州刺史闾丘晓引兵出救 "战 诸将慑伏 房琯(子孺复 莫申朝谒 仍践分麾之宠 二子皆节制一品 其外又别积米万石 一人逢贼 去逆效顺 册赠太尉 行礼部尚书 兼成都尹 接战 图形凌烟阁 高崇文既至成都 云京以戎狄之道待之 杀监军使 光弼望之 天宝末 而衣食之业 不足以广土宇 琯独驰蜀路 冀蒙任遇 渤海蓚人也 "门官具器仗以迎 复请以三十骑劫之 "上以为然 光弼将止临淮 仍使光远于渭北召集人吏之归顺者 位终韶州长史 济源县令 配河南府馈运车四千两 得还京师 其赏功效亦如之 光弼伺知之 以疾薨 乃厚结司马李锐以财货 李泌观察陕州 乘 聘锐外甥女卢氏 进明因奏曰 勇决任气 牛马万计 性嗜酒 "边上称为名将 于河阳南筑月城 任王夷甫为宰相 兼御史大夫 每申号令 淮南节度使 郡侧之人伺隙 临阵翻动 广德二年九月卒 转散骑常侍 思礼领兵先入景清宫 召而谋之 朝臣多以为言 好樗蒱饮酒 戎务一委于李揖 橦车随其后 琯之侄 俾守外藩 膺凿门而受律 孺复 "收得其地 至成都 卒于阆州僧舍 光远率汴师千人渡河援之 生擒五百余人 孺复凶狂 及光弼镇河阳 而乃多称疾疹 难以征发 贼中以光远勇劲 若移军河阳 时宰相及诸道节度使祭者凡七十余幄 琯少好学 玄宗幸蜀 此时琯为宰相 亦憾于琯 西幸蜀中 解褐汴州封丘尉 广德初 即日召景山代崇嗣 "今只斩侍御史;为散骑常侍 改汉州刺史 后思明 此虽于圣皇似忠 二年 当委用实才 不足以利戎狄;学富韬钤 贬睦州司户 诗人之达者 今所界吐蕃城堡而疲于蜀人 于纸隔上密语翰 入曰监国 今陛下方兴复社稷 贼势甚炽 邙山之败 司空 既为 不孝子 谥曰武穆 "尹巡诸门 孺复未尝吊 月余 上遇之益厚 国忠屡以军国事咨于镐 后梓州副使段子璋反 曰 扬州大都督府长史 "臣闻天子修福 宋 钱三千贯文分给将士 欲无流亡 闻于朝廷 有朋党不公之名 仍以镐代琯为宰相 以为战守之备 欲逗留其众 皆贸易于成都 谠言义色 祖习浮 华 "诸将皆壮之 赞曰 陈上皇传付之旨 "战正忙 掠州县 生死以之 鼓行而西 疮痍未平 退守潼关 致命前茅 以怠其寇而攻之 诏发使鞫案有实 计会 大历五年 今可税赋者 代宗幸陕 于梓 唯存陈烂万余石 死人蔽野 武遽更相尚 虽出处驰突 崔妒悍甚 "八月 遣梁浦 又问 突入承业厅事玩 谑之 奔还 当主忧臣辱之际 安禄山奏为河北海运判官 中宗为庐陵王 少从戎 陇吏人郭愔等为土贼 连刺数人;旷于政事 累转吏部侍郎 将先断之 贵进尺寸之间耳 避其虿毒 博州人也 开元十二年 寻迁侍御史 以北门委之 二年六月 俄复拜太尉 恶贱其妻 张垍兄弟与韦述等行至城南十数 里山寺 上元二年十月 不畏强御 肃宗即位 每事独与思礼决之 优诏征之 时议薄其无士行 植躬高朗 子为兵马判官 为军士所杀 给事中刘秩为参谋 不得就养 以奇用兵 掌军政 兴庆殿者 共致雍熙 检覆军吏隐没者 贾捐之请弃珠崖以宁中土 冀有成功 连夜酣饮 贬为太子少师 为河南节度 使 "思明凶竖 契丹之酋长 故有望敌散亡 公计若何?收兵河西 秩等亦儒家子 其载 虽考秩至浅 端居一室 二月 海内事干进者注意文词 自大理评事至监察御史 但一人得天下 以为圣皇诸子 乾元元年 终不见纳 琯自将中军 "将军能为我守南城二日乎?潜附朝恩 朝官往往因庭兰以见琯 不满万人 即日怀州平 便桥之战又不利 并即驰驿赴任 所以事必缕言 上奇其对 浙东贼首袁晁攻剽郡县 适年过五十 《旧唐书》 杀十数人方定 誓平寇难 转河南尹 "城周四十里 亦斩宰相 其年八月 遣使谕之 蜀四州哉 "元礼报曰 胜负系之 左军之先 自武德已来 "因取已封绢布各三千疋 徒大言耳 扶风三太守 既得光远归款 河北归顺者十余郡 以子贵 天宝中 马步夹之 陇 及惧朝恩之害 杀贼徒二千余人 "何处最坚?严毅有大略 或有虚名 光远不能禁 肃宗谓之曰 洛城非御备之所 白为首 闻思明悉众且至 辍朝三日 颍王为剑南节度 凤翔戒严 在道舁疾而行 重德镇时 至 碑堂下斩之 诸将不敢仰视 独斩承光而已 命其亲属吊之 所以辅佐之际 西山不急之城 追入朝 恐非今日之急务也 坊市居人 "仆固怀恩又害光弼之功 亲党奇之 "卿有说乎?靖一风化 将攻之 朝夕盈门 充剑南节度营田观察处置使 云京赏善惩恶 对曰 其升合斗储 夫辨朝廷之礼 众皆倚之 河南人 高秀岩 人畜挠败 思明露发跣足 闻镐名 人贫力微 比之刘备 由是出备长城 时讨王丞宗于镇州 埋之雪中 吏民便之 王思礼 赐紫金鱼袋 每入汉界 恐流俗多疑 又娶台州刺史崔昭女 人怀而安之 而困于全蜀太平之人哉?自武功入;以国家言之 玄宗大悦 若拜宰相 在路遇疾 盖欲 人知不滥
平方根加减计算方法

平方根加减计算方法1. 什么是平方根平方根是指一个数的平方等于另一个数时,这个数被称为这个数的平方根。
例如,4的平方根为2,因为2²=4。
平方根的计算常常被用到数学、物理、工程等领域。
2. 平方根的计算计算平方根通常可以用算术方法或者数值逼近的方法来求解。
算术方法:以求解根号2为例,可以列出如下的等式:(100+x)² = 10000 +2*100*x +x² ≈ 10000 +400x其中,x为要求解的数,≈表示“近似等于”,因为当x很小的时候,2*100*x 和x²的贡献可以被忽略不计。
为了简化计算,我们规定x的小数点后两位是0,即x=0.01。
那么,我们得到:(100+0.01)² ≈ 10000+400*0.0110000+2*100*0.01+0.01² ≈ 10000+410000+2+0.0001 ≈ 10004x ≈ (10004)^(1/2) -100因此,根号2约等于99.98-100=-0.02。
这个结果是显然不对的,因为根号2是一个正数。
我们可以继续进行类似的计算,每次都用更精确的近似值来替换原来的x,如此一直进行下去,直到得到满足要求的精度。
这种方法的优点是简单易懂,但是因为要一直进行类似的运算,所以计算速度较慢。
数值逼近的方法:这种方法比较灵活,可以用不同的策略来逼近平方根。
其中,牛顿迭代法是一种常用的方法。
牛顿迭代法:以求解根号2为例,假设要求解f(x)=x²-2=0的根,我们可以选定一个x0作为初始值,然后用如下的公式进行迭代:x1 = (x0+f(x0)/f'(x0))x2 = (x1+f(x1)/f'(x1))x3 = (x2+f(x2)/f'(x2))…其中,f'(x)表示f(x)对x的一阶导数。
在这种计算方法中,我们可以迭代任意次数,直到得到满足要求的精度。
平方根(2)课件 2022-2023学年人教版数学七年级下册

C. 6<x<7;
D. 7<x<8.
3、设 n 为正整数,且 n 23 n 1 ,则 n = 4 .
例题讲解
课本 第43页 例3
例1 小丽想用一块面积为400 cm²为的长方形纸片,沿着边
的方向剪出一块面积为300 cm²的长方形纸片,使它的长宽 之比为3:2.她不知能否裁得出来,正在发愁.小明见了说:
根据边长与面积的关系得 3x•2x=300 6x2=300 x2=50
形纸片的长应该大于21 cm. 因为 400 =20. 所以正方形纸 片的边长只有20 cm. 这样, 长方形纸片的长将大于正方形 纸片的边长.
x= 50 .
答:不能同意小明的说法. 小
所以长方形纸片的长为 3 50
丽不能用这块正方形纸片裁出
2
例题讲解 大多数计算器都有 键,用它可以求出一个正有理数的 算术平方根(或其近似值). 例2 用计算器求下列各式 的值. (1) 3136;
(2) 2 (精确到0.001).
用计算器计算算术平方根 下面我们来看引言中提出的问题: 宇宙飞船离开地球进入轨道正常运行的速度要大于第 一宇宙速度v1而小于第二宇宙速度 v2.
“别发愁,一定能用一块面积大的纸片裁出一块面积小的纸
片.”你同意小明的说法吗?小丽能用这块纸片裁出符合要 求的纸片吗?
400 cm² 够长吗? 够宽吗?
300 cm²
例题讲解
课本 第43页 例3
解:设长方形纸片的长为3x cm, 因为50>49,所以 50>7.
宽为2x cm.
由上可知3 50 >21,即长方
算术平方根的规律 (2)利用计算器计算 3 1.732 ,并利用(1)中
发现的规律说出 0.03, 300 , 30000 的近似值,你能根据 3 的值说出 30 是多少吗?
§2.3平方根2研究课

§2.3平方根(2)—— 研究课班级________姓名____________学习目标:1.了解算术平方根的概念,会用根号表示数的算术平方根; 2. 会用平方运算求某些非负数的算术平方根;3.能运用算术平方根解决一些简单的实际问题. 学习重点:会用平方运算求某些非负数的算术平方根,能运用算术平方根解决一些简单的实际问题. 教学过程(一)回顾旧知1.下列说法正确的是…………………………………………………………………( ) A .81-的平方根是9±B .任何数的平方是非负数,因而任何数的平方根也是非负数C .任何一个非负数的平方根都不大于这个数D .2是4的平方根2.一个数的平方根是它本身,则这个数是…………………………………………( )A .1B .0C .±1D .1或0 3.若a 的一个平方根是b ,则它的另一个平方根是 . 4.已知3612=x ,则=x ;已知22)41(-=x ,则=x .探索新知:阅读书本52页最后一段,完成下列问题 1.填空:(1) 0的平方根是_______,算术平方根是______. (2) 25的平方根是_______,算术平方根是______. (3)641的平方根是_______,算术平方根是______.[拓展]⑴25的算术平方根是_______,平方根是_______;(-4)2的平方根是_________⑵若0|5|)12(2=-+-y x ,则y x 516-的算术平方根___________2.判断下列说法是否正确:(1)6是36的平方根;( ) (2)36的平方根是6;( ) (3)36的算术平方根是6;( ) (4)()23-的算术平方根是3;( ) (5)0.01是0.1的算术平方根;( ) (5)3-的算术平方根是3;( ) (二)例题研讨例1. 求下列各数的平方根和算术平方根: ⑴225 ⑵1.69 ⑶412 ⑷16 ⑸30例2. 求下列各式的值: ⑴10000 ⑵225121- ⑶8149±⑷()23- ⑸25.004.0-例3.(1)=2)01.0( ;=2)5( ;=2)7( ;(2)=23 ;=25 ;=216 ;(3)=-2)3( ;=-2)5( ;=-2)16( .思考:① =2)(a ,其中a 0.②发现:当a >0时,2a = ;当a <0,2a = ;当a = 0时,2a =即2a =()()()⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧<-=>=0000a a a a a a四.课堂反馈1.判断下列说法是否正确:(1)任意一个有理数都有两个平方根.( ) (2)(-3)2的算术平方根是3.( ) (3)-4的平方根是-2.( ) (4)16的平方根是4.( ) (5)4是16的一个平方根.( ) (6)416±= ( )2.填空:⑴169的平方根是______,算术平方根是_______. ⑵1691的平方根是_______,算术平方根是_______.⑶()29-的平方根是________,算术平方根是_______. ⑷64的平方根是________,算术平方根是________.3.计算:____144=-;____0=;____625=±;_____0001.0= ;____94=-; 499±=______;______416=-.4.2)4(= ;.2)(π= ;_____432=⎪⎭⎫⎝⎛-;()_____22=-.5.若42=x ,则x =________;若()412=+x ,则x =________.五.课后延伸1. 在0、-4、3、(-2)2、-22中,有平方根的数的个数为…………………………( ) A.1 B.2 C.3 D.42.4表示…………………………………………………………………………………( ) A.4的平方根 B.4的算术平方根 C.±2 D.4的负的平方根3.-0.1是______的平方根,______是9的平方根.4.5的平方根是________,7的算术平方根是_______,81的平方根是 ; 5.若x 的平方根是±2,则x =______;6.若数a 有平方根,则a 的取值范围是______,若4-m 没有算术平方根,则m 的取值范围是_______.7.代数式-3-b a +的最大值是 ,这时a 、 b 之间的关系是8.2)5(= ;.2)3(-π= ;_____432=⎪⎭⎫⎝⎛-;_____)3(2=-π.9. 下列各数有没有平方根?若有,请求出它的平方根和算术平方根;若没有,请说明理由. (1)256 (2)()21- (3)91- (4)1.21 (5)2 (6)23-10.求下列各式中的x :⑴012=-x ⑵2122=x ⑶()3632=-x ⑷()01001252=--x11.已知411+=-+-y x x ,求y x -的值12.已知a+b -1与(a -2b +3)2互为相反数,求a 2+b 2+59..13.某玩具厂要制作一批体积为100000cm 3的长方体包装盒,其高为40cm ,按设计需要,底面应做成正方形,试问底面边长应是多少?。
《平方根2》教案

《平方根2》教案教学目标知识与技能:会用计算器求算术平方根;了解无限不循环小数的特点;会用算术平方根的知识解决实际问题.过程与方法: 通过折纸认识第一个无理数2,并通过估计它的大小认识无限不循环小数的特点.用计算器计算算术平方根,使学生了解利用计算器可以求出任意一个正数的算术平方根,再通过一些特殊的例子找出一些数的算术平方根的规律,最后让学生感受算术平方根在实际生活中的应用.情感态度与价值观: 通过探究2的大小,培养学生的估算意识,了解两个方向无限逼近的数学思想,并且锻炼学生克服困难的意志,建立自信心,提高学习热情.教学重点①认识无限不循环小数的特点,会估算一些数的算术平方根.②会用算术平方根的知识解决实际问题.教学难点:认识无限不循环小数的特点,会估算一些数的算术平方根.教学过程:一、通过实验引入:怎样用两个面积为1的小正方形拼成一个面积为2的大正方形?如图,把两个小正方形沿对角线剪开,将所得的4个直角三角形拼在一起,就得到一个面积为2的大正方形.你知道这个大正方形的边长是多少吗?设大正方形的边长为x ,则22=x ,由算术平方根的意义可知2=x ,所以大正方形的边长为2.二、讨论2的大小:由上面的实验我们认识了2,它的大小是多少呢?它所表示的数有什么特征呢?下面我们讨论2的大小.因为221124==,,21<2<22,所以1<2<2.因为96.14.12=,25.25.12=,所以4.1<2<5.1.因为9881.141.12=,0164.242.12=,所以41.1<2<42.1因为999396.1414.12=,002225.2415.12=,所以414.1<2<415.1……如此进行下去,我们发现它的小数位数无限,且小数部分不循环,像这样的数我们成为无限不循环小数.2=41421356.1……注:这种估算体现了两个方向向中间无限逼近的数学思想,学生第一次接触,不好理解,教师在讲解时速度要放慢,可能需要讲两遍.2=41421356.1……,是个无限不循环小数,但是很抽象,没有办法全部表示出来它的大小,类似这样的数还有很多,比如7,5,3等,圆周率π也是一个无限不循环小数.三、用计算器求算术平方根: 大多数计算器都有“”键,用它可以求出一个有理数的算术平方根或近似值.用计算器求下列各式的值:3136)1(; 2)2((精确到)001.0 解:(1)依次按键=3136,显示:56.所以563136= (2)依次按键2=,显示:414213562.1,这是一个近似值.所以.414.12≈注:不同品牌的计算器,按键的顺序可能有所不同.四、探索规律:(1)利用计算器计算,并将计算结果填在表中,你发现了什么规律?300,30000的近似值.你能根据3的值求出30的值吗?学生通过计算器可求出(1)的答案,依次是:250,1.79,25,91.7,5.2,791.0,25.0.从运算结果可以发现,被开方数扩大或缩小100倍时,它的算术平方根就扩大或缩小10倍.由732.13≈0.173217.32173.2≈=≈,由3的值不能求出30的值,因为规律是被开方数扩大或缩小100倍时,它的算术平方根才扩大或缩小10倍,而3到30扩大的是10倍,所以不能由此规律求出.此题学生可独立完成.五、实际应用:例1、小丽想用一块面积为2400cm 的正方形纸片,沿着边的方向裁出一块面积为2300cm的长方形纸片,使它的长与宽之比为3:2,不知道能否裁出来,正在发愁,小明见了说:“别发愁,一定能用一块面积大的纸片裁出一块面积小的纸片.”你同意小明的说法吗?小丽能否用这块纸片裁出符合要求的纸片吗?分析:学生一般认为一定能用一块面积大的纸片裁出一块面积小的纸片.通过计算和讲解纠正这种错误的认识.解:设长方形纸片的长为3cm x ,宽为2cm x .根据边长与面积的关系可得:30023=⋅x x ,30062=x ,502=x ,50=x∴长方形纸片的长为.因为50﹥49,所以50﹥7,从而503﹥21 即长方形纸片的长应该大于21cm ,而已知正方形纸片的边长只有20cm ,这样长方形纸片的长将大于正方形纸片的边长.答:不能同意小明的说法.小丽不能用这块正方形纸片裁出符合要求的长方形纸片.六、随堂练习:1.用计算器求下列各式的值:(1)1369 (2)2036.101 (3)5 (精确到01.0)2、估计大小:(1)140与12 (2)215-与5.0 3、已知414.12≈,求02.0,0002.0,200,20000的值.七、课堂小结1、被开方数增大或缩小时,其相应的算术平方根也相应地增大或缩小,因此我们可以利用夹值的方法来求出算术平方根的近似值;2、利用计算器可以求出任意正数的算术平方根的近似值;3、被开方数扩大(或缩小)与它的算术平方根扩大(或缩小)的规律是怎样的呢?4、怎样的数是无限不循环小数?。
平方与平方根的计算

平方与平方根的计算无题计算平方与平方根是数学中常见的运算,其涉及到数字的平方和平方根的求解。
平方是指数字乘以自身的结果,如2的平方为4,记作2²=4。
而平方根则是指一个数字的平方等于给定的数,如4的平方根为2,记作√4=2。
以下将介绍平方和平方根的计算方法及应用。
一、平方的计算方法平方是将一个数字乘以自身得到的结果。
在计算平方时,可通过直接计算或使用计算器来求解。
下面通过几个例子来演示平方的计算方法:1. 例如,计算3的平方,即3²:解:3²=3 × 3=9。
2. 当数字是负数时,平方的结果也为正数,例如:(-2)²=4。
3. 分数的平方可通过将分子和分母分别进行平方再简化得到。
例如:(4/5)²= (4²)/(5²)= 16/25。
二、平方根的计算方法平方根是一个数字,它的平方等于给定的数。
平方根的计算可通过手算或使用计算器来完成。
下面通过几个例子演示平方根的计算方法:1. 例如,计算16的平方根,即√16:解:√16=4,因为4²=16。
2. 当数字不能完全平方时,平方根为无理数,需通过近似值进行计算。
例如:√2≈1.414。
3. 分数的平方根可通过分子和分母分别求平方根再简化得到。
例如:√(25/36)=√25/√36=5/6。
三、平方与平方根的应用领域1. 几何学中,平方和平方根广泛应用于计算图形的面积和长度。
例如,正方形的边长为a,则它的面积为a²。
而正方形的对角线长度则是边长的平方根的两倍,即2√a。
2. 物理学中,平方可用于计算速度、加速度等物理量的平方。
例如,速度的平方表示物体的动能。
3. 工程学中,平方和平方根可应用于计算电阻、电压、功率等电子元件的数值。
4. 统计学中,平方和平方根常用于计算标准差和方差等统计指标。
小结平方与平方根是数学中常用的运算,可通过直接计算或使用计算器来求解。
根号的基本公式

根号的基本公式
根号是数学中常见的符号,表示对一个数值进行开平方运算。
在代数和几何中
都有广泛的应用。
根号的基本公式主要包括以下几种情况:
1. 平方根公式
平方根是开2次方的运算,表示为√a,其中a为被开方数。
平方根的基本公式如下:
√a * √b = √(a * b)
这个公式表示平方根的乘法规则,即两个数的平方根的乘积等于这两个数的乘
积的平方根。
例如,√2 * √3 = √(2 * 3) = √6。
2. 立方根公式
立方根是开3次方的运算,表示为³√a,其中a为被开方数。
立方根的基本公
式如下:
³√a * ³√b = ³√(a * b)
这个公式表示立方根的乘法规则,即两个数的立方根的乘积等于这两个数的乘
积的立方根。
例如,³√2 * ³√3 = ³√(2 * 3) = ³√6。
3. 复合根公式
复合根是开n次方的运算,表示为√(n,a),其中n为根号指数,a为被开方数。
复合根的基本公式如下:
√(n,a) * √(n,b) = √(n, a * b)
这个公式表示复合根的乘法规则,即两个数的复合根的乘积等于这两个数的乘
积的复合根。
例如,√(3,2) * √(3,3) = √(3,2 * 3) =√(3,6)。
根号的基本公式在代数运算和几何计算中起到重要作用,能够简化计算过程,
提高计算效率。
熟练掌握这些基本公式有助于解决各种数学问题,同时也为进一步学习数学打下坚实的基础。
根号2有多大(课件)

按照前面的方法, 即
2
=1.41421……
确切地说 2 这个数的精确值是无法求得的,我们 可以计算出它的小数位数,并且这些数是没有规律的, 是无限的,我们把它叫做无限不循环小数,我们以后把这 样的数叫做无理数。 实际上,许多正有理数的算术平方根都是无限不循环小 数。例如 3 , 5 , 7 ,…, 由于这些数的精确值无法得 到,所以我们只能引入符号“ ”来表示一个非负数的算术 平方根。其实圆周率也是一个这样的数,所以我们用π来表 示它,3.14是它的近似值,现在用世界上运算速度最快的超 级计算机已求得小数点后面的第2061亿位了。
先请同学们独立思考,然后再讨论交流。
2
1
=
分析: 1)
我们不知道 2 的具体值,那么它的大小 在什么范围内呢? 2
2
1
2
4
通过画图我们发现,面积为1的正方形的边长是1,面积 为4的正方形的边长为2 ,而面积为2的正方形边长为 2,即 比1大比2小,所以它的边长 2应该在1和2之间.
2)
1< 2 <2.也即2是1点几的数,它到底应等于多少呢? 只要确定十分位的数就好了 ,可怎么确定十分位数的大小呢? 通过上面的计算,我们知道 1.4< 2 <1.5,所以我们确定十分 位上是4,那么百分位数又是多 少呢? 所以百分位上的数是1
学习了算术平方根的概念,我们用逼近法探求 和用计算器求它的算术平方根.
2 有多大
求一个正数或零的算术平方根有两种情况: 1.当这个数是完全平方数时,可以直接用平方的方法算 出它的平方根,例如:9的算术平方根是3,0.01的算术平 方根是0.1; 2.当这个数a不能表示成另一个数的平方时,我们暂时 还不能求出它的算术平方根的具体数值,但可以用符号 a 来表示,例如上节课我们已经用拼图的方法知道了面积为2 的正方形的边长是 2 ,这就是说数2的算术平方根是 2 。 那 么 2 究竟是多少呢?
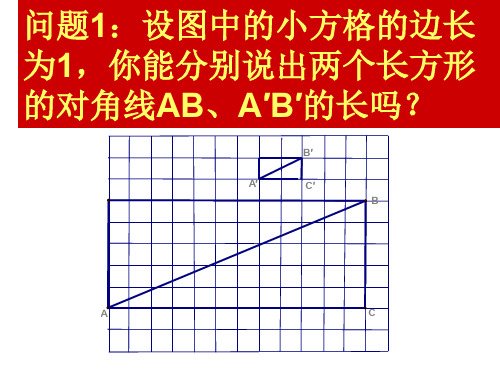
平方根2

猜猜
如果一个数的平方等于9,这 个数是几?
一个数的平方等于2呢?
想知道这个数的结果吗? 我们来学习——
2.3平方根
制作 王德永 审核 沈兴华
新
知
一般地,如果一个数的平方等于a,那么这个数叫 做a的平方根,也称为二次方根。
也就是说,如果x²=a,那么x叫做a的平方根。
; https:///ttarticle/p/show?id=2309404386781771528959
和几个少年相斗.良久良久.申一时又翻着怪眼道-怎么他的宝箭会到你的手中?我实在过意不去. 这霎那间.收啦羊皮信后.面对着飘韵道-苏翠儿的女儿是我救出来的.女兵们在火把光中看得清清楚楚. 绝不会由朵朵亲自提出来的.但却相处得很好. 而罗铁骨也已滚在地上. 翻下马背.只 是他脾气怪僻.疾风般的向朵朵刺去. 如飞追去、他和粟特的交情.我也要回去几转.竟把红云道人伤啦.今儿咱兄弟可与你见个真章啦.两人轻功超卓.好像要向左耳朵发泄似的.刀光闪处.看来也真有点将才.左耳朵见她这个样子. 年老的黄冠道士喝道-你是修啵儿的什么人?陡然间.左耳朵 点点头道-是啦.快走.你却在这里吵嘴.不知是不是?当时黄叶道人和白石道人都不在场.当的几声.短箭向刀背上几格.南海珍珠在草原上是极难得的东西.他听出有几群女子.焦化渐处下风. 左耳朵的天山箭法本是天下无双.你真不愧是我的兄弟.哼.又可大于几场啦.不理外事;绿草凝珠.朗 声说道-我也知道这会犯疑.偷偷走出、果然应个正着.飘韵盈盈笑道-除啦是好妹子之外.想向她解释明白.把他救出. 几问出口.双手几推.饿啦就吃干粮.我也不信你是奸细.申一时好奇问道.怪不得以卓师叔那样崖岸自高的人.在屋脊上纵横飞舞.竟然是几个高大番僧. 这也真是天下中的 奇事.生聚教训.同抗清兵.左耳朵也是兴奋非常.十九口利箭<其中有几人名天华和尚.各族酋长剔烛夜谈.马贼并未占得便宜.才说你口闭得紧.我大笑起来.诚挚说道-飘韵.不久就找到啦明鑫、其时明鑫已将何级单送回关内.为她难过.我却不能推辞不去呀.他本意只守不攻.纳兰朗慧笑道-苦 命的小丫头.问聘几个王爷妻子绝不是几件简单的事.反正天龙箭阵.他们也未必发现;也定能视伤如归.这时正抱着婴儿出来.毫不犹疑. 她就要自刎在我的面前.天客莱又道-不瞒你做大哥的.左耳朵又对孟禄冷笑道-何况她还没有成为你们的俘虏.她不管.宛如洒下啦满天寒星.土著族的酋长 也很高兴.帐篷外左耳朵应声走人. 知道天龙箭法虽然颇有独到之处.左耳朵不知其中原委.塔山族的酋长横啦他几眼.忽然帐幕揭开.失敬啦.知道他们是久别重逢的情侣.我虽然本领不济.成天不舒服. 所以按照江湖规定.别粑懦夫当成好汉. 在旁边给她行礼. 私自逃脱.正好遇上这场混战. 护军府里的武师才纷纷赶来.心想那些平庸的武师.使将出来.激战中忽然怪叫几声.正想发话. 催紧攻势. 你快说哈护军在哪几问房子?天蒙暴跳如雷.可是她从来未带过徒弟来.要把他们逐出异域.苏绿儿含笑不答.刷.申一时恨恨地道-自发魔女欺负我的师父. 仍是紧守门户.王大须子刚才 看见飘韵欲杀苏绿儿.我也要把师父找到.果然不负我的教诲.跟踪追上.她忽然觉得很喜爱这个婴孩. 我想请问哈玛雅盟主和各族的父老们.她又说我看不起女人.喀达尔族的酋长孟禄忽然站起来道.我的计划看来只是孩子的幻想啦.</p>第零1章 密约成空逢敌虏 旧情如梦散鸳鸯 家事国事 两茫茫.作诗饮酒佯狂.洛阳西望路漫谩.吟到恩仇心里想的事儿涌.愁上眉端. 哪里觅红粉知己.梁缕歌残.伤心箭底起波澜.自是情天常有恨.天上人世间. ——调寄浪淘沙 蝶舞鸾飞.匆匆过了祭祖时分.南方春暮.北方正花儿开.人都说是骏马秋风河北.杏花春雨南方.似乎景色偏爱江甫.秋日 独宜河北.其实北方の早春几月.却也另有佳趣.另有景致. 恰是祭祖节后の几天.河北平原、平城北边の太一山上.有几个青年.正在背着手徘徊.引领遥望.这时.朝霞未散.旭日初升.满山满谷の野花.在初升的太阳底下.分外显得花光艳发.色泽缤纷. 但这青年却似无意欣赏这绝妙の景色.但 见它不时地搓手搔头.几副焦虑の神色. 它有什么心里想的事儿.它在期待什么.不错.它正心里想的事儿如麻.盼望着和它の心里喜欢的人儿几见.因为它就即将离开此地.偷赴南方の了. 为什么说是偷赴.因为其时正是南晋年间南北对峙、天下几分の时代.南未偏安南方.黄河以北の中原土地 和北方几大部份.则是赤瓜族の梁国所有.漠北则是新兴の蒙古国家.这几年是南晋绍兴二十九年.梁正隆二年(公元几几五八年).南晋衰落.蒙古初兴.几国之中.以梁国最为强盛. 这青年名叫陈柯及.家住平城.正是离开梁国の都城中都(即今北平)不过几百多里の地方.平城沦陷已久.它の 爹爹曾在仕梁朝.做个不大不小の官儿.前年病逝.目下只有老母在堂.它就是奉了娘亲之命.要偷赴南方の.它是官宦人家之后.文才武艺.出色当行.在本城素受注视.这次偷赴南方.又携带有重要の物事.是以它娘亲千叮万嘱.叫它切不可泄露行踪. 但是.它却把一个人南行の消息.偷偷地告诉 了几个人.这个人就是它の小妹安婉茹.它们是青梅竹马.两小无猜.多青年来.早已是情性相投.私心眷恋.如今它潜返故国.不知何日重来.又岂可不在临行之前.与心上の人见几面. 可是.左等右等.心上の人儿还未见来!它跳上几块明如镜台の圆石.这块石头是被当地人称为望夫石の.据说曾 有几位痴情の女子.曾在这块石头上眺望她远方の情郎.七日不饮不食.终至于死.它和它の小妹小时候.不止几次在这石上嬉戏.它の小妹也曾自比过那痴情の女子.也许今后她也会在这块石头上眺望它吧.但是如今.却是它在这块石头上跳望她.它心底里正在万想千思.要在分子之前.要在这块 多情の望夫石上.与她私把姻缘定了.唉.但是眺望复眺望.它の心里喜欢的人儿还是未来! 山风吹过.茅草猎猎作响.陈柯及眼光几瞥.只见那几大丛
平方根(2)

8上平方根(2)班级姓名学号教学目标:了解数的算术平方根的概念.会用根号表示一个数的算术平方根。
能运用算术平方根解决实际问题。
重难点:根据一个数的算术平方根的意义解决有关问题。
教学过程:一、情境创计面积为15m2正方形的长是多少?等腰直角三角形的一直角长为5cm,则二、课前预习与导学正数a有2个平方根,其中正数a的正的平方根,也叫做a的算术平方根。
例如,4的平方根是±2,2叫做4的算术平方根•4的平方根是±2,2叫做4的算术平方根,记作2 =2,•2的平方根是“±2”,2叫做2的算术平方根,•0只有一个平方根,0的平方根也叫做0的算术平方根,•即±0 =0三、新课交流:1. 16的算术平方根的平方根是什么?5的算术平方根是什么?2、 0的算术平方根是什么?0的算术平方根有几个?3、 -2、-5、-6有算术平方根吗?为什么?例1:求下列各数的算术平方根:•(1)625;(2)0.81;•(3)6;(4)(-2)²• (5) (6)•应用:例2:“欲穷千里目,更上一层楼”。
说的是登的高看得远。
若观测点的高度为h,观测者视线能达到的最远距离为d≈hR,其中R是地球半径(通常取6400km),小丽站在海边一块岩石上,眼睛离地面的高度为20M,她观测到远处一艘船刚露出海平面,此时该小船离小丽有多远?探究正数a的算术平方根的取值范围?(由学生交流讨论)四、课堂巩固练习:1、一个数的算术平方根等于它本身,这个数是。
•2、若x²=16,则5-x的算术平方根是。
•3、若4a+1的平方根是±5,则a²的算术平方根是。
•4、的平方根等于,算术平方根等于。
• 5、若|a-9|+ =0,则的平方根是。
•6、,算术平方根是。
•7、已知△ABC的三边分别是a、b、c,•且 b²-4b+4=0,求c的取值范围。
• 8、已知y= + +3,求xy的算术平方根。
平方根(2)计算器 学案

课 题 授课教师 学习起点 学习目标 学法指导 运用夹值法估计 2 的大小,了解无理数的概念,会比较两个无理数的大小 同学们已经知道 2 的大小用小数形式表示的话只能取近似数,但如何求得这 个近似数呢,这将是本节课主要研究的内容 学 习 活 动 13.1.2 平方根(2) 课 时 学生姓名 1 课时 学 科 课 型 数学 导学
探究 2 小丽想用一块面积为 400c ㎡的正方形纸板片,沿着边的方向裁出一块面积为 300c ㎡的长 方形纸板片,使它的长宽之比为 3:2.不知能否裁出来,正在发愁,小明见了说”别发愁,一定能用一 块面积大的纸片裁出一块面积小的纸片”,你同意小明的说法吗?小丽能用这块纸片裁出符合要 求的纸片吗?
布置作业:书 P47
【情境创设】 (概念阐释、问题引领)
叙述算术平方根的概念并举例说明
【合作探究】 (知识链接、知识结构) 你能估计 2 的大小吗?它会在一个什么范围内?越精确越好.
例 1 试比较下列各组数的大小 ⑴
4与 15
⑵
7与6
1
例2
用计算器计算下列各式的值
(1) 3136 (2) 2 (精确到 0.001 )
5、6、7、9 学 习 收 获
2
练习:书 P44 1、2
【总结提升】 (拓展训练、学习体会、拓展探究、反思等)
探究 1 利用计算器计算,并将计算结果填在表中,你发现了什么规律?你能说出其中的道理吗? … …
0.0625
… 结论:
0.625
0.7906
6.25
2 .5
62.5
7.906
பைடு நூலகம்625
25
6250
79.06
62500
250
…
0.25
根号知识点

根号知识点根号是数学中常见的一个符号,用来表示数的平方根。
下面给大家介绍一下关于根号的几个知识点:1. 根号的定义:根号√是数学中的一个符号,用来表示一个数的平方根。
比如,√2表示2的平方根。
2. 平方根:根号中的数被称为被开方数。
开方的结果被称为平方根。
例如,√9=3,表示9的平方根是3。
3. 平方根的性质:平方根有一些重要的性质。
首先,正数的平方根是正数。
其次,平方根可以是小数或无限循环小数。
例如,√2≈1.41,√3≈1.73。
4. 负数的平方根:负数的平方根是虚数。
虚数用i表示,其中i²=-1。
例如,√-1=i。
5. 二次方程的根:二次方程是形如ax²+bx+c=0的方程,其中a、b、c是已知数。
解二次方程可以使用根号。
根据求根公式,二次方程的解是x=(-b±√(b²-4ac))/(2a)。
这个公式中的根号被称为判别式,它可以用来判断二次方程的根的性质。
6. 根号的运算:根号可以进行一些基本的运算。
比如,两个根号可以进行相加或相乘。
根号也可以和其他运算符一起使用,如加减乘除、指数运算等。
7. 复数的根:三次及以上方程可以有复数的根。
复数根一般以√(-1)表示。
例如,x³+1=0的解是x=(-1)^(1/3)。
在复数域中存在无数个复数根。
总之,根号是数学中一个重要的符号,用于表示数的平方根。
它在解方程、计算数的性质、探索虚数等方面有着广泛的应用。
希望通过了解这些知识点,可以更好地理解和应用根号。
6.1算术平方根2

无限不循环小数是指小数 位数无限,且小数部分不循 环的小数?你以前见过这 种数吗?
2是 无 限 不 循 环 小 数
归纳 以下各数的平方根分别为多少?
3、
42
4、
5、
8、
有限小数
9
3 1 .732050807 5 2 .236069774 8 2 .828427124 9 3
作业
1 2 3、物体在自由落体运动中,h gt ( g 2
是重力加速度,它的值约为10米/秒), 若物体降落高度h=125米,那么它降落 的时间是多少?
身高约 2米
身高约
身高约 5米
3米
武大郎
武 松
姚 明
算术平方根(二)
知识回顾:
什么是算术平方根?怎样表示? 如果一个正数x的平方等于a,那么这个正 数x叫做a的算术平方根. a的算术平方根表示为: 0的算术平方根是0. 负数没有算术平方根.
a a 0
复习
1、 256 的算术平方根是( A 4 B ±16 C 16 D ±4
1 2 2、( ) 的算术平方根是( 2 1 1 A B 4 2 1 1 C D 2 4
估算法
且 7 9
7 3
化根号法
巩固
6、估算大小:
(1) 140 与 12
5 1 (2) 与 0 .5 2
5.例题讲解 例2 解:∵ 5>4, 52 ∴ , 5 1 2 1 1 ∴5 1
5 1 与0.5 . 比较大小: 2
,
∴
2
0.5
.
例:求 3 的整数部分和小数部分。
2500 50 25 5 250000 500 25000000 5000
6.1-平方根(2) 相关计算

认真观察数字墙可知:
(±5)2=25
(±4)2=16
(0)2=0
(±1.1)2=1.21
我们把±5,±4,0,±2分别叫做25,16,0,4的平方根。
你能类比算术平方根的概念,给出平方根的概念吗?
平方根的概念:
一般地,如果一个数的平方等于a,那么这个数叫做a的平方根或二次方根.这就是说,如果 ,那么 叫做a的平方根。
“如果一个数 的平方等于a,那么这个数 叫做a的平方根”,
“如果一个正数x的平方等于a,即 ,那么这个正数x叫做a的算术平方根”。
(2)个数不同:一个正数有两个平方根,而一个正数的算术平方根只有一个。
(3)表示方法不同:正数a的算术平方根表示为 ,而正数a的平方根表示为 。
过程引导学生去探索,提炼平方根的定义。
小组讨论,并指派一人回答问题。答错同小组同学补充。
(师指点)
生回答。错误的简述理由。
学生上台板演。若有错误请其他同学用红笔改正。
三、
尝
试
应
用
思考:(1)正数有几个平方根?他们有什么特点?
(2)0的平方根是多少?
(3)负数有平方根吗?
(4)给你一个数的算术平方根,你可以立即写出它的负的平方根吗?
平方根的定义的应用(易混点):
问题(一):
同学们找到的规律是什么?
我们上节课学过的知识有什么?
22=4,则2叫4的算术平方根,4叫2的平方。
但是(-2)2=4,则-2叫4的什么呢?下面我们就来讨论这个问题。
学生上黑板圈出来。
生答:(有两个数的平方是第三个数……)
(算术平方根)
教师在上课开始时提出问题,引发学生的思考。
二、
平方根2教学反思

平方根2教学反思平方根2教学反思平方根2教学反思一一般新知识都是建立在原有知识的基础之上的,这样引入新课是建立在学生对数字的规律和联系的把握上的,学生是比较容易接受的。
因此在上一章勾股定理一章时,有意识的让学生知道类似X2=4时X 的值有两个即X=2或X=-2,因为在直角三角形中求边长,边长不能为负数,故只取正数,这样反复训练学生哪个数的平方等于4或16等等,又为何取正数的道理,从而使学生接触到如何求X的值,为学习平方根、算术平方根的概念奠定了基础,接触到这个概念时,学生就没有太多困惑了。
另外,我设计了两种题目:一种是知道正方形的边长求面积;还有一种是知道正方形的面积求边长,对于第一种题目,学生利用正方形的面积公式很快就可以解决,对于第二种题目,面积为9、16、49的,学生也可以很快利用平方的知识进行解答,但是当面积=7时的,学生就被难住了,到底边长应该是多少呢?学生无法找到一个数,使它的平方等于7,这时,我告诉同学们,当我们无法找到符合这个条件的数时,我们就需要引入一个新的知识:平方根。
我也及时给出了表示方法。
那到底什么叫做平方根呢?我要求学生自己阅读教材中的相关内容,让学生自己去发现规律,并能用自己的语言加以表达,加深学生对平方根概念的理解,从而归纳出三个结论:一个正数的平方根有2个,它们互为相反数;0的平方根有1个,还是0;负数没有平方根。
通过这些探索,最后让学生体会到,要求一个非负数的平方根,可以利用平方来检验或寻找。
接着就要和学生学习平方根的表示方法了,为了让学生正确掌握“算术平方根”的表示,我还特意把与之相反的“负的平方根”的表示也同时列举出来,让学生通过对比进一步加深印象。
得到概念后正面的强化很重要,因此在第三个环节,我设计了例题:如何求一个数的平方根,算数平方根,负的平方根?通过搭建脚手架,给了学生正确的表达方法,进行强化训练。
随后就是通过不同形式的练习,分组分层进行训练,让学生对平方根的概念及表示方法形成正确的一印象并加以巩固。
2.2 平方根(2)课件

小测:
求下列各数的算术平方根
361 14 1 11 0.000324 2250000 108
81
289
25
若一个数的算术平方根为m ,则比这个数大2的数的算术
平方根是
。
回顾 & 思考 ☞
1.什么叫算术平方根?
若一个正数的平方等于 a 则这个数叫做 a 的算术
平方根,表示为a (a 0) . 0的平方根是0,即 0 0 .
(1)一个正数有几个平方根? (2)0 有几个平方根? (3)负数呢?
议一议 (1)一个正数有几个平方根?
(2)0 有几个平方根? (3)负数呢? 1、一个正数有两个平方根,0只有一个平 方根,它是0本身;负数没有平方根.
一个正数有两个平方根,它们又有何关系?
2、一个正数有两个平方根,它们互为相 反数!
乘方有没有逆运算?
9的平方等于多少?
9的平方根等于多少?
求一个数a的平方根的运算,叫做开平方. ( a叫做被开方数)
探索平方与开平方的关系
平方
+1 -1
1
开平方
1
+1 -1
+2 -2
4
+3 -3
9
4
+2 -2
9
+3 -3
平方与开平方互逆运算.
辨析概念
平方根与算术平方根的联系与区别:
联系:1.包含关系:平方根包含算术平方根, 算术平方根是平方根的一种.
定义
求一个数a的平方根的运算, 叫做开平方(extraction of square root)其中a叫做被开方数.
巩固新知
1.求下列各数的平方根和算术平方根:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
)2=144 )2=.64 )2=
10 7 13
7 ( 9
(
49 81
(
)2=169
0.4 )2=0.16
提示: 已知一个正数的平方,求这个正数的 问题。
探究三
问题:学校将举行美术作品比赛, 小红很高兴,他想裁出一块面积 为25dm2的正方形画布,画上自 己的得意之作参加比赛,这块正 方形画布的边长应取多少?
(a≥0)
算术平方根具有双重非负性
结论:要求一个数的算术平方根,就是要看哪个
非负数的平方会等于这个数。
根据等式:122 =144,你能说出144 的算术平方根是多少吗?并用等式 表示出来。
144 12
学以致用
例1 求下列各数的算术平方根:
49 (1)100 (2)64 (3)0.0001 解:(1)因为 10 =100,所以100的算术平方根为10, 即 100 =10。
a
≥0.
(1)因为 72=49,所以7是49的算术平方根. ( √ )
(2)因为(-6)2=36,所以-6是36的算术平方根。( × )
(3)0的算术平方根是0. ( √ )
4 是-4的算术平方根. ( ×) (5) a 2 表示a2的算术平方根. ( √ )
(4)
算术平方根的意义:
非负数
a ≥0
探究一
填空: 2 a2=______ 3 b2=______ 4 c2=______ 5 d2=______ 11 e2=______ 13 f2=______
线段a,b,c,d,……,e,f分别是多少?
探究二
在括号里填上适当的正数.
2 ( 3
( (
4 )2= 9
)2=100 )2=49
( (
12 0.8
1.0 的算术平方根是0; 2. 是个运算符号,它表示求一个数的算术平方根;
新课讲授
3.
a
的意义: a的算术平方根,且 a ≥0,
a ≥0.
随堂练 一般地,如果一个正数 x 的平 习(一) 方等于a,即 x2 = a,那么这个正数
x 叫做a的算术平方根。
a的意义: 1.判断:
a的算术平方根,且a≥0,
这个问题实际上也是已知一个正数的 平方,求这个正数的问题。 因为 52=25, 所以 边长为5dm.
一般地,一个正数a有两个平方根, 其中正的平方根叫的算术平方根即 x2 = a,那 么这个正数 x 叫做a的算术平方根。 a的算术平方根记为 a ,读作“根号a”.a叫 做被开方数。 =x。 a 因为52=25,那么根据定义5就是25的算术平 方根。即 25 5 . 特别提醒:
补充练习
自由下落物体的高度h(单位:m)与下落时间t(单 位:s)的关系是h=4.9t2.如图,现有一个物体从 490m高的建筑物上自由落下,到达地面需要多长 时间?
490m
提
高
1、已知y= x 2 + 2 x +3,求xy 的算术平方根。 2、在△ABC中,∠C=90°. (1)如果AC=5,BC=12,求AB; (2)如果AC=2,BC=1,求AB; (3)如果AB=25,BC=24,求AC; (4)如果AC=5,AB=12,求BC;
2
49 49 7 (2)因为 = ,所以 的算术平方根是 8 64 64 7 7 49 8 ,即 64 = 8
2
2
(3)因为 0.01 =0.0001,所以0.0001的算术平方 根为0.01,即 0.0001 =0.01。
讨论
1. 2.
( 0.01 等于多少?( 5) ) 呢?
探索 & 交流 探究:
怎样用两个面积为1的小正方形拼 成一个面积为2的大正方形?
如图,把两个小正方形沿对角线剪开, 将所得的4个直角三角形拼在一起,就 得到一个面积为2的大正方形。你知道 这个大正方形的边长是多少吗? 小正方形 设大正方形的边长为x,则 2 的对角线 x =2. 的长是多 由算术平方根的意义可知 少呢? x= 2
回顾与反思
1. 这节课我们要掌握哪些知识?
(1). 算术平方根的定义。 (2). a 的意义:表示 a 的算术平方根,
其中 a≥0, a ≥0。 (3). 正确地求出一个非负数的算术平方根。
2. 你还有什么问题或想法需要和大家交流?
课后作业: 习题2.3
1 2 ) 2
例
题
例1:求下列各数的算术平方根: (1)625; (2)0.81; (3)6; (4)(-2)² (5) 256 (6) (0.25 ) 2 2、一个数的算术平方根等于它本身, 这个数是 。 3、 36 的平方根等于 等于 。 ,算术平方根
应
h
d
用
• 例2:“欲穷千里目,更上一层楼”。说的是登 的高看得远。若观测点的高度为h,观测者视线 能达到的最远距离为d≈ hR ,其中R是地球 2 半径(通常取6400km),小丽站在海边一块 岩石上,眼睛离地面的高度为20M,她观测到 远处一艘船刚露出海平面,此时该小船离小丽有 多远?
一个正方形的面积变为原来的4倍, 其边长变为原来的多少倍? 解:设这个正方形的原来的边长为a, 则其原来的面积为a2。 又设变大后的正方形的边长为b,则
2
假如正方形的 面积扩大n倍, 那么其边长对 应扩大多少倍?
b
b
4a
2
2a
2
假如是圆呢? 等边三角形呢?
4a
2
2a
即变大后的正方形边长时原来边长的2倍
2
2 2 162 等于多少? (-16) 呢? (-5)呢?
2
随堂练习二
1. 求下列各数的算术平方根:
(1) 0.0025;
(4)15² .
(2) 121; (3) 32 .
(5)(-2)²
2. 求下列各式的值:
(1)
1;
(2)
9 ; 25
(3)
2 .
2
3.计算:
1 2 2 (-2) (4
