江苏省灌南高级中学2018-2019学年高三上学期周练试卷(文)
灌南县高级中学2018-2019学年上学期高三期中数学模拟题
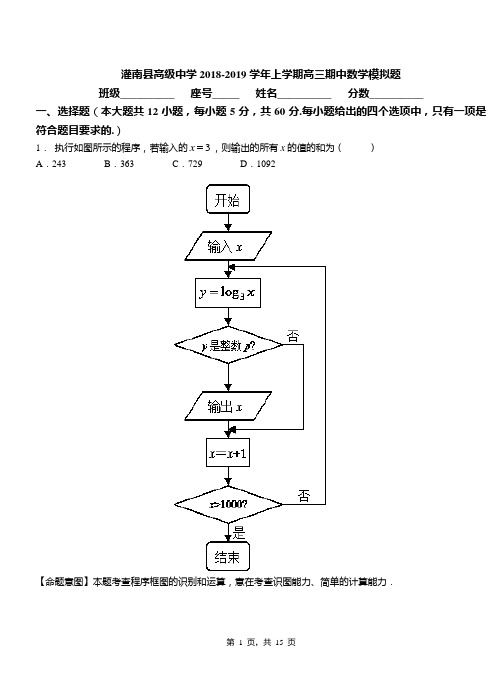
灌南县高级中学2018-2019学年上学期高三期中数学模拟题班级__________ 座号_____ 姓名__________ 分数__________一、选择题(本大题共12小题,每小题5分,共60分.每小题给出的四个选项中,只有一项是符合题目要求的.)x ,则输出的所有x的值的和为()1.执行如图所示的程序,若输入的3A.243B.363C.729D.1092【命题意图】本题考查程序框图的识别和运算,意在考查识图能力、简单的计算能力.2. 已知变量与正相关,且由观测数据算得样本平均数,,则由该观测的数据算得的线性回归方程可能是( ) ABC D3. 已知实数[1,1]x ∈-,[0,2]y ∈,则点(,)P x y 落在区域20210220x y x y x y +-⎧⎪-+⎨⎪-+⎩……… 内的概率为( )A.34B.38C.14D.18【命题意图】本题考查线性规划、几何概型等基础知识,意在考查数形结合思想及基本运算能力.4. 圆222(2)x y r -+=(0r >)与双曲线2213y x -=的渐近线相切,则r 的值为( ) AB .2 CD.【命题意图】本题考查圆的一般方程、直线和圆的位置关系、双曲线的标准方程和简单几何性质等基础知识,意在考查基本运算能力.5. 如图,在正方体1111ABCD A B C D -中,P 是侧面11BB C C 内一动点,若P 到直线BC 与直线11C D 的距离相等,则动点P 的轨迹所在的曲线是( )A 1CA B A.直线 B.圆C.双曲线D.抛物线【命题意图】本题考查立体几何中的动态问题等基础知识知识,意在考查空间想象能力.6. 复数i i -+3)1(2的值是( )A .i 4341+-B .i 4341-C .i 5351+-D .i 5351-【命题意图】本题考查复数乘法与除法的运算法则,突出复数知识中的基本运算,属于容易题. 7. ABC ∆中,“A B >”是“cos 2cos 2B A >”的( ) A. 充分必要条件 B. 充分不必要条件 C. 必要不充分条件 D. 既不充分也不必要条件【命题意图】本题考查三角函数的性质与充分必要条件等基础知识,意在考查构造函数的思想与运算求解能力. 8. 为调查某地区老人是否需要志愿者提供帮助,用简单随机抽样方法........从该地区调查了500位老年人,结果如由2()()()()()n ad bc K a b c d a c b d -=++++算得22500(4027030160)9.96720030070430K ⨯⨯-⨯==⨯⨯⨯ 附表:参照附表,则下列结论正确的是( )①有99%以上的把握认为“该地区的老年人是否需要志愿者提供帮助与性别无.关”; ②有99%以上的把握认为“该地区的老年人是否需要志愿者提供帮助与性别有.关”; ③采用系统抽样方法比采用简单随机抽样方法更好; ④采用分层抽样方法比采用简单随机抽样方法更好 A .①③ B .①④ C .②③ D .②④9. 已知抛物线C :y x 82=的焦点为F ,准线为l ,P 是l 上一点,Q 是直线PF 与C 的一个交点,若2=,则=QF ( ) A .6B .3C .38 D .34 第Ⅱ卷(非选择题,共100分)10.从1、2、3、4、5中任取3个不同的数、则这3个数能构成一个三角形三边长的概率为( ) A.110 B.15 C.310 D.253.841 6.635 10.828k 2() 0.050 0.010 0.001P K k ≥11.某三棱锥的三视图如图所示,该三棱锥的体积是( ) A . 2 B .4 C .34 D .38【命题意图】本题考查三视图的还原以及特殊几何体的体积度量,重点考查空间想象能力及对基本体积公式的运用,难度中等. 12.设为全集,是集合,则“存在集合使得是“”的( )A 充分而不必要条件B 必要而不充分条件C 充要条件D 既不充分也不必要条件二、填空题(本大题共4小题,每小题5分,共20分.把答案填写在横线上)13.已知x ,y 为实数,代数式2222)3(9)2(1y x x y ++-++-+的最小值是 .【命题意图】本题考查两点之间距离公式的运用基础知识,意在考查构造的数学思想与运算求解能力. 14.已知数列{}n a 的首项1a m =,其前n 项和为n S ,且满足2132n n S S n n ++=+,若对n N *∀∈,1n n a a +< 恒成立,则m 的取值范围是_______.【命题意图】本题考查数列递推公式、数列性质等基础知识,意在考查转化与化归、逻辑思维能力和基本运算能力.15.设变量y x ,满足约束条件22022010x y x y x y --≤⎧⎪-+≥⎨⎪+-≥⎩,则22(1)3(1)z a x a y =+-+的最小值是20-,则实数a =______.【命题意图】本题考查线性规划问题,意在考查作图与识图能力、逻辑思维能力、运算求解能力. 16.设向量a =(1,-1),b =(0,t ),若(2a +b )·a =2,则t =________.三、解答题(本大共6小题,共70分。
灌南高级中学周练试卷

江苏省灌南高级中学周练试卷(文科)命题人:袁中飞 2015年12月19日一、填空题(共14小题每小题5分共计70分.将正确答案填入答题纸的相应横线上.........) 1.设集合{}2,0,M x =,集合{}0,1N =,若N M ⊆,则x = . 2.已知复数z 满足()341i z +=(i 为虚数单位),则z 的模为 . 3.已知m 为实数,直线1:30l mx y ++=,2:(32)20l m x my -++=,则“1m =”是“12//l l ”的 条件(请在“充要、充分不必要、必要不充分、既不充分也不必要”中选择一个填空).4.根据如图所示的伪代码,最后输出的S 的值 为 .5.现有5道试题,其中甲类试题2道,乙类试题3道,现从中随机取2道试题,则至少有1道试题是乙类试题的概率为 .6.若实数,x y 满足约束条件2211x y x y x y -⎧⎪--⎨⎪+⎩≤≥≥,则目标函数2z x y =+的最小值为 .7.已知等比数列{}n a 的前n 项和为n S ,若283652,62a a a a S ==-,则1a 的值是 .8.已知1,2a b == ,a 与b 的夹角为120︒,0a b c ++= ,则a 与c的夹角为 .9.已知1cos(75)3α︒+=,则cos(302)α︒-的值为 . 10.设椭圆22221x y a b+=(0a b >>)的左右焦点分别为12F F 、,左准线为l ,P 为椭圆上的一点,PQ l ⊥于点Q ,若四边形12PQF F 为平行四边形,则椭圆离心率的取值范围是 .11.若x y 、均为正实数,且24x y +=,则22221x y x y +++的最小值是 . 12. 在ABC ∆中,已知2BC =,1AB AC ∙=,则ABC ∆面积的最大值是 .13.已知圆22:4O x y +=,直线:40l x y +-=,A 为直线l 上一点,若圆O 上存在两点B C 、,使得60BAC ∠=︒,则点A 的横坐标的取值范围是 .14.若函数223,1()32,1x a x f x x ax a x ⎧-<⎪=⎨-+≥⎪⎩恰有2个零点,则实数a 的取值范围是 .二、解答题(本大题共6小题,共90分.请在答题纸...指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.)15.(本小题满分14分)已知向量3(sin ,),(cos ,1)4a xb x ==-rr .(1)当//a b时,求tan()4x π-的值;(2)设函数()()2f x a b b =+?r r r ,当[0,]2x π∈时,求()f x 的值域.16.(本小题满分14分)如图,在多面体ABCDEF 中,四边形ABCD 是菱形,,AC BD 相交于点O ,//EF AB ,2AB EF =,平面BCF ⊥平面ABCD ,BF CF =,点G 为BC 的中点.(1)求证:直线//OG 平面EFCD ; (2)求证:直线AC ⊥平面ODE .17.(本小题满分15分)如图,椭圆2222:1x y C a b +=(0a b >>)的离心率e =,椭圆CC 的下顶点为D .(1)求椭圆C 的方程;(2)若过D 点作两条互相垂直的直线分别与椭圆C 相交于点P M 、.求证:直线PM 经过一定点.18.(本小题满分15分)如图,某广场中间有一块边长为2百米的菱形状绿化区ABCD ,其中BMN 是半径为1百米的扇形,23ABC π∠=.管理部门欲在该地从M 到D 修建小路:在 MN 上选一点P (异于M 、N 两点),过点P 修建与BC 平行的小路PQ . (1)设PBC θ∠=,试用θ表示修建的小路 MP与线段PQ 及线段QD 的总长度l ; (2)求l 的最小值.PDQCNBAM(第18题)19.(本题满分16分)已知数列{}n a 的前n 项和为n S ,且对一切正整数n 都有212n n S n a =+. (1)求证:142n n a a n ++=+(*n N ∈); (2)求数列{}n a 的通项公式;(3)是否存在实数a,使不等式212111(1)(1)(1)n a a a ---< 对一切正整数n 都成立?若存在,求出a 的取值范围;若不存在,请说明理由。
灌南县高级中学2018-2019学年高二上学期第二次月考试卷数学

灌南县高级中学2018-2019学年高二上学期第二次月考试卷数学 班级__________ 姓名__________ 分数__________一、选择题1. 如图是某几何体的三视图,正视图是等腰梯形,俯视图中的曲线是两个同心的半圆组成的半圆环,侧视图是直角梯形.则该几何体表面积等于( )A .12+B .12+23πC .12+24πD .12+π2. 已知向量=(2,1),=10,|+|=,则||=( )A .B .C .5D .253. 甲、乙两所学校高三年级分别有1 200人,1 000人,为了了解两所学校全体高三年级学生在该地区六校联考的数学成绩情况,采用分层抽样方法从两所学校一共抽取了110名学生的数学成绩,并作出了频数分布统计表如下: 甲校:乙校:则x ,yA、12,7B、10,7C、10,8D、11,94f x[14]f(x)的导函数y=f′(x)的图象如图所示.)A.2 B.3 C.4 D.55.“”是“一元二次方程x2+x+m=0有实数解”的()A.充分非必要条件B.充分必要条件C.必要非充分条件D.非充分非必要条件6.“x2﹣4x<0”的一个充分不必要条件为()A.0<x<4 B.0<x<2 C.x>0 D.x<47.下列说法正确的是()A.圆锥的侧面展开图是一个等腰三角形;B.棱柱即是两个底面全等且其余各面都是矩形的多面体;C.任何一个棱台都可以补一个棱锥使他们组成一个新的棱锥;D.通过圆台侧面上的一点,有无数条母线.8.圆心为(1,1)且过原点的圆的方程是()A.2=1 B.2=1 C.2=2 D.2=29.曲线y=在点(1,﹣1)处的切线方程为()A.y=x﹣2 B.y=﹣3x+2 C.y=2x﹣3 D.y=﹣2x+110.下列命题中正确的是()A.若命题p为真命题,命题q为假命题,则命题“p∧q”为真命题B.命题“若xy=0,则x=0”的否命题为:“若xy=0,则x≠0”C.“”是“”的充分不必要条件D .命题“∀x ∈R ,2x >0”的否定是“”11.已知函数f (x )=x 3+(1﹣b )x 2﹣a (b ﹣3)x+b ﹣2的图象过原点,且在原点处的切线斜率是﹣3,则不等式组所确定的平面区域在x 2+y 2=4内的面积为( )A .B .C .πD .2π12.若函数()y f x =的定义域是[]1,2016,则函数()()1g x f x =+的定义域是( )A .(]0,2016B .[]0,2015C .(]1,2016D .[]1,2017二、填空题13.已知实数x ,y 满足,则目标函数z=x ﹣3y 的最大值为14.计算sin43°cos13°﹣cos43°sin13°的值为 .15.如图,在长方体ABCD ﹣A 1B 1C 1D 1中,AB=AD=3cm ,AA 1=2cm ,则四棱锥A ﹣BB 1D 1D 的体积为 cm 3.16.双曲线x 2﹣my 2=1(m >0)的实轴长是虚轴长的2倍,则m 的值为 .17.已知双曲线﹣=1(a >0,b >0)的一条渐近线方程是y=x ,它的一个焦点在抛物线y 2=48x 的准线上,则双曲线的方程是 .18.已知直线l 的参数方程是(t 为参数),曲线C 的极坐标方程是ρ=8cos θ+6sin θ,则曲线C 上到直线l 的距离为4的点个数有 个.三、解答题19.已知函数,.(Ⅰ)求函数的最大值; (Ⅱ)若,求函数的单调递增区间.20.(本小题满分12分)如图, 矩形ABCD 的两条对角线相交于点()2,0M ,AB 边所在直线的方 程为360x y --=点()1,1T -在AD 边所在直线上. (1)求AD 边所在直线的方程; (2)求矩形ABCD 外接圆的方程.21.(本小题满分12分)某市拟定2016年城市建设,,A B C 三项重点工程,该市一大型城建公司准备参加这三个工程的竞标,假设这三个工程竞标成功与否相互独立,该公司对,,A B C 三项重点工程竞标成功的概率分别为a ,b ,14()a b >,已知三项工程都竞标成功的概率为124,至少有一项工程竞标成功的概率为34.(1)求a 与b 的值;(2)公司准备对该公司参加,,A B C 三个项目的竞标团队进行奖励,A 项目竞标成功奖励2万元,B 项目竞标成功奖励4万元,C 项目竞标成功奖励6万元,求竞标团队获得奖励金额的分布列与数学期望.【命题意图】本题考查相互独立事件、离散型随机变量分布列与期望等基础知识,意在考查学生的运算求解能力、审读能力、获取数据信息的能力,以及方程思想与分类讨论思想的应用.22.如图,四边形ABCD 与A ′ABB ′都是边长为a 的正方形,点E 是A ′A 的中点,AA ′⊥平面ABCD . (1)求证:A ′C ∥平面BDE ;(2)求体积V A ′﹣ABCD 与V E ﹣ABD 的比值.23.如图,在三棱柱111ABC A B C -中,111,A A AB CB A ABB =⊥. (1)求证:1AB ⊥平面1A BC ;(2)若15,3,60AC BC A AB ==∠=,求三棱锥1C AA B -的体积.24.已知椭圆G:=1(a>b>0)的离心率为,右焦点为(2,0),斜率为1的直线l与椭圆G交与A、B两点,以AB为底边作等腰三角形,顶点为P(﹣3,2).(Ⅰ)求椭圆G的方程;(Ⅱ)求△PAB的面积.灌南县高级中学2018-2019学年高二上学期第二次月考试卷数学(参考答案)一、选择题1.【答案】C【解析】解:根据几何体的三视图,得;该几何体是一半圆台中间被挖掉一半圆柱,其表面积为S=[×(2+8)×4﹣2×4]+[×π•(42﹣12)+×(4π×﹣π×)+×8π]=12+24π.故选:C.【点评】本题考查了空间几何体三视图的应用问题,也考查了空间想象能力与计算能力的应用问题,是基础题目.2.【答案】C【解析】解:∵|+|=,||=∴(+)2=2+2+2=50,得||=5故选C.【点评】本题考查平面向量数量积运算和性质,根据所给的向量表示出要求模的向量,用求模长的公式写出关于变量的方程,解方程即可,解题过程中注意对于变量的应用.3.【答案】B=60人,【解析】1从甲校抽取110× 1 2001 200+1 000从乙校抽取110× 1 000=50人,故x=10,y=7.1 200+1 0004.【答案】C【解析】解:根据导函数图象,可得2为函数的极小值点,函数y=f(x)的图象如图所示:因为f(0)=f(3)=2,1<a<2,所以函数y=f(x)﹣a的零点的个数为4个.故选:C.【点评】本题主要考查导函数和原函数的单调性之间的关系.二者之间的关系是:导函数为正,原函数递增;导函数为负,原函数递减.5.【答案】A【解析】解:由x2+x+m=0知,⇔.(或由△≥0得1﹣4m≥0,∴.),反之“一元二次方程x2+x+m=0有实数解”必有,未必有,因此“”是“一元二次方程x2+x+m=0有实数解”的充分非必要条件.故选A.【点评】本题考查充分必要条件的判断性,考查二次方程有根的条件,注意这些不等式之间的蕴含关系.6.【答案】B【解析】解:不等式x2﹣4x<0整理,得x(x﹣4)<0∴不等式的解集为A={x|0<x<4},因此,不等式x2﹣4x<0成立的一个充分不必要条件,对应的x范围应该是集合A的真子集.写出一个使不等式x2﹣4x<0成立的充分不必要条件可以是:0<x<2,故选:B.7.【答案】C【解析】考点:几何体的结构特征.8.【答案】D【解析】解:由题意知圆半径r=,∴圆的方程为2=2.故选:D.【点评】本题考查圆的方程的求法,解题时要认真审题,注意圆的方程的求法,是基础题.9.【答案】D【解析】解:y′=()′=,∴k=y′|x=1=﹣2.l:y+1=﹣2(x﹣1),则y=﹣2x+1.故选:D10.【答案】D【解析】解:若命题p为真命题,命题q为假命题,则命题“p∧q”为假命题,故A不正确;命题“若xy=0,则x=0”的否命题为:“若xy≠0,则x≠0”,故B不正确;“”⇒“+2kπ,或,k∈Z”,“”⇒“”,故“”是“”的必要不充分条件,故C不正确;命题“∀x∈R,2x>0”的否定是“”,故D正确.故选D.【点评】本题考查命题的真假判断,是基础题,解题时要认真审题,仔细解答.11.【答案】B【解析】解:因为函数f(x)的图象过原点,所以f(0)=0,即b=2.则f(x)=x3﹣x2+ax,函数的导数f′(x)=x2﹣2x+a,因为原点处的切线斜率是﹣3,即f′(0)=﹣3,所以f′(0)=a=﹣3,故a=﹣3,b=2,所以不等式组为则不等式组确定的平面区域在圆x2+y2=4内的面积,如图阴影部分表示,所以圆内的阴影部分扇形即为所求.∵k OB=﹣,k OA=,∴tan∠BOA==1,∴∠BOA=,∴扇形的圆心角为,扇形的面积是圆的面积的八分之一,∴圆x2+y2=4在区域D内的面积为×4×π=,故选:B【点评】本题主要考查导数的应用,以及线性规划的应用,根据条件求出参数a,b的是值,然后借助不等式区域求解面积是解决本题的关键.12.【答案】B【解析】二、填空题13.【答案】5【解析】解:由z=x﹣3y得y=,作出不等式组对应的平面区域如图(阴影部分):平移直线y=,由图象可知当直线y=经过点C时,直线y=的截距最小,此时z最大,由,解得,即C(2,﹣1).代入目标函数z=x﹣3y,得z=2﹣3×(﹣1)=2+3=5,故答案为:5.14.【答案】.【解析】解:sin43°cos13°﹣cos43°sin13°=sin(43°﹣13°)=sin30°=,故答案为.15.【答案】6【解析】解:过A作AO⊥BD于O,AO是棱锥的高,所以AO==,所以四棱锥A﹣BB1D1D的体积为V==6.故答案为:6.16.【答案】4.【解析】解:双曲线x2﹣my2=1化为x2﹣=1,∴a2=1,b2=,∵实轴长是虚轴长的2倍,∴2a=2×2b,化为a2=4b2,即1=,解得m=4.故答案为:4.【点评】熟练掌握双曲线的标准方程及实轴、虚轴的定义是解题的关键.17.【答案】【解析】解:因为抛物线y2=48x的准线方程为x=﹣12,则由题意知,点F(﹣12,0)是双曲线的左焦点,所以a2+b2=c2=144,又双曲线的一条渐近线方程是y=x,所以=,解得a2=36,b2=108,所以双曲线的方程为.故答案为:.【点评】本题考查双曲线的标准方程,以及双曲线的简单性质的应用,确定c和a2的值,是解题的关键.18.【答案】2【解析】解:由,消去t 得:2x ﹣y+5=0,由ρ=8cos θ+6sin θ,得ρ2=8ρcos θ+6ρsin θ,即x 2+y 2=8x+6y ,化为标准式得(x ﹣4)2+(y ﹣3)2=25,即C 是以(4,3)为圆心,5为半径的圆.又圆心到直线l 的距离是,故曲线C 上到直线l 的距离为4的点有2个, 故答案为:2.【点评】本题考查了参数方程化普通方程,考查了极坐标方程化直角坐标方程,考查了点到直线的距离公式的应用,是基础题.三、解答题19.【答案】【解析】【知识点】三角函数的图像与性质恒等变换综合【试题解析】(Ⅰ)由已知当 ,即, 时,(Ⅱ)当时,递增即,令,且注意到函数的递增区间为20.【答案】(1)320x y ++=;(2)()2228x y -+=.【解析】试题分析:(1)由已知中AB 边所在直线方程为360x y --=,且AD 与AB 垂直,结合点()1,1T -在直线AD 上,可得到AD 边所在直线的点斜式方程,即可求得AD 边所在直线的方程;(2)根据矩形的性质可得矩形ABCD 外接圆圆心纪委两条直线的交点()2,0M ,根据(1)中直线,即可得到圆的圆心和半径,即可求得矩形ABCD 外接圆的方程.(2)由360320x y x y --=⎧⎨++=⎩解得点A 的坐标为()0,2-,因为矩形ABCD 两条对角线的交点为()2,0M ,所以M 为距形ABCD 外接圆的圆心, 又AM ==从而距形ABCD 外接圆的方程为()2228x y -+=.1 考点:直线的点斜式方程;圆的方程的求解.【方法点晴】本题主要考查了直线的点斜式方程、圆的方程的求解,其中解答中涉及到两条直线的交点坐标,圆的标准方程,其中(1)中的关键是根据已知中AB 边所在的直线方程以及AD 与AB 垂直,求出直线AD 的斜率;(2)中的关键是求出A 点的坐标,进而求解圆的圆心坐标和半径,着重考查了学生分析问题和解答问题的能力,以及推理与运算能力. 21.【答案】【解析】(1)由题意,得11424131(1)(1)(1)44ab a b ⎧=⎪⎪⎨⎪----=⎪⎩,因为a b >,解得1213a b ⎧=⎪⎪⎨⎪=⎪⎩.…………………4分(Ⅱ)由题意,令竞标团队获得奖励金额为随机变量X ,则X 的值可以为0,2,4,6,8,10,12.…………5分而41433221)0(=⨯⨯==X P ;1231(2)2344P X ==⨯⨯=;1131(4)2348P X ==⨯⨯=; 1211135(6)23423424P X ==⨯⨯+⨯⨯=; 1211(8)23412P X ==⨯⨯=; 1111(10)23424P X ==⨯⨯=;1111(12)23424P X ==⨯⨯=.…………………9分所以X 的分布列为:于是,11()012345644824122424E X =⨯+⨯+⨯+⨯+⨯+⨯+⨯12=.……………12分 22.【答案】【解析】(1)证明:设BD 交AC 于M ,连接ME . ∵ABCD 为正方形,∴M 为AC 中点, 又∵E 为A ′A 的中点, ∴ME 为△A ′AC 的中位线, ∴ME ∥A ′C .又∵ME ⊂平面BDE ,A ′C ⊄平面BDE , ∴A ′C ∥平面BDE .(2)解:∵V E ﹣ABD ====V A ′﹣ABCD .∴V A ′﹣ABCD :V E ﹣ABD =4:1.23.【答案】(1)证明见解析;(2)【解析】试题分析:(1)有线面垂直的性质可得1BC AB ⊥,再由菱形的性质可得11AB A B ⊥,进而有线面垂直的判定定理可得结论;(2)先证三角形1A AB 为正三角形,再由于勾股定理求得AB 的值,进而的三角形1A AB 的面积,又知三棱锥的高为3BC =,利用棱锥的体积公式可得结果.考点:1、线面垂直的判定定理;2、勾股定理及棱锥的体积公式.24.【答案】【解析】解:(Ⅰ)由已知得,c=,,解得a=,又b2=a2﹣c2=4,所以椭圆G的方程为.(Ⅱ)设直线l的方程为y=x+m,由得4x2+6mx+3m2﹣12=0.①设A,B的坐标分别为(x1,y1),(x2,y2)(x1<x2),AB的中点为E(x0,y0),则x0==﹣,y0=x0+m=,因为AB是等腰△PAB的底边,所以PE⊥AB,所以PE的斜率k=,解得m=2.此时方程①为4x2+12x=0.解得x1=﹣3,x2=0,所以y1=﹣1,y2=2,所以|AB|=3,此时,点P(﹣3,2).到直线AB:y=x+2距离d=,所以△PAB的面积s=|AB|d=.。
江苏省连云港市灌南高级中学2023-2024学年高三上学期假期检测(一)语文试卷及参考答案

高三语文暑假检测时间:150分钟总分:150分一、现代文阅读(35分)(一)现代文阅读Ⅰ(本题共5小题,19分)阅读下面的文字,完成1~5小题。
我们常引以为豪的是,中华文明是世界四大古文明中唯一延续至今的伟大文明。
今天我们中国的种族和文化与五千多年前是一脉相承的,而古埃及、古巴比伦、古印度的文明后来都中断过。
人们会发现,四个文明都勃发于北纬30°左右的大河冲积平原,都是依靠栽培旱地粮作的灌溉农业,都创造了文字,都建立了等级制度,都面临着游牧民族的侵袭……大家既然拥有这么多共同点,那为何却有着不同的发展命运?还有古罗马文明,欧亚大陆另一端的发达农业文明,其发源地今天的文化样貌与当初相比已是面目全非。
倘使一个汉代人在一千年后的唐代复活,他仍会感到舒适自在,因为两个朝代从语言、文字、儒家学说、祖先崇拜到国家管理都是相同的。
如果有位公元前1世纪的罗马人于公元1000年的欧洲复活,他一定会惊讶于眼前崭新而奇特的一切。
假若换成是一位唐末的吴越人在一千年后的清末返生,他看到的那个江南依然大同小异,而如果是位欧洲人则会见到天翻地覆的反差,怕是要惊掉下巴。
为何中华文明走上了迥异的演进道路?众所周知,我们黄河流域早期靠的是粟作,其他三个文明靠麦作。
不过粟作文明与麦作文明的差别有限,小米常用作煮粥,小麦多用来磨面,况且我们的旱作是同时包含了粟和麦的旱作。
真正的差异在于,我们不是旱作独自在战斗,而是有水稻与之并肩作战。
水稻与旱作这一对好搭档,无论在旱涝还是寒暑上都是强烈互补关系。
在万邦并列的时代,一个小国去攻打另一个小国,不一定是因为有多么大的争霸雄心,可能只是为了夺取山下或对岸的一片与自己不一样的农田,这样就算是原有的田地歉收,还能指望收成较好的另一片。
那个时代,一个国家要长期生存,一个文明要延续不断,就必须同时掌控多种类型的农业区域。
在五千多年以前,是稻作发出的第一道文明曙光划破了东亚的漫长暗夜,有可能激发了,至少是影响了最早的黄河旱作文明。
灌南高级中学周练试卷

)
3. 已知 cos( A.1 3
1
)
,则 sin(
) 的值为(
)
63
3
B. 1 3
23 C.
3
D. 2 3 3
4.已知 sin
1a
3a 1
, cos
,若 为第二象限角,则下列结论正确的是(
)
1a
1a
( A) . a
1 ( 1, )
3
( B) . a 1 (C).
1
a 1或 a
(D).
9
1 a
9
5、圆弧长度等于圆内接正三角形的边长,则其圆心角弧度数为
8. sin2 120 cos180 tan 45 cos2( 330 ) sin( 210 ) =_______
9. 在 (0, 2 ) 内,使 sin x cos x 成立的 x 的取值范围为
10. 若定义域为 R 的偶函数 f ( x)在[ 0,+∞)上是增函数,
> 0 的 x 的集合是
.
.
1
12. 求函数 y 2 4sin x 4cos2 x 的最大值和最小值,并写出函数取最值时对应的
x 的值.
x
13. 已知函数 f ( x) 3sin(
) 3,
26
( 1)求 f ( x) 的周期、对称轴、对称中心、单调增区间
;
( 2)求 f ( x) 的最大值及取最大值时相应的 x 的值。
灌南高级中学周练试卷 (2019.11.30.)
一 . 选择题(每题 5 分)
制卷人:代传凤1. 集合 M Nhomakorabeak
x|x
2
,k 4
Z ,N
k
x|x
【解析版】江苏省连云港市灌南高级中学2013届高三数学上学期期中试题 理 苏教版

2012-2013学年某某省某某市灌南高级中学高三(上)期中数学试卷(理科)一、填空题:本大题共14小题,每小题5分,共70分.不需要写出解答过程,请把答案直接填在答题纸相应位置上.1.(5分)设集合U={1,2,3,4,5},A={1,2},B={2,3},则(∁U A)∩B={3} .考点:交、并、补集的混合运算.专题:计算题.分析:找出U中不属于A的元素,确定出A的补集,找出A补集与B的公共元素,即可求出所求的集合.解答:解:∵U={1,2,3,4,5},A={1,2},∴∁U A={3,4,5},又B={2,3},则(∁U A)∩B={3}.故答案为:{3}点评:此题考查了交、并、补集的混合运算,熟练掌握交、并、补集的定义是解本题的关键.2.(5分)若复数z=(是虚数单位),则复数z的虚部是.考点:复数的基本概念.专题:计算题.分析:利用两个复数代数形式的乘法,虚数单位i的幂运算性质,化简复数z等于+i,由此可得它的虚部.解答:解:∵复数z====+i,故它的虚部等于,故答案为.点评:本题主要考查复数的基本概念,两个复数代数形式的乘法,虚数单位i的幂运算性质,属于基础题.3.(5分)设S n是等差数列{a n}(n∈N+)的前n项和,且a1=1,a4=7,则S5= 25 .考点:等差数列的前n项和.专题:计算题;等差数列与等比数列.分析:先由d=求出公差d,然后代入等差数列的求和公式即可求解解答:解:∵a1=1,a4=7,∴d==2∴=25故答案为:25点评:本题主要考查了等差数列的通项公式及求和公式的简单应用,属于基础试题4.(5分)函数,则f(2)= 1 .考点:函数的值.专题:函数的性质及应用.分析:按照分段函数解析式的特点代入数值计算即可.解答:解:由f(x)解析式得,f(2)=f(2+3)=f(5)=5﹣4=1,故答案为:1.点评:本题考查分段函数求值,属基础题.5.(5分)平面向量与的夹角为60°,=(2,0),||=1,则|+|=.考点:数量积表示两个向量的夹角;向量的模.专题:平面向量及应用.分析:由条件利用两个向量的数量积的定义求出=1,求出=+2+的值,即可求得的值.解答:解:由题意可得||=2,||=1,向量与的夹角为60°,∴=2×1×cos60°=1,∴=+2+=4+2+1=7,∴=,故答案为.点评:本题主要考查两个向量的数量积的定义,求向量的模的方法,属于中档题.6.(5分)已知510°角的始边在x轴的非负半轴上,终边经过点P(m,2),则m= ﹣2.考点:任意角的概念.专题:三角函数的求值.分析:利用诱导公式求得cos510°=﹣,再由任意角的三角函数的定义可得m<0且﹣=,由此求得m的值.解答:解:∵510°=360°+150°,∴cos510°=cos150°=﹣cos30°=﹣.再由510°角的终边经过点P(m,2),可得m<0,且cos510°=﹣=,解得 m=﹣2,故答案为﹣2.点评:本题主要考查任意角的三角函数的定义,诱导公式,终边相同的角的性质,属于基础题.7.(5分)函数的定义域是.考点:对数函数的定义域.专题:计算题.分析:欲求函数的定义域,只需找到使函数解析式有意义的x的取值X围,因为函数中有对数,所以真数大于0,因为函数中有二次根式,所以被开方数大于等于0,解不等式组即可.解答:解:要使函数有意义,需满足,解得∴函数的定义域为故答案为点评:本题主要考察了函数定义域的求法,主要是求使函数成立的x的取值X围.8.(5分)(2012•某某)已知y=f(x)是奇函数,若g(x)=f(x)+2且g(1)=1,则g (﹣1)= 3 .考点:函数奇偶性的性质;函数的值.专题:计算题.分析:由题意y=f(x)是奇函数,g(x)=f(x)+2得到g(x)+g(﹣x)=f(x)+2+f(﹣x)+2=4,再令x=1即可得到1+g(﹣1)=4,从而解出答案解答:解:由题意y=f(x)是奇函数,g(x)=f(x)+2 ∴g(x)+g(﹣x)=f(x)+2+f(﹣x)+2=4又g(1)=1∴1+g(﹣1)=4,解得g(﹣1)=3故答案为3点评:本题考查函数奇偶性的性质,解题的关键是利用性质得到恒成立的等式,再利用所得的恒等式通过赋值求函数值9.(5分)已知函数f(x)=x2+bx的图象在点A(1,f(1))处的切线l与直线3x﹣y+2=0平行,若数列的前n项和为S n,则S2013的值为.考点:利用导数研究曲线上某点切线方程;数列的求和.专题:综合题;导数的概念及应用.分析:对函数求导,根据导数的几何意义可求切线在x=1处的斜率,然后根据直线平行时斜率相等的条件可求b,代入可求f(n),利用裂项求和即可求得结论.解答:解:由f(x)=x2+bx求导得:f′(x)=2x+b,∵函数f(x)=x2+bx的图象在点A(1,f(1))处的切线l与直线3x﹣y+2=0平行,∴f′(1)=2+b=3,∴b=1,∴f(x)=x2+x所以f(n)=n(n+1),∴=∴S2013的值为1﹣+﹣+…+﹣=1﹣=故答案为:点评:本题考查了导函数的几何意义,考查利用利用裂项相消法求数列的前n项和的方法,属于中档题.10.(5分)在锐角△ABC中,若A=2B,则的取值X围是(,).考点:正弦定理.专题:解三角形.分析:利用正弦定理列出关系式,将A=2B代入,利用二倍角的正弦函数公式化简,约分得到结果为2cosB,根据三角形的内角和定理及三角形ABC为锐角三角形,求出B的X 围,进而确定出cosB的X围,即可得出所求式子的X围.解答:解:∵A=2B,∴根据正弦定理=得:====2cosB,∵A+B+C=180°,∴3B+C=180°,即C=180°﹣3B,∵C为锐角,∴30°<B<60°,又0<A=2B<90°,∴30°<B<45°,∴<cosB<,即<2cosB<,则的取值X围是(,).故答案为:(,)点评:此题考查了正弦定理,余弦函数的图象与性质,以及特殊角的三角函数值,熟练掌握正弦定理是解本题的关键.11.(5分)已知函数存在单调递减区间,则实数a 的取值X围为(﹣1,0)∪(0,+∞).考点:利用导数研究函数的单调性.专题:计算题;导数的综合应用.分析:利用导数进行理解,即f'(x)<0在(0,+∞)上有解.可得ax2+2x﹣1>0在正数X围内至少有一个解,结合根的判别式列式,不难得到a的取值X围.解答:解:对函数求导数,得f'(x)=﹣,(x>0)依题意,得f'(x)<0在(0,+∞)上有解.即ax2+2x﹣1>0在x>0时有解.∴△=4+4a>0且方程ax2+2x﹣1=0至少有一个正根.∴a>﹣1,∴a≠0,∴﹣1<a<0,或a>0.故答案为:(﹣1,0)∪(0,+∞).…(5分)点评:本题主要考查函数与导数,以及函数与方程思想,体现了导数值为一种研究函数的工具,能完成单调性的判定和最值的求解方程,同时能结合常用数学思想,来考查同学们灵活运用知识解决问题的能力.12.(5分)(2010•马某某模拟)如图,在平面四边形ABCD中,若AC=3,BD=2,则= 5 .考点:向量在几何中的应用.专题:计算题;转化思想.分析:先利用向量的加法把转化为,再代入原题整理后即可求得结论.解答:解:因为=(+)+(+)=+()=.∴()•()=()•()=﹣=32﹣22=5.故答案为5点评:本题主要考查向量在几何中的应用以及向量的加法运算,是对基础知识的考查,属于基础题目.13.(5分)(2011•某某模拟)已知函数f(x)=|x2﹣6|,若a<b<0,且f(a)=f(b),则a2b的最小值是﹣16 .考点:利用导数求闭区间上函数的最值;二次函数的性质.专题:函数的性质及应用.分析:由题意可得 a2﹣6=6﹣b2,即 a2+b2=12,﹣2<b<0,故g(b)=a2b=(12﹣b2) b=12b ﹣b3.利用导数研究函数的单调性,根据函数的单调性求函数的最小值.解答:解:∵函数f(x)=|x2﹣6|,若a<b<0,且f(a)=f(b),∴a2﹣6=6﹣b2,即a2+b2=12.∴﹣<b<0,∴a2b=(12﹣b2) b=12b﹣b3.设g(b)=12b﹣b3,则 g'(b)=12﹣3b2,令 g'(b)=0,解得b=﹣2,所以,g(b)在(﹣,﹣2)上单调递减,g(b)在[﹣2,0)上单调增,故g(b)最小值是g(﹣2)=﹣24+8=﹣16,故答案为﹣16.点评:本题主要考查二次函数的性质应用,利用导数研究函数的单调性,根据函数的单调性求函数的最小值,属于基础题.14.(5分)(2011•某某模拟)设等差数列{a n}满足:公差d∈N*,a n∈N*,且{a n}中任意两项之和也是该数列中的一项.若a1=35,则d的所有可能取值之和为364 .考点:等差数列的性质.专题:计算题.分析:先求出数列的通项公式,求出数列{a n}中任意两项之和,根据数列{a n}中任意两项之和仍是该数列中的一项求出d=,再结合k,m,n,d∈N*,即可求出d的所有可能取值进而求出结论.解答:解:设等差数列的公差为d,若a1=35,=243,则a n=243+(n﹣1)d.所以数列{a n}中任意两项之和a m+a n=243+(m﹣1)d+243+(n﹣1)d=486+(m+n﹣2)d.设任意一项为a k=243+(k﹣1)d.则由a m+a n=a k可得 243+(m+n﹣k﹣1)d=0,化简可得 d=.再由k,m,n,d∈N*,可得 k+1﹣m﹣n=1,3,9,27,81,243,∴d=243,81,27,9,3,1,则d的所有可能取值之和为 364,故答案为 364.点评:本题主要考查等差数列的性质.解决问题的关键在于利用数列{a n}中任意两项之和仍是该数列中的一项求出d=,属于中档题.二.解答题:本大题共6小题,共90分.请在答题卡指定区域内作答,解答时应写出必要的文字说明,证明过程或演算步骤.15.(14分)(2011•日照模拟)设命题p:实数x满足x2﹣4ax+3a2<0,其中a>0,命题q:实数x满足.(Ⅰ)若a=1,且p∧q为真,某某数x的取值X围;(Ⅱ)若¬p是¬q的充分不必要条件,某某数a的取值X围.考点:充分条件;命题的真假判断与应用.分析:(1)p∧q为真,即p和q均为真,分别解出p和q中的不等式,求交集即可;(2)﹁p是﹁q的充分不必要条件⇔q是p的充分不必要条件,即q⇒p,反之不成立.即q中的不等式的解集是p中的不等式解集的子集.解答:解:(1)a=1时,命题p:x2﹣4x+3<0⇔1<x<3命题q:⇔⇔2<x≤3,p∧q为真,即p和q均为真,故实数x的取值X围是2<x<3(2)﹁p是﹁q的充分不必要条件⇔q是p的充分不必要条件,即q⇒p,反之不成立.即q中的不等式的解集是p中的不等式解集的子集.由(1)知命题q:2<x≤3,命题p:实数x满足x2﹣4ax+3a2<0⇔(x﹣a)(x﹣3a)<0由题意a>0,所以命题p:a <x<3a,所以,所以1<a≤2点评:本题考查复合命题的真假、充要条件的判断、解二次不等式等知识,考查知识点较多,但难度不大.16.(14分)(2011•某某二模)已知函数,其中=,.(1)求函数f(x )在区间上的单调递增区间和值域;(2)在△ABC中,a、b、c分别是角A、B、C 的对边,f(A)=﹣1,且b=1△ABC的面积,求边a的值.考点:正弦函数的定义域和值域;三角函数中的恒等变换应用;解三角形.专题:计算题.分析(1)利用向量的数量积,二倍角公式两角差的余弦函数化简函数的表达式,然后结合:余弦函数的单调增区间求函数的单调递增区间,确定函数在上的单调增区间,单调减区间,然后求出函数的最大值最小值,即可确定函数的值域.(2))由于f(A)=﹣1,求得又求得c=4最后由余弦定理得a值即可.解答:解:(1)==(2分)由得,又∴单调增区间为.(4分)由∴﹣1≤f(x)≤2∴f(x)∈[﹣1,2](6分)(2)∵f(A)=﹣1,∴,(8分)又,∴c=4(10分)由余弦定理得a2=b2+c2﹣2bccosA=13(12分)点评:本题是基础题,考查向量数量积的应用,三角函数的化简求值,单调区间的求法,最值的求法,考查计算能力,注意函数值域的确定中,区间的讨论,单调性的应用是解题的易错点.17.(15分)设数列{a n}的前n项和为S n,且满足S n=2﹣a n,n=1,2,3,….(1)求数列{a n}的通项公式;(2)若数列{b n}满足b1=1,且b n+1=b n+a n,求数列{b n}的通项公式;(3)设=n (3﹣b n),求数列{}的前n项和为T n.考点:数列的求和;数列的函数特性;等比数列的通项公式.专题:计算题.分析:(1)利用数列中a n与 Sn关系解决.(2)结合(1)所求得出b n+1﹣b n=.利用累加法求b n(3)由上求出=n (3﹣b n)=,利用错位相消法求和即可.解解:(1)因为n=1时,a1+S1=a1+a1=2,所以a1=1.答:因为S n=2﹣a n,即a n+S n=2,所以a n+1+S n+1=2.两式相减:a n+1﹣a n+S n+1﹣S n=0,即a n+1﹣a n+a n+1=0,故有2a n+1=a n.因为a n≠0,所以=( n∈N*).所以数列{a n}是首项a1=1,公比为的等比数列,a n=( n∈N*).(2)因为b n+1=b n+a n( n=1,2,3,…),所以b n+1﹣b n=.从而有b2﹣b1=1,b3﹣b2=,b4﹣b3=,…,b n﹣b n﹣1=( n=2,3,…).将这n﹣1个等式相加,得b n﹣b1=1+++…+==2﹣.又因为b1=1,所以b n=3﹣( n=1,2,3,…).(3)因为=n (3﹣b n)=,所以T n=.①=.②①﹣②,得=﹣.故T n=﹣=8﹣﹣=8﹣( n=1,2,3,…).点评:本题考查利用数列中a n与 Sn关系求数列通项,累加法、错位相消法求和,考查转化、变形构造、计算能力.18.(15分)(2012•某某)海事救援船对一艘失事船进行定位:以失事船的当前位置为原点,以正北方向为y轴正方向建立平面直角坐标系(以1海里为单位长度),则救援船恰好在失事船正南方向12海里A处,如图,现假设:①失事船的移动路径可视为抛物线;②定位后救援船即刻沿直线匀速前往救援;③救援船出发t小时后,失事船所在位置的横坐标为7t(1)当t=0.5时,写出失事船所在位置P的纵坐标,若此时两船恰好会合,求救援船速度的大小和方向.(2)问救援船的时速至少是多少海里才能追上失事船?圆锥曲线的综合.考点:专应用题.题:分(1)t=0.5时,确定P的横坐标,代入抛物线方程中,可得P的纵坐标,利析:用|AP|=,即可确定救援船速度的大小和方向;(2)设救援船的时速为v海里,经过t小时追上失事船,此时位置为(7t,12t2),从而可得vt=,整理得,利用基本不等式,即可得到结论.解解:(1)t=0.5时,P的横坐标x P=7t=,代入抛物线方程中,得P的纵坐答:标y P=3.…2分由|AP|=,得救援船速度的大小为海里/时.…4分由tan∠OAP=,得∠OAP=arctan,故救援船速度的方向为北偏东arctan 弧度.…6分(2)设救援船的时速为v海里,经过t小时追上失事船,此时位置为(7t,12t2).由vt=,整理得.…10分因为,当且仅当t=1时等号成立,所以v2≥144×2+337=252,即v≥25.因此,救援船的时速至少是25海里才能追上失事船.…14分点评:本题主要考查函数模型的选择与运用.选择恰当的函数模型是解决此类问题的关键,属于中档题.19.(16分)已知函数.(1)若a=1,求函数f(x)的极值;(2)若函数f(x)在[2,+∞)上是增函数,某某数a的取值X围;(3)若函数f(x)在[1,e]上的最小值为3,某某数a的值.考点:函数模型的选择与应用;利用导数研究函数的单调性;利用导数求闭区间上函数的最值.专题:导数的综合应用.分析:(1)把a=1代入函数解析式,求导后由导函数等于0把定义域分段,判断出各区间段内的导函数的符号,由导函数的符号得到原函数的单调性,从而判断出极值点并求出极值;(2)求出原函数的导函数,由导函数在[2,+∞)大于等于0恒成立得到x﹣2a≥0在[2,+∞)恒成立,分离变量a后即可得到a的取值X围;(3)由原函数的导函数等于0求出导函数的零点,由零点对定义域分段,然后根据原函数的极值点与给出的区间端点值得大小关系分析原函数在区间[1,e]上的单调性,由单调性求得原函数在[1,e]上的最小值,由最小值等于3解得a的值.解答:解:(1)当a=1时,f(x)=lnx+,定义域为(0,+∞),.所以,当x∈(0,2)时,f′(x)<0,f(x)为减函数;当x∈(2,+∞)时,f′(x)>0,f(x)为增函数,所以在(0,+∞)上f(x)有极小值,极小值为f(2)=1+ln2;(2)由,所以.若函数f(x)在[2,+∞)上是增函数,则在[2,+∞)恒成立,即x﹣2a≥0在[2,+∞)恒成立,也就是在[2,+∞)恒成立,所以a≤1.所以使函数f(x)在[2,+∞)上是增函数的实数a的取值X围是(﹣∞,1];(3)由(2)知,以,若a≤0,则f′(x)>0,f(x)在(0,+∞)上为增函数,f(x)在[1,e]上的最小值为f(1)=2a=3,,不合题意;若a>0,由f′(x)=0,得x=2a.当x∈(0,2a)时,f′(x)<0,f(x)为减函数,当x∈(2a,+∞)时,f′(x)>0,f(x)为增函数,所以当2a≤1,即时,f(x)在[1,e]上为增函数,最小值为f(1)=2a=3,,不合题意;当2a≥e,即a≥时,f(x)在[1,e]上为减函数,最小值为f(e)=1+=3,a=e,符合题意;当1<2a<e,即时,f(x)在[1,e]上的最小值为f(2a)=ln2a+1=3,a=不合题意.综上,使函数f(x)在[1,e]上的最小值为3的实数a的值为e.点评:本题考查了利用导数研究函数的单调性,考查了利用导数求函数在闭区间上的最值,考查了分类讨论的数学思想方法,训练了利用分离变量法求参数的X围,解答的关键是会求基本初等函数的导函数和对变量的正确分类,是难题.20.(16分)已知二次函数f(x)=ax2+bx+c.(1)设f(x)在[﹣2,2]上的最大值、最小值分别是M、m,集合{x|f(x)=x}={1},且a≥1,记h(a)=M+m,求h(d)的最小值.(2)当a=2,c=﹣1时,①设A=[﹣1,1],不等式f(x)≤0的解集为C,且C⊆A,某某数b的取值X围;②设g(x)=|x﹣t|﹣x2﹣bx(t∈R),求f(x)+g(x)的最小值.考点:二次函数在闭区间上的最值;集合的包含关系判断及应用;函数的值域.专题:函数的性质及应用.分析:(1)由题意可得方程ax2+bx+c=x存在两等根x1=x2=1,可得 b=1﹣2a,c=a,由此可得f(x)的解析式,可得 h(a)=M+m=f(﹣2)+f(1﹣)=9a﹣﹣1,再利用单调性求出 h(a)的最小值.(2)①由不等式f(x)≤0的解集为C,且C⊆A,可得,由此解得 b的X围.②根据f(x)+g(x)=x2+|x﹣t|﹣1,分t<﹣时、当﹣≤t≤时、t>时三种情况分别求得f(x)+g(x)的最小值.解答:解:(1)由题意可得方程ax2+bx+c=x 存在两等根x1=x2=1,可得 b=1﹣2a,c=a.∴f(x)=a +1﹣,它的对称轴为 x=1﹣∈[,1].∵x∈[﹣2,2],∴h(a)=M+m=f(﹣2)+f(1﹣)=9a﹣﹣1,∵a≥1,故函数 h(a)为增函数,∴函数 h(a)的最小值为 h(1)=.(2)当a=2,c=﹣1时,f(x)=2x2+bx﹣1,①由不等式f(x)≤0的解集为C,且C⊆A,可得,解得 b∈[﹣1,1].②f(x)+g(x)=x2+|x﹣t|﹣1=.当 t<﹣时,最小值为﹣t﹣,当﹣≤t≤时,最小值为 t2﹣1,当t>时,最小值为t﹣.点评:本题主要考查求二次函数在闭区间上的最值,二次函数的性质的应用,集合间的包含关系,体现了分类讨论的数学思想,属于中档题.。
江苏灌南高级中学2019高三上年中考试试题-政治
江苏灌南高级中学2019高三上年中考试试题-政治考试时间长度:100分钟总分值:120制卷人:程金忠审校人:杜华杰第|卷〔选择题共66分〕【一】单项选择题:本大题共33小题,每题2分,共计66分。
在每题给出的四个选项中,只有一项为哪一项最符合题意的。
1、技客一族,拿特长换生活,如用汽车陪驾交换电脑维修,用瑜珈招式交换摄影技术……越来越多的人参与到技能互换中成为“技客一族”。
从经济生活角度看,以下关于“技能互换”说法正确的选项是①“技能互换”属于商品流通②题中的“技能”是使用价值与价值的统一体③从消费目的看,“技能互换”属劳务消费④“技能互换”符合等价交换的原那么A、②③B、①④C、②④D、③④2、随着我国网购市场日趋成熟,大部分网购消费者已从最初单纯追求低价,逐渐过渡为对商品质量及服务的高要求,时下出现了团购网站专业化、细分化、地域化、个性化的进展趋势。
这说明A、消费模式变化使人们消费观念发生全然性改变B、新的消费需求能够引导生产经营的调整和升级C、生产方式的变化决定了人们的消费方式的改变D、消费方式的变化促进了人们消费水平的提高3、基于投资的风险,一位理财专家给工薪阶层的建议是:“理财方程式=50%稳守+25%稳攻+25%强攻”。
这一理财公式的合理之处在于A、兼顾投资的合法性和多样性B、幸免投资的风险性C、兼顾投资的风险性和收益性D、保证收益的最大化4.2018年,我国将接着完善结构性减税政策,对蔬菜的批发、零售免征增值税。
假设将这一政策产生的妨碍用图形描绘出来,你认为最有可能的是5、在国家一系列调控政策下,我国房价过快增长的势头得到了有效遏制。
你认为导致这一现象的缘故可能有①利率上调②保障房供给增加③上调房产税率④建筑成本上升A、①②③B、②③④C、①③④D、①②④6、国内某企业在国际市场上按5美元/件的价格售出20万件机电产品,该产品的生产成本为人民币10元/件。
依照下表,在其他条件不变的情况下,2017年12月28日结算比2017 年10月28日结算,该企业会人民币外汇牌价〔人民币元/100美元中间价〕A、少获利14400元人民币B、不受妨碍C、利润持平D、多获利14400元人民币7、右图描述的是一商品在某年1—6月份的价格走势,以下观点中对该图理解正确的选项是A、该商品逐步走向卖方市场B、该商品的生产者会扩大生产规模C、该商品的互补商品需求量会有所减少D、该商品的替代商品需求量会有所减少8、龙年春节过后,有市民将家中闲置物品“铺”上网,换取所需。
5.9江苏省灌南高级中学周练试卷(11次)含答案

江苏省灌南高级中学周练试卷总分:100分 考试时间:70分钟 制卷人:杨思佳 邵华川一、单选题(每题5分)1.在ABC ∆中,内角,,A B C 的对边分别为,,a b c ,若sin :sin 2:3A B =,则:a b =( ) A .3:2 B .2:3 C .4:9 D .9:4 2.已知:在△ABC 中,cos cos c C b B =,则此三角形为( ) A .直角三角形B .等腰直角三角形C .等腰三角形D .等腰或直角三角形3.已知ABC ∆的内角,,A B C 所对的边分别为,,a b c ,ABC ∆2cos 2b A a c +=,6a c +=则其周长为( )A .10B .9C .12D .4.设△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,(a +b +c )(a -b +c )=ac ,sinAsinC =4,则角C =( )A .C =15°或C =45°B .C =15°或C =30° C .C =60°或C =45°D .C =30°或C =60°5.在ABC ∆中,3B π=,AC =2AB BC +的最大值为( )A .B .C .3D .46.我国宋代数学家秦九韶(1202-1261)在《数书九章》(1247)一书中提出“三斜求积术”,即:以少广求之,以小斜幂并大斜幂减中斜幂,余半之,自乘于上;以小斜幂乘大斜幂减上,余四约之,为实;一为从隅,开平方得积. 其实质是根据三角形的三边长a ,b ,c 求三角形面积S ,即S =若ABC ∆的面积2S =,a =2b =,则sin A 等于( )A B C D .1120或1136二、填空题(每题5分)7.经过两条直线2310x y ++=和340x y -+=的交点,并且平行于直线3470x y +-=的直线方程是________.8.设1tan 2α=,4cos()((0,))5πββπ+=-∈,则tan 2()αβ-= 9.已知ABC ∆的内角A 、B 、C 的对边分别为a 、b 、c 其面积为S ,且()2243b c a S +-=,则角A =________10.在ABC ∆中,若sin :sin :sin 1:1:3A B C =,则ABC ∆中最大角的余弦值为_________.三、解答题(11,12每题10分,13,14每题15分)11.在△ABC 中,角A ,B ,C 所对的边分别是a ,b ,c ,且c sin2B ﹣b sin (A +B )=0 (1)求角B 的大小;(2)设a =4,c =6,求sin C 的值.12..ABC ∆的内角,,A B C 的对边分别为,,a b c ,已知26sin cossin 2A a B b A =. (1)求cos A ;(2)若21,5a b c =+=,求ABC ∆的面积.13如图,在ABC ∆中,33sin BAD ∠=,1cos 7ADC ∠=,7AD =,8AC =,D 在BC 边上,连接AD . (1)求角B 的大小;(2)求ACD ∆的面积.14已知直线1:2(1)20l mx m y -++=,2:230l x y -+=,3:10l x y -+=是三条不同的直线,其中m R ∈.(1)求证:直线1l 恒过定点,并求出该点的坐标;(2)若以2l ,3l 的交点为圆心,C 与直线1l 相交于,A B 两点,求AB 的最小值.答案一、单选题 BCBABC二、填空题7. 3x+4y+1119=0 8.247 9. 3π 10. 32π 三、解答题 11.12.13.14.。
2019届高三上学期文科数学第五周周练试题.docx

一、选择题二.填空题]3・ _____________ , 14. _____________ , 15. ____________ , 16. _____________每小题5分,共60分。
在每小题给出的四个选项中,只有一项符合题目要求。
集合A={2. 4. 5}. B = {1, 3. 5. 7}.则((:")A B =( )5.已知n 为直线,a 为平面,下列结论正确的是7.设c?eR,则“日=1”是“直线人:^+2y —1 =0与直线人:x+@+l)y+4 = 0平行”的 ()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件2&设珥丁2是双曲线亡・1=1的两个焦点,P 是双曲线上的一点,且3|PF]| = 4|PF 』,则APFR 的24一.选择题:本题共12小题, 1.己知全集U= {1234567}, C. {1. 3. 6. 7}2.设I 为虚数单位,则复数z = 回的共轨复数是()1 + 1A. {7}B. {3, 5}D. {], 3. 7}A. 1 +iB. l-iC. 一1 + i3.若幕函数/(x)的图像过点A g,4),贝Of(x)=( A. 16xB. x 1C. x 2D. x4.已知|a| = |b| = 2,(a+2b)«(a-b)=-2,则:与为的夹角为A. 30°B. 45°C. 60°D. 120°A. 若 m 丄 n, n c a,贝lj m 丄 aB. 若 m 丄 a> n 丄 a,贝U m II nC. 若 m II n, n II a,贝ij m II aD. 若 m II m 丄 m 贝ij n 丄 a (孑,b = 5 92(?, c = log 3-, 则H 、b 、c 大小关系是( A. a<b<cB. c<b<aC. a<c<bD. c<a<b10. 已知函数f(x) = sin(mx + cp) + cos(cnx +(p)(s > 0,0 < q) <兀)满足f(-x) = -f(x),且直线y =血与函数f(x)的图象的两个相邻交点的横坐标之差的绝对值为1则()2 A. f(x)在(0;)上单调递减B. f(x)在(;更)上单调递减4 8 8 JTJT 3 兀c. f(x)在(0,-)上单调递增D. f(x)在(:,〒)上单调递增48 811. 把边长为1的正方形ABCD 沿对角线BD 折起,使得平面ABD 丄平面CBD,形成三棱锥C-ABD 的正视图与俯视图如图所示,则侧视图的面积为()令AA. -B. —C. -D. 224412. 已知函数/(x)是定义在7?上的偶函数,设函数/(x)的导函数为广(x),若对任意兀>0都有2/(兀)+护(兀)> 0成立,则()A .4/(-2)<9/⑶ B. 4/(-2)>9/(3)C. 2/⑶ >3/(-2) D. 3/(-3)<2/(-2)二、填空题:本题共4小题,每小题5分,共20分。
灌南县高级中学2018-2019学年高二上学期数学期末模拟试卷含解析

灌南县高级中学2018-2019学年高二上学期数学期末模拟试卷含解析班级__________ 座号_____ 姓名__________ 分数__________一、选择题1. ,则( )4213532,4,25a b c ===A .B .C .D .b a c <<a b c <<b c a <<c a b<<2. 椭圆的左右顶点分别为,点是上异于的任意一点,且直线斜率的22:143x y C +=12,A A P C 12,A A 1PA 取值范围是,那么直线斜率的取值范围是( )[]1,22PA A . B . C . D .31,42⎡⎤--⎢⎥⎣⎦33,48⎡⎤--⎢⎥⎣⎦1,12⎡⎤⎢⎥⎣⎦3,14⎡⎤⎢⎥⎣⎦【命题意图】本题考查椭圆的标准方程和简单几何性质、直线的斜率等基础知识,意在考查函数与方程思想和基本运算能力.3. 某几何体的三视图如图所示(其中侧视图中的圆弧是半圆),则该几何体的表面积为()A .20+2πB .20+3πC .24+3πD .24+3π4. 在等差数列{a n }中,a 1+a 2+a 3=﹣24,a 10+a 11+a 12=78,则此数列前12项和等于( )A .96B .108C .204D .2165. 已知 m 、n 是两条不重合的直线,α、β、γ是三个互不重合的平面,则下列命题中 正确的是( )A .若 m ∥α,n ∥α,则 m ∥nB .若α⊥γ,β⊥γ,则 α∥βC .若m ⊥α,n ⊥α,则 m ∥nD .若 m ∥α,m ∥β,则 α∥β6. 已知函数f (x )=x (1+a|x|).设关于x 的不等式f (x+a )<f (x )的解集为A ,若,则实数a 的取值范围是( )A .B .C .D .7. 已知向量,,,若为实数,,则( )(1,2)a = (1,0)b = (3,4)c = λ()//a b c λ+λ=A . B . C .1D .214128. 集合U=R ,A={x|x 2﹣x ﹣2<0},B={x|y=ln (1﹣x )},则图中阴影部分表示的集合是()A .{x|x ≥1}B .{x|1≤x <2}C .{x|0<x ≤1}D .{x|x ≤1}9. 高三(1)班从4名男生和3名女生中推荐4人参加学校组织社会公益活动,若选出的4人中既有男生又有女生,则不同的选法共有( )A .34种B .35种C .120种D .140种10.若f (x )=x 2﹣2x ﹣4lnx ,则f ′(x )>0的解集为( )A .(0,+∞)B .(﹣1,0)∪(2,+∞)C .(2,+∞)D .(﹣1,0)11.已知函数f (x )=2x ﹣+cosx ,设x 1,x 2∈(0,π)(x 1≠x 2),且f (x 1)=f (x 2),若x 1,x 0,x 2成等差数列,f ′(x )是f (x )的导函数,则( )A .f ′(x 0)<0B .f ′(x 0)=0C .f ′(x 0)>0D .f ′(x 0)的符号无法确定12.已知双曲线C :﹣=1(a >0,b >0)的左、右焦点分别为F 1,F 2,过点F 1作直线l ⊥x 轴交双曲线C的渐近线于点A ,B 若以AB 为直径的圆恰过点F 2,则该双曲线的离心率为( )A .B .C .2D .13.,分别为双曲线(,)的左、右焦点,点在双曲线上,满足,1F 2F 22221x y a b-=a 0b >P 120PF PF ⋅=若 )12PF F ∆C. D. 11+【命题意图】本题考查双曲线的几何性质,直角三角形内切圆半径与外接圆半径的计算等基础知识,意在考查基本运算能力及推理能力.14.正方体的内切球与外接球的半径之比为( )A .B .C .D .15.如图所示,在三棱锥的六条棱所在的直线中,异面直线共有()111]P ABC -A .2对B .3对C .4对D .6对二、填空题16.已知,,那么.tan()3αβ+=tan(24πα+=tan β=17.命题“∃x ∈R ,2x 2﹣3ax+9<0”为假命题,则实数a 的取值范围为 .18.直线l 1和l 2是圆x 2+y 2=2的两条切线,若l 1与l 2的交点为(1,3),则l 1与l 2的夹角的正切值等于 _________ 。
2021-2022江苏省灌南高级中学高三年级第一学期第三次周练(B)(数学)(10.17)

高三年级第一学期第三次周练(B)(数学)一、单选题(本大题共8小题,共40.0分。
在每小题列出的选项中,选出符合题目的一项)1.设是虚数单位,若复数是纯虚数,则的值为()A. -3B. -1C. 1D. 32.下列命题中,真命题的是()A. 函数的周期是B. x R,>C. 周期函数一定是奇函数或偶函数.D. 已知服从正态分布N(0,),且P(-22)=0.4,则P(>2)=0.3;3.设,,,则()A. B. C. D.4.定义:将24小时内降水在平地上积水厚度(mm)来判断降雨程度;其中小雨(0mm-10mm),中雨(10mm-25mm),大雨(25mm-50mm),暴雨(50mm-100mm);小明用一个圆锥雉形容器接了24小时的雨水,则这天降雨属于哪个等级( )A. 小雨B. 中雨C. 大雨D. 暴雨5.在ABC中,=+,则= ()A. B. C. D. 26.如图⊙O与轴正半轴交点为A,点B,C在⊙O上,且,点C在第一象限,,则()A. B. C. D.7.已知点O(0,0),A(–2,0),B(2,0).设点P满足|PA|–|PB|=2,且P为函数y=图像上的点,则|OP|=()A. B. C. D.8.已知函数,函数有个零点,则实数的取值范围为()A. B. C. D.二、多选题(本大题共4小题,共20.0分。
在每小题有多项符合题目要求)9.已知为坐标原点,点,,,,,则A. B.C. D.10.若a>0,b>0,且a+b=4,则下列不等式恒成立的是( )A. 0<≤B. <2C.D.11.已知函数f(x)=则下列结论正确的是( )A. f(x)是偶函数B. =1C. f(x)是增函数D. f(x)的值域为[-1,+ ∞)12.将函数f(x)=2sin的图象向左平移个单位长度,再向上平移1个单位长度,得到函数g(x)的图象.若g(x1)g(x2)=9,且x1,x2∈[-2π,2π],则2x1-x2的可能取值为()A. -B. -C.D.三、填空题(本大题共4小题,共20.0分)13.已知向量=(1,2),=(2,m),若//(+2),则m=___________.14.已知点为抛物线上一点,点到的焦点的距离为,到轴的距离为,则 .15.已知函数关于点对称,,且函数在区间上单调,则的最大值为________.16.已知函数,若关于的不等式有且仅有两个整数解,则实数的取值范围是___________四、解答题(本大题共6小题,共70.0分。
江苏省灌南高级中学2019-2020学年高一下学期周练数学试题(含答案)

江苏省灌南高级中学2019—2020学年第二学期周练高一数学试卷一、选择题:本大题共12小题,在每小题给出的四个选项中,只有一个符合题目要求,请把答案填写在答题卡相应位置上......... 1.若直线//m α,n ⊂α,则直线,m n 间的位置关系是( )A. 平行B. 异面或平行C. 相交D. 异面2.已知直线30x my +-=的倾斜角为30°,则实数m 的值为( ) A. 3- B. 3- C. 3 D. 33.在ABC ∆中,若sin cos A B a b =,则角B 的大小为( ) A. 30° B. 45︒ C. 60︒ D. 75︒4.已知m 、n 是直线,α、β是平面,下列命题中正确的选项是( )A. 若m α⊥,n ⊂α,则m n ⊥B. 若m 平行于α,则m 平行α内所有直线C. 若m α⊂,n ⊂α,//m β,//n β,则//αβD. αβ⊥,m β⊥,则//m α5.已知直线20ax y a +-+=在两坐标轴上的截距相等,则实数a 等于( )A. 1B. ±1C. 2或1D. -2或16.如图,2AC R =为圆O 的直径,45PCA ∠=o ,PA 垂直于圆O 所在的平面,B 为圆周上不与点A 、C 重合的点,AS PC ⊥于S ,AN PB ⊥于N ,则下列不正确的是( )A. 平面ANS ⊥平面PBCB. 平面ANS ⊥平面PABC. 平面PAB ⊥平面PBCD. 平面ABC ⊥平面PAC7.在圆O 内接四边形ABCD 中,2AB =,6BC =,4CD AD ==,则四边形ABCD面积S 为( )A . 43 B. 63 C. 83 D. 1038.直线1l 过定点()2,1P -与直线2:240l x y +-=的交点位于第一象限,则直线1l 斜率k 的取值范围是( )A. 3122k -<< B. 12k >或32k <- C. 12k ≥或32k ≤- D. 1162k -<<9.如图,四棱锥P ABCD -的底面ABCD 为平行四边形,2=NB PN ,则三棱锥B ACN -与四棱锥P ABCD -的体积比值为( )A . 14 B. 23 C. 12 D. 13 10.在ABC ∆中,1a =,b x =,A ∠=30°则使ABC ∆有两解的x 的范围是( )A. 231,3⎛⎫ ⎪ ⎪⎝⎭B. ()1,+∞C. 23,23⎛⎫ ⎪ ⎪⎝⎭D. ()1,2 11.若点()3,4A 关于直线:l y kx =的对称点在x 轴上,则k 的值是( )A. 12或-2 B. 12-或2 C. 5或-5 D. 4或-412.我国南宋时期著名的数学家秦九韶在其著作《数书九章》中,提出了已知三角形三边长求三角形的面积的公式,与著名的海伦公式完全等价,由此可以看出我国古代已具有很高的数学水平,其求法是:“以小斜幂并大斜幂减中斜幂,余半之,自乘于上.以小斜幂乘大斜幂减上,余四约之,为实.一为从隔,开平方得积.”若把以上这段文字写成公式,即2222221()42a c b S a c ⎡⎤+-=-⎢⎥⎣⎦,其中a 、b 、c 分别为ABC V 内角A 、B 、C 的对边.若2b =,3sin tan 13cos B C B =-,则ABC V 面积S 的最大值为 A. 3 B. 5 C. 3 D. 2二、填空题:本大题共4小题,请把答案填写在答题卡相应位置上......... 13.已知两条直线12:330,:4610.l ax y l x y +-=+-=若12l l //,则a =14.圆柱的一个底面积为4,侧面展开图是一个正方形,那么这个圆柱的侧面积是______.15.在ABC ∆中,23B π=,2AB =,A 的角平分线3AD =,则AC =______. 16.已知钝角ABC ∆三边长,,a b c 满足1a b b c -=-=,其最大角A 不超过120°,则最小角C 的余弦值的取值范围为______.三、解答题:本大题共6小题,请把解答过程写在答题纸的相应位置上.17.在平面直角坐标系xOy 中,已知三角形三个顶点的坐标分别为()4,1A ,()6,3B -,()3,0C ,求:(1)BC 边上的中线AD 所在的直线方程;(2)若BC 边上的高为AE ,求点C 到直线AE 的距离.18.如图四边形ABCD 是正方形,PB ⊥平面ABCD ,MA ⊥平面ABCD ,2PB AB MA ==,(1)求证:平面//AMD 平面BPC ;(2)若点E 为线段PD 中点.证明:ME ⊥平面BDP .19.在ABC ∆中,已知3AB =,4AC =,60A =°.(1)求BC 的长;(2)求sin 2B 的值.20.如图,在四棱锥P ABCD -中,平面PAB ⊥平面ABCD ,BC//平面PAD ,PBC ∠90=o ,90PBA o ∠≠. 求证:(1)//AD 平面PBC ;(2)平面PBC ⊥平面PAB .21.如图为某公园的绿化示意图,准备在道路AB 的一侧进行绿化,线段AB 长为2km ,1OC OD OA OB km ====,设COB θ∠=.(1)为了类化公园周围的环境,现要在四边形ABCD 内种满郁金香,若3COD π∠=,则当θ为何值时,郁金香种植面积最大; (2)为了方便游人散步,现要搭建一条栈道,栈道由线段BC ,CD 和DA 组成,若BC CD =,则当θ为何值时,栈道的总长l 最长,并求l 的最大值.22.设直线l 的方程为()()1520a x y a a R ++--=∈.(1)求证:不论a 为何值,直线l 必过一定点P ;(2)若直线l 分别与x 轴正半轴,y 轴正半轴交于点(),0A A x ,()0,B B y ,当AOB ∆而积最小时,求AOB ∆的周长;(3)当直线l 在两坐标轴上截距均为整数时,求直线l 的方程.江苏省灌南高级中学2019—2020学年第二学期周练高一数学试卷一、(5分*12=60)1.B2.A3.B.4.A.5.C.6.B.7.C.8.D.9.D. 10.D. 11.A. 12.C二、填空题13.2 14.16π 15.6 16.413,514⎛⎤⎥⎝⎦三、解:(1)∵()6,3B -,()3,0C ,则线段BC 的中点为33,22D ⎛⎫- ⎪⎝⎭,∴BC 边上的中线AD 所在的直线方程为14331422y x --=---,整理得:11150x y +-=;(2)由已知得301633BC k -==---,则3AE k =,又()4,1A ,∴BC 边上的高AE 所在直线的方程为()341y x =-+,即3110x y --=,所以点C 到直线AE 的距离为233111031⨯-=+.18.证明:(1)因为PB ⊥平面ABCD ,MA ⊥平面ABCD ,所以PB //MA .因PB ⊂平面BPC ,MA 不在平面BPC 内,所以MA //平面BPC ,同理DA //平面BPC ,因为MA ⊂平面AMD ,AD ⊂平面AMD ,MA ∩AD =A ,所以平面AMD //平面BPC ;(2)连接AC ,设AC ∩BD =F ,连接EF .因ABCD 为正方形,所以F 为BD 中点.因为E 为PD 中点,所以1//2EF PB .因为1//2AM PB ,所以//AM EF , 所以AFEM 为平行四边形. 所以ME //AF .因为PB ⊥平面ABCD ,AF ⊂平面ABCD ,所以PB ⊥AF ,所以ME ⊥PB ,因为ABCD 为正方形,所以AC ⊥BD ,所以ME ⊥BD ,所以ME ⊥平面BDP .19.解:(1)∵在ABC ∆中.已知3AB =,4AC =,60A =°. ∴由余弦定理可得:2212cos 916234132BC AB AC AB AC A =+-⋅⋅=+-⨯⨯⨯=; (2)∵由正弦定理可得:34sin 2392sin 13AC A B BC ⨯⋅===,又22213cos 22313AB BC AC B AB BC +-===⋅⨯⨯Q , 2391343sin 22sin cos 2B B B ∴==⨯⨯=. 20.试题解析:(1)因为BC //平面PAD , 而BC ⊂平面ABCD ,平面ABCD I 平面PAD = AD ,所以BC //AD , 又因为AD ⊄平面PBC ,BC ⊂平面PBC ,所以//AD 平面PBC(2)过P 作PH ⊥AB 于H ,因为平面PAB ⊥平面ABCD ,且平面PAB I 平面ABCD =AB ,所以PH ⊥平面ABCD 因为BC ⊂平面ABCD , 所以BC ⊥PH .因为PBC ∠ 90=o , 所以BC ⊥PB , 而90PBA ∠≠o ,于是点H 与B 不重合,即PB I PH = H . 因为PB ,PH ⊂平面PAB ,所以BC ⊥平面PAB 因为BC ⊂平面PBC ,故平面PBC ⊥平面P A B .21.解:(1)由图可得:111sin sin sin sin 22323264ABCD BOC COD DOA S S S S πθππθθπ⎛⎫⎛⎫=++=++--=++ ⎪ ⎪⎝⎭⎝⎭V V V 203θπ∴<<,则5666ππθπ<+<, sin 16πθ⎛⎫∴+≤ ⎪⎝⎭,此时62ππθ+=,可得3πθ=, ∴则当3πθ=时,郁金香种植面积最大;(2)由余弦定理,2sin 2BC θ==,2cos DA θ==,4sin 2cos 022l θπθθ⎛⎫∴=+<< ⎪⎝⎭, 令sin 2t θ=,则02t <<, ()22214sin 212sin 421243222l t t t θθ⎛⎫⎛⎫∴=+-=+-=--+ ⎪ ⎪⎝⎭⎝⎭, 12t ∴=,即3πθ=时,l 的最大值为3. 22.解:(1)由()1520a x y a ++--=得()250a x x y -++-=,则2050x x y -=⎧⎨+-=⎩,解得23x y =⎧⎨=⎩, 所以不论a 为何值,直线l 必过一定点()2,3P ;(2)由()1520a x y a ++--=得,当0x =时,52B y a =+,当0y =时,521A a x a +=+, 又由5205201B A y a a x a =+>⎧⎪+⎨=>⎪+⎩,得1a >-, ()()119141+121212221252521AOB a a a S a a ⎡⎤⎡⎤∴=⋅++++⋅=≥=⎢⎥⎢⎥+⎣⎦⎣⎦+V , 当且仅当()9411a a +=+,即12a =时,取等号. ()4,0A ∴,()0,6B ,AOB ∴∆的周长为4610OA OB AB ++=+=+(3) 直线l 在两坐标轴上的截距均为整数,即52a +,521a a ++均为整数, 523211a a a +=+++Q ,4,2,0,2a ∴=--, 又当52a =-时,直线l 在两坐标轴上的截距均为零,也符合题意, 所以直线l 的方程为330x y --=,10x y -+=,50x y +-=,390x y +-=,320x y -=.。
最新-灌南高级中学2018学年度第一学期期末复习 精品

灌南高级中学2018-2018学年度第一学期期末复习高三物理试卷命题:审核:18/1/17 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
满分120分。
考试时间100分钟。
第Ⅰ卷(选择题共31分)一.单项选择题:本题共5小题,每小题3分,共15分。
1.16世纪纪末,伽利略用实验和推理,推翻了已在欧洲流行了近两千年的亚里士多德关于力和运动的理论,开启了物理学发展的新纪元.在以下说法中,与亚里士多德观点相反的是( )A.四匹马拉的车比两匹马拉的车跑得快:这说明,物体受的力越大,速度就越大B.一个运动的物体,如果不再受力了,它总会逐渐停下来,这说明,静止状态才是物体长时间不受力时的“自然状态”C.两物体从同—高度自由下落,较重的物体下落较快D.一个物体维持匀速直线运动,不需要受力2.如图所示谴一足够长的固定光滑斜面与水平面的夹角为530,物体A以初速度v1 从斜面顶端水平抛出,物体B在斜面上距顶端L=20m处同时以速度v2沿斜面向下匀加速运动,经历时间t物体A和物体B在斜面上相遇,则下列各组速度和时间中满足条件的是(cos530=0.6,sin530=0.8,g=l0m/s2) ( )A.v1=l5m/s,v2=4m/s,t=4sB.v1=15m/S,v2=6m/S,t=3sC.v1=18m/s,v2=4m/s,t=4sD.v1=18m/S,v2=6m/S,t=3s3.用一根细线一端系一小球(可视为质点),另一端固定在一光滑锥顶上,如图(1)所示,设小球在水平面内作匀速圆周运动的角速度为ω,线的张力为T,则T随ω变化的图像是图(2)中的( )4.一正弦交流电的电压随时间变化的规律如图所示。
由图可知( )A .该交流电的电压瞬时值的表达式为u =B .该交流电的频率为50 HzC .该交流电的电压的有效值为D .若将该交流电压加在阻值R=100 Ω 5.如图所示,一轻弹簧左端固定在长木板M 的左端,右端与小木块m 连接,且m ,M 及M 与地面间摩擦不计.开始时,m 和M 均静止,现同时对m ,M 施加等大反向的水平恒力F l 和F 2,设两物体开始运动以后的整个运动过程中,弹簧形变不超过其弹性限度.对于m ,M 和弹簧组成的系统 ( )A .由于F 1,F 2等大反向,故系统机械能守恒B .当弹簧弹力大小与F l ,F 2大小相等时,rn ,M 各自的动能最大C .由于F 1,F 2大小不变,所以m ,M 各自一直做匀加速运动D .由于F 1,F 2均能做正功。
灌南县高级中学2018-2019学年高三上学期11月月考数学试卷含答案

灌南县高级中学2018-2019学年高三上学期11月月考数学试卷含答案一、选择题1. 设函数的集合,平面上点的集合,则在同一直角坐标系中,P 中函数的图象恰好经过Q 中两个点的函数的个数是A4B6C8D102. 下列语句所表示的事件不具有相关关系的是( )A .瑞雪兆丰年B .名师出高徒C .吸烟有害健康D .喜鹊叫喜 3. 等差数列{a n }中,a 1+a 5=10,a 4=7,则数列{a n }的公差为( )A .1B .2C .3D .44. 设函数()''y f x =是()'y f x =的导数.某同学经过探究发现,任意一个三次函数()()320f x ax bx cx d a =+++≠都有对称中心()()00,x f x ,其中0x 满足()0''0f x =.已知函数()3211533212f x x x x =-+-,则1232016...2017201720172017f f f f ⎛⎫⎛⎫⎛⎫⎛⎫++++= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭( )A .2013 B .2014 C .2015 D .20161111]5. 下列命题正确的是()A .很小的实数可以构成集合.B .集合{}2|1y y x =-与集合(){}2,|1x y y x =-是同一个集合.C .自然数集 N 中最小的数是.D .空集是任何集合的子集.6. 已知函数在处取得最大值,则函数的图象( )sin(2)y x ϕ=+6x π=cos(2)y x ϕ=+A .关于点对称B .关于点对称(0)6π,(0)3π,C .关于直线对称D .关于直线对称6x π=3x π=7. 如图,长方形ABCD 的长AD=2x ,宽AB=x (x ≥1),线段MN 的长度为1,端点M 、N 在长方形ABCD 的四边上滑动,当M 、N 沿长方形的四边滑动一周时,线段MN 的中点P 所形成的轨迹为G ,记G 的周长与G 围成的面积数值的差为y ,则函数y=f (x )的图象大致为()班级_______________ 座号______ 姓名_______________ 分数__________________________________________________________________________________________________________________A .B .C .D .8. 已知函数f (x )=xe x ﹣mx+m ,若f (x )<0的解集为(a ,b ),其中b <0;不等式在(a ,b )中有且只有一个整数解,则实数m 的取值范围是( )A .B .C .D .9. 袋中装有红、黄、蓝三种颜色的球各2个,无放回的从中任取3个球,则恰有两个球同色的概率为( )A .B .C .D .10.已知集合A={﹣1,0,1,2},集合B={0,2,4},则A ∪B 等于( )A .{﹣1,0,1,2,4}B .{﹣1,0,2,4}C .{0,2,4}D .{0,1,2,4}11.若复数满足(为虚数单位),则复数的虚部为( )71i i z+=A .1 B . C .D .1-i-12.已知全集,集合,集合,则集合为R U ={|||1,}A x x x R =≤∈{|21,}xB x x R =≤∈U AC B I ( ) A.B.C.D.]1,1[-]1,0[]1,0()0,1[-【命题意图】本题考查集合的运算等基础知识,意在考查运算求解能力.二、填空题13.设函数f (x )=则函数y=f (x )与y=的交点个数是 .14.等差数列的前项和为,若,则等于_________.{}n a n S 37116a a a ++=13S 15.如图:直三棱柱ABC ﹣A ′B ′C ′的体积为V ,点P 、Q 分别在侧棱AA ′和CC ′上,AP=C ′Q ,则四棱锥B ﹣APQC 的体积为 .16.,分别为双曲线(,)的左、右焦点,点在双曲线上,满足,1F 2F 22221x y a b-=a 0b >P 120PF PF ⋅=u u u r u u u u r 若,则该双曲线的离心率为______________.12PF F ∆【命题意图】本题考查双曲线的几何性质,直角三角形内切圆半径与外接圆半径的计算等基础知识,意在考查基本运算能力及推理能力.17.平面向量,满足|2﹣|=1,|﹣2|=1,则的取值范围 .18.已知函数,则__________;的最小值为__________.三、解答题19.本小题满分10分选修:几何证明选讲41-如图,是⊙的内接三角形,是⊙的切线,切点为,交于点,交⊙于点,ABC ∆O PA O A PB AC E O D ,,,.PE PA =︒=∠45ABC 1=PD 8=DB Ⅰ求的面积;ABP ∆Ⅱ求弦的长.AC 20.已知函数(a ≠0)是奇函数,并且函数f (x )的图象经过点(1,3),(1)求实数a ,b 的值;(2)求函数f (x)的值域.21.(本小题满分12分)已知.1()2ln ()f x x a x a R x=--∈(Ⅰ)当时,求的单调区间;3a =()f x (Ⅱ)设,且有两个极值点,其中,求的最小值.()()2ln g x f x x a x =-+()g x 1[0,1]x ∈12()()g x g x -【命题意图】本题考查导数的应用等基础知识,意在考查转化与化归思想和综合分析问题、解决问题的能力.22.(本小题满分12分)设03πα⎛⎫∈ ⎪⎝⎭,αα+=(1)求cos 6πα⎛⎫+ ⎪⎝⎭的值;(2)求cos 212πα⎛⎫+ ⎪⎝⎭的值.23.已知函数f (x )=2cos 2ωx+2sin ωxcos ωx ﹣1,且f (x )的周期为2.(Ⅰ)当时,求f (x )的最值;(Ⅱ)若,求的值.24.某校举办学生综合素质大赛,对该校学生进行综合素质测试,学校对测试成绩(10分制)大于或等于7.5的学生颁发荣誉证书,现从A 和B 两班中各随机抽5名学生进行抽查,其成绩记录如下:A777.599.5B6x8.58.5y由于表格被污损,数据x,y看不清,统计人员只记得x<y,且A和B两班被抽查的5名学生成绩的平均值相等,方差也相等.(Ⅰ)若从B班被抽查的5名学生中任抽取2名学生,求被抽取2学生成绩都颁发了荣誉证书的概率;(Ⅱ)从被抽查的10名任取3名,X表示抽取的学生中获得荣誉证书的人数,求X的期望.灌南县高级中学2018-2019学年高三上学期11月月考数学试卷含答案(参考答案)一、选择题题号12345678910答案B D B D D A C C B A题号1112答案A C.二、填空题13. 4 .14.2615.V16117. [,1] .18.三、解答题19.20.21.22.(1;(2.23.24.。
江苏省灌南高级中学高三数学 高三数学周练试卷复习

FED 1C 1B 1BCD A 1A一.填空题1. 已知复数),(R y x yi x z ∈+=,且5)21(=+z i ,则=+y x . 2.集合{}*523M x x N=--∈,则M 的非空真子集的个数是 .3. 设函数()f x 是定义在R 上的偶函数,当0x ≥时,()21xf x =+,若()3f a =,则实数a 的值为 .4. 方程lg(2)1x x +=有 个不同的实数根5. 不等式11112-≥-x x 的解集为 6. 直线(2m 2+m-3)x+(m 2-m)y=4m-1与直线2x-3y=5平行,则m=7. 已知)2sin ,2(),sin ,1(2x b x a ==,其中()0,x π∈,若a b a b ⋅=⋅, 则tan x = .8. 在等腰三角形ABC 中, 底边2=BC , DC AD =, 12AE EB =, 若12BD AC ⋅=-, 则AB CE ⋅= .9.32121212()1,()[()()]0f x x x mx x x R x x f x f x =+++∈-->对任意满足(21x x ≠),则实数m 的取值范围是10. 已知B 为双曲线22221(0,0)x y a b a b-=>>的左准线与x 轴的交点, (0,)A b ,若满足2AP AB =的点P 在双曲线上,则该双曲线的离心率为 .11. 如图,在直四棱柱1111ABCD A B C D -中,点,E F 分别在11,AA CC 上,且134AE AA =,113CF CC =,点,A C 到BD 的距离之比为3:2,则三棱锥E BCD -和F ABD -的体积比E BCDF ABDV V --= ______.12. 已知函数ln ,1()1(2)(),1x x f x x x a x e≥⎧⎪=⎨+-<⎪⎩(a 为常数,e 为自然对数的底数)的图象在点(,1)A e 处的切线与该函数的图象恰好有三个公共点,则实数a 的取值范围是 . 二.解答题13.已知向量(cos ,sin )A A =-m ,(cos ,sin )B B =n ,cos2C ⋅=m n ,其中,,A B C 为ABC ∆的内角.(1)求角C 的大小;(2)若6AB =,且18CA CB ⋅=,求,AC BC 的长.15. 某建筑公司要在一块宽大的矩形地面(如图所示)上进行开发建设,阴影部分为一公共设施建设不能开发,且要求用栏栅隔开(栏栅要求在一直线上),公共设施边界为曲线f (x )=1﹣ax 2(a >0)的一部分,栏栅与矩形区域的边界交于点M 、N ,交曲线于点P ,设P (t ,f (t )).(1)将△OMN (O 为坐标原点)的面积S 表示成t 的函数S (t ); (2)若在t=处,S (t )取得最小值,求此时a 的值及S (t )的最小值.16.椭圆C :2222+1x y a b =(a >b >0)的离心率为12,其左焦点到点P(2,1)的距离为10.不过原点O 的直线l 与C 相交于A ,B 两点,且线段AB 被直线OP 平分.(Ⅰ)求椭圆C 的方程;(Ⅱ) 求∆ABP 的面积取最大时直线l 的方程.13. 解:(Ⅰ)cos cos sin sin cos()cos A B A B A B C ⋅=-=+=-m n , 所以cos cos2C C -=,即22cos cos 10C C +-=故1cos 2C =或cos 1C =-(舍), 又0C π<<,所以3C π=.(Ⅱ)因为18CA CB ⋅=,所以36CA CB ⨯=. ①由余弦定理2222cos60AB AC BC AC BC =+-⋅⋅︒,及6AB =得,12AC BC +=. ② 由①②解得6,6AC BC ==. 14.证明:(Ⅰ)取PD 中点G ,连,AG FG ,因为F 、G 分别为PC 、PD 的中点,所以FG ∥CD ,且12FG CD =. 又因为E 为AB 中点,所以AE ∥CD ,且12AE CD =. 所以AE ∥FG ,AE FG =.故四边形AEFG 为平行四边形.所以EF ∥AG ,又EF ⊄平面PAD ,AG ⊂平面PAD , 故EF ∥平面PAD . (Ⅱ)设ACDE H =,由AEH ∆∽CDH ∆及E 为AB 中点得12AG AE CG CD ==, 又因为2AB =,1BC =,所以3AC =,133AG AC ==.所以23AG AB AE AC ==,又BAC ∠为公共角,所以GAE ∆∽BAC ∆. 所以90AGE ABC ∠=∠=︒,即DE AC ⊥. 又DE PA ⊥,PAAC A =,所以DE ⊥平面PAC . 又DE ⊂平面PDE ,所以平面PAC ⊥平面PDE .15. 解:(1)∵曲线f (x )=1﹣ax 2(a >0) 可得f′(x )=﹣2ax ,P (t ,f (t )).直线MN 的斜率为:k=f′(t )=﹣2at ,可得 L MN :y ﹣f (t )=k (x ﹣t )=﹣2at (x ﹣t ), 令y=0,可得x M =t+,可得M (t+,0);令x=0,可得y M =1+at 2,可得N (0,1+at 2), ∴S(t )=S △OMN =×(1+at 2)×=;(2)t=时,S (t )取得最小值,S′(t )==,∴S′()=0,可得12a 2×﹣4a=0,可得a=,此时可得S (t )的最小值为S ()===;16. (Ⅰ)由题:12c e a ==; (1) 左焦点(﹣c ,0)到点P(2,1)的距离为:22(2)1d c =++=10. (2)由(1) (2)可解得:222431a b c ===,,.∴所求椭圆C 的方程为:22+143x y =.(Ⅱ)易得直线OP 的方程:y =12x ,设A(x A ,y A ),B(x B ,y B ),R(x 0,y 0).其中y 0=12x 0.∵A ,B 在椭圆上, ∴220220+12333434422+143A A A B A B AB A B A B B B x y x y y x x k x x y y y x y ⎧=⎪-+⎪⇒==-⨯=-⨯=-⎨-+⎪=⎪⎩.设直线AB 的方程为l :y =﹣32x m +(m ≠0),代入椭圆:2222+143333032x y x mx m y x m ⎧=⎪⎪⇒-+-=⎨⎪+⎪⎩=-.显然222(3)43(3)3(12)0m m m ∆=-⨯-=->. ∴﹣12<m <12且m ≠0.由上又有:A B x x +=m ,A B y y +=233m -.∴|AB|=1AB k +|A B x x -|=1AB k +2()4A B A B x x x x +-=1ABk +243m -. ∵点P(2,1)到直线l 的距离表示为:31211ABABm m d k k -+-+==++.∴S ∆ABP =12d|AB|=12|m +2|243m -,当|m +2|=243m -,即m =﹣3 或m =0(舍去)时,(S ∆ABP )max =12.此时直线l 的方程y =﹣3122x +. 17. 解:(1)设等差数列的公差为d ,等比数列的公比为q ,则123451,2,1,2,12a a a d a q a d ===+==+34,12(1)2,42S a d q d q =∴++=+=即又3542a a a +=+,(1)(12)22,32d d q d q ++=+=即,解得2,3d q ==∴对于k N *∈,有12121(1)221,23k k k a k k a --=+-⋅=-=⋅故12,21,23,2nn n n k a k N n k*-=-⎧⎪=∈⎨⎪⋅=⎩- (2)22(121)2(13)13213k k kk k S k +--=+=-+-(3)在数列{}n a 中,仅存在连续的三项123,,a a a ,按原来的顺序成等差数列,此时正整数m 的值为1,下面说明理由 若2m k a a =,则由212m m m a a a +++=,得123232(21)k k k -⋅+⋅=+化简得14321k k -⋅=+,此式左边为偶数,右边为奇数,不可能成立若21m k a a -=,则由212m m m a a a +++=,得1(21)(21)223k k k --++=⋅⋅化简得13k k -=令1,()3k k k T k N *-=∈,则111120333k k k k kk k k T T +-+--=-=<因此,1231T T T =>>>,故只有11T =,此时1,2111k m ==⨯-=综上,在数列{}n a 中,仅存在连续的三项123,,a a a ,按原来的顺序成等差数列,此时正整数m 的值为1。
江苏灌南高级中学2019高三上年中考试试题-语文

江苏灌南高级中学2019高三上年中考试试题-语文【一】语言文字运用〔15分〕1、以下词语中加点的字,每对读音都不相同的一组是〔3分〕〔〕A、遒劲.∕劲.头震颤.∕冷颤炮..制∕炮.烙纰.漏∕砒.霜B、伛偻.∕佝偻.积攒.∕攒.动剽.窃∕剽.悍祈.祷∕颀.长C、殷.切∕殷.忧冠.冕∕冠.军倾轧.∕轧.钢蛰.伏∕海蜇.D、拾.级∕捡拾巷..陌∕巷.道曲.折∕歌曲.笑靥.∕梦魇.2、以下加点词语运用正确的一项为哪一项〔3分〕〔〕A、特别的想象天赋成全了莫言,使他在从取材炼意乃至细节描写诸方面都获得了高度自由,在创作的“自由王国”里如鱼得水,几近达到了呼风唤雨、撒豆成兵、点石成金....的境界。
B、特别多同学总是认为,平时因为时间关系,马虎点没关系,考试时认真就能够了。
因而对卷面不以为然....。
殊不知,一个良好的适应的养成绝不是一朝一夕的功夫。
C、在久居大陆的人的眼里,大海的一吟一荡基本上诗。
可从小在海边长大的人,早已司.空见惯...了归帆片片,鸥影点点。
D、他的音质特别好,惋惜师出无名....,假如能有名师指点,他在音乐上确信会有光明的前途。
3、概括下面这段文字是从哪几方面来介绍莫言的小说《生死轮回》的。
〔4分〕小说表达了1950年到2000年中国农村50年的历史,围绕土地那个沉重的话题,阐释农民与土地的种种关系,并透过生死轮回的艺术图像,展示了建国以来中国农民饱经患难的生活和他们坚韧、乐观、坚韧的生命。
小说的表达者,在六道轮回中,一世为人、一世为马、一世为牛……从不同的视角讲述他所看到的故事。
故情况节极端、怪异、变形、荒诞,然而与寄寓其中的哲理浑然天成。
究其所达到的艺术境界而言,这是当今文坛一部划时代的史诗性作品,是中国文学终于跳出图解概念沼泽最辉煌的标志性著作。
答:4.南京名园瞻园中有一副对联,其下联的句序、有的句子内部结构已被打乱,请依照所给出的上联,进行适当的调整〔5分〕上联:大江东去,浪淘尽千古英雄,问楼外青山,山外白云,何处是唐宫汉阙?下联的内容:红雨树边,小苑西回,一庭佳丽莺唤起,看池边绿树,此间有尧天舜日。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
江苏省灌南高级中学2018-2019学年度高三年级上学期周练数学试卷(9.8)一、填空题:本大题共14个小题,每小题5分,共70分.1.函数1y x =-的定义域为A ,函数lg(2)y x =-的定义域为B ,则A B = .2.写出命题“0x ∃>,210x -≤”的否定: . 3.函数2(sin cos )y x x =+的最小正周期是 .4.设向量a ,b 不平行,向量a b λ+ 与2a b +平行,则实数λ= .5.已知复数 z =11i-,其中 i 是虚数单位,则z i += 6.已知角α的终边经过点(1,3)-,则sin()2πα+的值为 .7.函数1ln y x=(x e ≥)的值域是 . 8.“2πϕ=”是“函数sin()y x ϕ=+的图象关于y 轴对称的” 条件(填“充分必要”、“充分不必要”、“必要不充分”、“既不充分也不必要”).9.设函数2()sin f x a x x =+,若(1)0f =,则(1)f -的值为 . 10.若函数2()'(1)x f x x e f x =⋅+⋅,则'(1)f = .11. 如图,函数()2sin()f x x ωϕ=+(0ω>,2πϕπ≤≤)的部分图象,其中A ,B 分别是图中的最高点和最低点,且5AB =,那么ωϕ+的值为 .12.如图,在ABC ∆中,120BAC ∠=︒,2AB AC ==,D 为BC 边上的点,且0AD BC ⋅= ,2CE EB = ,则AD AE ⋅=.13.若关于x 的方程1ln kx x +=有解,则实数k 的取值范围是 .14.下列有关命题的说法正确的是 (请填写所有正确的命题序号). ①命题“若21x =,则1x =”的否命题为:“若21x =,则1x ≠”; ②命题“若x y =,则sin sin x y =”的逆否命题为真命题;③条件p :2x x ≥-,条件q :||x x =,则p 是q 的充分不必要条件;④已知0x >时,(1)'()0x f x -<,若ABC ∆是锐角三角形,则(sin )(cos )f A f B >.二、解答题 (本大题共6小题,共90分.解答应写出文字说明、证明过程或演算步骤.)15.已知m R ∈,复数22(23)1m z m m i m +=+--+(i 是虚数单位). (1)若复数z 是实数,求m 的值;(2)若复数z 对应的点位于复平面的第二象限,求m 的取值范围.16.(本小题满分14分)已知函数()22sin sin 6f x x x π⎛⎫=-- ⎪⎝⎭,[0,]2x π∈(1)求()f x 的值域;(2)若ABC ∆的面积为332,角C 所对的边为c ,且1()2f C =,7c =,求ABC ∆的周长.17.(本小题满分14分)二次函数2(0)y x bx b =+≠图像与x 轴交于O ,A 两点,交直线:l y x =于O ,B 两点,经过三点O ,A ,B 作圆C .(1)求证:当b 变化时,圆C 的圆心在一条定直线上; (2)求证:圆C 经过除原点外的一个定点.18. 因客流量临时增大,某鞋店拟用一个高为50cm (即50EF cm =)的平面镜自制一个竖直摆放的简易鞋镜,根据经验:一般顾客AB 的眼睛B 到地面的距离为x (cm )在区间[140,180]内,设支架FG 高为h (090h <<)cm ,100AG cm =,顾客可视的镜像范围为CD (如图所示),记CD 的长度为y (y GD GC =-).(I )当40h cm =时,试求y 关于x 的函数关系式和y 的最大值; (II )当顾客的鞋A 在镜中的像1A 满足不等关系1GC GA GD <≤(不计鞋长)时,称顾客可在镜中看到自己的鞋,若使一般顾客都能在镜中看到自己的鞋,试求h 的取值范围.19. 已知函数()ln 2f x a x ax =--(a R ∈). (1)当0a >时,求函数()f x 的单调区间;(2)若函数()y f x =的图象在点(2,(2))f 处的切线的倾斜角为45︒,且函数21()'()2g x x nx mf x =++(,m n R ∈)当且仅当在1x =处取得极值,其中'()f x 为()f x 的导函数,求m 的取值范围.20.已知函数()()()3244f x x a x a b x c =+--++(),,a b c ∈R 有一个零点为4,且满足()01f =. (1)求实数b 和c 的值;(2)试问:是否存在这样的定值0x ,使得当a 变化时,曲线()y f x =在点()()00,x f x 处的切线互相平行?若存在,求出0x 的值;若不存在,请说明理由; (3)讨论函数()()g x f x a =+在()0,4上的零点个数.试卷答案一、选择题1. [1,2)2.0x ∀>,210x ->3.π4.125.210 6.1-2 7.(0,1]8.充分不必要 9.210.2e -11.76π 12.113.21(,]e -∞ 14.②④二、解答题15.(1)m=-3,(2)(-2,-1)16. 解:(1)1cos 21cos211313()cos2sin 2cos2222222x x f x x x x π⎛⎫-- ⎪⎛⎫-⎝⎭=-=+- ⎪⎝⎭311sin 2cos 2sin 24426x x x π⎛⎫=--=- ⎪⎝⎭. [0,]2x π∈ ,52[,]666x πππ∴-∈-,故11()[,]42f x ∈-.(2)由已知,133sin C 22ab =.由1()2f C =,得C 3π=,所以6ab =. 由已知及余弦定理得,222cosC 7a b ab +-=.故2213a b +=,从而()225a b +=.所以C ∆AB 的周长为57+.17.解:(I )在方程y=x 2+bx 中.令y=0,y=x ,易得A (﹣b ,0),B (1﹣b ,1﹣b ) 设圆C 的方程为x 2+y 2+Dx+Ey=0,则⇒,故经过三点O ,A ,B 的圆C 的方程为x 2+y 2+bx+(b ﹣2)y=0, 设圆C 的圆心坐标为(x 0,y 0), 则x 0=﹣,y 0=﹣,∴y 0=x 0+1,这说明当b 变化时,(I )中的圆C 的圆心在定直线y=x+1上.(II )设圆C 过定点(m ,n ),则m 2+n 2+bm+(b ﹣2)n=0,整理得(m+n )b+m 2+n 2﹣2n=0,它对任意b ≠0恒成立,∴⇒或故当b 变化时,(I )中的圆C 经过除原点外的一个定点坐标为(﹣1,1).18.解(1)因为40FG =,100AG =,所以由GC GC AG FG AB +=,即10040GC GC x +=,解得400040GC x =-,同理,由GD GD AG EG AB +=,即10090GD GD x +=,解得900090GD x =-,所以2941000()500090401303600xy GD GC x x x x =-=⨯-=⨯---+,[140,180]x ∈因为2223600'50000(1303600)x y x x -=⨯<-+,所以y 在[140,180]上单调递减,故当140x cm =时,y 取得最大值为140cm (2)由100GC GC h x +=,得100h GC x h =-,由10050GD GD h x +=+,得100(50)50h GD x h +=--,所以由题意知1GC AG AG GD <=≤,即100100(50)10050h h x h x h +<≤---对[140,180]x ∈恒成立,从而2502xh x h ⎧<⎪⎪⎨⎪≥-⎪⎩对[140,180]x ∈恒成立,解得14070218050402h h ⎧<=⎪⎪⎨⎪≥-=⎪⎩,故h 的取值范围是[40,70)19.解:(1)(1)'()a x f x x-=(0x >),当0a >时,令'()0f x >得01x <<,令'()0f x <得1x >,故函数()f x 的单调递增区间为(0,1),单调递减区间为(1,)+∞; (2)由题意可知'(2)1f =,即2a =-;所以212()(2)2g x x nx m x =++-,所以322222'()m x nx mg x x n x x++=++=,因为()g x 在1x =处有极值,故'(1)0g =,从而可得12n m =--,则322222(1)(22)'()x nx m x x mx m g x x x ++---==,又因为()g x 仅在1x =处有极值,所以2220x mx m --≥在(0,)+∞上恒成立,当0m >时,由20m -<,显然0(0,)x ∃∈+∞,使得200220x mx m --<,所以0m >不成立,当0m ≤且(0,)x ∈+∞时,2220x mx m --≥恒成立,所以0m ≤.20.解:(1)由题意()()01440f c f b c =+⎧⎪⎨=-+=⎪⎩,解得141b c ⎧=⎪⎨⎪=⎩;(2)由(1)可知()()324f x x a x =+--1414a x ⎛⎫++ ⎪⎝⎭, ∴()()2132444f x x a x a ⎛⎫'=+--+⎪⎝⎭; 假设存在0x 满足题意,则()()2000132444f x x a x a ⎛⎫'=+--+ ⎪⎝⎭是一个与a 无关的定值, 即()2000124384x a x x -+--是一个与a 无关的定值, 则0240x -=,即02x =,平行直线的斜率为()1724k f '==-; (3)()()()324g x f x a x a x =+=+-1414a x a ⎛⎫-+++ ⎪⎝⎭, ∴()()2132444g x x a x a ⎛⎫'=+--+⎪⎝⎭, 其中()21441244a a ⎛⎫∆=-++= ⎪⎝⎭()224166742510a a a ++=++>, 设()0g x '=两根为1x 和()212x x x <,考察()g x 在R 上的单调性,如下表1°当0a >时,()010g a =+>,()40g a =>,而()152302g a =--<,∴()g x 在()0,2和()2,4上各有一个零点,即()g x 在()0,4有两个零点; 2°当0a =时,()010g =>,()40g a ==,而()15202g =-<, ∴()g x 仅在()0,2上有一个零点,即()g x 在()0,4有一个零点; 3°当0a <时,()40g a =<,且13024g a ⎛⎫=->⎪⎝⎭, ①当1a <-时,()010g a =+<,则()g x 在10,2⎛⎫ ⎪⎝⎭和1,42⎛⎫⎪⎝⎭上各有一个零点, 即()g x 在()0,4有两个零点;②当10a -≤<时,()010g a =+≥,则()g x 仅在1,42⎛⎫⎪⎝⎭上有一个零点, 即()g x 在()0,4有一个零点;综上:当1a <-或0a >时,()g x 在()0,4有两个零点; 当10a -≤≤时,()g x 在()0,4有一个零点.。
