2019年第十一届全国大学生数学竞赛
不动点定理与Picard迭代数列的收敛性--不动点方法在大学生数学竞赛试题解题中的应用

| | | xn - xn-1| = f (xn - 1) - f (xn-2) ≤ L| xn - 1 - | xn - 2 ,0 < L < 1 ,
{ 下证 xn} 为有界变差数列.事实上,
| | | | | | | | xn - xn - 1 ≤ r xn - 1 - xn - 2 ≤ r2 xn - 2 - xn - 3 ≤ ⋯ ≤ rn - 2 x2 - x1 (n ≥ 3) ,
第 42 卷第 3 期 2021 年 6 月
韩山师范学院学报 Journal of Hanshan Normal University
Vol.42 No.3 Jun.2021
不动点定理与 Picard 迭代数列的收敛性
——不动点方法在大学生数学竞赛试题解题中的应用
许绍元 1,程素玉 2
(1.韩山师范学院 数学与统计学院,广东 潮州 521041;2.韩山师范学院 图书馆,广东 潮州 521041)
( ) xn + 1 = f (xn) , 令 n → ∞ , 由 函 数 f (x) 的 连 续 性 有 nli→m∞xn + 1 = nli→m∞ f (xn) = f nli→m∞xn , 即 x0 = f (x0) . 下 证
x0 = 0 .反证法.若 x0≠ 0 则 0 < x0 < a ,再由题设可知 x0 = f (x0) < x0 ,矛盾.故 nli→m∞xn = 0 .证毕. 在定理 1 中,将 f (x) 的定义域扩大为 [0, +∞) ,得到下面的结论. 推论1 设函数 f (x) 在 [0, +∞) 上连续,且 0 < f (x) < x,x ∈(0, +∞) .作Picard迭代 xn + 1 = f (xn), x1∈(0, +∞) .
【2019年整理】全国大学生数学竞赛简介

全国大学生数学竞赛第一届2009年,第一届全国大学生数学竞赛由中国数学会主办、国防科学技术大学承办。
该比赛将推动高等学校数学课程的改革和建设,提高大学数学课程的教学水平,激励大学生学习数学的兴趣,发现和选拔数学创新人才。
第二届2011年3月,历时十个月的第二届全国大学生数学竞赛在北京航空航天大学落幕。
来自北京、上海、天津、重庆等26个省(区、市)数百所大学的274名大学生进入决赛,最终,29人获得非数学专业一等奖,15人获数学专业一等奖。
这次赛事预赛报名人数达3万余人,已成为全国影响最大、参加人数最多的学科竞赛之一。
竞赛用书该比赛指导用书为《大学生数学竞赛指导》,由国防科技大学大学数学竞赛指导组组织编写,已经由清华大学出版社出版。
竞赛大纲中国大学生数学竞赛竞赛大纲(2009年首届全国大学生数学竞赛)为了进一步推动高等学校数学课程的改革和建设,提高大学数学课程的教学水平,激励大学生学习数学的兴趣,发现和选拔数学创新人才,更好地实现“中国大学生数学竞赛”的目标,特制订本大纲。
1.竞赛的性质和参赛对象“中国大学生数学竞赛”的目的是:激励大学生学习数学的兴趣,进一步推动高等学校数学课程的改革和建设,提高大学数学课程的教学水平,发现和选拔数学创新人才。
“中国大学生数学竞赛”的参赛对象为大学本科二年级及二年级以上的在校大学生。
1.竞赛的内容“中国大学生数学竞赛”分为数学专业类竞赛题和非数学专业类竞赛题。
(一)中国大学生数学竞赛(数学专业类)竞赛内容为大学本科数学专业基础课的教学内容,即,数学分析占50%,高等代数占35%,解析几何占15%,具体内容如下:Ⅰ、数学分析部分1.集合与函数2. 1. 实数集、有理数与无理数的稠密性,实数集的界与确界、确界存在性定理、闭区间套定理、聚点定理、有限覆盖定理.3. 2. 上的距离、邻域、聚点、界点、边界、开集、闭集、有界(无界)集、上的闭矩形套定理、聚点定理、有限覆盖定理、基本点列,以及上述概念和定理在上的推广.4. 3. 函数、映射、变换概念及其几何意义,隐函数概念,反函数与逆变换,反函数存在性定理,初等函数以及与之相关的性质.5.极限与连续6. 1. 数列极限、收敛数列的基本性质(极限唯一性、有界性、保号性、不等式性质).7. 2. 数列收敛的条件(Cauchy准则、迫敛性、单调有界原理、数列收敛与其子列收敛的关系),极限及其应用.8. 3.一元函数极限的定义、函数极限的基本性质(唯一性、局部有界性、保号性、不等式性质、迫敛性),归结原则和Cauchy收敛准则,两个重要极限及其应用,计算一元函数极限的各种方法,无穷小量与无穷大量、阶的比较,记号O与o的意义,多元函数重极限与累次极限概念、基本性质,二元函数的二重极限与累次极限的关系.9. 4. 函数连续与间断、一致连续性、连续函数的局部性质(局部有界性、保号性),有界闭集上连续函数的性质(有界性、最大值最小值定理、介值定理、一致连续性).10.一元函数微分学11.1.导数及其几何意义、可导与连续的关系、导数的各种计算方法,微分及其几何意义、可微与可导的关系、一阶微分形式不变性.12.2.微分学基本定理:Fermat定理,Rolle定理,Lagrange定理,Cauchy定理,Taylor公式(Peano余项与Lagrange余项).13.3.一元微分学的应用:函数单调性的判别、极值、最大值和最小值、凸函数及其应用、曲线的凹凸性、拐点、渐近线、函数图象的讨论、洛必达(L'Hospital)法则、近似计算.14.多元函数微分学15.1. 偏导数、全微分及其几何意义,可微与偏导存在、连续之间的关系,复合函数的偏导数与全微分,一阶微分形式不变性,方向导数与梯度,高阶偏导数,混合偏导数与顺序无关性,二元函数中值定理与Taylor公式.16.2.隐函数存在定理、隐函数组存在定理、隐函数(组)求导方法、反函数组与坐标变换.17.3.几何应用(平面曲线的切线与法线、空间曲线的切线与法平面、曲面的切平面与法线).18.4.极值问题(必要条件与充分条件),条件极值与Lagrange乘数法.19.一元函数积分学20.1. 原函数与不定积分、不定积分的基本计算方法(直接积分法、换元法、分部积分法)、有理函数积分:型,型.21.2. 定积分及其几何意义、可积条件(必要条件、充要条件:)、可积函数类.22.3. 定积分的性质(关于区间可加性、不等式性质、绝对可积性、定积分第一中值定理)、变上限积分函数、微积分基本定理、N-L公式及定积分计算、定积分第二中值定理.23.4.无限区间上的广义积分、Canchy收敛准则、绝对收敛与条件收敛、非负时的收敛性判别法(比较原则、柯西判别法)、Abel判别法、Dirichlet 判别法、无界函数广义积分概念及其收敛性判别法.24.5. 微元法、几何应用(平面图形面积、已知截面面积函数的体积、曲线弧长与弧微分、旋转体体积),其他应用.25.多元函数积分学26.1.二重积分及其几何意义、二重积分的计算(化为累次积分、极坐标变换、一般坐标变换).27.2.三重积分、三重积分计算(化为累次积分、柱坐标、球坐标变换).28.3.重积分的应用(体积、曲面面积、重心、转动惯量等).29.4.含参量正常积分及其连续性、可微性、可积性,运算顺序的可交换性.含参量广义积分的一致收敛性及其判别法,含参量广义积分的连续性、可微性、可积性,运算顺序的可交换性.30.5.第一型曲线积分、曲面积分的概念、基本性质、计算.31.6.第二型曲线积分概念、性质、计算;Green公式,平面曲线积分与路径无关的条件.32.7.曲面的侧、第二型曲面积分的概念、性质、计算,奥高公式、Stoke公式,两类线积分、两类面积分之间的关系.33.无穷级数34.1. 数项级数级数及其敛散性,级数的和,Cauchy准则,收敛的必要条件,收敛级数基本性质;正项级数收敛的充分必要条件,比较原则、比式判别法、根式判别法以及它们的极限形式;交错级数的Leibniz判别法;一般项级数的绝对收敛、条件收敛性、Abel判别法、Dirichlet判别法.1.函数项级数函数列与函数项级数的一致收敛性、Cauchy准则、一致收敛性判别法(M-判别法、Abel判别法、Dirichlet判别法)、一致收敛函数列、函数项级数的性质及其应用.1.幂级数幂级数概念、Abel定理、收敛半径与区间,幂级数的一致收敛性,幂级数的逐项可积性、可微性及其应用,幂级数各项系数与其和函数的关系、函数的幂级数展开、Taylor级数、Maclaurin级数.1.Fourier级数三角级数、三角函数系的正交性、2及2周期函数的Fourier级数展开、 Beseel 不等式、Riemanm-Lebesgue定理、按段光滑函数的Fourier级数的收敛性定理. Ⅱ、高等代数部分1.多项式2. 1. 数域与一元多项式的概念3. 2. 多项式整除、带余除法、最大公因式、辗转相除法4. 3. 互素、不可约多项式、重因式与重根.5. 4. 多项式函数、余数定理、多项式的根及性质.6. 5.代数基本定理、复系数与实系数多项式的因式分解.7. 6. 本原多项式、Gauss引理、有理系数多项式的因式分解、Eisenstein判别法、有理数域上多项式的有理根.8.7. 多元多项式及对称多项式、韦达(Vieta)定理.9.行列式10.1. n级行列式的定义.11.2. n级行列式的性质.12.3. 行列式的计算.13.4. 行列式按一行(列)展开.14.5.拉普拉斯(Laplace)展开定理.15.6. 克拉默(Cramer)法则.16.线性方程组17.1.高斯(Gauss)消元法、线性方程组的初等变换、线性方程组的一般解.18.2. n维向量的运算与向量组.19.3. 向量的线性组合、线性相关与线性无关、两个向量组的等价.20.4. 向量组的极大无关组、向量组的秩.21.5.矩阵的行秩、列秩、秩、矩阵的秩与其子式的关系.22.6. 线性方程组有解判别定理、线性方程组解的结构.23.7.齐次线性方程组的基础解系、解空间及其维数24.矩阵25.1.矩阵的概念、矩阵的运算(加法、数乘、乘法、转置等运算)及其运算律.26.2. 矩阵乘积的行列式、矩阵乘积的秩与其因子的秩的关系.27.3. 矩阵的逆、伴随矩阵、矩阵可逆的条件.28.4. 分块矩阵及其运算与性质.29.5.初等矩阵、初等变换、矩阵的等价标准形.30.6. 分块初等矩阵、分块初等变换.31.双线性函数与二次型32.1. 双线性函数、对偶空间33.2. 二次型及其矩阵表示.34.3.二次型的标准形化二次型为标准形的配方法、初等变换法、正交变换法.35.4. 复数域和实数域上二次型的规范形的唯一性、惯性定理.36.5.正定、半正定、负定二次型及正定、半正定矩阵37.线性空间38.1. 线性空间的定义与简单性质.39.2. 维数,基与坐标.40.3. 基变换与坐标变换.41.4. 线性子空间.42.5. 子空间的交与和、维数公式、子空间的直和.43.线性变换44.1. 线性变换的定义、线性变换的运算、线性变换的矩阵.45.2. 特征值与特征向量、可对角化的线性变换.46.3.相似矩阵、相似不变量、哈密尔顿-凯莱定理.47.4. 线性变换的值域与核、不变子空间.48.若当标准形49.1.矩阵.50.2. 行列式因子、不变因子、初等因子、矩阵相似的条件.51.3. 若当标准形.52.欧氏空间53.1. 内积和欧氏空间、向量的长度、夹角与正交、度量矩阵.54.2. 标准正交基、正交矩阵、施密特(Schmidt)正交化方法.55.3. 欧氏空间的同构.56.4. 正交变换、子空间的正交补.57.5. 对称变换、实对称矩阵的标准形.58.6. 主轴定理、用正交变换化实二次型或实对称矩阵为标准形.59.7. 酉空间.Ⅲ、解析几何部分1.向量与坐标2. 1. 向量的定义、表示、向量的线性运算、向量的分解、几何运算.3. 2. 坐标系的概念、向量与点的坐标及向量的代数运算.4. 3. 向量在轴上的射影及其性质、方向余弦、向量的夹角.5. 4. 向量的数量积、向量积和混合积的定义、几何意义、运算性质、计算方法及应用.6. 5. 应用向量求解一些几何、三角问题.7.轨迹与方程8. 1.曲面方程的定义:普通方程、参数方程(向量式与坐标式之间的互化)及其关系.9. 2.空间曲线方程的普通形式和参数方程形式及其关系.10.3.建立空间曲面和曲线方程的一般方法、应用向量建立简单曲面、曲线的方程.11.4.球面的标准方程和一般方程、母线平行于坐标轴的柱面方程.12.平面与空间直线13.1.平面方程、直线方程的各种形式,方程中各有关字母的意义.14.2.从决定平面和直线的几何条件出发,选用适当方法建立平面、直线方程.15.3.根据平面和直线的方程,判定平面与平面、直线与直线、平面与直线间的位置关系.16.4. 根据平面和直线的方程及点的坐标判定有关点、平面、直线之间的位置关系、计算他们之间的距离与交角等;求两异面直线的公垂线方程.17.二次曲面18.1.柱面、锥面、旋转曲面的定义,求柱面、锥面、旋转曲面的方程.19.2.椭球面、双曲面与抛物面的标准方程和主要性质,根据不同条件建立二次曲面的标准方程.20.3.单叶双曲面、双曲抛物面的直纹性及求单叶双曲面、双曲抛物面的直母线的方法.21.根据给定直线族求出它表示的直纹面方程求动直线和动曲线的轨迹问题.22.二次曲线的一般理论23.1.二次曲线的渐进方向、中心、渐近线.24.2.二次曲线的切线、二次曲线的正常点与奇异点.25.3.二次曲线的直径、共轭方向与共轭直径.26.4.二次曲线的主轴、主方向,特征方程、特征根.27.5.化简二次曲线方程并画出曲线在坐标系的位置草图.(二)中国大学生数学竞赛(非数学专业类)竞赛内容为大学本科理工科专业高等数学课程的教学内容,具体内容如下:一函数、极限、连续1.函数的概念及表示法、简单应用问题的函数关系的建立.2.函数的性质:有界性、单调性、周期性和奇偶性.3.复合函数、反函数、分段函数和隐函数、基本初等函数的性质及其图形、初等函数.4.数列极限与函数极限的定义及其性质、函数的左极限与右极限.5.无穷小和无穷大的概念及其关系、无穷小的性质及无穷小的比较.6.极限的四则运算、极限存在的单调有界准则和夹逼准则、两个重要极限. 7.函数的连续性(含左连续与右连续)、函数间断点的类型.8.连续函数的性质和初等函数的连续性.9.闭区间上连续函数的性质(有界性、最大值和最小值定理、介值定理).二一元函数微分学1. 导数和微分的概念、导数的几何意义和物理意义、函数的可导性与连续性之间的关系、平面曲线的切线和法线.2. 基本初等函数的导数、导数和微分的四则运算、一阶微分形式的不变性.3. 复合函数、反函数、隐函数以及参数方程所确定的函数的微分法.4.高阶导数的概念、分段函数的二阶导数、某些简单函数的n阶导数.5.微分中值定理,包括罗尔定理、拉格朗日中值定理、柯西中值定理和泰勒定理.6 洛必达(L’Hospital)法则与求未定式极限.7. 函数的极值、函数单调性、函数图形的凹凸性、拐点及渐近线(水平、铅直和斜渐近线)、函数图形的描绘.8. 函数最大值和最小值及其简单应用.9. 弧微分、曲率、曲率半径.三一元函数积分学1. 原函数和不定积分的概念.2. 不定积分的基本性质、基本积分公式.3. 定积分的概念和基本性质、定积分中值定理、变上限定积分确定的函数及其导数、牛顿-莱布尼茨(Newton-Leibniz)公式.4. 不定积分和定积分的换元积分法与分部积分法.5. 有理函数、三角函数的有理式和简单无理函数的积分.6. 广义积分.7. 定积分的应用:平面图形的面积、平面曲线的弧长、旋转体的体积及侧面积、平行截面面积为已知的立体体积、功、引力、压力及函数的平均值.四.常微分方程1.常微分方程的基本概念:微分方程及其解、阶、通解、初始条件和特解等.2.变量可分离的微分方程、齐次微分方程、一阶线性微分方程、伯努利(Bernoulli)方程、全微分方程.3.可用简单的变量代换求解的某些微分方程、可降阶的高阶微分方程: .4.线性微分方程解的性质及解的结构定理.5.二阶常系数齐次线性微分方程、高于二阶的某些常系数齐次线性微分方程.6.简单的二阶常系数非齐次线性微分方程:自由项为多项式、指数函数、正弦函数、余弦函数,以及它们的和与积7.欧拉(Euler)方程.8.微分方程的简单应用9.五、向量代数和空间解析几何10.向量的概念、向量的线性运算、向量的数量积和向量积、向量的混合积.11.两向量垂直、平行的条件、两向量的夹角.12.向量的坐标表达式及其运算、单位向量、方向数与方向余弦.13.曲面方程和空间曲线方程的概念、平面方程、直线方程.14.平面与平面、平面与直线、直线与直线的夹角以及平行、垂直的条件、点到平面和点到直线的距离.15.球面、母线平行于坐标轴的柱面、旋转轴为坐标轴的旋转曲面的方程、常用的二次曲面方程及其图形.16.空间曲线的参数方程和一般方程、空间曲线在坐标面上的投影曲线方程.17.六、多元函数微分学18.多元函数的概念、二元函数的几何意义.19.二元函数的极限和连续的概念、有界闭区域上多元连续函数的性质.20.多元函数偏导数和全微分、全微分存在的必要条件和充分条件.21.多元复合函数、隐函数的求导法.22.二阶偏导数、方向导数和梯度.23.空间曲线的切线和法平面、曲面的切平面和法线.24.二元函数的二阶泰勒公式.25.多元函数极值和条件极值、拉格朗日乘数法、多元函数的最大值、最小值及其简单应用.26.七、多元函数积分学27.二重积分和三重积分的概念及性质、二重积分的计算(直角坐标、极坐标)、三重积分的计算(直角坐标、柱面坐标、球面坐标).28.两类曲线积分的概念、性质及计算、两类曲线积分的关系.29.格林(Green)公式、平面曲线积分与路径无关的条件、已知二元函数全微分求原函数.30.两类曲面积分的概念、性质及计算、两类曲面积分的关系.31.高斯(Gauss)公式、斯托克斯(Stokes)公式、散度和旋度的概念及计算.32.重积分、曲线积分和曲面积分的应用(平面图形的面积、立体图形的体积、曲面面积、弧长、质量、质心、转动惯量、引力、功及流量等)33.八、无穷级数34.常数项级数的收敛与发散、收敛级数的和、级数的基本性质与收敛的必要条件.35.几何级数与p级数及其收敛性、正项级数收敛性的判别法、交错级数与莱布尼茨(Leibniz)判别法.36.任意项级数的绝对收敛与条件收敛.37.函数项级数的收敛域与和函数的概念.38.幂级数及其收敛半径、收敛区间(指开区间)、收敛域与和函数.39.幂级数在其收敛区间内的基本性质(和函数的连续性、逐项求导和逐项积分)、简单幂级数的和函数的求法.40.初等函数的幂级数展开式.41.函数的傅里叶(Fourier)系数与傅里叶级数、狄利克雷(Dirichlei)定理、函数在[-l,l]上的傅里叶级数、函数在[0,l]上的正弦级数和余弦级数。
2019全国大学生数学建模竞赛河南赛区获奖名单(专科组)
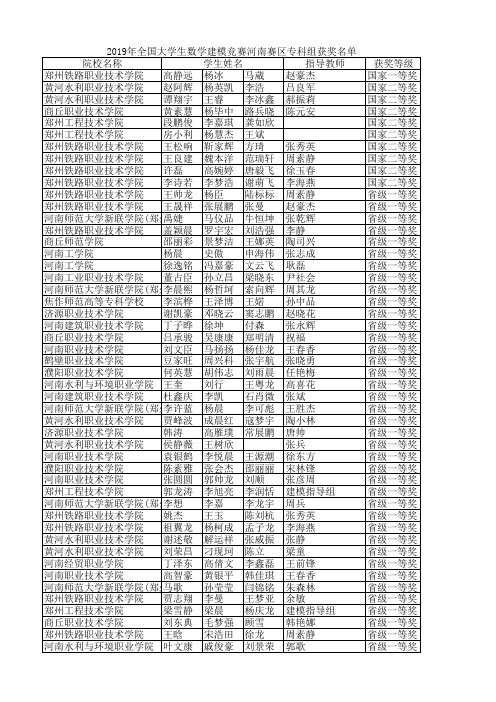
河南工业职业技术学院
李世祥
开封大学
张明坤
开封大学
李新元
鹤壁职业技术学院
党慧龙
河南建筑职业技术学院 谢金鑫
河南水利与环境职业学院 尚佳凝
黄河水利职业技术学院 史少聪
焦作师范高等专科学校 马沙沙
黄河水利职业技术学院 林晓峰
商丘职业技术学院
周雪枫
黄河水利职业技术学院 邓坤鹏
永城职业学院
莫伟
河南水利与环境职业学院 周泽宇
平顶山教育学院
赵醒醒 常新新
郑州铁路职业技术学院 张泽南 沈秋凤
商丘师范学院
刘胜楠 刘勤
黄河水利职业技术学院 张高潭 高尚
河南水利与环境职业学院 贾龙飞 楚东辉
黄河水利职业技术学院 周茹雪 李永虎
平顶山教育学院
张会洋 杨建荣
黄河水利职业技术学院 常浩迪 姜昆
郑州工程技术学院
焦劲夫 徐振家
河南水利与环境职业学院 黄浩杰 赵艺超
平顶山教育学院
孙梦丽
郑州工程技术学院
王亚林
濮阳职业技术学院
王广雨
河南水利与环境职业学院 张远冲
商丘职业技术学院
李晨
战略支援部队信息工程大学龚虎成
黄河水利职业技术学院 杨皓森
濮阳职业技术学院
高雅
黄河水利职业技术学院 韩雅湄
商丘职业技术学院
吴数德
商丘师范学院
陈东亮
战略支援部队信息工程大学吕贵生
开封大学
尹萍洋
2019年全国大学生数学建模竞赛河南赛区专科组获奖名单
院校名称
学生姓名
指导教师
郑州铁路职业技术学院 高静远 杨冰 马葳 赵豪杰
黄河水利职业技术学院 赵阿辉 杨英凯 李浩 吕良军
历年全国大学生数学竞赛初赛真题全(数学类)十一届试卷高清无水印(2009-2019)

(数学类)试卷第一题:(15分)求经过三平行直线1:L x y z ==,2:11L x y z -==+,3:11L x y z =+=-的圆柱面的方程.第二题:(20分)设n nC ⨯是n n ⨯复矩阵全体在通常的运算下所构成的复数域C 上的线性空间,12100010*******n n n a a a F a --⎛⎫- ⎪ ⎪ ⎪- ⎪ ⎪ ⎪ ⎪-= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪- ⎪⎝⎭. (1)假设111212122212n n n n nn aa a a a a A a a a ⎛⎫ ⎪ ⎪⎪ ⎪ ⎪= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭,若AF FA =,证明: 121112111n n n n A a F a F a F a E ---=++++ ;(2)求n nC⨯的子空间{}()|n n C F X C FX XF ⨯=∈=的维数.第三题:(15分)假设V 是复数域C 上n 维线性空间(0n >),,f g 是V 上的线性变换. 如果fg gf f -=,证明:f 的特征值都是0,且,f g 有公共特征向量.第四题:(10分)设{}()n f x 是定义在,a b ⎡⎤⎢⎥⎣⎦上的无穷次可微的函数序列且逐点收敛,并在,a b ⎡⎤⎢⎥⎣⎦上满足()nf x M '≤.(1)证明{}()n f x 在,a b ⎡⎤⎢⎥⎣⎦上一致收敛;(2)设()lim ()n n f x f x →∞=,问()f x 是否一定在,a b ⎡⎤⎢⎥⎣⎦上处处可导, 为什么?第五题:(10分)设320sin d sin n nt a t t t π=⎰,证明11nn a ∞=∑发散.第六题:(15分)(,)f x y 是{}22(,)|1x y x y +≤上二次连续可微函数,满足222222f f x y x y ∂∂+=∂∂,计算积分221d d x y I x y +≤⎛⎫=⎰⎰第七题:(15分)假设函数()f x 在[0,1]上连续,在()0,1内二阶可导,过点(0,(0))A f ,与点(1,(1))B f 的直线与曲线()y f x =相交于点(,())C c f c ,其中01c <<. 证明:在 ()0,1内至少存在一点ξ,使()0f ξ''=.(数学类)试卷一、(本题共10分)设(0,1)ε∈,0x a =,1sin 0,1,2).n n x a x n ε+=+= (证明lim n n x ξ→+∞=存在,且ξ为方程sin x x a ε-=的唯一根.二、(本题共15分)设01030002010000B ⎛⎫⎪ ⎪ ⎪ ⎪= ⎪ ⎪ ⎪ ⎪⎝⎭. 证明2X B =无解,这里X 为三阶未知复方阵.三、(本题共10分)设2D ⊂ 是凸区域,函数(,)f x y 是凸函数. 证明或否定:(,)f x y 在D 上连续.注:函数(,)f x y 为凸函数的定义是(0,1)α∀∈以及1122(,),(,)x y x y D ∈,成立12121122((1),(1))(,)(1)(,)f x x y y f x y f x y αααααα+-+-≤+-.四、(本题共10分) 设()f x 在0,1⎡⎤⎢⎥⎣⎦上黎曼(Riemann)可积,在1x =可导,(1)0,f =(1)f a '=. 证明:120lim ()d .n n n x f x x a →+∞=-⎰五、(本题共15分)已知二次曲面∑(非退化)过以下九点:(1,0,0),(1,1,2),(1,1,2),(3,0,0),(3,1,2),(3,2,4),(0,1,4),(3,1,2),(5,8).A B C D E F G H I ------问∑是哪一类曲面?六、(本题共20分) 设A 为n n ⨯实矩阵(未必对称),对任一n 维实向量T 1(,,),0n A ααααα=≥ (这里T α表示α的转置),且存在n 维实向量β使得T 0A ββ=. 同时对任意n 维实向量x 和y ,当T 0xAy ≠时有TT 0xAy yAx +≠. 证明:对任意n 维实向量v ,都有T0.vA β=七、(本题共10分) 设f 在区间0,1⎡⎤⎢⎥⎣⎦上黎曼(Riemann)可积,0 1.f ≤≤ 求证:对任何0ε>,存在只取值为0和1的分段(段数有限)常值函数()g x ,使得,0,1αβ⎡⎤⎡⎤∀⊆⎢⎥⎢⎥⎣⎦⎣⎦,()()().f x g x dxβαε-<⎰八、(10分) 已知:(0,)(0,)ϕ+∞→+∞是一个严格单调下降的连续函数,满足0lim (),t t ϕ+→=+∞且10()d ()d ,t t t t a ϕϕ+∞+∞-==<+∞⎰⎰其中1ϕ-表示ϕ的反函数. 求证:32212001()d ()d .2t t t t a ϕϕ+∞+∞-⎡⎤⎡⎤+≥⎢⎥⎢⎥⎣⎦⎣⎦⎰⎰(数学类)试卷一、(本题15分)已知四点(1,2,7),(4,3,3),(5,1,0).-试求过这四点的球面方程。
2018-2019全国大学生数学竞赛试题及答案(最完整版).pdf

y y→+∞ 0
五 、( 本 题 满 分 12 分 ) 设 函 数 f (x) 在 [0,1] 上 连 续 , 在 (0,1) 内 可 微 , 且
f (0) = f (1) = 0, f (1 ) = 1 。 证明:(1) 存在ξ ∈ (1 ,1) 使得 f (ξ ) = ξ ;(2) 存在η ∈ (0,ξ )
2
f (x)dx − 2 , 则 f (x) =
0
;
3.曲面 z = x2 + y2 − 2 平行平面 2x + 2 y − z = 0 的切平面方程是
;
2
4.设函数 y = y(x) 由方程 xe f ( y) = e y ln 29 确定,其中 f 具有二阶导数,且 f ′ ≠ 1 ,则
d2y =
知该抛物线与 x 轴及直线 x = 1所围图形的面积为 1 。试确定 a, b, c ,使此图形绕 x 轴旋转一 3
周而成的旋转体的体积最小。
七、(本题满分 15 分)已知 un (x) 满足 un′ (x) = un (x) + xn−1ex (n = 1,2,
∞
∑ 求函数项级数 un (x) 之和。 n=1 ∞
L
2
五、(本题满分 10 分)已知 y1 = xex + e2x , y2 = xex + e−x , y3 = xe x + e2x − e−x 是某二
阶常系数线性非齐次微分方程的三个解,试求此微分方程。
六、(本题满分 10 分)设抛物线 y = ax2 + bx + 2 ln c 过原点。当 0 ≤ x ≤ 1 时, y ≥ 0 ,又已
?若存在,请给出一个例子;若不存在,请给出证明。
2019 年全国大学生数学建模竞赛 浙江赛区获奖名单的通知
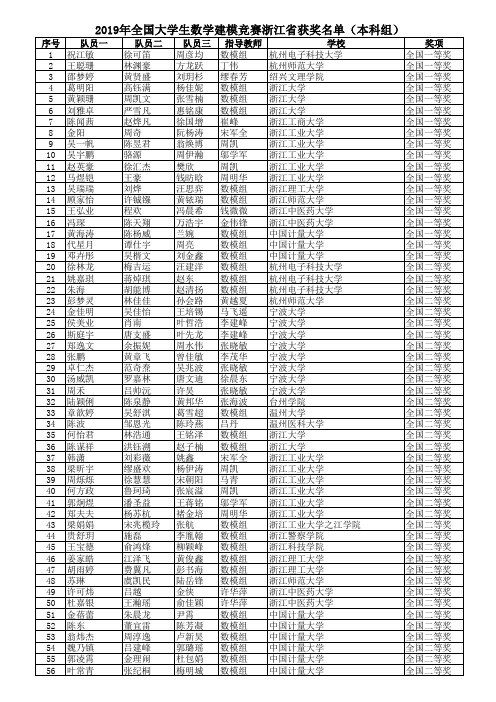
唐支盛 余振妮 黄章飞
叶先龙 周水伟 曾佳敏
李建峰 张晓敏 李茂华
宁波大学 宁波大学 宁波大学
全国二等奖 全国二等奖 全国二等奖
29 卓仁杰 30 汤威凯 31 周禾 32 陆颖俐
范奇焘 罗嘉林 吕帅沅 陈泉静
吴兆波 唐文迪 许昊 黄邦华
张晓敏 徐晨东 张晓敏 张海波
宁波大学 宁波大学 宁波大学 台州学院
浙江理工大学 浙江理工大学 浙江师范大学 浙江中医药大学
全国二等奖 全国二等奖 全国二等奖 全国二等奖
50 杜嘉银 51 金蓓蕾 52 陈东
王瀚瑶 朱晨龙 董宜雷
俞佳颖 尹霄 陈芳凝
许华萍 数模组 数模组
浙江中医药大学 中国计量大学 中国计量大学
全国二等奖 全国二等奖 全国二等奖
53 翁炜杰 54 魏乃镇 55 郭凌霄
ห้องสมุดไป่ตู้
绍兴文理学院 浙江大学 浙江大学
全国一等奖 全国一等奖 全国一等奖
6 刘雅卓 7 陈闻茜 8 金阳
严雪凡 赵烨凡 周奇
惠铭康 徐国增 阮杨涛
数模组 崔峰 宋军全
浙江大学 浙江工商大学 浙江工业大学
全国一等奖 全国一等奖 全国一等奖
9 吴一帆 10 吴宇鹏 11 赵英豪 12 马煜铠
陈昱君 骆源 徐汇杰 王豪
翁焕博 周伊瀚 樊欣 钱昉晗
周凯 邬学军 周凯 周明华
浙江工业大学 浙江工业大学 浙江工业大学 浙江工业大学
全国一等奖 全国一等奖 全国一等奖 全国一等奖
13 吴瑞瑞 14 顾家怡 15 王弘业
刘烨 许铖镪 程欢
汪思弈 黄铱瑞 冯晨希
数模组 数模组 钱微微
浙江理工大学 浙江师范大学 浙江中医药大学
2019年第十一届全国大学生数学竞赛初赛非数学专业试题

1 2019年第十一届全国大学生数学竞赛非数学专业竞赛试题一、填空题(本题满分30分,共5小题,每小题6分)(1)sin 0ln sin lim x x e x →+-= .(2)设隐函数()y y x =由方程22()y x y x -=所确定,则2d x y =⎰. (3)定积分20(1sin )d 1cos x e x x x π+=+⎰ .(4)已知22d d d (,)323y x x y u x y x xy y -=-+,则(),u x y =.(5)设,,,0a b c μ>,曲面xyz μ=与曲面2222221x y z a b c++=相切,则μ=. 二、(本题满分14分)计算三重积分22d d d xyz x y z x y Ω+⎰⎰⎰,其中Ω是由曲面()22222x y z xy ++=围成的区域在第一卦限部分.三、(本题满分14分) 设()f x 在[0,)+∞上可微,()00f =,且存在常数0A >,使得()()||||f x A f x '≤在[0,)+∞上成立,试证明在(0,)+∞上有()0.f x ≡四、(本题满分14分)计算积分2sin (cos sin )00d sin d .I e ππθφφφθθ-=⎰⎰ 五、(本题满分14分)设()f x 是仅有正实根的多项式函数,满足0()()n n n f x c x f x +∞='=-∑,证明:()00,n c n >≥极限lim n →+∞存在,且等于()f x 的最小根.六、(本题满分14分)设()f x 在[0,)+∞上具有连续导数,满足222233()()21()x f x f x f x e -⎡⎤⎡⎤'+=+⎢⎥⎢⎥⎣⎦⎣⎦, 且()01f ≤. 证明:存在常数0M >,使得[0,)x ∈+∞时,恒有()||.f x M ≤。
第十一届全国大学生数学竞赛预赛试题(非数类)

Z
2
ex (1 + sin x ) dx =
.
0 1 + cosx
y dx x dy
4. 已知 d u ( x; y ) = 3x 2
2 ,则 u ( x; y ) =
.
2xy + 3y
x 2 y 2 z2
5. 设 a; b; > 0,曲面 xyz = 与曲面 a2 + b2 + c2 = 1 相切,则 =
第2页 共6页
得分 评卷人 复核人
三、解答题 (本题满分 14 分 )
设 f ( x ) 在区间 [0; + 1 ) 上可微,f (0) = 0,且存在常数 A > 0,使得 jf 0( x ) j ? Ajf ( x) j 在 [0; + 1 ) 上成立,试证明 (0 ; + 1 ) 上有 f ( x ) á 0.
:
题
号
证
考
准
答
设 f ( x ) 是仅有正实根的多项式函数,且满足
f 0( x ) = f (x)
1
n 0,极限 lim
存在,且等于 f (x ) 的最小根 .
n !1
pn cn
1
X
cn x n . 证明: cn > 0,
n =0
要
不
: 名 姓
内
线
:
订
校
学
装
: 市
省
科目名称:非数类
微信公众号:八一考研数学竞赛
绝密 ? 启用前
试卷类型:数学竞赛
:
题
号
证
考
准
答
要
不
: 名 姓
整理2019全国卷三数学

2019全国卷三数学整理人尼克附件河海大学2019-2020学年省部级以上学科竞赛获奖指导教师名单1.2019年第十六届“挑战杯”大学生课外学术科技作品竞赛2.2020年第十三届全国大学生节能减排社会实践与科技竞赛3.2019年全国大学生电子设计竞赛4.2019年全国大学生数学建模竞赛5.2019年“宝治杯”第十三届全国大学生结构设计竞赛6.2020年全国大学生电子设计竞赛模拟电子专题邀请赛2020年全国大学生智能汽车竞赛7.8.2020年第九届“中国软件杯”大学生软件设计大赛9.2019年第十一届全国大学生广告艺术大赛10.2019年外研社杯全国大学生英语演讲大赛全国总决赛11.2020年美国大学生数学建模竞赛12.2019年第十三届iCAN国际创新创业大赛13.2019年第二十一届中国机器人及人工智能大赛大赛14.2019年第十届全国大学生数学竞赛15.2019年全国大学生环境资源模拟法庭大赛16.2020年第二届国际大学生工程力学竞赛(亚洲赛区)团体赛17.2020年国际企业管理挑战赛(GMC)18.2020年第十三届中国大学生计算机设计大赛19.2019年CCPC中国大学生程序设计竞赛20.2020年第十六届国际大学生工程力学竞赛个人赛21.2020年第十一届中国大学生服务外包创新创业大赛22.2020年全国大学生物联网设计竞赛(华为杯)23.2019年中国计算机设计大赛-网络技术挑战赛24.2020年“永冠杯”中国大学生铸造工艺设计大赛25.2019年第21届齐越朗诵艺术节暨全国大学生朗诵大赛26.2020年第六届江苏省“互联网+”大学生创新创业大赛27.2019年第一届全国大学生农业水利工程及相关专业创新设计大赛28.2020年第九届POCIB全国外贸从业能力大赛(2019-2020赛季春季赛)29.2019年全国高等学校土木工程专业本科生优秀创新实践成果竞赛30.2019年第三届全国大学生“茅以升公益桥——小桥工程”设计大赛31.2019年ESRI杯中国大学生GIS软件开发竞赛32.2019年第八届全国大学生GIS应用技能大赛33.2019年全国大学生可再生能源科技竞赛年“易居杯”第十一届全国大学生房地产策划大赛34.202036.2020年泰迪杯全国大学生数据挖掘挑战赛37.2020年数学中国“认证杯”数学建模网络挑战赛38.2020年企业竞争模拟大赛39.2019年第四届OCALE全国跨境电商创新创业能力大赛40.2019年“学创杯”全国大学生创业综合模拟大赛41.2020年全国海洋航行器设计与制作大赛42.2019年第十届“蓝桥杯”软件和信息技术大赛国赛43.2019年第七届“网中网杯”大学生财务决策大赛44.2019年第十届中国玩具和婴童用品创意设计大赛45.2020年第二届国际大学生工程力学竞赛(亚洲赛区)个人赛46.2019年第十三届iCAN国际创新创业大赛江苏赛区47.2019年第四届江苏省高校测绘地理信息创新创业大赛48.2019年全国三维数字化创新设计大赛年度竞赛(江苏赛区)49.2019年江苏省高校测绘本科生优秀毕业论文50.2019年外研社杯全国大学生英语写作大赛江苏赛区比赛51.2019年外研社杯全国大学生英语演讲大赛江苏赛区比赛52.2020年第十二届全国大学生广告艺术大赛(江苏赛区)53.2019年第七届江苏省大学生工程管理创新、创业与实践竞赛54.2019年外研社杯全国大学生英语阅读大赛江苏赛区比赛55.2019年全国第十二届3D大赛(江苏赛区)56.2019年江苏省高校第十六届大学生物理及实验科技作品创新竞赛57.2020年第十三届江苏省大学生计算机设计大赛整理丨尼克本文档信息来自于网络,如您发现内容不准确或不完善,欢迎您联系我修正;如您发现内容涉嫌侵权,请与我们联系,我们将按照相关法律规定及时处理。
第十一届大学生数学竞赛非数类预赛参考答案

������ = ∬Σ ������������−������������������
-------4 分
设平面������������ :
������−������ √2
= ������,
−1 ≤ ������
≤ 1,其中������为平面������������被球面截下部分中心到原点距离.
用平面������������分割球面������,球面在平面������������, ������������+������������之间的部分形如圆台外表面状,记为Σt,dt.被积
x(1 cos x)+ sin2 (1 cos x)2
x
dx
0
2
ex
dx sin xex
2
2
ex
dx e 2 .
0 1 cos x 1 cos x 0 1 cos x
0
4. 已知 du(x, y) ydx xdy ,则 u(x, y) 1 arctan 3 ( x 1) C .
f (x) f (x)
n0
cn xn
.
试证:cn
0,
(n 0),极限 lim 1 存在,且等于 f (x) 的最小根. c n n
n
证明:由������(������)为仅有正实根的多项式,不妨设 f (x) 的全部根为
0 < ������1 < ������2 < ⋯ < ������������,这样,
22
22 y 3
1
5.
设
a,
b,
c,
0
全国大学生数学竞赛

第十一届“全国大学生数学竞赛”简介全国大学生数学竞赛是由中国数学会主办的大学生专业技能竞赛活动,旨在进一步推动和促进高等学校数学的教学改革和课程建设,激发和培养广大学生学习数学的兴趣,发现和选拔数学创新人才,为青年学子提供一个展示自我的舞台。
一、竞赛的方式与时间安排第十一届全国大学生数学竞赛分初赛和决赛两个阶段。
分区初赛于2019年10月下旬在四川赛区进行,竞赛委员会负责统一命题,各赛区数学会组织考试。
全国决赛于2020年3月举行。
二、奖项的设立:设初赛(以省、市、自治区作为赛区)奖与决赛奖。
预赛奖:每个赛区的获奖总名额不超过总参赛人数的25%(其中一等奖、二等奖、三等奖分别占各类获奖总人数的20%、30%、50%)。
颁发“第八届全国大学生数学竞赛预赛*等奖”证书。
决赛奖:参加全国决赛的总人数不超过300人。
每个赛区参加决赛的名额不少于3名,由各赛区在赛区一等奖获得者中推选。
最后入选名单由竞赛工作小组批准。
决赛阶段的评奖等级按绝对分数评奖。
颁发“第八届全国大学生数学竞赛决赛*等奖”证书。
预赛奖和决赛奖证书均加盖“中国数学会普及工作委员会”的公章,获奖证书由承办单位统一印制。
三、全国竞赛内容:省级预赛只考高等数学内容。
全国决赛时在预赛的基础上增加线性代数内容。
(考分约占总分的15%--20%)。
四、全国大学生数学竞赛官网全国大学生数学竞赛网站/中国大学生数学竞赛(非数学专业类)竞赛内容一、函数、极限、连续1.函数的概念及表示法、简单应用问题的函数关系的建立。
2.函数的性质:有界性、单调性、周期性和奇偶性。
3.复合函数、反函数、分段函数和隐函数、基本初等函数的性质及其图形、初等函数。
4.数列极限与函数极限的定义及其性质、函数的左极限与右极限。
5.无穷小和无穷大的概念及其关系、无穷小的性质及无穷小的比较。
6.极限的四则运算、极限存在的单调有界准则和夹逼准则、两个重要极限。
7.函数的连续性(含左连续与右连续)、函数间断点的类型。
2019年第十一届全国大学生数学竞赛初赛数学专业(B类)试题

2019年第十一届全国大学生数学竞赛数学专业竞赛(B 卷)试题一、(本题15分)设1L 和2L 是空间中的两条不垂直的异面直线,点B 是它们公垂线段的中点。
点1A 和2A 分别在1L 和2L 上滑动,使得12A B A B ⊥. 证明直线12A A 的轨迹是单叶双曲面。
二、(本题10分)计算()()220190d 11x x x +∞++⎰三、(本题15分)设数列{}n x 满足:()110,ln 1,1,2,n n x x x n +>=+= . 证明:{}n x 收敛并求其极限值. 四、(本题15分)设{}1,,n 是n 维实线性空间V 的一组基,令1210n n +++++=证明:(1)对{}11111,2,,1,,,,,,i i n i n -++=+ 都构成V 的基;(2)V α∀∈,在(1)中的1n +组基中,必存在一组基使α在此基下的坐标分量均非负;(3)若1122n n a a a α=+++ ,且(1,2,,)i a i n = 互不相同,则在(1)中的1n +组基中,满足(2)中非负坐标表示的基是唯一的.五、(本题20分)设A 是数域F 上的n 阶矩阵,若(2n n A I I =表示单位矩阵),则称A 为对合矩阵. 试证:(1)若A 是n 阶对合矩阵,则()()rank rank n n I A I A n ++-=;(2)n 阶对合矩阵A 一定可以对角化,其相似对角形为00r n r I I -⎛⎫ ⎪ ⎪ ⎪- ⎪⎝⎭,其中 ()rank n A r I =+;(3)若A ,B 均是n 阶对合矩阵,且AB BA =,则存在可逆矩阵P ,使得1P AP -和1P BP -同时为对角矩阵.六、(本题15分)设函数()f x 为闭区间,a b ⎡⎤⎢⎥⎣⎦上的连续凹函数,满足()()0,0f a f b =>且()f x 在x a =处存在非零的右导数. 对2n ≥,记()11:(),[,]n n n k k k k k S kx kf x f b x a b ==⎧⎫⎪⎪⎪⎪==∈⎨⎬⎪⎪⎪⎪⎩⎭∑∑(1)证明对(0,())f b α∀∈,存在唯一(,)x a b ∈使得()f x α=;(2)求()lim sup inf .n n n S S →∞-七、(本题10分)设正项级数11n n a ∞=∑收敛. 证明级数221n n nn a S ∞=∑收敛,其中1n k k n a S ==∑.。
获奖信息:2019年第十一届全国大学数学竞赛你获奖了吗?

获奖信息:2019年第十一届全国大学数学竞赛你获奖了吗?
今年的数学竞赛
走出考场那一刻
那么今年的成绩到底怎样呢?貌似到现在为止各赛区获奖结果公布都不那么着急!那么咱们到底有没有获奖呢?多少分有可能获奖呢?小编根据学友分享的获奖信息,收集了两个985,211高校共1186份非数学专业的成绩分布供大家参考,同时内含的一个评奖信息分享给大家参考!以下数据有一个学校10分以下的成绩没有分享,估计不少于200人!最终获奖信息以赛区、学校通知到个人为准!
以下是其中一个学校在赛区获奖成绩参考,一等奖最后一名是14分,二等奖从13分开始,到9分结束,三等奖8分开始5分结束!
总结一句话
惊喜总在风雨后
大家对自己获奖要有充分的信心哦!历届全国、各省、市、校数学竞赛真题、参考解答、参赛经验分享和获奖名单请点击公众号会话框底部菜单“竞赛实验”下的“竞赛试题与通知”,其他更多历史推文分类列表点击底部各菜单选项.
•第十一届全国大学生数学竞赛经历感受、试题来源和备考经验分析
•全国大学生数学竞赛初赛非数学真题与专题、典型题教学视频内容详细目录列表
•第十一届全国大学生数学竞赛初赛(非数学专业真题)及参考解答
•第十一届全国大学生数学竞赛初赛数学类(A卷)试题及参考解答
•第十一届全国大学生数学竞赛初赛数学类(B卷)试题及参考解答。
2019年河南省第十一届大学生数学竞赛《非数学》复赛试题

1.2 克盐的盐水以每分钟 2 升的速度流入该容器并以相同速度从该容器中流出(该过程中持
续搅动以保持混合物浓度恒定),求 1 小时后容器中剩余的盐量.(已知e1 0.37 ).
五、(本题满分 10 分)设函数 f
x
在闭区间
a,
b
上具有一阶连续导数,且
f
a
f
b
,
4
b
证明: max f (x)
z2
u n 的方向导数
n
(规定:L 与 z 轴正向的夹角为锐角的方向为L 的正向).
x2 y2
dx dy
5、设 : 1 ,方向为逆时钟方向,则
49
|x ||y |
.
二、(本题满分 10 分)设z z x, y 具有一阶连续偏导数,w w u, v 是由方程组
u
x2
y2,
v
.
(1 x x 2 x3 )2
3 、 设 直 线 L 的 极 坐 标 方 程 为 r , 则 直 线 L 在 点 r, , 处 的 曲 率 半 径
为
.
4、设曲线 L
:
x3
z 2
1,
,则u cos2 xy y 在点 0, 0, 1 处沿直线L 的正向
y 2z 4 0
2019 年第十一届全国大学生数学竞赛河南赛区复赛 《非数学专业》竞赛试题
一、填空题(本题满分 25 分,每题 5 分)
x tan t ln
1 t2
sin
1
d
t
1、计算 lim
0
t
.
x 0
x
ln 1 arctan tdt
0
2、函数 1 2x 3x 2 的麦克劳林级数中x 2019 项的系数是
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
预赛模拟试题
一 、(15 分) 设点 P, Q, R 分别分三角形的边 AB, BC, CA 成定比 l, m, n, 证明: 三点 P, Q, R 共线的充要条件为 lmn = −1.
1
2
二
、(12 分) 已知方程
1 ln(1 + x)
−
·
·
·
,证明:
6
六 、(15 分) 设 A 是复数域上的一个 n 阶方阵,f (x) = |xE − A| 是 A 的特征多项式,g(x) 是一个复系数多项式. 证明:g(A) 是可逆的充分必 要条件为 g(x) 与 f (x) 互素.
7
七 、(20 分) 将 m 阶单位矩阵的第一行移到最后一行所得矩阵具有如下
1 x
= 2k
在区间 (0, 1)
内有实根,求常
数 k 的取值范围.
3
三 、(13 分) 设 f 是一连续函数
(a)
令
g(t1,
t2)
=
f
(t1)·f
(t2),证明
∫t
0
dt1
∫ t1
0
g(t1,
t2)dt2
=
1 2
(∫0t
f
(x)dx)2.
(b) 请把上述结果推广到 g 为 3 元函数的情形,并证明之.形式:Βιβλιοθήκη 01
0
... ...
1
(1)
1
0
特别地,m = 1 时,上式为 1 阶矩阵 (1). 设 n 阶矩阵 A 的每一行每
一列元素均为一个 1,其余元素均为 0,证明:A 与如下形式准对角矩
阵 J 相似,其中
J1 . . .
(2)
Js
其中 (2) 式中的 Ji(i = 1, 2, · · · , s) 均为形如 (1) 式的矩阵.
4
四
、(13
分)
设 f (x) 是
[0,
+∞)
上的单调递减函数,且
∫∞
0
f (x)dx
收敛,
试证 lim xf (x) = 0.
x→∞
5
五
、(12 分) 设 对于 |x| < 1
3
,a2幂=级a数1 =∑a∞ n>=10a,naxnn+−11=收a敛n +,2并an求−1其, n和=函2数, 3.,
