matlab非线性规划实例
matlab解决非线性规划问题(凸优化问题)

matlab解决⾮线性规划问题(凸优化问题)当⽬标函数含有⾮线性函数或者含有⾮线性约束的时候该规划问题变为⾮线性规划问题,⾮线性规划问题的最优解不⼀定在定义域的边界,可能在定义域内部,这点与线性规划不同;例如:编写⽬标函数,定义放在⼀个m⽂件中;编写⾮线性约束条件函数矩阵,放在另⼀个m⽂件中;function f = optf(x);f = sum(x.^2)+8;function [g, h] = limf(x);g = [-x(1)^2+x(2)-x(3)^2x(1)+x(2)^2+x(3)^3-20]; %⾮线性不等式约束h = [-x(1)-x(2)^2+2x(2)+2*x(3)^2-3]; %⾮线性等式约束options = optimset('largescale','off');[x y] = fmincon('optf',rand(3,1),[],[],[],[],zeros(3,1),[],...'limf',options)输出为:最速下降法(求最⼩值):代码如下:function [f df] = detaf(x);f = x(1)^2+25*x(2)^2;df = [2*x(1)50*x(2)];clc,clear;x = [2;2];[f0 g] = detaf(x);while norm(g)>1e-6 %收敛条件为⼀阶导数趋近于0p = -g/norm(g);t = 1.0; %设置初始步长为1个单位f = detaf(x+t*p);while f>f0t = t/2;f = detaf(x+t*p);end %这⼀步很重要,为了保证最后收敛,保持f序列为⼀个单调递减的序列,否则很有可能在极值点两端来回震荡,最后⽆法收敛到最优值。
x = x+t*p;[f0,g] = detaf(x);endx,f0所得到的最优值为近似解。
MATLAB优化应用非线性规划

MATLAB优化应用非线性规划非线性规划是一类数学优化问题,其中目标函数和约束条件都是非线性的。
MATLAB作为一种强大的数值计算软件,提供了丰富的工具和函数,可以用于解决非线性规划问题。
本文将介绍如何使用MATLAB进行非线性规划的优化应用,并提供一个具体的案例来演示。
一、MATLAB中的非线性规划函数MATLAB提供了几个用于解决非线性规划问题的函数,其中最常用的是fmincon函数。
fmincon函数可以用于求解具有等式约束和不等式约束的非线性规划问题。
其基本语法如下:x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)其中,fun是目标函数,x0是变量的初始值,A和b是不等式约束的系数矩阵和右端向量,Aeq和beq是等式约束的系数矩阵和右端向量,lb和ub是变量的上下界,nonlcon是非线性约束函数,options是优化选项。
二、非线性规划的优化应用案例假设我们有一个工厂,需要生产两种产品A和B,目标是最大化利润。
产品A 和B的生产成本分别为c1和c2,售价分别为p1和p2。
同时,我们需要考虑两种资源的限制,分别是资源1和资源2。
资源1在生产产品A和B时的消耗分别为a11和a12,资源2的消耗分别为a21和a22。
此外,产品A和B的生产量有上下限限制。
我们可以建立以下数学模型来描述这个问题:目标函数:maximize profit = p1 * x1 + p2 * x2约束条件:c1 * x1 + c2 * x2 <= budgeta11 * x1 + a12 * x2 <= resource1a21 * x1 + a22 * x2 <= resource2x1 >= min_production_Ax2 >= min_production_Bx1 <= max_production_Ax2 <= max_production_B其中,x1和x2分别表示产品A和B的生产量,budget是预算,min_production_A和min_production_B是产品A和B的最小生产量,max_production_A和max_production_B是产品A和B的最大生产量。
基于matlab求解非线性规划问题

计算结果为:
x =[ 3.0000 5.0000 0.0000 7.0000 0.0000 1.0000 0.0000 0.0000 4.0000 0.0000 6.0000 10.0000]’ fval = 136.2275
即 由 料 场 A、 B 向 6 个 工 地 运 料 方 案 为 : 1 料场 A 料场 B 3 0 2 5 0 3 0 4 4 7 0 5 0 6 6 1 10
(二)使用临时料场的情形
使用两个临时料场A(5,1),B(2,7).求从料场j向工地i的运送量 为Xij,在各工地用量必须满足和各料场运送量不超过日储量的 条件下,使总的吨千米数最小,这是线性规划问题. 线性规划模 型为:
min f
aa ( i , j ) X
j 1 i 1
2
6
ij
2、先建立M-文件 fun3.m: function f=fun3(x); f=-x(1)-2*x(2)+(1/2)*x(1)^2+(1/2)*x(2)^2
3、再建立主程序youh2.m: x0=[1;1]; A=[2 3 ;1 4]; b=[6;5]; Aeq=[];beq=[]; VLB=[0;0]; VUB=[]; [x,fval]=fmincon('fun3',x0,A,b,Aeq,beq,VLB,VUB) 4、运算结果为: x = 0.7647 1.0588 fval = -2.0294
工 地 位 置 ( a, b) 及 水 泥 日 用 量 d 1 a b d 1 .2 5 1 .2 5 3 2 8 .7 5 0 .7 5 5 3 0 .5 4 .7 5 4 4 5 .7 5 5 7 5 3 6 .5 6 6 7 .2 5 7 .2 5 11
MATLAB优化工具箱--线性规划-非线性规划

linprog输入参数说明: f, A, b, Aeq, beq lb,ub 边界设置 说明: 如果x(i)无边界,则 lb(i) = -inf, ub(i) = inf
6
linprog 输出参数说明: x 决策变量取值 fval 目标函数最优值
exitflag > 0 成功找到最优解 0 达到最大迭代次数也没有找到最优解 < 0 该线性规划问题不可行或者linprog计
10
fmincon函数求解形如下面的有约束非线性规 划模型
一般形式:
min f ( X ) s.t. AX b
Aeq X beq l X u c(X ) 0 ceq ( X ) 0
Matlab求解有约束非线性最小化 1.约束中可以有等式约束 2.可以含线性、非线性约束均可
数学实验
输入参数语法:
例子:某农场种植两种作物A、B,需要甲、乙两种化肥。种植 每亩作物A和作物B分别需用的化肥数,可得利润及农场现有化
肥数量如下表所示:
问在现有条件下,如何安排种植,才能使利润最大?
作物
每亩所需化肥 (百公斤)
现有化肥
AB (百公斤)
化肥
甲
23
100) 6 4
数学实验
例题建模
[x,fval,exitflag,output,lambda]=fmincon(fun,x0,...)
数学实验
输入参数的几点说明
模型中如果没有A,b,Aeq,beq,lb,ub的限制,则以空矩阵[ ]作为 参数传入; nonlcon:如果包含非线性等式或不等式约束,则将这些函数
编写为一个Matlab函数, nonlcon就是定义这些函数的程序文件名;
3
多元非线性规划Matlab,非线性规划MATLAB代码

多元⾮线性规划Matlab,⾮线性规划MATLAB代码下⾯是三个⾮线性规划领域的算法。
课堂上给予了详细的讲解,在实践环节让学⽣编程实现,从⽽可以实验复杂⼀些的例⼦,加深对算法的理解。
下⾯共有四个程序grad,simplelinesearch,bfgs和phr,全部使⽤MATLAB语⾔编写。
这些代码远未完善,可修改余地很⼤,仅供教学之⽤。
function gradf=grad(hfun,x)%GRAD 数值法求函数在给定点处的导数值(⼀元函数)或梯度(多元函数)% gradf = grad(hfun,x0) hfun是函数句柄或内联函数,x0是⼀定点或⼀批点(按列);返回% 值gradf是函数在该点处的导数或梯度。
% 要求函数能对成批的点求函数值。
⽐如:feval(hfun,X)返回⼀个与X同列的⾏向量,对应于以% X每⼀列作为函数⾃变量⽽求得的函数值。
%% Reference: 《最优化计算原理与算法程序设计》, 粟塔⼭等编著, 国防科技⼤学出版社% (湖南), 2001.%% $Author: WBC $ $Date: 2003/10/25 $n = length(x);h=1e-3; % 数值法求梯度的步长w1=zeros(n,1);%h/2w2=w1; %-h/2w3=w1; %hw4=w1; %-hfor i=1:nx(i)=x(i)+h/2;w1(i)=hfun(x);x(i)=x(i)-h;w2(i)=hfun(x);x(i)=x(i)-h/2;w4(i)=hfun(x);x(i)=x(i)+2*h;w3(i)=hfun(x);x(i)=x(i)-h;endgradf=(8*(w1-w2)-(w3-w4))/(6*h);function [fv,x,lambda,exitflag]=simplelinesearch(hf,rho,l,u,lambda0,fv0,x0,g,d)%LINESEARCH 简单线搜索%输⼊参数:% hf -- 函数句柄,⽬标函数% rho -- 实标量,简单线搜索的参数,介于0到0.5之间的数% l -- 实标量,简单线搜索的参数,介于0到1之间的数% u -- 实标量,简单线搜索的参数,介于0到1之间的数,满⾜u>l% alpha0 -- 实标量,步长的初始值% fv0 -- 实标量,⼀维搜索的初始⽬标函数值,即 hf(x0+alpha_0*d)% x0 -- 实列向量,当前点% g -- 实列向量,函数hf在当前点处的梯度% d -- 实列向量,函数hf在当前点处的搜索⽅向%输出参数:% fv -- 实标量,⼀维搜索完成后的⽬标函数值,即 hf(x0+alpha*d)% x -- 实列向量,下⼀个点% lambda -- 实标量,可接受步长% exitflag -- 整型标量,等于0表⽰线搜索成功,等于-1表⽰线搜索失败(内部迭代次数⼤于iterMax) %参考⽂献:倪勤,最优化⽅法与程序设计,科学出版社% Date: 2009/12/20lambda = lambda0;x = x0;i = 0;imax = 30; % 最⼤迭代次数,⽤户可以修改% 主循环gd = dot(g, d);while i <= imaxfv = hf(x + lambda*d);i = i + 1;if fv < fv0 + lambda * rho * gd;x = x + lambda*d;exitflag = 0;return;endlambda_bar = -gd*lambda^2*0.5/(fv-fv0-lambda*gd);lambda = min(lambda_bar, u*lambda);endexitflag=0;if i >= imax && fv >= fv0fv = fv0;x = x0;lambda = 0;exitflag = -1;endfunction [fv, x, exitflag] = bfgs(hf, x0, epsi)%BFGS ⽆约束问题的BFGS算法%输⼊参数:% hf -- 函数句柄,⽬标函数% x0 -- 实列向量,初始点% epsi -- 实标量,终⽌误差%输出参数:% fv -- 实标量,⼀维搜索完成后的⽬标函数值,即 hf(x0+alpha*d)% x -- 实列向量,下⼀个点% exitflag -- 整型标量,等于0表⽰成功,等于-1表⽰失败(迭代次数⼤于iter_max) %参考⽂献:倪勤,最优化⽅法与程序设计,科学出版社% Date: 2009/12/20%%初始化%k = 0;rho = 0.01;l = 0.15;u = 0.85;x =x0;fv = hf(x);n = length(x);H = eye(n);iter_max = 100;%检查终⽌条件%g = grad(hf, x);while norm(g) > epsi && k<= iter_maxd = -H*g;lambda0 = 1.0;%%做线搜索,如果成功,则返回更新当前点%[fv, x, lambda, exitflag] = simplelinesearch(hf, rho, l, u, lambda0, fv, x, g, d); if exitflag == -1 %重开始H = eye(n);else%%更新H%g_old = g;g = grad(hf, x);p = lambda*d;q = g- g_old;Hq = H*q;pq = p'*q;qHq = q'*Hq;v = sqrt(qHq) * (p/pq-Hq/qHq);H = H + p*p'/pq - Hq*Hq'/qHq + v*v';endk = k+1;endexitflag = 0;if k > iter_maxexitflag = -1;endfunction [fv, x, exitflag] = phr(hf, cf, x0)%输⼊参数:% hf -- 函数句柄,⽬标函数% cf -- 函数句柄,约束条件,包含等式约束和不等式约束% x0 -- 实列向量,初始点%输出参数:% fv -- 实标量,⼀维搜索完成后的⽬标函数值,即 hf(x0+alpha*d)% x -- 实列向量,下⼀个点% exitflag -- 整型标量,等于0表⽰成功,等于-1表⽰失败(迭代次数⼤于iter_max) %参考⽂献:倪勤,最优化⽅法与程序设计,科学出版社% Date: 2009/12/20%%初始化%epsi = 1.0e-4;k = 0;sigma = 0.8;c = 1.5;theta = 0.8;x = x0;[ce, ci] = cf(x);l = length(ce);li = length(ci);lambda = ones(l+li, 1) * 0.1;iter_max = 100;phi = 0;if lphi = phi + ce'*ce;endif liphi = phi + sum(min(ci,lambda(l+1:end)/sigma).^2);endwhile phi > epsi && k <= iter_max%%hmf = @(x) mfun(x, hf, cf,lambda, sigma);[fv, x] = bfgs(hmf, x, epsi);[ce, ci] = cf(x);phi_old = phi;phi = 0;if lphi = phi + ce'*ce;endif liphi = phi + sum(min(ci,lambda(l+1:end)/sigma).^2); endif phi > epsi%%更新罚因⼦%if k >= 2 && phi/phi_old > thetasigma = c * sigma;end%%更新乘⼦%if llambda(1:l) = lambda(1:l) - sigma*ce;endif lilambda(l+1:end) = max(0, lambda(l+1:end) - sigma*ci); endendk = k+1;endexitflag = 0;fv = hf(x);exitflag = -1;end%%乘⼦罚函数%function fv = mfun(x, hf, cf, lambda, sigma)[ce, ci] = cf(x);l = length(ce);li = length(ci);fv = 0;fv = fv + hf(x);if lfv = fv - lambda(1:l)'*ce + 0.5*sigma*ce'*ce;endif lifv = fv + 0.5/sigma*sum(max(0,lambda(l+1:end) - sigma*ci).^2 - lambda(l+1:end).^2); end这⾥是演⽰代码:%% bfgs演⽰%教材P328.1-3hf1 = @(x) 100 * (x(2) - x(1).^2).^2 + (1 - x(1)).^2; %banana函数hf2 = @(x) (6 + x(1) + x(2)).^2 + (2 - 3*x(1) - 3*x(2) - x(1)*x(2)).^2;hf3 = @(x) x(1).^2 - 2*x(1)*x(2) + 4*x(2).^2 + x(1) - 3*x(2);[fv,x,exitflag]=bfgs(hf1,[0;0],0.001);fvxexitflag[fv,x,exitflag]=bfgs(hf2,[4;6],0.001);fvxexitflag[fv,x,exitflag]=bfgs(hf3,[1;1],0.001);fvexitflag%% phr算法%教材P414.5hf1 = @(x) x(1).^2 + x(2).^2;cf1 = @(x) deal([], x(1) - 1);hf2 = @(x) x(1) + (x(2) + 1).^2/3;cf2 = @(x) deal([],[x(1); x(2) - 1]);%教材P392.2hf3 = @(x) x(1).^2 + x(1).*x(2) + 2*x(2).^2 - 6*x(1) - 2*x(2) - 12*x(3);cf3 = @(x) deal(x(1)+x(2)+x(3)-2,...[x(1) - 2*x(2) + 3; x(1); x(2); x(3)]);%其它例⼦hf4 = @(x) 6*x(2)*x(5) + 7*x(1)*x(3) + 3*x(2)^2;cf4 = @(x) deal([3*x(2)^2*x(5) + 3*x(1)^2*x(3) - 20.875;x(1) - 0.3*x(2)],...[-x(1) + 0.2*x(2)*x(5) + 71-0.9*x(3) + x(4)^2 + 67x(3)x(5) - 1-x(3) + 20x(4) - 0.1*x(5)-x(4) + 0.5*x(5)x(3) - 0.9*x(5)]);hf5 = @(x) exp(x(1)) * (4*x(1)^2 + 2*x(2)^2 + 4*x(1)*x(2) + 2*x(2) + 1);cf5 = @(x) deal([], [x(1) + x(2) - x(1)*x(2) - 1.5; x(1)*x(2) + 10]);[fv, x, exitflag] = phr(hf1, cf1, [3;2]); fv x exitflag [fv, x, exitflag] = phr(hf2, cf2, [3;2]); fv x exitflag [fv, x, exitflag] =phr(hf3, cf3, [1;1;0]); fv x exitflag [fv, x, exitflag] = phr(hf4, cf4, [1; 4; 5; 2; 5]); fv x exitflag [fv, x, exitflag] = phr(hf5, cf5, [-1; 1]); fv x exitflag。
遗传算法解决非线性规划问题的Matlab程序

非线性整数规划的遗传算法Matlab程序(附图)通常,非线性整数规划是一个具有指数复杂度的NP问题,如果约束较为复杂,Matlab 优化工具箱和一些优化软件比如lingo等,常常无法应用,即使能应用也不能给出一个较为令人满意的解。
这时就需要针对问题设计专门的优化算法。
下面举一个遗传算法应用于非线性整数规划的编程实例,供大家参考!模型的形式和适应度函数定义如下:这是一个具有200个01决策变量的多目标非线性整数规划,编写优化的目标函数如下,其中将多目标转化为单目标采用简单的加权处理。
function Fitness=FITNESS(x,FARM,e,q,w)%% 适应度函数% 输入参数列表% x 决策变量构成的4×50的0-1矩阵% FARM 细胞结构存储的当前种群,它包含了个体x% e 4×50的系数矩阵% q 4×50的系数矩阵% w 1×50的系数矩阵%%gamma=0.98;N=length(FARM);%种群规模F1=zeros(1,N);F2=zeros(1,N);for i=1:Nxx=FARM{i};ppp=(1-xx)+(1-q).*xx;F1(i)=sum(w.*prod(ppp));F2(i)=sum(sum(e.*xx));endppp=(1-x)+(1-q).*x;f1=sum(w.*prod(ppp));f2=sum(sum(e.*x));Fitness=gamma*sum(min([sign(f1-F1);zeros(1,N)]))+(1-gamma)*sum(mi n([sign(f2-F2);zeros(1,N)]));针对问题设计的遗传算法如下,其中对模型约束的处理是重点考虑的地方function [Xp,LC1,LC2,LC3,LC4]=MYGA(M,N,Pm)%% 求解01整数规划的遗传算法%% 输入参数列表% M 遗传进化迭代次数% N 种群规模% Pm 变异概率%% 输出参数列表% Xp 最优个体% LC1 子目标1的收敛曲线% LC2 子目标2的收敛曲线% LC3 平均适应度函数的收敛曲线% LC4 最优适应度函数的收敛曲线%% 参考调用格式[Xp,LC1,LC2,LC3,LC4]=MYGA(50,40,0.3)%% 第一步:载入数据和变量初始化load eqw;%载入三个系数矩阵e,q,w%输出变量初始化Xp=zeros(4,50);LC1=zeros(1,M);LC2=zeros(1,M);LC3=zeros(1,M);LC4=zeros(1,M);Best=inf;%% 第二步:随机产生初始种群farm=cell(1,N);%用于存储种群的细胞结构k=0;while k %以下是一个合法个体的产生过程x=zeros(4,50);%x每一列的1的个数随机决定for i=1:50R=rand;Col=zeros(4,1);if R<0.7RP=randperm(4);%1的位置也是随机的Col(RP(1))=1;elseif R>0.9RP=randperm(4);Col(RP(1:2))=1;elseRP=randperm(4);Col(RP(1:3))=1;endx(:,i)=Col;end%下面是检查行和是否满足约束的过程,对于不满足约束的予以抛弃 Temp1=sum(x,2);Temp2=find(Temp1>20);if length(Temp2)==0k=k+1;farm{k}=x;endend%% 以下是进化迭代过程counter=0;%设置迭代计数器while counter%% 第三步:交叉%交叉采用双亲双子单点交叉newfarm=cell(1,2*N);%用于存储子代的细胞结构Ser=randperm(N);%两两随机配对的配对表A=farm{Ser(1)};%取出父代AB=farm{Ser(2)};%取出父代BP0=unidrnd(49);%随机选择交叉点a=[A(:,1:P0),B(:,(P0+1):end)];%产生子代ab=[B(:,1:P0),A(:,(P0+1):end)];%产生子代bnewfarm{2*N-1}=a;%加入子代种群newfarm{2*N}=b;%以下循环是重复上述过程for i=1:(N-1)A=farm{Ser(i)};B=farm{Ser(i+1)};P0=unidrnd(49);a=[A(:,1:P0),B(:,(P0+1):end)];b=[B(:,1:P0),A(:,(P0+1):end)];newfarm{2*i-1}=a;newfarm{2*i}=b;endFARM=[farm,newfarm];%新旧种群合并%% 第四步:选择复制FLAG=ones(1,3*N);%标志向量,对是否满足约束进行标记%以下过程是检测新个体是否满足约束for i=1:(3*N)x=FARM{i};sum1=sum(x,1);sum2=sum(x,2);flag1=find(sum1==0);flag2=find(sum1==4);flag3=find(sum2>20);if length(flag1)+length(flag2)+length(flag3)>0FLAG(i)=0;%如果不满足约束,用0加以标记endendNN=length(find(FLAG)==1);%满足约束的个体数目,它一定大于等于N NEWFARM=cell(1,NN);%以下过程是剔除不满主约束的个体kk=0;for i=1:(3*N)if FLAG(i)==1kk=kk+1;NEWFARM{kk}=FARM{i};endend%以下过程是计算并存储当前种群每个个体的适应值SYZ=zeros(1,NN);syz=zeros(1,N);for i=1:NNx=NEWFARM{i};SYZ(i)=FITNESS2(x,NEWFARM,e,q,w);%调用适应值子函数endk=0;%下面是选择复制,选择较优的N个个体复制到下一代while k minSYZ=min(SYZ);posSYZ=find(SYZ==minSYZ);POS=posSYZ(1);k=k+1;farm{k}=NEWFARM{POS};syz(k)=SYZ(POS);SYZ(POS)=inf;end%记录和更新,更新最优个体,记录收敛曲线的数据minsyz=min(syz);meansyz=mean(syz);pos=find(syz==minsyz);LC3(counter+1)=meansyz;if minsyz Best=minsyz;Xp=farm{pos(1)};endLC4(counter+1)=Best;ppp=(1-Xp)+(1-q).*Xp;LC1(counter+1)=sum(w.*prod(ppp));LC2(counter+1)=sum(sum(e.*Xp));%% 第五步:变异for i=1:Nif Pm>rand%是否变异由变异概率Pm控制AA=farm{i};%取出一个个体POS=unidrnd(50);%随机选择变异位R=rand;Col=zeros(4,1);if R<0.7RP=randperm(4);Col(RP(1))=1;elseif R>0.9RP=randperm(4);Col(RP(1:2))=1;elseRP=randperm(4);Col(RP(1:3))=1;end%下面是判断变异产生的新个体是否满足约束,如果不满足,此次变异无效 AA(:,POS)=Col;Temp1=sum(AA,2);Temp2=find(Temp1>20);if length(Temp2)==0farm{i}=AA;endendendcounter=counter+1end%第七步:绘收敛曲线图figure(1);plot(LC1);xlabel('迭代次数');ylabel('子目标1的值');title('子目标1的收敛曲线'); figure(2);plot(LC2);xlabel('迭代次数');ylabel('子目标2的值');title('子目标2的收敛曲线'); figure(3);plot(LC3);xlabel('迭代次数');ylabel('适应度函数的平均值');title('平均适应度函数的收敛曲线'); figure(4);plot(LC4);xlabel('迭代次数');ylabel('适应度函数的最优值');title('最优适应度函数的收敛曲线');贴出一幅运行得到的收敛曲线。
MATLAB线性规划非线性规划

解 编写M文件xxgh1.m如下: c=[-0.4 -0.28 -0.32 -0.72 -0.64 -0.6]; A=[0.01 0.01 0.01 0.03 0.03 0.03;0.02 0 0 0.05 0 0;0 0.02 0 0 0.05 0;0 0 0.03 0 0 0.08]; b=[850;700;100;900];
返 回
解答
线性规划模型的一般形式
目标函数和所有的约束条件都是设计变量 的线性函数.
min u ci xi
i 1
n
n aik xk bi , i 1, 2,..., n. s.t. k 1 x 0, i 1, 2,..., n. i
矩阵形式: min u cx Ax b s.t. vlb x vub
Aeq=[]; beq=[];
vlb=[0;0;0;0;0;0]; vub=[];
To MATLAB (xxgh1)
[x,fval]=linprog(c,A,b,Aeq,beq,vlb,vub)
例2
min z 6x1 3x2 4x3 s.t. x1 x2 x3 120 x1 30 0 x2 50 x3 20
编写M文件xxgh3.m如下: f = [13 9 10 11 12 8]; A = [0.4 1.1 1 0 0 0 0 0 0 0.5 1.2 1.3]; b = [800; 900]; Aeq=[1 0 0 1 0 0 0 1 0 0 1 0 0 0 1 0 0 1]; To MATLAB (xxgh3) beq=[400 600 500]; vlb = zeros(6,1); vub=[]; [x,fval] = linprog(f,A,b,Aeq,beq,vlb,vub)
MATLAB非线性规划问题

一.非线性规划课题实例1 表面积为36平方米的最大长方体体积。
建立数学模型:设x、y、z分别为长方体的三个棱长,f为长方体体积。
max f = x y (36-2 x y)/2 (x+y)实例2 投资决策问题某公司准备用5000万元用于A、B两个项目的投资,设x1、x2分别表示配给项目A、B的投资。
预计项目A、B的年收益分别为20%和16%。
同时,投资后总的风险损失将随着总投资和单位投资的增加而增加,已知总的风险损失为2x12+x22+(x1+x2)2.问应如何分配资金,才能使期望的收益最大,同时使风险损失为最小。
建立数学模型:max f=20x1+16x2-λ[2x12+x22+(x1+x2)2]s.t x1+x2≤5000x 1≥0,x2≥0目标函数中的λ≥0是权重系数。
由以上实例去掉实际背景,其目标函数与约束条件至少有一处是非线性的,称其为非线性问题。
非线性规划问题可分为无约束问题和有约束问题。
实例1为无约束问题,实例2为有约束问题。
二.无约束非线性规划问题:求解无约束最优化问题的方法主要有两类:直接搜索法(Search method)和梯度法(Gradient method),单变量用fminbnd,fminsearch,fminunc;多变量用fminsearch,fminnuc 1.fminunc函数调用格式:x=fminunc(fun,x0)x=fminunc(fun,x0,options)x=fminunc(fun,x0,options,P1,P2)[x,fval]=fminunc(…)[x,fval, exitflag]=fminunc(…)[x,fval, exitflag,output]=fminunc(…)[x,fval, exitflag,output,grad]=fminunc(…)[x,fval, exitflag,output,grad,hessian]=fminunc(…)说明:fun为需最小化的目标函数,x0为给定的搜索的初始点。
非线性规划问题的Matlab实现求解

本科毕业论文(设计)论文题目:非线性规划问题的建模与Matlab求解实现的案例分析学生:许富豪学号:1204180137专业:信息与计算科学班级:计科1201指导教师:王培勋完成日期:2015年6月25日非线性规划问题的建模与Matlab求解实现的案例分析容摘要非线性规划问题通常极其抽象,并且求解计算极其复杂,本文举个别非线性规划问题案例,通过对抽象的非线性规划问题先建立数学模型,再利用Matlab软件高效快捷的实现非线性规划问题的求解,最后分析利用Matlab软件得出的案例结果。
关键词:非线性规划建立数学模型Matlab目录(三号黑体居中)空一行空一行一、※※※※※※ (1)(一)※※※※※※ (1)1.※※※※※※※※※※※※※ (1)2.※※※※※※※ (4)(二)※※※※ (7)(三)※※※※※※※※ (12)二、※※※※ (16)(一)※※※※※ (16)(二)※※※※※ (24)1.※※※※ (24)2.※※※※※ (30)3.※※※※ (31)(三)※※※※ (33)三、※※※※ (36)(一)※※※※※ (38)(二)※※※※ (43)四、※※※※ (45)参考文献 (48)附录 (50)(标题顺序号、容及其开始页码均为四号宋体,一级标题为黑体四号)序 言非线性规划问题通常难以用人力计算,所以我们一般利用Matlab 软件代替人去计算抽象的非线性规划问题,解决了耗费时间、耗费精力的问题,快速准确的得出计算结果。
因此,善于利用Matlab 实现非线性规划问题的求解非常重要,而求解非线性规划问题之前必须先对问题进行建立数学模型,才能准确的理解题意并快速的运用Matlab 求解。
一、非现性规划的基本概念(一)定义如果目标函数或约束条件中至少有一个是非线性函数,则最优化问题就叫做非线性规划问题,简记为NP 。
(二)一般形式min (),n f x x E ∈,()=0(=1,2,..()0(j=1,2i jh x j m s t g x l ⋯≤⎩⋯⎧⎨),,)其中:1,2,n =()Tx x x x ⋯称为模型(NP )的决策变量,f 称为目标函数,(=1,...,)i h i m 和(=1,...,)j g j l 称为约束函数;()=0(=1,...,)i h x i m 称为等式约束;()0(=1,...,)j g x j l ≤称为不等式约束。
MATLAB非线性规划问题样本

一.非线性规划课题实例1 表面积为36平方米的最大长方体体积。
建立数学模型:设x、 y、 z分别为长方体的三个棱长, f为长方体体积。
max f = x y (36-2 x y)/2 (x+y)实例2 投资决策问题某公司准备用5000万元用于A、 B两个项目的投资, 设x1、 x2分别表示配给项目A、 B的投资。
预计项目A、 B的年收益分别为20%和16%。
同时, 投资后总的风险损失将随着总投资和单位投资的增加而增加, 已知总的风险损失为2x12+x22+(x1+x2)2.问应如何分配资金, 才能使期望的收益最大, 同时使风险损失为最小。
建立数学模型:max f=20x1+16x2-λ[2x12+x22+(x1+x2)2]s.t x1+x2≤5000x 1≥0,x2≥0目标函数中的λ≥0是权重系数。
由以上实例去掉实际背景, 其目标函数与约束条件至少有一处是非线性的, 称其为非线性问题。
非线性规划问题可分为无约束问题和有约束问题。
实例1为无约束问题, 实例2为有约束问题。
二.无约束非线性规划问题:求解无约束最优化问题的方法主要有两类: 直接搜索法(Search method)和梯度法(Gradient method), 单变量用fminbnd,fminsearch,fminunc;多变量用fminsearch,fminnuc1.fminunc函数调用格式: x=fminunc(fun,x0)x=fminunc(fun,x0,options)x=fminunc(fun,x0,options,P1,P2)[x,fval]=fminunc(…)[x,fval, exitflag]=fminunc(…) [x,fval, exitflag,output]=fminunc(…)[x,fval, exitflag,output,grad]=fminunc(…)[x,fval, exitflag,output,grad,hessian]=fminunc(…)说明: fun 为需最小化的目标函数, x0为给定的搜索的初始点。
利用二层规划算法求解非线性问题(matlab)
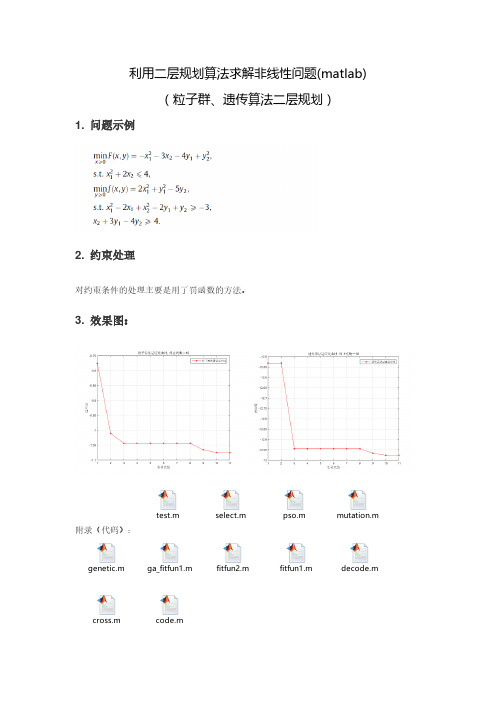
利用二层规划算法求解非线性问题(matlab)(粒子群、遗传算法二层规划)1. 问题示例2. 约束处理对约束条件的处理主要是用了罚函数的方法。
3. 效果图:test.m select.m pso.m mutation.m 附录(代码):genetic.m ga_fitfun1.m fitfun2.m fitfun1.m decode.mcross.m code.m代码有如上图附录所示11个文件,分别对应下面的code1-code11。
将code1-code11的代码分别保存为.m文件,名字为对应括号中的名字。
Code 1(code.m)%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%function ret = code(lenchrom, bound)% 本函数将变量编码成染色体,用于随机初始化一个种群% lenchrom input : 染色体长度% bound input : 变量的取值范围% ret output: 染色体的编码值flag = 0;while flag == 0pick = rand(1,length(lenchrom));ret = bound(:,1)' + (bound(:,2) - bound(:,1))'.*pick; % 线性插值,编码结果以实数向量存入ret中flag = test(lenchrom,bound,ret); % 检验染色体的可行性endCode 2(cross.m)function ret = cross(pcross, lenchrom, chrom, sizepop, bound)% 本函数完成交叉操作% pcorss input : 交叉概率% lenchrom input : 染色体的长度% chrom input : 染色体群% sizepop input : 种群规模% ret output : 交叉后的染色体for i = 1:sizepop % 每一轮for循环中,可能会进行一次交叉操作,染色体是随机选择的,交叉位置也是随机选择的,% 但该轮for循环中是否进行交叉操作则由交叉概率决定(continue控制)% 随机选择两个染色体进行交叉pick = rand(1,2);while prod(pick) == 0pick = rand(1,2);endindex = ceil(pick.*sizepop);% 交叉概率决定是否进行交叉pick = rand;while pick == 0pick = rand;endif pick > pcrosscontinue;endflag = 0;while flag == 0% 随机选择交叉位pick = rand;while pick == 0pick = rand;endpos = ceil(pick.*sum(lenchrom));% 随机选择进行交叉的位置,即选择第几个变量进行交叉,注意:两个染色体交叉的位置相同pick = rand; % 交叉开始v1 = chrom(index(1), pos);v2 = chrom(index(2),pos);chrom(index(1), pos) = pick*v2 + (1 - pick)*v1;chrom(index(2), pos) = pick*v1 + (1 - pick)*v2; % 交叉结束flag1 = test(lenchrom, bound, chrom(index(1),:)); % 检验染色体1的可行性flag2 = test(lenchrom, bound, chrom(index(2),:)); % 检验染色体2的可行性if flag1 * flag2 == 0flag = 0;elseflag = 1;end% 如果两个染色体不是都可行,则重新交叉endendret = chrom;Code 3(decode.m)%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%function ret=Decode(lenchrom,bound,code,opts)% 本函数对染色体进行解码% lenchrom input : 染色体长度% bound input : 变量取值范围% code input : 编码值% opts input : 解码方法标签% ret output: 染色体的解码值switch optscase 'binary'% binary codingfor i = length(lenchrom):-1:1data(i) = bitand(code, 2^lenchrom(i) - 1); % 并低十位,然后将低十位转换成十进制数存在data(i)里面code = (code-data(i))/(2^lenchrom(i)); % 低十位清零,然后右移十位endret = bound(:,1)' + data./(2.^lenchrom-1).*(bound(:,2) - bound(:,1))';%分段解码,以实数向量的形式存入ret中case 'grey' % grey codingfor i = sum(lenchrom):-1:2code = bitset(code, i - 1, bitxor(bitget(code,i), bitget(code,i - 1)));endfor i = length(lenchrom):-1:1data(i) = bitand(code, 2^lenchrom(i) - 1);code = (code - data(i))/(2^lenchrom(i));endret = bound(:,1)' + data./(2.^lenchrom - 1).*(bound(:,2) - bound(:,1))';%分段解码,以实数向量的形式存入ret中case 'float' % float codingret = code; % 解码结果就是编码结果(实数向量),存入ret中endCode 4(fitfun1.m)%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function y = fitfun1(x, penalty_num)x1 = x(1);x2 = x(2);y1 = x(3);y2 = x(4);% 公式1 - 顶层公式y = -x1^2 - 3*x2 - 4 * y1 + y2^2;% 约束条件测试if x1 < 0 | x2 < 0 | y1 < 0 | y2 < 0y = y + (min([x1, x2, y1, y2])).^2 * penalty_num; % 惩罚系数return;endif x2 + 3 * y1 - 4 * y2 < 4y = y + (4 - (x2 + 3 * y1 - 4 * y2)).^2 * penalty_num; % 惩罚系数return;endif (x1^2 + 2 * x2) > 4y = y + ((x1^2 + 2 * x2) - 4).^2 * penalty_num; % 惩罚系数return;endCode 5(fitfun2.m)function y = fitfun2(x, penalty_num)x1 = x(1);x2 = x(2);y1 = x(3);y2 = x(4);% 第2个公式y = 2 * x1^2 + y1^2 - 5 * y2;% - 检查约束条件if x1 < 0 | x2 < 0 | y1 < 0 | y2 < 0y = y + (min([x1, x2, y1, y2])).^2 * penalty_num; % 惩罚系数return;endif x2 + 3 * y1 - 4 * y2 < 4y = y + (4 - (x2 + 3 * y1 - 4 * y2)).^2 * penalty_num; % 惩罚系数return;endif (x1^2 + 2 * x2) > 4y = y + ((x1^2 + 2 * x2) - 4).^2 * penalty_num; % 惩罚系数return;endCode 6(ga_fitfun1.m)function [y, x_best_pso] = ga_fitfun2(x, penalty_num, limition_min, limition_max)[y2, x_best_pso] = pso(x, penalty_num, limition_min, limition_max); % 粒子算法进行计算并且获得优化后的x 和适应度y2% 按第一层公式进行评价y = fitfun1(x_best_pso, penalty_num);Code 7(genetic.m)% 清空环境变量clcclearclose all;% 遗传算法参数初始化maxgen = 10; % 进化代数,即迭代次数sizepop = 50; % 种群规模pcross = 0.2; % 交叉概率选择,0和1之间pmutation = 0.1; % 变异概率选择,0和1之间limition_max = 100; % 数值变化范围的最大值limition_min = 0; % 数值变化范围的最小值penalty_num = 1e10; % 惩罚系数numsum = 4; % 自变量总数% - 用global 变量来初始化一个最糟糕的初始化粒子个体来做全局最佳粒子个体global zbest;zbest = zeros(1, numsum) - 1; % 约束条件是: 4 个自变量都大于0, 为了违背都赋值为"- 1";global fitnesszbest;fitnesszbest = 100*penalty_num;% ------------------------lenchrom = ones(1,numsum);bound = [limition_min*ones(numsum,1), limition_max*ones(numsum,1)]; %数据范围%------------------------------------------------------种群初始化--------------------------------------------------------individuals = struct('fitness', zeros(1,sizepop), 'chrom',[]); % 将种群信息定义为一个结构体avgfitness = []; % 每一代种群的平均适应度bestfitness = []; % 每一代种群的最佳适应度bestchrom = []; % 适应度最好的染色体fprintf(['开始初始化\n']);% 初始化种群for i = 1:sizepop% 随机产生一个种群individuals.chrom(i,:) = code(lenchrom,bound); % 编码(binary和grey的编码结果为一个实数,float的编码结果为一个实数向量)x = individuals.chrom(i,:);% 计算适应度[individuals.fitness(i), x_best_pso] = ga_fitfun1(x, penalty_num, limition_min, limition_max); % 染色体的适应度individuals.chrom(i,:) = x_best_pso;end% 找最好的染色体[bestfitness, bestindex] = min(individuals.fitness);bestchrom = individuals.chrom(bestindex,:); % 最好的染色体avgfitness = sum(individuals.fitness)/sizepop; % 染色体的平均适应度% 记录每一代进化中最好的适应度和平均适应度trace_ga = [avgfitness, bestfitness];trace_pso = [fitnesszbest];% 迭代求解最佳初始阀值和权值% 进化开始fprintf(['开始进化\n']);for i = 1:maxgen% 选择individuals = select(individuals,sizepop);avgfitness = sum(individuals.fitness)/sizepop;% 交叉individuals.chrom = cross(pcross, lenchrom, individuals. chrom, sizepop, bound);% 变异individuals.chrom = mutation(pmutation, lenchrom, individuals. chrom, sizepop, i, maxgen, bound);% 计算适应度for j = 1:sizepopx = individuals.chrom(j,:); % 解码[individuals.fitness(j), x_best_pso] = ga_fitfun1(x, penalty_num, limition_min, limition_max);individuals.chrom(j,:) = x_best_pso;end% 找到最小和最大适应度的染色体及它们在种群中的位置[newbestfitness, newbestindex] = min(individuals.fitness);[worestfitness, worestindex] = max(individuals.fitness);% 代替上一次进化中最好的染色体if bestfitness > newbestfitnessbestfitness = newbestfitness;bestchrom = individuals.chrom(newbestindex,:);endindividuals.chrom(worestindex,:) = bestchrom;individuals.fitness(worestindex) = bestfitness;avgfitness = sum(individuals.fitness)/sizepop;trace_ga = [trace_ga; avgfitness, bestfitness]; % 记录每一代进化中最好的适应度和平均适应度- 遗传算法trace_pso = [trace_pso; fitnesszbest];fprintf(['遗传进化了', num2str(i), '代\n']);end% 遗传算法结果显示figure(1);[r_ga, c_ga] = size(trace_ga);plot([1:r_ga]', trace_ga(:,2), 'r-*');title(['遗传算法适应度曲线' '终止代数=' num2str(maxgen)]); xlabel('进化代数'); ylabel('适应度');legend('遗传算法最佳适应度');grid on;print(gcf, '-dpng', '遗传算法最佳适应度变化.png', '-r300');% 粒子算法结果显示figure(2)[r_pso, c_pso] = size(trace_pso);plot([1:r_pso]', trace_pso, 'r-*');title(['粒子算法适应度曲线' '终止代数=' num2str(maxgen)]); xlabel('进化代数'); ylabel('适应度');legend('粒子算法最佳适应度');grid on;print(gcf, '-dpng', '粒子算法最佳适应度变化.png', '-r300');% - 存储最佳结果x = bestchrom;dos('del Result.xls');xlswrite('Result.xls', [{'x1', 'x2', 'y1', 'y2', '公式1结果', '公式2结果'}; num2cell([x, fitfun1(x, penalty_num), fitfun2(x, penalty_num)])]);Code 8(mutation.m)function ret = mutation(pmutation, lenchrom, chrom, sizepop, num, maxgen, bound)% 本函数完成变异操作% pcorss input : 变异概率% lenchrom input : 染色体长度% chrom input : 染色体群% sizepop input : 种群规模% opts input : 变异方法的选择% pop input : 当前种群的进化代数和最大的进化代数信息% bound input : 每个个体的上届和下届% maxgen input : 最大迭代次数% num input : 当前迭代次数% ret output : 变异后的染色体for i = 1:sizepop% 每一轮for循环中,可能会进行一次变异操作,染色体是随机选择的,变异位置也是随机选择的,% 但该轮for循环中是否进行变异操作则由变异概率决定(continue控制)% 随机选择一个染色体进行变异pick = rand;while pick == 0pick = rand;endindex = ceil(pick*sizepop);% 变异概率决定该轮循环是否进行变异pick = rand;if pick > pmutationcontinue;endflag = 0;while flag == 0% 变异位置pick = rand;while pick == 0pick = rand;endpos = ceil(pick * sum(lenchrom)); % 随机选择了染色体变异的位置,即选择了第pos个变量进行变异pick = rand; % 变异开始fg = (rand*(1 - num/maxgen))^2;if pick > 0.5chrom(i, pos) = chrom(i, pos) + (bound(pos, 2) - chrom(i,pos))*fg;elsechrom(i,pos) = chrom(i, pos) - (chrom(i, pos) - bound(pos,1))*fg;end% 变异结束flag = test(lenchrom, bound, chrom(i,:)); % 检验染色体的可行性endendret = chrom;Code 9(pso.m)function [y, x_best] = pso(x, penalty_num, limition_min, limition_max)% 参数初始化% 粒子群算法中的两个参数c1 = 1.49445;c2 = 1.49445;maxgen = 100; % 进化次数sizepop = 50; % 种群规模pop_len = length(x); % 粒子个体长度Vmax = 1*limition_max;Vmin = -1*limition_max;popmax = limition_max;popmin = limition_min;pop = [];V = [];fitness = [];for i = 1:sizepop%pop(i,:) = 10*rand(1,4);pop(i,:) = x;V(i,:) = rand(1,4);fitness(i) = fitfun2(pop(i,:), penalty_num);end% 个体极值和群体极值global zbest; % 通过全局变量评比确保公式2获得最小值global fitnesszbest;[bestfitness, bestindex] = min(fitness);if bestfitness < fitnesszbestzbest = pop(bestindex,:); % 全局最佳fitnesszbest = bestfitness; % 全局最佳适应度值endgbest = pop; % 个体最佳fitnessgbest = fitness; % 个体最佳适应度值% 迭代寻优% fprintf(['粒子算法进化了: ']);for i = 1:maxgenfor j = 1:sizepop% 速度更新V(j,:) = V(j,:) + c1*rand*(gbest(j,:) - pop(j,:)) + c2*rand*(zbest - pop(j,:));V(j,find(V(j,:) > Vmax)) = Vmax;V(j,find(V(j,:) < Vmin)) = Vmin;% 种群更新pop(j,:) = pop(j,:) + 0.2*V(j,:);pop(j,find(pop(j,:) > popmax)) = popmax;pop(j,find(pop(j,:) < popmin)) = popmin;% 自适应变异pos = unidrnd(pop_len);if rand > 0.95pop(j,pos) = popmin + rand(1,1)*(popmax - popmin);end% 适应度值fitness(j) = fitfun2(pop(j,:), penalty_num);endfor j = 1:sizepop% 个体最优更新if fitness(j) < fitnessgbest(j)gbest(j,:) = pop(j,:);fitnessgbest(j) = fitness(j);end%群体最优更新if fitness(j) < fitnesszbestzbest = pop(j,:);fitnesszbest = fitness(j);endendyy(i) = fitnesszbest;%fprintf([num2str(i), ',']);end% fprintf(['\n']);% - 结果分析% plot(yy)% title(['适应度曲线' '终止代数=' num2str(maxgen)]); % xlabel('进化代数');ylabel('适应度');x_best = zbest;y = yy(end);Code 10(select.m)function ret = select(individuals, sizepop)% 本函数对每一代种群中的染色体进行选择,以进行后面的交叉和变异% individuals input : 种群信息% sizepop input : 种群规模% ret output : 经过选择后的种群%根据个体适应度值进行排序fitness1 = 10./individuals.fitness;sumfitness = sum(fitness1);sumf = fitness1./sumfitness;index = [];for i = 1:sizepop %转sizepop次轮盘pick = rand;while pick == 0pick = rand;endfor j = 1:sizepop% pick=pick-sumf(i);pick = pick - sumf(j);if pick < 0index = [index, j];break; % 寻找落入的区间,此次转轮盘选中了染色体i% 注意:在转sizepop次轮盘的过程中,有可能会重复选择某些染色体endendendindividuals.chrom = individuals.chrom(index,:);individuals.fitness = individuals.fitness(index);ret = individuals;Code 11(test.m)function flag = test(lenchrom, bound, code)% lenchrom input : 染色体长度% bound input : 变量的取值范围% code output: 染色体的编码值x = code; %先解码flag = 1;% if(x(1)<0)&&(x(2)<0)&&(x(3)<0)&&(x(1)>bound(1,2))&&(x(2)>bound(2,2))&&(x(3)>bound(3, 2))% flag=0;% end。
用MATLAB解二次型规划和一般非线性规划问题

实验报告11实验名称:用MATLAB 解二次型规划和一般非线性规划问题实验目的:学会如何运用MATLAB 解二次型规划和一般非线性规划问题; 实验内容:书P21111、试求解下面的二次型规划问题。
2122212136442min x x x x x x --+-⎪⎩⎪⎨⎧≥≤+≤+0943..2,12121x x x x x t s x解:>> f=[-6,-3];H=[4,-4;-4,8];>> A=[1,1;4,1];B=[3,9];Aeq=[];Beq=[];xm=zeros(2,1);>> [x,f_opt]=quadprog(H,f,A,B,Aeq,Beq,xm,[],[])Warning: Your Hessian is not symmetric. Resetting H=(H+H')/2.> In quadprog at 232Warning: Large-scale method does not currently solve this problem formulation, using medium-scale method instead.> In quadprog at 263Optimization terminated.x =1.95001.0500f_opt =-11.025012、试求解下面的非线性规划问题。
()12424min 22122211++++x x x x x e x⎪⎪⎩⎪⎪⎨⎧≤≤--≥≥++-≤+10,10105.10..2121212121x x x x x x x x x x t s x 解:function [c,ceq]=cdd01(x)c=[x(1)+x(2);x(1)*x(2)-x(1)-x(2)+1.5;-x(1)*x(2)-10];ceq=[];>> y=@(x)exp(x(1))*(4*x(1)*x(1)+2*x(2)*x(2)+4*x(1)*x(2)+2*x(2)+1);x0=[1;1];xm=[-10;-10];xM=[10;10];A=[];B=[];Aeq=[];Beq=[];[x,f_opt,c,d]=fmincon(y,x0,A,B,Aeq,Beq,xm,xM,@cdd01)Warning: Trust-region-reflective method does not currently solve this type of problem, using active-set (line search) instead.> In fmincon at 422Maximum number of function evaluations exceeded;increase OPTIONS.MaxFunEvals.x =3.1740-7.9967f_opt =1.2351e+003c =d =iterations: 54funcCount: 201lssteplength: 1stepsize: 5.6428algorithm: 'medium-scale: SQP, Quasi-Newton, line-search'firstorderopt: 390.0759constrviolation: 1.7857e-008message: [1x79 char]15、试求解下面的0-1线性规划问题解>> f=[5,7,10,3,1]>> A=[-1,1,-5,-1,4;2,-6,3,2,-2;0,-2,2,-1,-1] >> B=[-2;0;1]>> x_m=[0,0,0,0,0]>> x_M=[1,1,1,1,1]>> x=bintprog(f,A,B,[],[],x_m,x_M)x =11。
多目标非线性规划程序(Matlab)

function [errmsg,Z,X,t,c,fail] =BNB18(fun,x0,xstat,xl,xu,A,B,Aeq,Beq,nonlcon,setts,options1,options2,ma xSQPit,varargin);%·ÇÏßÐÔÕûÊý¹æ»®Ä£ÐÍÇó½â·ÖÖ§¶¨½çµü´úËã·¨¡£ÔÚMATLAB5.3ÖÐʹÓã¬ÐèOptimizat ion toolbox 2.0Ö§³Ö?% Minimize F(x)%subject to: xlb <= x <=xub% A*x <= B% Aeq*x=Beq% C(x)<=0% Ceq(x)=0%% x(i)¿ÉΪÁ¬Ðø±äÁ¿£¬ÕûÊý£¬»ò¹Ì¶¨Öµ% ʹÓøñʽ%[errmsg,Z,X]=BNB18('fun',x0,xstat,xl,xu,A,B,Aeq,Beq,'nonlcon',setts)%fun£º MÎļþÃû£¬±íʾ×îС»¯Ä¿±êº¯Êýf=fun(x)%x0: ÁÐÏòÁ¿£¬±íʾ±äÁ¿³õÖµ%xstat£º ÁÐÏòÁ¿£¬xstat(i)=0±íʾx(i)ΪÁ¬Ðø±äÁ¿£¬1±íʾÕûÊý£¬2±íʾ¹Ì¶¨Öµ%xl£º ÁÐÏòÁ¿£¬±íʾ±äÁ¿Ï½ç%xu: ÁÐÏòÁ¿£¬±íʾ±äÁ¿ÉϽç%A: ¾ØÕó, ±íʾÏßÐÔ²»µÈʽԼÊøϵÊý%B: ÁÐÏòÁ¿, ±íʾÏßÐÔ²»µÈʽԼÊøÉϽç%Aeq: ¾ØÕó, ±íʾÏßÐÔµÈʽԼÊøϵÊý%Beg: ÁÐÏòÁ¿, ±íʾÏßÐÔ²»µÈʽԼÊøÓÒ¶ËÖµ%nonlcon:MÎļþÃû£¬±íʾ·ÇÏßÐÔÔ¼Êøº¯Êý[C,Ceq]=nonlin(x),ÆäÖÐC(x)Ϊ²»µÈʽԼÊø,% Ceq(x)ΪµÈʽԼÊø%setts: Ëã·¨ÉèÖÃ%errmsq: ·µ»Ø´íÎóÌáʾ%Z: ·µ»ØÄ¿±êº¯Êý×îСֵ%X: ·µ»Ø×îÓŽâ%%ÀýÌâ% max x1*x2*x3% -x1+2*x2+2*x3>=0% x1+2*x2+2*x3<=72% 10<=x2<=20% x1-x2=10% ÏÈд Mº¯Êýdiscfun.m% function f=discfun(x)% f=-x(1)*x(2)*x(3);%Çó½â% clear;x0=[25,15,10]';xstat=[1 1 1]';% xl=[20 10 -10]';xu=[30 20 20]';% A=[1 -2 -2;1 2 2];B=[0 72]';Aeq=[1 -1 0];Beq=10;% [err,Z,X]=BNB18('discfun',x0,xstat,xl,xu,A,B,Aeq,Beq);% XMAX=X',ZMAX=-Z%% BNB18 Finds the constrained minimum of a function of several possibly integer variables.% Usage: [errmsg,Z,X,t,c,fail] =%BNB18(fun,x0,xstatus,xlb,xub,A,B,Aeq,Beq,nonlcon,settings,options1,opti ons2,maxSQPiter,P1,P2,...)%% BNB solves problems of the form:% Minimize F(x) subject to: xlb <= x0 <=xub% A*x <= B Aeq*x=Beq% C(x)<=0 Ceq(x)=0% x(i) is continuous for xstatus(i)=0% x(i) integer for xstatus(i)= 1% x(i) fixed for xstatus(i)=2%% BNB uses:% Optimization Toolbox Version 2.0 (R11) 09-Oct-1998% From this toolbox fmincon.m is called. For more info type help fmincon. %% fun is the function to be minimized and should return a scalar.F(x)=feval(fun,x).% x0 is the starting point for x. x0 should be a column vector.% xstatus is a column vector describing the status of every variable x(i). % xlb and xub are column vectors with lower and upper bounds for x.% A and Aeq are matrices for the linear constrains.% B and Beq are column vectors for the linear constrains.% nonlcon is the function for the nonlinear constrains.% [C(x);Ceq(x)]=feval(nonlcon,x). Both C(x) and Ceq(x) should be column vectors.%% errmsg is a string containing an error message if BNB found an erro r in the input.% Z is the scalar result of the minimization, X the values of the accompanying variables.% t is the time elapsed while the algorithm BNB has run, c is the number of BNB cycles and% fail is the number of unsolved leaf sub-problems.%% settings is a row vector with settings for BNB:% settings(1) (standard 0) if 1: use phase 1 by relaxation. This sometimes makes the algorithm% faster, because phase 1 means the algorithm first checks if there is a feasible solution% for a sub-problem before trying to find a best solution. If there is no feasible solution BNB% will not try to find a best solution.% settings(2) (standard 0) if 1: if the sub-problem did not converge do not branch. If a sub-% problem did not converge this means BNB did not find a solution for it. Normally BNB will% branch the problem so it can try again to find a solution.% A sub-problem that is a leaf of the branch-and-bound-three can not be branched. If such% a problem does not converge it will be considered unfeasible and the parameter fail will be% raised by one.% settings(3) (standard 0) if 1: if 1 a sub-problem that did not converge but did return a feasible% point will be considered convergent. This might be useful if fmincon is having a hard time with% a certain problem but you do want some results.% options1 and options2 are options structures for phase 1 and phase 2.% For details about the options structure type help optimset.% maxSQPiter is a global variable used by fmincon (if modified as described in bnb18.m).% maxSQPiter is 1000 by default.% P1,P2,... are parameters to be passed to fun and nonlcon.% F(x)=feval(fun,x,P1,P2,...). [C(x);Ceq(x)]=feval(nonlcon,x,P1,P2,...). % Type edit BNB18 for more info.% E.C. Kuipers% e-mail E.C.Kuipers@cpedu.rug.nl% FI-Lab% Applied Physics% Rijksuniversiteit Groningen% To get rid of bugs and to stop fmincon from hanging make the following chances:%% In optim/private/nlconst.m ($Revision: 1.20 $ $Date: 1998/08/24 13:46:15 $):% Get EXITFLAG independent of verbosity.% After the lines: disp(' less than 2*options.TolFun but constraints are not satisfied.')% end% EXITFLAG = -1;% end% end% status=1;% add the line: if (strncmp(howqp, 'i',1) & mg > 0), EXITFLAG = -1; end; %% In optim/private/qpsub.m ($Revision: 1.21 $ $Date: 1998/09/01 21:37:56 $):% Stop qpsub from hanging.% After the line: % Andy Grace 7-9-90. Mary Ann Branch 9-30-96.% add the line: global maxSQPiter;% and changed the line: maxSQPiters = Inf;% to the line: if exist('maxSQPiter','var'), maxSQPiters = maxSQPiter; else maxSQPiters=inf; end;% I guess there was a reason to put maxSQPiters at infinity, but this works fine for me.global maxSQPiter;% STEP 0 CHECKING INPUTZ=[]; X=[]; t=0; c=0; fail=0;if nargin<2, errmsg='BNB needs at least 2 input arguments.'; return; end; if isempty(fun), errmsg='No fun found.'; return; end;if isempty(x0), errmsg='No x0 found.'; return;elseif size(x0,2)>1, errmsg='x0 must be a column vector.'; return; end; xstatus=zeros(size(x0));if nargin>2 & ~isempty(xstat)if all(size(xstat)<=size(x0))xstatus(1:size(xstat))=xstat;else errmsg='xstatus must be a column vector the same size as x0.'; return;end;if any(xstatus~=round(xstatus) | xstatus<0 | 2<xstatus)errmsg='xstatus must consist of the integers 0,1 en 2.'; return;end;end;xlb=zeros(size(x0));xlb(find(xstatus==0))=-inf;if nargin>3 & ~isempty(xl)if all(size(xl)<=size(x0))xlb(1:size(xl,1))=xl;else errmsg='xlb must be a column vector the same size as x0.'; return;end;end;if any(x0<xlb)errmsg='x0 must be in the range xlb <= x0.'; return;elseif any(xstatus==1 & (~isfinite(xlb) | xlb~=round(xlb)))errmsg='xlb(i) must be an integer if x(i) is an integer variabele.'; return;end;xlb(find(xstatus==2))=x0(find(xstatus==2));xub=ones(size(x0));xub(find(xstatus==0))=inf;if nargin>4 & ~isempty(xu)if all(size(xu)<=size(x0))xub(1:size(xu,1))=xu;else errmsg='xub must be a column vector the same size as x0.'; return;end;end;if any(x0>xub)errmsg='x0 must be in the range x0 <=xub.'; return;elseif any(xstatus==1 & (~isfinite(xub) | xub~=round(xub)))errmsg='xub(i) must be an integer if x(i) is an integer variabale.'; return;end;xub(find(xstatus==2))=x0(find(xstatus==2));if nargin>5if~isempty(A) & size(A,2)~=size(x0,1), errmsg='Matrix A not correct.'; return; end;else A=[]; end;if nargin>6if~isempty(B) & any(size(B)~=[size(A,1) 1]), errmsg='Column vector B not correct.'; return; end;else B=[]; end;if isempty(A) & ~isempty(B), errmsg='A and B should only be nonempty together.'; return; end;if isempty(B) & ~isempty(A), B=zeros(size(A,1),1); end;if nargin>7 & ~isempty(Aeq)if size(Aeq,2)~=size(x0,1), errmsg='Matrix Aeq not correct.'; return; end;else Aeq=[]; end;if nargin>8if ~isempty(Beq) & any(size(Beq)~=[size(Aeq,1) 1]), errmsg='Column vector Beq not correct.'; return; end;else Beq=[]; end;if isempty(Aeq) & ~isempty(Beq), errmsg='Aeq and Beq should only be nonempty together'; return; end;if isempty(Beq) & ~isempty(Aeq), Beq=zeros(size(Aeq,1),1); end;if nargin<10, nonlcon=''; end;settings = [0 0 0];if nargin>10 & ~isempty(setts)if all(size(setts)<=size(settings))settings(setts~=0)=setts(setts~=0);else errmsg='settings should be a row vector of length 3.'; return; end; end;if nargin<12, options1=[]; end;options1=optimset(optimset('fmincon'),options1);if nargin<13, options2=[]; end;options2=optimset(optimset('fmincon'),options2);if nargin<14, maxSQPiter=1000;elseif isnumeric(maxSQPit) & all(size(maxSQPit))==1 & maxSQPit>0 &round(maxSQPit)==maxSQPitmaxSQPiter=maxSQPit;else errmsg='maxSQPiter must be an integer >0'; return; end;eval(['z=',fun,'(x0,varargin{:});'],'errmsg=''fun caused error.''; return;');if ~isempty(nonlcon)eval(['[C, Ceq]=',nonlcon,'(x0,varargin{:});'],'errmsg=''nonlcon caused error.''; return;');if size(C,2)>1 | size(Ceq,2)>1, errmsg='C en Ceq must be column vectors.'; return; end;end;% STEP 1 INITIALISATIONcurrentwarningstate=warning;warning off;tic;lx = size(x0,1);z_incumbent=inf;x_incumbent=inf*ones(size(x0));I =ceil(sum(log2(xub(find(xstatus==1))-xlb(find(xstatus==1))+1))+size(find (xstatus==1),1)+1);stackx0=zeros(lx,I);stackx0(:,1)=x0;stackxlb=zeros(lx,I);stackxlb(:,1)=xlb;stackxub=zeros(lx,I);stackxub(:,1)=xub;stacksize=1;xchoice=zeros(size(x0));if ~isempty(Aeq)j=0;for i=1:size(Aeq,1)if Beq(i)==1 & all(Aeq(i,:)==0 | Aeq(i,:)==1)J=find(Aeq(i,:)==1);if all(xstatus(J)~=0 & xchoice(J)==0 & xlb(J)==0 & xub(J)==1) if all(xstatus(J)~=2) | all(x0(J(find(xstatus(J)==2)))==0)j=j+1;xchoice(J)=j;if sum(x0(J))==0, errmsg='x0 not correct.'; return; end;end;end;end;end;end;errx=optimget(options2,'TolX');errcon=optimget(options2,'TolCon');fail=0;c=0;% STEP 2 TERMINIATIONwhile stacksize>0c=c+1;% STEP 3 LOADING OF CSPx0=stackx0(:,stacksize);xlb=stackxlb(:,stacksize);xub=stackxub(:,stacksize);x0(find(x0<xlb))=xlb(find(x0<xlb));x0(find(x0>xub))=xub(find(x0>xub));stacksize=stacksize-1;% STEP 4 RELAXATION% PHASE 1con=BNBCON(x0,A,B,Aeq,Beq,xlb,xub,nonlcon,varargin{:});if abs(con)>errcon & settings(1)~=0[x1 dummyfeasflag]=fmincon('0',x0,A,B,Aeq,Beq,xlb,xub,nonlcon,options1,varargin{ :});if settings(3) & feasflag==0con=BNBCON(x1,A,B,Aeq,Beq,xlb,xub,nonlcon,varargin{:});if con<errcon, feasflag=1; end;end;else x1=x0; feasflag=1; end;% PHASE 2if feasflag>0[x zconvflag]=fmincon(fun,x1,A,B,Aeq,Beq,xlb,xub,nonlcon,options2,varargin{ :});if settings(3) & convflag==0con=BNBCON(x,A,B,Aeq,Beq,xlb,xub,nonlcon,varargin{:});if con<errcon, convflag=1; end;end;else convflag=feasflag; end;% STEP 5 FATHOMINGK = find(xstatus==1 & xlb~=xub);separation=1;if convflag<0 | (convflag==0 & settings(2))% FC 1separation=0;elseif z>=z_incumbent & convflag>0% FC 2separation=0;elseif all(abs(round(x(K))-x(K))<errx) & convflag>0% FC 3z_incumbent = z;x_incumbent = x;separation = 0;end;% STEP 6 SELECTIONif separation == 1 & ~isempty(K)dzsep=-1;for i=1:size(K,1)dxsepc = abs(round(x(K(i)))-x(K(i)));if dxsepc>=errx | convflag==0xsepc = x; xsepc(K(i))=round(x(K(i)));dzsepc = abs(feval(fun,xsepc,varargin{:})-z);if dzsepc>dzsepdzsep=dzsepc;ixsep=K(i);end;end;end;% STEP 7 SEPARATIONif xchoice(ixsep)==0% XCHOICE==0branch=1;domain=[xlb(ixsep) xub(ixsep)];while branch==1xboundary=(domain(1)+domain(2))/2;if x(ixsep)<xboundarydomainA=[domain(1) floor(xboundary)];domainB=[floor(xboundary+1) domain(2)];elsedomainA=[floor(xboundary+1) domain(2)];domainB=[domain(1) floor(xboundary)];end;stacksize=stacksize+1;stackx0(:,stacksize)=x;stackxlb(:,stacksize)=xlb;stackxlb(ixsep,stacksize)=domainB(1);stackxub(:,stacksize)=xub;stackxub(ixsep,stacksize)=domainB(2);if domainA(1)==domainA(2)stacksize=stacksize+1;stackx0(:,stacksize)=x;stackxlb(:,stacksize)=xlb;stackxlb(ixsep,stacksize)=domainA(1);stackxub(:,stacksize)=xub;stackxub(ixsep,stacksize)=domainA(2);branch=0;elsedomain=domainA;branch=1;end;end;else% XCHOICE~=0L=find(xchoice==xchoice(ixsep));M=intersect(K,L);[dummy,N]=sort(x(M));part1=M(N(1:floor(size(N)/2)));part2=M(N(floor(size(N)/2)+1:size(N)));stacksize=stacksize+1;stackx0(:,stacksize)=x;O = (1-sum(stackx0(part1,stacksize)))/size(part1,1);stackx0(part1,stacksize)=stackx0(part1,stacksize)+O;stackxlb(:,stacksize)=xlb;stackxub(:,stacksize)=xub;stackxub(part2,stacksize)=0;stacksize=stacksize+1;stackx0(:,stacksize)=x;O = (1-sum(stackx0(part2,stacksize)))/size(part2,1);stackx0(part2,stacksize)=stackx0(part2,stacksize)+O;stackxlb(:,stacksize)=xlb;stackxub(:,stacksize)=xub;stackxub(part1,stacksize)=0;if size(part2,1)==1, stackxlb(part2,stacksize)=1; end;end;elseif separation==1 & isempty(K)fail=fail+1;end;end;% STEP 8 OUTPUTt=toc;Z = z_incumbent;X = x_incumbent;errmsg='';eval(['warning ',currentwarningstate]);function CON=BNBCON(x,A,B,Aeq,Beq,xlb,xub,nonlcon,varargin); if isempty(A), CON1=[]; else CON1 = max(A*x-B,0); end;if isempty(Aeq), CON2=[]; else CON2 = abs(Aeq*x-Beq); end; CON3 = max(xlb-x,0);CON4 = max(x-xub,0);if isempty(nonlcon)CON5=[]; CON6=[];else[C Ceq]=feval(nonlcon,x,varargin{:});CON5 = max(C,0);CON6 = abs(Ceq);end;CON = max([CON1; CON2; CON3; CON4; CON5; CON6]);。
(完整word版)matlab解非线性规划例题

关于非线性规划问题背景:线性规划问题,即目标函数和约束条件都是线性函数的规划问题,但在实际工作中,还常常会遇到另一类更一般的规划问题,即目标函数和约束条件中至少有一个是非线性函数问题,即非线性规划问题.求解方法:Matlab软件问题:某厂向用户提供发动机,合同规定,第一、二、三季度末分别交货50台、70台、90台。
每季度的生产费用为()^2=+(元),f x ax bx其中x是该季度生产的台数,若交货有剩余可用于下季度交货,但需支付存储费,每季度每台c元。
已知工厂每季度最大生产能力为100台,第一季度开始时无存货,设a=50,b=0。
2,c=4,问工厂如何安排每月生产计划,才能既满足合同又使总费用最低(包括生产费用和库存费用)。
问题分析与假设:目标函数是总费用,记为()F x.约束条件是生产合同和生产能力的限制.设第一季度生产1x台,第二季度生产2x台,则第三季度生产(21012)--台。
则:x x≤+≤x x12012210≤≤x501100≤≤x02100由a=50,b=0.2,c=4,第一季度生产费用15010.21^2=+,T x x剩余品存储到下一季度的费用14(150)=-,k x同理可得:25020.22^2T x x=+=+-24(12120)k x x350(21012)0.2(21012)^2=--+--T x x x x建模总费用=++++=+++--++-先建立M-文件: F x T T T k k x x x x x x()12312103000.2(1^22^2)0.2(21012)^24(212120)a=50;b=0.2;c=4;H=diag(2*b*ones(1,3));C=[a+2*c,a+c,a];A1=[-1,0,0;—1,-1,0];b1=[-50,—120]';A2=[1 1 1];b2=210;v1=[0 0 0]';v2=[100 100 100]’;[x,faval,exitflag,output,lambada]=quadprog(H,C,A1,b1,A2,b2,v1,v2,[])X2=x'*H*x/2+C*x-140*c再建立主程序:a=50;b=0。
数学实验报告——利用MALTAB进行非线性规划

㈡简要分析
本题是一道比较简单的非线性规划求解问题, 不涉及数学建模以及应用分析 等问题,只需要将所给问题转化为 MATLAB 代码进行处理。这里可以采用不同的 算法,并对比进行分析。
㈢方法与公式
1、求解规划方法
求解本题可以考虑几种规划。 对于第(1)组约束来说,仅含有上下界约束,可以考虑使用 SQP 方法或者置 信域方法;但是考虑到本题规模较小,这里仅采用 SQP 方法。(事实是,设定使 用大规模算法后,MATLAB 仍旧自动使用 SQP 完成计算,因而无法进行对比); 对第(2)组约束来说,仅可以使用 SQP 方法; 对第(3)组约束来说,可以使用 SQP 方法,也可以利用后两个等式把规划化 化简后再使用 SQP 方法。
5、脚本 2
5
v1 = -10*ones(1,4); v2 = 10*ones(1,4); x00 = [-3,-1,-3,-1]; x01 = -[-3,-1,-3,-1]; x02 = [10,-20,5,3]; x03 = [-5,10,15,-20]; opt = optimset('largeScale','off','MaxFunEvals',4000,'MaxIter', 1000,'Algorithm','active-set'); [x(1,:),f1,exitflag1,out(1)] = fmincon('fun',x00,[],[],[],[],v1,v2,@edge3,opt); [x(2,1:2),f2,exitflag2,out(2)] = fmincon('fun1',x00(2:3),[],[],[],[],v1(1:2),v2(1:2),@edge 31,opt); [x(3,:),f3,exitflag3,out(3)] = fmincon('fun',x01,[],[],[],[],v1,v2,@edge3,opt); [x(4,1:2),f4,exitflag4,out(4)] = fmincon('fun1',x01(2:3),[],[],[],[],v1(1:2),v2(1:2),@edge 31,opt); [x(5,:),f5,exitflag5,out(5)] = fmincon('fun',x02,[],[],[],[],v1,v2,@edge3,opt); [x(6,1:2),f6,exitflag6,out(6)] = fmincon('fun1',x02(2:3),[],[],[],[],v1(1:2),v2(1:2),@edge 31,opt); [x(7,:),f7,exitflag7,out(7)] = fmincon('fun',x03,[],[],[],[],v1,v2,@edge3,opt); [x(8,1:2),f8,exitflag8,out(8)] = fmincon('fun1',x03(2:3),[],[],[],[],v1(1:2),v2(1:2),@edge 31,opt); answer = zeros(1:8); for i = 1:8 out(i) end for j = 1:4 x(2*j,3)=x(2*j,1); x(2*j,1) = -x(2*j,2);
MATLAB非线性规划

MATLAB⾮线性规划MATLAB求解⾮线性规划可以使⽤ fmincon 函数,其数学模型可以写成如下形式:x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)其中,fun是⽬标函数,x0是初始值,A,b 规定线性不等式约束条件,Aeq,beq 规定线性等式约束条件,lb 规定可⾏解的数值下限,ub规定可⾏解的数值上限。
nonlcon是包含⾮线性约束条件(C(x),Ceq(x))的函数。
使⽤options所指定的优化选项执⾏最⼩化。
例如,使⽤MATLAB计算如下⾮线性规划。
x0 = [0.5,0];A = [1,-2];b = 1;Aeq = [2,1];beq = 1;x = fmincon(fun,x0,A,b,Aeq,beq)带有边界约束的,例如:fun = @(x)1+x(1)/(1+x(2)) - 3*x(1)*x(2) + x(2)*(1+x(1));lb = [0,0];ub = [1,2];% 没有线性约束,因此将这些参数设置为 []。
A = [];b = [];Aeq = [];beq = [];% 尝试使⽤⼀个位于区域中部的初始点。
x0 = (lb + ub)/2;x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub)带有⾮线性约束的,例如:%% 主函数options=optimset('largescale','off');x = fmincon(@fun,rand(3,1),[],[],[],[],zeros(3,1),[], @nonlcon, options)%% ⽬标函数function f=fun(x)f=sum(x.^2)+8;end%% ⾮线性约束条件function [c,ceq]=nonlcon(x)c=[-x(1)^2+x(2)-x(3)^2x(1)+x(2)^2+x(3)^3-20]; %⾮线性不等式约束ceq=[-x(1)-x(2)^2+2x(2)+2*x(3)^2-3]; %⾮线性等式约束end特别注意:⽬标函数为最⼩化函数,fun是⼀个函数,fun接受向量或数组 x,并返回实数标量 f,即在 x 处计算的⽬标函数值。
用Matlab求解非线性规划

用Matlab 求解非线性规划1.无约束优化问题)(min x f n Rx ∈,其中向量x 的n 个分量i x 都是决策变量,称)(x f 目标函数。
用Matlab 求解:先建立函数文件mbhs.m ,内容是)(x f 的表达式;再回到Matlab 命令区输入决策变量初值数据x0,再命令[x,fmin]=fminunc(@mbhs,x0) 如:)32(m in 22212x x R x +∈的最优解是.)0,0(T x = 用Matlab 计算,函数文件为 function f=mbhs(x)f=2*x(1)^2+3*x(2)^2;再输入初值 x0=[1;1]; 并执行上述命令,结果输出为 x =? fmin =? 略。
2.约束优化问题.),,...,2,1(,0)(),,...,2,1(,0)(..)(min U x L m i x h p i x g t s x f i i Rx n ≤≤===≤∈其中:向量x 的n 个分量i x 都是决策变量,称)(x f 目标函数、)(x g i 等式约束函数、)(x h i 不等式约束函数、L 下界、U 上界。
用Matlab 求解:先把模型写成适用于Matlab 的标准形式.,0)(,0)(,,..)(min U x L x h x g beq x Aeq b Ax t s x f n Rx ≤≤=≤=≤∈ 约束条件中:把线性的式子提炼出来得前两个式子;后三个式子都是列向量。
(如:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡===⨯⨯)()()([],[],,,11262x g x g x g beq Aeq b A p )再建立两个函数文件:目标函数mbhs.m ;约束函数yshs.m再回到Matlab 命令区,输入各项数据及决策变量初值数据x0,执行命令[x,fmin]=fmincon(@mbhs,x0,A,b,Aeq,beq,L,U,@yshs)例:单位球1222≤++z y x 内,曲面xy y x z 1.05.022--+=的上方,平面008.0=-++z y x 之上(不是上面),满足上述三个条件的区域记为D ,求函数)1cos()sin(2-+-+-z e z y x e xy xyz 在D 上的最大值、最大值点。
数学建模_非线性规划模型用MATLAB++LINGO

近似规划法的算法步骤如下
1 1 1 , x1 (1) 给定初始可行点 X 1 x1 2 ,, xn ,步长限制 j j 1,, n ,
步长缩小系数 0,1,允许误差 ,令 k=1;
(2)
在点 X k 处,将 f X , g i X , h j X 按泰勒级数展开并
2 2 min 0 , g X M h X i j i 1 j 1
(2)
将问题( 1 )转化为无约束问题: min T X , M n
X E
(3)
其中T(X,M)称为罚函数,M称为罚因子,带M的项称为罚项,这 里的罚函数只对不满足约束条件的点实行惩罚:当 X 足各 gi X 0, hi X 0 ,故罚项=0,不受惩罚.当 X D 时, gi X 0或hi X 0 的约束条件,故罚项>0,要受惩罚. 必有
2
min f(x1,x2)=-2x1-6x2+x12-2x1x2+2x22 s.t. x1+x2≤2 -x1+2x2≤2 x1≥0, x2≥0 T x 1 - 1 1 2 x1 1、写成标准形式:min z ( x , x )
简称为SUMT法.其一为SUMT外点法,其
二为SUMT内点法.
SUTM外点法
对一般的非线性规划: min f X
gi X 0 s.t. h j X 0
m
i 1,2,..., m; j 1,2,...,l.
l
(1)
可设:T X , M f X M
4
解(1)(2)(3)(4),得
1 1 x 2 4 ,3 6 20
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x= 0.7647 1.0588
fval = -2.0294
则有: ������1 = 0.7647; ������2 = 1.0588 最优解为-2.0294
用 MATLAB 求解非线性规划练习题目
题目一
Min
非线性规划
������ ������1 , ������2 = −2������1 − 6������2 + ������1 2 − 2������1 ������2 + 2������2 2
������1 + ������2 ≤ 2 s.t −������1 + 2������2 ≤ 2 ������1 ≥ 0, ������2 ≥ 0 运用 MATLAB 数学软件求解: 在界面中输入以下代码:
>> a=[1 -1 ;-1 2]; c=[-2;-6]; A=[1 1;-1 2]; b=[2;2]; Aeq=[]; >> beq=[]; >> VLB=[0;0];VUB=[]; >> [x,z]=quadprog(a,c,A,b,Aeq,beq,VLB,VUB)
运行结果:
Warning: Large-scale method does not currently solve this problem formulation, switching to medium-scale method. > In D:\MATLAB6p5\toolbox\optim\quadprog.m at line 213 Optimization terminated successfully. x= 0.6667 1.3333 z =-8.2222
运行结果为:
Warning: Large-scale (trust region) method does not currently solve this type of problem, switching to medium-scale (line search). > In D:\MATLAB6p5\toolbox\optim\fmincon.m at line 213 f= -2
建立 M 文件,并输入:
function f=fun3(x); f=-x(1)-2*x(2)+(1/2)*x(1)^2+(1/2)*x(2)^2
在界面中输入:
>> x0=[1;1];
A=[2 3;1 4];b=[6;5]; Aeq=[];beq=[]; VLB=[0;0];VUB=[]; [x,fval]=fmincon('fun3',x0,A,b,Aeq,beq,VLB,VUB)
则有 ������1 = 0.6667,������2 = 1.3333 最优解为 − 8.2222
题目 2 非线性规划
Min ������ = −������1 − 2������2 + ������1 2 + ������2 2
2 2
1
1
2������1 + 3������2 ≤ 6 s.t ������1 + 4������2 ≤ 5 ������1 ≥ 0, ������2 ≥ 0
f= -2
f= -2.0000
f= -2ቤተ መጻሕፍቲ ባይዱ0294
f= -2.0294
f= -2.0294 Optimization terminated successfully: First-order optimality measure less than options.TolFun and maximum constraint violation is less than options.TolCon Active Constraints: 4
