第三章矢量数据模型
合集下载
第三章空间数据模型第3节矢量数据模型
(xn,yn) (x(1x,ny,1y)n) (x1,y1)
(a) (xn,yn)
(b)
(xn,yn)
A
KI
H
J
BC
G
FE
D
(c)
第三章空间数据模型第3节矢量数据模型
一维矢量具有方向、长度
方向：即有起始结点和终止结点
长度：可以用以下方式表达：
引入欧氏空间的距离概念：
n
长度 [(xi xi1)2 ( yi yi1)2 ]1/2 i2
一．基本概念 二．关系数据模型和关系表 三．矢量数据模型（ Spaghetti Model ） 四．矢量数据模型（拓扑数据模型）
第三章空间数据模型第3节矢量数据模型
一、基本概念
• 现实世界和矢量表达 • 位置和边界被清楚地记录 • 对象可以被识别 • 属性值与对象相联系 • 空间关系可以清晰表达
第三章空间数据模型第3节矢量数据模型
(1) 地理要素被当成单个对象对待
空间边界可以被清晰的编码
(2)对象之间没有关系
要素间的空间拓扑不被记录
第三章空间数据模型第3节矢量数据模型
矢量表达法
• 不同的空间特征具有不同的矢量维数
– 0维矢量-点：即空间中的一个点，没有大小、 方向，二维和三维欧氏空间中为：（x,y),(x,y,z)
– 一维矢量-线：空间中的线划要素或空间对象间 的边界，也称为弧段、链
用的概念，是三维空间中曲面法向矢量的 另外一种描述方法
第三章空间数据模型第3节矢量数据模型
空间曲面
• 矢量实现方法多样 • 常用等值线法、剖面法
第三章空间数据模型第3节矢量数据模型
三维矢量-体
• 指三维空间中的实体
4.2矢量数据模型
5
f
2
b3
g
6
拓扑关系表见书66、67 页；应 用。
五、三维数据结构
• 对于地下矿体分布、大气流场在某一 时刻的状态等，需要一种能描述真三 维的数据结构来表达。
• 三维数据结构一般用八叉树结构编码。
八叉树结构编码
• 它是在四叉树结构直接发展而来的，其原 理是将空间区域不断地分解为八个同样大 小的区域，一直到同一区域的属性单一为 止。
一、基本概念
• 1、矢量数据： 地图图形离散化成计算机能 识别和处理的数据。代表地 图图形的各离散点的平面坐 标。
• 2、空间数据： 地图数据大多反映空间地物的地
理分布，具有空间定位的性质。
3、属性数据
• 用来描述地物的质量和数量特征的 数据。
二、基本表示方法
点——用一坐标对表示：（X,Y）; 线——用一串有序的坐标对表示：
（X1,Y1）、 （X2,Y2）…（Xn,Yn） 面——用一串有序的但首尾坐标相同的x,y
坐标表示其轮廓范围：即（X1,Y1）、 （X2,Y2）…（Xn,Yn），（X1,Y1）.
三、矢量数据组织方法
• 点实体数据结构：P60 • 线实体数据结构： • 面实体数据结构：
线实体数据结构
唯一 线标 起始 终止 坐标 显示 非几 非几 非几 非几
• 缺点：
• 1、对于邻域函数运算、消除无用 边、处理岛状信息及检查拓扑关系 等方面较为困难。
• 2、编码表均需要人工方式建立， 工作量大，容易出错。
四、拓扑关系及其应用
• 通过一幅地图，我们可以了解地理要 素的区域信息、属性信息和空间信息。
• 而在计算机中，地理信息可以用坐标 对表示，属性信息以一组特征码的数 字或字符形式存储。而空间关系只能 靠拓扑结构来定义。
地理信息系统课件05矢量数据模型来自华北科技学院魏志刚
1. 在监视器上显示更快
– 对用户比对数据库制作者更为重要
2. 非私有，可共用
– 可跨软件使用
35
A
9
223
4.链状双重独立式
• 链状双重独立式数据结构是DIME数据结构的 一种改进。
• 在DIME中，一条边只能用直线两端点的序号 及相邻的面域来表示，而在链状数据结构中， 将若干直线段合为一个弧段（或链段），每个 弧段可以有许多中间点。
• 在链状双重独立数据结构中，主要有四个文件： 多边形文件、弧段文件、弧段坐标文件、结点 文件
• 对空间数据而言，
– 则是地理实体的空间排列方式和相互关系的抽象描述。
• 数据编码是实现空间数据的计算机存储、处理和管理， 将空间实体（地理要素）按一定的数据结构转换为适 合于计算机操作的过程。
3
4
3.1 概述
• 数据模型是数据结构的概念模型，数据结构是数据模 型的物理实现。
• 数据结构是数据模型和数据文件格式的中间媒介，数 据模型需要通过数据结构来表达，同一种数据模型可 以用多种数据结构来表达。
• 面实体: 多边形、区域
13
点
• 零维 • 没有长度、宽度和高度，只暗含位置属性 • 由x，y坐标来定义 • 也可称为结点，顶点，或0-单元 • 例如：井、建筑物、测量标记 • 存储内容：
– 位置：坐标 – 属性：名称、类型、编码…
14
线
• 一维 • 具有长度和位置属性 • 由端点和所经过的节点的x，y坐标定义 • 也可称为边，链，1-单元 • 例如：道路、河流、等高线 • 存储内容：
2
3.1 概述
• 信息系统中：
– 数据模型：对客观实体及其关系的认识和数学描述。 – 目的是揭示客观实体的本质特征，并对它进行抽象化表
– 对用户比对数据库制作者更为重要
2. 非私有，可共用
– 可跨软件使用
35
A
9
223
4.链状双重独立式
• 链状双重独立式数据结构是DIME数据结构的 一种改进。
• 在DIME中，一条边只能用直线两端点的序号 及相邻的面域来表示，而在链状数据结构中， 将若干直线段合为一个弧段（或链段），每个 弧段可以有许多中间点。
• 在链状双重独立数据结构中，主要有四个文件： 多边形文件、弧段文件、弧段坐标文件、结点 文件
• 对空间数据而言，
– 则是地理实体的空间排列方式和相互关系的抽象描述。
• 数据编码是实现空间数据的计算机存储、处理和管理， 将空间实体（地理要素）按一定的数据结构转换为适 合于计算机操作的过程。
3
4
3.1 概述
• 数据模型是数据结构的概念模型，数据结构是数据模 型的物理实现。
• 数据结构是数据模型和数据文件格式的中间媒介，数 据模型需要通过数据结构来表达，同一种数据模型可 以用多种数据结构来表达。
• 面实体: 多边形、区域
13
点
• 零维 • 没有长度、宽度和高度，只暗含位置属性 • 由x，y坐标来定义 • 也可称为结点，顶点，或0-单元 • 例如：井、建筑物、测量标记 • 存储内容：
– 位置：坐标 – 属性：名称、类型、编码…
14
线
• 一维 • 具有长度和位置属性 • 由端点和所经过的节点的x，y坐标定义 • 也可称为边，链，1-单元 • 例如：道路、河流、等高线 • 存储内容：
2
3.1 概述
• 信息系统中：
– 数据模型：对客观实体及其关系的认识和数学描述。 – 目的是揭示客观实体的本质特征，并对它进行抽象化表
地理信息系统下的空间分析——第三章_空间分析的理论问题
4、顺序关系描述 顺序关系中的一类重要关系是方向关系，如东、西、 南、北等。 （1）方向关系的定量描述 方向关系的定量描述主要是使用方位角来进行
（2）方向关系的定性描述 方向关系的定性描述主要有投影法(projection)和锥形 法(cone)。 1）投影法：是将空间目标投影到特定的坐标轴上，通 过各目标投影间的关系去描述与定义方向关系。其中的投 影可以是正射投影，也可以是斜率投影。 2）锥形法：是将空间目标及其周围的区域分成带有方 向性的几个区域，通过各目标本身及方向区域之间的交的 结果来描述空间关系。
7）西南关系
South_West(Pi，Qj)=X(Pi)＜X(Qj) And Y(Pi)＜Y(Qj) 示意图如下：
8）东南关系
South_East(Pi，Qj)=X(Pi)＞X(Qj) And Y(Pi)＜Y(Qj) 示意图如下：
以上8种关系通过点的投影可以精确判断。对于任意两点， 上述8种关系必有一种满足。 这些关系具有传递性。 另外，一些关系可进行相互转换，如North_East(Pi，Qj)和 South_West(Qj，Pi)。
课堂练习： 请大家分别算 出8种面面关系 的4元组矩阵
8种面/面关系
………………….
三种点/线拓扑关系。 课堂练习：请大家分别算出3 种点线关系的4元组矩阵。
两种点/点拓扑关系。
课堂练习：请大家分别算出2种点 点关系的4元组矩阵。
三种点/面拓扑关系，请 写出4元组矩阵。
2、空间关系描述结果的评价： 完备性是指空间关系描述结果能包含目标间所有可能的定 性关系； 严密性是要求所推出的一组关系是实际存在的或正确的； 唯一性要求所有关系是互斥的； 通用性指描述方法应能处理各种形状的目标和各类关系。
地理信息系统GIS—第3章矢量数据
空间关系及其表达
绝对空间关系：坐标、角度、方位、距离等 相对空间关系：相邻、包含、关联（连接）
等
相对空间关系的类型
拓扑空间关系：描述空间对象的相邻、包含、关联 关系等。
顺序空间关系：描述空间对象在空间上的排列次序 ，如前后、左右、东、西、南、北等。
地图、遥感影像上的空间关系是通过图形识别的， 在GIS中的空间关系则必须显式的进行定义和表达
地理信息系统
第三章 矢量数据模型
第二章内容回顾
1、什么叫坐标系？ 2、为什么要建立坐标系？ 3、为什么要建立地球的坐标系？ 4、如何建立地球的坐标系统？ 5、坐标系统与地图绘制有什么关系？
第二章内容回顾
1. 什么是地图投影？ 2. 地图投影主要有几种分类方法？ 3. 中国、美国的地图投影主要有哪几种？ 4. 在地图投影过程中需要设置哪两部分内容？需要设
3.2 拓扑
Topology一词来自希腊文，它的原意是“形状 的研究”。拓扑学属于数学中几何学的内容， 最早由德国数学家莱布尼茨1679年提出。历 史上著名的哥尼斯堡七桥问题、多面体的欧 拉定理、四色问题等都是拓扑学发展史的重 要问题。
3.2 拓扑-哥尼斯堡七桥问题
问：能不能每座桥都 只走一遍，最后又回 到原来的位置？
空间数据结构
数据结构的概念：
数据结构即指数据组织的形式，是适于计算机存 储、管理和处理的数据逻辑结构。
对空间数据而言，数据结构则是地理实体的空间 排列方式和相互关系的抽象描述。
在地理系统中描述地理要素和地理现象的空间数 据主要包括：空间位置、拓扑关系和属性三个方 面的内容。
常用的空间数据结构
ArcGIS中的矢量数据模型
Coverage Shapefile
矢量数据模型适用范围
矢量数据模型适用范围1. 什么是矢量数据模型在地理信息系统（GIS）中，数据模型是描述和组织地理数据的方式。
矢量数据模型是其中的一种，它以点、线、面等几何对象来表示地理实体和属性。
2. 矢量数据模型的基本元素矢量数据模型的基本元素包括点、线、面和属性。
这些元素可以表示为几何对象和属性表。
2.1 几何对象•点（Point）：在地理坐标系中用一个坐标对表示，通常表示一个地理位置或地物的中心点。
•线（Line）：由一系列连续的点组成，可以表示道路、河流等线状地理实体。
•面（Polygon）：由一系列闭合的线组成，可以表示湖泊、建筑物等面状地理实体。
2.2 属性表属性表是一个包含特定属性的表格，每一行对应一个几何对象，每一列对应一个属性。
属性可以描述地理实体的特征，例如道路的名称、人口数量等。
3. 矢量数据模型的特点矢量数据模型具有以下特点：3.1 精确度高矢量数据模型能够精确表示地理实体的几何形状和空间关系，因此在精细化建模和分析方面有优势。
3.2 模型扩展性强矢量数据模型可以不断扩展，添加新的几何对象和属性，以适应数据的增长和需求的变化。
3.3 拓扑关系表达能力强矢量数据模型能够准确表达线与点、线与面、面与面之间的拓扑关系，例如相交、包含、相邻等。
3.4 空间分析功能强大矢量数据模型支持各种空间分析操作，如缓冲区分析、叠加分析等，可以对地理实体进行复杂的空间分析和处理。
4. 矢量数据模型的应用矢量数据模型广泛应用于各个领域，包括地理信息系统、测绘、城市规划、环境保护等。
4.1 地理信息系统地理信息系统是矢量数据模型的主要应用领域之一。
利用矢量数据模型，可以对地理实体进行建模、查询、分析和可视化等操作，为地理空间数据管理和决策提供支持。
4.2 测绘测绘是通过测量和绘制方法获取地理信息的过程。
矢量数据模型可以精确表示地理要素的几何形状和位置，可以用于测绘地物的绘制和更新。
4.3 城市规划城市规划涉及到对城市空间的分析和设计。
06 第三章 空间数据模型 4- 7节 TIN模型及模型比较
4
B C D E F
G K P
12
H
10
J M
9
11
G H I J ...
N
13 14
O
Q
S
15
Node Attribute Table
Node 1 2 3 X x1 x2 x3 Y y1 y2 y3 Z z1 z2 z3
...
...
...
...
三、TIN的生成
1. 如何选择点（How to pick points）？
一、模型的比较
1. 理解和感知的差异 2. 模型特性的差异
理解和感知的差异
现实世界
完全定义或可定义 的实体(如地籍)
概念模型
连续但可定义的对象 (如高程表面)
平滑和连续的空间变化 (如温度)
数据模型 及其表达
边界轮廓 (点、线、多边形)
矢量
表面 (三角形表面) TIN
镶嵌 (正方形, 像元)
栅格
3 3 3 3 3 3 2 3 3 3 3 3 3 3 3 1 3 3 3 3 3 3 3 2 3 3 3 3 3 3 3 1 3 3 3 3 3 3 3 2 3 3 3 3 3 3 1 7 3 3 3 3 3 3 3 2 3 3 3 3 3 1 7 7 3 3 3 3 3 3 3 2 3 3 3 3 3 1 7 7 3 3 3 3 3 3 3 2 3 3 3 3 1 7 7 7 3 3 3 3 3 3 3 3 2 3 3 1 7 7 7 7 3 3 3 3 3 3 3 3 2 3 3 1 7 7 7 7 3 3 3 3 3 3 3 3 2 3 1 7 7 7 7 7 3 3 3 3 3 3 3 3 2 1 7 7 7 7 7 7 3 3 3 3 3 3 3 3 2 1 7 7 7 7 7 7 3 3 3 1 1 1 1 1 1 1 1 4 6 6 6 6 2 7 7 7 7 7 7 7 4 4 4 4 6 6 6 6 6 2 7 7 7 7 7 7 4 4 4 4 4 6 6 6 6 2 7 7 7 7 7 7 4 4 4 4 4 6 6 6 6 2 7 7 7 7 7 7 4 4 4 4 4 6 6 6 6 2 7 7 7 7 7 7 4 4 4 4 4 6 6 6 6 6 2 7 7 7 7 7 4 4 4 4 4 6 6 6 6 6 2 7 7 7 7 7 4 4 4 4 4 6 6 6 6 6 2 7 7 7 7 7 4 4 4 4 4 6 6 6 6 6 2 7 7 7 7 7 4 4 4 4 4 6 6 6 6 6 6 2 7 7 7 7 4 4 4 4 4 6 6 6 6 6 6 2 7 7 7 7
第3章 空间数据模型
＊通过描述小面块的几何形态、相邻关系及面块内属性 特征的变化来建立空间数据的逻辑模型；
＊小面块之间不重叠且能完整铺满整个地理空间； ＊根据面块的形状，镶嵌数据模型可分为 规则镶嵌数据模型 不规则镶嵌数据模型
规则镶嵌数据模型
不规则镶嵌数据模型
TIN和Voronoi多边形数据模型
Voronoi 图又称为Dirichlet ( tessellation) ,其概念由 Dirichlet 于1850 年首先提出; 1907 后俄国数学家 Voronoi 对此作了进一步阐述,并提出高次方程化简; 1911 年荷兰气候学Thiessen为提高大面积气象预报 的准确度,应用Voronoi 图对气象观测站进行了有效 区域划分。因此在二维空间中,Voronoi 图也称为泰 森多边形。
2 作为两个面域之间的一个边界。
3 作为一个面域特征，精确表达河流的堤岸、辫 状河道以及河流上的运河。
4 作为一条曲线以构成表面模型上的沟槽。根据 地表上河流的路径，可以算出其横截面、落差度、 排水流域以及在预测降雨下的洪水爆发可能性。
针对真实的世界，每一个人都在创建他 自己的主观模型。GIS的观点是为真实世 界建立一个通用的模型。
泰森（Thiessen)多边形的特点： 1 组成多边形的边总是与两相邻样点的连线垂直； 2 多边形内的任意位置总是离该多边形内样点的距 离最近，离相邻多边形内样点距离远； 3 每个多边形内包含且仅包含一个样点。
（五）面向对象数据模型
为了有效地描述复杂的事物或现象，需要 在更高层次上综合利用和管理多种数据结构 和数据模型，并用面向对象的方法进行统一 的抽象。
空间逻辑数据模型作为概念模型向 物理模型转换的桥梁，是根据概念模型 确定的空间信息内容，以计算机能理解 和处理的形式，具体地表达空间实体及 其关系。
第三章 矢量数据模型
3.3.2 拓扑矢量数据
• 拓扑数据模型定义：不仅表达几何位置和属 性，还表示空间拓扑关系的矢量数据模型。 • 拓扑关系具体可由4个关系表来表示：
– （1）结点—弧段关系 – （2）弧段—结点关系 – （3）弧段—多边形关系 – （4）多边形—弧段关系
结点-弧
1
A b a 3 2
c
B e D 6 C 5 7
线：位置： (x1,y1),(x2,y2),„,(xn,yn) 属性：符号—形状、颜色、尺寸
面：位置： (x1,y1),(x2,y2),„,(xi,yi),„,(xn,yn) 属性：符号变化 等值线
点
抽象的点, 有位置，无宽度和长度；
美国佛罗里达洲地震监测站2002年9月该洲可 能的500个地震位置
1)关联性
• 关联性： 不同 类要素之间关 系
– 结点与弧段 如V9与L5,L6,L3 – 多边形与弧段 如P2与L3,L5,L2
2)邻接性
• 邻接性：同类元素 之间关系
– 多边形之间、结 点之间。 – 邻接矩阵 ： 重叠：-- 邻接：1 不邻接：0
P1 P2 P3 P4 P -1 1 1 P2 1 -1 0 P3 1 1 -0 P4 1 0 0 --
5 6
表中数字前负号为相反方向
7
B
—
空间拓扑关系表达：面与弧
1
A b a 3 2 c B
多边形-弧拓扑
e
D 7
面号
6
弧号 -1,-2,3 2,-7,5,0,-6 -3,-5,4 6
A B
C
5
4
d
a: 结点号 1: 弧段号
A: 多边形号 弧段数字化方向
C D
表中数字前负号为相反方向
矢量数据模型
35
图3.15 TIN的数据结构
2021/5/18
36
分区
分区在这里是指具有相似特征的地域范围。 分区数据模型应能处理好两个空间特征：第一，分 区可以在空间上相连和分离；第二，分区可重叠或涵 盖相同区域。
2021/5/18
37
图3.16 美国本土上的县和州形成的等级结构。
2021/5/18
线
不重叠, 不相交, 不交叉，没有悬挂弧段, 没有伪结点, 不相交
或内部接触，不与其它图层相交或内部接触，不与其它图层重叠,
必须被另一要素类覆盖, 必须被另一图层的边界覆盖，必须在内
部，终节点必须被覆盖, 不能自重叠, 不能自相交, 必须是单一
部分。
点
2021/5/18
必须与其它图层一致，不分离，必须被另一图层的边界覆盖，必 须位于多边形内部, 必须被另一图层的终节点覆盖, 必须被线覆 盖。
38
图3.17 分区数据模型允许分区相互重叠(a)，且可有空间上分离的多边形（b)。
2021/5/18
39
图3.18 分区亚类的数据结构
2021/5/18
40
路径
路径是诸如高速公路、自行车道或河流等线要 素，但它与其它线要素不同在于它有度量系统，可 使线性测量用于投影坐标系统中。
2021/5/18
图3.2 台湾台北市的地铁线路图 .
7
拓扑
拓扑是研究几何对象在弯曲或拉伸等变换下仍保 持不变的性质。 图和表用于研究空间几何对象的分布及其空间关 系。
2021/5/18矩阵。
2021/5/18
9
拓扑统一地理编码格式（TIGER）
拓扑在地理空间技术上的早期应用是来自美国人 口普查局的拓扑统一地理编码格式(TIGER)数据库。
p03第三章 空间数据模型-第六-八节1
第六节、 ArcGIS介绍
1. 厂家：ARCGIS是美国环境系统研究所（Environmental System Research Institute, Co.，简称ESRI）于20世纪80年 代初推出的一个通用GIS软件 。
2. 运行平台：uninx－NT(96年）（2000）－pc
Ar析
2、ArcCatalog
• 空间数据管理：
– ESRI coverage、 shape file
– CADData – 遥感图像 – 栅格 – TINS – Geodatabase – 属性表格
• 察看空间数据、源 数据等
3、ArcToolbox
• 超过140个工具，用 于进行geoprocessing 处理；
六、ARCGIS的开发环境
在Windows环境下以可编程控件(OCX)的形式为用户提 供在其应用中增加制图和GIS功能的可能性(MapObjects)；
在ArcView和MapObjects中提供Internet网上的GIS和制图 功能；
ArcObject和ArcEngineer面向组件的开发技术。 Arcsever开发工具
三、ArcGIS Workstation 的功能模块（1）
1. ARC是ARCGIS Workstartion的其他功能模块的运行环境；
① ARC主要完成对工作空间和数据单元的操作和管理； ② 进行空间数据操作； ③ 建立拓扑关系，进行数据格式和投影转换； ④ 进行某些基于矢量的空间分析。
2. INFO是一个完整的关系型数据库管理系统，用于完成对属 性数据库的管理和维护;
第三章 空间数据模型
空间数据模型是GIS的基础；
空间数据模型：指利用特定的数据结构来表达空间对 象的空间位置、空间关系和属性信息；是对空间对象 的数据描述。
矢量和栅格数据模型介绍课件
在环境监测中，栅格数据模型可以用 于分析空气质量、水质、土壤状况等 环境要素的空间分布和变化趋势。
在城市规划中，栅格数据模型可以用 于城市空间布局规划、交通规划、公 共设施布局等方面。
矢量和栅格数据模型的比 较
数据精度比 较
矢量数据模型
矢量数据模型通过记录坐标点之间的几何关系来表达空间实 体，能够精确表示点、线、面等几何要素的位置和形状。因 此，矢量数据模型在表示复杂几何形状和细节方面具有较高 的精度。
栅格数据模型
栅格数据模型通过将空间划分为规则的格网或像素来表达空 间实体，每个像素或格网表示一个离散的地理空间单元。栅 格数据模型的精度取决于格网的大小，格网越小，精度越高。
数据结构比较
矢量数据模型
矢量数据模型的数据结构通常包括要素类和特征类，分别用于表示空间实体和 几何要素。矢量数据模型的数据结构相对简单，但表达的空间关系和属性信息 较为丰富。
栅格数据模型
栅格数据模型的数据结构通常包括网格矩阵和栅格地图，分别用于表示地理空 间单元和地表覆盖信息。栅格数据模型的数据结构相对复杂，但表达的空间信 息和属性信息较为有限。
数据处理速度比较
矢量数据模型
矢量数据模型的数据处理速度通 常较快，因为矢量数据模型的数 据结构相对简单，可以进行高效 的几何运算和空间分析。
02
矢量数据模型以离散方式表示空 间信息，每个几何对象都有明确 的坐标信息，可以精确表示地理 实体的位置和形状。
矢量数据模型特点
数据精度高
数据结构紧凑
由于矢量数据模型基于几何对象表示，可 以精确表示地理实体的位置和形状，因此 具有较高的数据精度。
矢量数据模型采用高效的数据压缩和编码 技术，使得数据存储和传输更加紧凑，节 省存储空间和网络带宽。
地理信息系统原理第三章 空间数据模型与数据结构3.2
第1行第N列亮度值 波段2 第1行第1列亮度值
第1行第N列亮度值 波段n 波段1 第2行第1列亮度值 波段n
BSQ结构
BIP结构
BIL结构
星蓝海学习网13
以行为记录单位按行存储 地理数据。属性明显，位 置隐含。 缺点：存在大量冗余，精 度提高有限制。
星蓝海学习网14
0 0 0 0 0 4 4 4 记录1 0 0 0 0 0 4 4 4
星蓝海学习网
• 优点：
• 栅格加密时，数据量不会明显 增加，压缩效率高，最大限度 保留原始栅格结构，
• 编码解码运算简单，且易于检 索、叠加、合并等操作，得到 广泛应用。
• 缺点：
• 不适合于类型连续变化或类型 区域分散的数据。
星蓝海学习网
(2)压缩栅格数据结构
块码（二维游程编码）（行，列，半径，属性值）
弧段ID a b c d e
起始点 5 7 1 13 7
终结点 1 1 13 7 5
… … … 左多边形 Q A Q D D
右多边形 A B B B A
f
13
5
Qห้องสมุดไป่ตู้
D
点号 1 2
…… 25
坐标 （x1，y1） （x2，y2）
…… （x25，y25）
g
25
弧段ID
点号
a
5,4,3,2,1
b
7,8,1
c
1,9,10,11,12,13
• 采用方形区域作为记录单元，每个记录单元包括相邻的若干栅格，数据结构由初始位置(行、 列号)和半径，再加上记录单元代码组成。特点：
• 一个多边形所包含的正方形越大，多边形的边界越简单，块状编码的效率就越好。
• 块状编码对大而简单的多边形更为有效，而对那些碎部较多的复杂多边形效果并不好。
第1行第N列亮度值 波段n 波段1 第2行第1列亮度值 波段n
BSQ结构
BIP结构
BIL结构
星蓝海学习网13
以行为记录单位按行存储 地理数据。属性明显，位 置隐含。 缺点：存在大量冗余，精 度提高有限制。
星蓝海学习网14
0 0 0 0 0 4 4 4 记录1 0 0 0 0 0 4 4 4
星蓝海学习网
• 优点：
• 栅格加密时，数据量不会明显 增加，压缩效率高，最大限度 保留原始栅格结构，
• 编码解码运算简单，且易于检 索、叠加、合并等操作，得到 广泛应用。
• 缺点：
• 不适合于类型连续变化或类型 区域分散的数据。
星蓝海学习网
(2)压缩栅格数据结构
块码（二维游程编码）（行，列，半径，属性值）
弧段ID a b c d e
起始点 5 7 1 13 7
终结点 1 1 13 7 5
… … … 左多边形 Q A Q D D
右多边形 A B B B A
f
13
5
Qห้องสมุดไป่ตู้
D
点号 1 2
…… 25
坐标 （x1，y1） （x2，y2）
…… （x25，y25）
g
25
弧段ID
点号
a
5,4,3,2,1
b
7,8,1
c
1,9,10,11,12,13
• 采用方形区域作为记录单元，每个记录单元包括相邻的若干栅格，数据结构由初始位置(行、 列号)和半径，再加上记录单元代码组成。特点：
• 一个多边形所包含的正方形越大，多边形的边界越简单，块状编码的效率就越好。
• 块状编码对大而简单的多边形更为有效，而对那些碎部较多的复杂多边形效果并不好。
第三章矢量数据模型ppt课件
(2)拓扑元素 点：孤立点、线的端点、面的首尾点、链的连接点； 线：两结点之间的有序弧段，包括链、弧段和线段； 面：若干弧段组成的多边形。
点 :
线 :
起点
弧段 3
面 :
弧段 4
中间点
弧段 2
终点
弧段 1
(3)拓扑关系类型
• (3)拓扑关系类型
关联：不同拓扑元素之间的关系； 邻接：相同拓扑元素之间的关系； 包含：面与其他元素之间的关系； 连通：拓扑元素之间的通达关系； 层次：相同拓扑元素之间的层次关系；
拓扑关系的表示
结点 弧段
面域 弧段
A a, c, e
A
P0
P1 a, b, c, -g
B a, d, b
P2 b, d, f
C d, e, f
e
c
P1
P3 c, f, e
D b, f, c
P3 f C
P2 d
E
D
P4 g
b
B
P4 g
a
弧段 结点 a A,B b B,D c D,A d B,C e C,A
2、拓扑数据结构
(1)拓扑空间关系 拓扑空间关系是GIS中重点描述的空间关系。“拓 扑”（Topology）一词来源于希腊文，它的原意是 “形状的研究”。拓扑学是几何学的一个分支，它研 究在拓扑变换下能够保持不变的几何属性，即拓扑 属性。理解拓扑变换和拓扑变换属性时，可以设想 一块高质量的橡皮，它的表面时欧氏平面，这块橡 皮可以任意拉伸、压缩，但不能扭转和折叠，表面 上有点、线、面等组成的几何图形。在变换中，图 形的有些属性会消失，有的属性则保持不变。前者 称为非拓扑属性，后者称为拓扑属性。象拉伸、压 缩这样的变换，称为拓扑变换。
矢量数据模型名词解释
矢量数据模型名词解释
1. 啥是矢量数据模型呀？就好比是一幅精确的地图！比如说，你看城市的地图，那些线条清晰的道路、边界，那就是矢量数据模型的体现呀！它能准确地记录和表示各种地理要素的位置和形状呢！
2. 嘿，矢量数据模型啊，就像一个超级细致的记录员！好比你画一个房子的图形，每一条线、每一个角都被准确记录下来，这就是矢量数据模型在起作用啦！你说神奇不神奇？
3. 矢量数据模型哟，这可是个厉害的家伙！就好像是一个精准的导航仪，能指引你找到具体的地点。
比如你要找一家特定的商店，它就能通过矢量数据准确地定位呢！
4. 哎呀呀，矢量数据模型呀，相当于一个无比严谨的建筑师！举个例子，设计大楼的时候，它能把每根柱子、每堵墙的位置都精确呈现，是不是很牛？
5. 矢量数据模型，那可是如同一个聪明的侦探一样的存在！比如在追踪犯罪现场的线索时，它能把每个细节都清晰展现，帮助找到关键信息呢！
6. 哇塞，矢量数据模型呀，简直就是一个神奇的魔法盒！像画一幅美丽的插画，那些线条和形状都是通过矢量数据模型来完美呈现的呀！
7. 矢量数据模型呢，就好像是一个耐心的老师！比如说在地理课上，它能清楚地告诉我们山脉的走向、河流的路径，是不是很厉害？
8. 嘿哟，矢量数据模型啊，不就是个超棒的工具嘛！就像做手工时，用它来精确裁剪出各种形状，厉害得很呢！
9. 矢量数据模型，这可是个不能小瞧的角色呀！好比一场精彩的球赛，球员的位置和动作都可以通过矢量数据模型来记录和分析呢！
10. 矢量数据模型呀，那绝对是个超级实用的东西！就像你要去一个陌生的地方，它能准确地给你指引方向，太有用啦！
我的观点结论：矢量数据模型真的是非常重要且实用的，在各种领域都有着广泛的应用，能帮助我们更准确、更清晰地理解和处理各种信息。
相关主题
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
关系数据：实体间 的邻接、关联包含 等相互关系
属性数据：各种属 性特征和时间 元数据
2014.3.5
一、矢量数据结构
矢量数据的表示类型 从前面的内容知道，表示地理现象的空间矢量数据可以表示为 点、线、面三类。但按其表示的内容，又可进一步分为七种不 同的类型。它们表示的内容如下： 类型数据，如考古地点，道路线、土壤类型等； 面域数据，如多边形的中心点，行政区界线、行政单元等； 网络数据，地下管线的设施、管线网、供水区域等； 样本数据，气象站、航线、实验区等； 曲面数据，高程点、等高线、等值区域等； 文本数据，地名、河流名称和区域名称等； 符号数据，点状符号、线状符号和面状符号等。
（1）连接性：弧段间通过节点连接； （2）面定义：由一系列相连的弧段定义面 （3）邻接性：弧段有方向性，且有左右多边形
点的coveroverage数据结构 弧段-节点清单 弧段坐标清单
多边形的coverage数据结构 左/右多边形清单 多边形-弧段清单 弧段坐标清单
地图是地理空间实体的图形模型。它是按照一定 的比例、一定的投影原则，有选择地将复杂的三维 地理实体的某些内容投影绘制在二维平面媒体上， 并用符号将这些内容要素表现出来。地图上各种要 素之间的关系，是按照地图投影建立的数学规则， 使地表各点和地图平面上的相应各点保持一定的函 数关系，从而在地图上准确表达空间各要素的关系 和分布规律，反映它们之间的方向、距离和面积。
DEM
TIN,
GRID
矢量数据
栅格数据
数字高程
三、空间实体的表达
1、实体 • 地理系统：地理系统是一个开放的复杂巨系统。 • 地理实体：将地理系统中复杂的地理现象进行抽 象得到的地理对象称为地理实体或空间实体、空 间目标，简称实体（Entity）。实体是现实世界 中客观存在的，并可相互区别的事物。抽象程度 与研究区域的大小、规模不同而有所不同。实体 是一个具有概括性、复杂性、相对意义的概念。
邻接 点—点 点—线
相交
相离
包含
重合
点—面
线—线 线—面 面—面
在有向图中建立节点和弧段的邻接和关联关系。 一条弧段连接两个节点，则称这两个节点的弧段呈 邻接和关联 邻接矩阵：节点和节点做矩阵，用1表示邻接，用0 表示非邻接 关联矩阵：弧段和节点做矩阵，用1表示关联自， 用-1表示关联至，用0表示不关联。
拓扑关系的表示
面域
A P0 e P3 f C b P2 d B D c E a P4 g P1
结点
弧段
弧段 a, b, c, -g b, d, f
A
B C D E
弧段
a, c, e
a, d, b d, e, f b, f, c g
右邻面
P1 P2
P3
P4 弧段 a
c, f, e
g 结点 A, B
2、拓扑数据结构
空间关系 空间关系是指地理实体之间存在的与空间特 性有关的关系，如度量关系、顺序关系和拓 扑关系等。是刻画数据组织、查询、分析和 推理的基础。空间关系的描述和表达，是 GIS区别于CAD等计算机图形处理系统的主 要标志。空间关系的研究，直接影响GIS的 设计、开发与应用。
2、拓扑数据结构
图斑不能相互压盖 用地多边形的边界必须与用地红线完全重合 用地红线不能有悬挂结点 道路与公共汽车线路必须重合
（
（2）一维矢量表示空间中的一个线状要素， 或者空间实体对象之间的边界，包括线段、 弦列、拓扑连线、弧段、链、环等。 线段是两个结点之间的连线 。
一维矢量可以闭合，即弧段首尾相接， 存在x1=xn ,y1=yn ,或z1=zn。但弧 段不能自身相交。如果相交，则应以交 点为界，将该一维矢量分成几个一维矢 量。
左邻面
a b c
P0 P2 P3
P1 P1 P1
b
c d e f g
B,D
D,A B,C C,A C,D E,E
d
e f g
P0
P0 P3 P1
P2
P3 P2
1、拓扑关系能清楚地反映实体之间的逻辑结构关系，它 比集合关系具有更大的稳定性，不随地图投影而变化。 2、有助于空间要素的查询，利用拓扑关系可以解决许多 实际问题。如某县的邻接县（面面相邻问题）。又如供水 管网系统中某段水管破裂找关闭它的阀门，就需要查询该 线与哪些点关联。 3、根据拓扑关系可以重建地理实体。例如根据弧段构建 多边形，实现面域的选取；根据弧段与结点的关联关系重 建道路网络，进行最佳路径选择等。 总的来说，有两个目的：保证数据质量，保证空间对象表 达的合理性和正确性、一致性。二是提高空间分析的效率 。
在地图学上，把地理空 间实体分为点、线、 面三种地理要素，分 别用点状、线状、面 状符号来表示。
符号化表示的地形图
2、影像对地理空间的描述
影像是记录了地理实体分布的写照模型。写 真的程度受摄影比例尺的影响，或空间分辨 率的影响。
3、地理信息的数字化描述
在GIS中，地理信息是以数字化的形式 存在的。表达地理信息的地理数据的几何空 间数据主要有四种数据类型，即矢量数据、 栅格数据、属性数据和数字高程模型数据。
(1)拓扑空间关系 拓扑空间关系是GIS中重点描述的空间关系。“拓 扑”（Topology）一词来源于希腊文，它的原意 是“形状的研究”。拓扑学是几何学的一个分支， 它研究在拓扑变换下能够保持不变的几何属性，即 拓扑属性。理解拓扑变换和拓扑变换属性时，可以 设想一块高质量的橡皮，它的表面时欧氏平面，这 块橡皮可以任意拉伸、压缩，但不能扭转和折叠， 表面上有点、线、面等组成的几何图形。在变换中 ，图形的有些属性会消失，有的属性则保持不变。 前者称为非拓扑属性，后者称为拓扑属性。象拉伸 、压缩这样的变换，称为拓扑变换。
多边形环路法的缺点是，除了多边形轮廓外，其它 公共边均存储了两次，因而会产生数据在结点处不 重合、边界处易产生裂缝和重叠。点位字典法避免 了这些情况，但仍没有存储必需的拓扑关系。
矢量本身是数学上的概念，运用到GIS中， 则不同的空间特征具有不同的矢量维数。
1）零维矢量表示空间中的一个点，点在二 维欧氏空间中用唯一的实数对（x, y）来表 示，在三维空间中用唯一的实数组（x, y, z ）来表示。在数学上，点没有大小和方向。 在GIS中，点的类型包括实体点、标记点、 面标识点、结点和节点等
根据数据的来源不同分 为 • 几何图形数据 • 影像数据 • 属性数据 • 地形数据 地图数据 影像数据 文本数据
根据表示对象的不同 分为： • 类型数据 • 区域数据 • 网络数据 • 样本数据 • 曲面数据 • 文本数据 • 符号数据
按照数据结构
矢量数据 栅格数据
按照数据特征
在拓扑数据结构中，点是相互独立存储的，它们相
互连接构成线，线始于起结点，止于终结点。面由 线（线段、弧段、链、环等）构成。一个多边形可 以由一个外环和领个内环或多个内环组成，简单多 边形没有内环，复杂多边形由一个或多个内环组成。 这些内环所包围的区域称为“岛”或“洞”。前者 有实体意义，后者无实体意义。 在大多数的GIS软件中，仅存储部分的拓扑关系，主 要是关联关系（不同类元素之间的关系），其他关 系可以从这些关系导出，或通过空间运算得到。拓 扑关系可以有两种表达方式，全显式和半隐含表达。
(2)拓扑元素 点：孤立点、线的端点、面的首尾点、链的连接点； 线：两结点之间的有序弧段，包括链、弧段和线段； 面：若干弧段组成的多边形。
点 : 线 :
终点
中间点 起点
弧段 2
弧段 3
面 :
弧段 4
弧段 1
(3)拓扑关系类型
• (3)拓扑关系类型
关联：不同拓扑元素之间的关系； 邻接：相同拓扑元素之间的关系； 包含：面与其他元素之间的关系； 连通：拓扑元素之间的通达关系； 层次：相同拓扑元素之间的层次关系；
按照几何特征 点 线 面、曲面 体 按照数据发布形式 数字线画图 数字栅格图 数字高程模型 数字正射影像图
空间数据 非空间属性数据
1、基本特征 空间特征 属性特征 时间特征
2、基本信息 定位信息 属性信息 拓扑信息
二、地理空间的表达 1 地图对地理空间的描述
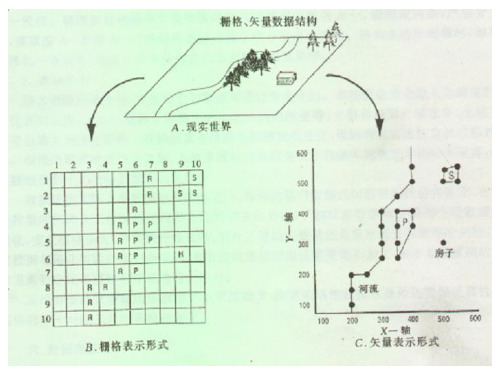
1、实体数据结构（简单数据结构、无拓扑关系的矢
量数据结构） 无拓扑关系的矢量数据结构是对Spaghetti数据模型 的具体定义和描述。它仅记录空间对象的位置坐标和 属性数据，而不记录空间关系。它有两种方式，一种 是每个点、线、面目标分别记录其坐标，称为多边形 环路法，另一种方式是一个文件记录点坐标对，其他 一些文件记录点与线、点与面的关系，称为点位字典 法。
从历史的观点来看拓扑关系的使用，过去拓 扑关系主要用于数据结构的创建，以保证具 有相关联的地理对象能够形成一致的、清晰 拓扑的数据结构。但随着面向对象的概念和 数据模型建模技术的发展，这个概念的使用 开始产生了一些变化。拓扑关系作为数据结 构的一部分开始弱化。主要是约束空间对象 的行为，以及定义一些描述表达规则。
矢量数据的简单数据结构分别是按照点线面三种基 本形式来描述的。 点：
标识码
X，y坐标对 坐标对数N X，Y坐标
线 面
标识码
标识码 链数N
链标识码集
1、实体数据结构
点 线
面
1、实体数据结构
矢量数据是用坐标对 、坐标串和封闭的坐 标串表示实体点、线 、面的位置及其空间 关系的一种数据格式 。
2、实体的描述及存储
描述内容 位置、形状、尺 寸 识别码（名称） 、实体的角色、 功能、行为、实 体的衍生信息 时间 测量方法、编码 方法、空间参考 系等 实体基本特征 属性特征：名 称、等级、类 别等 空间特征：地 理位置和空间 关系 时间特征 空间数据类型 几何数据（空间数 据、图形数据） 空间数据结构 矢量、栅格、TIN （专用于地表或特 殊造型） RDBMS属性表：采 用MIS较成熟 空间元数据