机械波课件PPT
大学物理机械振动和机械波ppt课件

2024/1/26
12
03
驻波形成条件及其性质分析
Chapter
2024/1/26
13
驻波产生条件及特点描述
产生条件
两列沿相反方向传播、振幅相同、频 率相同的波叠加。
特点描述
波形不传播,能量在波节和波腹之间 来回传递,形成稳定的振动形态。
2024/1/26
14
驻波能量分布规律探讨
能量分布
驻波的能量主要集中在波腹处,波节处能量为零。
2024/1/26
16
04
多普勒效应原理及应用举例
Chapter
2024/1/26
17
多普勒效应定义及公式推导
2024/1/26
定义
当波源与观察者之间存在相对运动时,观察者接收到的波的频率会发生变化,这种现象 称为多普勒效应。
公式推导
设波源发射频率为f0,波速为v,观察者与波源相对运动速度为vr,则观察者接收到的 频率为f=(v±vr)/v×f0,其中“+”号表示观察者向波源靠近,“-”号表示观察者远离
Chapter
2024/1/26
25
非线性振动概念引入和分类
非线性振动定义
描述系统振动特性不满足叠加原理的振动现象。
分类
根据振动性质可分为自治、非自治、周期激励和 随机激励等类型。
与线性振动的区别
线性振动满足叠加原理,而非线性振动则不满足 。
2024/1/26
26Biblioteka 混沌理论基本概念阐述混沌定义
确定性系统中出现的内在随 机性现象。
受迫振动
物体在周期性外力作用下所发生的振动。
共振现象
当外力的频率与物体的固有频率相等时,物体的振幅达到最大的现象。
《高三物理机械波》课件

通过实例,深入讲解机械波在不同领域中的应用,如声波在声学工程中的应用,光波在 光学通信中的应用等。
波穿过障碍物或通过开口
后的扩散现象。
纵波和横波
1 纵波和横波的定义
纵波是质点在振动方向上
2 纵波和横波的传播方
式
3 纵波和横波的区别
纵波的振动方向与波的传
传播的波,横波是质点在
传播的波。
向振动传播,横波通过介
方向垂直于波的传播方向。
质中质点的横向振动传播。
机械波通过介质中质点的振动传播。
机械波的特性
1 波长、频率、波速
波长表示波的长度,频率 表示波的振动次数,波速 表示波的传播速度。
2 振幅、周期
3 波的叠加、干涉和衍
射
振幅表示波的最大偏离值,
周期表示波的振动完成一
波的叠加是波与波相遇后
次所需时间。
形成新的波;波的干涉是
波与波叠加后产生增强或
减弱的现象;波的衍射是
《高三物理机械波》PPT 课件
本课件介绍高三物理中关于机械波的知识,包括机械波的定义、分类和传播 方式,并深入讨论了机械波的特性、纵波和横波的区别,以及声波和光波的 特点和传播方式。
介绍机械波
1 机械波的定义
机械波是由质点在介质中传播的能量和动量的传递。
2 机械波的分类
机械波分为横波和纵波两种。
3 机械波的传播方式
声波
1 声波的定义和特性
声波是由物体振动引起的 机械波,是一种纵波。声 波具有频率、波长和振幅 等特性。
2 声波的传播
声波通过介质中质点的纵 向振动传播,如空气、水 等。
3 声波的衍射和干涉
声波能够在障碍物后弯折 传播,也可以与波源发出 的声波叠加产生干涉现象。
大学物理(机械波篇)ppt课件

液晶显示
利用偏振光的特性,实现液晶 屏幕对图像的显示和控制。
科学研究
在物理学、化学、生物学等领 域中,利用偏振光研究物质的 光学性质和结构特征。
06
总结回顾与拓展延伸
机械波篇重点知识点总结
机械波的基本概念
机械波是介质中质点间相互作用力引起的振动在介质中的传播。机械波的产生条件、传播方 式、波动方程等基本概念是学习的重点。
驻波形成条件 两列波的频率相同、振幅相等、相位差恒定。
3
驻波特点
波形固定不动,节点和腹点位置固定;相邻节点 间距离等于半波长;能量在节点和腹点之间来回 传递。
03
非线性振动和孤立子简介
非线性振动概念及特点
非线性振动定义
指振动系统恢复力与位移之间不满足线 性关系的振动现象。
振幅依赖性
振动频率和波形随振幅变化而变化。
当障碍物尺寸远大于波长时,衍射现象不 明显。
衍射规律
衍射角与波长成正比,与障碍物尺寸成反 比。
双缝干涉实验原理及结果分析
实验原理:通过双缝让 单色光发生干涉,形成 明暗相间的干涉条纹。
01
干涉条纹间距与光源波 长、双缝间距及屏幕到
双缝的距离有关。
03
05 通过测量干涉条纹间距,
可以计算出光源的波长。
天文学领域
通过测量恒星光谱中谱线的多普勒频移,可以推断出恒星相对于观察 者的径向速度,进而研究恒星的运动和宇宙的结构。
05
光的衍射、干涉和偏振现 象
光的衍射现象及规律总结
衍射现象:光在传播过程中遇到障碍物或 小孔时,会偏离直线传播路径,绕到障碍 物后面继续传播的现象。
当障碍物尺寸与波长相当或更小时,衍射 现象显著。
多个孤立子相互作用后,各自保持 原有形状和速度继续传播。
10章机械波平面简谐波课件

机械波:机械振动在弹性介质中的传播.
一、机械波的形成:
1、弹性介质和波源——(机械波产生的条件)
弹性介质——由弹性力组合的连续介质。 波源——波源处质点的振动通过弹性介 质中的弹性力,将振动传播出去,从而形成 机械波。波动是振动状态的传播,是能量的 传播,而不是质点的传播。
2.传播
2 k 2
T
0
-
π 2
t 0 x 0 y 0, v y 0
t
y 1.0 cos[t - x - ] m
2
O
y
A
2)求 t 1.0s波形图.
y 1.0 cos[t - x - ] m
2
t 1.0s
波形方程
y 1.0 cos[ π - π x] 2
sin( x)
y/m
-
x) u
0 ]
a
2 y t 2
-2 Acos[(t
-
x) u
0]
二、 波函数的物理意义
y
A cos[ (t
-
x) u
0 ]
Acos[2π( t T
-
x
)
0 ]
1、 当 x 固定时,
波函数表示该点的简谐振动方程
波线上各点的简谐运动图
y(x,t) y(x,t T ) (波具有时间的周期性)
y
-
x) u
0 ]
y
A cos[ (t
x) u
0
]
u 沿 x 轴正向
u 沿x 轴负向
波函数的特征量
y
A cos
(t
-
x) u
0
相速度:单位时间内波传播过的距离
《机械波波动方程》课件
3
解多维波动方程的方法
解多维波动方程可以使用分离变量法和叠加原理等方法。
应用实例
机械波在弦上的传播
弦上的波动现象在音乐乐器和工 程结构设计等领域具有广泛的应 用。
声波在介质中的传播
声波的传播过程在声学及通信行 业等领域中发挥着重要作用。
电磁波在空气中的传播
电磁波的传播现象涉及到无线通 信、天文学等领域的研究和应用。
波动方程的概念
什么是波动方程
波动方程是描述波动现象的数 学表达式。
波动方程的类型
常见的波动方程包括一维和多 维波动方程。
波动方程的解法
解波动方程常用的方法有分离 变量法、叠加原理等。
一维波动方程
1 一维波动方程的表达式
一维波动方程可表示为∂²u/∂t² = v²(∂²u/∂x²)
2 一维波动方程的特征
一维波动方程描述了波在单一方向上的传播。
3 解一维波动方程的方法
解一维波动方程可以使用波函数分离变量法和叠加原理等方法。
多维波动方程
1
多维波动方程的表达式
多维波动方程可表示为∂²u/∂t² = v²(∂²u/∂x² + ∂²u/∂y² + ∂²u/∂z²)
2
多维波动方程的特征
多维波动方程描述了波在空间中的传播,在多个方向上具有振动。
总结
机械波波动方程的应用
机械波波动方程的理论与实践应用对科学研究和技 术发展具有重要意义。
未来发展及展望
随着科技的进步,机械波波动方程的研究将在更广 泛的领域及• 文献2 • 文献3
《机械波波动方程》PPT 课件
本课件将介绍机械波波动方程的基本概念、一维和多维波动方程的应用,以 及相关实例和未来发展展望。
机械波的产生和传播PPT课件

7.1 机械波的产生和传播
y
1 3 2 4
7
3 2
10
13
16
t0
t T 4
3 2
t 2T 4
3 2
t 3T 4
3 2
t T
3 2
t 5T 4
第5页/共21页
7.1 机械波的产生和传播
注意
波是运动状态的传播,介质 的质点并不随波传播.
第6页/共21页
7.1 机械波的产生和传播
三 波速、波长、频率(或周期) 波的特征:具有空间和时间上的周期性
7.1 机械波的产生和传播
2 波长
在波的传播方向上相邻的两个振动状态
相同(相位差为2 )的质点间的距离(一个完
整波的长度)
Ay
o
x
-A
第9页/共21页
7.1 机械波的产生和传播
横波:相邻 波峰——波峰 波谷—— 波谷 纵波:相邻 波疏——波疏 波密——波密
波长与介质有关
第10页/共21页
7.1 机械波的产生和传播
1 波速 v
在单位时间内振动状态(或相位)传播的 距离称为波的传播速度,也称为相速
大学物理 机械波ppt课件

3. 波速u : 单位时间波所传过的间隔
波速u又称相速度(相位传播速度)
三者关系
u
T
固体内横波和纵波的传播速度u分别为
u G (横波)
u E (纵波)
G:切变模量,E弹性模量, ρ 固体的密度
液体和气体内,纵波的传播速度为
u K (纵波)
K为体积模量
弹性绳上的横波 u T
T-绳的初始张力, -绳的线密度
u
y
u
P
O
x
x
动摇方程的另外两种常见方式
由 ω = 2π /T ,u = ν λ = λ /T
有 y(x,t)Aco2s(tx) 或
取角波数k k 2 有 u
y(x,t)Aco2s(T tx)
y (x ,t) A c ot s k)(x
假设知距O点为x0 的点Q的振动规律为 yQA co ts ()
y u
Q O
x0
x
P x
那么相应的波函数为 yAco stx ux0
沿Ox轴负方向传播的波
y
u
P
O
x
x
P点的振动比O点早t0= x/u. 当O点的相位是ωt 时, P点 的相位已是ω (t + x / u) .
所以
y(x,t)Acos(tx)
u
或 y(x,t)Aco2sT tx y (x ,t) A cot s k)(x
同理对D点 4. BC间的相位差
yD3co4st5 9 (S)I
C B 2 (x B x C ) 1 .6
CD间的相位差 2x4.4 C相位超前D4.4π
§3 波的能量
一. 弹性波的能量
动摇过程就是能量传播的过程
机械波的形成和传播(含flash和视频)ppt课件

学以致用
<1>.关于波下列说法正确的是( CD) A.有机械振动就有机械波 B.没有机械波就没有机械振动 C.有机械波就一定有机械振动 D.机械波是机械振动在介质中的传播过 程,它是传递能量的一种方式
<2>、区分横波和纵波是根据( C )
A.是否沿水平方向传播 B.质点振动的方向和波传播的远近
一、机械波的形成与传播
分组讨论:机械波在传播过程中的特点?
思考1:绳上的点有没有随波迁移? 思考2:绳上各点是不是同时开始振动的,它们
振动的步调一致吗? 思考3:绳上各点开始振动时的方向(起振方向)? 思考4:在波的传播过程中,介质中各点振动的周期
(频率)是否相同?
一、机械波的形成与传播
机械波的传播特点:
第二章 机械波
第一节 机械波的形成和传播
一生、活机中械的波机的械形波成与传播
请点击手
一、机械波的形成与传播
为什么绳上各点都能动起来呢?凹凸相间的波是怎样形成的呢?
设想:把绳分成很多小段 每一个小段可以看做一个质点
质点之间有相互作用力
精选ppt的形成与传播
波的形成过程是这样的
C.质点振动的方向和波传播的方向 D.质点振动的快慢
<3>、下列说法不正确的有( ACD)
A.声波在空气中传播时是纵波, 在水中传播时是横波
B.波不但传递能量,还能传递信息
C.质点振动的方向总是垂直于波 传播的方向
D.一切波的传播均需要介质
<4>.在机械波中,下列说法中错误的是( D )
A、各质点都在各自平衡位置附近振动 B、相邻质点间必有相互作用力 C、前一质点的振动带动相邻后一质点 的振动,后一质点的振动必定落后于前 一质点 D、各质点也随波的传播而迁移
波的形成ppt课件

三、横波和纵波
1、横波 ① 特征:质点的振动方向与波的传播方向垂直
②波形特点:凹波谷:
凹下部分的最低点叫波谷 横波只能在固体介质中传播
2、纵波
①特征:质点的振动方向与波的传播方向在一条直线上。 ②波形特点:质点分布较稀的部分叫疏部,质点分布较密的部分叫密部。
时刻:T/4
1 23 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
时刻:T/2
2 345 6
1
7 8 9 10 11 12 13 14 15 16 17 18
时刻:3T/4
678
5
9
4
10 11 12 13 14 15 16 17 18
123
时刻:T
1 2
34 5
8 7 6
波源(振源):能够维持振动的传播,不间断的输入 能量,并能发出波的物体或物体所在的初始位置。 介质:凡是能传播机械振动的媒介物质,都可以叫做 介质。
二、波的形成
设想:把绳分成很多小段 每一个小段可以看做一个质点
时刻:0
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
3.1 波的形成
1
2
目录
CONTENTS
3
机械波 波的形成 横波和纵波
在艺术体操的带操表演中,运
动员手持细棒抖动彩带的一端,彩 带随之波浪翻卷。彩带上的波浪向 前传播时,彩带上的每个点也在向 前运动吗?
一、机械波
1.机械波:机械振动在介质中由近及远的传播就形成了机械波。
2、产生条件:① 有振源。② 有可传播波的介质。
9
10
11 12
13 14 15 16 17 18
《机械波复习》课件

当波动从一种介质进入另一种介质时 ,波速、波长和频率都会发生变化, 这是由于介质的不同导致的。
当波动遇到不同介质或障碍物时,会 发生反射和折射现象,导致能量分布 的变化。
高难度题解析
在此添加您的文本17字
高难度题1: 求解复杂边界条件下的波动方程。
在此添加您的文本16字
对于复杂边界条件下的波动方程,需要采用数值方法进行 求解,如有限差分法、有限元法等。
THANKS
感谢观看
机械波的特性
01
02
03
波动性
机械波具有波动性,表现 为传播过程中的振动能量 会扩散和衰减。
周期性
机械波具有周期性,即质 点振动的周期与波的周期 相同。
干涉与衍射
当两列或多列机械波相遇 时,它们会产生干涉现象 ;当机械波遇到障碍物时 ,会产生衍射现象。
02
波动方程与波动现象
波动方程的推导
波动方程的推导方法
机械波的传播
机械波在介质中传播时,介质中的质 点不随波迁移,而是以平衡位置为中 心进行振动。波的传播需要介质,且 传播速度由介质决定。
机械波的分类
按振动方向分类
可分为横波和纵波两类。横波的质点振动方向与波的传播方向垂直,而纵波的 质点振动方向与波的传播方向一致。
按频率分类
可分为次声波、声波和超声波三类。次声波频率低于20Hz,声波频率在20Hz 到20kHz之间,而超声波频率高于20kHz。
式,如振动能发电。
04
机械波的干涉与衍射
机械波的干涉现象
干涉现象定义
两列或多列机械波在空间相遇时,会因叠加而产 生稳定的强弱分布现象。
干涉条件
频率相同、振动方向相同、相位差恒定。
干涉图样
机械波ppt课件

机械波ppt课件•机械波基本概念与分类•机械波产生与传播条件•机械波在各向同性介质中传播特性•机械波在各向异性介质中传播特性目•机械波检测技术应用领域及发展趋势•总结回顾与拓展延伸录机械振动在介质中的传播称为机械波。
机械波定义依赖于介质传播传播的是振动形式和能量周期、频率与振源相同机械波的传播需要介质,真空不能传声。
质点只在平衡位置附近振动,并不随波迁移。
波传播过程中,各质点的振动周期和频率都等于振源的振动周期和频率。
机械波定义及特点根据质点振动方向与波传播方向的关系,机械波可分为横波和纵波。
横波与纵波机械波分类与性质质点振动方向与波传播方向垂直的波。
横波质点振动方向与波传播方向在同一直线上的波。
纵波单位时间内波形传播的距离,反映了振动的传播快慢。
波速沿波的传播方向,两个相邻的、相位差为2π的质点间的距离。
波长单位时间内质点振动的次数,反映了振动的快慢。
频率通过演示绳波的形成过程,分析横波的特点和传播规律。
绳波的形成与传播通过演示声波的形成过程,分析纵波的特点和传播规律。
声波的形成与传播通过演示水波的形成过程,分析水波的波动性质和传播规律。
水波的形成与传播通过演示地震波的形成过程,分析地震波的波动性质和传播规律,以及地震波对地球结构和人类活动的影响。
地震波的形成与传播波动现象实例分析产生机械振动的物体或系统,为机械波提供能量。
振源介质作用关系传播机械振动的物质,如固体、液体或气体。
振源的振动通过介质中的质点间相互作用力传递,形成机械波。
030201振源与介质作用关系描述机械波传播规律的数学方程,通常为一阶或二阶偏微分方程。
波动方程根据机械波的传播规律,结合牛顿第二定律和介质本构关系,推导出波动方程。
建立方法采用分离变量法、行波法、驻波法等方法求解波动方程,得到波的传播速度、振幅、相位等参量。
求解方法波动方程建立与求解方法波动能量传递过程探讨波动能量01机械波传播过程中携带的能量,表现为质点振动的动能和势能之和。
大学物理机械波课件-PPT

2、t=t0为定值,y=y(x)
• 表示t0时刻波线上各质点离开各自平衡位置 得位移分布情况,称为该时刻得波形方程
• 对于横波,波形图就就是该时刻各质点在空 间得真实分布
• 对于纵波,波形图仅表示质点得位移分布
3、t与x都在变化
• 波动方程给出了各个质点在不同时刻得位
y 移,或者说包含了不同时刻得波形
结论:机械波传播得就是波 源得振动状态与能量
三、波线与波面
• 波传播到得空间——波场 • 波场中代表波传播方向得射线——波线 • 某时刻振动位相相同得点得轨迹——波面 • 最前方得波面——波前或波阵面 • 横波中,质元振动得轨迹与波线垂直,二者构
成得面——振动面或偏振面
波线
波线
平面波 球面波
波面
• P点t时刻得振动位移与原点 动位移相同
• P点振动方程为
时刻得振
沿x轴正向传播得平面简谐波得波函数
• 也就是x处质点得振ຫໍສະໝຸດ 方程沿x轴负向传播得平面简谐波得波函数
• 常用得波动表达式
(1)如图,已知 P 点得振动方程:
yP
A
y
cos( u
t
0
)
px Q x
O
x
求波动方程即波函数。
(2)如图,已知 P 点得振动方程:
平面简谐波——波面为平面得简谐波
?问题
• 如何用数学表达式描述一个前进中得波动?
• 如何描述各质点得振动位移y随平衡位置x与
t得变换规律
波函数
一、波函数得推导
• 平面简谐波沿x轴正方向传播 • 设原点得振动方程为
• 设平衡位置为x得P点在t时刻得振动位移为y • P点得振动落后于原点,晚了 • 也就就是原点得振动状态传到P点所需得时间 • P点在t时刻将重复原点在 时刻得振动状态
选修34第二讲机械波课件
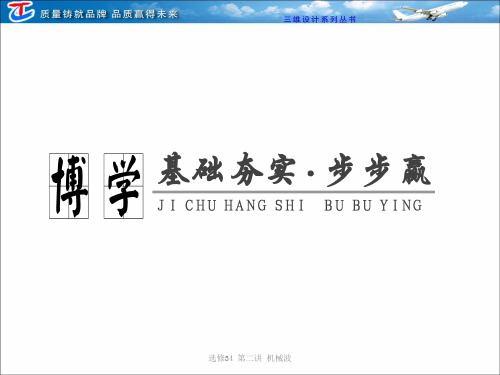
解析:由A、B两质点的的振动图象及传播可画出t=0时刻的
波动图象如图所示,由此可得λ= m,A正确;由振动图
象得周期T=4 s,故
B错误;由
振动图象知3 s末A质点位移为-2 cm,B质点位移为0,故C错
误;由振动图象知1 s末A质点处于波峰,振动速度为零,B质
点处于平衡位置,振动速度最大,故D错误.
图12-2-1
选修34 第二讲 机械波
⑤若知道波的传播方向,可知该时刻各质点的运动方向.如 图12-2-1所示,设波向右传播,则此时A、D质点沿y轴负方 向运动,B、C质点沿y轴正方向运动. ⑥若知道某时刻某质点的运动方向,可判断波的传播方 向.如图12-2-1所示,若D点向上运动,则该波向左传播.
所以波速v= =4 m/s.
(4)Δx=vΔt=14 m=3×4+ λ, 所以只需将波形向x轴负方向平移λ
图12-2-5 =2 m即可,如图
12-2-5所示.
选修34 第二讲 机械波
(5)求路程,因为n= 所以路程s=4nA=4×0.2×3.5 m=2.8 m. P点经3.5个周期后仍在平衡位置处,所以位移为零. [答案] 见解析
选修34 第二讲 机械波
2.某同学用一根弹性绳进行机械波的实验.用手握住绳 的一端做周期为1 s的简谐运动,在绳上形成一列简谐 波.以弹性绳为x轴,手握住的一端为坐标原点O,且 从波传到x=1 m处的M点开始计时,如图12-2-6所 示,求:
选修34 第二讲 机械波
图12-2-6 (1)当时间t为多少时,平衡位置在x=4.5 m处的N质点恰好第 一次从平衡位置向y轴正方向运动? (2)画出上问中t时刻弹性绳上的波形图.
2.机械波传播过程中,在固体和液体中的传播速度比在空气 中的传播速度大.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
频率--单位时间内质点振动的次数 1
T
u1 T
波动的频率,等于介质 中质点的振动频率。
--表示波在空间的周期性
--表示波在时间上的周期性
u 通过波速 联系起来
波的周期T:波传过一个波长的时间,或一个完整 的波通过波线上某一点所需要的时间叫做波的周期T。
物体的弹性和波速
机械波的传播速度完全取决于介质的弹性性质 和惯性性质。即介质的弹性模量和介质的密度, 亦 即决定于这种波在媒质中传播的机构。
传播方向
a·
b·
x
x
图中b点比a点的相位落后
波形曲线(波形图)
u
o
t
x
• 不同时刻对应有不同的波形曲线 • 波形曲线能反映横波、纵波的位移情况
波线、波面、波前
波场:波转播到的空间。 波线(或波射线)--波的传播方向称之为波射线或波线。 波面(或相面)--某时刻介质内振动相位相同的点组 成的面称为波面。 波前(波阵面)--某时刻处在最前面的波面。
左行波的波函数:
y0 Acos(t 0 )
p点运动传到 O 点需用时间:
t x
u
也即p点的相位超前于O点相位:
x
2x
u
所以 p点的运动方程,也就是左行波的波方程:
机械振动在弹性介质中的传播称为机械波。下面以 机械波为例介绍波的一些物理概念。
一、 机械波的产生和传播
弹性介质和波源——(机械波产生的条件)
弹性介质____由弹性力组合的连续介质。 波源____波源处质点的振动通过弹性介质中的 弹性力,将振动传播开去,从而形成机械波。波动 是振动状态的传播,是能量的传播,而不是质点的 传播。
可以证明:
对于柔软的绳索和弦线中横波波速为:
v T
T为绳索或弦线中张力;
为质量线密度
细长的棒状媒质中纵波波速为
v Y
Y为媒质的杨氏弹性模量; 为质量密度
各向同性均匀固体媒质横波波速
v G
G为媒质的切变弹性模量; 为质量密度
在同一种固体媒质中,横波波速比纵波波速小些。
在液体和气体只能传播纵波,其波速为:
纵波和横波:
纵波——振动方向与传播方向相同。 横波——振动方向与传播方向垂直。
任一波例如,水波、地表波,都能分解为横波与
纵波来进行研究。
·0 ··4····8····1·2···1·6···20 ···t = 0 ····························t = T/4 ························t = T/2 ··························t = 3T/4 ·························t = T
球面波
波线
平面波
波线
波面
波面
球面波平面波在各向同性均匀介质中,波线与波阵面垂直.
波的周期性和波速
波长、波速和频率:
波长--振动相位相同的两个相邻波阵面之间的距离是一 个波长。或振动在一个周期中传播的距离,称为波长,
用 表示。
波 位速) -所-传单播位的时距间离某称种为一定波的速振u动,状也态称(或之振相动速相。
y 设O点振动表达式: y0 Acos(t 0 )
y表示各质点在Y方向上的
位移,A是振幅, 是角频率或
叫圆频率, 0 为O点在零时刻的
相位。
u
pX Ox
O点运动传到 p点需用 P点比O点相位落后
t x u
x
u
P点在t时刻的位移等于原点处质点在 t x 时刻的位移
平面简谐波(plane harmonic waves):简
谐波的波面是平面。(可当作一维简谐波研究)
一维波动方程的一般表示:y y t, x
位移y是时间和空间的函数。
波函数
若波速v为恒量,则从整体上看,整个波以速度v向前推
进,所以又称这种波为行波(traveling waves)。
以横波为例说明平面简谐波的波函数:
p点的振动方程: y( x, t )
Acos[ (t
u
x u
)
0
]
y( x, t)
Acos[ (t
x u
)
0
]
2 /T
y( x, t)
Acos[(t
0 )
2
x]
即p点的相位落后于O点相位: 2x 。
这就是右行波的波动方程。
u /T
2 2 ;
结论: (1) 质元并未“随波逐流” 波的传播不是媒
质质元的传播 (2) “上游”的质元依次带动“下游”的质元振动 (3) 某时刻某质元的振动状态将在较晚时刻
于“下游”某处出现---波是振动状态的传播 (4) 同相点----质元的振动状态相同
波是相位的传播 沿波的传播方向,各质元的相位依次落后。
u
T
y u
pX
Tuu
Ox
因此下述几式等价:
y( x, t )
A cos[ (t
x u
)
0
]
y(x, t)
Acos[t
2x
0]
y(
x,
t)
Acos[2
(t
x
)
0]
y( x, t )
2
Acos[
(x
ut )
0]
y( x
x,
t
t )
V B
B为媒质的体变弹性模量;
为质量密度
1 V
B Vp
为压缩系数
理想气体纵波波速:
v P RT M
M为气体的质量;
T为热力学温度; R为气体的摩尔常数。
显然波速与温度有关。
8-2、平面简谐波的波动方程
简谐波(harmonic waves):波源的振动是简谐
振动,介质也不吸收波动的能量,那么介质中的质点 也将作简谐振动。
第八章 机械波
振动在空间的传播过程叫做波动
声波、水波、电磁波都是物理学中常见的波,它 对应一种物质波。波即可以是运动状态的传递而非物 质的自身运动,也可以是物质本身的运动结果,甚至 把波直接看作一种粒子。
各种类型的波有其特殊性,但也有普遍的共性, 例如,声波需要介质才能传播,电磁波却可在真空中 传播,至于光波有时可以直接把它看作粒子—光子的 运动。
A cos[ (t
t )
2
(x
x)
0
]
Acos[t
2x
2
(ut
x) 0 ]
若这两处相位相同,则有:
y(x x,t t) y(x,t)
y( x, t)
Acos(t
2x
0)
2
(ut x) 0
可见波速就是相位传播的速度
