27.1图形的相似练习题
27.1图形的相似同步练习
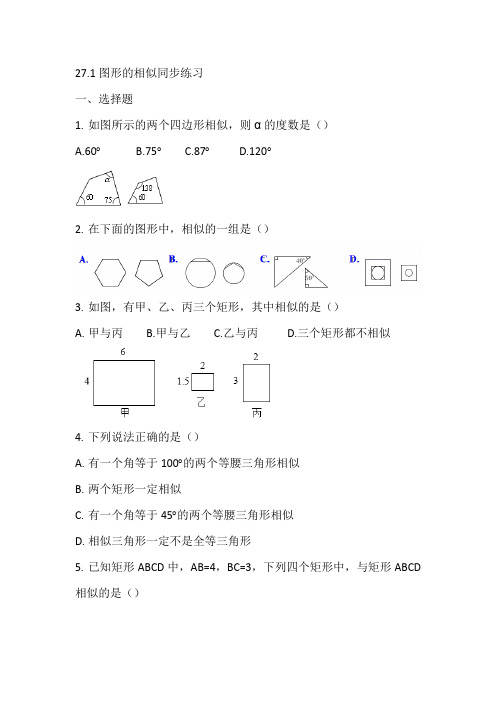
27.1图形的相似同步练习一、选择题1.如图所示的两个四边形相似,则α的度数是()A.60°B.75°C.87°D.120°2.在下面的图形中,相似的一组是()3.如图,有甲、乙、丙三个矩形,其中相似的是()A.甲与丙B.甲与乙C.乙与丙D.三个矩形都不相似4.下列说法正确的是()A.有一个角等于100°的两个等腰三角形相似B.两个矩形一定相似C.有一个角等于45°的两个等腰三角形相似D.相似三角形一定不是全等三角形5.已知矩形ABCD中,AB=4,BC=3,下列四个矩形中,与矩形ABCD 相似的是()6.如图所示,在长为8cm,宽为6cm的条形中,截去一个矩形(图中阴影部分),如果剩下的矩形与原矩形相似,那么剩下矩形的面积是()A.28cm2B.27cm2C.21cm2D.20cm27.两个相似多边形一组对应边分别为3cm,4.5cm,那么它们的相似比为()A.23B.32C.94D.498.一个多边形的边长为2,3,4,5,6,另一个和它相似的多边形最大边长为18,则最短边长为()A.6B. 8C. 12D. 109.下列说法正确的个数有()①同一底片印出来的不同尺寸的照片是相似的②放电影时胶片上的图象和它映射到屏幕上的图象是相似的③放大镜放大后的图形与原来的图形是相似的④水平观看装在带有水的透明玻璃杯中的金鱼所组成的像与金鱼本身的像是相似的A.1个B.2个C.3个D.4个10.用一个5倍的放大镜去观察一个三角形,对此,四位同学有如下说法:甲说:三角形的每个内角都扩大到原来的5倍;乙说:三角形的每条边都扩大到原来的5倍;丙说:三角形的面积扩大到原来的5倍;丁说:三角形的周长扩大到原来的5倍,上述说法中正确的是()A.甲和乙B.乙和丙C. 丙和丁D.乙和丁二、填空题1.一个多边形的边长依次为1,2,3,4,5,6,与它相似的另一个多边形的最大边长为8,那么另一个多边形的周长是_______.2.两个相似多边形的周长的比为2:3,较大多边形的面积为45cm2,则较小多边形的面积为_________cm23.如图,E,F分别为矩形ABCD的边AD,BC的中点,若矩形ABCD 与矩形EABF相似,则相似比等于________.4.秋天红透的枫叶,总能牵动人们无尽的思绪,所以诗人杜牧说:“停车坐爱枫林晚,霜叶红于二月花”如图是两片形状完全相同,大小不同的枫叶,则x的值为_______cm。
专题27.1 图形的相似(8个考点)(教师版) 2024-2025学年九年级数学下册(人教版)

专题27.1 图形的相似(8个考点)【考点1 比例性质】【考点2 比例线段】【考点3 成比例线段】【考点4 相似图形】【考点5相似多边形的性质】【考点6 黄金分割比】【考点7 由平行线判断成比例的线段】【考点8 由平行截线求相关相关线段的长或比值】【考点1 比例性质】1.如果ad=bc(a,b,c,d均不为零),那么下列比例式正确的是()A.bc =adB.ba=cdC.ab=cdD.cb=ad2.若mn =38,则m+nn的值是()A.118B.311C.113D.811【答案】A3.若xy =32,且x ≠0,则x+yy 的值为( )A .23B .32C .53D .524.若ab = 23,则下列式子不正确的是( )A .ba = 32B .a+bb= 53C .a 2 = b3D .a a−b = 23【答案】D【分析】本题主要考查比例的性质,熟练掌握比例的性质是解题的关键.根据比例的性质判断即可.【详解】解:A ,B ,C 选项分别对应比例的反比性质、合比性质、更比性质,只有D 选项不正确.故选D .5.若ab =23,则aa+b =.6.已知线段a、b、c满足a:b:c=3:2:6,且a+2b+c=26.(1)求a、b、c的值;(2)若线段a,b,c,d是成比例线段,求d的值.【答案】(1)6,4,12(2)8【分析】本题主要考查了比例线段,解一元一次方程,(1)利用a:b:c=3:2:6,可设a=3k,b=2k,c=6k,代入a+2b+c=26求出k的值,即可求出a、b、c的值;(2)根据题意得bc=ad,代入求得d即可.【详解】(1)解:∵a:b:c=3:2:6,∴设a=3k,b=2k,c=6k,又∵a+2b+c=26,∴3k+2×2k+6k=26,即3k+4k+6k=26,合并同类项,得:13k=26,系数化为1,得:k=2,∴a=3k=3×2=6,b=2k=2×2=4,c=6k=6×2=12;(2)解:∵线段a,b,c,d是成比例线段,∴bc=ad,∴4×12=6×d,即d=8,【考点2 比例线段】7.一种精密零件长2毫米,把它画在图纸上,图上零件长10厘米,这张图纸的比例尺是()A .1:500B .500:1C .1:50D .50:1【答案】D【分析】本题考查比例尺,关键是掌握比例尺的定义.比例尺=图上距离与实际距离的比,由此即可计算.【详解】解:∵10厘米=100毫米,∴100:2=50:1,∴这张图纸的比例尺是50:1.故选:D .8.若线段a =1m ,b =50cm ,则ba =( )A .2B .12cmC .12D .509.若在比例尺为1:10000的地图上,测得两地的距离为3.5厘米,则这两地的实际距离是 千米.【答案】0.35【分析】本题考查了比例尺的应用,设两地间的实际距离是x cm ,根据题意可得方程1:10000=3.5:x ,解方程即可求得x 的值,然后换算单位即可求得答案.【详解】解:设两地间的实际距离是x cm ,∵比例尺为1:10000,量得两地间的距离为3.5cm ,∴1:10000=3.5:x ,解得:x =35000,经检验,x =35000是原方程的解,∵35000cm=0.35km,∴两地间的实际距离是0.35千米,故答案为:0.35.10.已知线段a=9厘米,c=16厘米,则它们的比例中项b为.【答案】12厘米/12cm【分析】根据比例中项的性质:比例中项平方等于两外项的积直接求解即可得到答案;【详解】解:∵线段a=9厘米,c=16厘米,它们的比例中项为b,∴b2=9×16,解得:b=12(厘米),b=−12(厘米)(不符合题意舍去),故答案为:12厘米;11.如果线段a=4cm,b=5mm,那么a的值为.b【考点3 成比例线段】12.下列各组线段的长度成比例的是( )A.0.3m,0.6m,0.5m,0.9mB.30cm,20cm,90cm,60cmC.1cm,2cm,3cm,4cmD.2cm,3cm,4cm,5cm【答案】B【分析】本题主要考查相似图形,根据四条线段成比例的定义逐项判断即可.【详解】A、0.3×0.9≠0.6×0.5,各组线段的长度不成比例,该选项不符合题意;B、20×90=30×60,各组线段的长度成比例,该选项符合题意;C、1×4≠2×3,各组线段的长度不成比例,该选项不符合题意;D、2×5≠3×4,各组线段的长度不成比例,该选项不符合题意.故选:B13.下列各组中的四条线段成比例的是( )A.a=1,b=2,c=3,d=4B.a=2,b=3,c=4,d=5C.a=2,b=3,c=4,d=6D.a=2,b=4,c=6,d=8【答案】C【分析】此题考查了成比例线段,若ad=bc,则a,b,c,d成比例,据此进行计算判断即可.【详解】解:A、1×4≠2×3,故此选项中四条线段不成比例,不符合题意;B、2×5≠3×4,故此选项中四条线段不成比例,不符合题意;C、2×6=3×4,故此选项中四条线段成比例,符合题意;D、2×8≠4×6,故此选项中四条线段不成比例,不符合题意,故选:C.14.下列各组中的四条线段(单位:厘米)成比例线段的是()A.1、2、3、4;B.1、2、4、8;C.2、3、4、5;D.5、10、15、20.【答案】B【分析】本题主要考查了成比例线段的定义,熟练掌握对于给定的四条线段,如果其中两条线段的长度之比等于另外两条线段的长度之比,则这四条线段叫做成比例线段是解题的关键.根据比例线段的概念,让最小的和最大的相乘,另外两条相乘,看它们的积是否相等即可得出答案.【详解】解:A、4×1≠2×3,故本选项不符合题意;B、1×8=2×4,故本选项符合题意;C、2×5≠3×4,故本选项不符合题意;D、5×20≠10×15,故本选项不符合题意;故选:B.15.已知线段a,b,c,d成比例,且a=3b,c=12cm,则线段d的长为()A.4cm B.6cm C.9cm D.36cm16.已知四个数a,b,c,d成比例,且a=3,b=2,c=4,那么d的值为()A.2B.3C.43D.8317.已知四个数−3,9,2,d成比例,则d等于( )A.3B.6C.−3D.−6【答案】D【分析】本题主要考查了比例.熟练掌握比例的定义,比例的基本性质,是解决问题的关键.比例的定义:在四个数中,如果两个数的比等于另外两个数的比,就叫做这四个数成比例;比例的基本性质:两内项之比等于两外项之比.根据比例的定义,写出比例式,运用比例的基本性质解答.【详解】∵四个数−3,9,2,d成比例∴−3:9=2:d,∴−3d=18,解得,d=−6.故选:D.【考点4 相似图形】18.下列每个选项的两个图形,不是相似图形的是()A.B.C.D.【答案】D【分析】本题考查了图形相似的概念:形状相同,大小不同的两个图形;根据图形相似的概念即可作出判断.【详解】解:由图形相似的概念知,选项D中的两个图形不相似;故选:D.19.下列结论中正确的是()A.两个正方形一定相似B.两个菱形一定相似C.两个等腰三角形一定相似D.两个矩形一定相似【答案】A【分析】本题考查了相似形的判定,根据相似图形的定义逐项判断即可求解,掌握正方形、菱形、等腰三角形和矩形的性质是解题的关键.【详解】解:A、两个正方形角都是直角一定相等,四条边都相等一定成比例,所以一定相似,故A正确;B、两个菱形的边成比例,但角不一定相等,所以不一定相似,故B错误;C、两个等腰三角形的腰的比与底边的比不一定相等,角不一定相等,所以不一定相似,故C错误;D、两个矩形的角都是直角一定相等,但边不一定成比例,所以不一定相似,故D错误;故选:A.20.下列各组图形中,不一定相似的是()A.两个菱形B.两个有30°角的直角三角形C.两个正六边形D.两个正方形【答案】A【分析】题主要考查相似形.根据相似形的定义对各个选项进行分析,从而得到答案.【详解】解:A. 两个菱形得各边成比例,但角不一定相等,不一定相似,符合题意;B. 根据有两个角分别相等的两个三角形是相似三角形可知两个有30°角的直角三角形是相似性,不符合题意;C. 两个正六边形的各边成比例,各角相等,是相似形,不符合题意;D. 两个正方形的各边成比例,各角相等,是相似形,不符合题意;故选A.21.下列哪组图形是相似图形()A.B.C.D.【答案】C【分析】本题考查了相似图形的判定,属于简单题,熟悉相似图形的定义是解题关键.【详解】解:A、图形不是相似图形;B、图形不是相似图形;C、图形是相似图形;D、图形不是相似图形;故选:C.22.下列多边形一定相似的是()A.两个等腰三角形B.两个平行四边形C.两个正五边形D.两个六边形【答案】C【分析】本题主要考查了相似图形的判定,掌握相似形的定义(如果两个边数相同的多边形的对应角相等,对应边成比例,这两个多边形相似)是解题的关键.根据相似三角形的定义逐项判断即可.【详解】解:A、两个等边三角形相似,但是两个等腰三角形并不一定相似,三个角度没有确定,故A 不正确;B、两个平行四边形对应角度及对应边都不一定成比例,所以不一定相似,故B不正确;C、两个正五边形角度相等,放大缩小后可以完全重合,两图形相似,故C正确;D 、两个正六边形相似,但是两个六边形并不一定相似,故D 不正确.故选C .【考点5相似多边形的性质】23.两个相似多边形的面积之比为1:4,则它们的对应边之比为( )A .B .1:2C .1:4D .1:8【答案】B【分析】本题主要考查相似多边形的性质质.根据相似图形的面积比等于相似比的平方即可.【详解】解:两个相似多边形的面积之比为1:4,则它们的对应边之比为1:2,故选:B .24.若四边形ABCD ∽四边形A ′B ′C ′D ′,且AB:A ′B ′=3:5,已知B ′C ′=15,则BC 的长是( )A .25B .9C .20D .15【答案】B【分析】本题考查相似多边形的性质,关键是掌握相似多边形的性质:相似多边形的对应边成比例.由相似多边形的性质推出AB:A′B′=BC:B′C′,代入有关数据,即可求出BC 的值.【详解】解:∵四边形ABCD ∽四边形A ′B ′C ′D ′,∴AB:A ′B ′=BC:B ′C ′,∵AB:A ′B ′=3:5,B ′C ′=15,∴BC =9.故选:B .25.如图,已知五边形ABCDE ∽五边形A 1B 1C 1D 1E 1,若ABA 1B 1=25,则S 五边形ABCDES五边形A 1B 1C 1D 1E 1=( )A .52B .25C .254D .425【答案】D【分析】本题主要考查了相似多边形的性质,解题的关键在于熟知相似多边形的面积之比等于相似比26.如图,在矩形ABCD中,AB=6,点EF分别在AD、BC边上,且EF⊥BC,若矩形ABFE∽矩形DEFC,且面积比为1:9,则AD长为()A.20B.18C.12D.927.如图,把一张矩形纸片ABCD沿着AD和BC边的中点连线EF对折,对折后所得的矩形正好与原来的矩形相似,则原矩形纸片长与宽的比为( )A.4:1B.2:1CD.【答案】C【分析】本题考查的是相似多边形的性质,根据对应边的比相等列出比例式,计算即可,掌握相似多28.如图,四边形ABCD和EFGH相似,则α和x的大小分别为()A.75°30B.75°33C.80°30D.80°33【考点6 黄金分割比】29.射影中有一种拍摄手法叫黄金分割构图法,其原理是:如图,将正方形ABCD的边BC取中点O,以O为圆心,线段OD为半径作圆,其与边BC的延长线交于点E,这样就把正方形ABCD延伸为黄金矩形ABEF,若CE=4,则AB=.30.若点C是线段AB的一个黄金分割点,AB=2,且AC>BC,则AC=(结果保留根号).31.黄金分割是指将整体一分为二,较大部分与整体部分的比值等于较小部分与较大部分的比值,其比值.这个比例被公认为是最能引起美感的比例,因此被称为黄金分割.如图,乐器上的一根弦长为2AB=80cm,两个端点A,B固定在乐器面板上,支撑点C是靠近点B的黄金分割点,支撑点D是靠近点A的黄金分割点,则支撑点C,D之间的距离为cm.(结果保留根号)32.宽与长的比是黄金分割数计.如图,已知四边形ABCD是黄金矩形,若长AB+1,则该矩形ABCD的面积为.(结果保留根号)33.如图是意大利著名画家达・芬奇(daVinci,1452~1519年)的名画《蒙娜丽莎》.画面中脸部被围在矩形ABCD内,图中四边形BCEF为正方形.已知点F为线段AB的黄金分割点,且AF<FB,AB=20 cm.则FB=.【考点7 由平行线判断成比例的线段】34.在△ABC中,DE∥BC,AD:DB=2:3,AE=4,则EC等于( )A.10B.8C.9D.635.如图,直线AB ∥CD ∥EF ,则( )A .AC AE =BDBF B .AC AE =BDDFC .AC CE =BDBFD .AC CE =DFBD36.如图,在△ABC 中,D 、E 分别为AB 、AC 边上的点DE ∥BC ,点F 为BC 边上一点,连接AF 交DE 于点G .则下列结论中一定正确的是( )A.ADAB =AEECB.AGGF=AEBDC.BDAD=CEAED.AGGF=ACEC37.在△ABC中,点D、E、F分别在边BC、AB、AC上,连接DE、DF,如果DE∥AC,DF∥AB,且AE:EB=1:2,那么AF:FC的值是()A.3B.13C.2D.1238.如图,l 1∥l 2∥l 3,两条直线与这三条平行线分别交于点A 、B 、C 和D 、E 、F ,已知AB BC =32,若DF =10,则DE 的长为( )A .2B .3C .5D .639.如图,直线l 1∥l 2∥l 3,直线AC 分别交l 1,l 2,l 3于点A ,B ,C ,直线DF 分别交l 1,l 2,l 3于点D ,E ,F ,AC与DF 相交于点H ,则下列式子不正确的是( )A .AB BC =DEEFB .AH CH =DHFHC.ABAC =DEDFD.ABBC=BECF40.如图,AD∥BE∥CF,直线l1,l2与这三条平行线分别交于点A,B,C和点D,E,F.下列结论:①ABAC=DEDF ;②ADBE=BECF;③ABDE=BCEF;④BCAB=EFDE.其中正确的个数为()A.1个B.2个C.3个D.4个41.如图,AD 、BC 相交于点O ,点E 、F 分别在BC 、AD 上,AB∥CD∥EF .若CE =6,EO =4,BO =5,AF =6,则AD = .【考点8 由平行截线求相关相关线段的长或比值】42.如图,AB ∥CD ∥EF ,AC =2,AE =5,BD =1.5,那么BF 的长为( )A .154B .94C .52D .7【答案】A【分析】本题考查的是平行线分线段成比例定理,灵活运用定理、找准对应关系是解题的关键.根据平行线分线段成比例定理判断即可.43.已知,如图,直线l1∥l2∥l3,AB=3cm,BC=5cm,DE=2.4cm,则DF的长()A.3cm B.8cm C.6cm D.6.4cm44.如图,直线l1、l2与这三条平行线分别交于点A、D、F和点B、C、E.若BCCE=45,AD=4.4,则DF的长为()A.4.4B.5.5C.9.9D.10.145.如图,l1∥l2∥l3,DE=3,EF=4,AB=52,则BC的长为()A.3B.72C.103D.15846.已知l1∥l2∥l3,AM=3,BM=2,BC=4,DF=15,求DM,ED,EF.。
《图形的相似》专题练习含答案解析

图形的相似1.如图,在△ABC中,AB=AC=5,BC=6,点M为BC的中点,MN⊥AC于点N,则MN 等于()A.B.C.D.2.图中的两个三角形是位似图形,它们的位似中心是()A.点P B.点O C.点M D.点N3.已知△ABC∽△DEF,相似比为3:1,且△ABC的周长为18,则△DEF的周长为()A.2 B.3 C.6 D.544.如图,△ABC中,AB>AC,D,E两点分别在边AC,AB上,且DE与BC不平行.请填上一个你认为合适的条件:,使△ADE∽△ABC.(不再添加其他的字母和线段;只填一个条件,多填不给分!)5.如图,四边形ABCD和四边形ACED都是平行四边形,点R为DE的中点,BR分别交AC、CD于点P、Q.(1)请写出图中各对相似三角形(相似比为1除外);(2)求BP:PQ:QR.6.计算:|3﹣|+()0+(cos230°)2﹣4sin60°.7.计算:﹣2sin45°+(2﹣π)0﹣.8.计算:|﹣|﹣+(π﹣4)0﹣sin30°.9.如图,小明站在A处放风筝,风筝飞到C处时的线长为20米,这时测得∠CBD=60°,若牵引底端B离地面1.5米,求此时风筝离地面高度.(计算结果精确到0.1米,≈1.732)10.在我市迎接奥运圣火的活动中,某校教学楼上悬挂着宣传条幅DC,小丽同学在点A 处,测得条幅顶端D的仰角为30°,再向条幅方向前进10米后,又在点B处测得条幅顶端D的仰角为45°,已知测点A、B和C离地面高度都为1.44米,求条幅顶端D点距离地面的高度.(计算结果精确到0.1米,参考数据:≈1.414,≈1.732.)12.阳光明媚的一天,数学兴趣小组的同学们去测量一棵树的高度(这棵树底部可以到达,顶部不易到达),他们带了以下测量工具:皮尺,标杆,一副三角尺,小平面镜.请你在他们提供的测量工具中选出所需工具,设计一种测量方案.(1)所需的测量工具是: ;(2)请在图中画出测量示意图;(3)设树高AB 的长度为x ,请用所测数据(用小写字母表示)求出x .13.我国南方部分省区发生了雪灾,造成通讯受阴.如图,现有某处山坡上一座发射塔被冰雪从C 处压折,塔尖恰好落在坡面上的点B 处,在B 处测得点C 的仰角为38°,塔基A 的俯角为21°,又测得斜坡上点A 到点B 的坡面距离AB 为15米,求折断前发射塔的高.(精确到0.1米)14.如图,在Rt △ABC 中,∠ACB=90°,AC=5,CB=12,AD 是△ABC 的角平分线,过A 、C 、D 三点的圆O 与斜边AB 交于点E ,连接DE .(1)求证:AC=AE ;(2)求AD 的长.15.如图,矩形ABCD 的长,宽分别为和1,且OB=1,点E (,2),连接AE ,ED .(1)求经过A ,E ,D 三点的抛物线的表达式;(2)若以原点为位似中心,将五边形AEDCB 放大,使放大后的五边形的边长是原五边形对应边长的3倍,请在下图网格中画出放大后的五边形A′E′D′C′B′;(3)经过A′,E′,D′三点的抛物线能否由(1)中的抛物线平移得到?请说明理由.16.某县社会主义新农村建设办公室,为了解决该县甲,乙两村和一所中学长期存在的饮水困难问题,想在这三个地方的其中一处建一所供水站,由供水站直接铺设管道到另外两处.如图,甲,乙两村坐落在夹角为30°的两条公路的AB段和CD段(村子和公路的宽均不计),点M表示这所中学.点B在点M的北偏西30°的3km处,点A在点M的正西方向,点D在点M的南偏西60°的km处.为使供水站铺设到另两处的管道长度之和最短,现有如下三种方案:方案一:供水站建在点M处,请你求出铺设到甲村某处和乙村某处的管道长度之和的最小值;方案二:供水站建在乙村(线段CD某处),甲村要求管道铺设到A处,请你在图①中,画出铺设到点A和点M处的管道长度之和最小的线路图,并求其最小值;方案三:供水站建在甲村(线段AB某处),请你在图②中,画出铺设到乙村某处和点M处的管道长度之和最小的线路图,并求其最小值.综上,你认为把供水站建在何处,所需铺设的管道最短?17.如图,在Rt△ABC中,∠C=90°,AB=50,AC=30,D,E,F分别是AC,AB,BC的中点.点P从点D出发沿折线DE﹣EF﹣FC﹣CD以每秒7个单位长的速度匀速运动;点Q从点B出发沿BA方向以每秒4个单位长的速度匀速运动,过点Q作射线QK⊥AB,交折线BC﹣CA于点G.点P,Q同时出发,当点P绕行一周回到点D时停止运动,点Q 也随之停止.设点P,Q运动的时间是t秒(t>0).(1)D,F两点间的距离是;(2)射线QK能否把四边形CDEF分成面积相等的两部分?若能,求出t的值;若不能,说明理由;(3)当点P运动到折线EF﹣FC上,且点P又恰好落在射线QK上时,求t的值;(4)连接PG,当PG∥AB时,请直接写出t的值.18.如图,E是▱ABCD的边BA延长线上一点,连接EC,交AD于点F.在不添加辅助线的情况下,请你写出图中所有的相似三角形,并任选一对相似三角形给予证明.图形的相似参考答案与试题解析1.如图,在△ABC中,AB=AC=5,BC=6,点M为BC的中点,MN⊥AC于点N,则MN 等于()A.B.C.D.【考点】勾股定理;等腰三角形的性质.【分析】连接AM,根据等腰三角形三线合一的性质得到AM⊥BC,根据勾股定理求得AM的长,再根据在直角三角形的面积公式即可求得MN的长.【解答】解:连接AM,∵AB=AC,点M为BC中点,∴AM⊥CM(三线合一),BM=CM,∵AB=AC=5,BC=6,∴BM=CM=3,在Rt△ABM中,AB=5,BM=3,∴根据勾股定理得:AM===4,=MN•AC=AM•MC,又S△AMC∴MN==.故选:C.【点评】综合运用等腰三角形的三线合一,勾股定理.特别注意结论:直角三角形斜边上的高等于两条直角边的乘积除以斜边.2.图中的两个三角形是位似图形,它们的位似中心是()A.点P B.点O C.点M D.点N【考点】位似变换.【分析】根据位似变换的定义:对应点的连线交于一点,交点就是位似中心.即位似中心一定在对应点的连线上.【解答】解:点P在对应点M和点N所在直线上,故选A.【点评】位似图形的位似中心位于对应点连线所在的直线上,点M、N为对应点,所以位似中心在M、N所在的直线上,因为点P在直线MN上,所以点P为位似中心.考查位似图形的概念.3.已知△ABC∽△DEF,相似比为3:1,且△ABC的周长为18,则△DEF的周长为()A.2 B.3 C.6 D.54【考点】相似三角形的性质.【专题】压轴题.【分析】因为△ABC∽△DEF,相似比为3:1,根据相似三角形周长比等于相似比,即可求出周长.【解答】解:∵△ABC∽△DEF,相似比为3:1∴△ABC的周长:△DEF的周长=3:1∵△ABC的周长为18∴△DEF的周长为6.故选C.【点评】本题考查对相似三角形性质的理解.(1)相似三角形周长的比等于相似比;(2)相似三角形面积的比等于相似比的平方;(3)相似三角形对应高的比、对应中线的比、对应角平分线的比都等于相似比.4.如图,△ABC中,AB>AC,D,E两点分别在边AC,AB上,且DE与BC不平行.请填上一个你认为合适的条件:∠B=∠1或,使△ADE∽△ABC.(不再添加其他的字母和线段;只填一个条件,多填不给分!)【考点】相似三角形的判定.【专题】压轴题;开放型.【分析】此题属于开放题,答案不唯一.注意此题的已知条件是:∠A=∠A,可以根据有两角对应相等的三角形相似或有两边对应成比例且夹角相等三角形相似,添加条件即可.【解答】解:此题答案不唯一,如∠C=∠2或∠B=∠1或.【点评】此题考查了相似三角形的判定:有两角对应相等的三角形相似;有两边对应成比例且夹角相等三角形相似.要注意正确找出两三角形的对应边、对应角,根据判定定理解题.5.如图,四边形ABCD和四边形ACED都是平行四边形,点R为DE的中点,BR分别交AC、CD于点P、Q.(1)请写出图中各对相似三角形(相似比为1除外);(2)求BP:PQ:QR.【考点】相似三角形的判定与性质;平行四边形的性质.【专题】几何综合题.【分析】此题的图形比较复杂,需要仔细分析图形.(1)根据平行四边形的性质,可得到角相等.∠BPC=∠BRE,∠BCP=∠E,可得△BCP ∽△BER;(2)根据AB∥CD、AC∥DE,可得出△PCQ∽△PAB,△PCQ∽△RDQ,△PAB∽△RDQ.根据相似三角形的性质,对应边成比例即可得出所求线段的比例关系.【解答】解:(1)∵四边形ACED是平行四边形,∴∠BPC=∠BRE,∠BCP=∠E,∴△BCP∽△BER;同理可得∠CDE=∠ACD,∠PQC=∠DQR,∴△PCQ∽△RDQ;∵四边形ABCD是平行四边形,∴∠BAP=∠PCQ,∵∠APB=∠CPQ,∴△PCQ∽△PAB;∵△PCQ∽△RDQ,△PCQ∽△PAB,∴△PAB∽△RDQ.(2)∵四边形ABCD和四边形ACED都是平行四边形,∴BC=AD=CE,∵AC∥DE,∴BC:CE=BP:PR,∴BP=PR,∴PC是△BER的中位线,∴BP=PR,又∵PC∥DR,∴△PCQ∽△RDQ.又∵点R是DE中点,∴DR=RE.,∴QR=2PQ.又∵BP=PR=PQ+QR=3PQ,∴BP:PQ:QR=3:1:2【点评】此题考查了相似三角形的判定和性质:①如果两个三角形的三组对应边的比相等,那么这两个三角形相似;②如果两个三角形的两条对应边的比相等,且夹角相等,那么这两个三角形相似;③如果两个三角形的两个对应角相等,那么这两个三角形相似.6.计算:|3﹣|+()0+(cos230°)2﹣4sin60°.【考点】实数的运算;零指数幂;二次根式的性质与化简;特殊角的三角函数值.【专题】计算题.【分析】根据实数的有关运算法则计算.【解答】解:原式==﹣.【点评】本题考查实数的基本运算,难度适中.7.(2012•遂宁)计算:﹣2sin45°+(2﹣π)0﹣.【考点】实数的运算;零指数幂;负整数指数幂;二次根式的性质与化简;特殊角的三角函数值.【专题】计算题;压轴题.【分析】本题涉及零指数幂、负整数指数幂、特殊角的三角函数值、二次根式化简四个考点.在计算时,需要针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.【解答】解:原式==.【点评】本题考查实数的运算能力,解决此类题目的关键是熟记特殊角的三角函数值,熟练掌握负整数指数幂、零指数幂、二次根式等考点的运算.注意:负指数为正指数的倒数;任何非0数的0次幂等于1;二次根式的化简是根号下不能含有分母和能开方的数.8.计算:|﹣|﹣+(π﹣4)0﹣sin30°.【考点】特殊角的三角函数值;绝对值;零指数幂;二次根式的性质与化简.【专题】计算题.【分析】本题涉及零指数幂、特殊角的三角函数值、二次根式化简三个考点.在计算时,需要针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.【解答】解:原式=﹣3+1﹣=﹣2.【点评】本题考查实数的运算能力,解决此类题目的关键是熟记特殊角的三角函数值,熟练掌握零指数幂、二次根式、绝对值等考点的运算.注意:任何非0数的0次幂等于1;绝对值的化简;二次根式的化简是根号下不能含有分母和能开方的数.9.如图,小明站在A处放风筝,风筝飞到C处时的线长为20米,这时测得∠CBD=60°,若牵引底端B离地面1.5米,求此时风筝离地面高度.(计算结果精确到0.1米,≈1.732)【考点】解直角三角形的应用﹣仰角俯角问题.【专题】计算题;压轴题.【分析】由题可知,在直角三角形中,知道已知角以及斜边,求对边,可以用正弦值进行解答.【解答】解:在Rt△BCD中,CD=BC×sin60°=20×=10又DE=AB=1.5,∴CE=CD+DE=CD+AB=10+1.5≈18.8答:此时风筝离地面的高度约是18.8米.【点评】本题考查直角三角形知识在解决实际问题中的应用.10.在我市迎接奥运圣火的活动中,某校教学楼上悬挂着宣传条幅DC,小丽同学在点A 处,测得条幅顶端D的仰角为30°,再向条幅方向前进10米后,又在点B处测得条幅顶端D的仰角为45°,已知测点A、B和C离地面高度都为1.44米,求条幅顶端D点距离地面的高度.(计算结果精确到0.1米,参考数据:≈1.414,≈1.732.)【考点】解直角三角形的应用﹣仰角俯角问题.【专题】应用题.【分析】首先分析图形:根据题意构造直角三角形;本题涉及到两个直角三角形Rt△BCD、Rt△ACD,应利用其公共边DC构造方程关系式,进而可解即可求出答案.【解答】解:在Rt△BCD中,tan45°==1,∴CD=BC.在Rt△ACD中,tan30°=,∴.∴.∴3CD=CD+10.∴CD=+5≈13.66(米)∴条幅顶端D点距离地面的高度为13.66+1.44=15.1(米).【点评】本题要求学生借助仰角关系构造直角三角形,并结合图形利用三角函数解直角三角形.12.阳光明媚的一天,数学兴趣小组的同学们去测量一棵树的高度(这棵树底部可以到达,顶部不易到达),他们带了以下测量工具:皮尺,标杆,一副三角尺,小平面镜.请你在他们提供的测量工具中选出所需工具,设计一种测量方案.(1)所需的测量工具是:皮尺,标杆;(2)请在图中画出测量示意图;(3)设树高AB的长度为x,请用所测数据(用小写字母表示)求出x.【考点】相似三角形的应用.【专题】方案型;开放型.【分析】树比较高不易直接到达,因而可以利用三角形相似解决,利用树在阳光下出现的影子来解决.【解答】解:(1)皮尺,标杆;(2)测量示意图如图所示;(3)如图,测得标杆DE=a,树和标杆的影长分别为AC=b,EF=c,∵△DEF∽△BAC,∴,∴,∴.【点评】本题运用相似三角形的知识测量高度及考查学生的实践操作能力,应用所学知识解决问题的能力.本题答案有多种,测量方案也有多种,如(1)皮尺、标杆、平面镜;(2)皮尺、三角尺、标杆.13.我国南方部分省区发生了雪灾,造成通讯受阴.如图,现有某处山坡上一座发射塔被冰雪从C处压折,塔尖恰好落在坡面上的点B处,在B处测得点C的仰角为38°,塔基A的俯角为21°,又测得斜坡上点A到点B的坡面距离AB为15米,求折断前发射塔的高.(精确到0.1米)【考点】解直角三角形的应用﹣仰角俯角问题.【专题】应用题.【分析】首先分析图形,据题意构造直角三角形;本题涉及到两个直角三角形,应利用其公共边构造三角关系,进而可求出答案.【解答】解:作BD⊥AC于D.在Rt△ADB中,sin∠ABD=.∴AD=AB•sin∠ABD=15×sin21°≈5.38米.(3分)∵cos∠ABD=.∴BD=AB•cos∠ABD=15×cos21°≈14.00米.(5分)在Rt△BDC中,tan∠CBD=.∴CD=BD•tan∠CBD≈14.00×tan38°≈10.94米.(8分)∵cos∠CBD=.∴BC=≈≈17.77米(10分)∴AD+CD+BC≈5.38+10.94+17.77=34.09≈34.1米(11分)答:折断前发射塔的高约为34.1米.(12分)注意:按以下方法进行近似计算视为正确,请相应评分.①若到最后再进行近似计算结果为:AD+CD+BC=34.1;②若解题过程中所有三角函数值均先精确到0.01,则近似计算的结果为:AD+CD+BC≈5.40+10.88+17.66=33.94≈33.9.【点评】本题要求学生借助仰角关系构造直角三角形,并结合图形利用三角函数解直角三角形.14.如图,在Rt△ABC中,∠ACB=90°,AC=5,CB=12,AD是△ABC的角平分线,过A、C、D三点的圆O与斜边AB交于点E,连接DE.(1)求证:AC=AE;(2)求AD的长.【考点】圆周角定理;全等三角形的判定与性质;勾股定理.【专题】计算题;压轴题.【分析】(1)由圆O的圆周角∠ACB=90°,根据90°的圆周角所对的弦为圆的直径得到AD为圆O的直径,再根据直径所对的圆周角为直角可得三角形ADE为直角三角形,又AD是△ABC的角平分线,可得一对角相等,而这对角都为圆O的圆周角,根据同圆或等圆中,相等的圆周角所对的弦相等可得CD=ED,利用HL可证明直角三角形ACD与AED 全等,根据全等三角形的对应边相等即可得证;(2)由三角形ABC为直角三角形,根据AC及CB的长,利用勾股定理求出AB的长,由第一问的结论AE=AC,用AB﹣AE可求出EB的长,再由(1)∠AED=90°,得到DE与AB垂直,可得三角形BDE为直角三角形,设DE=CD=x,用CB﹣CD表示出BD=12﹣x,利用勾股定理列出关于x的方程,求出方程的解得到x的值,即为CD的长,在直角三角形ACD中,由AC及CD的长,利用勾股定理即可求出AD的长.【解答】解:(1)∵∠ACB=90°,且∠ACB为圆O的圆周角(已知),∴AD为圆O的直径(90°的圆周角所对的弦为圆的直径),∴∠AED=90°(直径所对的圆周角为直角),又AD是△ABC的∠BAC的平分线(已知),∴∠CAD=∠EAD(角平分线定义),∴CD=DE(在同圆或等圆中,相等的圆周角所对的弦相等),在Rt△ACD和Rt△AED中,,∴Rt△ACD≌Rt△AED(HL),∴AC=AE(全等三角形的对应边相等);(2)∵△ABC为直角三角形,且AC=5,CB=12,∴根据勾股定理得:AB==13,由(1)得到∠AED=90°,则有∠BED=90°,设CD=DE=x,则DB=BC﹣CD=12﹣x,EB=AB﹣AE=AB﹣AC=13﹣5=8,在Rt△BED中,根据勾股定理得:BD2=BE2+ED2,即(12﹣x)2=x2+82,解得:x=,∴CD=,又AC=5,△ACD为直角三角形,∴根据勾股定理得:AD==.【点评】此题考查了圆周角定理,勾股定理,以及全等三角形的判定与性质,利用了转化的思想,本题的思路为:根据圆周角定理得出直角,利用勾股定理构造方程来求解,从而得到解决问题的目的.灵活运用圆周角定理及勾股定理是解本题的关键.15.如图,矩形ABCD的长,宽分别为和1,且OB=1,点E(,2),连接AE,ED.(1)求经过A,E,D三点的抛物线的表达式;(2)若以原点为位似中心,将五边形AEDCB放大,使放大后的五边形的边长是原五边形对应边长的3倍,请在下图网格中画出放大后的五边形A′E′D′C′B′;(3)经过A′,E′,D′三点的抛物线能否由(1)中的抛物线平移得到?请说明理由.【考点】作图﹣位似变换;二次函数图象与几何变换;待定系数法求二次函数解析式;矩形的性质.【专题】压轴题;网格型.【分析】(1)A,E,D三点坐标已知,可用一般式来求解;(2)延长OA到A′,使OA′=3OA,同理可得到其余各点;(3)根据二次项系数是否相同即可判断两个函数是否由平移得到.【解答】解:(1)设经过A,E,D三点的抛物线的表达式为y=ax2+bx+c∵A(1,),E(,2),D(2,)(1分)∴,解之,得∴过A,E,D三点的抛物线的表达式为y=﹣2x2+6x﹣.(4分)(2)如图.(7分)(3)不能,理由如下:(8分)设经过A′,E′,D′三点的抛物线的表达式为y=a′x2+b′x+c′∵A′(3,),E′(,6),D′(6,)∴,解之,得a=﹣2,,∴a≠a′∴经过A′,E′,D′三点的抛物线不能由(1)中的抛物线平移得到.(8分)【点评】一般用待定系数法来求函数解析式;位似变化的方法应熟练掌握;抛物线平移不改变a的值.16.某县社会主义新农村建设办公室,为了解决该县甲,乙两村和一所中学长期存在的饮水困难问题,想在这三个地方的其中一处建一所供水站,由供水站直接铺设管道到另外两处.如图,甲,乙两村坐落在夹角为30°的两条公路的AB段和CD段(村子和公路的宽均不计),点M表示这所中学.点B在点M的北偏西30°的3km处,点A在点M的正西方向,点D在点M的南偏西60°的km处.为使供水站铺设到另两处的管道长度之和最短,现有如下三种方案:方案一:供水站建在点M处,请你求出铺设到甲村某处和乙村某处的管道长度之和的最小值;方案二:供水站建在乙村(线段CD某处),甲村要求管道铺设到A处,请你在图①中,画出铺设到点A和点M处的管道长度之和最小的线路图,并求其最小值;方案三:供水站建在甲村(线段AB某处),请你在图②中,画出铺设到乙村某处和点M处的管道长度之和最小的线路图,并求其最小值.综上,你认为把供水站建在何处,所需铺设的管道最短?【考点】作图—应用与设计作图.【专题】压轴题;方案型.【分析】(1)由题意可得,供水站建在点M处,根据垂线段最短、两点之间线段最短,可知铺设到甲村某处和乙村某处的管道长度之和的最小值为MB+MD,求值即可;(2)作点M关于射线OE的对称点M',则MM'=2ME,连接AM'交OE于点P,且证明P点与D点重合,即AM'过D点.求出AM'的值即是铺设到点A和点M处的管道长度之和最小的值;(3)作点M关于射线OF的对称点M',作M'N⊥OE于N点,交OF于点G,交AM于点H,连接GM,则GM=GM',可证得N,D两点重合,即M'N过D点.求GM+GD=M'D 的值就是最小值.【解答】解:方案一:由题意可得:∵A在M的正西方向,∴AM∥OE,∠BAM=∠BOE=30°,又∵∠BMA=60°∴MB⊥OB,∴点M到甲村的最短距离为MB,(1分)∵点M到乙村的最短距离为MD,∴将供水站建在点M处时,管道沿MD,MB线路铺设的长度之和最小,即最小值为MB+MD=3+(km);(3分)方案二:如图①,作点M关于射线OE的对称点M',则MM'=2ME,连接AM'交OE于点P,PE∥AM,PE=AM,∵AM=2BM=6,∴PE=3,(4分)在Rt△DME中,∵DE=DM•sin60°=×=3,ME=DM=×,∴PE=DE,∴P点与D点重合,即AM'过D点,(6分)在线段CD上任取一点P',连接P'A,P′M,P'M',则P'M=P′M',∵AP'+P'M'>AM',∴把供水站建在乙村的D点处,管道沿DA,DM线路铺设的长度之和最小,即最小值为AD+DM=AM'=;(7分)方案三:作点M关于射线OF的对称点M',作M'N⊥OE于N点,交OF于点G,交AM 于点H,连接GM,则GM=GM',∴M'N为点M'到OE的最短距离,即M'N=GM+GN在Rt△M'HM中,∠MM'N=30°,MM'=6,∴MH=3,∴NE=MH=3,∵DE=3,∴N,D两点重合,即M'N过D点,在Rt△M'DM中,DM=,∴M'D=(10分)在线段AB上任取一点G',过G'作G'N'⊥OE于N'点,连接G'M',G'M,显然G'M+G'N'=G'M'+G'N'>M'D,∴把供水站建在甲村的G处,管道沿GM,GD线路铺设的长度之和最小,即最小值为GM+GD=M'D=,(11分)综上,∵3+<,∴供水站建在M处,所需铺设的管道长度最短.(12分)【点评】此题主要考查线路最短问题的作图和求值问题,有一定的难度.17.如图,在Rt△ABC中,∠C=90°,AB=50,AC=30,D,E,F分别是AC,AB,BC的中点.点P从点D出发沿折线DE﹣EF﹣FC﹣CD以每秒7个单位长的速度匀速运动;点Q从点B出发沿BA方向以每秒4个单位长的速度匀速运动,过点Q作射线QK⊥AB,交折线BC﹣CA于点G.点P,Q同时出发,当点P绕行一周回到点D时停止运动,点Q 也随之停止.设点P,Q运动的时间是t秒(t>0).(1)D,F两点间的距离是25;(2)射线QK能否把四边形CDEF分成面积相等的两部分?若能,求出t的值;若不能,说明理由;(3)当点P运动到折线EF﹣FC上,且点P又恰好落在射线QK上时,求t的值;(4)连接PG,当PG∥AB时,请直接写出t的值.【考点】相似三角形的判定与性质;三角形中位线定理;矩形的判定与性质.【专题】压轴题.【分析】(1)由中位线定理即可求出DF的长;(2)连接DF,过点F作FH⊥AB于点H,由四边形CDEF为矩形,QK把矩形CDEF分为面积相等的两部分,根据△HBF∽△CBA,对应边的比相等,就可以求得t的值;(3)①当点P在EF上(2≤t≤5时根据△PQE∽△BCA,根据相似三角形的对应边的比相等,可以求出t的值;②当点P在FC上(5≤t≤7)时,PB=PF+BF就可以得到;(4)当PG∥AB时四边形PHQG是矩形,由此可以直接写出t.【解答】解:(1)Rt△ABC中,∠C=90°,AB=50,∵D,F是AC,BC的中点,∴DF为△ABC的中位线,∴DF=AB=25故答案为:25.(2)能.如图1,连接DF,过点F作FH⊥AB于点H,∵D,F是AC,BC的中点,∴DE∥BC,EF∥AC,四边形CDEF为矩形,∴QK过DF的中点O时,即过矩形CDEF的中点,QK把矩形CDEF分为面积相等的两部分此时QH=OF=12.5.由BF=20,△HBF∽△CBA,得HB=16.故t==.(3)①当点P在EF上(2≤t≤5)时,如图2,QB=4t,DE+EP=7t,由△PQE∽△BCA,得.∴t=4;②当点P在FC上(5≤t≤7)时,如图3,已知QB=4t,从而PB===5t,由PF=7t﹣35,BF=20,得5t=7t﹣35+20.解得t=7;(4)如图4,t=1;如图5,t=7.(注:判断PG∥AB可分为以下几种情形:当0<t≤2时,点P下行,点G上行,可知其中存在PG∥AB的时刻,如图4;此后,点G继续上行到点F时,t=4,而点P却在下行到点E再沿EF上行,发现点P在EF上运动时不存在PG∥AB;5≤t≤7当时,点P,G均在FC上,也不存在PG∥AB;由于点P比点G先到达点C并继续沿CD下行,所以在7<t<8中存在PG ∥AB的时刻,如图5当8≤t≤10时,点P,G均在CD上,不存在PG∥AB)【点评】本题主要运用了相似三角形性质,对应边的比相等,正确找出题目中的相似三角形是解题的关键.18.如图,E是▱ABCD的边BA延长线上一点,连接EC,交AD于点F.在不添加辅助线的情况下,请你写出图中所有的相似三角形,并任选一对相似三角形给予证明.【考点】相似三角形的判定;平行四边形的性质.【专题】压轴题;开放型.【分析】根据平行线的性质和两角对应相等的两个三角形相似这一判定定理可证明图中相似三角形有:△AEF∽△BEC;△AEF∽△DCF;△BEC∽△DCF.【解答】解:相似三角形有△AEF∽△BEC;△AEF∽△DCF;△BEC∽△DCF.(3分)如:△AEF∽△BEC.在▱ABCD中,AD∥BC,∴∠1=∠B,∠2=∠3.(6分)∴△AEF∽△BEC.(7分)【点评】考查了平行线的性质及相似三角形的判定定理.。
人教版数学九年级下册 27.1 ---27.3随堂练(含答案)

A B
C
二、填空题
6 / 36
9. (2020·盐城) 如图, BC / /DE, 且 BC DE, AD BC 4, AB DE 10 ,则 AE 的值 AC
为 .
10. (2020·吉林)如图, AB // CD // EF .若 AC 1 , BD 5 ,则 DF ______. CE 2
人教版数学九年级下册 27.1《图形的相似》
一、选择题 1.下图是大众汽车的标志示意图,下面的图形中与其相似的是( )
2.下列各组图形中,两个图形形状不一定相同的是( ) A.两个等边三角形 B.有一个角是 35°的两个等腰三角形 C.两个正方形 D.两个圆
3.一个多边形的边长为 2,3,4,5,6,另一个和它相似的多边形的最长边为 24,则这个多边形的 最短边为( )
A.6
B.8
C.10
D.12
4.要制作两个形状相同的三角形框架,其中一个三角形的三边长分别为 5 cm,6 cm 和 9 cm,另 一个三角形的最短边长为 2.5 cm,则它的最长边为( )
A.3 cm
B.4 cm
C.4.5 cm D.5 cm
5.小张用手机拍摄得到图(1),经放大后得到图(2),图(1)中的线段 AB 在图(2)中的对应线段是 ()
(1)如果四周的小路的宽均相等,都是 x,如图 1,那么小路四周所围成的矩形 A′B′C′D ′和矩形 ABCD 相似吗?请说明理由;
(2)如果相对着的两条小路的宽均相等,宽度分别为 x,y,如图 2,试问小路的宽 x 与 y 的 比值为多少时,能使得小路四周所围成的矩形 A′B′C′D′和矩形 ABCD 相似?请说明理由.
2023年人教版九年级数学下册第27章《相似》复习检测卷(一)附答案解析

2023年九年级数学下册第27章《相似》复习检测卷(一)考试范围:§27.1图形的相似~27.2相似三角形的判定满分:120分一、选择题(每小题3分,共30分)1.将△ABC 的每条边都扩大3倍得到△DEF ,其中点A 、B 、C 的对应点分别是D 、E 、F ,则∠D 与∠A 的关系为()A .∠D =∠AB .∠D =3∠AC .∠D =6∠AD .∠D =9∠A2.如图,在△ABC 中,∠A =78°,AB =4,AC =6,将△ABC 沿图中的虚线剪开,剪下的阴影三角形与原三角形不相似的是()3.如图,已知直线a ∥b ∥c ,直线m 、n 与a 、b 、c 分别交于点A 、C 、E ,B 、D 、F ,AC =8,CE =12,BD =6,则DF 的长为()A .4B .5C .9D .74.如图,在△ABC 中,D 、E 分别为AB 、AC 边上的点,DE ∥BC ,F 为BC 边上一点,连接AF交DE 于点G ,则下列结论中一定正确的是()A .AD AEAB CE=B .AC AEGF BD=C .BD CEAD AE=D .AG ACAF CE=5.如图,在正方形网格上有两个三角形,且△ABC 和△DEF 相似,则∠BAC 的度数为()A .135°B .125°C .115°D .105°6.如图,△ACP ∽△ABC ,若∠A =100°,∠ACP =20°,则∠ACB 的度数是()A .80°B .60°C .50°D .30°7.如图,在□ABCD 中,EF ∥AB ,DE ∶EA =2∶3,EF =4,则CD 的长为()A .6B .8C .9D .108.要制作两个形状相同的三角形框架,其中一个三角形的三边长分别为5cm 、6cm 和9cm ,另一个三角形的最短边长为2.5cm ,则它的最长边为()A .3cmB .4cmC .4.5cmD .5cm9.如图,在矩形ABCD 中,AB =a ,AD =3,按照图中的方式将它分成完全相同的三个矩形,如果每一个小矩形都与矩形ABCD 相似,则a 的值为()第5题第3题第4题第6题第7题第9题第10题A .22B .23C .33D .3210.如图,正方形ABCD 的边长为4,E 是BC 边上一点,过点E 作EF ⊥AE 交CD 边于点F ,则CF 的最大值是()A .0.5B .1C .1.5D .2二、填空题(每小题3分,共18分)11.如图,添加一个条件__________________,使△ADE ∽△ACB .12.如图,在□ABCD 中,E 是AD 的中点,EC 交对角线BD 于点F ,则BF ∶FD 的值为_________.13.如图,在△ABC 中,DE ∥BC ,若AD =1,BD =3,BC =8,则DE 的长为________.14.已知654a b c==,且a +b -2c =6,则a 的值为_______.15.如图,在Rt △OAC 中,O 为坐标原点,直角顶点C 在x 轴的正半轴上,反比例函数ky x=(k >0)在第一象限的图象经过OA 的中点B ,交AC 于点D ,连接OD ,若△OCD ∽△ACO ,则直线OA 的解析式为_______.16.如图,直线l 1∥l 2∥l 3,直线l 1与l 2之间的距离为2,直线l 2与l 3之间的距离为1,等边△ABC 的三个顶点分别在直线l 1、l 2、l 3上,则等边三角形的边长是______.三、解答题(共8题,共72分)17.(8分)如图,四边形ABCD ∽四边形A 'B 'C 'D ',∠BCD =125°,分别求x 、y 、α的值.18.(8分)如图,在矩形ABCD 中,点E 、F 分别在BC 、CD 上,AE ⊥BF 于点M ,若BC =2AB ,探究AE 与BF 的数量关系,并证明你的结论.第10题第11题第16题第12题第13题第15题19.(8分)如图,在四边形ABCD中,AC平分∠BAD,∠ADC=∠ACB=90°.(1)求证:AC2=AB·AD;(2)若BC=3,AB=5,求CD的长.20.(8分)如图,在矩形ABCD中,E是AD上一点,连接BE.(1)请用尺规在BE上求作一点P,使得△PCB∽△ABE(不写作法,保留作图痕迹);(2)若AE=3,AB=4,BC=6,求EP的长.21.(8分)如图,在△ABC中,AB=2,BC=4,D为BC边上一点,BD=1.(1)求证:△ABD∽△CBA;(2)作DE∥AB交AC于点E,请直接写出另一个与△ABD相似的三角形,并求出DE的长.22.(10分)在△ABC中,AB=6,AC=8,点D、E分别在AB、AC上,连接DE,设BD=x(0<x<6),CE=y(0<y<8).(1)当x=2,y=5时,求证:△AED∽△ABC;(2)若△ADE和△ABC相似,求y与x的函数表达式.23.(10分)如图,在△ABC中,∠ABC=90°,D是斜边AC的中点,连接DB.过点A作AE⊥BD于点F,交BC于点E.(1)求证:EB2=EF・EA;(2)若AB=4,CE=3BE,求AE的长.24.(12分)(1)【问题背景】如图1,D是等边△ABC中AB边上的点,以CD为边在CD的上方作等边△CDE,连接AE,求证:BD=AE;(2)【尝试应用】如图2,D是Rt△ABC中AB边上的一点,∠B=90°,∠BAC=30°,以CD为边在CD的上方作Rt△CDE,使∠CDE=90°,∠CED=30°,连接AE,请探究BD与AE的数量关系,并说明理由;(3)【拓展创新】如图3,在Rt△ABC中,∠ABC=90°,点D在AB边上,以CD为边在CD的上方作Rt△CDE,使∠CDE=90°,43DE ABCD BC==,DE交AC于F,若AD=3BD,求AFDF的值.《相似》阶段检测卷(一)考试范围:§27.1图形的相似~27.2相似三角形的判定满分:120分一、选择题(每小题3分,共30分)1.将△ABC 的每条边都扩大3倍得到△DEF ,其中点A 、B 、C 的对应点分别是D 、E 、F ,则∠D 与∠A 的关系为()A .∠D =∠AB .∠D =3∠AC .∠D =6∠A D .∠D =9∠A【答案】A .详解:依题意,△ABC 与△DEF 的三边成比例,∴△ABC ∽△DEF ,∴∠A =∠D ,故选A .2.如图,在△ABC 中,∠A =78°,AB =4,AC =6,将△ABC 沿图中的虚线剪开,剪下的阴影三角形与原三角形不相似的是()【答案】C .详解:由两个角分别相等的两个三角形相似,知选项A 和B 中的阴影三角形与原三角形相似,选项D 中,阴影三角形的∠A 的两边分别为4-1=3,6-4=2,∵4623=,∠A =∠A ,∴选项D 中的阴影三角形与原三角形相似.而选项C 中,不能保证∠B 的两边成比例,故选C .3.如图,已知直线a ∥b ∥c ,直线m 、n 与a 、b 、c 分别交于点A 、C 、E ,B 、D 、F ,AC =8,CE =12,BD =6,则DF 的长为()A .4B .5C .9D .7【答案】C .详解:∵a ∥b ∥c ,∴AC BD CE DF =,即8612DF=,解得DF =9,故选C . 4.如图,在△ABC 中,D 、E 分别为AB 、AC 边上的点,DE ∥BC ,F 为BC 边上一点,连接AF 交DE 于点G ,则下列结论中一定正确的是()A .AD AEAB CE=B .AC AEGF BD=C .BD CEAD AE=D .AG ACAF CE=【答案】C .详解:∵DE ∥BC ,∴BD CE AD AE =,故C 对;AD AEAB AC=,故A 错;AG AE ADAF AC AB==,故D 错;选项B 中的4条线段不成比例,故D 错.故选C .5.如图,在正方形网格上有两个三角形,且△ABC 和△DEF 相似,则∠BAC 的度数为()A .135°B .125°C .115°D .105°【答案】A .详解:∵△ABC 和△DEF 相似,观察角的大小,∠BAC =∠DEF =90°+45°=135°,故选A . 6.如图,△ACP ∽△ABC ,若∠A =100°,∠ACP =20°,则∠ACB 的度数是()A .80°B .60°C .50°D .30°【答案】B .详解:在△ACP 中,∵∠A =100°,∠ACP =20°,∴∠APC =60°.∵△ACP ∽△ABC ,∴∠ACB =∠APC =60°,故选B .7.如图,在□ABCD 中,EF ∥AB ,DE ∶EA =2∶3,EF =4,则CD 的长为()A .6B .8C .9D .10【答案】D .详解:∵EF ∥AB ,∴EF DEAB DA=,∵DE ∶EA =2∶3,EF =4,∴4223AB =+,∴AB =10,则CD =AB =10,故选D .8.要制作两个形状相同的三角形框架,其中一个三角形的三边长分别为5cm 、6cm 和9cm ,另一个三角形的最短边长为2.5cm ,则它的最长边为()A .3cmB .4cmC .4.5cmD .5cm【答案】C .详解:设所求的最长边为xcm ,则592.5x=,解得x =4.5,故选C .9.如图,在矩形ABCD 中,AB =a ,AD =3,按照图中的方式将它分成完全相同的三个矩形,如果每一个小矩形都与矩形ABCD 相似,则a 的值为()A .B .C .D .【答案】C .详解:小矩形的边边分别为13a 和3,∵小矩形与矩形ABCD 相似,∴13a ∶3=3∶a ,解得a =±(舍去负值),∴a =C .10.如图,正方形ABCD 的边长为4,E 是BC 边上一点,过点E 作EF ⊥AE交CD 边于点F ,则CF 的最大值是()A .0.5B .1C .1.5D .2【答案】B .详解:∵∠B =∠C =90°,AE ⊥EF ,可证△ABE ∽△ECF ,∴AB BECE CF=,设BE =x ,则CE =4-x ,∴44x x CF =-,∴CF =14x (4-x )=-14(x -2)2+1,当x =2时,CF 取得最大值1,故选B .二、填空题(每小题3分,共18分)11.如图,添加一个条件__________________,使△ADE ∽△ACB .【答案】答案不唯一,可以填下列中的一个:∠ADE =∠C ,∠AED =∠B ,AD AEAC AB=.12.如图,在□ABCD 中,E 是AD 的中点,EC 交对角线BD 于点F ,则BF ∶FD的值为_________.【答案】2.详解:∵四边形ABCD 为平行四边形,∴BC =AD ,BC ∥AD .∵E 为AD 的中点,∴BC =AD =2DE ,由AD ∥BC ,得△BCF ∽DEF ,∴BF ∶FD =BC ∶DE =2.13.如图,在△ABC 中,DE ∥BC ,若AD =1,BD =3,BC =8,则DE 的长为________.【答案】2.详解:∵DE ∥BC ,∴AD DE AB BC =,即1138DE=+,∴DE =2.14.已知654a b c==,且a +b -2c =6,则a 的值为_______.【答案】12.详解:∵654a b c==,故可设a =6x ,b =5x ,c =4x ,代入a +b -2c =6,得:6x +5x -2(4x )=6,解得x =2,∴a =6x =12.15.如图,在Rt △OAC 中,O 为坐标原点,直角顶点C 在x 轴的正半轴上,反比例函数ky x=(k >0)在第一象限的图象经过OA 的中点B ,交AC 于点D ,连接OD ,若△OCD ∽△ACO ,则直线OA 的解析式为_______.【答案】y =2x .详解:设B (t ,k t ),则直线OA 的解析式为y =2ktx .∵B 为OA 的中点,∴A (2t ,2k t ),∴D (2t ,2k t ),OC =2t ,CD =2k t ,CA =2kt.∵△OCD ∽△ACO ,∴OC CD AC OC =,∴OC 2=AC ·CD ,∴4t 2=2k t ·2k t,∴k 2=4t 4,∵k >0,∴k =2t 2,∴直线OA 的解析式为y =2x .16.如图,直线l 1∥l 2∥l 3,直线l 1与l 2之间的距离为2,直线l 2与l 3之间的距离为1,等边△ABC 的三个顶点分别在直线l 1、l 2、l 3上,则等边三角形的边长是______.【答案】2213.F详解:过C 作CE ⊥AC 交AB 的延长线于D ,过C 作CF ⊥l 1于F ,交l 3于H ,过E 作ED ⊥FC 交延长线于D ,∵∠AFC =∠ACE=∠CDE =90°,∴△ACF ∽△CED ,∴DE CD CECF AF AC==,∵△ABC 为等边△,∴CE ,AB =BC =BE ,则CD AF .依题意,FH =FC +CH =2+1=3,由AB =BE ,l 1∥l 3∥ED ,得DH =FH =3,CD =4,∴AF CD AC .三、解答题(共8题,共72分)17.(8分)如图,四边形ABCD ∽四边形A 'B 'C 'D ',∠BCD =125°,分别求x 、y 、α的值.【答案】∵四边形ABCD ∽四边形A 'B 'C 'D ',∴∠C ′=∠C =125°,∴∠α=360°-80°-75°-125°=80°,且AD AB BC A D A B B C =='''''',即45316x y==,解得x =20,y =12.答:x =20,y =12,α=80°.18.(8分)如图,在矩形ABCD 中,点E 、F 分别在BC 、CD 上,AE ⊥BF 于点M ,若BC ,探究AE 与BF 的数量关系,并证明你的结论.【答案】BF AE ,理由如下:∵四边形ABCD 是矩形,∴∠ABC =∠C ,∵AE ⊥BF ,∴∠AMB =∠BAM +∠ABM =90°,又∵∠ABM +∠CBF =90°,∴∠BAM =∠CBF ,∴△ABE ∽△BCF ,∴AE AB BF BC ==,∴BF AE .19.(8分)如图,在四边形ABCD 中,AC 平分∠BAD ,∠ADC =∠ACB =90°.(1)求证:AC 2=AB ·AD ;(2)若BC =3,AB =5,求CD 的长.【答案】(1)∵AC 平分∠BAD ,∴∠DAC =∠CAB .∵∠ADC =∠ACB =90°,∴△ADC ∽△ACB ,∴AD ACAC AB=,∴AC 2=AB ·AD .(2)在Rt △ABC 中,∵BC =3,AB =5,由勾股定理,得AC =4.∵AC 2=AB ·AD ,∴42=5AD ,∴AD =165.在Rt △ADC 中,CD 125.20.(8分)如图,在矩形ABCD 中,E 是AD 上一点,连接BE .(1)请用尺规在BE 上求作一点P ,使得△PCB ∽△ABE(不写作法,保留作图痕迹);(2)若AE =3,AB =4,BC =6,求EP 的长.【答案】(1)如图所示;(2)由勾股定理,得BE 5,由△PCB ∽△ABE ,得BP BC AE BE =,即635BP =,∴BP =185,∴EP =BE -BP =5-185=75.21.(8分)如图,在△ABC 中,AB =2,BC =4,D 为BC 边上一点,BD =1.(1)求证:△ABD ∽△CBA ;(2)作DE ∥AB 交AC 于点E ,请直接写出另一个与△ABD 相似的三角形,并求出DE 的长.【答案】(1)∵AB =2,BC =4,BD =1,∴AB BDBC AB=,又∠ABD =∠CBA ,∴△ABD ∽△CBA .(2)如图,∵DE ∥AB ,∴△CDE ∽△CBA ,∵△ABD ∽△CBA ,∴△CDE ∽△ABD ,∴DE CD BD AB =,即4112DE -=,∴DE =1.5.22.(10分)在△ABC 中,AB =6,AC =8,点D 、E 分别在AB 、AC 上,连接DE ,设BD =x (0<x <6),CE =y (0<y <8).(1)当x =2,y =5时,求证:△AED ∽△ABC ;(2)若△ADE 和△ABC 相似,求y 与x 的函数表达式.【答案】(1)∵AB =6,BD =x =2,∴AD =4.∵AC =8,CE =y =5,∴AE =3.∴AD AEAC AB=.又∵∠EAD =∠BAC ,∴△AED ∽△ABC .(2)分两种情况,1°当△ADE ∽△ABC 时,AD AE AB AC =,则6868x y --=,∴y =43x (0<x <6).2°当△ADE ∽△ACB 时,AD AE AC AB =,则6886x y --=,∴y =34x +72(0<x <6).23.(10分)如图,在△ABC 中,∠ABC =90°,D 是斜边AC 的中点,连接DB .过点A 作AE ⊥BD 于点F ,交BC 于点E .(1)求证:EB 2=EF ・EA ;(2)若AB =4,CE =3BE ,求AE 的长.【答案】(1)∵AE ⊥BD ,∴∠BFE =90°=∠ABC .又∵∠BEF =∠AEB ,∴△EBF ∽△EAB ,∴BE EFAE BE=,∴EB 2=EF ・EA .(2)在Rt △ABC 中,∵D 为斜边AC 的中点,∴BD =CD ,∴∠DBC =∠C .由(1),得△EBF∽△EAB,∴∠EBF=∠EAB,∴∠C=∠EAB.又∠ABE=∠CBA,∴△BAE∽△BCA,∴AB BEBC AB=,∴AB2=BE·BC.∵AB=4,CE=3BE,∴BC=4BE,42=BE(4BE),∴BE=2.∴AE=.24.(12分)(1)【问题背景】如图1,D是等边△ABC中AB边上的点,以CD为边在CD的上方作等边△CDE,连接AE,求证:BD=AE;(2)【尝试应用】如图2,D是Rt△ABC中AB边上的一点,∠B=90°,∠BAC=30°,以CD为边在CD的上方作Rt△CDE,使∠CDE=90°,∠CED=30°,连接AE,请探究BD与AE的数量关系,并说明理由;(3)【拓展创新】如图3,在Rt△ABC中,∠ABC=90°,点D在AB边上,以CD为边在CD的上方作Rt△CDE,使∠CDE=90°,43DE ABCD BC==,DE交AC于F,若AD=3BD,求AFDF的值.【答案】(1)∵△ABC与△CDE均为等边三角形,∴BC=AC,CD=CE,∠ACB=∠DCE=60°,∴∠BCD=∠ACE,∴△BCD≌△ACE,∴BD=AE.(2)AE=2BD,理由如下:∵∠BAC=∠DEC=30°,∠B=∠EDC=90°,∴△ABC∽△EDC,∴BC AC CD CE=.由条件得∠ACB=∠DCE,AC=2BC,∴∠BCD=∠ACE,∴△BCD∽△ACE,∴12BD BCAE AC==,∴AE=2BD.(3)由(2)得,△BCD∽△ACE,∴AE ACBD BC=,∵43DE ABCD BC==,∴53ACBC=,∴53AE ACBD BC==设BD=a,则AD=3BD=3a,AB=4a,BC=3a,CDa,AE=53BD=53a.∵△AFE∽△DFC ,∴53aAF AEDF CD=.。
人教版九年级下《27.1图形的相似》课时练习含答案解析

人教版数学九年级下册27.1图形的相似课时练习一、单选题(共15题)1.已知2x =5y (y≠0),则下列比例式成立的是( ) A.25x y = B.52x y= C.25x y = D.52x y =答案:B知识点:比例的性质 解析:解答:∵2x=5y ,知识点: 比例的性质 解析:解答: 由3a =2b ,得出23a b =于是可设a =2k ,则b =3k ,代入a b a-=232k kk -=12- 故选:A .分析: 本题考查了比例的基本性质,是基础题3. 不为0的四个实数a 、b ,c 、d 满足ab=cd ,改写成比例式错误的是( )A . a dc b = B . c b ad =C .d b a c =D .a c b d=答案:D知识点: 比例的性质. 解析:解答: A 、a dc b=ab cd ⇒=故A 正确B、c ba d=ab cd⇒=故B正确C、d ba c=ab cd⇒=故C正确D、a cb d=ad bc⇒=故D错误故选:D.分析: 本题考查了比例的性质,利用了比例的性质:分子分母交叉相乘,乘积相等.4. 如果a=3,b=2,且b是a和c的比例中项,那么c=()A.23±B.23C.43D.43±答案:C知识点: 比例线段解析:解答: 根据题意,可知a:b=b:c,b2=ac,当a=3,b=2时22=3c,3c=4,c=4 3故选:C.分析: 比例中项,也叫“等比中项”,即如果a、b、c三个量成连比例,即a:b=b:c,则b叫做a和c的比例中项.据此代数计算得解.5. 比例尺为1:1000的图纸上某区域面积400cm2,则实际面积为()A.4×105m2 B.4×104m2 C.1.6×105m2D.2×104 m2答案:B知识点:比例线段解析:解答: 设实际面积为x cm2,则400:x=(1:1000)2,解得x=4×108.4×108cm2=4×104m2.故选B.分析: 根据面积比是比例尺的平方比,列比例式求得该区域的实际面积.6、如图,画线段AB的垂直平分线交AB于点O,在这条垂直平分线上截取OC=OA,以A为圆心,AC为半径画弧于AB与点P,则线段AP与AB的比是()A.2B.C.D2答案:D知识点:比例线段.解析:解答: 连接AC,设AO=x,则BO=x,CO=x,故x,x∴线段AP与AB:22故选:D.分析: 利用已知表示出AC的长,即可得出AP以及AB的长,即可得出答案.7. 下列各组中得四条线段成比例的是()A.4cm、2cm、1cm、3cm B.1cm、2cm、3cm、5cmC.3cm、4cm、5cm、6cm D.1cm、2cm、2cm、4cm答案:D知识点:比例线段.解析:解答:A、从小到大排列,由于1×4≠2×3,所以不成比例,不符合题意;B、从小到大排列,由于1×5≠2×3,所以不成比例,不符合题意;C、从小到大排列,由于3×6≠4×5,所以不成比例,不符合题意;D、从小到大排列,由于1×4=2×2,所以成比例,符合题意.故选D.分析: 四条线段成比例,根据线段的长短关系,从小到大排列,判断中间两项的积是否等于两边两项的积,相等即成比例.8. 已知C 是线段AB 的黄金分割点(AC >BC ),则AC :AB=( )A .1):2B .1):2C .(3:2-D .(3:2+ 答案:A知识点: 黄金分割.解析:解答: 根据黄金分割的定义,知AC :AB=1):2故选A .分析: 此题主要考查了黄金分割比的概念.9. 若P 是线段AB 的黄金分割点(PA >PB ),设AB=1,则PA 的长约为( ) A .0.191 B .0.382 C .0.5 D .0.618 答案:D知识点: 黄金分割.解析:解答: 由于P 为线段AB=1的黄金分割点, 且PA >PB ,则PA=0.618×1=0.618. 故选D .分析: 根据黄金分割点的定义,知PA 是较长线段;则PA=0.618AB ,代入数据即可. 10. 主持人站在舞台的黄金分割点处最自然得体,如果舞台AB 长为20米,一个主持人现站在舞台AB 的黄金分割点点C 处,则下列结论一定正确的是( ) ∴AB :AC=AC :BC ; ∴AC≈6.18米;∴AC =1)米;∴BC =米或米. A .∴∴∴∴ B .∴∴∴ C .∴∴ D .∴ 答案:D知识点: 黄金分割.解析:解答: AB 的黄金分割点为点C 处,若AC >BC ,则AB :AC=AC :BC ,所以∴不一定正确;AC≈0.618AB≈12.36或AC≈20-12.36=7.64,所以②错误;若AC 为较长线段时,AC=12AB=10),BC=10(BC 为较长线段时,BC=12AB=10-1),AC=10(),所以③不一定正确,④正确. 故选D .分析:根据黄金分割的定义和AC 为较长线段或较短线段进行判断.11. 等腰∴ABC 中,AB=AC ,∴A=36°,D 是AC 上的一点,AD=BD ,则以下结论中正确的有( )∴∴BCD 是等腰三角形;∴点D 是线段AC 的黄金分割点;∴∴BCD∴∴ABC ;∴BD 平分∴ABC .A .1个B .2个C .3个D .4个 答案:D知识点: 黄金分割;等腰三角形的性质;相似三角形的判定与性质. 解析:解答: ∴AB=AC , ∴∴ABC=∴C=12(180°-∴A )=12(180°-36°)=72°, ∴AD=BD , ∴∴DBA=∴A=36°, ∴∴BDC=2∴A=72°, ∴∴BDC=∴C ,∴∴BCD 为等腰三角形,所以∴正确; ∴∴DBC=∴ABC-∴ABD=36°, ∴∴ABD=∴DBC ,∴BD 平分∴ABC ,所以∴正确; ∴∴DBC=∴A ,∴BCD=∴ACB , ∴∴BCD∴∴ABC ,所以∴正确; ∴BD :AC=CD :BD , 而AD=BD ,∴AD:AC=CD:AD,∴点D是线段AC的黄金分割点,所以∴正确.分析: 先根据等腰三角形的性质和三角形内角和定理计算出∴ABC=∴C=1 2(180°-∴A)=72°,再计算出∴BDC=72°,∴DBC=36°,则可对∴∴∴进行判断;利用∴BCD∴∴ABC得BD:AC=CD:BD,而AD=BD,则AD:AC=CD:AD,于是根据黄金分割的定义可对∴进行判断.12. 用一个2倍放大镜照一个△ABC,下面说法中错误的是()A.△ABC放大后,是原来的2倍B.△ABC放大后,各边长是原来的2倍C.△ABC放大后,周长是原来的2倍D.△ABC放大后,面积是原来的4倍答案:A知识点:相似图形解析:解答: ∴放大前后的三角形相似,∴放大后三角形的内角度数不变,面积为原来的4倍,周长和边长均为原来的2倍.故本题选A.分析: 用2倍的放大镜放大一个△ABC,得到一个与原三角形相似的三角形;根据相似三角形的性质:相似三角形的面积比等于相似比的平方,周长比等于相似比.可知:放大后三角形的面积是原来的4倍,边长和周长是原来的2倍,而内角的度数不会改变13. 对一个图形进行放缩时,下列说法中正确的是()A.图形中线段的长度与角的大小都保持不变B.图形中线段的长度与角的大小都会改变C.图形中线段的长度保持不变、角的大小可以改变D.图形中线段的长度可以改变、角的大小保持不变答案:D知识点:相似图形解析:解答:根据相似多边形的性质:相似多边形的对应边成比例,对应角相等,∴对一个图形进行收缩时,图形中线段的长度改变,角的大小不变,故选D.分析: 根据相似图形的性质得出相似图形的对应边成比例,对应角相等,即可得出答案.(1)菱形都相似;(2)等腰直角三角形都相似;(3)正方形都相似;(4)矩形都相似;(5)正六边形都相似.A.1 个B.2个C.3个D.4个答案: C解析:解答:(1)所有菱形的对应角不一定相等,故菱形不一定都相似;(2)等腰直角三角形都相似,正确;(3)正方形都相似,正确;(4)矩形对应边比值不一定相等,不矩形不一定都相似;(5)正六边形都相似,正确,故符合题意的有3个.故选:C.分析: 利用相似图形的性质分别判断得出即可.15. 下列说法不一定正确的是()A.所有的等边三角形都相似B.所有的等腰直角三角形都相似C.所有的菱形都相似D.所有的正方形都相似答案:C知识点:相似图形解析:解答:A、所有的等边三角形都相似,正确;B、所有的等腰直角三角形都相似,正确;C、所有的菱形不一定都相似,故错误;D、所有的正方形都相似,正确.故选C.分析: 利用“对应角相等,对应边的比也相等的多边形相似”进行判定即可.二、填空题(共5题)1. 给出下列几何图形:①两个圆;②两个正方形;③两个矩形;④两个正六边形;⑤两个等边三角形;⑥两个直角三角形;⑦两个菱形.其中,一定相似的有( )(填序号).答案: ①②④⑤知识点:相似图形解析:解答: 下列几何图形:∴两个圆;∴两个正方形;∴两个矩形;∴两个正六边形;⑤两个等边三角形;⑥两个直角三角形;⑦两个菱形.其中,一定相似的有①②④⑤.故答案为:①②④⑤.2. 在一张复印出来的纸上,一个多边形的一条边由原图中的2cm变成了6cm,这次复印的放缩比例是()答案: 1:3知识点:相似图形.解析:解答: 由题意可知,相似多边形的边长之比=相似比=2:6=1:3,故答案为:1:3分析:本题考查相似多边形的性质.相似多边形对应边之比、周长之比等于相似比.3. 若用一个2倍放大镜去看△ABC,则∠A的大小();面积大小为()答案:不变,4倍知识点:相似图形.解析:解答: ∵放大后的三角形与原三角形相似∴∠A的度数不变∵放大前后,两相似三角形的相似比为1:2∴它们的面积比为1:4即放大后面积为原来的4倍.分析: 本题考查相似三角形的性质:相似三角形的对应角相等,面积比等于相似比的平方.4、如果图形甲与图形乙相似,图形乙与图形丙相似,那么图形甲与图形丙()答案:相似知识点:相似图形.解析:解答:∵图形甲与图形乙相似,图形乙与图形丙相似,∴图形甲与图形丙相似.故答案为:相似分析:本题考查了相似图形,熟记相似图形具有传递性是解题的关键.5. 已知线段b是线段a、c的比例中项,且a=1,c=4,那么b=()答案:2知识点:比例线段解析:解答:∵b是a、c的比例中项,∴b2=ac,即b2=4,∴b=±2(负数舍去).故答案是:2.分析:根据比例中项的定义可得b2=ac,从而易求b.三、解答题(共5题)1. 如图,在△ABC中,若DE∥BC,12ADDB=,DE=4cm,求BC的长答案:12cm知识点:平行线分线段成比例解析:解答: 解:∵DE∥BC,∴DE ADBC AB=,又∵12ADDB=∴13ADAB=,∴413BC=∴BC=12cm.故答案为:12cm.分析:本题考查了平行线分线段成比例定理,找出图中的比例关系是解题的关键.2. 如图,已知AB∴CD∴EF,它们依次交直线l1、l2于点A、D、F和点B、C、E,如果AD=6,DF=3,BC=5,求BE的长答案:7.5知识点:平行线分线段成比例.解析:解答:∵AB∥CD∥EF,答案:m=2n+1知识点:平行线分线段成比例;旋转的性质.分析:本题考查了平行线分线段成比例定理的应用,解此题的关键是能根据定理得出比例式,注意:一组平行线截两条直线,所截得的线段对应成比例.也考查了旋转的性质和等腰三角形的性质.4.有一块三角形的草地,它的一条边长为25m.在图纸上,这条边的长为5cm,其他两条边的长都为4cm,求其他两边的实际长度答案:都是20m.知识点:比例线段即其他两边的实际长度都是20m.分析: 设其他两边的实际长度分别为x m、y m,然后根据相似三角形对应边成比例列式求解即可.5.如图,直线y=3x+3与x轴交于点A,与y轴交于点B.过B点作直线BP与x轴正半轴交于点P,取线段OA、OB、OP,当其中一条线段的长是其他两条线段长度的比例中项时,求P点的坐标。
初中数学人教版九年级下册第二十七章 相似27.1 图形的相似-章节测试习题(3)

章节测试题1.【题文】如图,矩形ABCD是一幅长3m,宽2m的国画,它的四周镶上宽度相等的一条金边.(1)金边宽度为10cm时,矩形ABCD与矩形EFGH是否相似?为什么?(2)是否存在装的金边宽度,使得矩形ABCD与矩形EFGH相似?如果存在,求出金边宽度;如果不存在,请说明理由.【答案】(1)不相似.理由见解答;(2)不存在装的金边宽度,使得矩形ABCD与矩形EFGH相似,理由见解答.【分析】本题考查的是相似多边形的判定、矩形的性质,熟练掌握相似多边形的判定方法是解题的关键.(1)求出,得出矩形ABCD与矩形EFGH不相似;(2)设金边宽度为x cm,若,则,解得x=0,即可得出结论.【解答】(1)不相似.理由如下:∵矩形ABCD中,AB=2 m,AD=3 m,金边宽度为10 cm=0.1 m,∴EF=2+2×0.1=2.2 m,EH=3+2×0.1=3.2 m,∴,∴,∴矩形ABCD与矩形EFGH不相似;(2)不存在装的金边宽度,使得矩形ABCD与矩形EFGH相似,理由如下:设金边宽度为x cm,若,则,解得x=0,∴不存在装的金边宽度,使得矩形ABCD与矩形EFGH相似.2.【答题】若某个直角三角形的两直角边之比为2:3,则确定了该三角形的()A. 形状B. 周长C. 面积D. 斜边【答案】A【分析】本题考查相似三角形的性质.【解答】∵直角三角形的两直角边之比为2:3,∴虽不能确定两直角边的值,但能确定其比值,∴能确定该直角三角形的形状,选A.3.【答题】下列图形中一定是相似形的是()A. 两个等边三角形B. 两个菱形C. 两个矩形D. 两个直角三角形【答案】A【分析】本题考查相似多边形的判定.【解答】∵等边三角形的对应角相等,对应边的比相等,∴两个等边三角形一定是相似形,又∵直角三角形,菱形的对应角不一定相等,矩形的边不一定对应成比例,∴两个直角三角形、两个菱形、两个矩形都不一定是相似形,选A.4.【答题】下列命题中,真命题是()A. 邻边之比相等的两个平行四边形一定相似B. 邻边之比相等的两个矩形一定相似C. 对角线之比相等的两个平行四边形一定相似D. 对角线之比相等的两个矩形一定相似【答案】B【分析】本题考查相似多边形的判定.【解答】A.邻边之比相等的两个平行四边形不一定相似,∴A选项错误;B.邻边之比相等,则四条边对应成比例,又四个角都是直角,∴两矩形相似,故本选项正确;C.对角线之比相等的两个平行四边形不一定相似,∴C选项错误;D.对角线之比相等的两个矩形不一定相似,∴D选项错误;选B.5.【答题】若两个相似多边形的面积之比为4:9,则这两个多边形的周长之比为()A. B. 2:3 C. 4:9 D. 16:81【答案】B【分析】本题考查相似多边形的性质.【解答】∵两个相似多边形的面积之比为4:9,∴两个相似多边形的对应边的比为2:3,∴两个相似多边形的周长的比为2:3,选B.6.【答题】下列四组图形中,不是相似图形的是()A. B.C. D.【答案】D【分析】本题考查相似多边形的判定.【解答】A.形状相同,但大小不同,符合相似形的定义,故不符合题意;B.形状相同,但大小不同,符合相似形的定义,故不符合题意;C.形状相同,但大小不同,符合相似形的定义,故不符合题意;D.形状不相同,不符合相似形的定义,故符合题意;选D.7.【答题】若一个三角形的各边长扩大为原来的5倍,则此三角形的周长扩大为原来的______倍.【答案】5【分析】本题考查相似多边形的性质.【解答】∵一个三角形的各边长扩大为原来的5倍,∴扩大后的三角形与原三角形相似,∵相似三角形的周长的比等于相似比,∴这个三角形的周长扩大为原来的5倍,故答案为5.8.【答题】某课外活动小组的同学在研究某种植物标本(如图所示)时,测得叶片①最大宽度是8 cm,最大长度是16 cm;叶片②最大宽度是7 cm,最大长度是14 cm;叶片③最大宽度约为6.5 cm,请你用所学数学知识估算叶片③的完整叶片的最大长度,结果约为______cm.【答案】13【分析】本题考查相似多边形的性质.【解答】根据叶片①②的最大长度和宽度,可得出这种植物的叶片的最大宽度:最大长度=1:2.由此可得出完整的叶片③的最大长度应是6.5×2=13 cm.故答案为13.9.【答题】如图,在矩形ABCD中,AD=2,CD=1,连接AC,以对角线AC为边,按逆时针方向作矩形ABCD的相似矩形AB1C1C,再连接AC1,以对角线AC1为边作矩形AB1C1C的相似矩形AB2C2C1,…,按此规律继续下去,则矩形AB n C n C n﹣1的面积为______.【答案】【分析】本题考查相似多边形的性质.【解答】∵四边形ABCD是矩形,∴AD⊥DC,∴AC,∵按逆时针方向作矩形ABCD的相似矩形AB1C1C,∴矩形AB1C1C的边长和矩形ABCD的边长的比为:2,∴矩形AB1C1C的面积和矩形ABCD的面积的比5:4,∵矩形ABCD的面积=2×1=2,∴矩形AB1C1C的面积,依此类推,矩形AB2C2C1的面积和矩形AB1C1C的面积的比5:4,∴矩形AB2C2C1的面积,∴矩形AB3C3C2的面积,按此规律第n个矩形的面积为,故答案为.10.【答题】一个多边形的边长依次为1,2,3,4,5,6,与它相似的另一个多边形的最大边长为8,那么另一个多边形的周长是______.【答案】28【分析】本题考查相似多边形的性质.【解答】设另一个多边形的周长是x.依题意,有x:(1+2+3+4+5+6)=8:6,解得x=28.故另一个多边形的周长是28.11.【答题】若两个相似多边形的相似比是2:3,则它们的面积比等于______.【答案】4:9【分析】本题考查相似多边形的性质.【解答】∵两个相似多边形的相似比为2:3,∴它们的面积比=22:32=4:9.故答案为4:9.12.【答题】若一个矩形截去两个以短边长为边长的正方形后得到的矩形与原矩形相似,则这个矩形的长与宽之比为______.【答案】1【分析】本题考查相似多边形的性质.【解答】设矩形的长是a,宽是b,则AE=EH=b,DH=a﹣2b,∵矩形ABCD∽矩形HDCG,∴,即,整理得a2﹣2ab﹣b2=0,两边同除以b2,得()21=0,解得或(舍去)∴长与宽的比为1,故答案为1.13.【题文】如图,一个矩形广场的长为100 m,宽为80 m,广场外围两条纵向小路的宽均为1.5 m,如果设两条横向小路的宽都为x m,那么当x为多少时,小路内、外边缘所围成的两个矩形相似.【答案】1.2.【分析】本题考查相似多边形的性质.【解答】当(100+3):100=(80+2x):80时,小路内、外边缘所围成的两个矩形相似.解得x=1.2.答:当x为1.2时,小路内、外边缘所围成的两个矩形相似.14.【题文】如图,四边形ABCD∽四边形A′B′C′D′.(1)α=______;(2)求边x、y的长度.【答案】(1)83°;(2)x=12,y.【分析】本题考查相似多边形的性质.【解答】(1)∵四边形ABCD∽四边形A′B′C′D′,∴∠A=∠A′=62°,∠B=∠B′=75°,∴α=360°﹣62°﹣75°﹣140°=83°,故答案为83°;(2)∵四边形ABCD∽四边形A′B′C′D′,∴,解得x=12,y.15.【答题】若两个相似多边形的面积之比为1:4,则它们的周长之比为()A. 1:4B. 1:2C. 2:1D. 1:16【答案】B【分析】本题考查相似图形的性质.【解答】∵两个相似多边形面积比为1:4,∴周长之比为1:2.选B.16.【答题】沿一张矩形纸较长两边的中点将纸一分为二,所得两张矩形与原来的矩形纸相似,那么原来那张纸的长和宽的比是()A. B. C. D.【答案】A【分析】本题考查相似图形的性质.【解答】设原来矩形的长为x,宽为y,则对折后的矩形的长为y,宽为,∵得到的两个矩形都和原矩形相似,∴x:y=y:,解得x:y:1.选A.17.【答题】下列说法正确的是()A. 所有菱形都相似B. 所有矩形都相似C. 所有正方形都相似D. 所有平行四边形都相似【答案】C【分析】本题考查相似图形的判定.【解答】∵相似多边形的对应边成比例,对应角相等,∴所有正方形都是相似多边形,选C.18.【答题】如图所示,长为8cm,宽为6cm的矩形中,截去一个矩形(图中阴影部分),如果剩下矩形与原矩形相似,那么剩下矩形的面积是()A. 28cm2B. 27cm2C. 21cm2D. 20cm2【答案】B【分析】本题考查相似图形的性质.【解答】依题意,在矩形ABDC中截取矩形ABFE,则矩形ABDC∽矩形FDCE,则,设DF=x cm,得到,解得x=4.5,则剩下的矩形面积是4.5×6=27cm2.选B.19.【答题】矩形的两边长分别为x和6(x<6),把它按如图方式分割成三个全等的小矩形,每一个小矩形与原矩形相似,则x的值为()A. B. C. D. 2.5【答案】B【分析】本题考查相似图形的性质.【解答】∵原矩形的长为6,宽为x,∴小矩形的长为x,宽为2,∵小矩形与原矩形相似,∴,解得x=2,选B.20.【答题】若△ABC的每条边长增加各自的10%得△A′B′C′,则∠B′的度数与其对应角∠B的度数相比()A. 增加了10%B. 减少了10%C. 增加了(1+10%)D. 没有改变【答案】D【分析】本题考查相似图形的性质.【解答】∵△ABC的每条边长增加各自的10%得△A′B′C′,∴△ABC与△A′B′C′的三边对应成比例,∴△ABC∽△A′B′C′,∴∠B′=∠B.选D.。
27.1 图形的相似 测试题2
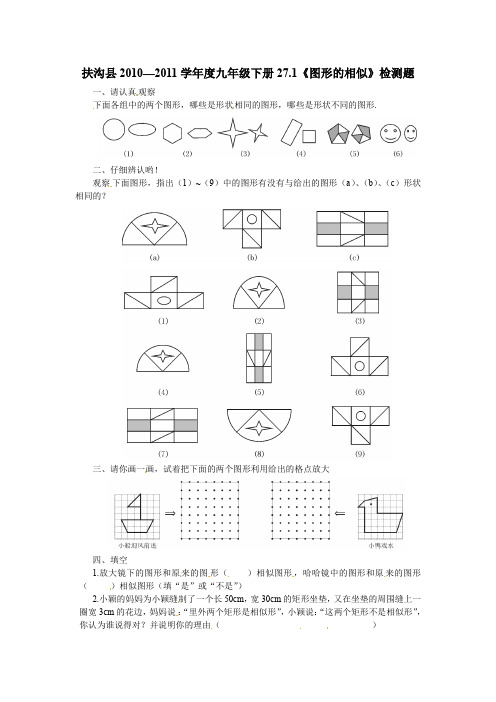
扶沟县2010—2011学年度九年级下册27.1《图形的相似》检测题一、请认真观察下面各组中的两个图形,哪些是形状相同的图形,哪些是形状不同的图形.二、仔细辨认哟!观察下面图形,指出(1)~(9)中的图形有没有与给出的图形(a)、(b)、(c)形状相同的?三、请你画一画,试着把下面的两个图形利用给出的格点放大四、填空1.放大镜下的图形和原来的图形()相似图形,哈哈镜中的图形和原来的图形()相似图形(填“是”或“不是”)2.小颖的妈妈为小颖缝制了一个长50cm,宽30cm的矩形坐垫,又在坐垫的周围缝上一圈宽3cm的花边,妈妈说:“里外两个矩形是相似形”,小颖说:“这两个矩形不是相似形”,你认为谁说得对?并说明你的理由()3.如果两个相似多边形的最长边分别为35cm 和14cm ,那么最短边分别为5cm 和( )cm五、想一想如图:已知A (0,-2),B (-2,1),C (3,2)图4—3—1(1)求线段AB 、BC 、AC 的长.(2)把A 、B 、C 三点的横坐标、纵坐标都乘以2,得到A ′、B ′、C ′的坐标,求 A ′B ′、B ′C ′、A ′C ′的长(3)以上六条线段成比例吗?(4)△ABC 与△A ′B ′C ′的形状相同吗?参考答案一、(3)、(5)组中的图形形状相同(1)、(2)、(4)、(6)组中的图形形状不同 二、图形(4)、(8)与图形(a )形状相同图形(6)与图形(b )形状相同图形(5)与图形(c )形状相同三、略四、1.是 不是 2.小颖说的对 3.2cm五、解:如图(见原题图)A (0,-2),B (-2,1),C (3,2)(1)由勾股定理得:AB =132322=+BC =261522=+ AC =2243+=5(2)由已知得A ′(0,-4),B ′(-4,2),C ′(6,4)由勾股定理得:A ′B ′=1326422=+B ′C ′=26221022=+A ′C ′=2286+=10(3)∵21=''=''=''C A AC C B BC B A AB ∴这六条线段成比例(4)△ABC 与△A ′B ′C ′的形状相同.。
人教版九年级数学下册第二十七章27.1 图形的相似

解:∠A=65° , ∠B=65° , ∠D=∠C=180° -65° =115° , 15 15 A′D′= 4 cm,B′C′=A′D′= 4 cm.
15. 在△ ABC 中,AB=12,点 E 在 AC 上,点 D AD AE 在 AB 上,若 AE=6,EC=4,且DB=EC. (1)求 AD 的长; DB EC (2)试问 AB =AC能成立吗?请说明理由.
13. 一个四边形的边长分别是 3,4,5,6,另一 个和它相似的四边形的最小边长为 6,那么另一个四 边形的周长为 36 .
14. 如 图所 示 , 等腰 梯 形 ABCD 与等 腰 梯 形 A′B′C′D′相似,∠A′=65° ,A′B′=6 cm,AB=8 cm, AD=5 cm,试求梯形 ABCD 各角的度数与 A′D′,B′C′ 的长.
(2)请归纳出相似体的 3 条主要性质: ①相似体的一切对应线段(或弧)长的比等 于
相似比
; ; .
②相似体表面积的比等于 相似比的平方 ③相似体体积的比等于 相似比的立方
17. (1)已知图①中的两个矩形相似,求它们的对 应边的比;
(2)如图②,两个六边形的边长分别都为 a 和 b, 且每一个六边形的内角均是 120° ,它们相似吗?为什 么?
S甲 6 a2 a2 则 =6b2 =b ,又设 V 甲、V 乙分别表示这两个正 S乙 V甲 a3 a3 方体的体积,则 =b3=b . V乙
(1)下列几何体中,一定属于相似体的是( A ) A.两个球体 C.两个圆柱体 B.两个圆锥体 D.两个长方体
8. 在比例尺为 1∶n 的某市地图上,A,B 两地相 距 5 cm,则 A,B 之间的实际距离为( C ) 1 A.5n cm C.5n cm 1 2 B.25n cm D是相似形的是 ( B )
中考数学《图形的相似》真题汇编含解析

图形的相似(29题)一、单选题1(2023·重庆·统考中考真题)如图,已知△ABC ∽△EDC ,AC :EC =2:3,若AB 的长度为6,则DE 的长度为()A.4B.9C.12D.13.5【答案】B【分析】根据相似三角形的性质即可求出.【详解】解:∵△ABC ∽△EDC ,∴AC :EC =AB :DE ,∵AC :EC =2:3,AB =6,∴2:3=6:DE ,∴DE =9,故选:B .【点睛】此题考查的是相似三角形的性质,掌握相似三角形的边长比等于相似比是解决此题的关键.2(2023·四川遂宁·统考中考真题)在方格图中,以格点为顶点的三角形叫做格点三角形.在如图所示的平面直角坐标系中,格点△ABC 、△DEF 成位似关系,则位似中心的坐标为()A.-1,0B.0,0C.0,1D.1,0【答案】A【分析】根据题意确定直线AD 的解析式为:y =x +1,由位似图形的性质得出AD 所在直线与BE 所在直线x 轴的交点坐标即为位似中心,即可求解.【详解】解:由图得:A 1,2 ,D 3,4 ,设直线AD 的解析式为:y =kx +b ,将点代入得:2=k +b 4=3k +b ,解得:k =1b =1 ,∴直线AD 的解析式为:y =x +1,AD 所在直线与BE 所在直线x 轴的交点坐标即为位似中心,∴当y =0时,x =-1,∴位似中心的坐标为-1,0 ,故选:A .【点睛】题目主要考查位似图形的性质,求一次函数的解析式,理解题意,掌握位似图形的特点是解题关键.3(2023·浙江嘉兴·统考中考真题)如图,在直角坐标系中,△ABC 的三个顶点分别为A 1,2 ,B 2,1 ,C 3,2 ,现以原点O 为位似中心,在第一象限内作与△ABC 的位似比为2的位似图形△A B C ,则顶点C 的坐标是()A.2,4B.4,2C.6,4D.5,4【答案】C【分析】直接根据位似图形的性质即可得.【详解】解:∵△ABC 的位似比为2的位似图形是△A B C ,且C 3,2 ,∴C 2×3,2×2 ,即C 6,4 ,故选:C .【点睛】本题考查了坐标与位似图形,熟练掌握位似图形的性质是解题关键.4(2023·四川南充·统考中考真题)如图,数学活动课上,为测量学校旗杆高度,小菲同学在脚下水平放置一平面镜,然后向后退(保持脚、镜和旗杆底端在同一直线上),直到她刚好在镜子中看到旗杆的顶端.已知小菲的眼睛离地面高度为1.6m ,同时量得小菲与镜子的水平距离为2m ,镜子与旗杆的水平距离为10m ,则旗杆高度为()A.6.4mB.8mC.9.6mD.12.5m【答案】B【分析】根据镜面反射性质,可求出∠ACB =∠ECD ,再利用垂直求△ABC ∽△EDC ,最后根据三角形相似的性质,即可求出答案.【详解】解:如图所示,由图可知,AB ⊥BD ,CD ⊥DE ,CF ⊥BD∴∠ABC =∠CDE =90°.∵根据镜面的反射性质,∴∠ACF =∠ECF ,∴90°-∠ACF =90°-∠ECF ,∴∠ACB =∠ECD ,∴△ABC ∽△EDC ,∴AB DE =BC CD.∵小菲的眼睛离地面高度为1.6m ,同时量得小菲与镜子的水平距离为2m ,镜子与旗杆的水平距离为10m ,∴AB =1.6m ,BC =2m ,CD =10m .∴1.6DE =210.∴DE =8m .故选:B .【点睛】本题考查了相似三角形的应用,解题的关键在于熟练掌握镜面反射的基本性质和相似三角形的性质.5(2023·安徽·统考中考真题)如图,点E 在正方形ABCD 的对角线AC 上,EF ⊥AB 于点F ,连接DE 并延长,交边BC 于点M ,交边AB 的延长线于点G .若AF =2,FB =1,则MG =()A.23B.352C.5+1D.10【答案】B 【分析】根据平行线分线段成比例得出DE EM =AF FB =2,根据△ADE ∽△CME ,得出AD CM =DE EM =2,则CM =12AD =32,进而可得MB =32,根据BC ∥AD ,得出△GMB ∽△GDA ,根据相似三角形的性质得出BG =3,进而在Rt △BGM 中,勾股定理即可求解.【详解】解:∵四边形ABCD 是正方形,AF =2,FB =1,∴AD =BC =AB =AF +FG =2+1=3,AD ∥CB ,AD ⊥AB ,CB ⊥AB ,∵EF ⊥AB ,∴AD ∥EF ∥BC∴DE EM =AFFB=2,△ADE∽△CME,∴AD CM =DEEM=2,则CM=12AD=32,∴MB=3-CM=32,∵BC∥AD,∴△GMB∽△GDA,∴BG AG =MBDA=323=12∴BG=AB=3,在Rt△BGM中,MG=MB2+BG2=322+32=352,故选:B.【点睛】本题考查了正方形的性质,平行线分线段成比例,相似三角形的性质与判定,勾股定理,熟练掌握以上知识是解题的关键.6(2023·湖北黄冈·统考中考真题)如图,矩形ABCD中,AB=3,BC=4,以点B为圆心,适当长为半径画弧,分别交BC,BD于点E,F,再分别以点E,F为圆心,大于12EF长为半径画弧交于点P,作射线BP,过点C作BP的垂线分别交BD,AD于点M,N,则CN的长为()A.10B.11C.23D.4【答案】A【分析】由作图可知BP平分∠CBD,设BP与CN交于点O,与CD交于点R,作RQ⊥BD于点Q,根据角平分线的性质可知RQ=RC,进而证明Rt△BCR≌Rt△BQR,推出BC=BQ=4,设RQ=RC=x,则DR=CD-CR=3-x,解Rt△DQR求出QR=CR=43.利用三角形面积法求出OC,再证△OCR∽△DCN,根据相似三角形对应边成比例即可求出CN.【详解】解:如图,设BP与CN交于点O,与CD交于点R,作RQ⊥BD于点Q,∵矩形ABCD中,AB=3,BC=4,∴CD =AB =3,∴BD =BC 2+CD 2=5.由作图过程可知,BP 平分∠CBD ,∵四边形ABCD 是矩形,∴CD ⊥BC ,又∵RQ ⊥BD ,∴RQ =RC ,在Rt △BCR 和Rt △BQR 中,RQ =RC BR =BR ,∴Rt △BCR ≌Rt △BQR HL ,∴BC =BQ =4,∴QD =BD -BQ =5-4=1,设RQ =RC =x ,则DR =CD -CR =3-x ,在Rt △DQR 中,由勾股定理得DR 2=DQ 2+RQ 2,即3-x 2=12+x 2,解得x =43,∴CR =43.∴BR =BC 2+CR 2=4310.∵S △BCR =12CR ⋅BC =12BR ⋅OC ,∴OC =CR ⋅BC BR =43×44310=2510.∵∠COR =∠CDN =90°,∠OCR =∠DCN ,∴△OCR ∽△DCN ,∴OC DC =CR CN ,即25103=43CN,解得CN =10.故选:A .【点睛】本题考查角平分线的作图方法,矩形的性质,角平分线的性质,全等三角形的判定与性质,勾股定理,相似三角形的判定与性质等,涉及知识点较多,有一定难度,解题的关键是根据作图过程判断出BP 平分∠CBD ,通过勾股定理解直角三角形求出CR .7(2023·四川内江·统考中考真题)如图,在△ABC 中,点D 、E 为边AB 的三等分点,点F 、G 在边BC 上,AC ∥DG ∥EF ,点H 为AF 与DG 的交点.若AC =12,则DH 的长为()A.1B.32C.2D.3【答案】C 【分析】由三等分点的定义与平行线的性质得出BE =DE =AD ,BF =GF =CG ,AH =HF ,DH 是△AEF 的中位线,易证△BEF ∽△BAC ,得EF AC =BE AB,解得EF =4,则DH =12EF =2.【详解】解:∵D 、E 为边AB 的三等分点,EF ∥DG ∥AC ,∴BE =DE =AD ,BF =GF =CG ,AH =HF ,∴AB =3BE ,DH 是△AEF 的中位线,∴DH =12EF ,∵EF ∥AC ,∴∠BEF =∠BAC ,∠BFE =∠BCA ,∴△BEF ∽△BAC ,∴EF AC =BE AB,即EF 12=BE 3BE ,解得:EF =4,∴DH =12EF =12×4=2,故选:C .【点睛】本题考查了三等分点的定义、平行线的性质、相似三角形的判定与性质、三角形中位线定理等知识;熟练掌握相似三角形的判定与性质是解题的关键.8(2023·湖北鄂州·统考中考真题)如图,在平面直角坐标系中,O 为原点,OA =OB =35,点C 为平面内一动点,BC =32,连接AC ,点M 是线段AC 上的一点,且满足CM :MA =1:2.当线段OM 取最大值时,点M 的坐标是()A.35,65B.355,655C.65,125D.655,1255 【答案】D【分析】由题意可得点C 在以点B 为圆心,32为半径的OB 上,在x 轴的负半轴上取点D -352,0 ,连接BD ,分别过C 、M 作CF ⊥OA ,ME ⊥OA ,垂足为F 、E ,先证△OAM ∽△DAC ,得OM CD =OA AD =23,从而当CD 取得最大值时,OM 取得最大值,结合图形可知当D ,B ,C 三点共线,且点B 在线段DC 上时,CD 取得最大值,然后分别证△BDO ∽△CDF ,△AEM ∽△AFC ,利用相似三角形的性质即可求解.【详解】解:∵点C 为平面内一动点,BC =32,∴点C 在以点B 为圆心,32为半径的OB 上,在x 轴的负半轴上取点D -352,0 ,连接BD ,分别过C 、M 作CF ⊥OA ,ME ⊥OA ,垂足为F 、E ,∵OA =OB =35,∴AD =OD +OA =952,∴OA AD=23,∵CM :MA =1:2,∴OA AD =23=CM AC,∵∠OAM =∠DAC ,∴△OAM ∽△DAC ,∴OM CD =OA AD=23,∴当CD 取得最大值时,OM 取得最大值,结合图形可知当D ,B ,C 三点共线,且点B 在线段DC 上时,CD 取得最大值,∵OA =OB =35,OD =352,∴BD =OB 2+OD 2=35 2+352 2=152,∴CD =BC +BD =9,∵OM CD=23,∴OM =6,∵y 轴⊥x 轴,CF ⊥OA ,∴∠DOB =∠DFC =90°,∵∠BDO =∠CDF ,∴△BDO ∽△CDF ,∴OB CF =BD CD 即35CF=1529,解得CF =1855,同理可得,△AEM ∽△AFC ,∴ME CF =AM AC =23即ME 1855=23,解得ME =1255,∴OE =OM 2-ME 2=62-1255 2=655,∴当线段OM 取最大值时,点M 的坐标是655,1255,故选:D .【点睛】本题主要考查了勾股定理、相似三角形的判定及性质、圆的一般概念以及坐标与图形,熟练掌握相似三角形的判定及性质是解题的关键.9(2023·山东东营·统考中考真题)如图,正方形ABCD 的边长为4,点E ,F 分别在边DC ,BC 上,且BF =CE ,AE 平分∠CAD ,连接DF ,分别交AE ,AC 于点G ,M ,P 是线段AG 上的一个动点,过点P 作PN ⊥AC 垂足为N ,连接PM ,有下列四个结论:①AE 垂直平分DM ;②PM +PN 的最小值为32;③CF 2=GE ⋅AE ;④S ΔADM =62.其中正确的是()A.①②B.②③④C.①③④D.①③【答案】D【分析】根据正方形的性质和三角形全等即可证明∠DAE =∠FDC ,通过等量转化即可求证AG ⊥DM ,利用角平分线的性质和公共边即可证明△ADG ≌△AMG ASA ,从而推出①的结论;利用①中的部分结果可证明△ADE ∽△DGE 推出DE 2=GE ⋅AE ,通过等量代换可推出③的结论;利用①中的部分结果和勾股定理推出AM 和CM 长度,最后通过面积法即可求证④的结论不对;结合①中的结论和③的结论可求出PM +PN 的最小值,从而证明②不对.【详解】解:∵ABCD 为正方形,∴BC =CD =AD ,∠ADE =∠DCF =90°,∵BF =CE ,∴DE =FC ,∴△ADE ≌△DCF SAS .∴∠DAE =∠FDC ,∵∠ADE =90°,∴∠ADG +∠FDC =90°,∴∠ADG +∠DAE =90°,∴∠AGD =∠AGM =90°.∵AE 平分∠CAD ,∴∠DAG =∠MAG .∵AG =AG ,∴△ADG ≌△AMG ASA .∴DG =GM ,∵∠AGD =∠AGM =90°,∴AE 垂直平分DM ,故①正确.由①可知,∠ADE =∠DGE =90°,∠DAE =∠GDE ,∴△ADE ∽△DGE ,∴DE GE=AE DE ,∴DE 2=GE ⋅AE ,由①可知DE =CF ,∴CF 2=GE ⋅AE .故③正确.∵ABCD 为正方形,且边长为4,∴AB =BC =AD =4,∴在Rt △ABC 中,AC =2AB =4 2.由①可知,△ADG ≌△AMG ASA ,∴AM =AD =4,∴CM =AC -AM =42-4.由图可知,△DMC 和△ADM 等高,设高为h ,∴S △ADM =S △ADC -S △DMC ,∴4×h 2=4×42-42-4 ⋅h 2,∴h =22,∴S △ADM =12⋅AM ⋅h =12×4×22=4 2.故④不正确.由①可知,△ADG ≌△AMG ASA ,∴DG =GM ,∴M 关于线段AG 的对称点为D ,过点D 作DN ⊥AC ,交AC 于N ,交AE 于P ,∴PM +PN 最小即为DN ,如图所示,由④可知△ADM 的高h =22即为图中的DN ,∴DN =2 2.故②不正确.综上所述,正确的是①③.故选:D .【点睛】本题考查的是正方形的综合题,涉及到三角形相似,最短路径,三角形全等,三角形面积法,解题的关键在于是否能正确找出最短路径以及运用相关知识点.10(2023·内蒙古赤峰·统考中考真题)如图,把一个边长为5的菱形ABCD 沿着直线DE 折叠,使点C 与AB 延长线上的点Q 重合.DE 交BC 于点F ,交AB 延长线于点E .DQ 交BC 于点P ,DM ⊥AB于点M ,AM =4,则下列结论,①DQ =EQ ,②BQ =3,③BP =158,④BD ∥FQ .正确的是()A.①②③B.②④C.①③④D.①②③④【答案】A【分析】由折叠性质和平行线的性质可得∠QDF =∠CDF =∠QEF ,根据等角对等边即可判断①正确;根据等腰三角形三线合一的性质求出MQ =AM =4,再求出BQ 即可判断②正确;由△CDP ∽△BQP 得CP BP =CD BQ=53,求出BP 即可判断③正确;根据EF DE ≠QE BE 即可判断④错误.【详解】由折叠性质可知:∠CDF =∠QDF ,CD =DQ =5,∵CD ∥AB ,∴∠CDF =∠QEF .∴∠QDF =∠QEF .∴DQ =EQ =5.故①正确;∵DQ =CD =AD =5,DM ⊥AB ,∴MQ =AM =4.∵MB =AB -AM =5-4=1,∴BQ =MQ -MB =4-1=3.故②正确;∵CD ∥AB ,∴△CDP ∽△BQP .∴CP BP =CD BQ=53.∵CP +BP =BC =5,∴BP =38BC =158.故③正确;∵CD ∥AB ,∴△CDF ∽△BEF .∴DF EF =CD BE =CD BQ +QE=53+5=58.∴EF DE =813.∵QE BE =58,∴EF DE ≠QE BE.∴△EFQ 与△EDB 不相似.∴∠EQF ≠∠EBD .∴BD 与FQ 不平行.故④错误;故选:A .【点睛】本题主要考查了折叠的性质,平行线的性质,等腰三角形的性质,相似三角形的判定和性质,菱形的性质等知识,属于选择压轴题,有一定难度,熟练掌握相关性质是解题的关键.11(2023·黑龙江·统考中考真题)如图,在正方形ABCD中,点E,F分别是AB,BC上的动点,且AF ⊥DE,垂足为G,将△ABF沿AF翻折,得到△AMF,AM交DE于点P,对角线BD交AF于点H,连接HM,CM,DM,BM,下列结论正确的是:①AF=DE;②BM∥DE;③若CM⊥FM,则四边形BHMF是菱形;④当点E运动到AB的中点,tan∠BHF=22;⑤EP⋅DH=2AG⋅BH.()A.①②③④⑤B.①②③⑤C.①②③D.①②⑤【答案】B【分析】利用正方形的性质和翻折的性质,逐一判断,即可解答.【详解】解:∵四边形ABCD是正方形,∴∠DAE=∠ABF=90°,DA=AB,∵AF⊥DE,∴∠BAF+∠AED=90°,∵∠BAF+∠AFB=90°,∴∠AED=∠BFA,∴△ABF≌△AED AAS,∴AF=DE,故①正确,∵将△ABF沿AF翻折,得到△AMF,∴BM⊥AF,∵AF⊥DE,∴BM∥DE,故②正确,当CM⊥FM时,∠CMF=90°,∵∠AMF=∠ABF=90°,∴∠AMF+∠CMF=180°,即A,M,C在同一直线上,∴∠MCF=45°,∴∠MFC=90°-∠MCF=45°,通过翻折的性质可得∠HBF=∠HMF=45°,BF=MF,∴∠HMF=∠MFC,∠HBC=∠MFC,∴BC∥MH,HB∥MF,∴四边形BHMF是平行四边形,∵BF=MF,∴平行四边形BHMF是菱形,故③正确,当点E运动到AB的中点,如图,设正方形ABCD的边长为2a,则AE=BF=a,在Rt △AED 中,DE =AD 2+AE 2=5a =AF ,∵∠AHD =∠FHB ,∠ADH =∠FBH =45°,∴△AHD ∽△FHB ,∴FH AH =BF AD=a 2a =12,∴AH =23AF =253a ,∵∠AGE =∠ABF =90°,∴△AGF ∽△ABF ,∴AE AF =EG BF =AG AB =a 5a=55,∴EG =55BF =55a ,AG =55AB =255a ,∴DG =ED -EG =455a ,GH =AH -AG =4515a ,∵∠BHF =∠DHA ,在Rt △DGH 中,tan ∠BHF =tan ∠DHA =DG GH=3,故④错误,∵△AHD ∽△FHB ,∴BH DH=12,∴BH =13BD =13×22a =223a ,DH =23BD =23×22a =423a ,∵AF ⊥EP ,根据翻折的性质可得EP =2EG =255a ,∴EP ⋅DH =255a ⋅423a =81015a 2,2AG ⋅BH =2⋅255a ⋅223a =81015a 2,∴EP ⋅DH =2AG ⋅BH =81015a 2,故⑤正确;综上分析可知,正确的是①②③⑤.故选:B .【点睛】本题考查了正方形的性质,翻折的性质,相似三角形的判定和性质,正切的概念,熟练按照要求做出图形,利用寻找相似三角形是解题的关键.二、填空题12(2023·湖北鄂州·统考中考真题)如图,在平面直角坐标系中,△ABC 与△A 1B 1C 1位似,原点O 是位似中心,且AB A 1B 1=3.若A 9,3 ,则A 1点的坐标是.【答案】3,1【分析】直接利用位似图形的性质得出相似比进而得出对应线段的长.【详解】解∶设A1m,n∵△ABC与△A1B1C1位似,原点O是位似中心,且ABA1B1=3.若A9,3,∴位似比为31,∴9 m =31,3n=31,解得m=3,n=1,∴A13,1故答案为:3,1.【点睛】此题主要考查了位似变换,正确得出相似比是解题关键.13(2023·吉林长春·统考中考真题)如图,△ABC和△A B C 是以点O为位似中心的位似图形,点A 在线段OA 上.若OA:AA =1:2,则△ABC和△A B C 的周长之比为.【答案】1:3【分析】根据位似图形的性质即可求出答案.【详解】解:∵OA:AA =1:2,∴OA:OA =1:3,设△ABC周长为l1,设△A B C 周长为l2,∵△ABC和△A B C 是以点O为位似中心的位似图形,∴l1l2=OAOA=13.∴l1:l2=1:3.∴△ABC和△A B C 的周长之比为1:3.故答案为:1:3.【点睛】本题考查了位似图形的性质,解题的关键在于熟练掌握位似图形性质.14(2023·四川乐山·统考中考真题)如图,在平行四边形ABCD中,E是线段AB上一点,连结AC、DE 交于点F .若AE EB =23,则S △ADF S △AEF =.【答案】52【分析】四边形ABCD 是平行四边形,则AB =CD ,AB ∥CD ,可证明△EAF ∽△DCF ,得到DF EF =CD AE =AB AE,由AE EB =23进一步即可得到答案.【详解】解:∵四边形ABCD 是平行四边形,∴AB =CD ,AB ∥CD ,∴∠AEF =∠CDF ,∠EAF =∠DCF ,∴△EAF ∽△DCF ,∴DF EF =CD AE =AB AE ,∵AE EB =23,∴AB AE =52,∴S △ADF S △AEF =DF EF =AB AE=52.故答案为:52【点睛】此题考查了平行四边形的性质、相似三角形的判定和性质等知识,证明△EAF ∽△DCF 是解题的关键.15(2023·江西·统考中考真题)《周髀算经》中记载了“偃矩以望高”的方法.“矩”在古代指两条边呈直角的曲尺(即图中的ABC ).“偃矩以望高”的意思是把“矩”仰立放,可测量物体的高度如图,点A ,B ,Q 在同一水平线上,∠ABC 和∠AQP 均为直角,AP 与BC 相交于点D .测得AB =40cm ,BD =20cm ,AQ =12m ,则树高PQ =m .【答案】6【分析】根据题意可得△ABD ∽△AQP ,然后相似三角形的性质,即可求解.【详解】解:∵∠ABC 和∠AQP 均为直角∴BD ∥PQ ,∴△ABD ∽△AQP ,∴BD PQ =AB AQ∵AB =40cm ,BD =20cm ,AQ =12m ,∴PQ =AQ ×BD AB=12×2040=6m ,故答案为:6.【点睛】本题考查了相似三角形的应用,熟练掌握相似三角形的性质与判定是解题的关键.16(2023·四川成都·统考中考真题)如图,在△ABC 中,D 是边AB 上一点,按以下步骤作图:①以点A 为圆心,以适当长为半径作弧,分别交AB ,AC 于点M ,N ;②以点D 为圆心,以AM 长为半径作弧,交DB 于点M ;③以点M 为圆心,以MN 长为半径作弧,在∠BAC 内部交前面的弧于点N :④过点N 作射线DN 交BC 于点E .若△BDE 与四边形ACED 的面积比为4:21,则BE CE的值为.【答案】23【分析】根据作图可得∠BDE =∠A ,然后得出DE ∥AC ,可证明△BDE ∽△BAC ,进而根据相似三角形的性质即可求解.【详解】解:根据作图可得∠BDE =∠A ,∴DE ∥AC ,∴△BDE ∽△BAC ,∵△BDE 与四边形ACED 的面积比为4:21,∴S △BDC S △BAC =421+4=BE BC2∴BE BC =25∴BE CE =23,故答案为:23.【点睛】本题考查了作一个角等于已知角,相似三角形的性质与判定,熟练掌握基本作图与相似三角形的性质与判定是解题的关键.17(2023·内蒙古·统考中考真题)如图,在Rt △ABC 中,∠ACB =90°,AC =3,BC =1,将△ABC 绕点A 逆时针方向旋转90°,得到△AB C .连接BB ,交AC 于点D ,则AD DC的值为.【答案】5【分析】过点D 作DF ⊥AB 于点F ,利用勾股定理求得AB =10,根据旋转的性质可证△ABB 、△DFB是等腰直角三角形,可得DF =BF ,再由S △ADB =12×BC ×AD =12×DF ×AB ,得AD =10DF ,证明△AFD ∼△ACB ,可得DF BC =AF AC ,即AF =3DF ,再由AF =10-DF ,求得DF =104,从而求得AD =52,CD =12,即可求解.【详解】解:过点D 作DF ⊥AB 于点F ,∵∠ACB =90°,AC =3,BC =1,∴AB =32+12=10,∵将△ABC 绕点A 逆时针方向旋转90°得到△AB C ,∴AB =AB =10,∠BAB =90°,∴△ABB 是等腰直角三角形,∴∠ABB =45°,又∵DF ⊥AB ,∴∠FDB =45°,∴△DFB 是等腰直角三角形,∴DF =BF ,∵S △ADB =12×BC ×AD =12×DF ×AB ,即AD =10DF ,∵∠C =∠AFD =90°,∠CAB =∠FAD ,∴△AFD ∼△ACB ,∴DF BC =AF AC,即AF =3DF ,又∵AF =10-DF ,∴DF =104,∴AD =10×104=52,CD =3-52=12,∴AD CD =5212=5,故答案为:5.【点睛】本题考查旋转的性质、等腰三角形的判定与性质、相似三角形的判定与性质、三角形的面积,熟练掌握相关知识是解题的关键.18(2023·河南·统考中考真题)矩形ABCD 中,M 为对角线BD 的中点,点N 在边AD 上,且AN =AB =1.当以点D ,M ,N 为顶点的三角形是直角三角形时,AD 的长为.【答案】2或2+1【分析】分两种情况:当∠MND =90°时和当∠NMD =90°时,分别进行讨论求解即可.【详解】解:当∠MND =90°时,∵四边形ABCD 矩形,∴∠A =90°,则MN ∥AB ,由平行线分线段成比例可得:AN ND =BM MD,又∵M 为对角线BD 的中点,∴BM =MD ,∴AN ND =BM MD=1,即:ND =AN =1,∴AD =AN +ND =2,当∠NMD =90°时,∵M 为对角线BD 的中点,∠NMD =90°∴MN 为BD 的垂直平分线,∴BN =ND ,∵四边形ABCD 矩形,AN =AB =1∴∠A =90°,则BN =AB 2+AN 2=2,∴BN =ND =2∴AD =AN +ND =2+1,综上,AD 的长为2或2+1,故答案为:2或2+1.【点睛】本题考查矩形的性质,平行线分线段成比例,垂直平分线的判定及性质等,画出草图进行分类讨论是解决问题的关键.19(2023·辽宁大连·统考中考真题)如图,在正方形ABCD 中,AB =3,延长BC 至E ,使CE =2,连接AE ,CF 平分∠DCE 交AE 于F ,连接DF ,则DF 的长为.【答案】3104【分析】如图,过F 作FM ⊥BE 于M ,FN ⊥CD 于N ,由CF 平分∠DCE ,可知∠FCM =∠FCN =45°,可得四边形CMFN 是正方形,FM ∥AB ,设FM =CM =NF =CN =a ,则ME =2-a ,证明△EFM ∽△EAB ,则FM AB=ME BE ,即a 3=2-a 3+2,解得a =34,DN =CD -CN =94,由勾股定理得DF =DN 2+NF 2,计算求解即可.【详解】解:如图,过F 作FM ⊥BE 于M ,FN ⊥CD 于N ,则四边形CMFN 是矩形,FM ∥AB ,∵CF 平分∠DCE ,∴∠FCM =∠FCN =45°,∴CM =FM ,∴四边形CMFN 是正方形,设FM =CM =NF =CN =a ,则ME =2-a ,∵FM ∥AB ,∴△EFM ∽△EAB ,∴FM AB =ME BE ,即a 3=2-a 3+2,解得a =34,∴DN =CD -CN =94,由勾股定理得DF =DN 2+NF 2=3104,故答案为:3104.【点睛】本题考查了正方形的判定与性质,勾股定理,相似三角形的判定与性质.解题的关键在于对知识的熟练掌握与灵活运用.20(2023·广东·统考中考真题)边长分别为10,6,4的三个正方形拼接在一起,它们的底边在同一直线上(如图),则图中阴影部分的面积为.【答案】15【分析】根据正方形的性质及相似三角形的性质可进行求解.【详解】解:如图,由题意可知AD =DC =10,CG =CE =GF =6,∠CEF =∠EFG =90°,GH =4,∴CH =10=AD ,∵∠D =∠DCH =90°,∠AJD =∠HJC ,∴△ADJ ≌△HCJ AAS ,∴CJ =DJ =5,∴EJ =1,∵GI ∥CJ ,∴△HGI ∽△HCJ ,∴GI CJ =GH CH=25,∴GI =2,∴FI =4,∴S 梯形EJIF =12EJ +FI ⋅EF =15;故答案为:15.【点睛】本题主要考查正方形的性质及相似三角形的性质与判定,熟练掌握正方形的性质及相似三角形的性质与判定是解题的关键.21(2023·天津·统考中考真题)如图,在边长为3的正方形ABCD 的外侧,作等腰三角形ADE ,EA =ED =52.(1)△ADE 的面积为;(2)若F 为BE 的中点,连接AF 并延长,与CD 相交于点G ,则AG 的长为.【答案】3;13【分析】(1)过点E 作EH ⊥AD ,根据正方形和等腰三角形的性质,得到AH 的长,再利用勾股定理,求出EH 的长,即可得到△ADE 的面积;(2)延长EH 交AG 于点K ,利用正方形和平行线的性质,证明△ABF ≌△KEF ASA ,得到EK 的长,进而得到KH 的长,再证明△AHK ∽△ADG ,得到KH GD =AH AD ,进而求出GD 的长,最后利用勾股定理,即可求出AG的长.【详解】解:(1)过点E作EH⊥AD,∵正方形ABCD的边长为3,∴AD=3,∵△ADE是等腰三角形,EA=ED=52,EH⊥AD,∴AH=DH=12AD=32,在Rt△AHE中,EH=AE2-AH2=522-32 2=2,∴S△ADE=12AD⋅EH=12×3×2=3,故答案为:3;(2)延长EH交AG于点K,∵正方形ABCD的边长为3,∴∠BAD=∠ADC=90°,AB=3,∴AB⊥AD,CD⊥AD,∵EK⊥AD,∴AB∥EK∥CD,∴∠ABF=∠KEF,∵F为BE的中点,∴BF=EF,在△ABF和△KEF中,∠ABF=∠KEF BF=EF∠AFB=∠KFE,∴△ABF≌△KEF ASA,∴EK=AB=3,由(1)可知,AH=12AD,EH=2,∴KH=1,∵KH∥CD,∴△AHK∽△ADG,∴KH GD =AH AD,∴GD=2,在Rt△ADG中,AG=AD2+GD2=32+22=13,故答案为:13.【点睛】本题考查了正方形的性质,等腰三角形的性质,全等三角形的判定和性质,相似三角形的判定和性质,勾股定理等知识,作辅助线构造全等三角形和相似三角形是解题关键.22(2023·四川泸州·统考中考真题)如图,E,F是正方形ABCD的边AB的三等分点,P是对角线AC上的动点,当PE+PF取得最小值时,APPC的值是.【答案】27【分析】作点F 关于AC 的对称点F ,连接EF 交AC 于点P ,此时PE +PF 取得最小值,过点F 作AD 的垂线段,交AC 于点K ,根据题意可知点F 落在AD 上,设正方形的边长为a ,求得AK 的边长,证明△AEP ∽△KF P ,可得KP AP=2,即可解答.【详解】解:作点F 关于AC 的对称点F ,连接EF 交AC 于点P ,过点F 作AD 的垂线段,交AC 于点K ,由题意得:此时F 落在AD 上,且根据对称的性质,当P 点与P 重合时PE +PF 取得最小值,设正方形ABCD 的边长为a ,则AF =AF =23a ,∵四边形ABCD 是正方形,∴∠F AK =45°,∠P AE =45°,AC =2a∵F K ⊥AF ,∴∠F AK =∠F KA =45°,∴AK =223a ,∵∠F P K =∠EP A ,∴△E KP ∽△EAP ,∴F K AE =KP AP=2,∴AP =13AK =292a ,∴CP =AC -AP =792a , ∴AP CP=27,∴当PE +PF 取得最小值时,AP PC 的值是为27,故答案为:27.【点睛】本题考查了四边形的最值问题,轴对称的性质,相似三角形的证明与性质,正方形的性质,正确画出辅助线是解题的关键.23(2023·山西·统考中考真题)如图,在四边形ABCD 中,∠BCD =90°,对角线AC ,BD 相交于点O .若AB =AC =5,BC =6,∠ADB =2∠CBD ,则AD 的长为.【答案】973【分析】过点A 作AH ⊥BC 于点H ,延长AD ,BC 交于点E ,根据等腰三角形性质得出BH =HC =12BC =3,根据勾股定理求出AH =AC 2-CH 2=4,证明∠CBD =∠CED ,得出DB =DE ,根据等腰三角形性质得出CE =BC =6,证明CD ∥AH ,得出CD AH=CE HE ,求出CD =83,根据勾股定理求出DE =CE 2+CD 2=62+83 2=2973,根据CD ∥AH ,得出DE AD =CE CH ,即2973AD=63,求出结果即可.【详解】解:过点A 作AH ⊥BC 于点H ,延长AD ,BC 交于点E ,如图所示:则∠AHC =∠AHB =90°,∵AB =AC =5,BC =6,∴BH =HC =12BC =3,∴AH =AC 2-CH 2=4,∵∠ADB =∠CBD +∠CED ,∠ADB =2∠CBD ,∴∠CBD =∠CED ,∴DB =DE ,∵∠BCD =90°,∴DC ⊥BE ,∴CE =BC =6,∴EH =CE +CH =9,∵DC ⊥BE ,AH ⊥BC ,∴CD ∥AH ,∴△ECD ~△EHA ,∴CD AH =CE HE ,即CD 4=69,解得:CD =83,∴DE =CE 2+CD 2=62+83 2=2973,∵CD ∥AH ,∴DE AD=CE CH ,即2973AD =63,解得:AD =973.故答案为:973.【点睛】本题主要考查了三角形外角的性质,等腰三角形的判定和性质,勾股定理,平行线分线段成比例,相似三角形的判定与性质,平行线的判定,解题的关键是作出辅助线,熟练掌握平行线分线段成比例定理及相似三角形的判定与性质.三、解答题24(2023·湖南·统考中考真题)在Rt △ABC 中,∠BAC =90°,AD 是斜边BC 上的高.(1)证明:△ABD ∽△CBA ;(2)若AB =6,BC =10,求BD 的长.【答案】(1)见解析(2)BD =185【分析】(1)根据三角形高的定义得出∠ADB =90°,根据等角的余角相等,得出∠BAD =∠C ,结合公共角∠B =∠B ,即可得证;(2)根据(1)的结论,利用相似三角形的性质即可求解.【详解】(1)证明:∵∠BAC =90°,AD 是斜边BC 上的高.∴∠ADB =90°,∠B +∠C =90°∴∠B +∠BAD =90°,∴∠BAD =∠C又∵∠B =∠B∴△ABD ∽△CBA ,(2)∵△ABD ∽△CBA∴AB CB =BD AB,又AB =6,BC =10∴BD =AB 2CB=3610=185.【点睛】本题考查了相似三角形的性质与判定,熟练掌握相似三角形的性质与判定是解题的关键.25(2023·湖南·统考中考真题)如图,CA ⊥AD ,ED ⊥AD ,点B 是线段AD 上的一点,且CB ⊥BE .已知AB =8,AC =6,DE =4.(1)证明:△ABC∽△DEB.(2)求线段BD的长.【答案】(1)见解析(2)BD=3【分析】(1)根据题意得出∠A=∠D=90°,∠C+∠ABC=90°,∠ABC+∠EBD=90°,则∠C=∠EBD,即可得证;(2)根据(1)的结论,利用相似三角形的性质列出比例式,代入数据即可求解.【详解】(1)证明:∵AC⊥AD,ED⊥AD,∴∠A=∠D=90°,∠C+∠ABC=90°,∵CE⊥BE,∴∠ABC+∠EBD=90°,∴∠C=∠EBD,∴△ABC∽△DEB;(2)∵△ABC∽△DEB,∴AB DE =AC BD,∵AB=8,AC=6,DE=4,∴8 4=6 BD,解得:BD=3.【点睛】本题考查了相似三角形的性质与判定,熟练掌握相似三角形的性质与判定是解题的关键.26(2023·四川眉山·统考中考真题)如图,▱ABCD中,点E是AD的中点,连接CE并延长交BA的延长线于点F.(1)求证:AF=AB;(2)点G是线段AF上一点,满足∠FCG=∠FCD,CG交AD于点H,若AG=2,FG=6,求GH的长.【答案】(1)见解析(2)65【分析】(1)根据平行四边形的性质可得AB∥CD,AB=CD,证明△AEF≅△DEC ASA,推出AF= CD,即可解答;(2)通过平行四边形的性质证明GC=GF=6,再通过(1)中的结论得到DC=AB=AF=8,最后证明△AGH∽△DCH,利用对应线段比相等,列方程即可解答.【详解】(1)证明:∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,∴∠EAF=∠D,∵E是AD的中点,∴AE=DE,∵∠AEF =∠CED ,∴△AEF ≅△DEC ASA ,∴AF =CD ,∴AF =AB ;(2)解:∵四边形ABCD 是平行四边形,∴DC =AB =AF =FG +GA =8,DC ∥FA ,∴∠DCF =∠F ,∠DCG =∠CGB ,∵∠FCG =∠FCD ,∴∠F =∠FCG ,∴GC =GF =6,∵∠DHC =∠AHG ,∴△AGH ∽△DCH ,∴GH CH =AG DC,设HG =x ,则CH =CG -GH =6-x ,可得方程x 6-x =28,解得x =65,即GH 的长为65.【点睛】本题考查了平行四边形的性质,等腰三角形的判定和性质,相似三角形的判定和性质,熟练运用上述性质证明三角形相似是解题的关键.27(2023·四川凉山·统考中考真题)如图,在▱ABCD 中,对角线AC 与BD 相交于点O ,∠CAB =∠ACB ,过点B 作BE ⊥AB 交AC 于点E .(1)求证:AC ⊥BD ;(2)若AB =10,AC =16,求OE 的长.【答案】(1)见详解(2)92【分析】(1)可证AB =CB ,从而可证四边形ABCD 是菱形,即可得证;(2)可求OB =6,再证△EBO ∽△BAO ,可得EO BO =BO AO,即可求解.【详解】(1)证明:∵∠CAB =∠ACB ,∴AB =CB ,∵四边形ABCD 是平行四边形,∴四边形ABCD 是菱形,∴AC ⊥BD .(2)解:∵四边形ABCD 是平行四边形,∴OA =12AC =8,∵AC ⊥BD ,BE ⊥AB ,∴∠AOB =∠BOE =∠ABE =90°,∴OB =AB 2-OB 2=102-82=6,∵∠EBO +∠BEO =90°,∠ABO +∠EBO =90°,∴∠BEO =∠ABO ,∴△EBO ∽△BAO ,∴EO BO =BO AO ,∴EO 6=68解得:OE =92.【点睛】本题考查了平行四边形的性质,菱形的判定及性质,勾股定理,三角形相似的判定及性质,掌握相关的判定方法及性质是解题的关键.28(2023·江苏扬州·统考中考真题)如图,点E 、F 、G 、H 分别是▱ABCD 各边的中点,连接AF 、CE 相交于点M ,连接AG 、CH 相交于点N .(1)求证:四边形AMCN 是平行四边形;(2)若▱AMCN 的面积为4,求▱ABCD 的面积.【答案】(1)见解析(2)12【分析】(1)根据平行四边形的性质,线段的中点平分线段,推出四边形AECG ,四边形AFCH 均为平行四边形,进而得到:AM ∥CN ,AN ∥CM ,即可得证;(2)连接HG ,AC ,EF ,推出S △ANH S △ANC =HN CN=12,S △FMC S △AMC =12,进而得到S △ANH +S △FMC =12S △ANC +S △AMC =12S ▱AMCN =2,求出S ▱AFCH =S △ANH +S △FMC +S ▱AMCN =2+4=6,再根据S ▱ABCD =2S ▱AFCH ,即可得解.【详解】(1)证明:∵▱ABCD ,∴AB ∥CD ,AD ∥BC ,AB =CD ,AD =BC ,∵点E 、F 、G 、H 分别是▱ABCD 各边的中点,∴AE =12AB =12CD =CG ,AE ∥CG ,∴四边形AECG 为平行四边形,同理可得:四边形AFCH 为平行四边形,∴AM ∥CN ,AN ∥CM ,∴四边形AMCN 是平行四边形;(2)解:连接HG ,AC ,EF ,∵H ,G 为AD ,CD 的中点,∴HG ∥AC ,HG =12AC ,∴△HNG ∽△CNA ,∴HN CN =HG AC =12,∴S △ANH S △ANC =HN CN=12,同理可得:S △FMC S △AMC =12∴S △ANH +S △FMC =12S △ANC +S △AMC =12S ▱AMCN =2,∴S ▱AFCH =S △ANH +S △FMC +S ▱AMCN =2+4=6,∵AH =12AD ,∴S ▱ABCD =2S ▱AFCH =12.【点睛】本题考查平行四边形的判定和性质,三角形的中位线定理,相似三角形的判定和性质,熟练掌握平行四边形的性质,以及三角形的中位线定理,证明三角形相似,是解题的关键.29(2023·上海·统考中考真题)如图,在梯形ABCD 中AD ∥BC ,点F ,E 分别在线段BC ,AC 上,且∠FAC =∠ADE ,AC =AD(1)求证:DE =AF(2)若∠ABC =∠CDE ,求证:AF 2=BF ⋅CE【答案】见解析【分析】(1)先根据平行线的性质可得∠DAE =∠ACF ,再根据三角形的全等的判定可得△DAE ≅△ACF ,然后根据全等的三角形的性质即可得证;(2)先根据全等三角形的性质可得∠AFC =∠DEA ,从而可得∠AFB =∠CED ,再根据相似三角形的判定可得△ABF ∼△CDE ,然后根据相似三角形的性质即可得证.【详解】(1)证明:∵AD ∥BC ,∴∠DAE =∠ACF ,在△DAE和△ACF中,∠DAE=∠ACF AD=CA∠ADE=∠CAF,∴△DAE≅△ACF ASA,∴DE=AF.(2)证明:∵△DAE≅△ACF,∴∠AFC=∠DEA,∴180°-∠AFC=180°-∠DEA,即∠AFB=∠CED,在△ABF和△CDE中,∠AFB=∠CED ∠ABF=∠CDE,∴△ABF∼△CDE,∴AF CE =BF DE,由(1)已证:DE=AF,∴AF CE =BF AF,∴AF2=BF⋅CE.【点睛】本题考查了三角形全等的判定与性质、相似三角形的判定与性质,熟练掌握相似三角形的判定与性质是解题关键.。
人教版数学九年级下27.1《图形的相似》测试(含答案及解析)
人教版数学九年级下27.1《图形的相似》测试(含答案及解析)1 / 11图形的相似测试时间:60 总分:100一、选择题(本大题共9小题,共36.0分)1. 下列四组图形中,一定相似的图形是A. 各有一个角是 的两个等腰三角形B. 有两边之比都等于2:3的两个三角形C. 各有一个角是 的两个等腰三角形D. 各有一个角是直角的两个三角形2. 下列说法正确的是A. 矩形都是相似图形B. 各角对应相等的两个五边形相似C. 等边三角形都是相似三角形D. 各边对应成比例的两个六边形相似3. 下列结论中,错误的有:所有的菱形都相似;放大镜下的图形与原图形不一定相似;等边三角形都相似;有一个角为110度的两个等腰三角形;所有的矩形不一定相似.A. 1个B. 2个C. 3个D. 4个4. 下列图形一定是相似图形的是A. 任意两个菱形B. 任意两个正三角形C. 两个等腰三角形D. 两个矩形5. 在下面的图形中,相似的一组是A.B.C.D.6. 如图,在矩形、锐角三角形、正五边形、直角三角形的外边加一个宽度一样的外框,保证外框的边与原图形的对应边平行,则外框与原图一定相似的有A. 1个B. 2个C. 3个D. 4个 7. 下列图形一定相似的是A. 两个矩形B. 两个等腰梯形C. 对应边成比例的两个四边形D. 有一个内角相等的菱形8.在下列命题中,正确的是A. 邻边之比相等的两个平行四边形一定相似B. 有一个角是两个等腰三角形一定相似C. 两个直角三角形一定相似D. 有一个角是的两个菱形一定相似9.用放大镜将图形放大,应该属于A. 平移变换B. 相似变换C. 对称变换D. 旋转变换二、填空题(本大题共8小题,共24.0分)10.若一个三角形的各边长扩大为原来的5倍,则此三角形的周长扩大为原来的______倍11.如图,的边长分别为1,,2,正六边形网格是由24个边长为2的正三角形组成,选择格点为顶点画,使得 ∽ 如果相似比,那么k的值可以是______ .12.如图,13个边长为1的小正方形,排列形式如图,把它们分割,使分割后能拼成一个大正方形请在如图所示的网格中网格的边长为中,用直尺作出这个大正方形.13.利用复印机的缩放功能,将原图中边长为5厘米的一个等边三角形放大成边长为20厘米的等边三角形,那么放大前后的两个三角形的周长比是______ .14.如图,______ 与______ 相似.15.如图,请在方格图中画出一个与相似且相似比不为1的、E、F必须在方格图的交叉点.人教版数学九年级下27.1《图形的相似》测试(含答案及解析)3 / 1116. 已知 在坐标平面内三顶点的坐标分别为 、、 以B 为位似中心,画出与 相似 与图形同向 ,且相似比是3的三角形,它的三个对应顶点的坐标分别是______ .17. 如图中的等腰梯形 是公园中儿童游乐场的示意图 为满足市民的需求,计划扩建该游乐场 要求新游乐场以MN 为对称轴,且新游乐场与原游乐场相似,相似比为2: 又新游乐场的一条边在直线BC 上,请你在图中画出新游乐场的示意图.三、解答题(本大题共5小题,共40.0分)18. 如图,在坐标系的第一象限建立网格,网格中的每个小正方形边长都为1,格点的顶点坐标分别为 、 、 .若 外接圆的圆心为P ,则点P 的坐标为______ .以点D 为顶点,在网格中画一个格点 ,使 ∽ ,且相似比为1: 画出符合要求的一个三角形即可19.已知,如图,中,,,D为BC边上一点,.求证: ∽ ;在原图上作交AC与点E,请直接写出另一个与相似的三角形,并求出DE的长.20.如图,已知,,请用尺规过点A作一条直线,使其将分成两个相似的三角形保留作图痕迹,不写作法21.已知:如图,在菱形ABCD中,垂足为E,对角线,,求边AB的长;的值.人教版数学九年级下27.1《图形的相似》测试(含答案及解析)5 / 1122. 如图,已知 , ,请用尺规过点A 作一条直线,使其将 分成两个相似的三角形 保留作图痕迹,不写作法答案和解析【答案】1. C2. C3. B4. B5. C6. C7. D8. D9. B10. 511. 2,,412. 解:如图所示:所画正方形即为所求.13. 1:414. ;15. 解:所画图形如下:就是所求的相似三角形.16. 、、17. 解:如图所示:18.19. 证明:,,,,,,,∽ ;解:,∽ ,∽ ,.人教版数学九年级下27.1《图形的相似》测试(含答案及解析)7 / 1120. 解:如图,AD 为所作.21. 解: 连接AC ,AC 与BD 相交于点O ,四边形ABCD 是菱形,, ,中, ,,;,菱形 ,,,,,.22. 解:如图所示:AD 即为所求.【解析】1. 解:A 、各有一顶角或底角是 的两个等腰三角形相似,故错误,不符合题意;B 、有两边之比为2:3的两个三角形不一定相似,故错误,不符合题意;C 、各有一个角是 的两个等腰三角形相似,正确,符合题意;D 、两个直角三角形不一定相似,故错误,不符合题意;故选C .利用相似图形的定义逐一判断后即可确定正确的选项.本题考查了相似图形的知识,能够了解相似图形的定义是解答本题的关键,难度不大. 2. 解: 矩形对应角相等,对应边不一定成比例,所以不一定是相似图形,故本选项错误;各角对应相等的两个五边形相似,对应角相等,对应边不一定成比例,所以不一定是相似图形,故本选项错误;C . 等边三角形对应角相等,对应边成比例,所以是相似三角形,故本选项正确; 各边对应成比例的六边形对应角不一定相等,所以不一定是相似六边形,故本选项错误;故选:C.根据相似图形的定义,对应边成比例,对应角相等对各选项分析判断后利用排除法求解.本题考查了相似图形的定义,熟记定义是解题的关键,要注意从边与角两个方面考虑解答.3. 解::菱形的两组对角不一定分别对应相等,故所有的菱形不一定都相似;即:选项错误.:放大镜下的图形与原图形只是大小不相等,但形状相同,所以它们一定相似;即:选项错误.:等边三角形的三个内角相等,三条边都相等,故所有的等边三角形都相似;即:选项正确:有一个角为110度的两个等腰三角形一定相似因为它们的顶角均为,两锐角均为,根据“两内角对应相等的两个三角形相似”即可判定故:选项正确.:只有长与宽对应成比例的两个矩形相似,故选项正确故:选B利用相似的定义逐一的对五个选项进行判定.本题考查了相似图形的判定,解题的关键是要掌握相似图形的概念与判定方法.4. 解:A、任意两个菱形,对应边成比例,对应角不一定相等,不符合相似的定义,故不符合题意;B、任意两个等边三角形,对应角相等,对应边一定成比例,符合相似的定义,故符合题意;C、两个两个等腰三角形,无法确定形状是否相等,故不符合题意;D、两个矩形,对应角相等,对应边不一定成比例,故不符合题意.故选:B.根据相似图形的定义和图形的性质对每一项进行分析,即可得出一定相似的图形.本题考查相似形的定义,熟悉各种图形的性质和相似图形的定义是解题的关键.5. 解:A、六边形与五边形不可能是相似图形,故本选项错误;B、两图形不是相似图形,故本选项错误;C、,两三角形相似,故本选项正确;D、直角梯形与等腰梯形不是相似图形,故本选项错误.故选C.根据相似图形的定义对各选项分析判断后利用排除法求解.本题考查了相似图形的判定,是基础题,准确识图是解题的关键.6. 解:矩形不相似,因为其对应角的度数一定相同,但对应边的比值不一定相等,不符合相似的条件;锐角三角形、直角三角形的原图与外框相似,因为其三个角均相等,三条边均对应成比例,符合相似的条件;正五边形相似,因为它们的边长都对应成比例、对应角都相等,符合相似的条件.故选C.根据相似多边形的判定定理对各个选项进行分析,从而确定最后答案.边数相同、各角对应相等、各边对应成比例的两个多边形是相似多边形.7. 解:A、两个矩形的对应角相等,但对应边的比不一定相等,故错误;B、两个等腰梯形不一定相似,故错误;C、对应边成比例且对应角相等的两个四边形是全等形,故错误;D、有一个内角相等的菱形是相似图形,故正确,故选D.根据相似图形的定义,结合选项,用排除法求解.本题考查相似形的定义,熟悉各种图形的性质是解题的关键.人教版数学九年级下27.1《图形的相似》测试(含答案及解析)9 / 11 8. 解:A 、邻边之比相等的两个平行四边形不一定相似,所以A 选项错误;B 、有一个角是 两个等腰三角形不一定相似,所以B 选项错误;C 、两个直角三角形不一定相似,所以C 选项错误;D 、有一个角是 的两个菱形一定相似,所以D 选项正确.故选:D .根据四边形相似要有对应角相等,对应边的比相等可对A 、D 进行判断;根据 的角可能为顶角,也可能为底角可以对B 进行判断;根据三角形判定方法对C 进行判断. 本题考查了命题与定理:判断一件事情的语句,叫做命题 许多命题都是由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,一个命题可以写成“如果 那么 ”形式;有些命题的正确性是用推理证实的,这样的真命题叫做定理. 9. 解:根据相似图形的定义知,用放大镜将图形放大,属于图形的形状相同,大小不相同,所以属于相似变换.故选:B .根据放大镜成像的特点,结合各变换的特点即可得出答案.本题考查的是相似形的识别,关键要联系图形,根据相似图形的定义得出.10. 解: 一个三角形的各边长扩大为原来的5倍,扩大后的三角形与原三角形相似,相似三角形的周长的比等于相似比,这个三角形的周长扩大为原来的5倍,故答案为:5.由题意一个三角形的各边长扩大为原来的5倍,根据相似三角形的性质及对应边长成比例来求解.本题考查了相似三角形的性质:相似三角形的周长的比等于相似比.11.解:的边长分别为1,,2为直角三角形, , ,根据等边三角形的三线合一,可作三边比为1: :2的三角形,故相似比 ,k 可取2, ,4.故答案为:2, ,4.根据题意可得:在正六边形网格找与 相似的三角形;即找三边的比值为1: :2的直角三角形;分析图形可得:共三种情况得出答案即可.此题主要考查了相似三角形的判定与性质,结合各边长得出符合题意的图形是解题关键. 12. 直接根据阴影部分面积得出正方形边长,进而得出答案.此题主要考查了应用设计与作图,正确得出正方形边长是解题关键.13. 解:因为原图中边长为5cm 的一个等边三角形放大成边长为20cm 的等边三角形, 所以放大前后的两个三角形的面积比为5: :4,故答案为:1:4.根据等边三角形周长的比是三角形边长的比解答即可.本题考查了相似三角形对应边比值相等的性质,关键是根据等边三角形面积的比是三角形边长的比的平方解答.14. 解:利用相似图形对应角相等,对应边成比例,只有,图形全等,符合题意.故答案为:,.根据相似图形的定义直接判断得出即可.本题考查的是相似形的定义,结合图形,即图形的形状相同,但大小不一定相同的变换是相似变换.15. 利用勾股定理计算出三角形的三边长,再让它的各边都乘以2,得到新三角形的三边长,从网格中画出即可.本题主要考查了作图中的相似变换问题,难度不大,注意看清题意是关键.16. 解:把原三角形的三边对应的缩小或放大一定的比例即可得到对应的相似图形.所画图形如下所示:它的三个对应顶点的坐标分别是:、、.故答案为:、、.根据把原三角形的三边对应的缩小或放大一定的比例即可得到对应的相似图形,在改变的过程中保持形状不变大小可变即可得出答案.本题考查了相似变换作图的知识,注意图形的相似变换不改变图形中每一个角的大小;图形中的每条线段都扩大或缩小相同的倍数.17. 先作轴对称图形,再把它利用位似变换放大为相似比为2:1的等腰梯形.考查了作图相似变换,作位似变换的图形的依据是相似的性质画位似图形的一般步骤为:确定位似中心,分别连接并延长位似中心和能代表原图的关键点;根据相似比,确定能代表所作的位似图形的关键点;顺次连接上述各点,得到放大或缩小的图形.18. 解:如图,点P即为所求,其坐标为,故答案为:;如图,即为所求三角形.分别作AC、AB的中垂线,两直线的交点即为所求点P;根据相似比为1:2可得,,,据此可得.本题主要考查三角形的外心和相似图形,熟练掌握三角形的外心到三顶点的距离相等及相似三角形的性质是解题的关键.19. 在与中,有,根据已知边的条件,只需证明夹此角的两边对应成比例即可;由知 ∽ ,又,易证 ∽ ,则: ∽ ,然人教版数学九年级下27.1《图形的相似》测试(含答案及解析)后根据相似三角形的对应边成比例得出DE的长.本题主要考查了相似三角形的判定及性质平行于三角形的一边的直线与其他两边相交,所构成的三角形与原三角形相似;两组对应边的比相等且相应的夹角相等的两个三角形相似;相似三角形的对应边成比例.20. 过点A作于D,利用等角的余角相等可得到,则可判断与相似.本题考查了作图相似变换:两个图形相似,其中一个图形可以看作由另一个图形放大或缩小得到解决本题的关键是利用有一组锐角相等的两直角三角形相似.21. 首先连接AC,AC与BD相交于点O,由四边形ABCD是菱形,可得,,又由,可求得OC的长,然后由勾股定理求得边AB的长;由,利用菱形,即可求得AE的长,在中可求得BE,则可求得的余弦值.本题主要考查菱形的性质、勾股定理以及三角函数等知识此题难度适中,注意掌握辅助线的作法、数形结合思想的应用.22. 直接利用直角三角形的性质过点A作,即可得出答案.此题主要考查了相似变换,正确应用直角三角形的性质是解题关键.11 / 11。
27.1图形的相似(基础练习)

巩固练习第27章 图形的相似27.1 图形的相似(1)1、在下面的图形中,形状相似的一组是( )2、下列图形一定是相似图形的是( )A .任意两个菱形B .任意两个正三角形C .两个等腰三角形D .两个矩形3、要做甲、乙两个形状相同(相似)的三角形框架,已知三角形框架甲的三边分别为50cm 、60cm 、80cm ,三角形框架乙的一边长为20cm ,那么,符合条件的三角形框架乙共有( )A .1种B .2种C .3种D .4种4、下列说法正确的是( )A .人们从平面镜及哈哈镜里看到的不同镜像相似.B .人们从平面镜里看到的像与人的关系是相似图形,但不是全等图形.C .拍照时,镜头的取景与照片上的画面是相似的D .放幻灯片时投在屏幕上的画面与幻灯片上的图形是全等的5、在比例尺是1:8000000的“中国政区”地图上,量得福州与上海之间的距离时7.5cm ,那么福州与上海之间的实际距离是多少?27.1图形的相似(2)巩固练习:1.△ABC 与△DEF 相似,且相似比是32,则△DEF 与△ABC 与的相似比是( ).A .32B .23C .52D .942.下列所给的条件中,能确定相似的有( )(1)两个半径不相等的圆;(2)所有的正方形; (3)所有的等腰三角形;(4)所有的等边三角形; (5)所有的等腰梯形;(6)所有的正六边形.A .3个B .4个C .5个D .6个3. 图中两个四边形是相似形,仔细观察这两个图形,它们对应边之间存在怎样的关系?对应角之间又有什么关系?4.如图,四边形EFGH相似于四边形ABCD,求∠A、∠C、∠H以及x、y、z的值.5.如图,△ABC与△DEF相似,求未知边x、y的长度。
6.如图,AB∥EF∥CD,CD=4,AB=9,若梯形CDEF与梯形EF AB相似,求EF的长.。
27.1图形的相似(2).

练习: 30 15 20 x
7、如图两矩形相似, 45 = .
x
8、在下面的两组图形中,各有两个相似三角形, 试确定x , y , m , n 的值。
X=32 x 20 33 22 30
( 1)
2
3a
n°
10
48
45°
85°
( 2)
° 2a 50 y m° ° 45
拓展:根据已知条件,找出图中相似三角形的对应边。
各对应角相等、各对应边成比例的两个多边形 叫做相似多边形(similar polygons);
相似多边形对应边的比叫做相似比 (similarity ratio) 相似比与叙述的顺序有关. 相似多边形的对应角相等,对应边成比例.
(1)如果两个多边形不相似,那么它们的各角可能对应相等
如:矩形
(2)如果两个多边形不相似,那么它们的各边可能对应成比例.
例3.如图已知△ABC∽△ADE , AE=50cm,EC=30cm,BC=70cm,∠BAC=450,∠C=400. (1)求∠AED和∠ADE的大小;(2)求DE的长.
解: (1)因为△ ABC ∽△ ADE, 所以由相似三角形对应 角相等,得∠AED=∠C=400. 在△ADE中, ∠ADE=1800-400-450=950. (2)由相似三角形对应边成比例,得
(2)线段AB、BC、CF、CD是否成比例? (3)矩形ABCD与矩形CFED相似吗?
解:(1) CF CD
4 7 43 3 4
A
E
D
AB 3 ( 2) BC 4
AB CF BC CD
3
F 7 (3)矩形ABCD与矩形CFED相似 4 4 思考:矩形ABCD与矩形ABFE相似吗?为什么?
27.1 图形的相似(知识解读+达标检测)(学生版) 2024-2025学年九年级数学下册(人教版)

27.1 图形的相似【考点1 比例性质】【考点2 比例线段】【考点3 成比例线段】【考点4 黄金分割比】【考点5 由平行线判断成比例的线段】【考点6 由平行截线求相关相关线段的长或比值】【考点7 相似图形】【考点8相似多边形的性质】知识点1 比例线段1.线段的比:如果选用同一长度单位量得两条线段a、b长度分别是m、n,那么就说这两条线段的比是a:b=m:n,或写成a mb n =.2.成比例线段:对于四条线段a、b、c、d,如果其中两条线段的比与另两条线段的比相等,如a:b=c:d,我们就说这四条线段是成比例线段,简称比例线段.3.比例的基本性质:(1)若a:b=c:d,则ad=bc;(2)若a:b=b:c,则2b =ac(b称为a、c的比例中项).【考点1 比例性质】【典例1】若x2=y3=z4≠0,则x−y+z2y=.【变式1-1】.若a4=b3,则ab的值是()A.34B.43C.12D.112【变式1-2】已知3a =5b,则3a+2ba−b的值为()A.−192B.−19C.192D.19【变式1-3】已知ab =cd=ef=12,则a−3c+2eb−3d+2f=()A.12B.13C.14D.15【考点2 比例线段】【典例2】已知线段a,b满足a5=b12,且a+b=34.(1)求a,b的值;(2)若线段x是线段a,b的比例中项,求x的值.【变式2-1】小红的爸爸是汽车制造厂的工程师.他要将一个长4毫米、宽2毫米的零件画在一张A3纸(42cm×29.7cm)上,适合的比例尺是( )A.1∶80B.80∶1C.1∶800D.800∶1【变式2-2】线段1cm、4cm的比例中项为cm.【变式2-3】点C在线段AB上,若ACCB =35,则ABCB=.【考点3 成比例线段】【典例3】下列各组中的四条线段成比例的是()A.1、2、3、4B.2、3、4、5C.3、4、6、9D.2、3、4、6【变式3-1】下面四组线段中不能成比例线段的是()A.3、6、2、4B.4、6、5、10C.1、2、3、6D.25、20、4、5【变式3-2】下列四组线段中,是成比例线段的一组是()A.a=1,b=2,c=3,d=4B.a=1,b=C.a=5,b=6,c=7,d=8D.a=4,b=6,c=6,d=8【变式3-3】下列四组长度的线段中,是成比例线段的是( )A .4cm ,5cm ,6cm ,7cm B .3cm ,4cm ,5cm ,8cm C .3cm ,5cm ,9cm ,15cmD .1cm ,3cm ,4cm ,8cm知识点2 黄金分割比1.黄金分割的定义: 点C 把线段AB 分割成AC 和CB 两段,如果AC BCAB AC=,那么线段AB 被点C 黄金分割,点C 叫做线段AB 的黄金分割点,AC 与AB 的比叫做黄金比.注意:AC AB =≈叫做黄金分割值).2.作一条线段的黄金分割点:如图,已知线段AB ,按照如下方法作图:(1)经过点B 作BD ⊥AB ,使BD =21AB .(2)连接AD ,在DA 上截取DE =DB .(3)在AB 上截取AC =AE .则点C 为线段AB 的黄金分割点.注意:一条线段的黄金分割点有两个.【考点4 黄金分割比】【典例4】射影中有一种拍摄手法叫黄金分割构图法,其原理是:如图,将正方形ABCD 的边BC 取中点O ,以O 为圆心,线段OD 为半径作圆,其与边BC 的延长线交于点E ,这样就把正方形ABCD 延伸为黄金矩形ABEF ,若CE =4,则AB = .【变式4-1】如图,点P 是线段AB 的黄金分割点,且PA >PB ,若AB =2,则PA 的长度是( )AB .C .D .1【变式4-2】宽与长的比是黄金分割数金矩形的设计.如图,已知四边形ABCD是黄金矩形,若长 AB =,则该矩形ABCD 的面积为.(结果保留根号)【变式4-3】如图,在△ABC 中,AB =AC ,∠A =108°,以B 为圆心,BA 为半径,两弧交BC 于点D ,此时,点D 为线段BC 的黄金分割点,若BC =2,则BD 的长为.知识点3 平行线分线段成比例类型1 平行线等分线段定理如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等.几何语言:,BD FDAC EC ==如图一:直线A B //C D //E F,直线A E 、B F 分别交A B 、C D 、E F 于A 、B 、C 、D 、E 、F.若则图一拓展:1).如果一组等距的平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等;1212=,BD FD=如图一:直线A B //C D //E F,直线A E 、B F 分别交A B 、C D 、E F 于A 、B 、C 、D 、E 、F.且A B 、C D 、E F 距离为d 、d 若d d 则A C =E C ,2).经过三角形一边中点且平行于另一边的直线平分第三边;∆如图二:在A B C 中,D 为A B 中点,D E //B C 交A C 于点F ,则A E =C E 。
人教版九年级下册27.1图形的相似课时练
人教版九年级下册27.1 图形的相像课时练(人教版)九年级下第二十七章图形的相像课时练(锦州中学)学校:姓名:班级:考号:评卷人得分一、选择题1.以下图形中 ,不是相像图形的有 ()A. 0组B.1组C.2组D. 3组2. 假如一个矩形与它的一半矩形是相像形,那么大矩形与小矩形的相像比是()A. ∶ 1B. ∶2C. 2∶1D. 1∶23. 以下各组中的四条线段成比率的是( )A. 4 cm,2 cm,1 cm,3 cmB. 1 cm,2 cm,3 cm,5 cmC. 3 cm,4 cm,5 cm,6 cmD. 1 cm,2 cm,2 cm,4 cm4.要做甲、乙两个形状同样 (相像 )的三角形框架 ,已知三角形框架甲的三边分别为50 cm,60 cm,80 cm, 三角形框架乙的一边长为20 cm,那么切合条件的三角形框架乙共有()A. 1种B.2种C.3种D. 4种5.如图 ,用放大镜将图形放大 ,应当属于 ()A. 相像变换B. 平移变换C. 对称变换D. 旋转变换6. 假如两个相像多边形的面积比为9∶ 4,那么这两个相像多边形的相像比为( )A. 9∶4B. 2∶3C. 3∶2D. 81∶167. 如图 ,六边形 ABCDEF ∽六边形 GHIJKL ,相像比为2∶1,则以下结论正确的选项是()1 / 8A. ∠E=2∠KB. BC=2HIC. 六边形ABCDEF的周长=六边形GHIJKL的周长D. S六边形ABCDEF=2S六边形GHIJKL8.手工制作课上,小盈利用一些花布的边角料,剪裁后装修手工画,下边四个图案是她剪裁出的空心不等边三角形,等边三角形,正方形,矩形花边,此中,每个图案花边的宽度都相等,那么,每个图案中花边的内外边沿所围成的几何图形不相像的是()A. B.C. D.9.在研究相像问题时,甲、乙同学的看法以下:甲:将边长为3, 4, 5 的三角形按图①的方式向外扩充,获得新三角形,它们的对应边间距均为 1,则新三角形与原三角形相像.乙:将邻边为 3 和 5 的矩形按图②的方式向外扩充,得到新矩形,它们的对应边间距均为1,则新矩形与原矩形不相像..第2页共8页人教版九年级下册27.1 图形的相像课时练关于两人的看法,以下说法正确的选项是()A. 两人都对B. 两人都不对C. 甲对,乙不对D. 甲不对,乙对10. 若2a=3b=4c,且abc≠0,则的值是()-A.2B.-2C.3D.-3评卷人得分二、填空题11. 如图,四边形ABCD∽四边形A'B'C'D' ,则∠1=,AD =.12. 已知 a,b,c,d 是成比率线段 ,此中 a=3 cm,b=2 cm,c=6 cm,则 d= cm.13.2小芳的房间有一面积为 3 m 的玻璃窗 ,她站在室内离窗子 4 m 的地方向外看 ,她能看到窗前面一幢楼房的面积有m2 (楼之间的距离为 20 m).14. 在比率尺为1∶200 的地图上 ,测得 A,B 两地间的图上距离为 4.5 cm,则 A,B 两地间的实质距离为m.15. 若一个三角形的各边长扩大为本来的 5 倍 ,则此三角形的周长扩大为本来的倍 .16. 如图 ,已知 P 是线段 AB 的黄金切割点 ,且 PA>PB,若 S1表示 PA 为一边的正方形的面积,S2表示长是 AB ,宽是 PB 的矩形的面积 ,则 S1 S2.( 填“ >”“或=“”<”)3 / 817. 以下图,一般书籍的纸张是在原纸张多次对开后获得.矩形 ABCD 沿 EF 对开后 ,再把矩形EFCD 沿 MN 对开 ,挨次类推 .假如各样开本的矩形都相像,那么=.评卷人得分三、解答题18. 已知四条线段a,b,c,d 的长度 ,试判断它们能否成比率:(1)a=16 cm,b=8 cm,c=5 cm,d=10 cm;(2)a=8 cm,b=5 cm, c=6 cm,d=10 cm.19. 已知矩形ABCD中,AD =3,AB =1.若EF把矩形分红两个小的矩形,以下图,此中矩形ABEF与矩形 ABCD 相像 .求 AF∶ AD 的值 .20.在平面直角坐标系中,已知点A(- 2, 0),点 B(0, 4),点 E 在 OB 上,且∠ OAE =∠ OBA.(1)如图①,求点 E 的坐标(2)如图②,将△AEO沿x轴向右平移获得△ A′E′O′,连结A′B,BE′.222 2①设 AA′= m,此中 0<m<2,试用含 m 的式子表示 A′B + BE′,并求出使 A′B + BE′获得最小值时点 E′的坐标;②当 A′B+ BE′获得最小值时,求点E′的坐标 (直接写出结果即可).第4页共8页人教版九年级下册27.1 图形的相像课时练参照答案1.【答案】 B【分析】此题考察了相像图形 .①②④的形状同样,是相像图形,③不是相像图形 .2. 【答案】A【分析】依据相像比的定义,相像多边形对应边的比称为相像比,由题可知 ,面积比为 2∶1,因此相像比为∶1.3.【答案】 D【分析】各数据比较可知 ,只有 D 中四条线段 ,1∶ 2=2∶ 4,能成比率 .4.【答案】 C【分析】三角形相像 ,则边长的比同样 ,均为 5∶ 6∶ 8,乙三角形 20 cm 的边能够当最短边、最长边和中间大小的边,因此共有 3 种状况 .应选 C.5.【答案】 A 【分析】依据相像图形的定义可知 ,用放大镜将图形放大 ,属于图形的形状同样、大小不同样 ,因此属于相像变换 .应选 A .6.【答案】 C【分析】此题考察了相像多边形 .面积比等于相像比的平方,因此相像比等于面积比的算术平方根,应选 C.7.【答案】 B【分析】∵六边形 ABCDEF ∽六边形 GHIJKL ,∴∠ E=∠ K,故 A 选项错误 ;∵六边形ABCDEF ∽六边形 GHIJKL ,相像比为 2∶ 1,∴ BC =2HI ,故 B 选项正确 ;∵六边形ABCDEF ∽六边形 GHIJKL ,相像比为 2∶1,∴六边形 ABCDEF 的周长 =六边形 GHIJKL 的周长×2,故 C 选项错误 ; ∵六边形 ABCDEF ∽六边形 GHIJKL ,相像比为 2∶ 1,∴ S六边形ABCDEF =4 S六边形GHIJKL ,故 D 选项错误 .8.【答案】 D【分析】由相像的性质知选 D.9.【答案】 A 【分析】图①中,新三角形和原三角形保持了三内角不变,依据两组角对应相等的两三角形相像,得新三角形和原三角形相像,图②中,原矩形的长宽比为,而新矩形的长宽比为,因此变化前后的矩形不相像 .5 / 810. 【答案】B【分析】设2a= 3b= 4c= 12k(k≠0),则有a= 6k,b= 4k,c= 3k,因此-=-= -=- 2.11.【答案】 70° 28【分析】∵四边形ABCD ∽四边形A'B'C'D' ,∴∠ 1=∠ B=70 °,即,解得 AD=28 .12.【答案】 4【分析】此题考察了比率线段.由题知= ,即 = ,解得 d=4.13. 【答案】108【分析】依据题意 ,她能看到窗前面一幢楼房的图形与玻璃窗的外形应当相像,且相像比为2 ==6,故面积的比为 36.故她能看到窗前面一幢楼房的面积为36×3=108(m ).故答案为 :108.14. 【答案】9【分析】设 A,B 两地间的实质距离为 x cm,由题意得 ,1∶∶x,解得 x= 900 cm.故 A,B 两地间的实质距离为 900 cm, 即 9 m.15.【答案】 5【分析】∵一个三角形的各边长扩大为本来的 5 倍 ,∴扩大后的三角形与原三角形相像.∵相像三角形的周长的比等于相像比,∴这个三角形的周长也扩大为本来的 5 倍 .故答案为 :5.16. 【答案】=【分析】依据黄金切割的定义获得2PA =PB·AB,2再利用正方形和矩形的面积公式有S1=PA ,S2=PB·AB,进而可得 S1=S2.17.【答案】【分析】设∵各开本的矩形都相像,因此有矩形ABCD 与矩形 BFEA 相像 ,即第6页共8页人教版九年级下册 27.1 图形的相像课时练=,∴ AB ·AB=AD ·BF. 又∵ BF= AD,22∴ AD=AB,∴ = = .18.(1) 【答案】 ∵ 8×10=80,16 ×5=80, ∴ bd=ac.∴能够成比率 .(2) 【答案】 ∵ 8×6=48,10 5=50,×∴不可以够成比率 .19. 【答案】 设 AF=x ,∵矩形 ABEF 与矩形 ABCD 相像 ,且 AD= 3,AB= 1,∴对应边成比率 ,即=,即 = ,解得 x= ,∴ AF ∶AD= ∶3= 1∶9.20.(1) 【答案】 ∵点 A 的坐标为 (- 2, 0),点 B 的坐标为 (0, 4),∴ OA = 2, OB = 4,∵∠ OAE =∠ OBA ,∠ EOA =∠ AOB = 90°, ∴△ OAE ∽△ OBA ,有= ,即 =,解得 OE = 1.∴点 E 的坐标为 (0, 1).(2) 【答案】 ①如图,连结 EE ′,由题设 AA ′= m ,则 A ′O =2- m.222在 Rt △ A ′BO 中,由 A ′B = A ′O + BO ,2222得 A ′B = (2- m) + 4 = m -4m + 20.∵△ A ′E ′O ′是将 △ AEO 沿 x 轴向右平移获得的, ∴ EE ′∥ AA ′,且 EE ′= AA ′. 有∠ BEE ′= 90°, EE ′= m.又 BE = OB - OE =3,222 2于是,在= E ′E+ BE = m + 9.Rt △ BE ′E 中, BE ′7 / 822 2∴A′B + BE′= 2m -4m+29(0< m<2).2 2 2配方,得 A′B + BE′= 2(m- 1) + 27,2 2当 m= 1 时, A′B +BE′能够获得最小值,∴当 E′的坐标为 (1, 1).②当 E′的坐标为 ( , 1).第8页共8页。
专题27.1 图形的相似(解析版)

专题27.1 图形的相似1.相似图形定义:形状相同的图形叫做相似图形。
2.相似多边形定义:两个边数相同的多边形,如果它们的角分别相等,边成比例,那么这两个多边形叫做相似多边形。
相似多边形对应边的比叫做相似比。
3.性质相似多边形的对应角相等,对应边成比例。
【例题1】在如图所示的相似四边形中,求未知边x、y的长度和角α的大小.【答案】x=31.5,y=27,α=83°.【解析】∵两个四边形相似,它们的对应边成比例,对应角相等. ∴67418y x ==, ∴27,5.31==y x .︒=︒+︒+︒-︒=83)1178377(360α.【点拨】利用图形相似,对应边成比例,对应角相等的性质来进行解题。
【例题2】要制作两个形状相同的三角形框架,其中一个三角形的三边长分别为5cm ,6cm 和9cm ,另一个三角形的最短边长为2.5cm ,则它的最长边为( )A .3cmB .4cmC .4.5cmD .5cm【答案】C .【解析】设另一个三角形的最长边长为xcm ,根据题意,得:=,解得:x=4.5,即另一个三角形的最长边长为4.5cm ,故选:C .【点拨】根据相似三角形的对应边成比例求解可得.【例题3】所有的正方形都相似吗?为什么?所有的矩形都相似吗?为什么?【答案】见解析。
【解析】所有的正方形都相似,因为正方形的每个角都是90°,因此对应角都相等,而每一个正方形的边长都相等,因此对应边成比例.所有的矩形不一定相似,虽然所有的矩形的角都相等,但对应的边不一定成比例,因此,矩形不一定相似.1. 图中的两个多边形相似吗?说说你的理由.【答案】见解析。
【解析】不相似.︒=︒-︒-︒-︒=∠587295135360D ,而︒=︒-︒-︒-︒=∠715995135360E ,不可能有“对应角相等”.2.已知图中的两个梯形相似,求出未知边x 、y 、z 的长度和βα∠∠、的度数.【答案】见解析。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
27.1 图形的相似
一.选择题:
1、下列各组数中,成比例的是( )
A .-7,-5,14,5
B .-6,-8,3,4
C .3,5,9,12
D .2,3,6,12 2、如果x:(x+y)=3:5,那么x:y =( )
A. B. C. D.
3、如图,F 是平行四边形ABCD 对角线BD 上的点,BF ∶FD=1∶3,
则BE ∶EC=( ) A 、
21 B 、31 C 、32 D 、4
1
4、下列说法中,错误的是( )
(A )两个全等三角形一定是相似形 (B )两个等腰三角形一定相似 (C )两个等边三角形一定相似 (D )两个等腰直角三角形一定相似 5、如图,Rt ΔABC 中,∠C =90°,D 是AC 边上一点,AB =5,AC =4, 若ΔABC ∽ΔBDC ,则CD = . A .2 B .32 C .43 D .94
二、填空题
6、已知a =4,b =9,c 是a b 、的比例中项,则c = .
7、如图,要使ΔABC ∽ΔACD ,需补充的条件是 .(只要写出一种) 8、如图,小东设计两个直角,来测量河宽DE ,他量得AD =2m ,BD =3m ,CE =9m ,则河宽DE 为
C
B
D
(第5题)
2383325
8
(第3题图)
9、一公园占地面积约为2m ,若按比例尺1∶2000缩小后,其面积约为 2m .
10、如图,点P 是Rt ΔABC 斜边AB 上的任意一点(A 、B 两点除外)过点P 作一条直线,使截得的三角形与Rt ΔABC 相似,这样的直线可以作 条. 三、解答题
11、如图18—95,AB 是斜靠在墙壁上的长梯,梯脚B 距墙80cm ,梯上点D 距墙70cm ,BD 长55cm .求梯子的长.(8分)
12、如图,已知AC ⊥AB ,BD ⊥AB ,AO =78cm ,BO =42cm ,CD =159cm ,求CO 和DO .(8分)
C
B
A
P
(第10题)
A
B
C
D
(第7题)
(第8题图)
13、如图,在正方形网格上有111C B A ∆∽222A C B ∆,这两个三角形相似吗?如果
相似,求出222111A C B A C B ∆∆和的面积比.(15分)
14、已知:如图,在△ABC 中,点D 、E 、F 分别在AC 、AB 、BC 边上,且四边形CDEF 是正方形,AC =3,BC =2,求△ADE 、△EFB 、△ACB 的周长之比和面积之比.(10分)
15、如图所示,梯形ABCD 中,AD ∥BC,∠A=90°,AB=7,AD=2,BC=3,试在腰AB 上确定点P 的位置,使得以P ,A,D 为顶点的三角形与以P ,B,C 为顶点的三角形相似.
P A
B D
C
参考答案
一、选择题:1.B 2.D 3.A 4.D 5.D 二、填空题:
6、±6;
7、∠ACD=∠B 或∠ADC=∠ACB 或AD :AC=AC :AB ;
8、6m ;
9、0.2;10、3 三、解答题: 11.梯子长为440cm 12.
cm
DO cm CO 65.55,35.103==(提示:设
xcm
DO =,则
()cm
x CO -=159,因为
AB BD AB AC ⊥⊥,,︒=∠=∠90B A ,BOD AOC ∠=∠,所以△AOC ∽△BDO ,所以DO
CO
BO AO
=即x x -=1594278,所以65.55=x )
13、相似,相似比为
(提示:,且222111135C A B C A B ∠=︒=∠)
14、周长之比:ADE ∆的周长:EFB ∆的周长:ACB ∆的周长5:2:3=;
25
:4:9::=∆∆∆ACB EFB ADE S S S .设x EF =,则x AD x EF -==3,.所以
5:2:3::=AC EF AD .因为△ADE ∽△EFB ∽△ACB ,所以可求得周长比等于相似比,面积比等于相似比的平方.
15、(1)若点A,P ,D 分别与点B,C,P 对应,即△APD ∽△BCP ,
∴
AD AP BP BC =, ∴273
AP
AP =-,
1
:4,
1:22
221
11=∆∆C B A C B A S S 222112211==B A B
A C A C A
∴AP 2-7AP+6=0, ∴AP=1或AP=6,
检测:当AP=1时,由BC=3,AD=2,BP=6, ∴
AP AD
BC BP
=
, 又∵∠A=∠B= 90°,∴△APD ∽△BCP . 当AP=6时,由BC=3,AD=2,BP=1, 又∵∠A=∠B=90°, ∴△APD ∽△BCP .
(2)若点A,P ,D 分别与点B,P ,C 对应,即△APD ∽△BPC.
∴
AP AD BP BC =,∴273AP AP =-, ∴AP=14
5
.
检验:当AP=145时,由BP=21
5
,AD=2,BC=3,
∴AP AD BP BC =, 又∵∠A=∠B=90°,∴△APD ∽△BPC.
因此,点P 的位置有三处,即在线段AB 距离点A 1、14
5
、6 处.。
