巴特沃斯滤波器的设计与仿真
巴特沃斯、切比雪夫滤波器的仿真与实现

华北科技学院课程设计任务书2013 — 2014 学年第二学期电子信息工程学院(系、部)通信工程专业 B111 班级课程名称:移动通信设计题目:巴特沃斯、切比雪夫滤波器的仿真与实现完成期限:自16 周至 18 周共 3 周目录1.前言 (3)1.1 MATLAB (3)1.2 滤波器的概念 (5)1.2.1滤波器的原理 (6)1.2.2理想滤波器与实际滤波器 (6)1.2.3 滤波器的分类 (7)2.设计目的 (9)3.设计原理 (9)3.1.模拟低通滤波器的设计指标及逼近方法 (9)3.2.巴特沃斯低通滤波器的设计方法 (10)3.3.切比雪夫滤波器的设计方法 (14)4.详细设计与系统分析 (21)4.1程序设计 (21)4.1.1巴特沃斯滤波器 (21)4.1.2切比雪肤滤波器 (23)4.2同一滤波器不同参数的比较 (25)4.2.1巴特沃斯滤波器 (25)4.2.2切比雪夫滤波器 (27)4.3不同滤波器同一阶数的比较 (30)4.3.1低通滤波器 (30)4.3.2高通滤波器 (30)4.3.3带通滤波器 (31)4.3.4带阻滤波器 (31)5.心得体会 (32)6.参考文献 (32)摘要:利用MATLAB设计滤波器,可以按照设计要求非常方便地调整设计参数,极大地减轻了设计的工作量,有利于滤波器设计的最优化。
MATLAB因其强大的数据处理功能被广泛应用于工程计算,其丰富的工具箱为工程计算提供了便利,利用MATLAB信号处理工具箱可以快速有效地设计各种数字滤波器,设计简单方便。
本文介绍了在MATLAB R2009a 环境下滤波器设计的方法和步骤。
关键词:滤波器,MATLAB1.前言1.1 MATLABMATLAB是美国MathWorks公司开发的一种功能极其强大的高技术计算语言和内容极其丰富的软件库,集数值计算、矩阵运算和信号处理与显示于一身。
该软件最初是由美国教授Cleve Moler 创立的。
数字信号处理实验数字巴特沃思滤波器的设计

数字信号处理实验数字巴特沃思滤波器的设计数字信号处理技术是现代通信、音频、图像等领域中不可或缺的一门技术。
数字信号处理的核心是数字滤波器设计,本文将介绍一种常用的数字滤波器——数字巴特沃斯滤波器的设计方法。
一、数字滤波器简介数字滤波器是将连续时间信号转换成离散时间信号,实现对离散时间信号的滤波处理,具有实时性好、精度高、可重复性强等优点。
数字滤波器有两种类型:有限冲激响应(FIR)滤波器和无限冲激响应(IIR)滤波器。
二、数字巴特沃斯滤波器数字巴特沃斯滤波器是一种常用的IIR滤波器,其主要特点是具有平坦的通/阻带,通/阻带边缘陡峭。
因此在实际应用中,数字巴特沃斯滤波器应用较为广泛。
数字巴特沃斯滤波器的设计方法一般包括以下步骤:确定滤波器类型、确定通/阻带的截止频率、确定滤波器的阶数、计算滤波器的系数。
1、确定滤波器类型在实际应用中,数字巴特沃斯滤波器有四种类型:低通、高通、带通和带阻滤波器,应根据实际需求选择。
2、确定通/阻带的截止频率通常情况下,固定本例中采用的是低通滤波器,需要确定的就是通带和阻带的截止频率。
对于低通滤波器,通带截止频率ωc应该比信号频率fs的一半小,阻带截止频率ωs 应该比ωc大一些,通常ωs/ωc取0.5~0.7比较好。
滤波器的阶数一般是与滤波器的性能相关的。
阶数越高,性能越好,但同时计算量也会更大。
在实际应用中,一般取4~8的阶数即可。
4、计算滤波器的系数根据上述参数计算滤波器的系数,这里介绍两种常用的方法:一种是脉冲响应不变法(Impulse Invariant Method),另一种是双线性变换法(Bilinear Transformation)。
脉冲响应不变法是一种较为简单的设计方法,但由于其数字滤波器与连续时间滤波器之间的不同,可能会引入一定程度的失真。
双线性变换法可以使二阶系统和一阶系统的增益分别为1和0dB,这是一种比较理想的设计方法。
四、实验步骤本实验采用Matlab软件进行数字滤波器的设计,具体步骤如下:1、打开Matlab软件,新建一个.m文件;2、输入需要滤波的数字信号,此处可以使用Matlab自带的signal工具箱中的一些模拟信号;4、使用filter函数实现数字滤波器对信号的滤波过程;5、通过比较信号的频谱图,评估滤波器的性能。
巴特沃斯滤波器的设计与仿真

信号与系统课程设计 题目巴特沃斯滤波器的设计与仿真学院英才实验学院学号2015180201019学生姓名洪 健指导教师王玲芳巴特沃斯滤波器的设计与仿真英才一班 洪健 2015180201019摘 要:工程实践中,为了得到较纯净的真实信号,常采用滤波器对真实信号进行处理。
本文对巴特沃斯模拟滤波器的幅频特性、设计方法及设计步骤进行了研究,并利用Matlab 程序和Multisim 软件,设计了巴特沃斯模拟滤波器,并分析了巴特沃斯模拟滤波器的幅频特性。
利用 Matlab 程序绘制了巴特沃斯模拟滤波器的幅频特性曲线,并利用Matlab 实现了模拟滤波器原型到模拟低通、高通、带通、带阻滤波器的转换。
通过Multisim 软件,在电路中设计出巴特沃斯滤波器。
由模拟滤波器原型设计模拟高通滤波器的实例说明了滤波器频率转换效果。
同时通过电路对巴特沃斯滤波器进行实现,说明了其在工程实践中的应用价值。
关键词:巴特沃斯滤波器 幅频特性 Matlab Multisim引言 滤波器是一种允许某一特定频带内的信号通过,而衰减此频带以外的一切信号的电路,处理模拟信号的滤波器称为模拟滤波器。
滤波器在如今的电信设备和各类控制系统里应用范围最广,技术最为复杂,滤波器的好坏直接决定着产品的优劣。
滤波器主要分成经典滤波器和数字滤波器两类。
从滤波特性上来看,经典滤波器大致分为低通、高通、带通和带阻等。
模拟滤波器可以分为无源和有源滤波器。
无源滤波器:这种电路主要有无源元件R、L 和C 组成。
有源滤波器:集成运放和R、C 组成,具有不用电感、体积小、重量轻等优点。
集成运放的开环电压增益和输入阻抗均很高,输出电阻小,构成有源滤波电路后还具有一定的电压放大和缓冲作用。
但集成运放带宽有限,所以目前的有源滤波电路的工作频率难以做得很高。
MATLAB 是美国MathWorks 公司出品的商业数学软件,用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言和交互式环境,主要包括MATLAB 和Simulink 两大部分。
(完整word版)巴特沃斯带阻数字滤波器设计matlab程序及仿真图 - 副本

fs=15000;T= 1/fs;rp=1;rs=40;wp1=0.11*pi;wp2=0.81*pi;ws1=0.31*pi;ws2=0.61*pi;%数字带阻滤波器技术指标wc1=(2/T)*tan(wp1/2);%频率预畸变wc2=(2/T)*tan(wp2/2);wr1=(2/T)*tan(ws1/2);wr2=(2/T)*tan(ws2/2);w0=sqrt(wc1*wc2);B=wc2-wc1;wp=1;%归一化通带截止频率ws=wp*(wr1*B) / (w0^2-wr1^2) ; %归一化阻带截止频率[N,wc]=buttord(wp,ws,rp,rs,'s')%求滤波器阶数和3dB截止频率[Z,P,K]=buttap(N)%设计模拟低通滤波器[Md,Nd]=zp2tf(Z,P,K)%将零极点形式转换为传输函数形式[M,N]=lp2bs(Md,Nd,w0,B)%对低通滤波器进行频率变换,转换为带阻滤波器[h,w]=freqs(M,N);%模拟带阻滤波器的幅频响应plot(w/(2*pi),abs(h));grid;xlabel('频率Hz');ylabel('幅度');title('模拟带阻滤波器');[b,a]=bilinear(M,N,15000)%对模拟滤波器双线性变换figure(1);freqz(b,a);[H,W]=freqz(b,a); %绘出频率响应;axis([0,1,-100,20]);figure(2);plot(W*fs/(2*pi),abs(H));grid on;xlabel('频率/Hz');ylabel('幅值');n=0:199;t=n/fs;x=sin(2*pi*400*t)+3*sin(2*pi*3000*t)+2*sin(2*pi*5000*t);figure(3);subplot(311);plot(t,x);axis([0,0.01,-5,5]);title('输入信号');grid on;y=filter(b,a,x);subplot(312);stem(y,'.');title('输出序列');grid on;ya=y*sinc(fs*(ones(length(n),1)*t-(n/fs)'*ones(1,length(t))));subplot(313);plot(t,ya);axis([0,0.01,-3,3]);title('输出波形');grid on;t=(0:100)/fs;figure(4)fs=1.5*10000;n=(0:100)/fs;f=sin(2*pi*400*t)+3*sin(2*pi*3000*t)+2*sin(2*pi*5000*t);y=fftfilt(b,x);[H1,f1]=freqz(f,[1]);[H2,f2]=freqz(y,[1]);f1=f1/pi*fs/2;f2=f2/pi*fs/2;subplot(2,1,1);plot(f1,abs(H1));title('输入信号的频谱');subplot(2,1,2);plot(f2,abs(H2));title('输出信号的频谱');基于Matlab 的带阻滤波器设计.10.20.30.40.50.60.70.80.91-800-600-400-2000N o r m a l i z e d Fre q u⨯π r a d /s a m p l e Ph a se(d e g r e e s )00.10.20.30.40.50.60.70.80.91-100-50N o r m a l i z e d Fr e q u⨯π r a d /s a m p l e M a g n i tu d e1000200030004000500060007000800000.20.40.60.811.21.4频率/Hz幅值00.0010.0020.0030.0040.0050.0060.0070.0080.0090.01-505输入信号020406080100120140160180200-22输出序列0.0010.0020.0030.0040.0050.0060.0070.0080.0090.01-202输出波形01000200030004000500060007000800050100150200输入信号的频谱010002000300040005000600070008000102030输出信号的频谱N =4wc =1.7947b =0.0186 -0.0410 0.1082 -0.1355 0.1810 -0.1355 0.1082 -0.0410 0.0186a =1.0000 -0.6707 -1.3750 0.5678 1.1964 -0.2996 -0.4631 0.0496 0.0762>。
常用模拟滤波器的设计方法

常用模拟滤波器的设计方法设计模拟滤波器常用的方法有很多种,如巴特沃斯滤波器、切比雪夫滤波器、脉冲响应滤波器等。
这些方法各有特点,适用于不同的滤波器设计需求。
下面将逐步介绍常用模拟滤波器的设计方法。
1. 巴特沃斯滤波器的设计方法巴特沃斯滤波器是一种最常用的模拟滤波器,其主要特点是通频带的频率响应是平坦的,也就是说在通过的频率范围内的信号不会被衰减或增强。
巴特沃斯滤波器的设计方法包括以下步骤:1.1 确定滤波器类型首先,根据滤波器的设计需求,确定滤波器的类型,包括低通滤波器、高通滤波器、带通滤波器和带阻滤波器。
不同类型的滤波器在频率响应和陡度上有一些差异。
1.2 确定滤波器模型根据滤波器类型,选择相应的滤波器模型。
比如,低通滤波器通常选择Butterworth滤波器模型、Elliptic滤波器模型或者Chebyshev滤波器模型。
1.3 确定滤波器参数确定滤波器的相关参数,包括截止频率、阻带衰减和通带波纹等。
这些参数的选择需要根据特定的滤波器性能需求决定。
1.4 开始设计根据确定的滤波器模型和参数,开始进行滤波器的设计。
可以使用电路设计软件进行模拟,或者手动计算和画图设计。
1.5 仿真和优化设计完成后,对滤波器进行仿真,检查其频率响应和时域特性。
根据仿真结果,可以调整一些参数以优化滤波器的性能。
1.6 实际搭建和测试在电路板上搭建设计好的滤波器电路,并进行实际测试。
测试结果比较与设计要求进行评估和调整,最终得到满足要求的滤波器。
2. 切比雪夫滤波器的设计方法切比雪夫滤波器是一种在通频带内具有较窄的波纹和较快的过渡带的滤波器。
其设计方法如下:2.1 确定滤波器类型和阶数选择滤波器的类型和阶数,通常切比雪夫滤波器可以选择类型Ⅰ和类型Ⅱ。
阶数的选择取决于滤波器对波纹的要求和频率范围。
2.2 确定滤波器参数确定滤波器的相关参数,包括截止频率、阻带衰减、通带波纹和过渡带宽度等。
这些参数的选择需要根据特定的滤波器性能需求决定。
巴特沃斯低通滤波器课程设计

电路基础课程设计巴特沃斯低通滤波器设计目标:通带边界频率ωc=4396rad/s (f c=700Hz);通带最大衰减αmax=3dB;阻带边界频率ωs=26376rad/s(f s=4200Hz); 阻带最小衰减αmin=30dB;1.设计步骤⑴设计电压转移函数①将给定的电压衰减技术指标进行频率归一化选取归一化角频率ωr=ωc,这样通带边界频率Ωc=ωc/ ωr=1,阻带边界频率Ωs=ωs/ ωr=ωs/ωc。
②根据归一化的技术指标求出电压转移函数巴特沃斯低通滤波器的阶数n=Log(100.1αmin−1) 2Log(Ωs)带入数据求得n=1.93 取整得n=2由a k=2sin(2k−1)π2n,b k=1和H(s)=U out(s)U in(s)=∏A ks2+a k s+b kn2k=1可得到电压转移函数H(s)=U out(s)U in(s)=1s2+√2s+1将转移函数进行反归一化,即另s=sωc 得到实际转移函数H(s)=U out(s)U in(s)=1s243962+√2s4396+1⑵转移函数的实现选取下图作为实现转移函数的具体电路:列节点方程求解转移函数节点1 U1(1R1+1R2+s∗C1)−1R1U in−1R2−s∗C1∗U2=0节点2 (1R2+s∗C2)U2−1R2U1=0又有U out=U3解得H(s)=U outU in=11+(R2+R2)s∗C2+C1C2R1R2s2对比解得的电压转移函数和推得的电压转移函数里各项的系数并且令R1= R2,C1=1μF,可以得到C1=11000000F=1μFR1=250000√21099Ω=321.705ΩR2=250000√21099Ω==321.705ΩC2=12000000F=0.5μF因实验室没有0.5μF的电容因此取C2=0.47μF2.计算机仿真⑴软件环境:Multisim 10⑵电路图:⑶仿真结果:①700Hz下的波形图②4200Hz下的波形图③波特图◎700Hz下衰减2.673dB◎4200Hz下衰减30.491dB3.实验室实际操作因实验室没有0.5μF的电容和321.705Ω的电阻,因此取C2=0.47μFR1=R2=330Ω实际连电路时,选取集成电路块的第1、2、3引脚分别作为放大器的输出端、负端和正端,第4和11引脚作为供电端,C2一端连接电压源的接地线。
巴特沃斯数字滤波器的设计与仿真实现

总770期第三十六期2021年12月河南科技Henan Science and Technology信息技术巴特沃斯数字滤波器的设计与仿真实现黄波(成都大学电子信息与电气工程学院,四川成都610106)摘要:数字通信系统传输数字信号时经常混杂着各种频率的干扰信号,数字滤波器可以利用数值运算,起到其他模拟滤波器根本无法实现的杂波滤除作用。
本文首先讨论了数字滤波器的原理,进一步给出了巴特沃斯数字滤波器的设计思路,然后利用MATLAB软件实现了对巴特沃斯数字滤波器的仿真试验,分析了巴特沃斯数字滤波器的各类幅频特性、相关的设计方法和对应的设计步骤等。
通过巴特沃斯数字滤波器的设计与实现,完成了低通滤波、高通滤波、带通滤波、带阻滤波的仿真试验,最后得到巴特沃斯数字滤波器的幅频特性曲线,并研究了巴特沃斯数字滤波器的相关幅频特性。
关键词:数字滤波器;巴特沃斯;MATLAB;幅频特性中图分类号:TN951文献标识码:A文章编号:1003-5168(2021)36-0010-03Design and Simulation of Butterworth Digital FilterHUANG Bo(School of electronic information and electrical engineering,Chengdu University,Chengdu Sichuan610106)Absrtact:When transmitting digital signals,digital communication systems are often mixed with interference signals of various frequencies.Digital filters can use numerical operation to achieve clutter filtering that other analog filters can not achieve at all.This paper first discusses the principle of digital filter,further gives the design idea of Butter⁃worth digital filter,then realizes the simulation of Butterworth digital filter by using MATLAB software,and analyzes various amplitude frequency characteristics,relevant design methods and corresponding design steps of Butterworth digital filter,through the design and implementation of Butterworth digital filter,the simulation of low-pass filter, high pass filter,band-pass filter and band stop filter are completed.Finally,the amplitude frequency characteristic curve of Butterworth digital filter is obtained,and the related amplitude frequency characteristics of Butterworth digi⁃tal filter are studied.Keywords:digital filter;butterworth;MATLAB;amplitude frequency characteristic数字滤波器作为数字信号处理的基础单元,可以完成对数字信号实现信号过滤、信号检测和相关参数估计等处理工作。
数字信号处理巴特沃斯滤波器设计

数字信号处理巴特沃斯滤波器设计数字信号处理在当今科技领域中扮演着至关重要的角色,滤波器作为数字信号处理领域中的重要组成部分,广泛应用于信号去噪、信号增强、信号分析等方面。
巴特沃斯滤波器作为数字信号处理领域中的一种重要类型,具有平滑的频率响应曲线和较陡的截止特性,被广泛应用于语音处理、图像处理、生物医学信号处理等领域。
本文将介绍数字信号处理中巴特沃斯滤波器的设计原理和方法。
在数字信号处理中,滤波器是一种通过对信号进行处理来实现滤除或增强某些频率成分的系统。
巴特沃斯滤波器是一种典型的低通滤波器,其特点是在通频带范围内频率响应平坦,截止频率处有较 steependifferentiation,可有效滤除非所需频率信号。
要设计一个巴特沃斯滤波器,首先需要确定滤波器的截止频率和阶数。
巴特沃斯滤波器的阶数决定了滤波器的频率选择性能,在实际应用中可根据信号处理的要求进行选择。
一般来说,阶数越高,滤波器的截止特性越陡,但相应的频率选择性能也会增强。
确定好阶数后,接下来需要进行巴特沃斯滤波器的参数计算,包括极点位置和幅频特性。
根据巴特沃斯滤波器的传递函数形式,可以通过公式计算各个极点的位置,并绘制出滤波器的幅频特性曲线。
设计完巴特沃斯滤波器的参数后,接下来是实现滤波器的数字化。
数字巴特沃斯滤波器一般通过模拟滤波器的模拟频率响应和数字频率响应之间的变换来实现。
常用的数字化方法包括脉冲响应不变法和双线性变换法,通过这些方法可以将模拟滤波器的参数转换为数字滤波器的参数,实现数字滤波器的设计。
在实际应用中,巴特沃斯滤波器的设计需要根据具体的信号处理要求和系统性能来选择合适的截止频率和阶数,确保滤波器设计的稳定性和性能。
同时,在设计过程中需要考虑到滤波器的实现复杂性和计算成本,选择合适的设计方法和参数计算技术,以实现滤波器设计的有效性和可靠性。
综上所述,巴特沃斯滤波器作为数字信号处理领域中的重要组成部分,在信号处理、通信系统、生物医学等领域中有着广泛的应用前景。
巴特沃斯低通滤波器设计

巴特沃斯低通滤波器一、设计要求(1)设计一巴特沃斯数字低通滤波器,在0.3π通带频率范围内,通带幅度波动小于1dB ,在0.5π~πrad 阻带频率范围内,阻带衰减大于12dB 。
二.设计过程巴特沃斯双线性变换法(1)数字指数:p w =0.3π,s w =0.5π,(2)求p Ω,s Ω利用频率预畸变公式得:p Ω=2T tan 2p w =2T tan 320π=1.019⨯1Ts Ω=2T tan 2s w =2T tan 4π=2T (3)确定滤波器阶数sp λ=s p ΩΩ=211.019TT ⨯=1.963 sp k≈0.132 N=—lg lg sp sp k λ=—lg 0.132lg1.963≈3.0023 N=4 (4)确定系统函数G(p)= 43212.613 3.4142 2.61311p p p p ++++ c Ω=p Ω()10.12101p a N --=1.019⨯1T⨯()10.1124101-⨯⨯-=1.2065T P=11211c s z s T z ---=Ω+=1c Ω⨯2T ⨯1111z z ---+=11211.20651z z ---+ H(z)=G(p)=12341234146434.1675441.3465432.542711.06234 1.69864z z z z z z z z--------++++-+-+三.软件仿真(1)将分子分母带入Matlab 验证b=[1 4 6 4 1];a=[34.16754 -41.34654 32.5427 -11.06234 1.69864];[H,w]=freqz(b,a,1000);plot(w,20*log10(abs(H)/max(H)),'-');grid;xlabel('frequency');ylabel('magnitude');-250-200-150-100frequency m a g n i t u d e图(a )频率——幅度衰减图0.3π≈0.940.9250.930.9350.940.9450.950.955frequency m a g n i t u d e图(b)0.5π≈1.57frequency m a g n i t u d e图(c)(2)用Matlab 直接仿真出低通滤波器wp=2*tan(0.3*pi/2)*1000;ws=2*tan(0.5*pi/2)*1000;ap=1;as=12;[n,wn]=buttord(wp,ws,ap,as,'s');[b,a]=butter(n,wn,'s');[bn,an]=bilinear(b,a,1000);[H,w]=freqz(bn,an);plot(w,abs(H),'-');grid;xlabel('frequency');ylabel('magnitude');legend('双线性变化法');figure(2);plot(w,20*log10(abs(H)/max(H)),'-');grid;00.51 1.522.533.5frequency m a g n i t u d e0.3π≈0.94图(d)0.5π≈1.57图(e)四.分析将计算得出的低通滤波器系统函数H(z)的分子分母各项系数用Matlab验证,得图(a)幅频关系图。
巴特沃斯滤波器设计
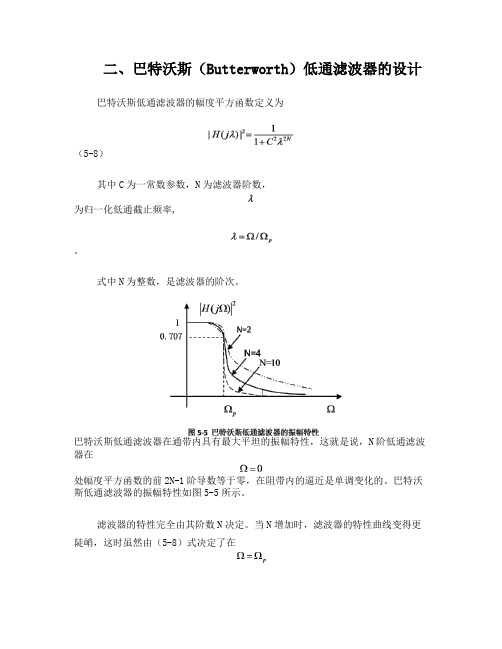
二、巴特沃斯(Butterworth)低通滤波器的设计巴特沃斯低通滤波器的幅度平方函数定义为(5-8)其中C为一常数参数,N为滤波器阶数,为归一化低通截止频率,。
式中N为整数,是滤波器的阶次。
巴特沃斯低通滤波器在通带内具有最大平坦的振幅特性,这就是说,N阶低通滤波器在处幅度平方函数的前2N-1阶导数等于零,在阻带内的逼近是单调变化的。
巴特沃斯低通滤波器的振幅特性如图5-5所示。
滤波器的特性完全由其阶数N决定。
当N增加时,滤波器的特性曲线变得更陡峭,这时虽然由(5-8)式决定了在处的幅度函数总是衰减3dB,但是它们将在通带的更大范围内接近于1,在阻带内更迅速的接近于零,因而振幅特性更接近于理想的矩形频率特性。
滤波器的振幅特性对参数N的依赖关系如图5-5所示。
设归一化巴特沃斯低通滤波器的归一化频率为,归一化传递函数为,其中,则由(5-6)式和(5-8)式得:由于(5-9)所以巴特沃斯滤波器属于全极点滤波器。
1、常用设计巴特沃斯低通滤波器指标:通带截止频率;:通带衰减,单位:dB;:阻带起始频率;:阻带衰减,单位:dB。
说明:(1)衰减在这里以分贝(dB)为单位;即(2)当时为通常意义上的截止频率。
(3)在滤波器设计中常选用归一化的频率,即2、巴特沃斯低通滤波器设计实质根据设计指标要求,,,确定归一化巴特沃斯低通滤波器幅度平方函数中的待定系数C及滤波器的阶数N;然后再根据幅度平方函数确定巴特沃斯低通滤波器的传递函数H(s)。
(1)将实际频率归一化得,,再根据已知的,,幅度平方函数确定C和N。
(2)求C和N由并带入,,,得即因为,所以由两边取对数得:其中这样可以求出C和N。
注意:当时,,即C=1,此时巴特沃斯滤波器只剩下一个参数N。
(3)确定巴特沃斯滤波器的传递函数H(p)。
由于由,解得极点为:将p左半平面的极点赋予即其中为了便于设计,工程上已将当时,各阶巴特沃斯低通滤波器系统函数设计成表格供查阅,该表如表5-1所示。
基于multisim和filtersolution的巴特沃斯滤波器的设计与仿真

基于m u ltisi m和filter so lu ti on的巴特沃斯滤波器的设计与仿真广东机电职业技术学院计算机系 程 光[摘 要]巴特沃斯滤波器因为具有最平坦的通带幅频特性,故广泛被电子设计者所应用,但其低阶的滤波器通带边界下降较慢。
高阶滤波电路通常都是以1阶和2阶滤波器的设计为基础,为此,本文从基础的2阶巴特沃斯低通滤波器的设计入手,详细介绍设计过程,然后在m ultisi m下给予验证,最后用filter so luti on设计高阶的,通带边界下降更快的低通滤波器。
[关键词]巴特沃斯滤波器 2阶 低通 m ultisi m filter so luti on——299—003——103—(上接第303页)是大都市,抢占大市场。
为此,作为地方中小企业应避免与这些强劲品牌产生正面冲突,不要在本已十分拥挤的都市道路上步履蹒跚,而应在潜在的广大农村市场上纵横驰骋,找出知名品牌无力顾及或仍未开发的市场空间,找准切入点,推出自己的品牌,在小市场中发展和壮大自己。
在市场竞争中,地方中小企业应注意保持低调务实的姿态,不要过多张扬自己的行动,以免惊动主导品牌。
3、搞好产品品牌的设计工作中小企业在进行产品品牌设计过程中,首先要突出产品品牌的个性。
品牌个性是品牌形象的核心,是消费者认知品牌的尺度和重心。
是品牌形象中最能体现差异、最活跃激进的部分。
为使品牌个性突出、鲜明,必须整合各种因素,使之加强消费者对品牌个性的认知,与消费者产生共鸣。
如:奔驰具有“自负、富有”的个性,百事可乐具有“年轻、活泼、刺激”的个性。
其次,要给产品命好名。
要使企业产品品牌的名字简洁醒目,易读易记;品牌构思巧妙,有所暗示;色彩美丽而富有个性;同时要尊重习俗、符合法律。
第三,要设计产品包装。
在设计产品包装时,充分考虑安全、便于携带、美观大方、色彩搭配协调等。
4、做好产品品牌的宣传和推广工作中小企业在进行产品品牌的宣传和推广工作过程中,切不能照搬大型企业的方法和模式,斥巨资大搞广告宣传。
巴特沃斯低通滤波器

巴特沃斯低通滤波器简介巴特沃斯低通滤波器(Butterworth low-pass filter)是一种常用的模拟滤波器,被广泛应用于信号处理和电子系统中。
它的设计原则是在通带中具有平坦的幅频特性,而在截止频率处具有最大衰减。
这种滤波器的设计目的是能够尽可能滤除高频噪声,而保留低频信号。
巴特沃斯滤波器的特性巴特沃斯低通滤波器具有以下特性:•通带幅度为1:在通带中,滤波器的增益保持不变,也就是幅度为1。
•幅度频率响应的过渡带是由通带到停带的渐变区域,没有任何波纹。
•幅度频率响应在通带之外都有指数衰减。
•巴特沃斯滤波器是最平滑的滤波器之一,没有任何截止角陡峭度。
巴特沃斯滤波器的传递函数巴特沃斯低通滤波器的传递函数由下式给出:H(s) = 1 / (1 + (s / ωc)^2n)^0.5其中,H(s)为滤波器的传递函数,s为复变量,ωc为截止频率,n为滤波器的阶数。
阶数决定了滤波器的过渡带宽度和滤波特性。
巴特沃斯滤波器设计步骤巴特沃斯滤波器的设计步骤如下:1.确定所需滤波器的阶数和截止频率。
2.根据阶数和截止频率选择巴特沃斯滤波器的标准传递函数,可以从经验图表或计算公式中得到。
3.将标准传递函数的复频域变量进行频率缩放,以得到实际的传递函数。
4.将传递函数进行因式分解,得到一系列一阶巴特沃斯滤波器的传递函数。
5.根据一阶传递函数设计电路原型。
6.将一阶电路原型按照阶数进行级联或并联,构成所需的滤波器电路。
巴特沃斯滤波器的优点和缺点巴特沃斯低通滤波器具有以下优点:•平坦的传递特性:在通带中,滤波器的增益保持不变,不会引入频率响应的波纹或衰减。
•平滑的过渡带:巴特沃斯滤波器的过渡带具有指数衰减特性,没有任何波纹或突变。
•简单的设计:巴特沃斯滤波器的设计步骤相对简单,可以通过标准传递函数和电路原型进行设计。
然而,巴特沃斯滤波器也具有一些缺点:•较大的阶数:为了达到较陡的阻带衰减,巴特沃斯滤波器需要较高的阶数,导致电路复杂度增加。
滤波器设计中的巴特沃斯滤波器

滤波器设计中的巴特沃斯滤波器滤波器在信号处理和电子通信中扮演着至关重要的角色,能够去除原始信号中的噪声或者限制信号在感兴趣频率范围内。
在滤波器的设计中,巴特沃斯滤波器是一种常用的滤波器类型,其具有平坦的幅频响应和极窄的过渡带宽。
本文将介绍巴特沃斯滤波器的原理和设计方法。
一、巴特沃斯滤波器的原理巴特沃斯滤波器基于巴特沃斯多项式来实现滤波功能。
巴特沃斯多项式的特点是它在通带内具有最平坦的幅频响应,即没有波纹或峰谷,而在过渡带和阻带中有最陡峭的衰减。
这使得巴特沃斯滤波器在高通和低通滤波器应用中非常有用。
巴特沃斯滤波器的频率响应函数可以通过以下公式表示:H(s) = 1 / (1 + (s/wc)^2N)^0.5其中,H(s)为频率响应函数,s为复变量,wc为截止频率,N为滤波器的阶数。
通过调整截止频率和阶数,可以实现不同类型的巴特沃斯滤波器,如低通滤波器、高通滤波器、带通滤波器和带阻滤波器。
二、巴特沃斯滤波器的设计方法巴特沃斯滤波器的设计过程可以通过以下步骤进行:1. 确定滤波器类型:根据实际需求确定滤波器的类型,例如低通滤波器或高通滤波器。
2. 确定滤波器的通带和阻带范围:根据信号的频率范围确定滤波器的通带和阻带范围。
通带是信号允许通过的频率范围,而阻带是信号被抑制的频率范围。
3. 确定滤波器的截止频率:根据滤波器类型和信号需求,确定滤波器的截止频率。
截止频率是信号通过滤波器时的临界点,可以控制滤波器的频率特性。
4. 确定滤波器的阶数:根据滤波器的要求,确定滤波器的阶数。
阶数越高,滤波器的衰减特性越陡。
5. 计算滤波器的巴特沃斯多项式:根据选择的滤波器类型、截止频率和阶数,计算滤波器的巴特沃斯多项式。
6. 实现滤波器:根据计算得到的巴特沃斯多项式,采用电路或者数字滤波器的方式来实现滤波器。
多种实现方式包括RC电路、LC电路、激励响应滤波器等。
三、巴特沃斯滤波器的应用巴特沃斯滤波器广泛应用于各个领域,包括通信系统、音频处理、图像处理等。
DSP_19巴特沃斯滤波器

2
1 p 1 c
2N
(2) 设 T=1,将数字域指标转换成模拟域指标得
20lg H a j 0.2 1 20lg H a j 0.3 15
代入巴特沃斯滤波器的幅度平方函数得
0.2 0.3 0.1 1.5 1 10 1 10 c c 解这两个方程得 N 5.8858 ,取 N 6,c 0.7032
2N 2N
0.3 100.11 c
2N
2N
0.2 101.5 , c
2N
0.3 100.1 c
2N
101.5 1
100.1 0.2 1.5 , lg 10 1 0.3
100.1 2
p 100.11 1 0.1 2 10 1 T
N
解 (1) 根据滤波器的指标得
20lg H e j 0.2 1 20lg H e j 0.3 15
16
巴特沃斯滤波器
Butterworth Filter
H a ( j p )
1 1
1 1
过渡带
1 p 1 c
2N
2 2
T
通带 阻带
p
2
15
c T
巴特沃斯滤波器
Butterworth Filter
p 1 c T 同理可得 1 c
2N
100.11
2N
这些极点对称于虚轴,而虚轴上无极点;N为奇数时, 实轴上有两个极点;N为偶数时,实轴上无极点;各个 极点间的角度为 / N 。图示为 N=3时各极点的分布 情况。
巴特沃斯滤波器的设计与仿真

信号与系统课程设计论文摘要传统的数字滤波器的设计过程复杂,计算工作量大,滤波特性调整困难,影响了它的应用。
本文介绍了一种利用matlab提供的巴特沃斯滤波器设计函数“buttord”可求出所需的滤波阶数和3dB 截止频率的方法。
利用matlab设计滤波器设计函数,可以随时对比设计要求和滤波器特性调整参数,直观简便,极大的减轻了工作量,有利于滤波器设计的最优化。
关键词:巴特沃斯滤波器 Matlab 截止频率I信号与系统课程设计论文AbstractDesign for traditional digital filteris very complicated ,count also very complicated.it is very hard to readjust filtering character, influence apply,the main body of the book introduce use matlab provide butwosto design function“buttord” filteris 3dB end e matlab to design could compete reqire parameter burden,contribute to optimize.Keywords: filteris matlab end frequencyII信号与系统课程设计论文目录摘要 (Ⅰ)Abstrct第1章绪论 (1)1.1 课题背景 (1)第2章巴特沃斯滤波器的设计 (2)2.1 巴特沃斯滤波器阶数的选择 (2)2.2 巴特沃斯滤波器系数计算 (2)2.2.1 巴特沃斯低通滤波器系数计算 (2)2.2.2巴特沃斯高通滤波器系数计算 (3)2.2.3巴特沃斯带通滤波器系数计算 (3)2.2.4巴特沃斯带阻滤波器系数计算 (4)第3章巴特沃斯滤波器设计仿真 (5)3.1巴特沃斯滤波器设计仿真 (5)3.1.1 巴特沃斯低通滤波器实例仿真 (5)3.1.2巴特沃斯高通滤波器实例仿真 (6)3.1.3巴特沃斯带通滤波器实例仿真 (7)3.1.4巴特沃斯带阻滤波器实例仿真 (8)结论 (9)参考文献 (10)III第1章绪论1.1课题背景巴特沃斯滤波器的特点是通频带内的频率响应曲线最大限度平坦,没有起伏,而在阻频带则逐渐下降为零。
巴特沃斯低通滤波器设计

L1'
2
600 1.304 104
0.7654H
5.61mH
C2
1 c RS
C2'
2
1 1.304 104
600
1.8478F
0.038uF
L3
RS c
L'3
2
600 1.304 104
1.8478H
13.53mH
C4
1 c RS
C4'
2
1 1.304 104
600
0.7654F
0.016uF
设计实现电路
巴特沃斯低通滤波器迅速设计总结
一:根据滤波器性
能指标(通带内旳
最大衰减 c ,阻带
内旳最小衰减 s ,
截至频率 c ,阻带
起始频率 s )利用
公式
N
lg
1
s2
-1
2 lg s / c
求巴特沃斯低通滤波 器旳阶次N。
二:根据阶次N和考尔 型电路
RS' 1
L1' 0.7654
L'3 1.8478
一般情况下,电路是在匹配情况下工作,所以取
信源内阻 Rs 和负载电阻 RL 相等。
此时满足
Ha ( j0)
RL RS RL
1 2
根据反射系数公式
(s)
(
s)=1- 4RS RL
s' s
H
a
s
H
a
-s
j
达林顿电路构造
Rs 源电阻 RL 负载电阻
RS
I1
Es
V1
1
2
LC
I2
无损
巴特沃斯阶跃阻抗低通滤波器设计

巴特沃斯阶跃阻抗低通滤波器设计引言巴特沃斯阶跃阻抗低通滤波器是一种常用于信号处理和电子电路设计中的滤波器类型。
它的设计原理是通过调整滤波器的阶数和截止频率,来实现对输入信号的频率成分进行筛选和衰减。
本文将详细介绍巴特沃斯阶跃阻抗低通滤波器的设计方法及其在实际应用中的一些注意事项。
巴特沃斯阶跃阻抗低通滤波器概述巴特沃斯阶跃阻抗低通滤波器是一种I IR(无无限冲激响应)滤波器,具有平坦的通带、陡峭的衰减特性以及相对较低的群延迟。
它广泛应用于音频处理、通信系统等领域。
巴特沃斯滤波器的设计步骤1.确定滤波器的阶数(n):阶数决定了滤波器的衰减程度和复杂度,一般取偶数值。
2.确定滤波器的截止频率(f c):截止频率即信号通过滤波器时频率衰减到原来的1/√2,是决定滤波器频率特性的关键参数。
3.计算滤波器的极点位置:根据巴特沃斯滤波器的特性方程,计算极点位置。
4.标准化滤波器:对计算得到的极点位置进行标准化处理,使得滤波器的截止频率为1。
巴特沃斯滤波器设计实例以下是一个以设计一个4阶巴特沃斯阶跃阻抗低通滤波器为例的设计过程。
步骤1:确定滤波器的阶数我们选择设计一个4阶的巴特沃斯阶跃阻抗低通滤波器。
步骤2:确定滤波器的截止频率假设我们需要将信号的截止频率设置在1k H z。
步骤3:计算滤波器的极点位置根据巴特沃斯滤波器的特性方程,我们可以计算出滤波器的极点位置。
对于一个4阶的巴特沃斯低通滤波器,其极点位置可以通过下式计算得到:p_k=-s in h(π*fc)*s in(π*(2k-1)/(2n)),k=1,2,...,n式中,f c是截止频率,n是滤波器阶数。
步骤4:标准化滤波器标准化滤波器是将计算得到的极点位置通过变换使得滤波器的截止频率为1。
标准化后的滤波器的特性方程为:H(s)=1/((s+p1)(s+p2)...(s+pn))巴特沃斯滤波器的应用注意事项-在实际设计中,应根据需要调整滤波器的阶数和截止频率,以满足对信号的频率特性要求。
巴特沃斯带通滤波器设计

做巴特沃斯带通滤波器设计模拟滤波器在测试系统或专用仪器仪表中是一种常用的变换装置。
例如:带通滤波器用作频谱分析仪中的选频装置;低通滤波器用作数字信号分析系统中的抗频混滤波;高通滤波器被用于声发射检测仪中剔除低频干扰噪声;带阻滤波器用作电涡流测振仪中的陷波器等等。
下面就在低频高阶滤波电路中应用较多的巴特沃斯滤波器的设计交流下自己的做法。
本设计只讨论有源带通滤波器的设计,因为带通包含了低通和高通的电路,暂不分别讨论。
设计中运放选择TI产品典型的通用双放LM358,LM358里面包括两个高增益、独立的、内部频率补偿的双运放,适用于电压范围很宽的单电源,而且也适用于双电源工作方式,特点方面具有低输入偏置电流、低输入失调电压和失调电流,它的共模输入电压范围较宽,差模输入电压范围等于电源电压范围,单电源供电电压3-32V,双电源供电±1.5-±16V,单位增益带宽为1MHz,适用于一般的带通滤波器的设计,同时具有低功耗的功能,对于设计阶数相对高一些的带通滤波器的话,可以选用TI的四运放LM324,其性能与LM358大体相同,应用起来节省空间。
对于运放的要求此设计不是特别高,只要运放的频率满足低通的截止频率即可,如果精确度要求高的话那么首先运放的供电电压要足够稳定,或者选择精密运放,如TLC274A,否则通用的即可,例如推荐TI的LM224四运放。
巴特沃斯带通滤波器幅频响应在通带中具有最平幅度特性,但是从通带到阻带衰减较慢,如果对于过渡带要求稍高,可以增加阶数来实现,否则改选用切比雪夫滤波电路。
下面讨论设计两种带通滤波器,其一为二阶低通滤波器和二阶高通滤波器组成的四阶带通滤波器,如下图:图1 四阶带通滤波器参数选择与计算:对于低通滤波器的设计,电容一般选取1000pF,对于高通滤波器的设计,电容一般选取0.1uF,然后根据公式R=1/2Πfc计算得出与电容相组合的电阻值,即得到此图中R2、R6和R7,为了消除运放的失调电流造成的误差,尽量是运放同相输入端与反向输入端对地的直流电阻基本相等,同时巴特沃斯滤波器阶数与增益有一定的关系(见表1),根据这两个条件可以列出两个等式:30=R4*R5/(R4+R5),R5=R4(A-1),36=R8*R9/(R8+R9),R8=R9(A-1)由此可以解出R4、R5、R8、R9,原则是根据现实情况稍调整电阻值保持在一定限度内即可,不要相差太大,注意频率不要超过运放的标定频率。
基于CFA的巴特沃斯低通滤波器设计和仿真

第41卷第3期2019年5月湖北大学学报(自然科学版)JournalofHubeiUniversity(NaturalScience)Vol.41㊀No.3㊀Mayꎬ2019㊀收稿日期:20180913作者简介:刘宛(1996)ꎬ女ꎬ本科生ꎻ赵柏树ꎬ通信作者ꎬ教授ꎬE ̄mail:zhaobaishu03@126.com文章编号:10002375(2019)03031305基于CFA的巴特沃斯低通滤波器设计和仿真刘宛ꎬ董金宁ꎬ池思慧ꎬ赵柏树(湖北大学计算机与信息工程学院ꎬ湖北武汉430062)摘要:选用一种典型的电流反馈型运放设计了巴特沃斯低通滤波器.详细论述电路结构㊁元件参数选择方法以及仿真结果.用巴特沃斯多项式逼近电路传递函数ꎬ得到巴特沃斯滤波器.结合数学方法和电路约束条件设计一种新的参数计算方法ꎬ该方法克服了常用方法中等值元件法和单位增益法的缺点.仿真结果表明ꎬ滤波器的通带增益为18dBꎬ上限截止频率为10MHzꎬ通带增益起伏为4dBꎬ过渡带下降速率为60dB/dec.关键词:巴特沃斯滤波器ꎻCFAꎻ电路仿真ꎻ网络函数中图分类号:TM919ꎻTN710㊀㊀文献标志码:A㊀㊀DOI:10.3969/j.issn.1000 ̄2375.2019.03.018DesignandsimulationofButterworthlowpassfilterbasedonCFALIUWanꎬDONGJinningꎬCHISihuiꎬZHAOBaishu(SchoolofComputerScienceandInformationEngineeringꎬHubeiUniversityꎬWuhan430062ꎬChina)Abstract:AtypicalcurrentfeedbackoperationalamplifierischosentodesignakindofButterworthlowpassfilter.Wediscussthecircuitstructureindetailꎬthemethodofselectingcomponentparametersandsimulationresults.ThemethodtodesignButterworthfilteristhatusingButterworthpolynomialtoapproximatethetransferfunctionofcircuitꎬcombiningmathmethodwithcircuitconstraintꎬwedesignakindofselectingcomponentparametersꎬwhichovercomesshortcomingofequalcomponentparametersandunity ̄gain.Thesimulationresultsshowthatgainofthefilteris18dBwithinpassbandandcut ̄offfrequencyis10MHzandpassbandrippleis4dBandrateofdescentis60dB/decwithintransitionband.Keywords:ButterworthfilterꎻCFAꎻcircuitsimulationꎻnetworkfunction0㊀引言在传统有源滤波器的设计中ꎬ有源器件通常为电压反馈运算放大器(VFA).然而ꎬVFA的增益带宽积为定值ꎬ不能同时兼顾滤波器的截止频率和增益.因此ꎬ基于VFA的有源滤波器仅限于低频应用(几百kHz以内)[1ꎬ2].随着微电子技术的高速发展ꎬ电流反馈运算放大器(CFA)应运而生ꎬCFA可以独立于增益来控制带宽ꎬ且闭环带宽大大增加ꎬ使有源滤波器的高频应用成为可能.但是ꎬ由于VFA 先入为主 的惯性作用ꎬ传统的教科书在论述低通滤波器的理论和应用电路时ꎬ均以VFA为例ꎬ并未涉及CFA.虽然近年来最新出版的电子技术教材论述了CFA的原理ꎬ但就如何应用CFA构成有源滤波器尚未涉及ꎬ各种期刊中有关CFA的应用研究时有报道ꎬ但相关研究仅限于具体问题的讨论[3 ̄4]ꎬ也见系统地研究使用CFA构成有源滤波器的文献ꎬ这与目前电子工程领域的应用要求大相径庭.为此ꎬ我们选用一种典型的CFA进行了研究ꎬ设计了六阶巴特沃斯低通滤波器.本文中将详细论述电路的结构㊁元件参数选314㊀湖北大学学报(自然科学版)第41卷择方法ꎬ以及仿真结果.1㊀滤波器网络函数巴特沃斯归一化的滤波器的网络函数为H(S)=1/B(S)ꎬ其中S=s/w0ꎬ当滤波器的阶数为6时ꎬ可以求得B(S)的表达式为B(S)=S6+3.864S5+7.464S4+9.141S3+7.464S2+3.864S+1(1)近年来ꎬ由于电子器件价格的大幅下降ꎬ单片运放的价格已经可与高性能阻容元件相比ꎬ使得用级联方式构成高阶滤波器的方法具有实用价值.为此ꎬ我们采用3个二阶滤波器级联的方法来实现六阶巴特沃斯低通滤波器.将(1)式进行因式分解ꎬ可得B(S)=(S2+0.51764S+1)(S2+1.414S+1)(S2+1.93185S+1)(2)为了方便表示ꎬ将(2)式中的一次项常数都抽象为bꎬ故B(S)的三个乘积因子都可以统一表示成S2+bS+1的形式ꎬ其中b为3个不同的常数ꎬ则每个二阶低通滤波器的网络函数均为H(S)=1S2+bS+1(3)根据S=sw0ꎬ将(3)式去归一化为H(s)=w20s2+bw0s+w20(4)2㊀电路结构为了能够提高滤波器的特征频率ꎬ我们选用一种典型的电流反馈运算放大器OPA603来实现ꎬOPA603工作频率可达几十兆赫兹以上.以OPA603为有源器件构成的二阶低通有源滤波器的原理电路图1㊀二阶KRC滤波器㊀如图1所示.其电路结构是最常见的压控电压源有源滤波器ꎬ或称KRC滤波器[5].虽然电流反馈运放和电压反馈运放的内部结构和工作原理有着巨大差异ꎬ但由电流反馈型运算放大器构成负反馈应用电路后ꎬ其输入电压约束条件(俗称 虚短 )和输入电流约束条件(俗称 虚断 )却是完全相同的[6].因此用电流反馈放大器设计二阶低通滤波电路的基本思路和方法ꎬ与使用电压反馈运放设计二阶低通电路的传统方法是基本相同的.根据图1电路ꎬ利用运放的输入电压约束条件和输入电流约束条件ꎬ可以求得传递函数(Vo/Vi)及通带放大倍数(K)的表达式如下:VoVi=KR1C1R2C2s2+1-K()R1C1+R1C2+R2C2[]s+1(5)K=1+R3R4(6)第3期刘宛ꎬ等:基于CFA的巴特沃斯低通滤波器设计和仿真315㊀3 元件参数计算将(5)式按照(4)式的形式进行化简ꎬ使两式相等即得到w0=1R1R2C1C2(7)b=1-K()R1C1R2C2+R1C2R2C1+R2C2R1C1(8)根据放大器的平衡条件可知R1+R2=R3R4R3+R4(9)由图1可知ꎬ一个二阶KRC滤波器的未知数个数为6ꎬ即电阻电容的值ꎬ而(6)(9)式可以理解为求解这6个未知数的4个独立方程ꎬ显然ꎬ还需要增加2个条件.通常先选定2个元件的值ꎬ然后根据(6)(9)式求出其他4个元件的值.而选定2个元件值的传统方法有等值元件法和单位增益法ꎬ分析表明ꎬ采用等值元件法时ꎬ上限截止频率无法设计得较高ꎬ过渡带的下降速度也达不到要求ꎻ采用单位增益法时ꎬ不能同时兼顾增益的要求.为此ꎬ我们设计了一种新的方法ꎬ在这里以一个二阶滤波电路为例来说明.由(2)式取b=1.414代入(8)式即有1.414=1-K()R1C1R2C2+R1C2R2C1+R2C2R1C1(10)令C1=C2ꎬ化简(7)㊁(10)式ꎬ使得t=R2R1ꎬ即两式分别为w0=1R1tC(11)t2-1.414t+2-K()=0(12)为了使得(12)有正根[7]ꎬ由根的判别式即得到K的约束条件为Kȡ1.5.由于电路的阻值较大时ꎬ整个电路的功耗较小ꎬ为降低功耗使得(12)式取得较大的根ꎬ即有t=1.414+1.414()2-4(2-K)2(13)由该根的规律可知随着放大倍数K的增大ꎬt也会增大.但由仿真规律可知ꎬ电阻和电容的值都不能取得太小ꎬ根据(11)式ꎬt有最大值ꎬ取R1=100ΩꎬC=50pFꎬ代入(11)式ꎬ得到t的最大值ꎬ代入(13)得到K的最大值.令上限截止频率为10MHzꎬ得到K的取值范围为1.5ɤKɤ7.61575ꎬ选择一个方便计算的K值ꎬ如K=2(只要在此范围内的K值都可根据实际电路的需要来自行选择)ꎬ来计算二阶KRC滤波器的6个元件值.将K=2代入(13)式得t=b=1.414ꎬ结合R1和R2的关系以及(9)可得R3由R1确定的表达式.由于电路的的闭环带宽仅依赖R3ꎬ如果取R3为千欧级别的电阻ꎬ则闭环带宽将达到100MHz数量级.根据这一限制条件ꎬ可以推出电阻R1的阻值范围ꎬ进而根据(11)式得到电容C的取值范围Cɤ67.8pF.当电容的容量取得较小时ꎬ必须考虑分布电容的影响ꎬ故需选择一个合适的电容Cꎬ电容确定以后根据(11)式得到R1ꎬ进而得到R2ꎬ由(6)和(9)即得R3和R4.当b=0.51764和b=1.93185时ꎬ具体计算过程也是类似的ꎬ其详细步骤不再赘述ꎬ我们得到的结论分别为1.933ɤKɤ10.466ꎬCɤ77.8pFꎻ1.069ɤKɤ5.967ꎬCɤ77.7pF.取3个二阶滤波器的电容的取值都为60pFꎬ得到六阶巴特沃斯低通滤波器如图2所示.316㊀湖北大学学报(自然科学版)第41卷图2㊀六阶巴特沃斯低通滤波器㊀4㊀仿真结果由上文可知ꎬ电容的容量存在一定的范围ꎬ选取几组容量ꎬ将得到的R1R3的值分别示于表1表3中.表1㊀第一级不同电容下的电阻值C/pFR1/ΩR2/ΩR3/R460513317166070439.5117.81114.675410109.91039.877399.51071013表2㊀第二级不同电容下的电阻值C/pFR1/ΩR2/ΩR3/R4601873741122651733461038671683361008当3个二阶滤波器的电容的容量依次取方案(1)方案(3)ꎬ(1)电容容量均为60pFꎻ(2)C1=70pFꎬC2=60pFꎬC3=70pFꎻ(3)C1=75pFꎬC2=67pFꎬC3=77pFꎬ电阻由表1表3可得ꎬ电路的幅频响应如图3图5所示.图3㊀电容均为60pF的幅频响应㊀图4㊀第二种电容取值方案的幅频响应㊀第3期刘宛ꎬ等:基于CFA的巴特沃斯低通滤波器设计和仿真317㊀图5㊀第三种电容取值方案的幅频响应㊀比较方案(1)方案(3)的仿真ꎬ将通带最大起伏㊁过渡带的下降速率㊁通带增益这三项的比较结果示于表4.表3㊀第三级不同电容下的电阻值C/pFR1/ΩR2/ΩR3/R460137513166070117.8439.51114675410109.91039.8771073991012表4㊀三个方案的仿真比较电容方案通带起伏/dB下降速率/(dB/dec)通带增益/dB(1)4.96017.968(2)3.96017.988(3)3.76017.988由表4可知ꎬ从方案(1)方案(3)ꎬ随着滤波器的电容的容量增大ꎬ通带起伏变小ꎬ过渡带下降速率㊁通带增益基本不变.5㊀结论1)基于CFA的有源滤波器可工作在高频频段ꎬ工作频率可达数十MHz以上.2)采用二阶KRC滤波器结构ꎬ用巴特沃斯低通滤波器的网络函数逼近其传递函数ꎬ用3节KRC滤波器级联得到六阶巴特沃斯低通滤波器ꎻ仿真结果表明ꎬ滤波器的通带增益为18dBꎬ通带起伏为4dBꎬ过渡带的下降速率为60dB/dec与理论计算相符.6㊀参考文献[1]林开司ꎬ张露ꎬ林开武.巴特沃斯低通滤波器优化设计与仿真研究[J].重庆工商大学学报(自然科学版)ꎬ2014ꎬ31(6):58 ̄62.[2]张涛ꎬ郑大威.基于FilterPro的有源滤波器的快速设计与分析[J].现代电子技术ꎬ2016ꎬ39(8):115 ̄117.[3]柳维玮ꎬ毛崎波.通过电流反馈运放模拟电感实现压电分流阻尼系统[J].组合机床与自动化加工技术ꎬ2017(9):73 ̄75.[4]洪庆辉ꎬ李志军ꎬ曾金芳ꎬ等.基于电流反馈运算放大器的忆阻混沌电路设计与仿真[J].物理学报ꎬ2014ꎬ63(18):90 ̄97.[5]赛尔吉欧 佛朗哥.基于运算放大器和模拟集成电路的电路设计[M].3版.西安:西安交通大学出版社ꎬ2009.[6]丰豪ꎬ王雅洁ꎬ赵柏树.基于CFA的运算电路设计与仿真[J].电子技术应用ꎬ2017ꎬ43(6):56 ̄59.[7]田聪.RC有源滤波器的优化设计[D].杭州:浙江师范大学ꎬ2016.(责任编辑㊀江津)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
信号与系统课程设计论文摘要传统的数字滤波器的设计过程复杂,计算工作量大,滤波特性调整困难,影响了它的应用。
本文介绍了一种利用matlab提供的巴特沃斯滤波器设计函数“buttord”可求出所需的滤波阶数和3dB 截止频率的方法。
利用matlab设计滤波器设计函数,可以随时对比设计要求和滤波器特性调整参数,直观简便,极大的减轻了工作量,有利于滤波器设计的最优化。
关键词:巴特沃斯滤波器 Matlab 截止频率I信号与系统课程设计论文AbstractDesign for traditional digital filteris very complicated ,count also very complicated.it is very hard to readjust filtering character, influence apply,the main body of the book introduce use matlab provide butwosto design function“buttord” filteris 3dB end e matlab to design could compete reqire parameter burden,contribute to optimize.Keywords: filteris matlab end frequencyII信号与系统课程设计论文目录摘要 (Ⅰ)Abstrct第1章绪论 (1)1.1 课题背景 (1)第2章巴特沃斯滤波器的设计 (2)2.1 巴特沃斯滤波器阶数的选择 (2)2.2 巴特沃斯滤波器系数计算 (2)2.2.1 巴特沃斯低通滤波器系数计算 (2)2.2.2巴特沃斯高通滤波器系数计算 (3)2.2.3巴特沃斯带通滤波器系数计算 (3)2.2.4巴特沃斯带阻滤波器系数计算 (4)第3章巴特沃斯滤波器设计仿真 (5)3.1巴特沃斯滤波器设计仿真 (5)3.1.1 巴特沃斯低通滤波器实例仿真 (5)3.1.2巴特沃斯高通滤波器实例仿真 (6)3.1.3巴特沃斯带通滤波器实例仿真 (7)3.1.4巴特沃斯带阻滤波器实例仿真 (8)结论 (9)参考文献 (10)III第1章绪论1.1课题背景巴特沃斯滤波器的特点是通频带内的频率响应曲线最大限度平坦,没有起伏,而在阻频带则逐渐下降为零。
在振幅的对数对角频率的波得图上,从某一边界角频率开始,振幅随着角频率的增加而逐步减少,趋向负无穷大。
巴特沃斯滤波器特别适用于低频应用,其对于维护增益的平坦性来说非常重要。
这种滤波器最先由英国工程师斯替芬·巴特沃斯(Stephen Butterworth)在1930年发表在英国《无线电工程》期刊的一篇论文中提出的。
在电力系统微机保护和二次控制中,很多信号的处理与分析都是基于对正弦基波和某些整次谐波的分析,而系统电压电流信号(尤其是故障瞬变过程)中混有各种复杂成分,所以滤波器一直是电力系统二次装置的关键部件。
目前微机保护和二次信号处理软件主要采用数字滤波器。
传统的数字滤波器设计使用繁琐的公式计算,改变参数后需要重新计算,在设计滤波器尤其是高阶滤波器时工作量很大。
利用matlab提供的巴特沃斯滤波器设计函数“buttord”可以快速有效的实现数字滤波器的设计与仿真。
巴特沃斯滤波器是电子滤波器的一种。
【1】第2章巴特沃斯滤波器的设计2.1巴特沃斯滤波器阶数的选择ω,sω,Rp,Rs之后,利用MATLAB提供的巴特在已知设计参数p沃斯滤波器设计函数“buttord”即可求出所需要的滤波器阶数和3dB 截止频率。
“buttord”命令的格式是:[n,Wn]= buttord(Wp,Ws,Rp,Rs)其中,Wp是通带截止频率,如Wp=500/4000或Wp=[650,1200]/4000等等。
Ws是阻带起始频率,Wp也可以是标量或2个元素的向量。
Rp是通带内波动(dB)。
Rs是阻带内最小衰减(dB)。
返回值n是巴特沃斯滤波器最低阶数,不同的n 有不同的频率响应。
n越大频率响应越理想,但n越大。
根据要求的指标是多少再选择相应的阶数。
这里我选用2阶就够了。
Wn是巴特沃斯滤波器截止频率,Wn可以是标量或2个元素的向量。
【2】2.2巴特沃斯滤波器系数计算[n,Wn]= buttord(Wp,Ws,Rp,Rs)其中Wp和Ws分别是通带和阻带的拐角频率(截止频率),其取值范围为0至1之间。
当其值为1时代表采样频率的一半。
Rp 和Rs分别是通带和阻带区的波纹系数。
不同类型(高通、低通、带通和带阻)滤波器对应的Wp和Ws值遵循一定的规则。
【3】2.2.1巴特沃斯低通滤波器系数计算低通滤波器遵循的规律:Wp和Ws为一元矢量且Wp<Ws。
稍后我会在仿真部分阐述设计一个巴特沃斯低通滤波器,通带截止频率为2KHz,阻带截止频率为3KHz,通带波纹系数为1,阻带衰减系数为20,采样频率为10KHz。
[b,a]= buttord(n,Wn) % n为低通滤波器阶数% Wn为低通滤波器截止频率% b为H(z)的分子多项式系数% a为H(z)的分母多项式系数2.2.2 巴特沃斯高通滤波器系数计算高通滤波器是容许高频信号通过、但减弱(或减少)频率低于截止频率信号通过的滤波器。
对于不同滤波器而言,每个频率的信号的减弱程度不同。
它有时被称为低频剪切滤波器;在音频应用中也使用低音消除滤波器或者噪声滤波器。
高通滤波器与低通滤波器特性恰恰相反。
一个滤波器滤除一个复杂信号中不想要的低频成份同时让高频信号通过是很有用的。
当然,'低'和'高'频率的含义是相对于滤波器设计者所选择的截止频率而言的。
利用巴特沃斯(Butterworth)高通滤波器对图像进行锐化处理。
高通滤波器遵循规律:Wp和Ws为一元矢量且Wp>Ws。
[b,a]= buttord(n,Wn,‘high’)% n为高通滤波器阶数% Wn为高通滤波器截止频率% b为H(z)的分子多项式系数% a为H(z)的分母多项式系数2.2.3 巴特沃斯带通滤波器系数计算带通滤波器是指能通过某一频率范围内的频率分量、但将其他范围的频率分量衰减到极低水平的滤波器,与带阻滤波器的概念相对。
这些滤波器也可以用低通滤波器同高通滤波器组合来产生。
实际上,并不存在理想的带通滤波器。
滤波器并不能够将期望频率范围外的所有频率完全衰减掉,尤其是在所要的通带外还有一个被衰减但是没有被隔离的范围。
这通常称为滤波器的滚降现象,并且使用每十倍频的衰减幅度dB来表示。
通常,滤波器的设计尽量保证滚降范围越窄越好,这样滤波器的性能就与设计更加接近。
然而,随着滚降范围越来越小,通带就变得不再平坦—开始出现“波纹”。
带通滤波器遵循规律:Wp和Ws为二元矢量且Wp<Ws,如Wp=[0.2,0.7],Ws=[0.1,0.8]。
[b,a]= buttord(n,[W1,W2])% n为buttord()设计出的带通滤波器阶数% 根据MATLAB帮组文件,butter(n,[W1,W2])将返回2*n阶滤波器系数% Wn为带通滤波器截止频率,Wn=[W1,W2],是2元向量% 注意,带通滤波器阶数是2倍关系% b为H(z)的分子多项式系数% a为H(z)的分母多项式系数【4】2.2.4 巴特沃斯带阻滤波器系数计算带阻滤波器(又称陷波器)的作用是抑制某一频率信号而通过其他频率的信号。
在Matlab中用[b,a]=butterord(n,Wn,′stop′,′s′)语句来实现带阻滤波器,其中[b,a]是滤波器传递函数多项式的系数;n为滤波器的阶数;wn=[fl*2*pi fu*2*pi]分别为阻带低端一3 dB和高端一3 dB处的角频率;′s′表示模拟滤波器的。
巴特沃特带阻滤波器返回分子分母多项式系数,还可以作出增益曲线,以及求出相位响应以及群延时响应。
带阻滤波器遵循规律:Wp和Ws为二元矢量且Wp>Ws,如Wp=[0.1,0.8],Ws=[0.2,0.7]。
[b,a]= buttord(ceil(n/2),[W1,W2],’stop’)% n为buttord()设计出的带阻滤波器阶数% 根据MATLAB帮组文件,butter(n,[W1,W2],‘stop’)将返回2*n阶滤波器系数% Wn为带通滤波器截止频率,Wn=[W1,W2],是2元向量% 注意,带通滤波器阶数是2倍关系% b为H(z)的分子多项式系数% a为H(z)的分母多项式系数【5】第3章巴特沃斯滤波器设计仿真3.1巴特沃斯滤波器设计仿真3.1.1 巴特沃斯低通滤波器实例仿真采样率为8000Hz,设计一个巴特沃斯低通滤波器,通带截止频率为2KHz,阻带截止频率为3KHz,通带波纹系数为1,阻带衰减系数为20,采样频率为10KHz,则只需在MATLAB的命令窗口下键入程序如下:f_N=8000;f_p=2100;f_s=2500;R_p=3;R_s=25;Ws=f_s/(f_N/2);Wp=f_p/ (f_N/2);[n,Wn]=buttord(Wp,Ws,R_p,R_s);[b,a]=butter(n,Wn);freqz(b,a,1000,8000)subplot(2,1,1);axis([0 4000 -30 3])程序运行后所设计出的巴特沃斯低通滤波器的频率响应如图1所示。
横坐标为:angular frequency(red/s) 纵坐标为:phase(degrees)和gain(dB)。
从图中可以得出,仿真后的频率响应满足的设计要求。
图一巴特沃斯低通滤波器的频率响应3.1.2 巴特沃斯高通滤波器实例仿真采样率为8000Hz,设计一个巴特沃斯高通滤波器,通带截止频率为2KHz,阻带截止频率为3KHz,通带波纹系数为1,阻带衰减系数为20,采样频率为10KHz,f_p=1000 Hz;f_s=700 Hz,Rp=3dB,Rs=20dB。
程序如下:f_N=8000;f_p=1000;f_s=700;R_p=3;R_s=20;Ws=f_s/(f_N/2);Wp=f_p/( f_N/2);[n,Wn]=buttord(Wp,Ws,R_p,R_s);[b,a]=butter(n,Wn,'high');freqz(b,a,1000,8000)subplot(2,1,1);axis([0 4000 -30 3])程序运行后所设计出的巴特沃斯高通滤波器的频率响应如图2所示。
横坐标为:frequency(Hz) 纵坐标为:phase(degrees)和Magnitude(dB)。
从仿真图中得出,仿真后的频率响应满足设计的要求。
