流体力学_龙天渝_绕流运动
流体力学 绕流运动

绕流运动绕流运动绕流运动,作用在物体上的力可以分为两个部份:(1)垂直于来流方向的作用力升力L(2) 平行于来流方向的作用力绕流阻力摩擦阻力形状阻力D摩擦阻力→主要发生在紧靠物体表面的一个流速梯度很大区域→边界层形状阻力→由于边界层分离,产生的压差阻力。
——都与边界层有关。
v 0v 0∂=∂xv 0yx K∂≠∂xv 0y1.边界层的形成边界层内:由于粘性影响,沿平板法线方向速度梯度大v ∂≠∂x0y主流区:v ∂≈∂xy ∴沿法线方向既存在剪切流动(边界层),又存在有势流动(主流区),一般把作为分界。
00.99v v =vv 0∂=∂xv 0yx K∂≠∂xv 0y2.流态边界层从开始,,长度逐渐增大,当,层流→紊流。
=x 0=⇒δ0δ=k x x 虽然出现紊流,但仍有一层紧靠壁面的层流底层(粘性力占主的区域)。
5Re 10k xk v x ==⨯0 3.5 5.0ν~Re 3000k δδν==0v ~35003. 边界层基本特性a.与物体长度相比,边界层厚度很小,δ小。
b.边界层内沿法向(厚度)方向速度变化大,梯度大,边界层内按层流或紊流计算,边界层外按势流理论计算。
c.由于边界层薄,先假设边界层不存在,全部按势流理论计算相应的速度及压强,得到的结果可认为是边界层外边界上的速度及压强。
边界层内边界是物体表面,速度为零;边界层很薄,边界层中各截面上沿Y方向压力不变,并且近似等于边界层边界上压力。
ACB D主流区边界层XV1. 有利压强梯度和不利压强梯度(以流体绕圆柱流动为例)在迎流面,沿流动方向,主流区v 增大,p 减小()0()0v p,x x∂∂⇒><∂∂主p px x∂∂=∂∂主边而()()()0px∂∴<∂边在背流面,沿流动方向,()0()0v p,x x ∂∂<>∂∂主主()()p px x ∂∂=∂∂主边由于()0p x∂∴>∂边前者称为有利压强梯度,后者称为不利压强梯度。
流体力学_龙天渝_一元气体动力学原理

第九章 一元气体动力学基础一、学习指导 1. 基本参数 (1) 状态方程气体的压强p ,密度ρ以及温度(绝对)T 满足状态方程p RT ρ=式中,R 为气体常数,对于空气,287/()R J kg K =⋅。
(2) 绝热指数k/p v k c c =式中,c p 和c v 分别是等压比热和等容比热,他们与气体参数地关系为1p k c R k =-,11p c R k =-(3) 焓和熵焓h 的定义是ph e ρ=+式中,e 是气体内能,v e c T =。
h 可一表示为 p h c T =熵的表达式为ln()kps cv c ρ=+常数(4) 音速cc =(5) 马赫数马赫数M 的定义是uM c =式中,u 是气流速度;c 是音速。
2. 一元恒定流动的运动方程 (1) 气体一元定容流动ρ=常数22pv g γ+=常数 (2) 气体一元等温流动T =常数,pRT cρ==2ln 2v c p +=常量2ln 2v RT p +=常量(3) 气体一元绝热流动k p cρ= 212k p v k ρ⋅+-=常量3. 滞止参数气流在某断面的流速,设想以无摩擦绝热过程降低至零时,断面各参数所达到的值,称为气流在该断面的滞止参数。
用p 0、ρ0、T 0、i 0、c 0表示滞止压强、滞止密度、滞止温度、滞止焓值、滞止音速。
0/T T ,0/p p ,0/ρρ,0/c c 与马赫数M 的函数关系:20112T k M T -=+11200112k kk k p T k M p T ---⎛⎫⎛⎫==+ ⎪⎪⎝⎭⎝⎭1111200112k k T k M T ρρ---⎛⎫⎛⎫==+ ⎪⎪⎝⎭⎝⎭1122200112c T k M c T -⎛⎫⎛⎫==+ ⎪ ⎪⎝⎭⎝⎭4. 气体一元恒定流动的连续性方程2(1)dA dv M A v =-(1) M<1为亚音速流动,v<c ,因此dv 与dA 正负号相反,速度随断面面积增大而减慢;随断面面积减小而加快。
流体力学第二版龙天渝课后答案

流体力学第二版龙天渝课后答案【篇一:流体力学_龙天渝_建环专业课程教案】>(建筑环境与设备工程专业)第一章绪论1.本章的教学目标及基本要求本章为绪论,涉及到流体的定义、作用在流体上的力、流体的基本物理性质和流体的力学模型。
通过本章的教学,要求学生了解流体力学在本学科及相关工程技术领域内的地位和作用,掌握流体与固体的典型区别,连续介质模型、不可压缩流体和理想流体的定义,了解流体的主要物理性质;掌握流体的受力分析方法,能够正确应用牛顿内摩擦定律分析解决液膜条件下流体的运动及及其与固体间的相互作用问题。
2.本章各节教学内容(列出节名)及学时分配本章教学内容分2单元,每单元2学时? 单元1:流体力学在本学科中的地位和作用,流体的定义与特点,,作用在流体上的力;流体的惯性, 流体的粘性;习题1-1, 4? 单元2:流体的粘性,压缩性与膨胀性, 不可压缩流体和理想流体的概念,流体的连续介质模型;习题1-7,8,123.本章教学内容的重点和难点本章的重点是:本章的教学任务是让学生初步建立起流体及流体力学的基本概念,重点放在流体与固体的本质区别,描述流体的基本模型及流体的主要物理性质。
本章的难点是:熟练、正确进行受力分析;正确运用牛顿内摩擦定律分析求解液膜条件下流体的运动及及其与固体间的相互作用问题。
4. 本章教学内容的深化和拓宽:介绍不可压缩流体的概念及其工程应用意义,说明粘性的外部特性与内部特性的区别。
5.本章教学方式(手段)及教学过程中应注意的问题;本章涉及到较多的物理基本概念,注意时刻提醒学生从最基本的物理现象出发去理解和把握物理概念,在受力分析及应用过程中注意结合以往课程的内容和知识,帮助学生逐步建立将所学知识与工程实际应用相结合的思维习惯。
教学方式以课堂教学为主。
6.本章的主要参考书目:? clayton t.crowe, donald f. elger and john a. roberson. engineering fluid mechanics. 7th ed. new york: john wiley sons,2001? vennard j k and r l street. elementary fluid mechanics. 6th ed. new york: john wiley sons,19827.本章的思考题和习题:习题1-1,4,7,8,12单元 11.教学内容:流体力学在本专业中的作用, 流体的定义,惯性、压缩性与膨胀性? 了解流体力学在学科中的地位和作用;? 明确流体的定义;? 了解流体的特点及流体的连续介质模型;? 了解流体惯性的度量方法;? 了解流体的压缩性与膨胀性的定义及数量级;? 明确不可压缩流体的概念。
流体力学_龙天渝_建环专业课程教案

《流体力学》课程教案(建筑环境与设备工程专业)第一章绪论1.本章的教学目标及基本要求本章为绪论,涉及到流体的定义、作用在流体上的力、流体的基本物理性质和流体的力学模型。
通过本章的教学,要求学生了解流体力学在本学科及相关工程技术领域内的地位和作用,掌握流体与固体的典型区别,连续介质模型、不可压缩流体和理想流体的定义,了解流体的主要物理性质;掌握流体的受力分析方法,能够正确应用牛顿内摩擦定律分析解决液膜条件下流体的运动及及其与固体间的相互作用问题。
2.本章各节教学内容(列出节名)及学时分配本章教学内容分2单元,每单元2学时单元1:流体力学在本学科中的地位和作用,流体的定义与特点,,作用在流体上的力;流体的惯性, 流体的粘性;习题1-1,4单元2:流体的粘性,压缩性与膨胀性, 不可压缩流体和理想流体的概念,流体的连续介质模型;习题1-7,8,12 3.本章教学内容的重点和难点本章的重点是:本章的教学任务是让学生初步建立起流体及流体力学的基本概念,重点放在流体与固体的本质区别,描述流体的基本模型及流体的主要物理性质。
本章的难点是:熟练、正确进行受力分析;正确运用牛顿内摩擦定律分析求解液膜条件下流体的运动及及其与固体间的相互作用问题。
4. 本章教学内容的深化和拓宽:介绍不可压缩流体的概念及其工程应用意义,说明粘性的外部特性与内部特性的区别。
5.本章教学方式(手段)及教学过程中应注意的问题;本章涉及到较多的物理基本概念,注意时刻提醒学生从最基本的物理现象出发去理解和把握物理概念,在受力分析及应用过程中注意结合以往课程的内容和知识,帮助学生逐步建立将所学知识与工程实际应用相结合的思维习惯。
教学方式以课堂教学为主。
6.本章的主要参考书目:●周光炯等编·流体力学·第2版·北京:高等教育出版社,2000●屠大燕主编·流体力学与流体机械·北京:中国建筑工业出版社,1999●刘鹤年编·水力学·北京:中国建筑工业出版社,1999●李玉柱苑明顺编·流体力学·北京:高等教育出版社,1998●陈卓如主编·工程流体力学·北京:高等教育出版社,1992●潘文全·工程流体力学·北京:清华大学出版社,1988●汪兴华·工程流体力学习题集·北京:机械工业出版社,1983●山东工学院东北电力学院·工程流体力学·北京:电力工业出版社,1980●Clayton T.Crowe, Donald F. Elger and John A. Roberson.Engineering Fluid Mechanics. 7th ed. New York: John Wiley& Sons,2001●Vennard J K and R L Street. Elementary Fluid Mechanics. 6thed. New York: John Wiley & Sons,19827.本章的思考题和习题:习题1-1,4,7,8,12单元11.教学内容:流体力学在本专业中的作用, 流体的定义,惯性、压缩性与膨胀性✧了解流体力学在学科中的地位和作用;✧明确流体的定义;✧了解流体的特点及流体的连续介质模型;✧了解流体惯性的度量方法;✧了解流体的压缩性与膨胀性的定义及数量级;✧明确不可压缩流体的概念。
流体力学 第1章

第1章 绪论
血液的流动、植物体内输送营养 液、鸟类的翱翔,鱼在水中的游动 等现象归属于生物流变学。
第1章 绪论
高尔夫球运动起源于15世纪的苏格兰, 当时人们认为表面光滑的球飞行阻力小, 因此用皮革制球。后来发现表面有很多划 痕的旧球反而飞得更远,这个谜直到20世 纪建立流体力学边界层理论后才解开。现 在的高尔夫球表面有很多窝坑,在同样大 小和重量下,飞行距离为光滑球的5倍。
第1章 绪论
地下水的利用,石油、天然气的开采,这些都是渗流力 学研究的主要对象。
沿海地区有较严重的海水入侵,使地下水质恶化,氯离 子含量增加,给这些地区工农业生产和人民生活造成危害。
第1章 绪论
气体参与的燃烧与爆炸所产生的瞬间能量变化和 传递过程,形成了爆炸力学。
第1章 绪论
煤粉输送、沙漠迁移、泥沙流动等,均为流体中带有固体 颗粒或液体中带有气泡等问题,都属于多相流体力学研究的范 畴。
第1章 绪论
1.5 流体力学的应用
(1)舰船、航空、航天(飞机的(风洞)实验、火箭上天); (2)城市给排水; (3)水利、水电(三峡水利工程); (4)矿山应用。
第1章 绪论
飞机的出现以及航天飞机的飞行,使人类的活 动范围扩展到地球之外的其他星球。航空航天事 业同流体力学的分支学科——空气动力学和气体 动力学的发展密不可分的。
粗糙表面可以减少 空气的阻力及提供 升力,让高尔夫球 飞得更远 。
第1章 绪论
汽车发明于19世纪末,当时人们认为汽车的阻力主要来自前部对空气的撞 击,因此早期的汽车后部是陡峭的,称为箱型车,阻力系数约为0.8。实际上 汽车阻力主要来自后部形成的尾流,称为形状阻力。20世纪30年代起,人们 开始运用流体力学原理改进汽车尾部形状,出现甲壳虫型,阻力系数降至0.6。 20世纪50-60年代改进为船型,阻力系数为0.45。80年代又改进为鱼型, 阻力系数为0.3,以后进一步改进为楔型,阻力系数为0.2。90年代后,科研 人员研制开发的未来型汽车,阻力系数仅为0.137。
流体力学龙天渝课后答案 一元流体动力学基础

1 一元流体动力学基础1.直径为150m m 的给水管道�输水量为h k N /7.980�试求断面平均流速。
解�由流量公式v A Q �� 注意���v A Q s k g h k N ����// A Q v��得�s m v /57.1� 2.断面为300m m ×400m m 的矩形风道,风量为2700m 3/h ,求平均流速.如风道出口处断面收缩为150m m ×400m m ,求该断面的平均流速 解�由流量公式v A Q � 得�AQv �由连续性方程知2211A v A v � 得�s m v /5.122� 3.水从水箱流经直径d 1=10c m ,d 2=5c m ,d 3=2.5c m 的管道流入大气中. 当出口流速10m / 时,求(1)容积流量及质量流量;(2)1d 及2d 管段的流速 解�(1)由s m A v Q /0049.0333�� 质量流量s k g Q /9.4�� (2)由连续性方程� 33223311,A v A v A v A v �� 得�s m v s m v /5.2,/625.021�� 4.设计输水量为h k g /294210的给水管道�流速限制在9.0∽s m /4.1之间。
试确定管道直径�根据所选直径求流速。
直径应是m m 50的倍数。
解�v A Q �� 将9.0�v ∽s m /4.1代入得343.0�d ∽m 275.0 ∵直径是m m 50的倍数�所以取m d 3.0� 代入v A Q �� 得m v 18.1� 5.圆形风道�流量是10000m 3/h ,�流速不超过20 m /s 。
试设计直径�根据所定直径求流速。
直径规定为50 m m 的倍数。
解�v A Q � 将s m v /20�代入得�m m d 5.420� 取m m d 450� 代入v A Q � 得�s m v /5.17� 6.在直径为d 圆形风道断面上�用下法选定五个点�以测局部风速。
流体力学_龙天渝_流动阻力、能量损失、孔口、管嘴与有压管流

第四章流动阻力、能量损失、孔口、管嘴与有压管流一、学习引导1.流动阻力与水头损失的两种型式:流体通过的边界不同,产生的阻力不同,流动阻力分为沿程阻力与局部阻力。
同样,克服这些阻力产生的能量损失也分为沿程水头损失与局部水头损失。
1)流动阻力沿程阻力:流体边界几何形状沿程不变,均匀分布在流程上的阻力称沿程阻力局部阻力:流体边界发生突变,集中分布在突变处的阻力,如转弯、阀门、进出口、突扩。
2)能量损失沿程水头损失:克服沿程阻力产生的能量损失,h f。
局部水头损失:克服局部阻力产生的能量损失h j。
2.流体的两种流动型态——层流和紊流1)层流与紊流层流:流体质点有条不紊,互不混掺的流动。
紊流:流体质点互相混掺的流动。
2)层流与紊流的判别标准层流与紊流的判别标准为临界雷诺数。
从层流到紊流时为上临界雷诺数,从紊流到层流时为下临界雷诺数。
上临界雷诺数不稳定,通常取下临界雷诺数作为层流与紊流的判别标准圆管流:ek R=2000 Re>2000紊流 Re<2000层流明渠流:ek R=500 Re>500 紊流 Re<500层流圆管流雷诺数:νυd ⋅=Re明渠流雷诺数:νυR ⋅=Re水力半径的计算: X A R =3.均匀流基本方程与沿程水头损失 1)均匀流基本方程RJ γτ=0适用范围:在压管流动,明渠流动。
圆管流中:2rJγτ=200Jr γτ=有: 00r r =ττ00r r ττ= 恒定均匀流中,有压管流的过流断面上切应力成线性分布,中心处τ最小,为零;边壁上τ最大,τ=0τ2)沿程水头损失的计算公式达西公式:圆管流中:g d l h f 22υλ⨯⨯= 明渠流动:g R l h f 242υλ⨯⨯= 达西公式适用:有压管流、明渠流, 层流 、紊流 4.圆管中的层流运动1)流速分布圆管中的层流运动流速分布为一个旋转抛物面:μγ4)(20r r J u -=最大流速位于圆管中心:r=0 ,μγ420m axJr u =平均流速:max22021328u Jd Jr ===μγμγυ2)动能修正系数与动量修正数 动能修正系数:2=α 动量修正数:33.1=β 5.紊流运动的特征和紊流阻力1)紊流运动的特征紊流运动最大的特点是具有脉动性与时均性。
重庆大学流体力学教学大纲

重庆大学流体力学教学大纲一、课程名称:流体力学二、课程代码:三、课程英文名称:FLUID MECHANICS四、课程负责人:龙天渝五、学时和学分:80学时 4.5学分六、课程性质:必修课程七、适用专业:建筑环境与设备工程八、选课对象:本科生九、预修课程:高等数学 工程力学十、使用教材:龙天渝、蔡增基编.流体力学.中国建筑工业出版社,2004十一、参考书目:李玉柱编..工程流体力学(上、下册).清华大学出版社,2007屠大燕编.流体力学与流体机械.中国建筑工业出版社,1999刘鹤年编.水力学.中国建筑工业出版社,1999Clayton T.Crowe, et al. Engineering Fluid Mechanics. 7th ed. New York: John Wiley & Sons,2001十二、开课单位:城市与环境工程学院十三、课程的目的和任务:本课程是建筑环境与设备工程专业的一门主要的技术基础课。
它的主要任务是通过各个教学环节,运用各种教学手段和方法,使学生掌握流体运动的基本概念、基本原理、基本计算方法;培养学生分析、解决问题的能力和实验技能,为学习后继课程,从事工程技术工作,科学研究以及开拓新技术领域,打下坚实的基础。
十四、课程的基本要求:1.绪论了解本课程在专业及工程中的应用,理解作用在流体上的力,理解流体主要物理性质,特别是粘性和牛顿内摩擦定律,理解连续介质、不可压缩流体及理想流体的概念。
2.流体静力学理解静压强的特性,掌握静力学基本方程、等压面以及液体中压强的计算、测量与表示方法,掌握总压力的计算方法,理解液体的相对平衡。
3.一元流体动力学基础理解描述流体运动的两种方法,理解流动类型和流束与总流等相关概念,掌握总流连续性方程、能量方程和动量方程及其应用。
4.流动阻力和能量损失掌握粘性流体的两种流态及判别准则,理解圆管层流的运动规律,理解紊流特性、处理方法和紊流切应力,理解沿程能量损失的成因和阻力系数的变化规律,掌握沿程能量损失的计算方法,理解局部能量损失的成因,掌握局部能量损失的计算方法。
流体力学课后习题答案龙天渝

(a)流动随时间按一定规律变化;
(b)流场中任意空间点的运动要素不随时间变化;
(c)各过流断面的流速分布不同;
(d)各过流断面的压强相同。
3-2非恒定流是:
(a)?u/?t=0;
(b)?u/?t≠0;
(c)?u/?s=0;
(d)?u/?s≠0。
3-3一元运动是:
(a)均匀流;
(b)速度分布按直线变化;
22求流线方程并画出若干条流线。(x+y=c)
3-15已知平面流动的速度场为u=(4y-6x)ti+(6y-9x)tj。求t=1时的流线方程并绘出x=0至x=4区间穿过x轴的4条流线图形。(1.5x-y=c)
3-16水管的半径r0=30mm,流量q=401l/s,已知过流断面上的流速分布为u=umax(y/r0)1/7。式中:umax是断面中心点的最大流速,y为距管壁的距离。试求:
求水头h。水头损失不计。(1.23m)
【篇二:流体力学_龙天渝_流体动力学基础】
ass=txt>一、学习指导1.主要概念:
流线,过流断面,均匀流,渐变流,恒定流
注:①流体是空间曲线。对恒定流其空间位置不变,对非恒定流随时间而变化。
②渐变流是将流速的大小和方向变化不大的流段看成均匀流所作的工程近似,与均匀流无明确的界定,根据经验而定。例:锥角较小的扩散段或收缩段,断面面积a(s)满足da/ds=0的断面附近的流段是渐变流。
(2)是几元流动?
(3)是恒定流还是非恒定流;
(4)是均匀流还是均匀定流?
3-13已知平面流动的速度分布为ux=a,uy=b,其中a、b为常数。求流线方程并画出若干条y0时的流线。((b/a)x-y=c)
3-14已知平面流动速度分布为ux=-cy/(x2+y2),uy= cx/(x2+y2),其中c为常数。
流体力学_龙天渝_流动阻力和能量损失

(2)光滑黄铜管的沿程水头损失
在Re<105时可用布拉修斯公式:
由图4-11和莫迪图可得出一致的结果.
(3)K=0.15mm工业管道的水头损失 根据Re=80000,K/d=0.15mm/100mm=0.0015,由莫迪图得 0.024。
第七节 非圆管的沿程损失
非圆管的沿程损失一般用到当量直径计算。 水力半径为过流断面面积A和湿周 之比。
( b) ( c) 图4-2 由紊流变为层流的临界流速 小于由层流转变为紊流的临界 流速 。称 为上临界流速, 为下临界流速。上临界流速 不稳定,下临界流速稳定,一般的临界流速指的是下临界流速。
( a)
流态的判别标准——临界雷诺数
பைடு நூலகம்
流动状态不仅和流速v有关,还和管径d、流体的动力黏度 和密度 有关,用一无因次数Re表示,称雷诺数:
式(4-30) 和式(4-32)都是半经验公式,还有两个应用 广泛的经验公式,光滑区的布拉休斯公式:
上式适用于Re<105的情况。还有粗糙区的希弗林松公式:
紊流过渡区和柯列勃洛克公式 柯列勃洛克根据大量的工业管道试验资料,整理出工业管道 过渡区曲线,并提出该曲线的方程:
K为工业管道的当量粗糙粒高度,可查4-1。该式为尼古拉兹 光滑区公式和粗糙区公式的机械组合。为简化计算,莫迪以 柯氏公式为基础绘制出反映Re、K/d和 对应关系的莫迪图, 在该图上可根据Re和K/d直接查出 。 此外,还有一些人为简化计算,在柯氏公式的基础上提出了
[例4-11]某钢板制风道,断面尺寸为400mm×200mm,管长 80m。管内平均流速v=10m/s。空气温度t=20℃,求压强损失 pf。 [解](1)当量直径
(2)求Re。查表,t=20 ℃时, =15.7×10-6m2/s
流体力学(第二版) 龙天渝 第八章 绕流运动习题答案
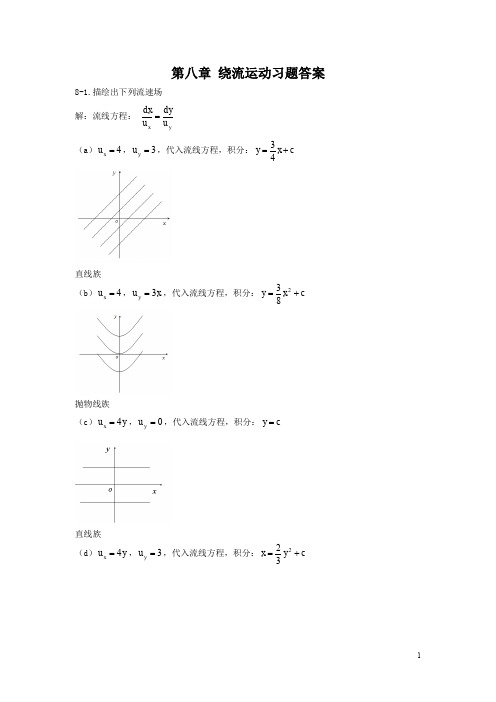
直线族 (d) u x 4 y , u y 3 ,代入流线方程,积分: x
2 2 y c 3
1
抛物线族 (e) u x 4 y , u y 3x ,代入流线方程,积分: 3x 2 4 y 2 c
椭圆族 (f) u x 4 y , u y 4 x ,代入流线方程,积分: x 2 y 2 c
5
u0 X k
(查表知 t=20ºC, 1.007 106 m / s )
Xk=
Re xk =0.1m<30m u0
可认为是紊流附面层:Re= 采用 C f
u0 X
=1.49×10
8
0.445 -3 ,则: C f =1.963×10 2.58 (lg Re )
2 u 0
u0 X k
,知
Xk=0.55m
8
(2)根据: =0.37 (
u0 x
) x,知 =0.0572m=57.2mm
1 5
(3) 根据:Re= 则: C f =
vx 6 知 Re =2.75×10 .
0.074 1700 -3 =3.196×10 1 Re Re 5
2 u 0
根据: D f C f A
解:叠加前
ux
Q y y (arctg arctg ) 2 xa xa
Q xa xa ( ) y 2 y 2 ( x a) 2 y 2 ( x a) 2 Q y y ( 2 2 ) 2 x 2 y ( x a) y ( x a) 2 uy Qy (y2 a2 )
Q y y (arctg arctg ) 2 xa xa
流体力学第八章绕流运动

流体⼒学第⼋章绕流运动第⼋章绕流运动⼀、应⽤背景1、问题的⼴泛存在性:在⾃然界和⼯程实际中,存在着⼤量的流体绕物体的流动问题(绕流问题),如:飞机在空⽓中的飞⾏、河⽔流过桥墩、⼤型建筑物周围的空⽓流动、植物护岸(消浪,船⾏波),粉尘颗粒在空⽓中的飞扬和沉降,⽔处理中固体颗粒污染物在⽔中的运动。
(⼀种:流体运动;另外⼀种:物体运动),我们研究,将坐标系固结于物体上,将物体看成静⽌的,讨论流体相对于物体的运动。
2、问题的复杂性上⼀章的内容中可以看出,流体⼒学的问题可以归结为求解在⼀定边界条件和初始条件下偏微分⽅程组的求解。
但描述液体运动的⽅程式⾮常复杂的:⼀⽅⾯,是⽅程的⾮线性性质,造成⽅程求解的困难;另⼀⽅⾯,复杂的边界条件和初始条件都给求解流体⼒学造成了很多⿇烦。
迄今为⽌,只有很少数的问题得到了解决。
平⾯泊萧叶流动,圆管coutte流动等等。
⽽我们所要解决的绕流问题正是有着⾮常复杂的边界条件。
3、问题的简化及其合理性流体⼒学对此的简化则是,简化原⽅程,建⽴研究理想液体的势流理论。
实际液体满⾜势流运动的条件:粘性不占主导地位,或者粘性还没有开始起作⽤。
正例:远离边界层的流体绕流运动、地下⽔运动、波浪运动、物体落⼊静⽌⽔体中,⽔的运动规律研究。
反例:研究阻⼒规律、能量损失、内能转换等等。
圆柱绕流(经典之⼀)半⽆限长平板绕流(经典之⼆)分成两个区域:⼀个区域是远离边界的地⽅,此区域剪切作⽤不明显,⽽且流体惯性⼒的影响远远⼤于粘性⼒的影响(理想液体)(引导n-s⽅程);另⼀个是靠近边界的地⽅(附⾯层,粘性底层),此区域有很强烈的剪切作⽤,粘性⼒的影响超强,据现代流体⼒学的研究表明,此区域是产⽣湍流的重要区域,有强烈的剪切涡结构,但此区域只有⾮常薄的厚度。
此区域对绕流物体的阻⼒、能量耗损、扩散、传热传质都产⽣重要影响。
4、本章的主要研究内容(1)外部:理想液体,(简化⽅法,求解⽅式)、(2)内部:附⾯层理论,(简化⽅法,求解⽅式,求解内容,现象描述)(3)两者的衔接。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
紧靠物体表面的一个流速梯度很大的流体薄层 内,这个薄层就叫附面层。形状阻力主要是指 流体绕曲面体或具有锐缘棱角的物体流动时, 附面层要发生分离,从而产生漩涡所造成的阻 力。这种阻力与物体形状有关,故称为形状阻 力。这两种阻力都与附面层有关。 一、附面层的形成及性质 二、管流附面层
第六节 附面层动量方程
因此,无旋流动的前提条件是
u z u y y z u x u z z x u y u x x y
由不可压缩流体的连续性方程 u x u y u z 0 x y z 得出拉普拉斯方程 2 2 2 2 2 0 2 x z y
四、直角内的流动
第四节 势流叠加
设有两势流1和 2,他们的连续性条件由满足拉普拉斯方程来 表征: 21 21 2 0 2 x y 2 2 2 2 0 2 2 x y 而这两势函数之和, 1 2也将适合拉普拉斯方程。因为 21 2 2 21 2 2 2 2 2 2 2 0 2 2 2 x x y y x y
一、绕流阻力的一般分析 以圆球绕流为例。 设圆球作匀速直线运动,如果流动的雷诺数 ud Re (d为圆球半径) 很小,在忽略惯性力的前提下,可以推 导出 FD 3du0 称为斯托克斯公式。
0
如用(8 - 68)式来表示,则 24 d 2 u0 24 u0 FD 3du0 . . A. u0 d 4 2 Re 2
绕流物体的摩擦阻力作用,主要表现在附面层 内流速的降低,引起动量的变化。
附面层的动量方程为 d d dp 2 0 u x dy U dx 0 u x dy dx 0 dx
附面层动量方程有五个未知数:、p、u x、U和 0。 dp 其中U可以用理想流体的势流理论求得, 可
一切不可压缩流体的平面运动,无论是有旋流 动或是无旋流动都存在流函数,但是,只有无 旋流动才存在势函数。
第三节 几种简单的平面无旋流动
一、均匀直线流动 在均匀直线流动中,流速及其在x, y方向上 的分速度保持为常数,即
u x a, u y b 则存在着势函数: d u x dx u y dy adx bdy
2 2
由此得 Cd 24 Re
(8-70)
二、悬浮速度 设在上升的气流中,小球的密度为 m,大于气体的密 度 ,即 m 。小球受力情况如下。 方向向上的力有: u0 2 1 2 FD Cd A Cd d 2 u0 绕流阻力 1 2 8 FB d 3 g 浮力 6 方向向下的力有: 1 重力 G d 3 m g
第八章 绕流运动
第一节 无旋流动 第二节 平面无旋流动 第三节 几种简单的平面无旋运动 第四节 势流叠加 第五节 绕流运动与附面层基本概念 第六节 附面层动量方程 第七节 平板上层流附面层的近似计算 第八节 平板上紊流附面层的近似计算 第九节 曲面附面层的分离现象与卡门涡街 第十节 绕流阻力和升力
2
1 u0 2 . xc 15 2 式中,c为积分常数,当x 0, 0, 代入后得到c 0。故 1 u0 2 . x 15 2 以
代入,并简化,得 x
u0
5.477
这便是附面层厚度沿x方向的变化关系。
平板上切应力沿平板长度方向的变化关系式为
0 0.365
L
u0
3
x 作用在平板上一面的总摩擦力FDF 为 FDF 0bdx 0.73b u0 L
3 0
如要求流体对平板两面的总摩擦力,只需乘2。
式中,b为平板垂直于纸面方向的宽度,L为平板长度。
第八节 平板上紊流附面层的近似计算
假设整个平板上都是紊流区。
附面层厚度沿平板长度x方向的变化关系为 0.37 u x x 0 平板切应力 0沿x方向的变化关系为 0 0.029 u0 u x 0
沿程增加的区段内,即增压减速区。 附面层分离后,物体后部形成许多无规则的漩涡,由 此产生的阻力称形状阻力。因为分离点的位置,漩涡 区的大小,都与物体的形状有关,故称形状阻力。对 于有尖角的物体,流动在尖角处分离,愈是流线型的 物体,分离点愈靠后。飞机、汽车、潜艇的外形尽量 做成流线型,就是为了推后分离点,缩小漩涡区,从 而达到减小形状阻力的目的。 二、卡门涡街 当流体绕圆柱体流动时,在圆柱体后半部分,流体处 于减速增压区,附面层要发生分离。物体后面形成有 规则的交错排列的漩涡组合,称为卡门涡街。
Qv Qv y 2 2 ln x y , arctan 2 2 x
可以看出,源流流线为从源点向外射出的射线, 而等势线则为同心圆周簇。
当流体反向流动,即流体从四方向某汇合点集 中,这种流动称为汇流。汇流的流量称为汇流
强度,它的和函数,是源流相应的函 数的负值。 Qv ln r 2 Qv 2 直角坐标系下相应函数 的表达式为 Qv ln x 2 y 2 2 QV y arctan 2 x
2 1 5 1 5
b为平板垂直于纸面方向的宽度,L为平板长度。
平板上的总摩擦力为 FDf b 0 dx 0.036 u0 bL u L 0 0
L 2 1 5
第九节 曲面附面层的分离现象 与卡门涡街
一、曲面附面层的分离现象 当流体绕曲面体流动时,沿附面层外边界上的 速度和压强不是常数。形成回流和前进两部分 运动情况。这两部分运动方向相反的流体相接 触,就形成漩涡。漩涡的出现势必使附面层与 壁面脱离,这种现象称为附面层的分离。 附面层的分离只能发生在断面逐渐扩大而压强
附面层理论用于探讨摩擦阻力的规律,而绕平 板的流动,是一种只有摩擦阻力而无形状阻力 的典型流动。 平板附面层的基本方程式为 0 d 2 d 0 ux dy u0 dx 0 u x dy dx
此方程式对层流和紊流均适用。
先研究层流附面层。在上一节已经提到,必须 补充两个方程,才能解出所需要的量。 第一个补充方程为附面层中的速度分布函数 2u0 y2 u x f1 y 。为 u x y
dx
以按能量方程求得,剩下三个未知数 0、 和 u x 因此要解附面层动量方程,还需两个补充方程。通常 的补充方程是 (1)附面层内的速度分布u x f1 y ;
(2) 0与的关系 0 f 2 , 该关系可根据附面层内的 速度分布求得。
第七节 平板上层流附面层的近视计算
第一节
无旋流动
流场中各点旋转角速度等于零的运动,称为无 旋流动。在无旋流动中,有
1 u z u y x 0 2 y z 1 u x u z y 0 2 z x 1 u y u x z 0 2 x y
将以上所得的两个补充方程代入层流附面层动量方程 中,有
2u0 2 u0 d y 2 d 2u0 y 2 y dy u0 y dy dx 0 2 dx 0 2 化简上式,并进行积分。得到附面层厚度沿x方向的变化关系。即
1 2
第五节 绕流运动与附面层基本概念
在绕流中,流体作用在物体上的力可以分为两 个分量:一是垂直于来流方向的作用力,叫做 升力;另一是平行于来流方向的作用力,叫做 阻力。本章主要讨论绕流阻力。 绕流阻力可以认为由两部分组成,即摩擦 阻力和形状阻力。实验证明,流体在大的雷诺 数下绕过物体运动时,其摩擦阻力组要发生在
这就是说,两势函数之和形成新势函数,代表新流动, 新流动的流速
1 2 ux u x1 u x 2 x x x 1 2 uy u y1 u y 2 y y y
是原两势流流速的叠加。 同样可以证明,复合流动的流函数等于原流动流 函数的代数和,即
第十节 绕流阻力和升力
绕流阻力包括摩擦阻力和形状阻力,附面层 理论用于求摩擦阻力。绕流阻力的计算式,和 平板阻力的计算式相同。
2 式中FD — 物体所受的绕流阻力; Cd — 无因次的阻力系数; A — 物体的投影面积。 u0 — 未受干扰时的来流速度; FD Cd A
u0 2
(8-68)
— 流体的密度。
adx bdy ax by
流函数根据
ay bx 得 二、源流和汇流 设想流体从通过O点垂直于平面的直线,沿 径向r均匀的四散流出,这种流动称为源流。O 点为源点。垂直单位长度所流出的流量为Qv, Qv称为源流强度。连续性条件要求,流经任一 半径r的圆周的流量Qv不变,则径向流速ur等于 流量Qv除以周长2πr 。即
满足拉普拉斯方程的函数称为调和函数。因此, 不可压缩流体势流的速度势函数,是坐标(x, y, z)的调和函数 ,而拉普拉斯方程本身,就 是不可压缩流体无旋流动的连续性方程。
第二节 平面无旋流动
在流场中,某一方向(取作z轴方向),uz=0, 而另两方向的流速ux、uy与上述坐标z无关的流 动,称为平面流动。 在不可压缩流体平面运动中,连续性方程简化 u x u y 0 为 x y 而旋转角速度只有分量ω z,如果ω z为零,则
2
第二个补充方程为平板上的切应力 0 和附面层 厚度 之间的函数关系,即 0 f 2 因为是层流,符合牛顿内摩擦定律。
du x 0 dy
y 0
d 2u0 y2 y dy 2
2u0 y 0
Qv ur , u 0 2r
d u x dy u y dx ady bdx
势函数用
流函数用
直角坐标下相应函数的表达式为
Qv ur dr u rd dr 0.rdr 2r Qv ln r 2 Qv ur rd u dr rd 0dr 2r Qv 2
