流体力学龙天渝课后答案 孔口管嘴管路流动
流体力学龙天渝课后答案 一元流体动力学基础

1 一元流体动力学基础1.直径为150m m 的给水管道�输水量为h k N /7.980�试求断面平均流速。
解�由流量公式v A Q �� 注意���v A Q s k g h k N ����// A Q v��得�s m v /57.1� 2.断面为300m m ×400m m 的矩形风道,风量为2700m 3/h ,求平均流速.如风道出口处断面收缩为150m m ×400m m ,求该断面的平均流速 解�由流量公式v A Q � 得�AQv �由连续性方程知2211A v A v � 得�s m v /5.122� 3.水从水箱流经直径d 1=10c m ,d 2=5c m ,d 3=2.5c m 的管道流入大气中. 当出口流速10m / 时,求(1)容积流量及质量流量;(2)1d 及2d 管段的流速 解�(1)由s m A v Q /0049.0333�� 质量流量s k g Q /9.4�� (2)由连续性方程� 33223311,A v A v A v A v �� 得�s m v s m v /5.2,/625.021�� 4.设计输水量为h k g /294210的给水管道�流速限制在9.0∽s m /4.1之间。
试确定管道直径�根据所选直径求流速。
直径应是m m 50的倍数。
解�v A Q �� 将9.0�v ∽s m /4.1代入得343.0�d ∽m 275.0 ∵直径是m m 50的倍数�所以取m d 3.0� 代入v A Q �� 得m v 18.1� 5.圆形风道�流量是10000m 3/h ,�流速不超过20 m /s 。
试设计直径�根据所定直径求流速。
直径规定为50 m m 的倍数。
解�v A Q � 将s m v /20�代入得�m m d 5.420� 取m m d 450� 代入v A Q � 得�s m v /5.17� 6.在直径为d 圆形风道断面上�用下法选定五个点�以测局部风速。
流体力学_龙天渝_流动阻力、能量损失、孔口、管嘴与有压管流

第四章流动阻力、能量损失、孔口、管嘴与有压管流一、学习引导1.流动阻力与水头损失的两种型式:流体通过的边界不同,产生的阻力不同,流动阻力分为沿程阻力与局部阻力。
同样,克服这些阻力产生的能量损失也分为沿程水头损失与局部水头损失。
1)流动阻力沿程阻力:流体边界几何形状沿程不变,均匀分布在流程上的阻力称沿程阻力局部阻力:流体边界发生突变,集中分布在突变处的阻力,如转弯、阀门、进出口、突扩。
2)能量损失沿程水头损失:克服沿程阻力产生的能量损失,h f。
局部水头损失:克服局部阻力产生的能量损失h j。
2.流体的两种流动型态——层流和紊流1)层流与紊流层流:流体质点有条不紊,互不混掺的流动。
紊流:流体质点互相混掺的流动。
2)层流与紊流的判别标准层流与紊流的判别标准为临界雷诺数。
从层流到紊流时为上临界雷诺数,从紊流到层流时为下临界雷诺数。
上临界雷诺数不稳定,通常取下临界雷诺数作为层流与紊流的判别标准圆管流:ek R=2000 Re>2000紊流 Re<2000层流明渠流:ek R=500 Re>500 紊流 Re<500层流圆管流雷诺数:νυd ⋅=Re明渠流雷诺数:νυR ⋅=Re水力半径的计算: X A R =3.均匀流基本方程与沿程水头损失 1)均匀流基本方程RJ γτ=0适用范围:在压管流动,明渠流动。
圆管流中:2rJγτ=200Jr γτ=有: 00r r =ττ00r r ττ= 恒定均匀流中,有压管流的过流断面上切应力成线性分布,中心处τ最小,为零;边壁上τ最大,τ=0τ2)沿程水头损失的计算公式达西公式:圆管流中:g d l h f 22υλ⨯⨯= 明渠流动:g R l h f 242υλ⨯⨯= 达西公式适用:有压管流、明渠流, 层流 、紊流 4.圆管中的层流运动1)流速分布圆管中的层流运动流速分布为一个旋转抛物面:μγ4)(20r r J u -=最大流速位于圆管中心:r=0 ,μγ420m axJr u =平均流速:max22021328u Jd Jr ===μγμγυ2)动能修正系数与动量修正数 动能修正系数:2=α 动量修正数:33.1=β 5.紊流运动的特征和紊流阻力1)紊流运动的特征紊流运动最大的特点是具有脉动性与时均性。
《流体力学》第五章孔口管嘴管路流动
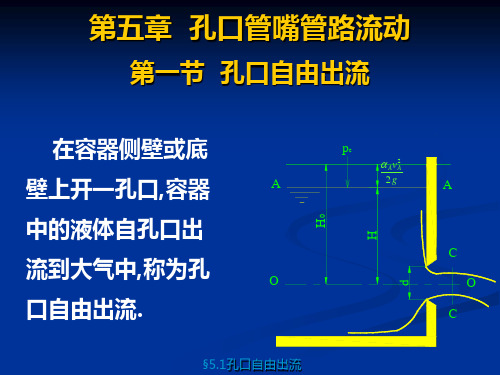
2g
A
C O
C
(C
1)
vc2 2g
(ZA
ZC )
pA
pC
Av
2 A
2g
令
H0
(Z A
ZC )
pA
pC
AvA2
2g
§5.1孔口自由出流
1
则有
vc
c 1
2gH0
H0
(Z A
ZC )
pA
pC
AvA2
2g
H0称为作用水头,是促使
力系数是不变的。
§5.4 简单管路
SH、Sp对已给定的管路是一个定数,它综合 反映了管路上的沿程和局部阻力情况,称为 管路阻抗。
H SHQ2
p SpQ2
简单管路中,总阻力损失与体积流量平方成 正比。
§5.4 简单管路
例5-5:某矿渣混凝土板风道,断面积为1m*1.2m, 长为50m,局部阻力系数Σζ=2.5,流量为14m3/s, 空气温度为20℃,求压强损失。
2v22
2g
1
vc2 2g
2
vc2 2g
令 H0 (H1 ζH12:局)液部体p阻1 经力p孔2系口数处1v的122g1 2v22
1
H1 H
H2
2
2
H0 (1 2 ) 2vcg2突ζ然2:液扩体大在的收局缩部断阻面力之系后数 C
C
§5.2 孔口淹没出流
1
c 1
2gH0
Q A 2gH0 A 2gH0
出流
H0
流体力学课后习题答案龙天渝

(a)流动随时间按一定规律变化;
(b)流场中任意空间点的运动要素不随时间变化;
(c)各过流断面的流速分布不同;
(d)各过流断面的压强相同。
3-2非恒定流是:
(a)?u/?t=0;
(b)?u/?t≠0;
(c)?u/?s=0;
(d)?u/?s≠0。
3-3一元运动是:
(a)均匀流;
(b)速度分布按直线变化;
22求流线方程并画出若干条流线。(x+y=c)
3-15已知平面流动的速度场为u=(4y-6x)ti+(6y-9x)tj。求t=1时的流线方程并绘出x=0至x=4区间穿过x轴的4条流线图形。(1.5x-y=c)
3-16水管的半径r0=30mm,流量q=401l/s,已知过流断面上的流速分布为u=umax(y/r0)1/7。式中:umax是断面中心点的最大流速,y为距管壁的距离。试求:
求水头h。水头损失不计。(1.23m)
【篇二:流体力学_龙天渝_流体动力学基础】
ass=txt>一、学习指导1.主要概念:
流线,过流断面,均匀流,渐变流,恒定流
注:①流体是空间曲线。对恒定流其空间位置不变,对非恒定流随时间而变化。
②渐变流是将流速的大小和方向变化不大的流段看成均匀流所作的工程近似,与均匀流无明确的界定,根据经验而定。例:锥角较小的扩散段或收缩段,断面面积a(s)满足da/ds=0的断面附近的流段是渐变流。
(2)是几元流动?
(3)是恒定流还是非恒定流;
(4)是均匀流还是均匀定流?
3-13已知平面流动的速度分布为ux=a,uy=b,其中a、b为常数。求流线方程并画出若干条y0时的流线。((b/a)x-y=c)
3-14已知平面流动速度分布为ux=-cy/(x2+y2),uy= cx/(x2+y2),其中c为常数。
流体力学课后习题答案(孔珑编)

2-5 解:如图示,设 A 点
距 1-2 等压面的距离为 h1 ,B 点距 3-4 等压面的
距离为 h2 ,1-2 等压面距基准面的距离为 h3 ,
在等压面 1-2 处列平衡方程, P1 P2 PA H2O gh1 在等压面 3-4 处列平衡方程, P3 P4 PB -H2O gh2 因为 P2 P3 Hg gh ,所以 PA H2O gh1 PB -H2O gh2 Hg gh , 故 Hg gh=PA -PB H2O g (h1+h2 ) , 又因为, h1 548102 - h3 , h2 h h3 - 304 102 ,所以
2
在容器顶部距中心 r 处取微圆环 dr ,则微圆环所受到的压力为
dF pdA 2 rpdr 2 r( gh 2 (r2 r02 ) )dr 2
所以整个容器顶盖受到的总压力为
F
d
2 dF
d 2
2
r(
gh
2 (r 2
r02
)
)dr
2 [
因为 P1 P2 ,所以, Pa PF oi gh1 H2O gh2 =Pa Hg gH , 所以
H
=
PF
oi gh1 H2O gh2 Hg g
=
46059.4+800 9.81 3010-2 103 13.6103 9.81
9.81 50 10-2
pA oi g (h1 hB ) p3 Hg gh1
在 3-3 等 压 面 处 列 等 压 面 方 程 得 P3 pB +oi g(hB - h2 )+Hg gh2 , 所 以
流体力学第二版龙天渝课后答案

流体力学第二版龙天渝课后答案【篇一:流体力学_龙天渝_建环专业课程教案】>(建筑环境与设备工程专业)第一章绪论1.本章的教学目标及基本要求本章为绪论,涉及到流体的定义、作用在流体上的力、流体的基本物理性质和流体的力学模型。
通过本章的教学,要求学生了解流体力学在本学科及相关工程技术领域内的地位和作用,掌握流体与固体的典型区别,连续介质模型、不可压缩流体和理想流体的定义,了解流体的主要物理性质;掌握流体的受力分析方法,能够正确应用牛顿内摩擦定律分析解决液膜条件下流体的运动及及其与固体间的相互作用问题。
2.本章各节教学内容(列出节名)及学时分配本章教学内容分2单元,每单元2学时? 单元1:流体力学在本学科中的地位和作用,流体的定义与特点,,作用在流体上的力;流体的惯性, 流体的粘性;习题1-1, 4? 单元2:流体的粘性,压缩性与膨胀性, 不可压缩流体和理想流体的概念,流体的连续介质模型;习题1-7,8,123.本章教学内容的重点和难点本章的重点是:本章的教学任务是让学生初步建立起流体及流体力学的基本概念,重点放在流体与固体的本质区别,描述流体的基本模型及流体的主要物理性质。
本章的难点是:熟练、正确进行受力分析;正确运用牛顿内摩擦定律分析求解液膜条件下流体的运动及及其与固体间的相互作用问题。
4. 本章教学内容的深化和拓宽:介绍不可压缩流体的概念及其工程应用意义,说明粘性的外部特性与内部特性的区别。
5.本章教学方式(手段)及教学过程中应注意的问题;本章涉及到较多的物理基本概念,注意时刻提醒学生从最基本的物理现象出发去理解和把握物理概念,在受力分析及应用过程中注意结合以往课程的内容和知识,帮助学生逐步建立将所学知识与工程实际应用相结合的思维习惯。
教学方式以课堂教学为主。
6.本章的主要参考书目:? clayton t.crowe, donald f. elger and john a. roberson. engineering fluid mechanics. 7th ed. new york: john wiley sons,2001? vennard j k and r l street. elementary fluid mechanics. 6th ed. new york: john wiley sons,19827.本章的思考题和习题:习题1-1,4,7,8,12单元 11.教学内容:流体力学在本专业中的作用, 流体的定义,惯性、压缩性与膨胀性? 了解流体力学在学科中的地位和作用;? 明确流体的定义;? 了解流体的特点及流体的连续介质模型;? 了解流体惯性的度量方法;? 了解流体的压缩性与膨胀性的定义及数量级;? 明确不可压缩流体的概念。
流体力学龙天渝课后答案第三章一元流体动力学基础.

第三章 一元流体动力学基础1.直径为150mm 的给水管道,输水量为h kN /7.980,试求断面平均流速。
解:由流量公式vA Q ρ= 注意:()vA Q s kg h kN ρ=⇒→// A Q v ρ=得:s m v /57.1= 2.断面为300mm ×400mm 的矩形风道,风量为2700m 3/h,求平均流速.如风道出口处断面收缩为150mm ×400mm,求该断面的平均流速解:由流量公式vA Q = 得:A Q v = 由连续性方程知2211A v A v = 得:s m v /5.122=3.水从水箱流经直径d 1=10cm,d 2=5cm,d 3=2.5cm 的管道流入大气中. 当出口流速10m/ 时,求(1)容积流量及质量流量;(2)1d 及2d 管段的流速解:(1)由s m A v Q /0049.0333==质量流量s kg Q /9.4=ρ(2)由连续性方程:33223311,A v A v A v A v ==得:s m v s m v /5.2,/625.021==4.设计输水量为h kg /294210的给水管道,流速限制在9.0∽s m /4.1之间。
试确定管道直径,根据所选直径求流速。
直径应是mm 50的倍数。
解:vA Q ρ= 将9.0=v ∽s m /4.1代入得343.0=d ∽m 275.0∵直径是mm 50的倍数,所以取m d 3.0=代入vA Q ρ= 得m v 18.1=5.圆形风道,流量是10000m 3/h,,流速不超过20 m/s 。
试设计直径,根据所定直径求流速。
直径规定为50 mm 的倍数。
解:vA Q = 将s m v /20≤代入得:mm d 5.420≥ 取mm d 450=代入vA Q = 得:s m v /5.17=6.在直径为d 圆形风道断面上,用下法选定五个点,以测局部风速。
设想用和管轴同心但不同半径的圆周,将全部断面分为中间是圆,其他是圆环的五个面积相等的部分。
流体力学龙天渝课后答案

流体力学龙天渝课后答案龙天渝课后答案第一章:流体力学基础概念在学习流体力学之前,我们首先需要了解一些基础概念。
流体力学是研究流体静力学和流体动力学的学科,它涉及了许多重要的概念和原理。
1. 流体的定义和特性:流体是指能够流动的物质,包括液体和气体。
与固体不同,流体具有流动性和粘滞性。
2. 流体静力学:流体静力学研究的是处于静止状态下的流体,它涉及了压力、密度、浮力等概念。
根据帕斯卡定律,流体中的压强是均匀的。
浮力是物体在液体中受到的向上的力,它的大小等于所排开的液体的重量。
3. 流体动力学:流体动力学研究的是流体在运动中的力学性质。
它基于质量守恒定律、动量守恒定律和能量守恒定律来描述流体的运动行为。
流体的运动可以通过速度场来描述,速度场是指在每个点上流体速度的矢量。
第二章:流体流动的方程了解了流体力学的基础概念后,我们来学习一些描述流体流动的方程。
1. 质量守恒方程:质量守恒方程是流体动力学的基本方程之一,它表达了流体质量在单位时间内在空间中的改变量等于流入或流出的质量通量与积累产生的差值。
2. 动量守恒方程:动量守恒方程描述了流体运动时动量守恒的原理。
它表达了流体单位时间内动量的改变量等于施加在流体上的外力与流体内部压力和重力之差。
3. 能量守恒方程:能量守恒方程用于描述流体在流动过程中能量的守恒性质。
它包括液体内能、压力能和动能等各种能量形式的转换和积累。
第三章:流体的稳定性和边界层在流体力学中,稳定性和边界层是两个重要的概念。
1. 稳定性:稳定性研究的是流体在受到扰动后是否能够恢复到原来的状态。
稳定性分析可以通过线性稳定性理论或非线性动力学方法来进行。
2. 边界层:边界层是指流体在与固体表面接触时的一层较薄的流动区域。
边界层内的速度变化很大,而在边界层外的流体速度几乎保持不变。
边界层对于流体流动的阻力有重要影响。
第四章:流体力学的应用领域流体力学广泛应用于许多领域,包括工程、地球科学和生物医学等。
流体力学龙天渝课后答案第五章孔口管嘴管路流动
�
L5
d
5 5
)
H并
�
S
2
Q
2 2
� 11.15m
H 1�5 � S1�5Q 2 � 13m 7
∴ H � 11.15 � 13 � 24.15m
23.管段 1 的管径为 20mm�管段 2 为 25mm�l1 为 20m�l2 为 10m��� 1 � �� 2 � 15 �� � 0.025 �
1
� �� �
1 l
� d � �� �1
证�∵ H 0
�
v2 2g
� ��
v2 2g
��
l d
v2 2g
∴ v � � 2 gH 0
其中� �
1 l
� d � �� �1
5.某诱导器的静压箱上装有圆柱形管嘴�管径为 4mm�长度 l =100mm�λ=0.02�从管嘴入 口到出口的局部阻力系数 �� � 0.5 �求管嘴的流速系数和流量系数�见上题图�。
由于 H 不变� Q3 减小�所以 Q 2 减小 25.三层供水管路�各管段的�值皆 106s2/m5� 层高均为 5m。设 a 点的压力水头为 20m�求 Q1、Q2、Q3�并比较三流量�得出结论来。�忽 略 a 处流速水头�
解� Q' � Q2 � Q3
Q � Q1 � Q' � Q1 � Q2 � Q3
解�Q= n�A 2 �p �得 n � 218.4 �所以需要 219 个 �
8.水从 A 水箱通过直径为 10cm 的孔口流入 B 水箱�流量系数为 0.62。设上游水箱的水面高
程 H 1 =3m 保持不变。
�1�B 水箱中无水时�求通过孔口的流量。
�2�B 水箱水面高程 H 2 =2m 时�求通过孔口的流量。
流体力学课后习题答案孔珑

流体力学课后习题答案孔珑流体力学课后习题答案流体力学是研究流体运动和力学性质的一门学科。
在学习流体力学的过程中,课后习题是巩固知识、提高理解能力的重要环节。
本文将为大家提供一些流体力学课后习题的答案,希望能够帮助大家更好地掌握这门学科。
一、流体的基本性质1. 什么是流体的黏度?如何度量黏度?答:流体的黏度是指流体的内部阻力,即流体分子之间的摩擦力。
黏度可以通过测量流体的粘流性来度量,常用的测量方法有旋转圆柱法、滴定法等。
2. 什么是压力?如何计算压力?答:压力是单位面积上的力的大小,可以用公式P=F/A来计算,其中P表示压力,F表示作用在某一面上的力,A表示该面的面积。
二、流体的运动1. 什么是流体的连续性方程?如何推导连续性方程?答:流体的连续性方程是指在流体运动中,质量守恒的表达式。
推导连续性方程的方法是通过质量守恒定律,即流体在单位时间内通过某一截面的质量相等。
2. 什么是流体的动量方程?如何推导动量方程?答:流体的动量方程是描述流体运动的力学方程。
推导动量方程的方法是通过牛顿第二定律和质量守恒定律,即流体在单位时间内动量的变化等于作用在流体上的力。
三、流体的静力学1. 什么是流体的静力学平衡?如何判断流体是否处于静力学平衡?答:流体的静力学平衡是指流体内部各点的压力和重力之间处于平衡状态。
判断流体是否处于静力学平衡的方法是通过判断流体内部各点的压力是否相等。
2. 什么是流体的浮力?如何计算浮力?答:流体的浮力是指流体对浸入其中的物体所产生的向上的力。
浮力可以通过阿基米德原理来计算,即浮力等于物体排开的流体的重量。
四、流体的流动1. 什么是流体的黏性?如何影响流体的流动?答:流体的黏性是指流体分子之间的内部摩擦力。
黏性会影响流体的流动,当黏性较小时,流体呈现无黏性流动;当黏性较大时,流体呈现黏性流动。
2. 什么是雷诺数?如何计算雷诺数?答:雷诺数是描述流体流动状态的无量纲参数,可以表示流体的惯性力和黏性力之间的比值。
流体力学课后习题答案解析自己整理孔珑4版

《工程流体力学》课后习题答案孔珑第四版第2章流体及其物理性质 (4)2-1 (4)2-3 (4)2-4 (6)2-5 (6)2-6 (6)2-7 (7)2-8 (7)2-9 (8)2-11 (8)2-12 (9)2-13 (9)2-14 (10)2-15 (10)2-16 (11)第3章流体静力学 (12)3-1 (12)3-2 (12)3-3 (13)3-5 (13)3-6 (14)3-9 (14)3-10 (15)3-21 (18)3-22 (19)3-23 (20)3-25 (20)3-27 (20)第4章流体运动学及动力学基础 (22)4-2 (22)4-5 (22)4-6 (23)4-8 (23)4-11 (24)4-12 (24)4-14 (25)4-22 (25)4-24 (26)4-26 (27)第6章作业 (28)6-1 (28)6-3 (28)6-7 (29)6-10 (29)6-11 (29)6-12 (30)6-17 (31)第2章流体及其物理性质2-1已知某种物质的密度ρ=2.94g/cm3,试求它的相对密度d。
【2.94】解:ρ=2.94g/cm3=2940kg/m3,相对密度d=2940/1000=2.942-2已知某厂1号炉水平烟道中烟气组分的百分数为,α(CO2)=13.5%α(SO2)=0.3%,α(O2)=5.2%,α(N2)=76%,α(H2O)=5%。
试求烟气的密度。
解:查课表7页表2-1,可知ρ(CO2)=1.976kg/m3,ρ(SO2)=2.927kg/m3,ρ(O2)=1.429kg/m3,ρ(N2)=1.251kg/m3,ρ(H2O)=1.976kg/m3,ρ(CO2)=1.976kg/m3,3ρ=∑i iαρ=341.1kg/m2-3上题中烟气的实测温度t=170℃,实测静计示压强Pe=1432Pa,当地大气压Pa=100858Pa。
试求工作状态下烟气的密度和运动粘度。
第六章流体力学课后答案

第六章流体力学课后答案第六章孔口、管嘴出流与有压管流6-1在水箱侧壁上有一直径d?50mm的小孔口,如图所示。
在水头H的作用下,收缩断面流速为VC?6.86m/s,经过孔口的水头损失hw?0.165m,如果流量系数??0.61,试求流速系数?和水股直径dc。
Vc2解:根据伯努利方程:H??hw?2.51m2g流速系数??Vc??0.967VQ???AVcc,dc?39.71mm6-2图示一船闸闸室,闸室横断面面积A?800m2,有一高h?2m、宽b?4m的矩形放水孔。
该孔用一个速度v?0.05m/s匀速上升的闸门开启。
假设初始水头H1?5m,孔口流量系数??0.65,孔口出流时下游水位保持不变。
试求(1)闸门开启完毕时闸室中水位降低值y;(2)闸室水位与下游平齐所需要的总时间T。
解:(1)闸门完全开启所用的时间:t?h?40sv此段时间内孔口的面积可用孔的平均面积来表示:A?4m2因为T??40s所以:H2?3.796m,y?H1?H2?1.204m(2)闸门完全打开后,防水孔的面积:A??bh?8m2液面降到与下游液面平齐所需要的时间因为T???135.41s所以T?t?T??175.41s6-3贮液箱中水深保持为h?1.8m,液面上的压强p0?70kPa(相对压强),箱底开一孔,孔直径d?50mm。
流量系数??0.61,求此底孔排出的液流流量。
p0V2解:根据伯努利方程:?h??g2g46-4用隔板将矩形水池中的水体分成左右两部分,如图所示,右半部分水Q??d2V??15.9L/s面保持恒定,隔板上有直径d1?0.1m的圆形孔口,位于右半部液面下H1?4.8m处。
在左半部分的侧面与前一孔口相同的高度处开有直径d2?0.125m的圆形孔口,当水池两半部分的水面稳定后,试求左半部水面高度计孔口出流流量。
解:当水池两半部分的水面稳定时:Q1?Q2Q1??AQ2??A??0.62?h?1.395m,Q?0.0398m3/s6-5图示水平圆柱状内插式管嘴,入口锐缘状,直径d?40mm,管嘴中心线离液面的距离h?1.5m,设管嘴较短,水流在管嘴内作自由出流如图示,各容器壁面上的压强可按静压规律分布。
流体力学龙天渝蔡增基版课后答案孔口管嘴管路流动

第五章孔口管嘴管路流动1.图中穿孔板上各孔眼的大小形状相同, 问每个孔口的出流量是否相同? 解:由 Q =MAj2gH 0与深度无关,所以每个孔口的出流量相同2. 有一水箱水面保持恒定 (5m ,箱壁上开一孔口,孔口直径10。
(1) 如果箱壁厚度S =3,求通过孔口的流速和流量。
(2)如果箱壁厚度S =40,求通过孔口的流速和流量。
解:(1)视作薄壁小孔口,W =0.97 ,」0.62V =®j 2gh =9.6m/s得: Q = ^vA = 4.82% 10^m 3/ s(2)视作管嘴,——0.82V =W J2gh =8.12m/s 得:Q = ^vA =6.38咒 10需3/s3. 一隔板将水箱分为A B 两格,隔板上有直径为 d i =40的薄壁图,B 箱底部有孔口,如题5-3第1题图一直径为d 2=30的圆柱形管嘴,管嘴长 0.1m , A 箱水深H=3m 恒 定不变。
(1)分析出流恒定性条件(H 2不变的条件)。
(2)在恒定出流时,B 箱中水深H 2等于多少?(3)水箱流量Q 为何值?解:(1)当Q 2时出流恒定(2)因为 Q 2,片A l j2g(H i -H 2)= 42A2j2g(H 2 +0.1)(3)解得 Q 1 =3.58 X 10-3m 34. 证明容器壁上装一段短管(如图所示),经过短管出流时的流其中-冬薦5.某诱导器的静压箱上装有圆柱形管嘴,管径为 4,长度1=100,入=0.02,从管嘴入口到出口的局部阻力系数 工匚=0.5,求管嘴的流速系数和流量系数(见上题图)。
解: 由题得,1— =0.707J 片吃匚+1查表得 片=0.6,馬=0.82,解得:H 2 =1.85m量系数卩与流速系数为2 2证一H 0计叫 +仝 d 2g解: ( 1)属孔口自由出流Q = H A j 2gH 0 , H 0 = H1得: Q=0.037m 3/s得: Q=0.0216m 3/s(3) Q =H A 72^ , H ^H ^H ^-20009807得:Q= 0.0236m 3/S6.如上题,当管嘴外空气压强为当地大气压强时,要求管嘴出流流速为30。
流体力学_龙天渝_孔口、管嘴出流和有压管流

第五章孔口、管嘴出流和有压管流一、复习思考题二、习题1、选择题2、计算题一、复习思考题1.孔口、管嘴出流和有压管流的水力特点有什么不同?2.正常工作条件下,作用水头相同,面积也相同的孔口和圆柱形外管嘴,过流能力是否相同?原因何在?3.怎样计算长管串联、并联管道及沿程均匀泄流管道的水头损失?4.有压管流,管道末端阀门瞬时关闭,水击波是怎样传播的?5.怎样选择离心泵?返回顶部目录二、习题1、选择题5-1比较在正常工作条件下,作用水头H、直径d相等时,小孔口的流量Q和圆柱形外管嘴的流量Q n():(a) Q>Q n(b) Q<Q n(c) Q=Q n(d) 不定5-2圆柱形外管嘴的正常工作条件是():(a) L=(3~4)d,H0>9m(b) L=(3~4)d,H0<9m(c) L>(3~4)d,H0>9m(d)Ll<(3~4)d,H0<9m5-3图示两根完全相同的长管道,只是安装高度不同,两管的流量关系为():(a) Q1<Q2(b) Q1>Q2(c) Q1=Q2(d) 不定返回顶部目录5-4并联管道1、2两管的直径相同,沿程阻力系数相同,长度L2=3L1,通过的流量为():(a) Q1=Q2(b) Q1=1.5Q2(c) Q1=1.73Q2(d) Q1=3Q25-5如图,并联管段1、2、3其中A、B之间的水头损失是():(a) h fAB=h f1+h f2+h f3(b) h fAB=h f1+h f2(c) h fAB= h f2+h f3(d) h fAB=h f1=h f2=h f35-6长管并联管道各并联支管的():(a) 水头损失相等(b) 水力坡度相等(c) 总能量损失相等(d) 通过的水量相等5-7并联管道阀门K全开时各段流量为Q1、Q2、Q3,现关闭小阀门K,其他条件不变,流量变化为()(a) Q1、Q2、Q3都减小(b) Q1减小、Q2不变、Q3减小(c) Q1减小、Q2增加、Q3减小(d) Q1不变、Q2增加、Q3减小返回顶部目录2、计算题5-8有一薄壁圆形孔口,直径d为10mm,水头H为2m,现测得射流收缩断面的直径d c为8mm,在32.8s时间内,经孔口流出的水量为0.01m3,试求该孔口的收缩系数μ,流速系数φ及孔口局部损失系数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
d=200mm�上游水面至管顶高度 h=1m。已知 λ�0.026,进口网 ζ=10�弯头 ζ=1.5�每个弯头�� 出口 ζ�1.0 �求� �1�虹吸管中的流量� �2�管中压强最低点的位置及其最大负压值。 解��1�方法一�
� d 2 2 gH
Q=
4
=0.
�
c
�
2� b
�
�
0
�
� �L1
�
1 :
S2
1 :
S3
1 �
S4
d
5 2
:
L2
dቤተ መጻሕፍቲ ባይዱ
5 3
:
L3
d
5 4
� 2185 :1743 : 3375
L4
Q2 � Q3 � Q4 � QA
S 2 � 3 4 6.8 s 2 m 5
Q2
�
2185
QA
2185 � 1743 � 3375
� 0.18 m 3
s
S 1� 5
�
8� � 2g
(
L1
d
5 1
解�并联管路 Q � 1 �如果要得到各支管流量相等必须各支管 S 相等 S
∴应设计成 S1=S2=S3 19. 有两长度尺寸相同的支管并联�如果在支管 2 中加一个调节阀�阻力系数为 ζ�� 则 Q1 和 Q 2 哪个大些�阻力 h f 1 和 h f 2 哪个大些�
解��1�S1 Q12
=S2
Q
�3�A 箱水面压力为 2000Pa� H 1 =3m 时�而 B 水箱水面
压力为 0� H 2 =2m 时�求通过孔口的流量。 解��1�属孔口自由出流 Q � �A 2 gH 0 � H 0 � H1
得� Q � 0.037 m 3 / s
�2�属孔口淹没出流� Q � �A 2 gH 0 � H 0 � H1 � H 2
解�Q1:Q2= S 2 :
S1 �Q�
1� S
S1
= 8�L1 d1
�
2
d
4 1
g
=3104.8 s2 /m5
S
2
=
8�L2 � 2d
d2
4 2
g
� 1862.9s 2
/ m5
解得� Q1 : Q2 � 0.774
Q2 � 45 � 10 �3 m 3 / s Q1 � 35 � 10 �3 m 3 / s
解�由题得� � � �
1 � 0.707
l
� d � �� �1
6.如上题�当管嘴外空气压强为当地大气压强时�要求管嘴出流流速为 30m/s。此时静压箱 内应保持多少压强�空气密度为 ρ=1.2kg/m3。
解� v � � 2 �p �得 �p � 1.08kN / m 2 �
7.某恒温室采用多孔板送风�风道中的静压为 200Pa�孔口直径为 20mm�空气温度为 20℃� μ=0.8。要求通过风量为 1m3/s。问需要布置多少孔口�
由于 H 不变� Q3 减小�所以 Q 2 减小 25.三层供水管路�各管段的�值皆 106s2/m5� 层高均为 5m。设 a 点的压力水头为 20m�求 Q1、Q2、Q3�并比较三流量�得出结论来。�忽 略 a 处流速水头�
解� Q' � Q2 � Q3
Q � Q1 � Q' � Q1 � Q2 � Q3
解�阻抗反映管路上沿程阻力和局部阻力情况。S H 用在液体管路�S P 用在气体管路。在紊
流粗糙区时� S 与管中流量无关�因为 � 此时与 v 以及流体状态无关��仅决定于管道的尺 寸和构造。
13.供热系统的凝结水箱回水系统如图。试写出水泵应具有的作用水头表达式。
解� H
�
p
, 2
�
p1,
� SQ 2 (如果冷却措施是开
解�Q= n�A 2 �p �得 n � 218.4 �所以需要 219 个 �
8.水从 A 水箱通过直径为 10cm 的孔口流入 B 水箱�流量系数为 0.62。设上游水箱的水面高
程 H 1 =3m 保持不变。
�1�B 水箱中无水时�求通过孔口的流量。
�2�B 水箱水面高程 H 2 =2m 时�求通过孔口的流量。
1
� �� �
1 l
� d � �� �1
证�∵ H 0
�
v2 2g
� ��
v2 2g
��
l d
v2 2g
∴ v � � 2 gH 0
其中� �
1 l
� d � �� �1
5.某诱导器的静压箱上装有圆柱形管嘴�管径为 4mm�长度 l =100mm�λ=0.02�从管嘴入 口到出口的局部阻力系数 �� � 0.5 �求管嘴的流速系数和流量系数�见上题图�。
=118.69s2 /m5
SH2
� 8�� � =�
L2 d2
��3 ��
�
2
d
4 1
g
4
� � 1��
�
=2106.1s2 /m5
�2� H � h � � S H1 + S H 2 � Q 2 � 23.56 m �其中 h � 17 � 3 � 20m �
�3�略 17.图为一水平安置的通风机�吸入管 d1=200m�l1=10m�λ=0.02。压出管为直径不同的两段 管段串联组成�d2=200mm� l2=50m�λ =0.02�l3=50m , λ=0.02。空气密度为 ρ=1.2kg/m3� 风量为 Q=0.15m3/s�不计局部阻力。试计算� �1�风机应产生的总压强为多少� �2�如风机与管道铅直安装�但管路情况不变�风机的总压有无变化� �3�如果流量提高到 0.16m3/s�风机总压变化多少� �4�绘出全压线与静压线图。
孔口管嘴管路流动 1.图中穿孔板上各孔眼的大小形状相同�问每个孔口的出流量是否相同� 解�由 Q � �A 2 gH 0 与深度无关�所以每个孔口的出流量相同
2.有一水箱水面保持恒定�5m��箱壁上开一孔口�孔口直径 d=10mm。�1�如果箱壁厚度 δ=3mm�求通过孔口的流速和流量。�2�如果箱壁厚度 δ=40mm�求通过孔口的流速和流量。 解��1�视作薄壁小孔口�� � 0.97 � � � 0.62 v � � 2 gh � 9.6m / s 得� Q � �vA � 4.82 � 10 �4 m 3 / s �2�视作管嘴�� � � � 0.82 v � � 2 gh � 8.12 m / s 得� Q � �vA � 6.38 � 10 �4 m 3 / s 3.一隔板将水箱分为 A、B 两格�隔板上有直径为 d1=40mm 的薄壁孔口�如题 5-3 图�B 箱底部有一直径为 d2=30mm 的圆柱形管嘴�管嘴长 l=0.1m�A 箱水深 H1=3m 恒定不 变。 �1�分析出流恒定性条件�H2 不变的条件�。 �2�在恒定出流时�B 箱中水深 H2 等于多少� �3�水箱流量 Q1 为何值� 解��1�当 Q1=Q2 时 出流恒定 �2�因为 Q1=Q2� �1 A1 2 g (H 1 � H 2 ) � � 2 A2 2 g (H 2 � 0.1) 查表得 �1 � 0.6 � � 2 � 0.82 �解得� H 2 � 1.85m �3�解得 Q1 � 3.58×10-3 m3/s 4.证明容器壁上装一段短管�如图所示��经过短管出 流时的流量系数 μ 与流速系数为
�g
式则需加上 h)
14.某供热系统�原流量为 0.005m3/s,总水头损 失 h=5mH 2O,现在要把流量增加到 0.0085m3/s, 试问水泵应供给多大压头。
解� H 1 � SQ12 即 5 � S � 0.005 2
∴ S � 2 �105 s 2 / m 5
H 2 � SQ 2 � 2 �105 � 0.0085 2 � 14.45m 15.两水池用虹吸管连通�上下游水位差 H=2m�管长 L��3m�L2�5m�L3�4m�直径
流量分配有何变化�
解�这样 Q1 更小� Q 2 更大�所以应将管段 1 的
管径改为 25mm �管段 2 的管径改为 20mm �两 管流量可接近。 24.已知某枝状管网的 Q1、Q2、Q3�若在支管 2 的末端再加一段管子�如图中所示。问 Q1 和 Q2、 Q3 各有何变化� 解�由于总阻抗加大�H � SQ 2 �使总流量 Q1 减小
解� �P � H �� � � �g � H � 0.37 � 2.744 N / m 2
Q= �内�A
2�p =12.96kg/s �内
�方法二��分别令上下部窗口外渐变流断面 2 和断面 1�根据气体能量方程�得
p1 � g (� a
� � )( z 2
� z1 ) �
� v1 2 2
�
p2
�
H1 � S1Q 2 � S 2Q 2 � 3.72m
21.如上题�若使 Q1 � Q2 如何改变第二支路�
解� d 2 减小或加调节阀等增加阻力的措施。
22.如图所示管路�设其中的流量 QA=0.6m3/s�λ=0.02�不计局部损失�其它已知条件如图� 求 A、D 两点间的水头损失。
解� Q2 : Q3 : Q4 �
2
得� Q � 0.0216 m 3 / s
�3� Q � �A
2 gH 0
�H0
�
H1
� H2
�
2000 9807
得� Q � 0.0236 m 3 / s
9.室内空气温度为 30℃�室外空气温度为 20℃�在厂房上下部各开有 8m2 的窗口�两窗口 的中心高程差为 7m�窗口流量系数 μ=0.64�气流在自然压头作用下流动�求车间自然通风 换气量�质量流量�。
L2 d
�
L3 �
05m3/S 方法二�
