最新流体力学龙天渝蔡增基版课后答案第五章孔口管嘴管路流动
流体力学 建工 课后作业答案 第五版

管进口到闸门总损失为1m,求管中平均流速v。
体
解:阀关时,由静力学方程
力 学
z1
p1
g
z2
p2
g
5mH2O
阀开时,由伯努利方程
1
1
2
z1
p1
g
v12 2g
z2
p2
g
v22 2g
hl
2
5 0 0.1 v2 1
2g
v 8.74m/s
50
3.28 管末端喷嘴d =10cm,D =40cm,Q=0.4m3/s,12 流
v3
2g
Q
Q/
4
v2 d32
4
d 2 67.2l/s 15.22m/s
v4
v2
Δh
2 d2 p 3
对3-3,4-4列能量方程
3d3
p4 v32 v42
g 2g
p4
(v32 v42 )
2
79.2kPa
H v32 11.82m
2g
49
3-18 阀关压力表读数时 p=49kPa,阀开时p=0.98kPa, 流
l=10m,d=50mm,λ=0.03。若AB两断面测压管水头 差Δh=0.629m,经2分钟流入水箱的水量为0.329m3。
流 体 力
解: Q 0.329 / 60 2 2.74103m3/s 学
v Q / d 2 1.4m/s
Δh
4
A
hf
l
d
v2 2g
0.03 10 1.42 0.6m
1
2 v1 2.572m/s, v2 =4.287m/s
列动量方程
F P1 P2 Q(2v2 1v1)
流体力学 第五章 孔口管嘴管路流动(第一次)

(a)突扩管 (c)突缩管
(b)渐扩管 (d)减缩管
(e)折弯管
(f)圆弯管
(g)锐角合流三通
(h)圆角分流三通
在局部阻碍范围内损失的能量,只占局部损失 中的一部分,另一部分是在局部阻碍下游一定长度 的管段上损耗掉的,这段长度称为局部阻碍的影响 长度。受局部阻碍干扰的流动,经过影响长度后, 流速分布和紊流脉动才能达到均匀流动的正常状态。
de
2ab ab
边长为a的正方形断面的水力半径为:
R A a2 a
4a 4
边长为a的正方形断面的当量直径为:
de a
有了当量直径,只要用de代替d.就可以计算非 圆管的沿程损失,即:
hf
l
d
2
2g
l 2
4R 2g
Re
de
v
(4R)
v
注意:流速的计算表达式仍为:u=Q/A
二、等效过程
(1)用实验方法对某种材料的管道进行沿程 损失实验,测出 和hf ;
(2)再用达西公式计算出λ;
hf
l d
2
2g
(3)用尼古拉兹阻力平方区公式计算出绝对
粗糙度K。
1
(1.74 2 lg d )2
2K
此时的K值在阻力的效果上是与人工粗糙管的管 道粗糙度相当的,故称其为当量粗糙度。
工业管道粗糙度
管道材料 表面光滑砖风道
K (mm)
4.0
管道材料 度锌钢管
K(mm) 0.15
矿渣混凝土板风道 1.5
钢管
0.046
钢丝网抹灰风道 10~15
铸铁管
0.25
胶合板风道
流体力学龙天渝课后答案 一元流体动力学基础

1 一元流体动力学基础1.直径为150m m 的给水管道�输水量为h k N /7.980�试求断面平均流速。
解�由流量公式v A Q �� 注意���v A Q s k g h k N ����// A Q v��得�s m v /57.1� 2.断面为300m m ×400m m 的矩形风道,风量为2700m 3/h ,求平均流速.如风道出口处断面收缩为150m m ×400m m ,求该断面的平均流速 解�由流量公式v A Q � 得�AQv �由连续性方程知2211A v A v � 得�s m v /5.122� 3.水从水箱流经直径d 1=10c m ,d 2=5c m ,d 3=2.5c m 的管道流入大气中. 当出口流速10m / 时,求(1)容积流量及质量流量;(2)1d 及2d 管段的流速 解�(1)由s m A v Q /0049.0333�� 质量流量s k g Q /9.4�� (2)由连续性方程� 33223311,A v A v A v A v �� 得�s m v s m v /5.2,/625.021�� 4.设计输水量为h k g /294210的给水管道�流速限制在9.0∽s m /4.1之间。
试确定管道直径�根据所选直径求流速。
直径应是m m 50的倍数。
解�v A Q �� 将9.0�v ∽s m /4.1代入得343.0�d ∽m 275.0 ∵直径是m m 50的倍数�所以取m d 3.0� 代入v A Q �� 得m v 18.1� 5.圆形风道�流量是10000m 3/h ,�流速不超过20 m /s 。
试设计直径�根据所定直径求流速。
直径规定为50 m m 的倍数。
解�v A Q � 将s m v /20�代入得�m m d 5.420� 取m m d 450� 代入v A Q � 得�s m v /5.17� 6.在直径为d 圆形风道断面上�用下法选定五个点�以测局部风速。
第五流体力学习题答案
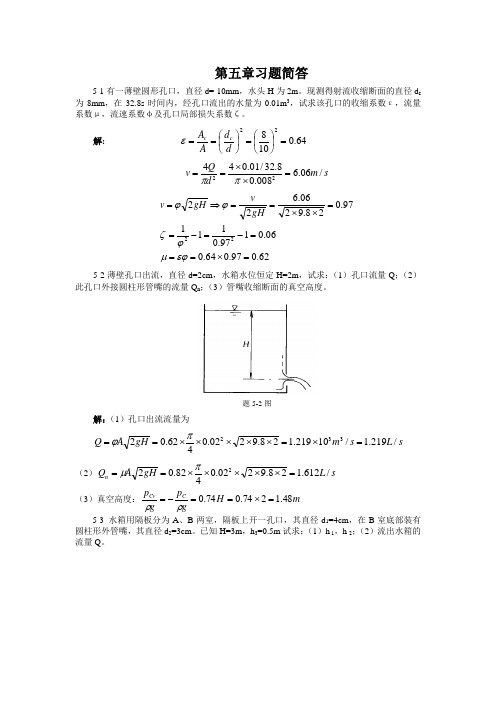
第五章习题简答5-1有一薄壁圆形孔口,直径d= 10mm ,水头H 为2m 。
现测得射流收缩断面的直径d c为8mm ,在32.8s 时间内,经孔口流出的水量为0.01m 3,试求该孔口的收缩系数ε,流量系数μ,流速系数φ及孔口局部损失系数ζ。
解: 64.010822=⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛==d d A A c c εs m d Q v /06.6008.08.32/01.04422=⨯⨯==ππ 62.097.064.006.0197.011197.028.9206.62222=⨯===-=-==⨯⨯==⇒=εϕμϕζϕϕgHvgH v5-2薄壁孔口出流,直径d=2cm ,水箱水位恒定H=2m ,试求:(1)孔口流量Q ;(2)此孔口外接圆柱形管嘴的流量Q n ;(3)管嘴收缩断面的真空高度。
题5-2图解:(1)孔口出流流量为s L s m gH A Q /219.1/10219.128.9202.0462.02332=⨯=⨯⨯⨯⨯⨯==πϕ(2)s L gH A Q n /612.128.9202.0482.022=⨯⨯⨯⨯⨯==πμ(3)真空高度:m H gpg p C Cv 48.1274.074.0=⨯==-=ρρ 5-3 水箱用隔板分为A 、B 两室,隔板上开一孔口,其直径d 1=4cm ,在B 室底部装有圆柱形外管嘴,其直径d 2=3cm 。
已知H=3m ,h 3=0.5m 试求:(1)h 1,h 2;(2)流出水箱的流量Q 。
题5-3图解:隔板孔口的流量 112gh A Q μ=圆柱形外管嘴的流量 ()()132222h H g A h h g A Q +=+=μμ由题意可得Q1=Q2,则()()1212122212111211303.082.004.062.022h h h H d h d h H g A gh A -⨯⨯=⨯⨯+=+=μμμμ解得m h 07.11=sL s m gh A Q mh h H h /56.3/1056.307.18.9204.0462.0243.15.007.1333211312=⨯=⨯⨯⨯⨯⨯==∴=--=--=∴-πμ5-4 有一平底空船,其船底面积Ω为8m 2,船舷高h 为0.5m ,船自重G 为9.8kN。
流体力学蔡增基_课后习题解析(1)

5.在封闭水箱中,水深
A 点上安
装一压力表,其中表距 A 点 Z=0.5m 压 力表读数为 其真空度。
6
4.9kN / m 2
,求水面相对压强及
解:
p0h MZ
p0 9.8071.5 4.9 9.807 0.5 p0−4.9kpa
真空度为 4.9 kPa
1 d dp dp 10at− 5at ∴
0.53810−9 m 2 / N
d 0.026%
13.体积为 5 m 的水,再温度不变的情况下,当压强从 1at
3
增加到 5at 时,体积
减少 1L,求水的压缩系数
3
及弹性模量。 解:− dV / V
dp E −(− 0.001) 5(5− 1) 9.80710 4 5.110−10 m 2 / N
dy
5 1 (0.4 0.5) 13 110−3
得 =0.105pa.S 10.一圆锥体绕其铅直中心轴等速旋转, 锥体与固定壁间的距离
1mm
,全部为
润滑油( =0.1pas)充满,当旋转速度
16s−1
,锥体底部半径 R=0.3m,高
H=0.5m 时,求作用于圆锥的阻力矩。 解: 其中
p1 Hg h p2h
Hg
∴ p 2 p2 p3 p4h‘ p3 Hg h’ p1
Hg
∴ p4 p3 p4 p3 p2 p1
2 1
∴ 13.
一封闭容器盛有(水银)(水)的两种不同的液体。试问
同一水平线上的 1,2,3,4,5 各点的压强哪点最大?哪点 最小?哪些点相等?
4
第2章;流体静力学
1. 试求图(a),( b),( c)中,A,B,C 各点相对压强,图
(完整word版)流体力学习题及答案-第五章

第五章 势流理论5-1流速为u 0=10m/s 沿正向的均匀流与位于原点的点涡叠加。
已知驻点位于(0,-5),试求: (1)点涡的强度;(2) (0,5)点的流速以及通过驻点的流线方程。
答:(1)求点涡的强度Γ:设点涡的强度为Γ,则均匀流的速度势和流函数分别为:x u 01=ϕ,y u 01=ψ;点涡的速度势和流函数为:xy arctg πϕ22Γ-=,r y x ln 2)ln(221222ππψΓ=+Γ=; 因此,流动的速度势和流函数为:θπθπϕϕϕ2cos 20021Γ-=Γ-=+=r u x y arctg x u , r y u y x y u ln 2sin )ln(202122021πθπψψψΓ+=+Γ+=+=;则速度分布为:2202y x yu y x u +⋅Γ+=∂∂=∂∂=πψϕ, 222yx x x y v +⋅Γ=∂∂-=∂∂=πψϕ; 由于)5,0(-为驻点,代入上式第一式中则得到:0)5(052220=-+-⋅Γ+πu , 整理得到:ππ100100==Γu 。
(2)求)5,0(点的速度:将π100=Γ代入到速度分布中,得到:222222050102100102y x y y x y y x y u u ++=+⋅+=+⋅Γ+=πππ,2222225021002y x x y x x y x x v +=+⋅=+⋅Γ=πππ; 将0=x 、5=y 代入上述速度分布函数,得到:201010505501022=+=+⨯+=u (m/s ),05005022=+⨯=v (m/s );(3)求通过)5,0(点的流线方程:由流函数的性质可知,流函数为常数时表示流线方程C =ψ,则流线方程为:C y x y u =+Γ+21220)ln(2π;将0=x 、5=y 代入,得到:5ln 5050)50ln(21005102122+=+⨯+⨯=ππC ;则过该点的流线方程为:5ln 5050)ln(2100102122+=++y x y ππ,整理得到:5ln 55)ln(52122+=++y x y5-2 平面势流由点源和点汇叠加而成,点源位于(-1,0),其流量为θ1=20m 3/s ,点汇位于(2,0)点,其流量为θ2=40m 3/s ,已知流体密度为ρ=1.8kg/m 3,流场中(0,0)点的压力为0,试求点(0,1)和(1,1)的流速和压力。
流体力学泵与风机(第五版) 蔡增基 课后习题答案(2)

绪论1.流体的容重及密度有何区别及联系?解:g 是流体的本身属性。
还与g 有关。
ργ=ργ2.已知水的密度1000kg/m ,求其容重。
若有这样的水1L ,=ρ3它的质量和重力各是多少?解:g=1000×9.807=9807N/m ργ=3m=v=1000×0.001=1kg G=mg=1×9.807=9.807Nρ3.什么是流体的粘滞性?它对流体流动有什么作用?动力粘滞系数和运动粘滞系数有何区别及联系?µυ答:流体内部质点间或流层间因为相对运动的性质叫粘滞性,它使流动的能量减少。
表征单位速度梯度作用下的切µ应力,反映粘滞性的动力性质。
是单位速度梯度作用下的υ切应力对单位体积质量作用产生的阻力加速度。
=/υµρ4.水的容重=9.17kN/m ,=0.599×10pa.s 求它的运动粘γ3µ3−滞系数υ解:=g/=6.046×10m /sυ=ρµµγ5−25.空气容重=11.5N/m ,=0.157cm /s,求它的动力粘滞系γ3υ2数。
µ解:=pa.sµ5410841.1807.9/10157.05.11−−×=××==g γυρυ6.当空气从0℃增加到20℃时,增加15%,容重减少υ10%,问此时增加多少?µ解:=µgg g 0000035.1%)151%)(101(υγυγγυρυ=+−==所以增加了3.5%µ7.水平方向运动的木板,其速度为1m/s,平板浮在油面上,,油的=0.09807pa.s 。
求作用于平板单位面积上mm 10=δµ的阻力。
解:2/807.901.0/109807.0m N dydu =×==µτ8.温度为20℃的空气,在直径为2.5cm 管中流动,距管壁上1mm 处的空气速度为3cm/s 。
流体力学第五章

蔡增基《流体力学》考点精讲及复习思路第五章 孔口管嘴管路流动1.本章考情分析本章主要介绍简单长管、复杂管路、短管的水力计算以及孔口和管嘴的水力计算等。
与先前学过的章节有密不可分的联系,是具有一定综合性的工程应用。
考试中主要以名词解释、简答和计算题的形式予以考察,题目综合性相对较强,考题一般会配以管路图形,需要考生深入理解题意,看懂管路图,梳理解题思路,综合运用所学知识。
2.本章框架结构本章首先介绍了简单长管的水力计算和复杂管路的水力计算,而后分别就短管的水力计算,孔口和管嘴的水力计算做了详尽的说明。
3.本章考点精讲考点一 简单长管的水力计算前面几章已经介绍了工程流体力学的基本理论和方法。
但是,在实际的工程设计计算中这些方法显得有些烦琐。
因此,有必要对管路进行分类,再根据不同情况对理论方法进行简化,总结出比较简便实用的方法,以提高设计计算工作的效率。
本章将给出工程实际中常见的压力管路、孔口出流及管嘴出流的水力设计计算的实用方法。
(1)压力管路压力管路:在一定压差下,液流充满全管的流动管路。
(管路中的压强可以大于大气压,也可以小于大气压)注:输送气体的管路都是压力管路。
压力管道水力计算的主要内容就是确定水头损失,包括沿程水头损失和局部水头损失。
压力管路的分类①按管路的结构特点,分为简单管路:等径无分支复杂管路:串联、并联、分支②按能量比例大小,分为长管:和沿程水头损失相比,流速水头和局部水头损失可以忽略的流动管路。
(如室外管路,如油田地面集输管路、外输管路)。
短管:流速水头和局部水头损失不能忽略的流动管路。
(如室内管路,如联合站、计量间内管件较多的管路)。
注意:①长管和短管不按管道绝对长度决定。
②当管道存在较大局部损失管件,例如局部开启闸门、喷嘴、底阀等。
即使管道很长,局部损失也不能略去,必须按短管计算。
③将压力管道按长管计算,可以简化计算过程。
但在不能判断流速水头与局部水头损失之和远小于沿程水头损失之前,按短管计算不会产生较大的误差。
流体力学第五章

一、名词解释1.边界层:黏性流体流经固体壁面时,在固体壁面法线方向上存在一速度急剧变化的薄层,称为边界层。
2.管道进口段:边界层相交以前的管段称为管道进口段(或称起始段),其长度以L*表示。
3、粘性底层:紧贴壁面有一因壁面限制而脉动消失的层流薄层,其粘滞力使流速使流速急剧下降,速度梯度较大,这一薄层称为粘性底层。
二、简答题1:何谓普朗特混合长理论?根据这一理论紊流中的切应力应如何计算?答:沿流动方向和垂直于流动方向上的脉动速度都与时均速度的梯度有关。
2:什么是水力光滑管与水力粗糙管?与哪些因素有关?答:当粘性底层厚度大于管壁的粗糙突出部分时,粘性底层完全淹没了管壁的粗糙突出部分。
这时紊流完全感受不到管壁粗糙度的影响,流体好像在完全光滑的管子中流动一样。
这种情况的管内流动称作“水力光滑”,或简称“光滑管”。
当粘性底层厚度小于管壁的粗糙突出部分时,管壁的粗糙突出部分有一部分或大部分暴露在紊流区中,当流体流过突出部分时,将产生漩涡,造成新的能量损失,管壁粗糙度将对紊流产生影响。
这种情况的管内紊流称作“水力粗糙”,或简称“粗糙管”。
对于同样的管子,其流动处于水力光滑或水力粗糙取要看雷诺数的大小。
3、黏性流体总体的伯努利方程及适用条件? 黏性流体总体的伯努利方程:g g g g v p z v p z a a 222222221111ααρρ++=++适用条件:⑴流动为定常流动;⑵流体为黏性不可压缩的重力流体;⑶列方程的两过流断面必须是缓变流截面,而不必顾及两截面间是否有急变流。
4、黏性流体在管内流动时产生的损失有哪几种?分别怎么计算? 答:沿程损失是发生在缓变流整个流程中的能量损失,是由流体的粘滞力造成的损失。
单位重力作用下流体的沿程损失可用达西—魏斯巴赫公式计算。
g d l v h f 22λ=。
局部损失发生在流动状态急剧变化的急变流中,单位重力作用下流体流过某个局部件时,产生的能量损失:g v h j 22ζ=。
流体力学第二版(蔡增基)第五章解析

所组成的管道系统,如图(b)。 2)并联管道:是指数段管道并列联接所组成的管道系统,
如图(c)所示。
管道系统分类
3)枝状管道:如图(d)所示,各不相同的出口管段在不同 位置分流,形状如树枝。
4)网状管道:如图(e)所示,通过多路系统相互连接组成 一些环形回路,而节点的流量来自几个回路的管道。
2
2
前者与自由出流的能量损失
相同,为 vc2 2g,后者可看成圆
管突扩的能量损失,为:
0
0
1 Ac
A2
2
vc 2 2g
vc 2 2g
11
注意到 1v12 2v22 0 ,可整理得
2g 2g
2
2
vc 2gz
其中速度系数 1 1 孔口淹没出流流量
q vc Ac 2gzA mA 2gz
如图,箱中水流的流线从各个方向趋 近孔口,由于水流运动的惯性,流线不 能成折角地改变方向,只能光滑、连续 地弯曲,因此在孔口断面上各流线
平行,使水流在出孔后继续收缩,直至距孔口约为d/2处收
缩完毕,形成断面最小的收缩断面。流线在此趋于平行,
然后扩散,c-c断面称为孔口出流的收缩断面。
取断面1-1和收缩断面C-C,列伯努利方程
L≈(3~4)d,或当孔壁厚等于 δ=(3~4)d,此时的出流称为圆柱
形外管嘴出流,如图所示。
水流进入管嘴后,同样形成收缩,
并在收缩断面c-c处主流与管壁分
离,形成旋涡区;然后又逐渐扩大, 在管嘴出口断面上,水流充满整个 断面流出。
管嘴自由出流的流速和流量公式与 孔口自由出流的流速和流量公式的形 式类似。
一、管道系统分类
最新流体力学龙天渝蔡增基版课后答案第五章孔口管嘴管路流动

第五章孔口管嘴管路流动1•图中穿孔板上各孔眼的大小形状相同,问每个孔口的出流量是否相同?解:由Q - A . 2gH0与深度无关,所以每个孔口的出流量相同2•有一水箱水面保持恒定(5m),箱壁上开一孔口,孔口直径d=10mm。
( 1)如果箱壁厚度S =3mm求通过孔口的流速和流量。
(2)如果箱壁厚度S =40mm求通过孔口的流速和流量。
解: (1 )视作薄壁小孔口,「=0.97 ,」•-0.62v 二2gh =9.6m/s 得:Q = S = 4.82 10^m3/s(2 )视作管嘴,—」=0.82v = .2gh=8.12m/s 得:Q =」vA=6.38 10“m3/s3•—隔板将水箱分为A、B两格,隔板上有直径为d1=40mm的薄壁孔口,如题5-3图,B箱底部有一直径为d2=30mm的圆柱形管嘴,管嘴长l=0.1m , A箱水深H1=3m恒定不变。
(1)分析出流恒定性条件(H2不变的条件)。
(2)在恒定出流时,B箱中水深H2等于多少?(3 )水箱流量Q1为何值?解: (1 )当Q1=Q2时出流恒定(2)因为Q1=Q2, g •. 2g(H1 -H2)= "2A2 .2g(H2 0.1)查表得f =0.6, J2=0.82,解得:H2 = 1.85m(3)解得Q1^3.58 X 10-3m3/s4•证明容器壁上装一段短管(如图所示) ,经过短管出流时的流量系数□与流速系数为护=P ■ __鳥八1证:••• H o••• v 二 2gH o5•某诱导器的静压箱上装有圆柱形管嘴,管径为 4mm ,长度l =100mm , ;=0.02,从管嘴入口到出口的局部阻力系数 0.5,求管嘴的流速系数和流量系数(见上题图) 。
10cm 的孔口流入B 水箱,流量系数为0.62。
设上游水箱的水面高程H 1 =3m 保持不变。
(1) B 水箱中无水时,求通过孔口的流量。
(2) B 水箱水面高程H 2=2m 时,求通过孔口的流量。
流体力学龙天渝课后答案

流体力学龙天渝课后答案龙天渝课后答案第一章:流体力学基础概念在学习流体力学之前,我们首先需要了解一些基础概念。
流体力学是研究流体静力学和流体动力学的学科,它涉及了许多重要的概念和原理。
1. 流体的定义和特性:流体是指能够流动的物质,包括液体和气体。
与固体不同,流体具有流动性和粘滞性。
2. 流体静力学:流体静力学研究的是处于静止状态下的流体,它涉及了压力、密度、浮力等概念。
根据帕斯卡定律,流体中的压强是均匀的。
浮力是物体在液体中受到的向上的力,它的大小等于所排开的液体的重量。
3. 流体动力学:流体动力学研究的是流体在运动中的力学性质。
它基于质量守恒定律、动量守恒定律和能量守恒定律来描述流体的运动行为。
流体的运动可以通过速度场来描述,速度场是指在每个点上流体速度的矢量。
第二章:流体流动的方程了解了流体力学的基础概念后,我们来学习一些描述流体流动的方程。
1. 质量守恒方程:质量守恒方程是流体动力学的基本方程之一,它表达了流体质量在单位时间内在空间中的改变量等于流入或流出的质量通量与积累产生的差值。
2. 动量守恒方程:动量守恒方程描述了流体运动时动量守恒的原理。
它表达了流体单位时间内动量的改变量等于施加在流体上的外力与流体内部压力和重力之差。
3. 能量守恒方程:能量守恒方程用于描述流体在流动过程中能量的守恒性质。
它包括液体内能、压力能和动能等各种能量形式的转换和积累。
第三章:流体的稳定性和边界层在流体力学中,稳定性和边界层是两个重要的概念。
1. 稳定性:稳定性研究的是流体在受到扰动后是否能够恢复到原来的状态。
稳定性分析可以通过线性稳定性理论或非线性动力学方法来进行。
2. 边界层:边界层是指流体在与固体表面接触时的一层较薄的流动区域。
边界层内的速度变化很大,而在边界层外的流体速度几乎保持不变。
边界层对于流体流动的阻力有重要影响。
第四章:流体力学的应用领域流体力学广泛应用于许多领域,包括工程、地球科学和生物医学等。
流体力学龙天渝课后答案第五章孔口管嘴管路流动
�
L5
d
5 5
)
H并
�
S
2
Q
2 2
� 11.15m
H 1�5 � S1�5Q 2 � 13m 7
∴ H � 11.15 � 13 � 24.15m
23.管段 1 的管径为 20mm�管段 2 为 25mm�l1 为 20m�l2 为 10m��� 1 � �� 2 � 15 �� � 0.025 �
1
� �� �
1 l
� d � �� �1
证�∵ H 0
�
v2 2g
� ��
v2 2g
��
l d
v2 2g
∴ v � � 2 gH 0
其中� �
1 l
� d � �� �1
5.某诱导器的静压箱上装有圆柱形管嘴�管径为 4mm�长度 l =100mm�λ=0.02�从管嘴入 口到出口的局部阻力系数 �� � 0.5 �求管嘴的流速系数和流量系数�见上题图�。
由于 H 不变� Q3 减小�所以 Q 2 减小 25.三层供水管路�各管段的�值皆 106s2/m5� 层高均为 5m。设 a 点的压力水头为 20m�求 Q1、Q2、Q3�并比较三流量�得出结论来。�忽 略 a 处流速水头�
解� Q' � Q2 � Q3
Q � Q1 � Q' � Q1 � Q2 � Q3
解�Q= n�A 2 �p �得 n � 218.4 �所以需要 219 个 �
8.水从 A 水箱通过直径为 10cm 的孔口流入 B 水箱�流量系数为 0.62。设上游水箱的水面高
程 H 1 =3m 保持不变。
�1�B 水箱中无水时�求通过孔口的流量。
�2�B 水箱水面高程 H 2 =2m 时�求通过孔口的流量。
《流体力学泵与风机》(蔡增基龙天渝)第3章课后题答案

一元流体动力学基础1.直径为150mm 的给水管道,输水量为h kN /7.980,试求断面平均流速。
解:由流量公式vA Q ρ= 注意:()vA Q s kg h kN ρ=⇒→//A Qv ρ=得:s m v /57.1=2.断面为300mm ×400mm 的矩形风道,风量为2700m 3/h,求平均流速.如风道出口处断面收缩为150mm ×400mm,求该断面的平均流速解:由流量公式vA Q = 得:A Q v =由连续性方程知2211A v A v = 得:s m v /5.122=3.水从水箱流经直径d 1=10cm,d 2=5cm,d 3=2.5cm 的管道流入大气中. 当出口流速10m/ 时,求(1)容积流量及质量流量;(2)1d 及2d 管段的流速解:(1)由s m A v Q /0049.0333==质量流量s kg Q /9.4=ρ (2)由连续性方程:33223311,A v A v A v A v ==得:s m v s m v /5.2,/625.021==4.设计输水量为h kg /294210的给水管道,流速限制在9.0∽s m /4.1之间。
试确定管道直径,根据所选直径求流速。
直径应是mm 50的倍数。
解:vA Q ρ= 将9.0=v ∽s m /4.1代入得343.0=d ∽m 275.0 ∵直径是mm 50的倍数,所以取m d 3.0= 代入vA Q ρ= 得m v 18.1=5.圆形风道,流量是10000m 3/h,,流速不超过20 m/s 。
试设计直径,根据所定直径求流速。
直径规定为50 mm 的倍数。
解:vA Q = 将s m v /20≤代入得:mm d 5.420≥ 取mm d 450= 代入vA Q = 得:s m v /5.17=6.在直径为d 圆形风道断面上,用下法选定五个点,以测局部风速。
设想用和管轴同心但不同半径的圆周,将全部断面分为中间是圆,其他是圆环的五个面积相等的部分。
流体力学课后习题答案龙天渝

在水管出口中心a点与盘中心b点立元流能量方程,并用v1代替ua,有:
【篇三:流体力学_龙天渝_流体静力学】
一、学习导引
=
,?y
=
,?z
=
(2-1)
(2)压强微分
质量力只有重力的条件下,液体的位置水头与压强水头之和等于常数,即
+
=(2-4)
式中,为液体的重度。如果液面的压强为
=
+
,
方向的投影面积;
的形心的淹没深度;是压力体的体积。
4、浮体的稳定性
设表示定倾半径,表示偏心距,它等于浮体平衡时,重心与浮心的距离,浮体的平衡有三种情况:
稳定平衡
=随遇平衡
不稳定平衡定倾半径的定义是
(2-9)
式中,是浮体被淹没的体积;是浮面对其转轴的面积惯性矩。
二、难点分析
1.通器内不同液体的压强传递
式中,
;
为左侧(上部)液体的总压力,
为左侧
为
(上部)液体的压力中心;为右侧(下部)液体的总压力,
右侧(下部)液体的压力中心。如图2-2(c)所示。
3.复杂曲面的பைடு நூலகம்力体
压力体是物体表面与液面或液面的延伸面以及铅垂面所围合的空间体积。压力体内不一定有液体。正确地识别压力体,可以使铅垂方向的总压力的计算得到简化。
22求流线方程并画出若干条流线。(x+y=c)
3-15已知平面流动的速度场为u=(4y-6x)ti+(6y-9x)tj。求t=1时的流线方程并绘出x=0至x=4区间穿过x轴的4条流线图形。(1.5x-y=c)
3-16水管的半径r0=30mm,流量q=401l/s,已知过流断面上的流速分布为u=umax(y/r0)1/7。式中:umax是断面中心点的最大流速,y为距管壁的距离。试求:
流体力学泵与风机-蔡增基-第五版-下-答案
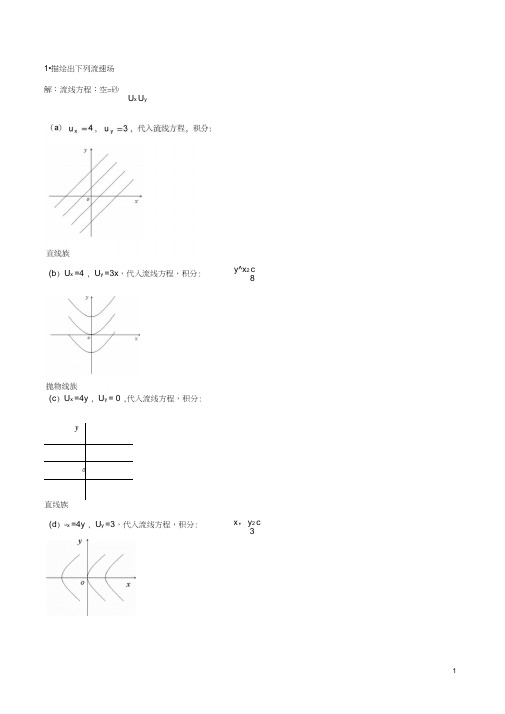
(c) U x =4y , U y = 0 ,代入流线方程,积分:y(d) U x =4y , U y =3,代入流线方程,积分:1•描绘出下列流速场解:流线方程:空=砂U x U y(b) U x =4 , U y =3x,代入流线方程,积分: y^x2 c8x,y2 c32(g ) U x =4y , U y - -4x ,代入流线方程,积分: x 2 y 2 =c(h ) u x =4 , U y =0,代入流线方程,积分: y=c直线族2x(i ) U x =4 , U y - -4x ,代入流线方程,积分: yc 抛物线族 代入流线方程,积分:2 23x 4y = c代入流线方程,积分:抛物线族(j) u x =4x , U y =0,代入流线方程,积分:y=cy直线族(k) u x =4xy , U y =0,代入流线方程,积分:y=cy直线族直线族(I ) u rru^=0,由换算公式:u x二u r COST -u^sin v , U y 二u r sin)UjCosvc x cU x 0r rexx2y2u ycyx2 y2代入流线方程积分:-=c(m ) u 「0 , u# , Ux^-C ^- 2Cy 2,u_0 叫—口 r r r x + yr r x + y代入流线方程积分: x 2 y 2 =c同心圆2•在上题流速场中,哪些流动是无旋流动,哪些流动是有旋流动。
如果是有旋流动,它的旋转角速度的表达 式是什么?解:无旋流有:呂二巴(或如二皀J ).y ;xr(a ) , ( f ),( h ),( j ),( l ),( m )为无旋流动,其余的为有旋流动 对有旋流动,旋转角速度:•=丄(—--—x )2 ex dy…、3 7(b )( c ) • - -2 ( d ) - - -2 ( e ) •=2(g ) ■- -4 ( i ) ■ - -2 ( k ) • - -2x3•在上题流速场中,求出各有势流动的流函数和势函数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第五章孔口管嘴管路流动1•图中穿孔板上各孔眼的大小形状相同,问每个孔口的出流量是否相同?解:由Q - A . 2gH0与深度无关,所以每个孔口的出流量相同2•有一水箱水面保持恒定(5m),箱壁上开一孔口,孔口直径d=10mm。
( 1)如果箱壁厚度S =3mm求通过孔口的流速和流量。
(2)如果箱壁厚度S =40mm求通过孔口的流速和流量。
解: (1 )视作薄壁小孔口,「=0.97 ,」•-0.62v 二2gh =9.6m/s 得:Q = S = 4.82 10^m3/s(2 )视作管嘴,—」=0.82v = .2gh=8.12m/s 得:Q =」vA=6.38 10“m3/s3•—隔板将水箱分为A、B两格,隔板上有直径为d1=40mm的薄壁孔口,如题5-3图,B箱底部有一直径为d2=30mm的圆柱形管嘴,管嘴长l=0.1m , A箱水深H1=3m恒定不变。
(1)分析出流恒定性条件(H2不变的条件)。
(2)在恒定出流时,B箱中水深H2等于多少?(3 )水箱流量Q1为何值?解: (1 )当Q1=Q2时出流恒定(2)因为Q1=Q2, g •. 2g(H1 -H2)= "2A2 .2g(H2 0.1)查表得f =0.6, J2=0.82,解得:H2 = 1.85m(3)解得Q1^3.58 X 10-3m3/s4•证明容器壁上装一段短管(如图所示) ,经过短管出流时的流量系数□与流速系数为护=P ■ __鳥八1证:••• H o••• v 二 2gH o5•某诱导器的静压箱上装有圆柱形管嘴,管径为 4mm ,长度l =100mm , ;=0.02,从管嘴入口到出口的局部阻力系数 0.5,求管嘴的流速系数和流量系数(见上题图) 。
10cm 的孔口流入B 水箱,流量系数为0.62。
设上游水箱的水面高程H 1 =3m 保持不变。
(1) B 水箱中无水时,求通过孔口的流量。
(2) B 水箱水面高程H 2=2m 时,求通过孔口的流量。
(3) A 箱水面压力为2000Pa , H 1 =3m 时,而B 水箱水面 压力为0, H 2=2m 时,求通过孔口的流量。
解:(1 )属孔口自由出流Q "A .2gH ° , H 。
二已得:Q = 0.037m 3/s(2)属孔口淹没出流, Q=・A.2gH 0 , H °=H 1-H 2解:由题得:=J ,1= 0.7076•如上题,当管嘴外空气压强为当地大气压强时,要求管嘴出流流速为 内应保持多少压强?空气密度为p =1.2kg/m 3。
30m/s 。
此时静压箱解:"• pv = 2 ,得=p =1.08kN/m 27.某恒温室采用多孔板送风, 风道中的静压为200Pa ,孔口直径为20mm ,空气温度为20C,尸0.8。
要求通过风量为1m 3/s 。
问需要布置多少孔口? 解:Q=nA 2:P ,得 n =218.4,所以需要219个8.水从A 水箱通过直径为精品文档得:Q =0.0216m3/s(3) Q“A2g H o ,叫十”齧得:Q=0.0236m3/s9•室内空气温度为30C,室外空气温度为20 C,在厂房上下部各开有8m2的窗口,两窗口的中心高程差为7m,窗口流量系数尸0.64,气流在自然压头作用下流动,求车间自然通风换气量(质量流量)。
解:g =H 0.37 =2.744N/m2Q=[内-A =12.96kg/s(方法二):分别令上下部窗口外渐变流断面2和断面1,根据气体能量方程,得P I g(—2 2因为p 1 =P 2 =P a , V1 =V2 : 0 ,所以P L =g('a - ')H又由于二P L = i p2根据气体孔口淹没出流的流量公式:Q M 1 = P aVQ M2= ^A j2g骨又由于连续性方程Q M 1 = Q M2查得烏=1.205kg/m3,匸=1.165kg/m3Q MI=Q M2-Q M =12.96kg/s10•如图示管路中输送气体,采用U形差压计测量压强差为h米液体。
试推导通过孔板的流量公式。
解::.p = _ .7 gh,,是U形压差计液体容重,?为气体容重Q = PAV2gH; = A A』2g 齐叫2g^% 叫2g舟h11. 如上题图孔板流量计,输送20C空气,测量h=100mmH20。
尸0.62, d=100mm,求Q。
解:将数据代入上题公式得Q =0.2m3/s12. 什么叫管路阻抗?(又称为综合阻力数)为什么有两种表示?在什么情况下,S与管中流量无关,仅决定于管道的尺寸及构造?解:阻抗反映管路上沿程阻力和局部阻力情况。
S H用在液体管路,S p用在气体管路。
在紊流粗糙区时,S与管中流量无关(因为•此时与v以及流体状态无关),仅决定于管道的尺寸和构造。
13. 供热系统的凝结水箱回水系统如图。
试写出水泵应具有的作用水头表达式。
“p2— p;2解:H 2 1SQ (如果冷却措施是开g式则需加上h)14. 某供热系统,原流量为0.005m3/s,总水头损失h=5mH 20,现在要把流量增加到0.0085m3/s, 试冋水泵应供给多大压头。
解:H1 二SQ2即5 二S 0.0052二S =2 105s2/m52 5 2H2 =SQ2=2 105 0.00852=14.45m15. 两水池用虹吸管连通,上下游水位差H=2m,管长L 1 = 3m, L2 = 5m, L3= 4m,直径d=200mm,上游水面至管顶高度h=1m。
已知匸0.026,进口网Z10,弯头Z1.5(每个弯头),出口t= 1.0,求:(1)虹吸管中的流量;(2)管中压强最低点的位置及其最大负压值。
解:(1 )方法一:d2..2gHQ= ----------------- 4—c -2- - '「八E L —8( ) d■: d g=SQ2,解得Q =0.05m3/s05m3/S方法二:h v 咤-Z i)g L||L2lH.a L2 L3)d=2.75m (C =10,b -1.5,0-1)•••负压值为-2.93m16. 如图水泵抽水系统,管长、管径单位为求:. 3 3m, Z给于图中,流量Q=40 X10" m /s, A=0.03。
(1) 吸水管及压水管的S数。
(2) 求水泵所需水头。
(3 )绘制总水头线。
8人L1十匚+匚2 ]解:(1) S Hl= -------- '=118.69s2/m5Tt digf I8 人匕+ J +J +1。
,2 丿 2 5S H2=-------- 厂飞-------- =2106.1s /m兀d i g(2) H =h ( S H1+S H2 ) Q2= 23.56m (其中h =17 3 = 20m)(3 )略17•图为一水平安置的通风机,吸入管d1=200m , l1=10m ,启0.02。
压出管为直径不同的两段管段串联组成,d2=200mm,b=50m,入=0.02; 250m , A=0.02。
空气密度为p=1.2kg/m3, 风量为Q=0.15m3/s,不计局部阻力。
试计算:(1)风机应产生的总压强为多少?(2)如风机与管道铅直安装,但管路情况不变,风机的总压有无变化?(3)如果流量提高到0.16m3/s,风机总压变化多少?(4)绘出全压线与静压线图。
解得:p=2500Pa(2 )铅直安装不会改变总压,因为同种气体位压等于零(3) p =S P Q2=2830Pa18. 并联管路中各支管的流量分配,遵循什么原理?如果要得到各支管中流量相等,该如何设计管路?1解:并联管路Q :「——,如果要得到各支管流量相等必须各支管S相等•••应设计成S1=S2=S319. 有两长度尺寸相同的支管并联,如果在支管2中加一个调节阀(阻力系数为Z), P8』解:⑴SP^^S p22dS P3「8(丄1)d32dS P二S P1 2p = S P Q2JI则Q1和Q2哪个大些?阻力h f1和h f2哪个大些?解: (1) S1Q12=S2Q;, S与Z有关因为S, ::: S2,故Q1 Q2 。
(2)h fi = h f220. 有一简单并联管路如下图,总流量Q =80 XW -3m 3/s , /=0.02,求各管段之间的流量及两节 点之间的水头损失。
第一支路 d 1 =200mm , L 仁600m ,第二支路d 2 =200mm , L2=360m 。
H 1 = S 1Q 2 = S 2Q 2 = 3.72m21. 如上题,若使Q j 二Q 2如何改变第二支路? 解:d 2减小或加调节阀等增加阻力的措施。
22.如图所示管路,设其中的流量 QA=0.6m 3/s , /=0.02,不计局部损失,其它已知条件如图, 求A 、D 两点间的水头损失。
1_ ____ 1 解牛:Q I :Q 2=S 2 : J S 〔 ( Q 川■v SS i =8 丄1 d id i 4g2 5=3104.8 s /m8' L 2 f d 225=1862.9s 2/m 5解得:Q 1 : Q^0.774Q 2 = 45 10'm 3 /s Q j =35 10 "m 3/s解:Q 2 Q 3 Q 4 二Q AS 2 =346.8s 2. m 5Q 2 2185-21851743 3375 Q A 一。
"山 sH 并=S 2Q ; - 11.15mI600( min j/iQ 2 :Q 3 :L 2d4=2185:1743:3375.L 4L 5hl350( m m//i 1000( m)8 兀L52爲矿評e2H i 5 =S i5Q13m二 H =11.15 13 =24.15m23. 管段 1 的管径为 20mm ,管段 2 为 25mm ,1 为 20m ,2 为 10m ,匕 7 ^15=0.025 , 流量分配有何变化? 解:这样Q 1更小,Q 2更大,所以应将管段 1的 管径改为25mm ,管段2的管径改为20mm ,两 管流量可接近。
24. 已知某枝状管网的 的末端再加一段管子, Q 3各有何变化?解:由于总阻抗加大,H 二SQ 2,使总流量Q 1 减小由于H 不变,Q 3减小,所以Q 2减小25. 三层供水管路,各管段的S 值皆 106s 2/m 5, 层高均为5m 。
设a 点的压力水头为 20m ,求Q 1、Q 2、Q 3,并比较三流量,得出结论来。
(忽 略a 处流速水头) 解:Q^Q 2 Q 3Q =Q1 Q^Q 1 Q 2 Q 3(1) 2O=SQ 2(2) 20= 5+S Q '2+SQ ;=5+S (Q 2 Q 3)2 SQ ; (3) 20= 10+S Q '2+2S Q 2联立(1) (2) (3) Q 1= 4.46X 10-3m 3/s Q 2= 2.41 x 10-3 m 3/s Q 3 = 0.63 x 10-3 m 3/s26. 如上题,若想得到相同的流量,在 a 点压力水头仍为20m 时,应如何改造管网? 解:加大底层阻力(如加阀门,减小管径) 。
