中考数学几何选择填空压轴题精选配答案
专题3 填空压轴题之几何求值-备战2022年中考数学满分真题模拟题分类之压轴题汇编(深圳专用解析版)
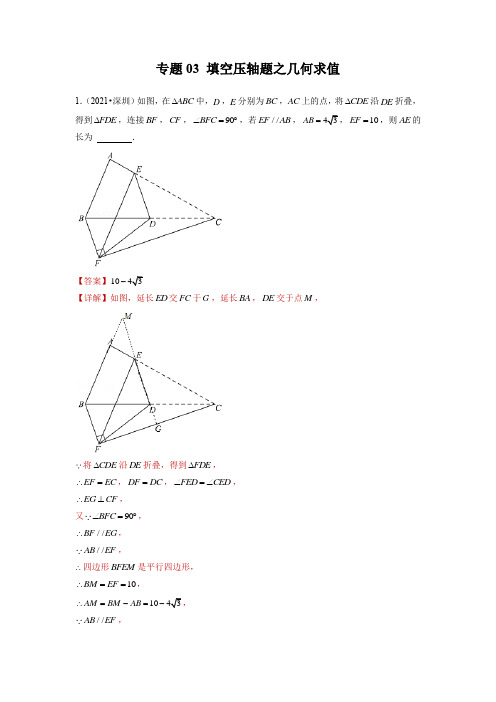
专题03 填空压轴题之几何求值1.(2021•深圳)如图,在ABC ∆中,D ,E 分别为BC ,AC 上的点,将CDE ∆沿DE 折叠,得到FDE ∆,连接BF ,CF ,90BFC ∠=︒,若//EF AB ,43AB =,10EF =,则AE 的长为 .【答案】1043-【详解】如图,延长ED 交FC 于G ,延长BA ,DE 交于点M ,将CDE ∆沿DE 折叠,得到FDE ∆,EF EC ∴=,DF DC =,FED CED ∠=∠,EG CF ∴⊥,又90BFC ∠=︒,//BF EG ∴,//AB EF ,∴四边形BFEM 是平行四边形,10BM EF ∴==,1043AM BM AB ∴=-=-,//AB EF ,M FED∴∠=∠,M CED AEM∴∠=∠=∠,1043 AE AM∴==-2.(2020•深圳)如图,在四边形ABCD中,AC与BD相交于点O ,90ABC DAC∠=∠=︒,1tan2ACB∠=,43BOOD=,则ABDCBDSS∆∆=.【答案】332【详解】如图,过点D作//DM BC,交CA的延长线于点M,延长BA交DM于点N,//DM BC,ABC ANM∴∆∆∽,OBC ODM∆∆∽,∴1tan2AB ANACBBC NM==∠=,43BC OBDM OD==,又90ABC DAC∠=∠=︒,90BAC NAD∴∠+∠=︒,90BAC BCA∠+∠=︒,NAD BCA∴∠=∠,ABC DAN∴∆∆∽,∴12AB DNBC NA==,设4BC a=,由43BC OBDM OD==得,3DM a=,2AB a∴=,35DN a=,65AN a=,616255NB AB AN a a a∴=+=+=,∴22313521323225ABDBCDaAB DNSS BC NB a∆∆⋅===⋅.3.(2019•深圳)如图,在正方形ABCD 中,1BE =,将BC 沿CE 翻折,使B 点对应点刚好落在对角线AC 上,将AD 沿AF 翻折,使D 点对应点刚好落在对角线AC 上,求EF = .【答案】6 【详解】如图,作FM AB ⊥于点M .四边形ABCD 是正方形,45BAC CAD ∴∠=∠=︒.将BC 沿CE 翻折,B 点对应点刚好落在对角线AC 上的点X ,1EX EB AX ∴===,90EXC B ∠=∠=︒,222AE AX EX ∴=+=.将AD 沿AF 翻折,使D 点对应点刚好落在对角线AC 上的点Y ,1AM DF YF ∴===,∴正方形的边长21AB FM ==+,21EM =-,2222(21)(21)6EF EM FM ∴=+=-++=.4.(2018•深圳)在Rt ABC ∆中,90C ∠=︒,AD 平分CAB ∠,BE 平分ABC ∠,AD 、BE 相交于点F ,且4AF =,2EF =,则AC = .【答案】8105 【详解】如图,过点E 作EG AD ⊥于G ,连接CF , AD ,BE 是分别是BAC ∠和ABC ∠的平分线, CAD BAD ∴∠=∠,CBE ABE ∠=∠,90ACB ∠=︒,2()90BAD ABE ∴∠+∠=︒,45BAD ABE ∴∠+∠=︒,45EFG BAD ABE ∴∠=∠+∠=︒,在Rt EFG ∆中,2EF =,1FG EG ∴==,4AF =,3AG AF FG ∴=-=,根据勾股定理得,2210AE AG EG =+=,AD 平分CAB ∠,BE 平分ABC ∠,CF ∴是ACB ∠的平分线,45ACF AFE ∴∠=︒=∠,CAF FAE ∠=∠,AEF AFC ∴∆∆∽,∴AE AF AF AC=, 216810510AF AC AE ∴===5.(2017•深圳)如图,在Rt ABC ∆中,90ABC ∠=︒,3AB =,4BC =,Rt MPN ∆,90MPN ∠=︒,点P 在AC 上,PM 交AB 于点E ,PN 交BC 于点F ,当2PE PF =时,AP = .【答案】3【详解】如图作PQ AB ⊥于Q ,PR BC ⊥于R .90PQB QBR BRP ∠=∠=∠=︒,∴四边形PQBR 是矩形,90QPR MPN ∴∠=︒=∠,QPE RPF ∴∠=∠,QPE RPF ∴∆∆∽, ∴2PQ PE PR PF ==, 22PQ PR BQ ∴==,//PQ BC ,::::3:4:5AQ QP AP AB BC AC ∴==,设4PQ x =,则3AQ x =,5AP x =,2BQ x =, 233x x ∴+=,35x ∴=, 53AP x ∴==.6.(2021•深圳模拟)如图,在四边形ABCD 中,AE 平分BAD ∠交CD 于点E ,且AB AE =,12CBA D BAD ∠=∠+∠,过点E 作EG AB ⊥,垂足为G .延长BC 和AE 交于点F ,若:2:1BF ED =,2EG =,三角形ABF 的面积为7,则AD = .【答案】72 【详解】解法一: 如图,过A 作AM BF ⊥于M ,作AN CD ⊥于N ,过E 作EH AD ⊥于H ,90AMB ANE ∴∠=∠=︒,AE 平分BAD ∠交CD 于点E ,12BAE DAE BAD ∴∠=∠=∠, 12CEA DAE ADE BAD ADE ∠=∠+∠=∠+∠, 12CBA D BAD ∠=∠+∠, CEA CBA ∴∠=∠,AED ABM ∴∠=∠,AB AE =,()ABM AEN AAS ∴∆≅∆,AM AN ∴=,12ABF S BF AM ∆=⋅,12AED S DE AN ∆=⋅,且2BF ED =, 2ABF AED S S ∆∆∴=, 7ABF S ∆=,72AED S ∆∴=, AE 平分BAD ∠,EG AB ⊥,EH AD ⊥,2EH EG ∴==,1722AED S AD EH ∆∴=⋅=, 72AD ∴=; 解法二:过D 作DM AE ⊥于M ,过F 作FN AB ⊥,交AB 的延长线于N , AE 平分BAD ∠交CD 于点E ,12BAE DAE BAD ∴∠=∠=∠, 12CEA DAE ADE BAD ADE ∠=∠+∠=∠+∠, 12CBA D BAD ∠=∠+∠, CEA CBA ∴∠=∠,AED FBN ∴∠=∠,90DME FNB ∠=∠=︒,DME FNB ∴∆∆∽,∴12ED DM BF FN ==, 2FN DM ∴=,112722ABF S AB FN AE DM ∆=⋅=⋅=, 7AE DM ∴⋅=,BAE DAE ∠=∠,90AGE AMD ∠=∠=︒,AGE AMD ∴∆∆∽,∴EG AE DM AD =, ∴2AE DM AD=,722DM AE AD ⋅∴==.7.(2021•龙岩模拟)将含30︒角且大小不等的两个三角板按如图摆放,使直角顶点重合,连接AE 、BD ,则AE BD = .【答案】3【详解】EDC ∆与ACB ∆为两个直角三角形,且30DEC BAC ∠=∠=︒,90ACB ECD ∠=∠=︒, ACB DCA ECD DCA ∴∠+∠=∠+∠,DCB ECA ∴∠=∠,在Rt ACB ∆中,tan tan30BC CAB AC∠==︒, 在Rt ECD ∆中,tan tan30DC CED EC ∠==︒, ∴BC DC AC EC=, ∴在ECA ∆与DCB ∆中,DC BC EC AC=, DCB ECA ∠=∠,ECA DCB ∴∆∆∽,∴AE AC BD BC=,在Rt ACB ∆中,tan tan 603AC ABC BC =∠=︒= 8.(2021•南山区一模)如图,在Rt ABC ∆中,90C ∠=︒,BE ,AF 分别是ABC ∠,CAB ∠平分线,BE ,AF 交于点O ,OM AB ⊥,10AB =,8AC =,则OM = .【答案】2【详解】过O 作OG AC ⊥于G ,OH BC ⊥于H ,连接OC ,AF 平分CAB ∠,BE 平分ABC ∠,OG OH OM ∴==,90C ∠=︒,10AB =,8AC =,221086BC ∴=-=11112222ABC S AC BC AB OM AC OG BC OH ∆∴=⋅=⨯⋅+⋅+⋅, ∴11118610862222OM OG OH ⨯⨯=⨯⨯+⨯⨯+⨯⨯, 2OM ∴=9.(2021•深圳模拟)如图,在ABC ∆中,45B ∠=︒,62AB =,D 、E 分别是AB 、AC 的中点,连接DE ,在直线DE 和直线BC 上分别取点F 、G ,连接BF 、DG .若3BF DG =,且直线BF 与直线DG 互相垂直,则BG 的长为 .【答案】4或2【详解】如图,过点B 作BT BF ⊥交ED 的延长线于T ,过点B 作BH DT ⊥于H .DG BF ⊥,BT BF ⊥,//DG BT ∴,AD DB =,AE EC =,//DE BC ∴,∴四边形DGBT 是平行四边形,BG DT ∴=,DG BT =,45BDH ABC ∠=∠=︒, 32AD DB ==, 3BH DH ∴==, 90TBF BHF ∠=∠=︒,90TBH FBH ∴∠+∠=︒,90FBH F ∠+∠=︒,TBH F ∴∠=∠,1tan tan 3BT DG F TBH BF BF ∴∠=∠===, ∴13TH BH =, 1TH ∴=,134DT TH DH ∴=+=+=,4BG ∴=.当点F 在ED 的延长线上时,同法可得312DT BG ==-=.10.(2021•福田区二模)如图,点M 是Rt ABC ∆斜边AB 的中点,过点M 作DM CM ⊥,交AC 于点D ,若2AD =,5BC =,则CD = .【答案】29【详解】延长CM,使CM MN=,连接AN,点M是Rt ABC∆斜边AB的中点,AM BM∴=,在AMN∆和BMC∆中,AM BMAMN BMCMN CM=⎧⎪∠=∠⎨⎪=⎩,()AMN BMC SAS∴∆≅∆,5BC AN∴==,NAM B∠=∠,//AN BC∴,90BCA∠=︒,90NAD∴∠=︒,22225229DN AN AD∴=+=+=,DM CM⊥,CM MN=,29CD DN∴==.11.(2021•深圳模拟)如图,在Rt ABC∆中,90BAC∠=︒,D为BC的中点,过点D作DE DF⊥,交BA的延长线于点E,交AC的延长线于点F.若72CF=,4AC=,2AB=.则AE=.【答案】10【详解】延长FD 至G ,使GD FD =,连接BG ,如图所示: D 为BC 的中点,BD CD ∴=,在BDG ∆和CDF ∆中,BD CD BDG CDF GD FD =⎧⎪∠=∠⎨⎪=⎩,()BDG CDF SAS ∴∆≅∆,72BG CF ∴==,G F ∠=∠, //BG CF ∴, BGH AFH ∴∆∆∽, ∴77271542GH BH BG FH AH AF ====+, ∴411DH FD =,15152211AH AB ==, 90BAC ∠=︒,152AF AC CF =+=, 221515755()()21122HF ∴=+=, 41051511DH FH ∴==, DE DF ⊥,90EDH BAC ∴∠=︒=∠,90E EHD F EHD ∴∠+∠=∠+∠=︒,E F ∴∠=∠,DHE AHF ∴∆∆∽,∴HE DH HF AH=,即10511157551122HE=,解得:12511HE=,12515101111AE HE AH∴=-=-=;12.(2021•宝安区二模)如图,在等腰Rt ABC∆中,90B∠=︒,BA BC=,D为BC上一点,且3BD=,E为AD上一点,连接CE,45CED∠=︒,2CE AE=,则CE的长为.【答案】1855【详解】过A作AN CE⊥的延长线于N,过C作CM AD⊥交AD延长线于M,2CE AE=,∴设AE a=,则2CE a=,3445∠=∠=︒,AN NE ∴=,45ECM ∠=︒,90B ∠=︒,BA BC =,45ACD ∴∠=︒,12∴∠=∠,AEN ∴∆,CEM ∆都是等腰直角三角形, 2CE a =,AE a =, CM EM a ∴==,22AN NE a ==, 12∠=∠,CDM CAN ∴∆∆∽,∴CM CD CN AC=, 22NE a =,2CE a =, 322NC a ∴=, 222213255222AC AN NC a a a a ∴=+=+==, ∴3252aCD a a =,103CD a ∴=, 1033BC a ∴=+, 在Rt ABC ∆中,45BAC ∠=︒,sin BC BAC AC∴∠=, sin45BC AC ∴=︒⋅,即1023532a a +=⨯, 9105a ∴=, 9101852255CE a ∴==⨯=. 13.(2021•宝安区期末)如图,在ABC ∆中,AB AC =,点D 、E 是BC 边上两点,连接AD ,以AD 为腰作等腰直角ADF ∆,90ADF ∠=︒,作FE BC ⊥于点E ,FE CE =,若2BD =,5CE =,则CDF S ∆=. 【答案】30 【详解】过点A 作AH BC ⊥于H ,90AHD ∴∠=︒,FE BC ⊥,90DEF ∴∠=︒,ADF ∆是等腰直角ADF ∆,AD DF ∴=,90ADF ADH EDF ∠=∠+∠=︒,90ADH DAH ∴∠+∠=︒,EDF DAH ∴∠=∠,在ADH ∆和DFE ∆中,DAH EDF AHD DEF AD FD ∠=∠⎧⎪∠=∠⎨⎪=⎩,()ADH DFE AAS ∴∆≅∆,5CE =,5DH EF ∴==,7BH CH ∴==(三线合一), ∴12CDF S DC EF ∆=⨯⨯11252=⨯⨯30=.14.(2021•罗湖区期末)如图,在ABC∆中,90ACB∠=︒,点D 是BC上的一点,AC DC=,AB AE⊥,且AE AB=,连接DE交AC的延长线于点F,32ACCF=,则BDCD=.【答案】43【详解】在DC上截取CG CF=,连接AG,32ACCF=,设3AC x=,2CF x=,AC DC=,3CD x∴=,CG CF=,2CG x∴=,90ACB∠=︒,在Rt ACG∆和Rt DCF∆中,AC CDACD DCFCG CF=⎧⎪∠=∠⎨⎪=⎩,()ACG DCF SAS∴∆≅∆,CAG CDF∴∠=∠,90AGB CAG∠=∠+︒,90EFA CDF∠=︒+∠,AGB EFA∴∠=∠,AB AE⊥,90EAB∴∠=︒,90ACD∠=︒,AC CD=,45CAD∴∠=︒,45EAF BAD ∴∠+∠=︒,45ADC ABC BAD ∠=︒=∠+∠,EAF ABC ∴∠=∠,在EAF ∆和ABG ∆中,EAF ABC EFA AGB AE AB ∠=∠⎧⎪∠=∠⎨⎪=⎩,()EAF ABG AAS ∴∆≅∆,5BG AF x ∴==,32GD x x x =-=,4BD x ∴=, ∴43BDCD =15.(2020•崇州市模拟)如果点P 是ABC ∆内一点,且它到三角形的三个顶点距离之和最小,则P 点叫ABC ∆的费马点.已经证明:在三个内角均小于120︒的ABC ∆中,当120APB APC BPC ∠=∠=∠=︒时,P 就是ABC ∆的费马点.若点P 是腰长为2的等腰直角三角形DEF 的费马点,则PD PE PF ++= .【答案】31+【详解】如图:过点D 作DM EF ⊥于点M ,在BDE ∆内部过E 、F 分别作30MEP MFP ∠=∠=︒,则120EPF FPD EPD ∠=∠=∠=︒,点P 就是费马点, 在等腰Rt DEF ∆中,2DE DF ==,DM EF ⊥,22EF DE ∴==1EM DM ∴==, 故cos30EM PE ︒=, 解得:233PE =,则33PM =, 故313DP =-,同法可得233PF = 则233213133PD PE PF ++=⨯+-=+.16.(2021•深圳模拟)如图,在ABC ∆中,5AB AC ==,45BC =,D 为边AB 上一动点(B 点除外),以CD 为一边作正方形CDEF ,连接BE ,则BDE ∆面积的最大值为 .【答案】8【详解】过点C 作CG BA ⊥于点G ,作EH AB ⊥于点H ,作AM BC ⊥于点M . 5AB AC ==,45BC =,25BM CM ∴==,易证AMB CGB ∆∆∽,∴BM AB GB CB=, 即25545GB = 8GB ∴=,设BD x =,则8DG x =-,易证()EDH DCG AAS ∆≅∆,8EH DG x ∴==-,2111(8)(4)8222BDE S BD EH x x x ∆∴==-=--+, 当4x =时,BDE ∆面积的最大值为8.17.(2021•光明区二模)如图,扇形OPQ 可以绕着正六边形ABCDEF 的中心O 旋转,若120POQ ∠=︒,OP 等于正六边形ABCDEF 边心距的2倍,2AB =,则阴影部分的面积为 .【答案】423π-【详解】连接OE ,OD ,OC .设EF 交OP 于T ,CD 交OQ 于J .120POQ EOC ∠=∠=︒,EOT COJ ∴∠=∠,OE OJ =,60OET OCJ ∠=∠=︒,()EOT COJ ASA ∴∆≅∆,2322234OTEDJ OEDC S S ∴==⨯⨯=五边形四边形, 2120(23)23423360OPQ OTEDJ S S S ππ⋅⋅∴=-=-=-阴扇形五边形 18.(2021•深圳二模)如图Rt ABC ∆中,90BAC ∠=︒,3AB =,4AC =,点P 为BC 上任意一点,连接PA ,以PA ,PC 为邻边作平行四边形PAQC ,连接PQ ,则PQ 的最小值为.【答案】12 5【详解】90BAC∠=︒,3AB=,4AC=,225BC AC AB∴=+=,四边形APCQ是平行四边形,PO QO∴=,CO AO=,PQ最短也就是PO最短,∴过O作BC的垂线OP',ACB P CO∠=∠',90CP O CAB∠'=∠=︒,CAB∴∆∽△CP O',∴CO OP BC AB'=,∴253OP' =,65 OP∴'=,∴则PQ的最小值为1225 OP'=,方法二:不用相似的方法,只利用等面积得,OC AB BC OP'=,求得OP',而其他部分的步骤共用.19.(2020•九龙坡区校级月考)如图,Rt ABC∆中,AB BC⊥,6AB=,4BC=,点D是ABC∆内一个动点,且满足DAB DBC∠=∠,当线段CD取最小值时,记BCDα∠=,线段AB 上一动点E绕着点D顺时针旋转得到点F,且满足EDFα∠=,则AF的最小值 .【答案】125 【详解】AB BC ⊥,6AB =、4BC =, 90DBC ABD ∴∠+∠=︒,DAB DBC ∠=∠,设DAB DBC β∠=∠=,90DAB ABD ∴∠+∠=︒,90ADB ∴∠=︒,∴点D 在以AB 为直径的圆上,设圆心为O ,半径为132AB =,则当O 、D 、C 三点共线时CD 最小,3OD OB OA ∴===,225OC OB BC ∴=+=,将DA 绕点D 逆时针旋转α,得到DG ,连接GE ,DG DA ∴=,GDA EDF α∠=∠=,GDE ADF ∴∠=∠,DE DF =,()GDE ADF SAS ∴∆≅∆,GE AF ∴=,∴当GE AB ⊥时,GE 最小,即AF 最小,过点D 作DM AB ⊥于M ,过点G 作GH DM ⊥,交DM 的延长线于点H ,//DM BC ∴,四边形GHME 为矩形.OMD OBC ∴∆∆∽,GE HM =,∴DM OM OD BC OB OC ==, ∴3435DM OM ==, 125DM ∴=,95OM =, 924355AM OM OA ∴=+=+=, DAB DBC β∠=∠=,OA OD =,ODA OAD β∴∠=∠=,2BOC ODA OAD β∴∠=∠+∠=.在Rt OBC ∆中,90OCB BOC ∠=︒-∠,902αβ∴=︒-,90MAD MDA ∠+∠=︒,90GDH βα∴++∠=︒,GDH DAM β∴∠==∠,90DHG AMD ∠=∠=︒,AD DG =,()GDH DAM AAS ∴∆≅∆.245DH AM ∴==, 125HM DH DM ∴=-=,即AF 的最小值为125. 20.(2021•南山区二模)矩形ABCD 中,4AB =,6BC =,点E 为BC 的中点,沿AE 将AEB ∆翻折得到AFE ∆,sin FCE ∠= .【答案】45【详解】如图,过E 作EH CF ⊥于H ,由折叠的性质得:BE EF =,BEA FEA ∠=∠,点E 是BC 的中点,3CE BE ∴==,3EF CE ∴==,FEH CEH ∴∠=∠,90AEB CEH ∴∠+∠=︒,在矩形ABCD 中,90B ∠=︒,90BAE BEA ∴∠+∠=︒,BAE CEH ∴∠=∠,B EHC ∠=∠,ABE EHC ∴∆∆∽, ∴AB AE EH CE =, 22435AE =+=,125EH ∴=, 4sin 5EH ECF CE ∴∠==. 21.(2021•龙岗区二模)如图,已知在菱形ABCD ,9BC =,60ABC ∠=︒,点E 在BC 上,且6BE =,将ABE ∆沿AE 折叠得到△AB E ',其中B E '交CD 于点F ,则CF = .【答案】95【详解】过点A 作AG BC ⊥交BC 于G ,取HG 使HG GE =,过H 作HM AE ⊥于H ,过F 作FN BC ⊥交BC 延长线于N ,四边形ABCD 是菱形,在Rt ABG ∆中,60B ∠=︒, 3sin sin 602AG B AB ∴=︒==, 39322AG AB ∴==, 1cos cos602BG B AB =︒==, 1922BG AB ∴==, 6BE =,922()2(6)32HE GE BE BG ∴==-=⨯-=, 在Rt AGE ∆中,222439633744AE AG GE =+=+==, 1122AHE S HE AG AE HM ∆=⨯⨯=⨯⨯, ∴131337222HM ⨯⨯=⨯⨯, 解得,92114HM =, HG GE =,AG HE ⊥,AHE ∴∆是等腰三角形,AH AE ∴=,AHE HEA ∠=∠,在Rt AHM ∆中,222229211064739763()1419614AM AH HM AE HM =-=-=-==, //AB CD ,60FCN B ∴∠=∠=︒,∴tan 603FN CN=︒=, 折叠,AEB HEA ∴∠'=∠,在Rt AHE ∆中,1801802HAE HEA AHE HEA ∠=︒-∠-∠=︒-∠,又1801802FEN HEA AEB HEA ∠=︒-∠-∠'=︒-∠,设CN x =,3FN x =, tan tan FN HM FEC HAM EN AM ∠=∠==,∴921314339714x x =+, ∴333313x x =+, 910x ∴=, 9931010CN FN ∴==, 22189105CF CN FN ∴=+==. 22.(2021•深圳模拟)如图,矩形ABCD 中,13AE AD =,将ABE ∆沿BE 折叠后得到GBE ∆,延长BG 交CD 于F 点,若3CF FD ==,则BC 的长为 .【答案】66【详解】延长BF 交AD 的延长线于点H ,四边形ABCD 是矩形,AD BC ∴=,//AD BC ,90A BCF ∠=∠=︒, H CBF ∴∠=∠,在BCF ∆和HDF ∆中,CBF H BCF DFH CF DF ∠=∠⎧⎪∠=∠⎨⎪=⎩,()BCF HDF AAS ∴∆≅∆,将ABE ∆沿BE 折叠后得到GBE ∆,90A BGE ∴∠=∠=︒,AE EG =,90EGH ∴∠=︒, 13AE AD =, ∴设AE EG x ==,则3AD BC DH x ===, 2ED x ∴=,5EH ED DH x ∴=+=, 在Rt EGH ∆中,1sin 55EG x H EH x ∠===, 1sin 5CF CBF BF ∴∠==, ∴315BF =, 15BF ∴=,222215366BC BF CF ∴=-=-=23.(2021•葫芦岛二模)如图,在矩形ABCD 中,15AB =,8AD =,E 为AB 边上一点,将BEC ∆沿CE 翻折,点B 落在点F 处,当AEF ∆为直角三角形时,AE = .【答案】7或515【详解】①如图,若90AEF ∠=︒,90B BCD AEF ∠=∠=︒=∠,∴四边形BCFE 是矩形,将BEC ∆沿着CE 翻折,∴四边形BCFE 是正方形,8BE BC AD ∴===,1587AE AB BE ∴=-=-=;②如图,若90AFE ∠=︒,将BEC ∆沿着CE 翻折,8CB CF ∴==,90B EFC ∠=∠=︒,BE EF =, 180AFE EFC ∠+∠=︒,∴点A ,点F ,点C 三点共线, 222215817AC AB BC ∴=+=+=,9AF AC CF ∴=-=,222AE AF EF =+,2281(15)AE AE ∴=+-,515AE ∴=, ③若90EAF ∠=︒,158CD CF BC =>==,∴点F 不可能落在直线AD 上,∴不存在90EAF ∠=︒,综上所述:7AE =或515. 24.(2020•青羊区校级期末)如图1,在矩形ABCD 中,8AB =,10BC =,P 是边AD 上一点,将ABP ∆沿着直线BP 翻折得到△A BP '.当8AP =时,A D '= .如图2,连接A C ',当2AP =时,此时△A BC '的面积为 .【答案】217;60017 【详解】如图1,当8AP =时,由折叠知AB AP =,APB BPA '∠=∠,ABP A BP '∠=∠,90A BA P '∠=∠=︒, ∴四边形ABA P '是正方形,8A P '∴=,2PD =,222282217A D A P PD ''∴=+=+=.如图2,当2AP =时,过点A '作//MN AB ,交AD 于点M ,交BC 于点N ,∴四边形ABNM 为矩形,8AB MN ∴==,AM BN =,90AMN BNM ∠=∠=︒, 设A M x '=,则8A N x '=-,设BN y =,则2PM y =-, 在Rt PMA '∆中,222PM A M PA ''+=,222(2)2y x ∴-+=①,在Rt BNA '∆中,222BN A N A B ''+=,222(8)8y x ∴+-=②,由①②可得,4y x =,把4y x =代入①得,222(42)2x x -+=, 解得,1617x =, 1612081717A N '∴=-=, 1112060010221717A BC S BC A N ''∴=⨯⨯=⨯⨯=. 25.(2021•坪山区二模)如图,在ABC ∆和ADE ∆中,90BAC DAE ∠=∠=︒,60C E ∠=∠=︒,点D 在BC 边上,AC 与DE 相交于点F ,3DF CF =,则AD BD= .【答案】3【详解】连接EC ,如图,90BAC DAE ∠=∠=︒,60ACB AED ∠=∠=︒, AED ACB ∴∆∆∽,∴AE AD AC AB=, 即AE AC AD AB=, 90BAC DAE ∠=∠=︒,BAC CAD DAE CAD ∴∠-∠=∠-∠,EAC DAB ∴∠=∠,EAC DAB ∴∆∆∽,∴AD BD AE EC=,ACE ABD ADE ∠=∠=∠, 在Rt EAD ∆中,60AED ∠=︒,∴3AD AE=,∴3BD EC =, ∴33EC BD=,EFCAFD ∠=∠,ECF ADF ∠=∠, EFC AFD ∴∆∆∽,∴3AD DF EC CF==, ∴3333AD AD EC BD EC BD =⋅=⨯= 26.(2021•深圳模拟)如图所示的网格是正方形网格,则BAC DAE ∠-∠= ︒(点A ,B ,C ,D ,E 是网格线交点).【答案】45【详解】如图,连接CG 、AG ,由勾股定理得:2222125AC AG ==+=,2221310CG =+=, 222AC AG CG ∴+=,90CAG ∴∠=︒,CAG ∴∆是等腰直角三角形,45ACG ∴∠=︒,//CF AB ,ACF BAC ∴∠=∠,在CFG ∆和ADE ∆中,90CF AD CFG ADE FG DE =⎧⎪∠=∠=︒⎨⎪=⎩,()CFG ADE SAS∴∆≅∆,FCG DAE∴∠=∠,45BAC DAE ACF FCG ACG∴∠-∠=∠-∠=∠=︒27.(2021•深圳模拟)如图,矩形ABCD中,E是AB上一点,连接DE,将ADE∆沿DE翻折,恰好使点A落在BC边的中点F处,在DF上取点O,以O为圆心,OF长为半径作半圆与CD相切于点G.若4AD=,则图中阴影部分的面积为.【答案】23 9【详解】连接OG,QG,将ADE∆沿DE翻折,恰好使点A落在BC边的中点F处,4AD DF∴==,2BF CF==,矩形ABCD中,90DCF∠=︒,30FDC∴∠=︒,60DFC∴∠=︒,O与CD相切于点G,OG CD∴⊥,BC CD⊥,//OG BC∴,DOG DFC∴∆∆∽,∴DO OG DF FC=,设OG OF x==,则442x x-=,解得:43x =,即O 的半径是43. 连接OQ ,作OH FQ ⊥, 60DFC ∠=︒,OF OQ =, OFQ ∴∆为等边三角形;同理OGQ ∆为等边三角形; 60GOQ FOQ ∴∠=∠=︒,32323OH OQ ==, 3232333QH ∴=⨯=, 23CQ ∴= 四边形OHCG 为矩形,233OH CG ∴==, 232311222339CGQ S S CQ CG ∆∴==⨯⨯=⨯⨯=阴影. 28.(2020•扬州)如图,在ABCD 中,60B ∠=︒,10AB =,8BC =,点E 为边AB 上的一个动点,连接ED 并延长至点F ,使得14DF DE =,以EC 、EF 为邻边构造EFGC ,连接EG ,则EG 的最小值为 .【答案】93【详解】作CH AB ⊥于点H ,在ABCD 中,60B ∠=︒,8BC =,43CH ∴=,四边形ECGF 是平行四边形,//EF CG ∴,EOD GOC ∴∆∆∽,∴EO DO ED GO OC GC==,14DF DE =, ∴45DE EF =, ∴45ED GC =, ∴45EO GO =, ∴当EO 取得最小值时,EG 即可取得最小值,当EO CD ⊥时,EO 取得最小值,CH EO ∴=,43EO ∴=,53GO ∴=,EG ∴的最小值是9329.(2021•锡山区一模)如图,在平行四边形ABCD 中,60B ∠=︒,4BC =,点E 为边AB上的一个动点,连接ED 并延长至点F ,使得13DF DE =,以EC 、EF 为邻边构造平行四边形EFGC ,连接EG ,则EG 的最小值为 .【答案】1433【详解】作CH AB ⊥于点H ,在ABCD 中,60B ∠=︒,4BC =,23CH ∴=,四边形ECGF 是平行四边形,//EF CG ∴,EOD GOC ∴∆∆∽, ∴EO DO ED GO CO GC ==, 13DF DE =, ∴34DE EF =, ∴34ED GC =, ∴34EO GO =, ∴当EO 取得最小值时,EG 即可取得最小值,当EO CD ⊥时,EO 取得最小值,CH EO ∴=,23EO ∴=,833GO ∴=, EG ∴的最小值是814233333+=30.(2021•龙岗区校级一模)如图,在矩形ABCD 中,5AC =,AE 平分DAC ∠交CD 于E ,CF 平分ACD ∠交AE 于点F ,且:1:2EF AF =,则CF = .【答案】10【详解】作FG AC ⊥于点G ,作FM CD ⊥于点M ,作FN AD ⊥于点N , CF 平分ACD ∠交AE 于点F ,且:1:2EF AF =,:1:2CE CA ∴=,5AC =, 52CE ∴=, AE 平分DAC ∠,CF 平分ACD ∠, FG FM FN ∴==, FM CD ⊥,AD CD ⊥,:1:2EF AF =, EMF EDA ∴∆∆∽,∴13MF EF DA EA ==, 设FM x =,则3AD x =,同理可得,ANF AED ∆∆∽,则32DE x =, 5322CD x ∴=+, 90D ∠=︒,3AD x =,5AC =, 22253()(3)522x x ∴++=, 解得11x =,253x =-(舍去), 1FM ∴=,5311322CM =+⨯-=, 又90CMF ∠=︒,221310CF ∴=+=,故答案为:10.。
江苏省无锡地区2019年中考数学选择填空压轴题专题8几何变换问题(含答案)70

专题08 几何变换问题例1.如图,斜边长12cm,∠A=30°的直角三角尺ABC绕点C顺时针方向旋转90°至△A′B′C的位置,再沿CB向左平移使点B′落在原三角尺ABC的斜边AB上,则三角尺向左平移的距离为______________.(结果保留根号)同类题型:1.1 把图中的一个三角形先横向平移x格,再纵向平移y格,就能与另一个三角形拼合成一个四边形,那么x+y()A.是一个确定的值B.有两个不同的值C.有三个不同的值D.有三个以上不同的值同类题型:1.2 已知:如图△ABC的顶点坐标分别为A(-4,-3),B(0,-3),C(-2,1),如将B点向右平移2个单位后再向上平移4个单位到达B1点,若设△ABC的面积为S1,△AB1C的面积为S2,则S1,S2的大小关系为()A.S1>S2 B.S1=S2 C.S1<S2 D.不能确定例2.如图,P是等边△ABC外一点,把BP绕点B顺时针旋转60°到BP′,已知∠AP′B=150°,P′A:P′C=2:3,则PB:P′A是()A . 2 :1B .2:1C . 5 :2D . 3 :1同类题型:2.1 如图,△ABC 为等边三角形,以AB 为边向形外作△ABD ,使∠ADB =120°,再以点C 为旋转中心把△CBD 旋转到△CAE ,则下列结论:①D 、A 、E 三点共线;②DC 平分∠BDA ;③∠E =∠BAC ;④DC =DB +DA ,其中正确的有( )A .1个B .2个C .3个D .4个同类题型:2.2 如图,在正方形ABCD 中,O 是对角线AC 与BD 的交点,M 是BC 边上的动点(点M 不与B ,C 重合),CN ⊥DM ,CN 与AB 交于点N ,连接OM ,ON ,MN .下列五个结论:①△CNB ≌△DMC ;②△CON ≌△DOM ;③△OMN ∽△OAD ;④AN 2+CM 2=MN 2 ;⑤若AB =2,则S △OMN 的最小值是12,其中正确结论的个数是( )A .2B .3C .4D .5同类题型:2.3 在平面直角坐标系中,已知点A (3,0),B (0,4),将△BOA 绕点A 按顺时针方向旋转得△CDA ,使点B 在直线CD 上,连接OD 交AB 于点M ,直线CD 的解析式为__________.同类题型:2.4 如图,在矩形ABCD中,AB=5,BC=3,将矩形ABCD绕点B按顺时针方向旋转得到矩形GBEF,点A落在矩形ABCD的边CD上,连结CE,CF,若∠CEF=α,∠CFE=β,则tanα﹒tanβ=___________.同类题型:2.5 如图,在Rt△ABC中,∠ACB=90°,将△ABC绕顶点C逆时针旋转得到△A′B′C,M是BC的中点,P是A′B′的中点,连接PM,若BC=2,∠BAC=30°,则线段PM的最大值是_____.同类题型:2.6 如图1,一副含30°和45°角的三角板ABC和DEF叠合在一起,边BC与EF重合,BC=EF=12,点G为边EF的中点,边FD与AB相交于点H,如图2,将三角板DEF绕点G按顺时针方向旋转到60°的过程中,BH的最大值是_________,点H运动的路径长是_________.例3.如图,折叠菱形纸片ABCD ,使得AD 的对应边A 1D 1 过点C ,EF 为折痕,若∠B =60°,当A 1 E ⊥AB 时,BE AE的值等于( ) A .36 B .3-16 C .3+18 D .3-12同类题型:3.1 如图,正方形ABCD 中,AD =4,点E 是对角线AC 上一点,连接DE ,过点E 作EF ⊥ED ,交AB 于点F ,连接DF ,交AC 于点G ,将△EFG 沿EF 翻折,得到△EFM ,连接DM ,交EF 于点N ,若点F 是AB 边的中点,则△EMN 的周长是_____________.同类题型:3.2 如图,∠MON =40°,点P 是∠MON 内的定点,点A 、B 分别在OM ,ON 上移动,当△PAB 周长最小时,则∠APB 的度数为( )A .20°B .40°C .100°D .140°同类题型:3.3 如图,矩形纸片ABCD 中,G 、F 分别为AD 、BC 的中点,将纸片折叠,使D 点落在GF 上,得到△HAE ,再过H 点折叠纸片,使B 点落在直线AB 上,折痕为PQ .连接AF 、EF ,已知HE =HF ,下列结论:①△MEH 为等边三角形;②AE ⊥EF ;③△PHE ∽△HAE ;④AD AB = 2 35,其中正确的结论是( ) A .①②③ B .①②④ C .①③④ D .①②③④同类题型:3.4 △ABC 中,∠BAC =90°,AB =3,AC =4,点D 是BC 的中点,将△ABD 沿AD 翻折得到△AE D .连CE ,则线段CE 的长等于_______.专题08 几何变换问题例1.如图,斜边长12cm ,∠A =30°的直角三角尺ABC 绕点C 顺时针方向旋转90°至△A ′B ′C 的位置,再沿CB 向左平移使点B ′落在原三角尺ABC 的斜边AB 上,则三角尺向左平移的距离为______________.(结果保留根号)解:如图:连接B ′B ″,∵在Rt △ABC 中,AB =12,∠A =30°,∴BC =12AB =6,AC =6 3 ,∴B ′C =6,∴AB ′=AC -B ′C =6 3 -6,∵B ′C ∥B ″C ″,B ′C =B ″C ″,∴四边形B ″C ″CB ′是矩形,∴B ″B ′∥BC ,B ″B ′=C ″C ,∴△AB ″B ′∽△ABC ,∴AB ′AC =B ″B ′BC, 即:63-663=B ″B ′6 , 解得:B ″B ′=6-2 3 .∴C ″C =B ″B ′=6-2 3 .同类题型:1.1 把图中的一个三角形先横向平移x 格,再纵向平移y 格,就能与另一个三角形拼合成一个四边形,那么x +y ( )A .是一个确定的值B .有两个不同的值C .有三个不同的值D .有三个以上不同的值解:(1)当两斜边重合的时候可组成一个矩形,此时x =2,y =3,x +y =5;(2)当两直角边重合时有两种情况,①短边重合,此时x =2,y =3,x +y =5; ②长边重合,此时x =2,y =5,x +y =7.综上可得:x +y =5或7.选B .同类题型:1.2 已知:如图△ABC 的顶点坐标分别为A (-4,-3),B (0,-3),C (-2,1),如将B 点向右平移2个单位后再向上平移4个单位到达B 1 点,若设△ABC 的面积为S 1 ,△AB 1 C 的面积为S 2 ,则S 1 ,S 2 的大小关系为( )A .S 1>S 2B .S 1=S 2C .S 1<S 2D .不能确定解:△ABC 的面积为S 1=12 ×4×4=8,将B 点平移后得到B 1 点的坐标是(2,1),所以△AB 1 C 的面积为S 2=12 ×4×4=8,所以S 1=S 2 .选B .同类题型:1.3同类题型:1.4例2. 如图,P 是等边△ABC 外一点,把BP 绕点B 顺时针旋转60°到BP ′,已知∠AP ′B =150°,P ′A :P ′C =2:3,则PB :P ′A 是( )A . 2 :1B .2:1C . 5 :2D . 3 :1解:如图,连接AP ,∵BP 绕点B 顺时针旋转60°到BP ′,∴BP =BP ′,∠ABP +∠ABP ′=60°,又∵△ABC 是等边三角形,∴AB =BC ,∠CBP ′+∠ABP ′=60°,∴∠ABP =∠CBP ′,在△ABP 和△CBP ′中,∵⎩⎨⎧BP =BP ′∠ABP =∠CBP ′AB =BC, ∴△ABP ≌△CBP ′(SAS ),∴AP =P ′C , ∵P ′A :P ′C =2:3,∴AP =32P ′A , 连接PP ′,则△PBP ′是等边三角形,∴∠BP ′P =60°,PP ′=PB ,∵∠AP ′B =150°,∴∠AP ′P =150°-60°=90°,∴△APP ′是直角三角形,设P ′A =x ,则AP =32x , 根据勾股定理,PP ′=AP 2-P ′A 2=94x 2-x 2=52x , 则PB =52x , ∴PB :P ′A =52x :x = 5 :2. 选C .同类题型:2.1 如图,△ABC 为等边三角形,以AB 为边向形外作△ABD ,使∠ADB =120°,再以点C 为旋转中心把△CBD 旋转到△CAE ,则下列结论:①D 、A 、E 三点共线;②DC 平分∠BDA ;③∠E =∠BAC ;④DC =DB +DA ,其中正确的有( )A.1个 B.2个 C.3个 D.4个解:①设∠1=x度,则∠2=(60-x)度,∠DBC=(x+60)度,故∠4=(x +60)度,∴∠2+∠3+∠4=60-x+60+x+60=180度,∴D、A、E三点共线;②∵△BCD绕着点C按顺时针方向旋转60°得到△ACE,∴CD=CE,∠DCE=60°,∴△CDE为等边三角形,∴∠E=60°,∴∠BDC=∠E=60°,∴∠CDA=120°-60°=60°,∴DC平分∠BDA;③∵∠BAC=60°,∠E=60°,∴∠E=∠BA C.④由旋转可知AE=BD,又∵∠DAE=180°,∴DE=AE+A D.∵△CDE为等边三角形,∴DC =DB +B A .同类题型:2.2 如图,在正方形ABCD 中,O 是对角线AC 与BD 的交点,M 是BC 边上的动点(点M 不与B ,C 重合),CN ⊥DM ,CN 与AB 交于点N ,连接OM ,ON ,MN .下列五个结论:①△CNB ≌△DMC ;②△CON ≌△DOM ;③△OMN ∽△OAD ;④AN 2+CM 2=MN 2 ;⑤若AB =2,则S △OMN 的最小值是12 ,其中正确结论的个数是( )A .2B .3C .4D .5解:∵正方形ABCD 中,CD =BC ,∠BCD =90°,∴∠BCN +∠DCN =90°,又∵CN ⊥DM ,∴∠CDM +∠DCN =90°,∴∠BCN =∠CDM ,又∵∠CBN =∠DCM =90°,∴△CNB ≌△DMC (ASA ),故①正确;根据△CNB ≌△DMC ,可得CM =BN ,又∵∠OCM =∠OBN =45°,OC =OB ,∴△OCM ≌△OBN (SAS ),∴OM =ON ,∠COM =∠BON ,∴∠DOC +∠COM =∠COB +∠BPN ,即∠DOM =∠CON ,又∵DO =CO ,∴△CON ≌△DOM (SAS ),故②正确;∵∠BON +∠BOM =∠COM +∠BOM =90°,∴∠MON =90°,即△MON 是等腰直角三角形,又∵△AOD 是等腰直角三角形,∴△OMN ∽△OAD ,故③正确;∵AB =BC ,CM =BN ,∴BM =AN ,又∵Rt △BMN 中,BM 2+BN 2=MN 2 ,∴AN 2+CM 2=MN 2 ,故④正确;∵△OCM ≌△OBN ,∴四边形BMON 的面积=△BOC 的面积=1,即四边形BMON 的面积是定值1, ∴当△MNB 的面积最大时,△MNO 的面积最小,设BN =x =CM ,则BM =2-x ,∴△MNB 的面积=12x (2-x )=-12x 2 +x , ∴当x =1时,△MNB 的面积有最大值12, 此时S △OMN 的最小值是1-12=12,故⑤正确; 综上所述,正确结论的个数是5个,选D .同类题型:2.3 在平面直角坐标系中,已知点A (3,0),B (0,4),将△BOA 绕点A 按顺时针方向旋转得△CDA ,使点B 在直线CD 上,连接OD 交AB 于点M ,直线CD 的解析式为__________.解:∵△BOA 绕点A 按顺时针方向旋转得△CDA ,∴△BOA ≌△CDA ,∴AB =AC ,OA =AD ,∵B 、D 、C 共线,AD ⊥BC ,∴BD =CD =OB ,∵OA =AD ,BO =CD =BD ,∴OD ⊥AB ,设直线AB 解析式为y =kx +b ,把A 与B 坐标代入得:⎩⎨⎧3k +b =0b =4 , 解得:⎩⎨⎧k =-43b =4 ,∴直线AB 解析式为y =-43x +4, ∴直线OD 解析式为y =34x , 联立得:⎩⎨⎧y =-43x +4y =34x ,解得:⎩⎨⎧x =4825y =3625 ,即M (4825 ,3625 ), ∵M 为线段OD 的中点,∴D (9625 ,7225), 设直线CD 解析式为y =mx +n ,把B 与D 坐标代入得:⎩⎨⎧9625m +n =7225n =4,解得:m =-724,n =4, 则直线CD 解析式为y =-724 x +4. 同类题型:2.4 如图,在矩形ABCD 中,AB =5,BC =3,将矩形ABCD 绕点B 按顺时针方向旋转得到矩形GBEF ,点A 落在矩形ABCD 的边CD 上,连结CE ,CF ,若∠CEF =α,∠CFE =β,则tan α﹒tan β=___________.解:过C 点作MN ⊥BF ,交BG 于M ,交EF 于N ,由旋转变换的性质可知,∠ABG =∠CBE ,BA =BG =5,BC =BE =3,由勾股定理得,CG =BG 2+DG 2 =4,∴DG =DC -CG =1,则AG =AD 2+DG 2=10 ,∵BA BC =BG BE ,∠ABG =∠CBE ,∴△ABG ∽△CBE ,∴CE AG =BC AB =35 ,解得,CE =3105 ,∵∠MBC =∠CBG ,∠BMC =∠BCG =90°,∴△BCM ∽△BGC ,∴CM CG =BC BG ,即CM4=35 ,∴CM =125 ,∴MN =BE =3,∴CN =3-125=35 ,∴EN =CE 2-CN 2=95 ,∴FN =EF -EN =5-95=165, ∴tan α﹒tan β=CN EN ﹒CN FN =3595×35165=116. 同类题型:2.5 如图,在Rt △ABC 中,∠ACB =90°,将△ABC 绕顶点C 逆时针旋转得到△A ′B ′C ,M 是BC 的中点,P 是A ′B ′的中点,连接PM ,若BC =2,∠BAC =30°,则线段PM 的最大值是_____.解:如图连接P C .在Rt △ABC 中,∵∠A =30°,BC =2,∴AB =4,根据旋转不变性可知,A ′B ′=AB =4,∴A ′P =PB ′,∴PC =12A ′B ′=2, ∵CM =BM =1,又∵PM ≤PC +CM ,即PM ≤3,∴PM 的最大值为3(此时P 、C 、M 共线).同类题型:2.6 如图1,一副含30°和45°角的三角板ABC 和DEF 叠合在一起,边BC 与EF 重合,BC =EF =12,点G 为边EF 的中点,边FD 与AB 相交于点H ,如图2,将三角板DEF绕点G按顺时针方向旋转到60°的过程中,BH的最大值是_________,点H运动的路径长是_________.解:如图1中,作HM⊥BC于M,设HM=a,则CM=HM=a.在Rt△ABC中,∠ABC=30°,BC=12,在Rt△BHM中,BH=2HM=2a,BM= 3 a,∵BM+FM=BC,∴ 3 a+a=12,∴a=6 3 -6,∴BH=2a=12 3 -12.如图2中,当DG⊥AB时,易证GH1⊥DF,此时BH1的值最小,易知BH1=BK+KH1=3 3 +3,∴HH 1=BH -BH 1=9 3 -15,当旋转角为60°时,F 与H 2 重合,此时BH 的值最大,易知最大值BH 2=6 3 , 观察图象可知,在∠CGF 从0°到60°的变化过程中,点H 相应移动的路径长=2HH 1+HH 2=18 3-30+[6 3-(12 3-12)]=12 3 -18. 例3.如图,折叠菱形纸片ABCD ,使得AD 的对应边A 1D 1 过点C ,EF 为折痕,若∠B =60°,当A 1 E ⊥AB 时,BE AE的值等于( )A .36B .3-16C .3+18D .3-12解:如图所示,延长AB ,D 1A 1 交于点G ,∵A1E⊥AB,∠EA1C=∠A=120°,∴∠G=120°-90°=30°,又∵∠ABC=60°,∴∠BCG=60°-30°=30°,∴∠G=∠BCG=30°,∴BC=BG=BA,设BE=1,AE=x=A1E,则AB=1+x=BC=BG,A1G=2x,∴GE=1+x+1=x+2,∵Rt△A1GE中,A1E2+GE2=A1G2,∴x2+(x+2)2=(2x)2,解得x=1+ 3 ,(负值已舍去)∴AE=1+ 3 ,∴BEAE=11+3=3-12,选D.同类题型:3.1 如图,正方形ABCD中,AD=4,点E是对角线AC上一点,连接DE,过点E作EF⊥ED,交AB于点F,连接DF,交AC于点G,将△EFG沿EF翻折,得到△EFM,连接DM,交EF于点N,若点F是AB边的中点,则△EMN的周长是_____________.解:解法一:如图1,过E作PQ⊥DC,交DC于P,交AB于Q,连接BE,∵DC ∥AB ,∴PQ ⊥AB ,∵四边形ABCD 是正方形,∴∠ACD =45°,∴△PEC 是等腰直角三角形,∴PE =PC ,设PC =x ,则PE =x ,PD =4-x ,EQ =4-x , ∴PD =EQ ,∵∠DPE =∠EQF =90°,∠PED =∠EFQ , ∴△DPE ≌△EQF ,∴DE =EF ,∵DE ⊥EF ,∴△DEF 是等腰直角三角形,易证明△DEC ≌△BEC ,∴DE =BE ,∴EF =BE ,∵EQ ⊥FB ,∴FQ =BQ =12BF , ∵AB =4,F 是AB 的中点,∴BF =2,∴FQ =BQ =PE =1,∴CE = 2 ,PD =4-1=3, Rt △DAF 中,DF =42+22=2 5 , DE =EF =10 ,如图2,∵DC ∥AB ,∴△DGC ∽△FGA ,∴CG AG =DC AF =DG FG =42=2, ∴CG =2AG ,DG =2FG ,∴FG =13×25=253, ∵AC =42+42=4 2 ,∴CG =23×42=823, ∴EG =823-2=523, 连接GM 、GN ,交EF 于H , ∵∠GFE =45°,∴△GHF 是等腰直角三角形,∴GH =FH =2532=103 ,∴EH =EF -FH =10-103=2103, 由折叠得:GM ⊥EF ,MH =GH =103 , ∴∠EHM =∠DEF =90°,∴DE ∥HM ,∴△DEN ∽△MNH ,∴DE MH =EN NH, ∴10103=EN NH=3, ∴EN =3NH ,∵EN +NH ═EH =2103, ∴EN =102, ∴NH =EH -EN =2103-102=106, Rt △GNH 中,GN =GH 2+NH 2=(103)2+(106)2=526, 由折叠得:MN =GN ,EM =EG ,∴△EMN 的周长=EN +MN +EM =102+526+523=52+102; 解法二:如图3,过G 作GK ⊥AD 于K ,作GR ⊥AB 于R ,∵AC 平分∠DAB ,∴GK =GR ,∴S △ADG S △AGF =12AD ﹒KG 12AF ﹒GR =AD AF =42 =2, ∵S △ADG S △AGF =12DG ﹒h12GF ﹒h =2, ∴DG GF=2, 同理,S △DNF S △MNF =DF FM =DN MN=3, 其它解法同解法一,可得:∴△EMN 的周长=EN +MN +EM =102+526+523=52+102; 解法三:如图4,过E作EP ⊥AP ,EQ ⊥AD ,∵AC 是对角线,∴EP =EQ ,易证△DQE 和△FPE 全等,∴DE =EF ,DQ =FP ,且AP =EP ,设EP =x ,则DQ =4-x =FP =x -2,解得x =3,所以PF =1,∴AE =32+32=3 2 ,∵DC ∥AB ,∴△DGC ∽△FGA ,∴同解法一得:CG =23×42=823, ∴EG =823-2=523, AG =13AC =423, 过G 作GH ⊥AB ,过M 作MK ⊥AB ,过M 作ML ⊥AD ,则易证△GHF ≌△FKM 全等,∴GH =FK =43 ,HF =MK =23, ∵ML =AK =AF +FK =2+43=103 ,DL =AD -MK =4-23=103, 即DL =LM ,∴∠LDM =45°∴DM 在正方形对角线DB 上,过N 作NI ⊥AB ,则NI =IB ,设NI =y ,∵NI ∥EP∴NI EP =FI FP∴y 3=2-y 1, 解得y =1.5,所以FI =2-y =0.5,∴I 为FP 的中点,∴N 是EF 的中点,∴EN =0.5EF =102, ∵△BIN 是等腰直角三角形,且BI =NI =1.5,∴BN =32 2 ,BK =AB -AK =4-103=23 ,BM =23 2 ,MN =BN -BM =322-232=562 , ∴△EMN 的周长=EN +MN +EM =102+526+523=52+102. 同类题型:3.2 如图,∠MON =40°,点P 是∠MON 内的定点,点A 、B 分别在OM ,ON 上移动,当△PAB 周长最小时,则∠APB 的度数为( )A .20°B .40°C .100°D .140°解:如图所示:分别作点P 关于OM 、ON 的对称点P ′、P ″,连接OP ′、OP ″、P ′P ″,P ′P ″交OM 、ON 于点A 、B ,连接PA 、PB ,此时△PAB 周长的最小值等于P ′P ″.如图所示:由轴对称性质可得,OP ′=OP ″=OP ,∠P ′OA =∠POA ,∠P ″OB =∠POB ,所以∠P ′OP ″=2∠MON =2×40°=80°,所以∠OP ′P ″=∠OP ″P ′=(180°-80°)÷2=50°,又因为∠BPO =∠OP ″B =50°,∠APO =∠AP ′O =50°,所以∠APB =∠APO +∠BPO =100°.选C .同类题型:3.3 如图,矩形纸片ABCD 中,G 、F 分别为AD 、BC 的中点,将纸片折叠,使D 点落在GF 上,得到△HAE ,再过H 点折叠纸片,使B 点落在直线AB 上,折痕为PQ .连接AF 、EF ,已知HE =HF ,下列结论:①△MEH 为等边三角形;②AE ⊥EF ;③△PHE ∽△HAE ;④AD AB = 2 35,其中正确的结论是( ) A .①②③ B .①②④ C .①③④ D .①②③④解:∵矩形纸片ABCD 中,G 、F 分别为AD 、BC 的中点,∴GF ⊥AD ,由折叠可得,AH =AD =2AG ,∠AHE =∠D =90°,∴∠AHG =30°,∠EHM =90°-30°=60°,∴∠HAG =60°=∠AED =∠MEH ,∴△EHM 中,∠EMH =60°=∠EHM =∠MEH ,∴△MEH 为等边三角形,故①正确;∵∠EHM =60°,HE =HF ,∴∠HEF =30°,∴∠FEM =60°+30°=90°,即AE ⊥EF ,故②正确;∵∠PEH =∠MHE =60°=∠HEA ,∠EPH =∠EHA =90°,∴△PHE ∽△HAE ,故③正确;设AD =2=AH ,则AG =1,∴Rt △AGH 中,GH=3AG= 3 ,Rt △AEH 中,EH=AH 3=233 =HF , ∴GF=533 =AB , ∴AD AB =2533=235 ,故④正确, 综上所述,正确的结论是①②③④,选D .同类题型:3.4 △ABC 中,∠BAC =90°,AB =3,AC =4,点D 是BC 的中点,将△ABD 沿AD 翻折得到△AE D .连CE ,则线段CE 的长等于_______. 解:如图连接BE 交AD 于O ,作AH ⊥BC 于H .在Rt △ABC 中,∵AC =4,AB =3,∴BC =32+42 =5,∵CD =DB ,∴AD =DC =DB =52,∵12﹒BC ﹒AH =12﹒AB ﹒AC , ∴AH =125, ∵AE =AB ,DE =DB =DC ,∴AD 垂直平分线段BE ,△BCE 是直角三角形, ∵12﹒AD ﹒BO =12﹒BD ﹒AH , ∴OB =125, ∴BE =2OB =245, 在Rt △BCE 中,EC =BC 2-BE 2=75 .。
2020年中考数学选择填空压轴题汇编几何综合结论含解析

几何综合结论1. (2020深圳)如图,矩形纸片個8中,AB=6. 5(7=12.将纸片折叠,使点3落在边"的延长线上的点 G 处,折痕为肪 点E 、尸分别在边血和边證上.连接%,交CD 于点、K, FG 交CD 于点、H.给出以下结 论: ① EF1BG ;② GE=GF :③ 冰和2X00的而积相等;④ 当点尸与点Q 重合时,Z/?£F=75° ,其中正确的结论共有( )【解答】解:如图,连接宓设EFG BG 交于点0,•••将纸片折叠,使点〃落在边〃的延长线上的点G 处,B. 2个 C. 3个D. 4个:.EFIBG, BO=GO. BE=EG, BF= FG,故①正确,AD//BC.:・ZEGO= ZFBO、又T ZEOG= ZBOF,:.、BOZ'GOE (ASA\:・BF=EG,:・BF=EG=GF、故②正确,•: BE=EG=BF=FG、・••四边形购沪是菱形,:•乙BEF= ZGEF,当点尸与点Q重介时,则BF=BC=BE=\2,TsinZ 遊「,•••ZM5=30° ,:・ZDEF=W,故④正确,由题意无法证明△宓和△GAZf的而积相等,故③错误:故选:C.2.(2020贵州铜仁)如图,正方形個力的边长为4,点厅在边曲上,BE=\,ZQLW=45°,点尸在射线刖上,且过点尸作“的平行线交BA的延长线于点H, 67■与初相交于点G,连接EC、EG、EF.下列结论:①尸的而积为S②△庇G的周长为&③必=亦+血:其中正确的是()A.①(D ③B. @@C.①②【解答】解:如图,在正方形個8中,AD//BC. AB=BC=AD=49AZZ£W=90° ,HF//AD.AZ J ^=90° ,VZ2£4F=90° - ZMQ45° >AAFH=AHAF.:.AH=HF=\=BE.:.EH=AE^AH=AB- BE ・AH=4 = BC 、:AEHFg'CBE (SAS'、:・EF=EC, ZHEF= ZBCE,•:乙BCE+乙BEC=9$ ,:・HEHZBEC=9y »:.ZFEC=9Q° ,:■ \ CEF 是等腰直角三角形, 在 R 仏CBE 中,BE=1. BC=A. H 刀D.②③ ZB=ZBAD=9Q Q ,:.EC=BE+BC = 17.=i=g =兰:£g云EF・EC 2EC 2\故①正确;过点尸作FQLBC于0,交.AD于P,•••Z 时=90° = ZH= ZHAD.・••四边形北明是矩形,•: AH=HF,.•・矩形册叨是正方形,:.AP=PH=AH=\,同理:四边形测是矩形,:.PQ=AB=\y BQ=AP1、FQ=FP-PQ=z. CQ=BO BQ=3、•: AD〃BC,•••△/TVs △磁,FP _况. 五一&在RtAEAG 中,根据勾股宦理得,EG°V/i^=4,=空 Is t 2旳工空 Is 产云 :・E C 羊D C+B E,故③错误,・•・正确的有①故选:C.:.AG=AP^PG'AEG 的周长为 AG-E&rAEI r 3=8,敬②正确; 25:.DG^BE 1£7•: EC= ( 3:.DG=AD- AG3. (2020黑龙江鹤岗)如图,正方形 馭7?的边长为⑦ 点&在边月万上运动(不与点川3重合),ADAM= 45°,点尸在射线凡『上,且AF ^^BE,仔■与血相交于点G,连接应'、EF 、EG.则下列结论: ① ZECF= 45° :② △近的周长为(1 <3:③ B »D C=E C ;④△轩的而积的最大值是肚其中正确的结论是( )•:BE=BH, Z 翊=90° ,:・AF=EH,⑤当BE 二;a 时,G 是线段初的中点.A.①②③B.②④⑤C.①®®D.①④⑤ 【解答】解:如图1中, 任BC 上截取BH=庞,连接筋•: ZDAM=ZEHB=45° , Z馳?=90° ,:・ZFAE=ZEHC=\35° ,•: BA=BC, BE= BH,:.AE=HC.:仏FAE^HEHC (SAS)、:・EF=EC, ZAEF= ZECH,•:乙EC出乙CEB=90° ,:.AAEF^ACEB=W y•••Z亦*90° ,:•乙ECF= ZEFC='M ,故①正确,如图2中.延长初到/ 使得BE,则厶CBMHCDH ISAS). :・ZECB= ZDCH、:.2LECH= ABCD=W ,:.ZECG=ZGCH=45° ,•: CG=CG、CE=CH.:.HGCE^HGCH (SAS),:・EG=GH,V GH=D&rDH. DH=BE、:・EG=BE+DG.故③错误,'AEG的周长=AE^EG-AG= AE-AH= AD-DH^AE= AE^E&vAD= A&rAD= 2a.故②错误,二屈 设殆F 贝^AE=a-x. AF 阳=—- 十一■ ■£> 2 W.Y ax解得-Y •:.AG=GD.故⑤正确,故选:D.4. (2020黑龙江绥化)如图,在Rt △磁中,G9为斜边初的中线,过点。
填空压轴题(几何篇)-2023年中考数学压轴题专项训练(解析版)

2023年中考数学压轴题专项训练--填空压轴题(几何篇)一、压轴题速练1一.填空题(共40小题)1(2023•龙湾区二模)如图,在△ABC 中,AB =13,BC =14,AC =15,点D 是线段AC 上任意一点,分别过点A 、C 作直线BD 的垂线,垂足为E 、F ,AE =m ,CF =n ,则n +m 的最大值是15,最小值是12.【答案】15,12.【分析】根据S △ABC =S △ABD +S △CBD 即可得到m +n 关于x 的反比例函数关系式.根据垂直线段最短的性质,当BD ⊥AC 时,x 最小,由面积公式可求得;因为AB =13,BC =14,所以当BD =BC =14时,x 最大.从而根据反比例函数的性质求出y 的最大值和最小值.【详解】解:在△ABC 中,AB =13,BC =14,AC =15,AH ⊥BC 于点H ,∴设AH =x ,则CH =14-x ,∴AB 2-AH 2=AC 2-CH 2,即132-x 2=152-(14-x )2,解得x =5,即AH =5,∴BH =AB 2-BH 2=132-52=12,∴S △ABC =12BC •AH =12×14×12=84,由三角形面积公式,得S △ABD =12BD •AE =12xm ,S △CBD =12BD •CF =12xn ,∴m =2S △ABD x ,n =2S △CBDx,∴y =m +n =2S △ABD x +2S △CBD x =2S △ABC x =168x,即y =168x.∵△ABC 中AC 边上的高为2S △ABC AC=16815=565,∴x 的取值范围为565≤x ≤14.∵m +n 随x 的增大而减小,∴当x =565时,y 的最大值为15,当x =14时,y 的最小值为12.故答案为:15,12.【点睛】本题考查三角形的面积,掌握三角形的面积公式,反比例函数的应用是解题的关键.2(2023•湖北模拟)如图,正方形ABCD 的对角线交于点O ,AB =22,现有半径足够大的扇形OEF ,∠EOF =90°,当扇形OEF 绕点O 转动时,扇形OEF 和正方形ABCD 重叠部分的面积为2.【答案】2.【分析】根据四边形ABCD 为正方形,得到∠OAG =∠OBH =45°,OA =OB ,∠AOB =90°;推出△AOG ≌△BOH ,于是得到结论.【详解】解:∵四边形ABCD 为正方形,∴∠OAG =∠OBH =45°,OA =OB ,∠AOB =90°,由题意得:∠GOH =90°,∴∠AOG =∠BOH ;在△AOG 与△BOH 中,∠AOG =∠BOH OA =OB∠OAG =∠OBH ,∴△AOG ≌△BOH (ASA ),∴扇形OEF 和正方形ABCD 重叠部分的面积=S △AOB =14S 正方形ABCD =14×AB 2=14×(22)2=2.故答案为:2.【点睛】本题考查了全等三角形的判定和性质,正方形的性质,熟练掌握全等三角形的判定和性质是解题的关键.3(2023•榆树市二模)如图是中国古代数学家赵爽用来证明勾股定理的弦图的示意图,它是由四个全等的直角三角形和一个小正方形EFGH 组成,恰好拼成一个大正方形ABCD ,连结EG 并延长交BC于点M .若AB =13,EF =1,则GM 的长为 425 .【答案】425.【分析】由大正方形ABCD 是由四个全等的直角三角形和一个小正方形EFGH 组成,在直角三角形AEB 中使用勾股定理可求出BF =AE =GC =DH =2,过点M 作MN ⊥FC 于点N ,由三角形EFG 为等腰直角三角形可证得三角形GNM 也为等腰直角三角形,设GN =NM =a ,则NC =GC -GN =2-a ,由tan ∠FCB =BF CF =23=NM CN=a 2-a ,可解得a =45.进而可得GM =2MN =425.【详解】解:由图可知∠AEB =90°,EF =1,AB =13,∵大正方形ABCD 是由四个全等的直角三角形和一个小正方形EFGH 组成,故AE =BF =GC =DH ,设AE =x ,则在Rt △AEB 中,有AB 2=AE 2+BE 2,即13=x 2+(1+x )2,解得:x 1=2,x 2=-3(舍去).过点M 作MN ⊥FC 于点N ,如图所示.∵四边形EFGH 为正方形,EG 为对角线,∴△EFG 为等腰直角三角形,∴∠EGF =∠NGM =45°,故△GNM 为等腰直角三角形.设GN =NM =a ,则NC =GC -GN =2-a ,∵tan ∠FCB =BF CF =23=NM CN=a2-a ,解得:a =45,∴GM =2GN =425.故答案为:425.【点睛】本题考查了勾股定理的证明,正方形的性质、勾股定理、锐角三角函数、等腰三角形的性质、正确作出辅助线是解决本题的关键.4(2023•道外区二模)如图,在四边形ABCD 中,AB =BC ,∠A =∠ABC =90°,以CD 为斜边作等腰直角△ECD ,连接BE ,若CD =213,BE =2,则AB =6.【答案】6.【分析】过点E 作EF ⊥AD 交AD 于点F ,延长FE 交BC 于点M ,从而可判定四边形ABMF 是矩形,则有AB =FM ,可得∠DFE =∠CME =90°,再求得∠DEF =∠ECM ,利用AAS 可判定△DEF ≌△ECM ,则有EF =CM ,从而可求得BM =EM ,利用勾股定理求得EM ,CE ,即可求CM ,从而可求解.【详解】解:过点E 作EF ⊥AD 交AD 于点F ,延长FE 交BC 于点M ,如图,∵∠A =∠ABC =90°,∠AFM =90°,∴四边形ABMF 是矩形,∴AB =FM ,∠DFE =∠CME =90°,∵△ECD 是等腰三角形,∴DE =CE ,∠CED =90°,∵∠ECM +∠CEM =90°,∠FED +∠CEM =180°-∠CED =90°,∴∠DEF =∠ECM ,在△DEF 和△ECM 中,∠EFD =∠CME =90°∠DEF =∠ECMDE =EC,∴△DEF ≌△ECM (AAS ),∴EF =CM ,∵EM =FM -EF ,BM =BC -CM ,AB =BC ,∴BM =EM ,∴△BME 是等腰直角三角形,∵CD =213,BE =2,∴CE =26,EM =1,∴BM =1,CM =CE 2-EM 2=5,∴BC =BM +CM =6,∴AB =BC =6.故答案为:6.【点睛】本题主要考查全等三角形的判定与性质,勾股定理,等腰直角三角形,解答的关键是作出适当的辅助线.5(2023•包河区二模)Rt △ABC 中,点D 是斜边AB 的中点.(1)如图1,若DE ⊥BC 与E ,DF ⊥AC 于F ,DE =3,DF =4,则AB =10;(2)如图2,若点P 是CD 的中点,且CP =52,则PA 2+PB 2=62.5.【答案】(1)10:(2)62.5.【分析】(1)首先证明四边形DECF 为矩形,得DE =CF =3,在Rt △DFC 中,由勾股定理得,CD =5,再利用直角三角形斜边上中线的性质可得答案;(2)过点D 作DE ⊥BC ,DF ⊥AC ,垂足分别为点E 、F ,过点P 作PG ⊥BC ,PH ⊥AC ,垂足分别为点G 、H ,则四边形CGPH 为矩形,说明BG =BE +EG =3EG =3CG =3PH ,同理可得AH =3PG ,再利用勾股定理即可.【详解】解:(1)∵DE ⊥BC ,DF ⊥AC ,∴∠DEF =∠DFC =∠ACB =90°,∴四边形DECF 为矩形,∴DE =CF =3,在Rt △DFC 中,由勾股定理得,CD =5,∵点D 是斜边AB 的中点,∴AB =2CD =10,故答案为:10;(2)如图,过点D 作DE ⊥BC ,DF ⊥AC ,垂足分别为点E 、F ,过点P 作PG ⊥BC ,PH ⊥AC ,垂足分别为点G 、H ,则四边形CGPH 为矩形,∴PG =CH ,CG =PH ,∵点D 为Rt △ABC 的斜边AB 的中点,∴CD =BD ,∴BE =CE ,∵点P 为CD 的中点,DE ⊥BC ,PG ⊥BC ,∴点G 为CE 的中点,即CE =2EG =2CG ,∴BE =CE =2EG ,∴BG =BE +EG =3EG =3CG =3PH ,同理可得AH =3PG ,∴PA 2+PB 2=BG 2+PG 2+AH 2+PH 2=(3PH )2+PG 2+(3PG )2+PH 2=10×522=62.5,故答案为:62.5.【点睛】本题主要考查了直角三角形斜边上中线的性质,等腰三角形的性质,勾股定理等知识,熟练掌握勾股定理是解题的关键.6(2023•庐江县三模)如图,四边形ABCD 中,AB =AC =AD ,点M 、N 分别是BC 、CD 的中点,连接MN ,若∠DAM =105°,∠BAN =75°,若AM AN=3+12,则∠ANM =75°.【答案】75.【分析】根据三角形中位线定理和二元一次方程组解答即可.【详解】解:四边形ABCD 中,AB =AC =AD ,点M 、N 分别是BC 、CD 的中点,设∠BAM =∠CAM =α,∠DAN =∠CAN =β,2α+β=75°α+2β=105° ,解得:α+β=60°,即:∠MAN =60°,过N 作NH ⊥AM 于H ,如图:可得:∠ANH =30°,设AH =x ,可得:HN =3x ,AN =2x ,∵AM AN=3+12,∴AM =3+12⋅AN =3+12⋅2x =(3+1)x ,∴MH =3x =NH ,∴∠MNH =45°,∴∠ANM =30°+45°=75°,故答案为:75.【点睛】此题考查三角形中位线定理,关键是根据三角形中位线定理解答.7(2023•中山市二模)如图,△ABC 与△BDE 均为等腰直角三角形,点A ,B ,E 在同一直线上,BD ⊥AE ,垂足为点B ,点C 在BD 上,AB =4,BE =10.将△ABC 沿BE 方向平移,当这两个三角形重叠部分的面积等于△ABC 面积的一半时,△ABC 平移的距离为2-2或5.【答案】2-2或5.【分析】根据平移的性质和等腰直角三角形的性质解答即可.【详解】解:∵△ABC 与△BDE 均为等腰直角三角形,∴AB =BC =4,DB =BE =10,∴△ABC 的面积=12AB •BC =12×4×4=8,当这两个三角形重叠部分的面积等于△ABC 面积的一半时,∴△A 'BE 的面积=12A 'B ⋅BE =12A 'B ⋅A 'B =1,∴A 'B =2,∴AA '=AB -A 'B =2-2,即平移的距离为2-2,当当点B 平移到与点E 重合时,也满足,此时平移的距离为:5,故答案为:2-2或5.【点睛】此题考查等腰直角三角形的性质,关键是根据等腰直角三角形的面积公式解答.8(2023•新都区模拟)青朱出入图,是魏晋时期数学家刘徽根据“割补术”运用数形关系证明勾股定理的几何证明法,即“勾自乘为朱方,股自乘为青方,令出入相补,各从其类,因就其余不动也,合成弦方之幂.开方除之,即弦也.”,若图中DF =1,CF =2,则AE 的长为310 .【答案】310.【分析】由勾股定理求出AF 的长,由△ADF ∽△ECF ,得到AF :FE =DF :FC =1:2,求出FE 的长,即可求出AE 的长.【详解】解∵四边形ABCD 是正方形,∴AD =DC ,∠D =90°,∵DF =1,FC =2,∴AD =DC =DF +FC =3,∴AF =AD 2+DF 2=32+12=10,∵AD ∥BE ,∴△ADF ∽△ECF ,∴AF :FE =DF :FC =1:2,∴FE =2AF =210,∴AE =AF +FE =310.故答案为:310.【点睛】本题考查勾股定理,相似三角形的判定和性质,掌握以上知识点是解题的关键.9(2023•黄埔区一模)△ABC 为等腰直角三角形,AB =AC =6,∠BAC =90°,动点D 在边BC 上运动.以A 为直角顶点,在AD 右侧作等腰直角三角形△ADE (如图).M 为DE 中点,N 为BC 三等分点,CN =13BC ,连接MN ,则线段MN 的最小值为1.【答案】1.【分析】连接CE ,证明△ABD ≌△ACE (SAS ),可得∠ACE =∠B =45°,CE =BD ,证明CE ⊥BD ,得出点E 始终在过点C 垂直于BC 的射线上,当BD =13BC =2时,MN 最小,根据三角形中位线定理可得MN =12CE ,结合已知条件即可得线段MN 的最小值.【详解】解:如图,连接CE ,∵△ABC 、△ADE 为等腰直角三角形,AB =AC =6,∴∠BAC =∠DAE =90°,AD =AE ,∴∠BAD =90°-∠DAC =∠CAE ,在△ABD 和△ACE 中,AB =AC ∠BAD =∠CAE AD =AE ,∴△ABD ≌△ACE (SAS ),∴∠ACE =∠B =45°,CE =BD ,∵∠ACB =∠B =45°,∴∠ECB =45°+45°=90°,∴CE ⊥BD ,因为点D 在BC 上运动,所以点M 在直线上运动,当BD =13BC =2时∵N 为BC 三等分点,CN =13BC ,此时MN ∥CE ,∵M 为DE 中点,∴N 为CD 中点,∴MN =12CE =1,故答案为:1.【点睛】本题考查了全等三角形的判定与性质,三角形中位线定理,等腰直角三角形的性质,解决本题的关键是判断出△ABD ≌△ACE .10(2023•雁塔区校级模拟)如图,菱形ABCD 的边长为5,将一个直角的顶点放置在菱形的中心O 处,此时直角的两边分别交边AD ,CD 于点E ,F ,当OE ⊥AD 时,OE 的长为2,则EF 的长是 412 .【答案】412.【分析】连接AC ,先证OF ∥AD ,再证OF 是△ACD 的中位线,得OF =12AD =52,然后在Rt △EOF 中,由勾股定理即可得出结论.【详解】解:如图,连接AC ,∵四边形ABCD 是菱形,∴OA =OC ,由题意可知,∠EOF =90°,∴OE ⊥OF ,∵OE ⊥AD ,∴OF ∥AD ,∵OA =OC ,∴DF =CF ,∴OF 是△ACD 的中位线,∴OF =12AD =52,在Rt △EOF 中,由勾股定理得:EF =OE 2+OF 2=22+522=412,故答案为:412.【点睛】本题考查了菱形的性质、平行线的判定与性质、三角形中位线定理以及勾股定理等知识,熟练掌握菱形的性质和三角形中位线定理是解题的关键.11(2023•奉贤区二模)如果四边形有一组邻边相等,且一条对角线平分这组邻边的夹角,我们把这样的四边形称为“准菱形”.有一个四边形是“准菱形”,它相等的邻边长为2,这两条边的夹角是90°,那么这个“准菱形”的另外一组邻边的中点间的距离是 2 .【答案】2.【分析】连接BD ,在Rt △ABD 中,由勾股定理得BD =22,再证EF 是△BCD 的中位线,即可得出结论.【详解】解:如图,四边形ABCD 是“准菱形”,且AB =AD ,∠BAD =90°,点E 、F 分别是CD 、BC 的中点,连接BD 、EF ,在Rt △ABD 中,由勾股定理得:BD =AB 2+AD 2=22+22=22,∵点E 、F 分别是CD 、BC 的中点,∴EF 是△BCD 的中位线,∴EF =12BD =2,即这个“准菱形”的另外一组邻边的中点间的距离是2,故答案为:2.【点睛】本题考查了“准菱形”的性质、勾股定理以及三角形中位线定理等知识,熟练掌握“准菱形”的性质和三角形中位线定理是解题的关键.12(2023•吕梁一模)如图,在正方形ABCD 中,点P 在对角线BD 上,点E ,F 分别在边AB 和BC 上,且∠EPF =45°,若CF =2DP =4,AE =12,则AB 的长度为 8+214 .【答案】8+214.【分析】过点P作MN⊥BC交BC于点M,交AD于点N;过点P作JG⊥AB交AB于点G,交DC 于点J;根据四边形ABCD是正方形,BD是对角线,则AD=BC=JG,AB=DC=MN;根据CF =2DP=4,由勾股定理得PJ=PN=2,则CM=MF=2,AG=2;过点E作EH⊥DB交BD于点H,设EH=x,根据勾股定理,EB=2x,根据相似三角形的判定和性质,得△PMF∽△PHE,得MF EH=PMPH,求出x,根据AB=AE+EB解答即可.【详解】解:过点P作MN⊥BC交BC于点M,交AD于点N;过点P作JG⊥AB交AB于点G,交DC于点J,∵四边形ABCD是正方形,BD是对角线,∴AD=BC=JG,AB=DC=MN,∠ADB=45°,∵CF=2DP=4,∴PJ=PN=2,∴CM=MF=2,AG=2,∵AE=12,∴GE=10,∵△PGB是等腰直角三角形,∴PG=GB,过点E作EH⊥DB交BD于点H,设EH=x,∴EH2+HB2=EB2,∴EB=2x,∴PG=GB=10+2x,∴PB=2(10+2x),∴PH=PB-HB=2(10+2x)-x,∵∠EPF=∠FPB+∠EPB=45°,∠MPB=∠MPF+∠FPB=45°,∴∠EPB=∠MPF,∴△PMF∽△PHE,∴MF EH=PM PH,∴2x=10+2x2(10+2x)-x,解得:x=27-22,∴EB=214-4,∴AB=8+214.故答案为:8+214.【点睛】本题考查正方形的性质,相似三角形的知识,解题的关键是掌握正方形的性质,相似三角形的判定和性质,勾股定理.13(2023•蚌埠二模)如图,点E为正方形ABCD的边CD上一点,以点A为圆心,AE长为半径画弧EF,交边BC于点F,已知正方形边长为1.(1)若∠DAE=15°,则DE的长为 2-3 ;(2)△AEF的面积为S的最大值是 12 .【答案】(1)2-3;(2)12.【分析】(1)由已知可证Rt △ADE ≌Rt △ABF (HL ),再利用勾股定理即可得出结论;(2)设DE =x ,表示出S =-12x 2+12,再利用二次函数的性质即可得出结论.【详解】解:(1)∵ABCD 是正方形,∴AD =AB ,∠D =∠B =90°,∵AE =AF ,∴Rt △ADE ≌Rt △ABF (HL ),∴∠DAE =∠BAF =15°,BF =DE ,∴∠EAF =60°,∴△AEF 为等边三角形,设DE =x ,则CE =CF =1-x ,在Rt △ADE 中,AE 2=AD 2+DE 2=1+x 2,在Rt △CFE 中,FE 2=CE 2+CF 2=2(1-x )2,∴1+x 2=2(1-x )2,解得:x =2±3,∵0≤x ≤1,∴x =2-3.故答案为:2-3,(2)设DE =x ,由(1)可知DE =BF =x ,则CE =CF =1-x ,∴S =S △AEF =S 正方形ABCD -S △ADE -S △ABF -S △CEF ,=1-12×1×x -12×1×x -12(1-x )2=-12x 2+12,∵0≤x ≤1,对称轴直线x =0,∴S 随x 增大而减小,∴当x =0时S 有最大值,此时S =12,故答案为:12.【点睛】本题主要考查正方形的性质、全等三角形的判定与性质、等边三角形的判定与性质、二次函数的应用,解题的关键是熟练掌握全等三角形的判定与性质、二次函数的性质等知识点.14(2023•兰考县一模)如图,方形ABCD 中,AB =8,点P 为射线BC 上任意一点(与点B 、C 不重合),连接AP ,在AP 的右侧作正方形APGH ,连接AG ,交射线CD 于E ,当ED 长为2时,点BP 的长为 245或403.【答案】245或403.【分析】由题可分两种情况,当交点E 在线段CD 上时,或当交点E 在线段CD 延长线上时,分别将△ADE 绕点A 顺时针旋转90°,可判定全等三角形,用勾股定理求出对应边的长度即可.【详解】解:由题意,分两种情况,如下(1)当交点E 在线段CD 上时,∵四边形ABCD 为正方形,∴将△ADE 绕点A 顺时针旋转90°,如图所示,AD 与AB 重合,且E ',B ,P 三点共线,∵四边形APGH 是正方形,∴∠PAG =45°,∴∠DAE +∠BAP =45°,由旋转可得,∴∠BAE '+∠BAP =45°,∴∠E 'AP =∠EAP =45°,连接EP ,在△E 'AP 和△EAP 中,∵AE '=AE ∠E 'AP =∠EAP AP =AP,∴△E 'AP ≌△EAP (SAS ),∴E 'P =EP ,设BP =x ,∵正方形ABCD 边长AB =8,DE =2,∴CE =8-2=6,PC =8-x ,EP =E 'P =2+x ,在Rt △ECP 中,有勾股定理得:PC 2+CE 2=EP 2,即:(8-x )2+62=(2+x )2,解得:x =245;(2)当交点E 在线段CD 延长线上时,同理旋转△ADE 到△ABE ',如图所示,并可得∠FAE =∠FAE '=45°,同理可证△FAE ≌△FAE ',∴E 'F =EF ,设CF =y ,∵正方形ABCD 边长AB =8,DE =2,∴CE '=8-2=6,E 'F =EF =DF +DE =8-y +2=10-y ,在Rt △E 'CF 中,有勾股定理得:CF 2+E 'C 2=E 'F 2,即:y 2+62=(10-y )2,解得:y =165;在△CPF 和△BPA 中,∵∠CPF =∠BPA ∠FCP =∠ABP =90°,∴△CPF ∽△BPA ,∴CP BP =CF AB ,即BP -8BP =1658,解得:BP =403;综上所述:BP =245或403.故答案为:245或403.【点睛】本题主要考查正方形的性质,利用旋转图形证三角形全等,根据勾股定理和相似图形求出对应线段的长度是解题的关键,本题难点在于利用旋转构造全等三角形.15(2023•本溪一模)由4个形状相同,大小相等的菱形组成如图所示的网格,菱形的顶点称为格点,点A ,B ,C ,D 都在格点上,∠A =60°,则cos ∠CDB 的值为 32 .【答案】32.【分析】根据菱形的性质证明△ECD 、△FCD 都是等边三角形,求得∠BCD =120°,利用等边对等角求得∠CDB =30°,据此即可求解.【详解】解:∵四边形ABCF 、CFDE 都是菱形,∠A =60°,∴△ECD 、△FCD 都是等边三角形,∴∠FCD =∠BCF =60°,CD =CF ,∴∠BCD =120°,BC =CF =CD ,∴∠CDB =12(180°-∠BCD )=30°,∴cos ∠CDB =cos30°=32,故答案为:32.【点睛】本题主要考查菱形的性质、等边三角形的性质与判定、锐角三角函数,熟练掌握相关理论是解答关键.16(2023•沂南县校级一模)如图,矩形ABCD 中,AC 、BD 相交于点O ,过点B 作BF ⊥AC 交CD 于点F ,交AC 与点M ,过点D 作DE ∥BF 交AB 于点E ,交AC 于点N ,连接FN 、EM ,则下列结论:①DN =BM ;②EM ∥FN ;③AE =FC ;④当AO =AD 时,四边形DEBF 是菱形.其中,正确结论的个数是4.【答案】4.【分析】根据矩形的性质得到AB =CD ,AB ∥CD ,∠DAE =∠BCF =90°,OD =OB =OA =OC ,AD =BC ,AD ∥BC ,根据平行线的性质得到DE ⊥AC ,根据垂直的定义得到∠DNA =∠BMC =90°,由全等三角形的性质得到DN =BM ,∠ADE =∠CBF ,故①正确;证△ADE ≌△CBF (ASA ),得出AE =FC ,DE =BF ,故③正确;证四边形NEMF 是平行四边形,得出EM ∥FN ,故②正确;证四边形DEBF 是平行四边形,证出∠ODN =∠ABD ,则DE =BE ,得出四边形DEBF 是菱形;故④正确;即可得出结论.【详解】解:∵四边形ABCD 是矩形,∴AB =CD ,AB ∥CD ,∠DAE =∠BCF =90°,OD =OB =OA =OC ,AD =BC ,AD ∥BC ,∴∠DAN =∠BCM ,∵BF ⊥AC ,DE ∥BF ,∴DE ⊥AC ,∴∠DNA =∠BMC =90°,在△DNA 和△BMC 中,,∴△DNA ≌△BMC (AAS ),∴DN=BM,∠ADE=∠CBF,故①正确;在△ADE和△CBF中,,∴△ADE≌△CBF(ASA),∴AE=FC,DE=BF,故③正确;∴DE-DN=BF-BM,即NE=MF,∵DE∥BF,∴四边形NEMF是平行四边形,∴EM∥FN,故②正确;∵AB=CD,AE=CF,∴BE=DF,∵BE∥DF,∴四边形DEBF是平行四边形,∵AO=AD,∴AO=AD=OD,∴△AOD是等边三角形,∴∠ADO=∠DAN=60°,∴∠ABD=90°-∠ADO=30°,∵DE⊥AC,∴∠ADN=∠ODN=30°,∴∠ODN=∠ABD,∴DE=BE,∴四边形DEBF是菱形;故④正确;故答案为:4.【点睛】本题考查了矩形的性质、菱形的判定、平行四边形的判定与性质、全等三角形的判定与性质、等边三角形的判定与性质、等腰三角形的判定等知识;熟练掌握矩形的性质和菱形的判定,证明三角形全等是解题的关键.17(2023•琼海一模)如图,菱形ABCD,AE⊥BC,点E为垂足,点F为AE的中点,连接BF并延长交AD于点G,连接CG,CE=2,CG=211,则DG=2,AG=6,AF= 7 .【答案】2,6,7.【分析】过点G作GH⊥BC,垂足为H,连接EG,证明△AGF≌△EBF,得到AG=BE,则DG= CE=2,然后可得四边形ABEG为平行四边形,设AG=BE=x,则AD=AB=GE=2+x,求出CH=x-2,在Rt△AGE和Rt△GCH中用勾股定理列方程进行求解.【详解】解:如图所示,过点G作GH⊥BC,交BC的延长线于H,连接EG,∵F 是AE 中点,∴AF =EF ,∵四边形ABCD 是菱形,∴AD ∥BC ,∵AE ⊥BC ,∴∠GAF =∠BEF =90°,在△AGF 与△EBF 中,∠GAF =∠BEF AF =EF ∠AFG =∠EFB,∴△AGF ≌△EBF (ASA ),∴AG =BE ,∴DG =CE =2,又∵AG ∥BE ,∴四边形ABEG 为平行四边形,∴GE =AB ,设AG =BE =x ,则AD =AB =GE =2+x ,∵∠GAE =∠AEH =∠H =90°,∴四边形AEHG 是矩形,∴AG =EH ,AE =GH ,∴CH =EH -CE =AG -CE =x -2,在Rt △AGE 和Rt △GCH 中,AE 2=GE 2-AG 2,GH 2=GC 2-CH 2,∴(x +2)2-x 2=(211)2-(x -2)2,解得x =6,即AG =6,∴AE =(6+2)2-62=27,∴AF =12AE =7.故答案为:2,6,7.【点睛】本题考查了菱形的性质、平行四边形的判定和性质、全等三角形的判定和性质、勾股定理等知识,设出线段长,寻找等量关系列出方程是解题的关键.18(2023•镇江一模)如图,在矩形ABCD 中,AB =6,BC=8,△BEF 的顶点E 在对角线AC 上运动,且∠BFE =90°,∠EBF =∠BAC ,连接AF ,则AF 的最小值为 7225 .【答案】7225.【分析】过点B 作BH ⊥AC 于点H ,连接FH .由∠BFE =∠BHE =90°推出E ,B ,F ,H 四点共圆,证明∠AHF =∠ACD =定值,推出点F 在射线HF 上运动,当AF ⊥FH 时,AF 的值最小,求出AH ,sin ∠AHF ,可得结论.【详解】解:过点B 作BH ⊥AC 于点H ,连接FH ,如图,∵∠BFE =∠BHE =90°,∴E ,B ,F ,H 四点共圆,∴∠FHB =∠FEB ,∵∠AHF +∠FHB =90°,∠FBE +FEB =90°∴∠AHF =∠EBF ,∵四边形ABCD 是矩形,∴ABC ∥CD ,∴∠BAC =∠ACD ,∵∠EBF =∠BAC ,∴∠EBF =∠ACD ,∴∠AHF =∠ACD =定值,∴点F 在射线HF 上运动,当AF ⊥FH 时,AF 的值最小,∵四边形ABCD 是矩形,∴AB =CD =6,BC =AD =8,∠D =90°.∴AC =CD 2+AD 2=62+82=10,∴sin ∠AHF =sin ∠ACD =AD AC =810=45,∵S △ACB =12•AB •CB =12•AC •BH ,∴BH =245,∴AH =AB 2-BH 2=62-245 2=185,∴AF 的最小值=AH ⋅sin ∠AHE =185×45=7225.故答案为:7225.【点睛】本题考查了矩形的性质、锐角三角函数的定义、勾股定理、四点共圆、圆周角定理、轨迹、三角形面积以及最小值问题等知识,本题综合性强,熟练掌握矩形的性质,利用垂线段最短解决最值问题是解题的关键.19(2023•泉州模拟)如图,在菱形ABCD 中,∠A =60°,点E 在边AD 上,以BE 为边在菱形ABCD 的内部作等边三角形BEF ,若∠DEF =α,∠EBD =β,则α与β之间的数量关系可用等式表示为α+β=60°.【答案】α+β=60°.【分析】根据菱形的性质得到∠C =∠A =60°,AD =AB =CD =BC ,求得∠ADB =∠CDB =∠DBC=60°,得到BD=BC,根据等边三角形的性质得到BE=BF,∠EBF=60°,根据全等三角形的性质得到∠DBE=∠CBF=β,∠BFC=∠BED=60°+α,根据三角形的内角和定理即可得到结论.【详解】解:在菱形ABCD中,∠A=60°,∴∠C=∠A=60°,AD=AB=CD=BC,∴∠ADB=∠CDB=∠DBC=60°,∴△BCD是等边三角形,∴BD=BC,∵△BEF是等边三角形,∴BE=BF,∠EBF=60°,∴∠DBE=∠CBF,∴△BDE≌△BCF(SAS),∴∠DBE=∠CBF=β,∠BFC=∠BED=60°+α,∵∠BFC+∠C+∠CBF=180°,∴β+60°+α+60°=180°,∴α+β=60°.故答案为:α+β=60°.【点睛】本题考查了菱形的性质,全等三角形的判定和性质,等边三角形的判定和性质,熟练掌握菱形的性质是解题的关键.20(2023•市南区一模)如图,正方形ABCD中,E、F分别为BC、CD边上的点,∠EAF=45°,则下列结论中正确的有①②③.(填序号)①BE+DF=EF;②tan∠AMD=CDDF; ③BM2+DN2=MN2;④若EF=1.5,S△AEF=3,则.S正方形ABCD=4.【答案】①②③.【分析】①将△ADF绕点A顺时针旋转90°使AD与AB重合,得△ABQ,根据正方形的性质及会等三角形的性质可得答案;②根据三角形的外角性质及三角函数可得答案;③在AQ上取一点H,使AH=AN.连接BH,利用全等三角形的性质及勾股定理可得答案;④过点A作AR⊥EF于点R,根据全等三角形的性质、角平分线的性质可得AR=AB,然后由三角形面积公式及正方形的面积公式可得答案.【详解】解:①将△ADF绕点A顺时针旋转90°使AD与AB重合,得△ABQ,∴△ABQ≌△ADF,∴∠QAB=∠DAF,AQ=AF,∠ABQ=∠ADF,BQ=DF,∵四边形ABCD是正方形,∴∠BAD=∠ABC=∠C=90°,AB=BC=CD=AD,∵∠EAB+∠DAF+∠EAF=∠BAD=90°,且∠EAF=45°,∴∠DAF +∠EAB =45°,∴∠QAB +∠EAB =45°,∴∠QAE =∠FAE =45°,∵∠ABQ +∠ABE =90°+90°=180°,∴点Q 、B 、E 共线,在△AEQ 和△AEF 中,AQ =EF∠QAE =∠FAE AE =AE,∴△AEQ ≌△AEF (SAS ),∴EQ =EF ,∵EQ =BE +BQ =BE +DF ,∴EF =BE +DF ,故①正确;②∵∠AND =∠EAF +∠AMD =∠BDC +∠AFD ,∴∠AMD =∠AFD ,∴tan ∠AMD =tan ∠AFD ,在Rt △AFD 中,tan ∠AFD =AD DF ,∴tan ∠AMD =CD DF ,故②正确;③在AQ 上取一点H ,使AH =AN .连接BH ,在△AMH 和△AMN 中,AH =AN∠HAM =∠NAM =45°AM =MN,∴△AMH ≌△AMN (SAS ),∴MH =MN ,同理,△ABH ≌△ADN (SAS ),∴BH =DN ,∠ABH =∠ADN =45°,∴∠HBM =∠ABH +∠ABD =90°,在Rt △BMH 中,MH 2=BH 2+BM 2,∴MN 2=DN 2+BM 2,故③正确;④假设EF ∥BD 时,过点A 作AR ⊥EF 于点R ,∴AR 在正方形对角线上,∴∠RAE =∠BAE ,∴EB =ER ,∵AE =AE ,∴Rt △AEB ≌Rt △AER (HL ),∴∠AEB =∠AEF ,∵AB ⊥BC ,AR ⊥EF ,∴AR=AB,∵S△AEF=12EF•AR,∴3=12×1.5•AR,∴AR=4,=42=16,∴S正方形ABCD故④错误,∴①②③正确,故答案为:①②③.【点睛】此题考查的是正方形的性质、全等三角形的判定与性质、角平分线的性质、勾股定理有解直角三角形,正确作出辅助线是解决此题关键.21(2023•大连一模)学习菱形时,我们从它的边、角和对角线等方面进行研究,可以发现并证明:菱形的每一条对角线平分一组对角.小明参考平行四边形、矩形判定方法的研究过程,得出下面的猜想:①一条对角线平分一组对角的四边形是菱形;②每一条对角线平分一组对角的四边形是菱形;③一条对角线平分一组对角的平行四边形是菱形.其中正确的是②③(填序号,填写一个即可).【答案】见试题解答内容【分析】由菱形的判定以及平行四边形的判定与性质分别对各个猜想进行判断即可.【详解】解:①一条对角线平分一组对角的四边形不一定是菱形,如筝形,故①不正确;②如图1,∵AC平分∠BAD和∠BCD,∴∠BAC=∠DAC,∠BCA=∠DCA,∵∠BAC+∠BCA+∠ABC=180°,∠DAC+∠DCA+∠ADC=180°,∴∠ABC=∠ADC,同理:∠BAD=∠BCD,∴四边形ABCD是平行四边形,∴AD∥BC,∴∠DAC=∠BCA,∴∠BAC=∠BCA,∴AB=BC,∴平行四边形ABCD是菱形,故②正确;③一条对角线平分一组对角的平行四边形是菱形,故③正确;故答案为:②③.【点睛】本题考查了菱形的判定、等腰三角形的判定以及平行四边形的判定与性质,熟练掌握菱形的判定是解题的关键.22(2023•石景山区一模)如图,在菱形ABCD中,点E,F分别在BC,AD上,BE=DF.只需添加一个条件即可证明四边形AECF是矩形,这个条件可以是AE⊥BC(答案不唯一)(写出一个即可).【答案】AE⊥BC(答案不唯一).【分析】证四边形AECF是平行四边形,再证∠AEC=90°,然后由矩形的判定即可得出结论.【详解】解:这个条件可以是AE⊥BC,理由如下:∵四边形ABCD是菱形,∴AD∥BC,AD=BC,∵BE=DF,∴BC-BE=AD-DF,即CE=AF,∴四边形AECF是平行四边形,又∵AE⊥BC,∴∠AEC=90°,∴平行四边形AECF是矩形,故答案为:AE⊥BC(答案不唯一).【点睛】本题考查了矩形的判定、菱形的性质以及平行四边形的判定与性质等知识,熟练掌握矩形的判定是解题的关键.23(2023•河东区一模)已知,如图,已知菱形ABCD的边长为6,∠ABC=60°,点E,F分别在AB,CB的延长线上,且BE=BF=13AB,G是DF的中点,连接GE,则GE的长是 39 .【答案】39.【分析】如图,延长EG到H,使GH=EG,连接CH,CG,DH,CE,过点F作PF∥DC,根据全等三角形的性质得到EF=HD,∠EFG=∠HDG,根据菱形的性质得到CD=CB,∠ADC=∠ABC= 60°,点A,B,E在同一直线上,根据全等三角形的性质得到CH=CE,∠DCH=∠BCE,根据等腰三角形的性质和含30°角的直角三角形的性质得到结论.【详解】解:如图,延长EG到H,使GH=EG,连接CH,CG,DH,CE,过点F作FP∥DC,过点E 作EQ⊥BC于Q,∵G是线段DF的中点,∴FG=DG,∵∠EGF=∠HGD,∴△GEF≌△GHD(SAS),∴EF=HD,∠EFG=∠HDG,∵∠EBF=∠ABC=60°,BE=BF,∴△BEF是等边三角形,∴∠BEF=60°,∵BE=BF=2,EQ⊥BC,∴∠QEB=30°,∴BQ=1,EQ=3,在Rt△CQE中,由勾股定理得:CE=CQ2+EQ2=72+(3)2=213,∵AB∥CD,CD∥FP,∴AB∥FP∥CD,∠GFP=∠CDG,∴∠AEF+∠EFP=180°,∴∠EFG+∠GFP=120°,∴∠CDH=∠HDG+∠GDC=120°,∵四边形ABCD是菱形,∴CD=CB=6,∠ADC=∠ABC=60°,点A,B,E在同一直线上,∴∠EBC=120°=∠CDH,∵△BEF是等边三角形,∴EF=BE,∴DH=BE,∴△HDC≌△EBC(SAS),∴CH=CE,∠DCH=∠BCE,∴∠DCH+∠HCB=∠BCE+∠HCB=120°,即∠HCE=120°,∵CH=CE,GH=GE,∴CG⊥GE,∠GCE=∠HCG=60°,∴∠GEC=30°,∵cos30°=EGCE=3 2,∴GE=32×213=39.故答案为:39.【点睛】本题主要考查了等边三角形的性质和判定,菱形的性质,全等三角形的判定和性质,解直角三角形,通过添加辅助线构造全等三角形是解题关键.24(2023•合肥模拟)如图,点P在正方形ABCD内,∠BPC=135°,连接PA、PB、PC、PD.(1)若PA=AB,则∠CPD=90°;(2)若PB=2,PC=3,则PD的长为 22 .【答案】(1)90°;(2)22.【分析】(1)根据正方形的性质得到AD=AB,求得PA=AD,设∠APB=α,则∠BAP=180°-2a,根据周角的定义即可得到结论;(2)如图,过C作CQ⊥CP,过P作PQ⊥PB,PQ与CQ相交于Q,连接BQ,推出△PCQ为等腰直角三角形,根据等腰直角三角形的性质得到PQ=32,根据全等三角形的性质得到BQ=PD,根据勾股定理即可得到结论.【详解】解:(1)∵四边形ABCD是正方形,∴AD=AB,∵PA=AB,∴PA=AD,设∠APB=α,则∠BAP=180°-2a,∴∠PAD=2α-90°,∠APD==135°-α,∵∠BPC=135°,∴∠CPD=360°-(135°-α)-a-135°=90°;故答案为:90°;(2)如图,过C作CQ⊥CP,过P作PQ⊥PB,PQ与CQ相交于Q,连接BQ,∵∠BPC=135°,∴∠CPQ=45°,∴△PCQ为等腰直角三角形,∵PC=3,∴PQ=32,∵CD=BC,∠PCD=∠QCB,PC=CQ,∴△DCP≌△BCQ(SAS),∴BQ=PD,在Rt△PBQ中,PB2+PQ2=BQ2,∵PB=2,∴PD=BQ=22.【点睛】本题考查了正方形的性质,全等三角形的判定和性质,等腰三角形的性质,正确地作出辅助线是解题的关键.25(2023•鄞州区一模)如图,Rt△ABC中,∠C=90°,AC=BC=8,作正方形CDEF,其中顶点E在边AB上.(1)若正方形CDEF的边长为26,则线段AE的长是 42-4 ;(2)若点D到AB的距离是2,则正方形CDEF的边长是 25 .【答案】(1)42-4;(2)25.【分析】(1)连接CE,过点E作EH⊥AC于点H,根据正方形的性质,可得CE的长,根据等腰直角三角形的性质可得AH=EH,设AH=EH=x,在Rt△EHC中,根据勾股定理列方程,求出x的值,进一步可得AE的长;(2)过点D作DM⊥AB于点M,连接BD,AF,过点F作FN⊥AB于点N,先证△MDE≌△NEF (AAS),根据全等三角形的性质可得EN=DM,ME=NF,再证△BCD≌△ACF(SAS),根据全等三角形的性质可得BD=AF,∠CAF=∠CBD,然后再证明△BMD≌△FNA(AAS),根据全等三角形的性质可得BM=NF,MD=NA,进一步可得BM=ME,EN=NA=MD,求出ME的长度,根据勾股定理可得DE的长度,即可确定正方形DCFE的边长.【详解】解:(1)连接CE,过点E作EH⊥AC于点H,如图所示:则∠AHE=90°,在正方形CDEF中,CD=DE=26,∠CDE=90°,根据勾股定理,得CE=(26)2+(26)2=43,在Rt△ABC中,∠C=90°,∴∠A=∠B=45°,∴∠AEH=45°,∴AH=EH,设AH=EH=x,∵AC=BC=8,∴CH=8-x,在Rt△EHC中,根据勾股定理,得x2+(8-x)2=(43)2,解得x1=4+22(舍去),x2=4-22,∴AH=EH=4-22,在Rt△AEH中,根据勾股定理,得AE=(4-22)2+(4-22)2=42-4,故答案为:42-4;(2)过点D作DM⊥AB于点M,连接BD,AF,过点F作FN⊥AB于点N,如图所示:则∠DME=∠FNE=90°,∴∠MDE+∠MED=90°,在正方形DCEF中,∠DEF=90°,DE=EF,∴∠MED+∠FEN=90°,∴∠MDE=∠FEN,在△MDE 和△NEF 中,∠DME =∠FNE ∠MDE =∠FEN DE =EF,∴△MDE ≌△NEF (AAS ),∴EN =DM ,ME =NF ,在Rt △ABC 中,BC =AC ,∠ACB =90°,在正方形EDCF 中,∠DCF =90°,CD =CF ,∴∠BCD =∠ACF ,在△BCD 和△ACF 中,BC =AC ∠BCD =∠ACF CD =CF,∴△BCD ≌△ACF (SAS ),∴BD =AF ,∠CAF =∠CBD ,∵∠ABC +∠BAC =90°,∴∠MBD +∠DBC +∠BAC =90°,∴∠MBD +∠CAF +∠BAC =90°,即∠MBD +∠BAF =90°,∵∠MBD +∠MDB =90°,∴∠MDB =∠BAF ,在△BMD 和△FNA 中,∠BMD =∠FNA ∠BDM =∠FAN BD =AF,∴△BMD ≌△FNA (AAS ),∴BM =NF ,MD =NA ,∴BM =ME ,EN =NA =MD ,∵点D 到AB 的距离是2,∴EN =NA =2,在Rt △ABC 中,AC =BC =8,∠ACB =90°,根据勾股定理,得AB =82+82=82,∴BM +ME =82-2-2=62,∴ME =32,在Rt △MDE 中,根据勾股定理,DE =(32)2+(2)2=25,∴正方形CDEF 的边长是25,故答案为:25.【点睛】本题考查了正方形的性质,全等三角形的判定和性质,等腰直角三角形的性质,勾股定理等,添加合适的辅助线构造全等三角形是解题的关键,本题综合性较强,难度较大.26(2023•郓城县校级模拟)如图,在平行四边形ABCD 中,对角线AC 、BD 交于点O .点M 是BC 边的中点,连接AM 、OM ,作CF ∥AM .已知OC 平分∠BCF ,OB 平分∠AOM ,若BD =32,则。
中考数学28道压轴题含答案解析

中考数学选填压轴题练习一.根的判别式(共1小题)1.(2023•广州)已知关于x的方程x2﹣(2k﹣2)x+k2﹣1=0有两个实数根,则的化简结果是()A.﹣1B.1C.﹣1﹣2k D.2k﹣3【分析】首先根据关于x的方程x2﹣(2k﹣2)x+k2﹣1=0有两个实数根,得判别式Δ=[﹣(2k﹣2)]2﹣4×1×(k2﹣1)≥0,由此可得k≤1,据此可对进行化简.【解答】解:∵关于x的方程x2﹣(2k﹣2)x+k2﹣1=0有两个实数根,∴判别式Δ=[﹣(2k﹣2)]2﹣4×1×(k2﹣1)≥0,整理得:﹣8k+8≥0,∴k≤1,∴k﹣1≤0,2﹣k>0,∴=﹣(k﹣1)﹣(2﹣k)=﹣1.故选:A.二.函数的图象(共1小题)2.(2023•温州)【素材1】某景区游览路线及方向如图1所示,①④⑥各路段路程相等,⑤⑦⑧各路段路程相等,②③两路段路程相等.【素材2】设游玩行走速度恒定,经过每个景点都停留20分钟,小温游路线①④⑤⑥⑦⑧用时3小时25分钟;小州游路线①②⑧,他离入口的路程s与时间t的关系(部分数据)如图2所示,在2100米处,他到出口还要走10分钟.【问题】路线①③⑥⑦⑧各路段路程之和为()A.4200米B.4800米C.5200米D.5400米【分析】设①④⑥各路段路程为x米,⑤⑦⑧各路段路程为y米,②③各路段路程为z米,由题意及图象可知,然后根据“游玩行走速度恒定,经过每个景点都停留20分钟,小温游路线①④⑤⑥⑦⑧用时3小时25分钟”可进行求解.【解答】解:由图象可知:小州游玩行走的时间为75+10﹣40=45(分钟),小温游玩行走的时间为205﹣100=105(分钟),设①④⑥各路段路程为x米,⑤⑦⑧各路段路程为y米,②③各路段路程为z米由图象可得:,解得:x+y+z=2700,∴游玩行走的速度为:(2700﹣2100)÷10=60 (米/分),由于游玩行走速度恒定,则小温游路线①④⑤⑥⑦⑧的路程为:3x+3y=105×60=6300,∴x+y=2100,∴路线①③⑥⑦⑧各路段路程之和为:2x+2y+z=x+y+z+x+y=2700+2100=4800(米).故选:B.三.动点问题的函数图象(共1小题)3.(2023•河南)如图1,点P从等边三角形ABC的顶点A出发,沿直线运动到三角形内部一点,再从该点沿直线运动到顶点B.设点P运动的路程为,图2是点P运动时y随x变化的关系图象,则等边三角形ABC的边长为()A.6B.3C.D.【分析】如图,令点P从顶点A出发,沿直线运动到三角形内部一点O,再从点O沿直线运动到顶点B,结合图象可知,当点P在AO上运动时,PB=PC,AO=,易知∠BAO=∠CAO=30°,当点P在OB上运动时,可知点P到达点B时的路程为,可知AO=OB=,过点O作OD⊥AB,解直角三角形可得AD=AO•cos30°,进而得出等边三角形ABC的边长.【解答】解:如图,令点P从顶点A出发,沿直线运动到三角形内部一点O,再从点O沿直线运动到顶点B,\结合图象可知,当点P在AO上运动时,,∴PB=PC,,又∵△ABC为等边三角形,∴∠BAC=60°,AB=AC,∴△APB≌△APC(SSS),∴∠BAO=∠CAO=30°,当点P在OB上运动时,可知点P到达点B时的路程为,∴OB=,即AO=OB=,∴∠BAO=∠ABO=30°,过点O作OD⊥AB,垂足为D,∴AD=BD,则AD=AO•cos30°=3,∴AB=AD+BD=6,即等边三角形ABC的边长为6.故选:A.四.反比例函数系数k的几何意义(共1小题)4.(2023•宁波)如图,点A,B分别在函数y=(a>0)图象的两支上(A在第一象限),连结AB交x 轴于点C.点D,E在函数y=(b<0,x<0)图象上,AE∥x轴,BD∥y轴,连结DE,BE.若AC =2BC,△ABE的面积为9,四边形ABDE的面积为14,则a﹣b的值为12,a的值为9.【分析】依据题意,设A(m,),再由AE∥x轴,BD∥y轴,AC=2BC,可得B(﹣2m,﹣),D (﹣2m,﹣),E(,),再结合△ABE的面积为9,四边形ABDE的面积为14,即可得解.【解答】解:设A(m,),∵AE∥x轴,且点E在函数y=上,∴E(,).∵AC=2BC,且点B在函数y=上,∴B(﹣2m,﹣).∵BD∥y轴,点D在函数y=上,∴D(﹣2m,﹣).∵△ABE的面积为9,∴S△ABE=AE×(+)=(m﹣)(+)=m••==9.∴a﹣b=12.∵△ABE的面积为9,四边形ABDE的面积为14,∴S△BDE=DB•(+2m)=(﹣+)()m=(a﹣b)••()•m=3()=5.∴a=﹣3b.又a﹣b=12.∴a=9.故答案为:12,9.五.反比例函数图象上点的坐标特征(共2小题)5.(2023•德州)如图,在平面直角坐标系中,四边形OABC是矩形,点B的坐标为(6,3),D是OA的中点,AC,BD交于点E,函数的图象过点B.E.且经过平移后可得到一个反比例函数的图象,则该反比例函数的解析式()A.y=﹣B.C.D.【分析】先根据函数图象经过点B和点E,求出a和b,再由所得函数解析式即可解决问题.【解答】解:由题知,A(6,0),B(6,3),C(0,3),令直线AC的函数表达式为y1=k1x+b1,则,解得,所以.又因为点D为OA的中点,所以D(3,0),同理可得,直线BD的函数解析式为y2=x﹣3,由得,x=4,则y=4﹣3=1,所以点E坐标为(4,1).将B,E两点坐标代入函数解析式得,,解得.所以,则,将此函数图象向左平移3个单位长度,再向下平移4个单位长度,所得图象的函数解析式为:.故选:D.6.如图,O是坐标原点,Rt△OAB的直角顶点A在x轴的正半轴上,AB=2,∠AOB=30°,反比例函数y=(k>0)的图象经过斜边OB的中点C.(1)k=;(2)D为该反比例函数图象上的一点,若DB∥AC,则OB2﹣BD2的值为4.【分析】(1)根据直角三角形的性质,求出A、B两点坐标,作出辅助线,证得△OPC≌△APC(HL),利用勾股定理及待定系数法求函数解析式即可解答.(2)求出AC、BD的解析式,再联立方程组,求得点D的坐标,分两种情况讨论即可求解.【解答】解:(1)在Rt△OAB中,AB=2,∠AOB=30°,∴,∴,∵C是OB的中点,∴OC=BC=AC=2,如图,过点C作CP⊥OA于P,∴△OPC≌△APC(HL),∴,在Rt△OPC中,PC=,∴C(,1).∵反比例函数y=(k>0)的图象经过斜边OB的中点C,∴,解得k=.故答案为:.(2)设直线AC的解析式为y=k1x+b(k≠0),则,解得,∴AC的解析式为y=﹣x+2,∵AC∥BD,∴直线BD的解析式为y=﹣x+4,∵点D既在反比例函数图象上,又在直线BD上,∴联立得,解得,,当D的坐标为(2+3,)时,BD2==9+3=12,∴OB2﹣BD2=16﹣12=4;当D的坐标为(2﹣3,)时,BD2=+=9+3=12,∴OB2﹣BD2=16﹣12=4;综上,OB2﹣BD2=4.故答案为:4.六.反比例函数与一次函数的交点问题(共1小题)7.(2023•湖州)已知在平面直角坐标系中,正比例函数y=k1x(k1>0)的图象与反比例函数(k2>0)的图象的两个交点中,有一个交点的横坐标为1,点A(t,p)和点B(t+2,q)在函数y=k1x的图象上(t≠0且t≠﹣2),点C(t,m)和点D(t+2,n)在函数的图象上.当p﹣m与q﹣n的积为负数时,t的取值范围是()A.或B.或C.﹣3<t<﹣2或﹣1<t<0D.﹣3<t<﹣2或0<t<1【分析】将交点的横坐标1代入两个函数,令二者函数值相等,得k1=k2.令k1=k2=k,代入两个函数表达式,并分别将点A、B的坐标和点C、D的坐标代入对应函数,进而分别求出p﹣m与q﹣n的表达式,代入解不等式(p﹣m)(q﹣n)<0并求出t的取值范围即可.【解答】解:∵y=k1x(k1>0)的图象与反比例函数(k2>0)的图象的两个交点中,有一个交点的横坐标为1,∴k1=k2.令k1=k2=k(k>0),则y=k1x=kx,=.将点A(t,p)和点B(t+2,q)代入y=kx,得;将点C(t,m)和点D(t+2,n)代入y=,得.∴p﹣m=kt﹣=k(t﹣),q﹣n=k(t+2)﹣=k(t+2﹣),∴(p﹣m)(q﹣n)=k2(t﹣)(t+2﹣)<0,∴(t﹣)(t+2﹣)<0.∵(t﹣)(t+2﹣)=•=<0,∴<0,∴t(t﹣1)(t+2)(t+3)<0.①当t<﹣3时,t(t﹣1)(t+2)(t+3)>0,∴t<﹣3不符合要求,应舍去.②当﹣3<t<﹣2时,t(t﹣1)(t+2)(t+3)<0,∴﹣3<t<﹣2符合要求.③当﹣2<t<0时,t(t﹣1)(t+2)(t+3)>0,∴﹣2<t<0不符合要求,应舍去.④当0<t<1时,t(t﹣1)(t+2)(t+3)<0,∴0<t<1符合要求.⑤当t>1时,t(t﹣1)(t+2)(t+3)>0,∴t>1不符合要求,应舍去.综上,t的取值范围是﹣3<t<﹣2或0<t<1.故选:D.七.二次函数图象与系数的关系(共3小题)8.(2023•乐至县)如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣2,且过点(1,0).现有以下结论:①abc<0;②5a+c=0;③对于任意实数m,都有2b+bm≤4a﹣am2;④若点A(x1,y1)、B(x2,y2)是图象上任意两点,且|x1+2|<|x2+2|,则y1<y2,其中正确的结论是()A.①②B.②③④C.①②④D.①②③④【分析】根据题意和函数图象,利用二次函数的性质,可以判断各个小题中的结论是否正确,从而可以解答本题.【解答】解:由图象可得,a>0,b>0,c<0,∴abc<0,故①正确,∵抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣2,且过点(1,0).∴﹣=﹣2,a+b+c=0,∴b=4a,∴a+b+c=a+4a+c=0,故5a+c=0,故②正确,∵当x=﹣2时,y=4a﹣2b+c取得最小值,∴am2+bm+c≥4a﹣2b+c,即2b+bm≥4a﹣am2(m为任意实数),故③错误,∵抛物线开口向上,对称轴为直线x=﹣2,若点A(x1,y1)、B(x2,y2)是图象上任意两点,且|x1+2|<|x2+2|,∴y1<y2,故④正确;故选:C.9.(2023•丹东)抛物线y=ax2+bx+c(a≠0)与x轴的一个交点为A(﹣3,0),与y轴交于点C,点D是抛物线的顶点,对称轴为直线x=﹣1,其部分图象如图所示,则以下4个结论:①abc>0;②E(x1,y1),F(x2,y2)是抛物线y=ax2+bx(a≠0)上的两个点,若x1<x2,且x1+x2<﹣2,则y1<y2;③在x轴上有一动点P,当PC+PD的值最小时,则点P的坐标为;④若关于x的方程ax2+b(x﹣2)+c =﹣4(a≠0)无实数根,则b的取值范围是b<1.其中正确的结论有()A.1个B.2个C.3个D.4个【分析】根据所给函数图象可得出a,b,c的正负,再结合抛物线的对称性和增减性即可解决问题.【解答】解:根据所给函数图象可知,a>0,b>0,c<0,所以abc<0,故①错误.因为抛物线y=ax2+bx的图象可由抛物线y=ax2+bx+c的图象沿y轴向上平移|c|个单位长度得到,所以抛物线y=ax2+bx的增减性与抛物线y=ax2+bx+c的增减性一致.则当x<﹣1时,y随x的增大而减小,又x1<x2,且x1+x2<﹣2,若x2<﹣1,则E,F两点都在对称轴的左侧,此时y1>y2.故②错误.作点C关于x轴的对称点C′,连接C′D与x轴交于点P,连接PC,此时PC+PD的值最小.将A(﹣3,0)代入二次函数解析式得,9a﹣3b+c=0,又,即b=2a,所以9a﹣6a+c=0,则c=﹣3a.又抛物线与y轴的交点坐标为C(0,c),则点C坐标为(0,﹣3a),所以点C′坐标为(0,3a).又当x=﹣1时,y=﹣4a,即D(﹣1,﹣4a).设直线C′D的函数表达式为y=kx+3a,将点D坐标代入得,﹣k+3a=﹣4a,则k=7a,所以直线C′D的函数表达式为y=7ax+3a.将y=0代入得,x=.所以点P的坐标为(,0).故③正确.将方程ax2+b(x﹣2)+c=﹣4整理得,ax2+bx+c=2b﹣4,因为方程没有实数根,所以抛物线y=ax2+bx+c与直线y=2b﹣4没有公共点,所以2b﹣4<﹣4a,则2b﹣4<﹣2b,解得b<1,又b>0,所以0<b<1.故④错误.所以正确的有③.故选:A.10.(2023•河北)已知二次函数y=﹣x2+m2x和y=x2﹣m2(m是常数)的图象与x轴都有两个交点,且这四个交点中每相邻两点间的距离都相等,则这两个函数图象对称轴之间的距离为()A.2B.m2C.4D.2m2【分析】求出三个交点的坐标,再构建方程求解.【解答】解:令y=0,则﹣x2+m2x=0和x2﹣m2=0,∴x=0或x=m2或x=﹣m或x=m,∵这四个交点中每相邻两点间的距离都相等,若m>0,则m2=2m,∴m=2,若m<0时,则m2=﹣2m,∴m=﹣2.∵抛物线y=x2﹣m2的对称轴为直线x=0,抛物线y=﹣x2+m2x的对称轴为直线x=,∴这两个函数图象对称轴之间的距离==2.故选:A.八.二次函数图象上点的坐标特征(共1小题)11.(2023•广东)如图,抛物线y=ax2+c经过正方形OABC的三个顶点A,B,C,点B在y轴上,则ac 的值为()A.﹣1B.﹣2C.﹣3D.﹣4【分析】过A作AH⊥x轴于H,根据正方形的性质得到∠AOB=45°,得到AH=OH,利用待定系数法求得a、c的值,即可求得结论.【解答】解:过A作AH⊥x轴于H,∵四边形ABCO是正方形,∴∠AOB=45°,∴∠AOH=45°,∴AH=OH,设A(m,m),则B(0,2m),∴,解得am=﹣1,m=,∴ac的值为﹣2,故选:B.九.二次函数与不等式(组)(共1小题)12.(2023•西宁)直线y1=ax+b和抛物线(a,b是常数,且a≠0)在同一平面直角坐标系中,直线y1=ax+b经过点(﹣4,0).下列结论:①抛物线的对称轴是直线x=﹣2;②抛物线与x轴一定有两个交点;③关于x的方程ax2+bx=ax+b有两个根x1=﹣4,x2=1;④若a >0,当x<﹣4或x>1时,y1>y2.其中正确的结论是()A.①②③④B.①②③C.②③D.①④【分析】根据直线y1=ax+b经过点(﹣4,0).得到b=4a,于是得到=ax2+4ax,求得抛物线的对称轴是直线x=﹣﹣=2;故①正确;根据Δ=16a2>0,得到抛物线与x轴一定有两个交点,故②正确;把b=4a,代入ax2+bx=ax+b得到x2+3x﹣4=0,求得x1=﹣4,x2=1;故③正确;根据a>0,得到抛物线的开口向上,直线y1=ax+b和抛物线交点横坐标为﹣4,1,于是得到结论.【解答】解:∵直线y1=ax+b经过点(﹣4,0).∴﹣4a+b=0,∴b=4a,∴=ax2+4ax,∴抛物线的对称轴是直线x=﹣﹣=2;故①正确;∵=ax2+4ax,∴Δ=16a2>0,∴抛物线与x轴一定有两个交点,故②正确;∵b=4a,∴方程ax2+bx=ax+b为ax2+4ax=ax+4a得,整理得x2+3x﹣4=0,解得x1=﹣4,x2=1;故③正确;∵a>0,抛物线的开口向上,直线y1=ax+b和抛物线交点横坐标为﹣4,1,∴当x<﹣4或x>1时,y1<y2.故④错误,故选:B.一十.三角形中位线定理(共1小题)13.(2023•广州)如图,在Rt△ABC中,∠ACB=90°,AB=10,AC=6,点M是边AC上一动点,点D,E分别是AB,MB的中点,当AM=2.4时,DE的长是 1.2.若点N在边BC上,且CN=AM,点F,G分别是MN,AN的中点,当AM>2.4时,四边形DEFG面积S的取值范围是3≤S≤4.【分析】依据题意,根据三角形中位线定理可得DE=AM=1.2;设AM=x,从而DE=x,由DE∥AM,且DE=AM,又FG∥AM,FG=AM,进而DE∥FG,DE=FG,从而四边形DEFG是平行四边形,结合题意可得DE边上的高为(4﹣x),故四边形DEFG面积S=4x﹣x2,进而利用二次函数的性质可得S的取值范围.【解答】解:由题意,点D,E分别是AB,MB的中点,∴DE是三角形ABM的中位线.∴DE=AM=1.2.如图,设AM=x,∴DE=AM=x.由题意得,DE∥AM,且DE=AM,又FG∥AM,FG=AM,∴DE∥FG,DE=FG.∴四边形DEFG是平行四边形.由题意,GF到AC的距离是x,BC==8,∴DE边上的高为(4﹣x).∴四边形DEFG面积S=2x﹣x2,=﹣(x﹣4)2+4.∵2.4<x≤6,∴3≤S≤4.故答案为:1.2;3≤S≤4.一十一.矩形的性质(共2小题)14.(2023•宁波)如图,以钝角三角形ABC的最长边BC为边向外作矩形BCDE,连结AE,AD,设△AED,△ABE,△ACD的面积分别为S,S1,S2,若要求出S﹣S1﹣S2的值,只需知道()A.△ABE的面积B.△ACD的面积C.△ABC的面积D.矩形BCDE的面积【分析】作AG⊥ED于点G,交BC于点F,可证明四边形BFGE是矩形,AF⊥BC,可推导出S﹣S1﹣S2=ED•AG﹣BE•EG﹣CD•DG=ED•AG﹣FG•ED=BC•AF=S△ABC,所以只需知道S△ABC,就可求出S﹣S1﹣S2的值,于是得到问题的答案.【解答】解:作AG⊥ED于点G,交BC于点F,∵四边形BCDE是矩形,∴∠FBE=∠BEG=∠FGE=90°,BC∥ED,BC=ED,BE=CD,∴四边形BFGE是矩形,∠AFB=∠FGE=90°,∴FG=BE=CD,AF⊥BC,∴S﹣S1﹣S2=ED•AG﹣BE•EG﹣CD•DG=ED•AG﹣FG•ED=BC•AF=S△ABC,∴只需知道S△ABC,就可求出S﹣S1﹣S2的值,故选:C.15.(2023•河南)矩形ABCD中,M为对角线BD的中点,点N在边AD上,且AN=AB=1.当以点D,M,N为顶点的三角形是直角三角形时,AD的长为2或1+.【分析】以点D,M,N为顶点的三角形是直角三角形时,分两种情况:如图1,当∠MND=90°时,如图2,当∠NMD=90°时,根据矩形的性质和等腰直角三角形的性质即可得到结论.【解答】解:以点D,M,N为顶点的三角形是直角三角形时,分两种情况:①如图1,当∠MND=90°时,则MN⊥AD,∵四边形ABCD是矩形,∴∠A=90°,∴MN∥AB,∵M为对角线BD的中点,∴AN=DN,∵AN=AB=1,∴AD=2AN=2;如图2,当∠NMD=90°时,则MN⊥BD,∵M为对角线BD的中点,∴BM=DM,∴MN垂直平分BD,∴BN=DN,∵∠A=90°,AB=AN=1,∴BN=AB=,∴AD=AN+DN=1+,综上所述,AD的长为2或1+.故答案为:2或1+.一十二.正方形的性质(共2小题)16.如图,在边长为4的正方形ABCD中,点G是BC上的一点,且BG=3GC,DE⊥AG于点E,BF∥DE,且交AG于点F,则tan∠EDF的值为()A.B.C.D.【分析】由正方形ABCD的边长为4及BG=3CG,可求出BG的长,进而求出AG的长,证△ADE∽△GAB,利用相似三角形对应边成比例可求得AE、DE的长,证△ABF≌△DAE,得AF=DE,根据线段的和差求得EF的长即可.【解答】解:∵四边形ABCD是正方形,AB=4,∴BC=CD=DA=AB=4,∠BAD=∠ABC=90°,AD∥BC,∴∠DAE=∠AGB,∵BG=3CG,∴BG=3,∴在Rt△ABG中,AB2+BG2=AG2,∴AG=,∵DE⊥AG,∴∠DEA=∠DEF=∠ABC=90°,∴△ADE∽△GAB,∴AD:GA=AE:GB=DE:AB,∴4:5=AE:3=DE:4,∴AE=,DE=,又∵BF∥DE,∴∠AFB=∠DEF=90°,又∵AB=AD,∠DAE=∠ABF(同角的余角相等),∴△ABF≌△DAE,∴AF=DE=,∴EF=AF﹣AE=,∴tan∠EDF=,故选:A.17.(2023•湖州)如图,标号为①,②,③,④的四个直角三角形和标号为⑤的正方形恰好拼成对角互补的四边形ABCD,相邻图形之间互不重叠也无缝隙,①和②分别是等腰Rt△ABE和等腰Rt△BCF,③和④分别是Rt△CDG和Rt△DAH,⑤是正方形EFGH,直角顶点E,F,G,H分别在边BF,CG,DH,AE上.(1)若EF=3cm,AE+FC=11cm,则BE的长是4cm.(2)若,则tan∠DAH的值是3.【分析】(1)将AE和FC用BE表示出来,再代入AE+FC=11cm,即可求出BE的长;(2)由已知条件可以证明∠DAH=∠CDG,从而得到tan∠DAH=tan∠CDG,设AH=x,DG=5k,GH =4k,用x和k的式子表示出CG,再利用tan∠DAH=tan∠CDG列方程,解出x,从而求出tan∠DAH 的值.【解答】解:(1)∵Rt△ABE和Rt△BCF都是等腰直角三角形,∴AE=BE,BF=CF,∵AE+FC=11cm,∴BE+BF=11cm,即BE+BE+EF=11cm,即2BE+EF=11cm,∵EF=3cm,∴2BE+3cm=11cm,∴BE=4cm,故答案为:4;(2)设AH=x,∵,∴可设DG=5k,GH=4k,∵四边形EFGH是正方形,∴HE=EF=FG=GH=4k,∵Rt△ABE和Rt△BCF都是等腰直角三角形,∴AE=BE,BF=CF,∠ABE=∠CBF=45°,∴CG=CF+GF=BF+4k=BE+8k=AH+12k=x+12k,∠ABC=∠ABE+∠CBF=45°+45°=90°,∵四边形ABCD对角互补,∴∠ADC=90°,∴∠ADH+∠CDG=90°,∵四边形EFGH是正方形,∴∠AHD=∠CGD=90°,∴∠ADH+∠DAH=90°,∴∠DAH=∠CDG,∴tan∠DAH=tan∠CDG,∴,即,整理得:x2+12kx﹣45k2=0,解得x1=3k,x2=﹣15k(舍去),∴tan∠DAH===3.故答案为:3.一十三.正多边形和圆(共1小题)18.(2023•河北)将三个相同的六角形螺母并排摆放在桌面上,其俯视图如图1,正六边形边长为2且各有一个顶点在直线l上.两侧螺母不动,把中间螺母抽出并重新摆放后,其俯视图如图2,其中,中间正六边形的一边与直线l平行,有两边分别经过两侧正六边形的一个顶点.则图2中:(1)∠α=30度;(2)中间正六边形的中心到直线l的距离为2(结果保留根号).【分析】(1)作图后,结合正多边形的外角的求法即可得到结论;(2)把问题转化为图形问题,首先作出图形,标出相应的字母,把正六边形的中心到直线l的距离转化为求ON=OM+BE,再根据正六边形的性质以及三角函数的定义,分别求出OM,BE即可.【解答】解:(1)作图如图所示,∵多边形是正六边形,∴∠ACB=60°,∵BC∥直线l,∴∠ABC=90°,∴α=30°;故答案为:30°;(2)取中间正六边形的中心为O,作图如图所示,由题意得,AG∥BF,AB∥GF,BF⊥AB,∴四边形ABFG为矩形,∴AB=GF,∵∠BAC=∠FGH,∠ABC=∠GFH=90°,∴△ABC≌△GFH(SAS),∴BC=FH,在Rt△PDE中,DE=1,PE=,由图1知AG=BF=2PE=2,OM=PE=,∵,∴,∴,∵,∴,∴.∴中间正六边形的中心到直线l的距离为2,故答案为:2.一十四.扇形面积的计算(共1小题)19.(2023•温州)图1是4×4方格绘成的七巧板图案,每个小方格的边长为,现将它剪拼成一个“房子”造型(如图2),过左侧的三个端点作圆,并在圆内右侧部分留出矩形CDEF作为题字区域(点A,E,D,B在圆上,点C,F在AB上),形成一幅装饰画,则圆的半径为5.若点A,N,M在同一直线上,AB∥PN,DE=EF,则题字区域的面积为.【分析】根据不共线三点确定一个圆,根据对称性得出圆心的位置,进而垂径定理、勾股定理求得r,连接OE,取ED的中点T,连接OT,在Rt△OET中,根据勾股定理即可求解.【解答】解:如图所示,依题意,GH=2=GQ,∵过左侧的三个端点Q,K,L作圆,QH=HL=4,又NK⊥QL,∴O在KN上,连接OQ,则OQ为半径,∵OH=r﹣KH=r﹣2,在Rt△OHQ中,OH2+QH2=QO2,∴(r﹣2)2+42=r2,解得:r=5;连接OE,取ED的中点T,连接OT,交AB于点S,连接PB,AM,过点O作OU⊥AM于点U.连接OA.由△OUN∽△NPM,可得==,∴OU=.MN=2,∴NU=,∴AU==,∴AN=AU﹣NU=2,∴AN=MN,∵AB∥PN,∴AB⊥OT,∴AS=SB,∴NS∥BM,∴NS∥MP,∴M,P,B共线,又NB=NA,∴∠ABM=90°,∵MN=NB,NP⊥MP,∴MP=PB=2,∴NS=MB=2,∵KH+HN=2+4=6,∴ON=6﹣5=1,∴OS=3,∵,设EF=ST=a,则,在Rt△OET中,OE2=OT2+TE2,即,整理得5a2+12a﹣32=0,即(a+4)(5a﹣8)=0,解得:或a=﹣4,∴题字区域的面积为.故答案为:.一十五.轴对称-最短路线问题(共1小题)20.(2023•安徽)如图,E是线段AB上一点,△ADE和△BCE是位于直线AB同侧的两个等边三角形,点P,F分别是CD,AB的中点.若AB=4,则下列结论错误的是()A.P A+PB的最小值为3B.PE+PF的最小值为2C.△CDE周长的最小值为6D.四边形ABCD面积的最小值为3【分析】延长AD,BC交于M,过P作直线l∥AB,由△ADE和△BCE是等边三角形,可得四边形DECM 是平行四边形,而P为CD中点,知P为EM中点,故P在直线l上运动,作A关于直线l的对称点A',连接A'B,当P运动到A'B与直线l的交点,即A',P,B共线时,P A+PB=P A'+PB最小,即可得P A+PB 最小值A'B==2,判断选项A错误;由PM=PE,即可得当M,P,F共线时,PE+PF 最小,最小值为MF的长度,此时PE+PF的最小值为2,判断选项B正确;过D作DK⊥AB于K,过C作CT⊥AB于T,由△ADE和△BCE是等边三角形,得KT=KE+TE=AB=2,有CD≥2,故△CDE周长的最小值为6,判断选项C正确;设AE=2m,可得S四边形ABCD=(m﹣1)2+3,即知四边形ABCD面积的最小值为3,判断选项D正确.【解答】解:延长AD,BC交于M,过P作直线l∥AB,如图:∵△ADE和△BCE是等边三角形,∴∠DEA=∠MBA=60°,∠CEB=∠MAB=60°,∴DE∥BM,CE∥AM,∴四边形DECM是平行四边形,∵P为CD中点,∴P为EM中点,∵E在线段AB上运动,∴P在直线l上运动,由AB=4知等边三角形ABM的高为2,∴M到直线l的距离,P到直线AB的距离都为,作A关于直线l的对称点A',连接A'B,当P运动到A'B与直线l的交点,即A',P,B共线时,P A+PB =P A'+PB最小,此时P A+PB最小值A'B===2,故选项A错误,符合题意;∵PM=PE,∴PE+PF=PM+PF,∴当M,P,F共线时,PE+PF最小,最小值为MF的长度,∵F为AB的中点,∴MF⊥AB,∴MF为等边三角形ABM的高,∴PE+PF的最小值为2,故选项B正确,不符合题意;过D作DK⊥AB于K,过C作CT⊥AB于T,如图,∵△ADE和△BCE是等边三角形,∴KE=AE,TE=BE,∴KT=KE+TE=AB=2,∴CD≥2,∴DE+CE+CD≥AE+BE+2,即DE+CE+CD≥AB+2,∴DE+CE+CD≥6,∴△CDE周长的最小值为6,故选项C正确,不符合题意;设AE=2m,则BE=4﹣2m,∴AK=KE=m,BT=ET=2﹣m,DK=AK=m,CT=BT=2﹣m,∴S△ADK=m•m=m2,S△BCT=(2﹣m)(2﹣m)=m2﹣2m+2,S梯形DKTC =(m+2﹣m)•2=2,∴S四边形ABCD=m2+m2﹣2m+2+2=m2﹣2m+4=(m﹣1)2+3,∴当m=1时,四边形ABCD面积的最小值为3,故选项D正确,不符合题意;故选:A.一十六.翻折变换(折叠问题)(共2小题)21.(2023•乐至县)如图,在平面直角坐标系xOy中,边长为2的等边△ABC的顶点A、B分别在x轴、y 轴的正半轴上移动,将△ABC沿BC所在直线翻折得到△DBC,则OD的最大值为+1.【分析】过点D作DF⊥AB,交AB延长线于点F,取AB的中点E,连接DE,OE,OD,在Rt△ABO 中利用斜边中线性质求出OE,根据OE+DE≥OD确定当D、O、E三点共线时OD最大,最大值为OD =OE+DE.【解答】解:如图,过点D作DF⊥AB,交AB延长线于点F,取AB的中点E,连接DE,OE,OD,∵等边三角形ABC的边长为2,∴AB=2,∠ABC=60°,由翻折可知:∠DBC=∠ABC=60°,DB=AB=2,∴∠DBF=60°,∵DF⊥AB,∴∠DFB=90°,∴∠BDF=30°,∴BF=BD=1,∴DF=BF=,∵E是AB的中点,∴AE=BE=OE=AB=1,∴EF=BE+BF=2,∴DE===,∴OD≤DE+OE=+1,∴当D、E、O三点共线时OD最大,最大值为+1.故答案为:+1.22.(2023•南京)如图,在菱形纸片ABCD中,点E在边AB上,将纸片沿CE折叠,点B落在B′处,CB′⊥AD,垂足为F.若CF=4cm,FB′=1cm,则BE=cm.【分析】作EH⊥BC于点H,由CF=4cm,FB′=1cm,求得B′C=5cm,由折叠得BC=B′C=5cm,由菱形的性质得BC∥AD,DC=BC=5cm,∠B=∠D,因为CB′⊥AD于点F,所以∠BCB′=∠CFD =90°,则∠BCE=∠B′CE=45°,DF==3cm,所以∠HEC=∠BCE=45°,则CH=EH,由=sin B=sin D=,=cos B=cos D=,得CH=EH=BE,BH=BE,于是得BE+BE =5,则BE=cm.【解答】解:作EH⊥BC于点H,则∠BHE=∠CHE=90°,∵CF=4cm,FB′=1cm,∴B′C=CF+FB′=4+1=5(cm),由折叠得BC=B′C=5cm,∠BCE=∠B′CE,∵四边形ABCD是菱形,∴BC∥AD,DC=BC=5cm,∠B=∠D,∵CB′⊥AD于点F,∴∠BCB′=∠CFD=90°,∴∠BCE=∠B′CE=∠BCB′=×90°=45°,DF===3(cm),∴∠HEC=∠BCE=45°,∴CH=EH,∵=sin B=sin D==,=cos B=cos D==,∴CH=EH=BE,BH=BE,∴BE+BE=5,∴BE=cm,故答案为:.一十七.旋转的性质(共1小题)23.(2023•西宁)如图,在矩形ABCD中,点P在BC边上,连接P A,将P A绕点P顺时针旋转90°得到P A′,连接CA′,若AD=9,AB=5,CA′=2,则BP=2.【分析】过A′点作A′H⊥BC于H点,如图,根据旋转的性质得到P A=P A′,再证明△ABP≌△PHA′得到PB=A′H,PH=AB=5,设PB=x,则A′H=x,CH=4﹣x,然后在Rt△A′CH中利用勾股定理得到x2+(4﹣x)2=(2)2,于是解方程求出x即可.【解答】解:过A′点作A′H⊥BC于H点,如图,∵四边形ABCD为矩形,∴BC=AD=9,∠B=90°,∵将P A绕点P顺时针旋转90°得到P A′,∴P A=P A′,∵∠P AB+∠APB=90°,∠APB+∠A′PH=90°,∴∠P AB=∠A′PH,在△ABP和△PHA′中,,∴△ABP≌△PHA′(AAS),∴PB=A′H,PH=AB=5,设PB=x,则A′H=x,CH=9﹣x﹣5=4﹣x,在Rt△A′CH中,x2+(4﹣x)2=(2)2,解得x1=x2=2,即BP的长为2.故答案为:2.一十八.相似三角形的判定与性质(共2小题)24.(2023•杭州)如图,在△ABC中,AB=AC,∠A<90°,点D,E,F分别在边AB,BC,CA上,连接DE,EF,FD,已知点B和点F关于直线DE对称.设=k,若AD=DF,则=(结果用含k的代数式表示).【分析】方法一:先根据轴对称的性质和已知条件证明DE∥AC,再证△BDE∽△BAC,推出EC=k•AB,通过证明△ABC∽△ECF,推出CF=k2•AB,即可求出的值.方法二:证明AD=DF=BD,可得BF⊥AC,设AB=AC=1,BC=k,CF=x,则AF=1﹣x,利用勾股定理列方程求出x的值,进而可以解决问题.【解答】解:方法一:∵点B和点F关于直线DE对称,∴DB=DF,∵AD=DF,∴AD=DB,∵AD=DF,∴∠A=∠DF A,∵点B和点F关于直线DE对称,∴∠BDE=∠FDE,∵∠BDE+∠FDE=∠BDF=∠A+∠DF A,∴∠FDE=∠DF A,∴DE∥AC,∴∠C=∠DEB,∠DEF=∠EFC,∵点B和点F关于直线DE对称,∴∠DEB=∠DEF,∴∠C=∠EFC,∵AB=AC,∴∠C=∠B,∵∠ACB=∠EFC,∴△ABC∽△ECF,∴=,∵DE∥AC,∴∠BDE=∠A,∠BED=∠C,∴△BDE∽△BAC,∴==,∴EC=BC,∵=k,∴BC=k•AB,∴EC=k•AB,∴=,∴CF=k2•AB,∴====.方法二:如图,连接BF,∵点B和点F关于直线DE对称,∴DB=DF,∵AD=DF,∴AD=DB=DF,∴BF⊥AC,设AB=AC=1,则BC=k,设CF=x,则AF=1﹣x,由勾股定理得,AB2﹣AF2=BC2﹣CF2,∴12﹣(1﹣x)2=k2﹣x2,∴x=,∴AF=1﹣x=,∴=.故答案为:.25.(2023•广东)边长分别为10,6,4的三个正方形拼接在一起,它们的底边在同一直线上(如图),则图中阴影部分的面积为15.【分析】根据相似三角形的性质,利用相似比求出梯形的上底和下底,用面积公式计算即可.【解答】解:如图,∵BF∥DE,∴△ABF∽△ADE,∴=,∵AB=4,AD=4+6+10=20,DE=10,∴=,∴BF=2,∴GF=6﹣2=4,∵CK∥DE,∴△ACK∽△ADE,∴=,∵AC=4+6=10,AD=20,DE=10,∴=,∴CK=5,∴HK=6﹣5=1,∴阴影梯形的面积=(HK+GF)•GH=(1+4)×6=15.故答案为:15.一十九.相似三角形的应用(共1小题)26.(2023•南京)如图,不等臂跷跷板AB的一端A碰到地面时,另一端B到地面的高度为60cm;当AB 的一端B碰到地面时,另一端A到地面的高度为90cm,则跷跷板AB的支撑点O到地面的高度OH是()A.36cm B.40cm C.42cm D.45cm【分析】过点B作BC⊥AH,垂足为C,再证明A字模型相似△AOH∽△ABC,从而可得=,过点A作AD⊥BH,垂足为D,然后证明A字模型相似△ABD∽△OBH,从而可得=,最后进行计算即可解答.【解答】解:如图:过点B作BC⊥AH,垂足为C,∵OH⊥AC,BC⊥AC,∴∠AHO=∠ACB=90°,∵∠BAC=∠OAH,∴△AOH∽△ABC,∴=,∴=,如图:过点A作AD⊥BH,垂足为D,∵OH⊥BD,AD⊥BD,∴∠OHB=∠ADB=90°,∵∠ABD=∠OBH,∴△ABD∽△OBH,∴=,∴=,∴+=+,∴+=,∴+=1,解得:OH=36,∴跷跷板AB的支撑点O到地面的高度OH是36cm,故选:A.二十.解直角三角形(共1小题)27.(2023•丹东)如图,在平面直角坐标系中,点O是坐标原点,已知点A(3,0),B(0,4),点C在x 轴负半轴上,连接AB,BC,若tan∠ABC=2,以BC为边作等边三角形BCD,则点C的坐标为(﹣2,0);点D的坐标为(﹣1﹣2,2+)或(﹣1+2,2﹣).【分析】过点C作CE⊥AB于E,先求处AB=5,再设BE=t,由tan∠ABC=2得CE=2t,进而得BC =,由三角形的面积公式得S△ABC=AC•OB=AB•CE,即5×2t=4×(3+OC),则OC=﹣3,然后在Rt△BOC中由勾股定理得,由此解出t1=2,t2=10(不合题意,舍去),此时OC=﹣3=2,故此可得点C的坐标;设点D的坐标为(m,n),由两点间的距离公式得:BC2=20,BD2=(m﹣0)2+(n﹣4)2,CD2=(m+2)2+(n﹣0)2,由△BCD为等边三角形得,整理:,②﹣①整理得m=3﹣2n,将m=3﹣2n代入①整理得n2﹣4n+1=0,解得n=,进而再求出m即可得点D的坐标.【解答】解:过点C作CE⊥AB于E,如图:∵点A(3,0),B(0,4),由两点间的距离公式得:AB==5,设BE=t,∵tan∠ABC=2,在Rt△BCE中,tan∠ABC=,∴=2,∴CE=2t,由勾股定理得:BC==t,∵CE⊥AB,OB⊥AC,AC=OC+OA=3+OC,∴S△ABC=AC•OB=AB•CE,即:5×2t=4×(3+OC),∴OC=﹣3,在Rt△BOC中,由勾股定理得:BC2﹣OB2=OC2,即,整理得:t2﹣12t+20=0,解得:t1=2,t2=10(不合题意,舍去),∴t=2,此时OC=﹣3=2,∴点C的坐标为(﹣2,0),设点D的坐标为(m,n),由两点间的距离公式得:BC2=(﹣2﹣0)2+(0﹣4)2=20,BD2=(m﹣0)2+(n﹣4)2,CD2=(m+2)2+(n﹣0)2,∵△BCD为等边三角形,∵BD=CD=BC,∴,整理得:,②﹣①得:4m+8n=12,∴m=3﹣2n,将m=3﹣2n代入①得:(3﹣2n)2+n2﹣8n=4,整理得:n2﹣4n+1=0,解得:n=,当n=时,m=3﹣2n=,当n=时,m=3﹣2n=,∴点D的坐标为或.故答案为:(﹣2,0);或.二十一.解直角三角形的应用(共1小题)28.(2023•杭州)第二十四届国际数学家大会会徽的设计基础是1700多年前中国古代数学家赵爽的“弦图”.如图,在由四个全等的直角三角形(△DAE,△ABF,△BCG,△CDH)和中间一个小正方形EFGH 拼成的大正方形ABCD中,∠ABF>∠BAF,连接BE.设∠BAF=α,∠BEF=β,若正方形EFGH与正方形ABCD的面积之比为1:n,tanα=tan2β,则n=()A.5B.4C.3D.2【分析】设AE=a,DE=b,则BF=a,AF=b,解直角三角形可得,化简可得(b﹣a)2=ab,a2+b2=3ab,结合勾股定理及正方形的面积公式可求得S正方形EFGH;S正方形ABCD=1:3,进而可求解n的值.【解答】解:设AE=a,DE=b,则BF=a,AF=b,∵tanα=,tanβ=,tanα=tan2β,∴,∴(b﹣a)2=ab,∴a2+b2=3ab,∵a2+b2=AD2=S正方形ABCD,(b﹣a)2=S正方形EFGH,∴S正方形EFGH:S正方形ABCD=ab:3ab=1:3,∵S正方形EFGH:S正方形ABCD=1:n,∴n=3.故选:C.。
2020年中考数学5.几何综合选择填空压轴题(含解析)

几何综合-填空选择压轴题51、以正方形ABCD勺边AD作等边△ ADE则/ BEC勺度数是 __________2、如图.在厶ABC中, / ACB=60 , AC=1, D是边AB的中点,E是边BC上一点.若DE平分△ ABC的周长,则DE的长是 ____ .3、已知CD是△ ABC的边AB上的高,若CD・3,AD=1AB=2AC则BC的长为__4、如图,将面积为32V2的矩形ABCC沿对角线BD折叠,点A的对应点为点P,连接AP交BC于点E.若BE=J,贝U AP的长为____ .p5、如图,△ ABC是等边三角形,△ ABD是等腰直角三角形,/ BAD=90 , AE L BD 于点E,连CD分别交AE AB于点F, G过点A作AH L CD交BD于点H.则下列结论:①/ ADC=15 :② AF=AG ③ AH=DF ④厶AF3A CBQ ⑤AF= (V3 - 1)EF.其中正确结论的个数为()A. 5 B . 4 C . 3 D . 26 已知O 0的半径为10cm AB CD是O O的两条弦,AB// CD AB=16cm CD=12cm则弦AB和CD之间的距离是cm513 13 13 7 77、如图,将矩形ABCD 沿 EF 折叠,使点B 落在AD 边上的点G 处,点C 落在点H 处,已知/ DGH=30,连接BG 则/ AGB ________ .8、如图,?ABCD 勺对角线相交于点 0,且A 》CD 过点0作OM L AC,交AD 于点 M.如果△ CDM 勺周长为8,那么?ABCD 勺周长是 _____ .9、如图,由四个全等的直角三角形围成的大正方形的面积是169,小正方形的面积为 49,则 sin a - COS a =( ) A 13 B10、如图,P是厶ABC的内心,连接PA PB PC, △ PAB △ PBG △ PAC的面积分别为S、S、S.则Si ____ S2+S3.(填“v” 或“二”或“〉”)11、如图,△ ABC中, AB=AC AD L BC 于D点,DEL AB 于点E, BF 丄AC 于点F,DE=3cryi 则BF= ______ cm12、如图,已知半圆O与四边形ABCD勺边AD AB BC都相切,切点分别为DE、C,半径OC=1 则AE?BE=_.13、《九章算术》是我国古代数学名著,书中有下列问题:“今有勾五步,股十二步,问勾中容方几何?”其意思为:“今有直角三角形,勾(短直角边)长为5步,股(长直角边)长为12步,冋该直角二角形能容纳的正方形边长最大是多少步?”该问题的答案是____________ 步.14、如图,以AB为直径的。
几何最值问题-2023年中考数学压轴题专项训练(全国通用)(解析版)

12023年中考数学压轴题专项训练1.几何最值问题一、压轴题速练1一、单选题1(2023·山东烟台·模拟预测)如图,在矩形ABCD 中,AB =8,AD =4,点E 是矩形ABCD 内部一动点,且∠BEC =90°,点P 是AB 边上一动点,连接PD 、PE ,则PD +PE 的最小值为()A.8 B.45 C.10 D.45-2【答案】A【分析】根据∠BEC =90°得到点的运动轨迹,利用“将军饮马”模型将PE 进行转化即可求解.【详解】解:如图,设点O 为BC 的中点,由题意可知,点E 在以BC 为直径的半圆O 上运动,作半圆O 关于AB 的对称图形(半圆O '),点E 的对称点为E 1,连接O 'E 1,则PE =PE 1,∴当点D 、P 、E 1、O '共线时,PD +PE 的值最小,最小值为DE 1的长,如图所示,在Rt △DCO '中,CD =8,CO '=6,∴DO '=82+62=10,又∵O 'E 1=2,∴DE 1=DO '-O 'E 1=8,即PD +PE 的最小值为8,故选:A .【点睛】本题考查线段和最短问题、轴对称的性质、勾股定理及圆周角定理,利用“将军饮马”模型将PE 进行转化时解题的关键.2(2023·安徽黄山·校考模拟预测)如图,在平面直角坐标系中,二次函数y =32x 2-32x -3的图象与x 轴交于点A ,C 两点,与y 轴交于点B ,对称轴与x 轴交于点D ,若P 为y 轴上的一个动点,连接PD ,则12PB +PD 的最小值为()2A.334B.32C.3D.543【答案】A【分析】作射线BA ,作PE ⊥BA 于E ,作DF ⊥BA 于F ,交y 轴于P ,可求得∠ABO =30°,从而得出PE =12PB ,进而得出PD +12PB =PD +EP ,进一步得出结果.【详解】解:如图,作射线BA ,作PE ⊥BA 于E ,作DF ⊥BA 于F ,交y 轴于P ,抛物线的对称轴为直线x =--322×32=12,∴OD =12,当x =0时,y =-3,∴OB =3,当y =0时,32x 2-32x -3=0,∴x 1=-1,x 2=2,∴A (-1,0),∴OA =1,∵tan ∠ABO =OA OB =13=33,∴∠ABO =30°,∴PE =12PB ,∴12PB +PD =PD +PE ≥DF ,当点P 在P 时,PD +PE 最小,最大值等于DF ,在Rt △ADF 中,∠DAF =90°-∠ABO =60°,AD =OD +PA =12+1=32,∴DF =AD ⋅sin ∠DAE =32×32-334,∴12PB +PD 最小=DF =334,故选:A .【点睛】本题以二次函数为背景,考查了二次函数与一元二次方程之间的关系,解直角三角形等知识,解决问题的关键是用三角函数构造12PB .3(2023秋·浙江金华·九年级统考期末)如图,正方形ABCD 的边长为4,点E 是正方形ABCD 内的动点,点P 是BC 边上的动点,且∠EAB =∠EBC .连结AE ,BE ,PD ,PE ,则PD +PE 的最小值为()3A.213-2B.45-2C.43-2D.215-2【答案】A【分析】先证明∠AEB =90°,即可得点E 在以AB 为直径的半圆上移动,设AB 的中点为O ,作正方形ABCD 关于直线BC 对称的正方形CFGB ,则点D 的对应点是F ,连接FO 交BC 于P ,交半圆O 于E ,根据对称性有:PD =PF ,则有:PE +PD =PE +PF ,则线段EF 的长即为PE +PD 的长度最小值,问题随之得解.【详解】解:∵四边形ABCD 是正方形,∴∠ABC =90°,∴∠ABE +∠EBC =90°,∵∠EAB =∠EBC ,∴∠EAB +∠EBA =90°,∴∠AEB =90°,∴点E 在以AB 为直径的半圆上移动,如图,设AB 的中点为O ,作正方形ABCD 关于直线BC 对称的正方形CFGB ,则点D 的对应点是F ,连接FO 交BC 于P ,交半圆O 于E ,根据对称性有:PD =PF ,则有:PE +PD =PE +PF ,则线段EF 的长即为PE +PD 的长度最小值,E∵∠G =90°,FG =BG =AB =4,∴OG =6,OA =OB =OE =2,∴OF =FG 2+OG 2=213,∴EF =OF -OE =213-2,故PE +PD 的长度最小值为213-2,故选:A .【点睛】本题考查了轴对称-最短路线问题,正方形的性质,勾股定理,正确的作出辅助线,得出点E 的运动路线是解题的关键.4(2022秋·安徽池州·九年级统考期末)如图,Rt △ABC 中,∠C =90°,AC =4,BC =3,点P 为AC 边上的动点,过点P 作PD ⊥AB 于点D ,则PB +PD 的最小值为()4 A.154 B.245 C.5 D.203【答案】B【分析】作点B 关于AC 的对称点B ,过点B 作B D ⊥AB 于点D ,交AC 于点P ,点P 即为所求作的点,此时PB +PD 有最小值,连接AB ,根据对称性的性质,可知:BP =B P ,△ABC ≅△AB C ,根据S △ABB =S △ABC +S △AB C =2S △ABC ,即可求出PB +PD 的最小值.【详解】解:如下图,作点B 关于AC 的对称点B ,过点B 作B D ⊥AB 于点D ,交AC 于点P ,连接AB ,点P 即为所求作的点,此时PB +PD 有最小值,根据对称性的性质,可知:BP =B P ,在Rt △ABC 中,∠ACB =90°,AC =4,BC =3,∴AB =AC 2+BC 2=5,根据对称性的性质,可知:△ABC ≅△AB C ,∴S △ABB =S △ABC +S △ABC =2S △ABC ,即12×AB ⋅B D =2×12BC ⋅AC ,∴5B D =24,∴B D =245,故选:B .【点睛】本题考查了轴对称一最短路线问题,解题的关键是掌握轴对称的性质.5(2023秋·甘肃定西·八年级校考期末)如图所示,在△ABC 中,∠ABC =68°,BD 平分∠ABC ,P 为线段BD 上一动点,Q 为 边AB 上一动点,当AP +PQ 的值最小时,∠APB 的度数是()A.118°B.125°C.136°D.124°【答案】D【分析】先在BC 上截取BE =BQ ,连接PE ,证明△PBQ ≌△PBE SAS ,得出PE =PQ ,说明AP +PQ =AP +PE ,找出当A 、P 、E 在同一直线上,且AE ⊥BC 时,AP +PE 最小,即AP +PQ 最小,过点A 作AE ⊥BC 于点E ,交BD 于点P ,根据三角形外角的性质可得答案.【详解】解:在BC 上截取BE =BQ ,连接PE ,如图:∵BD 平分∠ABC ,∠ABC =68°,∴∠ABD =∠CBD =12∠ABC =34°,∵BP =BP ,∴△PBQ ≌△PBE SAS ,∴PE =PQ ,∴AP +PQ =AP +PE ,∴当A 、P 、E 在同一直线上,且AE ⊥BC 时,AP +PE 最小,即AP +PQ最小,过点A作AE ⊥BC 于点E ,交BD 于点P ,如图:∵∠AEB =90°,∠CBD =34°,∴∠APB =∠AEB +∠CBD =124°.故选:D .5【点睛】本题主要考查了角平分线的定义,三角形全等的判定和性质,垂线段最短,三角形内角和定理与三角形的外角的性质,解题的关键是找出使AP +PQ 最小时点P 的位置.6(2022秋·重庆沙坪坝·八年级重庆市凤鸣山中学校联考期末)如图,E 为正方形ABCD 边AD 上一点,AE =1,DE =3,P 为对角线BD 上一个动点,则PA +PE 的最小值为()A.5B.42C.210D.10【答案】A【分析】连接EC 交BD 于P 点,根据“两点之间线段最短”,可知PA +PE 的最小值即为线段EC 的长,求出EC 的长即可.【详解】连接EC ,交BD 于P 点∵四边形ABCD 为正方形∴A 点和C 点关于BD 对称∴PA =PC∴PA +PE =PC +PE =EC根据“两点之间线段最短”,可知PA +PE 的最小值即为线段EC 的长.∵AE =1,DE =3∴AD =4∴DC =4∴CE =DE 2+CD 2=32+42=5∴PA +PE 的最小值为5故选:A【点睛】本题主要考查了正方形的性质和两点之间线段最短,这是一个将军饮马模型.熟练掌握正方形的性质并且能够识别出将军饮马模型是解题的关键.7(2023春·湖南张家界·八年级统考期中)如图,正方形ABCD 的边长为4,点M 在DC 上,且DM =1,N 是AC 上一动点,则DN +MN 的最小值为()A.4B.42C.25D.5【答案】D【分析】由正方形的对称性可知点B 与D 关于直线AC 对称,连接BM 交AC 于N ′,N ′即为所求在Rt △BCM 中利用勾股定理即可求出BM 的长即可.【详解】∵四边形ABCD 是正方形,∴点B 与D 关于直线AC 对称,6连接BD ,BM 交AC 于N ′,连接DN ′,∴当B 、N 、M 共线时,DN +MN 有最小值,则BM 的长即为DN +MN 的最小值,∴AC 是线段BD 的垂直平分线,又∵CD =4,DM =1∴CM =CD -DM =4-1=3,在Rt △BCM 中,BM =CM 2+BC 2=32+42=5故DN +MN 的最小值是5.故选:D .【点睛】本题考查的是轴对称-最短路线问题及正方形的性质,先作出D 关于直线AC 的对称点,由轴对称及正方形的性质判断出D 的对称点是点B 是解答此题的关键.8(2022秋·浙江杭州·九年级杭州外国语学校校考开学考试)如图,在平面直角坐标系中,二次函数y =-x 2+bx +3的图像与x 轴交于A 、C 两点,与x 轴交于点C (3,0),若P 是x 轴上一动点,点D 的坐标为(0,-1),连接PD ,则2PD +PC 的最小值是()A.4B.2+22C.22D.32+232【答案】A【分析】过点P 作PJ ⊥BC 于J ,过点D 作DH ⊥BC 于H ,根据2PD +PC =2PD +22PC =2PD +PJ ,求出DP +PJ 的最小值即可解决问题.【详解】解:连接BC ,过点P 作PJ ⊥BC 于J ,过点D 作DH ⊥BC 于H .∵二次函数y =-x 2+bx +3的图像与x 轴交于点C (3,0),∴b =2,∴二次函数的解析式为y =-x 2+2x +3,令y =0,-x 2+2x +3=0,解得x =-1或3,∴A (-1,0),令x =0,y =3,∴B (0,3),∴OB =OC =3,∵∠BOC =90°,∴∠OBC =∠OCB =45°,∵D(0,-1),∴OD =1,BD =4,∵DH ⊥BC ,∴∠DHB =90°,设DH =x ,则BH =x ,∵DH 2+BH 2=BD 2,7∴x =22,∴DH =22,∵PJ ⊥CB ,∴∠PJC =90°,∴PJ =22PC ,∴2PD +PC =2PD +22PC =2PD +PJ ,∵DP +PJ ≥DH ,∴DP +PJ ≥22,∴DP +PJ 的最小值为22,∴2PD +PC 的最小值为4.故选:A .【点睛】本题考查了二次函数的相关性质,以及等腰直角三角形的判定和性质,垂线段最短等知识,得到∠OBC =∠OCB =45°,PJ =22PC 是解题的关键.9(2022·山东泰安·统考中考真题)如图,四边形ABCD 为矩形,AB =3,BC =4.点P 是线段BC 上一动点,点M 为线段AP 上一点.∠ADM =∠BAP ,则BM 的最小值为()A.52 B.125 C.13-32 D.13-2【答案】D【分析】证明∠AMD =90°,得出点M 在O 点为圆心,以AO 为半径的圆上,从而计算出答案.【详解】设AD 的中点为O ,以O 点为圆心,AO 为半径画圆∵四边形ABCD 为矩形∴∠BAP +∠MAD =90°∵∠ADM =∠BAP∴∠MAD +∠ADM =90°∴∠AMD =90°∴点M 在O 点为圆心,以AO 为半径的圆上连接OB 交圆O 与点N∵点B 为圆O 外一点∴当直线BM 过圆心O 时,BM 最短∵BO 2=AB 2+AO 2,AO =12AD =2∴BO 2=9+4=13∴BO =13∵BN =BO -AO =13-2故选:D .【点睛】本题考查直角三角形、圆的性质,解题的关键是熟练掌握直角三角形和圆的相关知识.810(2022·河南·校联考三模)如图1,正方形ABCD 中,点E 是BC 的中点,点P 是对角线AC 上的一个动点,设AP =x ,PB +PE =y ,当点P 从A 向点C 运动时,y 与x 的函数关系如图2所示,其中点M 是函数图象的最低点,则点M 的坐标是()A.42,35B.22,35C.35,22D.35,42【答案】A【分析】根据图像,当P 与C 重合时,PB +PE =9即CB +CE =9,从而确定正方形的边长为6,根据将军饮马河原理,连接DE 交AC 于点G ,当点P 与点G 重合时,PE +PB 最小,且为DE 的长即点M 的纵坐标,利用相似三角形,计算AG 的长即为横坐标.【详解】如图,根据图像,当P 与C 重合时,PB +PE =9即CB +CE =9,∵点E 是BC 的中点,∴BC =6,连接DE 交AC 于点G ,当点P 与点G 重合时,PE +PB 最小,且为DE 的长即点M 的纵坐标,∵四边形ABCD 是正方形,AB =6,∴CE ∥AD ,AC =62+62=62,DE =62+32=35,∴△CGE ∽△AGD ,∴CG AG =CE AD =12,∴AC AG=32,∴AG =42,故点M 的坐标为(42,35),故A 正确.故选:A .【点睛】本题考查了正方形的性质,三角形相似的判定和性质,函数图像信息的获取,将军饮马河原理,熟练掌握正方形的性质,灵活运用三角形相似,构造将军饮马河模型求解是解题的关键.2二、填空题11(2023春·江苏宿迁·九年级校联考阶段练习)如图,矩形ABCD ,AB =4,BC =8,E 为AB 中点,F 为直线BC 上动点,B 、G 关于EF 对称,连接AG ,点P 为平面上的动点,满足∠APB =12∠AGB ,则DP 的最小值.【答案】210-22【分析】由题意可知,∠AGB =90°,可得∠APB =12∠AGB =45°,可知点P 在以AB 为弦,圆周角∠APB =45°的9圆上,(要使DP 最小,则点P 要靠近蒂点D ,即点P 在AB 的右侧),设圆心为O ,连接OA ,OB ,OE ,OP ,OD ,过点O 作OQ ⊥AD ,可知△AOB 为等腰直角三角形,求得OA =22AB =22=OP ,AQ =OQ =22OA =2,QD =AD -AQ =6,OD =OQ 2+QD 2=210,再由三角形三边关系可得:DP ≥OD -OP =210-22,当点P 在线段OD 上时去等号,即可求得DP 的最小值.【详解】解:∵B 、G 关于EF 对称,∴BH =GH ,且EF ⊥BG∵E 为AB 中点,则EH 为△ABG 的中位线,∴EH ∥AG ,∴∠AGB =90°,∵∠APB =12∠AGB ,即∠APB =12∠AGB =45°,∴点P 在以AB 为弦,圆周角∠APB =45°的圆上,(要使DP 最小,则点P 要靠近蒂点D ,即点P 在AB 的右侧)设圆心为O ,连接OA ,OB ,OE ,OP ,OD ,过点O 作OQ ⊥AD ,则OA =OB =OP ,∵∠APB =45°,∴∠AOB =90°,则△AOB 为等腰直角三角形,∴OA =22AB =22=OP ,又∵E 为AB 中点,∴OE ⊥AB ,OE =12AB =AE =BE ,又∵四边形ABCD 是矩形,∴∠BAD =90°,AD =BC =8,∴四边形AEOQ 是正方形,∴AQ =OQ =22OA =2,QD =AD -AQ =6,∴OD =OQ 2+QD 2=210,由三角形三边关系可得:DP ≥OD-OP =210-22,当点P 在线段OD 上时去等号,∴DP 的最小值为210-22,故答案为:210-22.【点睛】本题考查轴对称的性质,矩形的性质,隐形圆,三角形三边关系,正方形的判定及性质,等腰直角三角形的判定及性质,根据∠APB =12∠AGB =45°得知点P 在以AB 为弦,圆周角∠APB =45°的圆上是解决问题的关键.12(2023春·江苏连云港·八年级期中)如图,在边长为8的正方形ABCD 中,点G 是BC 边的中点,E 、F 分别是AD 和CD 边上的点,则四边形BEFG 周长的最小值为.【答案】2410【分析】作点G 关于CD 的对称点G ,作点B 关于AD 的对称点B ,连接B G ,根据两点之间线段最短即可解决问题.【详解】作点G 关于CD 的对称点G ,作点B 关于AD 的对称点B ,连接B G∵EB =EB ,FG =FG ,∴BE +EF +FG +BG =B E +EF +FG +BG ,∵EB +EF +FG ≥B G ,∴四边形BEFG 的周长的最小值=BG +B G ,∵正方形ABCD 的边长为8∴BG =4,BB =16,BG =12,∴B G =162+122=20,∴四边形BEFG 的周长的最小值为=4+20=24.故答案为:24.【点睛】本题考查轴对称求线段和的最短问题,正方形的性质,勾股定理,解题的关键是学会利用轴对称解决最短问题.13(2022·湖南湘潭·校考模拟预测)如图,菱形草地ABCD 中,沿对角线修建60米和80米两条道路AC <BD ,M 、N 分别是草地边BC 、CD 的中点,在线段BD 上有一个流动饮水点P ,若要使PM +PN 的距离最短,则最短距离是米.【答案】50【分析】作M 关于BD 的对称点Q ,连接NQ ,交BD 于P ,连接MP ,当P 点与P 重合时,MP +NP =MP +NP =NQ 的值最小,根据菱形的性质和勾股定理求出BC 长,即可得出答案.【详解】解:作M 关于BD 的对称点Q ,连接NQ ,交BD 于P ,连接MP ,当P 点与P 重合时,MP +NP =MP +NP =NQ 的值最小,∵四边形ABCD 是菱形,∴AC ⊥BD ,∠QBP =∠MBP ,即Q 在AB 上,∵MQ ⊥BD ,∴AC ∥MQ ,∴M 为BC 中点,∴Q 为AB 中点,∵N 为CD 中点,四边形ABCD 是菱形,∴BQ ∥CD ,BQ =CN ,∴四边形BQNC 是平行四边形,∴NQ =BC ,设AC 与BD 的交点为点O ,∵四边形ABCD 是菱形,∴AC ⊥BD,OC =12AC =30米,OB =12BD =40米,∴BC =OB 2+OC 2=50米,∴PM +PN 的最小值是50米.故答案为:50.11【点睛】本题考查了轴对称-最短路线问题,平行四边形的性质和判定,菱形的性质,勾股定理的应用,解此题的关键是能根据轴对称找出P 的位置.14(2023春·江苏·九年级校考阶段练习)如图,正方形ABCD 的边长为4,⊙B 的半径为2,P 为⊙B 上的动点,则2PC -PD 的最大值是.【答案】2【分析】解法1,如图:以PD 为斜边构造等腰直角三角形△PDM ,连接MC ,BD ,连接PM 、DM ,推得2PC -PD=2PC -22PD =2PC -PM ,因为PC -PM ≤MC ,求出MC 即可求出答案.解法2:如图:连接BD 、BP 、PC ,在BD 上做点M ,使BM BP =24,连接MP ,证明△BMP ∼△BPD ,在BC 上做点N ,使BN BP=12,连接NP ,证明△BNP ∼△BPC ,接着推导出2PC -PD =22MN ,最后证明△BMN ∼△BCD ,即可求解.【详解】解法1如图:以PD 为斜边构造等腰直角三角形△PDM ,连接MC ,BD ,∴∠PDM =45,DM =PM =22PD ,∵四边形ABCD 正方形∴∠BDC =45°,DB DC=2又∵∠PDM =∠PDB +MDB ,∠BDC =∠MDB +MDC∴∠PDB =∠MDC在△BPD 与△MPC 中∠PDB =∠MDC ,DB DC=DP DM =2∴△BPD ∼△MPC∴PB MC=2∵BP =2∴MC =2∵2PC -PD =2PC-22PD =2PC -PM ∵PC -PM ≤MC ∴2PC -PD =2PC -PM ≤2MC =2故答案为:2.解法2如图:连接BD 、BP 、PC根据题意正方形ABCD 的边长为4,⊙B 的半径为2∴BP =2,BD =BC 2+CD 2=42+42=42∵BP BD =242=2412在BD 上做点M ,使BM BP=24,则BM =22,连接MP 在△BMP 与△BPD 中∠MBP =∠PBD ,BP BD =BM BP∴△BMP ∼△BPD∴PM PD =24,则PD =22PM ∵BP BC =24=12在BC 上做点N ,使BN BP=12,则BN =1,连接NP 在△BNP 与△BPC 中∠NBP =∠PBC ,BN BP =BP PC∴△BNP ∼△BPC∴PN PC=12,则PC =2PN ∴如图所示连接NM ∴2PC -PD =2×2PN -22PM =22PN -PM ∵PN -PM ≤NM ∴2PC -PD =22PN -PM ≤22NM在△BMN 与△BCD 中∠NBM=∠DBC ,BM BC =224=28,BN BD =142=28∴BM BC=BN BD ∴△BMN ∼△BCD∴MN CD=28∵CD =4∴MN =22∴22MN =22×22=2∴2PC -PD ≤22NM =2故答案为:2.【点睛】本题考查正方形的性质,相似三角形,勾股定理等知识,难度较大,熟悉以上知识点运用是解题关键.15(2023秋·广东广州·九年级统考期末)如图,四边形ABCD 中,AB ∥CD ,AC ⊥BC ,∠DAB =60°,AD =CD =4,点M 是四边形ABCD 内的一个动点,满足∠AMD =90°,则△MBC 面积的最小值为.【答案】63-4【分析】取AD 的中点O ,连接OM ,过点M 作ME ⊥BC 交BC 的延长线于点E ,过点O 作OF ⊥BC 于F ,交CD 于G ,则OM +ME ≥OF ,通过计算得出当O ,M ,E 三点共线时,ME 有最小值,求出最小值即可.【详解】解:如图,取AD 的中点O ,连接OM ,过点M 作ME ⊥BC 交BC 的延长线于点E ,过点O 作OF ⊥BC 于F ,交CD 于G ,则13OM +ME ≥OF ,∵AB ∥CD ,∠DAB =60°,AD =CD =4,∴∠ADC =120°,∵AD =CD ,∴∠DAC =30°,∴∠CAB =30°,∵AC ⊥BC ,∴∠ACB =90°∴∠B =90°-30°=60°,∴∠B =∠DAB ,∴四边形ABCD 为等腰梯形,∴BC =AD =4,∵∠AMD =90°,AD =4,OA =OD ,∴OM =12AD =2,∴点M 在以点O 为圆心,2为半径的圆上,∵AB ∥CD ,∴∠GCF =∠B =60°,∴∠DGO =∠CGF =30°,∵OF ⊥BC ,AC ⊥BC ,∴∠DOG =∠DAC =30°=∠DGO ,∴DG =DO =2,∴OG =2OD ⋅cos30°=23,GF =3,OF =33,∴ME ≥OF -OM =33-2,∴当O ,M ,E 三点共线时,ME 有最小值33-2,∴△MBC 面积的最小值为=12×4×33-2 =63-4.【点睛】本题考查了解直角三角形、隐圆、直角三角形的性质等知识点,点M 位置的确定是解题关键.16(2023春·全国·八年级专题练习)如图,在等边△ABC 中,BD ⊥AC 于D ,AD =3cm .点P ,Q 分别为AB,AD 上的两个定点且BP =AQ =1cm ,点M 为线段BD 上一动点,连接PM ,QM ,则PM +QM 的最小值为cm .【答案】5【分析】如图所示,作点P 关于BD 的对称点P ,且点P 在BC 上,则PM +QM =P M+QM ,当P ,M ,Q 在同一条直线上时,有最小值,证明四边形PP QA 是平行四边形,P Q =AP =AB -BP ,由此即可求解.【详解】解:如图所示,作点P 关于BD 的对称点P ,∵△ABC 是等边三角形,BD ⊥AC ,∴∠ABD =∠DBC =12∠ABC =12×60°=30°,14∴点P 在BC 上,∴P M =PM ,则PM +QM =P M +QM ,当P ,M ,Q 在同一条直线上时,有最小值,∵点P 关于BD 的对称点P ,∠ABD =∠DBC =30°,∴PP ⊥BM ,BP =BP =1cm ,∴∠BP P =60°,∴△BPP 是等边三角形,即∠BP P =∠C =60°,∴PP ∥AC ,且PP =AQ =1cm ,∴四边形PP QA 是平行四边形,∴P Q =AP =AB -BP ,在Rt △ABD 中,∠ABD =30°,AD =3,∴AB =2AD =2×3=6,∴AP =P Q =P M +QM =PM +QM =AB -BP =6-1=5,故答案为:5.【点睛】本题主要考查动点与等边三角形,对称-最短路径,平行四边形的判定和性质的综合,理解并掌握等边三角形得性质,对称-最短路径的计算方法,平行四边形的判定和性质是解题的关键.17(2022秋·山东菏泽·九年级校考阶段练习)如图,在周长为12的菱形ABCD 中,DE =1,DF =2,若P 为对角线AC 上一动点,则EP +FP 的最小值为.【答案】3【分析】作F 点关于BD 的对称点F ,连接EF 交BD 于点P ,则PF =PF ,由两点之间线段最短可知当E 、P 、F 在一条直线上时,EP +FP 有最小值,然后求得EF 的长度即可.【详解】解:作F 点关于BD 的对称点F ,则PF =PF ,连接EF '交BD 于点P .∴EP +FP =EP +F P .由两点之间线段最短可知:当E 、P 、F '在一条直线上时,EP +FP 的值最小,此时EP +FP =EP +F P =EF .∵四边形ABCD 为菱形,周长为12,∴AB =BC =CD =DA =3,AB ∥CD ,∵AF =2,AE =1,∴DF =AE =1,∴四边形AEF D 是平行四边形,∴EF =AD =3.∴EP +FP 的最小值为3.故答案为:3.【点睛】本题主要考查的是菱形的性质、轴对称--路径最短问题,明确当E 、P 、F 在一条直线上时EP +FP 有最小值是解题的关键.18(2023春·上海·八年级专题练习)如图,直线y =x +4与x 轴,y 轴分别交于A和B ,点C 、D 分别为线段AB 、OB 的中点,P 为OA 上一动点,当PC +PD 的值最小时,点P 的坐标为.15【答案】(-1,0)【分析】直线y =x +4与x 轴,y 轴分别交于A 和B ,可求出点A ,B 的坐标,点C 、D 分别为线段AB 、OB 的中点,可求出点C 、D 的坐标,作点C 关于x 轴的对称点C ,连接C D 与x 轴的交点就是所求点P 的坐标.【详解】解:直线y =x +4与x 轴,y 轴分别交于A 和B ,∴当y =0,x =-4,即A (-4,0);当x =0,y =4,即B (0,4),∵点C 、D 分别为线段AB 、OB 的中点,∴C (-2,2),D (0,2),如图所示,过点C 关于x 轴的对称点C,∴C (-2,-2),∴直线C D 的解析式为:y =2x +2,当y =0,x =-1,即P (-1,0),故答案为:(-1,0).【点睛】本题主要考查一次函数与最短线段的综合,掌握对称中最短线段的解题方法是解题的关键.19(2023秋·黑龙江鸡西·九年级统考期末)如图,抛物线y =x 2-4x +3与x 轴分别交于A ,B两点(点A 在点B 的左侧),与y 轴交于点C ,在其对称轴上有一动点M ,连接MA ,MC ,AC ,则△MAC 周长的最小值是.【答案】32+10【分析】根据“将军饮马”模型,先求出A 1,0 ,B 3,0 ,C 0,3 ,由二次函数对称性,A ,B 关于对称轴对称,从而C △MAC =CA +CM +MA =CA +CM +MB ,AC =OA 2+OC 2=10,则△MAC 周长的最小值就是CM +MB 的最小值,根据两点之间线段最短即可得到CM +MB 的最小值为C ,M ,B 三点共线时线段CB 长,从而得到CB =OC 2+OB 2=32,即可得到答案.【详解】解:∵抛物线y =x 2-4x +3与x 轴分别交于A ,B 两点(点A 在点B 的左侧),与y 轴交于点C ,16∴当y =0时,0=x 2-4x +3解得x =1或x =3,即A 1,0 ,B 3,0 ;当x =0时,y =3,即C 0,3 ,由二次函数对称性,A ,B 关于对称轴对称,即MA =MB ,∴C △MAC =CA +CM +MA =CA +CM +MB ,∵AC =OA 2+OC 2=10,∴△MAC 周长的最小值就是CM +MB 的最小值,根据两点之间线段最短即可得到CM +MB 的最小值为C ,M ,B 三点共线时线段CB 长,∵CB =OC 2+OB 2=32,∴△MAC 周长的最小值为CA +CB =32+10,故答案为:32+10.【点睛】本题考查动点最值问题与二次函数综合,涉及“将军饮马”模型求最值、二次函数图像与性质、解一元二次方程、勾股定理求线段长等知识,熟练掌握动点最值的常见模型是解决问题的关键.20(2023秋·浙江温州·九年级校考期末)如图所示,∠ACB =60°,半径为2的圆O 内切于∠ACB.P 为圆O 上一动点,过点P 作PM 、PN 分别垂直于∠ACB 的两边,垂足为M 、N ,则PM +2PN 的取值范围为.【答案】6-23≤PM +2PN ≤6+23【分析】根据题意,本题属于动点最值问题-“阿氏圆”模型,首先作MH ⊥NP 于H ,作MF ⊥BC 于F ,如图所示,通过代换,将PM +2PN 转化为PN +12PM =PN +HP =NH ,得到当MP 与⊙O 相切时,MF 取得最大值和最小值,分两种情况,作出图形,数形结合解直角三角形即可得到相应最值,进而得到取值范围.【详解】解:作MH ⊥NP 于H ,作MF ⊥BC 于F ,如图所示:∵PM ⊥AC ,PN ⊥CB ,∴∠PMC =∠PNC =90°,∴∠MPN =360°-∠PMC -∠PNC -∠C =120°,∴∠MPH =180°-∠MPN =60°,∴HP =PM ⋅cos ∠MPH =PM ⋅cos60°=12PM ,∴PN +12PM =PN +HP =NH ,∵MF =NH ,∴当MP 与⊙O 相切时,MF 取得最大和最小,①连接OP ,OG ,OC ,如图1所示:可得:四边形OPMG 是正方形,∴MG =OP =2,在Rt △COG 中,CG =OG ⋅tan60°=23,∴CM =CG +GM =2+23,在Rt △CMF 中,MF =CM ⋅sin60°=3+3,∴HN =MF =3+3,即PM +2PN =212PM +PN =2HN =6+23;②连接OP ,OG ,OC ,如图2所示:可得:四边形OPMG 是正方形,17∴MG =OP =2,由上同理可知:在Rt △COG 中,CG =OG ⋅tan60°=23,∴CM =CG -GM =23-2,在Rt △CMF 中,MF =CM ⋅sin60°=3-3,∴HN =MF =3-3,即PM +2PN =212PM +PN =2HN =6-23,∴6-23≤PM +2PN ≤6+23.故答案为:6-23≤PM +2PN ≤6+23.【点睛】本题考查动点最值模型-“阿氏圆”,难度较大,掌握解决动点最值问题的方法,熟记相关几何知识,尤其是圆的相关知识是解决问题的关键.3三、解答题21(2022春·江苏·九年级专题练习)综合与探究如图,已知抛物线y =ax 2+bx +4经过A -1,0 ,B 4,0 两点,交y 轴于点C .(1)求抛物线的解析式,连接BC ,并求出直线BC 的解析式;(2)请在抛物线的对称轴上找一点P ,使AP +PC 的值最小,此时点P 的坐标是;(3)点Q 在第一象限的抛物线上,连接CQ ,BQ ,求出△BCQ 面积的最大值.【答案】(1)y =-x 2+3x +4;y =-x +4(2)32,52(3)8【分析】(1)将A -1,0 ,B 4,0 两点,代入抛物线解析式,可得到抛物线解析式,从而得到C 0,4 ,再设直线BC 的解析式为y =kx +b k ≠0 ,把点B 、C 的坐标代入,即可求解;(2)连接BC ,PB ,根据题意可得A 、B 关于抛物线的对称轴直线x =32对称,从而得到当P 在直线AB 上三点共线时,AP +CP 的值最小,把x =32代入直线BC 的解析式,即可求解;(3)过Q 作QD ⊥x 轴,交BC 于D ,设Q d ,-d 2+3d +4 ,其中0≤d ≤4,则D d ,-d +4 ,可得QD =-d 2+4d ,从而得到S ΔBCQ =12OB ×QD =-2d -2 2+8,即可求解;【详解】(1)解:(1)∵抛物线y =ax 2+bx +4经过A -1,0 ,B 4,0 两点,∴a -b +4=016a +4b +4=0,解得:a =-1b =3 ,18∴抛物线的解析式为y =-x 2+3x +4;∵抛物线与y 轴的交点为C ,∴C 0,4 ,设直线BC 的解析式为y =kx +b k ≠0 ,把点B 、C 的坐标代入得:4k +b =0b =4 ,解得:k =-1b =4 ,∴直线BC 的解析式为y =-x +4;(2)如图,连接BC ,PB ,∵y =-x 2+3x +4=-x -32 2+74,∴抛物线的对称轴为直线x =32,根据题意得:A 、B 关于抛物线的对称轴直线x =32对称,∴AP =BP ,∴AP +CP =BP +CP ≥BC ,即当P 在直线AB 上时,AP +CP 的值最小,∴当x =32时,y =-32+4=52,∴P 32,52 ,故答案是:32,52 ;(3)过Q 作QD ⊥x 轴,交BC 于D ,设Q d ,-d 2+3d +4 ,其中0≤d ≤4,则D d ,-d +4 ,∴QD =-d 2+3d +4 --d +4 =-d 2+4d ,∵B 4,0 ,∴OB =4,∴S ΔBCQ =12OB ×QD =-2d 2+8d =-2d -2 2+8,当d =2时,S ΔBCQ 取最大值,最大值为8,∴△BCQ 的最大面积为8;【点睛】本题主要考查了二次函数的图像和性质,利用数形结合思想和分类讨论思想是解题的关键.22(2023秋·江苏淮安·八年级统考期末)如图1,直线AB :y =-x +6分别与x ,y 轴交于A ,B 两点,过点B 的直线交x 轴负半轴于点C -3,0 .(1)请直接写出直线BC 的关系式:(2)在直线BC 上是否存在点D,使得S △ABD =S △AOD 若存在,求出点D 坐标:若不存请说明理由;(3)如图2,D 11,0 ,P 为x 轴正半轴上的一动点,以P 为直角顶点、BP 为腰在第一象限内作等腰直角三角形△BPQ ,连接QA ,QD .请直接写出QB -QD 的最大值:.19【答案】(1)y =2x +6(2)当D 185,665 或D -185,-65时,S △ABD =S △AOD (3)37【分析】(1)根据直线AB 与y 轴的交点,可求出点B 的坐标,再用待定系数法即可求解;(2)设D (a ,2a +6),分别用含a 的式子表示出出S △AOD ,S △ABD ,由此即可求解;(3)△BPQ 是等腰直角三角形,设P (m ,0)(m >0),可表示出QB ,再证Rt △BOP ≌Rt △PTQ (AAS ),如图所示,当点B ,R ,Q 在一条直线上时,QB -QD 的值最大,最大值为BR 的值,可求得点R 的坐标,根据勾股定理即可求解.【详解】(1)解:∵直线AB :y =-x +6分别与x ,y 轴交于A ,B 两点,令x =0,则y =6,∴B (0,6),且C -3,0 ,设直线BC 的解析式为y =kx +b ,∴b =6-3k +b =0,解得,k =2b =6 ,∴直线BC 的解析式为y =2x +6,故答案为:y =2x +6.(2)解:由(1)可知直线BC 的解析式为y =2x +6,直线AB 的解析式为y =-x +6,∴A (6,0),B (0,6),C (-3,0),∴OA =6,BO =6,OC =3,如图所示,点D 在直线BC 上,过点D 作DE ⊥x 轴于E ,∴设D (a ,2a +6),E (a ,0),∴S △ABC =12AC ·OB =12×(6+3)×6=27,S △ADC =12AC ·DE =12×(6+3)×a =92a ,S △AOD =12OA ·DE =12×6×a =3a ,∴S △ABD =S △ABC -S △ADC =27-92a ,若S △ABD =S △AOD ,则27-92a =3a ,当a >0时,27-92a =3a ,解得,a =185,即D 185,665 ;当a <0时,27+92a =-3a ,解得,a =-185,即D -185,-65 ;综上所述,当D 185,665 或D -185,-65时,S △ABD =S △AOD .(3)解:已知A (6,0),B (0,6),D (11,0),设P (m ,0)(m >0),∴在Rt △BOP 中,OB =6,OP =m ,∵△BPQ 是等腰直角三角形,∠BPQ =90°,∴BP =QP ;如图所示,过点Q 作QT ⊥x 轴于T ,20在Rt △BOP ,Rt △PTQ 中,∠BOP =∠PTQ =90°,∠BPO +∠QPA =∠QPA +∠PQT =90°,∴∠BPO =∠PQT ,∴∠BPO =∠PQT∠BOP =∠PTQ BP =QP,∴Rt △BOP ≌Rt △PTQ (AAS ),∴OP =TQ =m ,OB =PT =6,∴AT =OP +PT -OA =m +6-6=m ,∴AT =QT ,且QT ⊥x 轴,∴△ATQ 是等腰直角三角形,∠QAT =45°,则点Q 的轨迹在射线AQ 上,如图所示,作点D 关于直线AQ 的对称点R,连接QR ,BR ,AR ,A (6,0),B (0,6),D (11,0),∵△ATQ 是等腰直角三角形,即∠QAT =45°,根据对称性质,∴∠QAR =45°,∴RA ⊥x 轴,且△DQA ≌△RQA ,∴AR =AD =11-6=5,则R (6,5),如图所示,当点B ,R ,Q 在一条直线上时,QB -QD 的值最大,最大值为BR 的值;∴由勾股定理得:BR =62+(6-5)2=37,故答案为:37.【点睛】本题主要考查一次函数,几何的综合,掌握待定系数法求解析式,将军饮马问题,等腰直角三角形的性质,勾股定理是解题的关键.23(2023春·重庆沙坪坝·九年级重庆八中校考阶段练习)△ABC 中,∠B =60°.(1)如图1,若AC >BC ,CD 平分∠ACB 交AB 于点D ,且AD =3BD .证明:∠A =30°;(2)如图2,若AC <BC ,取AC 中点E ,将CE 绕点C 逆时针旋转60°至CF ,连接BF 并延长至G ,使BF =FG ,猜想线段AB 、BC 、CG 之间存在的数量关系,并证明你的猜想;(3)如图3,若AC =BC ,P 为平面内一点,将△ABP 沿直线AB 翻折至△ABQ ,当3AQ +2BQ +13CQ 取得最小值时,直接写出BPCQ的值.【答案】(1)见解析(2)BC =AB +CG ,理由见解析(3)213+33913【分析】(1)过点D 分别作BC ,AC 的垂线,垂足为E ,F ,易得DE =DF ,由∠B =60°,可得DE =DF =32BD ,由AD =3BD ,求得sin A =DE AD=12,可证得∠A =30°;(2)延长BA ,使得BH =BC ,连接EH ,CH ,易证△BCH 为等边三角形,进而可证△BCF ≌△HCE SAS ,可得BF =HE ,∠BFC =∠HEC ,可知∠AEH =∠CFG ,易证得△AEH ≌△CFG SAS ,可得AH =CG ,由BC =BH =AB +AH =AB +CG 可得结论;(3)由题意可知△ABC 是等边三角形,如图,作CM ⊥CA ,且CM =32CA ,作CN ⊥CQ ,且CN =32CQ ,可得CM CA=CN CQ =32,QN =CQ 2+CN 2=132CQ ,可知△ACQ ∽△MCN ,可得MN =32AQ ,由3AQ +2BQ +13CQ =232AQ +BQ +132CQ =2MN +BQ +QN ≥2BM 可知点Q ,N 都在线段BM 上时,3AQ +2BQ+13CQ 有最小值,过点C 作CR ⊥BM ,过点M 作MT ⊥BC 交BC 延长线于T ,可得CR =CQ ⋅sin ∠CQN =313CQ ,QR =CQ ⋅cos ∠CQN =213CQ ,可证△CBR ∽△MBT ,得BR CR =BT MT ,设BC =a 由等边三角形的性质,可得CM =32a ,进而可得CT =CM ⋅cos30°=334a ,MT =CM ⋅sin30°=34a ,结合BR CR=BTMT 可得:BQ +213CQ 313CQ =a +334a 34a ,可得BQ CQ =213+33913,由翻折可知,BP =BQ ,可求得BP CQ的值.【详解】(1)证明:过点D 分别作BC ,AC 的垂线,垂足为E ,F ,∵CD 平分∠ACB ,DE ⊥BC ,DF ⊥AC ,∴DE =DF ,又∵∠B =60°,∴DE =BD ⋅sin60°=32BD ,则DE =DF =32BD ,又∵AD =3BD ,∴sin A =DE AD =32BD3BD=12,∴∠A =30°;(2)BC =AB +CG ,理由如下:延长BA ,使得BH =BC ,连接EH ,CH ,∵∠ABC =60°,BH =BC ,∴△BCH 为等边三角形,∴CB =CH ,∠BCH =60°,∵CE 绕点C 逆时针旋转60°至CF ,∴CE =CF ,∠ECF =60°,则∠BCH -∠ACB =∠ECF -∠ACB ,∴∠ECH =∠FCB ,∴△BCF ≌△HCE SAS ,∴BF =HE ,∠BFC =∠HEC ,则∠AEH =∠CFG ,∵BF =FG ,∴BF =HE =FG ,又∵E 为AC 中点,∴AE =CE =CF ,∴△AEH ≌△CFG SAS ,∴AH =CG ,∴BC =BH =AB +AH =AB +CG ;(3)∵∠ABC =60°,AC =BC ,∴△ABC 是等边三角形,如图,作CM ⊥CA ,且CM =32CA ,作CN ⊥CQ ,且CN =32CQ ,则CM CA=CN CQ =32,QN =CQ 2+CN 2=132CQ ,∴sin ∠CQN =CN QN =313,cos ∠CQN =CQ QN =213,则∠ACM =∠QCN =90°,∴∠ACM -∠ACN =∠QCN -∠ACN ,则∠ACQ =∠MCN∴△ACQ ∽△MCN ,∴MN AQ =CM CA=32,即:MN =32AQ ,∴3AQ +2BQ +13CQ =232AQ +BQ +132CQ =2MN +BQ +QN ≥2BM即:点Q ,N 都在线段BM 上时,3AQ +2BQ +13CQ 有最小值,如下图,过点C 作CR ⊥BM ,过点M 作MT ⊥BC 交BC 延长线于T ,则∠BRC =∠BTM =90°,CR =CQ ⋅sin ∠CQN =313CQ ,QR =CQ ⋅cos ∠CQN =213CQ ,又∵∠CBR =∠MBT ,∴△CBR ∽△MBT ,∴BR CR=BT MT ,∵△ABC 是等边三角形,设BC =a ∴∠ACB =60°,AC =BC =a ,则CM =32a ,∵∠ACM =90°,∴∠MCT =30°,则CT =CM ⋅cos30°=334a ,MT =CM ⋅sin30°=34a ,则由BR CR=BT MT 可得:BQ +213CQ 313CQ =a +334a34a ,整理得:133BQ CQ +23=4+333,得BQ CQ=213+33913,由翻折可知,BP =BQ ,∴BP CQ =BQ CQ=213+33913.【点睛】本题属于几何综合,考查了解直角三角形,等边三角形的判定及性质,全等三角形的判定及性质,相似三角形的判定及性质,旋转的性质以及费马点问题,掌握费马点问题的解决方法,添加辅助线构造全等三角形和相似三角形是解决问题的关键.24(2023春·江苏·八年级专题练习)定义:既相等又垂直的两条线段称为“等垂线段”,如图1,在Rt △ABC 中,∠A =90°,AB =AC ,点D 、E 分别在边AB 、AC 上,AD =AE ,连接DE 、DC ,点M 、P 、N 分别为DE 、DC 、BC 的中点,且连接PM 、PN .(1)观察猜想线段PM 与PN 填(“是”或“不是”)“等垂线段”.(2)△ADE 绕点A 按逆时针方向旋转到图2所示的位置,连接BD ,CE ,试判断PM 与PN 是否为“等垂线段”,并说明理由.(3)拓展延伸把△ADE 绕点A 在平面内自由旋转,若DE =2,BC =4,请直接写出PM 与PN 的积的最大值.。
(完整版)九年级数学选择、填空压轴题训练(含答案)

九年级数学综合训练、选择题(本大题共9小题,共27.0分)1. 如图,在平面直角坐标系中2条直线为11 : y=-3x+3 , 12:y=-3x+9,直线l i交x轴于点A,交y轴于点B,直线12交x轴于点D,过点B作x轴的平行线交12于点C,点A、E关于y轴对称,抛物线y=ax2+bx+c 过E、B、C三点,下列判断中:①a-b+c=0:②2a+b+c=5;③抛物线关于直线x=1对称;④抛物线过点(b,c);⑤S四边形ABCD=5,其中正确的个数有()A. 5B. 4C. 32. 如图,10个不同的正偶数按下图排列,箭头上方的每个数都等于其下方两数的和,如 A :ci r小表示a1=a2+a3,贝y a1的最小值为()M是反比例函数y=??(x>0)的图象上位于直线上方的A. 32B. 36C. 38D. 403. 如图,直线y= v3x-6分别交x轴,y轴于A, B,一点,MC /x轴交AB于C, MD AMC交AB于D,AC?BD=4,则k 的值为()A. -3B. -4C. -5D. -64.在平面直角坐标系xOy中,将一块含有45。
角的直角三角板如图放置,直角顶点C的坐标为(1, 0),顶点A的坐标为(0, 2),顶点B恰好落在第一象限的双曲线上,现将直角三角板沿x轴正方向平移,当顶点A恰好落在该双曲线上时停止运动,则此时点C的对应点C'的坐标为()3A. (2,0)B. (2,0)5C. (2,0)D. (3,0)5.如图,在矩形ABCD中,AB v BC, E为CD边的中点,将△ADE绕点E顺时针旋转180°,点D的对应点为C,点A的对应点为F,过点E作ME丄AF交BC于点M , 连接AM、BD交于点N,现有下列结论:①AM=AD+MC;②AM=DE+BM;③DE2=AD?CM ;④点N为△ABM的外心.其中正确的个数为()A. 1个B. 2个C. 3个D. 4个6.规定:如果关于x的一元二次方程ax2+bx+c=0 (a工0有两个实数根,且其中一个根是另一个根的 2 倍,则称这样的方程为“倍根方程” •现有下列结论:①方程X2+2X-8=0是倍根方程;②若关于x的方程x2+ax+2=0是倍根方程,则a=±3;③ 若关于x 的方程ax 2-6ax+c=0( a ^0是倍根方程,则抛物线y=ax 2-6ax+c 与x 轴的公共点的坐标是 (2, 0)和(4,0);4④ 若点(m , n )在反比例函数y=?的图象上,则关于 x 的方程mx 2+5x+ n=0是倍根方程.12. 如图,正方形 ABCD 中,BE=EF=FC ,CG=2GD ,BG 分别交AE ,AF 于M ,N .下列结论:①AF 丄BG ;4???? 31② BN =§NF ; 四边形CGNF=[S 四边形ANGD .其中正确的结论的序号是 __________ .13. 已知:如图,在 A AOB 中,ZAOB=90 ° AO=3cm ,BO=4cm .将A AOB 绕顶点 0,按顺时针方向旋转到△A 1OB 1处,此时线段 OB 1与AB 的交点D 恰好为AB 的中点,则线段 B 1D= __________ cm .7. 上述结论中正确的有()A.①②B.③④C.②③D.②④如图,六边形 ABCDEF 的内角都相等,ZDAB=60 ° AB=DE ,则下列结论成立的个数是( ①AB/DE :②EF /AD /BC ;③AF=CD :④四边形 ACDF 是平行 四边形;⑤六边形ABCDEF 既是中心对称图形, 又是轴对称图 形.A. 2B. 3C. 4D. 58. 如图,在Rt A ABC 中,/C=90 °以A ABC 的一边为边画等腰三角形,他边上,则可以画出的不同的等腰三角形的个数最多为()A. 4B. 5C. 6D. 79. 如图,矩形ABCD 延长线于点F ,且中,AE _LBD 于点E ,CF 平分ZBCD ,交EA 的 BC=4,CD=2,给出下列结论:① ZBAE=ZCAD ;②/DBC=30°③AE=4v5;④AF=2需,其中正确结论的个数有(A. 1个B. 2个C. 3个 二、填空题(本大题共 10小题,共30.0分)10. D. 4个如图,在Rt A ABC 中,ZBAC=30 °以直角边AB 为直径作半圆交 AC 于点D , .(结果不取近似值)11. 延长ED 交BC 于点F , BC=2V 3,则图中阴影部分的面积为 1352斗23CS3 ah3如图,在6X 5的网格内填入1至6的数字后,使每行、每列、 每个小粗线宫中的数字不重复,则a>c= )使得它的第三个顶点在 △ABC 的其AB以AD 为边作等边A ADE , D G CB14. 如图,边长为4的正六边形ABCDEF 的中心与坐标原点 0重合,AF 仅轴,将正六边形 ABCDEF 绕原15.如图,在Rt ^ABC 中,BC=2 , /BAC=30 °斜边AB 的两个端点分别在相互垂直的射线OM 、ON 上滑动,下列结论:① 若C 、O 两点关于AB 对称,则OA=2霭; ② C 、O 两点距离的最大值为 4; ③ 若AB 平分CO ,贝U AB ±30;??④ 斜边AB 的中点D 运动路径的长为-?其中正确的是 _______ (把你认为正确结论的序号都填上).16. ____________________________________________________________________ 如图,ZAOB 的边OB 与x 轴正半轴重合,点 P 是OA 上的一动点,点 N ( 3, 0)是OB 上的一定点, 点M 是ON 的中点,Z AOB=30° ,要使PM+PN 最小,则点 P 的坐标为 _________________________________________________ .17.在一条笔直的公路上有 A 、B 、C 三地,C 地位于A 、B 两地之间,甲车从 A 地沿这条公路匀速驶向 C 地,乙车从B 地沿这条公路匀速驶向 A 地,在甲车 出发至甲车到达 C 地的过程中,甲、乙两车各自与C 地的距离y (km )与甲车行驶时间t ( h )之间的函数关系如图所示.下列结论:①甲车出发2h 时,两车相遇;②乙车出发 1.5h 时,两车相距170km ;③乙车出发2寸人时,两车 相遇;④甲车到达 C 地时,两车相距40km .其中正确的是 ___________ (填写所 有正确结论的序号) OA=AB , ZOAB=90 °反比例函数y=??(x > 0)的图象经过A , B 两点•若18.如图,在平面直角坐标系中,点0顺时针旋转n 次,每次旋转60°当n=2017时,顶点A 的坐标为点A 的坐标为(n , 1),则19.如图,在平面直角坐标系中,△ABC的顶点坐标分别为A (-1, 1), B (0, -2), C ( 1, 0),点P (0,2)绕点A旋转180。
2020年中考数学4.几何综合选择填空压轴题(含解析)

几何综合-填空选择压轴题41、如图,在菱形ABCD中,AB=2,∠B是锐角,AE⊥BC于点E,M是AB的中点,连结MD,ME.若∠EMD=90°,则cosB的值为.2、如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8cm,AE=2cm,则OF的长度是()A.3cm B.√6cm C.2.5cm D.√5cm3、定义:在平面直角坐标系中,一个图形先向右平移a个单位,再绕原点按顺时针方向旋转θ角度,这样的图形运动叫作图形的γ(a,θ)变换.如图,等边△ABC的边长为1,点A在第一象限,点B与原点O重合,点C在x轴的正半轴上.△A1B1C1就是△ABC经γ(1,180°)变换后所得的图形.若△ABC经γ(1,180°)变换后得△A1B1C1,△A1B1C1经γ(2,180°)变换后得△A2B2C2,△A2B2C2经γ(3,180°)变换后得△A3B3C3,依此类推……△An﹣1Bn﹣1Cn﹣1经γ(n,180°)变换后得△AnBnCn,则点A1的坐标是,点A2018的坐标是.4、我国古代伟大的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式.后人借助这种分割方法所得的图形证明了勾股定理,如图所示的矩形由两个这样的图形拼成,若a=3,b=4,则该矩形的面积为()A.20 B.24 C.994D.5325、如图,直线y=﹣√33x+4与x轴、y轴分别交于A,B两点,C是OB的中点,D 是AB上一点,四边形OEDC是菱形,则△OAE的面积为.6、小明发现相机快门打开过程中,光圈大小变化如图1所示,于是他绘制了如图2所示的图形.图2中六个形状大小都相同的四边形围成一个圆的内接正六边形和一个小正六边形,若PQ所在的直线经过点M,PB=5cm,小正六边形的面积为49√3cm2,则该圆的半径为cm.27、如图,在矩形ABCD中,AB=4,AD=2,点E在CD上,DE=1,点F是边AB上一动点,以EF为斜边作Rt△EFP.若点P在矩形ABCD的边上,且这样的直角三角形恰好有两个,则AF的值是.8、如图,AB是⊙O的直径,弦CD交AB于点P,AP=2,BP=6,∠APC=30°,则CD的长为()A.√15 B.2√5 C.2√15 D.89、如图,在矩形ABCD中,点E是边BC的中点,AE⊥BD,垂足为F,则tan∠BDE 的值是()A.√24 B.14C.13D.√2310、如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AF平分∠CAB,交CD于点E,交CB于点F.若AC=3,AB=5,则CE的长为()A.32B.43C.53D.8511、如图,在正方形ABCD中,AD=2√3,把边BC绕点B逆时针旋转30°得到线段BP,连接AP并延长交CD于点E,连接PC,则三角形PCE的面积为.12、如图,P为等边三角形ABC内的一点,且P到三个顶点A,B,C的距离分别为3,4,5,则△ABC的面积为()A.9+25√34 B.9+25√32C.18+25√3 D.18+25√3213、如图,点O 是▱ABCD 的对称中心,AD >AB ,E 、F 是AB 边上的点,且EF=12AB ;G 、H 是BC 边上的点,且GH=13BC ,若S 1,S 2分别表示△EOF 和△GOH 的面积,则S 1与S 2之间的等量关系是 .14、如图,已知∠POQ=30°,点A 、B 在射线OQ 上(点A 在点O 、B 之间),半径长为2的⊙A 与直线OP 相切,半径长为3的⊙B 与⊙A 相交,那么OB 的取值范围是( )A .5<OB <9 B .4<OB <9C .3<OB <7D .2<OB <715、如图,在矩形ABCD 中,按以下步骤作图:①分别以点A 和C 为圆心,以大于12AC 的长为半径作弧,两弧相交于点M 和N ;②作直线MN 交CD 于点E .若DE=2,CE=3,则矩形的对角线AC 的长为 .16、如图,在菱形ABCD中,tanA=43,M,N分别在边AD,BC上,将四边形AMNB沿MN翻折,使AB的对应线段EF经过顶点D,当EF⊥AD时,BNCN的值为.17、如图,△ABC的周长为19,点D,E在边BC上,∠ABC的平分线垂直于AE,垂足为N,∠ACB的平分线垂直于AD,垂足为M,若BC=7,则MN的长度为()A.32B.2 C.52D.318、如图,E,F是平行四边形ABCD对角线AC上两点,AE=CF=14AC.连接DE,DF并延长,分别交AB,BC于点G,H,连接GH,则S△ADGS△BGH的值为()A.12B.23C.34D.119、如图,平面直角坐标系中,矩形OABC的顶点A(﹣6,0),C(0,2√3).将矩形OABC绕点O顺时针方向旋转,使点A恰好落在OB上的点A1处,则点B的对应点B1的坐标为.20、如图,Rt△ABC中,∠C=90°,AC=2,BC=5,点D是BC边上一点且CD=1,点P是线段DB上一动点,连接AP,以AP为斜边在AP的下方作等腰Rt△AOP.当P从点D出发运动至点B停止时,点O的运动路径长为.21、如图,点O为正六边形ABCDEF的中心,点M为AF中点,以点O为圆心,以OM的长为半径画弧得到扇形MON,点N在BC上;以点E为圆心,以DE的长为半径画弧得到扇形DEF,把扇形MON的两条半径OM,ON重合,围成圆锥,将此圆锥的底面半径记为r1;将扇形DEF以同样方法围成的圆锥的底面半径记为r2,则r 1:r2= .22、对角线长分别为6和8的菱形ABCD如图所示,点O为对角线的交点,过点O 折叠菱形,使B,B′两点重合,MN是折痕.若B'M=1,则CN的长为()A.7 B.6 C.5 D.423、如图,一艘渔船正以60海里/小时的速度向正东方向航行,在A处测得岛礁P在东北方向上,继续航行1.5小时后到达B处,此时测得岛礁P在北偏东30°方向,同时测得岛礁P正东方向上的避风港M在北偏东60°方向.为了在台风到来之前用最短时间到达M处,渔船立刻加速以75海里/小时的速度继续航行小时即可到达.(结果保留根号)24、如图,点A1的坐标为(2,0),过点A1作x轴的垂线交直线l:y=√3x于点B 1,以原点O为圆心,OB1的长为半径画弧交x轴正半轴于点A2;再过点A2作x轴的垂线交直线l于点B2,以原点O为圆心,以OB2的长为半径画弧交x轴正半轴于点A3;….按此作法进行下去,则A2019B2018̂的长是.25、如图,正方形ABCD的边长为8,M是AB的中点,P是BC边上的动点,连结PM,以点P为圆心,PM长为半径作⊙P.当⊙P与正方形ABCD的边相切时,BP 的长为.26、如图,正方形ABCD的边长为1,点A与原点重合,点B在y轴的正半轴上,点D在x轴的负半轴上,将正方形ABCD绕点A逆时针旋转30°至正方形AB'C′D′的位置,B'C′与CD相交于点M,则点M的坐标为.27、如图,在△ABC中,已知AC=3,BC=4,点D为边AB的中点,连结CD,过点A作AE⊥CD于点E,将△ACE沿直线AC翻折到△ACE′的位置.若CE′∥AB,则CE′=.。
中考数学几何选择填空压轴题四边形难题(含答案))

1、 《求长度》 (答案)1、(容易)如图1的矩形ABCD 中,有一点E 在AD 上,今以BE 为折线将A 点往右折,如图2所示,再作过A 点且与CD 垂直的直线,交CD 于F 点,如图3所示,若AB= 36,BC=13,∠BEA=60°,则图3中AF 的长度为 4【解】作AH ⊥BC 于H2、(难)如图,矩形ABCD 与菱形EFGH 的对角线均交于点O ,且EG ∥BC ,将矩形折叠,使点C 与点O 重合,折痕MN 恰好过点G 若AB=6,EF=2,∠H=120°,则DN 的长为36-【解】长EG 交DC 于P 点,连接GC 、FH ;如图所示: 则CP=DP=21CD=26,△GCP 为直角三角形,∵四边形EFGH 是菱形,∠EHG=120°,∴GH=EF=2,∠OHG=60°,EG ⊥FH ,∴OG=GH•sin60°=2×23=3,由折叠的性质得:CG=OG=3,OM=CM ,∠MOG=∠MCG ,∴PG==26,∵OG ∥CM ,∴∠MOG+∠OMC=180°,∴∠MCG+∠OMC=180°,∴OM ∥CG ,∴四边形OGCM 为平行四边形,∵OM=CM ,∴四边形OGCM 为菱形,∴CM=OG=3,根据题意得:PG 是梯形MCDN 的中位线,∴DN+CM=2PG=6,∴DN=36-3、(中等)如图,△ABC 的周长为19,点D ,E 在边BC 上,∠ABC 的平分线垂直于AE ,垂足为N ,∠ACB 的平分线垂直于AD ,垂足为M ,若BC=7,则MN 的长度为25【解】△BNA ≅△BNE∴BA=BE ,∴△BAE 是等腰三角形,同理△CAD 是等腰三角形,∴点N 是AE 中点,点M 是AD 中点(三线合一),∴MN 是△ADE 的中位线, ∵BE+CD=AB+AC=19-BC=19-7=12,∴DE=BE+CD-BC=5,∴MN=21DE=25.4、(难度)如图,在菱形ABCD 中,∠ABC=120°,将菱形折叠,使点A 恰好落在对角线BD 上的点G 处(不与B 、D 重合),折痕为EF ,若DG=2,BG=6,则BE 的长为______2.8【解】作EH ⊥BD ,设BE=x在Rt △EHG 中,EG 2=EH 2+GH 2,即(8-x )2=(23x )2+(6-21x )2,解得,x =2.8,即BE=2.8, 故答案为:2.85、如图,▱ABCD 中,AB=7,BC=3,连接AC ,分别以点A 和点C 为圆心,大于21AC 的长为半径作弧, 两弧相交于点M ,N ,作直线MN ,交CD 于点E ,连接AE ,则△AED 的周长是_____ 10.6、(容易)如图,ABCD 的对角线相交于点O ,且AD CD ,过点O 作OM AC ,交AD 于点M .如果CDM 的周长为8,那么ABCD 的周长是_ 16【解】∵四边形ABCD 是平行四边形,∴OA=OC ,∵OM ⊥AC ,∴AM=CM ,∵△CDM 的周长为8, ∴CM+DM+CD=AM+DM+CD=AD+CD=8,∴平行四边形ABCD 的周长是:2×8=16.7、(中等)如图,正方形ABCD 的边长为12,点E 在边AB 上,BE=8,过点E 作EF ∥BC ,分别交BD 、CD 于G 、F 两点.若点P 、Q 分别为DG 、CE 的中点,则PQ 的长为_____ 1328、(难度)如图,在平行四边形ABCD 中,对角线AC 、BD 相交于点O ,AB=OB ,点E 、点F 分别是OA 、OD 的中点,连接EF ,∠CEF=45°,EM ⊥BC 于点M ,EM 交BD 于点N ,FN=,则线段BC 的长为_____249、(难度)如图,平行四边形ABCD 中,AM ⊥BC 于M ,AN ⊥CD 于N ,已知AB =10,BM =6,MC =3,则MN 的长为___________5734【方法】将目标量置入直角三角形中10、(容易)如上图,在矩形ABCD 中,AB =6,BC =8,点E 是BC 中点,点F 是边CD 上的任意一点,当△AEF 的周长最小时,则DF 的长为 4【解】以CD 为对称轴作对称变换11、如图,在矩形ABCD 中,E 是BC 边上的点,连接AE 、DE ,将△DEC 沿线段DE 翻折,点C 恰好落在线段AE 上的点F 处.若AB =6,BE : EC =4 : 1,则线段DE 的长为 ____102_______.【方法】AD = AE=10;勾股定理12、如图,矩形ABCD 中,AB =8,BC =4.点E 在边AB 上,点F 在边CD 上,点G 、H 在对角线AC 上.若四边形EGFH 是菱形,则AE 的长是 [5【解】连接EF 交AC 于O ,∵四边形EGFH 是菱形,∴EF ⊥AC ,OE =OF , ∵四边形ABCD 是矩形,∴∠B =∠D =90°,AB ∥CD ,∴∠ACD =∠CAB , 在△CFO 与△AOE 中,,∴△CFO ≌△AOE ,∴AO =CO ,A BDCM NAE BDC F∵AC ==4,∴AO =21AC =2,∵∠CAB =∠CAB ,∠AOE =∠B =90°,∴△AOE ∽△ABC ,∴,∴,∴AE =5.13、(难度)如图,矩形ABCD 中,AB =2,AD =2.点E 是BC 边上的一个动点,连接AE ,过点D 作DF ⊥AE 于点F .当△CDF 是等腰三角形时,BE 的长为 1、2、22-【解】①CF =CD 时,过点C 作CM ⊥DF ,垂足为点M ,则CM ∥AE ,DM =MF ,延长CM 交AD 于点G ,∴AG =GD =1,∴CE =1, ∵CG ∥AE ,AD ∥BC ,∴四边形AGCE 是平行四边形,∴CE =AG =1,∴BE =1 ∴当BE =1时,△CDF 是等腰三角形;②DF =DC 时,则DC =DF =2,∵DF ⊥AE ,AD =2,∴∠DAE =45°,则BE =2, ∴当BE =2时,△CDF 是等腰三角形;③FD =FC 时,则点F 在CD 的垂直平分线上,故F 为AE 中点. ∵AB =2,BE =x ,∴AE =,AF =,∵△ADF ∽△EAB ,∴=,,x 2﹣4x +2=0,解得:x =2±2,∴当BE =22-时,△CDF 是等腰三角形.综上,当BE =1、2、22-时,△CDF 是等腰三角形.14、如图,边长为1的菱形ABCD 中,∠DAB=60度.连接对角线AC ,以AC 为边作第二个菱形ACC 1D 1,使∠D 1AC=60°;连接AC 1,再以AC 1为边作第三个菱形AC 1C 2D 2,使∠D 2AC 1=60°;…,按此规律所作的第n 个菱形的边长为 1)3(-n .解:连接DB ,∵四边形ABCD 是菱形,∴AD=AB .AC ⊥DB , ∵∠DAB=60°,∴△ADB 是等边三角形,∴DB=AD=1,∴BM=21, ∴AM==23,∴AC=3,同理AC 1=3AC=(3)2,AC 2=3AC 1=33=(3)3, 按此规律所作的第n 个菱形的边长为1)3(-n15、如图,以Rt △ABC 的斜边BC 为一边在△ABC 的同侧作正方形BCEF ,设正方形的中心为O ,连接AO ,如果AB=4,AO=26,那么AC 的长等于 16 .【解】如图,过O 点作OG 垂直AC ,G 点是垂足.∵∠BAC=∠BOC=90°,∴ABCO 四点共圆,∴∠OAG=∠OBC=45° ∴△AGO 是等腰直角三角形,∴2AG 2=2GO 2=AO 2=2)26(=72, ∴OG=AG=6,∵∠BAH=∠OGH=90°,∠AHB=∠OHG ,∴△ABH ∽△GOH ,∴AB/OG=AH/(AG ﹣AH ),∵AB=4,OG=AG=6,∴AH=2.4 在直角△OHC 中,∵HG=AG ﹣AH=6﹣2.4=3.6,OG 又是斜边HC 上的高, ∴OG 2=HG×GC ,而OG=6,GH=3.6,∴GC=10.∴AC=AG+GC=6+10=16. 故AC 边的长是16.16、如图,在梯形ABCD 中,AD ∥BC ,∠B=90°,AD=2,BC=5,E 为DC 中点,tanC=34.则AE 的长度为265【解】过点E 作BC 的垂线交BC 于点F ,交AD 的延长线于点M , 在梯形ABCD 中,AD ∥BC ,E 是DC 的中点,∴∠M=∠MFC ,DE=CE ;在△MDE 和△FCE 中,∠M=∠MFC ,∠DEM=∠CEF ,DE=CE ;∴△MDE ≌△FCE ,∴EF=ME ,DM=CF . ∵AD=2,BC=5,∴DM=CF=23, 在Rt △FCE 中,tanC=CFEF =34,∴EF=ME=2,在Rt △AME 中,AE=265)232(222=++ 17、如图,平行四边形ABCD 中,AE 平分∠BAD 交BC 边于E ,EF ⊥AE 交CD 边于F ,延长BA 到点G ,使AG = CF ,连接GF .若BC = 7,DF = 3,tan ∠AEB =3 ,则GF 的长为 23【解】连接AC ,羊场AE 与DC 延长线交于一点H18、(容易)如图,梯形ABCD 中,AD ∥BC ,AB = 3,BC=4,连结BD ,∠BAD 的平分线交BD 于 点E ,且AE ∥CD ,则AD 的长为1DG ABCDEMABC DEF【解】构造平行四边形。
专项 几何图形选填压轴题(含特殊三角形、特殊平行四边形、圆等综合问题)中考数学

抢分通关02 几何图形选填压轴题(含特殊三角形、特殊平行四边形、圆等综合问题) 目录【中考预测】预测考向,总结常考点及应对的策略【误区点拨】点拨常见的易错点【抢分通关】精选名校模拟题,讲解通关策略(含新考法、新情境等)几何图形选填压轴题含特殊三角形、特殊平行四边形、圆等综合问题是全国中考的热点内容,更是全国中考的必考内容。
每年都有一些考生因为知识残缺、基础不牢、技能不熟、答欠规范等原因导致失分。
1.从考点频率看,以等腰三角形、直角三角形等为基础的多解题,特殊四边形与圆为载体的几何求解问题是高频考点、必考点,所以必须提高对几何图形性质的理解和掌握。
2.从题型角度看,以选择题、填空题最后一题为主,分值3分左右,着实不少!易错点一 等腰三角形多解题漏解【例1】(2024·辽宁锦州·模拟预测)如图,AB ⊥直线l 于点B ,点C 在直线l 上(不与点B 重合),连接AC ,将线段CA 绕点C 顺时针旋转90︒,得到线段CD ,连接AD ,点E 是AD 的中点,连接BE ,AB =ABE 是等腰三角形时,BC = .本题考查旋转的性质,涉及等腰直角三角形性质及应用,全等三角形的判定与性质,勾股定理逆定理的应用等知识,解题的关键是用含的代数式表示的三边长.m ABE【例2】(2024·辽宁盘锦·模拟预测)在矩形ABCD 中,6AB =,8BC =,M 是射线BD 上的动点,过点M 作ME BC ⊥于点E ,连接AM ,当ADM △是等腰三角形时,ME 的长为 .【例3】(2024·四川达州·一模)如图,ABC 和CEF 都是等腰直角三角形,90BAC CEF ∠=∠=︒,点E 在AC 边上.将CEF 绕点C 逆时针旋转(0180)αα︒<<︒,旋转过程中,直线EF 分别与直线AC ,BC 交于点M ,N ,若CMN 是等腰三角形,则α的值为 .【例4】(2024·河南·一模)如图,菱形ABCD 的边长为2,120BAD ∠=︒,将菱形纸片翻折,使点B 落在对角线BD 上的点B '处,折痕为MN ,连接AB ',当AB D 'V 为等腰三角形时,BM 的长为 .易错点二 直角三角形多解题漏解【例1】(2024·江苏常州·模拟预测)在平面直角坐标系中,已知A ()0,2,B ()4,0,点P 在x 轴上,把AP 绕点P 顺时针旋转90︒得到线段A P ',连接A B '.若A PB '△是直角三角形时,则点P 的横坐标为 .【例2】(2024·河南周口·一模)矩形ABCD 中,O 为对角线AC 的中点,点E 从点A 出发,沿A B C →→运动到点C,且1AB AD ==,当以点A E O ,,为顶点的三角形为直角三角形时,AE 的长为 .【例3】(2024·河南漯河·一模)ABC 是边长为4的等边三角形,点D 为高BF 上一个动点.连接AD ,将AD 绕点A 顺时针旋转60︒得到AE ,当CEF △是直角三角形时,EF =.本题考查旋转性质、全等三角形的判定与性质、坐标与图形、解直角三角形、解一元二次方程等知识,添加辅助线构造全等三角形,利用分类讨论和数形结合思想求解是解答的关键.【例4】(2023·江西·中考真题)如图,在ABCD Y 中,602B BC AB ∠=︒=,,将AB 绕点A 逆时针旋转角α(0360α︒<<︒)得到AP ,连接PC ,PD .当PCD 为直角三角形时,旋转角α的度数为 .题型一 平行线中求角的度数【例1】(2024·江苏宿迁·一模)如图,直线m n ∥,点A C 、在直线m 上,点B 在直线n 上,BC 平分ABD ∠,若122BAC ∠=︒,则ACB ∠的度数为( )A .58︒B .61︒C .30︒D .29︒【例2】(2024·河北沧州·一模)如图,直线a ,b 分别与ABC 的边相交,且a ∥AC ,b ∥BC ,根据图中标示的角度,可知C ∠的度数为()本题主要考查平行线的性质,角平分线的性质,掌握平行线的性质是解题的关键.A .30︒B .40︒C .50︒D .60︒1.(2024·广东珠海·一模)如图,12l l ∥,135∠=︒,250∠=︒,则3∠的度数为( )A .85︒B .95︒C .105︒D .116︒2.(2024·陕西西安·三模)如图,,145AB CD ABE ∠=︒∥,40DFE ∠=︒,则BEF ∠的度数为( )A .40︒B .50︒C .75︒D .70︒题型二 特殊平行四边形中求线段或角【例1】(新考法,拓视野)(2024·安徽合肥·一模)七巧板是我们祖先的一项伟大创造,被誉为“东方魔板”.在一次“美术制作”活动课上,小明用边长为4的正方形纸片制作了如图1所示的七巧板,并设计了一幅作品放入矩形ABCD 中(如图2),则AB 的长为 .【例2】(2024·陕西宝鸡·一模)如图,在菱形ABCD 中,过点A 作AG CD ⊥于点G ,过点G 作BC 的平行线EF ,连接AE 、DF ,EF AB =,四边形AEFD 的面积为48,若6AG =,则CG 的长为 .1.(2024·湖北孝感·一模)如图,平行四边形ABCD 中,4AB =,BC =120ABC ∠=︒,点E 在AD 上,将ABE 沿BE 折叠得到A BE ' ,若点A '恰好在线段CE 上,则AE 的长为 .题型三 多边形中求角度或线段长【例1】(新考法,拓视野)(2024·山西吕梁·一模)如图1,飞虹塔位于山西省洪洞县的广胜寺景区内,是第一批全国重点文物保护单位,呈三角形共十三层,图2所示的正八边形是其中一层的平面示意图,则α∠=.本题考查了七巧板的应用,掌握七巧板的相关结论是解题关键.【例2】(2024·陕西西安·二模)约1500年前,我国伟大的数学家和天文学家祖冲之计算出圆周率应在3.1415926和3.1415927之间,成为世界上第一个把圆周率精确到小数点后7位的人.如图,若O 的半径为2,若用O 的内接正六边形的周长来估计O 的周长,则O 的周长与其内接正六边形的周长的差值为 .(结果保留π)1.(2024·河北石家庄·一模)如图1的螺丝钉由头部(直六棱柱)和螺纹(圆柱)组合而成,其俯视图如图2所示.小明将刻度尺紧靠螺纹放置,经过点A 且交CD 于点P ,量得PC 长为1mm ,六边形ABCDEF 的边长为4mm .(1)AP 长为 mm ;(2)Q 为圆上一点,则AQ 的最小值为 mm .2.(2024·河北石家庄·一模)图1是一种拼装玩具的零件,它可以看作是底面为正六边形的六棱柱,其内部挖去一个底面为正方形的长方体后得到的几何体,图2是该零件的俯视图,正方形ABCD 的两个相对的顶点A ,C 分别在正六边形一组平行的对边上,另外两个顶点B ,D 在正六边形内部(包括边界),点E ,F 分别是正六边形的顶点.已知正六边形的边长为2,正方形边长为a.本题主要考查正多边形的内角和外角,与圆中边心矩,中心角等知识.(1)连接EF ,EF 的长为 ;(2)a 的取值范围是 .题型四 圆中求角度或线段长【例1】(2024·湖南永州·一模)如图,ABC 的边AC 与O 相交于C ,D 两点,且经过圆心O ,边AB 与O相切,切点为B .如果38A ∠=︒,那么C ∠等于 .【例2】(2024·河南鹤壁·模拟预测)如图,PA 与O ☉相切于点A ,PO 与弦AB 相交于点C ,OB OP ⊥,若3OB =,1OC =,则PA 的长为 .1.(2024·四川成都·一模)如图,在平面直角坐标系xOy 中,P 经过点O ,与y轴交于点(0,A ,与x轴交于点()B ,则OP 的长为 .本题考查切线的性质,圆周角定理,解题的关键是熟练掌握切线的性质和圆周角定理.2.(2024·安徽合肥·一模)如图所示,AB 是O 的直径,弦CE AB ⊥,垂足为M ,过点C 作O 的切线交BA 的延长线于点D ,若1AM =、5BM =,则AD =题型五 圆中求扇形或不规则图形的面积【例1】(2024·河南周口·二模)如图,从一张圆心角为45︒的扇形纸板剪出一个边长为1的正方形CDEF ,则图中阴影部分的面积为 .【例2】(2024·河南驻马店·一模)如图,已知扇形ACB 中,90ACB ∠=︒,以BC 为直径作半圆O ,过点O 作AC 的平行线,分别交半圆O ,弧AB 于点D E 、,若扇形ACB 的半径为4,则图中阴影部分的面积是.第一种是规则图形的面积,知圆心角,直接代入公式求值.第二种是不规则图形的面积,转化为规则图形或利用切割法把不规则转化为几个规则图形,进而求解.1.(2024·河北沧州·一模)马面裙(图1),又名“马面褶裙”,是我国古代女子穿着的主要裙式之一,如图2,马面裙可以近似地看作扇环ABCD (AD 和BC 的圆心为点O ),A 为OB 的中点,8dm BC OB ==,则该马面裙裙面(阴影部分)的面积为( )A .24πdmB .28πdmC .212πdmD .216πdm 2.(2024·山西吕梁·一模)如图,点A 、B 为O 上的点,O 的半径为2,128AOB ∠=︒,点C 在O 外,连接AC 、BC 与O 分别交于点D 、E ,若34C ∠=︒,则阴影部分的面积为( )A .23πB .43πC .23π-D .43π-题型六 网格中求某角的三角函数值【例1】(新考法,拓视野)(2024·江苏常州·模拟预测)如图,在44⨯的正方形网格中,每个小正方形的边长均为1,每个小正方形的顶点称为格点,ABC 的顶点均在格点上.则tan BAC ∠的值是 .【例2】(2024·贵州·一模)如图是54⨯的网格,每个格子都为正方形.点A B C D E ,,,,均为格点,线段AC DE ,交于点O .则sin COE ∠= .1.(2024·辽宁沈阳·模拟预测)如图,点,,A B C 为正方形网格中的3个格点,则tan ACB ∠= .2.(2024·宁夏·一模)如图,在64⨯网格正方形中,每个小正方形的边长为1,顶点为格点,若ABC 的顶点均是格点,则sin ABC ∠的值是 .抢分通关02 几何图形选填压轴题解析(含特殊三角形、特殊平行四边形、圆等综合问题)第一种是以原角构造直角三角形,求构造后的边长,再根据三角形函数的定义求值.第二种是转化角,找与原角相等的角构造直角三角形,求构造后的边长,再根据三角形函数的定义求值.【中考预测】预测考向,总结常考点及应对的策略【误区点拨】点拨常见的易错点【抢分通关】精选名校模拟题,讲解通关策略(含新考法、新情境等)几何图形选填压轴题含特殊三角形、特殊平行四边形、圆等综合问题是全国中考的热点内容,更是全国中考的必考内容。
2020年中考数学2几何综合选择填空压轴题(含解析)

几何综合-填空选择压轴题21、矩形ABCD中,AB=6,BC=8.点P在矩形ABCD的内部,点E在边BC±,满足△PBE s^DBC,若AAPD是等腰三角形,则PE的长为.2、如图,CE是q ABCD的边AB的垂直平分线,垂足为点0,CE与DA的延长线交于点E.连接AC,BE,DO,DO与AC交于点F,则下列结论:四边形ACBE是菱形;①②ZACD=ZBAE;③AF:BE=2:3;④S四边形AFOE:S a C0D=2: 3.其中正确的结论有..(填写所有正确结论的序号)3、如图,点P是菱形ABCD边上的一动点,它从点A出发沿在A-B-C—D路径匀速运动到点D,设APAD的面积为y,P点的运动时间为x,则y关于x的函数)图象大致为(4、如图,在菱形ABCD中,AC=6很,BD=6,E是BC边的中点,P,M分别是AC, AB上的动点,连接PE,PM,则PE+PM的最小值是()A.6B.3V3C.2V6D. 4.55、如图,在RtAABC中,ZACB=90°,AB=4,BC=2,将AABC绕点B顺时针方向旋转到AA,BJ的位置,此时点A,恰好在CB的延长线上,则图中阴影部分的面积为.(结果保留丸).6、如图,ZA0B=60°,OA=OB,动点C从点0出发,沿射线OB方向移动,以AC 为边在右侧作等边AACD,连接BD,则BD所在直线与0A所在直线的位置关系是()A.平行B,相交C,垂直 D.平行、相交或垂直7、如图,正六边形ABCDEF的边长是6+4扼,点0”0?分别是^ABF,ACDE的内心,贝I0i02=.8、已知。
0的直径CD=10cm,AB是。
0的弦,AB±CD,垂足为M,且AB=8cm,则AC的长为()A.2V5cmB.4V5cmC.2-\/5cm或4扼cmD.2-\/3cm或4V3cm9、正方形AiBCO,A2B2C2G,A3B3C3C2,…按如图的方式放置,点A”A2,A3…和点G,C2,C3…分别在直线y=x+l和x轴上,则点辟的坐标为10、如图,C为半圆内一点,0为圆心,直径AB长为2cm,ZB0C=60°,NBC0=90°,将△BOC绕圆心0逆时针旋转至AB,0C',点C'在0A上,则边BC扫过区域(图中阴影部分)的面积为cm2.A C O B11、如图,已知在AABC中,BC边上的高AD与AC边上的高BE交于点F,且/ BAC=45°,BD=6,CD=4,则AABC的面积为.12、如图,四边形ABCD中,AD〃BC,ZABC=90°,AB=5,BC=10,连接AC、BD,以BD为直径的圆交AC于点E.若DE=3,则AD的长为()C.3V5A.5B.4 D.2V513、如图,在菱形ABCD中,ZABC=120°,将菱形折叠,使点A恰好落在对角线BD上的点G处(不与B、D重合),折痕为EF,若DG=2,BG=6,则BE的长为.14、如图,已知口AOBC的顶点0(0,0), A (-1,2),点B在x轴正半轴上按以下步骤作图:①以点0为圆心,适当长度为半径作孤,分别交边0A,0B于点D, E;②分别以点D,E为圆心,大于fDE的长为半径作弧,两孤在ZA0B内交于点F;③作射线0F,交边AC于点G,则点G的坐标为()A.(V5-1,2)B.(V5,2)C.(3-扃2)D,(扼-2,2)15、如图,ZMAN=90°,点C在边AM上,AC=4,点B为边AN上一动点,连接BC,AA Z BC与AABC关于BC所在直线对称,点D,E分别为AC,BC的中点,连接DE并延长交A'B所在直线于点F,连接A' E.当△▲'EF为直角三角形时, AB的长为.16、如图,在AABC中,ZACB=90°,AC=BC=2,将AABC绕AC的中点D逆时针旋转90。
中考数学部分选填压轴

选填压轴题选集一.选择题(共16小题)1.函数y=和y=在第一象限内的图象如图,点P是y=的图象上一动点,PC⊥x轴于点C,交y=的图象于点B.给出如下结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积大小不会发生变化;④CA=AP.其中所有正确结论的序号是()A.①②③B.②③④C.①③④D.①②④2.如图,在直角坐标系中,直线y1=2x﹣2与坐标轴交于A、B两点,与双曲线y2=(x>0)交于点C,过点C作CD⊥x轴,垂足为D,且OA=AD,则以下结论:①S△ADB=S△ADC;②当0<x<3时,y1<y2;③如图,当x=3时,EF=;④当x>0时,y1随x的增大而增大,y2随x的增大而减小.其中正确结论的个数是()A.1B.2C.3D.43.如图,A、B是双曲线上的点,A、B两点的横坐标分别是a、2a,线段AB的延长线交x轴于点C,若S△AOC=6.则k的值为()A.1B.2C.4D.无法确定4.如图,是二次函数 y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:①a+b+c=0;②b>2a;③ax2+bx+c=0的两根分别为﹣3和1;④a﹣2b+c>0.其中正确的命题是()A.①②B.②③C.①③D.①②③④5.如图(1)所示,E为矩形ABCD的边AD上一点,动点P,Q同时从点B出发,点P沿折线BE﹣ED﹣DC运动到点C时停止,点Q沿BC运动到点C时停止,它们运动的速度都是1cm/秒.设P、Q同时出发t秒时,△BPQ的面积为ycm2.已知y与t的函数关系图象如图(2)(曲线OM为抛物线的一部分),则下列结论:①AD=BE=5;②;③当0<t≤5时,;④当秒时,△ABE∽△QBP;其中正确的结论是()A.①②③B.②③B.①③④D.②④6.如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为x=,且经过点(2,0),有下列说法:①abc<0;②a+b=0;③4a+2b+c<0;④若(0,y1),(1,y2)是抛物线上的两点,则y1=y2.上述说法正确的是()A.①②④B.③④C.①③④D.①②7.如图,已知A、B两点的坐标分别为(﹣2,0)、(0,1),⊙C 的圆心坐标为(0,﹣1),半径为1.若D是⊙C上的一个动点,射线AD与y轴交于点E,则△ABE面积的最大值是()A.3B.C.D.48.图1是用钢丝制作的一个几何探究工具,其中△ABC内接于⊙G,AB是⊙G的直径,AB=6,AC=2.现将制作的几何探究工具放在平面直角坐标系中(如图2),然后点A在射线OX上由点O开始向右滑动,点B在射线OY上也随之向点O滑动(如图3),当点B滑动至与点O重合时运动结束.在整个运动过程中,点C运动的路程是()A.4B.6C.4﹣2D.10﹣49.如图,AB为半圆O在直径,AD、BC分别切⊙O于A、B两点,CD切⊙O于点E,连接OD、OC,下列结论:①∠DOC=90°,②AD+BC=CD,③S△AOD:S△BOC=AD2:AO2,④OD:OC=DE:EC,⑤OD2=DE•CD,正确的有()A.2个B.3个C.4个D.5个10.如图,在矩形ABCD中,AB=4,AD=5,AD,AB,BC分别与⊙O相切于E,F,G三点,过点D作⊙O的切线BC于点M,切点为N,则DM的长为()A.B.C.D.2B.11.如图,⊙O的半径为2,AB、CD是互相垂直的两条直径,点P是⊙O上任意一点(P与A、B、C、D不重合),经过P作PM⊥AB于点M,PN⊥CD于点N,点Q是MN的中点,当点P沿着圆周转过45°时,点Q走过的路径长为()B.C.D.A.B.12.一张圆心角为45°的扇形纸板和圆形纸板按如图方式分别剪成一个正方形,边长都为1,则扇形和圆形纸板的面积比是()A.5:4B.5:2C.:2D.:13.如图,在平面直角坐标系中,⊙O的半径为1,点P在经过点A(﹣4,0)、B(0,4)的直线上,PQ切⊙O于点Q,则切线长PQ的最小值为()A.B.2C.3D.414.如图1,在矩形ABCD中,动点E从A出发,沿AB→BC方向运动,当点E到达点C时停止运动,过点E做FE⊥AE,交CD于F点,设点E运动路程为x,FC=y,如图2所表示的是y与x的函数关系的大致图象,当点E在BC上运动时,FC的最大长度是,则矩形ABCD的面积是()B.5C.6D.A.15.如图,在平面直角坐标系中,四边形OBCD是边长为4的正方形,平行于对角线BD的直线l从O出发,沿x轴正方向以每秒1个单位长度的速度运动,运动到直线l与正方形没有交点为止.设直线l扫过正方形OBCD的面积为S,直线l运动的时间为t(秒),下列能反映S与t之间函数关系的图象是()A.B.C.D.16.如图,动点P从点A出发,沿线段AB运动至点B后,立即按原路返回,点P在运动过程中速度不变,则以点B为圆心,线段BP长为半径的圆的面积S与点P的运动时间t的函数图象大致为()A.B.C.D.二.填空题(共7小题)17.如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数y=的图象上,若点A的坐标为(﹣2,﹣2),则k的值为.18.如图,已知点A,C在反比例函数y=(a>0)的图象上,点B,D在反比例函数y=(b<0)的图象上,AB∥CD∥x轴,AB,CD在x轴的两侧,AB=3,CD=2,AB与CD的距离为5,则a﹣b的值是.19.如图,在平面直角坐标系xOy中,四边形ODEF和四边形ABCD都是正方形,点F在x 轴的正半轴上,点C在边DE上,反比例函数y=(k≠0,x>0)的图象过点B,E.若AB=2,则k的值为.20.如图,点A1,A2依次在y=(x>0)的图象上,点B1,B2依次在x轴的正半轴上.若△A1OB1,△A2B1B2均为等边三角形,则点B2的坐标为.21.如图,若双曲线y=(k>0)与边长为3的等边△AOB(O为坐标原点)的边OA、AB 分别交于C、D两点,且OC=2BD,则k的值为.22.如图,在平面直角坐标系xOy中,△OAB的顶点A在x轴正半轴上,OC是△OAB的中线,点B,C在反比例函数y=(x>0)的图象上,则△OAB的面积等于.23.如图,已知点A1,A2,…,A n均在直线y=x﹣1上,点B1,B2,…,B n均在双曲线y=﹣上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,A n B n⊥x轴,B n A n+1⊥y 轴,…,记点A n的横坐标为a n(n为正整数).若a1=﹣1,则a2015=.2018年06月02日445****3977的初中数学组卷参考答案一.选择题(共17小题)1.C;2.C;3.C;4.C;5.C;6.A;7.B;8.D;9.C;10.A;11.A;12.A;13.A;14.B;15.D;16.B;二.填空题(共7小题)17.4;18.6;19.6+2;20.(6,0);21.;22.;23.2;。
初中中考数学几何选择填空压轴题精选配包括答案.doc

2 0 1 6中考数学几何选择填空压轴题精选(配答案)一.(共13 小)1.( 2013?春模)如,点O正方形 ABCD的中心, BE 平分∠ DBC 交 DC于点 E,延 BC到点F,使 FC=EC,接 DF交 BE的延于点 H,接 OH交 DC于点 G,接 HC.以下四个中正确的个数()①OH= BF;②∠ CHF=45°;③ GH= BC;④ DH2=HE?HB.A. 1 个B. 2 个C. 3 个D. 4 个2.(2013?云港模)如, Rt△ABC 中, BC= ,∠ ACB=90°,∠ A=30°, D1是斜 AB的中点,D1作 D1E1⊥AC 于 E1, BE1交 CD1于 D2;D2作 D2 E2⊥AC 于 E2, BE2交 CD1于 D3; D3作D3E3⊥AC 于 E3,⋯,如此,可以依次得到点E4、 E5、⋯、 E2013,分△ BCE1、△ BCE2、△BCE3、⋯、△ BCE2013的面 S1、 S2、 S3、⋯、 S2013. S2013的大小()A.B.C.D.3.如,梯形 ABCD中, AD∥BC,,∠ ABC=45°, AE⊥BC 于点 E,BF⊥AC 于点 F,交AE于点 G, AD=BE,接 DG、 CG.以下:①△ BEG≌△ AEC;②∠ GAC=∠GCA;③ DG=DC;④G AE 中点,△ AGC 的面有最大.其中正确的有()A. 1 个B. 2 个C. 3 个D. 4 个4.如,正方形ABCD中,在 AD的延上取点E, F,使 DE=AD, DF=BD,接 BF 分交 CD, CE于H, G下列:①EC=2DG;②∠ GDH=∠GHD;③S△CDG=S?DHGE;④ 中有 8 个等腰三角形.其中正确的是()A.①③B.②④C.①④D.②③5.( 2008? 州)如,直角梯形ABCD中,∠ BCD=90°, AD∥BC, BC=CD, E 梯形内一点,且∠BEC=90°,将△ BECC点旋90°使 BC 与 DC重合,得到△ DCF,EF 交 CD于 M.已知 BC=5,CF=3, DM: MC的()A. 5: 3 B. 3: 5 C. 4: 3 D. 3: 4 6.如,矩形ABCD的面5,它的两条角交于点O1,以 AB, AO1两作平行四形ABCO11,平行四形 ABCO11的角交 BD于点 02,同以 AB, AO2两作平行四形 ABCO22.⋯,依此推,平行四形ABC2009O2009的面()A.B.C.D.7.如,在角△ ABC 中, AB=6,∠ BAC=45°,∠ BAC 的平分交 BC 于点 D, M, N 分是 AD和 AB上的点, BM+MN的最小是()A.B. 6 C.D. 3 8.( 2013? 牡丹江)如,在△ ABC 中∠ A=60°, BM⊥AC 于点 M,CN⊥AB 于点 N, P BC的中点,接 PM, PN,下列:① PM=PN;②;③△ PMN等三角形;④当∠ ABC=45° ,BN= PC.其中正确的个数是()A. 1 个B. 2 个C. 3 个D. 4 个9.( 2012? 黑河) Rt△ABC 中, AB=AC,点 D BC中点.∠ MDN=90°,∠ MDN 点 D 旋, DM、 DN分与 AB、AC 交于 E、 F 两点.下列:①( BE+CF) =BC;②S△AEF≤S△ABC;③S四边形=AD?EF;AEDF④A D≥EF;⑤A D 与 EF 可能互相平分,其中正确的个数是()A. 1 个B. 2 个C. 3 个D. 4 个10.(2012? 无一模)如,在正方形片ABCD中,角AC、 BD交于点 O,折叠正方形片ABCD,使 AD落在 BD上,点 A 恰好与 BD上的点 F 重合,展开后折痕DE分交 AB、 AC于点 E、 G,接 GF.下列①∠ ADG=°;② tan ∠AED=2;③S△AGD=S△OGD;④四形 AEFG是菱形;⑤ BE=2OG.其中正确的有()A.①④⑤B.①②④C.③④⑤D.②③④11.如,正方形ABCD中, O BD中点,以 BC 向正方形内作等△ BCE,接并延AE 交 CD 于 F,接 BD分交 CE、AF 于 G、 H,下列:①∠ CEH=45°;② GF∥DE;③2OH+DH=BD;④ BG= DG;⑤.其中正确的是()A.①②③B.①②④C.①②⑤D.②④⑤12.如,在正方形ABCD中, AB=4, E CD上一点, AE交 BD 于 F, F 作 FH⊥AE 于 H, H 作GH⊥BD 于 G,下列有四个:① AF=FH,②∠ HAE=45°,③ BD=2FG,④△ CEH 的周定,其中正确的有()A.①②③B.①②④C.①③④D.①②③④13.(2013? 州模)正方形 ABCD、正方形 BEFG和正方形 RKPF的位置如所示,点G在段 DK上,正方形 BEFG的4,△ DEK 的面()A. 10 B. 12 C. 14 D. 16 二.填空(共 16 小)14.如,在梯形ABCD中, AD∥BC,EA⊥AD, M是 AE上一点, F、 G分是 AB、 CM的中点,且∠B AE=∠MCE,∠ MBE=45°,出以下五个:① AB=CM;② A E⊥BC;③∠ BMC=90°;④ EF=EG;⑤△ BMC是等腰直角三角形.上述中始正确的序号有_________ .15.(2012? 沟区一模)如,面 1 的△ ABC逐次行以下操作:第一次操作,分延AB、BC、 CA至 A1、 B1、 C1,使得 A1B=2AB, B1C=2BC, C1A=2CA,次接 A1、 B1、 C1,得到△A1B1C1,其面 S1;第二次操作,分延 A1B1, B1C1, C1 A1至 A2, B2, C2,使得 A2B1=2A1B1, B2C1=2B1C1,C2A1=2C1A1,次接 A2,B2, C2,得到△A2B2 C2,其面 S2⋯,按此律下去,可得到△A5B5C5,其面S5= _________ .第 n 次操作得到△A n B n C n,△A n B n C n的面 S n =_________ .16.( 2009? 黑河)如, 1 的菱形 ABCD中,∠ DAB=60 度.接角 AC,以 AC作第二个菱形 ACCD11,使∠D1AC=60°;接AC1,再以 AC1作第三个菱形 AC1C2D2,使∠D2AC1 =60°;⋯,按此律所作的第n 个菱形的_________ .17.( 2012? 通州区二模)如,在△ ABC 中,∠ A=α.∠ ABC 与∠ ACD的平分交于点 A1,得∠A1;∠A1BC与∠A1CD的平分相交于点A2,得∠A2;⋯;∠A2011BC与∠A2011CD的平分相交于点 A2012,得∠A2012,∠A2012= _________ .18.( 2009?湖州)如,已知 Rt△ABC, D1是斜 AB的中点, D1作 D1E1⊥AC 于 E1,接 BE1交 CD1于 D ; D 作D E ⊥AC 于 E ,接 BE 交 CD 于 D ; D 作 D E ⊥AC 于 E ,⋯,如此,可以依次22 2 222133 3 3 3得到点 D4, D5,⋯, D n,分△ BD 1E1,△ BD2E2,△ BD3E3,⋯,△ BD n E n的面 S1, S2,S3,⋯S n. S n= _________ S△ABC(用含 n 的代数式表示).19.( 2011? 丰台区二模)已知:如,在Rt△ABC 中,点 D1是斜 AB 的中点,点 D1作 D1 E1⊥AC 于点 E1,接 BE1交 CD1于点 D2;点 D2作 D2E2⊥AC于点 E2,接 BE2交 CD1于点 D3;点 D3作 D3E3⊥AC于点 E3,如此,可以依次得到点D4、 D5、⋯、 D n,分△ BD 1E1、△ BD2E2、△ BD3E3、⋯、△ BD n E n的面 S1、 S2、 S3、⋯S n.△ ABC 的面是1, S1= _________ , S n= _________ (用含 n 的代数式表示).20.( 2013?路北区三模)在△ ABC中, AB=6, AC=8, BC=10, PBC上一点, PE⊥AB 于 E,PF⊥AC于 F, M EF 中点, AM的最小_________ .21.如,已知 Rt△ABC中, AC=3, BC=4,直角点 C作 CA1⊥AB,垂足 A1,再 A1作 A1C1⊥BC,垂足 C1, C1作 C1 A2⊥AB,垂足A2,再 A2作 A2 C2⊥BC,垂足 C2,⋯,一直做下去,得到了一段 CA1, A1C1, C1A2,⋯,CA1= _________ ,= _________ .22.( 2013? 沐川二模)如,点A1, A2, A3, A4,⋯, A n在射 OA上,点 B1, B2, B3,⋯, B n﹣1在射 OB上,且 A1B1∥A2B2∥A3B3∥⋯∥A n﹣1B n﹣1, A2B1∥A3B2∥A4B3∥⋯∥A n B n﹣1,△A1A2 B1,△A2A3B2,⋯,△A n﹣ 1A n B n﹣ 1 阴影三角形,若△A 2B1B2,△A3B2B3 的面分1、 4,△A1A2B1的面_________ ;面小于2011 的阴影三角形共有_________ 个.23.( 2010?城区)如,已知点A1( a, 1)在直 l :上,以点 A1心,以半径画弧,交 x 于点 B1、 B2,点 B2作 A1B1的平行交直 l 于点 A2,在 x 上取一点 B3,使得A2B3=A2 B2,再点 B3作 A2B2的平行交直 l 于点 A3,在 x 上取一点B4,使得 A3B4 =A3B3,按此律作下去,① a= _________ ;②△A4 B4B5 的面是_________ .24.( 2013? 松北区二模)如,以Rt△ABC 的斜 BC 一在△ ABC 的同作正方形 BCEF,正方形的中心 O,接 AO,如果 AB=4, AO=6 ,那么 AC的等于_________ .25.( 2007? 淄川区二模)如,将矩形ABCD的四个角向内折起,恰好拼成一个既无隙又无重叠的四形 EFGH,若 EH=3, EF=4,那么段AD与 AB的比等于_________ .26.( 2009? 泰市模)梯形ABCD中 AB∥CD,∠ ADC+∠BCD=90°,以AD、 AB、 BC 斜向形外作等腰直角三角形,其面分是S1、 S2、 S3且 S1+S3 =4S2, CD= _________ AB.27.如,察中菱形的个数: 1 中有 1 个菱形, 2 中有 5 个菱形, 3 中有 14 个菱形, 4 中有 30 个菱形⋯,第 6 个中菱形的个数是_________ 个.28.(2012? 港一模)如, E、 F 分是平行四形 ABCD的 AB、 CD上的点, AF 与 DE相交于点 P,BF 与 CE 相交于点 Q,若 S△APD=15cm2,S△BQC=25cm2,阴影部分的面_________ cm2.29.( 2012? 天津)如,已知正方形ABCD的 1,以点 A、 B 心, 1 半径的两弧交于点E,以点 C、 D 心, 1 半径的两弧交于点F, EF 的_________ .30.如, ABCD是凸四形, AB=2, BC=4, CD=7,求段 AD 的取范().参考答案与试题解析一.(共 13 小)1.( 2013?春模)如,点O正方形 ABCD的中心, BE 平分∠ DBC 交 DC于点 E,延 BC到点F,使 FC=EC,接 DF交 BE的延于点H,接 OH交 DC于点 G,接 HC.以下四个中正确的个数()①OH= BF;②∠ CHF=45°;③ GH= BC;④ DH2=HE?HB.A. 1 个B. 2 个C. 3 个D. 4 个解答:解:作 EJ⊥BD 于 J,接 EF①∵ BE 平分∠ DBC∴E C=EJ,∴△ DJE≌△ ECF∴D E=FE∴∠ HEF=45°+°=°∴∠ HFE==°∴∠ EHF=180°﹣°﹣° =90°∵D H=HF, OH是△ DBF 的中位线∴OH∥BF∴O H= BF②∵四边形ABCD是正方形, BE 是∠ DBC的平分线,∴B C=CD,∠ BCD=∠DCF,∠ EBC=°,∵C E=CF,∴Rt△BCE≌Rt△DCF,∴∠ EBC=∠CDF=°,∴∠ BFH=90°﹣∠ CDF=90°﹣° =°,∵OH是△ DBF 的中位线, CD⊥AF,∴O H是 CD的垂直平分线,∴D H=CH,∴∠ CDF=∠DCH=°,∴∠ HCF=90°﹣∠ DCH=90°﹣° =°,∴∠ CHF=180°﹣∠ HCF﹣∠ BFH=180°﹣°﹣° =45°,故②正确;③∵ OH是△ BFD 的中位线,∴D G=CG= BC, GH= CF,∵C E=CF,∴G H= CF= CE∵C E< CG= BC,∴GH<BC,故此结论不成立;④∵∠ DBE=45°, BE 是∠ DBF 的平分线,∴∠ DBH=°,由②知∠ HBC=∠CDF=°,∴∠ DBH=∠CDF,∵∠ BHD=∠BHD,∴△ DHE∽△ BHD,∴=∴D H=HE?HB,故④成立;所以①②④正确.故选 C.2.(2013?云港模)如, Rt△ABC 中, BC=,∠ ACB=90°,∠A=30°,D1是斜AB的中点,D1作 D1E1⊥AC 于 E1, BE1交 CD1于 D2; D2作 D2 E2⊥AC 于 E2, BE2交 CD1于 D3; D3作D3E3⊥AC 于E3,⋯,如此,可以依次得到点E4、 E5、⋯、E2013,分△ BCE1、△ BCE2、△BCE3、⋯、△ BCE2013的面S1、 S2、 S3、⋯、 S2013.S2013的大小()A.B.C.D.解答:解:∵ Rt△ABC 中, BC=∴AC==BC=6,,∠ ACB=90°,∠ A=30°,∴S△ABC=AC?BC=6,∵D1 E1⊥AC,∴D1 E1∥BC,∴△ BD1E1与△ CD1E1同底同高,面相等,∵D1 是斜AB的中点,∴D1 E1=BC, CE1= AC,∴S1 =BC?CE1= BC×AC= ×AC?BC= S△ABC;∴在△ ACB 中, D2其重心,∴D2 E1=BE1,∴D E =2 2 BC, CE = AC, S =×22×AC?BC= S△,ABC∴D E =3 3BC, CE = AC, S = S△⋯;23ABC ∴S n = S△ABC;∴S2013= ×6= .故C.3.如,梯形ABCD中, AD∥BC,AE于点 G, AD=BE,接 DG、 CG.以下:①△,∠ ABC=45°, AE⊥BC 于点 E,BF⊥AC 于点BEG≌△ AEC;②∠ GAC=∠GCA;③ DG=DC;④GF,交AE中点,△ AGC 的面有最大.其中正确的有()A. 1 个B. 2 个C. 3 个D. 4 个解答:解:根据BE=AE,∠ GBE=∠CAE,∠ BEG=∠CEA可判定①△ BEG≌△AEC;用反法明②∠ GAC≠∠ GCA,假∠ GAC=∠GCA,有△ AGC等腰三角形,F AC 的中点,又BF⊥AC,可AB=BC,与不符;由①知△ BEG≌△ AEC 所以GE=CE 接 ED、四形ABED平行四形,∵∠ ABC=45°, AE⊥BC 于点 E,∴∠ GED=∠CED=45°,∴△ GED≌△ CED,∴D G=DC;④ AG X,易求出GE=EC=2 X 因此, S△=S S =+x=(x22x)AGC AEC GEC=﹣(x2﹣2x+1﹣1)=﹣(x﹣1)2+,当X取1时,面积最大,所以AG等于 1,所以 G是 AE 中点,故 G 为 AE 中点时, GF最长,故此时△ AGC 的面积有最大值.故正确的个数有 3 个.故选 C.4.如图,正方形ABCD中,在AD的延长线上取点E, F,使DE=AD, DF=BD,连接BF 分别交CD, CE于H, G下列结论:①EC=2DG;②∠ GDH=∠GHD;③S△CDG=S?DHGE;④图中有A.①③B.②④解答:解:∵ DF=BD,∴∠ DFB=∠DBF,8 个等腰三角形.其中正确的是(C.①④)D.②③∵AD∥BC, DE=BC,∴∠ DEC=∠DBC=45°,∴∠ DEC=2∠EFB,∴∠ EFB=°,∠ CGB=∠CBG=°,∴CG=BC=DE,∵DE=DC,∴∠ DEG=∠DCE,∵∠ GHC=∠CDF+∠DFB=90°+°=°,∠DGE=180°﹣(∠ BGD+∠EGF),=180°﹣(∠ BGD+∠BGC),=180°﹣( 180°﹣∠ DCG)÷ 2,=180°﹣( 180°﹣ 45°)÷ 2,=°,∴∠ GHC=∠DGE,∴△ CHG≌△ EGD,∴∠ EDG=∠CGB=∠CBF,∴∠ GDH=∠GHD,∴S△CDG=S?DHGE.故选D.5.( 2008? 荆州)如图,直角梯形ABCD中,∠ BCD=90°, AD∥BC,BC=CD, E 为梯形内一点,且∠BEC=90°,将△ BEC 绕 C点旋转90°使BC 与 DC重合,得到△DCF,连EF 交CD于M.已知BC=5,CF=3,则 DM: MC的值为()A.5: 3B.3: 5解答:解:由题意知△ BCE 绕点 C 顺时转动了∴△ BCE≌△ DCF,∠ ECF=∠DFC=90°,90 度,C.4: 3 D.3: 4∴CD=BC=5,DF∥CE,∴∠ ECD=∠CDF,∵∠EMC=∠DMF,∴△ECM∽△ FDM,∴D M: MC=DF: CE,∵DF==4,∴DM: MC=DF: CE=4: 3.故选 C.6.如,矩形ABCD的面5,它的两条角交于点O1,以AB, AO1两作平行四形ABC1O1,平行四形ABC1O1的角交BD于点02,同以AB, AO2两作平行四形ABC2O2.⋯,依此推,平行四形ABC O的面(20092009)A.B.C.D.解答:解:∵矩形ABCD的角互相平分,面5,∴平行四形ABC1O1的面,∵平行四形ABC1O1的角互相平分,∴平行四形ABC2O2的面×=,⋯,依此推,平行四形ABC2009O2009的面.故 B.7.如,在角△ABC 中, AB=6,∠ BAC=45°,∠ BAC 的平分交BC 于点D, M, N 分是AD和AB 上的点,BM+MN的最小是()A.解答:B. 6解:如,作BH⊥AC,垂足H,交 AD 于 M′点,最小.C.M′点作M′N′⊥ AB,垂足D. 3N′,BM′+M′N′ 所求∵A D是∠ BAC 的平分,∴M′H=M′N′,∴BH是点 B 到直 AC的最短距离(垂段最短),∵A B=4,∠ BAC=45°,∴BH=AB?sin45°=6×=3.∵BM+MN的最小是BM′+M′N′=BM′+M′H=BH=3.故 C.8.( 2013? 牡丹江)如,在△ ABC 中∠ A=60°, BM⊥AC 于点 M,CN⊥AB 于点 N, P BC的中点,接PM, PN,下列:①PM=PN;②;③△ PMN等三角形;④当∠ABC=45° ,BN= PC.其中正确的个数是()A. 1 个B. 2 个C. 3 个D. 4 个解答:解:①∵ BM⊥AC 于点 M,CN⊥AB 于点 N, P BC 的中点,∴P M= BC, PN= BC,∴P M=PN,正确;②在△ABM与△ ACN中,∵∠ A=∠A,∠ AMB=∠ANC=90°,∴△ ABM∽△ ACN,∴,正确;③∵∠ A=60°, BM⊥AC 于点 M,CN⊥AB 于点 N,∴∠ ABM=∠ACN=30°,在△ ABC中,∠ BCN+∠CBM═180° 60° 30°× 2=60°,∵点 P 是 BC 的中点, BM⊥AC,CN⊥AB,∴P M=PN=PB=PC,∴∠ BPN=2∠BCN,∠ CPM=2∠CBM,∴∠ BPN+∠CPM=2(∠ BCN+∠CBM)=2×60°=120°,∴∠ MPN=60°,∴△ PMN是等边三角形,正确;④当∠ ABC=45°时,∵ CN⊥AB于点N,∴∠ BNC=90°,∠ BCN=45°,∴B N=CN,∵P为 BC边的中点,∴P N⊥BC,△ BPN 为等腰直角三角形∴B N= PB= PC,正确.故选 D.9.( 2012? 黑河) Rt△ABC 中, AB=AC,点 D 为 BC中点.∠ MDN=90°,∠ MDN 绕点 D 旋转, DM、DN分别与边 AB、 AC 交于 E、 F 两点.下列结论:①( BE+CF) =BC;②S△AEF≤S△ABC;③S四边形 AEDF=AD?EF;④A D≥EF;⑤A D 与 EF 可能互相平分,其中正确结论的个数是()A. 1 解答:个B. 2 个解:∵ Rt△ABC 中, AB=AC,点 D 为∴∠ C=∠BAD=45°,AD=BD=CD,∵∠ MDN=90°,BC中点,C. 3 个D. 4 个∴∠ ADE+∠ADF=∠ADF+∠CDF=90°,∴∠ ADE=∠CDF.在△ AED与△ CFD中,∵,∴△ AED≌△ CFD( ASA),∴A E=CF,在 Rt△ABD 中, BE+CF=BE+AE=AB==BD=BC.故①正确;设AB=AC=a, AE=CF=x,则 AF=a﹣ x .∵S= AE?AF= x( a﹣ x) =﹣(x﹣a)2+a2,△AEF∴当 x= a 时, S△AEF有最大值a2,又∵ S△ABC= × a2= a2,∴S△AEF≤S△ABC.故②正确;EF2=AE2+AF2=x2+( a﹣ x)2 =2( x﹣a)2+a2,∴当 x= a 时, EF2取得最小值a2,∴EF≥a(等号当且仅当x= a 时成立),而AD= a,∴ EF≥AD.故④错误;由①的证明知△ AED≌△ CFD,∴S四边形=S△+S△=S△+S△=S△=AD2,AEDF AED ADF CFD ADF ADC∵E F≥AD,∴A D?EF≥AD 2,∴A D?EF> S 四边形AEDF故③错误;当E、 F 分别为 AB、 AC 的中点时,四边形 AEDF为正方形,此时 AD与 EF 互相平分.故⑤正确.综上所述,正确的有:①②⑤,共 3 个.故选 C.10.(2012? 无锡一模)如图,在正方形纸片ABCD中,对角线AC、 BD交于点 O,折叠正方形纸片ABCD,使 AD落在 BD上,点 A 恰好与 BD上的点 F 重合,展开后折痕DE分别交 AB、 AC于点 E、 G,连接 GF.下列结论①∠ ADG=°;② tan∠AED=2;③S△AGD=S△OGD;④四边形AEFG是菱形;⑤BE=2OG.其中正确的结论有()A.①④⑤B.①②④C.③④⑤D.②③④解答:解:∵四边形ABCD是正方形,∴∠ GAD=∠ADO=45°,由折叠的性质可得:∠ADG= ∠ADO=°,故①正确.∵tan ∠AED= ,由折叠的性质可得:AE=EF,∠ EFD=∠EAD=90°,∴A E=EF< BE,∴A E< AB,∴tan ∠AED=>2,故②错误.∵∠ AOB=90°,∴A G=FG> OG,△ AGD与△ OGD同高,∴S△AGD>S△OGD,故③错误.∵∠ EFD=∠AOF=90°,∴E F∥AC,∴∠ FEG=∠AGE,∵∠ AGE=∠FGE,∴∠ FEG=∠FGE,∴EF=GF,∵AE=EF,∴A E=GF,故④正确.∵AE=EF=GF, AG=GF,∴A E=EF=GF=AG,∴四边形 AEFG是菱形,∴∠ OGF=∠OAB=45°,∴E F=GF= OG,∴BE=EF=×OG=2OG.故⑤正确.∴其中正确结论的序号是:①④⑤.故选: A.11.如图,正方形ABCD中, O 为 BD中点,以 BC 为边向正方形内作等边△BCE,连接并延长于 F,连接BD分别交 CE、AF 于 G、 H,下列结论:①∠ CEH=45°;② GF∥DE;AE 交CD③2OH+DH=BD;④ BG= DG;⑤.其中正确的结论是()A.①②③B.①②④C.①②⑤D.②④⑤解答:解:①由∠ ABC=90°,△ BEC为等边三角形,△ ABE为等腰三角形,∠ AEB+∠BEC+∠CEH=180°,可求得∠CEH=45°,此结论正确;②由△ EGD≌△ DFE,EF=GD,再由△ HDE 为等腰三角形,∠ DEH=30°,得出△ HGF为等腰三角形,∠ HFG=30°,可得 GF∥DE,此结论正确;③由图可知2( OH+HD) =2OD=BD,所以 2OH+DH=BD此结论不正确;④如图,过点G作 GM⊥CD 垂足为 M,GN⊥BC 垂足为 N,设 GM=x,则 GN= x ,进一步利用勾股定理求得GD=BG= x,得出BG=GD,此结论不正确;⑤由图可知△BCE 和△ BCG同底不等高,它们的面积比即是两个三角形的高之比,由④可知△BCE 的高为(x+x )和△ BCG的高为x ,因此S△BCE:S△BCG= (x+x ):x= ,此结论正确;故正确的结论有①②⑤.故选 C.12.如图,在正方形ABCD中, AB=4, E 为 CD上一动点, AE交 BD 于 F,过GH⊥BD 于 G,下列有四个结论:① AF=FH,②∠ HAE=45°,③ BD=2FG,④△ CEH F 作 FH⊥AE 于 H,过 H 作的周长为定值,其中正确的结论有()A.①②③解答:解:( 1)连接B.①②④FC,延长 HF交 AD 于点L,C.①③④D.①②③④∵B D为正方形 ABCD的对角线,∴∠ ADB=∠CDF=45°.∵AD=CD, DF=DF,∴△ ADF≌△ CDF.∴FC=AF,∠ ECF=∠DAF.∵∠ ALH+∠LAF=90°,∴∠ LHC+∠DAF=90°.∵∠ ECF=∠DAF,∴∠ FHC=∠FCH,∴F H=FC.∴F H=AF.(2)∵ FH⊥AE,FH=AF,∴∠ HAE=45°.(3)连接 AC交 BD于点 O,可知: BD=2OA,∵∠ AFO+∠GFH=∠GHF+∠GFH,∴∠ AFO=∠GHF.∵AF=HF,∠ AOF=∠FGH=90°,∴△ AOF≌△ FGH.∴OA=GF.∵B D=2OA,∴B D=2FG.(4)延长 AD至点 M,使 AD=DM,过点 C 作 CI∥HL,则: LI=HC,根据△ MEC≌△ CIM,可得:CE=IM,同理,可得:AL=HE,∴HE+HC+EC=AL+LI+IM=AM=8.∴△ CEH的周长为8,为定值.故( 1)( 2)( 3)( 4)结论都正确.故选 D.13.(2013? 钦州模拟)正方形 ABCD、正方形BEFG和正方形RKPF的位置如图所示,点正方形 BEFG的边长为4,则△ DEK 的面积为()G在线段DK上,A.10 B.12 C.14 D.16解答:解:如图,连DB, GE, FK,则 DB∥GE∥FK,在梯形 GDBE中, S△DGE=S△GEB(同底等高的两三角形面积相等),同理 S△GKE=S△GFE.∴S阴影 =S△+S△,DGE GKE=S△GEB+S△GEF,=S 正方形GBEF,=4×4=16故选 D.二.填空题(共16 小题)14.如图,在梯形ABCD中, AD∥BC,EA⊥AD,M是 AE上一点, F、 G分别是AB、 CM的中点,且∠BAE=∠MCE,∠ MBE=45°,则给出以下五个结论:① AB=CM;② A E⊥BC;③∠ BMC=90°;④ EF=EG;⑤△ BMC是等腰直角三角形.上述结论中始终正确的序号有①②④.解答:解:∵梯形ABCD中, AD∥BC,EA⊥AD,∴A E⊥BC,即②正确.∵∠MBE=45°,∴B E=ME.在△ ABE 与△ CME中,∵∠ BAE=∠MCE,∠ AEB=∠CEM=90°,BE=ME,∴△ ABE≌△ CME,∴AB=CM,即①正确.∵∠ MCE=∠BAE=90° ∠ ABE<90° ∠ MBE=45°,∴∠ MCE+∠MBC<90°,∴∠ BMC>90°,即③⑤ .∵∠ AEB=∠CEM=90°,F、 G分是AB、 CM的中点,∴E F= AB, EG= CM.又∵ AB=CM,∴EF=EG,即④正确.故正确的是①②④.15.(2012? 沟区一模)如,面 1 的△ ABC逐次行以下操作:第一次操作,分延 AB、BC、 CA至 A1、 B1、 C1,使得 A1B=2AB, B1C=2BC, C1A=2CA,次接 A1、 B1、 C1,得到△A1B1C1,其面 S1;第二次操作,分延 A1B1,B1C1, C1 A1至 A2, B2, C2,使得 A2B1=2A1B1, B2C1=2B1C1,C2A1=2C1A1,次接A2, B2, C2,得到△A2B2 C2,其面S2⋯,按此律下去,可得到△A5B5C5,其面S5= 2476099.第n次操作得到△A n B n C n,△A n B n C n的面S n= 19 n.解答:解:接A1C;S△AA1C=3S△ABC=3,S△AA1C1=2S△AA1C=6,所以 S△=6×3+1=19;A1B1C1同理得 S△A2B2C2=19×19=361;S△A3B3C3=361×19=6859,S△A4B4C4=6859×19=130321,S△A5B5C5=130321×19=2476099,从中可以得出一个律,延各后得到的三角形是原三角形的19 倍,所以延第 n 次后,得到△A n B n C n,其面 S n=19n?S1 =19n故答案是: 2476099 ; 19n.16.( 2009? 黑河)如, 1 的菱形 ABCD中,∠ DAB=60 度.接角 AC,以 AC作第二个菱形 ACC1D1,使∠D1AC=60°;接AC1,再以 AC1作第三个菱形AC1C2D2,使∠D2AC1 =60°;⋯,按此律所作的第n 个菱形的() n﹣ 1 .解答:解:接 DB,∵四形 ABCD是菱形,∴AD=AB.AC⊥DB,∵∠ DAB=60°,∴△ ADB 是等三角形,∴D B=AD=1,∴B M= ,∴AM= = ,∴AC= ,同理可得 AC1 = AC=()2, AC2= AC1=3=()3,按此律所作的第n 个菱形的(n﹣ 1 )n﹣ 1 故答案().∠A BC与∠A CD的平分相交于点1 1ABC 中,∠ A=α.∠ ABC 与∠ ACD的平分交于点A1,得∠A1;A2,得∠A2;⋯;∠A2011BC与∠A2011CD的平分相交于点A2012,得∠A2012,∠A2012= .解答:解:∵∠ ABC 与∠ ACD的平分交于点A1,∴∠A1BC= ∠ABC,∠A1CD= ∠ACD,根据三角形的外角性,∠A+∠ABC=∠ACD,∠A1+∠A1BC=∠A1CD,∴∠A1+∠A1BC=∠A1 +∠ABC=(∠A+∠ABC),整理得,∠A1=∠A=,同理可得,∠A2=∠A1=×=,⋯,∠A2012=.故答案:.18.( 2009?湖州)如,已知Rt△ABC, D1是斜 AB的中点,D1作 D1E1⊥AC 于 E1,接 BE1交 CD1 于D2; D2作 D2E2⊥AC 于 E2,接 BE2交 CD1于 D3; D3作 D3E3⊥AC 于 E3,⋯,如此,可以依次得到点 D4,D5,⋯, D n,分△ BD 1E1,△ BD2E2,△ BD3E3,⋯,△ BD n E n的面 S1, S2,S3,⋯S n. S n =S△ABC(用含n 的代数式表示).解答:解:易知D1E1∥BC,∴△ BD 1E1与△ CD1 E1同底同高,面相等,以此推;根据直角三角形的性以及相似三角形的性可知:D1E1= BC, CE1= AC, S1=S△ABC;∴在△ ACB 中, D2其重心,∴D E = BE ,2 1 1∴D2E2=BC, CE2= AC, S2=S△ABC,∵D2E2:D1E1=2:3,D1E1:BC=1:2,∴B C: D2E2 =2D1 E1: D1E1=3,∴CD3: CD2 =D3E3: D2E2=CE3: CE2=3: 4,∴D3E3=D2E2=×BC= BC, CE3= CE2=×AC= AC, S3=S△ABC⋯;∴S n=S△ABC.19.( 2011? 丰台区二模)已知:如,在Rt△ABC 中,点 D1是斜 AB 的中点,点D1作 D1 E1⊥AC 于点 E1,接 BE1交 CD1于点 D2;点 D2作 D2E2⊥AC于点 E2,接 BE2交 CD1于点 D3;点 D3作 D3E3⊥AC于点 E3,如此,可以依次得到点D4、 D5、⋯、 D n,分△ BD 1E1、△ BD2E2、△ BD3E3、⋯、△ BD n E n的面S1、 S2、 S3、⋯S n.△ ABC 的面是1, S1=,S n=(用含n 的代数式表示).解答:解:易知 D1E1∥BC,∴△ BD 1E1与△ CD1 E1同底同高,面相等,以此推;∴S1=S△D1E1A= S△ABC,根据直角三角形的性以及相似三角形的性可知:D1E1= BC, CE1= AC, S1= S△ABC;∴在△ ACB 中, D2其重心,又D1E1三角形的中位,∴D1E1∥BC,∴△D2D1E1∽△ CD2B,且相似比 1: 2,即= ,∴D2E1=BE1,∴D2E2=BC, CE2= AC, S2=S△ABC,∴D E = BC, CE = AC, S =S△⋯;3 333ABC∴S=S△.n ABC故答案:,.20.( 2013?路北区三模)在△ ABC中, AB=6, AC=8, BC=10, P BC上一点, PE⊥AB 于 E,PF⊥AC 于 F, M EF 中点,AM的最小.解答:解:∵四形AFPE是矩形∴A M= AP,AP⊥BC , AP最短,同 AM也最短∴当 AP⊥BC ,△ ABP∽△ CAB∴A P: AC=AB: BC∴A P: 8=6: 10∴A P 最短, AP=∴当 AM最短, AM=AP÷2=.点:解决本的关是理解直外一点到直上任一点的距离,垂段最短,利用相似求解.21.如,已知 Rt△ABC中, AC=3, BC=4,直角点 C作 CA1⊥AB,垂足 A1,再 A1作 A1C1⊥BC,垂足 C1, C1作 C1 A2⊥AB,垂足 A2,再 A2作 A2 C2⊥BC,垂足 C2,⋯,一直做下去,得到了一段CA1, A1C1, C1A2,⋯,CA1=,=.解答:解:在 Rt△ABC 中, AC=3,BC=4,∴AB=,又因 CA1⊥AB,∴AB?CA=AC?BC,1即 CA1===.∵C4A5⊥AB,∴△ BA5C4∽△ BCA,∴,∴==.所以填和.22.( 2013? 沐川二模)如,点A1, A2, A3, A4,⋯, A n在射 OA上,点 B1, B2, B3,⋯, B n﹣1在射 OB上,且 A1B1∥A2B2∥A3B3∥⋯∥A n﹣1B n﹣1, A2B1∥A3B2∥A4B3∥⋯∥A n B n﹣1,△A1A2 B1,△A A B ,⋯,△A﹣ A B ﹣阴影三角形,若△A B B ,△A B B 的面分1、 4,△A A B 的面2 3 2n 1 n n 1 2 1 2 3 2 3 1 2 1;面小于2011 的阴影三角形共有6个.解答:解:由意得,△A2B1B2∽△A3B2B3,∴==,==,又∵A1B1∥A2B2∥A3B3,∴===,==,∴OA1=A1 A2, B1B2=B2B3而可得出律:A1A2= A2A3= A3A4⋯; B1B2= B2B3= B3 B4⋯又△A2B1B2,△A3B2B3 的面分1、 4,∴S△A1B1A2=,S△A2B2A3=2,而可推出S△A3B3A4=8, S△A,4B4A5=32, S△A5B5A6=128 ,S△A6B6A7=512, S△A7B7A8=2048 ,故可得小于2011 的阴影三角形的有:△A 1 B1A2,△A2B2A3,△A3B3A4,△A4B4A5,△A5 B5 A6,△A6 B6A7,共 6 个.故答案是:; 6.23.( 2010?城区)如,已知点A1( a, 1)在直l :上,以点A1心,以半径画弧,交x 于点B1、 B2,点 B2作 A1B1的平行交直l 于点 A2,在 x 上取一点B3,使得A2B3=A2 B2,再过点B3作A2B2的平行线交直线l 于点A3,在x 轴上取一点B4,使得A3B4 =A3B3,按此规律继续作下去,则①a= ;②△A4B4B5 的面积是.解答:解:如图所示:①将点A1( a,1)代入直线 1 中,可得,所以a= .②△A1B1B2 的面积为:S= =;因为△ OA1B1∽△ OA2B2,所以2A1 B1 =A2B2,又因为两线段平行,可知△A 1 B1B2∽△A2B2B3,所以△A 2B2B3 的面积为S1=4S;以此类推,△A4B4B5 的面积等于64S= .BCEF,设正方24.( 2013? 松北区二模)如图,以Rt△ABC 的斜边 BC 为一边在△ ABC 的同侧作正方形形的中心为O,连接 AO,如果AB=4, AO=6,那么AC的长等于16.解答:解:如图,过O点作 OG垂直 AC, G点是垂足.∵∠ BAC=∠BOC=90°,∴ABCO四点共圆,∴∠ OAG=∠OBC=45°∴△ AGO是等腰直角三角形,2 2 2∴2AG =2GO=AO==72,∴O G=AG=6,∵∠ BAH=∠0GH=90°,∠ AHB=∠OHG,∴△ ABH∽△ GOH,∴A B/OG=AH/( AG﹣AH),∵AB=4,OG=AG=6,∴A H=在直角△ OHC 中,∵ HG=AG﹣ AH=6﹣ =, OG又是斜边HC上的高,2∴OG=HG×GC,而OG=6,GH=,∴GC=10.∴AC=AG+GC=6+10=16.故 AC边的长是 16.25.( 2007? 淄川区二模)如图,将矩形ABCD的四个角向内折起,恰好拼成一个既无缝隙又无重叠的四边形 EFGH,若 EH=3, EF=4,那么线段 AD与 AB的比等于.解答:解:∵∠ 1=∠2,∠ 3=∠4,∴∠ 2+∠3=90°,∴∠ HEF=90°,同理四边形EFGH的其它内角都是90°,∴四边形EFGH是矩形.∴E H=FG(矩形的对边相等);又∵∠ 1+∠4=90°,∠ 4+∠5=90°,∴∠ 1=∠5(等量代换),同理∠ 5=∠7=∠8,∴∠ 1=∠8,∴R t△AHE≌Rt△CFG,∴A H=CF=FN,又∵ HD=HN,∴A D=HF,在 Rt△HEF 中, EH=3, EF=4,根据勾股定理得HF=,∴H F=5,又∵ HE?EF=HF?EM,∴E M= ,又∵ AE=EM=EB(折叠后A、 B 都落在M点上),∴A B=2EM= ,∴AD: AB=5:=.故答案:.26.( 2009? 泰市模)梯形ABCD中 AB∥CD,∠ ADC+∠BCD=90°,以等腰直角三角形,其面分是S1、 S2、 S3且 S1+S3 =4S2, CD= 3 解答:解:∵以AD、 AB、 BC斜向外作等腰直角三角形,其面分是S1、 S2、 S3,AD、 AB、 BC 斜向形外作AB.∴S1=,S2=,S3=∵S1+S3=4S2,∴A D2+BC2=4AB2点 B 作 BK∥AD 交 CD于点 K,∵A B∥CD∴AB=DK, AD=BK,∠ BKC=∠ADC∵∠ ADC+∠BCD=90°∴∠ BKC+∠BCD=90°∴B K2+BC2=CK2∴A D2+BC2=CK22 2∴C K =4AB∴C K=2AB∴C D=3AB.27.如,察中菱形的个数: 1 中有 1 个菱形, 2 中有 5 个菱形, 3 中有 14 个菱形, 4中有 30 个菱形⋯,第 6 个中菱形的个数是91个.2 222 214+4 =30 个菱形,第 5 个中菱形的个数是30+5 =55,第 6 个中菱形的个数是55+6 =91 个.4 中有故答案91.28.(2012? 港一模)如, E、 F 分是平行四形ABCD的 AB、 CD上的点, AF 与 DE相交于点22 2解答:解:如,接EFP,∵△ ADF 与△ DEF 同底等高,∴S△ADF=S△DEF即 S△﹣S△=S△﹣S△,ADF DPF DEF DPF即S△APD=S△EPF=15cm2,同理可得S△=S△=25cm2,BQC EFQ∴阴影部分的面积为S△EPF+S△EFQ=15+25=40cm2.故答案为40.29.( 2012? 天津)如图,已知正方形ABCD的边长为1,以顶点A、 B 为圆心, 1 为半径的两弧交于点E,以顶点C、 D 为圆心, 1 为半径的两弧交于点F,则解答:解:连接AE, BE, DF, CF.∵以顶点A、 B 为圆心, 1 为半径的两弧交于点∴AB=AE=BE,∴△ AEB 是等边三角形,EF 的长为E, AB=1,.∴边 AB上的高线为EN=,延长 EF 交 AB于 N,并反向延长EF 交 DC于 M,则 E、 F、 M, N 共线,则EM=1﹣ EN=1﹣,∴NF=EM=1﹣,∴EF=1﹣ EM﹣ NF=﹣1.故答案为﹣ 1.30.如图, ABCD是凸四边形,AB=2, BC=4, CD=7,求线段AD 的取值范围.解答:解:连接AC.∵AB=2, BC=4,在△ ABC 中,根据三角形的三边关系,4﹣ 2< AC< 2+4,即 2< AC< 6.∴﹣ 6<﹣ AC<﹣ 2, 1< CD﹣ AC< 5, 9< CD+AC< 13 ,在△ ACD 中,根据三角形的三边关系,得CD﹣ AC< AD<CD+AC,∴1< AD< 13.故 AD的取值范围是1< AD< 13.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2016中考数学几何选择填空压轴题精选(配答案)一 •选择题(共13小题) 1.( 2013?蕲春县模拟)如图,点 O 为正方形ABCD 的中心,BE平分/ DBC 交DC 于点E ,延长BC 到点 F ,使FC=EC 连接DF 交BE 的延长线于点 H,连接OH 交DC 于点G ,连接HC.则以下四个结论中正确 结论的个数为()① OH 丄BF ;②/ CHF=45 :③GH=J L BC ;④DH 2=HE?HB24A. 1个B . 2个C. 3个D . 4个2. (2013?连云港模拟)如图,Rt △ ABC 中,BC=2^1,/ ACB=90,/ A=30°, Di 是斜边 AB 的中点, 过D 作D1E 1丄AC 于巳,连结BE 1交CD 于6;过D 2作D^丄AC 于连结BR 交CD 于D 3;过D 3作 QE 3丄AC 于 母 …,如此继续,可以依次得到点曰、尽、…、E 2013,分别记厶BCE 1、A BCE 2、△ BCE 、…、△ BCE 2013的面积为 Si 、S2、S 3、…、S 2013.贝U S 2013的大小为( )A.B .C.D .3•如图,梯形 ABCD 中, AD// BC 壮=2 近严 EC ,/ ABC=45 , AE! BC 于点 E, BF 丄 AC 于点 F ,交 AE 于点G, AD=BE 连接DG C :G 以下结论:①△ BEG^^AEC ②/ GAC /GCA ③DG=D ;④G为AE中点时,△ AGC 的面积有最大值..其中正确的结论有( )A. 1个 B . 2个C. 3个D .4个4.如图,正方形 ABCD 中,在 AD 的延长线上取点 E , F ,使DE=AD DF=BD 连接BF 分别交CD CE 于H, G 下列结论:①EC=2DG ②/ GDH /GHD ③S△ CD=S ?DHGE ④图中有 8个等腰三角形•其中正确的是()A.①③B .②④C.①④D . ②③ 5.( 2008?荆州)如图,直角梯形 ABCD 中,/ BCD=90 , AD// BC BC=CDE 为梯形内一点, 且/ BEC=90,将△ BEC 绕C 点旋转90°使BC 与DC 重合,得到△ DCF 连 EF 交CD 于 M.已矢知BC=5, CF=3,贝U DM MC 的值为( ) A. 5: 3B . 3: 5C. 4: 3D . 3: 46•如图,矩形 ABCD 的面积为5,它的两条对角线交于点O,以AB, AO 为两邻边作平行四边形ABCO 1,平行四边形 ABCQ 的对角线交BD 于点0?,同样以AB, AQ 为两邻边作平行四边形 ABCQ •…, 依此类推,则平行四边形 ABC 009Q009的面积为( )A. B .C.D .7.如图,在锐角厶ABC 中,AB=6,Z BAC=45,/ BAC 的平分线交 BC 于点D , M N 分别是 AD 和AB 上的动点,贝U BM+MN 勺最小值是( ) 8. ( 2013?牡丹江)如图,在△ ABC 中/A=60°, BMLAC 于点M, CNL AB 于点N , P 为BC 边的中点,Air AN连接PM PN 则下列结论:①PM=PN ②竺q!;③A PMN 为等边三角形;④当/ ABC=45时,AB ACBN= 'PC.其中正确的个数是( ) 9. ( 2012?黑河)Rt △ ABC 中,AB=AC 点 D 为 BC 中点./ MDN=9°,/ MDN 绕点 D 旋转,DM DN 分 别与边AB AC 交于E 、F 两点•下列结论:A. B . 6 C. D . 3 A. 1个B . 2个C. 3个D . 4个©(BE+CF ^^BC;2②S △AEF^ —S^ABC;1③S四边形AED=AD?EF;④AD> EF;⑤AD与EF可能互相平分,其中正确结论的个数是()A. 1个B. 2个C. 3个D. 4个10. (2012?无锡一模)如图,在正方形纸片ABCD中,对角线AC BD交于点O,折叠正方形纸片ABCD 使AD落在BD上,点A恰好与BD上的点F重合,展开后折痕DE分别交AB AC于点E、G,连接GF.下列结论①/ ADG=/ AED=2③S △AG D=S MG D④四边形AEFG是菱形;⑤BE=2OG其中正确的结论有()A.①④⑤B.①②④C.③④⑤D.②③④11•如图,正方形ABCD中, O为BD中点,以BC为边向正方形内作等边厶BCE连接并延长AE交CD于F,连接BD分别交CE、AF于G H,下列结论:①/ CEH=45 •、②GF// DES空T G C_2其中正确的结论是()A.①②③B.①②④C.①②⑤D.②④⑤12 .如图,在正方形ABCD中, AB=4, E为CD上一动点,AE交BD于F,过F作FH±AE于H,过H作GHL BD于G,下列有四个结论:①AF=FH②/ HAE=45,③BD=2FG④厶CEH 的周长为定值,其中正确的结论有()A.①②③B.①②④C.①③④D.①②③④13 .(2013?钦州模拟)正方形ABCD正方形BEFG和正方形RKPF的位置如图所示,点G在线段DK上,正方形BEFG的边长为4,则△ DEK的面积为()A.10B. 12C.14D. 16二.填空题(共16小题)14. 如图,在梯形ABCD中, AD// BC EALAD M是AE上一点,F、G分别是AB CM的中点,且/ BAE K MCE/ MBE=45,则给岀以下五个结论:① AB=CM② A E L BQ ③/ BMC=90 :④ EF=EG⑤厶BMC是等腰直角三角形•上述结论中始终正确的序号有 ___________________ .15. (2012?门头沟区一模)如图,对面积为1的厶ABC逐次进行以下操作:第一次操作,分别延长ABBC CA至A1、B1、C1,使得A1B=2AB BQ=2BC GA=2CA 顺次连接A1、B1、G,得到AA 1B1C1,记其面积为S I;第二次操作,分别延长A1B1, B1G , GA 至A2, B2, C2,使得A2B1=2A1B1, BQ=2B1G ,CA1=2GA1,顺次连接A, B, C2,得到AA 2B2G,记其面积为3…,按此规律继续下去,可得到△ A5B5C5,则其面积为S5= ____________ •第n次操作得到AA n B nG,则AA n B n C n的面积$=_16. ___________________________________________ (2009?黑河)如图,边长为1的菱形ABCD中, / DAB=60度•连接对角线AC,以AC为边作第二个菱形ACCU,使/D 1AC=60 ;连接AG,再以AG为边作第三个菱形AGC2D2,使/D 2AG=60°;…,按此规律所作的第n个菱形的边长为.17. ________________________ (2012?通州区二模)如图,在△ ABC中,/ A=a./ ABC与/ ACD的平分线交于点A,得/A 1;/A1BC与/A 1CD的平分线相交于点A2,得/A 2;…;/A 2011BC与/A 2011CD的平分线相交于点A012,得/A 2012, 则/A 2012= ____________ .18. (2009?湖州)如图,已知Rt△ ABC D I是斜边AB的中点,过D作D1E1丄AC于日,连接BE1交CD 于过D2作DE?丄AC于E2,连接BE?交CD于b 过D3作D3E3丄AC于&,…,如此继续,可以依次得到点D4, &,•••,0,分别记△ BD1E1,A BD2E2,A BD3E3,•••,△BDnB 的面积为S1, S2,S3,…S n.贝U S I= _____________ S^ABC(用含n的代数式表示).③2OH+DH=BD@ BG=y^DG ⑤19.( 2011?丰台区二模)已知:如图,在 Rt △ ABC 中,点Di 是斜边AB 的中点,过点 Di 作DE i 丄AC于点E i ,连接BE i 交CD 于点D 2;过点D 2作D 2E 2丄AC 于点连接BE 交CD 于点0;过点0作QE 3丄AC 于点E 3,如此继续,可以依次得到点D 4、D 5、…、D n ,分别记△ BD iE i 、A BD 2E 2、A BD 3E 3、…、△ BD n E n的面积为 S i 、S 2、S 3、…S n .设厶ABC 的面积是1,贝U S i = _____________ ,S n = _____________ (用含n的代数式表示). 20.(2013?路北区三模)在厶ABC 中,AB=6, AC=8, BC=10, P 为边 BC 上一动点,PE!AB 于 E, PF 丄AC 于F , M 为EF 中点,贝U AM 的最小值为 — _ .21•如图,已知 Rt △ ABC 中,AC=3, BC=4,过直角顶点 C 作CA 丄AB 垂足为 A,再过 A 作AC 」BC 垂足为G,过C 1作GA 丄AB 垂足为 A 2,再过A ?作A P C 2丄BC 垂足为C 2,…,这样一直做下去,得到22. ( 2013?沐川县二模)如图,点 A 1, A ?, A 3,如 …,A 在射线0A 上,点B 1,B 3,…,B n -1在射线 0B 上,且 A 1B 1//A 2B 2//A 3B 3//-//A n - 1B n - 1, A 2B 1//A 3B 2//A 4B 3//-//A n B n-1, △A 1A 2B 1,△ A 2A 3B 2,…,AA n - 1A n B n - 1为阴影三角形,若AA 2B 1B 2,^A 3B 2B 3的面积分别为 1、4,则AA 1A 2B 1的面 积为 _ _ ;面积小于2011的阴影三角形共有 __ 个.23.( 2010?鲤城区质检)如图,已知点 ( a , 1)在直线丨:上,以点A 1为圆心,以一:-;为半径画弧,交x 轴于点Bi 、B ,过点B 2作AB 1的平行线交直线 丨于点A 2,在x 轴上取一点B 3,使得 A 2B 3=A 2B 2,再过点B 3作A 2B 2的平行线交直线丨于点A s ,在x 轴上取一点B 4,使得A s B^A^,按此规律 继续作下去,则①a= :②厶人4印氏的面积是 ______________________ . 24.( 2013?松北区二模)如图,以 Rt △ ABC 的斜边BC 为一边在厶ABC 的同侧作正方形 BCEF 设正方形的中心为 0,连接AQ 如果AB=4, AO=^?,那么AC 的长等于 _______________________ . 25.( 2007?淄川区二模)如图,将矩形 ABCD 的四个角向内折起,恰好拼成一个既无缝隙又无重叠的四边形EFGH 若EH=3, EF=4,那么线段 AD 与AB 的比等于 __________.26. ( 2009?泰兴市模拟)梯形 ABCD 中 AB// CD / ADC # BCD=90 ,以 AD AB BC 为斜边向形外作 等腰直角三角形,其面积分别是S 1、S 2、S 3且S 1+S 3=4S2 ,贝U CD= ____________ AB.27 •如图,观察图中菱形的个数:图1中有1个菱形,图2中有5个菱形,图3中有14个菱形,图4中有30个菱形…,则第 6个图中菱形的个数是 _________________ 个.28. (2012?贵港一模)如图,E 、F 分别是平行四边形 ABCD 的边AB 、CD 上的点,AF 与DE 相交于点P,2 2 ______________________________________ 2BF 与CE 相交于点Q ,若S ^APD=15cm , S ^BQ (=25cm ,则阴影部分的面积为 __________________ cm . 29. ( 2012?天津)如图,已知正方形 ABCD 的边长为1,以顶点 A 、B 为圆心,1为半径的两弧交于点 E ,以顶点C 、D 为圆心,1为半径的两弧交于点F ,贝U EF 的长为 _______________ .30•如图,ABCD 是凸四边形,AB=2, BC=4, CD=7,求线段 AD 的取值范围().参考答案与试题解析一 •选择题(共13小题)1. ( 2013?蕲春县模拟)如图,点 0为正方形ABCD 的中心,BE 平分/ DBC 交DC 于点E ,延长BC 到点 F ,使FC=EC 连接DF 交BE 的延长线于点 H,连接0H 交DC 于点G ,连接HC.则以下四个结论中正确 结论的个数为( ) ① 0H 丄BF ;②/ CHF=45 ; @GH=2B C ;④D M=HE?HB2 4了一组线段 CA , A1G , GA2,…,贝U CA=£^_5=A 5C 5A. 1个B. 2个C. 3个D. 4个解答:解:作EJ丄BD于J,连接EF①••• BE平分/ DBC••• EC=EJ•••△DJE^A ECF• DE=FE :丄 HEF=45 +°=°:丄 HFE= =°2•:Z EHF=180 -°-°=90°•/ DH=HF 0曰是厶DBF的中位线:OH/ BF:OHdBF2②•••四边形ABCD是正方形,BE是/ DBC的平分线,:BC=CD / BCD h DCF / EBC=,•/ CE=CF:Rt△ BCE^ Rt△ DCF•:Z EBC d CDF=,•:Z BFH=90 -Z CDF=90 -°=°,••• 0曰是厶DBF的中位线,CD!AF,•: OH是CD的垂直平分线,:DH=CH•:Z CDF Z DCH=,•:Z HCF=90 -Z DCH=90 -°=°,•:Z CHF=180 -Z HC-Z BFH=180 -°-° =45。
