2020年贵州省中考数学压轴题汇编解析:几何综合
2020年中考数学《几何综合》培优拔高专项复习讲义及解析

2020年中考数学《几何综合》培优拔高专项复习讲义及解析1.如图,△ABC是等边三角形,D,E分别是AC,BC边上的点,且AD=CE,连接BD,AE相交于点F.(1)∠BFE的度数是;(2)如果=,那么=;(3)如果=时,请用含n的式子表示AF,BF的数量关系,并证明.2.如图,∠BAD=90°,AB=AD,CB=CD,一个以点C为顶点的45°角绕点C旋转,角的两边与BA,DA交于点M,N,与BA,DA的延长线交于点E,F,连接AC.(1)在∠FCE旋转的过程中,当∠FCA=∠ECA时,如图1,求证:AE=AF;(2)在∠FCE旋转的过程中,当∠FCA≠∠ECA时,如图2,如果∠B=30°,CB=2,用等式表示线段AE,AF之间的数量关系,并证明.3.已知:如图,矩形ABCD中,AB>AD.(1)以点A为圆心,AB为半径作弧,交DC于点E,且AE=AB,联结AE,BE,请补全图形,并判断∠AEB 与∠CEB的数量关系;(2)在(1)的条件下,设a=,b=,试用等式表示a与b间的数量关系并加以证明.4.已知:△ABD和△CBD关于直线BD对称(点A的对称点是点C),点E,F分别是线段BC和线段BD上的点,且点F在线段EC的垂直平分线上,连接AF,AE,AE交BD于点G.(1)如图1,求证:∠EAF=∠ABD;(2)如图2,当AB=AD时,M是线段AG上一点,连接BM,ED,MF,MF的延长线交ED于点N,∠MBF=∠BAF,AF=AD,试探究FM和FN之间的数量关系,并证明你的结论.5.以AB为直径作半圆O,AB=10,点C是该半圆上一动点,连接AC、BC,并延长BC至点D,使DC=BC,过点D作DE⊥AB于点E、交AC于点F,连接OF.(1)如图①,当点E与点O重合时,求∠BAC的度数;(2)如图②,当DE=8时,求线段EF的长;(3)在点C运动过程中,若点E始终在线段AB上,是否存在以点E、O、F为顶点的三角形与△ABC相似?若存在,请直接写出此时线段OE的长;若不存在,请说明理由.6.如图①,P为△ABC内一点,连接P A、PB、PC,在△P AB、△PBC和△P AC中,如果存在一个三角形与△ABC 相似,那么就称P为△ABC的自相似点.(1)如图②,已知Rt△ABC中,∠ACB=90°,∠ABC>∠A,CD是AB上的中线,过点B作BE丄CD,垂足为E.试说明E是△ABC的自相似点;(2)在△ABC中,∠A<∠B<∠C.①如图③,利用尺规作出△ABC的自相似点P(写出作法并保留作图痕迹);②若△ABC的内心P是该三角形的自相似点,求该三角形三个内角的度数.7.在Rt△ABC中,∠ACB=90°,AC=BC,CD⊥AB于点D,点E为AC边上一点,连接BE交CD于点F,过点E作EG⊥BE交AB于点G,(1)如图1,当点E为AC中点时,线段EF与EG的数量关系是;(2)如图2,当,探究线段EF与EG的数量关系并且证明;(3)如图3,当,线段EF与EG的数量关系是.8.如图,已知点P是边长为4的正方形ABCD内一点,且PB=3,BF⊥BP,垂足是B.请在射线BF上找一点M,使以点B、M、C为顶点的三角形与△ABP相似.(请注意:全等图形是相似图形的特例)参考答案与试题解析1.如图,△ABC是等边三角形,D,E分别是AC,BC边上的点,且AD=CE,连接BD,AE相交于点F.(1)∠BFE的度数是60°;(2)如果=,那么=1;(3)如果=时,请用含n的式子表示AF,BF的数量关系,并证明.【分析】(1)易证△ABD≌△ACE,可得∠DAF=∠ABF,根据外角等于不相邻两个内角的和即可解题.(2)如图1中,当=时,由题意可知:AD=CD,BE=CE.利用等腰三角形的性质即可解决问题;(3)设AF=x,BF=y,AB=BC=AC=n.AD=CE=1,由△ABD≌△CAE,推出BD=AE,设BD=AE=m,利用相似三角形的性质,列出关系式即可解决问题;【解答】解:(1)∵△ABC是等边三角形,∴AB=AC,∠BAD=∠C=60°,在△ABD和△ACE中,,∴△ABD≌△ACE(SAS)∴∠DAF=∠ABD,∴∠BFE=∠ABD+∠BAF=∠DAF+∠BAF=∠BAD=60°,故答案为:60°.(2)如图1中,当=时,由题意可知:AD=CD,BE=CE.∵△ABC是等边三角形,BE=EC,AD=CD,∴∠BAE=∠BAC=×60°=30°,∠ABD=∠ABC=30°,∴∠F AB=∠FBA,∴F A=FB,∴=1.故答案为1.(3)设AF=x,BF=y,AB=BC=AC=n.AD=CE=1,∵△ABD≌△CAE,∴BD=AE,∠DAF=∠ABD,设BD=AE=m,∵∠ADF=∠BDA,∴△ADF∽△BDA,∴=,∴=①,∵∠FBE=∠CBD,∠BFE=∠C=60°,∴△BFE∽△BCD,∴=,∴=②,①÷②得到:=,∴=.【点评】本题属于三角形综合题,考查了等边三角形的性质,相似三角形的判定和性质的等知识,解题的关键是正确寻找相似三角形解决问题,学会利用参数解决问题,属于中考压轴题.2.如图,∠BAD=90°,AB=AD,CB=CD,一个以点C为顶点的45°角绕点C旋转,角的两边与BA,DA交于点M,N,与BA,DA的延长线交于点E,F,连接AC.(1)在∠FCE旋转的过程中,当∠FCA=∠ECA时,如图1,求证:AE=AF;(2)在∠FCE旋转的过程中,当∠FCA≠∠ECA时,如图2,如果∠B=30°,CB=2,用等式表示线段AE,AF之间的数量关系,并证明.【分析】(1)首先证明△ABC≌△ADC(SSS),推出∠BAC=∠DAC=45°,推出∠F AC=∠EAC=135°,再证明△ACF≌△ACE(ASA)即可解决问题;(2)由△ACF∽△AEC,推出=,可得AC2=AE•AF,求出AC即可解决问题;【解答】(1)证明:∵AB=AD,CB=CD,AC=AC,∴△ABC≌△ADC(SSS),∴∠BAC=∠DAC=45°,∴∠F AC=∠EAC=135°,∵∠FCA=∠ECA,∴△ACF≌△ACE(ASA),∴AE=AF.(2)证明:作CG⊥AB于G.∵BC=2,∠B=30°,∴CG=BC=1,∵AG=AC=1,∴AC=,∵∠F AC=∠EAC=135°,∴∠ACF+∠F=45°,∵∠ACF+∠ACE=45°,∴∠F=∠ACE,∴△ACF∽△AEC,∴=,∴AC2=AE•AF,∴AE•AF=2.【点评】本题考查旋转变换、全等三角形的判定和性质、解直角三角形等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.3.已知:如图,矩形ABCD中,AB>AD.(1)以点A为圆心,AB为半径作弧,交DC于点E,且AE=AB,联结AE,BE,请补全图形,并判断∠AEB 与∠CEB的数量关系;(2)在(1)的条件下,设a=,b=,试用等式表示a与b间的数量关系并加以证明.【分析】(1)根据题意画出图形,根据等腰三角形的性质即可得出结论;(2)作过点A作AF⊥BE于点F,根据AB=AE可知BF=BE,由∠AFB=∠C=90°,∠ABE=∠CEB,得出△ABF∽△BEC,再由相似三角形的对应边成比例即可得出结论.【解答】解:(1)如图1,∵AE=AB,∴∠AEB=∠CEB.(2)a=b.证明:如图2,作过点A作AF⊥BE于点F,∵AB=AE,∴BF=BE,∵∠AFB=∠C=90°,∠ABE=∠CEB,∴△ABF∽△BEC∴=,∴=,即a=b.【点评】本题考查的是相似三角形的判定与性质,根据题意画出图形,利用等腰三角形的性质求解是解答此题的关键.4.已知:△ABD和△CBD关于直线BD对称(点A的对称点是点C),点E,F分别是线段BC和线段BD上的点,且点F在线段EC的垂直平分线上,连接AF,AE,AE交BD于点G.(1)如图1,求证:∠EAF=∠ABD;(2)如图2,当AB=AD时,M是线段AG上一点,连接BM,ED,MF,MF的延长线交ED于点N,∠MBF=∠BAF,AF=AD,试探究FM和FN之间的数量关系,并证明你的结论.【分析】(1)如图1,连接FE、FC,构建全等三角形△ABF≌△CBF(SAS),则易证∠BAF=∠2,F A=FC;根据垂直平分线的性质、等量代换可知FE=F A,∠1=∠BAF,则∠5=∠6.然后由四边形内角和是360°、三角形内角和定理求得∠5+∠6=∠3+∠4,则∠5=∠4,即∠EAF=∠ABD;(2)FM=FN.理由如下:由△AFG∽△BF A,易得∠AGF=∠BAF,所以结合已知条件和图形得到∠MBG=∠BMG.易证△AGF∽△DGA,则对应边成比例:==.即==.设GF=2a(a>0),AG=3a,则GD=a,FD=a;利用平行线(BE∥AD)截线段成比例易得=,则==.设EG=2k(k>0),所以BG=MG=3k.如图2,过点F作FQ∥ED交AE于点Q.则===,又由FQ∥ED,易证得==,所以FM=FN.【解答】(1)证明:如图1,连接FE、FC.∵点F在线段EC的垂直平分线上,∴FE=FC,∴∠1=∠2.∵△ABD和△CBD关于直线BD对称(点A的对称点是点C),∴AB=CB,∠4=∠3,∵在△ABF与△CBF中,,∴△ABF≌△CBF(SAS),∴∠BAF=∠2,F A=FC,∴FE=F A,∠1=∠BAF,∴∠5=∠6.∵∠1+∠BEF=180°,∴∠BAF+∠BEF=180°∵∠BAF+∠BEF+∠AFE+∠ABE=360°,∴∠AFE+∠ABE=180°.又∵∠AFE+∠5+∠6=180°,∴∠5+∠6=∠3+∠4,∴∠5=∠4,即∠EAF=∠ABD;(2)FM=FN.理由如下:如图2,由(1)知,∠EAF=∠ABD.又∵∠AFB=∠GF A,∴△AFG∽△BF A,∴∠AGF=∠BAF.又∵∠MBF=∠BAF,∴∠MBF=∠AGF.∵∠AGF=∠MBG+∠BMG,∴∠MBG=∠BMG,∴BG=MG.∵AB=AD,∴∠ADB=∠ABD=∠EAF.又∵∠FGA=∠AGD,∴△AGF∽△DGA,∴==.∵AF=AD,∴==.设GF=2a(a>0),AG=3a,∴GD=a,∴FD=a∵∠CBD=∠ABD,∠ABD=∠ADB,∴∠CBD=∠ADB,∴BE∥AD,∴=,∴==.设EG=2k(k>0),∴BG=MG=3k.如图2,过点F作FQ∥ED交AE于点Q.则===,∴GQ=QE,∴GQ=EG=k,MQ=3k+k=k.∵FQ∥ED,∴==,∴FM=FN.【点评】本题综合考查了相似三角形的判定与性质,平行线分线段成比例,三角形内角和定理以及四边形内角和是360度等知识点.难度较大,综合性较强.5.以AB为直径作半圆O,AB=10,点C是该半圆上一动点,连接AC、BC,并延长BC至点D,使DC=BC,过点D作DE⊥AB于点E、交AC于点F,连接OF.(1)如图①,当点E与点O重合时,求∠BAC的度数;(2)如图②,当DE=8时,求线段EF的长;(3)在点C运动过程中,若点E始终在线段AB上,是否存在以点E、O、F为顶点的三角形与△ABC相似?若存在,请直接写出此时线段OE的长;若不存在,请说明理由.【分析】(1)连接OC.根据直角三角形的性质和圆的性质可得△OBC是等边三角形,再根据等边三角形的性质和直角三角形两锐角互余即可得到∠BAC的度数;(2)连接DA.根据垂直平分线的性质可得AB=AD=10,根据勾股定理和线段的和差关系可得AE和BE的长,通过AA证明△AEF∽△DEB,根据相似三角形的性质即可得到EF的长;(3)分两种情况:①当交点E在O、A之间时;②当交点E在O、B之间时;讨论即可求得线段OE的长.【解答】解:(1)连接OC.∵C为DB中点,∴OC=BC=OB,∴△OBC是等边三角形,∴∠B=60°,∵AB为直径,∴∠ACB=90°,∴∠BAC=30°;(2)连接DA.∵AC垂直平分BD,∴AB=AD=10,∵DE=8,DE⊥AB,∴AE=6,∴BE=4,∵∠F AE+∠AFE=90°,∠CFD+∠CDF=90°,∴∠CDF=∠EAF,∵∠AEF=∠DEB=90°,∴△AEF∽△DEB,∴=,∴EF=3;(3)①当交点E在O、A之间时,若∠EOF=∠BAC,此时,∵,∴,∴OE=AE,则OE=;若∠EOF=∠ABC,此时,∴,则OE=;②当交点E在O、B之间时,OE=.综上所述,OE=或或.【点评】考查了圆的综合题,涉及的知识点有直角三角形的性质和圆的性质,等边三角形的判定和性质,垂直平分线的性质,勾股定理,相似三角形的判定和性质,分类思想的运用,综合性较强,有一定的难度.6.如图①,P为△ABC内一点,连接P A、PB、PC,在△P AB、△PBC和△P AC中,如果存在一个三角形与△ABC 相似,那么就称P为△ABC的自相似点.(1)如图②,已知Rt△ABC中,∠ACB=90°,∠ABC>∠A,CD是AB上的中线,过点B作BE丄CD,垂足为E.试说明E是△ABC的自相似点;(2)在△ABC中,∠A<∠B<∠C.①如图③,利用尺规作出△ABC的自相似点P(写出作法并保留作图痕迹);②若△ABC的内心P是该三角形的自相似点,求该三角形三个内角的度数.【分析】(1)根据已知条件得出∠BEC=∠ACB,以及∠BCE=∠ABC,得出△BCE∽△ABC,即可得出结论;(2)①根据作一角等于已知角即可得出△ABC的自相似点;②根据∠PBC=∠A,∠BCP=∠ABC=∠2∠PBC=2∠A,∠ACB=2∠BCP=4∠A,即可得出各内角的度数.【解答】解:(1)在Rt△ABC中,∠ACB=90°,CD是AB上的中线,∴CD=AB,∴CD=BD,∴∠BCE=∠ABC,∵BE⊥CD,∴∠BEC=90°,∴∠BEC=∠ACB,∴△BCE∽△ABC,∴E是△ABC的自相似点;(2)①如图所示,作法:①在∠ABC内,作∠CBD=∠A,②在∠ACB内,作∠BCE=∠ABC,BD交CE于点P,则P为△ABC的自相似点;②∵P是△ABC的内心,∴∠PBC=∠ABC,∠PCB=∠ACB,∵△ABC的内心P是该三角形的自相似点,∴∠PBC=∠A,∠BCP=∠ABC=2∠PBC=2∠A,∠ACB=2∠BCP=4∠A,∴∠A+2∠A+4∠A=180°,∴∠A=,∴该三角形三个内角度数为:,,.【点评】此题主要考查了相似三角形的判定以及三角形的内心作法和作一角等于已知角,此题综合性较强,注意从已知分析获取正确的信息是解决问题的关键.7.在Rt△ABC中,∠ACB=90°,AC=BC,CD⊥AB于点D,点E为AC边上一点,连接BE交CD于点F,过点E作EG⊥BE交AB于点G,(1)如图1,当点E为AC中点时,线段EF与EG的数量关系是EF=EG;(2)如图2,当,探究线段EF与EG的数量关系并且证明;(3)如图3,当,线段EF与EG的数量关系是.【分析】(1)根据全等三角形的证明方法利用ASA得出△EFM≌△EGN,即可得出EF=EG;(2)根据已知首先求出∠ENG=∠FEM,再得出∠ENG=∠EMF,即可得出△EFM∽△EGN,再利用相似三角形的性质得出答案即可.【解答】解:(1)证明:如图1,过E作EM⊥AB于M,EN⊥CD于N,∵∠ACB=90°,AC=BC,∴∠A=∠ABC=45°,∴AD=CD,∵点E为AC的中点,CD⊥AB,EN⊥DC,∴EN=AD,∴EM=CD,∴EN=EM,∵∠GEB=90°,∠MEN=90°,∴∠NEF=∠GEM,∴,∴△EGM≌△EFN,(ASA)∴EG=EF(2)证明如图(2):过点E作EM⊥CD于点M,作EN⊥AB于点N,∴∠ENA=∠CME=∠EMF=90°.∵CD⊥AB于点D,∴∠CDA=90°.∴EM∥AD.∠A=∠CEM.∴△EMC∽△ANE.∴∵EM∥AD,∴∠NEM=90.即∠1+∠2=90°.∵EG⊥BE,∴∠3+∠2=90°,∴∠MEF=∠GEN.∴△EFM∽△EGN.∴.∵∠ACB=90°,AC=BC,∴∠A=45°,∴AN=EN.∴,∴∵,∴.(3)∴证明如图(3):过点E作EM⊥CD于点M,作EN⊥AB于点N,∴∠ENA=∠CME=∠EMF=90°.∵CD⊥AB于点D,∴∠CDA=90°.∴EM∥AD.∠A=∠CEM.∴△EMC∽△ANE.∴∵EM∥AD,∴∠NEM=90.即∠2+∠3=90°.∵EG⊥BE,∴∠3+∠2=90°,∴∠MEF=∠GEN.∴△EFM∽△EGN.∴.∵∠ACB=90°,AC=BC,∴∠A=45°,∴AN=EN.∴,∴∵∴,故答案为:(1)EF=EG,(3)【点评】本题考查了相似三角形的判定与性质,平行线的性质,等腰直角三角形的性质的运用.8.如图,已知点P是边长为4的正方形ABCD内一点,且PB=3,BF⊥BP,垂足是B.请在射线BF上找一点M,使以点B、M、C为顶点的三角形与△ABP相似.(请注意:全等图形是相似图形的特例)【分析】此题有两种情况,(1)当△CBM≌△ABP时,全等图形是相似图形的特例,此时BP和BM为一组对应边且相等,BM=BP=3;(2)当△MBC∽△ABP时,有MB:AB=BC:BP,从而求出BM的值.【解答】解:在射线BF上截取线段,连接M1C,⇒,⇒∠ABP=∠CBM1,∴△M1BC∽△ABP.在射线BF上截取线段BM2=BP=3,连接M2C,⇒△CBM2≌△ABP.(全等必相似)∴在射线BF上取或BM2=3时,M1,M2都为符合条件的M.(说明:其他解法请参照给分)【点评】此题主要是考查三角形相似的判定,属中等难度.。
2020年中考数学压轴题-专题28几何证明综合复习(判定四边形形状)(解析版)

专题28 几何证明综合复习(判定四边形形状)教学重难点1.培养学生通过探索和证明,发展推理意识和能力2.通过证明举例的学习和实践,懂得演绎推理的一般规则,并掌握规范表达的格式;了解证明之前进行分析的基本思路;3.体会用“分析综合法”探求解题思路;4.学习添置辅助线的基本方法,会添置常见的辅助线;5.会用文字语言、图形语言、符号语言三种数学语言进行证明说理。
【说明】:本部分为知识点方法总结性梳理,目的在于让学生能从题目条件和所证明结论,去寻找证明思路,用时大概 5-8 分钟左右。
【知识点、方法总结】:中考几何题证明思路总结几何证明题重点考察的是学生的逻辑思维能力,能通过严密的" 因为"、"所以 " 逻辑将条件一步步转化为所要证明的结论。
这类题目出法相当灵活,不像代数计算类题目容易总结出固定题型的固定解法,而更看重的是对重要模型的总结、常见思路的总结。
所以本文对中考中最常出现的若干结论做了一个较为全面的思路总结。
一、证明两线段相等1.两全等三角形中对应边相等。
2.同一三角形中等角对等边。
3.等腰三角形顶角的平分线或底边的高平分底边。
4.平行四边形的对边或对角线被交点分成的两段相等。
5.直角三角形斜边的中点到三顶点距离相等。
6.线段垂直平分线上任意一点到线段两段距离相等。
7.角平分线上任一点到角的两边距离相等。
8.过三角形一边的中点且平行于第三边的直线分第二边所成的线段相等。
9.同圆(或等圆)中等弧所对的弦或与圆心等距的两弦或等圆心角、圆周角所对的弦相等。
10.两前项(或两后项)相等的比例式中的两后项(或两前项)相等。
、证明两角相等1.两全等三角形的对应角相等。
2.同一三角形中等边对等角。
3.等腰三角形中,底边上的中线(或高)平分顶角。
4.两条平行线的同位角、内错角或平行四边形的对角相等。
5.同角(或等角)的余角(或补角)相等。
6.同圆(或圆)中,等弦(或弧)所对的圆心角相等;7.相似三角形的对应角相等;8.等于同一角的两个角相等。
几何综合(解析版)--中考数学抢分压轴题秘籍(全国通用)

几何综合--中考数学抢分秘籍(全国通用)几何综合问题在中考中以填空题和解答题的形式出现,考查难度较大.此类问题在中考中多考查面积平分、面积最值和几何变换的综合问题,一般要用到特殊三角形、特殊四边形、相似三角形、圆、锐角三角函数、勾股定理、图形变换的性质和二次函数的最值等相关知识,以及分类讨论、数形结合、转化与化归等数学思想.此类题型常涉及以下问题:①几何图形中的线段最值问题②探究图形面积的分割问题;③探究图形面积的最值问题.右图为几何综合问题中各题型的考查热度.题型1:线段最值问题①动点路径问题②“胡不归”问题③“将军饮马”问题④“造桥选址”问题解题模板:1.(2021秋•白云区校级月考)如图,正方形ABCD的边长为4,⊙O的半径为1.若⊙O在正方形ABCD内平移(⊙O可以与该正方形的边相切,则点A到⊙O上的点的距离的最大值为()A.B.C.D.【分析】由题意画出符合题意的图形,当⊙O与BC,CD相切时,点A到⊙O上的点的距离取得最大值,利用勾股定理即可求得结论.【解答】解:由题意,当⊙O与BC,CD相切时,点A到⊙O上的点的距离取得最大值,如图,由对称性可知:圆心O在AC上.AC==4.∵BC与⊙O相切于点E,∴OE⊥EC.∵四边形ABCD是正方形,∴∠ACB=45°.∴△OEC为等腰直角三角形.∴OC=OE=.∴CG=OC﹣OG=﹣1.∴AG=AC﹣CG=4﹣(﹣1)=3+1.故选:C.【点评】本题主要考查了切线的性质,正方形的性质,直线和圆的位置关系,勾股定理,连接OE,利用切线的性质得到OE⊥EC是解题的关键.【变式1-1】(2020•遵义)如图,在边长为4的正方形ABCD中,点E为对角线AC上一动点(点E与点A、C不重合),连接DE,作EF⊥DE交射线BA于点F,过点E作MN∥BC分别交CD、AB于点M、N,作射线DF交射线CA于点G.(1)求证:EF=DE;(2)当AF=2时,求GE的长.【分析】(1)要证明EF=DE,只要证明△DME≌△ENF即可,然后根据题目中的条件和正方形的性质,可以得到△DME≌△ENF的条件,从而可以证明结论成立;(2)根据勾股定理和三角形相似,可以得到AG和CG、CE的长,然后即可得到GE的长.【解答】(1)证明:∵四边形ABCD是正方形,AC是对角线,∴∠ECM=45°,∵MN∥BC,∠BCM=90°,∴∠NMC+∠BCM=180°,∠MNB+∠B=180°,∴∠NMC=90°,∠MNB=90°,∴∠MEC=∠MCE=45°,∠DME=∠ENF=90°,∴MC=ME,∵CD=MN,∴DM=EN,∵DE⊥EF,∠EDM+∠DEM=90°,∴∠DEF=90°,∴∠DEM+∠FEN=90°,∴∠EDM=∠FEN,在△DME和△ENF中,∴△DME≌△ENF(ASA),∴EF=DE;(2)解:如图1所示,由(1)知,△DME≌△ENF,∴ME=NF,∵四边形MNBC是矩形,∴MC=BN,又∵ME=MC,AB=4,AF=2,∴BN=MC=NF=1,∵∠EMC=90°,∴CE=,∵AF∥CD,∴△DGC∽△FGA,∴,∴,∵AB=BC=4,∠B=90°,∴AC=4,∵AC=AG+GC,∴AG=,CG=,∴GE=GC﹣CE==;如图2所示,同理可得,FN=BN,∵AF=2,AB=4,∴AN=1,∵AB=BC=4,∠B=90°,∴AC=4,∵AF∥CD,∴△GAF∽△GCD,∴,即,解得,AG=4,∵AN=NE=1,∠ENA=90°,∴AE=,∴GE=GA+AE=5.综上所述:GE的长为:,5.【点评】本题考查正方形的性质、全等三角形的判定与性质、三角形相似,解答本题的关键是明确题意,利用数形结合的思想解答.2.(2022春•广陵区期末)如图,在菱形ABCD中,AB=AC=10,对角线AC、BD相交于点O,点M在线段AC上,且AM=2,点P为线段BD上的一个动点,则MP+PB的最小值是4.【分析】过P点作PH⊥BC于H,过M点作MN⊥BC于N,如图,根据菱形的性质得到AB=BC,BO 平分∠ABC,AO⊥BD,再判断△ABC为等边三角形得到∠ABC=∠ACB=60°,则∠OBC=30°,所以PH=BP,则MP+PB=MP+PH,所以MP+PH的最小值为MN的长,然后利用含30度角的直角三角形三边的关系求出MN即可.【解答】解:过P点作PH⊥BC于H,过M点作MN⊥BC于N,如图,∵四边形ABCD为菱形,∴AB=BC,BO平分∠ABC,AO⊥BD,∵AB=AC=10,∴AB=AC=BC=10,∴△ABC为等边三角形,∴∠ABC=∠ACB=60°,∴∠OBC=30°,∴PH=BP,∴MP+PB=MP+PH,当M、P、H共线时,MP+PH的值最小,即MP+PH的最小值为MN的长,∵AM=2,∴CM=10﹣2=8,在Rt△MNC中,∵∠MCN=60°,∴CN=CM=4,∴MN=CN=4,即MP+PB的最小值为4.故答案为:.【点评】本题考查了胡不归问题:利用垂线段最短解决最短路径问题,把PB转化为PH是解决问题的关键.也考查了菱形的性质和等边三角形的性质.【变式2-1】(2021•郴州)如图,在△ABC中,AB=5,AC=4,sin A=,BD⊥AC交AC于点D.点P为线段BD上的动点,则PC+PB的最小值为.【分析】过点P作PE⊥AB于点E,过点C作CH⊥AB于点H,首先得出BD=4,AD=3,根据sin∠ABD=,得EP=,则PC+PB的最小值为PC+PE的最小值,即求CH的长,再通过等积法即可解决问题.【解答】解:过点P作PE⊥AB于点E,过点C作CH⊥AB于点H,∵BD⊥AC,∴∠ADB=90°,∵sin A==,AB=5,∴BD=4,由勾股定理得AD=,∴sin∠ABD=,∴EP=,∴PC+PB=PC+PE,即点C、P、E三点共线时,PC+PB最小,∴PC+PB的最小值为CH的长,=,∵S△ABC∴4×4=5×CH,∴CH=.∴PC+PB的最小值为.故答案为:.【点评】本题主要考查了锐角三角函数,垂线段最短、勾股定理等知识,将PC+PB的最小值转化为求CH的长,是解题的关键.3.(2022秋•朝阳区校级月考)如图,在Rt△ABO中,∠OBA=90°,A(4,4),点C在边AB上,且=,点D为OB的中点,点P为边OA上的动点,当点P在OA上移动时,使四边形PDBC周长最小的点P的纵坐标为.【分析】根据已知条件得到AB=OB=4,∠AOB=45°,求得BC=3,OD=BD=2,得到D(2,0),C(4,3),作D关于直线OA的对称点E,连接EC交OA于P,则此时,四边形PDBC周长最小,E (0,2),求得直线EC的解析式为y=x+2,解方程组即可得到结论.【解答】解:∵∠OBA=90°,A(4,4),∴AB=OB=4,∠AOB=45°,∵=,点D为OB的中点,∴BC=3,OD=BD=2,∴D(2,0),C(4,3),作D关于直线OA的对称点E,连接EC交OA于P,则此时,四边形PDBC周长最小,E(0,2),∵直线OA的解析式为y=x,设直线EC的解析式为y=kx+b,则,解得:,∴直线EC的解析式为y=x+2,解,得,∴P(,),故答案为:.【点评】本题考查了轴对称﹣最短路线问题,等腰直角三角形的性质,正确的找到P点的位置是解题的关键.【变式3-1】(2021•聊城)如图,在直角坐标系中,矩形OABC的顶点O在坐标原点,顶点A,C分别在x 轴,y轴上,B,D两点坐标分别为B(﹣4,6),D(0,4),线段EF在边OA上移动,保持EF=3,当四边形BDEF的周长最小时,点E的坐标为(﹣,0).【分析】在BC上截取BH=3,可证四边形BHEF是平行四边形,可得BF=EH,由对称性可得DE=D'E,则四边形BDEF的周长=EH+ED'+BD+EF,由EF和BD是定值,则当EH+D'E有最小值时,四边形BDEF 的周长有最小值,即当点E,点H,点D'共线时,EH+D'E有最小值,利用待定系数法可求HD'解析式,即可求解.【解答】解:在BC上截取BH=3,作点D关于x轴的对称点D',连接D'H交AO于点E,∴BH=EF=3,BC∥AO,∴四边形BHEF是平行四边形,∴BF=EH,∵点D与点D'关于x轴对称,∴DE=D'E,点D'坐标为(0,﹣4),∵四边形BDEF的周长=EF+BF+BD+DE,∴四边形BDEF的周长=EH+ED'+BD+EF,∵EF和BD是定值,∴当EH+D'E有最小值时,四边形BDEF的周长有最小值,∴当点E,点H,点D'共线时,EH+D'E有最小值,∵点B(﹣4,6),∴点H(﹣1,6),设直线D'H的解析式为y=kx+b,则,解得:,∴直线D'H的解析式为y=﹣10x﹣4,∴当y=0时,x=﹣,∴点E(﹣,0),故答案为:(﹣,0).【点评】本题考查了轴对称﹣最短路线问题,坐标与图形,平行四边形的判定和性质,一次函数的性质等知识,确定点E的位置是解题的关键.4.如图,正方形ABCD的边长为4,点E在边BC上且CE=1,长为的线段MN在AC上运动,当四边形BMNE的周长最小时,则tan∠MBC的值是.【分析】根据题意得出作EF∥AC且EF=,连接DF交AC于M,在AC上截取MN=,此时四边形BMNE的周长最小,进而利用相似三角形的判定与性质得出答案.【解答】解:作EF∥AC且EF=,连接DF交AC于M,在AC上截取MN=,延长DF交BC于P,作FQ⊥BC于Q,作出点E关于AC的对称点E′,则CE′=CE=1,将MN平移至E′F′处,则四边形MNE′F′为平行四边形,则当BM+EN=BM+FM=BF′时四边形BMNE的周长最小,由∠FEQ=∠ACB=45°,可求得FQ=EQ=1,∵∠DPC=∠FPQ,∠DCP=∠FQP,∴△PFQ∽△PDC,∴=,∴=,解得:PQ=,∴PC=,由对称性可求得tan∠MBC=tan∠PDC==.故答案为.【点评】此题主要考查了正方形的性质以及相似三角形的判定与性质,得出M,N的位置是解题关键.【变式4-1】如图,已知四边形ABCD四个顶点的坐标为A(1,3),B(m,0),C(m+2,0),D(5,1),当四边形ABCD的周长最小时,m的值为.【分析】因为AD,BC的长度都是固定的,所以求出AB+CD的长度就行了.问题就是AB+CD什么时候最短.把D点向左平移2个单位到D′点;作D′关于x轴的对称点D″,连接AD″,交x轴于P,从而确定C点位置,此时AB+CD最短.设直线AD″的解析式为y=kx+b,待定系数法求直线解析式.即可求得m的值.【解答】解:将C点向左平移2单位与B重合,点D向左平移2单位到D′(3,1),作D′关于x轴的对称点D″,根据作法知点D″(3,﹣1),设直线AD″的解析式为y=kx+b,则,解得k=﹣2,b=5.∴直线AD″的解析式为y=﹣2x+5.当y=0时,x=,即B(,0),m=.故答案为:.【点评】考查了轴对称﹣最短路线问题,关键是熟悉关于x轴的对称点,两点之间线段最短等知识.题型2:面积平分问题解题模板:技巧精讲1:利用中线平分图形面积的方法2.利用对称性平分图形面积的方法5.(1)问题提出:如图(1),在直角△ABC中,∠C=90°,AC=8,BC=6,点D为AC上一点且AD=2,过点D作直线DE交△ABC于点E,使得△ABC被分成面积相等的两部分,则DE的长为2.(2)类比发现:如图(2),五边形ABOCD,各顶点坐标为:A(3,4),B(0,2),O(0,0),C (4,0),D(4,2)请你找出一条经过顶点A的直线,将五边形ABOCD分为面积相等的两部分,求出该直线对应的函数表达式.(3)如图(3),王叔叔家有一块四边形菜地ABCD,他打算过D点修一条笔直的小路把四边形菜地ABCD 分成面积相等的两部分,分别种植不同的农作物,已知AB=AD=200米,BC=DC=200米,∠BAD =90°过点D是否存在一条直线将四边形ABCD的面积平分?若存在,求出平分该四边形面积的线段长:若不存在,请说明理由.【分析】(1)如图1中,取AC的中点F,连接BF,BD,作FE∥BD交BC于E,连接DE交BF于O.证明DE平分△ABC的面积,利用平行线分线段成比例定理求出CE即可解决问题.(2)如图2中,连接AO、AC,作BE∥AO交x轴于E,DF∥AC交x轴于F,EF的中点为M,则直线AM平分五边形ABCOD的面积,求出点M的坐标即可解决问题.(3)先求出四边形ABCD的面积,即可得出四边形ABQD的面积,从而求出QM,再用平行线分线段成比例定理求出BM,即可得出DM,最后用勾股定理即可.【解答】解:(1)如图1中,取AC的中点F,连接BF,BD,作FE∥BD交BC于E,连接DE交BF 于O.∵AF=FC,=S△BFC,∴S△AFB∵BD∥EF,=S△BDF,∴S△BDE=S△BOE,∴S△DFO=S四边形ABED,∴S△ECD∴DE平分△ABC的面积,∵AC=8,AD=2,∴AF=CF=4,DF=2,∵EF∥BD,∴=,∴=,∴CE=4,∴DE===2,故答案为2.(2)如图2中,连接AO、AC,作BE∥AO交x轴于E,DF∥AC交x轴于F,EF的中点为M,则直线AM平分五边形ABCOD的面积,∵直线AO的解析式为y=x,∴直线BE解析式为y=x+2,∴点E坐标(﹣,0),∵直线AC的解析式为y=﹣4x+16,∴直线DF的解析式为y=﹣4x+18,∴点F坐标为(,0)∴EF的中点M坐标为(,0),∴直线AM的解析式为:y=x﹣4.(3)如图3中,连接BD,AC交于点O.在BC上取一点Q,过Q作QM⊥BD,∵AB=AD=200、BC=CD=200,∴AC是BD的垂直平分线,在Rt△ABD中,BD=AB=200,∴DO=BO=OA=100,在Rt△BCO中,OC==300,=S△ABD+S△CBD=BD×(AO+CO)=×200×(100+300)=80000,∴S四边形ABCD∵在一条过点D的直线将筝形ABCD的面积二等分,=S四边形ABCD=40000,∴S四边形ABQD=×BD×OA=20000,∵S△ABD=BD×QM=×200×QM=100QM=S四边形ABQD﹣S△ABD=20000,∴S△QBD∴QM=100,∵QM∥CO.∴=,∴=,∴BM=,∴DM=BD﹣BM=,在Rt△MQD中,DQ===.【点评】此题是一次函数综合题,主要考查了等腰三角形的性质,三角形的中线,几何作图,勾股定理,等积问题等知识,解题的关键是把多边形转化为三角形是解决问题的关键,记住三角形的中线把三角形分成面积相等的两个三角形.【变式5-1】(2022•江北区模拟)新知学习:若一条线段把一个平面图形分成面积相等的两部分,我们把这条线段叫做该平面图形的二分线.解决问题:(1)①三角形的中线、高线、角平分线中,一定是三角形的二分线的是三角形的中线;②如图1,已知△ABC中,AD是BC边上的中线,点E,F分别在AB,DC上,连接EF,与AD交于=S△DGF,则EF是(填“是”或“不是”)△ABC的一条二分线.点G.若S△AEG(2)如图2,四边形ABCD中,CD平行于AB,点G是AD的中点,射线CG交射线BA于点E,取EB 的中点F,连接CF.求证:CF是四边形ABCD的二分线.(3)如图3,在△ABC中,AB=CB=CE=7,∠A=∠C,∠CBE=∠CEB,D,E分别是线段BC,AC上的点,且∠BED=∠A,EF是四边形ABDE的一条二分线,求DF的长.【分析】(1)①由平面图形的二分线定义可求解;②由面积的和差关系可得S△BEF=S△ABD=S△ABC,可得EF是△ABC的一条二分线;=S△CEF,由AB∥DC,G是AD的中点,证明△CDG≌△EAG,所(2)根据EB的中点F,所以S△CBF=S△CEF,所以S四边形AFCD=S△CBF,可得CF是四边形ABCD的二分线;以S四边形AFCD=S△DEC=S△ABE,可得S△HED=(3)延长CB使BH=CD,连接EH,通过全等三角形的判定可得S△BEHS四边形ABDE,即可得DF=DH=.【解答】解:(1)∵三角形的中线把三角形分成面积相等的两部分;∴三角形的中线是三角形的二分线,故答案为三角形的中线②∵AD是BC边上的中线=S△ACD=S△ABC,∴S△ABD=S△DGF,∵S△AEG+S△AEG=S四边形BDGE+S△DGF,∴S四边形BDGE=S△ABD=S△ABC,∴S△BEF∴EF是△ABC的一条二分线故答案为:是(2)∵EB的中点F,=S△CEF,∴S△CBF∵AB∥DC,∴∠E=∠DCG,∵G是AD的中点,∴DG=AG,在△CDG和△EAG中,∴△CDG≌△EAG(AAS),=S△DCG,∴S△AEG=S△CEF,∴S四边形AFCD=S△CBF,∴S四边形AFCD∴CF是四边形ABCD的二分线.(3)如图,延长CB使BH=CD,连接EH,AB=CB=CE=7,∠A=∠C,∠CBE=∠CEB,D,E分别是线段BC,AC上的点,且∠BED=∠A,∵BC=7∴BD+CD=7∴BD+BH=7=HD∵∠BED=∠A,∠BED+∠DEC=∠A+∠ABE∴∠ABE=∠CED,且AB=CE=7,∠A=∠C∴△ABE≌△CED(ASA)=S△EDC,∴AE=CD,BE=DE,∠AEB=∠EDC,S△ABE∴AE=BH,∵∠CBE=∠CEB∴∠AEB=∠EBH∴∠EBH=∠EDC,且BE=DE,BH=CD∴△BEH≌△DEC(SAS)、=S△DEC,∴S△BEH=S△DEC=S△ABE,∴S△BEH=S四边形ABDE,∴S△HED∵EF是四边形ABDE的一条二分线,=S四边形ABDE=S△HED,∴S△DEF∴DF=DH=【点评】本题是三角形综合题,考查了全等三角形的判定和性质,三角形中线的性质,平行线的性质,理解新定义是本题的关键.【变式5-2】(2021•西安一模)问题提出(1)如图①,在Rt△ABC中,∠A=90°,AB=3,AC=4,在BC上找一点D,使得AD将△ABC分成面积相等的两部分,作出线段AD,并求出AD的长度;问题探究(2)如图②,点A、B在直线a上,点M、N在直线b上,且a∥b,连接AN、BM交于点O,连接AM、BN,试判断△AOM与△BON的面积关系,并说明你的理由;解决问题(3)如图③,刘老伯有一个形状为筝形OACB的养鸡场,在平面直角坐标系中,O(0,0)、A(4,0)、B(0,4)、C(6,6),是否在边AC上存在一点P,使得过B、P两点修一道笔直的墙(墙的宽度不计),将这个养鸡场分成面积相等的两部分?若存在,请求出直线BP的表达式;若不存在,请说明理由.【分析】(1)当点D是BC的中点时,AD将△ABC分成面积相等的两部分,根据直角三角形斜边中线等于斜边的一般,可求出AD的长度;(2)根据同底等高的三角形面积相等,再减去相等的部分,就可以得出△AOM与△BON的面积相等;(3)连接AB,过点O作AB的平行线,交CA的延长线于点F,交OA于点G,则△OBG的面积等于△AFG的面积,则四边形OACB的面积转化为△BCF的面积,取CF的中点P,求出点P的坐标,即可求出直线BP的表达式.【解答】解:(1)如图①,取BC边的中点D,连接AD,则线段AD即为所求.在Rt△ABC中,∠BAC=90°,AB=3,AC=4,∴BC=,∵点D为BC的中点,∴AD=BC=.=S△BON,理由如下:(2)S△AOM=S△ABM﹣S△AOB,S△BON=S△ABN﹣S△AOB,由图可知,S△AOM如图②,过点M作MD⊥AB于点D,过点N作NE⊥AB于点E,∴MD∥NE,∠MDE=90°,又∵MN∥DE,∴四边形MDEN是矩形,∴MD=NE,=,S△ABN=,∵S△ABM=S△ABN,∴S△ABM=S△BON.∴S△AOM(3)存在,直线BP的表达式为:y=x+4.如图③,连接AB,过点O作OF∥AB,交CA的延长线于点F,交OA于点G,=S△AFG,由(2)的结论可知,S△OBG=S△BCF,∴S四边形OACB取CF的中点P,作直线BP,直线BP即为所求.∵A(4,0),B(0,4),C(6,6),∴线段AB所在直线表达式为:y=﹣x+4,线段AC所在直线的表达式为:y=3x﹣12,∴直线OF的表达式为:y=﹣x,联立,解得,∴F(3,﹣3),∵点P是CF的中点,∴P(,),∴直线BP的表达式为:y=x+4.【点评】主要考查了勾股定理,中点的性质,面积转化以及待定系数法求一次函数表达式等内容,熟练掌握勾股定理的内容,中点性质的应用,作出辅助线,进行面积的转化是解答本题的关键.题型3:面积最值问题6.(2019•无锡)如图,在△ABC中,AB=AC=5,BC=4,D为边AB上一动点(B点除外),以CD为一边作正方形CDEF,连接BE,则△BDE面积的最大值为8.得到BM=CM=2,易证△AMB∽△CGB,求得GB=8,设BD=x,则DG=8﹣x,易证△EDH≌△DCG,EH=DG=8﹣x,所以S△BDE===,当x=4时,△BDE面积的最大值为8.【解答】解:过点C作CG⊥BA于点G,作EH⊥AB于点H,作AM⊥BC于点M.∵AB=AC=5,BC=4,∴△AMB∽△CGB,∴,∴GB=8,设BD=x,则DG=8﹣x,∵ED=DC,∠EHD=∠DGC,∠HED=∠GDC,∴△EDH≌△DCG(AAS),∴EH=DG=8﹣x,===,∴S△BDE当x=4时,△BDE面积的最大值为8.故答案为8.【点评】本题考查了正方形,熟练运用正方形的性质与相似三角形的判定与性质以及全等三角形的判定与性质是解题的关键.;【变式6-1】(1)如图①,若BC=6,AC=4,∠C=60°,求△ABC的面积S△ABC;(2)如图②,若BC=a,AC=b,∠C=α,求△ABC的面积S△ABC(3)如图③,四边形ABCD,AC=m,BD=n,对角线AC交于O点,他们所成锐角为β,求四边形ABCD .的面积S四边形ABCD【分析】(1)过A作AM⊥BC于M,解直角三角形求出AM,再根据三角形面积公式求出即可;(2)过A作AM⊥BC于M,解直角三角形求出AM,再根据三角形面积公式求出即可;(3)过A作AE⊥BD于E,过C作CF⊥BD于F,解直角三角形求出AE、CF,根据三角形面积公式求出即可.【解答】解:(1)如图①,过A作AM⊥BC于M,则∠AMC=90°,∵∠C=60°,AC=4,∴AM=AC×sin60°=4×=2,∵BC=6,=×BC×AM=×6×2=6;∴△ABC的面积S△ABC(2)如图②,过A作AM⊥BC于M,则∠AMC=90°,∵∠C=α,AC=b,∴AM=AC×sinα=b×sinα=b sinα,∵BC=a,=×BC×AM=×a×b sinα=ab sinα;∴△ABC的面积S△ABC(3)如图3,过A作AE⊥BD于E,过C作CF⊥BD于F,BD=n,OA+OC=m,∵AC、BD夹角为β,∴AE=OA•sinβ,CF=OC•sinβ,=S△ABD+S△BDC∴S四边形ABCD=BD•AE+BD•CF=BD•(AE+CF)=BD•(OA•sinβ+OC•sinβ)=BD•AC•sinβ=mn sinβ.=mn sinβ.即四边形ABCD的面积S四边形ABCD【点评】本题考查了解直角三角形,三角形的面积的应用,此题比较难,解题时关键要找对思路,即原四边形的高已经发生了变化,只要把高求出来,一切将迎刃而解.【变式6-2】如图,正方形ABCD的边长为2,动点E从点A出发,沿边AB﹣BC向终点C运动,以DE为边作正方形DEFG(点D、E、F、G按顺时针方向排列).设点E运动的速度为每秒1个单位,运动的时间为x秒.(1)如图1,当点E在AB上时,求证:点G在直线BC上;(2)设正方形ABCD与正方形DEFG重叠部分的面积为S,求S与x之间的函数关系式;(3)直接写出整个运动过程中,点F经过的路径长.【分析】(1)由正方形的性质得出AD=CD,DE=DG,∠ADE+∠EDC=∠EDC+∠CDG=90°,证出∠ADE=∠CDG,由SAS证明△ADE≌△CDG,得出∠DCG=∠DAE=90°,证出∠DCG+∠DCB=180°,即可得出结论;(2)分情况讨论:①当点E在AB边上时,过点E作EK∥AD,交CD于点K,则AC∥EK∥AD,证明△ADE∽△BEH,由相似三角形的性质得出=,求出BH=,S=正方形ABCD的面积﹣△ADE的面积﹣△BEH的面积,即可得出结果;②当点E在BC边上时,S=△DEC的面积=4﹣x;(3)由(1)知,当点E在AB上时,点G在直线BC上,当点E与B点重合时,点F的位置如图2所示:点F运动的路径为BF;同理,点E在BC上时,当点E与C点重合时,点F运动的路径为FG;由勾股定理求出BD,即可得出结果.【解答】(1)证明:∵四边形ABCD与四边形DEFG都是正方形,∴AD=CD,DE=DG,∠ADE+∠EDC=∠EDC+∠CDG=90°,∴∠ADE=∠CDG,在△ADE和△CDG中,,∴△ADE≌△CDG(SAS),∴∠DCG=∠DAE=90°,∵∠DCB=90°,∴∠DCG+∠DCB=180°,∴点G在直线BC上;(2)解:①当点E在AB边上时,过点E作EK∥AD,交CD于点K,如图1所示:则AC∥EK∥AD,∴∠HEK=∠EHB,∠DEK=∠EDA,∵∠EHB+∠BEH=90°,∠EDA+∠AED=90°,∠HEK+∠DEK=90°,∴∠EDA=∠BEH,∠AED=∠EHB,∴△ADE∽△BEH,∴=,即=,∴BH=,S=正方形ABCD的面积﹣△ADE的面积﹣△BEH的面积=2×2﹣×2×x﹣×(2﹣x)×=;②当点E在BC边上时,S=△DEC的面积=×2×(4﹣x)=4﹣x;(3)解:由(1)知,当点E在AB上时,点G在直线BC上,当点E与B点重合时,点F的位置如图2所示:点F运动的路径为BF;同理,点E在BC上时,当点E与C点重合时,点F运动的路径为FG;∵BD===2,∴BF+FG=2BD=4,∴点F运动的路径长为4.【点评】本题是四边形综合题目,考查了正方形的性质、平行线的判定与性质、三角形面积的计算、全等三角形的判定与性质、相似三角形的判定与性质、勾股定理等知识;熟练掌握正方形的性质、全等三角形的判定与性质、相似三角形的判定与性质是解决问题的关键.1.如图,在边长为6的菱形ABCD中,∠BCD=60°,连接BD,点E、F分别是边AB、BC上的动点,且AE=BF,连接DE、DP、EF.(1)如图①,当点E是边AB的中点时,求∠EDF的度数;(2)如图②,当点E是边AB上任意一点时,∠EDF的度数是否发生改变?若不改变,请证明;若发生改变,请说明理由;(3)若点P是线段BD上一动点,求PF+DP的最小值.【分析】(1)由菱形的性质可得AB=BC=CD=AD=6,∠BCD=∠BAD=60°,可证△ABD,△BCD 是等边三角形,由等边三角形的性质可证DE=DF,∠EDF=60°,可得结论;(2)证明△ADE≌△BDF(SAS),根据全等三角形的性质得∠ADE=∠BDF,由角的和差即可得∠EDF =∠ADB=60°;(3)过点P作PG⊥AD于点G,连接PF,过点F作FG′⊥AD于点G′,交BD于点P′,可得GP=DP•sin60°=DP,则PF+DP=PF+GP,当点F、P、G三点共銭,且FG⊥AD时,PF+GP有最小值,最小值为FG′的长,过点D作DH⊥BC于点H,则DH=FG',PF+DP的最小值即为DH的长,由△BDC是等边三角形可得DH=CD•sin60°=3,即可求得PF+DP的最小值.【解答】解:(1)∵四边形ABCD是菱形,边长为6,∴AB=BC=CD=AD=6,∠BCD=∠BAD=60°,∴△ABD,△BCD是等边三角形,∵点E是边AB的中点,AE=BF,∴点F是边BC的中点,∴∠ADE=∠BDE=∠BDF=∠CDF=30°,∴∠EDF=∠BDE+∠BDF=60°;(2)∠EDF的度数不改变,证明:△ABD,△BCD是等边三角形,∴AD=BD,∠DAB=∠DBC=60°,∵AE=BF,∴△ADE≌△BDF(SAS),∴∠ADE=∠BDF,∴∠EDF=∠ADB=60°;(3)如图,过点P作PG⊥AD于点G,连接PF,过点F作FG′⊥AD于点G′,交BD于点P′,∵∠ADB=60°,∴GP=DP•sin60°=DP,∴PF+DP=PF+GP,∴当点F、P、G三点共銭,且FG⊥AD时,PF+GP有最小值,最小值为FG′的长,过点D作DH⊥BC于点H,∵四边形ABCD是菱形,∴DH=FG',∴PF+DP的最小值即为DH的长,∵DH⊥BC,△BDC是等边三角形,∴DH=CD•sin60°=3,∴PF+DP的最小值为3.【点评】本题考查了四边形的综合应用,掌握菱形的性质,等边三角形的判定和性质,全等三角形的判定和性质,最短路径等知识,添加恰当辅助线构造构造在直角三角形是解本题的关键.2.(2022•连云港)如图,四边形ABCD为平行四边形,延长AD到点E,使DE=AD,且BE⊥DC.(1)求证:四边形DBCE为菱形;(2)若△DBC是边长为2的等边三角形,点P、M、N分别在线段BE、BC、CE上运动,求PM+PN的最小值.【分析】(1)先证明四边形DBCE是平行四边形,再由BE⊥DC,得四边形DBCE是菱形;(2)作N关于BE的对称点N',过D作DH⊥BC于H,由菱形的对称性知,点N关于BE的对称点N'在DE上,可得PM+PN=PM+PN',即知MN'的最小值为平行线间的距离DH的长,即PM+PN的最小值为DH的长,在Rt△DBH中,可得DH=DB•sin∠DBC=,即可得答案.【解答】(1)证明:∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC,∵DE=AD,∴DE=BC,∵E在AD的延长线上,∴DE∥BC,∴四边形DBCE是平行四边形,∵BE⊥DC,∴四边形DBCE是菱形;(2)解:作N关于BE的对称点N',过D作DH⊥BC于H,如图:由菱形的对称性知,点N关于BE的对称点N'在DE上,∴PM+PN=PM+PN',∴当P、M、N'共线时,PM+PN'=MN'=PM+PN,∵DE∥BC,∴MN'的最小值为平行线间的距离DH的长,即PM+PN的最小值为DH的长,在Rt△DBH中,∠DBC=60°,DB=2,∴DH=DB•sin∠DBC=2×=,∴PM+PN的最小值为.【点评】本题考查平行四边形性质及应用,涉及菱形的判定,等边三角形性质及应用,对称变换等,解题的关键是掌握解决“将军饮马”模型的方法.3.(2014•海南)如图,对称轴为直线x=2的抛物线经过A(﹣1,0),C(0,5)两点,与x轴另一交点为B.已知M(0,1),E(a,0),F(a+1,0),点P是第一象限内的抛物线上的动点.(1)求此抛物线的解析式;(2)当a=1时,求四边形MEFP的面积的最大值,并求此时点P的坐标;(3)若△PCM是以点P为顶点的等腰三角形,求a为何值时,四边形PMEF周长最小?请说明理由.【分析】(1)利用待定系数法求出抛物线的解析式;(2)首先求出四边形MEFP面积的表达式,然后利用二次函数的性质求出最值及点P坐标;(3)四边形PMEF的四条边中,PM、EF长度固定,因此只要ME+PF最小,则PMEF的周长将取得最小值.如答图3所示,将点M向右平移1个单位长度(EF的长度),得M1(1,1);作点M1关于x 轴的对称点M2,则M2(1,﹣1);连接PM2,与x轴交于F点,此时ME+PF=PM2最小.【解答】方法一:解:(1)∵对称轴为直线x=2,∴设抛物线解析式为y=a(x﹣2)2+k.将A(﹣1,0),C(0,5)代入得:,解得,∴y=﹣(x﹣2)2+9=﹣x2+4x+5.(2)当a=1时,E(1,0),F(2,0),OE=1,OF=2.设P(x,﹣x2+4x+5),如答图2,过点P作PN⊥y轴于点N,则PN=x,ON=﹣x2+4x+5,∴MN=ON﹣OM=﹣x2+4x+4.S四边形MEFP=S梯形OFPN﹣S△PMN﹣S△OME=(PN+OF)•ON﹣PN•MN﹣OM•OE=(x+2)(﹣x2+4x+5)﹣x•(﹣x2+4x+4)﹣×1×1=﹣x2+x+=﹣(x﹣)2+∴当x=时,四边形MEFP的面积有最大值为,把x=时,y=﹣(﹣2)2+9=.此时点P坐标为(,).(3)∵M(0,1),C(0,5),△PCM是以点P为顶点的等腰三角形,∴点P的纵坐标为3.令y=﹣x2+4x+5=3,解得x=2±.∵点P在第一象限,∴P(2+,3).四边形PMEF的四条边中,PM、EF长度固定,因此只要ME+PF最小,则PMEF的周长将取得最小值.如答图3,将点M向右平移1个单位长度(EF的长度),得M1(1,1);作点M1关于x轴的对称点M2,则M2(1,﹣1);连接PM2,与x轴交于F点,此时ME+PF=PM2最小.设直线PM2的解析式为y=mx+n,将P(2+,3),M2(1,﹣1)代入得:,解得:m=,n=﹣,∴y=x﹣.当y=0时,解得x=.∴F(,0).∵a+1=,∴a=.∴a=时,四边形PMEF周长最小.方法二:(1)略.(2)连接MF,过点P作x轴垂线,交MF于点H,有最大值时,四边形MEFP面积最大.显然当S△PMF当a=1时,E(1,0),F(2,0),∵M(0,1),∴l MF:y=﹣x+1,设P(t,﹣t2+4t+5),H(t,﹣t+1),=(P Y﹣H Y)(F X﹣M X),∴S△PMF=(﹣t2+4t+5+t﹣1)(2﹣0)=﹣t2+t+4,∴S△PMF最大值为,∴当t=时,S△PMF=EF×MY=×1×1=,∵S△MEF的最大值为+=,∴S四边形MEFP∴P(,).(3)∵M(0,1),C(0,5),△PCM是以点P为顶点的等腰三角形,∴点P的纵坐标为3,∴﹣x2+4x+5=0,解得:x=2±,∵点P在第一象限,∴P(2+,3),PM、EF长度固定,当ME+PF最小时,PMEF的周长取得最小值,将点M向右平移1个单位长度(EF的长度),得M1(1,1),∵四边形MEFM1为平行四边形,∴ME=M1F,作点M1关于x轴的对称点M2,则M2(1,﹣1),∴M2F=M1F=ME,当且仅当P,F,M2三点共线时,此时ME+PF=PM2最小,∵P(2+,3),M2(1,﹣1),F(a+1,0),∴K PF=K M1F,∴,∴a=.【点评】本题是二次函数综合题,第(1)问考查了待定系数法;第(2)问考查了图形面积计算以及二次函数的最值;第(3)问主要考查了轴对称﹣最短路线的性质.试题计算量偏大,注意认真计算.4.(2021•靖江市校级一模)如图,在菱形ABCD中,AB=6,∠B=60°,点E在边AD上.若直线l经过点E,将该菱形的面积平分,并与菱形的另一边交于点F,若AE=2,则求EF的长.(请从“线段的长度或线段的位置关系”的方向设计条件及问题,并解答)【分析】过点A和点E作AG⊥BC,EH⊥BC于点G和H,可得矩形AGHE,再根据菱形ABCD中,AB=6,∠B=60°,可得BG=3,AG=3=EH,由题意可得,FH=FC﹣HC=2﹣1=1,进而根据勾股定理可得EF的长.【解答】若AE=2.则求EF的长.解:如图,过点A和点E作AG⊥BC,EH⊥BC于点G和H,得矩形AGHE,∴GH=AE=2,在菱形ABCD中,AB=6,∠B=60°,∴BG=3,AG=3=EH,∴HC=BC﹣BG﹣GH=6﹣3﹣2=1,∵EF平分菱形面积,EF经过菱形对角线交点,∴FC=AE=2,∴FH=FC﹣HC=2﹣1=1,在Rt△EFH中,根据勾股定理,得:EF===2.【点评】本题考查了菱形的性质,勾股定理,矩形的性质,解决本题的关键是掌握菱形的性质.5.(2012•新密市自主招生)如图,菱形ABCD的边长为4,∠BAD=60°,点E是AD上一动点(不与A、D重合),点F是CD上一动点,且AE+CF=4,则△DEF面积的最大值为.【分析】首先过点F作FG⊥AD,交AD的延长线于点G,由菱形ABCD的边长为4,∠BAD=60°,即=DE•FG)=﹣(x﹣2)2+,可求得AD=CD=4,∠FDG=60°,然后设AE=x,即可得S△DEF然后根据二次函数的性质,即可求得答案.【解答】解:过点F作FG⊥AD,交AD的延长线于点G,∵菱形ABCD边长为4,∠BAD=60°,∴AD=CD=4,∠ADC=180°﹣∠BAD=120°,∴∠FDG=180°﹣∠ADB=60°,设AE=x,∵AE+CF=4,∴CF=4﹣x;∴DE=AD﹣AE=4﹣x,DF=CD﹣CF=4﹣(4﹣x)=x,在Rt△DFG中,FG=DF•sin∠GDF=x,=DE•FG=×(4﹣x)×x=﹣x2+x=﹣(x2﹣4x)=﹣(x﹣2)2+,∴S△DEF∴当x=2时,△DEF面积的最大,最大值为.故答案为:.【点评】此题考查了菱形的性质、三角函数的性质以及二次函数的最值问题.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想与函数思想的应用.6.(2022•杭州模拟)将正方形ABCD的边AB绕点A逆时针旋转至AB′,记旋转角为α,连接BB′,过点D作DE垂直于直线BB′,垂足为点E,连接DB′,CE.(1)如图1,当α=60°时,△DEB′的形状为等腰直角三角形,连接BD,BB′与CE的数量关系是BB'=CE.(2)当0°<α<360°且a≠90°时,①(1)中的两个结论是否仍然成立?如果成立,请仅就图2的情形进行证明;如果不成立,请说明理由;②当以点E,C,D,B′为顶点的四边形是平行四边形时,请直接写出BE与B′E的数量关系.。
中考数学几何压轴题(有关三角形、四边形)的综合专题(含答案解析)
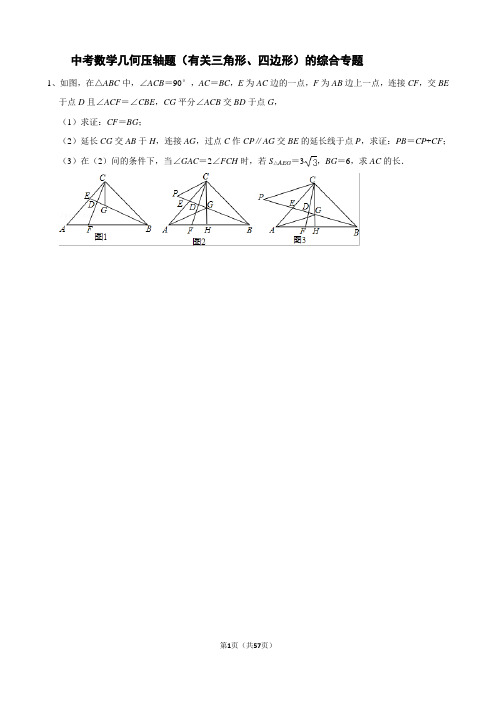
中考数学几何压轴题(有关三角形、四边形)的综合专题1、如图,在△ABC中,∠ACB=90°,AC=BC,E为AC边的一点,F为AB边上一点,连接CF,交BE于点D且∠ACF=∠CBE,CG平分∠ACB交BD于点G,(1)求证:CF=BG;(2)延长CG交AB于H,连接AG,过点C作CP∥AG交BE的延长线于点P,求证:PB=CP+CF;(3)在(2)问的条件下,当∠GAC=2∠FCH时,若S△AEG=3,BG=6,求AC的长.2、[问题背景]如图1所示,在△ABC中,AB=BC,∠ABC=90°,点D为直线BC上的一个动点(不与B、C重合),连结AD,将线段AD绕点D按顺时针方向旋转90°,使点A旋转到点E,连结EC.[问题初探]如果点D在线段BC上运动,通过观察、交流,小明形成了以下的解题思路:过点E作EF⊥BC 交直线BC于F,如图2所示,通过证明△DEF≌△,可推证△CEF是三角形,从而求得∠DCE=.[继续探究]如果点D在线段CB的延长线上运动,如图3所示,求出∠DCE的度数.[拓展延伸]连接BE,当点D在直线BC上运动时,若AB=,请直接写出BE的最小值.3、(2019秋•锦江区校级期末)在Rt△ABC中,∠ACB=90°,∠A=30°,BD是△ABC的角平分线.(1)如图1,求证:AD=2DC.(2)如图2,作∠CBD的角平分线交线段CD于点M,若CM=1,求△DBM的面积;(3)如图3,过点D作DE⊥AB于点E,点N是线段AC上一点(不与C、D重合),以BN为一边,在BN的下方作∠BNG=60°,NG交DE延长线于点G,试探究线段ND,DG与AD之间的数量关系,并说明理由.4、(2019•镇平县三模)如图1,已知直角三角形ABC,∠ACB=90°,∠BAC=30°,点D是AC边上一点,过D作DE⊥AB于点E,连接BD,点F是BD中点,连接EF,CF.(1)发现问题:线段EF,CF之间的数量关系为;∠EFC的度数为;(2)拓展与探究:若将△AED绕点A按顺时针方向旋转α角(0°<α<30°),如图2所示,(1)中的结论还成立吗?请说明理由;(3)拓展与运用:如图3所示,若△AED绕点A旋转的过程中,当点D落到AB边上时,AB边上另有一点G,AD=DG=GB,BC=3,连接EG,请直接写出EG的长度.5、(2017春•西城区校级期末)如图1,在等腰△ABC中,AB=AC,∠BAC=a,点P是线段AB的中点,点E是线段CB延长线上一点,且PE=PC,将线段PC绕点P顺时针旋转α得到PD,连接BD.(1)如图2,若α=60°,其他条件不变,先补全图形,然后探究线段BD和BC之间的数量关系,并说明理由.(2)如图3,若α=90°,其他条件不变,探究线段BP、BD和BC之间的等量关系,并说明理由.6、【发现问题】如图1,已知△ABC,以点A为直角顶点、AB为腰向△ABC外作等腰直角△ABE.请你以A为直角顶点、AC为腰,向△ABC外作等腰直角△ACD(不写作法,保留作图痕迹).连接BD、CE.那么BD与CE的数量关系是BD=CE.【拓展探究】如图2,已知△ABC,以AB、AC为边向外作正方形AEFB和正方形ACGD,连接BD、CE,试判断BD与CE之间的数量关系,并说明理由.【解决问题】如图3,有一个四边形场地ABCD,∠ADC=60°,BC=15,AB=8,AD=CD,求BD的最大值.7、(1)如图1,点C为线段AB外一个动点,已知AB=a,AC=b.当点C位于BA的延长线上时,线段BC取得最大值,则最大值为(用含a,b的式子表示);(2)如图2,点C为线段AB外一个动点,若AB=10,AC=3,分别以AC,BC为边,作等边三角形ACD和等边三角形BCE,连接AE,DB.①求证:AE=DB;②请直接写出线段AE的最大值;(3)如图3,AB=6,点M为线段AB外一个动点,且AM=2,MB=MN,∠BMN=90°,请直接写出线段AN的最大值.8、【初步探索】(1)如图1:在四边形ABC中,AB=AD,∠B=∠ADC=90°,E、F分别是BC、CD上的点,且EF =BE+FD,探究图中∠BAE、∠F AD、∠EAF之间的数量关系.小王同学探究此问题的方法是:延长FD到点G,使DG=BE.连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是;【灵活运用】(2)如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E、F分别是BC、CD上的点,且EF=BE+FD,上述结论是否仍然成立,并说明理由;【拓展延伸】(3)如图3,已知在四边形ABCD中,∠ABC+∠ADC=180°AB=AD,若点E在CB的延长线上,点F在CD的延长线上,如图3所示,仍然满足EF=BE+FD,请写出∠EAF与∠DAB的数量关系,并给出证明过程.9、(2018•大东区一模)如图,在Rt△ABC中,∠ACB=90°,∠A=30°,点O为AB中点,点P为直线BC上的动点(不与点B、点C重合),连接OC、OP,将线段OP绕点P逆时针旋转60°,得到线段PQ,连接BQ.(1)如图1,当点P在线段BC上时,请直接写出线段BQ与CP的数量关系.(2)如图2,当点P在CB延长线上时,(1)中结论是否成立?若成立,请加以证明;若不成立,请说明理由;(3)如图3,当点P在BC延长线上时,若∠BPO=45°,AC=,请直接写出BQ的长.10、模型发现:同学们知道,三角形的两边之和大于第三边,即如图1,在△ABC中,AB+AC>BC.对于图1,若把点C看作是线段AB外一动点,且AB=c,AC=b,则线段BC的长会因为点C的位置的不同而发生变化.因为AB、AC的长度固定,所以当∠BAC越大时,BC边越长.特别的,当点C位于时,线段BC的长取得最大值,且最大值为(用含b,c的式子表示)(直接填空).模型应用:点C为线段AB外一动点,且AB=3,AC=2,如图2所示,分别以AC,BC为边,作等边三角形ACD 和等边三角形BCE,连接BD,AE.(1)求证:BD=AE.(2)线段AE长的最大值为.模型拓展:如图3,在平面直角坐标系中,点A是y轴正半轴上的一动点,点B是x轴正半轴上的一动点,且AB =8.若AC⊥AB,AC=3,试求OC长的最大值.11、已知:△ABC中,∠ACB=90°,AC=BC.(1)如图1,点D在BC的延长线上,连AD,过B作BE⊥AD于E,交AC于点F.求证:AD=BF;(2)如图2,点D在线段BC上,连AD,过A作AE⊥AD,且AE=AD,连BE交AC于F,连DE,问BD与CF有何数量关系,并加以证明;(3)如图3,点D在CB延长线上,AE=AD且AE⊥AD,连接BE、AC的延长线交BE于点M,若AC =3MC,请直接写出的值.12、已知在△ABC中,AB=AC,射线BM、BN在∠ABC内部,分别交线段AC于点G、H.(1)如图1,若∠ABC=60°,∠MBN=30°,作AE⊥BN于点D,分别交BC、BM于点E、F.①求证:∠1=∠2;②如图2,若BF=2AF,连接CF,求证:BF⊥CF;(2)如图3,点E为BC上一点,AE交BM于点F,连接CF,若∠BFE=∠BAC=2∠CFE,求的值.13、已知,△ABC中,AB=AC,∠BAC=90°,E为边AC任意一点,连接BE.(1)如图1,若∠ABE=15°,O为BE中点,连接AO,且AO=1,求BC的长;(2)如图2,F也为AC上一点,且满足AE=CF,过A作AD⊥BE交BE于点H,交BC于点D,连接DF交BE于点G,连接AG;①若AG平分∠CAD,求证:AH=AC;②如图3,当G落在△ABC外时,若将△EFG沿EF边翻折,点G刚好落在AB边上点P,直接写出AG与EF的数量关系.14、如图所示,Rt△ABC中,∠ACB=90°,E为AC中点,作ED⊥AC交AB于D,连接CD;(1)如图1,求证:AB=2CD;(2)如图2,作CF⊥AB交AB于F,点G为CF上一点,点H为DE延长线上一点,分别连接AH、GH,若∠AHG=2∠B,求证:AH=GH;(3)如图3,在(2)的条件下,连接DG,且有DE=BF,∠EDG=90°,若AC=6,求AH的长度.15、【问题情境】一节数学课后,老师布置了一道课后练习题:如图:已知在Rt△ABC中,AC=BC,∠ACB=90°,CD⊥AB于点D,点E、F分别在A和BC上,∠1=∠2,FG⊥AB于点G,求证:△CDE≌△EGF.(1)阅读理解,完成解答本题证明的思路可用下列框图表示:根据上述思路,请你完整地书写这道练习题的证明过程;(2)特殊位置,证明结论若CE平分∠ACD,其余条件不变,求证:AE=BF;(3)知识迁移,探究发现如图,已知在Rt△ABC中,AC=BC,∠ACB=90°,CD⊥AB于点D,若点E是DB的中点,点F在直线CB上且满足EC=EF,请直接写出AE与BF的数量关系.(不必写解答过程)16、在正方形ABCD和等腰直角△BGF中,∠BGF=90°,P是DF的中点,连接PG、PC.(1)如图1,当点G在BC边上时,延长GP交DC于点E.求证:PG=PC;(2)如图2,当点F在AB的延长线上时,(1)中的结论是否成立?请证明你的结论;(3)如图3,若四边形ABCD为菱形,且∠ABC=60°,△BGF为等边三角形,点F在CB的延长线上时,线段PC、PG又有怎样的数量关系,请直接写出你的结论,并画出论证过程中需要添加的辅助线.17、在△ABC中,∠BAC=60°,点D、E分别在边AC、AB上,AD=AE,连接CE、BD相交于点F,且∠BEC=∠ADF,连接AF.(1)如图1,连接ED,求证:∠ABD=∠CED;(2)如图2,求证:EF+FD=AF;(3)如图3,取BC的中点G,连接AG交BD于点H,若∠GAC=3∠ABD,BH=7,求△ABH的面积.18、点D,E分别在△ABC的边AC,BD上,BD,CE交于点F,连接AF,∠F AE=∠F AD,FE=FD.(1)如图1,若∠AEF=∠ADF,求证:AE=AD;(2)如图2,若∠AEF≠∠ADF,FB平分∠ABC,求∠BAC的度数;(3)在(2)的条件下,如图3,点G在BE上,∠CFG=∠AFB若AG=6,△ABC的周长为20,求BC长.中考数学几何压轴题(有关三角形、四边形)的综合专题参考答案1、如图,在△ABC中,∠ACB=90°,AC=BC,E为AC边的一点,F为AB边上一点,连接CF,交BE于点D且∠ACF=∠CBE,CG平分∠ACB交BD于点G,(1)求证:CF=BG;(2)延长CG交AB于H,连接AG,过点C作CP∥AG交BE的延长线于点P,求证:PB=CP+CF;(3)在(2)问的条件下,当∠GAC=2∠FCH时,若S△AEG=3,BG=6,求AC的长.证明:(1)如图1,∵∠ACB=90°,AC=BC,∴∠A=45°,∵CG平分∠ACB,∴∠ACG=∠BCG=45°,∴∠A=∠BCG,在△BCG和△CAF中,∵,∴△BCG≌△CAF(ASA),∴CF=BG;(2)如图2,∵PC∥AG,∴∠PCA=∠CAG,∵AC=BC,∠ACG=∠BCG,CG=CG,∴△ACG≌△BCG,∴∠CAG=∠CBE,∵∠PCG=∠PCA+∠ACG=∠CAG+45°=∠CBE+45°,∠PGC=∠GCB+∠CBE=∠CBE+45°,∴∠PCG=∠PGC,∴PC=PG,∵PB=BG+PG,BG=CF,∴PB=CF+CP;(3)解法一:如图3,过E作EM⊥AG,交AG于M,∵S△AEG=AG•EM=3,由(2)得:△ACG≌△BCG,∴BG=AG=6,∴×6×EM=3,EM=,设∠FCH=x°,则∠GAC=2x°,∴∠ACF=∠EBC=∠GAC=2x°,∵∠ACH=45°,∴2x+x=45,x=15,∴∠ACF=∠GAC=30°,在Rt△AEM中,AE=2EM=2,AM==3,∴M是AG的中点,∴AE=EG=2,∴BE=BG+EG=6+2,在Rt△ECB中,∠EBC=30°,∴CE=BE=3+,∴AC=AE+EC=2+3+=3+3.解法二:同理得:∠CAG=30°,AG=BG=6,如图4,过G作GM⊥AC于M,在Rt△AGM中,GM=3,AM===3,∵∠ACG=45°,∠MGC=90°,∴GM=CM=3,∴AC=AM+CM=3+3.2、[问题背景]如图1所示,在△ABC中,AB=BC,∠ABC=90°,点D为直线BC上的一个动点(不与B、C重合),连结AD,将线段AD绕点D按顺时针方向旋转90°,使点A旋转到点E,连结EC.[问题初探]如果点D在线段BC上运动,通过观察、交流,小明形成了以下的解题思路:过点E作EF⊥BC 交直线BC于F,如图2所示,通过证明△DEF≌△ADB,可推证△CEF是等腰直角三角形,从而求得∠DCE=135°.[继续探究]如果点D在线段CB的延长线上运动,如图3所示,求出∠DCE的度数.[拓展延伸]连接BE,当点D在直线BC上运动时,若AB=,请直接写出BE的最小值.解:[问题初探]如图2,过点E作EF⊥BC交直线BC于F,∴∠DFE=90°=∠ABD,∴∠EDF+∠DEF=90°,由旋转知,AD=DE,∠ADE=90°,∴∠ADB+∠EDF=90°,∴∠ADB=∠DEF,∴△ABD≌△DFE(AAS),∴BD=EF,DF=AB,∵AB=BC,∴BC=DF,∴BD=CF,∴EF=CF,∴△CEG是等腰直角三角形,∴∠ECF=45°,∴∠DCE=135°,故答案为:ADB,等腰直角,135;[继续探究]如图3,过点E作EF⊥BC于F,∴∠DFE=90°=∠ABD,∴∠EDF+∠DEF=90°,由旋转知,AD=DE,∠ADE=90°,∴∠ADB+∠EDF=90°,∴∠ADB=∠DEF,∴△ABD≌△DFE(AAS),∴BD=EF,DF=AB,∵AB=BC,∴BC=DF,∴BD=CF,∴EF=CF,∴△CEG是等腰直角三角形,∴∠ECF=45°,∴∠DCE=45°;[拓展延伸]如图4,在△ABC中,∠ABC=90°,AB=BC=,∴∠ACB=45°当点D在射线BC上时,由[问题初探]知,∠BCM=135°,∴∠ACM=∠BCM﹣∠ACB=90°,当点D在线段CB的延长线上时,由[继续探究]知,∠BCE=45°,∴∠ACN=∠ACB+∠BCM=90°,∴点E是过点C垂直于AC的直线上的点,∴当BE⊥MN时,BE最小,∵∠BCE=45°,∴∠CBE=45°=∠BCE,∴BE=CE,∴BE最小=BC=,即:BE的最小值为.3、在Rt△ABC中,∠ACB=90°,∠A=30°,BD是△ABC的角平分线.(1)如图1,求证:AD=2DC.(2)如图2,作∠CBD的角平分线交线段CD于点M,若CM=1,求△DBM的面积;(3)如图3,过点D作DE⊥AB于点E,点N是线段AC上一点(不与C、D重合),以BN为一边,在BN的下方作∠BNG=60°,NG交DE延长线于点G,试探究线段ND,DG与AD之间的数量关系,并说明理由.证明:(1)如图1,过点D作DE⊥AB,∵BD是△ABC的角平分线,DE⊥AB,∠ACB=90°,∴DC=DE,∵∠A=30°,DE⊥AB,∴AD=2DE,∴AD=2DC;(2)如图2,过点M作ME∥BD,∵∠ACB=90°,∠A=30°,∴∠ABC=60°,∵BD是△ABC的角平分线,∴∠ABD=∠DBC=30°,∵BM平分∠CBD,∴∠CBM=15°=∠DBM,∵ME∥BD,∴∠MEC=∠CBD=30°,∠EMB=∠DBM=∠MBE,∴ME=BE,∵∠MEC=30°,∠C=90°∴CE=MC=,ME=2MC=2=BE,∴BC=+2,∵∠CBD=30°,∠C=90°,∴BC=CD,∴CD=1+,∴DM=,∴△DBM的面积=××(+2)=1+;(3)若点N在CD上时,AD=DG+DN,理由如下:如图3所示:延长ED使得DW=DN,连接NW,∵∠ACB=90°,∠A=30°,BD是△ABC的角平分线,DE⊥AB于点E,∴∠ADE=∠BDE=60°,AD=BD,∵DN=DW,且∠WDN=60°∴△WDN是等边三角形,∴NW=DN,∠W=∠WND=∠BNG=∠BDN=60°,∴∠WNG=∠BND,在△WGN和△DBN中,∴△WGN≌△DBN(SAS),∴BD=WG=DG+DN,∴AD=DG+DN.(3)若点N在AD上时,AD=DG﹣DN,理由如下:如图4,延长BD至H,使得DH=DN,连接HN,由(1)得DA=DB,∠A=30°.∵DE⊥AB于点E.∴∠2=∠3=60°.∴∠4=∠5=60°.∴△NDH是等边三角形.∴NH=ND,∠H=∠6=60°.∴∠H=∠2.∵∠BNG=60°,∴∠BNG+∠7=∠6+∠7.即∠DNG=∠HNB.在△DNG和△HNB中,∴△DNG≌△HNB(ASA).∴DG=HB.∵HB=HD+DB=ND+AD,∴DG=ND+AD.∴AD=DG﹣ND.4、如图1,已知直角三角形ABC,∠ACB=90°,∠BAC=30°,点D是AC边上一点,过D作DE⊥AB于点E,连接BD,点F是BD中点,连接EF,CF.(1)发现问题:线段EF,CF之间的数量关系为EF=CF;∠EFC的度数为120°;(2)拓展与探究:若将△AED绕点A按顺时针方向旋转α角(0°<α<30°),如图2所示,(1)中的结论还成立吗?请说明理由;(3)拓展与运用:如图3所示,若△AED绕点A旋转的过程中,当点D落到AB边上时,AB边上另有一点G,AD=DG=GB,BC=3,连接EG,请直接写出EG的长度.解:(1)如图1中,∵DE⊥AB,∴∠BED=90°,∵∠BCD=90°,BF=DF,∴FE=FB=FD=CF,∴∠FBE=∠FEB,∠FBC=∠FCB,∴∠EFC=∠EFD+∠CFD=∠FBE+∠FEB+∠FBC+∠FCB=2(∠FBE+∠FBC)=2∠ABC=120°,故答案为:EF=CF,120°.(2)结论成立.理由:如图2中,取AB的中点M,AD的中点N,连接MC,MF,ED,EN,FN.∵BM=MA,BF=FD,∴MF∥AD,MF=AD,∵AN=ND,∴MF=AN,MF∥AN,∴四边形MFNA是平行四边形,∴NF=AM,∠FMA=∠ANF,在Rt△ADE中,∵AN=ND,∠AED=90°,∴EN=AD=AN=ND,同理CM=AB=AM=MB,在△AEN和△ACM中,∠AEN=∠EAN,∠MCA=∠MAC,∵∠MAC=∠EAN,∴∠AMC=∠ANE,又∵∠FMA=∠ANF,∴∠ENF=∠FMC,在△MFC和△NEF中,,∴△MFC≌△NEF(SAS),∴FE=FC,∠NFE=∠MCF,∵NF∥AB,∴∠NFD=∠ABD,∵∠ACB=90°,∠BAC=30°,∴∠ABC=60°,△BMC是等边三角形,∠MCB=60°∴∠EFC=∠EFN+∠NFD+∠DFC=∠MCF+∠ABD+∠FBC+∠FCB=∠ABC+∠MCB=60°+60°=120°.(3)如图3中,作EH⊥AB于H.在Rt△ABC中,∵∠BAC=30°,BC=3,∴AB=2BC=6,在Rt△AED中,∠DAE=30°,AD=2,∴DE=AD=1,在Rt△DEH中,∵∠EDH=60°,DE=1,∴EH=ED•sin60°=,DH=ED•cos60°=,在Rt△EHG中,EG==.5、如图1,在等腰△ABC中,AB=AC,∠BAC=a,点P是线段AB的中点,点E是线段CB延长线上一点,且PE=PC,将线段PC绕点P顺时针旋转α得到PD,连接BD.(1)如图2,若α=60°,其他条件不变,先补全图形,然后探究线段BD和BC之间的数量关系,并说明理由.(2)如图3,若α=90°,其他条件不变,探究线段BP、BD和BC之间的等量关系,并说明理由.解:(1)BC=2BD,理由:如图2,连接CD,由旋转可得,CP=DP,∠CPD=60°,∴△CDP是等边三角形,∴∠CDP=60°=∠PCD,又∵P是AB的中点,AB=AC,∠A=60°,∴等边三角形ABC中,∠PCB=30°,CP⊥AB,∴∠BCD=30°,即BC平分∠PCD,∴BC垂直平分PD,∴∠BDC=∠BPC=90°,∴Rt△BCD中,BC=2BD.(2)如图3,取BC中点F,连接PF,∵∠A=90°,AB=AC,∴△ABC是等腰直角三角形,∵P是AB的中点,F是BC的中点,∴PF是△ABC的中位线,∴PF∥AC,∴∠PFB=∠ACB=45°,∠BPF=∠A=90°,∴△BPF是等腰直角三角形,∴BF=BP,BP=PF,∵∠DPC=∠BPF=90°,∴∠BPD=∠FPC,又∵PD=PC,∴△BDP≌△FCP,∴BD=CF,∵BC=BF+FC,∴BC=BD+BP.6、【发现问题】如图1,已知△ABC,以点A为直角顶点、AB为腰向△ABC外作等腰直角△ABE.请你以A为直角顶点、AC为腰,向△ABC外作等腰直角△ACD(不写作法,保留作图痕迹).连接BD、CE.那么BD与CE的数量关系是BD=CE.【拓展探究】如图2,已知△ABC,以AB、AC为边向外作正方形AEFB和正方形ACGD,连接BD、CE,试判断BD与CE之间的数量关系,并说明理由.【解决问题】如图3,有一个四边形场地ABCD,∠ADC=60°,BC=15,AB=8,AD=CD,求BD的最大值.【发现问题】解:延长CA到M,作∠MAC的平分线AN,在AN上截取AD=AC,连接CD,即可得到等腰直角△ACD;连接BD、CE,如图1所示:∵△ABE与△ACD都是等腰直角三角形,∴AB=AE,AD=AC,∠BAE=∠CAD=90°,∴∠BAD=∠EAC,在△BAD和△EAC中,,∴△BAD≌△EAC(SAS),∴BD=CE,【拓展探究】解:BD=CE;理由如下:∵四边形AEFB与四边形ACGD都是正方形,∴AB=AE,AD=AC,∠BAE=∠CAD=90°,∴∠BAD=∠EAC,在△BAD和△EAC中,,∴△BAD≌△EAC(SAS),∴BD=CE;【解决问题】解:以AB为边向外作等边三角形ABE,连接CE,如图3所示:则∠BAE=60°,BE=AB=AE=8,∵AD=CD,∠ADC=60°,∴△ACD是等边三角形,∴∠CAD=60°,AC=AD,∴∠CAD+∠BAC=∠BAE+∠BAC,即∠BAD=∠EAC,在△BAD和△EAC中,,∴△BAD≌△EAC(SAS),∴BD=CE;当C、B、E三点共线时,CE最大=BC+BE=15+8=23,∴BD的最大值为23.7、如图1,点C为线段AB外一个动点,已知AB=a,AC=b.当点C位于BA的延长线上时,线段BC取得最大值,则最大值为a+b(用含a,b的式子表示);(2)如图2,点C为线段AB外一个动点,若AB=10,AC=3,分别以AC,BC为边,作等边三角形ACD和等边三角形BCE,连接AE,DB.①求证:AE=DB;②请直接写出线段AE的最大值;(3)如图3,AB=6,点M为线段AB外一个动点,且AM=2,MB=MN,∠BMN=90°,请直接写出线段AN的最大值.(1)解:∵点C为线段AB外一动点,且AC=b,AB=a,∴当点C位于BA的延长线上时,线段BC的长取得最大值,且最大值为AC+AB=a+b,(2)①证明:如图2中,∵△ACD与△BCE是等边三角形,∴CD=AC,CB=CE,∠ACD=∠BCE=60°,∴∠DCB=∠ACE,在△CAD与△EAB中,,∴△CAD≌△EAB(SAS),∴AE=BD.②∵线段AE长的最大值=线段BD的最大值,由(1)知,当线段BD的长取得最大值时,点D在BA的延长线上,∴最大值为AD+AB=3+10=13;(3)如图3中,连接BN,∵将△AMN绕着点M顺时针旋转90°得到△PBM,连接AP,则△APM是等腰直角三角形,∴MA=MP=2,BP=AN,∴P A=2,∵AB=6,∴线段AN长的最大值=线段BP长的最大值,∴当P在线段BA的延长线时,线段BP取得最大值最大值=AB+AP=6+2.8、【初步探索】(1)如图1:在四边形ABC中,AB=AD,∠B=∠ADC=90°,E、F分别是BC、CD上的点,且EF =BE+FD,探究图中∠BAE、∠F AD、∠EAF之间的数量关系.小王同学探究此问题的方法是:延长FD到点G,使DG=BE.连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是∠BAE+∠F AD=∠EAF;【灵活运用】(2)如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E、F分别是BC、CD上的点,且EF=BE+FD,上述结论是否仍然成立,并说明理由;【拓展延伸】(3)如图3,已知在四边形ABCD中,∠ABC+∠ADC=180°AB=AD,若点E在CB的延长线上,点F在CD的延长线上,如图3所示,仍然满足EF=BE+FD,请写出∠EAF与∠DAB的数量关系,并给出证明过程.解:(1)∠BAE+∠F AD=∠EAF.理由:如图1,延长FD到点G,使DG=BE,连接AG,根据SAS可判定△ABE≌△ADG,进而得出∠BAE=∠DAG,AE=AG,再根据SSS可判定△AEF≌△AGF,可得出∠EAF=∠GAF=∠DAG+∠DAF=∠BAE+∠DAF.故答案为:∠BAE+∠F AD=∠EAF;(2)仍成立,理由:如图2,延长FD到点G,使DG=BE,连接AG,∵∠B+∠ADF=180°,∠ADG+∠ADF=180°,∴∠B=∠ADG,又∵AB=AD,∴△ABE≌△ADG(SAS),∴∠BAE=∠DAG,AE=AG,∵EF=BE+FD=DG+FD=GF,AF=AF,∴△AEF≌△AGF(SSS),∴∠EAF=∠GAF=∠DAG+∠DAF=∠BAE+∠DAF;(3)∠EAF=180°﹣∠DAB.证明:如图3,在DC延长线上取一点G,使得DG=BE,连接AG,∵∠ABC+∠ADC=180°,∠ABC+∠ABE=180°,∴∠ADC=∠ABE,又∵AB=AD,∴△ADG≌△ABE(SAS),∴AG=AE,∠DAG=∠BAE,∵EF=BE+FD=DG+FD=GF,AF=AF,∴△AEF≌△AGF(SSS),∴∠F AE=∠F AG,∵∠F AE+∠F AG+∠GAE=360°,∴2∠F AE+(∠GAB+∠BAE)=360°,∴2∠F AE+(∠GAB+∠DAG)=360°,即2∠F AE+∠DAB=360°,∴∠EAF=180°﹣∠DAB.9、如图,在Rt△ABC中,∠ACB=90°,∠A=30°,点O为AB中点,点P为直线BC上的动点(不与点B、点C重合),连接OC、OP,将线段OP绕点P逆时针旋转60°,得到线段PQ,连接BQ.(1)如图1,当点P在线段BC上时,请直接写出线段BQ与CP的数量关系.(2)如图2,当点P在CB延长线上时,(1)中结论是否成立?若成立,请加以证明;若不成立,请说明理由;(3)如图3,当点P在BC延长线上时,若∠BPO=45°,AC=,请直接写出BQ的长.解:(1)CP=BQ,理由:如图1,连接OQ,由旋转知,PQ=OP,∠OPQ=60°⊅∴△POQ是等边三角形,∴OP=OQ,∠POQ=60°,在Rt△ABC中,O是AB中点,∴OC=OA=OB,∴∠BOC=2∠A=60°=∠POQ,∴∠COP=∠BOQ,在△COP和△BOQ中,,∴△COP≌△BOQ(SAS),∴CP=BQ,(2)CP=BQ,理由:如图2,连接OQ,由旋转知,PQ=OP,∠OPQ=60°∴△POQ是等边三角形,∴OP=OQ,∠POQ=60°,在Rt△ABC中,O是AB中点,∴OC=OA=OB,∴∠BOC=2∠A=60°=∠POQ,∴∠COP=∠BOQ,在△COP和△BOQ中,,∴△COP≌△BOQ(SAS),∴CP=BQ,(3)如图3,在Rt△ABC中,∠A=30°,AC=,∴BC=AC•tan∠A=,过点O作OH⊥BC,∴∠OHB=90°=∠BCA,∴OH∥AB,∵O是AB中点,∴CH=BC=,OH=AC=,∵∠BPQ=45°,∠OHP=90°,∴∠BPQ=∠PQH,∴PH=OH=,∴CP=PH﹣CH=﹣=,连接BQ,同(1)的方法得,BQ=CP=.10、模型发现:同学们知道,三角形的两边之和大于第三边,即如图1,在△ABC中,AB+AC>BC.对于图1,若把点C看作是线段AB外一动点,且AB=c,AC=b,则线段BC的长会因为点C的位置的不同而发生变化.因为AB、AC的长度固定,所以当∠BAC越大时,BC边越长.特别的,当点C位于线段BA的延长线上时,线段BC的长取得最大值,且最大值为b+c(用含b,c的式子表示)(直接填空)模型应用:点C为线段AB外一动点,且AB=3,AC=2,如图2所示,分别以AC,BC为边,作等边三角形ACD 和等边三角形BCE,连接BD,AE.(1)求证:BD=AE.(2)线段AE长的最大值为5.模型拓展:如图3,在平面直角坐标系中,点A是y轴正半轴上的一动点,点B是x轴正半轴上的一动点,且AB =8.若AC⊥AB,AC=3,试求OC长的最大值.解:当点C位于线段BA的延长线上时,线段BC的长取得最大值,最大值为b+c,故答案为:线段BA的延长线上;b+c;模型应用:(1)证明:∵△ACD、△BCE都是等边三角形,∴CD=CA=AD,CB=CE,∠ACD=60°,∠BCE=60°,∴∠DCB=∠ACE,在△DCB和△ACE中,,∴△DCB≌△ACE(SAS)∴BD=AE;(2)当点D位于线段BA的延长线上时,线段BD的长取得最大值,最大值为AB+AD=AB+AC=3+2=5,∵AE=BD,∴线段AE长的最大值为5,模型拓展:取AB的中点G,连接OG、CG,在Rt△AOB中,G为AB的中点,∴OG=AB=4,在Rt△CAG中,CG===5,当点O、G、C在同一条直线上时,OC最大,最大值为4+5=9.11、已知:△ABC中,∠ACB=90°,AC=BC.(1)如图1,点D在BC的延长线上,连AD,过B作BE⊥AD于E,交AC于点F.求证:AD=BF;(2)如图2,点D在线段BC上,连AD,过A作AE⊥AD,且AE=AD,连BE交AC于F,连DE,问BD与CF有何数量关系,并加以证明;(3)如图3,点D在CB延长线上,AE=AD且AE⊥AD,连接BE、AC的延长线交BE于点M,若AC =3MC,请直接写出的值.(1)证明:如图1中,∵BE⊥AD于E,∴∠AEF=∠BCF=90°,∵∠AFE=∠CFB,∴∠DAC=∠CBF,∵BC=CA,∴△BCF≌△ACD,∴BF=AD.(2)结论:BD=2CF.理由:如图2中,作EH⊥AC于H.∵∠AHE=∠ACD=∠DAE=90°,∴∠DAC+∠ADC=90°,∠DAC+∠EAH=90°,∴∠DAC=∠AEH,∵AD=AE,∴△ACD≌△EHA,∴CD=AH,EH=AC=BC,∵CB=CA,∴BD=CH,∵∠EHF=∠BCF=90°,∠EFH=∠BFC,EH=BC,∴△EHF≌△BCF,∴FH=CF,∴BD=CH=2CF.(3)如图3中,同法可证BD=2CM.∵AC=3CM,设CM=a,则AC=CB=3a,BD=2a,∴==.12、已知在△ABC中,AB=AC,射线BM、BN在∠ABC内部,分别交线段AC于点G、H.(1)如图1,若∠ABC=60°,∠MBN=30°,作AE⊥BN于点D,分别交BC、BM于点E、F.①求证:∠1=∠2;②如图2,若BF=2AF,连接CF,求证:BF⊥CF;(2)如图3,点E为BC上一点,AE交BM于点F,连接CF,若∠BFE=∠BAC=2∠CFE,求的值.(1)①证明:如图1中,∵AB=AC,∠ABC=60°∴△ABC是等边三角形,∴∠BAC=60°,∵AD⊥BN,∴∠ADB=90°,∵∠MBN=30°,∠BFD=60°=∠1+∠BAF=∠2+∠BAF,∴∠1=∠2②证明:如图2中,在Rt△BFD中,∵∠FBD=30°,∴BF=2DF,∵BF=2AF,∴BF=AD,∵∠BAE=∠FBC,AB=BC,∴△BFC≌△ADB,∴∠BFC=∠ADB=90°,∴BF⊥CF(2)在BF上截取BK=AF,连接AK.∵∠BFE=∠2+∠BAF,∠CFE=∠4+∠1,∴∠CFB=∠2+∠4+∠BAC,∵∠BFE=∠BAC=2∠EFC,∴∠1+∠4=∠2+∠4∴∠1=∠2,∵AB=AC,∴△ABK≌CAF,∴∠3=∠4,S△ABK=S△AFC,∵∠1+∠3=∠2+∠3=∠CFE=∠AKB,∠BAC=2∠CEF,∴∠KAF=∠1+∠3=∠AKF,∴AF=FK=BK,∴S△ABK=S△AFK,∴=2.13、已知,△ABC中,AB=AC,∠BAC=90°,E为边AC任意一点,连接BE.(1)如图1,若∠ABE=15°,O为BE中点,连接AO,且AO=1,求BC的长;(2)如图2,F也为AC上一点,且满足AE=CF,过A作AD⊥BE交BE于点H,交BC于点D,连接DF交BE于点G,连接AG;①若AG平分∠CAD,求证:AH=AC;②如图3,当G落在△ABC外时,若将△EFG沿EF边翻折,点G刚好落在AB边上点P,直接写出AG与EF的数量关系.(1)解:如图1中,在AB上取一点M,使得BM=ME,连接ME.在Rt△ABE中,∵OB=OE,∴BE=2OA=2,∵MB=ME,∴∠MBE=∠MEB=15°,∴∠AME=∠MBE+∠MEB=30°,设AE=x,则ME=BM=2x,AM=x,∵AB2+AE2=BE2,∴(2x+x)2+x2=22,∴x=(负根已经舍弃),∴AB=AC=(2+)•,∴BC=AB=+1.方法二:作EH⊥BC于H,求出BH,CH即可解决问题.(2)证明:如图2中,作CP⊥AC,交AD的延长线于P,GM⊥AC于M.∵BE⊥AP,∴∠AHB=90°,∴∠ABH+∠BAH=90°,∵∠BAH+∠P AC=90°,∴∠ABE=∠P AC,在△ABE和△CAP中,,∴△ABE≌△CAP,∴AE=CP=CF,∠AEB=∠P,在△DCF和△DCP中,,∴△DCF≌△DCP,∴∠DFC=∠P,∴∠GFE=∠GEF,∴GE=GF,∵GM⊥EF,∴FM=ME,∵AE=CF,∴AF=CE,∴AM=CM,在△GAH和△GAM中,,∴△AGH≌△AGM,∴AH=AM=CM=AC(3)解:结论:AG=EF.理由:如图3中,作CM⊥AC交AD的延长线于M,连接PG交AC于点O.由(2)可知△ACM≌△BAE,△CDF≌△CDM,∴∠AEB=∠M=∠GEF,∠M=∠CFD=∠GFE,AE=CM=CF,∴∠GEF=∠GFE,∴GE=GF,∵△EFP是由△EFG翻折得到,∴EG=EP=GF=PF,∴四边形EGFP是菱形,∴PG⊥AC,OE=OF,∵AE=CF,∴AO=OC,∵AB∥OP,∴BP=PC,∵PF∥BE,∴EF=CF=AE,∵PB=PC,AO=OC,∴PO=OG=AB,∴AB=PG,AB∥PG,∴四边形ABPG是平行四边形,∴AG∥BC,∴∠GAO=∠ACB=45°,设EO=OF=a,则OA=OG=3a,AG=3a,∴==,∴AG=EF14、如图所示,Rt△ABC中,∠ACB=90°,E为AC中点,作ED⊥AC交AB于D,连接CD;(1)如图1,求证:AB=2CD;(2)如图2,作CF⊥AB交AB于F,点G为CF上一点,点H为DE延长线上一点,分别连接AH、GH,若∠AHG=2∠B,求证:AH=GH;(3)如图3,在(2)的条件下,连接DG,且有DE=BF,∠EDG=90°,若AC=6,求AH的长度.解:(1)∵E为AC中点,作ED⊥AC交AB于D,∴AD=CD,∵∠ACB=90°,∴BC∥DE,∴AD=BD,∴CD=BD,∴AB=2CD;(2)如图2,连接CH,∵点E是AC的中点,∴AE=CE,∵DE⊥AC,∴CH=AH,∴∠ACH=∠CAH,∵∠ACB=90°,∴∠B+∠BAC=90°,∵CF⊥AB,∴∠BAC+∠ACF=90°,∴∠ACF=∠B,∴∠HCG=∠ACH+∠ACF=∠CAH+∠B,∠AHG=2∠B∴在四边形AHGF中,∠AFG+∠FGH+∠AHG+∠F AH=360°,∴∠FGH=360°﹣(∠AFG+∠AHG+∠F AH)=360°﹣(90°+2∠B+∠CAH+∠BAC)=360°﹣(90°+2∠B+∠CAH+90°﹣∠B)=360°﹣(180°+∠B+∠CAH)=180°﹣(∠B+∠CAH),∵∠CGH=180°﹣∠FGH=∠B+∠CAH=∠HCG,∴CH=GH,∵CH=AH,∴AH=GH;(3)如图3,由(1)知,DE∥BC,∴∠B=∠ADE,在△BFC和△DEA中,,∴△BFC≌△DEA,∴BC=AD,∵AD=BD=CD,∴BC=BD=CD,∴△BCD是等边三角形,∴∠B=60°,在Rt△ABC中,AC=6,∴BC=2,AB=4,∵CF⊥BD,∴DF=,CF=3,∵∠BAC=30°,∴∠ADE=60°,∵∠EDG=90°,∠FDG=30°,在Rt△DFG中,DF=,∴FG=1,DG=2,∴CG=CF﹣FG=2过点H作HN⊥CF,由(2)知,CH=GH,∴NG=CG=1,∴FN=NG+FG=2,过点H作HM⊥AB,∴∠FMH=∠NFM=∠HNF=90°,∴四边形NFMH是矩形,∴HM=FN=2,在Rt△DMH中,∠ADE=60°,HM=2,∴DH=,在Rt△HDG中,根据勾股定理得,HG==.15、【问题情境】一节数学课后,老师布置了一道课后练习题:如图:已知在Rt△ABC中,AC=BC,∠ACB=90°,CD⊥AB于点D,点E、F分别在A和BC上,∠1=∠2,FG⊥AB于点G,求证:△CDE≌△EGF.(1)阅读理解,完成解答本题证明的思路可用下列框图表示:根据上述思路,请你完整地书写这道练习题的证明过程;(2)特殊位置,证明结论若CE平分∠ACD,其余条件不变,求证:AE=BF;(3)知识迁移,探究发现如图,已知在Rt△ABC中,AC=BC,∠ACB=90°,CD⊥AB于点D,若点E是DB的中点,点F在直线CB上且满足EC=EF,请直接写出AE与BF的数量关系.(不必写解答过程)(1)证明:∵AC=BC,∠ACB=90°,∴∠A=∠B=45°,∵CD⊥AB,∴∠CDB=90°,∴∠DCB=45°,∵∠ECF=∠DCB+∠1=45°+∠1,∠EFC=∠B+∠2=45°+∠2,∠1=∠2,∴∠ECF=∠EFC,∴CE=EF,∵CD⊥AB,FG⊥AB,∴∠CDE=∠EGF=90°,在△CDE和△EGF中,,∴△CDE≌△EGF(AAS);(2)证明:由(1)得:CE=EF,∠A=∠B,∵CE平分∠ACD,∴∠ACE=∠1,∵∠1=∠2,∴∠ACE=∠2,在△ACE和△BEF中,,∴△ACE≌△BEF(AAS),∴AE=BF;(3)AE=BF,作EH⊥BC与H,如图3所示:设DE=x,根据题意得:BE=DE=x,AD=BD=2x,CD=AD=2x,AE=3x,根据勾股定理得:BC=AC=2x,∵∠ABC=45°,EH⊥BC,∴BH=x,∴CH=BC﹣BH=x,∵EC=EF,∴FH=CH=x,∴BF=x﹣x=x,∴=,∴AE=.16、在正方形ABCD和等腰直角△BGF中,∠BGF=90°,P是DF的中点,连接PG、PC.(1)如图1,当点G在BC边上时,延长GP交DC于点E.求证:PG=PC;(2)如图2,当点F在AB的延长线上时,(1)中的结论是否成立?请证明你的结论;(3)如图3,若四边形ABCD为菱形,且∠ABC=60°,△BGF为等边三角形,点F在CB的延长线。
中考数学模拟题汇总《几何综合压轴题》练习

中考数学模拟题汇总《几何综合压轴题》练习(含答案解析)一、倍长八字共5小题1.在△ABC中,D是BC的中点,且∠BAD≠90°,将线段AB沿AD所在直线翻折,得到线段AB′,作CE//AB交直线AB′于点E.(1)如图,若AB>AC,①依题意补全图形;②用等式表示线段AB,AE,CE之间的数量关系,并证明;(2)若AB<AC,上述结论是否仍然成立?若成立,简述理由;若不成立,直接用等式表示线段AB,AE,CE 之间新的数量关系(不需证明).2.如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,EF垂直平分CD,分别交AC,BC于点E,F,连接DE,DF.(1)求∠EDF的度数;(2)用等式表示线段AE,BF,EF之间的数量关系,并证明.3.如图,在△ABC中,∠ACB=90°,AC=BC,点D为AB边上一点(不与点A,B重合),作射线C D,过点A作AE⊥CD于E,在线段AE上截取EF=EC,连接BF交CD于G.(1)依题意补全图形;(2)求证:∠CAE=∠BCD(3)判断线段BG与GF之间的数量关系,并证明.4.如图,在△ABC中,∠BAC=α,点D在边BC上(不与B,C重合),连接AD,以点A为中心,将线段AD逆时针旋转180°-α得到线段AE,连接BE.(1)∠BAC+∠DAE= °(2)取CD的中点F,连接AF,用等式表示线段AF与BE的数量关系,并证明。
5.如图,△ACB中,AC=BC,∠ACB=90°,D为边BC上一点(不与点C重合),CD<BD,点E在AD的延长线上,且ED=AD,连接BE,过点B作BE的垂线,交边AC于点F.(1)依题意补全图形;(2)求证:BE=BF;(3)用等式表示线段AF与CD的数量关系,并证明.二、一线三垂直共1小题 6.如图,在Rt △ACB 中, ∠ACB =90°,AC =BC .点D 是BC 延长线上一点,连接AD .将线段AD 绕点A 逆时针旋转90°,得到线段AE .过点E 作EF //BD ,交AB 于点F .(1)①直接写出∠AFE 的度数是____________;②求证:∠DAC =∠E ;(2)用等式表示线段AF 与DC 的数量关系,并证明.三、三线合一共1小题 7.已知:如图,OB =BA ,∠OBA =150°,线段BA 绕点A 逆时针旋转90°得到线段AC .连接BC ,OA ,OC ,过点O 作OD ⊥AC 于点D .(1)依题意补全图形;(2)求∠DOC 的度数.A B C D A B C D四、手拉手共5小题8.如图,在三角形ABC 中,AB =AC ,∠BAC <60°,AD 是BC 边的高线,将线段AC 绕点A 逆时针旋转60°得到线段AE ,连接BE 交AD 于点F .(1)依题意补全图形,写出∠CAE= °(2)求∠BAF+∠ABF 和∠FBC 的度数;(3)用等式表示线段AF ,BF ,EF 之间的数量关系,并证明.9.如图,在等边△ABC 中,将线段AC 绕点A 顺时针旋转α(0∘<α<60∘),得到线段AD ,连接CD ,作∠BAD 的平分线AE ,交BC 于E .(1)① 根据题意,补全图形;② 请用等式写出∠BAD 与∠BCD 的数量关系,并证明.(2)分别延长CD 和AE 交于点F ,用等式表示线段AF ,CF ,DF 的数量关系,并证明.10.已知:等边△ABC ,过点B 作AC 的平行线l .点P 为射线AB 上一个动点(不与点A,B 重合),将射线PC 绕点P 顺时针旋转60°交直线l 于点D .(1)如图1,点P 在线段AB 上时,依题意补全图形;①求证:∠BDP =∠PCB ;②用等式表示线段BC,BD,BP 之间的数量关系,并证明;(2)点P 在线段AB 的延长线上,直接写出线段BC,BD,BP 之间的数量关系.A B C A B C AB C11.在Rt△ABC中,∠ABC=90°,∠BAC=30°,D为边BC上一动点,点E在边AC上,CE=CD.点D关于点B 的对称点为点F,连接AD,P为AD的中点,连接PE,PF,EF.(1)如图1,当点D与点B重合时,写出线段PE与PF之间的位置关系与数量关系;(2)如图2,当点D与点B,C不重合时,判断(1)中所得的结论是否仍然成立?若成立,请给出证明,若不成立,请举出反例。
2020年中考数学4.几何综合选择填空压轴题(含解析)

几何综合-填空选择压轴题41、如图,在菱形ABCD中,AB=2,∠B是锐角,AE⊥BC于点E,M是AB的中点,连结MD,ME.若∠EMD=90°,则cosB的值为.2、如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8cm,AE=2cm,则OF的长度是()A.3cm B.√6cm C.2.5cm D.√5cm3、定义:在平面直角坐标系中,一个图形先向右平移a个单位,再绕原点按顺时针方向旋转θ角度,这样的图形运动叫作图形的γ(a,θ)变换.如图,等边△ABC的边长为1,点A在第一象限,点B与原点O重合,点C在x轴的正半轴上.△A1B1C1就是△ABC经γ(1,180°)变换后所得的图形.若△ABC经γ(1,180°)变换后得△A1B1C1,△A1B1C1经γ(2,180°)变换后得△A2B2C2,△A2B2C2经γ(3,180°)变换后得△A3B3C3,依此类推……△An﹣1Bn﹣1Cn﹣1经γ(n,180°)变换后得△AnBnCn,则点A1的坐标是,点A2018的坐标是.4、我国古代伟大的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式.后人借助这种分割方法所得的图形证明了勾股定理,如图所示的矩形由两个这样的图形拼成,若a=3,b=4,则该矩形的面积为()A.20 B.24 C.994D.5325、如图,直线y=﹣√33x+4与x轴、y轴分别交于A,B两点,C是OB的中点,D 是AB上一点,四边形OEDC是菱形,则△OAE的面积为.6、小明发现相机快门打开过程中,光圈大小变化如图1所示,于是他绘制了如图2所示的图形.图2中六个形状大小都相同的四边形围成一个圆的内接正六边形和一个小正六边形,若PQ所在的直线经过点M,PB=5cm,小正六边形的面积为49√3cm2,则该圆的半径为cm.27、如图,在矩形ABCD中,AB=4,AD=2,点E在CD上,DE=1,点F是边AB上一动点,以EF为斜边作Rt△EFP.若点P在矩形ABCD的边上,且这样的直角三角形恰好有两个,则AF的值是.8、如图,AB是⊙O的直径,弦CD交AB于点P,AP=2,BP=6,∠APC=30°,则CD的长为()A.√15 B.2√5 C.2√15 D.89、如图,在矩形ABCD中,点E是边BC的中点,AE⊥BD,垂足为F,则tan∠BDE 的值是()A.√24 B.14C.13D.√2310、如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AF平分∠CAB,交CD于点E,交CB于点F.若AC=3,AB=5,则CE的长为()A.32B.43C.53D.8511、如图,在正方形ABCD中,AD=2√3,把边BC绕点B逆时针旋转30°得到线段BP,连接AP并延长交CD于点E,连接PC,则三角形PCE的面积为.12、如图,P为等边三角形ABC内的一点,且P到三个顶点A,B,C的距离分别为3,4,5,则△ABC的面积为()A.9+25√34 B.9+25√32C.18+25√3 D.18+25√3213、如图,点O 是▱ABCD 的对称中心,AD >AB ,E 、F 是AB 边上的点,且EF=12AB ;G 、H 是BC 边上的点,且GH=13BC ,若S 1,S 2分别表示△EOF 和△GOH 的面积,则S 1与S 2之间的等量关系是 .14、如图,已知∠POQ=30°,点A 、B 在射线OQ 上(点A 在点O 、B 之间),半径长为2的⊙A 与直线OP 相切,半径长为3的⊙B 与⊙A 相交,那么OB 的取值范围是( )A .5<OB <9 B .4<OB <9C .3<OB <7D .2<OB <715、如图,在矩形ABCD 中,按以下步骤作图:①分别以点A 和C 为圆心,以大于12AC 的长为半径作弧,两弧相交于点M 和N ;②作直线MN 交CD 于点E .若DE=2,CE=3,则矩形的对角线AC 的长为 .16、如图,在菱形ABCD中,tanA=43,M,N分别在边AD,BC上,将四边形AMNB沿MN翻折,使AB的对应线段EF经过顶点D,当EF⊥AD时,BNCN的值为.17、如图,△ABC的周长为19,点D,E在边BC上,∠ABC的平分线垂直于AE,垂足为N,∠ACB的平分线垂直于AD,垂足为M,若BC=7,则MN的长度为()A.32B.2 C.52D.318、如图,E,F是平行四边形ABCD对角线AC上两点,AE=CF=14AC.连接DE,DF并延长,分别交AB,BC于点G,H,连接GH,则S△ADGS△BGH的值为()A.12B.23C.34D.119、如图,平面直角坐标系中,矩形OABC的顶点A(﹣6,0),C(0,2√3).将矩形OABC绕点O顺时针方向旋转,使点A恰好落在OB上的点A1处,则点B的对应点B1的坐标为.20、如图,Rt△ABC中,∠C=90°,AC=2,BC=5,点D是BC边上一点且CD=1,点P是线段DB上一动点,连接AP,以AP为斜边在AP的下方作等腰Rt△AOP.当P从点D出发运动至点B停止时,点O的运动路径长为.21、如图,点O为正六边形ABCDEF的中心,点M为AF中点,以点O为圆心,以OM的长为半径画弧得到扇形MON,点N在BC上;以点E为圆心,以DE的长为半径画弧得到扇形DEF,把扇形MON的两条半径OM,ON重合,围成圆锥,将此圆锥的底面半径记为r1;将扇形DEF以同样方法围成的圆锥的底面半径记为r2,则r 1:r2= .22、对角线长分别为6和8的菱形ABCD如图所示,点O为对角线的交点,过点O 折叠菱形,使B,B′两点重合,MN是折痕.若B'M=1,则CN的长为()A.7 B.6 C.5 D.423、如图,一艘渔船正以60海里/小时的速度向正东方向航行,在A处测得岛礁P在东北方向上,继续航行1.5小时后到达B处,此时测得岛礁P在北偏东30°方向,同时测得岛礁P正东方向上的避风港M在北偏东60°方向.为了在台风到来之前用最短时间到达M处,渔船立刻加速以75海里/小时的速度继续航行小时即可到达.(结果保留根号)24、如图,点A1的坐标为(2,0),过点A1作x轴的垂线交直线l:y=√3x于点B 1,以原点O为圆心,OB1的长为半径画弧交x轴正半轴于点A2;再过点A2作x轴的垂线交直线l于点B2,以原点O为圆心,以OB2的长为半径画弧交x轴正半轴于点A3;….按此作法进行下去,则A2019B2018̂的长是.25、如图,正方形ABCD的边长为8,M是AB的中点,P是BC边上的动点,连结PM,以点P为圆心,PM长为半径作⊙P.当⊙P与正方形ABCD的边相切时,BP 的长为.26、如图,正方形ABCD的边长为1,点A与原点重合,点B在y轴的正半轴上,点D在x轴的负半轴上,将正方形ABCD绕点A逆时针旋转30°至正方形AB'C′D′的位置,B'C′与CD相交于点M,则点M的坐标为.27、如图,在△ABC中,已知AC=3,BC=4,点D为边AB的中点,连结CD,过点A作AE⊥CD于点E,将△ACE沿直线AC翻折到△ACE′的位置.若CE′∥AB,则CE′=.。
2020年贵州省中考数学压轴题汇编解析:几何综合-最新推荐

2018年全国各地中考数学压轴题汇编(贵州专版)几何综合参考答案与试题解析一.选择题(共6小题)1.(2018•贵阳)如图,在菱形ABCD中,E是AC的中点,EF∥CB,交AB于点F,如果EF=3,那么菱形ABCD的周长为()A.24 B.18 C.12 D.9解:∵E是AC中点,∵EF∥BC,交AB于点F,∴EF是△ABC的中位线,∴EF=BC,∴BC=6,∴菱形ABCD的周长是4×6=24.故选:A.2.(2018•遵义)如图,点P是矩形ABCD的对角线AC上一点,过点P作EF∥BC,分别交AB,CD于E、F,连接PB、PD.若AE=2,PF=8.则图中阴影部分的面积为()A.10 B.12 C.16 D.18解:作PM⊥AD于M,交BC于N.则有四边形AEPM,四边形DFPM,四边形CFPN,四边形BEPN都是矩形,∴S△ADC =S△ABC,S△AMP=S△AEP,S△PBE=S△PBN,S△PFD=S△PDM,S△PFC=S△PCN,∴S△DFP=S△PBE=×2×8=8,∴S阴=8+8=16,故选:C.3.(2018•贵阳)如图,A、B、C是小正方形的顶点,且每个小正方形的边长为1,则tan∠BAC的值为()A.B.1 C.D.解:连接BC,由网格可得AB=BC=,AC=,即AB2+BC2=AC2,∴△ABC为等腰直角三角形,∴∠BAC=45°,则tan∠BAC=1,故选:B.4.(2018•遵义)如图,四边形ABCD中,AD∥BC,∠ABC=90°,AB=5,BC=10,连接AC、BD,以BD为直径的圆交AC于点E.若DE=3,则AD的长为()A.5 B.4 C.3D.2解:如图,在Rt△ABC中,AB=5,BC=10,∴AC=5过点D作DF⊥AC于F,∴∠AFD=∠CBA,∵AD∥BC,∴∠DAF=∠ACB,∴△ADF∽△CAB,∴,∴,设DF=x,则AD=x,在Rt△ABD中,BD==,∵∠DEF=∠DBA,∠DFE=∠DAB=90°,∴△DEF∽△DBA,∴,∴,∴x=2,∴AD=x=2,故选:D.5.(2018•安顺)已知⊙O的直径CD=10cm,AB是⊙O的弦,AB⊥CD,垂足为M,且AB=8cm,则AC的长为()A.2cm B.4cm C.2cm或4cm D.2cm或4cm解:连接AC,AO,∵⊙O的直径CD=10cm,AB⊥CD,AB=8cm,∴AM=AB=×8=4cm,OD=OC=5cm,当C点位置如图1所示时,∵OA=5cm,AM=4cm,CD⊥AB,∴OM===3cm,∴CM=OC+OM=5+3=8cm,∴AC===4cm;当C点位置如图2所示时,同理可得OM=3cm,∵OC=5cm,∴MC=5﹣3=2cm,在Rt△AMC中,AC===2cm.故选:C.6.(2018•铜仁市)在同一平面内,设a、b、c是三条互相平行的直线,已知a与b的距离为4cm,b与c的距离为1cm,则a与c的距离为()A.1cm B.3cm C.5cm或3cm D.1cm或3cm解:当直线c在a、b之间时,∵a、b、c是三条平行直线,而a与b的距离为4cm,b与c的距离为1cm,∴a与c的距离=4﹣1=3(cm);当直线c不在a、b之间时,∵a、b、c是三条平行直线,而a与b的距离为4cm,b与c的距离为1cm,∴a与c的距离=4+1=5(cm),综上所述,a与c的距离为3cm或3cm.故选:C.二.填空题(共8小题)7.(2018•贵阳)如图,点M、N分别是正五边形ABCDE的两边AB、BC上的点.且AM=BN,点O是正五边形的中心,则∠MON的度数是72度.解:连接OA、OB、OC,∠AOB==72°,∵∠AOB=∠BOC,OA=OB,OB=OC,∴∠OAB=∠OBC,在△AOM和△BON中,∴△AOM≌△BON,∴∠BON=∠AOM,∴∠MON=∠AOB=72°,故答案为:72.8.(2018•遵义)如图,△ABC中.点D在BC边上,BD=AD=AC,E为CD的中点.若∠CAE=16°,则∠B为37度.解:∵AD=AC,点E是CD中点,∴AE⊥CD,∴∠AEC=90°,∴∠C=90°﹣∠CAE=74°,∵AD=AC,∴∠ADC=∠C=74°,∵AD=BD,∴2∠B=∠ADC=74°,∴∠B=37°,故答案为37°.9.(2018•贵阳)如图,在△ABC中,BC=6,BC边上的高为4,在△ABC的内部作一个矩形EFGH,使EF在BC边上,另外两个顶点分别在AB、AC边上,则对角线EG长的最小值为.解:如图,作AQ⊥BC于点Q,交DG于点P,∵四边形DEFG是矩形,∴AQ⊥DG,GF=PQ,设GF=PQ=x,则AP=4﹣x,由DG∥BC知△ADG∽△ABC,∴=,即=,则EF=DG=(4﹣x),∴EG====,∴当x=时,EG取得最小值,最小值为,故答案为:.10.(2018•遵义)如图,在菱形ABCD中,∠ABC=120°,将菱形折叠,使点A恰好落在对角线BD上的点G处(不与B、D重合),折痕为EF,若DG=2,BG=6,则BE的长为 2.8.解:作EH⊥BD于H,由折叠的性质可知,EG=EA,由题意得,BD=DG+BG=8,∵四边形ABCD是菱形,∴AD=AB,∠ABD=∠CBD=∠ABC=60°,∴△ABD为等边三角形,∴AB=BD=8,设BE=x,则EG=AE=8﹣x,在Rt△EHB中,BH=x,EH=x,在Rt△EHG中,EG2=EH2+GH2,即(8﹣x)2=(x)2+(6﹣x)2,解得,x=2.8,即BE=2.8,故答案为:2.8.11.(2018•安顺)如图,C 为半圆内一点,O 为圆心,直径AB 长为2cm ,∠BOC=60°,∠BCO=90°,将△BOC 绕圆心O 逆时针旋转至△B′OC′,点C′在OA 上,则边BC 扫过区域(图中阴影部分)的面积为 π cm 2.(结果保留π)解:∵∠BOC=60°,△B′OC′是△BOC 绕圆心O 逆时针旋转得到的,∴∠B′OC′=60°,△BCO=△B′C′O ,∴∠B′OC=60°,∠C′B′O=30°, ∴∠B′OB=120°,∵AB=2cm ,∴OB=1cm ,OC′=, ∴B′C′=,∴S 扇形B′OB ==π, S 扇形C′OC ==,∵ ∴阴影部分面积=S 扇形B′OB +S △B′C′O ﹣S △BCO ﹣S 扇形C′OC =S 扇形B′OB ﹣S 扇形C′OC =π﹣=π; 故答案为:π.12.(2018•黔西南州)已知一个菱形的边长为2,较长的对角线长为2,则这个菱形的面积是 2 . 解:依照题意画出图形,如图所示.在Rt△AOB中,AB=2,OB=,∴OA==1,∴AC=2OA=2,=AC•BD=×2×2=2.∴S菱形ABCD故答案为:2.13.(2018•铜仁市)在直角三角形ABC中,∠ACB=90°,D、E是边AB上两点,且CE所在直线垂直平分线段AD,CD平分∠BCE,BC=2,则AB=4.解:∵CE所在直线垂直平分线段AD,∴CE平分∠ACD,∴∠ACE=∠DCE.∵CD平分∠BCE,∴∠DCE=∠DCB.∵∠ACB=90°,∴∠ACE=∠ACB=30°,∴∠A=60°,∴AB===4.故答案为:4.14.(2018•黔西南州)如图,已知在△ABC中,BC边上的高AD与AC边上的高BE交于点F,且∠BAC=45°,BD=6,CD=4,则△ABC的面积为60.解:∵AD⊥BC,BE⊥AC,∴∠AEF=∠BEC=∠BDF=90°,∵∠BAC=45°,∴AE=EB,∵∠EAF+∠C=90°,∠CBE+∠C=90°,∴∠EAF=∠CBE,∴△AEF≌△BEC,∴AF=BC=10,设DF=x.∵△ADC∽△BDF,∴=,∴=,整理得x2+10x﹣24=0,解得x=2或﹣12(舍弃),∴AD=AF+DF=12,=•BC•AD=×10×12=60.∴S△ABC故答案为60.三.解答题(共9小题)15.(2018•贵阳)如图,在平行四边形ABCD中,AE是BC边上的高,点F是DE的中点,AB 与AG关于AE对称,AE与AF关于AG对称.(1)求证:△AEF是等边三角形;(2)若AB=2,求△AFD的面积.解:(1)∵AB与AG关于AE对称,∴AE⊥BC,∵四边形ABCD是平行四边形,∴AD∥BC,∴AE⊥AD,即∠DAE=90°,∵点F是DE的中点,即AF是Rt△ADE的中线,∴AF=EF=DF,∵AE与AF关于AG对称,∴AE=AF,则AE=AF=EF,∴△AEF是等边三角形;(2)记AG、EF交点为H,∵△AEF是等边三角形,且AE与AF关于AG对称,∴∠EAG=30°,AG⊥EF,∵AB与AG关于AE对称,∴∠BAE=∠GAE=30°,∠AEB=90°,∵AB=2,∴BE=1、DF=AF=AE=,则EH=AE=、AH=,=××=.∴S△ADF16.(2018•遵义)如图,正方形ABCD的对角线交于点O,点E、F分别在AB、BC上(AE<BE),且∠EOF=90°,OE、DA的延长线交于点M,OF、AB的延长线交于点N,连接MN.(1)求证:OM=ON.(2)若正方形ABCD的边长为4,E为OM的中点,求MN的长.解:(1)∵四边形ABCD是正方形,∴OA=OB,∠DAO=45°,∠OBA=45°,∴∠OAM=∠OBN=135°,∵∠EOF=90°,∠AOB=90°,∴∠AOM=∠BON,∴△OAM≌△OBN(ASA),∴OM=ON;(2)如图,过点O作OH⊥AD于点H,∵正方形的边长为4,∴OH=HA=2,∵E为OM的中点,∴HM=4,则OM==2,∴MN=OM=2.17.(2018•贵阳)如图,AB为⊙O的直径,且AB=4,点C在半圆上,OC⊥AB,垂足为点O,P为半圆上任意一点,过P点作PE⊥OC于点E,设△OPE的内心为M,连接OM、PM.(2)当点P在半圆上从点B运动到点A时,求内心M所经过的路径长.解:(1)∵△OPE的内心为M,∴∠MOP=∠MOC,∠MPO=∠MPE,∴∠PMO=180°﹣∠MPO﹣∠MOP=180°﹣(∠EOP+∠OPE),∵PE⊥OC,即∠PEO=90°,∴∠PMO=180°﹣(∠EOP+∠OPE)=180°﹣(180°﹣90°)=135°,(2)如图,∵OP=OC,OM=OM,而∠MOP=∠MOC,∴△OPM≌△OCM,∴∠CMO=∠PMO=135°,所以点M在以OC为弦,并且所对的圆周角为135°的两段劣弧上(和);点M在扇形BOC内时,过C、M、O三点作⊙O′,连O′C,O′O,在优弧CO取点D,连DA,DO,∵∠CMO=135°,∴∠CDO=180°﹣135°=45°,∴∠CO′O=90°,而OA=2cm,∴O′O=OC=×2=,∴弧OMC的长==π(cm),同理:点M在扇形AOC内时,同①的方法得,弧ONC的长为πcm,所以内心M所经过的路径长为2×π=πcm.18.(2018•遵义)如图,AB是半圆O的直径,C是AB延长线上的点,AC的垂直平分线交半圆于点D,交AC于点E,连接DA,DC.已知半圆O的半径为3,BC=2.(1)求AD的长.(2)点P是线段AC上一动点,连接DP,作∠DPF=∠DAC,PF交线段CD于点F.当△DPF为等腰三角形时,求AP的长.解:(1)如图1,连接OD,∵OA=OD=3,BC=2,∴AC=8,∵DE是AC的垂直平分线,∴AE=AC=4,∴OE=AE﹣OA=1,在Rt△ODE中,DE==2;在Rt△ADE中,AD==2;(2)当DP=DF时,如图2,当DP=PF时,如图4,∴∠CDP=∠PFD,∵DE是AC的垂直平分线,∠DPF=∠DAC,∴∠DPF=∠C,∵∠PDF=∠CDP,∴△PDF∽△CDP,∴∠DFP=∠DPC,∴∠CDP=∠CPD,∴CP=CD,∴AP=AC﹣CP=AC﹣CD=AC﹣AD=8﹣2;当PF=DF时,如图3,∴∠FDP=∠FPD,∵∠DPF=∠DAC=∠C,∴△DAC∽△PDC,∴,∴,∴AP=5,即:当△DPF是等腰三角形时,AP的长为0或5或8﹣2.19.(2018•安顺)如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC 的平行线交BE的延长线于点F,连接CF.(1)求证:AF=DC;(1)证明:连接DF,∵E为AD的中点,∴AE=DE,∵AF∥BC,∴∠AFE=∠DBE,在△AFE和△DBE中,,∴△AFE≌△DBE(AAS),∴EF=BE,∵AE=DE,∴四边形AFDB是平行四边形,∴BD=AF,∵AD为中线,∴DC=BD,∴AF=DC;(2)四边形ADCF的形状是菱形,理由如下:∵AF=DC,AF∥BC,∴四边形ADCF是平行四边形,∵∴∵AD为中线∴AD=BC=DC,∴平行四边形ADCF是菱形;20.(2018•铜仁市)如图,在三角形ABC中,AB=6,AC=BC=5,以BC为直径作⊙O交AB于点D,交AC于点G,直线DF是⊙O的切线,D为切点,交CB的延长线于点E.(1)求证:DF⊥AC;(2)求tan∠E的值.(1)证明:如图,连接OC,∵BC是⊙O的直径,∴∠BDC=90°,∴CD⊥AB,∵AC=BC,∴AD=BD,∵OB=OC,∴OD是△ABC的中位线∴OD∥AC,∵DF为⊙O的切线,∴OD⊥DF,∴DF⊥AC;(2)解:如图,连接BG,∵BC是⊙O的直径,∴∠BGC=90°,∵∠EFC=90°=∠BGC,∴∠CBG=∠E,Rt△BDC中,∵BD=3,BC=5,∴CD=4,S△ABC=,6×4=5BG,BG=,由勾股定理得:CG==,∴tan∠CBG=tan∠E===.21.(2018•安顺)如图,在△ABC中,AB=AC,O为BC的中点,AC与半圆O相切于点D.(1)求证:AB是半圆O所在圆的切线;(2)若cos∠ABC=,AB=12,求半圆O所在圆的半径.解:(1)如图,作OE⊥AB于E,连接OD,OA,∵AB=AC,点O是BC的中点,∴∠CAO=∠BAO,∵AC与半圆O相切于D,∴OD⊥AC,∵OE⊥AB,∵AB径半圆O的半径的外端点,∴AB是半圆O所在圆的切线;(2)∵AB=AC,O是BC的中点,∴AO⊥BC,在Rt△AOB中,OB=AB•cos∠ABC=12×=8,根据勾股定理得,OA==4,=AB•OE=OB•OA,由三角形的面积得,S△AOB∴OE==,即:半圆O所在圆的半径为.22.(2018•贵阳)如图,在矩形ABCD中,AB═2,AD=,P是BC边上的一点,且BP=2CP.(1)用尺规在图①中作出CD边上的中点E,连接AE、BE(保留作图痕迹,不写作法);(2)如图②,在(1)的条件下,判断EB是否平分∠AEC,并说明理由;(3)如图③,在(2)的条件下,连接EP并廷长交AB的廷长线于点F,连接AP,不添加辅助线,△PFB能否由都经过P点的两次变换与△PAE组成一个等腰三角形?如果能,说明理由,并写出两种方法(指出对称轴、旋转中心、旋转方向和平移距离)解:(1)依题意作出图形如图①所示,(2)EB是平分∠AEC,理由:∵四边形ABCD是矩形,∴∠C=∠D=90°,CD=AB=2,BC=AD=,∴DE=CE=CD=1,在△ADE和△BCE中,,∴△ADE≌△BCE,∴∠AED=∠BEC,在Rt△ADE中,AD=,DE=1,∴tan∠AED==,∴∠AED=60°,∴∠BCE=∠AED=60°,∴∠AEB=180°﹣∠AED﹣∠BEC=60°=∠BEC,∴BE平分∠AEC;(3)∵BP=2CP,BC=,∴CP=,BP=,在Rt△CEP中,tan∠CEP==,∴∠CEP=30°,∴∠BEP=30°,∴∠AEP=90°,∵CD∥AB,∴∠F=∠CEP=30°,在Rt△ABP中,tan∠BAP==,∴∠PAB=30°,∴∠EAP=30°=∠F=∠PAB,∵CB⊥AF,∴AP=FP,∴△AEP≌△FBP,∴△PFB能由都经过P点的两次变换与△PAE组成一个等腰三角形,变换的方法为:将△BPF绕点B顺时针旋转120°和△EPA重合,①沿PF折叠,②沿AE折叠.23.(2018•黔西南州)如图1,已知矩形AOCB,AB=6cm,BC=16cm,动点P从点A出发,以3cm/s的速度向点O运动,直到点O为止;动点Q同时从点C出发,以2cm/s的速度向点B运动,与点P同时结束运动.(1)点P到达终点O的运动时间是s,此时点Q的运动距离是cm;(2)当运动时间为2s时,P、Q两点的距离为6cm;(3)请你计算出发多久时,点P和点Q之间的距离是10cm;(4)如图2,以点O为坐标原点,OC所在直线为x轴,OA所在直线为y轴,1cm长为单位长度建立平面直角坐标系,连结AC,与PQ相交于点D,若双曲线y=过点D,问k的值是否会变化?若会变化,说明理由;若不会变化,请求出k的值.解:(1)∵四边形AOCB是矩形,∴OA=BC=16,∵动点P从点A出发,以3cm/s的速度向点O运动,∴,此时,点Q的运动距离是cm(2)如图1,由运动知,AP=3×2=6cm,CQ=2×2=4cm,过点P作PE⊥BC于E,过点Q作QF⊥OA于F,∴四边形APEB是矩形,∴PE=AB=6,BE=6,∴EQ=BC﹣BE﹣CQ=16﹣6﹣4=6,根据勾股定理得,PQ=6,故答案为6;(3)设运动时间为t秒时,由运动知,AP=3t,CQ=2t,同(2)的方法得,PE=6,EQ=16﹣3t﹣2t=16﹣5t,∵点P和点Q之间的距离是10cm,∴62+(16﹣5t)2=100,∴t=或t=;(4)k的值是不会变化,理由:∵四边形AOCB是矩形,∴OC=AB=6,OA=16,∴C(6,0),A(0,16),∴直线AC的解析式为y=﹣x+16①,设运动时间为t,∴AP=3t,CQ=2t,∴OP=16﹣3t,∴P(0,16﹣3t),Q(6,2t),∴PQ解析式为y=x+16﹣3t②,联立①②得,﹣x+16=x+16﹣3t,∴x+x=3t,∴5tx﹣16x+16x=3t,∴x=,∴y=,∴D(,)∴k=×=是定值.。
贵州省贵阳市,2020~2021年中考数学压轴题精选解析

贵州省贵阳市,2020~2021年中考数学压轴题精选解析贵州省贵阳市中考数学压轴题精选~~第1题~~(2020贵阳.中考模拟) 如图,在平面直角坐标系中,抛物线y=-x +bx+c 经过点(0,6),其对称轴为直线x= .在x 轴上方作平行于x 轴的直线l 与抛物线交于A 、B 两点(点A 在对称轴的右侧),过点A 、B 作x 轴的垂线,垂足分别为D、C.设A 点的横坐标为m.(1) 求此抛物线所对应的函数关系式.(2) 当m 为何值时,矩形ABCD 为正方形.(3) 当m 为何值时,矩形ABCD 的周长最大,并求出这个最大值.~~第2题~~(2019贵阳.中考真卷) 如图(1) 数学理解:如图①,△ABC 是等腰直角三角形,过斜边AB 的中点D 作正方形DECF ,分别交BC ,AC 于点E ,F ,求AB ,BE ,AF 之间的数量关系;(2) 问题解决:如图②,在任意直角△ABC 内,找一点D ,过点D 作正方形DECF ,分别交BC ,AC 于点E ,F ,若A B =BE+AF ,求∠ADB 的度数;(3) 联系拓广:如图③,在(2)的条件下,分别延长ED ,FD ,交AB 于点M ,N ,求MN ,AM ,BN 的数量关系.~~第3题~~(2019贵阳.中考模拟) △ABC 是等边三角形,点D 是射线BC 上的一个动点(点D 不与点B 、C 重合),△ADE 是以AD 为边的等边三角形,过点E作BC 的平行线,分别交射线AB 、AC 于点F 、G ,连接BE.(1) 如图1,当点D 在线段BC 上时:①求证:△AEB ≌△ADC ;②求证:四边形BCGE 是平行四边形;(2) 如图2,当点D 在BC 的延长线上,且CD =BC 时,试判断四边形BCGE 是什么特殊的四边形?并说明理由.~~第4题~~2(2019白云.中考模拟) 在平面直角坐标系中,点是原点,四边形是矩形,点,点.以点 为中心,顺时针旋转矩形,得到矩形 ,点的对应点分别为.(1) 如图①,当点落在边上时,求点的坐标;(2) 如图②,当点落在线段上时, 与交于点.求点的坐标;(3) 记为矩形 对角线的交点, 为 的面积,求 的取值范围(直接写出结果即可).~~第5题~~(2018贵阳.中考真卷) 如图,在平面直角坐标系xOy 中,点A 是反比例函数y=(x >0,m >1)图象上一点,点A 的横坐标为m ,点B (0,﹣m )是y 轴负半轴上的一点,连接AB ,AC ⊥AB ,交y 轴于点C ,延长CA到点D ,使得AD=AC ,过点A 作AE 平行于x 轴,过点D 作y 轴平行线交AE 于点E .(1) 当m=3时,求点A 的坐标;(2) DE=,设点D 的坐标为(x ,y ),求y 关于x 的函数关系式和自变量的取值范围;(3) 连接BD ,过点A 作BD 的平行线,与(2)中的函数图象交于点F ,当m 为何值时,以A 、B 、D 、F 为顶点的四边形是平行四边形?~~第6题~~(2017贵阳.中考真卷) 我们知道,经过原点的抛物线可以用y=ax +bx (a≠0)表示,对于这样的抛物线:(1) 当抛物线经过点(﹣2,0)和(﹣1,3)时,求抛物线的表达式;(2) 当抛物线的顶点在直线y=﹣2x 上时,求b 的值;(3) 如图,现有一组这样的抛物线,它们的顶点A 、A 、…,A 在直线y=﹣2x 上,横坐标依次为﹣1,﹣2,﹣3,…,﹣n (n 为正整数,且n≤12),分别过每个顶点作x 轴的垂线,垂足记为B 、B ,…,B ,以线段A B 为边向左作正方形A B C D ,如果这组抛物线中的某一条经过点D ,求此时满足条件的正方形A B C D 的边长.~~第7题~~(2016贵阳.中考模拟) 如图,在平面直角坐标系xOy 中,Rt △OA C , Rt △OA C , Rt △OA C , Rt △OA C …的斜边都在坐标轴上,∠A OC =∠A OC =∠A OC =∠A OC …=30°.若点A 的坐标为(3,0),OA =OC , OA =OC , OA =OC …,则依次规律,点A 的纵坐标为( )212n 12n n n n n n n n n n n n 112233441122334411223342016A . 0B . ﹣3×( ) C . (2 ) D . 3×( )~~第8题~~(2016贵阳.中考模拟) 如图,四边形ABCD 中,AB ∥CD ,AB≠CD ,BD=AC .(1)求证:AD=BC ;(2)若E 、F 、G 、H 分别是AB 、CD 、AC 、BD 的中点,求证:线段EF 与线段GH 互相垂直平分.~~第9题~~(2016贵阳.中考模拟) 如图,矩形ABCD 中,AB=6,BC=8,点E 是射线CB 上的一个动点,把△DCE 沿DE 折叠,点C 的对应点为C′.(1)若点C′刚好落在对角线BD 上时,BC′=;(2)若点C′刚好落在线段AB 的垂直平分线上时,求CE 的长;(3)若点C′刚好落在线段AD 的垂直平分线上时,求CE 的长.~~第10题~~(2016贵阳.中考真卷) 如图,直线y=5x+5交x 轴于点A ,交y 轴于点C ,过A ,C 两点的二次函数y=ax +4x+c 的图象交x 轴于另一点B .2015201620152(1)求二次函数的表达式;(2)连接BC ,点N 是线段BC 上的动点,作ND ⊥x 轴交二次函数的图象于点D ,求线段ND 长度的最大值;(3)若点H 为二次函数y=ax +4x+c 图象的顶点,点M (4,m )是该二次函数图象上一点,在x 轴、y 轴上分别找点F ,E ,使四边形HEFM 的周长最小,求出点F ,E 的坐标.温馨提示:在直角坐标系中,若点P ,Q 的坐标分别为P (x ,y ),Q (x ,y ),当PQ 平行x 轴时,线段PQ 的长度可由公式PQ=|x ﹣x |求出;当PQ 平行y 轴时,线段PQ 的长度可由公式PQ=|y ﹣y |求出.贵州省贵阳市中考数学压轴题答案解析~~第1题~~答案:211221212解析:~~第2题~~答案:解析:~~第3题~~答案:解析:~~第4题~~答案:解析:~~第5题~~答案:解析:~~第6题~~答案:解析:~~第7题~~答案:解析:~~第8题~~答案:解析:~~第9题~~答案:解析:答案:解析:。
2023年中考数学真题汇编几何综合压轴问题专项练习(共40题)(解析版)

几何综合压轴问题专项练习答案(40题)(1)将CDE 绕顶点C 旋转一周,请直接写出点M ,N 距离的最大值和最小值;(2)将CDE 绕顶点C 逆时针旋转120︒(如图2),求MN 【答案】(1)最大值为3,最小值为1(2)7【分析】(1)根据直角三角形斜边上的中线,得出,CM CN 解;(2)过点N 作NP MC ⊥,交MC 的延长线于点P ,根据旋转的性质求得进而可得1CP =,勾股定理解Rt ,Rt NCP MCP ,即可求解.【详解】(1)解:依题意,112CM DE ==,12CN AB =当M 在NC 的延长线上时,,M N 的距离最大,最大值为(2)解:如图所示,过点N 作NP MC ⊥,交MC 的延长线于点∵CDE 绕顶点C 逆时针旋转∴120BCE ∠=︒,∵45BCN ECM ∠=∠=︒,∴MCN BCM ECM ∠=∠-∠=∴60NCP ∠=︒,∴30CNP ∠=︒,∴112CP CN ==,在Rt CNP 中,2NP NC =-在Rt MNP △中,MP MC CP =+∴2234MN NP MP =+=+【点睛】本题考查了直角三角形斜边上的中线等于斜边的一半,勾股定理,旋转的性质,含(1)如图1,求证:DE BF =;(2)如图2,若2AD BF =,的延长线恰好经过DE 的中点【答案】(1)见解析(2)22BE =+△∵点G 是DE 的中点,∴GH 是FCD 的中位线,∴11122GH CD AD ===,设BE a =,则CH EH ==(1)如图1,求AB边上的高CH的长.''.(2)P是边AB上的一动点,点,C D同时绕点P按逆时针方向旋转90︒得点,C D①如图2,当点C'落在射线CA上时,求BP的长.△是直角三角形时,求BP的长.②当AC D''∴90C PQ PC Q '∠+∠='︒∵90C PQ CPH ∠+∠='︒∴PC Q CPH ∠=∠'.由旋转知PC PC '=,设C D ''与射线BA 的交点为作CH AB ⊥于点H .∵PC PC ⊥',∴90CPH TPC ∠'+∠=︒,∵C D AT ''⊥,∴90PC T TPC ∠'+∠='︒,【答案】(1)①见解析;②AD DF BD =+,理由见解析;【分析】(1)①证明:ABE CBD ∠=∠,再证明ABE ≅△可得DF DC =.证明AE DF =,从而可得结论;(2)如图,过点B 作BE AD ⊥于点E ,得90BED ∠=︒,证明2DE BD =,证明2AB BC =,ABE CBD ∠=∠,可得②AD DF BD=+.理由如下:∵DF和DC关于AD对称,=.∴DF DC=,∵AE CD∴AE DF=.∴AD AE DE DF BD=+=+∵DF 和DC 关于AD 对称,∴DF DC =,ADF ADC ∠=∠.∵CD BD ⊥,∴45ADF ADC ∠=∠=︒,∴45EBD ∠=︒.∴2DE BD =.∵AB AC AF ==,∴()11222HF BF BD DF ==-=,222262210BC BD CD =+=+=∴2221022AF AC BC ===⨯=25HF (2)知识应用:如图2Y是菱形;①求证:ABCD②延长BC至点E,连接OE交【答案】(1)见解析5∴1BG BO GC OD==,∴115222CG BC AD ===,∴552OF GC .处从由60PC P C PCP ''=∠=︒,,可知PCP '△为①三角形,故PP PC '=,又P A PA ''=,故PA PB PC PA PB PP A B '''++=++≥,由②可知,当B ,P ,P ',A 在同一条直线上时,PA PB PC ++取最小值,如图2,最小值为(3)如图5,设村庄A ,B ,C 的连线构成一个三角形,且已知4km 23km AC BC ==,,建一中转站P 沿直线向A ,B ,C 三个村庄铺设电缆,已知由中转站P 到村庄A ,B ,C 元/km ,a 元/km ,2a 元/km ,选取合适的P 的位置,可以使总的铺设成本最低为___________用含的式子表示)∵ACP A CP ''∠=∠,∴ACP BCP A CP BCP ∠+∠=∠+∠''又∵60PCP '∠=︒过点A '作A H BC '⊥,垂足为H ,∵60ACB ∠=︒,90ACA '∠=︒,∴30A CH '∠=︒,1猜想证明:(1)如图2,试判断四边形AEDG的形状,并说明理由.问题解决;(2)如图3,将图2中左侧折叠的三角形展开后,重新沿MN折叠,使得顶点B与点∵1122 CHGS CH HG=⋅=∴154302CG HE⋅=⨯=,①求证:PD PB =;②将线段DP 绕点P 逆时针旋转,化时,DPQ ∠的大小是否发生变化?请说明理由;③探究AQ 与OP 的数量关系,并说明理由.【答案】(1)①见解析;②不变化,(2)AQ CP =,理由见解析【分析】(1)①根据正方形的性质证明②作,PM AB PN AD ⊥⊥,垂足分别为点∵四边形ABCD 是正方形,∴45DAC BAC ∠=∠=︒,∴四边形AMPN 是矩形,∴90MPN ∠=︒,∵四边形ABCD 是正方形,∴45BAC ∠=︒,90AOB ∠=∴45AEP ∠=︒,四边形OPEF=作PM AB⊥于点M,则QM MB=,∴QA BE=.∴AQ CP(1)求BCF ∠的度数;(2)求CD 的长.深入探究:(3)若90BAC ∠<︒,将BMN 绕点B 顺时针旋转α,得到BEF △,连接AE ,CF 满足0360α︒<<︒,点,,C E F 在同一直线上时,利用所提供的备用图探究BAE ∠与ABF ∠的数量关系,并说明理由.【答案】初步尝试:(1)1MN AC =;MN AC ∥;(2)特例研讨:(1)30BCF ∠=︒;(2)CD∵MN 是BAC 的中位线,∴MN AC ∥,∴90BMN BAC ∠=∠=︒∵将BMN 绕点B 顺时针旋转α∴,BE BM BF BN ==;BEF ∠=∵点,,A E F 在同一直线上时,2∵,ADN BDE ANB BED ∠=∠∠=∠∴ADN BDE ∽,∴2222DN AN DE BE ===,设DE x =,则2DN x =,在Rt ABE △中,2,2BE AE ==在Rt ADN △中,22AD DN AN =+∵AB AC =,∴A ABC CB =∠∠,设ABC ACB θ∠=∠=,则1802BAC θ∠=︒-,∵MN 是ABC 的中位线,∴MN AC∥∴MNB MBN θ∠=∠=,∵将BMN 绕点B 顺时针旋转α,得到BEF △,∴EBF MBN ≌,MBE NBF α∠=∠=,∴EBF EFB θ∠=∠=∴1802BEF θ∠=︒-,∵点,,C E F 在同一直线上,∴2BEC θ∠=∴180BEC BAC ∠+∠=︒,∴,,,A B E C 在同一个圆上,∴EAC EBC αθ∠=∠=-∴()()1802BAE BAC EAC θαθ∠=∠-∠=︒---180αθ=︒--∵ABF αθ∠=+,∴180BAE ABF ∠∠=+︒;如图所示,当F 在EC 上时,∵,BEF BAC BC BC∠=∠=∴,,,A B E C 在同一个圆上,设ABC ACB θ∠=∠=,则1802BAC BEF θ∠=∠=︒-,将BMN 绕点B 顺时针旋转α,得到BEF △,设NBF β∠=,则EBM β∠=,则360αβ+=︒,∴ABF θβ∠=-,∵BFE EBF θ∠=∠=,EFB FBC FCB∠=∠+∠∴ECB FCB EFB FBC θβ∠=∠=∠-∠=-,∵ EBEB =∴EAB ECB θβ∠=∠=-∴BAE ∠ABF=∠综上所述,BAE ABF ∠=∠或180BAE ABF ∠∠=+︒【点睛】本题考查了圆周角定理,圆内接四边形对角互补,相似三角形的性质与判定,旋转的性质,中位线的性质与判定,等腰三角形的性质与判定,三角形内角和定理,三角形外角的性质,勾股定理,熟练掌握以上知识是解题的关键.10.(2023·湖北黄冈·统考中考真题)【问题呈现】CAB △和CDE 都是直角三角形,90,,ACB DCE CB mCA CE mCD ∠=∠=︒==,连接AD ,BE ,探究AD ,BE 的位置关系.(1)如图1,当1m =时,直接写出AD ,BE 的位置关系:____________;(2)如图2,当1m ≠时,(1)中的结论是否成立?若成立,给出证明;若不成立,说明理由.【拓展应用】(3)当3,47,4m AB DE ===时,将CDE 绕点C 旋转,使,,A D E 三点恰好在同一直线上,求(2)解:成立;理由如下:∵90DCE ACB ∠=∠=︒,∴DCA ACE ACE ∠+∠=∠+(3)解:当点E 在线段AD设AD y =,则AE AD DE =+根据解析(2)可知,DCA △∴3BE BC m AD AC===,勾股定理,解题的关键是熟练掌握三角形相似的判定方法,画出相应的图形,注意分类讨论.(1)若点P 在AB 上,求证:A P AP '=;(2)如图2.连接BD .①求CBD ∠的度数,并直接写出当180n =时,x 的值;②若点P 到BD 的距离为2,求tan A MP '∠的值;∵PM 平分A MA '∠∴90PMA ∠=︒∴PM AB∥∴DNM DBA V V ∽∴DN DM MN DB DA BA ==∵8,6,90AB DA A ==∠=︒,∴2226BD AB AD =+=+∴2103sin 3BQ BP DBA ===∠,∵90PQB CBD DAB ∠=∠=∠=︒,∴90QPB PBQ DBA ∠=︒-∠=∠,∵A MP AMP ' ≌,∴90PA M A '∠=∠=︒,(2)如图②,在矩形ABCD 的BC 边上取一点E ,将四边形ABED 沿DE 翻折,使点B '处,若24,6BC CE AB ⋅==,求BE 的值;(3)如图③,在ABC 中,45,BAC AD BC ∠=︒⊥,垂足为点,10,D AD AE ==于点F ,连接DF ,且满足2DFE DAC ∠=∠,直接写出53BD EF +的值.∵EF BC ∥,∴2CDF DFE ∠=∠=∴CDH FDH ∠=∠,又∵DH DH =,CHD ∠∴(ASA CHD FHD ≌【点睛】本题考查矩形的性质、翻折性质、勾股定理、相似三角形的判定与性质、等腰三角形的判定与性质、全等三角形的判定与性质、锐角三角函数等知识,综合性强,较难,属于中考压轴题,熟练掌握相关知识的联系与运用,添加辅助线求解是解答的关键.13.(2023·湖南郴州·=,连接点E,使CE AD(1)如图1,当点D在线段AB上时,猜测线段CF与BD的数量关系并说明理由;(2)如图2,当点D在线段AB的延长线上时,①线段CF与BD的数量关系是否仍然成立?请说明理由;②如图3,连接AE.设4AB=,若AEB DEB∠=∠,求四边形BDFC的面积.【答案】(1)1CF BD=,理由见解析∴60,ADG ABC AGD ∠=∠=︒∠=∠∴ADG △为等边三角形,∴AD AG DG ==,∵AD CE =,AD AB AG AC -=-∴DG CE =,BD CG =,于点由①知:ADG △为等边三角形,∵ABC 为等边三角形,∴4,AB AC BC BH CH =====∴2223AH AB BH =-=,(1)若正方形ABCD 的边长为2,E 是AD 的中点.①如图1,当90FEC ∠=︒时,求证:AEF DCE ∽△△;②如图2,当2tan 3FCE ∠=时,求AF 的长;(2)如图3,延长CF ,DA 交于点G ,当1,sin 3GE DE FCE =∠=时,求证:,可得结论;正方形ABCD 中,①ADC BAD ∠=∠ ∴AEF CED ∠+∠=AEF ECD ∴∠=∠,延长DA ,CF 交于点G ,作GH CE ⊥,垂足为H ,90EDC EHG ∠=∠=︒ 且∠问题探究:(1)先将问题特殊化,如图(2),当90α=︒时,直接写出GCF ∠的大小;(2)再探究一般情形,如图(1),求GCF ∠与α的数量关系.问题拓展:(3)将图(1)特殊化,如图(3),当120α=︒时,若12DG CG =,求BE CE 的值.故答案为:45︒.(2)解:在AB上截取ANABC BAE AEB∠+∠+∠=∠=∠,ABC AEF22⎝⎭(3)解:过点A作CD的垂线交CD的延长线于点【点睛】此题考查菱形性质、三角形全等、三角形相似,解题的关键是熟悉菱形性质、三角形全等、三角形相似.16.(2023·山西·统考中考真题)问题情境:“综合与实践沿对角线剪开,得到两个全等的三角形纸片,表示为∠=∠=︒∠=∠.将ABCACB DEF A D90,和DFE△(1)数学思考:谈你解答老师提出的问题;(2)深入探究:老师将图2中的DBE绕点B逆时针方向旋转,使点问题.∠①“善思小组”提出问题:如图3,当ABE②“智慧小组”提出问题:如图AH的长.请你思考此问题,直接写出结果.【答案】(1)正方形,见解析(2)①AM BE=,见解析;【分析】(1)先证明四边形形;∠(2)①由已知ABE【点睛】本题考查了旋转的性质、全等三角形的判定与性质、正方形的判定与性质、相似三角形的判定与性质、三角函数、勾股定理等知识点,适当添加的辅助线、构造相似三角形是解题的关键.17.(2023·湖北十堰·统考中考真题)过正方形E ,连接AE ,直线AE 交直线(1)如图1,若25CDP ∠=︒,则DAF ∠=___________(2)如图1,请探究线段CD ,EF ,AF 之间的数量关系,并证明你的结论;(3)在DP 绕点D 转动的过程中,设AF a =,EF 【答案】(1)20︒。
2020年贵州省中考数学试卷汇编附答案解析

13. 在“抛掷正六面体”的试验中,正六面体的六个面分别标有数字 “1”“2”“3”“4”“5”“6”,在试验次数很大时,数字“6”朝上的频率的 变化趋势接近的值是______.
14. 如图,△ABC 是⊙O 的内接正三角形,点 O 是圆心,点 D,E 分别在边 AC,AB 上,若 DA=EB,则∠DOE 的度数是______ 度.
21. 脱贫攻坚工作让老百姓过上了幸福的生活.如图①是政府给贫困户新建的房屋,如 图②是房屋的侧面示意图,它是一个轴对称图形,对称轴是房屋的高 AB 所在的直 线,为了测量房屋的高度,在地面上 C 点测得屋顶 A 的仰角为 35°,此时地面上 C 点、屋檐上 E 点、屋顶上 A 点三点恰好共线,继续向房屋方向走 8m 到达点 D 时, 又测得屋檐 E 点的仰角为 60°,房屋的顶层横梁 EF=12m,EF∥CB,AB 交 EF 于点 G (点 C,D,B 在同一水平线上).(参考数据:sin35°≈0.6,cos35°≈0.8, tan35°≈0.7, ≈1.7) (1)求屋顶到横梁的距离 AG; (2)求房屋的高 AB(结果精确到 1m).
( )
A. 150°
B. 120°
C,下列分式没有意义的是( )
A.
B.
C.
D.
6. 下列四幅图中,能表示两棵树在同一时刻太阳光下的影子的图是( )
A.
B.
C.
D.
第 1 页,共 20 页
7. 菱形的两条对角线长分别是 6 和 8,则此菱形的周长是( )
第 2 页,共 20 页
15. 如图,△ABC 中,点 E 在边 AC 上,EB=EA, ∠A=2∠CBE,CD 垂直于 BE 的延长线于点 D,BD=8, AC=11,则边 BC 的长为______.
2020年部编人教版贵州省各市中考数学分类精析专题12押轴题

专题12:押轴题一、选择题1. (2020年贵州安顺3分)如图,A、B、C三点在⊙O上,且∠AOB=80°,则∠ACB等于【】A.100°B.80°C.50°D.40°2. (2020年贵州毕节3分)在等腰直角三角形ABC中,AB=AC=4,点O为BC的中点,以O为圆心作⊙O交BC于点M、N,⊙O与AB、AC相切,切点分别为D、E,则⊙O的半径和∠MND的度数分别为【】A.2,22.5°B.3,30°C.3,22.5°D.2,30°3. (2020年贵州贵阳3分)在矩形ABCD中,AB=6,BC=4,有一个半径为1的硬币与边AB、AD相切,硬币从如图所示的位置开始,在矩形内沿着边AB、BC、CD、DA滚动到开始的位置为止,硬币自身滚动的圈数大约是【】A.1圈B.2圈C.3圈D.4圈4. (2020年贵州六盘水3分)下列图形中,阴影部分面积最大的是【】5. (2020年贵州黔东南4分)如图,直线y=2x 与双曲线2y x在第一象限的交点为A ,过点A 作AB ⊥x 轴于B ,将△ABO 绕点O 旋转90°,得到△A′B′O ,则点A′的坐标为【 】A .(1.0)B .(1.0)或(﹣1.0)C .(2.0)或(0,﹣2)D .(﹣2.1)或(2,﹣1)6. (2020年贵州黔西南4分)如图所示,二次函数y=ax 2+bx+c 的图象中,王刚同学观察得出了下面四条信息:(1)b 2﹣4ac >0;(2)c >1;(3)2a ﹣b <0;(4)a+b+c <0,其中错误的有【 】A .1个B .2个C .3个D .4个7. (2020年贵州铜仁4分)如图,直线y=kx+b交坐标轴于A(﹣2,0),B(0,3)两点,则不等式kx+b>0的解集是【】A.x>3 B.﹣2<x<3 C.x<﹣2 D.x>﹣2∴不等式kx+b>0的解集是x>﹣2。
贵州省,2020~2021年中考数学压轴题精选解析

贵州省,2020~2021年中考数学压轴题精选解析贵州省中考数学压轴题精选~~第1题~~(2020赤水.九上期中) 如图,在平面直角坐标系中,二次函数的图象交坐标轴于A (﹣1,0),B (4,0),C (0,﹣4)三点,点P 是直线BC 下方抛物线上一动点.(1)求这个二次函数的解析式;(2)是否存在点P ,使△POC 是以OC 为底边的等腰三角形?若存在,求出P 点坐标;若不存在,请说明理由;(3)动点P 运动到什么位置时,△PBC 面积最大,求出此时P 点坐标和△PBC 的最大面积.~~第2题~~(2020贵州.中考模拟) 在平面直角坐标系中,抛物线y = ﹣6x+4的顶点A 在直线y =kx ﹣2上.(1) 求直线的函数表达式;(2) 现将抛物线沿该直线方向进行平移,平移后的抛物线的顶点为A′,与直线的另一交点为B′,与x 轴的右交点为C (点C 不与点A′重合),连接B′C 、A′C.ⅰ)如图,在平移过程中,当点B′在第四象限且△A′B′C 的面积为60时,求平移的距离AA′的长;ⅱ)在平移过程中,当△A′B′C 是以A′B′为一条直角边的直角三角形时,求出所有满足条件的点A′的坐标.~~第3题~~(2020贵州.中考模拟) 如图1,已知二次函数y=ax +x+c (a≠0)的图象与y 轴交于点A (0,4),与x 轴交于点B 、C,点C 坐标为(8,0),连接AB 、AC.2(1) 请直接写出二次函数y=ax + x+c 的表达式;(2) 判断△ABC 的形状,并说明理由;(3) 若点N 在x 轴上运动,当以点A 、N 、C 为顶点的三角形是等腰三角形时,请写出此时点N 的坐标;(4) 如图2,若点N 在线段BC 上运动(不与点B 、C 重合),过点N 作NM ∥AC ,交AB 于点M ,当△AMN 面积最大时,求此时点N 的坐标.~~第4题~~(2020贵州.中考真卷) 已知抛物线y =ax +bx+c (a≠0)与x 轴交于A 、B 两点(点A 在点B 的左边),与y 轴交于点C (0,﹣3),顶点D 的坐标为(1,﹣4).(1) 求抛物线的解析式.(2) 在y 轴上找一点E ,使得△EAC 为等腰三角形,请直接写出点E 的坐标.(3) 点P 是x 轴上的动点,点Q 是抛物线上的动点,是否存在点P 、Q ,使得以点P 、Q 、B 、D 为顶点,BD 为一边的四边形是平行四边形?若存在,请求出点P 、Q 坐标;若不存在,请说明理由.~~第5题~~(2020贵州.中考真卷) 已知抛物线y =ax +bx +6(a≠0)交x 轴于点A(6,0)和点B(-1,0),交y 轴于点C.(1) 求抛物线的解析式和顶点坐标;(2) 如图(1),点P 是抛物线上位于直线AC 上方的动点,过点P 分别作x 轴,y 轴的平行线,交直线AC 于点D ,E ,当PD +PE 取最大值时,求点P 的坐标;(3) 如图(2),点M 为抛物线对称轴l 上一点,点N 为抛物线上一点,当直线AC 垂直平分△AMN 的边MN 时,求点N 的坐标.~~第6题~~(2020贵州.中考真卷) 如图(1),在平面直角坐标系中,抛物线y =ax +bx+4(a≠0)与y 轴交于点A ,与x 轴交于点C (﹣2,0),且经过点B (8,4),连接AB ,BO ,作AM ⊥OB 于点M ,将Rt △OMA 沿y 轴翻折,点M 的对应点为点N.解答下列问题:2222(1) 抛物线的解析式为________,顶点坐标为________;(2) 判断点N 是否在直线AC 上,并说明理由;(3) 如图(2),将图(1)中Rt △OMA 沿着OB 平移后,得到Rt △DEF.若DE 边在线段OB 上,点F 在抛物线上,连接AF ,求四边形AMEF 的面积.~~第7题~~(2019贵州.中考真卷) 已知抛物线y=ax +bx+3经过点A(1,0)和点B(-3,0),与y 轴交于点C,点P 为第二象限内抛物线上的动点.(1) 抛物线的解析式为,抛物线的顶点坐标为;(2) 如图1,连接OP 交BC 于点D,当S :S =1:2时,请求出点D 的坐标;(3) 如图2,点E 的坐标为(0,-1),点G 为x 轴负半轴上的一点,∠OGE=15°,连接PE,若∠PEG=2∠OGE,请求出点P 的坐标;(4) 如图3,是否存在点P,使四边形BOCP 的面积为8?若存在,请求出点P 的坐标;若不存在,请说明理由~~第8题~~(2018贵州.中考模拟) 如图,在平面直角坐标系xOy 中,A 、B 为x 轴上两点,C 、D 为y 轴上的两点,经过点A 、C 、B 的抛物线的一部分c与经过点A 、D 、B 的抛物线的一部分c 组合成一条封闭曲线,我们把这条封闭曲线成为“蛋线”.已知点C 的坐标为(0,﹣),点M 是抛物线C :y=mx ﹣2mx ﹣3m (m <0)的顶点.(1) 求A 、B 两点的坐标;(2) “蛋线”在第四象限上是否存在一点P ,使得△PBC 的面积最大?若存在,求出△PBC 面积的最大值;若不存在,请说明理由;(3) 当△BDM 为直角三角形时,求m 的值.~~第9题~~(2018贵州.中考模拟) 已知,抛物线y=ax +ax+b (a≠0)与直线y=2x+m 有一个公共点M (1,0),且a <b .2△CPD △BPD 12222(1)求b与a的关系式和抛物线的顶点D坐标(用a的代数式表示);(2)直线与抛物线的另外一个交点记为N,求△DMN的面积与a的关系式;(3) a=﹣1时,直线y=﹣2x与抛物线在第二象限交于点G,点G、H关于原点对称,现将线段GH沿y轴向上平移t个单位(t>0),若线段GH与抛物线有两个不同的公共点,试求t的取值范围.~~第10题~~(2018贵州.中考真卷) 如图1,已知矩形AOCB,AB=6cm,BC=16cm,动点P从点A出发,以3cm/s的速度向点O运动,直到点O为止;动点Q同时从点C出发,以2cm/s的速度向点B运动,与点P同时结束运动.(1)点P到达终点O的运动时间是s,此时点Q的运动距离是cm;(2)当运动时间为2s时,P、Q两点的距离为cm;(3)请你计算出发多久时,点P和点Q之间的距离是10cm;(4)如图2,以点O为坐标原点,OC所在直线为x轴,OA所在直线为y轴,1cm长为单位长度建立平面直角坐标系,连结AC,与PQ相交于点D,若双曲线y= 过点D,问k的值是否会变化?若会变化,说明理由;若不会变化,请求出k的值.贵州省中考数学压轴题答案解析~~第1题~~答案:解析:~~第2题~~答案:解析:~~第3题~~答案:解析:答案:解析:答案:解析:答案:解析:答案:解析:~~第8题~~答案:解析:答案:解析:答案:解析:。
贵州省安顺市,2020~2021年中考数学压轴题精选解析

贵州省安顺市,2020~2021年中考数学压轴题精选解析贵州省安顺市中考数学压轴题精选~~第1题~~(2020安顺.中考真卷) 如图,四边形是正方形,点O 为对角线的中点.(1) 问题解决:如图①,连接,分别取,的中点P ,Q ,连接 ,则与的数量关系是________,位置关系是________;(2)问题探究:如图②, 是将图①中的绕点A 按顺时针方向旋转得到的三角形,连接,点P ,Q 分别为, 的中点,连接,.判断的形状,并证明你的结论;(3)拓展延伸:如图③, 是将图①中的绕点A 按逆时针方向旋转得到的三角形,连接,点P,Q 分别为,的中点,连接 , .若正方形 的边长为1,求 的面积.~~第2题~~(2019安顺.中考真卷) 如图,抛物线y = x +bx+c 与直线y = x+3分别相交于A,B 两点,且此抛物线与x 轴的一个交点为C ,连接AC,BC.已知A(0,3),C(-3,0).(1) 求抛物线的解析式;(2) 在抛物线对称轴l 上找一点M ,使|MB -MC|的值最大,并求出这个最大值;(3) 点P 为y 轴右侧抛物线上一动点,连接PA,过点P 作PQ ⊥PA 交y 轴于点Q ,问:是否存在点P 使得以A,P,Q 为顶点的三角形与△ABC 相似?若存在,请求出所有符合条件的点P 的坐标;若还在存在,请说明理由.~~第3题~~(2018安顺.中考模拟) 如图,平面直角坐标系中,点A 、B 、C 在x 轴上,点D 、E 在y 轴上,OA=OD=2,OC=OE=4,B 为线段OA 的中点,直线AD 与经过B 、E 、C 三点的抛物线交于F 、G 两点,与其对称轴交于M ,点P 为线段FG 上一个动点(与F 、G 不重合),PQ ∥y 轴与抛物线交于点Q .2(1)求经过B、E、C三点的抛物线的解析式;(2)判断△BDC的形状,并给出证明;当P在什么位置时,以P、O、C为顶点的三角形是等腰三角形,并求出此时点P的坐标;(3)若抛物线的顶点为N,连接QN,探究四边形PMNQ的形状:①能否成为菱形;②能否成为等腰梯形?若能,请直接写出点P的坐标;若不能,请说明理由.~~第4题~~(2018安顺.中考真卷) 如图,已知抛物线的对称轴为直线x=-1,且抛物线与x轴交于A、B两点,与y轴交于C点,其中A(1.0),C(0,3).(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;(2)在抛物线的对称轴x=-1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;(3)设点P为抛物线的对称轴x=-1上的一个动点,求使△BPC为直角三角形的点P的坐标.~~第5题~~(2017西秀.中考模拟) 如图,已知抛物线经过点A(﹣1,0)、B(3,0)、C(0,3)三点.(1)求抛物线的解析式.(2)点M是线段BC上的点(不与B,C重合),过M作MN∥y轴交抛物线于N,若点M的横坐标为m,请用m的代数式表示MN的长.(3)在(2)的条件下,连接NB、NC,是否存在m,使△BNC的面积最大?若存在,求m的值;若不存在,说明理由.~~第6题~~2(2017安顺.中考模拟) 如图,抛物线y= x+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).(1)求抛物线的解析式及顶点D的坐标;(2)判断△ABC的形状,证明你的结论;(3)点M是x轴上的一个动点,当△DCM的周长最小时,求点M的坐标.~~第7题~~(2017安顺.中考模拟) 如图,AB是⊙O的直径,点C是⊙O上一点,∠BAC的平分线AD交⊙O于点D,过点D垂直于AC的直线交AC的延长线于点E.(1)求证:DE是⊙O的切线;(2)如果AD=5,AE=4,求AC长.~~第8题~~(2017安顺.中考模拟) 如图,抛物线y= x+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).(1)求抛物线的解析式及顶点D的坐标;(2)判断△ABC的形状,证明你的结论;(3)点M是x轴上的一个动点,当△DCM的周长最小时,求点M的坐标.~~第9题~~22(2017安顺.中考真卷) 如图甲,直线y=﹣x+3与x 轴、y 轴分别交于点B 、点C ,经过B 、C 两点的抛物线y=x +bx+c 与x 轴的另一个交点为A ,顶点为P.(1)求该抛物线的解析式;(2)在该抛物线的对称轴上是否存在点M ,使以C ,P ,M 为顶点的三角形为等腰三角形?若存在,请直接写出所符合条件的点M 的坐标;若不存在,请说明理由;(3)当0<x <3时,在抛物线上求一点E ,使△CBE 的面积有最大值(图乙、丙供画图探究).~~第10题~~(2016安顺.中考真卷) 如图,抛物线经过A (﹣1,0),B (5,0),C (0,-)三点.(1)求抛物线的解析式;(2)在抛物线的对称轴上有一点P ,使PA+PC 的值最小,求点P 的坐标;(3)点M 为x 轴上一动点,在抛物线上是否存在一点N ,使以A ,C ,M ,N 四点构成的四边形为平行四边形?若存在,求点N 的坐标;若不存在,请说明理由.贵州省安顺市中考数学压轴题答案解析~~第1题~~答案:2解析:~~第2题~~答案:解析:答案:解析:答案:解析:~~第5题~~答案:解析:~~第6题~~答案:解析:答案:解析:答案:解析:~~第9题~~答案:解析:~~第10题~~答案:解析:。
倍半角,镜面相似,2020贵阳中考压轴题分析

倍半角,镜面相似,2020贵阳中考压轴题分析
传播知识,传播力量!
贵阳市是贵州的省会,贵州有9个地级行政区,2020年的中考有三各个地方考卷一样(贵阳,安顺,六盘水),其他地方各自为战。
今天做的是贵阳中考:
选择题:
结合图形来看,主要应用二函对称性
开口无所谓:
填空题:
本题为静态几何求长度
所用的策略是倍半角构造之先转移再构造!
关键把∠A转移到∠BFC
再倍半构造即
倍半角处理策略,依山势建城堡,含例题分析
解答题几何:
看着也就最后一题有难度
(1)略
(2)其实和(3)是连续性的,甚至可以得到一般性结论,即△ABO不轮转多少度,△PQB恒为等直的结论。
联结O'A 可发现模型:
(交互式)镜面相似模型
简单证明:
证毕!
(3)就根据等直很好算了!
感谢支持:分享、转发、右下角点“在看赞”
“知识”这个东西非常的神奇,你把它分享出去,它不但不会减少,反而会增加,所分享知识应当是快乐的,也能够让自己提升,这就是我每天分享知识的信念。
贵州省各市2020年中考数学分类解析 专题12:押轴题

贵州各市2020年中考数学试题分类解析汇编专题12:押轴题一、选择题1. (2020贵州贵阳3分)已知二次函数y=ax2+bx+c(a<0)的图象如图所示,当﹣5≤x≤0时,下列说法正确的是【】A.有最小值﹣5、最大值0 B.有最小值﹣3、最大值6C.有最小值0、最大值6 D.有最小值2、最大值6【答案】B。
【考点】二次函数的图象和最值。
【分析】由二次函数的图象可知,∵﹣5≤x≤0,∴当x=﹣2时函数有最大值,y最大=6;当x=﹣5时函数值最小,y最小=﹣3。
故选B。
2. (2020贵州安顺3分)下列说法中正确的是【】A.B.函数的自变量的取值范围是x>﹣1C.若点P(2,a)和点Q(b,﹣3)关于x轴对称,则a﹣b的值为1D.﹣8的立方根是2【答案】C。
【考点】无理数,函数自变量的取值范围,二次根式有意义的条件,关于x轴对称的点的坐标,立方根。
【分析】A是有理数,故此选项错误;B、函数的自变量的取值范围是x≥﹣1,故此选项错误;C、若点P(2,a)和点Q(b,﹣3)关于x轴对称,则b=2,a=3,故a﹣b=3﹣2=1,故此选项正确;D、﹣8的立方根式﹣2,故此选项错误。
故选C。
3. (2020贵州毕节3分)如图,在正方形ABCD中,以A为顶点作等边△AEF,交BC边于E ,交DC 边于F ;又以A 为圆心,AE 的长为半径作»EF。
若△AEF 的边长为2,则阴影部分的面积约是【 】1.414 1.732≈,π取3.14)A. 0.64B. 1.64C. 1.68D. 0.36【答案】A 。
【考点】正方形和等边三角形的性质,勾股定理,扇形和三角形面积。
【分析】由图知,AEF CEF AEF S S S S ∆∆=+-扇形影部分阴。
因此,由已知,根据正方形、等边三角形的性质和勾股定理,可得等边△AEF 的边长为2Rt △AEF 的两直角边长;扇形AEF 的半径为2圆心角为600。
∴2AEF CEF AEF 116022S S S S =20.64223603ππ∆∆⋅⋅=-⋅-≈扇形影部分阴。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2020年全国各地中考数学压轴题汇编(贵州专版)几何综合参考答案与试题解析一.选择题(共6小题)1.(2020•贵阳)如图,在菱形ABCD中,E是AC的中点,EF∥CB,交AB于点F,如果EF=3,那么菱形ABCD的周长为()A.24 B.18 C.12 D.9解:∵E是AC中点,∵EF∥BC,交AB于点F,∴EF是△ABC的中位线,∴EF=BC,∴BC=6,∴菱形ABCD的周长是4×6=24.故选:A.2.(2020•遵义)如图,点P是矩形ABCD的对角线AC上一点,过点P作EF∥BC,分别交AB,CD于E、F,连接PB、PD.若AE=2,PF=8.则图中阴影部分的面积为()A.10 B.12 C.16 D.18解:作PM⊥AD于M,交BC于N.则有四边形AEPM,四边形DFPM,四边形CFPN,四边形BEPN都是矩形,∴S△ADC =S△ABC,S△AMP=S△AEP,S△PBE=S△PBN,S△PFD=S△PDM,S△PFC=S△PCN,∴S△DFP=S△PBE=×2×8=8,∴S阴=8+8=16,故选:C.3.(2020•贵阳)如图,A、B、C是小正方形的顶点,且每个小正方形的边长为1,则tan∠BAC的值为()A.B.1 C.D.解:连接BC,由网格可得AB=BC=,AC=,即AB2+BC2=AC2,∴△ABC为等腰直角三角形,∴∠BAC=45°,则tan∠BAC=1,故选:B.4.(2020•遵义)如图,四边形ABCD中,AD∥BC,∠ABC=90°,AB=5,BC=10,连接AC、BD,以BD为直径的圆交AC于点E.若DE=3,则AD的长为()A.5 B.4 C.3D.2解:如图,在Rt△ABC中,AB=5,BC=10,∴AC=5过点D作DF⊥AC于F,∴∠AFD=∠CBA,∵AD∥BC,∴∠DAF=∠ACB,∴△ADF∽△CAB,∴,∴,设DF=x,则AD=x,在Rt△ABD中,BD==,∵∠DEF=∠DBA,∠DFE=∠DAB=90°,∴△DEF∽△DBA,∴,∴,∴x=2,∴AD=x=2,故选:D.5.(2020•安顺)已知⊙O的直径CD=10cm,AB是⊙O的弦,AB⊥CD,垂足为M,且AB=8cm,则AC的长为()A.2cm B.4cm C.2cm或4cm D.2cm或4cm 解:连接AC,AO,∵⊙O的直径CD=10cm,AB⊥CD,AB=8cm,∴AM=AB=×8=4cm,OD=OC=5cm,当C点位置如图1所示时,∵OA=5cm,AM=4cm,CD⊥AB,∴OM===3cm,∴CM=OC+OM=5+3=8cm,∴AC===4cm;当C点位置如图2所示时,同理可得OM=3cm,∵OC=5cm,∴MC=5﹣3=2cm,在Rt△AMC中,AC===2cm.故选:C.6.(2020•铜仁市)在同一平面内,设a、b、c是三条互相平行的直线,已知a与b的距离为4cm,b与c的距离为1cm,则a与c的距离为()A.1cm B.3cm C.5cm或3cm D.1cm或3cm解:当直线c在a、b之间时,∵a、b、c是三条平行直线,而a与b的距离为4cm,b与c的距离为1cm,∴a与c的距离=4﹣1=3(cm);当直线c不在a、b之间时,∵a、b、c是三条平行直线,而a与b的距离为4cm,b与c的距离为1cm,∴a与c的距离=4+1=5(cm),综上所述,a与c的距离为3cm或3cm.故选:C.二.填空题(共8小题)7.(2020•贵阳)如图,点M、N分别是正五边形ABCDE的两边AB、BC上的点.且AM=BN,点O是正五边形的中心,则∠MON的度数是72度.解:连接OA、OB、OC,∠AOB==72°,∵∠AOB=∠BOC,OA=OB,OB=OC,∴∠OAB=∠OBC,在△AOM和△BON中,∴△AOM≌△BON,∴∠BON=∠AOM,∴∠MON=∠AOB=72°,故答案为:72.8.(2020•遵义)如图,△ABC中.点D在BC边上,BD=AD=AC,E为CD的中点.若∠CAE=16°,则∠B为37度.解:∵AD=AC,点E是CD中点,∴AE⊥CD,∴∠AEC=90°,∴∠C=90°﹣∠CAE=74°,∵AD=AC,∴∠ADC=∠C=74°,∵AD=BD,∴2∠B=∠ADC=74°,∴∠B=37°,故答案为37°.9.(2020•贵阳)如图,在△ABC中,BC=6,BC边上的高为4,在△ABC的内部作一个矩形EFGH,使EF在BC边上,另外两个顶点分别在AB、AC边上,则对角线EG长的最小值为.解:如图,作AQ⊥BC于点Q,交DG于点P,∵四边形DEFG是矩形,∴AQ⊥DG,GF=PQ,设GF=PQ=x,则AP=4﹣x,由DG∥BC知△ADG∽△ABC,∴=,即=,则EF=DG=(4﹣x),∴EG====,∴当x=时,EG取得最小值,最小值为,故答案为:.10.(2020•遵义)如图,在菱形ABCD中,∠ABC=120°,将菱形折叠,使点A恰好落在对角线BD上的点G处(不与B、D重合),折痕为EF,若DG=2,BG=6,则BE的长为2.8.解:作EH⊥BD于H,由折叠的性质可知,EG=EA,由题意得,BD=DG+BG=8,∵四边形ABCD是菱形,∴AD=AB,∠ABD=∠CBD=∠ABC=60°,∴△ABD为等边三角形,∴AB=BD=8,设BE=x,则EG=AE=8﹣x,在Rt△EHB中,BH=x,EH=x,在Rt△EHG中,EG2=EH2+GH2,即(8﹣x)2=(x)2+(6﹣x)2,解得,x=2.8,即BE=2.8,故答案为:2.8.11.(2020•安顺)如图,C 为半圆内一点,O 为圆心,直径AB 长为2cm ,∠BOC=60°,∠BCO=90°,将△BOC 绕圆心O 逆时针旋转至△B′OC′,点C′在OA 上,则边BC 扫过区域(图中阴影部分)的面积为 π cm 2.(结果保留π)解:∵∠BOC=60°,△B′OC′是△BOC 绕圆心O 逆时针旋转得到的,∴∠B′OC′=60°,△BCO=△B′C′O ,∴∠B′OC=60°,∠C′B′O=30°, ∴∠B′OB=120°,∵AB=2cm ,∴OB=1cm ,OC′=, ∴B′C′=,∴S 扇形B′OB ==π,S 扇形C′OC ==, ∵∴阴影部分面积=S 扇形B′OB +S △B′C′O ﹣S △BCO ﹣S 扇形C′OC =S 扇形B′OB ﹣S 扇形C′OC =π﹣=π; 故答案为:π.12.(2020•黔西南州)已知一个菱形的边长为2,较长的对角线长为2,则这个菱形的面积是 2 . 解:依照题意画出图形,如图所示.在Rt△AOB中,AB=2,OB=,∴OA==1,∴AC=2OA=2,=AC•BD=×2×2=2.∴S菱形ABCD故答案为:2.13.(2020•铜仁市)在直角三角形ABC中,∠ACB=90°,D、E是边AB上两点,且CE 所在直线垂直平分线段AD,CD平分∠BCE,BC=2,则AB=4.解:∵CE所在直线垂直平分线段AD,∴CE平分∠ACD,∴∠ACE=∠DCE.∵CD平分∠BCE,∴∠DCE=∠DCB.∵∠ACB=90°,∴∠ACE=∠ACB=30°,∴∠A=60°,∴AB===4.故答案为:4.14.(2020•黔西南州)如图,已知在△ABC中,BC边上的高AD与AC边上的高BE交于点F,且∠BAC=45°,BD=6,CD=4,则△ABC的面积为60.解:∵AD⊥BC,BE⊥AC,∴∠AEF=∠BEC=∠BDF=90°,∵∠BAC=45°,∴AE=EB,∵∠EAF+∠C=90°,∠CBE+∠C=90°,∴∠EAF=∠CBE,∴△AEF≌△BEC,∴AF=BC=10,设DF=x.∵△ADC∽△BDF,∴=,∴=,整理得x2+10x﹣24=0,解得x=2或﹣12(舍弃),∴AD=AF+DF=12,=•BC•AD=×10×12=60.∴S△ABC故答案为60.三.解答题(共9小题)15.(2020•贵阳)如图,在平行四边形ABCD中,AE是BC边上的高,点F是DE的中点,AB与AG关于AE对称,AE与AF关于AG对称.(1)求证:△AEF是等边三角形;(2)若AB=2,求△AFD的面积.解:(1)∵AB与AG关于AE对称,∴AE⊥BC,∵四边形ABCD是平行四边形,∴AD∥BC,∴AE⊥AD,即∠DAE=90°,∵点F是DE的中点,即AF是Rt△ADE的中线,∴AF=EF=DF,∵AE与AF关于AG对称,∴AE=AF,则AE=AF=EF,∴△AEF是等边三角形;(2)记AG、EF交点为H,∵△AEF是等边三角形,且AE与AF关于AG对称,∴∠EAG=30°,AG⊥EF,∵AB与AG关于AE对称,∴∠BAE=∠GAE=30°,∠AEB=90°,∵AB=2,∴BE=1、DF=AF=AE=,则EH=AE=、AH=,=××=.∴S△ADF16.(2020•遵义)如图,正方形ABCD的对角线交于点O,点E、F分别在AB、BC上(AE <BE),且∠EOF=90°,OE、DA的延长线交于点M,OF、AB的延长线交于点N,连接MN.(1)求证:OM=ON.(2)若正方形ABCD的边长为4,E为OM的中点,求MN的长.解:(1)∵四边形ABCD是正方形,∴OA=OB,∠DAO=45°,∠OBA=45°,∴∠OAM=∠OBN=135°,∵∠EOF=90°,∠AOB=90°,∴∠AOM=∠BON,∴△OAM≌△OBN(ASA),∴OM=ON;(2)如图,过点O作OH⊥AD于点H,∵正方形的边长为4,∴OH=HA=2,∵E为OM的中点,∴HM=4,则OM==2,∴MN=OM=2.17.(2020•贵阳)如图,AB为⊙O的直径,且AB=4,点C在半圆上,OC⊥AB,垂足为点O,P为半圆上任意一点,过P点作PE⊥OC于点E,设△OPE的内心为M,连接OM、PM.(1)求∠OMP的度数;(2)当点P在半圆上从点B运动到点A时,求内心M所经过的路径长.解:(1)∵△OPE的内心为M,∴∠MOP=∠MOC,∠MPO=∠MPE,∴∠PMO=180°﹣∠MPO﹣∠MOP=180°﹣(∠EOP+∠OPE),∵PE⊥OC,即∠PEO=90°,∴∠PMO=180°﹣(∠EOP+∠OPE)=180°﹣(180°﹣90°)=135°,(2)如图,∵OP=OC,OM=OM,而∠MOP=∠MOC,∴△OPM≌△OCM,∴∠CMO=∠PMO=135°,所以点M在以OC为弦,并且所对的圆周角为135°的两段劣弧上(和);点M在扇形BOC内时,过C、M、O三点作⊙O′,连O′C,O′O,在优弧CO取点D,连DA,DO,∵∠CMO=135°,∴∠CDO=180°﹣135°=45°,∴∠CO′O=90°,而OA=2cm,∴O′O=OC=×2=,∴弧OMC的长==π(cm),同理:点M在扇形AOC内时,同①的方法得,弧ONC的长为πcm,所以内心M所经过的路径长为2×π=πcm.18.(2020•遵义)如图,AB是半圆O的直径,C是AB延长线上的点,AC的垂直平分线交半圆于点D,交AC于点E,连接DA,DC.已知半圆O的半径为3,BC=2.(1)求AD的长.(2)点P是线段AC上一动点,连接DP,作∠DPF=∠DAC,PF交线段CD于点F.当△DPF为等腰三角形时,求AP的长.解:(1)如图1,连接OD,∵OA=OD=3,BC=2,∴AC=8,∵DE是AC的垂直平分线,∴AE=AC=4,∴OE=AE﹣OA=1,在Rt△ODE中,DE==2;在Rt△ADE中,AD==2;(2)当DP=DF时,如图2,点P与A重合,F与C重合,则AP=0;当DP=PF时,如图4,∴∠CDP=∠PFD,∵DE是AC的垂直平分线,∠DPF=∠DAC,∴∠DPF=∠C,∵∠PDF=∠CDP,∴△PDF∽△CDP,∴∠DFP=∠DPC,∴∠CDP=∠CPD,∴CP=CD,∴AP=AC﹣CP=AC﹣CD=AC﹣AD=8﹣2;当PF=DF时,如图3,∴∠FDP=∠FPD,∵∠DPF=∠DAC=∠C,∴△DAC∽△PDC,∴,∴,∴AP=5,即:当△DPF是等腰三角形时,AP的长为0或5或8﹣2.19.(2020•安顺)如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A 作BC的平行线交BE的延长线于点F,连接CF.(1)求证:AF=DC;(2)若AC⊥AB,试判断四边形ADCF的形状,并证明你的结论.(1)证明:连接DF,∵E为AD的中点,∴AE=DE,∵AF∥BC,∴∠AFE=∠DBE,在△AFE和△DBE中,,∴△AFE≌△DBE(AAS),∴EF=BE,∵AE=DE,∴四边形AFDB是平行四边形,∴BD=AF,∵AD为中线,∴DC=BD,∴AF=DC;(2)四边形ADCF的形状是菱形,理由如下:∵AF=DC,AF∥BC,∴四边形ADCF是平行四边形,∵∴∵AD为中线∴AD=BC=DC,∴平行四边形ADCF是菱形;20.(2020•铜仁市)如图,在三角形ABC中,AB=6,AC=BC=5,以BC为直径作⊙O交AB于点D,交AC于点G,直线DF是⊙O的切线,D为切点,交CB的延长线于点E.(1)求证:DF⊥AC;(2)求tan∠E的值.(1)证明:如图,连接OC,∵BC是⊙O的直径,∴∠BDC=90°,∴CD⊥AB,∵AC=BC,∴AD=BD,∵OB=OC,∴OD是△ABC的中位线∴OD∥AC,∵DF为⊙O的切线,∴OD⊥DF,∴DF⊥AC;(2)解:如图,连接BG,∵BC是⊙O的直径,∴∠BGC=90°,∵∠EFC=90°=∠BGC,∴EF∥BG,∴∠CBG=∠E,Rt△BDC中,∵BD=3,BC=5,∴CD=4,S△ABC=,6×4=5BG,BG=,由勾股定理得:CG==,∴tan∠CBG=tan∠E===.21.(2020•安顺)如图,在△ABC中,AB=AC,O为BC的中点,AC与半圆O相切于点D.(1)求证:AB是半圆O所在圆的切线;(2)若cos∠ABC=,AB=12,求半圆O所在圆的半径.解:(1)如图,作OE⊥AB于E,连接OD,OA,∵AB=AC,点O是BC的中点,∴∠CAO=∠BAO,∵AC与半圆O相切于D,∴OD⊥AC,∵OE⊥AB,∴OD=OE,∵AB径半圆O的半径的外端点,∴AB是半圆O所在圆的切线;(2)∵AB=AC,O是BC的中点,∴AO⊥BC,在Rt△AOB中,OB=AB•cos∠ABC=12×=8,根据勾股定理得,OA==4,=AB•OE=OB•OA,由三角形的面积得,S△AOB∴OE==,即:半圆O所在圆的半径为.22.(2020•贵阳)如图,在矩形ABCD中,AB═2,AD=,P是BC边上的一点,且BP=2CP.(1)用尺规在图①中作出CD边上的中点E,连接AE、BE(保留作图痕迹,不写作法);(2)如图②,在(1)的条件下,判断EB是否平分∠AEC,并说明理由;(3)如图③,在(2)的条件下,连接EP并廷长交AB的廷长线于点F,连接AP,不添加辅助线,△PFB能否由都经过P点的两次变换与△PAE组成一个等腰三角形?如果能,说明理由,并写出两种方法(指出对称轴、旋转中心、旋转方向和平移距离)解:(1)依题意作出图形如图①所示,(2)EB是平分∠AEC,理由:∵四边形ABCD是矩形,∴∠C=∠D=90°,CD=AB=2,BC=AD=,∵点E是CD的中点,∴DE=CE=CD=1,在△ADE和△BCE中,,∴△ADE≌△BCE,∴∠AED=∠BEC,在Rt△ADE中,AD=,DE=1,∴tan∠AED==,∴∠AED=60°,∴∠BCE=∠AED=60°,∴∠AEB=180°﹣∠AED﹣∠BEC=60°=∠BEC,∴BE平分∠AEC;(3)∵BP=2CP,BC=,∴CP=,BP=,在Rt△CEP中,tan∠CEP==,∴∠CEP=30°,∴∠BEP=30°,∴∠AEP=90°,∵CD∥AB,∴∠F=∠CEP=30°,在Rt△ABP中,tan∠BAP==,∴∠PAB=30°,∴∠EAP=30°=∠F=∠PAB,∵CB⊥AF,∴AP=FP,∴△AEP≌△FBP,∴△PFB能由都经过P点的两次变换与△PAE组成一个等腰三角形,变换的方法为:将△BPF绕点B顺时针旋转120°和△EPA重合,①沿PF折叠,②沿AE 折叠.23.(2020•黔西南州)如图1,已知矩形AOCB,AB=6cm,BC=16cm,动点P从点A出发,以3cm/s的速度向点O运动,直到点O为止;动点Q同时从点C出发,以2cm/s 的速度向点B运动,与点P同时结束运动.(1)点P到达终点O的运动时间是s,此时点Q的运动距离是cm;(2)当运动时间为2s时,P、Q两点的距离为6cm;(3)请你计算出发多久时,点P和点Q之间的距离是10cm;(4)如图2,以点O为坐标原点,OC所在直线为x轴,OA所在直线为y轴,1cm长为单位长度建立平面直角坐标系,连结AC,与PQ相交于点D,若双曲线y=过点D,问k 的值是否会变化?若会变化,说明理由;若不会变化,请求出k的值.解:(1)∵四边形AOCB是矩形,∴OA=BC=16,∵动点P从点A出发,以3cm/s的速度向点O运动,∴,此时,点Q的运动距离是cm(2)如图1,由运动知,AP=3×2=6cm,CQ=2×2=4cm,过点P作PE⊥BC于E,过点Q作QF⊥OA于F,∴四边形APEB是矩形,∴PE=AB=6,BE=6,∴EQ=BC﹣BE﹣CQ=16﹣6﹣4=6,根据勾股定理得,PQ=6,故答案为6;(3)设运动时间为t秒时,由运动知,AP=3t,CQ=2t,同(2)的方法得,PE=6,EQ=16﹣3t﹣2t=16﹣5t,∵点P和点Q之间的距离是10cm,∴62+(16﹣5t)2=100,∴t=或t=;(4)k的值是不会变化,理由:∵四边形AOCB是矩形,∴OC=AB=6,OA=16,∴C(6,0),A(0,16),∴直线AC的解析式为y=﹣x+16①,设运动时间为t,∴AP=3t,CQ=2t,∴OP=16﹣3t,∴P(0,16﹣3t),Q(6,2t),∴PQ解析式为y=x+16﹣3t②,联立①②得,﹣x+16=x+16﹣3t,∴x+x=3t,∴5tx﹣16x+16x=3t,∴x=,∴y=,∴D(,)∴k=×=是定值.。
