数字电路实验三全加器应用技术
全加器及应用的实验原理

全加器及应用的实验原理全加器是一种逻辑电路,用于对两个二进制数相加时,同时考虑进位位以及和位。
它也是电路设计中的基本模块,广泛应用于计算机、数字信号处理等领域。
全加器的实验原理基于布尔代数和逻辑门的运算。
全加器由两个半加器和一个与门组成。
半加器用于计算两个输入位的和位和进位位,而全加器则在此基础上还考虑了上一位的进位。
半加器是全加器的基本组成部分之一。
它由一个异或门和一个与门组成。
异或门用于计算两个输入位的和位,而与门用于计算进位位。
半加器的输入包括两个待加数位A和B,输出为和位S和进位位C。
全加器由两个半加器和一个与门组成。
半加器1的输入为A和B,输出为和位S1和进位位C1;半加器2的输入为S1和Cin(上一位的进位),输出为和位S 和进位位C。
与门的输入为C1和Cin,输出为进位位C。
全加器的输出包括和位S和进位位C。
实验中可以使用门电路芯片(如74系列)来实现全加器。
门电路芯片中包含了多个逻辑门,如与门、或门、异或门等。
通过合理的连接和输入信号值,可以构建出全加器电路。
在实验中,可以利用开关或跳线来模拟输入信号。
将A、B和Cin分别连接到不同的开关或跳线上,模拟待加数和上一位的进位。
然后将开关或跳线连接到门电路芯片的输入引脚上,将门电路芯片的输出引脚连接到LED等显示装置上,以观察全加器的输出结果。
实验中还可以通过多个全加器的级联来实现多位加法器。
将多个全加器连续连接起来,将每一个全加器的进位位C连接到下一个全加器的Cin输入上,即可实现多位数的加法运算。
全加器的应用非常广泛。
在计算机中,全加器用于实现算术逻辑单元(ALU),负责执行加法操作。
在数字信号处理中,全加器可以用于实现滤波器、变换器、编码器等功能。
此外,全加器还可用于设计控制电路、编码器、译码器、计数器等。
总之,全加器是一种基本的逻辑电路,用于计算二进制数的和位和进位位。
实验中可以利用门电路芯片来搭建全加器电路,通过观察输出结果来验证其正确性。
全加器及其应用实验报告

一、实验目的1. 理解全加器的原理和结构。
2. 掌握全加器的逻辑功能及其实现方法。
3. 学习全加器在实际电路中的应用。
二、实验原理全加器是一种组合逻辑电路,用于实现两个二进制数相加,同时考虑来自低位的进位信号。
全加器由三个输入端和两个输出端组成,输入端分别为两个加数位(A、B)和来自低位的进位信号(Cin),输出端分别为和位(S)和进位输出信号(Cout)。
全加器的逻辑功能如下:- 当A、B和Cin都为0时,S为0,Cout为0;- 当A、B和Cin中有一个为1时,S为1,Cout为0;- 当A、B和Cin中有两个为1时,S为0,Cout为1;- 当A、B和Cin都为1时,S为1,Cout为1。
全加器可以通过半加器(HAdder)和与门(AND)来实现。
半加器实现两个一位二进制数相加的功能,而与门用于实现进位信号的产生。
三、实验器材1. 74LS系列集成电路芯片(如74LS00、74LS86等);2. 实验箱;3. 电源;4. 导线;5. 万用表;6. 示波器。
四、实验步骤1. 根据全加器的逻辑功能,设计全加器的原理图,包括半加器和与门;2. 将设计好的原理图连接到实验箱上,包括输入端(A、B、Cin)和输出端(S、Cout);3. 使用万用表检测各个芯片的引脚电压,确保电路连接正确;4. 使用示波器观察输入信号和输出信号的变化,验证全加器的逻辑功能;5. 改变输入信号,观察全加器的输出信号,进一步验证其逻辑功能;6. 将全加器应用于实际电路,如实现多位加法器等。
五、实验结果与分析1. 实验结果表明,全加器能够实现两个二进制数相加,同时考虑来自低位的进位信号;2. 通过示波器观察,发现全加器的输出信号与输入信号符合逻辑功能;3. 将全加器应用于实际电路,如实现多位加法器,实验结果表明电路能够正常工作。
六、实验心得1. 全加器是一种重要的组合逻辑电路,在数字电路中具有广泛的应用;2. 在实验过程中,需要掌握全加器的原理和结构,熟悉各个芯片的功能和引脚连接;3. 实验过程中,要注意电路的连接和信号的观察,确保实验结果的准确性;4. 通过本次实验,加深了对全加器的理解,为以后的学习和工作打下了基础。
实验三-数据选择器译码器全加器

实验三:数据选择器和译码器应用1. 能力培养目标● 理解数据选择器和译码器的逻辑功能● 运用数据选择器和译码器的逻辑关系设计实际应用2. 项目任务要求(1)测试4选1数据选择器的逻辑功能,通过示波器观测每种组合下数据选择器的输出波形(2)测试2-4线译码器的逻辑功能(3)将2-4线译码器扩展组成3-8线译码器,利用两个2-4线译码器扩展组成3-8线译码器(4)利用2-4线译码器设计并实现组合逻辑电路B A F ⊕=【选做】3. 项目分析(1) 数据选择器及主流芯片数据选择器是一种多输入、单输出的组合逻辑电路,其应用主要包括通过级联进行通道扩展数据输入端的个数;或者配合门电路实现逻辑函数,组成函数发生器。
数据选择器中常见的芯片有双4选1数据选择器74LS153芯片。
74LS153中的引脚G 用于控制输出。
当G 为高电平时,禁止输出,引脚Y 输出为低电平;当G 为低电平时,允许输出,由数据选择端B 、A 决定C 0、C 1、C 2、C 3中的哪个数据送往数据输出端Y 。
14131211109161234567双4选1数据选择器 74LS153Vcc2GA2C 32C 22C 12C 01Y1GB1C 31C 21C 11C 01582YGND图2-3-1 74LS153引脚结构图 表2-3-1 4选1数据选择器真值表选择输入 数据输入 选通 输出 B A C 0 C 1 C 2 C 3 G Y X X X X X X H L L L L X X X L L L L H X X X L H L H X L X X L L L H X H X X L H H L X X L X L L H L X X H X L H H H X X X L L L H HX X X HLH(2) 译码器及主流芯片译码器中常见的芯片有双2-4线译码器74LS139,其引脚结构图和真值表分别如下:14131211109161234567双2-4线译码器 74LS139Vcc2G2A2B2Y 02Y 12Y 21Y 31G1A1B1Y 01Y 11Y 21582Y 3GND图2-3-2 74LS139引脚结构图 表2-3-2 2-4线译码器真值表输入端输出端允许G选择B AY 0(____________________0BA G Y =) Y 1(_________________1B A G Y =) Y 2(_________________2B A G Y =)Y 3(______________3B A G Y =)H X X H H H H L L L L H H H L L H H L H H L H L H H L H LH HH H H L在74LS139中,引脚G 用于控制输出。
全加器应用实验报告

一、实验目的1. 理解全加器的逻辑功能和工作原理。
2. 掌握全加器的组成和电路结构。
3. 学习全加器在实际电路中的应用。
4. 培养动手实践能力和分析问题、解决问题的能力。
二、实验原理全加器是一种能够实现二进制加法运算的数字电路,它由半加器和与门组成。
全加器有三个输入端:两个加数输入端A和B,以及一个进位输入端Cin;三个输出端:进位输出端Cout,和输出端Sum,以及一个进位输入端Cin。
全加器的逻辑功能如下:- 当Cin为0时,全加器相当于一个半加器,即A和B相加,进位输出Cout为0,和输出Sum为A+B。
- 当Cin为1时,全加器将A、B和Cin相加,进位输出Cout为1,和输出Sum为A+B+Cin。
三、实验仪器与设备1. 数字电路实验箱2. 集成芯片(如74LS00、74LS86等)3. 导线4. 逻辑分析仪或示波器5. 实验指导书四、实验步骤1. 搭建全加器电路(1) 使用74LS86芯片搭建半加器电路,连接A、B和Sum端。
(2) 使用74LS00芯片搭建与门电路,连接Sum和Cin端,输出为Cout。
(3) 将半加器和与门电路连接起来,形成全加器电路。
2. 验证全加器功能(1) 将A、B和Cin端分别接入逻辑电平开关。
(2) 通过逻辑电平开关改变A、B和Cin端的电平,观察Cout和Sum端的输出。
(3) 将实验结果与理论计算结果进行对比,验证全加器的功能。
3. 全加器在实际电路中的应用(1) 使用全加器搭建一个4位加法器电路。
(2) 将A、B和Cin端分别接入4位二进制数输入端。
(3) 观察Cout和Sum端的输出,验证4位加法器电路的功能。
五、实验结果与分析1. 全加器功能验证通过实验验证,全加器能够实现二进制加法运算,其逻辑功能与理论计算结果一致。
2. 全加器在实际电路中的应用通过实验验证,全加器可以应用于4位加法器电路,实现多位二进制数的加法运算。
六、实验总结1. 全加器是一种能够实现二进制加法运算的数字电路,具有广泛的应用。
电工电子实验-全加器实验报告
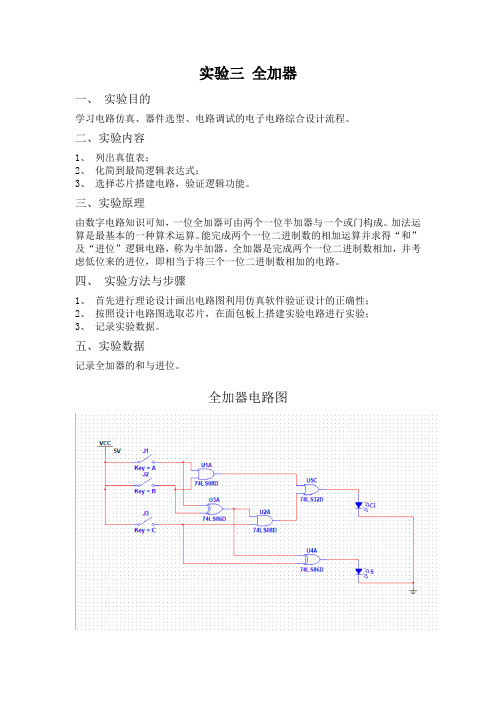
实验三全加器一、实验目的学习电路仿真、器件选型、电路调试的电子电路综合设计流程。
二、实验内容1、列出真值表;2、化简到最简逻辑表达式;3、选择芯片搭建电路,验证逻辑功能。
三、实验原理由数字电路知识可知,一位全加器可由两个一位半加器与一个或门构成。
加法运算是最基本的一种算术运算。
能完成两个一位二进制数的相加运算并求得“和”及“进位”逻辑电路,称为半加器。
全加器是完成两个一位二进制数相加,并考虑低位来的进位,即相当于将三个一位二进制数相加的电路。
四、实验方法与步骤1、首先进行理论设计画出电路图利用仿真软件验证设计的正确性;2、按照设计电路图选取芯片,在面包板上搭建实验电路进行实验;3、记录实验数据。
五、实验数据记录全加器的和与进位。
全加器电路图全加器真值表A iB iC i-1S i C i0 0 0 0 01 0 0 1 00 1 0 1 01 1 0 0 10 0 1 1 01 0 1 0 10 1 1 0 11 1 1 1 1表 1实验中使用的芯片分别为74LS08P,74LS32P,74LS86P,其分别为一个14针脚封装的4与门电路,14针脚封装的4或门电路,14针脚封装的4异或门电路。
实验目的为模拟并做出一个2进制的1位全加器。
根据其模拟要求列出了2进制的1位全加器的真值表(见表1)。
其输入分别为A i,B i,C i-1,分别代表着本位的两个加数A i,B i与上位进位C i-1,输出为S i和C i其代表为本位求和与本位进位。
根据逻辑代数化简规则对真值表进行化简,对于S i的化简其只能运用公式法而不能运用卡诺图化简,这是由于S i的卡诺图中并不能圈出2n个格子的矩形,而对于C i的化简则可使用卡诺图和公式法分别化简,在化简过程中发现卡诺图化简结果与公式法化简结果并不相同,但其结果是等效的。
其具体化简过程见图1,化简后的公式为S i=A i⊕B i⊕C i-1,C i-B i+C i-1(A i⊕B i)或C i-1=A i B i+C i-1(A i+B i)。
数字电路实验报告实验三加法器

实验三加法器一、实验目的1、掌握用SSI器件实现全加器的方法。
2、掌握用MSI组合逻辑器件实现全加器的方法。
3、掌握集成加法器的应用。
二、实验设备及器件1、数字逻辑电路实验板1块2、74HC(LS)00(四二输入与非门)1片3、74HC(LS)86(四二输入异或门)1片4、74HC(LS)153(双四选一数据选择器)1片5、74HC(LS)283(4位二进制全加器)1片6、万用表1块三、实验原理组合逻辑电路是数字电路中最常见的逻辑电路之一。
组合逻辑电路的特点,就是在任意时刻电路的输出仅取决于该时刻的输入信号,而与信号作用前电路所处的状态无关。
本实验是根据给定的逻辑功能,设计出实现这些功能的组合逻辑电路。
不考虑低位进位,只本位相加,称半加。
实现半加的电路,为半加器。
考虑低位进位的加法称为全加。
实现全加的电路,为全加器。
实现三个输入变量(一位二进制数)全加运算功能的电路称为1位全加器。
实现多位二进制数相加有串行多位加法和并行多位加法两种形式,其中比较简单的一种电路是采用多个1位全加器并行相加,逐位进位的方式。
实验用器件管脚介绍:1、74HC(LS)00(四二输入与非门)管脚如下图所示。
2、74HC(LS)86(四二输入异或门)管脚如下图所示。
3、74HC(LS)153(双四选一数据选择器)管脚如下图所示。
4、74HC(LS)283(4位二进制全加器)管脚如下图所示。
四、 实验内容与步骤1、用门电路实现全加器(基本命题)参照表达式i i i i C B A S ⊕⊕=,i i i i i i B A C B A C +⊕=+)(1,其中i S 为本位和,i C 为低位向本位的进位,1+i C 为本位向高位进位,设计用与非门74HC(LS)00及异或门74HC(LS)86实现1位全加器的实验电路图,搭接电路,用LED 显示其输出,并记录结果在下表中。
1.1电路图1.2实验结果(基本命题)2、用数选器实现全加器输出Sn参照和实验内容与步骤1完全相同的逻辑功能,设计用与非门74HC(LS)00和数选器74HC(LS)153实现1位全加器输出S n的实验电路图,搭接电路,用LED显示其输出,观察电路的逻辑功能是否与设计功能一致。
数字电路实验报告——全加器

数字电路实验报告——全加器
一、实验目的
本实验以PT5801数字电路模块为本,搭建全加器模块,通过实验表实验结果,分析和探究全加器的模块运作。
二、实验要点
(1)准备实验条件:PT5801数字电路模块,模块芯片,模块芯片胶结线,电源,模拟电路仪表和相关配件。
(2)搭建实验模块:将PT5801数字电路模块安装在试验板上,把它的芯片用胶结线接进芯片接口上,将它的上,下,左,右的输入信号用胶结线接到模拟电路板上,最后接上电源供电即可。
(3)进行实验:将上,下,左,右的输入信号分别为0,1,1,0的状态,测试出输出信号,1,保存实验表,观察相关参数趋势。
(4)分析实验结果:通过实验表,可以看出在四种不同组合输入时,只要输入任意一种组合,输出结果都会是1,这是由于全加器为一种位加法器,运行由机械加减器变更成位加法器,在进行两个或多个数据的加法操作时,此模块就可以起效作用,使计算机内部的计算速度大大提高。
三、小结
本次实验通过PT5801数字电路模块搭建全加器模块,通过四种不同组合输入,观察输出结果,分析出全加器是一种位加法器,对电脑中计算机内部计算速度有很大的提高。
数字电路实验报告——全加器

数字电路实验报告——全加器一、实验目的1.了解全加器的工作原理和应用。
2.掌握全加器的逻辑电路。
3.能够实现全加器的电路。
二、实验原理1.全加器的概念全加器是将三个二进制数相加的电路,其中两个输入用于加,另一个输入用于进位。
目前计算机中都采用二进制数系,因此采用全加器电路可以将二进制数计算的加、减、乘、除等运算转化为逻辑电路控制。
2.全加器电路原理全加器一般包括两个半加器,也就是相邻的两位之间的进/退位。
全加器的三个输入:A、B:相邻位的输入。
Cin:低一级的进位数。
输出:S:相邻位的和。
Cout:进位输出。
半加器(HA)是组成全加器的基本单元,其有两个输入和两个输出。
半加器的输出只考虑了A、B两个输入相加的进位情况,而对于进位需要从低一位的进位来考虑是否产生进位。
因此,需要将半加器和前一位的进位一起运算才能得到正确结果。
三、实验装置1.数字实验箱。
2.全加器IC 7483。
3.数字示波器。
四、实验步骤1. 将全加器IC 7483插在数字实验箱的插孔上。
2. 根据全加器的逻辑关系,接线如下图所示。
3. 输入逻辑信号,并观察全加器的输出结果。
4. 将输出结果接入数字示波器中,观察波形。
五、实验结果及分析本次实验使用全加器IC 7483进行数字电路的设计与实现,由于全加器具有计算机中常见的二进制数加法功能,因此在缺少专业计算机设备或软件的情况下,可以使用数字逻辑电路来进行二进制数的计算。
在实验中,传入的逻辑信号为001和010,分别作为相邻位的数字输入A、B,Cin输入为0,代表即不需要进位。
从输出结果中可以看出,在全加器电路的输出端正确得到了二进制数001和010的相加结果,即为011。
通过实验,可以发现全加器的工作原理和应用,掌握全加器的逻辑电路,并能够实现全加器电路。
六、实验结论1.全加器是一个能够将三个二进制数相加的电路。
2.全加器由两个半加器组成,每个半加器有两个输入和两个输出。
3.在计算机中常用全加器电路进行二进制数的计算。
全加器实验报告

全加器实验报告全加器实验报告引言:全加器是数字电路中的基本组件之一,用于实现两个二进制数的加法运算。
在本次实验中,我们将学习如何设计和实现一个全加器电路,并通过实验验证其正确性和可靠性。
实验目的:1. 理解全加器的原理和工作方式;2. 学习使用逻辑门实现全加器电路;3. 掌握实验仪器的使用方法;4. 验证全加器电路的正确性和可靠性。
实验器材:1. 实验板2. 逻辑门芯片(与门、或门、非门)3. 连线4. 电源实验步骤:1. 首先,我们需要了解全加器的原理。
全加器由两个半加器和一个额外的输入端组成。
半加器用于计算两个输入位的和与进位,而额外的输入端用于接收前一位的进位。
全加器的输出包括两个部分:当前位的和和当前位的进位。
2. 根据全加器的原理,我们可以使用逻辑门来实现它。
首先,使用与门计算当前位的进位。
将两个输入位和前一位的进位作为与门的输入,输出结果为当前位的进位。
3. 接下来,使用或门计算当前位的和。
将两个输入位和前一位的进位作为或门的输入,输出结果为当前位的和。
4. 最后,使用非门将当前位的进位取反,作为全加器的输出。
5. 按照上述设计,将逻辑门芯片连接到实验板上。
确保连接的正确性和稳定性。
6. 给实验电路供电,并输入测试数据。
观察输出结果是否符合预期。
实验结果:通过实验,我们成功实现了一个全加器电路,并验证了其正确性和可靠性。
输入不同的测试数据,我们得到了相应的输出结果。
这证明了全加器电路的功能和性能。
讨论与分析:全加器是数字电路中的重要组件,广泛应用于计算机和其他数字系统中。
它的设计和实现对于数字电路的正确运行至关重要。
通过本次实验,我们深入了解了全加器的原理和工作方式,并通过实验验证了其正确性和可靠性。
然而,在实际应用中,全加器电路可能会面临一些问题。
例如,输入信号的噪声、电源波动等因素都可能影响全加器的性能。
因此,在实际设计中,需要采取一些措施来提高全加器电路的抗干扰性和稳定性。
另外,全加器电路的设计还可以进一步优化。
全加器数电实验报告

全加器数电实验报告全加器数电实验报告引言:数电实验是电子信息工程专业的一门重要课程,通过实践操作,能够更好地理解和掌握数字电路的原理和设计方法。
本次实验主要是关于全加器的设计和实现,全加器是数字电路中的基本组成部分,用于实现两个二进制数的相加运算。
通过本次实验,我将深入了解全加器的工作原理和内部结构,并通过实际搭建电路和观察信号波形来验证其正确性。
一、实验目的:1. 理解全加器的工作原理;2. 掌握全加器的逻辑电路设计方法;3. 通过实验验证全加器的正确性。
二、实验原理:全加器是一种能够实现两个二进制数相加的电路,由于二进制数的相加可能会产生进位,所以全加器有三个输入端:两个二进制数的输入端和一个来自低位的进位输入端。
全加器的输出端有两个:一个是相加结果,另一个是向高位的进位输出。
全加器的逻辑电路设计如下:1. 对两个输入二进制数进行异或运算,得到相加结果;2. 对两个输入二进制数进行与运算,得到进位输出;3. 将进位输入与相加结果进行异或运算,得到最终的和输出。
三、实验步骤:1. 准备实验所需器材和元件:集成电路芯片、电路板、导线等;2. 根据实验原理,设计全加器的逻辑电路图;3. 将电路图转化为实际电路连接方式,搭建电路;4. 使用示波器观察输入信号和输出信号的波形;5. 调整输入信号,观察输出信号的变化;6. 验证全加器的正确性,比较输出信号和预期结果。
四、实验结果与分析:在实验过程中,我按照实验步骤搭建了全加器的电路,并通过示波器观察了输入信号和输出信号的波形。
通过调整输入信号,我可以清晰地观察到输出信号的变化。
在输入信号为0和0的情况下,输出信号为0,符合预期结果。
在输入信号为1和0的情况下,输出信号为1,也符合预期结果。
在输入信号为1和1的情况下,输出信号为0,但同时产生了一个进位输出信号,这也是全加器的特点。
通过对比输出信号和预期结果,可以验证全加器的正确性。
如果输出信号与预期结果一致,说明全加器的设计和实现是正确的。
数字电路实验报告_北邮

一、实验目的本次实验旨在通过实践操作,加深对数字电路基本原理和设计方法的理解,掌握数字电路实验的基本步骤和实验方法。
通过本次实验,培养学生的动手能力、实验技能和团队合作精神。
二、实验内容1. 实验一:TTL输入与非门74LS00逻辑功能分析(1)实验原理TTL输入与非门74LS00是一种常用的数字逻辑门,具有高抗干扰性和低功耗的特点。
本实验通过对74LS00的逻辑功能进行分析,了解其工作原理和性能指标。
(2)实验步骤① 使用实验箱和实验器材搭建74LS00与非门的实验电路。
② 通过实验箱提供的逻辑开关和指示灯,验证74LS00与非门的逻辑功能。
③ 分析实验结果,总结74LS00与非门的工作原理。
2. 实验二:数字钟设计(1)实验原理数字钟是一种典型的数字电路应用,由组合逻辑电路和时序电路组成。
本实验通过设计一个24小时数字钟,使学生掌握数字电路的基本设计方法。
(2)实验步骤① 分析数字钟的构成,包括分频器电路、时间计数器电路、振荡器电路和数字时钟的计数显示电路。
② 设计分频器电路,实现1Hz的输出信号。
③ 设计时间计数器电路,实现时、分、秒的计数。
④ 设计振荡器电路,产生稳定的时钟信号。
⑤ 设计数字时钟的计数显示电路,实现时、分、秒的显示。
⑥ 组装实验电路,测试数字钟的功能。
3. 实验三:全加器设计(1)实验原理全加器是一种数字电路,用于实现二进制数的加法运算。
本实验通过设计全加器,使学生掌握全加器的工作原理和设计方法。
(2)实验步骤① 分析全加器的逻辑功能,确定输入和输出关系。
② 使用实验箱和实验器材搭建全加器的实验电路。
③ 通过实验箱提供的逻辑开关和指示灯,验证全加器的逻辑功能。
④ 分析实验结果,总结全加器的工作原理。
三、实验结果与分析1. 实验一:TTL输入与非门74LS00逻辑功能分析实验结果表明,74LS00与非门的逻辑功能符合预期,具有良好的抗干扰性和低功耗特点。
2. 实验二:数字钟设计实验结果表明,设计的数字钟能够实现24小时计时,时、分、秒的显示准确,满足实验要求。
数电实验三加法器

实验三一.实验目的1.掌握全加器的工作原理与逻辑功能。
2.掌握全加器的应用。
二.实验设备及器材数字电路实验箱稳压电源 74LS00 CD4008B三.实验原理全加器是中规模组合逻辑器件,它实现二进制数码的加法运算。
CD4008B为四位加法器,其逻辑符号如图2,A3、A2、A1、A0和B3、B2、B1、B0为两个四位二进制数,CI为进位输入端,CO为进位输出端。
图2全加器主要用于数值运算,i位全加器可以实现两个i位二进制数的加法运算。
另外,全加器也可以实现组合逻辑函数,如用全加器实现四位二进制数向BCD码的转换。
四.实验内容1.按照全加器真值表,利用逻辑电平产生电路及逻辑电平指示电路验证CD4008B的逻辑功能,画出测试电路图。
A3、A2、A1、A0和B3、B2、B1、B0为两个四位二进制数:加数和被加数,CIN为进位输入,S3、S2、S1、S0为输出的和,CON为进位输出端。
2.连接 B/BCD码转换电路,验证其实验结果是否与真值表一致。
二进制码转换为BCD码时,9以前即0000—1001,二进制数B和BCD码二者相等。
但九以后,即1010—1111,需要给B加6(0110)才能和BCD码在数值上相等。
因此利用四位全加器实现转换时,以四位二进制数作为被加数,而加数在四位二进制数为0000—1001时为0000,为1001—1111时为0110,这样就可实现B/BCD的转换。
图3 B/BCD码转换电路验证得其实验结果与真值表一致3.设计电路,完成1位十进制数的相加运算,使实现7+9=?,6+4=?,和3+2=?,并用数码管显示电路。
可得图四真值表:图四真值表实验结果:数码管显示电路图如下图四五.实验结论与反思1.全加器主要用于数值运算,其有多种,也可用于实现逻辑函数。
2.用四位全加器实现四位二进制数向BCD码的转换,用逻辑函数实现,要注意函数的产生与电路的连接。
3.完成1位十进制数的加法器时,需根据相加得到的和的大小的不同来连接电路,和越大,电路越复杂,越难实现。
王利利三位全加器

计算机组成原理实验报告题目:__三位全加器___学号: 01111609_______姓名:_王利利_______ 教师: 孙丽________东南大学成贤学院计算机系2013年10月30日实验题目实验报告正文一律使用A4打印纸打印或手写,页眉上标明“《XXXX》课程实验”字样。
页面设置上边距2.5cm,下边距2 cm,右边距2 cm(左装订),多倍行距1.25倍。
正文用宋体5号字,页眉和页脚同宋体小5号字并居中。
1、实验内容三位全加器的设计与实现。
2、实验目的与要求a)通过课本的学习熟练掌握一下全加器和半加器的设计。
b)熟悉实验硬件平台的使用c) 、理解层次化的设计方法3、实验环境Max+plus II 的开发软件4、设计思路分析(包括需求分析、整体设计思路、概要设计)一个3位全加器可以由3个1位全加器构成,加法器间的进位可以串行方式实现,即将低位加法器的进位输出cout与相邻的高位加法器的最低进位输入信号cin相接5、详细设计1) 参考书本了解串行加法器的理论知识;2)之前已经做过一位全加器的设计,通过串行方法进行设计;3)设计步骤如下:a )由三位全加器可以看做3个1位全加器级联而成,首先采用基本逻辑门设计一位全加器,而后通过多个1位全加器级联实现3位全加器。
b )根据原理图链接好如图一 c )进行编译 d)进行仿真如图二6、实验结果与分析图一:电路图由三位全加器串联组成.(c4为和c3为进位)图二:仿真波形1仿真波形 2 :取了一个特例p7=0;p6=p5=p4=p3=p2=p1=1;则相应地结果为c4=0;c3=c2=c1=1.7、实验体会与建议通过这次实验学习并且掌握了QuartusⅡ开发平台的基本使用,学习了基于原理图输入设计法设计数字电路的方法,能用原理图输入设计法设计通过三个全加器串联可以设计三位全加器但是这种方法运行速度慢有较大的时延。
全加器实训报告

一、实验目的1. 理解全加器的原理和组成。
2. 掌握全加器电路的设计和搭建方法。
3. 通过实验验证全加器的逻辑功能。
4. 提高电子电路实验操作技能。
二、实验原理全加器是一种能够进行二进制加法运算的数字电路,它能够同时处理来自两个加数和一个来自低位的进位信号,并将结果输出。
全加器由两个半加器和一个或门组成,其中两个半加器分别负责处理加数和进位信号,或门则将两个半加器的输出相加得到最终结果。
三、实验仪器与材料1. 数字电路实验箱2. 74LS00(四路2-3-3-2输入与或非门)3. 74LS86(异或门)4. 导线5. 连接器四、实验步骤1. 设计电路图:根据全加器的原理,设计出电路图,包括半加器和或门的连接方式。
2. 搭建电路:按照电路图,在实验箱上搭建全加器电路。
3. 连接测试:将电路的输入端分别连接到数字电路实验箱的输入端口,将输出端连接到相应的输出端口。
4. 测试验证:通过改变输入端口的电平,观察输出端口的电平变化,验证全加器的逻辑功能。
五、实验结果与分析1. 半加器测试:通过将两个输入端分别连接到高电平和低电平,观察输出端口的电平变化,验证半加器的逻辑功能。
2. 全加器测试:将一个半加器的输出端连接到另一个半加器的进位输入端,将或门的输入端连接到两个半加器的输出端,通过改变输入端口的电平,观察输出端口的电平变化,验证全加器的逻辑功能。
六、实验心得体会1. 通过本次实验,我深入理解了全加器的原理和组成,掌握了全加器电路的设计和搭建方法。
2. 在实验过程中,我学会了如何使用数字电路实验箱和相应的元器件,提高了电子电路实验操作技能。
3. 通过实验验证全加器的逻辑功能,我对数字电路的基本概念有了更深入的理解。
七、实验总结本次全加器实训实验,让我对数字电路的基本原理和组成有了更深入的理解,提高了我的电子电路实验操作技能。
在实验过程中,我遇到了一些问题,但在老师和同学的指导下,我成功解决了这些问题,收获颇丰。
全加器及应用的实验原理

全加器及应用的实验原理1. 全加器的基本原理全加器是用来实现二进制数字相加的电路。
它接收两个输入信号A和B,以及一个进位信号Cin,输出一个和信号S和一个进位输出信号Cout。
1.1 全加器的真值表全加器的真值表如下:A B Cin S Cout0 0 0 0 00 0 1 1 00 1 0 1 00 1 1 0 11 0 0 1 01 0 1 0 11 1 0 0 11 1 1 1 11.2 全加器的逻辑电路图全加器的逻辑电路图如下所示:_______A ----| || |----- SB ----| Full || Adder |----- CoutCin ---| ||_______|2. 全加器的应用全加器是数字电路中非常重要的组件,它在多种数字电路中发挥着关键的作用。
以下是全加器的几个应用例子:2.1 加法器全加器可以用来构建加法器,实现多位二进制数字相加的功能。
多位加法器是将多个全加器串联起来的电路。
例如,一个4位加法器就需要四个全加器来完成。
2.2 二进制数减法器全加器也可以用于实现二进制数的减法。
减法器和加法器很相似,只是在输入信号上作了一些改变。
通过将被减数、减数和一个补码输入给减法器,可以实现减法运算。
2.3 乘法器全加器还可以用于构建乘法器。
乘法器是将多个加法器和逻辑门组合而成的电路,用来计算两个二进制数的乘积。
2.4 计数器计数器是一种电路,用于计数操作。
全加器可以被用来构建计数器电路,实现二进制计数功能。
3. 实验原理与步骤3.1 实验原理本实验通过使用全加器实现二进制数字相加的功能,展示全加器在数字电路中的应用。
实验中,我们将使用真值表和逻辑电路图来证明全加器的正确性。
3.2 实验步骤1.准备所需材料和工具,包括全加器芯片、电路板、电源以及逻辑电路图。
2.按照逻辑电路图,将全加器芯片正确连接到电路板上。
3.确保电源正常工作,并将其接入电路板。
4.根据真值表,依次输入不同的A、B和Cin的组合,并验证输出的S和Cout是否与真值表一致。
全加器的实验报告

一、实验目的1. 理解全加器的概念和组成原理。
2. 掌握全加器的逻辑功能及其在数字电路中的应用。
3. 通过实验,验证全加器的逻辑功能,加深对全加器电路的理解。
二、实验原理全加器是一种能够实现两个二进制数相加,同时考虑来自低位进位信号的加法器。
它由两个半加器和一个与门组成。
其中,两个半加器分别用于实现两个加数的加法运算,与门用于处理来自低位的进位信号。
全加器的逻辑表达式如下:S = A ⊕ B ⊕ CinCout = (A ∧ B) ∨ (B ∧ Cin) ∨ (Cin ∧ A)其中,S为全加器的和输出,Cout为进位输出,A和B为两个加数,Cin为进位输入。
三、实验器材1. 数字电路实验箱2. 集成芯片:74LS86(异或门)、74LS08(与门)、74LS32(或门)3. 导线四、实验步骤1. 搭建全加器电路(1)根据实验原理图,在实验箱上连接两个半加器和两个与门。
(2)将A、B、Cin分别接入相应的电平开关,将S和Cout分别接入发光二极管。
(3)检查电路连接是否正确。
2. 测试全加器功能(1)设置A、B、Cin的不同电平组合,观察发光二极管显示的S和Cout状态。
(2)记录实验数据,验证全加器的逻辑功能。
3. 比较实验结果与理论值(1)根据实验数据,分析全加器的逻辑功能是否与理论值相符。
(2)对实验过程中出现的问题进行分析和总结。
五、实验结果与分析1. 实验数据| A | B | Cin | S | Cout ||---|---|-----|---|-------|| 0 | 0 | 0 | 0 | 0 || 0 | 0 | 1 | 1 | 0 || 0 | 1 | 0 | 1 | 0 || 0 | 1 | 1 | 0 | 1 || 1 | 0 | 0 | 1 | 0 || 1 | 0 | 1 | 0 | 1 || 1 | 1 | 0 | 0 | 1 || 1 | 1 | 1 | 1 | 1 |2. 分析通过实验数据可以看出,全加器的逻辑功能与理论值相符。
实验三.全加器和奇偶判断资料

实验三组合逻辑电路请交实验报告(写上座位号)实验目的1.掌握组合集成电路元件的功能检查方法。
2.熟悉全加器和奇偶位判断电路的工作原理。
3.掌握组合逻辑电路的功能测试方法及设计方法。
用与非门74LS00、与或非门74LS55 设计P500 P503实验原理组合逻辑电路设计的一般步骤:a)根据给定的功能要求,列出真值表;b)求各个输出逻辑函数的最简“与-或”表达式;c)将逻辑函数形式变换为设计所要求选用逻辑门的形式;d)根据所要求的逻辑门,画出逻辑电路图。
一位半加器A iB iC i S i1110 1 0 1 0 1 1 0 0 0 0 0 C i S i B i A i输 出 输 入 ii i i i i i i B A C B A B A S =+=一位全加器A iB iC i-1C i S iiA iB 1-iC iS iC 0 1 1 0 0 111111 0 0 1 1 1 0 1 0 1 0 1 0 0 1 1 0 1 1 0 0 1 0 1 0 0 0 0 0 0 结果输出全加器输入 1111----+++=i i i i i i i i i i i i i C B A C B A C B A C B A S 1111----+++=i i i i i i i i i i i i i C B A C B A C B A C B A C一位全加器A B C C i S i一位半加器A BC i S i '1111----+++=i i i i i i i i i i i i i C B A C B A C B A C B A S一位全加器A B C C i S i一位半加器A B C i S i '))((AB B A B A AB ++=1111----+++=i i i i i i i i i i i i i C B A C B A C B A C B A C 11--++=i i i BC AC AB C )()()()(11--+'⋅+=++'+=i i i i i C S B A C B A S B A C数码奇偶位判断电路全加器和实验内容1.测试与非门74LS00、与或非门74LS55的逻辑功能。
全加器的实验报告

全加器的实验报告全加器的实验报告引言全加器是数字电路中的基本模块之一,用于实现数字加法运算。
本实验旨在通过实际搭建和测试全加器电路,加深对全加器原理的理解。
实验目的1. 掌握全加器的工作原理和电路结构;2. 熟悉数字电路实验中的实际搭建和测试方法;3. 分析全加器电路的性能和应用。
实验器材1. 电路实验箱;2. 电源模块;3. 逻辑门芯片(如74LS08、74LS32等);4. 连接线等。
实验原理全加器是一种能够实现三个输入和两个输出的数字电路。
它可以将两个二进制数的和以及进位输入作为输入,输出它们的和以及进位输出。
全加器的电路结构由两个半加器和一个或门组成。
半加器用于计算两个输入位的和以及进位输出,而或门用于将两个半加器的进位输出与输入的进位相加。
实验步骤1. 搭建全加器电路:根据全加器的电路结构,使用逻辑门芯片和连接线搭建全加器电路;2. 连接电源:将电源模块连接到电路实验箱上,确保电路供电正常;3. 输入信号:将两个二进制数和进位输入信号连接到全加器电路的输入端;4. 测试输出:通过示波器或LED灯等测试工具,检测全加器电路的输出信号;5. 记录实验数据:记录输入信号和对应的输出结果,以便后续分析。
实验结果与分析根据实验步骤,我们成功搭建了全加器电路并进行了测试。
以下是部分实验数据记录:输入信号:A=1, B=1, Cin=0输出信号:Sum=0, Cout=1输入信号:A=0, B=1, Cin=1输出信号:Sum=0, Cout=1输入信号:A=1, B=1, Cin=1输出信号:Sum=1, Cout=1通过对实验数据的分析,我们可以得出以下结论:1. 当输入信号A和B都为1时,无论进位信号Cin的值如何,输出信号Sum始终为1;2. 当输入信号A和B都为0时,无论进位信号Cin的值如何,输出信号Sum始终为0;3. 当输入信号A和B不同时,输出信号Sum的值取决于进位信号Cin的值。
三位全加器版图课程设计

三位全加器版图课程设计一、教学目标本课程的学习目标包括:1.知识目标:学生能够理解并掌握三位全加器的电路原理、功能和应用,了解数字电路的基本组成和设计方法。
2.技能目标:学生能够运用逻辑推理和分析能力,设计并搭建三位全加器电路,培养实验操作和问题解决能力。
3.情感态度价值观目标:培养学生对科学探究的兴趣,提高学生对电子技术的认识,培养学生团队协作和自主学习的能力。
二、教学内容本课程的教学内容主要包括:1.三位全加器的电路原理:介绍三位全加器的电路结构、工作原理和逻辑功能。
2.三位全加器的应用:讲解三位全加器在数字电路中的应用场景和实例。
3.数字电路设计方法:介绍数字电路的设计方法,包括逻辑门、逻辑函数和逻辑电路等。
4.实验操作:安排实验室实践环节,让学生亲自动手搭建三位全加器电路,并进行功能验证。
三、教学方法本课程的教学方法包括:1.讲授法:教师通过讲解三位全加器的电路原理和应用,引导学生掌握相关知识。
2.讨论法:学生进行小组讨论,促进学生对三位全加器设计和应用的深入理解。
3.案例分析法:分析实际案例,让学生了解三位全加器在数字电路中的应用。
4.实验法:安排实验室实践环节,让学生通过实际操作,加深对三位全加器原理和应用的理解。
四、教学资源本课程的教学资源包括:1.教材:选用权威、实用的教材,为学生提供系统、全面的学习材料。
2.参考书:提供相关领域的参考书籍,丰富学生的知识体系。
3.多媒体资料:制作精美的PPT、教学视频等多媒体资料,提高学生的学习兴趣。
4.实验设备:准备充足的实验设备,确保每个学生都能动手实践,提高实验操作能力。
五、教学评估本课程的评估方式包括:1.平时表现:评估学生的课堂参与度、提问回答和团队协作等情况,占总评的30%。
2.作业:布置相关作业,评估学生的理解和应用能力,占总评的20%。
3.考试:进行期中和期末考试,评估学生的知识掌握和运用能力,占总评的50%。
评估方式应客观、公正,能够全面反映学生的学习成果。
03实验三 加法器的设计与应用

4位二进制加 数A 输入端
向高位片的 进位输出 本位和输出端 相加结果读数为 C0S3S2S1S0
4位二进制加 数B 输入端 低位片进位输入端
74LS283逻辑符号
四、实验内容及步骤
1.用基本门电路实现全加器电路。
解:①逻辑抽象 输入变量: 被加数为A,加数为B 由低位来的进位为Ci 输出变量: 相加后本位和为S 往高位的进位为Co
i i
1
1
BCi A 00 01 0 1 1
11 1
1
10
1
Co A BC i A B C i AB C i ABC ( A B ) C i AB ( A B ) C i AB
四、实验内容及步骤
③逻辑电路图
用一片74LS00和一片74LS86即可实现。
四、实验内容及步骤
如:
要考虑低位 来的进位
0 0 0 1
全加器实现
+ 0 0 1 1
进位
1 1 01 0 0
不考虑低位 来的进位
半加器实现
三、实验原理
多个一位全加器进行级联可以得到多位全加器。 74ls283是采用快速进位的四位二进制全加器.与之 类似的还有 74ls83等。
83管脚图
三、实验原理
A4 A3 A2 A1 B4 B3 B2 B1 CI ∑ CO S4 S3 S2 S1 S4 S3 S2 S1
END
兰州交通大学 国家级电工电子实验教学示范中心
真值表
A 0 0 0 0 1 1 1 1
B 0 0 1 1 0 0 1 1
Ci 0 1 0 1 0 1 0 1
S 0 1 1 0 1 0 0 1
Co 0 0 0 1 0 1 1 1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验报告
课程名称:数字电路实验第 3 次实验实验名称:全加器应用
实验时间:2012 年 4 月 1 日
实验地点:组号
学号:
姓名:
指导教师:评定成绩:
一、实验目的:
1.了解算术运算电路的结构。
2.掌握74LS283先行进位全加器的逻辑功能和特点。
3.学习全加器的应用。
二、实验仪器:
三、实验原理:
算术运算电路是脉冲与数字电路的核心部件之一,工作模式有加、减、乘、除等运算,尤其以加法为最基本,其电路构成既有组合逻辑,也有时序逻辑。
本实验采用的逻辑器件4位全加器为TTL双极型数字集成电路74LS283,是组合逻辑电路,它的特点是先行进位,因此运算速度很快,其外形为双列直插,引脚排列如图3-1所示,逻辑符号如图3-2所示。
它有两组4位二进制数输入A4A3A2A1、B4B3B2B1,一个向最低位
的进位输入端CI,有一组二进制数输出S4S3S2S1,一个最高位的进
位输出端CO,算术加法运算关系式见左所列。
利用74LS283可以实
现一些算术运算。
(1)两个4位二进制数相加
因为74LS283本身是全加器,所以可以直接进行4位二进制数加法,例如令:A4A3A2A1=1001,B4B3B2B1=1101,CI=0,则输出为C4S4S3S2S1=10110。
有些码组变换存在加法关系,如8421BCD码转换至余3码,只要在8421BCD码基础上加3(0011)即可实现变换。
(2)两个1位8421BCD 码相加
1位BCD 码要用4位二进制数来表示,但是4位二进制数与1位BCD 码并不完全相应。
例如对4位二进制数1001,若加1则为1010,而对8421BCD 码1001(9)再加1后则为10000(10D ),即用4位二进制数表示1位8421BCD 码时禁止出现1010~1111这六个码组。
因此,用74LS283二进制全加器进行BCD 码运算时需要在组间进位方式上加一个校正电路,使原来的逢16进1自动校正为逢10进1。
所以,进行BCD 码加法时,分为两步,第一步将BCD 码按二进加法运算规则进行,第二步对运算结果进行判断,若和数大于9或有进位CO=1则电路加6(0110),并在组间产生进位,若和数小于或等于9,则保留该运算结果,保留该运算结果即加0(0000)。
二进制数6和0只有中间两位不同,可以设为0FF0,用校正电路使F=0或1来产生0或6,F 的设计如下,由表3-1得到卡诺图,见图3-3,经化简得到表达式:
F=S4S3+S4S2+C4
由此得到逻辑电路见图3-4,输出低4位是L4L3L2L1,高4位用L5表示,因为两个1位BCD 码相加最大是18,高位不会大于1。
其中,74LS10引脚排列如图3-5所示,逻辑符号如图3-6所示。
(3)两个4位二进制数相减
两个4位二进制数相减可以看做两个带符号的4位二进制数相加,即原码的相减变为补码的相加,而正数的补码就是本身,负数的补码是反码加1,这样,A-B=A+(-B),就可利用74LS283实现减法运算。
A数照常输入,B数通过反相器输入,加1可以使CI=1得到,这样输出的结果就是两数之差,但是这个结果为补码,要通过CO来判别结果正负。
例如7-3(原码0111-0011)转化为补码相加0111+1101=10100这里CO=1,结果为正数,补码0100等于原码,即结果为+4;而3-7(原码0011-0111)转化为补码相加0011+1001=01100这里CO=0,结果为负数,补码1100还要再求补一次才能得到正确的原码,1100求补为0100,即结果为-4。
按习惯,把CO通过非门作为符号位。
逻辑电路见图3-7。
其中,74LS86引脚排列如图3-8所示,逻辑符号如图3-9所示。
四、实验内容:
1.实现两个4位二进制数的加法
直接利用74LS283器件,分别用9个开关表示输入A、B及CI,这9个开关按次序从左到右代表A4A3A2A1、B4B3B2B1、CI(下面几个实验也是如此),输出分别接5个指示灯,也是按次序从左到右代表C4S4S3S2S1。
改变开关状态,观察5个指示灯的变化,记录五组数据:
(注意:保留此电路,下一个实验还要用)
答:电路图:
数据:
(2
利用上个实验的电路,把A当做8421BCD码输入,B和CI选取适当值。
输出为S4S3S2S1,要求是余3码。
依此改变A,观察指示灯的变化,记录:
答:只要取3的二进制码输入到B1~B4中,再按照电路输出即可。
(3)实现两个1位
答:电路如图3-4:
用两块74LS283及门电路完成联接,输入用9个开关,输出用5个指示灯,改变开关状态,观察5
(4
用两块74LS283及门电路完成联接,输入用9个开关,输出用5个指示灯,改变开关状态,观察5个指示灯的变化,记录:
电路就按下面的图3-7接:
五、实验思考:
1.如何实现余3码至8421BCD码的转换?
答:如下图中,A1~A4接余3码,B1~B4接-3的补码,把S1~S4输出即可。
2.如何实现两个1位8421BCD码的减法?
答:用下面的电路,把B1~B4取补码输入,A1~A4正常输入,输出L1~L5,其中L5=1时,得数为负值。
由于只做一位8421BCD码的减法,因而不涉及-6的转换。
