任意凸多边形的重心求解
识别多边形中心点的方法
识别多边形中心点的方法全文共四篇示例，供读者参考第一篇示例：多边形是一个平面图形，由若干个线段组成，每个线段都相邻接且不相交，而且首尾相连，形成一个封闭图形。
多边形的中心点是指多边形的质心，也是多边形的重心。
识别多边形中心点是在计算机视觉和图像处理中一个重要的问题，可以帮助我们进行图像分析、目标定位等相关任务。
本文将介绍几种常用的方法来识别多边形的中心点。
方法一：几何中心法在数学几何中，多边形中心点通常是指多边形的“几何中心”，也称几何质心。
几何中心法是最简单直观的方法，通过计算多边形的顶点坐标的平均值来得到多边形的中心点。
具体步骤如下：1. 对多边形的所有顶点坐标进行求和，并除以顶点的个数，得到一个平均坐标作为中心点的坐标。
2. 将得到的中心点坐标绘制在多边形的内部，即可得到多边形的中心点。
这种方法简单易行，适用于正规的凸多边形。
但对于不规则的凸多边形或凹多边形，可能会得到与我们期望不同的结果。
重心法也是一种常用的计算多边形中心点的方法。
重心是一个物理学和工程学概念，是指一个图形的“平均质量点”。
在数学上，一个多边形的重心定义为其所有小面积的中点的平均。
计算多边形的重心的方法是将多边形分解成多个三角形，计算每个三角形的重心，最后取所有三角形重心的平均值作为多边形的重心。
具体步骤如下：1. 将多边形分解成若干个三角形，可以采用三角剖分算法进行分解。
2. 计算每个三角形的重心，即三个顶点坐标的平均值。
通过重心法计算多边形中心点，可以更准确地反映多边形的形状和结构。
但对于复杂的多边形，计算过程可能比较复杂。
方法三：最小外接矩形法最小外接矩形法是另一种计算多边形中心点的方法。
这种方法不需要对多边形进行三角剖分，而是根据多边形的外包矩形来确定多边形的中心点。
计算多边形的最小外接矩形的步骤如下：1. 找到多边形的外包矩形，即包含多边形的最小矩阵。
最小外接矩形法适用于不规则多边形的中心点计算，并且计算效率高，较为简单。
三角形的重心坐标公式
三角形的重心坐标公式
三角形是几何学中最基本的图形之一，它的重心可以用简单的公式来求解。
三角形的重心坐标公式可以表示为：G=(x1+x2+x3)/3,(y1+y2+y3)/3。
这里G表示三角形的重心，而x1、x2、x3、y1、y2、y3分别表示三角形三个顶点的横纵坐标。
该公式可以用于求解任意多边形的重心，因为多边形也可以看作是由多个小三角形构成的。
在这种情况下，我们只需要将多边形各个小三角形的重心加权平均即可得出多边形整体重心的坐标。
此外，该公式还可以用于求凸多边形的内切圆半径。
将所有顶点连接成一条直线后，将直线上各顶点到重心G之间的距离加权平均即可得出内切圆半径R。
而R也是该凸多边形最大内接圆半径，它能帮助我们找出一个物体上最大化覆盖面积所需要使用最少数量物料所对应的圆周长。
总之，三角形的重心坐标公式不但能帮助我们求出任意图形的重心，还能帮助我们找到一个物体上最大化覆盖面积所对应使用物料最少数量时所对应圆周长。
它是一个高效便捷而又实用性强大的工具，也是几何学中不可或缺的部分。
多边形重心问题-计算几何
多边形重⼼问题-计算⼏何转重⼼和⾯积以及坐标的关系三⾓形的重⼼坐标是顶点坐标的平均值。
对于⼀般的多边形（包含⼀条线段的情形）⼀：⼀般适合凸多边形n边多边形可以分成n-2个三⾓形，将这些三⾓形看做质点（质点的位置是三⾓形的重⼼x1,x2,..，质量是⾯积s1,s2,..），那么多边形就由这些质点组成，质点坐标以其质量为权的加权算术平均数即是多边形重⼼坐标x。
x=(x1*s1+x2*s2+...)/(s1+s2+...)s=s1+s2+...算法⼆：任意多边形将算法⼀改进，n边多边形中每两个点（有顺序）加上原点可构成n个三⾓形,将这些三⾓形看做质点（质点的位置是三⾓形的重⼼x1,x2...，质量是⾯积(有正负)s1,s2,...），那么多边形就由这些质点组成，质点坐标以其质量为权的加权算术平均数即是多边形重⼼坐标x。
多边形的⾯积s是这n个三⾓形⾯积(有正负)的代数和的绝对值。
x=(x1*s1+x2*s2+...)/(s1+s2+...)s=|s1+s2+...|算法2代码1 #include<cstdio>2 #include<cmath>3 #include<iostream>4using namespace std;56double cross(double a[2],double b[2]){ //求向量a,b的叉积⼤⼩7return a[0]*b[1]-a[1]*b[0];8 }910int main(void){11int ncase;12 cin>>ncase;13while(ncase--){14int i,k;15double S,tS,a[10002][2],sx,sy;16 cin>>k;17for(i=1;i<=k;i++)18 cin>>a[i][0]>>a[i][1];19 S=0.;sx=0.;sy=0.; //S⾯积,xy横纵坐标和20for(i=1;i<=k;i++){21 tS=cross(a[i],a[i%k+1])/2.;22 S+=tS;23 sx+=tS*(a[i][0]+a[i%k+1][0])/3;24 sy+=tS*(a[i][1]+a[i%k+1][1])/3;25 }26if(fabs(S)<1e-7)27 puts("0.000 0.000");28else29 printf("%.3lf %.3lf\n",fabs(S),(sx+sy)/S);30 }31 system("pause");32return0;33 }。
多边形质心计算公式_c++_解释说明以及概述
多边形质心计算公式c++ 解释说明以及概述1. 引言1.1 概述本文主要介绍了多边形质心计算公式的C++实现，并对其进行了详细的解释说明。
在几何学中，多边形质心是指一个多边形内部所有点的平均值，也被称为重心或几何中心。
计算多边形质心具有广泛的应用领域，包括计算图形的属性、图像处理等。
本文将首先概述整篇文章的结构，然后介绍撰写本文的目的和意义。
1.2 文章结构本文按照如下结构进行组织：引言、多边形质心计算公式解释说明、C++实现多边形质心计算程序、结论与讨论。
在引言部分，我们将对本文进行简要介绍，并概述了各个章节内容。
随后，在第二部分中，我们将详细解释多边形质心的定义与意义，并推导出计算公式。
第三部分将介绍如何使用C++语言来实现这一计算过程，并提供具体代码实现步骤以及测试结果分析。
最后，在第四部分中，我们将总结本文所述内容，并对未来发展方向进行展望。
1.3 目的撰写此篇长文旨在通过对多边形质心计算公式的解释说明和C++实现方法的介绍，帮助读者更好地理解多边形质心的概念和计算过程，并能够利用C++编写程序来计算多边形的质心。
同时，通过对本文所述内容的总结和讨论，我们将进一步提升对该主题的理解，并展望未来在多边形质心计算方面的研究和应用前景。
2. 多边形质心计算公式解释说明:2.1 多边形质心定义与意义:多边形的质心，也称为重心或几何中心，是指位于多边形内部的一个点，其对于多边形各个顶点的欧氏距离之和最小。
质心在计算几何中具有广泛应用，可以用于确定多边形的位置、形状、曲率等特性。
2.2 多边形质心计算公式推导:假设有一个包围多边形的坐标系，并以该坐标系的原点作为参考点，那么可以通过以下步骤推导多边形质心计算公式：- 首先，将多边形分解成若干个三角形。
- 对于每个三角形，找到它的重心（三角形三个顶点坐标的平均值）。
- 对于每个三角形重心，根据其面积与坐标加权求和得出整个多边形质心。
综上所述，在平面上一个n边(n≥3)简单闭合多边形P(x1, y1), (x2, y2), ..., (xn,yn)，其中(xi, yi)表示多边形各顶点坐标。
平面几何证明 凸多边形内任意一点到多边形距离的最大值
平面几何证明凸多边形内任意一点到多边形距离的最大值
我们要证明在凸多边形内任意一点到多边形距离的最大值的相关性质。
首先，我们需要明确什么是凸多边形以及点到多边形的距离是如何定义的。
凸多边形定义：一个多边形，如果从它的一边到另一边的任何线段都完全位于该多边形内，则称该多边形为凸多边形。
点到多边形的距离：点到多边形上任意一点的距离的最小值，就是点到多边形的距离。
但是，这里有一个特殊情况，
就是当点位于多边形内部时，点到多边形的距离为0，因为点已经位于多边形内部了。
但考虑到题目的语境，我们可能更关心点到多边形边界的最大距离。
对于凸多边形内任意一点P，其到多边形各边的垂直距离中的最大值，即为点到多边形的距离的最大值。
为了找到这个最大值，我们可以分别计算点P到多边形每一条边的垂直距离，然后取其中的最大值。
然而，这里有一个更简单的直观理解：
凸多边形内任意一点到多边形距离的最大值一定出现在该点与多边形某个顶点的连线上。
因为对于凸多边形，任意一点到边的垂直距离都不会超过到该边两个端点的距离。
所以，为了找到这个最大值，我们只需计算点P到多边形每一个顶点的距离，然后取其中的最大值即可。
综上所述，凸多边形内任意一点到多边形距离的最大值可以通过计算该点到多边形每一个顶点的距离，然后取其中的最大值来得到。
注意：这里的结论是基于点到多边形边界的最大距离，而不是点到多边形内部的最小距离（这总是0，因为点已经在多边形内部了）。
形心坐标计算公式
形心坐标计算公式
求多边形重心坐标的计算公式如下：
多边形重心坐标=∑（各顶点坐标×该顶点所在边的反正切值之和
/4G)。
其中，G为多边形内接圆的半径，∑和求和符号分别表示多边形各顶点的坐标和反正切值进行的求和操作。
计算公式的求解步骤如下：
（1）求多边形的各边的反正切值，一般都是用tan-1(y/x)的方法求的；。
（2）计算多边形各顶点的坐标：x1，y1，x2，y2，……xn，yn；
（3）计算多边形内接圆的半径G；
（4）求多边形重心坐标：。
多边形重心坐标= ∑（x1*a1+x2*a2+…+xn*an）/4*G 。
（5）根据多边形重心坐标，可以求出多边形重心所在位置。
通过以上步骤，即可得到多边形重心的坐标，从而求出多边形重心所在位置。
计算几何-多边形重心公式
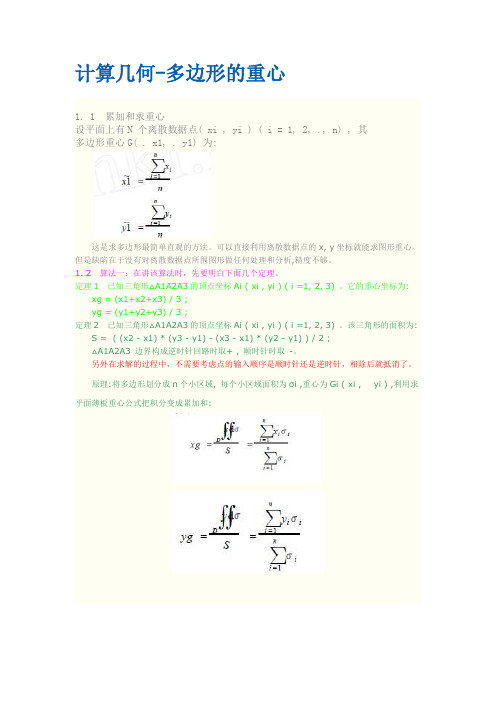
计算几何-多边形的重心1. 1 累加和求重心设平面上有N 个离散数据点( xi , yi ) ( i = 1, 2, ., n) , 其多边形重心G( . x1, . y1) 为:这是求多边形最简单直观的方法。
可以直接利用离散数据点的x, y坐标就能求图形重心。
但是缺陷在于没有对离散数据点所围图形做任何处理和分析,精度不够。
1. 2算法一：在讲该算法时，先要明白下面几个定理。
定理1已知三角形△A1A2A3的顶点坐标Ai ( xi , yi ) ( i =1, 2, 3) 。
它的重心坐标为: xg = (x1+x2+x3) / 3 ;yg = (y1+y2+y3) / 3 ;定理2已知三角形△A1A2A3的顶点坐标Ai ( xi , yi ) ( i =1, 2, 3) 。
该三角形的面积为: S = ( (x2 - x1) * (y3 - y1) - (x3 - x1) * (y2 - y1) ) / 2 ;△A1A2A3 边界构成逆时针回路时取+ , 顺时针时取-。
另外在求解的过程中，不需要考虑点的输入顺序是顺时针还是逆时针，相除后就抵消了。
原理:将多边形划分成n个小区域, 每个小区域面积为σi ,重心为Gi ( xi , yi ) ,利用求平面薄板重心公式把积分变成累加和:由前面所提出的原理和数学定理可以得出求离散数据点所围多边形的一般重心公式:以Ai ( xi , yi ) ( i = 1, 2, ., n) 为顶点的任意N边形A1A2 .An ,将它划分成N - 2个三角形(如图1) 。
每个三角形的重心为Gi (xi , . yi ) ,面积为σi。
那么多边形的重心坐标G( x2, .y2) 为:图1 多边形分解例题：HDU 1115 Lifting the Stone代码：如下。
1 #include<stdio.h>2 #include<math.h>3 #include<stdlib.h>4struct centre5 {6double x , y ;7 };8int cas , n ;9double Area( centre p0 , centre p1 , centre p2 )10 {11double area = 0 ;12 area = p0.x * p1.y + p1.x * p2.y + p2.x * p0.y - p1.x * p0.y - p2.x * p1.y - p0.x * p2.y;13return area / 2 ; // 另外在求解的过程中，不需要考虑点的输入顺序是顺时针还是逆时针，相除后就抵消了。
凸多边形的性质与计算
凸多边形的性质与计算一、凸多边形的定义与基本性质1.凸多边形：一个多边形如果它的所有角都是凸角，即多边形内部任意两点的连线段都完全包含在多边形内部，那么这个多边形就叫做凸多边形。
2.边：凸多边形相邻两个顶点之间的线段称为多边形的边。
3.顶点：凸多边形拐角的地方称为顶点。
4.内角：凸多边形中，顶点与相邻两边构成的角称为内角，内角的度数大于0度小于180度。
5.外角：凸多边形中，一个内角的非相邻角称为外角，外角的度数等于其所对的内角的补角，即外角为直角。
6.对边：凸多边形中，不相邻的两个顶点与它们之间的边称为对边。
7.对角线：凸多边形中，连接不相邻两个顶点的线段称为对角线。
8.边长：凸多边形的边长是指多边形边的长度。
9.面积：凸多边形的面积可以通过分割成三角形计算，也可以利用对角线分割成的三角形面积和计算。
二、凸多边形的计算1.边数：凸多边形的边数用n表示，n为正整数，且n≥3。
2.内角和：凸多边形的内角和为(n-2)×180度。
3.外角和：凸多边形的外角和为360度。
4.对角线数量：凸多边形的对角线数量为n(n-3)/2。
5.面积计算公式：–分割法：将凸多边形分割成n-2个三角形，每个三角形的面积为底乘以高除以2，凸多边形的面积为这些三角形面积之和。
–对角线法：凸多边形的面积等于其半周长与对角线乘积的一半。
其中半周长为(n-2)×180度/n，对角线乘积为所有对角线长度的乘积。
三、凸多边形的特殊性质1.正多边形：所有边长相等，所有内角相等的多边形称为正多边形。
2.圆：特殊的正多边形，当边数趋近于无穷大时，圆的形状越明显。
3.凸五边形：具有5条边和5个内角的凸多边形。
4.凸五边形的对角线数量为5(5-3)/2=5。
5.凸六边形：具有6条边和6个内角的凸多边形。
6.凸六边形的对角线数量为6(6-3)/2=9。
四、凸多边形的应用1.平面几何中的计算：在平面几何中，凸多边形的边长、面积、对角线等性质在计算和证明中起着重要作用。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
模型的建立与求解
一、计算凸多边形的重心
对于任意凸多边形，我们以其重心为蛛网的中枢区中心，也即蜘蛛的等待猎物点，以此点出发，先发出放射丝，再织捕丝。
1.计算任意凸多边形重心的理论基础
1.四边形的重心作法：连接出四边形的一条对角线，这样四边形就变成两个三角形的组合体，分别作出
两个三角形的重心，并连接两个重心成一条线段AB，同样，连接出四边形的另一条对角线，四边形就变成另外两个三角形的组合体，分别作出这两个三角形的重心，并连接两个重心成一条线段CD，则线段AB，CD的交点就是四边形的重心。
2.五边形的重心作法：连接出五边形的任一条对角线，将五边形分为1个三角形与一个四边形组合体，分
别作出三角形的重心，和四边形的重心，并连成线段AB；连接五边形的另外一条对角形，将五边形分为另1个三角形与四边形的组合体，分别作出三角形与四边形的重心，并连接成线段CD；则AB、CD的交点就是五边形的重心。
3、用数学归纳法，对于六边形、七边形，N边形，都可以用上述方法，先连接出一条对角线，将N边形化为一个三角形与(N-1)边形，或四边形与(N-2)边形，然后分别作出重心，并连接成线段，然后再连接另外一条对象线，分别作出两个组合体的重心并连接成线段，两条线段的交点就是N边形的重心。
2．重心计算的算法程序实现：
有了以上理论基础，我们通过C++语言编写了一个计算任意凸多边形的程序，算法思想如下，算法程序见附录一。
○1在平面上取一点(一般取原点)得到N个三角形OP[i]P[i+1](其中点的顺序为逆时针)
○2分别求出这N个三角形的重心Ci和面积Ai(注意此处面积是有向面积, 就是用叉乘求面积时保留其正负号)
○3求出A = A1+A2+...+AN(同样保留正负号的代数相加)
○4重心C = sigma(Ai+Ci)/A;
附录一：任意凸多边形重心C++算法
#include <iostream>
#include <cmath>
#include <iomanip>
using namespace std;
struct point
{
double x;
double y;
};
point gravity(point *p, int n)
{
double area = 0;
point center;
center.x = 0;
center.y = 0;
for (int i = 0; i < n-1; i++)
{
area += (p[i].x*p[i+1].y - p[i+1].x*p[i].y)/2;
center.x += (p[i].x*p[i+1].y - p[i+1].x*p[i].y) * (p[i].x + p[i+1].x);
center.y += (p[i].x*p[i+1].y - p[i+1].x*p[i].y) * (p[i].y + p[i+1].y);
}
area += (p[n-1].x*p[0].y - p[0].x*p[n-1].y)/2;
center.x += (p[n-1].x*p[0].y - p[0].x*p[n-1].y) * (p[n-1].x + p[0].x);
center.y += (p[n-1].x*p[0].y - p[0].x*p[n-1].y) * (p[n-1].y + p[0].y); center.x /= 6*area;
center.y /= 6*area;
return center;
}。