离散数学例题整理
离散数学复习题含答案

离散数学复习题含答案1. 集合论基础集合A和集合B的交集表示为A∩B,它包含所有既属于A又属于B的元素。
请写出集合{1, 2, 3}和{2, 3, 4}的交集。
答案:{2, 3}2. 逻辑运算设命题p为“今天是周一”,命题q为“明天是周三”。
请判断复合命题“p且q”的真值。
答案:假3. 图论初步在无向图中,若存在一条路径使得起点和终点相同,则称该图为欧拉图。
请判断一个有5个顶点且每个顶点的度均为2的无向图是否一定是欧拉图。
答案:是4. 组合数学从5个不同的球中选取3个,有多少种不同的选取方法?答案:10种5. 布尔代数在布尔代数中,逻辑或运算符表示为∨,逻辑与运算符表示为∧。
请计算表达式(A∨B)∧(¬A∨¬B)的值。
答案:¬(A∧B)6. 归纳与递归给定递归关系式T(n) = 2T(n-1) + 1,初始条件为T(1) = 1,求T(3)的值。
答案:T(3) = 2T(2) + 1 = 2(2T(1) + 1) + 1 = 2(2*1 + 1) + 1 =2(3) + 1 = 77. 有限状态机在有限状态机中,状态转移可以通过一个转移函数来描述。
若状态转移函数定义为δ(q, a) = q',其中q和q'是状态,a是输入符号,请说明该函数的作用。
答案:该函数定义了在给定当前状态q和输入符号a的情况下,有限状态机将转移到新的状态q'。
8. 正则表达式正则表达式用于描述字符串的模式。
请写出匹配任意长度的数字串的正则表达式。
答案:\d*9. 命题逻辑命题逻辑中的等价关系是指两个命题逻辑表达式在所有可能的真值赋值下具有相同的真值。
请判断命题p∨¬p和命题¬(p∧¬p)是否等价。
答案:是10. 树的遍历在计算机科学中,树的遍历有前序、中序和后序三种方式。
请简述后序遍历的步骤。
答案:后序遍历的步骤是先访问左子树,然后访问右子树,最后访问根节点。
《离散数学》试题及答案

《离散数学》试题及答案一、选择题(每题5分,共25分)1. 设集合A={1,2,3,4,5},B={2,4,6,8,10},则A∩B的结果是()A. {1,2,3,4,5}B. {2,4}C. {1,3,5}D. {1,2,3,4,5,6,8,10}答案:B2. 下列关系中,哪个是等价关系?()A. ≤B. ≠C. |D. ≠答案:A3. 设图G有5个顶点,每两个顶点之间都有一条边相连,则图G的边数是()A. 5B. 10C. 15D. 20答案:C4. 下列哪一个图是欧拉图?()A. 无向图B. 有向图C. 树D. 环答案:D5. 下列哪一个命题是正确的?()A. 若p→q为真,则p为真B. 若p∧q为假,则p为假C. 若p∨q为真,则q为真D. 若p→q为假,则p为假答案:B二、填空题(每题5分,共25分)1. 设集合A={a,b,c,d},B={c,d,e},则A-B=________。
答案:{a,b}2. 设p是命题“今天是晴天”,q是命题“我去公园玩”,则命题“如果今天不是晴天,那么我不去公园玩”可以表示为________。
答案:¬p→¬q3. 设图G有n个顶点,e条边,则图G的度数之和为________。
答案:2e4. 一个连通图至少有________个顶点。
答案:25. 设图G的邻接矩阵为A,则A的转置矩阵表示________。
答案:图G的转置图三、判断题(每题5分,共25分)1. 离散数学是研究离散结构的数学分支。
()答案:正确2. 两个集合的笛卡尔积是这两个集合的直积。
()答案:正确3. 有向图中,顶点u和顶点v之间的长度为2的路径是指路径上有3条边。
()答案:错误4. 树是一种无向图。
()答案:正确5. 哈夫曼编码是一种贪心算法。
()答案:正确四、应用题(每题25分,共50分)1. 设集合A={1,2,3,4,5},B={2,4,6,8,10},C={3,6,9,12,15},求A∪(B∩C)。
离散数学试题及答案

离散数学试题及答案一、选择题1. 设A、B、C为三个集合,下列哪个式子是成立的?A) \(A \cup (B \cap C) = (A \cup B) \cap (A \cup C)\)B) \(A \cap (B \cup C) = (A \cap B) \cup (A \cap C)\)C) \(A \cup (B \cup C) = (A \cup B) \cup (A \cup C)\)答案:B2. 对于一个有n个元素的集合S,S的幂集中包含多少个元素?A) \(n\)B) \(2^n\)C) \(2 \times n\)答案:B二、判断题1. 对于两个关系R和S,若S是自反的,则R ∩ S也是自反的。
答案:错误2. 若一个关系R是反对称的,则R一定是反自反的。
答案:正确三、填空题1. 有一个集合A,其中包含元素1、2、3、4和5,求集合A的幂集的大小。
答案:322. 设a和b是实数,若a \(\neq\) b,则a和b之间的关系是\(\__\_\)关系。
答案:不等四、解答题1. 证明:如果关系R是自反且传递的,则R一定是反自反的。
解答:假设关系R是自反的且传递的,即对于集合A中的任意元素x,都有(x, x) ∈ R,并且当(x, y) ∈ R和(y, z) ∈ R时,(x, z) ∈ R。
反证法:假设R不是反自反的,即存在一个元素a∈A,使得(a, a) ∉ R。
由于R是自反的,所以(a, a) ∈ R,与假设矛盾。
因此,R一定是反自反的。
答案完整证明了该结论。
2. 已知集合A={1, 2, 3},集合B={2, 3, 4},求集合A和B的笛卡尔积。
解答:集合A和B的笛卡尔积定义为{(a, b) | a∈A,b∈B}。
所以,集合A和B的笛卡尔积为{(1, 2), (1, 3), (1, 4), (2, 2), (2, 3), (2, 4), (3, 2), (3, 3), (3, 4)}。
离散数学例题整理

第一章定律证明:(1) A⋃B=B⋃A (交换律)证∀x x∈A⋃B⇒ x∈A 或 x∈B, 自然有 x∈B 或 x∈A⇒ x∈B⋃A得证 A⋃B⊆B⋃A.同理可证 B⋃A⊆A⋃B.(2) A⋃(B⋂C)=(A⋃B)⋂(A⋃C) (分配律)证∀x x∈A⋃(B⋂C)⇒ x∈A或(x∈B且 x∈C )⇒(x∈A或x∈B)且(x∈A或x∈C)⇒x∈(A⋃B)⋂(A⋃C)得证 A⋃(B⋂C)⊆(A⋃B)⋂(A⋃C).类似可证 (A⋃B)⋂(A⋃C)⊆A⋃(B⋂C).(3) A⋃E=E (零律)证根据并的定义, 有E⊆A⋃E.根据全集的定义, 又有A⋃ E⊆E.(4) A⋂E=A (同一律)证根据交的定义, 有A⋂E⊆A.又, ∀x x∈A,根据全集E的定义,x∈E, 从而 x∈A且x∈E,⇒ x∈A⋂E得证 A⊆A⋂E.例4 证明 A⋃(A⋂B)=A(吸收律)证利用例3证明的4条等式证明A⋃(A⋂B)= (A⋂E)⋃(A⋂B) (同一律)= A⋂(E⋃B) (分配律)= A⋂(B⋃E) (交换律)= A⋂E (零律)= A (同一律)例5 证明 (A-B)-C=(A-C)-(B-C)证 (A-C)-(B-C)= (A ⋂~C) ⋂ ~(B ⋂ ~C) (补交转换律)= (A ⋂~C) ⋂ (~B ⋃ ~~C) (德摩根律) = (A ⋂~C) ⋂ (~B ⋃ C) (双重否定律)= (A ⋂~C⋂ ~B)⋃(A ⋂~C⋂ C) (分配律)= (A ⋂~C⋂ ~B)⋃(A ⋂∅) (矛盾律)= A ⋂~C⋂ ~B (零律,同一律)= (A ⋂~B) ⋂ ~C (交换律,结合律)= (A – B) –C (补交转换律) 例6 证明 (A⋃B)⊕(A⋃C)= (B⊕C) - A证 (A⋃B)⊕(A⋃C)=((A⋃B) - (A⋃C))⋃((A⋃C) - (A⋃B)) =((A⋃B)⋂~A⋂~C)⋃((A⋃C)⋂~A⋂~B)= (B⋂~A⋂~C)⋃(C⋂~A⋂~B)=((B⋂~C)⋃(C⋂~B))⋂~A=((B-C)⋃(C-B))⋂~A= (B⊕C) - A例7 设A,B为任意集合, 证明:若A⊆B, 则P(A)⊆P(B)证∀x x∈P(A) ⇔x⊆A⇒x⊆B (已知A⊆B)⇔x∈P(B)例8 证明A⊕B=A⋃B-A⋂B.A⊕B=(A⋂~B)⋃(~A⋂B)=(A⋃~A)⋂(A⋃B)⋂(~B⋃~A)⋂(~B⋃B)=(A⋃B)⋂(~B⋃~A)=(A⋃B)⋂~(A⋂B)=A⋃B-A⋂B直接法若n是奇数, 则n2也是奇数.假设n是奇数, 则存在k∈N, n=2k+1.于是 n2 = (2k+1)2 = 2(2k2+2k)+1得证n2是奇数.间接法若n2是奇数, 则n也是奇数.只证:若n是偶数, 则n2也是偶数.假设n是偶数, 则存在k∈N, n=2k.于是 n2 = (2k)2= 2(2k2)得证n2是偶数.归谬法若A-B=A, 则A⋂B=∅证用归谬法, 假设A⋂B≠∅, 则存在x,使得x∈A⋂B ⇔x∈A且x∈B⇒x∈A-B且x∈B (A-B=A)⇔ (x∈A且x∉B)且x∈B⇒x∉B且x∈B, 矛盾构造性对每正整数n, 存n个连的正合数.证令x=(n+1)! +1考虑如下n个连续正整数:x+1, x+2,…, x+n,对于i(i=1,2,3,…,n),x+i=(n+1)! +(1+i),此式含有因子1+i,而1+i不等于1也不等于x+i,因此x+i是合数。
(完整版)离散数学题目及答案

数理逻辑习题判断题1.任何命题公式存在惟一的特异析取范式 ( √ ) 2. 公式)(q p p →⌝→是永真式 ( √ ) 3.命题公式p q p →∧)(是永真式 ( √ ) 4.命题公式r q p ∧⌝∧的成真赋值为010 ( × ) 5.))(()(B x A x B x xA →∃=→∀ ( √ )6.命题“如果1+2=3,则雪是黑的”是真命题 ( × ) 7.p q p p =∧∨)( ( √ )8.))()((x G x F x →∀是永真式 ( × ) 9.“我正在撒谎”是命题 ( × ) 10. )()(x xG x xF ∃→∀是永真式( √ )11.命题“如果1+2=0,则雪是黑的”是假命题 ( × ) 12.p q p p =∨∧)( ( √ )13.))()((x G x F x →∀是永假式 ( × )14.每个命题公式都有唯一的特异(主)合取范式 ( √ ) 15.若雪是黑色的:p ,则q →p 公式是永真式 ( √ ) 16.每个逻辑公式都有唯一的前束范式 ( × ) 17.q →p 公式的特异(主)析取式为q p ∨⌝ ( × ) 18.命题公式 )(r q p →∨⌝的成假赋值是110 ( √ ) 19.一阶逻辑公式)),()((y x G x F x →∀是闭式( × )单项选择题1. 下述不是命题的是( A )A.花儿真美啊! B.明天是阴天。
C.2是偶数。
D.铅球是方的。
2.谓词公式(∀y)(∀x)(P(x)→R(x,y))∧∃yQ(x,y)中变元y (B)A.是自由变元但不是约束变元B.是约束变元但不是自由变元C.既是自由变元又是约束变元D.既不是自由变元又不是约束变元3.下列命题公式为重言式的是( A )A.p→ (p∨q)B.(p∨┐p)→qC.q∧┐q D.p→┐q4.下列语句中不是..命题的只有(A )A.花儿为什么这样红?B.2+2=0C.飞碟来自地球外的星球。
离散数学练习题(含答案)

离散数学练习题(含答案)题目1. 对于集合 $A={1,2,3,...,10}$ 和 $B={n|n是偶数,2<n<8}$,求 $A \cap B$ 的元素。
2. 存在三个可识别的状态A,B,C。
置换群 $S_3$ 作用在状态集上。
定义四个动作:$α: A → C, β: A → B, γ: C→ A, δ: B→ C$。
确定式子,描述 $\{α,β,γ,δ\}$ 的乘法表。
3. 证明 $\forall n \in \mathbb{N}$,合数的个数不小于$n$。
4. 给定一个无向带权图,图中每个节点编号分别是$1,2,...,n$,证明下列结论:a. 如果从节点$i$到$j$只有一条权值最小的路径,则这条路径的任意子路径都是最短路径。
b. 如果从节点$i$到$j$有两条或两条以上权值相等的路径,则从$i$到$j$的最短路径可能不唯一。
答案1. $A \cap B = \{2,4,6\}$。
2. 乘法表:3. 对于任意$n$,我们可以选择$n+1$个连续的自然数$k+1,k+2,...,k+n,k+n+1$中的$n$个数,其中$k \in \mathbb{Z}$。
这$n$个数构成的$n$个正整数均为合数,因为它们都至少有一个小于它自身的因子,所以不是质数。
所以合数的个数不小于任意$n$。
4.a. 根据题意,从$i$到$j$只有一条权值最小的路径,即这条最短路径已被确定。
如果从这条路径中任意取出一段子路径,假设这段子路径不是这个节点到$j$的最短路径,那么存在其他从$i$到$j$的路径比这段子路径更优,又因为这条路径是最短路径,所以这段子路径也一定不优于最短路径,矛盾。
所以从这条路径中任意取出的子路径都是最短路径。
b. 如果从节点$i$到$j$有多条权值相等的路径,则这些路径权值都是最短路径的权值。
因为所有最短路径的权值相等,所以这些路径的权值就是最短路径的权值。
所以从$i$到$j$的最短路径可能不唯一。
《离散数学》典型例题
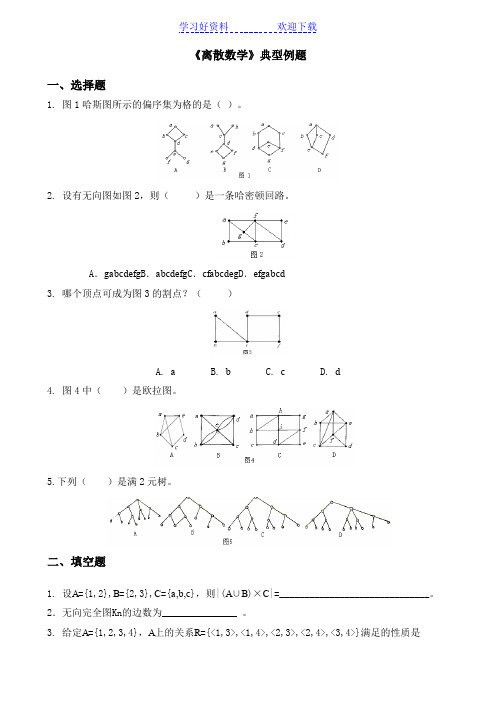
《离散数学》典型例题一、选择题1. 图1哈斯图所示的偏序集为格的是()。
2. 设有无向图如图2,则()是一条哈密顿回路。
A.gabcdefg B.abcdefg C.cfabcdeg D.efgabcd3. 哪个顶点可成为图3的割点?()A. aB. bC. cD. d4. 图4中()是欧拉图。
5.下列()是满2元树。
二、填空题1. 设A={1,2},B={2,3},C={a,b,c},则|(A∪B)×C|=______________________________。
2.无向完全图Kn的边数为_______________ 。
3. 给定A={1,2,3,4},A上的关系R={<1,3>,<1,4>,<2,3>,<2,4>,<3,4>}满足的性质是_________________________。
4. 设A ={a,b,c },F 是A 上的二元关系,F ={<a,a >,<b,b >,<c,c >},则其自反闭包为r (F )=______________________________。
5. 设A 和B 是有穷集合,|A |=m ,|B |=n ,A 到B 有_______多少个不同一对一映射。
三、判断题1.每个正整数都可以唯一地表示为素数的乘积。
( )2.集合X 上的关系R 如果是自反的、反对称的、传递的则称此关系为相容关系。
( )3.一条基本回路一定是简单回路,但一条简单回路不一定是基本回路。
( )4.树是不包含回路的连通图,在(n ,m )树中必有m=n+1( )5.一个有限群<G ,*>的阶n 一定被它的任一个子群的阶m 所等分。
( )四 、综合题1. 求公式(~P →Q) →(Q →~P)的主析取范式和主合取范式。
2. 6个人一起吃饭,围绕圆桌就餐,有多少种就座方式?如果要从4种不同的菜系中点足6道菜,问有多少种点法?3. 一个面包店里有5种不同口味的面包,要挑选8个面包,并且至少有2个奶油味面包和不超过2个咸味面包。
离散数学试题总汇及答案

离散数学试题总汇及答案一、单项选择题(每题2分,共20分)1. 在集合{1, 2, 3, 4}中,子集{1, 2}的补集是()。
A. {3, 4}B. {1, 3, 4}C. {2, 3, 4}D. {1, 2, 3, 4}答案:A2. 命题“若x > 0,则x² > 0”的逆否命题是()。
A. 若x² ≤ 0,则x ≤ 0B. 若x² > 0,则x > 0C. 若x ≤ 0,则x² ≤ 0D. 若x² ≤ 0,则x < 0答案:C3. 函数f(x) = x² + 2x + 1的值域是()。
A. {x | x ≥ 0}B. {x | x ≥ 1}C. {x | x ≥ 2}D. {x | x ≥ -1}答案:B4. 以下哪个图是无向图()。
A. 有向图B. 无向图C. 有向树D. 无向树答案:B5. 以下哪个图是二分图()。
A. 完全图B. 非完全图C. 任意两个顶点都相连的图D. 任意两个顶点都不相连的图答案:C6. 以下哪个是哈密顿回路()。
A. 经过每个顶点恰好一次的回路B. 经过每个顶点至少一次的回路C. 经过每个顶点恰好两次的回路D. 经过每个顶点至少两次的回路答案:A7. 以下哪个是欧拉回路()。
A. 经过每条边恰好一次的回路B. 经过每条边至少一次的回路C. 经过每条边恰好两次的回路D. 经过每条边至少两次的回路答案:A8. 以下哪个是二进制数()。
A. 1010B. 1020C. 1102D. 1120答案:A9. 以下哪个是格雷码()。
A. 0101B. 1010C. 1100D. 1110答案:B10. 以下哪个是素数()。
A. 4B. 6C. 7D. 8答案:C二、填空题(每题2分,共20分)11. 集合{1, 2, 3}与{2, 3, 4}的交集是______。
答案:{2, 3}12. 命题“若x > 0,则x² > 0”的逆命题是:若x² > 0,则______。
全版离散数学 练习题及答案.ppt

课件
例3 对任意两个集合A, B,试证 A (A B) A B
证明 对于任意的x
x A (A B)
x {x x A x ( A B)} x {x x A (x A B)} x {x x A (x A x B)} x {x x A (x A x B)} x {x x A x B}
课件
例10 求图的最小生成树
A 1B34 Nhomakorabea5
2 E
6
1A 2
B
E
4
6
C7 D
C
D
课件
例11
• 无向树T有7片树叶, 3个3度顶点,其余的 都是4度顶点,则T有几个4度顶点?
• 解:设T有x个4度顶点 顶点度数之和: 7+3*3+4x 由树的性质可得总边数: 7+3+x-1 由握手原理可得: 7+3*3+4x=2(7+3+x-1)
求g f
g f { 1,b , 2,b , 3,b }
课件
例12 求复合函数
X {1,2,3}, Y {p, q}, Z {a,b} f { 1, p , 2, p , 3, q } g { p,b , q,b }
求g f
g f { 1,b , 2,b , 3,b }
课件
例: 求幺元、零元、逆元
x A B 因为 x 是任意的,所以有
x ((x A (A B)) (x A B)) 的真值为T,
因此 A ( A B)课件 A B
例4 判断关系的性质
R1 { a, a , a,b , b,b , c,c }
a
1 1 0
M R 1 0 1 0
0 0 1
《离散数学》题库及答案

《离散数学》题库及答案一、选择或填空(数理逻辑部分)1、下列哪些公式为永真蕴含式?()(1)Q=>Q→P(2)Q=>P→Q(3)P=>P→Q(4)P(PQ)=>P答:(1),(4)2、下列公式中哪些是永真式?()(1)(┐PQ)→(Q→R)(2)P→(Q→Q)(3)(PQ)→P(4)P→(PQ)答:(2),(3),(4)3、设有下列公式,请问哪几个是永真蕴涵式()(1)P=>PQ(2)PQ=>P(3)PQ=>PQ(4)P(P→Q)=>Q(5)(P→Q)=>P(6)P(PQ)=>P答:(2),(3),(4),(5),(6)4、公式某((A(某)B(y,某))zC(y,z))D(某)中,自由变元是(变元是()。
答:某,y,某,z5、判断下列语句是不是命题。
若是,给出命题的真值。
((1)北京是中华人民共和国的首都。
(2)陕西师大是一座工厂。
),约束)(3)你喜欢唱歌吗?(4)若7+8>18,则三角形有4条边。
(5)前进!(6)给我一杯水吧!答:(1)是,T(2)是,F(3)不是(4)是,T(5)不是(6)不是6、命题“存在一些人是大学生”的否定是(),而命题“所有的人都是要死的”的否定是()。
答:所有人都不是大学生,有些人不会死7、设P:我生病,Q:我去学校,则下列命题可符号化为()。
(1)只有在生病时,我才不去学校(2)若我生病,则我不去学校(3)当且仅当我生病时,我才不去学校(4)若我不生病,则我一定去学校答:(1)QP(2)PQ(3)PQ(4)PQ8、设个体域为整数集,则下列公式的意义是()。
(1)某y(某+y=0)(2)y某(某+y=0)答:(1)对任一整数某存在整数y满足某+y=0(2)存在整数y对任一整数某满足某+y=09、设全体域D是正整数集合,确定下列命题的真值:(1)某y(某y=y)()(2)某y(某+y=y)()(3)某y(某+y=某)()(4)某y(y=2某)()答:(1)F(2)F(3)F(4)T10、设谓词P(某):某是奇数,Q(某):某是偶数,谓词公式某(P(某)Q(某))在哪个个体域中为真()2(1)自然数(2)实数(3)复数(4)(1)--(3)均成立答:(1)11、命题“2是偶数或-3是负数”的否定是()。
离散考试试题及答案

离散考试试题及答案一、选择题(每题5分,共20分)1. 在离散数学中,下列哪个概念不是布尔代数的基本运算?A. 与B. 或C. 非D. 模答案:D2. 集合论中,下列哪个符号表示“属于”关系?A. ∈B. ∉C. ⊆D. ⊂答案:A3. 命题逻辑中,下列哪个符号表示“蕴含”关系?A. ∧B. ∨C. →D. ↔答案:C4. 关系R在集合A上是自反的,意味着什么?A. 对于所有a∈A,(a, a)∈RB. 对于所有a∈A,(a, a)∉RC. 对于所有a∈A,(a, b)∈RD. 对于所有a∈A,(a, b)∉R答案:A二、填空题(每题5分,共20分)1. 一个集合的基数是集合中元素的________。
答案:数量2. 在有向图中,如果存在一条从顶点u到顶点v的路径,则称顶点v 是顶点u的________。
答案:可达的3. 一个图是连通的,当且仅当图中任意两个顶点都是________。
答案:连通的4. 在命题逻辑中,一个命题的否定是________。
答案:它的对立命题三、简答题(每题10分,共30分)1. 请解释什么是图的哈密顿回路。
答案:哈密顿回路是一个图中的闭合回路,它恰好访问图中的每个顶点一次。
2. 描述一下什么是二元关系,并给出一个例子。
答案:二元关系是定义在两个集合上的一个关系,它关联了第一个集合中的元素和第二个集合中的元素。
例如,小于关系是数字集合上的一个二元关系。
3. 什么是图的生成树?答案:图的生成树是图的一个子图,它包含图中的所有顶点,并且是一棵树,即它是连通的且没有环。
四、计算题(每题15分,共30分)1. 给定一个集合A={1,2,3,4,5},计算它的幂集。
答案:幂集P(A)={∅, {1}, {2}, {3}, {4}, {5}, {1,2}, {1,3}, {1,4}, {1,5}, {2,3}, {2,4}, {2,5}, {3,4}, {3,5}, {4,5},{1,2,3}, {1,2,4}, {1,2,5}, {1,3,4}, {1,3,5}, {1,4,5}, {2,3,4}, {2,3,5}, {2,4,5}, {3,4,5}, {1,2,3,4}, {1,2,3,5}, {1,2,4,5}, {1,3,4,5}, {2,3,4,5}, {1,2,3,4,5}, A}。
离散数学考试题及答案

离散数学考试题及答案一、选择题(每题5分,共20分)1. 下列哪个选项不是离散数学的研究对象?A. 图论B. 组合数学C. 微积分D. 逻辑学答案:C2. 在逻辑学中,下列哪个命题是真命题?A. 如果今天是周一,那么明天是周二。
B. 如果今天是周一,那么明天是周三。
C. 如果今天是周一,那么明天是周四。
D. 如果今天是周一,那么明天是周五。
答案:A3. 在集合论中,下列哪个符号表示集合的并集?A. ∩B. ∪C. ⊆D. ⊂答案:B4. 在图论中,下列哪个术语描述的是图中的顶点集合?A. 边B. 路径C. 子图D. 顶点答案:D二、填空题(每题5分,共20分)1. 如果一个集合A包含5个元素,那么它的子集个数是______。
答案:322. 在逻辑学中,如果命题P和命题Q都是真命题,那么复合命题“P且Q”的真值是______。
答案:真3. 在图论中,如果一个图的顶点数为n,那么它的最大边数是______。
答案:n(n-1)/24. 如果一个二叉树的深度为3,那么它最多包含______个节点。
答案:7三、简答题(每题10分,共30分)1. 请简述什么是图的连通性,并给出一个例子。
答案:图的连通性是指在图中任意两个顶点之间都存在一条路径。
例如,在一个完全图K3中,任意两个顶点之间都可以通过一条边直接连接,因此它是连通的。
2. 解释什么是逻辑蕴含,并给出一个例子。
答案:逻辑蕴含是指如果一个命题P为真,则另一个命题Q也必须为真。
例如,命题P:“如果今天是周一”,命题Q:“明天是周二”。
如果今天是周一,那么根据逻辑蕴含,明天必须是周二。
3. 请描述什么是二叉搜索树,并给出它的一个性质。
答案:二叉搜索树是一种特殊的二叉树,其中每个节点的左子树只包含小于当前节点的数,右子树只包含大于当前节点的数。
它的一个性质是中序遍历可以得到一个有序序列。
四、计算题(每题15分,共30分)1. 给定一个集合A={1, 2, 3, 4, 5},请计算它的幂集,并列出所有元素。
离散数学试题总汇及答案

离散数学试题总汇及答案一、单项选择题(每题2分,共20分)1. 在集合{1,2,3}和{3,4,5}的笛卡尔积中,元素(2,4)是否存在?A. 存在B. 不存在C. 无法确定D. 以上都不对2. 函数f: A→B是单射的,当且仅当对于任意的a1, a2∈A,若f(a1)=f(a2),则a1=a2。
A. 正确B. 错误C. 无法确定D. 以上都不对3. 以下哪个命题是真命题?A. 所有的狗都会游泳。
B. 有些狗不会游泳。
C. 所有的狗都不会游泳。
D. 以上都不是真命题。
4. 如果p蕴含q为假,那么p和q的真值可以是?A. p为真,q为假B. p为假,q为真C. p为真,q为真D. p为假,q为假5. 以下哪个图是连通图?A. 一个孤立点B. 两个不相连的点C. 一个包含三个点且每对点都相连的图D. 以上都不是连通图6. 在有向图中,如果存在从顶点u到顶点v的路径,那么称v是u的后继顶点。
A. 正确B. 错误C. 无法确定D. 以上都不对7. 以下哪个等价关系是集合{1,2,3}上的?A. {(1,1), (2,2), (3,3)}B. {(1,2), (2,1), (2,2), (3,3)}C. {(1,1), (2,3), (3,2), (3,3)}D. {(1,1), (2,2), (3,3), (1,3)}8. 以下哪个命题是假命题?A. 所有的鸟都有羽毛。
B. 有些鸟不会飞。
C. 所有的哺乳动物都是温血动物。
D. 以上都不是假命题。
9. 在图论中,一个图的生成树是包含图中所有顶点的最小连通子图。
A. 正确B. 错误C. 无法确定D. 以上都不对10. 如果命题p和q互为逆否命题,那么它们具有相同的真值。
A. 正确B. 错误C. 无法确定D. 以上都不对二、填空题(每题2分,共20分)1. 集合{1,2,3}和{3,4,5}的并集是________。
2. 函数f: A→B是满射的,当且仅当对于任意的b∈B,存在a∈A,使得f(a)=________。
离散数学试题及答案解析

离散数学试题及答案解析一、选择题1. 在集合{1,2,3,4}中,含有3个元素的子集有多少个?A. 4B. 8C. 16D. 32答案:B解析:含有3个元素的子集可以通过组合数公式C(n, k) = n! / [k!(n-k)!]来计算,其中n为集合的元素个数,k为子集中的元素个数。
在本题中,n=4,k=3,所以C(4, 3) = 4! / [3!(4-3)!] = 4。
2. 下列哪个命题是真命题?A. 所有偶数都是整数。
B. 所有整数都是偶数。
C. 所有整数都是奇数。
D. 所有奇数都是整数。
答案:A解析:偶数是指能被2整除的整数,因此所有偶数都是整数,选项A是真命题。
选项B、C和D都是错误的,因为并非所有整数都是偶数或奇数。
二、填空题1. 逻辑运算符“非”(NOT)的真值表是:当输入为真时,输出为______;当输入为假时,输出为真。
答案:假解析:逻辑运算符“非”(NOT)是一元运算符,它将输入的真值取反。
如果输入为真,则输出为假;如果输入为假,则输出为真。
2. 命题逻辑中,合取词“与”(AND)的真值表是:当两个命题都为真时,输出为真;否则输出为______。
答案:假解析:合取词“与”(AND)是二元运算符,只有当两个命题都为真时,输出才为真;如果其中一个或两个命题为假,则输出为假。
三、简答题1. 解释什么是等价关系,并给出一个例子。
答案:等价关系是定义在集合上的一个二元关系,它满足自反性、对称性和传递性。
例如,考虑整数集合上的“同余”关系。
对于任意整数a,b,如果a和b除以同一个正整数n后余数相同,则称a和b模n同余。
这个关系是自反的(a同余a),对称的(如果a同余b,则b同余a),并且是传递的(如果a同余b且b同余c,则a同余c)。
2. 什么是图的连通性?一个图是连通的需要满足什么条件?答案:图的连通性是指在无向图中,任意两个顶点之间都存在一条路径。
一个图是连通的需要满足以下条件:图中的任意两个顶点v和w,都可以通过图中的边相互到达。
离散数学初步例题和知识点总结

离散数学初步例题和知识点总结离散数学是现代数学的一个重要分支,它在计算机科学、信息科学、密码学等领域都有着广泛的应用。
下面我们通过一些例题来讲解离散数学中的部分重要知识点。
一、集合论集合是离散数学中的基本概念之一。
例 1:设集合 A ={1, 2, 3, 4},B ={3, 4, 5, 6},求 A ∪ B 和 A∩ B。
解:A ∪ B ={1, 2, 3, 4, 5, 6},A ∩ B ={3, 4}集合的运算包括并集、交集、差集等。
并集是将两个集合中的所有元素合并在一起,去掉重复的元素;交集是两个集合中共同拥有的元素组成的集合。
知识点:集合的基本运算规则1、交换律:A ∪ B = B ∪ A,A ∩ B =B ∩ A2、结合律:(A ∪ B) ∪ C = A ∪(B ∪ C),(A ∩ B) ∩ C = A ∩ (B ∩ C)3、分配律:A ∩ (B ∪ C) =(A ∩ B) ∪(A ∩ C),A ∪(B ∩C) =(A ∪ B) ∩ (A ∪ C)二、关系关系是集合元素之间的某种联系。
例 2:设集合 A ={1, 2, 3},R 是 A 上的关系,R ={(1, 1),(1, 2),(2, 2),(2, 3),(3, 3)},判断 R 是否具有自反性、对称性和传递性。
解:R 具有自反性,因为对于 A 中的每个元素 a,都有(a, a) ∈ R;R 不具有对称性,因为(1, 2) ∈ R 但(2, 1) ∉ R;R 具有传递性,因为(1, 2) ∈ R 且(2, 3) ∈ R ,同时(1, 3) ∈ R 。
知识点:1、自反关系:对于集合中的每个元素 a,都有(a, a) ∈ R 。
2、对称关系:若(a, b) ∈ R ,则(b, a) ∈ R 。
3、传递关系:若(a, b) ∈ R 且(b, c) ∈ R ,则(a, c) ∈ R 。
三、函数函数是一种特殊的关系。
例 3:设函数f: R → R ,f(x) = x^2 ,求 f(-2),f(0),f(3)。
同等学力离散数学经典题及答案

同等学力离散数学经典题及答案离散数学是计算机科学与数学领域的一门基础课程,它主要研究离散结构及其相互关系。
对于同等学力的考生来说,掌握离散数学的经典题型和解题方法是非常必要的。
下面,我们将通过几个经典题目来帮助考生更好地理解和应用离散数学知识。
一、集合与关系题目1:设集合A={a, b, c},B={1, 2, 3},求笛卡尔积A×B,以及集合A上的所有二元关系。
答案:笛卡尔积A×B是指从A中取一个元素,从B中取一个元素,所组成的所有有序对。
因此,A×B={(a, 1), (a, 2), (a, 3), (b, 1), (b, 2), (b, 3), (c, 1), (c, 2), (c, 3)}。
集合A上的所有二元关系是指A×A的子集。
由于A×A包含所有可能的有序对,因此A上的二元关系有2^9=512个。
二、图论题目2:给定一个有6个顶点的简单图,其中每个顶点的度数分别为3, 3, 2, 2, 2, 1。
问这个图是否连通?答案:由握手定理知,图中的总边数等于所有顶点度数之和的一半。
因此,这个图的总边数为(3+3+2+2+2+1)/2=7。
对于一个有6个顶点的图,如果它是连通的,那么它的边数应该大于或等于6-1=5。
由于这个图有7条边,因此它是连通的。
三、逻辑与布尔代数题目3:化简布尔表达式F=AB+AB'+A'B。
答案:根据布尔代数的基本定律,我们有:F = AB + AB' + A'B= A(B + B') + A'B (分配律)= A + A'B (B + B' = 1)= A +B (吸收律)因此,F的化简结果为A + B。
四、组合数学题目4:从数字1到10中,任取3个不同的数字,求取法总数。
答案:这是一个组合问题,可以使用组合公式C(n, k) = n!/ [k!(n-k)!]来求解,其中n是总的数字个数,k是每次取的数字个数。
(完整版)《离散数学》试题及答案解析,推荐文档

4. 设 I 是如下一个解释:D = {2, 3},
a
b
f (2) f (3)
3
2
3
2
试求 (1) P(a, f (a))∧P(b, f (b));
WORD 整理版
一、填空题 1 设集合 A,B,其中 A={1,2,3}, B= {1,2}, 则 A - B=____________________;
(A)
- (B)= __________________________ . 2. 设有限集合 A, |A| = n, 则 |(A×A)| = __________________________. 3. 设集合 A = {a, b}, B = {1, 2}, 则从 A 到 B 的所有映射是 __________________________ _____________, 其中双射的是
专业资料学习参考
WORD 整理版
0 1 1 1 1
15. 设图 G 的相邻矩阵为 1 0 1 0 0 ,则 G 的顶点数与边数分别为(
).
1 1 0 1 1
1 0 1 0 1
1 0 1 1 0
(A)4, 5 (B)5, 6 三、计算证明题
(C)4, 10
(D)5, 8.
1.设集合 A={1, 2, 3, 4, 6, 8, 9, 12},R 为整除关系。
则在解释 I 下取真值为 1 的公式是( ).
(A)xyP(x,y) (B)xyP(x,y) (C)xP(x,x) (D)xyP(x,y). 6. 若供选择答案中的数值表示一个简单图中各个顶点的度,能画出图的是( ).
离散数学例题

例1证明p→(q→r) ⇔ (p∧q)→r证p→(q→r)⇔⌝p∨(⌝q∨r) (蕴涵等值式,置换规则)⇔ (⌝p∨⌝q)∨r(结合律,置换规则)⇔⌝(p∧q)∨r(德摩根律,置换规则)⇔ (p∧q)→r(蕴涵等值式,置换规则)今后在注明中省去置换规则注意:用等值演算不能直接证明两个公式不等值例2 证明p→(q→r) 与(p→q)→r 不等值证方法一真值表法, 见例1(2)方法二观察法. 观察到000, 010是左边的成真赋值,是右边的成假赋值方法三先用等值演算化简公式,然后再观察p→(q→r) ⇔⌝p∨⌝q∨r(p→q)→r ⇔⌝(⌝p∨q)∨r⇔(p∧⌝q)∨r更容易看出前面的两个赋值分别是左边的成真赋值和右边的成假赋值例3 用等值演算法判断下列公式的类型(1) q∧⌝(p→q)(2) (p→q)↔(⌝q→⌝p)(3) ((p∧q)∨(p∧⌝q))∧r)解(1) q∧⌝(p→q)⇔q∧⌝(⌝p∨q) (蕴涵等值式)⇔q∧(p∧⌝q) (德摩根律)⇔p∧(q∧⌝q) (交换律,结合律)⇔p∧0 (矛盾律)⇔ 0 (零律)矛盾式(2) (p→q)↔(⌝q→⌝p)⇔ (⌝p∨q)↔(q∨⌝p) (蕴涵等值式)⇔ (⌝p∨q)↔(⌝p∨q) (交换律)⇔ 1重言式(3) ((p∧q)∨(p∧⌝q))∧r)⇔ (p∧(q∨⌝q))∧r(分配律)⇔p∧1∧r(排中律)⇔p∧r(同一律)可满足式,101和111是成真赋值,000和010等是成假赋值.例4 求下列公式的析取范式与合取范式(1) (p→⌝q)∨⌝r;(2) (p→⌝q)→r解(1) (p→⌝q)∨⌝r ⇔ (⌝p∨⌝q)∨⌝r(消去→)⇔⌝p∨⌝q∨⌝r(结合律)最后结果既是析取范式(由3个简单合取式组成的析取式),又是合取范式(由一个简单析取式组成的合取式)(2) (p→⌝q)→r⇔ (⌝p∨⌝q)→r(消去第一个→)⇔⌝(⌝p∨⌝q)∨r(消去第二个→)⇔ (p∧q)∨r(否定号内移——德摩根律) 析取范式⇔ (p∨r)∧(q∨r) (∨对∧分配律)合取范式例 5 求公式A=(p→⌝q)→r的主析取范式解(p→⌝q)→r⇔ (p∧q)∨r(析取范式)①⇔((p∧q)∧(⌝r∨r))∨((⌝p∨p)∧(⌝q∨q)∧r)⇔((p∧q∧⌝r)∨(p∧q∧r))∨((⌝p∧⌝q∧r)∨(⌝p∧q∧r)∨(p∧⌝q∧r)∨(p∧q∧r))⇔m6∨m7 ∨m1∨m3∨m5∨m7 ②排序,得(p→⌝q)→r⇔m1∨m3∨m5∨m6∨m7(主析取范式)注①:一个公式的真值为T的指派所对应的极小项的析取即为主析取范式例 6 结合下表求G:(P→Q)↔R的主析取范式P Q R(P→Q)↔R真值的指派所对应的极小项0 0 000 0 1 1 ⌝P∧⌝Q∧R0 1 000 1 11⌝P∧Q∧R1 0 01P∧⌝Q∧⌝R1 0 101 1 001 1 11P∧Q∧R将极小项全部进行析取后,便得到所求的主析取范式:G:(P→Q)↔R⇔(┐P∧┐Q∧R)∨(┐P∧Q∧R)∨(P∧┐Q∧┐R)∨(P∧Q∧R)注②:n个命题变项的极小项或极大项的关系为:⌝m i ⇔M i, ⌝M i ⇔m i注③:极小项(极大项)的性质:(1)每个极小项(极大项)的成真(成假)赋值有且仅有一个;(2)两个不同的极小项的合取(极大项的析取)构成的命题形式为矛盾式(重言式);(3)所有极小项的析取(极大项的合取)构成的命题形式为重言式(矛盾式)。
离散数学试题及答案解析

离散数学试题及答案解析一、单项选择题(每题2分,共10分)1. 集合A={1,2,3},集合B={2,3,4},则A∩B等于:A. {1,2,3}B. {2,3}C. {1,4}D. {3,4}答案:B2. 以下哪个命题是真命题?A. 所有天鹅都是白色的。
B. 有些天鹅不是白色的。
C. 所有天鹅都不是白色的。
D. 没有天鹅是白色的。
答案:B3. 函数f: A→B的定义域是A,值域是B,那么f是:A. 单射B. 满射C. 双射D. 既不是单射也不是满射答案:D4. 逻辑表达式(p∧q)→r的逆否命题是:A. ¬r→¬(p∧q)B. ¬r→¬p∨¬qC. r→(p∧q)D. ¬r∧¬p∨¬q答案:B5. 有限集合A={a, b, c}的子集个数为:A. 3B. 4C. 7D. 8答案:D二、填空题(每题3分,共15分)1. 如果一个关系R在集合A上是自反的,那么对于A中的每一个元素a,都有___________。
答案:(a, a)∈R2. 命题逻辑中,合取(AND)的逻辑运算符用___________表示。
答案:∧3. 在图论中,一个连通图是指图中任意两个顶点之间都存在___________。
答案:路径4. 集合{1, 2, 3}的幂集包含___________个元素。
答案:85. 如果一个函数f是单射,那么对于任意的x1, x2∈A,如果f(x1)=f(x2),则x1___________x2。
答案:=三、解答题(每题10分,共20分)1. 证明:若p是q的充分条件,q是r的充分条件,则p是r的充分条件。
证明:假设p成立,由于p是q的充分条件,所以q成立。
又因为q是r的充分条件,所以r成立。
因此,p成立可以推出r成立,即p是r的充分条件。
2. 给定一个有向图,其中包含顶点A、B、C、D,边为(A, B),(B, C),(C, D),(D, A),(A, C)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章定律证明:(1) A⋃B=B⋃A (交换律)证∀x x∈A⋃B⇒ x∈A 或x∈B, 自然有x∈B 或x∈A⇒ x∈B⋃A得证A⋃B⊆B⋃A.同理可证B⋃A⊆A⋃B.(2) A⋃(B⋂C)=(A⋃B)⋂(A⋃C) (分配律)证∀x x∈A⋃(B⋂C)⇒ x∈A或(x∈B且x∈C )⇒(x∈A或x∈B)且(x∈A或x∈C)⇒x∈(A⋃B)⋂(A⋃C)得证A⋃(B⋂C)⊆(A⋃B)⋂(A⋃C).类似可证(A⋃B)⋂(A⋃C)⊆A⋃(B⋂C).(3) A⋃E=E (零律)证根据并的定义, 有E⊆A⋃E.根据全集的定义, 又有A⋃ E⊆E.(4) A⋂E=A (同一律)证根据交的定义, 有A⋂E⊆A.又, ∀x x∈A,根据全集E的定义,x∈E, 从而x∈A且x∈E,⇒x∈A⋂E得证A⊆A⋂E.例4 证明A⋃(A⋂B)=A(吸收律)证利用例3证明的4条等式证明A⋃(A⋂B)= (A⋂E)⋃(A⋂B) (同一律)= A⋂(E⋃B) (分配律)= A⋂(B⋃E) (交换律)= A⋂E (零律)= A (同一律)例5 证明(A-B)-C=(A-C)-(B-C)证(A-C)-(B-C)= (A ⋂~C) ⋂ ~(B ⋂ ~C) (补交转换律)= (A ⋂~C) ⋂ (~B ⋃ ~~C) (德摩根律)= (A ⋂~C) ⋂ (~B ⋃ C) (双重否定律)= (A ⋂~C⋂ ~B)⋃(A ⋂~C⋂ C) (分配律)= (A ⋂~C⋂ ~B)⋃(A ⋂∅) (矛盾律)= A ⋂~C⋂ ~B (零律,同一律)= (A ⋂~B) ⋂ ~C (交换律,结合律)= (A – B) –C (补交转换律)例6 证明(A⋃B)⊕(A⋃C)= (B⊕C) - A证(A⋃B)⊕(A⋃C)=((A⋃B) - (A⋃C))⋃((A⋃C) - (A⋃B))=((A⋃B)⋂~A⋂~C)⋃((A⋃C)⋂~A⋂~B)= (B⋂~A⋂~C)⋃(C⋂~A⋂~B)=((B⋂~C)⋃(C⋂~B))⋂~A=((B-C)⋃(C-B))⋂~A= (B⊕C) - A例7 设A,B为任意集合, 证明:若A⊆B, 则P(A)⊆P(B)证∀x x∈P(A) ⇔x⊆A⇒x⊆B (已知A⊆B)⇔x∈P(B)例8 证明A⊕B=A⋃B-A⋂B.A⊕B=(A⋂~B)⋃(~A⋂B)=(A⋃~A)⋂(A⋃B)⋂(~B⋃~A)⋂(~B⋃B)=(A⋃B)⋂(~B⋃~A)=(A⋃B)⋂~(A⋂B)=A⋃B-A⋂B直接法若n是奇数, 则n2也是奇数.假设n是奇数, 则存在k∈N, n=2k+1.于是n2 = (2k+1)2 = 2(2k2+2k)+1得证n2是奇数.间接法若n2是奇数, 则n也是奇数.只证:若n是偶数, 则n2也是偶数.假设n是偶数, 则存在k∈N, n=2k.于是n2 = (2k)2= 2(2k2)得证n2是偶数.归谬法若A-B=A, 则A⋂B=∅证用归谬法, 假设A⋂B≠∅, 则存在x,使得x∈A⋂B ⇔x∈A且x∈B⇒x∈A-B且x∈B(A-B=A)⇔ (x∈A且x∉B)且x∈B⇒x∉B且x∈B, 矛盾构造性对每正整数n, 存n个连的正合数. 证令x=(n+1)! +1考虑如下n个连续正整数:x+1, x+2,…, x+n,对于i(i=1,2,3,…,n),x+i=(n+1)! +(1+i),此式含有因子1+i,而1+i不等于1也不等于x+i,因此x+i是合数。
所以x+1, x+2,…,x+n是n个连续的正合数。
非构造性对每个正整数n, 存在大于n的素数.令x等于所有小于等于n的素数的乘积加1,则x不能被所有小于等于n的素数整除.于是, x或者是素数, 或者能被大于n的素数整除.因此,存在大于n的素数.数学归:对所有n≥1, 1+3+5+ … +(2n-1)=n2归纳基础. 当n=1时, 1=12, 结论成立.归纳步骤. 假设对n(n≥1)结论成立,则考虑n+1的情况有1+3+5+ … +(2n-1)+(2n+1)=n2 +(2n+1) = (n+1)2得证当n+1时结论也成立.第二数学归任>=2的整数均可表成素数的乘积证归纳基础. 对于2, 结论显然成立.归纳步骤. 假设对所有的k(2≤k≤n)结论成立, 要证结论对n+1也成立. 若n+1是素数, 则结论成立; 否则n+1=ab, 2≤a,b<n. 由归纳假设, a,b均可表成素数的乘积, 从而n+1 也可表成素数的乘积. 得证结论对n+1成立.命题为假的证明——举反例例11 证明下述命题不成立:若A⋂B=A⋂C, 则B=C.证明反例: 取A={a,b}, B={a,b,c}, C={a,b,d},有A⋂B=A⋂C = {a,b}但B≠C, 故命题不成立.第二章例3 证明p→(q→r) ⇔ (p∧q)→r证p→(q→r)⇔⌝p∨(⌝q∨r) (蕴涵等值式)⇔ (⌝p∨⌝q)∨r(结合律)⇔⌝(p∧q)∨r(德摩根律)⇔ (p∧q) →r(蕴涵等值式)(1) q∧⌝(p→q)解q∧⌝(p→q)⇔q∧⌝(⌝p∨q) (蕴涵等值式)⇔q∧(p∧⌝q) (德摩根律)⇔p∧(q∧⌝q) (交换律,结合律)⇔p∧0 (矛盾律)⇔ 0 (零律)该式为矛盾式.(2) (p→q)↔(⌝q→⌝p)解(p→q)↔(⌝q→⌝p)⇔ (⌝p∨q)↔(q∨⌝p) (蕴涵等值式)⇔ (⌝p∨q)↔(⌝p∨q) (交换律)⇔ 1该式为重言式.⌝(p→q)∨⌝r 的析取范式与合取范式解⌝(p→q)∨⌝r⇔⌝(⌝p∨q)∨⌝r⇔ (p∧⌝q)∨⌝r析取范式⇔ (p∨⌝r)∧(⌝q∨⌝r) 合取范式⌝(p→q)∨⌝r 的主析取范式主合取范式解(1) ⌝(p→q)∨⌝r⇔ (p∧⌝q)∨⌝rp∧⌝q⇔ (p∧⌝q)∧1 同一律⇔ (p∧⌝q)∧(⌝r∨r) 排中律⇔ (p∧⌝q∧⌝r)∨(p∧⌝q∧r) 分配律⇔m4∨m5⌝r ⇔ (⌝p∨p)∧(⌝q∨q)∧⌝r 同一律, 排中律⇔ (⌝p∧⌝q∧⌝r)∨(⌝p∧q∧⌝r)∨(p∧⌝q∧⌝r)∨(p∧q∧⌝r) ⇔m0∨m2∨m4∨m6 分配律得⌝(p→q)∨⌝r⇔m0∨m2∨m4 ∨m5 ∨m6可记作⇔∑(0,2,4,5,6)(2) ⌝(p→q)∨⌝r⇔ (p∨⌝r)∧(⌝q∨⌝r)p∨⌝r⇔p∨0∨⌝r 同一律⇔p∨(q∧⌝q)∨⌝r 矛盾律⇔ (p∨q∨⌝r)∧(p∨⌝q∨⌝r)分配律⇔M1∧M3⌝q∨⌝r⇔ (p∧⌝p)∨⌝q∨⌝r 同一律, 矛盾律⇔ (p∨⌝q∨⌝r)∧(⌝p∨⌝q∨⌝r) 分配律⇔M3∧M7得⌝(p→q)∨⌝r⇔M1∧M3∧M7可记作⇔∏(1,3,7)快速求A ⇔ (⌝p∧q)∨(⌝p∧⌝q∧r)∨r的主析取范式(1) ⌝p∧q⇔ (⌝p∧q∧⌝r)∨(⌝p∧q∧r) ⇔m2∨m3⌝p∧⌝q∧r⇔m1r⇔(⌝p∧⌝q∧r)∨(⌝p∧q∧r)∨(p∧⌝q∧r)∨(p∧q∧r)⇔m1∨m3∨m5∨m7得A⇔m1∨m2∨m3∨m5∨m7 ⇔∑(1,2,3,5,7)(2) 求B⇔⌝p∧(p∨q∨⌝r)的主合取范式解⌝p⇔ (⌝p∨q∨r)∧(⌝p∨q∨⌝r)∧(⌝p∨⌝q∨r)∧(⌝p∨⌝q∨⌝r)⇔M4∧M5∧M6∧M7p∨q∨⌝r⇔M1得B⇔M1∧M4∧M5∧M6∧M7 ⇔∏(1,4,5,6,7)例3 用主析取范式判断公式的类型:(1) A⇔⌝(p→q)∧q (3) C⇔ (p∨q)→rA⇔⌝(⌝p∨q)∧q ⇔ ( p∧⌝q)∧q ⇔ 0 矛盾式(2) B⇔p→(p∨q)B⇔⌝p∨(p∨q) ⇔ 1 ⇔m0∨m1∨m2∨m3重言式(3) C⇔ (p∨q)→rC ⇔⌝(p∨q)∨r ⇔ (⌝p∧⌝q)∨r⇔ (⌝p∧⌝q∧r)∨(⌝p∧⌝q∧⌝r)∨(⌝p∧⌝q∧r)∨(⌝p∧q∧r)∨(p∧⌝q∧r)∨(p∧q∧r)⇔ m0∨m1∨m3∨m5∨m7非重言式的可满足式用主析取范式判断下面2组公式是否等值:(1) p与(⌝p∨q)→(p∧q)解p ⇔p∧(⌝q∨q) ⇔ (p∧⌝q)∨(p∧q) ⇔m2∨m3(⌝p∨q)→(p∧q) ⇔⌝(⌝p∨q)∨(p∧q)⇔ (p∧⌝q)∨(p∧q) ⇔m2∨m3故p ⇔ (⌝p∨q)→(p∧q)(2) (p∧q)∨r 与p∧(q∨r)解(p∧q)∨r⇔ (p∧q∧⌝r)∨(p∧q∧r) ∨(⌝p∧⌝q∧r)∨(⌝p∧q∧r)∨(p∧⌝q∧r)∨(p∧q∧r)⇔ m1∨m3∨m5∨m6∨m7p∧(q∨r) ⇔ (p∧q)∨(p∧r)⇔(p∧q∧⌝r)∨(p∧q∧r)∨(p∧⌝q∧r)∨(p∧q∧r)⇔ m5∨m6∨m7故(p∧q)∨r 不等于p∧(q∨r)例5 某单位要从A,B,C三人中选派若干人出国考察, 需满足下述条件:(1) 若A去, 则C必须去;(2) 若B去, 则C不能去;(3) A和B必须去一人且只能去一人.问有几种可能的选派方案?解记p:派A去, q:派B去, r:派C去(1) p→r, (2) q→⌝r, (3) (p∧⌝q)∨(⌝p∧q)求下式的成真赋值A=(p→r)∧(q→⌝r)∧((p∧⌝q)∨(⌝p∧q))求A的主析取范式A=(p→r)∧(q→⌝r)∧((p∧⌝q)∨(⌝p∧q))⇔ (⌝p∨r)∧(⌝q∨⌝r)∧((p∧⌝q)∨(⌝p∧q))⇔ ((⌝p∧⌝q)∨(⌝p∧⌝r)∨(r∧⌝q)∨(r∧⌝r))∧((p∧⌝q)∨(⌝p∧q))⇔ ((⌝p∧⌝q)∧(p∧⌝q))∨((⌝p∧⌝r)∧(p∧⌝q))∨((r∧⌝q)∧(p∧⌝q))∨((⌝p∧⌝q)∧(⌝p∧q))∨((⌝p∧⌝r)∧(⌝p∧q))∨((r∧⌝q)∧(⌝p∧q))⇔ (p∧⌝q∧r)∨(⌝p∧q∧⌝r)成真赋值:101,010结论: 方案1 派A与C去方案2派B去A=(⌝p∧⌝q∧r)∨(⌝p∧q∧r)∨(p∧q∧r)的主合取范式解 A ⇔m1∨m3∨m7⇔M0∧M2∧M4∧M5∧M6第二章判断若今天是1号, 则明天是5号.今天是1号. 所以, 明天是5号.解设p: 今天是1号, q: 明天是5号推理的形式结构为(p→q)∧p→q证明用等值演算法(p→q)∧p→q⇔⌝((⌝p∨q)∧p)∨q⇔ ((p∧⌝q)∨⌝p)∨q⇔⌝p∨⌝q∨q⇔ 1得证推理正确判断若下午气温超过30度, 则小燕必去游泳,若她去游泳她就不去看电影了. 所以若小燕没去看电影, 下午气温必定超过了30度. m1解设p: 下午气温超过30度, q: 小燕去游泳,r: 小燕去看电影.推理的形式结构为((p→q)∧(q→⌝ r) )→(⌝ r→p)证明主析取范式法((p→q)∧(q→⌝ r) )→(⌝ r→p)⇔p∨ r⇔m1∨m3∨m4∨m5∨m6 ∨m7主析取范式中缺少m0,m2,不是重言式,不正确。
