几何对象学习笔记及处理BUG(b—11.21)
布尔运算失败的原因及解决方法

布尔运算失败的原因及解决方法在实体建模的过程中,理解下列ANSYS所用的数学操作是很有帮助的。
这些知识在遇到实体退化和不连续处尤为有用。
例如,在实体模型布尔运算中遇到退化的错误提示。
数学术语知识对克服这样的错误会有帮助。
实体模型图元的内在数学表现为经修整过的参数表面。
修整过的参数化表面包括两部分:参数的几何形状和拓扑结构。
参数化几何形状定义模型的基本表面。
参数项是指数学上代表几何空间的参数空间。
图为几何模型与参数模型的关系。
非均匀有理B样条或NURBS用来定义参数的几何形状。
拓扑是指围成模型的几何形状的修整表面。
●退化布尔运算可能会由于实体退化而失败。
退化由几何形状或拓扑结构所引起。
ANSYS程序将退化(引起了布尔运算失败)归结为参数的(几何形状)或拓扑结构的退化。
Degenerate entities are those whose length, area or volume degenerate to ze ro because of the coincidence of one or more points or vertices.用基本参数空间来表示几何空间进会产生参数的退化。
当参数所表示的“阴影区”与真实的几何模型的维数不一致时,就会产生退化。
例如圆锥体的顶点,几何模型上的单个点却由参数空间体现为一个边。
这样的一个点称为一个退化边,或简称为退化。
这种退化本身并没有危害。
包含退化的模型仍可用来进行布尔运算,可以成功地进行网格划分,并产生良好的分析结果。
只有当退化使布尔运算出现问题时才需要注意它的存在。
▪从图形上识别单元退化用下列所述方法可以验证面或体的退化。
如果使用命令输入方法,包括DEGEN命令在内,会在退化的关键点处出现红星。
•显示面的退化:命令:APLOT, , , ,DEGEGUI : Main Menu>Preprocessor>Operate>Show Degeneracy>Plot Degen Areas•显示所选体的退化:命令:VPLOT, , , ,DEGEGUI : Main Menu>Preprocessor>Operate>Show Degeneracy>Plot Degen Volus▪退化的关键点列表可以选择退化的关键点列表:•面中参数退化的关键点列表:命令:ADGLGUI : Main Menu>Preprocessor>Operate>Show Degeneracy>List Degen Areas•体中参数退化的关键点列表:命令:VDGLGUI : Main Menu>Preprocessor>Operate>Show Degeneracy>List Degen Volus另一种退化可在布尔运算要生成退化的边界时被发现。
3DMAX课堂学习笔记

第一课:现成的三维物体建模1-1、3Dmax2010软件简介和快捷键3D Studio Max,常简称为3ds Max或MAX,是Autodesk公司开发的基于PC系统的三维模型制作和动画渲染软件,其广泛应用于室内设计、建筑设计、影视、工业设计、多媒体制作、游戏、辅助教学以及工程可视化等领域。
3Dmax为了便捷,我们还要记住一些快捷方式:改变到上(Top)视图【T】改变到底(Bottom)视图【B】改变到相机(Camera)视图【C】改变到前(Front)视图【F】改变到等大的用户(User)视图【U】改变到右(Right)视图【R】改变到透视(Perspective)图【P】显示/隐藏网格(Grids) 【G】新的场景【Ctrl】+【N】约束到X轴【F5】约束到Y轴【F6】约束到Z轴【F7】撤消场景*作【Ctrl】+【Z】渲染配置【F10】显示/隐藏光源(Lights) 【Shift】+【L】以下部分可以了解了解就好:最大化当前视图(开关) 【ALT】+【W】法线(Normal)对齐【Alt】+【N】偏移捕捉【Alt】+【Ctrl】+【空格】打开一个MAX文件【Ctrl】+【O】平移视图【Ctrl】+【P】交互式平移视图【I】放置高光(Highlight) 【Ctrl】+【H】播放/停止动画【/】快速(Quick)渲染【Shift】+【Q】回到上一场景*作【Ctrl】+【A】回到上一视图*作【Shift】+【A】旋转(Rotate)视图模式【Ctrl】+【R】或【V】1-2、3dmax2010界面组成和界面优化快速工具栏“文件”菜单3Dsmax2010界面优化:1、改变界面风格:自定义---加载自定义用户界面方案UI文件的位置在C:\Program Files\Autodesk\3ds Max 2010\ui2、隐藏动画轨迹栏:自定义---显示---3、隐藏石墨建模工具栏:4、以小图标来显示工具栏:自定义---首选项---常规---5、自定义布局:在“视图控制区”右击1-3、3dmax2010视图控制1-4、3Dmax2010标准基本体长方体、球体、圆柱体、圆环、茶壶、圆锥体、几何球体、管状体、四棱锥、平面1-5和1.6、实例:装饰品知识点:(1)、学习堆积木式的建模方法,(2)、学习“选择、移动、修改、复制”物体1-7、实例:桌几尺寸:1300*800 1000*500 25*480知识点:(1)、使用标准尺寸建模1-8、3Dmax2010扩展基本体异面体、切角长方体、油罐,纺锤,油桶、球棱柱、环形波,软管,环形结、切角圆柱体、胶囊、L-Ext , C-Ext、棱柱。
abaqus建模流程——学习笔记
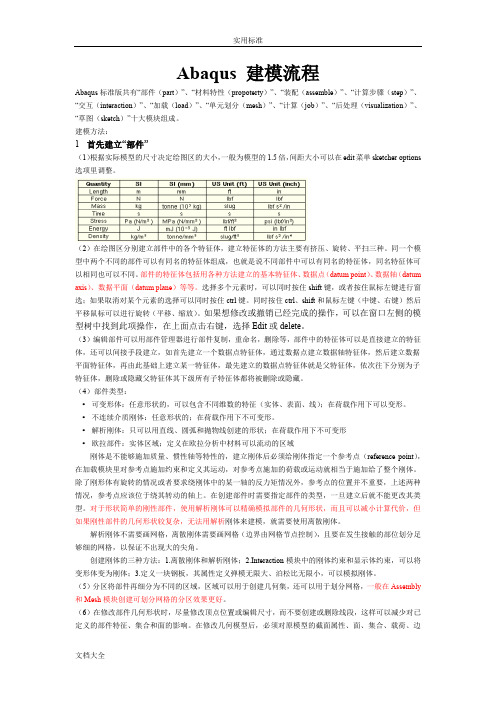
Abaqus 建模流程Abaqus标准版共有“部件(part)”、“材料特性(propoterty)”、“装配(assemble)”、“计算步骤(step)”、“交互(interaction)”、“加载(load)”、“单元划分(mesh)”、“计算(job)”、“后处理(visualization)”、“草图(sketch)”十大模块组成。
建模方法:1首先建立“部件”(1)根据实际模型的尺寸决定绘图区的大小,一般为模型的1.5倍,间距大小可以在edit菜单sketcher options 选项里调整。
(2)在绘图区分别建立部件中的各个特征体,建立特征体的方法主要有挤压、旋转、平扫三种。
同一个模型中两个不同的部件可以有同名的特征体组成,也就是说不同部件中可以有同名的特征体,同名特征体可以相同也可以不同。
部件的特征体包括用各种方法建立的基本特征体、数据点(datum point)、数据轴(datum axis)、数据平面(datum plane)等等。
选择多个元素时,可以同时按住shift键,或者按住鼠标左键进行窗选;如果取消对某个元素的选择可以同时按住ctrl键。
同时按住ctrl、shift和鼠标左键(中键、右键)然后平移鼠标可以进行旋转(平移、缩放)。
如果想修改或撤销已经完成的操作,可以在窗口左侧的模型树中找到此项操作,在上面点击右键,选择Edit或delete。
(3)编辑部件可以用部件管理器进行部件复制,重命名,删除等,部件中的特征体可以是直接建立的特征体,还可以间接手段建立,如首先建立一个数据点特征体,通过数据点建立数据轴特征体,然后建立数据平面特征体,再由此基础上建立某一特征体,最先建立的数据点特征体就是父特征体,依次往下分别为子特征体,删除或隐藏父特征体其下级所有子特征体都将被删除或隐藏。
(4)部件类型:•可变形体:任意形状的,可以包含不同维数的特征(实体、表面、线);在荷载作用下可以变形。
OSG学习过程中的笔记

一旋转其中trans->setMatrix(osg::Matrix::translate(0,0,20));就是用来平移物体,这个表示象Z轴正方向平移也就是屏幕正上方。
o sg::Matrix::scale(0.5,0.5,0.5)表示缩放的比例,也就是原来物体的一般大小osg::Matrix::rotate(osg::DegreesToRadians(90.0),0,1,0)该方法参数分别表示角度,x,y,z当xyz其中有值是那么物体会绕着物体旋转。
当角度为正值的时候,物体绕着x,y,z箭头指向向右旋转,否则物体绕着x,y,z箭头指向向左旋转osg笔记(一)2011-07-05 19:37:29| 分类:OSG | 标签:|字号大中小订阅场景图形采用一种自顶向下的,分层的树状数据结构来组织空间数据集,以提高渲染的效率场景图形树结构的顶部是一个根节点,从根节点向下延伸,各个组节点中均包含了几何信息和用于控制其外观的渲染状态信息。
根节点和各个组节点都可以有零个(实际上是没有执行任何操作)或多个子成员。
在场景图形的最底部,各个叶节点包含了构成场景中物体的实际几何信息。
Osg程序使用组节点来组织和排列场景中的几何体。
场景图形通常包含了多种类型的节点以执行各种各样的用户功能,例如开关节点可以设置其子节点可用或不可用,细节层次节点(LOD)可以根据观察者的距离调用不同的子节点,变换节点可以改变子节点几何体的坐标变换状态。
场景图形特征:1. 提供底层渲染API中具备的几何信息和状态管理功能之外,还兼备以下的附加特征和功能:2. 空间结构:3. 场景拣选,投影面剔除和隐藏面剔除。
4. 细节层次:5. 透明6. 状态改动最少化7. 文件I/O8. 更多高性能函数:全特征文字支持,渲染特效的支持,渲染优化,3d模型文件读写支持,跨平台输入渲染及显示设备的访问.场景图形渲染方式:三种遍历操作1. 更新2. 拣选3. 绘制Osg设计所采用的设计理念和工具:Ansi标准C++C++标准模板库设计模式Osg命名习惯:命名空间:小写字母开头,然后大写字母避免混淆。
小甲鱼《零基础入门学习Python》课堂笔记

[键入公司名称]人生苦短,我用Python [键入文档副标题]徐辉[选取日期]目录01讲:我和Python的第一次亲密接触 (12)02讲:用Python设计第一个游戏 (15)03讲:小插曲之变量和字符串 (17)04讲:改进我们的小游戏 (19)05讲:闲聊之Python的数据类型 (21)06讲:Pyhon之常用操作符 (22)07讲:了不起的分支和循环1 (23)08讲:了不起的分支和循环2 (25)09讲:了不起的分支和循环3 (27)10讲:列表,一个打了激素的数组1 (29)11讲:列表,一个打了激素的数组2 (31)12讲:列表,一个打了激素的数组3 (33)13讲:元组,戴上了枷锁的列表 (36)14讲:字符串:各种奇葩的内置方法 (38)15讲:字符串的格式语句与操作符 (43)16讲:序列相关内置函数介绍 (46)1-16讲:阶段总结 (51)17讲:函数:Python的乐高积木 (52)18讲:函数:灵活即强大 (53)18讲2:py文件打包成exe文件 (55)19讲:函数:我的地盘我做主 (56)20讲:函数:内嵌函数和闭包 (58)21讲:函数:lambda表达式 (60)22讲:函数:递归是神马 (61)23讲:递归:这帮小兔崽子 (62)24讲:递归:汉诺塔 (63)17-24讲:阶段性总结 (64)25讲:字典:当索引值不好用时 (65)26讲:字典:当索引值不好用时2 (66)27讲:集合:在我的世界里,你就是唯一 (69)28讲:文件:因为懂你,所以永恒 (70)29讲:文件:一个任务 (72)30讲:文件系统:介绍一个高大上的东西 (75)31讲:永久存储:腌制一缸美味的泡菜 (79)31讲:异常处理:你不可能总是对的 (80)33讲:异常处理:你不可能总是对的2 (82)34讲:丰富的else语句和简洁的with (85)35讲:图形界面用户入门:EasyGui (87)36讲:类和对象:给大家介绍对象 (87)37讲:类和对象:面向对象编程 (89)38讲:类和对象:继承 (90)39讲:类和对象:拾遗 (91)40讲:类和对象:一些相关的BIF (94)41讲:类和对象:构造和析构 (96)42讲:类和对象:算术运算符 (98)43讲:类和对象:算术运算符2 (100)44讲:魔法方法:简单定制 (101)45讲:魔法方法:属性访问 (103)46讲:魔法方法:描述符 (105)47讲:魔法方法:定制容器 (108)48讲:魔法方法:迭代器 (109)序----小甲鱼四件在我步入职业软件开发生涯那天起就该知道的事情我的软件开发生涯开始于大约15年以前。
Open_CASCADE学习笔记-曲面建模

直纹曲面(Ruled surfaces) 直纹曲面是通过将两条曲线利用直线连接起来生成的(例如连接这两条曲线上的 点,在另一种说法中直纹曲面是通过直线沿着两条曲线上的点运动生成的)。平 面是直纹曲面的特例(平面可以在两条平行直线的基础上通过直线连接生成)。假 如沿着两个平行的圆上的点用直线连接起来,就可以生成圆柱面或者锥面。
序
在 OpenCascade 的论坛上知道了 Roman Lygin 在他的博客上写了 Open CASCADE notes Geometry 和 Surface Modeling 两篇文章,拜读之后获益良多。如果大家发现文中翻译有错 误或不足之处,望不吝赐教,可以发到我的邮箱 fenghongkui@,十分感谢。
曲面对象只包含有最终的几何表示,而且不提供任何关于曲面是如何生成的信 息。这使得它相对于其他 CAD 核心部分显得很特别,例如 ACIS 使用一种非常 著名的过程曲面(procedural surface),其中不但包含生成曲面的技术,也有可供 选择的最终逼近(an optional final approximation)曲面。例如,蒙皮曲面(a skin surface)由一组截曲线(section curves)生成,整个曲面被扫过(skinned),从而生 成逼近 NURBS 的曲面。这要求建模软件支持更多的实体类型,也使得支持这些 模型的建模算法变得复杂。这也使我不得不在软件 CAD Exchanger 的转换器 (translator)中额外开发一些类来表示所有的这些变体(variety),并将它们转换到 OCC 中。我可以将 OCC 中导出的 SAT 文件再重新导入到 OCC 中,但是到目前 为止还不能支持所有的 SAT 类型。顺便说一下,如果有谁对 ACIS 非常熟悉, 就可以对 OCC 和 ACIS 做一个非常有价值对比测试报告。
UG个人学习总结

陕西科技大学UG学习总结毕业设计学习笔记WJG2014/4/15毕业设计学习笔记,练习打字以及论文排版。
UGNX6.0F8 视图快速摆正保存当前视图View-layout 设置布局艺术外观时才会显示材质局部着色:Object Display Ctrl+J对象的现实与隐藏有两种方法:1.图层2.通过命令显示与隐藏的快捷键:显示和隐藏Ctrl+W 隐藏Ctrl+B显示Ctrl+Shift+K 全部显示Ctrl+Shift+U 颠倒显示与隐藏Ctrl+Shift+BUG中选择方式:导航器,鼠标取消对象的选择shift+鼠标左击Esc可全部取消Preference-selection 设置快速选择及相关参数UG中坐标系:绝对坐标系,基准坐标系(可以有多个),工作坐标系WCS(只能有一个,其显示与否可用W键切换)工作坐标WCS的定制:Dynamic 可以动态移动和旋转移动:1鼠标按住原点不放,移动鼠标,可实现移动。
2若要使坐标沿某一坐标轴移动,则可以单击该轴,输入数值,也可以鼠标按住该轴不放,在Snap中输入数值可以每次以固定的值移动。
旋转:欲使坐标系绕某一坐标轴旋转,可在垂直于该轴的平面内单击小圆球,其亦可以使用输入数值和以固定值旋转两种。
关于图形变换中的圆形阵列:选择的第一个点是圆形阵列的参考点,第二个点是圆形阵列的阵列中心。
后面阵列参数中的起始角度角度如果是0,则阵列出来的图形中会有一个图形与原图重合。
WCS方向Format-WCS-Orient:Plane and vector(平面与矢量) CSYS基准坐标系1.UG中的坐标系ACS绝对坐标系系统默认坐标系,原点永远不会变,显示在视图的左下角WCS 工作坐标系用户使用的坐标系,可以自己设置。
快捷键W可以设置WCS的显示与否。
MCS 机械坐标系一般用于模具设计加工中2.装配约束Angle 角度Bond 胶合Fit 适合使具有两个等半径的圆柱面合起来。
高等数学笔记(含数一内容)

隐函数求导
参数方程确定的函数求导
分段函数求导
先讨论关键点是否连续,确定连续后再判断函数各个部分是否可导。
求函数高阶导
一般使用数学归纳法解决。
微分
可微
定义:设y=f(x) (x∈D),x₀∈D。若∆y=A∆x+৹(∆x),则称f(x)在x=x₀处可微。
性质
可微一定可导,可导一定可微(充要条件)
若∆y=A∆x+৹(∆x),则A=f'(x₀),即dy∣₍x=x₀₎=f'(x₀)dx
二阶线性微分方程解的结构 齐+齐=齐 齐 + 非齐 = 非齐 非齐 + 非齐 = 齐 (拆解性质)对于方程**,若f(x)=f1(x)+f2(x)(即可拆成两部分),则分别构造两个二阶非齐次线性微分方程,且φ1(x),φ2(x)分别为它们的特解,则 有原方程特解为:
y=φ1(x)+φ2(x) (系数和的特点)设φ1(x),φ2(x),...,φn(x),为方程**的解,则通解的组合形式为y=k1φ1(x)+k2φ2(x)+...+knφn(x) 若y为方程*的通解,则k1+k2+...+kn=0(系数和为0) 若y为方程**的通解,则k1+k2+...+kn=1(系数和为1) (二阶常系数线性微分方程通解形式推导定理)
函数f(x)∈ c【a,b】的性质(函数在区间内恒连续)
性质1:∃最大值 M 和最小值 m (最值); 性质2:∃M₀>0,使得∣f(x)∣≤M₀(有界);
性质3: ∀η ∈【m,M】,∃ξ∈【a,b】,使得f(ξ)=η(介值定理);
性质4:若 f(a)*f(b)<0,则∃c∈(a,b),使得f(c)=0(零点定理)。 连续函数的运算
Open_CASCADE学习笔记-拓扑和几何

OPEN CASCADE学习笔记——拓扑和几何著: Roman Lygin译:George Feng这是一篇关于开源三维建模软件O P E N C A S C A D E内核的博文:R O M A N L Y G I N是O P E N C A S C A D E的前程序开发员和项目经理,曾经写过许多关于该开源软件开发包的深入文章,可以在他的博客(H T T P://O P E N C A S C A D E.B L O G S P O T.C O M)上面找到这些文章。
序在OpenCascade的论坛上知道了Roman Lygin在他的博客上写了Open CASCADE notes系列文章,但是却无法访问他的博客,幸而百度文库已经收录了Topology and Geometry和Surface Modeling两篇文章,拜读之后获益良多。
如果大家发现文中翻译有错误或不足之处,望不吝赐教,可以发到我的邮箱fenghongkui@,十分感谢。
2012年6月28日星期四第1节概述下面首先介绍一下Open CASCADE的基本概念。
关于这些基本概念的问题经常在论坛中出现,我希望这篇文章能够帮助大家理解这些基本概念。
如果你要使用或者开发自己的建模算法,就更要理解这些基本概念。
或许你应该重新读一读Modeling Data User's Guide的各个章节,从而加深记忆。
拓扑抽象类Open CASCADE的拓扑结构是在参考STEP ISO-10303-42标准的基础上设计的。
也许读一读STEP标准也是有益的(我自己曾经在1997年读过一次)。
Open CASCADE的结构是面向单向图的(an oriented one-way graph),在该单向图中父类可以引用(refer to)他们的子类,而不能反向引用(reference)。
抽象结构在TopoDS包中的C++类中实现。
图1是由Doxygen生成的继承关系图。
几何变换的基本概念知识点总结

几何变换的基本概念知识点总结几何变换是几何学中非常重要的概念,用于描述图形在平面上的变化。
在学习几何变换的过程中,我们需要了解一些基本的概念和知识点。
本文将对几何变换的基本概念进行总结,并介绍其常见的几种类型。
一、几何变换的基本概念1. 点:几何变换的基本元素,是平面上最简单的图形表示。
2. 直线:由无数个点组成,是平面上最基本的线段。
3. 线段:由两个不同的点组成的线段。
4. 角度:由两条射线(直线的一种特殊情况)共享一个端点构成,用来描述两条直线之间的偏转程度。
5. 相似:指两个图形的形状相同,但大小可能不同。
6. 共线:指多个点位于同一条直线上。
7. 垂直:指两条直线或线段之间的夹角为90度。
8. 平行:指两条直线永远不会相交。
二、基本几何变换类型几何变换包括平移、旋转、缩放和翻转等。
下面将对这几种常见的几何变换类型进行介绍。
1. 平移:是指图形沿着平面上的平行线进行移动,保持形状和大小不变。
平移可以通过向量来描述,即将图形中的每个点按照给定的向量进行移动。
2. 旋转:是指图形绕着某个中心点进行旋转,保持形状和大小不变。
旋转可以通过角度来描述,即将图形中的每个点按照给定的角度和中心点进行旋转。
3. 缩放:是指按照比例因子,改变图形的大小。
缩放可以分为放大和缩小两种方式,分别通过比例因子大于1和小于1来实现。
4. 翻转:是指将图形沿着一条直线对称交换位置,保持形状不变,但是可能改变大小。
翻转可以分为水平翻转和垂直翻转两种方式。
三、几何变换的性质在进行几何变换时,有一些重要的性质需要我们了解。
1. 保持相似性:几何变换通常都会保持图形的相似性,即形状不变,只是发生了平移、旋转、缩放或翻转等变化。
2. 保持相对位置:几何变换会保持图形中各个点之间的相对位置关系不变,即平行线仍然平行,相交的角度不变。
3. 保持面积比例:几何变换通常会保持图形的面积比例不变,即如果一个图形的面积是另一个图形的两倍,那么经过几何变换后,面积比例仍然保持不变。
2.1坐标法课件-高二上学期数学人教B版(2019)选择性

坐标法
教材分析
平面解析几何简介
解析几何学是借助坐标系,用代数方法研究几何对象之间的 关系和性质的一门几何学分支,亦叫坐标几何. 由法国数学家 笛卡尔和费马等人创建.
解析几何的核心思想——数形结合
几何问题——代数化——处理代数问题——分析 代数结果的几何意义——解决几何问题
课程标准
1.掌握数轴上向量的坐标公式,会用向量法推导 出数轴上两点之间的距离公式,中点坐标公式; 2.了解并掌握平面直角坐标系内的两点之间的距 离公式,中点坐标公式及其推导过程 3.能用坐标法解决几何问题
2.已知平行四边形ABCD的两个顶点坐标分别为A(4,2),B(5,7),对角
线交点为E(-3,4),两顶点C,D的坐标为(-10,6)、(-11,1。)
当堂检测
3.已知AO是△ABC中BC边的中线,证明:|AB|2+|AC|2=2(|AO|2+|OC|2).
取BC边所在直线为x轴,边BC的中点为原点,建立直 角坐标系,如图所示. 设B(-a,0),C(a,0),A(m,n)(其中a>0), 则|AB|2+|AC|2=(m+a)2+n2+(m-a)2+n2=2(m2+a2+n2), |AO|2+|OC|2=m2+n2+a2, ∴|AB|2+|AC|2=2(|过数轴上两点间的距离公式、中点坐标公式
一 的探索,掌握平面直角坐标系中两点间的距离 公式和中点坐标公式.体现了逻辑推理的素养
学习 目标
二 通过对两点间距离公式的推导过程的探索,体 会算法。体现了数学抽象,逻辑推理的素养
进一步体会“坐标法”的基本思想,逐步学会
三 用“坐标法”解决有关问题.体现了数学运算,
求这个三角形AB边上中线的长.
y 4
B
几何学习中常见的困难有哪些如何克服

几何学习中常见的困难有哪些如何克服在数学学习的道路上,几何无疑是一座颇具挑战性的山峰。
许多同学在攀登这座山峰时,会遇到各种各样的困难。
那么,常见的困难有哪些呢?又该如何去克服它们呢?首先,空间想象力不足是一个常见的难题。
几何涉及到对空间图形的理解和想象,对于一些同学来说,将平面图形在脑海中转化为立体的、具有空间感的图形并非易事。
比如,在学习正方体、长方体的表面积和体积计算时,难以准确地想象出各个面的位置和大小关系。
要克服空间想象力不足的问题,我们可以多观察身边的几何形状。
例如,观察房屋的结构、盒子的形状、球类的特征等。
通过实际观察,将抽象的几何图形与现实生活中的物体联系起来。
同时,利用一些辅助工具,如积木、模型等,亲手搭建和摆弄,更直观地感受图形的特点。
其次,概念理解不清晰也是困扰同学们的一大障碍。
几何中有许多专业的术语和定义,如平行线、垂线、角平分线等等,如果对这些概念没有透彻的理解,在解题时就容易出现错误。
针对概念理解的问题,我们要学会多比较、多总结。
把相似的概念放在一起进行对比,找出它们的异同点。
同时,通过大量的实例来加深对概念的理解,不要仅仅死记硬背定义,而是要真正明白其内涵。
再者,几何证明题常常让同学们感到头疼。
不知道从何处入手,找不到证明的思路,或者在证明过程中逻辑混乱。
解决几何证明题的困难,关键在于掌握好基本的证明方法和逻辑推理规则。
平时要多做一些典型的证明题,学习别人的解题思路和方法。
在自己做题时,先仔细分析题目所给的条件,尝试从不同的角度去思考,找到解题的突破口。
并且要注意证明过程的严谨性,每一步都要有依据。
另外,几何计算中的错误也是常见的。
在计算图形的周长、面积、体积时,由于公式记错、单位换算错误等原因导致结果出错。
为了减少计算错误,一定要牢记各种图形的计算公式,并通过反复练习来加深记忆。
在计算过程中,要认真仔细,注意单位的统一和换算。
做完题目后,养成检查的好习惯,重新审视计算过程和结果。
《数学思维2:代数与几何》笔记

《数学思维2:代数与几何》阅读札记目录一、代数篇 (2)1.1 整数的性质 (2)1.2 有理数与无理数 (3)1.3 代数表达式与运算 (5)1.4 方程与不等式 (5)1.5 函数的概念与性质 (6)二、几何篇 (7)2.1 平面图形 (8)2.2 立体图形 (9)2.3 圆与弧 (11)2.4 角度与多边形 (12)2.5 地图与地理坐标 (13)三、代数与几何的联系 (13)3.1 代数在几何中的应用 (14)3.2 几何在代数中的应用 (15)3.3 代数与几何的交叉问题 (17)四、数学思维方法 (18)4.1 类比推理 (19)4.2 归纳推理 (20)4.3 模型法 (22)4.4 构造法 (23)五、总结与展望 (24)5.1 本书总结 (25)5.2 数学思维的重要性 (26)5.3 未来发展趋势 (27)一、代数篇由于您没有提供具体的《数学思维2:代数与几何》阅读札记文档,我无法直接给出“代数篇”的具体内容。
我可以为您提供一个关于代数篇可能的概述和结构,以帮助您理解这个部分可能包含的内容。
方程和不等式:解一元一次方程、二元一次方程组,以及不等式的应用。
函数:定义、性质、图象,以及一次函数、二次函数、反比例函数等的解析式和图像。
1.1 整数的性质整数是数学中最基本的数,它们具有许多独特的性质。
在《数学思维2:代数与几何》我们将学习一些关于整数的基本性质,这些性质对于理解代数和几何问题非常重要。
整数包括正整数、负整数和零。
正整数是大于零的整数,负整数是小于零的整数,而零既不是正整数也不是负整数、0都是整数的例子。
整数具有加法和乘法运算,加法是将两个整数相加以得到它们的和,例如3+ 58。
乘法是将一个整数与另一个整数相乘以得到它们的积,例如46 24。
乘法不满足交换律,即a a(除非b为零)。
整数具有除法运算,除法是将一个整数除以另一个整数以得到它们的商,例如124 3。
需要注意的是,当被除数不能被除数整除时,结果通常是一个带有小数部分的分数。
基于算法视角的解析几何例题教学——椭圆中一类非对称问题的处理策略

2
消元是关键•我们发现点MN在椭圆上,有⑷+
3 =1,⑷+3=1成立•仔细分析其中的差异,发
现条件式是二次, 目标式是一次, 需要将次数化成
同次才能便于消元,从而想到将②式平方,把一 次升为二次再代入消元 在解析几何的化简中,常 常需要我们具有结构观念,仔细观察式子的结构, 发现它们的差异,通过数学的方法架起联系的 桥梁.
x2 —2
kx1x2 + (2k + 2X] + (4k — 1X2 + 6=0 ①9将
X1X2 代入得—4k82 k+3 + (k + 2)・
一 4k+ 2712k2_+6烌 + 火—1)・
烆
4k2 +3
烎
一 4k—2712犽一十6 烌 +6= 0,化简得(18—12k ) +
(6 — 4k) X 712k2 +6 = 0 , 即 (3 —
4k2+3
化简得 64k4+48k3 + 18k —9=0,即(8k2+3) (8k2
+ 6k — 3) =0.因为 8k2 +3^0,所以 8k2 + 6k —
12k
3 =0.
从M 而而k, MN
; = kcN
= ---48万kk2—2+-—- 376---------4k2 +3
4k2 +12k+3 _ 8k2 — 6=
x2 一 2
(2k+2)得xx2 +
(2k +2)(x1 +x2) + (2k —3)x2 + 6 =0 .将 x1 +
数学几何问题的解决方案

数学几何问题的解决方案数学几何是数学的一个重要分支,它研究的是空间中的形状、结构和变换。
几何问题的解决方案可以帮助我们更好地理解和应用数学知识。
在本文中,我将介绍一些常见的数学几何问题,并探讨它们的解决方案。
一、平面几何问题平面几何是几何学的基础,它研究的是二维空间中的形状和结构。
在平面几何中,有许多经典的问题,如求两点之间的最短距离、求直线与曲线的交点等。
解决平面几何问题的一种常见方法是使用坐标系。
我们可以将平面上的点表示为坐标对(x, y),通过坐标系的建立,我们可以将几何问题转化为代数问题。
例如,求两点之间的最短距离,我们可以使用勾股定理来计算,根据两点的坐标差值求平方和再开方即可。
此外,解决平面几何问题还可以使用向量的方法。
向量是平面几何中的重要工具,它可以表示方向和大小。
通过向量的加减、点乘和叉乘等运算,我们可以解决许多几何问题。
例如,求两直线的夹角可以使用向量的点乘公式,求两直线的交点可以使用向量的叉乘公式。
二、立体几何问题立体几何是几何学的扩展,它研究的是三维空间中的形状和结构。
在立体几何中,有许多有趣的问题,如求立方体的体积、求球体的表面积等。
解决立体几何问题的一种常见方法是使用几何体的特性和性质。
每种几何体都有其独特的特点,通过了解这些特点,我们可以找到解决问题的关键。
例如,求立方体的体积,我们知道立方体的体积等于边长的立方,因此只需将边长代入公式即可。
此外,解决立体几何问题还可以使用投影的方法。
投影是将三维物体映射到二维平面上的过程。
通过投影,我们可以将立体几何问题转化为平面几何问题,然后使用平面几何的方法解决。
例如,求两个平行直线之间的距离,我们可以将其投影到一条直线上,然后使用平面几何的方法求解。
三、解决几何问题的策略除了具体的方法和技巧,解决几何问题还需要一定的策略。
在解决几何问题时,我们可以采取以下几个步骤:首先,仔细阅读问题,理解问题的要求和条件。
几何问题往往有很多条件,我们需要明确这些条件,然后将其转化为数学表达式。
CAD学习笔记

CAD学习笔记AutoCAD学习笔记一、选择常用的三种方法:1、从左到右拖动窗口选择,要框住才能选中;2、从右向左拖动窗口选择,只要接触到对象就能选中,包含在其内的也能选中;3、点选。
二、鼠标的操作:1、中键向外(上)滚动为放大窗口,向里(下)滚动为缩小窗口;2、按两次中键等于窗口全部显示;3、按住中键不放,等于移动窗口;快捷键:P4、按右键相当于键盘的空格键。
三、绘图工具:1、直线(快捷键:L)A、指定第一点,拉出角度,输入长度确定第二点。
B、相对直角坐标下,输入相对于第一点的X坐标,用“,(英文输入)”或“TAB 键”切换到Y坐标,空格即可。
C、极坐标下,指定第一点,输入线的长度,然后用“<”,切换到角度(该角度相对于x轴正方向,逆时针方向为正),空格即可。
D、可用快捷键LT导出线型管理器添加直线类型。
2、构造线(快捷键:XL)指定点或【水平(H)/垂直(V)/角度(A)/二等分(B)/偏移(O)】A、二等分(B):顶点+角的两边B、偏移(O):偏移距离+相对直线+向哪侧偏移3、多段线(快捷键:PL)指定起点,再指定下一个点或【圆弧(A)/半宽(H)/长度(L)/放弃(U)/宽度(W)】宽度(W):指定起点宽度+指定端点宽度。
若起点宽度=端点宽度,则画出的是矩形;若起点宽度≠端点宽度,画出的为等腰梯形或者三角形。
4、圆(快捷键:C)指定圆的圆心或【三点(3P)/两点(2P)/切点、切点、半径(T)】5、修剪工具(快捷键:TR)A、选择修剪工具,选择对象(可以框选),然后空格确定,选择要修剪的对象,再空格结束。
B、选择修剪工具,直接空格确定,选择要修剪的对象,再空格结束。
6、椭圆(快捷键:EL)指定椭圆的轴端点或【圆弧(A)/中心点(C)】椭圆弧:椭圆+起始角度+终止角度7、偏移(快捷键:O)指定偏移距离或【通过(T)/删除(E)/图层(L)】偏移距离+偏移对象+要偏移的那一侧8、倒圆角(快捷键:F)第一个对象或【弃(U)/多段线(P)/半径(R)/修剪(T)/多个(M)】半径+第一个对象+第二个对象9、复制(快捷键:CO或者Ctrl + C)选择对象+空格+指定基点或【位移(D)/模式(O)】10、旋转复制(快捷键:RO)选择对象+空格+指定基点(旋转中心点)+指定旋转角度或【复制(C)/参照(R)】注意:旋转角度之前可以选择复制(C)11、镜像(快捷键:MI)选择对象(需要对称过去的对象)+空格+指定镜像线的第一点+指定镜像线的第二点+要删除源对象吗?12、矩形(快捷键:REC)A、指定第一个角点或【倒角(C)/标高(E)/圆角(F)/厚度(T)/宽度(W)】B、利用相对坐标系(X坐标+“,”+Y坐标)指定另一个角点或【面积(A)/尺寸(D)/旋转(R)】C、尺寸(D):矩形的长度(X方向)+矩形的宽度(Y方向)+方向13、样条曲线(快捷键:SPL)14、正多边形(快捷键:POL)输入边的数目+指定正多边形的中心点或【边(E)】+输入选项【内接于圆(I)/外切于圆(C)】+圆的半径15、点(快捷键:PO)定数等分(快捷键:DIV):线+选择对象+分成的线段数目定距等分(快捷键:ME):线+选择对象+指定线段长度16、图案填充/渐变色(快捷键:H)封闭曲线类型+图案+样例(颜色)+添加拾取点(或添加选择对象)17、边界(快捷键:BO)拾取点,对象必须封闭。
(完整版)高等数学完全归纳笔记(全)

一、函数与极限 (2)1、集合的概念 (2)2、常量与变量 (3)2、函数 (4)3、函数的简单性态 (4)4、反函数 (5)5、复合函数 (6)6、初等函数 (6)7、双曲函数及反双曲函数 (7)8、数列的极限 (9)9、函数的极限 (10)10、函数极限的运算规则 (12)一、函数与极限1、集合的概念一般地我们把研究对象统称为元素,把一些元素组成的总体叫集合(简称集)。
集合具有确定性(给定集合的元素必须是确定的)和互异性(给定集合中的元素是互不相同的)。
比如“身材较高的人”不能构成集合,因为它的元素不是确定的。
我们通常用大字拉丁字母A、B、C、……表示集合,用小写拉丁字母a、b、c……表示集合中的元素。
如果a是集合A中的元素,就说a属于A,记作:a∈A,否则就说a不属于A,记作:a A。
⑴、全体非负整数组成的集合叫做非负整数集(或自然数集)。
记作N⑵、所有正整数组成的集合叫做正整数集。
记作N+或N+。
⑶、全体整数组成的集合叫做整数集。
记作Z。
⑷、全体有理数组成的集合叫做有理数集。
记作Q。
⑸、全体实数组成的集合叫做实数集。
记作R。
集合的表示方法⑴、列举法:把集合的元素一一列举出来,并用“{}”括起来表示集合⑵、描述法:用集合所有元素的共同特征来表示集合。
集合间的基本关系⑴、子集:一般地,对于两个集合A、B,如果集合A中的任意一个元素都是集合B的元素,我们就说A、B有包含关系,称集合A为集合B的子集,记作A B(或B A)。
⑵相等:如何集合A是集合B的子集,且集合B是集合A的子集,此时集合A中的元素与集合B中的元素完全一样,因此集合A与集合B相等,记作A=B。
⑶、真子集:如何集合A是集合B的子集,但存在一个元素属于B但不属于A,我们称集合A是集合B的真子集。
⑷、空集:我们把不含任何元素的集合叫做空集。
记作,并规定,空集是任何集合的子集。
⑸、由上述集合之间的基本关系,可以得到下面的结论:①、任何一个集合是它本身的子集。
天大《结构力学-1》学习笔记一

天⼤《结构⼒学-1》学习笔记⼀主题:《结构⼒学-1》学习笔记学习时间:整学期《结构⼒学-1》学习笔记⼀——绪论教学内容:⼀、绪论,结构⼒学的研究对象,荷载的分类,节点及⽀座的分类,结构的计算简图及分类⼆、⼏何组成分析的⽬的,⾃由度的概念,平⾯体系⾃由度的计算公式。
平⾯⼏何不变体系的基本组成规律及其运⽤。
瞬变体系的特征。
体系的⼏何组成与静定性的关系。
难点:平⾯⼏何体系的判断。
重点:平⾯⼏何体系的组成分析。
要求:⼏何不变体系的基本组成规则及应⽤教学⽬的要求:1、掌握:结构⼒学的研究对象,荷载的分类,节点及⽀座的分类,结构的计算简图及分类;平⾯⼏何不变体系的基本组成规律及其运⽤。
体系的⼏何组成与静定性的关系。
2、熟悉:⼏何组成分析的⽬的,⾃由度的概念,瞬变体系的特征。
体系的⼏何组成与静定性的关系。
3、了解:平⾯体系⾃由度的计算公式。
绪论1.1 结构⼒学的研究对象、任务和学习⽅法⼀、研究对象1、研究对象:结构⼒学以结构为研究对象。
(1)住宅、⼚房等⼯业民⽤建筑物;(2)涵洞、隧道、堤坝、挡⼟墙等构筑物;(3)桥梁、轮船、潜⽔艇、飞⾏器等结构物。
2、结构:承受荷载⽽起⾻架作⽤的部分称为⼯程结构,简称结构。
⼆、结构⼒学的任务1、研究结构的组成规律:保证结构能够承受荷载⽽不致发⽣相对运动;探讨结构的合理形式,以便有效地利⽤材料,充分发挥其性能。
2、计算结构在荷载、温度变化、⽀座移动等外部因素作⽤下的内⼒:为结构的强度计算提供依据,以保证结构满⾜安全和经济要求。
3、计算结构在荷载、温度变化、⽀座移动等外部因素作⽤下的变形和位移:为结构的刚度计算提供依据,以保证结构不致发⽣超过规范限定的变形⽽影响正常使⽤。
4、研究结构的稳定计算:确定结构丧失稳定性的最⼩临界荷载,以保证结构处于稳定的平衡状态⽽正常⼯作。
5、研究结构在动⼒荷载作⽤下动⼒特性。
三、结构⼒学与相关课程的关系1、“理⼒”、“材⼒”是“结构⼒学”的先修课。
小学优秀摘抄笔记数学(3篇)

第1篇一、整数运算1. 加法交换律:两个数相加,交换加数的位置,和不变。
例如:3 + 5 = 5 + 3。
2. 加法结合律:三个数相加,先把前两个数相加,或先把后两个数相加,和不变。
例如:2 + (3 + 4) = (2 + 3) + 4。
3. 减法的性质:一个数连续减去两个数,等于减去这两个数的和。
例如:8 - 3 - 5 = 8 - (3 + 5)。
4. 乘法交换律:两个数相乘,交换因数的位置,积不变。
例如:3 × 4 = 4 × 3。
5. 乘法结合律:三个数相乘,先把前两个数相乘,或先把后两个数相乘,积不变。
例如:2 × (3 × 4) = (2 × 3) × 4。
6. 乘法分配律:一个数乘以两个数的和,等于这个数分别乘以这两个数的积的和。
例如:2 × (3 + 4) = 2 × 3 + 2 × 4。
7. 除法的性质:一个数连续除以两个数,等于用这个数除以这两个数的积。
例如:12 ÷ 3 ÷ 2 = 12 ÷ (3 × 2)。
二、分数1. 分数与整数的关系:一个整数可以看作是分母为1的分数。
例如:3可以写作3/1。
2. 分数的基本性质:分数的分子和分母同时乘或除以相同的数(0除外),分数的大小不变。
3. 分数的加减法:同分母的分数相加减,只把分子相加减,分母不变。
异分母的分数相加减,先通分,再按照同分母分数加减法的计算方法进行计算。
4. 分数的乘除法:分数乘以分数,先把分子相乘的积作为新的分子,分母相乘的积作为新的分母;分数除以分数,先把除数的分子和分母颠倒位置后,再乘以被除数。
三、小数1. 小数与分数的关系:小数可以看作是分母为10、100、1000等10的幂次的分数。
2. 小数的基本性质:小数的末尾添上0或去掉0,小数的大小不变。
3. 小数的加减法:小数点对齐,按照整数加减法的计算方法进行计算。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
pGC.AddElement(pElement, 0);
pLineSymbol.Width = 2; pLineSymbol.Color = pRGBColor;
symbol = pLineSymbol; // 将图像绘制在地图上的参数 ILineElement pLineElement; pLineElement = new LineElementClass();//LineElementClass是 ESRI.ArcGIS.Carto
pSimpleFillSymbol.Outline = pLineSymbol;
同时添加代码:
pSimpleFillSymbol.Outline = pOutLine;
下面为改正后的代码(改动的地方有注释(红色字体)):
else if (radioButton2.Checked == true) { axToolbarControl1.CurrentTool = null; axToolbarControl1.Refresh();
(2) 加载地图后不能绘制图形是因为缺少一个将绘制好的图形传到地图文档的方法。 解决方法:
因此我们需要在 private void axMapControl1_OnMouseDown()的
最后添加一段代码:
axMapControl1.DrawShape(geomertry, ref symbol);
码:
if(e.button==1)
问题 2
在 axMapControl1 中不能画线,加载地图后不能绘制图形。 原因: (1) 画线完成后不显示的原因是pLineSymbol没有对象去存放画好的线, 解决方法:
需要新建一个SimpleLineSymbolClass对象。即:
pLineSymbol = new Sieometry = pPolygon;
//ILineSymbol pOutLine; //pOutLine = new SimpleLineSymbolClass(); //pOutLine.Width = 1; //pOutLine.Color = pColor;
ISimpleFillSymbol pSimpleFillSymbol; pSimpleFillSymbol = new SimpleFillSymbolClass(); pSimpleFillSymbol.Color = pRGBColor;
pSimpleFillSymbol.Style = esriSimpleFillStyle.esriSFSSolid;
symbol = pSimpleFillSymbol;
// pFillSymbol = pSimpleFillSymbol as IFillSymbol;
IFillShapeElement pFillShapeElement; pFillShapeElement = new PolygonElementClass(); pFillShapeElement.Symbol = pSimpleFillSymbol; //pFillShapeElement = pPolygon as IFillShapeElement; IElement pElement; pElement = pFillShapeElement as IElement; pElement.Geometry = pPolygon;
其中,geometry 和 symbol 这两个参数是将图形显示在图层上。 下面为改正后的代码(改动的地方有注释):
private void axMapControl1_OnMouseDown(object sender, ESRI.ArcGIS.Controls.IMapControlEvents2_OnMouseDownEvent e)
geometry = pPolygon;
定的颜色
ILineSymbol pOutLine; pOutLine = new SimpleLineSymbolClass(); pOutLine.Width = 1; pOutLine.Color = pColor; //将外廓线的颜色指向引用pColor ISimpleFillSymbol pSimpleFillSymbol; pSimpleFillSymbol = new SimpleFillSymbolClass(); pSimpleFillSymbol.Color = pRGBColor; pSimpleFillSymbol.Outline = pOutLine; //新增代码,使面的外廓线颜色为设
pSimpleFillSymbol.Color = pRGBColor; //pSimpleFillSymbol.Outline = pOutLine; pSimpleFillSymbol.Outline = pLineSymbol; pSimpleFillSymbol.Style = esriSimpleFillStyle.esriSFSSolid;
“pRgbColor”指向的不是同一个RgbColorClass对象。“color”按钮中的引用需要和绘制图形中
的“pRgbColor”共享同一个RgbColorClass对象,才能改变绘制图像的颜色;
(2)而且程序中因添加了颜色的初始化代码而无法改变颜色。
解决方法:
(1)定义一个颜色对象作为全局变量,同时将原程序中生成的两个RgbColorClass()
原因:程序中将面的外廓线的颜色(pOutLine.Color)指向了画线时颜色的引用 (pRgbColor),也就是说线的颜色改变,那么面的颜色随之改变。
解决方法: 解决此问题有两种方法: ●方法1: 在画面的代码中重新定义一个颜色对象,并对颜色引用pColor进行赋值来作为默认的 外廓线的颜色,同时将外廓线的颜色(pOutLine.Color)指向引用pColor; 删除代码:
geometry = pPolygon;// 将图像绘制在地图上的参数 ILineSymbol pOutLine; pOutLine = new SimpleLineSymbolClass(); pOutLine.Width = 1; pOutLine.Color = pRGBColor;
ISimpleFillSymbol pSimpleFillSymbol; pSimpleFillSymbol = new SimpleFillSymbolClass();
symbol = pSimpleFillSymbol; // 将图像绘制在地图上的参数
// pFillSymbol = pSimpleFillSymbol as IFillSymbol;
IFillShapeElement pFillShapeElement; pFillShapeElement = new PolygonElementClass(); pFillShapeElement.Symbol = pSimpleFillSymbol; //pFillShapeElement = pPolygon as IFillShapeElement; IElement pElement; pElement = pFillShapeElement as IElement; pElement.Geometry = pPolygon;
//IRgbColor pColor = new RgbColorClass(); //pColor.Red = 255; //pColor.Green = 0; //pColor.Blue = 0;
IGeometry pPolygon = new PolygonClass(); pPolygon = axMapControl1.TrackPolygon();
pGC.AddElement(pElement, 0); }
●方法2: 和问题3中解决画线问题的思想一样,始终将面的外廓线的颜色设置为默认颜色(黑 色),即不对外廓线的颜色进行初始化。代码如下(代码为绿色的都删除):
else if (radioButton2.Checked == true) { axToolbarControl1.CurrentTool = null; axToolbarControl1.Refresh();
pGC.AddElement(pElement, 0); } axMapControl1.DrawShape(geometry, ref symbol); 将图形画在地图的图层上。 } }
//必须有此代码,才能
问题 3
在老师提供的程序中,点击
改变绘制图形的颜色,操作无效。
原因:
(1)color按钮的代码中使用的颜色引用“pRgbColor”与绘制图形所使用的颜色引用
pPolyLine = axMapControl1.TrackLine();
geometry = pPolyLine;// 将图像绘制在地图上的参数
pLineSymbol = new SimpleLineSymbolClass(); //对照画面的方法,pLineSymbol缺少存放画好线的方法。 //SimpleLineSymbolClass是ESRI.ArcGIS.Display成员, pLineSymbol要用 SimpleLineSymbolClass对象来存放画好的线。
{ IGeometry geometry = null;//定义参数 object symbol = null; //定义参数
if (e.button == 1) {
if (radioButton1.Checked == true) {
axToolbarControl1.CurrentTool = null; axToolbarControl1.Refresh(); //IPolyline pPolyLine; IGeometry pPolyLine = new PolylineClass();
