1.1.2 程序框图
合集下载
1.1.2 程序框图
开始
①
பைடு நூலகம்
程序框图
输入n r =0? i=2
是
否
求n除以i的余数r i=i+1 i>n-1 或r=0?
是 ① 否
n不是质数
n是质数
结束
(1)给定大于 (1)给定大于 的整数n. 2的整数n.
(2)令i=2 令
(3)用 (3)用i除n,得余数r.判断余数r是否为0,若是,则n不是质数,结束 n,得余数r.判断余数r是否为0,若是, 得余数r.判断余数 0,若是 不是质数, 算法；否则, 的值增加1,仍用i表示这个数. 1,仍用 算法；否则,将i的值增加1,仍用i表示这个数. (4)判断i是否大于n 1,若是, (4)判断i是否大于n-1,若是,则n是质数；否则,返回第三步. 判断 若是 是质数；否则,返回第三步.
画流程图的规则
为了使大家彼此之间能够读懂各自画出的框图, 为了使大家彼此之间能够读懂各自画出的框图,必须遵守一些共 同的规则. 同的规则.
(1)使用标准的框图符号. 使用标准的框图符号. 框图一般按从上到下、从左到右的方向画. (2)框图一般按从上到下、从左到右的方向画. (3) 流程线是带有方向箭头的线, 用以连接框图, 直观地表 流程线是带有方向箭头的线 , 用以连接框图 , 示算法的流程.在程序框图中, 示算法的流程.在程序框图中,任意两个程序框之间都存在 流程线. 流程线. 在程序框图中,除起止框外, (4) 在程序框图中 , 除起止框外 , 任意一个程序框都只有一 条流程线“ 流进” 输入输出框、 条流程线 “ 流进 ” , 输入输出框 、 处理框都只有一条流程 线“流出”,但判断框一定是至少有两条流程线“流出”. 流出” 但判断框一定是至少有两条流程线“流出” 一个完整的程序框图包括以下几部分： (5) 一个完整的程序框图包括以下几部分 ： 表示相应操作 的程序框、带箭头的流程线、程序框外必要的文字说明.以 的程序框、带箭头的流程线、程序框外必要的文字说明 以 起止框表示开始,以终止框表示结束 以终止框表示结束. 起止框表示开始 以终止框表示结束
1.1.2程序框图
第三步：输出结果。
广东省东莞沙田中学 罗朝举
每天进步一点点,哪怕是1%的进步.
相应的程序框图为：
开始
a＝2，b＝3
计算 x y 1
ab
输出结果
结束
广东省东莞沙田中学 罗朝举
每天进步一点点,哪怕是1%的进步.
练习3： 1、写出过两点P1（3，5），P2（－1，2）的 直线的斜率的一个算法，并画出程序框图。 2、写出求A（x1，y1），B（x2，y2）的两点 距离的一个算法，并画出程序框图。
广东省东莞沙田中学 罗朝举 Nhomakorabea天进步一点点,哪怕是1%的进步.
三、本课小结 1、程序框图 （1）程序框图由程序框、流程线和程 序框外必要的文字说明组成。 （2）程序框有：终端框、输入输出框、 处理框和判断框。
广东省东莞沙田中学 罗朝举
每天进步一点点,哪怕是1%的进步.
2、算法的基本逻辑结构：顺序结构、条件结 构和循环结构。 3、画程序框图的规则 （1）使用标准的框图符号； （2）框图一般从上到下、从左到右的方向画； （3）除判断框外，大多数框图符号只有一个 进入点(入口)和一个退出点(出口)； （4）在框图符号内描述的语言要简练清楚。
广东省东莞沙田中学 罗朝举
每天进步一点点,哪怕是1%的进步.
基本的程序框和它们各自表示的功能如下:
图形符号
名称
功能
终端框 (起止框)
输入、输出 框
表示一个算法的起始 和结束
表示一个算法输入和 输出的信息
处理框 (执行框)
判断框
流程线
赋值、计算
判断某一条件是否成立,成立 时在出口处标明“是”或 “Y”；不成立时标明“否”
2、 ①有限性
②明确性
广东省东莞沙田中学 罗朝举
每天进步一点点,哪怕是1%的进步.
相应的程序框图为：
开始
a＝2，b＝3
计算 x y 1
ab
输出结果
结束
广东省东莞沙田中学 罗朝举
每天进步一点点,哪怕是1%的进步.
练习3： 1、写出过两点P1（3，5），P2（－1，2）的 直线的斜率的一个算法，并画出程序框图。 2、写出求A（x1，y1），B（x2，y2）的两点 距离的一个算法，并画出程序框图。
广东省东莞沙田中学 罗朝举 Nhomakorabea天进步一点点,哪怕是1%的进步.
三、本课小结 1、程序框图 （1）程序框图由程序框、流程线和程 序框外必要的文字说明组成。 （2）程序框有：终端框、输入输出框、 处理框和判断框。
广东省东莞沙田中学 罗朝举
每天进步一点点,哪怕是1%的进步.
2、算法的基本逻辑结构：顺序结构、条件结 构和循环结构。 3、画程序框图的规则 （1）使用标准的框图符号； （2）框图一般从上到下、从左到右的方向画； （3）除判断框外，大多数框图符号只有一个 进入点(入口)和一个退出点(出口)； （4）在框图符号内描述的语言要简练清楚。
广东省东莞沙田中学 罗朝举
每天进步一点点,哪怕是1%的进步.
基本的程序框和它们各自表示的功能如下:
图形符号
名称
功能
终端框 (起止框)
输入、输出 框
表示一个算法的起始 和结束
表示一个算法输入和 输出的信息
处理框 (执行框)
判断框
流程线
赋值、计算
判断某一条件是否成立,成立 时在出口处标明“是”或 “Y”；不成立时标明“否”
2、 ①有限性
②明确性
1.1.2程序框图
（2）构成程序框图的图形符号及其作用
图形符号
名称
终端框 (起止框) 输入、 输出框 处理框 (执行框)
功能
表示一个算法的起始和结束 表示一个算法输 它是唯一的具有 入和输出的信息 两个出口的符号 赋值、计算
判断某一条件是否成立 , 成立时 在出口处标明“是”或“ Y”, 不 成立时标明“否”或“N”.
算 法 的 基 本 逻 辑 结 构
开始 输入n i=2 求n除以i的余数
顺 序 结 构
i的值增加1,仍用i表示
i>n-1或r=0?
是 r=0? 是 否
否
循 环 结 构
条 件 结 构
n不是质数
结束
n是质数
从上面的程序框图中,不难看出以下三种不 同的逻辑结构.
r=0?
输入n 是 否
求n除以i 的余数r
判断框
流程线
连结点
连接程序框 连接程序框图的两部分
判断“整数n(n>2)是否是质数”的算法：
开始
自然语言描述
第二步，令i=2.
图形描述
输入n i=2 求n除以i的余数r
第一步，给定大于2的整数n.
第三步，用i除n，得到余数r. 第四步，判断“r=0”是否成 立.若是，则n不是质数，结束算 法；否则将i的值增加1，仍用i 表示. 第五步，判断“i>(n-1)”是否 成立.若是，则n是质数，结束算 法；否则返回第三步.
i=i+1
n是质数
i=2
n不是质数
否
i≥n或r=0? 是
尽管不同的算法千差万别 , 但它们都是由 三种基本的逻辑结构构成的 , 这三种逻辑结构 就是顺序结构、条件结构 、循环结构 . 下面分 别介绍这三种结构．
原创2：1.1.2程序框图
名称
名称
名称
输入、输出框
处理框或执行框
判断框
作用
作用
作用
表示算法的
起始和结束
表示算法的输入
和输出的信息
赋值、计算
判断某一条件是否成立，
成立在出口处标明“是”或“Y”
不成立标明“否”或“N”
画程序框图的规则如下：
1、使用标准的图形符号。
2、框图一般按从上到下、从左到右的方向画。
3、除判断框外，大多数流程图符号只有一个进入点和一个退出
三步。
开始
输入n
i=2
n除以i的余数r
i=i+1
否
i>n-1或r=0?
是
r=0?
是
n不是质数
结束
否
n是质数
上述表示算法的图形称为算法的程序框图又称流程图，其
中的多边形叫做程序框，带方向箭头的线叫做流程线，你
能指出程序框图的含义吗？
用程序框、流程线及文字说明来表示算法的图形.
二、新课
开始
输入n
i=2
不同的程序框有不同的含义
i=2
n除以i的余数r
i=i+1
否
i>n-1或r=0?
是
r=0?
是
n不是质数
结束
否
n是质数
开始
输入n
i=2
终端框（起止框），表示
一个算法的起始和结束
n除以i的余数r
i=i+1
否
i>n-1或r=0?
是
r=0?
是
n不是质数
结束
否
n是质数
开始
输入n
输入、输出框表示一个
算法输入和输出的信息
名称
名称
输入、输出框
处理框或执行框
判断框
作用
作用
作用
表示算法的
起始和结束
表示算法的输入
和输出的信息
赋值、计算
判断某一条件是否成立，
成立在出口处标明“是”或“Y”
不成立标明“否”或“N”
画程序框图的规则如下：
1、使用标准的图形符号。
2、框图一般按从上到下、从左到右的方向画。
3、除判断框外，大多数流程图符号只有一个进入点和一个退出
三步。
开始
输入n
i=2
n除以i的余数r
i=i+1
否
i>n-1或r=0?
是
r=0?
是
n不是质数
结束
否
n是质数
上述表示算法的图形称为算法的程序框图又称流程图，其
中的多边形叫做程序框，带方向箭头的线叫做流程线，你
能指出程序框图的含义吗？
用程序框、流程线及文字说明来表示算法的图形.
二、新课
开始
输入n
i=2
不同的程序框有不同的含义
i=2
n除以i的余数r
i=i+1
否
i>n-1或r=0?
是
r=0?
是
n不是质数
结束
否
n是质数
开始
输入n
i=2
终端框（起止框），表示
一个算法的起始和结束
n除以i的余数r
i=i+1
否
i>n-1或r=0?
是
r=0?
是
n不是质数
结束
否
n是质数
开始
输入n
输入、输出框表示一个
算法输入和输出的信息
1.1.2程序框图
思考6:用当型循环结构，上述算法的程 序框图如何表示？ 开始
i=1
S=0
i≤100？ 否
输出S
结束
S=S+i 是
思考6:用当型循环结构，上述算法的程 序框图如何表示？ 开始
i=1 S=0
i=i+1
i≤100？ 否
输出S
S=S+i 是
结束
小结
顺序结构的程序框图的基本特征：
（1）必须有两个起止框，穿插输入、输出框和 处理框，没有判断框.
开始
输入a，b，c
△= b2-4ac
△≥0？
是
p
b 2a
q 2a
△=0？ 否 x1=p+q x2=p-q
输出x1，x2
程序框图：
开始
输入a，b，c
△= b2-4ac
△≥0？
是
p
b 2a
q 2a
△=0？ 否 x1=p+q x2=p-q
输出x1，x2
结束
程序框图：
开始
输入a，b，c
△= b2-4ac
（2）各程序框从上到下用流程线依次连接.
小结
条件结构的程序框图的基本特征：
（1）程序框图中必须有两个起止框，穿插 输入、输出框和处理框，一定有判断框.
（2）条件结构的程序框图各有两种形式.
小结
循环结构的程序框图的基本特征：
（1）循环结构中包含条件结构，条件结构 中不含循环结构. （2）循环结构的程序框图各有两种形式.
程序框图：
程序框图：
开始 输入a，b，c
程序框图：
开始 输入a，b，c △= b2-4ac
程序框图：
开始 输入a，b，c △= b2-4ac
1.1.2 程序框图
算法初步
§1.1.2 程序框图
复习 1、算法的概念
2、算法的特点 3、常见的几个例子 4、判断一个正整数是否是质数的算法
算法的概念 算法是指解决给定问题的有穷操作步骤的 描述，简单的说，算法就是解决问题的步 骤和方法。
算法的基本特点
1、有穷性
一个算法应包括有限的操作步骤，能在执行有穷的操作 步骤之后结束。
思考：整个程序框图有什么特点？
输出面积S
结束
例2 已知一个三角形的三边长 确分别为2,3,4,利用海伧-秦九 韶公式设计一个算法,求出它的 面积,画出算法的程序框图.
开始
p=（2+3+4）/2
s=SQR(p*(p－2)*(p －3)*(p-4))
输出s
结束
例3 设计房租收费的算法,其要求是:住房面积80平方米 以内,每平方米收费3元,住房面积超过80平方米时,超过 部分,每平方米收费5元.输入住房面积数,输出应付的房租.
开始
输入a，b，c
a+b＞c，a+c ＞ b， b+c ＞ a是否同 时成立？ 是
否
存在这样的 三角形
不存在这样 的三角形
结束
例5 设计一个计算1＋2 ＋．．．＋１００的值的 算法，并画出程序框图．
开始
i=1
sum=0
i=i+1 sum=sum+1
i≤100?
否 输出sum 结束
是
练习巩固
１ 看下面的程序框图，分析算法的作用
2、确定性
算法的计算规则及相应的计算步骤必须是唯一确定的， 既不能含糊其词，也不能有二义性。 3、可行性 算法中的每一个步骤都是可以在有限的时间内完成的基 本操作，并能得到确定的结果 。
§1.1.2 程序框图
复习 1、算法的概念
2、算法的特点 3、常见的几个例子 4、判断一个正整数是否是质数的算法
算法的概念 算法是指解决给定问题的有穷操作步骤的 描述，简单的说，算法就是解决问题的步 骤和方法。
算法的基本特点
1、有穷性
一个算法应包括有限的操作步骤，能在执行有穷的操作 步骤之后结束。
思考：整个程序框图有什么特点？
输出面积S
结束
例2 已知一个三角形的三边长 确分别为2,3,4,利用海伧-秦九 韶公式设计一个算法,求出它的 面积,画出算法的程序框图.
开始
p=（2+3+4）/2
s=SQR(p*(p－2)*(p －3)*(p-4))
输出s
结束
例3 设计房租收费的算法,其要求是:住房面积80平方米 以内,每平方米收费3元,住房面积超过80平方米时,超过 部分,每平方米收费5元.输入住房面积数,输出应付的房租.
开始
输入a，b，c
a+b＞c，a+c ＞ b， b+c ＞ a是否同 时成立？ 是
否
存在这样的 三角形
不存在这样 的三角形
结束
例5 设计一个计算1＋2 ＋．．．＋１００的值的 算法，并画出程序框图．
开始
i=1
sum=0
i=i+1 sum=sum+1
i≤100?
否 输出sum 结束
是
练习巩固
１ 看下面的程序框图，分析算法的作用
2、确定性
算法的计算规则及相应的计算步骤必须是唯一确定的， 既不能含糊其词，也不能有二义性。 3、可行性 算法中的每一个步骤都是可以在有限的时间内完成的基 本操作，并能得到确定的结果 。
1.1.2程序框图
结束
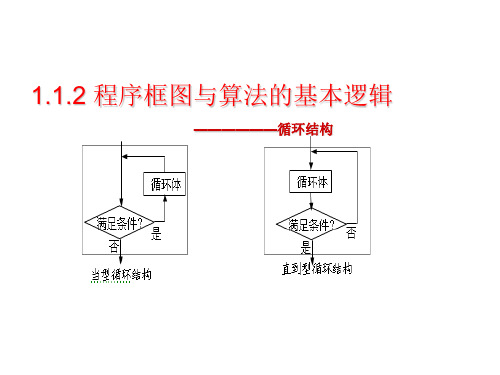
3.循环结构
需要重复执行同一操作的结构称为循 环结构。反复执行的处理步骤称为循环体。
循环体 循环体
是
满足条件？
否
满足条件？
否
是
当型结构
直到型结构
开始 i=1，S=0
设计一个算法：
1+2+3+…+100的程序框图。
循环结构就 可以解决！
i<＝100? 是 S=S + i i=i+1
否
输出S
结束
3三种基本结构示意图
是
条件
否 处理2
继续循环
A B
处理1
是
条件 否
顺序结构
条件结构
循环结构
1．(2012年高考课标全国卷)如果执行如图 所示的程序框图，输入正整数N(N≥2)和实 数a1，a2，…，aN，输出A，B，则( )
A．A＋B 为 a1，a2，„，aN 的和 A＋B B. 为 a1，a2，„，aN 的算术平均数 2 C．A 和 B 分别是 a1，a2，„，aN 中最大的数和最小的数 D．A 和 B 分别是 a1，a2，„，aN 中最小的数和最大的数
开始
图形描述：
输入n i=2 求n除以i的余数r i的值增加1,仍用i表示 i>n-1或r=0? 否
新的描述方法 —程序框图！
是 r=0? 是
否
输出“n不是质数” 输出“n是质数” 结束
知识要 点 程序框图
程序框图又称流程图，是一种 用规定的图形、指向线及文字说明 来准确、直观地表示算法的图形。
4．(2013年南昌模拟)若如下框图所给的程序运 行结果为S＝20，那么判断框中应填入的关于 k的条件是( ) A．k＝9？ B．k≤8? C．k<8? D．k>8?
1.1.2第1课时程序框图、顺序结构课件人教新课标
结果的传送，故选 A，其他选项皆不正确．
4．阅读如图所示
()
A．12
B．7
C．34
D．43
解析：选 A b＝a1·a2＝3×4＝12.故选 A.
对程序框图的认识和理解
[典例] (1)下列说法正确的是
()
A．程序框图中的图形符号可以由个人来确定
B． 也可以用来执行计算语句
(1)框图①中 x＝4 的含义是什么？ (2)框图②中 y1＝x3＋2x＋3 的含义是什么？ (3)框图④中 y2＝x3＋2x＋3 的含义是什么？ [解] (1)框图①的含义是初始化变量，令 x＝4. (2)框图②中 y1＝x3＋2x＋3 的含义：该框图是在执行① 的前提下，即当 x＝4 时，计算 x3＋2x＋3 的值，并令 y1 等 于这个值． (3)框图④中 y2＝x3＋2x＋3 的含义：该图框是在执行③ 的前提下，即当 x＝－2 时，计算 x3＋2x＋3 的值，并令 y2 等于这个值．
图示
[小试身手]
1．判断下列命题是否正确．(正确的打“√”，错误的打“×”)
(1)任何一个程序框图都必须有起止框
(√)
(2)输入框只能放在输出框之前
(×)
(3)判断框是唯一具有超过一个退出点的图形符号 ( √ )
解析：(1)正确，任何程序都必须有开始和结束，从而必须有
起止框；(2)错误，输入、输出框可以用在算法中任何需要输
[活学活用] 已知一个圆柱的底面半径为 R，高为 h，求圆柱的体积．设 计一个解决该问题的算法，并画出相应的程序框图． 解：算法如下： 第一步，输入 R，h. 第二步，计算 V＝πR2h. 第三步，输出 V. 程序框图如图所示：
顺序结构的读图问题 [典例] 阅读如图所示的程序框图，回答下面的问题：
1.1.2程序框图
复习: 复习
上节课例1:任意给定一个大于 的整数 上节课例 任意给定一个大于1的整数 试设计一个 任意给定一个大于 的整数n,试设计一个 算法判定n是否为质数 是否为质数. 算法判定 是否为质数
第一步 第二步 第三步 任意给定一个大于1的整数n 任意给定一个大于1的整数n 令i=2 用i除n得余数r 得余数r
开始 输入a、b、c 输入 、 、
A
B
a+b>c,a+c>b, b+c>a是否同时成立 是否同时成立
否
是
存在这样的三角形 不存在这样的三角形
结束
开始
输入系数 , 输入系数a,b,c 系数
∆ = b 2 − 4ac 计算
例3：设计算法,求一元二次 设计算法, 方程ax +bx+c=0（ 的根, 方程ax2+bx+c=0（a≠0）的根, 画出相应的流程图 是
Sum=1+2+3
否
输出sum 输出
结束
……Sum=1+2+3+…100
练习: 习
1+3+5+7+……+31=?
分析:只需要一个累加变量sum和计数变量 将累加 和计数变量i.将累加 分析 只需要一个累加变量 和计数变量
变量sum初值赋为 计数变量 从1到31变化 初值赋为0,计数变量 变化. 变量 初值赋为 计数变量i从 到 变化
2 + 3 + 4 p = 3
三角形面积为 s = 其中 p = p ( p − a )( p − b )( p − c ) a+b+c ( a、 b、 c为三角形三边长 ) 2
1.1.2程序框图
.2基本算法语句 1.3算法案例
1.1.2 程序框图 流程图） 程序框图(流程图） 流程图
算法可以用自然语言来描述， 算法可以用自然语言来描述，但为了使算法的 程序或步骤表达得更直观， 程序或步骤表达得更直观，我们更常用图形方 式来表示它。 式来表示它。
例1、任意给定一个大于1的整数n，试设计出一个程序 或步骤对n是否为质数做出判定
例2、用二分法设计一个求
3 近似值，并画出程序框图。
算法分析： 算法分析： 2 第一步：令f(x)= x − 3 。因为f(1)<0，f(2)>0，所以设
a=1，b=2。 第二步：令 所求；若否，则继续判断f(a) ·f(m)大于0还是小于0。 第三步：若f(a) ·f(b)>0，则令a=m；否则，令b=m。 第四步：判断︳a-b︳<0.005是否成立？若是，则a或b为 满足条件的近似根；若否，则返回第二步。
判断质数程序
n是质数
结束
x2 − 2 = 0
程序框图又称流程图，是一种规定的图形、 程序框图又称流程图，是一种规定的图形、指向 又称流程图 线及文字说明来准确、直观地表示算法的图形。 线及文字说明来准确、直观地表示算法的图形。 流程图的三种基本逻辑结构： 流程图的三种基本逻辑结构：
顺序结构 条件结构 循环结构
INPUT “输入一个实数a=”；a
开始
IF a≥0 THEN PRINT “|”;a;“|=”;a ELSE
输入a
PRINT “|”;a;“|=”;-a END IF END N
a ≥0
Y
输出 |a|=a
输出 |a|=-a
结束
求绝对值
x2 − 2 = 0
P.11练习 练习2 练习 ——二分法求平方根 二分法求平方根
1.1.2 程序框图 流程图） 程序框图(流程图） 流程图
算法可以用自然语言来描述， 算法可以用自然语言来描述，但为了使算法的 程序或步骤表达得更直观， 程序或步骤表达得更直观，我们更常用图形方 式来表示它。 式来表示它。
例1、任意给定一个大于1的整数n，试设计出一个程序 或步骤对n是否为质数做出判定
例2、用二分法设计一个求
3 近似值，并画出程序框图。
算法分析： 算法分析： 2 第一步：令f(x)= x − 3 。因为f(1)<0，f(2)>0，所以设
a=1，b=2。 第二步：令 所求；若否，则继续判断f(a) ·f(m)大于0还是小于0。 第三步：若f(a) ·f(b)>0，则令a=m；否则，令b=m。 第四步：判断︳a-b︳<0.005是否成立？若是，则a或b为 满足条件的近似根；若否，则返回第二步。
判断质数程序
n是质数
结束
x2 − 2 = 0
程序框图又称流程图，是一种规定的图形、 程序框图又称流程图，是一种规定的图形、指向 又称流程图 线及文字说明来准确、直观地表示算法的图形。 线及文字说明来准确、直观地表示算法的图形。 流程图的三种基本逻辑结构： 流程图的三种基本逻辑结构：
顺序结构 条件结构 循环结构
INPUT “输入一个实数a=”；a
开始
IF a≥0 THEN PRINT “|”;a;“|=”;a ELSE
输入a
PRINT “|”;a;“|=”;-a END IF END N
a ≥0
Y
输出 |a|=a
输出 |a|=-a
结束
求绝对值
x2 − 2 = 0
P.11练习 练习2 练习 ——二分法求平方根 二分法求平方根
人教A版 高中数学 必修3 第一章 1.1.2 循环结构的程序框图课件(共16张PPT)
巩固提高
1、设计一算法，求 积:1×2×3×…×100， 画出流程图
思考：该流程图与前面 的例1中求和的流程图有 何不同？
开始 i=0，S=1
i=i+1 S=S*i 否 i>=100?
是 输出S 结束
巩固提高
2、设计一算法输出1~1000以内能被3整除的整数
开始
算法：
i=0
S1：确定i的初始值为0；
开始 i=0，S=0
否 i<100? 是 i=i+1 S=S+ i
输出S 结束
思考:将步骤A和步骤B交换位 置，结果会怎样？能达到预期结果 吗？为什么？要达到预期结果，还 需要做怎样的修改？
步骤A
步骤B 答：达不到预期结果；
当i = 100时，退出循环，i 的值未能加入到S中；修 改的方法是将判断条件改 为i<101
1.1.2 程序框图与算法的基本逻辑
——————循环结构
复习回顾
1、程序框图（流程图）的概念： 2、算法的三种逻辑结构： 3、顺序结构的概念及其程序框图： 4、条件结构的概念及其程序框图：
复习回顾
i) 顺序结构
ii) 条件结构
Yp N A
A
B
B
循环结构
循环结构：在一些算法中，也经常会出现从某处开始，
小结：
4．画循环结构流程图前： ①确定循环变量和初始条件； ②确定算法中反复执行的部分，即循环体； ③确定循环的转向位置； ④确定循环的终止条件.
循环结构的三要素：
循环变量，循环体、循环的终止条件。
其中顺序结构是最简单的结构，也是最基 本的结构，循环结构必然包含条件结构，所以 这三种基本逻辑结构是相互支撑的，无论怎样 复杂的逻辑结构，都可以通过这三种结构来表 达。
1.1.2程序框图
开始 输入a，b，c
第二步，计算p=(a+b+c)/2..
第三步，计算 S 第四步，输出S..
p
abc 2
p( p a)( p b)( p c)
S p( p a)( p b)( p c)
输出S 结束
练习：
1.就（1）、（2）两种逻辑结构，说出各自的算
法功能 （1） 开始 输入a，b （2） 开始 输入a，b 2.已知梯形上底为2，下底为4，
1.1.2 程序框图与 算法的基本逻辑结构
复习: 上节课例:任意给定一个大于1的整数n,试设计一个算 法判定n是否为质数.
算法分析：
1.判断n是否等于2,如果n=2,则 n为质数,若n>2,则执行第2步. 2.依次从2到n-1检验是不是n的因数(即是否整除n).若存在这样 的数,则n不是质数,若不存在这样的数,则n为质数. 以上是用自然语言描述一个算法.为了使得算法的描述更为直观和 步骤化,下面介绍另一种描述算法的方法:程序框图.
任何算法都离不开顺序结构。
步骤n
步骤n+1
顺序结构：
例1： 已知一个三角形的三边分别为a，b，c，利用海伦-秦九韶公式设计 一个算法，求出它的面积，画出算法的程序框图． 程序框图： 分析：先算出p的值，再将它代入公式，最后输出
结果，只用顺序结构就能够表达出算法．
算法步骤如下： 第一步，输入三角形三边的边长a,b,c.
高为5，求其面积，设计出该
问题的流程图． 开始
a 2, b 4, h 5
S 1 ( a b) h 2
d a 2 b2
c d
输出
sum=a+b 输出sum 结束
1.1.2算法与程序框图
循环结构分为当型循环结构和 循环结构分为当型循环结构和直到型循环结构 当型循环结构
循环体 循环体 是 满足条件？ 满足条件？ 否 当型循环结构 满足条件？ 满足条件？ 是 直到型循环结构 否
差异:循环终止条件不同 检验条件是否成立的先后次序也不同 差异 循环终止条件不同,检验条件是否成立的先后次序也不同 循环终止条件不同 检验条件是否成立的先后次序也不同. 当型循环结构:先判断后执行循环体 先判断后执行循环体. 当型循环结构 先判断后执行循环体 直到型循环结构:先执行循环体后判断条件是否成立 先执行循环体后判断条件是否成立. 直到型循环结构 先执行循环体后判断条件是否成立
1.1.2 程序框图 与 算法的基本逻辑结构
程序框
名称
终端框 起止框） （起止框） 输入、 输入、输出框 处理框 执行框） （执行框）
功能
表示一个算法的起始和结束 表示一个算法输入和 输出的信息 赋值、 赋值、计算
判断框
判断某一条件是否成立, 判断某一条件是否成立,成立 时在出口处标明“ 时在出口处标明“是”或“Y”； ； 不成立时标明“ 不成立时标明“否”或“N”. . 连接程序框
结束
判断整数n(n>2)是否为质数”的算法： 判断整数n(n>2)是否为质数”的算法： n(n>2)是否为质数
开始 输入n 输入 i=2 设n是一个大 是一个大 的整数. 于2的整数 的整数
一般用i=i+1 一般用 表示. 表示
除以i的余数 求n除以 的余数 除以 的余数r
i=i+1 i的值增加 仍用 表示 的值增加1仍用 的值增加 仍用i表示
循环结构一定包含条件结构,用以控制循环过程 避免出现 循环结构一定包含条件结构 用以控制循环过程,避免出现 用以控制循环过程 死循环” 判断框内写上条件 判断框内写上条件,两个出口分别对应终止条件成 “死循环”.判断框内写上条件 两个出口分别对应终止条件成 立与否,其中一个指向循环体 经过循环体回到判断框的入口处. 其中一个指向循环体,经过循环体回到判断框的入口处 立与否 其中一个指向循环体 经过循环体回到判断框的入口处
1.1.2程序框图-顺序结构
解: 鸡兔同笼,设鸡兔总头数为H ,总脚数为F,求 鸡兔各有多少只.算法分析如下： X Y H, 设有X 只鸡,Y 只兔.则 2 X 4Y F .
X (4 H F ) / 2, 解方程组,得 Y ( F 2 H ) / 2.
主页
§1.1.2程序框图
主页
§1.1.2程序框图
4.画流程图的规则 为了使大家彼此之间能够读懂各自画出 的框图,必须遵守一些共同的规则,下面对一些 常用的规则作一简单的介绍. (1)使用标准的框图符号. (2)框图一般按从上到下、从左到右的方向画. (3)除判断框外，大多数程序框图符号只有一 个进入点和一个退出点，判断框是具有超过一 个退出点的唯一符号. (4)一类判断框是“是”与“否”两分支的判 断,而且有且仅有两个结果;另一类是多分支判 断,有几种不同的结果.
判断框
主页
§1.1.2程序框图
3.四种基本的框及其功能用法: (1)起止框:框内填写开始、结束,任何程序框 图中，起止框是必不可少的；
(2)输入、输出框:框内填写输入、输出的 字母、符号等;
(3)处理框(执行框):算法中需要的算式、 公式、对变量进行赋值等要用执行框表示. (4)判断框:当算法要求在不同的情况下执 行不同的运算时，需要判断框.框内填写 判断条件.
主页
§1.1.2程序框图
(5)在图形符号内描述的语言要非常简练清楚.
(6)起始框只允许一条流出线,终止框只允许一 条流入线,输入框、输出框、处理框只有一条流 入线和一条流出线,判断框有一条流入线和两条 流出线,但任何时候只有一条流出线起作用.
(7)一个程序框图包括以下几部分:表示相应操 作的程序框;带箭头的流程线;程序框外必要的 文字说明．
主页
X (4 H F ) / 2, 解方程组,得 Y ( F 2 H ) / 2.
主页
§1.1.2程序框图
主页
§1.1.2程序框图
4.画流程图的规则 为了使大家彼此之间能够读懂各自画出 的框图,必须遵守一些共同的规则,下面对一些 常用的规则作一简单的介绍. (1)使用标准的框图符号. (2)框图一般按从上到下、从左到右的方向画. (3)除判断框外，大多数程序框图符号只有一 个进入点和一个退出点，判断框是具有超过一 个退出点的唯一符号. (4)一类判断框是“是”与“否”两分支的判 断,而且有且仅有两个结果;另一类是多分支判 断,有几种不同的结果.
判断框
主页
§1.1.2程序框图
3.四种基本的框及其功能用法: (1)起止框:框内填写开始、结束,任何程序框 图中，起止框是必不可少的；
(2)输入、输出框:框内填写输入、输出的 字母、符号等;
(3)处理框(执行框):算法中需要的算式、 公式、对变量进行赋值等要用执行框表示. (4)判断框:当算法要求在不同的情况下执 行不同的运算时，需要判断框.框内填写 判断条件.
主页
§1.1.2程序框图
(5)在图形符号内描述的语言要非常简练清楚.
(6)起始框只允许一条流出线,终止框只允许一 条流入线,输入框、输出框、处理框只有一条流 入线和一条流出线,判断框有一条流入线和两条 流出线,但任何时候只有一条流出线起作用.
(7)一个程序框图包括以下几部分:表示相应操 作的程序框;带箭头的流程线;程序框外必要的 文字说明．
主页
1.1.2程序框图与顺序结构
顺序结构
条件结构
循环结构
尽管不同的算法千差万别,但它们都是由 三种基本的逻辑结构构成的。
顺序结构及框图表示
1.顺序结构:按照步骤依次执行的一个算法,称 为具有“顺序结构”的算法,或者称为算法的 顺序结构. 顺序结构是最简单的算 2.顺序结构的流程图
语句A
语句B
法结构,语句与语句之间,框 与框之间是按从上到下的顺 序进行的.它是由若干个处理 步骤组成的,这是任何一个算 法都离不开的基本结构.
n除以i的余数r
i=i+1 否
i>n-1或r=0?
是 否
r=0?
是 n不是质数 n是质数
结束
开始
输入n
输入、输出框 表示一个算法输入和 输出的信息
i=2
n除以i的余数r
i=i+1 否
i>n-1或r=0?
是 否
r=0?
是 n不是质数 n是质数
结束
开始
输入n i=2
处理框（执行框） 赋值、计算
n除以i的余数r
i=i+1 否
i>n-1或r=0?
是 否
r=0?
是 n不是质数 n是质数
结束
开始
输入n i=2
判断框 判断某一条件是否成立，成 立时在出口处标明“是”； 不成立时标明“否”
n除以i的余数r
i=i+1 否
i>n-1或r=0?
是 否
r=0?
是 n不是质数 n是质数
结束
开始
输入n
流程线
i=2
n除以i的余数r
画出程序框图．先算出p的值，再将它代入公式， 最后输出结果，只用顺序结构就能够表达出算法．
高一数学 1.1.2《程序框图》教案 新人教版必修3
1．1．2 程序框图(第二、三课时)一、教学目标：1、知识与技能：掌握程序框图的概念；会用通用的图形符号表示算法，掌握算法的三个基本逻辑结构；掌握画程序框图的基本规则，能正确画出程序框图。
2、过程与方法：通过模仿、操作、探索，经历通过设计程序框图表达解决问题的过程；学会灵活、正确地画程序框图。
3、情感态度与价值观：通过本节的学习，使我们对程序框图有一个基本的了解；掌握算法语言的三种基本逻辑结构，明确程序框图的基本要求；认识到学习程序框图是我们学习计算机的一个基本步骤，也是我们学习计算机语言的必经之路。
二、重点与难点：重点是程序框图的基本概念、基本图形符号和3种基本逻辑结构，难点是能综合运用这些知识正确地画出程序框图。
三、学法与教学用具：1、通过上节学习我们知道，算法就是解决问题的步骤，在我们利用计算机解决问题的时候，首先我们要设计计算机程序，在设计计算机程序时我们首先要画出程序运行的流程图，使整个程序的执行过程直观化，使抽象的问题就得十分清晰和具体。
有了这个流程图，再去设计程序就有了依据，从而就可以把整个程序用机器语言表述出来，因此程序框图是我们设计程序的基本和开端。
2、我们在学习这部分内容时，首先要弄清各种图形符号的意义，明确每个图形符号的使用环境，图形符号间的联结方式。
例如“起止框”只能出现在整个流程图的首尾，它表示程序的开始或结束，其他图形符号也是如此，它们都有各自的使用环境和作用，这是我们在学习这部分知识时必须要注意的一个方面。
另外，在我们描述算法或画程序框图时，必须遵循一定的逻辑结构，事实证明，无论如何复杂的问题，我们在设计它们的算法时，只需用顺序结构、条件结构和循环结构这三种基本逻辑就可以了，因此我们必须掌握并正确地运用这三种基本逻辑结构。
3、教学用具：电脑，计算器，图形计算器四、教学设想：1、创设情境：算法可以用自然语言来描述，但为了使算法的程序或步骤表达得更为直观，我们更经常地用图形方式来表示它。
1.1.2程序框图
判断某一条件是否成立,成立 时在出口处标明“是”或 “Y”；不”成立时标明“否” 或“N”.
连接程序框
连接程序框图的两部分
练习巩固
看右面的 程序，填 入框图
开始
输入x
y=3x2+4x+5
输出y
结束
开始
（2）
输入a，b
a<b？
是
否
输出a，b
输出b，a
结束
（3）
开始
输入a a>=0
是 输出∣a∣=a
第三步:输出S的值.
程序框图:
开始
输入a,b,h
s ( a b) h 2
算法分析:
第一步:输入上底a， 下底b和高h的值. 第二步:由面积公式 算出面积s的值. 第三步:输出S的值.
输出S
结束
开始
输入a,b
a,b为直角三角形的 边长
d a b
2
2
1输入a=3,b=4则输出 2输入a=7,b=24则输出
i=i+1 i≥n-1或r=0?
是 否 否
r=0?
是
n不是质数
结束
n是质数
语言描述 第一步，给定大于2的整数n。
第二步，令i=2。 第三步，用i除n，得到余数r。
开始 输入n
简单流程
i=2
求n除以i的余数r i=i+1
第四步，判断r=0是否成立， 若是，则n不是质数，结束 算法；否则，将i的值增加 1，仍用i表示。
例．“判断整数n(n>2)是否为质数”的算 法
第一步，给定大于２的整数n. 第二步，令i=2. 第三步，用i除n 得到余数r. 第四步，判断“r=0”是否成立．若是，则n不是质 数，结束算法；否则，将i的值增加１，仍用i表示. 第五步，判断“i>(n-1) ”是否成立．若是，则n是 质数,结束算法；否则，返回第三步．
连接程序框
连接程序框图的两部分
练习巩固
看右面的 程序，填 入框图
开始
输入x
y=3x2+4x+5
输出y
结束
开始
（2）
输入a，b
a<b？
是
否
输出a，b
输出b，a
结束
（3）
开始
输入a a>=0
是 输出∣a∣=a
第三步:输出S的值.
程序框图:
开始
输入a,b,h
s ( a b) h 2
算法分析:
第一步:输入上底a， 下底b和高h的值. 第二步:由面积公式 算出面积s的值. 第三步:输出S的值.
输出S
结束
开始
输入a,b
a,b为直角三角形的 边长
d a b
2
2
1输入a=3,b=4则输出 2输入a=7,b=24则输出
i=i+1 i≥n-1或r=0?
是 否 否
r=0?
是
n不是质数
结束
n是质数
语言描述 第一步，给定大于2的整数n。
第二步，令i=2。 第三步，用i除n，得到余数r。
开始 输入n
简单流程
i=2
求n除以i的余数r i=i+1
第四步，判断r=0是否成立， 若是，则n不是质数，结束 算法；否则，将i的值增加 1，仍用i表示。
例．“判断整数n(n>2)是否为质数”的算 法
第一步，给定大于２的整数n. 第二步，令i=2. 第三步，用i除n 得到余数r. 第四步，判断“r=0”是否成立．若是，则n不是质 数，结束算法；否则，将i的值增加１，仍用i表示. 第五步，判断“i>(n-1) ”是否成立．若是，则n是 质数,结束算法；否则，返回第三步．
1.1.2程序框图
不存在这样的三角
形。
结束
练习：
1.就逻辑结构,说 出其算法功能．
开始 max=a 输入b
max>b？ 否
是
max=b
输出max
结束 答案:1.求两个数中的最大值.
小结
3.程序框图的三种基本的逻辑结构：
顺序结构 条件结构 循环结构
注：条件后面要加“？”
【回顾】求函数
x2 2x, x 2 y
程序框图：
算法步骤:第一步，输入a,b,c.
第二步:计算p的值.
开始
第三步:由海伦-秦九韶公式
输入a，b，c 求出三角形的面积S. 第四步:输出S.
p abc 2
计算机完成
S p( p a)(p b)(p c)
输出S 结束
将确定的数值赋给变量的语句叫 做赋值语句。给变量a赋值一个数 为12，则格式为：a = 12
练习：观察下面两个逻辑结构，说出各自的算法功能
（1）
开始
（2）
开始
输入正数a，b
输入ห้องสมุดไป่ตู้，b
d a2 b2
c d
s=（a+b）÷2 输出s
输出c
结束
结束
（1）求直角三角形斜边长；（2）求两个数的平均值．
2.已知梯形上底为2,下底为4,高为5,求其面积, 设计出该问题的流程图．
开始
a 2,b 4, h 5
1、程序框图:
又称流程图,是一种用程序框、流 程线及文字说明来准确、直观的表示 算法的图形．
2.基本的程序框和它们各自表示的功能如下:
图形符号
名称 终端框 (起止框) 输入、输 出框 处理框 (执行框)
人教A版高中数学必修3课件：1.1.2程序框图与算法的基本逻辑结构
0(x 0)
设计一个算法计算分段函数 y 1(0 x 1)
画出程序框图。
x(x 1)
， 的函数值，并
第一步、输入x
第二步、判断“x<0”是否成立， 若
是，则输出y=0，否则执行第三步；
第三步、判断“x<1”是否成立， 若
是，则输出y=1，否则输出y=x。
1、设计一个算法判断任意给定一个整数N是 奇数还是偶数，并画出程序框图；
第三步：将所有步骤的程序框图用流程线连接起来，并加上 终端框，得到表示整个算法的程序框图.
2、算法的逻辑结构
（1）顺序结构
由若干个依次执行的处理步骤组成的结构.它是任 何一个算法都离不开的结构.
画顺序结构程序框图时注意事项
步骤n 步骤n＋1
(1)在程序框图中,开始框 和结束框不可少； (2)在算法过程中,第一步 输入语句是必不可少的; (3)顺序结构在程序框图中 的体现就是用流程线将程 序框自上而下地连接起来, 按顺序执行算法步骤.
循环结构的三要素 循环变量,循环体、循环的终止条件.
循环结构的设计步骤 (1)确定循环结构的循环变量和初始条件; (2)确定算法中需要反复执行的部分,即循环体； (3)确定循环的终止条件.
循环结构一定包含条件结构,用以控制循环过程,避免出现 “死循环”.判断框内写上条件,两个出口分别对应终止条件成 立与否,其中一个指向循环体,经过循环体回到判断框的入口处.
0 有两个不相等的实数根
b b2 4ac
b
0 有两个相等的实数根 x 0 没有实数根
2a
2a 2a
算法
第一步：输入三个系数 a, b, c
第二步：计算 b2 4ac
第三步：判断 0 是否成立.若是，计算
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
开始
1
输入n 输入
否
i=2
r=0? 是
n不是质数 不是质数 n是质数 是质数
除以i 求n除以 除以 的余数r 的余数 i=i+1
i≥n或r=0? 或
否
结束
是 1
从上面的程序框图中,不难看出以下三种不 从上面的程序框图中 不难看出以下三种不 同的逻辑结构. 同的逻辑结构
除以i 求n除以 除以 的余数r 的余数 输入n 输入
练习：
1.流程线的功能是:…………………..( A.表示算法的起始和结束. B.表示算法的输入和输出信息. C.赋值、运算. D.按照算法顺序连接程序图框. ).
2.对程序框 表示的功能描述正确的一项 是:…( ). A.表示算法的起始和结束. B.表示算法输入和输出的信息. C.赋值、计算. 答案:D,B 答案 D. 按照算法顺序连接程序图框.
输入a,b
S=(a+b)*0.5 否 S>=60? 是
credit=2
输出credit 结束
credit=0
小结： 1、程序框图的概念
2、程序框图图例的名称和意义（作用）
3、如何用程序框图表示顺序结构、选择结构
程序框图又称流程图， 一.程序框图又称流程图，是一种用规定的图形，指向线 程序框图又称流程图 是一种用规定的图形， 及文字说明来准确、直观地表示算法的图形。 及文字说明来准确、直观地表示算法的图形。 程序框 名称 功能
终端框（起 表示一个算法的起始和结束 止框） 输入、输出 表示算法的输入和输出的信 框 息 处理框（执 赋值、计算 行框） 判断框 判断一个条件是否成立，用 “是”、“否”或“Y”、 “N”标明
输入面积S 否 S<=80 是 M=3*S M=240+5*(S-80) 开始
输出租金M
结束
三、选择结构及框图表示 选择结构及框图表示
选择结构也叫条件结构， 选择结构也叫条件结构，是指在算法中通过对条件的 也叫条件结构 判断，根据条件是否成立而选择不同流向的算法结构． 判断，根据条件是否成立而选择不同流向的算法结构． 右图此结构中包含一个判断框， 右图此结构中包含一个判断框， 根据给定的条件P是否成立而选择 根据给定的条件 是否成立而选择 执行A框或 框或B框 无论P条件是否 执行 框或 框．无论 条件是否 成立，只能执行A框或 框之一， 框或B框之一 成立，只能执行 框或 框之一， 不可能同时执行A框和 框和B框 不可能同时执行 框和 框，也不 可能A框 框都不执行． 可能 框、B框都不执行． 框都不执行
以上是用自然语言描述一个算法.为了使得算法的描述更为直观和 以上是用自然语言描述一个算法 为了使得算法的描述更为直观和 步骤化,下面介绍另一种描述算法的方法 程序框图. 下面介绍另一种描述算法的方法:程序框图 步骤化 下面介绍另一种描述算法的方法 程序框图 由一些图框和有向箭头构成,表示算法 程序框图的通俗解释: 由一些图框和有向箭头构成 表示算法 按一定的顺序执行. 按一定的顺序执行
开始
（1）
开始
（2）
输入a,b
输入x a<b? y=3*x*x+4*x+5 是 输出a,b 输出y
否
输出b,a
结束
结束
练习2
开始
城区一中学生数学模块学分 认定由模块成绩决定，模块 成绩由模块考试成绩和平时 成绩构成，各占50%，若模 块成绩大于或等于60分，获 得2学分，否则不能获得学分 （为0分），设计一算法，通 过考试成绩和平时成绩计算 学分，并画出程序框图
例4 任意给定3个 正实数,设计一个 算法,判断分别以 这3个数为三边边 长的三角形是否 存在.画出这个算 法的程序框图..
开始 输入a，b，c
a+b＞c，a+c ＞ b， b+c ＞ a是否同 时成立？ 是 存在这样的 三角形
否
不存在这样 的三角形
结束
练习巩固 １ 看下面的程序框图，分析算法的作用
算法初步
§1.1.2 程序框图
复习: 复习 上节课例1:任意给定一个大于 的整数 上节课例 任意给定一个大于2的整数 试设计一个 任意给定一个大于 的整数n,试设计一个 算法判定n是否为质数 是否为质数. 算法判定 是否为质数
第一步：给定正整数n 第一步：给定正整数n
第二步： 第二步：令i=2 第三步： 是否成立， 第三步：用i除n，得到余数r。判断“r=0”是否成立，若是则n不是质数，结束 得到余数r 判断“r=0 是否成立 若是则n不是质数， 算法，否则将i的值增加1 仍用i 算法，否则将i的值增加1，仍用i表示 第四步：判断i是否大于（ 第四步：判断i是否大于（n-1），若是则n是质数，结束算法，否则返回第三 ），若是则n是质数，结束算法， 若是则 步
r=0?
是
否
i=i+1
i=2
否 i≥n或r=0? 或 是
n不是质数 不是质数
n是质数 是质数
尽管不同的算法千差万别, 尽管不同的算法千差万别 , 但它们都是由 三种基本的逻辑结构构成的, 三种基本的逻辑结构构成的 , 这三种逻辑结构 就是顺序结构、 循环结构、 选择结构. 就是顺序结构 、 循环结构 、 选择结构 . 以后分 别介绍这三种结构． 别介绍这三种结构．
计算S=Pi*R*R 定义Pi=3.14
输入半径R
思考：整个程序框图有什么特点？
输出面积S
结束
二、顺序结构及框图表示 顺序结构及框图表示 1.顺序结构 像上面这种算法是依次进行多个处 顺序结构:像上面这种算法是依次进行多个处 顺序结构 像上面这种算法 理的结构称为顺序结构 称为顺序结构. 理的结构称为顺序结构 2.顺序结构的流程图 顺序结构的流程图 顺序结构是最简单、 顺序结构是最简单 、 最基本的算法结构 的算法结构, 最基本的算法结构,语句与 语句之间, 语句之间,框与框之间是按 从上到下的顺序进行的. 从上到下的顺序进行的.它 是由若干个处理步骤组成 的,这是任何一个算法都离 不开的基本结构. 不开的基本结构.
例1 设计一算法：输入圆的半径,输出圆的面积，并画出流程图 算法分析：
开始
第一步：输入圆的半径 输入圆的半径 第二步：利用公式“圆的面 利用公式“ 利用公式 圆周率× 半径的平方） 积=圆周率×（半径的平方）” 圆周率 计算圆的面积； 计算圆的面积； 第三步：输出圆的面积。 输出圆的面积。 输出圆的面积
语句A 语句 语句B 语句
例2 已知一个三角形的三边长 确分别为2,3,4,利用海伧-秦九 韶公式设计一个算法,求出它的 面积,画出算法的程序框图.
开始
p=（2+3+4）/2
s=SQR(p*(p－2)*(p －3)*(p-4))
输出s
结束
例3 设计房租收费的算法,其要求是:住房面积80平方米 以内,每平方米收费3元,住房面积超过80平方米时,超过 部分,每平方米收费5元.输入住房面积数,输出应付的房租. 算法分析： 第一步：输入住房面积 输入住房面积S 输入住房面积 第二步：根据面积选择计费 根据面积选择计费 方式：如果S小于或等于 小于或等于80， 方式：如果 小于或等于 ， 则租金为M= 则租金为 s×3，否则为 ， M=240+(S-80)×5 × 第三步：输出房租 的值。 输出房租M的值 输出房租 的值。 思考：整个程序框图有什么特点？