含电容器电路的归类分析
2含电容器的电路分析1
含电容器的电路分析1
在教学中发现,学生对含有电容的直流电路问题,感到很头疼,一遇到计算题,就茫然失措。
分析其原因,是没有很好地理顺解题思路,那麽如何解决这类问题呢?对初学者,具体地说要做到“三能”:
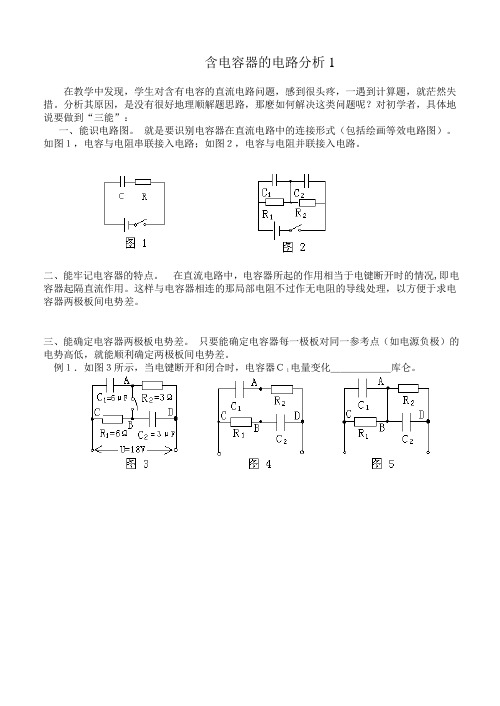
一、能识电路图。
就是要识别电容器在直流电路中的连接形式(包括绘画等效电路图)。
如图1,电容与电阻串联接入电路;如图2,电容与电阻并联接入电路。
二、能牢记电容器的特点。
在直流电路中,电容器所起的作用相当于电键断开时的情况,即电容器起隔直流作用。
这样与电容器相连的那局部电阻不过作无电阻的导线处理,以方便于求电容器两极板间电势差。
三、能确定电容器两极板电势差。
只要能确定电容器每一极板对同一参考点(如电源负极)的电势高低,就能顺利确定两极板间电势差。
例1.如图3所示,当电键断开和闭合时,电容器C1电量变化______库仑。
例2.如图6所示,R1=6Ω,R2=3Ω,R3=4Ω,UAB=12V,C1=3μF,C2=1μF,则他们带电量分别为____C和____C。
例3.如图8所示,已知电源电动势为ε=12V,内电阻为r=1Ω,R1=3Ω,R2=2Ω,R3=5Ω,C1=4μF,C2=1μF,则C1带电量为____C,C2带电量为____C。
高二物理电学专题提升专题20含容电路的分析及计算(2021年整理)

专题20 含容电路的分析及计算一:专题概述解决含电容器的直流电路问题的一般方法:(1) 不分析电容器的充、放电过程时,把电容器处的电路视为断路,简化电路时可以去掉,求电荷量时再在相应位置补上。
(2)电路稳定后,与电容器串联的电路中没有电流,同支路的电阻相当于导线,即电阻不起降压的作用,但电容器两端可能出现电势差.(3)电路中电流、电压的变化可能会引起电容器的充、放电。
若电容器两端电压升高,电容器将充电;若电压降低,电容器将通过与它连接的电路放电.(4)如果电容器与电源并联,且电路中有电流通过,则电容器两端的电压不是电源电动势E,而是路端电压U.(5) 如果变化前后极板带电的电性相同,那么通过每根引线的电荷量等于始、末状态电容器带电荷量之差;如果变化前后极板带电的电性改变,那么通过每根引线的电荷量等于始、末状态电容器带电荷量之和.二:典例精讲1.电容器与滑动变阻器的电路分析典例1:在如图所示的电路中,闭合电键S,将滑动变阻器滑片P向a端移动一段距离,下列结论正确的是A.灯泡L变亮B.电流表读数变大C.电容器C上的电荷量增多D.电压表读数变小【答案】C2.电容与传感器结合的电路分析典例2:如图所示的电路中,R1、R2、R3是固定电阻,R4是光敏电阻,其阻值随光照强度的增强而减小。
当开关S闭合且没有光照射时,电容器C不带电。
当用强光照射R4且电路稳定时,则与无光照射时比较A.电容器C的上极板带正电B.电容器C的下极板带正电C.通过R4的电流变小,电源的路端电压增大D.通过R4的电流变大,电源提供的总功率变小【答案】B3.电容器与二极管电路的分析典例3:如图所示的电路中,电源电动势E=6V,内阻r=1Ω,电阻R1=3Ω,R2=6Ω,电容器的电容C=3。
6μF,二极管D具有单向导电性。
开始时,开关S1闭合,S2断开.(1)合上S2,待电路稳定以后,求电容器上电荷量变化了多少.(2)合上S2,待电路稳定以后再断开S1,求断开S1后流过R1的电荷量是多少.【答案】(1) 减少1.8×10—6C(2) 9.6×10—6C【解析】(1) 设开关S1闭合,S2断开时,电容器两端的电压为U1,干路电流为I1,根据闭合电路欧姆定律有I1==1。
→总结归纳→高考含电容电路的分析

难点14 含电容电路的分析策略将电容器置于直流电路,创设复杂情景,是高考命题惯用的设计策略,借以突出对考生综合能力的考查,适应高考选拔性需要.应引起足够关注.●难点磁场1.(★★★★)在如图14-1电路中,电键S1、S2、S3、S4均闭合.C是极板水平放置的平行板电容器,板间悬浮着一油滴P,断开哪一个电键后P会向下运动A.S1B.S2C.S3D.S4图14—1 图14—22.(★★★)(2000年春)图14-2所示,是一个由电池、电阻R与平行板电容器组成的串联电路.在增大电容器两极板间距离的过程中A.电阻R中没有电流B.电容器的电容变小C.电阻R中有从a流向b的电流D.电阻R中有从b流向a的电流●案例探究[例1](★★★★★)如图14-3所示的电路中,4个电阻的阻值均为R,E为直流电源,其内阻可以不计,没有标明哪一极是正极.平行板电容器两极板间的距离为d.在平行极板电容器的两个平行极板之间有一个质量为m,电量为q的带电小球.当电键K闭合时,带电小球静止在两极板间的中点O上.现把电键打开,带电小球便往平行极板电容器的某个极板运动,并与此极板碰撞,设在碰撞时没有机械能损失,但带电小球的电量发生变化.碰后小球带有与该极板相同性质的电荷,而且所带的电量恰好刚能使它运动到平行极板电容器的另一极板.求小球与电容器某个极板碰撞后所带的电荷.图14-3命题意图:考查推理判断能力及分析综合能力,B级要求.错解分析:不能深刻把握该物理过程的本质,无法找到破题的切入点(K断开→U3变化→q所受力F变化→q运动状态变化),得出正确的解题思路.解题方法与技巧:由电路图可以看出,因R4支路上无电流,电容器两极板间电压,无论K是否闭合始终等于电阻R3上的电压U3,当K闭合时,设此两极板间电压为U,电源的电动势为E,由分压关系可得U=U3=E ①小球处于静止,由平衡条件得=mg ②当K断开,由R1和R3串联可得电容两极板间电压U′为U′=③由①③得U′=U④U′<U表明K断开后小球将向下极板运动,重力对小球做正功,电场力对小球做负功,表明小球所带电荷与下极板的极性相同,由功能关系mg-qmv2-0 ⑤因小球与下极板碰撞时无机械能损失,设小球碰后电量变为q′,由功能关系得q′U′-mgd=0-mv2 ⑥联立上述各式解得q′=q即小球与下极板碰后电荷符号未变,电量变为原来的.[例2](★★★★)如图14-4所示,电容器C1=6 μF,C2= 3μF,电阻R1=6 Ω,R2=3 Ω,当电键K断开时,A、B两点间的电压U AB=?当K闭合时,电容器C1的电量改变了多少(设电压U= 18 V)?图14-4命题意图:考查理解、推理、分析综合能力及解决实际问题的创新能力,B级要求.错解分析:没有依据电路结构的变化分析求出电容器充放电前后的电压变化,使问题难于求解.解题方法与技巧:在电路中电容C1、C2的作用是断路,当电键K断开时,电路中无电流,B、C等电势,A、D等电势,因此U AB=U DB=18 V,U AB=U AC=U DB=18 V,K断开时,电容器C1带电量为Q1=C1U AC=C1U DC=6×10-6×18 C=1.08×10-4 C.当K闭合时,电路R1、R2导通,电容器C1两端的电压即电阻R1两端的电压,由串联的电压分配关系得:U AC==12 V此时电容器C1带电量为:Q1′=C1U AC=7.2×10-5 C电容器C1带电量的变化量为:ΔQ=Q1-Q1′=3.6×10-5 C所以C1带电量减少了3.6×10-5●锦囊妙计电容器是一个储存电能的元件,在直流电路中,当电容器充、放电时,电路有充电、放电电流,一旦电流达到稳定状态,电容器在电路中就相当于一个阻值无限大(只考虑电容器是理想不漏电的情况)的元件,电容电路可看作是断路,简化电路时可去掉它,简化后若要求电容器所带电量时,可在相应的位置补上.分析和计算含有电容器的直流电路时,关键是准确地判断并求出电容器的两端的电压,其具体方法是:1.确定电容器和哪个电阻并联,该电阻两端电压即为电容器两端电压.2.当电容器和某一电阻串联后接在某一电路两端时,此电路两端电压即为电容器两端电压.3.对于较复杂电路,需要将电容器两端的电势与基准点的电势比较后才能确定电容器两端的电压.●歼灭难点训练1.(★★★)(1997年全国)如图14-5所示的电路中,电源的电动势恒定,要想使灯泡变暗,可以图14-5A.增大R1B.减小R1C.增大R2D.减小R22.(★★★)一平行板电容器C,极板是水平放置的,它和三个可变电阻及电源联接成如图14-6所示的电路.今有一质量为m的带电油滴悬浮在两极板之间静止不动.要使油滴上升,可采用的办法是图14-6A.增大R1B.增大R2C.增大R3D.减小R23.(★★★★)如图14-7所示,E=10 V,R1=4 Ω,R2=6 Ω,C=30 μF,电池内阻可忽略.(1)闭合开关K,求稳定后通过R1的电流;(2)然后将开关K断开,求这以后通过R1的总电量.图14—7 图14—84.(★★★★)如图14-8所示的电路,已知电池电动势E=90 V,内阻r=5 Ω,R1=10 Ω,R2=20 Ω,板面水平放置的平行板电容器的两极板M、N相距d=3 cm,在两板间的正中央有一带电液滴,其电量q=-2×10-7 C,其质量m=4.5×10-5 kg,取g=10 m/s2,问(1)若液滴恰好能静止平衡时,滑动变阻器R的滑动头C正好在正中点,那么滑动变阻器的最大阻值R m是多大?(2)将滑动片C迅速滑到A端后,液滴将向哪个极板做什么运动?到达极板时的速度是多大?5.(★★★★)如图14-9所示.两根相距为L的竖直金属导轨MN和PQ的上端接有一个电容为C的电容器,质量为m的金属棒ab可紧贴竖直导轨无摩擦滑动,且滑动中ab始终保持水平,整个装置处于磁感应强度为B的磁场中,不计电阻,求最后通过C的充电电流.图14—96.(★★★★★)图14-10所示,金属棒ab质量m=5 g,放在相距L=1 m的光滑金属导轨MN、PQ上,磁感应强度B=0.5 T,方向竖直向上,电容器的电容C=2μF,电源电动势E=16 V,导轨距地面高度h=0.8 m.当单刀双掷开关先掷向1后,再掷向2,金属棒被抛到水平距离s=6.4 cm的地面上,问电容器两端的电压还有多大?图14-10参考答案:[难点磁场]1.C2.BC[歼灭难点训练]1.AD2.CD3.电容器稳定后相当于断路,K断开前电容器相当于和R2并联,K 断开前,电容器相当于直接接到电源上,K断开前后通过R1的电量即为前后两状态下电容器带电量之差.电容器稳定后相当于断路,则:(1)I1=I总=A=1A(2)断开K前,电容器相当于和R2并联,电压为I2R2,储存的电量为Q1=CI1R2断开K稳定后,总电流为零,电容器上电压为E,储存电量为Q2=CE所以通过R1的电量为:ΔQ=Q2-Q1=C(E-I1R2)=1.2×10-3 C4.滑动变阻器R的滑动触头C正好在AB正中点时对液滴进行受力分析知,重力G与电场力Eq平衡,从而求得电容器两极电压,也就是BC 间电压,然后据闭合电路欧姆定律求得R BC,从而求得R m.将滑片C迅速滑到A端后,由闭合电路欧姆定律可求得AB间电压,即电容器两板间电压UAB=UMN′=×90即UMN′=77 V大于C在中央时电压,对液滴分析受力知电场力大于重力,所以向M板运动,由动量定理便可求得速度.(1)滑片C在AB中央时,对带电液滴由平衡条件得mg=q所以UMN== V=67.5(V)由题意知U MN=UBC=67.5 V由欧姆定律得=UBC即=67.5所以R m=90 Ω(2)滑片滑到A时,UMN′=V=77(V)>67.5 V所以液滴向M板运动,设达M板时速度为v由动能定理得q··=mv2 所以v=0.2 m/s5.经分析知最终ab棒做匀加速下滑,设最终充电电流为I,在Δt内电量、速率、电动势的变化量分别为ΔQ、Δv和ΔE则有I==C·=CBL·=CBLa由牛顿第二定律有mg-BIL=ma解得I=6.电容器充电后电量为Q=CE.开关掷向位置2时,电容器通过ab放电,其放电电量为ΔQ,则通过棒中电流为I=金属棒受安培力F=BIL=BL①据动量定理FΔt=mv-0②由平抛运动可知v=s/ ③由式①、②、③得BL·Δt=ms所以ΔQ==1.6×10-5C电容器所余电量Q′=Q-ΔQ=CE-ΔQ=1.6×10-5 C所以电容器两端电压为U′==8V。
电容归纳总结(通用3篇)

电容归纳总结第1篇(1)基本结构:由两块彼此绝缘互相靠近的导体组成。
(2)带电特点:两板电荷等量异号,分布在两板相对的内侧。
(3)板间电场:板间形成匀强电场(不考虑边缘效应),场强大小E=U/d,方向始终垂直板面。
充电与放电:使电容器带电叫充电;使充电后的电容器失去电荷叫放电。
充电过程实质上是电源逐步把正电荷从电容器的负极板移到正极板的过程。
由于正、负两极板间有电势差,所以电源需要克服电场力做功。
正是电源所做的这部分功以电能的形式储存在电容器中,放电时,这部分能量又释放出来。
电容器所带电量:电容器的一个极板上所带电量的绝对值。
击穿电压与额定电压:加在电容器两极上的电压如果超过某一极限,电介质将被击穿而损坏电容器,这个极限电压叫击穿电压;电容器长期工作所能承受的电压叫做额定电压,它比击穿电压要低。
电容归纳总结第2篇MLCC(Multi-layer CeramicCapacitors)是片式多层陶瓷电容器英文缩写。
是由印好电极(内电极)的陶瓷介质膜片以错位的方式叠合起来,经过一次性高温烧结形成陶瓷芯片,再在芯片的两端封上金属层(外电极),从而形成一个类似独石的结构体,故也叫独石电容器。
可以看到,内部电极通过一层层叠起来,来增大电容两极板的面积,从而增大电容量。
陶瓷介质即为内部填充介质,不同的介质做成的电容器的特性不同,有容量大的,有温度特性好的,有频率特性好的等等,这也是为什么陶瓷电容有这么多种类的原因。
陶瓷电容的基本参数:电容的单位:电容的基本单位是:F(法),此外还有μF(微法)、nF、pF(皮法),由于电容 F 的容量非常大,所以我们看到的一般都是μF、nF、pF 的单位,而不是 F 的单位。
它们之间的具体换算如下: 1F=1000000μF 1μF=1000nF=1000 000pF电容容量:常用陶瓷电容容量范围:。
实际生产的电容的陶瓷容量值也是离散的,常用电容容量如下表:陶瓷电容容量从起步,可以做到100uF,并且根据电容封装(尺寸)的不同,容量也会不同。
含电容器电路的分析与计算方法

含电容器电路的剖析与计算方法1、电路稳固后,因为电容器所在支路无电流经过,因此在此支路中的电阻上无电压降,因此电容器两极板间的电压就等于该支路两头的电压。
2、当电容器和电阻并联接入电路时,电容器两极板间的电压与其并联电阻两头的电压相等。
3、电路的电流、电压变化时,将会惹起电容器的充(放)电。
假如电容器两头的电压高升,电容器将充电,反之则放电。
1、如下图,电源两头电压为U=10 V保持不变, R1=Ω, R2=Ω, C= C=30μF.先闭合开关S,待电路稳固后,再将S 断1 2开,则 S 断开后,经过R1的电荷量为( )A.× 10 - 4 CB.× 10 - 4 CC.× 10 - 4 CD.× 10 - 4 C2、如图 16 所示,两个同样的平行板电容器C1、 C2用导线相连,开始都不带电.现将开关S 闭合给两个电容器充电,待充电均衡后,电容器C1两板间有一带电微粒恰巧处于均衡状态.再将开关S 断开,把电容器C2两板稍错开一些( 两板间距离保持不变) ,从头均衡后,以下判断正确的选项是A.电容器C1两板间电压减小B.电容器C2两板间电压增大C.带电微粒将加快上涨D.电容器C1所带电荷量增大3、在如下图,c1=6μ F,c2=3 μ F,R1=3Ω ,R2=6Ω,电源电动势E=18V,内阻不计,以下说法正确的选项是:A. 开关 s 断开时, a、 b 两点电势相等B. 开关 s 闭合后, a, b 两点间的电流时2AC.开关 s 断开时 C1带的电荷量比开关s 闭合后 C1 带的电荷量大D.无论开关s 断开仍是闭合,C1 带的电荷量总比C2 带的电荷量大。
原创1:含容电路的分析与计算

由欧姆定律得通过R1的电流
E
10
I
A 1A
R1 R2 4 6
(2)S断开前,C两端电压U1=IR2=6 V C所带电量Q1=CU1=30×10-6×6 C=1.8×10-4 C 开关S断开稳定后,总电流为零, 电容器两端电压为E, 所带电量Q2=CE=30×10-6×10 C=3×10-4 C 通过R1的电量,即为电容器增加的电量 ΔQ=Q2-Q1=1.2×10-4 C. 答案:(1)1 A (2)1.2×10-4 C 规律总结:处于稳定状态时,电容器相当于断路,与之串联的电阻不
例1.如图所示,电路中E=10 V,R1=4 Ω,R2=6 Ω,C=30 μF.电 池内阻可忽略. (1)闭合开关S,求稳定后通过R1的电流. (2)然后将开关S断开,求这以后通过R1的总电量.
解析:(1)电路稳定后,电容器所在的支路上无电流通过,
因此R1与R2串联,C两端的电压即为R2两端的电压.
R0为定值电阻,R1、R2为可调电阻,用绝缘细线 将质量为m、带正电的小球悬于电容器内部.闭合 电键S,小球静止时受到悬线的拉力为F,下列关 于F的大小变化的判断正确的是( ) A.保持R2不变,缓慢增大R1时,F将变大 B.保持R1不变,缓慢增大R2时,F将变小 C.保持R1、R2不变,减小平行板MN的间距,F将变大 D.保持R1、R2不变,减小平行板MN的间距,F将变小
·R2=3 V.
Q=CU2=12×10-6 C,且a板带正电,b板带负电.
SQ闭′=合C,U1C=两7端.2×电1压0-即6 RC1.两且端a电板压带,负由电电,路b分板析带:正U电1=.R1
R1 R2
·r
E R外
·R外=1.8 V.
据此通过电流表电量ΔQ=Q+Q′=1.92×10-5 C. 答案:1.92×10-5 C
人教版高中物理选修3-1 闭合电路习题课---含容电路 课件

解:由电路图可以看出,因R4支路上无电流,电容器两极板间 电压,无论K是否闭合始终等于电阻R3上的电压U3,当K闭合 时,设此两极板间电压为U,电源的电动势为E,由分压关系 可得U=U3= 2 E ①
3
小球处于静止,由平衡条件得 qU =mg
d
②
E ③ 2
当K断开,由R1和R3串联可得电容两极板间电压U′为U′= 由①③得U′= 3 U
例题3、电源内阻r=2Ω,R1=8Ω,R2=10Ω,K1闭合, K2断开时,在相距d=70cm,水平放置的固定金属板 AB间有一质量m=1.0g,带电量为q=7×10—5C的带负 电的微粒,恰好静止在AB两板中央的位置上,求 (1)电源的电动势(2)将K1断开0.1s后,又将K2闭 合,微粒再经过多长时间与极板相碰。(g=10m/s2)
G P A B
I=32μA 电流的方向自右向左
E r
s
(三)、电容器特殊问题 如图所示,电源电压200V,两个电容器完全相 同,静电计读数U和电压表读数U’,以下说法 正确的是(C) A.U=100V, U’=100V B.U=0, U’=200V V C1 C.U=200V, U’=0 C2 D.U=100V, U’=0
4
④
U′<U表明K断开后小球将向下极板运动,重力对小球做正功, 电场力对小球做负功,表明小球所带电荷与下极板的极性相 同,由功能关系 U 1 d Mg -q 2 2 mv2-0 ⑤ 2
因小球与下极板碰撞时无机械能损失,设小球碰后 电量变为q′,由功能关系得 q′U′-mgd=0-
1 mv2 2
R
80Ω,23w
Er S
P m
v0
A B
例题7、所示的电路,已知电池电动势E=90 V,内阻 r=5 Ω,R1=10 Ω,R2=20 Ω,板面水平放置的平 行板电容器的两极板M、N相距d=3 cm,在两板间的 正中央有一带电液滴,其电量q=-2×10-7 C,其质量 m=4.5×10-5kg,取g=10 m/s2,问 (1)若液滴恰好能静止平衡时,滑动变阻器R的滑动 头C正好在正中点,那么滑动变阻器的最大阻值Rm是 多大? (2)将滑动片C迅速滑到A端后, 液滴将向哪个极板做什么运动? 到达极板时的速度是多大?
电路分析基础第二章 电路元件及电路基本类型(完整)

2. 线性 & 非线性元件
元件的特性方程为线性函数(满足可加性 和齐次性)时为线性元件,否则为非线性元件。 可加性: f ( x1 + x2 ) = f ( x1 ) + f ( x2 ) 齐次性: f (α x ) = α f ( x ) eg1:定常电阻元件的特性方程为u(t)=f[i(t)]=5i(t),问
⑵
u
N
有源二端元件
---有可能不满足无源特性积分式的二端元件。 i
+
-
w (t ) =
∫− ∞
t
u (τ )i (τ ) d τ 有可能 <0
w(t )有可能<0 ,说明(-∞,t]内,吸收<供出, 该元件能将多于电源供给的能量送回,是能量 的提供者,这类元件称为有源元件。如:独立 电压源(流源)、受控电压源(流源)。 独立电压源,独立电流源亦称为供能元件。
t t
在 uc与i 为关联参考方向下,
上式说明: 输入能量总非负--释放的能量不超过以前所储存的能量 时刻t观看电容时,储能只与该时刻t的电压uc(t)有关。 即 WC(t)只随uc(t)变化。 C是无损元件。
例 求电流i、功率P (t)和储能W (t) 解
uS (t)的函数表示式为:
+ -
u/V 2
小结小结电流源端电压则随与之联接的外电路而改变电流源端电压则随与之联接的外电路而改变常数则称为直流常数则称为直流常用大写字母常用大写字母表示直流表示直流电流源电流源理想电压源和电流源统称理想电压源和电流源统称独立源独立源电压源的电压和电压源的电压和电流源的电流都不受外电路影响它们电流源的电流都不受外电路影响它们作为电源或作为电源或输入信号输入信号时在电路中起时在电路中起激励激励excitationexcitation作用作用将在电路中产生将在电路中产生电流和电压电流和电压即输出信号称为即输出信号称为响应响应responseresponse当线性定常电容元件上电压的参考方向规定电容元件上电压的参考方向规定由正极板指向负极板则任何时刻正极板上的由正极板指向负极板则任何时刻正极板上的与其端电压与其端电压之间的关系有
含电容器电路的分析与计算

含电容器电路的分析与计算电容器是一种重要的电子元件,广泛应用于电路中。
在电容器电路的分析与计算中,我们需要了解电容器的基本原理、参数和特性,以及如何计算电容器电路中的电压、电流和时间常数等。
首先,电容器是一种能够储存电荷的电子元件,由两个导体板和介质组成。
常用的电容器有金属箔电容器、陶瓷电容器和电解电容器等,其容值单位是法拉(F)。
电容器的容量取决于其两个导体板之间的面积、板间的距离和介质的电容常数。
在电容器电路中,电容器的两个导体板分别连接到电路的两个节点,形成一个开回路。
当电容器充电时,电容器两个板之间的电荷会积累,并且在两个板之间形成一个电势差。
根据库仑定律,电容器的电压与其所储存的电荷量成正比。
电容器的电压-电荷关系可以表示为V=Q/C,其中V 是电容器的电压,Q是电容器所储存的电荷量,C是电容器的容值。
在电容器电路中,常用于分析和计算的是RC电路和RLC电路。
1.RC电路:RC电路由电阻和电容器组成,常用于滤波和积分电路。
在RC电路中,电容器会充电和放电,形成一个充放电过程。
当电容器充电时,电流通过电阻,电压逐渐上升。
当电容器放电时,电流从电容器流向电阻,电压逐渐下降。
在RC电路中,电容器的充放电过程遵循指数衰减的规律,其电压变化可以用指数函数来描述。
2.RLC电路:RLC电路由电感、电阻和电容器组成,常用于振荡、滤波和谐振电路。
在RLC电路中,电容器和电感可以形成共振回路,当外部输入信号频率等于回路共振频率时,电流最大。
RLC电路的分析和计算可利用电压-电流关系和频率响应等进行求解。
在电容器电路分析和计算时,我们可以通过以下步骤进行:1.确定电容器电路的拓扑结构:确定电容器的连接方式、电阻和电感的位置等。
2.建立电容器电路的数学模型:通过电压和电流的关系、电容器的电压-电荷关系等,建立电容器电路的数学方程。
3.求解电容器电路的初始条件:根据电路的初始状态,确定初始电荷量、电压和电流。
1﹒种类﹕按极性可分为有极性电容...

1﹒种类﹕按极性可分为有极性电容...1﹒种类﹕按极性可分为有极性电容:铝电解电容和钽质电解电容(钽Tan:一种非常坚硬、密度很大的灰色金属元素,在摄氏150度以下能抗化学物质的强腐蚀。
)无极性电容:陶瓷电容(又称瓷片电容)和塑料电容(又称唛拉电容)。
2﹒电容的电路符号及字母表示法﹕(1) 电容的电路符号有两种﹕无极性电容,有极性电容 + -(2) 电容字母表示﹕C(3) 电容的特性﹕隔直通交。
(4) 作用﹕用于贮存电荷的组件﹐贮存电量充电放电﹑滤波﹑耦合﹑旁路。
3﹒电容的单位及换算公式﹕a、电容的单位﹕基本单位为法拉(F)。
常用的有微法(UF)﹑皮法(PF) 、(F)法拉。
b、换算公式﹕1F=103MF=106UF=109NF=1012PF4﹒电解电容(EC)的参数:容量﹑耐压系数﹑温度系数。
其中 10UF表示电容容量﹐50V表示耐压系数﹐105℃为温度系数。
电解电容的特点是容量大﹑漏电大﹑耐压低。
按其制作材料又分为铝电解电容及钽质电解电容。
前者体积大﹐损耗大;后者体积小﹐损耗小﹐性能较稳定。
极性区分﹕长脚为正﹐短脚为负﹔负极有一条灰带。
常用单位为UF级。
5﹒陶瓷电容﹕(CC)右上边的电容为常用的陶瓷电容﹐容量为0.022UF。
换算223J电容为﹕22×103PF=0.022UF “J”表示误差。
6﹒麦拉电容﹕(MC)常用的麦拉电容其表示法如104J/100V表示容量为0.1UF﹐J为误差﹐100V为耐压值。
7﹒色环电容(卧式)电容﹕材料一般为聚脂类﹐体积较小﹐数值与电阻读法相似﹐但后面单位为PF。
例如﹕(1) 棕红黄银容量为0.12UF 误差为﹕±10%(2) 棕红金容量为0.12UF色环电容与色环电阻的区别﹕色环电容本体底色一般为淡黄色或红色﹔中间部分比两端略高﹐而色环电阻一般两端隆起﹐中间部分略低。
8﹒电容常用字母代表误差﹕B: ±0.1﹪C: ±0.25﹪D: ±0.5﹪F: ±1﹪G: ±2﹪J: ±5﹪,K: ±10﹪M: ±20﹪N: ±30﹪ Z:+80﹪-20﹪。
第63讲 含电容器电路的动态分析(解析版)

第63讲 含电容器电路的动态分析1.(2019•北京)电容器作为储能器件,在生产生活中有广泛的应用。
对给定电容值为C 的电容器充电,无论采用何种充电方式,其两极间的电势差u 随电荷量q 的变化图象都相同。
(1)请在图1中画出上述u ﹣q 图象。
类比直线运动中由v ﹣t 图象求位移的方法,求两极间电压为U 时电容器所储存的电能E p 。
(2)在如图2所示的充电电路中,R 表示电阻,E 表示电源(忽略内阻)。
通过改变电路中元件的参数对同一电容器进行两次充电,对应的q ﹣t 曲线如图3中①②所示。
a .①②两条曲线不同是 R (选填E 或R )的改变造成的;b .电容器有时需要快速充电,有时需要均匀充电。
依据a 中的结论,说明实现这两种充电方式的途径。
(3)设想使用理想的“恒流源”替换(2)中电源对电容器充电,可实现电容器电荷量随时间均匀增加。
请思考使用“恒流源”和(2)中电源对电容器的充电过程,填写下表(选填“增大”、“减小”或“不变”)。
“恒流源”(2)中电源 电源两端电压增大 不变 通过电源的电流 不变减小 【解答】解:(1)根据电容的定义Q =UC 可知,U =q C ,故电压U 与电量为正比例关系,故图象如图所示;根据图象的性质可知,图象与q 轴所围成的面积表示电能,故有:E P =12qU =12CU 2;(2)a 、电源电阻不计,当电容器充满电后,电容器两端电压等于电源电动势。
由图可知,充电时间不同,而最大电量相等,故说明图象不同的原因是电阻R 的改变造成的; b 、由图象可知,当R 越小,充电时间越短;R越大,电荷量随时间变化趋向均匀,故需要快速充电时,R 越小越好;而需要均匀充电时,R 越大越好;(3)由于电容充电后两板间的电势差增大,因此需要恒流源的电压增大才能保证电量随时间均匀增加;而(2)中电源电动势不变,而内阻忽略不计,故两端电压不变;所以使用恒流源时,电流不变,而使用(2)中电源时电流减小。
含电容的电路分析

含电容的电路分析
含容电路分析计算
电容器是一个储存电能的元件.在直流电路中,当电容器充放电时,电路里有充放电电流,一旦电路达到稳定状态,电容器在电路中就相当于一个阻值无限大(只考虑电容器是理想的不漏电的情况)的元件,在电容器处电路看作是断路,简化电路时可去掉它。
简化后若要求电容器所带电荷量时,可在相应的位置补上。
分析和计算含有电容器的直流电路时,需注意以下几点:
(1)电路稳定后,由于电容器所在支路无电流通过.所以在此支路中的电阻上无电压降,因此电容器两极间的电压就等于该支路两端的电压.
(2)当电容器和用电器并联后接入电路时,电容器两极间的电压与其并联用电器两端的电压相等.
(3)电路的电流、电压变化时,将会引起电容器的充(放)电.如果电容器两端电压升高,电容器将充电,如果电压降低,电容器将通过与它并联的电路放电.电容器两根引线上的电流方向总是相同的,所以要根据正极板电荷变化情况来判断电流方向。
含容电路分析计算技巧和实例

含容电路分析计算技巧和实例电容器是一个储存电能的元件.在直流电路中,当电容器充放电时,电路里有充放电电流,一旦电路达到稳定状态,电容器在电路中就相当于一个阻值无限大(只考虑电容器是理想的不漏电的情况)的元件,在电容器处电路看作是断路,简化电路时可去掉它。
简化后若要求电容器所带电荷量时,可在相应的位置补上。
分析和计算含有电容器的直流电路时,需注意以下几点:(1)电路稳定后,由于电容器所在支路无电流通过.所以在此支路中的电阻上无电压降,因此电容器两极间的电压就等于该支路两端的电压.(2)当电容器和用电器并联后接入电路时,电容器两极间的电压与其并联用电器两端的电压相等.(3)电路的电流、电压变化时,将会引起电容器的充(放)电.如果电容器两端电压升高,电容器将充电,如果电压降低,电容器将通过与它并联的电路放电.电容器两根引线上的电流方向总是相同的,所以要根据正极板电荷变化情况来判断电流方向。
⑷如果变化前后极板带电的电性相同,那么通过每根引线的电荷量等于始末状态电容器电荷量的差;如果变化前后极板带电的电性改变,那么通过每根引线的电荷量等于始末状态电容器电荷量之和。
含有电容器的电路解题方法(1)先将含电容器的支路去掉(包括与它串在同一支路上的电阻),计算各部分的电流、电压值。
(2)电容器两极扳的电压,等于它所在支路两端点的电压。
(3)通过电容器的电压和电容可求出电容器充电电量。
(4)通过电容器的电压和平行板间距离可求出两扳间电场强度,再分析电场中带电粒子的运动。
例1:如图所示的电路,水平放置的平行板电容器中有一个带电液滴正好处于静止状态,现将滑动变阻器的滑片P向左移动,则()A.电容器中的电场强度将增大B.电容器上的电荷量将减少C.电容器的电容将减小D.液滴将向上运动由题意可知,电容器与R2并联,根据闭合电路欧姆定律可确定随着滑片左移,电阻的变化,导致电压的变化,从而判定电阻R2的电压变化,再根据可得,电容器的电量及由E=知两极间的电场强度如何变化.【解析】A、电容器两板间电压等于R2两端电压.当滑片P向左移动时,R2两端电压U 减小,由E=知电容器中场强变小,A错误;B、根据可得,电容器放电,电荷量减少,B项正确;C、电容器的电容与U的变化无关,保持不变,C项错误.D、带电液滴所受电场力变小,使液滴向下运动,D项错误;故选:B例2:在如图所示的电路中,电源两端A、B 间的电压恒定不变,开始时S断开,电容器上充有电荷.闭合S后,以下判断正确的是()A.C1所带电量增大,C2所带电量减小B.C1所带电量减小,C2所带电量增大C.C1、C2所带电量均减小D.C1、C2所带电量均增大S断开时,外电路中没有电流,两电容器的电压都等于电源的电动势,S闭合后,两电容器的电压都小于电源的电动势,根据Q=CU分析电容器电量的变化.【解析】S断开时,外电路中没有电流,两电容器的电压都等于电源的电动势.S闭合后,两电阻串联,电容器C1的电压等于R1的电压,电容器C2的电压等于R2的电压,可知两电容器的电压都小于电源的电动势,根据Q=CU分析可知两电容器电量均减小.故C正确,ABD错误.故选C例3:如图所示的电路中,R1、R2、R3是固定电阻,R4是光敏电阻,其阻值随光照的强度增强而减小.当开关S闭合且没有光照射时,电容器C不带电.当用强光照射R4且电路稳定时,则与无光照射时比较()A.电容器C的上极板带正电B.电容器C的下极板带正电C.通过R4的电流变小,电源的路端电压增大D.通过R4的电流变大,电源提供的总功率变小电容在电路稳定时可看作开路,故由图可知,R1、R2串联后与R3、R4并联,当有光照射时,光敏电阻的阻值减小,由闭合电路欧姆定律可得出电路中总电流的变化及路端电压的变化,再分析外电路即可得出C两端电势的变化,从而得出电容器极板带电情况;同理也可得出各电阻上电流的变化.【解析】因有光照射时,光敏电阻的阻值减小,故总电阻减小;由闭合电路的欧姆定律可知,干路电路中电流增大,由E=U+Ir可知路端电压减小;R1与R2支路中电阻不变,故该支路中的电流减小;则由并联电路的电流规律可知,另一支路中电流增大,即通过R2的电流减小,而通过R4的电流增大,故C、D错误;当没有光照时,C不带电说明C所接两点电势相等,以电源正极为参考点,R1上的分压减小,而R3上的分压增大,故上极板所接处的电势低于下极板的电势,故下极板带正电;故A错误,B正确;故选B.例4:如图所示的电路中,两平行金属板A、B水平放置,极板长L=80cm,两板间的距离d=40cm.电源电动势E=40V,内电阻r=1Ω,电阻R=15Ω,闭合开关S,待电路稳定后,将一带负电的小球从B板左端且非常靠近B板的位置以初速度v=4m/s水平向右射入两板高效课堂—实验微专题间,该小球可视为质点.若小球带电量q=1×10-2C,质量为m=2×10-2kg,不考虑空气阻力,电路中电压表、电流表均是理想电表.若小球恰好从A板右边缘射出(g取10m/s2).求:(1)滑动变阻器接入电路的阻值为多少?(2)此时电流表、电压表的示数分别为多少?(3)此时电源的输出功率是多少?(1)小球进入电场中做类平抛运动,小球恰好从A板右边缘射出时,水平位移为L,竖直位移为d,根据运动学和牛顿第二定律结合可求出板间电压,再根据串联电路分压特点,求解滑动变阻器接入电路的阻值.(2)根据闭合电路欧姆定律求解电路中电流,由欧姆定律求解路端电压,即可求得两电表的读数.(3)电源的输出功率P=UI,U是路端电压,I是总电流.【解析】(1)小球进入电场中做类平抛运动,水平方向做匀速直线运动,竖直方向做匀加速运动,则有:水平方向:L=vt竖直方向:d=由上两式得:a===20m/s2又根据牛顿第二定律得:a=联立得:U==V=24V根据串联电路的特点有:=代入得:=解得,滑动变阻器接入电路的阻值为R′=24Ω(2)根据闭合电路欧姆定律得电流表的示数为:I==A=1A电压表的示数为:U=E-Ir=(40-1×1)V=39V(3)此时电源的输出功率是P=UI=39×1W=39W.答:(1)滑动变阻器接入电路的阻值为24Ω.(2)此时电流表、电压表的示数分别为1A和39V.(3)此时电源的输出功率是39W.每日一练解析C为板间距离固定的电容器,电路连接如图所示,当滑动触头P向右缓慢滑动的过程中,下列说法中正确的是()A.电容器C充电B.电容器C放电C.流过电流计G的电流方向为a→G→bD.流过电流计G的电流方向为b→G→a首先明确含电容器的支路等效为断路,且两端的电压为并联部分的电压相等;当滑动触头P向右缓慢滑动的过程中,该电路的总电阻不变,但与电容器并联部分的电阻减少,即电容器两端的电压减少,根据C=可知,电容器极板电量减少,即放电;电容器右极板与电源负极相连,所以自由电子从a移动到b,故流过电流计G的电流方向为b→G→a.【解析】AB、含电容器的支路等效为断路,且两端的电压为并联部分的电压相等;当滑动触头P向右缓慢滑动的过程中,该电路的总电阻不变,但与电容器并联部分的电阻减少,即电容器两端的电压减少,根据C=可知,电容器极板电量减少,即放电,故A错误,B正确.CD、以上分析可知,电容器放电,且电容器右极板与电源负极相连,所以自由电子从a移动到b,电流的方向与电子的方向相反,故流过电流计G的电流方向为b→G→a,故C错误,D正确.。
《电容知识大全》PPT课件

整理ppt
7
• 3.电容的类别和符号
C表示电容
4.电解电容极性的判别:可用万用表的电阻挡测量其极性
测量时,先假定某极为“ + ”极,让其与万用表的黑表笔 相接,另一电极与万用表的红表笔相接,记下表针停止的 刻度(表针靠左阻值大),然后将电容器放电(既两根引 线碰一下),两只表笔对调,重新进行测量。两次测量中, 表针最后停留的位置靠左(阻值大)的那次,黑表笔接的 就是电解电容的正极。 测量时最好选用 R*100 或 R*1K 挡。 用万用表判断电容 器质量
为开么会出现这些现象呢?这是因为电容器是依靠它的充放电功能来工作的电容器产品标出的电容量值云母和陶瓷介质电容器的电容量较低大约在5000pf以下纸塑料和一些陶瓷介质形式的电容器居中大约在0005uf10uf电容器设计所确定的能连续工作的环境温度范围
电容知识大全
整理ppt
1
一、电容的特性
隔直通交 1.电容器是一种能储存电荷的容器.它是由两片靠得
云母和陶瓷介质电容器的电容量较低(大约在 5000pF 以下)
纸、塑料和一些陶瓷介质形式的电容器居中(大约在 0.005uF~1.0uF );
通常电解电容器的容量较大
2.类别温度范围 :电容器设计所确定的能连续工作的环境温 度范围。该范围取决于它相应类别的温度极限值,如上限 类别温度、下限类别温度、额定温度(可以连续施加额定 电压的最高环境温度)等
整理ppt
11
整理ppt
10
总结: 电子电路中,只有在电容器充电过程中,才有电流
流过,充电过程结束后,电容器是不能通过直流电 的,在电路中起着“隔直流”的作用。电路中,电 容器常被用作耦合、旁路、滤波等,都是利用它 “通交流,隔直流”的特性。 那么交流电为什么能够通过电容器呢?我们先来 看看交流电的特点。交流电不仅方向往复交变,它 的大小也在按规律变化。电容器接在交流电源上, 电容器连续地充电、放电,电路中就会流过与交流 电变化规律一致的充电电流和放电电流。 电容器的选用涉及到很多问题。首先是耐压的问题。 加在一个电容器的两端的电压超过了它的额定电压, 电容器就会被击穿损坏。一般电解电容的耐压分档 为6.3V,10V,16V,25V,50V等
浅谈解物理题的方法优秀获奖科研论文

浅谈解物理题的方法优秀获奖科研论文物理解题方法有很多, 本文重点介绍两种解题方法, 即分析法和综合法.一、分析法和综合法简介分析法的特点是从问题出发,逐层进行分析求解,直到求出待求量.综合法,就是将已知的各个量联系在一起,明确各部分的关系后,最后综合在一起进行整体解答.不管是“分析法”还是“综合法”,它们是密不可分的.分析是综合的基础,综合是分析的结果,两者是互补的.(2)受力分析步骤.首先,判断物体的受力情况并作图.其次,判断力的方向:①根据力的性质和产生的原因去判断.②根据物体的运动状态判断:a由牛顿第三定律判断;b由牛顿第二定律判断(有加速度的方向物体必受力).三、运动学解题的基本方法、步骤在解答运动学问题时,位移、速度、加速度等基本概念和基本规律是解题的依据.只有对这些概念和规律有深刻的认识后,才有利于我们解答相关问题.基本步骤如下:(1)审题.弄清题意,画草图,明确已知量,未知量,待求量.(2)明确研究对象.选择参考系、坐标系.(3)分析有关的时间、位移、初末速度,加速度等.(4)应用运动规律、几何关系等建立解题方程.(5)解方程.四、动力学解题的基本方法由于动力学规律较复杂,在解答此类问题时,要首先将这些问题进行归类处理,再进行具体的解答.1.应用牛顿定律求解的问题.(1)已知物体受力求物体运动情况.(2)已知物体运动情况求物体受力.这两种基本问题的综合题很多.从研究对象看,有单个物体也有多个物体.解答习题的基本方法:①确定研究对象.②分析物体受力情况,画受力图.③对物体的运动情况进行分析,确定加速度a.④根据牛顿定律、力的概念、规律、运动学公式等建立解题方程.⑤解方程.⑥验算,讨论.2.应用动能定理求解的问题.解题的基本方法:①选定研究的物体和物体的一段位移以明确m、s.②对物体受到的力进行受力分析.③对物体的初始速度和末速度进行分析,确定初末动能.3.应用机械能守恒定律求解的问题.解题的基本方法:①选定研究的系统和一段位移;②对系统进行受力分析,包括外力、内力,及他们做功情况,以判定系统机械能是否守恒;③对物体初始位置和最终的位置进行分析,然后根据机械能守恒定律等列方程,解方程,验算讨论.五、电路解题的基本方法1.针对电路问题,主要采用如下步骤:(1)确定所研究的电路;(2)将不规范的串并联电路改画为规范的串并联电路;(3)在所画图中标出已知量和待求量,以利分析;(4)应注意当某一电阻改变时,各部分电流、电压、功率都要改变.可以认为电源电动势和内电阻及其它定值电阻的数值不变.必要时先求出、r和定随电阻的大小;(5)根据欧姆定律,串、并联特性和电功率公式列方程求解;(6)学会用等效电路,会用数学方法讨论物理量的极值.2.含有电容器的电路解题方法.在直流电路中,电容器相当电阻为无穷大的电路元件,对电路是断路.解题步骤如下:(1)先将含电容器的支路去掉(包括与它串在同一支路上的电阻),计算各部分的电流、电压值;(2)电容器两极板的电压,等于它所在支路两端点的电压;(3)通过电容器的电压和电容可求出电容器充电电量;(4)求出两板间电场强度,再分析电场中带电粒子的运动.物理解题方法有很多,本文重点介绍两种解题方法,即分析法和综合法.一、分析法和综合法简介分析法的特点是从问题出发,逐层进行分析求解,直到求出待求量.综合法,就是将已知的各个量联系在一起,明确各部分的关系后,最后综合在一起进行整体解答.不管是“分析法”还是“综合法”,它们是密不可分的.分析是综合的基础,综合是分析的结果,两者是互补的.(2)受力分析步骤.首先,判断物体的受力情况并作图.其次,判断力的方向:①根据力的性质和产生的原因去判断.②根据物体的运动状态判断:a由牛顿第三定律判断;b由牛顿第二定律判断(有加速度的方向物体必受力).三、运动学解题的基本方法、步骤在解答运动学问题时,位移、速度、加速度等基本概念和基本规律是解题的依据.只有对这些概念和规律有深刻的认识后,才有利于我们解答相关问题.基本步骤如下:(1)审题.弄清题意,画草图,明确已知量,未知量,待求量.(2)明确研究对象.选择参考系、坐标系.(3)分析有关的时间、位移、初末速度,加速度等.(4)应用运动规律、几何关系等建立解题方程.(5)解方程.四、动力学解题的基本方法由于动力学规律较复杂,在解答此类问题时,要首先将这些问题进行归类处理,再进行具体的解答.1.应用牛顿定律求解的问题.(1)已知物体受力求物体运动情况.(2)已知物体运动情况求物体受力.这两种基本问题的综合题很多.从研究对象看,有单个物体也有多个物体.解答习题的基本方法:①确定研究对象.②分析物体受力情况,画受力图.③对物体的运动情况进行分析,确定加速度a.④根据牛顿定律、力的概念、规律、运动学公式等建立解题方程.⑤解方程.⑥验算,讨论.2.应用动能定理求解的问题.解题的基本方法:①选定研究的物体和物体的一段位移以明确m、s.②对物体受到的力进行受力分析.③对物体的初始速度和末速度进行分析,确定初末动能.3.应用机械能守恒定律求解的问题.解题的基本方法:①选定研究的系统和一段位移;②对系统进行受力分析,包括外力、内力,及他们做功情况,以判定系统机械能是否守恒;③对物体初始位置和最终的位置进行分析,然后根据机械能守恒定律等列方程,解方程,验算讨论.五、电路解题的基本方法1.针对电路问题,主要采用如下步骤:(1)确定所研究的电路;(2)将不规范的串并联电路改画为规范的串并联电路;(3)在所画图中标出已知量和待求量,以利分析;(4)应注意当某一电阻改变时,各部分电流、电压、功率都要改变.可以认为电源电动势和内电阻及其它定值电阻的数值不变.必要时先求出、r和定随电阻的大小;(5)根据欧姆定律,串、并联特性和电功率公式列方程求解;(6)学会用等效电路,会用数学方法讨论物理量的极值.2.含有电容器的电路解题方法.在直流电路中,电容器相当电阻为无穷大的电路元件,对电路是断路.解题步骤如下:(1)先将含电容器的支路去掉(包括与它串在同一支路上的电阻),计算各部分的电流、电压值;(2)电容器两极板的电压,等于它所在支路两端点的电压;(3)通过电容器的电压和电容可求出电容器充电电量;(4)求出两板间电场强度,再分析电场中带电粒子的运动.物理解题方法有很多,本文重点介绍两种解题方法,即分析法和综合法.一、分析法和综合法简介分析法的特点是从问题出发,逐层进行分析求解,直到求出待求量.综合法,就是将已知的各个量联系在一起,明确各部分的关系后,最后综合在一起进行整体解答.不管是“分析法”还是“综合法”,它们是密不可分的.分析是综合的基础,综合是分析的结果,两者是互补的.(2)受力分析步骤.首先,判断物体的受力情况并作图.其次,判断力的方向:①根据力的性质和产生的原因去判断.②根据物体的运动状态判断:a由牛顿第三定律判断;b由牛顿第二定律判断(有加速度的方向物体必受力).三、运动学解题的基本方法、步骤在解答运动学问题时,位移、速度、加速度等基本概念和基本规律是解题的依据.只有对这些概念和规律有深刻的认识后,才有利于我们解答相关问题.基本步骤如下:(1)审题.弄清题意,画草图,明确已知量,未知量,待求量.(2)明确研究对象.选择参考系、坐标系.(3)分析有关的时间、位移、初末速度,加速度等.(4)应用运动规律、几何关系等建立解题方程.(5)解方程.四、动力学解题的基本方法由于动力学规律较复杂,在解答此类问题时,要首先将这些问题进行归类处理,再进行具体的解答.1.应用牛顿定律求解的问题.(1)已知物体受力求物体运动情况.(2)已知物体运动情况求物体受力.这两种基本问题的综合题很多.从研究对象看,有单个物体也有多个物体.解答习题的基本方法:①确定研究对象.②分析物体受力情况,画受力图.③对物体的运动情况进行分析,确定加速度a.④根据牛顿定律、力的概念、规律、运动学公式等建立解题方程.⑤解方程.⑥验算,讨论.2.应用动能定理求解的问题.解题的基本方法:①选定研究的物体和物体的一段位移以明确m、s.②对物体受到的力进行受力分析.③对物体的初始速度和末速度进行分析,确定初末动能.3.应用机械能守恒定律求解的问题.解题的基本方法:①选定研究的系统和一段位移;②对系统进行受力分析,包括外力、内力,及他们做功情况,以判定系统机械能是否守恒;③对物体初始位置和最终的位置进行分析,然后根据机械能守恒定律等列方程,解方程,验算讨论.五、电路解题的基本方法1.针对电路问题,主要采用如下步骤:(1)确定所研究的电路;(2)将不规范的串并联电路改画为规范的串并联电路;(3)在所画图中标出已知量和待求量,以利分析;(4)应注意当某一电阻改变时,各部分电流、电压、功率都要改变.可以认为电源电动势和内电阻及其它定值电阻的数值不变.必要时先求出、r和定随电阻的大小;(5)根据欧姆定律,串、并联特性和电功率公式列方程求解;(6)学会用等效电路,会用数学方法讨论物理量的极值.2.含有电容器的电路解题方法.在直流电路中,电容器相当电阻为无穷大的电路元件,对电路是断路.解题步骤如下:(1)先将含电容器的支路去掉(包括与它串在同一支路上的电阻),计算各部分的电流、电压值;(2)电容器两极板的电压,等于它所在支路两端点的电压;(3)通过电容器的电压和电容可求出电容器充电电量;(4)求出两板间电场强度,再分析电场中带电粒子的运动.。
简明电工学课件:含电阻、电容、电感元件的直流电路分析

含电阻、电容、电感元件的 直流电路分Байду номын сангаас
3.4.3 RC 电路的全响应 RC 电路的全响应指电源激励、电容元件的初始能量均
不为零时电路的响应。全响应 分析可以应用叠加原理。 如图3.4.3所示,假设换路前电容元件存储能量且uC =U0。
在t = 0时,合上开关。 电容元件初始能量U0单独作用时,电路如图3.4.5所示,显
分析。
含电阻、电容、电感元件的 直流电路分 知识结构
含电阻、电容、电感元件的 直流电路分
3.1 电阻元件、 电容元件与电感元件
3.1.1 电阻元件 电阻元件是消耗电能的元件。如图3.1.1所示,用u、i表
示电压和电流均是随时间变化的瞬时值。根据欧姆定律可得
含电阻、电容、电感元件的 直流电路分
图3.1.1 电阻元件
理论上讲,指数衰减曲线只会无限逼近零。结合指数衰 减的规律,经过分析一般认为 3τ~5τ的时间,电路达到稳定状 态。
含电阻、电容、电感元件的 直流电路分 放电电流
其随时间变化的曲线同样绘制于图3.4.2中。负号表示其放电 实际方向和图3.4.1参考方向 相反。
含电阻、电容、电感元件的 直流电路分
电感元件均未储能。试求 电路中标注的电压、电流的初始 值和稳态值。
图3.3.1 例3.3.1的电路
含电阻、电容、电感元件的 直流电路分
含电阻、电容、电感元件的 直流电路分
图3.3.2 t=0+ 的电路
含电阻、电容、电感元件的 直流电路分
图3.3.3 t=∞的电路
含电阻、电容、电感元件的 直流电路分 【例3.3.2】 电路如图3.3.4所示,换路前已处于稳态。
含电阻、电容、电感元件的 直流电路分
电容器知识大全

电容器知识大全第1讲:电容的特性(隔直通交) 电容器是一种能储存电荷的容器.它是由两片靠得较近的金属片,屑湓俑粢跃 滴镏识 槌傻模 淳 挡牧喜煌 芍瞥筛髦指餮 牡缛萜?如:云母.瓷介.纸介,电解电容器等.在构造上,又分为固定电容器和可变电容器.电容器对直流电阻力无穷大,即电容器具有隔直流作用.电容器对交流电的阻力受交流电频率影响,即相同容量的电容器对不同频率的交流电呈现不同的容抗.为开么会出现这些现象呢\'这是因为电容器是依靠它的充放电功能来工作的,如图1,电源开关s未合上时.电容器的两片金属板和其它普通金属板—样是不带电的。
当开关S合上时,如图2所示,电容器正极板上的自由电子便被电源所吸引,并推送到负极板上面。
由于电容器两极板之间隔有绝缘材料,所以从正极板跑过来的自由电子便在负极板上面堆积起来.正极板便因电子减少而带上正电,负极板便因电子逐渐增加而带上负电。
电容器两个极板之间便有了电位差,当这个电位差与电源电压相等时,电容器的充电就停上了.此时若将电源切断,电容器仍能保持充电电压。
对已充电的电容器,如果我们用导线将两个极板连接起来,由于两极板间存在的电位差,电子便会通过导线,回到正极板上,直至两极板间的电位差为零.电容器又恢复到不带电的中性状态,导线中也就没电流了.电容器的放电过程如图3所示.加在电容器两个极板上的交流电频率高,电容器的充放电次数增多;充放电电流也就增强;也就是说.电容器对于频率高的交流电的阻碍作用就减小,即容抗小,反之电容器对频率低的交流电产生的容抗大.对于同一频率的交流电电.电容器的容量越大,容抗就越小,容量越小,容抗就越大. 第2讲:电容器的参数与分类 在电子产品中,电容器是必不可少的电子器件,它在电子设备中充当整流器的平滑滤波、电源的退耦、交流信号的旁路、交直流电路的交流耦合等。
电容器电路分析

电容器、电路专题(一)1.如图所示,用长L=0.50 m的绝缘轻质细线,把一个质量m=1.0 g带电小球悬挂在均匀带等量异种电荷的平行金属板之间,平行金属板间的距离d=5.0 cm,两板间电压U=1.0×103 V.静止时,绝缘细线偏离竖直方向θ角,小球偏离竖直线的距离a=1.0 cm.取g=10 m/s2.则下列说法正确的是().A.两板间电场强度的大小为2.0×104 V/mB.小球带的电荷量为1.0×10-8 CC.若细线突然被剪断,小球在板间将做类平抛运动D.若细线突然被剪断,小球在板间将做匀加速直线运动2.如图所示,M、N是平行板电容器的两个极板,R0为定值电阻,R1、R2为可调电阻,用绝缘细线将质量为m、带正电的小球悬于电容器内部.闭合开关S,小球静止时受到悬线的拉力为F.调节R1、R2,关于F的大小判断正确的是().A.保持R1不变,缓慢增大R2时,F将变大B.保持R1不变,缓慢增大R2时,F将变小C.保持R2不变,缓慢增大R1时,F将变大D.保持R2不变,缓慢增大R1时,F将变小3.如图所示电路,在平行金属板M,N内部左侧中央P有一质量为m的带电粒子(重力不计)以水平速度v0射入电场并打在N板的O点.改变R1或R2的阻值,粒子仍以v0射入电场,则().A.该粒子带正电B.减少R2,粒子还能打在O点C.减少R1,粒子将打在O点左侧D.增大R1,粒子在板间运动时间不变4.如图所示,平行板电容器与电动势为E′的直流电源(内阻不计)连接,下极板接地,静电计所带电荷量很少,可被忽略.一带负电油滴被固定于电容器中的P点.现将平行板电容器的下极板竖直向下移动一小段距离,则().A.平行板电容器的电容将变小B.静电计指针张角变小C.带电油滴的电势能将减少D.若先将上极板与电源正极的导线断开,再将下极板向下移动一小段距离,则带电油滴所受电场力不变5.如图所示,带电平行金属板相距为2R,在两板间有垂直纸面向里、磁感应强度为B的圆形匀强磁场区域,与两板及左侧边缘线相切.一个带正电的粒子(不计重力)沿两板间中心线O1O2从左侧边缘O1点以某一速度射入,恰沿直线通过圆形磁场区域,并从极板边缘飞出,在极板间运动时间为t0.若撤去磁场,质子仍从O1点以相同速度射入,则经t02时间打到极板上.(1)求两极板间电压U;(2)若两极板不带电,保持磁场不变,该粒子仍沿中心线O1O2从O1点射入,欲使粒子从两板左侧间飞出,射入的速度应满足什么条件?电容器、电路专题(二)1.如图所示的电路中,L1、L2是两个不同的小灯泡,a、b间有恒定的电压,它们都正常发光,当滑动变阻器的滑片向右滑动时,发生的现象是().A.L1亮度不变,L2变暗B.L1变暗,L2变亮C.电路消耗的总功率变小D.流过滑动变阻器的电流变小2.(单选)在图7-2-20所示的闭合电路中,当滑片P向右移动时,两电表读数的变化是().A.变大,变大B.变小,变大C.变大,变小D.变小,变小3.在如图7-2-22所示的电路中,E为电源的电动势,r为电源的内阻,R1、R2为可变电阻.在下列叙述的操作中,可以使灯泡L变暗的是 ().A.仅使R1的阻值增大B.仅使R1的阻值减小C.仅使R2的阻值增大D.仅使R2的阻值减小4.已知磁敏电阻在没有磁场时电阻很小,有磁场时电阻变大,并且磁场越强阻值越大.为探测磁场的有无,利用磁敏电阻作为传感器设计了如图7-2-23所示电路,电源的电动势E和内阻r不变,在没有磁场时调节变阻器R使电灯L正常发光,若探测装置从无磁场区进入强磁场区.则().A.电灯L变亮B.电灯L变暗C.电流表的示数减小D.电流表的示数增大5.如图所示的电路中,电源的电动势E和内阻r恒定不变,滑片P在变阻器正中位置时,电灯L正常发光,现将滑片P移到右端,则().A .电压表的示数变大B .电流表的示数变大C .电灯L 消耗的功率变小D .电阻R 1消耗的功率变小 6.在研究微型电动机的性能时,应用如图所示的实验电路.当调节滑动变阻器R 使电动机停止转动时,电流表和电压表的示数分别为0.5 A 和2.0 V .重新调节R 使 电动机恢复正常运转,此时电流表和电压表的示数分别为2.0 A 和24.0 V .则这台电动机正常运转时输出功率为( ).A .32 WB .44 WC .47 WD .48 W7.空间某区域内存在B 1=0.5T ,方向水平的匀强磁场,在磁场区域内有两根相距L 1=0.6m 的足够长的平行金属导轨PQ 、MN ,固定在竖直平面内(导轨所在平面与磁场垂直),如图所示。
电容的分类和应用

电容的分类和应⽤电容的分类和应⽤⼀、电容的分类和作⽤电容,由两个⾦属极,中间夹有绝缘材料(介质)构成。
由于绝缘材料的不同,所构成的电容器的种类也有所不同:按结构可分为:固定电容,可变电容按介质材料可分为:空⽓电容、液体电容、⽆机固体电容、有机固体电容、电解电容。
按极性分为:有极性电容和⽆极性电容。
电容在电路中具有隔断直流电,通过交流电的作⽤,因此常⽤于级间耦合、滤波、去耦、旁路及信号调谐⼆、电容的符号电容的符号同样分为国内标表⽰法和国际电⼦符号表⽰法,但电容符号在国内和国际表⽰都差不多,唯⼀的区别就是在有极性电容上,国内的是⼀个空筐下⾯⼀根横线,⽽国际的就是普通电容加⼀个"+"符号代表正极。
(见下图)三、电容的单位电阻的基本单位是:F (法),此外还有µF(微法)、pF(⽪法),另外还有⼀个⽤的⽐较少的单位,那就是:nF(纳法)。
电容 F 的容量很⼤,我们看到的⼀般都是µF、nF、pF的单位,⽽不是F的单位。
它们之间的具体换算关系如下:1F=1000000µF1µF=1000nF1nF=1000pF四、电容的耐压单位:V(伏特)每⼀个电容都有它的耐压值,这是电容的重要参数之⼀。
普通⽆极性电容的标称耐压值有:63V、100V、160V、250V、400V、600V、1000V等,有极性电容的耐压值相对要⽐⽆极性电容的耐压要低,⼀般的标称耐压值有:4V、6.3V、10V、16V、25V、35V、50V、63V、80V、100V、220V、400V等。
五、电容的种类电容的种类可以从原理上分为:⽆极性可变电容、⽆极性固定电容、有极性电容等,从材料上可以分为:CBB电容(聚⼄烯),涤纶电容、瓷⽚电容、云母电容、独⽯电容、电解电容、钽电容等。
各种电容的优缺点及⽤途⽆极性可变电容制作⼯艺: 1、可旋转动⽚为陶瓷⽚表⾯镀⾦属薄膜,定⽚为镀有⾦属膜的陶瓷底座;动⽚为同轴⾦属⽚,定⽚为有机薄膜⽚作介质优点:容易⽣产,技术含量低。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
含电容器电路的归类分析
山东潍坊寒亭一中 张启光 李瑞芳(邮编261100)
电容器是一个储能元件,在直流电路中,当电路稳定后,电容器相当于一个阻值无限大的元件,含有电容器的支路看作断路,关于电路中电容器的考查常见以下几方面:
一、考查电容器所带电荷量
例1 如图1所示电路中,已知电容器的电容C =2μF ,电源电动势E =12V ,内阻不计,1R :2R :3R :4R =1:2:6:3,
则S 闭合时电容器a 板所带电荷量为( ) A .-8×6
10- C B .4×6
10- C
C .-4×6
10- C D .8×6
10- C
解析:电源内阻不计则路端电压为12V ,电路稳定后电容器相当于断路,由串联正比分压有
2
1
2121==R R U U ,则2U =8V ,同理1
2
4343==R R U U ,则4U =4V ,取电源的负极电势为零,则a 板电势为8V ,b 板电势为4V ,故电容器两极板间电势差U =4V ,a 板带正电荷CU q ==8×6
10-C ,正确答案为D .
二、考查电路变化后流过用电器的电荷量
例2 如图2所示电路中1R =2R =3R =8Ω,电容器电容C =5μF ,电源电动势E =6V ,内阻不计,求电键S 由稳定的闭合状态断开后流过3R 的电荷量.
解析:电键闭合时电路结构为R 1和R 2串联后与R 3并联,电容器并在R 2两端,电源内阻不计,由串联正比分压得2U =3V ,b 板带正电,电荷量Q =CU 2=15×6
10-C ;电键断开后电路结构为R 1和R 2串联,电容器通过
R 3并在R 1两端,则电容器两端电压为1U =3V ,b 板带负电,电荷量1CU Q ='=15×6
10-C ,所以电键断开后电容器通过R 3先放电后反向充电,流过R 3的电荷量为两情况下电容器所带
电荷量之和Q Q Q '+=∆=3×10-
5C .
注意:求电路变化后流过用电器的电荷量的问题,一定要注意同一极板上所带电荷的电性是否变化,不变则流过用电器的电荷量为初、末状态电容器所带电荷量之差,变化则为二者之和.
三、以电容器为背景考查力电综合问题
例3 如图3所示,1R =2R =3R =4R =R ,电键S 闭合时,间距为d 的平行板电容器C 的正中间有一质量为m 、电荷量为q 的小球恰好处于静止状态;电键S 断开时,小球向电容器的一个极板运动并发生碰撞,碰后小球带上与极板同性质的电荷.设碰撞过程中没有机械能的损失,小球反弹后恰好能运动到电容器的另一极板,不计电源内阻,求电源的电动势和碰后小球所带的电荷量.
解析:电键S 闭合时1R 、3R 并联后与4R 串联(2R 中没有电流通过),电容器并在4
R 上,U C =4U =
E 3
2
,对带电小球有d U q mg C =,解得q mgd E 23=.电键S 断开时,仅1R 、
4R 串联,电容器仍并在4R 上,2
E
U C
=',故小球向下运动,设小球与下极板碰撞后带电荷量为q ',从小球开始运动到小球恰好运动到上极板的全过程由动能定理得
C C U q U q mgd ''+'--22=0,综合解得6
7q
q ='.
点评:分析和计算含有电容器的直流电路问题,关键是准确地判断和求出电容器两端的电压,具体方法是:
(1)明确电路结构,确定电容器和哪部分电路并联,该电路两端电压就是电容器两端
电压.
(2)当电容器与某一电阻串联后接入电路时,此支路中没有电流,所以与电容器串联的电阻看成导线,电路两端的电压就是电容器两极板间电压.
(3)对于较复杂电路,需要将电容器两端的电势与基准点的电势比较后才能确定电容器两端的电压.。
