索罗和拉姆齐模型
拉姆齐模型

第三章 无限期界模型(拉姆齐模型)
一、问题的提出
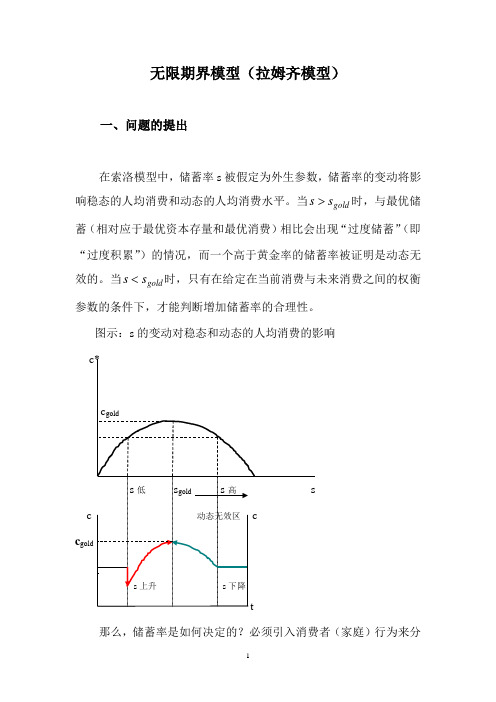
在索洛模型中,储蓄率s 被假定为外生参数,储蓄率的变动将影响稳态的人均消费和动态的人均消费水平。
当gold s s >时,与最优储蓄(相对应于最优资本存量和最优消费)相比会出现“过度储蓄”(即“过度积累”)的情况,而一个高于黄金率的储蓄率被证明是动态无效的。
当gold s s <时,只有在给定在当前消费与未来消费之间的权衡参数的条件下,才能判断增加储蓄率的合理性。
图示:s 的变动对稳态和动态的人均消费的影响
c c gol
d 那么,储蓄率是如何决定的?必须引入消费者(家庭)行为来分
析跨期预算约束条件下的消费和储蓄选择,即储蓄率的“内生化”。
二、模型假定
1.完全竞争市场结构
2.长生不老的不断扩展的家庭(有限寿命的个人和基于利他主义的代际转让)
3.家庭和个人完全同质
4.忽略资本的折旧
5.暂不考虑政府行为
在简单经济中,家庭与厂商之间的关系:
三、厂商行为。
拉姆齐模型

拉姆齐模型拉姆齐模型是一种用于分析企业资本结构和债务重组的理论模型。
拉姆齐模型以名字命名,是由经济学家弗兰克·拉姆齐(Frank P. Ramsey)在20世纪30年代提出的。
该模型用于探讨企业在决定自己的资本结构时所面临的权衡问题,帮助企业制定最佳的债务比例。
背景资本结构是指企业所采用的资本来源和组织方式。
一般来说,企业可以通过两种方式筹集资金:通过债务融资和通过股权融资。
债务融资指的是企业通过发行债券或贷款等方式借入资金,而股权融资则是通过发行股票或吸引投资者购买股权来筹集资金。
企业的资本结构选择对其经营和财务状况有着重要的影响。
合理的资本结构可以降低企业的融资成本、提高税务效益,并平衡利益相关者之间的关系。
这就引出了拉姆齐模型。
模型解释拉姆齐模型首先假设企业的资本结构通过对债务与股权的选择进行优化来实现最大化价值的目标。
在这个模型中,企业的价值受到利润、税收、资本结构和风险等多个因素的影响。
模型中最基本的假设是,企业的资本结构会影响其成本和价值。
企业选择债务的比例是为了最大化净利润,同时平衡税务和金融风险。
根据拉姆齐模型的理论,债务的选择可以通过计算企业的债务税盾等参数来进行。
债务税盾是指企业由于债务利息的抵扣而减少应纳税额的优势。
在拉姆齐模型中,债务税盾会对企业的价值产生积极的影响,因为它减少了企业的纳税额,提高了净现金流。
此外,模型还考虑了资本结构对企业风险的影响。
债务融资可以增加企业财务风险,因为债务必须偿还,而股权融资则可以减少财务风险,因为股票的回报没有偿还压力。
因此,企业需要权衡风险与税盾所带来的优势,以确定最佳的资本结构。
实践应用拉姆齐模型的应用可以帮助企业确定最佳的资本结构,以实现最大化的价值。
通过分析债务税盾和风险影响,企业可以选择适合自己的债务比例,从而降低融资成本,改善财务状况。
在实际应用中,企业可以通过以下步骤使用拉姆齐模型:1.确定企业的利润和税务情况。
中级宏观经济学第章拉姆齐模型

第一节 拉姆齐问题
家庭行为-效用最大化
B
et c
t 1 dt
0
1
k 0
eRtengt w t dt-
0
0
eRt
en
g
t
c
t
dt
( 5-16)
在每个时点家庭选择c,这样就会形成无限多个c(t)。对每一单 个c(t),其一阶条件是对于任意的t:
第一节 拉姆齐问题
厂商行为
厂商行为相对简单。在每个时点上,他们租用劳动与资本进行生
产,并按这些要素各自的边际产品支付报酬,并出售所生产的产出。
由于生产函数具有不变的规模报酬,经济是竞争性的,厂商因此获得
正常利润。我们知道,资本的边际产品F为K, AL =f ' k
K
。由于市场是
竞争性的,资本只能获得其边际产品。由于不存在折旧,资本的真实
C
t
Lt
H
dt
(可以是负值);
eRsRt 则表明从t时刻到s时刻该储蓄值的变动状况。
式(5-9)表达式是 eRs 与式(5-8)的大括号中的表达式的乘
积,预算约束写成下式:
第一节 拉姆齐问题
家庭行为-预算约束(续)
lim eRs K s 0( 5-10)
报酬率等于其每单位时间的收入,因此,在t时刻,真实利率为:
r t f ' k t( 5-3)
第一节 拉姆齐问题
厂商行为(续)
劳动的边际产品为 F K, AL ,它也等于 AF K, AL 。根据
L
AL
上述生产函数的紧凑形式,它可写成A f k kf ' k 。因此在c
拉姆齐模型1-2

第三章 无限期界模型(拉姆齐模型)一、问题的提出在索洛模型中,储蓄率s 被假定为外生参数,储蓄率的变动将影响稳态的人均消费和动态的人均消费水平。
当gold s s >时,与最优储蓄(相对应于最优资本存量和最优消费)相比会出现“过度储蓄”(即“过度积累”)的情况,而一个高于黄金率的储蓄率被证明是动态无效的。
当gold s s <时,只有在给定在当前消费与未来消费之间的权衡参数的条件下,才能判断增加储蓄率的合理性。
图示:s 的变动对稳态和动态的人均消费的影响c c gold 那么,储蓄率是如何决定的?必须引入消费者(家庭)行为来分析跨期预算约束条件下的消费和储蓄选择,即储蓄率的“内生化”。
二、模型假定1.完全竞争市场结构2.长生不老的不断扩展的家庭(有限寿命的个人和基于利他主义的代际转让)3.家庭和个人完全同质4.忽略资本的折旧5.暂不考虑政府行为在简单经济中,家庭与厂商之间的关系:三、厂商行为沿用新古典生产函数),(AL K F Y = 根据欧拉定理,AL AL Y K K Y Y )(∂∂+∂∂=其中,资本的边际产品为:r k f KY==∂∂)('(真实利率) 有效劳动的边际产品为:w k kf k f AL Y=-=∂∂)(')()((工资率)四、家庭行为1.一些假定和符号总人口为L ,以速率n 增长,e L t L nt )0()(=; 家庭的个数为H ,每个家庭有L/H 个人; 每个家庭成员在每一时点上提供1单位劳动;资本最初存量为K(0),每个家庭初始资本存量为K(0)/H 。
2. 家庭效用函数和即期效用函数定义家庭效用函数(也称作“幸福函数”)为:dt HL t C u dt H t L t C u U o t tn o t te e )0()]([)()]([)(⎰⎰∞=--∞=-==ρρ 其中,C(t)为每个家庭成员的消费,)(∙u 为即期效用函数,ρ为贴现率(ρ越大表明与现期消费相比远期消费的价值就越低)。
2-拉姆齐模型

七、修正的黄金资本存量
定理1:在拉姆齐模型中,人均资本存量k收敛于k*,且低于索洛模
型中的黄金资本存量k*, 因此k*被称作“修正的黄金资本存量”。
定理2:拉姆齐模型表明在索洛模型中高于黄金资本存量的平衡增
长路径是不可能的。
【证明】通过相位图可以证明当k(0)>k(gold)时,追求跨期最优化的
家庭将降低储蓄,使k收敛于k*,且k*<k(gold)。
定理3:经济不收敛于产生最大c(即c(gold))的平衡增长路径,而
是收敛于一个较低的水平c*。
【证明】c*<c(gold)的前提是,它表明贴现率较高,家庭和个人更
重视现期消费,而不是未来消费。
图示(在索洛模型中当s低于s(gold)时提高s的影响):
c(gold)
c*
c0
c0
t
t
s较大的提高
s较小的提高
思考:在动态转移过程中ρ、ln(Y/L)、c、k、s的轨迹是什么? 此外,贴现率下降将可以使人均消费达到黄金律水平的平衡增长。
九、基本结论
1.拉姆齐模型没有改变索洛模型关于经济增长平衡路径的基本结 论。
2.索洛模型可以被看作是拉姆齐模型的一个特例,它必须对应于 后者特殊的参数和稳态。
3.拉姆齐模型的特点在于从家庭和个人的跨期消费行为的微观基 础出发决定稳态的消费(储蓄),从厂商的微观基础出发决定稳态的资 本存量,因此c和k是同时决定的。在这样的过程中,储蓄的决定被内生 化了。
六、平衡增长路径
均衡点E(c*,k*)的解为: 因此模型中的各个变量的长期变动如下:
变量
含义
平衡增长速度
K
资本存量
n+g
绝 对
简答什么是拉姆齐模型

简答什么是拉姆齐模型
简单来说,拉姆齐模型与索罗模型不同,拉姆齐模型是研究在任何情况下,国民产出有多少应该分配给消费从而产生当前的效用,又有多少国民产出应该分配给储蓄并进而投资以提高未来的产出和消费,从而产生未来的效用。
与新古典增长模型或者说索罗模型不同,因为在新古典增长模型中,储蓄率是被假定为一个外生参数,并没有说明其是如何决定的。
对此,拉姆齐模型引入了消费者(家庭)行为来分析跨期预算约束条件下的消费和储蓄选择,从而将储蓄这个参数内生化了。
拉姆齐模型的基本假定主要是:
1)市场是完全竞争的;
2)家庭是不断延续的;
3)家庭和个人是完全同质的;
4)忽略了资本折旧;
5)不考虑政府行为。
拉姆齐模型研究的结论可归结为以下几点:
第一,拉姆齐模型并没有改变新古典增长模型关于经济平衡增长路径的基本结论。
第二,在对应于拉姆齐模型中的参数稳态下,新古典增长模型可以看作是拉姆齐模型的一个特例。
第三,拉姆齐模型的特点在于从家庭和个人的跨期消费行为
的微观基础出发决定稳态的消费和储蓄,从厂商的微观基础出发决定稳态的资本存量,所以消费和储蓄是同时决定的。
在这个过程中,储蓄的决定被内生化了。
第四,拉姆齐模型避免了新古典增长模型中的无效的过度资本积累。
第五,拉姆齐模型中的任意初始状态不一定会收敛到稳态,会存在发散的情况,而新古典增长模型则不会。
论述题

1.论述消费者行为分析的对偶原理对偶性原理:对偶性是指一些成对问题或概念,是目标和约束条件的表达正好相反。
需求分析中还存在下列四个重要的恒等关系,被称之为对偶性。
若效用函数u(.)是严格单调和连续的,且消费者效用最大和支出最小问题均有解,则:1.x(p,w)≡h[p,v(p,w)]2.h(p,u) ≡x[p,e(p,u)]3.e[p,v(p,w)] ≡w4.v[p,e(p,u)] ≡u上述四个关系式中,h(p,u) ≡x[p,e(p,u)]是最重要的。
因为他将客观车的瓦尔拉斯需求函数与不可观测的希克斯需求函数联系起来。
其意义为希克斯需求函数与瓦尔拉斯需求函数指的是同一件事。
这样需求即可用效用最大化解表示,也可用支出最小化解表示。
2.试论述宏观经济学一般研究规范与微观经济学相对而言,是一种现代经济学分析方法。
它以国民经济学作为考察对象,研究经济生活中有关总量的决定与变动,解释失业、通货膨胀、经济增长与波动、国际收支与汇率的决定与变动等经济中的宏观整体问题,所以称之为总量经济学,宏观经济学的中心和基础是总供给——总需求模型。
具体来说,宏观经济学主要包括总需求理论、总供给理论、失业和通货膨胀理论、经济周期与经济增长理论、开放经济理论、宏观经济政策等内容。
经济学在研究过程中会有一定的规范过程和方法:(1)宏观经济学的研究过程:代表性微观经济主体的确定,微观经济主体行为范式研究,微观经济变量向宏观经济变量的过渡,宏观经济变量之间的关系分析,宏观经济模型的构建,经验分析(2)宏观经济学的研究方法A.实证研究与规范研究方法实证方法是排斥价值判断,只研究经济变量之间的关系,探讨经济运行的内在规律,以分析和预测经济行为后果的。
它要解决“是什么”的问题。
规范方法则以一定的价值判断为基础,回答“应该是什么”的问题。
规范分析是实证分析的基础,离开了规范分析,实证分析就没有意义了。
B.均衡分析与非均衡分析方法均衡分析方法:均衡分析就是要揭示经济处于均衡状态所需要的前提条件,找出经济变量变动的动向,从而说明如何满足这些条件。
01--高级宏观:拉姆齐模型

复旦大学博士生宏观经济学讲义
第一章 拉姆齐模型
效劳动单位人均消费,ke (t)
=
k (t ) A(t)
为每有效劳动单位人均资本。资本积累的方程
可变为:
.
k e (t) = f (ke (t)) − ce (t) − (n + δ + g)ke (t) 代表性行为人的最大化问题
∫ max ∞ e− tU (c(t))dt
.
a t = wt + rat − ct − nat 5
2-3
2.非蓬齐对策条件(意义)
lim t − (rv−n)dv [a e ∫ t 0
]
≥
0
t→∞
2-4
这意味着,在长期,一个家庭的平均债务的增长速度不能大于 rt − n ,因此总债
∫ 务的增长速度不能超过 rt 。我们定义 rt = 1 t rvdv ,因此 2-4 又可被写为
ke**
ke
第二节 市场分散解
注意,第一节和第二节在使用符号上的区别
第一节
第二节
有效变量 技术增长率
ce (t) , ke (t) g
^
^
c(t) , k(t)
γ
时间
c(t) , k(t)
ct , kt
请原谅,并避免混淆,因为两节的制作时间不同。
1.效用函数
拉姆齐问题解决的是一个国家应该储蓄多少,即资源的跨期最佳分配。假定
那么 e−ρtU (c(t)) = e−ρt
c(t )1−θ 1−θ
= e−ρt
(ce (t)egt )1−θ 1−θ
= e−(ρ −(1−θ )g )tU (ce (t))
(1.4)
拉姆齐模型

模型说明
索洛模型主要从生产角度研究平衡增长路径, 空间是一维的;
R-C-K模型从生产者、家庭两个角度研究 增长路径,空间是二维的。
5
循环图
家庭
租让资本,获取利息 提供劳动,赚取工资 购买产品,进行消费
相互拥有
厂商
销售产品,获得利润
雇佣劳动,支付工资
租用资本,支付利息
6
模型所描述的经济体: 厂商租用资本雇佣劳动用以生产并销售产品, 而数量固定的长生不老家庭供给劳动、持有 资本、消费并储蓄。这回避了所有的市场不 完美性,以及由异质家庭和代际联系造成的 所有问题,因此提供了一个理论上的参照系。
16
如果趋近于零,则效用几乎是C的线性函数:
经济含义:因此家庭也就愿意消费的大的波动
以利用贴现率与储蓄报酬率之间小的差异。
具体而言,可以证明任意两时点的消费之间
的替代弹性为1 / 。
17
注释(1):为什么效用函数要除以 1
18
注释(2): 1的特殊情况
根据罗必塔 法则
19
根据:(ax)' ax ln a
的生产函数Y=F(K,AL) ;
✓ 要素市场、产品市场都是完全竞争的; ✓ A外生以速率g增长; ✓ 厂商追求最大化利润。
9
一、模型的基本假定
家庭
✓ 大量相同家庭(数量H),每一家庭规模 以速率n增长(长生不老且没有新家庭加 入)。
✓ 家庭每一成员在每一时点上供给1单位劳动, 将所拥有资本均租给厂商,家庭拥有企业, 因此,企业产生的利润归于家庭。
是时间偏好率,表示获得效用越晚价值 越低,越大,则相对于现期消费,家庭对
未来的消费估价越小
12
关于家庭效用函数的说明:
拉姆齐模型(第一部分)

储蓄的价值 从t期到s期 如何变化
t期的储蓄 (它可能为负)
51
52
非蓬齐博弈:将任意时刻s的财富 贴现到当前,应为非负。
limeR(s) K(s) 0
s
H
K kAL kA(0)L(0)e(ng)t
lim lim eR(s) K(s) 0
eR(s)e(ng)tk(s) 0
s
H
s
53
储蓄
每个家庭在 0 时期有
L0 / H 个成员
每个家庭在 0 时期拥有
K 0 / H 的资本
作出储蓄—消费决策
当期收入
消费
每将 人全
提部
产品市场
(完全竞争)
购提 买供 产产 品品
供 资 要素市场
1 单
本 (完全竞争) 租
位给
劳厂 动商
付出工资,一个家庭获得:
Lt At f kt kt f kt
H
付资本报酬,一个家庭获得:
20
关于家庭效用函数的说明:
2.家庭无限期的效用
21
22
关于家庭效用函数的说明:
3.家庭无限期效用函数的现值
23
u(Ct )
24
(1)连续的复利计算和贴现 计算
由于时间 t被假定为连续的,利息 率也被假定
按照复利连续计算
25
lim (1 / n)nt
n
lim[11/(n / )](n/ )t et n
新古典生产函数:Y F(K, AL) 根据欧拉定理:Y Y K Y AL
K (AL)
31
二、模型中决策主体的行为(厂商)
资本的边际产品:FK, AL f (k)
K
有效劳动的边际产品:f k kf k
拉姆齐模型
无限期界模型(拉姆齐模型)一、问题的提出在索洛模型中,储蓄率s 被假定为外生参数,储蓄率的变动将影响稳态的人均消费和动态的人均消费水平。
当gold s s >时,与最优储蓄(相对应于最优资本存量和最优消费)相比会出现“过度储蓄”(即“过度积累”)的情况,而一个高于黄金率的储蓄率被证明是动态无效的。
当gold s s <时,只有在给定在当前消费与未来消费之间的权衡参数的条件下,才能判断增加储蓄率的合理性。
图示:s 的变动对稳态和动态的人均消费的影响c c gold 那么,储蓄率是如何决定的?必须引入消费者(家庭)行为来分析跨期预算约束条件下的消费和储蓄选择,即储蓄率的“内生化”。
二、模型假定1.完全竞争市场结构2.长生不老的不断扩展的家庭(有限寿命的个人和基于利他主义的代际转让)3.家庭和个人完全同质4.忽略资本的折旧5.暂不考虑政府行为在简单经济中,家庭与厂商之间的关系:三、厂商行为沿用新古典生产函数),(AL K F Y = 根据欧拉定理,AL AL Y K K Y Y )(∂∂+∂∂=其中,资本的边际产品为:r k f KY==∂∂)('(真实利率) 有效劳动的边际产品为:w k kf k f AL Y=-=∂∂)(')()((工资率)四、家庭行为1.一些假定和符号总人口为L ,以速率n 增长,e L t L nt )0()(=; 家庭的个数为H ,每个家庭有L/H 个人; 每个家庭成员在每一时点上提供1单位劳动;资本最初存量为K(0),每个家庭初始资本存量为K(0)/H 。
2. 家庭效用函数和即期效用函数定义家庭效用函数(也称作“幸福函数”)为:dt HL t C u dt H t L t C u U o t tn o t te e )0()]([)()]([)(⎰⎰∞=--∞=-==ρρ 其中,C(t)为每个家庭成员的消费,)(•u 为即期效用函数,ρ为贴现率(ρ越大表明与现期消费相比远期消费的价值就越低)。
索罗和拉姆齐模型34页PPT

2、要冒一次险!整个生命就是一场冒险。走得最远的人,常是愿意 去做,并愿意去冒险的人。“稳妥”之船,从未能从岸边走远。-戴尔.卡耐基。
梦 境
3、人生就像一杯没有加糖的咖啡,喝起来是苦涩的,回味起来却有 久久不会退去的余香。
索罗和拉姆齐模型4、守业的最好办法就是不断的发展。 5、当爱不能完美,我宁愿选择无悔,不管来生多么美丽,我不愿失 去今生对你的记忆,我不求天长地久的美景,我只要生生世世的轮 回里有你。
பைடு நூலகம் 谢谢
11、越是没有本领的就越加自命不凡。——邓拓 12、越是无能的人,越喜欢挑剔别人的错儿。——爱尔兰 13、知人者智,自知者明。胜人者有力,自胜者强。——老子 14、意志坚强的人能把世界放在手中像泥块一样任意揉捏。——歌德 15、最具挑战性的挑战莫过于提升自我。——迈克尔·F·斯特利
用索洛模型来解释技术进步对经济增长的作用

用索洛模型来解释技术进步对经济增长的作用我们假设生产函数为:Y=F(K, L)(1)其中K表示资本总量,L表示劳动总量,Y表示产出总量。
随着技术的进步,劳动效率会提高。
我们用L×E衡量效率工人数,E代表每个工人的效率,这样生产函数就改写成:Y=F(K, L×E) (2)我们让k=K/( L×E)代表每个效率工人的资本,y=Y/ (L×E)代表每个效率工人的产出,这样(2)式就可以变换为:y=f(k),资本存量的变换△k= sf(k)-(δ+n+g)k,其中s为储蓄率,δ为折旧率,n为人口增长率,g为劳动效率的增长率也就技术进步的比率,sf(k)为投资,(δ+n+g)k表示收支相抵的投资。
收支相抵的投资包括三部分:为使人均资本不变,δk是替代折旧的资本所需要的,nk是为新工人提供资本所需要的,gk是为技术进步所创造的新的“效率工人”提供资本所需要的。
当sf(k)等于(δ+n+g)k时,经济是处于稳定状态的。
即稳定状态时效率工人的人均资本是不变的。
由于y=f(k),所以效率工人的人均产出也是不变的。
由于每个实际工人的效率是按g的比率增长,因此人均产出Y/L=y×E也是按g比率增长。
总产出Y=y×(E×L)是按n+g的比率增长。
索罗技术进步模型可以解释经济的长期增长。
如图,经济一旦达到稳定状态,高储蓄率已经不能引起经济的增长,人均产出的增长只取决于技术进步的比率。
可见,技术进步,也就是说科技成果转化是促进经济增长的最重要因素。
关于高级宏观经济学中的经济增长理论•经济增长理论可谓高级宏观经济学的核心。
罗默的《高级宏观经济学》索洛增长模型是几乎所有增长问题研究的出发点分,甚至于那些从根本上不同于索洛模型的理论通常也需在与索洛模型的比较中才能得到最好的理解。
索洛模型把技术进步看作是给定的,它探讨了产出在消费和投资之间的分割对资本积累和增长的影响。
索罗模型和拉姆齐模型的比较

Carl-Johan Dalgaard Institute of Economics University of Copenhagen
March 19, 2003
Abstract
This note shows formally that, under certain circumstances, the dynamic system of the Ramsey-Cass-Koopmans model can be expressed as the mirror image of the laws of motion guiding consumption and capital in the Solow model.
c
The only restriction we still haven’t used is αθ > 1. This condition is nessesary to insure that in fact the utility maximzation problem of the representative household is well defined. We require
ρ = αθ (n + δ + x) − (δ + θx)
C. αθ > 1. D. s ≡ 1/θ.
In order to see that (A)-(D) does the job, start by noting that the CD technology implies:
f 0 (k) = αkα−1 f (k) = kα−1
索罗模型的问题解答

*
黄金率状态水平下的人均资本量是通过最大化
c( s ) f (k ( s )) s f (k ( s )) f (k ( s )) (n g ) k ( s )
来确定的。通过一阶求导 c' ( s ) 0 可得, )) (n g )
在索罗模型中,saving rate 是外生给定的,并不能变化,所以不可能设定为 1. 对应于模型 初始给定的 saving rate, 模型对应地存在一个黄金率状态水平下的 k 。 拉姆齐模型是索罗 模型的延伸,设定储蓄率为内生变量,你可以进一步看看,从而加深对索罗模型的理解。
索罗模型的稳态应该是通过令 k sf ( k ) ( n g ) k 等于 0 来确定稳态下的人均资本水 平, k ,而不需要求导。且 k 满足 sf ( k ) ( n g ) k ,资本的边际产量为 f ' ( k ) .如
* * * * *
果有具体的生产函数,如科布-道格拉斯生产函数,可以具体求出 k 。
宏观考试要点(研二)

宏观经济学复习资料第一章索洛模型索洛模型基本内容、政策含义、主要说明什么问题、核心公式的理解,资本水平效应、资本增长效应、如何理解索洛模型中的A索洛模型包含四个变量:产量(Y),资本K,劳动L和知识或劳动的有效性A。
在任一时间,经济中有一定量的资本、劳动和知识,而这些被结合起来生产产品。
生产函数的形式为Y(t)=F(K(t),A(t)L(t)),其中t表示时间。
时间不直接进入生产函数,只是通过K,L,A进入。
这就是说,仅在生产投入变化时,产量才随时间变化。
具体而言,从一定的资本和劳动量中得到的产品量随时间增加—有技术进步—的唯一前提是知识量增加。
A和L以相乘形式影响Y,AL被称为有效劳动,而以这种形式引入的技术进步被称为劳动增进型或哈罗德中性的。
模型的基本假定:1)规模报酬不变。
即对于c≥0,有F(cK,cAL)=cF(K,AL),令c=1/AL,规模报酬不变的假定使我们可以使用生产函数的密集形式:F(K/AL,1)=F(K,AL)/AL,定义k=K/AL,y=Y/AL,f(k)=F(k,1),y=f(k),,y为单位有效劳动的平均产量,k为单位有效劳动的平均资本量。
f’(k)>0,f’(k)<0,边际报酬递减。
2)关于投入品的假设L(t)=nL(t),A(t)=gA(t),n为人口增长率,g为技术进步率,均为外生参数,表示不变增长速度。
资本的增长率K(t)=sY(t)- δK(t),其中s为储蓄率,δ为资本折旧率,均为外生变量。
索洛模型的核心公式:k(t)=sf(k(t))-(n+g+δ)k(t)它表明每单位有效劳动的平均资本量的变动率是两项之差。
第一项sf(k)是每单位有效劳动的平均实际投资:每单位有效劳动的平均产量为f(k),该产量中用于投资的比例为s。
第二项(n+g+δ)k是持平投资,即使得k保持在现有水平上所必须的投资量。
为防止k下降,必须进行一些投资。
其原因有二。
第一,现有资本有折旧,这一部分资本必须予以补足以防止资本存量下降,这就是δk项。
西北大学研究生宏观经济学 第一章 索罗增长模型

nt
• (3)资本的增长
•
新增资本 减去 折旧
K (t ) = [dK (t ) / dt] = sY (t ) − δK (t )
索罗模型是一个高度简化的模型: 一种产品 没有政府 没有就业波动 三种投入品的生产函数 储蓄率、折旧率、人口增长率、技术进步率不 变 • 忽视了现实世界的许多明显特征,其中部分特 征对于增长是重要的。 • • • • • •
• 二、关于生产函数的假设 • (1)规模报酬不变: • F(cK,cAL)=cF(K,AL),对于c≥0 • 含义: • (整体)经济足够大,专业化收益被穷尽;
• • • 其他投入品(如自然资源)相对不重要。 在自然资源有限的情况下,规模报酬递减。 马尔萨斯 罗马俱乐部
• • • • • • • • • •
• 生活水平在不同时间的巨大差异 • 中国 :30年的变化 • 城市:变大、变高、变多、变好 • 农村:楼上楼下,电灯电话
• 二、增长问题的重要性 • 生活水平差异——福利差异:营养、居住环 境、医疗、预期寿命 • 长期经济增长速度的差异对福利的影响更大: • 一般的衰退 真实收入 几个百分点 • 长期经济增长率降低一个百分点? • 1.09^30 = 13.267678 • 1.08^30 = 10.062657 • 1.07^30 = 7.612255 •
第一章 索罗增长模型
第一节 经济增长理论
• 一、关于增长的现象 • 世界各地巨大的生活水平差异 • (2009年人均GDP) 001 卢 森 堡 105350 002 挪 威 79089 006 美 国 46436 012 澳大利亚 42279 013 法 国 41051 014 德 国 40873 015 日 本 39727 016 加拿大 39599
经济增长模型

∆A = 0 ⇒ ∆A > 0
生的技术进步,即从 A
A。
令
g
=
∆A A
为技术进步引起的增长率,那么
g
产生的影响是:
1)使得 y = f (k) 以 g 的增长率增长(注意 A 的影响是对整个生产函数的影响)
2)使得人均储蓄 sy = sf (k) 以 g 的增长率增长 注意 P53 图 3-7,技术进步作为外生变量导致生产函数曲线整体上移。 此时在稳态, y 和 k 不是不变,而是均以 g 的速率增长——人均指标。而总
y
kA
为
∆y y
=θ
•
∆k k
+
(1−θ )
∆A(对应 A
P52
倒数第
6
行,参见专栏
3-3)。将
∆A A
=
∆k
k
代入该式,我们得到:
g = ∆y = θ • ∆k + (1 −θ ) ∆A = θ • ∆k + (1−θ ) ∆k = ∆k
y
k
A
k
kk
这说明,产出与资本以同样速率增长,人均产出的增长率 ∆y y 与人均资本的
sy* = (n + d )k * 用图表示为:
4
关于稳态的几个结论:因为在稳态有 ∆y = 0 ,表示人均 GDP 不增长,那么此 时总的 GDP 增长率( ∆Y Y )=人口增长率 n。即在稳态的增长率与储蓄率 s 无关 (仅仅与 n 有关)。 ※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※
3.戴蒙德模型 拉姆齐-卡斯-库普曼斯模型仍然存在缺陷,即其中的家庭都是神仙,长生 不老,显然与事实不符。戴蒙德修正了这一不足,引入新老家庭的更替,从而将 现实的人口生死更替引入增长模型,使增长模型与现实更为相符。在戴蒙德模型 下,平衡增长路径的资本存量又可以高于黄金律资本存量,维护了索洛模型的结 论。 4.新增长理论 虽然以上三类模型通过不断修正与现实越来越接近,但还是忽视了一个十分 核心的问题。这些模型里的核心变量——技术一直被假设是外生的,技术进步到 底如何发生、与增长是否有内在联系等重要问题都被回避。新增长理论正是针对 这一缺陷,将技术进步视为内生,研究经济增长,具体包括 R&D 模型和人力资 本模型,从而使得经济增长理论研究与现实世界之间的距离进一步得到了缩短。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.6.5 收敛速度 下图是假设生产函数是科布-道格拉斯生产函数,对不同的资本份额的 两个值0.3和0.75做出的收敛速度的数值估计,从图中可以看出,资本份 额小的其收敛速度上的变化更显著。
考虑一个任意规模譬如说有效劳动投入的企业,则该企业的利润可被 写成:
当r和w为给定的竞争性企业,满足 ,利润最大化。 在完全竞争市场上,利润为零。则工资w应满足:
2.3 均衡
在封闭经济模型中,a=k,r和w给定,则我们得到:
其中, 有效单位人均消费增长率为:
从ˆk角度来看横截性条件为:
2.5 稳态
1.2 索洛和斯旺的新古典模型
1.2.1 新古典生产函数 忽略了技术进步,Y=F(K,L) (1.4) 满足以下条件的生产函数是新古典的:第一,对所有的K>0,L>0,
第二,F呈现出不变的规模报酬:F(λK, λL, λT ) = λ · F(K, L, T ) 第三,
1.2.2 资本存量的基本动态方程 资本存量的持续变化有(1.2)式给出:
CH 1 有外生储蓄率的增长模型(索 洛—斯旺模型)
-------M201474028 张 悦
1.1基本结构
1、生产函数:Y(t)=F[K(t),L(t),t] (1.1)
假设:a. 经济是封闭的
b. s是外生给定的,是一个常数 c. >0,在一个时点上物资资本存量的净增加等于总投资减去折旧 K(t)=I(t) −δK(t)=s· F[K(t),L(t),T(t)]−δK(t)(1.2) d. 人口以不变、外生的速率增长, t时的人口和劳动力等于 ,
式是完全替代的,因此对它们必须支付相同的真实收益率r(t)。我们用 a(t)来表示家庭的人均净资产,w(t)为付给每单位劳动服务的工资率。 对家庭而言的流量预算约束是:
为了排除“拆东墙补西墙”似的连环信的可能性,我们假设信贷市场
对借款数额加了一重约束。适当的限制应该是资产的现值渐近于非负,
即:
2.1.2 一阶条件 汉密尔顿方程: 变量v是收入的现值影子价格,它表示t时所获得的累积收入以0时效用 单位衡量的价值。 U的最大值的一阶条件是:
2.2企业
假定生产函数为: ,,其中, 以不变的速度x增长。 对每单位有效劳动的数量,则生产函数写成: 要素的边际产品分别由下式给出: ,技术水平T(t)
企业从拥有资本的家庭那里租用资本服务,R为一单位资本服务的租金 价格,再假定资本存量以不变速度δ ≥0折旧。那么拥有一单位资本的一 个家庭的净收益率为R-δ。由于家庭也可以选择将一单位资本贷给其他 家庭,则r=R-δ。 企高 值表明家庭有一种很强的持平消费的偏好, 因此,他们将努力把消费从未来转移到现在进行。因此,此时的稳定臂 将靠近 (如下图所示)。相应的低投资意味着转移要花很长时间。
2.6.3 储蓄率的行为
在最优化消费者的拉姆齐模型中,s可以遵循一条复杂的路径,随着经 济的发展并趋于稳态。 由于储蓄率涉及来自替代效应和收入效应,那么储蓄率的行为是模糊 不确定的。首先,随着 上升, 的下降降低了储蓄的收益率r。其 远远低于该经济的长期或 上升,当前收入与持
1.2.3 稳态
稳态:各种数量都以不变速率增长的状况。
在新古典模型中,人均数量k,y,c在稳态中都不增长。人均数量的固定
意味着变量K,L,C的水平在稳态中以人口增长率n的速率增长。
1.2.4 资本积累的黄金律和动态无效率
黄金律水平时,k满足:
1.2.5 转移动态
1.2.6 政策实验 假设经济最初处在一个有人均资本 策提高储蓄率:
横截性条件为: 随时间选择消费的基本条件:
边际效应弹性值 有时被称作跨期替代弹性的倒数,为了 使这一弹性渐近于常数,假定如下函数形式:
则: 横截性条件:
时间积分
故横截性条件变为:
消费函数:考虑一个0到t之间的平均利润r(t):
此时现值因子等于: 一个对任何时间T>=0都成立的跨期预算约束:
当T趋于无穷大时,上式最左边消息,跨期预算约束为:
1.3 内生增长模型
1.3.1 AK模型 Y=AK (A是一个反应技术水平的正常数) 因此,
1.3.2 具有转移动态的内生增长
1.3.3 不变替代弹性生产函数
1.3.4 里昂惕夫生产函数与哈罗德—多马争论
1.3.5 有贫困陷阱的增长模型
CH 2 有消费者最优化的增长模型(拉姆 齐模型)
令 为 的稳态增长率, 为 的稳态增长率,在稳态中:
把这一条件对时间求导,则我们发现: 在稳态中一定成立。有横截性条件可知,大括号内的表达式为正,则 和 一定同号。由分析可知,两者均为零时才成立。 在稳态时,由 可以推出:
但是,在消费最大化时,即处于黄金率水平是,满足:
2.6 转移动态
2.6.1 相位图 拉姆齐模型相位图如下所示:
2.1 家庭
2.1.1 模型的建立 我们考虑的是一个长生不老的不断扩展的家庭。如果我们把0时的成人 数目标准化为1单位,则t时的家庭规模—它对应于成人人口数为: 每个家庭希望最大化总效用:
假设:1、 2、 3、
, ,意味则着效应获得越晚其价值越低,在这里假设
家庭拥有以对资本的所有要求权或贷款为形式的资产,那么这两种形
次,一个贫穷经济中的每有效工人的收入 持久收入。当
很低的时候储蓄率也很低,随着
久收入之间的差距缩小,因此相对于收入而言消费趋于下降而储蓄率上 升。
科布-道格拉斯情形中的稳态储蓄率为:
由横截性条件可知, ,也就是说稳态总储蓄率小于总资本份额。 附录证明储蓄率的转移动态模式要视 是大于、小于还是等于 。 下图是科布-道格拉斯情形中储蓄率的行为:
消费函数:
代入到上面的跨期预算约束中,得到0时的消费函数为: μ(0)是财富的消费倾向,由下式决定:
对于给定的财富来说,平均利率的增加对边际消费倾向有双重影响。 第一,更高的利率增加了当前消费相对于未来消费的成本,跨期替代效 应会刺激人们把消费从现期转移到未来。第二,更高的利率还有一个趋 于提高在所有时期消费的收入效应。
的稳定位置,政府导入某种政
1.2.8 绝对和条件收敛
绝对收敛:在人均量上穷国趋于比富国增长更快的假说——不以经济 的任何其他特征为条件。 条件收敛:一个经济离其自身的稳态值越远,增长就越快。
1.2.10 技术进步 1、希克斯称一个技术创新是中性的(希克斯中性),如果对于一给定 的资本/劳动比率其边际产品的比率保持不变,因此希克斯中性生产函 数被写成:
