第九章_空间分析的应用
第9章 状态空间分析法

根据A和b的上述特征,一般只要对微分方程式或传递
函数的观察,就能直接写出矩阵A和b及对应的动态方程。
第二节 传递函数与动态方程的关系
能控标准形状态图
第二节 传递函数与动态方程的关系
例9-3 已知一系统的传递函数为
试写出能控标准形的状态空间表达式。 解:根据矩阵A和b的特征,直接写出系统能控标准形的 状态空间表达式为:
第二节 传递函数与动态方程的关系
3、对角标准型实现
当系统的传递函数只含有相异的实极点时,还可化为 对角标准型实现。 设系统的传递函数为:
令 则上式变为
第二节 传递函数与动态方程的关系
式中: 则 令
Ci lims i W s
s i
则得
i
i
i
对上式取拉氏变换
第二节 传递函数与动态方程的关系
i
或写作
第二节 传递函数与动态方程的关系
上述状态方程的状态变量描述有如下特点: (1)矩阵A对角线上的元素为传递函数的极点,其余元素
全为零,各状态变量间没有耦合,彼此是独立的。
(2)矩阵b是一列向量,其元素均为1;矩阵C为一行向量, 它的元素为W(s)极点的留数。
第二节 传递函数与动态方程的关系
其中
D为m×r型矩阵
m×r
Wij s 为第i个输出与第j个输入间的传递函数。
第二节 传递函数与动态方程的关系
求系统的传递函数。 例9-2 已知系统的动态方程式如下,
解:
-
=
-
第二节 传递函数与动态方程的关系
二、由传递函数列写动态方程 设线性定常系统微分方程的一般形式为:
y为系统的输出量,u为系统的输入量,初始条件为零, 对上式取拉氏变换,得系统的传递函数为: -
《自动控制原理》线性定常连续系统状态方程的解

2
k!
= P −1IP + P −1 APt + 1 P −1 A2 Pt 2 + + 1 P −1 Ak Pt k +
2
k!
= P −1 (I + At + 1 A2t 2 + + 1 Ak t k + )P = P −1e At P
2
k!
因而式(9-39)成立。
性质10: 两种常见的状态转移矩阵。设 A = diag[1, 2 ,,n ],
2. 拉普拉斯变换法。将式(9-22)取拉氏变换有
sX (s) = AX (s) + x(0)
则
(sI − A) X (s) = x(0)
X (s) = (sI − A)−1 x(0)
(9-27)
进行拉氏反变换有
x(t) = −1[(sI − A)−1]x(0)
(9-28)
与(9-25)相比有
e At = −1[(sI − A)−1 ]
进行拉氏反变换有 x(t) = −1(sI − A)−1 x(0) + −1[(sI − A)−1 BU (s)]
由拉氏变换卷积定理
−1[F1(s)F2 (s)] =
t
0 f1 (t − ) f2 ( )d
=
t
0 f1 ( ) f2 (t − )d
在此将(sI − A)−1 视为F1 (s),将BU (s) 视为 F2 (s) ,则有
x(t) = eA(t) x(0) + t eA(t− )Bu( )d 0 t = (t)x(0) + 0 (t − )Bu( )d
结果与式(9-43)相同。上式又可表示为
第九章 三维分析

第九章三维分析相当长的一段时间里,由于GIS理论方法及计算机软硬件技术所限,GIS以描述二维空间为主,同时发展了较为成熟的基于二维空间信息的分析方法。
但是将三维事物以二维的方式来表示,具有很大的局限性。
在以二维方式描述一些三维的自然现象时,不能精确地反映、分析和显示有关信息,致使大量的三维甚至多维空间信息无法加以充分利用。
随着GIS技术以及计算机软硬件技术的进一步发展,三维空间分析技术逐步走向成熟。
三维空间分析相比二维分析,更注重对第三维信息的分析。
其中第三维信息不只是地形高程信息,已经逐步扩展到其它更多研究领域,如降雨量、气温等。
ArcGIS具有一个能为三维可视化、三维分析以及表面生成提供高级分析功能的扩展模块3D Analyst,可以用它来创建动态三维模型和交互式地图,从而更好地实现地理数据的可视化和分析处理。
利用三维分析扩展模块可以进行三维视线分析和创建表面模型(如TIN)。
任何ArcGIS 的标准数据格式,不论二维数据还是三维数据都可通过属性值以三维形式来显示。
例如,可以把平面二维图形突出显示成三维结构、线生成墙、点生成线。
因此,不用创建新的数据就可以建立高度交互性和可操作性的场景。
如果是具有三维坐标的数据,利用该模块可以把数据准确地放置在三维空间中。
ArcScene是ArcGIS三维分析模块3D Analyst所提供的一个三维场景工具,它可以更加高效地管理三维GIS数据、进行三维分析、创建三维要素以及建立具有三维场景属性的图层。
此外,还可以利用ArcGlobe模型从全球的角度显示数据,无缝、快速地得到无限量的虚拟地理信息。
ArcGlobe能够智能化地处理栅格、矢量和地形数据集,从区域尺度到全球尺度来显示数据,超越了传统的二维制图。
利用交互式制图工具,可以在任何比例尺下进行数据筛选、查询和分析,或者把比例尺放大到合适的程度来显示感兴趣区域的高分辨率空间数据,例如航空相片的细节。
本章主要介绍如何利用ArcGIS三维分析模块进行创建表面、进行各种表面分析及在ArcScene中数据的三维可视化。
第九章_状态空间分析方法

第九章状态空间分析方法第9章状态空间分析方法基本要求9-1 状态空间方法基础9-2 线性系统的可控性和可观性9-3 状态反馈和状态观测器9-4 有界输入、有界输出的稳定性9-5 李雅普诺夫第二方法引言:前面几章所学的内容称为经典控制理论;下面要学的内容称为现代控制理论。
两者作一简单比较。
经典控制理论(50年代前)现代控制理论(50年代后)研究对象单输入单输出的线性定常系统可以比较复杂数学模型传递函数(输入、输出描述)状态方程(可描述内部行为)数学基础运算微积、复变函数线性代数、矩阵理论设计方法的特点非唯一性、试凑成份多, 经验起很大作用。
主要在复数设计的解析性,与计算机结合,主要在时间域进行。
基本要求①掌握由系统输入—输出的微分方程式、系统动态结构图、及简单物理模型图建立系统状态空间模型的方法。
②熟练掌握矩阵指数的计算方法,熟练掌握由时域和复数域求解状态方程的方法。
熟练掌握由动态方程计算传递函数的公式。
③正确理解可逆线性变换, 熟练掌握可逆线性变换前、后动态方程各矩阵的关系。
④正确理解可控性和可观测性的概念,熟练掌握和运用可控性判据和可观性判据。
⑤熟练掌握可逆线性变换矩阵的构成方法, 能将可控系统化为可控标准形。
能将不可控系统进行可控性分解。
⑥正确理解对偶原理, 会将原系统的有关可观测性的问题转化为对偶系统的可控性问题来研究。
⑦正确理解单变量系统零、极点对消与动态方程可控、可观测的关系。
熟练掌握传递函数的可控性标准形实现、可观性标准形实现的构成方法。
⑧正确理解状态反馈对可控性,可观性的影响, 正确理解状态反馈可任意配置闭环极点的充要条件。
⑨熟练掌握全维状态观测器的公式和设计方法, 熟练掌握由观测器得到的状态估计值代替状态值构成的状态反馈系统, 可进行闭环极点配置和观测器极点配置。
⑩正确理解系统齐次方程渐近稳定和系统BIBO稳定的概念, 熟练掌握判别渐近稳定的方法和判别系统BIBO稳定的方法。
11正确理解李雅普诺夫方程正定对称解存在的条件和解法, 能通过解李雅普诺夫方程进行稳定性分析。
《自动控制原理》第九章 线性系统的状态空间分析与综合

第九章 线性系统的状态空间分析与综合在第一章至第七章中,我们曾详细讲解了经典线性系统理论以及用其设计控制系统的方法。
可以看到,经典线性理论的数学基础是拉普拉斯变换和z 变换,系统的基本数学模型是线性定常高阶微分方程、线性常系数差分方程、传递函数和脉冲传递函数,主要的分析和综合方法是时域法、根轨迹法和频域法,分析的主要内容是系统运动的稳定性。
经典线性系统理论对于单输入-单输出线性定常系统的分析和综合是比较有效的,但其显著的缺点是只能揭示输入-输出间的外部特性,难以揭示系统内部的结构特性,也难以有效处理多输入-多输出系统。
在50年代蓬勃兴起的航天技术的推动下,在1960年前后开始了从经典控制理论到现代控制理论的过渡,其中一个重要标志就是卡尔曼系统地将状态空间概念引入到控制理论中来。
现代控制理论正是在引入状态和状态空间概念的基础上发展起来的。
在现代控制理论的发展中,线性系统理论首先得到研究和发展,已形成较为完整成熟的理论。
现代控制理论中的许多分支,如最优控制、最优估计与滤波、系统辨识、随机控制、自适应控制等,均以线性系统理论为基础;非线性系统理论、大系统理论等,也都不同程度地受到了线性系统理论的概念、方法和结果的影响和推动。
现代控制理论中的线性系统理论运用状态空间法描述输入-状态-输出诸变量间的因果关系,不但反映了系统的输入—输出外部特性,而且揭示了系统内部的结构特性,是一种既适用于单输入--单输出系统又适用于多输入—多输出系统,既可用于线性定常系统又可用于线性时变系统的有效分析和综合方法。
在线性系统理论中,根据所采用的数学工具及系统描述方法的不同,又出现了一些平行的分支,目前主要有线性系统的状态空间法、线性系统的几何理论、线性系统的代数理论、线性系统的多变量频域方法等。
由于状态空间法是线性系统理论中最重要和影响最广的分支,加之受篇幅限制,所以本章只介绍线性系统的状态空间法。
9-1 线性系统的状态空间描述1. 系统数学描述的两种基本类型这里所谓的系统是指由一些相互制约的部分构成的整体,它可能是一个由反馈闭合的整体,也可能是某一控制装置或受控对象。
9章状态空间分析

状态空间分析法举例
例1求图示机械系统的状态空间表达式
外力 u(t)
K ---弹性系数 m
牛顿力学
阻 尼 系 数
b
y(t) u(t )
位移
m y y b ky
令
x1 y
x2 y
动态方程如下
x1 x2
k b 1 x2 y y y u (t ) m m m
k b 1 x1 x2 u (t ) m m m
y x1
状态空间表达式为:
x 1 x 2
0 1 x 0 1 b u k 1 x m m 2 m
x1 y 1 0 x2
1 0 0 a1
0 1 0 a2
0 0 1 an 1
0 0 b 0 0
c 1 0 0
例1设
...
y 5y 8y 6 y 3u
求(A,B,C,D)
.
..
(可加性), H (u1 ) H (u1 ) (齐次性),则该系统 称为线性的,否则为非线性. 定常性:1)定义: Qa -位移算子
2)一个松弛系统当且仅当对任何输入u和任意 实数 , 均有 y Hu HQau Qa Hu Qa y
u (t ) Qau(t ) u(t )
a0 a1 a2
0
y 1
0
x1 0 x 2 x3
作业
系统微分方程为
...
y 2 y 5 y 18 y 3u
..
第九章 平面与曲面相交 (3)

平面与圆柱相交
作图步骤如下:
(1)先作出完整基本形体的三面投影图。 (2)然后作出槽口三面投影图。 ( 3) 作出穿孔的三面投影图。
Q
P
平面与圆柱相交
例 例8 8:求 :求W W投影 投影
例9:求W投影
虚实分界点
例10:圆柱与四棱柱相交,求W投影
例11 已知圆柱截切后的两面投影,求作其W面投影
g'≡h' m'≡n'
a'≡c' o1'
Rv
b'≡d'
Qv
1'
h n 1 c e a g o1 d b m
例22 分析圆球打孔后的投影
㈣ 组合体的截交线
求组合体的截交线分两步 求出这些基本回转体的截交线,并依次将其连接。 一般情况下,两个基本几何体表面若相交,则截平 面截得的二截交线也相交,交点即为两基本形体表面 交线与截平面的交点 特殊情况下,若两个基本几何体表面相切, 二截 交线也相切,切点即为两基本切线与截平面的交点
5.整理轮廓线。
a
4
2
例15 分析并想象出圆锥穿孔后的投影
例15 分析并想象出圆锥穿孔后的投影
例16 分析六角螺母头部的曲线
1 2
例16 分析六角螺母头部的曲线
㈢ 圆球表面的截交线
圆
㈢ 圆球表面的截交线
求圆球截交线上点的方法——纬圆法
㈢ 圆球表面的截交线
平面与圆球相交,截交线的形状都是圆,但 根据截平面与投影面的相对位置不同,其截交线 的投影可能为圆、椭圆或积聚成一条直线。 例1:求半球体截切后的H投影和W投影。
例18
求圆球截交线
c'd'
第9章 两立体相交

由已知的三视图投影,可 分析出空间物体的形状。
基本 体为轴心 线正交的
圆柱体
被 公 切
两直径相
的
等的圆柱
球
体公切于
一个球。
空间分析::
椭圆曲线
被公切的球
椭圆曲线在V面投影积聚为一直线
例8-9:求圆柱穿孔后(方孔和圆孔
在轴4心、求线圆上柱穿相孔交后)的水的平水投平影及投侧影面及投影侧。面投 影。
二、利用辅助面法求作相贯线
圆柱和圆锥两轴心线 正交,两表面相交的共 有线(相贯线)。
空间曲线
辅助平面 直素线
空间分析:
三面共点 水平圆
辅 助 平 面 法
例8-7:求圆柱与圆锥的相贯线
扩展分析: 空间曲线
三、两曲面立体相贯线特殊情况 两曲面立体的相贯线,在一般情况
下是封闭的空间曲线;但在某些特殊情 况下,相贯线可能是平面曲(圆或者椭 圆)或直线。如果此时两曲面立体对投 影面恰又处于特殊位置,则它们的相贯 线在该投影面上的投影就具有一定的特 点和规律。了解和掌握这些特点和规律 有助于判断和绘制相贯线的投影,并可 以简化作图过程。
题目:补画第三视图
空间分析:四个简单形体的分割
题目:补画第三视图。 绘制底板
题目:补画第三视图。 绘制托架
题目:补画第三视图。 绘制圆筒
题目:补画第三视图 绘制支撑板
题目:补画第三视图 完成补画第三视图
小结
该题是用形体分析法读图和画图的典型题 目, 即将组合体假想分成若干基本形体,然后 一个一个形体分析,想象出简单形体的形状和 彼此之间的位置及组合关系.看图和画图的步 骤是:
1.平面立体与平面立体相交
2.平面立体与曲面立体相交
第九章欧氏空间分析

第八章 欧氏空间练习题1.证明:在一个欧氏空间里,对于任意向量ηξ,,以下等式成立:(1)2222||2||2||||ηξηξηξ+=-++; (2).||41||41,22ηξηξηξ--+=在解析几何里,等式(1)的几何意义是什么? 2.在区氏空间n R 里,求向量)1,,1,1(Λ=α与每一向量)0,,0,1,0,,0()(ΛΛi i =ε,n i ,,2,1Λ=的夹角.3.在欧氏空间4R 里找出两个单位向量,使它们同时与向量)4,5,2,3()2,2,1,1()0,4,1,2(=--=-=γβα 中每一个正交.4.利用内积的性质证明,一个三角形如果有一边是它的外接圆的直径,那么这个三角形一定是直角三角形.5.设ηξ,是一个欧氏空间里彼此正交的向量.证明:222||||||ηξηξ+=+(勾股定理)6.设βααα,,,,21n Λ都是一个欧氏空间的向量,且β是n ααα,,,21Λ的线性组合.证明:如果β与i α正交,n i ,,2,1Λ=,那么0=β. 7.设n ααα,,,21Λ是欧氏空间的n 个向量. 行列式><><><><><><><><><=n n n n n n n G ααααααααααααααααααααα,,,,,,,,,),,,(21222121211121ΛΛΛΛΛΛΛΛ 叫做n ααα,,,21Λ的格拉姆(Gram)行列式.证明),,,(21n G αααΛ=0,必要且只要n ααα,,,21Λ线性相关.8.设βα,是欧氏空间两个线性无关的向量,满足以下条件:><><ααβα,,2和><><βββα,,2都是0≤的整数.证明: βα,的夹角只可能是6543,32,2ππππ或. 9.证明:对于任意实数n a a a ,,,21Λ,23322211(||n ni ia a a a n a++++≤∑=Λ).10.已知)0,1,2,0(1=α,)0,0,1,1(2-=α, )1,0,2,1(3-=α,)1,0,0,1(4=α是4R 的一个基.对这个基施行正交化方法,求出4R 的一个规范正交基.11.在欧氏空间]1,1[-C 里,对于线性无关的向量级{1,x ,2x ,3x }施行正交化方法,求出一个规范正交组.12.令},,,{21n αααΛ是欧氏空间V 的一组线性无关的向量,},,,{21n βββΛ是由这组向量通过正交化方法所得的正交组.证明,这两个向量组的格拉姆行列式相等,即><>><=<=n n n n G G βββββββββααα,,,),,,(),,,(22112121ΛΛΛ13.令n γγγ,,,21Λ是n 维欧氏空间V 的一个规范正交基,又令},2,1,10,|{1n i x x V K ni i i i Λ=≤≤=∈=∑=γξξK 叫做一个n -方体.如果每一i x 都等于0或1,ξ就叫做K 的一个项点.K 的顶点间一切可能的距离是多少?14.设},,,{21m αααΛ是欧氏空间V 的一个规范正交组.证明,对于任意V ∈ξ,以下等式成立:∑=≤mi i122||,ξα.15.设V 是一个n 维欧氏空间.证明)(i 如果W 是V 的一个子空间,那么W W =⊥⊥)(.)(ii 如果21,W W 都是V 的子空间,且21W W ⊆,那么⊥⊥⊆12W W )(iii 如果21,W W 都是V 的子空间,那么⊥⊥⊥+=+2121)(W W W W16.证明,3R 中向量),,(000z y x 到平面}0|),,{(3=++∈=cz by ax R z y x W的最短距离等于222000||cb a cz by ax ++++.17.证明,实系数线性方程组∑===nj i j ijn i b x a1,,2,1,Λ有解的充分且必要条件是向量n n R b b b ∈=),,,(21Λβ与齐次线性方程组∑===nj j jin i x a1,,2,1,0Λ的解空间正交.18.令α是n 维欧氏空间V 的一个非零向量.令}0,|{>=<∈=αξξαV P .αP 称为垂直于α的超平面,它是V 的一个1-n 维子空间.V 中有两个向量ξ,η说是位于αP 的同侧,如果><><αηαξ,,与同时为正或同时为负.证明,V 中一组位于超平面αP 同侧,且两两夹角都2π≥的非零向量一定线性无关.[提示:设},,,{21r βββΛ是满足题设条件的一组向量.则)(0,j i j i ≠>≤<ββ,并且不妨设)1(0,r i i ≤≤>><αβ.如果∑==ri i i c 10β,那么适当编号,可设0,,,0,,,121≤≥+r s s c c c c c ΛΛ,)1(r s ≤≤,令∑∑+==-==rs j j j s i i i c c 11ββγ,证明0=γ.由此推出0=i c )1(r i ≤≤.] 19.设U 是一个正交矩阵.证明:)(i U 的行列式等于1或-1; )(ii U 的特征根的模等于1; )(iii 如果λ是U 的一个特征根,那么λ1也是U 的一个特征根; )(iv U 的伴随矩阵*U 也是正交矩阵.20.设02cos≠θ,且⎪⎪⎪⎭⎫⎝⎛-=θθθθcos sin 0sin cos 0001U . 证明,U I +可逆,并且⎪⎪⎪⎭⎫⎝⎛-=+--010*******tan ))((1θU I U I21.证明:如果一个上三角形矩阵⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=nn n n n a a a a a a a a a a A ΛΛΛΛΛΛΛΛΛ000000333223221131211 是正交矩阵,那么A 一定是对角形矩阵,且主对角线上元素ij a 是1或-1.22.证明:n 维欧氏空间的两个正交变换的乘积是一个正交变换;一个正交变换的逆变换还是一个正交变换.23.设σ是n 维欧氏空间V 的一个正交变换.证明:如果V 的一个子空间W 在σ之下不变,那么W 的正交补⊥W 也在σ下不变.24.设σ是欧氏空间V 到自身的一个映射,对ηξ,有,)(),(ηησξσ=证明σ是V 的一个线性变换,因而是一个正交变换. 25.设U 是一个三阶正交矩阵,且1det =U .证明:)(i U 有一个特征根等于1; )(ii U 的特征多项式有形状1)(23-+-=tx tx x x f这里31≤≤-t .26.设},,,{21n αααΛ和},,,{21n βββΛ是n 维欧氏空间V 的两个规范正交基.)(i 证明:存在V 的一个正交变换σ,使n i i i ,,2,1,)(Λ==βασ.)(ii 如果V 的一个正交变换τ使得11)(βατ=,那么)(,),(2n ατατΛ所生成的子空间与由n ββ,,2Λ所生成的子空间重合.27.设σ是n 维欧氏空间V 的一个线性变换.证明,如果σ满足下列三个条件的任意两个,那么它必然满足第三个:)(i σ是正交变换;)(ii σ是对称变换;)(iii ισ=2是单位变换.28.设σ是n 维欧氏空间V 的一个对称变换,且σσ=2.证明,存在V 的一个规范正交基,使得σ关于这个基的矩阵有形状⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛000101OO 29.证明:两个对称变换的和还是一个对称变换.两个对称变换的乘积是不是对称变换?找出两个对称变换的乘积是对称变换的一个充要条件.30.n 维欧氏空间V 的一个线性变换σ说是斜对称的,如果对于任意向量V ∈βα,, )(,),(βσαβασ-=.证明:)(i 斜对称变换关于V 的任意规范正交基的矩阵都是斜对称的实矩阵(满足条件A A -='的矩阵叫做斜对称矩阵))(ii 反之,如果线性变换σ关于V 的某一规范正交基的矩阵是斜对称的,那么σ一定是斜对称线性变换.)(iii 斜对称实矩阵的特征根或者是零,或者是纯虚数.31.令A 是一个斜对称实矩阵.证明,A I +可逆,并且1))((-+-=A I A I U 是一个正交矩阵.32.对于下列对称矩阵A,各求出一个正交矩阵U,使得AU U '是对角形式:)(i ⎪⎪⎪⎭⎫ ⎝⎛--=510810228211A ; )(ii ⎪⎪⎪⎭⎫⎝⎛----=114441784817A。
第九章_空间分析的应用

第九章_空间分析的应用空间分析是地理信息系统(GIS)中的一个重要概念,它通过利用空间数据的特征和关系,来研究地理现象和问题。
在不同领域和行业中,空间分析的应用非常广泛,例如城市规划、环境保护、农业决策等。
本文将重点介绍空间分析在城市规划和环境保护中的应用。
在城市规划方面,空间分析能够帮助规划师分析和评估城市的空间布局和发展趋势。
通过对城市土地利用、建筑物分布和人口分布等数据进行空间分析,规划师可以更好地了解城市的发展状况,并制定相应的城市发展计划。
例如,规划师可以利用空间分析来评估城市中不同地区的人口密度,以便更合理地规划住宅、商业和公共设施的布局。
此外,空间分析还可以帮助规划师分析城市的交通状况,包括道路拥堵情况、交通流量分布等,从而制定交通规划和交通管理策略。
此外,空间分析还可以应用在农业决策中。
农业是空间分析的一个重要应用领域,因为农业活动高度依赖于土地、气候和水资源等自然要素的地理分布。
空间分析可以帮助农民和农业专业人员分析土壤质量、气候变化、作物适应性等因素的关系,从而制定合理的农业种植和管理策略。
例如,农民可以利用空间分析技术,分析土地的肥力分布情况,从而合理选择不同地块的作物种植;同时,空间分析还可以帮助农民评估和优化灌溉系统,以便更有效地利用水资源。
综上所述,空间分析在城市规划和环境保护中的应用非常广泛和重要。
通过利用空间数据和空间分析技术,我们能够更好地了解和评估地理现象和问题,从而制定相应的规划和管理策略。
未来,随着技术的不断进步和数据的不断丰富,空间分析在各个领域中的应用将会进一步拓展和深化。
空间前方交会及其应用

水平像片对的前方交会公式
X x Y y Z f
BX BZ x2 f N1 p BX BZ x1 f N2 p
p x1 x2
理想像片对的前方交会公式
Z1
BX= XS2 –XS1 X1
X1
Z Y XS1 M
ZS1 Y1
(XA, YA, ZA) YS1
X
像点投影系数
S1 A X A X S1 YA YS1 Z A Z S1 N1 S1a1 X1 Y1 Z1
S1
Z1 X1
Y1
S2 A X A X S 2 YA YS 2 Z A Z S 2 N2 S2a2 X2 Y2 Z2
A
前方交会公式
BX Z 2 BZ X 2 N1 X 1Z 2 X 2 Z1
BX X S 2 X S 1 BY YS 2 YS 1 BZ Z S 2 Z S 1
X A X S1 N1 X 1 X S 2 N 2 X 2 1 YA [(YS1 N1Y1 ) (YS 2 N 2Y2 )] 2 Z A Z S1 N1Z1 Z S 2 N 2 Z 2
X x Y y Z f
BX X S 2 X S 1 B BY YS 2 YS1 0 BZ Z S 2 Z S1 0
N1 N 2
B p
p x1 x2
B B x1 X S1 B x2 p p B B YA YS1 y1 YS1 y2 p p y1 y 2 B B Z A Z S1 f Z S 2 f q y1 y 2 0 p p X A X S1
考研必备之自动化专业 自控原理 第九章 状态空间分析法答案-计算题
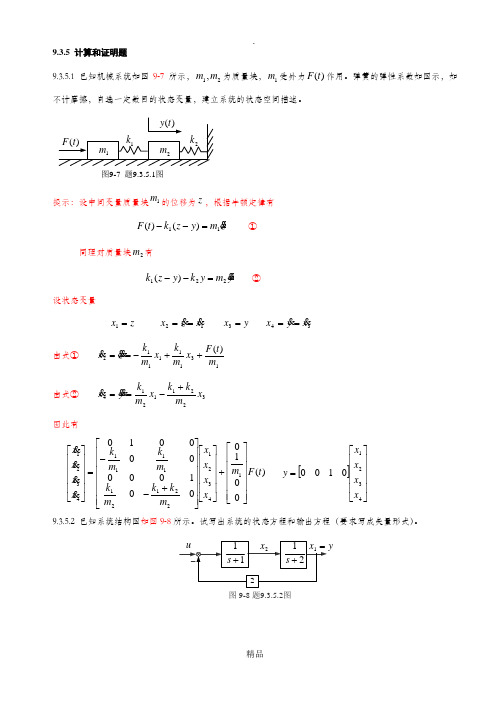
9.3.5 计算和证明题9.3.5.1 已知机械系统如图9-7所示,21,m m 为质量块,1m 受外力)(t F 作用。
弹簧的弹性系数如图示,如不计摩擦,自选一定数目的状态变量,建立系统的状态空间描述。
图9-7 题9.3.5.1图提示:设中间变量质量块1m 的位移为z ,根据牛顿定律有z m y z k t F 11)()( ①同理对质量块2m 有y m y k y z k 221)( ②设状态变量z x 1 12x z x y x 3 34x y x由式① 13111112)(m t F x m k x m k z x由式② 32211214x m k k x m k y x因此有)(001000100000001143212212111114321t F m x x x x m k k m k m k m k x x x x43210100x x x x y 9.3.5.2 已知系统结构图如图9-8所示。
试写出系统的状态方程和输出方程(要求写成矢量形式)。
y 图 9-8 题9.3.5.2图提示: xy u x x 011012129.3.5.3 已知系统的微分方程,试建立其相应的状态空间描述,并画出相应的状态结构图。
(1)u u u y y y y 86375 (2)u u u y y y y 23375提示:(1) x u x x 168100573100010 y ,状态结构图略 (2) ux u x x54110057310001y ,状态结构图略。
9.3.5.4判断下列矩阵是否满足状态转移矩阵的条件,如果满足,试求与之对应的A 阵。
(1)t t t t t sin cos 0cos sin 0001)(Φ (2)tt e e t 220)1(211)(Φ 提示:(1)不是状态转移矩阵,因为I )0(Φ。
(2)是。
2010)(0t t A Φ 9.3.5.5 线性系统u x x101000 ,11)0(x ,在单位阶跃输入时系统的响应x (t)。
作业空间设计

第九章作业空间设计作业空间包括作业者在操作时所需的空间及在作业中所需的机器、设备、工具和操作对象所占的空间范围。
作业空间的设计是指按照作业者的操作范围、视觉范围以及作业姿势等一系列生理、心理因素对作业对象、机器、设备、工具进行合理的布置、安排,并找出最适合本作业的人体最佳作业姿势、作业范围,以便为作业者创造一个最佳的作业条件。
一个设计优良的作业空间,不仅可以使作业者作业舒适、安全,操作简便,而且有助于提高人机系统的作业效率。
本章主要分析了影响作业空间设计的主要因素,在“人”方面有:作业者的操作范围、视觉范围、作业姿势等因素;在“机”方面有:单个机器设备的控制面板布置以及多个机器布置时局部与整体的关系等;在此基础上研究了坐姿作业空间与站姿作业空间,虚拟车间、工厂,以及作业空间的辅助用具如座椅、工作台的设计等;最后论述了作业空间的设计评价。
第一节作业空间设计概述研究作业空间的设计,首先要明确以下几个相关概念:一、近身作业空间是指作业者在某一固定的工作岗位上,保持站姿或坐姿等一定的作业姿势时,由于人体的静态或动态尺寸的限制,作业者为完成作业所及的空间范围。
如人在坐姿打字时,四肢(主要指上肢)所及的空间范围,就是近身作业空间。
近身作业空间作为作业空间设计的最基本内容,主要依据作业者在操作时四肢所及范围的静态尺寸和动态尺寸来确定。
根据人体的作业姿势不同,近身作业空间又可分为坐姿近身作业空间和站姿近身作业空间。
二、个体作业场所是指作业者周围与作业有关的、包含设备因素在内的作业区域,简称作业场所。
如电脑、计算机桌、电脑椅就构成一个完整的个体作业场所。
同近身作业空间相比,作业场所更复杂些,除了作业者的作业范围,还要包括相关设备所需的场地。
当仅有一台机器设备时,我们就可以把它当作个体作业场所来设计,而不必考虑多台设备布置时总体与局部的关系。
三、总体作业空间多个相互联系的个体作业场所布置在一起就构成了总体作业空间。
第九章 状态空间分析方法基础.ppt

上一页 下一页
§9-1 控制系统的状态空间描述
的、液压的、热力的等等。根据其物理定律,如基尔霍夫定 律、牛顿定律、能量守恒定律、热力学定律等,即可建立系统 的状态方程;当指定系统的输出后,可写出系统的输出方程。
3)利用输出反馈和调整系统的开环增益,只能使闭环极点沿 着一定得根轨迹移动,而利用状态反馈能使闭环系统任意配置 极点。这说明,状态反馈比一般的输出反馈对系统性能的综合
上一页 下一页
§9-6 状态反馈与状态观测器
更为方便。但在实际上实现起来,状态反馈比输出反馈要来的 复杂。
4)对单输入单输出系统,在一般情况下,利用状态反馈使闭 环系统极点与又性能指标给出的希望极点相一致的方法,以达 到改善系统性能的目的,是行之有效的。但状态反馈只能改变 极点的位置,却不能改变系统极点的个数和系统零点的位置, 有时单靠状态反行综合。
上一页 返回
§9-3 线性离散系统状态空间表达式
一、线性离散系统的状态空间表达式 线性定常离散系统状态空间表达式的结构图如图9-16所
示。 二、线性定常离散系统状态方程的解
1.迭代法求解 迭代法是一种递推的数值解法,其思路是:利 用初始时刻t0=0(即k=0)时的x(0)和u(0)求x(1);再根据求出的 x(1)和给定的u(1)求x(2);如此逐步迭代,即可求得所需的 x(k)。此法适于在计算机上求解。
上一页 下一页
§9-1 控制系统的状态空间描述
1.系统状态空间表达式的非唯一性 2.系统特征值的不变性及系统的不变量 对线性定常系统, 系统的特征值决定了系统的基本特性。 3.化状态方程为对角线规范型 化状态方程为某种形式的规 范型,是通过非奇异变化来实现的,所以求取该非奇异变化矩 阵是解决状态方程转化为某些规范型的关键。 4.化状态方程为约当规范型 五、状态空间表达式与传递函数阵间的变换
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
空间分析在地震灾害和损失估计中的应用主要包括: 3)估计建筑物的损害 需要收集地震区域内建筑和生命线的分布状况,然 后对每种建筑建立损失模型,该模型是一个函数, 与地表震动强度以及潜在的次要灾害有关。
18
空间分析在地震灾害和损失估计中的应用主要包括:
4)估计可以用金钱衡量和不可以用金钱衡量的损失
3)水污染监测;
4)洪水灾害分析;
5)道路交通管理; 6)地震灾害和损失估计;
7)输电网管理;
8)配电网管理;
9)地形地貌分析; 10)医疗卫生;
11)军事领域等。
2
空间分析在城市规划中的 应用
3
空间分析可提高城市规划的科学性和有效性 城市规划中的空间分析是指利用空间分析的理论和方法 对城市规划中含有空间信息(位置、形状、分布)的数 据进行统计、分类、比例计算、形成报表,同时绘制出 相应的分析结果图件的分析过程。 作为地理信息系统核心功能的空间分析技术方法,在城 市规划领域具有及其广阔的应用前景。
23
数据库是洪水灾害损失评估的基础,洪水灾害损失评 估数据库包括:
①数字地形数据; ②行政区划数据; ③洪灾区的土地利用数据; ④社会经济数据(包括以县为单位的人口、农作物 产量、投入、总产值等); ⑤历史洪水损失数据; ⑥水文气象数据等。
24
评估模型为利用数据库的数据进行快速评估提供方法, 这些评估模型包括: ➢受灾地区土地利用评估分析模型、 ➢受淹人口与房屋评估模型、 ➢受淹农作物损失估算模型、 ➢防洪抗灾辅助决策模型(洪灾行为的模拟模型、滞洪 区洪水演进模型、避险迁安分析模型等)。
8
(2)在空间分析研究的深度方面: 空间分析方法实现了空间数据和非空间数据的一体化 处理,能够透过城市空间现象的表面,对深层次的空 间关系进行研究分析。 在把握城市空间演变机制的基础上,预测模拟城市的 未来发展趋势,优化调整城市空间格局。 空间分析技术方法的应用,可以提高城市规划处理各 类规划基础数据的能力,提高未来城市发展的预测、 模拟和优化能力,使规划能够在理性的综合分析基础 上作出科学判断与决策。
29
利用空间分析的水文分析功能模块进行分析得出的 40小时分洪区水深分布图
30
利用统计分析模块进行统计分析所得出的北闸分洪40 小时时的洪水淹没情况统计表
31
空间分析在水污 染监测中的应用
32
水质污染是我国面临的最为严重的水环境问题之一, 防治水质污染已成为我国环境保护的一项紧迫的任务。
水环境污染防治问题涉及的区域范围广,数据量(空 间数据和属性数据)大,必须借助大量的科学合理的 水质模拟模型进行水质的预测和评价。
27
1、空间分析在洪水灾害评估中的应用 5)提供多种输出 GIS的空间分析计算结果可以在屏幕上以图形 或表格方式显示, 也可提供报告、报表、地图的硬拷贝。
28
2、洪水灾害评估GIS系统中的空间分析在荆江分滞洪 区的应用
荆江分洪区工程是长江防洪体系的重要组成部分,担负着削减洪 峰,分、蓄洪水的作用。 该工程由位于荆江河段沙市段南岸的荆江分洪区、涴市扩大区、 虎西备蓄区及长江北岸的人民大垸(上、下)组成。总蓄滞面积 1358KM2,有效容积71.6亿m3。
36
水环境可视化
监 监测点实测指标信息可视化包括时序对比和监测点对比
测
点
➢时序对比
实
测
指
标
信
息
可
视
化
通过选择站点和时间段来监视某个站点的某个指标在某 时间段的监测指标变化情况。
水环境可视化
监
➢监测点对比
测
点
实
测
指
标
信
息
可
视
化
显示多个站点的某个指标在某个时间点的对比情况
水环境可视化
35
4)知识库:知识库用于存放环保规划专家和水质评 价专家提供的专门知识(各种环保法律法规、各种水质 等级的评价标准、各种规划方案的指定经验),通过知 识库知识的自动获取为江河流域水污染防治规划辅助 决策支持系统提供有力支持。 这种具有大量数学模型的GIS系统进行空间分析时解 决的一个最重要的问题就是如何充分利用这些数学模 型,为空间分析任务服务。
充分利用GIS的空间分析功能进行洪水灾害 的评估是一个十分有效的“非工程措施”。
22
1、空间分析在洪水灾害评估中的应用 1)洪水灾害评估模型的建立 洪水灾害的研究涉及自然科学和社会科学的众多领域。 在洪水灾害损失评估信息系统中,利用建立的灾害数 据库和灾害评估模型,在地理信息系统的支持下,在 遥感监测的基础上,对洪水淹没的土地类型、受灾人 口和房屋、洪水淹没历时、作物损失程度等进行科学 而有效的评估。
可以用金钱衡量的损失包括受损建筑的修复和重建, 清除垃圾和重新安置等方面的费用损失,而不可以用 金钱衡量的损失包括人员伤亡、精神影响以及其它长 期或短期的影响等。
估算这些损失需要相应的社会经济信息。
可以针对不同的损失类型,建立不同的模型,分别估 计损失。
在地震损估计中,需要使用多种空间信息,如地质
9
城市规划空间分析的内容
城市规划的空间分析可以揭示城市空间对象间的相互 作用关系,如城市土地空间演变、城市结构以及空间 演变、人口与用地之间的关系,自然条件与城市结构 的关系,城市持续发展过程中物质、能量和信息流动 的空间规律等。
10
在实践应用中,城市规划空间分析有五种主要类型:
1)比较分析:分析城市规划要素的时间序列与空间 序列的变化,通过比较分析发现要素在不同时期的数 量变化,空间分布的模式及其演变。为规划人员提供 更加详细的规划信息以供决策,把握城市空间发展的 内在规律以及未来的时空演变趋势。
2)统计分析:城市规划要素的非空间信息的分析, 运用回归分析、相关分析、主成分分析等方法,确定 数据库属性之间存在的函数关系或相关关系,应用于 城市规划中的单因素不同状况统计、多因素交叉统计、 频率统计等运算。
11
3)预测分析:根据城市发展的时空演变规律,使用 各类预测模型,预测一定时期内的人口规模、城市 土地利用、城市灾害、区域增长等的发展变化趋势 以及演变过程。在预测分析的基础上,制定正确的 政策措施来引导城市结构要素在空间上的合理布局 与组合。
空间分析技术方法的应用,为城市规划空间研究提供 了新的技术手段,能解决这方面存在的不足。
5
《Nature》社论:科学家应为城市发展作出贡献 2010年10月21日出版的《Nature》杂志发表社论—— 《救救我们的城市》(Save our cities),称相关研究 领域的科学家们应该更多地将关注重点放在城市。同 期《自然》还刊登了关于科研与城市的系列文章。
16
空间分析在地震灾害和损失估计中的应用主要包括:
1)估计地表震动灾害
应急指挥需要识别地震源点,然后建立在该点发生 地震以及地震波传播的模型,估计地震破坏的分布, 最后根据地表的土壤条件得到最终的震动强度。
2)估计次生地震的灾害
次生地震灾害是直接灾害发生后,破坏了自然或社 会原有的平衡或稳定状态,从而引发的灾害。主要 有火灾、水灾、毒气泄漏、瘟疫等。评估这些灾害 需要收集相应区域的地质构造信息,计算地表运动 的强度和持续时间,以及在以前的地震发生过程中 发生这些灾害的历史情况。
4
城市规划空间分析的实践意义:分析和研究城市空间 实体的现状以及预测其发展,并以此作为编制城市规 划、指导城市建设的依据。
城市空间作为一个特殊的空间系统,是政治、经济、 社会、环境等人文、自然过程共同作用的结果,有其 独特的空间演变机制。在充分分析城市空间基础数据, 包括空间数据与非空间数据的基础上,发现空间演变 的规律,为城市规划奠定分析基础,使城市规划成果 有据可依。
26
1、空间分析在洪水灾害评估中的应用 4)洪灾场景模拟分析 洪水灾害分析信息系统可以对洪灾发生的不同阶段进 行分析。 ➢在洪灾发生前,模拟分析洪灾发生的可能性和空间 分布规律; ➢在洪灾发生过程中,实现洪灾信息的接收、处理和 分析,为防洪抗险提供即时的信息; ➢在洪灾发生后,利用多方面的信息,提供洪灾损失 的详细报告,辅助制定救灾计划和重建家园规划。
武汉大学遥感信息工程学院遥感科学与技术本科生教案(2012)
第九章 空间分析的应用
秦昆 qinkun163@
1
空间分析的应用是指空间分析的理论、方法和过程在 与空间数据处理有关的领域的具体应用。
空间分析可以应用到自然科学和社会科学的多个领域, 包括以下应用领域:
1)城市规划与管理; 2)厂址选择;
13
空间分析在地震灾害 和损失估计中的应用
14
地理信息系统的空间分析能够评估地震灾害以 及地震次生灾害,并且对临震地震和短期地震 进行分析预报。 对发生地震灾害的地区,及时分配资源援助, 提供应急决策方案具有重要的意义。
15
利用GIS的空间分析功能,分析地质构造、地形、地上 建筑物等信息,模拟地震发生过程,估计地震引起的损 失,并且可以分析地震实际发生时的灾害严重程度的空 间分布,帮助政府分配应急资源。 进行地震灾害评估时,要综合考虑地质构造、地形等各 种信息。
构造、建筑、地形等等,因此必须充分利用GIS的空
间分析功能进行地震损失的评估。
19
空间分析在洪水灾害 评估中的应用
20
洪水灾害是当今世界上的主要自然灾害,防治洪水 灾害是世界各国普遍关注的问题。
在过去相当长的时间内,世界各国的防洪战略主要 是依靠水利工程控制洪水,降低洪灾损失,
随着社会经济的发展,人类不断扩大对自然资源的 开发利用范围,洪水出现频数及其所造成的损失也 不断地增加,
4)优化分析:制定合理的城市规划涉及到社会、经 济、政治、环境等许多要素,优化分析就是通过对 大量规划数据的综合与概括,在多因素综合影响的 条件下,在多种规划方案中,选择最优的规划方案 或发展目标。城市土地利用功能区划、城市功能区 划分、规划方案评价、环境质量评价等问题都需要 进行优化分析。
