应用技术回归分析第九章部分完整答案
应用数值分析(第四版)课后习题答案第9章

应⽤数值分析(第四版)课后习题答案第9章第九章习题解答1.已知矩阵=???=4114114114,30103212321A A 试⽤格希哥林圆盘确定A 的特征值的界。
解:,24)2(,33)1(≤-≤-λλ2.设T x x x x ),...,,(321=是矩阵A 属于特征值λ的特征向量,若i x x =∞,试证明特征值的估计式∑≠=≤-n i j j ij ii aa 1λ.解:,x Ax λ=∞∞∞∞≤==x A x x Ax i λλ由 i x x =∞ 得 i n in i ii i x x a x a x a λ=++++ 11j n j i i ij i ii x ax a ∑≠==-1)(λj n j i i ij j n j i i ij i ii x a x ax a ∑∑≠=≠=≤=-11λ∑∑≠=≠=≤≤-nj i i ij i j n j i i ijii a x x a a 11λ3.⽤幂法求矩阵=1634310232A 的强特征值和特征向量,迭代初值取T y )1,1,1()0(=。
解:y=[1,1,1]';z=y;d=0;A=[2,3,2;10,3,4;3,6,1];for k=1:100y=A*z;[c,i]=max(abs(y));if y(i)<0,c=-c;endz=y/cif abs(c-d)<0.0001,break; endd=cend11.0000=c ,0.7500) 1.0000 0.5000(z 10.9999 =c ,0.7500) 1.0000 0.5000(z 11.0003 =c ,0.7500) 1.0000 0.5000(z 10.9989=c ,0.7500) 1.0000 0.5000(z 11.0040 =c ,0.7498) 1.0000 0.5000(z 10.9859=c ,0.7506) 1.0000 0.5001(z 11.04981 =c ,0.7478) 1.0000 0.4995(z 10.8316 =c ,0.7574) 1.0000 0.5020(z 11.5839 =c ,) 0.7260 1.0000 0.4928 (z 9.4706 =c ,0.8261) 1.0000 0.5280(z 17 = c ,0.5882) 1.0000 0.4118(z 11T (11)10T (10)9T (9)8T (8)7T (7)6T (6)5T (5)4T (4)3T (3)2T (2)1T (1)===========强特征值为11,特征向量为T 0.7500)1.0000 0.5000(。
《应用回归分析》课后习题部分答案-何晓群版

第二章 一元线性回归2.14 解答:(1)散点图为:(2)x 与y 之间大致呈线性关系。
(3)设回归方程为01y x ββ∧∧∧=+1β∧=12217()ni ii nii x y n x yxn x --=-=-=-∑∑0120731y x ββ-∧-=-=-⨯=-17y x ∧∴=-+可得回归方程为(4)22ni=11()n-2i i y y σ∧∧=-∑ 2n 01i=11(())n-2i y x ββ∧∧=-+∑=2222213⎡⎤⨯+⨯+⨯⎢⎥+⨯+⨯⎣⎦(10-(-1+71))(10-(-1+72))(20-(-1+73))(20-(-1+74))(40-(-1+75)) []1169049363110/3=++++=6.1σ∧=(5)由于211(,)xxN L σββ∧t σ∧==服从自由度为n-2的t 分布。
因而/2||(2)1P t n αασ⎡⎤⎢⎥<-=-⎢⎥⎣⎦也即:1/211/2(p t t ααβββ∧∧∧∧-<<+=1α-可得195%β∧的置信度为的置信区间为(7-2.3537+2.353 即为:(2.49,11.5)2201()(,())xxx Nn L ββσ-∧+t ∧∧==服从自由度为n-2的t 分布。
因而/2|(2)1P t n αα∧⎡⎤⎢⎥⎢⎥<-=-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦即0/200/2()1p βσββσα∧∧∧∧-<<+=- 可得195%7.77,5.77β∧-的置信度为的置信区间为()(6)x 与y 的决定系数22121()490/6000.817()ni i nii y y r y y ∧-=-=-==≈-∑∑(7)由于(1,3)F F α>,拒绝0H ,说明回归方程显著,x 与y 有显著的线性关系。
(8)t σ∧==其中2221111()22n ni i i i i e y y n n σ∧∧====---∑∑ 7 3.661==≈/2 2.353t α= /23.66t t α=>∴接受原假设01:0,H β=认为1β显著不为0,因变量y 对自变量x 的一元线性回归成立。
《应用回归分析》课后题答案解析

1.9 回归模型有那几个方面的应用? 答:回归模型的应用方面主要有:经济变量的因素分析和进行经济预测。
1.5 回归变量的设置理论根据是什么?在回归变量设置时应注意哪些问题? 答:理论判断某个变量应该作为解释变量,即便是不显著的,如果理论上无法判 断那么可以采用统计方法来判断,解释变量和被解释变量存在统计关系。应注意 的问题有:在选择变量时要注意与一些专门领域的专家合作,不要认为一个回归 模型所涉及的变量越多越好,回归变量的确定工作并不能一次完成,需要反复试 算,最终找出最合适的一些变量。
t /2
0
0
1 n
( x)2 Lxx
t
/
2
)
1
可得 1的置信度为95%的置信区间为( 7.77,5.77)
n
( yi y)2
(6)x 与 y 的决定系数 r 2
i 1 n
490 / 600 0.817
3
精品文档
(5)由于 1
N
(1,
2 Lxx
)
t
1 1 2 / Lxx
(1
)
Lxx
服从自由度为 n-2 的 t 分布。因而
P
|
(
1
)
Lxx
|
t
/
2
(n
2)
1
也即: p(1 t /2
Lxx
1 1 t /2
) =1 Lxx
可得
1
《应用回归分析》课后题答案要点

《应用回归分析》部分课后习题答案第一章回归分析概述1.1 变量间统计关系和函数关系的区别是什么?答:变量间的统计关系是指变量间具有密切关联而又不能由某一个或某一些变量唯一确定另外一个变量的关系,而变量间的函数关系是指由一个变量唯一确定另外一个变量的确定关系。
1.2 回归分析与相关分析的联系与区别是什么?答:联系有回归分析和相关分析都是研究变量间关系的统计学课题。
区别有 a.在回归分析中,变量y称为因变量,处在被解释的特殊地位。
在相关分析中,变量x和变量y处于平等的地位,即研究变量y与变量x的密切程度与研究变量x与变量y的密切程度是一回事。
b.相关分析中所涉及的变量y与变量x全是随机变量。
而在回归分析中,因变量y是随机变量,自变量x可以是随机变量也可以是非随机的确定变量。
C.相关分析的研究主要是为了刻画两类变量间线性相关的密切程度。
而回归分析不仅可以揭示变量x对变量y的影响大小,还可以由回归方程进行预测和控制。
1.3 回归模型中随机误差项ε的意义是什么?答:ε为随机误差项,正是由于随机误差项的引入,才将变量间的关系描述为一个随机方程,使得我们可以借助随机数学方法研究y与x1,x2…..xp的关系,由于客观经济现象是错综复杂的,一种经济现象很难用有限个因素来准确说明,随机误差项可以概括表示由于人们的认识以及其他客观原因的局限而没有考虑的种种偶然因素。
1.4 线性回归模型的基本假设是什么?答:线性回归模型的基本假设有:1.解释变量x1.x2….xp是非随机的,观测值xi1.xi2…..xip是常数。
2.等方差及不相关的假定条件为{E(εi)=0 i=1,2…. Cov(εi,εj)={σ^23.正态分布的假定条件为相互独立。
4.样本容量的个数要多于解释变量的个数,即n>p.1.5 回归变量的设置理论根据是什么?在回归变量设置时应注意哪些问题?答:理论判断某个变量应该作为解释变量,即便是不显著的,如果理论上无法判断那么可以采用统计方法来判断,解释变量和被解释变量存在统计关系。
《应用回归分析》课后题答案

《使用回归分析》部分课后习题答案第一章回归分析概述变量间统计关系和函数关系的区别是什么答:变量间的统计关系是指变量间具有密切关联而又不能由某一个或某一些变量唯一确定另外一个变量的关系,而变量间的函数关系是指由一个变量唯一确定另外一个变量的确定关系。
回归分析和相关分析的联系和区别是什么答:联系有回归分析和相关分析都是研究变量间关系的统计学课题。
区别有 a.在回归分析中,变量y称为因变量,处在被解释的特殊地位。
在相关分析中,变量x和变量y处于平等的地位,即研究变量y和变量x的密切程度和研究变量x和变量y的密切程度是一回事。
b.相关分析中所涉及的变量y和变量x全是随机变量。
而在回归分析中,因变量y是随机变量,自变量x可以是随机变量也可以是非随机的确定变量。
C.相关分析的研究主要是为了刻画两类变量间线性相关的密切程度。
而回归分析不仅可以揭示变量x对变量y的影响大小,还可以由回归方程进行预测和控制。
回归模型中随机误差项ε的意义是什么答:ε为随机误差项,正是由于随机误差项的引入,才将变量间的关系描述为一个随机方程,使得我们可以借助随机数学方法研究y和x1,x2…..xp的关系,由于客观经济现象是错综复杂的,一种经济现象很难用有限个因素来准确说明,随机误差项可以概括表示由于人们的认识以及其他客观原因的局限而没有考虑的种种偶然因素。
—线性回归模型的基本假设是什么答:线性回归模型的基本假设有:1.解释变量….xp是非随机的,观测值…..xip是常数。
2.等方差及不相关的假定条件为{E(εi)=0 i=1,2…. Cov(εi,εj)={σ^23.正态分布的假定条件为相互独立。
4.样本容量的个数要多于解释变量的个数,即n>p.回归变量的设置理论根据是什么在回归变量设置时应注意哪些问题答:理论判断某个变量应该作为解释变量,即便是不显著的,如果理论上无法判断那么可以采用统计方法来判断,解释变量和被解释变量存在统计关系。
应用回归分析(第三版)何晓群 刘文卿 课后习题答案 完整版

资料范本本资料为word版本,可以直接编辑和打印,感谢您的下载应用回归分析(第三版)何晓群刘文卿课后习题答案完整版地点:__________________时间:__________________说明:本资料适用于约定双方经过谈判,协商而共同承认,共同遵守的责任与义务,仅供参考,文档可直接下载或修改,不需要的部分可直接删除,使用时请详细阅读内容第二章一元线性回归分析思考与练习参考答案2.1 一元线性回归有哪些基本假定?答:假设1、解释变量X是确定性变量,Y是随机变量;假设2、随机误差项ε具有零均值、同方差和不序列相关性:E(εi)=0 i=1,2, …,nVar (εi)=s2 i=1,2, …,nCov(εi, εj)=0 i≠j i,j= 1,2, …,n假设3、随机误差项ε与解释变量X之间不相关:Cov(Xi, εi)=0 i=1,2, …,n假设4、ε服从零均值、同方差、零协方差的正态分布εi~N(0, s2 ) i=1,2, …,n2.2 考虑过原点的线性回归模型Yi=β1Xi+εi i=1,2, …,n误差εi(i=1,2, …,n)仍满足基本假定。
求β1的最小二乘估计解:得:2.3 证明(2.27式),Sei =0 ,SeiXi=0 。
证明:其中:即: Sei =0 ,SeiXi=02.4回归方程E(Y)=β0+β1X的参数β0,β1的最小二乘估计与最大似然估计在什么条件下等价?给出证明。
答:由于εi~N(0, s2 ) i=1,2, …,n所以Yi=β0 + β1Xi + εi~N(β0+β1Xi , s2 )最大似然函数:使得Ln(L)最大的,就是β0,β1的最大似然估计值。
同时发现使得Ln(L)最大就是使得下式最小,上式恰好就是最小二乘估计的目标函数相同。
值得注意的是:最大似然估计是在εi~N(0, s2 )的假设下求得,最小二乘估计则不要求分布假设。
所以在εi~N(0, s2 ) 的条件下,参数β0,β1的最小二乘估计与最大似然估计等价。
《应用回归分析》课后习题部分答案-何晓群版
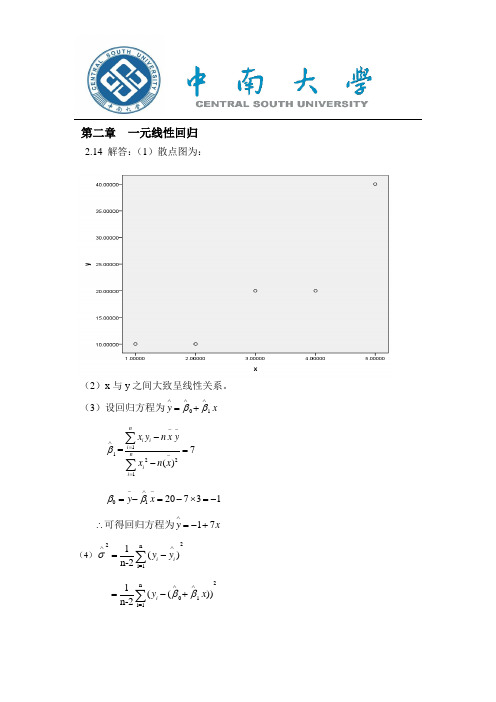
第二章 一元线性回归2.14 解答:(1)散点图为:(2)x 与y 之间大致呈线性关系。
(3)设回归方程为01y x ββ∧∧∧=+1β∧=12217()ni ii nii x y n x yxn x --=-=-=-∑∑0120731y x ββ-∧-=-=-⨯=-17y x ∧∴=-+可得回归方程为(4)22ni=11()n-2i i y y σ∧∧=-∑2n01i=11(())n-2i y x ββ∧∧=-+∑=2222213⎡⎤⨯+⨯+⨯⎢⎥+⨯+⨯⎣⎦(10-(-1+71))(10-(-1+72))(20-(-1+73))(20-(-1+74))(40-(-1+75)) []1169049363110/3=++++=6.1σ∧=≈ (5)由于211(,)xxN L σββ∧t σ∧==服从自由度为n-2的t 分布。
因而/2|(2)1P t n αασ⎡⎤⎢⎥<-=-⎢⎥⎣⎦也即:1/211/2(p t t ααβββ∧∧∧∧-<<+=1α-可得195%β∧的置信度为的置信区间为(7-2.3537+2.353 即为:(2.49,11.5)22001()(,())xxx N n L ββσ-∧+t ∧∧==服从自由度为n-2的t 分布。
因而/2|(2)1P t n αα∧⎡⎤⎢⎥⎢⎥<-=-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦即0/200/2()1p βσββσα∧∧∧∧-<<+=- 可得195%7.77,5.77β∧-的置信度为的置信区间为()(6)x 与y 的决定系数22121()490/6000.817()nii nii y y r y y ∧-=-=-==≈-∑∑由于(1,3)F F α>,拒绝0H ,说明回归方程显著,x 与y 有显著的线性关系。
(8)t σ∧==其中2221111()22n ni i i i i e y y n n σ∧∧====---∑∑ 3.66==≈/2 2.353t α= /23.66t t α=>∴接受原假设01:0,H β=认为1β显著不为0,因变量y 对自变量x 的一元线性回归成立。
最新《应用回归分析》课后题答案解析

《应用回归分析》部分课后习题答案第一章回归分析概述1.1 变量间统计关系和函数关系的区别是什么?答:变量间的统计关系是指变量间具有密切关联而又不能由某一个或某一些变量唯一确定另外一个变量的关系,而变量间的函数关系是指由一个变量唯一确定另外一个变量的确定关系。
1.2 回归分析与相关分析的联系与区别是什么?答:联系有回归分析和相关分析都是研究变量间关系的统计学课题。
区别有a.在回归分析中,变量y称为因变量,处在被解释的特殊地位。
在相关分析中,变量x和变量y处于平等的地位,即研究变量y与变量x的密切程度与研究变量x 与变量y的密切程度是一回事。
b.相关分析中所涉及的变量y与变量x全是随机变量。
而在回归分析中,因变量y是随机变量,自变量x可以是随机变量也可以是非随机的确定变量。
C.相关分析的研究主要是为了刻画两类变量间线性相关的密切程度。
而回归分析不仅可以揭示变量x对变量y的影响大小,还可以由回归方程进行预测和控制。
1.3 回归模型中随机误差项ε的意义是什么?答:ε为随机误差项,正是由于随机误差项的引入,才将变量间的关系描述为一个随机方程,使得我们可以借助随机数学方法研究y与x1,x2…..xp的关系,由于客观经济现象是错综复杂的,一种经济现象很难用有限个因素来准确说明,随机误差项可以概括表示由于人们的认识以及其他客观原因的局限而没有考虑的种种偶然因素。
1.4 线性回归模型的基本假设是什么?答:线性回归模型的基本假设有:1.解释变量x1.x2….xp是非随机的,观测值xi1.xi2…..xip是常数。
2.等方差及不相关的假定条件为{E(εi)=0 i=1,2…. Cov(εi,εj)={σ^23.正态分布的假定条件为相互独立。
4.样本容量的个数要多于解释变量的个数,即n>p.1.5 回归变量的设置理论根据是什么?在回归变量设置时应注意哪些问题?答:理论判断某个变量应该作为解释变量,即便是不显著的,如果理论上无法判断那么可以采用统计方法来判断,解释变量和被解释变量存在统计关系。
《应用回归分析》课后题答案

《使用回归分析》部分课后习题答案第一章回归分析概述1.1 变量间统计关系和函数关系的区别是什么?答:变量间的统计关系是指变量间具有密切关联而又不能由某一个或某一些变量唯一确定另外一个变量的关系,而变量间的函数关系是指由一个变量唯一确定另外一个变量的确定关系。
1.2 回归分析和相关分析的联系和区别是什么?答:联系有回归分析和相关分析都是研究变量间关系的统计学课题。
区别有 a.在回归分析中,变量y称为因变量,处在被解释的特殊地位。
在相关分析中,变量x和变量y处于平等的地位,即研究变量y和变量x的密切程度和研究变量x和变量y的密切程度是一回事。
b.相关分析中所涉及的变量y和变量x全是随机变量。
而在回归分析中,因变量y是随机变量,自变量x可以是随机变量也可以是非随机的确定变量。
C.相关分析的研究主要是为了刻画两类变量间线性相关的密切程度。
而回归分析不仅可以揭示变量x对变量y的影响大小,还可以由回归方程进行预测和控制。
1.3 回归模型中随机误差项ε的意义是什么?答:ε为随机误差项,正是由于随机误差项的引入,才将变量间的关系描述为一个随机方程,使得我们可以借助随机数学方法研究y和x1,x2…..xp的关系,由于客观经济现象是错综复杂的,一种经济现象很难用有限个因素来准确说明,随机误差项可以概括表示由于人们的认识以及其他客观原因的局限而没有考虑的种种偶然因素。
1.4 线性回归模型的基本假设是什么?答:线性回归模型的基本假设有:1.解释变量x1.x2….xp是非随机的,观测值xi1.xi2…..xip是常数。
2.等方差及不相关的假定条件为{E(εi)=0 i=1,2…. Cov(εi,εj)={σ^23.正态分布的假定条件为相互独立。
4.样本容量的个数要多于解释变量的个数,即n>p.1.5 回归变量的设置理论根据是什么?在回归变量设置时应注意哪些问题?答:理论判断某个变量应该作为解释变量,即便是不显著的,如果理论上无法判断那么可以采用统计方法来判断,解释变量和被解释变量存在统计关系。
《应用回归分析》课后题答案解析

《应用回归分析》部分课后习题答案第一章回归分析概述1.1 变量间统计关系和函数关系的区别是什么?答:变量间的统计关系是指变量间具有密切关联而又不能由某一个或某一些变量唯一确定另外一个变量的关系,而变量间的函数关系是指由一个变量唯一确定另外一个变量的确定关系。
1.2 回归分析与相关分析的联系与区别是什么?答:联系有回归分析和相关分析都是研究变量间关系的统计学课题。
区别有 a.在回归分析中,变量y称为因变量,处在被解释的特殊地位。
在相关分析中,变量x和变量y处于平等的地位,即研究变量y与变量x的密切程度与研究变量x与变量y的密切程度是一回事。
b.相关分析中所涉及的变量y与变量x全是随机变量。
而在回归分析中,因变量y是随机变量,自变量x可以是随机变量也可以是非随机的确定变量。
C.相关分析的研究主要是为了刻画两类变量间线性相关的密切程度。
而回归分析不仅可以揭示变量x对变量y的影响大小,还可以由回归方程进行预测和控制。
1.3 回归模型中随机误差项ε的意义是什么?答:ε为随机误差项,正是由于随机误差项的引入,才将变量间的关系描述为一个随机方程,使得我们可以借助随机数学方法研究y与x1,x2…..xp的关系,由于客观经济现象是错综复杂的,一种经济现象很难用有限个因素来准确说明,随机误差项可以概括表示由于人们的认识以及其他客观原因的局限而没有考虑的种种偶然因素。
1.4 线性回归模型的基本假设是什么?答:线性回归模型的基本假设有:1.解释变量x1.x2….xp是非随机的,观测值xi1.xi2…..xip是常数。
2.等方差及不相关的假定条件为{E(εi)=0 i=1,2…. Cov(εi,εj)={σ^23.正态分布的假定条件为相互独立。
4.样本容量的个数要多于解释变量的个数,即n>p.1.5 回归变量的设置理论根据是什么?在回归变量设置时应注意哪些问题?答:理论判断某个变量应该作为解释变量,即便是不显著的,如果理论上无法判断那么可以采用统计方法来判断,解释变量和被解释变量存在统计关系。
《应用回归分析》课后习题部分答案何晓群版

第二章 一元线性回归2.14 解答:(1)散点图为:(2)x 与y 之间大致呈线性关系。
(3)设回归方程为01y x ββ∧∧∧=+1β∧=12217()ni ii nii x y n x yxn x --=-=-=-∑∑0120731y x ββ-∧-=-=-⨯=-17y x ∧∴=-+可得回归方程为(4)22ni=11()n-2i i y y σ∧∧=-∑ 2n 01i=11(())n-2i y x ββ∧∧=-+∑=2222213⎡⎤⨯+⨯+⨯⎢⎥+⨯+⨯⎣⎦(10-(-1+71))(10-(-1+72))(20-(-1+73))(20-(-1+74))(40-(-1+75)) []1169049363110/3=++++=6.1σ∧=≈ (5)由于211(,)xxN L σββ∧t σ∧==服从自由度为n-2的t 分布。
因而/2|(2)1P t n αασ⎡⎤⎢⎥<-=-⎢⎥⎣⎦也即:1/211/2(p t t ααβββ∧∧∧∧-<<+=1α-可得195%β∧的置信度为的置信区间为(7-2.3537+2.353 即为:(2.49,11.5)2201()(,())xxx Nn L ββσ-∧+t ∧∧==服从自由度为n-2的t 分布。
因而/2(2)1P t n αα∧⎡⎤⎢⎥⎢⎥<-=-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦即0/200/2()1p βσββσα∧∧∧∧-<<+=- 可得195%7.77,5.77β∧-的置信度为的置信区间为()(6)x 与y 的决定系数22121()490/6000.817()nii nii y y r y y ∧-=-=-==≈-∑∑(7)由于(1,3)F F α>,拒绝0H ,说明回归方程显著,x 与y 有显著的线性关系。
(8)t σ∧==其中2221111()22n ni i i i i e y y n n σ∧∧====---∑∑ 7 3.661==≈ /2 2.353t α= /23.66t t α=>∴接受原假设01:0,H β=认为1β显著不为0,因变量y 对自变量x 的一元线性回归成立。
《应用回归分析》课后题答案

《应用回归分析》部分课后习题答案第一章回归分析概述1。
1 变量间统计关系和函数关系的区别是什么?答:变量间的统计关系是指变量间具有密切关联而又不能由某一个或某一些变量唯一确定另外一个变量的关系,而变量间的函数关系是指由一个变量唯一确定另外一个变量的确定关系。
1。
2 回归分析与相关分析的联系与区别是什么?答:联系有回归分析和相关分析都是研究变量间关系的统计学课题。
区别有a.在回归分析中,变量y称为因变量,处在被解释的特殊地位。
在相关分析中,变量x和变量y处于平等的地位,即研究变量y与变量x的密切程度与研究变量x与变量y的密切程度是一回事。
b.相关分析中所涉及的变量y与变量x全是随机变量.而在回归分析中,因变量y是随机变量,自变量x可以是随机变量也可以是非随机的确定变量。
C.相关分析的研究主要是为了刻画两类变量间线性相关的密切程度。
而回归分析不仅可以揭示变量x对变量y的影响大小,还可以由回归方程进行预测和控制。
1。
3 回归模型中随机误差项ε的意义是什么?答:ε为随机误差项,正是由于随机误差项的引入,才将变量间的关系描述为一个随机方程,使得我们可以借助随机数学方法研究y与x1,x2…。
.xp的关系,由于客观经济现象是错综复杂的,一种经济现象很难用有限个因素来准确说明,随机误差项可以概括表示由于人们的认识以及其他客观原因的局限而没有考虑的种种偶然因素。
1.4 线性回归模型的基本假设是什么?答:线性回归模型的基本假设有:1。
解释变量x1。
x2…。
xp是非随机的,观测值xi1.xi2…..xip是常数.2。
等方差及不相关的假定条件为{E(εi)=0 i=1,2…. Cov(εi,εj)={σ^23。
正态分布的假定条件为相互独立。
4。
样本容量的个数要多于解释变量的个数,即n>p。
1.5 回归变量的设置理论根据是什么?在回归变量设置时应注意哪些问题?答:理论判断某个变量应该作为解释变量,即便是不显著的,如果理论上无法判断那么可以采用统计方法来判断,解释变量和被解释变量存在统计关系.应注意的问题有:在选择变量时要注意与一些专门领域的专家合作,不要认为一个回归模型所涉及的变量越多越好,回归变量的确定工作并不能一次完成,需要反复试算,最终找出最合适的一些变量.1。
(完整word版)应用回归分析,第9章课后习题参考答案

第9章 含定性变量的回归模型思考与练习参考答案9.1 一个学生使用含有季节定性自变量的回归模型,对春夏秋冬四个季节引入4个0—1型自变量,用SPSS 软件计算的结果中总是自动删除了其中的一个自变量,他为此感到困惑不解。
出现这种情况的原因是什么?答:假如这个含有季节定性自变量的回归模型为:t t t t kt k t t D D D X X Y μαααβββ++++++=332211110其中含有k 个定量变量,记为x i 。
对春夏秋冬四个季节引入4个0—1型自变量,记为D i ,只取了6个观测值,其中春季与夏季取了两次,秋、冬各取到一次观测值,则样本设计矩阵为:⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛=000110010110001010010010100011)(616515414313212111k k k k k k X X X X X X X X X X X XD X,显然,(X ,D)中的第1列可表示成后4列的线性组合,从而(X ,D)不满秩,参数无法唯一求出。
这就是所谓的“虚拟变量陷井",应避免。
当某自变量x j 对其余p —1个自变量的复判定系数2j R 超过一定界限时,SPSS 软件将拒绝这个自变量x j 进入回归模型.称Tol j =1—2j R 为自变量x j 的容忍度(Tolerance ),SPSS 软件的默认容忍度为0。
0001。
也就是说,当2j R >0.9999时,自变量x j 将被自动拒绝在回归方程之外,除非我们修改容忍度的默认值。
而在这个模型中出现了完全共线性,所以SPSS 软件计算的结果中总是自动删除了其中的一个定性自变量。
⎪⎪⎪⎪⎪⎭⎫⎝⎛=k βββ 10β⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=4321ααααα9。
2对自变量中含有定性变量的问题,为什么不对同一属性分别建立回归模型,而采取设虚拟变量的方法建立回归模型?答:原因有两个,以例9.1说明。
一是因为模型假设对每类家庭具有相同的斜率和误差方差,把两类家庭放在一起可以对公共斜率做出最佳估计;二是对于其他统计推断,用一个带有虚拟变量的回归模型来进行也会更加准确,这是均方误差的自由度更多。
《应用回归分析》课后题答案-推荐下载

对全部高中资料试卷电气设备,在安装过程中以及安装结束后进行高中资料试卷调整试验;通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关,系电通,力1根保过据护管生高线产中0不工资仅艺料可高试以中卷解资配决料置吊试技顶卷术层要是配求指置,机不对组规电在范气进高设行中备继资进电料行保试空护卷载高问与中题带资2负料2,荷试而下卷且高总可中体保资配障料置2试时32卷,3各调需类控要管试在路验最习;大题对限到设度位备内。进来在行确管调保路整机敷使组设其高过在中程正资1常料中工试,况卷要下安加与全强过,看度并25工且52作尽22下可护都能1关可地于以缩管正小路常故高工障中作高资;中料对资试于料卷继试连电卷接保破管护坏口进范处行围理整,高核或中对者资定对料值某试,些卷审异弯核常扁与高度校中固对资定图料盒纸试位,卷置编工.写况保复进护杂行层设自防备动腐与处跨装理接置,地高尤线中其弯资要曲料避半试免径卷错标调误高试高等方中,案资要,料求编试技5写、卷术重电保交要气护底设设装。备备置管4高调、动线中试电作敷资高气,设料中课并技3试资件且、术卷料中拒管试试调绝路包验卷试动敷含方技作设线案术,技槽以来术、及避管系免架统不等启必多动要项方高方案中式;资,对料为整试解套卷决启突高动然中过停语程机文中。电高因气中此课资,件料电中试力管卷高壁电中薄气资、设料接备试口进卷不行保严调护等试装问工置题作调,并试合且技理进术利行,用过要管关求线运电敷行力设高保技中护术资装。料置线试做缆卷到敷技准设术确原指灵则导活:。。在对对分于于线调差盒试动处过保,程护当中装不高置同中高电资中压料资回试料路卷试交技卷叉术调时问试,题技应,术采作是用为指金调发属试电隔人机板员一进,变行需压隔要器开在组处事在理前发;掌生同握内一图部线纸故槽资障内料时,、,强设需电备要回制进路造行须厂外同家部时出电切具源断高高习中中题资资电料料源试试,卷卷线试切缆验除敷报从设告而完与采毕相用,关高要技中进术资行资料检料试查,卷和并主检且要测了保处解护理现装。场置设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况,然后根据规范与规程规定,制定设备调试高中资料试卷方案。
应用技术回归分析第九章部分完整答案

第9章 非线性回归9.1 在非线性回归线性化时,对因变量作变换应注意什么问题?答:在对非线性回归模型线性化时,对因变量作变换时不仅要注意回归函数的形式, 还要注意误差项的形式。
如:(1) 乘性误差项,模型形式为e y AK L αβε=, (2) 加性误差项,模型形式为y AK L αβε=+。
对乘法误差项模型(1)可通过两边取对数转化成线性模型,(2)不能线性化。
一般总是假定非线性模型误差项的形式就是能够使回归模型线性化的形式,为了方便通常省去误差项,仅考虑回归函数的形式。
9.2为了研究生产率与废料率之间的关系,记录了如表9.14所示的数据,请画出散点图,根据散点图的趋势拟合适当的回归模型。
表9.14生产率x (单位/周) 1000 2000 3000 3500 4000 4500 5000 废品率y (%)5.26.56.88.110.2 10.3 13.0解:先画出散点图如下图:5000.004000.003000.002000.001000.00x12.0010.008.006.00y从散点图大致可以判断出x 和y 之间呈抛物线或指数曲线,由此采用二次方程式和指数函数进行曲线回归。
(1)二次曲线 SPSS 输出结果如下:Mode l Sum mary.981.962.942.651R R SquareAdjusted R SquareStd. E rror of the E stim ateThe independent variable is x.ANOVA42.571221.28650.160.0011.6974.42444.2696Regression Residual TotalSum of Squares dfMean SquareF Sig.The independent variable is x.Coe fficients-.001.001-.449-.891.4234.47E -007.0001.4172.812.0485.843 1.3244.414.012x x ** 2(Constant)B Std. E rror Unstandardized Coefficients BetaStandardizedCoefficientstSig.从上表可以得到回归方程为:72ˆ 5.8430.087 4.4710yx x -=-+⨯ 由x 的系数检验P 值大于0.05,得到x 的系数未通过显著性检验。
应用回归分析课后习题参考答案_全部版__何晓群_刘文卿

第一章回归分析概述1.2 回归分析与相关分析的联系与区别是什么?答:联系有回归分析和相关分析都是研究变量间关系的统计学课题。
区别有 a.在回归分析中,变量y称为因变量,处在被解释的特殊地位。
在相关分析中,变量x和变量y处于平等的地位,即研究变量y与变量x的密切程度与研究变量x与变量y的密切程度是一回事。
b.相关分析中所涉及的变量y与变量x全是随机变量。
而在回归分析中,因变量y是随机变量,自变量x可以是随机变量也可以是非随机的确定变量。
C.相关分析的研究主要是为了刻画两类变量间线性相关的密切程度。
而回归分析不仅可以揭示变量x对变量y的影响大小,还可以由回归方程进行预测和控制。
1.3回归模型中随机误差项ε的意义是什么?答:ε为随机误差项,正是由于随机误差项的引入,才将变量间的关系描述为一个随机方程,使得我们可以借助随机数学方法研究y与x1,x2…..xp的关系,由于客观经济现象是错综复杂的,一种经济现象很难用有限个因素来准确说明,随机误差项可以概括表示由于人们的认识以及其他客观原因的局限而没有考虑的种种偶然因素。
1.4 线性回归模型的基本假设是什么?答:线性回归模型的基本假设有:1.解释变量x1.x2….xp是非随机的,观测值xi1.xi2…..xip是常数。
2.等方差及不相关的假定条件为{E(εi)=0 i=1,2…. Cov(εi,εj)={σ^23.正态分布的假定条件为相互独立。
4.样本容量的个数要多于解释变量的个数,即n>p.第二章一元线性回归分析思考与练习参考答案2.1一元线性回归有哪些基本假定?答:假设1、解释变量X是确定性变量,Y是随机变量;假设2、随机误差项ε具有零均值、同方差和不序列相关性:E(εi)=0 i=1,2, …,nVar (εi)=σ2i=1,2, …,nCov(εi,εj)=0 i≠j i,j= 1,2, …,n假设3、随机误差项ε与解释变量X之间不相关:Cov(X i, εi)=0 i=1,2, …,n假设4、ε服从零均值、同方差、零协方差的正态分布εi~N(0, σ2) i=1,2, …,n2.3 证明(2.27式),∑e i =0 ,∑e i X i =0 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第9章 非线性回归9.1 在非线性回归线性化时,对因变量作变换应注意什么问题?答:在对非线性回归模型线性化时,对因变量作变换时不仅要注意回归函数的形式, 还要注意误差项的形式。
如:(1) 乘性误差项,模型形式为e y AK L αβε=, (2) 加性误差项,模型形式为y AK L αβε=+。
对乘法误差项模型(1)可通过两边取对数转化成线性模型,(2)不能线性化。
一般总是假定非线性模型误差项的形式就是能够使回归模型线性化的形式,为了方便通常省去误差项,仅考虑回归函数的形式。
9.2为了研究生产率与废料率之间的关系,记录了如表9.14所示的数据,请画出散点图,根据散点图的趋势拟合适当的回归模型。
表9.14生产率x (单位/周) 1000 2000 3000 3500 4000 4500 5000 废品率y (%)5.26.56.88.110.2 10.3 13.0解:先画出散点图如下图:5000.004000.003000.002000.001000.00x12.0010.008.006.00y从散点图大致可以判断出x 和y 之间呈抛物线或指数曲线,由此采用二次方程式和指数函数进行曲线回归。
(1)二次曲线 SPSS 输出结果如下:Mode l Sum mary.981.962.942.651R R SquareAdjusted R SquareStd. E rror of the E stim ateThe independent variable is x.ANOVA42.571221.28650.160.0011.6974.42444.2696Regression Residual TotalSum of Squares dfMean SquareF Sig.The independent variable is x.Coe fficients-.001.001-.449-.891.4234.47E -007.0001.4172.812.0485.843 1.3244.414.012x x ** 2(Constant)B Std. E rror Unstandardized Coefficients BetaStandardizedCoefficientstSig.从上表可以得到回归方程为:72ˆ 5.8430.087 4.4710yx x -=-+⨯ 由x 的系数检验P 值大于0.05,得到x 的系数未通过显著性检验。
由x 2的系数检验P 值小于0.05,得到x 2的系数通过了显著性检验。
(2)指数曲线Mode l Sum mary.970.941.929.085RR SquareAdjusted R SquareStd. E rror of the E stim ateThe independent variable is x.ANOVA.5731.57379.538.000.0365.007.6096Regression Residual TotalSum of SquaresdfMean SquareF Sig.The independent variable is x.Coe fficients.000.000.9708.918.0004.003.34811.514.000x(Constant)B Std. E rror Unstandardized Coefficients BetaStandardizedCoefficientstSig.The dependent variable is ln(y).从上表可以得到回归方程为:0.0002t ˆ 4.003ye 由参数检验P 值≈0<0.05,得到回归方程的参数都非常显著。
从R 2值,σ的估计值和模型检验统计量F 值、t 值及拟合图综合考虑,指数拟合效果更好一些。
9.3 已知变量x与y的样本数据如表9.15,画出散点图,试用αeβ/x来拟合回归模型,假设:(1)乘性误差项,模型形式为y=αeβ/x eε(2)加性误差项,模型形式为y=αeβ/x+ε。
表9.15序号x y 序号x y 序号x y1 4.20 0.086 6 3.20 0.150 11 2.20 0.3502 4.06 0.090 7 3.00 0.170 12 2.00 0.4403 3.80 0.100 8 2.80 0.190 13 1.80 0.6204 3.60 0.120 9 2.60 0.220 14 1.60 0.9405 3.40 0.130 10 2.40 0.240 15 1.40 1.620解:散点图:(1)乘性误差项,模型形式为y=αeβ/x eε线性化:lny=lnα+β/x +ε令y1=lny, a=lnα,x1=1/x .做y1与x1的线性回归,SPSS 输出结果如下:Model Summ aryb.999a .997.997.04783Model 1RR SquareAdjusted R SquareStd. E rror of the EstimateP redictors: (Constant), x1a. Dependent Variable: y1b. ANOVA b10.930110.9304778.305.000a.03013.00210.96014Regression Residual TotalModel 1Sum of Squares dfMean SquareF Sig.P redictors: (Constant), x1a. Dependent Variable: y1b. Coe fficientsa -3.856.037-103.830.0006.080.088.99969.125.000(Constant)x1Model1B Std. E rror Unstandardized Coefficients BetaStandardizedCoefficientstSig.Dependent Variable: y1a.从以上结果可以得到回归方程为:y1=-3.856+6.08x1F 检验和t 检验的P 值≈0<0.05,得到回归方程及其参数都非常显著。
回代为原方程为:y=0.021e6.08/x(2)加性误差项,模型形式为y=αeβ/x+ε不能线性化,直接非线性拟合。
给初值α=0.021,β=6.08(线性化结果),NLS 结果如下:Parameter E stimates.021.001.020.0236.061.0445.9656.157P aram etera b E stim ateStd. E rrorLow er Bound Upper Bound95% Confidence I ntervalANOVA a4.4582 2.229.00113.0004.459152.46714Source Regression ResidualUncorrected Total Corrected TotalSum of SquaresdfMean SquaresDependent variable: yR squared = 1 - (Residual Sum of Squares) /(Corrected Sum of Squares) = 1.000.a.从以上结果可以得到回归方程为: y=0.021e 6.061/x根据R 2≈1,参数的区间估计不包括零点且较短,可知回归方程拟合非常好,且其参数都显著。
9.4 Logistic 回归函数常用于拟合某种消费品的拥有率,表8.17(书上239页,此处略)是北京市每百户家庭平均拥有的照相机数,试针对以下两种情况拟合Logistic 回归函数。
0111t y b b u=+(1)已知100u =,用线性化方法拟合,(2)u 未知,用非线性最小二乘法拟合。
根据经济学的意义知道,u 是拥有率的上限,初值可取100;b0>0,0<b1<1初值请读者自己选择。
解:(1),100u =时,的线性拟合。
对0111t y b b u=+函数线性化得到:11ln() 1.8510.264100y -=--0111ln()ln ln 100b t b y -=+,令311ln()100y y =-,作3y 关于t 的线性回归分析,SPSS 输出结果如下:Model Summ aryb.994a .988.987.16820Model 1RR SquareAdjusted R SquareStd. E rror of the EstimateP redictors: (Constant), t a. Dependent Variable: y3b.ANOVA b39.839139.8391408.165.000a.48117.02840.32018Regression Residual TotalModel 1Sum of Squares dfMean SquareF Sig.P redictors: (Constant), t a. Dependent Variable: y3b.Coe fficientsa -1.851.080-23.039.000-.264.007-.994-37.526.000(Constant)tModel1B Std. E rror Unstandardized Coefficients BetaStandardizedCoefficientstSig.Dependent Variable: y3a.由表Model Summary 得到,0.994R =趋于1,回归方程的拟合优度好,由表ANOVA 得到回归方程显著,由Coefficients 表得到,回归系数都是显著的,得到方程:11ln() 1.8510.264100y -=--,进一步计算得到:00.157b =,10.768b =(100u =)回代变量得到最终方程形式为: 1ˆ0.010.1570.768ty=+⨯ 最后看拟合效果,通过sequence 画图:由图可知回归效果比较令人满意。
(2)非线性最小二乘拟合,取初值100u =,00.157b =,10.768b =: 一共循环迭代8次,得到回归分析结果为:Parameter E stimates91.062 2.03586.74795.377.211.028.152.271.727.012.701.753P aram eteru b c E stim ate Std. E rrorLow er Bound Upper Bound95% Confidence I ntervalANOVA a60774.331320258.11085.36916 5.33660859.7001915690.38618Source Regression Residual Uncorrected TotalCorrected Total Sum ofSquares df MeanSquaresDependent variable: yR squared = 1 - (Residual Sum of Squares) /(Corrected Sum of Squares) = .995.a.0.995R =>0.994,得到回归效果比线性拟合要好,且:91.062u =,00.211b =,10.727b =,回归方程为:110.211*0.72791.062ty =+。
