蚁群算法路径规划MATLAB程序
蚁群算法路径优化matlab代码

蚁群算法路径优化matlab代码标题:蚁群算法路径优化 MATLAB 代码正文:蚁群算法是一种基于模拟蚂蚁搜索食物路径的优化算法,常用于求解复杂问题。
在路径优化问题中,蚂蚁需要从起点移动到终点,通过探索周围区域来寻找最短路径。
MATLAB 是一个常用的数值计算软件,可以用来实现蚁群算法的路径优化。
下面是一个基本的 MATLAB 代码示例,用于实现蚁群算法的路径优化:```matlab% 定义参数num_ants = 100; % 蚂蚁数量num_steps = 100; % 路径优化步数search_radius = 2; % 搜索半径max_iterations = 1000; % 最大迭代次数% 随机生成起点和终点的位置坐标start_pos = [randi(100), randi(100)];end_pos = [75, 75];% 初始化蚂蚁群体的位置和方向ants_pos = zeros(num_ants, 2);ants_dir = zeros(num_ants, 2);for i = 1:num_antsants_pos(i, :) = start_pos + randn(2) * search_radius; ants_dir(i, :) = randomvec(2);end% 初始化蚂蚁群体的速度ants_vel = zeros(num_ants, 2);for i = 1:num_antsants_vel(i, :) = -0.1 * ants_pos(i, :) + 0.5 *ants_dir(i, :);end% 初始时蚂蚁群体向终点移动for i = 1:num_antsans_pos = end_pos;ans_vel = ants_vel;for j = 1:num_steps% 更新位置和速度ans_pos(i) = ans_pos(i) + ans_vel(i);ants_vel(i, :) = ones(1, num_steps) * (-0.1 * ans_pos(i) + 0.5 * ans_dir(i, :));end% 更新方向ants_dir(i, :) = ans_dir(i, :) - ans_vel(i) * 3;end% 迭代优化路径max_iter = 0;for i = 1:max_iterations% 计算当前路径的最短距离dist = zeros(num_ants, 1);for j = 1:num_antsdist(j) = norm(ants_pos(j) - end_pos);end% 更新蚂蚁群体的位置和方向for j = 1:num_antsants_pos(j, :) = ants_pos(j, :) - 0.05 * dist(j) * ants_dir(j, :);ants_dir(j, :) = -ants_dir(j, :);end% 更新蚂蚁群体的速度for j = 1:num_antsants_vel(j, :) = ants_vel(j, :) - 0.001 * dist(j) * ants_dir(j, :);end% 检查是否达到最大迭代次数if i > max_iterationsbreak;endend% 输出最优路径[ans_pos, ans_vel] = ants_pos;path_dist = norm(ans_pos - end_pos);disp(["最优路径长度为:" num2str(path_dist)]);```拓展:上述代码仅仅是一个简单的示例,实际上要实现蚁群算法的路径优化,需要更加复杂的代码实现。
PythonMatlab实现蚂蚁群算法求解最短路径问题的示例

PythonMatlab实现蚂蚁群算法求解最短路径问题的⽰例⽬录1知识点1.1 蚁群算法步骤1.2 蚁群算法程序2蚂蚁算法求解最短路径问题——Python实现2.1源码实现2.2 ACA_TSP实现3 蚂蚁算法求解最短路径问题——Matlab实现3.1流程图3.2代码实现3.3结果1 知识点详细知识点见:我们这⼀节知识点只讲蚁群算法求解最短路径步骤及流程。
1.1 蚁群算法步骤设蚂蚁的数量为m,地点的数量为n,地点i与地点j之间相距Dij,t时刻地点i与地点j连接的路径上的信息素浓度为Sij,初始时刻每个地点间路径上的信息素浓度相等。
蚂蚁k根据各个地点间连接路径上的信息素决定下⼀个⽬标地点,Pijk表⽰t时刻蚂蚁k从地点i转移的概率,概率计算公式如下:上式中,为启发函数,,表⽰蚂蚁从地点i转移到地点j的期望程度;为蚂蚁k即将访问地点的集合,开始时中有n-1个元素(除出发地点),随时间的推移,蚂蚁每到达下⼀个地点,中的元素便减少⼀个,直⾄空集,即表⽰所有地点均访问完毕;a为信息素重要程度因⼦,值越⼤,表明信息素的浓度在转移中起到的作⽤越⼤,也就是说蚂蚁选择距离近的下⼀个地点的概率更⼤,β为启发函数重要程度因⼦。
蚂蚁在释放信息素的同时,每个地点间连接路径上的信息素逐渐消失,⽤参数表⽰信息素的挥发程度。
因此,当所有蚂蚁完成⼀次循环后,每个地点间连接路径上的信息素浓度需更新,也就是有蚂蚁路过并且留下信息素,有公式表⽰为:其中,表⽰第k只蚂蚁在地点i与j连接路径上释放的信息素浓度;表⽰所有蚂蚁在地点i与j连接路径上释放的信息素浓度之和;Q为常数,表⽰蚂蚁循环⼀次所释放的信息素总量;Lk表⽰第k只蚂蚁经过路径的长度,总的来说,蚂蚁经过的路径越短,释放的信息素浓度越⾼,最终选出最短路径。
1.2 蚁群算法程序(1)参数初始化在寻最短路钱,需对程序各个参数进⾏初始化,蚁群规模m、信息素重要程度因⼦α、启发函数重要程度因⼦β、信息素会发因⼦、最⼤迭代次数ddcs_max,初始迭代值为ddcs=1。
蚁群算法matlab代码讲解

蚁群算法matlab代码讲解蚁群算法(Ant Colony Algorithm)是模拟蚁群觅食行为而提出的一种优化算法。
它以蚁群觅食的方式来解决优化问题,比如旅行商问题、图着色问题等。
该算法模拟了蚂蚁在寻找食物时的行为,通过信息素的正反馈和启发式搜索来实现问题的最优解。
在蚁群算法中,首先需要初始化一组蚂蚁和问题的解空间。
每只蚂蚁沿着路径移动,通过信息素和启发式规则来选择下一步的移动方向。
当蚂蚁到达目标位置后,会根据路径的长度来更新信息素。
下面是一个用MATLAB实现蚁群算法的示例代码:```matlab% 参数设置num_ants = 50; % 蚂蚁数量num_iterations = 100; % 迭代次数alpha = 1; % 信息素重要程度因子beta = 5; % 启发式因子rho = 0.1; % 信息素蒸发率Q = 1; % 信息素增加强度因子pheromone = ones(num_cities, num_cities); % 初始化信息素矩阵% 初始化蚂蚁位置和路径ants = zeros(num_ants, num_cities);for i = 1:num_antsants(i, 1) = randi([1, num_cities]);end% 迭代计算for iter = 1:num_iterations% 更新每只蚂蚁的路径for i = 1:num_antsfor j = 2:num_cities% 根据信息素和启发式规则选择下一步移动方向next_city = choose_next_city(pheromone, ants(i, j-1), beta);ants(i, j) = next_city;endend% 计算每只蚂蚁的路径长度path_lengths = zeros(num_ants, 1);for i = 1:num_antspath_lengths(i) = calculate_path_length(ants(i, :), distances);end% 更新信息素矩阵pheromone = (1 - rho) * pheromone;for i = 1:num_antsfor j = 2:num_citiespheromone(ants(i, j-1), ants(i, j)) = pheromone(ants(i, j-1), ants(i, j)) + Q / path_lengths(i); endendend```上述代码中的参数可以根据具体问题进行调整。
matlab的蚂蚁算法的实现

matlab的蚂蚁算法的实现
在上述代码中,我们首先设置了一些参数,如蚂蚁数量、迭代次数、信息素和启发式信息 的重要程度等。然后,根据参数初始化了信息素矩阵,并进行了迭代优化过程。
在每次迭代中,我们先初始化蚂蚁的位置,然后根据信息素和启发式信息的重要程度,以 及当前城市和已访问城市的距离,计算每个城市被选择的概率。根据概率选择下一个城市, 直到完成整个路径的选择。然后,根据蚂蚁的路径更新信息素矩阵。重复迭代过程,直到达 到指定的迭代次数。
最后,输出最优路径和最优距离。
matlab的蚂蚁算法的实现
需要注意的是,上述代码只是一个简单的示例,实际应用中可能需要根据具体问题进行适 当的调整和扩展。蚂蚁算法的实现也可能因问题的复杂性和特点而有所不同。
Байду номын сангаас
matlab的蚂蚁算法的实现
以下是一个使用 MATLAB 实现蚂蚁算法的简单示例:
```matlab % 参数设置 numAnts = 10; % 蚂蚁数量 numIterations = 100; % 迭代次数 alpha = 1; % 信息素重要程度 beta = 5; % 启发式信息重要程度 rho = 0.5; % 信息素挥发率 Q = 1; % 信息素增量 numCities = 10; % 城市数量 distances = rand(numCities); % 城市之间的距离矩阵
蚁群算法matlab代码

蚁群算法matlab代码蚁群算法,英文名为Ant Colony Algorithm,缩写为ACO,是一种启发式算法,是一种模拟蚂蚁寻找食物路径的算法。
在实际生活中,蚂蚁找到食物并返回巢穴后,将其找到食物的路径上的信息素留下,其他蚂蚁通过检测信息素来指导寻路,成为了一种集体智慧行为。
ACO也是通过模拟蚂蚁寻找食物路径的方式来寻找优化问题的最优解。
在ACO算法中,信息素是一个重要的概念,代表了走过某一路径的“好概率”,用这个“好概率”更新一些路径上的信息素,使得其他蚂蚁更可能选择经过这条路径,从而实现路径优化的目的。
在本文中,我们将讨论如何使用Matlab实现蚁群算法来优化问题。
1. 设定问题首先,我们要选取一个优化问题,并将其转换为需要在优化过程中进行选择的决策变量。
例如,我们想要优化旅行商问题(TSP)。
在TSP中,我们需要让旅行商以最短的距离经过所有城市,每个城市仅经过一次,最终回到出发的城市。
我们可以将每个城市编号,然后将TSP转化为一个最短路径选择的问题,即最短路径从编号为1的城市开始,经过所有城市,最终回到编号为1的城市。
2. 设定ACO参数在使用ACO优化问题时,需要设定一些参数,这些参数会影响算法的表现。
ACO算法需要设定的参数有:1.信息素含量:初始信息素的大小,即每个路径上的信息素浓度。
2.信息素挥发速度:信息素的随时间“减弱”程度。
3.信息素加成强度:蚂蚁经过路径后增加的信息素量。
4.启发式权重:用于计算启发式因子,即节点距离的贡献值。
5.蚂蚁数量:模拟蚂蚁数量,即同时寻找路径的蚂蚁个数。
6.迭代次数:模拟的迭代次数,即ACO算法运行的次数。
7.初始节点:ACO算法开始的节点。
3. 创建ACO优化函数我们可以使用Matlab来创建一个函数来实现ACO算法。
我们称其为“ACOoptimization.m”。
function best_path =ACOoptimization(city_location,iter_num,ant_num,init ial_path,alpha,beta,rho,update_flag) %ACO优化函数 %输入: %city_location: 城市坐标矩阵,格式为[x1,y1;x2,y2;...;xn,yn] %iter_num: 迭代次数 %ant_num: 蚂蚁数量 %initial_path: 起始路径,即初始解 %alpha,beta,rho: 超参数,用于调节蚂蚁选择路径的概率 %update_flag: 是否更新信息素的标志(1表示更新,0表示否) %输出: %best_path: 最优解,即最短路径%初始化信息素 pheromone = 0.01 *ones(length(city_location),length(city_location)); %初始化路径权重 path_weight =zeros(ant_num,1); %城市数量 n_cities =length(city_location);%主循环 for iter = 1:iter_num %一个迭代里所有蚂蚁都寻找一遍路径 for ant =1:ant_num %初始化蚂蚁位置current_city = initial_path; %标记是否经过了某个城市 visit_flag =zeros(1,n_cities);visit_flag(current_city) = 1; %用来存储当前路径 current_path = [current_city];%蚂蚁找东西 for i =1:n_cities-1 %计算路径概率p =calculate_probability(current_city,visit_flag,phero mone,city_location,alpha,beta); %蚂蚁选择路径 [next_city,next_index] = select_path(p);%路径更新current_path = [current_path;next_city];visit_flag(next_city) = 1;current_city = next_city;%更新路径权重path_weight(ant) = path_weight(ant) +Euclidean_distance(city_location(current_path(end-1),:),city_location(current_path(end),:));end%加入回到起点的路径权重path_weight(ant) = path_weight(ant) +Euclidean_distance(city_location(current_path(end),:),city_location(current_path(1),:));%判断是否为最优解 ifant == 1 best_path = current_path; else if path_weight(ant) <path_weight(ant-1) best_path =current_path; end end%更新信息素 ifupdate_flag == 1 pheromone =update_pheromone(pheromone,path_weight,initial_path,current_path,rho); end end end end在函数中,我们首先定义了ACOalg函数的参数,包括城市坐标矩阵,迭代次数,蚂蚁数量,初始路径,超参数alpha,beta,rho,以及是否需要更新信息素。
(完整word版)基于蚁群算法的路径规划

MATLAB 实现基于蚁群算法的机器人路径规划1、问题描述移动机器人路径规划是机器人学的一个重要研究领域。
它要求机器人依据某个或某些优化原则(如最小能量消耗,最短行走路线,最短行走时间等),在其工作空间中找到一条从起始状态到目标状态的能避开障碍物的最优路径。
机器人路径规划问题可以建模为一个有约束的优化问题,都要完成路径规划、定位和避障等任务。
2 算法理论蚁群算法(Ant Colony Algorithm ,ACA ),最初是由意大利学者Dorigo M. 博士于1991 年首次提出,其本质是一个复杂的智能系统,且具有较强的鲁棒性,优良的分布式计算机制等优点。
该算法经过十多年的发展,已被广大的科学研究人员应用于各种问题的研究,如旅行商问题,二次规划问题,生产调度问题等。
但是算法本身性能的评价等算法理论研究方面进展较慢。
Dorigo 提出了精英蚁群模型(EAS ),在这一模型中信息素更新按照得到当前最优解的蚂蚁所构造的解来进行,但这样的策略往往使进化变得缓慢,并不能取得较好的效果。
次年Dorigo 博士给出改进模型(ACS ),文中改进了转移概率模型,并且应用了全局搜索与局部搜索策略,来得进行深度搜索。
Stützle 与Hoos 给出了最大-最小蚂蚁系统(MAX-MINAS ),所谓最大-最小即是为信息素设定上限与下限,设定上限避免搜索陷入局部最优,设定下限鼓励深度搜索。
蚂蚁作为一个生物个体其自身的能力是十分有限的,比如蚂蚁个体是没有视觉的,蚂蚁自身体积又是那么渺小,但是由这些能力有限的蚂蚁组成的蚁群却可以做出超越个体蚂蚁能力的超常行为。
蚂蚁没有视觉却可以寻觅食物,蚂蚁体积渺小而蚁群却可以搬运比它们个体大十倍甚至百倍的昆虫。
这些都说明蚂蚁群体内部的某种机制使得它们具有了群体智能,可以做到蚂蚁个体无法实现的事情。
经过生物学家的长时间观察发现,蚂蚁是通过分泌于空间中的信息素进行信息交流,进而实现群体行为的。
matlab基于蚁群算法的二维路径规划算法【matlab优化算法二十二】
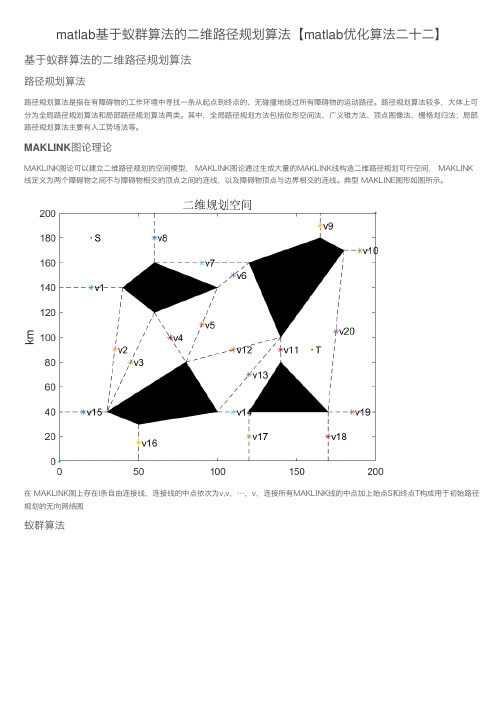
matlab基于蚁群算法的⼆维路径规划算法【matlab优化算法⼆⼗⼆】基于蚁群算法的⼆维路径规划算法路径规划算法路径规划算法是指在有障碍物的⼯作环境中寻找⼀条从起点到终点的、⽆碰撞地绕过所有障碍物的运动路径。
路径规划算法较多,⼤体上可分为全局路径规划算法和局部路径规划算法两类。
其中,全局路径规划⽅法包括位形空间法、⼴义锥⽅法、顶点图像法、栅格划归法;局部路径规划算法主要有⼈⼯势场法等。
MAKLINK图论理论MAKLINK图论可以建⽴⼆维路径规划的空间模型, MAKLINK图论通过⽣成⼤量的MAKLINK线构造⼆维路径规划可⾏空间, MAKLINK 线定义为两个障碍物之间不与障碍物相交的顶点之间的连线,以及障碍物顶点与边界相交的连线。
典型 MAKLINE图形如图所⽰。
在 MAKLINK图上存在l条⾃由连接线,连接线的中点依次为v,v,…,v,连接所有MAKLINK线的中点加上始点S和终点T构成⽤于初始路径规划的⽆向⽹络图蚁群算法蚁群算法是由 dorigo.M等⼈在20世纪90年代初提出的⼀种新型进化算法,它来源于对蚂蚁搜索问题的研究。
⼈们在观察蚂蚁搜索⾷物时发现,蚂蚁在寻找⾷物时,总在⾛过的路径上释放⼀种称为信息素的分泌物,信息素能够保留⼀段时间,使得在⼀定范围内的其他蚂蚁能够觉察到该信息素的存在。
后继蚂蚁在选择路径时,会选择信息素浓度较⾼的路径,并且在经过时留下⾃⼰的信息素这样该路径的信息素会不断增强,蚂蚁选择的概率也在不断增⼤蚁群算法最优路径寻找如图。
图表达了蚂蚁在觅⾷过程中的三个过程,其中点A是蚂蚁蚁巢,点D是⾷物所在地,四边形 EBFCE表⽰在蚁巢和⾷物之间的障碍物。
蚂蚁如果想从蚁巢点A达到点D,只能经过路径BFC或者路径BEC,假定从蚁巢中出来若⼲只蚂蚁去⾷物所在地D搬运⾷物,每只蚂蚁经过后留下的信息素为1,信息素保留的时间为1.⼀开始,路径BFC和BEC上都没有信息素,在点A的蚂蚁可以随机选择路径,蚂蚁以相同的概率选择路径BFC或BEC,如图(b)所⽰。
蚁群算法的Matlab程序

#include<iostream.h>#include<stdlib.h>#include<time.h>#include<math.h>#define citynumber 5#define Q 100#define p 0.5#define NM2 1000#define A 1#define B 5int ccdi=-1;//全局变量,用在myrand()中float myrand()//产生0-1随机数,100个,每调用一次,结果不同{srand(time(0));float my[100];ccdi++;if (ccdi==100)ccdi=0;for(int mi=0;mi<100;mi++){float fav=rand()%10000;my[mi]=fav/10000;}return my[ccdi];}double fpkij(double T[citynumber][citynumber],double n[citynumber][citynumber],int tabu[citynumber][citynumber],int k,int s,int i,int j )//定义函数用于计算Pij{//double A=0.5,B=0.5;double sumup,pkij,sumdown;sumdown=0;for(int aTi=0;aTi<citynumber;aTi++){for(int aTj=0;aTj<citynumber;aTj++)aT[aTi][aTj]=pow(T[aTi][aTj],A);}for(int bni=0;bni<citynumber;bni++){for(int bnj=0;bnj<citynumber;bnj++)bn[bni][bnj]=pow(n[bni][bnj],B);}for (int can=0;can<citynumber;can++)//判断,除掉已经走过的城市{if(can==tabu[k][ci]){aT[i][can]=0;bn[i][can]=0;}}sumup=aT[i][j]*bn[i][j];for(int tj=0;tj<citynumber;tj++)sumdown=aT[i][tj]*bn[i][tj]+sumdown;pkij=sumup/sumdown;return pkij;}void main(){ doublecity[citynumber][2]={{0,1},{0,2},{2,2},{2,4},{1,3}/*,{3,4},{4,7},{2,8},{3,9},{1,10},{1,0},{2,1},{3,0},{4,9},{5,2},{6,2},{7,1},{8,6},{9,0},{10,3}*/}; /*城市坐标*/ double d[citynumber][citynumber]; //L[j][k]是城市j to k距离for(int j=0;j<citynumber;j++){d[j][k]=sqrt((city[j][0]-city[k][0])*(city[j][0]-city[k][0])+(city[j][1]-city[k][1])*(city[j][1]-city[k] [1]));// cout<<d[j][k]<<" ";}//cout<<"\n";} /*计算距离,从j城市到k城市*//* for (int cj=0;cj<10;cj++){float c=myrand();cout<<c<<" "<<"\n";}*///输出随机数double n[citynumber][citynumber];for(int ni=0;ni<citynumber;ni++){for(int j=0;j<citynumber;j++)}//cout<<"\n";} /*初始化visibility nij*/double L[citynumber];int shortest[citynumber];double T[citynumber][citynumber];for(int ti=0;ti<citynumber;ti++){for (int j=0;j<citynumber;j++){//cout<<T[ti][j]<<" ";}//cout<<"\n";}/*初始化t*/double changT[citynumber][citynumber];//step2:for(int NC=0;NC<NM2;NC++){ for(int cti=0;cti<citynumber;cti++){for (int j=0;j<citynumber;j++){changT[cti][j]=0;//cout<<changT[cti][j]<<" ";}//cout<<"\n";} /*初始化changT*/int tabu[citynumber][citynumber];//tabu[k][s]表示第k只蚂蚁,第s次循环所在的城市for (int i=0;i<citynumber;i++)tabu[tai][i]=0;}for (int tabui1=0;tabui1<citynumber;tabui1++)tabu[tabui1][0]=tabui1;/*for (tai=0;tai<citynumber;tai++){for (int i=0;i<citynumber;i++)cout<<tabu[tai][i]<<" ";cout<<"\n";}*///初始化tabufor(int kk=0;kk<citynumber;kk++)L[kk]=0;//第三步开始for(int s=0;s<citynumber-1;s++){for(int k=0;k<citynumber;){int ci,can;float sumpk=0;float pkij;hq2: can++;if (can==citynumber) can=0;for (ci=0;ci<=s;ci++){if(can==tabu[k][ci]) goto hq2;}pkij=fpkij(T,n,tabu,k,s,tabu[k][s],can);sumpk=sumpk+pkij;else goto hq2;tabu[k][s+1]=can;k++;}} //第三步完成/*for (tai=0;tai<citynumber;tai++){for (int i=0;i<citynumber;i++) }*///输出一个循环后的tabu[][]//第四步开始for(int k4=0;k4<citynumber;k4++){s44=s4+1;if (s44==citynumber) s44=0;L[k4]+=d[tabu[k4][s4]][tabu[k4][s44]]; }//cout<<L[k4]<<" ";}//计算L[k]float shortest1=0; int short2=0;//最短距离for(ii=1;shorti<citber;shi++ ){shortest1=L[0];if(L[shorti]<=shortest1){shortest1=L[shorti];short2=shorti;}}//cout<<L[sort2]<<"\n";cout<<short2<<"\n";for(int shoi=0;shoi<ctynumber;shoi++){shortest[shoi]=tabu[short2][shoi];//cout<<shest[shoi]<<" ";}//cout<<"\n";for(int k41=0;k41<citynumber;k41++){for(int s41=0,ss=0;s41<citynumber;s41++){ss=s41+1;if (ss==citynumber) ss=0;changT[tabu[k41][s41]][tabu[k41][ss]]+=Q/L[k41];changT[tabu[k41][ss]][tabu[k41][s41]]=changT[tabu[k41][s41]][tabu[k41][ss]]; }}/* for(int cti4=0;cti4<citynumber;cti4++){for (int j=0;j<citynumber;j++){cout<<changT[cti4][j]<<" ";}cout<<"\n";}*///第四步完// 第五步开始for(int i5=0;i5<citynumber;i5++){for(int j5=0;j5<citynumber;j5++){// cout<<T[i5][j5]<<" ";}//cout<<"\n";}}for(int shoi1=0;shoi1<citynumber;shoi1++){cout<<city[shortest[shoi1]][0]<<" "<<city[shortest[shoi1]][1]<<" ";}}。
基于MATLAB的蚁群算法实验研究程序的应用

基于MATLAB的蚁群算法实验研究程序的应用%蚁周模型,解决TSP问题function AS()%clc%初始化format short;n=6; %n 城市数目m=30; %m 蚂蚁数量Nmax=100;%最大循环次数%d(i,j)城市i,j之间的距离,d is a n*n matrixd=[inf,1,inf,inf,8,inf;1,inf,8,inf,4,5;inf,8,inf,3,6,7;inf,inf,3,inf,inf,10;8,4,6, inf,inf,9;inf,5,7,10,9,inf];y=zeros(n,n);%y(i,j)=1/d(i,j) 在TSP问题中,启发信息for i=1:nfor j=1:ny(i,j)=1/d(i,j);endende=1;%信息启发因子f=1;%期望启发因子Q=20;%S=ones(n,n);%(i,j)路段初始化起始信息素for i=1:nfor j=1:nif d(i,j)==infS(i,i)=0;endendendS1=zeros(n,n);%(i,j)路段信息素增量s=zeros(n,n,m);%s(i,j,k)蚂蚁k在路径i,j上残留的信息素notallowed=ones(m,n);%禁忌表,0表示已经访问过a=zeros(m,n);%蚂蚁循环一次的路径for k=1:ma(k,1)=1+round(rand*(n-1));%将蚂蚁随机放到n个城市上endfor k=1:m % 将初始城市放入禁忌表中notallowed(k,a(k,1))=0;endfor N=1:Nmax %N 循环次数t=2;L=zeros(1,m);while t<=n %重复直至禁忌表满为止for k=1:m%计算蚂蚁k转移的概率i=a(k,t-1);p=zeros(1,n);%p(j)蚂蚁k选择路径i,j的概率for j=1:nif notallowed(k,j)~=0u=(S(i,j)^e)*(y(i,j)^f);v=0;for w=1:nv=v+(S(i,w)^e)*(y(i,w)^f)*notallowed(k,w);endif v~=0p(j)=u/v;endendend[pk,j]=max(p);notallowed(k,j)=0;L(k)=L(k)+d(i,j);a(k,t)=j;endt=t+1;endfor k=1:mL(k)=L(k)+d(a(k,n),a(k,1));end%一次循环结束,回到起始位置%更新for k=1:mfor i=1:n-1s(a(k,i),a(k,i+1),k)=Q/L(k);ends(a(k,n),a(k,1),k)=Q/L(k);endfor i=1:nfor j=1:nif d(i,j)~=inffor k=1:mS1(i,j)=S1(i,j)+s(i,j,k);endendendendfor i=1:nfor j=1:nif d(i,j)~=infS(i,j)=(1-rand)*S(i,j)+S1(i,j);endendendfor k=1:m %将禁忌表中除起始城市,全都置为未访问for t=1:nif t~=a(k,1)notallowed(k,t)=1;endendendS1=zeros(n,n);%(i,j)路段信息素增量清零s=zeros(n,n,m);%s(i,j,k)蚂蚁k在路径i,j上残留的信息素清零end %循环最大次数结束[result,k]=min(L)a(k,:)。
蚁群优化算法原理及Matlab编程实现

蚁群优化算法原理及Matlab编程实现
蚁群算法的提出:
人工蚂蚁与真实蚂蚁的异同比较
相同点比较
不同点比较
蚁群算法的流程图
基本蚁群算法的实现步骤
(i,j)的初始化信息量τij(t) = const,其中const表示常数,且初始时刻Δτij(0) = 0。
(2)循环次数。
(3)蚂蚁的禁忌表索引号k=1。
(4)蚂蚁数目。
(5)蚂蚁个体根据状态转移概率公式计算的概率选择元素(城市)j并前进,。
其中,表示在t时刻蚂蚁k由元素(城市)i转移到元素(城市)j的状态转
重要性,反映了蚂蚁在运动过程中启发信息在蚂蚁选择路径中的受重
视程度,其值越大,则该状态转移概率越接近于贪心规则;ηij(t)为启发函数,
表达式为。
式中,d ij表示相邻两个城市之间的距离。
(6)修改禁忌表指针,即选择好之后将蚂蚁移动到新的元素(城市),并把该τij(t + n) = (1 − ρ) * τij(t) + Δτij(t)
(9)若满足结束条件,即如果循环次数,则循环结束并输出程序计算结果,
]蚁群算法的matlab源程序1.蚁群算法主程序:main.m
2.蚁群算法寻找路径程序:path.m
[编辑]蚁群算法仿真结果。
蚁群算法整个程序(matlab)

蚁群算法整个程序(matlab)main:%function [bestroute,routelength]=Ant clccleartic% 读入城市间距离矩阵数据文件CooCity = load( 'CooCity.txt' ) ;% 城市网络图坐标数据文件,txt形式给出 NC=length(CooCity); % 城市个数for i=1:NC % 计算各城市间的距离for j=1:NCdistance(i,j)=sqrt((CooCity(i,2)-CooCity(j,2))^2+(CooCity(i,3)-CooCity(j,3))^2);endend% distance=xlsread('DistanceCity.xls'); % 城市间距离矩阵数据文件,excel形式给出MAXIT=10; % 最大循环次数Citystart=[]; % 起点城市编号tau=ones(NC,NC); % 初始时刻各边上的信息痕迹为1rho=0.5; % 挥发系数alpha=1; % 残留信息相对重要度beta=5; % 预见值的相对重要度Q=10; % 蚁环常数NumAnt=20; % 蚂蚁数量%bestroute=zeros(1,48); % 用来记录最优路径routelength=inf; % 用来记录当前找到的最优路径长度for n=1:MAXITfor k=1:NumAnt %考查第K只蚂蚁deltatau=zeros(NC,NC); % 第K只蚂蚁移动前各边上的信息增量为零%[routek,lengthk]=path(distance,tau,alpha,beta,[]); % 不靠率起始点[routek,lengthk]=path(distance,tau,alpha,beta,Citystart); % 指定起始点if lengthk<routelength % 找到一条更好的路径routelength=lengthk;bestroute=routek;endfor i=1:NC-1 % 第K只蚂蚁在路径上释放的信息量deltatau(routek(i),routek(i+1))=deltatau(routek(i),routek(i+1))+Q/le ngthk; % 信息素更新end%deltatau(routek(NC),1)=deltatau(routek(NC),1)+Q/lengthk; %endlength_n(n)=routelength; % 记录路径收敛tau=(1-rho).*tau; % 信息素挥发end%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% costtime=toc;subplot(1,2,1),plot([CooCity(bestroute,2)],[CooCity(bestroute,3)],'-*')subplot(1,2,2),plot([1:MAXIT],length_n,'-*')[routelength,costtime]inroute:function Y=inroute(n,A)% A 为已过城市点集合,如果n在A中返回1 Y=0;for i=1:length(A)if A(i)==nY=1;break;endendnextcitychoose:% % ,为何不直接以转移概率最大值对应节点为下一转移节点 % 随机决策原则确定下步转移节点, 转移概率累积序列大于某随机值方向 functionN=nextcitychoose(Cp)a=rand;s=0;for i=1:length(Cp)s=s+Cp(i);if a<=sN=i;break;endendnextcitychoose2:% % 直接以转移概率最大值对应节点为下一转移节点% 随机决策原则确定下步转移节点function N=nextcitychoose2(Cp)I=find(Cp==max(Cp));N=I(1);nextcitychoose3% % 直接以转移概率最大值对应节点为下一转移节点% 随机决策原则确定下步转移节点function N=nextcitychoose2(Cp)I=find(Cp==max(Cp));N=I(1);path:% 某只蚂蚁找到的某条路径routek,lengthk function [routek,lengthk]=path(distance,tau,alpha,beta,Citystart) [m,n]=size(distance);if isempty(Citystart) % 如果不确定起点p=fix(m*rand)+1; % 随机方式初始化起点,均匀概率 else p=Citystart; % 外部给定确定起点endlengthk=0; % 初始路径长度设为 0routek=[p]; % 蚂蚁路径点序列,即该蚂蚁已经过的城市集合,路径初始起点for i=1:m-1np=routek(end); % 蚂蚁路径城市序号,依次经过的城市编号np_sum=0; % 路由长度初始为 0for j=1:mif inroute(j,routek) % 判断城市节点j是否属于tabuk,即是否已经过continue;else % j为还未经过的点,对ada=1/distance(np,j); % 预见度np_sum=np_sum+tau(np,j)^alpha*ada^beta; % 路由表:信息痕迹、预见度endendcp=zeros(1,m); % 转移概率,基于路径长度及路由表for j=1:mif inroute(j,routek)continue;elseada=1/distance(np,j); % 预见度cp(j)=tau(np,j)^alpha*ada^beta/np_sum; % np到j的转移概率endendNextCity=nextcitychoose3(cp); % 根据转移概率确定下一个城市,% 这里采用不同的随机决策原则所得效果也不同:% nextcitychoose3 取转移概率最大值方向% nextcitychoose和nextcitychoose2 转移概率累积序列大于某随机值方向% 直观地,取转移概率最大值方向方法,决策结果稳定且收敛快routek=[routek,NextCity]; % 更新路径lengthk=lengthk+distance(np,NextCity); % 更新路径长度 end。
基于蚁群算法的机器人路径规划MATLAB源码收藏

基于蚁群算法的机器人路径规划MA TLAB源码收藏使用网格离散化的方法对带有障碍物的环境建模,使用邻接矩阵存储该环境,使得问题转化为蚁群算法寻找最短路径。
function [ROUTES,PL,Tau]=ACASPS(G,Tau,K,M,S,E,Alpha,Beta,Rho,Q)%% ---------------------------------------------------------------% ACASP.m% 蚁群算法动态寻路算法%% ---------------------------------------------------------------% 输入参数列表% G 地形图为01矩阵,如果为1表示障碍物% Tau 初始信息素矩阵(认为前面的觅食活动中有残留的信息素)% K 迭代次数(指蚂蚁出动多少波)% M 蚂蚁个数(每一波蚂蚁有多少个)% S 起始点(最短路径的起始点)% E 终止点(最短路径的目的点)% Alpha 表征信息素重要程度的参数% Beta 表征启发式因子重要程度的参数% Rho 信息素蒸发系数% Q 信息素增加强度系数%% 输出参数列表% ROUTES 每一代的每一只蚂蚁的爬行路线% PL 每一代的每一只蚂蚁的爬行路线长度% Tau 输出动态修正过的信息素%% --------------------变量初始化----------------------------------%loadD=G2D(G);N=size(D,1);%N表示问题的规模(象素个数)MM=size(G,1);a=1;%小方格象素的边长Ex=a*(mod(E,MM)-0.5);%终止点横坐标if Ex==-0.5Ex=MM-0.5;endEy=a*(MM+0.5-ceil(E/MM));%终止点纵坐标Eta=zeros(1,N);%启发式信息,取为至目标点的直线距离的倒数%下面构造启发式信息矩阵for i=1:Nix=a*(mod(i,MM)-0.5);if ix==-0.5ix=MM-0.5;endiy=a*(MM+0.5-ceil(i/MM));if i~=EEta(1,i)=1/((ix-Ex)^2+(iy-Ey)^2)^0.5;elseEta(1,i)=100;endendROUTES=cell(K,M);%用细胞结构存储每一代的每一只蚂蚁的爬行路线PL=zeros(K,M);%用矩阵存储每一代的每一只蚂蚁的爬行路线长度%% -----------启动K轮蚂蚁觅食活动,每轮派出M只蚂蚁-------------------- for k=1:K%disp(k);for m=1:M%% 第一步:状态初始化W=S;%当前节点初始化为起始点Path=S;%爬行路线初始化PLkm=0;%爬行路线长度初始化TABUkm(S)=0;%已经在初始点了,因此要排除DD=D;%邻接矩阵初始化%% 第二步:下一步可以前往的节点DW=DD(W,:);DW1=find(DW<inf);for j=1:length(DW1)if TABUkm(DW1(j))==0endendLJD=find(DW<inf);%可选节点集Len_LJD=length(LJD);%可选节点的个数%% 觅食停止条件:蚂蚁未遇到食物或者陷入死胡同while W~=E&&Len_LJD>=1%% 第三步:转轮赌法选择下一步怎么走PP=zeros(1,Len_LJD);for i=1:Len_LJDendPP=PP/(sum(PP));%建立概率分布Pcum=cumsum(PP);Select=find(Pcum>=rand);to_visit=LJD(Select(1));%下一步将要前往的节点%% 第四步:状态更新和记录Path=[Path,to_visit];%路径增加PLkm=PLkm+DD(W,to_visit);%路径长度增加W=to_visit;%蚂蚁移到下一个节点for kk=1:Nif TABUkm(kk)==0DD(W,kk)=inf;DD(kk,W)=inf;endendTABUkm(W)=0;%已访问过的节点从禁忌表中删除DW=DD(W,:);LJD=find(DW<inf);%可选节点集Len_LJD=length(LJD);%可选节点的个数end%% 第五步:记下每一代每一只蚂蚁的觅食路线和路线长度ROUTES{k,m}=Path;if Path(end)==EPL(k,m)=PLkm;elsePL(k,m)=inf;endend%% 第六步:更新信息素Delta_Tau=zeros(N,N);%更新量初始化for m=1:Mif PL(k,m)<infROUT=ROUTES{k,m};TS=length(ROUT)-1;%跳数PL_km=PL(k,m);for s=1:TSx=ROUT(s);y=ROUT(s+1);Delta_Tau(x,y)=Delta_Tau(x,y)+Q/PL_km;Delta_Tau(y,x)=Delta_Tau(y,x)+Q/PL_km;endendendTau=(1-Rho).*Tau+Delta_Tau;%信息素挥发一部分,新增加一部分end%% ---------------------------绘图--------------------------------plotif=0;%是否绘图的控制参数if plotif==1%绘收敛曲线meanPL=zeros(1,K);minPL=zeros(1,K);for i=1:KPLK=PL(i,:);Nonzero=find(PLK<inf);PLKPLK=PLK(Nonzero);meanPL(i)=mean(PLKPLK);minPL(i)=min(PLKPLK);endfigure(1)plot(minPL);hold onplot(meanPL);grid ontitle('收敛曲线(平均路径长度和最小路径长度)'); xlabel('迭代次数');ylabel('路径长度');%绘爬行图figure(2)axis([0,MM,0,MM])for i=1:MMfor j=1:MMif G(i,j)==1x1=j-1;y1=MM-i;x2=j;y2=MM-i;x3=j;y3=MM-i+1;x4=j-1;y4=MM-i+1;fill([x1,x2,x3,x4],[y1,y2,y3,y4],[0.2,0.2,0.2]);hold onelsex1=j-1;y1=MM-i;x2=j;y2=MM-i;x3=j;y3=MM-i+1;x4=j-1;y4=MM-i+1;fill([x1,x2,x3,x4],[y1,y2,y3,y4],[1,1,1]);hold onendendendhold onROUT=ROUTES{K,M};Rx=ROUT;Ry=ROUT;for ii=1:LENROUTRx(ii)=a*(mod(ROUT(ii),MM)-0.5);if Rx(ii)==-0.5Rx(ii)=MM-0.5;endRy(ii)=a*(MM+0.5-ceil(ROUT(ii)/MM));endplot(Rx,Ry)endplotif2=0;%绘各代蚂蚁爬行图if plotif2==1figure(3)axis([0,MM,0,MM])for i=1:MMfor j=1:MMif G(i,j)==1x1=j-1;y1=MM-i;x2=j;y2=MM-i;x4=j-1;y4=MM-i+1;fill([x1,x2,x3,x4],[y1,y2,y3,y4],[0.2,0.2,0.2]);hold onelsex1=j-1;y1=MM-i;x2=j;y2=MM-i;x3=j;y3=MM-i+1;x4=j-1;y4=MM-i+1;fill([x1,x2,x3,x4],[y1,y2,y3,y4],[1,1,1]);hold onendendendfor k=1:KPLK=PL(k,:);minPLK=min(PLK);pos=find(PLK==minPLK);m=pos(1);ROUT=ROUTES{k,m};LENROUT=length(ROUT);Rx=ROUT;Ry=ROUT;for ii=1:LENROUTRx(ii)=a*(mod(ROUT(ii),MM)-0.5);if Rx(ii)==-0.5Rx(ii)=MM-0.5;endRy(ii)=a*(MM+0.5-ceil(ROUT(ii)/MM));endplot(Rx,Ry)hold onendend。
蚁群算法最短路径matlab程序 - 副本

蚁群算法最短路径matlab程序 - 副本蚁群算法最短路径通用Matlab程序下面的程序是蚁群算法在最短路中的应用,稍加扩展即可应用于机器人路径规划function [ROUTES,PL,Tau]=ACASP(G,Tau,K,M,S,E,Alpha,Beta,Rho,Q) D=G2D(G);N=size(D,1);%N表示问题的规模(象素个数) MM=size(G,1);a=1;%小方格象素的边长Ex=a*(mod(E,MM)-0.5);%终止点横坐标if Ex==-0.5Ex=MM-0.5;endEy=a*(MM+0.5-ceil(E/MM)); Eta=zeros(1,N); for i=1:N if ix==-0.5 ix=MM-0.5;endiy=a*(MM+0.5-ceil(i/MM)); if i~=EEta(1,i)=1/((ix-Ex)^2+(iy-Ey)^2)^0.5;elseEta(1,i)=100;endendROUTES=cell(K,M);PL=zeros(K,M);%% -----------启动K轮蚂蚁觅食活动,每轮派出M只蚂蚁--------------------for k=1:Kdisp(k);for m=1:MW=S;Path=S;PLkm=0;TABUkm=ones(1,N);TABUkm(S)=0;DD=D;DW=DD(W,:);DW1=find(DW)for j=1:length(DW1)if TABUkm(DW1(j))==0 DW(j)=inf;endendLJD=find(DWLen_LJD=length(LJD); while W~=E&&Len_LJD>=1 PP=zeros(1,Len_LJD); for i=1:Len_LJDPP(i)=(Tau(W,LJD(i))^Alpha)*(Eta(LJD(i))^Beta);endPP=PP/(sum(PP)); Pcum=cumsum(PP);Select=find(Pcum>=rand);Path=[Path,to_visit]; PLkm=PLkm+DD(W,to_visit); W=to_visit;for kk=1:Nif TABUkm(kk)==0 DD(W,kk)=inf;DD(kk,W)=inf;endendTABUkm(W)=0;for j=1:length(DW1)if TABUkm(DW1(j))==0DW(j)=inf;endendLJD=find(DWLen_LJD=length(LJD);%可选节点的个数 end ROUTES{k,m}=Path; if Path(end)==EPL(k,m)=PLkm;elsePL(k,m)=inf;endendDelta_Tau=zeros(N,N);%更新量初始化for m=1:Mif PL(k,m) ROUT=ROUTES{k,m};TS=length(ROUT)-1;%跳数PL_km=PL(k,m);for s=1:TSx=ROUT(s);Delta_Tau(x,y)=Delta_Tau(x,y)+Q/PL_km;Delta_Tau(y,x)=Delta_Tau(y,x)+Q/PL_km;endendendTau=(1-Rho).*Tau+Delta_Tau;%信息素挥发一部分,新增加一部分 end %% ---------------------------绘图-------------------------------- plotif=1;%是否绘图的控制参数if plotif==1%绘收敛曲线meanPL=zeros(1,K);minPL=zeros(1,K);for i=1:KPLK=PL(i,:);Nonzero=find(PLKPLKPLK=PLK(Nonzero);meanPL(i)=mean(PLKPLK);minPL(i)=min(PLKPLK);endfigure(1)plot(minPL);hold onplot(meanPL);grid ontitle('收敛曲线(平均路径长度和最小路径长度)'); xlabel('迭代次数');ylabel('路径长度');%绘爬行图figure(2)axis([0,MM,0,MM])for i=1:MMfor j=1:MMif G(i,j)==1x1=j-1;y1=MM-i;x2=j;y2=MM-i;x3=j;y3=MM-i+1;x4=j-1;y4=MM-i+1;fill([x1,x2,x3,x4],[y1,y2,y3,y4],[0.2,0.2,0.2]); hold onelsex1=j-1;y1=MM-i;x2=j;y2=MM-i;x3=j;y3=MM-i+1;x4=j-1;y4=MM-i+1;fill([x1,x2,x3,x4],[y1,y2,y3,y4],[1,1,1]); hold onendendendhold onROUT=ROUTES{K,M};LENROUT=length(ROUT);Rx=ROUT;Ry=ROUT;for ii=1:LENROUTRx(ii)=a*(mod(ROUT(ii),MM)-0.5);if Rx(ii)==-0.5Rx(ii)=MM-0.5;endRy(ii)=a*(MM+0.5-ceil(ROUT(ii)/MM));endplot(Rx,Ry)endplotif2=1;%绘各代蚂蚁爬行图if plotif2==1figure(3)axis([0,MM,0,MM])for i=1:MMfor j=1:MMif G(i,j)==1x1=j-1;y1=MM-i;x2=j;y2=MM-i;x3=j;y3=MM-i+1;x4=j-1;y4=MM-i+1;fill([x1,x2,x3,x4],[y1,y2,y3,y4],[0.2,0.2,0.2]); hold onelsex1=j-1;y1=MM-i;x2=j;y2=MM-i;x3=j;y3=MM-i+1;x4=j-1;y4=MM-i+1;fill([x1,x2,x3,x4],[y1,y2,y3,y4],[1,1,1]);hold onendendendfor k=1:KPLK=PL(k,:);minPLK=min(PLK);pos=find(PLK==minPLK);m=pos(1);ROUT=ROUTES{k,m};LENROUT=length(ROUT);Rx=ROUT;Ry=ROUT;for ii=1:LENROUTRx(ii)=a*(mod(ROUT(ii),MM)-0.5);if Rx(ii)==-0.5Rx(ii)=MM-0.5;endRy(ii)=a*(MM+0.5-ceil(ROUT(ii)/MM));endplot(Rx,Ry)hold onendend将上述算法应用于机器人路径规划,优化效果如下图所示。
matlab蚁群算法代码

matlab蚁群算法代码以下是一个简单的MATLAB蚁群算法代码示例,其中使用了一个二维网格作为蚂蚁的住所,并在网格上放置了一些随机的节点作为蚂蚁的出发和目的地,每个蚂蚁沿着最短路径搜索路径从一个节点到另一个节点。
```matlab% 定义蚂蚁的参数num_nodes = 10; % 网格节点数num_tasks = 100; % 任务数num_neighbors = 50; % 蚂蚁之间的连接数% 随机放置节点nodes = randi(num_nodes, num_nodes);% 创建蚂蚁的基本队列蚂蚁_queue = queue();% 定义蚂蚁的基本策略def_蚂蚁_策略 = {[set_task(i, j, k)]= {1},[set_neighbor(i, j, k)]= {2},[set_task(i, j, k)]= {3},};% 更新蚂蚁的状态def_蚂蚁_update = {for i = 1:num_tasksfor j = 1:num_neighborsif get(蚂蚁_queue, -1, 1) == num_tasksget(蚂蚁_queue, -1, 1) = set_task(i, j, k);set(蚂蚁_queue, -1, 1) = set_neighbor(i, j, k); endendend};% 定义蚂蚁的搜索函数function 蚂蚁_function(i, j, k, task, target) % 计算当前蚂蚁的最短路径path = [zeros(1, num_neighbors); 1];path(end+1, -1) = target;path(end, num_nodes) = 1;path = path./zeros(1, num_neighbors);% 搜索蚂蚁的下一个节点for j = 1:num_neighborsif get(蚂蚁_queue, -1, j) == taskif get(蚂蚁_queue, -1, j) == target蚂蚁_function(i, j, k, task, target)endend% 计算蚂蚁的当前路径path_function = path(1:end-1, 1:end-1);end% 启动蚂蚁搜索蚂蚁_start(蚂蚁_queue);% 计算蚂蚁的最短路径function path_function = get_shortest_path(path_var) % 计算每个节点到目标节点的最短路径path_var = path_function;% 计算每个节点到每个邻居节点的最短路径for k = 1:num_neighborspath_var = cellfun(@(i,j) get(path_var, i, j, k), path_var);end% 返回所有节点的最短路径return path_var;```这是一个简单的例子,可以根据具体的需求进行修改和优化。
蚁群算法路径优化matlab代码

蚁群算法路径优化matlab代码蚁群算法是一种基于生物群体的智能算法,常用于路径优化等问题。
在这个问题中,蚂蚁在寻找食物时会根据周围的环境信息和食物的香味找到最短路径。
本文将介绍如何在 MATLAB 中使用蚁群算法进行路径优化,并提供一些拓展。
在 MATLAB 中实现蚁群算法需要用到三个主要函数:ants_logic.m、ants_move.m 和 ants_display.m。
以下是这三个函数的基本功能和代码实现。
1. ants_logic.m这个函数是蚁群算法的核心部分,负责计算蚂蚁的当前路径和更新路径搜索树。
函数的基本思路是每个蚂蚁根据当前环境和食物香味来选择前进方向,如果前方是死路或食物已经被其他蚂蚁找到,则蚂蚁会返回原路。
如果蚂蚁到达了食物位置,则它会将自己的信息传递给其他蚂蚁,并更新食物香味。
拓展:在路径优化问题中,通常会有多个不同的路径可供选择,而蚁群算法可以通过学习其他蚂蚁的路径来发现更短、更快的路径。
为了实现这一功能,可以在 ants_logic.m 函数中增加一个参数,指示当前蚂蚁应该学习其他哪个蚂蚁的路径。
2. ants_move.m这个函数负责控制蚂蚁的移动方向。
在函数中,我们需要给定蚂蚁的当前位置和食物位置,并计算蚂蚁应该移动到的新位置。
在MATLAB 中,我们可以使用 rand 函数生成一个随机数,然后将其作为新位置的坐标。
拓展:为了提高路径搜索的效率,我们可以在 ants_move.m 函数中加入一些随机因子。
例如,可以在蚂蚁移动方向上添加一个随机偏置,这样可以让蚂蚁更有可能探索新的区域。
3. ants_display.m这个函数用于可视化路径搜索的过程。
在函数中,我们可以给定蚂蚁的初始位置和食物位置,并使用 MATLAB 的图形处理函数绘制路径。
拓展:为了使路径搜索过程更加有趣,我们可以在ants_display.m 函数中添加一些动画效果。
例如,可以使用 MATLAB 的 animation 函数创建动画,让蚂蚁路径在屏幕上动态地显示。
蚁群算法在Matlab中的程序设计

f r ( t +1 )=( 1一P ) ( t )+△
k ㈤ :
2 . 1 . 1 数据的初始化 这个步骤主要完成 以下数据 的初始化 : ①通过 已知 的 n个城市 坐标 , 求 得 每 两个 城 市 间 的距 离并 保存在距离矩阵中; ②初始化信息素矩阵; ③初始化 算法参数 ; ④初始化记录数据的变量及矩阵。 2 . 1 . 2 通过算法寻找最优路径 运行算法 , 通过迭代来计算最优路径 , 直到满足
否则
S t e p 2, 否 则输 出结果 。 整 个步 骤的算 法框 图如 图 2所示 。
2 . 3 运 行结 果及分 析 式( 3 ) 中, Q为 常数 , 表 示蚂 蚁循 环 一次 所 释放 的信
息素的总量 ; 为蚂蚁 k 经过的路径长度 。
2 用M a t l a b实现蚁群 算法
Ma t l a b是一个 功 能强大 的科学 计算 和工 程计 算
结果 数 据 以 图表 的形 式 展示 出来 , 如 图 3和图 4所 示 分 别 为 蚁 群 算 法 最 短 路 径 和 各 代 的 收 敛 情况。 从 图 中可 以看 出 , 本 算 法 得 到 的最 短距 离 为 1 5 6 0 1 . 9 1 9 5 k m, 而最 短距 离 在 迭代 了 1 0 0次 以后 基 本上 就 接近最短 路 径 了 , 平 均 距 离也 在 迭代 次 数 达 到1 0 0次后趋 于平 缓 。程序运行 的输 出结果 为 :
蚁群算法求解TSP问题的MATLAB程序(较好的算例)

蚁群算法求解TSP问题的MATLAB程序(较好的算例) %蚁群算法求解TSP问题的matlab程序clear allclose allclc%初始化蚁群m=31;%蚁群中蚂蚁的数量,当m接近或等于城市个数n时,本算法可以在最少的迭代次数内找到最优解C=[1304 2312;3639 1315;4177 2244;3712 1399;3488 1535;3326 1556;3238 1229;4196 1004;4312 790;4386 570;3007 1970;2562 1756;2788 1491;2381 1676;1332 695;3715 1678;3918 2179;4061 2370;3780 2212;3676 2578;4029 2838;4263 2931;3429 1908;3507 2367;3394 2643;3439 3201;2935 3240;3140 3550;2545 2357;2778 2826;2370 2975];%城市的坐标矩阵Nc_max=200;%最大循环次数,即算法迭代的次数,亦即蚂蚁出动的拨数(每拨蚂蚁的数量当然都是m)alpha=1;%蚂蚁在运动过程中所积累信息(即信息素)在蚂蚁选择路径时的相对重要程度,alpha过大时,算法迭代到一定代数后将出现停滞现象beta=5;%启发式因子在蚂蚁选择路径时的相对重要程度rho=0.5;%0<rho<1,表示路径上信息素的衰减系数(亦称挥发系数、蒸发系数),1-rho表示信息素的持久性系数Q=100;%蚂蚁释放的信息素量,对本算法的性能影响不大%变量初始化n=size(C,1);%表示TSP问题的规模,亦即城市的数量D=ones(n,n);%表示城市完全地图的赋权邻接矩阵,记录城市之间的距离 for i=1:nfor j=1:nif i<jD(i,j)=sqrt((C(i,1)-C(j,1))^2+(C(i,2)-C(j,2))^2);endD(j,i)=D(i,j);endendeta=1./D;%启发式因子,这里设为城市之间距离的倒数pheromone=ones(n,n);%信息素矩阵,这里假设任何两个城市之间路径上的初始信息素都为1 tabu_list=zeros(m,n);%禁忌表,记录蚂蚁已经走过的城市,蚂蚁在本次循环中不能再经过这些城市。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
y=ROUT(s+1);
Delta_Tau(x,y)=Delta_Tau(x,y)+Q/PL_km;
Delta_Tau(y,x)=Delta_Tau(y,x)+Q/PL_km;
% passes
% Tau output updated pheromone
%% -------------------- variableinitialization-----------------------------
D=G2D(G);
N=size(D,1);%N is the peoblem scale(pixel number)
PLkm=PLkm+DD(W,to_visit);%Path length accumulation
W=to_visit;%move to the next point
for kk=1:N
if TABUkm(kk)==0
if i~=E
Eta(1,i)=1/((ix-Ex)^2+(iy-Ey)^2)^0.5;
else
Eta(1,i)=100;
end
end
ROUTES=cell(K,M);% use cell construct to load the passing route of every ant for every iteration
Len_LJD=length(LJD);%number of points can be selected
%% Colony stop condition:there is no food or go into a impass
while W~=E&&Len_LJD>=1
%% ---------------------------------------------------------------
% input parameters
% G gragh, which is 01 matrix, 1 represents obstcles
function [ROUTES,PL,Tau]=ACASP(G,Tau,K,M,S,E,Alpha,Beta,Rho,Q)
%% ---------------------------------------------------------------
% ACASP.m
% ACS for Path Planning
end
end
end
Tau=(1-Rho).*Tau+Delta_Tau;%pheromone evaporates some and accumulates some
end
%% ---------------------------PLOT--------------------------------
DW=DD(W,:);
DW1=find(DW<inf);
for j=1:length(DW1)
if TABUkm(DW1(j))==0
DW(j)=inf;
PLK=PL(i,:);
Nonzero=find(PLK<inf);
PLKPLK=PLK(Nonzero);
meanPL(i)=mean(PLKPLK);
minPL(i)=min(PLKPLK);
end
for j=1:length(DW1)
if TABUkm(DW1(j))==0
DW(j)=inf;
end
end
LJD=find(DW<inf);% set of points can be selected
% Alpha parameter indicates the importance of pheromone
% Beta parameter indicates the importance of visibility
% Rho pheromone evaporation rate
end
end
LJD=find(DW<inf);%set of optional points
Len_LJD=length(LJD);%number of optional points
end
%% Fifth Step:record the pate and length that every ant for every
%% iteration passes
ROUTES{k,m}=Path;
if Path(end)==E
plotif=1;%control parameter, determine if plot or not
if plotif==1
%plot convergence curve
meanPL=zeros(1,K);
minPL=zeros(1,K);
for i=1:K
end
PP=PP/(sum(PP));%construct probability distributing
Pcum=cumsum(PP);
Select=find(Pcum>=rand);
to_visit=LJD(Select(1));%the next step node
%% Fourth Step:status update and record
Path=[Path,to_visit];%Paths accumulation
% Q pheromone accumulation parameter
%
% output parameters
% ROUTES the route that every ant in every iteration
% passes
% PL the length that every ant in every iteration
PLkm=0;%initialize the passing length
TABUkm=ones(1,N);%initialize the forbbiden table
TABUkm(S)=0;% eliminate this point for it is the starting point
MM=size(G,1);
a=1;% edge length of pixel
Ex=a*(mod(E,MM)-0.5);% goal point coordinate
if Ex==-0.5
Ex=MM-0.5;
end
Ey=a*(MM+0.5-ceil(E/MM));% Y coordinate of goal point
DD(W,kk)=inf;
DD(kk,W)=inf;
end
end
TABUkm(W)=0;%eliminate the travelled point in the forbidden table
%% Third Step:the method to choose the next step
PP=zeros(1,Len_LJD);
for i=1:Len_LJD
PP(i)=(Tau(W,LJD(i))^Alpha)*(Eta(LJD(i))^Beta);
DD=D;%initialize adjacency matrix
%% Second Step:Choose the nodes that can step forward
DW=DD(W,:);
DW1=find(DW<inf);
figure(1)
plot(minPL);
hold on
plot(meanPL);
PL=zeros(K,M);% use matrix to load the passing length of every ant for every iteration
%% -----------iteration time is k, ant number is M--------------------
PL(k,m)=PLkm;
else
PL(k,m)=inf;
end
end
%% Sixth Step: update pheromone
Delta_Tau=zeros(N,N);%initialize updating ammount
for m=1:M
if PL(k,m)<inf
ROUT=ROUTES{k,m}; TS=length(Fra bibliotekOUT)-1;
PL_km=PL(k,m);
for s=1:TS
% Tau initial pheromone matrix
% K iterative times
% M ant number for once iteration
% S Start Point
% E Goal point
for k=1:K
disp(k);
for m=1:M
%% First step: status initialization
W=S;%set current point as the starting point
Path=S;%initialize the passing route
Eta=zeros(1,N);
%construct the initialization matrix
