实验探究题的解法与练习
2019版生物:热点题型一 含答案

一、鉴定酶的本质人的唾液中含有唾液淀粉酶,有人说:“唾液淀粉酶的化学本质是蛋白质”。
请设计一个实验以探究该酶的化学本质是否是蛋白质. (1)实验材料:质量浓度为0.1 g/mL的NaOH溶液、质量浓度为0.01 g/mL的CuSO4溶液、鸡蛋、人的口腔唾液(含有酶)、清水、小烧杯、玻璃棒、试管和滴管.(2)实验原理:鸡蛋的蛋清的主要成分是蛋白质,在碱性溶液中,蛋白质与CuSO4反应能产生紫色物质,即蛋白质的双缩脲反应。
如果能通过实验证明,酶能发生双缩脲反应,即可证明酶的化学本质是蛋白质。
(3)实验步骤:①制备蛋清液:取生鸡蛋一个,打破蛋壳(不要破坏蛋黄)。
取少许蛋清注入小烧杯中,加入30 mL的清水,用玻璃棒调匀。
②取两支试管,编号,在1号试管中注入第一步得到的________2 mL,2号试管中注入________________。
③向1号和2号试管中各加入 1 mL__________________________________,摇匀。
④分别向两试管中注入________________________________,摇匀。
⑤振荡摇匀后,静置一会,观察其颜色变化。
(4)实验结果与结论预测:①若____________________,则________________________________;②若_____________________________,则唾液淀粉酶的化学本质不是蛋白质。
审题关键(1)据题可知该实验的目的是探究唾液淀粉酶的化学本质是否是蛋白质。
(2)确定本实验的自变量为蛋白质和酶,因变量为是否出现紫色反应.(3)找出本实验的无关变量有:蛋清液和唾液的注入量、双缩脲试剂的使用量和方法等.(4)联想到鉴定蛋白质的方法:双缩脲试剂使用时,先加入NaOH 溶液(1 mL),振荡摇匀,造成碱性的反应环境,然后再加入4滴CuSO4溶液,振荡摇匀后观察现象。
(5)由题干信息可知本实验属于探究类实验,其结果与结论预测的一般语言表述模型是:若××××××,则××××××;若××××××,则××××××.答案(3)②蛋清液等量的口腔唾液③质量浓度为0.1 g/mL 的NaOH溶液④质量浓度为0.01 g/mL的CuSO4溶液4滴(4)①两支试管中都呈现紫色唾液淀粉酶的化学本质是蛋白质②1号试管中呈现紫色,2号试管没有呈现紫色鉴定酶本质的“试剂检测法”模型“试剂检测法”——从酶的化学本质上来讲,绝大多数的酶是蛋白质,少数的酶是RNA。
初中化学实验题

初中化学实验题篇一:中考化学实验探究题归类及解法中考化学实验探究题归类及解法实验探究活动是新课标理念中的一种全新的学习方法,也是中考考查的重点和热点,但不少同学对于实验探究类试题,往往不知如何入手去解答。
实验探究题中的许多内容都是平时学习(实验)或生活中司空见惯的,只是命题形式新颖,选择素材陌生度高,但基础知识或原型实验来源于教材的演示实验或学生实验。
很多同学做题时联想不到,这就要求我们在平时学习和生活中要多想多问几个为什么?要注意从化学的视角去观察思考学习和生产生活中的各种问题,并能根据自己已有的化学知识和经验对问题做出有意义的猜想和假设,并设法用实验去检验验证它。
在解答实验探究类试题时要①通读全题划出关键的语句,审清题意,明确要求;②回归教材确定知识点;③细心分析明确设计意图,灵活应用基础知识解决探究题中的问题(关键是分析题中的设计方案和实验装置图)。
现从近年来各地中考试题中选取数题,进行简要的归类与评析。
根据探究题的内容可分为以下几种类型:一、气体成分的探究如人吸入和呼出气体成分探究、酒精和蜡烛等可燃物燃烧后产生气体成分探究、两种物质反应后产生气体成分探究、鱼瞟内气体成分探究等。
涉及的知识点有空气、O2、N2、H2、CO、CO2等这些物质的制法及检验,以及它们与氧气、水、碱溶液等反应产生的特有现象。
例1.(07长春)请你阅读下列短文后,回答有关问题。
“二氧化碳本身没有毒性,但当空气中的二氧化碳超过正常含量时,会对人体产生有害影响,所以在人群密集的地方,应该注意通风换气,保持空气新鲜。
”(1)根据上述短文,提出一个你想探究的问题:。
(2)对你的问题做出一个比较合理的猜想:。
(3)请自选用品设计实验验证你的猜想,并填写下表。
[思路点拨]通过阅读短文“二氧化碳超过正常含量对人体有害,人群密集地应注意通风换气”,知道探究目的是“新鲜空气和人群密集地空气中二氧化碳含量高低问题”,再根据“人群密集地,应注意通风换气”提出猜想“人群密集地空气中二氧化碳含量高”。
河南数学中考题型汇总 几何探究题题型练习含答案

河南数学中考题型汇总几何探究题题型练习含答案类型 1 实践操作类探究题角度1 折叠类1.[2022河南]综合与实践综合与实践课上,老师让同学们以“矩形的折叠”为主题开展数学活动.(1)操作判断操作一:对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展平;操作二:在AD上选一点P,沿BP折叠,使点A落在矩形内部点M处,把纸片展平,连接PM,BM.根据以上操作,当点M在EF上时,写出图(1)中一个30°的角:.(2)迁移探究小华将矩形纸片换成正方形纸片,继续探究,过程如下.将正方形纸片ABCD按照(1)中的方式操作,并延长PM交CD于点Q,连接BQ.①如图(2),当点M在EF上时,∠MBQ= °,∠CBQ= °;②改变点P在AD上的位置(点P不与点A,D重合),如图(3),判断∠MBQ与∠CBQ的数量关系,并说明理由.(3)拓展应用在(2)的探究中,已知正方形纸片ABCD的边长为8 cm,当FQ=1 cm时,直接写出AP 的长.图(1)图(2)图(3)2.[2022河南省实验模拟]问题情境数学活动课上,同学们开展了以折叠为主题的探究活动,如图(1),已知矩形纸片ABCD(AD>AB),其中宽AB=8.动手实践(1)如图(1),威威同学将矩形纸片ABCD折叠,点A落在BC边上的点M处,折痕为BN,连接MN,然后将纸片展平,得到四边形ABMN,则折痕BN的长为;探究发现(2)如图(2),胜胜同学将图(1)中的四边形ABMN剪下,取AN边的中点E,将△ABE 沿BE折叠得到△A'BE,延长BA'交MN于点F.点Q为BM边的中点,点P是MN边上一动点,将△MQP沿PQ折叠,当点M的对应点M'落在线段BF上时,求此时tan∠PQM的值;反思提升(3)明明同学改变图(2)中点Q的位置,即点Q为BM边上一动点,点P仍是MN边上一动点,按照(2)中方式折叠△MQP,使点M'落在线段BF上,明明同学不断改变点Q 的位置,发现在某一位置∠QPM与(2)中的∠PQM相等,请直接写出此时BQ的长.图(1)图(2)备用图3.综合与实践——探究平行四边形折叠中的数学问题问题情境已知▱ABCD中,ÐA为锐角,AB<AD,点E,F分别是AB,CD边的中点,点G,H分别是AD,BC边上的点,分别沿EG和FH折叠▱ABCD,点A,C的对应点分别为点A',C'.操作分析(1)如图(1),点A'与点B重合,点C'与点D重合.①四边形BHDG 平行四边形(填“是”或“不是”).②当▱ABCD满足某个条件时,四边形BHDG能成为矩形.这个条件可以是.(2)点A',C'均落在▱ABCD内部(含边界),连接A'H,C'G,若AG=CH,则四边形A'HC'G是平行四边形吗?若是,请就图(2)进行证明;若不是,请说明理由.拓展探究(3)在(2)的条件下,若ÐA=60°,AD=2AB=8,且A'G与▱ABCD的一边平行,则此时四边形A'HC'G的面积为.图(1)图(2)备用图4.综合与实践数学活动课上,张老师找来若干张等宽的矩形纸条,让学生们进行折纸探究. (1)希望小组将如图(1)所示的矩形纸片ABCD沿过点A的直线折叠,使点D落在AB边上的点D'处,折痕为AE.填空:图(1)中四边形ADED'的形状是.(2)智慧小组准备了一张如图(2)所示的长、宽之比为3∶2的矩形纸片ABCD,用希望小组的方法折叠纸片,得到四边形ADED',接着沿过点B的直线折叠纸片,使点C落在ED'上的点M处,折痕为BF.求∠MBC的度数.(3)勤奋小组拿着一张如图(3)所示长为4,宽为2的矩形纸片ABCD,利用希望小组的方法折叠纸片,得到四边形ADED',在CE上取一点F(不与点C,E重合),沿BF 折叠△BCF,点C的对应点为N,射线FN交直线AB于点H.①HF与HB的数量关系为.②当射线FN经过△AED'的直角边的中点时,直接写出FC的长.图(1)图(2)图(3)5.综合与实践问题情境数学活动课上,老师让同学们以“矩形纸片的折叠”为主题,开展数学活动,如图(1),在矩形ABCD中,AB=8,BC=4.观察发现(1)如图(2),智慧小组连接对角线BD,将矩形纸片ABCD沿直线BD折叠,使点A落在点P的位置,PB交CD于点Q,连接AP.直接写出图中所有的等腰三角形:.(不再添加字母)探究证明(2)求实小组在智慧小组的启发下,又对矩形纸片ABCD进行了如下操作,并对其中所产生的问题进行了探究:如图(3),沿过点A的直线折叠,使点B的对应点F 落在CD上,折痕交BC于点E,过点F作FG∥BC交AE于点G,连接BG.①小组成员发现四边形BEFG是特殊四边形.请你判断四边形BEFG的形状,并说明理由.②小组成员通过计算求得四边形BEFG的面积.请你直接写出这个面积:.探索拓广(3)参照上面的探究方式,对图(1)进行一次折叠操作,使点B的对应点B'落在BD 的三等分点上,设折痕与AB交于点N.请直接写出BN的长.图(1)图(2)图(3)角度2 旋转类6.综合与实践——图形变换中的数学问题问题情境数学活动课上,老师出示了一个问题:如图(1),已知正方形ABCD、矩形BCEF,点E,F分别在边CD,AB上,且BF=k(3<k<5),BC=5.将矩形BCEF绕点B顺时针旋转得到矩形BGHK,点G,H,K分别是点C,E,F的对应点,如图(2).图(1)图(2)图(3)图(4)同学们通过小组合作,提出下列数学问题,请你解答.(1)在图(2)中,连接BE,BH,EH,CG,得到图(3),可以发现在旋转过程中存在一个三角形始终与△BCG相似,这个三角形是,它与△BCG的相似比为(用含k的式子表示).(2)如图(4),矩形BGHK的顶点K恰好落在正方形ABCD的对角线AC上,KH交DC 的延长线于点T.求证:BK=KT.(3)在旋转过程中,连接CH,CK.若k=23,则当CH=CK时,直接写出CK的长.备用图(1)备用图(2)角度3 平移类7.综合与实践问题背景如图(1),在矩形ABCD中,AB=10,BC=8,点E为边BC上一点,沿直线DE将矩形折叠,使点C落在AB边上的点C'处.问题解决(1)填空:AC'的长为.(2)如图(2),展开后,将△DC'E沿线段AB向右平移,使点C'的对应点与点B重合,得到△D'BE',D'E'与BC交于点F,D'B与DE交于点G.求EF的长.拓展探究(3)如图(3),在△DC'E沿射线AB向右平移的过程中,设点C'的对应点为C″,则当△D'C″E'在线段BC上截得的线段PQ(D'E',折线D'C″E'分别与BC交于点P,Q)的长度为2时,直接写出平移的距离.图(1)图(2)图(3)角度4 尺规作图类8.[2022南阳宛城区一调]下面是某数学兴趣小组探究用不同方法作线段AB的垂直平分线的讨论片段,请仔细阅读,并完成相应的任务.任务:(1)小明的作图依据是.(2)小军作图得到的直线CP是线段AB的垂直平分线吗?请判断并说明理由.(3)如图(3),已知△ABC中,CA=CB,∠ACB=30°,点D,E分别是射线CA,CB上的动点,且CD=CE,连接BD,AE,交点为P.当AB=6,∠PAB=45°时,请直接写出线段CD 的长.图(3)9.[2022开封二模]中华文明源远流长,图(1)是汉代数学家赵爽在注解《周髀算经》时给出的图形,人们称它为“赵爽弦图”.2002年北京国际数学家大会依据赵爽弦图制作了会标,该图由4个全等的直角三角形围成一个大正方形和中间一个小正方形,巧妙地证明了勾股定理.问题发现如图(1),若直角三角形的直角边BC=3,斜边AB=5,则中间小正方形的边长CD= ,连接BD,△ABD的面积为.知识迁移如图(2),P是正方形ABCD内一点,连接PA,PB,PC,当∠BPC=90°,BP=10时,△PAB的面积为.拓展延伸如图(3),已知∠MBN=90°,以点B为圆心,适当长为半径画弧,分别交射线BM,BN 于点A,C.(1)已知D为线段AB上一动点,连接CD,过点B作BE⊥CD,垂足为点E,在线段CE 上取一点F,使EF=BE,过点F作GF⊥CD交BC于点G,试判断BE,DE,GF这三条线段之间的数量关系,并说明理由.(2)在(1)的条件下,若D为射线BM上一动点,F为射线EC上一点,当AB=10,CF=2时,直接写出线段DE的长.图(1)图(2)图(3)备用图类型 2 阅读理解类探究题10.[2022许昌二模]问题情境数学课上,王老师出示了这样一个问题:如图(1),在矩形ABCD中,AD=2AB,点E是AB延长线上一点,且BE=AB,连接DE,交BC于点M,以DE为一边在DE的左下方作正方形DEFG,连接AM.试判断线段AM与DE的位置关系.探究展示小明发现,AM垂直平分DE,并展示了如下的证明方法:证明:∵BE=AB,∴AE=2AB.又∵AD=2AB,∴AD=AE.∵四边形ABCD是矩形,∴AD∥BC,∴.(平行线分线段成比例)∵BE=AB,∴EM=1,∴EM=DM,DM即AM是△ADE的边DE上的中线.又∵AD=AE,∴.(等腰三角形的“三线合一”)∴AM垂直平分DE.反思交流(1)请将上述证明过程补充完整;(2)小颖受到小明的启发,继续进行探究,如图(2),连接CE,以CE为一边在CE的左下方作正方形CEFG,发现点G在线段BC的垂直平分线上,请你给出证明;图(1)图(2)拓展应用(3)如图(3),连接CE,以CE为一边在CE的右上方作正方形CEFG,分别以点B,C 为圆心,m为半径作弧,两弧交于点M,连接MF.若MF=AB=1,请直接写出m的值.图(3)11.[2022商丘二模]如下是小明复习全等三角形时遇到的一个问题及由此引发的思考,请帮助小明完成以下学习任务.如图(1),OC平分∠AOB,点P在OC上,点M,N分别是OA,OB上的点,且OM=ON.求证:PM=PN.小明的思考:要证明PM=PN,只需证明△MOP≌△NOP即可.证明:如图(1),∵OC平分∠AOB,∴∠AOC=∠BOC.又∵OP=OP,OM=ON,∴△MOP≌△NOP,∴PM=PN.请仔细阅读并完成以下任务.(1)小明得出△MOP≌△NOP的依据是(填序号).①SSS ②SAS ③AAS ④ASA⑤HL(2)如图(2),在四边形ABCD中,AB=AD+BC,∠DAB的平分线和∠ABC的平分线交于CD边上的点P.求证:PC=PD.,当△PBC有一个内角是45°时,△PAD(3)在(2)的条件下,若AB=10,tan∠PAB=12的面积是.图(1)图(2)备用图(1)备用图(2)类型 3 类比、拓展探究题12.[2021湖北仙桃]已知△ABC和△DEC都为等腰三角形,AB=AC,DE=DC,∠BAC=∠EDC=n°.(1)当n=60时:①如图(1),当点D在AC上时,请直接写出BE与AD的数量关系:;②如图(2),当点D不在AC上时,判断线段BE与AD的数量关系,并说明理由.(2)当n=90时:①如图(3),探究线段BE 与AD 的数量关系,并说明理由; ②当BE ∥AC ,AB=3√2,AD=1时,请直接写出DC 的长.图(1) 图(2) 图(3)答案:1.(1)∠ABP ,∠PBM ,∠MBC 或∠BME (注:任意写出一个即可) (2)①15 15②∠MBQ=∠CBQ. 理由如下:∵四边形ABCD 是正方形,∴AB=BC ,∠A=∠C=90°. 由轴对称性质,得BM=AB ,∠BMP=∠A=90°,∴∠BMQ=90°=∠C ,BM=BC.又∵BQ 是公共边,∴Rt △MBQ ≌Rt △CBQ ,∴∠MBQ=∠CBQ.(3)4011 cm 或2413cm. 解法提示:由翻折的性质知AP=PM ,DF=CF=4. 由(2)可知,△MBQ ≌△CBQ ,∴MQ=CQ. 分两种情况讨论.①当点Q 在EF 下方时,如图(1),则MQ=CQ=4-1=3,DQ=4+1=5,PQ=AP+3,PD=8-AP. 由勾股定理,得PD 2+DQ 2=PQ 2,∴(8-AP )2+52=(AP+3)2,∴AP=4011.图(1)②当点Q 在EF 上方时,如图(2),则MQ=CQ=4+1=5,DQ=4-1=3,PQ=AP+5,PD=8-AP. 由勾股定理,得PD 2+DQ 2=PQ 2,∴(8-AP )2+32=(AP+5)2,∴AP=2413.图(2)综上所述,AP 的长为4011 cm 或2413cm. 2.(1)8√2(2)如图(1),连接MM'交PQ 于点O ,连接EF.图(1)由折叠的性质知,点O 为MM'的中点. 又∵点Q 为BM 边的中点,∴QO ∥BM',即QP ∥BF ,∴∠PQM=∠FBM.∵点E 是AN 边的中点,且将△ABE 沿BE 折叠得到△A'BE , ∴EN=EA',∠EA'F=∠N=90°. 又∵EF=EF ,∴Rt △NEF ≌Rt △A'EF. 设NF=x ,则A'F=x ,MF=8-x ,∴BF=BA'+A'F=BA+A'F=8+x.在Rt △BMF 中,由勾股定理,得BM 2+FM 2=BF 2, 即82+(8-x )2=(8+x )2,解得x=2,∴FM=6,∴tan ∠FBM=FM BM =68=34,∴tan ∠PQM=34. (3)BQ 的长为398. 解法提示:如图(2),连接MM'交PQ 于点G.图(2)由折叠的性质知,PQ 垂直平分MM',∴∠QPM+∠PMM'=90°.∵∠PMQ=90°,∴∠PMM'+∠M'MB=90°, ∴∠QPM=∠M'MB.由(2)知,(2)中∠PQM=∠M'BM. 又∵∠QPM 与(2)中的∠PQM 相等,∴∠M'BM=∠M'MB.过点M'作M'H ⊥BM 于点H ,则BH=MH=4,M'H BH =34, ∴M'H=3.设MQ=M'Q=a ,则HQ=4-a.在Rt △M'HQ 中,根据勾股定理,得M'H 2+HQ 2=M'Q 2, 即32+(4-a )2=a 2,解得a=258, ∴BQ=8-258=398. 3.(1)①是解法提示:∵四边形ABCD 是平行四边形,∴∠A=∠C ,∠ABC=∠ADC ,AD ∥BC. 如图(1),由折叠可知,∠A=∠1,∠C=∠2,图(1)∴∠1=∠2,∴∠ABC-∠1=∠ADC-∠2,即∠3=∠4. ∵AD ∥BC ,∴∠4+∠5=180°,∴∠3+∠5=180°, ∴BG ∥DH ,∴四边形BHDG 是平行四边形. ②∠A=45°(答案不唯一,正确即可) 解法提示:∵四边形BHDG 是矩形,∴∠BGD=90°,∴∠AGB=90°, 又由折叠可知,AG=A'G ,∴∠A=45°. (2)四边形A'HC'G 是平行四边形. 证明:如图(2),连接GH.图(2)∵四边形ABCD 是平行四边形, ∴∠A=∠C ,AB=CD ,AD ∥BC. ∵点E ,F 分别是AB ,CD 的中点,∴AE=12AB ,CF=12CD ,∴AE=CF. ∵AG=CH ,∴△AEG ≌△CFH , ∴∠1=∠3.由折叠可知,∠1=∠2,∠3=∠4,AG=A'G ,CH=C'H ,∴∠1=∠2=∠3=∠4,A'G=C'H. ∵AD ∥BC ,∴∠AGH=∠CHG ,∴∠5=∠6, ∴A'G ∥C'H ,∴四边形A'HC'G 是平行四边形. (3)2√3或4√3解法提示:当A'G ∥BC 时,如图(3),点A'落在AD 上,EG ⊥AD ,则A'G=AG=12AE=1,∴S 四边形A'HC'G =A'G ·AB sin 60°=1×4×√32=2√3.图(3)当A'G ∥AB 时,如图(4),则∠AGA'=120°,∴∠AGE=∠A'GE=60°,图(4)从而易得△AEG ,△A'EG ,△CHF ,△C'HF 均是等边三角形,EA'∥BC ,C'F ∥AD ,∴S 四边形A'HC'G =S ▱ABCD -4S △AEG -2S 四边形A'EBH=8×4×√32-4×√34×22-2×12×(2+6)×2×√32=4√3. 综上可知,四边形A'HC'G 的面积为2√3或4√3. 4.(1)正方形(2)由题意可知,AB∶AD=3∶2,∴设AD=2a ,AB=3a , ∴BM=BC=AD'=2a ,∴BD'=a ,∴sin ∠BMD'=a 2a =12,∴∠BMD'=30°.又ED'∥AD ∥BC ,∴∠MBC=∠BMD'=30°. (3)①HF=HB②FC 的长为3-√5或23. 解法提示:①∵DC ∥AB ,∴∠CFB=∠ABF. 由折叠可知∠CFB=∠NFB ,∴∠ABF=∠NFB ,∴HF=HB.②设FC=NF=x ,分两种情况讨论.a.当射线FN 经过AD'的中点时,点H 即为AD'的中点,如图(1),则HF=HB=3,∴HN=3-x.在Rt △HBN 中,由勾股定理,得HN 2+BN 2=HB 2,∴(3-x )2+22=32,解得x=3-√5(不合题意的值已舍去),∴FC=3-√5.图(1)b.当射线FN 经过ED'的中点P 时,如图(2), 易证△HD'P ≌△FEP ,∴HD'=EF=2-x ,∴HF=HB=2-x+2=4-x , ∴HN=4-x-x=4-2x.在Rt △HBN 中,由勾股定理,得BN 2+HN 2=HB 2,∴22+(4-2x )2=(4-x )2,解得x=23(不合题意的值已舍去),∴FC=23.图(2)综上可知,当射线FN 经过△AED'的直角边的中点时,FC 的长为3-√5或23. 5.(1)△ADP ,△ABP ,△BDQ (2)①四边形BEFG 是菱形. 理由如下:由折叠知∠BEG=∠FEG.∵FG ∥BC ,∴∠EGF=∠BEG , ∴∠EGF=∠FEG ,∴FG=FE. 又∵FE=BE ,∴FG=BE ,∴四边形BEFG 是平行四边形. 又∵FE=BE ,∴四边形BEFG 是菱形.②224-128√3解法提示:由折叠的性质知AF=AB=8.在Rt △ADF 中,由勾股定理得DF=√AF 2-AD 2=√82-42=4√3,∴CF=8-4√3. 设BE=y ,则EF=y ,CE=4-y.在Rt △CEF 中,由勾股定理得EF 2=CF 2+CE 2, 即y 2=(8-4√3)2+(4-y )2,解得y=16-8√3,∴S 四边形BEFG =BE ·CF=(16-8√3)×(8-4√3)=128-64√3-64√3+96=224-128√3.(3)BN 的长为103或53. 解法提示:分两种情况讨论.①当点B'落在离点D 较近的三等分点上时,如图(1),过点B'作B'H ⊥AB 于点H ,易知B'H=83,BH=163,B'N=BN ,∴HN=163-BN. 根据勾股定理,得B'H 2+HN 2=B'N 2,即(83)2+(163-BN )2=BN 2,∴BN=103.图(1) 图(2)②当点B'落在离点B 较近的三等分点上时,如图(2),同理可求得BN=53. 综上可知,BN 的长为103或53. 6.(1)△BEH√k 2+255(2)证明:如图(1),过点K 分别作KN ⊥BC 于点N ,KM ⊥CD 于点M , 则KN=KM ,∠MKN=90°=∠BKH ,∴∠TKM=∠BKN.又∠TMK=∠BNK=90°,∴△TMK ≌△BNK ,∴BK=KT.图(1)(3)CK 的长为√7或√67.解法提示:分如图(2)、图(3)所示的两种情况讨论,连接CG ,过点K 作KP ⊥BC ,垂足为点P.图(2)图(3)∵CK=CH ,∴∠CKH=∠CHK ,∴∠CKB=∠CHG. 又KB=HG ,∴△CKB ≌△CHG ,∴CG=CB=BG ,∴△CBG 是等边三角形, ∴∠CBG=60°. 图(2)中∠KBC=30°,∴KP=12KB=√3,BP=√32KB=3, ∴CP=2,∴CK=√(√3)2+22=√7. 图(3)中∠KBP=30°,∴KP=12KB=√3,BP=√32KB=3, ∴CP=8,∴CK=√(√3)2+82=√67. 综上可知,CK 的长为√7或√67. 7.(1)6(2)由(1)得AC'=6,∴BC'=AB -AC'=10-6=4.在Rt △BEC'中,设BE=x ,则EC'=EC=8-x ,根据勾股定理,得(8-x )2=x 2+42, 解得x=3,即BE=3,∴EC'=EC=5.连接EE',由平移可知,EE'=C'B=4,EE'∥AB ∥CD ,DE ∥D'E',∴△FEE'∽△FCD'∽△ECD , ∴EF∶EE'=EC∶DC=5∶10=1∶2, 又EE'=4,∴EF=2.(3)平移的距离为85或385. 解法提示:设平移的距离为x. 分两种情况讨论.①当点C″在BC 左侧时,如图(1),则BC″=4-x ,D'C=10-x ,∴CP=D'C ·tan ∠CD'P=D'C ·tan ∠CDE=510(10-x )=12(10-x ),BQ=BC″·tan ∠QC″B=BC″·tan ∠ADC'=68(4-x )=34(4-x ). 又CP+PQ+BQ=8,PQ=2,∴12(10-x )+2+34(4-x )=8,解得x=85.图(1) 图(2)②当点C″在BC 右侧时,如图(2),则BC″=x -4,D'C=10-x ,∴CP=D'C ·tan ∠CD'P=12(10-x ),BQ=BC″·tan ∠QC″B=BC″·tan ∠AC'D=43(x-4). 又CP+PQ+BQ=8,PQ=2,∴12(10-x )+2+43(x-4)=8,解得x=385.综上可知,平移的距离为85或385. 8.(1)等腰三角形的顶角平分线、底边上的高、底边上的中线互相重合 (2)是. 理由如下:由作图可知,CA=CB ,CD=CE. 又∵∠ACE=∠BCD ,∴△ACE ≌△BCD , ∴∠CAE=∠CBD. ∵CA=CB ,∴∠CAB=∠CBA , ∴∠PAB=∠PBA ,∴AP=BP ,∴直线CP 是线段AB 的垂直平分线. (3)线段CD 的长为√3+1或3√3+3. 解法提示:∵CD=CE ,∠C=∠C ,CA=CB ,∴△CAE ≌△CBD ,∴∠CAE=∠CBD. ∵CA=CB ,∠ACB=30°, ∴∠CAB=∠CBA=75°,∴∠PBA=∠PAB=45°,∴∠APB=90°, ∴PA=PB=√22AB=√3. 分两种情况讨论.①当点P 在AB 上方时,如图(1),图(1)则∠DAP=∠EBP=30°,∠APD=90°,∴DB=DC ,DP=√33AP=1,∴CD=DB=√3+1. ②当点P 在AB 下方时,如图(2), 则∠DAP=∠EBP=60°,∠APD=90°,∴∠ADP=30°,∴BD=BC,DP=√3AP=3,AD=2AP=2√3,∴BC=BD=√3+3,∴CD=CA+AD=CB+AD=√3+3+2√3=3√3+3.综上可知,线段CD的长为√3+1或3√3+3.图(2) 9.问题发现192知识迁移 5拓展延伸(1)BE=DE+GF.理由:如图(1),过点G作GH⊥BE于点H.图(1)∵BE⊥CD,GF⊥CD,∴∠HEF=∠EFG=∠EHG=90°,∴四边形EFGH为矩形,∴EH=GF,EF=GH.∵EF=BE,∴GH=BE.∵∠MBN=90°,∠BHG=90°,∴∠1+∠2=90°,∠2+∠3=90°,∴∠1=∠3.又∵∠BED=∠GHB=90°,BE=GH,∴△BDE≌△GBH(ASA),∴DE=BH,∴BE=BH+EH=DE+GF.(2)92或323. 解法提示:分两种情况讨论.①当点F 在线段EC 上时,如图(2).图(2)由(1)可得BE=DE+GF. 设BE=EF=m ,则EC=m+2.在Rt △BEC 中,根据勾股定理,得BE 2+CE 2=BC 2, 即m 2+(m+2)2=102,解得m=6(负值已舍),∴BE=EF=6.易证△CFG ∽△CEB ,∴CF CE =GF BE ,即22+6=GF 6, ∴GF=32,∴DE=BE -GF=6-32=92. ②当点F 在线段EC 的延长线上时,如图(3).图(3)同(1)中方法可得BE=DE-GF. 设BE=EF=n ,则EC=n-2.在Rt △BEC 中,根据勾股定理,得BE 2+CE 2=BC 2, 即n 2+(n-2)2=102,解得n=8(负值已舍),∴BE=EF=8.易证△CFG ∽△CEB ,∴CF CE =GF BE ,即28−2=GF 8, ∴GF=83,∴DE=BE+GF=8+83=323.10.(1)EM DM =EBAB AM ⊥DE(2)证明:如图(1),过点G 作GH ⊥BC 于点H.图(1)∵四边形ABCD 是矩形,点E 在AB 的延长线上, ∴∠CBE=∠GHC=90°,∴∠BCE+∠BEC=90°. ∵四边形CEFG 为正方形, ∴CG=CE ,∠GCE=90°,∴∠BCE+∠BCG=90°,∴∠BEC=∠BCG , ∴△GHC ≌△CBE ,∴HC=BE. ∵AD=BC=2AB ,BE=AB ,∴BC=2BE=2HC , ∴HC=BH ,∴GH 垂直平分BC , 即点G 在线段BC 的垂直平分线上. (3)√5或√17.解法提示:同(2)中思路可证得点F 在线段BC 的垂直平分线上.如图(2),过点F 作FN ⊥BC 于点N ,连接CF ,则CF=√2CE=√2×√22+12=√10,CN=1,∴NF=√(√10)2-12=3.图(2)由作图过程可知,点M 在线段BC 的垂直平分线上,故分两种情况讨论.①当点M 在点F 左侧时,如图(3),连接MC ,图(3)则NM=3-1=2,∴m=CM=√22+12=√5.②当点M在点F右侧时,如图(4),连接MC,图(4)则NM=3+1=4,∴m=CM=√42+12=√17.综上可知,m的值为√5或√17.11.(1)②(2)如图(1),在AB上取点E,使得AE=AD,连接PE.图(1)∵AP平分∠DAE,∴∠DAP=∠EAP.又∵AP=AP,AD=AE,∴△DAP≌△EAP,∴PD=PE.∵AD+BC=AB=AE+BE,AD=AE,∴BC=BE.∵BP平分∠CBE,∴∠CBP=∠EBP.又∵BP=BP,∴△EBP≌△CBP,∴PE=PC,∴PC=PD.(3)8或403解法提示:如图(1),由(2)可得△DAP ≌△EAP ,△EBP ≌△CBP ,∴∠DPA=∠EPA ,∠CPB=∠EPB ,∠D=∠AEP ,∠C=∠BEP. 又∵∠DPA+∠EPA+∠CPB+∠EPB=180°,∠AEP+∠BEP=180°,∴∠APB=∠EPA+∠EPB=90°,∠D+∠C=180°, ∴AD ∥BC.在Rt △PAB 中,tan ∠PAB=12,∠APB=90°, 故可设BP=x ,AP=2x ,∴AB=√x 2+(2x)2=√5x=10, 解得x=2√5,∴AP=4√5,sin ∠PAB=1√5. 易知∠PBC>45°,故分两种情况讨论.①当∠C=45°时,如图(2),图(2)过点P 作PM ⊥AD ,交AD 的延长线于点M ,则∠MDP=∠C=45°,∴MP=MD. 又∵tan ∠MAP=tan ∠PAB=12,∴AM=2MP , ∴AD=MD=MP=AP ·sin ∠MAP=4, ∴S △PAD =12×4×4=8. ②当∠BPC=45°时,如图(3),图(3)过点D 作DN ⊥AP 于点N ,则∠DPN=180°-45°-90°=45°,∴NP=ND.∵tan ∠DAP=tan ∠PAB=12,∴AN=2ND. 又∵AP=AN+NP ,∴4√5=2ND+ND ,∴ND=4√53,∴S △PAD =12×4√5×4√53=403. 综上可知,△PAD 的面积为8或403.12.(1)①BE=AD②BE=AD. 理由如下:当点D 不在AC 上时,∵∠ACB=∠ACD+∠DCB=60°,∠DCE=∠BCE+∠DCB=60°,∴∠ACD=∠BCE. 在△ACD 和△BCE中,{AC =BC,∠ACD =∠BCE,DC =EC,∴△ACD ≌△BCE ,∴AD=BE. (2)①BE=√2AD. 理由如下:当n=90时,在等腰直角三角形DEC 中,DC EC =sin 45°=√22, 在等腰直角三角形ABC 中,AC BC =sin 45°=√22.∵∠ACB=∠ACE+∠ECB=45°,∠DCE=∠ACE+∠DCA=45°,∴∠ECB=∠DCA. 在△DCA 和△ECB中,{DCEC=AC BC=√22,∠DCA =∠ECB,∴△DCA ∽△ECB ,∴AD BE =√22,∴BE=√2AD. ②5或√13.解法提示:当点D 在△ABC 外部时,设EC 与AB 交于点F ,如图(1)所示.图(1)∵AB=3√2,AD=1,由上可知:AC=AB=3√2,BE=√2AD=√2. 又∵BE ∥AC ,∴∠EBF=∠CAF=90°.而∠EFB=∠CFA ,∴△EFB ∽△CFA ,∴EF CF =BF AF =BE AC =√23√2=13,∴AF=3BF ,而AB=BF+AF=3√2,∴BF=14×3√2=3√24. 在Rt △EBF 中,EF=√EB 2+BF 2=(√2)2+(3√24)2=5√24. 又∵CF=3EF=3×5√24=15√24, ∴EC=EF+CF=5√24+15√24=5√2. 在等腰直角三角形DEC 中,DC=EC ·sin 45°=5√2×√22=5.当点D 在△ABC 内部时,设AB 延长线与CE 延长线交于点F ,如图(2),图(2)∵AB=3√2,AD=1,由上可知:AC=AB=3√2,BC=√2AB=6,BE=√2AD=√2. 又∵BE ∥AC ,∴△EFB ∽△CFA ,∴FB FA =BE AC =13, ∴BF=12AB=3√22,AF=AB+BF=3√2+3√22=9√22. 在Rt △ACF 中,CF=√AC 2+AF 2=3√262.CE=23CF=23×3√262=√26. 在等腰直角三角形DEC 中,DC=√22CE=√13. 综上所述,满足条件的CD 的值为5或√13.。
物理实验题答题技巧

物理实验题答题技巧实验题是物理试卷的一个重要组成部分。
关于实验题有哪些答题技巧呢?下面是店铺为你整理的物理实验题的答题技巧,一起来看看吧。
物理实验题答题技巧一、测量型实验题这种实验题是比较简单的,主要包括直接测量型实验和间接测量型实验,只要同学们不马虎,得满分是没问题的。
二、探究型实验题新课标的特点就是探究,探究型实验题也是中考物理实验题的主角。
教材上除了几个测量类实验和演示实验以外,都可以以探究的形式出现,课本上的实验是出题的一个重点。
解法分析:解探究题要深入了解课本上实验的原理和方法,做到了如指掌,才能对探究实验题做到万无一失;二是掌握探究的方法,要熟练运用“控制变量法”“等效替代法”“类比法”等方法。
三、开放型实验题有许多物理实验可以用不同的方法来做,用不同的实验方法、不同的验仪器能得出相同的实验结果,也就是说物理实验具有开放性。
开放型实验题是近年考题中的一个新亮点,特点是题设条件不确定、解题方法多样化、答案不惟一;在考查大家实验能力的同时还考查大家的创新能力、发散思维能力。
因为一题多解,考题的难度并不大。
解法分析:希望大家把做过的开放型实验题归纳在一起,找到解题方法和技巧,提高自己的创新能力、发散思维能力。
四、设计型实验题设计型实验让我们自行设计实验方案,能考查综合运用能力、创新能力和独立解决问题的能力。
常见设计型实验题多数考察密度和电学部分,并有以下特点:基础性:大部分题目以课本知识为依托,不脱离教材,考查我们对知识的灵活运用能力;开放性:设计题大部分没有惟一答案,只要求写出其中的一种或几种,还有就是贴近生产、生活,常把日用品作为实验仪器来验证物理规律,考查知识的迁移能力与运用能力。
解法分析:设计型实验题所能涵盖的内容较多,提供的信息较少,出题的知识点不好把握,要求我们要富有创新精神,能灵活运用所学知识去分析问题和解决问题,遇到问题需要充分发挥自己的想像力。
物理实验的基本思想方法1.等效法等效法是科学研究中常用的一种思维方法.对一些复杂问题采用等效法,可将其变换成理想的、简单的、已知规律的过程来处理,常使问题的解决得以简化.如在“验证力的平行四边形定则”的实验中,要求用一个弹簧秤单独拉橡皮条时,要与用两个互成角度的弹簧秤同时拉橡皮条时产生的效果相同——使结点到达同一位置O,即要在合力与两分力等效的条件下,才能找出它们之间合成与分解时所遵循的关系——平行四边形定则.2.转换法将某些不易显示、不易直接测量的物理量转化为易于显示、易于测量的物理量的方法称为转换法(间接测量法).如:弹簧测力计是把力的大小转换为弹簧的伸长量;打点计时器是把流逝的时间转换成振针的周期性振动;电流表是利用电流在磁场中受力,把电流转化为指针的偏转角;用单摆测定重力加速度g是通过公式T=2π把g的测量转换为T 和L的测量,等等.3.留迹法留迹法是利用某些特殊的手段,把一些瞬间即逝的现象(如位置、轨迹等)记录下来,以便于此后对其进行仔细研究的一种方法.如:用打点计时器打在纸带上的点迹记录小车的位移与时间之间的关系;用描迹法描绘平抛运动的轨迹;在描绘电场中等势线的实验中,用探针通过复写纸在白纸上留下的痕迹记录等势点的位置等等.4.累积法累积法是把某些难以直接准确测量的微小量累积后测量,以提高测量的准确度的一种实验方法.如:在缺乏高精密度的测量仪器的情况下测细金属丝的直径,常把细金属丝绕在圆柱体上测若干匝的总长度,然后除以匝数就可求出细金属丝的直径;测一张薄纸的厚度时,常先测出若干页纸的总厚度,再除以被测页数即所求每页纸的厚度等.5.模拟法模拟法是一种间接实验方法,它是通过与原型相似的模型来说明原型的规律性的.模拟法在中学物理实验中的典型应用是“用描迹法画出电场中平面上的等势线”这一实验,由于直接描绘静电场的等势线很困难,而恒定电流的电场与静电场相似,所以用恒定电流的电场来模拟静电场,通过它来了解静电场中等势线的分布情况.6.控制变量法在多因素的实验中,可以先控制一些量不变,依次研究某一个因素的影响.如在“验证牛顿第二定律”的实验中,可以先保持质量一定,研究加速度和力的关系;再保持力一定,研究加速度和质量的关系;最后综合得出加速度与质量、力的关系.。
中考生物 实验探究题

小试牛刀
(1)该实验设置①组目的是 对照 ,该实验 的变量是 有无蚂蚁 。 (2)根据实验数据,得出结论: 蚂蚁对金合欢 幼苗的生长有促进作用 。 (3)蚂蚁的发育过程有蛹期,此昆虫的发育过程 属于的发育类型是 完全变态 发育。
小试牛刀
(4)下列细胞结构中,蚂蚁体细胞不具有,而金
合欢叶肉细胞具有的是 ①④⑥ (多项选择)
样题示例
①用香烟和蒸馏水制成烟草浸出液。 ②通过稀释,得到25%、50%、75%的烟草浸出液。 ③取5个大培养皿,编号,铺上卫生纸,均放入结构完整、大小相当的 50粒黄豆种子。 ④在培养皿中分别加入等量的蒸馏水和不同浓度的烟草浸出液,将装置 放在室温条件下。 ⑤每天向培养皿中分别加入等量的相应浓度的烟草浸出液和蒸馏水。 ⑥5天后统计种子的发芽率。 实验结果如下表所示,请分析回答下列问题。
样题示例
(2)若A组菌落平均数较少,B组菌落平均数较多,C组无 菌落或菌落平均数较少,则说明“抗菌”洗手液具有抗菌抑 菌作用。 (3)对照实验是在探究某种条件对研究对象的影响时,对 研究对象进行的除了该条件不同以外,其他条件都相同的实 验。根据变量设置一组对照实验,使实验结果具有说服力。 一般来说,对实验变量进行处理的,就是实验组。没有处理 的就是对照组;所以设置C组的实验目的是对照作用。
样题示例
(4)每组用1个培养皿做实验,数量少偶然性大; 每组设置3个培养皿,取菌落的平均数,可以避免 偶然性,减小实验误差,使实验结果具有说服力。 (5)细菌通过分裂方式繁殖。
小试牛刀
1.为了研究蚂蚁对金合欢(被子植物)幼苗生长的 影响,某生物兴趣小组的同学进行了实验探究,得 到了如下表所示的实验结果。请据表分析,回答下 列问题:
生
物识
三类探究题解法例析

的由来, 如果是后者, 解答时必须先对实例进行分析 , 异中
()较陡” 做的有用功为— — 1“ 时, 机械效率为— — ; ; 总功为— — ; 求同, 抽象出研究方法的模式。 例3 (06 20 年盐城市) 小张同学在做“ 制作、 研究电磁 铁” 的实验中, 猜想电磁铁的磁性强弱应该与电流大小有 关, 还与线圈的匝数有关 。为此他用铁钉和漆包线绕制成 匝数不同的甲、 乙两个电磁铁, 并找来了相关的实验器材 ,
吗?
所示的电路接通后, 小 明同学发现电流 表 A 的读数 比电流 。 表 A 的读数要大一 些。于是他猜想: 当 图l
例 2 如 图 2所 示 ,
小明在探究串联电路电流 的实验时, 闭合开关后, 发 现电流表无示数 , L 与 灯 1
图2
电流通过灯泡( 电器) 能使灯泡工作 , 用 时, 因灯泡要消耗
维普资讯
《 探究 串、 并联电路 电流规律》 试题解析
对于串并联电路 中的电流规律, 各类试题中不再是简
单地考查是否能记住 ,而是特别注重考查实验探究的过 程和能力的发展。现举例加以说明。
例 1 当如 图 l
舞
湖南 欧忠祥
说明:在本题中,电流表 A 的读数比电流表 A 的读 “ 。
不能够被 吸 引的是木块 ;
方法四: 把它们都放入水中, 上浮的是木蛱 , 下沉的是 铁块。 小结: 这是一道要求用学过的知识设计探究方法的开 放性试题 , 方法有多种 , 要由此及彼 , 变通迁移。
图1
斜面螟 小 车 重量 斜面盔度 沿斜面控力 稿面 长 有用功 息 功 机槭 斜爱崖 I h・ , * I1 I 1 h 盯 f l 靛事 璇t
一
方法 一 : —
中考物理高频考点训练:探究电流与电压和电阻的关系实验

探究电流与电压和电阻的关系实验【考法综述】1.连接部分电路;2.设计实验电路图,实验记录表;3.连接电路时的注意事项:开关状态、滑动变阻器滑片位置、电表量程的选取、电表的正负接线柱;4.实验时的故障分析;5.实验数据分析;6.伏安曲线的绘制与解读;7.在探究电流与电阻关系时,电阻阻值变化与滑动变阻器的移动方向;8.在探究电流与电压关系时,电压值变化与滑动变阻器的移动方向;无法达到电压值的原因;9.滑动变阻器规格的选取方法;10.滑动变阻器的作用;11.其它问题。
【解法探讨】例1.(2018广元)如图甲,是张勇实验小组在探究“电流与电阻的关系”时的电路图,电源电压恒为6V.电压表、电流表无损坏,有阻值为5Ω、10Ω、20Ω、30Ω、40Ω定值电阻5个。
(1)根据图甲,用笔画线代替导线连接完成图乙的实物图。
(2)实验过程中,需要改变定值电阻,观察电流的变化,为了科学地得出实验结论,当每次更换电阻后,都要移动滑动变阻器的滑片,此时眼睛应注意观察_______(选填序号)。
A.变阻器滑片B.电压表C.电流表D.电源(3)某次实验,更换电阻R,合上开关后,电压表示数为0,电流表示数正常,其原因可能是_______。
(4)在老师的引导下,他们将5次实验数据描绘在图丙中。
图中阴影部分“面积”表示的物理量是_______(选填序号)。
A.电流B.电压C.电阻D.电功率(5)实验中,他们选择下列哪个滑动变阻器最合适_______(选填序号)。
A.10Ω 0.5A B.50Ω0.5A C.50Ω1A D.200Ω1A(6)请你用平滑曲线将图丙中5个点连接起来,观察图象你可以得出实验结论:当电压一定时,导体中的电流与导体的电阻_______。
【答案】. (1) (2) B (3) 电阻短路(4) B (5) C(6) 成反比【简析】(1)由图甲可以看出:当滑动变阻器的滑片向左移动时,连入电路的阻值变大;实物图中已连接上端的接线柱,所以另一端应该连接右下端,这样才能在滑动变阻器的滑片向左移动时连入电路的阻值变大。
【初中物理】中考物理实验探究专题真题训练大气压实验人教版
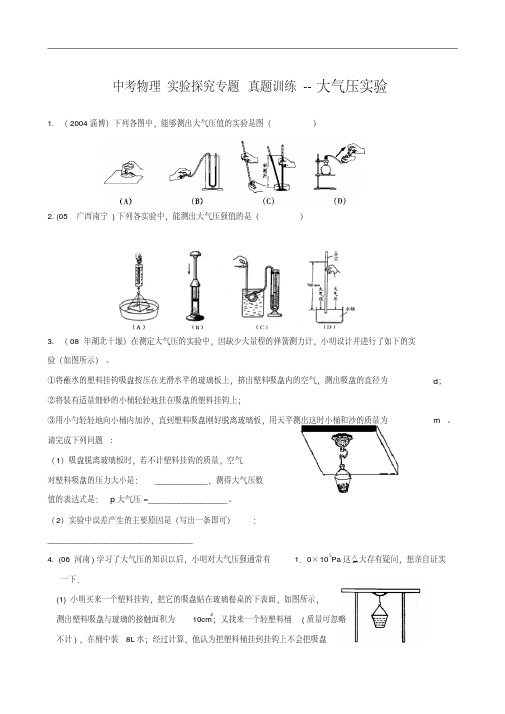
中考物理实验探究专题真题训练--大气压实验1. (2004淄博)下列各图中,能够测出大气压值的实验是图()2. (05广西南宁)下列各实验中,能测出大气压强值的是()3. (08年湖北十堰)在测定大气压的实验中,因缺少大量程的弹簧测力计,小明设计并进行了如下的实验(如图所示)。
①将蘸水的塑料挂钩吸盘按压在光滑水平的玻璃板上,挤出塑料吸盘内的空气,测出吸盘的直径为d;②将装有适量细砂的小桶轻轻地挂在吸盘的塑料挂钩上;③用小勺轻轻地向小桶内加沙,直到塑料吸盘刚好脱离玻璃板,用天平测出这时小桶和沙的质量为m。
请完成下列问题:(1)吸盘脱离玻璃板时,若不计塑料挂钩的质量,空气对塑料吸盘的压力大小是:____________,测得大气压数值的表达式是:p大气压=__________________。
(2)实验中误差产生的主要原因是(写出一条即可):_________________________________4.(06河南)学习了大气压的知识以后,小明对大气压强通常有1.0×105Pa这么大存有疑问,想亲自证实一下.(1)小明买来一个塑料挂钩,把它的吸盘贴在玻璃餐桌的下表面,如图所示,测出塑料吸盘与玻璃的接触面积为10cm2;又找来一个轻塑料桶(质量可忽略不计),在桶中装8L水;经过计算,他认为把塑料桶挂到挂钩上不会把吸盘拉掉.请你写出计算过程和判断依据.(g取10N/kg)(2)当小明把水桶挂到挂钩上时,吸盘却被拉掉了,是大气压没有那么大还是其他原因?请发表你的看法.5.(2005年苏州市)小明所设计的“估测大气压的值”的实验方案如下:①把注射器的活塞推至注射器筒的底端,然后用—个橡皮帽封住注射器的小孔;②如图所示,用细尼龙绳拴住注射器活塞的颈部,使绳的另一端与固定在墙上的弹簧测力计的挂钩相连,然后水平向右慢慢地拉动注射器筒. 当注射器中的活塞刚开始移动时,记下弹簧测力计的示数F;③观察并记录注射器筒上所标明的容积V,用刻度尺测出注射器的全部刻度长度L.(1)根据以上实验方案,用测得和记录的物理量计算大气压强的表达式应为p=___________________________.(2)按照上述实验方案测得的大气压强的值,往往会比大气压强的实际值偏小.你认为产生这种现象的主要原因是:___________________________________________________________.6.(2007年南通市)某学习小组利用注射器、弹簧测力计、刻度尺等器材粗测大气压值.(1)图甲是按1:1的比例拍摄的注射器上的全部刻度线,注射器的最大可读容积为_________,用刻度尺测量注射器全部刻度的总长为_____ cm,可算得活塞的横截面积为____cm2。
2021年合子配子致死的解题方法和习题答案

“合子、配子致死”遗传题的解法欧阳光明(2021.03.07)一、某基因使配子致死:某些致死基因可使雄配子死亡,从而使后代只出现某一性别的子代,所以若后代出现单一性别的问题,考虑是“雄配子致死”的问题。
例1、剪秋萝是一种雌雄异体的高等植物,有宽叶(B)和窄叶(b)两种类型,控制这两种性状的基因只位于X染色体上。
经研究发现,窄叶基因(b)可使花粉致死。
现将杂合子宽叶雌株与窄叶雄株杂交,其后代的表现型及比例正确的是()A、宽叶雄株:宽叶雌株:窄叶雄株:窄叶雌株=1:1:0:0B、宽叶雄株:宽叶雌株:窄叶雄株:窄叶雌株=1:0:0:1C、宽叶雄株:宽叶雌株:窄叶雄株:窄叶雌株=1:0:1:0D、宽叶雄株:宽叶雌株:窄叶雄株:窄叶雌株=1:1:1:1解析:由题意可知,杂合子宽叶雌株的基因型为XBXb,窄叶雄株的基因型为XbY,又知窄叶基因(b)可使花粉致死,则窄叶雄株只能产生一种花粉,即含有Y的花粉,雌株能产生含XB、Xb的两种卵细胞,则后代的表现型为宽叶雄株和窄叶雄株,无雌株。
选C。
例2、某种雌雄异株的植物女娄菜有宽叶和窄叶两种类型,宽叶由显性基因B控制,窄叶由隐性基因b控制,B和b均位于X染色体上,基因b使雄配子致死。
请回答:(1)若后代全为宽叶雄株个体,则其亲本基因型为)XBXB×XbY 。
(2)若后代全为宽叶,雌、雄植株各半时,则其亲本基因型为XBXB×XBY 。
(3)若后代全为雄株,宽叶和窄叶个体各半时,则其亲本基因型为 XBXb×XbY 。
(4)若后代性别比为1:1,宽叶个体占3/4,则其亲本基因型为XBXb×XBY 。
(5)能否出现后代全为窄叶,且雌雄各半的情况,若能写出亲本的基因型,若不能说明理由不能,因为亲本中基因型为XbXb的雌性个体不存在。
解析:(1)若后代全为宽叶雄株(XBY),则亲本雄株只产生Y 配子,雌株只产生XB配子,亲本基因组合必为XBXB×XbY。
初中物理探究实验题(含答案)

初中物理探究实验题(含答案)本文档为初中物理探究实验题,提供了一些适合初中学生进行实验的题目,并附有相应的答案。
以下是题目及答案的列表:题目1:重量与质量的关系题目:在实验中,小明用天平测量了一个物体的重量为10N,质量为1kg。
请问,重量和质量之间是否存在某种关系?如果存在,请写出你的观察结果和理由。
在实验中,小明用天平测量了一个物体的重量为10N,质量为1kg。
请问,重量和质量之间是否存在某种关系?如果存在,请写出你的观察结果和理由。
答案:是的,重量和质量之间存在一种简单的线性关系。
重量是物体受到重力作用的结果,而质量是物体自身的属性,二者之间存在以下关系:重量 = 质量 ×重力加速度。
根据题目中给出的数据,我们可以计算出重力加速度约为10 m/s^2,所以重量和质量的计算结果相等。
是的,重量和质量之间存在一种简单的线性关系。
重量是物体受到重力作用的结果,而质量是物体自身的属性,二者之间存在以下关系:重量 = 质量 ×重力加速度。
根据题目中给出的数据,我们可以计算出重力加速度约为10 m/s^2,所以重量和质量的计算结果相等。
题目2:摩擦力的影响题目:小明在实验中发现,当他用力拉扯一个木块时,木块的移动速度和木块与地面之间的摩擦力有关。
请写出你对这一现象的观察结果和解释。
小明在实验中发现,当他用力拉扯一个木块时,木块的移动速度和木块与地面之间的摩擦力有关。
请写出你对这一现象的观察结果和解释。
答案:我们观察到,当木块与地面之间的摩擦力增大时,木块的移动速度变慢;相反,当摩擦力减小时,木块的移动速度增加。
这是因为摩擦力会阻碍物体的运动,使其难以克服阻力而移动。
当摩擦力较大时,木块需要更多的力才能克服阻力移动,因此速度较慢;而当摩擦力较小时,木块受到的阻力较小,移动速度较快。
我们观察到,当木块与地面之间的摩擦力增大时,木块的移动速度变慢;相反,当摩擦力减小时,木块的移动速度增加。
初中物理实验题答题技巧

初中物理实验题答题技巧初中物理实验题怎么解答,解答得分技巧有哪些?不知道的考生看过来,下面由小编为你精心准备了“初中物理实验题答题技巧”仅供参考,持续关注本站将可以持续获取更多的资讯!初中物理实验题答题技巧初中物理实验题答题方法一、测量型实验测量型实验主要有直接测量型和间接测量型两种,共15个实验,这些是中考物理实验测试必不可少的组成部分。
1、测量型实验共10个实验:⑴用刻度尺测长度;⑵用秒表测时间;⑶用量筒测固、液体的体积;⑷用水表测家庭自来水使用量;⑸用天平测物体的质量;⑹用温度计测水的温度;⑺用弹簧测力计测力的大小;⑻用电流表测电流;⑼用电压表测电压;⑽用电能表测电功的大小。
直接测量型实验主要针对一些常用物理测量工具的使用方法、读数方法等,而这些知识和能力在课堂教学中已逐步渗入,常用物理测量工具的共性都需要看量程、分清分度值。
所以只要掌握好其一,便可基本无碍。
2、间接测量型实验共5个实验:⑴用刻度尺、秒表测平均速度;⑵用天平、量筒测物质密度;⑶用刻度尺、弹簧测力计测滑轮组的机械效率;⑷用电流表、电压表测电阻;⑸用电流表、电压表测小灯泡的电功率。
而且这五种实验都涉及到诸多的物理测量工具的使用,也同时具有相应的实验原理:⑴物体通过的某段路程或某段时间的平均速度测量实验原理是v=s/t。
⑵测物质密度的实验原理是ρ=m/v和排水法。
⑶测滑轮组的机械效率实验原理主要是η=W有/W总、W=F·S及二力平衡。
⑷测电阻的实验原理是欧姆定律I=U/R的推导式R=U/I。
⑸测小灯泡的电功率实验的原理有两种,①伏安法的实验原理即为P=U·I,②电能表、秒表测电功率实验的原理即为P=W/ t。
解决此类题时,一定要细心,确保基本的物理测量工具的使用、读数不出错。
同时还应注意题意的局部拓展性变化。
近年来各地的中考物理测量型实验在这类题中变化较多,要格外注意。
二、探究型实验题探究型实验题也是中考物理实验题的主角,因此教材中探究型的课题每个章节都有渗透。
七年级数学(人教)上册木杆和重物试验方程解法

分析问题
如图,在木杆右端挂一重物,支点左边挂n个重物,并使左右 平衡,设木杆长为l cm ,支点在木杆中点处,支点到木杆左边挂重 物处的距离为 x cm,把n, l作为已知数,列出关于x的一元一次方程.
问题1:题目中哪些量是已知的、哪些量是未知的?
分析问题
提出猜想
思考:木杆平衡与哪些因素有关? 木杆平衡与左右两端各自悬挂重物的多少有关; 木杆平衡与支点到左右挂重物处的距离有关.
实验探究
研究木杆平衡条件的实验
第一环节 准备器材 质地均匀的木杆(杠杆尺); 一些等重的小物体(钩码); 铁架台.
实验探究
研究木杆平衡条件的实验
第二环节 明确步骤
(1)调整木杆,保证其在不挂钩码时, 能保持水平并静止,达到平衡状态;
实验 次数
1 2 3 4 …
小物体数 (单位:个)
左
右
支点到左边挂 支点到右边挂
重(物单处位距:离cm)l1 重(物单处位距:离cm)l2
1
1
20
20
2
1
10
20
3
1
6.9
20
4
1
5
20
…
…
…
20
ห้องสมุดไป่ตู้
研究木杆平衡条件的实验
第四环节 分析数据
可以从上往下看, 观察每列 数据的变化;从左往右看,看 每行数据之间的关系
支点到右边挂重
物(处单距位离:cml2)
11
20
20
21
10
20
31
6.9
20
41
5
20
……
专题50 电流与电压关系实验探究问题-决战中考物理压轴题、高频题、高分值题解题技巧(解析版)

考点扫描☆名师点拨一、考点解析电磁学科学实验与探究是电学的重要内容,也是常考题型。
实验探究是一种认识科学、应用科学的物理方法。
进行科学探究活动的一般思维程序是:提出问题→建立假说(或猜想)→实验检验→归纳分析→解决问题(或得出结论)→实验修正。
探究性试题是考查学生综合分析能力、归纳总结能力、发散性思维和创造性思维能力的中考热点题型,是近年来中考必考内容。
探究性试题可分为:现象探究、方法探究、实验探究、数据探究、阅读情景探究等。
解答此类试题要具备定的知识基础、能力基础、生活经验基础。
思维方法是发掘物理现象与物理知识、物理过程与物理方法之间隐含的联系,找到物理知识、物理规律的应用原型,是学生能力得到锻炼与升华的过程。
实验探究题主要以选择、填空、解答、分析为主。
电学实验探究题的分类与解法:1.考查内容(1)基本测量仪器仪表使用与掌握情况,灵活使用电流表、电压表、滑动变阻器的能力。
(2)综合应用知识解决问题的能力。
(3)设计实验的能力。
(4)思维发展能力、创新能力。
2.考查形式:选择、填空、连线作图、电路故障分析、实验方案设计。
3.考查重点和热点:电学仪表的使用、滑动变阻器的作用、验证电学规律、电学量的测量、创新能力。
考查难点:创新设计实验和对实验过程进行评估。
4.题目分类及分类解法技巧(1)考查测量仪器的读数和使用:关于实验器材的读数是物理实验的一个基本要素,也是考察实验基本技能的一种重要手段。
新课程标准要求学生应熟练掌握刻度尺、秒表、温度计、托盘天平、量筒、弹簧测力计、电流表、电压表和电能表这九种测量工具的读数方法。
其中,电学主要是电流表、电压表读数和滑动变阻器的接线,有时也将电能表与秒表组合探究家用电器的功率。
攻略:读数前都应首先弄清测量工具的量程、分度值、零刻线的位置。
学生实验中电压表两个量程分别是0~3V 和0~15V ,分度值对应的是0.1V 和0.5V ;电流表量程分别0~0.6A 和0~3A 分度值对应的是0.02A 和0.1A 。
浅谈实验探究题的意义及解法

浅谈实验探究题的意义及解法作者:赵欣蕊来源:《学校教育研究》2017年第19期纵观近几年中考命题,都以能力立意为出发点,在考试大纲几项能力要求中,又特别突出考查实验能力和理解能力。
科学探究即是学习的目标,又是科学学习的方式。
实验探究题作为能力考查的载体,在中考中占有很大的比例,从仪器使用到具体操作方法,改正错误等多方面进行考查。
如何帮助学生深化对这一课程内容的理解,提高解答综合题目的能力,是我们教师一直思考的问题。
一、实验探究题的意义《义务教育物理课程标准(2011年版)》把发展科学探究能力作为义务教育物理课程的一项重要指标。
科学探究式学习方式是提高学生科学素养的一种重要而有效的途径。
通过参与科学探究活动,培养初步的科学探究能力,通过一系列的探究活动,使学生能独立思考、敢于质疑、尊重事实、勇于创新,进而培养了观察能力、提出问题的能力、收集信息的能力、分析概括能力、信息交流能力等多方面的能力。
实验探究题就是科学探究学习方式成果的具体体现,它是指利用给出的实验器材或从所给器材中选择适当的器材,设计实验方案,完成实验探究问题的题型。
遇到这样的题型,学生总有点摸不着头脑,无从下手。
下面我就如何解答这一类题提出几点简单的建议,希望对学生有所帮助。
二、关于实验探究题的解法指导(一)细读题文、明确探究问题读懂题目的要求是解题的第一步,在做题时由于读数粗糙信息理解不够造成的错误较多。
因此我们在学习过程中要将审题能力和对问题的语言文字表述能力进行强化培养,从而能快速有效的搜集、筛选、鉴别和处理信息。
(二)明确实验器材的作用和使用方法新课标课程目标中要求学生会使用简单的实验仪器,能测量一些基本的物理量。
会阅读简单仪器的使用说明书,了解仪器的用途、结构及原理、性能、使用方法、注意事项、保养方法等方面的知识,做到正确使用,具有安全操作的意识,以免损坏。
做到熟悉了解实验器材的使用方法,从而确定哪些物理量可以利用器材直接测量得出,哪些物理量需要间接测量。
针对初一学生的科学实验训练 (附答案)

针对初一学生的科学实验训练 (附答案)本文档旨在为初一学生提供一些科学实验训练,帮助他们在科学领域培养实验技能和科学思维能力。
以下是几个简单且适合初一学生的实验项目,附有相应的实验步骤和答案。
实验一:酸碱中和反应实验材料:- 醋、小苏打、红、蓝色花色试纸、盐、碗、勺子实验步骤:1. 取一小碗,倒入一些醋。
2. 用红色花色试纸蘸取少量醋。
3. 将红色花色试纸放入碗中,观察颜色变化。
4. 重复步骤2和3,使用蓝色花色试纸。
结果分析:- 红色花色试纸变为橙色或黄色:醋呈酸性。
- 蓝色花色试纸变为绿色:醋呈碱性。
实验二:空气中的氧气实验材料:- 蜡烛、竹签、盘子、玻璃杯实验步骤:1. 在盘子边缘插上一个竹签。
2. 点燃蜡烛,并将其放在盘子中心。
3. 将一个玻璃杯倒扣在竹签上,盖住蜡烛。
4. 观察玻璃杯内部的变化。
结果分析:- 玻璃杯内蜡烛熄灭:表示燃烧需要氧气。
- 玻璃杯内有水蒸气凝结:表示燃烧产生水蒸气。
实验三:水的沸点实验材料:- 水、锅、火源、温度计实验步骤:1. 在锅中倒入适量的水。
2. 将锅置于火源上加热。
3. 使用温度计测量水的温度。
4. 观察水沸腾时的温度。
结果分析:- 水开始沸腾的温度是100℃。
---该文档提供了三个针对初一学生的科学实验训练项目,并附有相应的实验步骤和答案。
这些实验可以帮助学生了解酸碱中和反应、空气中的氧气以及水的沸点等基本科学概念。
通过实验训练,学生可以培养实验技能和科学思维能力,进一步提升对科学的兴趣和理解。
初中物理实验题类型及解法

初中物理实验题的类型及解法分析类型一:测量型实验题1.直接测量型实验掌握各类常见仪器的读数和使用,是做好物理实验的前提,所以各省、市中考题中都要涉及此类实验题。
例1(2005,北京)在实验室里,用托盘天平测铜块的质量。
当天平平衡时,右盘中放有50g、20g、10g的砝码各一个,游码的位置如图1所示,该铜块的质量为_______g。
图1解法分析:本题考查的是基本测量仪器天平的使用,天平右盘内砝码质量加游码示数就是被测物体的质量,本题砝码80g,游码2.4g,铜块质量为82.4g。
解析:此类考题对能力要求并不高,但要求对仪器的使用必须有较高的熟练程度。
初中物理仪器不太多,主要包括:温度计、量筒、天平、电阻箱、刻度尺、秒表、弹簧测力计、密度计、电流表、电能表、电压表等,平时有目的的多练习即可。
2.间接测量型实验通过分析2005年各地中考实验题,间接测量型实验仍是中考实验题的主角,但是考点不多,一般有五个重点实验,它们分别是对密度、浮力、滑轮组机械效率、电阻、电功率的测量。
中考中这几个实验出现几率很高,“测定小灯泡的额定功率”几乎是每年必考的实验。
例2(2005,德阳课改)在“测定小灯泡的功率”的实验中,小明同学设计的电路如图2所示,他选用的小灯泡的额定电压为2.5V,电阻约为8Ω,电源为两节干电池。
图2(1)请用笔画线代替导线按电路图(如图2),将实物电路(如图3)连接完整(连线不得交叉,正确选用电表的量程)图3(2)正确连好电路后,闭合开关前应把滑动变阻器滑片的位置调到________(填写“最左边”或“最右边”)(3)连好电路后,闭合开关S,小明发现灯泡不发光,电流表的示数为零,电压表的示数为3V,产生故障的原因可能是下列的哪几种情况:_______________。
A.小灯泡短路;B.小灯泡的灯丝断了;C.小灯泡的灯座接触不良;D.电压表的正、负接线柱接反。
(4)排除故障后,调节滑动变阻器使小灯泡在额定电压下正常发光时,电流表的示数如图4所示,则灯泡的额定功率为__________W。
中考数学实验探究题的基本类型和解法技巧

中考数学实验探究题的基本类型和解法技
巧
中考数学实验探究题是中考数学中重要的一种题型,也是考生相对容易出现问题的一种题型。
下面将介绍中考数学实验探究题的基本类型和解法技巧。
基本类型
1. 统计类
这种类型的实验探究题通常是在观察和收集数据的基础上进行统计分析。
例如,某校初中一年级有80个学生,现在统计了80名学生的身高,然后分析身高的分布情况。
2. 对比类
这种类型的实验探究题通常是通过对比不同的数据进行分析比较。
例如,某超市推出了两款新的洗涤剂,现在请你用这两种洗涤剂分别处理同样的衣服,看看它们的清洁效果。
3. 推断类
这种类型的实验探究题通常是通过实验结果推断出结论,从而
得到一些新的认识。
例如,如果我们想知道三角形外角和等于多少度,我们可以做出多个不同形状的三角形,测量它们的外角和,然
后推断出外角和的大小规律。
解法技巧
1. 熟悉实验探究题的特点和分类方法,并学会根据题意将实验
探究题归类。
2. 做实验探究题时,一定要看清题意,理解实验的目的和意义,掌握实验的步骤和方法。
3. 在进行实验时,要认真记录实验数据,同时注意记录实验过
程中遇到的问题和解决方法。
4. 在进行数据统计和分析时,要运用数学知识和方法,进行合理的数据归纳和分析,从而得出正确的结论。
总之,中考数学实验探究题虽然难度较大,但只要我们掌握了基本类型和解题技巧,认真做好每道题目的分析和实验过程记录,相信我们一定可以在考试中获得不错的成绩。
实验探究试题说题

一道充分展示思维层次的实验探究试题每年中考结束之后,许多化学老师会想方设法搜集各地的中考题进行学习和研究,为下一学年教学中对各个知识、能力点的把握上提供一些方向和指导。
在研读过程中,许多题巧妙的构思、新颖的设计、合理的取材等都会让人拍手叫绝。
现与大家分享一道充分挖掘教材,激发师生问题意识;展现思维层次,评价学生能力的实验探究题。
[实验探究题]在高效复习课堂中,同学们利用“硫酸、硝酸钡、氢氧化钠、碳酸钾” 四种物质的溶液对 “复分解反应发生的条件”进行再探究。
【知识回放】通过判断上述四种溶液两两之间能否发生反应,我能写出其中符合下列条件的两个化学方程式:⑴一个中和反应 ;⑵一个有沉淀生成的反应 。
【挖掘实质】⑴图1是HCl和NaOH在水中解离出离子的示意图,小丽发现HCl在水中会解离出H+和Cl-,NaOH在水中会解离出Na+和OH-,以此类推硝酸钡在水中会解离出的离子是 (填离子符号)。
⑵图2是稀盐酸和氢氧化钠溶液发生化学反应的微观过程示意图,该化学反应的实质可以表示为 H++OH-=H2O我也能用同样的方式表示上述四种溶液两两之间发生反应时有气体生成的反应的实质 。
【实践运用】⑴通过上述探究发现,在溶液中H+和OH-不能大量共存,我还发现在溶液中 和 (填离子符号,下同)也不能大量共存。
⑵利用上述四种物质的溶液完成实验后,将所得物质混合并过滤,得到一种无色溶液。
经测定,该溶液显酸性。
则在该溶液中一定含有的离子是 。
为了验证该溶液中可能含有的离子是否存在,我设计如下实验进行验证。
溶液中可能含有的离子 设计实验验证(实验步骤、现象及对应的结论)【知识升华】对“复分解反应发生的条件”的再探究,我发现在分析多种溶液混合后所得溶液中离子的成分时,应考虑的因素是 。
[实验探究题说题]【说背景】本试题在中要求根据复分解发生的条件写化学方程式,其中中和反应即酸和碱发生的反应,也就只有硫酸和氢氧化钠了;而要有沉淀生成,根据所给物质把它们的成分组合的话,只可能得到硫酸钡和碳酸钡沉淀,因此,可以写硫酸和硝酸钡的反应,也可写碳酸钾与硝酸钡的反应。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验探究题的解法与练习一、科学探究的基本环节:提出问题——建立假设——设计实验方案——进行实验——得出结论——交流评价二、解题思路1、认真读题,划出关键的语句,审清题意,明确要求。
2 、找出题目中与教材相联系的知识点。
3、灵活应用基础知识解决探究题中的问题。
三、例题与练习例1、已知在溶液中氢氧化钙和碳酸钠反应生成碳酸钙和氢氧化钠。
现实验室中有一包白色粉末,可能是碳酸钠,也可能是氧化钙或氢氧化钙。
为确定其组成,某同学设计了以下实验方案进行探究,请你按要求帮助完成探究活动。
(1)提出假设:假设① 白色粉末是碳酸钠假设② 白色粉末是氧化钙假设③ 白色粉末是氢氧化钙(2)设计实验,通过实验分析进行判断并填空:(3)实验后思考:假定这包白色粉末是混有少量氧化钙的碳酸钠粉末,将混合物溶于水可观察到的现象是__________________________________________________;若将反应后的混合物进行固液分离,分离的方法是_______________;再将分离后的溶液蒸干,得到的固体物质是________________________(填化学式)。
例2、小森同学在滴加FeCI 3 溶液时,不小心把滴加FeCI 3溶液的滴管放入到盛“双氧水”(过氧化氢)的试剂瓶中,发现有大量的气泡产生。
小森联想FeCI 3 溶液能否也可以作过氧化氢分解的催化剂呢?于是他进行了探究。
得出结论:FeCI 3 溶液能作过氧化氢分解的催化剂。
小森同学知道FeCI 3溶液中含有H 2O 、Fe 3+和CI -三种微粒,于是又做了三种猜想: 猜想1:真正催化分解H 2O 2的是FeCI 3溶液中的H 2O猜想2:真正催化分解H 2O 2的是FeCI 3溶液中的Fe 3+猜想3:真正催化分解H 2O 2的是FeCI 3溶液中的CI -你认为最不可能的是猜想 ,理由是 。
小森同学又对余下的两种猜想,进行了实验探究,请你帮助他填写下表:例3、某校化学兴趣小组的同学对部分日常生活用品的酸碱度进行了测定,分析测定结果,发现各类洗发液的pH差别较大,约在7-9之间,护发素的pH均略小于7。
同学们联想到洗发、护发的程序,决定探究溶液的酸碱度对头发的影响。
【提出问题】溶液的酸碱度对头发有什么影响?【设计实验】⑴收集某人的5束头发,分别放在盛有不同pH的溶液的烧杯中,静置约30min。
⑵将各束头发取出,用纸巾吸干液体观察并实验.结果如下表。
【实验结论】。
【分析交流】洗发时使用洗发液和护发素的顺序是,。
原因是;。
解题时注意的问题:1、提出的猜想要准确合理,有利于方案的设计;合乎题意不能存在漏洞,不能信口开河;2、设计的实验方案要紧扣提出的假设,选用的实验用品要恰当;实验方案理论上合理,实际上可行,操作上简便易行、安全,还要经济环保。
3、结论一定是对假设的判定,交流评价一般是对实验方案、也是探究题中最难的地方。
练1、已知过氧化钠加入水中能发生如下反应:Na202+2H20=2NaOH+H202,过氧化氢又能分解放出氧气。
小华为了证明过氧化钠加入水中生成了氢氧化钠,在生成的溶液中滴加了几滴无色酚酞试液,观察到的现象是溶液先变红后褪为无色。
请你对此现象进行探究。
(只要提出假设、方案,不需要说出方案实施的具体结果) 假设一:生成的过氧化氢使溶液褪色。
方案一:在稀氢氧化钠中滴加酚酞试液,再滴加过氧化氢溶液,观察溶液颜色变化。
假设二:。
方案二:。
练2、实验室里某小组正在探究一个问题。
根据设计方案,小英向试管中加入2mL氢氧化钠溶液,滴入几滴酚酞溶液,溶液显红色。
然后她又用滴管连续滴入一定量的稀硫酸,溶液由红色变为无色。
(1)他们探究的问题是____________(填Ⅰ或Ⅱ)Ⅰ.酚酞溶液遇酸、碱溶液能显示不同颜色吗?Ⅱ.酸和碱溶液能发生反应吗?(2)大家对小英得到的无色溶液继续探究。
小斌认为反应后溶液中的溶质是硫酸钠,小亮认为溶质有两种,它们是______。
同学们根据以下两种方案进行实验后,一致认为小亮的观点是正确的。
请你补填下表的空缺。
练3、在做氢氧化钠的性质实验时,甲同学将稀盐酸滴入到装有氢氧化钠固体的试管中,触摸试管有灼热感,他马上得出结论:氢氧化钠与稀盐酸反应会放出大量的热。
但是乙同学提出异议:热量不一定是氢氧化钠与稀盐酸反应放出的。
(1)你认为乙同学提出异议的理由是。
(2)针对乙同学提出的异议,甲、乙同学对上述实验进行了探究:[提出问题]:氢氧化钠与稀盐酸反应是否会放出热量?[猜想与假设]:氢氧化钠与稀盐酸反应会放出热量。
[实验方案]:可能用到的实验仪器与药品:氢氧化钠固体、稀盐酸、蒸馏水、烧杯、温度计、玻璃棒、胶头滴管实验过程:(请补充完成下列空格)(3)丙同学取步骤②反应后所得的溶液,继续进行探究。
他向溶液中滴入无色酚酞试液,发现酚酞试液不变色。
因此他得出溶液呈中性的结论。
你认为他的结论是否正确?(填“是”或“否”),理由是。
练4、某化学兴趣小组按以下步骤探究某一温度下氯化钠饱和溶液的酸碱度。
[猜想或假设]溶液的pH可能为(请将你的假设填入空格中):①pH < 7 ,②____________ ,③____________ 。
[设计和实验]要测定该溶液的酸碱度,除有正确的操作步骤外,其中不能采用下列物质中的_________________(填序号)来进行实验。
①pH试纸②紫色石蕊试液③酚酞试液组内同学进行了如下实验:甲同学:取pH试纸放在玻璃片上,用玻璃棒蘸取氯化钠溶液沾在pH试纸上,把试纸显示的颜色与标准比色卡比较,测得pH=7。
乙同学:取pH试纸放在玻璃片上,先用蒸馏水将pH试纸湿润,然后用玻璃棒蘸取氯化钠溶液沾在pH试纸上,把试纸显示的颜色与标准比色卡比较,测得pH=7。
饱和石灰水浓NaOH溶液甲乙丙同学:将pH试纸直接浸入氯化钠溶液中,把试纸显示的颜色与标准比色卡比较,测得pH=7。
[评价]三位同学中操作规范的是___同学。
指出其余同学操作上的错误:_ 。
[结论和分析]丙同学得出:“凡是盐溶液的pH都等于7”,你认为该结论是否正确?___________,如不正确请举一例说明(如正确,此空不用填)。
_________________。
练5、某校进行化学实验考查时,教师给了同学们1小包黑色粉末,这种黑色粉末可能是氧化铜、炭粉或者是两者的混合物,让他们通过实验探究来确定。
某同学探究过程如下: (1)【提出假设】假设1:黑色粉末是炭粉;假设2:假设3.(2)【设计实验方案】他对实验做了如下设想和分析:取少量黑色粉末于烧杯中,并加入过量的稀硫酸。
则实验中可能出现的现象与对应结论如下表,请你完成下表。
(3)【进行实验】通过实验及分析,确定该黑色物质为炭粉和氧化铜的混合物。
(4)【拓展】为了进一步探究炭粉和氧化铜的性质,他又利用这种混合物补充做了如下实验:将此黑色粉末隔绝空气加热(若碳完全反应),待冷却到室温后,取剩余固体于烧杯中,再加入过量稀硫酸,反应完全后,静置。
请你回答:①烧杯中 (填“有”或“无)不溶物;②若静置后溶液呈无色,则该溶液中溶质是 (写作学式);③若静置后溶液呈蓝色,该反应的化学方程式为:练6、研究性学习小组中的小张同学在学习中发现:通常检验CO2用石灰水,吸收CO2用浓NaOH溶液。
【实验探究】在体积相同盛满CO2的两集气瓶中,分别加入等体积的饱和石灰水和浓NaOH 溶液。
实验装置和现象如图所示。
请你一起参与。
【现象结论】甲装置中产生的实验现象(用化学方程式表示),解释通常用石灰水而不用NaOH 溶液检验CO2的原因;乙装置中的实验现象是,吸收CO2较多的装置是。
【计算验证】另一位同学小李通过计算发现,等质量的Ca(OH)2和NaOH吸收CO2的质量,Ca(OH)2大于NaOH。
因此,他认为通常吸收CO2应该用饱和石灰水。
【思考评价】请你对小李同学的结论进行评价:。
参考答案:例1、(2)假设①:不成立;假设②:成立;假设③:不成立;(3)溶液温度升高、并出现白色沉淀;过滤;NaOH 。
例2例3、【实验结论】碱性溶液对头发有损害,酸性溶液对头发没有影响。
【分析交流】洗发时使用洗发液和护发素的顺序是,先用洗发液,后用护发素。
原因是:护发素和洗发液发生中和反应,使头发保持中性或酸性,对头发有利。
练1、假设二:生成的氧气使溶液褪色。
方案二:向稀NaOH 溶液中滴加几滴酚酞试液,通入氧气观察。
练2、(1练3、(1)你认为乙同学提出异议的理由是固体氢氧化钠溶于水放热。
(2)(3)否;理由是溶液呈酸性酚酞也是无色。
练4、 ①pH < 7 ,②pH > 7,③pH=7。
①pH 试纸[评价] 操作规范的是甲同学;乙同学:用蒸馏水将pH 试纸湿润,会改变PH ;丙同学:将pH 试纸直接浸入氯化钠溶液中,会导致溶液变质。
[结论和分析] 不正确;Na 2CO 3溶液呈碱性练5、(1)假设2:黑色粉末是氧化铜假设3.黑色粉末是氧化铜和炭粉的混合物(2)【设计实验方案】(4) 有;H 2SO 4;CuO+ H 2SO 4== CuSO 4+ H 2O练6、Ca(OH)2+CO 2=CaCO 3↓+H 2O 用NaOH 溶液检验CO 2观察不到任何现象 集气瓶中的小气球逐渐胀大 乙 小李同学没有考虑到石灰水的溶解度很小,吸收的CO 2也很小,所以不正确。
