探索与表达规律练习题
《探索与表达规律》专项练习【2020北师大版七年级数学上册】

试题汇编一一找规律1、如图所示,观察小圆圈的摆放规律,第一个图中有5个小圆圈,第二个图中有3个菱形,第3幅图中有5个菱形,则第4幅图中有______ 个菱形,第n幅图中有 _______ 个菱形.1 2 3 n3、用同样大小的黑色棋子按下图所示的方式摆图形,按照这样的规律摆下去,4、观察表一,寻找规律.表二、表三、表四分别是从表一中截取的一部分,其中a、b、c的值分别为________________ .5、如图①是一块瓷砖的图案,用这种瓷砖来铺设地面.如果铺成一个 2 2的正方形图案(如图②),其中完整的圆共有5个,如果铺成一个3 3的正方形有8个小圆圈,第100个图中有个小圆圈.2、(1) (2) (3)找规律.下列图中有大小不同的菱形, 第1幅图中有1个菱形,第2幅图中则第n个图形需棋子枚(用含n的代数式表示).第1个图• •第2个图第3个图O图案(如图③),其中完整的圆共有13个,如果铺成一个4 4的正方形图案(如图④),其中完整的圆共有25个•若这样铺成一个10 10的正方形图案,6 如下图,用同样大小的黑、白两种颜色的棋子摆设如下图所示的正方形图案,则第n个图案需要用白色棋子_____________ 枚(用含有n的代数式表示,并写成最简形式)•O O O O O O O O OO O O O••O O•••OO•O O••O O•••OO O O O O O O O•••OO O O O O7、用火柴棒按下图中的方式搭图形,按照这种方式搭下去,搭第334个图形需______ 根火柴棒。
8、将正整数按如图5所示的规律排列下去,若有序实数对(n ,m )表示第n排, 从左到右第m个数,如(4,2 )表示实数9,则表示实数17的有序实数对1第一排3 2 ",,,・,第二排4□56第三排1098 匚7第四排9、如图2 ,用n表示等边三角形边上的小圆圈,f(n)表示这个三角形中小圆圈的总数,那么f(n)和n的关系是___________则其中完整的圆共有 __________ 个.3J00 … o oo ooo o oo ooo oooo10、观察图4的三角形数阵,则第50行的最后一个数是( )1-2 3-4 5 -67 -8 9 -100 0 0 0 0 0 11、下列图案由边长相等的黑、白两色正方形按一定规律拼接而成, 依此规律, 第n 个图案中白色正方形的个数为 ___________ :12、观察下列各式:答案解析:1解析:n=1时,m=5 n 再每增加一个数时,m 就增加3个数•解答:根据所给 的具体数据,发现:8=5+3, 11=5+3X 2, 14=5+3X 3,….以此类推,第n 个圈 中,m=5+3( n-1 ) =3n+2.2解析:分析可得:第1幅图中有1X2-1=1个,第2幅图中有2X2-1=3个,第 3幅图中有3X2-1=5个,…,故第n 幅图中共有2n-1个3解析:在4的基础上,依次多3个,得到第n 个图中共有的棋子数.观察图形,发现:在4的基础上,依次多3个.即第n 个图中有4+3( n-1 )=3n+1.当 n=6时,即原式=19.故第6个图形需棋子19枚4解析:此题只要找出截取表一的那部分,并找出其规律即可解.解答:解:表二截取的是其中的一列:上下两个数字的差相等,所以a=15+3=18. 表猜.3 _3 _3 . . ._3 1 2 3 L L 10.3 .2 ,3 ^3 小2 1 11 2 3 62 ,3 小3 八2 1 2 3 ffl第一个,3 小3 八3 ,3 2 1 2 3 4 10三截取的是两行两列的相邻的四个数字:右边一列数字的差应比左边一列数字的差大1,所b=24+25-20+1=30.表四中截取的是两行三列中的6个数字:18是3的6倍,则c应是4的7倍,即28.故选D.认真观察表格,熟知各个数字之间的关系:第一列是1, 2,3,…;第二列是对应第一列的2倍;等三列是对应第一列的3倍5解析:据给出的四个图形的规律可以知道,组成大正方形的每个小正方形上有一个完整的圆,因此圆的数目是大正方形边长的平方,每四个小正方形组成一个完整的圆,从而可得这样的圆是大正方形边长减1的平方,从而可得若这样铺成一个10X 10的正方形图案,则其中完整的圆共有102+ (10-1 ) 2=181个.解答:解:分析可得完整的圆是大正方形的边长减1的平方,从而可知铺成一个, _ 2 210X 10的正方形图案中,完整的圆共有10+ (10-1) =181个.点评:本题难度中等,考查探究图形的规律.本题也只可以直接根据给出的四个图形中计数出的圆的个数,找出数字之间的规律得出答案.6解析:解:第1个正方形图案有棋子共32=9枚,其中黑色棋子有12=1枚,白色棋子有(32-12)枚;第2个正方形图案有棋子共42=16枚,其中黑色棋子有22=4枚,白色棋子有(42-22) 枚;…由此可推出想第n个图案的白色棋子数为(n+2)2-n2=4 (n+1).故第n个图案的白色棋子数为(n+2)2-n2=4 (n+1).点评:根据图形提供的信息探索规律,是近几年较流行的一种探索规律型问题.解决这类问题首先要从简单图形入手,抓住随着“编号”或“序号”增加时,后一个图形与前一个图形相比,在数量上增加(或倍数)情况的变化,找出数量上的变化规律,从而推出一般性的结论7解析:根据题意分析可得:搭第1个图形需12根火柴;搭第2个图形需12+6X仁18根;搭第3个图形需12+6X 2=24根;搭第n个图形需12+6 (n-1 )=6n+6根.解答:解:搭第334个图形需6X 334+6=2010根火柴棒8解析:寻找规律,然后解答.每排的数字个数就是排数;且奇数排从左到右,从小到大,而偶数排从左到右,从大到小.解答:解:观察图表可知:每排的数字个数就是排数;且奇数排从左到右,从小到大,而偶数排从左到右,从大到小.实数15=1+2+3+4+5则17在第6 排,第5个位置,即其坐标为(6, 5).故答案填:(6, 5).对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.9解析:根据题意分析可得:第n行有n个小圆圈.故f (n)和n的关系是?(n)=扌(n2+n).(^―11KR 10解析:根据题意可得:第n行有n个数;且第n行第一个数的绝对值为9(7i—+1,最后一个数的绝对值为 2 +n;奇数为正,偶数为负;故第50行的最后一个数是1275.(凱一1))<旧解答:解:第n行第一个数的绝对值为 2 +1,最后一个数的绝对值为+n,奇数为正,偶数为负,第50行的最后一个数是127511、第一个图中白色正方形的个数为3X3-1 ;第二个图中白色正方形的个数为3X5-2第三个图中白色正方形的个数为3X7-3 ;当其为第n个时,白色正方形的个数为3 (2n+1) -n=5n+312解析:根据所给的等式,可以发现右边的底数是前边的底数的和,指数是平方,则最后的底数是1+2+3+..+10=5 X 11=55,贝U原式M552•解答:解:根据分析最后的底数是1+2+3+..+10=5 X 11=55,则原式=552.故答案552。
七年级上探索与表达规律

19
20
21
22
23
24
25
26
27
28
29
30
31
日
一
二
三
四
五
六
8
如左图在月历中圈出的三个数: ①如果中间的数是8,那么前、后两个数分别是多少? 这三个数的和是__________ ②如果中间是23呢?则前、后两数分别是多少?这三个数的和是____________ ③如果中间是a呢?则前、后两数分别是____________ 这三个数的和是_____________
S2
S3
S4
图6
4、如图6,∠AOB=450,过OA到点O的距离分别为1,3,5,7,9,11,----的点作OA的垂线与OB相交,得到并标出一组黑色梯形,它们的面积分别为S1、S2、S3、S4--- 观察图中的规律,求出第10个黑色梯形的面积 S10=__________
5、一个巴尔末的中学教师成功地从光谱数据, ---中得到巴尔末公式,从而打开了光谱奥秘的大门,请你按照这种规律,写出第n(n≥1)个数据是___________________.
一、特例引入,揭示课题
01
添加标题
题1:观察下面的几个算式,你发现了什么?
02
添加标题
= 1
03
添加标题
112 = 121
04
添加标题
1112 = 12321
05
添加标题
11112 = 1234321
06
添加标题
利用上面的规律,猜想111112=____
题2:观察下面的几个算式,你发现了什么规律?
1+2+1 = 4
1+2+3+2+1 = 9
《探索与表达规律》练习题

(3n-2)×3n+1= (3n-1)2 可猜想第 n 个式子为____________________ .
探索表格的数字规律
5.(4 分)小何用计算机设下一个计算程序,输入和输出的数据如 下表: 输入 „ 输出 „ 1 1 2 2 2 5 3 3 10 4 4 17 5 5 26 „ „
那么当输入的数据是 8 时,输出的数据是( D ) 8 8 8 8 A.61 B.63 C.64 D.65
理由: 因为左边=(10a+b)×[100b+10(a+b)+a]=(10a+b)(100b +10a+10b+a)=(10a+b)(110b+11a)=11(10a+b)(10b+a);右边= [100a + 10(a + b) + b]×(10b + a) = (100a + 10a + 10b + b)(10b + a) = (110a+11b)(10b+a)=11(10a+b)(10b+a),所以左边=右边,所以表 示“数字对称等式”一般规律的式子为(10a+b)×[100b+10(a+b)+a] =[100a+10(a+b)+b]×(10b+a)
6.(8 分)把正整数从小到大依次排列成如下形式: 观察规律,求出第 10 行的最后一个数和第 20 行的第一个数.
第10行的最后一个数为55,第20行的第 一个数为191
探索图形规律
7.(4 分)一个由小菱形组成的装饰链,断去一部分,剩下部分如 图所示,则断去部分的小菱形的个数可能是( C ) A.3 个 B . 律填写的,根据此规律确定 x 的值为________
14.观察下列等式:9-1=8,16-4=12,25-9=16,36-16= 20,49-25=24,„„,这些等式反映出的自然数间的某种规律,设
2-n2=4n+4 (n + 2) n 表示自然数,用关于 n 的等式表示为___________________.
七年级数学上册《第三章探索与表达规律》练习题-带答案(北师大版)

七年级数学上册《第三章探索与表达规律》练习题-带答案(北师大版)一、选择题1.如图,用黑白两种颜色的纸片,按黑色纸片数逐渐增加1的规律拼成下列图案,若第n个图案中有2020个白色纸片,则n的值为( )A.671B.672C.673D.6742.下图是一个运算程序的示意图,若开始输入x的值为125,则第2 016次输出的结果为( )A.125B.25C.1D.53.观察下列各式: - 2x,4x2, - 8x3,16x4, - 32x5,…则第n个式子是( )A.- 2n - 1x nB.( - 2)n - 1x nC.- 2n x nD.( - 2)n x n4.观察如图所示图形,则第n个图形中三角形的个数是( )A.2n+2B.4n+4C.4nD.4n-45.下列图形都是按照一定规律组成,第一个图形中共有2个三角形,第二个图形中共有8个三角形,第三个图形中共有14个三角形…依此规律,第五个图形中三角形的个数是( )A.22B.24C.26D.286.下列是由一些火柴搭成的图案,图①用了5根火柴,图②用了9根火柴,图③用了13根火柴,按照这种方式摆下去,摆第n○个图案用多少根火柴( )A.4n+3B.5n-1C.4n+1D.5n-47.小明用棋子摆放图形来研究数的规律,图1中棋子围成三角形,其颗数3,6,9,12,…称为三角形数,类似地,图2中的4,8,12,16,…称为正方形数,下列数既是三角形数又是正方形数的是 ( )A.2010B.2012C.2014D.20168.下列图形都是由同样大小的小圆圈按一定规律所组成的,其中第①个图形中一共有6个小圆圈,第②个图形中一共有9个小圆圈,第③个图形中一共有12个小圆圈,…,按此规律排列,则第⑦个图形中小圆圈的个数为()A.21B.24C.27D.30二、填空题9.观察一组数2,5,10,17,26,37…则第n个数是.10.《庄子•天下篇》中写道:“一尺之棰,日取其半,万世不竭”意思是:一根一尺的木棍,如果每天截取它的一半,永远也取不完,如图.由图易得:= .11.当n等于1,2,3,…时,由白色小正方形和黑色小正方形组成的图形分别如图所示,则第n个图形中白色小正方形和黑色小正方形的个数总和等于 .(用含n的代数式表示,n是正整数)12.将从1开始的连续自然数按以下规律排列:第1行 1第2行 2 3 4第3行9 8 7 6 5第4行10 11 12 13 14 15 16第5行25 24 23 22 21 20 19 18 17 …则2023在第行.13.观察等式:1+3=4=22,1+3+5=9=32,1+3+5+7=16=421+3+5+7+9=25=52……猜想:(1)1+3+5+7…+99 =;(2)1+3+5+7+…+(2n﹣1)= _______.14.观察下列各式:13=1213+23=3213+23+33=6213+23+33+43=102…猜想13+23+33+…+103=.三、解答题15.探究题.用棋子摆成的“T”字形图如图所示:(1)填写下表:图形序号①②③④…⑩每个图案中棋子个数 5 8 …);(3)第20个“T”字形图案共有棋子多少个?(4)计算前20个“T”字形图案中棋子的总个数.(提示:请你先思考下列问题:第1个图案与第20个图案中共有多少个棋子?第2个图案与第19个图案中共有多少个棋子?第3个图案与第18个图案呢?)16.我们发现了一种“乘法就是减法”的非常有趣的运算:①1×12=1﹣12:②2×23=2﹣23;③3×34=3﹣34;…(1)请直接写出第4个等式是;(2)试用n(n为自然数,n≥1)来表示第n个等式所反映的规律是;(3)请说明(2)中猜想的结论是正确的.17.察下列各式:第1个:1×3=3=22﹣1第2个:2×4=8=32﹣1第3个:3×5=15=42﹣1第4个:4×6=24=52﹣1第5个:5×7=35=62﹣1…这些等式反映出自然数间的某种运算规律.(1)请你根据规律写出下一个等式:;(2)设n(n≥1)表示自然数,请根据这个规律把第n个等式表示出来,并通过你所学过的整式运算知识来验证这个等式成立.18.阅读解题:1111212=-⨯,3121321-=⨯,4131431-=⨯, ... 计算:+⨯+⨯+⨯431321211...200520041⨯+ =+-+-+-413131212111 (2005)120041-+=120051-=20052004 理解以上方法的真正含义,计算:(1)111 (10111112100101)+++⨯⨯⨯ (2)19.用三角形和六边形按如图所示的规律拼图案.(1)第4个图案中,三角形的个数有 个,六边形的个数有 个; (2)第n(n 为正整数)个图案中,三角形的个数与六边形的个数各有多少个? (3)第2018个图案中,三角形的个数与六边形的个数各有多少个?(4)是否存在某个符合上述规律的图案,其中有100个三角形与30个六边形?如果有,指出是第几个图案;如果没有,说明理由. (2027)20251531311⨯++⨯+⨯20.阅读材料:求1+2+22+23+24+…+22023的值.解:设S=1+2+22+23+24+…+22022+22023,将等式两边同时乘以2得:2S=2+22+23+24+25+…+22023+22024将下式减去上式得2S﹣S=22024﹣1即S=22024﹣1即1+2+22+23+24+…+22023=22024﹣1请你仿照此法计算:(1)1+2+22+23+24+…+210(2)1+3+32+33+34+…+3n(其中n为正整数).参考答案1.【答案】C2.【答案】D3.【答案】D4.【答案】C5.【答案】C6.【答案】C7.【答案】D8.【答案】B9.【答案】n2+1.10.【答案】1﹣.11.【答案】n2+4n.12.【答案】45.13.【答案】502;n2.14.【答案】55215.解:(1)11 14 32 (2)3n+2 (3)3n+2=3×20+2=62(个)(4)(5+62)×202=670(个).16.【答案】解:等式左侧乘积的第一个因数是从1开始的连续自然数,第二个因数的分子和这个自然数相同,分母比分子大1;右侧恰是左侧两个因数的差; (1)第4个等式:4×=4﹣ (2)第n 个等式:n ×=n ﹣ (3)证明:n ×=,n ﹣=∴n ×=n ﹣∴(2)中猜想的结论是正确的.17.【答案】解:(1)第6个:6×8=48=72﹣1;故【答案】6×8=48=72﹣1; (2)第n 个等式为n(n +2)=(n +1)2﹣1.n(n +2)=n 2+2n (n +1)2﹣1=n 2+2n +1﹣1=n 2+2n 所以n(n +2)=(n +1)2﹣1. 18.【答案】解:①根据题意得:1111111111011111210010110111112100101+++=-+-++-⨯⨯⨯ =1191101011010-= ②根据题意得:=21(1﹣20271)=20272013 19.【答案】解:(1)10 4;(2)观察发现,第1个图案中有4个三角形与1个六边形 以后每个图案都比它前一个图案增加2个三角形与1个六边形则第n 个图案中三角形的个数为4+2(n-1)=(2n +2)个,六边形的个数为n. (3)第2018个图案中,三角形的个数为2×2018+2=4038(个),六边形的个数为2018个.)(4)不存在.理由如下:假设存在这样的一个图案,其中有30个六边形,则这个图案是第30个图案 而第30个图案中三角形的个数为2×30+2=62≠100… 202720251531311⨯++⨯+⨯所以这样的图案不存在.20.【答案】解:(1)设S=1+2+22+23+24+…+210将等式两边同时乘以2得:2S=2+22+23+24+…+210+211 将下式减去上式得:2S﹣S=211﹣1,即S=211﹣1则1+2+22+23+24+…+210=211﹣1;(2)设S=1+3+32+33+34+…+3n①两边同时乘以3得:3S=3+32+33+34+…+3n+3n+1②②﹣①得:3S﹣S=3n+1﹣1,即S=12(3n+1﹣1)则1+3+32+33+34+…+3n=12(3n+1﹣1).。
《探索与表达规律》专项练习
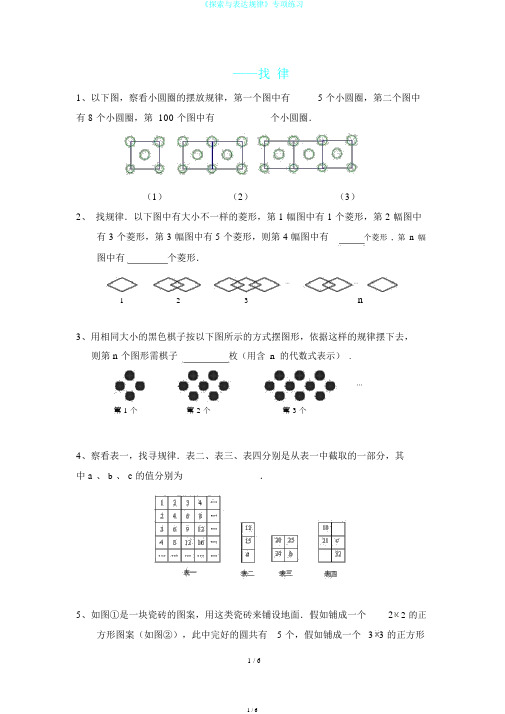
——找律1、以下图,察看小圆圈的摆放规律,第一个图中有 5 个小圆圈,第二个图中有 8 个小圆圈,第 100 个图中有 __________个小圆圈.(1)(2)(3)2、找规律.以下图中有大小不一样的菱形,第 1 幅图中有 1 个菱形,第 2 幅图中有 3 个菱形,第 3 幅图中有 5 个菱形,则第 4 幅图中有个菱形,第n幅图中有个菱形.⋯⋯123n3、用相同大小的黑色棋子按以下图所示的方式摆图形,依据这样的规律摆下去,则第 n 个图形需棋子枚(用含n的代数式表示).⋯第 1个第2个第3个4、察看表一,找寻规律.表二、表三、表四分别是从表一中截取的一部分,其中 a 、b、 c 的值分别为 ______________.5、如图①是一块瓷砖的图案,用这类瓷砖来铺设地面.假如铺成一个2 2 的正方形图案(如图②),此中完好的圆共有 5 个,假如铺成一个 3 3 的正方形图案(如图③),此中完好的圆共有 13 个,假如铺成一个 4 4 的正方形图案(如图④),此中完好的圆共有 25 个.若这样铺成一个 10 10 的正方形图案,则此中完好的圆共有个.6、以以下图 , 用相同大小的黑、白两种颜色的棋子陈设以以下图所示的正方形图案,则第 n 个图案需要用白色棋子枚(用含有 n 的代数式表示,并写成最简形式) .○○○○○○○○○○ ○ ○○●●○○●●●○○ ● ○○●●○○●●●○○ ○ ○○○○○○●●●○○○○○○7、用火柴棒按以下图中的方式搭图形,依据这类方式搭下去,搭第334 个图形需根火柴棒。
8、将正整数按如图 5 所示的规律摆列下去,如有序实数对( n ,m )表示第 n 排,从左到右第 m 个数,如( 4 , 2 )表示实数9 ,则表示实数17 的有序实数对是.1第一排32第二排456第三排10987第四排┅┅9、如图 2,用 n 表示等边三角形边上的小圆圈, f(n) 表示这个三角形中小圆圈的总数,那么 f(n)和 n 的关系是10、察 4 的三角形数,第50 行的最后一个数是()1-23-45-67-89 -10。
北师大版七年级上册 3.5 探索与表达规律(专题练习)

3.5 探索与表达规律(含答案)一.选择题:(四个选项中只有一个是正确的,选出正确选项填在题目的括号内)1.将正奇数按下表排成5列:第一列第二列第三列第四列第五列 第一行 1 3 5 7 第二行 15 13 11 9 第三行 17 19 21 23 第四行 31 29 27 25 根据上面规律,2019应在()A .125行,3列B .125行,2列C .251行,2列D .251行,5列2.如图所示的是某年5月的日历表,任意圈出一竖列上相邻的三个数,发现这三个数的和不可能是()A .27B .36C .40D .543.观察图中正方形四个顶点所标的数字规律,可知,数2019应标在()A .第504个正方形的左下角B .第504个正方形的右下角C .第505个正方形的左上角D .第505个正方形的右下角4.一根绳子弯曲成如图1所示的形状,当用剪刀像图2那样沿虚线a 把绳子剪断时,绳子被剪为5段;当用剪刀像图3那样沿虚线b (b ∥a )把绳子再剪一次时,绳子就被剪为9段.若用剪刀在虚线a ,b 之间把绳子再剪(n 2)次(剪刀的方向与a 平行),这样一共剪n 次时绳子的段数是()A .4n +1B .4n +2C .4n +3D .4n +55.如图所示,把同样大小的黑色棋子摆放在正多边形的边上,按照这样的规律摆下去,则第n (n 是大于0的整数)个图形需要黑色棋子的个数是( )A .3nB .n (n +2)C .n (n +1)D .2n -16.古希腊著名的毕达哥拉斯学派把1,3,6,10,……,这样的数称为“三角形数”,而把1,4,9,16,……,这样的数称为“正方形数”;从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和;则下列符合这一规律的等式是() A .20=4+16 B .25=9+16 C .36=15+21 D .40=12+283 2第1个正方形54 7 6第2个正方形 88 11 10第3个正方形 15 14第4个正方形日 一 二 三 四 五 六 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31图 1 图 2 a 图 2 a b7.同用样大小的黑色五角星按图所示的方式摆图案,按照这样的规律摆下去,第10个图案需要的黑色五角星的个数是()A .15B .16C .17D .188.下列图形都是由同样大小的五角星按一定的规律组成,其中第①个图形一共有2个五角星,第②个图形一共有8个五角星,第③个图形一共有18个五角星,……,则第⑥个图形中五角星的个数为()A .50B .64C .68D .729.如图,下列图案均是长度相同的火柴按一定的规律拼搭而成:第1个图案需7根火柴,第2个图案需13根火柴,……,依此规律,第11个图案需()根火柴 A .156 B .157 C .158 D .15910.如图,都是由边长为1的正方体叠成的立体图形,例如第(1)个图形由1个正方体叠成,第(2)个图形由4个正方体叠成,第(3)个图形由10个正方体叠成,依次规律,第(6)个图形由()个正方体叠成; A .36 B .37 C .56 D .84二.填空题:(将正确答案填在题目的横线上)11.观察下列算式:31=3,32=9,33=27,34=81,35=243,36=729,37=2187,38=6561,…,根据上述算式中的规律,32019的末位数字是_______;12.下面每个正方形中的五个数之间都有相同的规律,根据这种规律,则第4个正方形中间数字m 为,第n 个正方形的中间数字为;(用含n 的代数式表示)13.将一些半径相同的小圆按如图所示的规律摆放: ((14.观察下列图形,它们是按一定规律排列的,依照此规律,第n个图形有个;15.将一个正方体木块涂成红色,然后如图把它的棱三等分,再沿等分线把正方体切开,可以得到27个小正方体.观察并回答下列问题:(1)其中三面涂色的小正方体有________个,两面涂色的小正方体有______个,各面都没有涂色的小正方体有________个;145 32第1个581376第2个912211110第3个13m第4个图 ① 图 ② 图 ③(2)如果将这个正方体的棱n等分,所得的小正方体中三面涂色的有_________个,各面都没有涂色的有________个;(3)如果要得到各面都没有涂色的小正方体125个, 那么应该将此正方体的棱______等分;三.解答题:(写出必要的说明过程,解答步骤)16.观察下面数表:12343456745678 9 10(1)依此规律:第6行最后一个数字是________;第n行最后一个数字是________.(2)其中某一行最后一个数字可能是2019吗?若不可能,请说明理由;若可能,请求出是第几行?17.将连续的奇数1,3,5,7,9,……,排成如图所示的数阵.(1)十字框中的五个数的和与中间数15有什么关系?(2)设中间数为a,求出十字框中五个数之和;(3)十字框中五个数之和能等于2 015吗?若能,请写出这五个数;若不能,说明理由.18.如图1是一个三角形,分别连接这个三角形三变的中点得到图2,在分别连接图3中间的小三角形三边中点,得到图3,按此方法继续下去,请你根据每个图中三角形个数的规律,完成下列问题:(1(219.如图,将一张正方形纸片剪成四个小正方形,然后将其中的一个正方形再剪成四个小正方形,再将其中的一个正方形剪成四个小正方形,如此继续下去,……,请你根据以上操作方法得到的正方形的个数的规律完成各题;(1(2)a n =___________________(用含n的代数式表示);(3)按照上述方法,能否得到2019个正方形?如果能,请求出n;如果不能,请简述理由.20.用同样规格的黑白两色的正方形瓷砖铺设矩形地面,观察下列图形并解答有关问题.(1)在第n个图中,第一横行共_____________块瓷砖,第一竖列共有____________块瓷砖;(均用含n的代数式表示)(2)在第n个图中,铺设地面所用黑瓷砖的总块数为______________;(3)某商店黑瓷砖原价每块4元,则铺设第n个图的矩形地面,共需花多少元购买黑瓷砖?现在该商店举行“双11”促销活动,活动一:凡参加买黑瓷砖活动者赠送2块黑瓷砖;活动二:不赠送瓷砖,每块黑瓷砖打9折;现在需要购买黑瓷砖,铺设n=6时矩形地面,参加哪个活动合算?3.5 探索与表达规律参考答案:1~10DCDAB CBDBC11.7;12.29,8n-3;13.24,34,10104;14.1 (2)nn-+;15.(1)8,12,1;(2)8,3(2)n-;(3)7;16.(1)6,3n-2;(2)可能,672行;17.(1)15的5倍;(2)5a;(3)能;18.(1)13,17;(2)4n-3;19.(1)13,16;(2)a n =3n+1;(3)由3n+1=2019得:16723 n=这时,n不是整数,按照上述方法,不能得到2019个正方形;20.(1)(n+3),(n+2);(2)4n+6;(3)参加活动二合算;。
北师大版数学七年级上册3 5探索与表达规律同步练习(含解析)

第三章整式及其加减5探索与表达规律基础过关全练知识点探索规律的一般方法1.(2022湖北十堰房县一模)将正整数按如图所示的位置顺序排列:根据排列规律,知2021应在()A.A处B.B处C.C处D.D处2.观察下列等式:42-12=3×5;52-22=3×7;62-32=3×9;72-42=3×11;……则第n(n是正整数)个等式为(n+3)2-n2=.3.(2022山东济宁曲阜模拟)观察下面的变化规律:21×3=1−13,23×5=13−15,25×7=15−1 7,27×9=17−19,……,根据上面的规律计算:21×3+23×5+25×7+27×9+…+22 021×2 023.4.(教材P98变式题)如图为2022年8月的月历.在月历上任意圈出一个竖列上相邻的3个数.(1)设中间的一个数为a,则另外的两个数为,;(2)这三个数的和为,这三个数的和能为60吗?这三个数都在星期几?日一二三四五六123456789101112131415161718192021222324252627282930315.(教材P103变式题)图①②③是由火柴棒搭成的,按要求回答下列问题:(1)观察图形,并完成下表:图形标号①②③小正方形的个数1火柴棒的根数4(2)按照这种方式搭下去,搭第n个图形中小正方形有个,需要火柴棒根;(3)按照这种方式搭下去,求第50个图形需要的火柴棒根数.能力提升全练6.(2021山东济宁中考,10,)按规律排列的一组数据:12,35,□,717,926,1137,…,其中□内应填的数是()A.23B.511C.59D.127.(2022安徽合肥庐江期中,10,)下列图案是由长度相同的火柴棒按一定规律拼搭而成的,图案①需要8根火柴棒,图案②需要15根火柴棒,……,按此规律,图案n需要火柴棒的根数为()A.2+7nB.8+7nC.4+7nD.7n+18.(2022河北石家庄赵县月考,19,)如图,按此规律,第6行最后一个数字是,第行最后一个数是2020.素养探究全练9.[数学运算](2022江苏南京二十九中月考)探究规律,完成相关题目.定义“*”运算:(+2)*(+4)=+(22+42);(-4)*(-7)=+[(-4)2+(-7)2];(-2)*(+4)=-[(-2)2+(+4)2];(+5)*(-7)=-[(+5)2+(-7)2];0*(-5)=(-5)*0=(-5)2;(+3)*0=0*(+3)=(+3)2;0*0=02+02=0.(1)归纳“*”运算的法则:两数进行“*”运算时,(文字语言或符号语言均可).特别地,0和任何数进行“*”运算或任何数和0进行“*”运算,;(2)计算:(+1)*[0*(-2)];(3)是否存在有理数m,n,使得(m-1)*(n+2)=0?若存在,求出m,n的值,若不存在,请说明理由.答案全解全析基础过关全练1.D 因为2021÷4=505……1,所以2021应在1的位置,也就是在D处.故选D.2.3(2n+3)解析第n个等式为(n+3)2-n2=3(2n+3).3.解析原式=1-13+13−15+15−17+17−19+…+12 021−12 023=1−12 023=2 0222 023.4.解析(1)a-7;a+7.(2)这三个数的和为3a,这三个数的和可以为60.因为60÷3=20,所以这三个数都在星期六.5.解析(1)补全题表如下:图形标号①②③小正方形的个数149火柴棒的根数41224(2)第1个图形中小正方形的个数是1=12,需要火柴棒的根数是4=2×1×(1+1);第2个图形中小正方形的个数是4=22,需要火柴棒的根数是12=2×2×(2+1);第3个图形中小正方形的个数是9=32,需要火柴棒的根数是24=2×3×(3+1);……第n个图形中小正方形的个数是n2,需要火柴棒的根数是2n(n+1).故答案为n2;2n(n+1).(3)当n=50时,2n(n+1)=2×50×(50+1)=5100,即第50个图形需要的火柴棒根数为5100.能力提升全练6.D 观察这组数据可知,第n个数据为2n-1n2+1.当n=3时,2n-1n2+1=510=12.所以□内应填的数为12,故选D.7.D 因为图案①需要8根火柴棒;图案②需要8+7=15根火柴棒;图案③需要8+7+7=22根火柴棒;……所以图案n需要8+7(n-1)=(7n+1)根火柴棒.故选D.8.16;674解析因为每一行的最后一个数字分别是1,4,7,10,…,所以第n行最后一个数字为1+3(n-1)=3n-2,所以第6行最后一个数字为3×6-2=16.当3n-2=2020时,n=674,故答案为16;674.素养探究全练9.解析(1)同号得正,异号得负,并把两数的平方相加;都等于这个数的平方.(2)(+1)*[0*(-2)]=(+1)*(-2)2=(+1)*(+4)=+(12+42)=1+16=17.(3)存在.因为(m-1)*(n+2)=0,所以(m-1)2+(n+2)2=0,所以m-1=0,n+2=0,解得m=1,n=-2.。
北师大版数学7年级上册3.5《探索与表达规律》同步练习

《探索与表达规律》同步练习A 100 B. 125 C. 150 D.175答案:C解析:解答:∵2=1+1=13+12,12=8+4=23+22,36=27+9=33+32,80=64+16=43+42,∴下一个数是53+52=125+25=150.(第n个数为n3+n2).故选C分析:所给的数正好可以分成同一个数的立方与平方的和,从而得解.2.现定义一种变换:对于一个由有限个数组成的序列S0,将其中的每个数换成该数在S0中出现的次数,可得到一个新序列S1,例如序列S0:(4,2,3,4,2),通过变换可生成新序列S1:(2,2,1,2,2),若S0可以为任意序列,则下面的序列可作为S1的是()A.(1,2,1,2,2)B.(2,2,2,3,3)C.(1,1,2,2,3)D.(1,2,1,1,2)答案:D解析:解答:A.∵ 2有3个,∴不可以作为S1,故A选项错误;B.∵ 2有3个,∴不可以作为S1,故B选项错误;C.3只有1个,∴不可以作为S1,故C选项错误;D.符合定义的一种变换,故D选项正确.选:D.分析:根据题意可知,S1中2有2的倍数个,3有3的倍数个,据此即可作出选择3.将正奇数按下表排成5列:第一列第二列第三列第四列第五列第一行 1 3 5 7第二行15 13 11 9第三行17 19 21 23第四行31 29 27 25…根据上面规律,2007应在()A.125行,3列B.125行,2列C.251行,2列D.251行,5列答案:D解析:解答: 因为(2007+1)÷2=2008÷2=1004所以2007是第1004个奇数;因为1004÷4=251,所以2007在第251行;又因为奇数行的数从小到大排列,偶数行的数从大到小排列,所以2007应在第5列,综上,可得2007应在第251行第5列.选:D.分析: 首先判断出2007是第1004个奇数;然后根据每行有4个奇数,用1004除以4,判断出2007在第251行;最后根据奇数行的数从小到大排列,偶数行的数从大到小排列,可得2007应在第5列,据此判断4. 一组数1,1,2,x,5,y…满足“从第三个数起,每个数都等于它前面的两个数之和”,那么这组数中y表示的数为()A.8 B.9 C.13 D.15答案:A解析:解答:∵每个数都等于它前面的两个数之和,∴x=1+2=3,∴y=x+5=3+5=8,即这组数中y表示的数为8.故选:A分析: 根据每个数都等于它前面的两个数之和,可得x=1+2=3,y=x+5=3+5=8,据此解答即可.5.多位数139713…、684268…,都是按如下方法得到的:将第1位数字乘以3,积为一位数时,将其写在第2位;积为两位数时,将其个位数字写在第2位.对第2位数字进行上述操作得到第3位数字…后面的每一位数字都是由前一位数字进行如上操作得到的.当第1位数字为4时,所得多位数前2014位的所有数字之和是()A.10072 B.10066 C.10064 D.10060答案:B解析:解答:当第1位数字为4时,得到42684268…,每四个数字一循环,∵2014÷4=503…2,∴第2014位的数字是2,则(4+2+6+8)×503+4+2=20×503+6=10066.选:B.分析: 通过计算发现,每4位数为一个循环组依次循环,然后用2014除以4即可得出第2014位数字是第几个循环组的第几个数字,由此进一步计算得出答案6.小张在做数学题时,发现了下面有趣的结果:3-2=1,8+7-6-5=4,15+14+13-12-11-10=9,24+23+22+21-20-19-18-17=16,…根据以上规律可知,第20行左起第一个数是()A.360 B.339 C.440 D.483答案:C解析:解答: ∵3=22-1,8=32-1,15=42-1,24=52-1,…∴第20个式子左起第一个数是:212-1=440.选:C.分析: 根据左起第一个数3,8,15,24…的变化规律得出第n行左起第一个数为(n+1)2-1,由此求出7.四个小朋友站成一排,老师按图中的规则数数,数到2015时对应的小朋友可得一朵红花.那么得红花的小朋友是()A.小沈B.小叶C.小李D.小王答案:A解析:解答: 去掉第一个数,每6个数一循环,(2015-1)÷6=2014÷6=335…4,则2015时对应的小朋友与5对应的小朋友是同一个.选:C.分析: 从图上可以看出,去掉第一个数,每6个数一循环,用(2015-1)÷6算出余数,再进一步确定2015的位置8.观察下列数据:0,3,8,15,24…它们是按一定规律排列的,依照此规律,第201个数据是()A.40400 B.40040 C.4040 D.404答案:A解析:解答: ∵0=12-1,3=22-1,8=32-1,15=42-1,24=52-1,…,∴第201个数据是:2012-1=40400.选A.分析: 观察不难发现,各数据都等于完全平方数减1,然后列式计算即可得解9.对于每个正整数n,设f(n)表示n(n+1)的末位数字.例如:f(1)=2(1×2的末位数字),f(2)=6(2×3的末位数字),f(3)=2(3×4的末位数字),…则f(1)+f(2)+f(3)+…+f(2012)的值为()A.6 B.4022 C.4028 D.6708答案:C解析:解答:∵f(1)=2(1×2的末位数字),f(2)=6(2×3的末位数字),f(3)=2(3×4的末位数字),f(4)=0,f(5)=0,f(6)=2,f(7)=6,f(8)=2,f(9)=0,…,∴每5个数一循环,分别为2,6,2,0,0…∴2012÷5=402..2∴f(1)+f(2)+f(3)+…+f(2012)=2+6+2+0+0+2+6+2+…+2+6=402×(2+6+2)+8=4028.选:C.分析: 首先根据已知得出规律,f(1)=2(1×2的末位数字),f(2)=6(2×3的末位数字),f(3)=2(3×4的末位数字),f(4)=0,f(5)=0,f(6)=2,f(7)=6,f(8)=2,f(9)=0,…,进而求出10.两列数如下:7,10,13,16,19,22,25,28,31,…7,11,15,19,23,27,31,35,39,…第1个相同的数是7,第10个相同的数是()A.115 B.127 C.139 D.151答案:A解析:解答: 第一组数7,10,13,16,19,22,25,28,31,…第m个数为:3m+4,第二组数7,11,15,19,23,27,31,35,39,…第n个数为:4n+3,∵3与4的最小公倍数为12,∴这两组数中相同的数组成的数列中两个相邻的数的差值为12,∵第一个相同的数为7,∴相同的数的组成的数列的通式为12a-5,第10个相同的数是:12×10-5=120-1=115.选:A.分析: 根据两组数的变化规律写出两组数的通式,从而得到它们的相同数列中两个相邻的数的差值,再结合第一个相同的数写出通式,然后把序数10代入进行计算11.对正整数n,记n!=1×2×3×…×n,则1!+2!+3!+…+10!的末尾数为()A.0 B.1 C.3 D.5答案:C解析:解答: ∵1!=1,2!=1×2=2,3!=1×2×3=6,4!=1×2×3×4=24,而5!、…、10!的数中都含有2与5的积,∴5!、…、10!的末尾数都是0,∴1!+2!+3!+…+10!的末尾数为3.选C.分析: 根据n!=1×2×3×...×n得到1!=1,2!=1×2=2,3!=1×2×3=6,4!=1×2×3×4=24,且5!、...、10!的数中都含有2与5的积,则5!、...、10!的末尾数都是0,于是得到1!+2!+3!+ (10)的末尾数为312.一组数1,1,2,x,5,y…满足“从第三个数起,每个数都等于它前面的两个数之和”,那么这组数中y表示的数为()A.8 B.9 C.13 D.15答案:A解析:解答: ∵每个数都等于它前面的两个数之和,∴x=1+2=3,∴y=x+5=3+5=8,即这组数中y表示的数为8.选:A.分析: 根据每个数都等于它前面的两个数之和,可得x=1+2=3,y=x+5=3+5=8,据此解答13.下面每个表格中的四个数都是按相同规律填写的:根据此规律确定x的值为()A.135 B.170 C.209 D.252答案:C解析:解答: ∵a+(a+2)=20,∴a=9,∵b=a+1,∴b=a+1=9+1=10,∴x=20b+a=20×10+9=200+9=209选:C.分析: 首先根据图示,可得第n个表格的左上角的数等于n,左下角的数等于n+1;然后根据4-1=3,6-2=4,8-3=5,10-4=6,…,可得从第一个表格开始,右上角的数与左上角的数的差分别是3、4、5、…,n+2,据此求出a的值是多少;最后根据每个表格中右下角的数等于左下角的数与右上角的数的积加上左上角的数,求出x的值14.把所有正奇数从小到大排列,并按如下规律分组:(1),(3,5,7),(9,11,13,15,17),(19,21,23,25,27,29,31),…,现有等式Am=(i,j)表示正奇数m是第i组第j个数(从左往右数),如A7=(2,3),则A2015=()A.(31,50)B.(32,47)C.(33,46)D.(34,42)答案:B解析:解答:2015是第201512+=1008个数,设2015在第n组,则1+3+5+7+…+(2n-1)≥1008,即()1212n n+-≥1008,解得:当n=31时,1+3+5+7+…+61=961;当n=32时,1+3+5+7+…+63=1024;故第1008个数在第32组,第1024个数为:2×1024-1=2047,第32组的第一个数为:2×962-1=1923,则2015是(201512923-+1)=47个数.故A2015=(32,47).选B.分析:先计算出2015是第1008个数,然后判断第1008个数在第几组,再判断是这一组的第几个数15.意大利著名数学家斐波那契在研究兔子繁殖问题时,发现有这样一组数:1,1,2,3,5,8,13,…,请根据这组数的规律写出第10个数是()A.25 B.27 C.55 D.120答案:C解析:解答:1+1=2,1+2=3,2+3=5,3+5=8,5+8=13,8+13=21,13+21=34,21+34=55.所以第10个数是55.选C.分析: 观察发现,从第三个数开始,后一个数是前两个数的和,依次计算求解得之差在这两个数之间,可产生一个新数串:3,6,9,-1,8,这称为第一次操作;做第二次同样的操作后也可以产生一个新数串:3,3,6,3,9,-10,9,8,依此类推,则从数串,开始操作第100次以后所产生的那个新数串的所有数之和是___答案:520解析:解答:一个依次排列的n个数组成一个数串:a1,a2,a3,…,a n,依题设操作方法可得新增的数为:a2- a1,a3- a2,a4- a3,a n- a n -1,所以,新增数之和为:(a2- a1)+(a3- a2)+(a4- a3)+…+(a n - a n -1)= a n - a1,原数串为3个数:3,9,8,第1次操作后所得数串为:3,6,9,-1,8,根据(*)可知,新增2项之和为:6+(-1)=5=8-3,第2次操作后所得数串为:3,3,6,3,9,-10,-1,9,8,根据(*)可知,新增2项之和为:3+3+(-10)+9=5=8-3,按这个规律下去,第100次操作后所得新数串所有数的和为:(3+9+8)+100×(8-3)=520,答案为:520.分析: 根据题意,计算可得第1次操作后所得数串为:3,6,9,-1,8;进而可得第2次操作后所得数串;分析可得其规律,运用规律可得答案17.将全体正整数排成一个三角形数阵,根据上述排列规律,数阵中第10行从左至右的第5个数是______答案: 50解析:解答: 由排列的规律可得,第n-1行结束的时候排了1+2+3+…+n-1=12n(n-1)个数.所以第n行从左向右的第5个数12n(n-1)+5.所以n=10时,第10行从左向右的第5个数为50.答案为:50.分析:先找到数的排列规律,求出第n-1行结束的时候一共出现的数的个数,再求第n行从左向右的第5个数,即可求出第10行从左向右的第5个数18.甲、乙、丙、丁四位同学围成一圈依次循环报数,规定:①甲、乙、丙、丁首次报出的数依次为1、2、3、4,接着甲报5,乙报6…,后一位同学报出的数比前一位同学报出的数大1,按此规律,当报到的数是50时,报数结束;②若报出的数为3的倍数,则该报数的同学需拍手一次,在此过程中,甲同学需要拍手的次数为_________答案:4解析:解答: ∵甲、乙、丙、丁首次报出的数依次为1、2、3、4,接着甲报5,乙报6…按此规律,后一位同学报出的数比前一位同学报出的数大1.当报到的数是50时,报数结束;∴50÷4=12余2,∴甲共报数13次,分别为1,5,9,13,17,21,25,29,33,37,41,45,49,∴报出的数为3的倍数,则报该数的同学需拍手一次.在此过程中,甲同学需报到:9,21,33,45这4个数时,应拍手4次.答案为:4.分析: 根据报数规律得出甲共报数13次,分别为1,5,9,13,17,21,25,29,33,37,41,45,49,即可得出报出的数为3的倍数的个数,即可得出答案19.观察下列等式:1=12;1+3=22;1+3+5=32;1+3+5+7=42,…,则1+3+5+7+…+2015= _________ 答案:1016064解析:解答:因为1=12;1+3=22;1+3+5=32;1+3+5+7=42;…,所以1+3+5+…+2015=1+3+5+…+(2×1008-1)=10082=1016064答案为:1016064.分析: 根据1=12;1+3=22;1+3+5=32;1+3+5+7=42;…,可得1+3+5+…+(2n-1)=n2,据此求出1+3+5+…+2015的值20.古希腊数学家把数1,3,6,10,15,21,…叫做三角形数,其中1是第一个三角形数,3是第2个三角形数,6是第3个三角形数,…依此类推,那么第9个三角形数是________ 答案:45解析:解答: 第9个三角形数是1+2+3+4+5+6+7+8+9=45分析: 根据所给的数据发现:第n个三角形数是1+2+3+…+n,由此代入分别求得答案52-1=24=8×3,72-1=48=8×6,92-1=80=8×10,…你发现了什么?答案:(2n+1)2-1=8×(1+2+3+…+n)解答: (1)n=1时,(2×1+1)2-1=8×1;n=2时,(2×2+1)2-1=24=8×(1+2);n=3时,(2×3+1)2-1=48=8×(1+2+3);n=4时,(2×4+1)2-1=80=8×(1+2+3+4);…n=n时,(2n+1)2-1=8×(1+2+3+…+n).即发现的规律为:(2n+1)2-1=8×(1+2+3+…+n)解析:分析: 式子的左边是一个奇数的平方减去1;等式右边是8的倍数,即(2n+1)2-1=8×(1+2+3+…+n)22.观察下列各式你会发现什么规律?1×5=5,而5=32-222×6=12,而12=42-223×7=21,而21=52-22…(1)求10×14的值,并写出与题目相符合的形式;答案:解答: 10×14=140=122-22;(2)将你猜想的规律用只含一个字母n的等式表示出来,并说明等式的正确性.答案: n(n+4)=(n+2)2-22.解答:第n个等式为n(n +4)=(n+2)2-22.∵左边= n(n +4)=n2+4n右边=(n +2)2-22=n2+4n+4-4═n2+4n左边=右边∴n(n+4)=(n+2)2-22.解析:分析: 由1×5=5,而5=5=32-22;2×6=12,而12=42-22;3×7=21,而21=52-22…可以看出两个因数相差4,所得的积是大的因数减去2的差的平方再减去2的平方,由此规律计算23.有规律排列的一列数:2、4、6、8…它的每一项可用式子2n(n是正整数)来表示;有规律的一列数:1、-2、3、-4、5、-6、7、-8…它的第100个数是什么?第n个数是什么?答案:100个数是-100,第n个数,(-1)n+1n;解析:解答:(1)奇数为正数,偶数为负数,并且第n个数的绝对值为n,所以100个数是-100,第n个数,(-1)n+1n;分析: 先得到符号的规律,再得到绝对值的规律即可;24.观察下列等式:12-02 ①,22-12 ②,32-22 ③,42-32 ④,…(1)按此规律猜想写出第⑥和第⑩个算式;答案:观察所给的4个算式,可知⑥、⑩个算式为:62-52,102-92;(2)请用含自然数n的等式表示这种规律.答案:用含自然数n的式子表示这种规律为:n2-(n-1)2解析:解答:(1)观察所给的4个算式,可知⑥、⑩个算式为:62-52,102-92;(2)用含自然数n的式子表示这种规律为:n2-(n-1)2分析: 本题考查规律型终端额数字变化问题,比较简单,考查学生的观察和总结能力25.观察:4×6=24,14×16=224,24×26=624,34×36=1224…,(1)上面两数相乘后,其末尾的两位数有什么规律?答案:末尾都是24;(2)如果按照上面的规律计算:124×126(请写出计算过程).答案:124×126=12×(12+1)×100+24=15600+24=15624;答案:(10a+4)(10a+6)=100a2+100a+24=100a(a+1)+24.解析:分析:本题考查了数字的变化类问题,仔细观察算式发现规律是解答本题的关键。
七年级数学上册 3.5 探索与表达规律作业 试题

3.5 探究与表达规律1.用棋子按如图方式摆“小房子〞:照这样的规律摆下去,摆第10个“小房子〞需要多少颗棋子?摆第n个需要多少颗棋子?你是如何得到的?2.请你伸出左手,做下面的游戏:从大拇指开场,像图中显示的这只手那样依次数数字1、2、3、4、5、……,请问数字20落在哪个手指上?数字200落在哪个手指上?2000呢?大拇指食指中指无名指小指1 2 3 4 59 8 7 610 11 12 1317 16 15 14……励志赠言经典语录精选句;挥动**,放飞梦想。
厚积薄发,一鸣惊人。
关于努力学习的语录。
自古以来就有许多文人留下如头悬梁锥刺股的经典的,而近代又有哪些经典的高中励志赠言出现呢?小编筛选了高中励志赠言句经典语录,看看是否有些帮助吧。
好男儿踌躇满志,你将如愿;真巾帼灿烂扬眉,我要成功。
含泪播种的人一定能含笑收获。
贵在坚持、难在坚持、成在坚持。
功崇惟志,业广为勤。
耕耘今天,收获明天。
成功,要靠辛勤与汗水,也要靠技巧与方法。
常说口里顺,常做手不笨。
不要自卑,你不比别人笨。
不要自满,别人不比你笨。
高三某班,青春无限,超越梦想,勇于争先。
敢闯敢拼,**协力,争创佳绩。
丰富学校体育内涵,共建时代校园文化。
奋勇冲击,永争第一。
奋斗冲刺,誓要蟾宫折桂;全心拼搏,定能金榜题名。
放心去飞,勇敢去追,追一切我们为完成的梦。
翻手为云,覆手为雨。
二人同心,其利断金。
短暂辛苦,终身幸福。
东隅已逝,桑榆非晚。
登高山,以知天之高;临深溪,以明地之厚。
大智若愚,大巧若拙。
聪明出于勤奋,天才在于积累。
把握机遇,心想事成。
奥运精神,永驻我心。
“想”要壮志凌云,“干”要脚踏实地。
**燃烧希望,励志赢来成功。
楚汉名城,喜迎城运盛会,三湘四水,欢聚体坛精英。
乘风破浪会有时,直挂云帆济沧海。
不学习,如何养活你的众多女人。
不为失败找理由,要为成功想办法。
不勤于始,将悔于终。
不苦不累,高三无味;不拼不搏,高三白活。
不经三思不求教不动笔墨不读书,人生难得几回搏,此时不搏,何时搏。
第04讲 探索与表达规律(6类热点题型讲练)(原卷版)-七年级数学上册同步学与练(北师大版)

第04讲探索与表达规律(6类热点题型讲练)1.探索运用符号表示数字规律和图形规律的方法.2.提高观察图形、探索规律的能力,培养创新意识.知识点01规律探究常见的数字规律规律总结数列形式21n -1,3,5,7,9,···,21n -2n 2,4,6,8,10,···,2n 13+n 4,7,10,13,16,···,13+n 13-n 2,5,8,11,14,···,13-n n 22,4,8,16,32,···,n 212+n 3,5,9,17,33,···,12+n 21n +2,5,10,17,26,···,21n +21n -0,3,8,15,24,···,21n -(1)n x -x -,x +,x -,x +,x -,x +,···,(1)n x-1(1)n x+-x +,x -,x +,x -,x +,x -,···,1(1)n x+-(1)2n n +1,3,6,10,15,21,···,(1)2n n +斐波那契数列1,1,2,3,5,8,13,…,从第三个数开始每个数等于与它相邻的前两个数之和知识点02规律探究方法总结1.规律探究的核心是找出每个数与对应的位次(即n )之间的关系;2.若数列为分数数列,则分子分母分开找规律;3.若数列是正负交替排列,则在答案前加上n )1(-;若数列是负正交替排列,则在答案前加上1)1(+-n ;4.若是选择题,则可以用代值法,再利用排除法选出正确答案即可.知识点03高斯求和定理2)1(2)(14321nn n n ⋅+=⨯+=+-+⋅⋅⋅++++项数末项首项.题型01数字类规律探索之排列问题【典例1】(2023·浙江衢州·校考一模)观察下列数据:0,3,8,15,24,…,它们是按一定规律排列的,依照此规律,第201个数据是()A .40400B .40040C .4040D .404【变式1】(2022春·黑龙江哈尔滨·六年级校考期中)一组数据x ,23x -,35x ,47x -,59x …请按这种规律写出第十个数是.【变式2】(2022秋·浙江金华·七年级校考期中)从3开始的连续奇数按右图的规律排列,其余位置数字均为0.(1)第5行第10列的数字是.(2)数字2023在图中的第行,第列.题型02数字类规律探索之末尾数字问题【典例2】(2022秋·江苏连云港·七年级校考阶段练习)观察下列算式:031=,133=,239=,3327=,4381=,53243=,63729=,732187=…归纳各计算结果中个位数字的规律,可得20033的个位数字是()A .1B .3C .9D .7【变式1】(2023春·江苏南京·七年级校考阶段练习)观察下列算式:①2(1)(1)1x x x -+=-;②23(1)(1)1x x x x -++=-;③324(1)(1)1x x x x x -+++=-寻找规律,并判断(2011)(2017)222221++⋯+++的值的末位数字为()A .1B .3C .5D .7【变式2】(2023春·江苏泰州·七年级统考期中)发现规律解决问题是常见解题策略之一.已知数5555551234529a =++++++ ,则这个数a 的个位数为()A .3B .4C .5D .6【变式3】(2023春·江苏连云港·七年级统考期末)生物学中,描述、解释和预测种群数量的变化,常常需要建立数学模型.在营养和生存空间没有限制的情况下,某种细胞可通过分裂来繁殖后代,我们就用数学模型2n 来表示,即:122=,224=,328=,4216=,5232=,……,请你推算123452023222222+++++⋅⋅⋅⋅⋅⋅+的个位数字是()A .8B .6C .4D .2题型03数字类规律探索之新运算问题【典例3】(2022·湖南株洲·统考二模)定义一种关于整数n 的“F ”运算:(1)当n 是奇数时,结果为35n +;(2)当n 是偶数时,结果是2k n (其中k 是使2kn是奇数的正整数),并且运算重复进行.例如:取58n =,第一次经F 运算是29,第二次经F 运算是92,第三次经F 运算是23,第四次经F 运算是74,……;若9n =,则第2020次运算结果是()A .1B .2C .7D .8【变式1】(2022秋·江苏扬州·七年级校考阶段练习)a 是不为2的有理数,我们把22a-称为a 的“哈利数”.如:3的“哈利数”是2223=--,2-的“哈利数”是()21222=--,已知14a =,2a 是1a 的“哈利数”,3a 是2a 的“哈利数”,4a 是3a 的“哈利数”,...,依此类推,则2022a =()A .4B .1-C .23D .32【变式2】(2023秋·全国·七年级专题练习)已知整数1a ,2a ,3a ,4a ,……满足下列条件:10a =,211a a =-+,321a a =-+,431a a =-+…,以此类推,则6a 的值为,2022a 的值为题型04数字类规律探索之等式问题【典例4】(2022秋·江西九江·七年级统考期中)观察下面的变形规律:111122=-⨯;1112323=-⨯;1113434=-⨯;解答下面的问题:(1)若n 为正整数,请你猜想()11n n =+______;(2)计算111112233420222023+++⋯⋯+⨯⨯⨯⨯.(3)计算;111124466820202022+++⋯⋯+⨯⨯⨯⨯.【变式1】(2022秋·湖南永州·七年级校考期中)观察算式:()()()132153174131351357.,222,+⨯+⨯+⨯+=++=+++=按规律填空:135799+++++=.【变式2】(2023春·安徽合肥·七年级校考期末)观察算式:①213142⨯+==;②224193⨯+==;③2351164⨯+==;④2461255⨯+==;⋯,根据你发现的规律解决下列问题:(1)写出第5个算式:______;(2)写出第n 个算式:______;(3)计算:111111111324351820⎛⎫⎛⎫⎛⎫⎛⎫+⨯++⨯⨯+ ⎪ ⎪⎪ ⎪⨯⨯⨯⨯⎝⎭⎝⎭⎝⎭⎝⎭.题型05图形类规律探索之数字问题【典例5】(2022秋·湖北黄冈·七年级校考阶段练习)如图,根据图形中数的规律,可推断出a 的值为()A .128B .216C .226D .240【变式1】(2023春·贵州毕节·七年级统考期末)根据图中数字的规律,若第n 个图中A B C D ++-的值为196,则n =()A .12B .13C .14D .15【变式2】(2022秋·河南周口·七年级校考期中)如图所示,下列各三角形中的三个数之间均具有相同的规律,根据此规律,则第n (n 为正整数)个三角形中,用n 表示y 的式子为()A .21n +B .2n n +C .12n n ++D .21n n ++题型06图形类规律探索之数量问题【典例6】(2023·江苏·七年级假期作业)用大小一样的黑白两种颜色的小正方形纸片,按如图的规律摆放:(1)第5个图案有张黑色小正方形纸片;(2)第n 个图案有张黑色小正方形纸片;(3)第几个图案中白色纸片和黑色纸片共有81张?【变式1】(2023秋·全国·七年级专题练习)如图,用棋子摆方阵,那么,图⑥要摆枚棋子,图n 要摆枚棋子.【变式2】(2023·安徽淮北·淮北市第二中学校考二模)如图,利用黑白两种颜色的五边形组成的图案,根据图案组成的规律回答下列问题:(1)图案④中黑色五边形有______个,白色五边形有______个;(2)图案n中黑色五边形有______个,白色五边形有______个;(用含n的式子表示)(3)图案n中的白色五边形可能为2023个吗?若可能,请求出n的值;若不可能,请说明理由.1.(2023秋·全国·七年级专题练习)观察下列各单项式:234562481632a a a a a a ---,,,,,,…,根据你发现的规律,第10个单项式是()A .9102a -B .9102a C .11002a D .10102a -2.(2023秋·全国·七年级专题练习)一列数1a ,2a ,3a …n a ,其中11a =-,2111a a =-,3211a a =-,…,11n na a =-,则1232020a a a a ⨯⨯⨯⨯= ()A .1-B .1C .2020D .2020-3.(2023春·河南信阳·七年级校联考阶段练习)如图,用棋子摆出下列一组图形,如果按照这种规律摆下去,那么第10个图形里棋子的个数为()A .72B .66C .56D .784.(2023春·云南临沧·七年级统考期末)如图,用字母“C ”、“H ”按一定规律拼成图案,其中第1个图案中有4个H ,第2个图案中有6个H ,第3个图案中有8个H ,……,按此规律排列下去,第2023个图案中字母H 的个数为()A .4044B .4046C .6069D .40485.(2023春·福建宁德·七年级校联考期中)我国宋代数学文杨辉所著《详解九章算法》中记载了用如图所示的一角形解释了二项和的乘方展开式中的系数规律,我们把这种数字三角形叫做“杨辉三角”.请你利用杨辉三角,计算()6a b -的展开式中,含3b 项的系数是()()0a b +=1…………1()1a b +=a b +…………11()2a b +=222a ab b ++…………121()3a b +=322333a a b ab b +++ (1331)()4a b +=++++432234a 4a b 6a b 4ab b (14641)A .15-B .15C .20-D .20【答案】C【分析】根据图中规律,可得()2a b +的展开式中含3b 项的系数,再根据()6a b -的展开式中,系数的绝对值与()2a b +的展开式中的系数相同,符号从左往后为奇数项为正,偶数项为负.【详解】解:由题意可知,下排每个数等于上方两个数字的绝对值之和,∴5()a b +的展开式系数从左往右分别是1,5,10,10,5,1,6()a b ∴+的展开式系数从左往右分别是1,6,15,20,15,6,1,根据图中,可知()6a b -含有3b 项的项为从左往右第四项,且符号为负,故()6a b -的展开式中,含3b 项的系数是20-,故选:C .【点睛】本题考查了数字变化规律,通过观察、分析、归纳发现其中规律,并应用发现的规律是解题的关键.6.(2022秋·四川南充·七年级校考期中)正整数按图中的规律排列.由图知,数字6在第二行,第三列,请写出数字2021在第行,第列.7.(2023春·山东泰安·六年级校考期中)观察下列各式,探索规律:21321⨯=-;23541⨯=-;25761⨯=-;27981⨯=-;2911101⨯=-;用含正整数n 的等式表示你所发现的规律为.8.(2023春·黑龙江绥化·七年级校考期末)观察下列算式:133=,239=,3327=,4381=,53243=,⋯,根据上述算式中的规律,你认为20233的末位数字是.9.(2023春·河北石家庄·七年级行唐一中校考开学考试)观察下列图形的构成规律,按此规律,第6个图形中棋子的个数为个,第n 个图形中棋子的个数为个.10.(2022秋·江苏宿迁·七年级校考阶段练习)已知整数1234a a a a ⋅⋅⋅、、、、满足下列条件:11a =-,212a a =-+,323a a =-+,434a a =-+,…,11n n a a n +=-++(n 为正整数)依此类推,则2025a 的值为.11.(2022春·黑龙江哈尔滨·六年级哈尔滨市第十七中学校校考阶段练习)观察下列三行数:2-,4,8-,16,32-,64,……0,6,6-,18,30-,66, (1)2-,1,2-,4,8-,16……(1)第①行数第七个数是128-,那么第二行数第七个数是_____,第三行第七个数是_____.(2)列式计算:取每行的第9个数,求这三个数的和.12.(2023春·云南昭通·七年级统考期中)小明计算:2399100122222++++++L 的过程如下:解:令2399100122222S =++++++①L 则23100101222222S =+++++ ②②-①得10121S =-∴239910010112222221++++++=-L 请参照小明的方法,计算:2320222023155555++++++L .13.(2023春·安徽阜阳·七年级校考阶段练习)观察下列图形,完成下列问题.(1)数一数,完成下列表格.直线的条数2345交点的个数(2)若有n 条直线相交,则最多有交点__________个.(用含n 的代数式表示)14.(2022秋·江苏连云港·七年级校考阶段练习)观察下列各式:322111124==⨯⨯,33221129234+==⨯⨯,33322112336344++==⨯⨯,33332211234100454+++==⨯⨯L 回答下面的问题:(1)333331234100+++++=(写出算式即可);(2)计算33333312341920++++++ 的值;(3)计算333311121920++++ 的值.15.(2022秋·江苏宿迁·七年级校考阶段练习)探索规律:观察下面※由组成的图案和算式,解答问题:21342+==213593++==21357164+++==213579255++++==(1)请猜想135719++++⋅⋅⋅+=_________;(2)请猜想()135721n ++++⋅⋅⋅+-=_________;(3)请用上述规律计算:616365199+++⋅⋅⋅+的值.16.(2023秋·浙江·七年级专题练习)找规律,完成下列各题:(1)如图①,把正方形看作1,1111244+=-=.(2)如图②,把正方形看作1,111112488++=-=.(3)如图③,把正方形看作1,1111124816+++=-=.(4)计算:11111 2481632++++=.(5)计算:111111111 248163264128256512++++++++=.17.(2023春·安徽·九年级专题练习)用若干个“○”与“▲”按如图方式进行拼图:(1)观察图形,寻找规律,并将下面的表格填写完整:图1图2图3图4○的个数3921______▲的个数1410______(2)根据你所观察到的规律,分别写出图n中“○”与“▲”的个数(用含n的代数式表示).18.(2023·河北秦皇岛·统考一模)为迎接七一建党节,某社区党委在广场上设计了一座三角形展台,需在它的每条边上摆放上相等盆数的鲜花进行装饰.若每条边上摆放两盆鲜花,共需要3盆鲜花;若每条边上摆放3盆鲜花,共需要6盆鲜花;……,按此要求摆放下去(如图所示,每个小圆圈表示一盆鲜花).(1)填写下表:每条边上摆放的盆数(n)23456…需要的鲜花总盆数(y)369__________…(2)写出需要的鲜花总盆数y与n之间的关系式:__________(3)能否用2023盆鲜花作出符合要求的摆放?如果能,请计算出每条边上应摆放的盆数;如果不能,请说明理由.。
(新北师大)5_探索与表达规律_练习1
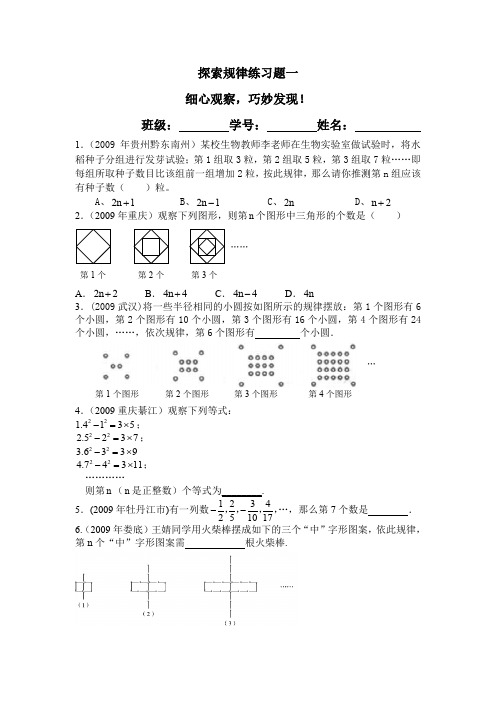
探索规律练习题一 细心观察,巧妙发现!班级: 学号: 姓名:1.(2009年贵州黔东南州)某校生物教师李老师在生物实验室做试验时,将水稻种子分组进行发芽试验;第1组取3粒,第2组取5粒,第3组取7粒……即每组所取种子数目比该组前一组增加2粒,按此规律,那么请你推测第n 组应该有种子数( )粒。
A 、12+n B 、12-n C 、n 2 D 、2+n 2.(2009年重庆)观察下列图形,则第n 个图形中三角形的个数是( )A .22n +B .44n +C .44n -D .4n3.(2009武汉)将一些半径相同的小圆按如图所示的规律摆放:第1个图形有6个小圆,第2个图形有10个小圆,第3个图形有16个小圆,第4个图形有24个小圆,……,依次规律,第6个图形有 个小圆.4.(2009重庆綦江)观察下列等式: 221.4135-=⨯; 222.5237-=⨯; 223.6339-=⨯ 224.74311-=⨯; …………则第n (n 是正整数)个等式为________.5.(2009年牡丹江市)有一列数1234251017--,,,,…,那么第7个数是 . 6.(2009年娄底)王婧同学用火柴棒摆成如下的三个“中”字形图案,依此规律,第n 个“中”字形图案需 根火柴棒.……第1个第2个第3个第1个图形第2个图形第3个图形第4个图形…7.(2009恩施市)观察数表根据表中数的排列规律,则字母A 所表示的数是____________. 8.(2009年益阳市)图6是一组有规律的图案,第1个 图案由4个基础图形组成,第2个图案由7个基础图形组成,……,第n (n 是正整数)个图案中由 个基础图形组成.-9.(2009年广州市)如图7-①,图7-②,图7-③,图7-④,…,是用围棋棋子按照某种规律摆成的一行“广”字,按照这种规律,第5个“广”字中的棋子个数是________,第n 个“广”字中的棋子个数是________10.(2009肇庆)观察下列各式:11111323⎛⎫=- ⎪⨯⎝⎭,111135235⎛⎫=- ⎪⨯⎝⎭,111157257⎛⎫=- ⎪⨯⎝⎭,…,根据观察计算:1111133557(21)(21)n n ++++⨯⨯⨯-+= .(n 为正整数)图6(1)(2) (3) …… 1 11 1 1 1 1 1 11-1-1-6-6-2-3-5-4-4-3 6 10 15 15 5 A 20- 111.(2009年济宁市)观察图中每一个大三角形中白色三角形的排列规律,则第5个大三角形中白色三角形有 个 . 12.(2009年广西梧州)下图是用火柴棍摆成的边长分别是1,2,3 根火柴棍时的正方形.当边长为n 根火柴棍时,设摆出的正方形所用的火柴棍的根数为s ,则s = . (用n 的代数式表示s )13.(2009年咸宁市)如图所示的运算程序中,若开始输入的x 值为48,我们发现第1次输出的结果为24,第2次输出的结果为12,……第2009次输出的结果为14.(2009年湖北荆州)将四张花纹面相同的扑克牌的花纹面都朝上,两张一叠放成两堆不变.若每次可任选一堆的最上面的一张翻看(看后不放回),并全部看完,则共有 种不同的翻牌方式. 15.(2009年山西省)下列图案是晋商大院窗格的一部分,其中“○”代表窗纸上所贴的剪纸,则第n 个图中所贴剪纸“○”的个数为 .(第13题)……n =1 n =2n =3第1个第2个第3个16.(2009年广东省)用同样规格的黑白两种颜色的正方形瓷砖,按下图的方式铺地板,则第(3)个图形中有黑色瓷砖 __________块,第n 个图形中需要黑色瓷砖__________块(用含n 的代数式表示).17.观察下表,回答问题:第 个图形中“△”的个数是“○”的个数的5倍.18.(2009年绵阳市)将正整数依次按下表规律排成四列,则根据表中的排列规律,数2009应排的位置是第行第 列.序号 1 2 3 …图形…(1) (2) (3)(1)(2)(3)…………探索规律练习题二班级:学号:姓名:1.(2009年河北)古希腊著名的毕达哥拉斯学派把1、3、6、10 … 这样的数称为“三角形数”,而把1、4、9、16 … 这样的数称为“正方形数”.从图1中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.下)A.13 = 3+10 B.25 = 9+16C.36 = 15+21 D.49 = 18+312.(2009年广西钦州)一组按一定规律排列的式子:-2a,52a,-83a,114a,…,(a≠0)则第n个式子是_ _(n为正整数).3.(2009成都)已知21(123...)(1)na nn==+,,,,记112(1)b a=-,2122(1)(1)b a a=--,…,122(1)(1) (1)n nb a a a=---,则通过计算推测出nb的表达式nb=_______.(用含n的代数式表示)4.(2009年广西南宁)正整数按图2的规律排列.请写出第20行,第21列的数字.5.(2009年宜宾)如图,菱形ABCD的对角线长分别为ba、,以菱形ABCD各边的中点为顶点作矩形A1B1C1D1,然后再以矩形A1B1C1D1的中点为顶点作菱形第一行第二行第三行第四行第五行第一列第二列第三列第四列第五列1 2 5 10 17 …4 3 6 11 18 …9 8 7 12 19 …16 15 14 13 20 …25 23 22 21 ………图24=1+3 9=3+6 16=6+10图1…A 2B 2C 2D 2,……,如此下去,得到四边形A 2009B 2009C 2009D 2009的面积用含 b a 、的代数式表示为 .第20题图36.(2009年青海)观察下面的一列单项式:x ,22x -,34x ,48x -,…根据你发现的规律,第7个单项式为 ;第n 个单项式为 . 7.(2009年台州市)将正整数1,2,3,…从小到大按下面规律排列.若第4行第2列的数为32,则①n = ;②第i 行第j 列的数为 (用i ,j 表示).第1列第2列 第3列 … 第n 列第1行 123 … n 第2行 1+n 2+n 3+n … n 2第3行 12+n 22+n 32+n …n 3 … … … … … …8.(2009丽水市)如图,图①是一块边长为1,周长记为P 1的正三角形纸板,沿图①的底边剪去一块边长为12的正三角形纸板后得到图②,然后沿同一底边依次剪去一块更小的正三角形纸板(即其边长为前一块被剪掉正三角形纸板边长的21)后,得图③,④,…,记第n (n ≥3) 块纸板的周长为P n ,则P n -P n-1= .9.(2009年四川省内江市)把一张纸片剪成4块,再从所得的纸片中任取若干块,每块又剪成4块,像这样依次地进行下去,到剪完某一次为止。
第7课 探索与表达规律

C.nxn+1
D.(n+1)xn
6.一列数 1 ,4 ,3 ,8 ,…,按此规律排列,第七个
2 9 8 25
数是
( B)
A.13
64
C. 5
28
B.7
32
D.3
16
7.将全体正奇数排成一个三角形数阵: 按照以上排列的规律,第12行第10个数是__1_5_1__.
8.标志(logo)代表的是一个企业或是产品的文化精髓,小明 模仿Windows95的logo设计思路,自己设计了一个logo. 他将图①中的正方形剪开得到图②,再将图②中右上角
所以第n个图形中有(4n+1)1 251,解得n=208.
2.观察图形的变化规律,则第10个小房子用石子的颗数
为 A.119
(C)
B.121
C.140
D.142
3. 某年8月份日历如图所示,任意选择其中上、下两行
的含4个数字的正方形部分,设右上角的数字为a,则
下列叙述中正确的是
( D)
A.左上角的数字为a+1
B.左下角的数字为a+7
C.右下角的数字为a+8
的正方形剪开得到图③,继续将图③中右上角的正方形 剪开得到图④,…,如此下去,他用正方形代表窗口, 一直按照这样的规律剪下去代表窗口可以根据需要一直 增加.按照小明的设计思路,图ⓝ中共有_(_3_n_-__2_)个正 方形.
9. 用黑、白两种颜色同样规格的正方形按如图所示的方 式铺成图形.
(1)铺第5个图形用黑色正方形__2_1_块,用白色正方形 __1_2_块;
D.方框中4个位置的数相加,结果是4的倍数
4.小明在翻阅往年的日历时,发现某一年的5月份,出 现5个星期五的日期,日期之和为80,请你判断一下 这个月的4日是星期_日___.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第7题图
14题
探索规律练习题
1、我们平常用的数是十进制数,如2639=2×103+6×102+3×101+9×100,表示十进制的数要用10个数码(又叫数字):0,1,2,3,4,5,6,7,8,9。
在电子数字计算机中用的是二进制,只要两个数码:0和1。
如二进制中101=1×22+0×21+1×20等于十进制的数5,10111=1×24+0×23+1×22+1×21+1×20等于十进制中的数23,那么二进制中的1101等于十进制的数 。
2、从1开始,将连续的奇数相加,和的情况有如下规律:1=1=12;1+3=4=22;1+3+5=9=32;1+3+5+7=16=42;1+3+5+7+9=25=52;…按此规律请你猜想从1开始,将前10个奇数(即当最后一个奇数是19时),它们的和是 。
3、小王利用计算机设计了一个计算程序,输入和输出的数据如下表:
A 、
618 B 、638 C 、65
8 D 、678
4、如下左图所示,摆第一个“小屋子”要5枚棋子,摆第二个要11枚棋子,摆第三个要17枚棋子,则摆第30个“小屋子”要 枚棋子
.
5、如下右图是某同学在沙滩上用石子摆成的小房子,观察图形的变化规律,写出第n 个小房子用了 块石子。
6、如下图是用棋子摆成的“上”字:
第一个“上”字 第二个“上”字 第三个“上”字
第九题图
如果按照以上规律继续摆下去,那么通过观察,可以发现:(1)第四、第五个“上”
字分别需用 和 枚
棋子;(2)第
n
个“上”字需用
枚棋子。
7、如图一串有黑有白,其排列有一定规律的珠子,被盒子遮住一部分,则这串珠子被盒子遮住的部分有_______
颗. 8、用边长为1cm 的小正方形搭成如下的塔状图形,则第n 次所搭图形的周长是_______________cm (用含n 的代数式表示)。
9、用“”定义新运算:对于任意实数a ,b ,都有a .b a b 2-=例如,4
,97472=-=
那么5
3=_____________,-1
(-1
2)=___________。
10、观察下列图形的排列规律(其中☆,□,●分别表示五角星、正方形、圆).●□☆●●□☆●□☆●●□☆●…….若
第一个图形是圆,则第2009个图形是________(填名称).
11、一组按规律排列的整数5,7,11,19,…,第6个整数为____ _,根据上述规律,第n 个整数为____ (n 为正整数). 12、下面是按照一定规律画出的一列“树型”图:
经观察可以发现:图(2)比图(1)多出2个“树枝”,图(3)比图(2)多出5个“树枝”,图(4)比图(3)多出10个“树枝”,照此规律,图(7)比图(6)多出 个“树枝”。
13、观察下面的点阵图和相应的等式,探究其中的规律:
(1)在④和⑤后面的横线上分别写出相应的等式;
(2)通过猜想写出与第n 个点阵相对应的等式_____________________。
14、如图用火柴摆去系列图案,按这种方式摆下去,当每边摆10根时(即10=n )时,需要的火柴棒总数为 根;
题图 15、如图,用同样规格的黑白两种正方形瓷砖铺设正方形地面,观察图形并猜想填空:
当黑色瓷砖为20块时,白色瓷砖为 块;当白色瓷砖为n 2
(n 为正整数)块时,黑色瓷砖为 块. 16、观察上图,我们可以发现:图⑴中有1个正方形;图⑵中有5个正方形,图⑶中共有14个正方形,按照这种规律继续下去,图⑹中共有_______个正方形。
17、某体育馆用大小相同的长方形木块镶嵌地面,第1次铺2块,如图1;第2次把第1次铺的完全围起来,如图2;第3次把第2次铺的完全围起来,如图3;…依此方法,第n 次铺完后,用字母n 表示第n 次镶嵌所使用的木块块数为 . (n 为正整数)
……
……
①1=12
; ②1+3=22③1+3+5=3
④ ; ⑤ ;
(1)
(2)
(3)
第4题
第1次 第2次 第3次 第4·
⑴ ⑵ ⑶
(1
) (2(3
) (4
) 18、分析如下图①,②,④中阴影部分的分布规律,按此规律在图③中画出其中的阴影部分.
19、根据上面5个图形及相应点的个数的变化规律:猜
想第6个图形有 个点,第n 个图形中有
个点。
20. 如图,将一块正方形纸片沿对角线折叠一次,然后在得到的三角形的三个角上各挖去一个圆洞,最后将正方形纸片展开,得到的图案是
第20题图
21.观察下表中三角形个数变化规律,填表并回答下面问题。
问题:如果图中三角形的个数是102个,则图中应有___________条横截线。
22.直线上现有n 个点,我们在每相邻两点间插入一个点,记作一次操作,经过10次操作后,直线上共有________个点. 23.我们把分子为1的分数叫做理想分数,如
21,31,4
1
,…,任何一个理想分数都可以写成两个不同理想分数的和,如613121+=,1214131+=,2015141+=,…根据对上述式子的观察,请你思考:如果理想分数b
a n 111+=(n 是不小于2的整数,且a <
b ),那么b -a =________.(用含n 的式子表示)
24.已知一列数:1,-2,3,-4,5,-6,7…,将这列数排成下列形式
第1行 1 第2行 -2 3 第3行 -4 5 -6 第4行 7 -8 9 -10 第5行 11 -12 13 -14 15 … …
按照上述规律排列下去,那么第10行从左边数第5个数等于( )A .50
B .-50
C .60
D .-60
25.把n 个正整数放在小正方形中并按照下图的形式排列,用一个虚线画的矩形框框住中间的一列数,若用a 表示这列数
的第八个数,则a 为________.
26. 如图,将边长为
2
1n
+(n =1,2,3,…)的正方形纸片从左到右顺次摆放,其对应的正方形的中心依次为A 1,A 2,A 3,…①若摆放前6个正方形纸片,则图中被遮盖的线段(虚线部分)之和为________;②若摆放前n (n 为大于1的正整数)个正方形纸片,则图中被遮盖的线段(虚线部分)之和为________.
27.观察下列有序数对:(3,-1),(-5,
21),(7,-31),(-9,4
1
),…,根据你发现的规律,第100个有序数对是________. 28、如图,都是由边长为1的正方体叠成的图形。
例如第(1)个图形的表面积为6个平方单位,第(2)个图形的表面积为18个平方单位,第(3)个图形的表面积是365)个图形的表面积 个平方单位。
29、图(1)是一个水平摆放的小正方体木块,图(2)、(3)是由这样的小正方体木块叠放而成,按照这样的规律继续叠放下去,至第七个叠放的图形中,小正方体木块总数应是( )A 25 B 66 C 91 D 120
30、如图是由大小相同的小立方体木块叠入而成的几何体,图⑴中有1个立方体,图⑵中有4个立方体,图⑶中有9个立
方体,……按这样的规律叠放下去, 第8个图中小立方体个数是 .
(1)
(2)
(3)。
