饿狼追兔问题数学建模
数学建模之兔子问题(出稿)

数学建模一周论文论文题目:野兔生长问题姓名1:李宝川学号:09023320姓名2:彭亚学号:09023308姓名3:刘新斌学号:09023304专业:勘查技术与工程班级:090233指导教师:虞先玉老师2010年1月1日、摘要参照题目,野兔生长属自然范畴,在生存条件良好,且无外力干扰的情况下,其种群数量是呈对数型增长的。
题中可读,野兔生长并不是处于理想的情况下的,考虑到自然的各种原因,诸如,天地的捕杀,自然灾害,疾病等。
对于这种种群生态学问题,我们可以用Logistic(逻辑斯蒂方程)模型来模拟。
Logistic模型是种群生态学的核心理论之一。
它可以用来描述种群生长规律,利用它可以表征种群的数量动态。
之所以选择该模型来研究野兔生长问题,是因为,该模型考虑并概括了,种群发展所遇到的各种外界条件,也就是说,它模拟了真实情况。
通过建立Logistic模型,我们小组得出T=10时,野兔数量为9.84194(十万)只。
该结果比较符合客观规律。
利用Logistic模型可以表征种群的数量动态;如鱼类种群的增长,收获与时间关系的确定。
描述某一研究对象的增长过程如生态旅游区环境容量的确定,森林资源的管理以及耐用消费品社会拥有量的预测、国民生产总值的预测等;也可作为其它复杂模型的理论基础如Lotka-Volterra两种群竞争模型;以上的大多数的工作都是拿逻辑斯蒂模型来用,但也由此可看出逻辑斯蒂方程不管在自然科学领域还是在社会科学中都具有非常广泛的用途。
关键字:Logistic模型生态学 MATLAB程序问题重述野兔生长问题。
首先,野兔是生长在自然环境中的。
自然很复杂,存在着许多影响种群发展的因素。
我们知道,假如给野兔一个理想的环境,野兔数量是呈J型增长的。
现实情况中,种群一般是呈S型增长的,从题中表格看出,野兔的数量并不是单一地增长,T=3,6.90568;T=4,6.00512;T=5,5.56495;T=6,5.32807。
《数学建模实验》

《数学建模》上机作业信科05-3韩亚0511010305实验1 线性规划模型一、实验名称:线性规划模型—设备的最优配备问题。
二、实验目的:掌握线性规划模型的建模方法,并能用数值算法或MATLAB 库函数求解。
三、实验题目:某商店拟制定某种商品7—12月的进货、售货计划,已知商店仓库最大容量为1500件,6月底已存货300件,年底的库存以不少于300件为宜,以后每月初进货一次,假设各月份该商品买进、售出单价如下表。
四、实验要求:1、若每件每月的库存费用为0.5元,问各月进货、售货各为多少件,才能使净收益最多?建立数学模型。
2、利用相应的数值方法求解此问题的数学模型。
3、谈一谈你对这类线性规划问题的理解。
4、举一个简单的二维线性规划问题,并针对此问题将你所了解的线性规划的求解方法作出总结。
5、用软件lindo 或lingo 求解上述问题。
(选做题)6、编写单纯形算法的MATLAB 程序。
(选做题) 五、实验内容:解:设第i 个月进货xi 件,销售yi 件,则下半年总收益为销售收入减去进货费和仓库储存费之和,所以目标函数为:1211109871211109711109871211109875.232427252628252528262729)2345(5.0)2345)300(6(5.07x x x x x x y y y y y y y y y y y x x x x x x z y ------+++++++++++++++++-=整理后得:90024255.28275.2831255.25295.27295.31121110987121110987-------+++++=x x x x x x y y y y y y z由于仓库的容量为1500件,每个月的库存量大于0,小于1500,所以有如下约束条件150030001500300015003000150030001500300015003000111210119108978710119108978791089787897877877≤-+-+-+-+-++≤≤-+-+-+-++≤≤-+-+-++≤≤-+-++≤≤-++≤≤+≤y x y x y x y x y x x y x y x y x y x x y x y x y x x y x y x x y x x x又有年底库存量不少于300则:300300121112101191089787≥--+-+-+-+-++y y x y x y x y x y x x化为抽象的线性规划模型为:90024255.28275.2831255.25295.27295.31max 121110987121110987-------+++++=x x x x x x y y y y y y z ,;12,,8,7;0,0120030012003001200300120030012003001200300121112101191089787111210119108978710119108978791089787897877877 =≥≥--+-+-+-+-+≤-+-+-+-+-+≤-≤-+-+-+-+≤-≤-+-+-+≤-≤-+-+≤-≤-+≤-≤≤-i y x y y x y x y x y x y x x y x y x y x y x y x x y x y x y x y x x y x y x y x x y x y x x y x x x STi i线性规划目标函数的系数:f = [31; 28.5; 27; 28.5;25;24;-31.5;-29;-27.5;-29;-25.5;-25]; 约束方程的系数及右端项: A=[1,0,0,0,0,0,0,0,0,0,0,0 1,1,0,0,0,0,-1,0,0,0,0,0 1,1,1,0,0,0,-1,-1,0,0,0,0 1,1,1,1,0,0,-1,-1,-1,0,0,0 1,1,1,1,1,0,-1,-1,-1,-1,0,0 1,1,1,1,1,1,-1,-1,-1,-1,-1,0 -1,0,0,0,0,0,0,0,0,0,0,0 -1,-1,0,0,0,0,1,0,0,0,0,0 -1,-1,-1,0,0,0,1,1,0,0,0,0 -1,-1,-1,-1,0,0,1,1,1,0,0,0 -1,-1,-1,-1,-1,0,1,1,1,1,0,0 -1,-1,-1,-1,-1,-1,1,1,1,1,1,0 -1,-1,-1,-1,-1,-1,1,1,1,1,1,1];b=[1200;1200;1200;1200;1200;1200; 300; 300; 300; 300; 300; 300;0]; lb=zeros(12,1);[x,fval,exitflag,output,lambda] = linprog(f,A,b,[],[],lb);实验2 非线性规划模型一、实验名称:非线性规划模型。
数学建模-猎狗追兔子问题

数学建模论文《数学建模》(2014春)课程期末论文摘要(一)对于问题一:自然科学中存在许多变量,也有许多常量,而我们要善于通过建立合适的模型找到这些变量之中的不变量。
猎狗追赶兔子的问题是我们在生活中常见的实例,而题目把我们生活中的普通的例子抽象成为高等数学中微分方程的例子,通过对高阶微分方程的分析,建立微分方程模型,并用数学软件编写程序求解,得出结论,解决生活中常见的实际问题。
(二)对于问题二:学习使用matlab进行数学模型的求解,掌握常用计算机软件的使用方法。
关键词微分方程导数的几何意义猎狗追兔子数学建模数学软件一、问题重述如图1所示,有一只猎狗在B 点位置,发现了一只兔子在正东北方距离它250m 的地方O 处,此时兔子开始以8m/s 的速度正向正西北方向,距离为150m 的洞口A 全速跑去. 假设猎狗在追赶兔子的时候,始终朝着兔子的方向全速奔跑。
请回答下面的问题:⑴ 猎狗能追上兔子的最小速度是多少? ⑵ 在猎狗能追上兔子的情况下,猎狗跑过的路程 是少?⑶ 假设猎狗在追赶过程中,当猎狗与兔子之间的距离为30m 时,兔子由于害怕导致奔跑速度每秒减半, 而狗却由于兴奋奔跑速度每秒增加0.1倍,在这种情 况下回答前面两个问题。
二、问题分析与假设在猎狗追赶兔子的时候猎狗一直朝着兔子的方向追赶,所以可以建立平面直角坐标系,通过导数联立起猎狗运动位移,速度和兔子的运动状态。
1.假设兔子的运动是匀速的。
2.假设猎狗的运动轨迹是一条光滑并且一阶导数存在的曲线。
3.猎狗的运动时匀速或者匀变速的。
4.猎狗运动时总是朝向兔子。
三、模型的建立及求解3.1 符号规定1.(x ,y ):猎狗或者兔子所在位置的坐标。
2. t :从开始到问题结束经过的时间。
3. a:猎狗奔跑的路程。
4. v:猎狗的奔跑速度。
3.2 模型一的建立与求解猎狗能够抓到兔子的必要条件:猎狗的运动轨迹在OA 要有交点以OA 为y 轴,以OB 为x 轴建立坐标系,则由图有O(0,0),A(0,150),B(250,0),兔子的初始位置0点,而猎狗初始位置是B 点,t (s )后猎狗到达了C (x ,y ),而兔子到达了D (0,8t ),则有CD 的连线是猎狗运动轨迹的一条切线,由导数的几何意义有:NW8dy y tdx x-=dav dt =da =三式联立消去t ,得到;设:若猎狗可以追上兔子则有当兔子在OA,猎狗在OB 之间运动时此方程有解,设:得到:得到:两式联立相加得到:1.如果q=1即v=8 m/s 得到所以此情况无交点,所以v=8m/s 猎狗无法追上兔子; 2.如果q<1即v>8m/s 得到此情况有交点,所以有可能能够追上兔子,如果要追上兔子需要y<=150; 解得到: 即所以这种情况下能够追上的最小速度是 .3.如果q>1 利用上式得到,所以这种情况不能追上兔子。
饿狼追兔模型研究

饿狼追兔模型研究数学建模辽宁工程技术大学数学建模课程成绩评定表学期姓名专业班级课程名称数学建模论文题目高阶常微分方程模型―饿狼追兔问题评定指标分值得分知识创新性 20 理论正确性 20 内容难易性 15 评结合实际性 10 知识掌握程度 15 定书写规范性 10 标工作量10 准总成绩 100 评语: 任课教师时间 09年月日备注 - 1 -年珊珊:饿狼追兔问题饿狼追兔模型研究摘要:本文建立狼的运动轨迹微分模型;在各种假设的情况下,通过数形结合的直观形象的画出兔子与狼的运动轨迹图形;采用解析方法和数值方法,研究兔子与狼的运行轨迹,编写matlab程序建立追击问题的数值模型。
关键词:饿狼追兔数值解析微分方程求解1 问题的背景1.1 问题的背景狼追兔子问题是欧洲文艺复兴时代的著名人物达.芬奇提出的一个数学问题。
现有一只兔子、一匹狼,兔子位于狼的正西100米处,假设兔子与狼同时发现对方并一起起跑,兔子往正北60米处的巢穴跑,而狼在追兔子。
已知兔子、狼是匀速跑且狼的速度是兔子的两倍。
建立狼的运动轨迹微分模型。
画出兔子与狼的运动轨迹图形。
用解析方法求解,问兔子能否安全回到巢穴,用数值方法求解,问兔子能否安全回到巢穴。
狼在追赶过程中所形成的轨迹就是追击曲线。
狼是否会在兔子跑回洞穴之前追赶上兔子呢?为了研究狼是否能够追上兔子,可以先考虑求出狼追兔子形成的追击曲线,然后根据曲线来确定狼是否能够追上兔子。
2 模型的假设2.1将问题转化为图形如下- 2 -数学建模2.1.1图形说明建立直角坐标系:兔子初始位置向东为x轴,兔子的正北方方向为y轴,设点A为狼的初始位置,点O为兔子的初始位置,点B为兔子巢穴的位置,参照图(1)。
2.2 主要假设2.2.1 假设狼始终以兔子为目标,将二者看做两个运动的点。
2.2.2 假设外界条件对饿狼和兔子的运行轨迹没有任何影响。
3 符号说明S0 狼初始位置距离兔子巢穴的位置B 兔子t时间后运行的位置 S B点距离O点距离 T 运行经历的时间 v 兔子的运行速度 V 狼的运行速度r 兔子与狼的速度比4 分析、建立模型及模型求解4.1 模拟方法:通过已假设的条件,可知狼始终对准兔子,用参数方程x=x(t);y=y(t) t>=0来描述饿狼的运动轨迹,兔子做匀速直线运动,在t时刻兔子的位置是O点距B点距离s=v*t,因此当饿狼追击到点D的位置时,其速度指向点B,由几何关系有dy/dt=tan(θ)=―(s-y)/x=―(v*t-y)/x,(1)这并不是一个常量微分方程,为了进行数值模拟,还需做进一步的变形。
追击问题解析解方法

两式消去 h,可得:
b
x
1 [ f ' (t )]2 dt 2[ y xf ' ( x)]
2 两边对 x 求导: 1 [ f ' ( x)] 2 xf ' ' ( x)
所以可得 y=f(x)满足下面的微x )]2 2 xf ' ' ( x ) f ' ( x ) | x b 0 f ( x ) | x b 0
基本假设: 狼跑动的方向应该是始终正对着兔子的, 所以狼的运动路线是一条曲线, 如下图:
y A(0,a) y=f(x) H(0,h) C(x,y) O(0,0) B(b,0) x
狼能追上兔子的条件:? 解决问题的关键:求出狼的运动轨迹为 y=f(x) 由于初始时刻兔子位于原点处,狼的运动方向应该是正对原点,所以有:
y'| x b 0, y | xb 0
设兔子跑到 H(0,h)处时,狼跑到 C(x,y)处,则(注意狼的速度是兔子的两倍, 狼跑的方向应该正对兔子,狼跑的距离是由弧长公式计算出来的) :
h y f ' ( x) 0 x b 1 [ f ' (t )]2 dt 2h x
用 matlab 解上面的微分方程可得:
y
1 2 1/ 2 ( 3 b x ) x b 3b1/ 2 3
2 2 所以当 x 0时, y b ,也就是说当 b a ,狼可以追上兔子。 3 3 附:求解微分方程的 matlab 代码: y=dsolve('2*x*D2y=(1+(Dy)^2)^(1/2)','y(b)=0','Dy(b)=0','x')
(完整word版)饿狼追兔问题

高阶常微分方程模型—饿狼追兔问题第一章摘要概述本文以狼追击兔子这一现实情况为背景,并合理的加以数学假设,着重实际与模型的结合,现有一只兔子和一匹狼,兔子位于狼的正西100米处,假设当狼发现兔子时,兔子同时也发现了狼,这时二者一起起跑,兔子往正北60米处的巢穴跑,狼朝同样的方向在追兔子。
已知兔子、狼是匀速跑且狼的速度是兔子的两倍。
建立狼的运动轨迹微分模型。
通过画出的兔子与狼的运动轨迹图形,用解析方法及数值方法求解,兔子能否安全回到巢穴?经过分析与求解,得知兔子无危险.在自然科学和技术科学中往往遇到大量的微分方程问题。
通过对高阶微分方程的分析,我们对题目里提出的问题建立了符合实际的数学模型,在模型的求解过程中应用数学软件MATLAB等计算工具,编写相应的程序,解决实际问题。
论文最后对模型的优缺点进行了分析和评价,并提出了模型的改进方向和思路。
关键字微分方程饿狼追兔数学建模第二章模型的背景问题描述随着课改的深入开展,实际情景问题应运而生,并迅速发展成为命题的亮点、热点。
实际情景问题是复杂多变的,它贴近生活,为学生所熟悉,且以一定的知识为依托。
恶狼追兔的问题属于实际的情景问题,具有一定的时代气息.数学模型一般是实际事物的一种数学简化。
它常常是以某种意义上接近实际事物的抽象形式存在的,但它和真实的事物有着本质的区别。
是研究现实世界数量关系和空间形式的科学,建立教学模型的过程,是把错综复杂的实际问题简化、抽象为合理的数学结构的过程。
有助于我们提高用数学理论和方法去分析和解决问题的全过程,提高我们分析问题和解决问题的能力,提高我们学习数学的兴趣和应用数学的意识与能力,使我们在今后的工作中能经常性地想到用数学去解决问题,提高我们尽量利用计算机软件及当代高新科技成果的意识,能将数学、计算机有机地结合起来去解决实际问题。
利用高阶常微分方程模型—饿狼追兔问题现有一只兔子、一匹狼,兔子位于狼的正西100米处,假设兔子与狼同时发现对方并一起起跑,兔子往正北60米处的巢穴跑,而狼在追兔子。
《数学建模与数学实验》期末考查试卷
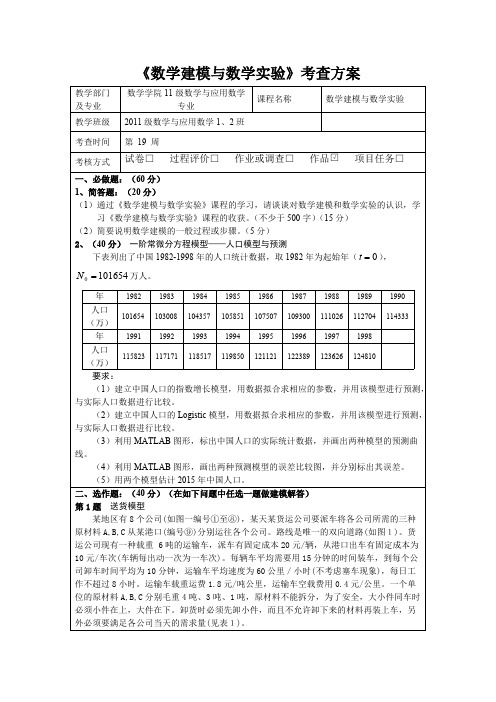
《数学建模与数学实验》考查方案教学部门及专业数学学院11级数学与应用数学专业课程名称数学建模与数学实验教学班级2011级数学与应用数学1、2班考查时间第 19 周考核方式试卷□ 过程评价□ 作业或调查□ 作品 项目任务□ □√一、必做题:(60分)1、简答题:(20分)(1)通过《数学建模与数学实验》课程的学习,请谈谈对数学建模和数学实验的认识,学习《数学建模与数学实验》课程的收获。
(不少于500字)(15分)(2)简要说明数学建模的一般过程或步骤。
(5分)2、(40分) 一阶常微分方程模型——人口模型与预测下表列出了中国1982-1998年的人口统计数据,取1982年为起始年(),0=t 万人。
1016540=N 年198219831984198519861987198819891990人口(万)101654103008104357105851107507109300111026112704114333年19911992199319941995199619971998人口(万)115823117171118517119850121121122389123626124810要求:(1)建立中国人口的指数增长模型,用数据拟合求相应的参数,并用该模型进行预测,与实际人口数据进行比较。
(2)建立中国人口的Logistic 模型,用数据拟合求相应的参数,并用该模型进行预测,与实际人口数据进行比较。
(3)利用MATLAB 图形,标出中国人口的实际统计数据,并画出两种模型的预测曲线。
(4)利用MATLAB 图形,画出两种预测模型的误差比较图,并分别标出其误差。
(5)用两个模型估计2015年中国人口。
二、选作题:(40分)(在如下问题中任选一题做建模解答)第1题 送货模型某地区有8个公司(如图一编号①至⑧),某天某货运公司要派车将各公司所需的三种原材料A,B,C 从某港口(编号⑨)分别运往各个公司。
路线是唯一的双向道路(如图1)。
一只狼追逐一只兔子,狼追兔问题解读及练习题

一只狼追逐一只兔子,狼追兔问题解读及练习题简介一只狼追逐一只兔子是一个常见的问题,用于解释追及一点的概念。
该问题基于以下背景:一只兔子以恒定速度向前跑动,而一只狼以更快的速度开始追逐兔子。
问题是,狼是否能追上兔子,并且若能追上,则需要多长时间。
解读该问题可以用简单的数学模型来解决。
假设兔子的速度为v1,狼的速度为v2,并且兔子与狼的初始距离为d。
根据这些条件,可以得出以下结论:- 如果v2大于v1,则狼能追上兔子并且需要的时间为d / (v2 - v1)。
- 如果v2小于或等于v1,则狼永远无法追上兔子。
练题下面是一些练题,帮助你巩固对狼追兔问题的理解。
问题一一只兔子以10 m/s的速度向前跑动,而一只狼以15 m/s的速度开始追逐兔子。
兔子与狼的初始距离为1000米。
狼需要多长时间才能追上兔子?解答一根据公式,狼需要的时间为1000米 / (15 m/s - 10 m/s) = 200秒。
问题二一只兔子以20 km/h的速度向前跑动,而一只狼以18 km/h的速度开始追逐兔子。
兔子与狼的初始距离为5公里。
狼能否追上兔子?解答二根据公式,狼需要的时间为5公里 / (18 km/h - 20 km/h) = -5公里 / 2 km/h = -2.5小时。
由于时间为负值,狼无法追上兔子。
总结一只狼追逐一只兔子是一个简单而有趣的问题,通过数学模型可以确定是否狼能追上兔子以及需要的时间。
记住,狼只有在速度比兔子快时才能追及兔子,否则狼将永远无法追上。
狼追兔子数据结构课程设计

狼追兔子数据结构课程设计青岛大学软件技术学院游戏算法实践报告姓名曹宁专业数字媒体艺术班级 10级 4班指导教师刘春秋2013年 1 月 16日目录1 问题定义与描述 (4)1.1 问题定义 (4)1.2 问题描述 (4)2 关键技术 (4)3 数据的组织 (4)3.1数据类型定义 (4)3.2数据存储结构 (5)4 总体设计 (5)4.1 系统模块图 (5)4.2栈的基本操作 (4)4.3顺序表的基本操作 (4)5 详细设计 (6)5.1顺序存储的线性表 (6)6 测试结果及分析 (7)7 心得体会 (8)附录:程序代码 (9)1问题定义与描述1.1 问题定义现实中很多利用顺序表,栈解决一些数学模型问题1.2 问题描述围绕着山顶有10个圆形排列的洞,狐狸要吃兔子,兔子说:“可以,但必须找到我,我就藏身于这十个洞中,你可以先到1号洞找我,第二次隔一个洞(即3号洞)找,第三次隔两个洞(即6号洞)找,以后如此类推,次数不限。
”但狐狸从早到晚进进出出1000次,但仍没有找到兔子,问兔子究竟藏身于哪个洞里2.关键技术顺序表一次申请多个空间,包括结构体定义的。
N为整数,这样得到的就是N个连续的空间。
顺序表可以利用类似于数组的形式访问,即通过下标访问。
当然定义的变量类型必须是指针类型的,很方便,当然也可以通过像链表一样的访问。
单链表只是将空间分散开了,这样的优点就是动态申请,需要多少就申请多少,一般一次申请一个空间结点,即N=1。
3 数据的组织3.1数据类型定义数据结构,顺序表,栈,单链表,数组。
在程序设计中,为了处理方便,把具有相同类型的若干变量按有序的形式组织起来。
这些按序排列的同类数据元素的集合称为数组。
在C语言中,数组属于构造数据类型。
一个数组可以分解为多个数组元素,这些数组元素可以是基本数据类型或是构造类型。
因此按数组元素的类型不同,数组又可分为数值数组、字符数组、指针数组、结构数组等各种类别。
3.2数据存储结构栈以顺序结构实现,队列以链表结构实现。
饿狼追兔问题 数学建模
实验报告专业:美术班级:(1)班指导老师:牛老师姓名:某某某学号:123456789 实验室:110实验名称:饿狼追兔问题时间:2012年10月3日一、实验目的及要求理解二阶微分法在建模过程中的应用,熟悉利用MATLAB软件求解微分方程的方法。
注意模型的普遍性和模型的广泛性二、问题的分析现有一只兔子、一匹狼,兔子位于狼的正西100米处,假设兔子与狼同时发现对方并一起起跑,兔子往正北60米处的巢穴跑,而狼在追兔子。
已知兔子、狼是匀速跑且狼的速度是兔子的两倍。
问兔子能否安全回到巢穴?(1)分析饿狼追野兔的运动模型。
饿狼追野兔过程中,野兔的目的是要在饿狼捉住自己之前跑到自己的巢穴,假如恶狼知道野兔巢穴的具体位置,根据题目所给,饿狼完全可以先兔子跑到其巢穴,然后在那里守株待兔,野兔则难逃饿狼之口。
那样饿狼的轨迹就是一条直线,只需简单的数学计算就可以完成。
(2)但这是一个理想化的实际问题,在这个问题中由于饿狼不可能知道兔子巢穴的具体位置,因此它的速度的方向永远是朝着兔子的,兔子一直向北跑,相对于饿狼来说兔的角度在时刻的变化,所以最终饿狼的轨迹是一条曲线。
而兔子能否活下来,还是一个需要经过具体较复杂计算的问题。
三、模型的建立与求解初始时刻(t=0)兔子位于原点(0,0),饿狼位于(100,0);兔子以常速度v0沿y轴跑,饿狼在t时刻的位置为(x,y),其速度为v1=2v0;饿狼在追兔子过程中一直向着兔子的方向,则:饿狼在t时刻其追赶曲线的切线方程为Y-y=(dy/dx)*(X-x)=[(dy/dt)/(dx/dt)]*(X-x)其中(X,Y)为切线上动点。
又饿狼在追兔子过程中一直向着兔子的方向,则t时刻兔子(0,v0t)在切线上,所以v0t-y=[(dy/dt)/(dx/dt)]*(0-x)从而饿狼追赶轨迹由下方程组确定(dx/dt)*( v0t-y)= (dy/dt)*(-x) (1)(dx/dt)2+(dy/dt)2=v12 (2)由(1)有(dy/dx)*(-x)= v0t-y,两边对t求导并化简(d2y/dx2)* (dx/dt) *(-x)= v0 (3)由(2)有(dx/dt)2{1+[(dy/dt)/(dx/dt)]2}=v12即dx/dt=-v1/[1+(dy/dx)2]1/2(注这里去负号,是由这个追赶曲线——上图,决定的) 代入(3),并把v1=2v0代入并化简得(d2y/dx2)*x=[1+(dy/dx)2]1/2/2 (4)这是一个二阶微分方程,它满足初始条件y(100)=0令p= dy/dx,这dp/dx= d2y/dx2,这(4)化为(dp/dx)*x=[1+p2]1/2/2,可分离变量求得ln{p+[1+p2]1/2/2}=0.5*lnx+c又p(100)=0,所以c=-ln10,从而p+[1+p2]1/2/2=x1/2/10这p=( x1/2/10-10/x1/2)/2即dy/dx=( x1/2/10-10/x1/2)/2,从而y=(x-300)*x1/2/30+c,又y(100)=0则y=(x-300)*x1/2/30+200/3令x=0,得y(0)=200/3>60故兔子没有有危险常微分方程高阶初值问题的MATLAB库函数为:ode45。
狼兔追击_数学建模

追击问题问题A 以1v 的速度向在自己正北方距离β处的目标前进,B 在A 的正东方以速度2v 追逐A 。
B 在追赶过程中所形成的轨迹就是追击曲线。
B 是否会在A 到达目标之前追赶上A ?变量说明1v :A 的速度(单位:m/s ) r :B 与A 速度的倍数;2v :B 的速度(单位:m/s ),显然有12rv v = t :B 追击A 的时刻1s :在时刻t ,A 跑过的路程(单位:m ),)(11t s s = 2s :在时刻t ,B 跑过的路程(单位:m ),)(22t s s = Q ),(11y x :表示在时刻t 时,A 的坐标 P ),(y x :表示在时刻t 时,B 的坐标模型假设1、B 在追击过程中始终朝向A ;2、B 追击A 的轨迹看作是一条光滑的曲线,即将动点P ),(y x 的轨迹看作一条曲线,曲线方程表示为)(x y y =。
模型建立(一)建模准备以t =0时,A 的位置作为直角坐标原点,A 朝向B 的方向为x 轴正向; 则显然有A 位置的横坐标α=1x 。
对B 来说,当α=x ,y =0,即0==αx y在t =0刚开始追击时,B 的奔跑方向朝向A ,此时即x 轴负方向, 则有0='=αx y(二)建立模型由于B 始终朝向A ,则在B 所在位置P ),(y x 点过B 的轨迹处的切线方向在y 轴上的截距为1y 。
设切线上的动点坐标为(X ,Y ),则切线方程为)(x X y y Y -'=- (1) 在(1)中,令X =0,则截距x y y Y '-=。
此时t v y 11=。
则此时截距等于A 所跑过的路程,即:1y Y =,从而可得 x y y y Y '-==1 (2)在t 时刻,A 跑过的路程为t v y s 111== (3)由于B 的速度是A 的r 倍,则B 跑的路程为112ry rs s == (4)B 跑过的路程可以用对弧长的曲线积分知识得到,如下。
狼追兔子数据结构课程设计

青岛大学软件技术学院游戏算法实践报告姓名曹宁专业数字媒体艺术班级 10级 4班指导教师刘春秋2013年 1 月 16日目录1问题定义与描述 (2)1.1 问题定义 (2)1.2 问题描述 (3)2.关键技术 (3)3 数据的组织 (3)3.1数据类型定义 (3)3.2数据存储结构 (3)4总体设计 (4)4.1 顺序表系统模块图 (4)4.2栈的基本操作 (4)4.3顺序表的基本操作 (4)5 详细设计 (5)5.1顺序存储的线性表 (5)6 测试结果及分析 (7)7心得体会 (8)附录:程序代码 (9)1问题定义与描述1.1 问题定义现实中很多利用顺序表,栈解决一些数学模型问题1.2 问题描述围绕着山顶有10个圆形排列的洞,狐狸要吃兔子,兔子说:“可以,但必须找到我,我就藏身于这十个洞中,你可以先到1号洞找我,第二次隔一个洞(即3号洞)找,第三次隔两个洞(即6号洞)找,以后如此类推,次数不限。
”但狐狸从早到晚进进出出1000次,但仍没有找到兔子,问兔子究竟藏身于哪个洞里2.关键技术顺序表一次申请多个空间,包括结构体定义的。
N为整数,这样得到的就是N个连续的空间。
顺序表可以利用类似于数组的形式访问,即通过下标访问。
当然定义的变量类型必须是指针类型的,很方便,当然也可以通过像链表一样的访问。
单链表只是将空间分散开了,这样的优点就是动态申请,需要多少就申请多少,一般一次申请一个空间结点,即N=1。
3 数据的组织3.1数据类型定义数据结构,顺序表,栈,单链表,数组。
在程序设计中,为了处理方便,把具有相同类型的若干变量按有序的形式组织起来。
这些按序排列的同类数据元素的集合称为数组。
在C语言中,数组属于构造数据类型。
一个数组可以分解为多个数组元素,这些数组元素可以是基本数据类型或是构造类型。
因此按数组元素的类型不同,数组又可分为数值数组、字符数组、指针数组、结构数组等各种类别。
3.2数据存储结构栈以顺序结构实现,队列以链表结构实现。
数学建模课程教学思考

数学建模课程教学思考作者:彭勇,钟鑫来源:《教育教学论坛》2013年第15期摘要:数学建模是联系实际问题与数学的桥梁,伴随着科技的蓬勃发展,数学建模被广泛地应用于众多科学领域中,高等教育必须重视对学生数学建模素质的培养。
本文分析了数学建模课程教学面临的课程定位、教学对象知识结构、教材内容与课时协调等问题,提出数学建模课程教学应注重案例引导,合理取舍教学内容;注重启发教学,促进学生积极思维;注重合作学习,保证教学效果。
关键词:数学建模;教学;能力培养中图分类号:G642.4 文献标志码:A 文章编号:1674-9324(2013)15-0033-03数学模型就是对于一个实际问题按其内在规律,进行一些合理的、必要的假设,运用适当的数学工具得到的一个数学结构。
而通过数学的分析与计算,求解此数学结构使其所得结果能成功解决原实际问题的过程即为数学建模。
自数学建模教学进入大学课堂,经过20多年的发展,现在大多本科、专科院校开设了各种形式的数学建模课程和讲座,为培养学生利用数学方法分析、解决实际问题的能力开辟了一条有效的途径。
数学建模是联系实际问题与数学的桥梁,伴随着科技的蓬勃发展,数学建模被广泛地应用于自然科学、工程技术、医学、经济学等众多科学领域中,必须重视数学建模素质的培养。
一、数学建模课程教学面临的问题1.数学建模课程定位问题。
数学建模课程教学目的应是通过一些具体实例引入使学生掌握数学建模基本思想、基本方法,学会进行科学研究的一般过程,并能进入一个实际操作的状态。
通过数学模型有关的概念、特征的学习和数学模型应用实例的分析,培养学生数学推导计算和简化分析能力,培养学生联想、洞察能力、综合分析能力,培养学生应用所学过数学知识解决实际问题的能力。
因此,数学建模课程教学应定位在培养用所掌握的数学知识解决实际问题的能力,而不是掌握某种新的数学工具。
2.教学对象知识结构问题。
要做好数学建模课程的教学,必须考虑教学对象所掌握的数学知识结构问题。
数模教材
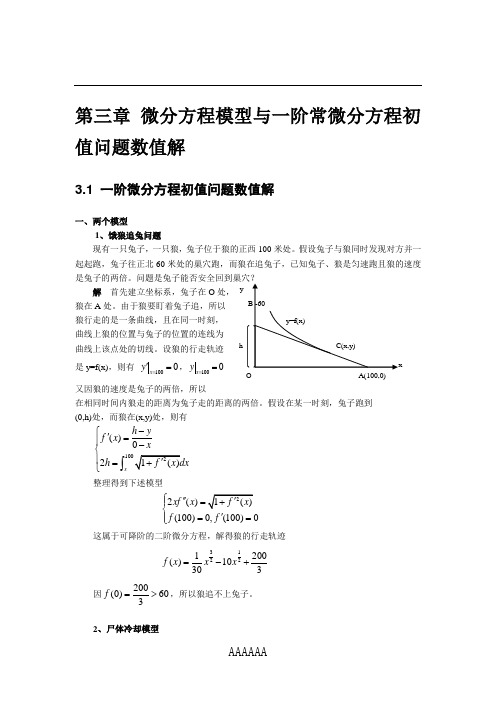
第三章 微分方程模型与一阶常微分方程初值问题数值解3.1 一阶微分方程初值问题数值解一、两个模型1、饿狼追兔问题现有一只兔子,一只狼,兔子位于狼的正西100米处。
假设兔子与狼同时发现对方并一起起跑,兔子往正北60米处的巢穴跑,而狼在追兔子,已知兔子、狼是匀速跑且狼的速度解 首先建立坐标系,兔子在O 处, 狼在A 处。
由于狼要盯着兔子追,所以 狼行走的是一条曲线,且在同一时刻, 曲线上狼的位置与兔子的位置的连线为 曲线上该点处的切线。
设狼的行走轨迹 是y=f(x),则有 1000x y ='=,1000x y == 又因狼的速度是兔子的两倍,所以在相同时间内狼走的距离为兔子走的距离的两倍。
假设在某一时刻,兔子跑到 (0,h)处,而狼在(x,y)处,则有()02x h y f x x h -⎧'=⎪-⎨⎪=⎩⎰ 整理得到下述模型2()(100)0,(100)0xf x f f ⎧''=⎪⎨'==⎪⎩ 这属于可降阶的二阶微分方程,解得狼的行走轨迹31221200()10303f x x x =-+因200(0)603f =>,所以狼追不上兔子。
2、尸体冷却模型y hA(100,0)O受害者的尸体于晚上7:30被发现,法医于晚上8:20赶到凶案现场,测得尸体温度为32.6℃;一小时后,当尸体即将被抬走时,测得尸体温度为31.4℃,室温在几个小时内始终保持21.1℃。
此案最大的嫌疑犯张某声称自己是无罪的,并有证人说:“下午张某一直在办公室上班,5:00时打完电话后就离开了办公室”。
从张某到受害者家(凶案现场)步行需5分钟,现在的问题是,张某不在凶案现场的证言能否被采信,使他排除在嫌疑犯之外。
解:首先应确定凶案的发生时间,若死亡时间在下午5点5分之前,则张某就不是嫌疑犯,否则不能将张某排除。
设T(t)表示t 时刻尸体的温度,并记晚上8:20为t=0,则T(0)=32.6℃,T(1)=31.4℃。
(完整word版)饿狼追兔问题

高阶常微分方程模型—饿狼追兔问题第一章摘要概述本文以狼追击兔子这一现实情况为背景,并合理的加以数学假设,着重实际与模型的结合,现有一只兔子和一匹狼,兔子位于狼的正西100米处,假设当狼发现兔子时,兔子同时也发现了狼,这时二者一起起跑,兔子往正北60米处的巢穴跑,狼朝同样的方向在追兔子。
已知兔子、狼是匀速跑且狼的速度是兔子的两倍。
建立狼的运动轨迹微分模型。
通过画出的兔子与狼的运动轨迹图形,用解析方法及数值方法求解,兔子能否安全回到巢穴?经过分析与求解,得知兔子无危险。
在自然科学和技术科学中往往遇到大量的微分方程问题。
通过对高阶微分方程的分析,我们对题目里提出的问题建立了符合实际的数学模型,在模型的求解过程中应用数学软件MATLAB等计算工具,编写相应的程序,解决实际问题。
论文最后对模型的优缺点进行了分析和评价,并提出了模型的改进方向和思路。
关键字微分方程饿狼追兔数学建模第二章模型的背景问题描述随着课改的深入开展,实际情景问题应运而生,并迅速发展成为命题的亮点、热点。
实际情景问题是复杂多变的,它贴近生活,为学生所熟悉,且以一定的知识为依托。
恶狼追兔的问题属于实际的情景问题,具有一定的时代气息。
数学模型一般是实际事物的一种数学简化。
它常常是以某种意义上接近实际事物的抽象形式存在的,但它和真实的事物有着本质的区别。
是研究现实世界数量关系和空间形式的科学,建立教学模型的过程,是把错综复杂的实际问题简化、抽象为合理的数学结构的过程。
有助于我们提高用数学理论和方法去分析和解决问题的全过程,提高我们分析问题和解决问题的能力,提高我们学习数学的兴趣和应用数学的意识与能力,使我们在今后的工作中能经常性地想到用数学去解决问题,提高我们尽量利用计算机软件及当代高新科技成果的意识,能将数学、计算机有机地结合起来去解决实际问题。
利用高阶常微分方程模型—饿狼追兔问题现有一只兔子、一匹狼,兔子位于狼的正西100米处,假设兔子与狼同时发现对方并一起起跑,兔子往正北60米处的巢穴跑,而狼在追兔子。
数学建模例题题

数学建模例题题数学建模试题⼀、传染病模型医学科学的发展已经能够有效地预防和控制许多传染病,但是仍然有⼀些传染病暴发或流⾏,危害⼈们的健康和⽣命。
社会、经济、⽂化、风俗习惯等因素都会影响传染病的传播,⽽最直接的因素是:传染者的数量及其在⼈群中的分布、被传染者的数量、传播形式、传播能⼒、免疫能⼒等。
⼀般把传染病流⾏范围内的⼈群分成三类:S类,易感者(Susceptible),指未得病者,但缺乏免疫能⼒,与感染者接触后容易受到感染;I类,感病者(Infective),指染上传染病的⼈,它可以传播给S类成员;R类,移出者(Removal),指被隔离或因病愈⽽具有免疫⼒的⼈。
要求:请建⽴传染病模型,并分析被传染的⼈数与哪些因素有关?如何预报传染病⾼潮的到来?为什么同⼀地区⼀种传染病每次流⾏时,被传染的⼈数⼤致不变?⼆、线性规划模型—销售计划问题某商店拟制定某种商品7—12⽉的进货、售货计划,已知商店仓库最⼤容量为1500件,6⽉底已存货300件,年底的库存以不少于300件为宜,以后每⽉初进货⼀次,假设各⽉份该商品买进、售出单价如下表。
要求:若每件每⽉的库存费⽤为0.5元,问各⽉进货、售货各为多少件,才能使净收益最多?建⽴数学模型,并⽤软件求解。
【注】线性规划在MATLAB的库函数为:linprog。
语法为:x = linprog(f,A,b)x = linprog(f,A,b,Aeq,beq,lb,ub,x0,options)[x,fval,exitflag,output,lambda] = linprog(...)例如:线性规划⽬标函数的系数:f = [-5; -4; -6]约束⽅程的系数及右端项:A = [1 -1 13 2 43 2 0];b = [20; 42; 30];lb = zeros(3,1);调⽤线性规划程序linprog求解,得:[x,fval,exitflag,output,lambda] = linprog(f,A,b,[],[],lb);x= 0.000015.00003.0000三、⼀阶常微分⽅程模型—⼈⼝模型与预测下表列出了中国1982-1998年的⼈⼝统计数据,取1982年为起始年(0=t ),1016540=N 万⼈,200000=m N 万⼈。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
饿狼追兔问题
摘要
本文研究饿狼追兔问题,是在给定狼兔相对位置,以及兔子巢穴位置的情况下求解的,狼的速度是兔子速度两倍,在不考虑其他任何因素的情况下研究狼能否追上兔子的问题。
首先,我们对问题进行了适当的分析,然后根据已知条件建立了狼的运动轨迹微分模型。
其次,根据建好的模型,运用MATLAB编程,然后仿真画出了饿狼和野兔的运动轨迹图。
再次,用解析方法将建立的模型求解,并给出该问题的结论,准确的回答题目。
最后,用数值方法求解,将所求与前面所求进行对比,也给出结论,回答题目。
并将两种方法做相应比较。
结论:野兔可以安全回巢
关键词:算法高阶常微分方程
§1.1问题的提出
在自然界中,各种生物都有它的生活规律,它们钩心斗角,各项神通,在饿狼追野兔的工程中,饿狼的速度是野兔的二倍,但是野兔有自己的洞穴,野兔在跑到自己洞穴之前被狼捉住,野兔就将会成为饿狼的囊中之物;如果野兔在饿狼捉住自己之前跑回到自己的洞穴,那么野兔就保住小命,得以生还。
图1-1-1为饿狼追野兔的两条曲线,其中绿线表示野兔,图中的箭头表示的是野兔的奔跑方向,野兔从远点开始沿y轴正方向运动,其洞穴在坐标为(0,60)的位置;红线为饿狼的运动轨迹,,图中的剪头表示饿狼追逐野兔的方向,饿狼从坐标为(100,0)的方向追逐野兔,饿狼的速度是野兔速度的二倍。
建立数学模型需研究一下几个问题:(1)设野兔的速度我v0,饿狼的速度为v1,野兔的奔跑方向是沿y轴正方向奔跑,而饿狼的方向是一直指向野兔的方向,即饿狼的运动的轨迹某一时候的切线指向同一时刻的野兔的位置。
建立饿狼追野兔的运动轨迹微分模型。
(2)根据建立的饿狼运动轨迹得微分模型,作出饿狼与野兔的运动轨迹图形。
(3)用解析方法求解,即根据第二步作出的饿狼渔业突地运动轨迹图形,分析兔子能否安全回到巢穴,即野兔的运动曲线与饿狼的运动曲线的交点是在点(0,60)-野兔巢穴的上面还是下面。
(4)用数值方法求解。
根据第一步建立的关于二郎追野兔的运动轨迹微分模型,进行数学运算,讨论兔子能否安全回到巢穴,即所求交点的y值大于60还是小于60.
§1.2问题的分析
(1)分析饿狼追野兔的运动模型。
在1.1中已经说了,饿狼追野兔过程中,野兔的目的是要在饿狼捉住自己之前跑到自己的巢穴,假如恶狼知道野兔巢穴的具体位置,根据题目所给,饿狼完全可以先兔子跑到其巢穴,然后在那里守株待兔,野兔则难逃饿狼之口。
那样饿狼的轨迹就是一条直线,只需简单的数学计算就可以完成。
(2)但这是一个理想化的实际问题,在这个问题中由于饿狼不可能知道兔子巢穴的具体位置,因此它的速度的方向永远是朝着兔子的,兔子一直向北跑,相对于饿狼来说兔的角度在时刻的变化,所以最终饿狼的轨迹是一条曲线。
而兔子能否活下来,还是一个需要经过具体较复杂计算的问题。
§1.3数值方法求解
初始时刻(t=0)兔子位于原点(0,0),饿狼位于(100,0);兔子以常速度v0沿y轴跑,饿狼在t时刻的位置为(x,y),其速度为v1=2v0;饿狼在追兔子过程中一直向着兔子的方向,则:
饿狼在t时刻其追赶曲线的切线方程为
Y-y=(dy/dx)*(X-x)=[(dy/dt)/(dx/dt)]*(X-x)
其中(X,Y)为切线上动点。
又饿狼在追兔子过程中一直向着兔子的方向,则t时刻兔子(0,v0t)在切线上,所以
v0t-y=[(dy/dt)/(dx/dt)]*(0-x)
从而饿狼追赶轨迹由下方程组确定
(dx/dt)*( v0t-y)= (dy/dt)*(-x) (1)
(dx/dt)2+(dy/dt)2=v12 (2)
由(1)有(dy/dx)*(-x)= v0t-y,两边对t求导并化简
(d2y/dx2)* (dx/dt) *(-x)= v0 (3)
由(2)有(dx/dt)2{1+[(dy/dt)/(dx/dt)]2}=v12
即dx/dt=-v1/[1+(dy/dx)2]1/2 (注这里去负号,是由这个追赶曲线——上图,决定的) 代入(3),并把v1=2v0代入并化简得
(d2y/dx2)*x=[1+(dy/dx)2]1/2/2 (4)
这是一个二阶微分方程,它满足初始条件y(100)=0
令p= dy/dx,这dp/dx= d2y/dx2,这(4)化为
(dp/dx)*x=[1+p2]1/2/2,可分离变量求得
ln{p+[1+p2]1/2/2}=0.5*lnx+c
又p(100)=0,所以c=-ln10,从而
p+[1+p2]1/2/2=x1/2/10
这p=( x1/2/10-10/x1/2)/2
即dy/dx=( x1/2/10-10/x1/2)/2,从而
y=(x-300)*x1/2/30+c,又y(100)=0
则
y=(x-300)*x1/2/30+200/3
令x=0,得
y(0)=200/3>60
故兔子没有有危险
§1.4解析方法求解(matlab创新求解)在本题题目中给出了参考的matlab的方程式
【注】常微分方程高阶初值问题的MATLAB库函数为:ode45。
语法为:[t,Y] =ode45(odefun,tspan,y0)
例如函数:function dy = rigid(t,y)
dy = zeros(3,1); % a column vector
dy(1) = y(2) * y(3);
dy(2) = -y(1) * y(3);
dy(3) = -0.51 * y(1) * y(2);
设置选项:
options = odeset('RelTol',1e-4,'AbsTol',[1e-4 1e-4 1e-5]);
求解得:
[t,Y] = ode45(@rigid,[0 12],[0 1 1],options);
画出解函数曲线图形:
plot(T,Y(:,1),'-',T,Y(:,2),'-.',T,Y(:,3),'.')
但是我们决定不用题目中给的函数,而是采用另一个函数:
r = dsolve('eq1,eq2,...', 'cond1,cond2,...', 'v'),这个函数的作用是把常微分方程(无论是一阶还是高阶)转化成不带有求导的一般性方程,但是一般情况下经过这种函数转化之后,得到的方程式比较复杂,但是如果把已知条件也带进dsolve函数中,得到的函数就会比较简单。
另外还要注意的一点就是在matlab中的Dy,D2y都默认为是对t的求导,所以在用desolve函数的时候,要把所有的x换成t,然后还要借助y=subs(y,t,’x’)函数,把求得的函数式的自变量改为x。
下面开始分析问题模型。
由§1.3中的(4)方程(d2y/dx2)*x=[1+(dy/dx)2]1/2/2,并且有已知条件:
y(100)=0;
dy/dx(100)=0。
故编写的matlab程序如下:
>>y=desolve(‘t*D2y=sqrt(1+Dy^2)/2’,’y(100)=0’‘Dy(100)=0’);
y=subs(y,t,‘x’);
得到y=sqrt(x).*(x-300)/30+200/3
在饿狼的运动曲线上取点x=25,并借助matlab:
>> y=sqrt(x).*(x-300)/30+200/3,x=25,y
得到y=20.833,并且求得切线在(25,20.833)点的斜率为-3/4,故求得饿狼运动曲线在点(25,20.833)处的切线方程:
z=0.75*(25-x)+20.833。
在matlab环境下运行得到函数y=sqrt(x).*(x-300)/30+200/3,然后再编辑elang.m 文件:
x=linspace(0,100,500);
y=sqrt(x).*(x-300)/30+200/3;
z=0.75*(25-x)+20.833;
plot(0,y,'y',x,y,'r',x,z,'c')
在matlab环境下调用elang.m文件
>>elang
得到如下图:
由题意知,野兔的巢穴在点(0,60)处,由图中可以看出,在野兔到达自己的巢穴点(0,60)时,饿狼的运动曲线与y轴还没有交点,即饿狼还没有追上兔子,所以,由此可以回答课题提出的问题:野兔可以安全回到巢穴。
§1.5 模型的优点与改进
优点:本模型适用范围较广,追击问题中可以较多应用,在辅助软件的求解下,结果很容易得出。
改进:由于问题有些理想化,没有考虑实际的具体环境因素和自然因素对野兔和饿狼速度的影响。
所以较问题复杂程度较低。
在真正的实际问题中,本模型可以作为参考,把相关因素考虑进来,同时借助辅助软件同样能很快求解。
参考文献:
[1]方道元(1958.4~) 编著
常微分方程
[2]刘会灯(计算机) 编著
MATLAB编程基础与典型应用
[3]数学建模原理与案例
冯杰(计算机教授) 编著。
