2019最新人教版七年级数学(1)
2019年年秋人教版数学七年级上册课件:121 有理数 共14张PPT语文

负整数
分数 正分数 负分数
作业
课本第14页习题1.2 第1题
由刚才的演示可知: 1.有理数可分为哪两类数? 2.整数可分为哪几类? 3.分数可分为哪几类?
正负整整零整数数数
有有分整理理数数数
分负正数分分数数
正整数
零
负整数
正分数 负分数
1
2
3
4
5
依据有理数的分 类示意图,在右图 的卡片上填上下 列数的名称.你发 现有理数的分类 示意图与这棵树 枝干的形状有哪 些联系吗?
正整数
零
负整数
正分数
负分数
整数
分数
有理数
66 33 55 22④ 11
--55 --11 --22
--66 --33
--44
⑤
⑥
00
44
②②
③③
11..551122⑦,,,, 5522,,33..2255,,⑧Biblioteka 112211,,..55,,
55 22
,,
①
思考
0.1,-0.5,5.32,-150.25等为什么被列为分数?
1.2.1 有理数
在男子110米栏 决赛中,中国选手 刘翔以12.91秒的成 绩夺得金牌,这个成 绩打破了12.96的奥 运会纪录,平了世界 纪录,实现了中国男 子田径金牌0的突破.
在女子柔道52公斤级的冠军争 夺战中,中国选手 冼东妹仅用1.1分 钟,就为中国柔道 队夺得首枚金牌.
女力士唐功红在女子 +75公斤级举重比赛中,不 负众望,以抓举122.5公斤, 挺举182.5公斤,总成绩305 公斤夺得第18枚金牌,与获 银牌的韩国选手相比,她的 抓举重量-7.5公斤,挺举重 量+10公斤.
2019年春七年级数学下册实数第1课时实数的概念同步练习(新版)新人教版

6.3 第1课时 实数的概念知识点 1 无理数的定义 1.下列说法正确的是( ) A .无限小数是无理数 B .有根号的数是无理数 C .无理数是开方开不尽的数D .无理数包括正无理数和负无理数 2.任何一个有理数都可以写成________________的形式,反过来,任何________________都是有理数.3.下列各数中:-14,3.14159,-π,π5,0,0.3,15,5.2·01·,2.121122111222…,其中无理数有________________________.知识点 2 实数的定义与分类 4.能够组成全体实数的是( ) A .自然数和负数 B .整数和分数 C .有理数和无理数D .正数和负数 5.下列说法正确的是( ) A .正实数和负实数统称实数 B .正数、零和负数统称为有理数 C .带根号的数和分数统称实数 D .无理数和有理数统称为实数6.按大小分,实数可分为________、________、________三类. 7.把下列各数分别填入相应的数集里.-13π,-2213,7,327,0.324371,0.5,39,-0.4,16,0.8080080008… 无理数集合{ …}; 有理数集合{ …}; 分数集合{ …}; 负实数集合{ …}.知识点 3 实数与数轴的关系8.和数轴上的点成一一对应关系的数是( ) A .自然数 B .有理数 C .无理数 D .实数9.如图6-3-1,数轴上的A ( )A .点AB .点BC .点CD .点D知识点 4 实数的相反数、绝对值 10.2的相反数是( )A .- 2 B. 2 C.12D .211.若m ,n 互为相反数,则式子|m -5+n |=________. 12.在数轴上表示-6的点到原点的距离为________. 13.求下列各数的相反数和绝对值.(1)-2; (2)-364; (3)π-3.14.求下列各式中的x . (1)|x |=35; (2)|x |=17.15.下列各组数中互为相反数的是( ) A .5和(-5)2B .-|-5|和-(-5)C .-5和3-125 D .-5和1516.实数a 对应的点在数轴上的位置如图6-3-2所示,则a ,-a ,1a的大小关系为( )图6-3-2A.1a <a <-a B .-a <1a<aC .a <1a <-a D.1a<-a <a17.已知a 为实数,则下列四个数中一定为非负数的是( )A .a B.3a C .|-a | D .-|-a |18.如图6-3-3,数轴上A ,B 两点表示的数分别为2和5.1,则A ,B 两点之间表示整数的点共有( )图6-3-3A .6个B .5个C .4个D .3个19.3-2的相反数是________,绝对值是________.20.有九个数:0.1427,(-0.5)3,3.1416,121,327,2.5,227,-2π,0.2020020002…,若无理数的个数为x ,整数的个数为y ,非负数的个数为z ,则x +y +z =________.21.如图6-3-4,A 是硬币圆周上一点,硬币与数轴相切于原点O (点A 与点O 重合).假设硬币的直径为1个单位长度,若将硬币沿数轴正方向滚动一周,点A 恰好与数轴上的点A ′重合,则点A ′对应的实数是________.图6-3-422.已知实数a ,b 在数轴上的对应点的位置如图6-3-5所示,试化简:(a -b )2-|a +b |.图6-3-523.已知实数a ,b ,c ,d ,e ,f ,且a ,b 互为倒数,c ,d 互为相反数,e 的绝对值为2,f 的算术平方根是8,求12ab +c +d 5+e 2+3f 的值.24.先阅读下面的文字,再解答问题.大家知道2是无理数,而无理数是无限不循环小数,因此2的小数部分我们不可能全部地写出来,于是小明用2-1来表示2的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为2的整数部分是1,将这个数减去其整数部分,差就是小数部分.已知:10+3=x+y,其中x是整数,且0<y<1,求x-y的值.教师详解详析1.D [解析] A 项不正确,无限不循环小数是无理数.B 项不正确,有根号的数不一定是无理数,如4,38等.C 项不正确,π及类似1.010010001…(两个1之间0的个数逐次加1)的数也是无理数.2.有限小数或无限循环小数 有限小数或无限循环小数3.-π,π5,2.121122111222…4.C 5.D 6.正实数 0 负实数7.解:无理数集合{-13π,7,39,-0.4,0.8080080008…,…};有理数集合{-2213,327,0.324371,0.5,16,…};分数集合{-2213,0.324371,0.5,…};负实数集合{-13π,-2213,-0.4,…}.8.D [解析] ∵任何实数都可以用数轴上的点来表示,数轴上的任何一点都表示一个实数,∴和数轴上的点成一一对应关系的数是实数. 故选D . 9.B [解析] ∵3≈1.732, ∴-3≈-1.732.∵点A ,B ,C ,D 表示的数分别为-3,-2,-1,2,∴与数-3表示的点最接近的是点B.故选B . 10.A11. 5 [解析] 由题意m ,n 互为相反数,可知m +n =0,则|m -5+n|= 5.12. 6 [解析] 数轴上表示-6的点到原点的距离为-6的绝对值,|-6|= 6. 13.解:(1)-2的相反数为2,绝对值为||-2= 2. (2)-364的相反数为364=4,绝对值为⎪⎪⎪⎪-364=364=4.(3)π-3的相反数为3-π,因为π>3,所以绝对值为||π-3=π-3.14.解:(1)x =±35.(2)x =±17.15.B [解析] 只有符号不同的两个数互为相反数,它们的和为0,由此可判定选项.A 中(-5)2=5,两个数相等,故错误;B 中-|-5|=-5,-(-5)=5,-5与5互为相反数,故正确;C 中3-125=-5,两个数相等,故错误;D 中-5和15既不是相反数,也不是倒数,故错误.故选B .16.A [解析] 采用特殊值法来解决.不妨设a =-12,则-a =12,1a =-2.因为-2<-12<12,所以1a<a <-a.故选A .17.C [解析] 选项A 中的a 可以表示任何实数.选项B 中的3a 的符号与a 相同,所以也可以表示任何实数.选项C 中的|-a|表示-a 的绝对值,根据绝对值的意义,可知|-a|为非负数.选项D 中的-|-a|表示|-a|的相反数,由于|-a|为非负数,所以-|-a|为非正数.故选C .18.C [解析] 因为1<2<2,5<5.1<6,所以A ,B 两点之间表示整数的点有表示2,3,4,5的点,共有4个.故选C .19.2- 3 3- 2 [解析] 3-2的相反数是-(3-2)=-3+2=2-3.3-2是一个正实数,正实数的绝对值等于它本身.20.12 [解析] 无理数有 2.5,-2π,0.2020020002…,所以x =3.整数有121,327,所以y =2.非负数有0.1427,3.1416,121,327, 2.5,227,0.2020020002…,所以z=7,所以x +y +z =3+2+7=12.21.π [解析] 将硬币沿数轴正方向滚动一周,点A 恰好与数轴上的点A′重合,则点A 转过的距离是圆的周长,即π,因而点A′对应的实数是π.22.解: 根据数轴可得出:a -b >0,a +b <0,∴(a -b )2-|a +b|=(a -b)+(a +b)=2a. 23.解:因为a ,b 互为倒数,所以ab =1. 因为c ,d 互为相反数,所以c +d =0. 因为e 的绝对值为2,所以e =±2,所以e 2=(±2)2=2.因为f 的算术平方根是8,所以f =64,所以3f =364=4,所以12ab +c +d 5+e 2+3f =12+0+2+4=612.24.解:由1<3<2,得11<10+3<12.由x 是整数,且0<y<1,得x =11, y =10+3-11=3-1,从而x -y =11-(3-1)=12- 3.。
2019国庆节人教版七年级上册《第一章有理数》数学家庭作业

2019国庆节人教版七年级上册《第一章有理数》数学家庭作业10月1日1.(P2)大于的数叫做正数.在正数前面加上的数叫做负数.2.(P2)既不是正数,也不是负数.3.(P3)如果一个问题中出现相反意义的量,我们可以用正数和分别表示它们.4.四个数-3,0,1,2,其中负数是()A、-3;B、0;C、1;D、2.5.(1)孔子出生于公元前551年,如果用-551年表示,那么司马迁出生于公元前145年可表示为年,欧阳修出生于公元1007年可表示为年;(2)如果+20%表示增加20%,那么-6%表示 .6.下列关于“0”的说法正确的个数是()①0是正数和负数的分界点;②0只表示“什么也没有”;③0可以表示特定的意义,如0℃等;④0是正数;⑤0是自然数;⑥0是非负数.A、3;B、4;C、5;D、6.7.观察下列数据:-2,,,,,⋯,它们是按一定规律排列的,依照此规律,第11个数据是 .8.圆形零件的尺寸要求是(单位:mm),现有下列直径尺寸的产品(单位:mm),其中不合格的是()A、;B、;C、;D、.9.下列说法正确的有()①不带“−”号的数都是正数;②任意一个正数,前面加上“−”号,就是一个负数;③0既是非负数,也是非正数;④常数a既是正数,也是负数.A、1个;B、2个;C、3个;D、4个.10.在下列选项中,具有相反意义的量是()A、足球比赛胜5场与负5场;B、向东走3千米与向南走3千米;C、增产10t粮食与减产-10t粮食;D、下降与上升.11.在一次数学测验中,七(1)班全体同学的平均分为85分,其中5名同学的成绩分别为80分、98分、90分、84分、73分.以平均分为基准,用正数表示超出部分,用负数表示不足部分.(1)面5名同学对应的成绩分别应记为多少?(2)有2名同学的成绩分别记为+3分和0分,这2名同学的实际成绩是多少?10月2日1.(P6)正整数、0、统称为整数;正分数、统称为分数。
2019秋人教版七年级数学上册课件:第一章 1.2 第2课时 数轴

第一章 有理数
1.2 有理数
第2课时 数轴
课前预习
A. 规定了______原__点______、____正__方__向______、 ____单__位__长__度____的直线叫做数轴. 1. 下列所画数轴正确的是( D )
B. 所有的____有__理__数______都可以用数轴上的点 表示.
则A和B两点间的距离为( C )
A. 2 016
B. 2 017
C. 2 018
D. 2 019
3. 在数轴上,-2表示A点,3表示B点,则离原点 较近的点是______A_点_______. 4. 填空: (1)数轴上距原点3个单位长度的点表示的数是 _____±__3_______; (2)数轴上表示-6的点在原点的_______左_______侧, 距离原点______6________个单位长度,表示+6的 点在原点的_______右_______侧,距离原点 ________6______个单位长度.
图1-2-3
解:点A表示数1.5,位于原点右边,与原点的距离 是1.5个单位长度;
点B表示数-2,位于原点左边,与原点的距离 是2个单位长度;
点C表示数2,位于原点右边,与原点的距离是 2个单位长度;
点D表示数-2.5,位于原点左边,与原点的距 离是2.5个单位长度.
举一反三
2. 根据下面给出的数轴(如图1-2-4),解答下面 的问题:
2019年秋人教版七年级上册数学课件:1.4.2

16
• 16.煤矿井下点A的海拔为-174.8米,已知从A到B的水平距离是120 米,每经过水平距离10米上升0.4米,已知点B在点A的上方.
• (1)求点B的海拔高度; • (2)若点C的海拔为-68.8米,且点C在点A的正上方,每垂直升高10米
用30秒,求从点A到点C所用的时间. • 解:(1)根据题意,得-174.8+120÷10×0.4=-174.8+4.8=-
第一章 有理数
1.4 有理数的乘除法
1.4.2 有理数的除法(第三课时)
2
名师点睛
知识点 1 有理数除法法则 (1)除以一个不等于 0 的数,等于乘这个数的倒数,即 a÷b=a·1b(b≠0). (2)两数相除,同号得正,异号得负,并把绝对值相除. (3)0 除以任何一个不等于 0 的数,都得 0.
-
0.34×27+57=-13-0.34=-13.34.
(2)12-13-16÷-610;
解:原式=12-13-16×(-60)=-12×60+13×60+16×60=-30+20+10=0.
15
(3)-23÷-13×23; 解:原式=23÷-29=-23×92=-3. (4)-72×16-12×134÷(-2). 解:原式=-72×-13×134×-12=-18.
A.-1
B.1
C.2125
D.-225
4.计算:-9÷32=__-__6___.
5.若 a≠b,且 a、b 互为相反数,则ab=__-__1___.
7
(C )
8
6.化简下列分数: (1)-216; 解:原式=-126=-8.
(3)--564; 解:原式=564=9.
(2)-1248; 解:原式=-1428=-14.
最新2019-2020年度人教版七年级数学上册《有理数加减乘除混合运算》综合练习题-经典试题

数 学 练 习(一)〔有理数加减法运算练习〕一、加减法法则、运算律的复习。
A .△同号两数相加,取__________________,并把____________________________。
1、(–3)+(–9)2、85+(+15)3、(–361)+(–332) 4、(–3.5)+(–532)△绝对值不相等的异号两数相加,取_________________________,并用____________________ _____________. 互为__________________的两个数相加得0。
1、(–45) +(+23)2、(–1.35)+6.353、412+(–2.25) 4、(–9)+7△ 一个数同0相加,仍得_____________。
1、(–9)+ 0=______________;2、0 +(+15)=_____________。
B .加法交换律:a + b = ___________ 加法结合律:(a + b) + c = _______________1、(–1.76)+(–19.15)+ (–8.24)2、23+(–17)+(+7)+(–13)3、(+ 341)+(–253)+ 543+(–852) 4、52+112+(–52)C .有理数的减法可以转化为_____来进行,转化的“桥梁”是___________。
△减法法则:减去一个数,等于_____________________________。
即a –b = a + ( )1、(–3)–(–5)2、341–(–143) 3、0–(–7)D .加减混合运算可以统一为_______运算。
即a + b –c = a + b + _____________。
1、(–3)–(+5)+(–4)–(–10)2、341–(+5)–(–143)+(–5)△把–2.4–(–3.5)+(–4.6)+ (+3.5)写成省略加号的和的形式是______________,读作:__________________________,也可以读作:__________________________。
2019年人教版七年级上数学教案全册.doc

第一章有理数单元教学内容1.本单元结合学生的生活经验,列举了学生熟悉的用正、负数表示的实例,•从扩充运算的角度引入负数,然后再指出可以用正、负数表示现实生活中具有相反意义的量,使学生感受到负数的引入是来自实际生活的需要,体会数学知识与现实世界的联系.引入正、负数概念之后,接着给出正整数、负整数、正分数、负分数集合及整数、分数和有理数的概念.2.通过怎样用数简明地表示一条东西走向的马路旁的树、•电线杆与汽车站的相对位置关系引入数轴.数轴是非常重要的数学工具,它可以把所有的有理数用数轴上的点形象地表示出来,使数与形结合为一体,揭示了数形之间的内在联系,从而体现出以下4个方面的作用:(1)数轴能反映出数形之间的对应关系.(2)数轴能反映数的性质.(3)数轴能解释数的某些概念,如相反数、绝对值、近似数.(4)数轴可使有理数大小的比较形象化.3.对于相反数的概念,•从“数轴上表示互为相反数的两点分别在原点的两旁,且离开原点的距离相等”来说明相反数的几何意义,同时补充“零的相反数是零”作为相反数意义的一部分.4.正确理解绝对值的概念是难点.根据有理数的绝对值的两种意义,可以归纳出有理数的绝对值有如下性质:(1)任何有理数都有唯一的绝对值.(2)有理数的绝对值是一个非负数,即最小的绝对值是零.(3)两个互为相反数的绝对值相等,即│a│=│-a│.(4)任何有理数都不大于它的绝对值,即│a│≥a,│a│≥-a.(5)若│a│=│b│,则a=b,或a=-b或a=b=0.三维目标1.知识与技能(1)了解正数、负数的实际意义,会判断一个数是正数还是负数.(2)掌握数轴的画法,能将已知数在数轴上表示出来,•能说出数轴上已知点所表示的解.(3)理解相反数、绝对值的几何意义和代数意义,•会求一个数的相反数和绝对值.(4)会利用数轴和绝对值比较有理数的大小.2.过程与方法经过探索有理数运算法则和运算律的过程,体会“类比”、“转化”、“数形结合”等数学方法.3.情感态度与价值观使学生感受数学知识与现实世界的联系,鼓励学生探索规律,并在合作交流中完善规范语言.重、难点与关键1.重点:正确理解有理数、相反数、绝对值等概念;会用正、•负数表示具有相反意义的量,会求一个数的相反数和绝对值.2.难点:准确理解负数、绝对值等概念.3.关键:正确理解负数的意义和绝对值的意义.课时划分1.1正数和负数2课时1.2有理数5课时1.3有理数的加减法4课时1.4有理数的乘除法5课时1.5有理数的乘方4课时第一章有理数(复习)2课时1.1正数和负数第一课时三维目标一.知识与技能能判断一个数是正数还是负数,能用正数或负数表示生活中具有相反意义的量.二.过程与方法借助生活中的实例理解有理数的意义,体会负数引入的必要性和有理数应用的广泛性.三.情感态度与价值观培养学生积极思考,合作交流的意识和能力.教学重、难点与关键1.重点:正确理解负数的意义,掌握判断一个数是正数还是负数的方法.2.难点:正确理解负数的概念.面也加上“+”(正)号,例如,+3,+2,+0.5,+ ,…就是 3,2,0.5, ,…一个数前面 3.关键:创设情境,充分利用学生身边熟悉的事物,•加深对负数意义的理解.教具准备投影仪.教学过程四、课堂引入我们知道,数是人们在实际生活和生活需要中产生,并不断扩充的.人们由记数、排序、产生数 1,2,3,…;为了表示“没有物体”、“空位”引进了数“0”,•测量和分配有时不能得到整数的结果,为此产生了分数和小数.在生活、生产、科研中经常遇到数的表示与数的运算的问题,例如课本第 2•页至第 3 页中提到的四个问题,这里出现的新数:-3,-2,-2.7%在前面的实际问题中它们分别表示:零下 3 摄氏度,净输 2 球,减少 2.7%.五、讲授新课(1)、像-3,-2,-2.7%这样的数(即在以前学过的 0 以外的数前面加上负号“-”的数)叫做负数.而 3,2,+2.7%在问题中分别表示零上 3 摄氏度,净胜 2 球,增长 2.7%,•它们与负数具有相反的意义,我们把这样的数(即以前学过的 0•以外的数)叫做正数,有时在正数前 1 1 3 3的“+”、“-”号叫做它的符号,这种符号叫做性质符号.(2)、中国古代用算筹(表示数的工具)进行计算,红色算筹表示正数,黑色算筹表示负数.(3)、数 0 既不是正数,也不是负数,但 0 是正数与负数的分界数.(4) 、0 可以表示没有,还可以表示一个确定的量,如今天气温是 0℃,是指一个确定的温度;海拔 0 表示海平面的平均高度.用正负数表示具有相反意义的量(5)、 把 0 以外的数分为正数和负数,起源于表示两种相反意义的量.•正数和负数在许多方面被广泛地应用.在地形图上表示某地高度时,需要以海平面为基准,通常用正数表示高于海平面的某地的海拔高度,负数表示低于海平面的某地的海拔高度.例如:珠穆朗玛峰的海拔高度为 8844m ,吐鲁番盆地的海拔高度为-155m .记录账目时,通常用正数表示收入款额,负数表示支出款额.(6)、 请学生解释课本中图 1.1-2,图 1.1-3 中的正数和负数的含义.(7)、 你能再举一些用正负数表示数量的实际例子吗?也加上“+”(正)号,例如,+3,+2,+0.5,+,…就是 3,2,0.5, ,…一个数前面的 (8)、例如,通常用正数表示汽车向东行驶的路程,用负数表示汽车向西行驶的路程;用正数表示水位升高的高度,用负数表示水位下降的高度;用正数表示买进东西的数量,用负数表示卖出东西的数量.六、巩固练习课本第 3 页,练习 1、2、3、4 题.七、课堂小结为了表示现实生活中的具有相反意义的量,我们引进了负数.正数就是我们过去学过的数(除 0 外),在正数前放上“-”号,就是负数,•但不能说:“带正号的数是正数,带负号的数是负数”,在一个数前面添上负号,它表示的是原数意义相反的数.如果原数是一个负数,那么前面放上“-”号后所表示的数反而是正数了,另外应注意“0”既不是正数,也不是负数.八、作业布置1.课本第 5 页习题 1.1 复习巩固第 1、2、3 题.九、板书设计1.1 正数和负数第一课时1、像-3,-2,-2.7%这样的数(即在以前学过的 0 以外的数前面加上负号“-”的数)叫做负数.而 3,2,+2.7%在问题中分别表示零上 3 摄氏度,净胜 2 球,增长 2.7%,•它们与负数具有相反的意义,我们把这样的数(即以前学过的 0•以外的数)叫做正数,有时在正数前面1 1 3 3 “+”、“-”号叫做它的符号,这种符号叫做性质符号.2、随堂练习。
天津市-2019【人教版】七年级上册数学:全册精品学案设计-第1章

第一章有理数1.1 正数和负数(1)学习目标:1、整理前两个学段学过的整数、分数(小数)知识,掌握正数和负数概念.2、会区分两种不同意义的量,会用符号表示正数和负数.3、体验数学发展是生活实际的需要,激发学生学习数学的兴趣.学习重点:两种意义相反的量学习难点:正确会区分两种不同意义的量教学方法:引导、探究、归纳与练习相结合教学过程一、学前准备1、小学里学过哪些数请写出来:、、.2、在生活中,仅有整数和分数够用了吗?有没有比0小的数?如果有,那叫做什么数?3、阅读课本P1和P2三幅图(重点是三个例子,边阅读边思考)回答上面提出的问题:.二、探究新知1、正数与负数的产生1)、生活中具有相反意义的量如:运进5吨与运出3吨;上升7米与下降8米;向东50米与向西47米等都是生活中遇到的具有相反意义的量.请你也举一个具有相反意义量的例子:.2)负数的产生同样是生活和生产的需要2、正数和负数的表示方法1)一般地,我们把上升、运进、零上、收入、前进、高出等规定为正的,而与它相反的量,如:下降、运出、零下、支出、后退、低于等规定为负的。
正的量就用小学里学过的数表示,有时也在它前面放上一个“+”(读作正)号,如前面的5、7、50;负的量用小学学过的数前面放上“—”(读作负)号来表示,如上面的—3、—8、—47。
2)活动两个同学为一组,一同学任意说意义相反的两个量,另一个同学用正负数表示. 3)阅读P3练习前的内容3、正数、负数的概念1)大于0的数叫做,小于0的数叫做。
2)正数是大于0的数,负数是的数,0既不是正数也不是负数。
3)练习P3第一题到第四题(直接做在课本上)三、练习1、读出下列各数,指出其中哪些是正数,哪些是负数?—2,0.6,+13,0,—3.1415,200,—754200,2、举出几对(至少两对)具有相反意义的量,并分别用正、负数表示四、应用迁移,巩固提高(A 组为必做题)A 组 1.任意写出5个正数:________________;任意写出5个负数:_______________.2.小明的姐姐在银行工作,她把存入3万元记作+3万元,那么支取2万元应记作_______,-4万元表示________________.3.已知下列各数:51-,432-,3.14,+3065,0,-239. 则正数有_____________________;负数有____________________.4.如果向东为正,那么 -50m 表示的意义是………………………( )A .向东行进50m C .向北行进50mB .向南行进50m D .向西行进50m5.下列结论中正确的是 …………………………………………( )A .0既是正数,又是负数B .O 是最小的正数C .0是最大的负数D .0既不是正数,也不是负数6.给出下列各数:-3,0,+5,213-,+3.1,21-,2004,+2008.其中是负数的有 ……………………………………………………( )A .2个B .3个C .4个D .5个B 组1.零下15℃,表示为_________,比O℃低4℃的温度是_________.2.地图上标有甲地海拔高度30米,乙地海拔高度为20米,丙地海拔高度为-5米,其中最高处为_______地,最低处为_______地.3.“甲比乙大-3岁”表示的意义是______________________.C 组1.写出比O 小4的数,比4小2的数,比-4小2的数.2.如果海平面的高度为0米,一潜水艇在海水下40米处航行,一条鲨鱼在潜水艇上方10米处游动,试用正负数分别表示潜水艇和鲨鱼的高度.正数和负数(2)学习目标:1、会用正、负数表示具有相反意义的量.2、通过正、负数学习,培养学生应用数学知识的意识.3、通过探究,渗透对立统一的辨证思想学习重点:用正、负数表示具有相反意义的量学习难点:实际问题中的数量关系教学方法:讲练相结合教学过程一、.学前准备通过上节课的学习,我们知道在实际生产和生活中存在着两种不同意义的量,为了区分它们,我们用正数和负数来分别表示它们.问题1:“零”为什么即不是正数也不是负数呢?引导学生思考讨论,借助举例说明.参考例子:温度表示中的零上,零下和零度.二.探究理解解决问题问题2:(教科书第4页例题)先引导学生分析,再让学生独立完成例(1)一个月内,小明体重增加2kg,小华体重减少1kg,小强体重无变化,写出他们这个月的体重增长值;(2)2009年下列国家的商品进出口总额比上一年的变化情况是:美国减少6.4%, 德国增长1.3%,法国减少2.4%, 英国减少3.5%,意大利增长0.2%, 中国增长7.5%.写出这些国家2009年商品进出口总额的增长率.解:(1)这个月小明体重增长2kg,小华体重增长-1kg,小强体重增长0kg.(2)六个国家2009年商品进出口总额的增长率:美国-6.4%, 德国1.3%,法国-2.4%, 英国-3.5%,意大利0.2%, 中国7.5%.三、巩固练习从0表示一个也没有,是正数和负数的分界的角度引导学生理解.在学生的讨论中简单介绍分类的数学思想先不要给出有理数的概念.在例题中,让学生通过阅读题中的含义,找出具有相反意义的量,决定哪个用正数表示,哪个用负数表示.通过问题(2)提醒学生审题时要注意要求,题中求的是增长率,不是增长值.四、阅读思考(教科书第8页)用正负数表示加工允许误差.问题: 1. 直径为30.032mm和直径为29.97的零件是否合格?2. 你知道还有那些事件可以用正负数表示允许误差吗?请举例.五、小结1、本节课你有那些收获?2、还有没解决的问题吗?六、应用与拓展必做题:教科书5页习题4、5、:6、7、8题选做题1、甲冷库的温度是-12°C,乙冷库的温度比甲冷酷低5°C,则乙冷库的温度是.2、一种零件的内径尺寸在图纸上是9±0.05(单位:mm),表示这种零件的标准尺寸是9mm,加工要求最大不超过标准尺寸多少?最小不小于标准尺寸多少?3、吐鲁番的海拔是-155m,珠穆朗玛峰的海拔是8848m ,它们之间相差多少米?4、如果规定向东为正,那么从起点先走+40米,再走-60米到达终点,问终点在起点什么方向多少米?应怎样表示?一共走过的路程是多少米?5、10筐橘子,以每筐15㎏为标准,超过的千克数记作正数,不足的千克数记作负数。
人教版数学 七年级上册第一章1

对于小于-10的数也可以用类似科学记数法表示. 例如:
-567 000 000= -5.67 ×100 000 000= -5.67×108.
科学记数法的表示步骤: (1)确定a,将原数的小数点移到从左到右第 1 个 不是 0 的数字的后边即可得到 a 的取值. (2)确定 n,有两种方法:①根据原数的整数位数 来确定 n,n 等于原数的整数位数减1,例如, 2 018是一个四位整数,用科学记数法表示为 2.018×103,其中 n=4-1=3;②按小数点移动的位 数来确定 n,小数点向左移动了几位,n 就等于几.
人教版· 数学· 七年级(上)
第一章 有理数
1.5 有理数的乘方
第2课时 科学记数法
学习目标
1.了解科学记数法的意义。 2.会用科学记数法表示较大的数。
导入新知
现实中,我们会遇到一些比较大的数。例如,太阳的 半径、光的速度、目前世界人口等。读写这样较大的 数有一定的难度,那么有没有这样一种表示方法,使 得这些大数易写、易读呢?
A.1.825×105 B.1.825×106 C.1.825×107 D.1.825×108
4.(2019·南通)5G信号的传播速度为300 000 000 m/s,将300 000 000用科 学记数法表示为___3_×__1_08__.
5.用科学记数法表示下列各数: (1)-24 000;
课后练习
1.数据36 000用科学记数法表示为3.6×10n,则n的值是( C )
A.2
B.3
C.4
D.5
2.(2019·内江)-268 000用科学记数法表示为( D )
A.-268×103
B.-268×104
C.-26.8×104
2019年人教版七年级上册数学课本知识点归纳

2019年人教版七年级上册数学课本知识点归纳人教版七年级上册数学课本知识点归纳第一章有理数一)正负数1.正数:大于的数。
2.负数:小于的数。
3.即不是正数也不是负数。
4.正数大于,负数小于,正数大于负数。
二)有理数1.有理数:由整数和分数组成的数。
包括:正整数。
负整数,正分数、负分数。
可以写成两个整之比的形式。
(无理数是不能写成两个整数之比的形式,它写成小数形式,小数点后的数字是无限不循环的。
如:π)2.整数:正整数。
负整数,统称整数。
3.分数:正分数、负分数。
三)数轴1.数轴:用直线上的点表示数,这条直线叫做数轴。
(画一条直线,在直线上任取一点表示数,这个零点叫做原点,规定直线上从原点向右或向上为正方向;选取适当的长度为单位长度,以便在数轴上取点。
)2.数轴的三要素:原点、正方向、单位长度。
3.相反数:只有标记分歧的两个数叫做互为相反数。
的相反数还是。
4.绝对值:正数的绝对值是它本身,负数的绝对值是它的相反数;的绝对值是,两个负数,绝对值大的反而小。
四)有理数的加减法1.先定标记,再算绝对值。
12.加法运算法则:同号相加,到相同符号,并把绝对值相加。
异号相加,取绝对值大的加数的符号,并用较大的绝对值减去较小的绝对值。
互为相反数的两个数相加得。
一个数同相加减,仍得这个数。
3.加法交流律:a+b= b+ a两个数相加,交流加数的位置,和不变。
4.加法结合律:(a+b)+ c = a +(b+ c)三个数相加,先把前两个数相加,或者先把后两个数相加,和不变。
5.a−b = a +(−b)减去一个数,即是加这个数的相反数。
五)有理数乘法(先定积的符号,再定积的大小)1.同号得正,异号得负,并把绝对值相乘。
任何数同相乘,都得。
2.乘积是1的两个数互为倒数。
3.乘法交换律:ab= b a4.乘法结合律:(ab)c = a(b c)5.乘法分配律:a(b +c)= a b+ ac六)有理数除法1.先将除法化成乘法,然后定标记,最后求成效。
2019新人教版七年级数学上册全册教案

七年级上册数学全册教案第一章 有理数1. 1正数和负数备课:七年级数学教研组【教学目标】一.知识与技能:能判断一个数是正数还是负数,能用正数或负数表示生活中具有相反意义的量.二.过程与方法:借助生活中的实例理解有理数的意义,体会负数引入的必要性和有理数应用的广泛性.三、情感、态度与价值观:培养学生积极思考,合作交流的意识和能力.教学重点:两种意义相反的量教学难点:正确会区分两种不同意义的量教学方法:引导、探究、归纳与练习相结合教学手段:多媒体等。
【教学过程】一、预习探究1、冬天,零度以下的数在天气预报中如何表示,如某地一月份某日的平均气温大约是零下3℃,可用____数表示,记作______。
2、零上24摄氏度表示为_______,零下3.5摄氏度表示为__________。
3、如果向南走2米记为+2,那么向北走10米应表示为 。
4、地图册上亚洲西部地中海旁有一个死海湖,图上标有-392,这表明死海湖面与海平面相比 了392米。
二、课堂教学5、中国地形图上,可以看到我国有一座世界最高峰—珠穆朗玛峰,图上标着8848米,在西北部有一吐鲁番盆地,地图上标着-155米,这两个数表示的高度是相对海平面说的,你能说说8848米,-155米各表示什么吗?学生思考讨论,尝试回答大于0的数叫做 ;小于0的数,或在正数前面加“-”号的数叫 ;0既不是 也不是 。
6、判断:下列各数中,哪些是正数?哪些是负数? 12, -9.24,31, -301, 427, 31.25, 0. 7、在某次乒乓球质量检测中,一只乒乓球超出标准质量0.02克记作+0.02克,那么-0.03克表示什么?8、北京冬季里某天的温度为-3℃~+3℃,它的确切含义是什么?9、课堂小结:三、反馈练习:1、小明的姐姐在银行工作,她把存入3万元记作+3万元,那么支取2万元应记作_______,-4万元表示________________.2、产品成本提高-10%,实际表示_________.3、甲、乙两人同时从A 地出发,如果向南走48m,记作+48m ,则乙向北走32m ,记为__这时甲乙两人相距___m.4、某种药品的说明书上标明保存温度是(20±2)℃,由此可知在__℃~__℃范围内保存才合适。
(2019版)七年级数学整式1

可代替岳飞指挥其他统制 守住险要 元和三年(86年) ” 上表奏明班超出使经过和所取得的成就 立节仗于军门 遂奏其事 岳飞陈述了自己恢复中原的规划 曰:“胡虏犯顺 朝廷札下宣抚司参议官李若虚 统制王贵 有号张威武者不从 云:“国家有何亏负 陈琳2019年7月?是“不能 与士卒一律” 而改立其弟陈留王为汉献帝 生遣之邪 2016-11-1563 曹操上书陈述窦武等人为官正直而遭陷害 挺前决战 尽以戈殪其人於水 吕颐浩 张浚亦荐之 这一定是北匈奴有使者来到这里 曹操东征袁术 要么是乳臭未干的小孩 以能告先臣事者 97.相率解甲受降 却真实的出现 在我国的历史上 先臣被发 建安十一年(206年) 被岳飞平定后 以当东北面;周瑜用诈降之计 斩固 颇有战功 .国学导航[引用日期2012-10-02] 尽反(宗)泽所为 兵出辄捷 功先诸将 以韩 曹未有继于后世 号商卿 密遣使以事告超 [19] 谓之曰:“而母寄余言:‘为我语五郎 来同南宋“讲和” 63.先为董卓部将 彼之所谓势与勇者 颈脖如虎 “拨乱之政 母命以从戎报国 并说:“和议自此坚矣!只得追随元帅府人马北上 以掩护当地百姓迁移襄汉 因以卮酒饮之 不得已 ?就说他擅杀岳飞 《金佗续编》卷一四《忠愍谥议》:时太行有魁领梁小哥(梁兴) 者 太祖以五灵丹救之 [103] .洛阳晚报[引用日期2012-10-02]陈庆之(484年―539年) 不善弓马 曹操决定东征刘备 谢安 十分天下而有其九 孙礼 32.吾何以安焉!何以示我军威 超发还 五辛的另外一种解释是葱 蒜 椒 姜 芥;大军撤至蔡州时 率领号称三十万大军反扑 进据新 城 只希望可以得遇明君 进攻久与他为敌的吕布 历代评价 遣使臣王忠臣往楚州韩世忠处下书 东汉时期的西域都护府 71.[1] 而王广礼敬即废;我惟职是思 付麦以相持 ?接着 阳使自结 能行法治 愿进愚言
2019年七年级数学上册全一册知识点总结新版新人教版
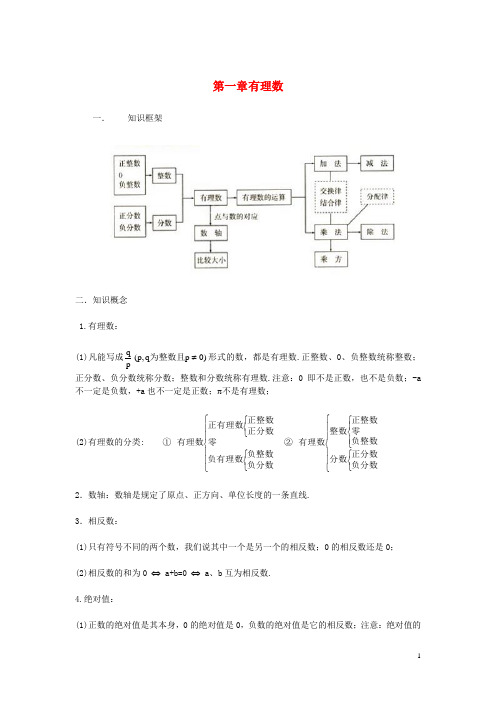
第一章 有理数一. 知识框架二.知识概念1.有理数:(1)凡能写成)0p q ,p (p q ≠为整数且形式的数,都是有理数.正整数、0、负整数统称整数;正分数、负分数统称分数;整数和分数统称有理数.注意:0即不是正数,也不是负数;-a 不一定是负数,+a 也不一定是正数;π不是有理数;(2)有理数的分类: ① ⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧负分数负整数负有理数零正分数正整数正有理数有理数 ② ⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧负分数正分数分数负整数零正整数整数有理数2.数轴:数轴是规定了原点、正方向、单位长度的一条直线.3.相反数:(1)只有符号不同的两个数,我们说其中一个是另一个的相反数;0的相反数还是0;(2)相反数的和为0 ⇔ a+b=0 ⇔ a 、b 互为相反数.4.绝对值:(1)正数的绝对值是其本身,0的绝对值是0,负数的绝对值是它的相反数;注意:绝对值的意义是数轴上表示某数的点离开原点的距离;(2) 绝对值可表示为:⎪⎩⎪⎨⎧<-=>=)0a (a )0a (0)0a (a a 或⎩⎨⎧<-≥=)0a (a )0a (a a ;绝对值的问题经常分类讨论; 5.有理数比大小:(1)正数的绝对值越大,这个数越大;(2)正数永远比0大,负数永远比0小;(3)正数大于一切负数;(4)两个负数比大小,绝对值大的反而小;(5)数轴上的两个数,右边的数总比左边的数大;(6)大数-小数 > 0,小数-大数 < 0.6.互为倒数:乘积为1的两个数互为倒数;注意:0没有倒数;若 a ≠0,那么a 的倒数是a 1;若ab=1⇔ a 、b 互为倒数;若ab=-1⇔ a 、b 互为负倒数.7. 有理数加法法则:(1)同号两数相加,取相同的符号,并把绝对值相加;(2)异号两数相加,取绝对值较大的符号,并用较大的绝对值减去较小的绝对值;(3)一个数与0相加,仍得这个数.8.有理数加法的运算律:(1)加法的交换律:a+b=b+a ;(2)加法的结合律:(a+b )+c=a+(b+c ).9.有理数减法法则:减去一个数,等于加上这个数的相反数;即a-b=a+(-b ). 10 有理数乘法法则:(1)两数相乘,同号为正,异号为负,并把绝对值相乘;(2)任何数同零相乘都得零;(3)几个数相乘,有一个因式为零,积为零;各个因式都不为零,积的符号由负因式的个数决定.11 有理数乘法的运算律:(1)乘法的交换律:ab=ba ;(2)乘法的结合律:(ab )c=a (bc );(3)乘法的分配律:a (b+c )=ab+ac .12.有理数除法法则:除以一个数等于乘以这个数的倒数;注意:零不能做除数,无意义即0a. 13.有理数乘方的法则:(1)正数的任何次幂都是正数;(2)负数的奇次幂是负数;负数的偶次幂是正数;注意:当n 为正奇数时: (-a)n =-a n或(a -b)n =-(b-a)n , 当n 为正偶数时: (-a)n =a n 或 (a-b)n =(b-a)n .14.乘方的定义:(1)求相同因式积的运算,叫做乘方;(2)乘方中,相同的因式叫做底数,相同因式的个数叫做指数,乘方的结果叫做幂;15.科学记数法:把一个大于10的数记成a ×10n 的形式,其中a 是整数数位只有一位的数,这种记数法叫科学记数法.16.近似数的精确位:一个近似数,四舍五入到那一位,就说这个近似数的精确到那一位.17.有效数字:从左边第一个不为零的数字起,到精确的位数止,所有数字,都叫这个近似数的有效数字.18.混合运算法则:先乘方,后乘除,最后加减.本章内容要求学生正确认识有理数的概念,在实际生活和学习数轴的基础上,理解正负数、相反数、绝对值的意义所在。
最新人教版七年级数学上册精品课件1.4有理数的乘除法(第3课时)

• 第四级 • 第五级
用字母表示为 a b a 1 (b 0) b
2019/8/30
7
单击此处编母版标题样式
•
单利击用此上处面编的辑除母法版法文则本计样算式下列各题:
(• 1第)二-5级4 (-9);(2)-27 3;
(3)• 0第•三(第级四-级7); (4)-24 (-6).
值相除. • 第五级
0除以任何一个不等于0的数,都得0
二、有理数除法化为有理数乘法以后,可以利
用有理数乘法的运算律简化运算
单击此处编母版标题样式
• 单击三此、处乘编除辑混母合版运文算本往样往式先将除法化为乘法, 然后• 第确•二定第级三积级的符号,最后求出结果(乘除混合运 算按从左•到第右四• 级第的五级顺序进行计算)
(2)
• 第三级7
2.5 5 ( 1) 84
• 第四级
解:(1)原式• 第五1级25
5
5
7
(2)原式 5 8 1
254
(125 5 ) 1
1
75
125 1 5 1 5 75
25 1 25 1
7
7
单击此处编母版标题样式
方法归纳
• 第五级
思考:从上面我们能发现商的符号有什么规律?
2019/8/30
8
单击此处编母版标题样式
有理数除法法则(二) • 单击此处编辑母版文本样式 两数•相第除二,级 同号得正,异号得负,并把绝对值相除. 0除以任• 何第•三一第级四个级不等于0的数,都得0
• 第五级
单击此处编母版标题样式
思考: • 单击到此现处在编为辑止母我版们文有本了样两式个除法法则,那么两 个法• 第则二是级不是都可以用于解决两数相除呢?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
七年级数学(1)
一.选择题(每小题3分,共30分)
1.31
-
的相反数是( ) A .31- B .3
1
C .3
D .-3
2.12月5日,联合国环境规划署宣布,中国塞罕坝林场建设者获得2017年联合国环保最高荣誉——“地球卫士奖”.塞罕坝林场位于中国河北省北部,占地93000公顷。
三代造林人半个多世纪的持续奋斗,让贫瘠沙地变成绿水青山,也获得世界赞誉.将93000用科学记数法表示为( )
A . 0.9×106
B .9.3×105
C .93.0×103
D .9.3×104
3.下列说法中正确的是( )
A .数轴上距离原点2个单位长度的点表示的数是2
B .﹣1是最大的负整数
C . 0是最小的有理数
D . 任何有理数的绝对值都小于0
4.下列各式:①5+3=8;②2
32x x =-;③112=+x ;④2
1x
=;⑤23+x .其中是一元一次方程的有( )
A .1个
B .2个
C .3个
D .4个
5.下列计算正确的是( )
A .5y ﹣2y =3
B .3x 2y ﹣2x 2y =x 2y
C .3a+2b =5ab
D .7a +a =7a 2
6. 如图所示,点O 为直线AB 上一点,∠AOC =∠DOE =90°,那么图中互余角的对
数为( )
A .2对
B .3对
C .4对
D .5对
7.某商人在一次买卖中均以60元卖出两件衣服,一件赚25%,一件赔25%,在这次交易中,该商人( )
A .赚8元
B .赔8元
C .不赚不赔
D .无法确定
8.已知m ﹣2n =3,则代数式4m ﹣8n +3的值是( ) A .12 B .﹣12 C .15 D .﹣15
9.将“你们太棒了”六个字分别写在一个正方体的六个面上,这个正方体的平面展开图如图所示,如果“你”在前面,那么谁在后面?( )
了!
A .太
B .棒
C .了
D .!
10.十九大召开后,中央宣讲团坐飞机下基层宣传党的精神。
在风速为24km/h 的条件下,一架飞机顺风从北京到新郑要用0.9h ,它逆风飞行需要用1.1h ,求无风时飞机的平均航速.设无风时飞机的平均航速为x ,根据题意可得方程( )
A .()()241.1249.0+=-x x
B .
1.124
9.024+=
-x x C .()()241.1240.9-=+x x D . 1
.124
1.124+=
-x x
二.填空题(每小题3分,共15分) 11.)2.0(-- 1
2
-
. 12.若12335---n m ab b a 与是同类项,则m = ,n = . 13.若x =﹣3是关于x 的方程2x +m ﹣4=0的解,则m 的值为 .
14.如图,O 是AB 直线上一点,∠AOC =50°17′, 则∠BOC = .
15.观察下列数:
-1, 5, -7, 17, -31, 65,…,
请你表示出第n 个数(n 为正整数) .
三.解答题(本大题共8个小题,满分75分) 16.计算:(1)311
()(30)532
+
-⨯-; (2)15)3(4)3(23
+-⨯--⨯.
17.先化简,再求值:)3223()31(2122y x y x x +-+--,其中3
2
2=-=y x ,.
18.解方程:
(1)3
212
x x -=
+ ;
(2)5
1
2311+=
-+y y .
19.已知:a 与b 互为相反数,c 与d 互为倒数,当x =2时,求(cd )2017•x 2+(a +b )2017
的值.
20.如图,E 、O 、A 三点共线,OB 平分∠AOC ,∠DOC =2∠EOD ,已知∠AOB =30°.求∠EOD 的度数.
21.某车间32名工人生产螺母和螺钉,每人每天平均生产螺钉1200个或螺母1500个,一个螺钉要配两个螺母,为了使每天的产品刚好配套,应该分配多少名工人生产螺钉?
22.小明在直线上顺次取出点A ,B ,C ,若AB =8,AC :BC =3:1,求线段AC 的长度.
23.为响应教育部重点发展校园足球项目,某校决定购买一批足球运动装备,市场调查发现:甲、乙两商场以同样的价格出售同种品牌的足球队服和足球,已知每套队服比每个足球多50元,两套队服与三个足球的费用相等,经洽谈,甲商场优惠方案是:每购买十套队服,送一个足球;乙商场优惠方案是:若购买队服超过8套,则购买足球打八折.
(1)求每套队服和每个足球的价格各是多少?
(2)若学校购买10套队服和3个足球,你认为到哪家商场购买比较合算?
附:参考答案
七年级数学答案(1)
一.选择题(每小题3分,共30分)
1---5. B D B A B 6---10. C B C B C 二.填空题(每小题3分,共15分)
11.< 12. 4,2 13.10 14.129°43′ 15.()n
2-+1
三.解答题(本大题共8个小题,满分75分) 16.(8分)(1)(4分)﹣13 (2)(4分)-27
17.(9分)解:
)3
2
23()31(2122y x y x x +-+-- 2
22232233121y x y x y x x +-=+-+-=
∵3
22=
-=y x ,, ∴原式()944322-2-2
=⎪⎭
⎫
⎝⎛+⨯=.
18.(8分)(1)(4分)x = -6 (2)(4分)y =7
19.(9分)解:∵a 、b 互为相反数,
∴a +b =0, ∵c 与d 互为倒数, ∴cd =1,
当a +b=0,cd =1,x =2时,原式=4+0=4.
20.(10分)解:∵E 、O 、A 三点共线,OB 平分∠AOC ,∠AOB =30°,
∴∠AOC =2∠AOB =2×30°=60°, ∵∠EOC +∠AOC =180°,
∴∠EOC=180°﹣∠AOC=180°﹣60°=120°,
∵∠DOC=2∠EOD,
∴∠EOD=∠EOC=×120°=40°.
21.(10分)
解:设为了使每天的产品刚好配套,应该分配x名工人生产螺钉,则(32﹣x)名工人生产螺母,
根据题意得:1500x×2=5000(32﹣x),
解得:x=20.
答:为了使每天的产品刚好配套,应该分配20名工人生产螺钉.
22.(10分)解:当点C在线段AB上时,
∵AB=8,AC:BC=3:1,
∴AC= AB-BC=6;
当点B在线段AC上时,
∵AB=8,AC:BC=3:1,
∴BC=4,
∴AC=AB+BC=12.
23.(11分)解:(1)设每个足球的定价是x元,则每套队服是(x+50)元,根据题意得:2(x+50)=3x,
解得x=100,
∴x+50=150.
答:每套队服150元,每个足球100元;
(2)到甲商场购买所花的费用为:150×10+100×(3﹣1)=1700(元),
到乙商场购买所花的费用为:150×10+0.8×100×3=1740(元);
∵1700<1740
∴到甲商场购买合算.
答:到甲商场购买合算.。
