高中数学数列基础知识
高中数学专题-数列

高中数学专题-数列一、基础知识1.等差数列的定义与性质定义:1n n a a d+-=(d 为常数),()11n a a n d=+-等差中项:x A y ,,成等差数列2A x y⇔=+前n 项和()()11122n n a a n n n S nad+-==+性质:{}n a 是等差数列(1)若m n p q+=+,则m n p q a a a a +=+;(2)数列{}{}{}12212,,+-n n n a a a 仍为等差数列,232n n n n n S S S S S --,,……仍为等差数列,公差为d n 2;(3)若三个成等差数列,可设为a d a a d-+,,(4)若n n a b ,是等差数列,且前n 项和分别为n n S T ,,则2121m m m m a S b T --=(5){}n a 为等差数列2n S an bn ⇔=+(a b ,为常数,是关于n 的常数项为0的二次函数)nS 的最值可求二次函数2n S an bn=+的最值;或者求出{}n a 中的正、负分界项,即:当100a d ><,,解不等式组100n n a a +≥⎧⎨≤⎩可得n S达到最大值时的n 值.当100a d <>,,由100n n a a +≤⎧⎨≥⎩可得n S达到最小值时的n 值.(6)项数为偶数n 2的等差数列{}n a ,有),)(()()(11122212为中间两项++-+==+=+=n n n n n n n a a a a n a a n a a n S ndS S =-奇偶,1+=n na a S S 偶奇.(7)项数为奇数12-n 的等差数列{}n a ,有)()12(12为中间项n n n a a n S -=-na S S =-偶奇,1-=n n S S 偶奇.2.等比数列的定义与性质定义:1n na q a +=(q 为常数,0q ≠),11n n a a q -=.等比中项:x G y 、、成等比数列2G xy ⇒=,或G xy =.前n 项和:()11(1)1(1)1n n na q S a q q q =⎧⎪=-⎨≠⎪-⎩(要注意!)性质:{}n a 是等比数列(1)若m n p q+=+,则m n p qa a a a =··(2)232n n n n n S S S S S --,,……仍为等比数列,公比为nq .注意:由nS 求na 时应注意什么?1n =时,11a S =;2n ≥时,1n n n a S S -=-.二、等差数列和等比数列对比等差数列等比数列定义a n-a n-1=常数(n≥2)a na n-1=常数(n≥2)通项公式a n=a1+(n-1)d a n=a1q n-1(q≠0)判定方法(1)定义法(2)中项公式法:2a n+1=a n+a n+2(n≥1)⇔{a n}为等差数列(3)通项公式法:a n=pn+q(pq为常数)⇔{a n}为等差数列(4)前n项和公式法:S n=An2+Bn(A、B为常数)⇔{a n}为等差数列(5){a n}为等比数列,a n>0⇔{log a a n}为等差数列(1)定义法(2)中项公式法:a2n+1=a n·a n+2(n≥1)(a n≠0)⇔{a n}为等比数列(3)通项公式法:a n=c·q n(c、q均是不为0的常数,n∈N*)⇔{a n}为等比数列(4){a n}为等差数列⇔{a an}为等比数列(a>0且a≠1)性质(1)若m、n、p、q∈N*,且m+n=p+q,则a m+a n=a p+a q特别:若m+n=2p,则a m+a n=2a p.(2)a n=a m+(n-m)d(3)数列S m,S2m-S m,S3m-S2m,…也是等差数列,即2(S2m-S m)=S m+(S3m-S2m)(1)若m、n、p、q∈N*,且m+n=p+q,则a m·a n=a p·a q特别地,若m+n=2p,则a m·a n=a2p.(2)a n=a m q n-m(3)若等比数列前n项和为S n则S m,S2m-S m,S3m-S2m仍成等比数列,即(S2m-S m)2=S m(S3m-S2m)(m∈N*,公比q≠-1).前n 项和S n=n a1+a n2=na1+n n-12d(1)q≠1,S n=a11-q n1-q=a1-a n q1-q(2)q=1,S n=na1三、考点方法归纳考点一求数列的通项公式1.由a n与S n的关系求通项公式:由S n与a n的递推关系求a n的常用思路有:①利用S n-S n-1=a n(n≥2)转化为a n的递推关系,再求其通项公式;数列的通项a n与前n项和S n的关系是a n S1,n=1,S n-S n-1,n≥2.当n=1时,a1若适合S n-S n-1,则n=1的情况可并入n≥2时的通项a n;当n=1时,a1若不适合S n-S n-1,则用分段函数的形式表示。
数列知识点总结(高中数学)

数列知识点总结 数列的概念与简单表示法知识点一、数列的定义按照一定顺序排列着的一列数称为数列,数列中的每一个数叫做这个数列的项。
数列中的每一项都和它的序号有关,排在第一位的数称为这个数列的第一项(通常称为首项),排在第二位的数称为这个数列的第2项……排在第n 位的数称为这个数列的第n 项,所以数列的一般形式可以写成: ,,,,,,321 n a a a a简记为{}n a 。
项数有限的数列叫做有穷数列,项数无限的数列叫做无穷数列。
1.从第2项起,每一项都大于它的前一项的数列叫做递增数列; 2.从第2项起,每一项都小于它的前一项的数列叫做递减数列; 3.各项相等的数列叫做常数列;4.从第2项起,有些项大于它的前一项,有些项小于它前一项的数列叫做摆动数列; 知识点二、通项公式如果数列{}n a 的第n 项与序号n 之间的关系可以用一个式子来表示,那么这个公式叫做这个数列的通项公式。
知识点三、数列的前n 项和1.数列的前n 项和的定义:我们把数列{}n a 从第一项起到第n 项止的各项之和,称为数列{}n a 的前n 项和,记作n S ,即n n a a a S +++= 21。
2.数列前n 项和n S 与通项公式n a 之间的关系:⎩⎨⎧≥-==-.2,,1,11n S S n S a n n n等差数列知识点一、等差数列的定义一般地,如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,那么这个数列就叫做等差数列,这个常数叫做等差数列的公差,公差通常用字母d 表示。
知识点二、等差中项有三个数b A a ,,组成的等差数列可以看成简单的等差数列,这时A 叫做b a 与的等差中项。
1.根据等差中项的定义:b A a ,,是等差数列,则2b a A +=;反之,若2ba A +=,则b A a ,,是等差数列。
2.在等差数列{}n a 中,任取相邻的三项()*+-∈≥N n n a a a n n n ,2,,11,则n a 是1-n a 与1+n a 的等差中项;反之,n a 是1-n a 与1+n a 的等差中项对一切*∈≥N n n ,2均成立,则数列{}n a 是等差数列。
高中数学必修二数列数列总知识点

高中数学必修二数列数列总知识点
1. 数列的定义与概念
- 数列是指由一系列按照一定规律排列的数构成的序列。
- 数列中的每个数称为项,用an表示第n项。
- 数列按照一定规律排列的规律称为通项公式,用an = f(n)表示。
- 数列的表示方法有通项公式、递推公式和图形表示等。
2. 等差数列
- 等差数列是指数列中相邻两项之间差相等的数列。
- 等差数列的通项公式为an = a1 + (n - 1)d,其中a1为首项,d 为公差,n为项数。
- 等差数列的前n项和公式为Sn = (a1 + an) * n / 2。
3. 等比数列
- 等比数列是指数列中相邻两项之间比相等的数列。
- 等比数列的通项公式为an = a1 * r^(n - 1),其中a1为首项,r 为公比,n为项数。
- 等比数列的前n项和公式为Sn = a1 * (1 - r^n) / (1 - r),当|r| <
1时成立。
4. 通项公式的推导
- 对于一些特定的数列,可以通过观察规律或利用数学方法推
导出通项公式。
- 例如,斐波那契数列的通项公式为an = (φ^n - (1 - φ)^n) / √5,其中φ为黄金分割比。
5. 常见数列的性质与应用
- 数列的性质包括单调性、有界性、极限等,这些性质在数学
应用中起到重要作用。
- 等差数列和等差中项数列常用于计算物体运动的位置和速度
等问题。
- 等比数列常用于计算复利、投资等涉及指数增长的问题。
以上是高中数学必修二数列的总知识点,希望对你的研究有所
帮助!。
高中数学数列知识点归纳

高中数学数列知识点归纳一、数列的概念数列是按照一定顺序排列的一列数。
例如,1,2,3,4,5……就是一个自然数列。
数列中的每一个数都叫做这个数列的项,排在第一位的数称为这个数列的第 1 项(通常也叫做首项),排在第二位的数称为这个数列的第 2 项……以此类推。
数列的一般形式可以写成 a₁,a₂,a₃,…,aₙ,…,其中 aₙ 是数列的第 n 项。
我们用{aₙ} 来表示一个数列。
二、数列的分类1、按项数分类(1)有穷数列:项数有限的数列。
例如,数列 1,2,3,4,5 就是一个有穷数列。
(2)无穷数列:项数无限的数列。
比如自然数列 1,2,3,4,……就是一个无穷数列。
2、按项的大小变化分类(1)递增数列:从第 2 项起,每一项都大于它的前一项的数列。
例如,数列 1,2,4,8,16,……就是一个递增数列。
(2)递减数列:从第 2 项起,每一项都小于它的前一项的数列。
比如数列 10,8,6,4,2 就是一个递减数列。
(3)常数列:各项都相等的数列。
例如,数列 3,3,3,3,……就是一个常数列。
(4)摆动数列:从第 2 项起,有些项大于它的前一项,有些项小于它的前一项的数列。
比如数列 1,-1,1,-1,1,……就是一个摆动数列。
三、数列的通项公式如果数列{aₙ} 的第 n 项 aₙ 与 n 之间的关系可以用一个公式来表示,那么这个公式叫做这个数列的通项公式。
例如,数列 1,3,5,7,9,……的通项公式为 aₙ = 2n 1 。
通项公式可以帮助我们快速求出数列中的任意一项,也能让我们更深入地了解数列的性质。
四、数列的递推公式如果已知数列{aₙ} 的第 1 项(或前几项),且从第二项(或某一项)开始的任一项 aₙ 与它的前一项 aₙ₋₁(或前几项)间的关系可以用一个公式来表示,那么这个公式叫做这个数列的递推公式。
例如,已知数列{aₙ} 的首项 a₁= 1 ,且 aₙ = aₙ₋₁+ 2 (n ≥2 ),则可以依次求出 a₂= a₁+ 2 =3 ,a₃= a₂+ 2 = 5 ,……五、等差数列1、定义如果一个数列从第二项起,每一项与它的前一项的差等于同一个常数,这个数列就叫做等差数列。
人教版高中数学必修五《数列》基础知识要点总结
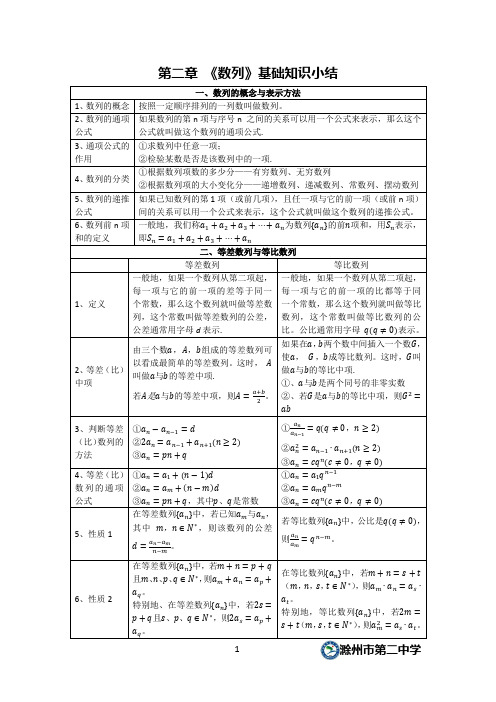
5、数列的递推公式
如果已知数列的第1项(或前几项),且任一项与它的前一项(或前n项)间的关系可以用一个公式来表示,这个公式就叫做这个数列的递推公式。
6、数列前n项和的定义
一般地,我们称 为数列 的前 项和,用 表示,即
二、等差数列与等比数列
已知三个数成等比数列,且已知三个数之积时,一般设此三个数分别为 , , ,其中 为公比。
若已知四个数成等比数列及这个四个数的积时,一般不设为 , , , ,因为这种设法使得四个数的公比为 ,就漏掉了公比为负数的情形,造成漏解。
2、求数列最大(小)值的方法
一般方法——解不等式 ;或
特别地,若 为等差数列, 为它的前n项的和时,求 的最大(小)值可以利用①二次函数的性质;② 中项的符号。
3、求数列通项的常用方法
①观察法:根据数列的前几项归纳出数列的通项公式;
②公式法:利用 求通项公式
③根据递推公式求通项公式:
(1)迭代法:对于形如 型的递推公式,采取逐次降低“下标”数值的反复迭代方式,最终使 与初始值 (或 )建立联系的方法就是迭代法.
(2)累加法:形如 的递推公式可用 求出通项;
①
②
③
①
②
③
4、等差(比)数列的通项公式
①
②
③ ,其中 、 是常数
①
②
③
5、性质1
在等差数列 中,若已知 与 ,其中 ,则该数列的公差 。
若等比数列 中,公比是 ,则 。
6、性质2
在等差数列 中,若 且 、 、 、 ,则 。
特别地、在等差数列 中,若 且 、 、 ,则 。
在等比数列 中,若 ( , , , ),则 。
高中数学数列知识点总结(精华版)

一、数列1.数列的定义:按照一定顺序排列的一列数称为数列,数列中的每个数称为该数列的项. ⑴数列中的数是按一定“次序”排列的,在这里,只强调有“次序”,而不强调有“规律”.因此,如果组成两个数列的数相同而次序不同,那么它们就是不同的数列.⑵在数列中同一个数可以重复出现. ⑶项a n 与项数n 是两个根本不同的概念.⑷数列可以看作一个定义域为正整数集(或它的有限子集)的函数当自变量从小到大依次取值时对应的一列函数值,但函数不一定是数列2.通项公式:如果数列{}n a 的第n 项与序号之间可以用一个式子表示,那么这个公式叫做这个数列的通项公式,即)(n f a n =.3.递推公式:如果已知数列{}n a 的第一项(或前几项),且任何一项n a 与它的前一项1-n a (或前几项)间的关系可以用一个式子来表示,即)(1-=n n a f a 或),(21--=n n n a a f a ,那么这个式子叫做数列{}n a 的递推公式. 如数列{}n a 中,12,11+==n n a a a ,其中12+=n n a a 是数列{}n a 的递推公式.4.数列的前n 项和与通项的公式①n n a a a S +++= 21; ②⎩⎨⎧≥-==-)2()1(11n S S n S a n nn .5. 数列的表示方法:解析法、图像法、列举法、递推法.6. 数列的分类:有穷数列,无穷数列;递增数列,递减数列,摆动数列,常数数列;有界数列,无界数列. ①递增数列:对于任何+∈N n ,均有n n a a >+1. ②递减数列:对于任何+∈N n ,均有n n a a <+1. ③摆动数列:例如: .,1,1,1,1,1 --- ④常数数列:例如:6,6,6,6,…….⑤有界数列:存在正数M 使+∈≤N n M a n ,.⑥无界数列:对于任何正数M ,总有项n a 使得M a n >. 1、已知*2()156n n a n N n =∈+,则在数列{}n a 的最大项为__(答:125); 2、数列}{n a 的通项为1+=bn ana n ,其中b a ,均为正数,则n a 与1+n a 的大小关系为___(答:n a <1+n a );3、已知数列{}n a 中,2n a n n λ=+,且{}n a 是递增数列,求实数λ的取值范围(答:3λ>-);4、一给定函数)(x f y =的图象在下列图中,并且对任意)1,0(1∈a ,由关系式)(1n n a f a =+得到的数列}{n a 满足)(*1N n a a n n ∈>+,则该函数的图象是()(答:A )二、 等差数列1、 等差数列的定义:如果数列{}a n 从第二项起每一项与它的前一项的差等于同一个常数,那么这个数列叫做等差数列,这个常数叫等差数列的公差。
高中数学数列知识点总结5篇

高中数学数列知识点总结5篇篇1一、数列的基本概念数列是一种特殊的函数,其定义域为自然数集或其自然数子集。
数列分为等差数列和等比数列两种基本形式,此外还有更为复杂的数列形式。
数列的通项公式是描述数列的一般规律的重要工具,对于等差数列和等比数列,其通项公式分别为an=a1+(n-1)d和an=a1×q^(n-1)。
掌握数列的基本概念对于后续的学习至关重要。
二、等差数列等差数列是一种常见且重要的数列形式,其任意两项之差都相等。
在等差数列中,需要掌握的主要知识点包括等差数列的通项公式、求和公式、中项公式等。
等差数列的求和公式为Sn=n(a1+an)/2或Sn=na1+[n(n-1)/2]d,这些公式在处理与等差数列相关的问题时非常实用。
等比数列的特点是任意两项之比都相等。
在等比数列中,需要掌握的知识点包括等比数列的通项公式、求和公式以及公比的概念。
等比数列的求和公式为Sn=a1(1-q^n)/(1-q),掌握这个公式对于解决涉及等比数列的问题非常关键。
四、数列的极限数列的极限是描述数列变化趋势的重要概念。
当n趋近于无穷大时,数列的项会趋近于一个固定的值,这个值就是数列的极限。
掌握数列极限的概念和计算方法是分析数列性质的重要工具。
五、数列的应用数列在实际生活中有着广泛的应用,如金融、物理、工程等领域。
例如,在金融领域,复利计算就涉及等比数列的应用;在物理领域,许多物理量的变化可以看作是等差或等比数列的形式。
掌握数列的应用对于解决实际问题具有重要意义。
除了等差数列和等比数列外,还有一些特殊数列需要了解,如斐波那契数列、三角数列等。
这些数列具有独特的性质和应用场景,了解这些数列有助于拓宽数学视野,提高数学素养。
七、数列的证明在数列的学习中,还需要掌握一些证明方法,如数学归纳法、反证法等。
这些证明方法在证明数列的性质和解决问题时非常有用。
掌握这些证明方法有助于提升数学思维和逻辑推理能力。
综上所述,高中数学中的数列知识点丰富且重要,需要掌握基本概念、等差数列和等比数列的性质、数列的极限、应用、特殊数列以及证明方法等方面的知识。
高中数列知识点归纳总结大全

高中数列知识点归纳总结大全数列是数学中一个基础而重要的概念,广泛应用于各个领域。
在高中数学学习中,数列的概念与应用也是不可或缺的内容。
本篇文章将对高中数列的知识点进行归纳总结,旨在帮助读者系统理解和掌握数列的相关概念和性质。
一、数列的基本概念和性质1. 数列的定义:数列是按照一定顺序排列的数,用字母a、b、c…表示。
2. 公式与通项公式:数列的通项公式是指数列中的第n个数与n的关系式,通常用an表示。
3. 数列的项和:数列的项和是指数列中前n项的和,常用Sn表示。
4. 等差数列:等差数列是指一个数列中的相邻两项之差等于同一个常数d。
5. 等差数列的通项公式与项和公式:对于等差数列an,它的通项公式为an = a1 + (n - 1)d,项和公式为Sn = (a1 + an)n/2。
6. 等比数列:等比数列是指一个数列中的相邻两项之比等于同一个常数q。
7. 等比数列的通项公式与项和公式:对于等比数列an,它的通项公式为an = a1 * q^(n - 1),项和公式为Sn = a1 * (q^n - 1)/(q - 1)。
二、数列的应用1. 等差数列的应用:等差数列可以描述各种线性变化的情况,例如描述自然数序列、等差数列求和、等差数列的推广等。
2. 等比数列的应用:等比数列常用于表示指数增长或指数衰减的情况,例如人口增长、物种繁殖、金融利率等方面。
3. 斐波那契数列:斐波那契数列是一个特殊的数列,其前两项为1,从第三项开始,每一项均为前两项之和。
斐波那契数列在自然界中普遍存在,如植物的叶子排列、蜂窝的排列等。
4. 数列与函数关系:数列与函数有着密切的联系,可以将数列看作离散的函数,通过数列的性质与函数的性质相互转化。
三、常见数列的特殊性质1. 等差数列的前n项和的性质:对于等差数列an,其前n项和为Sn = (n/2)(a1 + an)。
2. 等差数列的中项:对于等差数列an,当n为奇数时,中项为am= a((n+1)/2),当n为偶数时,不存在中项。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高中数学数列基础知识
高中数学数列基础知识:等差数列
定义
一般地,如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,这个数列就叫做等差数列(arithmetic sequence),这个常数叫做等差数列的公差(common difference),公差通常用字母d表示,前n项和用Sn表示。
等差数列可以缩写为A.P.(Arithmetic Progression)。
通项公式
an=a1+(n-1)d
n=1时 a1=S1
n≥2时 an=Sn-Sn-1
an=kn+b(k,b为常数) 推导过程:an=dn+a1-d 令d=k,a1-d=b 则得到an=kn+b
等差中项
由三个数a,A,b组成的等差数列可以堪称最简单的等差数列。
这时,A叫做a与b的等差中项(arithmetic mean)。
有关系:A=(a+b)÷2
前n项和
倒序相加法推导前n项和公式:
Sn=a1+a2+a3
+·····+an
=a1+(a1+d)+(a1+2d)+···· ··+[a1+(n-1)d] ①
Sn=an+an-1+an-2+····&mi ddot;·+a1
=an+(an-d)+(an-2d)+···· ··+[an-(n-1)d] ②
由①+②得
2Sn=(a1+an)+(a1+an)+···· ;··+(a1+an)(n个)=n(a1+an)
∴Sn=n(a1+an)÷2
等差数列的前n项和等于首末两项的和与项数乘积的一半:
Sn=n(a1+an)÷2=na1+n(n-1)d÷2
Sn=dn2÷2+n(a1-d÷2)
亦可得
a1=2sn÷n-an
an=2sn÷n-a1
有趣的是S2n-1=(2n-1)an,S2n+1=(2n+1)an+1
性质
一、任意两项am,an的关系为:
an=am+(n-m)d
它可以看作等差数列广义的通项公式。
二、从等差数列的定义、通项公式,前n项和公式还可推出:
a1+an=a2+an-1=a3+an-2=…=ak+an-k+1,k∈N*
三、若m,n,p,q∈N*,且m+n=p+q,则有
am+an=ap+aq
四、对任意的k∈N*,有
Sk,S2k-Sk,S3k-S2k,…,Snk-S(n-1)k…成等差数列。
高中数学数列基础知识:等比数列
定义
一般地,如果一个数列从第2项起,每一项与它的前一项的比等于同一个常数,这个数列就叫做等比数列(geometric sequence)。
这个常数叫做等比数列的公比(common ratio),公比通常用字母q表示。
缩写
等比数列可以缩写为G.P.(Geometric Progression)。
等比中项
如果在a与b中间插入一个数G,使a,G,b成等比数列,那么G叫做a与b的等比中项。
通项公式
an=a1*q^(n-1) (其中首项是a1 ,公比是q)
an=Sn-S(n-1) (n≥2)
前n项和
当q≠1时,等比数列的前n项和的公式为
Sn=a1(1-q^n)/(1-q)=(a1-a1*q^n)/(1-q) (q≠1)
当q=1时,等比数列的前n项和的公式为
Sn=na1
前n项和与通项的关系
an=a1=s1(n=1)
an=sn-s(n-1)(n≥2)
性质
(1)若 m、n、p、q∈N*,且m+n=p+q,则
am·an=ap·aq;
(2)在等比数列中,依次每 k项之和仍成等比数列。
(3)从等比数列的定义、通项公式、前n项和公式可以推出:
a1·an=a2·an-1=a3·an-2=…=ak&mi ddot;an-k+1,k∈{1,2,…,n}
(4)等比中项:q、r、p成等差数列,则
aq·ap=ar²,ar则为ap,aq等比中项。
记πn=a1·a2…an,则有π2n-1=(an)2n-1,
π2n+1=(an+1)2n+1
另外,一个各项均为正数的等比数列各项取同底对数后构成一个等差数列;反之,以任一个正数C为底,用一个等差数列的各项做指数构造幂Can,则是等比数列。
在这个意义下,我们说:一个正项等比数列与等差数列是“同构”的。
(5) 等比数列前n项之和Sn=a1(1-q^n)/(1-q)
(6)任意两项am,an的关系为an=am·q^(n-m)
(7)在等比数列中,首项a1与公比q都不为零。
注意:上述公式中a^n表示a的n次方。
高中数学数列基础知识:等和数列
定义
“等和数列”:在一个数列中,如果每一项与它的后一项的和都为同一个常数,那么这个数列叫做等和数列,这个常数叫做该数列的公和。
对一个数列,如果其任意的连续k(k≥2)项的和都相等,我们就把此数列叫做等和数列
性质
必定是循环数列
证明:对任意正整数n,有an + an+1 + … + an+k-1 = an+1 + an+2 + … + an+k,所以对任意正整数n,an = an+k,如果这个数列有n+k项的话。
