2017年全国初中数学联赛(初三组)初赛试卷参考答案及评分细则详解
2017年数学竞赛初中初赛答案

伊
1 006 1 007
伊…伊
2 004 2 005
伊
2 005 2 006
……………………………… 2 分
= 2 伊(1 + 2 + 3 + … + 2 005 + 2 006)
4分
= 2 006 伊 2 007
5分
= 4 026 042.
6分
14.(员)设爸爸追上乐乐用了 x 分钟援由题意列方程,得
5分
所以甲说的“801 班得第四”是对的;则丙说“803 班得第三”的对的;乙说“802 班得冠军”是对的.所以 804 班
是亚军.
9分
四、一鼓作气(本大题共 2 道小题,17 题 12 分,18 题 12 分,总计 24 分)
17. 当 a > 1 时,a >
1 a
;
1分
当 a = 1 时,a =
1 a
;当 a = 0 时,1a
不存在,没法比较;当 0 < a
< 1 或 a < -1 时,a <
1 a
.
12 分
18.(1)设年降水量为 x 万 m3,每人年平均用水量为 y m3.
1分
嗓 由题意,得
12 12
000 000
+ +
20x 15x
= 16 伊 20y, =(16 + 4)伊 15y.
9分
所以 a + b + c + d = 45,俞
11 分
将俞代入虞,愚,舆,余得
a = 3,b = 9,c = 12,d = 21,
13 分
所以 d - a = 21 - 3 = 18.
海南省澄迈县澄迈中学2017年4月九年级数学竞赛试题数学试题(含答案)

2017年4月海南省澄迈县澄迈中学九年级数学竞赛试题一、选择题(本大题满分50分,每小题5分)在下列各题的四个备选答案中,只有一个是正确的,请把你认为正确的答案的字母1.设xy <0,x >|y |,则x+y 的值是A. 负数B. 0C. 正数D. 非负数 2.若(x +3)(x +n )=x 2+mx -15,则m 等于 A. -2B. 2C. -5D. 53.若0||=+a a ,则化简22)1(a a +-的结果为A .1B .-1C .12-aD .a 21- 4.已知m 为任意实数,则直线y=x +m 与y=-x -4的交点不可能在A .第一象限B .第二象限C .第三象限D .第四象限 5.从1~9这九个自然数中随机取出一个数,取出的数是2的倍数的概率是 A .92 B .94 C .95D .32 6.A 地在河的上游,B 地在河的下游,若船从A 地开往B 地速度为v 1,从B 地返回A 地的速度为v 2,则A 、B 两地间往返一次的平均速度为A .221v v +B .21212v v v v +C .212v v + D .21212v v v v +7. 图1是韩老师早晨出门散步时,离家的距离(y )与时间(x )之间的函数图象.若用黑点表示韩老师家的位置,则韩老师散步行走的路线可能是B.图1A.C.D.8.如图2,AB是铅直地竖立在坡角为30°的山坡上的电线杆,当阳光与水平线成60°角时,电线杆的影子BC的长度为4米,则电线杆AB的高度为A.4米B.6米C.8米D.10米9.如图3,菱形ABCD中,点O是对角线AC上一点,OA=AD,且OB=OC=OD=1,则该菱形的边长为A.51+B.51-C.1 D.210.根据天气预报,某台风中心位于A市正东方向300 km的点O处(如图4),正以20 km/h的速度向北偏西60°方向移动,距离台风中心250 km范围内都会受到影响,若台风移动的速度和方向不变,则A市受台风影响持续的时间是A.10 h B.20 h C.30 h D.40 h二、填空题(本大题共8小题,每小题5分,满分40分)11.若n(0≠n)是关于x的方程022=++nmxx的根,则nm+的值为.12.若03=+ba(b≠0),则22222(1)24b a ab ba b a b++-÷=+-.13.图5是30名初三女学生1分钟内仰卧起坐次数的频数分布直方图(每组次数只含最小值而不含最大值),则仰卧起坐次数在25~45次的频率是________.14.如图6,每个小正方形的边长为1,A、B、C是小正方形的顶点,则∠ABC的度数为________.15.已知二次函数的图象经过原点及点1124⎛⎫--⎪⎝⎭,,且图象与x轴的另一交点到原点的距离为1,则该二次函数的解析式为.16.图7中的两个滑块A、B由一个连杆连接,分别可以在两条互相垂直的滑道上滑动.开始时,滑12953图51ABC图6A BCDO图3 图4图7图2块A 距O 点20 cm ,滑块B 距O 点15 cm .则当滑块A 向下滑到O 点时,滑块B 滑动了_________. 17.如图8,△COD 是△AOB 绕点O 顺时针旋转40°后得到的图形,点C 恰好在AB 上,∠AOD的度数是90°,则∠B 的度数是_________. 18.如图9,将长为4 cm 宽为2 cm 的矩形纸片ABCD 折叠,使点B 落在CD 边上的中点E 处, 压平后得到折痕MN ,则线段AM 的长度 为__________.三、解答题(本大题满分30分,每小题15分)19.如图10,正方形ABCD 的边长为1,对角线AC 与BD 相交于点O ,点P 是AB 边上的一个动点(点P 不与点A 、B 重合),CP 与BD 相交于点Q . (1)若CP 平分∠ACB ,求证:AP =2QO . (2)先按下列要求画出相应图形,然后求解问题.① 把线段PC 绕点P 旋转90°,使点C 落在点E 处,并连接AE .设线段BP 的长度为x ,△APE 的面积为S . 试求S 与x 的函数关系式; ② 求出S 的最大值,判断此时点P 所在的位置.图9BEACBDO图8ABC DPOQ 备用图ABCDP OQ图1020.文昌某校准备组织学生及学生家长到三亚进行社会实践,为了便于管理,所有人员必须乘坐在同一列火车上;根据报名人数,若都买一等座单程火车票需17010元,若都买二等座单程火车票且花钱最少.....,则需11220元;已知学生家长与教师的人数之比为2∶1,文昌到三亚的(1)参加社会实践的老师、家长与学生各有多少人?(2)由于各种原因,二等座火车票单程只能买x张(x小于参加社会实践的人数),其余的须买一等座火车票,在保证每位参与人员都有座位坐的前提下,请你设计最经济的购票方案,并写出购买火车票的总费用(单程)y与x之间的函数关系式.(3)请你做一个预算,按第(2)小题中的购票方案,购买一个单程火车票至少要花多少钱?最多要花多少钱?参考答案一、选择题(本大题满分50分,每小题5分)2. ∵3n =-15,∴n =-5,m =3+(-5)=-2. 故选A .3. ∵a +|a |=0, ∴|a |=-a , ∴a ≤0,进而a -1≤0∴22)1(a a +-=|a -1|+|a |=-(a -1)-a =1-2a . 故选D .4. ∵直线y =-x -4不经过第一象限,∴无论m 为何实数,直线y =x +m 与y =-x -4的交点不可能在第一象限,故选A .8. 如图2,由题意可知,∠ACB =90°,∠ABC =60°,则AB =2BC =8米,所以选择C .9. 如图3,由已知可知△ABC 与△BOC 相似,可得OCBC BCAC =,即BC 2=AC ·OC .设OA=BC=x ,可得方程x 2=x +1,解这个方程得2511+=x ,2512-=x (不合题意,舍去).故选A .10.如图4以点A 为圆心,250km 为半径画圆,交OM 于点B 、C ,作AN ⊥BC 于点N ,则可求出AN =150km ,又AC =250km ,利用勾股定理可求出CN =200km ,则BC =400km ,当台风中心在线段BC 上时,A 市都会受到台风的影响,所以A 市受台风影响持续的时间为400÷20=20小时,所以选择B . 二、填空题(本大题满分40分,每小题5分)11. 因为n 是关于x 的方程022=++n mx x 的根,所以022=++n mn n ,所以0)2(=++m n n ,又0≠n则02=++n m ,所以则n m +的值为-2.图4 ABCA B C D O 图3图212. 222222(2)(2)2(1)242()b a ab b a b a b a b a ba b a b a b a b a b++++---÷=⋅=+-+++, 又03=+b a 所以b a 3-= 所以原式=25323=+---b b b b .13. 由频率分布直方图可知,“25~45”的学生人数有21人,所以仰卧起坐次数在25~45次的频率是0.7.14. 如图6,连接AC 可知△ABC 是等腰直角三角形,所以∠ABC =45°. 15. 与原点的距离为1的交点有(1,0)或(-1,0),由此可求得该二次函数的解析式有两个,分别为:x x y +=2或x x y 31312+-=. 16. 如图7,由222222251520=+=+=OB AO AB ,可知连杆AB 的长度等于25cm ,当滑块A 向下滑到O 点时,滑块B 距O 点的距离是25 cm ,故滑块B 滑动了25-15 =10 cm . 17. △COD 是△AOB 绕点O 顺时针旋转40°后得到的图形,点C 恰好在AB 上,所以可知OA =OC ,∠AOC =∠BOD =40°, ∴∠ACO=70°,又∠AOD= 90°,∴∠BOC= 10°, ∴∠B= 60°. 18. 如图9,连接BM EM BE ,,.由题意得四边形ABNM 和四边形FENM 关于直线MN 对称. ∴MN 垂直平分BE .∴EM BM = ∵点E 是CD 的中点,DE =1∴ 在Rt ABM △和在Rt DEM △中,222AM AB BM +=,222DM DE EM +=,∴2222AM AB DM DE +=+.设x AM =,则x DM -=4,∴22221)4(2+-=+x x . 解得813=x ,即813=AM .三、解答题(本大题满分30分,每小题15分)19.(1)证明:过点O 作OM //AB 交PC 于点M ,则∠COM =∠CAB .∵ 四边形ABCD 是正方形,∴ OA =OC ,∠CAB =∠CBD =∠COM =45°, ∴ AP =2OM . 又∵ ∠1=∠2,∴ ∠1+∠COM =∠2+∠CBD , 即 ∠OMQ =∠OQM .∴ OM =OQ ∴ AP =2OQ .N ABCD EFM图9ABCDPEEOQM 1 2G F3图10(本小题也可以过点A 作直线平行于OQ 证明) (2)根据题意作出图形,如图10所示 ①ⅰ、当PC 绕点P 逆时针旋转90°时,作EF ⊥AB 交BA 延长线于点F ,则∠EFP =∠PBC =90°,∠3+∠CPB =90°. 又∠2+∠CPB =90°,∴∠3=∠2. 又PE 由PC 绕点P 旋转形成 ∴PE =PC ∴△EPF ≌△CPB .∴EF =BP =x , ∴AP =1-x ∴x x EF AP S APE )1(2121-=⋅=∆. ∴△APE 的面积S 与x 的函数关系式为x x S 21212+-= (10<x<).ⅱ、当PC 绕点P 顺时针旋转90°时,作EG ⊥AB 交AB 延长线于点G ,则同理可得△EPG ≌△CPB ,EG =BP =x .∴△APE 的面积S 与x 的函数关系式为x x S 21212+-= 由ⅰ、ⅱ可得△APE 的面积S 与x 的函数关系式为x x S 21212+-=,(10<x <)②由①知S 与x 的函数关系式为x x S 21212+-=,(10<x <)即81)21(212+--=x S ,(10<x <)∴当21=x 时S 的值最大,最大值为81.此时点P 所在的位置是边AB 的中点处.20.(1)设参加社会实践的老师有m 人,学生有n 人,则学生家长有m 2人,若都买二等座单程火车票且花钱最少.....,则全体学生都需买二等座学生票,依题意得: ⎩⎨⎧=+⨯=+112205136817010)3(81n m n m 解得⎩⎨⎧==18010n m 则202=m 答:参加社会实践的老师、家长与学生各有10、20与180人. (2)由(1)知所有参与人员总共有210人,其中学生有180人, ①当210180x <≤时,最经济的购票方案为:学生都买学生票共180张,(180-x )名成年人买二等座火车票,)210(x -名成年人买一等座火车票.∴火车票的总费用(单程)y 与x 之间的函数关系式为:)210(81)180(6818051x x y -+-+⨯= 即1395013+-=x y (210180x <≤)②当1800<x<时,最经济的购票方案为:一部分学生买学生票共x 张,其余的学生与家长老师一起购买一等座火车票共)210(x -张.∴火车票的总费用(单程)y 与x 之间的函数关系式为:)210(8151x x y -+=即1701030+-=x y (1800<x<)(3)由(2)小题知,当210180x <≤时,1395013+-=x y ,由此可见,当209=x 时,y 的值最小,最小值为11233元,当180=x 时,y 的值最大,最大值为11610元.当1800<x<时,1701030+-=x y ,由此可见,当179=x 时,y 的值最小,最小值为11640元,当1=x 时,y 的值最大,最大值为16980元.所以可以判断按(2)小题中的购票方案,购买一个单程火车票至少要花11233元,最多要花16980元.。
2017年全国初中数学联合竞赛试题(初三组)
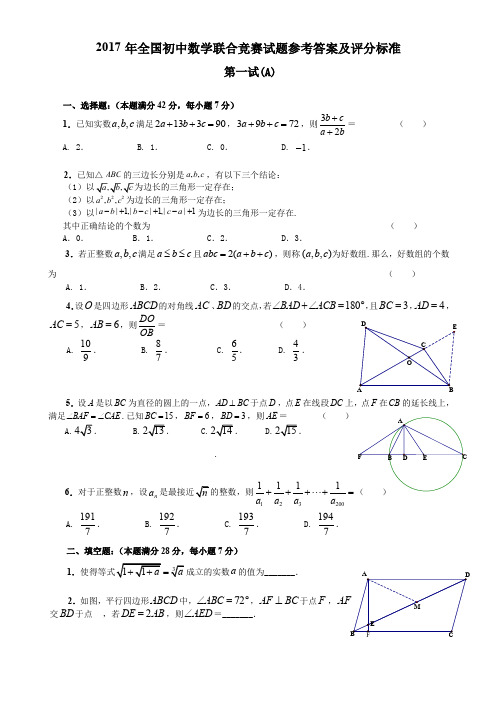
2017年全国初中数学联合竞赛试题参考答案及评分标准第一试(A) 一、选择题:(本题满分42分,每小题7分)1.已知实数满足213390a b c ++=,3972a b c ++=,则32b ca b++= ( )A. 2.B. 1.C. 0.D. 1-.2.已知△ABC 的三边长分别是,,a b c ,有以下三个结论: (1)以(2)以222,,a b c 为边长的三角形一定存在;(3)以||1,||1,||1a b b c c a -+-+-+为边长的三角形一定存在.其中正确结论的个数为 ( ) A .0. B .1. C .2. D .3.3.若正整数满足a b c ≤≤且2()abc a b c =++,则称为好数组.那么,好数组的个数为 ( )A. 1. B .2. C .3. D .4.,,a b c (,,)a b c 4.设O 是四边形ABCD 的对角线AC 、BD 的交点,若180BAD ACB ∠+∠=︒,且3BC =,4AD =,5AC =,6AB =,则DOOB= ( )A. 109.B. 87. C. 65. D. 43.5.设A 是以BC 为直径的圆上的一点,AD BC ⊥于点D ,点E 在线段DC 上,点F 在CB 的延长线上,满足BAF CAE ∠=∠.已知15BC =,6BF =,3BD =,则AE = ( ) A. B. C..D..6.对于正整数n ,设n a 1232001111a a a a ++++=A.1917. B. 1927. C. 1937. D. 1947.二、填空题:(本题满分28分,每小题7分) 1.=的值为_______.a 2.如图,平行四边形中,72ABC ∠=︒,AFBC ⊥于点F ,AF交于点,若2DE AB =,则AED ∠=_______.ABCD BD ,,a b c.3.设,m n 是正整数,且m n >.若9m与9n的末两位数字相同,则m n -的最小值为 .4.若实数,x y 满足3331x y xy ++=,则22x y +的最小值为 .第一试(B)一、选择题:(本题满分42分,每小题7分)1.已知二次函数2(0)y ax bx c c =++≠的图象与x 轴有唯一交点,则二次函数3233y a x b x c =++的图象与x 轴的交点个数为 ( )A .0.B .1.C .2.D .不确定.2.题目和解答与(A )卷第1题相同. 3. 题目和解答与(A )卷第3题相同. 4.已知正整数,,a b c 满足26390ab c --+=,260a b c -++=,则222a b c ++= ( )A. 424.B. 430.C. 441.D. 460. 5.设O 是四边形ABCD 的对角线AC 、BD 的交点,若180BAD ACB ∠+∠=︒,且3BC =,4AD =,5AC =,6AB =,则DOOB= ( ) A. 43. B. 65. C. 87. D. 109.6.题目和解答与(A )卷第5题相同.二、填空题:(本题满分28分,每小题7分) 1.题目和解答与(A )卷第1题相同. 2.设O 是锐角三角形ABC 的外心,,D E 分别为线段,BC OA 的中点,7ACB OED ∠=∠,5ABC OED ∠=∠,则OED ∠=_________.3. 题目和解答与(A )卷第3题相同.4. 题目和解答与(A )卷第4题相同.第二试 (A )一、(本题满分20分)已知实数,x y 满足3x y +=,221112x y x y +=++,求55x y +的值.二、(本题满分25分)如图,△ABC 中,AB AC >,45BAC ∠=︒,E 是BAC ∠的外角平分线与△ABC 的外接圆的交点,点F 在AB 上且EF AB ⊥.已1AF =,5BF =,求△ABC 的面积.三、(本题满分25分)求所有的正整数数对(,)a b ,使得34938b a=⨯+.第二试 (B )一、(本题满分20分)已知实数,,a b c 满足a b c ≤≤,16a b c ++=,22211284a b c abc +++=,求c 的值.二、(本题满分25分)求所有的正整数m ,使得21221m m --+是完全平方数.三、(本题满分25分)如图,O 为四边形ABCD 内一点,OAD OCB ∠=∠,OA OD ⊥,OB OC ⊥.求证:2222AB CD AD BC +=+.。
2017年全国初中数学联赛试题-含详细解析

2017年全国初中数学联合竞赛试题说明:评阅试卷时,请依据本评分标准.第一试,选择题和填空题只设7分和0分两档;第二试各题,请按照本评分标准规定的评分档次给分.如果考生的解答方法和本解答不同,只要思路合理,步骤正确,在评卷时请参照本评分标准划分的档次,给予相应的分数.第一试(A)一、选择题(本题满分42分,每小题7分)1. 已知实数a b c ,,满足2133903972a b c a b c ++=++= ,,则32b ca b+=+ ( ) A .2 B .1 C .0 D .1− 2. 已知△ABC 的三边长分别是a ,b ,c ,有以下三个结论:(1) (2)以a 2,b 2,c 2为边长的三角形一定存在;(3)以|a -b |+1,|b -c |+1,|c -a |+1为边长的三角形一定存在. 其中正确结论的个数为( )A .0B .1C .2D .33. 若正整数a ,b ,c 满足a b c ≤≤且()2abc a b c =++,则称(a ,b ,c )为好数组.那么,好数组的个数为( )A .1B .2C .3D .44. 设O 是四边形ABCD 的对角线AC ,BD 的交点,若∠BAD +∠ACB =180︒,且BC =3,AD =4,AC =5,AB =6,则DOOB=( ) A .109 B .87 C .65 D .435. 设A 是以BC 为直径的圆上的一点,AD ⊥BC 于点D ,点E 在线段DC 上,点F 在CB的延长线上,满足∠BAF =∠CAE .已知BC =15,BF =6,BD =3,则AE =( ) A .43 B .213 C .214 D .2156. 对于正整数n ,设a n 是最接近n 的整数,则1a 1+1a 2+1a 3+…+1a 200=( )A .1917B .1927C .1937D .1947二、填空题(本题满分28分,每小题7分)7.成立的实数a 的值为______.8. 如图,平行四边形ABCD 中,∠ABC =72︒,AF ⊥BC 于点F ,AF 交BD 于点E ,若DE =2AB ,则∠AED =______.9. 设m ,n 是正整数,且m >n .若9m 与9n 的末两位数字相同,则m -n 的最小值为____.10. 若实数x ,y 满足x 3+y 3+3xy =1,则x 2+ y 2的最小值为______.第一试(B)一、选择题(本题满分42分,每小题7分)1.已知二次函数y =ax 2+bx +c (c ≠0)的图象与x 轴有唯一交点,则二次函数y =a 3x 2+b 3x +c 3的图象与x 轴的交点个数为( )A .0B .1C .2D .不确定 2.题目与(A )卷第1题相同. 3.题目与(A )卷第3题相同.4.已知正整数a ,b ,c 满足a 2-6b -3c +9=0,-6a +b 2+c =0,则a 2+b 2+c 2=( ) A .424. B .430. C .441. D .460.5.设O 是四边形ABCD 的对角线AC ,BD 的交点,若∠BAD +∠ACB =180,且BC =3,AD =4,AC =5,AB =6,DOOB=( )A .43B .65C .87D .1096.题目与(A )卷第5题相同.二、填空题(本题满分28分,每小题7分) 1.题目与(A )卷第1题相同.2.设O 是锐角三角形ABC 的外心,D ,E 分别为线段BC ,OA 的中点,∠ACB =7∠OED ,∠ABC =5∠OED ,则∠OED =______. 3.题目与(A )卷第3题相同. 4.题目与(A )卷第4题相同.第二试(A)一、(本题满分20分)已知实数x ,y 满足x + y =3,1x +y 2+1x 2+y =12,求x 5+y 5的值.二、(本题满分25分)如图,△ABC 中,AB >AC ,∠BAC =45︒,E 是∠BAC 的外角平分线与△ABC 的外接圆的交点,点F 在AB 上且EF ⊥AB .已知AF =1,BF =5,求△ABC 的面积.三、(本题满分25分)求所有的正整数数对(a ,b ),使得a 3=49×3b +8.第二试(B)一、(本题满分20分)已知实数a ,b ,c 满足a ≤b ≤c ,a +b +c =16,a 2+b 2+c 2+14abc = ,求c 的值.二、(本题满分25分)求所有的正整数m ,使得22m -1-2m +1是完全平方数.三、(本题满分25分)如图,O 为四边形ABCD 内一点,∠OAD =∠OCB ,OA ⊥OD ,OB ⊥OC .求证:AB 2+CD 2=AD 2+BC 2.7。
2017年全国初中数学联合竞赛福建省赛区初赛试题参考答案及评分标准(1)

l 4a2b2 (a2 b2 c2 )2 ,则 l ( p a)( p b)( p c)
(D)
A. 8. 解析
B. 16.
C.32.
D.64.
l
4a2b2 (a2 b2 c2 )2
8(2ab a2 b2 c2 )(2ab a2 b2 c2 )
因此, AHE ≌ ABC ,则 HE BC , 所以
EG
GH
HE
BA BC
12 5 17 ,故 SBCE
1 2
BC EG
1 517 2
85 2
.
9. 设 A、B、C 为 1—9 中的任意数字, BC,CA, AB 都表示两位数, 那么
D
E H
D G
A BC BCA C AB 一定能被11 整除.
(a b c a)(a b c b)(a b c c)
(a b c)(a b c)(a b c)
2
2
2
8[(a b)2 c2 ][c2 (a b)2 ] 8(a b c)(a b c)(a b c)(a b c)
解析一 由二次函数的三项系数特征和 y1 0 ,可画出二次函数的图象,由图可得 y2 大
于 0.
解析二 由于 x m 时, y m2 2m a2 0 ,即
(m 1)2 (1 a2 ) 0 ,得到 1 a2 m 1 1 a2 ,
于是, m 2 1 1 a2 0 ,由此得到当 x m+2 时
(C)
A. 2015.
B.2016.
2017~2017年全国初中数学竞赛试题及答案.doc
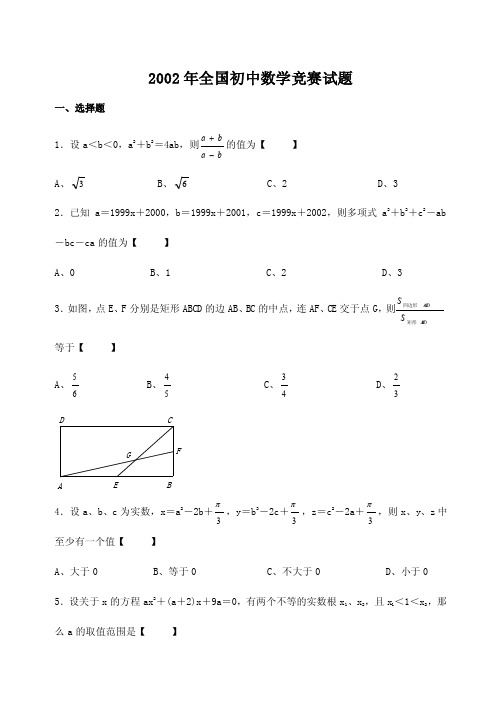
2002年全国初中数学竞赛试题一、选择题1.设a <b <0,a 2+b 2=4ab ,则ba b a -+的值为【 】A 、3B 、6C 、2D 、32.已知a =1999x +2000,b =1999x +2001,c =1999x +2002,则多项式a 2+b 2+c 2-ab -bc -ca 的值为【 】A 、0B 、1C 、2D 、33.如图,点E 、F 分别是矩形ABCD 的边AB 、BC 的中点,连AF 、CE 交于点G ,则A B C DA G C D S S 矩形四边形等于【 】A 、65 B 、54 C 、43 D 、32ABC D EFG4.设a 、b 、c 为实数,x =a 2-2b +3π,y =b 2-2c +3π,z =c 2-2a +3π,则x 、y 、z 中至少有一个值【 】A 、大于0B 、等于0C 、不大于0D 、小于0 5.设关于x 的方程ax 2+(a +2)x +9a =0,有两个不等的实数根x 1、x 2,且x 1<1<x 2,那么a 的取值范围是【 】A 、72-<a <52 B 、a >52 C 、a <72-D 、112-<a <06.A 1A 2A 3…A 9是一个正九边形,A 1A 2=a ,A 1A 3=b ,则A 1A 5等于【 】 A 、22b a + B 、22b ab a ++ C 、()b a +21 D 、a +b二、填空题7.设x 1、x 2是关于x 的一元二次方程x 2+ax +a =2的两个实数根,则(x 1-2x 2)(x 2-2x 1)的最大值为 。
8.已知a 、b 为抛物线y =(x -c)(x -c -d)-2与x 轴交点的横坐标,a <b ,则b c c a -+-的值为 。
9.如图,在△ABC 中,∠ABC =600,点P 是△ABC 内的一点,使得∠APB =∠BPC =∠CPA ,且PA =8,PC =6,则PB = 。
全国初中数学联合竞赛试题参考答案及评分标准

2017 年全国初中数学联合竞赛试题参考答案及评分标准 第 2 页(共 7 页)
2017 年全国初中数学联合竞赛试题参考答案及评分标准 第 3 页(共 7 页)
2017 年全国初中数学联合竞赛试题参考答案及评分标准 第 4 页(共 7 页)
2017 年全国初中数学联合竞赛试题参考答案及评分标准 第 5 页(共 7 页)
2017 年全国初中数学联合竞赛试题参考答案及评分标准 第 6 页(共 7 页)
2017 年全国初中数学联合竞赛试题参考答案及评分标准 第 7 页(共 7 页)
2017年全国初中数学联合竞赛试题及详细解答(含一试二试)

2. 设 O是 锐 角 三 角 形 ABC的 外 心 , D,E分 别 为 线 段 BC,OA的 中 点 ,
,
,则
_________.
3.题目与(A)卷第 3题相同. 4.题目与(A)卷第 4题相同
第二试 (A)
一、(本题满分 20分)已知实数 x,y满足 x+y=3,
,求
的值.
二、(本题满分25分)如图,△ABC中,AB AC, BAC 45,E是 BAC的 外角平分线与△ABC 的外接圆的交点,点F在AB 上且EF AB.已知AF 1,BF
1.已知二次函数 y ax2 bx c(c 0)的图象与x轴有唯一交点,则二次函
数
y a3x2 b3x c3 的图象与x轴的交点个数为 ( )
A.0
B.1
C.2
D.不确定.
2.题目与(A)卷第1 题相同.
3.题目与(A)卷第3 题相同.
4.已知正整数a,b,c满足 a2 6b 3c 9 0, 6a b2 c 0,则a2 b2 c2
CB的延长线上, 满足
.已知BC=15,BF=6,BD=3,则AE= ( )
A.
B.
C.
D.
6.对于正整数 n,设 an是最接近 的整数,则
A.191/7
B.192/7
C.193/7
() D.194/7
二、填空题(本题满分 28分,每小题 7分) (本题共有 4个小题,要求直接将答案写在横线上.)
1.使得等式
2017 年全国初中数学联合竞赛试题
2017年3月26日(星期日)上午8:30-11:30
第一试(A)
一、选择题(本题满分 42分,每小题 7分) (本题共有 6个小题,每题均给出了代号为 A,B,C,D的四个答案,其中有且仅
2017年全国初中数学联合竞赛试题参考答案和评分标准(1)

2017年全国初中数学联合竞赛试题参考答案和评分标准(1)2017年全国初中数学联合竞赛试题参考答案及评分标准说明:评阅试卷时,请依据本评分标准.第一试,选择题和填空题只设7分和0分两档;第二试各题,请按照本评分标准规定的评分档次给分.如果考生的解答方法和本解答不同,只要思路合理,步骤正确,在评卷时请参照本评分标准划分的档次,给予相应的分数.第一试(A)一、选择题:(本题满分42分,每小题7分)1.已知实数,,abc满足213390abc,3972abc,则32bcab??=()A.2.B.1.C.0.D.1?.【答】B.已知等式可变形为2(2)3(3)90abbc,3(2)(3)72abbc,解得218ab??,318bc??,所以32bcab1.2.已知△ABC的三边长分别是,,abc,有以下三个结论:(1)以,,abc为边长的三角形一定存在;(2)以222,,abc为边长的三角形一定存在;(3)以||1,||1,||1abbcca为边长的三角形一定存在.其中正确结论的个数为()A.0.B.1.C.2.D.3.【答】C.不妨设abc??,则有bca??.(1)因为bca??,所以2bcbca,即22()bca??(),即bca??,故以,,abc为边长的三角形一定存在;(2)以2,3,4abc为边长可以构成三角形,但以2224,9,16abc为边长的三角形不存在;(3)因为abc??,所以||11,||11,||11ababbcbccaac,故三条边中||1ca??大于或等于其余两边,而||1||111abbcabbc()()()()111||1acacca=,故以||1ab??,||1bc??,||1ca??为边长的三角形一定存在.3.若正整数,,abc满足abc??且2()abcabc,则称(,,)abc为好数组.那么,好数组的个数为()A.1.B.2.C.3.D.4.【答】C.若(,,)abc为好数组,则2()6abcabcc,所以6ab?.显然,a只能为1或2.若a=2,由6ab?可得2b?或3,2b?时可得4c?,3b?时可得52c?(不是整数);若a=1,则2(1)bcbc,于是可得(2)(2)6bc,可求得(,,)abc =(1,3,8)或(1,4,2017年全国初中数学联合竞赛试题参考答案及评分标准第1页(共7页)5).综合可知:共有3个好数组,分别为(2,2,4),(1,3,8)和(1,4,5).4.设O是四边形ABCD的对角线AC、BD的交点,若180BADACB,且3BC?,4AD?,5AC?,6AB?,则DOOB=()A.109.B.87.C.65.D.43.【答】A.过B作//BEAD,交AC的延长线于点E,则180ABEBAD ACB??,所以△ABC∽△AEB,所以ACBCABEB?,所以631855ABBCEBAC.再由//BEAD,得4101895DOADOBBE.5.设A是以BC为直径的圆上的一点,ADBC?于点D,点E在线段DC上,点F在CB的延长线上,满足BAFCAE.已知15BC?,6BF?,3BD?,则AE=()A.43.B.213.C.214.D.215.【答】B.如图,因为BAFCAE,所以BAFBAECAEBAE,即90FAEBAC.又因为ADBC?,故2ADDEDFDBDC.而639DFBFBD,15312DCBCBD,所以29312ADDE,所以6AD?,4DE?.从而222264213AEADDE.6.对于正整数n,设na是最接近n的整数,则1232001111aaaa()A.1917.B.1927.C.1937.D.1947.【答】A.对于任意自然数k,2211()24kkk不是整数,所以,对于正整数n,12n?一定不是整数.设m是最接近n的整数,则1||2mn??,1m?.易知:当1m?时,1||2mn2211()()mnm??221144mmnmm.于是可知:对确定的正整数m,当正整数n满足221mmnmm时,m是最接近n的整数,即nam?.所以,使得na=m的正整数n的个数为2m.注意到2213131822001414210,因此,12200,,,aaa?中,有:2个1,4个2,6个3,2017年全国初中数学联合竞赛试题参考答案及评分标准第2页(共7页)EOCBADCBFDE8个4,……,26个13,18个14.所以123200111111111191246261812313147aaaa.二、填空题:(本题满分28分,每小题7分)1.使得等式311aa成立的实数a的值为_______.【答】8.由所给等式可得32(11)aa.令1xa??,则0x?,且21ax??,于是有322(1)(1)xx,整理后因式分解得2(3)(1)0xxx,解得10x?,23x?,31x??(舍去),所以1a??或8a?.验证可知:1a??是原方程的增根,8a?是原方程的根.所以,8a?.2.如图,平行四边形ABCD中,72ABC,AFBC?于点F,AF交BD于点E,若2DEAB?,则AED?=_______.【答】66?.取DE的中点M,在Rt△ADE中,有12AMEMDEAB.设AED,则1802AME,18ABM.又ABMAMB,所以180218,解得66.3.设,mn是正整数,且mn?.若9m与9n的末两位数字相同,则mn?的最小值为.【答】10.由题意知,999(91)mnnmn是100的倍数,所以91mn??是100的倍数,所以9mn?的末两位数字是01,显然,mn?是偶数,设2mnt??(t是正整数),则29981mntt.计算可知:281的末两位数字是61,381的末两位数字是41,481的末两位数字是21,581的末两位数字是01.所以t的最小值为5,从而可得mn?的最小值为10.4.若实数,xy满足3331xyxy,则22xy?的最小值为.【答】12.因为333322031()(1)333xyxyxyxyxyxy22(1)[()()(1)(1)]3(1)xyxyxyxyxy2017年全国初中数学联合竞赛试题参考答案及评分标准第3页(共7页)MEFCBDA22(1)(1)xyxyxyxy2221(1)[()(1)(1)]2xyxyxy,所以1xy或1xy??.若1xy,则22xy?=2.若1xy??,则22222111[()()][1()]222xyxyxyxy,当且仅当12xy??时等号成立.所以,22xy?的最小值为12.第一试(B)一、选择题:(本题满分42分,每小题7分)1.已知二次函数2(0)yaxbxcc的图象与x轴有唯一交点,则二次函数3233yaxbxc的图象与x轴的交点个数为()A.0.B.1.C.2.D.不确定.【答】C.因为二次函数2yaxbxc的图象与x轴有唯一交点,所以2140bac,所以240bac??.故二次函数3233yaxbxc的判别式323363623211()4(4)()1616bacbacbb61516b?0?,所以,二次函数3233yaxbxc的图象与x轴有两个交点.2.题目和解答与(A)卷第1题相同.3.题目和解答与(A)卷第3题相同.4.已知正整数,,abc满足26390abc,260abc,则222abc??=()A.424.B.430.C.441.D.460.【答】C.由已知等式消去c整理得22(9)3(1)75ab,所以23(1)75b??,又b为正整数,所以16b??.若b=1,则2(9)75a??,无正整数解;若b=2,则2(9)72a??,无正整数解;若b=3,则2(9)63a??,无正整数解;若b=4,则2(9)48a??,无正整数解;若b=5,则2(9)27a??,无正整数解;若b=6,则2(9)0a??,解得9a?,此时18c?.2017年全国初中数学联合竞赛试题参考答案及评分标准第4页(共7页)因此,9a?,b=6,18c?,故222abc=441.5.设O是四边形ABCD的对角线AC、BD的交点,若180BADACB,且3BC?,4AD?,5AC?,6AB?,则DOOB=()A.43.B.65.C.87.D.109.【答】D.解答过程与(A)卷第4题相同.6.题目和解答与(A)卷第5题相同.二、填空题:(本题满分28分,每小题7分)1.题目和解答与(A)卷第1题相同.2.设O是锐角三角形ABC的外心,,DE分别为线段,BCOA的中点,7ACBOED,5ABCOED,则OED?=_________.【答】10?.如图,设OEDx??,则5ABCx??,7ACBx??,DOC??18012BACx,10AOCx??,所以1802AODx,180(1802)ODExxx,所以1122ODOEOAOC,所以60DOC,从而可得10x??.3.题目和解答与(A)卷第3题相同.4.题目和解答与(A)卷第4题相同.第二试(A)一、(本题满分20分)已知实数,xy满足3xy??,221112xyxy,求55xy?的值.解由221112xyxy可得2233222()xyxyxyxyxy.设xyt?,则222()292xyxyxyt,332()[()3]3(93)xyxyxyxyt,代入上式可得22(392)3(93)tttt,解得1t?或3t?.……………………10分当3t?时,3xy?,又3xy??,故,xy是一元二次方程2330mm的两实数根,但易知此方程没有实数根,不合题意.……………………15分当1t?时,1xy?,又3xy??,故,xy是一元二次方程2310mm的两实数根,符合题意.此时552233222()()()(92)[3(93)]3123xyxyxyxyxyttt.……………………20分2017年全国初中数学联合竞赛试题参考答案及评分标准第5页(共7页)DEOBAC二、(本题满分25分)如图,△ABC中,ABAC?,45BAC,E 是BAC?的外角平分线与△ABC的外接圆的交点,点F在AB上且EFAB?.已知1AF?,5BF?,求△ABC的面积.解在FB上取点D,使FD=AF,连接ED并延长,交△ABC的外接圆于点G.由EF⊥AD,AF=FD知△AED是等腰三角形,所以∠AED=1802??∠EAD=∠BAC,……………………10分所以??AGBC?,所以??ACBG?,所以AC=BG (15)分又∠BGE=∠BAE=∠ADE=∠BDG,所以BG=BD,所以AC=BD =5-1=4,……………………20分△ABC的AB边上的高sin4522hAC.所以,△ABC的面积116226222SABh (25)分三、(本题满分25分)求所有的正整数数对(,)ab,使得34938ba.解显然,4938b??为奇数,所以a为奇数.又因为33493849385ba,所以5a?.……………………5分由34938ba可得38493ba,即22(2)(24)73baaa.……………………10分设2(2,24)aaad,则d为奇数.注意到224(2)(4)12aaaa,所以|12d,所以d=1或3.……………………15分若d=1,则有22 27, 243,b aaa或22 23, 247, ba aa均无正整数解.……………………20分若d=3,则有221237,243,baaa?或12223,2437,baaa解得11a?,3b?.所以,满足条件的正整数对只有一个,为(11,3).……………………25分第二试(B)一、(本题满分20分)已知实数,,abc满足abc??,16abc,22211284abcabc,求c的值.解设abx??,aby?,依题意有2212(16)(16)1284xyxyx,整理得21(8)(8)8xyx,所以8x?或8(8)yx??.……………………10分2017年全国初中数学联合竞赛试题参考答案及评分标准第6页(共7页)FEABCD(1)若8x?,则8ab??,此时c=8.(2)若8(8)yx??,即8(8)abab,则(8)(8)0ab,所以8a?或8b?.当8a?时,结合abc??可得24abc,与16abc矛盾.当8b?时,结合abc??及16abc可得0a?,8c?.综合可知:8c?.……………………20分二、(本题满分25分)求所有的正整数m,使得21221mm 是完全平方数.解当m=1时,212211mm是完全平方数.……………………5分当1m?时,设212221mmn(n为正整数).注意到2112112122212(2)221(21)(2)mmmmmm,故可得12122(21)(2)mmn,……………………10分所以22212112(21)(21)(21)mmmmnnn.……………………15分设121mxn,121myn,则xy?,222mxy??,所以,xy均为2的方幂.……………………20分又22myx被4除余数为2,所以,只可能2x?,2my?,故22222mm,解得3m?.综上可知:满足条件的正整数m有两个,分别为1和3.……………………25分三、(本题满分25分)如图,O为四边形ABCD内一点,OADOCB,OAOD?,OBOC?.求证:2222ABCDADBC.证明由题设条件可知90AODBOC,又OADOCB,所以△AOD∽△COB,……………………5分所以ODAOOBCO?,从而OCAOOBOD?.……………………10分又AOCAOBBOCAOBAODDOB,所以△AOC∽△DOB,所以OACODB.……………………15分设AC和BD交于点P,则90APDAOD,所以ACDB?,……………………20分所以222222222222()()()()ABCDAPPBPDPCAPPDPBPCADBC .……………………25分2017年全国初中数学联合竞赛试题参考答案及评分标准第7页(共7页)PDAO CB。
2017年全国初中数学联合竞赛试题含答案

2017 年全国初中数学联合竞赛试题参考答案及评分标准说明:评阅试卷时,请依据本评分标准.第一试,选择题和填空题只设 7 分和 0 分两档;第二试各题,请按照本评分标准规定的评分档次给分.如果考生的解答方法和本解答不同,只要思路合理,步骤正确,在评卷时请参照本评分标准划分的档次,给予相应的分数.第一试(A)一、选择题:(本题满分 42 分,每小题 7 分)1.已知实数a,b,c满足2a+13b+3c=90,3a+9b+c=72,则3b+c=()a +2bA. 2.B. 1.C. 0.D.-1.【答】B.已知等式可变形为 2( a+ 2b) + 3(3b+c ) = 90 , 3( a+ 2b) + (3b+c ) = 72 ,解得a+2b=18,3b+c=18 ,所以3b+c=1.a +2b2.已知△ABC的三边长分别是a,b,c,有以下三个结论:(1)以a,b,c为边长的三角形一定存在;(2)以 a 2, b 2, c2为边长的三角形一定存在;(3)以 | a-b | +1,| b-c | +1,| c-a | +1 为边长的三角形一定存在.其中正确结论的个数为()A.0.B.1.C.2.D.3.【答】C.不妨设 a ≥ b ≥ c ,则有 b + c > a .(1)因为 b + c > a ,所以 b + c +222b +c > a ,故以a,b,c为bc > a ,即( b + c ) >( a),即边长的三角形一定存在;(2)以 a =2, b =3, c =4为边长可以构成三角形,但以 a 2= 4, b2= 9, c2=16 为边长的三角形不存在;(3)因为 a ≥ b ≥ c ,所以| a - b |+1= a - b +1,| b - c |+1= b - c +1,| c - a |+1= a - c +1,故三条边中| c - a |+1大于或等于其余两边,而(| a-b | +1)+(| b-c | +1)=(a-b+ 1)+(b-c+1)=a-c+ 1 + 1 >a -c+ 1 =| c-a | +1 ,故以 | a-b | +1 , | b-c | +1 , | c-a | +1 为边长的三角形一定存在.3.若正整数a,b,c满足a≤b≤c且abc=2(a+b+c),则称(a,b,c)为好数组.那么,好数组的个数为()A. 1.B.2.C.3.D.4.【答】C.若( a, b, c) 为好数组,则abc= 2( a+b+c ) ≤ 6c,所以ab≤6.显然,a只能为1或2.若a =2,由ab≤6可得b=2或3,b=2时可得c=4,b=3时可得c=52(不是整数);若a =1,则bc=2(1+b+c),于是可得(b-2)(c-2)=6,可求得(a,b,c)=(1,3,8)或(1,4,5).综合可知:共有 3 个好数组,分别为(2,2,4),(1,3,8)和(1,4,5).4.设 O 是四边形 ABCD 的对角线 AC 、BD 的交点,若 ∠BAD + ∠ACB = 180︒,且 BC = 3,AD = 4 ,AC = 5 , AB = 6 ,则 DO = ( )OB10 8 64A..B..C..D..D9 7 5 3E【答】A.C过 B 作 BE // AD ,交 AC 的延长线于点 E ,则 ∠ABE = 180︒ - ∠BAD= ∠ACB ,所以△ ABC ∽△ AEB ,所以AC = BC ,所以4O3AB EBAB ⋅ BC6 ⨯318BEB = = = .A6AC 5 5再由 BE // AD ,得 DO = AD = 4 = 10 .BEOB 18 955.设 A 是以 BC 为直径的圆上的一点,AD ⊥ BC 于点 D ,点 E 在线段 DC 上,点 F 在 CB 的延长线上,满足 ∠BAF = ∠CAE .已知 BC =15 , BF = 6 , BD = 3 ,则 AE = ( )AA. 4 3 .B. 2 13 .C. 2 14 .D. 2 15 .【答】B.FBDEC如图,因为 ∠BAF = ∠CAE ,所以 ∠BAF + ∠BAE = ∠CAE + ∠BAE ,即 6 3∠FAE = ∠BAC = 90︒ .又因为 AD ⊥ BC ,故 AD 2 = DE ⋅ DF = DB ⋅ DC .而 DF = BF + BD = 6 + 3 = 9 ,DC = BC - BD = 15 - 3 =12 ,所以 AD 2 = DE ⋅ 9 = 3 ⋅ 12 ,所以 AD = 6 ,DE= 4 . 从而 AE = AD 2 + DE 2 = 62 + 42 = 213 .6.对于正整数 n ,设 a 是最接近的整数,则 1 + 1 + 1 + +1 = ( n)na 1 a 2 a 3a200A. 191 .B. 192 .C. 193 .D. 194 .777 7 【答】A.对于任意自然数 k , ( k +1 )2 = k 2 + k + 1不是整数,所以,对于正整数 n ,- 1 一定不是整数.n24 2的整数,则| m - |< 1 , m ≥1.设 m 是最接近 nn2易知:当 m ≥1时,| m - |< 1 ⇔ ( m - 1 ) 2 < n < ( m + 1 )2⇔ m 2 - m + 1 < n < m 2 + m + 1 .n 2 2 24 4 于是可知:对确定的正整数 m ,当正整数 n 满足 m 2 - m + 1 ≤ n ≤ m 2+ m 时,m 是最接近的整数,n 即 a n = m .所以,使得 a n = m 的正整数 n 的个数为 2m .注意到132 + 13 = 182 < 200 < 14 2 + 14 = 210 ,因此, a , a , ,8 个 4,……,26 个 13,18 个 14.所以1+1+1+ +1= 2 ⨯1+ 4 ⨯1+ 6 ⨯1+ + 26 ⨯1+ 18⨯1=191.a a a a12313147 123200二、填空题:(本题满分 28 分,每小题 7 分)1.使得等式 1 + 1+a=3a 成立的实数 a 的值为_______.【答】 8 .由所给等式可得 (1 + 1 +a )3=a2.令 x =1+a,则 x ≥0,且a=x2-1,于是有(1+ x )3=( x2-1)2,整理后因式分解得x ( x -3)( x +1)2=0,解得 x= 0 ,x= 3 ,x= -1 (舍去),所以a= -1或a=8.123验证可知: a = -1是原方程的增根, a =8是原方程的根.所以, a =8.2.如图,平行四边形ABCD中,∠ABC=72︒,AF⊥BC于点F, AFM交 BD 于点 E ,若 DE =2AB ,则∠AED =_______.【答】 66︒.BE 取 DE 的中点 M ,在Rt△ ADE中,有 AM = EM =1DE = AB .2设∠AED =α,则∠AME =180︒ -2α,∠ABM =α-18︒.又∠ABM = ∠AMB ,所以180︒ -2α=α-18︒,解得α=66︒.3.设m,n是正整数,且m>n.若9m与9n的末两位数字相同,则m-n的最小值为.【答】10.由题意知,9m- 9n= 9n⋅ (9m-n-1) 是100的倍数,所以9m-n-1是100的倍数,所以9m-n的末两位数字是 01,显然,m-n是偶数,设m-n=2t(t是正整数),则9m-n=92t=81t .计算可知: 812的末两位数字是61, 813的末两位数字是41, 814的末两位数字是21, 815的末两位数字是 01.所以 t 的最小值为5,从而可得 m - n 的最小值为10.4.若实数 x, y 满足 x 3+ y 3+3 xy =1,则 x 2+ y2的最小值为.1【答】2 .因为0= x 3+ y 3+3 xy -1=( x + y )3+(-1)3-3 x 2 y -3 xy 2+3xy=( x+y- 1)( x2+y2-xy+x+y+1) =12(x+y-1)[(x-y)2+(x+1)2+(y+1)2],所以 x = y = -1或x+y=1.若x = y = -1,则 x 2+ y2=2.若x + y =1,则x2+y2=12[(x+y)2+(x-y)2]=12[1+(x-y)2]≥12,当且仅当x=y=12时等号成立.所以, x 2+ y2的最小值为12.第一试(B)一、选择题:(本题满分 42 分,每小题 7 分)1.已知二次函数y=ax2+bx+c(c≠0)的图象与x轴有唯一交点,则二次函数y=a3x2+b3x+c3的图象与 x 轴的交点个数为()A.0.B.1.C.2.D.不确定.【答】C.因为二次函数 y = ax 2+ bx + c 的图象与 x 轴有唯一交点,所以∆1=b2-4ac=0,所以b2=4ac≠0.故二次函数 y = a 3 x 2+ b3 x + c3的判别式∆2=(b3)2-4a3c3=b6-161(4ac)3=b6-161(b2)3=1615b6>0 ,所以,二次函数y=a3x2+b3x+c3的图象与x轴有两个交点.2.题目和解答与(A)卷第 1 题相同.3.题目和解答与(A)卷第 3 题相同.4.已知正整数a,b,c满足a2-6b-3c+9=0,-6a+b2+c=0,则a2+b2+c2=()A. 424.B. 430.C. 441.D. 460.【答】C.由已知等式消去 c 整理得( a -9)2+3(b -1)2=75,所以3(b -1)2≤75,又b为正整数,所以1≤b≤6.若b =1,则( a -9)2=75,无正整数解;若b =2,则( a -9)2=72,无正整数解;若b =3,则( a -9)2=63,无正整数解;若b =4,则( a -9)2=48,无正整数解;若b =5,则( a -9)2=27,无正整数解;若b =6,则( a -9)2=0,解得a=9,此时c=18.因此, a =9,b=6, c =18,故a2+b2+c2==441.5.设O是四边形ABCD的对角线AC、BD的交点,若∠BAD+ ∠ACB=180︒,且BC=3,AD=4,AC =5, AB =6,则DO=()OBA.4.B.6.C.8.D.10.3579【答】D.解答过程与(A)卷第 4 题相同.6.题目和解答与(A)卷第 5 题相同.二、填空题:(本题满分 28 分,每小题 7 分)1.题目和解答与(A)卷第 1 题相同.2 .设O是锐角三角形ABC的外心,D,E分别为线段BC,OA的中点,∠ACB=7∠OED,∠ABC =5∠OED ,则∠OED =_________.A 【答】10︒.如图,设∠OED = x ,则∠A B =C5,x ∠ACB =7x ,∠DOC= ∠BAC =180︒ -12x ,∠AOC =10x ,所以∠AOD =180︒ -2x ,∠ODE =180︒ - x -(180︒ -2 x)= x ,所以OD=OE=1OA =1OC ,所22B 以∠DOC =60︒,从而可得 x =10︒.3.题目和解答与(A)卷第 3 题相同.4.题目和解答与(A)卷第 4 题相同.EODC第二试(A)一、(本题满分20分)已知实数 x, y 满足x+y=3,1+1=1,求 x 5+ y5的值. x+ y 2x 2+ y2解由1+1=1可得 2( x+y+x2+ y 2)= x 3+ y 3+ x 2 y 2+ xy . x + y 2x 2+ y2设xy = t ,则 x 2+ y 2=( x + y )2-2xy =9-2t , x 3+ y 3=( x + y )[( x + y )2-3 xy ]=3(9-3t ),代入上式可得 2(3 + 9 - 2t ) = 3(9 - 3t ) +t2+t,解得t=1或t=3.……………………10分当 t =3时,xy=3,又x+y=3,故x,y是一元二次方程m2-3m+3=0的两实数根,但易知此方程没有实数根,不合题意.……………………15分当 t =1时,xy=1,又x+y=3,故x,y是一元二次方程m2-3m+1=0的两实数根,符合题意.此时x 5+ y 5=( x 2+ y 2)( x 3+ y 3)-( x + y ) x 2 y 2=(9-2t )⋅[3(9-3t )]-3t 2=123.……………………20分二(、本题满分 25 分)如图,△ ABC 中,AB > AC ,∠BAC = 45︒ ,E 是 ∠BAC的外角平分线与 △ ABC 的外接圆的交点,点 F 在 AB 上且 EF ⊥ AB . 已知 AF =1, BF = 5,求△ ABC 的面积.解 在 FB 上取点 D ,使 FD =AF ,连接 ED 并延长,交△ ABC 的外接圆于点 G.由 EF ⊥AD ,AF =FD 知△AED 是等腰三角形,所以∠AED =180︒ - 2 ∠EAD =∠BAC , ……………………10 分EAFDCGB……………………15 分 所以 AG = BC ,所以 AC = BG ,所以 AC =BG. 又∠BGE =∠BAE =∠ADE =∠BDG ,所以 BG =BD ,所以 AC =BD =5-1=4, ……………………20 分△ ABC 的 AB 边上的高 h = AC sin 45︒ = 2 2 .所以,△ ABC 的面积 S = 1 ⋅ AB ⋅ h = 1 ⨯ 6 ⨯ 2 = 6 .2 2 ……………………25 分22三、(本题满分 25 分)求所有的正整数数对 ( a , b ) ,使得 a 3 = 49 ⨯ 3b +8 . 解 显然, 49 ⨯ 3b +8 为奇数,所以 a 为奇数.又因为 a 3 = 49 ⨯ 3b + 8 ≥ 49 ⨯ 3 + 8 > 53 ,所以 a > 5 .……………………5 分由 a 3 = 49 ⨯ 3b +8 可得 a 3 - 8 = 49 ⨯3b ,即 ( a - 2)( a 2 + 2a + 4) = 7 2 ⨯3b . ……………………10 分设 ( a - 2, a 2 + 2a + 4) = d ,则 d 为奇数.注意到 a 2 + 2a + 4 = ( a - 2)( a + 4) +12 ,所以 d | 12 ,所以 d=1 或 3. ……………………15 分⎧a - 2 = 7 2,⎧a - 2 = 3b,均无正整数解.……………………20 分若 d =1,则有 ⎨a 2 + 2 a + 4 或 ⎨a 2 + 2 a + 4 = 7 2 ⎪ = 3b ,⎪ , ⎩⎩⎧a - 2 = 3 ⨯7 2, ⎧a - 2 = 3b -1,解得 a =11, b = 3 . 若 d =3,则有 ⎨ 2 + 2 a + 4 b -1或 ⎨ 2 + 2 a + 4 = 3 ⨯7 2 ⎪ a = 3 , ⎪ a ,⎩⎩所以,满足条件的正整数对只有一个,为(11,3).……………………25 分第二试 (B )一、(本题满分 20 分)已知实数 a , b , c 满足 a ≤ b ≤ c , a + b + c =16 , a 2 + b 2 + c 2 +14 abc =128 ,求 c 的值.解 设 a + b = x , ab = y ,依题意有 x 2 - 2 y + (16 - x ) 2 +14 y (16 - x ) =128 ,整理得( x - 8) 2 = 1y ( x -8) ,8所以 x = 8 或 y = 8( x -8) .……………………10 分(1)若 x =8,则 a + b =8,此时 c =8.(2)若 y =8( x -8),即 ab =8( a + b -8),则( a -8)(b -8)=0,所以a=8或b=8.当a =8时,结合 a ≤ b ≤ c 可得 a + b + c ≥24,与 a + b + c =16矛盾.当b =8时,结合 a ≤ b ≤ c 及 a + b + c =16可得 a =0, c =8.综合可知: c =8.……………………20分二、(本题满分 25 分)求所有的正整数m,使得22m-1-2m+1是完全平方数.解当 m =1时,22m-1-2m+1=1是完全平方数.……………………5分当 m >1时,设22m-1-2m+1=n2( n 为正整数).注意到 22m-1- 2m+ 1 = 2 ⋅ (2m-1 ) 2- 2 ⋅ 2 m-1+ 1 = (2 m-1- 1) 2+ (2 m-1 )2,故可得(2 m-1- 1) 2+ (2 m-1 )2=n2,……………………10分所以 22m-2=n2- (2m-1- 1) 2= ( n+ 2 m-1- 1)( n- 2 m-1+1) .……………………15分设 x = n -2m-1+1, y = n +2m-1-1,则x<y, xy =22m-2,所以x,y均为2的方幂.……………………20分又 y - x =2m-2被4除余数为2,所以,只可能x=2, y =2m,故2⨯2m=22m-2,解得m=3.综上可知:满足条件的正整数 m 有两个,分别为1和3.……………………25分三、(本题满分 25 分)如图,O为四边形ABCD内一点,∠OAD= ∠OCB,DOA ⊥ OD , OB ⊥ OC .求证:AB2+CD2=AD2+BC2.AOP 证明由题设条件可知∠AOD = ∠BOC =90︒,又∠OAD =∠OCB,所以△ AOD ∽△ COB ,……………………5分OD AO OC AOB所以OB=CO,从而OB=OD .……………………10分C 又∠AOC = ∠AOB + ∠BOC = ∠AOB + ∠AOD = ∠DOB ,所以△ AOC ∽ △ DOB ,所以∠OAC = ∠ODB .……………………15分设AC 和BD交于点P,则∠APD = ∠AOD =90︒,所以 AC ⊥ DB ,……………………20分所以 AB 2+ CD 2=( AP 2+ PB 2)+( PD 2+ PC 2)=( AP 2+ PD 2)+( PB 2+ PC 2)= AD 2+ BC2.……………………25分。
2017年全国初中数学竞赛试题及答案

“《数学周报》杯”2017年全国初中数学竞赛 (天津赛区)试题参考答案及评分标准一、选择题(共5小题,每小题7分,满分35分) (1)设x =(1)(2)(3)x x x x +++的值为( ). (A )0 (B )1(C )﹣1(D )2【答】C . 解:由已知得2310x x ++=, 于是2222(1)(2)(3)(3)(32)(31)1 1.x x x x x x x x x x +++=+++=++-=-(2)已知x y z ,,为实数,且满足253x y z +-=,25x y z --=-,则222x y z ++的最小值为( ).(A )111(B )0 (C )5 (D )5411【答】D .解:由 25325x y z x y z +-=⎧⎨--=-⎩,, 可得 312.x z y z =-⎧⎨=+⎩,于是 22221125xy z z z ++=-+.因此,当111z =时,222x y z ++的最小值为5411. (3)若1x >,0y >,且满足3yy xxy x x y==,,则x y +的值为( ). (A )1 (B )2(C )92(D )112【答】C .解:由题设可知1y yx -=,于是 341y y x yx x -==,所以411y -=.故12y =,从而4=x .于是92x y +=.(4)设333311111232011S =++++,则4S 的整数部分等于( ). (A )4 (B )5(C )6(D )7【答】A .解:当2 3 2011k =,,,,因为()()()32111112111k k k k k k k ⎡⎤<=-⎢⎥-+-⎣⎦, 所以333111111511123201122201120124S ⎛⎫<=++++<+-< ⎪⨯⎝⎭. 于是有445S <<,故4S 的整数部分等于4.(5)点D E ,分别在△ABC 的边AB AC ,上,BE CD ,相交于点F ,设1234BDF BCF CEF EADF S S S S S S S S ∆∆∆====四边形,,,,则13S S 与24S S 的大小关系为( ).(A )1324S S S S < (B )1324S S S S = (C )1324S S S S > (D )不能确定 【答】C .解:如图,连接DE ,设1DEF S S ∆'=, 则1423S S EF S BF S '==,从而有1324S S S S '=.因为11S S '>,所以1324S S S S >. 二、填空题(共5小题,每小题7分,共35分)(6)两条直角边长分别是整数a b ,(其中2011b <),斜边长是1b +的直角三角形的个数为 .【答】31.解:由勾股定理,得 12)1(222+=-+=b b b a .因为b 是整数,2011<b ,所以2a 第(5)题是1到4023之间的奇数,而且是完全平方数,这样的数共有31个,即2223 5 63,,,.因此a 一定是3,5,…,63,故满足条件的直角三角形的个数为31.(7)一枚质地均匀的正方体骰子的六个面上的数字分别是1,2,2,3,3,4;另一枚质地均匀的正方体骰子的六个面上的数字分别是1,3,4,5,6,8. 同时掷这两枚骰子,则其朝上的面两数之和为7的概率是 .【答】16. 解: 在36对可能出现的结果中,有6对:(1,6), (2,5), (2,5), (3,4),(3,4),(4,3)的和为7,所以朝上的面两数字之和为7的概率是61366=.(8)若y =a ,最小值为b ,则22a b +的值为 . 【答】32. 解:由1x -≥0,且12x -≥0,得12≤x ≤1.21122y =+=+ 由于13124<<,所以当34x =时,2y 取到最大值1,故1a =.当12x =或1时,2y 取到最小值12,故2b =.所以,2232a b +=.(9)如图,双曲线xy 2=(x >0)与矩形OABC 的边CB , BA 分别交于点E ,F ,且AF=BF ,连接EF ,则△OEF 的面积为 .【答】32. 解:如图,设点B 的坐标为a b (,),则点F 的坐标为2b a (,).因为点F 在双曲线2y x=上,所以 4.ab = 又点E 在双曲线上,且纵坐标为b ,所以点E 的坐标为2(,)b b.于是11212222221312.22OEF OEC FBEOFBC S S S S b b b a b a b b ab ∆∆∆=--=+-⨯⨯-⨯⨯-=+-=梯形()()() (10)如图,在Rt △ABC 中,斜边AB 的长为35,正方形CDEF 内接于△ABC ,且其边长为12,则△ABC 的周长为 .【答】84.解:如图,设BC =a ,AC =b , 则22235a b +==1225. ① 又Rt △AFE ∽Rt △ACB , 所以FE AF CB AC =,即1212b a b-=, 故12()a b ab +=. ②由①②得 2222122524a b a b ab a b +=++=++()(),解得a +b =49(另一个解-25舍去),所以 493584a b c ++=+=. 三、解答题(共4题,每题20分,共80分)(11)已知关于x 的一元二次方程20x cx a ++=的两个整数根恰好比方程20x ax b ++=的两个根都大1,求a b c ++的值.解:设方程20x ax b ++=的两个根为αβ,,其中αβ,为整数,且α≤β,则方程20x cx a ++=的两根为11αβ++,,由题意得 ()()11a a αβαβ+=-++=,, ………………………………5分两式相加,得2210αβαβ+++=,即 (2)(2)3αβ++=,第(10)题第(9)题所以,2123αβ+=⎧⎨+=⎩,; 或232 1.αβ+=-⎧⎨+=-⎩,………………………………10分解得 11αβ=-⎧⎨=⎩,; 或53.αβ=-⎧⎨=-⎩,又因为[11]a b c αβαβαβ=-+==-+++(),,()(), 所以012a b c ==-=-,,;或者8156a b c ===,,,故3a b c ++=-,或29. ………………………………………………20分 (12)如图,点H 为△ABC 的垂心,以AB 为直径的⊙1O 和△BCH 的外接圆⊙2O 相交于点D ,延长AD 交CH 于点P ,求证:点P 为CH 的中点.证明:如图,延长AP 交⊙2O 于点Q , 连接 AH BD QB QC QH ,,,,.因为AB 为⊙1O 的直径,所以∠ADB =∠90=︒BDQ .…………5分 故BQ 为⊙2O 的直径.于是CQ BC BH HQ ⊥⊥,. ……………………………………………………10分 又因为点H 为△ABC 的垂心,所以.AH BC BH AC ⊥⊥,所以AH ∥CQ ,AC ∥HQ ,四边形ACQH 为平行四边形. ………………………………………………15分 所以点P 为CH 的中点. ………………………………………………20分 (13) 如图,点A 为y 轴正半轴上一点,A B ,两点关于x 轴对称,过点A 任作直线交抛物线223y x =于P ,Q 两点. (Ⅰ)求证:∠ABP =∠ABQ ; (Ⅱ)若点A 的坐标为(0,1), 且∠PBQ =60º,试求所有满足条件的 直线PQ 的函数解析式.解:(Ⅰ)如图,分别过点P Q , 作y 轴的垂线,垂足分别为C D , . 设点A 的坐标为(0,t ),则点B 的坐标为(0,-t ). 设直线PQ 的函数解析式为y kx t =+,并设P Q ,的坐标分别为 P P x y (,),Q Q x y (,).由223y kx t y x =+⎧⎪⎨=⎪⎩,, 得2203x kx t --=,于是 32P Q x x t =-,即 23P Q t x x =-.于是,222323P P Q Qx t y t BC BD y t x t ++==++22222()333.222()333P P Q P P Q P Q Q P Q Q Q P x x x x x x x x x x x x x x --===--- …………5分又因为P Q x PC QD x =-,所以BC PCBD QD=. 因为∠BCP =∠90BDQ =︒,所以△BCP ∽△BDQ .故∠ABP =∠ABQ . …………………………………………………………10分(Ⅱ)解法一 设PC a =,DQ b =,不妨设a ≥b >0, 由(Ⅰ)可知∠ABP =∠30ABQ =︒,BC ,BD ,所以 AC 2-,AD =2. 因为PC ∥DQ ,所以△ACP ∽△ADQ .于是PC ACDQ AD=,即a b .所以a b +=.由(Ⅰ)中32P Q x x t =-,即32ab -=-,所以32ab a b =+=,于是,可求得2==a b将b =代入223y x =,得到点Q ,12). …………………15分再将点Q 的坐标代入1y kx =+,求得=k所以直线PQ 的函数解析式为1y x =+. 根据对称性知,所求直线PQ 的函数解析式为1y x =+,或1y =+. ………………20分 解法二 设直线PQ 的函数解析式为y kx t =+,其中1t =. 由(Ⅰ)可知,∠ABP =∠30ABQ =︒,所以2BQ DQ =.故 2Q x =将223Q Q y x =代入上式,平方并整理得 4241590Q Q x x -+=,即22(43)(3)0Q Q x x --=.所以 2Q x =又由(Ⅰ),得3322P Q x x t =-=-,32P Q x x k +=.若Q x =代入上式得P x = 从而2()3P Q k x x =+=.同理,若Q x =可得2P x =-从而2()3P Q k x x =+.所以,直线PQ 的函数解析式为1y =+,或1y x =+. ………………………………………20分 (14)已知0122011i a i >=,, , , ,且122011a a a <<<,证明:122011a a a ,,,中一定存在两个数i j a a i j <,(),使得(1)(1)2010i j j i a a a a ++-<.证明:令20101 2 20111i ix i a ==+,,,,, ……………………………………5分 则20112010102010x x x <<<<<. …………………………………10分故一定存在1≤k ≤2017, 使得11k k x x +-<,从而120102010111k k a a +-<++. …………………………………15分即 11(1)(1)2010k k k k a a a a ++++-<. …………………………………………20分。
全国初中数学联赛九年级第一试参考答案

2 1 1 2 则 c , m , AB m 1 1 m m
2 2
1 1 BC m m ,由题得 AB2 = BC 2 . m m
(
)
3 4
3 的距离. 4
这两条直线与 y 轴交点之间的距离为
7 7 . ,故直线间距离为 4 2 4
所以 a - c
教 州 奥 林
8x
2
2
得分
育
评卷人
((
) + (b - d ) )
2 2
=
min
49 . 32
二、填空题(本题满分 28 分,每小题 7 分) 本题共有 4 个小题,要求直接将答案写在横线上.
。
ww
(1,3) ,( 2,4) ,(3,1) ,(3,5) ,( 4,2) ,( 4,6) ,(5,3) ,(6,4) ,
ao
【解析】 a, b 共有 36 种情况,满足 a b 2 的只有 8 组: 所以 P =
li
2 9
C.
1 9
D.
1 18
奥 林
。
本题共有 6 小题,每题均给出了代号为 A,B,C,D 的四个答案, 其中有且仅有一个是正确的 .将你所选择的答案的代号填在 题后的括号内.每小题选对得 7 分;不选、错选或选出的代号 字母超过一个一律得 0 分.
.
考号
二○一六年全国初中数学联合竞赛试题(C) (九年级参考答案) 一试分 第一试
(12 月 18 日上午 8:30--9:30) 考生注意:1.本试两个大题共 10 个小题,全卷满分 70 分. 2.用圆珠笔或钢笔作答. 3.解题书写不要超出装订线. 一、选择题(本题满分 42 分,每小题 7 分) 二试分 总 分 计分人
初三全国数学竞赛题及答案

全国初中数学竞赛 试题参考答案及评分标准一、选择题(共5小题,每小题7分,满分35分) (1)设x =,则代数式(1)(2)(3)x x x x +++的值为( ). (A )0 (B )1 (C )﹣1 (D )2【答】C .解:由已知得2310x x ++=, 于是2222(1)(2)(3)(3)(32)(31)1 1.x x x x x x x x x x +++=+++=++-=-(2)已知x y z ,,为实数,且满足253x y z +-=,25x y z --=-,则222x y z ++的最小值为( ).(A )111(B )0 (C )5 (D )5411【答】D .解:由 25325x y z x y z +-=⎧⎨--=-⎩,, 可得 312.x z y z =-⎧⎨=+⎩,于是 22221125x y z z z ++=-+.因此,当111z =时,222x y z ++的最小值为5411. (3)若1x >,0y >,且满足3y y xxy x x y==,,则x y +的值为( ).(A )1 (B )2 (C )92(D )112【答】C .解:由题设可知1y y x -=,于是 341y y x yx x -==,所以411y -=.故12y =,从而4=x .于是92x y +=.(4)设333311111232011S =++++,则4S 的整数部分等于( ). (A )4 (B )5 (C )6 (D )7【答】A .解:当2 3 2011k =,,,,因为()()()32111112111k k k k k k k ⎡⎤<=-⎢⎥-+-⎣⎦, 所以333111111511123201122201120124S ⎛⎫<=++++<+-< ⎪⨯⎝⎭. 于是有445S <<,故4S 的整数部分等于4.(5)点D E ,分别在△ABC 的边AB AC ,上,BE CD ,相交于点F ,设1234BDF BCF CEF EADF S S S S S S S S ∆∆∆====四边形,,,,则13S S 与24S S 的大小关系为( ).(A )1324S S S S < (B )1324S S S S = (C )1324S S S S > (D )不能确定 【答】C .解:如图,连接DE ,设1DEF S S ∆'=, 则1423S S EF S BF S '==,从而有1324S S S S '=.因为11S S '>,所以1324S SSS >.二、填空题(共5小题,每小题7分,共35分)(6)两条直角边长分别是整数a b ,(其中2011b <),斜边长是1b +的直角三角形的个数为 .【答】31.解:由勾股定理,得 12)1(222+=-+=b b b a .因为b 是整数,2011<b ,所以2a 是1到4023之间的奇数,而且是完全平方数,这样的数共有31个,即2223 5 63,,,.因此a 一定是3,5,…,63,故满足条件的直角三角形的个数为31.(7)一枚质地均匀的正方体骰子的六个面上的数字分别是1,2,2,3,3,4;另一枚质地均匀的正方体骰子的六个面上的数字分别是1,3,4,5,6,8. 同时掷这两枚骰子,则其朝上的面两数之和为7的概率是 .【答】16.解: 在36对可能出现的结果中,有6对:(1,6), (2,5), (2,5), (3,4),(3,4),(4,3)的和为7,所以朝上的面两数字之和为7的概率是61366=.(8)若y =的最大值为a ,最小值为b ,则22a b +的值为 .【答】32.解:由1x -≥0,且12x -≥0,得12≤x ≤1.21122y =+=+ 由于13124<<,所以当34x =时,2y 取到最大值1,故1a =.当12x =或1时,2y 取到最小值12,故2b =.所以,2232a b +=.(9)如图,双曲线xy 2=(x >0)与矩形OABC 的边CB , BA 分别交于点E ,F ,且AF=BF ,连接EF ,则△OEF 的面积为 .【答】32.解:如图,设点B 的坐标为a b (,),则点F 的坐标为2ba (,).因为点F 在双曲线2y x=上,所以 4.ab = 又点E 在双曲线上,且纵坐标为b ,所以点E 的坐标为2(,)b b.于是11212222221312.22OEF OEC FBEOFBC S S S S b b b a b a b b ab ∆∆∆=--=+-⨯⨯-⨯⨯-=+-=梯形()()() (10)如图,在Rt △ABC 中,斜边AB 的长为35,正方形CDEF 内接于△ABC ,且其边长为12,则△ABC 的周长为 .【答】84.解:如图,设BC =a,AC =b , 则22235a b +==1225. ① 又Rt △AFE ∽Rt △ACB , 所以FE AF CB AC =,即1212b a b-=, 故12()a b ab +=. ②由①②得 2222122524a b a b ab a b +=++=++()(),解得a +b =49(另一个解-25舍去),所以 493584a b c ++=+=.三、解答题(共4题,每题20分,共80分)(11)已知关于x 的一元二次方程20x cx a ++=的两个整数根恰好比方程20x ax b ++=的两个根都大1,求a b c ++的值.解:设方程20x ax b ++=的两个根为αβ,,其中αβ,为整数,且α≤β,则方程20x cx a ++=的两根为11αβ++,,由题意得()()11a a αβαβ+=-++=,, ………………………………5分两式相加,得2210αβαβ+++=,即 (2)(2)3αβ++=, 所以,2123αβ+=⎧⎨+=⎩,;或232 1.αβ+=-⎧⎨+=-⎩,………………………………10分 解得 11αβ=-⎧⎨=⎩,; 或53.αβ=-⎧⎨=-⎩,又因为[11]a b c αβαβαβ=-+==-+++(),,()(), 所以012a b c ==-=-,,;或者8156a b c ===,,, 故3a b c ++=-,或29. ………………………………………………20分(12)如图,点H 为△ABC 的垂心,以AB 为直径的⊙1O 和△BCH 的外接圆⊙2O 相交于点D ,延长AD 交CH 于点P ,求证:点P 为CH 的中点.证明:如图,延长AP 交⊙2O 于点Q , 连接 AH BD QB QC QH ,,,,.因为AB 为⊙1O 的直径,所以∠ADB =∠90=︒BDQ .…………5分 故BQ 为⊙2O 的直径. 于是CQ BC BH HQ ⊥⊥,. ……………………………………………………10分又因为点H 为△ABC 的垂心,所以.AH BC BH AC ⊥⊥,所以AH ∥CQ ,AC ∥HQ , 四边形ACQH为平行四边形. ………………………………………………15分所以点P 为CH 的中点. ………………………………………………20分(13) 如图,点A 为y 轴正半轴上一点,A B ,两点关于x 轴对称,过点A 任作直线交抛物线223y x =于P ,Q 两点. (Ⅰ)求证:∠ABP =∠ABQ ; (Ⅱ)若点A 的坐标为(0,1), 且∠PBQ =60º,试求所有满足条件的 直线PQ 的函数解析式.解:(Ⅰ)如图,分别过点P Q , 作y. 设点A 的坐标为(0,t ),则点B 的坐标为(0,-t ). 设直线PQ 的函数解析式为y kx t =+,并设P Q ,的坐标分别为 P P x y (,),Q Q x y (,).由223y kx t y x =+⎧⎪⎨=⎪⎩,, 得2203x kx t --=,于是 32P Q x x t =-,即 23P Q t x x =-.于是,222323P P Q Qx t y t BC BD y t x t ++==++22222()333.222()333P P Q P P Q P Q Q P Q Q Q P x x x x x x x x x x x x x x --===--- …………5分又因为P Q x PC QD x =-,所以BC PCBD QD=. 因为∠BCP =∠90BDQ =︒,所以△BCP ∽△BDQ . 故∠ABP =∠ABQ . …………………………………………………………10分(Ⅱ)解法一 设PC a =,DQ b =,不妨设a ≥b >0, 由(Ⅰ)可知∠ABP =∠30ABQ =︒,BC,BD, 所以 AC2-,AD=2. 因为PC ∥DQ ,所以△ACP ∽△ADQ . 于是PC ACDQ AD=,即a b.所以a b +=. 由(Ⅰ)中32P Q x x t =-,即32ab -=-,所以322ab a b =+=,于是,可求得2==a b将2b =代入223y x =,得到点Q 的坐标,12). …………………15分再将点Q 的坐标代入1y kx =+,求得=k .所以直线PQ 的函数解析式为13y x =-+. 根据对称性知,所求直线PQ 的函数解析式为1y =+,或1y x =+. ………………20分解法二 设直线PQ 的函数解析式为y kx t =+,其中1t =. 由(Ⅰ)可知,∠ABP =∠30ABQ =︒,所以2BQ DQ =.故 2Q x =将223Q Q y x =代入上式,平方并整理得 4241590Q Q x x -+=,即22(43)(3)0Q Q x x --=.所以 2Q x =. 又由(Ⅰ),得3322P Q x x t =-=-,32P Q x x k +=.若2Q x =代入上式得 P x = 从而 2()3P Q k x x =+=.同理,若Q x = 可得2P x =-从而 2()33P Q k x x =+=.所以,直线PQ 的函数解析式为1y x =+,或1y x =+. ………………………………………20分(14)已知0122011i a i >=,, , , ,且122011a a a <<<,证明:122011a a a ,,,中一定存在两个数i j a a i j <,(),使得(1)(1)2010i j j i a a a a ++-<.证明:令20101 2 20111i ix i a ==+,,,,, ……………………………………5分则20112010102010x x x <<<<<. …………………………………10分故一定存在1≤k ≤2010, 使得11k k x x +-<,从而120102010111k k a a +-<++. …………………………………15分即11(1)(1)2010k k k k a a a a ++++-<. …………………………………………20分。
2017年第二十八届希望杯初赛初三试卷真题(PDF版,含解析)

第二十八届“希望杯”全国数学邀请赛初三 第1试试题一、选择题(每小题4分,共40分)1、在四个数,,,,5435432中,最大的是( )(A )2 (B )33 (C )44 (D )55 【答案】B【解析】2与33比较:()3622=,()26333=;44与33比较:()312444=,()412333=;55与33比较:()315555=,()515333=;2、函数xky =(k 是非零常数)图像的对称轴是( ) (A)x kky = (B )x k y = (C )kx y -= (D )kx y = 【答案】A3、无理数32+的小数部分是( )(A )232-+ (B )324-- (C )332-+ (D )[]232-+【答案】C【解析】 1.412≈。
1.733≈4、化简424242422222-++--++--+-++n n n n n n n n ,结果是( )(A )2n(B )n (C )n-2 (D )n+2 【答案】B 【解析】[]n nn n n n n n n n n n n n n n n n n n n n n n n n n n n n ==-++-++=-+++--+++--++-+++=-+++-+-++-+-+-+++44)2()2()2()2(2)22(2)22(2)22(2)22(2)2)(2(2)2)(2(2)2)(2(2)2)(2(25、若关于x 的二次三项式n x mx 322++在实数范围内不能分解因式,则(m.n )一定在( ) (A )第二象限 (B )第四象限 (C )第一或第三象限 (D )第二或第四象限 【答案】C【解析】实数范围内不能因式分解,即0322=++n x mx 无解,则0344<⨯-=∆n m31>∴mn 同为正数或者同为负数。
6、如图1,一次函数y=x 与二次函数c bx ax y ++=2的图像相交于点),(),,(2211y x Q y x P 两点,则函数c x b ax y +-+=)1(2的图像可能是( )(A ) (B ) (C ) (D ) 【答案】B【解析】由图可知有两个交点,则x c bx ax =++2有两个解,等价于函数c x b ax y +-+=)1(2与x 轴有两个交点,且由图可知,P ,Q 两点的横坐标为负,则c x b ax y +-+=)1(2与x 轴必在负半轴 7、若正整数c b a ,,满足1111=++cb a ,则这样的正整数组(a,b,c )共有( )组 (A )1 (B )3 (C )9 (D )10 【答案】D【解析】不妨设c b a c b a 11100≤≤<→>≥≥,311,31111c cc c b a c ≤<∴≤++<∴则c 可取的2,3当c=2时有两种情况: ① 1612131=++由轮换对称的结构可知,共6组② 1412141=++同理有三组c=3时,只有1313131=++这1组8、若二次函数c bx ax y ++=2(a,b,c 是常数)的图像如图2所示,对称轴是直线x=-2,则下列说法中不正确的是( )(A )0>abc (B )0<++c b a (C )05<+c a (D )0<+-c b a【答案】D【解析】由图可知,在1-=x 时,函数值在x 轴上半部分9、The radius of cricle O is 52,chord AB perpendicular chord CD at point E,and AE=6,ED=2,then the lengthof EB is( )(A )5 (B )2 (C )52 (D )4【答案】B【解析】设BC=x,EB=y,由相交弦定理可知,6y=2x ,则x=3y,分别由圆心向两条弦作垂线OM,ON, 则四边形MENO 为矩形,在Rt △ANO 中,222AN ON AE +=,即22)12()23(20-=+-xy 得y=210、关于x 的方程24222-=+-a ax x 有且仅有一个正根,则a 的取值范围是( ) (A )a<-12 (B )24≤a (C )a<-12或a=24 (D )a<12【答案】A【解析】方程有且仅有一个正根,即说明不存在两相等的正跟,又开口向上,120242,0)0(-<∴<+<a a f二、A 组填空题11、2007...4321-+++-+++-x x x x x 的最小值是______.【答案】2035152【解析】表示x 到1,-2,3,-4.....2016,-2017各个点之间的距离和,最中间点为1.当x=1时,整体最小将x =1代入即可12、在直角坐标系中,若x,y 都是整数,则称(x,y )是整点,满足不等式y x y x 4422-≤+的整点的个数是_______. 【答案】25【解析】化简式子:()()82222≤++-y x ,即以)2,2(-为圆心,22为半径的圆内有多少个整数点,画图,数点的数量即可13、方程组⎩⎨⎧==+65xy y x 的解是_______.【答案】⎩⎨⎧-=-=32y x 或者⎩⎨⎧-=-=23y x14、如图3,Rt △ABC 中,153090===∠BC AC C ,,,若以点C 为圆心,BC 为半径的圆交AB 于点D ,则AD 的长度是______ 【答案】59【解析】设AC 与圆左交点为F ,延长AC 交圆于右点E ,割线定理可知AF AE AB AD ⋅=⋅有勾股定理可得,515=AB 4515515⨯=⋅AD15、在正方形ABCD 中,点M,N 分别在BC ,CD 上,BM =4,DN =6,且MAN BAM ∠=∠,则AN 的长是_______【答案】10【解析】延长AN,DC 交于点E ,由平行可知,E MAN BAM ∠=∠=∠, 则有NE=NA,设NC=x,MC=y ,可得:MC MB NC DN AN DN AD +=+=+,222,代入数据即可得AN=1016、Suppose real numbers a and b satisfy ,0≠ab and 222)3()(10b a b a +=+,then the value of abb a 223+is_________ 【答案】328 【解析】化简式子:06922=+-b ab a 即a b b a 30)3(2=∴=-代入即可17、在△ABC 中,点D 在BC 上,点F 在AB 上,点E 在AC 上,四边形FDEA 是平行四边形,且BC AC AB 23==,,则△ABC 与四边形FDEA 的周长之比是________【答案】34【解析】 四边形FDEA 周长为AC+AB 两条线段长,设BC=2a ,则△ABC 周长为8a,四边形FDEA 周长6a.18、如图2,将面积为2的Rt △ABC 沿直线BC 翻折,再向左平移得到Rt △DCE ,延长AC 交DE 于点M ,则△AME 的面积是__________.【答案】3【解析】由翻折平移可知两三角形全等. 延长CM 使得C M=FM,连接FD,EF , 可证明四边形CEFD 为矩形19、若二次函数2017)1(2---=x y 的图像上有不同的两点A (m,-4036),B (n,-4036),则当点C(m+n ,p)在这函数图像上时,p =_________. 【答案】2018-【解析】点)4036,(),4036,(--n B m A 在函数图像上,代入即可知,n m ,是方程020182=-+-x x 的两根,则2=+n m ,代入得到2018-=p20、如图5,CD AB DE DC BE CB ACB ⊥===∠,,90,于点M,ED 的延长线交AC 于点N ,若AN =3,NC =5,则BC 的长度是____【答案】52【解析】由同余可知,2240CB ACCBCE NC E A =→=∴∠=∠ 21、若120163,2016201622=--=++x xy y y xy x 则y x -=_______或_______.【答案】-1或2017【解析】两式相加得:0201720162016222=-+--+y x xy y x化简:02017)(2016)(2=----y x y x22、如图6,在直角坐标系中,边长为1的正△ABC (C 与O 重合)的边BC 在x轴上,顶点A 在第一象限,现在进行以下操作:(1)把△ABC 沿X 轴向右平移一个单位,此时A 变为1A (2)将三角形沿X 轴翻折,此时1A 变为2A (3)将三角形绕点O 旋转180°,此时2A 变为3A (4)将三角形沿Y 轴翻折,此时3A 变为4A (5)将三角形绕点O 旋转180°,此时4A 变为5A按照此规律,重复以上五步,则17A 的坐标是(_______,______)【答案】)23,21(-【解析】)23,23()23,23()23,23()23,23()23,23()23,21(54321--→→-→-→→A A A A A A ⎪⎪⎭⎫ ⎝⎛→⎪⎪⎭⎫ ⎝⎛--→⎪⎪⎭⎫ ⎝⎛-→⎪⎪⎭⎫ ⎝⎛-→⎪⎪⎭⎫⎝⎛--→23,2123,2123,2123,2123,21109876A A A A A 从推导过程可知,10个一循环,则717A A =23、已知-2是三次方程03=++c bx x 的唯一实根,则b 的取值范围是______,c 的取值范围是______ 【答案】,3->b 2>c【解析】因为方程只有-2一个实根,则分解因式之后()()c bx x n mx x x ++=+++322对比系数,左边化简:2,2cn m =-=,且方程02=++n mx x ,化简得:n x n m x m x 2)2()2(23+-+-+ 没有实数根则0244<⨯-=∆c,3)4(2->→+=b b c 24、如图7,在边长为1的正方形ABCD 中,点E 在边AD 上运动(不与A ,D 重合),点A ,G 关于BE对称,连接EG 并延长交DC 于点F ,则∆DEF 的周长是_________,_____=∠EBF .【答案】2,45°【解析】连接BG ,可证三角形全等即可25、设21,x x 是一元二次方程02=++q x p x 的两根,若q 为质数,p =17q +4是完全平方数,则q=_________,______1121=+x x . 【答案】131513-,【解析】q x x p x x =⋅-=+2121,,417+=q p 且为完全平方数,设()()22174172-+=→+==k k q q p k ⎩⎨⎧=-=+∴q k k 2172或⎩⎨⎧=-=+1722k qk 则21,1321==q q (舍)225=∴p 则原方程可化为:013152=++x x。
全国初中数学联赛初三组初赛试卷及答案.doc

2014 年全国初中数学联赛 (初三组 )初赛试卷(3 月 7 日下午 4: 00—6:00)班级: :姓名:成绩:题号一二三四五合计得分评卷人复核人考生注意:1、本试卷共五道大题,全卷满分140 分;2、用圆珠笔、签字笔或钢笔作答;3、解题书写不要超出装订线;4、不能使用计算器。
一、选择题(本题满分42 分,每小题7 分)本题共有 6 个小题,每题均给出了代号为A、B、C、D 的四个答案,其中有且只有一个是正确的。
将你选择的答案的代号填在题后的括号内。
每小题选对得7 分;不选、错选或选出的代号字母超过一个(不论是否写在括号内),一律得0 分。
1、某件商品的标价为13200 元,若以 8 折降价出售,仍可获利10%(相对于进货价),则该商品的进货价是()A 、9504 元B、 9600 元C、 9900 元D、 10000 元2、如图,在凸四边形ABCD 中,AB BC BD ,ABC 80,则ADC 等于()A 、80B、100C、140D、160C D CDA B A B第 2 题图第4题图3、如果方程x 2 x 24x m 0 的三根可以作为一个三角形的三边之长,那么,实数m 的取值范围是()A 、0m 4B、m3C、m4D、3m 44、如图,梯形ABCD 中,AB // CD,BAD60 ,ABC 30,AB 6 且 AD CD ,那么BD 的长度是()A 、7B、 4C、 2 7 D 、 4 25、如果2014 a 0 ,那么| x a | | x 2014 | | x a 2014 | 的最小值是()A 、2014 B、a 2014 C、 4028 D、a 40286、方程x 2 xy y 2 3 x y 的整数解有()OD CA 、3 组B、4 组C、5 组D、 6 组 A B二、填空题(本大题满分28 分,每小题 7 分) E F1、如图,扇形AOB 的圆心角AOB 90 ,半径为5,正方形 CDEF 内接于该扇形,则正方形 CDEF 的边长为.2、已知四个自然数两两的和依次从小到大的次序是:23,28,33 ,39,x,y,则x y ____ .3、已知x y 6 ,x 2 xy xy y 2 9,则x2 xyxy y 2 的值是.4、有质地均匀的正方体形的红白骰子各一粒,每个骰子的六个面分别写有1、 2、 3、4、5、 6 的自然数,随机掷红、白两粒骰子各一次,红色骰子掷出向上面的点数比白色骰子掷出向上面的点数小的概率是.三、(本大题满分20 分)2 的值。
2008—2017年全国初中数学竞赛试题含答案

“《数学周报》杯”2008年全国初中数学竞赛试题班级__________学号__________姓名______________得分______________一、选择题(共5小题,每小题6分,满分30分.以下每道小题均给出了代号为A ,B ,C ,D 的四个选项,其中有且只有一个选项是正确的,请将正确选项的代号填入题后的括号里.不填、多填或错填都得0分)1.已知实数x ,y 满足:4x 4-2x 2=3,y 4+y 2=3,则4x4+y 4的值为( )(A )7 (B )1+132(C )7+132(D )52.把一枚六个面编号分别为1,2,3,4,5,6的质地均匀的正方体骰子先后投掷2次,若两个正面朝上的编号分别为m ,n ,则二次函数y =x 2+mx +n 的图象与x 轴有两个不同交点的概率是( )(A )512(B )49(C )1736(D )123.有两个同心圆,大圆周上有4个不同的点,小圆周上有2个不同的点,则这6个点可确定的不同直线最少有 ( )(A )6条(B )8条(C )10条(D )124.已知AB 是半径为1的圆O 的一条弦,且AB =a <1.以AB 为一边在圆O 内作正△ABC ,点D 为圆O 上不同于点A 的一点,且DB =AB =a ,DC 的延长线交圆O 于点E ,则AE 的长为 ( )(A )52a (B )1(C )32(D )a5.将1,2,3,4,5这五个数字排成一排,最后一个数是奇数,且使得其中任意连续三个数之和都能被这三个数中的第一个数整除,那么满足要求的排法有 ( ) (A )2种(B )3种(C )4种(D )5种二、填空题(共5小题,每小题6分,满分30分)6.对于实数u ,v ,定义一种运算“*”为:u *v =uv +v .若关于x 的方程x *(a *x )=-14有两个不同的实数根,则满足条件的实数a 的取值范围是_______.7.小王沿街匀速行走,发现每隔6分钟从背后驶过一辆18路公交车,每隔3分钟从迎面驶来一辆18路公交车.假设每辆18路公交车行驶速度相同,而且18路公交车总站每隔固定时间发一辆车,那么发车间隔的时间是_____分钟. 8.如图,在△ABC 中,AB =7,AC =11,点M 是BC 的中点,AD 是∠BAC 的平分线,MF ∥AD ,则FC 的长为______.9.△ABC 中,AB =7,BC =8,CA =9,过△ABC 的内切圆圆心I 作DE ∥BC ,分别与AB ,AC 相交于点D ,E ,则DE 的长为______.10.关于x ,y 的方程x 2+y 2=208(x -y )的所有正整数解为________.三、解答题(共4题,每题15分,满分60分)11.在直角坐标系xOy 中,一次函数y =kx +b (k ≠0)的图象与x 轴、y 轴的正半轴分别交FMD BA于A,B两点,且使得△OAB的面积值等于|OA|+|OB|+3.(1)用b表示k;(2)求△OAB面积的最小值.12.是否存在质数p,q,使得关于x的一元二次方程px2-qx+p=0有有理数根?13.是否存在一个三边长恰是三个连续正整数,且其中一个内角等于另一个内角2倍的△ABC?证明你的结论.14.从1,2,…,9中任取n个数,其中一定可以找到若干个数(至少一个,也可以是全部),它们的和能被10整除,求n的最小值.简答:一. 选择题 ACBBD ;二. 填空题 6. a > 0 或 a <-1; 7. 4; 8. 9; 9.163; 10. x =48, x =160,y =32; y =32. 三.解答题:11. (1)k =2b -b 22(b +3),b > 2; (2)当 b =2+10, k =-1时,△OAB 面积的最小值为7+210; 12. 存在满足题设条件的质数p ,q . 当p =2,q =5时,方程2x 2-5x + 2=0 的两根为 x 1=12, x 2=2. 它们都是有理数; 13. 存在满足条件的三角形. △ABC 的边 a =6,b =4,c =5,且∠A =2∠B ,证明略. 14. n 的最小值是5,证明略.中国教育学会中学数学教学专业委员会“《数学周报》杯”2009年全国初中数学竞赛试题参考答案一、选择题(共5小题,每小题7分,共35分. 以下每道小题均给出了代号为A ,B ,C ,D 的四个选项,其中有且只有一个选项是正确的. 请将正确选项的代号填入题后的括号里,不填、多填或错填都得0分)1.已知非零实数a ,b 满足 2242(3)42a b a b a -++-=,则a b +等于( ). (A )-1 (B )0 (C )1 (D )2 【答】C .解:由题设知a ≥3,所以,题设的等式为22(3)0b a b +-=,于是32a b ==-,,从而a b +=1.2.如图,菱形ABCD 的边长为a ,点O 是对角线AC 上的一点,且OA=a ,OB =OC =OD =1,则a 等于( ).(A)(B(C )1 (D )2【答】A .解:因为△BOC ∽ △ABC ,所以BO BCAB AC=,即11aa a =+, 所以, 210a a --=.由0a >,解得a =. 3.将一枚六个面编号分别为1,2,3,4,5,6的质地均匀的正方体骰子先后投掷两次,记第一次掷出的点数为a ,第二次掷出的点数为b ,则使关于x ,y 的方程组322ax by x y +=⎧⎨+=⎩,只有正数解的概率为( ). (A )121 (B )92 (C )185 (D )3613 【答】D .解:当20a b -=时,方程组无解.当02≠-b a 时,方程组的解为62,223.2b x a b a y a b -⎧=⎪⎪-⎨-⎪=⎪-⎩由已知,得⎪⎪⎩⎪⎪⎨⎧>-->--,0232,0226b a a b a b即⎪⎪⎩⎪⎪⎨⎧<>>-,3,23,02b a b a 或⎪⎪⎩⎪⎪⎨⎧><<-.3,23,02b a b a由a ,b 的实际意义为1,2,3,4,5,6,可得2345612a b =⎧⎨=⎩,,,,,,,共有 5×2=10种情况;或1456a b =⎧⎨=⎩,,,,共3种情况. 又掷两次骰子出现的基本事件共6×6=36种情况,故所求的概率为3613. 4.如图1所示,在直角梯形ABCD 中,AB ∥DC ,90B ∠=︒. 动点P 从点B 出发,沿梯形的边由B →C →D →A 运动. 设点P 运动的路程为x ,△ABP 的面积为y . 把y 看作x 的函数,函数的图像如图2所示,则△ABC 的面积为( ).(A )10 (B )16 (C )18 (D )32【答】B .解:根据图像可得BC =4,CD =5,DA =5,进而求得AB =8,故S △ABC =12×8×4=16.5.关于x ,y 的方程22229x xy y ++=的整数解(x ,y )的组数为( ). (A )2组 (B )3组 (C )4组 (D )无穷多组 【答】C .解:可将原方程视为关于x 的二次方程,将其变形为 22(229)0x yx y ++-=.由于该方程有整数根,则判别式∆≥0,且是完全平方数. 由 2224(229)7116y y y ∆=--=-+≥0, 解得 2y ≤11616.577≈.于是 2y0 1 4 9 16 ∆11610988534显然,只有216y =时,4∆=是完全平方数,符合要求. 当4y =时,原方程为2430x x ++=,此时121,3x x =-=-; 当y =-4时,原方程为2430x x -+=,此时341,3x x ==. 所以,原方程的整数解为111,4;x y =-⎧⎨=⎩ 223,4;x y =-⎧⎨=⎩ 331,4;x y =⎧⎨=-⎩ 443,4.x y =⎧⎨=-⎩ 二、填空题(共5小题,每小题7分,共35分)6.一个自行车轮胎,若把它安装在前轮,则自行车行驶5000 km 后报废;若把它安装在后轮,则自行车行驶 3000 km 后报废,行驶一定路程后可以交换前、后轮胎.如果交换前、(第4题)图1 图2后轮胎,要使一辆自行车的一对新轮胎同时报废,那么这辆车将能行驶 km .【答】3750.解:设每个新轮胎报废时的总磨损量为k ,则安装在前轮的轮胎每行驶1 km 磨损量为5000k ,安装在后轮的轮胎每行驶1km 的磨损量为3000k .又设一对新轮胎交换位置前走了x km ,交换位置后走了y km.分别以一个轮胎的总磨损量为等量关系列方程,有,50003000,50003000kxky k ky kx k ⎧+=⎪⎪⎨⎪+=⎪⎩ 两式相加,得()()250003000k x y k x y k +++=, 则 237501150003000x y +==+.7.已知线段AB 的中点为C ,以点A 为圆心,AB 的长为半径作圆,在线段AB 的延长线上取点D ,使得BD =AC ;再以点D 为圆心,DA 的长为半径作圆,与⊙A 分别相交于F ,G 两点,连接FG 交AB 于点H ,则AHAB的值为 .解:如图,延长AD 与⊙D 交于点E ,连接AF ,EF . 由题设知13AC AD =,13AB AE =,在△FHA 和△EFA 中,90EFA FHA ∠=∠=︒,FAH EAF ∠=∠所以 Rt △FHA ∽Rt △EFA ,AH AF AF AE=.而AF AB =,所以AH AB 13=. 8.已知12345a a a a a ,,,,是满足条件123459a a a a a ++++=的五个不同的整数,若b 是关于x 的方程()()()()()123452009x a x a x a x a x a -----=的整数根,则b 的值为 .【答】 10.解:因为()()()()()123452009b a b a b a b a b a -----=,且12345a a a a a ,,,,是五个不同的整数,所有12345b a b a b a b a b a -----,,,,也是五个不同的整数.(第7题)又因为()()2009117741=⨯-⨯⨯-⨯,所以1234541b a b a b a b a b a -+-+-+-+-=.由123459a a a a a ++++=,可得10b =.9.如图,在△ABC 中,CD 是高,CE 为ACB ∠的平分线.若AC =15,BC =20,CD =12,则CE 的长等于 .【答】6027. 解:如图,由勾股定理知AD =9,BD =16,所以AB =AD +BD =25 . 故由勾股定理逆定理知△ACB 为直角三角形,且90ACB ∠=︒.作EF ⊥BC ,垂足为F .设EF =x ,由1452ECF ACB ∠=∠=︒,得CF =x ,于是BF =20-x .由于EF ∥AC ,所以EF BFAC BC =, 即 201520x x-=,解得607x =.所以60227CE x ==.10.10个人围成一个圆圈做游戏.游戏的规则是:每个人心里都想好一个数,并把自己想好的数如实地告诉他两旁的两个人,然后每个人将他两旁的两个人告诉他的数的平均数报出来.若报出来的数如图所示,则报3的人心里想的数是 . 【答】2-.解:设报3的人心里想的数是x ,则报5的人心里想的数应是8x -.于是报7的人心里想的数是 12(8)4x x --=+,报9的人心里想的数是16(4)12x x -+=-,报1的人心里想的数是 20(12)8x x --=+,报3的人心里想的数是4(8)4x x -+=--.所以4x x =--, 解得2x =-.三、解答题(共4题,每题20分,共80分)(第9题)(第10题)11.已知抛物线2y x =与动直线c x t y --=)12(有公共点),(11y x ,),(22y x ,且3222221-+=+t t x x . (1)求实数t 的取值范围;(2)当t 为何值时,c 取到最小值,并求出c 的最小值. 解:(1)联立2y x =与c x t y --=)12(,消去y 得二次方程2(21)0x t x c --+= ①有实数根1x ,2x ,则121221,x x t x x c +=-=.所以2221212121[()()]2c x x x x x x ==+-+=221[(21)(23)]2t t t --+-=21(364)2t t -+. ②………………5分把②式代入方程①得221(21)(364)02x t x t t --+-+=. ③………………10分t 的取值应满足2221223t t x x +-=+≥0, ④且使方程③有实数根,即22(21)2(364)t t t ∆=---+=2287t t -+-≥0, ⑤解不等式④得 t ≤-3或t ≥1,解不等式⑤得 22-≤t ≤22+所以,t 的取值范围为2t ≤2+⑥ ………………15分(2) 由②式知22131(364)(1)222c t t t =-+=-+.由于231(1)22c t =-+在22-≤t ≤22+2t =-时,2min 3211162(21)2224c -=--+=. ………………20分12.已知正整数a 满足3192191a +,且2009a <,求满足条件的所有可能的正整数a 的和. 解:由3192191a +可得31921a -.619232=⨯,且()[]311(1)1(1)(1)(1)a a a a a a a a -=-++=-++-.………………5分因为()11a a ++是奇数,所以6321a -等价于621a -,又因为3(1)(1)a a a -+,所以331a -等价于31a -.因此有1921a -,于是可得1921a k =+.………………15分 又02009a <<,所以0110k =,,,.因此,满足条件的所有可能的正整数a 的和为11+192(1+2+…+10)=10571. ………………20分13.如图,给定锐角三角形ABC ,BC CA <,AD ,BE 是它的两条高,过点C 作△ABC 的外接圆的切线l ,过点D ,E 分别作l 的垂线,垂足分别为F ,G .试比较线段DF 和EG 的大小,并证明你的结论.解法1:结论是DF EG =.下面给出证明. ………………5分 因为FCD EAB ∠=∠,所以Rt △FCD ∽ Rt △EAB .于是可得CDDF BE AB=⋅. 同理可得 CEEG AD AB=⋅.………………10分又因为tan AD BEACB CD CE∠==,所以有BE CD AD CE ⋅=⋅,于是可得 DF EG =. ………………20分解法2:结论是DF EG =.下面给出证明.……………… 5分(第13A 题)连接DE ,因为90ADB AEB ∠=∠=︒,所以A ,B ,D ,E 四点共圆,故CED ABC ∠=∠.又l 是⊙O 的过点C 的切线,所以ACG ABC ∠=∠. ………………15分 所以,CED ACG ∠=∠,于是DE ∥FG ,故DF =EG .………………20分14.n 个正整数12n a a a ,,,满足如下条件:1212009n a a a =<<<=;且12n a a a ,,,中任意n -1个不同的数的算术平均数都是正整数.求n 的最大值.解:设12n a a a ,,,中去掉i a 后剩下的n -1个数的算术平均数为正整数i b ,12i n =,,,.即 12()1n ii a a a a b n +++-=-.于是,对于任意的1≤i j <≤n ,都有1j i i j a a b b n --=-,从而 1()j i n a a --. ………………5分由于 11200811n n a a b b n n --==--是正整数,故 312251n -⨯. ………………10分由于 ()()()112211n n n n n a a a a a a a ----=-+-++-≥()()()2111(1)n n n n -+-++-=-,所以,2(1)n -≤2008,于是n ≤45.结合312251n -⨯,所以,n ≤9. ………………15分另一方面,令123801,811,821a a a =⨯+=⨯+=⨯+,…,8871a =⨯+,982511a =⨯+,则这9个数满足题设要求.综上所述,n 的最大值为9. ………………20分中国教育学会中学数学教学专业委员会“《数学周报》杯”2010年全国初中数学竞赛试题参考答案一、选择题(共5小题,每小题7分,共35分.其中有且只有一个选项是正确的. 请将正确选项的代号填入题后的括号里,不填、多填或错填都得0分) 1.若20 10a b b c==,,则a bb c ++的值为( ). (A )1121 (B )2111 (C )11021 (D )21011解:D 由题设得12012101111110a ab bc b c b +++===+++. 代数式变形,同除b2.若实数a ,b 满足21202a ab b -++=,则a 的取值范围是 ( ).(A )a ≤2- (B )a ≥4 (C )a ≤2-或 a ≥4 (D )2-≤a ≤4 解.C因为b 是实数,所以关于b 的一元二次方程21202b ab a -++=的判别式 21()41(2)2a a ∆--⨯⨯+=≥0,解得a ≤2-或 a ≥4.方程思想,未达定理;要解一元二次不等式3.如图,在四边形ABCD 中,∠B =135°,∠C =120°,AB =23BC =422-CD =2,则AD 边的长为( ).(A )6(B )64(C )64+ (D )622+ 解:D如图,过点A ,D 分别作AE ,DF 垂直于直线BC ,垂足分别为E ,F .由已知可得BE =AE 6CF =22DF =6于是 EF =4+6.过点A 作AG ⊥DF ,垂足为G .在Rt △ADG 中,根据勾股定理得AD 222(46)(6)(224)=++=+226+(第3题)(第3题)勾股定理、涉及双重二次根式的化简,补全图形法4.在一列数123x x x ,,,……中,已知11=x ,且当k ≥2时,1121444k k k k x x -⎛--⎫⎡⎤⎡⎤=+-- ⎪⎢⎥⎢⎥⎣⎦⎣⎦⎝⎭ (取整符号[]a 表示不超过实数a 的最大整数,例如[]2.62=,[]0.20=),则2010x 等于( ).(A) 1 (B) 2 (C) 3 (D) 4 解:B由11=x 和1121444k k k k x x -⎛--⎫⎡⎤⎡⎤=+-- ⎪⎢⎥⎢⎥⎣⎦⎣⎦⎝⎭可得 11x =,22x =,33x =,44x =,51x =,62x =,73x =,84x =,……因为2010=4×502+2,所以2010x =2. 高斯函数;找规律。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2017年全国初中数学联赛(初三组)初赛试卷参考答案及评分细则详解2017年全国初中数学联赛(初三组)初赛试卷试题参考答案及评分标准说明:评阅试卷时,请依据本评分标准。
选择题和填空题只设7分和分两档;解答题,请严格按照本评分标准规定的评分档次给分,不要再增加其他中间档次。
如果考生的解答方法和本解答不同,只要思路合理,步骤正确,在评卷时请参照本评分标准划分的档次,给予相应的分数。
一、选择题(本题满分42分,每小题7分)1、设实数a、b满足a-b=-1,则a³-b³+3ab的值为(B)A、-3B、-1C、1D、3解析:a³-b³+3ab=(a-b)(a²+ab+b²)+3ab=-(a-b)=-12、若实数a为常数,关于x的不等式组{x+a²≤2a x≤-7}的整数解只有8个,则a的值为(C)A、-1B、0C、1D、2解析:{x+a²≤2a x≤-7}⇒-7≤x≤-a²+2a⇒1≤-a²+2a⇒(a-1)≤0⇒a≤1因为a是常数,所以a=13、在菱形ABCD中,AB=4,E为AB的中点,若在线段BD上取一点P,则PA+PE∠A=60°,的最小值是(D)A、23B、4C、25D、27解析:如图,连结AC,EC交BD于点P,则点P是所求的菱形ABCD中,AB=4,∠A=60°,E为AB的中点DE=√3×AB/2=2√3CE=DE+DC=2√3+4AE=√(CE²+AC²)=√(28²+16)=4√10PA+PE∠A=AE×sin(∠APE)=4√10×sin(60°+∠BPD)令∠BPD=θ,则∠APE=60°+θPA+PE∠A=4√10×(cosθ+√3sinθ)=4√10×(sinθ+√3cosθ+2)/24√10×(sin(θ-60°)+2)/2=2√10×(√3cosθ+sinθ+1)≥2√10所以最小值为2√10,即274、对于任意实数a,b,c,用M{a,b,c}表示三个数的平均数,用min{a,b,c}表示这三个数中最小的数,若M{2x+y+2,x+2y,2x-y}=min{2x+y+2,x+2y,2x-y},则x+y=(A)A、-4B、-2C、2D、4解析:不妨设a最小,则M{a,b,c}=aa+b+c=3ab-a)+(c-a)=ab-a≥0,c-a≥0b=a,c=a2x+y+2=x+2y=2x-yx=-3,y=-1x+y=-45、如图,RtΔABC的斜边AB与⊙O相切于点P,直角顶点C在⊙O上,若AC=22,BC=4,则⊙O的半径是(B)A、3B、23C、4D、26解析:如图,由射影定理得:BC²=AC×DCCD=4²/22BD²=CD²+BC²=48BO=BD/2=√48/2=2√3OP=OB-√AB²-AP²=2√3-√22²-4²=2√3-2r=OP=2√3-2=2(√3-1)=2∙236、不超过1142无明显问题的段落,不需修改)即有:x2kx5x 2x25x k x 2将两式相减,得:10x52x化XXX:2x210x50由于方程只有一个公共实根,所以判别式为0,即:24250解得:2或 5又因为x2kx k的实根为0或k,所以:当2时,实根为0,k,所以实根之和为k;当5时,实根为0,k,所以实根之和为k;综上所述,关于x的方程x2kx k所有的实根之和为k k0.题目一:已知方程组 $\begin{cases}\alpha^2-k\alpha+5=0 \\\alpha^2+5\alpha-k=0\end{cases}$,求所有实数根的和。
解:将两个方程相减,得 $(k+5)\alpha-(k+5)=0$。
因为当$k=-5$ 时两个方程相同,有两个公共的实根,不符合题意,所以 $k\neq-5$。
因此 $\alpha=1$,代入第一个方程解得 $k=6$。
所以方程 $x^2+kx=k$ 即为 $x^2+6x=6$ 或 $x^2+6x=-6$。
显然两个方程都有实根,因此所有实数根的和为 $-12$。
题目二:如图,已知圆 $O$ 的直径 $AB$ 与 $CD$ 互相垂直,$E$ 为 $OB$ 的中点,$CE$ 的延长线交圆 $O$ 于 $G$,$AG$ 交 $CD$ 于 $F$,求 $DF$ 的值。
解:设 $OE=a$,则 $OA=OB=OC=OD=2a$,$CE=5a$。
因为 $\triangle COE\sim\triangle CGD$,所以$\dfrac{CO}{CE}=\dfrac{CG}{CD}$,即 $\dfrac{2a\times4a}{5a\times 3a}=\dfrac{CG}{CD}$,解得$CG=\dfrac{12a^2}{5}$。
过 $G$ 作 $GH\perp AB$ 于点 $H$,则 $\triangle COE\sim\triangle GHE$,所以$\dfrac{CO}{OE}=\dfrac{GH}{HE}$,即$\dfrac{2a}{a}=\dfrac{GH}{a}$,解得 $GH=a$,$HE=a$,于是 $AH=a$。
因为 $\triangle AOF\sim\triangle AHG$,所以$\dfrac{OF}{AO}=\dfrac{HG}{AH}$,即$\dfrac{a}{2a+2a}=\dfrac{HG}{a}$,解得$HG=\dfrac{a}{3}$,$OF=\dfrac{2a}{3}$。
由于 $\triangle ADF\sim\triangle ACF$,所以 $\dfrac{DF}{FC}=\dfrac{AD}{AC}$,即$\dfrac{DF}{a}=\dfrac{a}{2a}$,解得 $DF=\dfrac{a}{2}$。
已知$a$、$b$、$c$、$d$、$x$、$y$、$z$、$w$是互不相等的非零实数,且frac{a^2}{y^2+b^2x^2+b^2z^2+c^2y^2}=\frac{abcd}{c^2d^ 2a^2b^2c^2d^2}$$求$\frac{y^2c^2w^2+d^2z^2x^2ywz}{abcdxw}$的值。
解:将等式两边通分,化简得a^2c^2d^2x^2y^2z^2w^2=b^4c^2d^2x^2y^4z^2+b^4c^2d^2 x^2y^2z^4+a^2c^4d^2y^2z^2+b^2c^2d^4x^2w^2$$将等式两边分别除以$a^2c^2d^2x^2y^2z^2w^2$,得frac{b^4}{a^2}(\frac{1}{x^2}+\frac{1}{z^2})+\frac{c^4}{a ^2}(\frac{1}{y^2}+\frac{1}{z^2})+\frac{d^4}{c^2}(\frac{1}{x^2 }+\frac{1}{w^2})=1$$注意到等式左边是对称的,于是不妨设$\frac{b^2}{a}=p,\frac{c^2}{a}=q,\frac{d^2}{c}=r$,则原等式化为p^2(\frac{1}{x^2}+\frac{1}{z^2})+q^2(\frac{1}{y^2}+\frac {1}{z^2})+r^2(\frac{1}{x^2}+\frac{1}{w^2})=1$$再设$\frac{1}{x^2}+\frac{1}{z^2}=m,\frac{1}{y^2}+\frac{1}{z^2}= n,\frac{1}{x^2}+\frac{1}{w^2}=k$,则有pm+qn+rk=1$$要求的值为frac{y^2c^2w^2+d^2z^2x^2ywz}{abcdxw}=\frac{d^2}{ac}\ cdot\frac{y^2}{xw}\cdot\frac{z^2}{xy}+\frac{c^2}{ad}\cdot\frac {z^2}{xy}\cdot\frac{w^2}{yz}+\frac{b^2}{cd}\cdot\frac{x^2}{y w}\cdot\frac{z^2}{xy}+\frac{b^2}{ac}\cdot\frac{x^2}{yw}\cdot\ frac{w^2}{yz}$$将$p,q,r$代入得frac{y^2c^2w^2+d^2z^2x^2ywz}{abcdxw}=\frac{d^2}{ac}\ cdot\frac{m}{k}+\frac{c^2}{ad}\cdot\frac{n}{k}+\frac{pb^2}{cd }\cdot\frac{m}{n}+\frac{qb^2}{ac}\cdot\frac{k}{n}$$ 将XXX代入得frac{y^2c^2w^2+d^2z^2x^2ywz}{abcdxw}=\frac{d^2m}{ac m+adn+cdk}+\frac{c^2n}{acm+adn+cdk}+\frac{pb^2m}{acm+ad n+cdk}+\frac{qb^2k}{acm+adn+cdk}$$frac{(d^2m+c^2n+pb^2m+qb^2k)x^2wy^2z^2wz}{abcdxw(a cm+adn+cdk)}$$由于$pm+qn+rk=1$,所以$mnk\neq 0$,故$\frac{y^2c^2w^2+d^2z^2x^2ywz}{abcdxw}=\frac{d^2m+c^2n+ pb^2m+qb^2k}{abcd(acm+adn+cdk)}$。
将$p,q,r$代回去,得frac{y^2c^2w^2+d^2z^2x^2ywz}{abcdxw}=\frac{d^2(\frac{ 1}{x^2}+\frac{1}{w^2})+c^2(\frac{1}{y^2}+\frac{1}{w^2})+b^ 2(\frac{1}{x^2}+\frac{1}{z^2})+b^2(\frac{1}{y^2}+\frac{1}{z^2 })}{abcd(\frac{1}{x^2}+\frac{1}{w^2}+\frac{1}{y^2}+\frac{1}{ z^2})}$$frac{(b^2+c^2)\frac{1}{w^2}+(c^2+d^2)\frac{1}{z^2}+(b^2 +d^2)\frac{1}{y^2}+(b^2+d^2)\frac{1}{x^2}}{abcd(\frac{1}{x^2 }+\frac{1}{w^2}+\frac{1}{y^2}+\frac{1}{z^2})}$$frac{(b^2+c^2)\frac{1}{w^2}+(c^2+d^2)\frac{1}{z^2}+(b^2 +d^2)\frac{1}{y^2}+(b^2+d^2)\frac{1}{x^2}}{(b+c)(c+d)(d+a)(a +b)}$$故所求的值为$\frac{(b^2+c^2)\frac{1}{w^2}+(c^2+d^2)\frac{1}{z^2}+(b^2+d ^2)\frac{1}{y^2}+(b^2+d^2)\frac{1}{x^2}}{(b+c)(c+d)(d+a)(a+b )}$。
