热点与圆有关的计算问题含答案
人教版2020年中考数学一轮复习《与圆有关的证明和计算》大题专项练习含答案解析

中考专题——与圆有关的证明和计算纵观近几年全国各地中考题,圆的有关概念以及性质等一般以填空题,选择题的形式考查并占有一定的分值;圆的有关性质,如垂径定理,圆周角,切线的判定与性质等综合性问题的运用一般以计算证明的形式考查;一般在10分-15分左右,以后发展中利用圆的知识与其他知识点如函数,方程等相结合作为中考压轴题将会占有非常重要的地位。
考查的类型:(1)线段、角以及切线的证明;(2)利用勾股定理、相似以及锐角三角函数进行线段,比值和阴影面积的求解.例题精讲:1、如图,点O为Rt△ABC斜边AB上一点,以OA为半径的⊙O与BC切于点D,与AC 交于点E,连接AD.(1)求证:AD平分∠BAC;(2)若∠BAC=60°,OA=2,求阴影部分的面积(结果保留π).2、如图,A,P,B,C是圆上的四个点,∠APC=∠CPB=60°,AP,CB的延长线相交于点D.(1)求证:△ABC是等边三角形;(2)若∠PAC=90°,AB=2,求PD的长.3、如图,∠BAC的平分线交△ABC的外接圆于点D,∠ABC的平分线交AD于点E,(1)求证:DE=DB;(2)若∠BAC=90°,BD=4,求△ABC外接圆的半径.4、如图,△ABC为等腰三角形,O是底边BC的中点,腰AB与⊙O相切于点D,OB与⊙O相交于点E.(1)求证:AC是⊙O的切线;(2)若BD=,BE=1.求阴影部分的面积.5、如图,AB是⊙O的直径,C是⊙O上一点,过点O作OD⊥AB,交BC的延长线于D,交AC于点E,F是DE的中点,连接CF.(1)求证:CF是⊙O的切线.(2)若∠A=22.5°,求证:AC=DC.补充练习:1、如图,在△ABC中,AB=AC,以AB为直径作⊙O,分别交BC,AC于点D,E,过点D作DF⊥AC于点F.(1)求证:DF是⊙O的切线;(2)若∠C=60°,⊙O的半径为2,求由弧DE,线段DF,EF围成的阴影部分的面积(结果保留根号和π)2、如图,在Rt△ABC中,∠C=90°,AC=BC,点O在AB上,经过点A的⊙O与BC相切于点D,交AB于点E.(1)求证:AD平分∠BAC;(2)若CD=1,求图中阴影部分的面积(结果保留π).3、如图,在△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,交AB于点E,过点D作DF⊥AB,垂足为F,连接DE.(1)求证:直线DF与⊙O相切;(2)若AE=7,BC=6,求AC的长.4、如图,AB为半圆O的直径,AC是⊙O的一条弦,D为的中点,作DE⊥AC,交AB 的延长线于点F,连接DA.(1)求证:EF为半圆O的切线;(2)若DA=DF=6,求阴影区域的面积.(结果保留根号和π)5、如图所示,以△ABC的边AB为直径作⊙O,点C在⊙O上,BD是⊙O的弦,∠A=∠CBD,过点C作CF⊥AB于点F,交BD于点G,过C作CE∥BD交AB的延长线于点E.(1)判断CE与⊙O的位置关系,并说明理由;(2)若∠DBA=30°,CG=8,求BE的长.6、如图,AB为⊙O的直径,C,E为⊙O上的两点,若AC平分∠EAB,CD⊥AE于点D.(1)求证:DC是⊙O的切线;3,求DE的长;(2)若AO=6,DC=33,求图中阴影部分面积.(3)过点C作CF⊥AB于F,如图2,若AD-OA=1.5,AC=3答案解析例题精讲:1、(1)证明:∵⊙O切BC于D,∴OD⊥BC,∵AC⊥BC,∴AC∥OD,∴∠CAD=∠ADO,∵OA=OD,∴∠OAD=∠ADO,∴∠OAD=∠CAD,即AD平分∠CAB;(2)设EO与AD交于点M,连接ED.∵∠BAC=60°,OA=OE,∴∠AEO是等边三角形,∴AE=OA,∠AOE=60°,∴AE=A0=OD,又由(1)知,AC∥OD即AE∥OD,∴四边形AEDO是菱形,则△AEM≌△DMO,∠EOD=60°,∴S△AEM=S△DMO,∴S阴影=S扇形EOD==.2、(1)证明:∵∵ABC=∵APC,∵BAC=∵BPC,∵APC=∵CPB=60°,∵∵ABC=∵BAC=60°,∵∵ABC是等边三角形.(2)解:∵∵ABC是等边三角形,AB=2,∵AC=BC=AB=2,∵ACB=60°.在Rt∵PAC中,∵PAC=90°,∵APC=60°,AC=2,∵AP=AC•cot∵APC=2.在Rt∵DAC中,∵DAC=90°,AC=2,∵ACD=60°,∵AD=AC•tan∵ACD=6.∵PD=AD﹣AP=6﹣2=4.3、(1)证明:∵BE平分∠BAC,AD平分∠ABC,∴∠ABE=∠CBE,∠BAE=∠CAD,∴,∴∠DBC=∠CAD,∴∠DBC=∠BAE,∵∠DBE=∠CBE+∠DBC,∠DEB=∠ABE+∠BAE,∴∠DBE=∠DEB,∴DE=DB;(2)解:连接CD,如图所示:由(1)得:,∴CD=BD=4,∵∠BAC=90°,∴BC是直径,∴∠BDC=90°,∴BC==4,∴△ABC外接圆的半径=×4=2.4、(1)证明:连接OD,作OF⊥AC于F,如图,∵△ABC为等腰三角形,O是底边BC的中点,∴AO⊥BC,AO平分∠BAC,∵AB与⊙O相切于点D,∴OD⊥AB,∵OF⊥AC,∴OF=OD,∴AC是⊙O的切线;(2)解:在Rt△BOD中,设⊙O的半径为r,则OD=OE=r,∴r2+()2=(r+1)2,解得r=1,∴OD=1,OB=2,∴∠B=30°,∠BOD=60°,∴∠AOD=30°,在Rt△AOD中,AD=OD=,∴阴影部分的面积=2S△AOD﹣S扇形DOF=2××1×﹣=﹣.5、(1)证明:∵AB 是⊙O 的直径,∴∠ACB =∠ACD =90°,∵点F 是ED 的中点,∴CF =EF =DF ,∴∠AEO =∠FEC =∠FCE ,∵OA =OC ,∴∠OCA =∠OAC ,∵OD ⊥AB ,∴∠OAC+∠AEO =90°, ∴∠OCA+∠FCE =90°,即OC ⊥FC ,∴CF 与⊙O 相切;(2)解:∵OD ⊥AB ,AC ⊥BD ,∴∠AOE =∠ACD =90°,∵∠AEO =∠DEC ,∴∠OAE =∠CDE =22.5°, ∵AO =BO ,∴AD =BD ,∴∠ADO =∠BDO =22.5°,∴∠ADB =45°,∴∠CAD =∠ADC =45°,∴AC =CD .补充练习:1、(1)如图,连接OD ∵AB 为⊙O 的直径∴AD ⊥BC ∵AB=AC ∴BD=CD ,D 为BC 中点∵O 为AB 中点∴OD ∥AC ∵DF ⊥AC ∴DF ⊥OD ∴DF 为⊙O 的切线(2)如图,连接OE 、OD ∵AB=AC ,∠C=60°∴△ABC 为等边三角形∴∠B=∠A=60°,AB=AC=BC=2⨯2=4∵OA=OB=OD=OE ∴△OAE ,△OBD 都是等边三角形∴∠ODB=∠BOD=∠AOE -∠OEA=∠C=60° ∴∠DOE=180°-2⨯60°=60°,OD ∥AC ,OE ∥BC ∴四边形ODCE 是平行四边形∴OD=CE=BD=CD=2∴DF=CDsin60°=3232=⨯,CF=CDcos60°=1212=⨯ ∴ππ32-323360260-3121-32--2=⨯⨯⨯⨯==∆ODE CDF S S S S 扇形平行四边形阴影2、(1)证明:连接DE 、OD ∵BC 相切⊙O 于点D ∴∠CDA=∠AED ∵AE 为直径∴∠ADE=90°∵AC ⊥BC ∴∠ACD=90°∴∠DAO=∠CAD ∴AD 平分∠BAC(3)在Rt △ABC 中,∠C=90°,AC=BC ∴∠B=∠BAC=45°∵BC 相切⊙O 于点D ∴∠ODB=90°∴OD=BD ,∠BOD=45°设BD=x ,则OD=OA=x ,0B=3x ∴BC=AC=x+1∵AC 2+BC 2=AB 2∴22)2()12x x x +=+( 所以x=2∴BD=OD=2 ∴()4-1360245-22212ππ=⨯⨯=-∆=DOE S BOD S S 扇形阴影3、(1)证明:连接OD ,∵AB=AC ,∴∠B=∠C 。
2024河南中考数学复习 与圆有关的计算(含阴影部分面积) 强化精练 (含答案)

2024河南中考数学复习与圆有关的计算(含阴影部分面积)强化精练基础题1.(2023兰州)如图①是一段弯管,弯管的部分外轮廓线如图②所示是一条圆弧AB ︵,圆弧的半径OA =20cm ,圆心角∠AOB =90°,则AB ︵=()第1题图A.20πcmB.10πcmC.5πcmD.2πcm2.(2023新疆维吾尔自治区)如图,在⊙O 中,若∠ACB =30°,OA =6,则扇形OAB (阴影部分)的面积是()第2题图A.12πB.6πC.4πD.2π3.(2023鄂州)如图,在△ABC 中,∠ABC =90°,∠ACB =30°,AB =4,点O 为BC 的中点,以O 为圆心,OB 长为半径作半圆,交AC 于点D ,则图中阴影部分的面积是()第3题图A.53-33πB.53-4πC.53-2πD.103-2π4.(2023连云港)如图,矩形ABCD 内接于⊙O ,分别以AB 、BC 、CD 、AD 为直径向外作半圆.若AB =4,BC =5,则阴影部分的面积是()第4题图A.414π-20B.412π-20C.20πD.205.(2023金华)如图,在△ABC 中,AB =AC =6cm ,∠BAC =50°,以AB 为直径作半圆,交BC 于点D ,交AC 于点E ,则弧DE 的长为________cm.第5题图6.如图,在2×3的网格图中,每个小正方形的边长均为1,点A ,B ,C ,D 都在格点上,线段CD 与AC ︵交于点E ,则图中AE ︵的长度为________.第6题图7.(2023重庆A 卷)如图,⊙O 是矩形ABCD 的外接圆,若AB =4,AD =3,则图中阴影部分的面积为________.(结果保留π)第7题图8.(2023包头)如图,正方形ABCD的边长为2,对角线AC,BD相交于点O,以点B为圆心,对角线BD的长为半径画弧,交BC的延长线于点E,则图中阴影部分的面积为________.第8题图9.(万唯原创)如图,在Rt△ABC中,∠BAC=90°,∠B=30°,AC=2,以点A为圆心,AC 长为半径作弧,分别交AB,BC于点D,E,则图中阴影部分的周长为________.第9题图10.(2023新乡一模)如图,△ABC中,∠C=90°,AC=BC=2.将△ABC绕着点A顺时针旋转90度到△AB1C1的位置,则边BC扫过区域的面积为________.第10题图11.(2023驻马店二模)如图,将扇形OAB沿OA方向平移得到对应扇形CDE,线段CE交AB︵于点F,当OC=CF时平移停止.若∠O=60°,OB=3,则阴影部分的面积为________.第11题图拔高题12.(2023通辽)如图,在扇形AOB中,∠AOB=60°,OD平分∠AOB交AB︵于点D,点C是半径OB 上一动点,若OA =1,则阴影部分周长的最小值为()A.2+π6B.2+π3C.22+π6 D.22+π3第12题图13.如图,两个半径长均为2的直角扇形的圆心分别在对方的圆弧上,扇形CFD 的圆心C 是AB ︵的中点,且扇形CFD 绕着点C 旋转,半径AE ,CF 交于点G ,半径BE ,CD 交于点H ,则图中阴影部分面积等于()第13题图A.π2-1B.π2-2C.π-1D.π-214.如图,AB 为⊙O 的直径,将BC ︵沿BC 翻折,翻折后的弧交AB 于点D.若BC =45,sin ∠ABC =55,则图中阴影部分的面积为()第14题图A.25πB.25πC.8D.1015.如图,在矩形ABCD中,AD=2,AB=22,对角线AC,BD交于点O,以A为圆心,AB的长为半径画弧,交CD于点F,连接FO并延长交AB于点M,连接AF,则图中阴影部分的面积是______.(结果保留π)第15题图参考答案与解析1.B 【解析】∵圆弧的半径OA =20cm ,圆心角∠AOB =90°,∴ AB 的长=90π×20180=10π(cm).2.B 【解析】∵∠ACB =30°,∴∠AOB =2∠ACB =60°,∴S 扇形AOB =60×π×62360=6π.3.C【解析】如解图,连接OD ,BD ,在Rt △ABC 中,tan 30°=AB BC ,∴BC =AB tan 30°=43,∵OC =OD ,∴∠OCD =∠ODC =30°,∴∠BOD =60°,∵BO =DO ,∴△BOD 是等边三角形,∴BD =BO =12BC =23,∠BDO =60°,∴∠BDC =90°,AD =BD ·tan 30°=2.∴S 阴影部分=S △ABD +S △BOD -S 扇形BOD =12×23×2+34×(23)2-60π×(23)2360=53-2π.第3题解图4.D 【解析】如解图,连接AC ,∵矩形ABCD 内接于⊙O ,AB =4,BC =5,∴AC 2=AB 2+BC 2,∴阴影部分的面积为S矩形ABCD +π×(AB 2)2+π×(BC 2)2-π×(AC 2)2=S 矩形ABCD +π×14(AB 2+BC 2-AC 2)=S 矩形ABCD =4×5=20.第4题解图5.56π【解析】如解图,连接OE ,OD ,∵OD =OB ,∴∠B =∠ODB ,∵AB =AC ,∴∠B =∠C ,∴∠C =∠ODB ,∴OD ∥AC ,∴∠EOD =∠AEO ,∵OE =OA ,∴∠OEA =∠BAC =50°,∴∠EOD =∠BAC =50°,∵OD =12AB =12×6=3(cm),∴ DE 的长为50π×3180=56π(cm).6.54π【解析】如解图,连接AC ,AD ,设AC 交网格线于点O ,连接OE .∵AD 2=22+12=5,AC 2=22+12=5,CD 2=12+32=10,∴AD =AC ,AD 2+AC 2=CD 2,∴△ACD 是等腰直角三角形,∴∠ACD =45°,∵∠ABC 是直角,∴AC 是⊙O 的直径,∴∠AOE =90°.∵AC =5,∴OE =OA =12AC =52,∴ AE 的长为90π×52180=54π.第6题解图7.254π-12【解析】如解图,连接BD ,由题知∠BAD =90°,∴BD 是⊙O 的直径,∵AB =4,AD =3,∴BD =AD 2+AB 2=32+42=5,∴S 阴影=S ⊙O -S 矩形ABCD =π×(52)2-3×4=254π-12.第7题解图8.π【解析】∵正方形ABCD 对角线相交于点O ,∴AO =BO ,CO =DO ,∠AOD =∠BOC ,∴△AOD ≌△BOC ,∴阴影部分的面积=扇形DBE 的面积,∵正方形的边长为2,∴由勾股定理得BD =22,∠DBC =45°,∴阴影部分的面积=45360×π·(22)2=π.9.π3+23【解析】如解图,连接AE ,∵在Rt △ABC 中,∠B =30°,∴BC =2AC =4,AB =23.∵ DE 是以点A 为圆心,AC 长为半径的弧,∴AD =AE =AC =2,∴BD =AB -AD=23-2,∠AEC =∠C =60°,∴△AEC 为等边三角形,∴AE =EC =2.,∴BE =2,∠BAE=∠B =30°,∴ DE 的长为30π×2180=π3,∴阴影部分的周长为2+π3+23-2=π3+23.10.π【解析】在△ABC 中,∠ACB =90°,AC =BC =2,由勾股定理得,AB =22+22=22,∵将△ABC 绕着点A 顺时针旋转90度到△AB 1C 1的位置,∴∠CAC 1=90°,∴阴影部分的面积S =S 扇形BAB 1+S △B 1AC 1-S △ACB -S 扇形CAC 1=S 扇形BAB 1-S 扇形CAC 1=90π×(22)2360-90π×22360=π.11.3π4-334【解析】如解图,连接OF ,过点C 作CH ⊥OF 于点H ,由平移性质知,CE ∥OB ,∴∠CFO =∠BOF ,∵CO =CF ,∴∠COF =∠CFO ,∴∠COF =∠BOF =12∠BOC =30°,在等腰△OCF 中,OH =12OF =12OB =32,∴CH =OH ·tan 30°=32×33=32,∴S 阴影=S 扇形AOF -S △COF =30·π×32360-12×3×32=3π4-334.第11题解图12.A 【解析】如解图,作D 点关于直线OB 的对称点E ,连接AE ,OE ,DE ,CE ,AE 与OB 的交点为C 点,则CD =CE ,OD =OE ,∠DOB =∠EOB ,∴AC +CD =AC +CE ≥AE ,当A ,C ,E 三点共线时,AC +CD 取得最小值,此时阴影部分周长最小,在扇形AOB 中,∠AOB =60°,OD 平分∠AOB 交 AB 于点D ,∴∠AOD =∠BOD =30°,由轴对称的性质,∠EOB =∠BOD =30°,OE =OD ,∴∠AOE =90°,∴△AOE 是等腰直角三角形,∵OA =1,∴AE =2, AD 的长=30π×1180=π6,∴阴影部分周长的最小值为2+π6.第12题解图13.D 【解析】两扇形的面积和为180π·(2)2360=π,如解图,过点C 作CM ⊥AE 于点M ,CN ⊥BE 于点N ,连接CE ,则四边形EMCN 是矩形,∵点C 是 AB 的中点,∴EC 平分∠AEB ,∴CM =CN ,∴矩形EMCN 是正方形,∵∠MCG +∠FCN =90°,∠NCH +∠FCN =90°,∴∠MCG =∠NCH ,在△CMG 与△CNH 中,MCG =∠NCH ,=CN ,CMG =∠CNH ,∴△CMG ≌△CNH (ASA),∴中间空白区域面积相当于对角线是2的正方形面积,∴空白区域的面积为12×2×2=1,∴图中阴影部分的面积=π-2.第13题解图14.C 【解析】如解图,连接AC ,CD ,过点C 作CH ⊥AB 于点H ,∵∠ABC =∠DBC ,∴ AC = CD,∴AC =CD ,∵CH ⊥AD ,∴AH =HD ,∵BC =45,sin ∠ABC =55,∴CH =BC ·sin ∠ABC =4,∵AB 为⊙O 的直径,∴∠ACB =90°,∵sin ∠ABC =AC AB =55,∴设AC =5m ,AB =5m ,根据勾股定理,AC 2+BC 2=AB 2,∴5m 2+80=25m 2,∴m =2(负值已舍去),∴AC =CD =25,∴AH =AC 2-CH 2=(25)2-42=2,∴AD =2AH =4,∴S 阴影=S △ACD =12AD ·CH =12×4×4=8.第14题解图15.π-22+2【解析】在矩形ABCD 中,AD =2,AB =22,∴∠ADC =90°,AB ∥CD ,OB =OD ,∴∠ABD =∠CDB ,∵AF =AB =22,AF 2=AD 2+DF 2,∴(22)2=22+DF 2,∴DF =2,∴AD =DF ,∴∠DAF =∠DFA =45°,∴∠BAF =45°,在△BOM 和△DOF 中,MBO =∠FDO=ODBOM =∠DOF ,∴△BOM ≌△DOF (ASA),∴BM =DF =2,∴AM =22-2,∴图中45π×(22)2360-12×(22-2)×2=π-22+2.阴影部分的面积为:。
中考数学复习专题24:圆的有关计算(含中考真题解析)
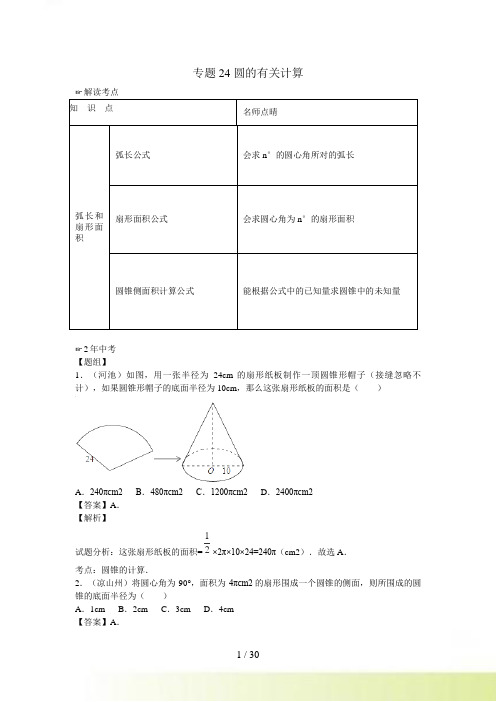
专题24 圆的有关计算☞解读考点知识点名师点晴弧长和扇形面积弧长公式会求n°的圆心角所对的弧长扇形面积公式会求圆心角为n°的扇形面积圆锥侧面积计算公式能根据公式中的已知量求圆锥中的未知量☞2年中考【题组】1.(河池)如图,用一张半径为24cm的扇形纸板制作一顶圆锥形帽子(接缝忽略不计),如果圆锥形帽子的底面半径为10cm,那么这张扇形纸板的面积是()A.240πcm2 B.480πcm2 C.1200πcm2 D.2400πcm2【答案】A.【解析】试题分析:这张扇形纸板的面积=12×2π×10×24=240π(cm2).故选A.考点:圆锥的计算.2.(凉山州)将圆心角为90°,面积为4πcm2的扇形围成一个圆锥的侧面,则所围成的圆锥的底面半径为()A.1cm B.2cm C.3cm D.4cm【答案】A.考点:圆锥的计算.3.(德州)如图,要制作一个圆锥形的烟囱帽,使底面圆的半径与母线长的比是4:5,那么所需扇形铁皮的圆心角应为()A.288° B.144° C.216° D.120°【答案】A.【解析】试题分析:∵底面圆的半径与母线长的比是4:5,∴设底面圆的半径为4x,则母线长是5x,设圆心角为n°,则524180n xxππ⨯⨯=,解得:n=288,故选A .考点:圆锥的计算.4.(宁波)如图,用一个半径为30cm,面积为300πcm2的扇形铁皮,制作一个无底的圆锥(不计损耗),则圆锥的底面半径r为()A.5cm B.10cm C.20cm D.5πcm【答案】B.考点:圆锥的计算.5.(苏州)如图,AB为⊙O的切线,切点为B,连接AO,AO与⊙O交于点C,BD为⊙O的直径,连接CD.若∠A=30°,⊙O的半径为2,则图中阴影部分的面积为()A .433π-B .4233π-C .3π-D .233π-【答案】A .【解析】试题分析:过O 点作OE ⊥CD 于E ,∵AB 为⊙O 的切线,∴∠ABO=90°,∵∠A=30°,∴∠AOB=60°,∴∠COD=120°,∠OCD=∠ODC=30°,∵⊙O 的半径为2,∴OE=1,CE=DE=3,∴CD=23,∴图中阴影部分的面积为:2120211233602⋅π⋅-⨯⨯=433π-.故选A .考点:1.扇形面积的计算;2.切线的性质.6.(成都)如图,正六边形ABCDEF 内接于⊙O ,半径为4,则这个正六边形的边心距OM 和BC 弧线的长分别为( )A .2,3πB .23,πC .3,23πD .23,43π【答案】D .考点:1.正多边形和圆;2.弧长的计算.7.(甘孜州)如图,已知扇形AOB的半径为2,圆心角为90°,连接AB,则图中阴影部分的面积是()A.π﹣2 B.π﹣4 C.4π﹣2 D.4π﹣4【答案】A.【解析】试题分析:S阴影部分=S扇形OAB﹣S△OAB=29021223602π⨯-⨯⨯=π﹣2.故选A.考点:扇形面积的计算.8.(攀枝花)如图,已知⊙O的一条直径AB与弦CD相交于点E,且AC=2,AE=3,CE=1,则图中阴影部分的面积为()A 239π439πC.29πD.49π【答案】D.考点:1.扇形面积的计算;2.勾股定理的逆定理;3.圆周角定理;4.解直角三角形. 9.(自贡)如图,AB 是⊙O 的直径,弦CD ⊥AB ,∠CDB =30°,CD =32,则阴影部分的面积为( )A .2πB .πC .3πD .32π【答案】D . 【解析】试题分析:连接OD .∵CD ⊥AB ,∴CE=DE=12CD=3(垂径定理),故S △OCE=S △ODE ,即可得阴影部分的面积等于扇形OBD 的面积,又∵∠CDB=30°,∴∠COB=60°(圆周角定理),∴OC=2,故S 扇形OBD=2602360π⨯=32π,即阴影部分的面积为32π.故选D .考点:1.扇形面积的计算;2.垂径定理;3.圆周角定理;4.解直角三角形. 10.(达州)如图,直径AB 为12的半圆,绕A 点逆时针旋转60°,此时点B 旋转到点B′,则图中阴影部分的面积是( )A .12πB .24πC .6πD .36π 【答案】B .考点:1.扇形面积的计算;2.旋转的性质.11.(德阳)如图,已知⊙O 的周长为4π,AB 的长为π,则图中阴影部分的面积为( )A .2π-B .3π-C .πD .2 【答案】A .考点:1.扇形面积的计算;2.弧长的计算.12.(梧州)如图,在边长为6的正方形ABCD中,E是AB的中点,以E为圆心,ED为半径作半圆,交A、B所在的直线于M、N两点,分别以直径MD、ND为直径作半圆,则阴影部分面积为()A.95 B.185 C.365 D.725【答案】B.【解析】试题分析:根据图形可知阴影部分的面积=两个小的半圆的面积+△DMN的面积﹣大半圆的面积.∵MN的半圆的直径,∴∠MDN=90°.在Rt△MDN中,MN2=MD2+DN2,∴两个小半圆的面积=大半圆的面积.∴阴影部分的面积=△DMN的面积.在Rt△AOD中,OD=22AD AO+=2263+=35,∴阴影部分的面积=△DMN的面积=12MN•AD=16562⨯⨯=185.故选B.考点:1.扇形面积的计算;2.勾股定理;3.综合题.13.(咸宁)如图,在△ABC中,CA=CB,∠ACB=90°,以AB的中点D为圆心,作圆心角为90°的扇形DEF,点C恰在EF上,设∠BDF=α(0°<α<90°),当α由小到大变化时,图中阴影部分的面积()A.由小到大 B.由大到小 C.不变 D.先由小到大,后由大到小【答案】C.考点:1.扇形面积的计算;2.定值问题;3.综合题.14.(常德)若两个扇形满足弧长的比等于它们半径的比,则这称这两个扇形相似.如图,如果扇形AOB 与扇形A1O1B1是相似扇形,且半径OA :O1A1=k (k 为不等于0的常数).那么下面四个结论:①∠AOB=∠A1O1B1;②△AOB ∽△A1O1B1;③11ABk A B ;④扇形AOB 与扇形A1O1B1的面积之比为2k . 成立的个数为( )A .1个B .2个C .3个D .4个【答案】D .考点:1.相似三角形的判定与性质;2.弧长的计算;3.扇形面积的计算;4.新定义;5.压轴题.15.(邵阳)如图,在矩形ABCD 中,已知AB=4,BC=3,矩形在直线l 上绕其右下角的顶点B 向右旋转90°至图①位置,再绕右下角的顶点继续向右旋转90°至图②位置,…,以此类推,这样连续旋转次后,顶点A 在整个旋转过程中所经过的路程之和是( )A .πB .3019.5πC .3018πD .3024π 【答案】D . 【解析】试题分析:转动一次A 的路线长是:90331802ππ⨯=,转动第二次的路线长是:90551802ππ⨯=,转动第三次的路线长是:9042180ππ⨯=,转动第四次的路线长是: 0,转动五次A 的路线长是:90331802ππ⨯=,以此类推,每四次循环,故顶点A 转动四次经过的路线长为:32π+52π+2π=6π,÷4=503余3,顶点A 转动四次经过的路线长为:6π×504=3024π.故选D .考点:1.旋转的性质;2.弧长的计算;3.规律型. 16.(北海)用一个圆心角为120°,半径为6的扇形作一个圆锥的侧面,这个圆锥的底面圆的半径是 . 【答案】2.考点:圆锥的计算.17.(贵港)如图,已知圆锥的底面⊙O的直径BC=6,高OA=4,则该圆锥的侧面展开图的面积为.【答案】15π.【解析】试题分析:∵OB=12BC=3,OA=4,由勾股定理,AB=5,侧面展开图的面积为:12×6π×5=15π.故答案为:15π.考点:圆锥的计算.18.(庆阳)如图,Rt△ABC中,∠ACB=90°,AC=BC=22,若把Rt△ABC绕边AB 所在直线旋转一周,则所得几何体的表面积为(结果保留π).【答案】2π.【解析】试题分析:过点C作CD⊥AB于点D,Rt△ABC中,∠ACB=90°,AC=BC,∴2,∴CD=2,以CD为半径的圆的周长是:4π.故直线旋转一周则所得的几何体得表面积是:2×12×4π×2282π.故答案为:82π.考点:1.圆锥的计算;2.点、线、面、体.19.(贺州)如图,在矩形ABCD中,AB=3,AD=4,将矩形ABCD绕点D顺时针旋转90°得到矩形A′B′C′D′,则点B经过的路径与BA,AC′,C′B′所围成封闭图形的面积是(结果保留π).【答案】2512 4π+.考点:1.扇形面积的计算;2.旋转的性质.20.(天水)如图,△ABC是正三角形,曲线CDEF叫做正三角形的渐开线,其中弧CD、弧DE、弧EF的圆心依次是A、B、C,如果AB=1,那么曲线CDEF的长是.【答案】4π.考点:1.弧长的计算;2.等边三角形的性质;3.综合题.21.(河南省)如图,在扇形AOB中,∠AOB=90°,点C为OA的中点,CE⊥OA交AB于点E,以点O为圆心,OC的长为半径作CD交OB于点D.若OA=2,则阴影部分的面积为.【答案】3 122π+.【解析】试题分析:连接OE、AE ,∵点C为OA的中点,∴∠CEO=30°,∠EOC=60°,∴△AEO为等边三角形,∴S扇形AOE=2602360π⨯=23π,S扇形ABO=2902360π⨯=π,S扇形CDO=2901360π⨯=14π,∴S阴影=S扇形ABO﹣S扇形CDO﹣(S扇形AOE﹣S△COE)=121(13)432πππ---⨯⨯=3122π+.故答案为:3122π+.考点:扇形面积的计算.22.(烟台)如图,将弧长为6π,圆心角为120°的圆形纸片AOB围成圆锥形纸帽,使扇形的两条半径OA与OB重合(粘连部分忽略不计)则圆锥形纸帽的高是.【答案】62.考点:圆锥的计算.23.(乐山)如图,已知A (23,2)、B (23,1),将△AOB 绕着点O 逆时针旋转,使点A 旋转到点A′(﹣2,23)的位置,则图中阴影部分的面积为 .【答案】34π.【解析】试题分析:∵A (232)、B (23,1),∴OA=4,13,∵由A (232)使点A 旋转到点A′(﹣2,23),∴∠A′OA=∠B′OB=90°,根据旋转的性质可得,''OB C OBC S S ∆∆=,∴阴影部分的面积等于S 扇形A'OA ﹣S 扇形C'OC=22114(13)44ππ⨯-⨯=34π,故答案为:34π.考点:1.扇形面积的计算;2.坐标与图形变化-旋转.24.(镇江)图①是我们常见的地砖上的图案,其中包含了一种特殊的平面图形﹣正八边形.(1)如图②,AE是⊙O的直径,用直尺和圆规作⊙O的内接正八边形ABCDEFGH(不写作法,保留作图痕迹);(2)在(1)的前提下,连接OD,已知OA=5,若扇形OAD(∠AOD<180°)是一个圆锥的侧面,则这个圆锥底面圆的半径等于.【答案】(1)作图见试题解析;(2)15 8.试题解析:(1)如图所示,八边形ABCDEFGH即为所求;(2)∵八边形ABCDEFGH是正八边形,∴∠AOD=3608×3=135°,∵OA=5,∴AD的长=1355180π⨯=154π,设这个圆锥底面圆的半径为R,∴2πR=154π,∴R=158,即这个圆锥底面圆的半径为158.故答案为:158.考点:1.正多边形和圆;2.圆锥的计算;3.作图—复杂作图.25.(宁德)图(1)是一个蒙古包的照片,这个蒙古包可以近似看成是圆锥和圆柱组成的几何体,如图(2)所示.(1)请画出这个几何体的俯视图;(2)图(3)是这个几何体的正面示意图,已知蒙古包的顶部离地面的高度EO1=6米,圆柱部分的高OO1=4米,底面圆的直径BC=8米,求∠EAO的度数(结果精确到0.1°).【答案】(1)答案见试题解析;(2)26.6°.(2)连接EO1,如图所示,∵EO1=6米,OO1=4米,∴EO=EO1﹣OO1=6﹣4=2米,∵AD=BC=8米,∴OA=OD=4米,在Rt△AOE中,tan∠EAO=2142EOOA==,则∠EAO≈26.6°.考点:1.圆锥的计算;2.圆柱的计算;3.作图-三视图.26.(玉林防城港)如图,在⊙O中,AB是直径,点D是⊙O上一点且∠BOD=60°,过点D作⊙O的切线CD交AB的延长线于点C,E为AD的中点,连接DE,EB.(1)求证:四边形BCDE是平行四边形;(2)已知图中阴影部分面积为6π,求⊙O的半径r.【答案】(1)证明见试题解析;(2)6.考点:1.切线的性质;2.平行四边形的判定;3.扇形面积的计算;4.综合题.27.(扬州)如图,已知⊙O的直径AB=12cm,AC是⊙O的弦,过点C作⊙O的切线交BA的延长线于点P,连接BC.(1)求证:∠PCA=∠B;(2)已知∠P=40°,点Q在优弧ABC上,从点A开始逆时针运动到点C停止(点Q与点C不重合),当△ABQ与△ABC的面积相等时,求动点Q所经过的弧长.【答案】(1)证明见试题解析;(2)53π或133π或233π.【解析】试题分析:(1)连接OC,由PC是⊙O的切线,得到∠1+∠PCA=90°,由AB是⊙O的直径,得到∠2+∠B=90°,从而得到结论;(2)△ABQ与△ABC的面积相等时,有三种情况,即:①当∠AOQ=∠AOC=50°时;②当∠BOQ=∠AOC=50°时;③当∠BOQ=50°时,即∠AOQ=230°时;分别求得点Q所经过的弧长即可.试题解析:(1)连接OC,∵PC是⊙O的切线,∴∠PCO=90°,∴∠1+∠PCA=90°,∵AB是⊙O的直径,∴∠ACB=90°,∴∠2+∠B=90°,∵OC=OA,∴∠1=∠2,∴∠PCA=∠B;考点:1.切线的性质;2.弧长的计算;3.分类讨论;4.综合题;5.轨迹.【题组】1.(·扬州)如图,已知正方形边长为1,若圆与正方形的四条边都相切,则阴影部分的面积与下列各数最接近的是()A.1.0 B.2.0 C.3.0 D.4.0【答案】B.【解析】试题分析:∵正方形的边长为1,圆与正方形的四条边都相切,∴22S S S10.510.250.215ππ=-=-⋅=-≈阴影正方形圆.∵0.215最接近0.2,∴阴影部分的面积与下列各数最接近的是0.2故选B.考点:1.圆和正方形的面积;2.无理数的大小估计;3.转换思想的应用.2.(·金华)一张圆心角为45°的扇形纸板和圆形纸板按如图方式剪得一个正方形,边长都为1,则扇形纸板和圆形纸板的面积比是()A.5:4 B.5:2 C52 D52【答案】A.故选A.考点:1.等腰直角三角形的判定和性质;2.勾股定理;3.扇形面积和圆面积的计算.3.(·辽宁省本溪市)底面半径为4,高为3的圆锥的侧面积是()A.12π B.15π C.20π D.36π【答案】B.【解析】试题分析:∵圆锥的底面半径为3,高为4,∴母线长为5,∴圆锥的侧面积为:πrl=π×3×5=15π,故选B.考点:圆锥的计算.4.(·山东省莱芜市)一个圆锥的侧面展开图是半径为R的半圆,则该圆锥的高是()A.R B.12R C3R D.32R【答案】D.【解析】试题分析:圆锥的底面周长是:πR;设圆锥的底面半径是r,则2πr=πR.解得:r=12R2213()22R R-=.故选D.考点:圆锥的计算.5.(·贵州安顺市)已知圆锥的母线长为6cm,底面圆的半径为3cm,则此圆锥侧面展开图的圆心角是()A . 30°B . 60°C .90°D .180°【答案】D .考点:圆锥的计算.6.(湖南衡阳市)圆心角为120,弧长为12π的扇形半径为 ( ) A .6 B .9 C .18 D .36 【答案】C .【解析】试卷分析:12012180rππ=,解得:r=18.故选C .考点:圆的计算.7. (南京) 如图,沿一条母线将圆锥侧面剪开并展开,得到一个扇形,若圆锥底面圆半径r=2cm ,扇形圆心角120θ=︒,则该圆锥母线长l 为 cm .【答案】6. 【解析】试题分析:∵圆锥底面圆半径r=2cm , ∴根据圆的周长公式,得圆的周长为2r 4ππ=,∵侧面展开后所得扇形弧长等于圆的周长,∴扇形弧长4π=.又∵侧面展开后所得扇形的圆心角为120°,∴根据扇形的弧长公式,侧面展开后所得扇形的弧长为()120l4l 6180cm ππ⋅⋅=⇒=.考点:圆锥和扇形的计算. 8.(·呼和浩特)一个底面直径是80cm ,母线长为90cm 的圆锥的侧面展开图的圆心角的度数为 . 【答案】1600.考点:圆锥的计算.9.(·潍坊)如图,两个半径均为3的⊙O1与⊙O2相交于A 、B 两点,且每个圆都经过另一个圆的圆心,则图中阴影部分的面积为 .(结果保留π)【答案】233π-.【解析】试题分析:如图,连接O1O2,过点O1作O1H ⊥AO2于点H ,由题意可得:AO1=O1O2=AO2=3,∴△AO1O2是等边三角形.∴11233HO O O sin60322=︒=⋅=.∴()12122AO O AO O 6031333S 3S 223,2460ππ∆⨯=⨯⨯===扇形.∴12212AO O AO AO O 33S S S 24π∆=-=-弓形扇形.∴图中阴影部分的面积为:33423324ππ⎛⎫-=- ⎪ ⎪⎝⎭ .考点:1.扇形面积的计算;2.等边三角形的判定和性质;3.相交两圆的性质;4. 锐角三角函数定义;5.特殊角的三角函数值;6.转换思想的应用. 10.(·重庆A )如图,△OAB 中,OA=OB=4,∠A=30°,AB 与⊙O 相切于点C ,则图中阴影部分的面积为 .(结果保留π)【答案】4433π-.考点:1.切线的性质;2.等腰三角形的性质;3.含30度角的直角三角形的性质;4.勾股定理;5.扇形面积的计算;6.转换思想的应用.☞考点归纳归纳 1:弧长公式 基础知识归纳:n °的圆心角所对的弧长l 的计算公式为180n r l π=注意问题归纳:①在弧长的计算公式中,n 是表示1°的圆心角的倍数,n 和180都不要带单位.②若圆心角的单位不全是度,则需要先化为度后再计算弧长. ③题设未标明精确度的,可以将弧长用π表示.④正确区分弧、弧的度数、弧长三个概念,度数相等的弧,弧长不一定相等,弧长相等的弧不一定是等弧,只有在同圆或等圆中,才有等弧的概念,才是三者的统一. 【例1】在半径为2的圆中,弦AB 的长为2,则AB 的长等于( )A .3πB .2πC .23πD .32π【答案】C .考点:弧长的计算. 归纳 2:扇形面积 基础知识归纳:扇形面积公式:lR R n S 213602==π扇注意问题归纳:其中n 是扇形的圆心角度数,R 是扇形的半径,l 是扇形的弧长.【例2】如图,将长为8cm 的铁丝AB 首尾相接围成半径为2cm 的扇形,则S 扇形= cm²【答案】4. 【解析】试题分析:设围成扇形的角度为n ,∵将长为8cm 的铁丝AB 首尾相接围成半径为2cm 的扇形,∴围成扇形的弧长为4cm .∴根据弧长公式,得n 23604n 180ππ⋅⋅=⇒=,∴根据扇形面积公式,得()223602S 4cm 360π⋅⋅==.考点:扇形的计算. 归纳 3:圆锥的侧面积 基础知识归纳:圆锥的侧面积:122S l r rlππ=•=,其中l 是圆锥的母线长,r 是圆锥的地面半径.注意问题归纳:①圆锥的母线与展开后所得扇形的半径相等.②圆锥的底面周长与展开后所得扇形的弧长相等.【例3】一个圆锥的高为4cm ,底面圆的半径为3cm ,则这个圆锥的侧面积为( ) A . 12πcm2 B .15πcm2 C .20πcm2 D .30πcm2考点:圆锥的计算.归纳 4:阴影部分面积基本方法归纳:求阴影面积常用的方法:①直接用公式法;②和差法;③割补法.注意问题归纳:求阴影面积的主要思路是将不规则图形面积转化为规则图形的面积.【例4】如图,扇形OAB中,∠AOB=60°,扇形半径为4,点C在AB上,CD⊥OA,垂足为点D,当△OCD的面积最大时,图中阴影部分的面积为.π-.【答案】24考点:扇形面积的计算.☞1年模拟1.(湖北省宜昌市兴山县校级模拟)劳技课上,小颖将一顶自制的圆锥形纸帽戴在头上,已知纸帽底面圆半径为10cm,母线长50cm,则这顶纸帽的侧面积为()cm2.A.250π B.500π C.750π D.1000π【解析】试题分析:底面圆的半径为10cm ,则底面周长=20πcm ,侧面面积=π×10×50=500πcm2.故选B .考点:圆锥的计算.2.(湖北省广水市校级模拟)如图,圆锥体的高h=2cm ,底面半径r=2cm ,则圆锥体的全面积为( )cm2.A .4π B .8π C .12π D .(4+4)π【答案】C . 【解析】试题分析:底面圆的半径为2,则底面周长=4π,因为底面半径为2cm 、高为23cm ,所以圆锥的母线长为4cm ,即可求得侧面面积=12×4π×4=8π;底面积为=4π,所以全面积为:8π+4π=12πcm2.故选C . 考点:圆锥的有关计算.3.(山东省高密市模拟考试)如果圆锥的母线长为5cm ,底面半径为2cm ,那么这个圆锥的侧面积是( )A .210cmB .210cm π C .220cm D .220cm π 【答案】B .考点:1.圆锥的侧面展开图;2.扇形的面积计算.4.(山东省新泰市模拟考试)如图,Rt ABC △中,90ACB ∠=,30CAB ∠=,2BC =,O H ,分别为边AB AC ,的中点,将ABC △绕点B 顺时针旋转120到11A BC △的位置,则整个旋转过程中线段OH 所扫过部分的面积(即阴影部分面积)为( )A .77π338-B .47π338+C .πD .4π33+【答案】C .【解析】试题分析:连接BH ,BH1,∵O 、H 分别为边AB ,AC 的中点,将△ABC 绕点B 顺时针旋转120°到△A1BC1的位置,∴△OBH ≌△O1BH1,利用勾股定理可求得BH=437+=,所以利用扇形面积公式可得()()22360132********BH BC πππ=⨯-=-.故选C .考点:扇形面积的计算.5.(江苏省兴化顾庄等三校校级模拟)若粮仓顶部是圆锥形,且这个圆锥的高为2m ,母线长为2.5m ,为防雨需在粮仓顶部铺上油毡,则这块油毡的面积是 m2.【答案】154π.考点:圆锥的计算.6.(河南省三门峡市模拟考试)如图,在Rt △ABC 中,∠ABC =90°,AB =8,BC =6,分别以A 、C 为圆心,以2AC的长为半径作圆,将Rt △ABC 截去两个扇形,则剩余(阴影)部分的面积为 .【答案】24-254πcm2.【解析】试题分析:如图:∵Rt△ABC中,∠ABC=90°,AB=8,BC=6,∴AC=2286+=10cm,△ABC的面积是:12AB•BC=12×8×6=24cm2.∴S阴影部分=12×6×8-2905360π⨯=24-254πcm2,故阴影部分的面积是:24-254πcm2.考点:扇形面积的计算.7.(湖北省武汉市校级模拟)如图,在边长为1的正方形组成的网格中,△ABC的顶点均在格点上,点A、B、C的坐标分别是A(-2,3)、B(-1,2)、C(-3,1),△ABC 绕点O顺时针旋转90°后得到△A1B1C1.(1)在正方形网格中作出△A1B1C1;(2)求点A经过的路径弧AA1的长度;(结果保留π)(3)在y轴上找一点D,使DB+DB1的值最小,并直接写出D点坐标.【答案】(1)图形详见解析;(2132;(3)(0,53).试题解析:解:(1)如图如下:考点:作图—旋转变换;待定系数法求解析式;弧长公式.8.(广东省中山市校级模拟)如图,AB是的直径,点D在上,∠DAB=45°,BC∥AD,CD∥AB.(1)、判断直线CD 与的位置关系,并说明理由;(2)、若的半径为1,求图中阴影部分的面积(结果保留π).【答案】(1)、相切;(2)、324.【解析】试题分析:(1)、连接OD,根据OA=OD,∠ODA=45°得出∠AOD=90°,根据CD∥AB 得出∠ODC=90°,从而说明切线;(2)、首先求出梯形OBCD的面积,然后利用梯形的面积减去扇形OBD的面积求出阴影部分的面积.考点:切线的判定、扇形的面积计算.9.(山东省博兴县校级模拟)如图,点B、C、D都在半径为6的⊙O上,过点C作AC∥BD交OB延长线于点A,连接CD,且∠CDB=∠OBD=30°.(1)求证:AC是⊙O的切线;(2)求弦BD的长;(3)求图中阴影部分的面积.【答案】(1)见解析;(2)3;(3)6π.【解析】试题分析:(1)连接OC交BD于点E,根据∠CDB=∠OBD=30°得出∠COB=60°,∠OEB=90°,根据AC∥BD得到∠OCA=90°;(2)根据OB=6,OE⊥BD,∠OEB=30°,求出OE和BE的长度,然后计算出BD的长度;(3)根据△OBE和△CDE全等,将阴影部分的面积转化成扇形OBC的面积,然后根据扇形的面积计算公式进行求解.试题解析:(1)证明:连接OC,交BD于点E.∵∠CDB=∠OBD=30°∴∠COB=60°,∠OEB=90°∵AC∥BD ∴∠OCA=∠OEB=90°∴OC⊥AC ∴AC是⊙O的切线.(2)∵∠OEB=90°,∠OBD=30°∴OC⊥BD,321==OB OE∴BE=DE=33273622==-∴362==DEBD(3)∵OE=CE,∠OEB=∠CED=90°,BE=DE,∴△OEB≌△CED∴ππ63606602=⋅==OBCSS扇形阴影考点:切线的判定、垂径定理、扇形的面积计算.10.(山东省高密市模拟考试)如图,BE是⊙O的直径,点A在EB的延长线上,弦PD⊥BE,垂足为C,连接OD,∠AOD=∠APC.(1)求证:AP是⊙O的切线.(2)若⊙O的半径是4,AP=43,求图中阴影部分的面积.【答案】(1)见解析(2)16433π-.考点:1.切线的证明;2.勾股定理;3.特殊角的三角函数值;4.扇形的面积计算.。
高中数学专题圆的方程:8+2个问题

圆的方程终极训练:10个常考热点问题类型1、标准方程知识梳理:1.若圆C的圆心落在直线y=2x上,且该圆与x轴相切,半径r=4,则圆C的方程是___________________2.类型2、一般方程知识梳理:1.2.3.已知圆的方程为2x²+2y²+2x+my+6=0,则m的范围是_____________.类型3、轨迹方程知识梳理:1.已知平面上有一动点P,点A(-2,0),点B(6,0),且满足PA⊥PB,求动点P所在的轨迹方程?2.已知圆的方程为x²+y²=4,点A(4,0),动点P在圆上,连结PA,点M是PA的中点,求点P的轨迹方程?类型4、点与圆的位置关系知识梳理:1.已知圆的方程为(x+1)²+(y-2)²=10,A、B、C、D四点的坐标分别为(0,3),(-2,-1),(3,4),(15 ,8),试判断这四点与圆的位置关系分别是什么?2.已知圆的方程为x²+(y+2)²=4,点A(1,m)在圆外,求m的范围?类型5、直线与圆的位置关系知识梳理:举一反三:在上一问题中,把“相切”改为“相交”,其他条件不变,求a的范围?类型6、圆与圆的位置关系、公切线知识梳理:类型7、求切线方程知识梳理:类型8、弦的有关计算:弦长,弦所在直线方程,公共弦知识梳理:求直线AB的方程及AB的弦长?类型9、直线、圆有关对称问题知识梳理:类型10、圆有关最值问题知识梳理:1.已知圆的方程为(x+1)²+y²=4,点A(-2,-1),点B(2,2),试在圆上找一动点P,分别求PA的最小值和PB的最大值各是多少?2.已知圆的方程为(x+1)²+(y-2)²=10,A的坐标分别为(0,3),求过点A的最大弦长和最小弦长分别是多少?。
2024中考数学全国真题分类卷 第二十一讲 与圆有关的计算 强化训练(含答案)

2024中考数学全国真题分类卷第二十一讲与圆有关的计算强化训练命题点1扇形的相关计算类型一弧长的计算1.(2023甘肃省卷)如图,一条公路(公路的宽度忽略不计)的转弯处是一段圆弧( AB ),点O 是这段弧所在圆的圆心,半径OA =90m ,圆心角∠AOB =80°,则这段弯路( AB )的长度为()第1题图A.20πmB.30πmC.40πmD.50πm2.(2023黄冈)如图,在Rt △ABC 中,∠C =90°,∠B =30°,AB =8,以点C 为圆心,CA 的长为半径画弧,交AB 于点D ,则弧AD 的长为()第2题图A.πB.43πC.53πD.2π3.(2023丽水)某仿古墙上原有一个矩形的门洞,现要将它改为一个圆弧形的门洞,圆弧所在的圆外接于矩形,如图.已知矩形的宽为2m ,高为23m ,则改建后门洞的圆弧长是()第3题图A.5π3mB.8π3mC.10π3m D.(5π3+2)m 4.(2023攀枝花)如图,在半径为1的⊙O 上顺次取点A ,B ,C ,D ,E ,连接AB ,AE ,OB ,OC ,OD ,OE .若∠BAE =65°,∠COD =70°,则 BC与 DE 的长度之和为________(结果保留π).第4题图5.(新趋势)·跨学科知识(2023衡阳)如图,用一个半径为6cm的定滑轮拉动重物上升,滑轮旋转了120°,假设绳索粗细不计,且与轮滑之间没有滑动,则重物上升了________cm.(结果保留π)第5题图6.(2023宜昌)如图,点A,B,C都在方格纸的格点上,△ABC绕点A顺时针方向旋转90°BB'的长为________.后得到△AB′C′,则点B运动的路径第6题图7.(2023福建)如图,△ABC内接于⊙O,AD∥BC交⊙O于点D,DF∥AB交BC于点E,交⊙O于点F,连接AF,CF.(1)求证:AC=AF;(2)若⊙O的半径为3,∠CAF=30°,求 AC的长(结果保留π).第7题图类型二扇形面积的计算8.(2023凉山州)家具厂利用如图所示直径为1米的圆形材料加工成一种扇形家具部件,已知扇形的圆心角∠BAC=90°,则扇形部件的面积为()A.1 2π米2B.14π米2 C.18π米2 D.116π米2第8题图9.(2023台州)一个垃圾填埋场,它在地面上的形状为长80m,宽60m的矩形,有污水从该矩形的四周边界....向外渗透了3m,则该垃圾填埋场外围受污染土地的面积为()A.(840+6π)m2B.(840+9π)m2C.840m2D.876m210.(2023玉林)数学课上,老师将如图边长为1的正方形铁丝框变形成以A为圆心,AB为半径的扇形(铁丝的粗细忽略不计),则所得扇形DAB的面积是________.第10题图11.(2023盐城)如图,在矩形ABCD中,AB=2BC=2,将线段AB绕点A按逆时针方向旋转,使得点B落在边CD上的点B′处,线段AB扫过的面积为________.第11题图命题点2与扇形有关的阴影部分面积计算类型一直接和差法12.(2023兰州)如图①是一块弘扬“社会主义核心价值观”的扇面宣传展板,该展板的部分示意图如图②所示,它是以O为圆心,OA,OB长分别为半径,圆心角∠O=120°形成的扇面,若OA=3m,OB=1.5m,则阴影部分的面积为()第12题图A.4.25πm 2B.3.25πm 2C.3πm 2D.2.25πm 213.(2023泰安)如图,四边形ABCD 中,∠A =60°,AB ∥CD ,DE ⊥AD 交AB 于点E ,以点E 为圆心,DE 为半径,且DE =6的圆交CD 于点F ,则阴影部分的面积为()第13题图A.6π-93B.12π-93C.6π-932D.12π-93214.(2023山西)如图,扇形纸片AOB 的半径为3,沿AB 折叠扇形纸片,点O 恰好落在 AB 上的点C 处,图中阴影部分的面积为()第14题图A.3π-33B.3π-932C.2π-33D.6π-93215.(2023重庆A 卷)如图,菱形ABCD 中,分别以点A ,C 为圆心,AD ,CB 长为半径画弧,分别交对角线AC 于点E ,F .若AB =2,∠BAD =60°,则图中阴影部分的面积为________.(结果不取近似值)第15题图类型二构造和差法16.(2023赤峰)如图,AB 是⊙O 的直径,将弦AC 绕点A 顺时针旋转30°得到AD ,此时点C 的对应点D 落在AB 上,延长CD ,交⊙O 于点E ,若CE =4,则图中阴影部分的面积为()第16题图A.2πB.22C.2π-4D.2π-2217.(2022资阳)如图,在矩形ABCD 中,AB =2cm ,AD =3cm ,以点B 为圆心,AB 长为半径画弧,交CD 于点E ,则图中阴影部分的面积为________cm 2.第17题图18.(2023河南)如图,将扇形AOB 沿OB 方向平移,使点O 移到OB 的中点O ′处,得到扇形A ′O ′B ′.若∠O =90°,OA =2,则阴影部分的面积为__________.第18题图19.(2023梧州)如图,四边形ABCD 是⊙O 的内接正四边形.分别以点A ,O 为圆心,取大于12OA 的定长为半径画弧,两弧相交于点M ,N ,作直线MN ,交⊙O 于点E ,F .若OA =1,则 BE,AE ,AB 所围成的阴影部分面积为________.第19题图类型三等积转化法20.(2023遵义)如图,在正方形ABCD 中,AC 和BD 交于点O ,过点O 的直线EF 交AB 于点E(E不与A,B重合),交CD于点F.以点O为圆心,OC为半径的圆交直线EF于点M,N.若AB=1,则图中阴影部分的面积为()A.π8-18B.π8-14C.π2-18D.π2-14第20题图21.(2022泰安)若△ABC为直角三角形,AC=BC=4,以BC为直径画半圆如图所示,则阴影部分的面积为________.第21题图22.(2023广元)如图,将⊙O沿弦AB折叠, AB恰经过圆心O,若AB=23,则阴影部分的面积为________.第22题图类型四容斥原理法23.(2022荆门)如图,正方形ABCD的边长为2,分别以B,C为圆心,以正方形的边长为半径的圆相交于点P,那么图中阴影部分的面积为________.第23题图命题点3圆切线与求阴影部分面积结合24.(2023齐齐哈尔)如图,在△ABC中,AB=AC,以AB为直径作⊙O,AC与⊙O交于点D,BC与⊙O交于点E,过点C作CF∥AB,且CF=CD,连接BF.(1)求证:BF是⊙O的切线;(2)若∠BAC=45°,AD=4,求图中阴影部分的面积.第24题图25.(2023益阳)如图,C是圆O被直径AB分成的半圆上一点,过点C的圆O的切线交AB 的延长线于点P,连接CA,CO,CB.(1)求证:∠ACO=∠BCP;(2)若∠ABC=2∠BCP,求∠P的度数;(3)在(2)的条件下,若AB=4,求图中阴影部分的面积(结果保留π和根号).第25题图命题点4圆锥、圆柱的相关计算26.(2023无锡)在Rt△ABC中,∠C=90°,AC=3,BC=4,以AC所在直线为轴,把△ABC 旋转1周,得到圆锥,则该圆锥的侧面积为()A.12πB.15πC.20πD.24π27.(2023赤峰)如图所示,圆锥形烟囱帽的底面半径为12cm,侧面展开图为半圆形,则它的母线长为()A.10cmB.20cmC.5cmD.24cm第27题图28.(2023云南)某中学开展劳动实习,学生到教具加工厂制作圆锥.他们制作的圆锥,母线长为30cm,底面圆的半径为10cm,这种圆锥的侧面展开图的圆心角度数是________.29.(2022广西北部湾经济区)如图,从一块边长为2,∠A=120°的菱形铁片上剪出一个扇形,这个扇形在以A为圆心的圆上(阴影部分).且圆弧与BC,CD分别相切于点E,F,将剪下来的扇形围成一个圆锥.则圆锥的底面圆半径是________.第29题图命题点5圆与正多边形的相关计算30.(2022贵阳)如图,⊙O与正五边形ABCDE的两边AE,CD相切于A,C两点,则∠AOC 的度数是()A.144°B.130°C.129°D.108°第30题图31.(2023雅安)如图,已知⊙O的周长等于6π,则该圆内接正六边形ABCDEF的边心距OG为()第31题图A.33B.32 C.332 D.332.(2022山西)如图,正六边形ABCDEF 的边长为2,以A 为圆心,AC 的长为半径画弧,得 EC ,连接AC ,AE ,则图中阴影部分的面积为()第32题图A.2πB.4πC.33πD.233π33.(2022绥化)边长为4cm 的正六边形,它的外接圆与内切圆半径的比值是________.参考答案与解析1.C 【解析】根据弧长公式l =n πr 180=80×π×90180=40π.2.B 【解析】如解图,连接CD ,∵∠B =30°,∠ACB =90°,AB =8,∴∠CAB =60°,AC =4.∵AC =CD ,∴△ACD 是等边三角形,∴∠ACD =60°.∴弧AD 的长为60π×4180=43π.第2题解图3.C 【解析】∵圆弧所在圆外接于矩形,且矩形四个角均为直角,∴直角所对的弦为直径,∴如解图,连接矩形对角线的交点O 即为圆心,∵AB =2,AD =23,∴BD =AB 2+AD 2=4,∴∠ADB =30°,∴∠ABD =60°,∵OA =OD =OB =OC =2,∴∠AOB =∠DOC =60°,∴圆弧长为300π×2180=10π3.第3题解图4.π3【解析】∵∠BAE =65°,∴∠BOE =2∠BAE =130°,∵∠COD =70°,∴∠BOC +∠DOE =∠BOE -∠COD =130°-70°=60°,∴ BC 与 DE 的长度之和为60π×1180=π3.5.4π【解析】由题意可知,重物上升的高度即为120°的圆心角所对应的弧长,∴重物上升的高度为120π×6180=4π.6.52π【解析】由题可得旋转角∠BAB ′=90°,AB =AB ′,∵在Rt △ABC 中,BC =3,AC=4,∴AB =5,∴路径 BB'的长为90π×5180=52π.7.(1)证明:∵AD ∥BC ,DF ∥AB ,∴四边形ABED 是平行四边形,∴∠B =∠D .又∵∠AFC =∠B ,∠ACF =∠D ,∴∠AFC =∠ACF ,∴AC =AF ;(2)解:如解图,连接AO ,CO .由(1)得∠AFC =∠ACF ,又∵∠CAF =30°,∴∠AFC =180°-30°2=75°,∴∠AOC =2∠AFC =150°.∴ AC 的长为150π×3180=52π.第7题解图8.C【解析】如解图,连接BC ,OA .∵∠BAC =90°,∴BC 为⊙O 的直径.∵BC =1米,∴OA =OB =12米,由题意可知AB =AC ,∴△ABC 为等腰直角三角形,∴AB =22米,∴S扇形=90π×(22)2360=18π米2.第8题解图9.B【解析】如解图,该垃圾填埋场外围受污染土地的面积=80×3×2+60×3×2+32π=(840+9π)m 2.第9题解图10.1【解析】∵正方形ABCD 的边长为1,∴AB =AD =1, BD的长为2,∴S 扇形DAB =12lr=12×2×1=1.11.π3【解析】如解图,过点B ′作B ′H ⊥AB 于点H ,∵B ′H =BC =1,AB ′=AB =2,∴∠B ′AH=30°,∴线段AB 所扫过的面积为30π×22360=π3.第11题解图12.D【解析】S 阴影=S 扇形AOD -S 扇形BOC =120π×32360-120π×1.52360=13×π×(9-2.25)=2.25π(m 2).13.B【解析】如解图,过点E 作EG ⊥CD 于点G ,∵∠A =60°,AD ⊥DE ,∴∠AED =30°.∵AB ∥CD ,∴∠EDF =∠AED =30°.又∵DE =EF ,∴∠DFE =∠EDF =30°,∴∠DEF =180°-∠DFE -∠EDF =120°.在Rt △DEG 中,DE =6,∠EDF =30°,∴EG =DE ·sin ∠EDF =3,DG =DE ·cos ∠EDF =33,∴DF =2DG =63,∴S 阴影=S 扇形DEF -S △DEF =120π×62360-12×63×3=12π-93.第13题解图14.B 【解析】如解图,连接OC ,∵扇形AOB 沿着AB 折叠,点O 落在 AB 上的点C 处,∴四边形OACB 是菱形.又∵OA =AC =OC ,∴△AOC 是等边三角形,∴∠AOC =60°,∴∠AOB =120°.∵S 菱形OACB =2S △AOC ,∴S 阴影=S 扇形AOB -S 菱形OACB =120π×32360-2×34×32=3π-932.第14题解图15.23-2π3【解析】如解图,连接BD 交AC 于点M .∵四边形ABCD 是菱形,∠BAD=60°,∴∠AMD =90°,∠DAM =12∠BAD =30°,AM =12AC ,DM =12BD ,∴在Rt △ADM中,DM =12AD =1,AM =32AD =3,∴AC =2AM =23,BD =2DM =2,∴S 菱形ABCD =12AC ·BD =12×23×2=23,S 扇形DAE =S 扇形BCF =30π×22360=π3,∴S 阴影=S 菱形ABCD -S 扇形DAE-S 扇形BCF =23-π3-π3=23-2π3.第15题解图16.C 【解析】如解图,连接OC ,OE ,过点O 作ON ⊥CE 于点N ,∵AC =AD 且∠A =30°,∴∠ADC =∠ACD =75°,∵OA =OC ,∴∠ACO =∠A =30°,∴∠OCD =∠ACD -∠ACO =45°,∵OC =OE ,∴∠OCE =∠OEC =45°,∴∠EOC =90°,∵CE =4,∴ON =EN =CN =2,OE =OC =22,∴S 阴影=S 扇形COE -S △OEC =90π×(22)2360-12×4×2=2π-4.第16题解图17.332-2π3【解析】如解图,连接BE ,由题意得BE =AB =2cm ,∵四边形ABCD是矩形,∴∠ABC =∠C =90°,BC =AD =3cm ,∴cos ∠EBC =BC BE =32,∴∠EBC =30°,∴∠ABE =60°,CE =1cm ,∴S 阴影=S 矩形ABCD -S 扇形ABE -S △ECB =2×3-60π×22360-12×1×3=(332-2π3)cm 2.第17题解图18.π3+32【解析】如解图,设O ′A ′与 AB 交于点C ,连接OC ,∵点O ′是OB 的中点,∴OO ′=12OB =12OA =1,由平移可得∠CO ′O =90°,∴cos ∠COO ′=OO ′OC =12,∴∠COO ′=60°,∴CO ′=3OO ′=3,∴S 阴影=S 扇形A ′O ′B ′+S △COO ′-S 扇形COB =90π×22360+12×3×1-60π×22360=π3+32.第18题解图19.π12-2-34【解析】如解图,连接OE ,OB ,∵四边形ABCD 是⊙O 的内接正四边形,∴∠AOB =90°,由尺规作图知MN 垂直平分OA ,∴AE =OE ,∵OA =OE ,∴△OAE 是等边三角形,∴AE =OE =OA =1,∠AOE =60°,设MN 与OA 交于点G ,则EG =OE ·sin ∠AOE =1×sin 60°=32,∴S 阴影=S 扇形AOB -S △OAB -S 弓形AE =S 扇形AOB -S △OAB -(S 扇形AOE -S △OAE )=90π×12360-12×1×1-(60π×12360-12×1×32)=π4-12-π6+34=π12-2-34.第19题解图20.B 【解析】如解图,以点O 为圆心,以OD 为半径作 DN,∵四边形ABCD 是正方形,AB =1,∴OB =OD =OC =22,∠DOC =90°,∵∠EOB =∠FOD ,∴S 扇形BOM =S 扇形DON ,易知△BOE ≌△DOF ,∴S 阴影=S 扇形COD -S △COD =90π×(22)2360-14×1×1=π8-14.第20题解图【一题多解】∵在正方形ABCD 中,AB =1,∴⊙O 的半径为OB =22AB =22,∵EF 过点O ,∴由中心对称可得四边形EBCF 的面积等于正方形面积的一半,又∵S △OBC =14S 正方形ABCD ,∴S阴影=S半圆-12S 正方形ABCD -(S扇形BOC -S △OBC )=12π×(22)2-12×1×1-90π×(22)2360+14×1×1=π4-12-π8+14=π8-14.21.4【解析】如解图,连接CD ,则阴影部分面积为△ABC 面积的一半,即12×4×4×12=4.第21题解图22.2π3【解析】如解图,过点O 作OD ⊥AB 于点D ,交劣弧AB 于点E ,连接AO ,AE ,根据垂径定理得AD =BD =12AB =3,∵将⊙O 沿弦AB 折叠, AB 恰经过圆心O ,∴OD=DE =12OA ,∴∠OAD =30°,∴∠OAE =60°,∵OA =OE ,∴△AOE 是等边三角形,∴∠E=60°,在Rt △AOD 中,AO =ADcos 30°=332=2,∵AD =BD ,∠ADE =∠BDO =90°,DE=OD ,∴△ADE ≌BDO (SAS),∴S 阴影=S 扇形AEO =60π×22360=2π3.第22题解图【一题多解】如解图,过点O 作OD ⊥AB 于点D ,交劣弧AB 于点E ,连接AO ,AE ,∴AD=BD =3,∠ODB =90°,由折叠可知,OD =DE =12OB ,可得∠OBD =30°,∠AOB =120°,∴OB =BD cos ∠OBD =2,∴S 扇形AOB =120π×22360=4π3,S △AOB =12×23×1=3,S 扇形AOB-S △AOB =4π3-3.OE 左边阴影部分面积为12(S 扇形AOB -S △AOB )=2π3-32,OE 右边阴影部分面积为12S △AOB =32,整体阴影部分面积为两部分阴影面积之和即为2π3.23.23-2π3【解析】如解图,连接PB ,PC ,过点P 作PF ⊥BC 于点F ,∵PB =BC =PC ,∴△PBC 为等边三角形,∴∠PBC =60°,∠PBA =30°,∴BF =PB ·cos 60°=12PB =1,PF =PB ·sin 60°=3,∴S 阴影=[S 扇形ABP -(S 扇形BPC -S △BPC )]×2=[30π×22360-(60π×22360-12×2×3)]×2=23-2π3.第23题解图24.(1)证明:如解图,连接BD ,第24题解图∵AB 是⊙O 的直径,∴∠BDA =90°,∴∠BDC =90°,∵AB =AC ,∴∠ABC =∠ACB .∵CF ∥AB ,∴∠FCB =∠ABC ,∠ABF +∠F =180°,∴∠FCB =∠ACB ,∵CF =CD ,BC =BC ,∴△BCF ≌△BCD (SAS).∴∠F =∠BDC =90°,又∵∠ABF +∠F =180°,∴∠ABF =90°,且AB 是⊙O 的直径,∴BF 是⊙O 的切线;(2)解:如解图,连接OE ,与BD 交于点M ,∵∠BDA =90°,∠BAC =45°,AD =4,∴BD =AD =4,∴AB =AD 2+BD 2=42,∴OB =22,∴OE =OB =22,∴∠OEB =∠ABC .∵AB =AC ,∠BAC =45°,∴∠BOE =∠BAC =45°,∴OE ∥AC ,∴∠OMB =∠ADB =90°,∴BM =OM =2,∴S 阴影=S 扇形BOE -S △OBE =45π×(22)2360-2×222=π-22.25.(1)证明:∵AB 为半圆O 的直径,∴∠ACB =90°,又∵CP 为半圆O 的切线,OC 为半圆O 的半径,∴∠OCP =90°,∴∠ACB =∠OCP ,∴∠ACO +∠OCB =∠OCB +∠BCP ,∴∠ACO =∠BCP ;(2)解:∵OA =OC ,∴∠OAC =∠OCA ,∴∠COB =∠OAC +∠OCA =2∠ACO ,∵∠ABC =2∠BCP ,∠ACO =∠BCP ,∴∠ABC =∠COB ,又∵OB =OC ,∴∠ABC =∠COB =∠OCB =60°,∴∠P =90°-∠COB =30°;(3)解:由(2)知∠OAC =30°,∴BC =12AB ,又∵AB =4,∴BC =2,∴AC =AB 2-BC 2=42-22=23,∴S △ABC =12×2×23=23,∴S 阴影=S 半圆-S △ABC =12π×22-23=2π-23.26.C 【解析】由题意得AB =32+42=5,∴以AC 所在直线为轴将△ABC 旋转一周得到一个圆锥,圆锥的底面圆半径为4,母线长为5,∴圆锥的侧面积为π×4×5=20π.27.D 28.120°【解析】由题意可知n π×30180=2π×10,解得n =120,即这种圆锥的侧面展开图的圆心角度数是120°.29.33【解析】如解图,连接AE ,AF ,AC .∵四边形ABCD 是菱形,∠BAD =120°,∴∠ACD =∠ACB =60°,∴AD =AB =BC =CD =AC =2,∵BC ,CD 是切线,∴AE ⊥BC ,AF ⊥CD ,∴AE =AF =AC ·sin 60°=3,设圆锥的底面圆半径为r ,则2πr =120π·AE180=120π×3180=23π3,解得r =33.第29题解图30.A【解析】正五边形的内角和为(5-2)×180°=540°,∴∠E =∠D =108°,∵AE ,CD分别与⊙O 相切于A ,C 两点,∴∠OAE =∠OCD =90°,∴∠AOC =540°-90°-90°-108°-108°=144°.31.C 【解析】如解图,连接OC ,OD ,∵圆的周长为6π,∴2πr =6π,∴r =3,∴OC =OD =3.∵六边形ABCDEF 是正六边形,∴∠COD =60°,∴∠OCD =60°.∵OG ⊥CD ,∴OG =OC ·sin ∠OCD =3×sin 60°=332.第31题解图32.A 【解析】如解图,过点B 作BG ⊥AC 于点G ,∵六边形ABCDEF 是正六边形,∴∠F =∠FAB =∠ABC =120°,AB =BC =AF =EF =2,∴∠BAC =∠EAF =30°,∴∠EAC =60°.∵BG ⊥AC ,∴AG =CG =AB ·cos 30°=2×32=3,∴AC =23,∴S 阴影=60π·(23)2360=2π.第32题解图33.233【解析】如解图,连接OA ,OB ,过点O 作OG ⊥AB 于点G ,∵正六边形的边长为4cm ,∴正六边形的外接圆的半径4cm ,内切圆的半径是正六边形的边心距,因而是GO =32×4=23,因而正六边形的外接圆的半径与内切圆的半径之比为423=233.第33题解图。
人教版九年级上册数学《与圆有关的弧长、面积计算》练习题(含答案)

与圆有关的弧长、面积计算一 、填空题(本大题共9小题)1.,圆心角等于的扇形内部作一个正方形,使点在上,点在上,点在上,则阴影部分的面积为____________.2.如图,⊙A 和⊙B 都与x 轴和y 轴相切,圆心A 和圆心B 都在反比例函数1y x=的图象上,则图中阴影部分的面积于 。
3.正n 边形内接于半径为R 的圆,这个n 边形的面积为23R ,则n 等于____________.4.如图,在等腰直角三角形中,,点为的中点,已知扇形和扇形的圆心分别为点、点,且,则图中阴影部分的面积为 (结果不取近似值).5.如图,点在直径为的上,,则图中阴影部分的面积等于 .(结果中保留π).545︒AOB CDEF C OA D E 、OB F AB FCA ABC 90C ∠=︒D AB EADFBD A B 2AC =FEBAC A B C 、、23O 45BAC ∠=︒6.如图7,在Rt ABC ∆中,9042C AC BC ∠=︒==,,分别以AC BC ,为直径画半圆,则图中阴影部分的面积为 .(结果保留)7.若一个扇形的圆心角为60°,面积为cm 2,则这个扇形的弧长为 cm (结果保留π).8.将绕点逆时针旋转到使在同一直线上,若,,则图中阴影部分面积为 cm 2.9.如图,等腰的直角边长为4,以为圆心,直角边为半径作弧1,交斜边于点,于点,设弧,,围成的阴影部分的面积为,然后以为圆心,为半径作弧,交斜边于点,于点,设弧围成的阴影部分的面积为,按此规律继续作下去,得到的阴影部分的面积= .OAπABC △B A BC ''△A B C '、、90BCA ∠=°4cm 30AB BAC ︒=∠=,A'C'ARt ABC △A AB BC AC 1C 11C B AB ⊥1B 1BC 11C B 1B B 1S A 1AB 22B C AC 2C 22C B AB ⊥2B 122221B C C B B B ,,2S 3S与圆有关的弧长、面积计算答案解析一 、填空题 1. 【解析】连结,由勾股定理可计算得正方形的边长为, 则正方形的面积为,等腰直角三角形的面积为, 扇形的面积为,所以阴影部分的面积为. 2.π【解析】根据反比例函数图像双曲线具有的性质,关于原点对称,从而可知把图中两块阴影归结在一个圆中,所以图中阴影部分的面积即为⊙A 或⊙B的面积.同时点A 、B 均在双曲线上1y x=,根据xy=1,且圆均与左边轴相切,可知圆的半径=1,所以阴影部分面积=π. 3.12 4..【解析】用三角形ABC 的面积减去扇形EAD 和扇形FBD 的面积,即可得出阴影部分的面积.∵, ∴, ∵点为的中点, ∴321A5382π-OF CDEF 1CDEF 1COD 12AOB 21588π⋅=π5382π-22π-902BC AC C AC =∠=︒=,,AB =D AB AD BD ==∴【点评】本题考查了扇形面积的计算以及等腰直角三角形的性质,熟记扇形的面积公式:.5.3342-π 【解析】首先连接,,即可求得,然后求得扇形的面积与的面积,求其差即是图中阴影部分的面积.连接, ∵, ∴, ∵的直径为,∴, ∴∴ 【点评】此题考查了圆周角的性质,扇形的面积与直角三角形面积得求解方法.此题难度不大,解题的关键是注意数形结合思想的应用. 6.542π-【解析】观察图形可知:图中阴影部分面积可分隔成两部分求解.设C 点到AB 的距离为CD ,第一部分:半圆AC 的面积-ACD S ∆,第二部分:半圆BC 的面积-BCD S ∆,最后两部分求和即可.7.3π;解:设扇形的半径为R ,弧长为l , 根据扇形面积公式得;=,解得:R =1, ∵扇形的面积=lR =,解得:l =π.=ABC FBD S S S -阴影扇形△24512222360π=⨯⨯-⨯22π=-2360n r s π=OB OC 90BOC ∠=︒OBC OBC △OB OC ,45BAC ∠=︒90BOC ∠=︒OBO CO =290313360422OBC OBCSS ππ⨯===扇形,△33=42OBC OBC S S S π-=-阴影扇形△8.3;【解析】此题需要把所在的圆补充完整,设它与线段的交点为,与的交点为.从而看出整个阴影部分可以割补成扇形的面积-扇形的面积.即.9.12-π; 【解析】每一个阴影部分的面积都等于扇形的面积减去等腰直角三角形的面积.此题的关键是求得的长.根据等腰直角三角形的性质即可求解. 根据题意,得. ∴. ∴. ∴. ∴阴影部分的面积. 【点评】此题综合运用了等腰直角三角形的性质和扇形的面积公式.πBC AB D 'A B E 'ABA BDE 221(42)34ππ-=23AB AB 、14AC AB ==21AC AB ==322AC AB ==3AB =345412136022S ππ⨯-⨯=-。
圆的有关计算与证明问题(真题10道+模拟30道)中考数学重难题型押题培优导练案【解析版】

专题15圆的有关计算与证明问题(北京真题10道+模拟30道)【方法归纳】题型概述,方法小结,有的放矢考点考查年份考查频率圆的有关计算与证明问题(大题) 2013.2014.2015.2016.2017十年10考2018.2019.2020.2021.2022圆的证明与计算是中考取的一类重要的问题,在北京市的2013-2022年10年中考中出现了10次,常见的圆的基础知识和解题技巧如下:1、圆中的重要定理:(1)圆的定义: 主要用来证明四点共圆和点到或直线圆的最值距离问题.(2)垂径定理: 主要用来证明——弧相等、线段相等、垂直关系等等.(3)三者之间的关系定理: 主要用来证明——弧相等、线段相等、圆心角相等.(4)圆周角性质定理及其推论 : 主要用来证明——直角、角相等、弧相等.(5)切线的性质定理: 主要用来证明垂直关系 .(6)切线的判断定理: 主要用来证明直线是圆的切线 .(7)切线长定理:线段相等、垂直关系、角相等 .2.圆中几个要点元素之间的相互转变 : 弧、弦、圆心角、圆周角等都能够经过相等来相互转变 . 这在圆中的证明和计算中常常用到 .3.判断切线的方法:( 1)若切点明确,则“连半径,证垂直”。
常有手法有:全等转变;平行转变;直径转变;中线转变等;有时可经过计算联合相像、勾股定理证垂直;( 2)若切点不明确,则“作垂直,证半径”。
常有手法:角均分线定理;等腰三角形三线合一,隐蔽角均分线;4、考题形式剖析:主要以解答题的形式出现, 第 1 问主要判断切线、证明角或线段相等;第2 问主要与圆有关的计算:①求线段长(或面积);②求线段比;③求角度的三角函数值(本质仍是求线段比)【典例剖析】典例精讲,方法提炼,精准提分【例1】(2021·北京·中考真题)如图,⊙O是△ABC的外接圆,AD是⊙O的直径,AD⊥BC于点E.(1)求证:∠BAD=∠CAD;(2)连接BO并延长,交AC于点F,交⊙O于点G,连接GC.若⊙O的半径为5,OE=3,求GC和OF的长.【答案】(1)见详解;(2)GC=6,OF=2511【解析】【分析】(1)由题意易得BD⌢=CD⌢,然后问题可求证;(2)由题意可先作图,由(1)可得点E为BC的中点,则有OE=12CG,OE//CG,进而可得△AOF∽△CGF,然后根据相似三角形的性质可进行求解.【详解】(1)证明:∵AD是⊙O的直径,AD⊥BC,∵BD⌢=CD⌢,∵∠BAD=∠CAD;(2)解:由题意可得如图所示:由(1)可得点E为BC的中点,∵点O是BG的中点,∵OE=12CG,OE//CG,∵△AOF∽△CGF,∵OA CG =OFGF,∵OE=3,∵CG=6,∵⊙O的半径为5,∵OA=OG=5,∵5 6=OFGF,∵OF=511OG=2511.【点睛】本题主要考查垂径定理、三角形中位线及相似三角形的性质与判定,熟练掌握垂径定理、三角形中位线及相似三角形的性质与判定是解题的关键.【例2】(2022·北京·中考真题)如图,AB是⊙O的直径,CD是⊙O的一条弦,AB⊥CD,连接AC,OD.(1)求证:∠BOD=2∠A;(2)连接DB,过点C作CE⊥DB,交DB的延长线于点E,延长DO,交AC于点F,若F为AC的中点,求证:直线CE为⊙O的切线.【答案】(1)答案见解析(2)答案见解析【解析】【分析】(1)设AB交CD于点H,连接OC,证明RtΔCOH≅RtΔDOH,故可得∠COH=∠DOH,于是BC⌢=BD⌢,即可得到∠BOD=2∠A;(2)连接,解出∠COB=60°,根据AB为直径得到∠ADB=90°,进而得到∠ABD=60°,即可证明OC//DB,故可证明直线CE为⊙O的切线.(1)证明:设AB交CD于点H,连接OC,由题可知,∴OC=OD,∠OHC=∠OHD=90°,∵OH=OH,∴RtΔCOH≅RtΔDOH(HL),∴∠COH=∠DOH,∴BC⌢=BD⌢,∴∠COB=∠BOD,∵∠COB=2∠A,∴∠BOD=2∠A;(2)证明:连接AD,∵OA=OD,∴∠OAD=∠ODA,同理可得:∠OAC=∠OCA,∠OCD=∠ODC,∵点H是CD的中点,点F是AC的中点,∴∠OAD=∠ODA=∠OAC=∠OCA=∠OCD=∠ODC,∵∠OAD+∠ODA+∠OAC+∠OCA+∠OCD+∠ODC=180°,∴∠OAD=∠ODA=∠OAC=∠OCA=∠OCD=∠ODC=30°,∴∠COB=2∠CAO=2×30°=60°,∵AB为⊙O的直径,∴∠ADB=90°,∴∠ABD=90−∠DAO=90°−30°=60°,∴∠ABD=∠COB=60°,∴OC//DE,∵CE⊥BE,∴CE⊥OC,∴直线CE为⊙O的切线.【点睛】本题主要考查三角形全等的判定与性质,同弧所对的圆周角相等,圆周角定理,直线平行的判定与性质,三角形的内角和公式,证明三角形全等以及证明平行线是解题的关键.【真题再现】必刷真题,关注素养,把握核心1.(2013·北京·中考真题)如图,AB是∵O的直径,PA,PC分别与∵O 相切于点A,C,PC交AB的延长线于点D,DE∵PO交PO的延长线于点E.(1)求证:∵EPD=∵EDO(2)若PC=6,tan∵PDA=,求OE的长.【答案】(1)见解析(2)√5【解析】【详解】试题分析:(1)根据切线长定理和切线的性质即可证明:∵EPD=∵EDO;(2)连接OC,利用tan∵PDA=34,可求出CD=4,再证明∵OED∵∵DEP,根据相似三角形的性质和勾股定理即可求出OE的长.试题解析:(1)证明:PA,PC与∵O分别相切于点A,C,∵∵APO=∵EPD且PA∵AO,∵∵PAO=90°,∵∵AOP=∵EOD,∵PAO=∵E=90°,∵∵APO=∵EDO,∵∵EPD=∵EDO;(2)解:连接OC,∵PA=PC=6,∵tan∵PDA=34,∵在Rt∵PAD中,AD=8,PD=10,∵CD=4,∵tan∵PDA=34,∵在Rt∵OCD中,OC=OA=3,OD=5,∵∵EPD=∵ODE,∵∵OED∵∵DEP,∵PD DO =PEDE=EDOE=2,∵DE=2OE在Rt∵OED中,OE2+DE2=OD2,即5OE2=52,∵OE=√5.考点:1.切线的性质;2.相似三角形的判定与性质.⌢的中点,⊙O的切线BD交AC的延长线于点D,E是2.(2014·北京·中考真题)如图,AB是⊙O的直径,C是ABOB的中点,CE的延长线交切线BD于点F,AF交⊙O于点H,连接BH.(1)求证:AC=CD;(2)若OB=2,求BH的长.【答案】(1)证明见解析(2)BH=4√55【解析】【分析】⌢的中点,可知OC∵AB,又BD是切(1)连接OC,若要证明C为AD的中点,只需证OC//BD,已知C是AB线,可知BD∵AB,问题得证(2)由(1)及E为OB中点可知∵COE∵∵FBE,从而可知BF=CO=BO=2,由勾股定理可得AF的长,由面积法即可求出BH的长【详解】(1)连接OC⌢的中点,AB是∵O的直径∵C是AB∵OC∵AB∵BD是∵O的切线∵BD∵AB∵OC//BD∵AO=BO∵AC=CD(2)∵E是OB的中点∵OE=BE在∵COE和∵FBE中{∠CEO=∠FEB OE=BE ∠COE=∠FBE∵∵COE∵∵FBE(ASA)∵BF=CO∵OB=2∵BF=2∵AF=√AB2+BF2=2√5∵AB是直径∵BH∵AFBH=AB⋅BFAF=2√5=4√55考点:1、平行线分线段成比例定理;2、切线的性质;3勾股定理;4、全等三角形3.(2015·北京·中考真题)如图,AB是∵O的直径,过点B作∵O的切线BM,弦CD//BM,交AB于点F,且DA⌢=DC⌢,连接AC,AD,延长AD交BM于点E.(l)求证:∵ACD是等边三角形;(2)连接OE,若DE=2,求OE的长.【答案】(1)见解析;(2)2√7【解析】【分析】(1)根据切线的定义可知AB∵BM,又∵BM//CD,∵AB∵CD,根据圆的对称性可得AD=AC,再根据等弧对等弦得DA=DC,即DA=DC=AC,所以可得∵ACD是等边三角形;(2)∵ACD为等边三角形,AB∵CD,由三线合一可得∵DAB=30°,连接BD,根据直径所对的角是直角和三角形的内角和可得∵∵EBD=∵DAB=30°,因为DE=2,求出BE=4,根据勾股定理得BD=2√3,直角三角形中30°角所对的直角边等于斜边的一半得,AB=4√3,OB=2√3,在Rt∵OBE中,根据勾股定理即可得出OE的长.【详解】解:(1)∵BM是∵O切线,AB为∵O直径,∵AB∵BM,∵BM//CD,∵AB∵CD,∵AD=AC,∵AD=AC,∵DA=DC,∵DC=AD,∵AD=CD=AC,∵∵ACD为等边三角形.(2)∵ACD为等边三角形,AB∵CD,∵∵DAB=30°,连结BD,∵BD∵AD.∵EBD=∵DAB=30°,∵DE=2,∵BE=4,BD=2√3,AB=4√3,OB=2√3,在Rt∵OBE中,OE=√OB2+BE2=√12+16=2√7.【点睛】本题考查圆的有关性质,直角三角形的性质;勾股定理.4.(2016·北京·中考真题)如图,AB为∵O的直径,F为弦AC的中点,连接OF并延长交AC⌢于点D,过点D作∵O的切线,交BA的延长线于点E.(1)求证:AC∵DE;(2)连接CD,若OA=AE=a,写出求四边形ACDE面积的思路.【答案】(1)证明见解析;(2)32a2.【解析】【详解】试题分析:(1)欲证明AC∵DE,只要证明AC∵OD,ED∵OD即可.(2)作DM∵OA于M,连接CD,CO,AD,首先证明四边形ACDE是平行四边形,根据S平行四边形ACDE=AE•DM,只要求出DM即可.试题解析:(1)∵ED与∵O相切于D,∵OD∵DE,∵F为弦AC中点,∵OD∵AC,∵AC∵DE.(2)作DM∵OA于M,连接CD,CO,AD.首先证明四边形ACDE是平行四边形,根据S平行四边形ACDE=AE•DM,只要求出DM即可.∵AC∵DE,AE=AO,∵OF=DF,∵AF∵DO,∵AD=AO,∵AD=AO=OD,∵∵ADO是等边三角形,同理∵CDO 也是等边三角形,∵∵CDO=∵DOA=60°,AE=CD=AD=AO=DD=a,∵AO∵CD,又AE=CD,∵四边形ACDE是平行四边形,易知DM=√32a,∵平行四边形ACDE面积=√32a2.考点:切线的性质.5.(2017·北京·中考真题)如图,AB是∵O的一条弦,E是AB的中点,过点E作EC∵OA于点C,过点B 作∵O的切线交CE的延长线于点D.(1)求证:DB=DE;(2)若AB=12,BD=5,求∵O的半径.【答案】(1)证明见解析;(2)152【解析】【详解】试题分析:(1)由切线性质及等量代换推出∵4=∵5,再利用等角对等边可得出结论;(2)由已知条件得出sin∵DEF和sin∵AOE的值,利用对应角的三角函数值相等推出结论.试题解析:(1)∵DC∵OA,∵∵1+∵3=90°,∵BD为切线,∵OB∵BD,∵∵2+∵5=90°,∵OA=OB,∵∵1=∵2,∵∵3=∵4,∵∵4=∵5,在∵DEB中,∵4=∵5,∵DE=DB.(2)作DF∵AB于F,连接OE,∵DB=DE,∵EF=12BE=3,在RT∵DEF中,EF=3,DE=BD=5,EF=3 ,∵DF=√52−32=4∵sin∵DEF=DFDE = 45,∵∵AOE=∵DEF,∵在RT∵AOE中,sin∵AOE=AEAO =45,∵AE=6,∵AO=152.【点睛】本题考查了圆的性质,切线定理,三角形相似,三角函数等知识,结合图形正确地选择相应的知识点与方法进行解题是关键.6.(2018·北京·中考真题)如图,AB是⊙O的直径,过⊙O外一点P作⊙O的两条切线PC,PD,切点分别为C,D,连接OP,CD.(1)求证:OP⊥CD;(2)连接AD,BC,若∠DAB=50°,∠CBA=70°,OA=2,求OP的长.【答案】(1)证明见解析;(2)4√33.【解析】【分析】(1)根据切线的性质定理得到PC=PD,OP平分∠CPD.根据等腰三角形的性质即可得到PQ⊥CD于Q,即OP⊥CD.(2)连接OC、OD.根据等腰三角形的性质和平角的性质得到∠COD=180°−∠AOD−∠BOC=60°.进而得到∠DOQ=12∠COD=30°.在Rt△ODP中,解直角三角形即可.【详解】(1)证明:∵PC、PD与⊙O相切于C、D.∵PC=PD,OP平分∠CPD.在等腰△PCD中,PC=PD,PQ平分∠CPD.∵PQ⊥CD于Q,即OP⊥CD.(2)解:连接OC、OD.∵OA=OD∵∠OAD=∠ODA=50°∵∠AOD=180°−∠OAD−∠ODA=80°同理:∠BOC=40°∵∠COD=180°−∠AOD−∠BOC=60°.在等腰△COD中,OC=OD.OQ⊥CD∵∠DOQ=12∠COD=30°.∵PD与⊙O相切于D.∵OD⊥DP.∵∠ODP=90°.在Rt△ODP中,∠ODP=90°,∠POD=30°∵OP=ODcos∠POD=OAcos30°=√32=43√3.【点睛】本题考查了切线的性质和判定,圆周角定理,解直角三角形等,题目比较典型,综合性比较强,难度适中.7.(2019·北京·中考真题)在平面内,给定不在同一直线上的点A,B,C,如图所示.点O到点A,B,C 的距离均等于a(a为常数),到点O的距离等于a的所有点组成图形G,∠ABC的平分线交图形G于点D,连接AD,CD.(1)求证:AD=CD;(2)过点D作DE⊥BA,垂足为E,作DF⊥BC,垂足为F,延长DF交图形G于点M,连接CM.若AD=CM,求直线DE与图形G的公共点个数.【答案】依题意画出图形G为∵O,如图所示,见解析;(1)证明见解析;(2)直线DE与图形G的公共点个数为1个.【解析】【分析】(1)根据线段垂直平分线的性质得出图形G为∵O,再根据在同圆或等圆中相等的圆周角所对的弧相等得⌢=CD⌢;从而得出弦相等即可.出AD(2)先根据HL得出△CDF∵∵CMF,得出DF=MF,从而得出BC为弦DM的垂直平分线,根据圆心角和圆周角之间的关系定理得出∵ABC=∵COD,再证得DE为∵O的切线即可【详解】如图所示,依题意画出图形G为∵O,如图所示(1)证明:∵BD平分∵ABC,∵∵ABD=∵CBD,⌢=CD⌢,∵AD=CD∵AD(2)解:∵AD=CD,AD=CM,∵CD=CM.∵DF∵BC,∵∵DFC=∵CFM=90°在Rt△CDF和Rt△CMF中{CD=CMCF=CF,∵Rt△CDF∵Rt△CMF(HL),∵DF=MF,∵BC为弦DM的垂直平分线∵BC为∵O的直径,连接OD∵∵COD=2∵CBD,∵ABC=2∵CBD,∵∵ABC=∵COD,∵OD∵BE.又∵DE∵BA,∵∵DEB=90°,∵∵ODE=90°,即OD∵DE,∵DE为∵O的切线.∵直线DE与图形G的公共点个数为1个.【点睛】本题考查了垂直平分线的性质,圆心角和圆周角之间的关系定理,切线的判定,熟练掌握相关的知识是解题的关键.8.(2020·北京·中考真题)如图,AB为∵O的直径,C为BA延长线上一点,CD是∵O的切线,D为切点,OF∵AD于点E,交CD于点F.(1)求证:∵ADC=∵AOF;(2)若sinC=13,BD=8,求EF的长.【答案】(1)见解析;(2)2.【解析】【分析】(1)连接OD,根据CD是∵O的切线,可推出∵ADC+∵ODA=90°,根据OF∵AD,∵AOF+∵DAO=90°,根据OD=OA,可得∵ODA=∵DAO,即可证明;(2)设半径为r,根据在Rt∵OCD中,sinC=13,可得OD=r,OC=3r,AC=2r,由AB为∵O的直径,得出∵ADB=90°,再根据推出OF∵AD,OF∵BD,然后由平行线分线段成比例定理可得OEBD =OAAB=12,求出OE,OFBD =OCBC=34,求出OF,即可求出EF.【详解】(1)证明:连接OD,∵CD是∵O的切线,∵OD∵CD,∵∵ADC+∵ODA=90°,∵OF∵AD,∵∵AOF+∵DAO=90°,∵OD=OA,∵∵ODA=∵DAO,∵∵ADC=∵AOF;(2)设半径为r,在Rt∵OCD中,sinC=13,∵OD OC =13,∵OD=r,OC=3r,∵OA=r,∵AC=OC-OA=2r,∵AB为∵O的直径,∵∵ADB=90°,又∵OF∵AD,∵OF∵BD,∵OE BD =OAAB=12,∵OE=4,∵OF BD =OCBC=34,∵OF=6,∵EF=OF−OE=2.【点睛】本题考查了平行线分线段成比例定理,锐角三角函数,切线的性质,直径所对的圆周角是90°,灵活运用知识点是解题关键.【模拟精练】押题必刷,巅峰冲刺,提分培优一、解答题1.(2022·北京市广渠门中学模拟预测)如图,AB是⊙O的直径,弦CD⊥AB,垂足为H,E为BC⌢上一点,过点E作⊙O的切线,分别交DC,AB的延长线于点F,G连接AE,交CD于点P.(1)求证:EF=FP;(2)连接AD,若AD∥FG,CD=8,cosF=45,求⊙O半径.【答案】(1)见解析(2)256【解析】【分析】(1)连接OE,要使EF=FP,需要∵FEP=∵FPE,通过切线和垂直的已知条件,利用等角的余角相等可得∵FEP=∵FPE,结论可得.(2)设圆的半径为r,在Rt∵ODH中,利用勾股定理可以求得半径r.(1)证明:连接OE,∵EF是圆的切线,∵OE∵EF.∵∵OEF=90°.∵∵OEA+∵AEF=90°.∵CD∵AB,∵∵AHC=90°.∵∵OAE+∵APH=90°.∵OA=OE,∵∵OAE=∵OEA.∵∵AEF=∵APH.∵∵APH=∵EPF,∵∵EPF=∵AEF.∵EF=PF.(2)连接OD,设圆的半径为r,∵直径AB∵CD于H,CD=8,∵CH=DH=4.∵AD∵FG,∵∵ADH=∵F.∵cos∵ADH=cos F=45∴AD=CHcos∠ADH=5∴AH=√AD2−DH2=3∵OH=OA-AH=r-3.在Rt∵ODH中,∵OH2+DH2=OD2,∵(r-3)2+42=r2.∴OE=r=25 6【点睛】本题主要考查了圆的切线的性质,勾股定理,垂径定理,圆周角定理和解直角三角形的知识.使用添加圆中常添加的辅助线是解题的关键.2.(2022·北京房山·二模)如图,已知AB是半⊙O的直径,点H在⊙O上,E是HB⌢的中点,连接AE,过点E作EC⊥AH交AH的延长线于点C.过点E作EF⊥AB于点F.(1)求证:CE是⊙O的切线;(2)若FB=2,EFAF =√22,求OF的长.【答案】(1)见解析(2)OF=1【解析】【分析】(1)连接OE,由于E为HB⌢的中点,根据圆周角定理可知∵1=∵2,而AO=EO,则∵3=∵2,于是∵1=∵3,根据平行线的判定知OE∥AC,而AC∵CE,根据平行线的性质知∵OEC=90°,即OE∵CE,根据切线的判定可知CE是∵O的切线;(2)由于AB是直径,故∵AED=90°,而EF∵AB,易知∵2=∵4=∵1,那么tan∵1=tan∵2=tan∵4=EFAF =√22,在Rt∵EFB中,利用正切可求出EF,同理在Rt∵AEF中,可求出AF,得半径OB=3,进而可求出OF.(1)证明:连结OE,∵点E为HB⌢的中点,∵ ∵1=∵2,∵OE=OA,∵∵3=∵2,∵∵3=∵1,∵OE∵AC,∵AC∵CE,∵OE∵CE,∵点E在∵O上,∵CE是∵O的切线.(2)连结EB,∵AB是∵O的直径,∵∵AEB=90°,∵EF∵AB于点F,∵∵AFE=∵EFB=90°,∵∵2+∵AEF=∵4+∵AEF=90°,∵∵2=∵4=∵1,∵EF AF =√22,∵tan∠1=√22,∵tan∵4 =√22,在Rt∵EFB中,∵EFB=90°,FB=2,tan∵4 =√22,∵EF=2√2,设OE=x,则OB= x.∵FB=2,∵OF=x-2,∵在Rt∵OEF中,∵EFO=90°,∵x2=(x-2)2+(2√2)2,∵x=3,∵OF=1.【点睛】本题主要考查了切线的判定,圆周角定理,平行线的性质,等腰三角形的性质,勾股定理,三角函数的定义,作出辅助线,熟练掌握圆的切线判定方法,是解题的关键.3.(2022·北京朝阳·二模)如图,AB为∵O的直径,C为∵O上的一点,OD⊥AB交AC于点E,DE=DC.(1)求证:DC是∵O的切线;(2)若OA=4,OE=2,求cos D.【答案】(1)见解析(2)35【解析】【分析】(1)连接OC.证∵OCD=90°,即可得出结论;(2)先求出OC=4.再同由勾股定理求出DC=3,OD=5,最后由余弦定义cosD=DC求解.OD(1)证明:如图,连接OC.∵OD⊥AB交AC于点E,∵∠AOD=90∘,∵∠A+∠AEO=90∘.∵∠AEO=∠DEC,∵∠A+∠DEC=90∘.∵DE=DC,∵∠DEC=∠DCE,∵OA=OC,∵∠A=∠ACO,∵∵OCD=∠ACO+∠DCE=90∘,∵DC⊥OC,∵DC是∵O的切线,(2)解:∵∠OCD=90∘,∵DC2+OC2=OD2,∵OA=4,∵OC=4.设DC=x,∵OE=2,∵x2+42=(x+2)2.解得x=3,∵DC=3,OD=5.∵在Rt∵OCD中,cosD=DCOD =35.【点睛】本师考查切线的判定,解直角三角形,掌握切线的判定定理是解题的关键.4.(2022·北京东城·二模)如图,在△ABC中,AB>AC,∠BAC=90°,在CB上截取CD=CA,过点D作DE⊥AB 于点E,连接AD,以点A为圆心、AE的长为半径作⊙A.(1)求证:BC是∵A的切线;(2)若AC=5,BD=3,求DE的长.【答案】(1)见解析(2)158【解析】【分析】(1)过点A作AF⊥BC于F,根据同旁内角互补证得DE//AC,可证得∠DAC=∠ADE,利用AAS可证得△ADE≅△ADF,则可证得AF=AE,根据切线的判定即可求证结论.(2)根据角相等即可得△BDE∼△BCA,利用相似三角形的性质即可求解.(1)过点A作AF⊥BC于F,如图所示,∵DE⊥AB,∴∠AED=90°,∵∠BAC=90°,∴∠AED+∠BAC=180°,∴DE//AC,∴∠DAC=∠ADE,∵CD=AC,∴∠DAC=∠ADC,∴∠ADE=∠ADC,在△ADE和△ADF中,{∠AED=∠AFD ∠ADE=∠ADFAD=AD,∴△ADE≅△ADF(AAS),∴AF=AE,且AE为⊙A的半径,∴AF是⊙A的半径,∴BC是⊙A的切线.(2)∵AC=5,∴CD=AC=5,∴BC=BD+CD=3+5=8,∵∠DEB=∠BAC=90°,∠B=∠B,∴△BDE∼△BCA,∴DEAC =BDBC,∴DE5=38,解得DE=158,∴DE的长为158.【点睛】本题考查了切线判定、三角形全等的判定及性质、相似三角形的判定及性质,熟练掌握全等三角形的判定及性质,切线的判定及相似三角形判定及性质是解题的关键.5.(2022·北京平谷·二模)如图,AB是∵O的直径,过B作∵O的切线,与弦AD的延长线交于点C,AD=DC,E是直径AB上一点,连接DE并延长与直线BC交于点F,连接AF.(1)求证:AD⌢=BD⌢;(2)若tan∠BAF=14,∵O的半径长为6,求EF的长.【答案】(1)证明见解析(2)√13【解析】【分析】(1)连接BD,根据圆周角定理、切线性质以及题中AD=DC可得∠BAD=∠ABD=∠CBD=∠C=45°,从而得出结论;(2)连接OD,由(1)知DO⊥AB,得出ΔDOE∼ΔFBE,得出DOBF =OEBE,在RtΔABF中,tan∠BAF=14,∵O的半径长为6,解得BF=3,从而63=OEBE,设BE=x,OE=2x,则BE+OE=OB=6,解得x=2,即BE=2,在RtΔEBF中,利用勾股定理得结论.(1)证明:连接BD,如图所示:∵AB是∵O的直径,∴∠ABD=90°,即BD⊥AC,∵过B作∵O的切线,∴AB⊥BC,∵AD=DC,∴∠BAD=∠ABD=∠CBD=∠C=45°,∴BD=AD,∴AD⌢=BD⌢;(2)解:连接OD,如图所示:在等腰RtΔABD中,∠ADB=90°,∴DO⊥AB,∵∠DEO=∠BEF,∠DOE=∠FBE=90°,∴ΔDOE∼ΔFBE,∴DOBF =OEBE,在RtΔABF中,tan∠BAF=14,∵O的半径长为6,则tan∠BAF=14=BFAB=BF12,解得BF=3,∴63=OEBE,设BE=x,OE=2x,则BE+OE=x+2x=OB=6,解得x=2,在RtΔEBF中,∠EBF=90°,BE=2,BF=3,则利用勾股定理得EF=√BE2+BF2=√22+32=√13.【点睛】本题考查圆综合,涉及到圆周角定理、直角三角形的性质、切线的性质、相似三角形的判定与性质、正切函数求线段长、勾股定理等知识点,根据题意准确作出辅助线是解决问题的关键.6.(2022·北京北京·二模)如图,AB为⊙O的直径,BD⌢=CD⌢,过点A作⊙O的切线,交DO的延长线于点E.(1)求证:AC∥DE;(2)若AC=2,t an E=1,求OE的长.2【答案】(1)见解析(2)5【解析】【分析】(1)根据同圆中,等弧相等性质可得∠BAD=∠CAD,再利用等边对等角及等量代换即可证得∠CAD=∠D从而证得结论.(2)连接BC,利用直径所对的圆周角是直角结合(1)中平行线的性质可求得∠B=∠E,从而得到tanB=tanE,根据直角三角形的锐角三角函数的值结合勾股定理即可求得答案.(1)⌢=CD⌢,证明:∵BD∵∠BAD=∠CAD,∵OA=OD,∵∠D=∠BAD,∵∠CAD=∠D,∵AC∥DE.(2)如图,连接BC,∵AB为⊙O的直径,∵∠C=90°,∵AC∥DE,∵∠BAC=∠AOE,∵AE是⊙O的切线,∵OA⊥AE,∵∠C=∠OAE=90°,∵∠B=∠E,∵tanB=tanE=12,在Rt△OAE中,tanB=12,AC=2,∵tanB=ACBC =2BC=12,解得BC=4,∴AB=√AC2+BC2=√22+C2=2√5,∵OA=√5,∵在Rt△OAE中,tanE=12,∵tanE=AOAE =√5AE=12,解得AE=2√5,∵OE=√OA2+AE2=√(√5)2+(2√5)2=5.【点睛】本题考查了平行线的判定及性质、切线的性质、圆周角定理、锐角三角函数值及勾股定理解直角三角形的应用,熟练掌握圆周角定理及平行线的判定及锐角三角函数值及勾股定理解直角三角形的应用是解题的关键.7.(2022·北京丰台·二模)如图,AB是∵O的直径,C为BA延长线上一点,过点C作∵O的切线,切点为D,过点B作BE∵CD于点E,连接AD,BD.(1)求证:∠ABD=∠DBE;(2)如果CA=AB,BD=4,求BE的长.【答案】(1)证明见解析;(2)43√6.【解析】【分析】(1)如图1,连接OD,由CD切∵O于点A得OD⊥CD,从而得OD∥BE,进而得∠ODB=∠DBE,另外由∠ODB=∠ABD即可得出结论;(2)解:设OA=x,则CA=AB=2x,CO=CA+OA=3x,先证明△COD∽△CBE,得ODBE =COCB=3x4x从而有x=34BE,另外由△ABD∽△DBE得ABBD =DBBE,即可求得BE=43√6.(1)证明:如图,连接OD,∵CD切∵O于点A,∴OD⊥CD,∵BE∵CD,∴OD∥BE,∴∠ODB=∠DBE,∵OD=OB,∴∠ODB=∠ABD,∴∠ABD=∠DBE;(2)解:如图,设OA=x,则CA=AB=2x,CO=CA+OA=3x,∵OD∥BE,∴∠CDO=∠E,∠COD=∠CBE,∴△COD∽△CBE,∴ODBE =COCB=3x4x即xBE=34,∴x=34BE,∵AB是∵O的直径,∴∠ADB=90°,∵BE∵CD,∴∠E=∠ADB=90°,∵∠ABD=∠DBE,∴△ABD∽△DBE,∴ABBD =DBBE,∵BD=4,∴2×34BE4=4BE,解得BE=43√6.【点睛】本题主要考查了圆的切线、勾股定理、相似三角形的判定及性质以及平行线的判定及性质,熟练掌握相似三角形的判定及性质是解题的关键.8.(2022·北京密云·二模)如图,在△ABC中,AB=BC,以BC为直径的∵O与AC交于点D,DE是∵O的切线.(1)计算∠AED的度数;(2)若tanA=12,BC=2√5,求线段DE的长.【答案】(1)90°(2)4√55【解析】【分析】(1)连接OD,BD,由直径所对圆周角等于90度得∵BDO+∵ODC=∵BDC=90°,再由切线的性质得∵BDE+∵BDO=∵ODE=90°,所以∵BDE=∵ODC,∵ADE=∵BDO,然后由OB-OC,则∵C=∵ODC,BA=BC,则∵C=∵A,所以∵A+∵ADE=90°,最后由三角形内角和定理即可求解;(2)由(1)知:∵AED=∵ADB=90°,则tan∵A=DEAE =BDAD=12,所以AD=2BD,AE=2DE,又因为AB=BC=2√5,在Rt△ADB中,由勾股定理,可求出BD=2,AD=4,再在Rt△ADE中,由勾股定理可求出DE长.(1)解:如图,连接OD,BD,∵BC是∵O的直径,∵∵BDO+∵ODC=∵BDC=90°,∵∵BDE+∵ADE=∵BDA=90°,∵DE是∵O的切线,∵∵BDE+∵BDO=∵ODE=90°,∵∵BDE=∵ODC,∵ADE=∵BDO,∵OD=OC,∵∵C=∵ODC,∵∵C+∵ADE=∵C+∵BDO=90°,∵BA=BC,∵∵C=∵A,∵∵A+∵ADE=90°,∵∵AED=180°-(∵A+∵ADE)=90°;(2)解:由(1)知:∵AED=∵ADB=90°,∵tan∵A=DEAE =BDAD=12,∵AD=2BD,AE=2DE,∵AB=BC=2√5,∵在Rt△ADB中,由勾股定理,得AD2+BD2=AB2,∵(2BD)2+BD2=(2√5)2,∵BD=2,∵AD=4,在Rt△ADE中,由勾股定理,得AE2+DE2=AD2,(2DE)2+DE2=42,∵DE=4√5.5【点睛】本题考查切线的性质,圆周角定理的推论,勾股定理,正切的定义,熟练掌握切线的性质、圆周角定理的推论、正切的定义是解题的关键.9.(2022·北京大兴·二模)如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,O是AB上一点,以OA 为半径的⊙O经过点D.(1)求证:BC是⊙O切线;(2)若BD=5,DC=3,求AC的长.【答案】(1)见解析(2)6【解析】【分析】(1)要证BC是∵O的切线,只要连接OD,再证OD∵BC即可.(2)过点D作DE∵AB,根据角平分线的性质可知CD=DE=3,由勾股定理得到BE的长,再通过证明△BDE∵∵BAC,根据相似三角形的性质得出AC的长.(1)连接OD;∵AD是∵BAC的平分线,∵∵1=∵3.∵OA=OD,∵∵1=∵2.∵∵2=∵3.∵OD∵AC.∵∵ODB=∵ACB=90°.∵OD∵BC.∵OD是∵O的半径,∵BC是∵O切线.(2)过点D作DE∵AB,∵AD是∵BAC的平分线,∵CD=DE=3.在Rt△BDE中,∵BED=90°,由勾股定理得:BE=√BD2−DE2=√52−32=4,∵∵BED=∵ACB=90°,∵B=∵B,∵∵BDE∵∵BAC.∵BE BC =DEAC.∵4 8=3AC.∵AC=6.【点睛】^$本题综合性较强,既考查了切线的判定,要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.同时考查了角平分线的性质,勾股定理得到BE的长,及相似三角形的性质.10.(2022·北京西城·二模)如图,AB是⊙O的直径,CB,CD分别与⊙O相切于点B,D,连接OC,点E 在AB的延长线上,延长AD,EC交于点F.(1)求证:FA∥CO;(2)若FA=FE,CD=4,BE=2,求F A的长.【答案】(1)见解析(2)3√5【解析】【分析】(1)连接OD,证明△CDO∵△CBO(SSS),得∵COD=∵COB,即∵BOD=2∵COB,又因为OD=OA,得∵OAD=∵ODA,所以∵BOD=∵OAD+∵ODA=2∵OAD,即可证得∵COB=∵OAD,即可由平行线的判定定理,得出结论;(2)由F A=FE,得∵F AE=∵FEA,又由(1)知:∵COB=∵OAD,所以∵COE=∵CEO,则CO=CE,又由切线的性质得OB∵CB,根据等腰三角形“三线合一”性质得OB=BE=2,从而求出AE=6,OE=4,再由切线性质得CB=CD=4,然后在Rt△CBE中,由勾股定理,得CF=√CB2+BE2=√42+22=2√5,最后证△EOC∵△EAF,得OEAE =CEFE,即46=2√5FE,可求得FE=3√5,即可由F A=FE得出答案.(1)证明:如图,连接OD,∵CB,CD分别与⊙O相切于点B,D,∵CD=CB,∵OD=OB,OC=OC,∵∵CDO∵△CBO(SSS),∵∵COD=∵COB,即∵BOD=2∵COB,∵OD=OA,∵∵OAD=∵ODA,∵∵BOD=∵OAD+∵ODA=2∵OAD,∵2∵COB=2∵OAD,即∵COB=∵OAD,∵F A∥OC;(2)解:∵F A=FE,∵∵F AE=∵FEA,由(1)知:∵COB=∵OAD,∵∵COE=∵CEO,∵CO=CE,∵CB是∵O的切线,∵OB∵CB,∵OB=BE=2,∵OA=OB=2,∵AE=6,OE=4,∵CB、CD是∵O的切线,∵CB=CD=4,在Rt△CBE中,由勾股定理,得CE=√CB2+BE2=√42+22=2√5,∵F A∥OC,∵∵EOC∵∵EAF,∵OE AE =CEFE,即46=2√5FE,∵FE=3√5,∵F A=FE=3√5.【点睛】本题考查切线的性质,全等三角形的判定与性质,相似三角形的判定与性质,等腰三角形的判定与性质,熟练掌握相关性质与判定是解题的关键.11.(2022·北京顺义·二模)如图,△ABC内接于⊙O,AB是⊙O的直径,点D在AB的延长线上,且∠BCD=∠A,点E为AC的中点,连接OE并延长与DC的延长线交于点F.(1)求证:CD是⊙O的切线;(2)若CD=4,tanA=12,求CF的长.【答案】(1)见解析(2)6【解析】【分析】(1)根据AB是⊙O的直径,可得∠ACB=90°,由OA=OC得∠A=∠ACO,结合已知条件,根据可得∠BCD+∠OCB=90°,即可得证;(2)证明△DCB∽△DAC,得出CDAD =DBDC=CBAC,根据tanA=12,可得CBAC=12,从而求得DB的长,进而求得OD的长,由点E为AC的中点,根据垂径定理以及∠ACB=90°,证明OF∥BC,根据平行线分线段成比例即可求解.(1)证明:如图,连接OC,∵OA=OC,∴∠A=∠ACO,∵∠BCD=∠A,∴∠BCD=∠ACO∵AB是⊙O的直径,∴∠ACB=90°,∴∠ACO+∠OCB=90°,∴∠BCD+∠OCB=90°,即∠OCD=90°,∵OC是半径,∴CD是⊙O的切线;(2)∵∠BCD=∠A,∠D=∠D,∴△DCB∽△DAC,∴CDAD =DBDC=CBAC,∵tanA=12,可得CBAC=12,∴4AD =DB4=12,∴AD=8,DB=2,∴OB=12AB=12(AD−BD)=3,∵点E为AC的中点,∴OF⊥AC,又∵∠ACB=90°,∴OF∥BC,∴DCCF =BDOB,即4CF=23,∴CF=6.【点睛】本题考查了切线的判定,直径所对的圆周角是直角,垂径定理的推论,相似三角形的性质与判定,正切,平行线分线段成比例,掌握以上知识是解题的关键.12.(2022·北京房山·二模)如图,在△ABC中,∠C=90°,∠ABC的平分线BE交AC于点E,过点E作直线BE 的垂线于交AB于点F,⊙O是△BEF的外接圆.(1)求证:AC是⊙O的切线;(2)过点E作EH⊥AB于点H,若CD=2,求HF的长度.【答案】(1)见详解(2)2【解析】【分析】(1)连接OE,先证明BF是圆的直径,OE是圆的半径,再证明OE∥BC在,则有∵OEA=∵C=90°,结论得证;(2)连接ED,根据角平分线的性质证明EH=EC,再证∵EHF∵∵ECD,则HF可求.(1)连接OE,如图,∵EF∵BE,∵∵BEF=90°,∵∵O是∵BEF的外接圆,∵BF是∵O的直径,OE是∵O的半径,∵∵OEB=∵OBE,∵BE是∵ABC的角平分线,∵∵OBE=∵CBE,∵∵OEB=∵CBE,∵OE∥BC,∵∵OEA=∵C=90°,即OE∵AC,∵OE是半径,∵AC是∵O的切线;(2)连接ED,如图,∵BE平分∵ABC,且EH∵BA,EC∵BC,∵EH=EC,∵四边形BDEF是∵O的内接四边形,∵∵EFH=∵EDC,∵∵EHF=∵C=90°,∵∵EHF∵∵ECD,∵HF=CD=2,即HF的值为2.【点睛】此题考查了圆的切线的判定、圆周角定理、平行线的判定与性质、全等三角形的判定与性质等知识,解题的关键是正确的作出所需辅助线.13.(2022·北京昌平·二模)如图,在△ABC中,∠C=90°,BC,AC与⊙O交于点F,D,BE为⊙O直径,点E在AB上,连接BD,DE,∠ADE=∠DBE.(1)求证:AC是⊙O的切线;(2)若sinA=35,⊙O的半径为3,求BC的长.【答案】(1)过程见详解(2)245【解析】【分析】(1)连接OD,OD=OB=OE,即有∵OBD=∵ODB,∵ODE=∵OED,再根据BE是直径,得到∵BDE=90°=∵DBE+∵DEB=∵ODB+∵ODE,即有∵DBE+∵ODE=90°,再根据∵ADE=∵DBE,有∵ADE+∵ODE=90°,即有OD∵AC,则结论得证;(2)先证OD∥BC,则有BCOD =ABOA,利用sinA=ODOA=35可求出OA,即可求出BC的值.(1)连接OD,如图,∵OD=OB=OE,∵∵OBD=∵ODB,∵ODE=∵OED,∵BE是直径,∵∵BDE=90°=∵DBE+∵DEB=∵ODB+∵ODE,∵∵DBE+∵ODE=90°,∵∵ADE=∵DBE,∵∵ADE+∵ODE=90°,∵OD∵AC,∵OD为半径,∵AC是∵O的切线;(2)根据(1)的结论,有OD∵AC,∵∵C=90°,∵BC∵AC,∵OD∥BC,∵BC OD =ABOA,∵在Rt△ADO中,sinA=ODOA =35,又∵OD=OB=3,∵OA=5,∵AB=OA+OB=8,∵BC OD =ABOA,∵BC=ABOA ×OD=85×3=245.即BC为245.【点睛】本题考查了切线的判定与性质、直径作对圆周角为90°、平行的性质、勾股定理、三角函数等知识,证明切线是解答本题的关键.14.(2022·北京海淀·二模)如图,AB为∵O的直径,CD为弦,CD∵AB于点E,连接DO并延长交∵O于点F,连接AF交CD于点G,CG =AG,连接AC.(1)求证:AC∵DF;(2)若AB = 12,求AC和GD的长.【答案】(1)见解析(2)AC =6,DG=4√3【解析】【分析】(1)根据圆周角定理得到∵C=∵F,由GA=GC推出∵CAF=∵C,得到∵CAF=∵F,即可得到结论AC∵DF.∠2,进而证得△AOD是等边三角形,(2)连接AD,利用AC∵DF推出∵C=∵1,根据圆周角定理得到∠C=12AB=6.利用垂径定理求出AC=AD=6,利用三角函数求出AG.得到AD=AO=12(1)证明:∵ C,F都在∵O上,∵ ∵C=∵F.∵ GA=GC,∵ ∵CAF=∵C.∵ ∵CAF=∵F.∵ AC∵DF.(2)解:连接AD.∵ AC∵DF,∵ ∵C=∵1,⌢=AD⌢,∵AD∠2.∵∠C=12∠2.∵∵∠1=12∵ AB∵CD于E,∵ ∵BED=90°.∵∠1+∠2=90°.∵∵由∵,∵得∵1=30°,∵2=60°.∵ OA=OD,∵ ∵AOD是等边三角形.AB=6.∵AD=AO=12∵直径AB∵CD于E,∵AC⌢=AD⌢.∵ AC=AD=6.∵ ∵AOD是等边三角形,∵ ∵ADO=60°,∵1=30°.∵ ∵3=∵AOD-∵1=30°∵ DF是∵O的直径,∵ ∵F AD=90°.=4√3.∵ 在Rt∵GAD中,DG=ADcos∠3【点睛】此题考查了圆周角定理,垂径定理,等边三角形的判定及性质,锐角三角函数,平行线的判定定理,熟记圆周角定理及垂径定理是解题的关键.15.(2022·北京市十一学校模拟预测)如图,AB 是⊙O 的弦,C 为⊙O 上一点,过点C 作AB 的垂线与AB 的延长线交于点D ,连接BO 并延长,与⊙O 交于点E ,连接EC ,CD 是⊙O 的切线.(1)求证:∠ABE =2∠E ;(2)若tanE =13,AB =8,求BD 的长.【答案】(1)证明见解析(2)1【解析】【分析】(1)连接OC ,根据切线的性质易得AD ∥CO ,由平行线的性质得到∠ABE =∠BOC ,再结合等腰三角形的性质得到∠OCE =∠OEC ,由三角形外角性质易得∠BOC =∠OCE +∠OEC =2∠BCE 即可求解;(2)连接BC 和AC ,CO ,根据BE 是⊙O 的直径和切线的性质易得∠BCD =∠E ,由圆周角定理得到∠A =∠E ,结合tanE =13得到BD CD =DC AD =13,进而可得CD =3BD ,将AB =8,AD =AB +BD =8+BD 代入即可求解.(1)证明:连接OC ,如下图.∵CD 是⊙O 的切线,过点C 作AB 的垂线与AB 的延长线交于点D ,∵∠CDA =∠DCO =90°,∵AD ∥CO ,∵∠ABE =∠BOC .∵OC =OE ,∵∠OCE =∠OEC ,∵∠BOC =∠OCE +∠OEC =2∠BCE,∵∠ABE=2∠E;(2)解:连接BC和AC,CO,如下图.∵BE是⊙O的直径,∵∠BCE=90°,∵∠OCE+∠OCB=90°.∵CD是⊙O的切线,∵∠OCB+∠BCD=90°,∵∠BCD=∠OCE,∵∠BCD=∠E,∵∠A=∠E,tanE=13,∵BDCD=DC AD =13,∵CD=3BD.∵AB=8,AD=AB+BD=8+BD,∵3BD8+BD=13,∵BD=1.【点睛】本题主要考查了圆周角定理、切线的性质,平行线的性质,等腰三角形的性质,三角形外角性质,锐角三角函数值的求法,作出辅助线是解答关键.16.(2022·北京东城·一模)如图,在△ABC中,AB=AC,以AB为直径作⊙O,交BC于点D,交AC于点E,过点B作⊙O的切线交OD的延长线于点F.(1)求证:∠A=∠BOF;(2)若AB=4,DF=1,求AE的长.【答案】(1)见解析(2)AE=83【解析】【分析】(1)首先根据等边对等角可证得∠C=∠ODB,再根据平行线的判定与性质,即可证得结论;(2)首先根据圆周角定理及切线的性质,可证得∠AEB=∠OBF,即可证得△ABE∽△OFB,再根据相似三角形的性质即可求得.(1)证明:∵AB=AC∴∠C=∠ABC∵OB=OD∴∠ODB=∠OBD∴∠C=∠ODB∴AC∥OD∴∠A=∠BOF(2)解:如图:连接BE∵AB是⊙O的直径,AB=4AB=2∴∠AEB=90°,OB=OD=12∵BF是⊙O的切线∴∠OBF=90°。
专题07圆的有关计算与证明问题(原卷版)
决胜2020年中考数学压轴题全揭秘()专题07圆的有关计算与证明问题【考点1】圆中有关角的计算问题【例1】(2019•台州)如图,AC是圆内接四边形ABCD的一条对角线,点D关于AC的对称点E在边BC 上,连接AE.若∠ABC=64°,则∠BAE的度数为.̂)上,若∠【例2】(2019•温州)如图,⊙O分别切∠BAC的两边AB,AC于点E,F,点P在优弧(EDFBAC=66°,则∠EPF等于度.【考点2】切线的有关线段计算问题【例3】(2019•舟山)如图,已知⊙O 上三点A ,B ,C ,半径OC =1,∠ABC =30°,切线P A 交OC 延长线于点P ,则P A 的长为( )A .2B .√3C .√2D .12 【例4】(2019•台州)如图,等边三角形ABC 的边长为8,以BC 上一点O 为圆心的圆分别与边AB ,AC 相切,则⊙O 的半径为( )A .2√3B .3C .4D .4−√3【考点3】扇形与弧长的有关计算问题【例5】(2019•宁波)如图所示,矩形纸片ABCD 中,AD =6cm ,把它分割成正方形纸片ABFE 和矩形纸片EFCD 后,分别裁出扇形ABF 和半径最大的圆,恰好能作为一个圆锥的侧面和底面,则AB 的长为( )A .3.5cmB .4cmC .4.5cmD .5cm【例6】(2019•绍兴)如图,△ABC 内接于⊙O ,∠B =65°,∠C =70°.若BC =2√2,则BC ̂的长为( )A .πB .√2πC .2πD .2√2π【考点4】圆锥的有关计算问题【例7】(2019•湖州)已知圆锥的底面半径为5cm ,母线长为13cm ,则这个圆锥的侧面积是( )A .60πcm 2B .65πcm 2C .120πcm 2D .130πcm 2【例8】(2019•金华)如图物体由两个圆锥组成.其主视图中,∠A =90°,∠ABC =105°,若上面圆锥的侧面积为1,则下面圆锥的侧面积为( )A .2B .√3C .32D .√2【考点5】圆与多边形的有关计算问题【例9】(2019•湖州)如图,已知正五边形ABCDE 内接于⊙O ,连结BD ,则∠ABD 的度数是( )A .60°B .70°C .72°D .144°【例10】(2018•温州)小明发现相机快门打开过程中,光圈大小变化如图1所示,于是他绘制了如图2所示的图形.图2中六个形状大小都相同的四边形围成一个圆的内接正六边形和一个小正六边形,若PQ 所在的直线经过点M ,PB =5cm ,小正六边形的面积为49√32cm 2,则该圆的半径为 cm .【考点6】圆中有关线段的最值问题【例11】(2019•嘉兴)如图,在⊙O中,弦AB=1,点C在AB上移动,连结OC,过点C作CD⊥OC交⊙O于点D,则CD的最大值为.【考点7】圆中有关计算与证明综合问题【例12】(2019•金华)如图,在▱OABC中,以O为圆心,OA为半径的圆与BC相切于点B,与OC相交于点D.̂的度数.(1)求BD(2)如图,点E在⊙O上,连结CE与⊙O交于点F,若EF=AB,求∠OCE的度数.【例13】(2019•衢州)如图,在等腰△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作DE⊥AB,垂足为E.(1)求证:DE是⊙O的切线.̂的长.(2)若DE=√3,∠C=30°,求AD1.(2020•温岭市一模)如图物体由两个圆锥组成.其主视图中,∠A=90°,∠ABC=105°,则上下两圆锥的侧面积之比为()A.1:2B.1:√3C.2:3D.1:√22.(2020•金华模拟)如图,一只蚂蚁要从圆柱体下底面的A点,沿圆柱表面爬到与A相对的上底面的B点,圆柱底面直径为4,母线为6,则蚂蚁爬行的最短路线长为()A.√36+4π2B.√4+36π2C.4πD.6π3.(2020•杭州模拟)如图,在△ABC中,以BC为直径的⊙O,交AB的延长线于点D,交AC于点E,连接OD,OE.若∠A=α,则∠DOE的度数为()A.180°﹣2αB.180°﹣αC.90°﹣αD.2α4.(2020•温州模拟)如图,△ABC,AC=3,BC=4√3,∠ACB=60°,过点A作BC的平行线1,P为直线l上一动点,⊙O为△APC的外接圆,直线BP交⊙O于E点,则AE的最小值为()A.√3−1B.7﹣4√3C.√3D.15.(2020•绍兴一模)如图,AB是⊙O的直径,DB,DE分别切⊙O于点B、C,若∠ACE=20°,则∠D 的度数是()A.40°B.50°C.60°D.70°二.填空题(共5小题)6.(2020•金华模拟)如图,BC是⊙O的弦,以BC为边作等边三角形ABC,圆心O在△ABC的内部,若BC=6,OA=√3,则⊙O的半径为.7.(2020•天台县模拟)如图,已知等边△ABC的边长为8,以AB为直径的⊙O与边AC、BC分别交于D、̂的长为.E两点,则劣弧DE8.(2020•绍兴一模)如图所示,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,若以点C为圆心,r为半径的圆与边AB所在直线有公共点,则r的取值范围为.9.(2020•拱墅区校级模拟)如图,P A,PB是⊙O的两条切线,A,B为切点,点D,E,F分别在线段AB,BP,AP上,且AD=BE,BD=AF,∠P=54°,则∠EDF=度.10.(2020•衢州模拟)如图,小圆O的半径为1,△A1B1C1,△A2B2C2,△A3B3C3,…,△A n B n∁n依次为同心圆O的内接正三角形和外切正三角形,由弦A1C1和弧A1C1围成的弓形面积记为S1,由弦A2C2和弧A2C2围成的弓形面积记为S2,…,以此下去,由弦A n∁n和弧A n∁n围成的弓形面积记为S n,其中S2020的面积为.三.解答题(共10小题)11.(2020•金华模拟)如图,在Rt△ABC中,∠C=90°,AC=BC,点O在AB上,以O为圆心,OA为半径作⊙O,与BC相切于点D,且交AB于点E.(1)连结AD,求证:AD平分∠CAB;(2)若BE=√2−1,求阴影部分的面积.12.(2020•鹿城区校级模拟)如图,在Rt△ABC中,∠BAC=90°,D是BC边上的一点,过A,B,D三点的⊙O交AC于点E,作直径AF,连结FD并延长交AC于点G,且FG∥BE,连结BE,BF﹒(1)求证:AB=BD;(2)若BD=2CD,AC=5,求⊙O的直径长﹒13.(2020•绍兴一模)如图,在正方形网格图中建立平面直角坐标系,一条圆弧经过格点A(0,4)、B(﹣4,4)、C(﹣6,2),若该圆弧所在圆的圆心为D点,请你利用网格图回答下列问题:(1)圆心D的坐标为;(2)若扇形ADC是一个圆锥的侧面展开图,求该圆锥底面圆的半径长(结果保留根号).14.(2020•上虞区校级一模)如图1 (1)已知△ABC中AB=AC,∠BAC=36°,BD是角平分线,求证:点D是线段AC的黄金分割点;(2)如图2,正五边形的边长为2,连结对角线AD、BE、CE,线段AD分别与BE和CE相交于点M、N,求MN的长;(3)设⊙O的半径为r,直接写出它的内接正十边形的边长=(用r的代数式表示).15.(2020•长安区模拟)如图1,在△ABC中,AC=BC,以BC为直径的⊙O交AB于点D.(1)求证:点D是AB的中点;(2)如图2,过点D作DE⊥AC于点E,求证:DE是⊙O的切线.16.(2020•衢州模拟)如图,以△ABC的BC边上一点O为圆心的圆,经过A、B两点,且与BC边交于点E,D为BE的下半圆弧的中点,连接AD交BC于F,若AC=FC.(1)求证:AC是⊙O的切线;(2)若BF=4,DF=√10,求⊙O的半径.17.(2020•温州模拟)如图,AB是O的直径,C是弧BD的中点,CE⊥AB,垂足为E,BD交CE于点F.(1)求证:CF=BF;(2)若AD=6,⊙O的半径为5,求BC的长.18.(2020•拱墅区校级模拟)如图,△ABC是的内接三角形,点C是优弧AB上一点,设∠OAB=α,∠C =β.(1)猜想:β关于α的函数表达式,并给出证明;(2)若α=30°,AB=6,S△ABC=6√3,求AC的长.19.(2019•泸县模拟)如图,已知⊙O的直径AB=10,弦AC=6,∠BAC的平分线交⊙O于点D,过点D 作DE⊥AC交AC的延长线于点E.(1)求证:DE是⊙O的切线;(2)求DE的长.20.(2019•泰顺县模拟)已知矩形ABCD,AB=10,AD=8,G为边DC上任意一点,连结AG,BG以AG 为直径作⊙P分别交BG,AB于点E,H,连结AE,DE.̂的中点,证明:AG=AB.(1)若点E为GH(2)若△ADE为等腰三角形时,求DG的长.(3)作点C关于直线BG的对称点C′.①当点C落在线段AG上时,设线段AG,DE交于点F,求△ADF与△AEF的面积之比;②在点G的运动过程中,当点C′落在四边形ADGE内时(不包括边界),则DG的范围是(直接写出答案)。
圆的培优专题(含解答)

第4题 第5题 第6题第1题 第2题 第3题圆的培优专题1——与圆有关的角度计算一 运用辅助圆求角度1、如图,△ABC 内有一点D ,DA =DB =DC ,假设∠DAB =20︒,∠DAC =30︒, 那么∠BDC = . 〔∠BDC = 12∠BAC =100︒〕2、如图,AE =BE =DE =BC =DC ,假设∠C =100︒,那么∠BAD = . 〔50︒〕3、如图,四边形ABCD 中,AB =AC =AD ,∠CBD =20︒,∠BDC =30︒,那么 ∠BAD = . 〔∠BAD =∠BAC +∠CAD =40︒+60︒=100︒〕解题策略:通过添加辅助圆,把问题转化成同弧所对的圆周角与圆心角问题,思维更明朗! 4、如图,□ABCD 中,点E 为AB 、BC 的垂直平分线的交点,假设∠D =60︒, 那么∠AEC = . 〔∠AEC =2∠B =2∠D =120︒〕5、如图,O 是四边形ABCD 内一点,OA =OB =OC ,∠ABC =∠ADC =70︒, 那么∠DAO +∠DCO = . 〔所求=360︒-∠ADC -∠AOC =150︒〕6、如图,四边形ABCD 中,∠ACB =∠ADB =90︒,∠ADC =25︒,那么∠ABC = . 〔∠ABC =∠ADC =25︒〕解题策略:第6题有两个直角三角形共斜边,由直角所对的弦为直径,易得到ACBD 共圆.第10题 第11题 第12题第7题 第8题 第9题 二 运用圆周角和圆心角相互转化求角度7、如图,AB 为⊙O 的直径,C 为AB 的中点,D 为半圆AB 上一点,那么∠ADC = . 8、如图,AB 为⊙O 的直径,CD 过OA 的中点E 并垂直于OA ,那么∠ABC = . 9、如图,AB 为⊙O 的直径,3BC AC =,那么∠ABC = .答案:7、45︒; 8、30︒; 9、22.5︒; 10、40︒; 11、150︒; 12、110︒ 解题策略:以弧去寻找同弧所对的圆周角与圆心角是解决这类问题的捷径!10、如图,AB 为⊙O 的直径,点C 、D 在⊙O 上,∠BAC =50︒,那么∠ADC = . 11、如图,⊙O 的半径为1,弦AB 2,弦AC 3∠BOC = . 12、如图,PAB 、PCD 是⊙O 的两条割线,PAB 过圆心O ,假设AC CD =,∠P =30︒, 那么∠BDC = . 〔设∠ADC =x ,即可展开解决问题〕解题策略:在连接半径时,时常会伴随出现特殊三角形——等腰三角形或直角三角形或等腰 直角三角形或等边三角形,是解题的另一个关键点!圆的四接四边形的外角等于内对角,是一个非常好用的一个重要性质!第1题 第2题 第3题圆的培优专题2——与垂径定理有关的计算1、如图,AB 是⊙O 的弦,OD ⊥AB ,垂足为C ,交⊙O 于点D ,点E 在⊙O 上,假设∠BED =30︒,⊙O 的半径为4,那么弦AB 的长是 . 略解:∵OD ⊥AB ,∴AB =2AC ,且∠ACO =90︒, ∵∠BED =30︒,∴∠AOC =2∠BED =60︒∴∠OAC =30︒,OC = 12 OA =2,那么AC =23AB =432、如图,弦AB 垂直于⊙O 的直径CD ,OA =5,AB =6,那么BC = . 略解:∵直径CD ⊥弦AB ,∴AE =BE =12 AB=3∴OE 22534-=,那么CE =5+4=9 ∴BC =2293310+=3、如图,⊙O 的半径为25弦AB ⊥CD ,垂足为P ,AB =8,CD =6,那么OP = . 略解:如图,过点O 作OE ⊥AB ,OF ⊥CD ,连接OB ,OD. 那么BE =12 AB =4,DF =12 CD =3,且OB =OD =25 OE 22(25)42-=,OF =22(25)311-= 又AB ⊥CD ,那么四边形OEPF 是矩形,那么OP 222(11)15+=4、如图,在⊙O 内,如果OA =8,AB =12,∠A =∠B =60︒,那么⊙O 的半径为 . 略解:如图,过点O 作OD ⊥AB ,连接OB ,那么AD =12 AB =4,因此,BD =8,OD =43∴OB 22(43)847+=.第4题 第5题 第6题5、如图,正△ABC 内接于⊙O ,D 是⊙O 上一点,∠DCA =15︒,CD =10,那么BC = 略解:如图,连接OC ,OD ,那么∠ODC =∠OCD∵△ABC 为等边三角形,那么∠OCA =∠OCE =30︒,∴∠ODC =∠OCD =45︒ ∴△OCD 是等腰三角形,那么OC =2 过点O 作OE ⊥BC ,那么BC =2CE =566、如图,⊙O 的直径AB =4,C 为AB 的中点,E 为OB 上一点,∠AEC =60︒,CE 的延 长线交⊙O 于点D ,那么CD = 略解:如图,连接OC ,那么OC =2∵C 为AB 的中点,那么OC ⊥AB ,又∠AEC =60︒,∴∠OCE =30︒ 如图,过点O 作OF ⊥CD ,那么OF =12 OC =1,CF =3,∴CD =2CF =237、如图,A 地测得台风中心在城正西方向300千米的B 处, 并以每小时10760︒的BF 方向移 动,距台风中心200千米范围内是受台风影响的区域. 问:A 地是否受到这次台风的影响?假设受到影响,请求 出受影响的时间?解:如图,过点A 作AC ⊥BF 交于点C ,∵∠ABF =30︒,那么AC =12 AB =150<200,因此A 地会受到这次台风影响;如图,以A 为圆心200千米为半径作⊙A 交BF 于D 、E 两点,连接AD , 那么DE =2CD =222001501007-= 所以受影响的时间为100710710=〔时〕圆的培优专题3——圆与全等三角形1、如图,⊙O 的直径AB =10,弦AC =6,∠ACB 的平分线交⊙O 于D ,求CD 的长. 解:如图,连接AB ,BD ,在CB 的延长线上截取BE =AC ,连接DE ∵∠ACD =∠BCD ,∴AD =BD 又∠CAD =∠EBD ,AC =BE ∴△CAD ≌△EBD 〔SAS 〕 ∴CD =DE ,∠ADC =∠BDE∵AB 为⊙O 的直径,那么∠ACB =∠ADB =90︒∴BC 221068-=;∠ADC +∠CDB =∠CDB +∠BDE =90︒,即∠CDE =90︒ ∴△CDE 是等腰直角三角形且CE =14,∴CD =22、如图,AB 是⊙O 的直径,C 是半圆的中点,M 、D 分别是CB 及AB 延长线上一点,且 MA =MD ,假设CM 2,求BD 的长.解:如图,连接AC ,那么AC =BC ,∠C =90︒,即△ABC 是等腰直角三角形 过点M 作MN ∥AD ,那么∠NMA =∠MAD那么△CMN 也是等腰直角三角形,那么MN 2CM =2 ∴∠ANC =∠MBD =135︒,又MA =MD ,∴∠D =∠NMA =∠MAD ∴△AMN ≌△BMD 〔AAS 〕 ∴BD =MN =23、如图,AB 为⊙O 的直径,点N 是半圆的中点,点C 为AN 上一点,NC 3 求BC -AC 的值.解:如图,连接AN ,BN ,那么△ABN 是等腰直角三角形 在BC 上截取BD =AC ,连接DN ∵AN =BN ,∠CAN =∠DBN ,AC =BD ∴△ACN ≌△BDN 〔SAS 〕∴CN =DN ,∠CNA =∠DNB ,∴∠CND =∠CNA +∠AND =∠ADN +∠DNB =90︒,即△CND 是等腰直角三角形 ∴CD 26,∴BC -AC =BC -BD =CD 64、如图,点A 、B 、C 为⊙O 上三点,AC BC =,点M 为BC 上一点,CE ⊥AM 于E , AE =5,ME =3,求BM 的长.解:如图,在AM 上截取AN =BM ,连接CN ,CM. ∵AC BC =,∴AC =BC ,又∠A =∠B ∴△ACN ≌△BCM 〔SAS 〕 ∴CN =CM ,又CE ⊥AM ∴NE =ME =3, ∴BM =AN =AE -NE =25、如图,在⊙O 中,P 为BAC 的中点,PD ⊥CD ,CD 交⊙O 于A ,假设AC =3,AD =1, 求AB 的长.解:如图,连接BP 、CP ,那么BP =CP ,∠B =∠C 过点P 作PE ⊥AB 于点E ,又PD ⊥CD ∴∠BEP =∠CDP ∴△BEP ≌△CDP 〔AAS 〕 ∴BE =CD =3+1=4,PE =PD连接AP ,那么Rt △AEP ≌Rt △ADP 〔HL 〕,那么AE =AD =1 ∴AB =AE+BE =56、如图,AB 是O 的直径,MN 是弦,AE ⊥MN 于E ,BF ⊥MN 于F ,AB =10,MN =8. 求BF -AE 的值.解:∵AE ⊥MN ,BF ⊥MN ,那么AE ∥BF ,∴∠A =∠ B如图,延长EO 交BF 于点G , 那么∠AOE =∠BOG ,AO =BO∴△AOE ≌△BOG 〔AAS 〕,那么OE =OG 过点O 作OH ⊥MN ,FG =2OH ,HN =4连接ON ,那么ON =5,OH =22543-=,那么BG -AE =FG =6.圆的培优专题4——圆与勾股定理1、如图,⊙O 是△BCN 的外接圆,弦AC ⊥BC ,点N 是AB 的中点,∠BNC =60︒, 求BNBC的值. 解:如图,连接AB ,那么AB 为直径,∴∠BNA =90︒ 连接AN ,那么BN =AN ,那么△ABN 是等腰直角三角形∴BN =22AB ;又∠BAC =∠BNC =60︒, ∴BC =32AB , ∴BN BC =63〔方法2,过点B 作BD ⊥CN ,即可求解〕2、如图,⊙O 的弦AC ⊥BD ,且AC =BD ,假设AD =22,求⊙O 半径. 解:如图,作直径AE ,连接DE ,那么∠ADE =90︒ 又AC ⊥BD ,那么∠ADB +∠DAC =∠ADB +∠EDB =90︒ ∴∠DAC =∠EDB ,那么CD BE =,∴DE BC =, ∵ AC =BD ,∴AC CD =,那么AD BC DE == ∴AD =DE ,即△ADE 是等腰直角三角形 ∴AE =2AD =4,即⊙O 的半径为23、如图,AB 为⊙O 的直径,C 为⊙O 上一点,D 为CB 延长线上一点,且∠CAD =45︒, CE ⊥AB 于点E ,DF ⊥AB 于点F.〔1〕求证:CE =EF ;〔2〕假设DF =2,EF =4,求AC. 〔1〕证:∵ AB 为⊙O 的直径,∠CAD =45︒,那么△ACD 是等腰直角三角形,即AC =DC 又CE ⊥AB ,那么∠CAE =∠ECB如图,过点C 作CG 垂直DF 的延长线于点G又CE ⊥AB ,DF ⊥AB ,那么四边形CEFG 是矩形,∠AEC =∠DGC =90︒ ∴EF =CG ,CE ∥DG ,那么∠ECB =∠CDG =∠CAE ∴△ACE ≌△DCG 〔AAS 〕,那么CE =CG =EF 〔2〕略解:AC =CD =2246213+=.4、如图,AB 为⊙O 的直径,CD ⊥AB 于点D ,CD 交AE 于点F ,AC CE =. 〔1〕求证:AF =CF ;〔2〕假设⊙O 的半径为5,AE =8,求EF 的长 〔1〕证:如图,延长CD 交⊙O 于点G ,连接AC ∵直径AB ⊥CG ,那么AG AC CE == ∴∠CAE =∠ACG ,那么AF =CF〔2〕解:如图,连接OC 交AE 于点H ,那么OC ⊥AE ,EH =AH =12 AE=4∴ OH =22543-=,那么CH =5-3=2 设HF =x ,那么CF =AF =4-x 那么2222(4)x x +=-,∴32x =,即HF =32∴EF =1125、如图,在⊙O 中,直径CD ⊥弦AB 于E ,AM ⊥BC 于M ,交CD 于N ,连接AD. 〔1〕求证:AD =AN ;〔2〕假设AB =42,ON =1,求⊙O 的半径. 〔1〕证:∵CD ⊥AB ,AM ⊥BC∴∠C +∠CNM =∠C +∠B =90︒ ∴∠B =∠CNM ,又∠B =∠D ,∠AND =∠CNM ∴∠D =∠AND ,即AD =AN (2)解:∵直径CD ⊥弦AB ,那么AE =22 又AN =AD ,那么NE =ED如图,连接OA ,设OE =x ,那么NE =ED =1x + ∴OA =OD =21x +∴222(22)(21)x x +=+,那么1x = ∴⊙O 的半径OA =3圆的培优专题5——圆中两垂直弦的问题1、在⊙O中,弦AB⊥CD于E,求证:∠AOD+∠BOC=180︒.证:如图,连接AC,∵AB⊥CD,那么∠CAB+∠ACD=90︒又∠AOD=2∠ACD,∠BOC=2∠BAC∴∠AOD+∠BOC=180︒.2、在⊙O中,弦AB⊥CD于点E,假设⊙O的半径为R,求证:AC2+BD2=4R2. 证:∵AB⊥CD,那么∠CAB+∠ACD=90︒如图,作直径AM,连接CM那么∠ACM=∠ACD+∠DCM=90︒∴∠CAB=∠DCM,=∴BC DM=,∴CM BD∴CM=BD∵AC2+CM2=AM2∴AC2+BD2=4R2.3、在⊙O中,弦AB⊥CD于点E,假设点M为AC的中点,求证ME⊥BD.证:如图,连接ME,并延长交BD于点F∵AB⊥CD,且点M为AC的中点∴ME为Rt△AEC斜边上的中线∴AM=ME∴∠A=∠AEM=∠BEF又∠B=∠C,∠A+∠C=90︒∴∠BEF+∠B=90︒,即∠BFE=90︒∴ME⊥BD.4、在⊙O中,弦AB⊥CD于点E,假设ON⊥BD于N,求证:ON =12 AC.证:如图,作直径BF,连接DF,那么DF⊥BD,又ON⊥BD,∴ON∥FD,又OB=OF∴ON=12DF连接AF,那么AF⊥AB,又CD⊥AB ∴AF∥CD∴AC FD=,那么AC=FD∴ON=12AC5、在⊙O中,弦AB⊥CD于点E,假设AC=BD,ON⊥BD于N,OM⊥AC于M. 〔1〕求证:ME//ON;〔2〕求证:四边形OMEN为菱形.证:〔1〕如图,延长ME交OD于点F∵OM⊥AC,那么点M为AC的中点∵AB⊥CD,那么ME为Rt△ACE的斜边上中线∴AM=EM,∴∠A=∠AEM=∠BEF又∠B=∠C,∠A+∠C=90︒∴∠B+∠BEF=90︒,那么∠BFE=90︒∴MF⊥BD,又ON⊥BD∴MF∥ON〔2〕由〔1〕知MF∥ON,同理可证OM∥NE,∴四边形OMEN是平行四边形∵AC=BD,∴OM=ON∴四边形OMEN为菱形.圆的培优专题6——圆与内角〔外角〕平分线一 圆与内角平分线问题往往与线段和有关,实质是对角互补的根本图形1、如图,⊙O 为△ABC 的外接圆,弦CD 平分∠ACB ,∠ACB =90︒. 求证:CA +CB 2CD.证:如图,在CA 的延长线上截取AE =BC ,连DE ,AD ,BD ∵CD 平分∠ACB ,∴AD =BD 又∠DAE =∠DBC ,AE =BC ∴△DAE ≌△DBC 〔SAS 〕 ∴CD =DE ,又∠ACD =45︒∴△CDE 是等腰直角三角形,那么CA +CB =CE 22、如图,⊙O 为△ABC 的外接圆,弦CD 平分∠ACB ,∠ACB =120︒,求CA+CBCD 的值.解:如图,在CA 的延长线上截取AE =BC ,连DE ,AD ,BD ∵CD 平分∠ACB ,∴AD =BD 又∠DAE =∠DBC ,AE =BC ∴△DAE ≌△DBC 〔SAS 〕 ∴CD =DE ,又∠ACD =60︒ ∴△CDE 是等边三角形∴CD =CE =CA +BC ,即CA+CBCD=13、如图,过O 、M (1,1)的动圆⊙1O 交y 轴、x 轴于点A 、B ,求OA +OB 的值. 解:如图,过点M 作ME y ⊥轴,MF ⊥x 轴,连AM 、BM 由M 〔1,1〕知:四边形OFME 是正方形 ∴OE =OF =4,EM =FM ,又∠MBF =∠MAE , ∴△AEM ≌△BFM 〔AAS 〕,那么AE =BF ∴OA +OB =AE +OE +OF -BF =8.二 圆中的外角问题往往与线段的差有关4、如图,⊙O 为△ABC 的外接圆,弦CP 平分△ABC 的外角∠ACQ ,∠ACB =90︒. 求证:〔1〕PA PB =;〔2〕AC -BC =2PC. 证:〔1〕如图,连接AP ,那么∠PCQ =∠PAB 又∠PCQ =∠PCA ,那么∠PAB =∠PCA ∴PA PB =〔2〕连接BP ,由〔1〕得,PA =PB在AC 上截取AD =BC ,连PD ,又∠PAD =∠PBC ∴△PAD ≌△PBC 〔SAS 〕,那么PD =PC又∠PCD =45︒,那么∴PCD 是等腰直角三角形,∴AC -BC =CD =2PC. 5、如图,⊙O 为△ABC 的外接圆,弦CP 平分△ABC 的外角∠ACQ ,∠ACB =120︒. 求BC -AC PC的值.解:如图,在BC 上截取BD =AC ,连AP 、BP 、DP ∵∠PCB =∠PCQ =∠PBA ∴AP =BP ,又∠CAP =∠DBP∴△CAP ≌△DBP 〔SAS 〕,那么CP =DP 又∠ACB =120︒,∴∠PCD =30︒, ∴BC -AC PC = CD PC=36、如图,A (4,0),B (0,4),⊙1O 经过A 、B 、O 三点,点 这P 为OA 上动点〔异于O 、A 〕. 求PB -PAPO的值.解:如图,在BP 上截取BC =AP∵A (4,0),B (0,4),那么OA =OB =4 又∠OAP =∠OBC ∴△OAP ≌△OBC 〔SAS 〕∴OC =OP ,且∠COP =∠AOB =90︒,那么PB -PA PO = PCPO =2.第6题一 切线与一个圆 答案:1、70︒;2、20︒;3、80︒;4、120︒;5、130︒;6、45︒1、如图,AD 切⊙O 于A ,BC 为直径,假设∠ACB =20︒,那么∠CAD = .2、如图,AP 切⊙O 于P ,PB 过圆心,B 在⊙O 上,假设∠ABP =35︒,那么∠APB = .3、如图,PA 、PB 为⊙O 的切线,C 为ACB 上一点,假设∠BCA =50︒,那么∠APB = .4、如图,PA 、PB 为⊙O 的切线,C 为AB 上一点, 假设∠BCA =150︒,那么∠APB = .5、如图,点O 是△ABC 的内切圆的的圆心,假设 ∠BAC =80︒,那么∠BOC = .6、如图,PA 切⊙O 于A ,假设PA =AB ,PD 平分∠APB 交AB 于D ,那么∠ADP = . 〔设元,列方程〕二 切线与两个圆7、如图,两同心圆的圆心为O ,大圆的弦AB 、AC 分别切小圆于D 、E ,小圆的DE 的度数为110︒, 那么大圆的BC 的度数为 .8、如图,⊙O 1和⊙O 2交于A 、B 两点,且点O 1在⊙O 2上,假设∠D =110︒,那么∠C = 9、如图,⊙O 1和⊙O 2外切于D ,AB 过点D ,假设∠AO 2D =100︒,C 为优弧BD 上任一点, 那么∠DCB = . 答案:7、140︒;8、40︒;9、50︒〔过点D 作两圆的切线〕第1题 第2题 第3题 第4题第5题第7题 第8题 第9题1、如图,在⊙O 的内接△ACB 中,∠ABC =30︒,AC 的延长线与过点D 的切线BD 交于 点D ,假设⊙O 的半径为1,BD //OC ,那么CD = . 〔CD =33〕2、如图△ABC 内接于⊙O ,AB =BC ,过点A 的切线与OC 的延长线交于D ,∠BAC =75︒, CD =3,那么AD = . 〔AD =3〕3、如图,⊙O 为△BCD 的外接圆,过点C 的切线交BD 的延长线于A ,∠ACB =75︒,∠ABC =45︒,那么 CD DB 的值为 . 〔CDDB =2〕4、如图,AB 为⊙O 的直径,弦DC 交AB 于E ,过C 作⊙O 的切线交DB 的延长线于M , 假设AB =4,∠ADC =45︒,∠M =75︒,那么CD = . 〔CD =23〕5、如图,等边△ABC 内接于⊙O ,BD 切⊙O 于B ,AD ⊥BD 于D ,AD 交⊙O 于E ,⊙O 的半径为1,那么AE = . 〔AE =1〕6、如图,△ABC 中,∠C =90︒,BC =5,⊙O 与ABC 的三边相切于D 、E 、F ,假设⊙O 的半径为2,那么△ABC 的周长为 . 〔C =30〕7、如图,△ABC 中,∠C =90︒,AC =12,BC =16,点O 在AB 上,⊙O 与BC 相切于D , 连接AD ,那么BD = . 〔示:过D 作DE ⊥AB ,设CD =DE =x ,BD =10〕第1题 第2题 第3题 第4题第5题 第6题第7题解题策略:连半径,有垂直;寻找特殊三角形;设元,构建勾股定理列方程.圆的培优专题9——圆的切线与垂径定理1、如图,AB 为⊙O 的直径,C 为AE 的中点,CD ⊥BE 于D. 〔1〕判断DC 与⊙O 的位置关系,并说明理由; 〔2〕假设DC =3,⊙O 的半径为5,求DE 的长. 解:〔1〕DC 是⊙O 的切线,理由如下:如图,连接OC ,BC ,那么∠ABC =∠CBD =∠OCB ∴OC ∥BD ,又CD ⊥BE ∴OC ⊥CD ,又OC 为⊙O 的半径 ∴DC 是⊙O 的切线〔2〕如图,过O 作OF ⊥BD ,那么四边形OFDC 是矩形,且BE =EF ∴OF =CD =3,DF =OC =5,∴EF =BF =22534-=,∴DE =DF -EF =12、如图,AB 为⊙O 的直径,D 是BC 的中点,DE ⊥AC 交AC 的延长线于E ,⊙O 的切线 BF 交AD 的延长线于点F. 〔1〕求证:DE 为⊙O 的切线;〔2〕假设DE =3,⊙O 的半径为5,求DF 的长. 〔1〕证:显然,∠CAD =∠OAD =∠ODA ∴OD ∥AE ,又DE ⊥AC , ∴OD ⊥DE ,又OD 为⊙O 半径 ∴DE 为⊙O 的切线〔2〕解:如图,过点O 作OG ⊥AC ,那么OGDE 是矩形,即OG =DE =3,DE =OD =5 ∴AG =22534-=,那么AE =5+4=9,∴2293310+= 连接BD ,那么BD ⊥AD ,∴BD =2210(310)10-=设DF =x ,那么22(10)x +=BF =22(310)10x +-,∴DF =103x =. 3、如图,四边形ABCD 内接于⊙O ,BD 是⊙O 的直径,AE ⊥CD 于E ,DA 平分∠BDE. 〔1〕求证:AE 是⊙O 的切线; 〔2〕假设AE =2,DE =1,求CD 的长.〔1〕证:如图,连接OA ,那么∠ADE =∠ADO =∠OAD ∴OA ∥CD ,又AE ⊥CD ∴OA ⊥AE ,又OA 为⊙O 的半径 ∴AE 是⊙O 的切线〔2〕解:如图,过点O 作OF ⊥CD ,那么CD =2DF ,且四边形OFEA 是矩形 ∴EF =OA =OD ,OF =AE =2 设DF =x ,那么OD =EF =1x + ∴2222(1)x x +=+,∴ 1.5x = ∴CD =2CF =23x =4、如图,AE 是⊙O 的直径,DF 切⊙O 于B ,AD ⊥DF 于D ,EF ⊥DF 于F. 〔1〕求证:EF +AD =AE ;〔2〕假设EF =1,DF =4,求四边形ADFE 的周长. 〔1〕证:如图,连接CE ,那么四边形CDFE 是矩形 连接OB 交CE 于点G , ∵DF 是⊙O 的切线 ∴OB ⊥DF ,OB ⊥CE∴BG =CD =EF ,OG ∥AC ,又AO =OE ∴AC =2OG∴EF +AD =AC +CD +EF =2OG +2BG =2OB =AE. 〔2〕解:显然CE =DF =4,CD =EF =1设AC =x ,那么AD =1x +,AE =2x +∴2224(2)x x +=+,那么3x =,那么AC =3,AD =4,AE =5 ∴四边形CDFE 的周长为14.圆的培优专题10——圆的切线与勾股定理1、如图,点A 是⊙O 上一点,半径OC 的延长线与过点A 的直线交于点B ,OC =BC , AC =12OB. 〔1〕求证:AB 是⊙O 的切线;〔2〕假设∠ACD =45︒,OC =2,求弦CD 的长. 〔1〕证:∵OC =OB ,∴AC 为OAB 的OB 边上的中线,又AC =12OB ∴△OAB 是直角三角形,且∠OAB =90︒,又OA 为⊙O 的半径 ∴AB 是⊙O 的切线〔2〕解:显然,OA =OC =AC ,即△OAC 是等边三角形 ∴∠AOC =60︒,∴∠D =30︒ 如图,过点A 作AE ⊥CD 于点E ,∵∠ACD =45︒,∴△AEC 是等腰直角三角形,∴AE =CE =22AC =22OC 2DE 3AE =6 ∴CD 622、如图,PA 、PB 切⊙O 于A 、B ,点M 在PB 上,且OM //AP ,MN ⊥AP 于N. 〔1〕求证:OM =AN ;〔2〕假设⊙O 的半径3r =,PA =9,求OM 的长. 〔1〕证:如图,连接OA ,∵PA 为⊙O 的切线, ∴OA ⊥AP ,又MN ⊥AP ∴OA ∥MN ,又OM //AP ,∴四边形OANM 是矩形,即OM =AN 〔2〕解:如图,连接OB ,∵PB 、PA 为⊙O 的切线 ∴∠OBM =∠MNP =90︒,PB =PA =9∵OM //AP ,∴∠OMB =∠P ,又OB =OA =MN ,∴△OBM ≌△MNP 〔AAS 〕 ∴OM =PM ,那么32+OM 2=〔9-OM 〕2,∴OM =53、如图,AB 为⊙O 的直径,半径OC ⊥AB ,D 为AB 延长线上一点,过D 作⊙O 的切线, E 为切点,连接CE 交AB 于F.〔1〕求证:DE =DF ;〔2〕连接AE ,假设OF =1,BF =3,求DE 的长. 〔1〕证:如图,连接OE ∵PE 为⊙O 的切线, ∴OE ⊥DE ,又OC ⊥AB∴∠C +∠CFO =∠OEF +∠DEF =90︒ 又∠C =∠OCF ,∠CFO =∠DFE ∴∠DEF =∠DFE ,∴DE =DF 〔2〕解:显然,OE =OB =OF +BF =4设BD =x ,那么DE =DF =3x +,OD =4x + ∴222(3)4(4)x x ++=+,∴x =4.5 ∴DE =7.54、如图,正方形ABCO 的顶点分别在y 轴、x 轴上,以AB 为弦的⊙M 与x 轴相切于F , A (0,8),求圆心M 的坐标.解:如图,连接FM 交延长交AB 于点E ∵⊙M 与x 轴相切,即OC 是⊙M 的切线∴EF ⊥OC ,又四边形ABCO 是正方形 ∴EF ⊥AB ,又A 〔0,8〕即AB =EM =OA =8 ∴ AE =4设MF =AM =x ,那么EM =8-x∴2224(8)x x +-=,∴5x =,即MF =5 ∴点M 的坐标为〔-4,5〕圆的培优专题11——圆的切线与全等三角形1、如图,BD 为⊙O 的直径,A 为BC 的中点,AD 交BC 于E ,过D 作⊙O 的切线,交BC 的延长线于F. 〔1〕求证:DF =EF ;〔2〕假设AE =2,DE =4,求DB 的长. 〔1〕证:如图,连接AB∵BD 为⊙O 的直径,DF 为⊙O 的切线 ∴∠BAD =∠BDF =90︒∴∠ABC +∠AEB =∠ADB +∠FDE =90︒ 又∠ABC =∠ADB ,∠AEB =∠DEF ∴∠DFE =∠DEF ,∴DE =EF〔2〕解:如图,过点F 作FG ⊥ED ,那么EG =GD =2=AE , 又∠BAE =∠FGE =90︒,∠AEB =∠GEF , ∴△ABE ≌△GFE 〔ASA 〕,∴BE =EF ,即DE 为R △BDF 的斜边上中线 ∴DF =EF =DE =4,BF =8,那么BD =432、如图,AB 为⊙O 的直径,C 、D 为⊙O 的一点,OC ⊥AD ,CF ⊥DB 于F. 〔1〕求证:CF 为⊙O 的切线;〔2〕假设BF =1,DB =3,求⊙O 的半径. 〔1〕证:∵AB 为⊙O 的直径 ∴DF ⊥AD ,又OC ⊥AD ∴OC ∥DF ,又CF ⊥DB ∴OC ⊥CF ,又OC 为⊙O 的半径 ∴CF 为⊙O 的切线〔2〕解:如图,过点C 作CE ⊥BD 于点E , 那么BE =DE =1.5,EF =2.5 又OC ⊥CF ,CF ⊥EF∴四边形OCFE 是矩形 ∴⊙O 有半径OC =EF =2.53、如图,以⊙O 的弦AB 为边向圆外作正方形ABCD. 〔1〕求证:OC =OD ; 〔2〕过D 作DM 切⊙O 于M ,假设AB =2,DM =22O 的半径. 〔1〕证:如图,连接OA 、OB ,那么OA =OB ∴∠OAB =∠OBA ∵四边形ABCD 是正方形∴AD =BC ,∠DAB =∠CBA =90︒ ∴∠OAD =∠OBC ∴△OAD ≌△OBC 〔SAS 〕 ∴OC =OD〔2〕解:如图,连接OM 、BD ,那么OM ⊥DM ,且BD 2=2=DM 又OM =OB ,OD =OD ,△ODM ≌△ODB 〔SSS 〕 ∴OB ⊥BD ,又∠ABD =45︒∴∠OAB =45︒,即△OAB 是等腰直角三角形 ∴OA =22AB 24、如图,在△ABC 中,AC =BC ,∠ACB =90︒,以BC 为直径的⊙O 交AB 于D. 〔1〕求证:AD =BD ;〔2〕弦CE 交BD 于M ,假设3ABCBCM S S=,求BD CE. 〔1〕略证:连接CD ,那么CD ⊥AB又AC =BC ,∠ACB =90︒,∴AD =BD 〔2〕解:如图,连接BE ,过A 作AN ⊥CE 于N , ∵3ABCBCMSS=,∴2ACMBCMSS=∴AN =2BE∵∠CAN =∠BCE ,AC =BC ,∠ANC =∠CEB ∴△ANC ≌△CEB 〔AAS 〕 ∴BE =CN ,CE =AN设CN =BE =x ,那么CE =AN =BE =2x , ∴BC 5x ,∴AB 210x ,即BD =102x∴BD CE =104. 圆的培优专题12——圆的切线与等腰三角形1、如图,在△ABC 中,AB =AC ,以AB 为直径的⊙O 与边BC 交于D ,与边AC 交于E , 过D 作DF ⊥AC 于F.〔1〕求证:DF 为⊙O 的切线;〔2〕假设DE =5,AB =5,求AE 的长. 〔1〕证:如图,连接AD ,OD , ∵AB 为⊙O 的直径,∴AD ⊥BC ,又AB =AC ,OA =OB ∴∠EAD =∠DAB =∠ADO ∴OD ∥AC ,又DF ⊥AC ∴OD ⊥DF ,又OD 为⊙O 的直径 ∴DF 为⊙O 的切线〔2〕解:∵∠EAD =∠DAB ,∴BD =DE =5,又AB =5,∴AD =225(5)25-= ∵DF ×AC =AD ×CD ,∴DF =2,CF =EF =52(5)21-=,∴AE =5-2=3 2、如图,在△ABC 中,AB =AC ,以边AB 为直径作⊙O ,交BC 于D ,过D 作DE ⊥AE. 〔1〕求证:DE 是⊙O 的切线;〔2〕连接OC ,假设∠CAB =120︒,求 DEOC的值. 〔1〕证:如图,连接AD ,OD ,那么AD ⊥BC 又AB =AC ,∴CD =BD ,又AO =OB ∴OD ∥AC ,又DE ⊥AE∴OD ⊥DF ,∴DE 是⊙O 的切线;〔2〕解:如图,过点O 作OF ⊥BD 于F ,那么BD =2BF ∵AB =AC ,∠CAB =120︒,∴∠B =30︒ 设OF =x ,那么BF =3x ,OB =2x ,∴AC =AB =4x ,CD =BD =23x ,那么CF =33x由勾股定理,得OC =7x ,由面积法,得DE 3x ,∴DEOC=2114. 3、如图,AB =AC ,点O 在AB 上,⊙O 过点B ,分别交BC 于D 、AB 于E ,DF ⊥AC. 〔1〕证:DF 为⊙O 的切线;〔2〕假设AC 切⊙O 于G ,⊙O 的半径为3,CF =1,求AC. 〔1〕证:如图,连接OD ,∵ AB =AC ,OB =OD ∴∠B =∠C =∠ODB ∴OD ∥AC ,又DF ⊥AC ∴OD ⊥DF ,又OD 为⊙O 的半径 ∴DF 为⊙O 的切线〔2〕解:如图,连接OG ,∵AC 为⊙O 的切线∴OG ⊥AC ,又OD ⊥DF ,DF ⊥AC ,OG =OD ∴四边形ODFG 是正方形,即OB =OG =GF =3 设AG =x ,那么AB =AC =4x +,那么AO =1x + ∴2323(1)x x +=+,∴4x =,那么AC =84、如图,CD 是⊙O 的弦,A 为CD 的中点,E 为CD 延长线上一点,EG 切⊙O 于G. 〔1〕求证:KG =GE ;〔2〕假设AC //EG ,DK CK = 35 ,AK =210,求⊙O 的半径.〔1〕证:如图,连接OG ,OA 交CD 于点F ∵A 为CD 的中点,EG 是⊙O 的切线 ∴OA ⊥CD ,OG ⊥GE∴∠OAG +∠AKF =∠OGA +∠EGK 又∠OAG =∠OGA ,∠AKF =∠EKG ∴∠EGK =∠EKG ∴KG =GE〔2〕解:∵AC ∥EG ,∴∠CAK =∠EGK ,又∠EGK =∠EKG =∠CKA ∴∠CAK =∠CKA ,∴CA =CK设CK =CA =5x ,那么DK =3x ,∴CD =8x ,CF =4x ,EG =x ∴AF =22(5)(4)3x x x -=在Rt △AFK 中,222(3)(210)x x +=,∴2x =∴CE =8,AE =6,设⊙O 的半径为R ,那么R 2=82+〔R -6〕2,∴R =253圆的培优专题13——圆与三角形的内心1、如图,AB 是⊙O 的直径,AC CE =,点M 为BC 上一点,且CM =AC.〔1〕求证:M 为△ABE 的内心;〔2〕假设⊙O 的半径为5,AE =8,求△BEM 的面积. 〔1〕证:如图,连接CE ,那么AC =CE =CM ∴∠CME =∠CEM ,∠CEA =∠CBE ∴∠CBE +∠BEM =∠CEA +∠AEM ∴∠AEM =∠BEM ,又∠ABC =∠CBE ∴点M 为△ABE 的内心.〔2〕解:如图,过点M 作MN ⊥BE 于点N ,那么MN 为△ABE 的内切圆的半径. ∵AB =10,AE =8,那么BE 221086-=∴MN =681022+-=, ★★ MN =2a b c +-=aba b c++=2 ∴BME 的面积为12×6×2=6.2、如图,⊙O 为△ABC 的外接圆,BC 为直径,AD 平分∠BAC 点M 是△ABC 的内心. 〔1〕求证:BC 2DM ;〔2〕假设DM =52AB =8,求OM 的长. 〔1〕证:如图,连接BD ,CD , ∵BC 为直径,AD 平分∠BAC ∴BD =CD ,∠BDC =90︒, ∴BC 2 连接CM ,那么∠ACM =∠BCM ,∠DAC =∠BCD∴∠DMC =∠ACM +∠DAC =∠BCM +∠BCD =∠DCM , ∴DM =CD ,即BC 2(2)解:显然,BC 2=10,AB =8,那么AC =6,且∠MAE =45︒如图,过M 作ME ⊥BC 于点N ,作MF ⊥AC 于点F ,那么ME =MF =AF =2∴ CF =CE =4,那么OE =1 ∴OM =22215+=.3、如图,AB 为⊙O 的直径,C 为⊙O 上一点,D 是BC 的中点,DE ⊥AB 于E ,I 是△ABD 的内心,DI 的延长线交⊙O 于N.〔1〕求证:DE 是⊙O 的切线;〔2〕假设DE =4,CE =2,求⊙O 的半径和IN 的长. 〔1〕证:∵D 是BC 的中点,OA =OD ∴∠CAD =∠DAO =∠ADO ∴OD ∥AE ,又DE ⊥AB ∴OD ⊥DE ,又OD 为⊙O 的半径 ∴DE 是⊙O 的切线.〔2〕解:如图,过点O 作OF ⊥AC ,那么AF =CF ∵DE ⊥AB ,OD ⊥DE∴四边形ODEF 是矩形,那么OF =DE =4设⊙O 的半径为R ,那么OA =OD =EF =R ,AF =CF =R -2 ∴〔R -2〕2+42 =R 2,∴R =5,∴AB =10,如图,连接BI ,AN ,BN ,那么IN =BN =AN =52 ★4、如图,在△ABC 中,AB =AC ,I 是△ABC 的内心,⊙O 交AB 于E ,BE 为⊙O 的直径. 〔1〕求证:AI 与⊙O 相切;〔2〕假设BC =6,AB =5,求⊙O 的半径. 〔1〕证:如图,延长AI 交BC 于点D ,那么AD ⊥BC , 连接OI ,那么∠OIB =∠OBI =∠OBD ∴OI ∥BC ,又AD ⊥BC ∴AD ⊥OI ,又OI 为⊙O 的半径 ∴AI 与⊙O 相切〔2〕显然BD =3,AB =5,那么AD =4如图,过点I 作IF ⊥AB 于点F ,那么BF =BD =3,AF =2,IF =ID ,设IF =ID =x ,那么AI =4x -,∴2222(4)x x +=-,那么IF =32x =设O 的半径为R ,那么OF =3-R ,∴〔3-R 〕2+〔32 〕2 =R 2,∴R =158圆的培优专题14——圆中动态问题1、如图,点P 是等边△ABC 外接圆BC 上的一个动点,求证PA =PB +PC. 证:如图,在AP 上截取PD =PC ,连接CD∵△ABC 是等边三角形,∠ABC =∠ACB =60︒ ∴∠DPC =∠ABC =60︒∴△PCD 是等边三角形,即CD =PC ∵∠ACD +∠BCD =∠BCP +∠BCD =60︒ ∴∠ACD =∠BCP ,又AC =BC ∴△ACD ≌△BCP 〔SAS 〕 ∴AD =BP∴PA =AD +DP =PB +PC.2、弦AD ⊥BD ,且AB =2,点C 在圆上,CD =1,直线AD 、BC 交于点E. 〔1〕如图1,假设点E 在⊙O 外,求∠AEB 的度数; 〔2〕如图2,假设C 、D 两点在⊙O 上运动,CD 的 长度不变,点E 在⊙O 内,求∠AEB 的度数. 解:〔1〕如图-1,连接OC ,OD ∵AD ⊥BD∴AB 为⊙O 的直径,且AB =2∴CD =OC =OD =1,即△OCD 是等边三角形 ∴∠COD =60︒∴∠CBD =12 ∠COD=30︒∴∠AEB =60︒ 〔2〕如图-2,连接OC ,OD图-1同理可得:∠ACD =60︒, ∴∠CBD =12 ∠COD=30︒又∠ADB =90︒,∴∠AED =120︒3、直线l 经过⊙O 的圆心O ,且交⊙O 于A 、B ,点C 在⊙O 上,且∠AOC =30︒,点 P 是直线l 上一个动点〔与O 不重合〕,直线CP 与⊙O 交于Q ,且QP =QO. 〔1〕如图1,当点P 在线段AO 上时,求∠OCP 的度数; 〔2〕如图2,当点P 在线段OA 的延长线上时,求∠OCP 的度数; 〔3〕如图3,当点P 在线段OB 的延长上时,求∠OCP 的度数. 解:〔1〕如图-1,设∠OCP =x ∵OC =OQ ,那么∠OQP =x 又∠AOC =30︒,QP =QO ∴∠QOP =∠QPO =30x +︒ ∴2(30)180x x +︒+=︒ ∴∠OCP =40x =︒〔2〕如图-2,设∠COQ =x , 又∠AOC =30︒,QP =QO ∴∠QOP =∠QPO =30x +︒ 又OC =OQ∴∠OQP =∠OCQ =60x +︒ ∴(60)2(30)180x x +︒++︒=︒ ∴∠COQ =20x =︒ ∴∠OCP =100︒ 〔3〕如图-3,设∠QPO =x∴QP =PO ,那么∠QOP =∠QPO =x ∴OC =OQ∴∠OCQ =∠OQC =2x图-1图-2图-3∴230x x +=︒ ∴∠QPO =x =10︒ ∴∠OCP =20︒圆的培优专题15——聚焦圆中无图多解题圆是中考数学考查的一个热点,题型较全,选择、填空、作图、计算与证明经常出现,常与三角形、四边形、相似形、二次函数等知识一起考查。
第十八讲 与圆有关的计算(含解答)-

第十八讲 与圆有关的计算【趣题引路】拿破仑是法国一位卓越的军事家、政治家,又是一个数学爱好者.一次他在远征埃及的航海途中,问部下:“怎样光用圆规把圆分成四等份?•”大家面面相觑,还是拿破仑自己解了这个谜.聪明的读者你知道他是怎样解的吗? 解析 (1)先用圆规画一个已知圆,如图 (1).(2)在已知圆中,画4个相同的小圆,它们的直径等于已知圆的半径,如图 (2) (3)在4个小圆相交的图形中,4个偏月牙形就是面积完全相同的图形,如图 (3).【知识延伸】与圆有关的计算,着重讲正多边形和圆、圆的面积、周长、弧长,扇形的面积以及圆柱和圆锥侧面展开图的计算问题.对于以上问题,首先要理解概念,熟记公式,法则,其次要会灵活运用各方面的知识.如正n 边形的计算可以集中在正n 边形的半径、边心距把正n 边形分成2n•个全等的直角三角形中,通过解直角三角形或三角形相似来解决.例1 如图,正五边形ABCDE 的边长为10,它的对角线分别交于点A 1,B 1,•C 1,D 1,E 1. (1)求证:D 1把线段AE 1分成黄金分割;(2)求五边形A 1B 1C 1D 1E 1的边长. 证明 (1)作正五边形的外接圆O, ∵AB=BC=CD=DE=EA=72°,∴∠D 1AB=∠D 1BA=•∠E 1BD 1=36°. 又∠BE 1D 1=∠BD 1E 1=72°, ∴AD 1=D 1B=BE.∵△ABE 1∽△B D 1E 1,∴11111AE BE BE D E =, 即11111AE AD AD D E =. ∴A D 12=AE 1·D 1E 1,即D 1把线段A E 1分成黄金分割. (2)设D 1E 1=x,则A E 1=AB=10,AD 1=10-D 1E 1=10-x,∴(10-x)2=10x,即x 2-30x+100=0. 解得,得x 1=15-55,x 2=15+55>10(舍去)∴D 1E 1=15-55.点评对于正多边形的计算,要注意利用相似三角形的性质去解,在本题的计算中,•用到了正五边形的两条对角线的交点是对角线的黄金分割点.在计算与面积有关问题时,等积变形,•把不规则图形的面积变成规则图形的面积去求,是经常使用的方法.例2 如图,已知在矩形ABCD 中,AB=1,BC=2,以B 为圆心,BC•为半径画弧交AD 于点F,交BA 的延长线于点F.求阴影部分的面积.解析 连结BF,∵BF=BC=2,AB=1,∠BAF=90°, ∴∠ABF=60°.在Rt △ABF 中,AF=22BF AB -=3,∴S 阴影=S 扇形BEF -S △ABF=2602360π-12×1×3 =23π-32. 点评阴影部分是不规则图形,无法直接计算,设法利用规则图形面积来计算,连结BF,则阴影部分的面积等于扇形面积减去三角形的面积.在处理展开图问题时,一定不要弄错对应关系,如圆锥侧面展开图是扇形,•这个扇形的半径等于圆锥的母线长,扇形的弧长等于圆锥底面圆的周长等.例2 如图,一个圆锥的高是10cm,侧面开展图是半圆,求圆锥的侧面积. 解析 设圆锥底面半径为r,扇形弧长为C,母线长为L. 由题意,得c=22lπ ,又∵c=2r π, ∴22lπ=2r π,得L=2r. ① 在Rt △SOA 中L 2=r 2+102. ② 由①,②解得r=1033cm, L=2033cm.∴所求圆锥的侧面积为S=πrL=π1033·2033=2003π(cm2).点评经过圆锥高(即轴)的截面所揭示的母线、高、底面半径.•锥角等元素之间的关系是解题的突破口,也是圆锥中几种量之间的基本关系.【好题妙解】佳题新题品味例1已知如图,AC切⊙O于点A,点B在⊙O上,AB=AC=AO,OC、BC分别交⊙O•于点E、F.求证:EF是⊙O的内接正二十四边形的一边.证明连结OB,OF,因AC是⊙O的切线,∴∠OAC=90°,∵AC=AO,∴∠AOC=45°.∵AB=AO=BD,∴△ABO是等边三角形.∴∠BAO=60°,∴∠BAC=60°+90°=150°,∵AB=AC,∴∠ABC=15°.∴∠AOF=2∠ABC=30°.∴∠EOF=∠AOC-∠AOF=45°-30°=15°.∵正二十四边形的中心角为360°÷24=15°,∴EF是正二十四边形的一边.点评证明一条弦是正多边形的一边.•需证这条弦所对的圆心角等于这个多边形的中心角.如证一条弦是正三角形的一边,需证这条边所对的圆心角为120°.证一条弦是正六边形的一边,需证这条弦所对的圆心角为60°.例2如图,⊙O1与⊙O2内切于点P,过P的直线交⊙O1于点A,交⊙O2于点B,•AC切⊙O2于点C,交⊙O1于点D,且PB、PD的长恰好是关于x的方程x2-16m+x=0的两根.求(1)PC的长;(2)若BP BC=,且S△PBC:S△APC=1:k,求代数式m(k2-k)的值.解析 (1)过P作两圆公切线PT,∵∠A=TPD,∠TPC=∠DCP,∠DCP=∠1+∠A,∠TPC=∠2+∠TPD.∴∠1=∠2.已知∠PBC=∠PCD,∴△PBC∽△PCD.∴P C2=PB·PD.而PB,PD是方程x2-16m+x+4=0的根. ∴PC2=4,∴PC=2.O2T21DCBAP O1(2)由BP=BC及∠1=∠2,知BC∥PD,PB=BC.∴AB BCAP PD=,∵1PBCAPCSPBPA S k∆∆==,∴1BC AB kPD AP k-==.∴PB2=4(1)kk-·PD2=41kk-.又由根与系数关系知PB+PD=16m+,∴m+16=PB2+PD2+2PB·PD=4(1)kk-+41kk-+8.∴m=24k k-,∴m(k2-k)=4.点评(1)小题仅涉及PB、PD的长是方程x2-16m+x+4=0的根,故易知PB·PD,从而须找PC•与PB·PD的关系;(2)由题意可知PB·PD均可用字母K表示,由根与系数的关系可知K 与m的关系,由此求出m,代入m(k2-k)中即可.例3如图有一直径是1m的圆形铁皮,要从中剪出一个最大的圆心角是90°的扇形ABC.求(1)被剪掉阴影部分的面积.(2)用所得的扇形铁皮围成一个圆锥,该圆锥的底面半径是多少?(结果可用根号表示).解析 (1)连结BC,∵∠BAC=90°,∴BC为⊙O的直径.又∵AB=AC,∴AB=AC=BC.sin45°=1×22=22.∴S阴=S⊙O-S扇形BAC=π(12)2-2290()2180π⨯=18π(m)2.(2)设圆锥的底面圆的半径为r,∴2902180π⨯=2πr ∴r=28.点评用和差法求图形中阴影部分的面积是最基本的方法,也是应用最广泛的方法.中考真题欣赏例1 (2003年吉林省中考题)圆心角都是90°的扇形OAB与扇形OCD,如图那样叠放在一起,连结AC、BD.(1)求证:△AOC≌△BOD;(2)若OA=3cm,OC=1cm,求阴影部分的面积.证明 (1)∵∠COD=∠AOB=90°.∴∠AOC=∠BOD.∵OA=OB,OC=OD,∴△AOC≌△BOD.(2)S阴影=S扇形AOB-S扇形COD=14π×32-14π×12=2π.点评(1)只需证∠DOB=∠COA即可;(2)将阴影部分转化为两个扇形面积的差,•再进行计算.例2 (2003年桂林市中考题)如图,AB是⊙O的直径,过圆上一点D作⊙O的切线DE,与过点A的直线垂直于E,弦BD的延长线与直线AE交于点C.(1)求证:点D为BC的中点;(2)设直线EA与⊙O的另一交点为F.求证:C A2-AF2=4CE·EA;(3)若AD=12DB,⊙O的半径为r,求由线段DE,AE和AD所围成的阴影部分的面积.证明 (1)连结OD,∵ED为⊙O的切线, ∴OD⊥DE,∵DE⊥AC,∴OD∥AC.∵O为AB中点,∴D为BC中点.(2)连结BF,∵AB为⊙O的直径,∴∠CFB=∠CED=90°.∴ED∥BF,∵D为BC中点,∴E为CF中点.∴CA2-AF2=(CA-AF)(CA+AF)=(CE+AE-EF+AE)·CF=2AE·2CE.∴CA2-AF2=4CE·AE.(3)解析:∵AD=12DB,∴∠AOD=60°.连结DA,可知△OAD为等边三角形.∴OD=AD=r. 在Rt△DEA中,∠EDA=30°,∴EA=12r,ED=32r,EDCA BF∴S 阴影=S 梯形DOAE -S 扇形OAD =13()222r r +-16πr 2=338r 216πr 2. 点评(1)由O 为圆心,设法证CF ∥OD,可得结论;(2)由D 为BC 的中点,证E 为CF 的中点,证得ED ∥BF,然后进行线段的恒等变形,•可得结论.(3)由图形的差可得阴影部分.竞赛样题展示例1 (2002年全国数学竞赛试题)如图,7•根圆形筷子的横截面圆的半径为r,求捆扎这7根筷子一周的绳子长度.解析:设⊙O 1,⊙O 2和绳子切A,B,C 点,知∠A O 1B =60°,∴AB 的长为601803r ππ=r, ∴AB 和线段BC 和的长为3πr,故整个绳长为6(AB+BC)=6(13r π+2r)=2(π+6)r.点评绳长由两部分组成,一部分是直线长,另一部分是弧线长,只要计算出AB•的长和O 1O 2的长,其余类推即可. 例2 (汉城国际数学竞赛试题)把3根长为1cm 的火柴杆和三根长为3cm 的火柴杆,摆放在如左图的圆周上构成六边形,此六边形的面积是由三根1cm 的火柴杆所构成的等边三角形面积的多少倍?解析 如图 (1),因为六边形ABCDEF 内接于⊙O,连结OA,OB,OC,OD,OE,OF, 显然△AOB ≌△AOF ≌△EOF;△BOC ≌△COD ≌△DOE.把底边长为1和3的等腰三角形作间隔排列拼成如图 (2),• 并向两端延长边长为3的边,得边长为5的等边三角形.边长为5的等边三角形可分割为25个边长为1的等边三角形,•于是此六边形可分割为22个边长为1的等边三角形.故此六边形的面积是边长为1的等边三角形面积的22倍.点评几何计算常建立在几何证明的基础之上,通过证明,•解决有关图形的位置关系和数量关系,从而使问题获得解决.全能训练A卷1.两圆相交,公共弦长为且在一圆中为内接正三角形的一边,在另一圆中为内接正六边形的一边,求这两圆的面积之比.2.已知三个正多边形的边数分别是a,b,c,从中各取一个内角相加,其和为360°.求111a b c++的值.3.已知半径为1的圆内接正五边形ABCDE中,P是AE的中点.求AP·BP的值.4.已知一个正三角形,一个正方形,一个圆的周长相等,•正三角形和正方形的外接圆半径为r1,r2,圆的半径为R,则r1,r2,R的大小关系是( ).A.r1>r2>RB.r2>R>r1C.R>r1>r2D.r2>r1>R5.如图,已知一个边长为2cm的正六边形,若要剪一张圆形纸片完全盖住这个图形,则这个圆形纸片的最小半径是_________.6.如图,大小两个同心圆的圆心为O,现任作小圆的三条切线分别交于A、B、C点,记△ABC的面积为S,以A、B、C为顶点的三个阴影部分的面积分别为S1,S2,S3,•试判断S1+S2+S3-S是否为定值,若是,求出这个值;若不是,说明理由.A卷答案:1.设正三角形外接圆O1的半径为R3,正三角形边长是AB,正六边形外接圆O2的半径为R6,∴R3=33AB,R6=AB.∴R3:R6=3:3 ,∴S⊙O1:S⊙O2=R32:R62=1:3.2.由180(2)aa︒-+180(2)bb︒-+180(2)cc︒-=360°,得111a b c++=12.3.连结OA交BP于F,证AP=PF,再证△OPF∽△BPO.∴PF·BP=O P2,∴AP·BP=PF·BP=OP2=14.A5.2cm6.如图,设大小圆半径分别为R和r(R和r为定值).小圆的每条切线与大圆所夹小弓形的面积相等且为定值,设这个定值为p,则有S1+S2+S3′=P;S2+S3+S1′=•P;•S3+S1+S2′=P. ∴(S1+S2+S3)·2+(S1′+S2′+S3′)=3P.又∵S1+S2+S3+S1′+S2′+S3′+S=πR2.∴S1′+S2′+S3′= -(S1+S2+S3)-S代入①式得:S1+S2+S3-S=3P- πR2 (定值)故S1+S2+S3-S为定值,这个定值为3P-πR2.B卷1.如图1,两个半圆,大圆的弦CD平行于直径AB,且与小圆相切,已知CD=24,•则在大半圆中挖去小半圆后剩下部分的面积为________.(1) (2)2.如图2,圆心在原点,半径为2的圆内一点P(22,22) ,过P作弦AB与劣弧AB组成一个弓形,则该弓形面积的最小值为___________.3.小伟在半径为1cm,圆心角为60°的扇形铁皮上剪取一块尽可能大的正方形铁皮,小伟在扇形铁皮上设计如图所示的甲,乙两种剪取方案,请你帮小伟计算一下,按甲、乙两种方案剪取所得的正方形面积,并估算哪个正方形的面积较大(•估算时3=1.73,结果保留两位有效数字).4.如图,在圆周内部有一凸四边形,其边的延长线分别交圆周于A 1,•A 2,B 1,B 2,C 1,C 2,D 1,D 2. 求证:若A 1B 2=B 1C 2=C 1D 2=D 1A 2,则由直线A 1A 2,B 1B 2,C 1C 2,D 1D 2所围成的四边形是圆内接四边形.5.如图,给定正七边形A 1A 2…A 7.证明:121314111A A A A A A =+.- 11 - B 卷答案:1.可将小半圆的圆心移至大半圆圆心重合.此时小半圆与CD 切于M 点,•同心圆圆心设为O, 则S 阴=12πOD 2-12πOM 2=12π(O D 2-OM 2)= 12πMD 2=12π×122=72π。
考点20 与圆有关的位置关系及计算(精讲)(解析版)

考点20.与圆有关的位置关系及计算(精讲)【命题趋势】与圆相关的位置关系也是各地中考数学中的必考考点之一,主要内容包括点、直线与圆的位置关系、切线的性质和判定、三角形的内切圆和外接圆三块,在解答题中想必还会考查切线的性质和判定,和直角三角形结合的求线段长的问题和三角函数结合的求角度的问题等知识点综合,考查形式多样,多以动点、动图的形式给出,难度较大。
关键是掌握基础知识、基本方法,力争拿到全分。
【知识清单】1:点、直线与圆的位置关系类(☆☆)1)点和圆的位置关系:已知⊙O的半径为r,点P到圆心O的距离为d,则:图1图2(1)d<r⇔点在⊙O内,如图1;(2)d=r⇔点在⊙O上,如图2;(3)d>r⇔点在⊙O外,如图3.解题技巧:掌握已知点的位置,可以确定该点到圆心的距离与半径的关系,反过来已知点到圆心的距离与半径的关系,可以确定该点与圆的位置关系。
2)直线和圆的位置关系:设⊙O的半径为r,圆心到直线l的距离为d,则直线和圆的位置关系如下:图1图2图3(1)d>r⇔相离,如图1;(2)d=r⇔相切,如图2;(3)d<r⇔相交,如图3。
2:切线的性质与判定(☆☆☆)1)切线的性质:(1)切线与圆只有一个公共点;(2)切线到圆心的距离等于圆的半径;(3)切线垂直于经过切点的半径。
解题技巧:利用切线的性质解决问题时,通常连过切点的半径,利用直角三角形的性质来解决问题。
2)切线的判定(1)与圆只有一个公共点的直线是圆的切线(定义法);(2)到圆心的距离等于半径的直线是圆的切线(数量关系法);(3)经过半径外端点并且垂直于这条半径的直线是圆的切线(判定定理法)。
切线判定常用的证明方法:①知道直线和圆有公共点时,连半径,证垂直;②不知道直线与圆有没有公共点时,作垂直,证垂线段等于半径。
3)切线长定理定义:在经过圆外一点的圆的切线上,这点和切点之间的线段的长,叫做这点到圆的切线长。
定理:从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角。
圆的难题汇编及答案

一、选择题
1.如图, 是一块绿化带,将阴影部分修建为花圃.已知 , , ,阴影部分是 的内切圆,一只自由飞翔的小鸟将随机落在这块绿化带上,则小鸟落在花圃上的概率为().
A. B.
C. D.
【答案】B
【解析】
【分析】
由AB=5,BC=4,AC=3,得到AB2=BC2+AC2,根据勾股定理的逆定理得到△ABC为直角三角形,于是得到△ABC的内切圆半径= =1,求得直角三角形的面积和圆的面积,即可得到结论.
上所述,PD的最小值为
故选D.
【点睛】
本题考查菱形的性质、等边三角形的性质、等腰三角形的判定和性质等知识,解题的关键是学会用分类讨论的思想思考问题,属于中考常考题型.
14.如图,AB是⊙O的直径,AC是⊙O的切线,OC交⊙O于点D,若∠ABD=24°,则∠C的度数是( )
A.48°B.42°C.34°D.24°
为 的中点,
由切线长定理得:
四边形 为正方形,
故选D.
【点睛】
本题考查的动态问题中的线段的最小值,三角形的内心的性质,等腰直角三角形的性质,锐角三角函数的计算,掌握相关知识点是解题关键.
5.已知⊙O的直径CD=10cm,AB是⊙O的弦,AB=8cm,且AB⊥CD,垂足为M,则AC的长为( )
A.2 cmB.4 cmC.2 cm或4 cmD.2 cm或4 cm
A.1B. C. D.
【答案】D
【解析】
【分析】
根据三角形角平分线的交点是三角形的内心,得到 最小时, 为三角形 内切圆的半径,结合切线长定理得到三角形为等腰直角三角形,从而得到答案.
【详解】
解: , 分别平分 和 ,交于 点,
初三中考一轮复习(24)与圆有关的计算 题型分类 含答案(全面 非常好)

考点一:正多边形和圆例1 如图,正三角形的内切圆半径为1,那么这个正三角形的边长为() A. 2 B. 3 C.3D.32OD对应训练1.正六边形的边心距与边长之比为()A.3:3 B.3:2 C.1:2 D.2:21.B考点二:圆周长与弧长例2 如图,矩形ABCD中,AB=4,BC=3,边CD在直线l上,将矩形ABCD沿直线l 作无滑动翻滚,当点A第一次翻滚到点A1位置时,则点A经过的路线长为6π.解:如图,∵四边形ABCD 是矩形,AB=4,BC=3,∴BC=AD=3,∠ADC=90°,对角线AC (BD )=5. ∵根据旋转的性质知,∠ADA ′=90°,AD=A ′D=BC=3, ∴点A 第一次翻滚到点A ′位置时,则点A ′经过的路线长为:90331802ππ⨯=. 同理,点A ′第一次翻滚到点A ″位置时,则点A ′经过的路线长为:904180π⨯=2π. 点″第一次翻滚到点A 1位置时,则点A ″经过的路线长为:90551802ππ⨯=. 则当点A 第一次翻滚到点A 1位置时,则点A 经过的路线长为:35222πππ++=6π. 故答案是:6π. 对应训练2.如图,将边长为1cm 的等边三角形ABC 沿直线l 向右翻动(不滑动),点B 从开始到结束,所经过路径的长度为( ) A .32πcmB .(2+32π)cm C .43πcmD .3cm2.C考点三:扇形面积与阴影部分面积π⨯,解得:r=1cm.2πr=1203180故选D.对应训练4.一个圆锥的左视图是一个正三角形,则这个圆锥的侧面展开图的圆心角等于()A.60°B.90°C.120°D.180°4.D考点五:圆的综合题例5如图,PA为⊙O的切线,A为切点,直线PO交⊙O与点E,F过点A作PO的垂线AB垂足为D,交⊙O与点B,延长BO与⊙O交与点C,连接AC,BF.(1)求证:PB与⊙O相切;(2)试探究线段EF,OD,OP之间的数量关系,并加以证明;,求cos∠ACB的值.(3)若AC=12,tan∠F=12解答:(1)证明:连接OA,∵PA 与圆O 相切, ∴PA ⊥OA ,即∠OAP=90°, ∵OP ⊥AB ,∴D 为AB 中点,即OP 垂直平分AB , ∴PA=PB ,∵在△OAP 和△OBP 中,AP BP OP OP OA OB =⎧⎪=⎨⎪=⎩, ∴△OAP ≌△OBP (SSS ), ∴∠OAP=∠OBP=90°, ∴BP ⊥OB ,则直线PB 为圆O 的切线;(2)答:EF 2=4DO •PO .证明:∵∠OAP=∠ADO=90°,∠AOD=∠POA , ∴△OAD ∽△OPA , ∴OA ODOP OA=,即OA 2=OD •OP , ∵EF 为圆的直径,即EF=2OA ,【聚焦中考】1.若正方形的边长为6,则其外接圆半径与内切圆半径的大小分别为( ) A .6,32 B .3 2,3 C .6,3 D .62,321.B2.如图,正方形ABCD 中,分别以B 、D 为圆心,以正方形的边长a 为半径画弧,形成树叶形(阴影部分)图案,则树叶形图案的周长为( ) A .πaB .2πaC .12πaD .3a2.A3.如图,扇形AOB 的半径为1,∠AOB=90°,以AB 为直径画半圆,则图中阴影部分的面积为( ) A .4πB .π-12C .12D .4π + 12.C4.将半径为3cm 的圆形纸片沿AB 折叠后,圆弧恰好能经过圆心O ,用图中阴影部分的扇形围成一个圆锥的侧面,则这个圆锥的高为( )A .22B .2C .10D .32.A5.在半径为5的圆中,30°的圆心角所对的弧长为 (结果保留π). .56π6.已知一个扇形的半径为60cm ,圆心角为150°,用它围成一个圆锥的侧面,那么圆锥的底面半径为 cm . 257.如图,AB 是⊙O 的直径,弦AC=2,∠ABC=30°,则图中阴影部分的面积是 ..433π- 8.若扇形的半径为6,圆心角为120°,则此扇形的弧长是( ) A .3π B .4π C .5π D .6π.B9.如果一个扇形的弧长是43π,半径是6,那么此扇形的圆心角为( )A.40°B.45°C.60°D.80°A10.已知圆锥的底面半径为6cm,高为8cm,则这个圆锥的母线长为()A.12cm B.10cm C.8cm D.6cm.B11.如图是某几何体的三视图,则该几何体的体积是()A.πB.2πC.3πD.4π.A12.用如图所示的扇形纸片制作一个圆锥的侧面,要求圆锥的高是4cm,底面周长是6πcm,则扇形的半径为()A.3cm B.5cm C.6cm D.8cm12.B,13.如图,已知圆锥的母线长为6,圆锥的高与母线所夹的角为θ,且sinθ=13则该圆锥的侧面积是()A.242πB.24πC.16πD.12π.D14.如图,以AD 为直径的半圆O 经过Rt △ABC 斜边AB 的两个端点,交直角边AC 于点E 、B ,E 是半圆弧的三等分点,弧BE 的长为23π,则图中阴影部分的面积为( )A .9πB .39πC .33322π-D .33223π-D二、填空题1.已知扇形的圆心角为120°,弧长为10πcm ,则扇形的半径为 cm . .152.如图,一个圆心角为90°的扇形,半径OA=2,那么图中阴影部分的面积为(结果保留π) ..π-23.如图,在正八边形ABCDEFGH中,四边形BCFG的面积为20cm2,则正八边形的面积为 cm2..404.△OAB是以正多边形相邻的两个顶点A,B与它的中心O为顶点的三角形,若△OAB的一个内角为70°,则该正多边形的边数为..95.如图,正六边形硬纸片ABCDEF在桌面上由图1的起始位置沿直线l不滑行地翻滚一周后到图2位置,若正六边形的边长为2cm,则正六边形的中心O运动的路程为 cm..4π6.如图,Rt△ABC中,∠C=90°,AC=8,BC=6,两等圆⊙A,⊙B外切,那么图中两个扇形(即阴影部分)的面积之和为.π6.2547.如图,在平面直角坐标系中,边长为6的正六边形ABCDEF的对称中心与原点O 重合,点A在x轴上,点B在反比例函数k=位于第一象限的图象上,则k的值yx为..93三、解答题1.如图,圆锥的侧面展开图是一个半圆,求母线AB与高AO的夹角.参考公式:圆锥的侧面积S=πrl,其中r为底面半径,l为母线长.`.解:设圆锥的母线长为l,底面半径为r,则:πl=2πr,∴l=2r,∴母线与高的夹角的正弦值=12r l =,∴母线AB 与高AO 的夹角30°.2.如图,在矩形ABCD 中,AB=2DA ,以点A 为圆心,AB 为半径的圆弧交DC 于点E ,交AD 的延长线于点F ,设DA=2.(1)求线段EC 的长;(2)求图中阴影部分的面积.2.解;(1)∵在矩形ABCD 中,AB=2DA ,DA=2,∴AB=AE=4,∴DE=2223AE AD -=,∴EC=CD-DE=4-23;(2)∵sin ∠DEA=12AD AE =, ∴∠DEA=30°,∴∠EAB=30°,∴图中阴影部分的面积为:S 扇形FAB -S △DAE -S 扇形EAB=290413602π⨯-×2×23-2304360π⨯=83π-23.3.如图,AB是⊙O的直径,AC是弦,直线EF经过点C,AD⊥EF于点D,∠DAC=∠BAC.(1)求证:EF是⊙O的切线;(2)求证:AC2=AD•AB;(3)若⊙O的半径为2,∠ACD=30°,求图中阴影部分的面积.3.(1)证明:如图,连接OC,∵OA=OC,∴∠BAC=∠OCA,∵∠DAC=∠BAC,∴∠OCA=∠DAC,∴OC∥AD,∵AD⊥EF,∴OC⊥EF,∵OC为半径,∴EF是⊙O的切线.。
2024年中考数学复习重难点题型训练—圆的相关证明与计算(含答案解析)

2024年中考数学复习重难点题型训练—圆的相关证明与计算(含答案解析)类型一基本性质有关的1.(2022·湖南省郴州市)如图,在△ABC中,AB=AC.以AB为直径的⊙O与线段BC交于点D,过点D作DE⊥AC,垂足为E,ED的延长线与AB的延长线交于点P.(1)求证:直线PE是⊙O的切线;(2)若⊙O的半径为6,∠P=30°,求CE的长.【答案】(1)连接OD,根据AB=AC,OB=OD,得∠ACB=∠ODB,从而OD//AC,由DE⊥AC,即可得PE⊥OD,故PE是⊙O的切线;(2)连接AD,连接OD,由DE⊥AC,∠P=30°,得∠PAE=60°,又AB=AC,可得△ABC 是等边三角形,即可得BC=AB=12,∠C=60°,而AB是⊙O的直径,得∠ADB=90°,可得BD=CD=12BC=6,在Rt△CDE中,即得CE的长是3.本题考查圆的综合应用,涉及圆的切线,等腰三角形性质及应用,含特殊角的直角三角形三边关系等,解题的关键是判定△ABC是等边三角形.2.(2022·辽宁省盘锦市)如图,△ABC内接于⊙O,∠ABC=45°,连接AO并延长交⊙O于点D,连接BD,过点C作CE//AD与BA的延长线交于点E.(1)求证:CE与⊙O相切;(2)若AD=4,∠D=60°,求线段AB,BC的长.【答案】(1)连接OC,根据圆周角定理得∠AOC=90°,再根据AD//EC,可得∠OCE=90°,从而证明结论;(2)过点A作AF⊥EC交EC于F,由AD是圆O的直径,得∠ABD=90°,又AD=4,60°,即得AB=3BD=23,根据∠ABC=45°,知△ABF是等腰直角三角形,AF=BF=2AB= 6,又△AOC是等腰直角三角形,OA=OC=2,得AC=22,故CF=AC2−AF2=2,从而BC=BF+CF=6+2.本题主要考查了圆周角定理,切线的判定与性质,含30°角的直角三角形的性质等知识,作辅助线构造特殊的直角三角形是解题的关键.3.(2021·山东临沂市·中考真题)如图,已知在⊙O中,==,OC与AD相交于点AB BC CDE.求证:(1)AD∥BC(2)四边形BCDE为菱形.【答案】(1)见解析;(2)见解析【分析】(1)连接BD ,根据圆周角定理可得∠ADB=∠CBD ,根据平行线的判定可得结论;(2)证明△DEF ≌△BCF ,得到DE=BC ,证明四边形BCDE 为平行四边形,再根据 BCCD =得到BC=CD ,从而证明菱形.【详解】解:(1)连接BD ,∵ AB BCCD ==,∴∠ADB=∠CBD ,∴AD ∥BC ;(2)连接CD ,∵AD ∥BC ,∴∠EDF=∠CBF ,∵ BCCD =,∴BC=CD ,∴BF=DF ,又∠DFE=∠BFC ,∴△DEF ≌△BCF (ASA ),∴DE=BC ,∴四边形BCDE 是平行四边形,又BC=CD ,∴四边形BCDE 是菱形.【点睛】本题考查了垂径定理,圆周角定理,弧、弦、圆心角的关系,全等三角形的判定和性质,菱形的判定,解题的关键是合理运用垂径定理得到BF=DF .4.(2021·四川南充市·中考真题)如图,A ,B 是O 上两点,且AB OA =,连接OB 并延长到点C ,使BC OB =,连接AC .(1)求证:AC 是O 的切线.(2)点D ,E 分别是AC ,OA 的中点,DE 所在直线交O 于点F ,G ,4OA =,求GF 的长.【答案】(1)见解析;(2)【分析】(1)先证得△AOB 为等边三角形,从而得出∠OAB=60°,利用三角形外角的性质得出∠C=∠CAB=30°,由此可得∠OAC=90°即可得出结论;(2)过O 作OM ⊥DF 于M ,DN ⊥OC 于N ,利用勾股定理得出AC=30°的直角三角形的性质得出DN ,再根据垂径定理和勾股定理即可求出GF 的长.【详解】(1)证明:∵AB=OA ,OA=OB∴AB=OA=OB∴△AOB 为等边三角形∴∠OAB=60°,∠OBA=60°∵BC=OB∴BC=AB∴∠C=∠CAB又∵∠OBA=60°=∠C+∠CAB∴∠C=∠CAB=30°∴∠OAC=∠OAB+∠CAB=90°∴AC 是⊙O 的切线;(2)∵OA=4∴OB=AB=BC=4∴OC=8∴AC=∵D 、E 分别为AC 、OA 的中点,∴OE//BC ,DC=过O 作OM ⊥DF 于M ,DN ⊥OC 于N则四边形OMDN 为矩形∴DN=OM在Rt △CDN 中,∠C=30°,∴DN=12DC=∴OM=3连接OG ,∵OM ⊥GF∴GF=2MG=222OG OM -=()22243-=213【点睛】本题考查了切线的判定、垂径定理、等边三角形的性质和判定,熟练掌握相关的知识是解题的关键.5.(2021·安徽中考真题)如图,圆O 中两条互相垂直的弦AB ,CD 交于点E .(1)M 是CD 的中点,OM =3,CD =12,求圆O 的半径长;(2)点F 在CD 上,且CE =EF ,求证:AF BD ⊥.【答案】(1)35;(2)见解析.【分析】(1)根据M 是CD 的中点,OM 与圆O 直径共线可得OM CD ⊥,OM 平分CD ,则有6MC =,利用勾股定理可求得半径的长;(2)连接AC ,延长AF 交BD 于G ,根据CE EF =,AE FC ⊥,可得AF AC =,12∠=∠,利用圆周角定理可得2D ∠=∠,可得1D ∠=∠,利用直角三角形的两锐角互余,可证得90AGB ∠=︒,即有AF BD ⊥.【详解】(1)解:连接OC ,∵M 是CD 的中点,OM 与圆O 直径共线∴OM CD ⊥,OM 平分CD ,90OMC ∴∠=︒12CD = 6MC ∴=.在Rt OMC △中.OC ===∴圆O 的半径为(2)证明:连接AC ,延长AF 交BD 于G .CE EF = ,AE FC⊥AF AC∴=又CE EF= 12∠∠∴= BCBC = 2D∴∠=∠1D∴∠=∠中在Rt BED∠+∠=︒90D B∴∠+∠=︒B190AGB∴∠=︒90∴⊥AF BD【点睛】本题考查了垂径定理,圆周角定理,直角三角形的两锐角互余,勾股定理等知识点,熟练应用相关知识点是解题的关键.∠是 AD所对的圆周角,6.(2021·浙江中考真题)如图,已知AB是⊙O的直径,ACD∠=︒.30ACD∠的度数;(1)求DABAB=,求DF的(2)过点D作DE AB⊥,垂足为E,DE的延长线交⊙O于点F.若4长.【答案】(1)60︒;(2)23【分析】(1)连结BD ,根据圆周角性质,得B ACD ∠=∠;根据直径所对圆周角为直角、直角三角形两锐角互余的性质计算,即可得到答案;(2)根据含30°角的直角三角形性质,得12AD AB =;根据垂径定理、特殊角度三角函数的性质计算,即可得到答案.【详解】(1)连结BD ,30ACD ∠=︒30B ACD \Ð=Ð=°AB Q 是O 的直径,90ADB ∴∠=︒,9060DAB B ∴∠=︒-∠=︒(2)90ADB ∠=︒ ,30B ∠=︒,4AB =∴122AD AB ==60DAB ∠=︒ ,DE AB ⊥,且AB 是直径sin 60EF DE AD︒∴===2DF DE =∴=.【点睛】本题考查了圆、含30°角的直角三角形、三角函数的知识;解题的关键是熟练掌握圆周角、垂径定理、含30°角的直角三角形、三角函数、直角三角形两锐角互余的性质,从而完成求解.7.(2021·湖南中考真题)如图,ABC 是O 的内接三角形,AC 是O 的直径,点D 是 BC的中点,//DE BC 交AC 的延长线于点E .(1)求证:直线DE 与O 相切;(2)若O 的直径是10,45A ∠=︒,求CE 的长.【答案】(1)见解析;(2)5CE =.【分析】(1)连接OD ,由点D 是 BC的中点得OD ⊥BC ,由DE//BC 得OD ⊥DE ,由OD 是半径可得DE 是切线;(2)证明△ODE 是等腰直角三角形,可求出OE 的长,从而可求得结论.【详解】解:(1)连接OD 交BC 于点F ,如图,∵点D 是 BC的中点,∴OD ⊥BC ,∵DE//BC∴OD ⊥DE∵OD 是O 的半径∴直线DE 与O 相切;(2)∵AC 是O 的直径,且AB=10,∴∠ABC=90°,152OC OA AB ===∵OD ⊥BC∴∠OFC=90°∴OD//AB 45BAC ∠=︒∴45DOE ∠=︒∵90ODE ∠=︒∴45OED ∠=∴5DE OD OC ===由勾股定理得,OE =∴5CE OE OC =-=.【点睛】此题主要考查了切线的判定与性质的综合运用,熟练掌握切线的判定与性质是解答此题的关键.8.(2021·湖南张家界市·中考真题)如图,在Rt AOB 中,90∠=︒ABO ,30OAB ∠=︒,以点O 为圆心,OB 为半径的圆交BO 的延长线于点C ,过点C 作OA 的平行线,交O 于点D ,连接AD .(1)求证:AD 为O 的切线;(2)若2OB =,求弧CD 的长.【答案】(1)见解析;(2)23π【分析】(1)连接OB ,先根据直角三角形的性质得到∠AOB=60°,再运用平行线的性质结合已知条件可得60AOD ∠=︒,再证明AOB AOD △≌△可得90ADO ABO ∠=∠=︒即可;(2)先求出∠COD ,然后再运用弧长公式计算即可.【详解】(1)证明:连接OD∵30OAB ∠=︒,90B ∠=︒∴60AOB ∠=︒又∵//CD AO∴60C AOB ∠=∠=︒∴2120BOD C ∠=∠=︒∴60AOD ∠=︒又∵,OB OD AO AO==∴()AOB AOD SAS ≌∴90ADO ABO ∠=∠=︒又∵点D 在O 上∴AD 是O 的切线;(2)∵120BOD ∠=︒∴60COD ∠=︒∴602223603l ππ=⨯⨯=.【点睛】本题主要考查了圆的切线的证明、弧长公式等知识点,掌握圆的切线的证明方法成为解答本题的关键.9.(2020•齐齐哈尔)如图,AB 为⊙O 的直径,C 、D 为⊙O 上的两个点,AC=CD =DB ,连接AD ,过点D 作DE ⊥AC 交AC 的延长线于点E .(1)求证:DE 是⊙O 的切线.(2)若直径AB =6,求AD 的长.【分析】(1)连接OD ,根据已知条件得到∠BOD =13×180°=60°,根据等腰三角形的性质得到∠ADO=∠DAB=30°,得到∠EDA=60°,求得OD⊥DE,于是得到结论;(2)连接BD,根据圆周角定理得到∠ADB=90°,解直角三角形即可得到结论.【解析】(1)证明:连接OD,=CD =DB ,∵AC∴∠BOD=13×180°=60°,=DB ,∵CD∴∠EAD=∠DAB=12∠BOD=30°,∵OA=OD,∴∠ADO=∠DAB=30°,∵DE⊥AC,∴∠E=90°,∴∠EAD+∠EDA=90°,∴∠EDA=60°,∴∠EDO=∠EDA+∠ADO=90°,∴OD⊥DE,∴DE是⊙O的切线;(2)解:连接BD,∵AB为⊙O的直径,∴∠ADB=90°,∵∠DAB=30°,AB=6,∴BD=12AB=3,∴AD=62−32=33.10.(2020•深圳)如图,AB为⊙O的直径,点C在⊙O上,AD与过点C的切线互相垂直,垂足为D.连接BC并延长,交AD的延长线于点E.(1)求证:AE=AB;(2)若AB=10,BC=6,求CD的长.【分析】(1)证明:连接AC、OC,如图,根据切线的性质得到OC⊥CD,则可判断OC∥AD,所以∠OCB=∠E,然后证明∠B=∠E,从而得到结论;(2)利用圆周角定理得到∠ACB=90°,则利用勾股定理可计算出AC=8,再根据等腰三角形的性质得到CE=BC=6,然后利用面积法求出CD的长.【解析】(1)证明:连接AC、OC,如图,∵CD为切线,∴OC⊥CD,∴CD⊥AD,∴OC∥AD,∴∠OCB=∠E,∵OB=OC,∴∠OCB=∠B,∴∠B=∠E,∴AE=AB;(2)解:∵AB为直径,∴∠ACB=90°,∴AC=102−62=8,∵AB=AE=10,AC⊥BE,∴CE=BC=6,∵12CD•AE=12AC•CE,∴CD=6×810=245.11.(2020•陕西)如图,△ABC是⊙O的内接三角形,∠BAC=75°,∠ABC=45°.连接AO并延长,交⊙O于点D,连接BD.过点C作⊙O的切线,与BA的延长线相交于点E.(1)求证:AD∥EC;(2)若AB=12,求线段EC的长.【分析】(1)连接OC,由切线的性质可得∠OCE=90°,由圆周角定理可得∠AOC=90°,可得结论;(2)过点A作AF⊥EC交EC于F,由锐角三角函数可求AD=83,可证四边形OAFC是正方形,可得CF=AF=43,由锐角三角函数可求EF=12,即可求解.【解析】证明:(1)连接OC,∵CE与⊙O相切于点C,∴∠OCE=90°,∵∠ABC=45°,∴∠AOC=90°,∵∠AOC+∠OCE=180°,∴∴AD∥EC(2)如图,过点A作AF⊥EC交EC于F,∵∠BAC=75°,∠ABC=45°,∴∠ACB=60°,∴∠D=∠ACB=60°,∴sin∠ADB=AB AD==83,∴AD=∴OA=OC=43,∵AF⊥EC,∠OCE=90°,∠AOC=90°,∴四边形OAFC是矩形,又∵OA=OC,∴四边形OAFC是正方形,∴CF=AF=43,∵∠BAD=90°﹣∠D=30°,∴∠EAF=180°﹣90°﹣30°=60°,∵tan∠EAF=EF AF=3,∴EF=3AF=12,∴CE=CF+EF=12+43.类型二与三角形全等、相似有关的12.(2022·辽宁省营口市)如图,在△ABC中,AB=AC,以AB为直径作⊙O与AC交于点E,过点A作⊙O的切线交BC的延长线于点D.(1)求证:∠D=∠EBC;(2)若CD=2BC,AE=3,求⊙O的半径.【答案】(1)根据切线的性质可得∠DAO=90°,从而可得∠D+∠ABD=90°,根据直径所对的圆周角是直角可得∠BEC=90°,从而可得∠ACB+∠EBC=90°,然后利用等腰三角形的性质可得∠ACB=∠ABC,从而利用等角的余角相等即可解答;(2)根据已知可得BD=3BC,然后利用(1)的结论可得△DAB∽△BEC,从而利用相似三角形的性质可得AB=3EC,然后根据AB=AC,进行计算即可解答.本题考查了圆周角定理,等腰三角形的性质,切线的性质,相似三角形的判定与性质,熟练掌握切线的性质,以及相似三角形的判定与性质是解题的关键.13.(2022·北部湾)如图,在△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作DE⊥AB,垂足为E,延长BA交⊙O于点F.(1)求证:DE是⊙O的切线(2)若AE DE=23,AF=10,求⊙O的半径.【答案】(1)证明:连接OD;∵OD=OC,∴∠C=∠ODC,∵AB=AC,∴∠B=∠C,∴∠B=∠ODC,∴OD∥AB,∴∠ODE=∠DEB;∵DE⊥AB,∴∠DEB=90°,∴∠ODE=90°,即DE⊥OD,∴DE是⊙O的切线(2)解:连接CF,由(1)知OD⊥DE,∵DE⊥AB,∴OD∥AB,∵OA=OC,∴BD=CD,即OD是△ABC的中位线,∵AC是⊙O的直径,∴∠CFA=90°,∵DE⊥AB,∴∠BED=90°,∴∠CFA=∠BED=90°,∴DE∥CF,∴BE=EF,即DE是△FBC的中位线,∴CF=2DE,∵AE DE=23,∴设AE=2x,DE=3k,CF=6k,∵AF=10,∴BE=EF=AE+AF=2k+10,∴AC=BA=EF+AE=4k+10,在Rt△ACF中,由勾股定理,得AC2=AF2+CF2,即(4k+10)2=102+(6k)2,解得:k=4,∴AC=4k+10=4×4+10=26,∴OA=13,即⊙O的半径为13.【知识点】平行线的判定与性质;等腰三角形的性质;圆周角定理;切线的判定;三角形的中位线定理【解析】【分析】(1)连接OD ,根据等腰三角形的性质可得∠C=∠ODC ,∠B=∠C ,则∠B=∠ODC ,推出OD ∥AB ,由平行线的性质可得∠ODE=∠DEB=90°,即DE ⊥OD ,据此证明;(2)连接CF ,由(1)知OD ⊥DE ,则OD ∥AB ,易得OD 是△ABC 的中位线,根据圆周角定理可得∠CFA=90°,根据垂直的概念可得∠BED=90°,则DE ∥CF ,推出DE 是△FBC的中位线,得CF=2DE ,设AE=2x ,DE=3k ,CF=6k ,则BE=EF=2k+10,AC=BA=4k+10,根据勾股定理可得k 的值,然后求出AC 、OA ,据此可得半径.14.(2021·江苏无锡市·中考真题)如图,四边形ABCD 内接于O ,AC 是O 的直径,AC 与BD 交于点E ,PB 切O 于点B .(1)求证:PBA OBC ∠=∠;(2)若20PBA Ð=°,40ACD ∠=︒,求证:OAB CDE V V ∽.【答案】(1)见详解;(2)见详解【分析】(1)由圆周角定理的推论,可知∠ABC=90°,由切线的性质可知∠OBP=90°,进而即可得到结论;(2)先推出20OCB OBC ∠=∠=︒,从而得∠AOB=40°,继而得∠OAB=70°,再推出∠CDE=70°,进而即可得到结论.【详解】证明:(1)∵AC 是O 的直径,∴∠ABC=90°,∵PB 切O 于点B ,∴∠OBP=90°,∴90PBA ABO OBC ABO ∠+∠=∠+∠=︒,∴PBA OBC ∠=∠;(2)∵20PBA Ð=°,PBA OBC ∠=∠,∴20OBC ∠=︒,∵OB=OC ,∴20OCB OBC ∠=∠=︒,∴∠AOB=20°+20°=40°,∵OB=OA ,∴∠OAB=∠OBA=(180°-40°)÷2=70°,∴∠ADB=12∠AOB=20°,∵AC 是O 的直径,∴∠ADC=90°,∴∠CDE=90°-20°=70°,∴∠CDE=∠OAB ,∵40ACD ∠=︒,∴40ACD AOB ∠=∠=︒,∴OAB CDE V V ∽.【点睛】本题主要考查圆的性质以及相似三角形的判定定理,掌握圆周角定理的推论,相似三角形的判定定理,切线的性质定理,是解题的关键.15.(2020•衢州)如图,△ABC 内接于⊙O ,AB 为⊙O 的直径,AB =10,AC =6,连结OC ,弦AD分别交OC,BC于点E,F,其中点E是AD的中点.(1)求证:∠CAD=∠CBA.(2)求OE的长.【分析】(1)利用垂径定理以及圆周角定理解决问题即可.(2)证明△AEC∽△BCA,推出CE AC=AC AB,求出EC即可解决问题.【解析】(1)证明:∵AE=DE,OC是半径,=CD ,∴AC∴∠CAD=∠CBA.(2)解:∵AB是直径,∴∠ACB=90°,∵AE=DE,∴OC⊥AD,∴∠AEC=90°,∴∠AEC=∠ACB,∴△AEC∽△BCA,∴CE AC=AC AB,∴CE6=610,∴CE=3.6,∵OC=12AB=5,∴OE=OC﹣EC=5﹣3.6=1.4.16.(2020•铜仁市)如图,AB是⊙O的直径,C为⊙O上一点,连接AC,CE⊥AB于点E,D 是直径AB延长线上一点,且∠BCE=∠BCD.(1)求证:CD是⊙O的切线;(2)若AD=8,BE CE=12,求CD的长.【分析】(1)连接OC,根据圆周角定理得到∠ACB=90°,根据余角的性质得到∠A=∠ECB,求得∠A=∠BCD,根据等腰三角形的性质得到∠A=∠ACO,等量代换得到∠ACO=∠BCD,求得∠DCO=90°,于是得到结论;(2)设BC=k,AC=2k,根据相似三角形的性质即可得到结论.【解析】(1)证明:连接OC,∵AB是⊙O的直径,∴∠ACB=90°,∵CE⊥AB,∴∠CEB=90°,∴∠ECB+∠ABC=∠ABC+∠CAB=90°,∴∠A=∠ECB,∵∠BCE=∠BCD,∴∠A=∠BCD,∵OC=OA,∴∠A=∠ACO,∴∠ACO=∠BCD,∴∠ACO+∠BCO=∠BCO+∠BCD=90°,∴∠DCO=90°,∴CD是⊙O的切线;(2)解:∵∠A=∠BCE,∴tanA=BC AC=tan∠BCE=BE CE=12,设BC=k,AC=2k,∵∠D=∠D,∠A=∠BCD,∴△ACD∽△CBD,∴BC AC=CD AD=12,∵AD=8,∴CD=4.17.(2020•衡阳)如图,在△ABC中,∠C=90°,AD平分∠BAC交BC于点D,过点A和点D的圆,圆心O在线段AB上,⊙O交AB于点E,交AC于点F.(1)判断BC与⊙O的位置关系,并说明理由;(2)若AD=8,AE=10,求BD的长.【分析】(1)连接OD,根据平行线判定推出OD∥AC,推出OD⊥BC,根据切线的判定推出即可;(2)连接DE,根据圆周角定理得到∠ADE=90°,根据相似三角形的性质得到AC=325,根据勾股定理得到CD=AD2−AC2==根据相似三角形的性质即可得到结论.【解析】(1)BC与⊙O相切,理由:连接OD,∵OA=OD,∴∠OAD=∠ODA,∵AD平分∠BAC,∴∠BAD=∠CAD,∴∠ODA=∠CAD,∴OD∥AC,∵∠C=90°,∴∠ODC=90°,∴OD⊥BC,∵OD为半径,∴BC是⊙O切线;(2)连接DE,∵AE是⊙O的直径,∴∠ADE=90°,∵∠C=90°,∴∠ADE=∠C,∵∠EAD=∠DAC,∴△ADE∽△ACD,∴AE AD=AD AC,108=8AC,∴AC=325,∴CD=AD2−AC2==245,∵OD⊥BC,AC⊥BC,∴△OBD∽△ABC,∴OD AC=BD BC,∴5325=BD BD+245,∴BD=1207.18.(2020•遵义)如图,AB是⊙O的直径,点C是⊙O上一点,∠CAB的平分线AD交BC 于点D,过点D作DE∥BC交AC的延长线于点E.(1)求证:DE是⊙O的切线;(2)过点D作DF⊥AB于点F,连接BD.若OF=1,BF=2,求BD的长度.【分析】(1)连接OD,由等腰三角形的性质及角平分线的性质得出∠ADO=∠DAE,从而OD∥AE,由DE∥BC得∠E=90°,由两直线平行,同旁内角互补得出∠ODE=90°,由切线的判定定理得出答案;(2)先由直径所对的圆周角是直角得出∠ADB=90°,再由OF=1,BF=2得出OB的值,进而得出AF和BA的值,然后证明△DBF∽△ABD,由相似三角形的性质得比例式,从而求得BD2的值,求算术平方根即可得出BD的值.【解析】(1)连接OD,如图:∵OA=OD,∴∠OAD=∠ADO,∵AD平分∠CAB,∴∠DAE=∠OAD,∴∠ADO=∠DAE,∴OD∥AE,∵DE∥BC,∴∠E=90°,∴∠ODE=180°﹣∠E=90°,∴DE是⊙O的切线;(2)∵AB是⊙O的直径,∴∠ADB=90°,∵OF=1,BF=2,∴OB=3,∴AF=4,BA=6.∵DF⊥AB,∴∠DFB=90°,∴∠ADB=∠DFB,又∵∠DBF=∠ABD,∴△DBF∽△ABD,∴BD BA=BF BD,∴BD2=BF•BA=2×6=12.∴BD=23.19.(2019•陕西)如图,⊙O的半径OA=6,过点A作⊙O的切线AP,且AP=8,连接PO 并延长,与⊙O交于点B、D,过点B作BC∥OA,并与⊙O交于点C,连接AC、CD.(1)求证:DC∥AP;(2)求AC的长.【分析】(1)根据切线的性质得到∠OAP=90°,根据圆周角定理得到∠BCD=90°,根据平行线的性质和判定定理即可得到结论;(2)根据勾股定理和相似三角形的判定和性质定理即可得到结论.【解析】(1)证明:∵AP是⊙O的切线,∴∠OAP=90°,∵BD是⊙O的直径,∴∠BCD=90°,∵OA∥CB,∴∠AOP=∠DBC,∴∠BDC=∠APO,∴DC∥AP;(2)解:∵AO∥BC,OD=OB,∴延长AO交DC于点E,则AE⊥DC,OE=12BC,CE=12CD,在Rt△AOP中,OP=62+82=10,由(1)知,△AOP∽△CBD,∴DB OP=BC OA=DC AP,即1210=BC6=DC8,∴BC=365,DC=485,∴OE=185,CE=245,在Rt△AEC中,AC=AE2+CE2==20(2021·云南中考真题)如图,AB 是O 的直径,点C 是O 上异于A 、B 的点,连接AC 、BC ,点D 在BA 的延长线上,且DCA ABC ∠=∠,点E 在DC 的延长线上,且BE DC ⊥.(1)求证:DC 是O 的切线:(2)若2,33OA BE OD ==,求DA 的长.【答案】(1)见解析;(2)910【分析】(1)连接OC ,根据圆周角定理得到∠ACB=90°,根据等量代换得到∠DCO=90°,即可证明DC 是圆O 的切线;(2)根据已知得到OA=2DA ,证明△DCO ∽△DEB ,得到DO CO DB EB =,可得DA=310EB ,即可求出DA 的长.【详解】解:(1)如图,连接OC ,由题意可知:∠ACB 是直径AB 所对的圆周角,∴∠ACB=90°,∵OC ,OB 是圆O 的半径,∴OC=OB ,∴∠OCB=∠ABC ,又∵∠DCA=∠ABC ,∴∠DCA=∠OCB ,∴∠DCO=∠DCA+∠ACO=∠OCB+∠ACO=∠ACB=90°,∴OC ⊥DC ,又∵OC 是圆O 的半径,∴DC 是圆O 的切线;(2)∵23OA OD =,∴23OA OA DA =+,化简得OA=2DA ,由(1)知,∠DCO=90°,∵BE ⊥DC ,即∠DEB=90°,∴∠DCO=∠DEB ,∴OC ∥BE ,∴△DCO ∽△DEB ,∴DO CO DB EB =,即33255DA OA DA DA DA OA OB DA EB+===++,∴DA=310EB ,∵BE=3,∴DA=310EB=3931010⨯=,经检验:DA=910是分式方程的解,∴DA=910.【点睛】本题考查了圆周角定理,相似三角形的判定和性质,切线的判定,正确的作出辅助线,证明切线,得到相似三角形是解题的关键.21.(2021·江苏扬州市·中考真题)如图,四边形ABCD 中,//AD BC ,90BAD ∠=︒,CB CD =,连接BD ,以点B 为圆心,BA 长为半径作B ,交BD 于点E .(1)试判断CD 与B 的位置关系,并说明理由;(2)若AB =,60BCD ∠=︒,求图中阴影部分的面积.【答案】(1)相切,理由见解析;(2)π-【分析】(1)过点B 作BF ⊥CD ,证明△ABD ≌△FBD ,得到BF=BA ,即可证明CD 与圆B 相切;(2)先证明△BCD 是等边三角形,根据三线合一得到∠ABD=30°,求出AD ,再利用S △ABD -S 扇形ABE 求出阴影部分面积.【详解】解:(1)过点B 作BF ⊥CD ,∵AD ∥BC ,∴∠ADB=∠CBD ,∵CB=CD ,∴∠CBD=∠CDB ,∴∠ADB=∠CDB ,又BD=BD ,∠BAD=∠BFD=90°,∴△ABD ≌△FBD (AAS ),∴BF=BA ,则点F 在圆B 上,∴CD 与圆B 相切;(2)∵∠BCD=60°,CB=CD ,∴△BCD 是等边三角形,∴∠CBD=60°∵BF ⊥CD ,∴∠ABD=∠DBF=∠CBF=30°,∴∠ABF=60°,∵AB=BF=,∴AD=DF=tan30AB ⋅︒=2,∴阴影部分的面积=S △ABD -S 扇形ABE=(230122360π⨯⨯⨯-=π-.【点睛】本题考查了切线的判定,全等三角形的判定和性质,等边三角形的判定和性质,扇形面积,三角函数的定义,题目的综合性较强,难度不小,解题的关键是正确做出辅助线.22.(2020•上海)如图,△ABC中,AB=AC,⊙O是△ABC的外接圆,BO的延长线交边AC 于点D.(1)求证:∠BAC=2∠ABD;(2)当△BCD是等腰三角形时,求∠BCD的大小;(3)当AD=2,CD=3时,求边BC的长.【分析】(1)连接OA.利用垂径定理以及等腰三角形的性质解决问题即可.(2)分三种情形:①若BD=CB,则∠C=∠BDC=∠ABD+∠BAC=3∠ABD.②若CD=CB,则∠CBD=∠CDB=3∠ABD.③若DB=DC,则D与A重合,这种情形不存在.分别利用三角形内角和定理构建方程求解即可.(3)如图3中,作AE∥BC交BD的延长线于E.则AE BC=AD DC=23,推出AO OH=AE BH=43,设OB=OA=4a,OH=3a,根据BH2=AB2﹣AH2=OB2﹣OH2,构建方程求出a即可解决问题.【解析】(1)证明:连接OA.A∵AB=AC,=AC ,∴AB∴OA⊥BC,∴∠BAO=∠CAO,∵OA=OB,∴∠ABD=∠BAO,∴∠BAC=2∠BAD.(2)解:如图2中,延长AO交BC于H.①若BD=CB,则∠C=∠BDC=∠ABD+∠BAC=3∠ABD,∵AB=AC,∴∠ABC=∠C,∴∠DBC=2∠ABD,∵∠DBC+∠C+∠BDC=180°,∴8∠ABD=180°,∴∠C=3∠ABD=67.5°.②若CD=CB,则∠CBD=∠CDB=3∠ABD,∴∠C =4∠ABD ,∵∠DBC+∠C+∠CDB =180°,∴10∠ABD =180°,∴∠BCD =4∠ABD =72°.③若DB =DC ,则D 与A 重合,这种情形不存在.综上所述,∠C 的值为67.5°或72°.(3)如图3中,作AE ∥BC 交BD 的延长线于E .则AE BC =AD DC =23,∴AO OH =AE BH =43,设OB =OA =4a ,OH =3a ,∵BH 2=AB 2﹣AH 2=OB 2﹣OH 2,∴25﹣49a 2=16a 2﹣9a 2,∴a 2=2556,∴BH =∴BC =2BH =23.(2021·云南中考真题)如图,AB 是O 的直径,点C 是O 上异于A 、B 的点,连接AC 、BC ,点D 在BA 的延长线上,且DCA ABC ∠=∠,点E 在DC 的延长线上,且BE DC ⊥.(1)求证:DC是O的切线:(2)若2,33OA BEOD==,求DA的长.【答案】(1)见解析;(2)9 10【分析】(1)连接OC,根据圆周角定理得到∠ACB=90°,根据等量代换得到∠DCO=90°,即可证明DC是圆O的切线;(2)根据已知得到OA=2DA,证明△DCO∽△DEB,得到DO CODB EB=,可得DA=310EB,即可求出DA的长.【详解】解:(1)如图,连接OC,由题意可知:∠ACB是直径AB所对的圆周角,∴∠ACB=90°,∵OC,OB是圆O的半径,∴OC=OB,∴∠OCB=∠ABC,又∵∠DCA=∠ABC,∴∠DCA=∠OCB,∴∠DCO=∠DCA+∠ACO=∠OCB+∠ACO=∠ACB=90°,∴OC⊥DC,又∵OC 是圆O 的半径,∴DC 是圆O 的切线;(2)∵23OA OD =,∴23OA OA DA =+,化简得OA=2DA ,由(1)知,∠DCO=90°,∵BE ⊥DC ,即∠DEB=90°,∴∠DCO=∠DEB ,∴OC ∥BE ,∴△DCO ∽△DEB ,∴DO CO DB EB =,即33255DA OA DA DA DA OA OB DA EB +===++,∴DA=310EB ,∵BE=3,∴DA=310EB=3931010⨯=,经检验:DA=910是分式方程的解,∴DA=910.【点睛】本题考查了圆周角定理,相似三角形的判定和性质,切线的判定,正确的作出辅助线,证明切线,得到相似三角形是解题的关键.类型三与锐角三角函数有关24.(2022·辽宁省铁岭市)如图,△ABC内接于⊙O,AC是⊙O的直径,过OA上的点P作PD⊥AC,交CB的延长线于点D,交AB于点E,点F为DE的中点,连接BF.(1)求证:BF与⊙O相切;(2)若AP=OP,cosA=45,AP=4,求BF的长.【答案】(1)连接OB,根据直径所对的圆周角是直角可得∠ABC=90°,从而可得∠ABD=90°,进而利用直角三角形三角形斜边上的中线可得BF=EF=12AD,然后利用等腰三角形的性质可得∠FEB=∠FBE,从而可得∠FBE=∠AEP,最后根据垂直定义可得∠EPA=90°,从而可得∠A+∠AEP=90°,再利用等腰三角形的性质可得∠A=∠OBA,从而可得∠OBA+∠FBE= 90°,进而可得∠OBF=90°,即可解答;(2)在Rt△AEP中,利用锐角三角函数的定义求出AE的长,从而利用勾股定理求出PE的长,然后利用同角的余角相等可得∠AEP=∠C,从而可证△APE∽△DPC,进而利用相似三角形的性质可求出DP的长,最后求出DE的长,即可解答.本题考查了解直角三角形,切线的判定与性质,圆周角定理,三角形的外接圆与外心,直线与圆的位置关系,熟练掌握解直角三角形,以及切线的判定与性质是解题的关键.25.(2022·四川省广安市)如图,AB为⊙O的直径,D、E是⊙O上的两点,延长AB至点C,连接CD ,∠BDC =∠BAD .(1)求证:CD 是⊙O 的切线.(2)若tan∠BED =23,AC =9,求⊙O 的半径.【答案】(1)连接OD ,由圆周角定理得出∠ADB =90°,证出OD ⊥CD ,由切线的判定可得出结论;(2)证明△BDC∽△DAC ,由相似三角形的性质得出CD AC =BC CD =BD DA =23,由比例线段求出CD 和BC 的长,可求出AB 的长,则可得出答案.本题考查了切线的判定,相似三角形的判定与性质,锐角三角函数的定义,圆周角定理,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.26.(2021·山东菏泽市·中考真题)如图,在O 中,AB 是直径,弦CD AB ⊥,垂足为H ,E 为 BC上一点,F 为弦DC 延长线上一点,连接FE 并延长交直径AB 的延长线于点G ,连接AE 交CD 于点P ,若FE FP =.(1)求证:FE 是O 的切线;(2)若O 的半径为8,3sin 5F =,求BG 的长.【答案】(1)见解析;(2)=2BG 【分析】(1)连接OE ,证明OE ⊥EF 即可;(2)由3sin 5F =证得4sin 5G =,运用正弦的概念可得结论.【详解】解:(1)证明:连接OE ,如图,∵OA=OE∴∠OAE=∠OEA .∵EF=PF ,∴∠EPF=∠PEF∵∠APH=∠EPF ,∴∠APH=∠EPF ,∴∠AEF=∠APH .∵CD ⊥AB ,∴∠AHC=90°.∴∠OAE+∠APH=90°.∴∠OEA+∠AEF=90°∴∠OEF=90°∴OE ⊥EF .∵OE 是O 的半径∴EF 是圆的切线,(2)∵CD ⊥AB∴FHG ∆是直角三角形∵3sin 5F =∴35GH FG =设3GH x =,则5FG x=由勾股定理得,4FH x=由(1)得,OEG ∆是直角三角形∴4sin 5OE FH x G OG FG x===∴45OE OG =,即45OE OE BG =+∵8OE =∴8485BG =+解得,2BG =【点睛】此题主要考查了圆的切线的判定,勾股定理和解直角三角形等知识,熟练掌握切线的判定是解答此题的关键.27.(2022·黔东南)(1)请在图中作出△ABC 的外接圆⊙O (尺规作图,保留作图痕迹,不写作法);的中点,过点B的(2)如图,⊙O是△ABC的外接圆,AE是⊙O的直径,点B是CE切线与AC的延长线交于点D.①求证:BD⊥AD;②若AC=6,tan∠ABC=34,求⊙O的半径.【答案】(1)解:如下图所示(2)解:①如下图所示,连接OC、OB∵BD是⊙O的切线∴OB⊥BD对应的圆周角,∠COE是CE 对应的圆心角∵∠CAE是CE∴∠COE=2∠CAE的中点∵点B是CE∴∠COE=2∠BOE∴∠CAE=∠BOE∴∠CAE=∠BOE∴AD//OB∴BD⊥AD②如下图所示,连接CE对应的圆周角∵∠ABC与∠AEC是AC∴∠ABC=∠AEC∵AE是⊙O的直径∴∠ACE=90°∴tan∠AEC=AC CE=34∴CE=8∵AE2=CE2+AC2∴AE=10∴⊙O的半径为5.【知识点】圆周角定理;三角形的外接圆与外心;切线的性质;解直角三角形;作图-线段垂直平分线【解析】【解答】(1)∵△ABC的外接圆⊙O的圆心为任意两边的垂直平分线的交点,半径为交点到任意顶点的距离,∴做AB、AC的垂直平分线交于点O,以OB为半径,以O为圆心做圆即可得到△ABC 的外接圆;【分析】(1)利用尺规作图分别作出AC,AB的垂直平分线,两垂直平分线交于点O,然后以点O为圆心,OB的长为半径画圆即可.(2)①连接OC,OB,利用切线的性质可证得OB⊥BD,利用圆周角定理可证得∠COE=2∠CAE,由点B是弧CE的中点,可推出∠CAE=∠BOE,利用平行线的判定定理可证得AD∥OB,由此可证得结论;②连接CE,利用同弧所对的圆周角相等,可证得∠ABC=∠AEC,利用直径所对的圆周角是直角,可推出∠ACE=90°;再利用解直角三角形求出CE的长,利用勾股定理求出AE的长.28.(2022·鄂州)如图,△ABC内接于⊙O,P是⊙O的直径AB延长线上一点,∠PCB=∠OAC,过点O作BC的平行线交PC的延长线于点D.(1)试判断PC与⊙O的位置关系,并说明理由;(2)若PC=4,tanA=12,求△OCD的面积.【答案】(1)解:PC与⊙O相切,理由如下:∵AB是圆O的直径,∴∠ACB=90°,∴∠OCB+∠OCA=90°,∵OA=OC,∴∠OCA=∠OAC,∵∠PCB=∠OAC,∴∠PCB=∠OCA,∴∠PCB+∠OCB=∠OCA+∠OCB=90°,即∠PCO=90°,∴PC与⊙O相切(2)解:∵∠ACB=90°,tanA=12,∴BC AC=12,∵∠PCB=∠OAC,∠P=∠P,∴△PBC∽△PCA,∴PC PA=PB PC=BC CA=12,∴PA=8,PB=2,∴AB=6,∴OC=OB=3,∴OP=5,∵BC∥OD,∴△PBC∽△POD,∴PB OP=PC PD,即25=4PD,∴PD=10,∴CD=6,∴S△OCD=12OC⋅CD=9【知识点】等腰三角形的性质;圆周角定理;切线的判定;相似三角形的判定与性质;锐角三角函数的定义【解析】【分析】(1)由圆周角定理得∠ACB=90°,根据等腰三角形的性质可得∠OCA=∠OAC,结合∠PCB=∠OAC得PCB=∠OCA,结合∠OCB+∠OCA=90°可得∠PCO=90°,据此证明;(2)根据三角函数的概念可得BC AC=12,易证△PBC∽△PCA,根据相似三角形的性质可得PA、PB,然后求出AB、OP,证明△PBC∽△POD,根据相似三角形的性质可得PD,由PD-PC=CD可得CD,然后根据三角形的面积公式进行计算.29.(2022·毕节)如图,在△ABC中,∠ACB=90∘,D是AB边上一点,以BD为直径的⊙O与AC相切于点E,连接DE并延长交BC的延长线于点F.(1)求证:BF=BD;(2)若CF=1,tan∠EDB=2,求⊙O直径.【答案】(1)证明:连接OE,如下图所示:∵AC为圆O的切线,∴∠AEO=90°,∵AC⊥BC,∴∠ACB=90°,∴OE∥BC,∴∠F=∠DEO,又∵OD=OE,∴∠ODE=∠DEO,∴∠F=∠ODE,∴BD=BF.(2)解:连接BE,如下图所示:由(1)中证明过程可知:∠EDB=∠F,。
中考数学点对点-涉及圆的证明与计算问题(解析版)

专题27 涉及圆的证明与计算问题专题知识点概述圆的证明与计算是中考必考点,也是中考的难点之一。
纵观全国各地中考数学试卷,能够看出,圆的证明与计算这个专题内容有三种题型:选择题、填空题和解答题。
一、与圆有关的概念1.圆:平面上到定点的距离等于定长的所有点组成的图形叫做圆。
定点称为圆心,定长称为半径。
圆的半径或直径决定圆的大小,圆心决定圆的位置。
2.圆心角:顶点在圆心上的角叫做圆心角。
圆心角的度数等于它所对弧的度数。
3.圆周角:顶点在圆周上,并且两边分别与圆相交的角叫做圆周角。
4. 外接圆和外心:经过三角形的三个顶点可以做一个圆,这个圆叫做三角形的外接圆。
外接圆的圆心,叫做三角形的外心。
外心是三角形三条边垂直平分线的交点。
外心到三角形三个顶点的距离相等。
5.若四边形的四个顶点都在同一个圆上,这个四边形叫做圆内接四边形,这个圆叫做这个四边形的外接圆。
6.和三角形三边都相切的圆叫做这个三角形的内切圆,其圆心称为内心。
内心是三角形三个角的角平分线的交点。
内心到三角形三边的距离相等。
二、与圆有关的规律1.圆的性质:(1)圆具有旋转不变性;(2)圆具有轴对称性;(3)圆具有中心对称性。
2.垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧。
3.推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.4.在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦心距也相等。
在同圆或等圆中,如果两条弧相等,那么他们所对的圆心角相等,所对的弦相等,所对的弦心距也相等。
在同圆或等圆中,如果两条弦相等,那么他们所对的圆心角相等,所对的弧相等,所对的弦心距也相等。
5.在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.6.半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.7.圆内接四边形的特征①圆内接四边形的对角互补;②圆内接四边形任意一个外角等于它的内对角。
2020年中考(通用)复习专题:圆的有关计算与证明(解答题,含答案)
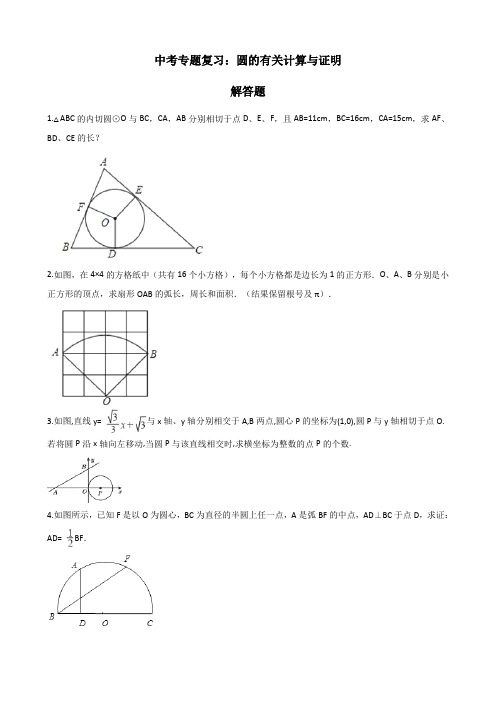
中考专题复习:圆的有关计算与证明解答题1.△ABC的内切圆⊙O与BC,CA,AB分别相切于点D、E、F,且AB=11cm,BC=16cm,CA=15cm,求AF、BD、CE的长?2.如图,在4×4的方格纸中(共有16个小方格),每个小方格都是边长为1的正方形.O、A、B分别是小正方形的顶点,求扇形OAB的弧长,周长和面积.(结果保留根号及π).3.如图,直线y= 与x轴、y轴分别相交于A,B两点,圆心P的坐标为(1,0),圆P与y轴相切于点O.若将圆P沿x轴向左移动,当圆P与该直线相交时,求横坐标为整数的点P的个数.4.如图所示,已知F是以O为圆心,BC为直径的半圆上任一点,A是弧BF的中点,AD⊥BC于点D,求证:AD= BF.5.如图,在△ABC 中,BE 是它的角平分线,∠C=90°,点D 在AB 边上,以DB 为直径的半圆O 经过点E ,交BC 于点F(1)求证:AC 是⊙O 的切线;(2)已知sinA=,⊙O 的半径为3,求图中阴影部分的面积 6.如图,已知是△ 的外角 的平分线,交 的延长线于点 ,延长 交△ 的外接圆于点 ,连接 , .(1)求证:.(2)已知,若 是△ 外接圆的直径, ,求 的长.7.已知:如图,在△ABC 中,AB=BC=10,以AB 为直径作⊙O 分别交AC ,BC 于点D ,E ,连接DE 和DB ,过点E 作EF ⊥AB ,垂足为F ,交BD 于点P .(1)求证:AD=DE ;(2)若CE=2,求线段CD 的长;(3)在(2)的条件下,求△DPE 的面积.8.如图,AB 是半圆O 的直径,AD 为弦,∠DBC=∠A .(1)求证:BC 是半圆O 的切线;(2)若OC ∥AD ,OC 交BD 于E ,BD=6,CE=4,求AD 的长.9.如图1,在正方形ABCD中,以BC为直径的正方形内,作半圆O,AE切半圆于点F交CD于点E,连接OA、OE.(1)求证:AO⊥EO;(2)如图2,连接DF并延长交BC于点M,求的值.10.如图,AD是⊙O的切线,切点为A,AB是⊙O的弦.过点B作BC∥AD,交⊙O于点C,连接AC,过点C作CD∥AB,交AD于点D.连接AO并延长交BC于点M,交过点C的直线于点P,且∠BCP=∠ACD.(1)判断直线PC与⊙O的位置关系,并说明理由;(2)若AB=9,BC=6.求PC的长.11.如图,点A在⊙O上,点P是⊙O外一点,PA切⊙O于点A,连接OP交⊙O于点D,作AB⊥OP于点C,交⊙O于点B,连接PB.(1)求证:PB是⊙O的切线;(2)若PC=9,AB=6 ,①求图中阴影部分的面积;12.如图,AB是⊙O的直径,过点A作⊙O的切线并在其上取一点C,连接OC交⊙O于点D,BD的延长线交AC于E,连接AD.(1)求证:△CDE∽△CAD;(2)若AB=2,AC=2 ,求AE的长.13.如图,AB是⊙O的直径,C是⊙O是一点,过点B作⊙O的切线,与AC延长线交于点D,连接BC,OE//BC 交⊙O于点E,连接BE交AC于点H.(1)求证:BE平分∠ABC;(2)连接OD,若BH=BD=2,求OD的长.14.如图①,在平面直角坐标系中,圆心为P(x,y)的动圆经过点A(2,8),且与x轴相切于点B.图①图②(1)当x>0,y=5时,求x的值;(2)当x = 6时,求⊙P的半径;(3)求y关于x的函数表达式,请判断此函数图象的形状,并在图②中画出此函数的图象(不必列表,画草图即可).15.如图,△OAB的底边经过⊙O上的点C,且OA=OB,CA=CB,⊙O与OA、OB分别交于D、E两点.(1)求证:AB是⊙O的切线;(2)若D为OA的中点,阴影部分的面积为,求⊙O的半径r.16.如图,在△ABC中,∠C=90°,∠ABC的平分线交AC于点E,过点E作BE的垂线交AB于点F,⊙O是△BEF 的外接圆.(1)求证:AC是⊙O的切线;(2)过点E作EH⊥AB,垂足为H,求证:CD=HF;(3)若CD=1,EH=3,求BF及AF长.17.如图,CD为⊙O的直径,CD⊥AB,垂足为点F,AO⊥BC,垂足为点E,CE=2.(1)求AB的长;(2)求⊙O的半径.18.如图,在△ABC中,∠ABC=90°,以AB的中点O为圆心,OA为半径的圆交AC于点D,E是BC的中点,连接DE,OE.(1)判断DE与⊙O的位置关系,并说明理由;(2)求证:BC2=2CD•OE;(3)若cos∠BAD= ,BE= ,求OE的长.19.如图,AB为⊙O的直径,点C在⊙O上,过点C作⊙O的切线交AB的延长线于点D,已知∠D=30°.(1)求∠A的度数;(2)若点F在⊙O上,CF⊥AB,垂足为E,CF=,求图中阴影部分的面积.20.如图,在Rt△ABC中,∠C=90°,点D,E,F分别在AC,BC,AB边上,以AF为直径的⊙O恰好经过D,E,且DE=EF.(1)求证:BC为⊙O的切线;(2)若∠B=40°,求∠CDE的度数;(3)若CD=2,CE=4,求⊙O的半径及线段BE的长.21.如图,⊙的圆心在反比例函数的图像上,且与轴、轴相切于点、,一次函数的图像经过点,且与轴交于点,与⊙的另一个交点为点.(1)求的值及点的坐标;(2)求长及的大小;(3)若将⊙沿轴上下平移,使其与轴及直线均相切,求平移的方向及平移的距离.参考答案解答题1.解:∵△ABC的内切圆⊙O与BC,CA,AB分别相切于点D、E、F,∴AF=AE,BF=BD,CD=CE.设AF=AE=x,则BF=BD=11﹣x,EC=DC=15﹣x.根据题意得11﹣x+15﹣x=16.解得;x=5cm.∴AF=5cm.BD=11﹣x=11﹣5=6cm,EC=15﹣x=10cm.∴AF=5cm,BD=6cm,EC=10cm.2.解:由图形可知,∠AOB=90°,∴OA=OB==2,∴==,扇形OAB的面积==2π.弧AB的长是:=π∴周长=弧AB的长+2OA=π+4.综上所述,扇形OAB的弧长是π,周长是π+4,面积是2π.3.解:∵直线y= 与x轴、y轴分别相交于A,B两点,∴A点的坐标为(-3,0),B点的坐标为(0, ),∴AB=2 .如图,将圆P沿x轴向左移动,当圆P与该直线相切于C1时,连结P1C1,则P1C1=1,易知△AP1C1∽△ABO,∴= ,∴AP1=2,∴P1的坐标为(-1,0),同理可得P2的坐标为(-5,0).-5与-1之间的整数(不含-5和-1)有:-4,-3,-2,故满足题意的点P的个数是34.证明:连接OA,交BF于点E,∵A是弧BF的中点,O为圆心,∴OA⊥BF,∴BE= BF,∵AD⊥BC于点D,∴∠ADO=∠BEO=90°,在△OAD与△OBE中,,∴△OAD≌△OBE(AAS),∴AD=BE,∴AD= BF5. (1)证明:连结OE,[MISSING IMAGE: , ]∵BE平分∠ABC,∴∠ABC=2∠ABE,∵OB=OE,∴∠OBE=∠OEB,∴∠AOE=∠OEB+∠OBE=2∠ABE,∴∠ABC=∠AOE,又∵∠C=90°,∴∠A+∠ABC=90°,∴∠A+∠AOE=90°,∵∠AEO=90°,即OE⊥AC,∴AC为⊙O的切线.(2)解:连结OF,∵sinA=,∴∠A=30°,由(1)知OE⊥AC,∴∠AOE=∠ABC=60°,∵⊙O半径为3,∴OD=OE=OF=OB=BF=3,∴∠BOF=∠EOF=∠ABC=60°,∴S扇形OEF=,在Rt△AOE中,∴AO=6,AE=3,在Rt△ACB中,∴AB=9,BC=,AC=,∴CE=AC-AE=-3,CF=BC-BF=-3=,∴S梯形OFCE===,∴S阴=S梯形OFCE-S扇形OEF=-.6.(1)解:∵四边形内接于圆,∴,∵,∴,∵是△的外角平分线,∴,,∴,又∵,∴(2)解:由()得,又∵,∴△∽△,∴,∴,∴,又∵,∴,,∵是直径,∴,∴BD= ,又∵∠D=∠D,∴△DBF∽△DAC,∴,∴CD=24,解得:CD= .7.(1)解:∵AB是⊙O的直径,∴∠ADB=90°,即BD⊥AC∵AB=BC,∴△ABD≌CBD∴∠ABD=∠CBD在⊙O中,AD与DE分别是∠ABD与∠CBD所对的弦∴AD=DE;(2)解:∵四边形ABED内接于⊙O,∴∠CED=∠CAB,∵∠C=∠C,∴△CED∽△CAB,∴,∵AB=BC=10,CE=2,D是AC的中点,∴CD= ;(3)解:延长EF交⊙O于M,在Rt△ABD中,AD= ,AB=10,∴BD=3 ,∵EM⊥AB,AB是⊙O的直径,∴,∴∠BEP=∠EDB,∴△BPE∽△BED,∴,∴BP= ,∴DP=BD-BP= ,∴S△DPE:S△BPE=DP:BP=13:32,∵S△BCD= × ×3 =15,S△BDE:S△BCD=BE:BC=4:5,∴S△BDE=12,∴S△DPE= .8.(1)证明:∵AB是半圆O的直径∴∠D=90°∴∠A+∠DBA=90°∵∠DBC=∠A∴∠DBC+∠DBA=90°∴BC⊥AB∴BC是半圆O的切线(2)解:∠BEC=∠D=90∘,∵BD⊥AD,BD=6,∴BE=DE=3,∵∠DBC=∠A,∴△BCE∽△BAD,∴,即∴AD=4.59.(1)证明:∵四边形ABCD为正方形,∴∠B=∠C=90°,AB∥CD,∴AB和CD为⊙O的切线,∵AE切半圆于点F,∴OA平分∠BAE,OE平分∠AEC,而AB∥CD,∴∠BAE+∠AEC=180°,∴∠OAE+∠OEA=90°,∴∠AOE=90°,∴OA⊥OE(2)解:作FH⊥CD于H,如图,设正方形ABCD的边长为4a,则AF=AB=4a,OB=OC=2a,∵∠AOE=90°,∴∠AOB+∠COE=90°,∵∠AOB+∠OAB=90°,∴∠OAB=∠EOC,∴Rt△ABO∽Rt△OCE,∴AB:OC=OB:CE,即4a:2a=2a:CE,解得CE=a,∴EF=EC=a,∴EA=5a,ED=3a,∵FH∥AD,∴△EFH∽△EAD,∴= = ,即= = ,∴FH= a,EH= a,∴DH=3a﹣a= a,∴CH=4a﹣a= a,∵FH∥CM,∴= = .10.(1)解:PC与圆O相切,理由为:过C点作直径CE,连接EB,如图,∵CE为直径,∴∠EBC=90°,即∠E+∠BCE=90°,∵AB∥DC,∴∠ACD=∠BAC,∵∠BAC=∠E,∠BCP=∠ACD.∴∠E=∠BCP,∴∠BCP+∠BCE=90°,即∠PCE=90°,∴CE⊥PC,∴PC与圆O相切;(2)解:∵AD是⊙O的切线,切点为A,∴OA⊥AD,∵BC∥AD,∴AM⊥BC,∴BM=CM= BC=3,∴AC=AB=9,在Rt△AMC中,AM= =6 ,设⊙O的半径为r,则OC=r,OM=AM﹣r=6 ﹣r,在Rt△OCM中,OM2+CM2=OC2,即32+(6 ﹣r)2=r2,解得r= ,∴CE=2r= ,OM=6 ﹣= ,∴BE=2OM= ,∵∠E=∠MCP,∴Rt△PCM∽Rt△CEB,∴= ,即= ,∴PC= .11.(1)证明:如图1,连接OB,∵OP⊥AB,OP经过圆心O,∴AC=BC,∴OP垂直平分AB,∴AP=BP,∵OA=OB,OP=OP,∴△APO≌△BPO(SSS),∴∠PAO=∠PBO,∵PA切⊙O于点A,∴AP⊥OA,∴∠PAO=90°,∴∠PBO=∠PAO=90°,∴OB⊥BP,又∵点B在⊙O上,∴PB与⊙O相切于点B;(2)解:如图1,∵OP⊥AB,OP经过圆心O,∴BC= AB=3 ,∵∠PBO=∠BCO=90°,∴∠PBC+∠OBC=∠OBC+∠BOC=90°,∴∠PBC=∠BOC,∴△PBC∽△BOC,∴∴OC= = =3,∴在Rt△OCB中,OB= = =6,tan∠COB= = ,∴∠COB=60°,∴S△OPB= ×OP×BC= × =18 ,S扇DOB= =6π,∴S阴影=S△OPB﹣S扇DOB=18 ﹣6π;②若点E是⊙O上一点,连接AE,BE,当AE=6 时,BE= .3 ﹣3 或3 +312.(1)证明:∵AB是⊙O的直径,∴∠ADB=90°,∴∠B+∠BAD=90°,∵AC为⊙O的切线,∴BA⊥AC,∴∠BAC=90°,即∠BAD+∠CAD=90°,∴∠B=∠CAD,∵OB=OD,∴∠B=∠ODB,而∠ODB=∠CDE,∴∠B=∠CDE,∴∠CAD=∠CDE,而∠ECD=∠DCA,∴△CDE∽△CAD(2)解:∵AB=2,∴OA=1,在Rt △AOC 中,AC=2,∴OC= =3,∴CD=OC ﹣OD=3﹣1=2,∵△CDE ∽△CAD ,∴ = ,即 = ,∴CE= .∴AE=AC ﹣CE=2﹣ = . 13.(1)证明:∵AB 为⊙O 的直径,∴∠ACB=90°,∵OE//BC ,∴OE ⊥AC ,∴ = ,∴∠1=∠2,∴BE 平分∠ABC(2)解:∵BD 是⊙O 的切线,∴∠ABD=90°,∵∠ACB=90°,BH=BD=2,∴∠CBD=∠2,∴∠1=∠2=∠CBD ,∴∠CBD=30°,∠ADB=60°,∵∠ABD=90°,∴AB=2 ,OB= ,∵OD 2=OB 2+BD 2 ,∴OD= .14.(1)解: 由y=5,得到P(x,5),连接AP,PB,∵圆P与x轴相切,∴PB⊥x轴,即PB=5,由AP=PB,由勾股定理得,x=2+ =2+4=6,∴x=6(2)解: 由x=6,得到P(6,y),连接AP,PB,∵圆P与x轴相切,∴PB⊥x轴,即PB=y,由AP=PB,得到=y,解得:y=5,则圆P的半径为5(3)解: 同(2),由AP=PB,得到(x﹣2)2+(8﹣y)2=y2,整理得:= ,即图象为抛物线,画出函数图象,如图②所示;15.(1)证明:连OC,如图,∵OA=OB,CA=CB,∴OC⊥AB,∴AB是⊙O的切线;(2)解:∵D为OA的中点,OD=OC=r,∴OA=2OC=2r,∴∠A=30°,∠AOC=60°,AC= r,∴∠AOB=120°,AB=2 r,∴S阴影部分=S△OAB﹣S扇形ODE= •OC•AB﹣= ﹣,∴•r•2 r﹣r2= ﹣,∴r=1,即⊙O的半径r为116. (1)证明:如图,连接OE.∵BE⊥EF,∴∠BEF=90°,∴BF是圆O的直径.∵BE平分∠ABC,∴∠CBE=∠OBE,∵OB=OE,∴∠OBE=∠OEB,∴∠OEB=∠CBE,∴OE∥BC,∴∠AEO=∠C=90°,∴AC是⊙O的切线;(2)证明:如图,连结DE.∵∠CBE=∠OBE,EC⊥BC于C,EH⊥AB于H,∴EC=EH.∵∠CDE+∠BDE=180°,∠HFE+∠BDE=180°,∴∠CDE=∠HFE.在△CDE与△HFE中,,∴△CDE≌△HFE(AAS),∴CD=HF(3)由(2)得CD=HF,又CD=1,∴HF=1,在Rt△HFE中,EF= = ,∵EF⊥BE,∴∠BEF=90°,∴∠EHF=∠BEF=90°,∵∠EFH=∠BFE,∴△EHF∽△BEF,∴= ,即= ,∴BF=10,∴OE= BF=5,OH=5﹣1=4,∴Rt△OHE中,cos∠EOA= ,∴Rt△EOA中,cos∠EOA= = ,∴= ,∴OA= ,∴AF= ﹣5=17.(1)解:∵,∴在中∴∴∵,∴∵是的直径,∴∴(2)解:∵是的半径,,∴,∵,∴.∵,∴又∵∴∴即的半径是18.(1)证明:连接OD,BD,∵AB为圆O的直径,∴∠ADB=90°,在Rt△BDC中,E为斜边BC的中点,∴CE=DE=BE= BC,∴∠C=∠CDE,∴∠A=∠ADO,∵∠ABC=90°,即∠C+∠A=90°,∴∠ADO+∠CDE=90°,即∠ODE=90°,∴DE⊥OD,又OD为圆的半径,∴DE为圆O的切线;(2)证明:∵E是BC的中点,O点是AB的中点,∴OE是△ABC的中位线,∴AC=2OE,∵∠C=∠C,∠ABC=∠BDC,∴△ABC∽△BDC,∴,即BC2=AC•CD.∴BC2=2CD•OE(3)解:∵cos∠BAD= ,∴sin∠BAC= = ,又∵BE= ,E是BC的中点,即BC= ,∴AC= .又∵AC=2OE,∴OE= AC=19.(1)解:连接OC,∵CD切⊙O于点C∴∠OCD=90°∵∠D=30°∵OA=OC∴∠A=∠ACO=30°;(2)解:∵CF⊥直径AB,CF=4∴CE=2∴在Rt△OCE中,tan∠COE= ,OE= =2,∴OC=2OE=4∴S扇形BOC= ,S△EOC= ×2×2 =2∴S阴影=S扇形BOC-S△EOC= -2 .20.(1)证明:连接OD、OE、DF,如图,∵AF为直径,∴∠ADF=90°,而∠C=90°,∴DF∥BC,∵DE=EF,∴=∴OE⊥DF,∴OE⊥BC,∴BC为⊙O的切线(2)解:∵∠OEB=90°,∠B=40°,∴∠BOE=90°﹣40°=50°,∴∠OFE= (180°﹣50°)=65°,∴∠CDE=∠AFE=65°(3)解:易得四边形CDHE为矩形,∴HE=CD=2,DH=CE=4,设⊙O的半径为r,则OH=OE﹣HE=r﹣2,OD=r,在Rt△OHD中,(r﹣2)2+42=r2,解得r=5,∵OH⊥DF,∴HF=DH=4,∵HF∥BE,∴△OHF∽△OEB,∴HF:BE=OH:OE,即4:BE=3:5,∴BE=21.(1)解:如图1中,连接AC、AB.∵⊙A与x轴、y轴相切于点B、C,∴AC⊥OC,AB⊥OB,AC=AB,四边形ABOC是正方形,设A(m,m),∵点A在y= 上,∴m2=3,∵m>0,∴点A坐标(,),∴OC= ,∴点C坐标(0,),∵一次函数y= x+b的图象经过点C,∴b= ,∴一次函数的解析式为y= ,令y=0得x=-3,∴D(-3,0),b=(2)解:如图2中,连接BC、BE,作AM⊥CE于M.在Rt△DOC中,∵tan∠CDO= ,∴∠CDO=30°,∵AC∥BD,∴∠ECA=∠CDO=30°,∠CAM=60°,∵AM⊥CE,∴∠CAM=∠EAM=60°,∴∠CAE=120°,在Rt△AMC中,CM=AC•cos30°= ,∴CE=2CM=3,∴∠CBE= ∠CAE=60°(3)解:如图3中,①当⊙A″与直线y= 相切于点E,AB与直线CD交于点K,∵AB∥OC,∴∠A″KE=∠DKB=∠DCO=60°,在Rt△A″EK中,A″E= ,A″K=A″E÷cos30°=2,在Rt△CKA中,AK=CA•tan30°=1,∴AA″=A″K+AK=1+2=3,∴⊙A向上平移3的单位⊙A与y轴及直线y= 均相切.②同理可得⊙A向下平移1个单位⊙A与y轴及直线y= 均相切。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
热点18 与圆有关的计算问题
(时间:100分钟总分:100分)
一、选择题(本大题共10小题,每小题3分,共30分,在每小题给出的四个选项中,只有一个是符合题目要求的)
1.已知圆心角为120°,所对的弧长为5 cm,则该弧所在圆的半径R=()
A.7.5cm B.8.5cm C.9.5cm D.10.5cm
2.一条弦分圆周为5:4两部分,则这条弦所对的圆周角的度数为()
A.80° B.100° C.80°或100° D.以上均不正确
3.⊙O的半径R=3cm,直线L与圆有公共点,且直线L和点O的距离为d,则()
A.d=3cm B.d≤3cm C.d>3cm D.d<3cm
4.如图1,AB是⊙O的直径,CD是弦,若AB=10cm,CD=8cm,那么A,•B•两点到直线CD 的距离之和为()
A.12cm B.10cm C.8cm D.6cm
(1)(2)(3)(4)
5.如图2,同心圆中,大圆的弦AB交小圆于C、D,AB=4,CD=2,AB•的弦心距等于1,那么两个同心圆的半径之比为()
A.3:2 B5 2 C52.5:4
6.正三角形的外接圆的半径为R,则三角形边长为()
A3R B.
3
2
R C.2R D.
1
2
R
7.已知如图3,圆内一条弦CD与直径AB相交成30°角,且分直径成1cm和5cm两部分,则这条弦的弦心距是()
A.1
2
cm B.1cm C.2cm D.2.5cm
8.∠AOB=30°,P为OA上一点,且OP=5cm,若以P为圆心,r为半径的圆与OB相切,则半径r为()
A.5cm B 5
3
2
.
5
2
cm D
5
3
3
cm
9.如图4,∠BAC=50°,则∠D+∠E=()
A.220° B.230° C.240° D.250°
10.秋千拉绳长3米,静止时踩板离地面0.5米,某小朋友荡该秋千时,秋千在最高处踩板离地面高2米(左右对称),则该秋千所荡过的圆弧长为()
A.π米 B.2π米 C.π米 D
.
3
2
π米
二、填空题(本大题共8小题,每小题3分,共24分)
11.已知两圆的直径分别为5+a与5-a,如果它们的圆心距为a,则这两个圆的位置关系是_________.
12.两等圆半径为5,圆心距为8,则公共弦长为__________.
13.⊙O的直径为50cm,弦AB∥CD,且AB=40cm,CD=48cm,则AB•和CD•之间的距离为_________ 14.如图5,有一圆弧形拱桥,拱的跨度AB=16m,拱高CD=4m,那么拱形的半径为_______m.
(5)(6)(7)(8)
15.如图6,⊙O的半径OA与弦AB和切线BC的长都相等,AC、OC与圆分别相交于D、E,那么
»BD的度数是__________.
16.如图7,半圆的直径AB=8cm,∠CBD=30°,则弦DC=________.
17.如图8,矩形ABCD中,AB=3cm,AD=4cm,若以A为圆心作圆,使B、C、D三点中至少有一点在圆内且至少有一点在圆外,则⊙A的半径r的取值范围为________.
18.某人用如下方法测一槽钢的内径:将一小段槽钢竖直放
在平台上,•向内放入两个半径为5cm的钢球,测得上面
一个钢球顶部高CD=16cm(槽钢的轴截面如图所示),则
槽钢的内直径AD长为________.
三、解答题(本大题共46分,19~23题每题6分,24题、
25题每题8分,解答题应写出文字说明、证明过程或演
算步骤)
19.如图,半径为4的⊙O中有弦AB,以AB为折痕对折,劣弧
恰好经过圆心O,•则弦AB的长度是多少?
20.如图,已知点C在以AB为直径的半圆上,连结AC、BC,AB=10,tan∠BAC=
3
4
,求阴影部分的面积.
21.如图21-12所示,有一弓形钢板ACB,
»AB的度数为120°,弧长为L,•现要用它剪出一个最大的圆形板料,求这个圆形板料的周长.
22.已知如图21-13,四边形ABCD内接于⊙A,AC为⊙O的直径,弦DB⊥AC,垂足为M,过
点D作⊙O的切线,交BA的延长线于点E,若AC=10,tan∠DAE=4
3
,求DB的长.
23.用半径R=8mm,r=5mm的钢球测量口小内大的零件的直径D,测得钢球顶点与孔口平面的距离分别为a=12.5mm,b=10.5mm(如图21-14),计算出内孔直径D的大小.
24.若⊙O的直径AB为2,弦AC2,弦3S扇形OCD.(其中2S扇形OCD<S⊙O)
25.如图,射线OA⊥射线OB,半径r=2cm的动圆M与OB相切于点Q(圆M与OA•没有公共
点),P是OA上的动点,且PM=3cm,设OP=xcm,OQ=ycm.
(1)求x、y所满足的关系式,并写出x的取值范围.
(2)当△MOP为等腰三角形时,求相应的x的值.
(3)是否存在大于2的实数x,使△MQO∽△OMP?若存在,求相应x的值,若不存在,•请说明理由.
答案:
一、选择题
1.A 2.C 3.B 4.D 5.C 6.A 7.B 8.C 9.B 10.B
二、填空题
11.内切 12.6 13.22cm或8cm 14.10 15.30° 16.4cm 17.3cm<r<5cm •18.18cm
三、解答题
19.解:过点O作OC⊥AB,由题意知,OC=1
2
×4=2,
连结OA,在Rt△AOC中,AC2=A O2-OC2=16-4=12,3.∵OC⊥AB⇒AC=BC⇒3
20.解:tan∠BAC=
3
4
BC
AC
=,可设BC=3x,AC=4x,
AB是直径⇒∠ACB=90°⇒A B2=9x2+16x2=100⇒x=2.∴AC=8,BC=6.
S阴=S半圆-S△ACB=1
2
π×(
10
2
)2-
1
2
×6×8=
25
2
π-24.
21.解:L=120
360
·2πR⇒R =
3
2
l
π
,则弓形的高为
3
4
l
π
,故周长为
3
4
L.
22.解:连结OD,由四边形ABCD内接于⊙O可知∠DAE=∠DCB.
∵AC 为⊙O 的直径,弦DB ⊥AC ,∴DB=2DM ,AD=AB . ∴∠DCA=∠BCA ,AD=AB ,又∠DOA=2∠DCA . ∴∠DOA=∠DCB=∠DAE . ∴tan ∠DOA=tan ∠DAE=
43
. 在Rt △ODM 中,可设DM=4x ,OM=3x ,由勾股定理得DM 2
+OM 2
=OD 2
,得x=1. ∴OM=3,DM=4,DB=2DM=8.
23.解:连结O 1、O 2,则O 1O 2=R+r=13mm . O 1A=D-R-r=D-13,O 2A=a +2R-b-r-R=5, 在Rt △O 1O 2A 中,O 1O 22=O 1A 2+O 2A 2, 即132=52+(D-13)2,∴D=25mm .
24.解:①当点C 、点D 在直径AB 的异侧时,过点O 作OE ⊥AC ,过点O 作OF ⊥AD ,
则,
故cos ∠OAC=
AE AO =2
,∴∠OAC=45°;
cos ∠OAD=
2
,∴∠COD=150°. S 扇形OCD =
150360·π·12=5
12
π. ②当点C 、点D 在直径AB 的同侧时,同法可得∠COD=30°. 此时S 扇形OCD =
30360·π·12=
1
12
π. 25.解:(1)过点M 作MD ⊥OA ,垂足为D ,显然ODMQ 为矩形,
∴OD=MQ=2,MD=OQ=•y ,•
∴PD=x-2.在Rt △MDP 中,y 2+(x-2)2=32,
∴x 2-4x+y 2=5.∴x 取值范围为2<x ≤
(2)若△MOP 为等腰三角形,①若OM=MP ,此时x=4; ②若MP=OP 时,x=3;③若OM=OP 时, ∵OM=4+y 2,∴4+y 2=x 2,于是
22
22
4,
45,
y x x x y ⎧+=⎪⎨-+=⎪⎩ 解得x=22 (3)分三种情况依次讨论:
①假设两三角形相似,若∠OPM=90°,则MP=y ,OP=2=x ,得x=2, 不是大于2的实数,故∠OPM 不可能是90°;
②若∠MOP=90°,由于圆M 在第一象限,所以这不可能.
③假设△QMO ∽△MOP ,此时∠OMP=90°,则
OQ OM MQ
MP OP OM ==
,∴3y =
得4+y 2
=2x ,于是2
2242,
45,
y x x x y ⎧+=⎪⎨-+=⎪⎩ 得
∴存在这样的实数x ,并且。
