第10章脉冲波形的产生
第十章 脉冲波形的产生和整形

进入传输特性的放大区,因而: vA ↑ vO1↓ vO↑
使输出vO 迅速跳变到vO = VOH≈VDD 西安工程大学
数字电子技术基础
求vI 在上升过程中电路
状态发生转换时对应的输入 电平VT+
v A VTH v I VT R2 vI R1 R2 R1 R 2 R1 VTH 1 VTH R2 R2 VT :正向阈值电压
10.3 单稳态触发器
特点:
①有一个稳态和一个暂稳态。 ②在外界触发信号作用下,能从稳态→暂稳态,在暂稳态维持一段时间 tw后自动返回稳态,并在输出端产生一个宽度为tw的矩形脉冲。 ③暂稳态维持的时间长短取决于电路内部参数,而与触发脉冲的宽度和 幅度无关。 可广泛应用于脉冲整形、延时以及定时电路。
10.3.1 用门电路组成的单稳态触发器 一、积分型
R1>R2 ,VT+>VDD,VT-为负 R1<R若 ,否则电路将进入自锁状态, 2 值,而 v I 变化范围在 0~VDD 之间, 不能正常的工作 ? 即达不到阈值而使电路不能翻转。 西安工程大学
数字电子技术基础
【10.2.1】在CMOS反相器构成的施密特触发器中,要求
VT+=7.5V,ΔVT=5V,试求R1、R2和VDD的值 。 R1 R1 解:由 VT (1 )VTH 7.5V 和 ΔVT 2 VTH 5V R2 R2
数字电子技术基础 2. 性能参数计算 输出脉宽:
v C ( ) v C ( 0) VOH t w RCln RCln vC ( ) vC ( t ) VTH )C t re ( 3 ~ 5)( R RO 恢复时间
t d t TR t re
脉冲与数字电路第十章 脉冲波形的产生和定时
C
uo2
0
输出信号的周 期近似为: T = 2.2 RC
t
t
uA
UT
0
U
T
(3)施密特振荡器
(4) 带石英晶体的环行多谐振荡器
1. 阻抗频率特性和符号
2. 特性: 品质因数Q很大
固定振荡频率
(4) 带石英晶体的环行多谐振荡器
三、555定时器的原理和应用
555定时器是将模拟电路和数字电路集成于 一体的 电子器件。它使用方便,带负载能力较强, 目前得到了 非常广泛的应用。
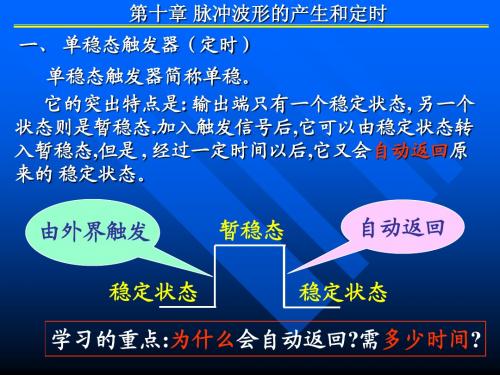
第十章 脉冲波形的产生和定时 一、 单稳态触发器(定时) 单稳态触发器简称单稳。 它的突出特点是: 输出端只有一个稳定状态, 另一个 状态则是暂稳态.加入触发信号后,它可以由稳定状态转 入暂稳态,但是 , 经过一定时间以后,它又会自动返回原 来的 稳定状态。
由外界触发 稳定状态
暂稳态
自动返回
稳定状态
R
1
0
三、555定时器的原理和应用
VCC
8
RD
4
RS 触发器功能表
R
1
3
TH CO TR
6 5 2 7
R + R + A1
S 0 1
Q 0 1
Q 1 0
RQ S Q
uo
0 0 1
R
1
D
A2 T
0 保持 保持
1 禁止 禁止
R 1 0 0
晶体管T uo 0 1 0 导通 1 0 1 截止 0 保持 保持 保持
S Q
2、555定时பைடு நூலகம்的应用
(1). 双稳态触发器: 微电机起动停车控制电路。
VCC S2 4
数字电子技术10脉冲波形的产生与变换资料

vR
vO2
vO1
vo1
t1
t
所以,一旦 vR = Vth ,立即 0 回到稳态:vO2= 0, vO1=1。 vR
vO1
vO2
Vth
0
t
t
G1 ≥1
C
1 G2 vR
R
VDD
vo2
vI
0
t
21
vO1 G1 ≥1
C
vO2 1 G2 vR
R VDD
vi
vo 1
vR
0
t1
t
vI
0
t
t tW
2. 主要参数计算:
常用的整形电路有单稳态触发器和施 密特触发器 。
3
图10.1.1 描述矩形脉冲特性的主要参数
1、脉冲周期T; 2、脉冲幅度Vm 3、脉冲宽度tw 4、上升时间tr
5、下降时间tf
6、占空比q q = tw / T
4
10. 2 施密特触发器 施密特触发器(Schmitt Trigger)的特点:
(1)属于电平触发,当输入信号达到一定电压值时,输 出电压会发生突变,输入信号增加和减少时,电路有不 同的阈值电平。 (2)在电路状态转换时,通过电路内部的正反馈过程, 使输出电压波形的边沿变得很陡。 VO VOH
1
G2
vI
vO1
vR
vR VDD
vO1 = 0 ,vO2 = 1, 同时: +5V
R4
vI
电容C应 该充电
vo2
vR
0
T4 T5
t
vo 1
C
R
VDD
t 只要 vR < Vth ,仍 然维持暂稳态。
0
数字电子技术-脉冲波形的产生与变换

3
锯齿波变换的应用
在数字电子技术中,锯齿波的变换常用于产生矩 形波等脉冲波形,这些波形在信号处理、测量和 控制等领域有广泛的应用。
04
脉冲波形产生与变换的方法
数字方法
数字方法是指通过数字电路和数字信号处理技术来产生 和变换脉冲波形。
数字方法可以通过编程实现各种不同的脉冲波形,如矩 形波、三角波、正弦波等。
数字电子技术-脉冲波形 的产生与变换
• 引言 • 脉冲波形的产生 • 脉冲波形的变换 • 脉冲波形产生与变换的方法 • 脉冲波形产生与变换的实际应用 • 结论
01
引言
主题简介
01
脉冲波形是指具有特定形状、幅 度、宽度和重复频率的波形,广 泛应用于数字电子技术中。
02
脉冲波形的产生与变换是数字电 子技术中的重要内容,涉及到信 号处理、通信、控制等多个领域 。
光纤通信
在光纤通信中,脉冲波形产生与变换技术用于生成高速光脉冲,实现大容量、高速的光信号传输。通 过调制技术,将数字信号加载到光脉冲上,提高通信系统的传输效率和可靠性。
在测量技术中的应用
时间测量
利用脉冲波形产生与变换技术,可以生成精确的时间间隔和频率,用于时间测量和计时 应用。例如,高精度计数器和频率计等测量仪器利用脉冲波形产生与变换技术实现高精
数字方法具有精度高、稳定性好、易于实现复杂波形等 优点。
数字方法还可以实现脉冲波形的调制和解调,广泛应用 于通信、雷达、测控等领域。
模拟方法
01
模拟方法是指通过模拟 电路和模拟信号处理技 术来产生和变换脉冲波 形。
02
模拟方法具有简单、直 观、易于实现等优点。
03
模拟方法可以通过简单 的RC电路、LC电路等实 现矩形波、锯齿波等基 本脉冲波形。
脉冲波形产生与变换电路(课件)

2
矩形脉冲波形的主要参数
图6.1.2 矩形脉冲波形的主要特征参数
3
主要参数
六个特征参数定义: ①脉冲周期 T:周期性脉冲序列中,两个相邻脉冲 出现的时间间隔。 ②脉冲幅值Um :脉冲信号的最大变化幅值。 ③占空比D :脉冲信号的正脉冲宽度与脉冲周期的 比值,即 D=tW / T 。 ④脉冲宽度 tW :从脉冲波形上升沿的 0.5Um 到下降 沿的 0.5Um所需的时间。 ⑤上升时间tr:脉冲波形由0.1Um上升到0.9Um所 需的时间。 ⑥下降时间tf:脉冲波形由0.9Um下降到0.1Um所需 的时间。
4
6.2 单稳态触发器
特点: ①有一个稳态和一个暂稳态 ②在外界触发信号作用下,能从稳态→暂稳态 ,维持一段时间后自动返回稳态 ③暂稳态维持的时间长短取决于电路内部参数 单稳态触发器的暂稳态通常都由RC电路的充放电 过程来维持。按电路中决定暂态时间的电路连接形式 不同,单稳态触发器可分为积分型和微分型两种,如 图6.2.1、6.2.5所示。
41
随着充电过程的进行,电容电压逐渐升高, 因此uI也逐渐增大。一旦uI 达到非门G1的阈值 电压UTH,多谐振荡器必将发生如下正反馈过 程:
这一正反馈过程促使G1瞬间导通、G2瞬间截止,可
得uO1 =UOL, uO =UOH。该状态被定义为第二暂稳
态。
42
②第二暂稳态自动翻转至第一暂稳态
当多谐振荡器进入第二暂稳态的瞬间,电路输
其中,74121的电路符号如图。
14
图6.2.10 集成单稳态触发器的两种工作波形
15
图6.2.12 集成单稳态触发器74121 的外部元件连接方法 (a)使用外接电阻Rext 且采用下降沿触发 (b)使用内部电 阻Rint 且采用上升沿触发
第十章——脉冲波形的产生与整型

电路结构
vO
1
vO 1 D vI2 R G2
vI
vO1 G1 1 Cd vd Rd C 1
vO G2
G1 vI Cd
& vd Rd
C vC
D v I2 v C R VDD
(CMOS门,与非,负脉冲触发)
(CMOS门,或非,正脉冲触发)
1、CMOS或非门电路构成的微分型单稳态触发器 (1)电路结构 正脉冲触发 (2)工作原理分析 解决三个问题: ①什么是稳态? ②如何在外部触 发脉冲作用下,由 稳态进入暂态?
vI
同相ST传输特性
反相ST传输特性
10.2 施密特触发器
4、施密特触发器应用
1. 波形变换
vI
0
vO1 VOH
VT VT
t
vo
0
t
vI
VOL o
VT_ VT+
2. 波形整形
vI
vI VT+ VT– 0 vO VOH VOL 0
1
vO
vI vI VT+ VT–
t
1
vO
0 vO VOH VOL 0
(3)当VI 1 至VTH , 又返回第一个暂稳态。
二、电压波形
脉冲宽度计算: TW T1 T2 T1 : C放电,从VTH VDD 放至VTH T2 : C充电,从VTH VDD 充至VTH
V( ) V( 0) tw RC ln V( ) V( t )
【题10-1】 在图题10-1所示的电路中,已知R1=10kW,R2=30kW, 其中CMOS非门电路的电源电压VCC=6V。 ① 计算该电路的正向阈值电压VT+、负向阈值电压VT-和回差电压ΔVT。 ② 画出该电路的传输特性曲线。
脉冲波形的产生和整形
UI
C1 R1
C2 R2
UO1
t
1ቤተ መጻሕፍቲ ባይዱ
B
74121
(1)
UO
A2
UI A1
UO
B
74121
(2)
UO
UO2
A2 A1
UO
UO1 UO2
TW1
t t
TW2
触发后,电路延时TW1 时间再输出。
t
TW1 = 0.69 R1C1
TW2 = 0.69 R2C2
§ 6-4 多谐振荡器
特点:不需要外加触发信号,电路自激振荡,没有稳态。
RF1
RF2
这就解决了多谐振荡器的稳频问题。
3、参数选择
各种固有振荡频率fo的石英晶体已做成成品,
可根据所购晶体的fo选择电路的外接RF 和C,
fo一般都很高,应利用分频器将fo分频为所需频率。
例如,需要频率为1HZ的秒脉冲,
可选购 fo=32768HZ的晶振,通过15次二分频获得1HZ。
§ 6-5 555定时器及其应用
74121的电路符号:
10 11
9
Cext Rext Rint
3B
4 A2 5 A1
Cext 74121
GND
7
14
Vcc Uo 6
Uo 1
74121的功能表 P.325.
电平 触发
脉冲 触发
集成单稳态触发器74121的功能表
输入
A1
A2
B
0
X
1
X
0
1
X
X
0
1
1
X
1
1
1
1
1
0
脉冲波形的产生

梯形脉冲具有抗干扰能力强、传输距离远等优点,适用于长距离通信和高速数据传 输。
THANKS
感谢观看
04
脉冲波形的产生方法
数字方法产生脉冲波形
脉冲宽度调制(PWM)
通过数字方式设定脉冲的宽度,以调节输出 电压或电流的大小。
相位调制(PM)
通过数字方式改变脉冲的相位,实现信号的 合成与解调。
频率调制(FM)
通过数字方式改变脉冲的频率,以实现不同 的控制效果。
脉位调制(PPM)
通过数字方式改变脉冲的位序,实现多路信 号的编码与解码。
脉冲。
三角脉冲的宽度和幅度可以通过 调节电路中的电阻、电容等元件
来改变。梯形脉冲的产生源自梯形脉冲是一种常见的脉冲波形,其特点 是脉冲的幅度从零开始逐渐上升到最大值 ,然后保持不变,最后逐渐下降到零。
梯形脉冲的宽度和幅度可以通过调节 电路中的电阻、电容等元件来改变。
梯形脉冲可以通过数字逻辑门电路或施密 特触发器产生,当数字逻辑门电路的输入 信号发生变化时,就会产生梯形脉冲。
01
02
03
三角脉冲是一种介于矩 形脉冲和正弦波之间的 波形,具有对称的波形
曲线。
三角脉冲在信号处理中 常被用作滤波器、信号 发生器等设备的输入信
号。
通过调整三角脉冲的频 率和幅度,可以生成不 同特性的信号,用于信 号的调制、解调和滤波
等操作。
梯形脉冲在通信系统中的应用
梯形脉冲具有对称的上升沿和下降沿,能够快速地切换信号状态。
05
脉冲波形的应用实例
矩形脉冲在电机控制中的应用
01
矩形脉冲具有高电平与低电平之间切换的特性,适用于电机控 制中的开关信号。
202X年数电-07-脉冲波形的变换与产生

※ 11
1 vO 1
vO
vI
0
G1 ≥1
00
≥1 G2
vO1
- + vI2Vth
vI
VDD
vI2
vO由1变0vO1=1(注意(zhù yì):
∵此时vI的正脉冲已撤消)
VTH
VDD+VTH VDD+Δ+
电容电压不能突变(tūbiàn)vC=Vth
vO
vI2上升到VDD+Vth
暂态过程结束
v如果G2是CMOS门,由于保护二极管的钳位作用 vI2只能(zhī nénɡ)上升到VDD+Δ+
预备知识:
TTL与非门
1、门坎(ménkǎn)电平(阈值电压):VTH
TTL与非门或反相器的电压传输(chuán shū)特性为:
输出低电平(逻辑0) ——与非门开通 输出高电平(逻辑1) ——与非门关闭
开门电平VON:使与非门开通的输入高电平的最小值。 关门电平VOFF:使与非门关闭的输入低电平的最大值。
(4)用TTL与非门组成微分型单稳态触发器,考虑到输入(shūrù)电流,
则应R <Roff,而Rd >Ron。CMOS门组成的单稳态触发器中R、
Rd 不受此限制。
第十七页,共九十二页。
※ 16
二、 积分(jīfēn)型单稳态触发器
两个与非门+RC积分电路 工作(gōngzuò)原理:
1 vO1 R
输出宽脉冲。
第十四页,共九十二页。
VDD+VTH VDD+Δ+
※ 13
3、主要参数计算(jìsuàn):
vO
vO
1
பைடு நூலகம்
脉冲波形的产生与变换

脉冲波形的产生与变换脉冲信号是数字电路中最常用的工作信号。
脉冲信号的获得经常采用两种方法:一是利用振荡电路直接产生所需的矩形脉冲。
这一类电路称为多谐振荡电路或多谐振荡器;二是利用整形电路,将已有的脉冲信号变换为所需要的矩形脉冲。
这一类电路包括单稳态触发器和施密特触发器。
这些脉冲单元电路可以由集成逻辑门构成,也可以用集成定时器构成。
下面先来介绍由集成门构成的脉冲信号产生和整形电路。
9.1 多谐振荡器自激多谐振荡器是在接通电源以后,不需外加输入信号,就能自动地产生矩形脉冲波。
由于矩形波中除基波外,还含有丰富的高次谐波,所以习惯上又把矩形波振荡器叫做多谐振荡器。
多谐振荡器通常由门电路和基本的RC电路组成。
多谐振荡器一旦振荡起来后,电路没有稳态,只有两个暂稳态,它们在作交替变化,输出矩形波脉冲信号,因此它又被称作无稳态电路。
9.1.1门电路组成的多谐振荡器多谐振荡器常由TTL门电路和CMOS门电路组成。
由于TTL门电路的速度比CMOS门电路的速度快, 故TTL门电路适用于构成频率较高的多谐振荡器,而CMOS门电路适用于构成频率较低的多谐振荡器。
(1)由TTL门电路组成的多谐振荡器由TTL门电路组成的多谐振荡器有两种形式:一是由奇数个非门组成的简单环形多谐振荡器;二是由非门和RC延迟电路组成的改进环形多谐振荡器。
①简单环形多谐振荡器uo(a) (b)图9-1 由非门构成的简单环形多谐振荡器把奇数个非门首尾相接成环状,就组成了简单环形多谐振荡器。
图9-1(a)为由三个非门构成的多谐振荡器。
若uo的某个随机状态为高电平,经过三级倒相后,uo跳转为低电平,考虑到传输门电路的平均延迟时间tpd,uo输出信号的周期为6tpd。
图9-1(b)为各点波形图。
简单环形多谐振荡器的振荡周期取决于tpd,此值较小且不可调,所以,产生的脉冲信号频率较高且无法控制,因而没有实用价值。
改进方法是通过附加一个RC延迟电路,不仅可以降低振荡频率,并能通过参数 R、C控制振荡频率。
《电子技术基础与技能》(张金华主编)习题答案
《电子技术基础与技能》(主编:张金华)各章复习与考工模拟题答案第1章 二极管及其应用一、判断题 1.√ 2.× 3.× 4.× 5.√ 6.√二、选择题 1.B 2.D 3.C 4.C 5.A三、综合题1.U AB =0 U AB =6V 2.3.亮 亮 4.(1)桥式整流 电容滤波 (2(3)U L =0.9U 2 (4)U L =1.2U 2L第2章 三极管及放大电路基础 一、判断题 1.√ 2.× 3.×二、选择题 1.C 2.A 3.C三、填空题1.正偏电压 反偏电压 2.各电极电流 极间电压 3.高 低 略小于1 4.20dB 四、综合题 1.2.3.(a )饱和失真 一般调节偏置电阻R b ,使其阻值减小。
(b )截止失真 一般调节偏置电阻R b ,使其阻值增大。
(c )饱和与截止失真 减小输入信号的幅度或更换三极管。
第三章 常用放大器 一、判断题 1.√ 2.× 3.× 4.× 5.×二、选择题 1.C 2.A1.01mA β=100 5mA β=50 u 0u iu 0 u i R 1 R 3 R 4VT 1 VT 2+ +- -3.B4.C5.D6.B三、综合题1.u0=8(u I2-u I1)2.t2.×3.×4.5.×二、填空题1.负载输出2.78××79××输出为正12V的集成稳压器输出为负12V的集成稳压器3.(U Z=14V)14 15 14 4 10三、综合题为了保证稳压管的正常工作,在稳压管电路中必须串联一个电阻来限制电流的大小,只有在R取值合适时,稳压管才能安全地工作在稳压状态。
其稳压过程:U I升高或R L变大→U0升高→I Z变大→I R变大→U R变大→U0减小,使输出电压U0稳定;当U I降低或R L变小,同理分析输出电压U0也能基本保持稳定。
脉冲波形的产生与整形详解

④CMOS型555在传输过渡时间里产生的尖 峰电流小,仅为2~3mA;而双极型555的尖峰电 流高达300~400mA。 ⑤CMOS型555的输人阻抗比双极型的要高 出几个数量级,高达1010Ω。 ⑥CMOS型555的驱动能力差,输出电流仅 为1~3mA,而双极型的输出驱动电流可达200mA.
一般说来,在要求定时长、功耗小、负载轻的场 合宜选用CMOS型555;而在负载重、要求驱动电流 大、电压高的场合,宜选用双极型的555。
二、用门电路组成的施密特触发器
将两级反相器串接起来,同时通过分压电阻把输出端的 电压反馈到输入端,就构成了施密特触发器电路。 CMOS门,阈值电压
1 VTH VDD,且R1 R2 2
R2
vI
R1
1
v O1
1 G2
vO
' vO
v 'I
G1
6.3.3 用CMOS反相器构成的施密特触发器
6.3.4 图6.3.3电路的电压传输特性 (a)同相输出 (b)反相输出
单稳态触发器
单稳态触发器的工作特性具有如下的显著特点: (1)电路在无外加触发信号作用期间,处于稳态; (2)在外界触发脉冲作用下,能从稳态翻转到暂稳 态,在暂稳态维持一段时间以后,再自动返回 稳态; (3)暂稳态维持时间的长短取决于电路本身的参数 (阈值电压及外接R、C),与触发脉冲的宽度和 幅度无关。
§6.3
施密特触发器
Schmitt Trigger
施密特触发器(电路)是一种特殊的双稳态时序 电路,与一般双稳态电路比较,它具有两个明显的特点: 1.施密特触发器是一种优良的波形整形电路, 只要输入信号电平达到触发电平,输出信号就会从一 个稳态转变到另一个稳态,且通过电路内部的正反馈 过程可使输出电压的波形变得很陡。 2.对正向和负向增长的输入信号,电路有不同 的阈值电平,这是施密特触发器的滞后特性或回差特 性,提高了干扰能力,可有效滤除噪声。
第10章 脉冲波形

uO的下降沿比uI的下降沿延迟了tw的时间。
数字电子技术
单稳态触发器小结
单稳态触发器可以由门电路构成,也可以由 555定时器构成。在单稳态触发器中,由一个暂稳 态过渡到稳态,其“触发”信号也是由电路内部 电容充(放)电提供的,暂稳态的持续时间即脉 冲宽度也由电路的阻容元件决定。
单稳态触发器不能自动地产生矩形脉冲,但 却可以把其它形状的信号变换成为矩形波,用途 很广。
对称式 多谐振荡器
数字电子技术
二、工作原理
假定接通电源后,由于某种原因使uI1有微小正跳变,则 必然会引起如下的正反馈过程 :
使uO1迅速跳变为低电平、uO2迅速跳变为高电平, 电路进入第一暂稳态。 此后,uO2的高电平对C1电容充电使uI2升高,电容 C2放电使uI1降低。由于充电时间常数小于放电时间常数, 所以充电速度较快,uI2首先上升到G2的阈值电压UTH, 并引起如下的正反馈过程:
为数字—模拟混合集成电路。 可产生精确的时间延迟和振荡,内部有 3 个 5KΩ的电阻分压器,故称555。
在波形的产生与变换、测量与控制、家用电
器、电子玩具等许多领域中都得到了应用。
数字电子技术
各公司生产的 555 定时器的逻辑功能与外引线 排列都完全相同。
双极型产品 单555型号的最后几位数码 双555型号的最后几位数码 优点 电源电压工作范围 负载电流 555 556 驱动能力较大 5~16V 可达200mA CMOS产品 7555 7556 低功耗、高输入阻抗 3~18V 可达4mA
数字电子技术
10.4 多谐振荡器
1. 多谐振荡器没有稳定状态,只有两个暂稳态。 • 通过电容的充电和放电,使两个暂稳态相互交替, 从而产生自激振荡。 • 输出周期性的矩形脉冲信号,由于含有丰富的谐 波分量,故称作多谐振荡器。
数电第十篇-脉冲波形的产生与整形

03
锯齿波的线性整形
通过调整锯齿波的斜率, 使其线性化,从而改善脉 冲的形状。
锯齿波的幅度整形
通过改变锯齿波的幅度, 可以调整脉冲的宽度和高 度,实现脉冲的整形。
锯齿波的对称整形
通过调整锯齿波的上升沿 和下降沿,使其对称,从 而改善脉冲的形状。
三角波的整形
01
三角波的对称整形
时间测量
01
利用脉冲波形产生与整形技术,测量系统可以精确测量时间间
隔、速度和加速度等参数。
频率和周期测量
02
通过脉冲波形产生与整形技术,测量系统能够实现高精度的频
率和周期测量。
距离和位移测量
03
利用脉冲波形产生与整形技术,测量系统能够实现非接触式距
离和位移测量。
在控制系统中的应用
伺服电机控制
脉冲波形产生与整形技术 用于控制伺服电机的运动, 实现精确的位置和速度控 制。
三角波的产生
一种常见的脉冲波形,其形状类似于三角形,具有对 称性。
输入 标题
差分电路
利用差分电路可以产生三角波。差分电路将输入的矩 形脉冲进行差分运算,形成三角波。
三角波
波形发生器
通过模拟电路(如运算放大器等)也可以产生三角波。 模拟电路将输入信号进行线性放大或缩小,形成三角
波波形。
模拟电路
波形发生器(如函数发生器)也可以产生三角波。波 形发生器内部通常包含差分电路,将输入信号进行差 分运算,形成三角波波形。
02
脉冲波形的整形
矩形脉冲的整形
矩形脉冲的对称整形
通过调整矩形脉冲的上升沿和下降沿, 使其对称,从而改善脉冲的形状。
矩形脉冲的幅度整形
矩形脉冲的延迟整形
通过引入适当的延迟,可以调整矩形 脉冲的起始时间和持续时间,实现脉 冲的整形。
脉冲的产生与波形

要点二
详细描述
脉冲宽度定义为高电平持续的时间,通常以时间单位(如 秒、毫秒等)表示。在数字电路中,脉冲宽度是一个关键 参数,因为它决定了信号的逻辑状态和传输速率。较窄的 脉冲宽度可能导致信号的逻辑状态不稳定,而较宽的脉冲 宽度则可能使信号在传输过程中发生畸变。因此,选择合 适的脉冲宽度对于确保信号的正确传输和识别至关重要。
脉冲幅度
总结词
脉冲幅度是衡量脉冲电压或电流高低的标准,它决定了信号的能量和强度。
详细描述
脉冲幅度定义为脉冲的最大电压或电流值,通常以伏特或安培表示。在电子设备和系统中,脉冲幅度对于信号的 传输质量和系统性能具有重要影响。较大的脉冲幅度意味着更高的能量和更强的信号,但同时也可能导致信号失 真和干扰。因此,选择合适的脉冲幅度需要根据具体的应用需求和系统限制进行权衡。
电子脉冲
电子脉冲是由电子设备产生的。当电子设备中的电路状态发生变化时,会产生电 流的突然变化,形成脉冲。
电子脉冲通常用于控制和驱动各种电子设备,如计算机、电视、音响等。它们在 通信、数据处理、控制系统中也有广泛应用,如数字信号传输、开关电源控制等 。
03
脉冲的波形
矩形波
矩形波是一种常见的脉冲波形, 其特点是具有明确的上升沿和 下降沿,以及相对平坦的顶部 和底部。
脉冲频率
总结词
脉冲频率是衡量单位时间内脉冲数量的参数 ,它决定了信号的速度和动态特性。
详细描述
脉冲频率定义为单位时间内脉冲重复的次数, 通常以赫兹(Hz)表示。在通信和控制系统 等应用中,脉冲频率是关键参数之一。较高 的脉冲频率意味着更快的传输速度和更高的 响应能力,但同时也可能增加信号的噪声和 干扰。因此,选择合适的脉冲频率需要根据 实际应用的需求和限制进行优化。
10第一节 几种常用的脉冲波形的产生和整形电路

0 ×
× 0 上页
25
下页
返回
第一节 几种常用的脉冲波形的产生和整形电路
集成单稳态触发器74121的外部连接方法
Cext
Rext VCC
Cext
VCC
10 11 9 14 C ext R ext R intVCC C ext
10 11 9 14 C ext R ext R intVCC C ext 3 A 1 4 A 2 5
vO1
上页
17
下页
返回
第一节 几种常用的脉冲波形的产生和整形电路
2. 工作原理
Cd v d G1
VDD R
vO1 C vI2
G2
vO
vI Rd
微分型单稳态触发器
如果这时触发脉冲已消失( vd已回到低电平),则 vO1 、vI2迅速跳变为高电平,并使输出返回vO=0的 状态。 同时,电容C通过电阻R和门G2的输入保护电路向 VDD放电,直至电容上的电压为0,电路恢复到稳定 状态。
不需要外加触发信号,便能自动产生矩形脉冲, 由于矩形脉冲中含有丰富的高次谐波分量, 所以习惯上把矩形波振荡器叫做多谐振荡器。
上页
27
下页
返回
第一节 几种常用的脉冲波形的产生和整形电路
对称式多谐振荡器
vI1
C2
G1 vO1
C1 RF1
vI2 G2
RF2
vO
假定由于某种原因使vI1 有微小的正跳变,则必然 会引起如下的正反馈过程
可通过施密特触发器整形获得比较理想的矩形脉冲波形。
3. 用于脉冲鉴幅
施密特触发器能将幅度大于VT+的脉冲选出,具有脉冲鉴幅能力。 4. 构成多谐振荡器
脉冲波形的产生与变换

02
脉冲波形的产生
矩形脉冲的产生
矩形脉冲:通过将电压快速地加到高 电平然后减到低电平,再重复这个过 程,可以产生矩形脉冲。
矩形脉冲的宽度和高度可以通过改变 电压的上升和下降速度以及高低电平 的电压值来调整。
三角脉冲的产生
三角脉冲:三角脉冲可以通过比较器电路产生,当输入信号大于某个阈值时,比 较器输出高电平,否则输出低电平。
脉冲波形产生与变换技术的实际应用
为了更好地发挥脉冲波形产生与变换技术的优势,未来研究可以加强该技术在各领域的实 际应用研究。通过与产业界的合作,推动脉冲波形产生与变换技术的成果转化,为经济发 展和产业升级提供技术支持。
感谢您的观看
THANKS
压力传感器
通过检测压力变化产生的 脉冲波形,实现对压力的 测量。
温度传感器
利用热敏元件产生的脉冲 波形,实现对温度的测量。
在医学领域的应用
超声成像
利用超声波产生的脉冲波形,通 过接收反射回的脉冲信号进行成
像。
核磁共振成像
通过施加脉冲磁场和射频脉冲, 获取组织中的氢原子核磁矩信息,
重建图像。
脉冲激光治疗
目的和意义
随着科技的发展,脉冲波形在各个领 域的应用越来越广泛,对脉冲波形产 生与变换的研究具有重要的实际意义。
此外,脉冲波形的产生与变换也是信 号处理领域的重要研究方向之一,对 于推动相关领域的发展具有重要意义。
研究脉冲波形的产生与变换,有助于 深入了解信号的特性和传播规律,为 信号处理、通信系统设计等领域提供 理论支持和技术指导。
够将输入的脉冲波形进行变换,得到所需的输出波形。实验结果表明,
该算法具有快速、准确和稳定的特点。
03
脉冲波形在各领域的应用
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
10.4.3环形振荡器
利用闭合回路中的正反馈作用可以产生自激振荡,其实只 要负反馈足够强,利用闭合回路中的延迟负反馈作用也能 产生自激振荡。
图10.4.10 最简单的环形振荡器
不难看出,这个电路是没有稳态的。因为在静态(假定没有 振荡)时任何一个反相器的输入和输出都不可能稳定在高电平 或低电平,而只能处于高、低电平之间,即处于放大状态。
VC(0)=VOH,VC(∞)=VOL, =(R+RO)C
VC(t)=VC ()- [VC( ) -VC (0)]e-t/
VC(tw)=VTH=VOL-(VOL-VOH) e-t/
tW
(
R
RO
)C
ln
VOL VOL
VOH VTH
输出脉冲幅度:Vm=VOH-VOL 图10.3.7 图10.3.5电路中电容C的放电回路和vA的波形
C充电 Vi2
VO
Vi1
VO1
结果使G1迅速截止,G2很快导通,电路回到稳态。 VO1=1,VO=0
假设输入波形已知,根据以上的分析可画出图10.3.1电路 中各点的电压波形,如下:
为了定量描述单稳态触发器 的性能,经常使用输出脉冲 宽度tW 、输出脉冲幅度VM、 恢复时间tre和分辨时间td等 参数。
10.4.1对称式多谐振荡器
1.电路组成及工作原理
RF取值 0.5~1.9K
图10.4.1 对称式多谐振荡 图10.4.2 TTL反相器
器电路
(7404)的电压传输特性
图10.4.1 对称式多谐 振荡器电路
图10.4.5 图10.4.1电路中各点电 压的波形
在 RF1= RF2= RF、C1= C2=C的条件下,电路 的振荡周期为:
门G1~G4组成的输入控制电路用于实现上升沿触发或下降沿触 发的控制。
输入
输出
电路处于 稳定状态
A1
A2
0
X
X
0
X
X
B
vO
vO’
1
0
1
1
0
1
0
0
1
1
1
X
0
1
电路由下 降沿触发
1
↓
1
↓
1
1
电路由 上升沿 触发
↓
↓
1
0
X
↑
X
0
↑
表10.3.1 集成单稳态触发器74121的功能
图10.3.10 集成单稳态触发器74121的 工作波形图
假定电路中CMOS反相器的阈值电压Vth=VDD/2,R1<R2,输入信 号VI为三角波,分析工作过程:
根据叠加原 理可写出:
Vi1=
R2
R1+R2
VI + R1 V0 R1+R2
*10.2.2 集成施密特触发器
由于施密特触发器的应用非常广泛,所以无论是在TTL电路 中还是在MOS电路中,都有单片集成的施密特触发器产品。
图10.4.11 图6.4.10电路的工作波形图 振荡周期为: T=6tpd
基于上述原理可知,将任何大于、等于3的奇数个 反相器首尾相连接成环形电路,都能产生自激振荡, 而且振荡周期为:T=2ntpd
用这种方法构成的振荡器虽然很简单,但不实用。 因为门电路的传输延迟时间极短,TTL电路只有几 十纳秒,CMOS电路也只有一二百纳秒,所以想获 得稍低一些的振荡频率很困难,而且频率不易调节。
为了保证VO1为低电平时VA在VTH 以下,R的阻值不能取得太大。
稳态时,由于VI=0,所以 VO=VOH,VA=VO1=VOH。
当输入正脉冲以后,VO1跳变为 低电平,但由于电容C上的电压 不能突变,所以在一段时间里VA 仍在VTH以上。G2两个输入为1, 使vO跳变为0,电路进入暂态。
暂稳时间tW为从电容开始放电到VA下降至VTH所需的时间。 所以有:
图10.3.2 图10.3.1电路的电压波形图
二、积分型单稳态触发器
电路进入暂态后,电容C开始放 电,VA电位开始下降,当下降到 VTH时,VO回到高电平。待VI返 回低电平以后,VO1又重新变成 高电平,并向C充电,VA恢复为 高电平,电路回到稳态。
该电路是用TTL与非门和反相
器以及RC积分电路组成的。
图中RP为CMOS电路的保护电阻
图10.4.6 非对称式多谐振荡器电路
由于RF跨接在G1的输入和输出之间,又CMOS电路输入
电流在正常的输入高、低电平范围内几乎等于零,所以RF
上没有压降, G1必然工作在vo1=vI1状态。因此,表示vo1=vI1
的直线与电压传输特性的交点就是G1的静态工作点,如图
图10.2.3 带与非功能的TTL集成施密特触发器—7413 因为在电路的输入部分附加了与的逻辑功能,同时
输出端附加了反相器,所以它也叫施密特触发的与非 门,集成电路手册中将其归入与非门类。
图10.2.4 集成施密特触发器7413的 电压传输特性
图10.2.5 CMOS集成施密特触发器 CC40106
输出脉冲宽度: tW=RextCextln2=0.69RextCext
通常Rext的取值在2~30K之间,Cext的取值在10pF~10µF 之间,得到tW可达20ns~200ms。内置电阻Rint=2K 。
图10.3.11 集成单稳态触发器74121的外部连接方 法(a)使用外接电阻Rext (下降沿触发)
V0 VOH
(1) 属于电平触发,当输入信号达到某一定 电压值时,输出电压会发生突变;
(2)输入信号增加和减少时,电路有不同
的v阈i1 值电压。
0
VT- VT+
利用这两个特点不仅能将边沿变化缓慢 VI 的信号波形整形为边沿陡峭的矩形波,而
电压传输特性
且可以将叠加在脉冲信号高低电平上的噪
10.2.1门电路组成的施声密有特效触地发清器除。
图10.4.12 带RC延迟电路的环形振荡器
(a)原理性电路(b)实用的改进电路
10.4.4 用施密特触发器构成的多谐振荡器
施密特触发器的电压传输特性有一个滞回区。由此可以设想, 若能使它的输入电压在VT+和VT-之间不停的往复变化,那么在它 的输出端就可以得到矩形脉冲,即实现了多谐振荡的功能。
实现上述设想的方法,只需在施密特触发器的反相输出端经 RC积分电路接回输入端即可,如图10.4.15所示。
10.4.7所示。
通常CMOS门的VTH=1/2VDD,
这时静态工作点P刚好处在电
压传输特性的中点,即
vo1=vI1=1/2VDD的地方。因为 vO1=vI2,所以这时G2的静态 工作点也在电压传输特性的
中点。
由于流过RF上静态电流基本 等于零,所以对RF阻值没有 严格地限制。 图10.4.7 图10.4.6电路中CMOS反相器静态工作点的确定
图10.2.6 集成施密特触发器CC40106的特性
( a)电压传输特性(b)VDD对VT+、VT-的影响
10.2.3施密特触发器的应用
一、用于波形变换 利用施密特触发器状态转换过程中的正反馈作用,可
以把边沿缓慢的周期性信号变换为边沿很陡的矩形脉 冲信号。
V0 VOH
0 VT- VT+ VI
图10.2.7 用 施密特触发器实 现波形变换
图10.4.15 用施密特触 发器构成的多谐振荡器
占空比q——脉冲宽度与脉
冲周期的比值,即q=tw/T
上升时间tr——脉冲前沿从 0.1VM上升到0.9VM所需要 的时间。
下降时间tf——脉冲后沿从
图10.1.1 描述矩形脉冲特0的性.9时的VM间主下。要降到参0数.1VM所需要
10.2施密特触发器(Schmitt Trigger)
它是脉冲波形变换中经常使用的一种电路具有下述特点:
假定由于某种原因使vi1产生了微小的正跳变,则经过G1的传 输延迟时间tpd之后vi2产生一个幅度更大的负跳变,再经过G2的 传输延迟时间tpd使vi3得到更大的正跳变。可以推想,再经过3 tpd 以后vi1又将跳变为高电平。如此周而复始,就产生了自激振荡。
稳定振荡后,可以假设各门电路的输入、输出电平均为高、 低电平。于是可画出上述自激振荡的工作波形图。
(b)使用内部电阻Rint (上升沿触发)
74121、74221、74LS221都是不可重复触发的单稳态触 发器。74122、74123等是可重复触发的单稳态触发器。
*二、CMOS集成单稳态触发器
10.4多谐振荡器 Astable Multivibrator
多谐振荡器是一种自激振荡电路,该电路在电源接通后,无需 外接触发信号就能产生一定频率和幅值的矩形波或方波。
(a)放电回路 (b) vA的波形
恢复时间是从VO1跳变为高电平后电容C充电至VOH所经过的时 间。若取充电时间常数的3~5倍,则得tre=(3~5)辨时间为:td=tTR+tre 与微分型单稳态触发器相比,积分型单稳态触发器具有抗干 扰能力强的优点。同时这也是这种电路的缺点,因为它不适应 窄脉冲触发。
10.3.2 集成单稳态触发器 一、TTL集成单稳态触发器
微分型单稳 态触发器
输入控 制电路
输出缓冲电路
图10.3.9 集成单稳态触发器74121简化的逻辑图
如果把G5和G6合在一起视为一个具有施密特触发特性的或非门, 则这个电路与前面所讨论的微分型单稳态触发器基本相同。它用
门G4给出的正脉冲触发,暂稳时间由Rext和Cext决定。
(2)当外加触发信号时,电路由稳态翻转到暂态暂
当Vi正跳变来时,在Rd、Cd组成的微分电路输出端得到很窄的 正脉冲,使 G1输出V01由高变为低电平,经电容C耦合,使Vi2 为D低电平,于是G2的输出变为高电平。即,VO1=0,VO=1。 由于G2的输出与G1的输入端相连,这时即使触发信号再变为 低电平,G1输出暂时也不会变回高电平。即,维持暂态。 (3)电容C充电,电路由暂态自动返回稳态 在暂稳期间,电源经G1的导通管及电阻R对电容充电。随着电 容两端的电压的增长,当Vi2上升到G2的阈值电压Vth时,电路 发生下述正反馈过程:
