计算机图形学(简单多边形裁剪算法)
4.6.3 多边形裁剪_计算机图形学教程(第2版)_[共3页]
![4.6.3 多边形裁剪_计算机图形学教程(第2版)_[共3页]](https://img.taocdn.com/s3/m/a0cbdc0749649b6649d74720.png)
153 作为新的P 1P 2线段从算法的第一步重新开始执行。
反之,则以线段P m P 2为新的线段P 1P 2(如图4.83中的线段c )从算法的第一步重新开始执行。
反复执行上述3步,直至找到离P 1点最远的可见点为止。
这个过程确定了距离P 1点最远的可见点。
然后对调该线段的两个端点,以线段P 2P 1为新的P 1P 2线段,重新开始实施该算法过程,就可以确定出距离P 2点最远的可见点。
这样,位于窗口内可见段的两个可见端点就确定了。
从这个算法我们可以看到,整个裁剪过程总是在执行第一步或第二步时结束。
这种结果表明:被裁剪的线段要么完全处于窗口之外而被排除掉;要么能在窗口内得到一个距对应端点最远的可见点,这个可见点可能是原直线段的一个端点,也可能是线段在被不断地中点再分过程中,最终得到的刚好和窗口边框相重的那个中点。
这里要注意的是:在判断中点和窗口边框相重时,一般不需要坐标值一定相等,也不大可能,只要在精度许可的前提下,给出一个误差允许范围即可。
4.6.3 多边形裁剪前面我们讨论了直线段裁剪,多边形裁剪是以直线段裁剪为基础,但又不同于直线段的裁剪。
多边形裁剪要比一条直线段裁剪复杂得多。
图4.84所示为用一个矩形窗口去裁剪多边形将会遇到各种不同情况,其中图4.84(a )所示为一个完整的多边形被裁剪成两个独立的多边形;图4.84(b )所示为一个凹多边形被裁剪成几个小多边形;图4.84(c )所示为多边形G 经矩形窗口裁剪后出现G 1和G 2两个多边形,究竟是G 1还是G 2呢?裁剪多边形要解决两个问题,一是一个完整的封闭多边形经裁剪后一般不再是封闭的,需要用窗口边界适当部分来封闭它;二是矩形窗口的4个角点在裁剪中是否要与其他交点连线。
由于这两个问题使得我们不能简单地应用直线段裁剪方法,而需要去研究适合多边形裁剪特点的算法。
图4.84 多边形裁剪多边形裁剪方法很多,例如逐边裁剪法、双边裁剪法、分区编码裁剪法等,这里仅介绍逐边裁剪法。
weiler-atherton多边形裁剪算法

weiler-atherton多边形裁剪算法weileratherton多边形裁剪算法,又称为weiler-atherton算法,是一种用于对多边形进行裁剪的算法。
它可以被用于计算机图形学中的裁剪任务,如可视化、图像处理和计算机辅助设计等领域。
本文将详细介绍weileratherton多边形裁剪算法的原理、步骤和实现方法。
1. 算法原理:weileratherton多边形裁剪算法是基于边界点的引入和处理的。
该算法将两个多边形相互之间进行裁剪,并生成裁剪结果。
算法使用四个边界点集合,分别为输入多边形的边界点集合(输入多边形顶点经过一系列处理得到),裁剪多边形的外部边界点集合和内部边界点集合,以及裁剪结果的边界点集合。
2. 算法步骤:weileratherton多边形裁剪算法的具体步骤如下:(1) 初始化:创建输入多边形的边界点集合、裁剪多边形的外部边界点集合和内部边界点集合,并将输入多边形的边界点添加至外部边界点集合中。
(2) 遍历输入多边形的每条边:对于输入多边形的每条边,判断其与裁剪多边形的相交情况。
(3) 相交情况处理:若相交情况为内部相交或外部相交,则根据交点生成新的内部边界点,并添加至相应的边界点集合中。
(4) 构造裁剪结果:根据输入多边形的边界点集合和裁剪多边形的内部边界点集合,生成裁剪结果的边界点集合。
(5) 根据边界点集合构造裁剪结果:根据裁剪结果的边界点集合,绘制裁剪结果多边形。
3. 算法实现:weileratherton多边形裁剪算法的实现可以使用编程语言来完成。
一种常用的实现方法是通过遍历输入多边形的每个边,利用线段与裁剪多边形的边界的相交情况判断是否产生交点,并根据交点生成新的边界点。
具体的实现步骤如下:(1) 初始化输入和裁剪多边形的边界点集合。
(2) 遍历输入多边形的每条边,对于每条边,判断其与裁剪多边形的每条边的相交情况。
(3) 根据相交情况,判断是否生成交点,如果有生成交点,则根据交点生成新的边界点,并添加至相应的边界点集合中。
简单多边形裁剪算法

摘 要 :为 了尽量 降低任意 多边形裁剪复杂度,提 出了一种基 于多边形顶点遍历 的简单 多边形裁 剪算 法。该 算法将 多边形
交 点插 入 到裁 剪 多边 形 和 被 裁 减 多边 形 顶 点 矢 量数 组 中 ,通 过 记 录 交 点及 其 前 驱 、 后 继 信 息 ,可 快 速 生 成 结 果 多边 形 。其
2 .C h i n a C e n t r e f o r R e s o u r c e s S a t e l l i t e Da t a a n d Ap p l i c a t i o n , B e i j i n g 1 0 0 0 9 4 , C h i n a ;3 .C h i n a C o a l Te c h n o l o g i e s G r o u p or C p o r a t i o n ,B e i j i n g 1 0 0 0 1 3 , C h i n a ; 4 .B e i j i n g I n s t i t u t e o f A p p l i e d Me t e o r o l o g y , B e i j i n g 1 0 0 0 2 9 , C h i n a )
中,时间复杂度 为 ( ) ( ( m+k ) ×k ) ,m 是两 多边形 中顶点数较 大者 ,k是 两 多边形的 交点数 。该算 法简化 了交点的数据 结 构 ,节省 了存储 空间,降低 了算法的时间复杂度 ,具有 简单 、易于编程 实现 、运行效 率高的特点 。
关 键 词 : 多边 形 裁 剪 ; 交点 ;前 驱 ;后 继 ;矢 量数 组 中图 法 分 类 号 :TP 3 9 1 文 献 标 识 号 :A 文章 编 号 :1 0 0 0 — 7 0 2 4( 2 0 1 4 )0 1 - 0 1 9 2 - 0 6
计算机图形学(简单多边形裁剪算法)

简单多边形裁剪算法摘要:多边形裁剪算法与线性裁剪算法具有更广泛的实用意义,因此它是目前裁剪研究的主要课题。
本文主要介绍了一种基于多边形顶点遍历的简单多边形裁剪算法,它有效降低了任意多边形裁剪复杂度。
通过记录交点及其前驱、后继信息,生成结果多边形,该算法简化了交点的数据结构,节省了存储空间,降低了算法的时间复杂度,具有简单、易于编程实现、运行效率高的特点。
关键词:多边形裁剪;交点;前驱;后继;矢量数组一、技术主题的基本原理简单多边形裁剪算法综合考虑现有多边形裁剪算法的优缺点,它是一种基于多边形顶点遍历来实现简单多边形裁剪工作的。
其主要的原理是遍历多边形并把多边形分解为边界的线段逐段进行裁剪,输出结果多边形。
二、发展研究现状近年来,随着遥感绘图、CAD辅助设计、图象识别处理技术的发展,图形裁剪算法从最初在二维平面上线和图形的裁剪扩展到三维空间里体和场的裁剪,国内外相继提出不少行之有效的算法,但越来越复杂的图形和计算也对算法的速度和适用性提出了越来越高的要求。
因此,不断简化算法的实现过程,完善细节处理,满足大量任意多边形的裁剪也就成了当今算法研究的焦点之一。
以往多边形裁剪算法不是要求剪裁多边形是矩形,就是必须判断多边形顶点的顺时针和逆时针性,即存在不实用或者是增加了多边形裁剪算法的难度。
为了解决现在的问题,我们研究现在的新多边形算法,其中,裁剪多边形和被裁剪多边形都可以是一般多边形,且不需要规定多边形输入方向。
它采用矢量数组结构,只需遍历剪裁多边形和被裁剪多边形顶点即完成多边形的裁剪,具有算法简单、运行效率高的特点。
三、新算法设计1、算法的思想本算法是为了尽量降低任意多边形裁剪算法复杂度而提出的,其主要思想是采用矢量数组结构来遍历裁剪多边形和被裁多边形顶点,记录裁剪多边形和被裁减多边形交点及其前驱、后继信息,并通过记录相邻交点的线段,然后通过射线法选择满足条件的线段,之后进行线段连接,输出对应的裁剪结果。
了解电脑显卡的多边形剪裁和裁剪

了解电脑显卡的多边形剪裁和裁剪随着计算机图形学的不断发展,电脑显卡在图像处理方面的性能也逐渐提升。
而多边形剪裁和裁剪则是电脑显卡中重要的技术之一。
本文将介绍多边形剪裁和裁剪的定义、作用以及相关的算法与技术。
一、多边形剪裁和裁剪的定义多边形剪裁是指根据视口和裁剪窗口的位置,将位于裁剪窗口外的多边形剪除,只保留位于窗口内的部分。
而裁剪是指将多边形按照裁剪窗口的形状进行修剪,以适应显示设备的输出。
二、多边形剪裁的作用多边形剪裁的作用主要有以下几个方面:1. 提高渲染效率:多边形剪裁可以剔除位于屏幕外的多边形,避免不必要的计算和绘制,从而提高渲染效率。
2. 减少像素填充:在3D渲染中,所有多边形都要经过像素填充来生成最终的图像。
通过剪裁掉屏幕外的多边形,可以减少不必要的像素填充操作,提高渲染速度。
3. 实现可视化效果:多边形剪裁可以确保只显示用户所需的图像内容,可以实现视点的选择、物体的隐藏和透视等视觉效果。
三、多边形剪裁的算法与技术在实际应用中,多边形剪裁通常使用的算法包括:1. 逐边裁剪算法(Cohen-Sutherland算法):该算法通过将裁剪窗口划分为9个区域,将多边形的每条边与裁剪窗口的边界相交,并根据交点位置来确定多边形是否可见以及如何修剪多边形。
2. 多边形切割算法(Sutherland-Hodgman算法):该算法通过对多边形的每条边进行切割,生成新的多边形。
这些新的多边形通过裁剪窗口切割并连接,最终得到位于裁剪窗口内的多边形。
四、裁剪的应用和技术裁剪不仅可以应用于多边形,还可以应用于曲线、曲面和体素等图形对象的裁剪。
裁剪的技术也不仅仅局限于多边形剪裁算法,还包括对二维和三维对象的参数化、位图和文本的裁剪处理等。
在实际应用中,常用的裁剪技术包括:1. 区域编码算法:区域编码算法通过给定的区域码来标识物体所在的位置,从而对物体进行裁剪。
常见的算法有四叉树编码和八叉树编码。
2. 软件裁剪和硬件裁剪:软件裁剪是指在计算机的主机CPU上通过算法进行裁剪操作;而硬件裁剪则是指使用专门的图形处理器(GPU)来完成裁剪操作,通过并行计算提高裁剪效率。
多边形裁剪算法

Cohen-Sutherland 直线裁剪算法小结
• 本算法的优点在于简单,易于实现。可以简单 的描述为将直线在窗口左边的部分删去,按左, 右,下,上的顺序依次进行,处理之后,剩余 部分就是可见的了。在这个算法中求交点是很 重要的,决定了算法的速度。另外,本算法对 于其它形状的窗口未必同样有效。
• 特点:用编码方法可快速判断线段的完全可见 和显然不可见。
• 为快速判断,采用如下编码方法:
Cohen-Sutherland裁剪
实现方法:
1001
1000 1010 A
C
0001 0101 0000 0100
ቤተ መጻሕፍቲ ባይዱ
0010
0110
D B
将窗口边线两边沿长,得到九个区域,每一个区 域都用一个四位二进制数标识,直线的端点都 按其所处区域赋予相应的区域码,用来标识出 端点相对于裁剪矩形边界的位置。
直接求交算法
直线与窗口边都 写成参数形式, 求参数值。
Cohen-Sutherland裁剪
• 基本思想:
对于每条线段P1P2分为三种情况处理: (1)若P1P2完全在窗口内,则显示该线段P1P2。 (2)若P1P2明显在窗口外,则丢弃该线段。 (3)若线段不满足(1)或(2)的条件,则在交点 处把线段分为两段。其中一段完全在窗口外,可弃 之。然后对另一段重复上述处理。
梁友栋-Barsky算法
线段的参数表示
x=x0+t△x
y=y0+t△y △x=x1-x0 0<=t<=1 △y=y1-y0
P0 A
Pm B P1
中点分割裁剪算法
中点分割裁剪算法
• 对分辩率为2N*2N的显示器,上述二分过 程至多进行N次。 • 主要过程只用到加法和除法运算,适合 硬件实现,它可以用左右移位来代替乘 除法,这样就大大加快了速度。
计算机图形学多边形裁剪

}
}
s=p;
}
}
bool CPaintView::inside(CPoint testvertex,CPoint* clipboundary)
{
if(clipboundary[1].x<clipboundary[0].x)
{
p=invertexlist[j];//p为当前要处理的顶点,前面已处理过的顶点为s
if(inside(p,clipboundary))//若p在裁剪边clipboundary的内侧,则inside()返回值为真
{ if(inside(s,clipboundary))//如果s在裁剪边clipboundary的内侧,则inside()返回值为真
if(testvertex.y >=clipboundary[0].y)
return true;
if(clipboundary[1].x>clipboundary[0].x)
if(testvertex.y<=clipboundary[0].y)
return true;
outvertexlist.insert(outvertexlist.begin( )+(*outlength),outvertex);
(*outlength)++;
}
void CPaintView::intersect(CPoint p1,CPoint p2,CPoint *clipboundary,CPoint *intersectpt)
{
if(clipboundary[0].y==clipboundary[1].y)
计算机图形学课程设计 多边形的裁剪算法

河南理工大学万方科技学院课程设计报告2010 — 2011学年第二学期课程名称计算机图形学设计题目多边形裁剪算法学生姓名孙晓芳学号**********专业班级计算机科学与技术10升指导教师侯守明2011 年6 月29 日目录目录目录 (I)第1章程序运行环境................................................................................... 错误!未定义书签。
1.1 程序运行环境的简单介绍................................................................. 错误!未定义书签。
1.2 程序运行环境的安装......................................................................... 错误!未定义书签。
1.3 多边形裁剪算法设计的内容........................................................................... 第2章直线裁剪和多边形裁剪的简单比较 (4)2.1 直线裁剪的介绍 (4)2.1.1 直线裁剪的基本原理………………………………………......................................2.1.2 直线裁剪算法的分类以及和窗口交点参数值的计算……………………………..2.2 多边形裁剪介绍 (9)2.2.1 多边形裁剪的基本思想……………………………………………………………..2.2.2 多边形和窗口相交的判定方法…………………………………………..第3章多边形裁剪方法的详细介绍 (12)3.1 Sutherland-Hodgman算法………………………………………………………………….3.2 多边形裁剪算法的流程图 (12)3.3多边形裁剪算法的实现 (13)第4章代码的实现 (14)第5章总结 (21)参考文献 (22)第1章程序的运行环境1.1 程序运行环境的简单介绍本次设计主要是运用了程序设计语言主要以C/C++语言为主,开发平台为Visual C++。
多边形裁剪

多边形裁剪刘世光天津大学计算机学院天津大学计算机科学与技术学院主要内容•多边形裁剪Sutherland Hodgman多边形裁剪算法;Weiler Sutherland-Hodgman;Weiler-Atherton算法;•曲线裁剪、字符裁剪曲线裁剪字符裁剪天津大学计算机科学与技术学院多边形裁剪与线段裁剪•使用线段裁剪进行多边形裁剪,则裁剪后的边使用线段裁剪进行多边形裁剪则裁剪后的边界将显示为一系列不连接的线段,没有关于如何形成裁剪后的封闭多边形的完整信息何形成裁剪后的封闭多边形的完整信息。
天津大学计算机科学与技术学院多边形裁剪•新的问题:–边界不再封闭–产生多个部分天津大学计算机科学与技术学院多边形裁剪天津大学计算机科学与技术学院Sutherland-Hodgman算法•Sutherland和Hodgman提出的裁剪凸多边形由S therland填充区的高效算法。
•其总体策略是顺序地将每一线段的一对顶点送给一组裁剪器(左、右、下、上)。
一个裁剪器完成一对顶点的处理后,该边裁剪后留下的坐标值送给下一个裁剪器。
天津大学计算机科学与技术学院•用裁剪边界对多边形的边裁剪时的四种情况:外内输出'12,V V 内内输出2V 内外输出'1V 外外输出: 无天津大学计算机科学与技术学院:实现步骤输入边:左裁剪右裁剪下裁剪上裁剪天津大学计算机科学与技术学院Sutherland-Hodgmang算法小结:•:–逐边裁剪:两次分解•第一次分解:将多边形关于矩形窗口的裁剪分解第次分解将多边形关于矩形窗口的裁剪分解为它关于窗口四条边所在直线的裁剪;•第二次分解:将多边形关于一条直线的裁剪分解第二次分解将多边形关于条直线的裁剪分解为多边形各边关于该直线的裁剪。
天津大学计算机科学与技术学院:举例天津大学计算机科学与技术学院:其他例子天津大学计算机科学与技术学院Sutherland-Hodgman算法g–推广•关于任意凸多边形窗口的裁剪天津大学计算机科学与技术学院练习:天津大学计算机科学与技术学院Sutherland-Hodgman算法•算法的不足之处:算法的不足之处裁剪凹多边形时,可能显示一条多余的直线,原因是该算法只有一个输出顶点队列。
多边形裁剪的Sutherland—Hodgman算法(计算机图形学)

多边形裁剪的Sutherland—Hodgman算法1>. Sutherland—Hodgman多边形裁剪算法思想该算法的基本思想是每次用窗口的一条边界及其延长线来裁剪多边形的各边。
多边形通常由它的顶点序列来表示,经过裁剪规则针对某条边界裁剪后,结果形成新的顶点序列,又留待下条边界进行裁剪,…,直到窗口的所有边界都裁剪完毕,算法形成最后的顶点序列,才是结果多边形(它可能构成一个或多个多边形)。
当多边形一个顶点Pi相对于窗口某条边界及其延长线进行剪裁时,不外乎下列四种情况(即裁剪规则):1、顶点Pi在内侧,前一顶点Pi-1也在内侧,则将Pi纳入新的顶点序列;2、顶点Pi在内侧,前一顶点Pi-1在外侧,则先求交点Q,再将Q、Pi依次纳入新的顶点序列;3、顶点Pi在外侧,前一顶点Pi-1在内侧,则先求交点Q,再将Q纳入新的顶点序列;4、顶点Pi与前一顶点Pi-1均在外侧,则顶点序列中不增加新的顶点。
2>. Sutherland—Hodgman多边形裁剪算法步骤考虑多边形相对于一条边界及其延长线进行裁剪的算法:1.从主函数得到待裁剪多边形的顶点序列P[][2]、顶点序列数n、窗口一条边界参数xl(假如为矩形窗口的左边界);2.赋初值:将顶点序列中的最后一个顶点赋给前一顶点S;设置初始标志flag:if(S在边界内侧)flag=0;else flag=1;设新的顶点序列数j=0;3.对多边形各顶点进行裁剪规则处理,结果放入新的多边形顶点序列Q[][2]中:for(对第一个顶点直到最后一个顶点,逐一处理){if(Pi在边界内侧){if(flag!=0){flag=0;求交点并放入新的多边形顶点序列Qj中;j++;}将当前顶点放入新的多边形顶点序列Qj中:Qj=Pi;j++;}else{if(flag==0){flag=1;求交点并放入新的多边形顶点序列Qj中;j++;}}将当前顶点赋给S:S=Pi;}4.做返回准备:将新的多边形顶点序列Q又逐一放回原多边形顶点序列P中:P=Q;将新的多边形顶点数j放回原多边形顶点数n中:n=j;///////////////////////////////////////////////////////////////////// ///////////////////-----多边形裁剪的Sutherland—Hodgman算法---------/////////////////////////////////////////////////////////////////////// ////////////////void CMyClip_AView::ClipedgeL(CPoint polypoint[], CPoint clipwindow[], UINT polynum)/*其中参数polypoint[]为多边形顶点,clipwindow[]为裁剪窗口顶点,polynum 为多边形顶点数目*/{//找出裁剪窗口边界long xl,xr,yt,yb;UINT i;xl=clipwindow[0].x;xr=clipwindow[0].x;yt=clipwindow[0].y;yb=clipwindow[0].y;for(i=1;i<=4;i++){if(xl>clipwindow[i].x)xl=clipwindow[i].x;if(xr<clipwindow[i].x)xr=clipwindow[i].x;if(yb>clipwindow[i].y)yb=clipwindow[i].y;if(yt<clipwindow[i].y)yt=clipwindow[i].y;}//CPoint B[Polygon_Num],C[Polygon_Num];UINT m_nA,m_nB;int x,y;long tem1,tem2;m_nA=polynum;/*记载原始多边形顶点顶点个数*/m_nB=0;/*记载新生成多边形顶点顶点个数*/for(i=0;i<m_nA;i++){if(polypoint[i].x<xl && polypoint[i+1].x<xl) /*判断的多边形边两个端点都在外部,不做处理*/{continue;/*如果是这种情况,那么就对继续对下一条多边形边作判断,也就是说下面的判断不用做了*/}if(polypoint[i].x>=xl && polypoint[i+1].x>=xl) /*边两个端点都在内部,保留*//*因为每个保留的点在数组中只出现一次,且下一次判断时第二个端点一定会要取到,因此只保留的两个点中的第一个*/{B[m_nB].x =polypoint[i].x ;B[m_nB].y =polypoint[i].y ;m_nB=m_nB+1;continue;}if(polypoint[i].x<xl && polypoint[i+1].x>=xl)/*边两个端点起点在外部,终点在内部,求交点,然后交点,终点都应该送入临时数组*/{/*保留交点*/x=xl;tem1=(xl-polypoint[i].x);//tem2=(xl-x1)*dy/dx+y1;//y/x=dy/dx---->y=x*dy/dxtem2=tem1*(polypoint[i+1].y-polypoint[i].y)/(polypoint[i+1].x-polypoint[i].x)+polypoi nt[i].y;y=tem2;B[m_nB].x =x;B[m_nB].y =y;m_nB=m_nB+1;continue;}if(polypoint[i].x>=xl && polypoint[i+1].x<xl)/*起点在内部,终点在外,求交点,然后起点,交点送入临时数组*/{ /*保留内部点*/B[m_nB].x =polypoint[i].x ;B[m_nB].y =polypoint[i].y ;m_nB=m_nB+1;/*保留交点*/tem1=(xl-polypoint[i].x);tem2=tem1*(polypoint[i+1].y-polypoint[i].y)/(polypoint[i+1].x-polypoint[i].x)+polypoi nt[i].y;y=tem2;B[m_nB].x =x;B[m_nB].y =y;m_nB=m_nB+1;continue;}}//把第一个点的数据拷贝到最后//形成裁剪后的多边形if(i==m_nA){B[m_nB]=B[0];}//下------------------m_nA=0;for(i=0;i<m_nB;i++){if(B[i].y<yb && B[i+1].y<yb)//两个点全在下方{continue;//下一条边}if(B[i].y>=yb && B[i+1].y>=yb)//p1,p2都在yb上方{C[m_nA].x =B[i].x;C[m_nA].y =B[i].y;m_nA++;continue;}if(B[i].y<yb && B[i+1].y>=yb)//p1在下,P2在上,留交点,外->内{y=yb;tem1=yb-B[i].y;//tem2=x1+(yb-y1)*dx/dytem2=tem1*(B[i+1].x-B[i].x)/(B[i+1].y-B[i].y) + B[i].x;C[m_nA].x =x;C[m_nA].y =y;m_nA++;continue;}if(B[i].y>=yb && B[i+1].y<yb)//p1在上方,P2在下方,留P1和交点,内-外{//save p1C[m_nA].x=B[i].x;C[m_nA].y=B[i].y;m_nA++;//留交点y=yb;tem1=yb-B[i].y;//tem2=x1+(yb-y1)*dx/dytem2=tem1*(B[i+1].x-B[i].x)/(B[i+1].y-B[i].y)+B[i].x;x=tem2;C[m_nA].x =x;C[m_nA].y =y;m_nA++;continue;}}//形成第二次裁剪多边形if(i==m_nB){C[m_nA]=C[0];}//右------------------m_nB=0;for(i=0;i<m_nA;i++){if(C[i].x>xr && C[i+1].x>xr)//P1,P2都在右方--go next{continue;}if(C[i].x<=xr && C[i+1].x<=xr)//P1,P2都在左方,留P1{B[m_nB].x =C[i].x;B[m_nB].y =C[i].y;m_nB++;continue;}if(C[i].x>xr && C[i+1].x<=xr)//P1在右方,P2在左方,留交点{x=xr;tem1=C[i].x-xr;tem2=C[i].y-tem1*(C[i+1].y-C[i].y)/(C[i+1].x-C[i].x);y=tem2;B[m_nB].x =x;B[m_nB].y =y;m_nB++;continue;}if(C[i].x<=xr && C[i+1].x>xr)//P1在内,P2在外,留P1和交点{//save p1B[m_nB].x =C[i].x;B[m_nB].y =C[i].y;m_nB++;//save 交点x=xr;tem1=C[i].x-xr;tem2=C[i].y-tem1*(C[i+1].y-C[i].y)/(C[i+1].x-C[i].x);y=tem2;B[m_nB].x =x;B[m_nB].y =y;m_nB++;continue;}}//三次裁剪后的新多边形if(i==m_nA){B[m_nB]=B[0];}//上-------------------m_nA=0;for(i=0;i<m_nB;i++){if(B[i].y>yt && B[i+1].y>yt)//p1,p2都在上方,next{continue;}if(B[i].y<=yt && B[i+1].y<=yt)//p1,p2都在下方,留P1{C[m_nA].x =B[i].x;C[m_nA].y =B[i].y;m_nA++;continue;}if(B[i].y>yt && B[i+1].y<=yt)//P1在上方,P2在下方外->内,留交点{y=yt;tem1=B[i].y-yt;//tem2=x1+(yb-y1)*dx/dytem2=B[i].x-tem1*(B[i+1].x-B[i].x)/(B[i+1].y-B[i].y);x=tem2;C[m_nA].x =x;C[m_nA].y =y;m_nA++;continue;}if(B[i].y<=yt && B[i+1].y>yt)//P1在下方,P2在上方,内->外,留P1和交点{//save p1,,,C[m_nA].x =B[i].x;C[m_nA].y =B[i].y;m_nA++;//save 交点y=yt;tem1=B[i].y-yt;//tem2=x1+(yb-y1)*dx/dytem2=B[i].x-tem1*(B[i+1].x-B[i].x)/(B[i+1].y-B[i].y);x=tem2;C[m_nA].x =x;C[m_nA].y =y;m_nA++;continue;}}//形成裁剪后的多边形if(i==m_nB){C[m_nA]=C[0];}CClientDC dc(this);CPen tempen;tempen.CreatePen(PS_SOLID,1,RGB(255,0,0));dc.SelectObject(tempen);dc.MoveTo(C[0]);for(i=1;i<=m_nA;i++){dc.LineTo(C[i]);}}//.....。
计算机图形学裁剪算法

一、实验目标1.了解Cohen-SutherLand线段裁剪算法、Liang-Barsky线段裁剪算法、SutherLand-Hodgeman多边形裁剪算法的基本思想;2.掌握Cohen-SutherLand线段裁剪算法、Liang-Barsky线段裁剪算法、SutherLand-Hodgeman多边形裁剪算法的算法实现;二、实验内容本次实验主要是实现Cohen-SutherLand线段裁剪算法、Liang-Barsky线段裁剪算法、SutherLand-Hodgeman多边形裁剪算法。
Cohen-sutherland线段裁剪算法思想:该算法也称为编码算法,首先对线段的两个端点按所在的区域进行分区编码,根据编码可以迅速地判明全部在窗口内的线段和全部在某边界外侧的线段。
只有不属于这两种情况的线段,才需要求出线段与窗口边界的交点,求出交点后,舍去窗外部分。
对剩余部分,把它作为新的线段看待,又从头开始考虑。
两遍循环之后,就能确定该线段是部分截留下来,还是全部舍弃。
Cohen-sutherland线段裁剪算法步骤:1、分区编码延长裁剪边框将二维平面分成九个区域,每个区域各用一个四位二进制代码标识。
各区代码值如图中所示。
四位二进制代码的编码规则是:(1)第一位置1:区域在左边界外侧(2)第二位置1:区域在右边界外侧(3)第三位置1:区域在下边界外侧(4)第四位置1:区域在上边界外侧裁剪窗口内(包括边界上)的区域,四位二进制代码均为0。
设线段的两个端点为P1(x1,y1)和P2(x2,y2),根据上述规则,可以求出P1和P2所在区域的分区代码C1和C2。
2、判别根据C1和C2的具体值,可以有三种情况:(1)C1=C2=0,表明两端点全在窗口内,因而整个线段也在窗内,应予保留。
(2)C1&C2≠0(两端点代码按位作逻辑乘不为0),即C1和C2至少有某一位同时为1,表明两端点必定处于某一边界的同一外侧,因而整个线段全在窗外,应予舍弃。
多边形裁剪算法

多边形裁剪算法多边形裁剪算法多边形裁剪是用线段对一些形状进行处理的一种常见算法。
它通常用于地图显示、机械加工以及其他基于图形的计算机图形系统中。
裁剪有一个边界框,其中包含可被裁剪的部分,以及无法被裁剪的区域。
多边形裁剪指的是在边界框内裁剪掉不符合要求的部分,只保留符合边界框的多边形。
下面将介绍一种基本的多边形裁剪算法——贝尔格罗夫多边形裁剪算法。
贝尔格罗夫多边形裁剪算法(Brelgorff Polygon Clipping Algorithm)是一种用于生成裁剪多边形轮廓的算法,由荷兰科学家Berlgorff于1890年发明。
它主要用于多边形裁剪。
贝尔格罗夫多边形裁剪算法的思想是:从一个多边形的起点,每次移动到下一个顶点,v,判断是否在裁剪区域内,若在裁剪区域内,则标记当前顶点v为可视边界,否则为不可视边界;然后,从v移动到下一个顶点,只要发现在裁剪区域外的边界,就必须标记下一个顶点为可视边界;最后,当发现多边形完全不在裁剪区域内时,就会将多边形的所有顶点都标记为不可视边界。
贝尔格罗夫多边形裁剪算法的实现方式如下:第一步:设置多边形的顶点序列。
第二步:从多边形的起点开始遍历顶点,检查每个顶点是否在裁剪区域内,将在裁剪区域内的顶点标记为可视边界,将在裁剪区域外的顶点标记为不可视边界。
第三步:对不可视边界进行处理,若两个不可视边界之间有一个可视边界,则以可视边界为结束位置,将不可视边界之间的边加入到多边形的边界框中;若两个不可视边界之间没有可视边界,则以最后一个不可视边界为结束位置,将不可视边界之间的边加入到多边形的边界框中。
第四步:对可视边界进行处理,遍历可视边界,将可视边界添加到多边形的边界框中。
第五步:根据多边形的边界框计算出裁剪后的多边形轮廓,即裁剪后的多边形。
贝尔格罗夫多边形裁剪算法具有以下特点:实现简单,复杂度较低,多边形裁剪时不要求多边形的顶点按边界框顺序排列,且可以处理任意多边形。
贝尔格罗夫多边形裁剪算法是一种常用的多边形裁剪算法,它对图形的显示、机械加工以及其他基于图形的计算机图形系统有着重要的应用。
多边形裁剪算法
y y
yB为始边,y yB为终边,y
yT为终边。 yT为始边。
梁友栋-Barsky算法:交点计算
– 求出P0P1与两条始边的交点
参数t0, t1 , 令tl=max(t0 ,t1,0),
则tl即为三者中离p1最近的
t2
点的参数
– 求出p0p1与两条终边的交点
t0 t1
参数t2, t3, 令tu=min(t2,t3,1) ,
满足下列不等式:
xL <= x <= xR • 并且yB <= y <= yT
否则,P点就在窗口外。
(xL,yB )
• 问题:对于任何多边形窗口, 如何判别?
(xR,yT )
5.6直线段裁剪
• 直线段裁剪算法是复杂图形裁剪的基础。 复杂的曲线可以通过折线段来近似,从 而裁剪问题也可以化为直线段的裁剪问 题。
• 从P1出发找距离P1最近可见点采用上面类似方法。
P0
A
Pm
B P1
中点分割裁剪算法
中点分割裁剪算法
• 对分辩率为2N*2N的显示器,上述二分过 程至多进行N次。
• 主要过程只用到加法和除法运算,适合 硬件实现,它可以用左右移位来代替乘 除法,这样就大大加快了速度。
梁友栋-Barsky算法
设要裁剪的线段是P0P1。 P0P1和 窗口边界交于A,B,C,D四点,见图。 算法的基本思想是从A,B和P0三点中 找出最靠近的P1点,图中要找的点 是P0。从C,D和P1中找出最靠近P0的 点。图中要找的点是C点。那么P0C 就是P0P1线段上的可见部分。
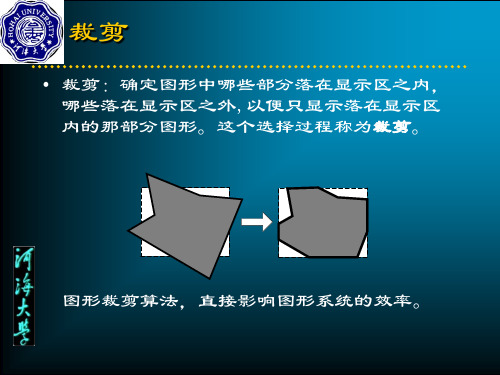
裁剪
• 裁剪:确定图形中哪些部分落在显示区之内, 哪些落在显示区之外,以便只显示落在显示区 内的那部分图形。这个选择过程称为裁剪。
sutherland算法表示方法

sutherland算法表示方法Sutherland算法:计算机图形学的里程碑引言计算机图形学是一门研究如何使用计算机生成和处理图像的学科。
在图形学的发展历史中,Sutherland算法是一个具有重要意义的里程碑。
本文将介绍Sutherland算法的基本原理、应用领域以及对计算机图形学的影响。
一、Sutherland算法的基本原理Sutherland算法,全称为Sutherland-Hodgman算法,是一种用于计算多边形裁剪的算法。
其基本原理是通过对多边形进行逐边裁剪,最终得到裁剪后的多边形。
这个过程可以简单地分为四个步骤:边界框检测、边界相交检测、多边形顶点分类以及多边形边界点的计算。
边界框检测是指通过与裁剪窗口的边界进行比较,确定多边形是否在裁剪窗口内部。
如果多边形完全位于裁剪窗口之外,则可以直接舍弃。
如果多边形与裁剪窗口有交集,则继续进行下一步操作。
接下来,边界相交检测是指确定多边形与裁剪窗口的边是否相交。
如果多边形的边与裁剪窗口的边没有相交,则舍弃该边。
如果有相交,则进行下一步操作。
然后,多边形顶点分类是指根据多边形的顶点与裁剪窗口的边界相对位置,将多边形的顶点分为内部点、外部点和交点。
内部点是指位于裁剪窗口内部的点,外部点是指位于裁剪窗口外部的点,交点是指位于裁剪窗口边界上的点。
根据多边形顶点的分类结果,计算出多边形的边界点。
这些边界点将组成裁剪后的多边形。
二、Sutherland算法的应用领域Sutherland算法在计算机图形学中有广泛的应用。
它可以用于多边形的裁剪,将多边形限制在指定的区域内,从而实现对图像的剪裁和切割。
这在计算机辅助设计(CAD)和计算机游戏中非常有用。
在CAD中,Sutherland算法可以用于对设计图形进行裁剪。
例如,在建筑设计中,可以使用Sutherland算法将建筑物的平面图限制在指定的区域内,以便更好地展示和分析。
在计算机游戏中,Sutherland算法可以用于实现视景裁剪。
图形学中的多边形裁剪与扫描线算法

图形学中的多边形裁剪与扫描线算法一、多边形裁剪与扫描线算法多边形裁剪和扫描算法是计算机图形学中常用的技术,用于处理在屏幕上显示的多边形的裁剪和填充。
裁剪是指将多边形中超出指定区域的部分去除,而扫描算法则是用来填充多边形的内部区域。
这两种算法通常结合使用,以实现对图形的精确裁剪和填充。
二、裁剪算法1. Cohen-Sutherland算法Cohen-Sutherland算法是一种常用的线段裁剪算法,它将平面分成九个部分,并用四位编码来表示线段的位置关系。
当线段与裁剪区域相交时,根据编码判断线段的起点和终点位置,然后将线段裁剪到裁剪区域内。
这样就可以快速有效地进行线段裁剪。
2. Sutherland-Hodgman算法Sutherland-Hodgman算法是用来对多边形进行裁剪的算法,它通过对多边形的每条边进行裁剪,最终得到裁剪后的多边形。
该算法的优势在于可以处理凸多边形和凹多边形,并且可以处理不规则的裁剪区域。
三、扫描线填充算法1.扫描线填充算法的原理扫描线填充算法是一种经典的多边形填充算法,其基本原理是从上到下逐行扫描屏幕,并根据扫描线与多边形边界的交点来确定每个像素点的颜色。
通过这种方法,可以有效地填充多边形的内部区域,并且可以处理复杂的多边形。
2.扫描线算法的实现步骤扫描线填充算法的实现步骤包括扫描线的生成、边界与扫描线的交点计算、交点排序、填充颜色等过程。
在每一行扫描时,通过计算扫描线与多边形的交点,然后对这些交点进行排序,最后通过填充算法来填充多边形的内部。
四、多边形裁剪与扫描算法的应用多边形裁剪与扫描算法在计算机图形学中有着广泛的应用。
例如,在计算机辅助设计(CAD)领域,这些算法被用于对图形进行裁剪和填充,以实现图形的精确显示和编辑。
另外,在计算机游戏开发中,多边形裁剪与扫描算法也被用于实现场景的渲染和光照效果。
五、总结多边形裁剪与扫描算法是计算机图形学中重要的技朧,通过裁剪算法可以实现对图形的剪切和编辑,而扫描算法则可以实现对图形的填充和显示。
计算机图形学-5

e旳交点I 否
(b)
输出I
退出
图(b)
用图(b)中旳算法对最终一条边PnP1作裁剪。裁 剪好一条边便输出一条边。
上述算法仅用一条裁剪边对多边形进行裁剪, 得到一种顶点序列,作为下一条裁剪边处理 过程旳输入。
裁剪成果旳顶点构成:裁剪边内侧旳原
顶点;多边形旳边与裁剪边旳交点。顺
e旳交点I 否
(a)
输出I SP
设封闭多边形旳顶点为 P1,P2,…Pn,框图中e是表达窗 口旳四条边中正在裁剪旳一条边,
每次裁剪时第一种点存储在F中, 以便对最终一条边裁剪时使用。
用图(a)中旳算法对边P1P2,
P2P3, …Pn-1Pn作裁剪。
是 输出S
S在e旳可见侧 否
退出
图(a)
取点F为P
怎样求窗口边界与线段P1P2旳交点?
怎样鉴定线段应该与窗口旳哪条边求交呢?
编码中相应位为1旳窗口边。
计算线段P1(x1,y1)P2(x2,y2)与窗口边界旳交点 Code代表线段某个端点旳编码。 if(LEFT&code !=0)
{ x=XL; y=y1+(y2-y1)*(XL-x1)/(x2-x1);} else if(RIGHT&code !=0) { x=XR; y=y1+(y2-y1)*(XR-x1)/(x2-x1);} else if(BOTTOM&code !=0) { y=YB; x=x1+(x2-x1)*(YB-y1)/(y2-y1);} else if(TOP & code !=0) { y=YT; x=x1+(x2-x1)*(YT-y1)/(y2-y1);}
多边形分割算法

多边形分割算法一、引言多边形分割算法是计算机图形学中的一个重要问题。
在实际应用中,多边形分割算法被广泛应用于计算机游戏、建筑设计、CAD等领域。
本文将介绍多边形分割的基本概念和常见算法。
二、多边形分割基本概念1. 多边形多边形是由若干个线段组成的封闭图形。
每条线段称为多边形的一条边,相邻两条边之间的夹角称为内角。
多边形可以分为凸多边形和凹多边形两种。
2. 多边形分割将一个凸或凹多边形划分成若干个不相交的子多边形,使得每个子多边形都是凸多边形,这个过程就称为多边形分割。
3. 三角剖分三角剖分是指将一个复杂的凸或凹多边形划分成若干个三角形。
三角剖分是一种特殊的多边形分割方法,它可以使得每个子图元(三角形单元)面积最小且相互之间没有重叠部分。
三、常见的多变性分割算法1. 三角剖分法三角剖分是最常见的多边形分割算法,它将多边形划分成若干个三角形。
三角剖分有很多种方法,如Delaunay三角剖分、Ear Clipping Triangulation等。
2. 对角线交换法对角线交换法是一种将凸多边形划分为若干个凸子多边形的算法。
该算法首先选择一个顶点,然后从该点开始依次连接其他顶点,如果连接的线段不在多边形内部,则将其作为对角线,将多边形划分为两个子多边形。
接下来再对每个子多边形递归进行划分。
3. 梯形切割法梯形切割法是一种利用梯形进行切割的算法。
该算法首先将多边形按照从上到下的顺序排序,然后依次连接相邻两条线段所在的梯形的上底和下底,直到所有的梯形都被覆盖。
这样就可以将凸或凹多边形划分为若干个凸子多边形。
4. 空间扫描线算法空间扫描线算法是一种基于扫描线的算法。
该算法首先将多边形按照从上到下的顺序排序,然后从上到下依次扫描每一条水平线段,同时记录当前扫描线段与多边形相交的所有线段。
当扫描到某个顶点时,如果该点是凸顶点,则将其加入划分结果中,并删除与该顶点相邻的所有线段;如果该点是凹顶点,则选择与该点相邻的两条线段中跨越最小角度的一条作为对角线,并将多边形划分为两个子多边形。
计算机图形学-实验五直线和多边形的裁剪

大学实验报告学院:计算机科学与信息学院专业:软件工程班级:102班** 实验组实验时间指导教师成绩实验工程名称实验五直线和多边形的裁剪实验目的掌握直线段的裁剪算法以及多边形的裁剪算法实验要求熟练掌握直线段的裁剪算法以及多边形的裁剪算法的根本原理,并编写测试代码进展实验。
实验原理Cohen-Sutherland直线剪裁算法以区域编码为根底,将窗口及其周围的,8个方向以4 bit的二进制数进展编码。
右图所示的编码方法将窗口及其邻域分为5个区域:⑴域:区域(0000)。
⑵上域:区域(1001, 1000, 1010)。
⑶下域:区域(0101, 0100, 0110)。
⑷左域:区域(1001, 0001, 0101)。
⑸右域:区域(1010, 0010, 0110)。
当线段的两个端点的编码的逻辑"与〞非零时,线段为显然不可见的,对*线段的两个端点的区号进展位与运算,可知这两个端点是否同在视区的上、下、左、右;Cohen-Sutherland直线剪裁算法的算法思想是:对于每条线段P1P2分为三种情况处理。
〔1〕假设P1P2完全在窗口,则显示该线段P1P2简称"取〞之。
〔2〕假设P1P2明显在窗口外,则丢弃该线段,简称"弃〞之。
〔3〕假设线段既不满足"取〞的条件,也不满足"弃〞的条件,则在交点处把线段分为两段。
其while (code1 != 0 || code2 != 0) {if ((code1 & code2) != 0) {// 两端点的编码相与不为0,表示直线在窗口外return;}if (code1 != 0) {code = code1;} else {code = code2;}if ((LEFT & code) != 0) {// 直线的端点与矩形窗口的左边编码相与!=0* = *L;y = y1 + (y2 - y1) * (*L - *1) / (*2 - *1);// 求直线与矩形窗口的左边界的交点} elseif ((RIGHT & code) != 0) {// 直线的端点与矩形窗口的右边编码相与!=0* = *R;y = y1 + (y2 - y1) * (*R - *1) / (*2 - *1);// 求直线与矩形窗口的右边界的交点} elseif ((BOTTOM & code) != 0) {// 直线的端点与矩形窗口的下边编码相与!=0y = YB;* = *1 + (*2 - *1) * (YB - y1) / (y2 - y1);// 求直线与矩形窗口的下边界的交点} elseif ((TOP & code) != 0) {// 直线的端点与矩形窗口的上边编码相与!=0y = YT;* = *1 + (*2 - *1) * (YT - y1) / (y2 - y1);// 直线的端点与矩形窗口的上// 边编码相与!=0}if (code == code1) {*1 = *;y1 = y;code1 = encode(*, y);} else {*2 = *;y2 = y;code2 = encode(*, y);}}g.drawLine((int) (*1 + 0.5), (int) (y1 + 0.5), (int) (*2 + 0.5),(int) (y2 +0.5));}二、多边形裁剪的核心代码为:通过点集画直线或者多边形:privatevoid draw() {//通过点集画直线或者多边形for (int i = 1; i < points.size(); i++) {Point p1 = new Point();p1 = points.get(i);int *1 = (int) p1.get*();int y1 = (int) p1.getY();Point p2 = new Point();p2 = points.get(i - 1);int *2 = (int) p2.get*();int y2 = (int) p2.getY();g.drawLine(*1, y1, *2, y2);}}多边形的裁剪函数:private Point[] cutPicture(Point[] point, Point[] edge) {// 剪裁函数,参数为〔点集,边〕Point[] intersectPoint = new Point[20];//存放交点的集合for (int j = 0; j < 20; j++) {intersectPoint[j] = new Point();}Point s = new Point();Point p = new Point();Point t = new Point();int i = 0;int length = point.length;s = point[length - 1];for (int j = 0; j < length; j++) {p = point[j];if (inside(p, edge)) {// sp在窗口,情况1if (inside(s, edge)) {intersectPoint[i] = p;i += 1;} else {// s在窗口外,情况4t = intersect(s, p, edge);intersectPoint[i] = t;i += 1;intersectPoint[i] = p;i += 1;}} elseif (inside(s, edge)) {// s在窗口,p在窗口外,情况3t = intersect(s, p, edge);intersectPoint[i] = t;i += 1;}// 情况2没有输出s = p;}List<Point> tempList = new ArrayList<Point>();for (int k = 0; k < i; k++) {if (intersectPoint[k] != null) {Point pt = intersectPoint[k];tempList.add(pt);}}Point[] temp = new Point[tempList.size()];for (int j = 0; j < tempList.size(); j++) {temp[j] = new Point();temp[j] = tempList.get(j);}intersectPoint = temp;return intersectPoint;}判断点是否在裁剪边的可见侧:privateboolean inside(Point point, Point[] edge) {//判断点是否在裁剪边的可见侧// 裁剪边为窗口下边if ((edge[0].y == edge[1].y) && (edge[0].* < edge[1].*)) {if (point.y >= edge[0].y) {returntrue;}}// 裁剪边为窗口上边if ((edge[0].y == edge[1].y) && (edge[0].* > edge[1].*)) {if (point.y <= edge[0].y) {returntrue;}}// 裁剪边为窗口右边if ((edge[0].* == edge[1].*) && (edge[0].y < edge[1].y)) {if (point.* <= edge[0].*) {returntrue;}}// 裁剪边为窗口左边if ((edge[0].* == edge[1].*) && (edge[0].y > edge[1].y)) {if (point.* >= edge[0].*) {returntrue;}}returnfalse;}直线段与窗口边界求交:private Point intersect(Point s, Point p, Point[] edge) {//直线段与窗口边界求交,并返回交点Point t = new Point();if (edge[0].y == edge[1].y) {// 水平裁剪边t.y = edge[0].y;t.* = s.* + (edge[0].y - s.y) * (p.* - s.*) / (p.y - s.y);} elseif (edge[0].* == edge[1].*) {// 垂直裁剪边t.* = edge[0].*;t.y = s.y + (edge[0].* - s.*) * (p.y - s.y) / (p.* - s.*);}return t;}鼠标的监听类〔部类〕:class MouseMonitor e*tends MouseAdapter {//通过鼠标的单击获取点,并画出直线或者多边形publicvoid mouseClicked(MouseEvent e) {points.add(e.getPoint());if (points.size() > 1) {draw();}}}键盘的监听类〔部类〕:class KeyMonitor e*tends KeyAdapter {// 键盘控制publicvoid keyPressed(KeyEvent e) {switch (e.getKeyCode()) {case KeyEvent.VK_R:// 清空画布和点集panel.repaint();points.removeAll(points);break;case KeyEvent.VK_W://对裁剪窗口的处理g.setColor(Color.RED);g.drawRect(*L, YB, *R - *L, YT - YB);//存放裁剪窗口的边top = new Point[2];// 存放裁剪窗口的上边top[0] = new Point(*L, YB);top[1] = new Point(*R, YB);right = new Point[2];//存放裁剪窗口的右边right[0] = new Point(*R, YB);right[1] = new Point(*R, YT);bottom = new Point[2];//存放裁剪窗口的下边bottom[0] = new Point(*R, YT);bottom[1] = new Point(*L, YT);left = new Point[2];//存放裁剪窗口的左边left[0] = new Point(*L, YT);left[1] = new Point(*L, YB);break;case KeyEvent.VK_A://对直线段进展裁剪g.setColor(Color.GREEN);Point p1 = points.get(0);Point p2 = points.get(1);lineCut(p1.get*(), p1.getY(), p2.get*(), p2.getY()); break;case KeyEvent.VK_B://对多边形进展裁剪source = new Point[points.size()];//得到多边形的点for (int i = 0; i < points.size(); i++) {source[i] = points.get(i);}g.setColor(Color.GREEN);wT = cutPicture(source, top);//得到多边形与裁剪窗口上边的交点wR = cutPicture(wT, right);//得到多边形与裁剪窗口右边的交点wB = cutPicture(wR, bottom);//得到多边形与裁剪窗口下边的交点wL = cutPicture(wB, left);//得到多边形与裁剪窗口左边的交点第二种情况:线段在裁剪窗口的部,线段完全可见。
计算机图形学-多边形区域裁剪

P1被裁减多边形 P2为裁剪边框
多边形的边界均用其定点序列来表示,多边形的外部边界取顺时针方向(其内部 边界或内孔取逆时针方向),保证当遍历环形顶点表时,多边形内部总是位于前进 方向的右侧,依次定义了多边形边界的正方向。 交点判定规则: ①当主多边形的一条边位于窗口多边形 的一条边上时,两条边看作没有交点。 ②当主多边形的一个顶点位于窗口多边 形上时,作为主多边形的一条边的起点, 这个顶点应看作不是交点。 ③当主多边形的一个顶点位于窗口多边 形上时,,作为主多边形的一条交点,这 个顶点应看做一个交点。 ④ 当主多边形的一条边与窗口多边形的 交点不是主多边形的一个顶点时,是一个 正常的交点。 其类型为:如果该边的起点在裁剪 多边形外,则该交点是进入交点;反之如 果该边的起点在裁剪多边形内,则该交点 是离开交点。
记录顶点的判断 逐边裁剪法的实质使用四条边依次对多边形各边进行裁剪。每次裁剪的结果 都是输出一个多边形的顶点表。 ( 多边形的每一个顶点都是一条边的终点,又是下一条边的起点,我们统一 当多边形的一条边被窗口的一条边的延长线裁剪后需输出裁剪结果,即记录 将顶点作为边的终点进行判断和处理。) 需要保留的顶点(或交点)但应保留哪些点取决于该边与裁剪线的位置关系。 被裁多边形的边与裁剪线之间的位置关系存在四种可能的情况: ① 边的起点在不可见区域,终点在可见区域,此时,需保留边与裁剪线 的交点和边的终点。 ②边的起点和终点都在可见区域,此时,只需保留边与裁剪线的交点和 边的终点。 ③变得起点在可见区域,终点在不可见区域,此时只需保留边与裁剪线 的交点。 ④边到起点和终点都在不可见区域,此时,没有需要保留的点。
p1被裁减多边形p2为裁剪边框多边形的边界均用其定点序列来表示多边形的外部边界取顺时针方向其内部边界或内孔取逆时针方向保证当遍历环形顶点表时多边形内部总是位于前进方向的右侧依次定义了多边形边界的正方向
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
简单多边形裁剪算法摘要:多边形裁剪算法与线性裁剪算法具有更广泛的实用意义,因此它是目前裁剪研究的主要课题。
本文主要介绍了一种基于多边形顶点遍历的简单多边形裁剪算法,它有效降低了任意多边形裁剪复杂度。
通过记录交点及其前驱、后继信息,生成结果多边形,该算法简化了交点的数据结构,节省了存储空间,降低了算法的时间复杂度,具有简单、易于编程实现、运行效率高的特点。
关键词:多边形裁剪;交点;前驱;后继;矢量数组一、技术主题的基本原理简单多边形裁剪算法综合考虑现有多边形裁剪算法的优缺点,它是一种基于多边形顶点遍历来实现简单多边形裁剪工作的。
其主要的原理是遍历多边形并把多边形分解为边界的线段逐段进行裁剪,输出结果多边形。
二、发展研究现状近年来,随着遥感绘图、CAD辅助设计、图象识别处理技术的发展,图形裁剪算法从最初在二维平面上线和图形的裁剪扩展到三维空间里体和场的裁剪,国内外相继提出不少行之有效的算法,但越来越复杂的图形和计算也对算法的速度和适用性提出了越来越高的要求。
因此,不断简化算法的实现过程,完善细节处理,满足大量任意多边形的裁剪也就成了当今算法研究的焦点之一。
以往多边形裁剪算法不是要求剪裁多边形是矩形,就是必须判断多边形顶点的顺时针和逆时针性,即存在不实用或者是增加了多边形裁剪算法的难度。
为了解决现在的问题,我们研究现在的新多边形算法,其中,裁剪多边形和被裁剪多边形都可以是一般多边形,且不需要规定多边形输入方向。
它采用矢量数组结构,只需遍历剪裁多边形和被裁剪多边形顶点即完成多边形的裁剪,具有算法简单、运行效率高的特点。
三、新算法设计1、算法的思想本算法是为了尽量降低任意多边形裁剪算法复杂度而提出的,其主要思想是采用矢量数组结构来遍历裁剪多边形和被裁多边形顶点,记录裁剪多边形和被裁减多边形交点及其前驱、后继信息,并通过记录相邻交点的线段,然后通过射线法选择满足条件的线段,之后进行线段连接,输出对应的裁剪结果。
算法数据结构简单,即没有用常用的数据结构,如线性链表结构、双向链表结构和树形结构,这样就节省了存储空间,增加算法的效率。
2、主要数据结构多边形裁剪算法的核心是数据结构,它决定了算法的复杂度和计算效率。
兼顾数据结构简单和节省存储空间的目的,简单多边形裁剪算法是基于矢量数组vector的数据结构进行裁剪的,多边形矢量数组的每个元素表示多边形顶点,且按顶点输入的顺序存储。
裁剪多边形和被裁剪多边以下我们分别用S和C表示,其涉及的数据结构主要如下:1)顶点或交点的数据结构:Vertex={double x,y;bool IslnPolygon;}说明:Vertex用来存储多边形的顶点或交点,x,y表示顶点的坐标,IsInPolygon为true表示该点在多边形内部或在多边形边上,否则,表示该点在多边形外部。
2)交点的前驱后继数据结构如下:CrossPointIndex{int nPredecessorlndex=0//前驱序号int nSuccessorIndex=0//后继序号}说明:CrossPointIndex用于记录交点在多边形中的前驱与后继的序号信息,以及记录同一交点在两个多边形中顶点序号。
即若P为多边形S与多边形C的交点,为了表示P在S和C中为同一点,则可用CrossPointIndex记录用nPredecessorIndex记录P在S中的序号、用nSuccessorIndex记录P在C中序号。
3)线段的数据结构如下:Segment{int nStartIndex=0int nEndIndex=0int* pIndexes;int nIndexCount;}说明:Segment表示多边形在另一个多边形内(外)的线段,nStartaIndex 为Segment起始顶点的序号,nEndIndex为Segment终止顶点的序号,pIndexes 为起始顶点与终止顶点之间的顶点序号集合,nIndexCount为pIndexes中元素个数。
3、算法设计1)第一阶段:采用射线法计算并判断S(或C)在C(或S)内,并修改S(或C)顶点Vertex的IsInPolygon的值。
由于射线可以任意选取,为了方便可以将射线定为从被测点开始射向X轴坐标正方向的水平射线。
由于多边形的一条边与射线的交点最为1个,因此可以循环遍历每条边并判断边与射线有无交点,若有交点,计数器加1,。
最后得到的计数器的值即多边形与射线的交点个数。
若交点个数为奇数,则被测点在多边形内部,若交点个数为偶数,则被测点在多边形外部。
对于多边形的任意一条边,为了尽量避免求交点时用到乘除法,将判断该边与射线有无交点的算法可以包含3步:1)判断边的两个顶点是否均在被测点左方或者下方或者上方,若是则无交点,返回假并退出;2)若不满足第一条原则,且满足两个顶点均在被测点右方,则一定有顶点,返回真并退出;3)若以上两条都不满足,求出边与射线的交点,比较交点的X坐标与被测点的X坐标,若前者大于后者则返回真并退出,否则返回假并退出。
设边的两个顶点坐标分别为(x1,y1)和(x2,y2),则边的直线方程可写为: X=m(y-y1)+x1其中,m=(x2-x1)/(y2-y1)为直线斜率的倒数。
使用该方程时需要两次乘除法,效率较低。
为了尽量避免求交点,第三部可以采用二分法将边分成两段,对其中两个端点分别跨过射线两侧的边段重新进行以上第一步和第二步的判断,若以上两步中还没有推出,再继续二分,直到能够被第一步和第二步判断并退出。
采用二分法则避免了乘除法,算法中只有除2运算和一些判断,适合于硬件处理,二分法的循环次数一般较少,当被测点位于边上时,循环次数组最多。
其具体的算法如下:(Point为被测点变量,point1、point2为一条边的两个端点变量)If(piont2.y<point1.y){P1=point2;p2=point1}Else{p1=point1;p2=point2;}if(p1.y>point.y||p2.y<point.y) //两个端点都在被测点上方或者下方Return false;//无交点Else If(p1.x<point.x&&p2.x<point.x) //当两个端点都在被测点左方时 Return false ;无交点Else if (p1.x>point.x&&p2.x>point.x){Return true;有交点Count++;}Else {M=MyPoint((p1.x+p2.x)/2,(p1.y+p2.y)/2)//得到边的中点If(M.y>point.y)P2=M;ElseP1=M;If(p2.x>p1.x) //当p2在p1的右方时{If(p2.x<point.x) //当p2在被测点左方时,无交点Return false;If(P1.x>point.x)//当p1在被测点右方时,有交点{ Return true;count++;}}Else //当P2在P1右方时{If(P1.X<point.x)//当P1在被测点左方时,无交点Return false;If(p2.x>point.x)//当P2在被测点右方时,有交点{Return true;count++ ;}}}图1.射线法判断点的位置2)第二阶段按正方向遍历S与C,计算S与C的交点集,交点的前驱后继信息、交点在S 和C中的对应关系,以及相交多边形弧段集;﹡步骤1:按正向方向遍历S与C并计算交点集Vector<Vertex>CrossPointSet,同时生成交点在S和C中前驱,后继信息Vector<CrossPointIndex>CrossPointIndexSetS 和Vector<CrossPointIndex>CrossPointIndexSetC.其中,CrossPointSet中元素IsInPolygon的值为true。
﹡步骤2 ;判断CrossPointIndexSetS或CrossPointIndexSetC中首尾元素的nPredecessorIndex与nSuccessorIndex值是否相等。
若想等,则将尾部元素放置到首部位置。
重复判断操作,直到首尾元素值不相等为止。
﹡步骤3:按倒序将CrossPointIndexSetS和CrossPointIndexSetC中元素插入到S 和Czhong ,计算原多边形顶点的序号信息,并建立交点在两个多边形中顶点序号关系集合。
假设插入交点后的S和C成为S’和C’。
插入同时,建立交点在S’和C’中顶点序号对应集合Vector<CrossPointlndex>CorrespondingCrossPointlndexSe t,并用nPredecessorlndex记录S’中顶点序号、nSuccessorlndex记录C’中顶点序号。
其中,以CrossPointlndexSetS和CrossPointlndexSetC中前驱序号为0的元素开始,交点序号在前驱序号的基础上顺序递增。
根据交点的前驱后继集合信息,S和C点在S’和C’中的序号具有如下变化规律:NPredecessorIndex[0]=0Successorlndex[i]=nPredecessorlndex[i]+ni+1nPredecessorIndex[i+1]=nSuccessorIndex[i]+1i<N,N为原多边形顶点数式中:nPredecessorlndex[i]、nSuccessorIndex[i]——S、C序号为i的顶点在S’和C’中序号,ni——S和C中序号为i与i+1之间的交点个数﹡步骤4 :释放CrossPointIndexSetS和CrossPointIndexSetC空间,修改交点对应集合CorrespondingCrossPointIndexSet的元素值。
﹡步骤5 :按正方向分别连接S’和C’中Vertex的IsInPolygon为true且相邻的顶点,生成线段集Vector<Segnment>SegmentSetS和Vector<Segment>SegmentSetC.步骤6 遍历SegmentSetS元素并取第i号元素的中点Pi,采用射线法判断Pi是否在C中,若不在C中,则删除SegmentSetS中第i号元素。
同理,删除SegmentSetC 中元素的中点不在S’中的项,﹡步骤7 分别合并SegmentSetS和SegmentSetC中为相邻元素。
流程图如图2 第二阶段流程。
第三阶段对弧段集进行合并,生成并输出结果多边形。
