水平宽铅垂高求三角形面积
三角形水平宽铅垂高面积公式

三角形水平宽铅垂高面积公式在我们学习数学的奇妙旅程中,三角形这个家伙可是个常客。
今天咱们就来聊聊三角形的水平宽铅垂高面积公式,这可是个相当有趣又实用的小知识!先来说说啥是三角形的水平宽和铅垂高。
想象一下,有一个三角形稳稳地躺在平面直角坐标系里。
水平宽呢,就是三角形底边在 x 轴上的投影长度;铅垂高呢,则是从三角形的顶点向 x 轴作垂线,垂线的长度就是铅垂高。
我记得有一次给学生们讲这个知识点的时候,有个小家伙瞪着大眼睛一脸懵地问我:“老师,这水平宽和铅垂高怎么就跟面积有关系啦?”我笑着告诉他:“别着急,咱们一起来探究探究。
”咱们来看个具体的例子。
假设有个三角形,三个顶点的坐标分别是A(1, 2),B(3, 4),C(5, 1)。
首先,咱们来找出底边,假设底边是线段BC,那它在 x 轴上的投影长度就是水平宽。
B 点和 C 点的横坐标分别是 3 和 5,所以水平宽就是 5 - 3 = 2。
接下来找铅垂高。
咱们从 A 点向 x 轴作垂线,与 x 轴交点设为 D,那 AD 的长度就是铅垂高。
A 点的纵坐标是 2,所以铅垂高就是 2。
这时候,根据三角形水平宽铅垂高面积公式,面积就等于水平宽乘以铅垂高的一半。
也就是 2×2÷2 = 2。
再比如,还有个三角形,顶点坐标是 E( -1, 3),F(2, 5),G(4, -1)。
同样的方法,先找底边 FG 在 x 轴上的投影,也就是水平宽,4 - 2 = 2。
再找顶点 E 到 x 轴的垂线长度,也就是铅垂高,是 3。
那这个三角形的面积就是 2×3÷2 = 3。
同学们在做这类题的时候,可一定要仔细看准坐标,别把数值弄混了。
有个同学就因为粗心,把横坐标看成纵坐标,算出的面积差了十万八千里,自己还纳闷怎么不对呢!其实啊,这个公式的妙处就在于,它能让我们在面对一些复杂的三角形时,不用费力地去分割或者转化,就能轻松算出面积。
在实际生活中,这个公式也有大用处。
直角坐标系下三角形面积求法——水平宽铅垂高

直角坐标系下三角形面积求法——水平宽铅垂高前一阶段我们探讨了一次函数和三角形的面积问题,后台有一些同仁提出了一些宝贵的看法,在此笔者表示感谢。
我们知道对于不规则三角形的面积肯定是用割补法,由此引申出一种水平宽铅垂高的做法,也就是铅垂法。
今天我们来深入地探讨一下铅垂法的做法依据。
我们先从三个顶点都确定的三角形来看。
如图,在直角坐标系中,△ABC三个顶点的坐标为A(1,1)、B (3,4)、C(5,2),试求△ABC的面积。
显然这个三角形属于我们说的所谓不规则三角形(三条边均不和坐标轴平行,且不在坐标轴上),所以我们的基本思路是割补法。
由于此题相对来讲比较简单,我就简单用图形罗列一下各种不同的解法。
方法一:方法二:方法三:方法三是过点B作AC的平行线将不规则的△ABC转化为规则的△ADC从而来求解的过程,其实我们还可以过点A作BC的平行线或者过点C作AB的平行线来进行转化。
鉴于这不是本文研究的重点,另外两种方法在此略过。
方法四:方法五:方法六:方法七:方法八:方法九:方法四、方法五都是在点B处处理,方法四是在点B处作y轴的平行线,方法五是在点B处作x轴的平行线;方法六、方法七都是在点A处处理,方法六是在点A处作y轴的平行线,方法七是在点A处作x轴的平行线;方法八、方法九都是在点C处处理,方法八是在点C处作y轴的平行线,方法九是在点C处作x轴的平行线。
我们再来研究这六个图:如果我们对这六种方法都进行运算、思考,我们就会发现△ABC的面积为图中两个红色线段(一横一竖)乘积的一半。
这就是所谓的铅垂法求面积。
那么如何构造这些线呢?我的看法是选三角形的两个顶点(比如A和B),将AB之间的横坐标体现的横着的线段找出来(图5中的AM),最后一个顶点C作竖着的直线交AB边于点D,此时竖着的线段就是CD,然后利用AM和CD乘积的一半来求解。
或者将AB之间的纵坐标体现的竖着的线段找出来(图6中的AM),过第三个顶点C 作横着的直线交AB边于点D,此时横着的线段就是CD,然后利用AM和CD乘积的一半来求解。
中考专题复习--浅谈水平宽铅锤高求三角形面积+课件+-2023-2024学年人教版数学九年级下册+

1
s3
o•
-2 -1
1
2
3
4
5P
x
-1
-2
y
5
S=S梯形OPMB– S1 –S2
4
B(•3,4)
M
s1
3
2
•A(5,2)
1
s2
o•
-2 -1
1
2
3
4
5P
x
-1
-2
牛刀小试:1.如图,在直角坐标系中,点A的坐标为 (-2,0),连结OA,将线段OA绕原点O顺时针旋转 120°,得到线段OB.
(1)求点B的坐标;
3.如图1,抛物线y=-x+bx+c与x轴交于A(1,0),B(-3,
0)两点。 (3)如图2,在(1)中的抛物线上的第二象限上是否存在一点P, 使△PBC的面积最大?若存在,求出点P的坐标及△PBC的面 积最大值;若没有,请说明理由。
谢谢!
小结
我们可以得到一种计算三角形面积新方法:即三角 形的面积等于水平宽与铅锤高乘积的一半。
谢谢大家,再见!
例如图所示, 求△ OAB的面 积。
AM平行于x轴
y 4x OB 3
当y=2 x 3Βιβλιοθήκη 2所以M(3 2
,2
)
y
5
4
3
2
M
h2 1
o•
-2 -1
1
-1
-2
B(•3,4)
h1
S S S
OAB
ABM
2.如图,抛物线与x轴交于A(1,0),B(- 3,0)两点.
(1)求该抛物线的解析式;
(2)设(1)中的抛物线交y轴于C点,在该抛物线的对 称轴上是否存在点Q,使得△QAC的周长最小?若存在, 求出Q点的坐标;若不存在,请说明理由.
水平宽铅垂高求三角形面积

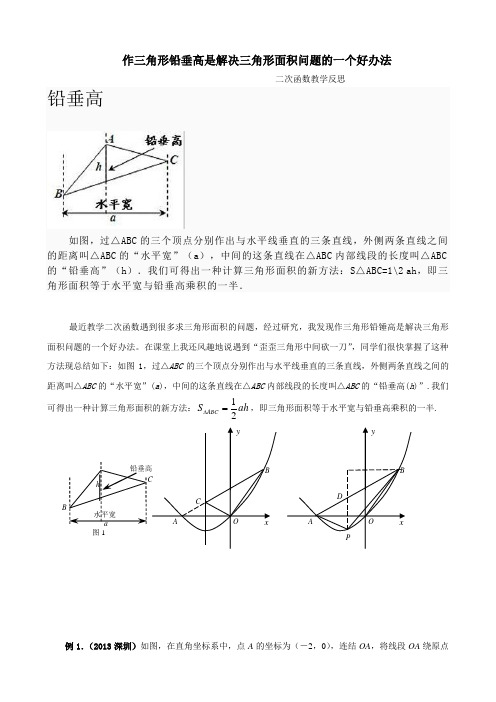
水平宽铅垂高求三角形面积文档编制序号:[KK8UY-LL9IO69-TTO6M3-MTOL89-FTT688]作三角形铅垂高是解决三角形面积问题的一个好办法------------二次函数教学反思铅垂高如图,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高”(h).我们可得出一种计算三角形面积的新方法:S△ABC=1\2 ah,即三角形面积等于水平宽与铅垂高乘积的一半.最近教学二次函数遇到很多求三角形面积的问题,经过研究,我发现作三角形铅锤高是解决三角形面积问题的一个好办法。
在课堂上我还风趣地说遇到“歪歪三角形中间砍一刀”,同学们很快掌握了这种方法现总结如下:如图1,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高(h)”.我们可得出一种计算三角形面积的新方法:ahSABC21=∆,即三角形面积等于水平宽与铅垂高乘积的一半.C铅垂hCByDBy例1.(2013深圳)如图,在直角坐标系中,点A的坐标为(-2,0),连结OA,将线段OA绕原点O顺时针旋转120°,得到线段OB.(1)求点B的坐标;(2)求经过A、O、B三点的抛物线的解析式;(3)在(2)中抛物线的对称轴上是否存在点C,使△BOC的周长最小若存在,求出点C的坐标;若不存在,请说明理由.(4)如果点P是(2)中的抛物线上的动点,且在x轴的下方,那么△PAB是否有最大面积若有,求出此时P点的坐标及△PAB的最大面积;若没有,请说明理由.解:(1)B(1(2)设抛物线的解析式为y=ax(x+a),代入点B(a=,因此2y=+(3)如图,抛物线的对称轴是直线x=—1,当点C位于对称轴与线段AB的交点时,△BOC的周长最小.设直线AB为y=kx+b.所以20.kk bk bb⎧=⎪⎧+=⎪⎪⎨⎨-+=⎪⎩⎪=⎪⎩解得,因此直线AB为y=+,当x=-1时,y=C的坐标为(-1).(4)如图,过P作y轴的平行线交AB于D.2221()()2132********331932PAB PAD PBD D P B A S S S y y x x x x x x x x ∆∆∆=+=--⎡⎤⎛⎫⎛⎫=+-+⨯⎢⎥ ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦=--+⎛⎫=-++⎪⎝⎭当x =-12时,△PAB 的面积的最大值为93,此时13,2P ⎛⎫--⎪ ⎪⎝⎭. 例2.(2014益阳) 如图2,抛物线顶点坐标为点C (1,4),交x 轴于点A (3,0),交y 轴于点B .(1)求抛物线和直线AB 的解析式;(2)点P 是抛物线(在第一象限内)上的一个动点,连结PA ,PB ,当P 点运动到顶点C 时,求△CAB 的铅垂高CD 及CAB S ∆;(3)是否存在一点P ,使S △PAB =89S △CAB ,若存在,求出P 点的坐标;若不存在,请说明理由. 解:(1)设抛物线的解析式为:4)1(21+-=x a y 把A(3,0)代入解析式求得1-=a 所以324)1(221++-=+--=x x x y 设直线AB 的解析式为:b kx y +=2由3221++-=x x y 求得B 点的坐标为)3,0( 把)0,3(A ,)3,0(B 代入b kx y +=2中解得:3,1=-=b k 所以32+-=x y(2)因为C 点坐标为(1,4)所以当x =1时,y 1=4,y 2=2所以CD =4-2=232321=⨯⨯=∆CAB S (平方单位)(3)假设存在符合条件的点P ,设P 点的横坐标为x ,△PAB 的铅垂高为h ,则x x x x x y y h 3)3()32(2221+-=+--++-=-=由S △PAB =89S △CAB 得389)3(3212⨯=+-⨯⨯x x 化简得:091242=+-x x 解得,23=x 将23=x 代入3221++-=x x y 中,解得P 点坐标为)415,23( 图-2xC O yABD11例3.(2015江津)如图,抛物线c bx x y ++-=2与x 轴交于A(1,0),B(- 3,0)两点,(1)求该抛物线的解析式;(2)设(1)中的抛物线交y 轴于C 点,在该抛物线的对称轴上是否存在点Q ,使得△QAC 的周长最小若存在,求出Q 点的坐标;若不存在,请说明理由.(3)在(1)中的抛物线上的第二象限上是否存在一点P ,使△PBC 的面积最大,若存在,求出点P 的坐标及△PBC 的面积最大值.若没有,请说明理由.解:(1)将A(1,0),B(-3,0)代2y x bx c =-++中得10930b c b c -++⎧⎨--+=⎩=∴23b c =-⎧⎨=⎩∴抛物线解析式为:223y x x =--+(2)存在。
水平宽铅垂高求三角形面积
作三角形铅垂高是解决三角形面积问题的一个好办法------------二次函数教学反思铅垂高如图,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC 的“铅垂高”(h).我们可得出一种计算三角形面积的新方法:S△ABC=1\2 ah,即三角形面积等于水平宽与铅垂高乘积的一半.最近教学二次函数遇到很多求三角形面积的问题,经过研究,我发现作三角形铅锤高是解决三角形面积问题的一个好办法。
在课堂上我还风趣地说遇到“歪歪三角形中间砍一刀”,同学们很快掌握了这种方法现总结如下:如图1,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高(h)”.我们可得出一种计算三角形面积的新方法:ahSABC21=∆,即三角形面积等于水平宽与铅垂高乘积的一半.例1.(2013深圳)如图,在直角坐标系中,点A的坐标为(-2,0),连结OA,将线段OA绕原点图1O 顺时针旋转120°,得到线段OB .(1)求点B 的坐标;(2)求经过A 、O 、B 三点的抛物线的解析式;(3)在(2)中抛物线的对称轴上是否存在点C ,使△BOC 的周长最小?若存在,求出点C 的坐标;若不存在,请说明理由.(4)如果点P 是(2)中的抛物线上的动点,且在x 轴的下方,那么△P AB 是否有最大面积?若有,求出此时P 点的坐标及△P AB 的最大面积;若没有,请说明理由. 解:(1)B (1(2)设抛物线的解析式为y =ax (x+a ),代入点B (1,,得a =,因此2y =(3)如图,抛物线的对称轴是直线x =—1,当点C 位于对称轴与线段AB 的交点时,△BOC 的周长最小.设直线AB 为y =kx +b .所以20.k k b k b b ⎧=⎪⎧+=⎪⎪⎨⎨-+=⎪⎩⎪⎪⎩解得因此直线AB为y =+,当x =-1时,y =,因此点C 的坐标为(-1).(4)如图,过P 作y 轴的平行线交AB 于D. 2221()()213212PAB PAD PBD D P B A S S S y y x x x ∆∆∆=+=--⎡⎤⎫=+-+⨯⎢⎥⎪⎪⎢⎥⎝⎭⎝⎭⎣⎦=+⎫=+⎪⎝⎭当x =-12时,△P AB,此时1,2P ⎛- ⎝⎭. 例2.(2014益阳) 如图2,抛物线顶点坐标为点C (1,4),交x 轴于点A (3,0),交y 轴于点B .(1)求抛物线和直线AB 的解析式;(2)点P 是抛物线(在第一象限内)上的一个动点,连结P A ,PB ,当P 点运动到顶点C 时,求△CAB 的铅垂高CD 及CAB S ∆;(3)是否存在一点P ,使S △P AB =89S △CAB ,若存在,求出P 点的坐标;若不存在,请说明理由.解:(1)设抛物线的解析式为:4)1(21+-=x a y 把A (3,0)代入解析式求得1-=a 所以324)1(221++-=+--=x x x y 设直线AB 的解析式为:b kx y +=2由3221++-=x x y 求得B 点的坐标为)3,0( 把)0,3(A ,)3,0(B 代入b kx y +=2中解得:图-2xC Oy ABD 113,1=-=b k 所以32+-=x y(2)因为C 点坐标为(1,4)所以当x =1时,y 1=4,y 2=2所以CD =4-2=232321=⨯⨯=∆CAB S (平方单位) (3)假设存在符合条件的点P ,设P 点的横坐标为x ,△P AB 的铅垂高为h ,则x x x x x y y h 3)3()32(2221+-=+--++-=-=由S △P AB =89S △CAB 得389)3(3212⨯=+-⨯⨯x x 化简得:091242=+-x x 解得,23=x 将23=x 代入3221++-=x x y 中,解得P 点坐标为)415,23(例3.(2015江津)如图,抛物线c bx x y ++-=2与x 轴交于A(1,0),B(- 3,0)两点,(1)求该抛物线的解析式;(2)设(1)中的抛物线交y 轴于C 点,在该抛物线的对称轴上是否存在点Q ,使得△QAC 的周长最小?若存在,求出Q 点的坐标;若不存在,请说明理由.(3)在(1)中的抛物线上的第二象限上是否存在一点P ,使△PBC 的面积最大?,若存在,求出点P 的坐标及△PBC 的面积最大值.若没有,请说明理由.解:(1)将A(1,0),B(-3,0)代2y x bx c =-++中得10930b c b c -++⎧⎨--+=⎩=∴23b c =-⎧⎨=⎩∴抛物线解析式为:223y x x =--+(2)存在。
水平宽铅垂高求三角形面积完整版

解:(1)将B、C两点的坐标代入得
解得: 所以二次函数的表达式为:
(2)存在点P,使四边形POP C为菱形.设P点坐标为(x, ),PP 交CO于E若四边形POP C是菱形,则有PC=PO.
连结PP 则PE⊥CO于E,∴OE=EC= = .
∴ = 解得 = , = (不合题意,舍去)
∴P点的坐标为( , )
(3)过点P作 轴的平行线与BC交于点Q,与OB交于点F,设P(x, ),易得,直线BC的解析式为 则Q点的坐标为(x,x-3).
图① 图②
3.(2015年恩施) 如图11,在平面直角坐标系中,二次函数 的图象与x轴交于A、B
两点,A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,-3)点,
点P是直线BC下方的抛物线上一动点.
(1)求这个二次函数的表达式.
(2)连结PO、PC,并把△POC沿CO翻折,得到四边形POP C,那么是否存在点P,使四边形POP C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
水平宽铅垂高求三角形面积
作三角形铅垂高是解决三角形面积问题的一个好办法
------------二次函数教学反思
铅垂高
如图,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高”(h).我们可得出一种计算三角形面积的新方法:S△ABC=1\2 ah,即三角形面积等于水平宽与铅垂高乘积的一半.
例1.(2013深圳)如图,在直角坐标系中,点A的坐标为(-2,0),连结OA,将线段OA绕原点O顺时针旋转120°,得到线段OB.(1)求点B的坐标;(2)求经过A、O、B三点的抛物线的解析式;(3)在(2)中抛物线的对称轴上是否存在点C,使△BOC的周长最小?若存在,求出点C的坐标;若不存在,请说明理由.(4)如果点P是(2)中的抛物线上的动点,且在x轴的下方,那么△PAB是否有最大面积?若有,求出此时P点的坐标及△PAB的最大面积;若没有,请说明理由.
水平宽铅垂高求三角形面积

做三角形铅垂下是办理三角形里积问题的一个佳办法之阳早格格创做------------二次函数教教深思 铅垂下如图,过△ABC 的三个顶面分别做出与火仄线笔曲的三条曲线,中侧二条曲线之间的距离喊△ABC 的“火仄宽”(a ),中间的那条曲线正在△ABC 里里线段的少度喊△ABC 的“铅垂下”(h ).咱们可得出一种估计三角形里积的新要领:S △ABC=1\2 ah ,即三角形里积等于火仄宽与铅垂下乘积的一半.迩来教教二次函数逢到很多供三角形里积的问题,通过钻研,尔创造做三角形铅锤下是办理三角形里积问题的一个佳办法.正在课堂上尔还风趣天道逢到“正正三角形中间砍一刀”,共教们很快掌握了那种要领现归纳如下:如图1,过△ABC的三个顶面分别做出与火仄线笔曲的三条曲线,中侧二条曲线之间的距离喊△ABC 的“火仄宽”(a),中间的那条曲线正在△ABC 里里线段的少度喊△ABC 的“铅垂下(h)”.咱们可得出一种估计三角形里积的新要领:ah S ABC 21=∆,即三角形里积等于火仄宽与铅垂下乘积的一半.例1.(2013深圳)如图,正在曲角坐标系中,面A 的坐标为(-2,0),连结OA ,将线段OA绕本面O 逆时针转动120°,得到线段OB.(1)供面B 的坐标;(2)供通过A 、O 、B 三面的扔物线的剖析式;(3)正在(2)中扔物线的对于称轴上是可存留面C ,使△BOC 的周少最小?若存留,供出面C 的坐标;若不存留,请证明缘由.(4)如果面P 是(2)中的扔物线上的动面,且正在x 轴的下圆,那么△PAB 是可有最大里积?若有,供出此时P 面的坐标及△PAB 的最大里积;若不,请证明缘由. 解:(1)B (1,(2)设扔物线的剖析式为y=ax(x+a),代进面B (1,,得a =,果此2y x =+ (3)如图,扔物线的对于称轴是曲线x=—1,当面C 位于对于称轴与线段AB 的接面时,△BOC 的周少最小.20.k k b k b b ⎧=⎪⎧+=⎪⎪⎨⎨-+=⎪⎩⎪=⎪⎩解得AB为y =+,当x=-1时,y =,果此面C 的坐标为(-1).(4)如图,过P 做y 轴的仄止线接AB 于D.当x=-12时,△PAB,此时1,2P ⎛-⎝⎭. 例2.(2014益阳) 如图2,扔物线顶面坐标为面C(1,4),接x 轴于面A(3,0),接y 轴于面B.(1)供扔物线战曲线AB 的剖析式;(2)面P 是扔图1物线(正在第一象限内)上的一个动面,连结PA ,PB ,当P 面疏通到顶面C 时,供△CAB 的铅垂下CD 及CAB S ∆;(3)是可存留一面P ,使S △PAB=89S △CAB ,若存留,供出P 面的坐标;若不存留,请证明缘由.解:(1)设扔物线的剖析式为:4)1(21+-=x a y 把A (3,0)代进剖析式供得1-=a 所以324)1(221++-=+--=x x x y 设曲线AB 的剖析式为:b kx y +=2由3221++-=x x y 供得B 面的坐标为)3,0(把)0,3(A ,)3,0(B 代进b kx y +=2中解得:3,1=-=b k 所以32+-=x y(2)果为C 面坐标为(1,4)所以当x =1时,y1=4,y2=2所以CD =4-2=232321=⨯⨯=∆CAB S (仄圆单位)(3)假设存留切合条件的面P ,设P 面的横坐标为x ,△PAB 的铅垂下为h ,则x x x x x y y h 3)3()32(2221+-=+--++-=-=由S △PAB=89S △CAB 得389)3(3212⨯=+-⨯⨯x x 化简得:091242=+-x x 解得,23=x 将23=x 代进3221++-=x x y 中,解得P 面坐标为)415,23(例3.(2015江津)如图,扔物线c bx x y ++-=2与x 轴接于A(1,0),B(- 3,0)二面,(1)供该扔物线的剖析式;(2)设(1)中的扔物线接y 轴于C 面,正在该扔物线的对于称轴上是可存留面Q ,使得△QAC 的周少最小?若存留,供出Q 面的坐标;若不存留,请证明缘由.(3)正在(1)中的扔物线上的第二象限上是可存留一面P ,使△PBC 的里积最大?,若存留,供出面P 的坐标及△PBC 的里积最大值.若不,请证明缘由.图-2xC Oy ABD1 1解:(1)将A(1,0),B(-3,0)代2y x bx c =-++中得10930b c b c -++⎧⎨--+=⎩=∴23b c =-⎧⎨=⎩∴扔物线剖析式为:223y x x =--+(2)存留. 缘由如下:由题知A 、B 二面闭于扔物线的对于称轴1x =-对于称∴曲线BC 与1x =-的接面即为Q 面, 此时△AQC 周少最小 ∵223y x x =--+∴C 的坐标为:(0,3) 曲线BC 剖析式为:3y x =+ Q 面坐标即为13x y x =-⎧⎨=+⎩的解 ∴12x y =-⎧⎨=⎩∴Q(-1,2) (3)问:存留.缘由如下:设P 面2(23) (30)x x x x --+-<<,∵92BPC BOC BPCO BPCO S S S S ∆∆=-=-四边形四边形若BPCOS 四边形有最大值,则BPCS ∆便最大,∴BPE BPCO PEOC S S S ∆+Rt 四边形直角梯形=11()22BE PE OE PE OC =⋅++=2211(3)(23)()(233)22x x x x x x +--++---++=233927()2228x -+++当32x =-时,BPCO S 四边形最大值=92728+∴BPC S ∆最大=9279272828+-=当32x =-时,215234x x --+=∴面P 坐标为315( )24-, 共教们不妨干以下训练:1.(2015浙江湖州)已知如图,矩形OABC 的少OA=宽OC=1,将△AOC 沿AC 翻合得△APC. (1)挖空:∠PCB=____度,P 面坐标为( , );(2)若P ,A二面正在扔物线y=-43x2+bx+c 上,供b ,c的值,并证明面C正在此扔物线上;(3)正在(2)中的扔物线CP段(不包罗C,P面)上,是可存留一面M,使得四边形MCAP的里积最大?若存留,供出那个最大值及此时M面的坐标;若不存留,请证明缘由.2.(湖北省十堰市2014)如图①,已知扔物线32++axy(a≠0)与x轴接于面A(1,0)=bx战面B(-3,0),与y轴接于面C.(1) 供扔物线的剖析式;(2) 设扔物线的对于称轴与x轴接于面M ,问正在对于称轴上是可存留面P,使△CMP为等腰三角形?若存留,请间接写出所有切合条件的面P的坐标;若不存留,请证明缘由.(3) 如图②,若面E为第二象限扔物线上一动面,对接BE、CE,供四边形BOCE里积的最大值,并供此时E面的坐标.图①图②3.(2015年恩施) 如图11,正在仄里曲角坐标系中,二次函数cy+=2+xbx的图象与x轴接于A、B二面,A面正在本面的左侧,B面的坐标为(3,0),与y轴接于C(0,-3)面,面P是曲线BC下圆的扔物线上一动面.(1)供那个二次函数的表白式.(2)连结PO、PC,并把△POC沿CO翻合,得到四边形POP/C,那么是可存留面P,使四边形POP/C为菱形?若存留,哀供出此时面P 的坐标;若不存留,请证明缘由.(3)当面P 疏通到什么位子时,四边形ABPC 的里积最大并供出此时P 面的坐标战四边形ABPC 的最大里积.解:(1)将B 、C 二面的坐标代进得⎩⎨⎧-==+303c c b解得:⎩⎨⎧-=-=32c b 所以二次函数的表白式为:322--=x x y(2)存留面P ,使四边形POP /C 为菱形.设P 面坐标为(x ,322--x x ),PP /接CO 于E 若四边形POP /C 是菱形,则有PC =PO .连结PP /则PE ⊥CO 于E ,∴OE=EC=23y =23-.∴322--x x =23-解得1x =2102+,2x =2102-(分歧题意,舍来)∴P 面的坐标为(2102+,23-)(3)过面P 做y 轴的仄止线与BC 接于面Q ,与OB 接于面F ,设P (x ,322--x x ),易得,曲线BC 的剖析式为3-=x y 则Q 面的坐标为(x ,x -3).EB QP OE QP OC AB S S S S CPQ BPQ ABC ABPC ⋅+⋅+⋅=++=∆∆∆212121四边形 3)3(2134212⨯+-+⨯⨯=x x =87523232+⎪⎭⎫ ⎝⎛--x 图11当23=x 时,四边形ABPC 的里积最大此时P 面的坐标为⎪⎭⎫⎝⎛-415,23,四边形ABPC 的里积875的最大值为.25.(2015绵阳)如图,扔物线y = ax2 + bx + 4与x 轴的二个接面分别为A (-4,0)、B (2,0),与y 轴接于面C ,顶面为D .E (1,2)为线段BC 的中面,BC 的笔曲仄分线与x 轴、y 轴分别接于F 、G .(1)供扔物线的函数剖析式,并写出顶面D 的坐标;(2)正在曲线EF 上供一面H ,使△CDH 的周少最小,并供出最小周少;(3)若面K 正在x 轴上圆的扔物线上疏通,当K 疏通到什么位子时,△EFK 的里积最大?并供出最大里积.【剖析】(1)由题意,得 ⎩⎨⎧=++=+-,0424,04416b a b a解得21-=a ,b =-1. 所以扔物线的剖析式为4212+--=x xy ,顶面D 的坐标为(-1,29).(2)设扔物线的对于称轴与x 轴接于面M .果为EF 笔曲仄分BC ,即C 闭于曲线EG 的对于称面为B ,连结BD 接于EF 于一面,则那一面为所供面H ,使DH + CH 最小,即最小为 DH + CH = DH + HB = BD =132322=+DMBM . 而 25)429(122=-+=CD .∴△CDH 的周少最小值为CD + DR + CH =21335+.设曲线BD 的剖析式为y = k1x + b ,则⎪⎩⎪⎨⎧=+-=+,29,021111b k b k 解得 231-=k ,b1 = 3. 所以曲线BD 的剖析式为y =23-x + 3.由于BC = 25,CE = BC∕2 =5,Rt △CEG ∽△COB ,得 CE : CO = CG : CB ,所以 CG = 2.5,GO = 1.5.G (0,1.5).共理可供得曲线EF 的剖析式为y =21x +23.联坐曲线BD 与EF 的圆程,解得使△CDH 的周少最小的面H (43,815).(3)如图所示,设K (t ,4212+--t t),xF <t <xE .过K 做x 轴的垂线接EF 于N .则 KN = yK -yN =4212+--t t-(21t +23)=2523212+--t t.所以 S △EFK = S △KFN + S △KNE =21KN (t + 3)+21KN (1-t )= 2KN= -t2-3t + 5 =-(t +23)2 +429.即当t =-23时,△EFK 的里积最大,最大里积为429,此时K (-23,835).仄里曲角坐标系中三角形里积的供法咱们时常会逢到正在仄里曲角坐标系中供三角形里积的问题.解题时咱们要注意其中的解题要领妥协题本领.1. 有一边正在坐标轴上:例1:如图1,仄里曲角坐标系中,△ABC 的顶面坐标分别为(-3,0),(0,3),(0,-1),供△ABC 的里积.分解:根据三个顶面的坐标特性不妨瞅出,△ABC 的边BC 正在y 轴上,由图形可得BC =4,面A 到BC 边的距离便是A 面到y 轴的距离,也便是A 面横坐目标千万于值3,而后根据三角形的里积公式供解.2. 有一边与坐标轴仄止:例2:如图2,三角形ABC 三个顶面的坐标分别为A (4,1),B (4,5),C (-1,2),供△ABC 的里积.分解:由A (4,1),B (4,5)二面的横坐标相共,可知边AB与y 轴仄止,果而AB 的少度易供.做AB 边上的下CD ,便可供得线段 CD 的少,从而可供得三角形ABC 的里积.3. 三边均不与坐标轴仄止:例3:分解:由于三边均不仄止于坐标轴,所以咱们无法间接供边少,也无法供下,果此得另设念子.4. 三角形里积公式的推广:过△ABC 三个顶面分别做与火仄线笔曲的三条曲线,中侧二条 曲线之间的距离喊△ABC 的“火仄宽”(a ),中间的那条曲线正在 △ABC 里里线段的少度喊△ABC 的“铅垂下”(h ).咱们可得出 一种估计三角形里积的新要领:S △ABC=21ah即三角形里积等于火仄宽与铅垂下乘积的一半例4:已知:曲线l1:y=﹣2x+6与x 轴接于面A ,曲线l2:y=x+3与y 轴接于面B ,曲线l1、l2接于面C .(Ⅰ)修坐仄里曲角坐标系,绘出示企图并供出C 面的坐标; (Ⅱ)利用阅读资料提供的要领供△ABC 的里积.5. 坚韧训练:(1)已知:如图,曲线b kx y +=与反比率函数'k y x=(x <0)的图象相接于面A 、面B ,与x 轴接于面C ,其中面A 的坐标为(-2,4),面B 的横坐标为-4.(Ⅰ)试决定反比率函数的闭系式; (Ⅱ)供△AOC的里积.(2)如图,正在曲角坐标仄里内,函数m y x=(0x >,m 是常数)的图象通过(14)A ,,()B a b ,,其中1a >.过面A 做x 轴垂线,垂脚为C ,过面B 做y 轴垂线,垂脚为D ,连结AD ,DC ,CB . 若ABD △的里积为4,供面B 的坐标; (3)已知,曲线与x 轴、y 轴分别接于面A 、B ,以线段AB 为曲角边正在第一象限内做等腰Rt △ABC ,∠BAC=90°.且面P (1,a )为坐标系中的一个动面.(Ⅰ)供三角形ABC 的里积S △ABC ;(Ⅱ)请证明不管a 与所有真数,三角形BOP 的里积是一个常数; (Ⅲ)要使得△ABC 战△ABP 的里积相等,供真数a 的值.。
角形面积公式——之水平宽铅垂高
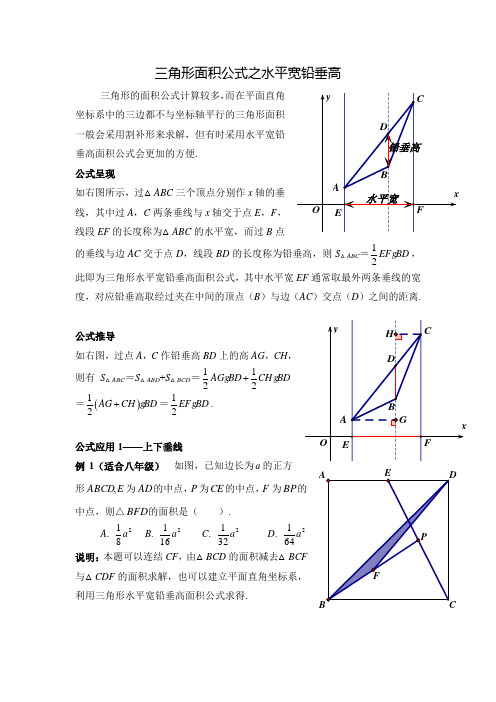
三角形的面积公式计算较多,垂高面积公式会更加的方便. 公式呈现如右图所示,过△ABC 三个顶点分别作x 线,其中过A ,C 两条垂线与x 轴交于点E ,F 线段EF 的长度称为△ABC 的水平宽,而过B 的垂线与边AC 交于点D ,线段BD 度,对应铅垂高取经过夹在中间的顶点(B公式推导如右图,过点A ,C 作铅垂高BD 上的高AG ,则有S △ABC =S △ABD +S △BCD =1122AG BD CH +g g =()12AG CH BD +g =12EF BD g .公式应用1——上下垂线例1(适合八年级) 如图,已知边长为a 形E ABCD ,为AD 的中点,P 为CE 的中点,F 为中点,则△BFD 的面积是( ).A .281a B . 2161a C . 2321a D .说明:本题可以连结CF ,由△BCD 的面积减去与△CDF 利用三角形水平宽铅垂高面积公式求得.解析:不妨以B 为原点,BC 为x 轴,BA 为y 轴建立平面直角坐标系,则点C 坐标为(a ,0),点D 坐标为(a ,a ),∵E 为AD 的中点,∴点E 坐标为(12a ,a ), ∵P 为CE 的中点,∴点P 坐标为(34a ,12a ),∵F 为BP 的中点,∴点F 坐标为(38a ,14a ).过F 点作BC 的垂线交BD 于点G ,则点G 的横坐标为38a ,又直线BD 的解析式为y x =,∴点G 的纵坐标为38a ,∴△BDF 的铅垂高FG =38a -14a =18a ,∴S △BDF =2111122816BC FG a a a ==g g .公式应用2——左右垂线例2(适合八年级) 如图,直线13y x =-+与x 轴,y 轴分别交于点A ,B ,以线段AB 为直角边在第一象限内作等腰直角△ABC ,且∠BAC =90°.如果在第二象限内有一点P 1,2a ⎛⎫⎪⎝⎭,且△ABP 的面积与Rt △ABC 的面积相等,求a 的值.说明:本题常见解法有三,一是连结OP ,△ABP 的面积=△AOB 面积+△BOP 面积-△AOP 面积,然后用a 的代数式表示,与Rt △ABC相等列方程求解;二是将点C 沿AB 翻折到C ’位置,则△ABC △ABC ’面积相等,若△ABP 的面积与Rt △ABC P相等,则可得PC ’三是考虑水平宽铅垂高公式来计算,但如果从A ,B ,P 三点向x 轴作垂线,较为复杂,不妨换个角度应用公式,即从A ,B ,P 向y 轴作垂解.解析:过线,则OB 而PE 度)由AB 的解析式可以得OA ,OB =1,而P的纵坐标为12,所以E 为AB 的中点, 所以PE =-a 从而有11221222a ⎛⨯⨯=⨯⨯-+ ⎝⎭, 解得42a =-.公式应用3——内外垂线从例2可以看到,三条垂线不一定作向x 轴,也可以作向y 轴,仿公式用即可.一般地,水平宽取的是最外的两条直线的距离,但这个做法不是绝对的,有12EF CG g . 简单推导:S △ABC =S △ACG -S △BCG =1122CG EH CG FH -g g =12EF CG g . 说明:当取相邻两条垂线距离为水平宽时,第三条垂线将与第三边(AB )的延长线相交,此时顶点(C )到交点(G )的距离为铅垂高(CG ).例3(适合九年级) 如图所示,直线l :y =3x +3与x 轴交于点A ,与y 轴交于点B .把△AOB 沿y 轴翻折,点A 落到点C ,抛物线过点B ,C 和D (3,0). (1)求直线BD 和抛物线的解析式.(2)若BD 与抛物线的对称轴交于点M ,点N 在坐标轴上,以点N ,B ,D 为顶点的三角形与△MCD 相似,求所有满足条件的点N 的坐标.(3)在抛物线上是否存在点P ,使S △PBD =6?若存在,求出点P 的坐标;若不存在,说明理由.(4)点Q 使得CQ BQ 的值最大,若存在,请直接写出点Q 解析:本题只解(3),由已知条件可以得抛物线解析式为243y x x =-+,BD 解析式为3y x =-+,由于问题中并未交待P 点在BD 的上方或下方,故要分类讨论:当P 在BD 下方时,如右上图,水平宽为OD =3,铅垂高为PE =224333x x x x x -++-=-; 当P 在BD 上方时,P 可能在左,也可以在右,但两者本质相同,如右下图,此时依然取OD =3为水平宽,则铅垂高PE =223433x x x x x -+-+-=-+.两种情况合起来就是213362x x ⨯⨯-=,即234x x -=±.当234x x -=-时,方程无实数根,即P 在BD 下方时,不可能面积为6;当234x x -=时,解得121,4x x =-=,xyEDBA C OPxy EDBCOP即当P(-1,8)或P(4,3)时,S△PBD=6.解后:从以上几例可以看到,灵活运用水平宽与铅垂高公式,可以有效解决三角形面积问题,尤其是在例3,可以将P点的两种不同的位置分类统一为PE长(绝对值)问题求解,可以有效回避原本点P在BD上方时,几何法要构造高等繁杂作法,使得问题解决简洁而快捷.老叶2015年1月26日记于温十七中。
数学类铅高乘以水宽

数学类铅高乘以水宽
铅垂线定理公式是三角形面积=铅锤高×水平宽的一半三角形面积。
物体重心与地球重心的连线称为铅垂线(用圆锥形铅垂测得)。
多用于建筑测量。
用一条细绳一端系重物,在相对于地面静止时,这条绳所在直线就是铅垂线,又称重垂线。
铅垂线地球重力场中的重力方向线。
它与水准面正交,是野外观测的基准线。
悬挂重物而自由下垂时的方向,即为此线方向,包含它的平面则称铅垂面。
判断物体是否与地面垂直,可用铅垂线法,即一根线加上一个重物。
此重物称为铅锤,铅锤受重力作用,即受万有引力的一个分力作用,让线与地面垂直,成90度角度。
水平宽铅垂高求三角形面积

作三角形铅垂高是解决三角形面积问题的一个好办法------------二次函数教学反思铅垂高 如图,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高”(h).我们可得出一种计算三角形面积的新方法:S△ABC=1\2 ah,即三角形面积等于水平宽与铅垂高乘积的一半.最近教学二次函数遇到很多求三角形面积的问题,经过研究,我发现作三角形铅锤高是解决三角形面积问题的一个好办法。
在课堂上我还风趣地说遇到“歪歪三角形中间砍一刀”,同学们很快掌握了这种方法现总结如下:如图1,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高(h)”.我们可得出一种计算三角形面积的新方法:,即三角形面积等于水平宽与铅垂高乘积的一半.DBAOyxPCBAOyxBC铅垂高水平宽ha图1例1.(2013深圳)如图,在直角坐标系中,点A的坐标为(-2,0),连结OA,将线段OA绕原点O顺时针旋转120°,得到线段OB.(1)求点B的坐标;(2)求经过A、O、B三点的抛物线的解析式;(3)在(2)中抛物线的对称轴上是否存在点C,使△BOC的周长最小?若存在,求出点C的坐标;若不存在,请说明理由.(4)如果点P 是(2)中的抛物线上的动点,且在x轴的下方,那么△PAB是否有最大面积?若有,求出此时P点的坐标及△PAB的最大面积;若没有,请说明理由.解:(1)B(1,)(2)设抛物线的解析式为y=ax(x+a),代入点B(1, ),得,因此(3)如图,抛物线的对称轴是直线x=—1,当点C位于对称轴与线段AB 的交点时,△BOC的周长最小.设直线AB为y=kx+b.所以,因此直线AB为,当x=-1时,,因此点C的坐标为(-1,/3).(4)如图,过P作y轴的平行线交AB于D.当x=-时,△PAB的面积的最大值为,此时.例2.(2014益阳)如图2,抛物线顶点坐标为点C(1,4),交x轴于点A(3,0),交y轴于点B.(1)求抛物线和直线AB的解析式;(2)点P是抛物线(在第一象限内)上的一个动点,连结PA,PB,当P点运动到顶点C时,求△CAB的铅垂高CD及;(3)是否存在一点P,使S△PAB=S△CAB,若存在,求出P点的坐标;若不存在,请说明理由.解:(1)设抛物线的解析式为:把A(3,0)代入解析式求得所以设直线AB的解析式为:由求得B点的坐标为把,代入中解得:所以图-2xCOyABD11(2)因为C点坐标为(1,4)所以当x=1时,y1=4,y2=2所以CD=4-2=2(平方单位)(3)假设存在符合条件的点P,设P点的横坐标为x,△PAB的铅垂高为h,则由S△PAB=S△CAB得化简得:解得,将代入中,解得P点坐标为例3.(2015江津)如图,抛物线与x轴交于A(1,0),B(- 3,0)两点,(1)求该抛物线的解析式;(2)设(1)中的抛物线交y轴于C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.(3)在(1)中的抛物线上的第二象限上是否存在一点P,使△PBC的面积最大?,若存在,求出点P的坐标及△PBC的面积最大值.若没有,请说明理由.解:(1)将A(1,0),B(-3,0)代中得∴∴抛物线解析式为:(2)存在。
水平宽铅垂高求三角形面积.doc
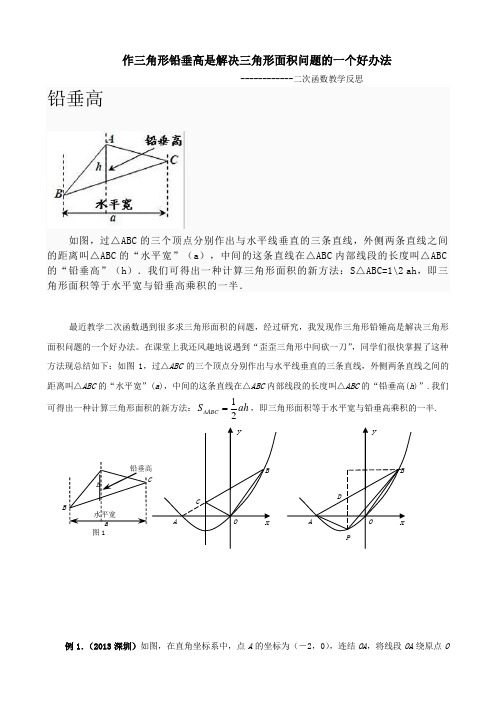
作三角形铅垂高是解决三角形面积问题的一个好办法------------二次函数教学反思铅垂高如图,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC 的“铅垂高”(h).我们可得出一种计算三角形面积的新方法:S△ABC=1\2 ah,即三角形面积等于水平宽与铅垂高乘积的一半.最近教学二次函数遇到很多求三角形面积的问题,经过研究,我发现作三角形铅锤高是解决三角形面积问题的一个好办法。
在课堂上我还风趣地说遇到“歪歪三角形中间砍一刀”,同学们很快掌握了这种方法现总结如下:如图1,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高(h)”.我们可得出一种计算三角形面积的新方法:ahSABC21=∆,即三角形面积等于水平宽与铅垂高乘积的一半.例1.(2013深圳)如图,在直角坐标系中,点A的坐标为(-2,0),连结OA,将线段OA绕原点O 图1顺时针旋转120°,得到线段OB .(1)求点B 的坐标;(2)求经过A 、O 、B 三点的抛物线的解析式;(3)在(2)中抛物线的对称轴上是否存在点C ,使△BOC 的周长最小?若存在,求出点C 的坐标;若不存在,请说明理由.(4)如果点P 是(2)中的抛物线上的动点,且在x 轴的下方,那么△PAB 是否有最大面积?若有,求出此时P 点的坐标及△PAB 的最大面积;若没有,请说明理由. 解:(1)B (1(2)设抛物线的解析式为y =ax (x+a ),代入点B (,得a,因此2y =+ (3)如图,抛物线的对称轴是直线x =—1,当点C 位于对称轴与线段AB 的交点时,△BOC 的周长最小.设直线AB 为y =kx +b .所以20.k k b k b b ⎧=⎪⎧+=⎪⎪⎨⎨-+=⎪⎩⎪=⎪⎩解得,因此直线AB为y =+,当x =-1时,y =,因此点C 的坐标为(-1). (4)如图,过P 作y 轴的平行线交AB 于D. 2221()()213212PAB PAD PBD D P B A S S S y y x x x x x x ∆∆∆=+=--⎡⎤⎫=+-+⨯⎢⎥⎪⎪⎢⎥⎝⎭⎝⎭⎣⎦=⎫=+⎪⎝⎭当x =-12时,△PAB,此时1,2P ⎛- ⎝⎭. 例2.(2014益阳) 如图2,抛物线顶点坐标为点C (1,4),交x 轴于点A (3,0),交y 轴于点B .(1)求抛物线和直线AB 的解析式;(2)点P 是抛物线(在第一象限内)上的一个动点,连结PA ,PB ,当P 点运动到顶点C 时,求△CAB 的铅垂高CD 及CAB S ∆;(3)是否存在一点P ,使S △PAB =89S △CAB ,若存在,求出P 点的坐标;若不存在,请说明理由.解:(1)设抛物线的解析式为:4)1(21+-=x a y 把A (3,0)代入解析式求得1-=a 所以324)1(221++-=+--=x x x y 设直线AB 的解析式为:b kx y +=2由3221++-=x x y 求得B 点的坐标为)3,0( 把)0,3(A ,)3,0(B 代入b kx y +=2中解得:图-2xCOy ABD113,1=-=b k 所以32+-=x y(2)因为C 点坐标为(1,4)所以当x =1时,y 1=4,y 2=2所以CD =4-2=232321=⨯⨯=∆CAB S (平方单位) (3)假设存在符合条件的点P ,设P 点的横坐标为x ,△PAB 的铅垂高为h ,则x x x x x y y h 3)3()32(2221+-=+--++-=-=由S △PAB =89S △CAB 得389)3(3212⨯=+-⨯⨯x x 化简得:091242=+-x x 解得,23=x 将23=x 代入3221++-=x x y 中,解得P 点坐标为)415,23(例3.(2015江津)如图,抛物线c bx x y ++-=2与x 轴交于A(1,0),B(- 3,0)两点,(1)求该抛物线的解析式;(2)设(1)中的抛物线交y 轴于C 点,在该抛物线的对称轴上是否存在点Q ,使得△QAC 的周长最小?若存在,求出Q 点的坐标;若不存在,请说明理由.(3)在(1)中的抛物线上的第二象限上是否存在一点P ,使△PBC 的面积最大?,若存在,求出点P 的坐标及△PBC 的面积最大值.若没有,请说明理由.解:(1)将A(1,0),B(-3,0)代2y x bx c =-++中得10930b c b c -++⎧⎨--+=⎩=∴23b c =-⎧⎨=⎩∴抛物线解析式为:223y x x =--+(2)存在。
三角形面积铅直高乘水平宽

您所指的公式是指三角形的面积,当三角形的高度是从基底到相反顶点的垂直线时,三角形的宽度是基点两个端点之间的水平距离。
公式是:
面积=(1/2)x底座x高度
其中底座是三角形的水平宽度,高度是从底座到相反顶点的垂直距离。
这被称为“按基数和高度划分的三角形面积”公式,它适用于任何三角形,无论其形状或大小。
该公式之所以有效,是因为三角形的面积等于其基数和高度乘积的一半。
需要注意的是,只有当高度是从基底到相反顶点的垂直线,并且宽度是基座两个端点之间的水平距离时,这个公式才有效。
如果高度不是垂直的或宽度不是水平的,公式将不起作用,应使用其他方法来找到区域。
铅垂高水平宽求三角形面积例题

铅垂高水平宽求三角形面积例题在阳光明媚的下午,咱们来聊聊三角形的面积吧。
说到三角形,大家肯定脑海里会浮现出那种简单的形状,有点像一块比萨饼对吧?三角形其实特别有趣,它的面积计算方法可不是随便来的哦。
咱们得提到一个重要的概念——铅垂高和水平宽。
听起来高大上,其实很简单。
想象一下,你在草地上用手指画出一个三角形,底边是宽宽的,顶尖儿高高的。
这个时候,铅垂高就像是从三角形的顶点垂下来的一条线,正好碰到底边的中间。
就好像是你在给三角形“量身高”,是不是很有意思?再说说那水平宽,它就是底边的长度,宽宽的,能让你坐下去的那种。
这两个东西的关系可重要了,正是它们让我们能算出这个三角形的面积。
哎,你知道吗?算三角形的面积其实也不难。
只要你把底边的长度和铅垂高的长度相乘,然后再除以二,简单吧?就像你在切蛋糕,先量好每块蛋糕的宽度,然后把它们的高度也量好,再除个二,嘿!这就搞定了。
公式看起来是这样的:面积=(底边×铅垂高)÷2。
就这么简单,人人都能学会!不过话说回来,面积这个概念其实在生活中到处都有。
你有没有想过,为什么房子要有面积?因为咱们得知道房子能住多少人,对吧?当你在厨房里忙活的时候,想想你做饭的那片地方,面积也在告诉你能放多少锅碗瓢盆,真是无处不在的数字。
回过头来,三角形的面积也能让我们理解更多事物,比如一些艺术作品的设计,或者是风景中的山丘,甚至是纸飞机的造型,都少不了这个简单的计算。
说到这里,不禁让我想起小时候学数学的那些日子。
记得那时候,数学老师会拿着黑板,兴致勃勃地给我们讲解这些概念,有时还会用一些生动的例子。
她说,三角形就像是站在高处的守护者,脚下稳稳的,顶上又高又尖。
而我们就是要学会利用这些知识,去探索更大的世界。
三角形的形状让人感到一种力量,那种尖锐的感觉让人觉得无所不能。
哎,别以为我光在说三角形,其实这也是个哲理的寓言。
人生不就是一个个三角形吗?有高有低,有宽有窄。
我们在这个世界上拼搏,就像在量三角形的高和宽,最终才能找到自己的位置,算出自己生活的“面积”。
水平宽铅垂高求三角形面积
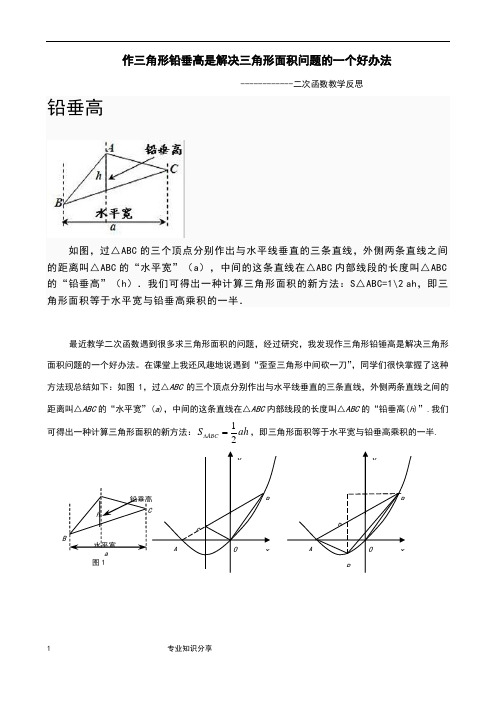
v1.0 可编辑可修改作三角形铅垂高是解决三角形面积问题的一个好办法------------二次函数教学反思铅垂高如图,过△ABC 的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC 的“水平宽”(a ),中间的这条直线在△ABC 内部线段的长度叫△ABC 的“铅垂高”(h ).我们可得出一种计算三角形面积的新方法:S△ABC=1\2 ah ,即三角形面积等于水平宽与铅垂高乘积的一半.最近教学二次函数遇到很多求三角形面积的问题,经过研究,我发现作三角形铅锤高是解决三角形面积问题的一个好办法。
在课堂上我还风趣地说遇到“歪歪三角形中间砍一刀”,同学们很快掌握了这种方法现总结如下:如图1,过△ABC 的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC 的“水平宽”(a ),中间的这条直线在△ABC 内部线段的长度叫△ABC 的“铅垂高(h )”.我们可得出一种计算三角形面积的新方法:ah S ABC 21=∆,即三角形面积等于水平宽与铅垂高乘积的一半.B铅垂高水平宽ha图1CBAOyxDBAOyxP例1.(2013深圳)如图,在直角坐标系中,点A 的坐标为(-2,0),连结OA ,将线段OA 绕原点O 顺时针旋转120°,得到线段OB .(1)求点B 的坐标;(2)求经过A 、O 、B 三点的抛物线的解析式;(3)在(2)中抛物线的对称轴上是否存在点C ,使△BOC 的周长最小若存在,求出点C 的坐标;若不存在,请说明理由.(4)如果点P 是(2)中的抛物线上的动点,且在x 轴的下方,那么△PAB 是否有最大面积若有,求出此时P 点的坐标及△PAB 的最大面积;若没有,请说明理由. 解:(1)B (1(2)设抛物线的解析式为y =ax (x+a ),代入点B(,得a,因此2y =+ (3)如图,抛物线的对称轴是直线x =—1,当点C 位于对称轴与线段AB 的交点时,△BOC 的周长最小. 设直线AB 为y =kx +b.所以20.k k b k b b ⎧=⎪⎧+=⎪⎪⎨⎨-+=⎪⎩⎪=⎪⎩解得,因此直线AB为y =+,当x =-1时,y =,因此点C 的坐标为(-1). (4)如图,过P 作y 轴的平行线交AB 于D .2221()()213212PAB PAD PBD D P B A S S S y y x x x x x x ∆∆∆=+=--⎡⎤⎫=+-+⨯⎢⎥⎪⎪⎢⎥⎝⎭⎝⎭⎣⎦=⎫=+⎪⎝⎭ 当x =-12时,△PAB,此时1,2P ⎛- ⎝⎭. 例2.(2014益阳) 如图2,抛物线顶点坐标为点C (1,4),交x 轴于点A (3,0),交y 轴于点B .(1)求抛物线和直线AB 的解析式;(2)点P 是抛物线(在第一象限内)上的一个动点,连结PA ,PB ,当P 点运动到顶点C 时,求△CAB 的铅垂高CD 及CAB S ∆;(3)是否存在一点P ,使S △PAB =89S △CAB ,若存在,求出P 点的坐标;若不存在,请说明理由.解:(1)设抛物线的解析式为:4)1(21+-=x a y 把A (3,0)代入解析式求得1-=a 所以324)1(221++-=+--=x x x y 设直线AB 的解析式为:bkx y +=2由3221++-=x x y 求得B 点的坐标为)3,0( 把)0,3(A ,)3,0(B 代入b kx y +=2中解得:3,1=-=b k 所以32+-=x y(2)因为C 点坐标为(1,4)所以当x =1时,y 1=4,y 2=2所以CD =4-2=232321=⨯⨯=∆CAB S (平方单位) (3)假设存在符合条件的点P ,设P 点的横坐标为x ,△PAB 的铅垂高为h ,则x x x x x y y h 3)3()32(2221+-=+--++-=-=由S △PAB =89S △CAB 得389)3(3212⨯=+-⨯⨯x x 化简得:091242=+-x x 解得,23=x 将23=x 代入3221++-=x x y 中,解得P 点坐标为)415,23(例3.(2015江津)如图,抛物线c bx x y ++-=2与x 轴交于A(1,0),B(- 3,0)两点,(1)求该抛物线的解析式;(2)设(1)中的抛物线交y 轴于C 点,在该抛物线的对称轴上是否存在点Q ,使得△QAC 的周长最小若存在,求出Q 点的坐标;若不存在,请说明理由.(3)在(1)中的抛物线上的第二象限上是否存在一点P ,使△PBC 的面积最大,若存在,求出点P 的坐标及△PBC 的面积最大值.若没有,请说明理由.解:(1)将A(1,0),B(-3,0)代2y x bx c =-++中得10930b c b c -++⎧⎨--+=⎩=∴23b c =-⎧⎨=⎩∴抛物线解析式为:223y x x =--+(2)存在。
三角形面积公式——之水平宽铅垂高

三角形面积公式——之水平宽铅垂高三角形是几何学中最基本的形状之一,它由三个边和三个角组成。
理解三角形面积的公式对于解决各类几何问题至关重要。
有几种不同的方法可以计算三角形的面积,其中一种基本方法是使用三角形的底和高的长度。
在本文中,我将详细介绍水平宽和垂直高的概念,并展示如何使用这些概念来计算三角形的面积。
水平宽是指从一个顶点到另一个顶点的水平距离,也就是三角形的底边。
垂直高是指从三角形的一个顶点到底边上的垂直距离。
水平宽和垂直高之间的关系可以用来计算三角形的面积。
首先,我们需要明确水平宽和垂直高对于三角形面积的重要性。
在一个三角形中,两个相邻边形成一个角,而这个角的大小取决于它们之间的夹角。
为了计算这两个边之间的角度,我们需要引入正弦和余弦等三角函数。
在一个直角三角形中,正弦函数定义为垂直高与斜边之间的比例,即sin(θ) = h/c,其中θ是角度,h是垂直高,c是斜边的长度。
正弦函数在大多数三角函数表中都有详细的值,可以通过查表或计算器来获得。
现在,让我们考虑如何使用水平宽和垂直高来计算三角形的面积。
首先,我们需要将水平宽和垂直高表示为变量。
假设水平宽为b,垂直高为h。
根据三角形的面积公式,三角形的面积等于底边的长度乘以垂直高的长度的一半,即A=(1/2)*b*h。
这个公式的推导可以用几何方法或三角函数来解释。
从几何的角度来看,可以将三角形划分为两个直角三角形,每个直角三角形的面积等于底边长度乘以垂直高的长度再除以2、因此,整个三角形的面积等于这两个直角三角形的面积之和。
另一种推导方法是使用三角函数。
根据正弦函数的定义,sin(θ) =h / c,其中h是垂直高,c是斜边的长度。
我们可以通过将等式两边都乘以c来得到h = c * sin(θ)。
由于三角形的面积等于底边乘以高的一半,所以A = (1/2) * b * h = (1/2) * b * c * sin(θ)。
这个公式的意义在于,我们可以用底边长度、斜边长度和夹角的正弦值来计算三角形的面积。
水平宽铅垂高求三角形面积 (2)

作三角形铅垂高是解决三角形面积问题的一个好办法------------二次函数教学反思铅垂高如图,过△ABC 的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC 的“水平宽”(a ),中间的这条直线在△ABC 内部线段的长度叫△ABC 的“铅垂高”(h ).我们可得出一种计算三角形面积的新方法:S△ABC=1\2 ah ,即三角形面积等于水平宽与铅垂高乘积的一半.最近教学二次函数遇到很多求三角形面积的问题,经过研究,我发现作三角形铅锤高是解决三角形面积问题的一个好办法。
在课堂上我还风趣地说遇到“歪歪三角形中间砍一刀”,同学们很快掌握了这种方法现总结如下:如图1,过△ABC 的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC 的“水平宽”(a ),中间的这条直线在△ABC 内部线段的长度叫△ABC 的“铅垂高(h )”.我们可得出一种计算三角形面积的新方法:ah S ABC 21=∆,即三角形面积等于水平宽与铅垂高乘积的一半.2,0),)求点B )中抛物的坐标;x轴的下方,那么△PAB 是否有最大面积?若有,求出此时P 点的坐标及△PAB 的最大面积;若没有,请说明理由.解:(1)B (1,(2)设抛物线的解析式为y =ax (x+a ),代入点B (1,a ,因此2y = (3)如图,抛物线的对称轴是直线x =—1,当点C 位于对称轴与线段AB 的交点时,△BOC 的周长最小.设直线AB 为y =kx +b .所以20.k k b k b b ⎧=⎪⎧+⎪⎪⎨⎨-+=⎪⎩⎪⎪⎩解得,因此直线AB 为y =,当x =-1时,y =,因此点C 的坐标为(-1).(4)如图,过P 作y 轴的平行线交AB 于D .图1当x =-12时,△PAB 的面积的最大值为938,此时13,24P ⎛⎫-- ⎪ ⎪⎝⎭. 例2.(2014益阳) 如图2,抛物线顶点坐标为点C (1,4),交x 轴于点A (3,0),交y 轴于点B .(1)求抛物线和直线AB 的解析式;(2)点P 是抛物线(在第一象限内)上的一个动点,连结PA ,PB ,当P 点运动到顶点C 时,求△CAB 的铅垂高CD 及CAB S ∆;(3)是否存在一点P ,使S △PAB =89S △CAB ,若存在,求出P 点的坐标;若不存在,请说明理由.解:(1)设抛物线的解析式为:4)1(21+-=x a y 把A (3,0)代入解析式求得1-=a 所以324)1(221++-=+--=x x x y 设直线AB 的解析式为:b kx y +=2由3221++-=x x y 求得B 点的坐标为)3,0( 把)0,3(A ,)3,0(B 代入b kx y +=2中解得:3,1=-=b k 所以32+-=x y(2)因为C 点坐标为(1,4)所以当x =1时,y 1=4,y 2=2所以CD =4-2=232321=⨯⨯=∆CAB S (平方单位) (3)假设存在符合条件的点P ,设P 点的横坐标为x ,△PAB 的铅垂高为h ,则x x x x x y y h 3)3()32(2221+-=+--++-=-=由S △PAB =89S △CAB 得389)3(3212⨯=+-⨯⨯x x 化简得:091242=+-x x 解得,23=x 将23=x 代入3221++-=x x y 中,解得P 点坐标为)415,23(例3.(2015江津)如图,抛物线c bx x y ++-=2与x 轴交于A(1,0),B(- 3,0)两点,(1)求该抛物线的解析式;(2)设(1)中的抛物线交y 轴于C 点,在该抛物线的对称轴上是否存在点Q ,使得△QAC 的周长最小?若存在,求出Q 点的坐标;若不存在,请说明理由.(3)在(1)中的抛物线上的第二象限上是否存在一点P ,使△PBC 的面积最大?,若存在,求出点P 的坐标及△PBC 的面积最大值.若没有,请说明理由. 解:(1)将A(1,0),B(-3,0)代2y x bx c =-++中得10930b c b c -++⎧⎨--+=⎩=∴23b c =-⎧⎨=⎩∴抛物线解析式为:223y x x =--+(2)存在。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
作三角形铅垂高是解决三角形面积问题的一个好办法------------二次函数教学反思铅垂高如图,过△ABC 的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC 的“水平宽”(a ),中间的这条直线在△ABC 内部线段的长度叫△ABC 的“铅垂高”(h ).我们可得出一种计算三角形面积的新方法:S△ABC=1\2 ah ,即三角形面积等于水平宽与铅垂高乘积的一半.最近教学二次函数遇到很多求三角形面积的问题,经过研究,我发现作三角形铅锤高是解决三角形面积问题的一个好办法。
在课堂上我还风趣地说遇到“歪歪三角形中间砍一刀”,同学们很快掌握了这种方法现总结如下:如图1,过△ABC 的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC 的“水平宽”(a ),中间的这条直线在△ABC 内部线段的长度叫△ABC 的“铅垂高(h )”.我们可得出一种计算三角形面积的新方法:ah S ABC 21=∆,即三角形面积等于水平宽与铅垂高乘积的一半.A 的旋转120°,得到线段OB .(1)求点B 的坐标;(2)求经过A、O、B三点的抛物线的解析式;(3)在(2)中抛物线的对称轴上是否存在点C,使△BOC的周长最小?若存在,求出点C的坐标;若不存在,请说明理由.(4)如果点P是(2)中的抛物线上的动点,且在x轴的下方,那么△PAB是否有最大面积?若有,求出此时P点的坐标及△PAB的最大面积;若没有,请说明理由.解:(1)B(1(2)设抛物线的解析式为y=ax(x+a),代入点B(a,因此2y x=(3)如图,抛物线的对称轴是直线x=—1,当点C位于对称轴与线段AB的交点时,△BOC的周长最小.设直线AB为y=kx+b.所以20.kk bk bb⎧⎪⎧+=⎪⎪⎨⎨-+=⎪⎩⎪=⎪⎩解得,因此直线AB为y,当x=-1时,y=,因此点C的坐标为(-1).(4)如图,过P作y轴的平行线交AB于D.当x=-12时,△PAB,此时1,2P⎛-⎝⎭.例2.(2014益阳)如图2,抛物线顶点坐标为点C(1,4),交x轴于点A(3,0),交y轴于点B.(1)求抛物线和直线AB的解析式;(2)点P是抛物线(在第一象限内)上的一个动点,连结PA,PB,当P点运动到顶点C时,求△CAB的铅垂高CD及CAB S ∆;(3)是否存在一点P ,使S △PAB =89S △CAB ,若存在,求出P 点的坐标;若不存在,请说明理由.解:(1)设抛物线的解析式为:4)1(21+-=x a y 把A (3,0)代入解析式求得1-=a 所以324)1(221++-=+--=x x x y 设直线AB 的解析式为:b kx y +=2由3221++-=x x y 求得B 点的坐标为)3,0( 把)0,3(A ,)3,0(B 代入b kx y +=2中解得:3,1=-=b k 所以32+-=x y(2)因为C 点坐标为(1,4)所以当x =1时,y 1=4,y 2=2所以CD =4-2=232321=⨯⨯=∆CAB S (平方单位)(3)假设存在符合条件的点P ,设P 点的横坐标为x ,△PAB 的铅垂高为h ,则x x x x x y y h 3)3()32(2221+-=+--++-=-=由S △PAB =89S △CAB 得389)3(3212⨯=+-⨯⨯x x 化简得:091242=+-x x 解得,23=x 将23=x 代入3221++-=x x y 中,解得P 点坐标为)415,23(例3.(2015江津)如图,抛物线c bx x y ++-=2与x 轴交于A(1,0),B(- 3,0)两点,(1)求该抛物线的解析式;(2)设(1)中的抛物线交y 轴于C 点,在该抛物线的对称轴上是否存在点Q ,使得△QAC 的周长最小?若存在,求出Q 点的坐标;若不存在,请说明理由.(3)在(1)中的抛物线上的第二象限上是否存在一点P ,使△PBC 的面积最大?,若存在,求出点P 的坐标及△PBC 的面积最大值.若没有,请说明理由.解:(1)将A(1,0),B(-3,0)代2y x bx c =-++中得10930b c b c -++⎧⎨--+=⎩=∴23b c =-⎧⎨=⎩∴抛物线解析式为:223y x x =--+(2)存在。
理由如下:由题知A 、B 两点关于抛物线的对称轴1x =-对称 ∴直线BC 与1x =-的交点即为Q 点, 此时△AQC 周长最小 ∵223y x x =--+∴C 的坐标为:(0,3) 直线BC 解析式为:3y x =+ Q 点坐标即为13x y x =-⎧⎨=+⎩的解∴12x y =-⎧⎨=⎩∴Q(-1,2)(3)答:存在。
理由如下:设P 点2(23) (30)x x x x --+-<<,∵92BPC BOC BPCO BPCO S S S S ∆∆=-=-四边形四边形若BPCO S 四边形有最大值,则BPC S ∆就最大,∴BPE BPCO PEOC S S S ∆+Rt 四边形直角梯形=11()22BE PE OE PE OC =⋅++ =2211(3)(23)()(233)22x x x x x x +--++---++=233927()2228x -+++ 当32x =-时,BPCO S 四边形最大值=92728+ ∴BPC S ∆最大=9279272828+-= 当32x =-时,215234x x --+=∴点P 坐标为315( )24-, 同学们可以做以下练习:OABC 的长1.(2015浙江湖州)已知如图,矩形OC=1,将△AOC 沿AC 翻折得△APC 。
(1)填空:∠PCB=____度,P 点坐标为( , );(2)若P ,A 两点在抛物线y=-43x 2+bx+c 上,求b ,c 的值,并说明点C 在此抛物线上;(3)在(2)中的抛物线CP 段(不包括C ,P 点)上,是否存在一点M ,使得四边形MCAP 的面积最大?若存在,求出这个最大值及此时M 点的坐标;若不存在,请说明理由。
2.(湖北省十堰市2014)如图①, 已知抛物线32++=bx ax y (a ≠0)与x 轴交于点A (1,0)和点B (-3,0),与y 轴交于点C .(1) 求抛物线的解析式;(2) 设抛物线的对称轴与x 轴交于点M ,问在对称轴上是否存在点P ,使△CMP 为等腰三角形?若存在,请直接写出所有符合条件的点P 的坐标;若不存在,请说明理由.(3) 如图②,若点E 为第二象限抛物线上一动点,连接BE 、CE ,求四边形BOCE 面积的最大值,并求此时E 点的坐标.图① 图②3.(2015年恩施) 如图11,在平面直角坐标系中,二次函数c bx x y ++=2的图象与x 轴交于A 、B两点, A 点在原点的左侧,B 点的坐标为(3,0),与y 轴交于C (0,-3)点, 点P 是直线BC 下方的抛物线上一动点.(1)求这个二次函数的表达式.(2)连结PO 、PC ,并把△POC 沿CO 翻折,得到四边形POP /C , 那么是否存在点P ,使四边形POP /C 为菱形?若存在,请求出此时点P 的坐标;若不存在,请说明理由.(3)当点P 运动到什么位置时,四边形 ABPC 的面积最大并求出此时P 点的坐标和四边形ABPC 的最大面积.解:(1)将B 、C 两点的坐标代入得⎩⎨⎧-==+303c c b解得:⎩⎨⎧-=-=32c b 所以二次函数的表达式为:322--=x x y(2)存在点P ,使四边形POP /C 为菱形.设P 点坐标为(x ,322--x x ),PP /交CO 于E 若四边形POP /C 是菱形,则有PC=PO .连结PP /则PE ⊥CO 于E ,∴OE=EC =23 y =23-.∴322--x x =23- 解得1x =2102+,2x =2102-(不合题意,舍去) ∴P 点的坐标为(2102+,23-) (3)过点P 作y 轴的平行线与BC 交于点Q ,与OB 交于点F ,设P (x ,322--x x ),易得,直线BC 的解析式为3-=x y 则Q 点的坐标为(x ,x -3).图=87523232+⎪⎭⎫ ⎝⎛--x当23=x 时,四边形ABPC 的面积最大 此时P 点的坐标为⎪⎭⎫⎝⎛-415,23,四边形ABPC 的面积875的最大值为.25.(2015绵阳)如图,抛物线y = ax 2 + bx + 4与x 轴的两个交点分别为A (-4,0)、B (2,0),与y 轴交于点C ,顶点为D .E (1,2)为线段BC 的中点,BC 的垂直平分线与x 轴、y 轴分别交于F 、G .(1)求抛物线的函数解析式,并写出顶点D 的坐标;(2)在直线EF 上求一点H ,使△CDH 的周长最小,并求出最小周长; (3)若点K 在x 轴上方的抛物线上运动,当K 运动到什么位置时,△EFK 的面积最大?并求出最大面积.【解析】(1)由题意,得 ⎩⎨⎧=++=+-,0424,04416b a b a 解得21-=a ,b =-1. 所以抛物线的解析式为4212+--=x x y ,顶点D 的坐标为(-1,29).(2)设抛物线的对称轴与x 轴交于点M .因为EF 垂直平分BC ,即C 关于直线EG 的对称点为B ,连结BD 交于EF 于一点,则这一点为所求点H ,使DH + CH 最小,即最小为DH + CH = DH + HB = BD =132322=+DM BM . 而 25)429(122=-+=CD .∴ △CDH 的周长最小值为CD + DR + CH =21335+.设直线BD 的解析式为y = k1x + b ,则 ⎪⎩⎪⎨⎧=+-=+,29,021111b k b k 解得 231-=k ,b1 = 3. 所以直线BD 的解析式为y =23-x + 3.由于BC = 25,CE = BC ∕2 =5,Rt △CEG ∽△COB ,得 CE : CO = CG : CB ,所以 CG = 2.5,GO = 1.5.G (0,1.5).同理可求得直线EF 的解析式为y =21x +23.联立直线BD 与EF 的方程,解得使△CDH 的周长最小的点H (43,815).(3)如图所示,设K (t ,4212+--t t ),xF <t <xE .过K 作x 轴的垂线交EF 于N .则 KN = yK -yN =4212+--t t -(21t +23)=2523212+--t t .所以 S △EFK = S △KFN + S △KNE =21KN (t + 3)+21KN (1-t )= 2KN = -t 2-3t+ 5 =-(t +23)2 +429.即当t =-23时,△EFK 的面积最大,最大面积为429,此时K (-23,835).平面直角坐标系中三角形面积的求法我们常常会遇到在平面直角坐标系中求三角形面积的问题.解题时我们要注意其中的解题方法和解题技巧.1.有一边在坐标轴上:例1:如图1,平面直角坐标系中,△ABC的顶点坐标分别为(-3,0),(0,3),(0,-1),求△ABC的面积.分析:根据三个顶点的坐标特征可以看出,△ABC的边BC在y轴上,由图形可得BC=4,点A到BC边的距离就是A点到y轴的距离,也就是A点横坐标的绝对值3,然后根据三角形的面积公式求解.2.有一边与坐标轴平行:例2:如图2,三角形ABC三个顶点的坐标分别为A(4,1),B(4,5),C(-1,2),求△ABC的面积.分析:由A(4,1),B(4,5)两点的横坐标相同,可知边AB与y轴平行,因而AB的长度易求.作AB边上的高CD,就可求得线段CD的长,进而可求得三角形ABC的面积.??????????????????????3.三边均不与坐标轴平行:例3:分析:由于三边均不平行于坐标轴,所以我们无法直接求边长,也无法求高,因此得另想办法.4.三角形面积公式的推广:过△ABC三个顶点分别作与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高”(h).我们可得出一种计算三角形面积的新方法:S△ABC =21ah即三角形面积等于水平宽与铅垂高乘积的一半例4:已知:直线l1:y=﹣2x+6与x轴交于点A,直线l2:y=x+3与y轴交于点B,直线l1、l2交于点C.(Ⅰ)建立平面直角坐标系,画出示意图并求出C点的坐标;(Ⅱ)利用阅读材料提供的方法求△ABC的面积.5.巩固练习:(1)已知:如图,直线bkxy+=与反比例函数'kyx=(x<0)的图象相交于点A、点B,与x轴交于点C,其中点A的坐标为(-2,4),点B的横坐标为-4.(Ⅰ)试确定反比例函数的关系式;(Ⅱ)求△AOC的面积.(2)如图,在直角坐标平面内,函数m y x=(0x >,m 是常数)的图象经过(14)A ,,()B a b ,,其中1a >.过点A 作x 轴垂线,垂足为C ,过点B 作y 轴垂线,垂足为D ,连结AD ,DC ,CB .若ABD △的面积为4,求点B 的坐标;(3)已知,直线与x 轴、y 轴分别交于点A 、B ,以线段AB 为直角边在第一象限内作等腰Rt△ABC,∠BAC=90°.且点P (1,a )为坐标系中的一个动点.(Ⅰ)求三角形ABC 的面积S △ABC ;(Ⅱ)请说明不论a 取任何实数,三角形BOP 的面积是一个常数; (Ⅲ)要使得△ABC 和△ABP 的面积相等,求实数a 的值.。
