宁夏师范学院数学与计算机科学学院

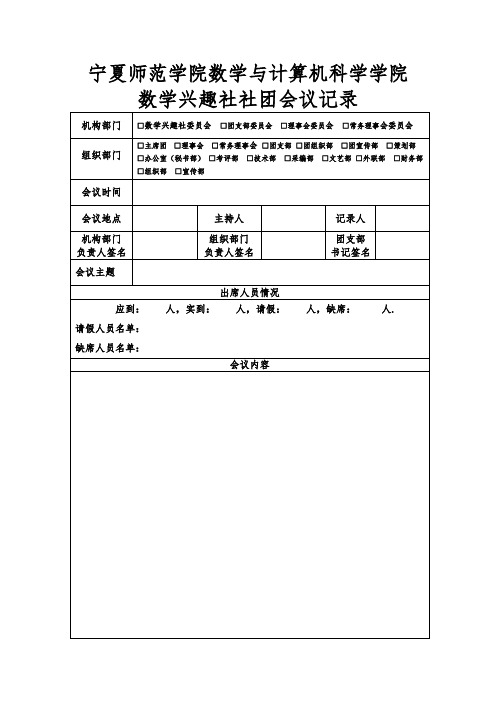
宁夏师范学院数学与计算机科学学院
《计算机图形学》实验报告
实验序号：2 实验项目名称：直线的扫描转换学号77 姓名王艳艳专业、班级14计本一班
实验地点文科楼206 指导教师罗晓丽时间2017.3.17 一、实验目的：
学会使用MFC，能够运用直线的三种扫描算法即数值微分算法（DDA算法）、中点画线算法和Bresenham画线算法绘制直线，并熟悉掌握制作过程。

二、实验环境：
Windows 7
VC++ 6.0
三、实验内容：
打开vc6.0,点击新建—>工程—>MFC AppWizard [exe]，创建项目名称（随便写），确定位置，然后点击确定。

选择创建的应用类型—>单文档—>完成。

点击确定。

DDA算法：
添加成员函数：
1.展开Wangyanyan classes—>右击WangyanyanView—>选择Add Member Funtion （添加成员函数）—>函数类型定义为void，函数描述为：DDAline—>点击确定
2.展开Wangyanyan classes—>CWangyanyanView—>在DDAline（）函数里添加形参int x0,int y0,int x1,int y1,int color,CClientDC & dc
3.双击CWangyanyanView，在public中添加代码：
void CWangyanyanjView::DDAline(int x0,int y0,int x1,int y1,int color,CClientDC & dc);
记住最后加分号
4.展开CWangyanyan—>双击OnDraw—>添加代码：
CClientDC dc(this);
DDAline(8,12,20,20,RGB(255,145,200),dc);
5.双击DDAline，在函数体内编写如下代码：
void CDWangyanyanView::DDAline(int x0,int y0,int x1,int y1,int color,CClientDC & dc)
{
CPen newpen(PS_SOLID,1,color);
dc.SelectObject(&newpen);
int x,dx,dy,y,k;
dx=x1-x0;
dy=y1-y0;
k=dy/dx;
y=y0;
for(x=x0;x<=x1;x++)
{
dc.SetPixel(x,int(y+0.5),color);
y=y+k;
}
}
调试程序：
运行结果：
中点画线算法：添加成员函数
1.展开Wangyanyan classes—>右击CWangyanyanView—>选择Add Member Funtion（添加成员函数）—>函数类型定义为void，函数描述为：MidpointLine —>点击确定
2.展开classes—>CWangyanyanview，在MidpointLine函数里添加形参int x0,int y0,int x1,int y1,int color,CClientDC & dc
3.双击CWangyanyanView，在public中添加代码：
void CWangyanyanView::MidpointLine(int x0,int y0,int x1,int y1,int color,CClientDC & dc);最后加分号
4.展开CWangyanyanView—>双击OnDraw—>添加代码：
MidpointLine(20,15,200,485,RGB(80,120,255), dc);
5.双击MidpointLine，在函数体内编写如下代码：
调试程序：
运行结果：
Bresenham算法：
添加成员函数
1.展开Wangyanyan classes—>右击CWangyanyanView—>选择Add Member Funtion，函数类型定义为void，函数描述为：Bresenham_Line—>点击确定
2.点击classes—>CWangyanyanview，在Bresenham_Line函数里添加形参int x0,int y0,int x1,int y1,int color,CClientDC & dc
3.双击CWangyanyanView，在public中添加代码：
void CWangyanyanView::Bresenham_Line(int x0,int y0,int x1,int y1,int color,CClientDC & dc)，最后加分号
4.展开CPwjView—>双击OnDraw—>添加代码：
Bresenham_Line(65,12,400,450,RGB(20,180,250), dc);
5.双击Bresenham_Line，在函数体内编写如下代码：
int x,y,dx,dy,e,i;
dx=x1-x0;
dy=y1-y0;
e=-dx;
x=x0;
y=y0;
for(i=0;i<=dx;i++)
{
dc.SetPixel(x,y,color);
x=x+1;
e=e+2*dy;
if(e>=0)
{
y=y+1;
e=e-2*dx;
}
}
调试程序：
运行结果：
. 11 / 11'.
教师评语
签名：
日期： 年 月 日
成绩。