结构力学计算题及问题详解
结构力学习题及答案

结构力学习题及答案结构力学习题及答案结构力学是工程学中的重要学科之一,它研究物体在外力作用下的变形和破坏。
在工程实践中,结构力学的应用广泛,涉及到建筑、桥梁、航空航天等领域。
在学习结构力学时,练习解答一些习题是非常重要的,下面我将给大家提供一些常见的结构力学习题及其答案。
题目一:简支梁的弯矩计算已知一根长度为L的简支梁,两端受到均布载荷q。
求梁的中点处的弯矩M。
解答一:根据简支梁的受力分析,可以得出梁的弯矩与距离中点的距离x之间的关系为M=qL/8-x^2/2,其中x为距离中点的距离。
因此,中点处的弯矩M=qL/8。
题目二:悬臂梁的挠度计算已知一根长度为L的悬臂梁,端部受到集中力F作用。
求梁的端部挠度δ。
解答二:根据悬臂梁的受力分析,可以得出梁的端部挠度与力F之间的关系为δ=FL^3/3EI,其中F为作用力,E为梁的杨氏模量,I为梁的截面惯性矩。
因此,梁的端部挠度δ=FL^3/3EI。
题目三:刚度计算已知一根长度为L的梁,截面形状为矩形,宽度为b,高度为h,梁的杨氏模量为E。
求梁的刚度K。
解答三:梁的刚度可以通过计算梁的弯曲刚度和剪切刚度得到。
弯曲刚度Kb可以通过梁的截面惯性矩I和杨氏模量E计算得到,即Kb=E*I/L。
剪切刚度Ks可以通过梁的剪切模量G和梁的截面面积A计算得到,即Ks=G*A/L。
因此,梁的刚度K=Kb+Ks=E*I/L+G*A/L。
题目四:破坏载荷计算已知一根长度为L的梁,截面形状为圆形,直径为d,梁的杨氏模量为E。
求梁的破坏载荷P。
解答四:梁的破坏载荷可以通过计算梁的破坏弯矩和破坏挠度得到。
破坏弯矩Mf可以通过梁的截面惯性矩I和杨氏模量E计算得到,即Mf=π^2*E*I/L^2。
破坏挠度δf可以通过梁的破坏弯矩Mf和梁的刚度K计算得到,即δf=Mf/K。
因此,梁的破坏载荷P=Mf/L=π^2*E*I/L^3。
结构力学是一门综合性较强的学科,掌握结构力学的基本原理和解题方法对于工程师来说非常重要。
结构力学计算题及结构力学练习题含答案

结构力学计算题及结构力学练习题含答案结构力学是研究结构在外力作用下内力和变形规律的科学,以下是一篇结构力学计算题及练习题,包括答案的示例。
结构力学计算题题目:一简支梁AB,跨度为4米,受到均布荷载q=2 kN/m,梁的截面惯性矩I=1.2×10^6 mm^4,弹性模量E=210 GPa。
求梁的最大弯矩和最大挠度。
解题步骤:1. 计算梁的最大弯矩Mmax。
根据简支梁受均布荷载的弯矩公式:\[ M_{max} = \frac{ql^2}{8} \]代入已知数据:\[ M_{max} = \frac{2 \times 4^2}{8} = 4 \text{ kN·m} \]2. 计算梁的最大挠度y_max。
根据简支梁受均布荷载的挠度公式:\[ y_{max} = \frac{ql^4}{384EI} \]代入已知数据:\[ y_{max} = \frac{2 \times 4^4}{384\times 1.2 \times 10^6 \times 210 \times 10^9} = 0.00017 \text{ m} = 0.17 \text{ mm} \]答案:梁的最大弯矩Mmax为4 kN·m,最大挠度y_max为0.17 mm。
---结构力学练习题1. 一悬臂梁CD,长度为3米,受到集中力F=5 kN作用在自由端,梁的截面惯性矩I=1.5×10^6 mm^4,弹性模量E=200 GPa。
求悬臂梁的最大弯矩和最大挠度。
答案:最大弯矩Mmax为5 kN·m,最大挠度y_max为0.013 mm。
2. 一连续梁EF,跨度为6米,分为两段,每段长度为3米,中间有一支点G。
梁上受到均布荷载q=1.5kN/m,梁的截面惯性矩I=2×10^6 mm^4,弹性模量E=220 GPa。
求支点G的反力及中间梁段的最大弯矩。
答案:支点G的反力为4.5 kN,中间梁段的最大弯矩为2.25 kN·m。
结构力学重点题目及解析分享

结构力学重点题目及解析分享结构力学是工程学中的重要学科,主要研究物体的力学性能和结构行为。
在学习结构力学过程中,解析重点题目是提高理解和掌握能力的关键。
本文将分享一些结构力学的重点题目及解析方法,希望对您的学习有所帮助。
1. 弹性力学题目及解析题目:一根长为L、截面积为A的均匀细棒,两端悬挂在两个支点上,求当棒受到作用力P时,支点的反力和棒的变形。
解析:根据均匀细棒的悬挂条件,棒在两个支点处受到反力R1和R2,且棒沿着重力方向存在变形。
应用弹性力学原理,可以得到以下解析步骤:1) 根据受力平衡条件,得到R1 + R2 = P;2) 利用弹性力学公式σ = Eε,其中σ为应力,E为弹性模量,ε为应变,根据变形计算得到棒的伸长量;3) 根据材料的本构关系,得到变形与应力的关系,进一步计算出R1和R2。
通过解析上述弹性力学题目,可以深入理解均匀细棒的受力分析和变形计算方法。
2. 梁的挠曲问题题目及解析题目:一根长度为L、截面形状为矩形的梁,在其一端施加一个力F,求梁的挠曲程度。
解析:梁的挠曲问题是结构力学中的经典问题之一。
解析该题目的步骤如下:1) 根据梁受力平衡条件,得到力F在梁上的均匀分布;2) 假设梁在y轴上的挠曲程度为y(x),并应用梁的挠曲方程EI(d^2y/dx^2) = M(x),其中E为弹性模量,I为截面惯性矩,M(x)为弯矩分布;3) 根据力F在梁上的均匀分布,得到弯矩M(x)的表达式;4) 解微分方程EI(d^2y/dx^2) = M(x),得到梁的挠曲函数y(x);5) 利用边界条件,求解得到梁的挠曲程度。
通过解析上述梁的挠曲问题,可以学习到梁的挠曲方程的应用和求解方法。
3. 桁架结构力学问题题目及解析题目:一个由杆件连接而成的平面桁架结构,已知每个杆件的长度和受力情况,求解整个桁架结构的受力分析。
解析:桁架结构是一种广泛应用于工程和建筑领域的结构形式。
解析该题目的步骤如下:1) 根据每个杆件的长度和连接方式,建立杆件的几何模型;2) 根据受力平衡条件和杆件内力的平衡条件,构建整个桁架结构的联立方程组;3) 利用方法求解联立方程组,得到每个杆件的受力情况;4) 进一步进行应力、变形等的计算和分析。
结构力学专题习题解答_图文

圆盘转动时的惯性力偶为 平衡方程
其中 利用初始条件得
16-13试求图示梁的自振频率和主振型。梁承重可略去不计 EI=常数
P1=1
解:(1)计算自振频率 分别画出该梁在P1=1,P2=1作用 下的弯矩图M1,M2
P2=1
(2)计算主振型
16-21用振型分解法重作题16-19
解:由于此刚架振动时,各横梁不 能竖向地移动和转动而只能作水 平移动。故只有三个自由度。 (1)按刚度系数如图
(2)确定主振型
由于上式的系数行列式为0。故三个方程中只有两个是独立 的,可有三个方程中任取两个计算得
(3) 求广义质量
(4)广义荷载为
由于荷载为简谐振动, 其正则坐标幅值为
(5)求位移幅值
得 :
, ,
试求下图楔形悬臂梁的自振频率。设梁的截面宽度b=1,截面高度为
直线变化
。
:
解 截面惯性矩 :
单位长的质量
设其振型函数为 :
因
,满足边界条件,
所以
如图所示为一圆轴AB,a端有一圆盘。设圆轴质量远比圆盘小 当t=0时,圆轴受有扭转变形,圆,盘具有初始角位移 和初始速度
,然后体系作自由振动,圆盘在任一时刻t的转角为 ,转动 惯量 ,试出体系自由振动的微分方程及其解答。
该刚架的极限荷载pu=32Mu/5L
θ
机构四
15-9 试用静力法求图示结构的稳定方程及临界荷载
l
l
l
解 :
• 平衡微分方程为:
• 边界条件为 :
• 因此得齐次方程为 :
• 特征方程
16-9 图示悬臂梁具有一重量G=12KN的集中质量,其上受有振动荷载 其中p=5KN。若不考虑阻尼,试分别计算该梁在 振动
结构力学试题答案

结构力学试题答案结构力学是一门研究结构受力和变形规律的学科,对于工程领域的学生来说,掌握这门学科的知识至关重要。
以下是一套结构力学试题的答案及详细解析。
一、选择题1、关于静定结构的内力,下列说法正确的是()A 内力与杆件的材料性质无关B 内力与杆件的截面形状无关C 内力与结构所受的荷载有关D 以上都对答案:D解析:静定结构的内力只与结构的几何形状、约束条件和所受荷载有关,而与杆件的材料性质和截面形状无关。
2、图示刚架,支座 A 发生竖向位移 a,支座 B 发生水平位移 b,不计杆件的轴向变形,利用单位荷载法求 C 点的竖向位移时,应在 C 点施加的单位力是()A 竖向单位集中力B 水平单位集中力C 顺时针单位集中力偶D 逆时针单位集中力偶答案:A解析:要求 C 点的竖向位移,应在 C 点施加竖向单位集中力。
3、力法的基本未知量是()A 多余约束力B 广义位移C 结点位移D 杆件内力答案:A解析:力法是以多余约束力为基本未知量,将超静定结构转化为静定结构进行分析。
二、填空题1、平面桁架在计算杆件内力时,通常采用__________法。
答案:节点法、截面法解析:节点法是依次取桁架的节点为研究对象,利用平衡条件求出杆件内力;截面法是用一截面截取桁架的一部分作为研究对象,利用平衡条件求出杆件内力。
2、梁在集中力作用处,剪力图发生__________,弯矩图发生__________。
答案:突变、转折解析:集中力会使剪力发生突变,弯矩发生转折。
3、结构的稳定性是指结构在__________作用下,保持其原有平衡状态的能力。
答案:微小干扰解析:稳定性指结构在微小干扰作用下不发生显著的变形或失去平衡。
三、计算题1、图示简支梁,受均布荷载 q 作用,跨度为 l ,求支座 A、B 的反力。
解:对整体进行受力分析,由平衡方程∑Fy = 0 可得:RA + RB ql = 0 (1)对 A 点取矩,由∑MA = 0 可得:RB × l ql × l/2 = 0 (2)联立(1)(2)解得:RA = ql/2 ,RB = ql/22、用力法计算图示超静定梁,EI 为常数。
结构力学计算题经典(有答案)
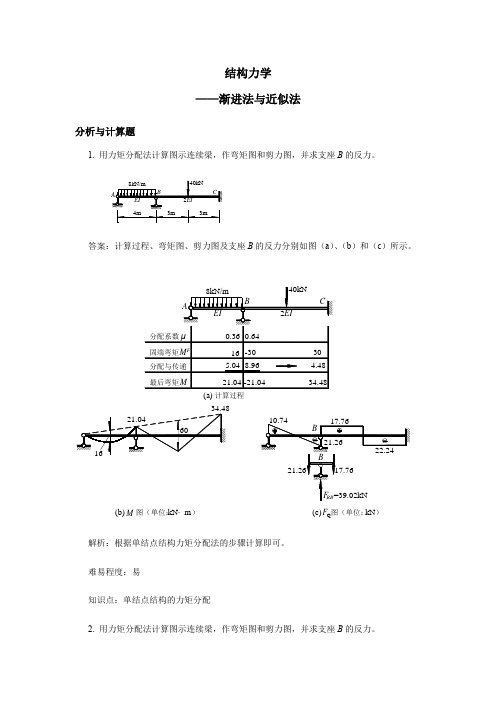
结构力学 ——渐进法与近似法分析与计算题1. 用力矩分配法计算图示连续梁,作弯矩图和剪力图,并求支座B 的反力。
答案:计算过程、弯矩图、剪力图及支座B 的反力分别如图(a )、(b )和(c )所示。
解析:根据单结点结构力矩分配法的步骤计算即可。
难易程度:易知识点:单结点结构的力矩分配2. 用力矩分配法计算图示连续梁,作弯矩图和剪力图,并求支座B 的反力。
A60kN 40kN·m EIEI B C4m4m6m(b)M 图(单位: )kN·m 图(单位: )(c)kNQ F (a)计算过程答案:图(a )为求解结点B 约束力矩的受力分析图。
计算过程、弯矩图、剪力图及支座B 的反力分别如图(b )、(c )和(d )所示。
解析:根据单结点结构力矩分配法的步骤计算即可。
难易程度:中知识点:单结点结构的力矩分配3. 用力矩分配法计算图示连续梁,作弯矩图和剪力图,并求支座B 的反力。
答案:CD 段为静定悬臂梁,将其截开并暴露出截面C 的弯矩,用力矩分配法计算如图(a )所示结构。
弯矩图和剪力图如图(b )、(c )所示。
BCEIN/m2EI m3m3m40kN(b)计算过程F BM (a)图(单位: )(c)M kN·m图(单位: )Q F (d)kN10kN20kN12kN/m ABCDEI 2EI 2m 4m4m解析:根据单结点结构力矩分配法的步骤计算即可。
本题中悬臂段CD 若不切除,则可按B 、C 两个刚结点的结构进行计算。
难易程度:中知识点:单结点结构的力矩分配4. 用力矩分配法计算图示连续梁,作弯矩图和剪力图,并求支座B 的反力。
答案:AB 段为静定悬臂梁,将其截开并暴露出截面B 的弯矩,用力矩分配法计算过程如图(a )所示。
弯矩图和剪力图图(b )、(c )所示。
kNQ F (c)图(单位: )m M 图(单位: )(b)RB F =63.02kN ( )计算过程(a)mkN·10kN/m 60kN EI 2IB CD2m6m2m解析:根据单结点结构力矩分配法的步骤计算即可。
《结构力学》习题解答(内含解答图)

解:将固定铰支座换为单铰,如图(b),由于与基础的约束多余三个,故基础作为刚片Ⅰ。铰结BF为刚片Ⅱ,铰结△CDE为刚片Ⅲ。刚片Ⅰ与刚片Ⅱ是由杆AB和支撑杆F相连,虚铰在无穷远处,刚片Ⅰ与刚片Ⅲ是由杆AC和支撑杆E相连,虚铰在两杆的延长线的交点处,而刚片Ⅱ与刚片Ⅲ是由杆BC和杆FD相连,虚铰在两杆的延长线的交点处。此时,三铰不共线,该体系为几何不变体,且无多余约束。
所以,体系是几何不变得,且无多余约束。
习题2-2试对图示体系进行几何组成分析。
解:从图2-15(b)可知,杆件CD和链杆3及铰D构成二元体,可以去掉;取杆件CB为刚片Ⅰ,基础作为刚片Ⅱ,根据规则一,两刚片是通过杆AB、链杆1、2组成几何不变体。所以,整个体系为几何不变体系,且无多余约束。
习题2-2图习题2-2解答图
习题2-10试对图示体系进行几何组成分析。
习题2-10图习题2-10解答图
解:由于与基础的约束多余三个,故基础作为刚片Ⅰ。铰结△ABF为刚片Ⅱ,铰结△BCD为刚片Ⅲ。刚片Ⅰ与刚片Ⅱ是由杆EA和支撑杆F相连,虚铰在两杆的延长线的交点处,刚片Ⅰ与刚片Ⅲ是由杆EC和支撑杆D相连,虚铰在两杆的延长线的交点处,而刚片Ⅱ与刚片Ⅲ是铰B相连。此时,三铰不共线,该体系为几何不变体,且无多余约束。
习题2-26图习题2-26解答图
解:将链杆截断,截断一处,去掉一个约束,共去掉四个约束;再将刚性联结杆截断,截断一处,去掉三个约束,共去掉十二个约束,如图(b)。此时,体系变成与基础独立相连的三个单一杆件,见图(b)。所以,该体系具有十六个多余约束的几何不变体。
2.3.2提高题
提高题2-1 试对图示体系作几何组成分析。
所以,由规则一知,体系是几何不变体,且无多余约束。
结构力学计算题及问题详解

标准文档《结构力学》计算题61.求以以下图所示刚架的弯矩图。
DCqaBa Aa a62.用结点法或截面法求图示桁架各杆的轴力。
63. 请用叠加法作以以下图所示静定梁的M 图。
64.作图示三铰刚架的弯矩图。
65.作图示刚架的弯矩图。
66. 用灵巧法作以以下图中M E、F L、 F R的影响线。
QB QBFp = 1A EBC D1m 1m2m2m2m67.作图示结构 M F、F QF的影响线。
68. 用灵巧法作图示结构影响线M F , F QB L。
69. 用灵巧法作图示结构M C , F QB R的影响线。
70. 作图示结构 F QB、M E、 F QE的影响线。
71.用力法作以以下图所示刚架的弯矩图。
PCB DlAEI =常数l l72.用力法求作以以下图所示刚架的M 图。
73.利用力法计算图示结构,作弯矩图。
74.用力法求作以以下图所示结构的M 图 ,EI= 常数。
75. 用力法计算以以下图所示刚架,作M 图。
76.77.78.79.80.81.82.83.84.85.答案61. 解:D 2qa 2/ 32qa 2/ 32C2qa/ 3qq ( 2a ) 2/ 8 = qa 2 / 2BF xBF xAF yBA F yA取整体为研究对象,由M A 0 ,得2aF yB aF xB 2qa 2 0 ( 1)(2 分)取 BC 部分为研究对象,由M C 0 ,得aF yB aF xB ,即 F yBF xB ( 2) (2 分 )由 (1) 、 (2) 联立解得 F xBFyB2qa (2 分 )34F x 0 有F xA 2qaFxBFxA由解得qa (1 分 )3由F y 0 有 F yAFyB解得FyAFyB2qa (1 分)4 223则 M D2aF yB aF xBqa 2 qa 2 qa 2 ()(2 分)3 3 3弯矩图 (3 分)62. 解:( 1)判断零杆( 12 根)。
( 4 分)( 2)节点法进行内力计算,结果如图。
结构力学精彩试题与问题详解汇总情况(完整版)

院(系) 学号 姓名 .密封线内不要答题 密封……………………………………………………………………………………………………………………………………………………结构力学试题答案汇总结构力学课程试题 ( B )卷考 试 成 绩题号 一二三四成绩得分一、选择题(每小题3分,共18分)1. 图 示 体 系 的 几 何 组 成 为 : ( ) A. 几 何 不 变 , 无 多 余 联 系 ; B. 几 何 不 变 , 有 多 余 联 系 ; C. 瞬变 ; D. 常 变 。
2. 静 定 结 构 在 支 座 移 动 时 , 会 产 生 : ( )A. 力 ;B. 应 力 ;C. 刚 体 位 移 ;D. 变 形 。
3. 在 径 向 均 布 荷 载 作 用 下 , 三 铰 拱 的 合 理 轴 线 为: ( )A .圆 弧 线 ;B .抛 物 线 ;C .悬 链 线 ;D .正 弦 曲 线 。
4. 图 示 桁 架 的 零 杆 数 目 为 : ( )A. 6;B. 7;C. 8;D. 9。
5. 图a 结构的最后弯矩图为:()A.图b;B.图c ;C.图d ;D.都不对。
6. 力法方程是沿基本未知量方向的:()A.力的平衡方程;B.位移为零方程;C.位移协调方程;D.力的平衡及位移为零方程。
二、填空题(每题3分,共9分)1.从几何组成上讲,静定和超静定结构都是_________体系,前者_________多余约束而后者_____________多余约束。
2. 图b 是图a 结构________ 截面的_______ 影响线。
3. 图示结构AB 杆B 端的转动刚度为________, 分配系数为________, 传递系数为_____。
三、简答题(每题5分,共10分)1.静定结构力分析情况与杆件截面的几何性质、材料物理性质是否相关?为什么?2.影响线横坐标和纵坐标的物理意义是什么?四、计算分析题,写出主要解题步骤(4小题,共63分)1.作图示体系的几何组成分析(说明理由),并求指定杆1和2的轴力。
结构力学试题答案

结构力学试题答案结构力学是一门研究结构的受力、变形和稳定性的学科,对于工程设计和建筑领域具有重要意义。
以下是一套结构力学试题的答案及详细解析。
一、选择题1、平面桁架在节点荷载作用下,各杆内力()A 均为压力B 均为拉力C 只有轴力D 只有剪力答案:C解析:平面桁架在节点荷载作用下,各杆只承受轴力,不承受剪力和弯矩。
2、三铰拱在竖向荷载作用下,其合理拱轴线为()A 二次抛物线B 圆弧线C 悬链线D 任意曲线答案:A解析:在竖向荷载作用下,三铰拱的合理拱轴线是二次抛物线。
3、梁的挠曲线近似微分方程在()条件下成立。
A 小变形B 材料服从胡克定律C 同时满足 A 和 BD 大变形答案:C解析:梁的挠曲线近似微分方程的成立需要同时满足小变形和材料服从胡克定律这两个条件。
4、用力法求解超静定结构时,基本未知量为()A 多余约束力B 广义位移C 节点位移D 内力答案:A解析:力法的基本未知量是多余约束力。
5、位移法的基本未知量是()A 多余约束力B 节点位移C 广义位移D 内力答案:B解析:位移法是以节点位移作为基本未知量来求解结构的内力。
二、填空题1、结构的计算简图应能反映结构的实际受力情况,又要便于计算。
其简化的主要内容包括:_____、_____、_____。
答案:杆件的简化、支座的简化、荷载的简化2、平面体系的几何组成分析中,三个刚片用三个铰两两相连,且三个铰不在一直线上,则组成_____体系。
答案:无多余约束的几何不变3、静定梁在集中力作用处,剪力图发生_____,弯矩图发生_____。
答案:突变、转折4、影响线是表示单位移动荷载作用下,某一量值的变化规律,其横坐标表示_____,纵坐标表示_____。
答案:移动荷载的位置、某一量值的大小5、用位移法计算有侧移刚架时,在基本未知量中加入_____,以考虑侧移的影响。
答案:侧移未知量三、简答题1、简述静定结构和超静定结构的区别。
答:静定结构是指在几何组成上没有多余约束,仅用静力平衡方程就能求出全部支座反力和内力的结构。
《结构力学》典型习题与解答

《结构力学》经典习题及详解一、判断题(将判断结果填入括弧内,以√表示正确,以×表示错误。
)1.图示桁架结构中有 3 个杆件轴力为0 。
(×)F P2。
(×) 2.图示悬臂梁截面 A 的弯矩值是qlq Al l3.静定多跨梁中基本部分、附属部分的划分与所承受的荷载无关。
(√)4.一般来说静定多跨梁的计算是先计算基本部分后计算附属部分。
(×)5.用平衡条件能求出全部内力的结构是静定结构。
(√)6.求桁架内力时截面法所截取的隔离体包含两个或两个以上的结点。
(√)7.超静定结构的力法基本结构不是唯一的。
(√)8.在桁架结构中,杆件内力不是只有轴力。
(×)9.超静定结构由于支座位移可以产生内力。
(√)10.超静定结构的内力与材料的性质无关。
(×)11.力法典型方程的等号右端项不一定为0。
(√)12.计算超静定结构的位移时,虚设力状态可以在力法的基本结构上设。
(√)13.用力矩分配法计算结构时,汇交于每一结点各杆端分配系数总和为1,则表明分配系数的计算无错误。
(×)14.力矩分配法适用于所有超静定结构的计算。
(×)15.当AB 杆件刚度系数S AB 3i 时,杆件的 B 端为定向支座。
(×)二、单项选择题(在每小题的四个备选答案中选出一个正确答案,并将其代号填在题干后面的括号内。
不选、错选或多选者,该题无分。
)1.图示简支梁中间截面的弯矩为( A )ql2 2ql qlA.8 B . 42qlql 2C. 2D.2.超静定结构在荷载作用下产生的内力与刚度(B)A.无关 B .相对值有关C.绝对值有关D.相对值绝对值都有关3.超静定结构的超静定次数等于结构中( B )A.约束的数目B.多余约束的数目C.结点数 D .杆件数4.力法典型方程是根据以下哪个条件得到的(C)。
A.结构的平衡条件B.结构的物理条件C.多余约束处的位移协调条件D.同时满足A、B两个条件5.图示对称结构作用反对称荷载,杆件EI 为常量,利用对称性简化后的一半结构为(A )。
结构力学自由度的计算例题及解析

1. 对于一个简单的平面桁架结构,若共有6个节点和10根构件,那么其自由度为多少?- A. 6- B. 8- C. 10- D. 122. 在一个平面梁结构中,每个支座具有多少个约束?- A. 1- B. 2- C. 3- D. 43. 计算一个刚性连接的平面框架结构的自由度时,若结构有8个节点和12根构件,自由度公式为:自由度 = 3n - 2j,其中n是节点数,j是构件数。
该结构的自由度是多少?- A. 4- B. 6- C. 8- D. 104. 一个平面结构中,假设有4个节点,6根构件,所有构件都在一个平面上,计算其自由度时需考虑:- A. 3自由度每节点,减去2自由度每构件- B. 2自由度每节点,减去1自由度每构件- C. 2自由度每节点,减去2自由度每构件- D. 3自由度每节点,减去1自由度每构件5. 对于一个三维空间的桁架结构,若有10个节点和20根构件,其自由度计算应使用的公式是:- A. 自由度 = 6n - 3j- B. 自由度 = 3n - 2j- C. 自由度 = 3n - 3j- D. 自由度 = 6n - 6j6. 在平面框架结构中,如果节点数为5,构件数为8,计算其自由度时,正确的自由度为: - A. 6- B. 8- C. 10- D. 127. 对于一个有10个节点和15根构件的平面结构,其自由度为:- A. 15- B. 18- D. 248. 一个简单的平面框架结构中有6个节点,8根构件,计算自由度时,如果框架是完全支撑的,结果是:- A. 3- B. 6- C. 9- D. 129. 对于一个空间框架结构,其中有5个节点和12根构件,计算自由度时所用的公式为: - A. 自由度 = 6n - 3j- B. 自由度 = 3n - 2j- C. 自由度 = 6n - 2j- D. 自由度 = 3n - 3j10. 若一个平面结构中节点数为7,构件数为10,且结构为刚性框架,计算其自由度时,结果为:- A. 5- B. 7- C. 9- D. 11。
结构力学考试题及答案

结构力学考试题及答案题一:某桥梁由钢材制成,其主要构件为一根长度为6m的梁。
梁的宽度为10cm,高度为20cm。
在距离每个端点2m处集中施加垂直力F。
结构力学考试题请回答以下问题:1. 梁的截面面积是多少?2. 梁的惯性矩是多少?3. 施加力F后,梁的变形位移是多少?答案一:1. 梁的截面面积:梁的截面面积可以通过宽度与高度的乘积计算得出。
即:截面面积 = 宽度 ×高度= 10cm × 20cm= 200cm²2. 梁的惯性矩:梁的惯性矩可以通过以下公式计算:惯性矩 = (宽度 ×高度³) / 12= (10cm × 20cm³) / 123. 梁的变形位移:根据结构力学中的梁理论,当在梁上施加集中力时,梁会发生弯曲变形。
其位移可以通过以下公式计算:位移 = (F × L³) / (48 × E × I)其中,F为施加力,L为梁的长度,E为梁的杨氏模量,I为梁的惯性矩。
因此,梁的变形位移为:位移 = (F × (6m)³) / (48 × E × 3333.33cm⁴)题二:某建筑物由木材梁柱构成,其中一根木材梁的长度为8m,截面为矩形,宽度为15cm,高度为30cm。
结构力学考试题请回答以下问题:1. 木材梁的截面面积是多少?2. 木材梁的惯性矩是多少?3. 若在梁的中点施加垂直力F,梁的最大弯曲应力为多少?答案二:1. 木材梁的截面面积:截面面积 = 宽度 ×高度= 450cm²2. 木材梁的惯性矩:惯性矩 = (宽度 ×高度³) / 12= (15cm × 30cm³) / 12= 11250cm⁴3. 最大弯曲应力:最大弯曲应力可以通过以下公式计算:最大弯曲应力 = (M × c) / I其中,M为弯矩,c为梁的最大距离到中性轴的距离,I为梁的惯性矩。
结构力学习题讲解精选全文
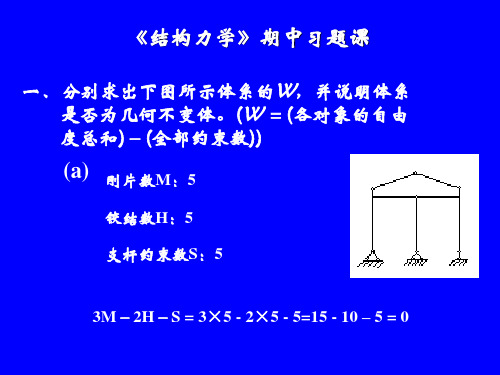
一、分别求出下图所示体系的W,并说明体系 是否为几何不变体。(W =(各对象的自由
度总和)-(全部约束数))
(a) 刚片数M:5
铰结数H:5 支杆约束数S:5
3M-2H-S = 3×5 - 2×5 - 5=15 - 10 – 5 = 0
(b) 刚片数M:5
铰结数H:6 支杆约束数S:3
超静定结构力法
<2>去掉一个单铰,相对于去掉两个约束:
超静定结构力法
<3>将刚结改成单铰联结,相对于去掉一个约束:
超静定结构力法
<4>在刚性联结处剪开,相对于去掉三个约束:
超静定结构力法 § 4.1超静定结构的基本概念和计算方法 2. 力法的基本概念
力法是计算超静定结构的最基本的方法
超静定结构力法 § 4.1超静定结构的基本概念和计算方法 2. 力法的基本概念
3M-2H-S = 3×5 - 2×6 - 3=15 - 12 – 3 = 0
题2. 试作图示结构中 横梁ABC的内力图 ( M, Q, N图 )
支座反力
支座反力 竖向分量
轴力N图
由Y方向的平衡条件:竖向载荷与竖向支座力平衡 处于水平位置的轴力,需分析支座反力的竖向分量。
剪力Q图
弯矩M图
题3:
过小时B处下陷
1 0 时,基本体系中的变力 X1 =超静定结构中常量
超静定结构力法
基本体系转化原来超静定结构的条件: 基本体系沿多余未知力,X1 方向的位移 1 与原结构相同, 即:1 0 这个转化条件是一个变形条件, 计算未知力需补充方程。称力法的基本方程。
超静定结构力法
讨论:线性变形体系
XA, XB, MA
结构力学习题含答案解析

第三章 静定结构的位移计算一、判断题:1、虚位移原理等价于变形谐调条件,可用于求体系的位移。
2、按虚力原理所建立的虚功方程等价于几何方程。
3、在非荷载因素(支座移动、温度变化、材料收缩等)作用下,静定结构不产生内力,但会有位移且位移只与杆件相对刚度有关。
4、求图示梁铰C 左侧截面的转角时,其虚拟状态应取:A.;; B.D.C.M =15、功的互等、位移互等、反力互等和位移反力互等的四个定理仅适用于线性变形体系。
6、已知M p 、M k 图,用图乘法求位移的结果为:()/()ωω1122y y EI +。
M k M p7、图a 、b 两种状态中,粱的转角ϕ与竖向位移δ间的关系为:δ=ϕ 。
8、图示桁架各杆E A 相同,结点A 和结点B 的竖向位移均为零。
9、图示桁架各杆EA =常数,由于荷载P 是反对称性质的,故结点B 的竖向位移等于零。
二、计算题:10、求图示结构铰A 两侧截面的相对转角ϕA ,EI = 常数。
q l l l /211、求图示静定梁D 端的竖向位移∆DV 。
EI = 常数,a = 2m 。
a a a 10kN/m12、求图示结构E 点的竖向位移。
EI = 常数。
l l l /3/3q13、图示结构,EI=常数,M =⋅90kN m , P = 30kN 。
求D 点的竖向位移。
P 3m 3m 3m14、求图示刚架B 端的竖向位移。
ql15、求图示刚架结点C 的转角和水平位移,EI = 常数。
16、求图示刚架中D点的竖向位移。
EI=常数。
l/217、求图示刚架横梁中D点的竖向位移。
EI =常数。
18、求图示刚架中D 点的竖向位移。
E I = 常数 。
ql l/219、求图示结构A、B两截面的相对转角,EI =常数。
l/23l/320、求图示结构A 、B 两点的相对水平位移,E I = 常数。
l l21、求图示结构B 点的竖向位移,EI =常数。
l l22、图示结构充满水后,求A 、B 两点的相对水平位移。
结构力学试题及答案

结构力学试题及答案第一题:一个竖立的、长度为L的悬臂梁上承受均布载荷w,各截面的弯曲半径r随其距左端的水平距离x的变化规律为r=2x,试求该梁各截面的弯矩M和剪力V的分布情况。
解答:对于悬臂梁来说,在截面x处的剪力V和弯矩M可以通过以下公式计算得出:剪力V = -wx弯矩M = -wx^2/2由于此题中弯曲半径和$x$之间的关系为$r=2x$,我们可以得到:$wR = EIκIz$即$-wx = E\frac{2x}{R}Iz$解方程可得$V = -\frac{6}{5} \frac{wL}{R}$$M = \frac{3}{10} \frac{wL^2}{R}$第二题:一根横截面为矩形的固定梁,长度为L,底部宽度为b,高度为h,悬臂长度为a,已知梁的材料力学特性,试求梁在距离左端x的位置的截面上的弯矩M和剪力V的分布情况。
解答:由于梁是固定梁,可以得知横截面上的弯矩M和剪力V的计算公式如下:剪力V = -qh弯矩M = -\frac{qh}{2}(x-a)^2其中,q为单位长度上的载荷。
由于题目中给出了梁的材料力学特性,可以知道梁的弹性模量为E,截面惯性矩为I,可以得到剪应力τ和最大剪应力τmax的计算公式:剪应力τ = \frac{V}{I} \cdot \frac{h}{2}最大剪应力τmax = \frac{Vmax}{I} \cdot \frac{h}{2}通过以上公式,可以计算出横截面上的剪力V、弯矩M、剪应力τ和最大剪应力τmax的具体数值。
第三题:一个跨度为L的简支梁上均匀分布有较长的集中荷载,如何确定梁上各部位的最大弯矩位置和最大弯矩值?解答:对于简支梁,可以通过以下步骤来确定各部位的最大弯矩位置和最大弯矩值:1. 计算梁的支点反力。
根据梁的简支边界条件,可以求得支点的反力,反力的大小等于荷载的大小。
根据反力的大小和荷载的位置,可以推算出反力的具体数值。
2. 根据荷载分布确定载荷大小。
结构力学理论试题及答案

结构力学理论试题及答案一、选择题(每题2分,共20分)1. 梁在均布荷载作用下的最大弯矩公式为:A. M = wL^2/8B. M = wL^2/6C. M = wL^2/4D. M = wL^2/2答案:B2. 悬臂梁自由端受到集中荷载P时,其最大弯矩为:A. M = PLB. M = PL/2C. M = PL/3D. M = PL/4答案:A3. 简支梁在跨中受到集中荷载P时,其最大弯矩为:A. M = PL/2B. M = PL/4C. M = PL/3D. M = PL/6答案:A4. 梁的剪力图和弯矩图的关系是:A. 剪力图的斜率等于弯矩图B. 弯矩图的斜率等于剪力图C. 剪力图的斜率等于弯矩图的导数D. 弯矩图的斜率等于剪力图的导数答案:D5. 梁的挠度计算公式中,通常需要考虑的因素不包括:A. 荷载类型B. 梁的截面特性C. 梁的支撑条件D. 梁的颜色答案:D6. 梁的剪力和弯矩之间的关系是:A. 剪力是弯矩的积分B. 弯矩是剪力的积分C. 剪力是弯矩的微分D. 弯矩是剪力的微分答案:B7. 梁的挠度计算中,通常采用的方法是:A. 能量法B. 弯矩分配法C. 叠加法D. 以上都是答案:D8. 梁在集中荷载作用下的剪力图是:A. 一条直线B. 一条曲线C. 一条折线D. 一条水平线答案:C9. 梁在均布荷载作用下的弯矩图是:A. 一条直线B. 一条曲线C. 一条抛物线D. 一条水平线答案:C10. 梁的剪力和弯矩的正负号规定是:A. 剪力向上为正,弯矩上凸为正B. 剪力向上为正,弯矩下凸为正C. 剪力向下为正,弯矩上凸为正D. 剪力向下为正,弯矩下凸为正答案:A二、简答题(每题5分,共30分)1. 简述梁的剪力和弯矩的定义及其物理意义。
2. 描述简支梁在均布荷载作用下的最大弯矩和剪力的分布情况。
3. 悬臂梁和简支梁在受到相同荷载时,其内力分布有何不同?4. 什么是梁的挠度?挠度的计算有何工程意义?5. 简述叠加法在梁的挠度计算中的应用。
结构力学力法习题及答案

结构力学力法习题及答案结构力学力法习题及答案结构力学是一门研究物体在外力作用下产生的应力和变形的学科。
在工程学中,结构力学是非常重要的一门学科,它为我们设计和分析各种建筑和机械结构提供了基础。
在学习结构力学的过程中,习题是必不可少的一部分。
下面将给出一些结构力学的力法习题及其答案,希望对读者有所帮助。
1. 一个悬臂梁上有一个集中力作用在梁的自由端,求该梁的弯矩分布图。
解答:根据悬臂梁的特点,自由端处的弯矩最大。
假设集中力为F,梁的长度为L,弹性模量为E,梁的截面惯性矩为I。
根据悬臂梁的弯矩公式M = F * L,可以得到弯矩分布图为一个从自由端开始逐渐减小的直线。
2. 一个等截面的梁上有一个均布载荷作用,求该梁的剪力分布图。
解答:假设均布载荷为q,梁的长度为L,根据梁的受力平衡条件,可以得到梁上任意一点的剪力大小为V = q * x,其中x为距离梁的一端的距离。
因此,该梁的剪力分布图为一个线性增长的直线。
3. 一个梁上有多个集中力作用,求该梁的弯矩和剪力分布图。
解答:对于每个集中力,可以分别求出其在梁上的弯矩和剪力分布图。
然后将所有的弯矩和剪力分布图叠加在一起,即可得到梁的总弯矩和总剪力分布图。
4. 一个悬臂梁上有一个集中力和一个均布载荷同时作用,求该梁的弯矩和剪力分布图。
解答:首先,根据集中力的大小和悬臂梁的长度,可以求出集中力在悬臂梁上的弯矩分布图。
然后,根据均布载荷的大小和悬臂梁的长度,可以求出均布载荷在悬臂梁上的剪力分布图。
最后,将两者叠加在一起,即可得到梁的总弯矩和总剪力分布图。
5. 一个梁上有多个集中力和多个均布载荷同时作用,求该梁的弯矩和剪力分布图。
解答:对于每个集中力和均布载荷,可以分别求出其在梁上的弯矩和剪力分布图。
然后将所有的弯矩和剪力分布图叠加在一起,即可得到梁的总弯矩和总剪力分布图。
通过以上习题的解答,我们可以看到结构力学中力法的应用。
在实际工程中,我们需要根据具体的结构形式和受力情况,运用结构力学的理论知识,求解结构的受力分布,从而保证结构的安全可靠。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《结构力学》计算题61.求下图所示刚架的弯矩图。
aaaaqABCD62.用结点法或截面法求图示桁架各杆的轴力。
63.请用叠加法作下图所示静定梁的M图。
64.作图示三铰刚架的弯矩图。
65.作图示刚架的弯矩图。
66.用机动法作下图中EM、LQBF、RQBF的影响线。
1m2m2mFp1=1mE BA2mC D67.作图示结构FM、QFF的影响线。
68.用机动法作图示结构影响线LQBFFM,。
69.用机动法作图示结构RQBCFM,的影响线。
70.作图示结构QBF、EM、QEF的影响线。
71.用力法作下图所示刚架的弯矩图。
l BD PACllEI=常数72.用力法求作下图所示刚架的M图。
73.利用力法计算图示结构,作弯矩图。
74.用力法求作下图所示结构的M图,EI=常数。
75.用力法计算下图所示刚架,作M图。
76.77.78.79.80.81.82.83.84.85.答案qABCDF xBF yBF yAF xA2qa32/2qa32/q2a()2/82qa32/=/qa22取整体为研究对象,由0AM=,得2220yB xBaF aF qa+-=(1)(2分)取BC部分为研究对象,由0CM=∑,得yB xBaF aF=,即yB xBF F=(2)(2分)由(1)、(2)联立解得23xB yBF F qa==(2分)由0xF=∑有20xA xBF qa F+-=解得43xAF qa=-(1分)由0yF=∑有0yA yBF F+=解得23yA yBF F qa=-=-(1分) 则2224222333D yB xBM aF aF qa qa qa=-=-=()(2分)弯矩图(3分)62.解:(1)判断零杆(12根)。
(4分)(2)节点法进行力计算,结果如图。
每个力3分(3×3=9分)63.解:(7分)(6分)64. 解:由0B M =∑,626P RA F F =⨯,即2PRA F F =(↓)(2分) 由0y F =∑,2PRB RA F F F ==(↑)(1分) 取BE 部分为隔离体0EM=∑,66yB RB F F =即2PyB F F =(←)(2分) 由0x F =∑得2PyA F F =(←)(1分) 故63DE DA yA P M M F F ===(侧受拉)(2分)63CB CE yB P M M F F ===(外侧受拉)(2分)(3分)65. 解:(1)求支座反力。
对整体,由0x F =∑,xA F qa =(←)(2分)0AM=∑,22308RC F a qa qa ⨯--=,178RC F qa =(↑)(2分)(2)求杆端弯矩。
0AB DC M M ==(2分)2BA BC xA M M F a qa ==⨯=(侧受拉)(2分) 2248CB CD a a qa M M q ==⨯⨯=(外侧受拉)(2分)(3分)66. 解:(1)C M 的影响线(4分)EBADC23/23/23/2(2)LQBF的影响线(4分)E BADC 123/1/3(2)RQB F 的影响线(4分)E BA D C 1167. 解:(1)F M 的影响线(6分)(2)QF F 的影响线(6分)68. 解:F M 影响线(6分)LQBF 影响线(6分) 69. 解:QBc F M ,影响线(6分)RQB c F M ,影响线(6分)70. 解:(1)QB F 的影响线。
(4分)E M 的影响线。
(4分)QE F 的影响线。
(4分)71. 解:(1)本结构为一次超静定结构,取基本体系如图(a )所示。
(2分)(2)典型方程11110P X δ+∆=(2分)(3)绘制P M 、1M 分别如图(b )、(c )所示。
(3分)基本体系PX 1M PP2Pl(a ) (b )MPl 8/PPl Pl 8/(c ) (d )(4)用图乘法求系数和自由项。
333111433l l l EI EIδ=+=(2分)232112217()22336P l Pl Pl Pl l Pl EI EI-⨯∆=++⨯=-(2分)(5)解方程得1178PX =(1分) (6)利用11P M M X M =+绘制弯矩图如图(d )所示。
(2分)72. 解:1)选择基本体系(2分)这是一次超静定刚架,可去掉B 端水平约束,得到如下图所示的基本体系。
2)列力法方程(2分)11110P X δ+∆=3)绘制基本体系的Mp 图和单位弯矩图,计算系数、自由项(6分,Mp 图和单位弯矩图各2分,系数每个1分,结果错误得一半分)31121711()2()2326l l l l l l l EI EI EI δ=⨯⨯⨯+⨯⨯=421211()38224l ql p ql l EI EI =-⨯⨯⨯=-∆解方程得: 1128ql X =(1分)作M 图:11P X M M M =+(3分)73. 解:(2分)(3分)(1分)(2*4=8分)74. 解:取基本体系如图(2分)列力法基本方程:11110p X δ+∆=(2分)1M 图(1.5分) p M 图(1.5分)3113l EI δ= (2分) 418p ql EI∆=-(2分) 代入力法方程得 138ql X =(1分) AB 28ql 216ql M 图(2分)75. 解:(1)选取基本体系如图(a )所示(2分)(a )(2)列力法方程。
11112210P X X δδ++∆=(1分) 21122220P X X δδ++∆=(1分) (3)分别作P M 、1M 和2M 图(1*3=3分)(4)求系数和自由项。
2241111315()32428P qa a qa a a a qa EI EI ∆=-⋅⋅⋅+⋅⋅=-⋅(1分) 422111()224P qa qa a a EI EI∆=-⋅⋅⋅=-(1分) 3111124()233a a a a a a a EI EIδ=⋅⋅⋅+⋅⋅=(1分) 322112()233a a a a EI EIδ=⋅⋅⋅=(0.5分) 3122111()22a a a a EI EIδδ==⋅⋅⋅=(0.5分) 将上述数据代入基本方程得137X qa =,2328X qa =(1分) (5)利用叠加法作弯矩图如图。
(2分)76.图中,刚片AB、BE、DC由不共线的三个铰B、D、E连接,组成一个大刚片,再和地基基础用不相交也不全平行的三链杆相连,组成没有多余约束的几何不变体系(5分)。
77.如图所示的三个刚片通过不在同一直线上的A、B、C三个铰两两相连构成无多余约束的扩大刚片,在此基础上依次增加二元体(1,2)、(3,4)、(5,6)、(7,8)组成无多余约束的几何不变体系。
(5分)ⅠⅡⅢ43125687ABC78.如图所示的三个刚片通过同一直线上的A、B、C三个铰两两相连构成了瞬变体系。
(5分)79.如图刚片Ⅰ、Ⅱ、Ⅲ通过不共线的三铰两两相连组成了无多余约束的几何不变体系。
(5分)80.如图依次拆除二元体(1,2)、(3,4)、剩下刚片Ⅰ和刚片Ⅱ通过一铰和不过该铰的链杆组成了几何不变体系,故原体系是无多余约束的几何不变体系。
(5分)81.如图刚片Ⅰ、Ⅱ、Ⅲ通过不共线的三铰两两相连组成了无多余约束的几何不变体系。
(5分)82.如图刚片Ⅰ、Ⅱ、Ⅲ通过不共线的三铰两两相连组成了无多余约束的几何不变体系。
(5分)83.如图以铰接三角形ABC为基本刚片,并依次增加二元体(1,2)、(3,4)、(5,6)、(7,8)、(9,10)形成扩大刚片,其和刚片通过铰A和节点B处链杆组成了几何不变体系,11杆为多余约束,故原体系为含有1个多余约束的几何不变体系。
(5分)84.如图依次拆除二元体(1,2)、(3,4)、(5,6),刚片Ⅱ和刚片Ⅰ通过相交于同一点的三根链杆组成了瞬变体系。
(5分)85.如图依次拆除二元体(1,2)、(3,4)、(5,6)、(7,8)、(9,10)、(11,12)后只剩下刚片,故原体系是无多余约束的几何不变体系。
(5分)。
