多聚甲醛-蔗糖溶液(20%)
浙江省温州市2024届高三二模语文试卷及答案

浙江省温州市2024届高三二模语文试卷及答案一、现代文阅读(35分)(一)现代文阅读Ⅰ(本题共5小题,18分)阅读下面的文字,完成1~5题。
材料一:和朋友这类后天选择的关系不同,以血缘为基础形成的亲缘关系是与生俱来的。
过去,人们讲求“血浓于水”,而到了今天,越来越多的人意识到,亲缘关系无法选择,但并不意味着无法舍弃。
尤其当亲缘关系只剩下困扰和伤害,却带不来一丝温暖和慰藉时,“断亲”就成了许多人的共同选择。
南京大学社会学院副教授胡小武将“断亲”定义为“懒于、疏于、不屑于同二代以内的亲戚互动和交往的一种现象”。
即年轻人很少和亲戚互动或基本不走亲戚,而非绝对的断绝往来。
早在十年前,胡小武就开始关注“断亲”话题,真正从个体经验走向学术研究,则要到2021年10月,他注意到网上有越来越多的人讲述自己和亲戚之间不愉快的经历,“断亲”已然成为一个社会性话题。
胡小武发现在“90后”特别是“00后”青年群体中,“断亲”已经成为越来越普遍的一个现象。
“我们同亲戚之间的冷漠、疏离状态,事实上正在成为个体乃至更广泛意义上群体的一种日常生活。
”胡小武分析。
为什么越来越多的年轻人选择“断亲”?《看天下》与胡小武展开了一场有关“断亲”话题的探讨。
《看天下》:距离你开展青年“断亲”研究已经过去两年,这两年中,“断亲”现象有发生新的变化吗?胡小武:现象本身没有太大变化,但“断亲”的话题引发了更多的关注和思考。
对年长一辈来说,站在传统价值观的立场,他们对这种现象表露出一种乡愁式的担忧,为当前的亲情淡漠感到失落,怀恋过去的其乐融融。
但对年轻人来说,他们往往从更加正面的角度来看待和接受“断亲”现象,访谈中,大多数选择“断亲”的年轻人也表示这是一种解脱和自在。
《看天下》:在未来一段时间内,“断亲”的趋势还会持续加剧吗?胡小武:根据我这两年来的持续观察和思考,“断亲”的趋势依然会加剧,或者说,“断亲”的人群规模还会逐渐扩大。
一个重要原因就是中国城市化比例还在持续增长。
Z型钢规格

Z型钢规格Z型钢就是一种常见的冷弯薄壁型钢,加工材料为热轧(喷漆),镀锌。
加工标准按GB50018-2002 执行。
它广泛用于汽车、铁道车辆、建筑门窗、交通运输、货架、公路护栏、建筑钢结构、集装箱、钢模板和脚手架、太阳能支架造船、桥梁、输电铁塔、蔬菜大棚、管道支架等领域。
由于Z型钢坚固耐用、经济适用,不污染环境,所以是目前我国大力推广应用的高附加值稀缺钢材品种。
既然Z型钢的用途这么广泛,而且还在大力推广,对于它的规格是不是要求也很严格?主要规格有哪些呢?由于Z型钢规格太多,只列出部分:型号断面尺寸 SeZtion sizeModel h(mm) b(mm) a(mm) s(mm)Z100 100 40 20 1.6-3.2Z120 120 40 20 1.6-3.2Z120 120 50 20 1.6-3.2Z120 120 60 20 1.6-3.2Z140 140 50 20 1.6-3.2Z140 140 60 20 1.6-3.2Z160 160 50 20 1.6-3.2Z160 160 60 20 1.6-3.2Z180 180 60 20 1.6-3.2Z180 180 75 20 1.6-3.2Z200 200 60 20 1.6-3.2Z200 200 70 20 1.6-3.2Z220 220 60 20 1.6-3.2Z220 220 70 20 1.6-3.2Z260 260 75 20 1.6-3.2Z280 280 80 20 1.6-3.2Z300 300 100 20 1.6-3.Z320 320 100 20 1.6-3.2我们可以知道,Z型钢主要用于护栏,那么在制作的时候,它就应该一个范围。
Z型钢可做规格有:(26-400)X(25-200)X (9-20)X(1.5-3.75)底宽 X 侧高 X 小边 X 壁厚 = 可定制可在下列尺寸中任意调节:80~300(mm) b:40~100(mm) t:1.5~5.0(mm)。
资产组合习题解答

第二章1、 假设你正考虑从以下四种资产中进行选择:资产1市场条件收益% 概率 好 16 1/4 一般 12 1/2 差8 1/4资产2市场条件收益 概率 好 4 1/4 一般 6 1/2 差8 1/4资产3市场条件收益 概率 好 20 1/4 一般 14 1/2 差8 1/4资产4市场条件收益 概率 好 16 1/3 一般 12 1/3 差81/3解答:111116%*12%*8%*12%424E =++= 10.028σ==同理 26%E = 20.014σ= 314%E = 30.042σ= 412%E = 40.033σ= 2、 下表是3个公司7个月的实际股价和股价数据,单位为元。
证券A证券B证券C时间价格股利价格股利价格股利1 6578 333 610682 7598368210883 3598 0.72543688 1.35 1240.404 4558 2382821228 5 256838641358 6 590.725 639781.35 61418 0.42 7260839261658A. 计算每个公司每月的收益率。
B. 计算每个公司的平均收益率。
C. 计算每个公司收益率的标准差。
D. 计算所有可能的两两证券之间的相关系数。
E. 计算下列组合的平均收益率和标准差:1/2A+1/2B 1/2A+1/2C 1/2B+1/2C 1/3A+1/3B+1/3C解答:A 、1.2%2.94%7.93%A B C R R R === C 、4.295%4.176%7.446%A B C σσσ=== D 、()()()0.140.2750.77A B A C B C ρρρ===- E 、3、已知:期望收益标准差证券1 10% 5% 证券24%2%在P P R σ-_空间中,标出两种证券所有组合的点。
假设ρ=1 ,-1,0。
对于每一个相关系数,哪个组合能够获得最小的Pσ?假设不允许卖空,Pσ最小值是多少?解答:设证券1比重为w122222(1,2)1112111,212(1)2(1)w w w w σσσρσσ=+-+-1ρ= m i n 2%σ= 10w = 21w = 1ρ=- m i n 0σ= 12/7w = 25/7w =0ρ= m i n 1.86%σ= 14/29w = 225/29w =4、分析师提供了以下的信息。
Z2直线双杆材料表
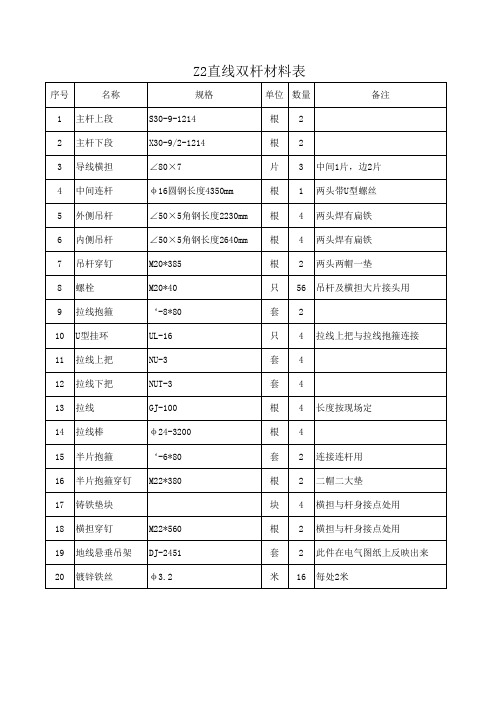
序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 名称 主杆上段 主杆下段 导线横担 中间连杆 外侧吊杆 内侧吊杆 吊杆穿钉 螺栓 拉线抱箍 U型挂环 拉线上把 拉线下把 拉线 拉线棒 半片抱箍 半片抱箍穿钉 铸铁垫块 横担穿钉 地线悬垂吊架 镀锌铁丝 M22*560 DJ-2451 φ 3.2 规格 S30-9-1214 X30-9/2-1214 ∠80×7 φ 16圆钢长度4350mm ∠50×5角钢长度2230mm ∠50×5角钢长度2640mm M20*385 M20*40 ‘-8*80 UL-16 NU-3 NUT-3 GJ-100 φ 24-3200 ‘-6*80 M22*380 单位 数量 根 根 片 根 根 根 根 只 套 只 套 套 根 根 套 根 块 根 套 米 2 2 3 1 4 4 2 56 2 4 4 4 4 4 2 2 4 2 2 16
材料表
备注
中间1片,边2片 两头带U型螺丝 两头焊有扁铁 两头焊有扁铁 ቤተ መጻሕፍቲ ባይዱ头两帽一垫 吊杆及横担大片接头用
拉线上把与拉线抱箍连接
长度按现场定
连接连杆用 二帽二大垫 横担与杆身接点处用 横担与杆身接点处用 此件在电气图纸上反映出来 每处2米
典型二阶系统的z变换

典型二阶系统的z变换在控制系统中,二阶系统是一种常见的系统结构,它由两个一阶子系统级联而成。
这种系统在许多实际应用中都有广泛的应用,例如机械控制、电路控制等领域。
在控制系统中,我们常常使用z变换来对系统进行分析和设计。
z变换是一种重要的数学工具,它能够将离散时间域函数转换为复平面上的函数。
在二阶系统中,我们可以使用z变换来描述系统的传递函数和频率响应。
通过对系统进行z变换,我们可以得到系统的离散时间域方程和频域特性。
二阶系统的传递函数通常可以表示为:H(z) = (b0 + b1z^(-1) + b2z^(-2)) / (1 + a1z^(-1) + a2z^(-2))其中,b0、b1、b2为输入信号的系数,a1、a2为输出信号的系数。
通过对传递函数进行z变换,我们可以得到系统的差分方程,从而可以分析系统的稳定性、阶跃响应和频率响应等特性。
对于二阶系统的稳定性分析,我们通常会计算系统的极点。
极点是传递函数的根,它决定了系统的稳定性。
在z平面上,稳定系统的极点应该位于单位圆内。
通过计算传递函数的极点,我们可以判断系统的稳定性。
在阶跃响应分析中,我们关注系统的响应时间和超调量。
通过对系统的传递函数进行部分分式展开,我们可以得到系统的阶跃响应。
阶跃响应可以描述系统对阶跃输入信号的响应情况,包括响应时间和超调量。
通过分析阶跃响应,我们可以了解系统的动态特性。
频率响应分析是控制系统设计中的重要一环。
通过对系统的传递函数进行z变换,并将z变量替换为复平面上的点,我们可以得到系统的频率响应。
频率响应描述了系统在不同频率下的增益和相位特性。
通过分析频率响应,我们可以了解系统对不同频率输入信号的响应情况,并进行系统的合理设计。
二阶系统的z变换在控制系统分析和设计中具有重要的作用。
通过对系统进行z变换,我们可以得到系统的离散时间域方程和频域特性,从而进行系统的稳定性分析、阶跃响应分析和频率响应分析。
掌握二阶系统的z变换方法,对于控制系统的设计和优化具有重要意义。
定性性状的连锁研究

二、IBD/IBS介绍
12
12
12
12
IBD= IBS=2
二、IBD/IBS介绍
12 12
IBD=2
Prob 1/2
12 12
12 12
12 12
12 12
IBD=0
12 12
1 2 1 2 Prob 1/2
12 12
二、IBD/IBS介绍-缺失数据
1/2
2/3
2/2
2/3
二、IBD/IBS介绍-缺失数据
• The average number of shared alleles is: (0.25 * 2) + (0.5 * 1) + (0.25 * 0) = 1
However, if the marker is linked to the disease locus the overall amount of sharing between affected sibs will be increased !
• IBS sharing probabilities: 依赖于标记位点的 等位频率,一个常见(common)的等位比一个 稀少(rare)的等位在同胞对之间更可能是共享 的IBS。
• 由于IBS没有用到父母的信息所以比IBD分析的 检验效能要低,而且如果等位频率错误可能会产 生偏倚。
三、受累同胞对数据分析
二、IBD/IBS介绍
12
13
12
12
IBD=2 IBS=2
二、IBD/IBS介绍
12
11
12
12
IBD=? IBS=2
二、IBD/IBS介绍
1/2 1/3
1/2 1/3
机械设计基础试题(含答案)

机械设计基础试卷1一、选择题:本大题共15个小题,每小题3分,共45分。
在每小题给出的四个选项中,只有一项符合题目的要求,把所选择项前的字母填在题后的括号内。
1.下列铰链四杆机构中,能实现急回运动的是A.双摇杆机构 B.曲柄摇杆机构C.双曲柄机构 D.对心曲柄滑块机构【】2.平面连杆机构中,当传动角γ较大时,则A.机构的传力性能较好 B. 机构的传力性能较差C.可以满足机构的自锁要求 D.机构的效率较低3.当一对渐开线齿轮制成后,即使两轮的中心距稍有改变,其角速度比仍保持原值不变,原因是:A. 压力角不变B. 啮合角不变C.节圆半径不变 D. 基圆半径不变【】4.渐开线齿轮实现连续传动时,其重合度为A.ε<0 B.ε=0 C.ε<1 D. ε≥1 【】5. 塑性材料制成的零件进行静强度计算时,其极限应力为A.σB B. σs C. σ0 D. σ-1【】6. 下列四种螺纹中,自锁性能最好的是A.粗牙普通螺纹 B.细牙普通螺纹C.梯形螺纹 D.锯齿形螺纹【】7.普通平键联接在选定尺寸后,主要是验算其A.挤压强度 B. 剪切强度C.弯曲强度 D. 耐磨性【】8.一对相啮合的圆柱齿轮的Z2>Z1,b1>b2,其接触应力的大小是A.σH1<σH2 B. σH1 >σH2C. σH1=σH2D. 可能相等,也可能不等【】9.实际齿数相同时,直齿圆柱齿轮、斜齿圆柱齿轮和直齿圆锥齿轮三者齿形系数之间的关系为A.直齿圆柱齿轮的最大 B. 斜齿圆柱齿轮的最大C.直齿圆锥齿轮的最大 D. 三者数值相同【】10.在润滑良好的条件下,为提高蜗杆传动的啮合效率,可采用的方法为:A.减小齿面滑动速度υs B. 减少蜗杆头数Z1C.增加蜗杆头数Z1 D. 增大蜗杆直径系数q 【】11. 带传动中,弹性滑动A.在张紧力足够时可以避免B.在传递功率较小时可以避免C.在小带轮包角足够大时可以避免D.是不可避免【】12.带传动作减速传动时,带的最大应力σmax等于A.σ1+σb1+σ cB. σ1+σb2+σ cC. σ2+σb1+σ cD. σ2+σb2+σc 【】13. 转轴的变曲应力为A.对称循环变应力 B.脉动循环变应力C.非对称循环变应力 D.静应力【】14.在基本额定动载荷C作用下,滚动轴承的基本额定寿命为106转时,其可靠度为A.10% B. 80% C.90% D.99% 【】15.在圆柱形螺旋拉伸(压缩)弹簧中,弹簧指数C是指A.弹簧外径与簧丝直径之比值B.弹簧内径与簧丝直径之比值C.弹簧自由高度与簧丝直径之比值D.弹簧中径与簧丝直径之比值【】二、填空题:本大题共10个小题,每空1分,共20分。
5包壳材料详解

Zr-3 过多的锡含量会影响加工成型性,同 时研究证明,在350℃水中和400 ℃蒸汽 中的吸氢与镍的含量有很大关系。因此, 降低了锡含量和镍含量,把镍含量由原来 的0.05%降低到了0.007%,研制了锆-3合 金。
Zr-4
由于减少了镍含量,抗腐蚀性能有所下降,研 究表明:铁、铬、镍的总量保持在0.3%左右可以 得到合适的第二相,获得较好的抗腐蚀性能。因 而把铁含量由原来的0.12%增加到0.18%-0.24% ,这就形成了锆-4合金。 锆-4合金在350 ℃高温水中和400 ℃蒸汽中有更 好的耐腐蚀性能,而吸氢量仅为锆-2合金的1/21/3,其余性能与锆-2相似。它已广泛被用于压水 堆和重水堆中做燃料包壳材料和堆芯结构材料。
2)锆-2.5铌合金
含有2.5 wt%铌的锆合金在高温水中的耐腐蚀 性虽不如锆-锡合金,但吸氢率低,径向蠕变速 率很小,同时可以热处理强化。 锆-2.5铌合金在重水堆上主要用于制作压力管, 在动力堆中用于元件盒壳体的板材及堆芯部件 的结构材料。 锆-2.5铌合金在使用中一个比较大的问题是氢 化物的延迟开裂(DHC)。其原因是在应力梯 度的影响下,氢向裂纹尖端扩散所引起的。
5.1.2 常用的包壳材料
1)铝、镁、锆的合金(中子吸收截面小、 熔点高) 水堆中应用最普遍的是锆-2和锆-4合金 2)不锈钢和镍基合金(优异的高温性能 和价格优势)。快堆中主要考虑高温性能 和抗辐照损伤性能,目前多采用奥氏体不 锈钢,有时也使用镍基合金。
5.2 锆及其合金
5.2.1 金属锆的性能 纯锆是一种银白色,有光泽的延性金属, 473K时理论密度为6.55Mg/m3,熔点为 2125K。 自然界中锆与铪共生,其含量为50:1,铪 的中子吸收截面约为400b,因此锆与铪必 须分离才能用于反应堆做包壳材料。
信息工程大学815误差理论与测量平差基础(2)2015-2016年考研专业课真题试卷

第1页 共5页 815误差理论与测量平差基础(2)(共五大题,满分150分)一、填空题(35分,1-10每空1分,11-20每空2分,21空5分)1. 测量误差按其性质可分为 (1) 、 (2) 和 (3) ,其中 (4) 是测量平差的主要对象。
2. 参数平差中,未知参数的选取要求满足 (5) 、 (6) 。
3. 衡量估计量优劣的标准有 (7) 、 (8) 、 (9) 。
4. 平均误差t 与中误差m 之间的近似关系为 (10) 。
5. 设观测值L 及其真值为X ,则均方误差的定义为MSE(L)= (11) ,当X = (12) 时,均方误差即为方差。
6. 设⎥⎦⎤⎢⎣⎡=21x x X ,⎥⎦⎤⎢⎣⎡--=∑10162121X , 20±=σ, 211x x z += ,212x x z -=, 则 =11x p (13) , =1z σ (14) ,=21z z σ (15) 。
7. 已知某观测量y 及其中误差y m ,且知12+=x y ,则x m = _(16) 。
8. 对同一观测量进行重复观测,每次观测独立等精度,两次观测结果之差的最大允许值为6±mm ,设x 是9次观测结果的平均值,则观测值的中误差为 (17) ,x 的中误差=x m (18) 。
9. 设n L L L ,,,21 为某量n 次独立非等精度观测值, 中误差分别为n m m m ,,,21 , 则该量的最小二乘平差值等于 (19) 。
10. 设共有n 个观测误差,W 表示误差列中同号交替次数与异号交替次数之差,根据误差检验原理,W 的限差公式为:<W (20) 。
11. 已知坐标转换的布尔莎模型为信息工程大学2016年考研专业课真题试卷(原版)。
2022年全国乙卷数学(理科)高考真题参考答案

绝密★启用前2022年普通高等学校招生全国统一考试(全国乙卷)数学(理科)参考答案一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设全集{1,2,3,4,5}U =,集合M 满足{1,3}U M =ð,则()A.2M ∈ B.3M∈ C.4M∉ D.5M∉【答案】A【解析】由题知{2,4,5}M =,对比选项知,A 正确,BCD 错误,故选:A 2.已知12z i =-,且0z az b ++=,其中a ,b 为实数,则()A.1,2a b ==- B.1,2a b =-= C.1,2a b == D.1,2a b =-=-【答案】A【解析】先算出z ,再代入计算,实部与虚部都为零解方程组即可12iz =+12i (12i)(1)(22)i z az b a b a b a ++=-+++=+++-由0z az b ++=,得10220a b a ++=⎧⎨-=⎩,即12a b =⎧⎨=-⎩故选:A3.已知向量,a b 满足||1,||2|3a b a b ==-=,则a b ⋅=()A.2-B.1- C.1D.2【答案】C【解析】根据给定模长,利用向量的数量积运算求解即可.∵222|2|||44-=-⋅+a b a a b b ,又∵||1,||2|3,==-=a b a b ∴91443134=-⋅+⨯=-⋅ a b a b ,∴1a b ⋅= 故选:C.4.嫦娥二号卫星在完成探月任务后,继续进行深空探测,成为我国第一颗环绕太阳飞行的人造行星,为研究嫦娥二号绕日周期与地球绕日周期的比值,用到数列{}n b :1111b α=+,212111b αα=++,31231111b ααα=+++,…,依此类推,其中(1,2,)k k α*∈=N .则()A.15b b <B.38b b < C.62b b < D.47b b <【答案】D 【解析】解:∵()*1,2,k k α∈=N,∴1121ααα<+,112111ααα>+,得到12b b >,同理11223111ααααα+>++,可得23b b <,13b b >又∵223411,11αααα>++112233411111ααααααα++<+++,∴24b b <,34b b >;以此类推,可得1357b b b b >>>>…,78b b >,故A 错误;178b b b >>,故B 错误;26231111αααα>++…,得26b b <,故C 错误;11237264111111αααααααα>++++++…,得47b b <,故D 正确.故选:D.5.设F 为抛物线2:4C y x =的焦点,点A 在C 上,点(3,0)B ,若AF BF =,则AB =()A.2B. C.3D.【答案】B 【解析】根据抛物线上的点到焦点和准线的距离相等,从而求得点A 的横坐标,进而求得点A 坐标,即可得到答案.由题意得,()1,0F ,则2AF BF ==,即点A 到准线1x =-的距离为2,所以点A 的横坐标为121-+=,不妨设点A 在x 轴上方,代入得,()1,2A ,所以AB ==.故选:B6.执行下边的程序框图,输出的n =()A.3B.4C.5D.6【答案】B【解析】执行第一次循环,2123b b a =+=+=,312,12a b a n n =-=-==+=,222231220.0124b a -=-=>;执行第二次循环,2347b b a =+=+=,725,13a b a n n =-=-==+=,222271220.01525b a -=-=>;执行第三次循环,271017b b a =+=+=,17512,14a b a n n =-=-==+=,2222171220.0112144b a -=-=<,此时输出4n =.故选:B7.在正方体1111ABCD A B C D -中,E ,F 分别为,AB BC 的中点,则()A.平面1B EF ⊥平面1BDD B.平面1B EF ⊥平面1A BD C.平面1//B EF 平面1A AC D.平面1//B EF 平面11AC D【答案】A【解析】证明EF ⊥平面1BDD ,即可判断A ;如图,以点D 为原点,建立空间直角坐标系,设2AB =,分别求出平面1B EF ,1A BD ,11AC D 的法向量,根据法向量的位置关系,即可判断BCD .解:在正方体1111ABCD A B C D -中,AC BD ⊥且1DD ⊥平面ABCD ,又∵EF ⊂平面ABCD ,∴1EF DD ⊥,∵,E F 分别为,AB BC 的中点,∴EF AC ,∴EF BD ⊥,又∵1BD DD D = ,∴EF ⊥平面1BDD ,∵EF ⊂平面1B EF ,∴平面1B EF ⊥平面1BDD ,故A 正确;如图,以点D 为原点,建立空间直角坐标系,设2AB =,则()()()()()()()112,2,2,2,1,0,1,2,0,2,2,0,2,0,2,2,0,0,0,2,0B E F B A A C ,()10,2,2C ,则()()11,1,0,0,1,2EF EB =-= ,()()12,2,0,2,0,2DB DA ==,()()()1110,0,2,2,2,0,2,2,0,AA AC A C ==-=-设平面1B EF 的法向量为()111,,m x y z =,则有11111020m EF x y m EB y z ⎧⋅=-+=⎪⎨⋅=+=⎪⎩ ,可取()2,2,1m =- ,同理可得平面1A BD 的法向量为()11,1,1n =--,平面1A AC 的法向量为()21,1,0n =,平面11AC D 的法向量为()31,1,1n =-,则122110m n ⋅=-+=≠,所以平面1B EF 与平面1A BD 不垂直,故B 错误;因为m 与2n uu r 不平行,所以平面1B EF 与平面1A AC 不平行,故C 错误;因为m 与3n不平行,所以平面1B EF 与平面11AC D 不平行,故D 错误,故选:A.8.已知等比数列{}n a 的前3项和为168,2542a a -=,则6a =()A.14 B.12C.6D.3【答案】D【解析】设等比数列{}n a 的公比为,0q q ≠,易得1q ≠,根据题意求出首项与公比,再根据等比数列的通项即可得解.解:设等比数列{}n a 的公比为,0q q ≠,若1q =,则250a a -=,与题意矛盾,所以1q ≠,则()31123425111168142a q a a a qa a a q a q ⎧-⎪++==⎨-⎪-=-=⎩,解得19612a q =⎧⎪⎨=⎪⎩,所以5613a a q ==.故选:D .9.已知球O 的半径为1,四棱锥的顶点为O ,底面的四个顶点均在球O 的球面上,则当该四棱锥的体积最大时,其高为()A.13B.12C.33D.22【答案】C【解析】先证明当四棱锥的顶点O 到底面ABCD 所在小圆距离一定时,底面ABCD 面积最大值为22r ,进而得到四棱锥体积表达式,再利用均值定理去求四棱锥体积的最大值,从而得到当该四棱锥的体积最大时其高的值.设该四棱锥底面为四边形ABCD ,四边形ABCD 所在小圆半径为r ,设四边形ABCD 对角线夹角为α,则2111sin 222222ABCD S AC BD AC BD r r r α=⋅⋅⋅≤⋅⋅≤⋅=即当四棱锥的顶点O 到底面ABCD 所在小圆距离一定时,底面ABCD 面积最大值为22r 又22r h 1+=则21432327O ABCDV r h -=⋅⋅=当且仅当222r h =即h 时等号成立,故选:C10.某棋手与甲、乙、丙三位棋手各比赛一盘,各盘比赛结果相互独立.已知该棋手与甲、乙、丙比赛获胜的概率分别为123,,p p p ,且3210p p p >>>.记该棋手连胜两盘的概率为p ,则()A.p 与该棋手和甲、乙、丙的比赛次序无关 B.该棋手在第二盘与甲比赛,p 最大C.该棋手在第二盘与乙比赛,p 最大 D.该棋手在第二盘与丙比赛,p 最大【答案】D【解析】该棋手连胜两盘,则第二盘为必胜盘.分别求得该棋手在第二盘与甲比赛且连胜两盘的概率p 甲;该棋手在第二盘与乙比赛且连胜两盘的概率p 乙;该棋手在第二盘与丙比赛且连胜两盘的概率p 丙.并对三者进行比较即可解决该棋手连胜两盘,则第二盘为必胜盘,记该棋手在第二盘与甲比赛,且连胜两盘的概率为p 甲则2132131231232(1)2(1)2()4p p p p p p p p p p p p p =-+-=+-甲记该棋手在第二盘与乙比赛,且连胜两盘的概率为p 乙则1231232131232(1)2(1)2()4p p p p p p p p p p p p p =-+-=+-乙记该棋手在第二盘与丙比赛,且连胜两盘的概率为p 丙则1321323121232(1)2(1)2()4p p p p p p p p p p p p p =-+-=+-丙则[]()1231232131231232()42()420p p p p p p p p p p p p p p p p p -=+--+-=-<甲乙[]()2131233121232312()42()420p p p p p p p p p p p p p p p p p -=+--+-=-<乙丙即p p <甲乙,p p <乙丙,则该棋手在第二盘与丙比赛,p 最大.选项D 判断正确;选项BC 判断错误;p 与该棋手与甲、乙、丙的比赛次序有关.选项A 判断错误.故选:D11.双曲线C 的两个焦点为12,F F ,以C 的实轴为直径的圆记为D ,过1F 作D 的切线与C 交于M ,N 两点,且123cos 5F NF ∠=,则C 的离心率为()A.B.32C.132D.2【答案】C【解析】依题意不妨设双曲线焦点在x 轴,设过1F 作圆D 的切线切点为G ,可判断N 在双曲线的右支,设12F NF α∠=,21F F N β∠=,即可求出sin α,sin β,cos β,在21F F N 中由()12sin sin F F N αβ∠=+求出12sin F F N ∠,再由正弦定理求出1NF ,2NF ,最后根据双曲线的定义得到23b a =,即可得解;解:依题意不妨设双曲线焦点在x 轴,设过1F 作圆D 的切线切点为G ,所以1OG NF ⊥,因为123cos 05F NF ∠=>,所以N 在双曲线的右支,所以OG a =,1OF c =,1GF b =,设12F NF α∠=,21F F N β∠=,由123cos 5F NF ∠=,即3cos 5α=,则4sin 5α=,sin a c β=,cos b c β=,在21F F N 中,()()12sin sin sin F F N παβαβ∠=--=+4334sin cos cos sin 555b a a bc c c αβαβ+=+=⨯+⨯=,由正弦定理得211225sin sin sin 2NF NF c cF F N αβ===∠,所以112553434sin 2252c c a b a b NF F F N c ++=∠=⨯=,2555sin 222c c a a NF c β==⨯=又12345422222a b a b aNF NF a +--=-==,所以23b a =,即32b a =,所以双曲线的离心率221312c b e a a ==+=故选:C12.已知函数(),()f x g x 的定义域均为R ,且()(2)5,()(4)7f x g x g x f x +-=--=.若()y g x =的图像关于直线2x =对称,(2)4g =,则221()k f k ==∑()A.21-B.22-C.23-D.24-【答案】D【解析】根据对称性和已知条件得到()(2)2f x f x +-=-,从而得到()()()352110f f f +++=- ,()()()462210f f f +++=- ,然后根据条件得到(2)f 的值,再由题意得到()36g =从而得到()1f 的值即可求解.∵()y g x =的图像关于直线2x =对称,∴()()22g x g x -=+,∵()(4)7g x f x --=,∴(2)(2)7g x f x +--=,即(2)7(2)g x f x +=+-,∵()(2)5f x g x +-=,∴()(2)5f x g x ++=,代入得[]()7(2)5f x f x ++-=,即()(2)2f x f x +-=-,∴()()()()35212510f f f +++=-⨯=- ,()()()()46222510f f f +++=-⨯=- .∵()(2)5f x g x +-=,∴(0)(2)5f g +=,即()01f =,∴()(2)203f f =--=-.∵()(4)7g x f x --=,∴(4)()7g x f x +-=,又∵()(2)5f x g x +-=,联立得,()()2412g x g x -++=,∴()y g x =的图像关于点()3,6中心对称,因为函数()g x 的定义域为R ,∴()36g =∵()(2)5f x g x ++=,所以()()1531f g =-=-.∴()()()()()()()()221123521462213101024()k f f f f f f f f f k =+++++++++=----=-⎡⎤⎡⎤⎣⎦⎣⎦=∑ 故选:D二、填空题:本题共4小题,每小题5分,共20分.13.从甲、乙等5名同学中随机选3名参加社区服务工作,则甲、乙都入选的概率为____________.【答案】310或0.3【解析】从5名同学中随机选3名的方法数为35C 10=甲、乙都入选的方法数为13C 3=,所以甲、乙都入选的概率310P =故答案为:31014.过四点(0,0),(4,0),(1,1),(4,2)-中的三点的一个圆的方程为____________.【答案】()()222313x y -+-=或()()22215x y -+-=或224765339x y ⎛⎫⎛⎫-+-= ⎪ ⎪⎝⎭⎝⎭或()2281691525x y ⎛⎫-+-= ⎪⎝⎭;【解析】依题意设圆的方程为220x y Dx Ey F ++++=,若过()0,0,()4,0,()1,1-,则01640110F D F D E F =⎧⎪++=⎨⎪+-++=⎩,解得046F D E =⎧⎪=-⎨⎪=-⎩,所以圆的方程为22460x y x y +--=,即()()222313x y -+-=;若过()0,0,()4,0,()4,2,则01640164420F D F D E F =⎧⎪++=⎨⎪++++=⎩,解得042F D E =⎧⎪=-⎨⎪=-⎩,所以圆的方程为22420x y x y +--=,即()()22215x y -+-=;若过()0,0,()4,2,()1,1-,则0110164420F D E F D E F =⎧⎪+-++=⎨⎪++++=⎩,解得083143F D E ⎧⎪=⎪⎪=-⎨⎪⎪=-⎪⎩,所以圆的方程为22814033x y x y +--=,即224765339x y ⎛⎫⎛⎫-+-= ⎪ ⎪⎝⎭⎝⎭;若过()1,1-,()4,0,()4,2,则1101640164420D E F D F D E F +-++=⎧⎪++=⎨⎪++++=⎩,解得1651652F D E ⎧=-⎪⎪⎪=-⎨⎪=-⎪⎪⎩,所以圆的方程为2216162055x y x y +---=,即()2281691525x y ⎛⎫-+-= ⎪⎝⎭;故答案为:()()222313x y -+-=或()()22215x y -+-=或224765339x y ⎛⎫⎛⎫-+-= ⎪ ⎪⎝⎭⎝⎭或()2281691525x y ⎛⎫-+-= ⎪⎝⎭;15.记函数()()cos (0,0π)f x x ωϕωϕ=+><<的最小正周期为T ,若3()2f T =,9x π=为()f x 的零点,则ω的最小值为____________.【答案】3【解析】解:因为()()cos f x x ωϕ=+,(0>ω,0πϕ<<)所以最小正周期2πT ω=,因为()()2π3cos cos 2πcos 2f T ωϕϕϕω⎛⎫=⋅+=+==⎪⎝⎭,又0πϕ<<,所以π6ϕ=,即()πcos 6f x x ω⎛⎫=+ ⎪⎝⎭,又π9x =为()f x 的零点,所以ππππ,Z 962k k ω+=+∈,解得39,Z k k ω=+∈,因为0>ω,所以当0k =时min 3ω=;故答案为:316.已知1x x =和2x x =分别是函数2()2e x f x a x =-(0a >且1a ≠)的极小值点和极大值点.若12x x <,则a 的取值范围是____________.【答案】1,1e ⎛⎫ ⎪⎝⎭【解析】由12,x x 分别是函数()22e x f x a x =-的极小值点和极大值点,可得()()12,,x x x ∈-∞⋃+∞时,()0f x '<,()12,x x x ∈时,()0f x '>,再分1a >和01a <<两种情况讨论,方程2ln 2e 0x a a x ⋅-=的两个根为12,x x ,即函数ln x y a a =⋅与函数e y x =的图象有两个不同的交点,构造函数()ln xg x a a =⋅,根据导数的结合意义结合图象即可得出答案.解:()2ln 2e xf x a a x '=⋅-,∵12,x x 分别是函数()22e xf x a x =-的极小值点和极大值点,∴函数()f x 在()1,x -∞和()2,x +∞上递减,在()12,x x 上递增,∴当()()12,,x x x ∈-∞⋃+∞时,()0f x '<,当()12,x x x ∈时,()0f x '>,若1a >时,当0x <时,2ln 0,2e 0x a a x ⋅><,则此时()0f x '>,与前面矛盾,故1a >不符合题意,若01a <<时,则方程2ln 2e 0x a a x ⋅-=的两个根为12,x x ,即方程ln e x a a x ⋅=的两个根为12,x x ,即函数ln x y a a =⋅与函数e y x =的图象有两个不同的交点,令()ln xg x a a =⋅,则()2ln ,01xg x a a a '=⋅<<,设过原点且与函数()y g x =的图象相切的直线的切点为()00,ln x x a a ⋅,则切线的斜率为()020ln xg x a a '=⋅,故切线方程为()0020ln ln x x y a a a a x x -⋅=⋅-,则有0020ln ln x x a a x a a -⋅=-⋅,解得01ln x a=,则切线的斜率为122ln ln eln aa aa ⋅=,因为函数ln x y a a =⋅与函数e y x =的图象有两个不同的交点,所以2eln e a <,解得1e ea <<,又01a <<,所以11ea <<,综上所述,a 的范围为1,1e ⎛⎫ ⎪⎝⎭.三、解答题:共0分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.(一)必考题:共60分.17.记ABC 的内角,,A B C 的对边分别为,,a b c ,已知sin sin()sin sin()C A B B C A -=-.(1)证明:2222a b c =+;(2)若255,cos 31a A ==,求ABC 的周长.【答案】(1)见解析(2)14【解析】(1)证明:∵()()sin sin sin sin C A B B C A -=-,∴sin sin cos sin sin cos sin sin cos sin sin cos C A B C B A B C A B A C -=-,∴2222222222222a c b b c a a b c ac bc ab ac bc ab +-+-+-⋅-⋅=-⋅,即()22222222222a cb a bc b c a +-+--+-=-,∴2222a b c =+;(2)解:∵255,cos 31a A ==,由(1)得2250bc +=,由余弦定理可得2222cos a b c bc A =+-,则50502531bc -=,∴312bc =,故()2222503181b c b c bc +=++=+=,∴9b c +=,∴ABC 的周长为14a b c ++=.18.如图,四面体ABCD 中,,,AD CD AD CD ADB BDC ⊥=∠=∠,E 为AC 的中点.(1)证明:平面BED ⊥平面ACD ;(2)设2,60AB BD ACB ==∠=︒,点F 在BD 上,当AFC △的面积最小时,求CF 与平面ABD 所成的角的正弦值.【答案】(1)证明过程见解析(2)CF 与平面ABD所成的角的正弦值为7【解析】(1)∵AD CD =,E 为AC 的中点,∴AC DE ⊥;在ABD △和CBD 中,∵,,B A C D CD ADB DB DB D ∠=∠==,∴ABD CBD ≌△△,∴AB CB =,又∵E 为AC 的中点,所以AC BE ⊥;又∵,DE BE ⊂平面BED ,DE BE E ⋂=,∴AC ⊥平面BED ,∵AC ⊂平面ACD ,∴平面BED ⊥平面ACD .(2)如图连接EF ,由(1)知,AC ⊥平面BED ,∵EF ⊂平面BED ,∴AC EF ⊥,∴1=2AFC S AC EF ⋅△,当EF BD ⊥时,EF 最小,即AFC △的面积最小.∵ABD CBD ≌△△,∴2CB AB ==,又∵60ACB ∠=︒,∴ABC 是等边三角形,∵E 为AC 的中点,∴1AE EC ==,BE =,∵AD CD ⊥,∴112DE AC ==,在DEB 中,222DE BE BD +=,∴BE DE ⊥.以E 为坐标原点建立如图所示的空间直角坐标系E xyz -,则()()()1,0,0,,0,0,1A B D ,∴()()1,0,1,AD AB =-=-,设平面ABD 的一个法向量为(),,n x y z =,则00n AD x z n AB x ⎧⋅=-+=⎪⎨⋅=-+=⎪⎩,取y =,则()n = ,又∵()331,0,0,0,44C F ⎛⎫- ⎪ ⎪⎝⎭,∴331,,44CF ⎛⎫= ⎪ ⎪⎝⎭,∴cos,7n CFn CFn CF⋅==,设CF与平面ABD所成的角的正弦值为02πθθ⎛⎫≤≤⎪⎝⎭,∴43sin cos,7n CFθ==,∴CF与平面ABD 所成的角的正弦值为437.19.某地经过多年的环境治理,已将荒山改造成了绿水青山.为估计一林区某种树木的总材积量,随机选取了10棵这种树木,测量每棵树的根部横截面积(单位:2m)和材积量(单位:3m),得到如下数据:样本号i12345678910总和根部横截面积i x0.040.060.040.080.080.050.050.070.070.060.6材积量i y0.250.400.220.540.510.340.360.460.420.403.9并计算得10101022i i i ii=1i=1i=10.038, 1.6158,0.2474x y x y===∑∑∑.(1)估计该林区这种树木平均一棵的根部横截面积与平均一棵的材积量;(2)求该林区这种树木的根部横截面积与材积量的样本相关系数(精确到0.01);(3)现测量了该林区所有这种树木的根部横截面积,并得到所有这种树木的根部横截面积总和为2186m.已知树木的材积量与其根部横截面积近似成正比.利用以上数据给出该林区这种树木的总材积量的估计值.附:相关系数i i(1.377)(nx x y yr--=≈∑.【答案】(1)20.06m;30.39m(2)0.97(3)31209m 【解析】(1)样本中10棵这种树木的根部横截面积的平均值0.60.0610x ==样本中10棵这种树木的材积量的平均值 3.90.3910y ==据此可估计该林区这种树木平均一棵的根部横截面积为20.06m ,平均一棵的材积量为30.39m (2)()()1010iii i10x x y y x y xyr ---=∑∑0.01340.970.01377=≈则0.97r ≈(3)设该林区这种树木的总材积量的估计值为,又已知树木的材积量与其根部横截面积近似成正比,可得,解之得.则该林区这种树木的总材积量估计为31209m 20.已知椭圆E 的中心为坐标原点,对称轴为x 轴、y 轴,且过()30,2,,12A B ⎛--⎫ ⎪⎝⎭两点.(1)求E 的方程;(2)设过点()1,2P -的直线交E 于M ,N 两点,过M 且平行于x 轴的直线与线段AB 交于点T ,点H 满足MT TH =.证明:直线HN 过定点.【答案】(1)22143y x +=(2)(0,2)-【解析】(1)解:设椭圆E 的方程为221mx ny +=,过()30,2,,12A B ⎛--⎫ ⎪⎝⎭,则41914n m n =⎧⎪⎨+=⎪⎩,解得13m =,14n =,所以椭圆E 的方程为:22143y x +=.(2)3(0,2),(,1)2A B --,所以2:23+=AB y x ,①若过点(1,2)P -的直线斜率不存在,直线1x =.代入22134x y+=,可得(1,3M,(1,3N -,代入AB 方程223y x =-,可得263,)3T +,由MT TH =得到265,)3H .求得HN 方程:26(2)23y x =--,过点(0,2)-.②若过点(1,2)P -的直线斜率存在,设1122(2)0,(,),(,)kx y k M x y N x y --+=.联立22(2)0,134kx y k x y --+=⎧⎪⎨+=⎪⎩得22(34)6(2)3(4)0k x k k x k k +-+++=,可得1221226(2)343(4)34k k x x k k k x x k +⎧+=⎪⎪+⎨+⎪=⎪+⎩,12222228(2)344(442)34k y y k k k y y k -+⎧+=⎪⎪+⎨+-⎪=⎪+⎩,且1221224(*)34kx y x y k -+=+联立1,223y y y x =⎧⎪⎨=-⎪⎩可得111113(3,),(36,).2y T y H y x y ++-可求得此时1222112:()36y y HN y y x x y x x --=-+--,将(0,2)-,代入整理得12121221122()6()3120x x y y x y x y y y +-+++--=,将(*)代入,得222241296482448482436480,k k k k k k k +++---+--=显然成立,综上,可得直线HN 过定点(0,2).-21.已知函数()()ln 1exf x x ax -=++(1)当1a =时,求曲线()y f x =在点()()0,0f 处的切线方程;(2)若()f x 在区间()()1,0,0,-+∞各恰有一个零点,求a 的取值范围.【答案】(1)2y x =(2)(,1)-∞-【解析】(1)()f x 的定义域为(1,)-+∞当1a =时,()ln(1),(0)0e x x f x x f =++=,所以切点为(0,0)11(),(0)21exx f x f x ''-=+=+,所以切线斜率为2所以曲线()y f x =在点(0,(0))f 处的切线方程为2y x =(2)()ln(1)e xax f x x =++()2e 11(1)()1e (1)e x xxa x a x f x x x '+--=+=++设()2()e 1xg x a x=+-①若0a >,当()2(1,0),()e 10xx g x a x∈-=+->,即()0f x '>所以()f x 在(1,0)-上单调递增,()(0)0f x f <=故()f x 在(1,0)-上没有零点,不合题意②若,当,()0x ∈+∞,则()e 20x g x ax '=->所以()g x 在(0,)+∞上单调递增所以()(0)10g x g a >=+,即()0f x '>所以()f x 在(0,)+∞上单调递增,()(0)0f x f >=故()f x 在(0,)+∞上没有零点,不合题意③若1a <-a .当,()0x ∈+∞,则()e 20x g x ax '=->,所以()g x 在(0,)+∞上单调递增(0)10,(1)e 0g a g =+<=>所以存在(0,1)m ∈,使得()0g m =,即()0'=f m 当(0,),()0,()x m f x f x '∈<单调递减当(,),()0,()x m f x f x '∈+∞>单调递增所以当(0,),()(0)0x m f x f ∈<=当,()x f x →+∞→+∞所以()f x 在(,)m +∞上有唯一零点又(0,)m 没有零点,即()f x 在(0,)+∞上有唯一零点b.当()2(1,0),()e 1xx g x a x ∈-=+-设()()e 2x h x g x ax'==-()e 20x h x a '=->所以()g x '在(1,0)-单调递增1(1)20,(0)10eg a g ''-=+<=>所以存在(1,0)n ∈-,使得()0g n '=当(1,),()0,()x n g x g x '∈-<单调递减-21-既然已经出发,就一定能到达!当(,0),()0,()x n g x g x '∈>单调递增,()(0)10g x g a <=+<又1(1)0eg -=>所以存在(1,)t n ∈-,使得()0g t =,即()0f t '=当(1,),()x t f x ∈-单调递增,当(,0),()x t f x ∈单调递减有1,()x f x →-→-∞而(0)0f =,所以当(,0),()0x t f x ∈>所以()f x 在(1,)t -上有唯一零点,(,0)t 上无零点即()f x 在(1,0)-上有唯一零点所以1a <-,符合题意所以若()f x 在区间(1,0),(0,)-+∞各恰有一个零点,求a 的取值范围为(,1)-∞-(二)选考题,共10分.请考生在第22、23题中任选一题作答.如果多做,则按所做的第一题计分.[选修4-4:坐标系与参数方程]22.在直角坐标系xOy 中,曲线C 的参数方程为322sin x ty t⎧=⎪⎨=⎪⎩,(t 为参数),以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,已知直线l 的极坐标方程为sin 03m πρθ⎛⎫⎪⎝+⎭+=.(1)写出l 的直角坐标方程;(2)若l 与C 有公共点,求m 的取值范围.-22-2022高考文科数学(全国乙卷)【答案】(120++=y m (2)195122-≤≤m 【解析】(1)∵l :sin 03m πρθ⎛⎫ ⎪⎝+⎭+=,∴13sin cos 022ρθρθ⋅+⋅+=m ,又∵sin ,cos y x ρθρθ⋅=⋅=,∴化简为13022++=y x m ,整理得l20++=y m (2)联立l 与C的方程,即将2=x t ,2sin y t =代入20++=y m 中,可得3cos 22sin 20++=t t m ,所以23(12sin )2sin 20-++=t t m ,化简为26sin 2sin 320-+++=t t m ,要使l 与C 有公共点,则226sin 2sin 3=--m t t 有解,令sin =t a ,则[]1,1a ∈-,令2()623=--f a a a ,(11)a -≤≤,对称轴为16a =,开口向上,所以(1)623()5=-=+-=max f f a ,min 11219(())36666==--=-f f a ,所以19256-≤≤m m 的取值范围为195122-≤≤m .[选修4-5:不等式选讲]23.已知a ,b ,c 都是正数,且3332221a b c ++=,证明:(1)19abc ≤;(2)a b c b c a c a b ++≤+++;-23-既然已经出发,就一定能到达!【答案】(1)证明见解析(2)证明见解析【解析】(1)证明:因为0a >,0b >,0c >,则32a >,32b >,320c >,所以3332223a b c ++≥,即()1213abc ≤,所以19abc ≤,当且仅当333222a b c ==,即a b c ===(2)证明:∵0a >,0b >,0c >,∴b c +≥a c +≥,a b +≥,∴32a b c ≤=+32b a c ≤=+,32c a b ≤=+333333222222a b c b c a c a b ++≤+++当且仅当a b c ==时取等号.。
齿轮箱原理和维修-PPT全文

fm
zr (nr 60
nc )
(Hz)
nc - 转臂得回转速度,当与参考齿轮转向相反时取正号,否则就取负号。
之越大。 d、离合功能:我们可以通过分开两个原本啮合得齿轮,达到把发动机与负载分开得
目得。比如刹车离合器等。 e、分配动力。例如我们可以用一台发动机,通过齿轮箱主轴带动多个从轴,从而实
现一台发动机带动多个负载得功能。
3、齿轮箱分类:
a、按齿轮形状分类
齿轮齿轮箱
蜗杆齿轮箱 行星齿轮箱
圆柱齿轮齿轮箱 圆锥齿轮齿轮箱 圆锥—圆柱齿轮齿轮箱
×
×
×
×
√
×
×
×
×
×
△
×
×
×
×
√
○
×
注:√——最有效 ○——尚有效 △——有可能 ×——不适用
1、齿轮箱故障得特征频率与边频带
在生产条件下很难直接检测某一个齿轮得故障信号,一般就是在轴承箱体有关部位 测量。当齿轮旋转时,无论齿轮发生了异常与否,齿得啮合都会发生冲击啮合振动, 其振动波形表现出振幅受到调制得特点,甚至既调幅又调频。
d、输入方式:电机联接法兰、轴输入。 c、采用吸音箱体结构、较大得箱体表面积与大风扇、圆柱齿轮与低、运转得可靠性得到提高,传递功率增大。 e、输出方式:带平键得实心轴、带平键得空心轴、胀紧盘联结得空心轴、花键联结得空心
轴、花键联结得实心轴与法兰联结得实心轴。 f、齿轮箱安装方式:卧式、立式、摆动底座式、扭力臂式。
圆柱蜗杆齿轮箱 圆弧齿蜗杆齿轮箱 锥蜗杆齿轮箱 蜗杆—齿轮齿轮箱 渐开线行星齿轮齿轮箱 摆线齿轮齿轮箱 谐波齿轮齿轮箱
b、按变速次数分类
大家学习辛苦了,还是要坚持
精编机械设计-滑动轴承习题与参考答案资料
习题与参考答案一、选择题(从给出的A、B、C、D中选一个答案)1 验算滑动轴承最小油膜厚度h min的目的是。
A. 确定轴承是否能获得液体润滑B. 控制轴承的发热量C. 计算轴承内部的摩擦阻力D. 控制轴承的压强P2 在题2图所示的下列几种情况下,可能形成流体动力润滑的有。
3 巴氏合金是用来制造。
A. 单层金属轴瓦B. 双层或多层金属轴瓦C. 含油轴承轴瓦D. 非金属轴瓦4 在滑动轴承材料中,通常只用作双金属轴瓦的表层材料。
A. 铸铁B. 巴氏合金C. 铸造锡磷青铜D. 铸造黄铜5 液体润滑动压径向轴承的偏心距e 随 而减小。
A. 轴颈转速n 的增加或载荷F 的增大 B. 轴颈转速n 的增加或载荷F 的减少 C. 轴颈转速n 的减少或载荷F 的减少 D. 轴颈转速n 的减少或载荷F 的增大6 不完全液体润滑滑动轴承,验算][pv pv ≤是为了防止轴承 。
A. 过度磨损 B. 过热产生胶合 C. 产生塑性变形 D. 发生疲劳点蚀7 设计液体动力润滑径向滑动轴承时,若发现最小油膜厚度h min 不够大,在下列改进设计的措施中,最有效的是 。
A. 减少轴承的宽径比d l /B. 增加供油量C. 减少相对间隙ψD. 增大偏心率χ 8 在 情况下,滑动轴承润滑油的粘度不应选得较高。
A. 重载 B. 高速C. 工作温度高D. 承受变载荷或振动冲击载荷 9 温度升高时,润滑油的粘度 。
A. 随之升高B. 保持不变C. 随之降低D. 可能升高也可能降低 10 动压润滑滑动轴承能建立油压的条件中,不必要的条件是 。
A. 轴颈和轴承间构成楔形间隙 B. 充分供应润滑油C. 轴颈和轴承表面之间有相对滑动D. 润滑油温度不超过50℃11 运动粘度是动力粘度与同温度下润滑油 的比值。
A. 质量B. 密度C. 比重D. 流速 12 润滑油的 ,又称绝对粘度。
A. 运动粘度B. 动力粘度C. 恩格尔粘度D. 基本粘度 13 下列各种机械设备中, 只宜采用滑动轴承。
场地平整土方量计算例题

V32 26 7 47 30 110(m3 )
V13 5810916 69 252(m3 )
②两挖、两填方格,由式(1-8);
V
() 11
202 0.292 0.032 292 32 ( ) 28.35(m2 ) 4 0.29 0.01 0.03 0.25 29 1 3 25
1) 试确定场地设计标高(不考虑土的可松 性的影响,余土加宽边坡) 2) 计算场地边坡的土方量
1)计算场地设计标H0
Z1 9.45 10.71 8.65 9.52 38.33
2 Z2 2 9.7510.14 9.1110.27 8.80 9.86 8.91 9.14 151.96
Z6 Z5 20 0.3% 9.40 0.06 9.46m
Z9 Z0 30 0.3% 10 0.2% 9.47 0.09 0.02 9.36m
其余各角点设计标高均可求出,详见图
3)计算各角点的施工高度 由式(1-6)得各角点的施工高度(以+为填方,-为挖方)
V
( ) 11
12 252 22.35(m3 ) 1 29 25 3
72 302 29.38(m3 ) 7 32 30 2
322 22 26.38(m3 ) 32 7 30 2
V
() 33
V
( ) 33
③三填一挖或三挖一填方格,由式(1-9);
2 3 3 20 0 . 03 2 3 () 3 V1 ( ) .25)(0.03 0.16) 3 (3 25)(3 16)
) V1( 2
内蒙古自治区通辽市第一中学2024-2025学年高一上学期12月月考语文试题(含答案)

通辽一中2024级高一上学期第三次月考语文试题考试时间:150分钟满分:150分注意事项:1、答卷前,考生务必将自己的姓名、考生号涂写在答题卡上。
2、做选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
写在本试卷上无效。
3、回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
一、现代文阅读(共37分)(一)阅读下面的文字,完成小题。
材料一:“什么时候结婚啊?”“每月工资多少啊?”每至年关,亲戚们的“嘘寒问暖”让年轻人叫苦不迭。
近年来,新世代的“90后”特别是“00后”青年群体的“断亲”,已成为越来越普遍的现象。
主要表现为懒于、疏于、不屑于同二代以内的亲戚互动和交往的一种现象,简单讲就是基本不走亲戚,而不是一种正式声明的断绝亲戚关系。
青年“断亲”背后的原因不能简单化理解,需要从中国社会结构嬗变的大环境和新世代生活方式变化等多重因素去思考。
在漫长的传统社会中,由于生产力低下和市场经济体制缺失,很多家庭都需要依托家族、宗族来获取谋生的资源。
中国经过40多年的改革开放,总体实现了国民经济的巨大发展,大量的核心家庭都有车有房,进入中产阶层群体。
与此同时,国家先后推动的全民医保、社保,九年义务教育等保障性制度,银行推出的各种贷款工具,使几乎每个核心家庭都能够在经济上实现自由独立,而不再需要依托亲戚网络的帮助。
这种因经济独立而带来的安全感,冲淡了中国社会堂表兄弟这种“二代亲”“三代亲”的心理认知。
城市化和社会流动加速了城市居民的跨区域形态的居住分离。
城市化是一个人口不断聚居于城市,最终导致社会结构变迁的过程。
随着高等教育的普及,城——城流动持续增加,加速了居民的居住分离。
核心家庭与爷爷奶奶、外公外婆、兄弟姐妹的分离,导致下一代从小就形成了亲戚之间因空间距离而情感疏离的社会交往状态。
城市化解构了传统社会中的大家庭小范围空间的相邻居住形态,为青年世代之间的面对面交往带来更大难度。
20式班用轻机枪首次试用新闻稿

20式班用轻机枪首次试用新闻稿摘要:一、前言二、20 式班用轻机枪的特点1.设计理念2.主要性能参数3.创新点与技术优势三、首次试用情况1.试验背景2.试验过程3.试验结果与评价四、20 式班用轻机枪的应用前景1.对我国军队战斗力的提升2.国内外市场需求3.对我国轻武器发展的影响五、结语正文:一、前言我国自主研发的20 式班用轻机枪首次试用成功,标志着我国轻武器研发取得了新的重要成果。
20 式班用轻机枪凭借其先进的设计理念、卓越的性能参数和创新点,为我国军队提供了一种具有世界先进水平的班用轻机枪。
二、20 式班用轻机枪的特点1.设计理念:20 式班用轻机枪的设计理念是立足我国军队的实际需求,结合现代战争的特点,以高可靠性、高机动性、高精确性、高火力持续性为原则,打造一款适应多样化作战环境的轻机枪。
2.主要性能参数:20 式班用轻机枪采用5.8mm 口径,全枪长940mm,枪管长460mm,全枪质量3.8kg,有效射程600m,理论射速650-750 发/分钟。
3.创新点与技术优势:20 式班用轻机枪具有以下创新点和技术优势:(1)采用了新型的材料和工艺,大幅减轻了全枪质量;(2)采用了可调节的枪托和握把,使射手可以根据自己的舒适度进行调整;(3)采用了模块化设计,方便拆卸和维护;(4)具有较高的射击精度和稳定性。
三、首次试用情况1.试验背景:为了全面检验20 式班用轻机枪的性能,我国军方组织了一系列严格的试验。
试验涵盖了各种环境、气候和地形条件,以模拟真实的战场环境。
2.试验过程:试验过程中,20 式班用轻机枪表现出了出色的性能。
其高可靠性、高机动性、高精确性和高火力持续性得到了充分验证。
试验人员对其易操作性、维护性以及模块化设计给予了高度评价。
3.试验结果与评价:经过严格的试验,20 式班用轻机枪顺利通过了所有测试项目,获得了试验人员的一致好评。
评价认为,20 式班用轻机枪性能优异,完全符合我国军队的实际需求,具有很高的作战效能。
自组装型分子光开关

自组装型分子光开关
佚名
【期刊名称】《光学仪器》
【年(卷),期】2005(27)1
【摘要】Tobin Marks和同事在2005年1月出版的《自然一材料学》上报告说,他们研制的一种有机分子薄膜开关可提供一种简单、廉价的方法,让信息在光纤网络中传播,而所需时间只是以前时间的一小部分。
【总页数】1页(P27-27)
【关键词】光开关;光纤网络;廉价;薄膜开关;有机分子;自组装;材料学;时间;传播
【正文语种】中文
【中图分类】TH-39;TN92
【相关文献】
1.基于酞菁光控自组装的超分子三阶非线性光开关材料 [J], 陈子辉;张复实
2.苝酰亚胺微米棒的自组装及其光开关应用 [J], 廉拓;栗叶芬;刘振东;吴义室;刘会
影
3.具有分子机器、分子开关功能的自组装超分子体系 [J], 陈慧兰
4.MEMS光开关及其与光纤组装方式的研究 [J], 朱晓蕊;罗元;李向东;黄尚廉
5.激发态质子转移型有机分子7-羟基喹啉的光开关效应 [J], 肖东;张桂兰;汤国庆;
陈文驹
因版权原因,仅展示原文概要,查看原文内容请购买。
食管癌组织微RNA-634、锌指蛋白ZBTB20表达与食管癌临床特征及预后的关系

食管癌组织微RNA-634、锌指蛋白ZBTB20表达与食管癌临床特征及预后的关系姜明泽;王磊;杨树博【期刊名称】《安徽医药》【年(卷),期】2024(28)2【摘要】目的分析食管癌组织中微RNA-634(miR-634)和锌指蛋白ZBTB20的表达水平,并分析二者是否与食管癌发生发展及预后相关。
方法选取2018年1月至2019年4月湖北医药学院附属国药东风总医院接受手术的食管癌病人102例,从病人根治切除术手术标本切取癌组织及癌旁正常组织。
实时荧光定量PCR(qRT-PCR)检测miR-634、ZBTB20 mRNA相对表达水平。
Pearson相关性分析食管癌组织中miR-634与ZBTB20 mRNA表达水平的相关性。
Kaplan-Meier生存曲线分析miR-634、ZBTB20与预后的关系。
Cox回归分析食管癌病人预后危险因素。
结果与癌旁正常组织(1.02±0.06、1.01±0.05)相比,食管癌组织中miR-634低表达(0.69±0.15)(P<0.05),ZBTB20 mRNA高表达(1.64±0.26)(P<0.05)。
Pearson相关性分析显示,miR-634、ZBTB20 mRNA在食管癌病人的组织样本中表达水平负相关(r=-0.65,P<0.05);两者均与TNM分期、淋巴结转移、组织分化程度相关(P<0.05)。
Kaplan-Meier法显示,miR-634高表达组(64.71%)无进展生存率较低表达(29.41%)高(χ^(2)=14.41,P<0.001),ZBTB20低表达组(62.75%)无进展生存率较高表达组(31.37%)高(χ^(2)=9.48,P=0.002)。
多因素Cox回归分析表明,TNM分期(Ⅲ)、淋巴结转移、miR-634低表达、ZBTB20高表达是影响食管癌病人不良预后的危险因素(P<0.05)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
多聚甲醛-蔗糖溶液(20%)
简介:
固定的目的在于保存细胞和组织的原有形态结构,固定剂能阻止内源性溶酶体酶对自身组织和细胞的自溶、抑制细菌和霉菌的生长。
固定剂通过凝固、生成添加化合物等使蛋白质内部结构发生改变,从而使酶失活。
固定液分为醛类固定液、汞类固定液、醇类固定液、氧化剂类固定液、苦味酸盐类固定液等,较为常用的是醛类中的福尔马林、醇类中的乙醇。
Leagene 多聚甲醛-蔗糖溶液(20%)由多聚甲醛、磷酸盐、蔗糖组成,pH 为7.4,该固定液适合于特殊要求的细胞或组织的固定,亦可作为特殊样本的脱水剂。
组成:
操作步骤(仅供参考):
1、 按实验具体要求操作。
注意事项:
1、 Leagene 多聚甲醛溶液有一定刺激性和腐蚀性,请在通风环境下小心操作。
2、 一经开启,尽快用完,储存过久的液体固定效果易下降。
3、 避免过度延长固定时间,否则易引起细胞内生物大分子过度交联。
4、 组织取材的厚度不同,固定时间也不同。
5、 固定液的容量应足够,一般固定液与组织块的体积比率应大于10:1。
6、 温度对固定的影响很明显,提高温度可以加速固定作用,但温度不宜过高。
7、 取出新鲜组织后,应及时固定,无法及时固定时,应保存于生理盐水中及时送检。
有效期: 12个月有效。
相关:
编号 名称 DF0143 Storage 多聚甲醛-蔗糖溶液(20%) 500ml 4℃ 避光 使用说明书 1份
编号 名称 DC0032 Masson 三色染色液 PE0103 Acr-Bis(30%,29:1)。
