三视图(小学)PPT课件
合集下载
《三视图》课件(共55张PPT)

如果物体向三个互相垂直 的投影面分别投影,所得到 的三个图形摊平在一个平面 上,则就是三视图。
练习: 根据三视图想 像物体的形状。
圆柱
圆台
手电筒
从左向右看
圆柱
正六棱柱
螺丝杆
从左向右看
柱
四棱柱
螺丝杆
从左向右看
圆柱
半圆球
螺丝钉
从左向右看
圆柱
圆台
圆柱
热水瓶
从上向下看
N
S
前后看 从上向下看
左右看
马蹄形磁铁
从下向上看
环的形成
有关概念
物体向投影面投影所得 到的图形称为视图。
接下一张幻灯片
在主视图、俯视 图中都体现形体的长 度,且长度在竖直方 向上是对正的,我们 称之为长对正。
返回
在主视图、左视 图上都体现形体的高 度,且高度在水平方 向上是平齐的,我们 称之为高平齐。
返回
在左视图、俯视 图上都体现形体的宽 度,且是同一形体的 宽度,是相等的,我 们称之为宽相等。
错误的三视图 —长未对正1
错误的三视图 —长未对正2
错误的三视图 —高不平齐1
错误的三视图 —高不平齐2
错误的三视图 —宽不相等1
错误的三视图 —宽不相等1
错误的三视图
错误的三视图
体验三视 图的作法
三视图的作图步骤
俯视图方向 1.确定视图方向 2.先画出能反映物体 真实形状的一个视图 左视图方向
三视图欣赏
观察左图:说 说下列三副 图是从哪个 角度看的?
甲、乙、丙、丁四人分别面向 桌坐在一张四方形桌子旁边。 桌上一张纸上写着数字“9”, 甲看到“6”,乙看到“ ” ,丙看到“ ”,丁看到 “9”,问四人是怎样的座次 丁正对着数字“9”;甲坐在丁的对面 ? ,
练习: 根据三视图想 像物体的形状。
圆柱
圆台
手电筒
从左向右看
圆柱
正六棱柱
螺丝杆
从左向右看
柱
四棱柱
螺丝杆
从左向右看
圆柱
半圆球
螺丝钉
从左向右看
圆柱
圆台
圆柱
热水瓶
从上向下看
N
S
前后看 从上向下看
左右看
马蹄形磁铁
从下向上看
环的形成
有关概念
物体向投影面投影所得 到的图形称为视图。
接下一张幻灯片
在主视图、俯视 图中都体现形体的长 度,且长度在竖直方 向上是对正的,我们 称之为长对正。
返回
在主视图、左视 图上都体现形体的高 度,且高度在水平方 向上是平齐的,我们 称之为高平齐。
返回
在左视图、俯视 图上都体现形体的宽 度,且是同一形体的 宽度,是相等的,我 们称之为宽相等。
错误的三视图 —长未对正1
错误的三视图 —长未对正2
错误的三视图 —高不平齐1
错误的三视图 —高不平齐2
错误的三视图 —宽不相等1
错误的三视图 —宽不相等1
错误的三视图
错误的三视图
体验三视 图的作法
三视图的作图步骤
俯视图方向 1.确定视图方向 2.先画出能反映物体 真实形状的一个视图 左视图方向
三视图欣赏
观察左图:说 说下列三副 图是从哪个 角度看的?
甲、乙、丙、丁四人分别面向 桌坐在一张四方形桌子旁边。 桌上一张纸上写着数字“9”, 甲看到“6”,乙看到“ ” ,丙看到“ ”,丁看到 “9”,问四人是怎样的座次 丁正对着数字“9”;甲坐在丁的对面 ? ,
《三视图》精品课件

3.如图,是由两个大小不同的长方体组成的几何体, 则该几何体的左视图是( C )
A
B
C
D
课堂小结
三 视 图
主视图
在正面内得到的由前向 后观察物体的视图
俯视图
在水平面内得到的由上 向下观察物体的视图
左视图
在侧面内得到的由左向 右观察物体的视图
简单几何体的三视图
对接中考
1.直六棱柱如图所示,它的俯视图是( )
主视图
左视图 俯视图
主视图
正面
左
主视图 左视图
视 图
高
长
宽
俯视图 水平面
侧面
宽 俯视图
将三个投影面展开在一个平面内,得到这一物体的一张 三视图.
1.物体的三视图中的各个视图,分别从不同角度表 示物体的形状,三者合起来能够较全面地反映物体 的形状. 2.三视图与投影的关系:物体的主视图、左视图、 俯视图可以看成一束平行光线分别从物体的正面、 左面、上面照射,在垂直于这一方向光线的平面上 所形成的正投影. 3.在生产实践中常用三视图描述物体,如机械零件, 建筑物等.
C
A.
B.
C.
D.
2.下列立体图形中,主视图是圆的 是( D )
A. B.
C.
D.
主视图是 角形
主视图 是圆
3.如图是由4个相同的小正方体构成的一个组合体,该组合
体的三视图中完全相同的是( )
A
A.主视图和左视图 B.主视图和俯视图
C.左视图和俯视图 D.三个视图均相同
单一的视图通常只能反映物体一个方面的形状.为了全面 地反映物体的形状,生产实践中往往采用多个视图来反映 同一物体不同方面的形状.
下图为某飞机的设计图,你能指出这些设计图是从哪 几个方向来描绘物体的吗?
三视图的画法PPT课件

*
作 业 作业: 1、P12练习1(2)(3) 2、P18、A1 3、P19、A6 4、P19、B1 探究:P11课本
*
返回
侧视图方向
俯视图方向
正视图方向
正视图 侧视图
俯视图
长
高
宽
画一个物体的三视图时,正视图,侧视图,俯视图所画的位置如图所示,且要符合如下原则:
*
从正面看到的图
从左边看到的图
从上面看到的图
三视图:我们从不同的方向观察同一物体时,可能看到不同的图形。其中,把从正面看到的图叫做正视图,从左面看到的图叫做侧视图,从上面看到的图叫做俯视图。三者统称三视图。
正视图 侧视图
俯视图
*
侧视图方向
俯视图方向
正视图方向
*
下面各图中物体形状分另可以看成什么样的几何体?
圆柱 圆锥 球
从正面,侧面,上面看这些几何体,它们的形状各是什么样的?
正面看:长方体 等腰三角形 圆
侧面看:长方体 等腰三角形 圆
上面看: 圆 圆 圆
六棱锥的三视图
*
例3:画出下面几何体的三视图。
简单组合体的三视图
*
正视图
侧视图
俯视图
简单组合体的三视图
注意:不可见的轮廓线,用虚线画出。
*
正视图
侧视图
俯视图
简单组合体的三视图
*
小 结
三视图 正视图——从正面看到的图 侧视图——从左面看到的图 俯视图——从上面看到的图 画物体的三视图时,要符合如下原则: 位置:正视图 侧视图 俯视图 大小:长对正,高平齐,宽相等. 挑战“自我”,提高画三视图的能力.
三视图的作图步骤
1.确定正视图方向
作 业 作业: 1、P12练习1(2)(3) 2、P18、A1 3、P19、A6 4、P19、B1 探究:P11课本
*
返回
侧视图方向
俯视图方向
正视图方向
正视图 侧视图
俯视图
长
高
宽
画一个物体的三视图时,正视图,侧视图,俯视图所画的位置如图所示,且要符合如下原则:
*
从正面看到的图
从左边看到的图
从上面看到的图
三视图:我们从不同的方向观察同一物体时,可能看到不同的图形。其中,把从正面看到的图叫做正视图,从左面看到的图叫做侧视图,从上面看到的图叫做俯视图。三者统称三视图。
正视图 侧视图
俯视图
*
侧视图方向
俯视图方向
正视图方向
*
下面各图中物体形状分另可以看成什么样的几何体?
圆柱 圆锥 球
从正面,侧面,上面看这些几何体,它们的形状各是什么样的?
正面看:长方体 等腰三角形 圆
侧面看:长方体 等腰三角形 圆
上面看: 圆 圆 圆
六棱锥的三视图
*
例3:画出下面几何体的三视图。
简单组合体的三视图
*
正视图
侧视图
俯视图
简单组合体的三视图
注意:不可见的轮廓线,用虚线画出。
*
正视图
侧视图
俯视图
简单组合体的三视图
*
小 结
三视图 正视图——从正面看到的图 侧视图——从左面看到的图 俯视图——从上面看到的图 画物体的三视图时,要符合如下原则: 位置:正视图 侧视图 俯视图 大小:长对正,高平齐,宽相等. 挑战“自我”,提高画三视图的能力.
三视图的作图步骤
1.确定正视图方向
【小学课件】《物体的三视图》优质PPT课件

物体的三视图
猜 猜 他 们 是 什 么 关 系 ?
看 事 物 不 能 只 看 单 方 面
猜一猜
在太阳底下你只看影子能判断出是什么实物吗?
在生活中我们应从不同角度,多方面地去看待一件事 物,分析一件事情。
A B
C
A B
C
A B
C
A
B
C
视图
三视 图
观察物体—图形 正投影—图形
主视图—从前向后观察 俯视图—从上向下观察 左视图—从左向右观察
分别说出下列物体的三视图
圆柱的三视图:
正视图:由前向后看到的 左视图:由左向右看到的 俯视图:由上向下看到的
主视图
左视图
俯视图
三视图位置有规定, 主视图要在左上边,它 的下方应是俯视图,左 视图坐落在右边
大小:与图上物体尺寸相 同或成比例.
主视图
左视图 高
长
宽
宽 俯视图
想一想,再动手画一画:
(A)
(B)
(C)
(D)
小结
三视图 正视图——从正面看到的图 左视图——从左面看到的图 俯视图——从上面看到的图 画物体的三视图时,要符合如下原则: 位置:正视图 侧视图 俯视图 大小:长对正,高平齐,宽相等.
练习:下面的四组图中,如图所示的圆 柱体的三视图是( )
主视图 俯视图
左视图
A
主视图 俯视图
左视图
C
主视图
左视图
B
俯视图思
球的三视图:
主视图
左视图
俯视图
高平30齐
15
长对正
圆锥体
宽相 等
点不要漏画哦!
正三菱柱的三视图:
可见轮廓线用粗实 线绘制
猜 猜 他 们 是 什 么 关 系 ?
看 事 物 不 能 只 看 单 方 面
猜一猜
在太阳底下你只看影子能判断出是什么实物吗?
在生活中我们应从不同角度,多方面地去看待一件事 物,分析一件事情。
A B
C
A B
C
A B
C
A
B
C
视图
三视 图
观察物体—图形 正投影—图形
主视图—从前向后观察 俯视图—从上向下观察 左视图—从左向右观察
分别说出下列物体的三视图
圆柱的三视图:
正视图:由前向后看到的 左视图:由左向右看到的 俯视图:由上向下看到的
主视图
左视图
俯视图
三视图位置有规定, 主视图要在左上边,它 的下方应是俯视图,左 视图坐落在右边
大小:与图上物体尺寸相 同或成比例.
主视图
左视图 高
长
宽
宽 俯视图
想一想,再动手画一画:
(A)
(B)
(C)
(D)
小结
三视图 正视图——从正面看到的图 左视图——从左面看到的图 俯视图——从上面看到的图 画物体的三视图时,要符合如下原则: 位置:正视图 侧视图 俯视图 大小:长对正,高平齐,宽相等.
练习:下面的四组图中,如图所示的圆 柱体的三视图是( )
主视图 俯视图
左视图
A
主视图 俯视图
左视图
C
主视图
左视图
B
俯视图思
球的三视图:
主视图
左视图
俯视图
高平30齐
15
长对正
圆锥体
宽相 等
点不要漏画哦!
正三菱柱的三视图:
可见轮廓线用粗实 线绘制
《三视图》PPT课件

影。
案例二
通过三视图还原组合体的空间 形状,理解辅助线和辅助面在 投影中的作用。
案例三
比较不同辅助线和辅助面对投 影结果的影响,掌握其使用技 巧。
案例四
针对复杂组合体,综合运用辅 助线和辅助面进行投影分析。
05
CATALOGUE
尺寸标注与技术要求在三视图 中体现
尺寸标注基本原则和方法
基本原则
01
中心线平行。
辅助面构造方法及作用
基本辅助面
通过平移或旋转基本投影 面得到,用于生成新的投 影。
局部辅助面
根据需要截取形体的一部 分而构造,用于表达形体 的局部结构。
综合辅助面
结合基本辅助面和局部辅 助面的特点构造,用于解 决复杂形体的投影问题。
案例分析:组合体三视图
案例一
分析组合体的结构特点,选择 合适的辅助线和辅助面进行投
04
CATALOGUE
辅助线与辅助面在三视图中的 应用
辅助线类型及使用场景
中心线
用于表示对称形体的中 心,或用于定位非对称
形体的主要部分。
轮廓线
用于表示形体的外轮廓 或内轮廓,通常与视图
的主要轮廓线重合。
剖面线
用于表示形体被剖切后 的内部结构,通常与剖
视图的剖面线对应。
尺寸线
用于标注形体的尺寸, 通常与形体的轮廓线或
圆锥体主视图为三角形,俯视 图为圆形和圆心点,左视图为
三角形和一条斜线。
球体的三视图
球体主视图、俯视图和左视图 均为圆形。
03
CATALOGUE
物体表面交线与三视图绘制技 巧
物体表面交线类型及特点
截交线
截平面与立体表面的交线。特点 :截交线的形状取决于立体的几 何性质及其与截平面的相对位置
案例二
通过三视图还原组合体的空间 形状,理解辅助线和辅助面在 投影中的作用。
案例三
比较不同辅助线和辅助面对投 影结果的影响,掌握其使用技 巧。
案例四
针对复杂组合体,综合运用辅 助线和辅助面进行投影分析。
05
CATALOGUE
尺寸标注与技术要求在三视图 中体现
尺寸标注基本原则和方法
基本原则
01
中心线平行。
辅助面构造方法及作用
基本辅助面
通过平移或旋转基本投影 面得到,用于生成新的投 影。
局部辅助面
根据需要截取形体的一部 分而构造,用于表达形体 的局部结构。
综合辅助面
结合基本辅助面和局部辅 助面的特点构造,用于解 决复杂形体的投影问题。
案例分析:组合体三视图
案例一
分析组合体的结构特点,选择 合适的辅助线和辅助面进行投
04
CATALOGUE
辅助线与辅助面在三视图中的 应用
辅助线类型及使用场景
中心线
用于表示对称形体的中 心,或用于定位非对称
形体的主要部分。
轮廓线
用于表示形体的外轮廓 或内轮廓,通常与视图
的主要轮廓线重合。
剖面线
用于表示形体被剖切后 的内部结构,通常与剖
视图的剖面线对应。
尺寸线
用于标注形体的尺寸, 通常与形体的轮廓线或
圆锥体主视图为三角形,俯视 图为圆形和圆心点,左视图为
三角形和一条斜线。
球体的三视图
球体主视图、俯视图和左视图 均为圆形。
03
CATALOGUE
物体表面交线与三视图绘制技 巧
物体表面交线类型及特点
截交线
截平面与立体表面的交线。特点 :截交线的形状取决于立体的几 何性质及其与截平面的相对位置
人教版《三视图》ppt-精美1

人教版《三视图》ppt-精美1
第二十九章 投影与视图
29.2 三视图
第3课时 与三视图有关 的计算
人教版《三视图》ppt-精美1
人教版《三视图》ppt-精美1
名师点金
对于由几何体的三种视图求它的表面积、体积等相 关数据的题目,首先由几何体的三种视图想象出该几何 体的形状,再利用三视图中的相关数据确定立体图形的 相关数据.
人教版《三视图》ppt-精美1
人教版《三视图》ppt-精美1
类型 1 利用视图确定构成几何体中小正方体的个数
1. 用小正方体搭一个几何体,使它的主视图和俯视图 如图.俯视图中小正方形中的字母表示在该位置上 小正方体的个数,请回答下列问题:
人教版《三视图》ppt-精美1
人教版《三视图》ppt-精美1
人教版《三视图》ppt-精美1
方法总结: 由几何体的三视图求它的表面积的方法:先由几
何体的三视图想象出该几何体的形状,再进一步画出 展开图,从而计算出表面积.
人教版《三视图》ppt-精美1
人教版《三视图》ppt-精美1
类型 4 利用三视图想象几何体的展开图求最短问题
4. 如图是一个几何体的三视图(单位:厘米): (1)写出这个几何体的名称; (2)根据所示数据计算这个几何体的表面积; (3)如果一只蚂蚁要从这个几何体中的点B出发,沿表 面爬到AC的中点D,请你求出最短线路的路程.
(1)a,b,c各表示几? (2)这个几何体最少由几个小正方体搭成?最多呢? (3)当d=e=1,f=2时,画出这个几何体的左视图. 思路导引: 由主视图与俯视图可知a为3,b与c均为1,而d,e,f中 至少有一个应为2.当均为2时,共有11个小正方体;当其 中两个为2,一个为1时,共有10个小正方体;当其中一 个为2,另外两个为1时,共有9个小正方体.当a,b,c, d,e,f的值确定时,就只有一种情况,由此即可画出它 的左视图.
第二十九章 投影与视图
29.2 三视图
第3课时 与三视图有关 的计算
人教版《三视图》ppt-精美1
人教版《三视图》ppt-精美1
名师点金
对于由几何体的三种视图求它的表面积、体积等相 关数据的题目,首先由几何体的三种视图想象出该几何 体的形状,再利用三视图中的相关数据确定立体图形的 相关数据.
人教版《三视图》ppt-精美1
人教版《三视图》ppt-精美1
类型 1 利用视图确定构成几何体中小正方体的个数
1. 用小正方体搭一个几何体,使它的主视图和俯视图 如图.俯视图中小正方形中的字母表示在该位置上 小正方体的个数,请回答下列问题:
人教版《三视图》ppt-精美1
人教版《三视图》ppt-精美1
人教版《三视图》ppt-精美1
方法总结: 由几何体的三视图求它的表面积的方法:先由几
何体的三视图想象出该几何体的形状,再进一步画出 展开图,从而计算出表面积.
人教版《三视图》ppt-精美1
人教版《三视图》ppt-精美1
类型 4 利用三视图想象几何体的展开图求最短问题
4. 如图是一个几何体的三视图(单位:厘米): (1)写出这个几何体的名称; (2)根据所示数据计算这个几何体的表面积; (3)如果一只蚂蚁要从这个几何体中的点B出发,沿表 面爬到AC的中点D,请你求出最短线路的路程.
(1)a,b,c各表示几? (2)这个几何体最少由几个小正方体搭成?最多呢? (3)当d=e=1,f=2时,画出这个几何体的左视图. 思路导引: 由主视图与俯视图可知a为3,b与c均为1,而d,e,f中 至少有一个应为2.当均为2时,共有11个小正方体;当其 中两个为2,一个为1时,共有10个小正方体;当其中一 个为2,另外两个为1时,共有9个小正方体.当a,b,c, d,e,f的值确定时,就只有一种情况,由此即可画出它 的左视图.
教学课件——三视图

三视图
情景引入
概念形成:
• 1、 满足什么条件的平行投影是正投影? 正投影除了平行投影的性质以外还具有 哪些性质? • 2、选取的三个投射面是什么位置关系? 它们分别是如何放置的? • 3、三视图是怎样定义的?一般按照怎 样的布局排列? • 4、物体被遮住的轮廓线应该怎样作? • 5、你是怎样理解“长对正、高平齐、 宽相等”的?
4
4
典型例题
• 题型 一.根据直观图求三视图 • 例1 你能说出下列几何体的三视图 分别是什么图形吗?
圆柱的三视图
俯
左
圆锥的三视图
俯
左
.
圆台的三视图
俯
左
三棱柱的三视图
俯
左
思考:
• (1)已知一个几何体的三视图,
怎样判断该几何体是多面体还是旋 转体? • (2)哪种几何体它的三视图都是 一样的图形?
2、下面是空心圆柱在指定方向上的视图, 正确的是…( )
课后练习
作业:A组2 B组1
深化提高
A组
• 1、一个四棱柱的俯视图如右图所示,则这 个四棱柱的主视图和左视图可个几何体自 上而下依次为 ( )
主视图
左视图
俯视图
A、四棱台、圆台 C、四棱柱、四棱柱
B、四棱台、四棱台 D、不能判断
• 例2.一个零件的直观图如图所示, 请画出这个几何体的三视图。
题型二根据三视图画直观图
例3 一个几何体的三视图如下,你能说出它 是什么立体图形吗?
4
4
4
课堂小结
1、三视图的概念; 2、三视图的应用; (1) 由直观图得三视图; (2)由三视图得直观图; (3)识图
当堂检测
1、请将六棱柱的三视图名称填在相应的横线上.
情景引入
概念形成:
• 1、 满足什么条件的平行投影是正投影? 正投影除了平行投影的性质以外还具有 哪些性质? • 2、选取的三个投射面是什么位置关系? 它们分别是如何放置的? • 3、三视图是怎样定义的?一般按照怎 样的布局排列? • 4、物体被遮住的轮廓线应该怎样作? • 5、你是怎样理解“长对正、高平齐、 宽相等”的?
4
4
典型例题
• 题型 一.根据直观图求三视图 • 例1 你能说出下列几何体的三视图 分别是什么图形吗?
圆柱的三视图
俯
左
圆锥的三视图
俯
左
.
圆台的三视图
俯
左
三棱柱的三视图
俯
左
思考:
• (1)已知一个几何体的三视图,
怎样判断该几何体是多面体还是旋 转体? • (2)哪种几何体它的三视图都是 一样的图形?
2、下面是空心圆柱在指定方向上的视图, 正确的是…( )
课后练习
作业:A组2 B组1
深化提高
A组
• 1、一个四棱柱的俯视图如右图所示,则这 个四棱柱的主视图和左视图可个几何体自 上而下依次为 ( )
主视图
左视图
俯视图
A、四棱台、圆台 C、四棱柱、四棱柱
B、四棱台、四棱台 D、不能判断
• 例2.一个零件的直观图如图所示, 请画出这个几何体的三视图。
题型二根据三视图画直观图
例3 一个几何体的三视图如下,你能说出它 是什么立体图形吗?
4
4
4
课堂小结
1、三视图的概念; 2、三视图的应用; (1) 由直观图得三视图; (2)由三视图得直观图; (3)识图
当堂检测
1、请将六棱柱的三视图名称填在相应的横线上.
《三视图》PPT课件_人教版1

《三视图 》优秀 课件人 教版1- 精品课 件ppt( 实用版)
根据三视图想象其表示的几何体
《三视图 》优秀 课件人 教版1- 精品课 件ppt( 实用版)
《三视图 》优秀 课件人 教版1- 精品课 件ppt( 实用版)
根据三视图想象它们表示的几何体的结构特征
正视图
侧视图
俯视图
《三视图 》优秀 课件人 教版1- 精品课 件ppt( 实用版)
《三视图 》优秀 课件人 教版1- 精品课 件ppt( 实用版)
正视图
俯视图
侧视图 光线从几何 体的左面向 右面正投影 所得的投影 图称为“侧 视图”
光线从几何体的上面向下面正投影所得的投 影图称为“俯视图”.
三视图的平面位置
正视图、侧视图、俯视图在平面图中的一般位置
正视图 侧视图
俯视图 正视图、侧视图、俯视图统称为三视图
三视图的关系
定义:长、宽、高
长:左、右方向的长度 宽:前、后方向的长度 高:上、下方向的长度
空间几何体的三视图 和直观图
主要内容
中心投影与平行投影 空间几何体的三视图 空间几何体的直观图
空间几何体的三视图
三视图概念
三个互相垂直的投影面
从前向后方 向的投影线
从左向右方 向的投影线
从上到下方 向的投影线
“视图”是将物体按正投影法向投影面投射时所得 到的投影图.
三视图的形成
光线从几何体的前面向后面正投影 所得的投影图称为“正视图”
《三视图 》优秀 课件人 教版1- 精品课 件ppt( 实用版) 《三视图 》优秀 课件人 教版1- 精品课 件ppt( 实用版)
《三视图 》优秀 课件人 教版1- 精品课 件ppt( 实用版) 《三视图 》优秀 课件人 教版1- 精品课 件ppt( 实用版)
《三视图》_PPT完整版人教版1

正视图
侧视图
正视图
侧视图
俯视图
圆台
俯视图
三棱锥
一个几何体的三视图如下,则这个几 何体是六__棱__锥__
正视图
主视图
左视图
俯视图
俯视图
画法说明
1、同一张图样中,同类图线的宽度应基本一致。 2、虚线、点划线相交时,应使两小段相交。
3、两直线相交处要避免间隙或线段出界。 4、两线相切的切点处,应画成一条线粗。
简单组合体的三视图
例题讲解
例题讲解
口答:桌上放着一个圆柱和一个长方体, 请说出三幅图分别是从哪个方向看到的?
(1)
(2)
(3)
口答:一个几何体某一方向的视图是圆, 则它不可能是(D )
A球
B 圆锥
C 圆柱 D 长方体
从上面看
俯视图
从左面看 左视图
从正面看 主视图
主视图
左视图
俯视图
相交于O点.画直观图时,把它画成对应的x 轴、
y 轴,使 xO y= 45或 135,它确定的平面表示水平
平面. (2)已知图形中平行于x轴或y轴的线段,在直观
图中分别画成平行于x′轴或y′轴的线段. (3)已知图形中平行于x 轴的线段,在直观图中保
持原长度不变;平行于y 轴的线段,长度为原来的一 半.
空间几何体的 三视图和直观图
➢中心投影和平行投影 ➢空间几何体的三视图 ➢空间几何体的直观图
1.2.1 平行投影和中心投影
概念
投影:光线通过物体,向选定的面 投射,并在该面上得到图形的方法.
概念
中心投影: 投射线交于一点的投影
Y
X
光光
概念
Y X
平行投影:投射线相互平行的投影 可以分为:
三视图教学PPT课件
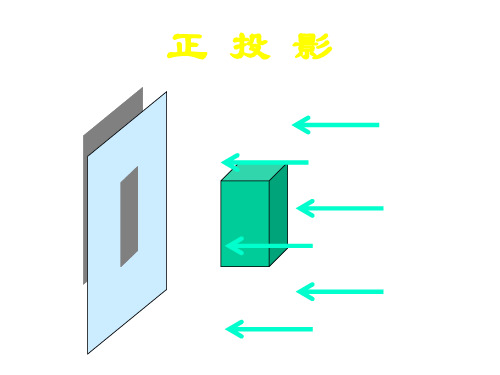
,侧棱长为
2的正四棱锥叠放而成.故该几何体的体积为
V 12 1 ( 2 )2 3
3
2 2 3.
3
[答案] C
│要点探究 要点探究
探究点3 三视图的画法 例3 画出如图36-1所示几何体的三视图.
│要点探究
【思路】 图36-1(1)为正六棱柱,可按棱柱画法画出; 图36-1(2)为一个圆锥和一个圆台的组合体,按圆锥、圆台 的三视图画法画出它们的组合形状.
左视图
能看见的轮廓线 和棱用实线表示,不 能看见的轮廓线和棱 用虚线表示。
圆锥的三视图
主视图
左视图
俯视图
圆台
俯
左
圆台
正视图
侧左视视图图
俯视图
棱锥的三视图
俯
左
正四棱锥
四棱锥的三视图
主
左
视
视
图
图
主视
俯 视
图
总结:三视图的概念
1.视图:将物体按正投影向投影 面投射所得到的图形.
正视图
c
侧 视
ba
答案:D
三基能力强化
3.关于如图所示几何体的正确说 法为( )
①这是一个六面体 ②这是一个 四棱台
③这是一个四棱柱 ④这是一个 四棱柱和三棱柱的组合体 ⑤这是一 个被截去一个三棱柱的四棱柱
三基能力强化
A.①②③④⑤ ④⑤
C.①④⑤ D.①③④
答案:A
B.①③
三视图是新课标新增的内容,是一个知识交汇的载 体,因而是高考的重点内容之一.但新课标对这部分内 容的要求较低,一般不会直接考查画图的问题,而经常 会与立体几何中有关的计算问题融合在一起考查.2009年 广东高考将三视图与几何体的体积计算、空间位置关系 融为一体,考查了学生的空间想象能力,是一个新的考 查方向.)
机械制图三视图ppt课件
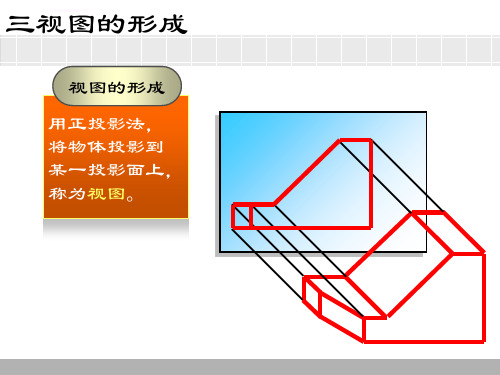
V
H
W
三个投影面的名称 为深入学习习近平新时代中国特色社会主义思想和党的十九大精神,贯彻全国教育大会精神,充分发挥中小学图书室育人功能
V
主视图
左视图 W
45 0
H 俯视图
第三分角 为深入学习习近平新时代中国特色社会主义思想和党的十九大精神,贯彻全国教育大会精神,充分发挥中小学图书室育人功能
第II分角
两个视图 为深入学习习近平新时代中国特色社会主义思想和党的十九大精神,贯彻全国教育大会精神,充分发挥中小学图书室育人功能
也不能唯一确定物体的形状
三个视图 为深入学习习近平新时代中国特色社会主义思想和党的十九大精神,贯彻全国教育大会精神,充分发挥中小学图书室育人功能
V
H
W
三投影面体系: 在两投影面体
右视图 W
三视图的投影规律 为深入学习习近平新时代中国特色社会主义思想和党的十九大精神,贯彻全国教育大会精神,充分发挥中小学图书室育人功能
图和物 体方位 的关系
视图与 视图的 关系
2.三视图的投影规律 为深入学习习近平新时代中国特色社会主义思想和党的十九大精神,贯彻全国教育大会精神,充分发挥中小学图书室育人功能
已知一立体的轴测图,按箭头所指方向的视图是 为深入学习习近平新时代中国特色社会主义思想和党的十九大精神,贯彻全国教育大会精神,充分发挥中小学图书室育人功能
投影方向
(1)
(2)
(3)
(4)
已知一立体的轴测图,按箭头所指方向的视图是 为深入学习习近平新时代中国特色社会主义思想和党的十九大精神,贯彻全国教育大会精神,充分发挥中小学图书室育人功能
为深 入 学习习近 平 新 时代 中 国特 色社会主 义思 想和党 的十九 大精神 ,贯彻全 国教育 大会精 神,充 分发挥中 小学图书室 育 人功 能
H
W
三个投影面的名称 为深入学习习近平新时代中国特色社会主义思想和党的十九大精神,贯彻全国教育大会精神,充分发挥中小学图书室育人功能
V
主视图
左视图 W
45 0
H 俯视图
第三分角 为深入学习习近平新时代中国特色社会主义思想和党的十九大精神,贯彻全国教育大会精神,充分发挥中小学图书室育人功能
第II分角
两个视图 为深入学习习近平新时代中国特色社会主义思想和党的十九大精神,贯彻全国教育大会精神,充分发挥中小学图书室育人功能
也不能唯一确定物体的形状
三个视图 为深入学习习近平新时代中国特色社会主义思想和党的十九大精神,贯彻全国教育大会精神,充分发挥中小学图书室育人功能
V
H
W
三投影面体系: 在两投影面体
右视图 W
三视图的投影规律 为深入学习习近平新时代中国特色社会主义思想和党的十九大精神,贯彻全国教育大会精神,充分发挥中小学图书室育人功能
图和物 体方位 的关系
视图与 视图的 关系
2.三视图的投影规律 为深入学习习近平新时代中国特色社会主义思想和党的十九大精神,贯彻全国教育大会精神,充分发挥中小学图书室育人功能
已知一立体的轴测图,按箭头所指方向的视图是 为深入学习习近平新时代中国特色社会主义思想和党的十九大精神,贯彻全国教育大会精神,充分发挥中小学图书室育人功能
投影方向
(1)
(2)
(3)
(4)
已知一立体的轴测图,按箭头所指方向的视图是 为深入学习习近平新时代中国特色社会主义思想和党的十九大精神,贯彻全国教育大会精神,充分发挥中小学图书室育人功能
为深 入 学习习近 平 新 时代 中 国特 色社会主 义思 想和党 的十九 大精神 ,贯彻全 国教育 大会精 神,充 分发挥中 小学图书室 育 人功 能
《三视图》PPT教学课文课件

【例题1】一个几何体的三视图如图所示,其中主视图和左视图都是边长
为4的等边三角形,则这个几何体的侧面积为_________.
分析: 该几何体是底面直径和母线长都是4的圆锥.
圆锥侧面展开图
∴ 侧= 扇=
扇形
1
×
2
弧长
圆锥底面圆周长
半径
圆锥母线长
4 × 4 = 8.
4
4
【例题2】如图是某几何体的三视图,根据图中所标的数据,该几何体的
主视图
图和俯视图宽相等,知俯视图是长和宽分别为
4cm和3的矩形(如图).
所以俯视图的面积为:4 × 3 = 12(2).
俯视图
左视图
1.如图,是一个工件的三视图,则此工件的全面积
是( )
A. 85πcm2
B. 90πcm2 C. 155πcm2
D. 165πcm2
2.长方体的主视图、俯视图如图所示(单位:m),则其左视图面积是( )
三视图
由三视图确定几何体的形状以后,根据尺寸就可以进行有关的计算.
根据三视图的有关计算
根据三视图的有关计算
1. 根据三视图求与几何体有关的面积、体积:
(1)根据三视图还原出几何体;
(2)根据三视图“长对正,高平齐,宽相等”的关系确定几何体的尺寸;
(3)根据几何体的面积、体积等公式进行有关的计算.
体积为__________.
136
分析:由三视图知道,该几何体
是两个圆柱的组合体(如图).
∴ 体= 22 × 2 + 42 × 8
= 136.
8
2
4
8
根据三视图的有关计算
2. 求组合体的表面积:
《三视图》课件(共55张PPT)

四棱锥
圆台
体验三视 图的作法
俯
左
圆台
六棱柱
体验三视 图的作法
俯
左
六棱柱
练一练: 画出左图 的三视图 请同学 自己做
先布局定作图基准,从俯视图 开始画起,后画主、左视图。
请同学 自己做
先布局定作图基准,从俯视图 开始画起,后画主、左视图。
Φ
Φ
练习3
Φ
冰淇淋
Φ
三通水管
图1 图2 如果要做一个水管的三叉接头,工人事先 看到的不是图1,而是图2,然后根据这三 个图形制造出水管接头.
练习: 根据三视图想 像物体的形状。
圆柱
圆台
手电筒
从左向右看
圆柱
正六棱柱
螺丝杆
从左向右看
圆锥
圆柱
圆台
冰淇淋 从左向右看
圆柱
四棱柱
螺丝杆
从左向右看
圆柱
半圆球
螺丝钉
从左向右看
圆柱
圆台
圆柱
热水瓶
从上向下看
N
S
前后看 从上向下看
左右看
马蹄形磁铁
从下向上看
环的形成
有关概念
物体向投影面投影所得 到的图形称为视图。
4.运用长对正、高平 齐、宽相等的原则画 出其它视图 5.检查,加深, 加粗。
主视图方向
练一练: 画出圆柱 的三视图
圆柱的形成
俯
左
圆柱
练一练: 画出球体 的三视图
球 体
球的形成
俯
左
球体
圆锥体
圆锥 的 形成
俯
左
圆锥
正六棱柱三视图
•正五棱柱
先布局定作图基准,从俯视图开 始画起,后画主、左视图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
----高斯
图
俯 视 图
你能根据下面的三视图画出它的原立体图形吗?
正视图
俯视图
左视图
原图形
下面是一个组合图形的三视图,请描述物体形状
正视图 俯视图
左视图 物体形状
用小方块搭成一个几何体,使它的主视图和俯视 图如图所示,它最少需要多少个小立方块,最多 需要多少个小立方块?
正视图
俯视图
给我最大快乐的, 不是已懂的知识, 而是不断的学习.
三视图及其画法
巨人学校 徐增华
万里长城—中国
天坛祈年殿—中国
国家体育馆—中国
金字塔—埃及
泰姬陵—印度
圆形斗兽场—意大利
猜 猜 他 们 是 什 么 关 系 ?
看 事 物 不 能 只 看 单 方 面
从上面看
从左边看
长方体
从正面看
从上面看
从左面看
从正面看
从左面看
从上面看 从正面看
从上面看 从左面看
从正面看
从上面看
从左面看
从Байду номын сангаас面看
从正面看
从左面看
从上面看
利用小正方体,摆成下面的图形,分别从正 面、左面、上面观察这个图形,各能得到什 么平面图形?
从正面看
从上面看 从左面看
2.由视图到立体图形
现在我们要想做的事情是根据视图来描述物 体的形状。让我们先看一个较为简单的、熟 悉的物体。
正
左
视
视
图
图
俯 视 图
你能根据下面的三视图画出它的原立体图形吗?
正视图
俯视图
左视图
原图形
下面是一个组合图形的三视图,请描述物体形状
正视图 俯视图
左视图 物体形状
用小方块搭成一个几何体,使它的主视图和俯视 图如图所示,它最少需要多少个小立方块,最多 需要多少个小立方块?
正视图
俯视图
给我最大快乐的, 不是已懂的知识, 而是不断的学习.
三视图及其画法
巨人学校 徐增华
万里长城—中国
天坛祈年殿—中国
国家体育馆—中国
金字塔—埃及
泰姬陵—印度
圆形斗兽场—意大利
猜 猜 他 们 是 什 么 关 系 ?
看 事 物 不 能 只 看 单 方 面
从上面看
从左边看
长方体
从正面看
从上面看
从左面看
从正面看
从左面看
从上面看 从正面看
从上面看 从左面看
从正面看
从上面看
从左面看
从Байду номын сангаас面看
从正面看
从左面看
从上面看
利用小正方体,摆成下面的图形,分别从正 面、左面、上面观察这个图形,各能得到什 么平面图形?
从正面看
从上面看 从左面看
2.由视图到立体图形
现在我们要想做的事情是根据视图来描述物 体的形状。让我们先看一个较为简单的、熟 悉的物体。
正
左
视
视
图
