多边形内角和与外角和模型专题
多边形内角和与外角和PPT教学课件

多种酶、 [H] 、ATP
物质变化:
CO2的固定: CO2+C5
酶 2C3
酶
C3的还原:
2C3 NADPH 、ATP
(CH2O) ADP+Pi 糖类
C5的再生:
酶 2C3NADPH 、ATP
ADP+PCi 5
能量变化:
ATP和NADPH中活跃的化学能转变为糖
类等 有机物中稳定的化学能
进行部位
光反应阶段
• 过程:
用于暗反应
水的光解:
2H2O
光 色素
O2+4H++4e-
酶
NADPH的形成: NADP++2e+H+
NADPH
ATP的形成: ADP+Pi + 电能
酶(A活TP跃化学能)
碳反应
二氧化碳还原为糖的一系列反应成为碳循环 ,又称卡尔文循环。
(二)碳反应阶段
碳反应总结
场所: 叶绿体的基质中
条件:
的内角和为1125 ° ,当发现错了之后,重
新检查,发现是少加了一个内角,求:
(1)这个多边形是几边形?
(2)这个内角是多少度?
某四边形有一个60°的角,剪去这个角 后,剩下的图形内角和为多少?
540º
360º
180º
光反应
光反应包括多个反应,最重要的是发生在两种 叶绿素蛋白质复合体(光系统Ⅰ和光系统Ⅱ) 中的电子被光激发的反应。
叫做这个多边形的外角(exterior angle)
在每个顶点处取这个多边形的一个外角,它们的和叫做
这个多边形的外角和.
1
一般地,在多边形的任一顶点处按
2
多边形内角和与外角和(共12张PPT)

A.90° C.210°
B.180° D.270°
3.若一个多边形的内角和等于它 的外角和,则它的边数是_________ 。 4.一个多边形的每个外角都是120°,则这个多边形是 _________边形。
8
挑战自我
(1)一个正多边形每个外角都是60°,求这个 多边形的边数;
(2)一个正多边形每个内角都是135°,求这 个多边形的边数;
八年级下
第4节 多边形的内角和与外角和(2)
1
1、n边形内角和计算公式是什么? 2、正n边形每个内角计算公式是什么?
2
练习:
1、正n 边形的一个内角为135°,那么n为( )
A.5
B.6
C.7
D.8
2、正六边形的每个内角都是( )
A.60° B.80° C.100° D.120°
3、过某个多边形一个顶点的所有对角线,将这个多
6
小试牛刀
一个多边形的内角和等于它的外角和的3倍,它 是几边形?
7
随堂练习
1.一个正多边形的每个外角都等于36°,那么它是( )
A.正六边形
B.正八边形
C.正十边形
D.正十二边形
2.如图,五边形ABCDE中,AB∥CD,∠1、∠2、∠3分别是
∠BAE、∠AED、∠EDC的外角,则∠1+∠2+∠3等于( )
1
n·180°-(n-2)·180°=
B
°
2
定理:多边形的外角和等于360° C 3
5
E
4
D
5
一个多边形的内角和等于它外角和的5倍, 它是几边形?
解:设多边形的边数为n,则它的内角和等于(n-2)·180°
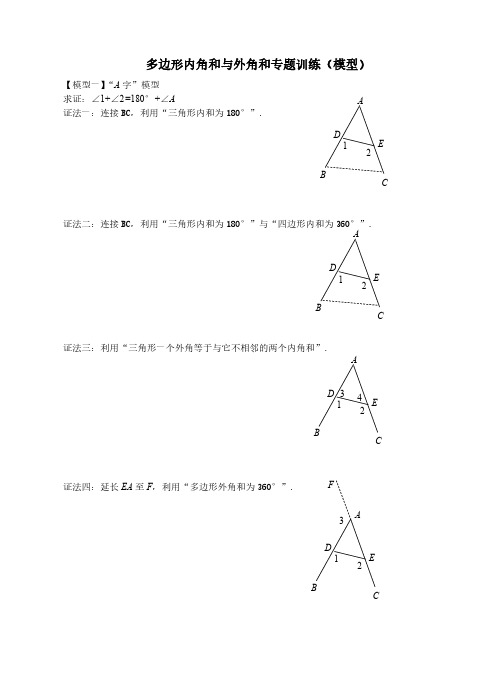
多边形内角和与外角和专题训练(模型)
2.☆如图,∠1+∠2=260°,则∠A= ° 3.☆如图,∠1=25°,∠2=75°,∠C=65°,则∠D=
A D F 1 B 第1题 C D A F 2 第2题 C F
° O A
1 2 B
B D 第3题
C °
4. ☆如图,在△ABC 中,∠A=62°,∠1=20°,∠2=35°,则∠BDC= 5. ☆如图,若∠A=∠B=∠C=∠D=∠E,则∠A= ° 6. ☆如图,若∠A=40°,则∠P= ° A A A B D 1 B 第4题 E 2 C C D 第5题 B 第6题 P C
D 3 1 B
4 E 2 C
证法四:延长 EA 至 F,利用“多边形外角和为 360°”.
F A
3 D 1 B
2
E
C
【模型二】飞镖模型 求证:∠A+∠B+∠C=∠D 证法一、 证明:连接 BC, 1
A D B 2 C
A 证法二、连接并延长 AD, 1 2 D 3 4 B C
证法三、连接并延长 BD,交 AC 于点 E,
多边形内角和与外角和专题训练(模型)
【模型一】 “A 字”模型 求证:∠1+∠2=180°+∠A 证法一:连接 BC,利用“三角形内和为 180°”. D 1 B 2 A
E
C
证法二:连接 BC,利用“Fra bibliotek角形内和为 180°”与“四边形内和为 360°”. A
D 1 B 2
E
C
证法三:利用“三角形一个外角等于与它不相邻的两个内角和”. A
A E
1 D B
C
【模型三】 “8 字”模型 求证:∠A+∠B=∠C+∠D 证法一、利用“三角形内角和为 180°”
多边形的内角和与外角和典型热点考题

多边形的内角和与外角和典型热点考题例1 已知:四边形的四个外角度数比为1∶2∶3∶4,求各外角的度数? 点悟:考查四边形外角和定理,由四边形外角和定理和各外角之间的比例关系很容易求出各角.解:设四边形的最小外角为x°,则其他三角分别为2x°,3x°,4x°,根据四边形外角和定理:x°+2x°+3x°+4x°=360°.∴ x°=36°, 2x°=72°, 3x°=108°, 4x°=144°.∴ 四边形各外角度数分别为36°,72°,108°,144°.点拨:本例应用了设参数x 的代数方法求出四边形四个外角的度数,不少的几何线段的计算,角的计算以及证明题,如果应用代数方法求解,可使过程简洁,清晰,特别是已知条件中如果出现比例关系时,采用设参数法是最常见的解题思路,通过设参数,结合几何知识,把问题转化为解方程,学生一定要掌握这种技巧.例 2 多边形的内角和与某一个外角的度数总和为1350°,求多边形的边数?解法一:设边数为n ,这个外角为x 度,则0<x <180,依题意有:(n-2)·180+x=1350,∴18090921801350x x n -+=+-=.又∵ 0<x <180, ∴-90<90-x <90,∴ n=9.解法二:∵0<x <180;∴ 1350-180<1350-x <1350;即 1170<1350-x <1350,又∵ (n-2)·180=1350-x ,∴ 1170<(n-2)·180<1350.∴ 8.5<n <9.5;∵ n 的边数必为整数, ∴ n=9.注:此类题都隐含着边数为正整数这个条件.解法一是利用整数方程来解的.解法二是利用不等式确定边数范围然后通过边数为整数来解的.例 3 如图,已知在四边形ABCD 中,AB=3,BC=4,CD=13,AD=12,∠B=90°.求:四边形ABCD 的面积.点悟:由∠B=90°,AB=3,BC=4,想到连接AC ,利用勾股定理解题得AC=5,又AD=12,CD=13由勾股定理的逆定理有∠DAC 为直角,从而ACD ABC ABCD S S S ∆∆+=四边形.解:连结AC .在Rt △ABC 中,有254322222=+=+=BC AB AC ∴ AC=5.∵ CD=13,AD=12,有22213512=+即 222CD AC AD =+.∴ △ACD 是直角三角形,∠DAC=90°,∴ A C D ABC ABCD S S S ∆∆+=四边形=AC AD BC AB ⋅+⋅2121=36512214321=⨯⨯+⨯⨯点拨:当题目中有线段长度时,一般利用勾股定理的逆定理判定某三角形是否为直角三角形.四边形问题通常转化为三角形问题来解决,在构造三角形时必须同已知条件结合起来,不要随意连线.例4 一个n 边形每个内角都是150°,则这个多边形的内角和是多少? 点悟:由于这个n 边形每个内角都是150°,所以可以推知它的每个外角都为30°,而任意多边形的外角和都为360°,从而可以知道这个n 边形的边数,再利用多边形内角和定理即可.解:方法一:∵ 这个n 边形的每个内角都为150°,∴ 此n 边形的每个外角为30°,又∵ 任意多边形的外角和为360°,∴ n=360°÷30°=12.∴ 此n 边形的内角和为180°(n-2)=180°×10=1800°.方法二:设这个多边形的边数为n ,由题意得:150°·n=180°(n-2).解这个方程,得n=12.则此多边形的内角和为:180°(n-2)=180°×10=1800°.点悟:如图,在n 边形内部取一点O ,连接O 与各个顶点的线段,把n 边形分成n 个三角形,因为这n个三角形的内角和等于n·180°,以O 为公共顶点的n个角的和是360°,即2×180°,所以n 边形的内角和是n·180°-2×180°=(n-2)×180°.我们还可以这样求n 边形内角和,如下图所示,作经过n 边形某一个顶点的所有对角线,把n 边形分成(n-2)个三角形,则n 边形的内角和即为(n-2)个三角形的内角和.即(n-2)·180°.例5 已知一个多边形的每个内角都为钝角,则这样的多边形有多少个?边数最少的一个是几边形?点悟:此题首先要利用多边形内角和定理表示出每一个内角,然后列出不等式.解:设多边形是n 边形,由题意得:︒<︒⋅-<︒180180)2(90n n即 ⎪⎪⎩⎪⎪⎨⎧︒>︒⋅-︒<︒⋅-,90n 180)2n (,180n 180)2n ( 解得 ⎩⎨⎧>>.4,0n n∴n>4.∴内角都为钝角的多边形有无数个.又∵ n>4,n为整数,∴n的最小值为5,即边数最少的一个是五边形.注:对于此题的最后一个问题,实际上是对不等式附加某些条件,然后可求出具体未知数,但要注意的是,五个角都是钝角的五边形是存在的,但五四形不一定五个角都是钝角.点拨:如果有4个或4个以上内角为锐角,那么与这些锐角相邻的外角都是钝角,所以这些外角的和将大于360°,这与多边形外角和恒等于360°相矛盾,故在多边形的内角中,锐角的个数不能多于3个.。
多边形的内角和与外角和公开课课件ppt

为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
《多边形的内角和与外角和》知识清单

《多边形的内角和与外角和》知识清单一、多边形的定义在平面内,由一些线段首尾顺次相接组成的封闭图形叫做多边形。
如果一个多边形有 n 条边,那么就称这个多边形为 n 边形。
比如,三角形就是有 3 条边的多边形,四边形就是有 4 条边的多边形,以此类推。
二、多边形的内角和1、三角形的内角和三角形的内角和是 180°。
这是一个基本且重要的定理,可以通过多种方法来证明,比如将三角形的三个角剪下来拼在一起,可以形成一个平角,也就是 180°。
2、四边形的内角和四边形可以分成两个三角形,因为三角形内角和是 180°,所以四边形的内角和是 360°。
3、 n 边形的内角和从 n 边形的一个顶点出发,可以引出(n 3)条对角线,将 n 边形分成(n 2)个三角形。
所以 n 边形的内角和为(n 2)×180°。
例如:五边形的内角和=(5 2)×180°= 540°六边形的内角和=(6 2)×180°= 720°三、多边形的外角和1、外角的定义多边形的一边与另一边的延长线所组成的角叫做多边形的外角。
2、外角和的定义在每个顶点处取一个外角,这些外角的和叫做多边形的外角和。
3、多边形外角和的性质任意多边形的外角和都为 360°。
不管是三角形、四边形还是 n 边形,它们的外角和始终是 360°。
例如,三角形的三个外角和为 360°,四边形的四个外角和也是 360°。
四、内角和与外角和的应用1、已知内角和求边数如果已知一个多边形的内角和,可以通过内角和公式(n 2)×180°来求出边数 n。
例如,一个多边形的内角和为1080°,则有(n 2)×180°=1080°,解得 n = 8,所以这个多边形是八边形。
2、已知边数求内角和如果已知多边形的边数 n,可以直接使用公式(n 2)×180°求出内角和。
多边形的外角和与内角和PPT教学课件

乃瞻衡宇,载欣载奔。僮仆欢迎,稚子候门。三径就荒,松菊犹 存。携幼入室,有酒盈樽。引壶觞以自酌,眄庭柯以怡颜。倚南 窗以寄傲,审容膝之易安。园日涉以成趣,门虽设而常关。策扶 老以流憩,时矫首而遐观。
云无心以出岫,鸟倦飞而知还。景翳翳以将入,抚孤松而盘桓。 归去来兮,请息交以绝游。世与我而相违,复驾言兮焉求?悦
陶渊明的诗歌,以歌咏田园生活的居多,后世称他为田园诗人。陶渊明的 田园诗主要见于他的组诗《饮酒》、《归园田居》、《拟古》、《和郭主簿》。 他的五言诗成就最高,诗歌的意境下平和、静穆、深远,在中国诗歌史上有着 重要的地位。他那种淡泊明志的人生态度,对读书人的影响很深。
通过虚构(
)一
个和平、美好、没有剥…削、没有压迫、人
文章线索 抒情
自责自悔
自安自乐
乐天安命
Hale Waihona Puke 叙事 辞官 归途 家中生活 纵情山水 抒发情怀
全文主旨
《归去来兮辞》 是陶渊明辞官归隐之际与上流社 会公开决裂的政治宣言。文章以 绝大篇幅写了他脱离官场的无限 喜悦,想家归隐田园的无限乐趣, 表现了作者对大自然和隐居生活
的向往和热爱。
少无适俗韵,性本爱丘山。误落尘网中,一去三十年。 羁鸟恋旧林,池鱼思故渊。开荒南野际,守拙归园田。 方宅十余亩,草屋八九间。榆柳荫后檐,桃李罗堂前。 暧暧远人村,依依墟里烟。狗吠深巷中,鸡鸣桑树颠。 户庭无尘杂,虚室有余闲。久在樊笼里,复得反自然。
赞曰:黔娄之妻有言:“不戚戚于贫贱, 不汲汲于富贵。”其言兹若人之俦乎?衔 觞赋诗,以乐其志。无怀氏之民欤?葛天 氏之民欤?
五柳先生传(译文)
五柳先生不知道是什么地方的人,也不知道他的姓名和表字,由 于他的住宅旁边有五棵柳树,因此用它做了自己的号。他悠闲安静, 沉默寡言,不羡慕荣华利禄。喜欢读书,只求领会要旨,不在一字 一句的理解上过分下功夫;每当对书中的意旨有独到的体会,便高 兴得忘了吃饭。(他)生性特别喜好喝酒,但却因家里贫穷,不能 常常有酒喝。亲戚朋友知道他这种境况,有时就准备好酒邀请他去 喝;他一去就要喝个尽兴, 愿望就是一定要喝醉。 醉了便离去, 并不装模作样, 说来就来, 想走就走。 简陋的居室里冷冷清清, 遮不住风和阳光;粗布短衣上打了补钉,盛饭的竹筒、水瓢经常是 空的,但他却安然自若。他经常写文章来消遣时光,也颇能表达自 己的心态。他从不把得失放在心上,他愿意这样度过自己的一生。
多边形的内角和外角和ppt课件

精选ppt课件
33
5.小明绕五边形各边走一圈,他共转了_ 3_6_0度。
6.下列正多边形(1)正三角形(2)正方形(3)正 五边形(4)正六边形,其中用一种正多边形能 镶嵌成平面图案的是 (1)、(2)、(4);
7.如下图,AD是BC边上的高,BE是 △ ABD 的角平分线,∠1=40°,∠2=30°,则 ∠C=_ 60_°_∠BED= 65°。
精选ppt课件
27
例3 一个六边形如图,已知AB∥DE,BC∥EF,
CD∥AF,求∠A+∠C+∠E的度数。
如图所示:可向两个方向分别延长AB, P
CD,EF三条边,构成△PQR。
解:∵ DE∥AB
E1D
∴∠1=∠R,同理∠2=∠R
∴∠1=∠2,
F
C
∴∠CDE=∠FAB
2
同理∠AFE=∠BCD,∠ABC=∠DEF A
结论:多边形的外角和都等于360°.
精选ppt课件
21
多边形 三角形 四边形 五边形 六边形 n边形
图形
1 3
2
1
2
4
3
1
2
5
34
1
2
6
3
5
4
多边形的外角和
多边形的外角和
3×180o-1×180o=360o 4×180o-2×180o=360o
5×180o-3×180o=360o
6×180o-4×180o=360o
9
例:求十边形的内角和的度数。
解:(10-2)×180°=8 ×180°=1440°
答:十边形的内角和是1440°
练:1、已知一个多边形的内角和为720o ,则这
个多边形是___6___边形
多边形的内角和与外角和PPT精品课件

成蛙
受精卵
幼蛙
胚胎
蛙的生活周期
蝌蚪
死亡
中年期 青春期
受精卵
儿童期
婴儿期
幼儿期
成蛙 幼蛙
受精卵 蝌蚪
成虫
蛹
受精卵 幼虫
死亡
成虫
受精卵
若虫
蝌蚪和成蛙的比较:
生活环境 运动器官 运动方式 呼吸器官
蝌蚪 水中
鳍
游泳
鳃
成蛙 陆上和水中
四肢
跳跃 肺和皮肤
像青蛙从幼体到成体的发育过程中, 在生活和形态结构上要发生很大的改变,
3、青蛙属于(B )
A、鱼类 C、跳跃类
B、两栖类 D、爬行类
小明学习了“动物的生命周期”后,想探究环境因素 对动物的寿命是否有较大的影响。他设计了下面的 实验:分别在甲、乙、丙三个金鱼缸中放入等量的、 未经处理过的自来水(含有漂白粉)、煮沸并冷却 的自来水和静置几天后的自来水。然后,在每个金 鱼缸中放入5条健康的、大小相近的小鱼,观察小鱼 的生活情况。一段时间后,发现只有丙缸中的小鱼 还活着,甲缸和乙缸中的小鱼都陆续死亡了。请分 析小鱼死亡的原因。
。
今天你学到了什么知识?你 能用自己的话说说吗?
3、生物结构和功能的基本单位是__细__胞____ 它是由_细__胞__膜___、 _细__胞_质____和细__胞__核____等 基本结构组成的。
人的生长过程的顺序排列应是:_婴_儿__期__、 _幼_儿__期__、_儿_童__期___、青__春_期_____、中年期 _老__年_期___、 _______。
植物能_利_用__太__阳_光__制_造__营_养__物__质_______,
动物___需_要__从_外__界_摄__取__营_养__物_质________。
多边形的内角和与外角和共36张课件

问题4:多边形的外角和是多少呢?
多边形的边数 3 4 5 6 7 … n
多边形的内角 与外角的总和
3180 4 180 5 180 6 180 7 180 …
540 720 900 1080 1260
n 180
多边形的内角和 1 8 0 3 6 0 5 4 0 7 2 0 9 0 0 … (n2)180
第二十二页,共36页。
2. 多边形内角和为1620°则它为_____边形,
3. 多边形每个内角都 等于120°,则它为_____边 形。
4. 四边形的内角的度数之比为2∶3∶5∶8,则
各角度数为 ____
第二十三页,共36页。
5.已知过m边形的一个顶点有7条对角线,n边 形没有对角线,p边形有p条对角线,求 ( m p )n 的
(3)你能否根据这样划分多边形的方法来说明 n边形的内角和等于 (n2)180 ?
当n=6时,多边形的内角和为: 6180360 6 1802 180(62)180
第十六页,共36页。
方法三
在n边形某边上任取一点P,连结点P与多边形的每一个顶
点,可得多少个三角形?你能否根据这样划分多
边形的方法来说明n边形的内角和等于 (n2)180 ? (图中取n=5的情形)
每一条都重复计算一次,所以n边形一共有
n(n-3) 2
条对角线.
第十三页,共36页。
❖问题3. 三角形,四边形,五边形…...
❖
n边形的内角和是多少呢?
第十四页,共36页。
方 法 一
多边形的边数
3
分成的三角形个数 1
4 5 6 7… n 2 3 4 5 … n-2
多边形的内角和 1180 2 180
7.5.2多边形的内角和与外角和-三角形有关的角度模型(同步课件)七年级数学下册(苏科版)

03
典例精析
例3、如图,已知∠CGE=110°,则
220°
∠A+∠B+∠C+∠D+∠E+∠F=________。
【分析】∵∠BGF=∠B+∠A+∠F,
∠CGE=∠C+∠D+∠E,且∠BGE=∠CGE=110°,
∴∠A+∠B+∠C+∠D+∠E+∠F
=∠BGE+∠CGE
=220°。
角平分线模型
情境引入
∠ACD的平分线,两条平分线交于点A1,得∠A1;∠A1BC和
∠A1CD的平分线交于点A2,得∠A2;…以此类推得到∠A11的度
°
数是________。
【分析】∵∠A1= ∠A,∠A2= ∠A1= ∠A,
∴∠A11= ∠A= ×60°=
°。
03
典例精析
在AC边上(不与端点重合),则∠AEF+∠AFE=________;
180°-ɑ
∠BEF+∠CFE=________。
180°+ɑ
A
E
B
F
C
法二:∵∠BEF=∠AEF+∠A,∠CFE=∠AFE+∠A,
∴∠BEF+∠CFE=∠AEF+∠AFE+∠A+∠A=180°+ɑ。
知识精讲
02
A字模型
A
E
B
F
C
B.35°
C.80°
D.85°
【分析】∵∠BEC=130°,
多边形内角和与外角和模型收集

多边形内角和与外角和专题训练(模型)【模型一】S字〃模型求证:zl+z2=180°证法一:连接BC ,利用"三角形内和为180°".证法二:连接BC ,利用〃三角形内和为180。
"与〃四边形内和为360^・证法三:利用〃三角形一个外角等于与它不相邻的两个内角和〃A 证法四:延长£4至[利用〃多边形外角和为360。
〃・【模型二]飞镖模型求证:Z/4+z^+zC=z£?证法一、证明:连接BC ,证法二连接并延长AD ,证法三.连接并延长BD ,交AC于点E,【模型三】〃8字〃模型求证:乙A+乙B二乙C十乙D证法一、利用"三角形内角和为180°"证法二、利用"三角形任意一个外角等于与它不相邻的两个内角和〃B 注意:"8字〃模型的变式.如图,zl+z2=zC*z£?【模型四】“五角星〃模型求证:乙A+乙B+乙C+乙D十zF二180°【模型五】〃角平分线〃模型1、两条内角平分线已知:如图,乙B、zU的平分线BP、CP交于点P求证:zBPC=90°+lz/l22、两条外角平分线已知:如图,乙CBE、乙BCF的平分线BP、CP交于点P 求证:ZQ90。
丄"23、一条内角平分线和一条外角平分线已知:如图,A ABC. A ACD的平分线BP、CP交于点P求证:2[模型六]“高线角平分线”模型求证:zDCE二丄("一).(其中">")2【模型七】〃折角〃模型B M CN求证:zl+z2=2z>4求证:z2-zl=2z/4求证:zl-z2=2z/4【直艇用】在〃填空题〃.〃选择题〃的客观题型中,可以直接运用模型结论解题•注意结论的准确性.1 •汝如图z在"BU中,二50° , zB=65°z贝^ACD=4.汝如图z在"3U中z二62° , zl=20° , z2二35° f贝UBDC= _______________ '5.汝如图z若乙A二乙B二乙C二乙D二乙E,贝!Jz4二°7.汝如图z'ABC中,CD丄AB, UF平分乙ACB、z^50° f z/4 二20°,则zQUF=10. 小如11. 12. 吹法如图z 乙ABD 与z/C 的角平分线相交于应P t 若"二50。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
.多边形内角和与外角和模型专题————————————————————————————————作者:————————————————————————————————日期:23多边形内角和与外角和专题训练(模型)【模型一】“A 字”模型 求证:∠1+∠2=180°+∠A证法一:连接BC ,利用“三角形内和为180°”.证法二:连接BC ,利用“三角形内和为180°”与“四边形内和为360°”.证法三:利用“三角形一个外角等于与它不相邻的两个内角和”.证法四:延长EA 至F ,利用“多边形外角和为360°”.CABDE 21 CABDE 21 CABD E 21 3 4 CABDE 21 3 F4【模型二】飞镖模型求证:∠A +∠B +∠C=∠D 证法一、证明:连接BC ,证法二、连接并延长AD ,证法三、连接并延长BD ,交AC 于点E,【模型三】“8字”模型 求证:∠A +∠B=∠C+∠D证法一、利用“三角形内角和为180°”证法二、利用“三角形任意一个外角等于与它不相邻的两个内角和”AB CDOAB CD1 2 A BCD 1 2 3 4ABCD 1E ABCDO15注意:“8字”模型的变式. 如图,∠1+∠2=∠C+∠D【模型四】“五角星”模型求证:∠A +∠B +∠C+∠D +∠E =180°【模型五】“角平分线”模型 1、 两条内角平分线已知:如图,∠B 、∠C 的平分线BP 、CP 交于点P求证:∠BPC=90°+21∠A2、两条外角平分线已知:如图,∠CBE 、∠BCF 的平分线BP 、CP 交于点P 求证:∠P =90°-21∠AA B CP12 PA B C 1 2 EFDAB O C1 2 C DE A B63、一条内角平分线和一条外角平分线已知:如图,∠ABC 、∠ACD 的平分线BP 、CP 交于点P 求证:∠P =21∠A【模型六】“高线角平分线”模型求证:∠DCE=21(∠B -∠A ).(其中∠B >∠A )【模型七】“折角”模型 求证:∠1+∠2=2∠A求证:∠2-∠1=2∠A求证:∠1-∠2=2∠APA BC1 2DCA BD E AB C MNA ’2 1MBA ’23D C1N A ABCM N A ’123 D7 在“填空题”、“选择题”的客观题型中,可以直接运用模型结论解题.注意结论的准确性. 1.☆如图,在△ABC 中,∠A =50°,∠B=65°,则∠ACD= °2.☆如图,∠1+∠2=260°,则∠A= °3.☆如图,∠1=25°,∠2=75°,∠C=65°,则∠D= °4. ☆如图,在△ABC 中,∠A =62°,∠1=20°,∠2=35°,则∠BDC= °5. ☆如图,若∠A=∠B=∠C=∠D=∠E ,则∠A= °6. ☆如图,若∠A=40°,则∠P= °7. ☆如图,△ABC 中,CD ⊥AB ,CE 平分∠ACB ,∠B =50°,∠A =20°,则∠DCE= ° 8. ☆如图,纸片△ABC 中,∠A =55°,∠B=75°,将纸片的一角折叠,使C 点落在△ABC 内的C’处,则∠1+∠2= °9. ☆☆如图,∠A +∠B +∠C+∠D +∠E+∠F +∠G= °10. ☆☆如图,∠A +∠B +∠C+∠D = °11. ☆☆如图,BE 、CF 交于点O ,∠EOF =105°,则∠A +∠B +∠C+∠D +∠E+∠F= °. 12. ☆☆如图,∠ABD 与∠ACB 的角平分线相交于点P ,若∠A =50°,∠D =10°,则∠P = °.AB C D 第1题A BCD12 第2题 D ABOC 1 2 第3题ABCD1 2 第4题ABCPCD EAB第5题第6题C ABD E 第7题2CABC’1第8题AB C D E FG 第9ABCD11第ABCDP第12ABC105° ODE F第118在“解答题”中,重现模型证明过程.注意方法的选择.1. ☆☆如图,在∠AMB 的两边AM 、BM 上分别取点P 、Q ,在∠AMB 内取一点N ,连接PN 、QN ,探索∠PNQ 、∠AMB 、∠MPN 、∠MQN 之间的数量关系,并证明你的结论.2. ☆☆如图,∠MON=90°,点A 、B 分别在射线PM 、PN 上,∠MAB 和∠NBA 的平分线相交于点P .点A 和点B 在运动过程中,∠P 的大小是否发生变化?请说明你的理由.3. ☆☆如图,已知AB ∥CD ,BD 平分∠ABC 交AC 于点O ,CE 平分∠DCG .若∠ACE=90°,试判断BD 与AC 的位置关系,并说明理由.A BNO M PAB C DEFAM BA MB AM B94. ☆☆在△ABC 中,内角∠ABC 、∠ACB 的平分线夹角为α,外角∠DBC 、∠ECB 的平分线夹角为β.(1)若α=110°,则∠A = °, (2)若∠A =40°,则β= °, (3)猜想α与β之间的关系,并说明理由.【探索新知】在模型的基础上探索新知,或用与探索模型类似的方法探索新知.注意的模型生成过程. 1. ☆☆如图①,则∠1+∠2+∠3+∠4 = °;如图②,则∠1+∠2+∠3+∠4 +∠5 = °;如图③,则∠1+∠2+∠3+∠4 +∠5+∠6 = °.2. ☆☆(1)如图(1),则∠A +∠B +∠C+∠D +∠E+∠F J= °;(2)如图(2),则∠A +∠B +∠C+∠D +∠E+∠F +∠G +∠H J= °;(3)如图(3),则∠A +∠B +∠C+∠D +∠E+∠F +∠G +∠H +∠I +∠J= °.3. ☆☆☆已知:如图,在△ABC 中,BO 1、BO 2是∠ABC 的三等分线,CO 1、CO 2是∠ACB 的三等分线.(1)当∠A =60°时,∠BO 2C = °;(2)探索∠BO 1C 与∠BO 2C 之间的数量关系,并证明你的结论.51 2 3 4 1 2 3 4 6 1 2 3 5 4①②③A BC D E F H GF E D C B AA BCD E G HI JF(1)(2)(3)ABCO 1 O 2DA BCEPO104. ☆☆☆已知:如图,∠ABC 和∠ACB 的平分线相交于点E . (1)若∠D =140°,∠E =110°,则∠A °; (2)求证:∠E =21(∠A +∠D )5. ☆☆☆☆如图,线段AB 、CD 交于点O ,连接AD 、BC ,我们把形如图1的图形称为“8字形”. (1)如图(1),直接写出∠A +∠D 与∠B+∠C 的关系; (2)如图(2),∠DAB 和∠BCD 的平分线AP 、CP 交于点P ,且分别与AB 、CD 交于点M 、N ,∠D=46°,∠B=30°. 先观察图中还有哪些“8字形”,再利用(1)的结论求∠P 的度数; (3)在(2)中,若∠D=α,∠B=β,直接写出∠P 的度数(用含有α、β的式子表示).6. ☆☆☆☆如图,在△ABC 中,将点A 向下拖动,依次可以得到图1、图2、图3.分别探究图(1)、图(2)、图(3)中∠EAD 、∠B 、∠C 、∠D 与∠E 之间有什么数量关系?A BCE DABC ABC D EAB C D EABCD E (1)(2)(3)AD BCOPM NA D BCO(2)(1)7. ☆☆☆☆如图,线段AB 、CD 交于点O .将图(1)中线段AD 上一点E (点A 、D 除外)向下拖动,依次可以得到图(2)、图(3)、图(4).分别探究图(2)、图(3)、图(4)中∠A 、∠B 、∠C 、∠D 与∠AED 之间有什么数量关系?8. ☆☆☆☆转化是数学中的重要思想,即把陌生的问题转化成熟悉的问题,把复杂的问题转化简单的问题,把复杂的问题转化为简单的问题,把抽象的问题转化为具体的问题. (1)请你根据学过的知识求出下面星形中∠A +∠B +∠C+∠D +∠E 的度数; (2)若将图(1)中的星形截去一个角,如图(2),请你求出∠A +∠B +∠C+∠D +∠E+∠F 的度数;(3)若再将图(2)中角进一步截去,如图(2),你能由题(2)中的方法或规律,猜想出图(3)中∠A +∠B +∠C+∠D +∠E+∠F +∠G +∠H +∠I +∠J 的度数?(直接写出结果,不需要写出解题过程)CD EABABC DEFGA BC DEF H I J (1)(2)(3)ADBCOABCDEOA DC BE OA BCD OE(2)(3)(4)(1)10. ☆☆☆☆☆如图,四边形ABCD 中,内角∠ABC 的角平分线与外角∠DCE 的角平分线交于点F ,且∠F 为锐角.设∠A =α,∠D =β.(1) 如图①,α+β>180°,试用α、β表示∠F ;(2) 如图②,α+β<180°,请在图中画出∠F ,并试用α、β表示∠F ;(3) 一定存在∠F 吗?如有,求出∠F 的值;如不一定,指出α、β满足什么条件时,不存在∠F .9. ☆☆☆☆☆如图①,把三角形纸片ABC 折叠,使3个顶点重合于点P ,这时∠α+∠β+∠γ= °,∠1+∠2+∠3+∠4 +∠5 +∠6 = °.如果三角形纸片ABC 折叠后,3个顶点并不重合于点P (如图②),那么(1)中关于“∠1+∠2+∠3+∠4 +∠5 +∠6 ”的结论是否仍然成立?请说明理由.ABCDEF①AB CDE②G 1 2 A B CD E F H I3 456 αβ γP A’ B’ C’ A B CD E F GIH 12 3654 4①②。
