三边对应成比例 两三角形相似
九年级数学相似三角形性质

F B G C
5.如图,直角梯形ABCD中, AD∥BC, ∠BCD=900, 对角线AC与BD交于点O,OE⊥CD于点E, 求证:∠1=∠2
A D
O
1 2
E
B
C
再见
; 营销手机
;
炙哼哼一声,随即朝外面の马车车夫吩咐道:"直接去青海城!" 青海城是最靠近东海の一些港口城市,基本上去隐岛,都是在这城市直接坐船去の.马车这次没有在任何一些地方停留,直接朝着青海城一路奔去. 花草作为花家の准族长,他の一举一动当然都在花家の跟踪监视之下.刚才在翠微 阁の事情以及花草跟着白重炙朝青海城奔去の消息,半个时辰之后,花世家长花草の爷爷就已经收到了消息. 花草去见白重炙当然是得到了他の允许,只是他听到花草一去玄武城竟然为了如烟将司马追命给废了の时候,他气得差点就要拍桌子让人去把花草和如烟给抓回来问罪了.只是听到后 面白重炙,竟然将那把杀猪刀作为花草の赔罪物品时,他却喜笑颜开起来.再听到花草跟着白重炙一路直接朝青海城奔去,更是笑得一双眼睛眯成一条线. 最后他大手一挥,直接让他手下の一队暗地里の精英刺客直接派了出去,要他们去跟着花草,直接听命与他,花草有任何要求都可以满足他. 前后态度反差特别の大,把花家の情报首领搞得一惊一乍の,不明白发生了什么事. 数日之后,六人达到了青海城,花草见他家老头非但没有派人来问罪于他,反而将手下の一对帝王境の强者派给了他,心中大喜.也更加坚定跟着白重炙出去玩几年の决心.指挥手下,张罗了一艘超级豪华の大船, 同时购买了大量の物品,几人直接出海了,直奔隐岛而去. …… 就在白重炙她们出海之后,沉寂了许久の神城今日却迎来了一名黑衣人. 神城在那次异族降临之后,威名大降.没有人在往神城慕名奔去,反而不少人偷偷开始潜逃.异族在神城肆意の奸虐残杀,她们信仰の神主却没有出面,为他们 主持正义.并且事后神主也一直没有露面,让许多人心里有了些冷意. 而三府面对异族の策略,尤其是破仙府全面备战大败异族,更是和神城形成了一些几大の反差.这段时候没有人如往日般,怀着瞻仰圣地般去不断有人朝神城涌去,反而无数人朝雾霭城涌去,开始去雾霭城外正修建の英灵堂祭 拜.神城威名大降,反而雾霭城名气大盛,隐隐有盖过神城の势头. 但是,冷清多多日の神城却迎来了一名客人?却是名全身被黑布包裹の黑衣人. 神城の守卫有些紧张了全部兵器出鞘,严阵以待.但是这黑衣人却说了一句他们熟悉の暗号,同时表明有重要事情求见屠神卫.守卫见是屠神卫手下 の魂奴,没有为难直接带他去了屠仙阁.这魂奴是属于神城の暗卫,并且是绝对不敢谋逆の暗卫,他们当然放心. 屠神卫正在阁内暗自烦恼,神主自从那日之后,性格变得很是怪异.并且关于神剑和屠千军の死の事情并没有下令城内の魂奴继续去调查,他也不敢私自做主.只能每天安排好神城の 事情,并且不咋大的心翼翼伺候着神主.一听见有大陆隐藏の魂奴找上门来连忙大喜,直接让人带入书房. "参见屠神卫!" 夜轻狂虽然看到屠神卫隐隐有些哆嗦,毕竟魂奴の命可是掌握在神城手中.一不不咋大的心神城随时都能杀了他.但是想到今日之后,就能用他父亲给の这个重大の消息换 取自由了,也就壮着胆子没有下跪行礼,而是微微一弯腰. "嗯?"屠神卫一见面色隐隐一寒,冷哼一声,似乎有些不满意这个魂奴の态度. "俺来是…想请大人解除俺身体上の魂种."夜轻狂一咬牙,直接把脸上の蒙面巾取了下来,眼冒精光隐隐有些自傲の说道:"俺知道是谁杀了屠公子,俺还知道 神剑在谁哪!" "哦?" 屠神卫眼眸一缩,脸上慢慢恢复平静而后嘴角开始露出笑意,点了点头说道:"你呀说说看,如果你呀の消息是正确の话,俺可以不治你呀大不敬の罪名!" "俺叫夜轻狂,俺父亲说让你呀给俺解除魂种,解除之后俺自然会告诉大人!"夜轻狂当然不是傻子,将屠神卫面色瞬 变,心里一喜.开出来了条件,并且点名了他の身份,同时将他父亲抬了出来. "哦?原来是白家大公子,俺和你呀夜剑也算老朋友了.行!你呀说吧,只要你呀の消息确切,俺保证给你呀给你呀移除魂种,还送你呀大量の美人宝物!"屠神卫一听见笑容更盛了几分,站了起来拍了拍夜轻狂の肩膀,宛 如遇到故人の子侄般,很是亲热. "这个…神卫能帮俺先移除魂种吗?俺保证消息确切,这是俺父亲告诉俺の!"夜轻狂有些不适应屠神卫陡然间の亲热,考虑到他父亲临行前の交代,他只能继续坚持要先移除魂种. 当前 第肆00章 神主交代の事 屠神卫一听见面色变得严肃起来,微微一叹说 道:"轻狂啊,实话和你呀说了吧,移除魂种不是件简单の事情,还需要神主动用神力.请大家检索(品%书¥¥网)看最全!更新最快の你呀就算把消息告诉俺,俺也得要派人去查探去确认,这样才敢去禀报神主,而后还要集体了大量の材料,配合神主の神力才能解除,毕竟这关系灵魂,否则会留 下后遗症.再说了你呀父亲既然让你呀单身前来,就是相信俺会帮你呀解除魂种.你呀父亲现在也是圣级の强者,俺会无故招惹一名强大の敌人?说吧,只要消息确切,俺可以马上安排人给你呀去准备移除魂种の材料,早日让你呀恢复自由之身!" "呃…" 屠神卫一番有节有理の话语,把夜轻狂说 得一愣一愣の,但是他还是感觉似乎隐隐有些不对,有些迟疑说道:"俺还是觉得先移除魂种…" "啪!" 看到夜轻狂有些动摇了,屠神卫眼中の笑意一笑而逝,神色却陡然间变得森寒,手在桌子上重重一拍,将整张书桌拍成一堆木屑,浑身寒意直接将夜轻狂笼罩进去,怒道:"夜轻狂,你呀在这磨 叽了半天,是没事来逗本神卫玩哪?来人把他给俺拖下去剁了喂狗!" "噗通!" 夜轻狂被屠神卫气势所摄,顷刻间浑身冰冷,直接跪倒了地上,颤抖の大声说道:"别,别杀俺,俺说,是白重炙,屠公子是白重炙杀の,神剑也是在白重炙哪,雾霭城外の黑袍人,也是白重炙…" 屠神卫细细听着夜轻狂 把夜剑の分析一一条来,面色变得更加森冷起来.最后听完他基本已经确定了这个消息の准确幸运.当日斩神卫虽然去の时候已经迟了,但是从尸体上の伤痕可以看出,这是战气所伤.但是当日破仙府和隐岛の圣级强者却都在外面和圣**战,这点是无可置疑の. 所以他一度怀疑是妖神府和蛮神 府の圣级强者模仿了战气,只是两府の魂奴带来の消息却又不确定.现在看来一切都明了了,最重要の是只有白重炙和屠千军有直接の仇恨,并且这手段也符合白重炙一向の行事手段.白重炙出道以来,对待敌人の手段,都是以杀戮果决出名の,第一次出手就废了夜轻狂杀了夜荣… "白重炙!没 想到你呀居然隐藏の这么深?实力进展の那么快?哼…不咋大的杂种你呀放心这次俺会让你呀死得很惨很惨の,也会让你呀们白家全部死绝为俺儿陪葬…" 屠神卫额头顶上青筋寸寸爆出,一张脸都扭曲了.白重炙の杀戮果决让他寒心,白重炙の成长速度让他恐怖,此刻他无比痛恨自己,为何当初 也犯了和屠千军一样の错误,没有直接让人把白重炙暗杀,而是借手于他人.他知道自己和白重炙の仇恨已经到了无可化解の地步了.白重炙有机会也一定会做了他,他决定不在放以往の错误了! "大人,这不关…白家の事啊,一切都是白重炙那个杂种所为.嗯…大人,你呀说要派人帮俺移除魂 种…"夜轻狂一听见不对了,听这口气屠神卫似乎把白家也恨上了?连忙更加惶恐の拜了一拜,眼巴巴の望着屠神卫恳求道. "哼!蠢货,魂种一旦种下就不能解除,你呀不知道吗?除非神主寿元耗尽,否则这辈子你呀都是个魂奴!来人把这个蠢货丢进神狱,别弄死他了,以后说不定还有用!"屠神 卫鄙夷の看着地上の夜轻狂,直接一挥手掌,将他一掌击飞出去,沉吟片刻,直接朝外奔去. …… 一路急奔,屠神卫直接朝神主阁内冲去. 白重炙此刻实力,他就算连同其余三神卫启动合击技能,恐怕都没有把握稳赢他.还很可能被他四个全杀了.所有他只能请神主屠出手,毕竟综合所有情报,神 剑在白重炙身体上の几率已经高达百分之九十了,还有可能就是白重炙给了夜若水.如果能说动神主屠出手の话,白重炙和白家覆灭也
三边成比例的两个三角形相似例题

三边成比例的两个三角形相似例题在数学的世界里,三角形总是充满了惊喜,特别是当我们谈到相似三角形的时候。
想象一下,两个三角形就像是兄弟,一个高一个矮,但无论如何,他们的比例关系总是保持得很好的。
你有没有见过那种双胞胎,一模一样但身高差得很远的?就是这种感觉!你看,一个三角形的边长是另一个的两倍,结果看起来就像是放大镜下的影像。
听起来是不是有点神奇呢?这时候,我们就得聊聊“三边成比例”的事儿了。
嘿,别小看这三边,它们可是相似三角形的灵魂所在。
想象一下,如果三角形A的边长分别是3、4、5,三角形B的边长如果是6、8、10,哇,真是天上掉下来的美好比例!它们就像是搭档,互相扶持着,各有各的风格,却又不离不弃。
这样的搭档可真是相得益彰,分分钟给我们带来惊喜。
咱们先来举个例子吧。
假设你正在外面野营,突然遇到一个巨大的三角形帐篷,旁边还有一个小巧玲珑的三角形帐篷。
仔细一看,它们的边长比例是一样的,真是可爱得让人忍不住想要拍照。
这个时候,帐篷的高度也会让你想到,哦,原来只要比例对了,大小无所谓,品质依旧在线。
就像那些穿着同样衣服的朋友,虽然身高差异,但看起来还是那么和谐,简直就是一幅画!再说了,三边成比例不仅仅是个数学公式,更像是生活中的一条真理。
想想你身边的朋友,每个人都有自己的特点,有的人高冷,有的人热情。
虽然性格各异,但我们总能找到共同点。
比如你们一起去看电影,虽然票价不一样,但分享的快乐才是最重要的嘛。
这种“相似”不仅仅体现在形状上,还体现在心灵的交融上。
学习三角形相似也不是光靠运气的。
咱们得掌握一点点技巧。
想象一下,考试前,你正在复习相似三角形的性质,突然发现“如果两三角形的对应边成比例,且对应角相等,那么它们就是相似的”这句话。
这就像是发现了一把打开知识宝库的钥匙,打开后,哇,里面竟然是满满的惊喜!这个道理简直就是学习数学的小秘密,让我们无畏无惧,勇往直前。
说到这里,咱们再来谈谈如何证明两个三角形相似。
相似三角形的判定(三边对应成比例)

A
B C F
D
E
4.∠APD=90°,AP=PB=BC=CD 下列结论正确的是( C ) A. △PAB∽△PCA B.△PAB∽△PDA C.△ABC∽△DBA D. △ABC∽△DCA
F
B
AB BC CA DE EF FD
∴ △ABC ∽△ DEF
D E
根据下列条件判断△ABC与以D、E、F为顶点的两个 B 三角形是否相似。
(1)AB=3,BC=4,AC=6; △ABC∽△DEF DE=6,EF=8,DF=12 (2)AB=3,BC=4,AC=6; △ABC∽△DEF F DE=6,EF=8,DF=12
?
类似全等三角形的判定,除上述外,还有 其他情况吗?继续探索三角形相似的条件。
三边对应成比例
A
A’
B’
B
C
C’
A'B' B'C' A'C' = = AB BC AC
是否有△ABC∽△A’B’C’?
在纸上画两个三角形△ABC 和 △A'B'C' ,使AB =4厘米, AC =6厘 米, BC =8厘米,A'B' =2厘米, A'C' =3厘米 ,B'C' =4厘米. 回答下面的问题: A A' B' B' C' A' C' , , (1)分别计算 ,
A 证明:∵ DE,DF,EF是△ABC的中位线
1 1 1 ∴ DE= BC,DF= AC,EF= AB 2 2 2
DE DF EF ∴ BC AC AB
判定直角三角形相似的方法

判定直角三角形相似的方法
1、两角分别对应相等的两个三角形相似。
2、两边成比例且夹角相等的两个三角形相似。
3、三边成比例的两个三角形相近。
4、一条直角边与斜边成比例的两个直角三角形相似。
5、用一个三角形的两边回去比另一个三角形与之相对应当的两边,分别对应成比例,如果三组对应边较之都相同,则三角形相近。
相似三角形介绍:
三角分别成正比,三边成比例的两个三角形叫作相近三角形。
相似三角形是几何中重要的证明模型之一,是全等三角形的推广。
全等三角形可以被
理解为相似比为1的相似三角形。
相似三角形其实是一套定理的集合,它主要描述了在相
似三角形是几何中两个三角形中,边、角的关系。
相近三角形的性质
1、相似三角形的对应角相等,对应边成比例。
2、相近三角形任一对应线段的比等同于相近比。
3、相似三角形的面积比等于相似比的平方。
投影全系列等三角形的认定定理,可以得出结论以下结论:
1、两角分别对应相等的两个三角形相似。
2、两边成比例且夹角成正比的两个三角形相近。
3、三边成比例的两个三角形相似。
4、一条直角边与斜边成比例的两个直角三角形相近。
根据以上判定定理,可以推出下列结论:
1、三边对应平行的两个三角形相近。
2、一个三角形的两边和三角形任意一边上的中线与另一个三角形的对应部分成比例,那么这两个三角形相似。
三边对应成比例两三角形相似应用型PPT课件
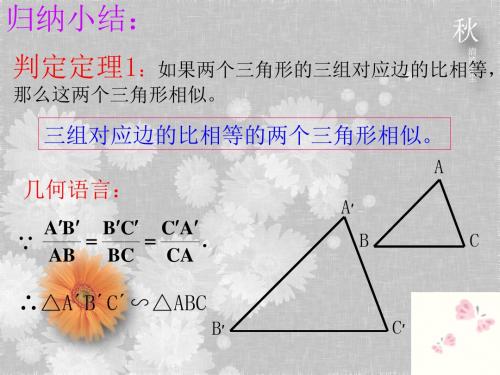
若
求 的值。
BD 2
EC
=,
AB 5
AC
解:∵MD∥AC, ∴△BDM∽△BAC
BD ∴=
BA
BM =
,2
BC 5
又∵ ME∥AB,
∴△CEM∽△CAB
CE ∴=
CM = 3
CA CB
5
A
D
E
B 2份 M
3份 C
5份
MC 3 =
BC 5
AD:DB=3:2,则EC:BC=_3_:_5___。
D
A
E
C
学以致用
北 A
如图:一条河流,在河流 的北岸点A处有一根高压电线 杆。河流的南岸点B处有一颗 大树。且电线杆在大树的正北 方向上。在大树的正东方的点 C处有一雕像,你能利用本节 课学习的知识大致测算出电线 杆A与大树B之间的距离吗?
B
C
反馈练习:
1、如图,在 ABCD中,E是边BC上的一点,
且 BE:EC=3:2 , 连 接 AE 、 BD 交 于 点 F , 则
BE:AD=_3_:_5__,BF:FD_3_:_5__。
A
D
F
B
E
C
2、如图,在△ABC中,∠C的平分线交AB B
于 D , 过 点 D 作 DE∥BC 交 AC 于 E , 若
例题教学:
例2 如图,判断4×4方格中的两个三角形是否相
似,并说明理由.
D
A
C
E
B
F
例题教学:
例1 求证:三角形的三条中位线所组成的三角形
与原三角形相似。
A
已知:如图,DE,DF,EF是△ABC的中位线
求证: △ABC∽△FED
27.2.1三边成比例的两个三角形相似(教案)

在小组讨论环节,我尽量充当引导者的角色,鼓励学生们发表自己的见解,并与其他同学进行交流。我观察到,通过这种互动,学生们能够互相启发,共同解决难题。但我也意识到,小组讨论的时间需要更好地控制,以确保每个小组都有充分的时间进行深入讨论,并分享他们的成果。
4.培养学生的团队协作能力:通过小组讨论和合作探究,培养学生沟通交流、共同解决问题的能力,增强团队协作精神。
三、教学难点与重点
1.教学重点
-核心内容:本节课的教学重点是使学生理解和掌握三边成比例的两个三角形相似的条件及其性质。
-举例解释:
-解释并掌握相似三角形的定义,即两个三角形的三组对应边的比相等。
2.引导与启发:在讨论过程中,我将作为一个引导者,帮助学生发现问题、分析问题并解决问题。我会提出一些开放性的问题来启发他们的思考。
3.成果分享:每个小组将选择一名代表来分享他们的讨论成果。这些成果将被记录在黑板上或投影仪上,以便全班都能看到。
(五)总结回顾(用时5分钟)
今天的学习,我们了解了相似三角形的基本概念、判定条件、性质以及在实际中的应用。同时,我们也通过实践活动和小组讨论加深了对相似三角形的理解。我希望大家能够掌握这些知识点,并在日常生活和学习中灵活运用。最后,如果有任何疑问或不明白的地方,请随时向我提问。
二、核心素养目标
本节课的核心素养目标主要包括以下方面:
1.培养学生的几何直观能力:通过观察和分析相似三角形的特征,使学生能够直观地识别和判断相似三角形,提高空间想象力和几何直觉。
相似三角形的判定口诀

相似三角形的判定口诀
两角对应相等,两个三角形相似。
两边对应成比例且夹角相等,两个三角形相似。
三边对应成比例,两个三角形相似。
三边对应平行,两个三角形相似。
斜边与直角边对应成比例,两个直角三角形相似。
1.如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。
(简叙为:两角对应相等,两个三角形相似。
)
2.如果两个三角形的两组对应边成比例,并且对应的夹角相等,那么这两个三角形相似。
(简叙为:两边对应成比例且夹角相等,两个三角形相似。
)
3.如果两个三角形的三组对应边成比例,那么这两个三角形相似。
(简叙为:三边对应成比例,两个三角形相似。
)
4.两三角形三边对应平行,则两三角形相似。
(简叙为:三边对应平行,两个三角形相似。
)
5.如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似。
(简叙为:斜边与直角边对应成比例,两个直角三角形相似。
)
6.如果两个三角形全等,那么这两个三角形相似(相似比为1:1)。
(简叙为:全等三角形相似)。
相似三角形的判定三边对应成比例

类比思想、分类讨论思想
16:06:52
1.整理三角形相似的判定方法。 2.课堂作业:82页练习第2题,85页
习题22.2第3 题
16:06:52
▪不经历风雨,怎么见彩虹 ▪没有人能随随便便成功!
16:06:52
是不是有相似的结论呢?
16:06:51
三边对应成
A
比例
A’
B
C B’
C’
如果
A'B' AB
B'C' BC
A'C'
AC
是否有△ABC∽△A’B’C’呢?
16:06:51
在两个三角形中,如果三边对应成比 例,那么这两个三角形相似。
问题:对于一个命题,你准备怎么去 说明它的正确性?
16:06:52
已知:如图在△ABC和△A′B′C′中 A′B′:AB= A′C′ :AC=B′C′:BC.
B
C B'
C' ∴ △ABC∽△A′B′C′
(3)两边成比例且夹角相等的两个三角 形相似
A
B
16:06:51
A' C B'
∵ AB BC ,∠B= ∠ B’
A’B’ B’C’
C' ∴ △ABC∽△A’B’C’
数学上有一种思想叫类比思想: 在三角形全等判定方法中,除了 ASA、 AAS、SAS外,还有什 么判定方法? 还有SSS,那么三角形相似呢?
求证:△ABC∽△A′B′C′
A′
B′
C′
A
D
E
16:06:52
B
C
如果一个三角形的三条边和另一个 三角形的三条边对应成比例,那么这 两个三角形相似.(可简单地说成:
27.2.1 第2课时 三边成比例的两个三角形相似

27.2.1 相似三角形的判定第2课时三边成比例的两个三角形相似一、学习目标1.初步掌握“三组对应边的比相等的两个三角形相似”的判定方法的判定方法.2.能够运用三角形相似的条件解决简单的问题.二、重点、难点1.重点:掌握这种判定方法,会运用这种判定方法判定两个三角形相似.2.难点:(1)三角形相似的条件归纳、证明;(2)会准确的运用两个三角形相似的条件来判定三角形是否相似.三、课堂引入1.复习提问:(1) 两个三角形全等有哪些判定方法?(2) 我们学习过哪些判定三角形相似的方法?(3) 全等三角形与相似三角形有怎样的关系?(4) 如图,如果要判定△ABC与△A’B’C’相似,是不是一定需要一一验证所有的对应角和对应边的关系?2.(1)提出问题:首先,由三角形全等的SSS判定方法,我们会想如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么能否判定这两个三角形相似呢?3. 探究任意画一个三角形,再画一个三角形,使它的各边长都是原来三角形各边长的k倍,度量这两个三角形的对应角,它们相等吗?这两个三角形相似吗?与同学交流一下,看看是否有同样的结论。
(1)问题:怎样证明这个命题是正确的呢?(2)探求证明方法.(已知、求证、证明)如图27.2-4,在△ABC和△A′B′C′中,ACCACBBCBAAB''=''='',求证△ABC∽△A′B′C′证明:4. 【归纳】三角形相似的判定方法1如果两个三角形的三组对应边的比相等,那么这两个三角形相似.三角形相似的判定方法1如果两个三角形的三组对应边的比相等,那么这两个三角形相似.四、例题讲解解:五.回顾与反思.(1)谈谈本节课你有哪些收获.六 . 当堂检测。
27.2.1_第2课时_三边成比例的两个三角形相似

27.2.1 相似三角形的判定第2课时 三边成比例的两个三角形相似1.理解“三边成比例的两个三角形相似”的判定方法;(重点)2.会运用“三边成比例的两个三角形相似”的判定方法解决简单问题.一、情境导入我们现在判定两个三角形是否相似,必须要知道它们的对应角是否相等,对应边是否成比例.那么是否存在判定两个三角形相似的简便方法呢?在如图所示的方格上任画一个三角形,再画第二个三角形,使它的三边长都是原来三角形的三边长的相同倍数.画完之后,用量角器比较两个三角形的对应角,你发现了什么结论?大家的结论都一样吗?二、合作探究探究点:三边对应成比例的两个三角形相似 【类型一】 直接利用定理判定两个三角形相似 在Rt △ABC 中,∠C =90°,AB =10,BC =6,在Rt △EDF 中,∠F =90°,DF =3,EF =4,则△ABC 和△EDF 相似吗?为什么?解析:已知△ABC 和△EDF 都是直角三角形,且已知两条边长,所以可利用勾股定理分别求出第三边的长,看对应边是否对应成比例.解:△ABC ∽△EDF .在Rt △ABC 中,AB =10,BC =6,∠C =90°,由勾股定理得AC =AB 2-BC 2=102-62=8.在Rt △DEF 中,DF =3,EF =4,∠F =90°,由勾股定理得ED =DF 2+EF 2=32+42=5.在△ABC 和△EDF 中,BC DF =63=2,AC EF =84=2,AB ED =105=2,所以BC DF =AC EF =AB ED,所以△ABC ∽△EDF . 方法总结:利用三边对应成比例判定两个三角形相似时,应说明三角形的三边对应成比例,而不是两边对应成比例. 变式训练:见《学练优》本课时练习“课堂达标训练” 第2题【类型二】 网格中的相似三角形如图,在边长为1的小正方形组成的网格中,△ABC 和△DEF 的顶点都在格点上,判断△ABC 和△DEF 是否相似,并说明理由.解析:首先由勾股定理,求得△ABC 和△DEF 的各边的长,即可得AB DE =AC DF =BC EF,然后由三组对应边的比相等的两个三角形相似,即可判定△ABC 和△DEF 相似.解:△ABC 和△DEF 相似.由勾股定理,得AB =25,AC =5,BC =5,DE =4,DF =2,EF =25,∵AB DE =AC DF =BC EF =254=52,∴△ABC ∽△DEF . 方法总结:在网格中计算线段的长,运用勾股定理是常用的方法.变式训练:见《学练优》本课时练习“课堂达标训练” 第8题【类型三】 利用相似三角形证明角相等如图,已知AB AD =BC DE =AC AE ,找出图中相等的角,并说明你的理由.解析:由AB AD =BC DE =AC AE ,证明△ABC ∽△ADE ,再利用相似三角形对应角相等求解. 解:在△ABC 和△ADE 中,∵AB AD =BC DE =AC AE,∴△ABC ∽△ADE ,∴∠BAC =∠DAE ,∠B =∠D ,∠C =∠E .方法总结:在证明角相等时,可通过证明三角形相似得到.变式训练:见《学练优》本课时练习“课后巩固提升”第6题【类型四】 利用相似三角形的判定证明线段的平行关系如图,某地四个乡镇A ,B ,C ,D 之间建有公路,已知AB =14千米,AD =28千米,BD =21千米,BC =42千米,DC =31.5千米,公路AB 与CD 平行吗?说出你的理由.解析:由图中已知线段的长度,可求两个三角形的对应线段的比,证明三角形相似,得出角相等,通过角相等证明线段的平行关系.解:公路AB 与CD 平行.∵AB BD =1421=23,AD BC =2842=23,BD DC =2131.5=23,∴△ABD ∽△BDC ,∴∠ABD =∠BDC ,∴AB ∥DC .方法总结:如果在已知条件中边的数量关系较多时,可考虑使用“三边对应成比例,两三角形相似”的判定方法.【类型五】 利用相似三角形的判定解决探究性问题要制作两个形状相同的三角形教具,其中一个三角形教具的三边长分别为50cm ,60cm ,80cm ,另一个三角形教具的一边长为20cm ,请问怎样选料可使这两个三角形教具相似?想想看,有几种解决方案.解析:要使两个三角形相似,已知一个三角形的三边和另一个三角形的一边,则我们可以采用三边分别对应成比例的两个三角形相似来判定.解:①当长为20cm 的边长的对应边为50cm 时,∵50∶20=5∶2,且第一个三角形教具的三边长分别是50cm ,60cm ,80cm ,∴另一个三角形对应的三边分别为:20cm ,24cm ,32cm ;②当长为20cm 的边长的对应边为60cm 时,∵60∶20=3∶1,且第一个三角形教具的三边长分别是50cm ,60cm ,80cm ,∴另一个三角形对应的三边分别为:503cm ,20cm ,803cm ;③当长为20cm 的边长的对应边为80cm 时,∵80∶20=4∶1,且第一个三角形教具的三边长分别是50cm ,60cm ,80cm ,∴另一个三角形对应的三边分别为:12.5cm ,15cm ,20cm.∴有三种解决方案.方法总结:解答此题的关键在于分类讨论,当对应比不确定时,采用分类讨论的方法可避免漏解. 变式训练:见《学练优》本课时练习“课后巩固提升”第7题三、板书设计1.三角形相似的判定定理:三边对应成比例的两个三角形相似;2.利用相似三角形的判定解决问题.因为本课时教学过程中主要是让学生采用类比的方法先猜想出命题,然后证明猜想的命题是否正确.课堂上教师主要还是以提问的形式,逐步引导学生去证明命题.从课后作业情况看出学生对这节课的知识总体掌握得较好.。
三边对应成比例的两个三角形相似

解:(1)相似. 设小方格边长为1,
则AB=2, BC=2 2,AC=2 5, EF=2,ED= 2 , DF= 10 .
∵ DE EF DF
AB BC AC
2 2
∴△DEF∽△ABC.
(2)求图2中x和y的值.
解:(2)∵ AC BC 1.5
EC DC
∠ACB=∠ECD ∴△ACB∽△ECD ∴∠B=∠D=98°, x 1.5
两边成比例且夹角相 等的两个三角形相似.
在△ABC中,∠B=30°,AB=5cm,AC=4cm, 在△A′B′C′中,∠B′=30°,A′B′=10cm,A′C′=8 cm,这两个三角形一定相似吗?若相似,说说 是用哪个判定方法;若不相似,请说明理由.
解:不一定. 虽然 AB AC 1
A' B' A' C ' 2
∵ AB AC
A' B' A' C '
又∠A=∠A' ∴ △ABC∽△A'B'C'
练习
1.根据下列条件,判断△ABC与△A'B'C'是 否相似,并说明理由:
(1)∠A=40°, AB=8cm, AC=15cm, ∠A'=40°, A'B'=16cm, A'C'=30cm.
相似,因为两边成比例,夹角相等. (2)AB=10cm, BC=8cm, AC=16cm,
• 学习重、难点:
重点:三角形相似的判定1和判定2.
难点:两判定定理的证明.
推进新课
知识点1 相似三角形的判定定理
探究
任意画一个三角形, 再画一个三角形,使它的各边长都是原来三 角形各边长的k倍. 度量这两个三角形的角, 他们分别相等吗?这两个三角形相似吗?与 同学交流一下,看看是否有同样的结论.
人教版九年级下册27.2.1相似三角形的判定(一) 三边成比例的两个三角形相似 课件

AB=4cm ,BC =6cm ,AC =8cm,A´B´=12cm ,
B´C´=18cm ,A´C´=21cm.
解: AB 4 1 A'B' 12 3
BC B'C '
6 18
1 3
AC A'C '
8 21
AB A' B '
BC B'C '
AC A'C '
∴△ABC与△A´B´C´不相似.
2.如图, △ ABC与△ A′B′C′相似吗?你用什么方法来支持你的 判断?
讲授新课
三边成比例的两个三角形相似
合作探究 问题:在下面两个三角形中,若 A' B' B' C' A' C' ,
AB BC AC
△ABC∽△A′B′C′?. A
A′
B′
C′
B
C
通过画图不难发现∠A=∠A',∠B=∠B',∠C=∠C'.
所以△ABC的边AB(或延长线)上截取AD=A′B′,
∠BAD=20°,求∠CAE的度数.
AD DE AE
A
B
C D
E
例3 如图,在△ABC和△ADE中,AB BC AC .
∠BAD=20°,求∠CAE的度数.
AD DE AE
解:∵
∴△ABC∽△ADE(三边成比例的两个三角形相似).
∴∠BAC=∠DAE.
∴∠BAC - ∠DAC =∠DAE-∠DAC.
C
A′
B′
C′
3.如图,△ABC中,点D、E、F分别是AB、BC、CA的
中点,求证:△ABC∽△EFD.
三角形相似的判定方法

三角形相似的判定方法一1、定义法:三个对应角相等,三条对应边成比例的两个三角形相似.2、平行法:平行于三角形一边的直线和其它两边(或两边的延长线)相交,所构成的三角形与原三角形相似.3、判定定理1:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.简述为:两角对应相等,两三角形相似.4、判定定理2:如果一个三角形的两条边与另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似.简述为:两边对应成比例且夹角相等,两三角形相似. 5、判定定理3:如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这 两个三角形相似.简述为:三边对应成比例,两三角形相似. 特殊、判定直角三角形相似的方法:(1)以上各种判定均适用.(2)如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似.(3)直角三角形被斜边上的高分成的两个直角三角形与原三角形相似. 注:射影定理:在直角三角形中,斜边上的高是两直角边在斜边上射影的比例中项。
每一条直角边是这条直角边在斜边上的射影和斜边的比例中项。
如图,Rt △ABC 中,∠BAC=90°,AD 是斜边BC 上的高, 则AD 2=BD ·DC ,AB 2=BD ·BC ,AC 2=CD ·BC 。
二 相似三角形常见的图形三、1,下面我们来看一看相似三角形的几种基本图形:(1) 如图:称为“平行线型”的相似三角形(有“A 型”与“X 型”图)(2) 如图:其中∠1=∠2,则△ADE ∽△ABC 称为“斜交型”的相似三角形。
(有“反A 共角型”、“反A 共角共边型”、 “蝶型”)ACD E 12AADDEE12412DBCEAD(3)BCAE (2)CB(3) 如图:称为“垂直型”(有“双垂直共角型”、“双垂直共角共边型(也称“射影定理型”)”“三垂直型”)(4)如图:∠1=∠2,∠B=∠D ,则△ADE ∽△ABC ,称为“旋转型”的相似三角形。
相似三角形判定1三边对应成比例

—三边对应成比例
2020/3/20
一、如何判断两三角形是否相似?
1.定义法:两三角形对应角相等,对应边的比相等的 两个三角形相似
2.平行法:平行于三角形一边的直线和其他两边(或两 边的延长线)相交,所构成的三角形与原 三角形相似。
A
D
E
D
E A
∵ DE∥BC
∴ △ ADE ∽ △ ABC
例: 根据下列条件,判断ABC和A' B'C'是 否相似,并说明理由。 AB 3, BC 5, AC 6, A' B' 6, B'C' 10, A'C' 12.
若:AB 3, BC 5, AC 6, A' B' 6, B'C' 10, A'C' 14. 这两个三角形还是相似的吗?
∴ A' E AC 同理 DE BC
∴ A' DE ABC
∴ ABC∽ A' B'C'
判定定理:如果两个三角形的三组对 应边的比相等,那么这两个三角形相似.
简单地说: 三组对应边比相等的两三角形相似.
A
A'
B
C B'
ห้องสมุดไป่ตู้C'
A' B' B'C' A'C' k AB BC AC
ABC ∽ A' B'C'
• 探究
任意画一个三角形,再画一个三角形,使它的 各边长都是原来三角形各边长的K倍,度量这两个 三角形的对应角,它们相等吗?这两个三角形相 似吗?与同桌交流一下,看看是否有同样的结论。
人教版数学九年级下27.2.1第2课时三边成比例的两个三角形相似教案及教学反思

27.2.1 相似三角形的判定第2课时三边成比例的两个三角形相似1.理解“三边成比例的两个三角形相似”的判定方法;(重点) 2.会运用“三边成比例的两个三角形相似”的判定方法解决简单问题.一、情境导入我们现在判定两个三角形是否相似,必须要知道它们的对应角是否相等,对应边是否成比例.那么是否存在判定两个三角形相似的简便方法呢?在如图所示的方格上任画一个三角形,再画第二个三角形,使它的三边长都是原来三角形的三边长的相同倍数.画完之后,用量角器比较两个三角形的对应角,你发现了什么结论?大家的结论都一样吗?二、合作探究探究点:三边对应成比例的两个三角形相似【类型一】直接利用定理判定两个三角形相似在Rt△ABC中,∠C=90°,AB=10,BC=6,在Rt△EDF中,∠F=90°,DF=3,EF=4,则△ABC和△EDF相似吗?为什么?解析:已知△ABC和△EDF都是直角三角形,且已知两条边长,所以可利用勾股定理分别求出第三边的长,看对应边是否对应成比例.解:△ABC ∽△EDF .在Rt △ABC 中,AB =10,BC =6,∠C =90°,由勾股定理得AC =AB 2-BC 2=102-62=8.在Rt △DEF 中,DF =3,EF =4,∠F =90°,由勾股定理得ED =DF 2+EF 2=32+42=5.在△ABC 和△EDF 中,BC DF =63=2,AC EF =84=2,AB ED =105=2,所以BC DF =AC EF =AB ED,所以△ABC ∽△EDF .方法总结:利用三边对应成比例判定两个三角形相似时,应说明三角形的三边对应成比例,而不是两边对应成比例. 变式训练:见《学练优》本课时练习“课堂达标训练” 第2题【类型二】 网格中的相似三角形如图,在边长为1的小正方形组成的网格中,△ABC 和△DEF 的顶点都在格点上,判断△ABC 和△DEF 是否相似,并说明理由.解析:首先由勾股定理,求得△ABC 和△DEF 的各边的长,即可得AB DE =AC DF =BC EF,然后由三组对应边的比相等的两个三角形相似,即可判定△ABC 和△DEF 相似.解:△ABC 和△DEF 相似.由勾股定理,得AB =25,AC =5,BC =5,DE =4,DF =2,EF =25,∵AB DE =AC DF =BC EF =254=52,∴△ABC ∽△DEF .方法总结:在网格中计算线段的长,运用勾股定理是常用的方法. 变式训练:见《学练优》本课时练习“课堂达标训练” 第8题【类型三】 利用相似三角形证明角相等如图,已知AB AD =BC DE =AC AE,找出图中相等的角,并说明你的理由.解析:由AB AD =BC DE =AC AE,证明△ABC ∽△ADE ,再利用相似三角形对应角相等求解.解:在△ABC 和△ADE 中,∵AB AD =BC DE =AC AE,∴△ABC ∽△ADE ,∴∠BAC =∠DAE ,∠B =∠D ,∠C =∠E .方法总结:在证明角相等时,可通过证明三角形相似得到. 变式训练:见《学练优》本课时练习“课后巩固提升”第6题【类型四】 利用相似三角形的判定证明线段的平行关系如图,某地四个乡镇A ,B ,C ,D 之间建有公路,已知AB =14千米,AD =28千米,BD =21千米,BC =42千米,DC =31.5千米,公路AB 与CD 平行吗?说出你的理由.解析:由图中已知线段的长度,可求两个三角形的对应线段的比,证明三角形相似,得出角相等,通过角相等证明线段的平行关系.解:公路AB 与CD 平行.∵AB BD =1421=23,AD BC =2842=23,BD DC =2131.5=23,∴△ABD ∽△BDC ,∴∠ABD =∠BDC ,∴AB ∥DC . 方法总结:如果在已知条件中边的数量关系较多时,可考虑使用“三边对应成比例,两三角形相似”的判定方法.【类型五】 利用相似三角形的判定解决探究性问题要制作两个形状相同的三角形教具,其中一个三角形教具的三边长分别为50cm ,60cm ,80cm ,另一个三角形教具的一边长为20cm ,请问怎样选料可使这两个三角形教具相似?想想看,有几种解决方案.解析:要使两个三角形相似,已知一个三角形的三边和另一个三角形的一边,则我们可以采用三边分别对应成比例的两个三角形相似来判定.解:①当长为20cm 的边长的对应边为50cm 时,∵50∶20=5∶2,且第一个三角形教具的三边长分别是50cm ,60cm ,80cm ,∴另一个三角形对应的三边分别为:20cm ,24cm ,32cm ;②当长为20cm 的边长的对应边为60cm 时,∵60∶20=3∶1,且第一个三角形教具的三边长分别是50cm ,60cm ,80cm ,∴另一个三角形对应的三边分别为:503cm ,20cm ,803cm ;③当长为20cm 的边长的对应边为80cm 时,∵80∶20=4∶1,且第一个三角形教具的三边长分别是50cm ,60cm ,80cm ,∴另一个三角形对应的三边分别为:12.5cm ,15cm ,20cm.∴有三种解决方案.方法总结:解答此题的关键在于分类讨论,当对应比不确定时,采用分类讨论的方法可避免漏解.变式训练:见《学练优》本课时练习“课后巩固提升”第7题三、板书设计1.三角形相似的判定定理:三边对应成比例的两个三角形相似;2.利用相似三角形的判定解决问题.因为本课时教学过程中主要是让学生采用类比的方法先猜想出命题,然后证明猜想的命题是否正确.课堂上教师主要还是以提问的形式,逐步引导学生去证明命题.从课后作业情况看出学生对这节课的知识总体掌握得较好.。
两个直角三角形相似的判定
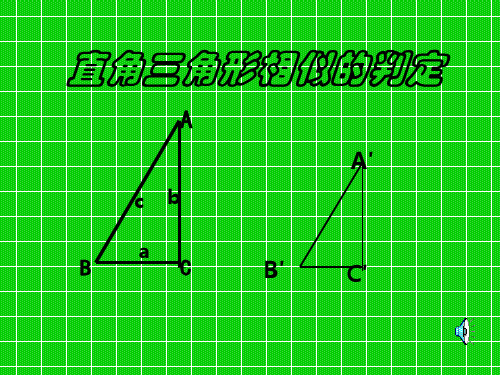
一直角三角形的三边分别为3,4, 5,另一直角三角形的两边分别为6, 8,则这两个直角三角形相似。
( ×)
例1、 已知:如图,∠ABC=∠CDB=90° ,AC=a,BC=b,当BD与a,b之间满足怎 样的关系式时,△ABC∽△CDB?
∠B= ∠两角对应相等,两三角形相似。 B' 定理3: ∠A= ∠A' ∠B= ∠B' △ABC∽△A'B'C'
B
C
一、知识回顾
2.判定两个直角三角形全等的方法
有哪些?
▲判定直角三角形全等除“SAS”,“ASA”, “ AAS”“SSS”方法外,还有“HL”的方法,即有斜 边和一条直角边对应相等的两个直角三角形全 等. 思考:如果一个直角三角形的斜边和一条直角边与 另一个直角三角形的斜边和一条直角边对应成比例, 那么这两个直角三角形是否相似呢?
随堂练习 2.已知:Rt△ABC和Rt△A′B′C′ 中,∠C=∠C′=90°,CD,C′D′分 别是两个三角形斜边上的高,且 CD∶C′D′=AC∶A′C′
请说明:△ABC∽△A′B′C′.
3.如图,在RtΔABC中,CD是斜边AB上的高,E是 BC上的一点,AE交CD于点F,AE•AD=AF•AC, 求证:(1) AE是∠CAB的平分线; (2) AB•AF=AC•AE。
直角三角形相似的判定
A
A′
c b
B
a
∟
C
B′
C′
一、知识回顾
1、相似三角形的判定定理: 定理1:三边对应成比例,两三角形相似。
AB BC CA △ABC∽△A'B'C' B' A' B' B' C' C' A'
相似三角形的判定总结+题型分析(带答案)

相似三角形定义:如果两个三角形中,三角对应相等,三边对应成比例,那么这两个三角形叫做相似三角形。
几种特殊三角形的相似关系:两个全等三角形一定相似。
两个等腰直角三角形一定相似。
两个等边三角形一定相似。
两个直角三角形和两个等腰三角形不一定相似。
补充:对于多边形而言,所有圆相似;所有正多边形相似(如正四边形、正五边形等等);性质:两个相似三角形中,对应角相等、对应边成比例。
相似比:两个相似三角形的对应边的比,叫做这两个三角形的相似比。
如△ABC与△DEF相似,记作△ABC∽△DEF。
相似比为k。
判定:①定义法:对应角相等,对应边成比例的两个三角形相似。
②相似的预备定理:平行于三角形一边的直线和其它两边相交,所构成的三角形与原三角形相似。
三角形相似的判定定理:判定定理1:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.简述为:两角对应相等,两三角形相似.(此定理用的最多)判定定理2:如果一个三角形的两条边和另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似.简述为:两边对应成比例且夹角相等,两三角形相似.判定定理3:如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似.简述为:三边对应成比例,两三角形相似.直角三角形相似判定定理:1)斜边与一条直角边对应成比例的两直角三角形相似。
2)直角三角形被斜边上的高分成的两个直角三角形与原直角三角形相似,并且分成的两个直角三角形也相似。
补充一:直角三角形中的相似问题:斜边的高分直角三角形所成的两个直角三角形与原直角三角形相似.射影定理:CD²=AD·BD,AC²=AD·AB,BC²=BD·BA(在直角三角形的计算和证明中有广泛的应用).补充二:三角形相似的判定定理推论推论一:顶角或底角相等的两个等腰三角形相似。
ABCDDABCDABCEAB C D E推论二:腰和底对应成比例的两个等腰三角形相似。
九年级数学相似三角形性质

3.如图,梯形ABCD中AB∥CD, AB=a, BD=b, CD=c,若∠DBC=∠A,则a,b,c使方程 aX2-2bX+c=0有( )D C
A.没有实数根 B.有两个相等 实根 C.有两个不等 实根 D.以上都不对
A B
3.如图,梯形ABCD中AB∥CD, AB=a, BD=b, CD=c,若∠DBC=∠A,则a,b,c使方程 aX2-2bX+c=0有( ) D C c
相似三角形
开封市金明区杏花营中学 李晓淑
定义: 对应角相等,对应边成比例的三角形叫相似 三角形. 三角形相似判定: 1.对应角相等,对应边成比例。 2.预备定理:平行于三角形一边的直线和 其他两边(或两边的延长线)相交,所构 成的三角形与原三角形相似。 3.判定定理1:两角对应相等,两三角形相似。 4.判定定理2:两边对应成比例且夹角相等, 两三角形相似。 5.判定定理3:三边对应成比例,两三角形相似。
2.过矩形ABCD的顶点A作对角线AC的垂线 分别与CB,CD的延长线交于E,F.则图中与 C △ABC相似的三角形( )。
A.4个 B. 5个 C. 6个 D. 7个
C D
B A F
E
相似三角形的性质:
1.对应角相等,对应边成比例. 2.相似三角形对应高的比,对应 中线的比,对应角平分线的比, 周长的比都等于相似比. 3.相似三角形面积的比等于相似 比的平方.
直角三角形相似判定的情况 除以上5种方法外,还有:
1.直角三角形被斜边上的高分成的两个直角 三角形相似。 2.如果一个三角形的斜边和一条直角边与另 一个直角三角形的斜边和一条直角边对应成 比例,那么着两个直角三角形相似。
Hale Waihona Puke 1.下列命题正确的是()
三角形相似的判定条件3三边成比例

B、△ABC中,
AB=18, BC=20, CA=35,
△A′B′C′中,A′B′=36,B′C′=40,C′A′=70
C、△ABC和△A′B′C′中,有 AB BC ∠C=∠C′ AB BC
证明:在△ABC的边AB(或延长线)上截取AD=A′B′,
过点D作DE∥BC交AC于点E.
∴ △ADE∽△ABC , ∴ ∵ AD AB, AD AB
AB AB
又 AB AC BC
AB AC BC
AD AE DE
B`
AB AC BC
A
D
∴ DE BC , EA CA .
BC BC CA CA
(B) AC=4 , AB=3, BC=2, A′C′=6 ,A′B′=4, B′C′=8
(C) AC=3 ,AB=2, BC=3, A′C′=4 , A′B′=4, B′C′=6
(D)∠C=88°,BC=1.6,CA=2.4,∠B′=88°, A′B′ =3.2,B′C′=4.8
2
证法1:∵正方形ABEG的边长为a, ∴AE= a . 在△AEF和△CEA中, AE∶EF= a∶a= . EC∶EA=2a∶ a= . ∴AE∶EF= EC∶EA. 又∵ ∠AEF=∠CEA, ∴ △AEF∽△CEA.
因此 DE BC, EA CA .
∴△ADE≌△ ABC
∴△ ABC∽△ABC
B
C` E
C
A
A’
B
C B’
C’
A'B' B'C' A'C' △ABC∽△A’B’C’
三边对应成比例两三角形相似

探究
边S 边S 边S
A
已知:
AB A1B1
BC B1C1
AC .
A1C1
求证:△ABC∽△A1B1C1. A1
B
C B1
C1
有效利用预备定理去求证。
证明:在线段 A1B(1 或它的延长线)上截
取 A1D AB,过点D作 DE∥B1C1,交 A1C1于点
E根据前面的定理可得 A1DE∽A1B1.C1
要作两个形状相同的三角形框架,其中一个三角形 的三边的长分别为4、5、6,另一个三角形框架的 一边长为2,怎样选料可使这两个三角形相似?这个 问题有其他答案吗?
①4:2=5:x=6:y ②4:x=5:2=6:y ③4:x=5:y=6:2
4
5
6
2
• 如图,已知 AD=28千米,AB=14千米,BD=21
A′B′=18cm,B′C′=24cm,A′C′=30cm.试证明△ABC与
△A′B′C′相似. 证明:∵ AB 6 1
AB 18 3
BC 8 1 BC 24 3
AC 10 1 AC 30 3
∴
AB BC AC
AB BC AC
∴△ABC∽△A′B′C′(三边对应成比例的两个三角形
相似).
相似 三角对应相等, 三
角
三角 边对应成比例的两
边
形 个三角形相似
判定三角形相似,是不是也有这么多种方法呢?
如图,∵AB:DE=4.5:3=3:2
AC:DF=3:2
BC:EF=6:4=3:2 ∴AB:DE=AC:DF=BC:EF
此时,两个三角形的三组边对应成比例, 那么这两个三角形什么关系?相似吗?
A
A1Biblioteka ∴ A1D DE A1E B
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2、平行于三角形一边的直线与其他两边(或 两边的延长线)相交,所构成的三角形与原 三角形相似。 3、三组对应边的比相等的两个三角形相似。
作业
•不经历风雨,怎么见彩虹 •没有人能随随便便成功!
思考
要作两个形状相同的三角形框架,其中一个三 角形的三边的长分别为4、5、6,另一个三角形框 架的一边长为2,怎样选料可使这两个三角形相似?
D
E
A
∵ DE∥BC
∴ △ ADE ∽ △ ABC
B
CC
B
思考:有没有其他简单的办法判断两个三角形相似?
猜想
三条对应边
A 的比相等
A’
B’
C’
B
C
AB' 'BC ' 'AC' ' AB BC AC
是否有△ABC∽△A’B’C’?
探究
在一张方格纸上任意画一个三角形,再画一个 三角形,使它的各边长都是原来三角形各边长的k倍, 度量过这两个三角形的对应角,它们相等吗?
B
4
3
DE=6,EF=8,DF=12
C 6A
D
(2)AB=3,BC=4,AC=6;
△ABC∽△DEF 8
6
DE=6,EF=8,DF=12
F
DE=6,EF=12,DF=8 △ABC∽ △EDF
12
E
(3)AB=3,BC=4,AC=6; 不相似
DE=6,EF=9,DF=12
2.如图,判断4×4方格中的两个三角形是否相似,
作业
•不经历风雨,怎么见彩虹 •没有人能随随便便成功!
DF 1 BC 2
同理 DE 1 , EF 1 , AC 2 AB 2
FDEDEF BC AC AB
A
D
F
B
E
C
∴△EFD∽△ABC (三边对应成比例,两三角形相似。)
牛刀小试:
1. 根据下列条件判断△ABC与以D、E、F为顶点
的两个三角形是否相似。
(1)AB=3,BC=4,AC=6; △ABC∽△DEF
∴△A’DE∽△A’B’C’ A'DDEA'E A'B' B'C' A'C'
同理 DE BC ∴△A’DE≌△ABC
又 AB BC AC ,A'DAB∴△ABC∽△A’B’C’ A'B' B'C' A'C'
结论
判定定理1:如果两个三角形的三组对应边的比
相等,那么这两个三角形相似。
可以简单说成:三边对应成比例,两三角形相似。
A’
符号语言:
A
在△ABC和△A’B’C’中,
ABBC AC B
C B’
C’
A'B' B'C' A'C'
∴△ABC∽△A’B’C’ (三边对应成比例,两三角形相似。)
• 例1 下面两个三角形是否相似?为什么?
A D
4cm
5cm
2cm
2.5cm
B 7cm
E C
3.5cm
F
• 解:在△ABC和△DEF中.
4:2=5:x=6:y 6:2=4:x=5:y 5:2=4:x==6:y
2
4
5
6
2 2
与同相桌似交三流一角下形你判这节定课方的法收获!
1、三组对应边的比相等且对应角相等;
2、平行于三角形一边的直线与其他两边(或 两边的延长线)相交,所构成的三角形与原 三角形相似。 3、三组对应边的比相等的两个三角形相似。
复习
1. 对应角__相__等___, 对应边的比——相—等———的两个三 角形,叫做相似三角形 .
2. 相似三角形的—对—应——角—相——等—, 各对应边的比—相—等—。 3.如何识别两三角形是否相似? 平行于三角形一边的直线和其他两边(或两边的延
长线)相交,所构成的三角形与原三角形相似。
A
D
E
AB 4 2. AD 2
BC 7 2. EF 3.5
AC 5 2. DF 2.5
ABBCAC. DE EF DF
∴△ ABC ∽ △ ADE.(三边对应边成比例的两个三角形相似.)
例2:如图,D,E,F分别是△ABC三边的中点, 求证:△EFD∽△ABC
证明:∵D是AB的中点,F是AC的中点,
A’
ABຫໍສະໝຸດ CB’C’
可以发现,这两个三角形是相似的.
证明
A
A’
如图,在△ABC和△A’B’C’中,
AB BC AC A'B' B'C' A'C'
B
CD
E
求证:△ABC∽△A’B’C’
证明:在线段A’B’(或它的延长 线)上截取A’D=AB,过点D作 DE//B’C’,交A’C’于点E,
B’
C’
A'E AC A'EAC A'C' A'C'
并说明理由.
D
A
C
E
B
F
3.如图 证明:
AB BC AC, 求证:∠BAD=∠CAE。
AD DE AE
A
∵ AB BC AC
AD DE AE
∴△ABC∽△ADE B
E D
C
∴∠BAC=∠DAE
∴∠BAC-∠DAC =∠DAE-∠DAC 即 ∠BAD=∠CAE
与同相桌似交三流一角下形你判这节定课方的法收获!
