FFT算法的c++实现

c语言dft算法

在C语言中实现DFT（离散傅里叶变换）算法可以使用库函数fft（Fast Fourier Transform，快速傅里叶变换），也可以自己实现。

以下是一个简单的DFT算法的C语言实现：
void idft(double *x, int n)
{
double complex *y;
int i;
for (i = 0; i < n; i++) {
y[i] = creal(x[i]);
y[i] *= pow(-1.0, i * 2) * x[i];
}
for (i = 0; i < n; i++) {
x[i] = creal(y[i]);
y[i] = complex_conj(y[i]);
}
}
这个算法的基本思路是：首先将输入向量x中的所有元素求实部和虚部，然后将虚部乘以-1.0的i*2次方，再将实部和虚部相加，得到DFT输出向量y中的每个元素。

最后将y中的实部和虚部交换，得到原始向量x的反转DFT输出。

在这个算法中，我们使用了C语言中的complex类型来表示复数，使用creal()函数来获取复数的实部，使用complex_conj()函数来计算复数的共轭。

需要注意的是，这个算法只适用于n为偶数的情况，因为DFT输出向量中的元素需要和输入向量中的元素一一对应。

如果n为奇数，则需要对输入向量进行填充或删除，以使其满足偶数长度。

FFT快速算法C程序

FFT快速算法C程序以下是一个使用C语言实现的FFT（快速傅里叶变换）算法的程序：```c#include <stdio.h>#include <stdlib.h>#include <math.h>typedef structdouble real;double imag;if (size == 1)output[0].real = input[0].real;output[0].imag = input[0].imag;return output;}for (int i = 0; i < size / 2; i++)even[i].real = input[2 * i].real;even[i].imag = input[2 * i].imag;odd[i].real = input[2 * i + 1].real;odd[i].imag = input[2 * i + 1].imag;}free(even);free(odd);for (int i = 0; i < size / 2; i++)double angle = 2 * PI * i / size;t.real = cos(angle);t.imag = -sin(angle);u.real = oddResult[i].real * t.real - oddResult[i].imag * t.imag;u.imag = oddResult[i].real * t.imag + oddResult[i].imag * t.real;output[i].real = evenResult[i].real + u.real;output[i].imag = evenResult[i].imag + u.imag;output[i + size / 2].real = evenResult[i].real - u.real;output[i + size / 2].imag = evenResult[i].imag - u.imag;}free(evenResult);free(oddResult);return output;int maiint size;printf("请输入需要进行FFT变换的序列长度：");scanf("%d", &size);printf("请输入待变换序列的实部和虚部：\n");for (int i = 0; i < size; i++)scanf("%lf %lf", &input[i].real, &input[i].imag);}printf("傅里叶变换后的结果为：\n");for (int i = 0; i < size; i++)printf("%f + %fi\n", output[i].real, output[i].imag);}free(input);free(output);return 0;```在 `main` 函数中，首先获取用户输入的序列长度，然后依次输入序列的实部和虚部。

fft的C语言实现

算法原理：按时间抽取（DIT）FFT算法将时间序列x(n)的次序重排，并利用W i n函数的特性，将长序列的离散傅里叶变换运算逐渐分解成较短序列的离散傅里叶变换计算，从而提高运算效率。

基2DIT FFT的特点（1）倒位序输出频谱抽样值X(K)是按照顺序出现的，但是输入时间序列x(n)的顺序被打乱了。

可以使用“二进制码位倒置法”对输入的时间序列x(n)进行排序。

比如对N=8，用三位二进制码n2n1n0表示。

对于正序来说，十进制数序号n的二进制数的关系为n=22n2+2n1+n0倒位序的序号为n=22n0+2n1+n2（2）运算结构FFT的运算结构式由大量的蝶形流图组成的。

基2DIT FFT运算是将N点的DFT先分成2个N/2点DFT，再是4个N/4点DFT，直至N/2个2点DFT。

每分一次，称为一“级”运算，前一级的输出时候一级的输入。

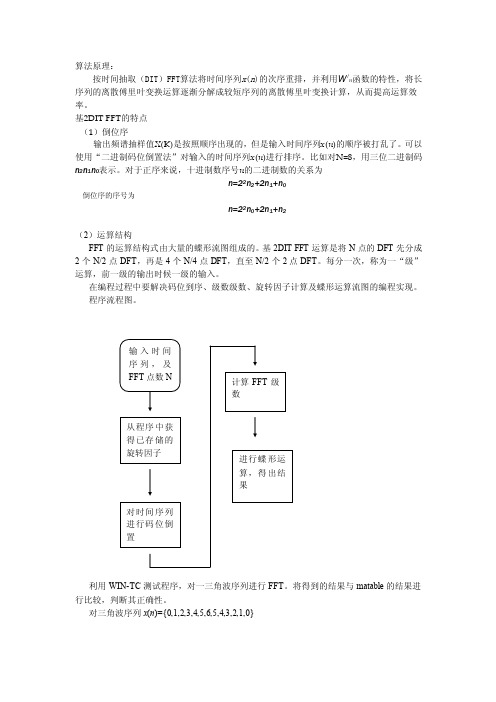
在编程过程中要解决码位到序、级数级数、旋转因子计算及蝶形运算流图的编程实现。

程序流程图。

利用WIN-TC测试程序，对一三角波序列进行FFT。

将得到的结果与matable的结果进行比较，判断其正确性。

对三角波序列x(n)={0,1,2,3,4,5,6,5,4,3,2,1,0}在WIN-TC进行128点FFT，得到前6个结果Matable仿真的前6个结果是XKN2 =Columns 1 through 636.0000 34.2084 -10.3770i 29.1007 -19.4445i 21.4292 -26.1115i 12.2946 -29.6817i 2.9501 -29.9525i前半段波形对比显示WIN-TC结果能保证小数点后2位的精度。

对方波序列x(n),长度为64，前32为1，幅值为1的序列在WIN-TC进行128点FFT，得到前6个结果Matable仿真的前6个结果是Columns 1 through 632.0000 20.8677 -19.8677i 1.0000 -20.3555i -6.2783 - 7.2783i 04.5539 - 3.5539i仿真波形对比显示WIN-TC结果能保证小数点后2位的精度。

FFT算法的C语言编程

#include <stdio.h>#include <math.h>#include <stdlib.h>#define PI 3.1415926/*This program is used to conduct FFT or IFFT transform based on 2 discomposition data can be loaded by typing on the keyboard or from file.*/typedefstruct{double real;doubleimag;}complex;long NN;long t2t(long n, int M){longnn=0;for(inti=0;i<M;i++){nn=nn+n%2*pow(2,M-1-i);n=n/2;}returnnn;}intdefM(long n){int M=0;while(pow(2,M)<n){M++;}return M;}voiddatain(complex x[],long N){int flag;longi;char s[20];FILE *fpi;doublea,b;printf("Load data from keybord(input 0) or file(input 1)\n");scanf("%d",&flag);if(flag==0){printf("Please enter the data in the form of a,b--a+j*b ending with'*'\n");for(i=0;getchar()!='*';i++)scanf("%lf%lf",&x[i].real,&x[i].imag);while(i<N){x[i].real=0;x[i].imag=0;i++;}}elseif(flag==1){printf("Please input the name of the file with its File type suffix-(eg:data.txt)\n");gets(s);gets(s);//To avoid the quick response to enterfpi=fopen(s,"r");if(!fpi){printf("Open file error");}i=0;while(!feof(fpi)){fscanf(fpi,"%lf",&a);fscanf(fpi,"%lf",&b);x[i].real=a;x[i].imag=b;i++;}fclose(fpi);while(i<N){x[i].real=0;x[i].imag=0;i++;}}}voiddataout(complex x[],long N){longi;for(i=0;i<N;i++)printf("%.3lf+j*%.3lf\n",x[i].real,x[i].imag);}void reverse(complex x[],complex xi[],long n,int m) {longi;long temp;for(i=0;i<n;i++){temp=t2t(i,m);xi[i].real=x[temp].real;xi[i].imag=x[temp].imag;}}complexcom_add(complex x1,complex x2){complex y;y.real=x1.real+x2.real;y.imag=x1.imag+x2.imag;return y;}complexcom_sub(complex x1,complex x2){complex y;y.real=x1.real-x2.real;y.imag=x1.imag-x2.imag;return y;}complexcom_mul(complex x1,complex x2){complex y;y.real=x1.real*x2.real-x1.imag*x2.imag;y.imag=x1.real*x2.imag+x2.real*x1.imag;return y;}complexcom_div(complex x1,complex x2){complex y;double down=x2.real*x2.real+x2.imag*x2.imag;y.real=(x1.real*x2.real+x1.imag*x2.imag)/down;y.imag=(x2.real*x1.imag-x1.real*x2.imag)/down;return y;}voidfft(complex x[],long NN, int M){intm,i,j;longNw,Ni;complexWm,temp;for(m=0;m<M;m++){Nw=pow(2,m+1);Ni=pow(2,m);for(i=0;i<Ni;i++){for(j=i;j<NN;j=j+Nw){Wm.real=cos(2*i*PI/Nw);Wm.imag=-sin(2*i*PI/Nw);temp=com_mul(x[j+Ni],Wm);x[j+Ni]=com_sub(x[j],temp);x[j]=com_add(x[j],temp);}}}}voidifft(complex x[],long NN, int M){intm,i,j;longNw,Ni;complexWm,temp;for(m=0;m<M;m++){Nw=pow(2,m+1);Ni=pow(2,m);for(i=0;i<Ni;i++){for(j=i;j<NN;j=j+Nw){Wm.real=cos(2*i*PI/Nw);Wm.imag=-sin(2*i*PI/Nw);temp=com_mul(x[j+Ni],Wm);x[j+Ni]=com_sub(x[j],temp);x[j]=com_add(x[j],temp);}}}for(i=0;i<NN;i++){x[i].real=x[i].real/NN;x[i].imag=-x[i].imag/NN;}}int main(){longN,i;intM,flag;doublea,b;printf("Please enter the length of the sequence\n");scanf("%ld",&N);M=defM(N);NN=pow(2,M);complexxy[NN];complex xyi[NN];datain(xy,N);for(i=N;i<NN;i++){xy[i].real=0;xy[i].imag=0;}reverse(xy,xyi,NN,M);printf("Please choose FFT(1) or IFFT(-1)\n");scanf("%d",&flag);if(flag==1)fft(xyi,NN,M);elseif(flag==-1)ifft(xyi,NN,M);printf("The initial sequence is:\n");dataout(xy,N);printf("The FFT results are as follows:\n"); dataout(xyi,N);return 0;}。

实序列FFT算法的C语言实现word文档良心出品

实序列FFT算法的C语言实现学生：XX 指导教师：XX内容摘要：DFT和IDFT是数字信号分析与处理中的一种重要运算和变换，但直接根据定义计算DFT时，运算量大，不能实时得到计算结果。

特别是在实际应用中，N都取得比较大，此时，由于乘法和加法的次数都近似与N的平方成正比，这将极大增加DFT计算所需时间。

为此，提出了许多DFT和IDFT的快速算法，称为快速傅里叶变换（FFT）和快速傅里叶反变换（IFFT）。

本文较为系统地阐述了快速傅里叶变换的算法原理然后用MATLA实现了快速傅里叶变换。

论文首先首要介绍了FT与DFT的定义、DFT与FFT的关系,然后重点介绍基2时域抽取FFT算法以及其原理和运算流图，再应用C语言实现了实序列的FFT。

最后在Matlab 软件上进行仿真，仿真结果验证了设计的正确性。

关键词：傅里叶变换快速傅立叶变换Matlab 仿真Realization of FFT algorithm for real sequenceWith C p rogramAbstract : DFTand IDFT are important transform and processing in digital signalprocessing. However, there are large amount of computation by directly calculati ng accord ing to the defi niti on of DFT. Esp ecially in the p racticalapp licati on, N is bigger, at this time, because the time of mult ip licatio n andadditi on are app roximately prop orti onal to the square of N, which will greatlyin crease the calculatio n time n eeded for DFT. Therefore, man yDFTa nd IDFT fastalgorithm are raised, which are called FFT and IFFT.In this paper relatively systematically elaborated the fast Fourier tran sform algorithm principle and use MATLABoftware to realize the fast Fourier tran sform. The paper first introduces the definition of FT and DFT,the relationship betwee n DFT and FFT, and the n mainly in troduces DIT-FFT ,in clud ing its principle andop erati on flow diagram, and fin ally used C Ian guage to realize the real sequeneeFFT.The desig ns are simulated in Matlab software, the results of the simulationcon firm the exact ness of the desig n.Keywords : Fourier transformation fast Fourier tran sformatio n Matlab simulati on、F —前言序列的FT 和DFT.1.1 序列的FT1.2 序列的DFT1.2.1 DFT 的定义和计算1.2.2 实序列的DFTFFT 算法2.1 基2时域抽取FFT算法2.2 实序列的FFT算法实序列FFT算法的C语言实现目录3.1 3.2 3.3 3.4 VS20103.1.13.1.2实序列3.2.13.2.2实序列3.3.13.3.2简介新建项目新建文件FFT算法子程序倒序蝶形运算FFT算法主程序原始序列的产生和读取计算结果的显示和输出运行结果分析结束语录：参考文献：101215151616 3.4.1 计算结果数据分析342 N 点DFT波形分析1717202127 2.1.1 基本原理2.1.2 DIT-FFT 算法的运算流图2.1.3 DIT-FFT 算法的运算量和存储量实序列FFT 算法的C 语言实现1刖言在实际的数字系统中, DFT 是一种得到了广泛的应用的、重要的信号处理手段，但它的运算效率非常低。

fft算法c语言实现

fft算法c语言实现快速傅里叶变换（FFT）是一种高效的离散傅里叶变换算法，用于计算信号在频域的表示。

下面是一个简单的使用 C 语言实现的 FFT 算法示例，它可以用于对输入的时域信号进行离散傅里叶变换。

```c#include <stdio.h>#include <stdlib.h>#include <math.h>#define N 16// 复数结构体typedef struct {double real;double imag;} Complex;// 初始化复数void initComplex(Complex *c, double real, double imag) {c->real = real;c->imag = imag;}// FFT 算法void fft(Complex *c, int n) {int i, j, k;Complex w, u, v;// 层次遍历for (i = 1; i < n; i <<= 1) {// 旋转因子w.real = cos(2 * M_PI * i / n);w.imag = -sin(2 * M_PI * i / n);for (j = 0; j < n; j += i) {for (k = 0; k < i / 2; k++) {u.real = c[j + k].real;u.imag = c[j + k].imag;v.real = c[j + i / 2 + k].real;v.imag = c[j + i / 2 + k].imag;c[j + k].real = u.real + w.real * v.real - w.imag * v.imag; c[j + k].imag = u.imag + w.real * v.imag + w.imag * v.real; c[j + i / 2 + k].real = u.real - w.real * v.real + w.imag * v.imag; c[j + i / 2 + k].imag = u.imag - w.real * v.imag - w.imag * v.real; }}}}// 打印复数void printComplex(Complex c) {printf("%f + %fi\n", c.real, c.imag);}int main() {Complex c[N];// 输入的时域信号for (int i = 0; i < N; i++) {c[i].real = rand() / RAND_MAX;c[i].imag = rand() / RAND_MAX;}printf("输入的时域信号：\n");// 打印输入的时域信号for (int i = 0; i < N; i++) {printComplex(c[i]);}fft(c, N);printf("经过 FFT 变换后的频域信号：\n");// 打印经过 FFT 变换后的频域信号for (int i = 0; i < N; i++) {printComplex(c[i]);}return 0;}```上述代码是一个简单的 C 语言实现的 FFT 算法示例。

C语言实现FFT

C语言实现FFT快速傅里叶变换（Fast Fourier Transform, FFT）是一种高效进行离散傅里叶变换（Discrete Fourier Transform, DFT）计算的算法。

它通过利用对称性和递归的方法，将O(n^2)的计算复杂度优化为O(nlogn)。

本文将介绍C语言实现FFT的基本步骤和代码。

首先，需要定义一个复数结构体来表示复数，包含实部和虚部两个成员变量：```ctypedef structdouble real; // 实部double imag; // 虚部```接着，需要实现FFT的关键函数，包括以下几个步骤：1. 进行位逆序排列（bit-reversal permutation）：FFT中的输入数据需要按照位逆序排列，这里使用蝶形算法来实现位逆序排列。

先将输入序列按照索引位逆序排列，再将复数序列按照实部和虚部进行重新排列。

```cint i, j, k;for (i = 1, j = size / 2; i < size - 1; i++)if (i < j)temp = data[j];data[j] = data[i];data[i] = temp;}k = size / 2;while (j >= k)j=j-k;k=k/2;}j=j+k;}```2. 计算旋转因子（twiddle factor）：FFT中的旋转因子用于对复数进行旋转变换，这里采用的旋转因子为e^( -2*pi*i/N )，其中N为DFT点数。

```cint i;double angle;for (i = 0; i < size; i++)angle = -2 * M_PI * i / size;twiddleFactors[i].real = cos(angle);twiddleFactors[i].imag = sin(angle);}```3.执行蝶形算法计算DFT：蝶形算法是FFT算法的核心部分，通过递归地将DFT问题一分为二，并将计算结果根据旋转因子进行两两合并，最终得到FFT结果。

FFT相位差算法的C语言实现

/*此算法为FFT相位差算法的C语言实现，经验证可用（网上有很多此类程序无法运行）；前半部分为FFT算法的子程序，也可用作其它用途*/#include <stdio.h>#include <stdlib.h>#include <math.h>typedef struct {double real,imag;} complex;complex cexp(complex a){complex z;z.real=exp(a.real)*cos(a.imag);z.imag=exp(a.real)*sin(a.imag);return(z);}void mcmpfft(complex x[],int n,int isign){complex t,z,ce;double pisign;int mr,m,l,j,i,nn;for(i=1;i<=16;i++) /*n must be power of 2 */{nn=(int)pow(2,i);if(n==nn) break;}if(i>16){printf(" N is not a power of 2 ! \n");return;}z.real=0.0;pisign=4*isign*atan(1.); /*pisign的值为+180度或-180度*/mr=0;for(m=1;m<n;m++){l=n;while(mr+l>=n) l=l/2;mr=mr%l+l;if(mr<=m) continue;t.real=x[m].real;t.imag=x[m].imag;x[m].real=x[mr].real;x[m].imag=x[mr].imag;x[mr].real=t.real;x[mr].imag=t.imag;}l=1;while(1){if(l>=n){if(isign==-1) /*isign=-1 For Forward Transform*/return;for(j=0;j<n;j++) /* Inverse Transform */{x[j].real=x[j].real/n;x[j].imag=x[j].imag/n;}return;}for(m=0;m<l;m++) /*完成当前级所有蝶形运算*/{for(i=m;i<n;i=i+2*l)/*完成当前级相同W因子的所有蝶形运算*/{z.imag=m*pisign/l;ce=cexp(z);t.real=x[i+l].real*ce.real-x[i+l].imag*ce.imag;t.imag=x[i+l].real*ce.imag+x[i+l].imag*ce.real;x[i+l].real=x[i].real-t.real; /*原位运算*/x[i+l].imag=x[i].imag-t.imag;x[i].real=x[i].real+t.real;x[i].imag=x[i].imag+t.imag;}}l=2*l; /*确定下一级蝶形运算中W因子个数*/}}void main(){ int i,N=1024,k;float pi=3.14159265,x[10000],A[10000],fi=3,f0=89,fs=450,max=0,o,oo,fi1,f00;complex s[2000];for (i=0;i<N;i++){x[i]=1*sin(2*pi*f0*i/fs+fi*pi/180);s[i].real=x[i];s[i].imag=0;}mcmpfft(s,N,-1);for (i=0;i<N;i++){ A[i]=sqrt(s[i].real*s[i].real+s[i].imag*s[i].imag);if(A[i]>max){max=A[i];k=i;}} max=max*2/N;fi1=atan(s[k].imag/s[k].real)*180/pi+90;if(s[k].real>s[k].imag){o=(s[k+1].real-s[k-1].real)/(2*s[k].real-s[k-1].real-s[k+1].real);} else {o=(s[k+1].imag-s[k-1].imag)/(2*s[k].imag-s[k-1].imag-s[k+1].imag);}f00=(k-o)*fs/N;oo=(f00-f0)/f0*100;printf("fi=%f\nA=%f\nk0=%d\nf0=%f\n%f%",fi1,max,k,f00,oo);getch();}。

FFT相位差算法的C语言实现

/*此算法为FFT相位差算法的C语言实现，经验证可用（网上有很多此类程序无法运行）；前半部分为FFT算法的子程序，也可用作其它用途*/#include<stdio.h>#include<stdlib.h>#include<math.h>typedef struct{double real,imag;}complex;complex cexp(complex a){complex z;z.real=exp(a.real)*cos(a.imag);z.imag=exp(a.real)*sin(a.imag);return(z);}void mcmpfft(complex x[],int n,int isign){complex t,z,ce;double pisign;int mr,m,l,j,i,nn;for(i=1;i<=16;i++)/*n must be power of2*/{nn=(int)pow(2,i);if(n==nn)break;}if(i>16){printf("N is not a power of2!\n");return;}z.real=0.0;pisign=4*isign*atan(1.);/*pisign的值为+180度或-180度*/mr=0;for(m=1;m<n;m++){l=n;while(mr+l>=n)l=l/2;mr=mr%l+l;if(mr<=m)continue;t.real=x[m].real;t.imag=x[m].imag;x[m].real=x[mr].real;x[m].imag=x[mr].imag;x[mr].real=t.real;x[mr].imag=t.imag;}l=1;while(1){if(l>=n){if(isign==-1)/*isign=-1For Forward Transform*/return;for(j=0;j<n;j++)/*Inverse Transform*/{x[j].real=x[j].real/n;x[j].imag=x[j].imag/n;}return;}for(m=0;m<l;m++)/*完成当前级所有蝶形运算*/{for(i=m;i<n;i=i+2*l)/*完成当前级相同W因子的所有蝶形运算*/{z.imag=m*pisign/l;ce=cexp(z);t.real=x[i+l].real*ce.real-x[i+l].imag*ce.imag;t.imag=x[i+l].real*ce.imag+x[i+l].imag*ce.real;x[i+l].real=x[i].real-t.real;/*原位运算*/x[i+l].imag=x[i].imag-t.imag;x[i].real=x[i].real+t.real;x[i].imag=x[i].imag+t.imag;}}l=2*l;/*确定下一级蝶形运算中W因子个数*/}}void main(){int i,N=1024,k;float pi=3.14159265,x[10000],A[10000],fi=3,f0=89,fs=450,max=0,o,oo,fi1,f00;complex s[2000];for(i=0;i<N;i++){x[i]=1*sin(2*pi*f0*i/fs+fi*pi/180);s[i].real=x[i];s[i].imag=0;}mcmpfft(s,N,-1);for(i=0;i<N;i++){A[i]=sqrt(s[i].real*s[i].real+s[i].imag*s[i].imag);if(A[i]>max){max=A[i];k=i;}}max=max*2/N;fi1=atan(s[k].imag/s[k].real)*180/pi+90;if(s[k].real>s[k].imag){o=(s[k+1].real-s[k-1].real)/(2*s[k].real-s[k-1].real-s[k+1].real);} else{o=(s[k+1].imag-s[k-1].imag)/(2*s[k].imag-s[k-1].imag-s[k+1].imag);}f00=(k-o)*fs/N;oo=(f00-f0)/f0*100;printf("fi=%f\nA=%f\nk0=%d\nf0=%f\n%f%",fi1,max,k,f00,oo);getch();}。

快速傅里叶变换FFT的C程序代码实现

快速傅⾥叶变换FFT的C程序代码实现标签：傅⾥叶变换(27)C程序(60) ⼀、彻底理解傅⾥叶变换快速傅⾥叶变换(Fast Fourier Transform)是离散傅⾥叶变换的⼀种快速算法，简称FFT，通过FFT可以将⼀个信号从时域变换到频域。

模拟信号经过A/D转换变为数字信号的过程称为采样。

为保证采样后信号的频谱形状不失真，采样频率必须⼤于信号中最⾼频率成分的2倍，这称之为采样定理。

假设采样频率为fs，采样点数为N，那么FFT结果就是⼀个N点的复数，每⼀个点就对应着⼀个频率点，某⼀点n(n从1开始)表⽰的频率为：fn=(n-1)*fs/N。

举例说明：⽤1kHz的采样频率采样128点，则FFT结果的128个数据即对应的频率点分别是0，1k/128，2k/128，3k/128，…，127k/128 Hz。

这个频率点的幅值为：该点复数的模值除以N/2(n=1时是直流分量，其幅值是该点的模值除以N)。

⼆、傅⾥叶变换的C语⾔编程 1、对于快速傅⾥叶变换FFT，第⼀个要解决的问题就是码位倒序。

假设⼀个N点的输⼊序列，那么它的序号⼆进制数位数就是t=log2N. 码位倒序要解决两个问题：①将t位⼆进制数倒序;②将倒序后的两个存储单元进⾏交换。

如果输⼊序列的⾃然顺序号i⽤⼆进制数表⽰，例如若最⼤序号为15，即⽤4位就可表⽰n3n2n1n0，则其倒序后j对应的⼆进制数就是n0n1n2n3，那么怎样才能实现倒序呢?利⽤C语⾔的移位功能! 程序如下，我不多说，看不懂者智商⼀定在180以下! 复数类型定义及其运算 #define N 64 //64点 #define log2N 6 //log2N=6 /*复数类型*/ typedef struct { float real; float img; }complex; complex xdata x[N]; //输⼊序列 /*复数加法*/ complex add(complex a,complex b) { complex c; c.real=a.real+b.real; c.img=a.img+b.img; return c; } /*复数减法*/ complex sub(complex a,complex b) { complex c; c.real=a.real-b.real; c.img=a.img-b.img; return c; } /*复数乘法*/ complex mul(complex a,complex b) { complex c; c.real=a.real*b.real - a.img*b.img; c.img=a.real*b.img + a.img*b.real; return c; } /***码位倒序函数***/ void Reverse(void) { unsigned int i,j,k; unsigned int t; complex temp;//临时交换变量 for(i=0;i<N;i++)//从第0个序号到第N-1个序号 { k=i;//当前第i个序号 j=0;//存储倒序后的序号，先初始化为0 for(t=0;t<log2N;t++)//共移位t次，其中log2N是事先宏定义算好的 { j<<=1; j|=(k&1);//j左移⼀位然后加上k的最低位 k>>=1;//k右移⼀位，次低位变为最低位 } if(j>i)//如果倒序后⼤于原序数，就将两个存储单元进⾏交换(判断j>i是为了防⽌重复交换) { temp=x; x=x[j]; x[j]=temp; } } } 2、第⼆个要解决的问题就是蝶形运算 ①第1级(第1列)每个蝶形的两节点“距离”为1，第2级每个蝶形的两节点“距离”为2，第3级每个蝶形的两节点“距离”为4，第4级每个蝶形的两节点“距离”为8。

用C语言实现FFT算法

sin(pi/lei); for(j=1;j=lei;j++) { /*double p=pow(2,m-l)*j; double ps=2*pi/N*p;
w.real=cos(ps); w.imag=-sin(ps);*/ for(i=j;i=N;i=i+le) { /* w.real=cos(ps); w.imag=-
main(){ int i=1 ; for(;i0x101;i++) { s[i].real=sin(pp*i/32); s[i].imag=0 ; }
FFT(s,Num);
for(i=1;i0x101;i++)
{
result[i]=sqrt(pow(s[i].real,2)+pow(s[i].imag,2)); }}
b3.real=b1.real*b2.real-b1.imag*b2.imag
;
b3.imag=b1.real*b2.imag+b1.imag*b2.real ; return(b3);}
void FFT(struct compx*xin,int N){ int f,m,nv2,nm1,i,k,j=1,l ; /*int
int le,lei,ip ; float pi ; for(l=1;l=m;l++) { le=pow(2,l); // 这里用的是 L 而不是 1 !!!!
lei=le/2 ; pi=3.14159 ; v.real=1.0 ; v.imag=0.0 ; w.real=cos(pi/lei); w.imag=-
用 C 语言实现 FFT 算法
/*****************fft programe*********************/#include typedef.h

fft 滤波算法 c

FFT（快速傅里叶变换）滤波算法是一种在信号处理中常用的技术，用于分析信号的频谱。

它是一种快速算法，可以有效地计算离散傅里叶变换（DFT）和其逆变换。

以下是一个使用C语言实现的基本FFT滤波算法：```c#include <stdio.h>#include <math.h>#include <complex.h>#include <math_constants.h>void fft(double complex buf[], int n, int step) {if (step < n) {fft(buf, n, step * 2);fft(buf + step, n, step * 2);for (int i = 0; i < n; i += 2 * step) {double complex t = cexp(-I * M_PI * i / n) * buf[i + step];buf[i / 2] = buf[i] + t;buf[(i + n)/2] = buf[i] - t;}}}void ifft(double complex buf[], int n, int step) {if (step < n) {ifft(buf, n, step * 2);ifft(buf + step, n, step * 2);for (int i = 0; i < n; i += 2 * step) {double complex t = cexp(I * M_PI * i / n) * buf[i + step];buf[i / 2] = buf[i] + t;buf[(i + n)/2] = buf[i] - t;}}}```以上代码中，`fft`函数实现了正向FFT变换，`ifft`函数实现了逆向FFT变换。

这两个函数都接受一个复数数组`buf`，数组的长度`n`以及递归的深度`step`。

FFT相位差算法的C语言实现

FFT相位差算法的C语言实现要实现FFT（快速傅里叶变换）相位差算法的C语言实现，涉及到以下几个步骤：1.实现FFT算法；2.计算两个信号的频谱；3.计算频谱的相位差。

1.实现FFT算法FFT算法可以通过递归地将问题划分为更小的子问题来实现，其中每个子问题都包含两个信号的FFT运算。

```c#include <stdio.h>#include <math.h>#ifndef M_PI#endiftypedef structdouble real;double imag;if (n <= 1)return;}for (int i = 0; i < n / 2; i++)even[i] = data[2 * i];odd[i] = data[2 * i + 1];}fft(even, n / 2);fft(odd, n / 2);for (int k = 0; k < n / 2; k++)double angle = -2 * M_PI * k / n;data[k] = { even[k].real + t.real, even[k].imag + t.imag };data[k + n / 2] = { even[k].real - t.real, even[k].imag - t.imag };}```2.计算两个信号的频谱频谱可以通过将信号进行FFT变换来获取，我们需要将信号转换为复数形式，并填充到长度为2的次方的数组中。

```cfor (int i = 0; i < size; i++)data[i] = { signal[i], 0 };}fft(data, size);for (int i = 0; i < size; i++)spectrum[i] = data[i];}```3.计算频谱的相位差频谱的相位差可以通过计算两个频谱中每个频点处的相位差来获得。

FFT的C语言算法实现

FFT的C语言算法实现程序如下：/************FFT***********/#include <stdio.h>#include <math.h>#include <stdlib.h>#define N 1000typedef struct{double real;double img;}complex;void fft(); /*快速傅里叶变换*/void ifft(); /*快速傅里叶逆变换*/void initW();void change();void add(complex ,complex ,complex *); /*复数加法*/void mul(complex ,complex ,complex *); /*复数乘法*/void sub(complex ,complex ,complex *); /*复数减法*/void divi(complex ,complex ,complex *);/*复数除法*/void output(); /*输出结果*/complex x[N], *W;/*输出序列的值*/int size_x=0;/*输入序列的长度，只限2的N次方*/ double PI;int main(){int i,method;system("cls");PI=atan(1)*4;printf("Please input the size of x:\n");/*输入序列的长度*/scanf("%d",&size_x);printf("Please input the data in x[N]:(such as:5 6)\n");/*输入序列对应的值*/for(i=0;i<size_x;i++)scanf("%lf %lf",&x[i].real,&x[i].img);initW();/*选择FFT或逆FFT运算*/printf("Use FFT(0) or IFFT(1)?\n");scanf("%d",&method);if(method==0)fft();elseifft();output();return 0;}/*进行基-2 FFT运算*/void fft(){int i=0,j=0,k=0,l=0;complex up,down,product;change();for(i=0;i< log(size_x)/log(2) ;i++) {l=1<<i;for(j=0;j<size_x;j+= 2*l ){for(k=0;k<l;k++){mul(x[j+k+l],W[size_x*k/2/l],&product); add(x[j+k],product,&up);sub(x[j+k],product,&down);x[j+k]=up;x[j+k+l]=down;}}}}void ifft(){int i=0,j=0,k=0,l=size_x;complex up,down;for(i=0;i< (int)( log(size_x)/log(2) );i++) /*蝶形运算*/{l/=2;for(j=0;j<size_x;j+= 2*l ){for(k=0;k<l;k++){add(x[j+k],x[j+k+l],&up);up.real/=2;up.img/=2;sub(x[j+k],x[j+k+l],&down);down.real/=2;down.img/=2;divi(down,W[size_x*k/2/l],&down);x[j+k]=up;x[j+k+l]=down;}}}change();}void initW(){int i;W=(complex *)malloc(sizeof(complex) * size_x); for(i=0;i<size_x;i++){W[i].real=cos(2*PI/size_x*i);W[i].img=-1*sin(2*PI/size_x*i);}}void change(){complex temp;unsigned short i=0,j=0,k=0;double t;for(i=0;i<size_x;i++){k=i;j=0;t=(log(size_x)/log(2));while( (t--)>0 ){j=j<<1;j|=(k & 1);k=k>>1;}if(j>i){temp=x[i];x[i]=x[j];x[j]=temp;}}}void output() /*输出结果*/{int i;printf("The result are as follows\n"); for(i=0;i<size_x;i++){printf("%.4f",x[i].real);if(x[i].img>=0.0001)printf("+%.4fj\n",x[i].img);else if(fabs(x[i].img)<0.0001)printf("\n");elseprintf("%.4fj\n",x[i].img);}}void add(complex a,complex b,complex *c) {c->real=a.real+b.real;c->img=a.img+b.img;}void mul(complex a,complex b,complex *c) {c->real=a.real*b.real - a.img*b.img;c->img=a.real*b.img + a.img*b.real;}void sub(complex a,complex b,complex *c) {c->real=a.real-b.real;c->img=a.img-b.img;}void divi(complex a,complex b,complex *c) {c->real=( a.real*b.real+a.img*b.img )/(b.real*b.real+b.img*b.img);c->img=( a.img*b.real-a.real*b.img)/(b.real*b.real+b.img*b.i mg);}。

FFT算法源代码（C++）#include <iostream>#include <iomanip>#include "math.h"using namespace std;double pi = 3.1415926535897932;class complex{public://无参构造函数complex(){re=0;im=0;}//有参构造函数complex(double real,double imag){re=real;im=imag;}//加法complex operator + (complex& c){return complex( re + c.re , im + c.im );}//减法complex operator - (complex& c){return complex( re - c.re , im - c.im );}//乘法complex operator * (complex& c){return complex( (re * c.re)-(im * c.im) , (re * c.im)+(im * c.re) );}//除法complex operator / (complex& c){return complex( ( re*c.re + im*c.im )/( c.re*c.re + c.im*c.im ),((im * c.re)-(re * c.im))/((c.re*c.re)+(c.im*c.im)) );}//除2void half(){re=re/2;im=im/2;}//输出到ostreamvoid insert(ostream& out){if(re>=0) cout<<" ";out<<re<< ((im>=0)?'+':'-') <<'j'<< ((im>=0)?im:(0-im));}//显示void show(){cout<<re<< ((im>=0)?'+':'-') <<'j'<< ((im>=0)?im:(0-im)) ;}//设值void setValue(double real,double imag){if(real>0.00000001||real< -0.00000001) re=real;else re=0;if(imag>0.00000001||imag< -0.00000001) im=imag;else im=0;}friend complex c_pow(complex c,int y);private:double re,im;};//流输出ostream& operator << (ostream& out, complex c){c.insert(out);return out;}//乘方complex c_pow(complex c,int y){complex returnValue = c ;for(int i = 1 ; i < y ; i++ ){returnValue = returnValue * c ;}return returnValue;}//获得Wnvoid getW(complex w[],int len){for(int i=0 ; i<len ; i++ ){w[i].setValue( cos(0 - pi*2*(i)/len) , sin(0 - pi*2*(i)/len) );}}//获得mWnvoid getMW(complex w[],int len){for(int i=0 ; i<len ; i++ ){w[i].setValue( cos(pi*2*(i)/len) , sin(pi*2*(i)/len) );}}//倒序重排void resort(complex x[],int len){//初始化int half=len/2;int p1=0,p2;int k;complex temp;//重排for( p2=0 ; p2+1<len ; p2++ ){if(p2<p1 && p1+1<len){temp=x[p1];x[p1]=x[p2];x[p2]=temp;}k=half;while(k<p1+1 && p1+1<len){p1=p1-k;k=k/2;}p1=p1+k;}}//基2时间FFTvoid FFT2t(complex x[],complex y[],int len){//初始化int m=0,n,k,j,q;int tlen=len/2;while(tlen!=0){m++;tlen=tlen/2;}resort(x,len); //倒序重排for(j=0;j<len;j++){y[j]=x[j];}complex *xt = new complex[len];complex *w = new complex[len];getW(w,len);//开始迭代运算q=len;for(int i=1;i<=m;i++){q=q/2;n=len/q/2;for(j=0;j<len;j++){xt[j]=y[j];}if(i!=1){ for(j=0;j<q;j++){for(k=0;k<n;k++){xt[n+j*2*n+k]=xt[n+j*2*n+k]*w[k*q];}}for(j=0;j<n;j++){for(k=0;k<q;k++){y[j+k*2*n]=xt[j+k*2*n]+xt[j+n+k*2*n];}}for(;j<2*n;j++){for(k=0;k<q;k++){y[j+k*2*n]=xt[j-n+k*2*n]-xt[j+k*2*n];}}}delete[]xt,w;}//基2频率FFT和IFFTvoid FFT(complex x[],complex y[],int len,bool IFFT = false) {//初始化int m=0,n,k,j,q;int tlen=len/2;while(tlen!=0){m++;tlen=tlen/2;}for(j=0;j<len;j++){y[j]=x[j];}complex *xt = new complex[len];complex *w = new complex[len];if(IFFT==true) //若是IFFT则获取Wn序列{getMW(w,len);}else //若是FFT则获取mWn序列{getW(w,len);}//开始迭代运算for(int i=1;i<=m;i++){n=n/2;q=len/n/2;for(j=0;j<len;j++){xt[j]=y[j];}for(j=0;j<n;j++){for(k=0;k<q;k++){y[j+k*2*n]=xt[j+k*2*n]+xt[j+n+k*2*n];}}for(;j<2*n;j++){for(k=0;k<q;k++){y[j+k*2*n]=xt[j-n+k*2*n]-xt[j+k*2*n];}}if(i!=m){ for(j=0;j<q;j++){for(k=0;k<n;k++){y[n+j*2*n+k]=y[n+j*2*n+k]*w[k*q];}}}if(IFFT==true)//若是IFFT则除以2{for(j=0;j<len;j++){y[j].half();}}}resort(y,len); //倒序重排delete[]xt,w;}void main(){//初始化complex q(0.9,0.3);complex x[32],y[32],z[32],w[32],v[32],w1;w1.setValue(1,0);getW(w,32); //获取Wn序列x[0].setValue(1,0);for(int i=1;i<32;i++)//定原序列的值{x[i]=x[i-1]*q;}//输出原序列cout<<"原序列："<<endl;for(i=0;i<32;i+=2){cout<<setiosflags(ios::fixed)<<setprecision(6)<<x[i]<<"\t"<<x[i+1]<<endl;}for(i=0;i<32;i++) //进行公式计算{complex a=w1-(x[31]*q),b=w1-q*w[i];v[i]=a/b;}//输出公式计算值cout<<"公式计算值："<<endl;for(i=0;i<32;i+=2){cout<<v[i]<<"\t"<<v[i+1]<<endl;}FFT2t(x,y,32); //进行基2时间变换//输出基2时间变换后序列cout<<"基2时间变换后序列："<<endl;for(i=0;i<32;i+=2){cout<<y[i]<<"\t"<<y[i+1]<<endl;}FFT(y,z,32,1); //进行反变换//输出反变换后的序列cout<<"反变换后的序列："<<endl;for(i=0;i<32;i+=2)cout<<z[i]<<"\t"<<z[i+1]<<endl;}}运行结果。

实现FFT算法的C语言程序

实现FFT算法的C语言程序目前在许多嵌入式系统中要用到FFT运算，如以单片机为核心的交流采样系统、谐波运算、频谱分析等。

本文首先分析实数FFT算法的推导过程，然后给出一种验证过的具体实现FFT算法的C语言程序，可以直接应用于需要FFT 运算的单片机或DSP等嵌入式系统中。

一、倒位序算法分析按时间抽取（DIT）的FFT算法通常将原始数据倒位序存储，最后按正常顺序输出结果X（0），X（1），...，X（k），...。

假设一开始，数据在数组float dataR[128]中，我们将下标i表示为（b6b5b4b3b2b1b0）b，倒位序存放就是将原来第i个位置的元素存放到第（b0b1b2b3b4b5b6）b的位置上去.由于C语言的位操作能力很强，可以分别提取出b6、b5、b4、b3、b2、b1、b0，再重新组合成b0、b1、b2、b3、b4、b5、b6，即是倒位序的位置。

程序段如下（假设128点FFT）：/* i为原始存放位置，最后得invert_pos为倒位序存放位置*/int b0=b1=b2=b3=b4=b5=6=0;b0=i&0x01; b1=(i/2)&0x01; b2=(i/4)&0x01;b3=(i/8)&0x01; b4=(i/16)&0x01; b5=(i/32)&0x01;b6=(i/64)&0x01; /*以上语句提取各比特的0、1值*/invert_pos=x0*64+x1*32+x2*16+x3*8+x4*4+x5*2+x6;对比教科书上的倒位序程序，会发现这种算法充分利用了C语言的位操作能力，非常容易理解而且位操作的速度很快。

二、实数蝶形运算算法的推导首先看一下图1所示的蝶形图。

图1：蝶形图蝶形公式：X(K) = X’(K) + X’(K+B)W PN ,X(K+B) = X’(K) - X’(K+B) W PN其中W PN= cos（2πP/N）- jsin（2πP/N）。

FFT快速算法C程序

FFT快速算法C程序FFT（快速傅里叶变换）算法是一种用于计算离散傅里叶变换的高效算法。

它通过分治策略将长度为N的序列递归地分解为两个长度为N/2的子序列，然后将计算结果合并在一起。

这个算法的时间复杂度为O(NlogN)，比传统的DFT（离散傅里叶变换）算法要高效许多。

以下是一个使用C语言实现的FFT算法的示例代码：#include <stdio.h>#include <math.h>//定义复数类型typedef structdouble real;double imag;//计算序列长度为N的FFTif (N <= 1)return;}//将输入序列划分为偶数项和奇数项for (int i = 0; i < N/2; i++)even[i] = x[2*i];odd[i] = x[2*i+1];}//递归计算偶数项和奇数项的FFTFFT(even, N/2);FFT(odd, N/2);//计算每个频谱点的值for (int k = 0; k < N/2; k++)W.real = cos(2*M_PI*k/N);W.imag = -sin(2*M_PI*k/N);t.real = W.real * odd[k].real - W.imag * odd[k].imag; t.imag = W.real * odd[k].imag + W.imag * odd[k].real; x[k].real = even[k].real + t.real;x[k].imag = even[k].imag + t.imag;x[k+N/2].real = even[k].real - t.real;x[k+N/2].imag = even[k].imag - t.imag;}//输出复数序列for (int i = 0; i < N; i++)printf("(%f + %fi) ", x[i].real, x[i].imag);}printf("\n");int maiint N = 4;x[0].real = 1;x[0].imag = 0;x[1].real = 2;x[1].imag = 0;x[2].real = 3;x[2].imag = 0;x[3].real = 4;x[3].imag = 0;printf("输入序列: ");FFT(x,N);printf("FFT结果: ");return 0;以上代码实现了一个简单的FFT算法，通过输入一个长度为N的复数序列，计算其FFT结果并输出。

FFT的C语言算法实现

FFT的C语言算法实现FFT算法的基本思想是将一个N点离散信号转换成N个频率分量。

它使用了分治思想，通过递归将问题分解为较小规模的子问题，最终合并子问题的结果得到最终结果。

以下是FFT的C语言算法实现：```#include <stdio.h>#include <math.h>//计算复数的实部double real(double x)return x;//计算复数的虚部double imag(double x)return -x; // i的平方为-1//复数相加return a + b;//复数相乘return a * b;//快速傅里叶变换主函数void fft(double* real_input, double* imag_input, int N, double* real_output, double* imag_output)//如果输入序列长度为1，直接返回if (N == 1)real_output[0] = real(real_input[0]);imag_output[0] = imag(imag_input[0]);return;}//创建长度为N/2的偶数序列和奇数序列输入double* even_real_input = (double*)malloc(sizeof(double) * (N/2));double* even_imag_input = (double*)malloc(sizeof(double) * (N/2));double* odd_real_input = (double*)malloc(sizeof(double) * (N/2));double* odd_imag_input = (double*)malloc(sizeof(double) * (N/2));//将输入序列按奇偶分组for (int i = 0; i < N/2; i++)even_real_input[i] = real_input[2*i];even_imag_input[i] = imag_input[2*i];odd_real_input[i] = real_input[2*i+1];odd_imag_input[i] = imag_input[2*i+1];}//计算偶数序列的FFTdouble* even_real_output = (double*)malloc(sizeof(double) * (N/2));double* even_imag_output = (double*)malloc(sizeof(double) * (N/2));fft(even_real_input, even_imag_input, N/2, even_real_output, even_imag_output);//计算奇数序列的FFTdouble* odd_real_output = (double*)malloc(sizeof(double) * (N/2));double* odd_imag_output = (double*)malloc(sizeof(double) * (N/2));fft(odd_real_input, odd_imag_input, N/2, odd_real_output, odd_imag_output);//合并子问题的结果for (int i = 0; i < N/2; i++)double k_real = cos(2 * M_PI * i / N);double k_imag = sin(2 * M_PI * i / N);}//释放内存free(even_real_input);free(even_imag_input);free(odd_real_input);free(odd_imag_input);free(even_real_output);free(even_imag_output);free(odd_real_output);free(odd_imag_output);int mai//测试数据double real_input[] = {1, 2, 3, 4};double imag_input[] = {0, 0, 0, 0};int N = sizeof(real_input) / sizeof(double);double* real_output = (double*)malloc(sizeof(double) * N); double* imag_output = (double*)malloc(sizeof(double) * N);fft(real_input, imag_input, N, real_output, imag_output);//输出傅里叶变换结果for (int i = 0; i < N; i++)printf("%.2f + %.2fi\n", real_output[i], imag_output[i]);}//释放内存free(real_output);free(imag_output);return 0;```在FFT函数中，先判断输入序列的长度，如果长度为1，直接返回结果。

用C实现FFT

%清除命令窗口及变量clc;clear all;%输入f、N、T、是否补零（补几个零）f=input('Input frequency of the signal: f\n');N=input('Input number of pointsl: N\n');T=input('Input sampling time: T\n');flag=input('Add zero too sampling signal or not? yes=1 no=0\n'); if(flag)ZeroNum=input('Input nmber of zeros\n');elseZeroNum=0;end%生成信号，signal是原信号。

signal为采样信号。

fs=1/T;t=0:0.00001:T*(N+ZeroNum-1);signal=sin(2*pi*f*t);t2=0:T:T*(N+ZeroNum-1);signal2=sin(2*pi*f*t2);if (flag)signal2=[signal2 zeros(1, ZeroNum)];end%画出原信号及采样信号。

figure;subplot(2,1,1);plot(t,signal);xlabel('Time(s)');ylabel('Amplitude(volt)');title('Singnal');hold on;subplot(2,1,1);stem(t2,signal2,'r');axis([0 T*(N+ZeroNum) -1 1]);%作FFT变换，计算其幅值，归一化处理，并画出频谱。

Y = fft(signal2,N);Pyy = Y.* conj(Y) ;Pyy=(Pyy/sum(Pyy))*2;f=0:fs/(N-1):fs/2;4subplot(2,1,2);bar(f,Pyy(1:N/2));xlabel('Frequency(Hz)');ylabel('Amplitude');title('Frequency compnents of signal');axis([0 fs/2 0 ceil(max(Pyy))])grid on; ———————————————————————————————————————这是一个傅里叶变化的子函数，你可以自己做主函数传递你这里的参数验证// 入口参数：// l: l = 0, 傅立叶变换; l = 1, 逆傅立叶变换// il: il = 0,不计算傅立叶变换或逆变换模和幅角；il = 1,计算模和幅角// n: 输入的点数，为偶数，一般为32，64，128， (1024)// k: 满足n=2^k(k>0),实质上k是n个采样数据可以分解为偶次幂和奇次幂的次数// pr[]: l=0时，存放N点采样数据的实部// l=1时, 存放傅立叶变换的N个实部// pi[]: l=0时，存放N点采样数据的虚部// l=1时, 存放傅立叶变换的N个虚部//// 出口参数：// fr[]: l=0, 返回傅立叶变换的实部// l=1, 返回逆傅立叶变换的实部// fi[]: l=0, 返回傅立叶变换的虚部// l=1, 返回逆傅立叶变换的虚部// pr[]: il = 1,l = 0 时，返回傅立叶变换的模// il = 1,l = 1 时，返回逆傅立叶变换的模// pi[]: il = 1,l = 0 时，返回傅立叶变换的辐角// il = 1,l = 1 时，返回逆傅立叶变换的辐角void kbfft(double *pr,double *pi,int n,int k,double *fr,double *fi,int l,int il){int it,m,is,i,j,nv,l0;double p,q,s,vr,vi,poddr,poddi;//排序for (it=0; it<=n-1; it++){ m=it; is=0;for (i=0; i<=k-1; i++){ j=m/2; is=2*is+(m-2*j); m=j;fr[it]=pr[is]; fi[it]=pi[is];}}//蝶形运算pr[0]=1.0; pi[0]=0.0;p=6.283185306/(1.0*n);pr[1]=cos(p); pi[1]=-sin(p);if (l!=0) pi[1]=-pi[1];for (i=2; i<=n-1; i++){ p=pr[i-1]*pr[1]; q=pi[i-1]*pi[1];s=(pr[i-1]+pi[i-1])*(pr[1]+pi[1]);pr[i]=p-q; pi[i]=s-p-q;}for (it=0; it<=n-2; it=it+2){ vr=fr[it]; vi=fi[it];fr[it]=vr+fr[it+1]; fi[it]=vi+fi[it+1];fr[it+1]=vr-fr[it+1]; fi[it+1]=vi-fi[it+1]; }m=n/2; nv=2;for (l0=k-2; l0>=0; l0--){ m=m/2; nv=2*nv;for (it=0; it<=(m-1)*nv; it=it+nv)for (j=0; j<=(nv/2)-1; j++){ p=pr[m*j]*fr[it+j+nv/2];q=pi[m*j]*fi[it+j+nv/2];s=pr[m*j]+pi[m*j];s=s*(fr[it+j+nv/2]+fi[it+j+nv/2]);poddr=p-q; poddi=s-p-q;fr[it+j+nv/2]=fr[it+j]-poddr;fi[it+j+nv/2]=fi[it+j]-poddi;fr[it+j]=fr[it+j]+poddr;fi[it+j]=fi[it+j]+poddi;}}if (l!=0)for (i=0; i<=n-1; i++){ fr[i]=fr[i]/(1.0*n);fi[i]=fi[i]/(1.0*n);}if (il!=0)for (i=0; i<=n-1; i++){ pr[i]=sqrt(fr[i]*fr[i]+fi[i]*fi[i]);pr[i]=(pr[i]/(n/2)); //各次谐波幅值，其中pr[1]为基波幅值if (fabs(fr[i])<0.000001*fabs(fi[i]))//fabs()是取绝对值函数,浮点型的0 在内存中并不是严格等于0,可以认为当一个浮点数离原点足够近时,也就是f>0.00001 && f<-0.00001,认为f是0{ if ((fi[i]*fr[i])>0) pi[i]=90.0;else pi[i]=-90.0;}elsepi[i]=atan(fi[i]/fr[i])*360.0/6.283185306;}return;}FFT in C code 用C语言实现FFT#include <stdio.h>#include <math.h>//此代码来源《数字信号处理C语言程序集》殷福亮、宋爱军，沈阳：辽宁科学技术出版社，1997.7//数组x存储时域序列的实部，数组y存储时域序列的虚部//n代表N点FFT，sign=1为FFT，sign=-1为IFFTvoid FFT(double x[],double y[],int n,int sign){int i,j,k,l,m,n1,n2;double c,c1,e,s,s1,t,tr,ti;//Calculate i = log2Nfor(j = 1,i = 1; i<16; i++){m = i;j = 2*j;if(j == n)break;}//计算蝶形图的输入下标（码位倒读）for(j=0,i=0; i<n1; i++){if(i<j){tr = x[j];ti = y[j];x[j] = x[i];y[j] = y[i];x[i] = tr;y[i] = ti;}k = n/2;while(k<(j+1)){j = j - k;k = k/2;}j = j + k;}//计算每一级的输出，l为某一级，i为同一级的不同群，使用同一内存（即位运算）n1 = 1;for(l=1; l<=m; l++){n1 = 2*n1;n2 = n1/2;e = 3.1415926/n2;c = 1.0;s = 0.0;c1 = cos(e);s1 = -sign*sin(e);for(j=0; j<n2; j++){for(i=j; i<n; i+=n1){k = i + n2;tr = c*x[k] - s*y[k];ti = c*y[k] + s*x[k];x[k] = x[i] - tr;y[k] = y[i] - ti;x[i] = x[i] + tr;y[i] = y[i] + ti;t = c;c = c*c1 - s*s1;s = t*s1 + s*c1;}}//如果是求IFFT，再除以Nif(sign == -1){for(i=0; i<n; i++){x[i] /= n;y[i] /= n;}}}int main(){double x[4] = {1,2,-1,3};//郑君里《信号与系统》上的例子，下P145double y[4] = {0};int i;for(i=0; i<4; i++)printf("%d %f %f\n",i,x[i],y[i]);FFT(x,y,4,1);for(i=0; i<4; i++)printf("%d %f %f\n",i,x[i],y[i]);FFT(x,y,4,-1);for(i=0; i<4; i++)printf("%d %f %f\n",i,x[i],y[i]);return 1;}《数字信号处理C语言程序集》殷福亮、宋爱军pdf下载地址/d/%e6%95%b0%e5%ad%97%e4%bf%a1%e5%8f%b7%e5 %a4%84%e7%90%86C%e8%af%ad%e8%a8%80%e7%a8%8b%e5%ba%8f%e9%9b %86.pdf/6aee5dc4904b19993bf9d8405859957965e992723a6c0d01以前信号与系统学得很浅，目前正在学习，代码只是看懂了个大概，对于是如何实现W的计算的没看懂，希望有谁看懂了解释一下，呵呵......还有一点我没有看懂就是，变换出来的频域序列和频率是怎么对应的，好像是N/2=采样频率的一半，正好满足耐奎斯特，N/2以后和以前是对称的，不知道理解的正确与否，希望牛人指点....C语言FFT和IFFT实现(2007-05-07 18:40:15)转载标签：基_2fft(频率抽取dif 法)c语言算法程序分类：学习资料基- 2 FFT ( 频率抽取DIF 法) 算法程序/* 基2-DIF-FFT的C语言算法程序*//* 输入: 序列点数、序列值* //* 输出: 输入序列FFT变换后的数值及又把FFT结果反变换得到原输入序列(与输入序列相同)，*//* 还输出输入序列的IFFT结果(应与原序列相同) */#include "conio.h"#include "math.h"#include "stdio.h"#define N 64#define PI 3.1415926#define w0 (0.125*PI)#define Cmul(a,b,c) a.x=b.x*c.x-b.y*c.y;a.y=b.x*c.y+b.y*c.x; /*利用结构体做复数乘法*/#define Cequal(a,b) a.x=b.x;a.y=b.y; /*结构体a的值赋给b*/#define Cadd(a,b,c) a.x=b.x+c.x;a.y=b.y+c.y; /*结构体实现复数的加减*/#define Csub(a,b,c) a.x=b.x-c.x;a.y=b.y-c.y;#define Wn(w,r) w.x=cos(2.0*PI*r/n);w.y=-sin(2.0*PI*r/n); /*旋转因子的分解*/ struct comp{float x;float y;};void main(){int i,j,nu2,nm1,n,m,le,le1,k,ip,z;int flag,f,n1;struct comp a[N],t,t1,w,d;float a_ipx,m1;printf("\nThis program is about FFT by DIF way. ");printf("\nplease enter N : ");scanf("%d",&n1);n=n1;m1=log(n1)/log(2);m=log(n1)/log(2); /*级数*/if (m!=m1) n=pow(2,m+1);for(i=0;i<n;i++) {a[i].x=a[i].y=0.0;} /*所有存储单元清零*/printf("\n");for(i=0;i<n1;i++) /*录入数据到存储单元，以结构体的形式分别存储实部和虚部*/{printf("\nplease enter data(%d)_[Re]: ",i);scanf("%f",&a[i].x);printf("\nplease enter data(%d)_[Im]: ",i);scanf("%f",&a[i].y);}for(z=0;z<=2;z++) /*z=0,时计算FFT；z=1时计算新序列的IFFT；z=2时计算原序列的IFFT*/{flag=-1; /*flag控制r的增加*/for (m=(log(n)/log(2));m>=1;m--) /*此循环控制级数m*/{le=pow(2,m); /*le控制同一级中具有相同的碟形结的距离*/flag++;le1=le/2; /*le1控制在同一级中有不同的个数*/for( j=0;j<le1;j++) /*此循环控制同一级中r的增加，实现一级不同的蝶形运算*/{for (i=j;i<=(n-1);i+=le) /*此循环控制一级中具有相同的碟形运算*/{ip=i+le1;Cequal(t,a[i]);Cequal(t1,a[ip]);f=(int) (i*pow(2,flag))%n;Wn(w,f);Cadd(a[i],t,t1); /*计算*/Csub(a[ip],t,t1); /*计算a_ipx=a[ip].x; */if (z==1){w.y*=-1;}if (z==2){w.y*=-1;}a[ip].x=a[ip].x*w.x-a[ip].y*w.y;a[ip].y=a_ipx*w.y+a[ip].y*w.x; /*计算，反变换则取反*/}}}nu2=n/2; /*用雷德算法将倒位序输出变为自然序输出*/nm1=n-2;j=0;i=0;while(i<=nm1){if (i<j){Cequal(d,a[j]);Cequal(a[j],a[i]);Cequal(a[i],d);}k=nu2;while(k<=j){j=j-k;k=k/2;}j=j+k;i=i+1;}if(z==0){printf("\n input num fft:\n\n");}else if(z==1)printf("\n sheng cheng xin num ifft(input):\n\n" ) ;elseprintf("\n input num ifft");for(i=0;i<n;i++)if(z==0){printf(" %7.4f",a[i].x);if (a[i].y>=0)printf(" + %7.4f j \n",a[i].y);elseprintf(" - %7.4f j \n",fabs(a[i].y));}else if(z==1){a[i].x=a[i].x/n; /*IFFT需将结果除以n*/printf(" %7.4f",a[i].x);a[i].y=a[i].y/n;if (a[i].y>=0)printf(" + %7.4f j \n",a[i].y);elseprintf(" - %7.4f j \n",fabs(a[i].y));}else{printf(" %7.4f",a[i].x/n);a[i].y=a[i].y/n;if (a[i].y>=0)printf(" + %7.4f j \n",a[i].y);elseprintf(" - %7.4f j \n",fabs(a[i].y));}}printf("\n");}。

用c语言实现的FFT

一、对FFT得介绍1、 FFT(Fast Fourier Transformation),即为快速傅里叶变换,就是离散傅里叶变换得快速算法,它就是根据离散傅里叶变换得奇、偶、虚、实等特性,对离散傅里叶变换得算法进行改进获得得。

2、FFT算法得基本原理FFT算法就是把长序列得DFT逐次分解为较短序列得DFT。

按照抽取方式得不同可分为DIT-FFT(按时间抽取)与DIF-FFT(按频率抽取)算法。

按蝶形运算得构成不同可分为基2,基4,基8,以及任意因子得类型。

3、迭代关系4、本次程序得基本过程我们这次所研究得就是数字信号处理中得FFT算法,我们这次所用得数字信号就是复数类型得。

(1)所以首先,我们先定义了一个复数结构体,因为就是进行复数得运算,我们又相继定义复数得加减乘运算得函数。

(2)紧接着,我们定义了进行FFT计算得fft()快速傅里叶变换函数initW() 初始化变换核函数即旋转因子得计算,change() 变址函数,output()输出傅里叶变换得结果得函数。

(3)定义主函数,并调用定义好得相关子函数,利用fft()中得蝶形运算以及change()函数来完成从时间域上选取得DIT-FFT。

EbodE。

二、FFT中码位倒置排序1、码位倒置得实现方法:(1)简单得利用按位与、或循环实现(2)利用公式推导得迭代方法2、为什么要进行码位倒置因为由于FFT得计算特性,如果按照正常顺序输入,而没有进行码位倒置得话,就会以乱序输出,就不便于我们后续对信号得相关性质进行研究了,所以DIT-FFT算法就就是在进行FFT计算之前,进行分奇偶后得码位倒置运算,即二进制数得倒位。

3、倒位序由奇偶分组造成,以N=8为例,说明如下:rAY2v。

三、蝶形运算由按照上述公式得规律进行逐级分解,直到2点DFT,如下就是N=8时得蝶形算法分析图:四、FFT算法中蝶形算法得基本思想分析(1)我们知道N点FFT运算可以分成log2(N)级,每一级都有N/2个碟形,FFT得基本思想就是用3层循环完成全部运算(N点FFT)。